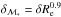| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423495 | |
| Published online | 18 July 2014 | |
Scaling relations of cluster elliptical galaxies at z~ 1.3
Distinguishing luminosity and structural evolution⋆
1
INAF – Osservatorio Astronomico di Brera, via Brera 28,
20121
Milano,
Italy
e-mail:
paolo.saracco@brera.inaf.it
2
Università Statale di Milano, via Celoria 22, 20133
Milano,
Italy
3
Università degli Studi dell’Insubria, via Valleggio 11, 22100
Como,
Italy
4
Università degli Studi di Padova, Vicolo dell’Osservatorio 5, 35141
Padova,
Italy
5
INAF – Osservatorio Astronomico di Padova, Vicolo
dell’Osservatorio 5, 35141
Padova,
Italy
6
INAF – Osservatorio Astronomico di Roma, via Frascati 33,
00040
Monte Porzio Catone,
Italy
7
INAF – IASF, via E. Bassini 15, 20133
Milano,
Italy
8
INAF - Osservatorio Astrofisico di Arcetri, Largo Entrico Fermi 5,
50125
Firenze,
Italy
Received:
23
January
2014
Accepted:
29
April
2014
Context. We studied the size–surface brightness and the size–mass relations of a sample of 16 cluster elliptical galaxies in the mass range ~ 1010−2 × 1011 M⊙, which were morphologically selected in the cluster RDCS J0848+4453 at z = 1.27.
Aims. Our aim is to assess whether they have completed their mass growth at their redshift or significant mass, and/or size growth can or must still take place until z = 0. This will enable us to know whether the elliptical galaxies of clusters follow or not the observed size evolution of passive galaxies.
Methods. To compare our data with the local universe we considered the Kormendy relation derived from the early-type galaxies of a local Coma Cluster reference sample and the WINGS survey sample. The comparison with the local Kormendy relation shows that the luminosity evolution due to the aging of the stellar content already assembled at z = 1.27 brings them on the local relation. Moreover, this stellar content places them on the size–mass relation of the local cluster ellipticals. These results imply that for a given mass, the stellar mass at z ~ 1.3 is distributed within these ellipticals according to the same stellar mass profile of local ellipticals. We find that a pure size evolution, even mild, is ruled out for our galaxies since it would lead them away from both the Kormendy and the size–mass relation. If an evolution of the effective radius takes place, this must be compensated by an increase in the luminosity, hence of the stellar mass of the galaxies, to keep them on the local relations. We show that to follow the Kormendy relation, the stellar mass must increase as the effective radius. However, this mass growth is not sufficient to keep the galaxies on the size–mass relation for the same variation in effective radius. Thus, if we want to preserve the Kormendy relation, we fail to satisfy the size–mass relation and vice versa.
Results. The combined analysis of the size–surface brightness relation with the size–mass relation leads to the result that these galaxies cannot increase solely in size and cannot significantly grow in mass.
Conclusions. We conclude that these 16 cluster ellipticals at z = 1.27 have, for the most part, completed their stellar mass growth at the redshift they are and that consequently, their evolution at z < 1.27 will be dominated by the aging of their stellar content. If this result is generalizable, then it shows that elliptical galaxies in the above mass range do not contribute to the observed size evolution of passive galaxies, as also found by other authors. This evolution would be instead mainly driven by disk galaxies. We do not find hints of differences between the properties of these cluster ellipticals and those of field ellipticals at comparable redshift, even if this last comparison is still based on a low number statistics.
Key words: galaxies: elliptical and lenticular, cD / galaxies: evolution / galaxies: high-redshift / galaxies: formation
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
It is now widely accepted that the mean size of early-type galaxies (ETGs; that is, of elliptical (E) and spheroidal galaxies (S0) as a population) has increased with time. This view arises from many authors having found that the average effective radius of high-z passive and/or massive galaxies, not necessarily early types, is smaller than the average effective radius of local early-type galaxies (e.g., Daddi et al. 2005; Trujillo et al. 2006, 2007; Longhetti et al. 2007; van der Wel et al. 2008; McGrath et al. 2008; van Dokkum et al. 2008; Buitrago et al. 2008; Cimatti et al. 2008; Bezanson et al. 2009; Damjanov et al. 2009, 2011; Cassata et al. 2011; Szomoru et al. 2012; Newman et al. 2012). The local comparison samples of galaxies are always selected from the Sloan Digital Sky Survey (SDSS), often on the basis of their Sérsic index n. This size evolution is found to be strong even at moderate redshift: the effective radius should increase by a factor two since z ~ 1 (e.g., Trujillo et al. 2011; Huertas-Company et al. 2013; Cimatti et al. 2012; Delaye et al. 2014). On the other hand, some studies do not confirm this result, in particular when samples of early-type galaxies are considered strictly defined on the basis of their morphology (e.g., Mancini et al. 2010; Saracco et al. 2011; Stott et al. 2011; Jørgensen & Chiboucas 2013) and when the progenitor bias is taken into account in the comparison between local and high-z samples (e.g., Saglia et al. 2010).
Progenitor bias represents a difficult limitation to treat, and the more heterogeneous the sample of selected galaxies, the more difficult it is to account for this bias. Progenitor bias has been treated in different ways by different authors according to the selection of galaxies considered. To compare the whole population of galaxies at different epochs in a meaningful way, some authors have selected galaxies at a constant number density at different redshift (e.g., van Dokkum et al. 2010). To compare early-type galaxies or passive galaxies some authors have selected galaxies progressively older with decreasing redshift, according to their passive aging (e.g., Saglia et al. 2010; Poggianti et al. 2013a; Carollo et al. 2013). Other authors try to get rid of this bias by selecting galaxies at fixed stellar velocity dispersion assuming that this quantity (defined in the same way for disks and for spheroids) is largely unaffected by the merger history of the galaxies (e.g., Belli et al. 2014).
The size evolution of passive/massive galaxies has been widely interpreted as the size evolution of the individual early types, that is to say, elliptical galaxies would increase their size individually during their lives. However, it was soon realized that this increase in size cannot be the result of a stellar mass growth since independent studies of the evolution of the luminosity and galaxy stellar mass function show that massive ETGs have already been assembled at z ~ 0.8 and that they have not grown further at lower redshift both in the field (e.g., Pozzetti et al. 2010) and in clusters (e.g., Andreon et al. 2008). Thus, early types should enlarge their size during their life but not grow significantly in mass, at least from z ~ 1. The mechanisms proposed to increase the size of ETGs, leaving their mass almost unchanged are principally two: a pure expansion due to a significant mass loss via quasar or stellar winds (Fan et al. 2008, 2010; Damjanov et al. 2009) and dry minor mergers whose main effect should be adding a low stellar mass density envelope re-arranging the stars in the outskirts of the galaxy enlarging the size (e.g., Hopkins et al. 2009; Naab et al. 2009; Bezanson et al. 2009; see also Nipoti et al. 2009 and 2012 for an analysis of the influence of dry mergers on size and velocity dispersion evolution of ETGs). Unless to only hypothesize dry minor mergers with particular orbital conditions (Naab et al. 2009), a pure increase in the effective radius of ETGs would imply a decrease in their stellar mass density within the same effective radius as the cube of the radius itself: if ETGs increase by a factor two since z = 1, their effective stellar mass density should decrease by a factor 8, a macroscopic effect that has not yet been observed (e.g., Saracco et al. 2012).
In fact, the study of the evolution of the mean size of passive and/or massive galaxies did not help much in constraining the evolution of proper elliptical galaxies or of their mass-assembly history. This may be for two main reasons. The first is that selecting passive and/or massive galaxies provides samples with a high fraction of disk galaxies. It is well established that at least 30–40 per cent of the passive galaxies at any redshift between 0.6 < z < 2.0 are disk galaxies (e.g., Ilbert et al. 2010; van der Wel et al. 2011; Cassata et al. 2011; Tamburri et al. 2014). Moreover, the remaining fraction (60–70 per cent) of early-type galaxies misses more than 20 per cent of the population of spheroidal galaxies (Tamburri et al. 2014). The selection of passive/massive galaxies therefore fails to produce representative samples of strictly defined ETGs, while it selects samples of disks and spheroids.
Disk galaxies and elliptical galaxies do not share the same formation and evolution history. In a hierarchical universe, elliptical galaxies are byproducts or descendants since their formation is directly linked to merger events of progenitor disk-like or irregular galaxies (e.g., Khochfar & Burkert 2003; De Lucia et al. 2006; Hopkins et al. 2010). Moreover, since merging controls the buildup and the growth of galaxies independently of their morphology, in a hierarchical universe it is reasonable to expect that the average size of galaxies increases with time because progenitors, which are smaller by definition, disappear to form the merger descendants which are by definition more massive, hence larger. In this possibly naive scheme, sampling both progenitors and descendants together as in a passive/massive galaxy selection to monitor the change of their mean properties (such as their mean size) makes it difficult to gain information about the mass assembly and the evolution either of early-type galaxies or of passive disk galaxies. It is difficult to understand which is evolving and what kind of evolution is taking place. The second reason for the poor effectiveness of the study of the mean size of passive/massive galaxies in constraining the evolution of proper ellipticals is that, independently of and in addition to the above progenitor bias, it is not clear whether the apparent change in the mean size of the whole population of passive/massive galaxies, that is disks and spheroids, is dominated by the size evolution of individual galaxies (each galaxy increases its effective radius) or rather by the appearance of new-born larger galaxies, by the disappearance of smaller ones, or by the combination of the two. van der Wel et al. (2008) suggests, among the first, the possibility that a combination of structural evolution of individual galaxies and the continuous formation of early-type galaxies may account for the observed size evolution. Actually, observations suggest that most of the observed size evolution is due to the size evolution of the compact disk-like galaxies observed at z ~ 2 (van der Wel et al. 2011). However, when disks and spheroids are mixed in the same sample, it is even more difficult to distinguish between the evolution of the individual galaxies and the evolution of the mean properties of the population.
A way to distinguish individual size evolution from other effects could be to compare the number density of compact early-type galaxies once selected at high and at low redshift consistently. Evidence of the presence of compact ETGs in the local Universe similar to those observed at high-z has come out recently (Valentinuzzi et al. 2010a,b; Poggianti et al. 2013a,b). Defining compact those early-types both at low-z and at high-z having a radius at least a factor two smaller than the radius derived by the mean size–mass relation by Shen et al. (2003), Saracco et al. (2010) find that the number density of compact high-z ETGs averaged over the interval 0.9 < z < 1.9 is accounted for by their local counterparts showing that size evolution, if it takes place, cannot affect the majority of the high-z ETGs. Recently, Carollo et al. (2013) have found no change in the number density of compact quenched early-type galaxies with masses < 1011 M⊙ at 0.2 < z < 1 and a 30 per cent decrease at higher masses, suggesting that the possible evolution of the mean size is driven mainly by the appearance of new-born larger early types. Poggianti et al. (2013a,b) find that no more than half and possibly a smaller fraction of the compact high-z galaxies has evolved in size.
Hints that the environment may affect the size of early-type galaxies and hence their evolution, in the sense that at a given redshift cluster ETGs are larger than field ETGs with the same mass, have also been recently claimed by some authors (e.g., Papovich et al. 2012; Delaye et al. 2014) even if not found by others (e.g., Damjanov et al. 2011; Rettura et al. 2010; Raichoor et al. 2012).
The studies of the size evolution of galaxies conducted and collected so far leave us with two basic questions about the assembly and evolution of elliptical galaxies: do individual elliptical galaxies grow their stellar mass and change continuously during their life, or is their morphological modeling the final stage of a process after which the elliptical evolves unperturbed in luminosity? The second question is: does the destiny of an elliptical galaxy depend significantly on the environment? We are trying to assess these by adopting a systematic approach based on the selection of early-type galaxies strictly defined morphologically at intermediate redshift both in the field and in cluster.
In this paper we study a sample of 16 elliptical galaxies in the cluster RDCS J0848+4453 at z = 1.27 to constrain their evolutionary status through comparing their size–surface brightness and size–stellar mass relations with those of a local sample of cluster ETGs selected according to the same criteria. In Sect. 2 we describe the data and the sample selection. In Sect. 3 we derive the physical (stellar mass, absolute magnitude, and age) and structural (effective radius, surface brightness) parameters for our galaxies. In Sect. 4 we derive the Kormendy relation at z ~ 1.3 and compare it with the local relation. In Sect. 5 we derive the luminosity evolution that the stars already formed at that redshift will experience and the consequences of this evolution. Then, combining the study of the size–mass relation to the size–surface brightness relation, we constrain the evolutionary status of our 16 ellipticals and their future evolution. Finally, in Sect. 6, we summarize the results and present our conclusions. Throughout this paper we use a standard cosmology with H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. All the magnitudes are in the Vega system, unless otherwise specified.
 |
Fig. 1 i775 − z850 color of galaxies. Left: the expected i775 − z850 color of galaxies is shown as a function of redshift for 4 different ages. The different solid lines refer to (from top to bottom) 7 Gyr old (red line), 4 Gyr old (green line), 2 Gyr old (blue line), and 1 Gyr old (cyan line). The dashed line refers to a 2 Gyr old template obtained with the Maraston (2005) models. The color is always i775 − z850 < 0.8 (horizontal black line) for redshift z < 0.8, and it is always larger than 0.8 for z > 0.8, this independently of the age of the stellar population considered. Right: the i775 − z850 color distribution of the 467 galaxies brighter than z850 < 24 falling within 1 Mpc from the cluster center is shown. The solid red line marks the mean color ⟨ i775 − z850 ⟩ = 1.1 ± 0.09 of the 5 ETGs cluster members spectroscopically identified by Stanford et al. (1997). The dashed lines represent ±1σ. A second peak is evident in the distribution at the mean color of the 5 ETGs. |
2. Data description
2.1. Observations
The analysis presented in this paper is based on Hubble Space Telescope (HST) and Spitzer archival data and on ground-based optical observations that we obtained at the Large Binocular Telescope (LBT). The HST data retrieved from the archive are composed of optical ACS observations and near-IR NICMOS observations. ACS observations (ID 9919) covering a field of about 11 arcmin2 surrounding the cluster RDCS J0848+4453 were obtained in 2004 in the F775W (7300 s) and F850LP (12 200 s) filters and they are described in Postman et al. (2005; see also Raichoor et al. 2011). The ACS images we used have a pixel scale of 0.05 arcsec/pix and a resolution of FWHM850 ≃ 0.12 arcsec. NICMOS observations (ID 7872) sampling a field of about 3 arcmin2 centered on the same cluster were obtained with the NIC3 camera in the F160W filter (11 200 s) and are described in van Dokkum et al. (2001). The NIC3 images have a pixels scale of 0.2 arcsec/pix and a resolution of FWHM160 ≃ 0.22 arcsec. Spitzer data (PI S. A. Stanford) were obtained in the four IRAC band passes [3.6, 4.5, 5.8, 8.0] μm. We used the fully co-added mosaics (0.6 arcsec/pix) produced by the standard Spitzer reduction pipeline resulting in a mean exposure time of ~2200 s in the 3.6 μm and 5.8 μm bands and in about 1900 s in the 4.5 μm and 8.0 μm.
Our LBT observations were carried out between 14 and 17 of February 2013 under poor and unstable seeing conditions (1.0–1.8 arcsec) with the Large Binocular Cameras (LBCs1) in the four Bessel U,B,V and R filters. LBCs are two wide-field imaging cameras located at the Prime Focus stations of LBT. Each LBC camera has a wide field of view equivalent to ~ 23′ × 23′, and it provides images with a sampling of 0.23 arcsec/pixel. The two LBC cameras are optimized for the UV-blue wavelengths (LBC-blue, from 0.3 μm to 0.5 μm) and for the red-IR bands (LBC-red, from 0.5 μm 1.0 μm), respectively. Observations have been carried out in the full binocular configuration, i.e., with the two LBC cameras operating simultaneously and pointing in the same direction of the sky. An integration of ~4 h in each filter has been obtained in 8 h of binocular configuration time (4 h in U at LBC-blue and simultaneously in V at LBC-red, plus 4 h in B (LBC-blue) and simultaneously in R (LBC-red)). Observations consist of short exposures of six minutes each dithered by 30 arcsec in a random pattern to cover the gap between the CCDs. The standard reduction procedure (bias and flat-field correction and cosmic ray removal) has been applied to the single frames before combining them to produce the final stacked mosaic. Given the large variation in the seeing conditions during the observations, we decided to consider only those images taken under seeing conditions better than 1.4 arcsec to construct final stacked images of good quality. Thus, the final co-added mosaics have different effective exposure times ranging from 1 h (U and V, FWHM ~ 1.0 arcsec) to almost 3 h (B and R, FWHM ~ 1.4 arcsec). The final mosaic has been produced with SWarp (v.2.19.1, Bertin 2010).
2.2. Sample selection
The sample of ellipticals used in this analysis is composed of 16 galaxies selected to belong to the cluster RDCS J0848+4453 at z = 1.27 (Stanford et al. 1997). Many authors have found that compact galaxies preferentially host older stellar populations (e.g., Gargiulo et al. 2009; Saracco et al. 2009, 2011; Valentinuzzi et al. 2010a; Poggianti et al. 2013a; Taylor et al. 2010). Consequently, selection criteria (directly or indirectly) dealing with the age could introduce a bias in favor of compact galaxies. For instance, the median mass-size relation of galaxies is found to shift towards smaller radii for galaxies with older stars (Poggianti et al. 2013a,b), and colors bracketing the Balmer break, such as the R-K, tend to select an increasingly higher fraction of compact galaxies going toward redder colors (Saracco et al. 2011). A selection based on the passivity as resulting from the specific star formation rate (sSFR) deals with the age of the stellar population since, at fixed stellar mass and for a fixed sSFR threshold, a galaxy may or not may be passive depending on the SFR of the best-fitting model, i.e., on its age. Our attempt is to select elliptical galaxies by avoiding selection criteria based on (or related to) the age of their stellar population. Thus, we selected our final sample on the basis of their morphology without introducing any selection based on the age of their stellar population or on their passivity.
To this end, we first detected all the sources (~2200 up to a magnitude in the F850LP filter z850 < 27.6) in the ~11 arcmin2 region surrounding the cluster covered by the F850LP image. We used SExtractor (Bertin & Arnouts 1996) both to detect sources and to measure their magnitude MAG_BEST. Magnitudes in the F775W filter (i775 hereafter) were obtained by running the procedure in double-image mode using the F850LP image as reference. To perform a reliable and robust visual morphological classification, we selected galaxies with magnitudes z850 ≤ 24. At this magnitude limit, the sample is 100% complete. From this flux-limited sample we removed stars identified by the SExtractor stellar index CLASS_STAR > 0.9 and restricted the selection to those galaxies within a projected radius D ≤ 1 Mpc (~2 arcmin) from the cluster center. We thus obtained a sample of 467 galaxies, 105 of which are also covered by NICMOS-F160W observations. This sample contains the six cluster member galaxies spectroscopically identified by Stanford et al. (1997) within a diameter region of ~0.7 Mpc. One of them (galaxy #237 in their Table 1) appears irregular in the F850LP image. The remaining five member galaxies are clearly ETGs, as confirmed by their morphology (see below for the morphological classification). The mean color of these five cluster member ETGs is ⟨ i775 − z850 ⟩ = 1.1 with a dispersion σiz = 0.09. At the redshift of the cluster, this color roughly corresponds to UV − U, so it is a measure of the slope of the spectral energy distribution (SED) of galaxies at λrest < 4000 Å.
In the left-hand panel of Fig. 1 the expected apparent i775 − z850 color of galaxies with different ages is shown as a function of redshift. It can be seen that this color clearly shows two different behaviors depending on whether it samples the spectrum at λrest> 4000 Å or at shorter wavelengths. In particular, the observed color is always i775 − z850 < ~0.8 for z < ~0.8 independently of the age of the galaxy. At redshift z ~ 0.8–0.9, when the region at 0.4–0.5 μm enters the filter F775W, the i775 − z850 color changes rapidly, thereby increasing its value. For z > 0.9, the color is always i775 − z850 > 0.8. The other important property of this color is its extremely weak dependence on the age of the stellar population as clearly demonstrated by the small color variations (<0.1 mag) for different ages. As a result, the observed i775 − z850 trace the redshift of the galaxies well without introducing any dependence on their age. In the right hand panel of Fig. 1 the i775 − z850 color distribution of the 467 galaxies with z850 ≤ 24 is shown.
The observed distribution clearly reflects the behavior shown in the left hand panel with the bulk of the z850 ≤ 24 galaxies having a color i775 − z850 < ~0.8 centered on 0.3–0.4 mag suggesting that they are all at z < 1. The remaining galaxies form a second peak centered on i775 − z850 ≃ 1.1 suggesting that they are at z> 1. This second peak is centered on the mean color of the five elliptical cluster members marked in Fig. 1. Thus, on the basis of these considerations we selected all the galaxies having a color 0.9 < i775 − z850 < 1.3 according to the color distribution shown in Fig. 1. This color range corresponds to two sigmas from the mean color of the 5 ETGs cluster members. For the resulting 44 galaxies we performed a morphological classification to identify the ellipticals.
The morphological classification is based on the visual inspection of the galaxies carried out independently by two of us on the ACS-F850LP image and on the fitting to their luminosity profile described below. In particular, we classified as ETG those galaxies having a regular shape with no signs of disk on the F850LP images and no irregular or structured residuals resulting from the profile fitting. On the basis of this morphological classification, 16 galaxies out of the 44 with zz850 < 24 and i775 − z850 = 1.1 ± 0.2 turned out to be ellipticals. The selected sample is summarized in Table 1. The F850LP images of the 16 ellipticals are shown in Appendix B.
Selected sample of 16 cluster elliptical galaxies.
2.3. Multiwavelength photometry
Magnitudes for these 16 galaxies have been measured in all the bands using SExtractor. We adopted the MAG_BEST as best estimator of the magnitude. Given the large difference in the PSF among the images (from ~0.12 arcsec of the ACS images to >2.7–3 arcsec of Spitzer images) and the relative crowding of the field, many sources isolated in the highest resolution images are affected by blending with neighboring sources in the less resolved (ground-based and Spitzer) images. As a consequence of this, magnitudes, hence colors, measured within apertures scaled according to the different PSF would be affected by this blending in the lowest resolution images, which is difficult to quantify. Instead of using aperture magnitudes, we therefore preferred to measure the colors using the MAG_BEST estimator that, in the case of blending, tries to recover the true flux of the target source. We also verified that for unblended sources, the colors derived from MAG_BEST are consistent with those measured within scaled apertures by comparing them for a sample of points sources isolated in all the images.
 |
Fig. 2 Color–magnitude relation. The i775 − z850 (upper panel) and the z850 − H160 (lower panel) colors of the selected ETGs galaxies (red filled symbols) as a function of z850 (16 galaxies) and of H160 (15 galaxies) are shown together with those of the 105 galaxies (black crosses) covered by NICMOS observations. The five ETGs with spectroscopic redshift are marked by red filled circles and the remaining 11 ETGs cluster members are marked by red filled triangles. Red open circles mark all the galaxies selected in the color range 0.9 < i775 − z850 < 1.3. The solid red line in the upper panel is the color–magnitude relation (i775 − z850) = 2.1 − 0.044z850 best-fitting the 16 ellipticals. |
NICMOS-F160W observations cover 15 out of the 16 ETGs selected above (and 30 out of the 44 galaxies in the color range 0.9 < i775 − z850 < 1.3), with galaxy #471 falling outside. In Fig. 2, the i775 − z850 and the z850 − H160 colors of the 16 selected ETGs are shown as a function of z850 (upper panel) and of H160 (lower panel) together with those of the 105 galaxies in common between NICMOS and ACS observations, and galaxies selected according to the color cut 0.9 < i − z < 1.3. It is worth noting that they span a wide color range, 1.7 < z850 − H160 < 3.6, as visible in the lower panel of Fig. 2. Once the morphology of these galaxies is defined, it turns out that ellipticals are mostly distributed within a narrower range of z850 − H160 color and that they define a red sequence, as expected. However, there is also an exception: one of the bluest galaxy, z850 − H160 = 1.7, has an elliptical morphology.
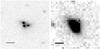 |
Fig. 3 Three galaxies, #5, #626, and #657 that are clearly resolved in the F850LP band image (left) thanks to both the resolution (FWHM ~ 0.11 arcsec) and to the small pixel size (0.05 arcsec/pix). They are not resolved in the NIC3-F160W band image (right) because of the lower resolution (FWHM ~ 0.22 arcsec) and pixel size (0.2 arcsec/pix). Both the images are 6′ × 6′. The black line represents 1 arcsec. |
Photometry in the 11 photometric bands.
The upper panel shows the color–magnitude relation (i775 − z850) = 2.1 − 0.044z850 best fitting the 16 selected ellipticals. It is worth noting the good agreement with the relations found by Holden et al. (2005) for a cluster at z = 1.23 and by Mei et al. (2012) for the clusters in the Linx structure. For the 15 ellipticals covered by NICMOS observations, we also derived structural parameters in the F160W band (see Sect. 3.2) besides measuring magnitudes. Three of them (#5, #626 and #657, see Fig. 3) are blended in the NICMOS images because of the large pixel size and the low resolution of the NIC3 camera. For the same reasons these galaxies are not resolved either in the LBC U-, B-, V-, and R-band images or in the Spitzer images. For these galaxies, the magnitudes in those filters in which they are not resolved have been derived by redistributing the total flux of the resulting blended object according to the flux measured for each of them in the nearest filter in which they are resolved. For instance, the H160 magnitude for each of these three galaxies has been derived redistributing the total F160W flux measured for them blended (i.e., considered as a single object) on the basis of the flux measured for each of them in the F850LP filter.
The LBC observations cover the whole sample of 16 ETGs. As previously said, three galaxies are not resolved in the LBC images. For them, U,B,V, and R magnitudes have been derived by redistributing the total U,B,V, and R fluxes on the basis of the flux measured for each of the galaxies in the F775W filter.
Spitzer-IRAC observations cover the whole sample of ETGs. Magnitudes were estimated in the four IRAC bands using SExtractor in double-image mode and adopting the 3.6 μm image as reference. The reliability of the flux measurement was checked by comparing the flux measured with SExtractor for some stars in the field with the flux obtained using the IRAF task phot. For the IRAC images, besides the three galaxies above, galaxies #2 and #1260 are also not resolved due to the low resolution (FWHM> 2.5 arcsec). For them, we estimated the magnitudes in the four IRAC bands, using the fluxes measured in the F160W filter as reference. In Table 2 we report the photometry in the 11 photometric bands for the 16 ellipticals of the sample.
2.4. Comparison data in the local universe
As comparison data in the local universe we considered two independent data sets relating to local cluster early-type galaxies. The first data set comprises the well defined local Kormendy relation, the first comparison that we face in Sect. 4. For this comparison, we used the Kormendy relation derived from the sample of 147 elliptical (E) and S0 galaxies belonging to the Coma cluster (z = 0.024) studied by Jørgensen et al. (1995a, 1996). The morphological classification of this sample is based on a visual analysis, as for our sample. Also, the structural parameters were derived in the Johnson B and in the Gunn r filters matching the F850LP and F160W filters at the redshift of our galaxies. We applied a correction of –0.38 mag to pass from Gunn r to Cousins R magnitudes (Fukugita et al. 1995; see also Longhetti et al. 2007). The stellar mass range covered by this sample is approximately 0.8 × 1010−3 × 1011 M⊙, as derived from their stellar velocity dispersion measurements (Jørgensen et al. 1995b), so it covers the same mass range as covered by our galaxies. It is worth noting that this sample comprises both elliptical and S0 galaxies, while our sample should only include elliptical galaxies. However, the scaling relations and, in particular, the zero point and the slope obtained using the whole sample of E and S0 galaxies do not differ from those obtained separately from S0 and E (Jørgensen et al. 1996). This relation is the one most commonly used as reference for the local cluster galaxies (e.g., La Barbera et al. 2003, 2010; Di Serego Alighieri et al. 2005; Saglia et al. 2010; Raichoor et al. 2012) and it is best suited to comparison with the one we derive from our galaxies at z = 1.27, given their properties.
The other data set that we consider is composed of local cluster ellipticals extracted from the Wide-field Nearby Galaxy Cluster Survey (WINGS; Fasano et al. 2006; Valentinuzzi et al. 2010a). The survey core is based on optical imaging of 78 nearby (0.04 < z < 0.07) clusters in B and V, matching the F850LP imaging of our sample. The morphology of the WINGS galaxies was derived on optical images using the automated dedicated tool MORPHOT (Fasano et al. 2012). The morphological indicators of MORPHOT were calibrated using a control sample of about 1000 visually classified galaxies to provide a fine classification resembling the one performed visually (see Fasano et al. 2012, for a comprehensive description). The effective radius of the WINGS galaxies were derived from optical images using GASPHOT (Pignatelli et al. 2006), an automated tool that performs a simultaneous fit to the major and minor axis light growth curves using a Sérsic low convoluted with the PSF.
Stellar masses are derived, as for our sample, from the Bruzual & Charlot (2003) stellar population synthesis models using the Salpeter IMF (Salpeter 1955), then rescaled to Kroupa IMF, according to the recipe in Longhetti & Saracco (2009). We did not apply any correction to these masses since the scaling between Kroupa and Chabrier IMF stellar masses is lower than a factor 1.1 (Longhetti & Saracco 2009). From the WINGS catalog, we selected all the elliptical galaxies and the transition class of E/S0 galaxies, namely galaxies of morphological type −5.0 < TM < −4.0, according to the morphological classification of the WINGS survey (see Table 1 in Fasano et al. 2012). We included the transition class of E/S0 since we believe that they cannot be distinguished in our sample at z ~ 1.3, given the difficulty in distinguishing these galaxies from pure ellipticals in the local universe. The resulting sample is composed of ~400 ellipticals with stellar masses in the range 109 − 1012 M⊙ and absolute magnitude –21 < MB < −15.5.
3. Deriving physical and structural parameters
3.1. Age, stellar masses, and absolute magnitudes
For each galaxy of the sample, we derived the mean age of its stellar population, the stellar mass ℳ∗, and the B- and R-band absolute magnitudes, MB and MR. These quantities were derived by fitting the 11 available photometric points of the observed (SED) at the redshift of the cluster, z = 1.27, with a large set of templates built with different models. In particular, we considered Bruzual & Charlot models (2003, hereafter BC03), the later release by Charlot & Bruzual (2007, hereafter CB07) and the models of Maraston (2005, hereafter MA05). We considered a Salpeter initial mass function (IMF) for the MA05 and BC03 models and Chabrier (Chabrier 2003) IMF for the BC03 and CB07 models. In all the cases we considered four exponentially declining star formation histories (SFHs) with e-folding time τ = [0.1, 0.3, 0.4, 0.6] Gyr and solar metallicity Z⊙.
Extinction AV has been considered and treated as a free parameter in the fitting. We adopted the extinction curve of Calzetti et al. (2000) and allowed AV to vary in the range 0 < AV < 0.6 mag. For 12 galaxies out of the 16 of the sample, the best-fitting template is defined by SFHs with τ = 0.1 Gyr independently of the model and of the IMF used. The remaining four galaxies of the sample are best fit by SFHs with τ = 0.3 Gyr (#1, #590) and τ = 0.4 Gyr (#719 and #1160). The stellar mass ℳ∗ we derived is the mass locked into stars at the epoch of their observation after the gas fraction returned to the interstellar medium.
The MB and MR absolute magnitudes have been derived using the observed apparent magnitudes in the filters closest to the rest-frame B and R of the galaxies, i.e., filters F850LP and F160W sampling λrest ~ 4000 Å and λrest ~ 7000, respectively, at the redshift of the cluster. The color k-correction term that takes the different filters response (e.g., F160W vs. Rcousin) into account was derived from the best-fitting template.
In Table A.1 we report the age, the stellar mass,
and the absolute magnitudes obtained for each galaxy with the different IMFs and models
considered. The mean values of the parameters are reported in the last row of the table.
It can be seen that the different models MA05, BC03, and CB07 do not provide significantly
different values of age, stellar mass, and absolute magnitudes at fixed IMF. In contrast,
a Salpeter IMF provides stellar masses systematically higher than a Chabrier IMF (see,
e.g., Longhetti et al. 2009). In particular, as to
our 16 galaxies, we obtained 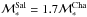 on
average.
on
average.
In the following, we consider the values obtained with BC03 models and Chabrier IMF
summarized in Table 3. The 16 ellipticals have
stellar masses in the range 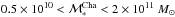 with a median
value ℳ∗ ≃ 6 ×
1010 M⊙. Their ages are in the
range 0.7–4.3 Gyr with a median value of about 1.7 Gyr. Since the sample is
magnitude-limited and all the galaxies are at the same redshift, the minimum stellar mass
for which the sample is complete depends on the M/L ratio. According to the method used by
Pozzetti et al. (2010) we estimated, for each
galaxy, the limiting mass log (ℳlim)
= log (ℳ∗) + 0.4(z −
zlim) that a galaxy would have if its
magnitude was equal to the limiting magnitude of the sample, zlim = 24 in our
case. Considering the distribution of the values of ℳlim for the whole sample, the
minimum mass ℳmin
above which 95% of them lie is log (ℳmin/M⊙) ≃
9.8. A similar result is obtained if we consider only the three (#173,
#471, and #1260) faintest galaxies of the samples, which is the 20% faintest galaxies for
which we estimated log (ℳlim/M⊙) =
10.52,10.02,9.56. The galaxy in our
sample with the lowest mass has a stellar mass log (ℳ∗/M⊙) =
9.7, so we can consider our sample nearly complete over the whole mass
range covered.
with a median
value ℳ∗ ≃ 6 ×
1010 M⊙. Their ages are in the
range 0.7–4.3 Gyr with a median value of about 1.7 Gyr. Since the sample is
magnitude-limited and all the galaxies are at the same redshift, the minimum stellar mass
for which the sample is complete depends on the M/L ratio. According to the method used by
Pozzetti et al. (2010) we estimated, for each
galaxy, the limiting mass log (ℳlim)
= log (ℳ∗) + 0.4(z −
zlim) that a galaxy would have if its
magnitude was equal to the limiting magnitude of the sample, zlim = 24 in our
case. Considering the distribution of the values of ℳlim for the whole sample, the
minimum mass ℳmin
above which 95% of them lie is log (ℳmin/M⊙) ≃
9.8. A similar result is obtained if we consider only the three (#173,
#471, and #1260) faintest galaxies of the samples, which is the 20% faintest galaxies for
which we estimated log (ℳlim/M⊙) =
10.52,10.02,9.56. The galaxy in our
sample with the lowest mass has a stellar mass log (ℳ∗/M⊙) =
9.7, so we can consider our sample nearly complete over the whole mass
range covered.
Physical parameters of the sample.
3.2. Surface brightness profile fitting
The effective radius Re [kpc] (re [arcsec]) of
our galaxies has been derived by fitting a Sérsic profile
![\begin{eqnarray} I(R)=I_{\rm e} \exp \left[-b_n\left[\left({R\over R_{\rm e}}\right)^{1/n}-1\right]\right] \end{eqnarray}](/articles/aa/full_html/2014/07/aa23495-14/aa23495-14-eq122.png) (1)to
the observed light profile both in the ACS-F850LP image and in the NIC3-F160W image, i.e.,
in the rest-frame B and R bands of the galaxies. The fitting was performed
both assuming n as a free parameter and assuming n = 4, i.e., a de
Vaucouleurs profile. The two-dimensional fitting was performed using Galfit
software (v. 3.0.4, Peng et al. 2002).
The point spread function (PSF) convolved with the Sérsic profile in the F850LP image was
chosen among five PSFs represented by four high signal-to-noise ratio stars identified in
the field plus a mean PSF obtained averaging the profile of these four stars. The PSFs
used in the NIC3 images were generated at different positions on the array using the Tiny
Tim software since the pixel size of the camera (0.2 arcsec/pix) does not provide a
sufficient sampling of the FWHM.
(1)to
the observed light profile both in the ACS-F850LP image and in the NIC3-F160W image, i.e.,
in the rest-frame B and R bands of the galaxies. The fitting was performed
both assuming n as a free parameter and assuming n = 4, i.e., a de
Vaucouleurs profile. The two-dimensional fitting was performed using Galfit
software (v. 3.0.4, Peng et al. 2002).
The point spread function (PSF) convolved with the Sérsic profile in the F850LP image was
chosen among five PSFs represented by four high signal-to-noise ratio stars identified in
the field plus a mean PSF obtained averaging the profile of these four stars. The PSFs
used in the NIC3 images were generated at different positions on the array using the Tiny
Tim software since the pixel size of the camera (0.2 arcsec/pix) does not provide a
sufficient sampling of the FWHM.
We derived the effective radius 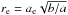 where ae is the semi-major axis of the projected
elliptical isophote containing half of the total light provided by Galfit
and b/a is the axial
ratio. In all the cases considered the fit converged for all the galaxies. In Appendix B
for each galaxy we show the Galfit two-dimensional fitting model
and the resulting residual. The goodness of the fit can be seen from the residuls shown in
Fig. B.1 and from the one-dimensional surface
brightness profiles shown in Fig. B.2. For all the
galaxies the fit to the surface brightness profile extends over more than five magnitudes
and, apart from the largest galaxy (#4), up to >2 Re. In Table
4 we report the best-fitting parameters
n,
Re [kpc], and the best-fitting apparent
magnitudes,
where ae is the semi-major axis of the projected
elliptical isophote containing half of the total light provided by Galfit
and b/a is the axial
ratio. In all the cases considered the fit converged for all the galaxies. In Appendix B
for each galaxy we show the Galfit two-dimensional fitting model
and the resulting residual. The goodness of the fit can be seen from the residuls shown in
Fig. B.1 and from the one-dimensional surface
brightness profiles shown in Fig. B.2. For all the
galaxies the fit to the surface brightness profile extends over more than five magnitudes
and, apart from the largest galaxy (#4), up to >2 Re. In Table
4 we report the best-fitting parameters
n,
Re [kpc], and the best-fitting apparent
magnitudes, 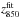 and
H
and
H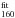 .
The values in parentheses, were obtained by fixing n = 4 in the fit. The
surface brightness in the B and in the R bands was obtained from
the B- and
R- band
absolute magnitudes reported in Table 3 and
corrected for
.
The values in parentheses, were obtained by fixing n = 4 in the fit. The
surface brightness in the B and in the R bands was obtained from
the B- and
R- band
absolute magnitudes reported in Table 3 and
corrected for 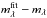 , the difference
between the best fitting apparent magnitude resulting from the surface brightness profile
fitting and the observed apparent magnitude reported in Table 2. (see Sect. 4). The effective radii Re, as derived
by fitting the Sérsic profile in the ACS-F850LP images,
are in the range 0.5–8 kpc, with the exception of the dominant elliptical galaxy of the
cluster that has an effective radius Re = 16.7 kpc. The Sérsic index varies
in the range 2.2
< n <
6 with a median value n = 4.2. As can be seen from Table 4 the typical uncertainty on the effective radius
derived from the F1850LP image is
about 10%, sligthly more (15%) in the F160W image.
, the difference
between the best fitting apparent magnitude resulting from the surface brightness profile
fitting and the observed apparent magnitude reported in Table 2. (see Sect. 4). The effective radii Re, as derived
by fitting the Sérsic profile in the ACS-F850LP images,
are in the range 0.5–8 kpc, with the exception of the dominant elliptical galaxy of the
cluster that has an effective radius Re = 16.7 kpc. The Sérsic index varies
in the range 2.2
< n <
6 with a median value n = 4.2. As can be seen from Table 4 the typical uncertainty on the effective radius
derived from the F1850LP image is
about 10%, sligthly more (15%) in the F160W image.
Morphological parameters of galaxies.
Some authors find that the sizes derived in near-IR bands for galaxies at z> 1 appear about 10% to 20% smaller than the sizes measured in optical bands (e.g., Cassata et al. 2011; Gargiulo et al. 2012). These works deal with field galaxies. In fact, we do not detect this systematic in our data. However, we have to consider that for a typical effecive radius of ~2 kpc (as for our galaxies), this systematic corresponds to 0.2–0.4 kpc, equal to the uncertainties (at one sigma) on our estimates of the effective radii. Most importantly, the NIC3 camera with its pixel size (0.2 arcsec) sampling a physical size of ~1.7 kpc at z = 1.3 is most probably not suited to detecting variations on the order of a tenth of its pixel size. The works showing differences between optical and UV rest-frame size of galaxies are indeed based on WFC3 data having a pixel size almost half of the pixel size of the NIC3 camera. We are therefore not in the position to assess whether there is a trend of the size with wavelength in our data and consequently to probe a possible dependence of this effect on the environment.
 |
Fig. 4 Kormendy relation in the rest-frame B band (left panel) and R band (right panel). Red filled symbols are our 16 cluster ellipticals at z = 1.27 (upper panels) and evolved to z = 0 (lower panels) according to the passive luminosity evolution as described in Sect. 5.1 and reported in Table 4. The red lines are the Kormendy relation reported in Table 5 obtained by fitting Eq. (4) to our 16 ellipticals assuming the slope β at z = 0 (solid line) and leaving β as free parameter (dashed line). The open squares are the sample of early-type galaxies in the Coma cluster studied by Jørgensen et al. (1995a). The black lines represent the Kormendy relation at z = 0 derived from this sample and reported in Eqs. (7) and (8). |
4. The Kormendy relation at z = 1.3
The mean effective surface brightness ⟨
μ ⟩ e [mag/arcsec2] of a galaxy can be computed from
the apparent magnitude m and the area included within the effective radius
re
[arcsec]: 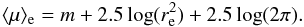 (2)By
substituting the observed quantities with those in the rest frame of the galaxy, we obtain
(2)By
substituting the observed quantities with those in the rest frame of the galaxy, we obtain
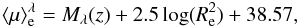 (3)where
Mλ(z) is
the absolute magnitude of the galaxy at the rest-frame wavelength λ at redshift z, and Re is in [kpc],
after correcting for the cosmological dimming term 10log (1 + z). This relation
can be used to trace the evolution that ellipticals undergo through time. The mean surface
brightness ⟨ μ ⟩
e is indeed expected to change with redshift because of the
passive luminosity evolution of the stellar populations that affects the absolute magnitude
in Eq. (3). Moreover, if elliptical galaxies grow with time due to merging, then their
surface brightness will change further, both due to the change in their luminosity
(proportional to the mass increase) and to the consequent increase in their effective
radius. The variation in Re will add up to the luminosity evolution
as the square of its variation, significantly affecting the observed change of
⟨ μ ⟩
e. We come back to this issue in the next section.
(3)where
Mλ(z) is
the absolute magnitude of the galaxy at the rest-frame wavelength λ at redshift z, and Re is in [kpc],
after correcting for the cosmological dimming term 10log (1 + z). This relation
can be used to trace the evolution that ellipticals undergo through time. The mean surface
brightness ⟨ μ ⟩
e is indeed expected to change with redshift because of the
passive luminosity evolution of the stellar populations that affects the absolute magnitude
in Eq. (3). Moreover, if elliptical galaxies grow with time due to merging, then their
surface brightness will change further, both due to the change in their luminosity
(proportional to the mass increase) and to the consequent increase in their effective
radius. The variation in Re will add up to the luminosity evolution
as the square of its variation, significantly affecting the observed change of
⟨ μ ⟩
e. We come back to this issue in the next section.
Best-fitting α and β values of Eq. (4) for the B and R band rest-frame data.
The evolution of the surface brightness Δμ of elliptical galaxies is usually quantified by
using the Kormendy relation (KR, Kormendy 1977), a
linear scaling relation between the logarithm of the effective radius Re [Kpc] and the
mean surface brightness ⟨ μ ⟩
e within Re:
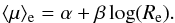 (4)Elliptical
galaxies both in field and in clusters follow this tight relation with a slope close to
three out to z ~
1 (Hamabe & Kormendy 1987;
Schade et al. 1996; Ziegler et al. 1999; La Barbera et al. 2003, 2004; Reda et al. 2004; di Serego Alighieri et al. 2005). On the other hand, the zero point α is found to vary with the
redshift of the galaxies, reflecting their luminosity evolution and the possible evolution
of Re over time. Since the value of
α strictly
depends on the photometric band and system selected to derive magnitudes and morphological
parameters, its value needs to be transformed into that of a common rest-frame wavelength
when comparisons at different z are performed. Since morphological parameters have
been derived in the F850LP and
F160W bands, the
comparison with the local scaling relations will be done considering the rest-frame
B-band and
R-band. For
each galaxy of our sample, we therefore computed the mean surface brightness in the
B-band,
(4)Elliptical
galaxies both in field and in clusters follow this tight relation with a slope close to
three out to z ~
1 (Hamabe & Kormendy 1987;
Schade et al. 1996; Ziegler et al. 1999; La Barbera et al. 2003, 2004; Reda et al. 2004; di Serego Alighieri et al. 2005). On the other hand, the zero point α is found to vary with the
redshift of the galaxies, reflecting their luminosity evolution and the possible evolution
of Re over time. Since the value of
α strictly
depends on the photometric band and system selected to derive magnitudes and morphological
parameters, its value needs to be transformed into that of a common rest-frame wavelength
when comparisons at different z are performed. Since morphological parameters have
been derived in the F850LP and
F160W bands, the
comparison with the local scaling relations will be done considering the rest-frame
B-band and
R-band. For
each galaxy of our sample, we therefore computed the mean surface brightness in the
B-band,
 (5)and
in the R-band,
(5)and
in the R-band,
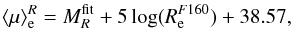 (6)where
(6)where
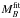 and
and
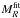 are the
absolute magnitudes derived from the Galfit best-fitting apparent
magnitudes
are the
absolute magnitudes derived from the Galfit best-fitting apparent
magnitudes 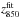 and
H
and
H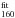 .
The surface brightnesses thus obtained are reported in Table 4. In the upper panels of Fig. 4 the surface
brightness of our 16 galaxies is plotted as a function of their Re on the
B-band
[Re; ⟨ μ ⟩ e] plane
(left) and on the R-band plane (right). The Kormendy relations derived
from the sample of early-type galaxies belonging to the Coma cluster at z = 0.024 studied by
Jørgensen et al. (1995a, 1996; see Sect. 2.4 for a description of the data) are also shown. In
particular, the KR in the B-band,
.
The surface brightnesses thus obtained are reported in Table 4. In the upper panels of Fig. 4 the surface
brightness of our 16 galaxies is plotted as a function of their Re on the
B-band
[Re; ⟨ μ ⟩ e] plane
(left) and on the R-band plane (right). The Kormendy relations derived
from the sample of early-type galaxies belonging to the Coma cluster at z = 0.024 studied by
Jørgensen et al. (1995a, 1996; see Sect. 2.4 for a description of the data) are also shown. In
particular, the KR in the B-band,
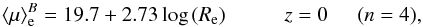 (7)and
in the R-band,
(7)and
in the R-band,
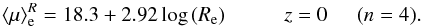 (8)Figure
4 shows the KR we obtained at z = 1.27 by fitting Eq. (4)
to our 16 ellipticals fixing the slope at z = 0 (βz = 0) (solid line) and
considering β
as free parameter (dashed line). The resulting best fitting relation we obtained (for a free
n index) is
(8)Figure
4 shows the KR we obtained at z = 1.27 by fitting Eq. (4)
to our 16 ellipticals fixing the slope at z = 0 (βz = 0) (solid line) and
considering β
as free parameter (dashed line). The resulting best fitting relation we obtained (for a free
n index) is
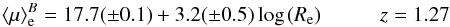 (9)in
the B band and
(9)in
the B band and
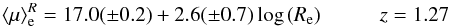 (10)in
the R band. The
slope β of the
KR we obtain agrees within the errors with the slope of the KR at z = 0 (Eqs. (7) and (8)). In
Table 5 we report the parameters α and β of the KR relation obtained
by fitting the (Re, ⟨ μ ⟩ e) data
obtained both for a free n index and for n = 4. The good agreement
between the slope obtained at z
~ 1.3 and the local value in the case of n = 4 is worth noting. We
also report the value of α obtained by fixing the β slope at the value at
z = 0 and the
resulting amount of evolution Δμ
= ⟨ μ ⟩ e(z = 1.27) − ⟨ μ ⟩
e(z = 0) between z = 0 and z = 1.27. That the slope of
the relation is not significantly changed in the past 9 Gyr means that the luminosity and
the effective radius of these elliptical galaxies scale according to the same rule seen in
the local Universe. In contrast, the zero point α of the relations at z = 1.27 is significantly
brighter than at z =
0, 1.8 mag brighter in the B-band and 1.3 mag brighter in the R-band (see Table 5). These offsets agree with those found by Holden et al.
(2005) and by Rettura et al. (2010) for the cluster RDCS J1252.9-2927 at z = 1.237 and with what was
found by Raichoor et al. (2012) on a sample of
cluster and group galaxies belonging to the Linx supercluster at z ≃ 1.27 including 7 out of
the 16 ellipticals of our sample. These offsets account for the evolution that galaxies
underwent and can be affected by any change that galaxies experience caused by the passive
luminosity evolution, by the possible evolution of the effective radius, and by the possible
mass accretion. In the next section we consider how these evolutionary terms can affect the
resulting Kormendy relation.
(10)in
the R band. The
slope β of the
KR we obtain agrees within the errors with the slope of the KR at z = 0 (Eqs. (7) and (8)). In
Table 5 we report the parameters α and β of the KR relation obtained
by fitting the (Re, ⟨ μ ⟩ e) data
obtained both for a free n index and for n = 4. The good agreement
between the slope obtained at z
~ 1.3 and the local value in the case of n = 4 is worth noting. We
also report the value of α obtained by fixing the β slope at the value at
z = 0 and the
resulting amount of evolution Δμ
= ⟨ μ ⟩ e(z = 1.27) − ⟨ μ ⟩
e(z = 0) between z = 0 and z = 1.27. That the slope of
the relation is not significantly changed in the past 9 Gyr means that the luminosity and
the effective radius of these elliptical galaxies scale according to the same rule seen in
the local Universe. In contrast, the zero point α of the relations at z = 1.27 is significantly
brighter than at z =
0, 1.8 mag brighter in the B-band and 1.3 mag brighter in the R-band (see Table 5). These offsets agree with those found by Holden et al.
(2005) and by Rettura et al. (2010) for the cluster RDCS J1252.9-2927 at z = 1.237 and with what was
found by Raichoor et al. (2012) on a sample of
cluster and group galaxies belonging to the Linx supercluster at z ≃ 1.27 including 7 out of
the 16 ellipticals of our sample. These offsets account for the evolution that galaxies
underwent and can be affected by any change that galaxies experience caused by the passive
luminosity evolution, by the possible evolution of the effective radius, and by the possible
mass accretion. In the next section we consider how these evolutionary terms can affect the
resulting Kormendy relation.
5. The evolution of cluster ellipticals since z = 1.3
In this section we discuss the possible evolution that the 16 cluster ellipticals of our sample may experience since z ~ 1.3. The aim of this analysis is twofold. On one hand, we are interested in constraining the evolution that brings these ellipticals on the local scaling relations. On the other hand, we want to understand whether they have completed their mass growth at the redshift they are observed or significant structural changes (mass accretion and/or size increase) can or even must take place in the last 9 Gyr. Before considering different possible evolutionary paths we have to consider the passive luminosity evolution. Indeed, the stars already formed (the stellar mass already assembled) at z = 1.27 will passively evolve till z = 0 due to their aging.
5.1. The unavoidable luminosity evolution
The zero point α of the KR relation is expected to change because of the change in ⟨ μ ⟩ e with time. The surface brightness is expected to change since the luminosity of a galaxy changes with time. This is due to the aging of the stars already formed and assembled at the time the galaxy has been observed. This luminosity evolution will take place and will affect the stellar mass of the galaxy. It is well known that the aging of a stellar population implies a dimming of its luminosity with time. The magnitude of this dimming at a given wavelength over a time Δt depends primarily on the age of the stellar population at the beginning of this interval and it is greater for younger ages. As shown in Table 3, our galaxies have different ages. Instead of computing a mean evolution for all of them, we thus computed its own luminosity evolution EvB,R = [ MB,R(z = 1.27) − MB,R(z = 0) ] for each of them , i.e., the difference between the absolute magnitude of the best-fitting model at z = 1.27 and the absolute magnitude of the same model aged 8.6 Gyr, the time elapsed from z = 1.27 to z = 0.
The evolutionary terms EvB,R thus obtained are reported in Table 4. They are in the ranges 1.21 mag < | EvB | < 2.98 mag for the B band and 1.03 mag < | ER | < 2.25 mag for the R band and, as expected, are greater for younger galaxies. It is worth noting that these evolutionary terms are almost independent of the IMF and the models. Indeed, in Table 4 we also report (in parenthesis) the evolutionary terms derived with the MA05 models and Salpeter IMF to be compared with those obtained with BC03 and Chabrier IMF.
 |
Fig. 5 Upper panels: size–surface brightness relation in the rest-frame B-band. Red circles are our 16 cluster ellipticals evolved to z = 0. Filled circles represent the values obtained using GASPHOT, consistently with the WINGS sample, while open circles are the values derived using GALFIT. Crosses are local cluster ellipticals selected from the WINGS sample in the same absolute magnitude range (−21 < MB < −17, left panel) of the 16 galaxies evolved to z = 0 and in the same stellar mass range (5 × 1010 M⊙ < ℳ∗ < 2 × 1011 M⊙, right panel). Lower panels: the distributions of the effective radius of the 16 ETGs at z = 1.27 (red histogram) and of the WINGS galaxies selected according to the luminosity (left) and stellar mass (right) criteria are shown and compared using the K-S test. In the small insets the cumulative distributions are shown together with the probability that they belong to the same parent populations. Effective radii have been computed using the same procedures for the high-z and the low-z samples (see text). |
For a given model, the Salpeter IMF produces differences in the range 0.04–0.06 mag with
respect to the Chabrier IMF. Thus, if our galaxies evolve solely in luminosity since
z = 1.27
according to their SFH, their surface brightness at z = 0 would be
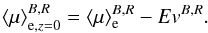 (11)In
the lower panels of Fig. 4 the surface brightness
evolved to z =
0, ⟨ μ ⟩
e,z = 0, of our 16 galaxies is plotted
as a function of their Re in the B-band (left) and in the
R-band
(right). Symbols are as in the upper panels. Our galaxies occupy the locus occupied by the
Coma cluster ETGs with comparable mass. The expected Kormendy relation at z = 0 obtained by fitting
Eq. (4) to our evolved data is also shown. We obtained
(11)In
the lower panels of Fig. 4 the surface brightness
evolved to z =
0, ⟨ μ ⟩
e,z = 0, of our 16 galaxies is plotted
as a function of their Re in the B-band (left) and in the
R-band
(right). Symbols are as in the upper panels. Our galaxies occupy the locus occupied by the
Coma cluster ETGs with comparable mass. The expected Kormendy relation at z = 0 obtained by fitting
Eq. (4) to our evolved data is also shown. We obtained
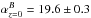 and
and
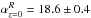 , in
agreement with the Kormendy relation in the local universe. Hence, the luminosity
evolution that the stars already assembled in the 16 ellipticals will necessarily
experience between z =
1.27 to z =
0 brings them on the local Kormendy relation; that is, it accounts for
the observed surface brightness evolution Δμ reported in Table 5.
, in
agreement with the Kormendy relation in the local universe. Hence, the luminosity
evolution that the stars already assembled in the 16 ellipticals will necessarily
experience between z =
1.27 to z =
0 brings them on the local Kormendy relation; that is, it accounts for
the observed surface brightness evolution Δμ reported in Table 5.
It is worth noting that a similar evolution of the KR (≃1.5–2 mag/arcsec2) was also observed by Holden et al. (2005), Raichoor et al. (2012), and Rettura et al. (2010) for cluster ellipticals at similar redshifts. Analogously to our findings, Holden et al. and Raichoor et al. find that this surface brightness evolution is consistent with the expected luminosity evolution due to aging and a similar result is also found at z < 0.9 from the study of the evolution of the fundamental plane (FP; Saglia et al. 2010).
This result has an important and constraining implication: the stellar mass underlying the luminosity of these ellipticals at z = 1.27 and responsible for the observed surface brightness must be distributed according to the same profile of the stellar mass responsible for the corresponding luminosity in ellipticals at z = 0. This means that the stellar mass assembled at z = 1.27 is not more concentrated than at z = 0; otherwise, once evolved to z = 0, the underlying stellar mass would result in a higher surface brightness with respect to that of ellipticals with the same luminosity at z = 0.
Indeed, comparing the size–surface brightness relation of our 16 ellipticals evolved to z = 0 with the one described by a sample of cluster ellipticals at z = 0 selected in the same absolute magnitude range and in the same stellar mass range, we obtain what it is shown in Fig. 5. The sample of local cluster ellipticals has been extracted from the Wide-field Nearby Galaxy Cluster Survey (WINGS; Fasano et al. 2006; Valentinuzzi et al. 2010a) as described in Sect. 2.4. To homogenize high-z with low-z data, we computed the effective radius of our 16 ellipticals again at z = 1.27 using GASPHOT the same software as was used to derive the structural parameters of WINGS galaxies. For completeness, in Fig. 5 we also show our 16 galaxies in the case of GALFIT estimates, even if the proper comparison is the one based on the same procedure as used to estimate the structural parameter. However, it can be seen that the result is robust with respect to the software used to derive the structural parameters.
The evolved B-band absolute magnitudes of our 16 ellipticals are in the range −21 < MB < −17, as can be derived from Tables 3 and 4 while their stellar masses are in the range 0.5 × 1010 M⊙< ℳ∗< 2 × 1011 M⊙. In the left hand panel of Fig. 5 crosses represent the WINGS cluster ETGs selected in the same absolute magnitude range, while in the right hand panel represent those selected in the same mass range. In both the cases, the high-z and the low-z samples occupy the same region. In the lower panels of Fig. 5, the distribution of the effective radius of the selected samples at different redshifts are shown and compared. The agreement between the distributions of the high-z and the low-z samples is also quantitatively confirmed by the KS test we performed, whose probability P is reported in the insets. The stellar mass of our 16 ellipticals at z = 1.27 is not more concentrated than the stellar mass of local cluster ETGs with the same luminosity and stellar mass. The lower-right panel of Fig. 5, compares the effective radius of ETGs selected in the same stellar mass range and shows quantitatively that the mean effective radius of the population of high-z cluster ETGs does not differ from the mean effective radius of local cluster ETGs with the same mass; that is, they follow the same size–mass relation. This is explicitly shown in Fig. 6 where the size–mass relation described by our galaxies is compared with the one defined by the WINGS ETGs. It is worth noting that the effect of the secular decrease in the galaxy stellar mass due to the stellar evolution (Poggianti et al. 2013b), which is the gas fraction returned to the interstellar medium due to the evolution of the stars, would be negligible in our case. This is shown in Table 3 where we report the correcting factors ℳ∗(z = 0) / ℳ∗ for each galaxy, namely the ratio between the stellar mass ℳ∗(z = 0) that the galaxy would have at z = 0 owing to the evolution of the stars and the stellar mass we estimated that they have at z = 1.27.
In Fig. 6 the size–mass relation for a sample of field ellipticals in the redshift range 0.9 <z< 1.9 (cyan filled triangles; Saracco et al. 2010) is also shown for comparison. It can be seen that, as also found by Raichoor et al. (2012), field and cluster elliptical galaxies seem to follow the same size–mass relation and no appreciable differences in their effective radii are visible. However, we refer to a forthcoming paper for a detailed and quantitative comparison between field and cluster ellipticals at z> 1.
In this section we have shown that since the passive evolution experienced by the stars present at z = 1.27 moves the 16 ETGs on the Kormendy relation of local ETGs and that they follow the same size–mass relation their stellar mass profile at z = 1.27 is the same as local cluster ellipticals with the same stellar mass. On the other hand, this does not imply that they cannot change their structure, e.g., grow further at z< 1.27 moving along the Kormendy and the size–mass relation. In the next section we tackle the possible structural evolution that they may experience.
 |
Fig. 6 Size–stellar mass relation for elliptical galaxies. The different symbols are as follows: red circles are our 16 cluster ellipticals at z = 1.27 (filled circles represent the Re derived using GASPHOT consistently with the WINGS sample, open circles are those derived with GALFIT); blue filled triangles are field ellipticals selected from the sample of Saracco et al. (2010, Sar10) at 1.1 <z< 1.5, crosses are local cluster ellipticals selected from the WINGS survey, and open squares are the local high-mass cluster ellipticals with σv> 330 km s-1 selected by Bernardi et al. (2008, hereafter Ber08). |
5.2. Size evolution, mass accretion, and structural evolution
We have seen that our 16 cluster ellipticals at z ~ 1.3 share the same scaling relations as local cluster ellipticals; that is, they follow the local size–mass relation and also the local Kormendy relation, once the aging of their stars is taken into account. Any further evolution that may occur at z< 1.27 (stellar mass accretion and/or effective radius evolution), in addition to the aging of the stellar mass already assembled, thus must keep them in the local scaling relations. In practice, any variation in Re of individual galaxies must be accompanied by a compensating variation of their absolute magnitude and of their stellar mass otherwise galaxies would move away from the local relations. This implies that an almost pure evolution of Re of individual galaxies, i.e., an expansion of the galaxy without the compensating variation of the luminosity/mass, is ruled out for our galaxies since it would turn them away from the local relations.
To clearly show this effect we considered the mild size evolution found by Delaye et al. (2014; see also Papovich et al. 2012) for cluster ETGs, Re ∝ (1 + z)b with b = −0.53. This rate of evolution means that the effective radius of our galaxies at z = 1.27 is on average 0.65 times the effective radius of the galaxies at z = 0 with the same stellar mass; that is, our galaxies should expand by a factor 1.5 since z = 1.27. We applied this evolution to each of the 16 galaxies, and the results are shown in Fig. 7. The left hand panel shows the best-fitting relation to our 16 galaxies once evolved according to the above size evolution in addition to the passive luminosity evolution. The offset with respect to the observed local KR relation is about Δμ ≃ 0.8 mag arcsec-2.
The middle and the right hand panels are the same plots as in Fig. 5 (lower panels), showing the comparison between the local WINGS sample and our 16 galaxies once expanded. It is evident in the right hand panel of Fig. 7 the large discrepancy of our galaxies with respect to the local size–mass relation produced by the size evolution, a discrepancy even greater than the one with the local KR shown in the middle panel. The above mild size evolution can be ruled out at more than 4σ as shown by the KS probabilities obtained. A size evolution even stronger than this with rates in the range −2 <b< − 1 is claimed for field early-type galaxies (Damjanov et al. 2011; Huertas-Company et al. 2013; Cimatti et al. 2012). If applied to cluster galaxies this size evolution would imply factors 2–5 of increase in the effective radius of galaxies since z = 1.27.
 |
Fig. 7 Effects of a pure size evolution of the form Re ∝ (1 + z)b with b = − 0.53 applied to the 16 cluster ETGs at z = 1.27. In the left panel the resulting Kormendy relation evolved to z = 0 (red filled circles and red line) is compared to the local one (black line). The middle and right panels are similar to the lower panels of Fig. 5: they show the distributions of the evolved effective radii of the 16 ETGs (red histogram) and of the WINGS galaxies selected in the same luminosity range (−21 <MB< −17; left panel) and stellar mass range (5 × 1010 M⊙< ℳ∗< 2 × 1011 M⊙; right). The effective radii have been computed using GASPHOT as for the WINGS sample. |
 |
Fig. 8 Left: size–surface brightness relation described by the 16 cluster
ellipticals (filled red circles) for pure luminosity evolution (upper
panel) and for stellar mass and effective radius evolution (lower
panel) according to the relation |
We now see what the variation in absolute magnitude required to hold our galaxies on the
local Kormendy relation should be in the case of a variation in Re. The
relationship between the variation in the effective radius and in the absolute magnitude
(hence in the stellar mass) of galaxies that satisfies this constraint can be derived from
Eqs. (3) and (4) as follows. Let M′ and R′ be the
evolved absolute magnitude and effective radius of a galaxy, that is their values at
z = 0;
M the
absolute magnitude of the stellar mass at z ~ 1.3 passively evolved to z = 0; ΔM = M′ −
M the variation in the absolute magnitude due to the
stellar mass grown at z< 1.27; and
δRe =
R′/Re
the variation in the effective radius. The corresponding surface brightness
⟨ μ ⟩
′, according to Eq. (3), can be written as
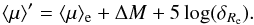 (12)On
the other hand, ⟨ μ ⟩
′ must satisfy the KR relation, so from Eq. (4) it follows
that
(12)On
the other hand, ⟨ μ ⟩
′ must satisfy the KR relation, so from Eq. (4) it follows
that 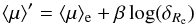 (13)and
if the last two equations are made equal we obtain
(13)and
if the last two equations are made equal we obtain
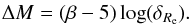 (14)We
can distinguish two different cases: the case where the fraction of the accreted stellar
mass at z< 1.27 has a mass-to-light
ratio (an age) at z =
0 comparable to the one of the stellar mass already present and the
case in which the mass-to-light ratio is significantly lower, that is the accreted
component is much younger than the bulk of the mass. Let us consider the first case. If
the accreted stellar mass is characterized by a mass-to-light ratio similar to the ratio
of the bulk of the mass, since the luminosity L is proportional to the stellar mass
ℳ∗, it follows
that ΔM =
M′ − M = −2.5log (δℳ∗) where
δℳ∗ =
ℳ′∗/ ℳ∗ and Eq.
(14) provides the sought relationship
(14)We
can distinguish two different cases: the case where the fraction of the accreted stellar
mass at z< 1.27 has a mass-to-light
ratio (an age) at z =
0 comparable to the one of the stellar mass already present and the
case in which the mass-to-light ratio is significantly lower, that is the accreted
component is much younger than the bulk of the mass. Let us consider the first case. If
the accreted stellar mass is characterized by a mass-to-light ratio similar to the ratio
of the bulk of the mass, since the luminosity L is proportional to the stellar mass
ℳ∗, it follows
that ΔM =
M′ − M = −2.5log (δℳ∗) where
δℳ∗ =
ℳ′∗/ ℳ∗ and Eq.
(14) provides the sought relationship
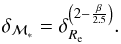 (15)The
values of β
are included in the range 2.5
<β<
3, hence
(15)The
values of β
are included in the range 2.5
<β<
3, hence 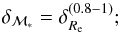 (16)that
is, the variation in Re must follow a variation of the same
magnitude of the stellar mass. Thus, the study of the evolution of the size–surface
brightness relation for these 16 cluster ellipticals establishes that if their
size increases, then so does their stellar mass. Actually, this result is
neither new nor surprising. For instance, Jørgensen & Chiboucas (2013) on the basis of optical spectroscopy of galaxies
in clusters, find no evidence of evolution of their velocity dispersion at a given galaxy
mass up to z ~
0.9. Since effective radius and velocity dispersion are linked by the
relation σ
(16)that
is, the variation in Re must follow a variation of the same
magnitude of the stellar mass. Thus, the study of the evolution of the size–surface
brightness relation for these 16 cluster ellipticals establishes that if their
size increases, then so does their stellar mass. Actually, this result is
neither new nor surprising. For instance, Jørgensen & Chiboucas (2013) on the basis of optical spectroscopy of galaxies
in clusters, find no evidence of evolution of their velocity dispersion at a given galaxy
mass up to z ~
0.9. Since effective radius and velocity dispersion are linked by the
relation σ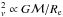 , it follows that a
simple expansion of individual galaxies would imply a decrease in their velocity
dispersion unless one hypothesizes of a corresponding growth in their (total) mass. In
fact, a decrease in the velocity dispersion of cluster ellipticals is not observed.
, it follows that a
simple expansion of individual galaxies would imply a decrease in their velocity
dispersion unless one hypothesizes of a corresponding growth in their (total) mass. In
fact, a decrease in the velocity dispersion of cluster ellipticals is not observed.
 |
Fig. 9 Left: same as right panel of Fig. 8 but considering only the 11 ETGs of the RDCS0848 cluster in the (non-evolved) mass range 2 × 1011−1.5 × 1011 M⊙. The distribution of the effective radius of these 11 cluster ETGs evolved to z = 0 according to mass and effective radius evolution is compared with the distribution of local WINGS ETGs selected in the same range of evolved stellar masses. Central: the stellar mass distribution of one of the 100 random sample extracted from the WINGS sample is compared with distribution of the 16 ETGs. Right: the effective radius distribution of the random sample shown in the central panel is compared with the distribution of the 16 ETGs. |
Returning to the earlier, if we assume that each galaxy increases its size as Re ∝ (1 + z)b with b = −0.5, it follows that its stellar mass must increase as δℳ∗ = [ (1 + z)b ] (0.9), having assumed the value β = 2.7 in Eq. (15). This is the structural evolution that fulfills the constraints imposed by the Kormendy relation; i.e., that leaves galaxies on the relation by moving them along it. This is shown in the left hand panel of Fig. 8 where our 16 galaxies are shown for the above stellar mass and size evolution (lower panel). For comparison, in the upper panel, the case of pure luminosity evolution is shown. In the central panel of Fig. 8 we show the effect of this structural evolution when we consider the size–mass relation. In this case, the 16 ETGs still significantly deviate from the local size–mass relation described by the WINGS sample in spite of the increase in mass. This is more clearly shown in the right hand panel where the distributions of the effective radius for the two samples selected in the same stellar mass range are compared. The median effective radius of the two samples differs at about four sigmas: the mass of our 16 galaxies has not grown enough to remain on the size–mass relation. For obvious reasons, when the accreted stellar component is much younger (mass-to-light ratio lower) than the bulk of the mass, the disagreement will be even larger than this (an even lower mass increase is sufficient to provide the compensating absolute magnitude variation).
These comparisons do not take into account that the two samples, even if selected in the same mass range, could not follow the same mass distribution, which could affect the comparison of the size distributions. In Fig. 6 and the central panel of Fig. 8, it seems that the difference between the effective radius distributions of the two samples may be due to the three lowest mass galaxies (< 2 × 1010 M⊙ in Fig. 6) and by the two most massive galaxies of the cluster RDCS0848. Repeating the comparison between the effective radius distributions shown in Fig. 8, considering only the 11 galaxies of the RDCS0848 sample in the (non-evolved) mass range 2 × 1010 −1.5 × 1010 M⊙, we obtain the same result: the two distributions differ at 97% confidence level, as shown in the left hand panel of Fig. 9 (at more than 99% in the extreme case of pure size evolution). However, the most proper way to perform this comparison without arbitrarily selecting the mass range and the number of galaxies considered, is to extract a sample of galaxies having the same mass distribution of the 16 ETGs at z = 1.27 from the WINGS catalog. We thus randomly extracted 100 samples of 48 galaxies each, following the stellar mass distribution of the 16 RDCS0848 ETGs and compared their effective radius distribution using the KS test.
We considered both the case of pure size evolution Re ∝ (1 + z)-0.5 shown in Fig. 7 and the case of size and mass growth shown in Fig. 8. As to the pure size evolution, the distribution of the effective radius of the 16 evolved ETGs deviates at 95% confident level from the one of the local WINGS early-type galaxies in 96 cases out of the 100 considered. This confirms that a pure size evolution cannot be experienced by these 16 ETGs since they would be significantly offset from the local Kormendy and size–mass relations. If the 16 ETGs increase the mass besides their size to continue to stay in the Kormendy relation, their effective radius distribution deviates from the one of the local WINGS galaxies in 87 cases out of the 100 considered. In Fig. 9, the mass distribution (central panel) and the size distribution (right panel) of the 16 ETGs is compared with one of the 100 WINGS random samples as an example. Even if at a lower significance level, this result therefore confirms that the constraint imposed by the Kormendy relation on the mass increase is not sufficient to keep them on the size–mass relation.
Actually, this result was expected since the size–mass relation establishes a different relationship between effective radius and stellar mass with respect to the one imposed by the Kormendy relation. If we want to preserve the size–surface brightness relation, we fail to satisfy the size–mass relation and vice versa. Similar conclusions about the size and luminosity/mass evolution up to z< 0.9 have already been reached after studying the evolution of the FP of cluster elliptical galaxies (Saglia et al. 2010).
The last result, based on Eq. (15) and on the comparison with the local scaling relations, puts a constraint on the maximum mass accretion and size increase that these galaxies could experience between z = 1.27 and z = 0. It follows that they can increase their mass and their size no more than 30% to not depart significantly from the size–mass distribution of local cluster ellipticals.
The study of the size–surface brightness relation for these 16 cluster ellipticals thus rules out the possibility of pure size evolution. The combined study of the size–surface brightness relation with the size–mass relation leads to the conclusion that these 16 ETGs have in general completed their stellar mass accretion at z ≃ 1.3 and that, consequently, their evolution will be dominated by the luminosity evolution.
6. Summary and conclusions
We studied the relations between surface brightness, effective radius, and stellar mass for a complete sample of 16 elliptical galaxies belonging to the cluster RDCS J0848+4453 at z = 1.27. The aim of our analysis was to define the evolutionary status of these galaxies by assessing whether they have completed their mass growth at the redshift where they are observed or they will experience significant structural changes due to mass accretion and/or size growth until z = 0.
The selection of the sample has been done on the basis of a pure morphological criterion based on the visual inspection of their luminosity profile in the ACS-F850LP image and of the residuals resulting from the profile fitting with a regular Sérsic profile. Their stellar mass and ages have been obtained through the best fitting of their SED composed of 11 photometric points in the range 0.38–8.0 μm with different stellar population synthesis models and IMF. We show that the results are independent of the models used as well as of the IMF adopted. Taking as reference the Chabrier IMF, the 16 ETGs have stellar masses in the range 0.5 × 1010−3 × 1011 M⊙ and ages in the range 1–4 Gyr.
We found that the size–surface brightness relation, which is the Kormendy relation defined by these 16 cluster ellipticals at z = 1.27, has the same slope as the local Kormendy relation. This means that the luminosity and the effective radius of these elliptical galaxies scaled according to the same rule in the past 9 Gyr. The zero point of the Kormendy relation at z = 1.27 is 1.8 mag brighter in the B-band and 1.3 mag brighter in the R-band than at z = 0. We found that the luminosity evolution that the stars already assembled at z = 1.27 will experience up to z = 0 brings the galaxies exactly to the local relation accounting for these different zero-point values. We showed that this result has important implications for the stellar mass profile at z ~ 1.3. In particular, we showed that the stellar mass underlying the luminosity of these ellipticals was distributed according to the same stellar mass profile of local ellipticals having the same evolved luminosity and stellar mass. This is confirmed by comparison of the size–mass relation of our galaxies with the relation described by the local WINGS sample of elliptical galaxies: the effective radius of the galaxies of the two samples follow the same distribution. Actually, we did not see any differences either between cluster and field ellipticals even if the samples used here are still too small to firmly assess it.
We find that since the simple luminosity evolution leads our galaxies to the local Kormendy relation, any further evolution that may occur at z< 1.27 must keep them on the relation. This implies that any variation in the effective radius must be accompanied by a compensating variation in the absolute magnitude that is in the stellar mass. Indeed, a pure evolution of the effective radius for these cluster ellipticals is ruled out. We explicitly show this by applying to our sample the mild size evolution Re ∝ (1 + z)-0.53 reported in the literature for passive cluster galaxies since z ~ 1, in addition to the passive luminosity evolution. The resulting Kormendy relation differs at more than four sigmas from the local Kormendy relation.
Thus, we are left with two possibilities. Either the 16 ellipticals have completed their
stellar mass accretion at redshift z ~ 1.3 or they grow in such a way that they follow
the local Kormendy relation. We found that the relation satisfying this last condition is
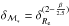 with
β ~ 3 the
slope of the Kormendy relation, which is an increase in the effective radius that must be
accompanied by an equivalent stellar mass increase. We applied this condition to our
galaxies assuming the mild size evolution above. As expected, the growth of the stellar mass
and of the effective radius leads to consistency between the galaxies and the local Kormendy
relation. On the other hand, considering the size–mass relation, we see that this mass and
size growth would lead these galaxies away from the size–mass relation described by local
ellipticals. If we want to preserve the size–surface brightness relation, we fail to satisfy
the size–mass relation and vice versa.
with
β ~ 3 the
slope of the Kormendy relation, which is an increase in the effective radius that must be
accompanied by an equivalent stellar mass increase. We applied this condition to our
galaxies assuming the mild size evolution above. As expected, the growth of the stellar mass
and of the effective radius leads to consistency between the galaxies and the local Kormendy
relation. On the other hand, considering the size–mass relation, we see that this mass and
size growth would lead these galaxies away from the size–mass relation described by local
ellipticals. If we want to preserve the size–surface brightness relation, we fail to satisfy
the size–mass relation and vice versa.
After combining the study of the size–surface brightness relation with the size–mass relation, we reached the conclusion that these 16 cluster elliptical galaxies have in general completed their stellar mass accretion at z ≃ 1.3 and that, consequently, they will mainly evolve in luminosity until z = 0.
Our results suggest that elliptical galaxies in the mass range < 2 × 1011 M⊙ do not take part in the observed size evolution of galaxies. They do not increase their size beyond z ~ 1.3 either individually or as a population (due to newly added galaxies). This result agrees with the results already found by other authors and with the view that size evolution is mainly driven by disk galaxies. van der Wel et al. (2011) find that most (65%) of the massive (> 1010.8 M⊙) compact galaxies at high-z (z> 1.5) are disk-dominated with a disk scale that is substantially smaller than the disks of equal-mass galaxies in the present universe. As already noticed, Jørgensen & Chiboucas (2013) studied early-type galaxies in three clusters at 0.5 <z< 0.9 and found no evolution of their size with respect to z = 0 cluster galaxies. Stott et al. (2011) studied the brightest galaxies in clusters at 0.8 <z< 1.3 finding little or no evolution with respect to counterparts at z ~ 0.2. Huertas-Company et al. (2013) homogeneously select and study elliptical galaxies in the redshift range 0.3 <z< 1.2 showing that no size evolution takes place for ellipticals with masses 5 × 1010−2 × 1011 M⊙ in this redshift range, as clearly shown in their Figs. 12 and 13. The evolution appears at z< 0.3 when they compare with the SDSS data. Looking at Fig. 2 in Cimatti et al. (2012), no size evolution of ETGs in the redshift range 0.3 <z< 1.6 is visible. Also in this case the evolution appears when the local SDSS data is considered.
The known bias against small galaxies that affects the SDSS data and the effect that it has on studies of the size evolution of galaxies is discussed in many works (see, e.g., Gargiulo et al. 2014; Damjanov et al. 2013). When revisiting the analysis performed by Belli et al. (2014), Gargiulo et al. (2014) use a sample of elliptical galaxies instead of passive galaxies to show that old early-type galaxies at high-z have local counterparts with similar structural properties, while the most massive and largest ones in the local universe were not present at high-z. Our result therefore suggests that ellipticals galaxies, at least in the mass range probed by our sample, do not individually grow their stellar mass and their size continuously during their lifetimes, leading to a null contribution to the observed size evolution of galaxies. Whether this conclusion can be generalized to the whole population of ellipticals (field and cluster ETGs) at these redshifts cannot be assessed from these data. We will assess this issue in a forthcoming paper.
Online material
Appendix A: Stellar masses, age and absolute magnitudes for different models
Age, stellar mass, and absolute magnitudes obtained for each galaxy.
| BC03 | Cha | CB07 | Cha | |||||
|
|
||||||||
| ID | age | log M∗ | M B | M R | age | log M∗ | M B | M R |
| [Gyr] | [M⊙] | |||||||
|
|
||||||||
| 1 | 3.75 | 11.31 | –21.55 | –23.39 | 4.50 | 11.32 | –21.55 | –23.40 |
| 2 | 1.43 | 11.16 | –22.24 | –23.65 | 3.25 | 11.27 | –22.26 | –23.66 |
| 3 | 2.60 | 11.01 | –21.94 | –23.00 | 2.60 | 10.94 | –21.93 | –23.00 |
| 4 | 1.68 | 11.25 | –22.65 | –23.80 | 2.20 | 11.18 | –22.64 | –23.81 |
| 5 | 1.43 | 10.78 | –21.49 | –22.71 | 1.70 | 10.68 | –21.46 | –22.71 |
| 606 | 1.43 | 10.70 | –21.32 | –22.53 | 2.75 | 10.78 | –21.34 | –22.54 |
| 590 | 2.30 | 10.84 | –21.18 | –22.50 | 2.50 | 10.72 | –21.16 | –22.52 |
| 568 | 2.00 | 10.57 | –20.81 | –22.15 | 2.60 | 10.56 | –20.81 | –22.16 |
| 719 | 3.50 | 10.82 | –20.67 | –22.10 | 3.75 | 10.76 | –20.67 | –22.11 |
| 1250 | 1.28 | 10.24 | –20.38 | –21.57 | 1.02 | 10.15 | –20.34 | –21.58 |
| 1260 | 0.71 | 9.70 | –20.03 | –20.79 | 0.77 | 9.64 | –20.04 | –20.79 |
| 173 | 4.25 | 10.55 | –20.02 | –21.53 | 4.50 | 10.50 | –20.01 | –21.54 |
| 1160 | 3.00 | 10.77 | –20.89 | –22.08 | 1.61 | 10.44 | –20.86 | –22.10 |
| 657 | 1.43 | 10.77 | –21.52 | –22.73 | 1.70 | 10.70 | –21.51 | –22.73 |
| 626 | 1.43 | 10.76 | –21.48 | –22.73 | 1.70 | 10.69 | –21.47 | –22.73 |
| 471 | 1.61 | 10.11 | –20.04 | –21.27 | 1.02 | 9.86 | –19.99 | –21.02 |
|
|
||||||||
| Mean | 2.10 | 10.86 | –21.41 | –22.70 | 2.35 | 10.83 | –21.40 | –22.70 |
Notes. For each galaxy of the sample we report the age [Gyr], the stellar mass [log (M/M⊙)] and the absolute magnitudes in the B and R bands derived through the best-fitting of their SED with the stellar population synthesis models of Maraston (2005; MA05), Bruzual & Charlot (2003; BC03), Charlot & Bruzual (2007; CB07), and with the two Salpeter and Chabrier stellar initial mass functions. The last row reports the mean values of the best-fitting parameters. The typical variation in the best fitting parameters due to the different models and IMF is about 18% in stellar mass and 25% in age.
The table reports the age [Gyr], the stellar mass [log (M/M⊙)], and the absolute magnitudes for each galaxy of the sample in the B and R bands derived by best-fitting their spectral energy distribution with the stellar population synthesis models of Maraston (2005, MA05), Bruzual & Charlot (2003; BC03), and the later release by Charlot & Bruzual (2007; CB07). The last row reports the mean values. We considered two different initial mass functions (IMFs): the Salpeter IMF for the MA05 and BC03 models and the Chabrier IMF for the BC03 and CB07 models. As expected, the absolute magnitudes depend neither on the model nor on the IMF adopted since the color k-correction term can vary with different models of hundredth of a magnitude. It can be seen that also the mean age of the stellar population is very stable with respect to the model used and to the IMF adopted. In contrast, the IMF, as is known, systematically affects the stellar mass with the Salpeter IMF producing masses about 1.7 times higher than the Chabrier IMF.
Appendix B: Surface-brightness profile fitting
The structural parameters of the galaxies were derived by fitting the observed surface brightness profile in the F850LP-band image with a Sérsic profile convoluted with the PSF using Galfit, as described in Sect. 3.2. In this appendix the 16 ellipticals of the sample selected according to the criteria described in Sect. 2.2 are shown (upper panels), together with the best-fitting surface brightness model (middle panels) and the residuals (lower panels). The images are 3 × 3 arcsec. The convolution box and the fitting box (6 × 6 arcsec) were defined by repeatedly fitting the observed profile with increasing values of the box until the convergence of the best-fitting parameter values. The goodness of the fit is shown by the lack of residuals obtained for all the galaxies. It is also worth noting that no structures are visible in the residuals, showing the regularity and the symmetry of the true profile. The good fitting is also shown in Fig. B.2 where the observed surface brightness profile measured on the F850LP image is compared with the best fitting model profile. In all cases, the profile of the galaxies were fit over at least five magnitudes in surface brightness. The observed surface brightness profiles of galaxies #5, #626, and #657 depart from the model profiles at r ~ 0.5 arcsec, the mean distance between them.
 |
Fig. B.1 Each column shows the GALFIT input and output for the 16 cluster ellipticals at z = 1.27: ACS − F850LP band image of the galaxy (upper box), best-fitting Sérsic model profile (middle box) and residual image (lower box) obtained by subtracting the model from the image. Galaxies are (from top left to bottom right): (upper panel) ID. #1, #2, #3, #4, #5 #626 and #657, #606, #590; (lower panel) #568, #719, #1250, #173, #1160, #1471. Each image is 3 × 3 arcsec. |
 |
Fig. B.2 Surface brightness in the F850LP band measured within circular annulus centered on each galaxy (black points), compared with the surface brightness resulting from the best fitting Sérsic model profile (red points). The dotted line marks the radius of the FWHM while the dot-dashed line marks the effective radius. In the lower panels the residuals of the fitting obtained as the difference between the data points and the models are shown. |
Acknowledgments
This work is partially based on data collected at the European Southern Observatory (ESO) telescopes and with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Science Institute which is operated by the Association of Universities for Research in Astronomy. This work is also based on observations carried out at the Large Binocular Telescope (LBT). The LBT is an international collaboration among institutions in the US, Italy, and Germany. We acknowledge the support from the LBT-Italian Coordination Facility for the execution of observations, data distribution, and reduction. We thank the anonymous referee for the useful comments and the constructive criticism. This work has received financial support from Prin-INAF 1.05.09.01.05.
References
- Andreon, S., Puddu, E., de Propris, R., & Cuillandre, J.-C. 2008, MNRAS, 385, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Belli, S., Newman, A. B., & Ellis, R. S., 2014, ApJ, 783, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Bezanson, R., van Dokkum, P. G., Tal, T., et al. 2009, ApJ, 697, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, A. G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago, F., Trujillo, I., Conselice, C. J., et al. 2008, ApJ, 687, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C., Bschorr, T. J., Renzini, A., et al. 2013, ApJ, 773, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Giavalisco, M., Guo, Y., et al. 2011, ApJ, 743, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Bruzual, A. G. 2007, unpublished [Google Scholar]
- Cimatti, A., Cassata, P., Pozzetti, L., et al. 2008, A&A, 482, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cimatti, A., Nipoti, C., & Cassata, P. 2012, MNRAS, 422, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., McCarthy, P. J., Abraham, R. G., et al. 2009, ApJ, 695, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Abraham, R. G., Glazebrook, K., et al. 2011, ApJ, 739, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Chilingarian, I., Hwang, H. S., & Geller, M. J. 2013, ApJ, L48 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Delaye, L., Huertas-Company, M., Mei, S., et al. 2014, MNRAS, 441, 203 [NASA ADS] [CrossRef] [Google Scholar]
- di Serego Alighieri, S., Vernet, J., Cimatti, A., et al. 2005, A&A, 442, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fasano, G., Marmo, C., Varela, J., et al. 2006, A&A, 445, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fasano, G., Vanzella, E., & Wings Team, 2007, ASP Conf. Ser., 374, 495 [NASA ADS] [Google Scholar]
- Fan, L., Lapi, A., De Zotti, G., & Danese, L. 2008, ApJ, 689, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, L., Lapi, A., Bressan, A. et al. 2010, ApJ, 718, 1460 [NASA ADS] [CrossRef] [Google Scholar]
- Gargiulo, A., Haines, C. P., Merluzzi, P., et al., 2009, MNRAS, 397, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Gargiulo, A., Saracco, P., Longhetti, M., La Barbera, F., & Tamburri, S. 2012, MNRAS, 425, 2698 [NASA ADS] [CrossRef] [Google Scholar]
- Gargiulo, A., Saracco, P., Longhetti, M., et al. 2014, A&A, submitted [Google Scholar]
- Hamabe, M., & Kormendy, J. 1987, Proc. IAU Symp., 127, 379 [Google Scholar]
- Holden, B. P., Blakeslee, J. P., Postman, M., et al. 2005, ApJ, 626, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P., Bundy, K., Murray, N., et al. 2009, MNRAS, 398, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Mei, S., Shankar, F., et al. 2013, MNRAS, 428, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., & Chiboucas, K. 2013, AJ, 145, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., Franx, M., & Kjaergaard, P. 1995a, MNRAS, 273, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., Franx, M., & Kjaergaard, P. 1995b, MNRAS, 276, 1341 [NASA ADS] [Google Scholar]
- Jørgensen, I., Franx, M., & Kjaergaard, P. 1996, MNRAS, 280, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar, S., & Burkert, A. 2003, ApJ, 597, L11 [Google Scholar]
- Kormendy, J. 1977, ApJ, 218, 333 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Busarello, G., Massarotti, M., Merluzzi, P., & Mercurio, A. 2003, A&A, 409, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Barbera, F., Merluzzi, P., Busarello, G., Massarotti, M., & Mercurio, A. 2004, A&A, 425, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., de la Rosa, I. G., & Lopes, P. A. A. 2010, MNRAS, 408, 1335 [NASA ADS] [CrossRef] [Google Scholar]
- Longhetti, M., & Saracco, P. 2009, MNRAS, 394, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Longhetti, M., Saracco, P., Severgnini, P., et al. 2007, MNRAS, 374, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, C., Daddi, E., Renzini, A., et al. 2010, MNRAS, 401, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- McGrath, E., Stockton, A., Canalizo, G., Iye, M., & Maihara, T. 2008, ApJ, 682, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Stanford, S. A., Holden, B. P., et al. 2012, ApJ, 754, 141 [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., Bundy, K., & Treu, T. 2012, ApJ, 746, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Treu, T., Auger, M. W., & Bolton, A. S. 2009, ApJ, 706, L86 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Treu, T., A.Leauthaud, K., et al. 2012, MNRAS, 422, 1714 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Bassett, R., Lotz, J. M., et al. 2012, ApJ, 750, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatelli, E., Fasano, G., & Cassata, P. 2006, A&A, 446, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poggianti, B. M., Calvi, R., Bindoni, D., et al. 2013a, ApJ, 762, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Moretti, A., Calvi, R., et al. 2013b, ApJ, 777, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Postamn, M., Franx, M., Cross, N. J. G., et al. 2005, ApJ, 623, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raichoor, A., Mei, S., Nakata, F., et al. 2011, ApJ, 732, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Raichoor, A., Mei, S., Stanford, S. A., et al. 2012, ApJ, 745, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Reda, F. M., Forbes, D. A., Beasley, M. A., O’Sullivan, E. J., & Goudfrooij, P. 2004, MNRAS, 354, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Rettura, A., Rosati, P., Nonino, M., et al. 2010, ApJ, 709, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Saglia, R. P., Sańchez-Blaźquez, P., Bender, R., et al. 2010, A&A, 524, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Saracco, P., Longhetti, M., & Andreon, S., 2009, MNRAS, 392, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Saracco, P., Longhetti, M., & Gargiulo, A. 2010, MNRAS, 408, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Saracco, P., Longhetti, M., & Gargiulo, A. 2011, MNRAS, 412, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Saracco, P., Gargiulo, A., & Longhetti, M. 2012, MNRAS, 422, 3107 [NASA ADS] [CrossRef] [Google Scholar]
- Schade, D., Carlberg, R. G., Yee, H. K. C., Lopez-Cruz, O., & Ellingson, E. 1996, ApJ, 464, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Mo, H. J., White Simon, D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, S. A., Elston, R., Eisenhardt, P. R., et al. 1997, AJ, 114, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Stott, J. P., Collins, C. A., Burke, C., Hamilton-Morris, V., & Smith, G. P. 2011, MNRAS, 414, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Szomoru, D., Franx, M., & van Dokkum, P. G. 2012, ApJ, 749, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Tamburri, S., Saracco, P., Longhetti, M., et al. 2014, A&A, submitted [Google Scholar]
- Taylor, E. N., Franx, M., Blazebrook, K., et al. 2010, ApJ, 720, 741 [Google Scholar]
- Trujillo, I., Feulner, G., Goranova, Y., et al. 2006, MNRAS, 373, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Ferreras, I., & de La Rosa, I. G. 2011, MNRAS, 415, 3903 [NASA ADS] [CrossRef] [Google Scholar]
- Valentinuzzi, P., Fritz, J., Poggianti, B. M., et al. 2010a, ApJ, 712, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Valentinuzzi, P., Poggianti, B. M., Saglia, R. P., et al. 2010b, ApJ, 721, L19 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Holden, B. P., Zirm, A. W., et al. 2008, ApJ, 688, 48 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Rix, H.-W., Wuyts, S., et al. 2011, ApJ, 730, 38 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Stanford, S. A., Holden, B. P., et al. 2001, ApJ, 552, L101 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Franx, M., Kriek, M., et al. 2008, ApJ, 677, L5 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Whitaker, K. E., Brammer, G., et al. 2010, ApJ, 709, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, B. L., Saglia, R. P., Bender, R., et al. 1999, A&A, 346, 13 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 i775 − z850 color of galaxies. Left: the expected i775 − z850 color of galaxies is shown as a function of redshift for 4 different ages. The different solid lines refer to (from top to bottom) 7 Gyr old (red line), 4 Gyr old (green line), 2 Gyr old (blue line), and 1 Gyr old (cyan line). The dashed line refers to a 2 Gyr old template obtained with the Maraston (2005) models. The color is always i775 − z850 < 0.8 (horizontal black line) for redshift z < 0.8, and it is always larger than 0.8 for z > 0.8, this independently of the age of the stellar population considered. Right: the i775 − z850 color distribution of the 467 galaxies brighter than z850 < 24 falling within 1 Mpc from the cluster center is shown. The solid red line marks the mean color ⟨ i775 − z850 ⟩ = 1.1 ± 0.09 of the 5 ETGs cluster members spectroscopically identified by Stanford et al. (1997). The dashed lines represent ±1σ. A second peak is evident in the distribution at the mean color of the 5 ETGs. |
| In the text | |
 |
Fig. 2 Color–magnitude relation. The i775 − z850 (upper panel) and the z850 − H160 (lower panel) colors of the selected ETGs galaxies (red filled symbols) as a function of z850 (16 galaxies) and of H160 (15 galaxies) are shown together with those of the 105 galaxies (black crosses) covered by NICMOS observations. The five ETGs with spectroscopic redshift are marked by red filled circles and the remaining 11 ETGs cluster members are marked by red filled triangles. Red open circles mark all the galaxies selected in the color range 0.9 < i775 − z850 < 1.3. The solid red line in the upper panel is the color–magnitude relation (i775 − z850) = 2.1 − 0.044z850 best-fitting the 16 ellipticals. |
| In the text | |
 |
Fig. 3 Three galaxies, #5, #626, and #657 that are clearly resolved in the F850LP band image (left) thanks to both the resolution (FWHM ~ 0.11 arcsec) and to the small pixel size (0.05 arcsec/pix). They are not resolved in the NIC3-F160W band image (right) because of the lower resolution (FWHM ~ 0.22 arcsec) and pixel size (0.2 arcsec/pix). Both the images are 6′ × 6′. The black line represents 1 arcsec. |
| In the text | |
 |
Fig. 4 Kormendy relation in the rest-frame B band (left panel) and R band (right panel). Red filled symbols are our 16 cluster ellipticals at z = 1.27 (upper panels) and evolved to z = 0 (lower panels) according to the passive luminosity evolution as described in Sect. 5.1 and reported in Table 4. The red lines are the Kormendy relation reported in Table 5 obtained by fitting Eq. (4) to our 16 ellipticals assuming the slope β at z = 0 (solid line) and leaving β as free parameter (dashed line). The open squares are the sample of early-type galaxies in the Coma cluster studied by Jørgensen et al. (1995a). The black lines represent the Kormendy relation at z = 0 derived from this sample and reported in Eqs. (7) and (8). |
| In the text | |
 |
Fig. 5 Upper panels: size–surface brightness relation in the rest-frame B-band. Red circles are our 16 cluster ellipticals evolved to z = 0. Filled circles represent the values obtained using GASPHOT, consistently with the WINGS sample, while open circles are the values derived using GALFIT. Crosses are local cluster ellipticals selected from the WINGS sample in the same absolute magnitude range (−21 < MB < −17, left panel) of the 16 galaxies evolved to z = 0 and in the same stellar mass range (5 × 1010 M⊙ < ℳ∗ < 2 × 1011 M⊙, right panel). Lower panels: the distributions of the effective radius of the 16 ETGs at z = 1.27 (red histogram) and of the WINGS galaxies selected according to the luminosity (left) and stellar mass (right) criteria are shown and compared using the K-S test. In the small insets the cumulative distributions are shown together with the probability that they belong to the same parent populations. Effective radii have been computed using the same procedures for the high-z and the low-z samples (see text). |
| In the text | |
 |
Fig. 6 Size–stellar mass relation for elliptical galaxies. The different symbols are as follows: red circles are our 16 cluster ellipticals at z = 1.27 (filled circles represent the Re derived using GASPHOT consistently with the WINGS sample, open circles are those derived with GALFIT); blue filled triangles are field ellipticals selected from the sample of Saracco et al. (2010, Sar10) at 1.1 <z< 1.5, crosses are local cluster ellipticals selected from the WINGS survey, and open squares are the local high-mass cluster ellipticals with σv> 330 km s-1 selected by Bernardi et al. (2008, hereafter Ber08). |
| In the text | |
 |
Fig. 7 Effects of a pure size evolution of the form Re ∝ (1 + z)b with b = − 0.53 applied to the 16 cluster ETGs at z = 1.27. In the left panel the resulting Kormendy relation evolved to z = 0 (red filled circles and red line) is compared to the local one (black line). The middle and right panels are similar to the lower panels of Fig. 5: they show the distributions of the evolved effective radii of the 16 ETGs (red histogram) and of the WINGS galaxies selected in the same luminosity range (−21 <MB< −17; left panel) and stellar mass range (5 × 1010 M⊙< ℳ∗< 2 × 1011 M⊙; right). The effective radii have been computed using GASPHOT as for the WINGS sample. |
| In the text | |
 |
Fig. 8 Left: size–surface brightness relation described by the 16 cluster
ellipticals (filled red circles) for pure luminosity evolution (upper
panel) and for stellar mass and effective radius evolution (lower
panel) according to the relation |
| In the text | |
 |
Fig. 9 Left: same as right panel of Fig. 8 but considering only the 11 ETGs of the RDCS0848 cluster in the (non-evolved) mass range 2 × 1011−1.5 × 1011 M⊙. The distribution of the effective radius of these 11 cluster ETGs evolved to z = 0 according to mass and effective radius evolution is compared with the distribution of local WINGS ETGs selected in the same range of evolved stellar masses. Central: the stellar mass distribution of one of the 100 random sample extracted from the WINGS sample is compared with distribution of the 16 ETGs. Right: the effective radius distribution of the random sample shown in the central panel is compared with the distribution of the 16 ETGs. |
| In the text | |
 |
Fig. B.1 Each column shows the GALFIT input and output for the 16 cluster ellipticals at z = 1.27: ACS − F850LP band image of the galaxy (upper box), best-fitting Sérsic model profile (middle box) and residual image (lower box) obtained by subtracting the model from the image. Galaxies are (from top left to bottom right): (upper panel) ID. #1, #2, #3, #4, #5 #626 and #657, #606, #590; (lower panel) #568, #719, #1250, #173, #1160, #1471. Each image is 3 × 3 arcsec. |
| In the text | |
 |
Fig. B.2 Surface brightness in the F850LP band measured within circular annulus centered on each galaxy (black points), compared with the surface brightness resulting from the best fitting Sérsic model profile (red points). The dotted line marks the radius of the FWHM while the dot-dashed line marks the effective radius. In the lower panels the residuals of the fitting obtained as the difference between the data points and the models are shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.