| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201323002 | |
| Published online | 13 May 2014 | |
Revealing the large nuclear dust structures in NGC 1068 with MIDI/VLTI⋆,⋆⋆,⋆⋆⋆
1
Leiden Observatory, Leiden University,
PO Box 9513
2300 RA
Leiden
The Netherlands
e-mail:
nlopez@strw.leidenuniv.nl
2
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312,
Gießenbachstr., 85741
Garching,
Germany
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
4
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
Received:
7
November
2013
Accepted:
13
January
2014
Aims. The aim of this paper is to understand the relation in active galactic nuclei (AGNs) between the small obscuring torus and dusty structures at larger scales (5−10 pc).
Methods. The dusty structures in AGNs are best observed in the mid-infrared. To achieve the necessary spatial resolution (20−100 millarcsec) we use ESO’s Mid-Infrared Interferometer (MIDI) with the 1.8 m Auxiliary Telescopes. We use the chromatic phases in the data to improve the spatial fidelity of the analysis.
Results. We present interferometric data for NGC 1068 obtained in 2007 and 2012. We find no evidence of source variability. Many (u,v) points show non-zero chromatic phases indicating significant asymmetries. Gaussian model fitting of the correlated fluxes and chromatic phases provides a three-component best fit with estimates of sizes, temperatures, and positions of the components. A large, warm, offcenter component is required at a distance approximately 90 mas to the northwest at a position angle (PA) of ~−18°.
Conclusions. The dust at 5−10 pc in the polar region contributes four times more to the mid-infrared flux at 12 μm than the dust located at the center. This dust may represent the inner wall of a dusty cone. If similar regions are heated by the direct radiation from the nucleus, then they will contribute substantially to the classification of many Seyfert galaxies as Type 2. Such a region is also consistent in other Seyfert galaxies (the Circinus galaxy, NGC 3783, and NGC 424).
Key words: techniques: interferometric / galaxies: active / galaxies: nuclei / galaxies: Seyfert / galaxies: individual: NGC 1068 / radiation mechanisms: thermal
Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 080.B-0928 and 089.B-0099. Based on data obtained from the ESO Science Archive Facility.
Appendices are available in electronic form at http://www.aanda.org
The reduced visibilities (UVFITS tables) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/565/A71
© ESO, 2014
1. Introduction.
Active galactic nuclei (AGNs) have been intensely studied because they host many interesting physical processes, such as accretion of material and formation of jets. Many subclasses of AGNs have been defined based on observational criteria; the earliest of these was defined by Seyfert (Seyfert 1943) by the presence of high ionization forbidden lines. They additionally show low ionization lines and very high ionization coronal lines. The similar line ratios from galaxy to galaxy suggest that they are powered by the engines of the same type, but they also show differences that have led to a dual classification: Type 1 galaxies show broad optical permitted lines absent in Seyfert Type 2. The idea that Type 1 and Type 2 share an underlying engine is strongly supported by the detection of polarized broad lines in 3C 234 (Antonucci 1984) and NGC 1068 (Antonucci & Miller 1985). These polarized spectra, most probably caused by electron scattering, revealed the existence of a broad line region (BLR) in Type 2 galaxies.
To explain the different appearances of various types of AGN, the existence of an axisymmetric dusty structure, a torus, was proposed in the context of AGN unified models (Antonucci 1993; Urry & Padovani 1995). The general concept is that the Type 2 galaxies are absorbed Type 1 galaxies, where the orientation and absorption of the torus play a major role in shaping the apparent properties. The energy absorbed by the torus will be re-emitted mainly in the mid-infrared wavelength regime, giving rise to a pronounced peak in the spectral energy distribution of many AGNs (Sanders et al. 1989). Resolving the morphology of this mid-infrared radiation is the key to understanding the physical properties of the dust structures. However, they are typically too small to be resolved even with the largest single-dish telescopes. Only with the availability of powerful techniques such as mid-infrared interferometry has further progress been possible. Several interferometric studies in the mid-infrared have been published for individual galaxies. They include the brightest AGNs, the Circinus galaxy (Tristram et al. 2007), NGC 1068 (Jaffe et al. 2004; Poncelet et al. 2006; Raban et al. 2009), and Centaurus A (Meisenheimer et al. 2007; Burtscher et al. 2010), and the brightest Type 1 Seyfert galaxy, NGC 4151 (Burtscher et al. 2009). Recently, two fainter sources, NGC 424 (Hönig et al. 2012) and NGC 3783 (Beckert et al. 2008; Hönig et al. 2013) were observed with a very well sampled (u,v) coverage. Studies with the intention of getting general properties of the objects have also been published. Kishimoto et al. (2009) claimed evidence for a “common radial structure” for the nearby AGN tori. Tristram et al. (2007) demonstrated that weak AGNs can also be observed with MIDI and saw the first evidence for a size-luminosity relation (Tristram et al. 2009). Burtscher et al. (2013) modeled 23 AGNs and found that there is a large diversity in nuclear mid-infrared structures that is not attributable to luminosity of the source or resolution of the observations.
This paper extends our previous work on the near-nuclear, parsec scale dust structures in NGC 1068 in order to investigate the connection with the larger scale structures. We achive this by making use of low spatial frequency interferometric observations. The outline of this paper is the following: in Sect. 2 we give a summary of the previous mid-infrared observations of the nuclear dust in NGC 1068. We describe the new observations and data reduction process in Sect. 3. In Sect. 4 we present the interferometric data with emphasis on the chromatic phases that give insights into asymmetric morphologies. We investigate the radial profile of the correlated fluxes and the possibility for variability. In Sect. 5 we explain the Gaussian model used to reproduce the interferometric data and the parameters that best fit. We discuss the best models in Sect. 6, analyze the properties of the components of the model and identify the dust regions associated with each component. In Sect. 7 we study the possible heating mechanism for the two mid-infrared northern components found from the modeling. In Sect. 8 we discuss the asymmetry of the mid-infrared nuclear region in NGC 1068 and its implications. Finally, we present our conclusions in Sect. 9.
2. Previous infrared observations of the nucleus of NGC 1068
The galaxy NGC 1068, at a distance of only 14.4 Mpc, is a prototype Seyfert 2 galaxy that has been intensively studied. Its proximity and infrared brightness make it a suitable target to study the dusty structures that obscure the nucleus. Previous high spatial resolution single telescope studies revealed the existence of an infrared extended emission region around the central engine (Bock et al. 1998, 2000; Tomono et al. 2001; Galliano et al. 2005 in the mid-infrared, and Rouan et al. 1998, 2004; Gratadour et al. 2006 in the near-infrared). In the mid-infrared regime, single-dish observations indicate that the extended emission has an elongation of about 1′′ in the north-south direction and is unresolved in the east-west direction (Bock et al. 2000). The emission shows a strong asymmetry, with a larger emission area extending more to the north than to the south.
Jaffe et al. (2004) demonstrated the existence of a central parsec-sized circumnuclear dust structure in NGC 1068 using mid-infrared (λ = 8−13 μm) interferometric observations from ESO’s VLTI/MIDI. Raban et al. (2009) reported additional MIDI observations with a more extensive (u,v) coverage of sixteen baselines which allowed them to investigate the structure of the inner regions of the obscuring disk with greater detail. In both cases, a two-component model, each with a Gaussian brightness distribution, was used to fit the correlated fluxes obtained from MIDI. The size and orientation of the hot component (~800 K), associated with the inner funnel of the obscuring disk, were well fitted with an elongated Gaussian 1.35 parsec long and 0.45 parsec thick (FWHM) at a position angle (PA) of −42°. The data strongly suggest that the dusty disk and the optical ionization cones from the jet are misaligned in NGC 1068. The disk is co-linear with the H2O megamaser disk (Greenhill et al. 1996).
A second, more extended component was also detected. This component was over-resolved by the interferometer and its geometrical parameters were not well constrained. The analysis implied a warm (~300 K) structure of ~3 × 4 pc in size. While the position angle could not be determined, the authors suggest that a north-south elongated structure could be identified with the elongation of the mid-infrared region of NGC 1068, seen by Bock et al. (2000), who attribute it to re-emission by dust of UV radiation concentrated in the ionization cone. This component is part of the environment surrounding the inner hot dust region, and according to Poncelet et al. (2007) it represents a large fraction of the emission within the MIDI field of view. Using single-dish telescope VISIR data, they find a compact component <85 milliarcseconds (mas) in size directly associated with the dusty torus, and an elliptical component of size (<140) mas ×1187 mas at PA ~ −4°. They suggest that the extended environment surrounding the compact 800 K dust region contributes more than 83% of the total core emission.
3. The current observations
3.1. Motivation
Since the extended component was overresolved in the observations reported by Raban et al. (2009), little is known about the physical nature of the structures on 5−10 parsec scales and different models could describe this region. The cooler emission on these scales may simply represent an extension of the inner dust accretion disk on larger scales. It may also arise in the intermediate region between the inner dust accretion disk and the outer circumnuclear starforming regions as suggested by the co-evolution scenario of nuclear starbursts and tori from Vollmer et al. (2008) and modeled for the case of NGC 1068 by Schartmann et al. (2009, 2010). We may also have a region where interactions between the accreting dust structures and infalling material (Müller Sánchez et al. 2009) and winds originating near the nucleus are present. To clarify these questions we obtained a new set of mid-infrared interferometric observations with MIDI/VLTI, using smaller baselines to better map these larger scale components.
3.2. Description of the observations
Our interferometric observations were performed in the N band in a wavelength range from 8 μm to 13 μm with the MID-Infrared Interferometric Instrument (MIDI, Leinert et al. 2003) at the Very Large Telescope Interferometer (VLTI) located on Cerro Paranal in Chile and operated by the European Southern Observatory (ESO).
The MIDI instrument is a two beam Michelson interferometer that combines the light from two 8.2-m Unit Telescopes (UTs) or two 1.8-m Auxiliary Telescopes (ATs). The main observables from MIDI are the single-dish spectra and the correlated flux spectra that are obtained from the interference pattern generated by the two beams. For our new observations we used only the ATs. They are movable, allowing the observation of more and shorter baselines than can be observed with the UTs. Their adequate sensitivity and available baselines from 10 to 50 m makes them suitable to study the region of 1−10 parsec of NGC 1068. For our observations we used the low resolution NaCl prism with spectral resolution R ≡ λ/ Δλ ~ 30 to disperse the light of the beams.
Observations were carried out on the nights of October 7 and 8, 2007, and September 19, 20, and 23−26, 2012, using guaranteed time observations (GTO). Two nights of observation (September 23 and 26) were discarded because of bad weather conditions. A log of the observations and instrument parameters can be found in Appendix B. Because of the near-zero declination of NGC 1068 the baseline tracks in the (u,v)-plane are parallel to the u-axis (see Fig. 1). This figure shows the previous UT observations together with the new AT observations. During our observation period we also tried the new MIDI + PRIMA fringe sensor unit (FSU) mode (Müller et al. 2010; Pott et al. 2012). This was done for two main reasons: 1) to stabilize the fringes on the long baselines and 2) to use the FSU to get an estimate of the K-band visibility on new (u,v) points. Previous VLTI/VINCI observations of Wittkowski et al. (2004) are available for one baseline along PA = 45°. Unfortunately the PRIMA FSU was not sensitive enough to improve upon the self-fringe tracking by MIDI.
 |
Fig. 1 (u,v) coverage for NGC 1068 showing both UT and AT configurations. Blue dots show the measurements taken with the UTs and red dots represent the (u,v) points measured with the ATs in 2007 and 2012. |
3.3. Calibration and data reduction
The calibrators used were HD 10380 and HD 18322. We choose them because they were close in airmass to the target with Δ(secz) ≤ 0.25. We started each observation night using HD 10380 as calibrator and when the altitude of the calibrator was less than the altitude of NGC 1068, we changed to HD 18322, which at that point was located 10 ° higher than NGC 1068.
We have applied the techniques developed during the MIDI AGN Large Program (Burtscher et al. 2012) to plan our observing strategy, data reduction process, and analysis of the data. Based on their experience we have optimized our observing sequence by switching as quiclky as possible between target and calibrator fringe track. This was done by omitting single-dish observations and also avoiding fringe searches. For each (u,v) point we performed a sequence of CAL-SCI-CAL, i.e., calibration measurements were taken just before and after a science fringe track; this allowed us to have a much better estimate of the correlated flux of NGC 1068 than using standard observing procedures (CAL-SCI). The additional calibration observations allow more reliable estimates of the instrumental visibility and therefore of the calibrated correlated flux. To correct for correlation losses due to atmospheric phase jitter we performed dilution experiments similar to those done for the MIDI AGN Large Program (Burtscher et al. 2013). Correlation losses for our faintest fluxes are less than 10% of the correlated fluxes, which is less than the uncertainties (see Sect. 4.1) The reduction of the data was performed with the interferometric data reduction software MIDI Interactive Analysis and Expert Work Station (MIA+EWS1, Jaffe 2004) which implement the method of coherent integration for MIDI data. Calibration of the correlated fluxes was computed by dividing the correlated fluxes of the target by those of the calibrator and multiplying by the known flux of the calibrator. For HD 10380 and HD 18322 we used the spectral template of Cohen et al. (1999). In the remainder of this paper we follow the radio astronomical custom of using correlated fluxes rather than visibilities which are defined as the correlated flux divided by the total or photometric flux. At short infrared wavelengths visibilities are less susceptible to changes in atmospheric conditions than correlated fluxes, but at longer wavelengths, i.e., in the mid-infrared, the difficulties of measuring photometric fluxes against the fluctuations of the bright sky favor the use of correlated fluxes.
 |
Fig. 2 Amplitudes of correlated fluxes measured with ATs and grouped by their separation in the (u,v) plane (see text for the selection criterion). The group numbers are given in the top left corner. The different correlated fluxes are displayed in gray lines and the average computed spectrum is shown with a black line. The red lines represent the region of the 1-sigma uncertainty of a single observation. Blue bars represent the 2-sigma uncertainty of the average computed spectrum at 8.5, 10.5, and 12.5 μm. The region between 9 μm and 10 μm has higher uncertainty because of the atmospheric O3 absorption feature in this region. |
 |
Fig. 3 Chromatic phases grouped by their separation in the (u,v) plane. The chromatic phases of each independent observation in the group are given in gray lines and the average computed signal is shown with a black line. The red lines represent the region of the 1-sigma uncertainty of a single observation. Blue bars represent the 2-sigma uncertainty of the average chromatic phase at 8.5, 10.5, and 12.5 μm. |
 |
Fig. 4 Comparison of the correlated flux observed with a projected baseline of 40 m and PA = 36° using UTs (observed in 2005, Raban et al. 2009) and using ATs (observed in 2012). The red line with error bars represents the correlated flux obtained with the UTs. The black line with a gray shaded region represents the correlated flux obtained with ATs. |
4. Results
4.1. Correlated fluxes
In total, 40 correlated fluxes measured under good weather conditions were reduced and calibrated2. We have divided these visibility points into 11 groups using the criterion that visibility points of the same group be located within the AT diameter (1.8 m) of each other. Figure 2 shows the correlated fluxes for each group, sorted by baseline length. The group number is indicated in the top left corner of each plot as a reference for the discussion below. The plots include (1) spectra of the individual measurements (gray); (2) the average of the measurements in the group (black); (3) the mean formal errors (average of the individual formal errors from EWS) (red); and (4) the formal errors in the means (blue error bars).
To check the consistency of calibrated interferometric fluxes with different baselines or telescopes, under different atmospheric conditions and in different epochs, we have taken multiple, independently calibrated measurements of the target at equivalent (u,v) positions. Fluxes measured at two adjacent (u,v) points cannot differ significantly if LΔu/λ ≪ 1, where L is the overall source angular size, and Δu the separation in the (u,v) plane. A single telescope of diameter D is only sensitive to emission within a region of size L ≲ λ/D, so we conclude that two points are equivalent if Δu<D. In our case D = 1.8 m. If the source is smaller, L ≪ λ/D, then (u,v) points separated by larger than D should still yield the same flux.
For the spectra shown in Fig. 2, we observe that all
correlated fluxes fall inside, or very close to, the 1-sigma uncertainty, thus verifying
the formal estimates. The flux uncertainties in a single independent measurement at 8.5,
10.5, and 12.5 μm are typically of the order of 13%, 20%, and 17%; uncertainties vary depending on the
weather conditions. Even when observations of equivalent (u,v) points were taken on
different days and under different weather conditions, the correlated fluxes are
consistent with each other. Computing the average of the measurements (see Sect. 4.1) should give us a proper estimate of the correlated
flux and we can lower the uncertainty of the error by a factor of
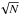 ,
where N is
the number of visibility points used to compute the average. The uncertainties for the
average computed flux are of the order of 6%, 11%,
and 8% at 8.5, 10.5, and 12.5
μm,
respectively.
,
where N is
the number of visibility points used to compute the average. The uncertainties for the
average computed flux are of the order of 6%, 11%,
and 8% at 8.5, 10.5, and 12.5
μm,
respectively.
4.2. Chromatic phases
The EWS software gives the amplitude of the (complex) source visibilities and the chromatic phases. The chromatic phases are identical to the true interferometric phases except that the constant and linear dependencies of phase on wavenumber k ≡ 2π/λ have been removed. This occurs because the fluctuations in the atmospheric refractivity introduce phase shifts that are linear functions of wavenumber. In the absence of a phase-stable external fringe tracker the removal of these atmospheric fluctuations in the reduction process inevitably removes the linear components of the true source phases. This leaves only the second and higher order phase components. Chromatic phases cannot be used directly in image reconstruction, but still constrain the source structure. Most directly, inversion symmetric sources, averaged over the entire wavelength band, will always have zero chromatic phase3. Thus non-zero chromatic phases imply asymmetric structures (Deroo et al. 2007).
The grouped chromatic phases of MIDI measurements are given in Fig. 3. In each group the chromatic phases of every independent observation fall almost entirely within the 1-sigma region meaning that the observations are consistent with each other. As in Sect. 4.1 a similar computation of the average chromatic phase of each group was calculated in order to obtain a proper estimate. The typical uncertainties for the measured chromatic phases of an independent observation at 8.5, 10.5, and 12.5 are 4°, 10°, and 7°, respectively.
The (u,v) points labelled with the number 2, 3, 7, and 8 located at position angles between 69° and 114° show no chromatic phases, while points located between 7° and 39° show significant chromatic phases4. This is clear evidence for non-symmetric structure. In a first approach this suggests that the asymmetry axis is located close to the north-south direction. We observe that within the range where the chromatic phases are observed (7° and 39°), the largest amplitude of the chromatic phases is reached in the lowest projected baseline length (BL); there is a decrease in the amplitude around BL ≈ 20 m and then the chromatic phases increase slightly in amplitude until BL ≈ 40 m. This change in the amplitude indicates that the asymmetries can be found at intermediate and larger scale sizes (relative to the compact central disk). The change in the amplitude of the chromatic phases as a function of baseline length makes it difficult to explain this behavior only using color gradients, i.e., having a chromatic photocenter shift of a brightness distribution, like in the dusty region of the Circinus galaxy (Tristram et al. 2014). This reasoning motivates us to use asymmetric shifts to explain the behavior of the chromatic phases on NGC 1068.
4.3. Variability
The interferometric data of NGC 1068 was taken over a period of seven years and there is some evidence that the nucleus of this source is variable (Glass 1997; Taranova & Shenavrin 2006). Therefore, we need to investigate whether source variability may influence our measurements before we attempt to model our data. To this end we compare a (u,v) point measured at two different epochs. This can provide us with information about the source evolution and/or the reliability of the instrument itself. In our dataset we have a visibility point measured using the ATs in 2012 at a projected baseline BL = 40 m at a position angle of 36°. This point was measured in 2005 by Raban et al. (2009) using the 8.2 m UTS. Figure 4 shows the correlated fluxes and chromatic phases of this point at both epochs. The general trend of the spectra are consistent with each other; we only see some small deviations between the 9.7−10.7μm and 12.5−13.0μm, close to the regions with atmospheric absorption. The chromatic phases are mostly similar except for some small deviations around 10.5 μm and 12 μm. This (u,v) point includes most of the flux of the small hot region5. We expect any variability to arise from the central accretion disk and the effects of a change of luminosity from this heating source to first influence the hot dust located close to the center and only later on the more distant dust. The flux from this component outside the silicate absorption feature is ~5 Jy (see Fig. 4 and the modeling below) and the change in this flux as estimated from Fig. 4 is <0.5 Jy. So we can conclude that the mid-infrared nuclear flux variation in this seven-year period did not exceed ~10%. Given this upper limit we include all MIDI data, regardless of epoch, in our modeling.
 |
Fig. 5 Correlated fluxes of NGC 1068 at
λ = 12.5
μm as a function of the projected baseline
length BL. Left: the data are colored according to their respective
position angles. The solid lines represent the correlated fluxes obtained at two
different position angles from the Gaussian modeling (model 1). The contribution of
each component is represented by different lines: the dotted line represents the
first component, the dashed line is the second component, and the dash-dotted line
the third component for a PA = 70°. Right: expected radial plot
using the photometry from Bock et al. (2000)
for NGC 1068 if the source is placed at a
distance |
4.4. Radial profile of the correlated fluxes
Figure 5 shows the radial profile of the correlated fluxes at 12.5 μm as a function of the projected baseline length BL. The total single-dish flux is obtained from the masked total flux obtained with MIDI as reported in Burtscher et al. (2013). This flux is limited by a mask with a FWHM of ~500 mas and includes the nuclear core emission.
The correlated fluxes show a rapid drop from values around 13 Jy at BL ≈ 10 m to less than 3 Jy at a BL ≈ 50 m. Longer projected baselines (50−140 m) show an almost constant value between 1.0 Jy and 3.0 Jy. The nearly constant behavior of the correlated flux as we go from 50 m to 140 m projected baseline length means that the source of emission cannot be resolved and it must consist of one or more regions that are smaller than the resolution limit of the interferometer λ/(2BL), i.e., less than 9 mas. On the other hand, we can also set a size limit for the large-scale structures that can be observed with the interferometer. Since our lowest projected baseline length is approximately 10 m, the largest structures that can still be resolved correspond to emission regions with a diameter of ~260 mas.
We observe that 14% of the MIDI masked flux corresponds to the emission regions with a size smaller than 50 mas in diameter while the remaining 86% corresponds to the large-scale structures inside the core region with sizes between 50 mas and 500 mas in diameter; the upper limit is given by the resolution limit of the single-dish telescope.
The scatter seen in Fig. 5 for similar projected baseline lengths is caused by the position angle dependency of the correlated fluxes. Since the (u,v) coverage of NGC 1068 is not equally mapped in all directions we cannot make a proper analysis to infer information about the source size in different directions. Still at the lowest projected baseline lengths we can find three (u,v) points with a similar length (BL = 10, 11, and 15 m), but observed with different position angles (at 28°, 72°, and 113° respectively). The point with the longest projected baseline length at PA = 72° has the highest correlated flux. This indicates that the source is less resolved in this direction than the others.
4.5. NGC 1068 in the context of the Large Program (LP) study
Results from a large survey of AGNs using mid-infrared interferometry to resolve the
small-scale structures of their nuclear regions were presented in Burtscher et al. (2013). The sources NGC
1068 and Circinus are a factor of 10 brighter than the rest of the sources
analyzed in that work and they seem to have significant differences compared to the rest
of the sample. A rescaling of these two bright sources was performed in Burtscher et al. (2013) to observe the radial behavior
of the correlated fluxes with a resolution and flux similar to the more distant, weak
sources. In the case of NGC 1068 the source was
placed at a distance 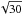 times farther away than its current location so that its fluxes would match the median
flux of the weak sources.
times farther away than its current location so that its fluxes would match the median
flux of the weak sources.
With our new short baseline observations we can more accurately repeat the rescaling experiment and give a quantitative description of the resulting properties when observed under conditions similar to the weak targets. To make this experiment as realistic as possible we only look at the rescaled baseline lengths that are available with the UTs. Figure 5 shows the radial plot of NGC 1068 after applying the rescaling at λ = 12.5μm.
To completely match the conditions of the observations of NGC 1068 with the weak sources we have to take a photometric flux with a
similar resolution to the rest of the targets. For some of the weak sources the total flux
was extracted from MIDI single-dish observations using a window of size
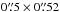 or by taking high spatial resolution
spectra or photometry obtained from the VLT spectrometer and imager for the mid-infrared
(VISIR) using a 0.̋53 window in the spatial direction. If we rescale NGC 1068 to a distance which is
or by taking high spatial resolution
spectra or photometry obtained from the VLT spectrometer and imager for the mid-infrared
(VISIR) using a 0.̋53 window in the spatial direction. If we rescale NGC 1068 to a distance which is
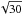 times farther away, then the 0.̋53 window corresponds to a ~3′′ window in the normal space. From Bock et al. (2000) we know that the flux at 12.5
μm does not
vary too much from a beam of a diameter of 4′′ to a beam of a diameter of 2′′, since we need a beam of
diameter of 3′′ we
take the value of the 4′′ diameter beam, FBock = 36 Jy
scaled to 1.2 Jy to be a reasonable approximation. Although the results from Burtscher et al. (2013) were obtained at
λ = 12
μm and we are going to use λ = 12.5μm for our experiment6, the results do not vary within this wavelength range
since the emission is mostly determined by the continuum and no absorption effects come in
to play.
times farther away, then the 0.̋53 window corresponds to a ~3′′ window in the normal space. From Bock et al. (2000) we know that the flux at 12.5
μm does not
vary too much from a beam of a diameter of 4′′ to a beam of a diameter of 2′′, since we need a beam of
diameter of 3′′ we
take the value of the 4′′ diameter beam, FBock = 36 Jy
scaled to 1.2 Jy to be a reasonable approximation. Although the results from Burtscher et al. (2013) were obtained at
λ = 12
μm and we are going to use λ = 12.5μm for our experiment6, the results do not vary within this wavelength range
since the emission is mostly determined by the continuum and no absorption effects come in
to play.
Fitting a radial model to the rescaled data, following Burtscher et al. (2013), by using a two-component model with an unresolved point source and a Gaussian component we find that the point source fraction (fp), of the total flux is of the order of 24% and the FWHM of the Gaussian must be ≳36 mas (the data only provide a lower limit to the size). At the rescaled distance the rescaled limit of the Gaussian component corresponds to structures larger than 14 pc. Figure 5 shows that the flux that we attribute to a point source comes from a partially resolved structure showing a position angle dependence that could be attributed to an elongation.
Burtscher et al. (2013) classified NGC 1068 as consisting of a resolved plus an unresolved emitter. In our rescaling experiment, where we match the fluxes and conditions of observation to the other weak sources, we now classify the rescaled version of NGC 1068 as an unresolved plus an overresolved emitter. We can now compare the results of our experiment with the results of Burtscher et al. (2013, cf. Figs. 30–32, and 34), where the principle difference with the earlier work is that fp has increased from 0.1 to 0.24. This rescale value of fp is no longer detached from the sample distribution, but appears at the lower edge, similar to Seyfert galaxies NGC 4507 and MCG-5-23-16. Thus in the context of the survey, NGC 1068 has a large but not extraordinary flux fraction in well-resolved structures.
Our experiment shows that the difference between the value of fp of NGC 1068 and the typical values for Seyfert Type 2 sources in Burtscher et al. (2013) can be attributed in part to resolution effects. This becomes more evident in a plot of the fp versus intrinsic resolution (see Fig. 32 in Burtscher et al. 2013). However, the new rescaling experiment does not contradict the conclusion of Burtscher et al. (2013) that the spread in morpholgies observed in the survey is instrinsic and not a resolution effect; NGC 1068 still shows some structural differences from the rest of the LP sample. It shows significantly non-zero chromatic phases at baselines of 10−20 m. These correspond to baselines of 60−120 m at the rescaled distance. None of the more distant LP galaxies shows non-zero chromatic phases at these baselines. Circinus seems to resemble NGC 1068 in this respect.
5. Gaussian fits
5.1. Motivation
Direct image reconstruction techniques cannot be applied to our interferometric data for two reasons: the limited (u,v) coverage and the lack of true phases. Still, information can be recovered by using simple analytical forms, such as Gaussians or point sources, to describe the source brightness distribution. The reason for using this approach is to describe the brightness distribution as accurately as possible with a small number of parameters while making few specific physical assumptions. In this section we present model fits for the recent observations, that allow us to specify the mid-infrared geometry of the 1−10 pc region of NGC 1068.
5.2. Graybody Gaussian models
Graybody Gaussian models have been used in earlier papers to model the amplitudes of the correlated flux and get estimates of the sizes, temperature, and inclinations for components in different AGN (e.g., NGC 1068, Jaffe et al. 2004; Raban et al. 2009; Circinus, Tristram et al. 2007, 2012; and Centaurus A, Burtscher et al. 2009). So far the modeling only included the amplitude of the correlated flux and thus by necessity assumed that the Gaussian components were concentric and therefore symmetric.
Raban et al. (2009) showed that the hot small emission region can be described by a Gaussian graybody with an absorption screen in front that reproduces the silicate feature. The authors described the larger scale emission region with a second component, but not enough short baseline information was available to constrain the parameters correctly. This concentric two-component model agreed well with the amplitudes of the correlated fluxes, but by definition cannot reproduce the non-zero chromatic phases described here.
For this work we again use a multi-component graybody Gaussian model to fit the
mid-infrared interferometric observations of NGC
1068. The model treats the infrared emission as coming from Gaussian graybody
components of a fixed size, temperature, and orientation, each one behind a uniform
absorption screen, but we no longer require the components to be concentric. The
contribution to the correlated flux of each component for a (u,v) point is given by
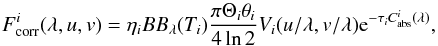 (1)where Ti, τi, and ηi are the dust
temperature, the optical depth, and the scaling factor of the component i, respectively. The
scaling factor ηi can be considered
to be a surface filling or emissivity factor, which is independent of the wavelength and
limited to values of 0
<η ≤ 1; Vi is the contribution of
the visibility of an elongated Gaussian component, described by a FWHM(Θi) along the
major axis, a FWHM(θi) along the minor
axis and a position angle (ψ). The visibility function Vi(u/λ,v/λ)
is obtained by computing the Fourier transform of a Gaussian intensity distribution
function described as
(1)where Ti, τi, and ηi are the dust
temperature, the optical depth, and the scaling factor of the component i, respectively. The
scaling factor ηi can be considered
to be a surface filling or emissivity factor, which is independent of the wavelength and
limited to values of 0
<η ≤ 1; Vi is the contribution of
the visibility of an elongated Gaussian component, described by a FWHM(Θi) along the
major axis, a FWHM(θi) along the minor
axis and a position angle (ψ). The visibility function Vi(u/λ,v/λ)
is obtained by computing the Fourier transform of a Gaussian intensity distribution
function described as ![\begin{equation} G_i(\alpha,\delta,\psi) = \exp\left\{-4 \ln 2 \left[ \left(\frac{\alpha_i'}{\theta_{i}}\right)^2 +\left(\frac{\delta_i'}{\Theta_{i}}\right)^2 \right] \right\}, \end{equation}](/articles/aa/full_html/2014/05/aa23002-13/aa23002-13-eq75.png) (2)where
(2)where
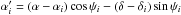 and
and
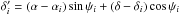 are the positional
coordinates of the Gaussians, and (αi,δi)
is the center of the ith Gaussian component. The absorption curve for the
chemical composition associated with the i-component is described by
are the positional
coordinates of the Gaussians, and (αi,δi)
is the center of the ith Gaussian component. The absorption curve for the
chemical composition associated with the i-component is described by
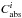 . For the dust
absorption curves we have selected three dust absorption templates, including
Ca2Al2SiO7 (gehlenite; Mutschke et
al. 1998) which was found as the best fit in Jaffe et al. (2004); the standard galactic dust as observed towards the center
of our Galaxy (Kemper et al. 2004); and
α-SiC
(Laor & Draine 1993) suggested by Köhler & Li (2010) as a better explanation for
the anomalous absorption feature present in NGC
1068. The dust template used for each component is made from a linear
combination of the three mentioned dust templates. The coefficients for each component are
fitted along with the rest of the parameters.
. For the dust
absorption curves we have selected three dust absorption templates, including
Ca2Al2SiO7 (gehlenite; Mutschke et
al. 1998) which was found as the best fit in Jaffe et al. (2004); the standard galactic dust as observed towards the center
of our Galaxy (Kemper et al. 2004); and
α-SiC
(Laor & Draine 1993) suggested by Köhler & Li (2010) as a better explanation for
the anomalous absorption feature present in NGC
1068. The dust template used for each component is made from a linear
combination of the three mentioned dust templates. The coefficients for each component are
fitted along with the rest of the parameters.
The final form of the complex correlated flux will be given by
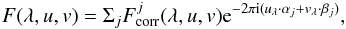 (3)where αj and βj are the offset in
right ascension and declination, respectively, and uλ =
u/λ and
vλ =
v/λ. The total
single-dish flux can be recovered by using the coordinates u = 0 and v = 0, i.e., BL
= 0 m.
(3)where αj and βj are the offset in
right ascension and declination, respectively, and uλ =
u/λ and
vλ =
v/λ. The total
single-dish flux can be recovered by using the coordinates u = 0 and v = 0, i.e., BL
= 0 m.
Parameters found for the graybody Gaussian models.
5.3. Offset components
In addition to the amplitude of the correlated fluxes, we have also measured the chromatic phases. As already mentioned in Sect. 4.2, these phases are not the true phases, but they still provide some spatial constraints. The properties of the chromatic phases observed in NGC 1068 and their distribution on the (u,v) plane excludes the possibility that all major components are concentric. Non-concentric components are required to reproduce the asymmetries observed, which are present for a wide range of projected baselines in our AT observations and there are also a few in longer baselines (see Appendix for plots of the UT data). The longest UT baselines, which respond primarily to the emission from the hot core, show small phases indicating that this core is essentially symmetric. The intermediate and short baselines respond to both the core and the larger structures and in the current models the non-zero phases indicate displacements between these components.
We can use Eq. (2) to calculate the complex correlated flux not only for the computation of the amplitude, but also for the calculation of the chromatic phases. For each modeled visibility point, the constant and linear dependencies on wavenumber are removed from the complex correlated flux. By doing this we lose some information of the exact position of each component in real space, but the information about the positions with respect to each other is preserved. To reduce the degeneracy of solutions we have fixed the position of the smallest component to be at the center of our plane, i.e., α1 = 0 and β1 = 0.
We have spectra of the amplitudes and chromatic phases for 30 (u,v) points, which include information from projected baselines between 10 m and 130 m. We have attempted to fit three-component models to these data, but we have not been able to find a reasonable fit to all the data. In these attempts we can find reasonable fits for either the chromatic phases or the correlated fluxes, but not both together. Apparently a more complicated model is necessary. Because our immediate goal was to describe the emission morphology with a limited number of parameters, we have chosen not to add a fourth or additional components to improve the fit.
Instead we will focus our attention on describing only the spatial information contained in the AT observations. This approach ignores the details of the small-scale structures, but describes the relative positions of the three components with respect to each other. The result from this procedure can be interpreted as a low resolution image of the emission of NGC 1068. It is our intention to present at a later date representations of our data using more general image reconstruction techniques constrained by physically motivated emission models.
The parameters reported in this paper are the least-squares solution found using the Levenberg-Marquardt technique to fit all 30 amplitude spectra and the 11 chromatic phase spectra from AT observations reported here. The reason for not using the chromatic phases measured with the UTs is to give an equal weight to the chromatic phases in all the scales, otherwise the fitting routine would focus more on the intermediate scale regime while the aim of this work is to disentangle the large structures from the small scales. Additionaly, we do not try to fit the single-dish MIDI masked flux since it was measured using the UTs. As mentioned in Sect. 4.4, the masked flux could also be capturing part of the emission coming from regions farther than 250 mas away.
There is a difference in the field of view of the UTs and ATs, which means that the region observed by the ATs might include regions which are not captured by the UTs. This does not seriously affect the interferometric observations since the UTs observe the small scales and in Sect. 4.3 we showed that the UTs and ATs observe the same structures on the small size regime (>30 mas). The large-scale structures are over-resolved with the UT baselines and thus depend only on the information obtained from the AT baselines.
To estimate the errors in the parameters, we fixed the value of all but one parameter at a time. The uncertainties that we report represent the range of variation of each parameter sufficient to cause a significant change in the quality of fit. We saw that parameters with a reduced chi-square larger than 15% of our best reduced chi-square begin to show significant differences.
We first attempted to fit a two-component model as Raban et al. (2009) but relaxing their assumption of concentricity. We were unable to get a reasonable fit of our data. We then tried three-component models.
We found two sets of parameters which can describe the source brightness distribution and the chromatic phases to a reasonable degree; these two sets of parameters can be seen in Table 1. Both models consist of two warm components using a standard galactic dust template and one hot small component using a mixture of gehlenite and galactic dust as the dust template. Contrary to what Köhler & Li (2010) report from their study, we find that the contribution of SiC in the dust templates is at most very small. Köhler & Li (2010) used the spectra of only one (u,v) point in their modeling, and the optical depth of the SiC feature can be chosen to fit well this one point, but it cannot fit the ensemble of observations. In Figs. A.1 and A.2 of Appendix A we also plot best-fit curves obtained for a model using only SiC as the template. The poor match to most of the data indicates why the least-squares routine avoided this component to the fits.
The size of the major and minor axes, and position angle of the hot component for both models agree with the parameters previously reported by Raban et al. (2009). This is not surprising since we left out the chromatic phases measured with the UTs, i.e., long projected baseline; therefore the hot small emission region will be treated as a symmetric Gaussian component. The 660 K temperature for one of our models is clearly lower than the one reported by Raban et al. (2009); the differences might be attributed to the dust absorption templates used in each model.
The two best fitting models differ primarily in the position of the intermediate-sized component. In our first model (see Fig. 7) we find this component to be associated with emission of dust around 257 K with a size of 3.7 × 1.6 pc elongated at a position angle of 120°. The position of its center is 19 mas to the north of the hot component. The third component is a large emission region with a temperature around 360 K. The center of the Gaussian which represents this large region is ~100 mas to the north of the hot component and at an angle of − 18° (measured from north to east). It is a highly elongated structure with an axis ratio of ~1:3.7 and a position angle of −36°.
 |
Fig. 6 Best-fit model for the (u,v) points observed with the ATs. Left: correlated fluxes and right: chromatic phases. The red line shows the corresponding correlated fluxes and chromatic phases for our non-concentric model no. 1 while the dashed blue line represents our non-concentric model no. 2. Light green lines (only on the first four plots of each panel) show the curves obtained by taking the parameters of our first-best model, and taking the lower limit of the uncertainty in the offset declination for the third component, we observe some significant deviations in some of the plots. |
Model no. 2 also has an intermediate- and large-sized Gaussian component. The second component for this model consists of emission at 300 K with an intermediate size of 2.9×2 pc elongated at a PA of 102° and located 17 mas south of the hot component. It is absorbed by a screen with a larger optical depth close to 3. The third and biggest component with a temperature around 370 K has a FWHM of 200 mas along the major axis and a FWHM of 52 along the minor axis. The position angle of this large component is similar to the one for our first model, −35°. The center of this large emission region is also located to the northwest of the small hot component, but with a slightly different position from our first model, it can be found at a distance of ~80 mas from the center and 16° in the NW direction. The ratio between the major and minor axis is also close to ~1:4.
The main differences between our best-fit models lie in the parameters of the intermediate size component. In the second model this component lies to the south rather than to the north, and it has a much larger absorption optical depth. The degeneracy of the modeling, i.e., the existence of two equally good fits is caused by the limitations of using chromatic phases. The contribution of this component to the phases changes sign when it is moved to the south, but this effect is cancelled, after removal of the linear phase gradient, by the absorption-diminished emission of this component near 10 μm. This ambiguity would be removed if true phase or closure phase observations were available. These possibilities should be available with future VLTI instruments, e.g. MATISSE (Lopez et al. 2008).
The fitted correlated fluxes and the chromatic phases for both models can be seen in Fig. 6. The correlated fluxes fit well; deviations are mainly caused by the assumption of a Gaussian shape. The largest deviations are seen in the mid- and long- baseline range where the resolved structures are probably more complex. This is also seen in the chromatic phases; the shortest baselines are fitted well with our model. In the long baseline regime (see Appendix A online for plots of UT chromatic phases) the chromatic phases are mostly zero and thus our model is consistent in that regime, while in the intermediate regime the model fits poorly.
 |
Fig. 7 Images of the three component models for the mid-infrared emission at 12.0 μm of the nuclear region of NGC 1068 corresponding to model 1 (left) and model 2 (right). The image was scaled using the square root of the brightness. Center: comparison between our first best model and the 12.5 μm image of Bock et al. (2000), taken with the 10 m Keck Telescope. The dashed circles represent the FWHM of the field of view for MIDI using the UTs (blue) or the ATs (orange). The letters indicate the positions of the [OIII] clouds according to Evans et al. (1991). |
6. Discussion
6.1. Summary of modeling
Our three graybody models provide us with a general image of the main emission regions of NGC 1068 using information from the short baselines and chromatic phases. The main differences between our models and the work by Raban et al. (2009) are the new short spatial frequency observations and the use of chromatic phases to get spatial information of the nuclear mid-infrared region. A sketch of the emission region can be seen in Fig. 7. Although our models are not able to reproduce the chromatic phases completely, especially in the intermediate baseline regime, we observe a reasonable consistency in the lower and higher baseline regime which fit much better than purely concentric models. The poor fits observed in the intermediate baseline regime would suggest that the link between the small scales and the large scales is more complex than can be fitted with a limited number of Gaussians and has to be modeled more carefully in order to understand the relations between the various size scales. Still, our 3-Gaussian model represents reasonably well the global variation of surface brightness with position in the nuclear region of NGC 1068. The resolution of these variations into discrete components may be an artefact of the modeling. More sophisticated image reconstruction techniques may remove these artificial transitions, but reliable multiwavelength image reconstruction algorithms that can accommodate the chromatic phase information are not yet available.
Both models show that the maximum separation, in the north-south direction, between the center of the Gaussian components must be approximately 100 mas. Since we identify the component at (0,0) with the radiation from near-nuclear dust (see Sect. 6.3), the large flux from the northern offset component must come from the regions located near the narrow line ionization region. This northern component is large relative to the other components in both models and the absorption optical depth and scaling factor are small. The total flux of this component reaches 10 Jy at 12 μm. Figure 8 shows the total flux of each component as a function of wavelength, the ratio of the total fluxes of each component varies depending on the wavelength. We observe a ratio of the fluxes of 1:0.4:1.2 for the first, second and third components, respectively at 8 μm, 1:1.6:7 at 10 μm, and 1:2:3.5 at 12 μm. Thus, our third (the largest component) contributes with 46%, 73%, and 55% of the total flux of structures with sizes below 260 mas in diameter, i.e., the ones that are resolved with the interferometer7.
The position and absorption profile of the intermediate component are ambiguous in our models. The foreground absorption required in the second model (τ ~ 3) is larger than that in front of the central component. This is counter-intuitive, but cannot be excluded in models where the dust is distributed in irregular clumps (Nenkova et al. 2008; Schartmann et al. 2008). This ambiguity can be removed if additional (u,v) coverage at intermediate baselines is obtained. Still, it is interesting to see that when comparing our two best models, the general trend seems to be consistent with a gradient in the silicate absorption, which decreases when going from south to north. Tristram et al. (2014) used this gradient in the silicate absorption to explain the behavior of the phases observed in the Circinus galaxy in the low spatial frequency regime. In NGC 1068, the lowest spatial frequency regime also seems to be consistent with a gradient in the silicate absorption while the chromatic phases observed in the intermediate spatial frequency regime are caused by offset components that together form a non-Gaussian shape region.
We conclude this summary by reiterating that the resolution of the emission from the galaxy into three distinct components, as seen in Fig. 7, is an approximation to the actual brightness distribution of the mid-infrared nuclear region of NGC 1068. If the a priori assumption of Gaussian components is relaxed, the components may blend into one continuous feature. The brightness distribution function for model no. 1 can be approximately represented by a continuous distribution where the brightness decreases as r−γ, with r being the distance from the center of the first component and γ ≈ 1.
6.2. The tongue
Single-dish mid-infrared images of NGC 1068 display a primarily N-S elongation dominated by a specific feature that Bock et al. (2000) have named the Tongue. This coincides with the regions IR-1/1b seen by Gratadour et al. (2006) in short wavelength infrared single-dish images, and component C in the VLBA radio maps of Gallimore et al. (2004). This region extends to the north of the core, bends to the west about 0.2′′ above the core, and then bends to the east. It seems to be associated with part of the [OIII] emission (Evans et al. 1991) and the radio continuum emission (Gallimore et al. 1996). According to Galliano et al. (2005), the Tongue region (identified as the NE1) has a flux of 11.2 ± 2 Jy at 12.8 μm and is thus the second brightest mid-infrared region in NGC 1068 after the core region. Because at least part of this feature lies within the AT/VLTI field of view, we need to explore its relationship to our measurements and models. The 1.8 m diameter ATs have a field of view (FOV) of radius ~1.14 arcsec at 12 μm while the 8 m UTs have a FOV of ~250 mas. From the images in Galliano et al. (2005) and Poncelet et al. (2007) we estimate the NE1 component to be 400−500 mas from the core. The existence of NE1 within our FOV raises two questions: (1) is component 3 in our model fits in fact identical with NE1, but incorrectly positioned due to our limited (u,v) coverage and (2) even if component 3 is distinct from NE1, do our observations place useful constraints on the morphology of NE1?
 |
Fig. 8 Total flux of the three best-fit model components as a function of wavelength. |
We have investigated whether positions of component 3 near NE1 are consistent with our AT data. There are such solutions, but we have discarded them as unphysical because (1) the third component then requires very high temperatures (>800 K) to fit the short baseline spectra and (2) the total flux of the third component exceeds the values reported by Galliano et al. (2005) and also the ones reported by Poncelet et al. (2008) at the two closest northern quadrants (3.4 Jy, 4.8 Jy, and 7.5 Jy at 9.0 μm, 10.8 μm, and 12.8 μm for their 1NO region and 1.2 Jy, 1.8 Jy, and 3.1 Jy at the same wavelengths for the 2NO region). Evidence in favor of the existence of a near-in third component is that the first two interferometric components do not provide the large flux (25 Jy) measured by these authors inside the 0.6′′ diameter central aperture.
We conclude that a third component <100 mas from the core is necessary to fit the spectra at the shortest projected baselines. We now investigate whether a new extra component at the position of the Tongue could improve the fits. To avoid adding an excessive number of degrees of freedom to our model we have fixed a priori several Gaussian parameters of the fourth component. From the flux values reported by Poncelet et al. (2008) we think it is reasonable to fix the temperature of this component to 300 K with a very small optical depth and place it 400 mas to the north of the hot core. From the mid-infrared images reported by Bock et al. (2000) we fix the PA of the emission region to ~−40°. We allow the modeling routines to fit the major and minor axes, and adjust the scale factor of this component to fit the single-dish fluxes. We found that including this fourth component with these characteristics does not improve the fits. A component with a large offset (more than 100 mas) and with similar or smaller size than our component 3 would produce phase steps in the 8−13 μm region that are not observed in the data. The existence of this component is consistent with the short baseline data only if it is so large as to be essentially resolved out by the interferometer. This places lower limits of ~160 mas and ~200 mas for the minor and major axes, respectively.
6.3. Cross-identification of the components
Previous single-dish observations (Bock et al. 2000) have clearly revealed an elongated region of the mid-infrared emission which extends up to 1′′ to the north, but their resolution was not sufficient to resolve the central emission of the core. From our interferometric observations we inferred that the emission of the core can be divided into two distinct regions: one consistent with a hot emission surrounded by warm dust (first and second components) and a large warm diffuse region approximately 100 mas (~7 pc) away from the other. We do not have absolute astrometric information about these components and cannot identify one with the nucleus without further assumptions.
We identify the first, most compact component with the nucleus for the following reasons: the hot temperature obtained for the small component is consistent with the temperatures obtained from dust in thermal equilibrium close to the sublimation radius in dusty clump tori (Schartmann et al. 2008) and also consistent with the temperature of the warm (>600 K) molecular dust that is expected to embed the water masers (Neufeld et al. 1994). If we attempt to locate the nucleus in components 2 or 3 it is difficult to explain the high temperature of component 1 without invoking a new, powerful heating source. Additionally, the size and orientation of component 1 closely match those of the water maser, which must be orbiting the nucleus.
With this identification we note that at lower resolution, the peak of the mid-infrared emission will not be at the position of the small hot dust component, but near our third component, whose flux exceeds that of the nucleus by a factor of 3.5 at 12 μm. In Fig. 7 we sketch the positions of our components on the contour map of (Bock et al. 2000). We observe that the inclination of our large component is roughly similar to the bend that is located to the north of the 12 μm image. Our components 1/2/3 cannot be resolved in this image. Gratadour et al. (2006) show deconvolved adaptive optics images of this region taken with the NAOS-CONICA instrument at the K-, L- and M-bands. It is possible that our component 3 is identical with the component labelled IR-CN on their Fig. 4a, but the limits of the resolution and dynamic range of this data make this identification uncertain.
Our estimates of the total flux for the large component show a similar behavior to the results of Poncelet et al. (2007) who found that part of a large north-south component enters the MIDI field of view and contributes 83% of the emission of the mid-infrared from the core (within 500 mas). The ratios of the 12 μm emission for our components can be summarized approximately as 1:2:3 for the first, second, and third components respectively, meaning that the flux due to the large component should be 55% of the core emission. The differences in percentage is possibly due to the additional components outside the central MIDI field of view that contribute to the component found by these authors.
This is not the first time that a large mid-infrared emission along or close to the polar region is observed in AGNs. Recently, interferometric observations of Circinus (Tristram et al. 2012), NGC 424 (Hönig et al. 2012), and NGC 3783 (Hönig et al. 2013) indicate the presence of mid-infrared emission along the outflow direction with a fairly big contribution to the total flux. In Hönig et al. (2012) a radiatively driven dusty wind scenario was proposed to explain the large contributions to the mid-infrared flux by polar dust.
7. The energetics of the mid-infrared emission
The primary scientific results from these observations are the detection of the intermediate components 2 and 3 at 1.3 and 7 parsec north of the core, and the non-detection of the Tongue at about 35 parsec to the north of the core. In this section we consider the possible heating mechanisms for the dust in these components.
The usual suspects are radiative heating and shock heating. These mechanisms collaborate. The hot gas in a strong shock will destroy the local dust by sputtering and conductive heating, but it will also emit ultraviolet light that efficiently heats dust in the surrounding environment. The morphology of the emission from the Tongue region supports this combined scenario. The VLBA radio images, (Gallimore et al. 2004), show a small bright component (C) with a sharp edge near this position, suggesting a shock. Most of the radio emission comes from a region less than 30 mas in diameter. Our data, and the imagesfrom Gratadour et al. (2006) indicate that the dust emission comes from a much larger region, probably displaced from radio component C. In particular the MIDI data excludes a narrow ridge morphology that might be associated with a shock. This extended emission presumably arises from radiatively heated dust.
Wang et al. (2012) describe a similar scenario based on relatively high-resolution (300 mas) Chandra X-ray data. The X-ray and radio bright region HST-G about 1′′ north of the nucleus shows an X-ray spectrum containing both photoionized and high-density thermal components. Detailed X-ray spectra for the other X-ray components in the region are not available, but the ratio of [OIII] to soft X-ray continuum indicates that some (labelled HST-D, -E, and -F) are radiation heated, while others (HST-G, -H, and the near-nuclear regions HST-A, -B, and -C) contain shocked gas. The HST-A, -B, and -C regions contain the nucleus (to the extent not blocked by Compton scattering), our components 1, 2, and 3, and the Tongue. Unfortunately the spatial resolution of the X-ray and [OIII] data cannot distinguish between these subcomponents. The very high-resolution VLBA data of Gallimore et al. (2004) show a flat-spectrum nuclear component, presumably coinciding with our component 1, but no emission at our positions 2 or 3. They find strong synchrotron emission at the Tongue and at their NE component, which curiously shows no enhanced X-ray, [OIII], or infrared emission. There are several regions (e.g., HST-D, E, F in Evans et al. 1991) that show X-ray, [OIII], and infrared emission, but where there is no sign of shock enhancement of the synchrotron jet (Gallimore et al. 2004). Regions NE-5, 6, and 7 of Galliano et al. (2005) show the same features. There is no evidence at these positions of direct interaction with the radio jet, although they lie at the edge of a radio cocoon (Wilson & Ulvestad 1983).
This summary indicates the complexity of the region and suggests that different mechanisms dominate at different positions. The data from the Tongue region seems to support the shock plus radiative heating in this area. On the other hand, our region 3 shows no signature of shocks in the radio. This and the proximity to the nucleus favor heating by UV-radiation from the nucleus.
We can examine whether the infrared spectral information in the region is consistent with
this hypothesis. The luminosity produced by the nucleus is sufficient to obtain the dust
temperature measured at this position. The expected temperature of dust (assuming silicate
grains) heated directly by the central engine is given by
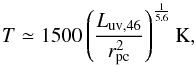 (4)where Luv,46 is the luminosity of
the heating source in units of 1046 erg s-1 (Barvainis 1987).
For the central source of NGC 1068 we take the UV
luminosity Luv = 1.5
× 1045 erg s-1 previously used by Gratadour et al. (2003) to reproduce the central K-band flux and continuum.
Dust at a distance of r ~
7 pc (100 mas) can be heated to T = 530 K. The color
temperatures in our wavelength range are lower (~400 K).
(4)where Luv,46 is the luminosity of
the heating source in units of 1046 erg s-1 (Barvainis 1987).
For the central source of NGC 1068 we take the UV
luminosity Luv = 1.5
× 1045 erg s-1 previously used by Gratadour et al. (2003) to reproduce the central K-band flux and continuum.
Dust at a distance of r ~
7 pc (100 mas) can be heated to T = 530 K. The color
temperatures in our wavelength range are lower (~400 K).
The spectra of the various infrared components show various, sometime quite high color temperatures, but it is difficult to use this to distinguish radiative from shock heating. The dust in the shock heated Tongue region shows short wavelength fluxes with color temperatures ~700 K (Gratadour et al. 2006), but some of the shortest wavelength data may represent scattered nuclear light rather than local thermal emission. The spatial resolution of the data in Gratadour et al. (2006) is not sufficient to unambiguously determine a short wavelength color temperature for our component 3. They report aperture fluxes for the non-deconvolved K-band image of the nucleus that increase from ~70 mJy at 80 mas radius to ~130 mJy at 130 mas radius and ~190 mJy at 270 mas. If we extrapolate our N-band flux of component 3 to the K-band with the same flux ratio as the Tongue region, it would have a flux of ~50 mJy, which is consistent with the fluxes just quoted. The speckle data in Weigelt et al. (2004) also give some indication of short wavelength radiation from our component, but the resolution is again marginal, and the same problem of scattered light exists. In conclusion, the infrared data do not exclude N- to K-band color temperatures up to ~700 K, which would be difficult to explain by radiative heating from the nucleus.
We anticipate that high-resolution interferometric mapping of NGC 1068 at 3 μm and 5 μm with the MATISSE interferometer (Lopez et al. 2008) will determine accurate infrared spectra for these regions and allow disentanglement of the thermal emission and scattering. Here we assume on the basis of the lack of radio emission in component 3 that it is heated radiatively by the nucleus. This component emits about 60% of the near nuclear mid-infrared flux. Hence this structure must absorb most of the nuclear UV-emission. Thus, the dust that extinguishes the nuclear emission in this Seyfert 2 galaxy is not distributed in a disk- or torus-like structure, cloudy or otherwise, but in a narrow cylindrical or conical structure generally in the jet direction, which is, however, not symmetric around the jet. Müller-Sánchez et al. (2011) similarly found that the coronal line ionization cone in NGC 1068 was also quite narrow. They estimate the half-opening angle to the north to be ~27°. If the simple unified models of Seyfert galaxies is in fact true, and the opening angles for viewing the direct emission from the nucleus were as small as that in NGC 1068, only about 10% of Seyfert would be of Type 1, instead of the observed value of ~50%. A spread in the values for the opening angles was earlier noted by studying the kinematics of the narrow line region using the HST (Fischer et al. 2013) and VLT/SINFONI (Müller-Sánchez et al. 2011), and for the case of NGC 1068 the relatively narrow opening angle of the ionization cone reported in both studies is in agreement with our observations. Thus, there is evidence for a large spread of the opening angles of AGNs, and that the actual difference between Types 1 and 2 may be more complicated than a simple inclination angle effect.
8. The north/south asymmetry
It is noteworthy that the majority of the emission in the immediate circumnuclear neighborhood is highly asymmetric, lying to the north of the nucleus itself. This is the same side where most of the radio, near-infrared emission and optical ionization cone emission is seen. At shorter wavelengths, the asymmetry is usually attributed to foreground absorption from the inclined dust structure, but a similar mechanism in the mid-infrared requires very high dust opacities. If we suppose that an additional component identical to component 3 were present in the south, we would need several optical depths at 12 μm at a position 7 parsec south of the nucleus to obscure this component. This dust needs to be quite cold, i.e., <200 K, in order that its own emission not dominate our picture. A similar picture, but with lower forground opacity is presented by Tristram et al. (2014) for Circinus. In view of the complexity of this source, it cannot be ruled out that a cold cloud or disk structure at large radius extinguishes the southern infrared emission. This would not explain the north-south asymmetry of the radio emission, which may represent accidental circumstances of the interception of the jet by clouds.
Tristram et al. (2014) have found a similar picture in the Circinus galaxy. They find non-torus emission aligned with radio jet. The mid-infrared continuum emission is more or less symmetric in these regions, but the 10 μm silicate absorption is much stronger on the side where optical emission is missing. This may represent a case where the foreground dust thickness is enough to block the center of the silicate band, but not enough to absorb most of the N-band continuum. In this picture the dust column density in NGC 1068 would be at least three times higher, so that both the continuum and the silicate feature are blocked.
9. Conclusions
We present new interferometric data from MIDI/VLTI using the Auxiliary Telescopes that allow us to investigate the structure of the 5−10 pc scale mid-infrared nuclear emission from NGC 1068. Our observations complement the previous UT interferometric observations, that trace the small-scales structures, and the single-dish images of the extended region. The ATs, which have an effective area smaller by a factor of ~20 than the UTs, were able to track fringes for NGC 1068 measuring fluxes close to the limit of the instrument.
We summarize our results as follows:
-
Fits using non-concentric Gaussian components indicate that most of the mid-infrared emission is attributed to the large-scale structures. This emission is associated with warm dust distributed in two major components, one close to the center and one with a distance larger than 80 mas and close to 16°–18° in the NW direction. The central warm region would mostly be seen as the extension of the hot emission region, while the offset region may be attributed to dusty clouds located close the northern ionization cone. The parameters found for this component indicate a size of ~14 parsec, strong elongation along a position angle of ~−35°, and a contribution to the total flux at 12 μm which is more than three times that of the central hot region.
-
The non-zero chromatic phases on the shorter baselines indicate major asymmetries in the emission on the 10 parsec scale, primarily along the north-south axis.
-
The 3-Gaussian model does not fit well the intermediate baseline data, probably because of the complexity of the structures in the equivalent size scales. This, combined with the limited information from the chromatic phases, leads to uncertainty in the description of the structures on equivalent scales. The displacement, size, and orientation of the large northern component is determined from the data at the shortest baselines, where the quality of the Gaussian fits is good.
-
The low resolution picture derived from the Gaussian fits indicates that the near-nuclear (<10 pc) emission is strongly asymmetric with respect to the nucleus, with the major components to the north agreeing in orientation with those seen in near-infrared NACO images. The north-south asymmetric may be caused by strong extinction of the southern components, or by intrinsic asymmetry of the dust components.
-
The warm component 3, located ~7 parsec north of the hotter nuclear disk, apparently intercepts a large fraction of the nuclear UV emission. Thus there are several obscuring components at different disk latitudes that can cause Seyfert 2 appearance in AGNs. The volume that is heated by this emission is quite narrow; the viewing angles from which this galaxy would be classified as Seyfert 1 cover only ~10% of the sky.
-
We do not observe evidence for variability effects in the mid-infrared emission of the small-scales structures in the nuclear region of NGC 1068. Similar (u,v) points observed with a difference of 7 years do not show significant differences (less than 10%).
-
Independently calibrated observations with the ATs over periods of several days show a high level of repeatability.
Online material
Appendix A: Plots of UT data
 |
Fig. A.1 Correlated fluxes of observations taken with UTs. The red and dashed blue lines are the curves obtained with our first and second best-fit models. The light blue curve shows the correlated fluxes of our best-fit model found using SiC as the dust template for all the components. We observe that the main reason of discarding SiC as the best option is mostly due to the shape of the absorption feature. |
Appendix B: Log of observations
continued.
EWS is available for download from: http://home.strw.leidenuniv.nl/~jaffe/ews/index.html
The same stacking method was applied to the fringe tracks as in Burtscher et al. (2013). Fringe tracks were reduced together when they were less than 30 min apart and were calibrated with the same star.
From the 23 sources analyzed in Burtscher et al. (2013) only NGC 1068 and Circinus show clearly visible non-zero chromatic phases. Circinus chromatic phases are analyzed in Tristram et al. (2014).
We refer to the small hot region as the 800 K component reported by Raban et al. (2009).
Acknowledgments
The authors thank the anonymous referee for thoughtful and helpful comments. This work was based on observations with ESO telescopes at the La Silla Paranal Observatory under programs: 074.A-9015, 076.B-0743, 277.B-5014, 080.B-0928, 087.C-0824 and 089.B-0099. N. López-Gonzaga was supported by grant 614.000 from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek and acknowledges support from a CONACyT graduate fellowship.
References
- Antonucci, R. R. J. 1984, ApJ, 278, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Beckert, T., Driebe, T., Hönig, S. F., & Weigelt, G. 2008, A&A, 486, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bock, J. J., Marsh, K. A., Ressler, M. E., & Werner, M. W. 1998, ApJ, 504, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Bock, J. J., Neugebauer, G., Matthews, K., et al. 2000, AJ, 120, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Jaffe, W., Raban, D., et al. 2009, ApJ, 705, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Meisenheimer, K., Jaffe, W., Tristram, K. R. W., & Röttgering, H. J. A. 2010, PASA, 27, 490 [NASA ADS] [Google Scholar]
- Burtscher, L., Tristram, K. R. W., Jaffe, W. J., & Meisenheimer, K. 2012, in Proc. SPIE, 8445, 1G [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Deroo, P., van Winckel, H., Verhoelst, T., et al. 2007, A&A, 467, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, I. N., Ford, H. C., Kinney, A. L., et al. 1991, ApJ, 369, L27 [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., & Schmitt, H. R. 2013, ApJS, 209, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, E., Pantin, E., Alloin, D., & Lagage, P. O. 2005, MNRAS, 363, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Baum, S. A., & O’Dea, C. P. 1996, ApJ, 464, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Baum, S. A., & O’Dea, C. P. 2004, ApJ, 613, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Glass, I. S. 1997, Ap&SS, 248, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Gratadour, D., Clénet, Y., Rouan, D., Lai, O., & Forveille, T. 2003, A&A, 411, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratadour, D., Rouan, D., Mugnier, L. M., et al. 2006, A&A, 446, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenhill, L. J., Gwinn, C. R., Antonucci, R., & Barvainis, R. 1996, ApJ, 472, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Antonucci, R., et al. 2012, ApJ, 755, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Tristram, K. R. W., et al. 2013, ApJ, 771, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. J. 2004, in Proc. SPIE 5491, ed. W. A. Traub, 715 [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kemper, F., Vriend, W. J., & Tielens, A. G. G. M. 2004, ApJ, 609, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Tristram, K. R. W., & Weigelt, G. 2009, A&A, 493, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., & Li, A. 2010, MNRAS, 406, L6 [NASA ADS] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Graser, U., Przygodda, F., et al. 2003, Ap&SS, 286, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, B., Antonelli, P., Wolf, S., et al. 2008, in Proc. SPIE, 7013, 2B [Google Scholar]
- Meisenheimer, K., Tristram, K. R. W., Jaffe, W., et al. 2007, A&A, 471, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, A., Pott, J.-U., Morel, S., et al. 2010, in Proc. SPIE, 7734, 20 [Google Scholar]
- Müller Sánchez, F., Davies, R. I., Genzel, R., et al. 2009, ApJ, 691, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Mutschke, H., Begemann, B., Dorschner, J., et al. 1998, A&A, 333, 188 [NASA ADS] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Ivezić, Ž., & Elitzur, M. 2008, ApJ, 685, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Maloney, P. R., & Conger, S. 1994, ApJ, 436, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Poncelet, A., Perrin, G., & Sol, H. 2006, A&A, 450, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poncelet, A., Doucet, C., Perrin, G., Sol, H., & Lagage, P. O. 2007, A&A, 472, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poncelet, A., Sol, H., & Perrin, G. 2008, A&A, 481, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pott, J.-U., Müller, A., Karovicova, I., & Delplancke, F. 2012, in Proc. SPIE, 8445, 0Q [Google Scholar]
- Raban, D., Jaffe, W., Röttgering, H., Meisenheimer, K., & Tristram, K. R. W. 2009, MNRAS, 394, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Rouan, D., Rigaut, F., Alloin, D., et al. 1998, A&A, 339, 687 [NASA ADS] [Google Scholar]
- Rouan, D., Lacombe, F., Gendron, E., et al. 2004, A&A, 417, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, D. B., Phinney, E. S., Neugebauer, G., Soifer, B. T., & Matthews, K. 1989, ApJ, 347, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., et al. 2008, A&A, 482, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Klahr, H., et al. 2009, MNRAS, 393, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Schartmann, M., Burkert, A., Krause, M., et al. 2010, MNRAS, 403, 1801 [NASA ADS] [CrossRef] [Google Scholar]
- Seyfert, C. K. 1943, ApJ, 97, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Taranova, O. G., & Shenavrin, V. I. 2006, Astron. Astrophys. Trans., 25, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Tomono, D., Doi, Y., Usuda, T., & Nishimura, T. 2001, ApJ, 557, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2007, A&A, 474, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Raban, D., Meisenheimer, K., et al. 2009, A&A, 502, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Schartmann, M., Burtscher, L., et al. 2012, J. Phys. Conf. Ser., 372, 012035 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Beckert, T., & Davies, R. I. 2008, A&A, 491, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J., Fabbiano, G., Karovska, M., Elvis, M., & Risaliti, G. 2012, ApJ, 756, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Wittkowski, M., Balega, Y. Y., et al. 2004, A&A, 425, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, A. S., & Ulvestad, J. S. 1983, ApJ, 275, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Kervella, P., Arsenault, R., et al. 2004, A&A, 418, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 (u,v) coverage for NGC 1068 showing both UT and AT configurations. Blue dots show the measurements taken with the UTs and red dots represent the (u,v) points measured with the ATs in 2007 and 2012. |
| In the text | |
 |
Fig. 2 Amplitudes of correlated fluxes measured with ATs and grouped by their separation in the (u,v) plane (see text for the selection criterion). The group numbers are given in the top left corner. The different correlated fluxes are displayed in gray lines and the average computed spectrum is shown with a black line. The red lines represent the region of the 1-sigma uncertainty of a single observation. Blue bars represent the 2-sigma uncertainty of the average computed spectrum at 8.5, 10.5, and 12.5 μm. The region between 9 μm and 10 μm has higher uncertainty because of the atmospheric O3 absorption feature in this region. |
| In the text | |
 |
Fig. 3 Chromatic phases grouped by their separation in the (u,v) plane. The chromatic phases of each independent observation in the group are given in gray lines and the average computed signal is shown with a black line. The red lines represent the region of the 1-sigma uncertainty of a single observation. Blue bars represent the 2-sigma uncertainty of the average chromatic phase at 8.5, 10.5, and 12.5 μm. |
| In the text | |
 |
Fig. 4 Comparison of the correlated flux observed with a projected baseline of 40 m and PA = 36° using UTs (observed in 2005, Raban et al. 2009) and using ATs (observed in 2012). The red line with error bars represents the correlated flux obtained with the UTs. The black line with a gray shaded region represents the correlated flux obtained with ATs. |
| In the text | |
 |
Fig. 5 Correlated fluxes of NGC 1068 at
λ = 12.5
μm as a function of the projected baseline
length BL. Left: the data are colored according to their respective
position angles. The solid lines represent the correlated fluxes obtained at two
different position angles from the Gaussian modeling (model 1). The contribution of
each component is represented by different lines: the dotted line represents the
first component, the dashed line is the second component, and the dash-dotted line
the third component for a PA = 70°. Right: expected radial plot
using the photometry from Bock et al. (2000)
for NGC 1068 if the source is placed at a
distance |
| In the text | |
 |
Fig. 6 Best-fit model for the (u,v) points observed with the ATs. Left: correlated fluxes and right: chromatic phases. The red line shows the corresponding correlated fluxes and chromatic phases for our non-concentric model no. 1 while the dashed blue line represents our non-concentric model no. 2. Light green lines (only on the first four plots of each panel) show the curves obtained by taking the parameters of our first-best model, and taking the lower limit of the uncertainty in the offset declination for the third component, we observe some significant deviations in some of the plots. |
| In the text | |
 |
Fig. 7 Images of the three component models for the mid-infrared emission at 12.0 μm of the nuclear region of NGC 1068 corresponding to model 1 (left) and model 2 (right). The image was scaled using the square root of the brightness. Center: comparison between our first best model and the 12.5 μm image of Bock et al. (2000), taken with the 10 m Keck Telescope. The dashed circles represent the FWHM of the field of view for MIDI using the UTs (blue) or the ATs (orange). The letters indicate the positions of the [OIII] clouds according to Evans et al. (1991). |
| In the text | |
 |
Fig. 8 Total flux of the three best-fit model components as a function of wavelength. |
| In the text | |
 |
Fig. A.1 Correlated fluxes of observations taken with UTs. The red and dashed blue lines are the curves obtained with our first and second best-fit models. The light blue curve shows the correlated fluxes of our best-fit model found using SiC as the dust template for all the components. We observe that the main reason of discarding SiC as the best option is mostly due to the shape of the absorption feature. |
| In the text | |
 |
Fig. A.2 The same as Fig. A.1, but chromatic phases are plotted instead of correlated fluxes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


