| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322861 | |
| Published online | 14 April 2014 | |
Proper horizontal photospheric flows in a filament channel⋆
1
LESIA, Observatoire de Paris, CNRS, UMR 8109,
92190
Meudon,
France
e-mail:
brigitte.schmieder@obspm.fr
2
Institut de Recherche en Astrophysique et Planétologie, Université
de Toulouse, CNRS, 14 avenue
Édouard Belin, 31400
Toulouse,
France
3
Department of Physics, DSB Campus, Kumaun
University, Nainital,
263002
Ultarakhand,
India
Received: 16 October 2013
Accepted: 29 January 2014
Context. An extended filament in the central part of the active region NOAA 11106 crossed the central meridian on Sept. 17, 2010 in the southern hemisphere. It has been observed in Hα with the THEMIS telescope in the Canary Islands and in 304 Å with the EUV imager (AIA) onboard the Solar Dynamic Observatory (SDO). Counterstreaming along the Hα threads and bright moving blobs (jets) along the 304 Å filament channel were observed during 10 h before the filament erupted at 17:03 UT.
Aims. The aim of the paper is to understand the coupling between magnetic field and convection in filament channels and relate the horizontal photospheric motions to the activity of the filament.
Methods. An analysis of the proper photospheric motions using SDO/HMI continuum images with the new version of the coherent structure tracking (CST) algorithm developed to track granules, as well as the large scale photospheric flows, was performed for three hours. Using corks, we derived the passive scalar points and produced a map of the cork distribution in the filament channel. Averaging the velocity vectors in the southern hemisphere in each latitude in steps of 3.5 arcsec, we defined a profile of the differential rotation.
Results. Supergranules are clearly identified in the filament channel. Diverging flows inside the supergranules are similar in and out of the filament channel. Converging flows corresponding to the accumulation of corks are identified well around the Hα filament feet and at the edges of the EUV filament channel. At these convergence points, the horizontal photospheric velocity may reach 1 km s-1, but with a mean velocity of 0.35 km s-1. In some locations, horizontal flows crossing the channel are detected, indicating eventually large scale vorticity.
Conclusions. The coupling between convection and magnetic field in the photosphere is relatively strong. The filament experienced the convection motions through its anchorage points with the photosphere, which are magnetized areas (ends, feet, lateral extensions of the EUV filament channel). From a large scale point-of-view, the differential rotation induced a shear of 0.1 km s-1 in the filament. From a small scale point-of-view, any convective motions favored the interaction of the parasitic polarities responsible for the anchorages of the filament to the photosphere with the surrounding network and may explain the activity of the filament.
Key words: Sun: filaments, prominences / Sun: photosphere / Sun: UV radiation / Sun: magnetic fields
Two movies are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Prominences, which are filaments when observed on the disk, are large structures in the solar corona filled with cool dense plasma suspended above magnetic polarity inversion lines (reviews of Mackay et al. 2010; Labrosse et al. 2010). The formation, the dynamics, and the eruption of solar filaments and prominences are important parts of our understanding of coronal physics and more specifically, the behavior of magnetic fields as they are transported across the solar surface through corona towards the heliosphere via the coronal mass ejections (CME). Recent observations show that surface motions acting on nonpotential magnetic fields may play an important role in the formation of large scale filaments, while magnetic flux emergence may be part of the formation of small filaments (Lites & Low 1997). Even though prominences are frequently observed, their formation process is still unclear. Three kinds of models have been proposed. Filament plasma can be formed by condensation of coronal material along magnetic field lines, which may be accumulated in coronal cavities (Karpen et al. 2005; Luna et al. 2012; Berger et al. 2010, 2012). A filament may be lifted through the photosphere by a levitation process (Okamoto et al. 2008; Lites et al. 2010) or formed by successive reconnections between magnetic field lines (van Ballegooijen & Martens 1989; Schmieder et al. 2006).
From a theoretical point of view, a dynamical photosphere is the common boundary of MHD models forming filaments or flux tubes, such as by emergence of flux (Chen 1996; Chen et al. 2000), by shearing motions (Aulanier et al. 2010), by converging flows towards the inversion lines (Priest et al. 1994; Forbes 1990), or by diffusion of magnetic field (Amari et al. 2000). MHD simulations are useful tools for testing these different mechanisms, which are able to produce a filament and then bring it into an unstable state until the eruption. The physical conditions leading to filament eruptions and CMEs have been recently reviewed by Schmieder et al. (2013a). They are based on the existence of flux ropes in the corona, where the electric currents increase and the magnetic tension that restrains the flux rope decreases. Twists, shears, and canceling flux in the photosphere are involved in the MHD models for producing instabilities of the filament/flux rope. Commonly it is found that eruptions are due to converging flows and canceling polarities in typical locations, where filaments are anchored in the photosphere, which is called footpoints.
Footpoints, feet or barbs of filaments have been morphologically defined in the review of Berger (2014). Three types of filaments are observed in Hα: active region filaments, intermediate filaments, and polar crown filaments (Mackay et al. 2008). The question is to define the footpoints feet uniquely for the three cited types of filaments. Martin et al. (1994), and Martin (1998) adopted the word “barb” for all the filament structures connecting the filament spines with the photosphere. They claimed that fine structures are “rooted” in parasitic polarities. Lin et al. (2005a) did a statistical study that links each filament fibril, end of barbs to magnetic concentrations using the G band observations as proxy of the magnetic field. The result was not conclusive with only a low percentage of correlation. An other study (López Ariste et al. 2006) showed the existence of different kinds of footpoints feet existing according to the different types of filaments. An active filament consists of long threads with two ends anchored in magnetic concentrations. They are similar to chromospheric fibrils, and correspond to the barb definition of Martin (1998). For intermediate filaments, recent extrapolation models (Aulanier & Démoulin 1998; Aulanier et al. 1998; Mackay & van Ballegooijen 2009; Dudík et al. 2008, 2012) have clearly shown that the feet of filaments consist of small threads that are part of long magnetic field lines. These threads are formed by accumulating plasma in dips of the field lines (Heinzel & Anzer 2001; Hillier & van Ballegooijen 2013). In this type of filament, feet are related to parasitic polarities, however they are not rooted in them. This explains the poor correlation found by Lin et al. (2005a). Nevertheless the word “barb” is often used for this kind of feet with dips. Polar crown filaments also have footpoints feet that appear as dark spots or bushes of threads in good spatial resolution Hα images. Recently, a new name has appeared for the structures connecting prominences with the photosphere, “pillars” when they are observed at the limb (Wedemeyer et al. 2013; Schmieder et al. 2013c). However, the identification as footpoints feet has not yet been established. Nevertheless, all the filaments have connections with the photosphere and should react to any motion in the photosphere.
Understanding surface motion on long term, as well as on short term scales is therefore important for the formation and the stability of filaments. Photospheric motions are due to the coupling of the convection motions with the diffusion of the magnetic field at the solar surface. Any changes in magnetic polarities or heating due to photosphere motions and/or emergence would disturb the footpoints and create activity in the filament itself, e.g., flows, counterstreaming, and even eruption (Aulanier et al. 1998; Schmieder et al. 2006, 2008). It is important to be able to quantify the horizontal flows in the photosphere and relate them to the evolution of filaments.
Very few analyses of surface motions have been done with high cadence and high spatial resolution observations. The local correlation tracking (LCT) method is mainly applied to magnetic field polarities to explain eruptions or flares with MDI data (1.96 arcsec pixel size) and only recently with HMI data (0.5 arcsec pixel size). The aim of these analyses mainly concerns the onsets of the eruptions or flares (Ahn et al. 2010; Zhou et al. 2006; Green et al. 2011; Liu et al. 2012). The LCT method has also been applied to tracking granules. Lites et al. (2010) demonstrate that filament formation resulted from the emergence of a flux rope through the photosphere and not from shearing photospheric motions in their studied case. In another study (Lin et al. 2005b), the LCT method was used to relate the fine structures of Hα filament barbs observed with the Swedish Solar Telescope (SST) to accumulations of corks driven by the photospheric motions. Roudier et al. (2008) studied the flow pattern in a filament channel in a bipolar region. From MDI magnetograms and Dopplergrams supergranular flow pattern using LCT, it was found that the flow field changes significantly during the eruption phase measuring an increase in the shear below the point where the eruption starts and a decrease after (Roudier et al. 2008). They found a pattern in the large scale horizontal flows at the solar surface that interacts with the differential rotation. The local photospheric flows were also measured with a higher spatial resolution (0.5 arcsec) in the filament channel during its eruption phase using TRACE 1600 Å to show the coupling between convection and magnetic field (Rondi et al. 2007). It was shown that the disappearance of the filament originates in a filament gap. Both parasitic and normal polarities were continuously swept into the gap by the diverging super granular flow. They also observed the interaction of opposite polarities in the same region, which could be responsible of the destabilization of the filament
The LCT technique (November & Simon 1988; Title et al. 1992; Shine et al. 2000; Chae & Sakurai 2008) has been developed in two ways: either by tracing the surface flows with the differential affine velocity estimator for vector magnetograms (DAVE4VM; Schuck 2008) or by tracking coherent structures (CST) on various scales (spatial and temporal) with a new algorithm (Rieutord et al. 2007). The CST has already been applied to full disk maps using the Solar Dynamic Observatory (SDO) Magnetic Imager (HMI) data (Schou et al. 2012).
We propose in this paper to compute the horizontal photospheric flows in an active region containing a long filament extended in the quiet Sun and detect any relationship between the photospheric flows and the filament structure and dynamics. In Sect. 2 we describe the observations of the Hα filament with the THEMIS telescope in the Canary Islands and its EUV filament channel observed by the SDO/AIA (Lemen et al. 2012) instrument. In Sect. 3 the new CST algorithm allows us to compute the solar horizontal photospheric velocities in the filament channel. The results are discussed in the framework of the filament morphology and its activity.
 |
Fig. 1 Active region NOAA 11106 with a long Hα filament on September 17, 2010 (BBSO at 16:17 UT) (top panel). The arrows indicate the limit of the different sections of the filament (F1, F2, F3, F4). HMI longitudinal magnetic field at 09:00 UT saturated at +/−100 G (middle panel), Active region and filament channel in 304 Å (AIA) at 08:06 UT (bottom). |
2. Observations of the filament
2.1. Overview
The Meudon survey observations allow us to follow the evolution of a filament over four rotations from August to November 2010 (Mandrini et al. 2013). The active region NOAA 11106, located in the southern hemisphere (S20), was crossing the central meridian on September 17, 2010. The leading part still had a positive magnetic polarity spot while the following part was formed by disperse and extended negative magnetic polarities of kilo Gauss (Fig. 1). Inside the trailing negative polarity of the active region, new positive polarities continued to emerge. An emergence of mixed weak polarities (<500 G) led to several jets in November 2010 (Guo et al. 2013; Schmieder et al. 2013b).
On September 17, 2010 the filament was lying in the central part of the active region and extending in a wide filament channel of low longitudinal magnetic field out of the active region between magnetic polarities of the network (S30) towards the quiet Sun close to the limb. Figure 1 shows the observations of the active region AR 11106 and the extended filament in different wavelengths (SDO/AIA at 304 Å and at 1600 Å). The filament extends over 600 arcsec (50 degrees in longitude). In the Hα image, different sections can be identified according to their shape and orientation. They have around 5 to 15 degrees of length each (about 150 arcsec or 100 Mm), and each section has a different apparent shape. Section F1 has elongated threads along the filament axis and are between strong magnetic field polarities of the active region. F1 belongs to the type of active region filament with no lateral feet. The sections F2, F3, and F4 have one or two apparent lateral feet and are classified as intermediate filaments.
The filament channel is well observed in 304 Å (SDO/AIA). It consists of a dark channel relatively wide out of the active region overlaid by elongated bright tiny threads from time to time and moving blobs or jets (Fig. 1 bottom panel and the two movies). In 171 Å (SDO/AIA), the channel (not shown in Fig. 1) is a long dark area. Large connecting loops between the two polarities in the north and south of the AR 11106 with bright legs are observed in 171 Å.
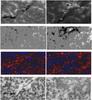 |
Fig. 2 MSDP (Hα) between 08:52 -09:02 UT (left column) and between 07:48-0758 UT (right column); (from top to bottom) Hα in the line center, HMI corresponding magnetic field saturated at +/−50 G, Dopplershifts in Hα +/−0.27 Å, Hα in the wing (+/−0.41 Å). The size of the images is 320 × 160 arcsec. Letters A, B1, and B2 indicate different parts of F1. Letters C and D point the feet of the filament shown in F2 (Fig. 1). North makes an angle of 10 degrees with the vertical. |
2.2. Dynamics and eruption of the filament
This long filament was observed well by the Canary Islands telescopes during an international campaign. The DOT observed the southeast on part (F4) of the filament (Martin et al. 2012), THEMIS, sects. F1 and F2 in two fields-of-view. We focus our study on the THEMIS observations.
2.2.1. Hα flows
THEMIS observed in two different modes in September 17, 2010 with the Multi-channel-Subtractive-Double-Pass (MSDP) spectrograph and with the MulTi-Raies (MTR) spectropolarimeter. Two maps (320 × 160 arcsec) were obtained with the MSDP between 07:48 UT and 07:58 UT and between 08:52 UT and 09:02 UT (Fig. 2) and one vector magnetogram between 09:37 UT and 10:37 UT with the MTR. We present the intensity maps in the Hα line center and in the wing (+/−0.41 Å). In the wing images the chromospheric threads (called fibrils, mottles, or spicules by the different observers) surround the supergranules. The MSDP allows us to reconstruct the profile of Hα in each point of the field of view. From the profiles, Dopplershifts in different wavelengths from the line center can be obtained. Figure 2 presents the Dopplershifts obtained in Hα +/−0.27 Å. The dynamics along the filament shows counterstreaming flows along long distances indicated by blue and red strands along the filament axis. Blue (or black) means material moving primarily toward the disk center (northwest), and red (white) moving towards the limb (southeast). We measured the shifts in the central points of the profiles at a given wavelength using the bisector method. They are on the order of +/−2 km s-1 in Hα +/−0.27 Å in the strands along the filament axis. Owing to the location of the filament far from the disk center, these measurements are minimum values, and they should be multiplied by a factor 2 to correct the projection effect. Moreover, if we consider that the filament is high enough and thick enough to be considered as a cloud, we may apply the cloud model method to derive the Dopplershifts (Mein & Mein 1988). In that case, the Dopplershifts could be estimated to be in the range of +/−10 km s-1 after also the projection effects taking into account, especially in section F2 between C and D (Mein et al. 2014).
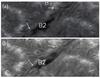 |
Fig. 3 Evolution of the fine structures of the Hα filament in B1 and B2 (section F1) observed with the MSDP in a small field of view (210 × 90 arcsec) a) at 07:48 UT and b) 08:52 UT. The arrows indicate the chromospheric fibrils turning towards the direction of the filament spine forming a thicker filament. |
 |
Fig. 4 EUV filament channel observed at at 17:30 UT in 304 Å (SDO/AIA) with the approximative overlay of the four slits used for the time slice analysis (see Fig. 5). S1 and S2 are the cuts along the section F1 (from east to west), S4 is following sections F2 and F3, S3 the section F4 (see Fig. 1). Between S4 and S3 we see a bright area in the network (around x = −400 and y = −600) where the onset of the eruption occurs. We detect an elongated bright strand below the right part of S3 and an dark absorbing strand below the left part of S3. They correspond to material of the eruption. The temporal evolution is shown in the two movies. The first movie corresponds to the field of view (red box) of S1 and S2 between 09:00 UT and 10:30 UT, and the second movie to the field of view (yellow box) of the slits S3 and S4 between 15:30 UT and 19:00 UT showing the eruption (online movies). |
2.2.2. Formation of an Hα filament section
During the MSDP observations, we noticed the formation of the section F1 as an active region filament. Filament threads were aligned along the filament axis with an S shape in the central part of the active region rooted in the positive magnetic polarities in the west and in the negative magnetic polarities in the east (see arrows in Fig. 3a). We notice that the filament threads were rotating and merging with the filament spine between 07:48 and 08:52 UT to form a longer and wider filament between the two arrows. This part of filament corresponds to the region B2 in Fig. 2.
THEMIS/MTR allows us to obtain the Stokes parameters in Fe 6302 Å and Hα image in a small field of view (160 × 120 arcsec). We detect different weak polarities in the filament channel, the magnetic field where the fibrils were anchored. The fibrils parallel to the filament again merged with it to form a thicker and thicker filament (F1).
2.2.3. AIA 304 Å
The EUV filament in 304 Å (around 50 arcsec wide) is a dark elongated area, much wider than the Hα filament (15 arcsec wide) by a factor three. The lateral extensions of the EUV filament are at different locations than the Hα filament feet or ends. In Fig. 1, the EUV channel seems to consist of two parts, one of which concerns sections F1, F2, and F3, the other one section F4.
The AIA/304 Å movies between 09:00 and 10:30 UT, and between 15:30 UT and 19:00 UT show bright blobs running along threads in the different sections of the filament channel (Figs. 4 and 5). Some flaring pattern close to the lateral extension of the filament could be the signature of reconnections.
Between 16:32 UT and 16:46 UT, a brightening started from a bright network point between the two parts of the EUV channel corresponding to the western end of F4. At 17:03 UT the filament underwent an eruption. In fact, the brightening seemed to propagate all along the spine of the EUV filament from the center of the active region to the eastern end of the EUV channel. The bright blobs were moving along threads or field lines. Their traveling distance may reach 200 arcsec during the time of the eruption (17 UT to 17:30 UT). Then the filament extended rapidly with untwisted threads towards the limb. The material was lifted up in 30 min, and part of it came back in the filament at 17:37 UT. It was apparently a failed eruption because we do not see a consequent prominence over the limb; however, the density of the escaped material may be too low to have a detectable emission.
The proper motion of the blobs was estimated by a time slice analysis. The slit positions for the slice analysis are drawn in Fig. 4. We rotated the cubes of 304 Å filament data to compute the velocity for each slit to follow the propagation of the blobs (Fig. 5). We did this study around two time intervals between 09:00 and 10:30 UT and between 16:30 to 17:30 UT. During the first interval, ejections of plasmoids were observed recurrently (every two or three minutes), moving with a projected velocity of propagation of 50 to 100 km s-1. They travelled from 60 to 120 arcsec. These plasmoids or jets were identified in an area where the opposite polarities were close to each other in the channel of the active region filament F1. They are brighter than the surroundings, indicating that the plasma is heated. It could be due to successive reconnections. During the previous rotation, similar jets were identified in the same region of the filament channel (Wang & Muglach 2013). During the “failed” eruption, ejected plasma escaped with an estimated projected velocity of 110 km s-1 to 130 km s-1. They may be even greater (Fig. 5). The extension was 200 arcsec long in projection. It could correspond to the projected height of the erupted material. The returning plasma has a projected velocity on the order of 130 km s-1.
3. Photospheric structures and motions in the filament channel
3.1. CST
The coherent structure tracking (CST) method is described in (Rieutord et al. 2007; Roudier et al. 2012, 2013). The method consists of tracking the horizontal motions of granules in a surface area (a window) and gives a mean value in this area over a given integration time. The area may be a square of 3.5, 7, 14, 28, 56 arcsec2. The CST method measures the velocities by following the trajectory of each granule, i.e. solar plasma, during the life of the coherent object, which is defined by its appearance and disappearance, if the granule does not split or merge. The introduction of the multi-resolution analysis on the velocity field, based on Daubechies wavelets, provides a view of the horizontal velocity field on different scales (from 3.5 to 56 arcsec2). “Daubechies wavelets” are used for each extrapolation computation in order to minimize the propagation of these errors during the extrapolations (Rieutord et al. 2007). The last properties allow us to learn the large scale flow field with confidence.
Accordingly, we estimate that an error of δV = 0.25 km s-1 for the HMI/SDO data for a time sequence of 30 min is acceptable since most of the granules show velocities in the range 0.3 and 1.6 km s-1 in our analysis. After three hours of integration, the result was robust.
 |
Fig. 5 Time slices through four slits (S1, S2, S3, S4) in different sections of the filament channel observed in 304 Å (SDO/AIA) during the recurrent jet activity from 09:00 UT to 10:30 UT (1.5 h) (top panels) and during the failed eruption between 16:30 UT and 18:30 UT (2 h) (bottom panels). The slit positions are drawn approximatively in Fig. 4. The origin zero is at the southeast end of each slit in the filament, near the limb for the bottom panels. The velocities indicated in the bottom panels are projected velocities. |
 |
Fig. 6 Distribution of the passive scalar “corks” (red dots) in the filament environment after 14:30 UT derived by using the mean photospheric motion velocity obtained over 3 h superimposed on respectively an SDO/AIA image 304 Å at 11:55 UT (top panel) and at 1600 Å (middle panel), proper velocity vector map integrated over 3 h and detected in the SDO/HMI images with a spatial resolution of 3.5 arcsec using the CST method overlaid by a contour of the 304 Å filament in a schematic channel (bottom panel). The corks are accumulated at the borders of the diverging flows in regions of convergence. They are concentrated in the supergranule boundaries (like the blue circle). Two blue arrows indicate two alignments of vectors crossing the filament channel. The origin of the graphs corresponds approximatively to the point (−250, −525) in the solar coordinates of Fig. 1. |
 |
Fig. 7 Proper velocity vector map integrated over 3 h detected in the SDO/HMI images with a spatial resolution of 56 arcsec computed by the CST algorithm overlying the 304 Å SDO/AIA image at 11:55 UT. The supergranules (red circles) are represented by divergence flows from their center. We see, in two locations, velocity vectors going in a direction perpendicular to the filament channel. It looks like flows are crossing the channel (blue arrows). The white spots on the right are saturated points where the computation cannot be done. |
 |
Fig. 8 Histograms of the horizontal photospheric velocities derived with the CST algorithm with a 3.5 arcsec window (left panel) and in the case of a 56 arcsec window (right panel) after three hours of integration and measured in a large field-of-view of Fig. 11. |
 |
Fig. 9 Zoom maps of the EUV filament channel observed with SDO/AIA 304 Å and the cork distribution (red-white dots) overlaid by the horizontal proper photospheric velocity field (arrows) after taking out the differential rotation (left top panel), the same data without the overlay of the velocity field for a better visibility (left middle panel). The red circles indicate some supergranules, and the large red dots indicate the locations of convergence velocity vectors at the edges of the filament channel in the top left panel. Right top panel: magnetic map overlaid by the EUV filament contour and the cork distribution. Middle and bottom right panels: Hα images (MSDP) (presented in Fig. 2) overlaid by the cork distribution. Blue arrows indicate the accumulation of corks at the edges of the EUV filament (bottom left panel) and close to the Hα feet C and D (bottom right panel). The unit of the coordinates are in arcsec. |
 |
Fig. 10 Divergence (white small areas) and convergence (dark line areas) map overlaid on a transparent SDO/304 Å image in a large field of view in solar coordinates. The bright large regions correspond to the plage regions. We notice dark lines in the edges of the filament channel, mainly on the northern edge, corresponding to areas of convergence close to the footpoints of the different sections of the filament (see the dashed lines corresponding to F2, F3, F4 filament sections). The short dashed lines in F3 correspond to convergence areas in the network (around − 400, − 600) from which the eruption may have started (Fig. 4). |
 |
Fig. 11 Top left panel: filament contour of the SDO/AIA 304 Å at 08:55 UT after applying the measured nominal differential rotation rate during 14.5 h (pink contour). The green contour is the contour of the filament drawn in the image 304 Å at 23:34 UT in both top panels. The superposition of both contours in the top left panel are in good agreement despite the filament evolution. Top right panel: filament contour of the SDO/AIA image 304 Å at 08:55 UT, after applying a second model of differential rotation rate, blocked for latitudes greater than 56 arcsec during 14.5 h (pink contour). The abscissae/ordinates of the top panels and the left bottom panel are the longitude/latitude. The origin of the latitudes in arcsec corresponds approximatively to x = −350 arcsec, y = −575 arcsec in Fig. 1. The superposition of the resulting images with the filament contour at 23:32 UT shows that the filament is clearly extended toward the West by the nominal differential rotation rate. Bottom left panel: the comparison of the contours of the filament with the two different rotation rates (green for the nominal differential rotation and pink for the blocked differential rotation) shows this extension. Bottom right panel: the two models of differential rotation rate. The solid line is computed for all the latitudes with the CST method. The dashed line is the blocked differential rotation rate for latitudes higher than 56 arcsec. |
3.2. Horizontal photospheric flows at small and large scales
The photospheric proper horizontal motions with the CST algorithm was analyzed by using the full disk SDO/HMI white light images (λ = 6173 Å) during an integration time of three hours (between 10:13 UT and 13:13 UT). We successively used two windows, one corresponding to the small scales (3.5 arcsec2) (Fig. 6 bottom panel), the other to the large scales (56 arcsec2) (Fig. 7). With the velocity vectors derived with the small scale window, we defined the passive scalar points or “saddle points” similarly to the cork stagnation points. We obtained a map of the distribution of the corks after the integration time of three hours. We co-aligned the full disk horizontal velocity map (Vx, Vy) with the full disk EUV images of SDO/AIA in 304 Å and in 1600 Å at 11:55 UT (middle time of the integration time). Then we extracted a large field-of-view containing the Hα filament and the EUV channel. The accuracy of the co-alignment is around one pixel of our analysis (3.5 arcsec or 0.2 degree). Two different sizes of field of views are presented in this study: a large one containing the whole filament channel and a smaller one containing the field of view of the Hα THEMIS observations.
Figure 6 (top panels) shows the cork distribution superimposed on parts of the AIA maps, respectively at 304 Å and 1600 Å after the three hours integration. Comparing SDO/AIA images at 304 Å and SDO/AIA images at 1600 Å (Fig. 6), we identified the supergranules as dark areas surrounded by brighter lines that correspond to magnetic regions. The filament channel in 1600 Å appears as a dark corridor because of the weak magnetic field along the magnetic inversion line. The corks delineate the boundaries of the supergranules (bright regions in 1600 Å). They have a typical size of 20 to 30 Mm. It corresponds to the maximum of the distribution of the super granule sizes (Hagenaar et al. 1997; Rieutord & Rincon 2010). They overlaid the maxima of the 1600 Å brightness on the faculae very well. It is not so clear for the 304 Å map. The image in 1600 Å is a better proxy for localizing the magnetic field structures.
Figure 6 (bottom panel) shows the velocity flow with diverging flows. The diverging cells correspond to the supergranules. Between the supergranules, the flow is converging. Accumulations of corks are detected in these locations. In the F1 filament channel, we notice horizontal flows crossing the filament channel in opposite directions (Fig. 6 bottom). It could create some rotation effect or large scale vorticity.
Figure 7 presents the proper velocity vector map computed with the CST algorithm with a large scale spatial resolution (56 arcsec) when comparing this map with the proper velocity vector map obtained with a low scale spatial resolution (3.5 arcsec), we notice that the supergranules are larger. We also notice some flows crossing the channels at the same locations as in the previous map. The locations of the super granules and the crossing flows are robust results after the three hours of integration.
The histogram of the velocity vectors for the two spatial scales that we analyzed are presented in Fig. 8. For the small scale, the maximum of the horizontal photospheric velocity reaches 1 km s-1. The mean velocity is 0.35 km s-1. These are relatively high velocity values. For the large scale, the velocities are much reduced (maximum =0.3 km s-1). It is interesting to note the apparent asymmetry in the plots that seem to show more convergence in the flow field rather than divergence. This is presumably because converging flows have higher velocities in granulation flows. The lane flows are always faster.
3.3. Velocity vectors and corks distribution in the filament channel
Figure 9 shows the distribution of the passive scale corks obtained as described in Sect. 3.2, overlaid respectively on a AIA 304 Å, a HMI magnetogram, and a Hα image. The left column panels are zooms of the Fig. 6 (top panel), centered on the filament channel. In Fig. 9 (top right panel) the cork distribution is over a magnetic field map. The corks are associated with magnetic concentrations in the network and surround the faculae. In Fig. 9 (middle and bottom right panels) accumulation areas of corks are observed over the brightest regions corresponding to the network. Some accumulation of corks are close to the Hα ends (B1 and B2 in F1) surrounding small supergranules and the Hα feet C and D in F2 (bottom right panel). This confirms the paper results of Lin et al. (2005b). They show clearly that the ends of what they called barbs (in this case the feet of filament) are close to accumulations of corks. They have done a statistical study with six filaments observed with the Swedish telescope each involving half a dozen barbs. They conclude that 65 percent of the end points of barbs falls in a concentration of corks.
In Fig. 9 (left column panels) the cork distribution was overlaid on AIA maps at 304 Å. Accumulations of corks are observed at the boundaries of the supergranules. The size of super granules is relatively uniform inside and outside the filament channel. Areas of higher concentrations of corks have been overlaid by big red dots. They correspond to high convergence flows between super granules. The edges of the EUV filament are associated with accumulation areas of corks. Concentrations of corks at the edges of the EUV channel are indicated in Fig. 9 (bottom left panel). The alignments of corks surround the dark lateral extensions of the EUV filament. It is also visible in the figure showing the divergence in a larger field of view including F3 and F4 (Fig. 10). Dark areas, the sites of convergence, are observed along the northern edge of the EUV filament, along F2, F3, and F4 in Fig. 10. Our study shows that there are accumulations of corks all over the map, but some of them are located on the edges of the EUV filament channel around the lateral extensions of the filament channel.
The interpretation of our results depends on the morphology of EUV filaments, EUV channels and their lateral extensions. Their identifications are not very clear. Different hypotheses have been proposed. One of them is that the transition region below the filament is less emissive than the transition region surrounding the filament (Schmieder et al. 2004). This hypothesis has been supported by extrapolation works showing that field lines supporting the Hα filament may be attracted by parasitic polarities located far away from the PIL (Aulanier & Schmieder 2002). They could form the lateral extensions of the EUV filament. These parasitic polarities would be completely different from the parasitic polarities responsible for the Hα footpoints. The other idea is that there is cool plasma in the environment of the filament that is less dense than the plasma of the filament (Schwartz et al. 2004). This hypothesis is supported by the new observations of “horns” near the top of the EUV filament structures (Berger et al. 2012). Viewed from above they could explain the lateral extensions of the EUV filament.
We looked carefully at the overlay of the filament channel and the Hα filament. We observe that the EUV channel (between y = 30 and 55 arcsec at x = 0) lies in a relative lower latitude than the Hα filament spine (y = 35 arcsec for x = 0) in Fig. 9 (bottom panels). Because the filament is in the southern hemisphere, we conclude that the EUV channel lies at lower altitudes than the Hα filament. The areas of the EUV extensions are definitely related to converging flows on the northern side of the filament channel between supergranules and may be the anchorage of the EUV filament in the photosphere (Fig. 9). The lateral extensions on the southern edge may still be due to EUV plasma in the surroundings or at the top of the filament (like the horns). It is not really possible to determine their real structure. We looked at the velocity vector map (Fig. 9 left top panel) to detect rotations of the velocity vector related to the feet of the filament or lateral extensions of the filament channel, as suspected in some papers (Wedemeyer et al. 2013). We did not find any clear case at the scale of the supergranule.
3.4. Influence of the differential rotation on the filament in 304 Å
Using the velocity vector (Vx,Vy) computed during the three hours of integration time with the CST algorithm, we derived the differential rotation in the southern hemisphere by averaging the Vx component for each latitude with a step of 3.5 arcsec (Fig. 11 right bottom panel). We performed three experiments to show the influence of the convection on the filament. We compared the shape of the 304 filament after experiencing the computed differential rotation rate (nominal) during 14.5 h with the shape of the 304 filament at 23:34 UT, and then we blocked the rotation rate in its northern part. We found that the differential rotation has a direct impact on the shape. It produces an extension of its northern part toward the west. We could quantify this extension to give a value of the shear involving the filament for the first time.
The first experiment applied the nominal differential rotation rate to the filament observed at 08:55 UT, which spans nearly 250 arcsec in longitude, during 14.5 h. The resulting contour (pink contour) is compared to the contour of the observed filament at 23:34 UT in Fig. 11 (left top panel). The two contours are superimposed well, if we do not take the changes due to the filament evolution into account during this time period. It means that the rotation rate we computed is correct. The second experiment blocked the differential rotation rate for the latitudes greater than 56 arcsec (Fig. 11 right bottom panel) and again applied this new differential rotation model to the filament observed observed at 08:55 UT during 14.5 hours. We obtained a new pink contour that we again compared to the contour of the filament observed at 23:32 UT. We observed a shift of the northern part of the filament between the two contours (Fig. 11 right top panel). The third experiment compared the two pinkish contours of the filament that we had computed previously. For convenience, we drew the contour of the filament with the nominal differential rotation rate in green and left the other one in pink (Fig. 11 bottom left panel). We observed a shift in the northern part of the filament on the order of 7 arcsec in 14.5 h (5100 km). This corresponds to a relative velocity of 0.1 km s-1 between the northern and the southern parts. This is a direct measurement of the shear of the filament induced by the differential rotation.
These experiments proved the influence of the differential rotation (large scale convection) on the filament. This can occur because the filament is tied to the photosphere by its anchorage points (ends, feet, lateral extensions). The photospheric convection motions are pushing the anchorage points of the filament and could induce a shear in the filament. Shear favors the formation and the stability of filaments (Mackay et al. 2010).
3.5. Filament activity
The EUV channel consists of two components: one the normal transition region that is not as bright as the surroundings, owing horizontal structures (flux tube or magnetic arcades). The lateral extensions on the northern edge are located in the low atmosphere and may be related directly to the photosphere if we adopt the MHD model of Aulanier & Schmieder (2002). The second component consists of the intermittent brightenings occurring along threads parallel to the filament axis. These brightenings are moving along magnetic field lines of the flux tube or the arcades. As we have shown with the time slice analysis, they are initiated at the edges of the filament channel. We suggest that they are due to canceling flux occurring in the network at the border of the channel. The eruption may be due to the destabilization of one lateral extension of the EUV filament after reconnection in the network (bright region between F3 and F4 in Fig. 10. Canceling flux producing eruptions are therefore mainly at the edges of the EUV channels and not always along the main inversion line of the filament (PIL).
4. Conclusion and discussion
We analyzed the horizontal proper photospheric motions in a filament channel and its surroundings using the new coherent structure tracking (CST) algorithm (Rieutord et al. 2007) and the white light images of SDO/HMI during an integration time of three hours on September 17, 2010 (between 10:13 UT and 13:13 UT) with successively two different scale windows (3.5 arcsec2 and 56 arcsec2). The supergranules with diverging flows are observed well in the whole field of view. The size of the supergranules is similar inside and outside the filament channel (around 30 Mm) even they are not displayed as regularly in the filament channel, as in the quiet Sun. Inside the filament channel, large scale photospheric horizontal flows cross the channel, thereby disturbing the supergranule pattern.
Using the velocity vectors derived with the small scale window (3.5 arcsec2), we defined the passive scalar points or “saddle points” similarly to the cork stagnation points. We obtained a map of the distribution of the corks after the integration time of three hours. The cork accumulation regions correspond to the network, which is a region of strong magnetic field. It confirms that the cork accumulation points are good proxies for identifing magnetic flux concentrations or polarities (Title et al. 1992).
The filament observations were obtained by the THEMIS/ MSDP spectrograph operating in the Canaries Islands in Hα and by the SDO/AIA instrument in 304 Å. Counterstreamings are observed in the Dopplershift maps of the Hα filament. The EUV filament channel consisted of a dark region with superimposed intermittent brightenings. The EUV filament underwent a “failed” eruption around 17:00 UT. We measured projected velocities of the ejected plasma on the order of 130 km s-1 going away and coming back.
We showed the unambiguity of the relationship between the convection with the filament on large scale. For that we computed the differential rotation rate by averaging the horizontal proper photospheric vectors computed with the CST for each latitude and showed its influence on the shape of the 304 filament. We could derive the existence of a shear of 0.1 km s-1. The filament experienced this shear because of its anchorage points in the photosphere. We inspected the photospheric velocity field and the cork distributions related to the anchorages of the filaments.
-
The two feet of the Hα filament that we identified in the THEMIS/ MSDP observations are related to regions of converging flows, regions of accumulation of corks, and magnetized regions. This confirms previous studies (Lin et al. 2005b). The horizontal velocities are high at these points (1 km s-1).
-
Accumulation of corks surround the EUV filament edges and lateral extensions mainly on the northern edge. We proposed that they are the anchorage points of the EUV filament in the photosphere.
Online material
Movie 1 Access here
Movie 2 Access here
Acknowledgments
We would like to thank the team of THEMIS and, particularly, the Director Bernard Gelly for adjusting the telescope to work in two different modes and for assisting us during the observations. We thank the team of SDO for putting all the data already reduced in Level-1 on line. This work was granted access to the HPC resources of CALMIP under the allocation 2013-P1115. We would like to thank the anonymous referee who helped us to improve the manuscripts and highlight the conclusions.
References
- Ahn, K., Chae, J., Cao, W., & Goode, P. R. 2010, ApJ, 721, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Amari, T., Luciani, J. F., Mikic, Z., & Linker, J. 2000, ApJ, 529, L49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Archontis, V., & Hood, A. W. 2009, A&A, 508, 1469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Archontis, V., & Török, T. 2008, A&A, 492, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aulanier, G., & Démoulin, P. 1998, A&A, 329, 1125 [Google Scholar]
- Aulanier, G., & Schmieder, B. 2002, A&A, 386, 1106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aulanier, G., Demoulin, P., van Driel-Gesztelyi, L., Mein, P., & Deforest, C. 1998, A&A, 335, 309 [NASA ADS] [Google Scholar]
- Aulanier, G., Török, T., Démoulin, P., & DeLuca, E. E. 2010, ApJ, 708, 314 [Google Scholar]
- Berger, T. 2014, IAU Symp., 300, 15 [NASA ADS] [Google Scholar]
- Berger, T. E., Slater, G., Hurlburt, N., et al. 2010, ApJ, 716, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Liu, W., & Low, B. C. 2012, ApJ, 758, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., & Sakurai, T. 2008, ApJ, 689, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J. 1996, J. Geophys. Res., 101, 27499 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J., Santoro, R. A., Krall, J., et al. 2000, ApJ, 533, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Dudík, J., Aulanier, G., Schmieder, B., Bommier, V., & Roudier, T. 2008, Sol. Phys., 248, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dudík, J., Aulanier, G., Schmieder, B., Zapiór, M., & Heinzel, P. 2012, ApJ, 761, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, T. G. 1990, J. Geophys. Res., 95, 11919 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., Kliem, B., & Wallace, A. J. 2011, A&A, 526, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Y., Démoulin, P., Schmieder, B., et al. 2013, A&A, 555, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hagenaar, H. J., Schrijver, C. J., & Title, A. M. 1997, ApJ, 481, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., & Anzer, U. 2001, A&A, 375, 1082 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, A., & van Ballegooijen, A. 2013, ApJ, 766, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Tanner, S. E. M., Antiochos, S. K., & DeVore, C. R. 2005, ApJ, 635, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J. E., & Berger, T. E. 2005a, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Wiik, J. E., Engvold, O., Rouppe van der Voort, L., & Frank, Z. A. 2005b, Sol. Phys., 227, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., & Low, B. C. 1997, Sol. Phys., 174, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Kubo, M., Berger, T., et al. 2010, ApJ, 718, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., & Low, B. C. 2012, ApJ, 745, L21 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A., Aulanier, G., Schmieder, B., & SainzDalda, A. 2006, A&A, 456, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luna, M., Karpen, J. T., & DeVore, C. R. 2012, ApJ, 746, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., & van Ballegooijen, A. A. 2009, Sol. Phys., 260, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Gaizauskas, V., & Yeates, A. R. 2008, Sol. Phys., 248, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Mandrini, C. H., Schmieder, B., Démoulin, P., Guo, Y., & Cristiani, G. D. 2013, Sol. Phys., 289, 2041 [Google Scholar]
- Martin, S. F. 1998, Sol. Phys., 182, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F., Bilimoria, R., & Tracadas, P. W. 1994, in Solar Surface Magnetism, eds. R. J. Rutten, & C. J. Schrijver (Springer-Verlag), 303 [Google Scholar]
- Martin, S. F., Panasenco, O., Berger, M. A., et al. 2012, in ASP Conf. Ser. 463, eds. T. R. Rimmele, A. Tritschler, F. Wöger, et al., 157 [Google Scholar]
- Mein, P., & Mein, N. 1988, A&A, 203, 162 [NASA ADS] [Google Scholar]
- Mein, N., Mein, P., Schmieder, B., Malherbe, J.-M., & Roudier, T. 2014, IAU Symp., 300, 451 [NASA ADS] [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Okamoto, T. J., Tsuneta, S., Lites, B. W., et al. 2008, ApJ, 673, L215 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., Parnell, C. E., & Martin, S. F. 1994, ApJ, 427, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 2 [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rondi, S., Roudier, T., Molodij, G., et al. 2007, A&A, 467, 1289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Švanda, M., Meunier, N., et al. 2008, A&A, 480, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J. M., et al. 2012, A&A, 540, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Prat, V., et al. 2013, A&A, 552, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Lin, Y., Heinzel, P., & Schwartz, P. 2004, Sol. Phys., 221, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Aulanier, G., Mein, P., & López Ariste, A. 2006, Sol. Phys., 238, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Bommier, V., Kitai, R., et al. 2008, Sol. Phys., 247, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Démoulin, P., & Aulanier, G. 2013a, Adv. Space Res., 51, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Guo, Y., Moreno-Insertis, F., et al. 2013b, A&A, 559, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Kucera, T. A., Knizhnik, K., et al. 2013c, ApJ, 777, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Borrero, J. M., Norton, A. A., et al. 2012, Sol. Phys., 275, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Schuck, P. W. 2008, ApJ, 683, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, P., Heinzel, P., Anzer, U., & Schmieder, B. 2004, A&A, 421, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shine, R. A., Simon, G. W., & Hurlburt, N. E. 2000, Sol. Phys., 193, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., Topka, K. P., Tarbell, T. D., et al. 1992, ApJ, 393, 782 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., & Martens, P. C. H. 1989, ApJ, 343, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., & Muglach, K. 2013, ApJ, 763, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer, S., Scullion, E., Rouppe van der Voort, L., Bosnjak, A., & Antolin, P. 2013, ApJ, 774, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G., Wang, Y., & Wang, J. 2006, Adv. Space Res., 38, 466 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Active region NOAA 11106 with a long Hα filament on September 17, 2010 (BBSO at 16:17 UT) (top panel). The arrows indicate the limit of the different sections of the filament (F1, F2, F3, F4). HMI longitudinal magnetic field at 09:00 UT saturated at +/−100 G (middle panel), Active region and filament channel in 304 Å (AIA) at 08:06 UT (bottom). |
| In the text | |
 |
Fig. 2 MSDP (Hα) between 08:52 -09:02 UT (left column) and between 07:48-0758 UT (right column); (from top to bottom) Hα in the line center, HMI corresponding magnetic field saturated at +/−50 G, Dopplershifts in Hα +/−0.27 Å, Hα in the wing (+/−0.41 Å). The size of the images is 320 × 160 arcsec. Letters A, B1, and B2 indicate different parts of F1. Letters C and D point the feet of the filament shown in F2 (Fig. 1). North makes an angle of 10 degrees with the vertical. |
| In the text | |
 |
Fig. 3 Evolution of the fine structures of the Hα filament in B1 and B2 (section F1) observed with the MSDP in a small field of view (210 × 90 arcsec) a) at 07:48 UT and b) 08:52 UT. The arrows indicate the chromospheric fibrils turning towards the direction of the filament spine forming a thicker filament. |
| In the text | |
 |
Fig. 4 EUV filament channel observed at at 17:30 UT in 304 Å (SDO/AIA) with the approximative overlay of the four slits used for the time slice analysis (see Fig. 5). S1 and S2 are the cuts along the section F1 (from east to west), S4 is following sections F2 and F3, S3 the section F4 (see Fig. 1). Between S4 and S3 we see a bright area in the network (around x = −400 and y = −600) where the onset of the eruption occurs. We detect an elongated bright strand below the right part of S3 and an dark absorbing strand below the left part of S3. They correspond to material of the eruption. The temporal evolution is shown in the two movies. The first movie corresponds to the field of view (red box) of S1 and S2 between 09:00 UT and 10:30 UT, and the second movie to the field of view (yellow box) of the slits S3 and S4 between 15:30 UT and 19:00 UT showing the eruption (online movies). |
| In the text | |
 |
Fig. 5 Time slices through four slits (S1, S2, S3, S4) in different sections of the filament channel observed in 304 Å (SDO/AIA) during the recurrent jet activity from 09:00 UT to 10:30 UT (1.5 h) (top panels) and during the failed eruption between 16:30 UT and 18:30 UT (2 h) (bottom panels). The slit positions are drawn approximatively in Fig. 4. The origin zero is at the southeast end of each slit in the filament, near the limb for the bottom panels. The velocities indicated in the bottom panels are projected velocities. |
| In the text | |
 |
Fig. 6 Distribution of the passive scalar “corks” (red dots) in the filament environment after 14:30 UT derived by using the mean photospheric motion velocity obtained over 3 h superimposed on respectively an SDO/AIA image 304 Å at 11:55 UT (top panel) and at 1600 Å (middle panel), proper velocity vector map integrated over 3 h and detected in the SDO/HMI images with a spatial resolution of 3.5 arcsec using the CST method overlaid by a contour of the 304 Å filament in a schematic channel (bottom panel). The corks are accumulated at the borders of the diverging flows in regions of convergence. They are concentrated in the supergranule boundaries (like the blue circle). Two blue arrows indicate two alignments of vectors crossing the filament channel. The origin of the graphs corresponds approximatively to the point (−250, −525) in the solar coordinates of Fig. 1. |
| In the text | |
 |
Fig. 7 Proper velocity vector map integrated over 3 h detected in the SDO/HMI images with a spatial resolution of 56 arcsec computed by the CST algorithm overlying the 304 Å SDO/AIA image at 11:55 UT. The supergranules (red circles) are represented by divergence flows from their center. We see, in two locations, velocity vectors going in a direction perpendicular to the filament channel. It looks like flows are crossing the channel (blue arrows). The white spots on the right are saturated points where the computation cannot be done. |
| In the text | |
 |
Fig. 8 Histograms of the horizontal photospheric velocities derived with the CST algorithm with a 3.5 arcsec window (left panel) and in the case of a 56 arcsec window (right panel) after three hours of integration and measured in a large field-of-view of Fig. 11. |
| In the text | |
 |
Fig. 9 Zoom maps of the EUV filament channel observed with SDO/AIA 304 Å and the cork distribution (red-white dots) overlaid by the horizontal proper photospheric velocity field (arrows) after taking out the differential rotation (left top panel), the same data without the overlay of the velocity field for a better visibility (left middle panel). The red circles indicate some supergranules, and the large red dots indicate the locations of convergence velocity vectors at the edges of the filament channel in the top left panel. Right top panel: magnetic map overlaid by the EUV filament contour and the cork distribution. Middle and bottom right panels: Hα images (MSDP) (presented in Fig. 2) overlaid by the cork distribution. Blue arrows indicate the accumulation of corks at the edges of the EUV filament (bottom left panel) and close to the Hα feet C and D (bottom right panel). The unit of the coordinates are in arcsec. |
| In the text | |
 |
Fig. 10 Divergence (white small areas) and convergence (dark line areas) map overlaid on a transparent SDO/304 Å image in a large field of view in solar coordinates. The bright large regions correspond to the plage regions. We notice dark lines in the edges of the filament channel, mainly on the northern edge, corresponding to areas of convergence close to the footpoints of the different sections of the filament (see the dashed lines corresponding to F2, F3, F4 filament sections). The short dashed lines in F3 correspond to convergence areas in the network (around − 400, − 600) from which the eruption may have started (Fig. 4). |
| In the text | |
 |
Fig. 11 Top left panel: filament contour of the SDO/AIA 304 Å at 08:55 UT after applying the measured nominal differential rotation rate during 14.5 h (pink contour). The green contour is the contour of the filament drawn in the image 304 Å at 23:34 UT in both top panels. The superposition of both contours in the top left panel are in good agreement despite the filament evolution. Top right panel: filament contour of the SDO/AIA image 304 Å at 08:55 UT, after applying a second model of differential rotation rate, blocked for latitudes greater than 56 arcsec during 14.5 h (pink contour). The abscissae/ordinates of the top panels and the left bottom panel are the longitude/latitude. The origin of the latitudes in arcsec corresponds approximatively to x = −350 arcsec, y = −575 arcsec in Fig. 1. The superposition of the resulting images with the filament contour at 23:32 UT shows that the filament is clearly extended toward the West by the nominal differential rotation rate. Bottom left panel: the comparison of the contours of the filament with the two different rotation rates (green for the nominal differential rotation and pink for the blocked differential rotation) shows this extension. Bottom right panel: the two models of differential rotation rate. The solid line is computed for all the latitudes with the CST method. The dashed line is the blocked differential rotation rate for latitudes higher than 56 arcsec. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


