| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322367 | |
| Published online | 04 April 2014 | |
Planck intermediate results. XIV. Dust emission at millimetre wavelengths in the Galactic plane
1
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3,
CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet,
75205
Paris Cedex 13,
France
2
Aalto University Metsähovi Radio Observatory and Dept of Radio
Science and Engineering, PO Box
13000, 00076
Aalto,
Finland
3
African Institute for Mathematical Sciences,
6-8 Melrose road, Muizenberg, Cape
Town, 7701
Rondebosch, South
Africa
4
Agenzia Spaziale Italiana Science Data Center,
via del Politecnico snc,
00133
Roma,
Italy
5
Agenzia Spaziale Italiana, viale Liegi 26, 00198
Roma,
Italy
6
Astrophysics Group, Cavendish Laboratory, University of
Cambridge, J J Thomson
avenue, Cambridge
CB3 0HE,
UK
7
Astrophysics & Cosmology Research Unit, School of Mathematics,
Statistics & Computer Science, University of KwaZulu-Natal,
Westville Campus, Private Bag
X54001, 4000
Durban, South
Africa
8
Atacama Large Millimeter/submillimeter Array, ALMA Santiago Central
Offices, Alonso de Córdova 3107, Vitacura, Casilla
763 0355, Santiago, Chile
9
CITA, University of Toronto, 60 St. George St., Toronto ON
M5S 3H8,
Canada
10
CNRS, IRAP, 9 Av.
colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
11
California Institute of Technology, Pasadena, USA
12
Centro de Estudios de Física del Cosmos de Aragón
(CEFCA), plaza San Juan 1, planta
2, 44001
Teruel,
Spain
13 Computational Cosmology Center,
Lawrence Berkeley National Laboratory, Berkeley, USA
14
Consejo Superior de Investigaciones Científicas
(CSIC), 28037
Madrid,
Spain
15
DSM/Irfu/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
16
DTU Space, National Space Institute, Technical University of
Denmark, Elektrovej
327, 2800
Kgs. Lyngby,
Denmark
17 Département de Physique Théorique,
Université de Genève, 24 Quai E.
Ansermet, 1211Genève 4, Switzerland
18
Departamento de Física Fundamental, Facultad de Ciencias,
Universidad de Salamanca, 37008
Salamanca,
Spain
19
Departamento de Física, Universidad de Oviedo,
Avda. Calvo Sotelo s/n,
33007
Oviedo,
Spain
20
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
21 Department of Electrical Engineering
and Computer Sciences, University of California, Berkeley, USA
22
Department of Physics & Astronomy, University of British
Columbia, 6224 Agricultural
road, Vancouver,
Canada
23
Department of Physics and Astronomy, Dana and David Dornsife College
of Letter, Arts and Sciences, University of Southern California,
Los Angeles
CA
90089,
USA
24
Department of Physics and Astronomy, University College
London, London
WC1E 6BT,
UK
25
Department of Physics, Gustaf Hällströmin katu 2a, University of
Helsinki, Helsinki,
Finland
26
Department of Physics, Princeton University,
Princeton,
USA
27 Department of Physics, University of
California, Santa
Barbara, USA
28
Department of Physics, University of Illinois at Urbana-
Champaign, 1110 West Green
street, Urbana,
USA
29
Dipartimento di Fisica e Astronomia G. Galilei, Università degli
Studi di Padova, via Marzolo
8, 35131
Padova,
Italy
30
Dipartimento di Fisica e Scienze della Terra, Università di
Ferrara, via Saragat
1, 44122
Ferrara,
Italy
31
Dipartimento di Fisica, Università La Sapienza,
P. le A. Moro 2, 00185
Roma,
Italy
32
Dipartimento di Fisica, Università degli Studi di
Milano, via Celoria
16, 20133
Milano,
Italy
33
Dipartimento di Fisica, Università degli Studi di
Trieste, via A. Valerio
2, 34127
Trieste,
Italy
34
Dipartimento di Fisica, Università di Roma Tor
Vergata, via della Ricerca Scientifica
1, 00133
Roma,
Italy
35
Discovery Center, Niels Bohr Institute, Blegdamsvej 17, 2100
Copenhagen,
Denmark
36
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206, La Laguna, Tenerife,
Spain
37
European Southern Observatory, ESO Vitacura,
Alonso de Córdova 3107, Vitacura,
Casilla
19001, Santiago, Chile
38
European Space Agency, ESAC, Planck Science Office, Camino bajo del
Castillo s/n, Urbanización Villafranca del Castillo, Villanueva de la
Cañada, Madrid,
Spain
39
European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ
Noordwijk, The
Netherlands
40
Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University
of Helsinki, 00014
Helsinki,
Finland
41
INAF – Osservatorio Astronomico di Padova,
vicolo dell’Osservatorio 5,
35122
Padova,
Italy
42
INAF – Osservatorio Astronomico di Roma,
via di Frascati 33, 00040
Monte Porzio Catone,
Italy
43
INAF – Osservatorio Astronomico di Trieste,
via G.B. Tiepolo 11, 34143
Trieste,
Italy
44
INAF/IASF Bologna, via Gobetti 101, 40129
Bologna,
Italy
45
INAF/IASF Milano, via E. Bassini 15, 20133
Milano,
Italy
46
INFN, Sezione di Bologna, via Irnerio 46, 40126
Bologna,
Italy
47
INFN, Sezione di Roma 1, Università di Roma Sapienza,
piazzale Aldo Moro 2,
00185
Roma,
Italy
48
INFN/National Institute for Nuclear Physics,
via Valerio 2, 34127
Trieste,
Italy
49
IPAG: Institut de Planétologie et d’Astrophysique de Grenoble,
Université Joseph Fourier, Grenoble 1/CNRS-INSU, UMR 5274 , 38041
Grenoble,
France
50
IUCAA, Post Bag 4, Ganeshkhind, Pune University
Campus, 411 007
Pune,
India
51
Imperial College London, Astrophysics group, Blackett
Laboratory, Prince Consort
road, London
SW7 2AZ,
UK
52
Infrared Processing and Analysis Center, California Institute of
Technology, Pasadena
CA
91125,
USA
53
Institut Universitaire de France, 103 Bd Saint-Michel, 75005
Paris,
France
54
Institut d’Astrophysique Spatiale, CNRS (UMR8617) Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay,
France
55
Institut d’Astrophysique de Paris, CNRS (UMR7095),
98 bis boulevard Arago,
75014
Paris,
France
56
Institute for Space Sciences, 077125
Bucharest-Magurale,
Romania
57
Institute of Astronomy and Astrophysics, Academia
Sinica, 10617
Taipei,
Taiwan
58
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
59
Institute of Theoretical Astrophysics, University of
Oslo, Blindern,
0315
Oslo,
Norway
60
Instituto de Astrofísica de Canarias, C/vía Láctea s/n, 38205, La
Laguna, Tenerife, Spain
61
Instituto de Física de Cantabria (CSIC-Universidad de
Cantabria), Avda. de los Castros
s/n, 39005
Santander,
Spain
62
Jet Propulsion Laboratory, California Institute of
Technology, 4800 Oak Grove
drive, Pasadena,
USA
63
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School
of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester
M13 9PL,
UK
64
Kavli Institute for Cosmology Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
65
LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
66
LERMA, CNRS, Observatoire de Paris, 61 avenue de
l’Observatoire, 75014
Paris,
France
67
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
68
Laboratoire Traitement et Communication de l’Information, CNRS (UMR
5141) and Télécom ParisTech, 46 rue
Barrault, 75634
Paris Cedex 13,
France
69
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble, 53 rue des
Martyrs, 38026
Grenoble Cedex,
France
70
Laboratoire de Physique Théorique, Université Paris-Sud 11 &
CNRS, Bâtiment 210,
91405
Orsay,
France
71
Lawrence Berkeley National Laboratory, Berkeley, USA
72
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching,
Germany
73
National University of Ireland, Department of Experimental
Physics, Maynooth,
Co. Kildare,
Ireland
74
Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
75
Observational Cosmology, Mail Stop 367-17, California Institute of
Technology, Pasadena
CA
91125,
USA
76
Optical Science Laboratory, University College London,
Gower Street, London, UK
77
SISSA, Astrophysics Sector, via Bonomea 265, 34136
Trieste,
Italy
78
School of Physics and Astronomy, Cardiff University,
Queens Buildings, The Parade,
Cardiff
CF24 3AA,
UK
79
Space Sciences Laboratory, University of California,
Berkeley, California, USA
80
Special Astrophysical Observatory, Russian Academy of
Sciences, Nizhnij Arkhyz,
Zelenchukskiy region, 369167
Karachai- Cherkessian Republic,
Russia
81
UPMC Univ Paris 06, UMR7095, 98 bis boulevard Arago, 75014
Paris,
France
82
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
83
Universities Space Research Association, Stratospheric Observatory
for Infrared Astronomy, MS
232-11, Moffett Field
CA
94035,
USA
84
University of Granada, Departamento de Física Teórica y del Cosmos,
Facultad de Ciencias, Granada, Spain
85
Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478
Warszawa,
Poland
* Corresponding author: M. I. R. Alves
marta.alves@ias.u-psud.fr
Received:
25
July
2013
Accepted:
28
January
2014
We use Planck HFI data combined with ancillary radio data to study the emissivity index of the interstellar dust emission in the frequency range 100–353 GHz, or 3–0.8 mm, in the Galactic plane. We analyse the region l = 20°–44° and |b| ≤ 4° where the free-free emission can be estimated from radio recombination line data. We fit the spectra at each sky pixel with a modified blackbody model and two opacity spectral indices, βmm and βFIR, below and above 353 GHz, respectively. We find that βmm is smaller than βFIR, and we detect a correlation between this low frequency power-law index and the dust optical depth at 353 GHz, τ353. The opacity spectral index βmm increases from about 1.54 in the more diffuse regions of the Galactic disk, |b| = 3°–4° and τ353 ~ 5 × 10-5, to about 1.66 in the densest regions with an optical depth of more than one order of magnitude higher. We associate this correlation with an evolution of the dust emissivity related to the fraction of molecular gas along the line of sight. This translates into βmm ~ 1.54 for a medium that is mostly atomic and βmm ~ 1.66 when the medium is dominated by molecular gas. We find that both the two-level system model and magnetic dipole emission by ferromagnetic particles can explain the results. These results improve our understanding of the physics of interstellar dust and lead towards a complete model of the dust spectrum of the Milky Way from far-infrared to millimetre wavelengths.
Key words: ISM: general / Galaxy: general / radiation mechanisms: general / radio continuum: ISM / submillimeter: ISM
© ESO, 2014
1. Introduction
The frequency coverage of Planck1 is
opening new windows in our understanding of Galactic emission. This is especially the case
for the high frequency data that provide an all-sky view of the Rayleigh-Jeans regime of the
thermal dust spectrum. The emission at the Planck high frequency bands
(350 μm–3 mm) is dominated by the contribution of big grains
(radius larger than 0.05 μm), which heated by stellar photons are in thermal
equilibrium with the interstellar radiation field (ISRF). The spectral energy distribution
(SED) of big dust grains is usually approximated by a modified blackbody emission law of the
form  (1)where τν0 is the dust
optical depth at a reference frequency ν0, β the spectral index of the
opacity, and Bν the Planck function,
which depends on both the frequency and the dust temperature Td. However, early
observations by the Cosmic Background Explorer (COBE) indicated that the modified blackbody
spectrum does not provide a good description of the dust SED from far-infrared (FIR) to
millimetre wavelengths (Reach et al. 1995). Later
works have confirmed that β appears to vary with frequency, the SED flattening in
the millimetre relative to the best single modified blackbody fit and also varying with
environment (Finkbeiner et al. 1999; Galliano et al. 2005; Paladini et al. 2007; Planck Collaboration XVII
2011; Planck Collaboration XIX 2011).
Studies of dust analogues (e.g., Agladze et al. 1996;
Boudet et al. 2005; Coupeaud et al. 2011) have characterized the FIR and millimetre emission of
different types of amorphous silicates. These show a frequency, as well as temperature,
dependence of β
not unlike the astronomical results. The astrophysical interpretation of this flattening is
under study as new observations become available, and some possible explanations have been
suggested. One possibility is a description of the opacity of the big grains in terms of a
two-level system (TLS, Meny et al. 2007).
Alternatively, it might be attributed to magnetic dipole emission from magnetic particles
(Draine & Hensley 2013) or to the evolution of
carbon dust (Jones et al. 2013).
(1)where τν0 is the dust
optical depth at a reference frequency ν0, β the spectral index of the
opacity, and Bν the Planck function,
which depends on both the frequency and the dust temperature Td. However, early
observations by the Cosmic Background Explorer (COBE) indicated that the modified blackbody
spectrum does not provide a good description of the dust SED from far-infrared (FIR) to
millimetre wavelengths (Reach et al. 1995). Later
works have confirmed that β appears to vary with frequency, the SED flattening in
the millimetre relative to the best single modified blackbody fit and also varying with
environment (Finkbeiner et al. 1999; Galliano et al. 2005; Paladini et al. 2007; Planck Collaboration XVII
2011; Planck Collaboration XIX 2011).
Studies of dust analogues (e.g., Agladze et al. 1996;
Boudet et al. 2005; Coupeaud et al. 2011) have characterized the FIR and millimetre emission of
different types of amorphous silicates. These show a frequency, as well as temperature,
dependence of β
not unlike the astronomical results. The astrophysical interpretation of this flattening is
under study as new observations become available, and some possible explanations have been
suggested. One possibility is a description of the opacity of the big grains in terms of a
two-level system (TLS, Meny et al. 2007).
Alternatively, it might be attributed to magnetic dipole emission from magnetic particles
(Draine & Hensley 2013) or to the evolution of
carbon dust (Jones et al. 2013).
To study the low frequency flattening of the dust SED in the Galactic plane, we need to take the free-free emission from the ionized gas into account. Free-free emission is a principal foreground contaminant of the cosmic microwave background (CMB), not only at radio frequencies, where it is comparable to other Galactic components such as synchrotron, but also at millimetre wavelengths where the thermal dust emission dominates. It becomes a major component in the Galactic plane where it is produced by the gas ionized by recently formed massive stars. All-sky maps of the free-free emission, derived in the context of CMB foreground studies, have been obtained directly from Hα measurements (Dickinson et al. 2003; Finkbeiner 2003). However, this optical line suffers from large dust absorption along the Galactic plane, and thus fails to provide a reliable measure of the thermal emission at low Galactic latitudes. A free-free map that includes the Galactic plane is essential, not only to correctly evaluate the CMB power spectrum at low angular frequency, but also for Galactic star formation studies. The WMAP satellite has provided all-sky maps at five microwave frequencies that have been combined to estimate the contribution of free-free, synchrotron, thermal dust and anomalous microwave emission (AME) using a maximum entropy method (MEM, Bennett et al. 2013). Another approach using hydrogen radio recombination lines (RRLs) has been presented recently by Alves et al. (2010, 2012). In contrast to Hα, these radio lines at a frequency of 1.4 GHz are optically thin and are not absorbed by dust or the radio emitting plasma. The RRL method has provided the first direct measure of the diffuse free-free emission along the Galactic plane, in the longitude range l = 20°–44° and for latitudes |b| ≤ 4° (Alves et al. 2012).
The free-free emission has a spectral index α ≡ dln(Iν) /dlnν, varying from −0.10 at 1.4 GHz to −0.15 at 100 GHz. The free-free emission dominates at frequencies between 60 and 100 GHz, but there the other Galactic components, namely synchrotron, dust and AME, also contribute to the total intensity. The AME is an additional Galactic component observed in the frequency range 10–60 GHz (e.g., Kogut et al. 1996; Leitch et al. 1997; de Oliveira-Costa et al. 1997; Planck Collaboration XX 2011; Planck Collaboration Int. XII 2013; Planck Collaboration Int. XV 2014) which cannot be explained by free-free, synchrotron or thermal dust emission and is thought to arise from small spinning dust grains (Draine & Lazarian 1998; Ali-Haïmoud et al. 2009; Ysard & Verstraete 2010; Hoang et al. 2010, 2011). In a spectral decomposition of the four Galactic emission components along the plane, Planck Collaboration Int. XXII (in prep.) find that the AME contribution is comparable to that of the free-free in the frequency range 20–40 GHz. On the other hand, and due to its steeper spectral index, −1.2 ≲ α ≲ −0.7 (Davies et al. 1996; Ghosh et al. 2012), the synchrotron emission is mostly dominant at frequencies less than a few gigahertz.
This paper aims to characterize for the first time the dust emissivity in the frequency range 100–353 GHz of the diffuse emission in the Galactic plane. For this purpose, we remove the free-free emission contribution using the RRL data (Sect. 3.1). We start by describing the Planck and ancillary data used in this work in Sects. 2 and 3. In Sect. 4 we present the data analysis techniques, followed by the main results of the paper in Sect. 5. These are discussed further and interpreted in Sect. 6, followed by the conclusions in Sect. 7.
2. Planck HFI data
Planck (Tauber et al. 2010; Planck Collaboration I 2011; Planck Collaboration Int.
XXII, in prep.) is the third-generation space mission to measure the anisotropy of the CMB.
It observed the sky in nine frequency bands covering 28.5–857 GHz with high sensitivity and
angular resolution from  to
to 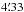 .
The Low Frequency Instrument (LFI; Mandolesi et al.
2010; Bersanelli et al. 2010; Mennella et al. 2011; Planck Collaboration II 2014) covered the 28.4, 44.1, and 70.4 GHz bands with
amplifiers cooled to 20 K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team
2011; Planck Collaboration VI 2014) covered
the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1 K. Polarization
is measured in all but the highest two bands (Leahy et al.
2010; Rosset et al. 2010).
.
The Low Frequency Instrument (LFI; Mandolesi et al.
2010; Bersanelli et al. 2010; Mennella et al. 2011; Planck Collaboration II 2014) covered the 28.4, 44.1, and 70.4 GHz bands with
amplifiers cooled to 20 K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team
2011; Planck Collaboration VI 2014) covered
the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1 K. Polarization
is measured in all but the highest two bands (Leahy et al.
2010; Rosset et al. 2010).
In the present work we use data from the Planck 2013 data release which
can be obtained from the Planck Legacy Archive2. We use the HFI data acquired between 13 August 2009 and 27 November 2010. These
are converted to intensity units of MJy sr-1 following the IRAS SED convention (Beichman et al. 1988), which assumes a spectral index α = −1. Colour corrections
based on the observed emission spectrum and on the spectral response of the receiver, are
applied to derive the specific intensity at the effective frequency of each band (Planck Collaboration IX 2014). The Planck
CMB map is derived from the SMICA component separation method and presented in
Planck Collaboration XII (2014). Close to the plane
of the Galaxy, it is not possible to correctly separate the CMB fluctuations from the much
brighter Galactic emission. Hence, this region of the SMICA map has been replaced by a
constrained realization of the CMB fluctuations. For this reason we derive our results using
the data uncorrected for the CMB fluctuations, which we compare with those obtained when the
SMICA CMB map is subtracted from the data (Sect. 5.4).
The lowest HFI frequency band also has the lowest angular resolution, of
 .
However we smooth the Planck data to a common resolution of
15′, assuming Gaussian beams,
to match the lower resolution of the RRL data (Sect. 3.1).
.
However we smooth the Planck data to a common resolution of
15′, assuming Gaussian beams,
to match the lower resolution of the RRL data (Sect. 3.1).
The 100 GHz data are significantly contaminated by the CO J = 1 → 0 line at 115 GHz and the 217 GHz data by the CO J = 2 → 1 line at 230 GHz. At 353 GHz the contribution of the CO J = 3 → 2 line is small, but not negligible compared to dust emission. The CO line emission is subtracted using the Plancktype 1 CO maps from the MILCA (Modified Independent Linear Combination Algorithm, Hurier et al. 2013) bolometer solution (Planck Collaboration XIII 2014). These are converted from line integrated units to intensity units as described in Planck Collaboration XIII (2014). The calibration uncertainties on these maps are of 10, 2, and 5% at 100, 217, and 353 GHz, respectively. The 100 GHz MILCA map has been compared with ground-based data, in particular the Dame et al. (2001)12CO J = 1 → 0 survey along the Galactic plane, for which there is an overall agreement of 16% (Planck Collaboration XIII 2014). However, in the Galactic plane region of the present study, both datasets agree within 25%. This discrepancy can be explained by the shifting of the CO line frequency due to Doppler effects, that is to say, the rotation of the Galactic disk (Planck Collaboration XIII 2014).
The overall calibration uncertainties for the Planck HFI maps are 10% at 857 and 545 GHz, 1.2% at 353 GHz, and 0.5% at lower frequencies. These values are increased at the lowest frequencies due to the subtraction of the CO and free-free emission. We did not subtract the zodiacal dust emission from the maps, because it is a negligible contribution in the Galactic plane (Planck Collaboration XIV 2014). Moreover, the cosmic infrared background (CIB) monopole was removed from all the HFI maps as described in Planck Collaboration XI (2014).
3. Ancillary data
Along with Planck HFI we need to use ancillary data, namely RRL observations for the removal of the free-free emission and IRAS data to constrain the dust temperature. All data sets are in HEALPix format (Górski et al. 2005), at Nside = 512, and are smoothed to a common resolution of 15′.
3.1. Radio Recombination Line data
A fully-sampled map of the free-free emission in the Galactic plane region
l = 20°–44° and |b| ≤ 4° has been derived by Alves et al. (2012) using RRL data. These data are from the H i
Parkes All-Sky Survey and associated Zone of Avoidance Survey (Staveley-Smith et al. 1996, 1998) at 1.4 GHz and 15′ resolution. One source of uncertainty on these data is the
conversion from the observed antenna temperature to intensity units, which requires a
detailed knowledge of the observing beam (Rohlfs &
Wilson 2000). The RRL data presented in Alves et
al. may need a correction downwards of 5–10%, since they were converted to a
scale appropriate for point sources; this correction depends on the angular size of the
source relative to the main beam of 15′. The free-free brightness temperature3 estimated from the RRL integrated line emission depends on the electron
temperature of the ionized gas as 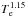 (Gordon
& Sorochenko 2009). Alves et al. used
an average value of Te = 6000 K; an increase of this value
by 500 K (1000 K) would increase the brightness temperature by 10% (19%).
(Gordon
& Sorochenko 2009). Alves et al. used
an average value of Te = 6000 K; an increase of this value
by 500 K (1000 K) would increase the brightness temperature by 10% (19%).
The RRL free-free data are similarly used in the work of Planck Collaboration Int. XXII (in prep.) to separate the different emission components in the Galactic plane and to determine the contribution of the AME. In that work, the free-free map estimated from the radio data are compared to two other free-free solutions, given by the Planck fastMEM (Planck Collaboration Int. XXII, in prep.) and WMAP MEM (Bennett et al. 2013) component separation methods. The fastMEM and WMAP results agree within 2% but they are about 20% higher than the RRL estimation. The proposed solution to this difference is to scale the free-free map from Alves et al. (2012) upwards by 10%, which is equivalent to increasing the electron temperature to 7000 K (Planck Collaboration Int. XXII, in prep.). In this paper we use the same electron temperature of 7000 K and adopt an overall calibration uncertainty of 10% in the free-free continuum estimated from the RRL data.
3.2. IRAS data
We use the IRIS (Improved Reprocessing of the IRAS survey) data at 100 μm (Miville-Deschênes & Lagache 2005) to constrain the peak of the thermal dust emission. The calibration uncertainty for these data is 13.5%.
3.3. H I data
The H i data from the Galactic All-Sky Survey (GASS, McClure-Griffiths et al. 2009) are used to estimate the column density
of the atomic medium. The GASS survey mapped the 21-cm line emission in the southern sky,
δ < 1°,
at 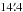 angular resolution and 1 km s-1 velocity resolution. We use the data corrected for
instrumental effects, stray radiation and radio frequency interference from Kalberla et al. (2010). The average temperature
uncertainties for these data are below 1%. The H i line is integrated as
described in Planck Collaboration Int. XVII (2014)
and converted to H i column density assuming that the line is optically thin. The
optically thin limit is a simplistic approach in the Galactic plane and results in an
underestimation of the true column density, by about 30–50% as found in H i
continuum absorption studies (Strasser & Taylor
2004).
angular resolution and 1 km s-1 velocity resolution. We use the data corrected for
instrumental effects, stray radiation and radio frequency interference from Kalberla et al. (2010). The average temperature
uncertainties for these data are below 1%. The H i line is integrated as
described in Planck Collaboration Int. XVII (2014)
and converted to H i column density assuming that the line is optically thin. The
optically thin limit is a simplistic approach in the Galactic plane and results in an
underestimation of the true column density, by about 30–50% as found in H i
continuum absorption studies (Strasser & Taylor
2004).
4. Analysis
The aim here is to determine the power-law index of the interstellar dust opacity at the lowest HFI frequencies, which we do by fitting the dust SED.
As mentioned in Sect. 1, β appears to be frequency dependent with a break observed at frequencies around 600 GHz, or (Paradis et al. 2009; Gordon et al. 2010; Galliano et al. 2011). Planck Collaboration XXV (2011) also found that a single modified blackbody curve accurately fits the FIR spectrum of Galactic molecular clouds, but leaves large residuals at frequencies below 353 GHz. For this reason we decided to fit the dust SED using a modified blackbody model, but allowing β to vary with frequency, having β = βFIR for ν ≥ 353 GHz and β = βmm for ν < 353 GHz. Using the Planck HFI bands along with the IRAS 100 μm data, we also solve for the other parameters in Eq. (1), namely Td and τ353, where we take the reference frequency as 353 GHz for the dust optical depth.
The Planck maps at frequencies above 353 GHz contain mainly dust emission and also CIB emission. The CIB fluctuations have a power spectrum flatter than that of the interstellar dust (Miville-Deschênes et al. 2002; Lagache et al. 2007; Planck Collaboration XVIII 2011), thus contributing mostly at small angular scales and producing a statistically homogeneous signal. This signal only represents a significant fraction of the total brightness in the most diffuse high latitude regions of the sky, and thus can be neglected in the Galactic plane.
In the range 100–353 GHz, even though most of the emission comes from interstellar dust, both the CMB and free-free components also contribute to the total brightness. The fluctuations of the CMB are faint, rms of about 80 μK at scales of 15′, compared to the brightest emission in the Galactic plane. Therefore, we can neglect the contribution from the CMB fluctuations, since its rms temperature is about 5% of the total emission in the thin disk of the Galaxy. However, at latitudes |b| ≳ 2° the CMB fluctuations at 100 GHz are about 10 times brighter than the free-free emission. The effects of neglecting the CMB component at these higher latitudes will be investigated via simulations in Sect. 5.3, as well as using the SMICA CMB map in Sect. 5.4.
At |b| ≲ 1°, the contribution of the free-free emission can be as high as 20–40% to the total emission at 100 GHz, from both the diffuse and the individual H ii regions. Therefore, we need to remove the free-free emission if we are to fit the dust spectrum only with a modified blackbody model. For this purpose, we use the free-free map estimated from the RRLs (Sect. 3.1), as this is currently the only direct measure of this emission in the Galactic plane, in particular in the 24° × 8° region centred on (l, b) = (32°, 0°). This region is shown in Fig. 1, in the Planck 353 GHz channel. The free-free continuum, estimated from the RRL data at 1.4 GHz, is extrapolated to the HFI frequencies using a frequency dependent Gaunt factor (Eq. (10.9) of Draine 2011) and an electron temperature of 7000 K.
 |
Fig. 1 HFI 353 GHz map of the Galactic plane region l = 20°–44°, |b| ≤ 4°, in units of MJy sr-1 and at 15′ resolution. |
We used the IDL MPFIT routine to fit the final SEDs pixel-by-pixel in the 24°×8° region. This routine performs weighted least-squares fitting of the data (Markwardt 2009), taking into account the noise (both statistical noise and systematic uncertainties) for each spectral band. We also include a noise term from the CMB fluctuations, typically 80 μK, which will be dominant outside the Galactic plane and at the lowest frequencies. These uncertainties are used to give weights to the spectral points. Colour corrections based on the local spectral index across each band were applied to both Planck and IRAS data during the model-fitting procedure (Planck Collaboration IX 2014).
 |
Fig. 2 Spectra towards the H ii region complex W42 (red) and a diffuse region in
the Galactic plane centred at (l, b) = |
5. The dust spectral index from FIR to millimetre wavelengths
In this section we present the main results of this work, namely the difference between βFIR and βmm in the Galactic plane and how the latter relates to changes in dust temperature and optical depth. Several tests are performed to assess the robustness of the results, including a validation of the analysis techniques via simulations.
 |
Fig. 3 Histograms of the dust temperature a) and dust opacity indices b) for the 24° × 8° region. The dashed lines in both panels correspond to the pixels where τ353 ≥ 4×10-4. In panel a) the dashed histogram is scaled up by a factor of four. |
 |
Fig. 4 Comparison of the results on βmma) when the CO and free-free corrections vary by 10%; b) when Td is allowed to vary in the fit and also when Td is fixed to a single value of 19 K. |
5.1. Flattening of the dust SED
The spectra at the position of a complex of H ii regions, G24.5+0.0 (W42), and
towards a diffuse region in the Galactic plane centred at
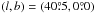 are shown in Fig. 2. The fitted models are also
shown. The effect of subtracting the free-free emission is clearly visible at 100 GHz in
the spectrum of the H ii region (compare the circles with the squares); at
frequencies above 143 GHz this subtraction is negligible. The spectral indices of the
H ii region are βFIR = 1.9 ± 0.2 and βmm = 1.7±0.1, while for the diffuse region, βFIR = 1.9±0.2 and βmm = 1.6±0.1. These values suggest that the diffuse region has a flatter
millimetre spectrum than the H ii region. The uncertainties on the parameters
reflect the likely mixture of dust components along the line of sight, which have a range
of temperatures and different properties. The χ2 values of the fits are 3.1 and 1.1,
for the H ii region and the diffuse region respectively, with 4Nd.o.f. = 3.
The χ2/Nd.o.f.
values across the map are usually lower than one, meaning that the fits are within the
uncertainties of each point. The uncertainties on the data at frequencies of 217 GHz and
above are dominated by the calibration uncertainties, which are correlated across the
channels. At these frequencies, the median value of our fit residuals across the map is
close to zero and within the overall uncertainties of the data, thus indicating that the
fits are a good representation of the data. At 100 and 143 GHz the histograms of the
percentage residual emission are centred at 2% and −3%, respectively. These values are higher
than the 0.5% calibration uncertainty at these frequencies but lower than the final
uncertainties once the noise contribution from CMB and the uncertainties associated with
free-free and CO templates are included.
are shown in Fig. 2. The fitted models are also
shown. The effect of subtracting the free-free emission is clearly visible at 100 GHz in
the spectrum of the H ii region (compare the circles with the squares); at
frequencies above 143 GHz this subtraction is negligible. The spectral indices of the
H ii region are βFIR = 1.9 ± 0.2 and βmm = 1.7±0.1, while for the diffuse region, βFIR = 1.9±0.2 and βmm = 1.6±0.1. These values suggest that the diffuse region has a flatter
millimetre spectrum than the H ii region. The uncertainties on the parameters
reflect the likely mixture of dust components along the line of sight, which have a range
of temperatures and different properties. The χ2 values of the fits are 3.1 and 1.1,
for the H ii region and the diffuse region respectively, with 4Nd.o.f. = 3.
The χ2/Nd.o.f.
values across the map are usually lower than one, meaning that the fits are within the
uncertainties of each point. The uncertainties on the data at frequencies of 217 GHz and
above are dominated by the calibration uncertainties, which are correlated across the
channels. At these frequencies, the median value of our fit residuals across the map is
close to zero and within the overall uncertainties of the data, thus indicating that the
fits are a good representation of the data. At 100 and 143 GHz the histograms of the
percentage residual emission are centred at 2% and −3%, respectively. These values are higher
than the 0.5% calibration uncertainty at these frequencies but lower than the final
uncertainties once the noise contribution from CMB and the uncertainties associated with
free-free and CO templates are included.
The distributions of temperature and spectral indices fitted for the 24° × 8° region under study are shown in Fig. 3. The dust temperature ranges from 16 to 24 K, with a median value of 19 K. Even though we are describing the SED with only a single temperature whilst a range of temperatures are expected along the line of sight especially in the Galactic plane, the higher temperature regions found here are associated with H ii regions, as expected from local heating by their OB stars. Similarly, colder regions are associated with molecular clouds.
The histograms of βFIR and βmm are compared in Fig. 3b for the whole 24° × 8° region. The βFIR distribution has a median value of 1.76 and a standard deviation (σ, corresponding to the 68.3% confidence interval) of 0.08 and that of βmm has a median value of 1.55 with σ = 0.12. This indicates that the βmm distribution is centred at a lower value and is also broader. If we select the pixels within |b| ≲ 1°, which represents regions with an optical depth τ353 ≥ 4 × 10-4, the corresponding βFIR and βmm histograms, shown as dashed lines, have median values of 1.88, σ = 0.08, and 1.60, σ = 0.06 respectively. The shift in the mean values of both βmm and βFIR is related to a variation of these parameters from the diffuse to the denser medium, as will be discussed in Sect. 6.2. The βmm values fitted outside the narrow Galactic plane are affected by CMB fluctuations, which become brighter than the free-free and are not taken into account in the fit. The impact of the CMB in the βmm results will be further analysed in Sects. 5.3 and 5.4. The dust temperature distribution is similar between the 24° × 8° region and the thin Galactic disk (full and dashed lines in Fig. 3a), with a sharper decrease of the latter below 19 K.
The histogram of βFIR in Fig. 3 does not include the effects of the calibration uncertainties, namely its width only takes into account the variations across the map. This is an important point when assessing the difference between βFIR and βmm, as given by Fig. 3. At frequencies of 353 GHz and above, where the contribution of CO, free-free and CMB are negligible compared to dust emission, the data uncertainties are dominated by calibration uncertainties. We performed Monte Carlo simulations to estimate this effect on βFIR and found that, in 1000 simulations, the dispersion around an input value of 1.75 is 0.17. This value is about twice that measured from the βFIR histograms of Fig. 3. Nevertheless, in the thin Galactic disk, this does not affect the difference measured between βFIR and βmm. A further check on the quality of the SED fits and the importance of including a second spectral index, βmm, is given by comparing the residuals with those resulting from a model with a single β. When only one spectral index is fit for from 100 to 3000 GHz, the median value of the residuals across the map is larger at all frequencies, relative to the two-β model. In particular, the median value of the residuals at 857 GHz, 11%, is higher than the calibration uncertainty. We also note that, if we choose the reference frequency of 545 GHz, instead of 353 GHz for the break in the spectral index, the fits also result in larger residuals at all frequencies.
We tested the robustness of the fitted βmm against calibration uncertainties in both the CO and the free-free templates by varying the subtraction of the CO and RRL contributions, at all frequencies, by 10% (Sects. 2 and 3.1). An under-subtraction of either the CO or the free-free emission could in principle result in a lower βmm. However, as Fig. 4a illustrates, βmm is essentially insensitive to these variations. This is due to the fact that dust is the dominant emission component at these frequencies, combined with the higher uncertainties of the data at 143 and 100 GHz.
 |
Fig. 5 Dust spectral indices as a function of temperature. a) βFIR versus Td for the whole 24° × 8° region. b) βFIR versus Td for points where τ353 ≥ 4 × 10-4. c) βmm versus Td for points where τ353 ≥ 4 × 10-4. The triangle and square in panels b) and c) indicate the values obtained by fitting the emissivities predicted by the TLS model (Paradis et al. 2011) for Td = 17 and 25 K (see Sect. 6.1.2). The colour scale is logarithmic and it represents the density of points. The contours show the densities for the cumulated fractions, given by the values in each panel, of the data points, from red to yellow. |
In order to investigate the impact of the dust temperature on βmm, we compare the results when Td is fixed to 19 K with those when Td is allowed to vary in the SED fit. These are shown in Fig. 4b, where it is seen that the distribution of βmm is unaffected when using a constant or varying value of Td across the region.
5.2. Variations with temperature and optical depth
An anti-correlation between β and Td has been detected in previous observations in a variety of Galactic regions (Dupac et al. 2003; Désert et al. 2008; Paradis et al. 2010; Planck Collaboration XXV 2011). This seems to indicate that the dust opacity index decreases with temperature, even if part of this effect can be attributed to data noise and to temperature mixing along the line of sight (Sajina et al. 2006; Shetty et al. 2009b,a; Juvela & Ysard 2012b,a). Kelly et al. (2012) show that the former can be mitigated by using a hierarchical Bayesian technique. The distribution of βFIR as a function of Td is shown in Fig. 5a, for all the points in the 24° × 8° region. The Pearson correlation coefficient5 between the uncertainties on these two parameters is around −0.95 across the map. However, such a strong anti-correlation is not observed in Fig. 5a, nor in Fig. 5b, where βFIR − Td is plotted for the thin Galactic disk, |b| ≲ 1°. Therefore, there is a real variation of βFIR across this region which decreases the anti-correlation trend generated by the data noise.
The distribution of βmm as a function of Td, for the thin Galactic disk, where τ353 ≥ 4 × 10-4, is shown in Fig. 5c. For this region, the correlation coefficient between the uncertainties on βmm and Td varies between −0.06 and −0.03. A value of −0.5 is reached outside the Galactic disk, where the signal-to-noise ratio decreases due to the CMB noise term included in the data uncertainties. Thus, Fig. 5c indicates that there is no evident trend of βmm with Td (as it is also seen by comparing the corresponding maps in Fig. 8). We note that the range of temperatures that we are probing is limited, about 6 K, which may be due to temperature mixing along the line of sight and local temperature increases around the heating sources present in the Galactic plane.
 |
Fig. 6 Distribution of βmm as a function of τ353, for the whole region. The red line gives the best linear fit for τ353 ≥ 4 × 10-4 (see text). The colour scale is logarithmic and it represents the density of points. The three contours show the densities for a cumulated fraction of 11, 31, and 62% of the data points, from red to yellow. |
 |
Fig. 7 Dust opacity index βmm recovered from the simulated maps, as a function of the input τ353. The simulated maps in a) have dust emission and CMB, and in b) consist of dust, free-free and CO emission. The black line shows the input βmm of 1.52 in each case; the red lines give the βmm–τ353 relationship derived in Sect. 5. The colour scale is logarithmic and it represents the density of points. The three contours show the densities for the cumulated fractions, given by the values in each panel, of the data points, from red to yellow. |
We find a correlation between βmm and the optical depth τ353, which is shown in Fig. 6. We note that βmm is an intrinsic parameter related to the physics of dust while τ353 scales with the column density of interstellar matter. In Sect. 6 we will describe this empirical correlation in terms of the type of matter rather than the quantity of matter along the line of sight, given by τ353. The scatter in βmm at low optical depth values, or |b| ≳ 1°, is due to the CMB, as discussed above. For τ353 ≥ 4 × 10-4, βmm increases in the highest optical depth regions, as foreshadowed by the results of Fig. 2, which showed an increase of βmm from the diffuse to the H ii region. A linear fit to the data, for τ353 ≥ 4 × 10-4, gives βmm = (1.52± 0.01) + (128 ± 2) ×τ353, where we have used the IDL routine regress to perform the linear regression fit, including only the errors on βmm. We note that the errors on τ353 are much lower than those on βmm. Moreover, the Pearson correlation coefficient between the uncertainties on these two parameters for τ353 ≥ 4 × 10-4, varies between 0.03 and 0.08. This indicates that it is unlikely that the correlation observed is due to data noise.
The uncertainty on βmm is statistical; including the
systematic uncertainties introduced by the CMB, CO and free-free components, which are
presented in Sect. 5.3, the correlation is
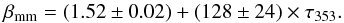 (2)
(2)
5.3. Validation with simulations
In order to test the robustness of our fitting procedure against possible biases on βmm associated with the separation of dust emission from CMB, free-free and CO, we apply our routine to simulated maps.
The first simulated maps include dust emission and CMB. We fix Td to 19 K, βFIR to 1.75 and βmm to 1.52 across the region. The distribution of τ353 is that obtained from the fit to the data. We reproduce the dust maps at each frequency with a modified blackbody law and add them to the CMB map, reproduced from the best-fit ΛCDM model. We then apply the SED fitting routine and recover βmm as a function of the input optical depth as shown in Fig. 7a. A linear fit to the points with τ353 ≥ 4 × 10-4 gives βmm = 1.53−8×τ353. As discussed in Sect. 5, the scatter on the βmm values for τ353 ≲ 4 × 10-4 is created by the CMB when this component is not taken into account in the fit. Moreover, even though it is a minor contributor in the Galactic disk, the CMB also affects the results for higher values of τ353, broadening the βmm distribution around the input value of 1.52 by 0.01. Thus this result shows that if there is no intrinsic correlation between these two parameters only a limited correlation will be detected. More importantly, Fig. 7a shows that the CMB is not responsible for the βmm–τ353 correlation derived in the previous section.
We also tested our results for a possible bias introduced by incorrect subtraction of CO and free-free emission from simulated dust maps produced as described above. For that we use the MILCA CO maps (Sect. 2) and subtract 10% of their emission at 100, 217, and 353 GHz. Similarly we remove 10% of the RRL free-free emission from the simulated dust maps at all frequencies. Such a correction steepens the dust spectrum, as we can see from the results of Fig. 7b. A linear fit to the points gives βmm = 1.53+22 × τ353. This is not, however, capable of reproducing the much steeper slope of βmm with the dust optical depth. For that to be the case, both the CO and RRL maps would have to be systematically underestimated by 30%.
 |
Fig. 8 Maps of the dust parameters. Top: βmm, which results from the best linear fit to the correlation with optical depth given by Eq. (2); middle: τ353; bottom: Td. |
We thus conclude that neither the uncertainty in the CO and free-free correction of the maps nor omitting the CMB in the spectral fits is responsible for the correlation of βmm with τ353. Finally, Fig. 8 shows the map of βmm, estimated using Eq. (2), which presents the same structure as the map of τ353. On the other hand, there is no apparent correlation between the maps of βmm and Td, as it was discussed in Sect. 5.2.
 |
Fig. 9 Distribution of βmm as a function of τ353, for the whole region, when the SMICA CMB map is subtracted from each channel map. The black line gives the βmm–τ353 relationship derived from a fit to the points where τ353 ≥ 4 × 10-4, compared to that estimated in Sect. 5 and given by the red line. The colour scale is logarithmic and it represents the density of points. The three contours show the densities for a cumulated fraction of 5, 30, and 56% of the data points, from red to yellow. |
5.4. Using the Planck SMICA CMB map
In this section we compare our results with those obtained when the SMICA CMB map is subtracted from each channel map before fitting the dust spectra with a modified blackbody. The resulting βmm as a function of τ353 is shown in Fig. 9. As expected, the scatter on βmm at low values of τ353 decreases, due to the subtraction of the CMB from the total emission. A linear fit to the points with τ353 ≥ 4 × 10-4 gives βmm = (1.54 ± 0.01) + (116 ± 1) × τ353, consistent with Eq. (2). This confirms that the CMB fluctuations, here measured with the SMICA solution, are indeed a small contribution in the Galactic disk and do not affect the main results of the work.
6. Towards a physical interpretation of the millimetre dust emission
In this section we compare our results with predictions from current dust models and interpret the empirical relation found between βmm and τ353.
6.1. Dust models
6.1.1. Silicate-carbon models
We start by comparing our results with the predictions of two commonly used dust models, DL07 (Draine & Li 2007) and DustEM (Compiègne et al. 2011). In particular, we want to investigate whether such models, with two populations of grains dominating the emission at long wavelengths, can explain the flattening of the dust spectrum detected in the present work. Both models use the same optical properties for silicates, for which the opacity scales as ν1.6, for λ ≳ 250 μm or ν ≲ 1200 GHz. For the carbon grains DL07 uses the optical properties of graphite, with a spectral index of 2, whereas DustEM uses the laboratory measurements of amorphous carbon, for which the spectral index is 1.6. We use both models to predict the emission in the photometric bands considered in this work, namely IRAS 100 μm and HFI, taking the standard size distribution for the diffuse Galactic emission. In order to reproduce conditions closer to those in the Galactic plane, we generate the SEDs for G0 values of 1, 2 and 4, where G0 is the scaling applied to the standard ISRF of Mathis et al. (1983). We then fit the spectra in the same way as the data, namely with a modified blackbody law and two spectral indices, βFIR and βmm. The results are shown in Table 1. First we note that when the radiation field is higher, the peak of the SED is moved to higher frequencies, where the opacity spectral index of silicate grains is larger than 1.6. This can explain the slight increase in βFIR with G0. The results also show that βmm is lower than βFIR, for both models. Moreover, βmm does not seem to vary with G0 or with Td. We find that such models, including two dust components with different opacities can in principle explain the flattening of the dust emission, even if the β values recovered from their spectra are lower than those measured from the data.
Results from a modified blackbody fit to the DL07 and DustEM spectra for different scalings of the ISRF, given by G0.
6.1.2. Two-level system
The TLS (Meny et al. 2007) model has been proposed to explain the flattening of the dust emission and its evolution with temperature. This model consists of three mechanisms which describe the interaction of electromagnetic waves with an amorphous solid. These are temperature-dependent and important in the sub-millimetre, for the range of temperatures relevant to this work. Paradis et al. (2011) use the TLS model to fit the spectrum of the diffuse Galactic emission as well as the spectra of the Archeops sources (Désert et al. 2008). Within this model, the opacity spectral index decreases with increasing temperature. We compare the emissivities predicted by TLS and given in Paradis et al. (2011) with our results for the relevant photometric bands. In particular, we select two spectra, with Td of 17 and 25 K, within the range of temperatures probed in the present work. We apply our fitting routine to the TLS SEDs to recover βFIR and βmm, which are shown in Figs. 5b and c. The resulting βFIR values are within the range found in this work, showing a small variation with temperature. However, that is not the case for βmm. The values predicted by the TLS model are not within the range of values found in the Galactic disk, and show a steep dependence with temperature. We note that the TLS emissivities used here were computed for a given set of parameters, derived from the combined fit of the diffuse medium emission and the SEDs of the Archeops compact sources (third set of parameters in Table 4 of Paradis et al. 2011). Moreover, they are derived for a single grain, rather than for a grain size distribution. We could argue that the dust temperature estimated from the modified blackbody fit used here is not comparable with that derived from the TLS model. However Paradis et al. (2012) show that both temperatures agree up to about 25 K. Still, we note that Td obtained from their modified blackbody fit assumes βFIR = 2. We conclude that the TLS model predicts variations of βmm which are not apparent in the data. We note, however, that the range of temperatures sampled by the data is limited and that if spatial variations of the TLS amplitude, related to the amorphous structure of the grains, were allowed they could easily hide the temperature dependence of βmm in the data.
6.1.3. Magnetic dipole emission
The dust emission of the Small Magellanic Cloud (SMC) shows a pronounced flattening towards millimetre wavelengths (Israel et al. 2010; Bot et al. 2010; Planck Collaboration XVII 2011), which, as proposed by Draine & Hensley (2012), can be explained by magnetic dipole emission from metallic particles. In this section we test the magnetic dipole emission model with the Galactic plane data, which also show excess emission at millimetre wavelengths, even if not as substantial as that observed in the SMC. According to the model of Draine & Hensley (2012), the iron missing from the gas phase can be locked up in solid grains, either as inclusions in larger grains, in which case they are at the same temperature as the other dust in the diffuse interstellar medium (ISM), Td ≈ 18 K, or as free-flying nanoparticles, which then have a higher temperature, Td ≈ 40 K. The emission spectrum of these particles above a resonance frequency, ν ~ 15 GHz, and below 353 GHz, is close to that of a blackbody. In order to test this model, we fit the dust SEDs in the region under study with a modified blackbody of a single opacity index βFIR. Its value is determined using the IRAS and HFI 857, 545, and 353 GHz points and then used to extrapolate the emission to lower frequencies. We include a blackbody spectrum, at the same temperature Td, to represent the metallic particles as inclusions in larger grains, which will account for the excess emission. We find that, at 100 GHz, the ratio between the emission from the iron dust particles and that from the modified blackbody, r100, has a median of 63% across the thin Galactic disk, with a standard deviation of 24%. The spectra of the same H ii and diffuse regions as in Fig. 2 are shown in Fig. 10, for which r100 is (41 ± 8)% and (63 ± 7)%, respectively. The contribution by the metallic particles is higher for the diffuse region since its SED is flatter at lower frequencies than that of the H ii region (Sect. 5). The fraction obtained here is within the range of plausible values for magnetic dipole emission within the model of Draine & Hensley (2013), and smaller than that fitted for the SMC (Draine & Hensley 2012). In a similar analysis performed at high Galactic latitudes, Planck Collaboration Int. XVII (2014) find r100 = 26 ± 6%. The lower ratio follows the lower difference between their mean values for the FIR and millimetre spectral indices, βFIR = 1.65 and βmm = 1.53.
 |
Fig. 10 Spectra towards the H ii region complex W42 (red) and a diffuse region
in the Galactic plane centred at |
6.2. Correlation between βmm and τ353
In this section we attempt to provide a phenomenological interpretation of the empirical correlation detected between βmm and τ353. As mentioned in Sect. 5.2, the dust optical depth provides a measure of the quantity of matter along the line of sight, which may be atomic or molecular and which has the contribution of both dense and diffuse media. We suggest that this variation of βmm with the dust optical depth can be translated into an evolution with the fraction of molecular gas along the line of sight.
The fraction of molecular gas is given by  . The column density of molecular hydrogen
can be estimated by using the conversion factor XCO = NH2/ICO,
where ICO is the 12CO J = 1 → 0 integrated line
intensity. The Galactic XCO conversion factor has been estimated
in a variety of ways, including the use of optically thin tracers of column density such
as dust emission, molecular and atomic lines, as well as using γ-ray emission. Bolatto et al. (2013) give XCO = 2.0 × 1020 cm-2 (K km s-1)-1, with 30% uncertainty, as the
recommended value to use in Galactic studies. We can obtain an estimate of XCO with the
present data using the dust optical depth and the CO emission provided by the MILCA map.
For that we need to include the dust specific opacity, or absorption cross-section per
unit gas mass, of the molecular gas after removing the contribution of the atomic gas to
the dust optical depth. Dust properties are known to evolve from the diffuse ISM to the
higher density environment of molecular clouds, giving rise to an enhancement of the dust
specific opacity (Planck Collaboration XXIV 2011;
Planck Collaboration XXV 2011; Planck Collaboration XI 2014). One possible explanation
is grain coagulation (Stepnik et al. 2003; Köhler et al. 2012). The dust specific opacity appears
to be a factor of 1.5–2 times higher than the average value in the high Galactic latitude
diffuse atomic ISM (Planck Collaboration XI 2014).
We define the ratio between the dust opacity in the molecular and atomic media,
R, and
solve for XCO as follows
. The column density of molecular hydrogen
can be estimated by using the conversion factor XCO = NH2/ICO,
where ICO is the 12CO J = 1 → 0 integrated line
intensity. The Galactic XCO conversion factor has been estimated
in a variety of ways, including the use of optically thin tracers of column density such
as dust emission, molecular and atomic lines, as well as using γ-ray emission. Bolatto et al. (2013) give XCO = 2.0 × 1020 cm-2 (K km s-1)-1, with 30% uncertainty, as the
recommended value to use in Galactic studies. We can obtain an estimate of XCO with the
present data using the dust optical depth and the CO emission provided by the MILCA map.
For that we need to include the dust specific opacity, or absorption cross-section per
unit gas mass, of the molecular gas after removing the contribution of the atomic gas to
the dust optical depth. Dust properties are known to evolve from the diffuse ISM to the
higher density environment of molecular clouds, giving rise to an enhancement of the dust
specific opacity (Planck Collaboration XXIV 2011;
Planck Collaboration XXV 2011; Planck Collaboration XI 2014). One possible explanation
is grain coagulation (Stepnik et al. 2003; Köhler et al. 2012). The dust specific opacity appears
to be a factor of 1.5–2 times higher than the average value in the high Galactic latitude
diffuse atomic ISM (Planck Collaboration XI 2014).
We define the ratio between the dust opacity in the molecular and atomic media,
R, and
solve for XCO as follows  (3)where τ353/NH i = σH i = 7 × 10-27 cm2 H-1 (Planck Collaboration XI 2014; Planck
Collaboration Int. XVII 2014) and σH2 = RσH i.
We remove the contribution of the atomic medium to the dust optical depth using the
NH i data from the GASS survey
(Sect. 3.3) and the above value of σH i.
The GASS data only cover a fraction of the region under study, l = 20°–
(3)where τ353/NH i = σH i = 7 × 10-27 cm2 H-1 (Planck Collaboration XI 2014; Planck
Collaboration Int. XVII 2014) and σH2 = RσH i.
We remove the contribution of the atomic medium to the dust optical depth using the
NH i data from the GASS survey
(Sect. 3.3) and the above value of σH i.
The GASS data only cover a fraction of the region under study, l = 20°– at b = 0°,
which is nevertheless sufficient to derive the correlation between CO emission and dust
optical depth.
at b = 0°,
which is nevertheless sufficient to derive the correlation between CO emission and dust
optical depth.
The distribution of ICO as a function of the
H i-corrected τ353 is shown in Fig. 11. A linear fit to the data passing through the origin,
combined with Eq. (3), gives
XCO = 1.7 × 1020 × (2/R) cm-2 (K km s-1)-1. The uncertainty on this value
is of 13%, estimated from the scatter of the points. In order to assess the effect of a
possible underestimation of the true column density of the atomic gas (Sect. 3.3), we scale NH i by a factor of 1.5 and
repeat the analysis. We find that the uncertainties on the NH i
template do not affect XCO by more than ~9%. We note that the MILCA CO data in
this region of the Galactic plane are about 25% higher than the CO data from Dame et al. (2001) (Sect. 2). Since the XCO values in the literature refer to
the Dame et al. data, we scale our result by 25%
which gives XCO = 2.1 × 1020 × (2/R) cm-2 (K km s-1)-1. If we assume R = 2 then we obtain
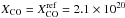 cm-2 (K km s-1)-1, which is consistent with the
recommended value for the Galaxy given by Bolatto et al.
(2013).
cm-2 (K km s-1)-1, which is consistent with the
recommended value for the Galaxy given by Bolatto et al.
(2013).
 |
Fig. 11 The MILCA CO line intensity as a function of the dust optical depth τ353,
corrected for the atomic gas contribution, along b = 0° in the
l = 20°– |
 |
Fig. 12 Opacity spectral indices as a function of the fraction of molecular gas along the line of sight. a)βmm versus fH2. b) βFIR versus fH2. The points correspond to the thin Galactic disk, |b|< ~1° or τ353 ≥ 4 × 10-4. Here fH2 is estimated assuming that the dust opacity in the molecular phase is twice that of the atomic medium, R = 2, and using XCO = 2.1 × 1020 cm-2 (K km s-1)-1. |
We can write the fraction of molecular gas along the line of sight as a function of
XCO, or R, as 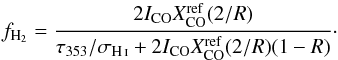 (4)The correlation between βmm and
fH2 for R = 2 is shown in Fig.
12a, where βmm is seen to
increase from atomic to molecular dominated regions. A linear fit to the data gives
βmm = (1.54 ± 0.01) + (0.12 ± 0.01)fH2,
meaning that βmm = 1.54 and 1.66 at low and high values
of fH2, respectively. If we assume
R = 1.5
then XCO = 2.8 × 1020 cm-2 (K km s-1)-1, which is somewhat higher than
the typical values for the Galaxy (Bolatto et al.
2013). Nevertheless, the correlation between βmm and
fH2, βmm = (1.53 ± 0.01) + (0.13 ± 0.01)fH2
is essentially unchanged. We note that we have assumed a single Td value in the
SED fit, ignoring the fact that Td is likely to be systematically lower
in molecular clouds than in the diffuse atomic medium (Planck Collaboration XIX 2011; Planck
Collaboration XI 2014). However, since Td and βmm are
anti-correlated, using a lower Td in the fit would result in an even
higher βmm in molecular media. This would thus
increase the difference in βmm between atomic and molecular
dominated regions. We also note that unphysical values of fH2
greater than one can be reached due to data noise as well as to the assumed values of
σH i and R. In Fig. 12, where R = 2 and σH i = 7 × 10-27 cm2 H-1, only 4% of the points have
fH2 > 1.
(4)The correlation between βmm and
fH2 for R = 2 is shown in Fig.
12a, where βmm is seen to
increase from atomic to molecular dominated regions. A linear fit to the data gives
βmm = (1.54 ± 0.01) + (0.12 ± 0.01)fH2,
meaning that βmm = 1.54 and 1.66 at low and high values
of fH2, respectively. If we assume
R = 1.5
then XCO = 2.8 × 1020 cm-2 (K km s-1)-1, which is somewhat higher than
the typical values for the Galaxy (Bolatto et al.
2013). Nevertheless, the correlation between βmm and
fH2, βmm = (1.53 ± 0.01) + (0.13 ± 0.01)fH2
is essentially unchanged. We note that we have assumed a single Td value in the
SED fit, ignoring the fact that Td is likely to be systematically lower
in molecular clouds than in the diffuse atomic medium (Planck Collaboration XIX 2011; Planck
Collaboration XI 2014). However, since Td and βmm are
anti-correlated, using a lower Td in the fit would result in an even
higher βmm in molecular media. This would thus
increase the difference in βmm between atomic and molecular
dominated regions. We also note that unphysical values of fH2
greater than one can be reached due to data noise as well as to the assumed values of
σH i and R. In Fig. 12, where R = 2 and σH i = 7 × 10-27 cm2 H-1, only 4% of the points have
fH2 > 1.
Recent results from Tabatabaei et al. (2014) show an increase of the opacity spectral index, βFIR, from the outer to the inner disk of M33. In addition, they find this trend to be associated with tracers of star formation and molecular gas. Their analysis is based on data between 70 and 500 μm, which they fit with a single and a double, cold and warm, component model. The results on βFIR from both models are consistent. We find that βFIR is also linearly correlated with fH2 in the Galactic plane, as shown in Fig. 12b. A linear fit to the data gives βFIR = (1.75 ± 0.01) + (0.23 ± 0.01)fH2, which translates into an increase of βFIR from 1.75 in atomic medium to 1.98 in molecular medium. This result compares with that found in M33, even if the wavelength range covered in our analysis does not allow the comprisal of two dust components in the fit. The same trend is found by Draine et al. (2014) in M31, where βFIR increases from ~2.0 at a distance of 15 kpc from the centre of the galaxy to ~2.3 at 3 kpc.
6.3. Dust evolution
The flattening of the dust emission towards millimetre wavelengths in the plane of the Galaxy found here, is accompanied by the results of Planck Collaboration Int. XVII (2014), where the same phenomenon is detected at high Galactic latitudes. In the present work βFIR − βmm ~ 0.2 for the atomic ISM, comparable to the value measured at high Galactic latitudes. One possibility to explain the observed change in spectral index is an increasing contribution from carbon dust at millimetre wavelengths. In the model of Jones et al. (2013) the spectral index of the carbon dust emission at 1 mm depends on the degree of hydrogenation and aromaticity of the grains.
It is not clear if the change of spectral index βmm from atomic to molecular media is related to the observed variation of the dust specific opacity (Planck Collaboration XI 2014). Grain coagulation is a possible interpretation of the change in dust opacity. Coagulation models indicate that dust aggregation produces an overall increase of the dust specific opacity in molecular clouds, without significantly changing the apparent βmm (Köhler et al. 2012). Further, there is evidence of variations in the dust opacity within the local atomic ISM (Planck Collaboration XXIV 2011; Planck Collaboration Int. XVII 2014), where grain coagulation is unlikely to occur.
Further studies are needed to explain the correlation with the molecular material observed here, which remains phenomenological and whose origin does not rely on a physical model. In particular, Planck polarization data will be a first test of the nature of the dust SED flattening.
7. Conclusions
We have used Planck HFI data to derive the power-law index of the interstellar dust opacity in the frequency range 100 to 353 GHz, in a 24°(l) × 8°(b) region of the Galactic plane. This is possible to achieve after the removal of the free-free emission contribution at these frequencies, which can be as high as 20–40% of the total emission in the thin and ionized disk of the Galaxy. Here we summarize our results:
-
The spectral index of the dust opacity in the millimetrewavelength range, βmm, and in the Galactic plane has a median value of 1.60 ± 0.06. Thus βmm is smaller than that at FIR frequencies, βFIR, for which we determine a median value of 1.88 ± 0.08.
-
We find that there is no apparent trend of βmm with temperature, as opposed to βFIR, for which the anti-correlation has been examined in several previous studies.
-
We find that βmm is, however, correlated with the derived dust optical depth at 353 GHz. We interpret this correlation as an evolution of βmm with the fraction of molecular gas along the line of sight, fH2. Within this scenario, βmm ~ 1.54 when the medium is mostly atomic, whereas it increases to about 1.66 when the medium is predominantly molecular.
-
The results on βmm are compared with predictions from two different physical models, TLS and emission by ferromagnetic grains, which have been suggested to explain the flattening of the dust emission observed at long wavelengths. We find that both models can in principle explain the results. The same applies to the standard, two dust component models, such as DL07 and DustEM.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Following the definition of brightness temperature by Spitzer (1978), in the Rayleigh-Jeans regime.
Acknowledgments
We acknowledge the use of the HEALPix (Górski et al. 2005) package and IRAS data. The Planck Collaboration acknowledges support from: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and DEISA (EU). A detailed description of the Planck Collaboration and a list of its members can be found at http://www.rssd.esa.int/index.php?project=PLANCK&page=Planck_Collaboration. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n° 267934.
References
- Agladze, N. I., Sievers, A. J., Jones, S. A., Burlitch, J. M., & Beckwith, S. V. W. 1996, ApJ, 462, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Ali-Haïmoud, Y., Hirata, C. M., & Dickinson, C. 2009, MNRAS, 395, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, M. I. R., Davies, R. D., Dickinson, C., et al. 2010, MNRAS, 405, 1654 [NASA ADS] [Google Scholar]
- Alves, M. I. R., Davies, R. D., Dickinson, C., et al. 2012, MNRAS, 422, 2429 [NASA ADS] [CrossRef] [Google Scholar]
- Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J. 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, Explanatory supplement, 1 [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boudet, N., Mutschke, H., Nayral, C., et al. 2005, ApJ, 633, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coupeaud, A., Demyk, K., Meny, C., et al. 2011, A&A, 535, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. D., Watson, R. A., & Gutierrez, C. M. 1996, MNRAS, 278, 925 [NASA ADS] [CrossRef] [Google Scholar]
- de Oliveira-Costa, A., Kogut, A., Devlin, M. J., et al. 1997, ApJ, 482, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, F.-X., Macías-Pérez, J. F., Mayet, F., et al. 2008, A&A, 481, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Draine, B. T., & Hensley, B. 2012, ApJ, 757, 103 [CrossRef] [Google Scholar]
- Draine, B. T., & Hensley, B. 2013, ApJ, 765, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998, ApJ, 494, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J.-P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, T., Banday, A. J., Jaffe, T., et al. 2012, MNRAS, 422, 3617 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, M. A., & Sorochenko, R. L. 2009, Radio Recombination Lines (Springer Verlag), Astrophys. Space Sci. Lib. [Google Scholar]
- Gordon, K. D., Galliano, F., Hony, S., et al. 2010, A&A, 518, L89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Draine, B. T., & Lazarian, A. 2010, ApJ, 715, 1462 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Lazarian, A., & Draine, B. T. 2011, ApJ, 741, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Israel, F. P., Wall, W. F., Raban, D., et al. 2010, A&A, 519, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., & Ysard, N. 2012a, A&A, 541, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., & Ysard, N. 2012b, A&A, 539, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., McClure-Griffiths, N. M., Pisano, D. J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelly, B. C., Shetty, R., Stutz, A. M., et al. 2012, ApJ, 752, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Banday, A. J., Bennett, C. L., et al. 1996, ApJ, 464, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagache, G., Bavouzet, N., Fernandez-Conde, N., et al. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitch, E. M., Readhead, A. C. S., Pearson, T. J., & Myers, S. T. 1997, ApJ, 486, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- McClure-Griffiths, N. M., Pisano, D. J., Calabretta, M. R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, A., Butler, R. C., Curto, A., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meny, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]
- Miville-Deschênes, M., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., Lagache, G., & Puget, J.-L. 2002, A&A, 393, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladini, R., Montier, L., Giard, M., et al. 2007, A&A, 465, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Bernard, J.-P., & Mény, C. 2009, A&A, 506, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Bernard, J.-P., Mény, C., & Gromov, V. 2011, A&A, 534, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Paladini, R., Noriega-Crespo, A., et al. 2012, A&A, 537, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2011, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVII. 2011, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2011, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2011, A&A, 536, A24 [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XII. 2013, A&A, 557, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration II. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321550 [Google Scholar]
- Planck Collaboration VI. 2014, A&A, submitted [arXiv:1303.5067] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321531 [Google Scholar]
- Planck Collaboration XI. 2014, A&A, submitted [Google Scholar]
- Planck Collaboration XII. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321580 [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, submitted [arXiv:1303.5073] [Google Scholar]
- Planck Collaboration XIV. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321562 [Google Scholar]
- Planck Collaboration Int. XV. 2014, A&A, in press [arXiv:1309.1357] [Google Scholar]
- Planck Collaboration Int. XVII. 2014, A&A, submitted DOI: 10.1051/0004-6361/201323270 [Google Scholar]
- Planck HFI Core Team. 2011, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reach, W. T., Dwek, E., Fixsen, D. J., et al. 1995, ApJ, 451, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Rohlfs, K., & Wilson, T. L. 2000, Tools of Radio Astronomy (New York: Springer) [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sajina, A., Scott, D., Dennefeld, M., et al. 2006, MNRAS, 369, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., & Goodman, A. A. 2009a, ApJ, 696, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009b, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1978, Physical processes in the interstellar medium (New York: Wiley) [Google Scholar]
- Staveley-Smith, L., Wilson, W. E., Bird, T. S., et al. 1996, Publ. Astron. Soc. Aust., 13, 243 [Google Scholar]
- Staveley-Smith, L., Juraszek, S., Koribalski, B. S., et al. 1998, AJ, 116, 2717 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strasser, S., & Taylor, A. R. 2004, ApJ, 603, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., Braine, J., Xilouris, E. M., et al. 2014, A&A, 561, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., & Verstraete, L. 2010, A&A, 509, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Results from a modified blackbody fit to the DL07 and DustEM spectra for different scalings of the ISRF, given by G0.
All Figures
 |
Fig. 1 HFI 353 GHz map of the Galactic plane region l = 20°–44°, |b| ≤ 4°, in units of MJy sr-1 and at 15′ resolution. |
| In the text | |
 |
Fig. 2 Spectra towards the H ii region complex W42 (red) and a diffuse region in
the Galactic plane centred at (l, b) = |
| In the text | |
 |
Fig. 3 Histograms of the dust temperature a) and dust opacity indices b) for the 24° × 8° region. The dashed lines in both panels correspond to the pixels where τ353 ≥ 4×10-4. In panel a) the dashed histogram is scaled up by a factor of four. |
| In the text | |
 |
Fig. 4 Comparison of the results on βmma) when the CO and free-free corrections vary by 10%; b) when Td is allowed to vary in the fit and also when Td is fixed to a single value of 19 K. |
| In the text | |
 |
Fig. 5 Dust spectral indices as a function of temperature. a) βFIR versus Td for the whole 24° × 8° region. b) βFIR versus Td for points where τ353 ≥ 4 × 10-4. c) βmm versus Td for points where τ353 ≥ 4 × 10-4. The triangle and square in panels b) and c) indicate the values obtained by fitting the emissivities predicted by the TLS model (Paradis et al. 2011) for Td = 17 and 25 K (see Sect. 6.1.2). The colour scale is logarithmic and it represents the density of points. The contours show the densities for the cumulated fractions, given by the values in each panel, of the data points, from red to yellow. |
| In the text | |
 |
Fig. 6 Distribution of βmm as a function of τ353, for the whole region. The red line gives the best linear fit for τ353 ≥ 4 × 10-4 (see text). The colour scale is logarithmic and it represents the density of points. The three contours show the densities for a cumulated fraction of 11, 31, and 62% of the data points, from red to yellow. |
| In the text | |
 |
Fig. 7 Dust opacity index βmm recovered from the simulated maps, as a function of the input τ353. The simulated maps in a) have dust emission and CMB, and in b) consist of dust, free-free and CO emission. The black line shows the input βmm of 1.52 in each case; the red lines give the βmm–τ353 relationship derived in Sect. 5. The colour scale is logarithmic and it represents the density of points. The three contours show the densities for the cumulated fractions, given by the values in each panel, of the data points, from red to yellow. |
| In the text | |
 |
Fig. 8 Maps of the dust parameters. Top: βmm, which results from the best linear fit to the correlation with optical depth given by Eq. (2); middle: τ353; bottom: Td. |
| In the text | |
 |
Fig. 9 Distribution of βmm as a function of τ353, for the whole region, when the SMICA CMB map is subtracted from each channel map. The black line gives the βmm–τ353 relationship derived from a fit to the points where τ353 ≥ 4 × 10-4, compared to that estimated in Sect. 5 and given by the red line. The colour scale is logarithmic and it represents the density of points. The three contours show the densities for a cumulated fraction of 5, 30, and 56% of the data points, from red to yellow. |
| In the text | |
 |
Fig. 10 Spectra towards the H ii region complex W42 (red) and a diffuse region
in the Galactic plane centred at |
| In the text | |
 |
Fig. 11 The MILCA CO line intensity as a function of the dust optical depth τ353,
corrected for the atomic gas contribution, along b = 0° in the
l = 20°– |
| In the text | |
 |
Fig. 12 Opacity spectral indices as a function of the fraction of molecular gas along the line of sight. a)βmm versus fH2. b) βFIR versus fH2. The points correspond to the thin Galactic disk, |b|< ~1° or τ353 ≥ 4 × 10-4. Here fH2 is estimated assuming that the dust opacity in the molecular phase is twice that of the atomic medium, R = 2, and using XCO = 2.1 × 1020 cm-2 (K km s-1)-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.