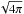| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322451 | |
| Published online | 03 December 2013 | |
Radiation magnetohydrodynamics in global simulations of protoplanetary discs
1 CEA, Irfu, SAp Centre de Saclay 91191 Gif-sur-Yvette France
e-mail: Mario.Flock@cea.fr
2 UMR AIM, CEA-CNRS-Univ. Paris Diderot, Centre de Saclay, 91191 Gif-sur-Yvette, France
3 Université Paris Diderot, Sorbonne Paris Cité, AIM, UMR 7158, CEA, CNRS, 91191 Gif-sur-Yvette, France
4 Laboratoire de radioastronomie, UMR 8112 du CNRS, École normale supérieure et Observatoire de Paris, 24 rue Lhomond, 75231 Paris Cedex 05, France
Received: 6 August 2013
Accepted: 18 October 2013
Aims. Our aim is to study the thermal and dynamical evolution of protoplanetary discs in global simulations, including the physics of radiation transfer and magneto-hydrodynamic turbulence caused by the magneto-rotational instability.
Methods. We have developed a radiative transfer method based on the flux-limited diffusion approximation that includes frequency dependent irradiation by the central star. This hybrid scheme is implemented in the PLUTO code. The focus of our implementation is on the performance of the radiative transfer method. Using an optimized Jacobi preconditioned BiCGSTAB solver, the radiative module is three times faster than the magneto-hydrodynamic step for the disc set-up we consider. We obtain weak scaling efficiencies of 70% up to 1024 cores.
Results. We present the first global 3D radiation magneto-hydrodynamic simulations of a stratified protoplanetary disc. The disc model parameters were chosen to approximate those of the system AS 209 in the star-forming region Ophiuchus. Starting the simulation from a disc in radiative and hydrostatic equilibrium, the magneto-rotational instability quickly causes magneto-hydrodynamic turbulence and heating in the disc. We find that the turbulent properties are similar to that of recent locally isothermal global simulations of protoplanetary discs. For example, the rate of angular momentum transport α is a few times 10-3. For the disc parameters we use, turbulent dissipation heats the disc midplane and raises the temperature by about 15% compared to passive disc models. The vertical temperature profile shows no temperature peak at the midplane as in classical viscous disc models. A roughly flat vertical temperature profile establishes in the optically thick region of the disc close to the midplane. We reproduce the vertical temperature profile with viscous disc models for which the stress tensor vertical profile is flat in the bulk of the disc and vanishes in the disc corona.
Conclusions. The present paper demonstrates for the first time that global radiation magneto-hydrodynamic simulations of turbulent protoplanetary discs are feasible with current computational facilities. This opens up the window to a wide range of studies of the dynamics of the inner parts of protoplanetary discs, for which there are significant observational constraints.
Key words: accretion, accretion disks / radiative transfer / magnetohydrodynamics (MHD) / protoplanetary disks / methods: numerical
© ESO, 2013
1. Introduction
The understanding of planet formation requires a deep insight into the physics of protoplanetary discs. Recent observations of young discs in nearby star-forming regions (Furlan et al. 2009; Andrews et al. 2009) have been able to constrain important physical parameters, like the disc mass and radial extent, its flaring index, or the dust-to-gas mass ratio. Our understanding of these observations is mainly based on 2D radiative viscous disc models (Chiang & Goldreich 1997; D’Alessio et al. 1998; Dullemond et al. 2002) that include proper dust opacities and irradiation by the star. The energy released by the accretion process is an important source for determining the structure and the evolution of the inner disc regions. The magneto-rotational instability (MRI) is the most likely candidate to drive accretion by an effective viscosity from magnetic turbulence (Balbus & Hawley 1998). Up to now there has been no global model which combines both magneto-hydrodynamics (MHD) turbulence driven by the MRI and the radiative transfer including irradiation by the star and proper dust opacities. The main challenge to performing these simulations is the computational effort. Global MHD simulations need high resolutions to resolve the MRI properly (Fromang & Nelson 2006; Flock et al. 2010; Sorathia et al. 2012) and the computational cost required to solve additional radiative transfer equations remains a challenge. The first full radiation magneto-hydrodynamics (RMHD) of that problem were performed in local box simulations by Turner et al. (2003) using a flux-limited diffusion (FLD) approach (Levermore & Pomraning 1981). Over the past few years, several accretion disc simulations have been performed using similar numerical schemes (Turner 2004; Hirose et al. 2006; Blaes et al. 2007; Krolik et al. 2007; Flaig et al. 2009) and have recently included irradiation heating (Hirose & Turner 2011). More sophisticated radiation hydrodynamics (RHD) methods, like the two-moment method (González et al. 2007), are usually very time demanding because they require large matrix inversion. In this work we develop a radiative transfer method based on the two-temperature grey1 FLD approach by Commerçon et al. (2011) and the hybdrid FLD approach (Kuiper et al. 2010) that includes frequency dependent irradiation by the star. This hybrid scheme accurately captures the irradiation energy by the star and performs well compared to computational expensive Monte Carlo radiative transfer methods (Kuiper & Klessen 2013). We particularly focus on the serial and parallel performance of our method. The model we design is especially suited for global RMHD disc calculations. Our paper is split into the following parts. In Sect. 2 we describe the RMHD equations, the numerical scheme, and a performance test. In Sect. 3 we explain our initial conditions for global RMHD disc calculations, the iteration method for calculating the disc’s radiative hydrostatic equilibrium, and the boundary conditions. In Sect. 4 we present the results, followed by the discussion and the conclusion. In the Appendix we show details of the discretization of the FLD method, the numerical developments, and tests.
2. Numerical implementations
2.1. Equations and numerical scheme
In this paper we solve the ideal RMHD equations using the FLD approximation. We use a spherical coordinate system (r,θ,φ) which has advantages for the treatment of stellar irradiation by means of a simple ray-tracing approach and because it is well adapted to the flared structure of protoplanetary discs. The set of equations reads
![\begin{eqnarray} && \frac{\partial \rho}{\partial t} + \nabla \cdot \left [\rho \boldsymbol{v}\right ]=0 , \label{eq:MDH_RHO} \\ && \frac{\partial \rho \boldsymbol{v}}{\partial t} + \nabla \cdot \left [ \rho \boldsymbol{v} \boldsymbol{v}^T - \boldsymbol{B}\boldsymbol{B}^T \right ] + \nabla P_{\rm t} = - \rho \nabla \Phi , \label{eq:MDH_MOM} \\ &&\frac{\partial E}{\partial t} + \nabla \cdot \left [ (E + P_t)\boldsymbol{v} - (\boldsymbol{v}\cdot\boldsymbol{B})\boldsymbol{B} \right ] = - \rho \boldsymbol{v} \cdot \nabla \Phi \nonumber\\& & \hspace*{48mm} - \kappa_\mathrm{P}( {T}) \rho c ( a_{\rm R} T^4 - E_{\rm R} )\nonumber\\ & & \hspace*{48mm}- \nabla \cdot {F}_* , \label{eq:MDH_EN} \\ && \partial_t E_{\rm R} - \nabla \frac{c \lambda}{\kappa_\mathrm{R}({T}) \rho} \nabla E_{\rm R} = + \kappa_\mathrm{P}({T}) \rho {c} (a_{\rm R} T^4 -E_{\rm R}) , \label{eq:ER} \\ && \frac{\partial B}{\partial t} + \nabla \times (\boldsymbol{v} \times \boldsymbol{B}) = 0 , \label{eq:MDH_MAG} \end{eqnarray}](/articles/aa/full_html/2013/12/aa22451-13/aa22451-13-eq7.png) in which the two coupled equations for the radiation transfer are
in which the two coupled equations for the radiation transfer are
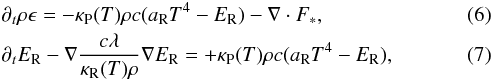 with the density ρ, the velocity vector v, the magnetic field vector2B, the total pressure Pt = P + 0.5B2, the gas pressure P = ρkBT/(μgu) with the gas temperature T, the mean molecular weight μg, the Boltzmann constant kB, the atomic mass unit u, the gravitational potential Φ = GM∗/r with the gravitational constant G, stellar mass M∗, r the radial distance to the star, the total energy E = ρϵ + 0.5ρv2 + 0.5B2 with the gas internal energy ρϵ, the radiation energy ER, the irradiation flux F∗, the Rosseland and Planck mean opacity κR and κP, the radiation constant aR = (4σ)/c with the Stefan-Boltzmann constant σ = 5.6704 × 10-5 erg cm-2 s-1 K-4, and c the speed of light. To enforce causality, we use the flux limiter λ = (2 + R)/(6 + 3R + R2) by Levermore & Pomraning (1981, Eq. (28) therein) with R = |∇ER|/(κRρER). The closure relation between gas pressure and internal energy is provided by the ideal gas equation of state P = (Γ − 1)ρϵ, with the adiabatic index Γ. We choose a mixture of hydrogen and helium with solar abundance (Decampli et al. 1978; Bitsch et al. 2013a) so that μg = 2.35 and Γ = 1.42.
with the density ρ, the velocity vector v, the magnetic field vector2B, the total pressure Pt = P + 0.5B2, the gas pressure P = ρkBT/(μgu) with the gas temperature T, the mean molecular weight μg, the Boltzmann constant kB, the atomic mass unit u, the gravitational potential Φ = GM∗/r with the gravitational constant G, stellar mass M∗, r the radial distance to the star, the total energy E = ρϵ + 0.5ρv2 + 0.5B2 with the gas internal energy ρϵ, the radiation energy ER, the irradiation flux F∗, the Rosseland and Planck mean opacity κR and κP, the radiation constant aR = (4σ)/c with the Stefan-Boltzmann constant σ = 5.6704 × 10-5 erg cm-2 s-1 K-4, and c the speed of light. To enforce causality, we use the flux limiter λ = (2 + R)/(6 + 3R + R2) by Levermore & Pomraning (1981, Eq. (28) therein) with R = |∇ER|/(κRρER). The closure relation between gas pressure and internal energy is provided by the ideal gas equation of state P = (Γ − 1)ρϵ, with the adiabatic index Γ. We choose a mixture of hydrogen and helium with solar abundance (Decampli et al. 1978; Bitsch et al. 2013a) so that μg = 2.35 and Γ = 1.42.
After the MHD step, the method solves the two coupled radiative transfer Eqs. (6) and (7). We neglect in the equations all terms of the order v/c (Krumholz et al. 2007), including the radiation pressure terms and the radiation force in the momentum equations since ER ≪ ρϵ. These approximations are well suited to our applications (v ≪ c), but not necessarily to other regimes like the dynamic diffusion (Krumholz et al. 2007). A similar method was presented in Bitsch et al. (2013b) and Kolb et al. (2013).
 |
Fig. 1 Dust absorption opacity over wavelengths. |
It has recently been shown that frequency dependent irradiation is more accurate in the context of protoplanetary discs for capturing irradiation heating (Kuiper et al. 2010; Kuiper & Klessen 2013). The irradiation flux F∗ at a radius r is calculated as 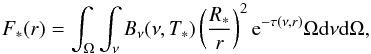 (8)with the Planck function Bν(ν,T∗), the solid angle Ω, the surface temperature of the star T∗, the radius of the star R∗, the frequency ν, and the radial optical depth for the irradiation flux
(8)with the Planck function Bν(ν,T∗), the solid angle Ω, the surface temperature of the star T∗, the radius of the star R∗, the frequency ν, and the radial optical depth for the irradiation flux 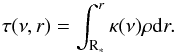 (9)The irradiation by the star is used as a source term in Eq. (3). This approximation is valid because of the short penetration time for stellar rays through the domain compared to the longer hydrodynamical timescale.
(9)The irradiation by the star is used as a source term in Eq. (3). This approximation is valid because of the short penetration time for stellar rays through the domain compared to the longer hydrodynamical timescale.
Figure 1 shows the frequency dependent dust absorption opacity. The opacity tables are derived for particle sizes of 1 μm and below (Draine & Lee 1984). We note that for the setup presented in this paper the temperature stays below the dust evaporation temperature of about 1000 K so that we can neglect the gas opacities. To calculate the opacity involved in the RMHD equations we take into account the dust-to-gas mass ratio for small particles which we define as 1% of the total dust-to-gas mass ratio ϵd2g (Birnstiel et al. 2012).
The ideal MHD equations are solved using the PLUTO code (Mignone 2009). The PLUTO code is a highly modular, multidimensional, and multi-geometry code that can be applied to relativistic or non-relativistic (magneto-)hydrodynamics flows. For this work we chose the Godunov-type finite volume configuration which consists of a second order space reconstruction, a second-order Runge-Kutta time integration, the constrained transport (CT) method (Gardiner & Stone 2005), the orbital advection scheme FARGO MHD (Masset 2000; Mignone et al. 2012), the HLLD Riemann solver (Miyoshi & Kusano 2005), and a Courant number of 0.3. In this work we neglect the magnetic dissipation which would appear at the right-hand side of Eq. (5). The effect of magnetic dissipation is discussed in the Conclusion.
To solve Eqs. (6) and (7) we use an implicit method because the gas velocities are small compared to the speed of light. The implicit discretized equations in spherical coordinates can be found in the Appendix A.1. We rewrite the radiative transfer equations in the matrix form Ax = b where x is the solution vector. The solution of this system involves a matrix inversion and is solved by an iterative method to minimize the residual r = Ax − b until a given accuracy is reached. We use the Jacobi-preconditioned BiCGSTAB solver based on the work by Van der Vorst (1992). As a convergence criteria we use the reduction of the L2 norm of the residual, ||r||2/||rinit||2 < 10-4.
2.2. Validation of the radiative transfer method
As a validation of our algorithm, we performed the radiation transfer test for discs described by Pascucci et al. (2004). We computed the spatial distribution of the equilibrium temperature of a static disc irradiated by a star using different radiative transfer methods. We compared the results of our method with the results obtained using the Monte Carlo radiative transfer code RADMC-3D3 (Dullemond 2012). Following Pascucci et al. (2004), we used the opacity table of Draine & Lee (1984), a dust-to-gas mass ratio of 0.01, and frequency dependent irradiation with 61 frequency bins. The star parameters are T∗ = 5800 K with R∗ = 1 R⊙ and M∗ = 1M⊙. The gas density follows 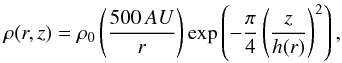 (10)with
(10)with 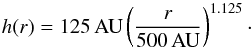 (11)We present here the most optically thick disc configuration of Pascucci et al. (2004) for which ρ0 = 8.321 × 10-18 g cm-3. The initial temperature is set to 10 K. The domain size ranges from 1 to 1000 AU in radius and from 0 to π in θ. We use a grid with logarithmically increasing cell size in radius and uniform in θ. The overall grid contains 240 × 100 cells. The boundary conditions of the radiation energy are fixed to 10 K in the poloidal direction and zero gradient in the radial direction. We solve the radiative transfer equations with a fixed time-step until we reach thermal equilibrium. The convergence criterion is |res|2/|resinit|2 < 10-8. In RADMC-3D we use 2.1 × 1010 photons. We plot the temperature profile over radius and height in Fig. 2. Both profiles agree very well with the results by RADMC-3D. In Appendix A.2, we describe a resolution study of this test to determine the order of the scheme. We also perform an additional diffusion test for our FLD method, which we present for completeness.
(11)We present here the most optically thick disc configuration of Pascucci et al. (2004) for which ρ0 = 8.321 × 10-18 g cm-3. The initial temperature is set to 10 K. The domain size ranges from 1 to 1000 AU in radius and from 0 to π in θ. We use a grid with logarithmically increasing cell size in radius and uniform in θ. The overall grid contains 240 × 100 cells. The boundary conditions of the radiation energy are fixed to 10 K in the poloidal direction and zero gradient in the radial direction. We solve the radiative transfer equations with a fixed time-step until we reach thermal equilibrium. The convergence criterion is |res|2/|resinit|2 < 10-8. In RADMC-3D we use 2.1 × 1010 photons. We plot the temperature profile over radius and height in Fig. 2. Both profiles agree very well with the results by RADMC-3D. In Appendix A.2, we describe a resolution study of this test to determine the order of the scheme. We also perform an additional diffusion test for our FLD method, which we present for completeness.
2.3. Serial and parallel performance
 |
Fig. 2 Top: θ-temperature profile at a radius of 2 AU. Bottom: radius-temperature profile at the midplane. |
An important emphasis of our work was to develop a module with high computational efficiency. During the development, we focused on reducing the number of operations per iteration cycle of the implicit method. By increasing the memory usage we substantially improved the performance of the algorithm. We performed an analysis of our module for the fiducial disc model (see Sect. 4). The MHD part takes 76.3%, while the radiation module consumes 22.5% of a full RMHD step. In our module each matrix vector multiplication per iteration in the BiCGSTAB method has the main computational cost with 8.2% from the full RMHD step, followed by the frequency dependent irradiation with 5.9%. In the following we present a weak scaling test. The number of iterations by the matrix solver was fixed to 30 which is a typical value for reaching convergence in our global high-resolution model. We used 323 cells per cpu as in this model, for which we used 1024 cores. Figure 3 shows the parallel performance of the RMHD module using an Intel Xeon 2.27 Ghz system. With 1024 cores we reached a scaling efficiency of 70.3% which is acceptable given the non-local nature of the algorithm. Nevertheless, the parallel performance is lower than the pure Godunov scheme (Mignone et al. 2007). This is largely due to the important amount of communications inside the BiCGSTAB method. Here one has to distribute all neighboring cells three times for each core per iteration to compute the new residual. As the number of iterations strongly depends on the physical problem, we do not a priori know the serial and the parallel performance for a given application. We note that the parallel performance also depends on the ratio between the number of grid cells to communicate over the grid cells per core. Reducing the number of cells below 323 per core would result in reduced scaling performance.
 |
Fig. 3 Weak scaling of the RMHD method (blue line) compared with optimal scaling (black line). Units are given in total number of grid cells per step per second. |
3. Initial disc structure and boundary conditions
As an illustration of the possibilities offered by our numerical implementation of a FLD scheme within the PLUTO code, we present in the remaining of this paper a series of 3D RMHD simulations of a fully turbulent protoplanetary disc. In this section, we describe the disc model parameters and the iterative procedure we designed to construct an initial setup that is in hydrostatic equilibrium. Boundary conditions in these simulations turned out to be subtle, so we also detail the set of conditions we used in this particular case. We caution that finding a proper set of boundary conditions is delicate and likely to be problem dependent.
3.1. An iterative procedure
Finding an irradiated disc structure in hydrostatic equilibrium is not a straightforward task. For a given irradiation source, the disc temperature depends on the spatial density distribution which itself depends on temperature (because of the pressure force). We thus solved for the hydrostatic disc structure iteratively: assuming a given density in the disc, we calculated the temperature as a result of disc irradiation using the hybrid FLD module described above. To calculate the new radiation and temperature field we used the typical diffusion time for this problem. The diffusion time can be estimated by Δtdif ~ 3κρΔx2/c. Using typical values at 1 AU with solar parameters ρ = 10-10 g cm-3, κ = 1 cm2 g-1, and Δx = 1 AU, we obtain Δtdif ~ 106 s. After the temperature and radiation field have reached equilibrium, a new density profile is calculated and the algorithm iterates until convergence.
 |
Fig. 4 Initial temperature distribution for different amounts of small dust particles (≤1 μm), calculated from radiative hydrostatic equilibrium. From top to bottom: Σdust(1 AU) = 0.17,0.017,0.0017 g cm-2. We overplot the radial integrated τ = 1 line for the irradiation (black solid line) and the vertically integrated τ = 1 for the local thermal emission (red solid line). |
The following input parameters are needed: the surface density over radius Σ(r), the opacity including the dust-to-gas mass ratio, and the stellar parameters T∗, M∗, and R∗. The density and the azimuthal velocity vφ are updated integrating the equations of hydrostatic equilibrium in spherical coordinates using a second-order Runge Kutta method. In hydrostatic equilibrium these are, for the radial and poloidal direction, respectively,
 Once ρ(r,θ0) is known for a given value of θ0 (e.g. θ0 = π/2 for the midplane) and for all r, Eq. (12) can be used to calculate vφ(r,θ0). The second equation is then integrated to give the density field at the next interface θ0 + Δθ/2 for any value of r, and we can repeat the cycle. Using the mid-point integral method we reach second-order accuracy. We impose the midplane gas density using
Once ρ(r,θ0) is known for a given value of θ0 (e.g. θ0 = π/2 for the midplane) and for all r, Eq. (12) can be used to calculate vφ(r,θ0). The second equation is then integrated to give the density field at the next interface θ0 + Δθ/2 for any value of r, and we can repeat the cycle. Using the mid-point integral method we reach second-order accuracy. We impose the midplane gas density using 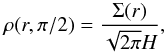 (14)where
(14)where 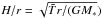 and
and 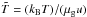 . The above relation is only valid for a constant vertical temperature and so a Gaussian vertical density profile. We do not expect this to be the case here since the temperature can vary with distance to the midplane. However, the bulk of the disc around the midplane has a constant vertical temperature (see Fig. 4 and Sect. 3.2 below). Since this is the location where most of the mass is located, the actual surface density is close to the targeted value with small deviations of 10-3. To reach a higher accuracy, we multiply the density in each grid cell by a constant factor Σtarget/Σ so that we reach the target value before calculating the new temperature. We iterate the procedure until both the temperature and density field have converged to better than max((Tn + 1 − Tn)/Tn,(ρn + 1 − ρn)/ρn) ≤ 10-8, where n is the number of iterations. A validation of this iterative method is presented in Appendix B by reproducing the passive disc model of Chiang & Goldreich (1997).
. The above relation is only valid for a constant vertical temperature and so a Gaussian vertical density profile. We do not expect this to be the case here since the temperature can vary with distance to the midplane. However, the bulk of the disc around the midplane has a constant vertical temperature (see Fig. 4 and Sect. 3.2 below). Since this is the location where most of the mass is located, the actual surface density is close to the targeted value with small deviations of 10-3. To reach a higher accuracy, we multiply the density in each grid cell by a constant factor Σtarget/Σ so that we reach the target value before calculating the new temperature. We iterate the procedure until both the temperature and density field have converged to better than max((Tn + 1 − Tn)/Tn,(ρn + 1 − ρn)/ρn) ≤ 10-8, where n is the number of iterations. A validation of this iterative method is presented in Appendix B by reproducing the passive disc model of Chiang & Goldreich (1997).
3.2. Simulation parameters: the case of AS 209
We used the scheme detailed above to calculate the initial disc structure of the series of simulations presented in Sect. 4. We chose stellar and disc parameters inspired from those of the circumstellar disc AS 209 in the Ophiuchus star-forming region, for which there are a number of observational constraints (Koerner & Sargent 1995; Andrews et al. 2009; Pérez et al. 2012). Stellar mass, radius, and surface temperature are well constrained parameters and we adopted the same values as Andrews et al. (2009) with 0.9 M⊙, 2.3 R⊙, and 4250 K. The gas surface density Σ in the inner region of AS 209 is nearly a free parameter and only constrained indirectly by the dust surface density. Andrews et al. (2009) estimated for this system a total dust surface density (including all particle sizes) of less than 1 g cm-2 at 1 AU from the star.
For radiation hydrodynamics, the distribution of the small particles (≤1 μm) is very important because these particles dominate the opacity at optical, near and mid-infrared wavelengths. They contain most of the dust surface, which is the controlling parameter for the opacity. By contrast, most of the dust mass, almost 99%, is stored in larger particles (Birnstiel et al. 2012). Roughly speaking, the dust surface density of the small particles can be estimated to be less than 0.01 g cm-2, using the parameters by Andrews et al. (2009). We have calculated our disc structure for three different amounts of small dust particles: Σdust(1 AU) = 0.17,0.017,0.0017 g cm-2. The initial temperature distribution in radiative hydrostatic equilibrium for the three cases is shown in Fig. 4. In the top panel, Σdust(1 AU) = 0.17 g cm-2 and the disc displays a large optically thick region. In the bottom panel, where Σdust(1 AU) = 0.0017 g cm-2, we find a very extended heated upper region while the disc midplane is completely optically thin to its own thermal radiation. Between these two extrema we chose our fiducial model with a dust surface density of Σdust(1 AU) = 0.017 g cm-2. In this configuration (shown in the middle panel in Fig. 4), both an optically thick midplane and an extended optically thin corona fit within the computational domain. The gas surface density is set to Σ(r) = 1700 g cm-2(r/1 AU)-0.9, such that it equals the minimum mass solar nebula (MMSN) value at 1 AU, but it displays a shallower slope than the MMSN suggested by Andrews et al. (2009), even if those constraints come from larger radial distances. Assuming again that small particles carry only 1% of the total dust mass, we obtain a total dust-to-gas mass ratio ϵd2g of 10-3 in our fiducial model.
Summary of model parameter.
The simulation spans the radial range r = 0.5 − 1.5 AU, the poloidal range θ = π/2 ± 0.13, and the azimuthal range φ = 0 − π/3. For the fiducial model in initial equilibrium, we obtain H/r = 0.02 at 0.5 AU which results in ±6.5 scale heights fitting in the computational domain at its inner boundary. Because of the disc flaring the value of H/r at the outer radius is larger, with H/r = 0.03 corresponding to ±4.3 scale heights at the outer boundary.
3.3. Boundary conditions
Finding suitable boundary conditions for a stable and physically reasonable global simulation such as presented in this paper is already difficult in ideal MHD. Radiative transfer makes the problem even more difficult. In this section we describe in detail the boundary conditions we have designed for that purpose. Straightforward periodic boundary conditions are used for all variables in the azimuthal direction, so we focus on the radial and poloidal boundaries.
In the radial direction we extrapolated linearly the density and azimuthal velocity. Radial and poloidal velocities were all set to zero gradient. In the case of inflowing gas with a Mach number of 0.1 or higher, we forced the radial velocity boundary condition to be reflective. The poloidal and toroidal magnetic field components were set to follow a 1/r profile, while the radial magnetic field was calculated to ensure ∇·B = 0 in the ghost cells. Temperature was set to zero gradient and we used 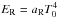 for the radiation energy density ER with T0 being the initial radiative hydrostatic equilibrium temperature. In order to avoid irradiation from directly illuminating the first radial cell of the computational domain, we set a vertical dependent optical depth τinit(θ) = κ0(θ)ρ0(θ)(r0 − 6R∗) with the subscript 0 corresponding to the first cell in the radial direction. Using six stellar radii as the inner disc edge is a reasonable approximation to absorb most of the irradiation at the disc midplane, as would be done by the inner parts of the disc4. Accordingly, the Rosseland opacity at the radial boundary was modified in the optically thick region so that κ0ρ0Δr < 0.1. Even if this boundary condition seems unrealistic it will prevent an artificial pile up of the radiation energy density near the boundary, and so permits the correct disc flaring (see Appendix B).
for the radiation energy density ER with T0 being the initial radiative hydrostatic equilibrium temperature. In order to avoid irradiation from directly illuminating the first radial cell of the computational domain, we set a vertical dependent optical depth τinit(θ) = κ0(θ)ρ0(θ)(r0 − 6R∗) with the subscript 0 corresponding to the first cell in the radial direction. Using six stellar radii as the inner disc edge is a reasonable approximation to absorb most of the irradiation at the disc midplane, as would be done by the inner parts of the disc4. Accordingly, the Rosseland opacity at the radial boundary was modified in the optically thick region so that κ0ρ0Δr < 0.1. Even if this boundary condition seems unrealistic it will prevent an artificial pile up of the radiation energy density near the boundary, and so permits the correct disc flaring (see Appendix B).
In the poloidal direction we forced the density to drop exponentially. The velocities are set to zero gradient. In the case of inflowing poloidal velocities we reflect vθ in the ghost cells. Tangential magnetic fields are set to zero gradient, while we calculated the poloidal field so as to enforce ∇·B = 0. The temperature was set to zero gradient and the radiation energy density was fixed to 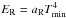 with Tmin = 10 K. The temperature in the poloidal direction has to be small Tmin ≪ Tgas to ensure that the disc can cool by radiating its energy away.
with Tmin = 10 K. The temperature in the poloidal direction has to be small Tmin ≪ Tgas to ensure that the disc can cool by radiating its energy away.
 |
Fig. 5 Snapshot of turbulent rms velocity (left panel) and magnetic field strength (right panel) at the final time of the full RMHD simulation H3D. |
4. Results
Table 1 summarizes the models we performed and provides an overview of the integrated angular momentum transport properties we obtain. Models L3D and L3Dl are low-resolution RMHD simulations, with (Nr,Nθ,Nφ) = (256,64,256). Such a low resolution enables long integration times of about 650 inner orbits. While the dust-to-gas mass ratio in model L3D is equal to our fiducial value of 10-3, it is reduced by one order of magnitude in model L3Dl. To save computational time, we interpolate the results of model L3D after 300 inner orbits on a grid twice as fine. After this time, the MRI has saturated, and we use the interpolated magnetic fields to restart the simulation, which constitutes model H3D. This represents the fiducial model of the present paper and is described in detail in the following sections. In Appendix C we describe the procedure of interpolation and restarting. To connect with previous work, its properties are compared with model H3D-ISO which is a locally isothermal model that uses an azimuthal- and time-averaged temperature profile calculated from the results of model H3D (see Sect. 4.2). Finally, we compare our results with a couple of 2D radiative hydrodynamic simulations (performed in the disc poloidal plane) of viscous discs, namely models H2D and H2D∗, that use different prescriptions for the viscous stress tensor (see Sect. 4.1.2). All MHD simulations are initialized with a pure toroidal magnetic field with a uniform plasma beta value β = 2P/B2 = 40. Initial random velocity fluctuations are added to the initial disc configuration with an amplitude equal to 10-3 of the local speed of sound.
4.1. Model H3D
4.1.1. Turbulent properties
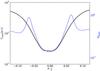 |
Fig. 6 Vertical profile of turbulent rms velocities for model H3D in units of m s-1 (black) and the corresponding turbulent Mach number (blue). The space average is calculated over azimuth at 1 AU with a time average of 100 inner orbits. |
 |
Fig. 7 Vertical stress profile for model H3D in units of dyn cm-2 (black) and normalized using the local pressure (blue). The space average is calculated over azimuth at 1 AU with a time average of 100 inner orbits. |
We start with a general description of the integrated properties of the turbulence in model H3D. The turbulent nature of the flow is best illustrated by Fig. 5 which shows two snapshots of the gas velocity fluctuations and the magnetic field strength in the disc. The root-mean-squared (rms) velocities in the disc midplane range from 1 m s-1 up to 100 m s-1. In the corona the turbulent velocities increase above 1000 m s-1. This is consistent with the azimuthal and time-averaged vertical profile of the gas turbulent velocities shown in Fig. 6 (black curve). When normalized by the local sound speed (blue curve), the plot shows a local Mach number around 0.15 at the midplane. This is typical of values obtained in isothermal simulations (Fromang & Nelson 2006; Flock et al. 2010). However, in contrast with such simulations, the turbulent Mach number reaches a peak (with roughly sonic velocity fluctuations) at around θ − π/2 = 0.07, which corresponds to around two pressure scale heights.
The right panel of Fig. 5 shows the magnetic field strength spatial distribution. In the midplane, it ranges from 0.01 Gauss up to 5 Gauss. In the corona, the field shows larger and smoother fluctuations with values below 1 Gauss. In Fig. 7, we plot the vertical profile of the accretion stress which is the sum of Reynolds and Maxwell stresses 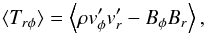 (15)where
(15)where 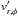 is the radial and azimuthal velocity fluctuations and ⟨ . ⟩ represents the time average. The black curve corresponds to the absolute values of the stress (in cgs units). It displays a peak of ~0.3 dyn cm-2 at about θ − π/2 ~ 0.06, a plateau with a small drop close to the midplane (~0.1 dyn cm-2), and decreases in the disc corona. This profile is in qualitative agreement with results of isothermal local simulations (Simon et al. 2012), as well as in radiative MHD local simulations (Hirose et al. 2006; Flaig et al. 2010), and in locally isothermal global MHD simulations (Fromang & Nelson 2006). By normalizing the stress over the local pressure (blue curve), we also obtain a vertical profile and absolute α values similar to isothermal simulations (Flock et al. 2011). The accretion stress α amounts to about 10-3 in the disc equatorial plane and increases up to a few times 10-1 in the corona. Table 1 also shows the value of the accretion stress volume averaged over the entire computational domain. Following Flock et al. (2011), its normalized value ⟨ α ⟩ is defined according to
is the radial and azimuthal velocity fluctuations and ⟨ . ⟩ represents the time average. The black curve corresponds to the absolute values of the stress (in cgs units). It displays a peak of ~0.3 dyn cm-2 at about θ − π/2 ~ 0.06, a plateau with a small drop close to the midplane (~0.1 dyn cm-2), and decreases in the disc corona. This profile is in qualitative agreement with results of isothermal local simulations (Simon et al. 2012), as well as in radiative MHD local simulations (Hirose et al. 2006; Flaig et al. 2010), and in locally isothermal global MHD simulations (Fromang & Nelson 2006). By normalizing the stress over the local pressure (blue curve), we also obtain a vertical profile and absolute α values similar to isothermal simulations (Flock et al. 2011). The accretion stress α amounts to about 10-3 in the disc equatorial plane and increases up to a few times 10-1 in the corona. Table 1 also shows the value of the accretion stress volume averaged over the entire computational domain. Following Flock et al. (2011), its normalized value ⟨ α ⟩ is defined according to 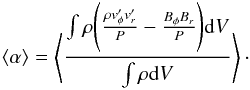 (16)The time average is calculated using between 400 and 500 inner orbits. Again, we find typical values of about a few times 10-3, very similar to transport coefficients measured in locally isothermal global simulations of turbulent protoplanetary discs in the last few years. We note that the changes in the turbulence properties over radius remain small during the simulation. Nevertheless, there are regions of increased activity. This is the case for the region that is about 0.1 AU broad visible in the 3D snapshots close to R ~ 1 AU at the midplane (Fig. 5), where turbulent velocities and magnetic fields are larger. These zones of increased turbulent activity could be connected to long-lived zonal flows such as those observed in local (Johansen et al. 2009; Dittrich et al. 2013) and global simulations (Dzyurkevich et al. 2010; Flock et al. 2011) when using an isothermal equation of state. We now move in the following to the specificities of the present work that are associated with radiative transfer.
(16)The time average is calculated using between 400 and 500 inner orbits. Again, we find typical values of about a few times 10-3, very similar to transport coefficients measured in locally isothermal global simulations of turbulent protoplanetary discs in the last few years. We note that the changes in the turbulence properties over radius remain small during the simulation. Nevertheless, there are regions of increased activity. This is the case for the region that is about 0.1 AU broad visible in the 3D snapshots close to R ~ 1 AU at the midplane (Fig. 5), where turbulent velocities and magnetic fields are larger. These zones of increased turbulent activity could be connected to long-lived zonal flows such as those observed in local (Johansen et al. 2009; Dittrich et al. 2013) and global simulations (Dzyurkevich et al. 2010; Flock et al. 2011) when using an isothermal equation of state. We now move in the following to the specificities of the present work that are associated with radiative transfer.
4.1.2. Temperature evolution
 |
Fig. 8 Top: vertical temperature profile of the RMHD run (black line) and the viscous RHD runs (green lines) for the high-resolution models at 1 AU. Model H2D uses a constant alpha. Model H2D∗ uses a vertical dependence of α ~ 1/ρ which is more similar to the RMHD run. Bottom: relative temperature profile compared to the initial passive disc, for models H2D∗ and H3D. On both panels, the background colour shows the region of the disc where the gas is optically thin to its own thermal radiation and to the irradiation by the star. The grey background colour shows the region where the gas is optically thick to its own radiation. We note that there is also a small region in the disc where the gas is optically thin to its own radiation but still optically thick for the irradiation by the star. |
The time-averaged vertical temperature profile at 1 AU in model H3D is shown in Fig. 8 and is compared with the temperature vertical profile at the start of the simulation (i.e., when the disc is in hydrostatic equilibrium). As a consequence of turbulent heating, the disc midplane temperature increases from around 140 K to 160 K for model H3D. This corresponds to an increase in the disc pressure scale height of 7%. The temperature profile remains flat in the optically thick part of the disc. The temperature rises in the upper layers because of the stellar irradiation. We find a small reduction in the temperature in the upper layers of a few percentage points (bottom panel in Fig. 8) because the disc vertical density profile is flattened in the upper layers as a result of magnetic support (in agreement with previous results; see e.g. Hirose & Turner 2011). This shields the disc corona from the incoming irradiation at a given height compared to the initial model and leads to a small drop in the temperature.
We next investigated whether this vertical temperature profile can be accounted for in the framework of standard α-disc models. We performed an axisymmetric 2D RHD simulation (model H2D) in the disc poloidal plane using a constant α viscosity ν = αcsH with α = 4.6 × 10-3 and the local sound speed cs. The 2D model was initialized using azimuthally averaged values of the density, pressure, temperature, azimuthal velocity, and radiation energy density as obtained in model H3D. The temperature in the 2D viscous RHD model quickly relaxes into a steady state that is overplotted on the top panel in Fig. 8. As we see, a classical α disc prescription does not reproduce the correct midplane temperature. It predicts a midplane temperature of about T = 180 K, which is higher than that of model H3D and does not display the flat temperature profile in the optically thick part of the disc. Here, most of the heat is released at the midplane vicinity because of the scaling of the viscous stress tensor with density. By contrast, the turbulent stress tensor in our simulation is rather flat for | θ − π/2 | ≤ 0.05 (see Fig. 7) with variations of only a factor of ~2. We thus performed an additional 2D RHD simulation, model H2D∗, that uses a different prescription for viscosity5, such that the viscous stress tensor remains constant with height below <± 2 scale heights but vanishes above that location. This α prescription to model the turbulence in 1D or 2D simulations has been used by Kretke & Lin (2010) and Landry et al. (2013). The vertical temperature profile we obtain in that model is also shown in Fig. 8. It shows midplane temperature and vertical profile in much better agreement with the full 3D RMHD model H3D. Besides the gas temperature, one can define the radiation temperature as TER = (ER/aR)1/4. In Fig. 9 we plot the vertical profile of both temperatures after 480 inner orbits. In the optically thick midplane, the two temperatures are well coupled because of the high opacity. In the optically thin upper layers the two temperatures start to diverge owing to the irradiation. The radiation temperature stays at the level of the midplane value. Figure 9 also shows the temperature fluctuations (red dotted line) which are small. The maximum relative temperature fluctuations are close to the τ = 1 line of the irradiation with values between 6 and 7%. In Fig. 10 we plot the time evolution of the azimuthally averaged total stress Trφ over height. The blue contour lines show the peak of stress at each time. They follow the butterfly motions of the mean toroidal field which is triggered by the MRI dynamo (Gressel 2010). The peak of relative temperature fluctuations are close to the azimuthally averaged τ = 1 absorption layer of the irradiation (white line). It suggests that the peak of relative temperature fluctuations is triggered by the fluctuations of the τ = 1 surface.
 |
Fig. 9 Vertical profile of radiation temperature TER = (ER/aR)1/4 (dashed line) and gas temperature (solid line) line at 1 AU. We overplot the range of the temperature fluctuations (red dotted line). The peak of relative temperature fluctuations ΔT/T are around 6−7% at the τ = 1 line (θ ≈ 0.07) for the irradiation (cf. Fig. 10). |
 |
Fig. 10 Time evolution of the azimuthally averaged total stress Trφ over height at 1 AU. We overplot the location of largest stress (blue contour), largest relative temperature fluctuations (black contour), the vertical location of the τ = 1 position of the irradiation (white contour), and the vertical location of the τ = 1 position for the local thermal radiation (green contour) for each time bin. |
4.1.3. Heating and cooling rates
In this section we take a closer look at the heating and cooling rates in the RMHD model H3D. To do so, we proceeded as follows: over any given timestep, we recorded the change in internal energy ΔPMHD/(Γ − 1) that occurred during the MHD step, as well as the change in internal energy ΔPrad/(Γ − 1) that occurred during the radiative step. The former captures all dynamical heating and cooling mechanisms, including the advection of energy or the transfers from kinetic, magnetic, or gravitational energy into thermal energy (see Eq. (3)). We then summed these fractional internal energy changes (divided by the timestep Δt and multiplied by the corresponding cell volume) over a large time interval to compute the heating and cooling rates associated with dynamical and radiative processes. These are respectively labelled QMHD and QRad. Figure 11 shows meridional snapshots of both quantities, in the top (QMHD) and bottom (QRad) panels. Both quantities are azimuthally and time averaged over 40 inner orbits starting after 380 inner orbits. The plots show that most of the disc is being heated with a rate of the order of 1013 erg/s that is mostly released in the disc upper layers, θ − (π/2) ~ 0.05. This corresponds to around two pressure scale heights above the disc midplane. Radiative cooling (bottom panel) roughly balances that heating, showing that the disc is approximately in steady state. To investigate how much of that heat can be attributed to turbulent dissipation, we calculate the expected theoretical heating rate QStress following Balbus & Papaloizou (1999). Figure 12, left, shows a meridional snapshot of the turbulent heating QStress that can be computed according to 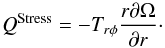 (17)The vertical profiles of the heating rates, plotted in Fig. 12, right, show a good correlation between QStress and QMHD. Most of the disc heating can be attributed to MHD turbulence locally dissipated into heat. In the upper disc layers, the energy is partly transported away by waves.
(17)The vertical profiles of the heating rates, plotted in Fig. 12, right, show a good correlation between QStress and QMHD. Most of the disc heating can be attributed to MHD turbulence locally dissipated into heat. In the upper disc layers, the energy is partly transported away by waves.
4.2. Effect of resolution, equation of state, and dust-to-gas mass ratio
We have focused so far on the high-resolution model H3D. However, both the vertical profile of the turbulent stress and the turbulent velocity depend on several factors, both numerical and physical.
First, the spatial resolution of the grid is known to be of importance. This is a particularly constraining problem in global simulations. Recently, the convergence and the effect of resolution in global adiabatic (Hawley et al. 2013) and locally isothermal (Parkin & Bicknell 2013) simulations were investigated. A convergence study in fully radiative global simulations is difficult to achieve and would go beyond the scope of this paper. As a first step in that direction, we nevertheless present the results of model L3D in which the resolution is reduced by a factor of two, compared to model H3D. In these low-resolution simulations, there are seven grid cells per pressure scale height. This is not enough to properly resolve the MRI (Flock et al. 2010; Sorathia et al. 2012), which leads to a reduction of the total accretion stress. The normalized total accretion stress α varies between 4.6 × 10-3 for model H3D and 2.6 × 10-3 for model L3D. As shown in Fig. 13, the stress vertical profiles of Trφ in both models are significantly different. At the midplane the stress in model L3D drops by one order of magnitude. This is expected, as in stratified MRI simulation it becomes more difficult to properly resolve the MRI at the midplane because of its low magnetization (Fromang & Nelson 2006; Flock et al. 2011).
Second, the isothermal model H3D-ISO shows a reduced stress compared to the full RMHD model H3D. It decreases from 4.6 × 10-3 to 2.5 × 10-3. This trend of increased turbulence in radiative models was also suggested by Flaig et al. (2010). Nevertheless, as shown in Fig. 13, the vertical profile of the stress has a similar shape for both models.
 |
Fig. 11 2D contour plot of the MHD heating and cooling QMHD (top) and the radiative heating and cooling QRad (bottom) in units of 1023, azimuthally and time averaged over 40 inner orbits. |
 |
Fig. 12 Top: 2D contour plot of expected theoretical heating QStress in units of 1023, azimuthally and time averaged over 40 inner orbits. Bottom: vertical profile of the MHD heating QMHD (solid line), radiative cooling − QRad (dashed line), and theoretically expected MHD heating QStress (dotted line). |
 |
Fig. 13 Vertical stress profile in units of dyn cm-2 for the high-resolution models H3D (solid line), H3D-ISO (dotted line), the low-resolution models L3D (dashed line), and L3Dl (dashed-dotted line) with reduced amounts of dust. |
 |
Fig. 14 Vertical profile of gas temperature (solid line) and radiation temperature TER = (ER/aR)0.25 (dashed line) for models L3Dl (red line) and L3D (black line). |
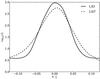 |
Fig. 15 Vertical profile of plasma beta β = 2P/B2 for models L3D (solid line) and L3Dl (dashed line). |
The last effect we want to discuss is the influence of the dust-to-gas mass ratio. In model L3Dl, we reduce it by one order of magnitude to 10-4. As shown in Fig. 4, this shifts the irradiated hotter disc region down to the midplane. In Fig. 14, we plot the temperature profiles at 1 AU, averaged over azimuth and time between 200 and 400 inner orbits. As the disc becomes hotter, the sound speed increases and a higher saturation level of the MRI is expected (Balbus & Hawley 1998). An effect of increased turbulence can be seen by comparing model L3D (dashed line) and model L3Dl (dashed-dotted line) in Fig. 13: the vertical profile of model L3Dl shows an overall larger stress than model L3D. The total normalized stress is increased by 25% (see Table 1), but more important is the position of the maximum stress. The hotter temperature region has shifted by Δθ ~ 0.02 down to the midplane, but the peak stress is still located at θ − π/2 ~ 0.05. This result indicates again that the position of the maximum stress due to MRI is independent of the vertical temperature profile. This position also seems independent of resolution when comparing model L3D and model H3D.
The position of the maximum of the stress is connected to the plasma beta. The vertical profiles of β for the models L3D and L3Dl are shown in Fig. 15, using the same time and space average. Even if the temperature profiles are quite different, the plasma beta value drops at the same height (θ ~ 0.05) in both models. All these results indicate that the vertical shape and especially the location of the peak of MRI turbulent magnetic fields are independent of the vertical temperature profile.
5. Conclusion and future work
In this paper, we successfully implemented in the PLUTO code a FLD method in spherical coordinates, including frequency dependent irradiation by a star. It is well adapted to performing global simulations of irradiated accretion discs such as protoplanetary discs. The FLD module has serial performances that are three times faster than the MHD part even for a mainly optically thin disc setup. We performed the first global 3D radiation magneto-hydrodynamics simulations of an irradiated and turbulent protoplanetary disc. The disc parameters were inspired by that of the system AS 209 in the star-forming region Ophiuchus (Andrews et al. 2009) for which there are strong observational constraints. The simulations started from a radiative hydrostatic disc which becomes MRI unstable, turbulent, and finally develops into a steady state with typical α values of a few times 10-3, comparable to published simulations of the same kind that use a locally isothermal equation of state. We investigated the turbulent properties and compared the disc structure with classical viscous disc models. Our findings are as follows:
-
The vertical temperature profile showed no tempera-ture peak at the midplane as in classical viscous disc models (D’Alessio et al. 1998). Aroughly flat vertical temperature profile established in the optically thick region of the disc close to the midplane. We re-produced the midplane temperature from the full 3D RMHD run using 2D viscous disc simulations in which the stresstensor is constant in the bulk of the disc and vanishes in thedisc corona. A simple prescription is given with the turbulent stress being constant in the vertical direction within two pres- sure scale heights of the midplane, and vanishing above. The simple prescription gives a satisfying account of the results.
-
The main heating in the turbulent discs was dominated by the Trφ stress tensor. We observed a heating of the order of 1023 erg s-1, mainly released in the disc upper heights.
-
The temperature fluctuations in the disc were small and of the order of 1%. A small increase was observed close to the transition region where the disc was heated by the irradiation from the star with fluctuations up to 6%.
-
The turbulent magnetic fields reached field strengths of about 1 to 10 Gauss at the midplane. The turbulent velocity of the gas was around 10 to 100 m/s at the midplane, and up to 1000 m/s in the upper heights of the disc.
We want to point out some limitations of our work. The first is the distribution and abundance of small dust particles. Indeed, the latter strongly affects the disc temperature vertical profile (see Fig. 4). For our model we choose the disc AS 209, which has a relative low dust abundance compared to other protostellar systems (Andrews et al. 2009). For the dust surface density we used 0.017 g cm-2 at 1 AU for grain sizes ≤1 μm. A much larger amount of small dust particles is difficult to include as it needs a much larger vertical extent to obtain the optically thin irradiated region. At the same time such large extents in stratified MHD turbulent simulation are difficult to perform. In our simulations we used a fixed dust-to-gas mass ratio. In contrast, a smaller dust amount over most of the disc height is expected in weakly turbulent discs, e.g. αturb < 10-2 (Zsom et al. 2011; Akimkin et al. 2013). All these points show that the total amount and distribution of small dust particles is rather uncertain. These simulations should be thought of as a proof of concept that RMHD simulations of turbulent protoplanetary discs are now feasible given the current computational resources.
Another limitation is our use of the ideal MHD approximation. It is well known that the electron fraction is so low at 1 AU in protoplanetary discs that dissipation terms (Ohmic resistivity, ambipolar diffusion, and Hall term) are important (Okuzumi & Hirose 2011; Bai 2011; Dzyurkevich et al. 2013). These dissipative processes are expected to stabilize the MRI in the bulk of the disc, producing a laminar dead zone around the equatorial plane of the disc (Gammie 1996). The presence of a dead zone and the consequences of the various dissipative processes at play will mainly affect the vertical profiles of the turbulent stress and heating rate (Hirose & Turner 2011). These are key aspects of protoplanetary discs dynamics that should be included in future simulations performed in the planet forming regions of protoplanetary discs.
Our current implementation assumes that the gas and dust temperatures are perfectly coupled. Recent models by Akimkin et al. (2013) predict photoelectric heating as a dominant heating source for the gas affected by UV flux. We thus expect that the gas temperature and even the dust temperature (Akimkin et al. 2011) to be higher in the irradiated regions than presently estimated in our models. Detailed studies of the flow in the corona (for example, reconnection and heating events) should include this effect to be meaningful. This would be the purpose of future developments of our numerical scheme.
Young stellar objects have dominant magnetic fields inside a few stellar radii, which destroy the disc structure (Günther 2013).
Acknowledgments
We thank Rolf Kuiper for several helpful comments and discussions during this project. We thank Andrea Mignone for supporting us with the newest PLUTO code including the FARGO advection scheme. Parallel computations have been performed on the Genci supercomputer curie at the calculation center of CEA TGCC. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC Grant agreement nr. 258729.
References
- Akimkin, V. V., Pavlyuchenkov, Y. N., Vasyunin, A. I., et al. 2011, Ap&SS, 335, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Akimkin, V., Zhukovska, S., Wiebe, D., et al. 2013, ApJ, 766, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N. 2011, ApJ, 739, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Balbus, S. A., & Papaloizou, J. C. B. 1999, ApJ, 521, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Boley, A., & Kley, W. 2013a, A&A, 550, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013b, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaes, O., Hirose, S., & Krolik, J. H. 2007, ApJ, 664, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Alessio, P., Canto, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Decampli, W. M., Cameron, A. G. W., Bodenheimer, P., & Black, D. C. 1978, ApJ, 223, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Dittrich, K., Klahr, H., & Johansen, A. 2013, ApJ, 763, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Dullemond, C. P. 2012, RADMC-3D: A multi-purpose radiative transfer tool, astrophysics Source Code Library [Google Scholar]
- Dullemond, C. P., van Zadelhoff, G. J., & Natta, A. 2002, A&A, 389, 464 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, T. 2010, A&A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzyurkevich, N., Turner, N. J., Henning, T., & Kley, W. 2013, ApJ, 765, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Flaig, M., Kissmann, R., & Kley, W. 2009, MNRAS, 282 [Google Scholar]
- Flaig, M., Kley, W., & Kissmann, R. 2010, MNRAS, 409, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Dzyurkevich, N., Klahr, H., & Mignone, A. 2010, A&A, 516, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Dzyurkevich, N., Klahr, H., Turner, N. J., & Henning, T. 2011, ApJ, 735, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., & Nelson, R. P. 2006, A&A, 457, 343 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Furlan, E., Watson, D. M., McClure, M. K., et al. 2009, ApJ, 703, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gardiner, T. A., & Stone, J. M. 2005, J. Comput. Phys., 205, 509 [Google Scholar]
- González, M., Audit, E., & Huynh, P. 2007, A&A, 464, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gressel, O. 2010, MNRAS, 404 [Google Scholar]
- Günther, H. M. 2013, Astron. Nachr., 334, 67 [NASA ADS] [Google Scholar]
- Hawley, J. F., Richers, S. A., Guan, X., & Krolik, J. H. 2013, ApJ, 772, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S., & Turner, N. J. 2011, ApJ, 732, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S., Krolik, J. H., & Stone, J. M. 2006, ApJ, 640, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Y.-F., Stone, J. M., & Davis, S. W. 2012, ApJS, 199, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Youdin, A., & Klahr, H. 2009, ApJ, 697, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Koerner, D. W., & Sargent, A. I. 1995, AJ, 109, 2138 [NASA ADS] [CrossRef] [Google Scholar]
- Kolb, S. M., Stute, M., Kley, W., & Mignone, A. 2013, A&A, 559, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2010, ApJ, 721, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., Hirose, S., & Blaes, O. 2007, ApJ, 664, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., & Bolstad, J. 2007, ApJ, 667, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., & Klessen, R. S. 2013, A&A, 555, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Klahr, H., Dullemond, C., Kley, W., & Henning, T. 2010, A&A, 511, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landry, R., Dodson-Robinson, S. E., Turner, N. J., & Abram, G. 2013, ApJ, 771, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A. 2009, Nuovo Cimento C Geophysics Space Physics C, 32, 37 [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Flock, M., Stute, M., Kolb, S. M., & Muscianisi, G. 2012, A&A, 545, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., & Hirose, S. 2011, ApJ, 742, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Parkin, E. R., & Bicknell, G. V. 2013, MNRAS, 435, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Wolf, S., Steinacker, J., et al. 2004, A&A, 417, 793 [Google Scholar]
- Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Beckwith, K., & Armitage, P. J. 2012, MNRAS, 422, 2685 [NASA ADS] [CrossRef] [Google Scholar]
- Sorathia, K. A., Reynolds, C. S., Stone, J. M., & Beckwith, K. 2012, ApJ, 749, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J. 2004, ApJ, 605, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Stone, J. M., Krolik, J. H., & Sano, T. 2003, ApJ, 593, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Vorst, H. A. 1992, SIAM J. Sci. Stat. Comput, 13, 631 [Google Scholar]
- Zsom, A., Ormel, C. W., Dullemond, C. P., & Henning, T. 2011, A&A, 534, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Flux-limited-diffusion method
Appendix A.1: Numerical scheme
We discretize Eqs. (6), (7) in spherical coordinates using a finite volume formulation and a fully implicit scheme 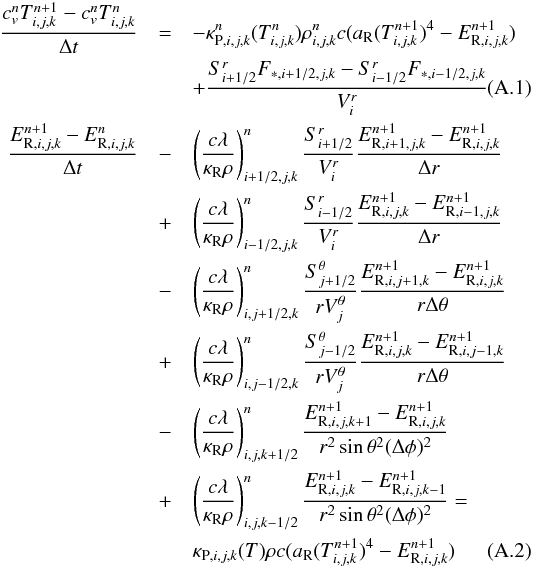 with the specific heat capacity cv = ρkB/(μgu(Γ − 1)), the geometrical terms
with the specific heat capacity cv = ρkB/(μgu(Γ − 1)), the geometrical terms 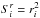 ,
, 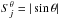 ,
, 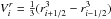 ,
, 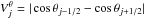 , and the irradiation flux F∗. Equations (A.1) and (A.2) are coupled by linearizing the term proportional to T4 that appears in both equations and neglecting the high-order term (Commerçon et al. 2011)
, and the irradiation flux F∗. Equations (A.1) and (A.2) are coupled by linearizing the term proportional to T4 that appears in both equations and neglecting the high-order term (Commerçon et al. 2011) 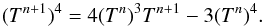 (A.3)This approximation is valid if the change in temperature T = (Tn + 1 − Tn) is small. The maximum change in relative temperature ΔT/T per time-step during our RMHD disc simulations is always below 0.01. Using this expression we can combine Eqs. (A.1) and (A.2) and construct the matrix that needs to be inverted. We note that in this version the scheme is first order in time because of the first-order backward Euler step, used for the time integration.
(A.3)This approximation is valid if the change in temperature T = (Tn + 1 − Tn) is small. The maximum change in relative temperature ΔT/T per time-step during our RMHD disc simulations is always below 0.01. Using this expression we can combine Eqs. (A.1) and (A.2) and construct the matrix that needs to be inverted. We note that in this version the scheme is first order in time because of the first-order backward Euler step, used for the time integration.
Appendix A.2: Test in spherical geometry
Appendix A.2.1: Diffusion test
In this section we test the diffusion operator in spherical coordinates 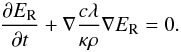 (A.4)We set up a domain of r:θ:φ = (0.5 − 1.5 AU):(0.507 − π/2):(0.5 − 1.5) with different resolutions of 163, 323, 643, and 1283. We use a logarithmic increasing grid in radius so that Δr ~ rΔθ ~ rΔφ. The domain is shifted in the θ direction, to test all the geometrical terms. As initial conditions we use the Gauss function
(A.4)We set up a domain of r:θ:φ = (0.5 − 1.5 AU):(0.507 − π/2):(0.5 − 1.5) with different resolutions of 163, 323, 643, and 1283. We use a logarithmic increasing grid in radius so that Δr ~ rΔθ ~ rΔφ. The domain is shifted in the θ direction, to test all the geometrical terms. As initial conditions we use the Gauss function
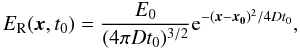 with E0 = 3.0 × 1047erg, D = c/(3κρ) and the Cartesian position vector x. The position x0 is placed at r = 1.0 AU, θ = 1.0, and φ = 1.0; κ is fixed to 1 cm2g-1 and ρ to 10-10 g cm-3. We set the flux limiter λ to 1/3, the initial time to t0 = 5000 s, and the boundary conditions to the analytical value for the given time. We evolve until tfinal = 55 000 s. The timestep for the 163 model is set to 500 s which represents a Courant number6 of 0.11. The timestep is decreased by a factor of 4 each time the resolution is doubled to keep the Courant number constant. Figure A.1 presents the profile of ER along each direction at low resolution, left column, and the profile of the relative error in each direction and resolution, right column. The low resolution run matches with the analytical profile with relative error around 2%. We note that this test problem is difficult to handle in spherical coordinates because of the different grid spacing and especially because of the change in volume over radius. As this test problem is time dependent, we observe a first-order convergence rate which is expected, using a first-order time integration (Jiang et al. 2012).
with E0 = 3.0 × 1047erg, D = c/(3κρ) and the Cartesian position vector x. The position x0 is placed at r = 1.0 AU, θ = 1.0, and φ = 1.0; κ is fixed to 1 cm2g-1 and ρ to 10-10 g cm-3. We set the flux limiter λ to 1/3, the initial time to t0 = 5000 s, and the boundary conditions to the analytical value for the given time. We evolve until tfinal = 55 000 s. The timestep for the 163 model is set to 500 s which represents a Courant number6 of 0.11. The timestep is decreased by a factor of 4 each time the resolution is doubled to keep the Courant number constant. Figure A.1 presents the profile of ER along each direction at low resolution, left column, and the profile of the relative error in each direction and resolution, right column. The low resolution run matches with the analytical profile with relative error around 2%. We note that this test problem is difficult to handle in spherical coordinates because of the different grid spacing and especially because of the change in volume over radius. As this test problem is time dependent, we observe a first-order convergence rate which is expected, using a first-order time integration (Jiang et al. 2012).
 |
Fig. A.1 Left: final profiles of ER (dots) over radius, θ and φ (top to bottom) at low resolution. Overplotted is the analytical value (solid line). Right: relative error from the analytical profile for the different resolution runs and as a function of radius, θ and φ. |
 |
Fig. A.2 Left: vertical temperature profiles at 2 AU for different resolutions. Right: L2 norm of the relative error (black dots) over the typical cell size Δr = (rout − rin)/Nr. The dotted line shows the theoretical second-order scheme slope ∝(Δr)2. |
Appendix A.2.2: Full hybrid scheme
In this second test we repeat the equilibrium setup (see Sect. 2.2) to determine the order of the full hybrid scheme and to verify the equilibrium temperature at low resolution. We perform a resolution study using five different resolutions 60 × 25, 120 × 50, 240 × 100, 480 × 200, and 960 × 400. In this test we set the convergence criteria to |res|2/(NrNθ) < 10-10. Figure A.2, left, shows the vertical temperature profile at 2 AU for the different resolutions. Even the lowest resolution (blue dots) matches very well with the reference solution (black solid line). The temperature profile from the highest resolution is taken as reference temperature Tref. The order of the scheme can be tested by comparing the L2 norm as a function of the grid spacing. We define the L2 norm as ![\appendix \setcounter{section}{1} \begin{equation} L_2=\sqrt{\frac{1}{N_{\rm cell}} \overset{N_{\rm cell}}{{\sum}} \left[ T^{\rm c} - \frac{ \overset{V^{\rm c}}{{\sum}} T^{\rm ref}{\rm d}V^{\rm ref} }{V^{\rm c}} \right]^2 }, \end{equation}](/articles/aa/full_html/2013/12/aa22451-13/aa22451-13-eq258.png) (A.5)with the number of cells Ncell for a given coarse resolution, the temperature and the corresponding volume of the coarse grid cell Tc and Vc, and the temperature and volume of the highest resolution run Tref and Vref. We average the reference temperature Tref over the given volume
(A.5)with the number of cells Ncell for a given coarse resolution, the temperature and the corresponding volume of the coarse grid cell Tc and Vc, and the temperature and volume of the highest resolution run Tref and Vref. We average the reference temperature Tref over the given volume 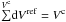 of the coarse resolution. Using this volume average becomes important here as the method and so the divergence terms are written in the finite volume approach (see Eq. (A.2)). In Fig. A.2, right, we show the L2 norm (black dots) overplotted with the theoretical slope of a second-order scheme. As this test problem is time independent, we are able to obtain second-order space accuracy. We note that the irradiation, the heating source, is only radius dependent and so is a 1D problem.
of the coarse resolution. Using this volume average becomes important here as the method and so the divergence terms are written in the finite volume approach (see Eq. (A.2)). In Fig. A.2, right, we show the L2 norm (black dots) overplotted with the theoretical slope of a second-order scheme. As this test problem is time independent, we are able to obtain second-order space accuracy. We note that the irradiation, the heating source, is only radius dependent and so is a 1D problem.
Appendix B: Validation of radiative hydrostatic equilibrium
In this section we test the iterative method presented in Sect. 3.1. To do so, we compare the hydrostatic disc structure we obtained using that procedure for a given set of disc parameters with the simple model described by Chiang & Goldreich (1997). The disc parameters, chosen to match that work, are as follows: T∗ = 4000 K, M∗ = 2.5 M⊙, R∗ = 2.5 R⊙, and 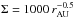 g cm-2, where rAU stands for the distance to the star in astronomical units. We fix the opacity to 1 cm2 g-1. We use a logarithmically increasing grid with 384 × 64 cells. The radial domain extends from 1 to 50 AU and the poloidal domain covers the range θ = ± 0.4. We follow the iteration procedure presented in Sect. 3.1 to compute the hydrostatic structure of that disc. The resulting 2D radiative hydrostatic temperature profile is plotted in Fig. B.1. The black solid line in Fig. B.1 shows the location of the photosphere.
g cm-2, where rAU stands for the distance to the star in astronomical units. We fix the opacity to 1 cm2 g-1. We use a logarithmically increasing grid with 384 × 64 cells. The radial domain extends from 1 to 50 AU and the poloidal domain covers the range θ = ± 0.4. We follow the iteration procedure presented in Sect. 3.1 to compute the hydrostatic structure of that disc. The resulting 2D radiative hydrostatic temperature profile is plotted in Fig. B.1. The black solid line in Fig. B.1 shows the location of the photosphere.
As mentioned, some of the basic properties of irradiated discs can be estimated well using the model of Chiang & Goldreich (1997), the basic physics of which we review here. The disc is irradiated at the photosphere Hph. The heating at that location by the incoming irradiation can be written 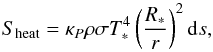 (B.1)where ds = r2sinθΔθΔφ is the irradiated surface element at the disc surface. If we assume isotropic blackbody cooling at the photosphere we can write the cooling as
(B.1)where ds = r2sinθΔθΔφ is the irradiated surface element at the disc surface. If we assume isotropic blackbody cooling at the photosphere we can write the cooling as 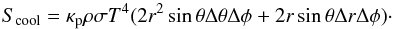 (B.2)Since irradiation hits the disc surface with a small angle one can approximate rΔθ + Δr ~ Δr (in other words, most of the cooling is done through disc emission in the vertical direction). Assuming that heating and cooling balance each other, we find (see also Chiang & Goldreich 1997,Eq. (1))
(B.2)Since irradiation hits the disc surface with a small angle one can approximate rΔθ + Δr ~ Δr (in other words, most of the cooling is done through disc emission in the vertical direction). Assuming that heating and cooling balance each other, we find (see also Chiang & Goldreich 1997,Eq. (1)) 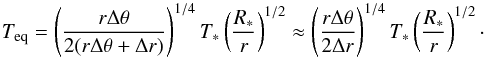 (B.3)The term rΔθ/Δr is often called the flaring angle αflare, and can be expressed as
(B.3)The term rΔθ/Δr is often called the flaring angle αflare, and can be expressed as 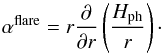 (B.4)Using Eq. (B.4), we can calculate the flaring angle of our disc model and derive the expected equilibrium temperature in our model using Eq. (B.3). In Fig. B.2 (top panel), we plot the temperature in the corona Tcorona (red dotted line at θ − π/2 = 0.4) and in the midplane Tmidplane (red solid line), overplotted with the corresponding blackbody temperature T∗(R∗/r)1/2 (black dotted line) and the equilibrium temperature Teq (black solid line). The two curves we obtained using our iterative procedure are in good agreement with the approximate expressions provided by the Chiang & Goldreich (1997) model.
(B.4)Using Eq. (B.4), we can calculate the flaring angle of our disc model and derive the expected equilibrium temperature in our model using Eq. (B.3). In Fig. B.2 (top panel), we plot the temperature in the corona Tcorona (red dotted line at θ − π/2 = 0.4) and in the midplane Tmidplane (red solid line), overplotted with the corresponding blackbody temperature T∗(R∗/r)1/2 (black dotted line) and the equilibrium temperature Teq (black solid line). The two curves we obtained using our iterative procedure are in good agreement with the approximate expressions provided by the Chiang & Goldreich (1997) model.
In Fig. B.2 (bottom panel), we plot in addition the disc scale height H/r over radius. When combining Eq. (B.4) with the Gaussian vertical profile of the disc (in the case of an isothermal disc), a simple formulae for its radial profile is obtained (Chiang & Goldreich 1997): 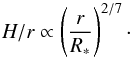 (B.5)This analytical prediction is compared in the bottom panel in Fig. B.2 (solid line) with our numerical estimate of the same quantity. Again, the agreement between the two curves validates our iterative procedure.
(B.5)This analytical prediction is compared in the bottom panel in Fig. B.2 (solid line) with our numerical estimate of the same quantity. Again, the agreement between the two curves validates our iterative procedure.
 |
Fig. B.1 Final 2D temperature distribution in radiation hydrostatic equilibrium. The black solid line shows the τ = 1 line for the irradiation. |
 |
Fig. B.2 Top: temperature at the disc photosphere (red dotted line) and the midplane (red solid line) overplotted with the analytical prediction (black lines). Bottom: scale height H/r at the midplane (dotted line), overplotted with the analytical prescription by Chiang & Goldreich (1997) (solid line). |
Appendix C: Restarting the H3D model
As mentioned, we restarted our high-resolution model from a magnetic field configuration after MRI saturation from model L3D. This requires interpolating the simulation data from a coarse grid to a refined grid (with refined cells about twice as small as the coarse cells). In MHD, this is not an immediate procedure if one wants to retain the solenoidal nature of the magnetic field. In the constraint transport MHD method, the magnetic fields are located at cell interfaces. Coarse cell interfaces are refined, and the magnetic field on the refined surfaces is simply injected from those coarse cell interfaces. In addition, new interfaces appear in the refined grid that do not exist in the coarse grid. At these locations, we perform a linear interpolation of r2Br,sinθBθ,Bφ and we use that interpolation to reconstruct the new magnetic field. This ensures ∇·B = 0 on the refined grid.
We restart the model first with pure isothermal MHD using the initial density and temperature profiles derived from hydrostatic equilibrium. We let the system relax for around 1000 steps, then we take the velocities and the magnetic fields from the relaxed state, but the density and temperature profiles again from the hydrostatic equilibrium. Restarting from this with full radiative RMHD will result after around 10 outer orbits in a new saturated state avoiding the linear MRI phase.
All Tables
All Figures
 |
Fig. 1 Dust absorption opacity over wavelengths. |
| In the text | |
 |
Fig. 2 Top: θ-temperature profile at a radius of 2 AU. Bottom: radius-temperature profile at the midplane. |
| In the text | |
 |
Fig. 3 Weak scaling of the RMHD method (blue line) compared with optimal scaling (black line). Units are given in total number of grid cells per step per second. |
| In the text | |
 |
Fig. 4 Initial temperature distribution for different amounts of small dust particles (≤1 μm), calculated from radiative hydrostatic equilibrium. From top to bottom: Σdust(1 AU) = 0.17,0.017,0.0017 g cm-2. We overplot the radial integrated τ = 1 line for the irradiation (black solid line) and the vertically integrated τ = 1 for the local thermal emission (red solid line). |
| In the text | |
 |
Fig. 5 Snapshot of turbulent rms velocity (left panel) and magnetic field strength (right panel) at the final time of the full RMHD simulation H3D. |
| In the text | |
 |
Fig. 6 Vertical profile of turbulent rms velocities for model H3D in units of m s-1 (black) and the corresponding turbulent Mach number (blue). The space average is calculated over azimuth at 1 AU with a time average of 100 inner orbits. |
| In the text | |
 |
Fig. 7 Vertical stress profile for model H3D in units of dyn cm-2 (black) and normalized using the local pressure (blue). The space average is calculated over azimuth at 1 AU with a time average of 100 inner orbits. |
| In the text | |
 |
Fig. 8 Top: vertical temperature profile of the RMHD run (black line) and the viscous RHD runs (green lines) for the high-resolution models at 1 AU. Model H2D uses a constant alpha. Model H2D∗ uses a vertical dependence of α ~ 1/ρ which is more similar to the RMHD run. Bottom: relative temperature profile compared to the initial passive disc, for models H2D∗ and H3D. On both panels, the background colour shows the region of the disc where the gas is optically thin to its own thermal radiation and to the irradiation by the star. The grey background colour shows the region where the gas is optically thick to its own radiation. We note that there is also a small region in the disc where the gas is optically thin to its own radiation but still optically thick for the irradiation by the star. |
| In the text | |
 |
Fig. 9 Vertical profile of radiation temperature TER = (ER/aR)1/4 (dashed line) and gas temperature (solid line) line at 1 AU. We overplot the range of the temperature fluctuations (red dotted line). The peak of relative temperature fluctuations ΔT/T are around 6−7% at the τ = 1 line (θ ≈ 0.07) for the irradiation (cf. Fig. 10). |
| In the text | |
 |
Fig. 10 Time evolution of the azimuthally averaged total stress Trφ over height at 1 AU. We overplot the location of largest stress (blue contour), largest relative temperature fluctuations (black contour), the vertical location of the τ = 1 position of the irradiation (white contour), and the vertical location of the τ = 1 position for the local thermal radiation (green contour) for each time bin. |
| In the text | |
 |
Fig. 11 2D contour plot of the MHD heating and cooling QMHD (top) and the radiative heating and cooling QRad (bottom) in units of 1023, azimuthally and time averaged over 40 inner orbits. |
| In the text | |
 |
Fig. 12 Top: 2D contour plot of expected theoretical heating QStress in units of 1023, azimuthally and time averaged over 40 inner orbits. Bottom: vertical profile of the MHD heating QMHD (solid line), radiative cooling − QRad (dashed line), and theoretically expected MHD heating QStress (dotted line). |
| In the text | |
 |
Fig. 13 Vertical stress profile in units of dyn cm-2 for the high-resolution models H3D (solid line), H3D-ISO (dotted line), the low-resolution models L3D (dashed line), and L3Dl (dashed-dotted line) with reduced amounts of dust. |
| In the text | |
 |
Fig. 14 Vertical profile of gas temperature (solid line) and radiation temperature TER = (ER/aR)0.25 (dashed line) for models L3Dl (red line) and L3D (black line). |
| In the text | |
 |
Fig. 15 Vertical profile of plasma beta β = 2P/B2 for models L3D (solid line) and L3Dl (dashed line). |
| In the text | |
 |
Fig. A.1 Left: final profiles of ER (dots) over radius, θ and φ (top to bottom) at low resolution. Overplotted is the analytical value (solid line). Right: relative error from the analytical profile for the different resolution runs and as a function of radius, θ and φ. |
| In the text | |
 |
Fig. A.2 Left: vertical temperature profiles at 2 AU for different resolutions. Right: L2 norm of the relative error (black dots) over the typical cell size Δr = (rout − rin)/Nr. The dotted line shows the theoretical second-order scheme slope ∝(Δr)2. |
| In the text | |
 |
Fig. B.1 Final 2D temperature distribution in radiation hydrostatic equilibrium. The black solid line shows the τ = 1 line for the irradiation. |
| In the text | |
 |
Fig. B.2 Top: temperature at the disc photosphere (red dotted line) and the midplane (red solid line) overplotted with the analytical prediction (black lines). Bottom: scale height H/r at the midplane (dotted line), overplotted with the analytical prescription by Chiang & Goldreich (1997) (solid line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.