| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 33 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322073 | |
| Published online | 11 November 2013 | |
Combined IRAM and Herschel/HIFI study of cyano(di)acetylene in Orion KL: tentative detection of DC3N⋆,⋆⋆,⋆⋆⋆
1 Centro de Astrobiología (CSIC-INTA), Ctra. de Torrejón-Ajalvir, km. 4, 28850 Torrejón de Ardoz, Madrid, Spain
e-mail: espluguesbg@cab.inta-csic.es
2 Department of Physics & Astronomy, University College London, Gower St., London WC1E 6BT, UK
3 National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
4 Institut de Ciències de l’Espai (CSIC-IEEC), Campus UAB-Facultat de Ciències, Torre C5-parell 2, 08193 Bellaterra, Barcelona, Spain
5 Department of Astronomy, University of Michigan, 500 Church St, Ann Arbor, MI 48109, USA
Received: 13 June 2013
Accepted: 2 September 2013
Context. We present a study of cyanoacetylene (HC3N) and cyanodiacetylene (HC5N) in Orion KL using observations from two line surveys performed with the IRAM 30-m telescope and the HIFI instrument onboard the Herschel telescope. The frequency ranges covered are 80−280 GHz and 480−1906 GHz.
Aims. This study (divided by families of molecules) is part of a global analysis of the physical conditions of Orion KL and the molecular abundances in the different components of this cloud.
Methods. We modeled the observed lines of HC3N, HC5N, their isotopologues (including DC3N), and vibrational modes using a non-local thermodynamic equilibrium (non-LTE) radiative transfer code. In addition, to investigate the chemical origin of HC3N and DC3N in Orion KL, we used a time-dependent chemical model.
Results. We detect 40 lines of the ground vibrational state of HC3N and 68 lines of its 13C isotopologues. We also detect 297 lines of six vibrational modes of this molecule (ν7, 2ν7, 3ν7, ν6, ν5, and ν6+ν7) and 35 rotational lines of the ground vibrational state of HC5N. We report the first tentative detection of DC3N in a giant molecular cloud. We have obtained a DC3N/HC3N abundance ratio of 0.015 ± 0.009, similar to typical D/H ratios of cold dark clouds. We provide column densities for all species and derived isotopic and molecular abundances. We also made a 2′ × 2′ map around Orion IRc2 and present maps of the HC3N lines with energies from 34 to 154 K and of the HC3N vibrational modes ν6 and ν7 with energies between 354 and 872 K. In addition, a comparison of our results for HC3N with those in other clouds has allowed us to derive correlations between the column density, the FWHM, the mass, and the luminosity of the clouds.
Conclusions. The high column densities of HC3N obtained in the hot core, in particular of the ground vibrational state and the vibrational mode ν7, make this molecule an excellent tracer of hot and dense gas. In addition, the wide frequency range covered reveals the need to consider a temperature and density gradient in the hot core to obtain better line fits. The high D/H ratio (similar to that obtained in cold clouds) that we derive suggests a deuterium enrichment. Our chemical models indicate that the possible deuterated HC3N in Orion KL is formed during the gas-phase. This fact provides new hints concerning the processes leading to deuteration.
Key words: ISM: clouds / ISM: molecules / ISM: abundances / radio lines: ISM
Based on observations carried out with the IRAM 30-m telescope and with the Herschel telescope (HIFI instrument). IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain). Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendix A (except Table A.1) is available in electronic form at http://www.aanda.org
Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/559/A51
© ESO, 2013
1. Introduction
The Orion region is one of the best places to study the formation of high-mass stars due to its proximity (≃414 pc, Menten et al. 2007) and the presence of compact radio sources, molecular outflows (Wright et al. 1996), a molecular hot core, and an IR luminosity of ~105 L⊙ in the central part of the region, indicating the presence of embedded massive protostars (Nissen et al. 2007). The Becklin-Neugebauer (BN) object was the first source of infrared radiation discovered in the Orion nebula (Becklin & Neugebauer 1967). The luminosity of the BN object is L ≃ 1500 L⊙ and it lies about 12″ north of the Kleinmann-Low (KL) nebula. Menten & Reid (1995) detected the radio continuum emission of the IR source n and the very embedded radio source I (located a few arcseconds to the south of the young and massive star IRc2), which could be a binary system with a total mass of ~20 M⊙, according to measurements of the proper motions of this source and the object BN (Goddi et al. 2011). Source I has been proposed as a possible driver of the two outflows observed in Orion KL: a high-velocity (30−100 km s-1), wide-angle (~1 rad) outflow that extends northwest-southeast over 0.3 pc, and a low-velocity (~18 km s-1) elongated northeast-southwest outflow (Genzel & Stutzki 1989; Greenhill et al. 1998; Zapata et al. 2009).
Orion BN/KL contains a large amount of dense gas, indicated by the presence of H2O, OH, and SiO masers. In fact, source I coincides with the centroid of the SiO maser distribution (Plambeck et al. 2009). These high densities and the high dust extinction (AV ~ 1000) obscure the innermost regions in the near- and mid-IR. To study the innermost regions of the hot core, it is therefore necessary to observe at radio wavelengths rotational transitions excited by collisions in these high density zones. Moreover, the observation of highly vibrationally excited states can provide information on the infrared radiation field in the same regions.
Orion KL also constitutes an excellent astrochemical laboratory because of its rich and complex chemistry. Many molecules (tracers of shocks, cold gas, hot and dense gas, etc.) have been observed in this cloud, in particular, organic molecules associated mainly with the hot core (richer in N-bearing organics) and the compact ridge component (richer in O-bearing organics) (Wang et al. 2009). One very abundant molecule in the hot core of Orion KL is HC3N. Interstellar cyanoacetylene, HC3N, was discovered by Turner (1971), who detected emission in the J = 1 − 0 line toward Sgr B2. This molecule is an excellent tracer of hot and dense regions affected by high extinction; its vibrational levels are mainly excited by mid-IR radiation (de Vicente et al. 2000) and the relatively low energy of its bending modes makes them easy to detect in many vibrationally excited states. Another advantage of studying HC3N is that, although it is abundant in warm clouds, the radio lines are usually optically thin (Morris et al. 1976). In addition, these low optical depths allow an accurate determination of the 12C/13C abundance ratio from the observation of the 13C isotopologues. The deuterated counterpart of cyanoacetylene (DC3N) was detected for the first time in the cold interstellar cloud Taurus Molecular Cloud 1 by Langer et al. (1980). Later it has been observed in L1498, L1544, L1521B, L1400K, and L1400G by Howe et al. (1994), in L1527 by Sakai et al. (2009), and in Cha-MMS1 by Cordiner et al. (2012). However, DC3N has so far never been observed so far in giant molecular clouds.
Most deuterated species are produced in molecular environments characterized by low temperatures (T ≤ 20 K) (Millar et al. 1989). Although these temperatures are typical of low-mass pre-stellar cores, many deuterated molecules such as DCN (Jacq et al. 1999), DNC (Tatematsu et al. 2010), CHD2OH (Parise et al. 2002), or D2CO (Fuente et al. 2005) have been detected in hot cores, where the gas kinetic temperature is >100 K. In the case of Orion, some of the first detected deuterated molecules were CH3OD (Mauersberger et al. 1988) and CH2DOH (Jacq et al. 1993). The formation of deuterated molecules occurs through exchange reactions (Howe & Millar 1993) where deuterated ions transfer the deuterium to neutral species in ion-molecule reactions. These reactions normally dominate at low temperatures, but there are some reactions such as 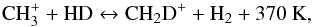 (1)that are energetically favorable at high temperatures that can lead to a variety of deuterated molecules in regions with temperatures up to 100 K (Howe & Millar 1993).
(1)that are energetically favorable at high temperatures that can lead to a variety of deuterated molecules in regions with temperatures up to 100 K (Howe & Millar 1993).
In this paper we focus on the IRAM line survey, first presented by Tercero et al. (2010), and on Herschel/HIFI observations (from the HEXOS program, Bergin et al. 2010; Crockett et al. 2010), covering the frequency ranges 80−280 and 480−1910 GHz, respectively. Observations are described in Sect. 2. We study the molecules HC3N, its isotopologues, and HC5N, and report the first detection of DC3N in Orion KL. Here we present (Sect. 3) more than 400 lines from HC3N for the ground state, different vibrational states (ν5, ν6, ν7, 2ν7, 3ν7, and ν6 + ν7), and isotopologues, and 35 lines of HC5N. We also present (Sect. 3.2) maps over a region 2′ × 2′ around Orion IRc2 of two transitions of HC3N, two of HC3N ν7, and one of HC3N ν6. Unlike previous works, we used an LVG (large velocity gradient) code, MADEX, to derive physical and chemical parameters, such as column densities or abundances (Sect. 4). In addition, we compare some of our results for HC3N with results obtained by other authors in a sample of 22 molecular cloud cores (Sect. 5). We study possible correlations between the line widths, the mass of the cloud cores, the infrared luminosity, the galactocentric distance, and the column density of HC3N. In Sects. 6 we present chemical models of the hot core of Orion KL to study the origin of HC3N and DC3N, and we discuss the results. Finally, in Sect. 7 we summarize our conclusions.
2. Observations
2.1. IRAM 30-m
The observations were carried out using the IRAM 30-m radiotelescope during September 2004 and March 2005. Four SiS receivers operating at 1.3, 2, and 3 mm were used simultaneously with image sideband rejections. The intensity scale was calibrated using two absorbers at different temperatures and using the atmospheric transmission model (ATM, Cernicharo 1985; Pardo et al. 2001). Observations were made in the balanced wobbler-switching mode, with a wobbling frequency of 0.5 Hz and a beam throw in azimuth of ±240″. As backends we used two filter banks with 512x1 MHz channels and a correlator providing two 512 MHz bandwidths and 1.25 MHz resolution (see Esplugues et al. 2013 for more details). We pointed the telescope toward the IRc2 source at αJ2000 = 5h35m14.5s, δJ2000 = −5°22′30.0″.
IRAM 30-m telescope efficiency data of the covered frequency range.
To analyze the survey we considered only the lines with antenna temperatures higher than 0.02 K (i.e., >3σ). The data were processed using the IRAM GILDAS software1 (developed by the Institut de Radioastronomie Millimétrique). We present the spectra in units of main-beam temperature TMB, which is defined as 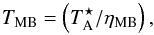 (2)where ηMB is the main-beam efficiency and
(2)where ηMB is the main-beam efficiency and 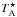 the antenna temperature. Table 1 shows the half power beam width (HPBW) and the mean beam efficiencies over the covered frequency range.
the antenna temperature. Table 1 shows the half power beam width (HPBW) and the mean beam efficiencies over the covered frequency range.
We also used the 30-m telescope to map a region around Orion IRc2 at 1.3 mm. We covered the whole frequency range (216−250 GHz) using the HERA heterodyne receiver, and the ranges 200−216 GHz and 250−285 GHz using EMIR E230 and E330 receivers, over a region of 2′ × 2′ with a 4″ spacing. The survey was performed in on-the-fly mode using position-switching with a emission-free reference position at an offset (− 600″,0) from IRc2. As backends we used WILMA with 2 MHz spectral resolution. The maps presented in Sect. 3.2 were observed using HERA (tuned at frequencies of 227.9 and 236.9 GHz), and the E090 receivers (at 109.983 GHz). Observations at 1.3 mm were performed in December 2008, with opacities ~0.1 at 1.3 mm and 1−1.5 mm of precipitable water vapor. The 3-mm data were collected in February 2010, under poorer weather conditions (opacities of 0.3−0.4 and 5 mm of pwv). Pointing was checked every 1−1.5 h on nearby and strong quasars, with errors better than 4−5″. Data reduction was also performed using the IRAM GILDAS software.
2.2. Herschel/HIFI
The HIFI line survey was observed as part of the HEXOS Guaranteed Time Key Program. The HIFI instrument (de Graauw et al. 2010), onboard Herschel, observed a bandwidth of approximately 1.2 THz in the frequency range 488−1902 GHz, with gaps between 1280−1430 GHz and 1540−1570 GHz. Most observations were carried out between March 2010 and March 2011. The spectral resolution is 1.1 MHz, corresponding to 0.2−0.7 km s-1. HIFI is a double-sideband system where, in the conversion to frequencies detectable by the spectrometers, spectral features in the opposite sideband appear superposed at a single frequency. As a part of the spectral scan observation, different settings of the local oscillator (LO) are observed and the double sideband is deconvolved to isolate the observed sideband. We applied the standard HIFI deconvolution using the doDeconvolution task within HIPE (see Bergin et al. 2010; and Crockett et al. 2010, for more details). The spectral scans for each band were taken in dual-beam-switch (DBS) mode, using the wide-band spectrometer (WBS). For bands 1−5, the telescope was pointed toward coordinates αJ2000 = 5h35m14.3s, δJ2000 = −5°22′33.7″, midway between the Orion hot core and the compact ridge. For bands 6−7, where the beam size is smaller (see Table 2), the telescope was pointed directly toward the hot core at coordinates αJ2000 = 5h35m14.5s, δJ2000 = −5°22′30.9″. We assumed the nominal absolute poiting error (APE) for Herschel of 2.0″ (Pilbratt et al. 2010). The data were reduced using the standard HIPE (Ott 2010) pipeline version 5.0. We also present the spectra in units of main-beam temperature TMB.
HIFI efficiency data of the covered frequency range.
3. Results
3.1. Line profiles
Cyanoacetylene is a linear molecule, therefore its rotational spectrum is very simple. Owing to its large moment of inertia, it has a small rotational constant B and its rotational transitions J → J − 1 are relatively close in frequency. Like other species containing 14N, cyanoacetylene has a hyperfine structure due to the interaction of the nitrogen nuclear spin with the rotation of the molecule.
 |
Fig. 1 Observed pure rotational lines of HC3N (black histogram) in the IRAM line survey. Best-fit LVG model results are shown in red. |
 |
Fig. 2 Observed pure rotational lines of HC3N (black histogram spectra) with the HIFI survey. Best-fit LVG model results are shown in red. |
3.1.1. HC3N
Figures 1 and 2 show the lines of HC3N (together with our best-fit LVG model, see Sect. 4) observed with the IRAM and the Herschel/HIFI survey, respectively. The 18 observed pure rotational lines between 3−1.3 mm belong to transitions between J = 9–8 and J = 30–29 with an energy range of Eup = 19 − 230 K (see Table A.1). All these lines are strong, with 8 < TMB < 31 K, and are barely blended with other species. The observed lines with HIFI are much weaker than those obtained with IRAM-30-m, TMB < 1.5 K, due to their high energies Eup = 624–1826 K. Assuming that the line emission is optically thin and the level populations are thermalized (Goldsmith & Langer 1999), we fitted the observed lines with Gaussian profiles using the CLASS software to derive the contribution of each cloud spectral component (see Table A.2). We treated the radial velocity (VLSR), the line-width and the antenna temperature as free parameters in the fits. We took into account the typical velocity ranges of each component of Orion KL to consider the best-fit and avoid possible degeneracy. The contribution to the intensity arises from different velocity components: a wide component present in all lines, a very narrow component centered at ≃10 km s-1 that mainly affects the lowest transitions, and another component wider (≃10 km s-1) than the previous which affects mainly the transitions with J > 20 and that is centered at about 5 km s-1. For the HIFI case, the contribution to the emission from a wide (~25 km s-1) component dominates the observed line profiles.
We also detected rotational lines from six vibrational states of HC3N: ν7, 2ν7, 3ν7, ν6, ν6 + ν7, and ν5. The modes ν5, ν6, and ν7 are doubly degenerate in order of decreasing energy (954, 718, and 320 K, respectively). With rotation, their degeneracy is broken, which is known as l-doubling. The modes ν1, ν2, and ν3 have energies higher than 2000 K and have not been detected in this study, nor has the ν4 mode. We observed 36 rotational transitions of HC3N ν7 in our IRAM line survey between J = 9–8 and J = 30–29 (see Fig. 3 and Sect. 4 for the best-fit LTE model). In the HIFI data, 30 lines from J = 53–52 to J = 77–76 are detected in the range of the survey (see Fig. A.1). From line profiles at mm frequencies, we see that the line intensity increases with the rotational quantum number J, whereas in the HIFI lines the opposite occurs (see Table A.1 where spectroscopic parameters for HC3N and its vibrational modes2 are shown). The intensity of each line depends (among other paremeters) on the energy of the level and mainly on the frequency, but the covered frequency range for a given transition range is broader for HIFI than in IRAM-30-m. This behavior produces different trends in the lines observed with both telescopes. On the other hand, it is evident that a wide component as well as a narrow compontent centered at ≃5 km s-1 play an important role in the contribution to the emission of all these lines.
There are 46 detected lines of the mode 2ν7 of HC3N in the range covered by the IRAM survey. These transitions cover the range J = 9–8 to J = 30–29 and are shown in Fig. A.2 (see the appendix and Sect. 4 for the best-fit LTE model). Within the Herschel line survey, there are 19 detected lines (see Fig. A.3) covering the frequency range of 484−660 GHz (higher transitions are too weak and/or blended by stronger emission from other species). From all line profiles and the range of energy (Eup = 665–1800 K), we deduce that the main contribution must arise from a narrow and hot component.
 |
Fig. 3 Observed pure rotational lines of HC3N ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
Twenty-seven transitions of HC3N 3ν7 are found in the frequency range of the survey at 3, 2 and 1.3 mm (Table A.1). Figure A.4 shows some of these lines. In this vibrational mode there are four l-transitions, although our spectral resolution cannot always resolve all of them. The lines observed with Herschel are very weak and mostly hidden by stronger species, therefore we did not consider detecting this vibrational mode of HC3N with the Herschel telescope.
We detected 15 transitions of HC3N ν6 in the IRAM line survey and 13 in the HIFI survey. Lines at 3 mm are weak, with TMB ~ 0.3 K, while lines at 2 and 1.3 mm present intensities between 0.5 and 2.5 K (see Fig. A.6). Similar to the two previous cases, lines from the Herschel survey are weak and/or blended with stronger species (see Fig. A.8). We also detected 42 transitions of ν6 + ν7 (Fig. A.9), dominated by contributions coming from narrow components. We do not detect lines from these vibrational modes with HIFI, because of the high energies of the levels (up to 1500 K) and the stronger lines.
We detect twenty-two lines of HC3N ν5 in total (see Table A.1, and a selection of these lines in Fig. A.5). The rest of them are hidden by species with higher intensity, which we do not consider them in this work. Given the high energies (>970 K) of these transitions, we deduce that the emission probably arises from a very hot component. In addition, according to the line profiles, this component must be narrow (≤10−11 km s-1).
We also observed several lines of both the ground and the vibrational state ν7, arising from the 13C isotopic substitutions of HC3N. In Table A.1, we list all detected transitions for the 13C isotopologues of the ground state and their energies. Within the IRAM survey, we detected 13 lines of H13CCCN (Fig. A.10), 18 lines of HC13CCN (Fig. A.11), and 16 lines of HCC13CN (Fig. A.12). From the Herschel line survey, we detected 21 lines from isotopologues in total. From their line profiles, we infer a contribution from a very narrow component that mainly affects the lowest frequencies, and a wide component important for transitions with J > 20. For the mode ν7 we detected (only in the IRAM survey) 47 isotopic lines (see Figs. A.16–A.18, and Table A.1). The temperatures of these lines are TMB < 0.7 K and some of them are blended with other species. We did not detect any transition arising from the 15N isotopologue.
 |
Fig. 4 Tentative detection of four lines of DC3N. The horizontal green line indicates the 3σ threshold used for line identification. |
3.1.2. DC3N
There are 20 rotational transitions (listed in Table A.3 together with their spectroscopic parameters3) of deuterated cyanoacetylene, that fall in the range of the IRAM survey. Four of these lines do not overlap with other species and they are identified as DC3N (see Fig. 4). However, in this figure we also observe that two of the four lines are very close to the detection limit, 3σ, (green horizontal line). To increase the signal-to-noise ratio and turn more confident of a possible detection of DC3N, we averaged the four spectra (accounting for the width of the channels in each spectrum). The result is shown in Fig. 5, where the red arrow indicates the resulting line profile of the average of the four DC3N lines. This profile presents a Gaussian shape (centered at 7.76 km s-1), is not blended with other species, and its main-beam temperature is >0.07 K (>5σ). This suggests that there is a molecule with emission lines at the frequencies listed in Table A.3, producing emission consistent with the expected velocity (5−10 km s-1, corresponding to the typical velocity range of the Orion KL components). We also checked using the MADEX catalog (see Sect. 4) that no lines from other species are expected at the frequencies of DC3N. Hence, altogether this suggests that the molecule responsible for this emission is very likely DC3N. The four transitions, their frequencies, energies (whose range is Eup = 26–122 K), and their observed velocities VLSR are listed in Table 3. For the ground state of DC3N, we show in Fig. 6 all DC3N lines within the IRAM survey, together with our best-fit LVG model (see Sect. 4). The line profiles of the four features, that do not overlap with other species indicate that the contribution comes from narrow (<11 km s-1) velocity components (typical line width range of the compact ridge and the hot core). We did not detect lines of vibrational states or isotopologues of DC3N. Neither we detected lines of this species in the frequency range covered by Herschel because their weakness and/or the presence of stronger species.
3.1.3. HC5N
Like HC3N, cyanodiacetylene (HC5N) is a linear molecule, H-C≡C-C≡C-C≡N, with a large dipole moment. It was detected for the first time in the interstellar medium by Avery et al. (1976) in Sgr B2. Later it was also detected in several dark clouds and in Orion KL by Bujarrabal et al. (1981) at wavelengths near 3 mm.
Tentative lines of DC3N.
We detected 35 rotational lines of HC5N in Orion KL in the IRAM line survey. Figure 7 shows a sample of transitions together with our best-fit LVG model lines (see Sect. 4). The transitions of HC5N cover the range J = 30 to J = 103 and their energies (listed in Table A.4, together with other spectroscopic parameters4) range between Eup = 63–685 K. All lines present a narrow line width (≲10 km s-1), especially lines at 3 mm, therefore the emission must arise from narrow components, such as the ridge or the hot core. We did not detect lines in the HIFI data because of the high energies, Eup > 2100 K, involved in these transitions. No lines arising from the 13C isotopologues of HC5N were detected.
 |
Fig. 6 Observed spectra of DC3N (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. The horizontal green line indicates the 3σ threshold used for line identification. |
 |
Fig. 7 Sample of observed lines of HC5N (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
3.2. 2′ × 2′ maps around IRc2
From the 2D survey data of Orion KL (Marcelino et al., in prep.) taken with the IRAM 30-m telescope, we present maps of the integrated intensity of HC3N over different velocity ranges. Figure 8 shows the mapped transitions J = 12–11 and J = 26–25, which correspond to energy levels Eup = 34.1 and 153.3 K, respectively. In both transitions, the highest integrated intensity is found in the velocity range 3−7 km s-1 (typical velocities of the hot core). However, whereas at low energies the peak is located around the IRc2 position (in agreement with the HC3N interferometric observations from Wright et al. 1996), at higher energies (lower panel) it is slightly shifted to the east for all velocity ranges. In the upper panel we can see extended emission along the molecular ridge in the N-S direction. In the velocity range 7−14 km s-1 there is a clear elongation of the emission towards the NE, corresponding to the extended ridge. All this extended emission is the result of the low energy of this transition (~34 K). Maps of the J = 26–25 transition represented in the lower panels, with an energy level four times higher, show the same elongation, but the emission is less extended. In addition, we observe a second emission peak centered at ~20″ east and ~25″ north of IRc2. In Sect. 6 we explain its possible origin. At velocities higher than 14 km s-1, the integrated intensity decreases and becomes more compact.
 |
Fig. 8 HC3N-line integrated intensity maps for different velocity ranges (indicated at the bottom of each panel). Row 1 shows the transition J = 12–11 with Eup = 34.1 K. The interval between contours is 4 K km s-1 and the lowest contour is 2 K km s-1. Row 2 shows the transition J = 26–25 with Eup = 153.3 K. The interval of contours is 7 K km s-1 and the lowest contour is 3 K km s-1. The white plus indicates the position of the hot core and the black cross the position of the compact ridge. The beam size is also shown with a blue circle. |
 |
Fig. 9 HC3N ν7-line integrated intensity maps for different velocity ranges (indicated at the bottom of each panel). Row 1 shows the transition J=12-1–11-1 with Eup = 354.2 K. The interval between contours is 0.4 K km s-1 and the lowest contour is 0.7 K km s-1. Row 2 shows the transition J = 25-1–24-1 with Eup = 462.3 K. The interval of contours is 1.5 K km s-1 and the lowest contour is 2 K km s-1. The white plus indicates the position of the hot core and the black cross the position of the compact ridge. The beam size is also shown with a blue circle. The velocity ranges 14−18 and 18−22 km s-1 show the integrated intensity contaminated by CH2CHCN since there is an overlap of this species with the line of HC3N ν7J = 25-1–24-1. |
Figure 9 shows integrated intensity maps for two transitions of the vibrational mode HC3N ν7 (J = 12-1–11-1 and J = 25-1–24-1). Similar to the ground state of HC3N, the peak of emission is observed in the range 3−7 km s-1. In this case, however, the emission presents a circular shape centered around IRc2, with the peak shifted a few arcseconds (~3″) toward the NE of IRc2 for the high-energy transition. The same behavior was found for the mapped transition at high energy of the ground state of HC3N, indicating the possible presence of a warmer region in this direction. Another feature is that for high velocities (VLSR > 14.5 km s-1), we barely found emission of HC3N ν7 from the low-frequency transition (upper panel), while for the high-frequency transition we observed a considerable contribution from this species. This line is overlapped with CH2CHCN (24(5,19)–23(5,18)) at high velocities (15−25 km s-1), see Fig. 3. Therefore, the emission we obtain in the maps in these ranges is emission from CH2CHCN instead of HC3N ν7.
We also present an integrated emission map for the transition J = 26-1–25-1 of HC3N ν6 (see Fig. 10). The largest contribution to the emission also comes from the velocity range 3−7 km s-1. All the emission is located to the NE of IRc2; unlike the ground state of HC3N and its vibrational mode ν7, there is no emission from the west of IRc2. We did not find emission in the range 14−22 km s-1 either.
4. Analysis
We have analyzed the non-LTE excitation and radiative transfer of the DC3N, HC3N, and HC5N lines using the code MADEX. Only we considered LTE approximation for the hot core because of the higher gas density so that most of transitions are thermalized to the gas temperature (Trot ≃ TK). MADEX has been developed by Cernicharo (2012) and includes corrections for the beam dilution of each line, depending on the different beam sizes at different frequencies. In addition, this code takes into account the size of each component and its offset position with respect to IRc2. The LVG models are based on the Goldreich & Kwan (1974) formalism.
To apply the LVG code, we considered the same cloud components for Orion KL as were used in Esplugues et al. (2013) for the analysis of SO and SO2. Most of these cloud components were also considered in previous Orion KL interferometric studies such as those of Wright et al. (1996) and Beuther et al. (2005). Taking into account the mapped transitions and the parameters obtained from the Gaussian fits (see Sect. 5) of the line profiles of HC3N, we assumed uniform physical conditions of density, kinetic temperature, line width, and radial velocity for each component (see Table 4), so that the column density of each observed species is the only free parameter. However, to fit the line profiles of HC3N (ground and vibrational states) obtained with Herschel observations, a density and temperature stratification or gradient in the hot core is needed (as was predicted by Esplugues et al. (2013) with IRAM observations of SO2 transitions with high energies, >700 K). This gradient was simulated by adding a hotter inner component to the typical hot core conditions (see Table 4). The final considered fit reproduces more line profiles better from transitions covering a wide energy range within about 20% of the uncertainty in the line intensity. Given the different sources of uncertainty, such as spatial overlap of the cloud components, modest angular resolution, and the lack of collisional rates for some vibrational modes such as ν7, 2ν7, and 3ν7 to consider LVG instead of LTE in components different to the hot core discussed in Esplugues et al. (2013), we estimate the uncertainty in the model intensity predictions to be 25% for the HC3N results, 30% for HC5N (higher uncertainty for HC5N than for HC3N because the lines are weaker and more blended with other species), and 35% for DC3N (due to the overlap with other species) and for the vibrational modes of HC3N (because of considering LTE instead of LVG). In all the fits, we determined the contribution of each component separately from the rest. The adopted fit is that which best reproduces the majority of the observed line profiles for both surveys (IRAM and HIFI) within ~15% of uncertainty in the intensity (see Esplugues et al. 2013 for more details about the technique used to fit the line profiles).
 |
Fig. 10 HC3N v6-line integrated intensity maps for different velocity ranges (indicated at the bottom of each panel) for the transition J = 26-1–25-1 with energy Eup = 871.2 K. The interval between contours is 0.5 K km s-1 and the lowest contour is 0.35 K km s-1. The white plus indicates the position of the hot core and the black cross the position of the compact ridge. The beam size is also shown with a blue circle. |
Physical parameters adopted in the radiative transfer code for the Orion KL cloud components.
4.1. HC3N
The results of the LVG code indicate that the HC3N lines present typical optical depths τ < 0.5. The column density of this molecule was derived using HC3N-pH2 collisonal rates from Wernli (2007), and the modeled line profiles are shown in Figs. 1 (IRAM) and 2 (Herschel). The cloud component with the highest HC3N column density is the hot core HC1, with N(HC3N) = (1.0 ± 0.2) × 1015 cm-2. This agrees with the result obtained by Wright et al. (1996), White et al. (2003), and Persson et al. (2007), who found HC3N column densities of 2 × 1015, 1015, and 1.5 × 1015 cm-2, respectively. The inner hot core (HC2) and the plateau (PL), with assumed temperatures of Tk = 310 and 150 K, respectively, present the same column density: N(HC3N) = (7 ± 1) × 1014 cm-2. The HC2 component is most visible in the transitions observed with HIFI (transitions with high energy), whereas the HC1 and PL components mainly affect lines at 1.3 and 2 mm. Another component with a strong contribution to the emission is the high-velocity plateau, whose column density is N(HC3N) = (5 ± 1) × 1014 cm-2. This component contributes significantly to the line intensity at 3 mm. To obtain a good fit to the lines at low frequencies, we also considered a contribution from the extended ridge, with a column density of N(HC3N) = (8 ± 2) × 1013 cm-2. In addition, similar to the analysis of SO and SO2 emission in Esplugues et al. (2013), we also found a contribution from the component centered at 20.5 km s-1, with N(HC3N) = (3.4 ± 0.6) × 1014 cm-2. This contribution is negligible in the isotopologues or vibrational modes of HC3N, but it is significant for ground-state transitions, as we can see in the line profiles in Fig. 1, in particular for J ≥ 15.
Column densities, N, for HC3N (its isotopologues and vibrationally excited states, including DC3N) and HC5N.
For the vibrational mode ν7 there are no collisional rates available, therfore we adopted an LTE approximation. As for the ground state of HC3N, we found the highest column density in the outer hot core, HC1, with a value of (8 ± 2) × 1014 cm-2. In HC2, the component with the highest temperature, we found a similar column density, (6 ± 1) × 1014 cm-2. The plateau component with higher temperature (PL) mainly contributes to the line emission at 2 and 3 mm with N(HC3N) = (4.0 ± 0.8) × 1014 cm-2. This value is about twice as low that obtained for the ground state. In the extended and compact ridge, the column densities are similar to those obtained for the 13C isotopologues of HC3N (discussed below). Figure 3 shows our best LTE model fits for lines observed in the IRAM survey. Fits for lines from HIFI are shown in the appendix (Fig. A.1). From Fig. 3, we observe that lines at 3 mm present a poor fit at negative velocities. The same behavior is also observed in Fig. 1 for the ground state of HC3N. This could be due to contributions from other blended species, as in the case of J = 11–10, which is blended with HCOOCH3, but emission arising from a component centered at VLSR ~ 0 km s-1 seems the more likely explanation. We are able to fit this part of the line profiles by introducing a new component in the model centered at − 1 km s-1, with n(H2) = 105 cm-3, Tk = 60 K, and a line-width of 10 km s-1. Given the low temperature, this component seems to represent a gradient of the extended ridge. However, ΔVFWHM = 10 km s-1 is more than twice the typical line width for the ridge, which could indicate effects from outflows. Finally, we did not include this component in the final model because of its unknown origin and the low certainty of its real existence, since it could also be due to contamination from other species.
We assumed LTE excitation due to the lack of collisional rates for the vibrational modes 2ν7 and 3ν7 of HC3N. They present column densities similar to the ν7 mode in the inner hot core HC2, in particular the mode 2ν7, with N = (5 ± 1) × 1014 cm-2. However, in HC1, the contribution to the emission of 2ν7 and 3ν7 is up to eight times lower than that of ν7 (see Table 5). The lowest contributions for both modes come from the extended and the compact ridge. HC3N 2ν7 is between 1.6 and 8 times more abundant than HC3N 3ν7. Figures A.2 and A.3 show our best-fit lines of 2ν7 from IRAM and HIFI, respectively, and Fig. A.4 shows the fits to lines of 3ν7 from the IRAM line survey.
Figures A.5–A.8 show the modeled profiles for the vibrational modes ν5 and v6 of HC3N, observed with the IRAM and Herschel surveys. These fits were also made considering LTE approximation, because of the lack of collisional rates. For both vibrational states, the emission comes mainly from the hottest region (HC2), with column densities ~3 × 1014 cm-2 (see Table 5). This component mainly affects the lines in the HIFI range and the lines at 1.3 mm. For ν6, we also found a contribution from the plateau (PL), with a column density of (1.0 ± 0.2) × 1014 cm-2. For ν5, the line profiles are very narrow and it was not necessary to include any contribution from the plateau.
We also fitted the lines of the state ν6 + ν7 of HC3N (Fig. A.9) with LTE models owing to the absence of collisional rates. We found that the largest contribution arises from the hot core (HC2), with N(HC3N ν6 + ν7) = (1.5 ± 0.5) × 1013 cm-2. Due to the high energies of all transitions, the contribution from the component HC1 is negligible compared with that from HC2. We found that the lines in the HIFI data were blended with stronger species, therefore we did not consider a detection of HC3N ν6 + ν7 with this instrument.
The emission from the 13C isotopologues of HC3N is dominated by the contribution from the inner hot core with N = (0.9 − 2.4) × 1014 cm-2 for all of them, followed by emission from the HC1, where we found N = (6 ± 1) × 1013 cm-2. To fit the line profiles at 2 and 3 mm it was necessary to consider a contribution from the plateau PL, where N = (3.3 ± 0.6) × 1013 cm-2 for H13CCCN and N = (1.0 ± 0.2) × 1013 cm-2 for the other two 13C isotopologues. These values are very similar to those obtained for the high-velocity plateau as well. The column densities obtained for the extended ridge are about one order of magnitude lower, N = (1 − 3) × 1012 cm-2 for the 13C isotopologues. Figures A.10–A.12 show our best-fit LVG model for each isotopologue observed with the IRAM-30-m, and Figs. A.13–A.15 show the results for the 13C isotopologue lines from HIFI. The collisional rates were taken from HC3N-pH2 (Wernli et al. 2007). All lines from HC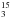 N except one are hidden by other stronger species. Therefore, we consider the column density obtained, N(HC
N except one are hidden by other stronger species. Therefore, we consider the column density obtained, N(HC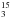 N) = 4.5 × 1013 cm-2, as an upper limit. We also calculated the column densities of the 13C isotopologues of HC3N ν7. The main contribution to the emission arises from the hot core (HC1 and HC2), while in the ridge (compact and extended) we found column densities about one order of magnitude lower (see Table 5 and Figs. A.16–A.18).
N) = 4.5 × 1013 cm-2, as an upper limit. We also calculated the column densities of the 13C isotopologues of HC3N ν7. The main contribution to the emission arises from the hot core (HC1 and HC2), while in the ridge (compact and extended) we found column densities about one order of magnitude lower (see Table 5 and Figs. A.16–A.18).
We also calculated the rotation temperature for the vibrational lines (vibrational temperature) in the hot core (HC1+HC2). We represent in Fig. 11 the column densities obtained for the ground state and the vibrational modes ν5, ν6, ν7, and 2ν7 (see Table 5) versus their vibrational energies (0, 954.48, 718.13, 320.45, and 642.67 K, respectively). From a linear fit of the points, we obtain a vibrational temperature of Tvib = 360 ± 50 K. This value is similar to the kinetic temperature we adopted for the hot core HC2 (310 K). Since vibrational excitation is expected to strongly depend on the temperature and density gradients in the region, it is consistent that we find the strongest emission from vibrational modes in the hot core.
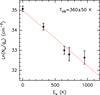 |
Fig. 11 Column densities, Ln(Nu/gu), of HC3N ν0, ν5, ν6, ν7, and 2ν7 vibrational states versus vibrational energy Eu (K). gu is the degeneracy of each mode. |
4.2. DC3N
To model the lines of DC3N we assumed LTE conditions for the hot core and LVG calculations for the rest of the components, as we did for HC3N, using collisional rates from Wernli et al. (2007) (HC3N-p-H2). Given that this molecule has previously only been detected in dark clouds, we first tried to use only components with rather low temperatures (TK ~ 60 K). However, it was impossible to fit the lines at high frequencies, so we had to consider hotter components in our model. In addition, these hot components needed to be narrow (given the observed line widths). For DC3N we found that only the hot core (HC1) and the compact ridge (CR) are responsible for the emission. The CR affects only the lines at 2 and 3 mm, whereas HC1 contributes to all lines, although mainly to lines at 1.3 mm (Fig. 6). In this case we changed the line width for the hot-core (HC1) component with respect to the parameters given in Table 4 to better reproduce the line profiles. The adopted value is ΔVFWHM = 8 km s-1. The column densities obtained are (1.5 ± 0.5) × 1013 cm-2 and (2.7 ± 0.8) × 1012 cm-2 for HC1 and CR, respectively (see Table 5). The value of the column density for the CR is very similar to the values obtained by Howe et al. (1994) in the dark clouds TMC-1, N = (5.9 ± 0.3) × 1012 cm-2, and L1544 N = (2.2 ± 0.5) × 1012 cm-2, although it is higher than the value obtained by Cordiner et al. (2012) in Cha-MMS1, N = 9 × 1011 cm-2. The column density for HC1, however, is one order of magnitude higher than the values found in these dark clouds.
Sample of molecular cloud cores.
4.3. HC5N
Column densities for HC5N were derived using LVG models with collisional rates from Deguchi & Uyemura (1984). We only found emission from three components: the hot core (HC1), the compact ridge, and the extended ridge. The hot core (HC1) presents the highest HC5N column density, with N(HC5N) = (7 ± 2) × 1013 cm-2, while the column densities for both ridges are an order of magnitude lower (see Table 5). Comparing these results with other sources, Broten et al. (1976) found a column density of 1.5 × 1014 cm-2 in Sgr B2, whereas in dark clouds such as L1489, L1521E, or TMC-2 the column density is ~1012 cm-2 (Suzuki et al. 1992). In Orion A (KL), Bujarrabal et al. (1981) found N(HC5N) = (5 ± 2) × 1012 cm-2 for the ridge component, consistent with our values.
5. HC3N in other sources
In this section we compare our results for HC3N with results obtained by other authors in a sample of 18 molecular cloud cores: 11 belong to giant clouds (GMCs) and 7 (MCLD123.5+24.9, Cha-MMS1, CrA C, TMC1, B1-b, L1544, and L183) to small dark clouds (SMCs). Table 6 shows the properties of each source. In addition, we study possible correlations between the column density of HC3N, the observed line width of this species, the cloud core mass, and the distance from the Galactic center.
First we considered the cloud cores of the sample with results for the column density of N(HC3N). These values (see references in Table 6) were calculated considering LTE approximation. To be able to compare with the other sources, for Orion KL we also calculated the column density of the ground state of HC3N for the dominant (hot core) component, assuming that the source fills the beam and that the lines are optically thin. With the data from Table A.2 we obtain a rotational diagram by applying the expression 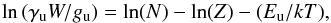 (3)where W is the integrated line intensity, gu is the statistical weight of each level, N the column density, Z is the partition function at temperature T, Eu the energy of the upper level, k is the Boltzman constant, T the rotational temperature, and γu a constant that depends on the transition frequency and the Einstein coefficient Aul (see Goldsmith & Langer 1999, for more details). Figure 12 shows the column density of HC3N for each source against its infrared luminosity. We observe an increasing trend of the column density of HC3N with the luminosity. A linear fit of these points provides a determination coefficient R2 = 0.79.
(3)where W is the integrated line intensity, gu is the statistical weight of each level, N the column density, Z is the partition function at temperature T, Eu the energy of the upper level, k is the Boltzman constant, T the rotational temperature, and γu a constant that depends on the transition frequency and the Einstein coefficient Aul (see Goldsmith & Langer 1999, for more details). Figure 12 shows the column density of HC3N for each source against its infrared luminosity. We observe an increasing trend of the column density of HC3N with the luminosity. A linear fit of these points provides a determination coefficient R2 = 0.79.
Figure 13 shows the observed line widths of HC3N (J = 10–9) in 17 cloud cores according to their masses. Considering only the cores that belong to giant clouds, we no find apparent correlation between these parameters. But including the dark clouds, we see a trend (R2 = 0.60), also increasing, between the FWHM of the HC3N lines and the mass of the sources. A bigger sample (including more cores of dark cloud cores) could confirm the correlation, but we did not include them due to the lack of observations of this transition of HC3N in these types of clouds.
 |
Fig. 12 Correlation between the column density of HC3N observed in different cloud cores and their infrared luminosity (L⊙). |
We also studied a possible correlation between the luminosity of the cloud cores and the line widths for the transition J = 10–9 (see Fig. 14). In this case, the FWHM increases as the luminosity increases (determination coefficient is R2 = 0.76). We therefore obtain the highest FWHMs, luminosities, and HC3N column densities in the cloud cores with higher masses. This suggests that these cores harbor the most massive stars which are responsible for their high luminosities. However, another posibility should be considered, mainly because of the trend of Fig. 14. We see that some of the cores present high FWHMs, and since line widths depend on the kinematics of the gas and mainly on the dispersion velocity, these results could suggest the presence of many lower mass sources within these massive cores, yielding higher velocity dispersions and therefore higher FHWMs. More studies of these cores could provide new hints concerning the high-mass star formation and the role of low-mass stars in this process. Observations of HC3N in a larger sample of SMCs are required to obtain firmer conclusions about the HC3N properties in GMCs and SMCs.
Isotopic and molecular ratios.
 |
Fig. 13 Correlation between the observed line widths of HC3N J = 10 − 9 in different cloud cores and their mass (M⊙). |
6. Discussion
We have shown that cyanoacetylene is an excellent dense-gas tracer (see also Morris et al. 1976; Chung et al. 1991; Bergin 1996). In particular, we found that the column density of HC3N in the hot core is up to two orders of magnitude higher than in the other Orion cloud components. The large number of high-energy transitions of HC3N (especially from the vibrational modes ν5, ν6, and ν7) observed with the Herschel telescope has revealed a temperature and density gradient in the hot core (the HC2 component), that probably would not have been detected from the IRAM-30-m data alone, because the emission from this component only affects the highest energy transitions. Moreover, the high vibrational temperature obtained in Sect. 4.1 shows the possible presence of an inner region even hotter than HC2 within the hot core.
 |
Fig. 14 Correlation between observed line width, FWHM, and infrared luminosity (L⊙) of different cloud cores. |
From the 2′ × 2′ maps (Sect. 3.2), we found that the emission for the ground state and the ν7 vibrational mode reaches its peak in the velocity range associated with the hot core and the high-velocity plateau (a hot region affected by shocks). These maps also show the kinematics of the gas from two low-energy transitions of HC3N. The transition J = 12–11 shows that the emission is elongated in the NE direction toward the extended ridge, with the emission toward the SW being much weaker. This elongation toward the NE could originate from the interaction of the hot spot situated at ~18″ east and ~25″ north of IRc2 (that we observe in the mapped transition J = 26–25), with the ambient gas in the ridge component. The hot spot could be associated with the CS1 condensation in the extended ridge noted by Mundy et al. (1988).
6.1. Isotopic and molecular abundances
Column density ratios were calculated for the different isotopologues of HC3N as well as molecular ratios (see Table 7). We showed only the cases where the column densities were obtained considering LVG approximation to avoid large uncertainties in the ratio values.
12C/13C: in the ground state we derived the same ratio in the high-velocity plateau for the three 13C isotopologues. In the hot core (HC1) we also obtained similar ratios for the three isotopologues, but in the plateau (PL) and in the extended ridge we obtained a larger difference (a factor ~3) between the abundance of H13CCCN and the other two 13C isotopologues than for HC3N. These last agree with the solar abundance (12C/13C = 90) from Anders & Grevesse (1989) in the plateau (PL) and extended ridge. In the rest of the regions, the results are much lower than the solar abundance, in particular in the hot core (HC2). In this region with the smallest size and the highest temperature of Orion KL, we obtained the largest abundance of the 13C isotopologue with respect to 12C. From observations of OCS, C34S, and H2CS in Orion KL, Tercero et al. (2010) obtained a 12C/13C ratio of 15, 18, and 20, respectively, in the hot core, while in the plateau the ratio is 25, and 7−14 in the compact ridge. These values agree with our results (considering the uncertainty), especially those obtained from the C34S molecule. Comparing this with other sources, Milam et al. (2004) found 12C/13C = 20.5 in the molecular cloud W31 and 12C/13C = 47.8 in G49.2, while in the cloud WB391 the value was 12C/13C ~ 135.
In Table 7, we also list the column density ratios for HC3N with respect to its deuterated counterpart (DC3N) and HC5N. For HC3N/HC5N, we obtained ratios >14. Comparing this with other authors, Bujarrabal et al. (1981) obtained HC3N/HC5N = 13 ± 7 in the ridge component of Orion KL, Cernicharo et al. (1984) obtained a ratio HC3N/HC5N between 3 and 8 in TMC-1, and HC3N/HC5N = 66 in IRC+10216 according to results from Bujarrabal et al. (1981) and Jewell & Snyder (1984). But especially interesting is the obtained D/H ratio (0.015), which is similar to that for dark clouds, like the ratio obtained by Langer et al. (1980) in TMC1, D/H = 0.02−0.08.
Table 8 shows the derived molecular abundances of HC3N, HC5N, and DC3N with respect to hydrogen in each component (see Tercero et al. (2011) for the assumed values of NH2). We found that the highest abundance of HC3N is obtained in the high-velocity plateau, whereas in the hot core this abundance is twice as low. The extended ridge has the lowest abundance of cyanoacetylene. HC5N is up to four times more abundant in the hot core than in the rest of components, and DC3N presents a similar abundance in the hot core and in the compact ridge.
Molecular abundances, X, with respect to H2.
6.2. Origin of the DC3N emission
We presented here a tentative detection of DC3N in a giant molecular cloud. Prior to this work, it was only observed in dark clouds, where deuterium fractionation is very effectively enhanced above the deuterium cosmic abundance, D/H ~ 10-5, due to their low temperatures and large CO depletion (see e.g. Roberts et al. 2005). We obtained a ratio D/H = 0.015 ± 0.009 in the hot core of Orion KL. In the same cloud, Walmsley et al. (1987) obtained D/H = 0.003 (from NH2D observations), Mauersberger et al. (1988) deduced D/H = 0.01−0.06 (from CH3OD), Jacq et al. (1993) D/H = 0.01−0.09 (from CH2DOH), and Bergin et al. (2010) D/H = 0.02 (from HDO/H2O), which all in broadly agree with our result. Other authors such as Persson et al. (2007) and Neill et al. (2013) obtained lower ratios of D/H (0.001 and 0.003, respectively), however. Deuterium enrichment is expected to be produced in cold clouds or during the cold phase (prior to the hot core stage) of giant clouds (Fontani et al. 2011). To obtain high ratios of D/H (as obtained in this work, which is similar to that obtained in cold clouds), low temperatures and high densities (>104 cm-3) are required. In our case, since the temperature of the hot core of Orion is >200 K, one of the most plausible mechanisms to explain the presence of DC3N is to consider that the formation of this molecule occurred prior to the gas phase, that is, the fractionation occurred on grain surfaces when the cloud was much colder, and then the deuterated compounds were released into the gas phase when the icy mantles sublimated. However, taking into account that HC3N is not mainly formed on grain surfaces, we should also consider other possible mechanisms for the formation of DC3N, which imply higher temperatures. If we analyze the different ways of forming deuterated molecules, we observe that deuterium is mainly locked into HD and transferred to other species by exothermic ion-molecule reactions (Howe et al. 1994) 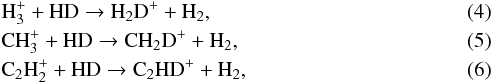 H2D+, CH2D+, and C2HD+ are molecules that can transfer their deuterium to other species. However, depending on the temeperature of the cloud, some may be more important than others. Equation (4) is only important at low temperatures (≤25 K), because the reverse reaction is exothermic and inefficient, whereas (5) and (6) (with exothermicities ~390 and ~550 K respectively) are efficient at temperatures up to 100 K.
H2D+, CH2D+, and C2HD+ are molecules that can transfer their deuterium to other species. However, depending on the temeperature of the cloud, some may be more important than others. Equation (4) is only important at low temperatures (≤25 K), because the reverse reaction is exothermic and inefficient, whereas (5) and (6) (with exothermicities ~390 and ~550 K respectively) are efficient at temperatures up to 100 K.
If we consider the case where HC3N is formed on grains, HC3N can be considered a reservoir from which DC3N could be formed subsequently in the gas phase, as a result of deuterated ions reacting with HC3N (Langer et al. 1980): 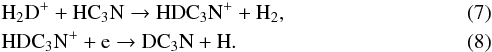 However, if the DC3N/HC3N ratio is higher than that of DCO+/HCO+, the formation of HC3N primarily on grains is ruled out (Langer et al. 1980). The ratio for DCO+/HCO+ observed in Orion is <0.009 (Rodríguez-Kuiper et al. 1978). This would suggest that the formation of HC3N did not take place during the cold phase. In this case, some of the mechanisms for the gas-phase production of HC3N are the reactions of H2CN+ with C2H2, followed by dissociative recombination, are proposed by Mitchell et al. (1979), or reactions of CH
However, if the DC3N/HC3N ratio is higher than that of DCO+/HCO+, the formation of HC3N primarily on grains is ruled out (Langer et al. 1980). The ratio for DCO+/HCO+ observed in Orion is <0.009 (Rodríguez-Kuiper et al. 1978). This would suggest that the formation of HC3N did not take place during the cold phase. In this case, some of the mechanisms for the gas-phase production of HC3N are the reactions of H2CN+ with C2H2, followed by dissociative recombination, are proposed by Mitchell et al. (1979), or reactions of CH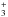 with C2H or C2 to produce C3H
with C2H or C2 to produce C3H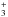 , followed by a reaction of this ion with nitrogen (Langer et al. 1980). The production of DC3N would then be through ion-molecule reactions, for example
, followed by a reaction of this ion with nitrogen (Langer et al. 1980). The production of DC3N would then be through ion-molecule reactions, for example 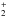 (9)In fact, other routes of formation may also be important. To investigate the origin of the deuterated cyanoacetylene in Orion KL in more detail, we used a gas-grain time-dependent chemical model (see Sect. 6.2.1).
(9)In fact, other routes of formation may also be important. To investigate the origin of the deuterated cyanoacetylene in Orion KL in more detail, we used a gas-grain time-dependent chemical model (see Sect. 6.2.1).
 |
Fig. 15 Time evolution of the column densities of HC3N, DC3N, H2D+, and CH2D+ for selected hot-cores chemical models. The input parameters for the mass of the formed star, the depletion efficiency (fr), and the sulphur solar abundance are indicated at the top of each panel. |
6.2.1. Chemical model
We modeled the hot core of Orion KL using the chemical model UCL_CHEM (Viti et al. 2004), a time-dependent gas-grain model where the chemistry, density, and temperature are calculated at each time-step, producing chemical abundances. This is a two-phase calculation: phase I simulates the free-fall collapse of the core, until densities typical of hot cores (~107 cm-3) are reached. In this phase atoms and molecules are frozen onto grain surfaces. Phase II follows the chemical evolution of the core once a source of radiation is present. We simulated the effect of an infrared source in the center of the core or in its vicinity by increasing the gas and dust temperature to T = 300 K. This increase of temperature is based on the luminosity of the protostar by using the observational luminosity function of Molinari et al. (2000).
We considered a source diameter of 10 arcsec, a final volume density nH = 2 × 107 cm-3, an efficiency of freeze out fr in phase I of 50% and 85%, and a mass for the star of 10 M⊙ and 15 M⊙ (see Table 9). The initial elemental abundances of the main species (H, He, C, O, N, Mg, S) are also input parameters. We adopted solar abundance for all of them, except for sulphur which we depleted by a factor 10 and 100, because it is well known that it may be depleted onto grains in star-forming regions (Bergin et al. 2001; Pagani et al. 2005). Figure 15 shows the time evolution of HC3N, DC3N, H2D+, and C2HD+ for selected hot-core models during phase II.
Hot-core chemical models and their parameters.
From Fig. 15 we find that the initial abundance of sulphur barely affects the time evolution of the column densities shown here. Comparing the theoretical and observed (Table 5) column densities of HC3N and DC3N, we find that the models that best reproduce our observations correspond to those for a hot core with a star of mass 10 M⊙ and with a depletion efficiency of 85%. In this case, the observations are reproduced at t ~ 6 × 104 years after the central star switches on. In the models with fr = 50%, we obtain (at t ~ 105 years) values for the column density of HC3N similar to those obtained from our line fits; however, the values for DC3N are too low. For all models with 15 M⊙, the column densities obtained for both HC3N and DC3N are too low.
It is interesting to note, however, that DC3N reaches the observed value during phase II, that is, its enhancement occurs during the hot core and not the cold phase, in conjunction with an increase in HC3N. A chemical analysis of these two species after 104 years (when they start to increase for the best-fit models) shows that their main route of formation is via reactions of CN with C2H2 and C2HD; in fact, when the core temperature starts to increase above 50 K, C2H2 and C2HD increase by several orders of magnitudes, because they evaporate from the icy mantles. At later stages however, these species are destroyed, leading to a decrease in HC3N and DC3N as well. We note that the time at which the different species sublimate from the mantle is a function of the mass of the star, as well as their binding (on the grains) properties (see Collings et al. 2004; and Viti et al. 2004, for more details). Hence, our treatment of the time and mass dependence of the increase of the temperature once the protostar is born is crucial to the interpretation of our results (Viti & Williams 1999); we therefore refrain from drawing any conclusion on the age of the core, but note that a too fast increase of temperature (as occurs for a 15 M⊙ star) leads to a more efficient destruction chemistry, hence misses the enhancement phase for HC3N and DC3N. Regardless of the details of the individual models, it is clear that the DC3N that forms during the cold phase is not enough to account for what is observed in the Orion KL hot core and that DC3N must partly form during the hot-core phase.
7. Summary and conclusions
We have reported a tentative detection of DC3N in Orion KL with the IRAM 30-m line survey. We also studied HC5N and HC3N in this region with IRAM 30-m and Herschel/HIFI observations, covering a total frequency range from 80 to 1907 GHz. We detected 35 lines of HC5N and 41 lines of HC3N in its ground state as well as 68 transitions of its 13C isotopologues and a large number of lines (297) from six vibrational states, ν5, ν6, ν7, 2ν7, 3ν7, and ν6 + ν7 of HC3N. This large number of observed lines has allowed us to consider a temperature and density gradient in the hot core of Orion KL, which would probably not be possible with observations from ground-based telescopes only.
For HC3N, we found the emission to arise mainly from the hot core. But unlike other works, we concluded, by applying an LVG code that the emission comes from the outer part of the hot core, where the temperature is TK ~ 220 K. For the vibrational modes ν5, ν6, 2ν7, and 3ν7, we detected emission from the innermost part of the hot core with TK ~ 310 K, which is the component most responsible for the emission of these modes. Their column densities are 1–6 × 1014 cm-2. Similar to HC3N, we obtained from LVG models that most of the emission of HC5N is coming from the outer hot core, although its column density in this region is ~15 times lower than that of HC3N. Comparing this with other sources, the derived column density of HC5N is a factor 3 higher than the column densities of HC3N found in dark clouds by Cernicharo et al. (1984). For DC3N, our best-fit model indicates that the emission comes from the hot core and from the compact ridge. Calculating the ratio R = DC3N/HC3N from the column densities of both molecules, we obtained R = 0.015 ± 0.009 for the hot core. To study the possible origin of DC3N in this region and to explain the high level of deuteration in the warm gas, we ran several chemical models. We reproduced the observed column densities of HC3N and DC3N in the gas-phase with models of a hot core, with a central star of 10 M⊙ and high depletion efficency (85%). From these results, we concluded that the tentatively observed DC3N in Orion KL is mainly formed during the warm gas-phase.
From maps of HC3N, we confirmed that the peak of the emission is found at velocities associated with the hot core, in agreement with the results of our best-fit models, and observed at low energies a northest-southwest gradient in the gas excitation, which traces the ridge component. For higher energies (E ~ 150 K), we detected a second peak of emission to the NE of the hot core that may represent the shocked ridge material, similar to the CH3CN study by Bell et al. (2013). For the vibrational modes ν6 and ν7 we found a compact distribution of the emission centered on the hot core.
Finally, we compared the results for HC3N in Orion KL with those for other sources. With a sample of 18 cloud cores, we found correlations between their masses, HC3N column densities, the line widths, and their infrared luminosities. We deduced that the most massive cloud cores present the highest column densities and broadest line widths of HC3N.
Online material
Appendix A: Figures and tables
HC3N parameters from Gaussian fits.
Lines of DC3N with emission frequencies whithin the 30-m IRAM survey.
Observed lines of HC5N.
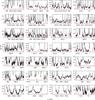 |
Fig. A.1 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N ν7 are shown in red. |
 |
Fig. A.2 Observed lines of HC3N 2ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.3 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N 2ν7 are shown in red. |
 |
Fig. A.4 Observed lines of HC3N 3ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.5 Detected lines of HC3N ν5 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.6 Observed lines of HC3N ν6 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.7 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N ν5 are shown in red. |
 |
Fig. A.8 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N ν6 are shown in red. |
 |
Fig. A.9 Observed lines of HC3N ν6 + ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.10 Observed lines of H13CCCN (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
 |
Fig. A.11 Observed lines of HC13CCN (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
 |
Fig. A.12 Observed lines of HCC13CN (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
 |
Fig. A.13 Observed spectra (black histogram) in the HIFI survey. Best-fit LVG model results for H13CCCN are shown in red. |
 |
Fig. A.14 Observed spectra (black histogram) in the HIFI survey. Best-fit LVG model results for HC13CCN are shown in red. |
 |
Fig. A.15 Observed spectra (black histogram) in the HIFI survey. Best-fit LVG model results for HCC13CN are shown in red. |
 |
Fig. A.16 Observed lines of H13CCCN ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.17 Observed lines of HC13CCN ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
 |
Fig. A.18 Observed lines of HCC13CN ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
Spectroscopic parameters for HC3N (dipole moment μ = 3.73 D) were obtained from DeLeon et al. (1985), de Zafra (1971), Mbosei (2000), Creswell et al. (1977), Chen et al. (1991), Yamada (2005), and Thorwirth et al. (2000). For 13C isotopologues the parameters were obtained from Creswell et al. (1977), Mallinson & de Zafra (1978), and Thorwirth et al. (2001). For the vibratonal mode ν7 and its 13C isotopologues, the parameters were obtained from Thorwirth et al. (2000) and Thorwirth et al. (2001), while the spectroscopic parameters for the rest of the vibrational modes were obtained from Yamada & Creswell (1986), Thorwirth et al. (2000), and Mbosei (2000).
Acknowledgments
We thank the Spanish MINECO for funding support through grants AYA2006-14876, CSD2009-00038, AYA2009-07304, and AYA2012-32032. G.B.E. is supported by a CSIC grant JAE PreDoc2009. J.R.G. is supported by a Ramón y Cajal research contract. A.P. is supported by a JAE-Doc CSIC fellowship co-funded with the European Social Fund under the program “Junta para la Ampliación de Estudios”, by the Spanish MICINN grant AYA2011-30228-C03-02 (co-funded with FEDER funds), and by the AGAUR grant 2009SGR1172 (Catalonia). T.A.B. is supported by a JAE-Doc research contract. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Anders, E., & Gevesse, N. 1989, GeCoA, 53, 197 [Google Scholar]
- Avery, L. W., Broten, N. W., MacLeod, J. M., & Oka, T. 1976, ApJ, 205, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Becklin, E. E., & Neugebauer, G. 1967, ApJ, 147, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. A., Cernicharo, J., Viti, S., et al. 2013, A&A, submitted [Google Scholar]
- Bergin, E. A., Snell, R. L., & Goldsmith, P. F. 1996, ApJ, 460, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Ungerechts, H., Goldsmith, F., et al. 1997, ApJ, 482, 267 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bergin, E. A., Ciardi, D. R., Lada, C. J., et al. 2001, ApJ, 557, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Zhang, Q., Greenhill, L. J., et al. 2005, ApJ, 632, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Esposti, D., & Botschwina, P. 2004, J. Mol. Spectr., 225, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Böttner, C., & Heithausen, A. 2003, Astron. Nachr. Suppl., 32, 63 [NASA ADS] [Google Scholar]
- Broten, N. W., MacLeod, M., Oka, T., & Avery, L. W. 1976, ApJ, 209, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Bujarrabal, V., Guélin, M., Morris, M., & Thaddeus, P. 1981, A&A, 99, 239 [NASA ADS] [Google Scholar]
- Cernicharo, J. 1985, ATM, A Program to compute atmospheric absorption for frequencies below 1000 GHz, IRAM Internal Report No. 52 [Google Scholar]
- Cernicharo, J. 2012, in ECLA-2011: Proc. Eur. Conf. Laboratory Astrophysics, EAS Publ. Ser. [Google Scholar]
- Cernicharo, J., Guélin, M., & Askne, J. 1984, A&A, 138, 371 [NASA ADS] [Google Scholar]
- Chen, W., Bocquet, R., Wlodarczak, G., & Boucher, D. 1991, Int. J. Infrared Millimeter Waves, 12, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, H. S., Kameya, O., & Morimoto, M. 1991, J. Kor. Astron. Soc., 24, 217 [Google Scholar]
- Cordiner, M. A., Charnley, S. B., Wirström, E. S., & Smith, R. G. 2012, ApJ, 744, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Creswell, R. A., Winnewisser, G., & Gerry, M. C. L. 1977, J. Mol. Spectr., 65, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Crockett, N. R., Bergin, E. A., Wang, S., et al. 2010, A&A, 521, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Helmich, F. P., & Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeLeon, R. L., & Muenter, J. S. 1985, J. Chem. Phys., 82, 1702 [NASA ADS] [CrossRef] [Google Scholar]
- de Vicente, P., Martín-Pintado, J., Neri, R., & Colom, P. 2000, A&A, 361, 1058 [NASA ADS] [Google Scholar]
- de Zafra, R. L. 1971, ApJ, 170, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Doty, S. D., Everett, S. E., Shirley, Y. L., et al. 2005, MNRAS, 359, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Esplugues, G. B., Tercero, B., Cernicharo, J., et al. 2013, A&A, 556, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Palau, A., Caselli, P., et al. 2011, A&A, 529, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Neri, R., & Caselli, P. 2005, A&A, 444, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., & Stutzki, J. 1989, A&A, 27, 41 [CrossRef] [Google Scholar]
- Gezari, D. Y. 1982, ApJ, 259, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, D. Y., Backman, D. E., & Werner, M. W. 1998, ApJ, 509, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Goddi, C., Humphreys, E. M. L., Greenhill, L. J., et al. 2011, ApJ, 728, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Greenhill, L. J., Gwinn, C. R., Schwartz, C., et al. 1998, Nature, 396, 650 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hachisuka, K., Brunthaler, A., Menten, K. M., et al. 2006, ApJ, 645, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Heithausen, A., Böttner, C., & Walter, F. 2008, A&A, 488, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirano, N., Kamazaki, T., & Mikami, H., et al. 1999, in Proc. Star Formation 1999, 181 [Google Scholar]
- Howe, D. A., & Millar, T. J. 1993, MNRAS, 262, 868 [NASA ADS] [Google Scholar]
- Howe, D. A., Millar, T. J., Schilke, P., & Walmsley, C. M. 1994, MNRAS, 267, 59 [NASA ADS] [Google Scholar]
- Howe, D. A., Taylor, S. D., & Williams, D. A. 1996, MNRAS, 279, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Jacq, T., Walmsley, C. M., Mauersberger, R., et al. 1993, A&A, 271, 276 [NASA ADS] [Google Scholar]
- Jacq, T., Baudry, A., Walmsley, C. M., & Caselli, P. 1999, A&A, 347, 957 [NASA ADS] [Google Scholar]
- Jewell, P. R., & Snyder, L. E. 1984, ApJ, 278, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, J. H., & Masson, C. R. 1998, ApJ, 509, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S. J., Kim, H. D., Lee, Y., et al. 2006, ApJS, 162, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kontinen, S., Harju, J., Heikkilä, A., & Haikala, L. K. 2000, A&A, 361, 704 [NASA ADS] [Google Scholar]
- Kroto, H. W. 1976, J. Mol. Spectr., 72, 175 [Google Scholar]
- Lada, C. 1976, ApJS, 32, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Schloerb, P., Snell, R. L., & Young, J. S. 1980, ApJ, 239, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Wang, J., Gu, Q., et al. 2012, ApJ, 745, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Q., Yang, J., Sun, Y., & Xu, Y. 2011, Res. Astron. Astrophys., 11, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Mallinson, P. D., & de Zafra, R. L. 1978, Mol. Phys., 36, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N. 2007, Ph.D. Thesis, Universidad de Granada, Spain [Google Scholar]
- Mauersberger, R., Henkel, C., Jacq, T., & Walmsley, C. M. 1988, A&A, 194, L1 [NASA ADS] [Google Scholar]
- Mbosei, L. 2000, J. Mol. Spectr., 65, 420 [NASA ADS] [Google Scholar]
- Menten, K. M., & Reid, M. J. 1995, ApJ, 445, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millar, T. J., Bennett, A., & Herbst, E. 1989, ApJ, 340, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, G. F., Huntress, W. T., & Prasad, S. S. 1979, ApJ, 233, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Brand, J., Cesaroni, R., & Palla, F. 2000, A&A, 355, 617 [NASA ADS] [Google Scholar]
- Morris, M., Turner, B. E., Plamer, P., & Zuckerman, B. 1976, ApJ, 205, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mundy, L. G., Cornwell, T. J., Masson, C. R., et al. 1988, ApJ, 325, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Wang, S., Bergin, E. A., et al. 2013, ApJ, 770, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Nielbock, M., Chini, R., & Müller, S. A. H. 2003, A&A, 408, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, ASPC, 434, 1390 [Google Scholar]
- Pagani, L., Pardo, J. R., Apponi, A. J., et al. 2005, A&A, 429, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J. R., Encrenaz, P. J., & Breton, D. 2001, IAU Symp., 196 [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2002, A&A, 393, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, T. C., Zapata, L. A., Wyrowski, F., et al. 2012, A&A, 544, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., Olofsson, A. O. H., Koning, N., et al. 2007, A&A, 476, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., Friedel, D. N., et al. 2009, ApJ, 704, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Polychroni, D., Moore, T. J. T., & Allsopp, J. 2012, MNRAS, 422, 2992 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R., & van den Bergh, S. 1970, IAU Symp. (Dordrecht: Reidel), 38, 219 [NASA ADS] [Google Scholar]
- Ridge, N. A., Wilson, T. L., Megeath, S. T., et al. 2003, ApJ, 126, 286 [Google Scholar]
- Roberts, H., Herbst, E., & Millar, T. J. 2003, ApJ, 591, 41 [Google Scholar]
- Rodriguez-Kuiper, E. N., Zuckerman, B., & Kuiper, T. B. H. 1978, ApJ, 219, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2009, ApJ, 702, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Sandell, G. 2000, A&A, 358, 242 [NASA ADS] [Google Scholar]
- Sargent, A. I., van Duinen, R. J., Nordh, H. L., et al. 1983, AJ, 88, 88S [NASA ADS] [CrossRef] [Google Scholar]
- Shimoikura, T., Dobashi, K., Sakurai, T., et al. 2012, ApJ, 745, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, ApJS, 97, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Tack, & Kukolich 1983, J. Chem. Phys., 78, 6512 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Bachiller, R., Wright, M. C. H., & Welch, W. J. 1997, ApJ, 474, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Tatematsu, K., Umemoto, T., Kameya, O., et al. 1993, ApJ, 404, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Tatematsu, K., Hirota, T., Kandori, R., & Umemoto, T. 2010, PASJ, 62, 1473 [NASA ADS] [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J. R., & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Vincent, L., Cernicharo, J., Viti, S., & Marcelino, N. 2011, A&A, 528, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tieftrunk, A. R., & Megeath, S. T., 1998, Msngr, 93, 36 [NASA ADS] [Google Scholar]
- Thorwirth, S., Müller, H. S. P., & Winnewisser, G. 2000, J. Mol. Spectr., 204, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Thorwirth, S., Müller, H. S. P., & Winnewisser, G. 2001, Phys. Chem. Chem. Phys., 3, 1236 [CrossRef] [Google Scholar]
- Thronson, H. A., Harper, D. A., Keene, J., et al. 1978, ApJ, 83, 5 [Google Scholar]
- Thronson, H. A., Gatley, I., Harvey, P. M., et al. 1980, ApJ, 237, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E. 1971, ApJ, 163, L35 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bout, P. A., Loren, R. B., Snell, R., & Wooten, A. 1983, ApJ, 271, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., & Williams, D. A. 1999, MNRAS, 305, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Collings, M. P., Dever, J. W., et al. 2004, MNRAS, 354, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Hermsen, W., Henkel, C., et al. 1987, A&A, 172, 311 [NASA ADS] [Google Scholar]
- Wang, Y., Jaffe, D. T., Evans II, et al. 1993, ApJ, 419, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K. S., Kuan, Y. J., Liu, S. Y., et al. 2009, ASPC, 420, 49 [NASA ADS] [Google Scholar]
- Wernli, M., Wiesenfeld, L., Faure, A., & Valiron, P. 2007, A&A, 464, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, G. J., Araki, M., Greaves, J. S., et al. 2003, A&A, 407, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, M. C. H., Plambeck, R. L., & Wilner, D. J. 1996, ApJ, 469, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, K. M. T. 2005, Z. Naturforsch, A50, 1179 [Google Scholar]
- Yamada, K. M. T., & Creswell, R. A. 1986, J. Mol. Spectr., 116, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Zapata, L. A., Schmid-Burgk, J., Ho, P. T. P., et al. 2009, ApJ, 704, L45 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Physical parameters adopted in the radiative transfer code for the Orion KL cloud components.
Column densities, N, for HC3N (its isotopologues and vibrationally excited states, including DC3N) and HC5N.
All Figures
 |
Fig. 1 Observed pure rotational lines of HC3N (black histogram) in the IRAM line survey. Best-fit LVG model results are shown in red. |
| In the text | |
 |
Fig. 2 Observed pure rotational lines of HC3N (black histogram spectra) with the HIFI survey. Best-fit LVG model results are shown in red. |
| In the text | |
 |
Fig. 3 Observed pure rotational lines of HC3N ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. 4 Tentative detection of four lines of DC3N. The horizontal green line indicates the 3σ threshold used for line identification. |
| In the text | |
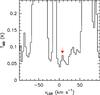 |
Fig. 5 Average of the spectra shown in Fig. 4. The red arrow indicates the resulting DC3N emission. |
| In the text | |
 |
Fig. 6 Observed spectra of DC3N (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. The horizontal green line indicates the 3σ threshold used for line identification. |
| In the text | |
 |
Fig. 7 Sample of observed lines of HC5N (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
| In the text | |
 |
Fig. 8 HC3N-line integrated intensity maps for different velocity ranges (indicated at the bottom of each panel). Row 1 shows the transition J = 12–11 with Eup = 34.1 K. The interval between contours is 4 K km s-1 and the lowest contour is 2 K km s-1. Row 2 shows the transition J = 26–25 with Eup = 153.3 K. The interval of contours is 7 K km s-1 and the lowest contour is 3 K km s-1. The white plus indicates the position of the hot core and the black cross the position of the compact ridge. The beam size is also shown with a blue circle. |
| In the text | |
 |
Fig. 9 HC3N ν7-line integrated intensity maps for different velocity ranges (indicated at the bottom of each panel). Row 1 shows the transition J=12-1–11-1 with Eup = 354.2 K. The interval between contours is 0.4 K km s-1 and the lowest contour is 0.7 K km s-1. Row 2 shows the transition J = 25-1–24-1 with Eup = 462.3 K. The interval of contours is 1.5 K km s-1 and the lowest contour is 2 K km s-1. The white plus indicates the position of the hot core and the black cross the position of the compact ridge. The beam size is also shown with a blue circle. The velocity ranges 14−18 and 18−22 km s-1 show the integrated intensity contaminated by CH2CHCN since there is an overlap of this species with the line of HC3N ν7J = 25-1–24-1. |
| In the text | |
 |
Fig. 10 HC3N v6-line integrated intensity maps for different velocity ranges (indicated at the bottom of each panel) for the transition J = 26-1–25-1 with energy Eup = 871.2 K. The interval between contours is 0.5 K km s-1 and the lowest contour is 0.35 K km s-1. The white plus indicates the position of the hot core and the black cross the position of the compact ridge. The beam size is also shown with a blue circle. |
| In the text | |
 |
Fig. 11 Column densities, Ln(Nu/gu), of HC3N ν0, ν5, ν6, ν7, and 2ν7 vibrational states versus vibrational energy Eu (K). gu is the degeneracy of each mode. |
| In the text | |
 |
Fig. 12 Correlation between the column density of HC3N observed in different cloud cores and their infrared luminosity (L⊙). |
| In the text | |
 |
Fig. 13 Correlation between the observed line widths of HC3N J = 10 − 9 in different cloud cores and their mass (M⊙). |
| In the text | |
 |
Fig. 14 Correlation between observed line width, FWHM, and infrared luminosity (L⊙) of different cloud cores. |
| In the text | |
 |
Fig. 15 Time evolution of the column densities of HC3N, DC3N, H2D+, and CH2D+ for selected hot-cores chemical models. The input parameters for the mass of the formed star, the depletion efficiency (fr), and the sulphur solar abundance are indicated at the top of each panel. |
| In the text | |
 |
Fig. A.1 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N ν7 are shown in red. |
| In the text | |
 |
Fig. A.2 Observed lines of HC3N 2ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.3 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N 2ν7 are shown in red. |
| In the text | |
 |
Fig. A.4 Observed lines of HC3N 3ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.5 Detected lines of HC3N ν5 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.6 Observed lines of HC3N ν6 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.7 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N ν5 are shown in red. |
| In the text | |
 |
Fig. A.8 Observed spectra (black histogram) in the HIFI survey. Best-fit LTE model results for HC3N ν6 are shown in red. |
| In the text | |
 |
Fig. A.9 Observed lines of HC3N ν6 + ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.10 Observed lines of H13CCCN (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
| In the text | |
 |
Fig. A.11 Observed lines of HC13CCN (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
| In the text | |
 |
Fig. A.12 Observed lines of HCC13CN (black histogram) in the IRAM survey. Best-fit LVG model results are shown in red. |
| In the text | |
 |
Fig. A.13 Observed spectra (black histogram) in the HIFI survey. Best-fit LVG model results for H13CCCN are shown in red. |
| In the text | |
 |
Fig. A.14 Observed spectra (black histogram) in the HIFI survey. Best-fit LVG model results for HC13CCN are shown in red. |
| In the text | |
 |
Fig. A.15 Observed spectra (black histogram) in the HIFI survey. Best-fit LVG model results for HCC13CN are shown in red. |
| In the text | |
 |
Fig. A.16 Observed lines of H13CCCN ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.17 Observed lines of HC13CCN ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
 |
Fig. A.18 Observed lines of HCC13CN ν7 (black histogram) in the IRAM survey. Best-fit LTE model results are shown in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


