| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321686 | |
| Published online | 03 October 2013 | |
The evolution of amorphous hydrocarbons in the ISM: dust modelling from a new vantage point
1 CNRS, Institut d’Astrophysique Spatiale, UMR 8617, 91405 Orsay, France
e-mail: Anthony.Jones@ias.u-psud.fr
2 Université Paris Sud, Institut d’Astrophysique Spatiale, UMR 8617, 91405 Orsay, France
Received: 12 April 2013
Accepted: 15 July 2013
Context. The evolution of amorphous hydrocarbon materials, a-C(:H), principally resulting from ultraviolet (UV) photon absorption-induced processing, are likely at the heart of the variations in the observed properties of dust in the interstellar medium.
Aims. The consequences of the size-dependent and compositional variations in a-C(:H), from aliphatic-rich a-C:H to aromatic-rich a-C, are studied within the context of the interstellar dust extinction and emission.
Methods. Newly-derived optical property data for a-C(:H) materials, combined with that for an amorphous forsterite-type silicate with iron nano-particle inclusions, a-SilFe, are used to explore dust evolution in the interstellar medium.
Results. We present a new dust model that consists of a power-law distribution of small a-C grains and log-normal distributions of large a-SilFe and a-C(:H) grains. The model, which is firmly anchored by laboratory-data, is shown to quite naturally explain the variations in the infrared (IR) to far-ultraviolet (FUV) extinction, the 217 nm UV bump, the IR absorption and emission bands and the IR-mm dust emission.
Conclusions. The major strengths of the new model are its inherent simplicity and built-in capacity to follow dust evolution in interstellar media. We show that mantle accretion in molecular clouds and UV photo-processing in photo-dominated regions are likely the major drivers of dust evolution.
Key words: dust, extinction / photon-dominated region / ISM: molecules
© ESO, 2013
1. Introduction
The evolution of interstellar dust is a key but complex issue that is now receiving some well-focussed attention. In particular, hydrocarbon solids (i.e., a-C:H and a-C, also known as HAC) present a particular challenge because of their inherent complexity and also because they appear to be rather vulnerable to destruction (e.g., Serra Díaz-Cano & Jones 2008; Jones & Nuth 2011). Further, they appear to undergo rather complex, size-dependent evolution arising, principally, from ultraviolet (UV) photon absorption leading to photo- or thermal-processing (e.g., Jones 2009, 2012a,b,c) and incident ion and electron collisions in shock waves and in a hot gas (e.g., Micelotta et al. 2010a,b; Bocchio et al. 2012). The evolution of their properties have received quite some interest as a model for the solid carbonaceous matter in the interstellar medium (ISM, e.g., Jones et al. 1990; Duley 1995; Duley et al. 1997; Dartois et al. 2004a,b, 2005; Pino et al. 2008; Serra Díaz-Cano & Jones 2008; Jones 2009; Godard & Dartois 2010; Godard et al. 2011; Compiègne et al. 2011), in circumstellar media (e.g., Goto et al. 2003; Sloan et al. 2007) and in the Solar System (e.g., Dalle Ore et al. 2011).
By dust evolution we here mean a change in the observable properties of the dust arising from processes such as accretion, coagulation, (photo-)fragmentation, erosion and grain charge effects. This evolution may be constructive, as for accretion and coagulation and lead to an increase in the total dust mass and/or its mean size, or destructive, as for (photo-)fragmentation and erosion and lead to a decrease in the total dust mass and/or its mean size.
The evolution of hydrocarbon solids was recently elucidated in detail in the series of preceding papers and their corrigenda (Jones 2012a,b,c, hereafter called Papers I, II and III) and this work builds upon these foundations in order to explore some of the consequences arising from the use of the optEC(s)(a) optical property data to explain the observed interstellar dust extinction and emission properties. As described in Papers I to III, amorphous hydrocarbon particles are macroscopically-structured (i.e., a contiguous network of atoms), solid-state materials consisting of only carbon and hydrogen atoms. For reference, a-C:H materials are H-rich (~15–60 at. %H), aliphatic-rich and wide band gap (>1 eV), whereas a-C materials are H-poor (≲15 at. %H), aromatic-rich and narrow band gap (~− 0.1 to 1 eV). The designation a-C(:H) is used here to cover the whole family of H-rich a-C:H to H-poor a-C carbonaceous solids, whose properties have been well-studied within both the physics and astrophysics communities (e.g., Phillips 1979; Döhler et al. 1980; Thorpe 1983; Robertson 1986, 1988, 1991, 2001, 2002; Robertson & O’Reilly 1987; Angus & Jansen 1988; Angus & Hayman 1988; Tamor & Wu 1990; Mennella et al. 1995, 1996, 2003; Ferrari & Robertson 2000, 2004; Kassavetis et al. 2007; Llamas-Jansa et al. 2007; Mennella 2008; Gadallah et al. 2011).
This paper uses a slightly-modified version of the laboratory-constrained optEC(s)(a) data presented in Paper III, which naturally explain many of the observed properties attributed to carbonaceous dust in the ISM. Here we insert these data into the DustEM dust extinction and emission calculator (Compiègne et al. 2011) in order to quantitatively examine and explore their viability as a tool in explaining the range of interstellar hydrocarbon dust extinction and emission observables and their associated (non-)correlations.
This work is a departure from the “traditional” interstellar dust modelling methodology because it adopts a “holistic” or “global” approach, in which we are able to coherently vary the dust properties over extreme-ultraviolet (EUV) to cm wavelengths. The result is a dust model that self-consistently explains almost all dust observables. This is important because it paves the way for an investigation of the interdependencies between the dust observables and, hence, their variations, correlations and non- or anti-correlations.
This paper is organised as follows: Sects. 2 and 3 summarise a-C(:H) dust photo-processing and its re-formation and re-accretion in the ISM, Sect. 4 briefly summarises the constraints imposed on dust models by experimental data and diffuse ISM dust observations, Sect. 5 presents our new evolutionary dust model, Sect. 6 discusses the astrophysical implications of the new model, Sect. 7 gives a schematic view of the a-C(:H) dust life-cycle and explores its evolution and variation in the ISM and Sect. 8 concludes this work.
2. Carbon dust photo-processing
Carbonaceous dust will be processed (evolve) as it traverses the ISM from its sites of formation to its demise in energetic regions and its eventual re-birth in some dense phase of the ISM (e.g., Jones & Nuth 2011). For small hydrocarbon grains and polycyclic aromatic hydrocarbons (PAHs), species of molecular dimensions, this processing can be catastrophic because high-energy photon absorption and electron collisions will result in highly electronically-excited particles that undergo dissociation before they can relax radiatively (e.g., Micelotta et al. 2010a,b; Bocchio et al. 2012).
Principal among the processes that affect the structure and composition of a-C(:H) dust is the photolytic and/or thermal processing arising from UV-EUV photon absorption (e.g., Papers II and III). As shown in Papers II and III the relevant time-scales for a-C(:H) photo-processing will be composition-dependent (i.e., depend on the H content, XH, which is directly proportional to the optical band gap, Eg) and also size-dependent. The characteristic time-scale for the direct photo-processing (photo-darkening or aromatisation) of a-C(:H) grains in the diffuse ISM appears to be relatively short and of the order of a million years for a-C(:H) nano-particles (see Papers II and III and their corrigenda). Thus, it is to be expected that small grains and thin mantles, of a-C(:H), ought to be maximally-aromatised in the diffuse ISM1. Large a-C(:H) grains (a ≥ 200 nm) will, however, remain predominantly aliphatic-rich because their cores, which are not UV photo-processed, make up ≥70% of the grain volume. This appears to be qualitatively consistent with observations, i.e., that the smaller carbonaceous particles are “aromatic-rich” while the larger carbonaceous grains are “aliphatic-rich” and that the carbon mantle/coating on amorphous silicate dust must be rather aromatic (e.g., Brooke et al. 1999).
Adamson et al. (1999) showed that the 3.4 μm absorption band is not polarised along the line of sight towards the Galactic centre source Sagittarius A IRS 7. At the time there were no spectropolarimetric observations of the 9.7 μm silicate band along this line of sight. This led Li & Greenberg (2002) to conclude that there was, at that time, no reason to reject a silicate core-carbonaceous organic mantle interstellar dust model. The modelling work by Li & Greenberg (2002) showed that, although both the 3.4 μm CH and 9.7 μm silicate bands are expected to be polarised, they are unlikely to be polarised to the same degree. However, Chiar et al. (2006) found that the 3.4 μm band is essentially unpolarised along the same Galactic centre lines of sight towards GCS 3-II and GCS 3-IV where the 9.7 μm silicate band is polarised. Thus, it is clear that any carbonaceous material associated with the silicate dust cannot be aliphatic-rich because of the lack of polarisation of the 3.4 μm absorption band. This then implies that there must be a population of large (a ≫ 20 nm) carbonaceous grains in the ISM that contain a significant aliphatic-rich component that is the origin of the 3.4 μm absorption band (e.g., Jones 2012a,c) and that this dust component is separate from the large, amorphous silicate grain population.
However, the exact nature of, and time-scale for, UV photon-induced processing is rather difficult to quantify because of uncertainties in the wavelength-dependence of the photo-dissociation cross-sections, and the importance of competing channels, such as UV photon absorption leading to heating or fluorescence (e.g., Paper III). In this work we therefore keep an open mind on this subject, construct a viable model for interstellar carbonaceous dust, using the optEC(s)(a) data, that best fits the observations and the variations in those observations.
3. a-C:H re-formation/accretion in the ISM
The work presented in Paper II indicates that enhanced large particle (a ≥ 100 nm) scattering at near-IR to IR wavelengths (1−5 μm) occurs in wide band gap a-C:H materials (i.e., aliphatic-rich a-C:H with Eg > 1.25 eV). Carbon accretion from the gas phase in a moderately extinguished medium (AV ≳ 1) will tend to form wide band gap a-C:H mantles on all grains. Such mantles, accreted in cloud cores, could be an explanation for the “cloudshine” observed predominantly in the H (1.6 μm) and Ks (2.2 μm) bands and explained as starlight scattered by the dust in cloud interiors (Foster & Goodman 2006). Possibly also related to a-C:H mantling is the observed “coreshine” effect observed in the Spitzer IRAC 3.6 and 4.5 μm bands, which is assumed to arise from cloud core dust emission (Pagani et al. 2010; Steinacker et al. 2010). It is possible that the observed “coreshine” could also be due to the scattering of starlight by a-C:H grain mantles or it could be due to luminescence from H-rich, a-C:H nano-particles recently released from carbonaceous mantles accreted within molecular clouds. The latter scenario is similar to the recently-proposed mechanism for fullerene formation around planetary nebulae via the photo-processing and vibrational excitation of “arophatic” clusters derived from a-C:H particles formed in denser regions (Bernard-Salas et al. 2012; Micelotta et al. 2012).
The observed “cloudshine” and “coreshine” can therefore be re-interpreted in terms of the scattering and/or emission by H-rich, carbonaceous grains formed by the accretion of gas phase carbon into aliphatic-rich mantles within molecular clouds. An initially-accreted a-C(:H) mantle will probably be rather H-poor (i.e., a-C) where the ambient radiation field is only weakly attenuated because of UV photon-driven dehydrogenation. However, with increasing density and extinction the accreting mantle will be H-rich (i.e., a-C:H). The maximum thickness of an a-C(:H) mantle is likely to be of the order of a few nm (e.g., Jones et al. 1990). This carbonaceous mantle accretion-transformation scenario could quite naturally explain the observed variations in the far-infrared (FIR) to mm dust emission in the transition between high-density/low-excitation molecular clouds and low-density/high-excitation photon-dominated regions (PDRs, see Sect. 7.2).
4. Diffuse ISM dust constraints
Observations, complimented by fundamental solid-state physics, optical property modelling and experimental data, impose stringent constraints on interstellar dust analogue materials and the models that use these data. Any viable dust model must therefore be carefully constructed within the framework of these constraints.
Observational constraints include the:
-
1.
λ-dependent EUV to FIR extinction;
-
2.
λ-dependent albedo and scattering;
-
3.
uniformity of the curvature of the far-ultraviolet (FUV) extinction;
-
4.
fixed UV bump position and limited variations in width;
-
5.
FUV, UV bump, visible/near-IR (NIR) and mid-IR (MIR) (non-)correlations;
-
6.
FUV and UV bump (non-)correlations with (C/H)dust;
-
7.
λ-dependent polarisation; polarisation-to-extinction ratio;
-
8.
NIR-FIR absorption and emission bands;
-
9.
extended red emission (ERE) and blue luminescence (BL);
-
10.
full EUV-cm dust spectral energy distribution (SED);
-
11.
cosmic abundance constraints (O, C, Si, Mg, Fe ...);
-
12.
known dust sources and pre-solar grain compositions;
-
13.
X-ray halo and absorption data;
-
14.
inferable dust (re-)formation processes in the ISM; and
-
15.
physical reasonableness and survivability in the ISM.
Experimental constraints include the measured behaviours of:
-
1.
material optical properties;
-
2.
T-dependence of dust analogue optical properties;
-
3.
quantum efficiency of likely ERE and BL carriers; and
-
4.
material deposition onto a substrate (accretion).
Modelling constraints include the:
-
1.
shape (irregularity) and structure (core-mantle, aggregate);
-
2.
dust size distribution (power law, log-normal, ...);
-
3.
small size (a ≲ 10 nm) of FUV and UV bump carriers; and
-
4.
a de-coupling of the FUV, UV bump and visible extinction.
As shown by Greenberg & Chlewicki (1983), particles that produce the UV bump at 217 nm, apparently, cannot contribute significantly to the FUV extinction and, further, the particles that are responsible for the UV bump can only make a small contribution to the extinction longwards of ~170 nm. They also infer that the physical characteristics of the FUV extinction carriers “remain fairly stable once the grains have emerged from the molecular cloud phase of their evolution.” Greenberg & Chlewicki (1983) also convincingly show that any dust model for which the FUV extinction is a sum of carbonaceous/graphite and silicate contributions is inconsistent with observations. The Mathis et al. (1977) and Draine & Lee (1984) models, and also the more recent Li & Draine (2001) and Compiègne et al. (2011) models, do not satisfy this constraint.
Fitzpatrick (2004) and Fitzpatrick & Massa (2007, 2009) have undertaken the most recent and detailed series of analyses of the extinction curve component (non-)correlations and we will use these studies as the basis for comparison of the optEC(s)(a) model data with observations. From these works we note that the major observed trends and variations that need to be explained by any viable dust model are:
-
1.
The FUV extinction rise (or curvature) and the intercept of anunderlying linear component at infinite wavelength, in anE(λ − V)/E(B − V) vs. 1/λ plot, are very well correlated.
-
2.
The 217 nm UV bump characteristics:
-
small peak position variations: 4.5903 ± 0.0085 μm-1 (217.85 ± 0.91 nm).
-
a range of UV bump widths: FWHM 1.00 ± 0.15 μm-1.
-
no correlation between peak position and width.
-
broader where the FUV curvature is greater.
-
strongest for intermediate levels of FUV extinction.
-
weaker for high or low FUV extinction.
-
weaker for low or high values of RV.
-
-
3.
The FUV extinction rise and UV bump do not appear to correlatewith the abundance of the mid-IR (12 and25 μm) emitters (Boulanger et al. 1994).
-
4.
The IR extinction, for λ > 1 μm, exhibit a power-law-like behaviour that is a function of RV (Fitzpatrick & Massa 2009).
5. Towards a more realistic interstellar dust model
Model dust compositions based on the optEC(s)(a) data and the dust observables.
Based on earlier considerations (e.g., Jones et al. 1990; Jones 2001; Jones & Nuth 2011), the work of Köhler et al. (2011, 2012), Planck satellite observations (Planck Collaboration 2011b,a), and the optEC(s)(a) model data (Papers I to III), we suggest that the usual decomposition of the interstellar dust species into two major populations of amorphous carbonaceous and silicate grains remains the most viable explanation. However, the newly-available optEC(s)(a) data imply that material composition and size effects likely play an important role. The a-C(:H) component is the detailed subject of this, and Papers I–III, and has properties determined by and calibrated against the available laboratory data.
5.1. Interstellar dust components
In the ISM it is hard to see how the silicate and carbonaceous dust populations could be completely segregated because mixing, even at some minor (contaminant) level, must occur. Thus, the amorphous silicates must be mixed, to some degree, with a carbonaceous dust component (e.g., Mathis & Whiffen 1989; Jones et al. 1990). In Table 1 and Fig. 1 we summarise our assumed dust properties as a function of size and in the following we describe these in more detail:
-
a-C(:H) grains with size-dependent properties2: this population represents a fundamentalcontinuity in composition and size distribution, which is quali-tatively consistent with a-C:H dust that has been exposed to the“equilibriating effects” of the local ISRF for at least 106 yr (see Fig. 18 in the Corrigendum to Paper III), i.e., long enough for any sub-nm particles to be aromatised to a-C3. Any particles larger than a few tens of nm in radius will be incompletely aromatised or will consist of an aliphatic-rich core surrounded by a more absorbing, aromatised mantle layer. (Therefore, carbonaceous mantles ≲20 nm thick will be completely aromatised, see following.)
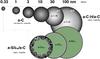
Fig. 1 Model dust populations, as seen in cross-section. In the upper part the a-C:H/a-C grains are shown, where black represents aromatic-rich material and white aliphatic-rich material. In the lower part amorphous silicate grains (green) are shown with a 5 nm thick coagulated/accreted a-C mantle. The particle radii are indicated on a logarithmic scale.
-
a-Sil grains ± a-C(:H) mantles: the interpretation of recent observations made by the Planck satellite (Planck Collaboration 2011b,a), coupled with Herschel and IRAS data, shows that the observed dust emission SED in the diffuse ISM can be empirically, and extremely well, fit with a single temperature (Tdust ~ 18 K), emissivity-modified (β ≃ 1.8) black-body. This strongly suggests that the dust emission at long wavelengths is dominated by emission from a single dust population that mixes, predominantly, amorphous silicate (a-Sil) materials (e.g., Coupeaud et al. 2011) with a carbonaceous (a-C or a-C:H) component in the form of mantles or accreted small grains (e.g., Köhler et al. 2011, 2012). The surface a-C(:H), whether accreted as a mantle or formed by the coagulation of small a-C particles, must be ≲20 nm thick (the depth at which the optical depth for the FUV processing photons is unity) otherwise it will be incompletely photolysed to a-C (see Paper II). An a-C:H mantle would be traceable through the polarisation of the aliphatic C−H 3.4 μm absorption band, which will follow that of the host a-Sil. The presence of an a-C:H mantle on a-Sil dust is inconsistent with observations (Adamson et al. 1999; Chiar et al. 2006). In our model we assume 5 nm thick a-C mantles (Eg = 0.1 eV) on the a-Sil grains. For the amorphous silicate optical properties we use those for an amorphous forsterite-type silicate with iron incorporated into the material as nano-particle inclusions, a-SilFe, which is equivalent to incorporating iron directly into the silicate lattice structure. In Appendix A we discuss the consequences of this form of amorphous silicate, in relation to those of the usually-adopted optical properties for “astronomical silicates” (e.g., Draine & Lee 1984; Greenberg & Li 1996). We will investigate the optical properties of the range of likely interstellar amorphous silicate dust analogue materials in a future paper.
-
3)
Coagulated, a-C(:H)-mantled a-Sil grains: enhanced dust emissivities in denser regions of the ISM perhaps indicate the onset of dust coagulation into larger inhomogeneous aggregates, which is consistent with recent modelling results (e.g., Köhler et al. 2011, 2012). This component therefore represents a coagulated mixing of all dust components, possibly with an additional a-C:H mantle material accreted from the remnant carbon in the gas phase, and also ice mantles in dense molecular clouds.
Comparing these dust populations with those used in the Compiègne et al. (2011) DustEM model, we find that there is no direct one-for-one correspondence because of overlapping properties. However, and in general, the small carbonaceous grains (a ≲ 20 nm) are the carriers of the same observables as the combined DustEM PAH and small amorphous carbon, SamC, grains. (Taken together we note that the combined DustEM PAH+SamC particles have a similar size distribution to our small a-C(:H) particles with a power-law size distribution.) The large a-C:H/a-C grains are equivalent to the DustEM large amorphous carbon, LamC, grains and the large carbon-coated amorphous silicates equivalent to the DustEM amorphous silicate, aSil, grains. Compared to most other dust models, we use a naturally-continuous distribution of carbonaceous grain properties rather than separate and disconnected populations of small carbon grains and PAHs. For the model proposed here we find it necessary to add an a-C mantle to the Fe-containing amorphous silicate grains in order to increase their emissivity and decrease their temperature (see Appendix A and Sect. 6.2.6).
The proposed dust model has the advantage of adding a carbonaceous component to the large (a ~ 10 − 4000 nm) silicate population (see Fig. 1) that does not exhibit a 3.4 μm aliphatic carbon band but which ought to show a weak 3.3 μm aromatic CH band and other associated CH and CC bands. However, as we show later (see Sect. 6.1), the a-C mantles on the a-Sil grains do not appear to manifest any absorption features in the 3 μm region. In any event, the IR absorption signatures of the a-C mantles will not be observable in the diffuse ISM because they will be swamped by emission bands at the same wavelengths. Observations of a 3.3 μm aromatic CH band in absorption would be possible along lines of sight where the emission bands are weak or absent (e.g., towards young stellar objects and the Galactic centre, Smith et al. 1989; Sellgren et al. 1995; Brooke et al. 1999; Chiar et al. 2000). Brooke et al. (1999) find that the optical depth of the 3.25 μm “aromatic” absorption feature in their spectra correlates better with the optical depth of the silicate feature than with the water ice feature, perhaps indicating an aromatic carbon component more intimately associated with the amorphous silicate grains than with their accreted ice mantles.
6. Astrophysical implications
The Li & Greenberg (1997) three-component dust model consists of large organic refractory-coated silicates (responsible for the visible extinction and polarisation), empirical UV bump-carrying particles (with a weak contribution to the visible extinction) and PAHs (responsible for the FUV extinction). In this model the extinction can naturally be decomposed into three separate populations and it thus satisfies the observed extinction constraints and (non-)correlations. It also satisfies the observed wavelength-dependent polarisation and extinction-to-polarisation ratio. As we shall see the dust model that we have developed bears some qualitatively-similar traits to the Li & Greenberg (1997) model. However, our model uses only two dust materials, i.e., a-SilFe and a-C(:H). In the model two of the dust observables, the FUV extinction and the UV bump, are due to the size-dependent properties of a-C(:H).
In order to illustrate the utility of the optEC(s)(a) data for ISM dust modelling we present a surprisingly-simple dust model, based on the discussion presented in the previous section. This model uses three dust populations but only two dust materials (see Figs. 1 and 2):
-
1.
A power-law distribution, with an exponential tail4, ofsmall (0.4 to ≃100 nm), a-C(:H) particles that have been photo-processed to depths of 20 nm and that show a continuity of size-dependent optical properties,
-
2.
a log-normal size distribution of large (≃200 nm) a-C:H grains (Eg = 2.5 eV)5 with an outer, photo-processed, a-C layer (20 nm thick, Eg = 0.1 eV), and
-
3.
a log-normal size distribution of large (≃200 nm) amorphous forsterite-type silicate grains, with Fe nano-particle inclusions (containing ~70% ≡ 22 ppm of the cosmic iron)6, that are coated with 5 nm thick a-C mantles (Eg = 0.1 eV).
With this model we are able to achieve an excellent fit to the dust observables using a coherent set of physically-realistic a-C(:H) and a-SilFe data that are based on laboratory measurements. In order to maximise the usefulness of the model we have “astronomicalised” the optEC(s)(a) data. All of the required adjustments are rather minor and physically-justified (see Appendix C). With these modified data we have re-visited the comparison of the optical properties of nm-sized a-C(:H) particles with those of “astronomical PAHs” (as per Paper III, i.e., see Sect. C.4).
The model results are not particularly sensitive to the large a-C:H/a-C grain size distribution, which contains a relatively small fraction of the dust mass. We find that removing the large a-C:H/a-C dust component and extending the small a-C:H/a-C grain power law to 4900 nm gives an equally good fit to the dust observables. However, at mm wavelengths the fit is not so good but we note that this is in a region where the amorphous silicate emission is not yet well constrained.
In the following sub-sections we present the detailed extinction and emission predictions for our dust model and compare them to the observations of dust in the diffuse ISM.
 |
Fig. 2 Standard dust model size distributions. a-C-coated (Eg = 0.1 eV, mantle depth 5 nm) amorphous forsterite-type silicate grains with ~70% of the available iron in metallic, nano-particle inclusions (triple dot-dashed). Core/mantle, a-C:H/a-C (Eg = 2.5/0.1 eV) particles: large, log-normal (dotted) and small, power-law with an exponential tail (dash-dotted). The grey line shows the overall a-C(:H) grain size distribution, with physically-continuous properties, which is only separated into “large” and “small” components for modelling convenience. |
6.1. A diffuse ISM dust model
 |
Fig. 3 Standard dust model for NH = 1020 H cm-2: NIR-UV extinction (top left), IR extinction (top right), albedo (bottom left) and the full dust SED (bottom right). The grain types are: a-SilFe/a-C core/mantle grains (triple dot-dashed), a-C:H/a-C core/mantle grains (dotted) and small a-C grains (dash-dotted). In each plot the totals are shown by the solid lines (red). The extinction data in the upper figures are taken from Mathis (1990). The observational data in the lower right plot are: ~5–15 μm ISOCAM/CVF ISO spectrum, ~100–1000 μm FIRAS/COBE spectrum, 3.3 μm AROME narrow band measurement (triangle) and DIRBE/COBE photometry (squares) (for details see Compiègne et al. 2011). |
The use of the optEC(s)(a) data, as derived in Papers II and III, is quite naturally able to explain the major dust observables. However, the fit to the UV bump, the 6–9 μm emission bands and the ~10–40 μm MIR continuum emission is not entirely satisfactory. We note that the latter two deficiencies are related, for a better account for the 6–9 μm emission bands leads to increased energy-loss via band emission for the larger a-C:H particles, which are then cooler and show weaker continuum emission in the ~10–40 μm region. Also, an increase in the IR band intensities in the 6–9 μm region leads to a slight increase in the extinction on the short wavelength side of the 9.7 μm silicate band (see Fig. 3 top right). We note that the 9.7 μm band in our laboratory data-derived a-SilFe is too narrow in comparison with the Mathis (1990) extinction profile (see Fig. 3, top right, and Appendix A), even with the addition of carbonaceous mantles. However, the extinction towards the Galactic centre observed by Lutz et al. (1996) looks rather different in that the short wavelength dip appears to be filled in, tantalisingly exhibiting what could be broad absorption bands in the 3–4 and 6–8 μm regions (similar to but much stronger than those of the a-C:H materials seen in Fig. 3 top right).
As mentioned above, we have adjusted the optEC(s)(a) data in a physically-meaningful way in order to get a good fit to the astronomical data7. Following our use of the published optEC(s)(a) data we find that it is difficult to interpolate for intermediate particle sizes because of the sharp IR bands, which are composition- and size-dependent. Thus, the optical property data ideally need to be calculated from scratch for each required particle size8.
Using the DustEM tool (Compiègne et al. 2011) we have calculated the predicted properties for our dust model. The small and large a-C(:H) grain size distributions are shown separately in Fig. 2 but they do in fact form a single grain population with size-dependent properties (the grey line in Fig. 2), which are important for a ≲ 30 nm (the separation into two distributions is simply a modelling convenience). Figure 3 shows the UV-visible extinction curve, the albedo9, the IR extinction and the emission spectrum (i.e., the SED). In this model the large a-C(:H) grain mass is about one tenth of that of the amorphous silicates, which reflects the lower resilience of carbonaceous dust to ISM dust processing, compared to silicate dust (see later, and also Serra Díaz-Cano & Jones 2008; Jones & Nuth 2011). Figure 4 gives the relative dust component contributions at each wavelength and shows that for λ ≈ 1 − 60 μm the emission is dominated by the small (power-law) a-C grains, for λ ≈ 60 μm–1 mm by the a-SilFe/a-C grains and for λ ≳ 1 mm by the large a-C:H/a-C grains. Figure 3 indicates that the model gives an extremely good fit to all of the major dust extinction and emission features observed in the diffuse ISM.
 |
Fig. 4 Dust component relative contributions to the SED: the line designations are as per Fig. 2. Note that the small a-C(:H) grain population contributes ≈45% of the total emission at 60 μm and ≈13% of the total emission at 100 μm. |
Note that the a-C:H to a-C dust mass ratio, an indicator of the sp3/sp2 C atom ratio, is ≈1/4 for our model (≡R = Xsp3/(Xsp3 + Xsp2) ≃ 0.2 and Eg ≃ 0.9 eV)10, indicating that in the diffuse ISM the grains are aromatic-rich in character, in agreement with the recent work by Li & Draine (2012) and Chiar et al. (2013). In fact, for the a-C nano-particles (Eg ≃ 0.1 eV), which are responsible for the IR emission bands in our model, ~90% of the carbon atoms are in sp2 aromatic clusters. This is consistent with the finding of Li & Draine (2012) that the emission band carriers contain <15% of aliphatic carbon. Chiar et al. (2013) interpret the observational evidence for the diffuse ISM carbonaceous dust as resulting from grain processing leading to the a-C:H mantling of aromatic-rich stardust grains.
We note that this dust model requires similar silicate-element depletion (321 ≡ 50, 22, 50, 199 ppm for Mg, Fe, Si and O, respectively) but more carbon depletion (233 ppm) than the Compiègne et al. (2011) model (315 ≡ 45, 45, 45 and 180 for Mg, Fe, Si and O, respectively, and 200 ppm for C). For bulk, crystalline olivine minerals the density ranges from 3.2 g cm-3 for forsterite (Mg2SiO4) to 4.4 g cm-3 for fayalite (Fe2SiO4). However, for sub-μm, amorphous materials that have been ion-irradiated through the effects of cosmic rays and shocks in the ISM the material densities will be significantly lower. We therefore adopt a density of 2.5 g cm-3 for our interstellar amorphous forsterite-type silicate, compared to the bulk, crystalline mineral density of 3.2 g cm-3. For iron in the form of nano-particles we assume a density of 7.87 g cm-3. Adopting Mg:Fe = 2.3:1 for the silicate, the same quantity of iron, as was assumed to be in Fe nano-particles (i.e., 22 ppm), can be incorporated into the silicate structure11. In this case all of the required silicate-forming elemental depletions (314 ppm) are similar to those of the Compiègne et al. (2011) model, i.e., 67, 22, 45, 180 ppm for Mg, Fe, Si and O, respectively. Nevertheless, the nature of amorphous silicates and the solid material into which iron is bound in the ISM, i.e., silicate, oxide or metal, remains something of an open question that awaits new laboratory and observational data.
In Fig. 5 we show a zoom into the extinction in the 3.4 μm region for each of the three dust components in our standard model. Note that the data have been scaled for comparison. Figure 5 shows that the large a-C:H/a-C grains exhibit a predominantly aliphatic 3.4 μm band with a peak at ≃3.42 μm, a shoulder at ≃3.5 μm and weak absorption in the 3.28 μm region, which resemble the band profile seen towards the Galactic centre (see Jones 2012a,c). Any small a-C:H/a-C grains, seen in absorption, will exhibit a dominant 3.28 μm aromatic CH band with sub-bands or shoulders at 3.37, 3.42 and 3.5 μm but all of these are significantly weaker than the large a-C:H/a-C grain absorption bands. Further, the large a-SilFe/a-C core/mantle grains appear to show no spectroscopic evidence of their a-C mantles in this wavelength region. The non-linear baseline seen in the a-SilFe/a-C extinction data is due to the narrow size range used to derive the Qext data. In our model the carbonaceous 3.4 μm and the amorphous silicate 9.7 μm bands are due to distinct dust populations and some variation in their relative band strengths is therefore to be expected (e.g., Gao et al. 2010).
 |
Fig. 5 Scaled dust model extinction in the 3.4 μm region: small a-C:H/a-C (× λ1.5, dash-dotted), large a-C:H/a-C (× λ1.65 − 2.9 × 104, dotted) and large a-SilFe/a-C (× λ1.7 − 8.2 × 103, triple dot-dashed). |
From the predicted dust SED in Fig. 3 it is clear that the emission bands in the 3 − 4 μm region have the correct spectral signatures, i.e., a dominant 3.3 μm with a side-band at ≃3.4 μm with a shoulder at ≃3.5 μm, but that they are too strong. However, we note that this model does not yet take into account the effects of grain charge, which (as in astronomical PAH models) will reduce the band strengths of the predominantly aromatic carriers that are the originators of the emission bands in this wavelength region. In a follow-up paper we will look at the detailed effects of grain charge and the anomalous microwave emission from spinning a-C(:H) grains.
With our proposed model we expect little silicate grain fragmentation, in shock waves and turbulent regions, for two reasons. Firstly, there are too few sufficiently-large grains (a ≃ 10 nm) for catastrophic collisions with silicate grains to be important (Jones et al. 1996) and, secondly, the silicate grains are protected from erosion-type, cratering fragmentation by their encasing a-C mantles. In contrast, the less resistant a-C(:H) grains will experience some fragmentation (Serra Díaz-Cano & Jones 2008) and we propose that our small a-C grain size distribution is the product of fragmentation in the ISM. We will investigate these fragmentation/cratering effects in detail in a follow-up paper. Further, we adopt log-normal size distributions for the large a-C:H/a-C and a-SilFe grains because, firstly, they are typical of dust condensation from the vapour phase, e.g., in the dust shells around evolved stars. Secondly, they appear to be consistent with the sizes of the pre-solar amorphous and crystalline silicate grains of evolved star origin that have been analysed in meteorites (e.g., Nguyen et al. 2007). Also, a theoretical study of cloud fragmentation and collapse prior to star formation shows that a log-normal distribution is a characteristic product of multiplicative processes acting on a size distribution (e.g., Larson 1973). This would appear to be similar to the case for the multiple processing of dust in turbulent and shocked interstellar regions.
6.2. The optEC(s)(a) model: diffuse ISM dust and beyond
Following on from Papers I to III, we consider the usefulness of the optEC(s)(a) data as a tool to interpret interstellar dust observations. In the following sub-sub-sections we compare the predicted properties, derived using the modified optEC(s)(a) data (see Appendix C), with the major constraints imposed by interstellar dust observations. The model-observation comparisons are presented in order of increasing wavelength.
 |
Fig. 6 Dust model normalised extinction, E(λ − V)/E(B − V) for fixed dust mass and for varying band gap, Eg [eV]: 0.1 (dark grey), 0.5 (pink), 1.0 (brown), 2.0 (blue) and 2.6 (violet). The solid (dotted) vertical grey lines mark the model (observed) UV bump positions. The yellow band indicates the observed extinction and its range of variation (Fitzpatrick & Massa 2007). |
 |
Fig. 7 Dust model extinction for fixed dust mass as a function of Eg (top), a− (middle) and α (bottom). The solid (dotted) vertical grey lines mark the model (observed) UV bump peak positions. The symbols indicate the observed extinction for RV = 3.1 (grey open squares) and 5.1 (black filled squares) (Savage & Mathis 1979; Mathis 1990). The orange line shows the intensity of the adopted ISRF plotted as Jλ/λ and normalised to unity. |
 |
Fig. 8 Dust size distributions for fixed mass in each component: large a-C:H/a-C particles (black dotted), large a-SilFe/a-C particles (black tripple-dot-dashed), for varying small a-C(:H) grain size distribution power-law index, α. |
6.2.1. The FUV extinction rise
In Fig. 6 we show the model extinction, for fixed dust component masses, normalised in the usual E(B − V) manner, as a function of the “outer” material band gap. These data are compared to the observed diffuse ISM extinction variations from the work of Fitzpatrick & Massa (2007). Here we vary the band gap of the outer 20 nm of all of the carbonaceous grains and, therefore, particles with a < 20 nm, which dominate the FUV extinction, are homogeneous. For particles with a > 20 nm the core material gap is fixed at 2.5 eV (see Footnote 5) and only the gap of the outer 20 nm deep layer is varied.
Figure 6 indicates that the observed FUV extinction (in normalised form) is only consistent with a-C:H dust with a band gap ≲2 eV. Nevertheless, care must be exercised in the use of E(B − V)-normalised extinction data because of the strong leverage by the V and B band data point anchors. Thus, in Fig. 7 we show the un-normalised FUV extinction for the model as a function of Eg (upper plot), a− (middle plot) and α (lower plot), along with the Savage & Mathis (1979) and Mathis (1990) extinction data (arbitrarily-scaled for qualitative comparison). Plotting the data in this way, we note that, for a fixed dust mass, the FUV extinction is intrinsically invariant in the 6−8 μm-1 region, as noted by Greenberg & Chlewicki (1983). Thus, for fixed dust mass and size distributions, the shape and intensity of the FUV extinction is independent of the band gap and hence the composition of the a-C(:H) dust component. This behaviour arises because the FUV optical properties, which are dominated by the σ − σ⋆ band of small a-C(:H) particles, are material independent. The FUV extinction shown in Fig. 7 is then qualitatively consistent with all of the plotted a-C(:H) band gap materials (Eg = 0.1−2.6 eV). Thus, it appears that the FUV extinction could be a direct tracer of the small particle dust mass. Parvathi et al. (2012) find a gradual decrease in the FUV extinction with decreasing density, which they interpret as indicating the disruption of small grains in the diffuse ISM.
In the lower plot in Fig. 7 we show how the extinction is affected by varying the power-law index, α, of the small a-C particles (see Fig. 8). As α decreases the FUV extinction flattens because of the increasing loss of small particles from the size distribution. The middle plot in Fig. 7 shows the effects of varying the minimum particle size, a−, which must be in the range 0.4−1 nm (for α = 5) in order to obtain a satisfactory fit to the FUV extinction12. We find that the form of 6 − 8 μm-1 (8−11 μm-1) FUV extinction in the diffuse ISM predicted by our model does not vary as long as a− < 5 nm (a− ≲ 3 nm) as indicated in Fig. 7 (middle). For a− > 3 nm the FUV extinction turns over for λ-1 > 8 μm-1 and for a− > 5 nm it is flatter in the λ-1 = 6−8 μm-1 region.
The form of the FUV extinction and the observed “tight” FUV rise-intercept correlation (Fitzpatrick 2004; Fitzpatrick & Massa 2007) seems to imply a “lever effect” with a “pivot point” at FUV wavelengths. Consistent with this constraint, we note that the optEC(s)(a) Qabs data, for particles smaller than 10 nm and for all band gap materials, have a “pivot point” in the ≈7.0–7.5 eV region, for small a-C(:H) dust size distributions with α ≥ 3 (Fig. 7 here, and Figs. 7 and D.2 to D.5 in Paper III).
We conclude that the variations in the FUV extinction, predicted by our model, are consistent with the FUV extinction characteristics determined by Greenberg & Chlewicki (1983) and the range of variations noted by Fitzpatrick & Massa (2009).
Dust model parameters as input into DustEM.
6.2.2. The 217 nm UV bump
The size dependence inherent in the optEC(s)(a) data naturally leads to a UV bump for small (a ≲ 1 nm), narrow band gap (Eg = −0.1 to 0.5 eV), a-C particles, as can clearly be seen in Fig. 3 and the extinction plots in Figs. 6 and 7. This occurs because the UV bump in a-C is carried by a restricted-range of aromatic (or PAH-like) clusters with 1–3 rings. In large particles (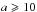 nm) the feature is very broad and peaks in the λ-1 < 4 μm region. We emphasise that the aromatic clusters intrinsic to a-C(:H) materials are not strictly PAHs because they form a cohesive part of a much larger network structure, within which they are bound to other clusters by aliphatic and olefinic bridging groups (Jones 2012c; Micelotta et al. 2012).
nm) the feature is very broad and peaks in the λ-1 < 4 μm region. We emphasise that the aromatic clusters intrinsic to a-C(:H) materials are not strictly PAHs because they form a cohesive part of a much larger network structure, within which they are bound to other clusters by aliphatic and olefinic bridging groups (Jones 2012c; Micelotta et al. 2012).
It is clear that the derived UV bump at ≈4.7 μm-1 is slightly too large with respect to the observed interstellar feature (e.g., see Figs. 3, 6 and 7). For varying band gap, but fixed dust mass, the predicted UV bump position is practically unvarying, which is in agreement with the immovable position of the observed bump (e.g., Fitzpatrick 2004; Fitzpatrick & Massa 2007). However, it does shift to positions as short as ≈4 μm-1, compared to the observed range of ≃4.58 − 4.60 μm-1 (Fitzpatrick & Massa 2007), but only in the case of extreme size distributions, i.e., for large a− or small-α distributions (see Fig. 7, middle and lower panels, and Sect. 7). We have investigated the width and postion of the UV bump extinction as a function of a−, as predicted by our diffuse ISM dust model (Fig. 3), and find no significant variations as long as a− < 1 nm. For a− > 1 nm the UV bump is broader and the peak shifts to longer wavelengths (see Fig. 7, middle). We then note that, in the absence of extreme size distribution variations, it is encouraging that the predicted variations in the UV bump position and width are rather small, in accordance with observations.
Fitzpatrick (2004) and Fitzpatrick & Massa (2007) have undertaken a detailed study of the UV extinction bump and its variations as seen in the E(B − V)-normalised extinction data. They find the UV bump peak positions and widths are uncorrelated, broader bumps for greater FUV curvature, stronger bumps for intermediate levels of FUV extinction (i.e., weaker for high or low FUV extinction), stronger FUV extinction as the bump weakens, and weaker bumps for low or high values of RV. Using the optEC(s)(a) data to model the UV bump we find that the peak position and width are not correlated. We also find broader bumps for larger band gap materials that exhibit more curvature in their FUV extinction and that the FUV extinction strengthens and the bump weakens with increasing Eg (see Fig. 6). The weaker bump associated with low FUV extinction could be explained by a “flatter”, i.e., high RV, size distribution, see Figs. 6 and 7. Conversely, a weak UV bump for high FUV extinction is consistent with large band gap a-C:H materials, which show basically no UV bump (Figs. 6 and 7).
In the un-normalised extinction plots in Fig. 7 (upper and middle panels) we can see that the FUV extinction shows little or no variation with Eg or a− but does depend, rather sensitively, on the assumed power law, α, for the small a-C grains (Fig. 7, lower panel). Thus, the observed UV extinction variations seen in the E(λ − V)/E(B − V) plot (Fig. 6), can be explained by variations in the visible extinction slope (Fig. 7, upper panel), which biases the E(B − V)-normalised data. The visible extinction and the UV bump are determined by the a-C(:H) composition and, for fixed dust mass, both increase in strength as Eg decreases, which leads to an anti-correlation between the UV bump strength and the FUV continuum in E(B − V)-normalised data (e.g., Fitzpatrick 2004). Further, the range of FUV extinction variations predicted by the model are in very good agreement with the observed FUV extinction dispersion seen in the diffuse ISM (Fitzpatrick 2004; Fitzpatrick & Massa 2007).
For our standard model parameter set (Table 2) the UV bump and the FUV extinction rise are due to a-C particles with <250 C atoms (≡a < 1 nm) and <7 × 103 C atoms (≡a < 3 nm), respectively. This could then explain why the UV bump and FUV extinction are partially de-coupled (e.g., Greenberg & Chlewicki 1983; Fitzpatrick 2004; Fitzpatrick & Massa 2007). As shown in Sects. 4, 6.2.1 and 6.2.2 the UV bump and FUV extinction produced by our model depend on the adopted minimum size for the a-C grains, a−, and their power law index, α (see Fig. 7 middle and lower panels). The upper panel of Fig. 7 shows that the UV bump intensity is sensitive to the material band gap. However, given that the aromatisation time-scale in the diffuse ISM seems to be short (e.g., ≃105/G0 yr, Jones 2012b) most small a-C(:H) particles with radii ≲20 nm will be a-C. The partial de-coupling of the UV bump and FUV extinction in the diffuse ISM would then be due to variations in the a-C dust mass for 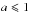 nm (UV bump carriers) with respect to somewhat larger particles (
nm (UV bump carriers) with respect to somewhat larger particles (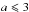 nm, the FUV extinction carriers), as shown in Fig. 7. In particular, we propose that the diffuse ISM FUV extinction is principally characterised by variations in α and that the IR-MIR SED is determined by the minimum particle size, a−, and that both are a function of the local ISRF intensity and hardness (e.g., Jochims et al. 1994; Bocchio et al. 2012). This is in agreement with the conclusions of the astronomical PAH model, i.e., that the IR emission band profiles are sensitive to the number of C atoms in the smallest PAHs (Verstraete et al. 2001).
nm, the FUV extinction carriers), as shown in Fig. 7. In particular, we propose that the diffuse ISM FUV extinction is principally characterised by variations in α and that the IR-MIR SED is determined by the minimum particle size, a−, and that both are a function of the local ISRF intensity and hardness (e.g., Jochims et al. 1994; Bocchio et al. 2012). This is in agreement with the conclusions of the astronomical PAH model, i.e., that the IR emission band profiles are sensitive to the number of C atoms in the smallest PAHs (Verstraete et al. 2001).
In conclusion, it is evident that the UV extinction bump, which is reasonably well fit with 0–0.22 eV band gap materials, appears to provide a stronger constraint on the composition of the small a-C dust particles than does the rather invariant FUV extinction rise. However, as noted by Parvathi et al. (2012) the intensity of the UV bump extinction appears to be essentially uncorrelated with the degree of carbon depletion into dust, (C/H)dust.
6.2.3. Visible-NIR extinction and variations
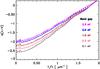 |
Fig. 9 NIR extinction predicted by the model (solid lines) and the parameterised fits (as per Fitzpatrick & Massa 2009) for varying band gap, Eg [eV] (dashed lines), for a column density NH = 5 × 1021 cm-2. The model data colour-coding is as per Fig. 7. The sinusoidal structure is due to the adopted narrow silicate size range and will not be present in real, irregular and non-spherical particles. |
The extinction data shown in Fig. 7 indicate that, for fixed dust mass, this model predicts a significant dispersion in the B and V band extinction, which is due to variations in the dust composition (i.e., decreasing (B − V) as Eg increases) or its size distribution (i.e., increasing (B − V) as α decreases or a− increases). Unfortunately, it is exactly these interesting variations that are “damped out” by the normalisation of the observed extinction by E(B − V). Thus, based on the above it appears that normalising the interstellar extinction in the FUV at ≃7 μm-1 (≡143 nm) would render the data in much more diagnostically-useful manner.
Fitzpatrick (2004), Fitzpatrick & Massa (2009) and Fritz et al. (2011) note that the IR extinction longward of 1 μm generally has a power-law type of behaviour. As Fig. 9 demonstrates, the range of a-C(:H) grain material optical properties, with Eg ≃ 0.0−2.6 eV (≡XH = 0.0 − 0.6), in combination with the adopted amorphous silicate, are consistent with this important observational constraint.
The NIR extinction can be fit with a two-parameter model, where the free parameters are a power law, αNIR, and RV, i.e., ![\begin{equation} k(\lambda-V) = \left[ \frac{0.349+2.087R_{\rm V}}{1 + (\lambda/0.507)^{\alpha_{\rm NIR}}} \right]- R_{V}, \label{eq_NIRext_fit} \end{equation}](/articles/aa/full_html/2013/10/aa21686-13/aa21686-13-eq161.png) (1)as determined by Fitzpatrick & Massa (2009). As they noted, and as we also find with our model, the good fits to the data extend out to shorter and longer wavelengths than those used by Fitzpatrick & Massa (2009) in deriving their NIR extinction law (Fig. 9). In fitting the observations Fitzpatrick & Massa (2009) show that αNIR generally decreases as RV increases. However, for our dust model we find good fits with αNIR ≃ 2 for all RV. In Fig. 10 we show αNIR as a function of RV, as per Fitzpatrick & Massa (2009), and find that the lower RV values derived for our model span the same range as those for the Fitzpatrick & Massa (2009) fits to their data. Discrepancies between the model and observational data are also apparent in Fig. 3 where the model data show slight curvature that is not apparent in the observations. This indicates that the model does not yet include all of the elements necessary to explain the exact form of the NIR extinction. This could be related to an underestimate of the absorption in the 5−10 μm region compared to observations (e.g., Lutz et al. 1996). The discrepancy could also be due to grain charge effects, which we do not take into account here. For example, aromatic cation species show NIR absorption in the ~0.8 to >2 μm region (Mattioda et al. 2008), which is not apparent in astronomical PAH models.
(1)as determined by Fitzpatrick & Massa (2009). As they noted, and as we also find with our model, the good fits to the data extend out to shorter and longer wavelengths than those used by Fitzpatrick & Massa (2009) in deriving their NIR extinction law (Fig. 9). In fitting the observations Fitzpatrick & Massa (2009) show that αNIR generally decreases as RV increases. However, for our dust model we find good fits with αNIR ≃ 2 for all RV. In Fig. 10 we show αNIR as a function of RV, as per Fitzpatrick & Massa (2009), and find that the lower RV values derived for our model span the same range as those for the Fitzpatrick & Massa (2009) fits to their data. Discrepancies between the model and observational data are also apparent in Fig. 3 where the model data show slight curvature that is not apparent in the observations. This indicates that the model does not yet include all of the elements necessary to explain the exact form of the NIR extinction. This could be related to an underestimate of the absorption in the 5−10 μm region compared to observations (e.g., Lutz et al. 1996). The discrepancy could also be due to grain charge effects, which we do not take into account here. For example, aromatic cation species show NIR absorption in the ~0.8 to >2 μm region (Mattioda et al. 2008), which is not apparent in astronomical PAH models.
We also note that the tail, extending to high RV and low αNIR in Fig. 10, cannot be explained by our model. This is probably because the dust along these lines of sight has undergone significant evolution (accretion and coagulation) and thus the constant mass assumption that we adopt here is no longer valid.
 |
Fig. 10 Fitzpatrick & Massa (2009) NIR extinction parameter αNIR as a function of RV (large black squares), see Eq. (1). The fit parameters for our model as a function of Eg (α) are shown by the coloured squares (crosses), the colour-coding as per Fig. 7. The thick squares use the model RV and the thin squares the best fit RV values from Eq. (1), shown as the dashed lines in Fig. 9. The vertical grey band shows the typical diffuse ISM value of RV. |
The NIR-MIR optical properties of a-C(:H) materials can also be fit with a two free-parameter Urbach tail model (see Paper II). However, in the optEC(s)(a) data the observed wavelength-dependent behaviour arises naturally from the physics and no empirical wavelength-dependence is imposed.
The IR extinction is generally rather invariant but we conclude that variations will arise with compositional and size distribution variations in the ISM, for example, due to the accretion of wide band gap a-C:H material, and also due to particle coagulation in dense regions and erosion in energetic regions. We have yet to fully explore this aspect of our dust model and leave this to targeted studies of particularly well-studied lines of sight.
6.2.4. The IR absorption bands
As discussed in detail in Papers I to III, the optEC(s)(a) data is consistent with the profile of the absorption bands observed towards the Galactic centre in the 3−4 μm wavelength region. The predicted absorption band profiles (see Fig. 5) are similar to those calculated in emission, as shown in Fig. 11. Using the optEC(s)(a) data it is possible to explain, in detail, all of the structure in the observed absorption bands with rather wide band gap (Eg ≳ 2.3 eV), a-C:H carbonaceous grains with radii ≳20 nm. As pointed out in Sect. 5.1 in Paper III, a-C nano-particles, with band gaps as low as 0.5 eV, also appear to have 3−4 μm IR absorption spectra which match the observed absorption features. However, such small particles are expected to be rapidly UV-photolysed in the ISM and so the good match may simply be fortuitous.
It is interesting to note that the nature of the bands in the 3 − 4 μm region can be used to constrain the emission properties at FIR-mm wavelengths because of the strong optical property coupling at all wavelengths. For example, and as noted above, the absorption band profiles in the 3 − 4 μm region indicate the presence of a significant H-rich, wide band gap (Eg ≳ 2.3 eV), a-C:H dust mass, which ought to be apparent in the long wavelength emission behaviour but this is not the case (see the following section for an explanation).
 |
Fig. 11 Dust model 3−14 μm and 3.1−3.7 μm emission band spectra as a function of the a-C(:H) material band gap, Eg [eV]. |
6.2.5. The IR emission bands
In Fig. 11 we show the IR emission band spectrum in the 2.5−14 μm (upper panel) and 3.1−3.7 μm (lower panel) wavelength regions. It is clear, from the lower plot in Fig. 11, that a-C materials with band gaps in the range 0.1–0.5 eV exhibit a 3.3 μm aromatic emission band that is always accompanied by a side-band at ~3.4 μm with a shoulder at ~3.5 μm. As pointed out in Sect. 5.1 in Paper III, this kind of band structure, as predicted by the optEC(s)(a) data, is consistent with the observed emission bands in many regions, e.g., across the Orion bar (Sloan et al. 1997; Verstraete et al. 2001), M17-SW, NGC 2023 (Verstraete et al. 2001) and in M 82 (Yamagishi et al. 2012), where both aromatic and aliphatic CH bands appear in the 3 − 4 μm spectral region, even in these energetic environments.
Our new dust modelling approach, using a-C(:H) optical property data, therefore offers an alternative view to the origin of observed IR emission bands, which are well-matched by astronomical PAH, thermal emission profile models (e.g., Verstraete et al. 2001; Pech et al. 2002). However, in our model it is small (a ≲ 0.5 nm), 3D, a-C particles that are the carriers of the observed IR emission bands. As proposed in Paper III, these 30 − 40 C atom, aromatic/aliphatic, cage-like particles (Micelotta et al. 2012), that we call “arophatics”, represent the “end of the road” for a-C(:H) grain evolution because their disintegration products, viz., small free-flying, PAH-like species and short hydrocarbon chains, will quickly be destroyed in the diffuse ISM (e.g., Jochims et al. 1994; Micelotta et al. 2010a,b, 2011; Bocchio et al. 2012). The IR emission band-carrying a-C particles are also responsible for the UV bump and FUV extinction, which is consistent with their limited range of variation and the constancy of the IR emission band profiles. Thus, these “end of the road”-particles, with a narrow range of optical properties, could explain the noted “stability” of the FUV extinction carriers in the diffuse ISM (Greenberg & Chlewicki 1983). As shown above, in Sect. 6.2.2, a partial de-correlation of the UV extinction components (bump and FUV) and the IR emission bands is predicted by our model.
The thermal emission from the wide band gap materials observed in absorption (see above) and the low band gap, UV photolysed a-C material component observed in emission should both be evident in the FIR-mm dust emission. However, we find that the predicted dust emissivity at these wavelengths is dominated by the photolysed outer surfaces of the a-C:H/a-C particles, i.e., the narrow band gap a-C material (Eg ≃ 0.1 − 0.25 eV), that dominates the emission because its emissivity at mm wavelengths is more than four orders of magnitude greater than that for wide band gap a-C(:H) materials (e.g., see Fig. 16 in Paper II and Fig. 10 in Paper III). Thus, and although there may be a significant mass in a-C:H carbonaceous dust, these wide band gap materials are apparently hard to detect and thus there significance has probably been underestimated.
6.2.6. MIR-FIR-mm emission
 |
Fig. 12 Dust model SEDs, for fixed dust mass, as a function of Eg (upper panel), a− (middle panel) and α (lower panel). The line designations are as per Fig. 7. |
In Fig. 12 we show the dust SED as a function of the band gap, Eg (upper), of the photo-processed dust components, i.e., the small a-C(:H) grains and the outer layer/mantle of the large a-C:H grains. Figure 12 also shows the SEDs as a function of the minimum grain size, a− (middle), and the small a-C(:H) grain size distribution power-law index, α (lower). As the band gap increases we note a decrease in the emission at FIR-mm wavelengths, a significant change in the MIR emission to a peak in the 20−30 μm region and a decrease in the continuum underlying the shortest wavelength emission bands. The decrease in the long wavelength emission is due to the fact that wide band gap a-C:H grains are less emissive, and therefore hotter, and their emission peaks at MIR rather than FIR wavelengths, which explains the broad 20−30 μm emission peak for Eg = 1.0 eV.
As the small a-C grain size distribution α decreases the FIR-mm emission increases and the IR emission bands and MIR emission decrease substantially and eventually disappear. Decreasing α is equivalent to a “flattening” and “narrowing” of the size distribution, which is equivalent to a transfer of mass to the larger particles. It is this that is responsible for the increase in the FIR-mm emission (see Figs. 8 and 12), while the loss of the IR emission bands and MIR continuum is simply due to the reduced abundance of their carriers, i.e., grains with a ≲ 10 nm (see Fig. 8).
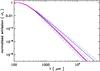 |
Fig. 13 Normalised FIR-cm SEDs show that the emissivity slopes segregate into two band-gap groups, one with β ~ 1.3 for Eg ~ 0 eV and the other with β ~ 2 for Eg ≳ 0.5 eV. The line designations are as per Fig. 7. The dashed blue lines indicate slopes of −1.0, −1.3, −1.5, −1.8 and − 2.0, from top to bottom. |
Figure 13 shows a zoom into the FIR-cm wavelength region, where the model SEDs have been normalised to the peak of the emission to allow a direct comparison of the slopes of the emissivity. This figure shows that the emissivity falls into two well-separated band-gap groups, in effect a two-state system, one with Eg ≳ 0.5 eV and β ≃ 2 that “switches” to an Eg ≃ 0 eV state with β ≃ 1.3 as a result of EUV photo-processing.
We note that variations in the FIR-mm emissivity slope for a-C(:H) particles are reduced for particles smaller than 3 nm and that the wavelength-dependence is dominated by the wings of the Drude profiles, i.e., β ≃ 2 for λ ≳ 20 μm (see Fig. 14). However, the emission at these wavelengths is a combination of that from amorphous silicate and carbon grains. Thus, in Fig. 14 we show the summed emissivity slopes of all the dust components, βeff, which is derived directly from the optical properties and is therefore independent of any assumed dust temperature. Figure 14 again reflects the two-state system mentioned above. In detail this figure shows that the switch to the narrow band gap state results in a wavelength-dependent β behaviour i.e., β ≃ 1.9, 1.8, 1.5 and 1.2 at 60−100 μm, 250 μm, 1 mm and 1 cm, respectively. The EUV processing-driven jump in the optical properties occurs between Eg = 0.1 and 0.5 eV and in Fig. 14 we show the results for an intermediate case where Eg = 0.25 eV. We note that the optical property jump is not related to the transition between the eRCN and DG models, which occurs at a band gap of ≃1 eV.
Figure 14 shows that the effective emissivity slope, βeff, varies significantly with wavelength over the FIR-cm range for EUV photo-processed a-C(:H) materials. Thus, an interpretation of the observed interstellar dust emissivity as arising from a single-emissivity-slope material would appear to be too simplistic because it neglects the combination of materials that contribute to the emission at long wavelengths. As Fig. 4 shows, the FIR emission is dominated by silicates but at wavelengths longer than a few mm the carbonaceous dust emission is dominant. Carbonaceous and silicate materials make about equal contributions to the emission in the mm region.
An important prediction of this model arising from the two-state system behaviour is that, at FIR wavelengths (e.g., ≈60–100 μm), βeff should be ~2 ± 0.1. However, at longer wavelengths βeff must be either ~2 or ≲1.8, with intermediate values unlikely. In the latter case, βeff decreases smoothly from ~1.8 at 250 μm to ~1.2–1.3 at cm wavelengths. In general, low (high) values of βeff indicate a “mature” aromatic-rich (“young” aliphatic-rich) carbonaceous dust component. We note that for mature materials the βeff at ~80–500 μm wavelengths is dominated by that of the silicate material optical properties, which are not yet well-determined. Hence, observed values of βeff significantly different from ~2 at λ ~ 100 μm (or different from ~1.8 at 250 μm) could be an indication that the interstellar silicates are not as we currently model them.
In a future paper we plan to explore the mm-cm dust emission predicted by our model within the context of the latest results from the Planck mission.
 |
Fig. 14 Upper plot: βeff vs. λ, as a function of Eg, where βeff is the effective emissivity slope resulting from a combination of the a-SilFe/a-C and a-C:H/a-C dust population optical properties. The green triple dot-dashed line shows the data for only the a-SilFe/a-C grains, which do not depend on the band gap of the thin a-C(:H) coating. The λ-dependence and variations are therefore only due to the a-C(:H) dust properties. The line colour-coding is as per Fig. 11. The horizontal grey lines and wide yellow bands show βeff = 1.80 ± 0.05 and 1.60 ± 0.05. Lower plot: the emissivity slope, β, for a-C(:H) dust, for λ = 100 μm, 300 μm, and 1 mm, as a function of Eg, for a = 100, 10 and 1 nm. The vertical grey dashed line shows the experimentally-derived “block” on band gap evolution (see Paper II). The grey area indicates the range of a-C materials that are consistent with many diffuse ISM dust properties (Sect. 6). The coloured squares at the bottom indicate the band gap colour coding scheme. |
6.2.7. Band gap evolution and the long wavelength emission
Figure 14 shows the band gap and size-dependence of the slope of the a-C(:H) dust emissivity, β, at λ = 100 μm, 300 μm and 1 mm. The black line indicates the behaviour of β based on the band gap dependence of γ, the long-wavelength slope of the imaginary part of the refractive index, k (see Eq. (22), Paper II). An upturn in β, for Eg = −0.1 to 0.1 eV, is due to a power-law dependence of n on wavelength and the peak at ≈0.9 eV is due to a reduced IR band contribution. Figure 14 shows that a-C(:H), whether in grains or mantles, could have a significant effect on the FIR-mm dust emissivity and that this will be superimposed any effects due to amorphous silicate variations (e.g., Agladze et al. 1996; Mennella et al. 1998; Boudet et al. 2005; Meny et al. 2007; Coupeaud et al. 2011).
The data in Fig. 14 indicate that in the diffuse ISM large, homogeneous a-C particles (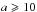 nm, Eg = 0.1 − 0.2 eV) would have a rather flat emissivity slope, β ≃ 1.2−1.3 (see Paper II). However, particles with radii >20 nm will exhibit a core material composition that can be different from that of a photo-processed outer mantle (see Footnote 1). In contrast, small a-C particles (a ≃ 1 nm, Eg(bulk) = 0.1 − 0.2 eV) will have a steeper emissivity slope, β ≃ 2.2−2.4. This is determined by the particle size limitation on the aromatic cluster sizes, which elevates the effective band gap to ≳0.7 eV and suppresses the long wavelength absorptivity (see Paper III). Within molecular clouds small particle coagulation and a-C:H mantle accretion will lead to materials with β ≃ 1.8 − 2.5 (for Eg = 0.5 − 2.6 eV). However, as discussed above (Sect. 6.2.5) a-C:H materials are so much less emissive than a-C that their effects on the FIR-mm emissivity may be hard to observe.
nm, Eg = 0.1 − 0.2 eV) would have a rather flat emissivity slope, β ≃ 1.2−1.3 (see Paper II). However, particles with radii >20 nm will exhibit a core material composition that can be different from that of a photo-processed outer mantle (see Footnote 1). In contrast, small a-C particles (a ≃ 1 nm, Eg(bulk) = 0.1 − 0.2 eV) will have a steeper emissivity slope, β ≃ 2.2−2.4. This is determined by the particle size limitation on the aromatic cluster sizes, which elevates the effective band gap to ≳0.7 eV and suppresses the long wavelength absorptivity (see Paper III). Within molecular clouds small particle coagulation and a-C:H mantle accretion will lead to materials with β ≃ 1.8 − 2.5 (for Eg = 0.5 − 2.6 eV). However, as discussed above (Sect. 6.2.5) a-C:H materials are so much less emissive than a-C that their effects on the FIR-mm emissivity may be hard to observe.
6.2.8. FIR-to-AV extinction ratio in the diffuse ISM
 |
Fig. 15 Dust model extinction, τi, in the V band (blue) and at 250 μm (green) and 1 mm (red) wavelengths for an assumed column density NH = 1021 H cm-2. The upper plot shows the variations as a function of the a-C(:H) material band gap, Eg, and the lower plot as a function of the power-law, α, component of the small a-C dust population. The filled data points indicate the values for the best-fit DHGL dust model. The crosses with error bars show τ250 = 5.8 ± 1.7 × 10-4 E(B − V), from Eq. (2), multiplied by 104. |
Here we consider the extinction in the diffuse ISM where the dust exhibits only limited variations in temperature and opacity.
Figure 15 shows the model optical depths (opacity) for NH = 1021 H cm-2 at the V band (blue), 250 μm (green) and 1 mm (red) wavelengths as a function of the photo-processed material band gap, Eg (for grain radii <20 nm or 20 nm thick mantles on larger grains, upper plot), and the small a-C grain power-law, α (lower plot). This figure shows that changes in the optical depth are significant for small band gap materials (Eg < 0.5 eV) and are more apparent as the wavelength increases and as the power-law index, α, decreases.
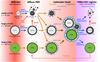 |
Fig. 16 A schematic view of the life-cycle of interstellar dust in terms of evolutionary tracks: “parallel-processing” tracks that lead to a smooth evolution are horizontal (i.e., accretion and photo-processing) and “cross-talk” tracks that lead to significant mass-transfer between grains sizes (i.e., coagulation and disaggregation) are diagonal and vertical. Qualitatively, the red shading reflects the density, nH, and the violet shading, on the extreme right, represents high G0 radiation fields. |
Variations in the FIR opacity and in the E(B − V) extinction must, at some level, be coupled because the dust optical properties at these disparate wavelengths vary in tandem (e.g., see Fig. 16 in Paper II and Figs. 10–13 in Paper III). As shown above, variations in E(B − V) and in the FIR opacity appear to be significant, while the FUV is practically invariant for fixed dust mass. In order to investigate the inter-dependence between the FIR emissivity and E(B − V) we take the standard extinction-column density relationship from Bohlin et al. (1978), NH = 5.8 × 1021 E(B − V) cm-2 mag-1, and combine this with the recent results from the Planck mission. From a fitting of the FIR to sub-mm dust emissivity in the local diffuse ISM the Planck data yield τ250 = 1.0 ± 0.3 × 10-25 NH (Planck Collaboration 2011b). We then find 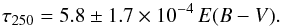 (2)This expression of τ250, calculated using our model results for E(B − V) substituted into Eq. (2) and multiplied by104, is shown in Fig. 15, as a function of Eg (upper) and α (lower), by the crosses with error bars. It is clear that the model and the recent Planck observational results are in good agreement and that variations in the FIR-mm opacity are rather limited when normalised in this way.
(2)This expression of τ250, calculated using our model results for E(B − V) substituted into Eq. (2) and multiplied by104, is shown in Fig. 15, as a function of Eg (upper) and α (lower), by the crosses with error bars. It is clear that the model and the recent Planck observational results are in good agreement and that variations in the FIR-mm opacity are rather limited when normalised in this way.
The major conclusion here is that, for a given dust composition and size distribution, variations in the FIR opacity go hand-in-hand with variations in E(B − V) because of the in-tandem evolution of the dust optical properties at visible and FIR wavelengths.
6.2.9. Some further points of note
As noted above, it appears that many of the distinct dust observables are attributable to carbonaceous matter. Further, our use of the optEC(s)(a) data indicates that the carriers of the FUV extinction, UV bump, NIR absorption and the IR emission bands are only weakly coupled.
We also note that there appears to be some degeneracy in the extinction, in that variations in a− and α often lead to similar extinction curves. For example, our investigations show that increasing a− from 0.4 nm to 3 nm gives essentially the same extinction curve as changing α from 5.0 to 4.0 (see Fig. 7). However, a look at the dust SEDs for the different size distributions show very different behaviour in the two cases, with a complete lack of IR emission bands in the case of increasing a− to 3 nm (see Fig. 12). Thus, a combined analysis of the observed extinction and emission, for a given line of sight, is required in order to constrain the exact dust composition and size distribution. In general, the dust SED is a more powerful constraint on the nature of dust in the ISM than the extinction curve.
Table 3 summarises the consistency of the model results with the observational constraints. Clearly the un-normalised FUV extinction does not appear to be a strong constraint. However, this table clearly indicates that the IR extinction, and the associated absorption bands, arise from an a-C:H dust component while the bulk of the dust extinction and emission features arise from a-C dust.
Observation-model coherency check: Eg characterisation as a function of the λ-dependent extinction and emission features.
7. Interstellar dust evolution
Here we outline a scenario for dust evolution as it transits from the dust-forming shells around evolved (asymptotic giant branch, AGB) stars, into the diffuse ISM and then, via cloud collapse, on into the dense star-forming regions of the ISM where dust accretion/(re-)formation is important. It is in star-forming, photon-dominated environments (e.g., HII regions and PDRs) that dust undergoes significant processing, which plays a key role in determining the course of its subsequent evolution. The constructive (destructive) processes inherent to dust evolution during its lifetime are accretion and coagulation (photo-processing and dis-aggregation/fragmentation).
A schematic view of the dust evolutionary sequence, as a function of environment, is given in Fig. 16. This figure introduces the idea of interstellar dust evolutionary tracks, which are very different for a-C(:H) and a-SilFe grains because of their differing susceptibilities and reactions to processing. Observational evidence indicates that the evolutionary processes have a stronger effect on a-C(:H) dust than on amorphous silicate dust (e.g., Serra Díaz-Cano & Jones 2008; Jones & Nuth 2011; Parvathi et al. 2012). Nevertheless, the evolutionary tracks are coupled because of dust component mixing, as indicated in Fig. 16 by the “parallel-processing” and “cross-talk” pathways. Seemingly, the most important evolutionary tracks for ISM dust are accretion and coagulation in an increasing density ISM (diffuse → dense molecular cloud phase change) and photon-driven fragmentation/destruction and disaggregation in intense radiation field, star-forming environments (i.e., HII regions and PDRs).
Dust evolution evidently leads to observable variations in the dust composition, structure and size distribution. Here we discuss the major a-C(:H) evolutionary processes in the ISM and how these are consistent with, or can be constrained by, the observational evidence.
In the following, and within the framework of the schematic dust life-cycle shown in Fig. 16, we explore dust evolution under the assumption of constant dust mass within each dust component. Thus, coagulation and accretion affects are not rigorously-treated because they lead to a net dust mass increase and to mass transfer between the different components. Nevertheless, within the framework of a constant mass assumption and evolving size distributions, we can qualitatively explore the effects of evolution on the dust observables.
7.1. a-C(:H) UV photo-processing and time-scale issues
The evolution of the a-C(:H) dust between the aliphatic-rich (a-C:H) and aromatic-rich (a-C) end members is accompanied by a narrowing of the band gap (Eg ≳ 2.3 eV → ≃ 0.1 eV) and by photo-fragmentation. This process occurs when a-C:H, accreted in the molecular ISM or formed around evolved stars, is exposed to the ambient radiation field. EUV-UV photon-induced processing (aromatisation) in the diffuse ISM (G0 = 1), and particularly in PDRs (G0 ≃ 10 − 104), on time-scales ≳106 yr/ G0 leaves an imprint on the dust extinction and emission (Jones 2012c). The observable effects of photo-processing (top left and right hand side of Fig. 16) are to increase the bump strength and to steepen the NIR-visible extinction (Fig. 7, upper plot), significant modifications to the IR emission band profiles (Fig. 11) and to enhance the MIR-mm emission (Fig. 12, upper plot).
Here we do not re-visit the time-scale-dependent aspects of photo-processing and photo-fragmentation but leave this until we have a better understanding of how they operate on a-C(:H) nano-particles in intense radiation fields. For example, it is not yet clear whether the aromatisation of a-C:H particles is a direct C−H bond photo-dissociation process or whether the transformation is driven by stochastic heating, or a combination of the two13. Dust models used in the interpretation of astronomical observations therefore need to be time-dependent in order to characterise the UV photon-induced transformation of a-C(:H) and must take into account its origin and prior history. This kind of study is probably best undertaken on a case-by-case basis, which compares model predictions with the astronomical observations (e.g., Compiègne et al. 2008; Arab et al. 2012).
7.2. Accretion
Carbon accretion from the gas phase leads to the formation of a-C(:H) mantles on all grains, with material composition depending on the local density and extinction. For example, if the onset of accretion is in the diffuse ISM, where most species are atomic or singly-ionised (e.g., Si+, S+, C+), the extinction is low and UV photo-processing still a significant hazard, then a-C mantles will form. However, for intermediate levels of extinction, AV < 3, i.e., before ice mantle formation, the mantles will be of a-C:H14. The onset of accretion is not restricted to C and H and other abundant gas phase atomic species, such as O and N, are also expected to accrete and to leave their observable signatures (Jones 2013). In high extinction regions, i.e., AV > 3 (≳ 6), the accreted carbon mantles will be submerged under H2O (H2O+CO) ice layers.
The observable effects of accretion (the “parallel-processing” tracks in the middle of Fig. 16) are to increase all grain sizes (Fig. 7, middle plot), to increase the total dust mass and to steepen the small grain mass distribution (Fig. 7, lower plot). However, small particles (a < 10 nm) will undergo temperature excursions, resulting from stochastic photon absorption, which is likely to inhibit accretion onto the smallest particles in low extinction regions.
7.3. Coagulation
Accretion is a key process in dust evolution, however, it does not occur in isolation but pre-dates and aids in coagulating grains into mixed-composition aggregates in low-velocity grain-grain collisions. The early stages of coagulation, in a quiescent cloud filament in Taurus, were observed and modelled by Stepnik et al. (2003), where it was shown that the disappearance of small particles is consistent with reduced dust temperatures, enhanced emissivity and their coagulation into and onto larger particles. More recently Köhler et al. (2011, 2012) found a factor of about 2.7 enhancement in the emissivity at FIR wavelengths, resulting from grain coagulation. Further, this emissivity gain is rather rapidly achieved, i.e., sticking only a few large grains together yields a doubling of the dust emissivity before saturation sets in; additional coagulation then only leads to incremental gains in emissivity.
The observable effects of coagulation (“cross-talk” tracks in the middle of Fig. 16) are a mass re-distribution towards larger grains (smaller grains remain but decrease in abundance, i.e., a− is fixed, see Fig. 8). The effects of coagulation on the dust extinction and emission can be mimicked by progressively decreasing the power law index, α, of the small a-C(:H) grain population from 5 to 2 as small grains are subsumed into the large grain population (Figs. 7 and 12, lower plots). As can be seen the extinction in the FUV flattens, the UV bump broadens and the NIR-visible extinction flattens. In emission these changes manifest as a diminution of the IR emission bands and the MIR continuum accompanied by an increase in the FIR-mm emission.
These evolutionary changes agree well with observations and their interpretation (e.g., Stepnik et al. 2003; Köhler et al. 2011, 2012) and are in general agreement with the evolution of the extinction curve with increasing RV (e.g., Mathis 1990, and Fig. 7 above).
 |
Fig. 17 UV bump parameter, c3 (diamonds), and FUV extinction parameter, c4 × 25 (squares), intensity data normalised by the depletion into dust, (C/H)dust, as a function of NH. The y value uncertainties are only illustrative. The data are taken from Parvathi et al. (2012). |
7.4. Destructive processing – UV photo-fragmentation
A bottom-up coagulation process appears to be unlikely in the diffuse ISM given the local conditions. In the dust coagulation kernel, nH σ vrel, the dust cross-section, σ, is “fixed” and the grain-grain collision velocities are low (vrel < 1 km s-1). Thus, higher densities than those typical of the diffuse ISM are required for efficient coagulation in time-scales ≲3 × 107 yr, the typical star formation time-scale in molecular clouds (e.g., McKee 1989).
Dust evolution in the diffuse ISM could be more straight-forwardly be explained by a “top-down” scenario, where the major dust growth processes (accretion and coagulation) only occur in dense molecular clouds. The observed extinction and emission variations can then be explained by the de-construction of the accreted/coagulated particles, formed in the dense ISM, as they are subsequently (photo-)processed in HII regions and PDRs.
Consistent with of a “top-down” dust evolution scenario is the observation that large RV sight-lines, usually taken to be an indicator of prior dust coagulation, are found in PDRs such as the Orion Trapezium region (e.g., Fitzpatrick & Massa 2007). Here we are observing dense molecular cloud dust ablated from a parent cloud and exposed to the intense radiation field of a PDR. Dust evolution here is driven by EUV-UV photo-processing, which drives off low-volatile mantles, triggers disaggregation and aromatises and photo-fragments a-C(:H) grains and mantles. The dust processing time-scale is generally longer than the local dynamical time-scale and so the dust will therefore not be in equilibrium with the local conditions.
Recent work by Parvathi et al. (2012) supports the idea that carbonaceous dust undergoes significant processing in the neutral ISM and shows that the intensity of the UV bump extinction does not correlate with carbon depletion into dust, (C/H)dust. This lack of correlation can naturally be explained by our model because (C/H)dust is determined by accretion in dense cloud interiors (i.e., by cloud volume), whereas the intensity of the bump and the FUV extinction reflect the abundance of UV photo-processed small grains in the low density surface regions of clouds. The UV bump and FUV extinction per unit dust mass should therefore decrease with cloud (line of sight) column density. In Fig. 17 we show the UV bump intensity parameter, c3 (diamonds), and FUV extinction parameter, c4 (squares), data from Parvathi et al. (2012), normalised by their derived carbon depletion into dust, (C/H)dust, and plotted as a function of NH. The indicated trends in the UV extinction observations do seem to be consistent with this kind of cloud geometry effect15. Parvathi et al. (2012) also note that the FUV extinction appears to show a gradual decrease with decreasing gas density, nH, which they interpret as due to the preferential fragmentation of small grains in the diffuse ISM. This observation seemingly lends support to the idea that small carbonaceous dust mass variations are driven by photo-fragmentation in low nH regions. A study by Pilleri et al. (2012) finds that the photo-fragmentation of very small carbon grains into PAHs occurs in relatively dense, nH = [100,105] cm-3, and UV irradiated PDRs, G0 = [100,5 × 104], where H2 rotational line emission is observed, i.e., where 0.5 < G0/nH < 1.0. This could be observational evidence for H2 formation via a-C(:H) grain photo-processing, as proposed by Jones (2012b).
In PDRs EUV/UV photo-processing (a-C:H → a-C) progressively destroys the aliphatic component that binds the growing aromatic domains, eventually leading to photo-fragmentation and the release of daughter species (e.g., Pety et al. 2005, and as discussed in Paper III)16. Thus, the observable effects of photo-processing in PDRs arise from dust dis-aggregation, a-C:H grain aromatisation and photo-fragmentation, which (re-)generates a power law distribution of small a-C(:H) particles (“cross-talk” tracks on the right of Fig. 16), leading to a progressive “steepening” of the UV extinction (Fig. 7, lower plot), increased MIR emission from nano-particles and decreased FIR-mm emission (Fig. 12, lower plots). This evolutionary scenario seems to be supported by Spitzer and ISO data for the Horsehead Nebula and NGC 2023 North (Compiègne et al. 2008) and Herschel observations of the Orion Bar (Arab et al. 2012), which indicate lower relative abundances of the IR band emitters and the small grain MIR continuum carriers, by up to an order of magnitude compared to the diffuse ISM.
In a future paper we plan to explore the effects of grain-grain collisional fragmentation and sputtering erosion on the SED in supernova-generated shocks.
8. Concluding summary
We propose a new two-material dust model, consisting of amorphous silicate and hydrocarbon dust, a-C(:H), with the optical properties of the latter determined by the particle size and material band gap. This dust model consists of three dust components: small (a ≃ 0.4 to ~100 nm) and large a-C(:H) grains, modelled using the optEC(s)(a) optical property data, and large carbon-coated, amorphous forsterite-type silicate grains with metallic iron nano-particle inclusions (a-SilFe). The large grains are assumed to have log-normal size distribution peaking at radii ≃200 nm.
Using the DustEM tool, to calculate the extinction and emission, we find that this model gives a good fit to astronomical observations of the diffuse ISM extinction, emission and albedo, with only a minimal “fine-tuning” of the laboratory-derived data. The fit to these observational data, without the use of “astronomical” silicates, graphite or PAHs, is rather remarkable and illustrates the viability of the adopted optEC(s)(a) and a-SilFe data.
The most innovative aspect of this dust model is that most of the observed extinction and emission, and their evolution, can quite naturally be explained by the size- and composition-dependent optical properties of a-C(:H) dust, with amorphous silicate dust playing only a subordinate role. We propose that the aliphatic-to-aromatic transformation (i.e., wide band gap a-C:H → narrow band gap a-C) is accompanied by photo-fragmentation. The evolution of the large a-C(:H) grains formed around evolved stars and the mantles formed by accretion in the dense ISM is then driven EUV-UV photo-processing and photo-fragmentation in HII regions and PDRs. These processes are likely to be critical for understanding dust evolution in the ISM.
Our understanding in interstellar dust modelling is currently limited by a lack of suitable, wide-wavelength coverage (EUV-cm) laboratory data for analogues of amorphous silicate and hydrocarbon dust. In particular, a major hindrance to the “holistic” dust modelling approach is the current lack of suitable optical property data for analogues of interstellar amorphous silicates, and also the means to validate the optEC(s)(a) data. A definitive quantitative analysis of astronomical observations must await these data and so some care should currently be exercised in order to avoid over-interpretation. Nevertheless, the fact that this model is able to explain so many FUV-mm dust observables, and their inter-correlations, is encouraging.
Note added in proof. In Sect. 4 we should also have made reference to the work of Viktor Zubko et al. (2004, ApJ, 152, 211) who present a wide array of PAH, bare-grain and composite (but not core-mantle) dust models that are consistent with the extinction, emission and abundance constraints. In all of the dust models proposed by Zubko et al. (2004) the wavelength-dependence of the FUV extinction is due to the combined effects of PAHs, carbonaceous/graphite and/or silicate dust components, which appears to be inconsistent with observations (Greenberg & Chlewicki 1983).
For a-C(:H) particles, with fewer than several thousand atoms, surface hydrogenation becomes important. Also, the aromatic cluster sizes are limited by the particle radius and the band gap for small ( nm) a-C particles can be significantly higher than expected. For example, for a-C the band gap can be as low as eV but for a 1 nm radius a-C particle the band gap cannot be smaller than 0.7 eV (for full details see Paper III).
Aromatised a-C nano-particles consist of small aromatic clusters, with a few aromatic rings per cluster, that are covalently-linked together by aliphatic and olefinic bridging structures. They are three-dimensional networks that intimately mix predominantly aromatic carbon but which also contain a significant aliphatic and olefinic carbon component in a single, contiguous chemical structure. The term PAH cannot be applied to them because they are not purely aromatic carbon structures.
This exponential cut-off is required in order to limit the size of the largest a-C particles when we explore variations in the power-law index due to dust evolution (see Sect. 6.2.1).
The dust extinction and emission results are not sensitive to the core a-C:H material band gap as long as it is 0 eV. However, the observed IR absorption bands in the m region and the derived aliphatic CH/CH ratio both require that the large a-C(:H) grain core material has a wide band gap, i.e., eV (see Paper I and Paper III and the corrigendum to Paper III).
The required modifications to the IR bands, and the and bands are minor and are explained in full detail in Appendix C.
The observational data are from Lillie & Witt (1976), Morgan et al. (1976), Morgan (1980), Chlewicki & Laureijs (1988), Hurwitz et al. (1991), Witt et al. (1997).
The optical properties for this silicate are very similar to those of a-Sil (see Appendix A). Further, as shown by Chiar & Tielens (2006), a mix of amorphous olivine-type and pyroxene-type silicate materials can equally well explain the profiles of the interstellar silicate bands. Hence, the Planck extinction and polarisation data will be critical in constraining the optical and physical properties of the large interstellar silicate and carbon dust populations.
However, as we show in Sect. 6.2.6, increasing leads to a progressive loss, and eventual disappearance, of the IR emission bands.
Particles with nm, where the grain heating is predominantly stochastic, in the standard interstellar radiation field (e.g., Draine & Anderson 1985), will undergo temperature excursions large enough to drive the dehydrogenation of a-C:H materials but the relevant time-scales are not yet determined. However, we have undertaken a preliminary study of a-C:H dust evolution in planetary nebulae within the context of fullerene formation (Bernard-Salas et al. 2012; Micelotta et al. 2012).
It is perhaps this accreted carbonaceous matter that could help to explain “coreshine” phenomena (Pagani et al. 2010; Steinacker et al. 2010, see also Paper II).
The high FUV extinction line of sight with a weak UV bump, the square at [0.68, 0.04], is the HD 207198 line of sight with the highest (C/H) value in the Parvathi et al. (2012) sample, i.e., (C/H) ppm. Strong FUV extinction associated with a weak UV bump is a characteristic of the wide band gap a-C:H materials expected to accrete in the denser regions of the diffuse ISM.
We note that carbon dust shattering in grain-grain collisions in shock waves results in fragments with a power-law mass distribution index of order 1.8–2.0 (e.g., Jones et al. 1996; Serra Díaz-Cano & Jones 2008), which is similar to the aromatic cluster mass distribution assumed in Paper III and similar to that derived for astronomical PAHs by Pech et al. (2002).
Assuming a cosmic abundance of 32 ppm for Fe, of which 22 ppm is incorporated into a silicate matrix as metallic Fe nano-particles or into the silicate as cations. For Mg we require an abundance of 50 ppm if the Fe is in metal or 67 ppm if the Fe is present as cations in the silicate (see Sect. 6.1).
Acknowledgments
We thank the anonymous referee for a very careful reading of this manuscript and Papers I-III, and for many useful and insightful remarks. We would like to thank our colleagues at the IAS and elsewhere for many interesting discussions on cosmic dust. This research was, in part, made possible through the financial support of the Agence National de la Recherche (ANR) through the programs Cold Dust (ANR-07-BLAN-0364-01) and CIMMES (ANR-11-BS56-029-02).
References
- Adamson, A. J., Whittet, D. C. B., Chrysostomou, A., et al. 1999, ApJ, 512, 224 [Google Scholar]
- Agladze, N. I., Sievers, A. J., Jones, S. A., Burlitch, J. M., & Beckwith, S. V. W. 1996, ApJ, 462, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, J. C., & Hayman, C. C. 1988, Science, 241, 913 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Angus, J. C., & Jansen, F. 1988, J. Vac. Sci. Technol., 6, 1778 [Google Scholar]
- Arab, H., Abergel, A., Habart, E., et al. 2012, A&A, 541, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard-Salas, J., Cami, J., Peeters, E., et al. 2012, ApJ, 757, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchio, M., Micelotta, E. R., Gautier, A.-L., & Jones, A. P. 2012, A&A, 545, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Boudet, N., Mutschke, H., Nayral, C., et al. 2005, ApJ, 633, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Prevot, M. L., & Gry, C. 1994, A&A, 284, 956 [NASA ADS] [Google Scholar]
- Brooke, T. Y., Sellgren, K., & Geballe, T. R. 1999, ApJ, 517, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Y. K., Hsieh, H. H., Pong, W. F., et al. 1999, Phys. Rev. Lett., 82, 5377 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, S. Z. D. 2002, Handbook of Thermal Analysis and Calorimetry: Applications to Polymers and Plastics, eds. P. K. Gallagher, & S. Z. D. Cheng (Elsevier Science BV) [Google Scholar]
- Chiar, J. E., & Tielens, A. G. G. M. 2006, ApJ, 637, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Chiar, J. E., Tielens, A. G. G. M., Whittet, D. C. B., et al. 2000, ApJ, 537, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Chiar, J. E., Adamson, A. J., Whittet, D. C. B., et al. 2006, ApJ, 651, 268 [CrossRef] [Google Scholar]
- Chiar, J. E., Tielens, A. G. G. M., Adamson, A. J., & Ricca, A. 2013, ApJ, 770, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Chlewicki, G., & Laureijs, R. J. 1988, A&A, 207, L11 [NASA ADS] [Google Scholar]
- Compiègne, M., Abergel, A., Verstraete, L., & Habart, E. 2008, A&A, 491, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coupeaud, A., Demyk, K., Meny, C., et al. 2011, A&A, 535, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalle Ore, C. M., Fulchignoni, M., Cruikshank, D. P., et al. 2011, A&A, 533, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Marco, O., Muñoz-Caro, G. M., et al. 2004a, A&A, 423, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Muñoz Caro, G. M., Deboffle, D., & d’Hendecourt, L. 2004b, A&A, 423, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Muñoz Caro, G. M., Deboffle, D., Montagnac, G., & D’Hendecourt, L. 2005, A&A, 432, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davoisne, C., Djouadi, Z., Leroux, H., et al. 2006, A&A, 448, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Döhler, G. H., Dandaloff, R., & Bilz, H. 1980, J. Noncryst. Solids, 42, 87 [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Draine, B. T., & Anderson, N. 1985, ApJ, 292, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. W. 1995, ApJ, 445, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. W., Seahra, S., & Williams, D. A. 1997, ApJ, 482, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, A. C., & Robertson, J. 2000, Phys. Rev. B, 61, 14095 [Google Scholar]
- Ferrari, A. C., & Robertson, J. 2004, Phil. Trans. R. Soc. Lond. A, 362, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 33 [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2009, ApJ, 699, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, J. B., & Goodman, A. A. 2006, ApJ, 636, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gadallah, K. A. K., Mutschke, H., & Jäger, C. 2011, A&A, 528, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, J., Jiang, B. W., & Li, A. 2010, Earth Planets Space, 62, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, M., & Dartois, E. 2010, A&A, 519, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godard, M., Féraud, G., Chabot, M., et al. 2011, A&A, 529, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, M., Gaessler, W., Hayano, Y., et al. 2003, ApJ, 589, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M., & Chlewicki, G. 1983, ApJ, 272, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M., & Li, A. 1996, A&A, 309, 258 [NASA ADS] [Google Scholar]
- Hurwitz, M., Bowyer, S., & Martin, C. 1991, ApJ, 372, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. 2001, in Tetons 4: Galactic Structure, Stars and the Interstellar Medium, eds. C. E. Woodward, M. D. Bicay, & J. M. Shull, ASP Conf. Ser., 231, 171 [Google Scholar]
- Jones, A. P. 2009, in Cosmic Dust – Near and Far, eds. T. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., 414, 473 [Google Scholar]
- Jones, A. P. 2012a, A&A, 540, A1 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2012b, A&A, 540, A2 (Paper II); 545, C2 (Corrigendum Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2012c, A&A, 542, A98 (Paper III); 545, C3 (Corrigendum Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2013, A&A, 555, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., & Nuth, J. A. 2011, A&A, 530, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Duley, W. W., & Williams, D. A. 1990, QJRAS, 31, 567 [NASA ADS] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Kassavetis, S., Patsalas, P., Logothetidis, S., Robertson, J., & Kennou, S. 2007, Diamond & Related Materials, 16, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, M., Guillet, V., & Jones, A. 2011, A&A, 528, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kwok, S., & Zhang, Y. 2011, Nature, 479, 80 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kwok, S., & Zhang, Y. 2013, ApJ, 771, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1973, MNRAS, 161, 133 [NASA ADS] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Li, A., & Draine, B. T. 2012, ApJ, 760, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Greenberg, J. M. 1997, A&A, 323, 566 [NASA ADS] [Google Scholar]
- Li, A., & Greenberg, J. M. 2002, ApJ, 577, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Lillie, C. F., & Witt, A. N. 1976, ApJ, 208, 64 [Google Scholar]
- Llamas-Jansa, I., Jäger, C., Mutschke, H., & Henning, T. 2007, Carbon, 45, 1542 [CrossRef] [Google Scholar]
- Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269 [NASA ADS] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., & Whiffen, G. 1989, ApJ, 341, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mattioda, A. L., Hudgins, D. M., & Allamandola, L. J. 2005, ApJ, 629, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Mattioda, A. L., Rutter, L., Parkhill, J., et al. 2008, ApJ, 680, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. 1989, in Interstellar Dust, eds. L. J. Allamandola, & A. G. G. M. Tielens, IAU Symp., 135, 431 [Google Scholar]
- Mennella, V. 2008, ApJ, 682, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Colangeli, L., Bussoletti, E., et al. 1995, ApJS, 100, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Colangeli, L., Palumbo, P., et al. 1996, ApJ, 464, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Brucato, J. R., Colangeli, L., et al. 1998, ApJ, 496, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Baratta, G. A., Esposito, A., Ferini, G., & Pendleton, Y. J. 2003, ApJ, 587, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meny, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010a, A&A, 510, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010b, A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2011, A&A, 526, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., Cami, J., et al. 2012, ApJ, 761, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, D. H. 1980, MNRAS, 190, 825 [NASA ADS] [Google Scholar]
- Morgan, D. H., Nandy, K., & Thompson, G. I. 1976, MNRAS, 177, 531 [NASA ADS] [Google Scholar]
- Nguyen, A. N., Stadermann, F. J., Zinner, E., et al. 2007, ApJ, 656, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Ordal, M. A., Long, L. L., Bell, R. J., et al. 1983, Appl. Opt., 22, 1099 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ordal, M. A., Bell, R. J., Alexander, Jr., R. W., Long, L. L., & Querry, M. R. 1985, Appl. Opt., 24, 4493 [NASA ADS] [CrossRef] [Google Scholar]
- Ordal, M. A., Bell, R. J., Alexander, Jr., R. W., Newquist, L. A., & Querry, M. R. 1988, Appl. Opt., 27, 1203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pagani, L., Steinacker, J., Bacmann, A., Stutz, A., & Henning, T. 2010, Science, 329, 1622 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Parvathi, V. S., Sofia, U. J., Murthy, J., & Babu, B. R. S. 2012, ApJ, 760, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Pech, C., Joblin, C., & Boissel, P. 2002, A&A, 388, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Teyssier, D., Fossé, D., et al. 2005, A&A, 435, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, J. C. 1979, Phys. Rev. Lett., 42, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Pilleri, P., Montillaud, J., Berné, O., & Joblin, C. 2012, A&A, 542, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pino, T., Dartois, E., Cao, A., et al. 2008, A&A, 490, 665 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A24 [Google Scholar]
- Robertson, J. 1986, Adv. Phys., 35, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, J. 1988, Philos. Mag. Lett., 57, 143 [Google Scholar]
- Robertson, J. 1991, Prog. Solid State Chem., 21, 199 [CrossRef] [Google Scholar]
- Robertson, J. 2001, Phys. Status Sol. Appl. Res., 186, 1521 [Google Scholar]
- Robertson, J. 2002, Mat. Sci. Eng., 37, 129 [Google Scholar]
- Robertson, J., & O’Reilly, E. P. 1987, Phys. Rev. B, 35, 2946 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, A., & Duley, W. W. 1996, ApJS, 105, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Sellgren, K., Brooke, T. Y., Smith, R. G., & Geballe, T. R. 1995, ApJ, 449, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Serra Díaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sloan, G. C., Bregman, J. D., Geballe, T. R., Allamandola, L. J., & Woodward, C. E. 1997, ApJ, 474, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sloan, G. C., Jura, M., Duley, W. W., et al. 2007, ApJ, 664, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. G., Sellgren, K., & Tokunaga, A. T. 1989, ApJ, 344, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Steinacker, J., Pagani, L., Bacmann, A., & Guieu, S. 2010, A&A, 511, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamor, M. A., & Wu, C. H. 1990, J. Appl. Phys., 67, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Tauc, J., Grigorovici, R., & Vancu, A. 1966, Phys. Status Sol. B Basic Res., 15, 627 [CrossRef] [Google Scholar]
- Thorpe, M. 1983, J. Non Cryst. Solids, 57, 355 [Google Scholar]
- Verstraete, L., Pech, C., Moutou, C., et al. 2001, A&A, 372, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witt, A. N., Friedmann, B. C., & Sasseen, T. P. 1997, ApJ, 481, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Yamagishi, M., Kaneda, H., Ishihara, D., et al. 2012, A&A, 541, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeidler, S., Posch, T., Mutschke, H., Richter, H., & Wehrhan, O. 2011, A&A, 526, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Interstellar silicates
The optical properties of interstellar silicates have been modelled by empirical fits to observations (Draine & Lee 1984) and also using laboratory-constrained organic-refractory and amorphous silicate data for core-mantle particles (Greenberg & Li 1996). Both approaches have been shown to give a good fit to the observations. However, these models have a problem in that they require essentially all of the available cosmic iron to be incorporated into the silicate but appear to add it for “free”. In that, they include its atomic fraction and mass but, apparently, neglect its important contribution to the imaginary part of the refractive index in the NIR region, e.g., see Fig. 3 in Draine & Lee (1984) and Fig. 1 in Greenberg & Li (1996). However, the inclusion of the cosmic abundance of iron into a silicate is far from “free” but leads to very significant absorption in the NIR (e.g., Zeidler et al. 2011) regardless of whether the iron is within the silicate structure or present as metallic nano-particles (e.g., see Fig. A.1). If the effect of the neglected iron on the optical constants of Draine & Lee (1984) and Greenberg & Li (1996) were to be included then the predicted silicate dust temperatures would be hotter than indicated by observations because of the enhanced absorption in the NIR region, where the interstellar radiation field peaks. Thus, the amorphous astronomical silicate data derived by Draine & Lee (1984) and Greenberg & Li (1996) are not without significant problems.
It is clear that, ideally, the recent laboratory data for amorphous silicates by Coupeaud et al. (2011) should be used to constrain the temperature-dependence of its long-wavelength properties. However, the currently-available data does not have a wide enough wavelength coverage to be used in amorphous silicate dust extinction and emission models.
 |
Fig. A.1 Black lines show the imaginary (solid) and real (dashed) parts of the complex refractive index of our newly-constructed amorphous silicate/Fe nano-particle material, a-SilFe. This is a composite constructed using the amorphous forsterite-type silicate data (green) from Scott & Duley (1996) and the metallic iron data (grey) from Ordal et al. (1983, 1985, 1988), see text for details. For comparison we show the experimental data for iron-containing amorphous olivine-type silicates, MgFeSiO4 (orange) and Mg0.8Fe1.2SiO4 (brown), from Dorschner et al. (1995) and the astronomical data of Draine & Lee (1984) (cobalt blue). |
For amorphous interstellar silicates, and until such time as suitable full wavelength-coverage optical property data are available for interstellar silicate analogue materials, we adopt an approach that allows for a range of silicate metal depletions. We first consider the available laboratory data for amorphous olivine-type silicates with iron incorporated into the silicate structure (Mg:Fe = 1:1 or 1:1.5, Dorschner et al. 1995). Secondly, following the work of Davoisne et al. (2006) on annealed silicates, where the iron is reduced to metal in the presence of carbon, we consider an amorphous forsterite-type silicate (Scott & Duley 1996) with ~70% of the cosmic iron17 is incorporated in the form of metallic iron (Ordal et al. 1983, 1985, 1988) nano-particle inclusions, equivalent to a metal ratio Mg:Fe = 2.3:1. The complex refractive index for the latter amorphous silicate/Fe mix, a-SilFe, was calculated using the Maxwell-Garnett effective medium theory (EMT)18. In Fig. A.1 we show our derived amorphous, Fe nanoparticle-containing, forsterite-type silicate complex refractive index data in comparison with other available silicate data. In the NIR wavelength region (0.2 − 8.0 μm) the a-SilFe data are close to those for the amorphous olivine-type silicate, (Mg,Fe)2SiO4, of Dorschner et al. (1995), as alluded to above, and allow for a range of silicate metal depletions.
We note that adding ~70% of the cosmic iron, as metallic nano-particles, into an amorphous silicate matrix has about the same effect on the optical properties in the NIR as incorporating the iron into the silicate structure (Fig. A.1). Hence, the presence of iron as metallic inclusions or as cations within the silicate structure leads to significant NIR absorption in the 0.3 − 3 μm region where the ISRF peaks.
In conclusion, dust modelling is currently hampered by the lack of laboratory-measured optical constants for appropriate amorphous interstellar silicate analogue materials over a sufficiently wide wavelength range (i.e., FUV to mm wavelengths). Further, our uncertain knowledge as to where, and in what solid form, the bulk of the cosmic iron is to be found in interstellar dust is also a severe limitation.
Appendix B: a-C(:H) material heat capacities
As proposed in Paper III we assume that the heat capacity of a-C(:H) materials is the linear sum of the abundance-weighted heat capacities of the constituent atoms in the given bonding configurations. We therefore calculate the particle heat capacities using Eq. (A.3) from Paper III, i.e., ![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{C_{\rm V}}{N_{\rm C}} &=& \frac{1}{(1-X_{\rm H})} \nonumber\\[2mm] &&\hskip-3mm \times\, \Bigg\{ X_{\rm H}^\prime C_{\rm V}({\rm CH}) \ + \ X_{\rm sp^3} \left[ \frac{C_{\rm V}({\rm CC})_{\rm sp^2}}{R} + C_{\rm V}({\rm CC})_{\rm sp^3} \right] \Bigg\}, \label{eq_Cv_4} \end{eqnarray}](/articles/aa/full_html/2013/10/aa21686-13/aa21686-13-eq253.png) (B.1)which includes the contributions from surface and interior H atoms,
(B.1)which includes the contributions from surface and interior H atoms,  , sp2 aromatic/olefinic and sp3 aliphatic C atoms, the left, centre and right terms in the lower line of Eq. (B.1), respectively. For the CH bond heat capacity, CV(CH), and for the aromatic/olefinic C atom heat capacity, CV(CC)sp2, we adopt the Draine & Li (2001) approach used to determine the heat capacities of free-flying PAHs in the ISM. However, we are interested in the aromatic domains within solid a-C(:H) and therefore use the number of carbon atoms per aromatic domain rather than the total number of C atoms in the particle in our determination of CV(CC)sp2. For the sp3 component heat capacity, CV(CC)sp3, we adopt the values for polyethylene (Cheng 2002, Fig. 10, p. 18).
, sp2 aromatic/olefinic and sp3 aliphatic C atoms, the left, centre and right terms in the lower line of Eq. (B.1), respectively. For the CH bond heat capacity, CV(CH), and for the aromatic/olefinic C atom heat capacity, CV(CC)sp2, we adopt the Draine & Li (2001) approach used to determine the heat capacities of free-flying PAHs in the ISM. However, we are interested in the aromatic domains within solid a-C(:H) and therefore use the number of carbon atoms per aromatic domain rather than the total number of C atoms in the particle in our determination of CV(CC)sp2. For the sp3 component heat capacity, CV(CC)sp3, we adopt the values for polyethylene (Cheng 2002, Fig. 10, p. 18).
Appendix C: “Astronomicalisation” of the optEC(s)(a) data
Appendix C.1: IR band profiles and the emission bands
In order to better fit the observed astronomical IR emission and absorption band profile intensities and widths we needed to make only a few, rather minor, modifications to the previously-published optEC(s)(a) band profile data (Jones 2012a). These changes are: the re-assignment of four aliphatic C-C bands to aromatic C ≃ C, and adjustments to the intensities (widths) of nine (six) bands. The new band profile intensity and width values are shown in boldface in Table C.1; otherwise the data are the same as in Table 2 of Paper I.
Adopted C-H and C-C band modes for eRCN and DG bulk materials: band centre (ν0), width (δ) and integrated cross-section (σ).
Appendix C.2: The π − π⋆ band and the UV extinction bump
We find that the optEC(s)(a) data gives a better fit to the observed 217 nm UV bump when the single aromatic ring (NR = 1), benzene-like clusters are not included in the aromatic cluster distribution summation (Sect. B.1.1 in Paper III). This was already hinted at in the discussion of the C6 band in Appendix B of Paper III. There the abundance scaling factor for NR = 1 aromatic species was taken to be 0.08 rather than 1 and the astronomical observation requirements seemingly justify that supposition. Hence, and for particles with a ≤ 30 nm, the summation in the denominator of Eq. (B.5) in Paper III should run from NR = 2 (rather than NR = 1) up to the largest aromatic cluster size, NR(max), which is equivalent to setting the relative abundance for NR = 1 to zero rather than the value of 0.08 asumed in Paper III.
As shown in Paper III, the as-is use of the optEC(s)(a) data predicts a UV bump that is too large by about a factor of two and it was concluded there that we do not yet have a complete understanding of the physics of the likely UV bump carriers. Here we attempt to, in part, fill this gap by adopting an empirical approach. We find that, for nanoparticles with a < 3 nm, a narrowing of the contributing aromatic bands is required to get a reasonable fit to the UV bump width and adopt the following empirical relationship 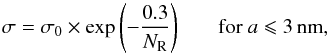 (C.1)where
(C.1)where 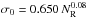 , as per Paper III, and the exponential term gives the aromatic cluster size-dependence.
, as per Paper III, and the exponential term gives the aromatic cluster size-dependence.
Appendix C.3: The σ − σ⋆ band and the FUV extinction
As suggested in Paper III, the σ − σ⋆ band in a-C:H materials should exhibit size-dependent effect, as per the π − π⋆ band (see Paper III for details and also Sect. C.2) but, to date and as far as we are aware, no such effect has been measured for a-C(:H).
However, the observation of quantum-size effects that can significantly alter the electronic properties of semiconductor materials when they exist as nano-crystals or nanoparticles would have major implications for the optical properties of interstellar dust particles. For example, in diamond, the conduction band and valence band energies (ECB and EVB) are, respectively, observed to shift to higher and lower energies as the particle size decreases. This leads to an increase in the band gap and a consequent shift in the absorption edge to shorter wavelengths as the particle size decreases. This effect was well-demonstrated for micro- and nanodiamond particles by Chang et al. (1999). They showed that for diamond particles with radii <1.8 nm (with <4300 C atoms) ECB does not remain bulk-like. From the results of Chang et al. the shift in the conduction band energy, ΔECB, can be expressed as, 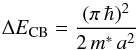 (C.2)where m∗ is the electron effective mass (0.10me, where me is the electron mass), ħ= h/2π where h is Planck’s constant and a is the particle radius. Figure C.1 plots ΔECB as a function of radius for nanodiamonds and indicates that the pre-solar, meteoritic nanodiamonds (mean radii ~1.4 nm) will clearly have electronic properties that differ markedly from those of bulk diamond. In fact, nanodiamonds may have band gap energies (ECB − EVB) shifted by about 1 eV from the bulk diamond value of 5.5 eV (226 nm, 4.4 μm-1), to in excess of 6.4 eV (190 nm, 5.3 μm-1).
(C.2)where m∗ is the electron effective mass (0.10me, where me is the electron mass), ħ= h/2π where h is Planck’s constant and a is the particle radius. Figure C.1 plots ΔECB as a function of radius for nanodiamonds and indicates that the pre-solar, meteoritic nanodiamonds (mean radii ~1.4 nm) will clearly have electronic properties that differ markedly from those of bulk diamond. In fact, nanodiamonds may have band gap energies (ECB − EVB) shifted by about 1 eV from the bulk diamond value of 5.5 eV (226 nm, 4.4 μm-1), to in excess of 6.4 eV (190 nm, 5.3 μm-1).
 |
Fig. C.1 Shift in the conduction band energy, ECB, as a function of radius for nanodiamonds, calculated using Eq. (C.2). The thick, solid portion of the curve indicates the behaviour supported by the experimental results of Chang et al. (1999) and the dashed portion is the extrapolation to smaller sizes using Eq. (C.2). For reference, the vertical solid line marks the mean radius of the meteoritic pre-solar nanodiamonds (~1.4 nm). The vertical dashed line marks the radius of the smallest diamond-type entity, the molecule adamantane, C10H16. |
 |
Fig. C.2 λ2Qabs/a for a-C(:H) particles with Eg(bulk) = 0.1 eV (black lines) and of radii 0.33 nm (solid), 0.5 nm (dashed), 1 nm (dotted) and 3 nm (dash-dotted). The data for neutral and cation PAHs, with the same number of C atoms (dark and light grey solid lines, respectively, Desert et al. 1990; Draine & Li 2001, 2007; Compiègne et al. 2011) are shown for comparison. The dashed, vertical, grey line shows the peak position of the UV bump and the solid, vertical, grey line shows the upper wavelength limit for the well-constrained a-C(:H) IR features. |
Given that the σ − σ⋆ band in a-C(:H) materials is determined by the carbon atom 2s electrons, exactly as in diamond, we use the above approach to determine the size-dependent shift in the band gap. For a-C(:H) materials at nanoparticle sizes we follow Chang et al. (1999) and shift the a-C(:H) σ − σ⋆ band peak energy by 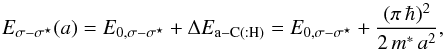 (C.3)where we here set ΔEa − C(:H) = ΔECB. Recalling that, from Paper III, E0,σ − σ⋆ = 13.0 eV, we limit the band peak position to a maximum of 14 eV, i.e., a maximum band shift of 1 eV, coherent with that measured in diamond (Chang et al. 1999).
(C.3)where we here set ΔEa − C(:H) = ΔECB. Recalling that, from Paper III, E0,σ − σ⋆ = 13.0 eV, we limit the band peak position to a maximum of 14 eV, i.e., a maximum band shift of 1 eV, coherent with that measured in diamond (Chang et al. 1999).
In order to get a reasonable fit to the observed slope and intensity of the FUV extinction we also needed to increase the peak intensity of the intrinsic a-C(:H) σ − σ⋆ band, I0,σ − σ⋆, but only for sub-10 nm radius particles, i.e., ![\appendix \setcounter{section}{3} \begin{equation} I_{\sigma-\sigma^\star} = I_{0,\sigma-\sigma^\star} \times \bigg\{ 1 + 0.06\, \left[ 10 - \left(\frac{a}{\rm 1\,nm}\right) \right] \bigg\} \ {\rm for} \ a \leqslant 10\,{\rm nm}, \label{eq_sigma_mult_factor} \end{equation}](/articles/aa/full_html/2013/10/aa21686-13/aa21686-13-eq306.png) (C.4)which corresponds to an increase by a factor of ≃1.5, 1.4, 1.3 for a = 1, 3 and 5 nm, respectively.
(C.4)which corresponds to an increase by a factor of ≃1.5, 1.4, 1.3 for a = 1, 3 and 5 nm, respectively.
Appendix C.4: Comparison of nm-sized a-C(:H) particles with PAHs
As per Sect. 4.1 of Paper III, we compare the modified a-C(:H) data with those for astronomical PAHs containing the same number of carbon atoms. Even with the assumed band strength and width modifications, used to give a better match to the astronomical data, it is clear that the discrepancy between the optEC(s)(a) data for a-C(:H) and the astronomical PAHs, as pointed out in Paper III, is still apparent. In the NIR regions (~1 − 5 μm) we note that laboratory data do indeed show enhanced extinction with respect to interstellar PAH models (Mattioda et al. 2005, 2008). Adding more longer wavelength bands, as per the Draine & Li (2007) model, could perhaps bring the optEC(s)(a) model data into closer correspondence with other models. However, the exact material/size origin of the bands is not yet completely clear and so this aspect has yet to be fully explored.
In a recent critical analysis of the interstellar PAH hypothesis Kwok & Zhang (2013) have shown that it is not without rather severe problems. As a response to this they proposed mixed organic and aliphatic nano-particles, MOANs, as a viable carrier of the observed IR emission bands and underlying continua (Kwok & Zhang 2011, 2013). These MOANs are, in essence, part of the same family of materials as a-C(:H). However, the MOANs appear to be much more open and less cross-linked structures than a-C(:H), and require the presence of O, N and S in the structure (Kwok & Zhang 2013), which is perhaps not supported by interstellar depletion studies.
All Tables
Observation-model coherency check: Eg characterisation as a function of the λ-dependent extinction and emission features.
Adopted C-H and C-C band modes for eRCN and DG bulk materials: band centre (ν0), width (δ) and integrated cross-section (σ).
All Figures
 |
Fig. 1 Model dust populations, as seen in cross-section. In the upper part the a-C:H/a-C grains are shown, where black represents aromatic-rich material and white aliphatic-rich material. In the lower part amorphous silicate grains (green) are shown with a 5 nm thick coagulated/accreted a-C mantle. The particle radii are indicated on a logarithmic scale. |
| In the text | |
 |
Fig. 2 Standard dust model size distributions. a-C-coated (Eg = 0.1 eV, mantle depth 5 nm) amorphous forsterite-type silicate grains with ~70% of the available iron in metallic, nano-particle inclusions (triple dot-dashed). Core/mantle, a-C:H/a-C (Eg = 2.5/0.1 eV) particles: large, log-normal (dotted) and small, power-law with an exponential tail (dash-dotted). The grey line shows the overall a-C(:H) grain size distribution, with physically-continuous properties, which is only separated into “large” and “small” components for modelling convenience. |
| In the text | |
 |
Fig. 3 Standard dust model for NH = 1020 H cm-2: NIR-UV extinction (top left), IR extinction (top right), albedo (bottom left) and the full dust SED (bottom right). The grain types are: a-SilFe/a-C core/mantle grains (triple dot-dashed), a-C:H/a-C core/mantle grains (dotted) and small a-C grains (dash-dotted). In each plot the totals are shown by the solid lines (red). The extinction data in the upper figures are taken from Mathis (1990). The observational data in the lower right plot are: ~5–15 μm ISOCAM/CVF ISO spectrum, ~100–1000 μm FIRAS/COBE spectrum, 3.3 μm AROME narrow band measurement (triangle) and DIRBE/COBE photometry (squares) (for details see Compiègne et al. 2011). |
| In the text | |
 |
Fig. 4 Dust component relative contributions to the SED: the line designations are as per Fig. 2. Note that the small a-C(:H) grain population contributes ≈45% of the total emission at 60 μm and ≈13% of the total emission at 100 μm. |
| In the text | |
 |
Fig. 5 Scaled dust model extinction in the 3.4 μm region: small a-C:H/a-C (× λ1.5, dash-dotted), large a-C:H/a-C (× λ1.65 − 2.9 × 104, dotted) and large a-SilFe/a-C (× λ1.7 − 8.2 × 103, triple dot-dashed). |
| In the text | |
 |
Fig. 6 Dust model normalised extinction, E(λ − V)/E(B − V) for fixed dust mass and for varying band gap, Eg [eV]: 0.1 (dark grey), 0.5 (pink), 1.0 (brown), 2.0 (blue) and 2.6 (violet). The solid (dotted) vertical grey lines mark the model (observed) UV bump positions. The yellow band indicates the observed extinction and its range of variation (Fitzpatrick & Massa 2007). |
| In the text | |
 |
Fig. 7 Dust model extinction for fixed dust mass as a function of Eg (top), a− (middle) and α (bottom). The solid (dotted) vertical grey lines mark the model (observed) UV bump peak positions. The symbols indicate the observed extinction for RV = 3.1 (grey open squares) and 5.1 (black filled squares) (Savage & Mathis 1979; Mathis 1990). The orange line shows the intensity of the adopted ISRF plotted as Jλ/λ and normalised to unity. |
| In the text | |
 |
Fig. 8 Dust size distributions for fixed mass in each component: large a-C:H/a-C particles (black dotted), large a-SilFe/a-C particles (black tripple-dot-dashed), for varying small a-C(:H) grain size distribution power-law index, α. |
| In the text | |
 |
Fig. 9 NIR extinction predicted by the model (solid lines) and the parameterised fits (as per Fitzpatrick & Massa 2009) for varying band gap, Eg [eV] (dashed lines), for a column density NH = 5 × 1021 cm-2. The model data colour-coding is as per Fig. 7. The sinusoidal structure is due to the adopted narrow silicate size range and will not be present in real, irregular and non-spherical particles. |
| In the text | |
 |
Fig. 10 Fitzpatrick & Massa (2009) NIR extinction parameter αNIR as a function of RV (large black squares), see Eq. (1). The fit parameters for our model as a function of Eg (α) are shown by the coloured squares (crosses), the colour-coding as per Fig. 7. The thick squares use the model RV and the thin squares the best fit RV values from Eq. (1), shown as the dashed lines in Fig. 9. The vertical grey band shows the typical diffuse ISM value of RV. |
| In the text | |
 |
Fig. 11 Dust model 3−14 μm and 3.1−3.7 μm emission band spectra as a function of the a-C(:H) material band gap, Eg [eV]. |
| In the text | |
 |
Fig. 12 Dust model SEDs, for fixed dust mass, as a function of Eg (upper panel), a− (middle panel) and α (lower panel). The line designations are as per Fig. 7. |
| In the text | |
 |
Fig. 13 Normalised FIR-cm SEDs show that the emissivity slopes segregate into two band-gap groups, one with β ~ 1.3 for Eg ~ 0 eV and the other with β ~ 2 for Eg ≳ 0.5 eV. The line designations are as per Fig. 7. The dashed blue lines indicate slopes of −1.0, −1.3, −1.5, −1.8 and − 2.0, from top to bottom. |
| In the text | |
 |
Fig. 14 Upper plot: βeff vs. λ, as a function of Eg, where βeff is the effective emissivity slope resulting from a combination of the a-SilFe/a-C and a-C:H/a-C dust population optical properties. The green triple dot-dashed line shows the data for only the a-SilFe/a-C grains, which do not depend on the band gap of the thin a-C(:H) coating. The λ-dependence and variations are therefore only due to the a-C(:H) dust properties. The line colour-coding is as per Fig. 11. The horizontal grey lines and wide yellow bands show βeff = 1.80 ± 0.05 and 1.60 ± 0.05. Lower plot: the emissivity slope, β, for a-C(:H) dust, for λ = 100 μm, 300 μm, and 1 mm, as a function of Eg, for a = 100, 10 and 1 nm. The vertical grey dashed line shows the experimentally-derived “block” on band gap evolution (see Paper II). The grey area indicates the range of a-C materials that are consistent with many diffuse ISM dust properties (Sect. 6). The coloured squares at the bottom indicate the band gap colour coding scheme. |
| In the text | |
 |
Fig. 15 Dust model extinction, τi, in the V band (blue) and at 250 μm (green) and 1 mm (red) wavelengths for an assumed column density NH = 1021 H cm-2. The upper plot shows the variations as a function of the a-C(:H) material band gap, Eg, and the lower plot as a function of the power-law, α, component of the small a-C dust population. The filled data points indicate the values for the best-fit DHGL dust model. The crosses with error bars show τ250 = 5.8 ± 1.7 × 10-4 E(B − V), from Eq. (2), multiplied by 104. |
| In the text | |
 |
Fig. 16 A schematic view of the life-cycle of interstellar dust in terms of evolutionary tracks: “parallel-processing” tracks that lead to a smooth evolution are horizontal (i.e., accretion and photo-processing) and “cross-talk” tracks that lead to significant mass-transfer between grains sizes (i.e., coagulation and disaggregation) are diagonal and vertical. Qualitatively, the red shading reflects the density, nH, and the violet shading, on the extreme right, represents high G0 radiation fields. |
| In the text | |
 |
Fig. 17 UV bump parameter, c3 (diamonds), and FUV extinction parameter, c4 × 25 (squares), intensity data normalised by the depletion into dust, (C/H)dust, as a function of NH. The y value uncertainties are only illustrative. The data are taken from Parvathi et al. (2012). |
| In the text | |
 |
Fig. A.1 Black lines show the imaginary (solid) and real (dashed) parts of the complex refractive index of our newly-constructed amorphous silicate/Fe nano-particle material, a-SilFe. This is a composite constructed using the amorphous forsterite-type silicate data (green) from Scott & Duley (1996) and the metallic iron data (grey) from Ordal et al. (1983, 1985, 1988), see text for details. For comparison we show the experimental data for iron-containing amorphous olivine-type silicates, MgFeSiO4 (orange) and Mg0.8Fe1.2SiO4 (brown), from Dorschner et al. (1995) and the astronomical data of Draine & Lee (1984) (cobalt blue). |
| In the text | |
 |
Fig. C.1 Shift in the conduction band energy, ECB, as a function of radius for nanodiamonds, calculated using Eq. (C.2). The thick, solid portion of the curve indicates the behaviour supported by the experimental results of Chang et al. (1999) and the dashed portion is the extrapolation to smaller sizes using Eq. (C.2). For reference, the vertical solid line marks the mean radius of the meteoritic pre-solar nanodiamonds (~1.4 nm). The vertical dashed line marks the radius of the smallest diamond-type entity, the molecule adamantane, C10H16. |
| In the text | |
 |
Fig. C.2 λ2Qabs/a for a-C(:H) particles with Eg(bulk) = 0.1 eV (black lines) and of radii 0.33 nm (solid), 0.5 nm (dashed), 1 nm (dotted) and 3 nm (dash-dotted). The data for neutral and cation PAHs, with the same number of C atoms (dark and light grey solid lines, respectively, Desert et al. 1990; Draine & Li 2001, 2007; Compiègne et al. 2011) are shown for comparison. The dashed, vertical, grey line shows the peak position of the UV bump and the solid, vertical, grey line shows the upper wavelength limit for the well-constrained a-C(:H) IR features. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


