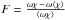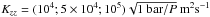| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321132 | |
| Published online | 14 October 2013 | |
3D mixing in hot Jupiters atmospheres
I. Application to the day/night cold trap in HD 209458b⋆
1 Université de Nice-Sophia Antipolis, Observatoire de la Côte d’Azur, CNRS UMR 6202, BP 4229, 06304 Nice Cedex 4, France
e-mail: vivien.parmentier@oca.eu
2 Department of Planetary Sciences, Lunar and Planetary Laboratory, University of Arizona, Tucson AZ, USA
3 Ashima Research, Suite 104, 600 South Lake Ave., Pasadena, CA 91106, USA
Received: 18 January 2013
Accepted: 12 August 2013
Context. Hot Jupiters exhibit atmospheric temperatures ranging from hundreds to thousands of Kelvin. Because of their large day-night temperature differences, condensable species that are stable in the gas phase on the dayside – such as TiO and silicates – may condense and gravitationally settle on the nightside. Atmospheric circulation may counterbalance this tendency to gravitationally settle. This three-dimensional (3D) mixing of condensable species has not previously been studied for hot Jupiters, yet it is crucial to assess the existence and distribution of TiO and silicates in the atmospheres of these planets.
Aims. We investigate the strength of the nightside cold trap in hot Jupiters atmospheres by investigating the mechanisms and strength of the vertical mixing in these stably stratified atmospheres. We apply our model to the particular case of TiO to address the question of whether TiO can exist at low pressure in sufficient abundances to produce stratospheric thermal inversions despite the nightside cold trap.
Methods. We modeled the 3D circulation of HD 209458b including passive (i.e. radiatively inactive) tracers that advect with the 3D flow, with a source and sink term on the nightside to represent their condensation into haze particles and their gravitational settling.
Results. We show that global advection patterns produce strong vertical mixing that can keep condensable species aloft as long as they are trapped in particles of sizes of a few microns or less on the nightside. We show that vertical mixing results not from small-scale convection but from the large-scale circulation driven by the day-night heating contrast. Although this vertical mixing is not diffusive in any rigorous sense, a comparison of our results with idealized diffusion models allows a rough estimate of the effective vertical eddy diffusivities in these atmospheres. The parametrization Kzz=5 × 104/ Pbar m2s-1, valid from ~1 bar to a few μbar, can be used in 1D models of HD 209458b. Moreover, our models exhibit strong spatial and temporal variability in the tracer concentration that could result in observable variations during either transit or secondary eclipse measurements. Finally, we apply our model to the case of TiO in HD 209458b and show that the day-night cold trap would deplete TiO if it condenses into particles bigger than a few microns on the planet’s nightside, keeping it from creating the observed stratosphere of the planet.
Key words: planets and satellites: atmospheres / methods: numerical / diffusion
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The year 1988 was marked by the discovery of the first substellar object outside our solar system (Becklin & Zuckerman 1988). This discovery was followed by numerous other discoveries of cool brown dwarfs, whose spectra differ significantly from stars. This led to the definition of three new spectral classes beyond the stellar classes O to M: the L, T, and Y dwarfs, ranging from temperatures of 2300 K to 350 K (Cushing et al. 2011). To understand of these brown dwarfs and the mechanisms that cause the transition from one spectral class to another, it is fundamental to take condensation processes into account: in cold atmospheres molecules can form, condense, and rain out, affecting the observed spectral features of these objects. In particular, the M to L transition is marked by the disappearance of the titanium oxide (TiO) bands, which is understood by its transformation into titanium dioxide (TiO2) and condensation into perovskite (CaTiO3; Lodders 2002). The L to T transition is understood as the switch from a cloudy atmosphere to a cloud-free atmosphere as the cloud layer migrates into the deep, unobservable regions of the star (see Kirkpatrick 2005, for a review). Because brown dwarfs produce their own light, high-quality spectra of their atmosphere can be measured. Numerous atmospheric models have been built to fit the data, from simple models with a reduced set of free parameters (Ackerman & Marley 2001) to sophisticated models including the detailed physics of condensation, growth, and settling of particles (Woitke & Helling 2004).
The discovery and characterization of exoplanets followed close behind. The first detection of a planet around a main sequence star by Mayor & Queloz (1995) opened the trail for discovering hundreds of exoplanets. Some years later, atmospheric characterization of these objects became available, both from transit spectroscopy (Charbonneau et al. 2002) and from direct detection of the planet’s thermal emission (Charbonneau et al. 2005). Although the global-mean effective temperatures of these planets are similar to those on brown dwarfs, a major difference is that hot Jupiters are strongly irradiated. Depending on the incident stellar flux, planetary rotation rate, and other factors, atmospheric circulation models show that this day-night heating gradient can lead, at low pressures, to nightside temperatures that are at least ~1000 K colder than dayside temperatures (e.g., Showman et al. 2008, 2009; Dobbs-Dixon et al. 2010; Rauscher & Menou 2010, 2012a; Heng et al. 2011a,b; Perna et al. 2012). As a result, a wide variety of condensable species that are stable in the gas phase on the dayside may condense on the nightside, leading to the formation of particles there. In the absence of atmospheric vertical mixing, such particles would gravitationally settle, depleting the atmosphere of these species on both the dayside and the nightside. Sufficiently strong vertical mixing, anywhere on the planet, however, may keep these particles suspended in the atmosphere, allowing them to sublimate into the gas phase in any air transported from nightside to dayside. Thus, the existence of this nightside “cold trap” is crucial for understanding not only the existence of hazes on hot Jupiters (e.g., Pont et al. 2013) but also the gas-phase composition of the atmosphere on both the dayside and the nightside.
These arguments are relevant to a wide range of titanium and vanadium oxides, silicate oxides, and other species. In particular, chemical-equilibrium calculations show that, at temperatures of ~1000–2000 K, there exist a wealth of condensates including Ti2O3, Ti3O5, and Ti4O7 (among other titanium oxides), MgAl2O4, Mg2SiO4, MgSiO3, NaAlSi3O8, KAlSi3O8, and several phosphorus oxides (Burrows & Sharp 1999; Lodders 2002). Understanding the possible existence of gas-phase TiO, Na, K, and other species on the dayside therefore requires an understanding of the nightside cold trap.
A particularly interesting problem in this regard is the existence of exoplanet stratospheres. For some transiting hot Jupiters, Spitzer/IRAC secondary-eclipse observations indicate the presence of thermal inversions (stratospheres) on these planets’ daysides (Knutson et al. 2008). These stratospheres are generally thought to result from absorption of starlight by strong visible/ultraviolet absorbers, but debate exists about the specific chemical species that are responsible. Hubeny et al. (2003) and Fortney et al. (2008) showed that, because of their enormous opacities at visible wavelengths, the presence of gaseous titanium and vanadium oxides can lead to stratospheres analogous to those inferred on hot Jupiters. This hypothesis is supported by the possible detection of TiO by Désert et al. (2008) in the atmospheric limb of HD 209458b. Then, a crucial question is whether the nightside cold trap would deplete the atmosphere of TiO, preventing this species from serving as the necessary absorber (Showman et al. 2009; Spiegel et al. 2009).
As pointed out by several authors, there exists another possible cold trap. 1D radiative-transfer models suggest that, on some hot Jupiters, the global-mean temperature-pressure profile becomes sufficiently cold for condensation of gaseous TiO to occur at pressures of tens to hundreds of bars (e.g., Fortney et al. 2008). Even though a stratosphere on such a planet would be sufficiently hot for TiO – if present – to exist in the gas phase, the condensation of TiO and downward settling of the resulting grains at ~10–100 bars might prevent the existence of TiO in the atmosphere (Showman et al. 2009; Spiegel et al. 2009). The strength of these two cold traps is given by a competition between gravitational settling and upward mixing. The vertical mixing results from complex 3D flows and can be inhomogeneous over the planet (Cooper & Showman 2006; Heng et al. 2011a). When using a 1D-model, the vertical mixing is usually considered to be diffusive only, and parametrized by a diffusion coefficient Kzz. Several studies give an estimate for this vertical diffusion coefficient in hot Jupiters atmospheres. Heng et al. (2011a) uses the magnitude of the Eulerian mean streamfunction as a proxy for the strength of the vertical motions and derived a vertical mixing coefficient of the order of Kzz ≈ 106 m2s-1. Other authors used an estimate based on the root mean squared vertical velocity either the local value (Cooper & Showman 2006) or the planet-averaged value (Moses et al. 2011). However these estimates are crude and there is a need for theoretical work to more rigorously characterize the vertical mixing rates in hot Jupiters atmospheres.
In this study we focus in the dynamical mixing of condensable species. We therefore neglect all the potential feedback of the condensable species on the atmospheric flow such as the radiative effects of the condensates (Heng et al. 2012; Dobbs-Dixon et al. 2012), non-equilibrium chemistry due to the depletion of a particular species, latent heat release during condensation among others. We present three-dimensional general circulation model (GCM) experiments of HD 209458b to model a chemical species that condenses and settles on the nightside of the planet. We show that mixing in hot Jupiters atmospheres is dominated by large-scale circulation flows resolved by the GCM. Finally, from the 3D model, we derive the values of an effective vertical mixing coefficient, representing the averaged vertical mixing in the planet atmosphere. We also compare these 3D models to an idealized 1D model parameterizing the mixing using an eddy diffusivity, with the goal of estimating an effective eddy diffusivity for the mixing rates in the 3D models. These are the first circulation models of hot Jupiters to include the influence of the dynamics on condensable species.
2. 3D model
Here, we use a state-of-the-art 3D circulation model, coupled to a passive tracer representing a condensable species, to determine how the interplay between dynamical mixing and vertical settling controls the spatial distribution of condensable species on hot Jupiters. Although the day/night cold trap should be present in most hot Jupiters, for concreteness, we must select a particular system to investigate. HD 209458b is among the best studied hot Jupiters. It is believed to harbor a stratosphere (Knutson et al. 2008) and a strong day-night temperature contrast (Showman et al. 2009). We decided to use it as our reference model in this study, keeping in mind that most of the mechanisms discussed here should apply to all hot Jupiters. To model the atmosphere of HD 209458b we use the 3D Substellar and Planetary Atmospheric Radiation and Circulation (SPARC/MITgcm) model of Showman et al. (2009), which couples the plane-parallel, multi-stream radiative transfer model of Marley & McKay (1999) to the MITgcm (Adcroft et al. 2004).
2.1. Dynamics
To model the dynamics of the planet we solve the global, three-dimensional primitive equations in spherical geometry using the MITgcm, a general circulation model for atmosphere and oceans developed and maintained at the Massachusetts Institute of Technology. The primitive equations are the standard equations used in stably stratified flows where the horizontal dimensions greatly exceed the vertical ones. In hot Jupiters, the horizontal scales are 107 − 108 m whereas the vertical scale height fall between 200 and 500 km leading to an aspect ration of 20 to 500. In order to minimize the constraints on the timestep by the CFL criterion, we solve the equations on the cubed-sphere grid as described in Adcroft et al. (2004). The simulations do not contain any explicit viscosity nor diffusivity. However, in order to smooth the grid noise and ensure the stability of the code we use a horizontal fourth-order Shapiro filter (Shapiro 1970). In the vertical direction, no filtering process is applied. Kalnay (2003) provide a more detailed description of the equations (see Showman et al. 2009 for the numerical method used to solve them).
We use a gravity of 9.81 m s-2, a planetary radius of 9.44 × 107 m, and a rotation rate of 2.06 × 10-5 s-2 (implying a rotation period of 3.5 days). The average pressure ranges from 200 bars at the bottom of the atmosphere to ptop at the top of the second-highest level, with the uppermost level extending from a pressure of ptop to zero. In most models, ptop is 2 μbar with 53 vertical levels. In some models – particularly those with the largest cloud particle size – we adopt Ptop of 20 µbar with 47 vertical levels. In either case, this leads to a resolution of almost three levels per scale height. We use a horizontal resolution of C32, equivalent to an approximate resolution of 128 cells in longitude and 64 in latitude and a timestep of 15 s. We reran some models at C64 resolution (equivalent to an approximate resolution of 256 × 128 in longitude and latitude) to check convergence.
It is worth mentioning that, although the primitive equations are hydrostatic in nature, it does not imply an absence of vertical motion (see Sect. 3.5 of Holton 1992). In the primitive equations, the horizontal divergence is generally non-zero, which requires the presence of vertical motions. Indeed, the dayside radiative heating and nightside radiative cooling are balanced by a combination of horizontal and vertical thermal advection. In many cases, including Earth’s tropics, the vertical advection dominates; in such cases, vertical motions play a crucial, zeroth-order role in the thermodynamic energy balance. For conditions relevant to hot Jupiters, GCMs and order-of-magnitude calculations show that vertical motions of 10 − 100 ms-1 or more are expected, despite the fact that the atmosphere is stably stratified. Further discussion can be found in Showman & Guillot (2002) and in Sect. 6.2 of Showman et al. (2008).
2.2. Radiative transfer
The radiative transport of energy is calculated with the plane-parallel radiative transfer code of Marley & McKay (1999). The code was first developed for Titan’s atmosphere (McKay et al. 1989) and since then has been extensively used for the study of giant planets (Marley et al. 1996), brown dwarfs (Marley et al. 2002; Burrows et al. 1997), and hot Jupiters (e.g., Fortney et al. 2005, 2008; Showman et al. 2009). We use the opacities developed by Freedman et al. (2008), including more recent updates, and the molecular abundances described by Lodders & Fegley (2002) and Visscher et al. (2006).
As in the models of HD 209458b presented by Showman et al. (2009), our opacity tables include gas-phase TiO and VO whenever temperatures are locally high enough for TiO to reside in gas phase. Note that, because of the assumption of local chemical equilibrium, we do not consider the effect of cold traps on the atmospheric composition, and thus on the opacities. TiO opacities are always taken into account where temperatures are high enough for TiO to exist in the gas phase. This causes a warm stratosphere on the dayside of our modeled planet, regardless of the 3D distribution of our tracers (to be described below).
Metallicities are solar, as given by Freedman et al. (2008). A metal enhanced atmosphere should modestly change the day-night temperature difference (at a given pressure) and the pressure of the photosphere itself, as shown in Showman et al. (2009). Cloud opacities are ignored in this study and might alter the flow more significantly (Dobbs-Dixon & Agol 2012).
Opacities are described using the correlated-k method (e.g., Goody 1961). We consider 11 frequency bins for the opacities ranging from 0.26 to 300 μm; within each bin, opacity information from typically 10 000 to 100 000 frequency intervals is represented statistically over 8 k-coefficients. This is radically different from other methods in the literature. In particular, Dobbs-Dixon & Agol (2012) uses a multi-bin approach for the opacity, but inside each of their 30 frequency bins they use a single average opacity. However, inside each bin of frequency, the line by line opacity varies by several orders of magnitudes and no mean, neither the Planck mean nor the Rosseland mean opacity (see Parmentier & Guillot 2013 and Parmentier et al., in prep., for more details) can take into account this large variability. Thus, as stated in Dobbs-Dixon & Agol (2012), our correlated-k radiative transfer is today’s most sophisticated radiative transfer approach implemented in a hot Jupiters GCM. Showman et al. (2009) provide a detailed description of the radiative-transfer model and its implementation in the GCM.
2.3. Tracer fields
Our target species is represented by a passive tracer field. Tracer fields are often used in GCMs to follow the concentration of a chemical species such as water vapor or cloud amount in the atmosphere or salinity in the oceans. Cooper & Showman (2006) were the first to include a passive tracer in a circulation model of hot Jupiters, in their case to investigate the quenching of CO and CH4 due to atmospheric mixing.
The tracer field is advected by the flow calculated in the GCM. Thus the tracer abundance χ is given by the continuity equation: 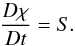 (1)Here, χ represents the mole fraction of the tracer, i.e., the number of molecules of the species in a given volume, either in gaseous phase or trapped in condensed particles, with respect to the total number of atmospheric molecules in that volume. For simplicity the value of χ is normalized to its initial value in the deep layers of the planet. In the equation, S is a source term and the total derivative is defined by
(1)Here, χ represents the mole fraction of the tracer, i.e., the number of molecules of the species in a given volume, either in gaseous phase or trapped in condensed particles, with respect to the total number of atmospheric molecules in that volume. For simplicity the value of χ is normalized to its initial value in the deep layers of the planet. In the equation, S is a source term and the total derivative is defined by 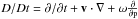 , where t is time, v is the horizontal velocity, ∇ is the horizontal gradient operator on the sphere, ω = DP/Dt is the vertical velocity in pressure coordinates, and P is pressure. We model the simplest possible horizontal cold trap in hot Jupiters atmospheres: a situation where the day/night temperature contrast is so strong that our target species is gaseous in the dayside of the planet but condenses and is incorporated in particles of size a in the nightside. Thus the source term S represents the gravitational settling of these particles and is given by
, where t is time, v is the horizontal velocity, ∇ is the horizontal gradient operator on the sphere, ω = DP/Dt is the vertical velocity in pressure coordinates, and P is pressure. We model the simplest possible horizontal cold trap in hot Jupiters atmospheres: a situation where the day/night temperature contrast is so strong that our target species is gaseous in the dayside of the planet but condenses and is incorporated in particles of size a in the nightside. Thus the source term S represents the gravitational settling of these particles and is given by 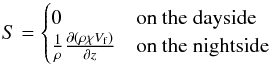 (2)where z is the height, increasing upward, ρ is the density of the air and Vf is the settling velocity of the particles defined by Eq. (3). This velocity depends on the size of the particles, which is determined by the complex microphysics of condensation, out of the scope of this study (see Woitke & Helling 2003). Thus we treat a as a free parameter in our model. We model spherical particles of radii 0.1, 0.5, 1, 2.5, 5, and 10 μm. Equation (2)describes a simple, bimodal mechanism for the condensation of chemical species on the nightside. Although this scheme is highly simplified (ignoring the detailed temperature and pressure dependence of the condensation curves of possible condensates in hot Jupiters atmospheres), it reflects the fact that a wide range of species will reside in gaseous form on the dayside yet condensed form at low pressures on the nightside.
(2)where z is the height, increasing upward, ρ is the density of the air and Vf is the settling velocity of the particles defined by Eq. (3). This velocity depends on the size of the particles, which is determined by the complex microphysics of condensation, out of the scope of this study (see Woitke & Helling 2003). Thus we treat a as a free parameter in our model. We model spherical particles of radii 0.1, 0.5, 1, 2.5, 5, and 10 μm. Equation (2)describes a simple, bimodal mechanism for the condensation of chemical species on the nightside. Although this scheme is highly simplified (ignoring the detailed temperature and pressure dependence of the condensation curves of possible condensates in hot Jupiters atmospheres), it reflects the fact that a wide range of species will reside in gaseous form on the dayside yet condensed form at low pressures on the nightside.
We consider several independent passive tracers, representing species that condenses in different particle size. Thus, they do not influence either the dynamics or the radiative transfer of the simulation and does not interact with each others. This ignores a role for possible radiative feedback mechanisms – discussed in Sect. 6 – or particle growth but represents a necessary first step toward understanding how dynamics controls the 3D distribution of a condensable species.
2.4. Settling velocity
We assume that the target chemical species condenses, in the nightside only, into spherical particles of radius a that reach immediately their terminal fall speed, which is given by (Pruppacher & Klett 1978): 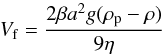 (3)where η is the viscosity of the gas, g is the gravitational acceleration of the planet, ρp is the density of the particle, and ρ the density of the atmosphere. Vf is positive when the particles goes downward. The Cunningham slip factor, β, accounts for gas kinetic effects that become relevant when the mean free path of the atmospheric molecules is bigger than the size of the falling particle. This factor has been measured experimentally by numerous experiments. We adopt the expression from Li & Wang (2003) as done by Spiegel et al. (2009).
(3)where η is the viscosity of the gas, g is the gravitational acceleration of the planet, ρp is the density of the particle, and ρ the density of the atmosphere. Vf is positive when the particles goes downward. The Cunningham slip factor, β, accounts for gas kinetic effects that become relevant when the mean free path of the atmospheric molecules is bigger than the size of the falling particle. This factor has been measured experimentally by numerous experiments. We adopt the expression from Li & Wang (2003) as done by Spiegel et al. (2009). 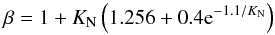 (4)where the Knudsen number KN is the ratio of the mean free path to the size of the particle:
(4)where the Knudsen number KN is the ratio of the mean free path to the size of the particle: 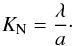 (5)For a perfect gas, the mean free path can be expressed as (Chapman & Cowling 1970):
(5)For a perfect gas, the mean free path can be expressed as (Chapman & Cowling 1970): 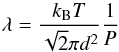 (6)with d the diameter of the gas molecules, P and T the pressure and temperature of the gas, and kB the Boltzmann constant. In the limit of a high-density atmosphere, β → 1 and the terminal speed Vf becomes the Stokes velocity VStokes.
(6)with d the diameter of the gas molecules, P and T the pressure and temperature of the gas, and kB the Boltzmann constant. In the limit of a high-density atmosphere, β → 1 and the terminal speed Vf becomes the Stokes velocity VStokes.
For low density gases, the dynamical viscosity is independent of pressure and can be expressed as a power law of the local temperature with an exponent varying between 1/2 in the hard-sphere model to near unity, depending on the strength of the interactions between the molecules. Following Ackerman & Marley (2001), we use the analytical formula given by Rosner (2000) for the viscosity of hydrogen: 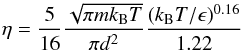 (7)with d the molecular diameter, m the molecular mass, and ϵ the depth of the Lennard-Jones potential well (for H2 we use 2.827 × 10-10 m and 59.7kB K respectively). The power law behavior of the viscosity remains valid for temperatures ranging from 300 K to 3000 K and for pressures less than 100 bar (Stiel & Thodos 1963). At higher temperature, ionization of hydrogen becomes relevant and the viscosity reaches a plateau. However the temperatures of the model are everywhere less than 3000 K and so Eq. (7)remains valid.
(7)with d the molecular diameter, m the molecular mass, and ϵ the depth of the Lennard-Jones potential well (for H2 we use 2.827 × 10-10 m and 59.7kB K respectively). The power law behavior of the viscosity remains valid for temperatures ranging from 300 K to 3000 K and for pressures less than 100 bar (Stiel & Thodos 1963). At higher temperature, ionization of hydrogen becomes relevant and the viscosity reaches a plateau. However the temperatures of the model are everywhere less than 3000 K and so Eq. (7)remains valid.
Figure 1 displays the resulting terminal velocity as a function of pressure and particle size. Two different regimes are observed. For Knudsen numbers smaller than unity, the terminal velocity is independent of pressure, whereas for Knudsen numbers exceeding unity, the terminal velocity is inversely proportional to the pressure. At low pressure and for particles bigger than a few tens of micrometers, the Reynolds number becomes higher than unity, and Eq. (3)is no longer valid. However, we show in Appendix A that these differences remain smaller than one order of magnitude and confined to a small parameter space thus we decided to neglect them for this work.
 |
Fig. 1 Terminal velocity of a falling particle as a function of pressure and particle size for an H2-atmosphere at 1000 K and a value of the gravitational acceleration of 15 m s-2. |
2.5. Integration time-limitation of the study
A challenge for any 3D numerical integrations of hot Jupiters dynamics is the wide range of timescales exhibited by these atmospheres. This is true for the radiative time constant, which varies significantly from low to high pressure (Iro et al. 2005; Showman et al. 2008). Nevertheless, Showman et al. (2009) showed that the computed light-curve of HD189733b changes little for integration time longer than hundreds of days, indicating that the dynamics in the millibar regime has stabilized. As we integrate ~1400 days, we consider the dynamics of the planet to be spun up at pressures less than ~100 mbar. For the settling of particles, another timescale must be taken into account. The particle settling timescale can be defined as the time for the particles to fall one atmospheric scale height. To obtain a correct picture of the problem at a given location of the planet, we need to integrate the simulation for at least several times longer than the settling timescale at this location. As we can see in Fig. 2 the settling timescale ranges from tens of seconds for big particles at low pressure to tens of years for small particles at high pressure. Due to computational limitation it is not possible to run the simulation long enough to ensure that every considered tracer field has reached a statistical steady state for the full range of particle sizes we consider. The integration during 1400 days allows us to calculate the steady state for every particle size at pressure lower than 10 bar and at every pressure for nightside condensates bigger than 2 μm.
We define the advective timescale as the time for a parcel in the main jet stream (see Sect. 3.1) to cross one hemisphere of the planet. If the advective timescale exceeds the settling timescale at a given level, the particles at these levels will fall several scale heights while on the nightside. We thus expect that these levels will be depleted. Conversely when the advective timescale is shorter than the settling timescale, the coupling between the flow and the particle is essential and particles’ behavior cannot be predicted easily. Typical advective times in our models are ~24 h; this is marked by the upper thick black curve in Fig. 2. We expect depletion to occur above this line.
Our initial conditions for the tracer field correspond to a tracer that is spatially constant everywhere at a normalized mole fraction of 1. The final tracer abundance in our models at low pressures (less than ≈0.1−1 bar) is qualitatively insensitive to the initial abundance at those low pressures. This results from the short vertical mixing and settling timescales at low pressures (e.g., Fig. 2).
 |
Fig. 2 Settling timescale as a function of pressure and particle size for the same conditions as in Fig. 1. Also shown are the advective timescale (black curve) and the simulation timescale (blue curve). In the shaded region (below 1 bar), the tracers are considered gaseous and the settling timescale is not relevant for our study. |
 |
Fig. 3 Temperature (left panel, colorscale), vertical velocities (right panel, colorscale), and horizontal winds (arrows) in our model of HD 209458b. Positive velocities are upward. The top three panels show the flow at three different pressure (0.1 mbar, 1 mbar, and 10 mbar). The bottom panel shows the vertical velocities versus longitude and pressure along the equator. The substellar point is at longitude, latitude (0°, 0°), the dayside is between -90° and +90°. All the quantities are time averaged. |
3. Results
3.1. Dynamical regime
We run the simulations for 1400 days and calculate the time average for all the variables over the last 400 days only, once the simulation reaches a statistical steady state at upper levels. Understanding the flow structure is essential to understanding the Lagrangian advection of particles, thus we first present a brief description of the dynamics. A more complete description of the circulation in our simulations is presented in Showman et al. (2009). The temperature structure is shown in Fig. 3. A hot stratosphere is visible at altitudes above the 10-mbar level, due to the strong visible-wavelength absorption by titanium oxide present in solar abundances in the simulation. Titanium oxide abundances should be affected by the horizontal cold trap. However, as explained in Sect. 2.2, we consider its radiative effects as if it was in local chemical equilibrium, regardless of the behavior of our passive tracers. Temperatures reach ~ 2200 K at low pressures near the substellar point. By contrast, the temperatures deeper than 10 mbar in the dayside are relatively temperate. This could lead to the presence of a vertical cold trap, not considered in this study. The day-night temperature contrast becomes significant at pressures less than ~100 mbar, reaching 1600 K near the top of the model. This large temperature difference results from the short radiative timescale at low pressures in comparison to dynamical timescales (Iro et al. 2005; Cooper & Showman 2005; Showman et al. 2008).
The horizontal flow on isobars comprises an eastward (superrotating) jet close to the equator and a day-to-night flow pattern at higher latitude. As the pressure increases, the radiative time constant increases and the jet extends to higher latitudes. As seen in Fig. 3, the mean vertical velocities exhibit planet-wide variations. The highest velocities coincide with strong horizontal convergence of the flow and occur mostly at the equator. West of the anti-stellar point, the convergence of the day-to-night circulation forces strong downwelling motions. As described in Rauscher & Menou (2010), this convergence point appears in a range of hot Jupiters GCMs of varying complexity. It is usually associated with a shock-like feature (Heng 2012). Our simulations assume local hydrostatic equilibrium and thus can not treat properly the physics of shocks. To date, no global model of hot Jupiters atmospheric dynamics can handle shocks properly. Yet, a similar wind convergence pattern appears when considering the non-hydrostatic nature of the flow as can be seen in Dobbs-Dixon et al. (2010). Between the substellar point and the west terminator, there are additional convergence/divergence points associated with the jet, leading to a region of strong ascending motion ~40° of longitude west of the substellar point, and a broad region of descending motion west of that. These vertical flows remain coherent over several orders of magnitude in pressure, giving them the potential to transport vertically large quantities of material. Outside of these points of strong vertical motions, the vertical velocities are more than one order of magnitude smaller. They are mostly upward on the dayside and downward on the nightside.
3.2. Spatial distribution of condensable species
Our simulations show that, as expected, condensation and particle settling on the nightside deplete the tracer from upper levels relative to the abundances at depth-an effect that is stronger for larger particles. This is illustrated in Fig. 4 (solid curves), which shows the global-mean tracer abundance (averaged horizontally on isobars) versus pressure for simulations with nightside condensates sizes ranging from 0.1 μm to 10 μm. In all cases, the horizontally averaged tracer abundance decreases with altitude. The depletion is modest for the smallest particle size (0.1 μm), but for the largest particle sizes, tracer abundances at the top are almost two orders of magnitude smaller than abundances at the bottom. A useful metric is the “50% depletion pressure”, that is, the pressure above which the global-mean tracer abundance is less than 50% of the deep abundance. This pressure is only 10 μbar for a particle size of 0.5 μm but is 0.1 bar for a particle size of 10 μm. We also note that, for all the models shown in Fig. 4, the particles settling times near the top of the model are much less than our integration times; at low pressures, the tracer abundances have reached a statistical equilibrium where downward transport of tracer due to particle settling is balanced by upward mixing of tracer by the large-scale dynamics.
 |
Fig. 4 Planet-wide, time averaged tracer abundances on isobars. The abundances are normalized to the abundance in the deepest layer. We compare the value of the 3D model (solid lines) and the fit using the 1D model (dashed lines). |
The tracer abundance on isobars exhibits a strong spatial variation as can be seen in Fig. 6. Although a day/night pattern is imposed in the tracer source/sink (with particle settling on the nightside but not the dayside), the three-dimensional advection of the tracer field by the atmospheric winds leads to a complex tracer distribution that does not exhibit an obvious day-night geometry. The main pattern appears to be an equator-to-pole gradient, with large zonal-mean abundances at the poles, and smaller zonal-mean abundances at the equator. This is particularly true around 0.1 mbar. Significant longitudinal tracer variations also occur; at ~1 mbar (Fig. 6), these variations are particularly prominent at high latitudes. Interestingly, these variations are phase shifted in longitude relative to the day-night pattern with maximum (minimum) peak tracer abundances occurring ~60–80° of longitude east of the substellar (antistellar) point.
On top of these main patterns, we clearly see two points depleted in tracers at the equator. These two points correspond to points of horizontal convergence of the flow and high downwelling motions as discussed in the previous section. This correlation between strong downwelling motions and low tracer abundances arises naturally in the presence of a background vertical gradient of tracer abundances. Due to their settling on the nightside, the local tracer abundance generally decreases with height and thus any downwelling motion would carry parcels of gas depleted in tracers whereas any upwelling motion should carry parcels of gas enhanced in tracers.
 |
Fig. 5 Time averaged fluxes of tracers across isobars. Upwelling fluxes due to the dynamics (solid lines) balance the downwelling fluxes due to the gravitational settling of the tracers (dashed lines). Negative values are upward fluxes. |
 |
Fig. 6 Time averaged tracer abundance relative to the deep abundance (χ/χ0) at two different pressures and for different particle sizes. |
3.3. Geometry of the mixing
As discussed in the previous section, the tracer abundance is not null everywhere in the planet, which implies that tracers did not rain out during the simulation time. Yet the integration time greatly exceeds the fall times at low pressure for all particle sizes considered, and everywhere throughout the domain for particle sizes exceeding a few μm. Therefore vertical mixing must happen in order to keep these particles aloft. This vertical mixing is characterized by an upward dynamical flux of tracers that balances the downward flux due to the gravitational settling in the nightside. The upward dynamical flux of tracers across isobars can be calculated as 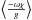 where ω is the vertical velocity in pressure coordinates, χ the tracer abundance, g the gravity of the planet and the brackets denote the average on isobars. As seen in Fig. 5, the upward flux of tracers due to the dynamics (solid lines) balances nicely the downward flux due to settling (dashed lines), showing that the simulation did reached a quasi steady-state.
where ω is the vertical velocity in pressure coordinates, χ the tracer abundance, g the gravity of the planet and the brackets denote the average on isobars. As seen in Fig. 5, the upward flux of tracers due to the dynamics (solid lines) balances nicely the downward flux due to settling (dashed lines), showing that the simulation did reached a quasi steady-state.
Hot Jupiters atmospheres are heated from above and thus are believed to be stably stratified. Then, vertical mixing cannot be driven by small scale convection as it is the case in the deep atmosphere of brown dwarfs (Freytag et al. 2010) and the gas giants of the solar system. As explained in Sect. 2.1, our model does not use any parametrization of sub-grid scale mixing. Thus we do not account for mixing induced by small-scale turbulence and gravity wave breaking, two mechanisms that are believed to dominate the mixing in the radiative part of brown dwarfs atmospheres (Freytag et al. 2010). Rather, the upward flux of tracers in our model is due to the large-scale, resolved flow of the simulation.
Given that mass is conserved, any upward flux of gas is compensated by a downward flux of gas. Thus, if the tracers concentrations were horizontally homogeneous on isobars, there would be no net upward flux of tracer through that isobar. For a net upward flux of tracers across isobars to occur, there must be a correlation between the horizontal distribution of the tracers and the vertical velocities. Dynamics will produce an upward flux if – on an isobar – ascending regions exhibit greater tracer abundance than descending regions. In other words, an upward tracer flux due to dynamics will occur only if (χ − ⟨ χ ⟩ )ω < 0 where ω is the upward velocity in pressure coordinates, χ is the tracer abundance and the brackets are the mean over one isobar (note that negative ω implies upward motion). Given a vertical gradient of ⟨ χ ⟩ such that the abundance of ⟨ χ ⟩ decreases upward, an upward flux of gas will naturally bring enhanced material whereas a downward flux will naturally advect parcels of gas depleted in tracers, thereby creating the correlation between ω and χ favorable for upward tracer transport. Figure 7 shows the relative contribution to the upward mixing versus longitude and latitude at a given isobar, which can be estimated by the quantity: 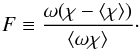 (8)Mass conservation in the primitive equations implies that ⟨ω ⟨ χ ⟩ ⟩ = 0: the advection of ⟨ χ ⟩ does not contribute to the net (horizontally averaged) upward flux of material and so we remove the contribution of this term when defining F in Eq. (8). The quantity
(8)Mass conservation in the primitive equations implies that ⟨ω ⟨ χ ⟩ ⟩ = 0: the advection of ⟨ χ ⟩ does not contribute to the net (horizontally averaged) upward flux of material and so we remove the contribution of this term when defining F in Eq. (8). The quantity 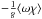 is the mean upward flux of material across isobars, thus the quantity F represents the local contribution to the total upward flux on isobars. It is normalized such that ⟨ F ⟩ = 1.
is the mean upward flux of material across isobars, thus the quantity F represents the local contribution to the total upward flux on isobars. It is normalized such that ⟨ F ⟩ = 1.
The strength of the mixing varies significantly with longitude and latitude. Both upward and downward fluxes are one order of magnitude greater than typical values in a handful of specific small areas across the planet – particularly at the two points of horizontal convergence and strong vertical velocities described in Sect. 3.1. This vertical flow remains coherent over several order of magnitude in pressure (see Fig. 3), acting like a vertical “chimney” where efficient transport of material can be achieved.
In summary, the mechanism by which the large-scale, resolved atmospheric circulation transports tracers upward is extremely simple and straightforward. The settling of particles leads to a mean vertical gradient of tracer abundance, with, on average, small tracer mixing ratios aloft and large tracer mixing ratios at depth. Given this background gradient, advection by vertical atmospheric motions – whatever their geometry – automatically produces a correlation between ω and (χ − ⟨ χ ⟩) on isobars, with ascending regions exhibiting larger values of (χ − ⟨ χ ⟩) than descending regions. In turn, this correlation automatically causes an upward dynamical net flux of tracers when averaged globally over isobars. In statistical steady state, this upward dynamical flux balances the downward transport due to particle settling and allows the atmospheric tracer abundance to equilibrate at finite (non-zero) values despite the effect of particle settling. The mechanism does not require convection, and indeed, the vertical motions that cause the upward transport in our models are resolved, large-scale motions in the stably stratified atmosphere. These vertical motions are a key aspect of the global-scale atmospheric circulation driven by the day-night heating contrast.
 |
Fig. 7 2D distribution of the mixing efficiency on the 1mbar isobar. We plot |
3.4. Time variability
Besides the spatial variability at a given time, the model exhibits significant temporal variability, both in the 3D flow and especially in the tracer field. The equatorial jet exhibits an oscillation pattern at planetary scale as seen in Fig. 9. At the convergence point west of the substellar point, the jet orientation can be toward the north, the south or well centered on the equator. Whereas Dobbs-Dixon et al. (2010) described a variation in longitude with time of the convergence point of the flow in the nightside, we see a variation in latitude of this convergence point and interpret it as a result of the larger oscillation of the jet itself.
 |
Fig. 8 Time dependence of the mean tracer abundance averaged between 1mbar and 0.1mbar. The abundances are averaged horizontally over a circular region of radius 45° centered on the substellar point (top) and averaged horizontally around the terminator, including all regions within ± 5° of the terminator (bottom). The top panel is relevant for inferring the presence of a stratosphere (see Sect. 6.1), albedo variations (see Sect. 6.2) or secondary eclipse measurements (see Sect. 6.3). The bottom panel is relevant for transit spectroscopy measurements. |
 |
Fig. 9 Tracer abundance (colorscale) and winds (arrows) at two different pressure levels and three different times of the simulation for the case a = 2.5 μm. |
The tracers abundances at specific locations on the planet exhibit strong temporal variability. This is illustrated in Fig. 9, which shows the tracer abundance at 0.1 and 1 mbar over the globe at several snapshots in time for a model where the radius of particles on the nightside is 2.5 μm. Significant variations in tracer abundance are advected by the equatorial jet and, at high latitudes, by the day-to-night flow, leading to large local variations in time. In many cases, the strongest tracer variability seems to involve regional-scale structures with typical sizes of ~1–3 × 104 km but also includes hemispheric-scale fluctuations (e.g., in the abundance averaged over the day or night) and between the northern and southern hemispheres. Around the substellar point, the tracer abundance can vary by up to 50%, whereas along the terminator, this temporal variation can reach 75% relative to the mean value. Such variability – if it occurs in radiatively active species like TiO – has important implications for secondary-eclipse and transit observations, which probe the dayside and terminator, respectively.
Figure 8 sheds light on the different timescales at which this variability occurs. The top panel shows the tracer abundance averaged vertically between 0.1 and 1 mbar and horizontally over a circular patch of 45° centered on the substellar point; this gives a sense of how the tracer abundance would vary in secondary-eclipse measurements probing the dayside. The bottom panel shows the tracer abundance averaged vertically between 0.1–1 mbar and horizontally around the terminator, including all regions within 5° of the terminator itself; this gives a sense of how the tracer might vary in transit measurements. The variability exhibits two characteristic timescales: a short (fast) timescale of order of days and a long (slower) timescale of ~50 to 100 days. The bigger the particles on the nightside, the bigger the amplitude of the variations. This comes from the smaller settling timescale of bigger particles. In these models, the amplitude of the long-period variations exceeds those of the short-period variations by a factor of ~2–3. The long-timescale variations exhibit similar amplitudes in the dayside and terminator time series. The short-period oscillations exhibit stronger amplitude at the terminator and seem related to variations of the flow itself, such as the oscillation of the jet described previously. Figure 8 suggests that radiatively active tracer species that can condense on the nightside, such as TiO or silicates, could lead to detectable time variations in transit or secondary eclipse spectra. The amplitude of this variability will depend on the type of tracer being considered (see Sect. 6) and may vary from planet to planet depending on the availability of the considered species. However we can predict the expected period of these variations: some days for the small amplitude ones and fifty to one hundred days for the biggest ones.
 |
Fig. 10 Limb profiles of our tracer field from 200 bar to 1 μbar as seen during transit. Black circles are situated at 100 bar, 10 bar, 1 bar, 0.1 bar, 0.01 mbar, 1 mbar, 0.1 mbar, 0.01 mbar, and 1 μbar. The north pole is on top and the leading limb on the right. The abundances are normalized to the abundance of the deepest level. |
3.5. Limb profile
Transit observations are sensitive to atmospheric composition near the terminator, thus we want to characterize the distribution of our tracer species at the terminator. The possibility of variations in chemical composition between the leading and trailing limbs (as seen during transit) has been discussed in a variety of studies (e.g., Iro et al. 2005; Fortney et al. 2010). However, these studies did not investigate the particular depletion of species due to the interaction between their condensation and the atmospheric dynamics. Our model leads to the first quantitative estimate of how dynamics affects the spatial distribution of condensable species at the day-night terminators, relevant to the interpretation of transit observations. Figure 11 shows the tracer abundance at the terminator at a snapshot in time for our models with particle sizes of 0.1, 0.5, 1, 2.5, 5, and 10 μm. Angle represents angle around the terminator and the radial coordinate represents the logarithm of the pressure. In agreement with Fig. 4, the tracers tend to be depleted from upper levels, particularly in models where the particles on the nightside are larger. Moreover, Fig. 11 demonstrates that significant spatial variations occur along the terminator. Depletion occurs first at the equator along the leading limb, corresponding to the terminator 90° west of the substellar point. The superrotating jet carries air depleted in tracer from the nightside directly to this region of the terminator, explaining why abundances are particularly depleted there. In contrast, air along most of the remainder of the terminator has arrived from the dayside, where no particle settling occurs, so depletion is less strong-particularly for particle sizes ≲1 μm. Once the particle size becomes sufficiently large, however, depletion occurs everywhere along the terminator at upper levels regardless of whether the air arrived there from the dayside or nightside.
Considering now the depth dependence of the terminator abundances, our results suggest two different zones (see Figs. 10 and 11):
-
At altitudes above the 1-mbar level, the tracer abundance is homogeneous over most of the limb except for the east (trailing) equatorial limb that is strongly depleted.
-
At altitudes below the 1-mbar level, the east and west equatorial limb are rather homogeneous; however, the east/west dichotomy shifts to higher latitudes and the west limb above 45° is more depleted than the equivalent region of the east limb.
 |
Fig. 11 Mean tracer abundance along the terminator for the case with nightside condensates of 1 μm. The different colors correspond to different latitudes along the terminator as shown in the legend. The colorwheel represents the terminator of the planet as seen during a transit, with the eastern hemisphere to the left. The mean profiles are almost symmetrical with respect to the equator, so only the profiles of the northern hemisphere are shown here. |
4. 1D model of the day-night cold trap
Although hot Jupiters atmospheres are inherently three-dimensional, 1D models continue to play a useful role for understanding the vertical thermal and chemical structure of these atmospheres. In particular, many groups have explored the chemistry of hot Jupiters using 1D models in which the vertical mixing caused by the large-scale dynamics is parameterized by a specified eddy diffusivity (e.g., Spiegel et al. 2009; Zahnle et al. 2009a,b; Youdin & Mitchell 2010; Line et al. 2010, 2011; Madhusudhan & Seager 2011). In these studies, the chosen eddy diffusivity is ad hoc, with no convincing theoretical support. Although the vertical mixing in our 3D models is not diffusive in any rigorous sense, there is merit in comparing the results of our 3D models with 1D models parameterized by eddy diffusivity. This allow us to make approximate estimates of the magnitudes of eddy diffusivity – in the context of a 1D model – that produce similar horizontal-mean behavior as our 3D models. Such estimates of eddy diffusivity should guide the parameter choices in 1D chemical models like those cited above. A comparison between our 3D models and 1D diffusive models also allow us to investigate how the horizontal-mean tracer depletion relates to the amplitudes of spatial tracer variation.
Therefore, in this section, we present a simple 1D model, including particle settling, with atmospheric mixing represented as an eddy diffusivity.
4.1. System studied
The presence of a superrotating, eastward equatorial jet is a dominant dynamical feature of many 3D circulation models of hot Jupiters. This superrotating jet was first predicted by Showman & Guillot (2002), and later emerges from almost all 3D simulations of hot Jupiters atmospheres (Cooper & Showman 2005; Showman et al. 2008, 2009, 2013; Dobbs-Dixon & Lin 2008; Rauscher & Menou 2010, 2012b,a; Perna et al. 2010, 2012; Heng et al. 2011a,b; Lewis et al. 2010; Kataria et al. 2013) including ours (see Sect. 3.1) and has been theoretically understood (Showman & Polvani 2011). A shift of the hottest point of the planet eastward from the substellar point has been directly observed in several exoplanets (Knutson et al. 2007, 2009, 2012; Crossfield et al. 2010) and interpreted as a direct consequence of this jet. Thus we believe that any study of the day/night cold trap in hot Jupiters atmospheres must account for this feature.
To include the presence of this jet in our model, we choose as a study system a vertical column of gas homogeneously advected around the equator by the superrotating jet. Such a column is transported from day to night and from night to day with a period 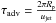 where τadv is the advective timescale, Rp is the planetary radius and ujet the equatorial jet velocity. τadv is around 48h for HD 209458b.
where τadv is the advective timescale, Rp is the planetary radius and ujet the equatorial jet velocity. τadv is around 48h for HD 209458b.
As in the 3D case, we focus on a hypothetical chemical species which is gaseous on the dayside and trapped in condensates of size a on the nightside. This species freely diffuses with a vertical diffusion coefficient Kzz on both the dayside and the nightside. Because we envision the species as condensed on the nightside, we additionally include downward settling via Stokes-Cunningham drift on the nightside (Eq. (3)) but not on the dayside. The model includes no horizontal dimensions. Rather, we model a single column of gas that is advected from day to night. The horizontal variations therefore translate into a time-dependant settling term. We assume this chemical species to be a minor constituent of a H2-atmosphere and neglect the latent heat released during the condensation.
4.2. 1D diffusion equation
As before, χ is the local mole fraction of the target chemical species i.e. the number of moles of tracer species (whether in gaseous or condensed form) to the total moles of air in a given volume. On the dayside, the molecules of the target chemical species can freely diffuse with a diffusion coefficient Kzz, according to the equation: 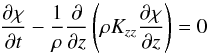 (9)with ρ the density of the atmosphere and z the vertical coordinate.
(9)with ρ the density of the atmosphere and z the vertical coordinate.
On the nightside, the molecules of the target species are trapped into particles that both diffuse and settle with the velocity Vf described in Sect. 2.4. Thus χ follows the same equation as Eq. (9), plus a source term describing the settling: 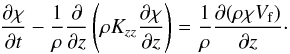 (10)We can define the diffusive time scale as
(10)We can define the diffusive time scale as 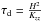 and a reference free fall time scale τs = H/Vs with
and a reference free fall time scale τs = H/Vs with 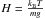 the atmospheric scale height and Vs the Stokes velocity (see Sect. 2.4). We note that τd is a reference time scale and is not equal to the effective free fall time scale for high Knudsen numbers. Assuming hydrostatic balance, we can use the pressure P as the vertical coordinate and using the perfect gas law the system to solve become:
the atmospheric scale height and Vs the Stokes velocity (see Sect. 2.4). We note that τd is a reference time scale and is not equal to the effective free fall time scale for high Knudsen numbers. Assuming hydrostatic balance, we can use the pressure P as the vertical coordinate and using the perfect gas law the system to solve become: 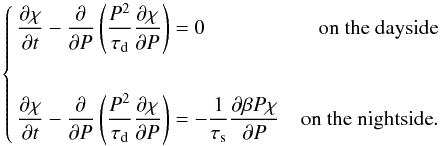 (11)
(11)
4.3. Time-dependent solution
In order to solve the system of Eq. (11)for χ(P,t), we need two boundary conditions. We assume the species to be well mixed below P1 = 1 bar with a molecular abundance χ0. At the top of the atmosphere, we assume that no molecule crosses the upper boundary (i.e. 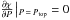 ). Then we can solve the system with an implicit time stepping code using GNU OCTAVE1, an open-source, free software equivalent to MATLAB. Assuming that the column of gas spends in each hemisphere, we can reach a periodic behavior where the initial condition is forgotten. While on the dayside, there is no settling and, at upper levels, the tracer diffuses upward. Thus at a given pressure the molecular abundance increases with time. This is shown by the red curves in Fig. 12. While on the nightside, the particles both diffuse vertically and settle downward at their terminal velocity and thus, at at given pressure level, the abundance decreases with time. This is shown by the blue curves in Fig. 12. In the upper atmosphere, the settling timescale and the diffusion timescale become smaller than the advective timescale. The particles have time to settle several scale heights during the time required for the air column to cross the dayside. Thus, at upper levels, the molecular abundance vary strongly throughout the diurnal cycle, and the vertical profiles vary widely around the mean value.
). Then we can solve the system with an implicit time stepping code using GNU OCTAVE1, an open-source, free software equivalent to MATLAB. Assuming that the column of gas spends in each hemisphere, we can reach a periodic behavior where the initial condition is forgotten. While on the dayside, there is no settling and, at upper levels, the tracer diffuses upward. Thus at a given pressure the molecular abundance increases with time. This is shown by the red curves in Fig. 12. While on the nightside, the particles both diffuse vertically and settle downward at their terminal velocity and thus, at at given pressure level, the abundance decreases with time. This is shown by the blue curves in Fig. 12. In the upper atmosphere, the settling timescale and the diffusion timescale become smaller than the advective timescale. The particles have time to settle several scale heights during the time required for the air column to cross the dayside. Thus, at upper levels, the molecular abundance vary strongly throughout the diurnal cycle, and the vertical profiles vary widely around the mean value.
 |
Fig. 12 Tracer abundance in the advected column of gas from the 1D model as a function of time. From bottom to top we used |
4.4. Steady-state solutions
Our system being forced periodically, there is no steady-state solution stricto sensu. However, the mean of the tracer abundance over one period should remain constant. We can thus integrate Eqs. (11)over one period and get an equation for 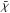 , the mean molecular abundance over one period. Then, once the periodic state is reached, the mean over one period of the tracer abundance in our column of gas,
, the mean molecular abundance over one period. Then, once the periodic state is reached, the mean over one period of the tracer abundance in our column of gas, 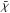 , is the same as the mean over longitude at a given time, ⟨ χ ⟩ and we obtain:
, is the same as the mean over longitude at a given time, ⟨ χ ⟩ and we obtain: 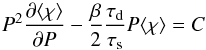 (12)where the factor
(12)where the factor 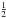 appears because the source term is only integrated during the night. To derive Eq. (12)we assumed that the mean tracer abundance on the nightside is close to the global-mean tracer abundance. This is true given than βτs and τd are much bigger than τadv. This approximation breaks down at low pressure and our analytical solution diverges from the real one as can be seen by comparing the black and the green curves in Fig. 12. However, the discrepancy is small such that the analytic solution is still a good representation of the time-mean of the full numerical solution of the 1D model everywhere deeper than the ~ 10 μbar level. C is a constant coming from the integration over pressure. When P goes to 0, χ goes to 0. Moreover we assume that
appears because the source term is only integrated during the night. To derive Eq. (12)we assumed that the mean tracer abundance on the nightside is close to the global-mean tracer abundance. This is true given than βτs and τd are much bigger than τadv. This approximation breaks down at low pressure and our analytical solution diverges from the real one as can be seen by comparing the black and the green curves in Fig. 12. However, the discrepancy is small such that the analytic solution is still a good representation of the time-mean of the full numerical solution of the 1D model everywhere deeper than the ~ 10 μbar level. C is a constant coming from the integration over pressure. When P goes to 0, χ goes to 0. Moreover we assume that 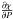 does not go to infinity. Then the constant must be zero and we obtain:
does not go to infinity. Then the constant must be zero and we obtain: 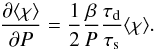 (13)To simplify the problem, we neglect the transitional regime for β from Eq. (4)and use the expression:
(13)To simplify the problem, we neglect the transitional regime for β from Eq. (4)and use the expression: 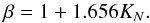 (14)Then choosing a functional form Kzz = Kzz0(P0/P)α, where α is a constant, we can solve Eq. (13). For α ≠ 0 and α ≠ 1, we get:
(14)Then choosing a functional form Kzz = Kzz0(P0/P)α, where α is a constant, we can solve Eq. (13). For α ≠ 0 and α ≠ 1, we get: 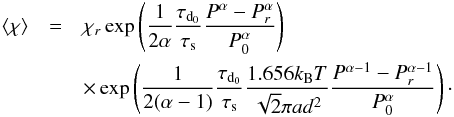 (15)For the particular case of a constant Kzz (α = 0) the formula becomes:
(15)For the particular case of a constant Kzz (α = 0) the formula becomes: 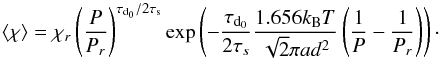 (16)In the case where Kzz is inversely proportional to P (α = 1):
(16)In the case where Kzz is inversely proportional to P (α = 1): 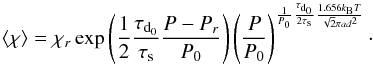 (17)Where χr is the abundance of ⟨ χ ⟩ at P = Pr and τd0 ≡ H/Kzz0.
(17)Where χr is the abundance of ⟨ χ ⟩ at P = Pr and τd0 ≡ H/Kzz0.
4.5. Diffusivities needed to keep the tracers suspended
Because particle settling acts to transport condensates downward, the tracers only exhibit significant abundances in the upper regions of the atmosphere if the eddy diffusion coefficient exceeds some critical value, which depends on the particle size of the condensates. Here we solve for an approximate analytical expression for this critical magnitude as a function of particle size and other parameters.
Assuming a constant vertical diffusion coefficient, we can use Eq. (16)to derive an expression for the Kzz needed to achieve a given molecular abundance χlim at a given pressure Plim. Like in Spiegel et al. (2009), we use Plim = 1 mbar and χlim = 0.5. We first note that Eq. (16)is composed of two terms. The first exponential is given by the Stokes regime (β ≈ 1) whereas the second term is given by the Cuningham regime (β ≫ 1). As can be seen in Fig. 1, particles smaller than 10 μm should be in the Cunhingham regime at P = 1 mbar. Thus the second term in Eq. (16)is dominant and we can use as a condition: 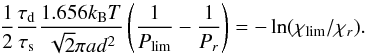 (18)As in the 3D model, we assume that below 1 bar the tracers are no more trapped into condensates and no more subject to settling. Thus we choose χr = 1 at Pr = 1 bar. Then, for Pr ≫ Plim, replacing τd and τs by their expressions, using Eq. (7) for the viscosity and Eq. (6) for the mean free path, we obtain a condition on the diffusion coefficient:
(18)As in the 3D model, we assume that below 1 bar the tracers are no more trapped into condensates and no more subject to settling. Thus we choose χr = 1 at Pr = 1 bar. Then, for Pr ≫ Plim, replacing τd and τs by their expressions, using Eq. (7) for the viscosity and Eq. (6) for the mean free path, we obtain a condition on the diffusion coefficient: 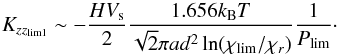 (19)For big particles, the Stokes regime become dominant thus we neglect the second term of Eq. (16)and the condition turns to be:
(19)For big particles, the Stokes regime become dominant thus we neglect the second term of Eq. (16)and the condition turns to be: 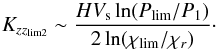 (20)As the relevant range of particle size span several order of magnitudes, a good approximation of Kzzlim can be obtained by taking the sum of these two coefficient:
(20)As the relevant range of particle size span several order of magnitudes, a good approximation of Kzzlim can be obtained by taking the sum of these two coefficient: 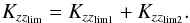 (21)Again we note that these limits for the diffusion coefficient are independent of the planet considered. Spiegel et al. (2009) stated that an abundance of half the solar composition at 1mbar would be necessary to produce an observable stratosphere. Applying formula (21)with χlim = 0.5 and Plim = 1 mbar and assuming a well mixed layer below 1 bar (i.e. Pr = 1 bar and χr = 1) we obtain Kzzlim = 1.4 × 104 m2 s-1 for a = 0.1 μm, Kzzlim = 1.4 × 105 m2 s-1 for a = 1 μm and Kzzlim = 1.6 × 106 m2 s-1 for a = 10 μm. These results are of the same order of magnitude as the ones found by Spiegel et al. (2009) for the vertical cold trap. This is expected, since we compare two similar mechanisms: settling and diffusion of particles. However, this similarity of the results shows that the day-night cold trap is at least as important as the vertical one in hot Jupiters atmospheres. Moreover, the condition on Kzzlim we derived is independent of the planet studied and holds for very hot Jupiters such as WASP-12b or WASP-33b where the vertical cold trap could be inefficient or nonexistent.
(21)Again we note that these limits for the diffusion coefficient are independent of the planet considered. Spiegel et al. (2009) stated that an abundance of half the solar composition at 1mbar would be necessary to produce an observable stratosphere. Applying formula (21)with χlim = 0.5 and Plim = 1 mbar and assuming a well mixed layer below 1 bar (i.e. Pr = 1 bar and χr = 1) we obtain Kzzlim = 1.4 × 104 m2 s-1 for a = 0.1 μm, Kzzlim = 1.4 × 105 m2 s-1 for a = 1 μm and Kzzlim = 1.6 × 106 m2 s-1 for a = 10 μm. These results are of the same order of magnitude as the ones found by Spiegel et al. (2009) for the vertical cold trap. This is expected, since we compare two similar mechanisms: settling and diffusion of particles. However, this similarity of the results shows that the day-night cold trap is at least as important as the vertical one in hot Jupiters atmospheres. Moreover, the condition on Kzzlim we derived is independent of the planet studied and holds for very hot Jupiters such as WASP-12b or WASP-33b where the vertical cold trap could be inefficient or nonexistent.
5. Effective vertical diffusion coefficient
As described previously, 1D models have been extensively used to investigate chemistry and vertical structure of hot Jupiter atmospheres, with the 3D dynamics parameterized as vertical eddy diffusion with a specified diffusivity (e.g Spiegel et al. 2009; Zahnle et al. 2009b,a; Youdin & Mitchell 2010; Line et al. 2010, 2011; Madhusudhan et al. 2011; Moses et al. 2011; Venot et al. 2012).
There is no theoretical reason for the mixing by the large scale flow patterns in hot Jupiters atmospheres to behave like a one-dimensional diffusion process. However, deriving an a posteriori effective diffusion coefficient that describes as closely as possible the averaged vertical mixing within the atmosphere can be a useful way to roughly characterize the strength of the vertical fluxes of material and guide 1D modelers in their choice of vertical mixing parameters.
A first way to define a vertical mixing coefficient from our simulation is to choose the Kzz that best reproduces the planet averaged tracer profiles. The 1D model developed in Sect. 4 describes the equilibrium between vertical diffusion of tracers with a specified height-dependent Kzz and their settling on the nightside. We tune the diffusivities to obtain a good match between the solutions of our 1D model and the horizontal-mean tracer abundance versus pressure from the 3D models. To use Eq. (15)we must specify the temperature of the atmosphere, constant in the analytical model. The temperature appears in the expression for the Knudsen number and in the expression for the viscosity of hydrogen. Both quantities are related to the settling of the particles. Thus the temperature to consider is the nightside temperature. In our GCM nightside temperatures range from 600 to ≈1500 K and we decided to use a mean temperature of 1000 K. However, we note that the derived value of Kzz does not depend strongly on this choice. Then using a Kzz value proportional to the inverse square root of the pressure (α = 0.5 in Eq. (15)), we obtain a remarkably good agreement between our 1D model (dotted lines in Fig. 4) and the horizontal average of the 3D model (solid lines of Fig. 4). The resulting value for the vertical mixing coefficient that best fits the different tracer field used in the simulation is: 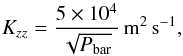 (22)which is valid over a pressure range from ~1 bar to a few μbar (see Fig. 13). Fundamentally, this represents an ad-hoc fitting of our simulation results, although we find it a good match to the overall mixing properties of our 3D models over a wide range of particle sizes. Note that the upward-increasing mixing rates captured in Eq. (22)arise naturally from the fact that the radiative heating rates and vertical velocities tend to increase with decreasing pressure in our models, leading to greater mixing rates at lower pressure. The 3D models adopt the stellar insolation and other properties for HD 209458b, so the results are most germane to that planet; the mixing rates are likely to be higher for hotter planets and lower for cooler planets than implied by Eq. (22).
(22)which is valid over a pressure range from ~1 bar to a few μbar (see Fig. 13). Fundamentally, this represents an ad-hoc fitting of our simulation results, although we find it a good match to the overall mixing properties of our 3D models over a wide range of particle sizes. Note that the upward-increasing mixing rates captured in Eq. (22)arise naturally from the fact that the radiative heating rates and vertical velocities tend to increase with decreasing pressure in our models, leading to greater mixing rates at lower pressure. The 3D models adopt the stellar insolation and other properties for HD 209458b, so the results are most germane to that planet; the mixing rates are likely to be higher for hotter planets and lower for cooler planets than implied by Eq. (22).
 |
Fig. 13 Vertical diffusion coefficient from the 3D model estimated from the different tracer fields separately (black lines), from the 1D fit to the 3D model (red line) and the root mean square of the vertical velocity times the vertical scale height, a common estimate of Kzz in the literature (blue line) (see Lewis et al. 2010; Moses et al. 2011, for example). |
Another way to define a one dimensional vertical mixing coefficient from the three-dimensional simulation is to find the Kzz that leads to an upward diffusive flux of material that matches the averaged vertical flux produced by the dynamics. This can be written (e.g., Chamberlain & Hunten 1987, p. 90): 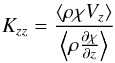 (23)where the brackets represent the horizontal average along isobars over the whole planet. This expression does not necessitate any assumption on the functional form of Kzz nor on the nightside mean temperature. It also has the advantage that no comparisons or fits to a 1D diffusion model are necessary; the effective values of Kzz can be derived directly from the 3D GCM data via Eq. (23). As a trade-off, this expression depends on the vertical tracer gradients that are affected by long term temporal variability (see Sect. 3.4), which are not smoothed out completely given the limited integration time of the simulation. This leads to some strong vertical variation of Kzz. The profile of Kzz calculated from Eq. (23)are shown in the black curves of Fig. 13. Despite the vertical fluctuations, the overall shape of Kzz obtained with this method is close to the estimate using the planet averaged tracer profile (see the red curve in Fig. 13). Like before, we note that the derived value does not depend strongly on the particle size, consistent with the fact that Eq. (22)leads to a good fit between 1D models and our 3D model for a wide range of particle sizes.
(23)where the brackets represent the horizontal average along isobars over the whole planet. This expression does not necessitate any assumption on the functional form of Kzz nor on the nightside mean temperature. It also has the advantage that no comparisons or fits to a 1D diffusion model are necessary; the effective values of Kzz can be derived directly from the 3D GCM data via Eq. (23). As a trade-off, this expression depends on the vertical tracer gradients that are affected by long term temporal variability (see Sect. 3.4), which are not smoothed out completely given the limited integration time of the simulation. This leads to some strong vertical variation of Kzz. The profile of Kzz calculated from Eq. (23)are shown in the black curves of Fig. 13. Despite the vertical fluctuations, the overall shape of Kzz obtained with this method is close to the estimate using the planet averaged tracer profile (see the red curve in Fig. 13). Like before, we note that the derived value does not depend strongly on the particle size, consistent with the fact that Eq. (22)leads to a good fit between 1D models and our 3D model for a wide range of particle sizes.
Several previous studies have attempted to estimate the vertical diffusion coefficient in hot Jupiters atmospheres (Cooper & Showman 2006; Moses et al. 2011; Heng et al. 2011a; Lewis et al. 2010). Cooper & Showman (2006) adopted an estimate for Kzz based on the product of a root-mean-square vertical velocity from their 3D GCMs and an appropriately chosen vertical length scale following the formulation of Smith (1998). Moses et al. (2011) and Lewis et al. (2010) followed a similar procedure but adopted an atmospheric scale height for the vertical length scale. These estimates are crude, although Cooper & Showman (2006) showed that this formulation for Kzz allows 1D models to match the full tracer profiles from 3D GCMs reasonably well. More recently, Heng et al. (2011a) used the magnitude of the Eulerian mean streamfunction as a proxy for the strength of the vertical motions and derived a vertical mixing coefficient of Kzz ~ 106 m2 s-1. Note, however, that the Eulerian-mean velocities are known to be a poor descriptor of tracer advection rates in planetary atmospheres, since mixing by large scale eddies (potentially resolved by GCMs) often dominates over transport due to the Eulerian-mean circulation (see, e.g., Andrews et al. 1987, Chap. 9).
Although we confirm that mixing in hot Jupiters atmospheres is strong, we find a value that is significantly smaller than the previous ones. In particular, our value is two orders of magnitude smaller than what is obtained when multiplying the vertical scale height by the root mean square of the vertical velocity (blue curve in Fig. 13), a common estimate for Kzz in the literature (e.g., Lewis et al. 2010; Moses et al. 2011).
As stated in Sect. 2.1, the model does not include any sub-grid vertical diffusion coefficient. Yet, given the large values for Kzz that we derive from the resolved flow, it seems unlikely that sub-grid turbulent mixing would contribute significantly to the total mixing. However, the interaction between small-scale turbulence and the global flow might not be trivial and a more detailed study would be required to draw a firm conclusion.
We emphasize that vertical mixing by the global circulation appears to be planet-wide and differs from region to region. Although the globally averaged dynamics seem to be reasonably described by a vertical mixing coefficient, that is not the case for the local flow in the simulation. It is therefore difficult to define mixing coefficient values for particular locations in the planet.
Along the equator, where the strong flow efficiently mixes the tracers longitudinally, we expect a good agreement of our 1D model to the 3D flow. Indeed, using the value of Kzz derived in Sect. 5 we realize that the spread of the tracer profiles along the equator (Fig. 14) is of the same order of magnitude as the spread predicted by the 1D model (middle panel of Fig. 12). However, in the 1D model, profiles from equally sampled longitude are equally spaced in abundances whereas the profiles obtained from the 3D model are sometimes packed together and sometimes widely spread, denoting an unequal strength of the vertical mixing longitudinally.
 |
Fig. 14 Time averaged tracer abundance along the equator for nightside condensate of 1 μm. The profiles are equally spaced in longitude by 2.8° The dayside profiles are in red whereas the nightside profiles are in blue. We highlight the profiles at the antistellar point (dotted line), the west terminator (dot-dashed line), the substellar point (dashed line) and the east terminator (plain line). |
 |
Fig. 15 Approximate growth time scale of TiO2 grains in HD 209458b. The bottom black line shows the advective timescale and the top one is ten times the advective timescale. |
6. Applications
6.1. Presence of a stratosphere on hot Jupiters
TiO is a leading hypothesis for the absorber needed to create temperature inversions in hot Jupiters atmospheres (Hubeny et al. 2003; Fortney et al. 2008). However, TiO condenses at temperatures lower than ≈2000 K. On most hot Jupiters, while gaseous TiO can be stable on the dayside, it should condense on the nightside. Thus, our results allow us to address the question of whether TiO can remain suspended in the atmospheres of hot Jupiters, and hence whether TiO-induced stratospheres are indeed viable. Spiegel et al. (2009) predicted that for a solar abundance of TiO in the planet, an abundance of 0.5 times the deep abundance at 1 mbar is necessary to maintain a temperature inversion on the dayside. Our simulations suggest that if TiO condenses into particles bigger than several micrometers, the day-night cold trap will be sufficiently efficient to deplete it from the dayside. If, on the contrary, TiO cannot condense in particles bigger than several micrometers, it should remain present on the dayside and produce a stratosphere (see Figs. 4 and 6).
The size of the condensate, a free parameter in our study, results from complex microphysical processes. Once on the nightside, TiO is over-saturated, and thus Ti-bearing condensates are expected to appear. We used the formalism of Woitke & Helling (2003) to calculate the characteristic growth time scale of TiO2 particles assuming that all the titanium is contained in TiO2(g) and that this last fully saturates the atmosphere. If the condensate growth time scale exceeds the advective time scale – the time for the jet to travel across one hemisphere – the condensate will be back in the dayside before reaching it’s full size and will vaporize. Thus, all the particles above the black line in Fig. 15 are unlikely to form. The low elemental abundance of titanium – solar abundance is 10-7 compared to H (Lodders 2002) – kinetically inhibits the formation of micrometer size particles above 10 mbar.
However, titanium is not the only element that can form condensates on the nightside of hot Jupiters. Silicates are believed to condense and could incorporate titanium atoms into their grains. Sub-micron size TiO2 particles could even be used as seeds for the formation of silicates grains. In that case the relevant time scale is not tied to the growth of TiO2 grains but rather to the growth of SiO2 based grains (MgSiO2 for example). We calculated the growth time scale of SiO2-based grains using the same formalism as for TiO2 grains, assuming that SiO2(g) is fully saturated and that all the silica atoms are in SiO2(g) molecules. As can be seen in Fig. 16, particles as big as 10 μm can form at pressures as low as 10 mbar in that case.
The estimates in Fig. 16 show that the growth time of silicate particles is comparable to the time for the jet to cross an hemisphere in the pressure range where the stratosphere forms (~0.01–1 mbar). This comparison suggests that more detailed calculations, coupling the 3D dynamics to microphysics that allow self-consistent prediction of particle growth, may be necessary to obtain a firm conclusion about whether particle growth timescales are sufficiently long to inhibit loss of TiO from the atmosphere.
 |
Fig. 16 Approximate growth time scale of SiO2 grains in HD 209458b. The bottom black line shows the advective timescale and the top one is ten times the advective timescale. |
Spiegel et al. (2009) studied the deep cold trap in the deep layer of the planet, at pressures exceeding tens of bars, where dynamical mixing rates are probably low. In planets that exhibit such a cold trap, mixing TiO upward to altitudes where it could be affected by the day-night cold trap may be difficult. On the other hand, the opacities and therefore temperature structure in these deep regions are rather uncertain; moreover, hot Jupiters that are particularly highly irradiated would exhibit warmer temperatures and would therefore be less likely to exhibit such a vertical cold trap. On these planets, the day-night cold trap at low pressure (P ≲ 1 bar) would then dominate.
The spatial variations in the gaseous tracer abundance in our 3D models (Fig. 6) suggest that the TiO abundance on the dayside, and hence the stratosphere itself, could be patchy, with some regions of the dayside exhibiting a stronger temperature inversion than others. This would have interesting consequences for the interpretation of dayside infrared spectra.
The time variability described in Sect. 3.4 could affect the presence of the stratosphere, leading to strong temporal variability in the upper atmospheric temperatures. In particular, the tracer abundance averaged over much of the dayside exhibits large-amplitude fluctuations (Fig. 8), particularly for larger particle sizes. This suggests that, at least for some planets, the TiO abundance could fluctuate between values large enough to generate a stratosphere and values too small for a stratosphere to form. The stratosphere itself might then fluctuate episodically in time, leading to variations of a factor two in the thermal flux emitted by the planet at some wavelength (see Fig. 12 of Fortney et al. 2008). Although not included in our current models, there is the possibility of feedbacks with the flow itself, since the presence (or absence) of a stratosphere exerts a significant impact on the flow structure and vertical mixing rates. If the feedback is positive, i.e. if the presence of high temperatures in the upper atmosphere enhances the mixing, then hot Jupiters could oscillate between a state with strong vertical mixing and stratospheric heating by TiO and a state with no stratospheric heating and less vertical mixing. This is a two-state atmosphere analogous to that described by Hubeny et al. (2003). However, this possibility remains speculative and further models that include the feedback of the tracer field on the flow are necessary to draw a firm conclusion.
TiO is thought to be the major Ti-bearing gas in hot Jupiters atmospheres (see Lodders 2002). However, other Ti-bearing gases, TiO2 being the most abundant, are believed to be the condensable Ti-bearing species. Thus, a parcel of gas experiencing a sudden drop in temperature due to its advection to the nightside might not see all its titanium incorporated into condensates, but rather only the titanium atoms that already reside in other Ti-bearing molecules such as TiO2(g). The reaction between gaseous species TiO + H2O ⇌ TiO2 + H2 is fast under the conditions relevant to the dayside of hot Jupiters (see Fortney et al. 2008). However, the reaction might be kinetically inhibited on the nightside of the planet where the temperature drops significantly, leading to a smaller depletion of Ti than in the hypothetical case where TiO(g) could condense by itself.
6.2. Clouds in hot Jupiters atmospheres
The huge day-night temperature difference and cold nightside temperatures predicted on many hot Jupiters at low pressure (e.g., Showman et al. 2009) suggest that, in addition to TiO, a wide range of other chemical species, including silicates and iron, will condense on the nightside. Some of them could also stay in a condensed state in part or all of the dayside hemisphere. The Rayleigh scattering slope in the transmission spectrum of HD189733b, first observed by Lecavelier Des Etangs et al. (2008) and later confirmed by numerous observations (see Pont et al. 2013, for a review of the different observations of this planet) is best fitted by models including sub-micron sized particles. Then the strong spatial and temporal variations observed in our model can also be interpreted as spatial variation of the cloud coverage in the atmospheres of hot Jupiters. This could lead to albedo variations along the dayside of the planet. As the hottest point of the planet is shifted to the east, the western part of the dayside is colder than the eastern one (see Fig. 3). Therefore, the western part of the dayside could be colder than the condensation temperature of some species whereas the eastern part could be at higher temperatures, leading to a more cloudy atmosphere west of the substellar point than east of it. Moreover, due to the eastward superrotating jet, material west of the substellar point arrives from the cold nightside – where condensation is thought to happen – whereas material east of the substellar point arrives from the hot substellar point – where the material is thought to have sublimated. Thus, clouds, if present on the dayside of the planet, should form more easily west of the substellar point than east of it, leading to a longitudinal variation of the albedo that contributes to the spatial variation described before. The large amount of data in the visible from the Kepler space telescope is ideal to search for such a spatial and temporal variability in albedo pattern of tidally locked planets.
6.3. Parameter retrieval
Atmospheric characteristics of hot Jupiters are usually derived from disk-integrated fluxes (for secondary eclipses measurements) or limb-integrated transmission (for transits spectroscopy). Therefore, interpretation of the data is usually done using one dimensional atmospheric models, assuming an homogenous atmosphere, both in term of temperature structure and composition (e.g., Madhusudhan & Seager 2009; Lee et al. 2012; Benneke & Seager 2012, among others). However, given the strong spatial variability in the tracer distribution both on the dayside hemisphere and in the limb profiles observed, some future exoplanet spectra – obtained with more and better data than nowadays – might be better understood by considering spatial variation in the atmospheric profiles and chemical composition along the planet (see also Agúndez et al. 2012, on the longitudinal variability in the chemical composition of HD 209458b). For example, an inhomogeneous distribution of TiO would lead to strong brightness differences in the emitted flux from the different locations of the planet, which could affect features such as the apparent eastward offset of the brightest spot of the planet. Hazes could also show a similar behavior, leading to planetary spectra that might be better explained with the combination of two different (cloudy and cloudless) 1D models-as is the case in recent models of brown dwarfs (e.g., Marley et al. 2010; Burrows et al. 2011). The rising technique of secondary eclipse mapping (see Majeau et al. 2012; De Wit et al. 2012), combined with the accuracy of telescopes like EChO (Tinetti et al. 2012) or JWST might soon allow us to constrain better the spatial inhomogeneities in the disk of the planet.
7. Conclusion
We presented global, three-dimensional numerical simulations of the atmospheric circulation of HD 209458b including a passive tracer. This is the first circulation model of a hot Jupiter to include the dynamical mixing of condensable species. We applied our model to chemical species that are gaseous on the dayside but condense on the nightside of the planet and are trapped in particles of a given size. Given the strong day/night contrast present in hot Jupiters, our model applies to a wealth of different chemical species such as titanium, vanadium, and silicate oxides among others.
Prior studies of hot Jupiters circulation demonstrate the presence of 3D circulation patterns including both strong horizontal and vertical velocities that are necessary for mixing to happen (e.g., Showman & Guillot 2002; Cooper & Showman 2005, 2006; Showman et al. 2008, 2013; Rauscher & Menou 2012b,a, 2013; Heng et al. 2011a,b, 2012; Lewis et al. 2010; Dobbs-Dixon & Lin 2008; Dobbs-Dixon et al. 2010, 2012; Perna et al. 2010, 2012). While preliminary attempts have been made to quantify the mixing rates (Cooper & Showman 2006; Heng et al. 2011b), these methods are approximate and do not lead to a rigorous quantification of the mixing rate. Here we demonstrate that, although hot Jupiters atmospheres are believed to be stably stratified (i.e. locally non-convective), they are strongly mixed. In the presence of a background gradient of chemical species, large-scale circulation patterns naturally create upward mixing. This mixing, resolved by the GCM, is strong and likely dominates over molecular, convective or turbulent mixing. In HD 209458b, the mixing is strong enough to keep a condensable species aloft if it condenses into particles smaller than a few microns on the nightside of the planet.
The coupling between 3D flow and particle settling leads to strong spatial and temporal variations in the abundance of a given condensable species. Around 0.1 mbar, the tracer abundance is homogeneous in longitude but exhibits a large latitudinal variation, the equator being more depleted than the poles. Around 1 mbar, at high latitudes, the day/night contrast becomes important. According to our models, variability of up to ~50% in the dayside tracer abundance, and of up to ~75% in the tracer abundance along the limb, can occur for sufficiently large particle sizes (~5 μm). This variability characteristic periods ranging from days to ~50–100 days. The observability of such a variation depends on the radiative properties of the considered species and will be quantified in a future work.
These results can be applied to a wide range of molecules in hot Jupiters atmospheres. Titanium oxide, the best candidate for creating a temperature inversion in the dayside of hot Jupiters, should condense on the nightside of most planets. Our results imply that the day/night cold trap could impede the formation of a stratosphere in the dayside if TiO condenses into particles bigger than a few microns on the nightside. Growing particles to such a size seems difficult when TiO alone is considered due to its small abundance. However, TiO can be incorporated into condensates from more abundant gases such as silicate oxides. In that case the day/night cold trap could be strong enough to impede the formation of a hot stratosphere on the dayside. Spatial variability of TiO could significantly affect the dayside temperature structure and exert interesting effects on infrared spectra and lightcurves. For example, mid-to-high latitudes might keep enough TiO to create an inversion whereas the equator, more depleted, might not be able to sustain the inversion. Such a latitudinal contrast could be observed using the secondary eclipse mapping technique (e.g., Majeau et al. 2012; De Wit et al. 2012). The temporal variability observed in the model could lead to the appearance and disappearance of the stratosphere on timescales of ~10–100 earth days. Highly irradiated planets have significant thermal emission in the Kepler bandpass (e.g., Spiegel & Burrows 2010, for Hat-P-7b). Using the long photometric series from the Kepler Space Telescope, such a variability might be observable.
Our results also apply to silicate hazes. Temporal and spatial variability in the cloud coverage could strongly affect the albedo and the thermal emission of the planet. For moderately irradiated planets, the Kepler spacecraft observes the reflected light of the star by the planet (e.g., Demory et al. 2011, for Kepler-7b). Thus, the time series from Kepler could be used to build albedo, and therefore cloud maps of the planet.
Although there is no theoretical reason for the upward mixing driven by the global circulation to be diffusive, it is interesting to quantify the averaged vertical mixing with a diffusive model. The parameterization Kzz value of 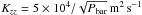 or
or 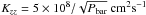 , between ~ 1 bar and ~ 1 μbar, can be used in 1D models of HD 209458b.
, between ~ 1 bar and ~ 1 μbar, can be used in 1D models of HD 209458b.
This study, the first one to include the influence of the dynamics on condensable species in a GCM of a hot Jupiter, confirms that hot Jupiters atmospheres are strongly mixed and that large scale spatial and temporal variability are expected in any condensable chemical constituents. Today, observers can already detect longitudinal variations in the emitted thermal flux of the planet. In the next decade, both longitudinal and latitudinal variations in thermal emission and albedo of the hot Jupiters will be observable, expanding the study of weather to extra-solar planets.
Online material
Appendix A: Departure from the Cunningham velocity
The Stokes-Cunningham velocity defined in Eq. (3)is derived under the assumption of low Reynolds number. Therefore it is not valid for turbulent flow and other expressions may be used when the Reynolds number increases. Here we derive better laws for intermediate and large Reynolds number.
Appendix A.1: Low Knudsen number
For small Reynolds number and small Knudsen number, the drag force exerted by a fluid on a sphere at rest is considered proportional to the kinetic energy of the fluid and the projected area of the sphere. The coefficient of proportionality, or drag coefficient, CD is given by: 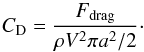 (A.1)Then, equating gravity and drag forces leads to the settling velocity of a particle in an atmosphere:
(A.1)Then, equating gravity and drag forces leads to the settling velocity of a particle in an atmosphere: 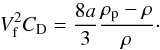 (A.2)Where ρp is the density of the particle. For small Reynolds numbers and high Knudsen number, CD = 24 is constant and the settling velocity is the Stokes velocity. When increasing the Reynolds number, the non linear terms of the Navier-Stokes equation become important and CD is no longer constant. We used tabulated values of the drag coefficient as a function of the Reynolds number given by Pruppacher & Klett (1978). We assume that CD = 24 when the Reynolds number reaches 1 to stay consistent with Stokes flow and that CD reaches its asymptotic value, CD = 0.45, when NRe ≡ 2Re = 1000 and fit the relationship:
(A.2)Where ρp is the density of the particle. For small Reynolds numbers and high Knudsen number, CD = 24 is constant and the settling velocity is the Stokes velocity. When increasing the Reynolds number, the non linear terms of the Navier-Stokes equation become important and CD is no longer constant. We used tabulated values of the drag coefficient as a function of the Reynolds number given by Pruppacher & Klett (1978). We assume that CD = 24 when the Reynolds number reaches 1 to stay consistent with Stokes flow and that CD reaches its asymptotic value, CD = 0.45, when NRe ≡ 2Re = 1000 and fit the relationship: 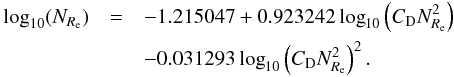 (A.3)Then we follow the same method as Ackerman & Marley (2001). Noting that:
(A.3)Then we follow the same method as Ackerman & Marley (2001). Noting that: 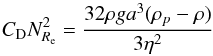 (A.4)is independent of the velocity, we use the fit of Eq. (A.3) and extract the velocity:
(A.4)is independent of the velocity, we use the fit of Eq. (A.3) and extract the velocity: 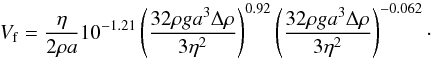 (A.5)
(A.5)
Appendix A.2: High Knudsen number
In the free-molecular regime, calculations have been made by Probstein (1968) leading to an expression for the drag coefficient: 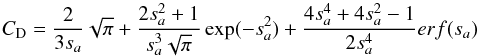 (A.6)
(A.6)
where sa is the ratio of the object velocity over the thermal speed of the gas (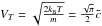 where
where 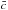 is the sound speed) and erf is the error function.
is the sound speed) and erf is the error function.
For velocities much smaller than the sound speed, sa → 0 and we can use an equivalent of the error function in 0: 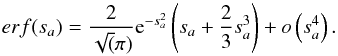 (A.7)Using this equation inside Eq. (A.6)and taking the limit sa → 0, the term e−sa2 goes to 1 and the terms proportional to
(A.7)Using this equation inside Eq. (A.6)and taking the limit sa → 0, the term e−sa2 goes to 1 and the terms proportional to 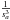 cancels out leading to:
cancels out leading to: 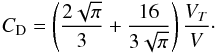 (A.8)For velocities much greater than the sound speed, the limit of Eq. (A.6)when sa → ∞ is:
(A.8)For velocities much greater than the sound speed, the limit of Eq. (A.6)when sa → ∞ is: 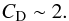 (A.9)In order to simplify Eq. (A.6)we use the following expression for the drag coefficient at high Knudsen number:
(A.9)In order to simplify Eq. (A.6)we use the following expression for the drag coefficient at high Knudsen number: 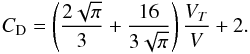 (A.10)Our approximation fits correctly the exact expression in the limit of low and high velocities. In between the difference to the exact expression is at most 30%. Replacing CD by its value in Eq. (A.2)we obtain a second order equation for the velocity:
(A.10)Our approximation fits correctly the exact expression in the limit of low and high velocities. In between the difference to the exact expression is at most 30%. Replacing CD by its value in Eq. (A.2)we obtain a second order equation for the velocity: 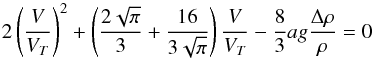 (A.11)which leads to:
(A.11)which leads to: 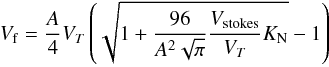 (A.12)with
(A.12)with 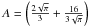 . When the speed becomes small compared to the sound speed (Vstokes ≪ VT) we obtain:
. When the speed becomes small compared to the sound speed (Vstokes ≪ VT) we obtain: 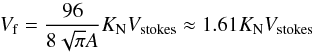 (A.13)which is in good agreement with Eq. (3), derived for high Knudsen number and small Reynolds numbers.
(A.13)which is in good agreement with Eq. (3), derived for high Knudsen number and small Reynolds numbers.
Appendix A.3: Comparison with the Cunningham velocity
Figure A.1 shows the ratio of the Cunningham velocity (see Eq. (3)) to the ones we just derived. The difference is noticeable only for particles of the order of 100 μm at pressures less than the 10-4 bar level and exceeding the 10 bar level. This difference is always less than one order of magnitude and concern only a tiny portion of the parameter space which has little relevance to our study (the largest particle sizes considered in our 3D models is 10 μm). Thus we decided to neglect this discrepancy in the main study.
 |
Fig. A.1 Ratio of the Cunningham velocity to the more sophisticated model of the particle settling velocity considered in the Appendix. |
Acknowledgments
The authors wish to thank the ISIMA program (http://isima.ucsc.edu) where this project was initiated. This project was supported by NASA Planetary Atmospheres and Origins grants to APS. We thank Christiane Helling for discussions on dust formation, Franck Hersant for discussions on the Kzz calculations, Nikole Lewis for sharing her Matlab routines and Franck Selsis for useful input. We also acknowledge the anonymous referee whose numerous comments improved the clarity of this paper.
References
- Ackerman, A. S., & Marley, M. S. 2001, ApJ, 556, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Adcroft, A., Campin, J.-M., Hill, C., & Marshall, J. 2004, Mon. Weather Rev., 132, 2845 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Venot, O., Iro, N., et al. 2012, A&A, 548, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, D. G., Holton, J. R., & Leovy, C. B. 1987, Middle atmosphere dynamics (New York: Academic Press) [Google Scholar]
- Becklin, E. E., & Zuckerman, B. 1988, Nature, 336, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Benneke, B., & Seager, S. 2012, ApJ, 753, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., & Sharp, C. M. 1999, ApJ, 512, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Marley, M., Hubbard, W. B., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Heng, K., & Nampaisarn, T. 2011, ApJ, 736, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, J. W., & Hunten, D. M. 1987, Theory of planetary atmospheres. An introduction to their physics andchemistry (Orlando: Academic Press Inc) [Google Scholar]
- Chapman, S., & Cowling, T. 1970, The mathematical theory of non-uniform gases, 3rd edn. (Cambridge mathematical library) [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, C. S., & Showman, A. P. 2005, ApJ, 629, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, C. S., & Showman, A. P. 2006, ApJ, 649, 1048 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Hansen, B. M. S., Harrington, J., et al. 2010, ApJ, 723, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Cushing, M. C., Kirkpatrick, J. D., Gelino, C. R., et al. 2011, ApJ, 743, 50 [NASA ADS] [CrossRef] [Google Scholar]
- De Wit, J., Gillon, M., Demory, B.-O., & Seager, S. 2012, A&A, 548, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demory, B.-O., Seager, S., Madhusudhan, N., et al. 2011, ApJ, 735, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Vidal-Madjar, A., Lecavelier Des Etangs, A., et al. 2008, A&A, 492, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs-Dixon, I., & Agol, E. 2012 [arXiv:1211.1709] [Google Scholar]
- Dobbs-Dixon, I., & Lin, D. N. C. 2008, ApJ, 673, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs-Dixon, I., Cumming, A., & Lin, D. N. C. 2010, ApJ, 710, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs-Dixon, I., Agol, E., & Burrows, A. 2012, ApJ, 751, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Astron. Nachr., 326, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Shabram, M., Showman, A. P., et al. 2010, ApJ, 709, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, R. S., Marley, M. S., & Lodders, K. 2008, ApJS, 174, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Allard, F., Ludwig, H.-G., Homeier, D., & Steffen, M. 2010, A&A, 513, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goody, Y. 1961, Atmospheric Radiation Theoretical Basis (Oxford University Press) [Google Scholar]
- Heng, K. 2012, ApJ, 761, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., Frierson, D. M. W., & Phillipps, P. J. 2011a, MNRAS, 418, 2669 [Google Scholar]
- Heng, K., Menou, K., & Phillipps, P. J. 2011b, MNRAS, 413, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., Hayek, W., Pont, F., & Sing, D. K. 2012, MNRAS, 420, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Holton, J. R. 1992, An introduction to dynamic meteorology (New York: Academic Press) [Google Scholar]
- Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Iro, N., Bézard, B., & Guillot, T. 2005, A&A, 436, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalnay, E. 2003, Atmospheric modeling, data assimilation, and predictability (Cambridge, UK, New York: Cambridge University Press) [Google Scholar]
- Kataria, T., Showman, A. P., Lewis, N. K., et al. 2013, ApJ, 767, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D. 2005, ARA&A, 43, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., Burrows, A., & Megeath, S. T. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Cowan, N. B., et al. 2009, ApJ, 690, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Lewis, N., Fortney, J. J., et al. 2012, ApJ, 754, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-M., Fletcher, L. N., & Irwin, P. G. J. 2012, MNRAS, 420, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, N. K., Showman, A. P., Fortney, J. J., et al. 2010, ApJ, 720, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., & Wang, H. 2003, Phys. Rev. E, 68, 061206 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Liang, M. C., & Yung, Y. L. 2010, ApJ, 717, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Vasisht, G., Chen, P., Angerhausen, D., & Yung, Y. L. 2011, ApJ, 738, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2002, ApJ, 577, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Fegley, B. 2002, Icarus, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., & Seager, S. 2009, ApJ, 707, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., & Seager, S. 2011, ApJ, 729, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Mousis, O., Johnson, T. V., & Lunine, J. I. 2011, ApJ, 743, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Majeau, C., Agol, E., & Cowan, N. B. 2012, ApJ, 747, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Marley, M. S., & McKay, C. P. 1999, Icarus, 138, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Marley, M. S., Saumon, D., Guillot, T., et al. 1996, Science, 272, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Marley, M. S., Seager, S., Saumon, D., et al. 2002, ApJ, 568, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Marley, M. S., Saumon, D., & Goldblatt, C. 2010, ApJ, 723, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- McKay, C. P., Pollack, J. B., & Courtin, R. 1989, Icarus, 80, 23 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Moses, J. I., Visscher, C., Fortney, J. J., et al. 2011, ApJ, 737, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, V., & Guillot, T. 2013, A&A, submitted [Google Scholar]
- Perna, R., Menou, K., & Rauscher, E. 2010, ApJ, 719, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., Heng, K., & Pont, F. 2012, ApJ, 751, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Sing, D. K., Gibson, N. P., et al. 2013, MNRAS [Google Scholar]
- Probstein, R. F. 1968, Problems of hydrodynamics and continuum mechanics (Society for industrial and applied mathematics) [Google Scholar]
- Pruppacher, H., & Klett, J. 1978, Microphysics of clouds and precipitation (D. Reidel publishing compagny) [Google Scholar]
- Rauscher, E., & Menou, K. 2010, ApJ, 714, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., & Menou, K. 2012a, ApJ, 750, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., & Menou, K. 2012b, ApJ, 745, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., & Menou, K. 2013, ApJ, 764, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Rosner, D. E. 2000, Transport processes in chemically reacting flow systems (Dover: Mineola) [Google Scholar]
- Shapiro, R. 1970, Rev. Geophys., 8, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., & Polvani, L. M. 2011, ApJ, 738, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Cooper, C. S., Fortney, J. J., & Marley, M. S. 2008, ApJ, 682, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Fortney, J. J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Fortney, J. J., Lewis, N. K., & Shabram, M. 2013, ApJ, 762, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. D. 1998, Icarus, 132, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., & Burrows, A. 2010, ApJ, 722, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Stiel, L., & Thodos, G. 1963, Indus. Eng. Chem. Fundamentals, 2, 233 [CrossRef] [Google Scholar]
- Tinetti, G., Beaulieu, J. P., Henning, T., et al. 2012, Exp. Astron., 34, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Venot, O., Hébrard, E., Agúndez, M., et al. 2012, A&A, 546, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visscher, C., Lodders, K., & Fegley, Jr., B. 2006, ApJ, 648, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., & Helling, C. 2003, A&A, 399, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., & Helling, C. 2004, A&A, 414, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Youdin, A. N., & Mitchell, J. L. 2010, ApJ, 721, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Zahnle, K., Marley, M. S., & Fortney, J. J. 2009a, ApJ, submitted [arXiv:0911.0728] [Google Scholar]
- Zahnle, K., Marley, M. S., Freedman, R. S., Lodders, K., & Fortney, J. J. 2009b, ApJ, 701, L20 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Terminal velocity of a falling particle as a function of pressure and particle size for an H2-atmosphere at 1000 K and a value of the gravitational acceleration of 15 m s-2. |
| In the text | |
 |
Fig. 2 Settling timescale as a function of pressure and particle size for the same conditions as in Fig. 1. Also shown are the advective timescale (black curve) and the simulation timescale (blue curve). In the shaded region (below 1 bar), the tracers are considered gaseous and the settling timescale is not relevant for our study. |
| In the text | |
 |
Fig. 3 Temperature (left panel, colorscale), vertical velocities (right panel, colorscale), and horizontal winds (arrows) in our model of HD 209458b. Positive velocities are upward. The top three panels show the flow at three different pressure (0.1 mbar, 1 mbar, and 10 mbar). The bottom panel shows the vertical velocities versus longitude and pressure along the equator. The substellar point is at longitude, latitude (0°, 0°), the dayside is between -90° and +90°. All the quantities are time averaged. |
| In the text | |
 |
Fig. 4 Planet-wide, time averaged tracer abundances on isobars. The abundances are normalized to the abundance in the deepest layer. We compare the value of the 3D model (solid lines) and the fit using the 1D model (dashed lines). |
| In the text | |
 |
Fig. 5 Time averaged fluxes of tracers across isobars. Upwelling fluxes due to the dynamics (solid lines) balance the downwelling fluxes due to the gravitational settling of the tracers (dashed lines). Negative values are upward fluxes. |
| In the text | |
 |
Fig. 6 Time averaged tracer abundance relative to the deep abundance (χ/χ0) at two different pressures and for different particle sizes. |
| In the text | |
 |
Fig. 7 2D distribution of the mixing efficiency on the 1mbar isobar. We plot |
| In the text | |
 |
Fig. 8 Time dependence of the mean tracer abundance averaged between 1mbar and 0.1mbar. The abundances are averaged horizontally over a circular region of radius 45° centered on the substellar point (top) and averaged horizontally around the terminator, including all regions within ± 5° of the terminator (bottom). The top panel is relevant for inferring the presence of a stratosphere (see Sect. 6.1), albedo variations (see Sect. 6.2) or secondary eclipse measurements (see Sect. 6.3). The bottom panel is relevant for transit spectroscopy measurements. |
| In the text | |
 |
Fig. 9 Tracer abundance (colorscale) and winds (arrows) at two different pressure levels and three different times of the simulation for the case a = 2.5 μm. |
| In the text | |
 |
Fig. 10 Limb profiles of our tracer field from 200 bar to 1 μbar as seen during transit. Black circles are situated at 100 bar, 10 bar, 1 bar, 0.1 bar, 0.01 mbar, 1 mbar, 0.1 mbar, 0.01 mbar, and 1 μbar. The north pole is on top and the leading limb on the right. The abundances are normalized to the abundance of the deepest level. |
| In the text | |
 |
Fig. 11 Mean tracer abundance along the terminator for the case with nightside condensates of 1 μm. The different colors correspond to different latitudes along the terminator as shown in the legend. The colorwheel represents the terminator of the planet as seen during a transit, with the eastern hemisphere to the left. The mean profiles are almost symmetrical with respect to the equator, so only the profiles of the northern hemisphere are shown here. |
| In the text | |
 |
Fig. 12 Tracer abundance in the advected column of gas from the 1D model as a function of time. From bottom to top we used |
| In the text | |
 |
Fig. 13 Vertical diffusion coefficient from the 3D model estimated from the different tracer fields separately (black lines), from the 1D fit to the 3D model (red line) and the root mean square of the vertical velocity times the vertical scale height, a common estimate of Kzz in the literature (blue line) (see Lewis et al. 2010; Moses et al. 2011, for example). |
| In the text | |
 |
Fig. 14 Time averaged tracer abundance along the equator for nightside condensate of 1 μm. The profiles are equally spaced in longitude by 2.8° The dayside profiles are in red whereas the nightside profiles are in blue. We highlight the profiles at the antistellar point (dotted line), the west terminator (dot-dashed line), the substellar point (dashed line) and the east terminator (plain line). |
| In the text | |
 |
Fig. 15 Approximate growth time scale of TiO2 grains in HD 209458b. The bottom black line shows the advective timescale and the top one is ten times the advective timescale. |
| In the text | |
 |
Fig. 16 Approximate growth time scale of SiO2 grains in HD 209458b. The bottom black line shows the advective timescale and the top one is ten times the advective timescale. |
| In the text | |
 |
Fig. A.1 Ratio of the Cunningham velocity to the more sophisticated model of the particle settling velocity considered in the Appendix. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.