| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 25 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321204 | |
| Published online | 10 September 2013 | |
The dynamical state of the first hydrostatic core candidate Chamaeleon-MMS1⋆
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail:
atsitali@mpifr-bonn.mpg.de
2
Laboratoire de radioastronomie, UMR 8112 du CNRS, École Normale
Supérieure et Observatoire de Paris, 24 rue Lhomond, 75231
Paris Cedex 5,
France
Received:
31
January
2013
Accepted:
10
June
2013
Context. First hydrostatic cores represent a theoretically predicted intermediate evolutionary link between the prestellar and protostellar phases. Studying the observational characteristics of first core candidates is therefore vital for probing and understanding the earliest phases of star formation.
Aims. We aim to determine the dynamical state of the first hydrostatic core candidate Chamaeleon-MMS1 (Cha-MMS1).
Methods. We observed Cha-MMS1 in various molecular transitions with the APEX and Mopra telescopes. Continuum data retrieved from the Spitzer Heritage Archive were used to estimate the internal luminosity of the source. The molecular emission was modelled with a radiative transfer code to derive constraints on the kinematics of the envelope, which were then compared to the predictions of magneto-hydrodynamic simulations.
Results. We derive an internal luminosity of 0.08 L⊙−0.18 L⊙ for Cha-MMS1. An average velocity gradient of 3.1 ± 0.1 km s-1 pc-1 over ~0.08 pc is found perpendicular to the filament in which Cha-MMS1 is embedded. The gradient is flatter in the outer parts and, surprisingly, also at the innermost ~2000 AU to 4000 AU. The former features are consistent with solid-body rotation beyond 4000 AU and slower, differential rotation beyond 8000 AU, but the origin of the flatter gradient in the innermost parts is unclear. The classical infall signature is detected in HCO+ 3−2 and CS 2−1. The radiative transfer modelling indicates a uniform infall velocity in the outer parts of the envelope. In the inner parts (at most 9000 AU), an infall velocity field scaling with r-0.5 is consistent with the data, but the shape of the profile is less well constrained and the velocity could also decrease toward the centre. The infall velocities are subsonic to transonic, 0.1 km s-1−0.2 km s-1 at r ≥ 3300 AU, and subsonic to supersonic, 0.04 km s-1−0.6 km s-1 at r ≤ 3300 AU. Both the internal luminosity of Cha-MMS1 and the infall velocity field in its envelope are consistent with predictions of MHD simulations for the first core phase. There is no evidence of any fast, large-scale outflow stemming from Cha-MMS1, but excess emission from the high-density tracers CS 5−4, CO 6−5, and CO 7−6 suggests the presence of higher velocity material at the inner core.
Conclusions. Its internal luminosity excludes Cha-MMS1 being a prestellar core. The kinematical properties of its envelope are consistent with Cha-MMS1 being a first hydrostatic core candidate or a very young Class 0 protostar.
Key words: stars: protostars − stars: formation − stars: low-mass − stars: kinematics and dynamics − ISM: kinematics and dynamics
Tables 6−9, 11, Figs. 2, 3, 12, 13, 15, 16, 18, 19, and Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Many advances have recently been made in the field of early low-mass star formation, spanning from the prestellar phase to the formation and evolution of Young Stellar Objects (YSOs), e.g., with the Spitzer c2d Legacy Project (“From Molecular Cores to Planet-Forming Disks”, Evans et al. 2003) and the Herschel Gould Belt Survey (André et al. 2010). In particular, Herschel (Pilbratt et al. 2010) has provided valuable insight into the early star formation processes. Most dense starless cores in molecular clouds appear to be located along a complex network of long, thin filaments, suggesting that filament formation precedes the core formation process (Arzoumanian et al. 2011; Hill et al. 2011; André et al. 2010; Men’shchikov et al. 2010; Molinari et al. 2010). The study of these early stages is necessary in order to address open questions such as the origin of the stellar initial mass function (IMF), its relationship with the prestellar phase and the core mass function (CMF; e.g., André et al. 2009), and the initial conditions needed for star formation to occur. Recent results from the Herschel survey confirm the resemblance of the prestellar CMF to the stellar IMF in the Aquila and Polaris clouds (Könyves et al. 2010; André et al. 2010). Such a resemblance has already been seen in various molecular clouds with ground-based single-dish telescopes, such as in the Ophiuchus molecular cloud (Motte et al. 1998) or in the Pipe nebula (Rathborne et al. 2009).
It has recently become common to split the population of the starless cores in molecular clouds into two categories, the gravitationally bound and unbound cores. Prestellar cores represent the subset of starless cores that are self-gravitating and will thus very likely form stars (e.g., di Francesco et al. 2007; André et al. 2009), while the gravitationally unbound starless cores may be transient objects (“failed” cores) or objects on the verge of becoming prestellar (e.g. Belloche et al. 2011b). The gravitational collapse of a prestellar core leads to the formation of a stellar embryo, the protostar. This marks the beginning of the Class 0 phase, during which the central object accretes mass from its protostellar envelope (André et al. 2000). Theoretically, the early work of Larson (1969) already showed that the formation of the central protostar must be preceded by the formation of a larger, less dense, first hydrostatic core (FHSC). The FHSC thus represents an intermediate evolutionary stage between the prestellar and protostellar phases. The detection of FHSCs is observationally very challenging because of their very short expected lifetime.
1.1. FHSC: a theoretical background
The formation of the first hydrostatic core emerged from theory for the first time with Larson (1969), but only a handful of objects have recently been observed and suggested as likely candidates. Larson (1969) describes the process of forming a protostar from a parent molecular core using a spherical collapse model that ignores magnetic fields and rotation. The initial phase is characterised by an isothermal contraction of the molecular core. When the central density exceeds 10-13 g cm-3 the radiative cooling ceases to be efficient and an opaque, adiabatic core forms at the centre. The rise in temperature results in an increase in the thermal pressure, and finally, when the pressure balances the gravitational force the collapse ceases and the first hydrostatic core is formed. The initial central temperature of the FHSC is estimated to be around 170 K with an initial central density of 2 × 10-10 g cm-3. The so-called second, more compact (protostellar) core is formed after the dissociation of H2 and subsequent collapse, when the central temperature reaches 2 × 104 K and the density reaches 2 × 10-2 g cm-3 (Larson 1969).
Various theoretical studies predict observational characteristics of the first core phase. Internal luminosities of up to ~0.1 L⊙ (Masunaga et al. 1998; Saigo & Tomisaka 2011) or ~0.25 L⊙ (Commerçon et al. 2012) have been predicted. First cores are characterised by radii and masses in the ranges of ~5 AU−10 AU and 0.05 M⊙−0.1 M⊙, respectively (Masunaga et al. 1998; Saigo et al. 2008). Their lifetimes range from a few 100 yr to a few 1000 yr, increasing with the rate of rotation. Commerçon et al. (2012) derive lifetimes ranging from ~1000 yr to >4000 yr for rotating, magnetised 1 M⊙ cores with 3D radiation-MHD simulations. The FHSC lifetime is shorter for higher levels of magnetisation owing to the stronger magnetic braking that increases the mass accretion rate. These short lifetimes imply that first cores are rare and thus difficult to observe, although we note that Tomida et al. (2010) predict much longer lifetimes (>104 yr) for first cores formed in very low-mass cloud cores (0.1 M⊙).
Outflows at the first core phase are thought to be a significant observational signature characterising this evolutionary stage. Machida et al. (2008) used 3D resistive MHD simulations to study the driving mechanisms of outflows in the star formation process. Their predictions distinguish between an extended, slow molecular outflow driven by the first core and a highly collimated, fast jet later driven by the protostellar core that exhibit typical velocities of ~3 km s-1 and 30 km s-1, respectively. The outflow driven by the first core is predicted to be extremely compact, spanning ~200 AU−800 AU in extent just before the start of the second collapse (Commerçon et al. 2012, 2010; Machida et al. 2008). The first core outflows are thought to result from the twisting of the magnetic field lines due to the rotation of the collapsing core, whose amplified toroidal component leads to the subsequent transfer of angular momentum to the gas outside of the core (Tomisaka & Tomida 2011).
1.2. Cha-MMS1 and its evolutionary stage
Chamaeleon-MMS1 (hereafter Cha-MMS1 for short) is a dense core embedded in a filament (~0.5 pc in length) within the Chamaeleon I molecular cloud (Belloche et al. 2011a) at a distance of 150 pc (Whittet et al. 1997; Knude & Høg 1998). Several previous studies of Cha-MMS1 suggest that it is an object at a very early evolutionary stage.
Reipurth et al. (1996) discovered Cha-MMS1 in dust continuum emission at 1.3 mm. They suggested that Cha-MMS1 is the driving source of the nearby HH 49/50 objects and identified it as a Class 0 protostar based on that association. During the Class 0 protostellar phase, the central object is deeply embedded within its collapsing envelope, which comprises more than half of the system’s mass (André et al. 1993). Lehtinen et al. (2001) confirms this classification based on a tentative far-infrared detection, but Lehtinen et al. (2003) argues that Cha-MMS1 possibly represents an evolutionary stage earlier than Class 0 based on its lack of thermal free-free emission at cm wavelengths. Cha-MMS1 is embedded in a gravitationally-bound C18O core (Haikala et al. 2005). High deuterium fractionations of HCO+ and N2H+ were derived, consistent with Cha-MMS1 being an evolved prestellar core or a young protostellar envelope (Belloche et al. 2006).
A faint Spitzer 24 μm and 70 μm detection indicates the presence of a central object in Cha-MMS1, either an FHSC or a protostar (Belloche et al. 2006). Belloche et al. (2011a) derived a very low internal luminosity of ~0.015 L⊙ for this object based on the correlation between the 70 μm flux density and internal luminosity established by Dunham et al. (2008) for protostellar objects. As most Class 0 protostars feature an outflow (André et al. 2000), a search for a large-scale outflow driven by Cha-MMS1 was performed in CO 3−2 with APEX but none was found (Belloche et al. 2006). The non-detection of an outflow around Cha-MMS1 on scales of ~104 AU suggests that the central object may be less evolved than a Class 0 object. It could possess an outflow that is too compact to have been detected with the resolution of the previous studies, which would agree with the predictions of the FHSC observational signatures. Furthermore, Cha-MMS1, the Class 0 protostar IRAM 04191+1522 (hereafter, IRAM 04191) and the very low luminosity object (VeLLO) L1521F (Crapsi et al. 2004; Bourke et al. 2006) are located at approximately the same distance, and a direct comparison of their Spitzer fluxes supports the idea that Cha-MMS1 is less evolved (Belloche et al. 2006). Bearing all this in mind, Cha-MMS1 could be at the stage of the FHSC between the prestellar and Class 0 phases. However, its classification as such is very difficult to observationally confirm until a compact (200 AU−800 AU; Commerçon et al. 2010, 2012), slow outflow with velocities in the range of 2 km s-1−4 km s-1 (Tomisaka 2002; Machida et al. 2008; Commerçon et al. 2010; Hennebelle & Fromang 2008) is detected. We therefore merely consider it as an FHSC candidate.
1.3. FHSC candidates
The detection of seven candidate first cores has been claimed so far: Cha-MMS1 (Belloche et al. 2006, 2011a), L1448-IRS2E (Chen et al. 2010), Per-Bolo 58 (Enoch et al. 2010; Dunham et al. 2011), L1451-mm (Pineda et al. 2011), CB17-MMS (Chen et al. 2012), B1-bS, and B1-bN (Pezzuto et al. 2012). All but one (B1-bS) are VeLLOs (internal luminosity Lint < 0.1 L⊙), in agreement with the range of luminosities predicted for FHSCs. With Lbol ~ 0.49 L⊙, B1-bS might be too luminous for an FHSC. L1448-IRS2E, Per-Bolo 58, and L1451-mm drive outflows that have been interferometrically detected. L1448-IRS2E drives an outflow with velocities of ~25 km s-1, one order of magnitude higher than predicted for a first core by MHD simulations (Machida et al. 2008). This suggests that it is at the more evolved second-core stage so is likely ruled out as a first core candidate. Per-Bolo 58, L1451-mm, and CB17-MMS all have outflow velocities in agreement with theoretical predictions (see Sect. 1.1). However, the outflows of Per-Bolo 58 and CB17-MMS extend over 6000 AU−8000 AU, with dynamical times ~104 yr, about one order of magnitude longer than the expected first core lifetime in a magnetised collapsing dense core. Lifetimes in the range ~4000 yr−10 000 yr are produced by non- or very-weakly magnetised simulations, but no outflow is produced at the FHSC stage in these cases (e.g, Commerçon et al. 2012). L1451-mm is therefore the only candidate driving an outflow with properties (maximum velocity 2.3 km s-1, dynamical time 1.6 × 103 yr) consistent with current theoretical predictions at the first-core stage. There has been no outflow detection for the B1-bS and B1-bN condensations in Perseus, but the SED fitting of their Herschel and Spitzer (where applicable) fluxes seems to be consistent with the presence of a central object surrounded by a dusty envelope that is younger than the Class 0 phase (Pezzuto et al. 2012).
The goal of this study is to set constraints on the kinematics of the envelope of Cha-MMS1 to test that it is consistent with Cha-MMS1 being in the FHSC stage. The structure of this paper is as follows. In Sect. 2 we summarise the observational details, we then present our results in Sect. 3 and in Sect. 4 we perform radiative transfer modelling of the spectra towards Cha-MMS1. The discussion and conclusions follow in Sects. 5 and 6, respectively.
2. Observations
 |
Fig. 1 a) 870 μm map of the filament in which Cha-MMS1 is
embedded, obtained with LABOCA as part of an unbiased survey of Chamaeleon I (Belloche et al. 2011a). The contour levels
correspond to − a, a, 2a,
4a, 6a, 8a, 12a,
16a, 24a, 32a, with
a = 36 mJy/21″-beam (3σ). The white cross at
αJ2000 = 11h06m33 |
We performed observations towards the dense core Cha-MMS1 at
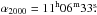 13,
δ2000 = −77°23′35.1′′1 with the APEX and Mopra telescopes on the central core
position as well as on offset positions close to the core along directions parallel and
perpendicular to the filament in which it is embedded (see Fig. 1). The data were reduced with the CLASS software2.
13,
δ2000 = −77°23′35.1′′1 with the APEX and Mopra telescopes on the central core
position as well as on offset positions close to the core along directions parallel and
perpendicular to the filament in which it is embedded (see Fig. 1). The data were reduced with the CLASS software2.
Parameters of 2010 APEX CHAMP+ observations.
Parameters of 2011 APEX observations.
Parameters of Mopra observations.
2.1. 2010 APEX observations
Observations with APEX3 using the CHAMP+ 4 heterodyne SSB receiver were carried out in 2010 July, in the following molecular transitions: 13CO 6−5, CO 6−5, and CO 7−6. CHAMP+ is a 2 × 7 pixel array receiver connected to a fast-fourier-transform spectrometer backend array (FFTS). It operates in two frequency bands simultaneously, around 690 GHz and 810 GHz. The channel spacing is 183 kHz. The corresponding velocity resolution for each transition is given in Table 1. All three transitions were observed with the central CHAMP+ pixel pointed on the central core position at αJ2000 = 11h06m33s.13, δJ2000 = −77°23′35.1′′. In addition to the central position, CO 6−5 and CO 7−6 were also observed with the central CHAMP+ pixel being centred on an offset position (Δα, Δδ) = (5.3′′, 8.3′′) relative to the centre of Cha-MMS1 (see Fig. 1b). The observations were done in position-switching mode with the reference position at (Δα, Δδ) = (−600′′, 4′′). The reference position was checked to be free of emission with an rms sensitivity of 0.06 K and 0.24 K for the central pixel in CO 6−5 and CO 7−6, respectively, and for the spectral resolution given in Table 1.
The observations were carried out on four different days, in the last two of which 13CO 6−5 was observed in parallel to CO 7−6. A comparison to the CO 7−6 spectra of the first two days of observation suggests that there is a pointing offset in the south-west direction parallel to the filament of up to ~5″ between the CO 6−5/CO 7−6 and 13CO 6−5/CO 7−6 datasets. The forward and beam efficiencies used to convert antenna temperatures Ta⋆ into main-beam temperatures can be found in Table 1 along with further information on line frequencies, system temperatures, and noise levels. The focus was optimised on Saturn and Mars and the pointing in CO 6−5 emission on the star IRAS 07454-7112.
2.2. 2011 APEX observations
We carried out observations with the APEX telescope in 2011 April, June, and December in
the following molecular transitions: CS 5−4, H13CO+ 3−2,
HCO+ 3−2, H13CO+ 4−3, CO 4−3, C18O 2−1, and
C17O 2−1. The observations were done in position-switching mode with the
reference position at
αJ2000 = 11h05m23 7,
δJ2000 = −77°11′02.2′′.
The reference position is free of emission with an rms of 0.12 K in HCO+ 3−2
and 0.33 K and CO 4−3 for the spectral resolution given in Table 2. The corresponding beamwidth, forward, and main beam efficiencies are
listed in Table 2. The positions observed for each
transition are shown in Figs. 1c to e, overlaid on
the 870 μm map of the filament seen in Fig. 1a. All positions lie either perpendicular (position angle − 35° east
from north) or parallel to the filament. The transitions CS 5−4,
H13CO+ 4−3, CO 4−3, C18O 2−1, and C17O 2−1
were only observed perpendicular to the filament, while H13CO+ 3−2
and HCO+ 3−2 were also observed parallel to it. Table 2 gives information about the frontend and backend used for each
transition, their respective spectral resolutions, the resulting system temperatures, and
rms noise levels. The telescope pointing was checked every 1 h to 1.5 h and was performed
on IRAS 07454-7112. The pointing accuracy is ~2′′ (rms). The focus was
optimised on either Saturn, Jupiter, or Mars, and repeated approximately every 3 h.
7,
δJ2000 = −77°11′02.2′′.
The reference position is free of emission with an rms of 0.12 K in HCO+ 3−2
and 0.33 K and CO 4−3 for the spectral resolution given in Table 2. The corresponding beamwidth, forward, and main beam efficiencies are
listed in Table 2. The positions observed for each
transition are shown in Figs. 1c to e, overlaid on
the 870 μm map of the filament seen in Fig. 1a. All positions lie either perpendicular (position angle − 35° east
from north) or parallel to the filament. The transitions CS 5−4,
H13CO+ 4−3, CO 4−3, C18O 2−1, and C17O 2−1
were only observed perpendicular to the filament, while H13CO+ 3−2
and HCO+ 3−2 were also observed parallel to it. Table 2 gives information about the frontend and backend used for each
transition, their respective spectral resolutions, the resulting system temperatures, and
rms noise levels. The telescope pointing was checked every 1 h to 1.5 h and was performed
on IRAS 07454-7112. The pointing accuracy is ~2′′ (rms). The focus was
optimised on either Saturn, Jupiter, or Mars, and repeated approximately every 3 h.
2.3. Mopra observations
We observed with the Mopra telescope towards the central position of Cha-MMS1 along with
eight other offset positions perpendicular and parallel to the filament (see Fig. 1f) in 2011 May in several molecular transitions using
the zoom mode of the high-resolution spectrometer MOPS. The receiver was tuned at two
different frequencies, 94 554 MHz and 87 190 MHz. Only the central position was observed
for the latter. Position-switching observations were done with the reference position at
αJ2000 = 11h05m23 7,
δJ2000 = −77°11′02.2′′.
It was checked that it was free of emission with an rms sensitivity ranging from 46 mK−52
mK in all transitions for the spectral resolution given in Table 3. The transitions that are used for the analysis in this paper are
listed here: CS 2−1, C34S 2−1, 13CS 2−1, C33S 2−1,
HC3N 10−9, HN13C 1−0, N2H+ 1−0,
HCO+ 1−0, H13CO+ 1−0, HC18O+ 1−0,
HNCO 4−3, c-C3H2
32,2−31,3,
CH3OH−A
20,2−10,1, and
CH3OH−E
21,2−11,1. The final reduced
dataset was obtained after averaging both polarisations. We did, however, notice some
differences in integrated intensity for the two polarisations of up to ~10% (see Appendix
A for more details about this discrepancy). The
channel spacing was 34 kHz. The range of system temperatures
Tsys for each transition is given in Table 3. The beam efficiency used to convert antenna
temperatures Ta⋆ into main-beam
temperatures is 0.34. This value was derived from a detailed calibration analysis (see
Appendix A). The telescope pointing was checked
approximately every hour on U Men for Cha-MMS1, and AH Sc and IK Tau for the calibration
sources Oph A SM1N and IRAM 04191, respectively. The transitions, their rest frequencies,
and the number of observed positions are listed in Table 3.
7,
δJ2000 = −77°11′02.2′′.
It was checked that it was free of emission with an rms sensitivity ranging from 46 mK−52
mK in all transitions for the spectral resolution given in Table 3. The transitions that are used for the analysis in this paper are
listed here: CS 2−1, C34S 2−1, 13CS 2−1, C33S 2−1,
HC3N 10−9, HN13C 1−0, N2H+ 1−0,
HCO+ 1−0, H13CO+ 1−0, HC18O+ 1−0,
HNCO 4−3, c-C3H2
32,2−31,3,
CH3OH−A
20,2−10,1, and
CH3OH−E
21,2−11,1. The final reduced
dataset was obtained after averaging both polarisations. We did, however, notice some
differences in integrated intensity for the two polarisations of up to ~10% (see Appendix
A for more details about this discrepancy). The
channel spacing was 34 kHz. The range of system temperatures
Tsys for each transition is given in Table 3. The beam efficiency used to convert antenna
temperatures Ta⋆ into main-beam
temperatures is 0.34. This value was derived from a detailed calibration analysis (see
Appendix A). The telescope pointing was checked
approximately every hour on U Men for Cha-MMS1, and AH Sc and IK Tau for the calibration
sources Oph A SM1N and IRAM 04191, respectively. The transitions, their rest frequencies,
and the number of observed positions are listed in Table 3.
2.4. Spitzer archive data
We used MIPS1 24 μm and MIPS2 70 μm continuum data taken from the Spitzer Heritage Archive5 (AORkeys: 19978496, 3962112, 19979264).
2.5. CO 3−2 data
Cha-MMS1 was observed in CO 3−2 in 2005 with the APEX telescope, and the data were presented in Belloche et al. (2006). We used the CO 3−2 data along the direction perpendicular to the filament in conjuction with the other CO transitions and isotopologues when modelling the spectra in Sect. 4.
3. Results
3.1. Internal luminosity derivation
We performed aperture photometry on MIPS1 24 μm and MIPS2 70 μm Spitzer data, and derived flux densities for the dense core Cha-MMS1. We used the IDL procedure aper.pro6 with the following aperture and background inner and outer radii: 16′′ (18′′−39′′) and 13′′ (20′′−32′′) for the 70 μm and 24 μm data, respectively. Fine-scale aperture corrections of 2.16 for MIPS1 and 1.17 for MIPS2 were taken from the MIPS Instrument Handbook7. The flux densities derived before and after correction are given in Table 4. In the following, we use the average value of the two independent, aperture-corrected 70 μm flux density measurements to estimate the internal luminosity of Cha-MMS1. We determine the internal luminosity of Cha-MMS1 with two methods.
3.1.1. Method 1
Dunham et al. (2008) calculated the internal
luminosity of low-luminosity protostars based on a parametric model consisting of a
protostellar envelope, a disk, and an outflow cone, coupled to a 2D radiative transfer
code. They derived the following empirical relation between the internal luminosity of a
protostar and its observed 70 μm flux:
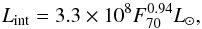 (1)where
F70 is normalised to 140 pc and is in cgs units (cm-2
s-1). With this equation, we derive an internal luminosity of 0.025 ± 0.003
L⊙ after correction for the distance of Cha-MMS1.
(1)where
F70 is normalised to 140 pc and is in cgs units (cm-2
s-1). With this equation, we derive an internal luminosity of 0.025 ± 0.003
L⊙ after correction for the distance of Cha-MMS1.
3.1.2. Method 2
Commerçon et al. (2012) have recently presented the evolution of the 24 μm and 70 μm flux densities in the course of the first core lifetime, as well as the time evolution of the FHSC internal luminosity via 3D radiation-magnetohydrodynamic (hereafter, RMHD) simulations of a 1 M⊙ dense core collapse. A 3D RMHD simulation for the case of a 5 M⊙ dense core collapse was also computed (see Sect. 5.4.2). Both models have a strong initial magnetisation level (MU2 model; Commerçon et al. 2012).
We looked for a correspondence between Cha-MMS1’s 24 μm and 70 μm flux densities and the model flux density predictions of FHSC obtained for the 1 M⊙ and 5 M⊙ dense cores. In the case of the 1 M⊙ model, we find consistent flux densities within a factor of ~2 for inclinations to the line-of-sight 45° < i < 60°, and a first core age of 850 yr. In this case, the internal luminosity prediction is ~0.08 L⊙−0.13 L⊙, at least three times higher than the internal luminosity derived using the relation by Dunham et al. (2008).
In the 5 M⊙ case at inclinations 30° < i < 45° and for a first core age of ~2680 yr, the observed and predicted 24 μm flux densities are consistent within a factor of ~2.5, and we thus obtain an internal luminosity estimate of ~0.13 L⊙−0.18 L⊙.
In the framework of this MHD model, the overall range is ~0.08 L⊙−0.18 L⊙ for inclinations of 30° ≤ i < 60°. The internal luminosity derived from the empirical relation of Dunham et al. (2008) is therefore lower by a factor of ~3−7 compared to the predictions of 3D RMHD simulations.
We adopt an internal luminosity of ~0.1 L⊙ as an approximation, which is within the luminosity range we derived based on the RMHD simulations. We use this value for the radiative transfer modelling that follows in Sect. 4. Even if we were to adopt the upper limit of 0.18 L⊙, the temperature profile of the inner envelope would not significantly change (Eq. (7), Sect. 4.1).
Flux densities of Cha-MMS1 from aperture photometry.
3.2. Spectra towards Cha-MMS1
Figures 2 and 3 show the spectra of the transitions observed with APEX and Mopra towards the central position of Cha-MMS1. Apart from 13CS 2−1 and C33S 2−1 for which we can only draw upper limits, most transitions are detected. Tables 5 to 9 give the centroid velocities derived for these transitions after performing Gaussian or hyperfine-structure fits in CLASS to the observed spectra (“GAUSS” and “HFS” methods). Only the spectra that have either a Gaussian shape or a well-defined hyperfine structure and no self-absorption features can be fitted in this way. Tables 5 to 9 list the systemic velocities of groups of transitions observed at the same offset positions (see Fig 1). The centroid velocities of transitions that were only observed at the central position of the core are given in Table 6.
3.2.1. Issues with the systemic velocity
It is apparent from Fig. 3 that all the APEX spectra are redshifted by 0.1 km s-1 compared to the systemic velocity derived from a hyperfine-structure fit to the N2H+ 1−0 multiplet observed with Mopra. There is therefore a problem with one of the two datasets. As the shift is seen for both the high and low-density APEX tracers (e.g., H13CO+ 4−3 and C18O 2−1), it is not likely to be an intrinsic characteristic of the source, but rather an instrumental effect.
We compared the spectra of the calibration source IRAM 04191, observed with APEX, Mopra, and with the IRAM 30-m telescope, to pinpoint the source of the systemic velocity inconsistency. In addition, because we have Mopra observations of the central position of Cha-MMS1 from both 2010 and 2012 (as part of a survey targeting starless cores in Cha I and III, Tsitali et al. in prep.), we compared them to the 2011 data that we present in this paper. The N2H+ 1−0 IRAM 04191 spectra are consistent with each other, and consequently, we cannot draw any conclusions about the velocity shift. However, the N2H+ 1−0 central spectrum of Cha-MMS1 observed with Mopra in 2010 and 2012 gives a velocity estimate consistent with the APEX data, i.e. 4.4 kms-1, but inconsistent with the 2011 Mopra data, i.e. 4.3 kms-1. We therefore assume that the Mopra 2010, 2012, and APEX 2011 datasets are correct and apply a correction of 0.1 kms-1 to the systemic velocity derived from the 2011 Mopra N2H+ 1−0 transition whenever we use it along with the 2011 APEX spectra. We explicitly mention it in the text whenever this correction is applied.
Mopra centroid velocities at positions perpendicular and parallel to the filament.
3.3. Rotation
We produced position–velocity (P−V) diagrams for the Mopra C34S 2−1, HC3N 10−9, N2H+ 1−0, CH3OH−A 20,2−10,1, and CH3OH−E 21,2−11,1 transitions and the APEX CS 5−4, H13CO+ 3−2, H13CO+ 4−3, C17O 2−1, and C18O 2−1 transitions (Figs. 4 and 5) based on the centroid velocities measured in Sect. 3.2. We performed linear fits to these P−V diagrams to search for velocity gradients. The results are listed in Table 10 and shown in Figs. 4 and 5. After combining all tracers, there is no clear velocity gradient parallel to the filament (≤2 km s-1 pc-1, see Figs. 4b and 5d).
The P−V diagrams for the direction perpendicular to the filament are given in Figs. 4a and 5a−c. There is a clear velocity gradient along this direction with an amplitude of ~2 km s-1−4.5 km s-1 pc-1 up to ~8000 AU. The average velocity gradient is ~3.1 ± 0.1 km s-1 pc-1. However, the C17O 2−1 and C18O 2−1 curves are significantly flatter at the inner, r ≤ 4000 AU radii, compared to the range 4000 AU−8000 AU (Fig. 5c), with velocity gradients ≤2 km s-1 pc-1. The H13CO+ 4−3 and H13CO+ 3−2 P−V curves are also consistent with no gradient for the inner ~4000 AU.
The P−V curves of C17O 2−1 and C18O 2−1 depart from a straight line for radii larger than ~8000 AU. The weighted average velocity gradient for the two transitions between the two outermost positions (at ±12 500 AU) is ~1.5 ± 0.2 km s-1 pc-1, i.e. smaller by a factor of ~2 than within 8000 AU. Such an “S” shape was reported by Belloche et al. (2002) for the Class 0 protostar IRAM 04191 and was interpreted as an indication of differential rotation in the envelope beyond a certain radius. If the velocity gradient of Cha-MMS1 perpendicular to the filament is due to rotation, then the bulk of the envelope is roughly in solid-body rotation between ~4000 AU and 8000 AU, and the outermost parts of the filament are rotating more slowly. After correcting for an inclination of 60°−30° (Sect. 3.1), the average angular velocity for radii between 4000 AU and 8000 AU is Ω ~ 3.6 km s-1 pc-1−6.2 km s-1 pc-1. At 12 500 AU, and for the same inclinations, we obtain Ω ~ 1.8 km s-1 pc-1−3.0 km s-1 pc-1.
The P−V diagram of CS 5−4 (Fig. 5a) shows a centrally peaked shape. The profile is not well resolved, but the centroid velocity at the central position is significantly higher than at one beam spacing on each side. This velocity shift is because there is an excess of redshifted emission toward the central position that is not reproduced by our radiative transfer modelling (see Sect. 4 and Fig. 10). This issue is discussed in Sect. 5.2.
Velocity gradients perpendicular and parallel to the filament.
 |
Fig. 4 Position–velocity diagrams of the Mopra C34S 2−1 (black), HC3N 10−9 (blue), N2H+ 1−0 (red), CH3OH−A 20,2−10,1 (green), and CH3OH−E 21,2−11,1 (pink) transitions, a) perpendicular and b) parallel to the filament. The error bars represent standard deviations (1σ). Linear fits to the velocities for each transition are shown with the same colour as in panel a). |
 |
Fig. 5 Position–velocity diagrams of the APEX CS 5−4, H13CO+ 3−2, H13CO+ 4−3, C17O 2−1, and C18O 2−1 transitions perpendicular a), b), c) and parallel d) to the filament. Linear fits are shown as straight lines. For C17O 2−1 and C18O 2−1 in c) the two outer points from either side of the curve were excluded from the fits. Fits to the innermost positions of C17O 2−1 and C18O 2−1 are also displayed. |
3.4. Turbulence
The spatial variation of the non-thermal velocity dispersion is shown in Fig. 6 for several transitions. The FWHM linewidths were
estimated using the “GAUSS” and “HFS” fitting methods in CLASS (see Table 11), as mentioned in Sect. 3.2. We computed the thermal velocity dispersion of each molecule as
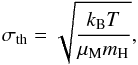 (2)where
μM is the molecular weight of the molecule,
kB the Boltzmann’s constant, mH
the hydrogen mass, and T the kinetic temperature that we assume to be 9 K
(see Sect. 4). The non-thermal linewidths are
computed as
(2)where
μM is the molecular weight of the molecule,
kB the Boltzmann’s constant, mH
the hydrogen mass, and T the kinetic temperature that we assume to be 9 K
(see Sect. 4). The non-thermal linewidths are
computed as 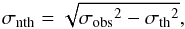 (3)while their respective
uncertainties, denoted as δσ, are calculated using
(3)while their respective
uncertainties, denoted as δσ, are calculated using
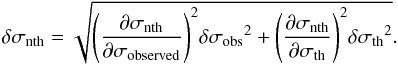 (4)If we assume that
δσth = 0, the above relation gives
(4)If we assume that
δσth = 0, the above relation gives
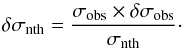 (5)We compare the
non-thermal velocity dispersion to the thermal dispersion of the mean particle, with
μ = 2.37:
(5)We compare the
non-thermal velocity dispersion to the thermal dispersion of the mean particle, with
μ = 2.37: 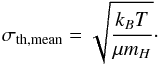 (6)For
T = 9 K, σth,mean ~ 0.18 km
s-1, or FWHMth,mean ~ 0.42 km
s-1. Table 11 lists the observed
linewidths and the derived thermal and non-thermal velocity dispersions for all
transitions that have a low optical depth.
(6)For
T = 9 K, σth,mean ~ 0.18 km
s-1, or FWHMth,mean ~ 0.42 km
s-1. Table 11 lists the observed
linewidths and the derived thermal and non-thermal velocity dispersions for all
transitions that have a low optical depth.
From Table 11 we infer that the non-thermal velocity dispersion is comparable to the mean thermal velocity dispersion. Therefore, there is almost an equipartition between thermal and non-thermal motions, provided that our asumption of T = 9 K is valid.
The non-thermal dispersion does not vary significantly along or across the filament (Figs. 6 and 7). One exception is, however, CS 5−4. Its non-thermal linewidth peaks at the centre and decreases at the outer parts. This is due to the excess redshifted emission observed at the central position (see Sect. 3.3, and Sects. 4 and 5.2 for further discussion).
Average values for the linewidths and non-thermal velocity dispersions over all positions are given in Table 12. The non-thermal dispersions, σnth, have typical values of 0.2 km s-1, comparable to the mean thermal dispersion. Uniform non-thermal dispersions on scales ~0.1 pc similar to the thermal dispersions have also been previously observed in other dense cores (e.g., Tafalla et al. 2004; Barranco & Goodman 1998).
Linewidths and non-thermal velocity dispersions averaged over all positions.
 |
Fig. 6 Non-thermal velocity dispersion, σnth, versus position perpendicular to the filament for a) CS 5−4 (black), H13CO 4−3 (red), and H13CO+ 3−2 (green), b) C17O 2−1 and C18O 2−1, all observed with the APEX telescope, and c) C34S 2−1 (black), HC3N 10−9 (green), N2H+ 1−0 (dark blue), CH3OH−E 21,2 − 11,1 (light blue), and CH3OH−A 20,2 − 10,1 (pink) observed with Mopra. The errorbars are standard deviations. The thermal dispersion was calculated assuming a temperature of T = 9 K. |
 |
Fig. 7 Non-thermal velocity dispersion, σnth, versus position parallel to the filament for a) C34S 2−1 (black), HC3N 10−9 (green), N2H+ 1−0 (dark blue), CH3OH−E 21,2 − 11,1 (light blue), and CH3OH−A 20,2 − 10,1 (pink) observed with Mopra, and b) H13CO+ 3−2 observed with the APEX telescope. The errorbars are standard deviations. The thermal dispersion was calculated assuming a temperature of T = 9 K. |
3.5. Infall signature
Cha-MMS1 exhibits the classical signature of infall in various transitions (Fig. 8). The infall signature manifests itself as a self-absorbed asymmetric, optically thick line with the blue peak stronger than the red one, and an optically thin line peaking in between these two peaks. This profile is indicative of inward motions as long as the excitation temperature increases towards the centre (e.g., Walker et al. 1986; Zhou 1992).
Figure 8 shows that the absorption dips of CS 2−1 and HCO+ 3−2 are redshifted with respect to the systemic velocity. The systemic velocity was estimated by a seven-component hyperfine-structure fit to the N2H+ 1−0 multiplet, using the HFS method in CLASS, giving a value of 4.299 ± 0.002 km s-1. As discussed in Sect. 3.2.1, we apply a correction of 0.1 km s-1 to this systemic velocity to compare it to the APEX spectra. The self-absorption dip of the optically thick CS 2−1 transition has a velocity of 4.50 ± 0.05 km s-1, which gives a velocity shift of 0.20 ± 0.05 km s-1. Using the corrected value of the systemic velocity we derive a velocity shift of 0.18 ± 0.05 km s-1 for the optically thick HCO+ 3−2 line, whose absorption dip has a velocity of 4.58 ± 0.06 km s-1. Since the self-absorption dips are produced by the outer parts of the envelope where the opacity of the CS and HCO+ lines becomes unity, this observed redshift points to the fact that the outer layers of Cha-MMS1 undergo inward motions with velocities of the order of 0.2 km s-1.
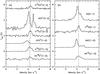 |
Fig. 8 Spectra obtained toward the central position of Cha-MMS1 in the optically thick CS 2−1, HCO+ 3−2, HCO+ 1−0, and HNC 1−0 transitions and the low optical depth C34S 2−1, H13CO+ 1−0, H13CO+ 3−2, H13CO+ 4−3, HC18O+ 1−0, and HN13C 1−0 transitions. The dashed line corresponds to the systemic velocity derived from a seven-component hyperfine fit to the N2H+ 1−0 multiplet (4.3 km s-1). It is corrected to 4.4 km s-1 for the APEX transitions HCO+ 3−2, H13CO+ 3−2, and H13CO+ 4−3 (see Sect. 3.2.1). |
3.6. Overview of CHAMP+ data
We probed Cha-MMS1 in the CO 6−5, CO 7−6, and 13CO 6−5 molecular transitions with the APEX CHAMP+ 2 × 7-pixel heterodyne receiver array in order to search for emission indicative of outflowing material. Figure 9 shows position maps of all spectra obtained for each transition. The CO 6−5 and 7−6 spectra along the filament have slightly higher intensities toward the north-east as opposed to the south-west. This could be due to contamination from the outflow of the Class I object IRAS 11051-7706 lying close to Cha-MMS1 at the north-east direction (Belloche et al. 2006), and it is further discussed in Sect. 5.2.
4. Radiative transfer modelling
We used the Monte Carlo radiative transfer code MAPYSO (Blinder 1997; Belloche et al. 2002), which assumes spherical symmetry, to derive kinematic constraints on the dense core Cha-MMS1 by modelling the observed spectra. We modelled the emission of three sets of molecules, namely CS, HCO+, and CO with their respective isotopologues.
We model all molecular transitions with the same density, temperature, and turbulence distributions, as described below. These distributions are shown in Figs. 11a, c, and e, respectively. Given the shape of the continuum emission, we assume that Cha-MMS1 is embedded in a filament and that the physical structure perpendicular to the filament in the plane of the sky is similar to the structure along the line-of-sight. We thus model the spectra taken along the direction perpendicular to the filament in addition to the central spectra. We perform the fit optimisation by eye, by focussing on three main features of the spectra: the peak temperature, the position of the self-absorption dip (when there is one), and the linewidth of each spectrum.
4.1. Input parameters
4.1.1. Temperature profile
Using the internal luminosity derived in Sect. 3.1 we can constrain the inner dust temperature profile of the source, which
we assume is dominated by the central heating. Following Terebey et al. (1993) and Motte &
André (2001), we assume that in the inner part the dust temperature behaves as
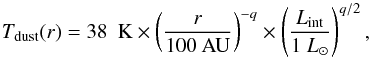 (7)with
(7)with
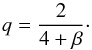 (8)The constant
β depends on the dust properties and the values 2, 1.5, and 1 are
often used for molecular clouds, protostellar envelopes, and protostellar disks,
respectively. Because this source is possibly at a very early evolutionary stage,
perhaps before the protostellar phase, we adopt an intermediate value between the first
two, 1.85, which gives q ~ 0.34.
(8)The constant
β depends on the dust properties and the values 2, 1.5, and 1 are
often used for molecular clouds, protostellar envelopes, and protostellar disks,
respectively. Because this source is possibly at a very early evolutionary stage,
perhaps before the protostellar phase, we adopt an intermediate value between the first
two, 1.85, which gives q ~ 0.34.
We assume that the gas and dust are coupled well for densities above ~105 cm-3 (Lesaffre et al. 2005), and we use Eq. (7) to define the kinetic temperature in the inner part. We assume a uniform temperature in the outer parts. We find from the modelling that a uniform kinetic temperature of 9 K produces spectra in agreement with the observations. More specifically, the optically thick CS 2−1 line sets the major constraints on the outer kinetic temperature, since this transition shows a strong asymmetry in the blue-red peak strengths (infall signature) with the blue peak stronger by about a factor of ~2. Its absorption dip and asymmetry require uniform outer temperatures to be well fitted. The radius at which the temperature drops to 9 K is fixed by the central heating (Eq. (7)).
4.1.2. Density profile
We use a power-law density profile with an external radius of 60 000 AU. We adopt a spherically symmetric r-2 density profile for the envelope, as is expected from models of spherical gravitational collapse of non-singular isothermal spheres during the core formation either without the effect of magnetic fields (e.g., Masunaga et al. 1998; Foster & Chevalier 1993; Bodenheimer & Sweigart 1968; Larson 1969; Penston 1969) or from models of axisymmetric, isothermal cloud contraction with magnetic fields (e.g., Tassis & Mouschovias 2007; Fiedler & Mouschovias 1993). Very recently, a 3D radiation hydrodynamic simulation of the collapse of an axisymmetric cloud core towards the formation of a first core led to a r-2 density distribution for the first core for r > 100 AU (Furuya et al. 2012). Since we do not resolve the inner r < 700 AU of Cha-MMS1, a simple, r-2 density profile is probably adequate for describing the envelope of Cha-MMS1.
 |
Fig. 9 CO 6−5, CO 7−6, and 13CO 6−5 spectra observed with the APEX telescope. The central position of Cha-MMS1 is at (0,0). The directions parallel and perpendicular to the filament are shown as dashed and dotted arrows, respectively. The central spectra of the three transitions are plotted in the rightmost panel on the scale of the main-beam brightness temperature. The dotted line shows the systemic velocity of Cha-MMS1 derived from a seven-component hyperfine fit to the N2H+ 1−0 multiplet and corrected for the 0.1 km s-1 velocity shift (see Sect. 3.2.1). |
Such density profiles have also been observed in dense cores. Density distributions close to a r-2 profile were derived for the starless cores L1498 and L1517B in Taurus (Tafalla et al. 2004). Bacmann et al. (2000) and Alves et al. (2001) also concluded that low-mass prestellar cores are described well by a density profile following an r-2 dependence, but excluding the sharp edges and flattened centre. Sharp density edges have been observed at the edges of starless cores, with exponents as steep as r-3.5 (Nielbock et al. 2012). For simplicity, we do not account for steep outer density slopes.
The mass of Cha-MMS1 was derived from the LABOCA 870 μm continuum map of the Chamaeleon I cloud. The flux density measured within a radius of 3750 AU gives a mass of ~1.44 M⊙ for the Cha-MMS1 core (Belloche et al. 2011a). We use this value to scale our input density profile.
4.1.3. Inner turbulent broadening and isotopic ratios
In Sect. 3.4, we found that the non-thermal dispersion for all the observed transitions shows no significant spatial variations for radii up to ~12 500 AU (~0.06 pc). We adopt a uniform turbulent broadening up to this radius and keep the shape of the outer profile for 12 500 AU < r < 60 000 AU (~0.3 pc) as a free parameter. The non-thermal dispersion appears to be uniform on scales ~0.1 pc within the interiors of dense cores (e.g., Barranco & Goodman 1998; Goodman et al. 1998) with increasing dispersion on larger scales (e.g., Goodman et al. 1998) that follows the Larson scaling law (Larson 1981).
We assume the local ISM abundance isotopic ratios: 12C/13C ~ 77 (Wilson & Rood 1994), 32S/34S ~ 22 (Frerking et al. 1980), 16O/18O ~ 560 (Wilson & Rood 1994), and 18O/17O ~ 4.11 (Wouterloot et al. 2005).
4.2. CS Modelling
The following transitions of CS and its isotopologues were modelled: CS 2−1 (Mopra), C34S 2−1 (Mopra), and CS 5−4 (APEX). 13CS 2−1 and C33S 2−1 were only used as upper limits due to their non-detections and are not presented here. We perform the modelling of the spectra for the direction perpendicular to the filament, along which five positions were observed for CS 5−4 and seven for the other transitions. Figure 10 shows one of the “best fit” models (hereafter “MCS” model) for the CS molecular transitions. The distributions of density, abundance, kinetic temperature, radial velocity, and turbulent broadening characterising “MCS” can be seen in Fig. 11.
 |
Fig. 10 Best fit model “MCS” for the CS and C34S molecular transitions. The black lines represent the observed spectra, while the red spectra are generated by the MAPYSO radiative transfer code. The dotted line shows the systemic velocity of Cha-MMS1 derived from a seven-component hyperfine fit to the N2H+ 1−0 multiplet. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). The angular separation of the different positions with respect to the central spectrum is shown on top of the respective spectra. The model assumes spherical symmetry, so the model spectra at symmetric positions are identical. The telescope used for conducting the obervations is shown at the leftmost box of each row. The spectra from left to right correspond to the south-east to north-west direction perpendicular to the filament. |
 |
Fig. 11 Input profiles for the best-fit models “MCS”, “MHCOP”, and “MCO”: a) density, b) CS (solid), HCO+ (dash-dot), and CO (dot) abundance; c) kinetic temperature; d) radial velocity; and e) turbulent linewidth. |
4.2.1. Abundance
The outer and inner abundances are constrained by the CS 2−1 absorption dip and the CS 5−4 intensity, respectively. In between, the abundance distribution is constrained by the C34S 2−1 spectra, which require a CS abundance of 2.5 × 10-9 at a radius of 8000 AU. The depth of the CS 2−1 self-absorption is mostly determined by the outer abundance distribution of the low-excitation material at radii ~10 000 AU < r < 30 000 AU. We do not constrain the CS abundance at radii larger than 30 000 AU. CS 5−4 probes the innermost parts of the core and sets constraints on the abundance at radii r < 2000 AU. As a result, the CS abundance increases up to 8000 AU and drops by a factor of 4 in the outer parts. As long as the temperature is low enough, CS and other sulphur-bearing molecules are expected to be strongly depleted towards the centre of dense cores where the density is high (e.g., Tafalla et al. 2004; Bergin et al. 2001). Depletion occurs due to the freezing-out process onto the dust grains (e.g., Tafalla et al. 2002; Stahler & Yen 2010) and observations of starless cores, such as L1544, or Class 0 protostars, such as IRAM 04191, also showed CS depletion towards the centre by a factor of ~20 (Tafalla et al. 2002; Belloche et al. 2002).
4.2.2. Turbulence
We keep the turbulent broadening uniform at 0.3 km s-1 (FWHM) up to ~12 600 AU as we see no clear variations in our diagrams of turbulent linewidth versus position up to this radius (see Fig. 6). We then let the turbulent linewidth double its value from 12 600 AU to the outermost envelope radius at 60 000 AU. This is a constraint we derive from both the width of the CS 2−1 absorption dip and the CO 3−2 modelling (see Sect. 4.4).
4.2.3. Opacities and excitation temperatures
All transitions of CS and its isotopologue are optically thin on all positions apart from CS 2−1 (see Fig. 12). The model excitation temperatures are shown in Fig. 13. CS 2−1, C34S 2−1, and CS 5−4 are thermalised up to ~2500 AU, ~1500 AU, and ~400 AU, respectively.
4.2.4. Discrepancies between model and observations
The model reproduces the absorption dip of CS 2−1 well for all positions, but, the intensity of the blue peak at the central position and at − 17.5′′ is higher compared to the observations. The discrepancy is not that strong at + 17.5′′, and the model fits the peak temperature well at the outer positions, i.e., ± 35′′ and ± 52.5′′. A peculiarity of the observed CS 2−1 spectra is the existence of velocity wings at all positions. The velocity wings are not reproduced by the model and may partly arise from extended emission stemming from the outflow of the nearby Class I object (see Fig. 1). It is, however, unclear whether this can explain both the redshifted and blueshifted wing emissions. The C34S 2−1 model is weaker at the outermost ± 52.5′′ positions while matching the intensity of the spectra at the other positions well. CS 5−4, on the other hand, shows one more peculiar feature: the model does not account for the excess of redshifted emission that is prominent toward the central position.
4.2.5. Testing the infall velocity field
Despite the discrepancies, the “MCS” model provides a consistent overall fit to the data. As we are interested in the infall velocity structure of the core we input different infall velocity profiles to “MCS” in order to test and constrain its value. The linewidths of the low optical depth lines and the position of the absorption dip of the optically thick lines can be used to place relatively tight constraints on the velocity structure of the source. We first test different uniform infall velocity profiles and then velocity profiles with a free-fall, power-law (v ∝ r-0.5) dependence in the inner parts.
In the case of uniform velocities, the best agreement is found for velocities in the range 0.1 km s-1−0.2 km s-1. For velocities less than 0.1 km s-1 the peak asymmetry of the CS 2−1 spectra reduces considerably with the red peak becoming too strong in comparison to the observations. In addition, the linewidths of both the CS 2−1 and C34S 2−1 lines become narrower than the observed linewidths. In contrast, when the infall velocities exceed 0.2 km s-1, the blue peak of CS 2−1 becomes much broader and the central C34S 2−1 spectrum starts showing a double-peaked structure (also seen in the opacity profile), which is inconsistent with the observations.
We then apply a power law with an exponent of −0.5 for the inner parts at gradually increasing radii while keeping the velocity constant at the outer parts in order to test whether higher inner velocities are consistent with the observations. From now on, we refer to the radius at which the velocity profile changes from a power-law to a uniform r dependence as the “breakpoint”. Our tests suggest that such a power law velocity distribution matches the observations for radii up to 9000 AU for velocities in the range of vbreak = 0.1 km s-1−0.2 km s-1, after which we let the velocity remain uniform. For breakpoint radii exceeding 9000 AU, the wide spatial range of high infall velocities produces broader CS 2−1 linewidths and stronger red peak intensities than the observed spectra. The CS 5−4 and C34S 2−1 models also start showing a double-peaked structure, which disagrees with the observations.
Therefore, the CS modelling suggests that the core’s envelope is infalling with subsonic to transonic outer velocities of 0.1 km s-1−0.2 km s-1. Inner free-fall power-law velocity distributions are possible with breakpoints at r ≤ 9000 AU, with infall velocities reaching supersonic values at r ≤ 3500 AU in this case. We do not constrain the infall velocity structure of the envelope for radii greater than 30 000 AU. The infalling motions at the outer parts of the envelope (<30 000 AU) contradict the Shu (1977) assumption of a static envelope in the inside-out collapse model.
The radial velocity structure of the “MCS” model shown in Fig. 11 corresponds to an r-0.5 dependence for radii <3000 AU, and a uniform infall velocity of 0.15 km s-1 for 3000 AU ≤ r ≤ 60 000 AU (see Fig. 11d).
4.3. HCO+ Modelling
The following molecular transitions of HCO+ and its isotopologues were modelled: HCO+ 1−0, HCO+ 3−2, H13CO+ 1−0, H13CO+ 3−2, H13CO+ 4−3, and HC18O+ 1−0. The 1−0 transitions were observed with Mopra, the other ones with APEX. We have central position spectra for HCO+, H13CO+, and HC18O+ 1−0, while HCO+ and H13CO+ 3−2 were also observed at seven and H13CO+ 4−3 at five positions along the direction perpendicular to the filament (see Fig. 1). One of the models that provides a good fit to the data is shown in Fig. 14, and hereafter we refer to it as “MHCOP”. The distributions of density, abundance, kinetic temperature, radial velocity, and turbulent broadening characterising “MHCOP” can be seen in Fig. 11.
4.3.1. Abundance
We take the following observational constraints into account to define the input abundance profile (Fig. 11b). The inner profile is constrained by the intensities of the optically thin H13CO+ 3−2, H13CO+ 4−3, and HC18O+ 1−0 spectra.
A decrease in the HCO+ abundance by a factor of ~20 from a radius of 20 000 AU down to the centre fits the intensities of the optically thin lines well. As a test, we extended the plateau of uniform outer abundance towards the centre to radii r < 20 000 AU, and found that this produced model intensities that were too high for the optically thin spectra. By varying the abundance profile between 20 000 AU and 60 000 AU, we conclude that we do not constrain the outer, r ≥ 20 000 AU, abundance profile with our current HCO+ transitions. We therefore use a uniform outer abundance for r ≥ 20 000 AU as an approximation.
4.3.2. Opacities and excitation temperatures
Figures 15 and 16 show the resulting opacity and excitation temperature profiles of the model for each transition. HCO+ 3−2, HCO+ 1−0, and H13CO+ 1−0 are optically thick, while H13CO+ 4−3, H13CO+ 3−2, and HC18O+ 1−0 are in the optically thin range. HCO+ 1−0 is thermalised up to ~10 000 AU and HCO+ 3−2, H13CO+ 1−0, and HC18O+ 1−0 are thermalised up to ~3000 AU. H13CO+ 4−3 and H13CO+ 3−2 cease to be thermalised for radii larger than ~500 AU. HCO+ 1−0 is thermalised up to a much larger radius than H13CO+ and HC18O+ 1−0 because of its much higher optical depth.
4.3.3. Discrepancies between model and observations
One of the major discrepancies between model and observations is the failure of the model to reproduce the emission of the red peak of the HCO+ 3−2 transition. Raising the outer temperature of the core does not have a significant effect on the red peak of the model spectrum since this transition is not thermally excited at radii larger than 3000 AU. This disagreement might then be a density effect instead, if the true density profile deviates from the spherically symmetric, r-2 dependence. The observed H13CO+ 3−2 spectra show higher intensities in the north-west (− 11.4′′, − 22.8′′, − 34.2′′) direction than in the south-east direction. H13CO+ 3−2 is not the only transition that does not peak at the central position. Higher intensities toward the north-west are also seen in our N2H+ 1−0 spectra. The N2H+ 1−0 emission in the maps presented by Ladd et al. (2011) is similarly not peaked at Cha-MMS1. “MHCOP” fits the spectra on the north-west side well, but it does not fit the excess emission on the south-east side. We cannot yet pinpoint the reason for this intensity difference on each side of the central spectrum. H13CO+ 4−3 and the central spectrum of HC18O+ 1−0 are reproduced rather well, as is H13CO+ 1−0, even though the exact lineshape of the observed spectrum is not reproduced. The observed H13CO+ 1−0 is broader than the model at the redshifted part of the spectrum, like CS 5−4 (see Sect. 4.2).
The model strongly overestimates the peak temperature of the observed HCO+ 1−0 transition which is even weaker than H13CO+ 1−0. HCO+ 1−0 is very optically thick and thermalised up to large radii. It is certainly affected by significant absorption from the low-density material in the ambient cloud at r ≥ 60 000 AU, which is not included in the modelling.
4.3.4. Testing the infall velocity field
There is a range of infall velocity profiles that give consistent fits to the data. In the case of uniform, constant velocities up to 60 000 AU the range 0.1 km s-1−0.2 km s-1 agrees well with the observations. For values higher than 0.2 km s-1 the HCO+ 3−2, H13CO+ 3−2, H13CO+ 4−3, and HC18O+ 1−0 spectra become too broad while for velocities lower than 0.1 km s-1 the absorption dip is not redshifted enough. We then tested a velocity profile described by a power law following an r-0.5 dependence in the inner part of the core up to a certain radius, after which the infall velocity remains uniform, as we did for CS. For a breakpoint at 3000 AU infall velocities of vbreak = 0.1 km s-1−0.2 km s-1 give consistent fits. When we increase the breakpoint radius, the range of consistent infall velocities decreases. At 6000 AU the breakpoint velocities still consistent with the data are 0.1 km s-1−0.15 km s-1 and at 9000 AU, 0.1 km s-1. Overall, inner power-law profiles at radii larger than 9000 AU produce spectra with too broad linewidths for all transitions, apart from H13CO+ 1−0, and inconsistent double-peaked spectra for H13CO+ 3−2, H13CO+ 4−3, and HC18O+ 1−0. We also varied the outer infall velocity profile to check whether it is constrained by our data. To accomplish this we let the infall velocity drop sharply to zero at gradually increasing radii and found that the model does not constrain the velocities for radii greater than 35 000 AU. Even though the dip in the HCO+3−2 model spectrum in Fig. 14 is not as redshifted as in the observed spectrum, a velocity drop to zero at radii smaller than 35 000 AU makes this discrepancy even stronger by producing model spectra with almost no apparent redshift of the HCO+3−2 absorption dip. We therefore cannot accurately constrain the infall velocity structure of the core for r ≥ 35 000 AU from the HCO+ modelling.
The velocity distribution corresponding to model “MHCOP” is the same as the one of “MCS” (see Fig. 11d).
4.4. CO Modelling
We modelled the following molecular transitions of CO and its isotopologues: CO 3−2, CO 4−3, CO 6−5, CO 7−6, 13CO 6−5, and C18O 2−1. Figure 17 shows one of the models that fits the data relatively well, hereafter “MCO”. The distributions of density, abundance, kinetic temperature, radial velocity, and turbulent broadening characterising “MCO” can be seen in Fig. 11.
4.4.1. Abundance
The abundance profile of CO down to a radius of ~1000 AU is mainly constrained by the intensity variations of the C18O and C17O 2−1 transitions. The ratio of the C17O and C18O 2−1 integrated intensities yields C18O 2−1 opacities ranging from ~1.6 toward the centre to less than ~0.5 toward the outer parts (see Appendix B.1). We take these opacity values into account to further constrain our model. Finally, the optically thin 13CO 6−5 transition, which traces higher densities and is spatially better resolved, sets strong constraints on the abundance in the inner parts of the envelope (r < 1500 AU). Overall, we obtain the abundance profile shown in Fig. 11b, with a maximum of 5 × 10-5 at 9000 AU, depletion by a factor of ~10 from ~9000 AU to ~700 AU, and also a decrease in the abundance by a factor ~7 from ~9000 AU to ~20 000 AU, in order to match the lower outer C18O opacity. We constrain the CO abundance up to 20 000 AU. CO depletion has previously been observed towards the inner parts of various prestellar cores (e.g., Bacmann et al. 2002; Christie et al. 2012).
Furuya et al. (2012) coupled a gas-grain chemical network to 3D radiation hydrodynamic simulations to derive molecular abundances at the first core stage. In their model, CO desorbs to the gas phase at a temperature of 25 K, somewhat higher than the commonly used 20 K value, due to the high density of the first-core envelope. The density at which their simulation reaches 25 K is ~109 cm-3, which is similar in our model. We tested the effect of an inner CO desorption region at r ≤ 54 AU (from Eq. (7)), at which radius the temperature reaches 25 K in our model. We used an inner CO abundance of 1 × 10-4 for the desorption region, which is consistent with the predicted abundance for the first core stage (Furuya et al. 2012). At radii larger than 54 AU, and therefore at temperatures T < 25 K, CO depletion takes place. We found that the model is not sensitive to the abundance within the inner 54 AU and the presence or the absence of a desorption region on these smaller scales has no apparent effect on the spectra. Therefore, we do not account for inner desorption.
4.4.2. Turbulence
The self-absorption of the CO 3−2 spectra is very broad, suggesting a large turbulent broadening in the outer parts (radii r ≥ 12 500 AU). We therefore raise it by a factor of ~2 from 12 500 AU to 60 000 AU. In this way, the blueshifted side of the self-absorption is reproduced well, but the redshifted side of the model is still too narrow. The turbulent broadening is kept uniform for radii r ≤ 12 500 AU (see Fig. 11), as derived in Sect. 3.4.
4.4.3. Model opacities and excitation temperatures
Figures 18 and 19 show the model opacities and excitation temperatures for all the transitions. CO 3−2, CO 4−3, and C18O 2−1 remain thermalised out to ~20 000 AU, ~13 000 AU, and ~9000 AU, respectively, while CO 6−5 and CO 7−6 cease to be thermalised at ~2000 AU. Moreover, all the transitions are optically thick with the exception of 13CO 6−5 at all positions, CO 7−6 at offset positions, and C18O 2−1 at the outermost position (see Fig. 18).
4.4.4. Discrepancies between model and observations
The spectra of CO 3−2 at 15′′, 30′′, 45′′, and 60′′ show strong emission in the blueshifted part of the spectrum, while the spectra at − 15′′, − 30′′, − 45′′, and − 60′′ show much weaker blueshifted emission. Excess emission in the redshifted part of the spectra is also seen at all positions. We expect the outflow of the neighbouring Class I protostar (see Fig. 1) to contaminate the low-density tracers such as CO 3−2, especially at the offset positions, thereby broadening the observed emission. Belloche et al. (2006) presented a CO 3−2 intensity map of the region toward Cha-MMS1 (see Fig. 1 of their paper). The blueshifted emission they show reaches our offset positions, and especially affects the spectra towards the south-east of Cha-MMS1. They also discuss the possible presence of two separate outflows in this region. The highly broadened blue and red peaks of CO 3−2 might partly result due to these outflows if they have a wide opening angle and lie close to the plane of the sky (see Cabrit & Bertout 1990).
The model reproduces the C18O 2−1 emission well, and its opacity, as well as the 13CO 6−5 emission. However, the model fails to reproduce the strong redshifted emission of the CO 6−5 and 7−6 transitions, similar to the CS 5−4 emission. Because these transitions probe regions of high densities, this extra emission may be an indication of additional warmer, high-velocity material in the inner core (see Fig. 10). This emission may stem from a very compact outflow. To address this question, however, we would need to resolve the very inner part of the core on small scales of a few hundred AU (see Sect. 1.1).
4.4.5. Testing the infall velocity field
From the CO modelling we draw the following conclusions on the infall velocity structure across the envelope. We find that uniform infall velocities of up to 0.2 km s-1 give fits relatively consistent with the data. Velocities above 0.2 km s-1 produce C18O 2−1 linewidths that are too broad compared to observed values. We test an inner power-law velocity dependence (v ∝ r-0.5), with uniform outer velocities. We find that the power-law profile is consistent with the observations up to ~6000 AU if the infall velocity is in the range of vbreak = 0.1 km s-1−0.15 km s-1 at this radius, after which it remains constant. A radius of 9000 AU is also consistent when vbreak = 0.1 km s-1 at this breakpoint and onwards. For larger radii the model spectra are much broader than the observed spectra due to the extended spatial range of high inner infall velocities. However, the opacity of the optically thick transition CO 3−2 does not allow us to set constraints on the lower limit of the infall velocity.
The velocity profile that coresponds to the “MCO” model is shown in Fig. 11, and it is identical to the ones used for “MHCOP” and “MCS”.
4.5. Infall velocity distribution of Cha-MMS1: combining modelling results
We obtain slightly different constraints on the infall velocity structure of Cha-MMS1 from the radiative transfer modelling of the CS, HCO+, and CO molecular transitions. We take the envelope of the infall velocity profiles that are consistent with all three datasets as the overall range of possible infall velocities for Cha-MMS1. The consistent velocities are shown as the area enclosed in Fig. 20.
The infall velocity is relatively well constrained over the range of radii 3300 AU to 30 000 AU, with subsonic/transonic velocities in the range 0.1 km s-1 to 0.2 km s-1. Our data do not constrain the velocity field beyond ~30 000 AU. Below 3300 AU, there are more degeneracies, and the spectra are consistent with an increase in the infall velocity as r-0.5, but also with a flat velocity profile, or even a decrease below a radius of ~3000 AU.
 |
Fig. 20 Infall velocity field of the envelope of Cha-MMS1 based on the radiative transfer modelling with MAPYSO. The solid black line corresponds to the velocity profile of the “MCS”, “MHCOP”, and “MCO” models. The dashed lines show the range of velocity fields that are still consistent with the observations. The red solid and dashed curves correspond to the average radial velocity at the equatorial plane of a magnetised FHSC with core masses of 1 M⊙ and 5 M⊙, and ages of 850 yr and 2684 yr, respectively. (Commerçon et al. 2012, see details in Sect. 5.4.2). |
5. Discussion
5.1. Far-infrared emission and luminosity
Recent radiation-MHD simulations predict that strongly or weakly magnetised FHSCs are expected not only to emit at 70 μm but also to produce detectable emission at wavelengths down to 20 μm, especially during the latest phase of their evolution (Commerçon et al. 2012). Previous simulations that found no significant first-core emission below 30 μm−50 μm were either spherical (e.g., Masunaga et al. 1998; Omukai 2007) or did not take the magnetic field into account and used a barotropic equation of state (Saigo & Tomisaka 2011). A first core can therefore also be identified by a Spitzer 24 μm (and 70 μm) detection at late phases if its inclination is less than 60° and there is no detection at wavelengths smaller than 20 μm (Commerçon et al. 2012). As seen in Sect. 3.1, the 24 μm and 70 μm Spitzer fluxes of Cha-MMS1 are consistent with the predictions of the RMHD simulation of Commerçon et al. (2012) for a magnetised FHSC with a normalised mass-to-magnetic-flux ratio of 2 seen at an inclination lower than 60°. The SED of Cha-MMS1 is therefore consistent with Cha-MMS1 being at the FHSC stage. However, if its actual inclination is higher than 60° then Cha-MMS1 would have to be in a more advanced stage (Class 0).
5.2. Outflows
Class 0 protostars usually drive fast, extended, and easily detectable outflows, whereas FHSCs are predicted to drive very compact, slow outflows (see Sect. 1.1). This is a major observational signature that can be used to distinguish between the two and break the degeneracies that remain in their SEDs when their inclination is not known.
A search for a fast, large-scale outflow driven by Cha-MMS1 in CO 3−2 with APEX was negative (Belloche et al. 2006). We observed the CO 6−5, CO 7−6, and 13CO 6−5 transitions in order to search for signs of a compact, unresolved outflow. The modelling of these transitions gave ambiguous, but maybe promising results (see Sect. 4.4). Our model does not reproduce the redshifted part of the CO 6−5 and 7−6 emission, while it fits the C18O 2−1 transition well. This excess emission might point to the presence of unresolved, higher-velocity material at the inner core (see Shinnaga et al. 2009, for a similar case of excess emission in CO 6–5 and 7–6 toward the more evolved protostar L1521F). In addition to this, the CS 5−4 model in Sect. 4.2 shows a similar discrepancy. Its observed spectrum has an excess of redshifted emission that the model fails to reproduce, while it fits the lower-J CS and C34S transitions well. CS 5−4 probes material at higher densities, so that its broad spectrum indicates higher velocity, dense material close to the centre of the core, which cannot be seen with the other, lower density transitions.
Despite hints of the presence of dense, higher velocity material confined to the centre of the core, there is also an alternative explanation. Figure 21 compares the CO 6−5 spectra at the centre and in the north-east direction of the filament (hence toward the nearby Class I outflow) to the central spectrum of CS 5−4. The CO 6−5 red peak emission becomes stronger as we move up along the filament. It peaks at a velocity where CS 5−4 has some wing emission. This suggests that at least part of the excess emission in the CS 5−4 spectrum is not confined to the inner parts of Cha-MMS1 but instead extends towards the nearby Class I outflow lobe. The bulk of the CS 5−4 excess emission, however, peaks at a lower velocity, and it is unclear whether it represents a similar extended component. Higher-angular resolution observations are certainly needed to make any reliable conclusions about the presence of a compact, slow outflow driven by Cha-MMS1.
 |
Fig. 21 Comparison of the CS 5−4 spectrum (solid) toward the central position of Cha-MMS1 and CO 6−5 spectra (dotted) taken at the central position and in the north-east direction toward the nearby Class I protostar. The offset position of each spectrum is given in arcseconds relative to the central position. The CO 6−5 spectra are shifted vertically by a step of 1 K for clarity. The solid vertical line roughly corresponds to the velocity of the CO 6−5 red peak, while the dashed line marks the velocity of the peak of the CS 5−4 excess emission. |
As mentioned in Sect. 4.2.4, all CS 2−1 spectra in Fig. 10 show blueshifted and redshifted wing emissions that are not accounted for by our model. Such wing emissions are even more pronounced in CO 3−2 (Fig. 17), the blueshifted one being clearly associated with emission from the outflow driven by the nearby Class I protostar (Belloche et al. 2006). Hiramatsu et al. (2007) and Ladd et al. (2011) propose that the curved shape of the blue lobe of this outflow is due to its partial interaction with the Cha-MMS1 dense core. This would explain the presence of the extended blueshifted CS 2−1 emission around Cha-MMS1. As recalled by Ladd et al. (2011), the HH objects 49 and 50, which are thought to be associated with this outflow, are redshifted. This suggests that the outflow axis lies close to the plane of the sky and, provided its opening angle is large enough, it could also explain the presence of extended, redshifted, wing emission in CS 2−1 in the vicinity of Cha-MMS1. This emission is, however, difficult to disentangle from the ambient cloud emission in CO 3−2, and it was excluded from the range of velocities used by Belloche et al. (2006) to produce their map of the redshifted outflow lobe.
5.3. Interpretation of the P–V diagrams
Determining the nature of the velocity gradients in position-velocity diagrams is not straightforward because many processes such as rotation, infall, outflow, and turbulence can influence their shape (e.g., Tobin et al. 2012; Burkert & Bodenheimer 2000). Tobin et al. (2012) suggest that projected infall in filamentary protostellar envelopes can dominate the velocity gradients for scales larger than 1000 AU. Burkert & Bodenheimer (2000) show that turbulence can produce velocity gradients that can be mistaken for rotation. In Sect. 3.3 we found no significant velocity gradient in the direction parallel to the filament in which Cha-MMS1 is embedded, but a significant one in the perpendicular direction. If we can approximate the filamentary geometry of the continuum emission as axisymmetric, and if infall plays a significant role in producing these velocity shifts, we would expect to see its contribution in the P−V diagrams in the filament direction. That this is not the case enhances the probability that the velocity gradients we observe perpendicular to the filament are due to rotation.
The P−V diagrams of C18O 2−1 and C17O 2−1 cover almost the same extent as the width of the filament (~0.1 pc). As the outermost positions of C18O 2−1 and C17O 2−1 reach the edges of the filament (see Fig. 1d), we cannot exclude the possibility that turbulent motions influence the shape of the velocity gradients on these scales. However, the “S” shape of the C18O 2−1 and C17O 2−1 P−V curve at the outermost positions on either side of the central position is relatively symmetric (see Fig. 5c) and therefore, probably indicative of rotation rather than random turbulent motions. If the interpretation in terms of rotation is valid, then the “S” shape of the P−V curve indicates that the filament is rotating in a differential manner, the outer parts (r > 8000 AU) rotating more slowly than the inner parts. The turn-over of the C18O and C17O P−V curves occurs very close to the edge of the filament as traced with LABOCA. We speculate that this behaviour is related to the formation process of the filament, but the physics of this process would have to be investigated.
We obtained a velocity gradient of 3.1 ± 0.1 km s-1 pc-1 over r < 8000 AU for Cha-MMS1. This is similar to the velocity gradients often found in dense cores and attributed to rotation, with magnitude typically ranging from ~0.3 km s-1 pc-1 to ~6 km s-1 pc-1 on typical scales of ~0.1 pc (e.g., Goodman et al. 1993; Caselli et al. 2002; Belloche et al. 2002; Tafalla et al. 2004). The “S” shape of the C17O 2−1 and C18O 2−1 P−V diagrams of Cha-MMS1 is very reminiscent of the P−V diagrams of the young Class 0 protostar IRAM 04191 located in Taurus. Belloche et al. (2002) derive a rotational angular velocity of 9 ± 3 km s-1 pc-1 at a radius of 2800 AU and 1.9 ± 0.2 km s-1 pc-1 at 7000 AU. They conclude that IRAM 04191 shows clear signs of differential rotation in the envelope. On scales of ~1000 AU, the envelope rotates even faster (Belloche & André 2004). As mentioned in the previous paragraph, the P−V diagram of Cha-MMS1 is also consistent with differential rotation, but a major difference compared to IRAM 04191 is that this concerns only the outer parts of the envelope (r > 8000 AU). At smaller radii down to ~4000 AU, the velocity profile is consistent with solid-body rotation. However, a puzzling feature of the P−V diagrams of Cha-MMS1 is the even flatter velocity gradient in the inner parts of the envelope below 4000 AU, with an amplitude lower than 2 km s-1 pc-1.
If the velocity gradients really trace rotation, then the envelope of Cha-MMS1 has a very peculiar rotational structure: the inner parts rotate more slowly than the bulk of the envelope, and the outer parts also rotate more slowly. A collapsing, magnetised core is expected to have an angular velocity increasing toward the centre (Basu & Mouschovias 1995), the exact shape of the profile depending on the initial angular momentum distribution. Since we see evidence of infall motions in the envelope of Cha-MMS1, its peculiar rotational structure suggests that an efficient mechanism removing angular momentum during the collapse is at work over the range of radii 2000 AU to 8000 AU. It would be interesting to investigate whether magnetic braking is efficient enough to account for this angular momentum removal in Cha-MMS1. Measuring the magnetic field structures and ionisation levels of the Cha-MMS1 and IRAM 04191 envelopes would then be necessary to compare the two sources and understand why they behave so differently in terms of rotation.
5.3.1. Centrifugal acceleration and rotational energy
If we interpret the velocity gradients in the P−V
diagrams as rotation, then we can estimate the dynamical importance of rotation for
Cha-MMS1. We assume solid-body rotation for the inner envelope at
r < 8000 AU and an inclination of the
rotation axis in the range 45°−60°, as derived in Sect. 3.1. The angular velocity then ranges from 4.4 km
s-1 pc-1 to 3.6 ± 0.1 km s-1 pc-1. We
compute the centrifugal acceleration and the local gravitational field as
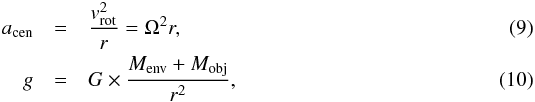 where
acen, vrot, Ω,
g, G, Menv,
Mobj, and r are the centrifugal
acceleration, the rotational velocity, the angular velocity, the gravitational
acceleration, the gravitational constant, the envelope mass, the mass of the central
object, and the radius, respectively. We assume that the envelope mass is proportional
to the radius (density proportional to r-2) and that a mass
of 1.44 M⊙ is enclosed within a radius of 3750 AU, as
derived from the LABOCA 870 μm dust continuum map (Belloche et al. 2011a).
where
acen, vrot, Ω,
g, G, Menv,
Mobj, and r are the centrifugal
acceleration, the rotational velocity, the angular velocity, the gravitational
acceleration, the gravitational constant, the envelope mass, the mass of the central
object, and the radius, respectively. We assume that the envelope mass is proportional
to the radius (density proportional to r-2) and that a mass
of 1.44 M⊙ is enclosed within a radius of 3750 AU, as
derived from the LABOCA 870 μm dust continuum map (Belloche et al. 2011a).
Figure 22 shows the variation of acen/g as a function of radius. Within the framework of our assumptions, the centrifugal acceleration represents at most 20% of the gravitational acceleration. Thus rotation does not provide significant support to the envelope on scales of a few thousand AU. A similar conclusion was drawn by, say, Caselli et al. (2002) for their sample of dense cores, while Belloche et al. (2002) found that the centrifugal acceleration was a sizeable fraction of the gravitational acceleration on such scales in IRAM 04191 (up to ~40%).
The ratio of rotational kinetic energy to the core’s gravitational energy for a
centrally peaked r-2 density profile,
βrot, is given by (Goodman
et al. 1993): 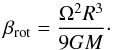 (11)We obtain
values of βrot ~ 0.02 and ~0.006 at 8000 AU for inclinations
of 30° and 60° degrees, respectively.
(11)We obtain
values of βrot ~ 0.02 and ~0.006 at 8000 AU for inclinations
of 30° and 60° degrees, respectively.
 |
Fig. 22 Ratio of centrifugal to gravitational accelerations for the inner part of Cha-MMS1 that may be undergoing solid-body rotation. The upper and lower curves are for an inclination of 30° and 60°, respectively. |
5.4. Implications of the infall velocity structure of Cha-MMS1
In this section we compare the infall velocity distribution of Cha-MMS1 with predictions from theory and observations of other collapsing cores. The number of uncertainties involved is large, both in constraining the velocity profile of Cha-MMS1 from the radiative transfer modelling, as well as in the various existent theoretical collapse models in terms of initial and boundary conditions, and the inclusion or omission of either magnetic fields or rotation. Therefore, a comparison of our source with theoretical models is not straightforward and we only aim to qualitatively discuss which collapse models provide better agreement with the infall profile we derived for Cha-MMS1.
5.4.1. Infall in Cha-MMS1 and in other observed cores
Figure 20 shows the infall velocities consistent with the envelope of Cha-MMS1 as derived from the radiative transfer modelling in Sect. 4. We can discern two distinct regimes in terms of the envelope motions of Cha-MMS1, one below 3300 AU and one within 3300 AU ≤ r ≤ 30 000 AU. At radii larger than 3300 AU we constrain the velocity profile of Cha-MMS1 better (more tightly). The velocities are sub- to transonic within the range of 0.1 km s-1−0.2 km s-1. At radii below 3300 AU, where the model degeneracies are greater, Cha-MMS1 is consistent both with increasing and decreasing central velocities, ranging from 0.04 km s-1 to 0.6 km s-1. Therefore, the inner (r < 3300 AU) envelope is characterised by velocities that can reach supersonic values compared to the outer (r > 3300 AU), more quiescent regions.
We also found that an inner, free-fall velocity distribution proportional to
r-0.5 is consistent with the envelope of Cha-MMS1 with an
upper limit of r ~ 9000 AU. If we assume that the latter radius
signifies the distance that the reflected expansion wave has so far covered while
travelling outwards at the speed of sound, as described in the inside-out collapse
scenario (Shu 1977), then we can estimate an
upper limit to the age of Cha-MMS1 as 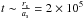 years or 0.2 Myr.
The sound speed, as ~ 0.2 km s-1, is computed for
a temperature of 9 K and assumes isothermality. In our models we have an isothermal
temperature of 9 K only for r > 2000 AU, so
this condition does not hold for the very inner radii. However, we only use the derived
value as a crude estimate. Since this lifetime is an upper limit, it is consistent with
both a first core (see Sect. 1.1 for FHSC
lifetimes) or a Class 0 protostar. The prestellar phase lifetime is estimated to be ~0.5
Myr (Evans et al. 2009), and Class 0 objects have
estimated lifetimes ranging from ~4−9 × 104 yr (Maury et al. 2011) to ~1.6 × 105 yr (Evans et al. 2009).
years or 0.2 Myr.
The sound speed, as ~ 0.2 km s-1, is computed for
a temperature of 9 K and assumes isothermality. In our models we have an isothermal
temperature of 9 K only for r > 2000 AU, so
this condition does not hold for the very inner radii. However, we only use the derived
value as a crude estimate. Since this lifetime is an upper limit, it is consistent with
both a first core (see Sect. 1.1 for FHSC
lifetimes) or a Class 0 protostar. The prestellar phase lifetime is estimated to be ~0.5
Myr (Evans et al. 2009), and Class 0 objects have
estimated lifetimes ranging from ~4−9 × 104 yr (Maury et al. 2011) to ~1.6 × 105 yr (Evans et al. 2009).
Belloche et al. (2002) similarly performed radiative transfer modelling of their molecular transitions towards the young Class 0 IRAM 04191 protostar using the MAPYSO code. They obtained an infall velocity of 0.15 km s-1 at a radius of 1500 AU and 0.1 km s-1 up to ~11 000 AU for their “best” fit. Their range of consistent infall velocities is similar to ours, albeit better constrained at small radii. For r ≥ 2000 AU they find infall velocities in the range of ~0.07 and ~0.15 km s-1, similar to the range 0.1 km s-1−0.2 km s-1 that we obtain for Cha-MMS1 at r ≥ 3300 AU. Nevertheless, they constrain the inner r ≤ 3000 AU velocity profile to that of a power law, whereas in the case of Cha-MMS1 power law, uniform and decreasing velocity distributions are consistent with our data below 3300 AU. Therefore, the infall velocity structures of both Cha-MMS1 and IRAM 04191 cover a similar range of velocities for r > 3000 AU, with Cha-MMS1 being additionally consistent with a wider range of velocity profiles at small radii. The flat, or decreasing velocity distributions at the inner core of Cha-MMS1 could represent a younger evolutionary phase than that of a protostar, if central free-fall has not yet taken place on these scales. The age of IRAM 04191 was estimated to be ≤3 × 104 yr, assuming 2000 AU is the radius below which there is a free fall velocity field structure, while we previously estimated an age of ≤2 × 105 yr for Cha-MMS1.
The infall velocities we derive are mostly within the sub- to transonic range for r ≥ 3300 AU (≥0.02 pc). Lee et al. (1999) found subsonic inward velocities of 0.04 km s-1−0.1 km s-1 for a sample of 17 starless cores showing evidence of infall motions. L1544 is one of the starless cores that has been extensively studied (e.g., Tafalla et al. 1998; Williams et al. 1999). These studies have shown that L1544 is undergoing inward motions with velocities up to ~0.1 km s-1 over ~0.1 pc. Such extended inward velocities imply that the velocity fields of Cha-MMS1, like that of L1544, are consistent with each other but inconsistent with the static SIS Shu (1977) model.
5.4.2. Comparison to theoretical models
In this section, we compare the infall velocity field derived for Cha-MMS1 with the velocities predicted by theoretical models. We resolve radii r ≥ 700 AU from our observations and find an infall velocity range of ~0.05 km s-1−0.5 km s-1 for this radius (r ~ 700 AU). We used 3D radiation-magneto-hydrodynamic models to extract the radial velocity structure for a 1 M⊙ (MU2 model; Commerçon et al. 2012) and 5 M⊙ dense core (Fig. 20). The mass estimate of Cha-MMS1 from continuum observations yields 1.44 M⊙ within a radius of 3750 AU (Belloche et al. 2011a).
Both models have a normalised mass-to-magnetic-flux ratio of 2. They employ an azimuthal density perturbation to assist fragmentation. The ratio of thermal to gravitational energy is 0.37 for the 1 M⊙ model and 0.35 for the 5 M⊙ model, the ratio of rotational to gravitational energies 0.045 and 0.03 (~2 and ~1.5 times greater than the upper limit of Cha-MMS1’s βrot, respectively), and the initial temperatures are 11 K and 10 K, respectively. Their corresponding initial radii are 3300 AU and 20 000 AU. The density profile of the 1 M⊙ case is initially uniform, whereas it scales as r-2 at the outer radii in the 5 M⊙ case. The 1 M⊙ and 5 M⊙ models are denser at the equatorial plane of the cores by a factor of ~3 and ~4, respectively, compared to the density profile we used for Cha-MMS1 in Sect. 4.
The models predict the evolution of the 24 μm and 70 μm flux densities during the first core phase. The 3D radiative transfer code RADMC-3D by Dullemond8 is used for the post-processing of the RMHD calculations (see Commerçon et al. 2012 for more details). The flux densities of Cha-MMS1 are, within a factor of ~2, consistent with a first core age of ~850 yr based on the 1 M⊙ model, and 2680 yr based on the 5 M⊙ model (see Sect. 3.1.2). The average radial velocity distribution of both first-core models close to the equatorial plane (to avoid outflow contamination) are shown in Fig. 20. We can only explore the velocity profile of the 1 M⊙ model for r < 2500 AU due to its smaller initial radius (3300 AU). The radial velocities it predicts up to ~2000 AU are within the range of velocities we constrain for Cha-MMS1. For r > 2000 AU the velocities decrease to zero as we approach the boundary of the core. The average velocity extracted from the 5 M⊙ model exhibits a velocity profile that follows the upper limit of Cha-MMS1’s velocity range up to ~8000 AU, and is within this range for 8000 AU < r < 12 000 AU. The slightly higher velocities predicted by the model compared to our upper limit for Cha-MMS1 may be due to the higher densities of the model.The velocity dip that peaks at ~18 000 AU in Fig. 20 is a remnant of a small initial expansion at the initial core radius of ~20 000 AU that preceded the first core collapse, and therefore is of no physical importance for interpretating of the collapse process in the model compared to the observational constraints.
We now compare our results with other first core models that show reasonable agreement with the properties of Cha-MMS1. Masunaga et al. (1998) explored the protostellar collapse of a cloud core via radiation hydrodynamic simulations assuming spherical symmetry, and specifically focussed on the formation of the first hydrostatic core. For the typical case of 1 M⊙ and 10 K they find a homogeneous density structure inside the first core and an outer density distribution proportional to r-2. The velocity field structure after the first core formation (ρ ~ 10-13 g cm-3) does not change for scales larger than ~1000 AU for the different evolutionary times they present. They find supersonic velocities out to radii of ~3000 AU, in very good agreement with the radius of ~3300 AU below which supersonic motions are compatible with the envelope of Cha-MMS1. The infall velocities at 1000 AU, 3000 AU, and 9000 AU they predict are ~0.25 km s-1, ~0.2 km s-1, and ~0.1 km s-1. At the same radii we obtain velocity ranges of 0.06−0.5 km s-1, 0.1−0.25 km s-1, and 0.1−0.2 km s-1. The velocity structure of Cha-MMS1 is therefore also consistent with the predictions of Masunaga et al. (1998) for a first core resulting from the collapse of a 1 M⊙ non-rotating, non-magnetised cloud.
Saigo et al. (2008) investigated the effect of different initial rotation speeds during protostellar collapse and the formation of the first and second hydrostatic cores by performing 3D hydrodynamical simulations of cores with slow, moderate, and fast initial rotation. For a slowly rotating cloud (βrot ~ 0.015−0.09, i.e., consistent with the respective ratio of Cha-MMS1), the infall velocity structure during the first core phase is described by supersonic motions below a radius of ~3000 AU, and infall velocities of ~0.4 km s-1, ~0.3 km s-1, and ~0.15 km s-1 at radii of 1000 AU, 3000 AU, and 9000 AU. The infall velocity predictions of Saigo et al. (2008) for the model with slow initial rotation is therefore consistent with the velocity ranges of 0.06−0.5 km s-1, 0.1−0.25 km s-1, and 0.1−0.2 km s-1 that we obtain for Cha-MMS1 at the same radial distances.
Finally, Ciolek & Basu (2000) presented an ambipolar diffusion model incorporating the observational constraints and physical parameters previously derived for the protostellar core L1544. They presented a non-rotating, ambipolar diffusion model with a lower background magnetic field strength (initial mass-to-flux ratio 0.8 in units of the critical value), which could reproduce the extended observed infall velocities of L1544, and concluded that L1544 might be a supercritical core undergoing magnetically diluted collapse. Their model predicts infall velocities of ~0.2 km s-1 and ~0.15 km s-1 at late times (approaching the first core densities), at 3000 AU and 9000 AU from the supercritical core, respectively, which are consistent with the infall velocity field structure we derive for Cha-MMS1 (Fig. 20). The spatial scale for supersonic infall velocities they predict at late times is ~2000 AU. The agreement between the velocities of the two cores, especially for the late-time evolution models (approaching first core densities), might be indicating that the initial conditions of the model for L1544 adequately describes the initial conditions of Cha-MMS1. Cha-MMS1 might therefore be undergoing collapse that is physically similar to that of the prestellar dense core L1544.
In general, the velocities of the RMHD model agree with the inner envelope (r < 2000 AU) of Cha-MMS1 for a 1 M⊙ collapsing dense core and for r < 12 000 AU for a 5 M⊙ dense core at the FHSC stage. In the innermost 2000 AU, the velocity predictions of both models “bracket” the upper limit of the observationally constrained velocities for Cha-MMS1, and for larger radii the 5 M⊙ predictions closely follow this upper limit. Non-magnetised, rotating, as well as non-rotating models for the first core phase (Saigo et al. 2008; Masunaga et al. 1998) also produce infall velocity structures that are consistent with the infall motions of Cha-MMS1 on scales of ~10 000 AU (~0.05 pc). Consequently, the collapse motions in the envelope of Cha-MMS1 are consistent with first core predictions.
Since our observations are not sensitive to the very inner part of Cha-MMS1, where rapid infall velocity changes are expected, we cannot distinguish between an evolved prestellar core, a first core, and a young Class 0 object based on the kinematics alone. The 24 μm and 70 μm detections of Cha-MMS1 rule out its prestellar nature, and thus shift the dilemma between a first core and a young Class 0 protostar. This dilemma can be solved by detecting a slow, compact outflow stemming from Cha-MMS1 via interferometric studies, which would differentiate between the two evolutionary phases. In any case, our kinematic and dynamical study has so far shown that its properties do not contradict the first-core predictions, and it is an interesting target for exploring the early protostellar stages of star-formation.
6. Summary and conclusions
We performed observations of the dense core Cha-MMS1 in various molecular transitions and conducted an analysis of the kinematics within the core in order to investigate its physical properties and dynamical state. We utilised a 1D radiative transfer code to constrain the infall velocity structure of the core. Our conclusions can be summarised as follows.
-
1.
The internal luminosity of Cha-MMS1 is estimated from the predicted inclination-dependent time evolution of SEDs for the first core phase for a 1 M⊙ (Commerçon et al. 2012) and a 5 M⊙ model. The 24 μm and 70 μm flux densities imply inclinations within the range of 30° ≤ i < 60° and an internal luminosity range of 0.08 L⊙−0.18 L⊙.
-
2.
The classical infall signature is detected in optically thick transitions, suggesting that the envelope of Cha-MMS1 is undergoing inward motions.
-
3.
The position-velocity diagrams of optically thin transitions show velocity gradients perpendicular to the filament in which Cha-MMS1 is embedded. The average gradient over an extent of ~16 000 AU in diameter is 3.1 ± 0.1 km s-1 pc-1, while we found no significant gradient along the filament. Interpreted in terms of rotation, these velocity variations imply solid-body rotation in the envelope up to a radius of ~8000 AU, and slower, differential rotation from ~8000 AU to ~12 500 AU. The average velocity gradient in the range 2000 AU−4000 AU is surprisingly flatter, which is difficult to understand in terms of rotation.
-
4.
The turbulent velocity dispersion in the core is uniform within a radius of r ~ 5000 AU parallel to the filament and ~12 500 AU perpendicular to the filament. The non-thermal dispersion is similar to the mean thermal dispersion at a temperature of 9 K, therefore implying an equipartition between thermal and non-thermal motions.
-
5.
Our radiative transfer modelling yields subsonic to transonic infall velocities in the range 0.1 km s-1−0.2 km s-1 for 3300 AU < r < 30 000 AU. The velocity field is less well constrained in the inner parts for r < 3300 AU. A velocity increasing as r-0.5 toward the centre is consistent with the data, but we cannot exclude a decrease either. We find subsonic to supersonic velocities in the range 0.04 km s-1−0.6 km s-1 for r ≤ 3300 AU.
-
6.
Part of the redshifted emission of the high-density tracers CS 5−4, CO 7−6, and CO 6−5 is not reproduced by the radiative transfer model. This excess emission may indicate the presence of unresolved, higher velocity material at the inner core originating in a compact outflow driven by Cha-MMS1, or alternatively, it could arise due to contamination from the outflow of the nearby Class I protostar.
-
7.
We find relatively good agreement between the infall velocity profile derived for Cha-MMS1 and predictions of 3D RMHD simulations for the first hydrostatic core phase.
Both the kinematic agreement with the predictions of RMHD simulations and the possible presence of a compact outflow suggested above are consistent with Cha-MMS1 being at the stage of the first hydrostatic core. However, we cannot affirm the object’s nature without high-resolution interferometric observations to search for and image a compact, slow outflow. With the early prestellar core phase ruled out due to the object’s 24 μm and 70 μm detection, Cha-MMS1 is either a first core or a young Class 0 protostar, and our kinematical study cannot exclude either possibility.
Online material
Mopra centroid velocities toward the central position, P1.
CS 5−4 and H13CO+ 4−3 centroid velocities (APEX) at positions perpendicular to the filament.
H13CO+ 3−2 centroid velocities (APEX) at positions parallel and perpendicular to the filament.
C17O 2−1 and C18O 2−1 centroid velocities (APEX) at positions perpendicular to the filament.
Observed linewidth, thermal, and non-thermal velocity dispersions toward the central position.
 |
Fig. 2 Transitions observed with Mopra towards the central position of Cha-MMS1, in main-beam brightness temperature scale. The dotted line shows the systemic velocity of Cha-MMS1, derived from a seven component hyperfine fit to the N2H+ 1−0 multiplet. |
 |
Fig. 3 Transitions observed with APEX towards the central position of Cha-MMS1, in main-beam brightness temperature scale. The dotted line shows the systemic velocity of Cha-MMS1, derived from a seven component hyperfine fit to the N2H+ 1−0 multiplet observed with Mopra without correcting for the +0.1 km s-1 velocity shift (see Sect. 3.2.1). |
 |
Fig. 12 Transition opacities for the best fit model “MCS”. The dotted line shows the systemic velocity of Cha-MMS1. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). |
 |
Fig. 13 Kinetic (black) and excitation temperature (colour) for all the transitions of the best fit model “MCS”. |
 |
Fig. 15 Transition opacities for the best fit model “MHCOP”. The dotted line shows the systemic velocity of Cha-MMS1. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). |
 |
Fig. 18 Transition opacities for the best fit model “MCO”. The dotted line shows the systemic velocity of Cha-MMS1. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). |
Appendix A: Mopra calibration and efficiency
Appendix A.1: Calibration ambiguities
Some of our Mopra data show differences in the peak temperatures of the two polarisations, POL0 and POL1. The differences are not systematic for all the transitions observed. The two polarisations in some cases differ up to ~10%. The CS 2−1 POL1 intensity for position P6 is stronger by ~5% within the uncertainties, while C34S 2−1 has a stronger POL0 intensity by ~9%. POL0 also shows higher intensities for positions P1 and P6 of the N2H+ 1−0 transition by ~7% and ~6%, respectively. Most of the other transitions (and positions) do not show any significant differences. As the observed discrepancies are not systematic and are only seen in very few cases, we use the average of both polarisations per transition for the analysis in this paper.
Pronounced differences in intensity are seen when comparing a pair of spectra belonging to the same transition that was observed with different tuning frequencies. HC3N 10−9 and HNC 1−0 are the two transitions observed in both setups and show intensity differences of ~38% and ~33%. Unfortunately, we have not yet found a satisfactory explanation for these discrepancies.
Appendix A.2: Efficiency
Even though the expected Mopra beam efficiency at the 90 GHz band is ~0.59, we derive a value that is lower by ~30% after performing independent calibration tests. IRAM 04191 in Taurus and OPH A SM1N in Ophiuchus were observed with both the
Mopra and the IRAM 30 m telescopes (Belloche et al. 2002; André et al. 2007). IRAM 04191 was observed in the molecular transitions CS 2−1, N2H+ 1−0, C34S 2−1, and H13CO+ 1−0, while OPH A SM1N was observed in N2H+ 1−0. After smoothing the 30 m data to the Mopra angular resolution we directly compared their integrated intensities with the equivalent Mopra intensities. We derived lower efficiencies for most of the observed transitions (see Table A.1) with the overall weighted average efficiency being ~0.34.
Mopra beam efficiencies.
Appendix B: Calculation of opacities
Appendix B.1: Opacity of the C18O 2−1 line
We observed both C18O 2−1 and C17O 2−1 at 13 positions
perpendicular to the filament (Fig. 1). An
isotopic ratio of [18O]/[17O] ~ 4.11 was found for the nearby
(140 pc) low-mass cloud ρ Ophiuchus (Wouterloot et al. 2005). We use this value to derive the opacity of
C18O 2−1 using the following relation:
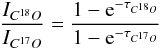 (B.1)where
IC18O and IC17O are the intensities of
the two transitions,
τC18O and
τC17O their
opacities and
τC17O = τC18O/4.11.
We find opacities that gradually increase from ≤0.5 at the outermost position to ~1.6
at the centre of the core for the C18O 2−1 transition.
(B.1)where
IC18O and IC17O are the intensities of
the two transitions,
τC18O and
τC17O their
opacities and
τC17O = τC18O/4.11.
We find opacities that gradually increase from ≤0.5 at the outermost position to ~1.6
at the centre of the core for the C18O 2−1 transition.
Position from Spitzer observations (Belloche et al. 2011a).
From the IDL Astronomy User’s Library (http://idlastro.gsfc.nasa.gov/contents.html).
Acknowledgments
We thank Bérengère Parise, Philippe André, and Tyler Bourke for their insightful comments and suggestions, the APEX and Mopra staff for their support during the observations, and the referee for the feedback that helped in improving the quality of this paper. AET was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.
References
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 2000, in Protostars and Planets IV (Arizona: University of Arizona Press), 59 [Google Scholar]
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Basu, S., & Inutsuka, S. 2009, in The formation and evolution of prestellar cores, ed. G. Chabrier (Cambridge University Press), 254 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barranco, J. A., & Goodman, A. A. 1998, ApJ, 504, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Mouschovias, T. C. 1994, ApJ, 432, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Mouschovias, T. C. 1995, ApJ, 452, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2011, MNRAS, 417, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., & André, P. 2004, A&A, 419, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., André, P., Despois, D., & Blinder, S. 2002, A&A, 393, 927 [Google Scholar]
- Belloche, A., Parise, B., van der Tak, F. F. S., et al. 2006, A&A, 454, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011a, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Parise, B., Schuller, F., et al. 2011b, A&A, 535, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benson, P. J., & Myers, P. C. 1983, ApJ, 270, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Ciardi, D. R., Lada, C. J., Alves, J., & Lada, E. A. 2001, ApJ, 557, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Blinder, S. 1997, Ph.D. Thesis, Université de Bordeaux I [Google Scholar]
- Bodenheimer, P., & Sweigart, A. 1968, ApJ, 152, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Bourke, T. L., Myers, P. C., Evans, II, N. J., et al. 2006, ApJ, 649, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Burkert, A., & Bodenheimer, P. 2000, ApJ, 543, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S., & Bertout, C. 1990, ApJ, 348, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Arce, H. G., Zhang, Q., et al. 2010, ApJ, 715, 1344 [Google Scholar]
- Chen, X., Arce, H. G., Dunham, M. M., et al. 2012, ApJ, 751, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Christie, H., Viti, S., Yates, J., et al. 2012, MNRAS, 422, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolek, G. E., & Basu, S. 2000, ApJ, 529, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2010, A&A, 510, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Launhardt, R., Dullemond, C., & Henning, T. 2012, A&A, 545, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2004, A&A, 420, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- di Francesco, J., Evans, II, N. J., Caselli, P., et al. 2007, in Protostars and Planets V (Arizona: University of Arizona Press), 17 [Google Scholar]
- Dunham, M. M., Crapsi, A., Evans, II, N. J., et al. 2008, ApJS, 179, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Chen, X., Arce, H. G., et al. 2011, ApJ, 742, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Lee, J.-E., Harvey, P., Dunham, M. M., & Schnee, S. 2010, ApJ, 722, L33 [Google Scholar]
- Evans, II, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fiedler, R. A., & Mouschovias, T. C. 1993, ApJ, 415, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, P. N., & Chevalier, R. A. 1993, ApJ, 416, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Frerking, M. A., Wilson, R. W., Linke, R. A., & Wannier, P. G. 1980, ApJ, 240, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Furuya, K., Aikawa, Y., Tomida, K., et al. 2012, ApJ, 758, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Barranco, J. A., Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Haikala, L. K., Harju, J., Mattila, K., & Toriseva, M. 2005, A&A, 431, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hiramatsu, M., Hayakawa, T., Tatematsu, K., et al. 2007, ApJ, 664, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, C. 1977, ApJ, 218, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J., & Høg, E. 1998, A&A, 338, 897 [NASA ADS] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ladd, E. F., Wong, T., Bourke, T. L., & Thompson, K. L. 2011, ApJ, 743, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 1999, ApJ, 526, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Lehtinen, K., Haikala, L. K., Mattila, K., & Lemke, D. 2001, A&A, 367, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehtinen, K., Harju, J., Kontinen, S., & Higdon, J. L. 2003, A&A, 401, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesaffre, P., Belloche, A., Chièze, J.-P., & André, P. 2005, A&A, 443, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Machida, M. N., & Matsumoto, T. 2011, MNRAS, 413, 2767 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S.-I., & Matsumoto, T. 2008, ApJ, 676, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Masunaga, H., & Inutsuka, S.-I. 1999, ApJ, 510, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Masunaga, H., Miyama, S. M., & Inutsuka, S.-I. 1998, ApJ, 495, 346 [Google Scholar]
- Maury, A. J., André, P., Men’shchikov, A.,Könyves, V., & Bontemps, S. 2011, A&A, 535, A77 [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2010, A&A, 518, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omukai, K. 2007, PASJ, 59, 589 [NASA ADS] [Google Scholar]
- Penston, M. V. 1966, Roy. Greenwich Obs. Bull., 117, 299 [Google Scholar]
- Penston, M. V. 1969, MNRAS, 144, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzuto, S., Elia, D., Schisano, E., et al. 2012, A&A, 547, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Arce, H. G., Schnee, S., et al. 2011, ApJ, 743, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., Tricco, T. S., & Bate, M. R. 2012, MNRAS, 423, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., et al. 2009, ApJ, 699, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., Nyman, L.-A., & Chini, R. 1996, A&A, 314, 258 [NASA ADS] [Google Scholar]
- Saigo, K., & Tomisaka, K. 2011, ApJ, 728, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Saigo, K., Tomisaka, K., & Matsumoto, T. 2008, ApJ, 674, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Shinnaga, H., Phillips, T. G., Furuya, R. S., & Kitamura, Y. 2009, ApJ, 706, L226 [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., & Yen, J. J. 2010, MNRAS, 407, 2434 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Mardones, D., Myers, P. C., et al. 1998, ApJ, 504, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takano, S., Masuda, A., Hirahara, Y., et al. 1998, A&A, 329, 1156 [NASA ADS] [Google Scholar]
- Tassis, K., & Mouschovias, T. C. 2007, ApJ, 660, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Terebey, S., Chandler, C. J., & André, P. 1993, ApJ, 414, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Hartmann, L., Bergin, E., et al. 2012, ApJ, 748, 16 [Google Scholar]
- Tomida, K., Machida, M. N., Saigo, K., Tomisaka, K., & Matsumoto, T. 2010, ApJ, 725, L239 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K. 2002, ApJ, 575, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K., & Tomida, K. 2011, PASJ, 63, 1151 [NASA ADS] [Google Scholar]
- Walker, C. K., Lada, C. J., Young, E. T., Maloney, P. R., & Wilking, B. A. 1986, ApJ, 309, L47 [Google Scholar]
- Whittet, D. C. B., Prusti, T., Franco, G. A. P., et al. 1997, A&A, 327, 1194 [NASA ADS] [Google Scholar]
- Williams, J. P., Myers, P. C., Wilner, D. J., & di Francesco, J. 1999, ApJ, 513, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wouterloot, J. G. A., Brand, J., & Henkel, C. 2005, A&A, 430, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, S. 1992, ApJ, 394, 204 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mopra centroid velocities at positions perpendicular and parallel to the filament.
CS 5−4 and H13CO+ 4−3 centroid velocities (APEX) at positions perpendicular to the filament.
H13CO+ 3−2 centroid velocities (APEX) at positions parallel and perpendicular to the filament.
C17O 2−1 and C18O 2−1 centroid velocities (APEX) at positions perpendicular to the filament.
Observed linewidth, thermal, and non-thermal velocity dispersions toward the central position.
All Figures
 |
Fig. 1 a) 870 μm map of the filament in which Cha-MMS1 is
embedded, obtained with LABOCA as part of an unbiased survey of Chamaeleon I (Belloche et al. 2011a). The contour levels
correspond to − a, a, 2a,
4a, 6a, 8a, 12a,
16a, 24a, 32a, with
a = 36 mJy/21″-beam (3σ). The white cross at
αJ2000 = 11h06m33 |
| In the text | |
 |
Fig. 4 Position–velocity diagrams of the Mopra C34S 2−1 (black), HC3N 10−9 (blue), N2H+ 1−0 (red), CH3OH−A 20,2−10,1 (green), and CH3OH−E 21,2−11,1 (pink) transitions, a) perpendicular and b) parallel to the filament. The error bars represent standard deviations (1σ). Linear fits to the velocities for each transition are shown with the same colour as in panel a). |
| In the text | |
 |
Fig. 5 Position–velocity diagrams of the APEX CS 5−4, H13CO+ 3−2, H13CO+ 4−3, C17O 2−1, and C18O 2−1 transitions perpendicular a), b), c) and parallel d) to the filament. Linear fits are shown as straight lines. For C17O 2−1 and C18O 2−1 in c) the two outer points from either side of the curve were excluded from the fits. Fits to the innermost positions of C17O 2−1 and C18O 2−1 are also displayed. |
| In the text | |
 |
Fig. 6 Non-thermal velocity dispersion, σnth, versus position perpendicular to the filament for a) CS 5−4 (black), H13CO 4−3 (red), and H13CO+ 3−2 (green), b) C17O 2−1 and C18O 2−1, all observed with the APEX telescope, and c) C34S 2−1 (black), HC3N 10−9 (green), N2H+ 1−0 (dark blue), CH3OH−E 21,2 − 11,1 (light blue), and CH3OH−A 20,2 − 10,1 (pink) observed with Mopra. The errorbars are standard deviations. The thermal dispersion was calculated assuming a temperature of T = 9 K. |
| In the text | |
 |
Fig. 7 Non-thermal velocity dispersion, σnth, versus position parallel to the filament for a) C34S 2−1 (black), HC3N 10−9 (green), N2H+ 1−0 (dark blue), CH3OH−E 21,2 − 11,1 (light blue), and CH3OH−A 20,2 − 10,1 (pink) observed with Mopra, and b) H13CO+ 3−2 observed with the APEX telescope. The errorbars are standard deviations. The thermal dispersion was calculated assuming a temperature of T = 9 K. |
| In the text | |
 |
Fig. 8 Spectra obtained toward the central position of Cha-MMS1 in the optically thick CS 2−1, HCO+ 3−2, HCO+ 1−0, and HNC 1−0 transitions and the low optical depth C34S 2−1, H13CO+ 1−0, H13CO+ 3−2, H13CO+ 4−3, HC18O+ 1−0, and HN13C 1−0 transitions. The dashed line corresponds to the systemic velocity derived from a seven-component hyperfine fit to the N2H+ 1−0 multiplet (4.3 km s-1). It is corrected to 4.4 km s-1 for the APEX transitions HCO+ 3−2, H13CO+ 3−2, and H13CO+ 4−3 (see Sect. 3.2.1). |
| In the text | |
 |
Fig. 9 CO 6−5, CO 7−6, and 13CO 6−5 spectra observed with the APEX telescope. The central position of Cha-MMS1 is at (0,0). The directions parallel and perpendicular to the filament are shown as dashed and dotted arrows, respectively. The central spectra of the three transitions are plotted in the rightmost panel on the scale of the main-beam brightness temperature. The dotted line shows the systemic velocity of Cha-MMS1 derived from a seven-component hyperfine fit to the N2H+ 1−0 multiplet and corrected for the 0.1 km s-1 velocity shift (see Sect. 3.2.1). |
| In the text | |
 |
Fig. 10 Best fit model “MCS” for the CS and C34S molecular transitions. The black lines represent the observed spectra, while the red spectra are generated by the MAPYSO radiative transfer code. The dotted line shows the systemic velocity of Cha-MMS1 derived from a seven-component hyperfine fit to the N2H+ 1−0 multiplet. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). The angular separation of the different positions with respect to the central spectrum is shown on top of the respective spectra. The model assumes spherical symmetry, so the model spectra at symmetric positions are identical. The telescope used for conducting the obervations is shown at the leftmost box of each row. The spectra from left to right correspond to the south-east to north-west direction perpendicular to the filament. |
| In the text | |
 |
Fig. 11 Input profiles for the best-fit models “MCS”, “MHCOP”, and “MCO”: a) density, b) CS (solid), HCO+ (dash-dot), and CO (dot) abundance; c) kinetic temperature; d) radial velocity; and e) turbulent linewidth. |
| In the text | |
 |
Fig. 14 Same as Fig. 10 but for the best fit model “MHCOP”. |
| In the text | |
 |
Fig. 17 Same as Fig. 10 but for the best fit model “MCO” of the CO transitions. |
| In the text | |
 |
Fig. 20 Infall velocity field of the envelope of Cha-MMS1 based on the radiative transfer modelling with MAPYSO. The solid black line corresponds to the velocity profile of the “MCS”, “MHCOP”, and “MCO” models. The dashed lines show the range of velocity fields that are still consistent with the observations. The red solid and dashed curves correspond to the average radial velocity at the equatorial plane of a magnetised FHSC with core masses of 1 M⊙ and 5 M⊙, and ages of 850 yr and 2684 yr, respectively. (Commerçon et al. 2012, see details in Sect. 5.4.2). |
| In the text | |
 |
Fig. 21 Comparison of the CS 5−4 spectrum (solid) toward the central position of Cha-MMS1 and CO 6−5 spectra (dotted) taken at the central position and in the north-east direction toward the nearby Class I protostar. The offset position of each spectrum is given in arcseconds relative to the central position. The CO 6−5 spectra are shifted vertically by a step of 1 K for clarity. The solid vertical line roughly corresponds to the velocity of the CO 6−5 red peak, while the dashed line marks the velocity of the peak of the CS 5−4 excess emission. |
| In the text | |
 |
Fig. 22 Ratio of centrifugal to gravitational accelerations for the inner part of Cha-MMS1 that may be undergoing solid-body rotation. The upper and lower curves are for an inclination of 30° and 60°, respectively. |
| In the text | |
 |
Fig. 2 Transitions observed with Mopra towards the central position of Cha-MMS1, in main-beam brightness temperature scale. The dotted line shows the systemic velocity of Cha-MMS1, derived from a seven component hyperfine fit to the N2H+ 1−0 multiplet. |
| In the text | |
 |
Fig. 3 Transitions observed with APEX towards the central position of Cha-MMS1, in main-beam brightness temperature scale. The dotted line shows the systemic velocity of Cha-MMS1, derived from a seven component hyperfine fit to the N2H+ 1−0 multiplet observed with Mopra without correcting for the +0.1 km s-1 velocity shift (see Sect. 3.2.1). |
| In the text | |
 |
Fig. 12 Transition opacities for the best fit model “MCS”. The dotted line shows the systemic velocity of Cha-MMS1. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). |
| In the text | |
 |
Fig. 13 Kinetic (black) and excitation temperature (colour) for all the transitions of the best fit model “MCS”. |
| In the text | |
 |
Fig. 15 Transition opacities for the best fit model “MHCOP”. The dotted line shows the systemic velocity of Cha-MMS1. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). |
| In the text | |
 |
Fig. 16 Same as Fig. 13 for the best fit model “MHCOP”. |
| In the text | |
 |
Fig. 18 Transition opacities for the best fit model “MCO”. The dotted line shows the systemic velocity of Cha-MMS1. For the APEX spectra, a correction of 0.1 km s-1 was added (see Sect. 3.2.1). |
| In the text | |
 |
Fig. 19 Same as Fig. 13 for the best-fit model “MCO”. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


