| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 50 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321285 | |
| Published online | 09 August 2013 | |
A line confusion-limited millimeter survey of Orion KL⋆
III. Sulfur oxide species
1
Centro de Astrobiología (CSIC-INTA), Ctra. de Torrejón-Ajalvir, km. 4,
28850 Torrejón de Ardoz,
Madrid
Spain
e-mail: espluguesbg@cab.inta-csic.es
2
Institut de Cències de l’Espai (CSIC-IEEC), Campus UAB-Facultat de Ciencies, Torre C5-parell 2, 08193 Bellaterra,
Barcelona,
Spain
3
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA
22903,
USA
Received: 13 February 2013
Accepted: 28 May 2013
Context. We present a study of the sulfur-bearing species detected in a line confusion-limited survey towards Orion KL performed with the IRAM 30-m telescope in the frequency range 80−281 GHz.
Aims. This study is part of an analysis of the line survey divided into families of molecules. Our aim is to derive accurate physical conditions, as well as molecular abundances, in the different components of Orion KL from observed SO and SO2 lines.
Methods. As a starting point, we assumed local thermodynamic equilibrium (LTE) conditions obtain rotational temperatures. We then used a radiative transfer model, assuming either LVG or LTE excitation to derive column densities of these molecules in the different components of Orion KL.
Results. We have detected 68 lines of SO, 34SO, 33SO, and S18O and 653 lines of SO2, 34SO2, 33SO2, SO18O, and SO2ν2 = 1. We provide column densities for all of them and also upper limits for the column densities of S17O, 36SO, 34S18O, SO17O, and 34SO2ν2 = 1 and for several undetected sulfur-bearing species. In addition, we present 2′ × 2′ maps around Orion IRc2 of SO2 transitions with energies from 19 to 131 K and also maps with four transitions of SO, 34SO, and 34SO2. We observe an elongation of the gas along the NE-SW direction. An unexpected emission peak appears at 20.5 km s-1 in most lines of SO and SO2. A study of the spatial distribution of this emission feature shows that it is a new component of a few arcseconds (~5″) in diameter, which lies ~4″ west of IRc2. We suggest the emission from this feature is related to shocks associated to the BN object.
Conclusions. The highest column densities for SO and SO2 are found in the high-velocity plateau (a region dominated by shocks) and in the hot core. These values are up to three orders of magnitude higher than the results for the ridge components. We also find high column densities for their isotopologues in both components. Therefore, we conclude that SO and SO2 are good tracers, not only of regions affected by shocks, but also of regions with warm dense gas (hot cores).
Key words: astrochemistry / ISM: abundances / ISM: clouds / ISM: molecules / radio lines: ISM
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The hot core phase of massive star formation shows a particularly rich chemistry that results from gas-phase chemical reactions and dust grain mantle evaporation. During cloud collapse, depletion of molecules onto dust surfaces takes place. When a new protostar forms, the surrounding gas and dust are heated and molecules sublimate from the grain mantles, giving rise to new species in the warm gas and to enhanced abundances of pre-existing species. The existence of molecular outflows and associated shocked regions also plays an important role in the chemical evolution, because they heat up the gas significantly and modify its chemistry.
Orion KL is the closest high-mass star-forming region (≃ 414 pc, Menten et al. 2007). It is one of the most studied regions owing to its chemical complexity and high gas temperature, which lead to a dense and bright line spectrum. In the Orion KL cloud it is useful to differentiate five distinct components, characterized by different physical and chemical conditions (Blake et al. 1987; Persson et al. 2007; Tercero et al. 2010, and references therein): i) the hot core (HC) with 10″ diameter, which contains a high abundance of complex species (Wilson et al. 2000). It is characterized by line widths of 7 ≤ Δv ≤ 15 km s-1 at vLSR ≃ 5 km s-1. It contains dense and warm gas with TK ≃ 200 K and n(H2) ≃ 107 cm-3. ii) The plateau (PL), a component with 30″ diameter, is affected by shocks with typical line widths of Δv ≃ 20−25 km s-1 at vLSR ≃ 6 km s-1. Typical temperatures and densities are TK ≃ 150 K and n(H2) ≃ 106 cm-3, respectively. iii) The high velocity plateau, HVP, (component affected by shocks, with similar temperature and densitity to the PL) with line widths of Δv ≃ 30−55 km s-1 at vLSR ≃ 11 km s-1. iv) The compact ridge (CR), with 15″ diameter, centered on vLSR ≃ 7.5 km s-1 with line widths of ~4 km s-1. Temperatures are about 110 K and densities ≃ 106 cm-3. And v) an extended component, the extended ridge (ER) or ambient cloud, whose emission is characterized by low temperature and density (60 K and 105 cm-3, respectively), and line widths similar to the compact ridge, but centered on a velocity of vLSR ≃ 9 km s-1. The luminosity of the Orion Becklin-Neugebauer/Kleinmann-Low complex is ~105 L⊙ (Gezari et al. 1998). From the model proposed by Wynn-Williams et al. (1984) and without observational evidence, IRc2 was thought to be the main source of luminosity, heating, and dynamics within the region. However, with the detection of two radio continuum point sources, B (coincident with the BN Object) and I (centroid of the Orion SiO maser), it was concluded that the intrinsic luminosity of IRc2 is only a fraction (L ≃ 1000 L⊙) of the total luminosity of the complex (Gezari et al. 1998), with source I being the main contributor.
In this paper, we continue our analysis of the line survey towards Orion IRc2 in the frequency range 80−281 GHz, first presented by Tercero et al. (2010). Here we concentrate on SO, SO2, and their isotopologues; we model the different cloud components (hot core, plateau, ridge) and derive their physical and chemical conditions, such as column densities and temperatures. Since Gottlieb & Ball (1973) discovered SO in Orion A, there have been many studies of this molecule, as well as SO2, in this region, including studies of the gas kinematics (Plambeck et al. 1982), molecular abundances (Blake et al. 1987), and spatial distribution (Sutton et al. 1995). Also we find several interferometric studies of these two molecules such as those from Wright et al. (1996) and Beuther et al. (2005). sulfur-bearing species are especially sensitive to physical and chemical variations during the lifetime of a hot core (Viti et al. 2001), and therefore are considered good probes of their time evolution (Hatchell et al. 1998). As such, they can be used as tools for investigating the chemistry and physical properties of complex star-forming regions (SFRs) located in dense molecular clouds. On the other hand, it is known that some molecules (SiO, H2CS, SO, SO2) show increased abudances in regions affected by shocks (Bachiller et al. 1996) as a result of the action of outflows on the surrounding gas. The study of molecular lines from shocked areas provides valuable information about chemical processes and the physical conditions of the shocked components.
The observations are described in Sect. 2. We present more than 700 detected lines of SO, SO2, their isotopologues, and their vibrationally excited states. In Sect. 3 we present the data and compute rotational temperatures as a first local thermodynamic equilibrium (LTE) approximation. In addition, we present maps of eight emission lines of SO2, SO, 34SO2, and 34SO in the 1.3 mm window, over a 2′ × 2′ region around Orion IRc2 (Sect. 3.4). Unlike other studies of SO, we use a non-LTE radiative transfer code (LVG) to derive physical and chemical parameters (Sect. 4). We provide column density calculations for SO and SO2, and isotopic abundance ratios, which have been improved over previous works due to the much larger number of available lines and to the up-to-date information on the physical properties of the region and molecular constants. Discussions on our results are included in Sect. 5, while Sect. 6 summarizes the main conclusions.
2. Observations
We continue our analysis of the line survey towards Orion IRc2 covering frequency ranges 80−115.5 GHz, 130−178 GHz, and 197−281 GHz, first presented by Tercero et al. (2010). The observations were carried out using the IRAM 30-m radiotelescope during September 2004 (1.3 mm and 3 mm windows), March 2005 (full 2 mm window), and April 2005 (completion of the 1.3 mm and 3 mm windows). Four SiS receivers operating at 1.3, 2, and 3 mm were used simultaneously, with image sideband rejections within ~13 dB (1.3 mm receivers), 12−16 dB (2 mm receivers), and 20−27 dB (3 mm receivers). System temperatures were in the range 200−800 K for the 1.3 mm receivers, 200−500 K for the 2 mm receivers, and 100−350 K for the 3 mm receivers, depending on the particular frequency, weather conditions, and source elevation. For the spectra between 172−178 GHz, the system temperature was significantly higher, 1000−4000 K, owing to proximity of the atmospheric water line at 183.31 GHz. The intensity scale was calibrated using two absorbers at different temperatures and using the atmospheric transmission model (ATM, Cernicharo 1985; Pardo et al. 2001).
IRAM 30 m telescope efficiency data along the covered frequency range.
Pointing and focus were regularly checked on the nearby quasars 0420-014 and 0528+134. Observations were made in the balanced wobbler-switching mode, with a wobbling frequency of 0.5 Hz and a beam throw in azimuth of ± 240″. No contamination from the off position affected our observations, except for a marginal amount at the lowest elevations (25°) for molecules showing low-J emission along the extended ridge. Two filter banks with 512 × 1 MHz channels and a correlator providing two 512 MHz bandwidths and 1.25 MHz resolution were used as backends. We pointed the observations towards IRc2 at α(J2000) = 5h35m14.5s, δ(J2000) = −5°22′30.0″.
The data were processed using the IRAM GILDAS software1 (developed by the Institut de Radioastronomie Millimétrique). In our analysis we only considered lines with intensities ≥ 0.02 K, covering three or more channels. Spectra with Gaussian line fits are shown in units of antenna temperature 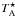 corrected for atmospheric absorption and spillover losses. Figures with results from LVG/LTE analysis are shown in units of main beam temperature TMB, which is defined as
corrected for atmospheric absorption and spillover losses. Figures with results from LVG/LTE analysis are shown in units of main beam temperature TMB, which is defined as 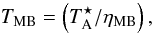 (1)where ηMB is the main beam efficiency. Table 1 shows the half power beam width (HVPBW) and the mean beam efficiencies over the covered frequency range. For further information about the data reduction and line identification, see Tercero et al. (2010).
(1)where ηMB is the main beam efficiency. Table 1 shows the half power beam width (HVPBW) and the mean beam efficiencies over the covered frequency range. For further information about the data reduction and line identification, see Tercero et al. (2010).
We also used the 30-m telescope to map a 2′ × 2′ region around IRc2 at 1.3 mm. In this two-dimensional (2D) line survey (Marcelino et al., in prep.), we covered the 1.3 mm window using the nine pixel HERA receiver array (216−250 GHz) and the EMIR single-pixel heterodyne receivers (200−216 and 250−282 GHz). We also mapped a small fraction of the 3 mm band taking advantage of simultaneous observations with the E230 and E090 receivers. Fully sampled maps over 140 × 140 arcsec2, centered on the position of IRc2, were performed in the on-the-fly (OTF) mapping mode, scanning both in α and δ with a 4″ spacing, and using position-switching to an emission-free reference position at an offset (−600″, 0″) with respect to IRc2. The observations presented here were obtained in February and December 2008 (HERA), February 2010, and January 2012 (EMIR). We used local oscillator settings at frequencies of 109.983, 221.600, 226.100, 235.100, 239.100, and 258.000 GHz, depending on the observed transition. We used short Wobbler-switching observations on the central position with a slightly different frequency for each setting, in order to remove all features arising from the image side band. We used the WILMA spectrometer backend, with a total bandwidth of 4 GHz (EMIR), 1 GHz (HERA), and a spectral resolution of 2 MHz, corresponding to velocity resolutions of 5.4 km s-1 at 3 mm and 2.7−2.3 at 1.3 mm. Weather conditions were the typically good winter conditions (with opacities ~0.1−0.2 at 1.3 mm and 1.3−2 mm of precipitable water vapor) resulting in system temperatures of 230−250 K (EMIR) and 300−400 K (HERA), except for observations in February 2010, when conditions were τ ~ 0.3−0.4 and 5 mm of pwv. In this case, system temperatures of 150 K and 300−400 K were obtained at 110 and 239 GHz, respectively. Pointing was checked every hour on strong and nearby quasars, and found to have errors of typically less than 3−4 arcsec.
The basic data reduction consisted of fitting and removing first-order polynomial baselines, checking for image sideband contamination and emission from the reference position. HERA data needed further reduction analysis due to the different performance of each pixel in the array. Spectra from all pixels were averaged to obtain a uniform map gridding of 4″, taking their different flux calibration and internal pointing errors into account (see Marcelino et al., in prep. for details).
 |
Fig. 1 Gaussian fits to the observed SO lines. Dashed line for the plateau, cyan (solid line) for the high-velocity plateau, black for hot core, green for extended ridge, and red for the contribution of the component at 20.5 km s-1. The total fit is shown in magenta. The data are the black histogram spectra. |
 |
Fig. 2 Gaussian fits for the SO2 lines (2 mm data). The total fit is shown in magenta. Plateau is represented with the dashed line, high-velocity plateau in cyan (solid line), hot core in black, compact ridge in blue, extended ridge in green, and 20.5 km s-1 component in red. The data are the black histogram spectra. |
 |
Fig. 3 Gaussian fits for the SO2 lines (1.3 mm data). The total fit is shown in magenta. Plateau is represented with the dashed line, high-velocity plateau in cyan (solid line), hot core in black, compact ridge in blue, extended ridge in green, and 20.5 km s-1 component in red. The data are the black histogram spectra. |
 |
Fig. 4 Gaussian fits for the SO2 lines (3 mm data). The total fit is shown in magenta. Plateau is represented with the dashed line, high-velocity plateau in cyan (solid line), hot core in black, compact ridge in blue, extended ridge in green, and 20.5 km s-1 component in red. The data are the black histogram spectra. |
3. Results
In total, the survey covers a bandwidth of 168 GHz, and of the 15 200 detected spectral features, about 10 700 have been identified and attributed to 45 molecules, including 191 isotopologues and vibrationally excited states (Tercero et al. 2010). We identify 20 lines of SO, 21 lines of 34SO, 13 lines of 33SO, and 14 lines of S18O. We also detect 166 lines of SO2, 129 lines of 34SO2, 85 lines of 33SO2, 129 lines of SO18O, 74 lines of SO17O, and 78 lines of SO2v2. Observed transitions of SO have a range of energy Eup between 16 and 100 K and a full width at half maximum (FWHM) of 40 km s-1. In the case of SO2 the energy range for the observed transitions is 12−1480 K and FWHM of 30−40 km s-1 for transitions J < 25 and FWHM ~ 10−20 km s-1 for transitions J > 25. All these identifications are shown in Tables A.8 and A.9. Those tables list the spectroscopic parameters2 of each transition, together with the observed line properties of the detected lines.
SO was the first molecule with a 3Σ electronic ground-state detected in space by radio techniques (Gottlieb & Ball 1973). Its rotational levels are characterized by the rotational angular momentum quantum number, N, and the total angular momentum quantum number, J, which includes the contribution of the angular momentum of two unpaired electrons. For 33S and 17O, the nuclear quadrupolar momentum couples with the rotation to produce a hyperfine splitting of the rotational levels. Selection rules for the electric dipole transitions are: ΔN = ± 1, ΔF = 0, ± 1, and ΔJ = 0, ± 1, in the absence of external fields. In the case of intermediate coupling, transitions are allowed for ΔN = ± 3. The magnetic dipole transitions occur with the selection rules: ΔN = 0, ± 2 and ΔJ = 0, ± 1. However, these transitions are extremely weak compared to the electric dipole transitions. We have estimated that the magnetic dipole allowed transitions SO will have intensities ~1−6 mK, i.e., lines within the confusion limit of Orion (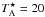 mK).
mK).
SO2 is an asymmetric molecule. The rotational energy levels are characterized by the three quantum numbers J, K-1, and K + 1. Since triatomic molecules are planar, the dipole moment components can only occur in the a- and b-axis directions. The selection rules for a-type transitions are ΔJ = 0, ± 1, ΔK-1 = 0, ± 2, and ΔK + 1 = ± 1, ± 3. For b-type transitions: ΔJ = 0, ± 1, ΔK-1 = ± 1, ± 3, and ΔK + 1 = ∓ 1, ∓ 3. SO2 has its dipole moment along the b axis of the molecule. The nuclear quadrupolar momentum of 33S and 17O also couples with the rotation leading to hyperfine structure.
As a starting point, we fitted each observed line with Gaussian profiles using CLASS to derive the contribution of each cloud spectral component (see Sect. 3.1). We assumed that the emission is optically thin and the observed lines are thermalized at a given temperature that was derived from rotational diagrams (see Goldsmith & Langer 1999), providing rotational temperatures for the different components of the cloud (Sect. 3.3). In Sect. 4 we use a radiative transfer code for a more advanced analysis of the LTE and non-LTE emission of SO and SO2 species.
3.1. Line profiles
Figures 1−4 show the line profiles of some observed transitions of SO and SO2, together with Gaussian fit results. To avoid degeneration, we fixed radial velocities (vLSR) considering the characteristic values of each component of Orion KL. And we left the line width, the integrated intensity, and the antenna temperature as free parameters in the fits (in the results, we took the typical ranges of line widths into account for each component found in the bibliography, discarding those with large differences). In addition to the contribution from the usual components listed above, we also observe an unexpected emission peak centered on a velocity of ≃ 20.5 km s-1. We discuss its origin in Sects. 3.2 and 5.2.
We have detected 20 rotational transitions of SO, eight of which are blended with lines of other species. Figure 1 shows the contribution of the different cloud components to the emerging profile. We tried to fit the lines by considering only one plateau instead of two (at high and low velocity). First we centered this single plateau component on a velocity around 6−7 km s-1, but with this we could not fit the part of the line profiles covering high (>20 km s-1) velocities. With an increase in the line width of the fit, we reproduced this part of the profiles, but we overestimated the part of the lines that covers negative velocities. We found the opposite behavior if we fixed the single plateau component at higher velocities. Therefore we deduced that the best fits were obtained by considering two plateau components: one at low velocity, PL, (~6.5 km s-1) and the other at high velocity, HVP, (~12 km s-1). We observe that the emission mainly arises from these both plateau components. For transitions with angular momentum quantum number N ≲ 5, the strongest emission is found from the HVP, while for N ≳ 5 PL presents the highest contribution to the emission. The contribution from the ER is very small. In this LTE analysis of SO, we have not considered the compact ridge component since its contribution is difficult to distinguish from the contribution from the HC. The parameters obtained from Gaussian fits for some of the SO lines are listed in Table A.1.
For SO2 we have clearly identified 166 rotational transitions (see Figs. 2−4). As indicated by their broad line profiles, we see that most of the emission comes from the plateau components, especially for transitions J < 20 where the HVP plays an important role. However, for transitions J > 20 the HC dominates. The parameters obtained for each component from Gaussian fits for SO2 lines are listed in Tables A.2 and A.3. Comparing this with SO lines, we see that the line profiles of both species are very similar.
3.2. The 20.5 km s-1 feature and absorption at 15 km s-1
Unlike the other species detected in the survey, we clearly observe an emission peak at ≃ 20.5 km s-1 in most SO and SO2 lines. From Gaussian fits, we find that the line widths are ~7.5 km s-1. This feature presents an increase in the line intensity with frequency (i.e., with smaller beam). Figure 5 shows the integrated intensity, W, as a function of the frequency for the 20.5 km s-1 component for SO lines. We see that, for the same line width, W increases with frequency with a dependence as ν2. This means that the size of the region responsible for this velocity componenent is only a few arcseconds in diameter (<9″, smaller than the IRAM 30-m beam at the highest frequencies). The emission of this component could come from the interaction of the outflow with the ambient cloud; however, it should be noted that while in Orion-KL the vLSR of the different components varies approximately between 3 and 10 km s-1, Scoville et al. (1983) inferred that the BN (Becklin-Neugebauer) object in Orion presents a significantly higher LSR velocity of around 21 km s-1, therefore another possibility is that this feature located at 20.5 km s-1 arises from the BN source.
On the other hand, between the main emission peak of the line profiles of SO and SO2 and this emission peak at 20.5 km s-1, we observe a dip at ≃ 15 km s-1. Tercero et al. (2011) also find a velocity component at 15.5 km s-1 in SiS emission lines (ν = 0), and one component of the SiO maser emission (ν = 1). Since the opacity is high for some lines of SO and SO2, as well as for SiO, another possibility is that this dip may be the result of self-absorption. This could suggest that the SO and SO2 dips at 15.5 km s-1 are produced by the same gas observed in SiS. In Sect. 5 we draw firmer conclusions about the origin of the dip at 15.5 km s-1 and of the peak at 20.5 km s-1 from maps of SO and SO2.
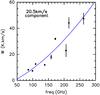 |
Fig. 5 Integrated line intensities of the 20.5 km s-1 component as a function of the line frequency for SO transitions. |
3.3. Rotational diagrams
 |
Fig. 6 SO-integrated intensity maps over different velocity ranges (indicated at the bottom of each panel in km s-1). Row 1 shows the transition 32−21 (Eup = 21.1 K, Aul = 1.1 × 10-5 s-1, S = 1.5). The interval between contours is 8 K km s-1 and the minimum contour is 15 K km s-1. Row 2 shows the transition 66−55 (Eup = 56.5 K, Aul = 2.2 × 10-4 s-1, S = 5.8). The interval between contours is 20 K km s-1 and the minimum contour is 15 K km s-1. The white cross indicates the position of the hot core and the black cross the position of the compact ridge. |
 |
Fig. 7 SO2-integrated intensity maps over different velocity ranges (indicated at the bottom of each panel in km s-1). Row 1 shows the transition 4(2,2)−3(1,3) (energy Eup = 19 K, Einstein coefficient Aul = 7.7 × 10-5 s-1, and line strength S = 1.7), row 2 the transition 11(1,11)−10(0,10) (Eup = 60.4 K, Aul = 1.1 × 10-4 s-1, S = 7.7), and the last row shows the transition 14(3,11)−14(2,12) (Eup = 119 K, Aul = 1.1 × 10-4 s-1, S = 8.1). The interval between contours is 10 K km s-1, the minimum contour is 5 K km s-1 and the maximum 155 K km s-1. The white cross indicates the position of the hot core and the black cross the position of the compact ridge. |
The results from the Gaussian fits have been used to build rotational diagrams for each species. This method involves the representation of the upper level column density normalized by the statistical weight of each rotational level versus the upper level energy, assuming optically thin emission filling the beam (see, e.g., Goldsmith & Langer et al 1999). The expression used to obtain the rotational diagrams, taking an optical depth (Cτ) different to unity into account, is 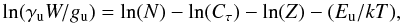 (2)where W is the integrated line intensity, gu is the statistical weight of each level, N the column density, Z the partition function, Eu the level energy, k the Boltzman constant, T the temperature considering LTE, and γu a constant that depends on the transition frequency and the Einstein coefficient Aul (see Goldsmith & Langer 1999 for more details). Each cloud component is considered separately in the analysis. The rotational diagrams, shown in Figs. A.1 and A.2, were obtained considering only lines without contamination from other species. The rotational temperatures obtained from SO2 lines are plateau (PL) = 120 ± 20 K, hot core (HC) = 190 ± 60 K, high-velocity plateau (HVP) = 110 ± 20 K, compact ridge (CR) = 80 ± 30 K, extended ridge (ER) = 83 ± 40 and 20.5 km s-1 component = 90 ± 20 K. The results from SO lines are (PL) = 130 ± 20 K, (HC) = 288 ± 90 K, (HVP) = 111 ± 15 K, (ER) = 107 ± 40 K, and 20.5 km s-1 component = 51 ± 10 K. These results are shown in Table A.4, together with the derived column densities and the optical depths. For each component, the obtained rotational temperatures for both molecules are consistent with each other, except for the HC where we obtain a large difference between both temperatures. This could indicate a temperature gradient in the hot core, or simply that the obtained rotational temperature could be overestimated due to the high scatter in the SO data. It would be necessary to have values of this species at higher energies in order to obtain firmer conlcusions. We observe that HVP presents a similar rotational temperature to the component of the plateau with lower velocity (PL). For the CR, we obtained a low temperature, probably due to the beam dilution, which is not corrected for in the rotational diagrams. From the diagrams, we also deduce that the new component at 20.5 km s-1 is not a very warm region.
(2)where W is the integrated line intensity, gu is the statistical weight of each level, N the column density, Z the partition function, Eu the level energy, k the Boltzman constant, T the temperature considering LTE, and γu a constant that depends on the transition frequency and the Einstein coefficient Aul (see Goldsmith & Langer 1999 for more details). Each cloud component is considered separately in the analysis. The rotational diagrams, shown in Figs. A.1 and A.2, were obtained considering only lines without contamination from other species. The rotational temperatures obtained from SO2 lines are plateau (PL) = 120 ± 20 K, hot core (HC) = 190 ± 60 K, high-velocity plateau (HVP) = 110 ± 20 K, compact ridge (CR) = 80 ± 30 K, extended ridge (ER) = 83 ± 40 and 20.5 km s-1 component = 90 ± 20 K. The results from SO lines are (PL) = 130 ± 20 K, (HC) = 288 ± 90 K, (HVP) = 111 ± 15 K, (ER) = 107 ± 40 K, and 20.5 km s-1 component = 51 ± 10 K. These results are shown in Table A.4, together with the derived column densities and the optical depths. For each component, the obtained rotational temperatures for both molecules are consistent with each other, except for the HC where we obtain a large difference between both temperatures. This could indicate a temperature gradient in the hot core, or simply that the obtained rotational temperature could be overestimated due to the high scatter in the SO data. It would be necessary to have values of this species at higher energies in order to obtain firmer conlcusions. We observe that HVP presents a similar rotational temperature to the component of the plateau with lower velocity (PL). For the CR, we obtained a low temperature, probably due to the beam dilution, which is not corrected for in the rotational diagrams. From the diagrams, we also deduce that the new component at 20.5 km s-1 is not a very warm region.
3.4. 2′ × 2′maps around IRc2
From the 2D line survey data of Orion KL, (Marcelino et al., in prep.), we produced integrated intensity maps of several SO and SO2 transitions over different velocity ranges. Figure 7 shows the transitions 4(2,2)−3(1,3), 11(1,11)−10(0,10), and 14(3,11)−14(2,12) of SO2; Fig. 6 shows the transitions 66−55 and 32−21 of SO; and Fig. 8 shows the transition 67−56 of 34SO and the transition 28(3,25)−28(2,26) of 34SO2. Velocity intervals in the figures have been chosen to represent different source components. For all species and transitions, the strongest contribution arises from the velocity ranges 3−7 km s-1 and 10−14 km s-1, belonging to the HC and the HVP, respectively. The range 3−7 km s-1 also includes PL velocities. These maps show elongated emission along the direction NE-SW. This agrees with Plambeck et al. (2009), who find (from SiO J = 2−1 observations with an angular resolution of 0.45″) that the strongest emission arises from a bipolar outflow covering velocities from −13 to 16 km s-1 along the NE-SW direction. This distribution is clearly seen in the maps of 34SO and of SO (see lower panel in Fig. 6), especially in the ranges 7−10 km s-1 (ridge) and 10−14 km s-1 (HVP). Since the line widths corresponding to the HVP are the widest, with FWHM ~ 30−40 km s-1, altogether this suggests that the gas of the HVP is expanding in the direction NE-SW. On the other hand, the spatial distribution of 34SO2 is less extended and usually shows a peak to the NE of IRc2 (also seen in SO2 and SO at velocities 3−7 km s-1). For this species, the NE-SW distribution is better traced by the 20.5 component. This different behavior should be due to the high energy level (Eup = 402.1 K) compared to the other mapped transitions, revealing the most compact and hottest regions in the KL cloud. Also evident on the maps is the new component at 20.5 km s-1. From Figs. 7 and 6 we observe that its emission peak is located between the HC and BN positions.
 |
Fig. 8 34SO and 34SO2-integrated intensity maps over different velocity ranges (indicated at the bottom of each panel in km s-1). Row 1 shows the transition 67−56 of 34SO (Eup = 46.7 K, Aul = 2.2 × 10-4 s-1). The contour interval is 7 K km s-1 and the minimum contour is 8 K km s-1. Row 2 shows the transition 28(3,25)−28(2,26) of 34SO2 (Eup = 402.1 K, Aul = 1.5 × 10-4 s-1). The interval between contours is 0.9 K km s-1, and the minimum contour is 1.2 K km s-1. The white cross indicates the position of the hot core and the black cross the position of the compact ridge. |
4. Analysis
4.1. LVG models of the SO lines
In this section we analyze the non-LTE excitation and radiative transfer of SO lines. Following the study started by Tercero et al. (2010), we use an LVG (large velocity gradient) code, MADEX, developed by Cernicharo (2012) assuming that the width of the lines is due to the existence of large velocity gradients across the cloud, so that the radiative coupling between two relatively close points is negligible, and the excitation problem is local. The LVG models are based on the Goldreich & Kwan (1974) formalism. The final considered fit is the one that reproduces more line profiles better from transitions covering a wide energy range, within a ~30% of the uncertainty in line intensity. For each component of the cloud, we assume uniform physical conditions (kinetic temperature, density, line width, radial velocity, and source size) that we choose taking into account the parameters obtained from the Gaussians fits of the line profiles, the rotational diagrams (with the derived rotational temperatures), and the mapped transitions.
Only for the HC do we consider LTE, which means that most transitions will be thermalized to the same temperature (Trot ≃ TK). If this condition was not satisfied, but we kept considering LTE approxmation, the temperatures would be overestimated, and this would produce a variation in the column densities. We cannot estimate whether they would be overestimated or underestimated since we do not know the population of each level. However, the HC of Orion presents a condition of temperature (TK > 200 K) and density (n(H2) ≃ 107 cm-3), which make the LTE assumption in this component feasible. Corrections for beam dilution are also applied for each line depending on the different beam sizes at different frequencies. Therefore, we fix all the above parameters (see Table 2) leaving only as a free parameter the column density fo each component. For the densitiy, n(H2), we have adopted fixed values taken from typical values quoted in the literature. In order to determine the uncertainty of the values of hydrogen density and of temperature (TK), we have run several models varying only the values for these parameters and fixing the rest.
Comparing the intensity differences between the spectra and the obtained line profiles for each case of T and n, we deduce an uncertainty of 20 and 15% for the temperature and the hydrogen density, respectively. Although the parameter which could introduce higher uncertainty in the line profiles is the considered source size for each component, due to it varies depending on the molecular emission used for its determination. We fixed this parameter, as well as the hydrogen density, taking into account also the values used by Tercero et al. (2011) in her models of SiO and SiS. Other sources of uncertainty in the model predictions arise from the spatial overlap of the different cloud components. However, it has been possible to model their contribution thanks to the wide range of frequency and to the large number of lines from different isotopologues. We also find as a source of uncertainty the modest angular resolution of any single-dish line survey, pointing errors (errors as small as 2″ could introduce important changes in the contribution from each cloud component to the observed line profiles, especially at 1.3 mm), and line opacity effects. This last source of uncertainty becomes important when lines arising from the plateau are optically thick, causing an underestimation of the column densities of the components that are surrounded by the plateau (compact ridge, hot core, and the 20.5 km s-1 component) along the line of sight (Schultz et al. 1999). In Tercero et al. (2010), these sources of uncertainty are explained in more detail. We estimate an uncertainty in our model intensity predictions of 25% for SO and 34SO, and 35% for SO2, 34SO2, 33SO, S18O, 33SO2, and SO18O lines (higher uncertainty for SO2 with respect to SO because of considering LTE instead of LVG approximation).
Physical parameters adopted for the Orion KL cloud components.
4.1.1. SO
 |
Fig. 9 Observed lines of SO (black histogram) and best fit LVG model results (red). |
 |
Fig. 10 Observed lines of 34SO (black histogram) and best fit LVG model results (red). |
To model the rotational lines of SO (listed in Table A.8), we used the collisional rates from Lique et al. (2006) for collisions with H2. Figure 9 shows our best fit model. The component with the highest SO column density is the HVP, with N(SO) = (5 ± 1) × 1016 cm-2 (see Table 3), although in the HC we also find a high column density with N(SO) = (9 ± 3) × 1015 cm-2. We find that the PL and the 20.5 km s-1 component also contribute to the emission, but with a column density that is one order of magnitude lower than the HVP. We did not need to consider any contribution from the CR for SO. We could fit the narrow component by considering only the contribution from a single ridge (the extended ridge) at a temperature TK = 60 K. This agrees with the previous SO analysis in Sect. 3.1.
The model indicates that some SO lines with emission coming mainly from the HVP are optically thick. The optical depths are τ = 1.1−1.4 for the transitions 65−54 and 66−55, and τ = 1.4−1.8 for the transitions 56−45 and 67−56. This means that the column densities obtained for the HC and 20.5 km s-1 components, which are surrounded by the plateau, must be considered as lower limits, because the gas in the plateau components can absorb the emission from them. The HVP column density also has to be considered as a lower limit due to this opacity effect. We have also calculated the SO column density from the column density of 34SO, whose lines are optically thin, and from the solar abundance ratio 32S/34S = 23 (Anders & Grevesse 1989). As we expected, Table 3 shows that the column densities of SO obtained from 34SO are higher than those obtained from the fits. This confirms the presence of opacity effects on SO lines. We notice that the SO lines 21−12, 54−44, 65−, and 98−88 present a poor fit. This is because of the low Einstein coefficients Aul and, mainly, to the low line strengths S (<4 × 10-6 s-1 and <0.35, respectively) of these lines, which provides small fits. The profile lines that we observe for these transitions are probably caused by stronger emission from other species.
Compared with values obtained in previous studies, such as those of Turner et al. (1991) or Blake et al. (1987), who derived (from source-averaged) N(SO) ~ 3 × 1016 cm-2 in the plateau and N ~ 3 × 1015 cm-2 in the HC, we see our results agree. If we compare these results with our obtained column densities from 34SO, we see that the plateau remains in agreement with these previous studies, but our column density in the HC is one order of magitude higher.
From the spatial distribution of the SO emission (Fig. 6), we find the integrated intensity peak to be in the velocity ranges 3−7 km s-1 and 10−14 km s1 for both transitions. These ranges correspond to emission arising mainly from the HC and the HVP, respectively, which agrees with the results obtained for the column densities in these regions. The transition with lowest energy (upper panel) shows a concentric emission distribution around IRc2, while for the transition with higher energy, the emission distribution is elongated toward NE-SW direction. We also observe that, for high energies, the emission peak in the velocity range 3−7 km s1 is shifted toward the NE of the HC.
4.1.2. 34SO, 33SO, and S18O
Figure 10 shows our best fit model for several rotational lines of 34SO, which are listed in Table A.8. We find that the HVP is also responsible for most of the emission, together with the PL and the 20.5 km s-1 component. According to our models, all transitions are optically thin with τ < 0.4, therefore this result is not considered to be a lower limit. The 20.5 km s-1 component presents a similar column density to the HVP, and as for SO, its contributon is greater for higher J. In the HC we also find a strong contribution to the emission, however in the ER we find the lowest column density with N(34SO) = (7 ± 2) × 1012 cm-2.
For the case of 33SO we observe in Fig. A.3 that lines are partially blended with other species, which produces a large uncertainty in the derived fit. In addition, the hyperfine structure is noticeable in these transitions, adding more complexity to the line profiles. The fits for this isotopologue were done by adopting the calculated frequencies, intensities, and energies for hyperfine levels up to N = 30 provided by the CDMS catalogs. We obtain similar column densities for all components, with N(33SO) = (3−6) × 1014 cm-2 (see Table 3).
As was the case for 33SO, some lines of S18O are blended with other species (Fig. A.4 and Table A.8). In this case we also find similar column densities for all the components, N(S18O) = (1−5) × 1014 cm-2, except for the CR, the ER, and the 20.5 km s-1 component, where we do not find contribution to the emission.
Column densities, N, for SO and its isotopologues obtained from LVG model fits.
4.1.3. S17O, 36SO, and 34S18O
Owing to the presence of other more intense species, we have detected neither S17O nor 36SO in this survey, but from our data we derive upper limits for their column densities of N(S17O) < 1.3 × 1014 cm-2 and N(36SO) < 1.6 × 1014cm-2, respectively. We note that C36S was detected by Mauersberger et al. (1996) in Orion. They found 32S/36S ≃ 3500 which is consistent with our upper limit. We have not detected 34S18O either; however, assuming the same physical conditions as those for the main isotopologue, we obtain an upper limit for its column density of N(34S18O) < 1.4 × 1014cm-2.
Column densities, N, for SO2 and its isotopologues, obtained from LTE model analysis.
4.2. LTE models of the SO2 lines
Due to the lack of collisional rates for levels with energies higher than 90 K, we have assumed LTE excitation to derive the SO2 column densities. As stated before, this can overestimate or underestimate the calculated column densities. Given that we have collisional rates for SO, we ran our SO models again but considering LTE approximation, in order to compare the results. We observed that the new fits underestimated the line profiles, especially for low transitions. Probably this also happens with the SO2 case, so we should consider our SO2 column densities as lower limits. Table A.9 lists the 166 observed rotational lines. Figures 11−14 show a sample of 90 observed lines (ordered by increasing energy) with our best fits overlaid.
The main contribution to the emission of SO2 comes from the HVP (affecting mainly the lines with energies E < 400 K), with a column density of N(SO2) = (1.3 ± 0.5) × 1017 cm-2. The hottest region (the HC) also presents a similar high value, N(SO2) = (1.0 ± 0.4) × 1017 cm-2. We find that the CR presents a column density of N(SO2) ~ 1015 cm-2, whereas the 20.5 km s-1 component presents the lowest contribution to the emission (Table 4).
If we compare our results for SO2 with those of SO, we find that SO2 column densities are about one order of magintude larger in all components, except in the 20.5 km s-1 component, where SO presents a higher contribution to the emission. As for SO, we also calculated the SO2 column densities from 34SO2 (optically thin lines) and the 32S/34S solar abundance ratio (Table 4). Except for the plateau components, we obtain that the column densities of SO2 obtained from 34SO2 are larger than those obtained from fits, suggesting they are opacity effects on the SO2 lines. Comparing with previous results, Blake et al. (1987) obtained (source-averaged) that SO2 presents a column density in the plateau, N ~ 1016 cm-2. Schilke et al. (2001) derived (beam-averaged) for the same region N(SO2) = 9.7 × 1016 cm-2, which is very similar to our result in the HVP. For the HC, Sutton et al. (1995) found (also source-averaged) a column density, N(SO2) ~ 9 × 1016 cm-2. Our results agree with these values; however, the large number of transitions that we observed let us determine more accurately that it is the lower temperature plateau component, i.e. the HVP, which contributes more to the emission of SO2.
From the spatial distribution of the SO2 emission (Fig. 7), we find the maximum integrated line intensity between the velocity ranges 3−7 km s-1 and 10−14 km s-1, as well as for SO. These velocity ranges correspond to emission of the HC and the HVP, respectively, which agrees with the column density results obtained above. The emission peak is located towards the NE of IRc2 for the range 3−7 km s-1, while the emission peak for the HVP range is located ~4″ to the SW of IRc2. Emission from the 20.5 km s-1 component presents similar integrated intensity to the ridge (range of 7−10 km s-1). On the other hand, the map of 34SO2 (Fig. 8) shows the strongest peak emission located northeast of IRc2 for all velocity ranges, although extended emission is seen to the southwest of IRc2, between 10 km s-1 and 22 km s-1. The 34SO2 transition shown in Fig. 8 has an upper energy level of ~400 K and therefore may trace only the hottest component of the gas.
 |
Fig. 11 Observed lines (black histogram) of SO2 with upper state energies lower than 400 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
 |
Fig. 12 Observed lines of SO2 (black histogram) with upper state energies lower than 400 K (continued), ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
 |
Fig. 13 Observed lines of SO2 (black histogram) with upper state energies between 400 K and 700 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
 |
Fig. 14 Observed lines of SO2 (black histogram) with energies higher than 700 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
 |
Fig. 15 Observed lines of 34SO2 (black histogram). Best fit LTE model results are shown in red. Boxes with black, blue and green borders correspond to lines observed at 1.3, 2, and 3 mm, respectively. |
 |
Fig. 16 Observed lines of SO2ν2 = 1 (black histogram). Best fit LTE model results are shown in red. |
4.2.1. 34SO2
We have detected 130 rotational lines of 34SO2 (Table A.9). A sample of more than 30 lines is shown in Fig. 15.
This isotopologue, whose lines are optically thin, has the highest contribution to its emission from the HC, with N(34SO2) = (1.0 ± 0.4) × 1016 cm-2. The other components with high column densities are the HVP and the PL with N(34SO2) = (7 ± 2) × 1015 cm-2 and N(34SO2) = (6 ± 2) × 1014cm-2, respectively. Particulary interesting is the column density found in the ER, which presents the same order of magnitude as the PL. The same behavior is also observed in the isotopologues 33SO2 and SO18O, where the column densities in the ER are only 3 to 12 times lower than in PL. This could be due to the strong emission emerging from the HVP and HC affecting the excitation of the energy levels of this isotopologue in the ER, which means that line photons emitted from the inner components will be scattered by the lower density gas in the ER component (radiative scattering). For the compact ridge, we find the emission contributes mainly to the lines at low frequencies. The column density for 34SO2 obtained in the 20.5 km s-1 component is about 100 times lower than for 34SO (see Table 4).
4.2.2. 33SO2, SO18O, and SO17O
Figure A.5 shows transitions of 33SO2 in the frequency range covered at 1.3, 2, and 3 mm. Several of these are blended with other species, which makes the derived fits a bit biased. As for 33SO, hyperfine structure affects the line profiles; however, we did not consider it in the 33SO2 model, so the derived column densities could be underestimated.
The most important contribution to the emission of 33SO2 comes from the hot core, with N(33SO2) = (4 ± 1) × 1015 cm-2, and from the HVP. The lowest contribution to the emission arises from the 20.5 km s-1 component, with N(33SO2) = (9 ± 3) × 1012 cm-2.
For SO18O (Fig. A.6), the highest column density is also found in the HC, with N(SO18O) = (1.5 ± 0.5) × 1015 cm-2. The HVP also presents an important contribution to the emission across the frequency range, whereas the PL mainly affects lines at 2 mm. The weakest contribution is from the ER, with N(SO18O) ~ 1013 cm-2.
Figure A.7 shows the spectra that contain some frequencies of SO17O, together with our best model. The maximum contribution to the emission of this isotopologue arises from the hot core with N(SO17O) = (8 ± 3) × 1014 cm-2. We find that the PL and HVP also contribute to the emission, but about four to eight times less than the HC. However, because all lines are weak (TMB < 0.3 K) and blended with other species, we should consider these results as upper limits.
4.2.3. SO2ν2 = 1
Figure 16 shows some of the detected lines of vibrationally excited SO2ν2, which are also listed in Table A.9. The hot core is responsible for most of the emission of this vibrational mode, with a column densitiy one order of magnitude higher than in the other components. From the column densities in the HC for SO2 in its ground and vibrationally excited states, we can estimate a vibrational temperature, considering that 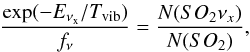 (3)where Eνx is the energy of the vibrational state (Eν2 = 745.1 K), Tvib is the vibrational temperature, N(SO2νx) is the column density of SO2 in the excited vibrational state, N(SO2) the total column density, and fν is the vibrational partition function, given by
(3)where Eνx is the energy of the vibrational state (Eν2 = 745.1 K), Tvib is the vibrational temperature, N(SO2νx) is the column density of SO2 in the excited vibrational state, N(SO2) the total column density, and fν is the vibrational partition function, given by 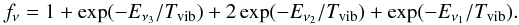 (4)Taking into account that N(SO2) = N(ground) × fν, we only need the energy of the vibrational state and the calculated column densities to derive the vibrational temperature.
(4)Taking into account that N(SO2) = N(ground) × fν, we only need the energy of the vibrational state and the calculated column densities to derive the vibrational temperature.
We obtain Tvib = (230 ± 40) K for SO2ν2 = 1. This value is similar to the kinetic temperature we assumed for the HC component (220 K). It is unlikely that the ν2 = 1 level at 745 K above the ground is excited by collisions. The main pumping mechanism could be IR radiation from the HC. A similar situation was found by Tercero et al. (2010) for OCS and other species.
4.2.4. 34SO2ν2 = 1
Figure A.8 shows some observed lines of 34SO2ν2 = 1. The strongest emission comes from the hot core with N(34SO2ν2 = 1) = (7 ± 2) × 1014 cm-2, although we also find a small contribution from the HVP and the CR, with N(34SO2ν2 = 1) ~ 5 × 1013 cm-2 for both. These contributions mainly affect the lines at 2 mm. Since all the lines we detect are very weak and mixed with other species, we should consider these results as upper limits.
4.3. Isotopic and molecular abundances
From the derived column densities of SO, SO2, and their isotopologues, we can estimate abundance ratios. These are shown in Table A.5. We compare these ratios with solar isotopic abundance values from Anders & Grevesse (1989).
32S/34S: from the SO2 lines we obtain a column density ratio for the PL of 32S/34S = 16 ± 10, in agreement with previous studies (32S/34S ≃ 16 by Johansson et al. 1984, 32S/34S ≃ 13−16 by Blake et al. 1987, and 32S/34S = 15 ± 5 by Tercero et al. 2010). For the HVP, 32S/34S = 20 ± 13, which is similar to the value for the solar isotopic abundance ratio and to the result deduced by Persson et al. (2007) where 32S/34S ≃ 23 ± 7. From the SO lines, with the exception of the HVP, we obtain low ratios for 32S/34S in comparison with the solar abundance, which could be due to opacity effects on the SO lines.
32S/33S: from N(SO)/N(33SO) we obtain 32S/33S = 180 ± 80 for the HVP. This value agrees with the solar isotopic abundance ratio, 127, from Anders & Grevesse (1989). For the other three components, the obtained ratios are very low compared to the solar abundance, probably also due to the opacity effects for SO lines. These values should be considered as lower limits. We find similar behavior for the ratio N(SO2)/N(33SO2).
34S/33S: from N(34SO2)/N(33SO2) we obtain 34S/33S = 4 ± 3 for the 20.5 km s-1 component and 34S/33S = 3−7 for the ridge (ER and CR), the HVP, and the HC. These values are similar to the solar abundance ratio (5.5). From N(34SO)/N(33SO) the obtained ratio is 34S/33S = 6 ± 3 for the HC and both plateau components.
16O/18O: our results for this ratio in the plateau agree with those obtained by Tercero et al. (2010), who derived 16O/18O = 250 ± 135 in the plateau from a study of OCS in this region. The compact ridge also presents similar ratio to that obtained by them. However, all these values are lower than the solar isotopic abundance (≃ 500).
SO/SO2: in Fig. 18 we present the ratio N(SO)/N(SO2) for the different components, as well as for the different isotopologues of SO and SO2. We find that SO2 is more abundant than SO in all components, except in the 20.5 km s-1 component. In the HVP, SO2 is three times more abundant than SO, while in the HC is up to 11 times more. However, in the 20.5 km s-1 component, SO is ~30 times more abundant than SO2.
34SO/34SO2: in the region affected by shocks, this ratio implies that 34SO2 is more abundant (~1.7 times) than 34SO. In the hot core, we also find that 34SO2 is more abundant (5 times) than 34SO, whereas in the ER the ratio is much larger (34SO2 is 14 times more abundant). As was found for SO/SO2, the main difference is in the 20.5 km s-1 component, where 34SO is ~100 times more abundant than 34SO2.
Table A.6 shows the molecular abundances, X, of SO and SO2 with respect to hydrogen in each component. They were derived using H2 column density by means of the C18O column density, from the isotopic abundance 16O/18O, and assuming that CO is a good tracer of H2 and therefore their abundance ratio is roughly constant. The column densities for H2 are 7.5 × 1022, 7.5 × 1022, 2.1 × 1023, 6.2 × 1022, 4.2 × 1023 cm-2, and 1.0 × 1023 for the ER, CR, PL, HVP, HC, and the 20.5 km s-1 component, respectively (see Tercero et al. 2011). We observe that the highest abundance of SO is obtained in the HVP, whereas in the HC and in the PL this abundance is ~30 times lower. The extended ridge presents the lowest abundance of sulfur monoxide. The abundance of this molecule in the 20.5 km s-1 component is about twice larger than in the HC. SO2 is also more abundant in the HVP (between 8 and 600 times more abundant than in the rest of components). With respect to hydrogen, SO2 is about one order of magnitude more abundant than SO in the HC and in the ER, while in both plateaus sulfur dioxide is only two-three times more abundant than SO.
4.4. Other sulfur-bearing molecules
We provide here upper limits for the column densities of several sulfur-bearing molecules not detected in our survey. We have assumed the same spectral components as for SO and SO2 (HC, PL, HVP, CR, and ER) and an LTE approximation, due to the lack of available collision rates. Table 2 shows the adopted temperature values, among other parameters, for each component, and Table A.7 shows the results obtained, the dipole moment of each species, and references for the spectroscopic constants. The upper limit of column density for each species were obtained summing the contribution of all the components.
SO+: first detected in the interstellar medium towards the supernova remnant IC443 (Turner et al. 1992), it was proposed as a tracer of dissociative shocks, although later surveys carried out in dark clouds, SFRs, and high velocity molecular outflows suggest that this reactive ion is not associated with shock chemistry (Turner et al. 1994). SO+ presents a high abundance in PDRs like NGC 7023 and in the Orion Bar (Fuente et al. 2003). In Orion KL, we obtain an upper limit to its column density of N(SO+) ≤ 2.5 × 1014 cm-2, providing an abundance ratio of N(SO)/N(SO+) ≥ 2080. This result implies that UV radiation does not play an important role in this region.
 |
Fig. 17 Observed lines of SO2 (black histogram) with energies higher than 700 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results considering a hot core at TK = 220 K (green curve) and with a hot core at TK = 280 K (red curve). |
(cis)-HOSO+: it is the most stable isomeric form of this ion. This species has not yet been detected in the interstellar medium, but its large dipole moment (1.74 D), its easy formation through H reacting with SO2 and the fact that it does not react with H2 make this ion an excellent candidate for being detected, mainly in hot regions where the parent SO2 is very abundant. The upper limit calculated for this ion is N(cis-HOSO+) ≤ 3.6 × 1013 cm-2.
reacting with SO2 and the fact that it does not react with H2 make this ion an excellent candidate for being detected, mainly in hot regions where the parent SO2 is very abundant. The upper limit calculated for this ion is N(cis-HOSO+) ≤ 3.6 × 1013 cm-2.
SSO: this molecule has not been detected yet in the interstellar medium, but it is a plausible candidate, since the oxides SO and SO2 are particulary abundant, especially in SFRs. Disulfur monoxide (SSO) was spectroscopically studied first by Meschi & Myers (1959) who detected rotational transitions in the ground vibrational state and in the ν2 = 1 state. Later, Thorwirth et al. (2006) carried out a millimeter and submillimeter wave investigation of SSO in the ground vibrational state to frequencies as high as 470 GHz. We have not detected SSO in our line survey, but we obtain an upper limit for its column density of N(SSO) ≤ 7.6 × 1014 cm-2, providing an abundance ratio of N(SO)/N(SSO) ≥ 1155.
OSiS: silicon oxysulfide was first characterized in the gas phase at high spectral resolution by Thorwirth et al. (2011). It prosseses a large dipole moment (μa = 1.47 D) and its bond distances are very short in comparison with those of SiO and SiS. It has not been detected yet in the interstellar medium, and we obtained an upper limit for the column density of this molecule in Orion KL of N(OSiS) ≤ 6.3 × 1013 cm-2. Tercero et al. (2010) found that in Orion KL the total column density for SiS in the ground state is N(SiS) = (1.4 ± 0.4) × 1015 cm-2. This result provides an abundance ratio of N(SiS)/N(OSiS) ≥ 22.
S3: thiozone is a bent chain with a bond to the apex S whose rotational spectrum was first measured by McCarthy et al. (2004a). S3 has not yet been observed in the interstellar medium; however, it is an excellent candidate for astronomical detection in rich interstellar sources. In addition, S3 may also exist in the atmosphere of Io, where S2 has already been detected in the ultraviolet. Owing to the presence of more intense lines from other species we have not detected S3 in our line survey. We provide an upper limit for its column density of N(S3) ≤ 1 × 1015 cm-2.
S4: tetrasulfur is a singlet planar trapezoid whose rotational spectrum was observed for the first time by McCarthy et al. (2004a). S4 has a substantial dipole moment, 0.87 D, hence an intense rotational spectrum across the entire radio band. The upper limit column density we calculated for this molecule is N(S4) ≤ 7 × 1014 cm-2.
CH3SOCH3: Barnes et al. (1994) obtained this molecule in the laboratory while investigating the gas-phase reaction of OH with the oxidation of dimethyl sulfide at room temperature. Dimethyl sulfoxide has not been observed yet in the interstellar medium, but we provide an upper limit for its column density of N(CH3SOCH3) ≤ 1 × 1014 cm-2.
H2CSO: sulfine was first identified in 1976 as a product of the pyrolysis of a variety of sulfur-bearing precursors. H2CSO is a planar molecule of Cs symmetry. Joo et al. (1995) analyzed its infrared spectrum at high resolution. We provide an upper limit for the column density for this undetected molecule in the interstellar medium of N(H2CSO) ≤ 3 × 1013 cm-2.
HNSO: thionylimide is a semi-stable molecule that adopts a cis-planar structure of Cs symmetry in the ground state. HNSO is the simplest molecule in the group of organic nitrogen-sulfur compounds. We calculated an upper limit for its column density of N(HNSO) ≤ 4.1 × 1014 cm-2, which provides an abundance ratio N(SO)/N(HNSO) ≥ 2600.
o-H2S2: the rotational spectrum of disulfane (H2S2) has been measured in the far-infrared, millimeter, and submillimeter (Winnewisser et al. 1966). The density of its spectrum is enhanced by the presence of low-lying torsional and S-S stretching modes. We did not observe this molecule in our line survey but we provide an upper limit for its column density of N(o-H2S2) ≤ 1.6 × 1014 cm-2.
SSH and H2SO4: these molecules have not yet been detected in the interstellar medium. The calculated upper limits for their column densities are N(SSH) ≤ 7.1 × 1013 cm-2 and N(H2SO4) ≤ 1.3 × 1014 cm-2, respectively.
CH3SSH: methyl hydrodisulfide has not been observed in the interstellar medium. Tyblewski et al. (1986) studied its rotational spectrum, together with that of CH3SSD, between 18 and 40 GHz providing rotational constants. We derive an upper limit for its column density of N(CH3SSH) ≤ 2.6 × 1014 cm-2.
(tr)-HCSSH: the spectrum of dithioformic acid has been studied by Bak et al. (1978), who assigned the rotational transitions of this species in its ground state to a trans and cis rotamer. We provide an upper limit for the column densitiy of (tr)-HCSSH (more stable) N ≤ 3.6 × 1013 cm-2.
5. Discussion
There have been many spectral line surveys of Orion KL aimed at determining the physical and chemical structure of this region (e.g., Blake et al. 1987, Sutton et al. 1995; Schilke et al. 2001). The survey analyzed here was first presented by Tercero et al. (2010), covers the widest frequency range of all of them (80−281 GHz). Due to this wide range and to the large number of observed transitions of SO, and particularly of SO2, it has been possible not only to determine the structure of the cloud (gas temperature, gas density, size of components, etc.) with better accuracy (the 3 mm window shows best the coldest regions, such as the ER, whereas the 1.3 mm window probes the warmest regions), but also to demonstrate the need for considering a density and temperature gradient in the HC of Orion KL. From rotational diagrams, we found a large difference (~100 K) between the rotational temperatures of SO and SO2, indicating the possibility of a hotter inner region to the HC. We draw the same conclusion from the fits for SO2 lines with energies E > 400 K. To obtain better fits for lines with energies E > 700 K, we considered a high column density for the HC, which overestimates in the fit for the lines with energy around 400 K (see Figs. 12 and 13). But by considering an additional inner component to the HC with higher temperature, it would probably be possible to obtain a better fit to the lines with high energies, while avoiding overestimation of lines with intermediate energies. To test this possibility, we fit the SO2 line profiles with energies E > 700 K considering a hotter (TK = 280 K) HC (affecting only the highest energy transitions), with n(H2) = 5 × 106 cm-3, located at 5.5 km s-1, and with △ vFWHM = 7 km s-1. For a SO2 column density of (4 ± 1) × 10m16 cm-2, we improve the line profile fits of these high energies transitions (see Fig. 17). This shows the existence of a temperature and density gradient in the HC of Orion KL. However, its structure should be determined accurately with observations of SO and SO2 (and mainly of its isotopologues3, which are optically thin) at higher frequencies with telescopes such as APEX.
 |
Fig. 18 Ratio N(SO)/N(SO2) for each component and for the different isotopologues of SO and SO2. |
On the other hand, the large number of observed lines of the 34S and 33S isotopologues has allowed us to calculate column densities and isotopic and molecular abundances that are key to understanding the chemical evolution of this region.
5.1. SO and SO2 as tracers of shocks and hot gas
In Sect. 4 we showed that an important contribution to the emission of SO and SO2 comes from the HC component of Orion KL. In Fig. 18 we plotted the ratio of N(SO)/N(SO2) for the different components, as well as for the different isotopologues of SO and SO2. The figure shows that the column density of SO2 in the HC is higher than that for SO. We should take into account that our column densities for SO2 may have been slightly underestimated because of using an LTE model to infer the column density (instead of LVG, as was used for SO). For that reason, we considered a higher uncertainty (35%) in the model intensity predictions for SO2, than for SO (20%), as said previously. Moreover, the opacity may affect SO and SO2 differently, which would in turn affect their column density ratio. But if we consider the result of the ratio 34SO/34SO2 in the hot core, we observe that SO2 continues to be more abundant than SO. This could indicate that SO2 is a better tracer of warm gas than SO.
Our results are consistent with predictions from chemical models of hot cores (e.g., Hatchell et al. 1998). Viti et al. (2004a) modeled the evaporation of ices near massive stars and found that SO2 becomes more abundant than SO in the hot core from 31.500 years after the formation of a high-mass star. For shorter timescales, SO is much more abundant than SO2. Thus, the SO/SO2 ratio could be regarded as a chemical clock (which should decrease with time), and our results showing a lower SO/SO2 ratio for the HC component seem to suggest a late stage for the hot core evolution in Orion KL.
On the other hand, the ratio of SO/SO2 is higher in the PL and the HVP than in the HC and the ER (see Fig. 18), and in particular for the PL, this ratio reaches values close to or even higher than 1. Since SO is a well-known outflow tracer (e.g., Chernin et al. 1994; Codella & Scappini 2003; Lee et al. 2010; Tafalla et al. 2010), and SO seems to be more enhanced than SO2 in shocks (from an observational point of view, e.g., Codella & Bachiller 1999, Jiménez-Serra et al. 2005, and from a theoretical point of view, e.g., Viti et al. 2004b; Benedettini et al. 2006, for timescales ~10 000 yr), it seems very feasible that the high SO/SO2 ratios measured in the (high velocity) plateau are the consequence of a definite enhancement of the SO abundance with respect to SO2, due to shocks propagating into the surrounding medium of Orion KL.
5.2. Nature of the 15 km s-1 dip and 20.5 km s-1 velocity component
To properly fit the SO and SO2 spectra in Orion KL, a new velocity component at 20.5 km s-1 had to be included in the model (see Sect. 3.2). In addition, a possible dip at 15.5 km s-1 in the SO and SO2 spectra has been identified. The dip at 15.5 km s-1 could be self-absorption due to the high opacity of the observed transitions. However, in all cases, the line strength S is uncorrelated with the amount of absorption. For example, the transition 11(1,11)−10(0,10) of SO2, with a line strength of S = 7.7 and Einstein coefficient Aul = 1.1 × 10-4 s-1, would be expected to display more self-absorption and therefore a lower integrated intensity than the transition 4(2,2)-3(1,3) with S = 1.7 and Aul = 7.7 × 10-5 s-1, but we see the opposite (especially in the range at 14.5−16.5 km s-1). In addition, we obtain in Fig. 7 a high integrated intensity in the velocity range 14−18 km s-1, when the integrated intensity in the ranges 10−14 km s-1 and 18−22 km s-1 is also large. Altogether, this suggests that the emission at 15 km s-1 is only the sum of contributions of emission coming from the HVP and the 20.5 km s-1 component.
With respect to the nature of the emission at 20.5 km s-1, Fig. 18 shows that the column density ratio of SO/SO2 of this component is about two to three orders of magnitude higher than the other velocity components in Orion KL. This is also true for the 34SO/34SO2 and 33SO/33SO2 ratios, suggesting that it is not an opacity effect. Such a high ratio could be due in part to filling factor problems, if the 20.5 km s-1 component is much more compact in SO2 than in SO4, and/or could be the result of applying a different method (LVG for SO vs LTE for SO2) to infer the column densities. However, the large difference compared to the other components suggests that it is a definite chemical effect, and since the SO/SO2 ratio is higher in regions associated with shocks such as the HVP and the PL (Sect. 5.1), the 20.5 km s-1 component could be related to shocks as well, maybe associated with the explosive dynamical interaction that took place in Orion KL (Gómez et al. 2005; Zapata et al. 2011a) and more especifically to shocks associated with the BN object. This is consistent with the fact that the BN object in Orion presents significantly high CO and 13CO emission at ~20 km s-1 (Scoville et al. 1983). Observations combining both single-dish and interferometric data are required to definitely identify the spatial region in Orion KL emitting the bulk of emission at 20 km s-1 .
6. Summary and conclusions
This study is part of a series of papers with the goal of analyzing the physical and chemical conditions of Orion KL. The study is divided into different molecular families, and here we have focused on the emission lines of SO and SO2 and their isotopologues. We have analyzed the IRAM 30-m line survey of Orion KL observed by Tercero et al. (2010), which covers the frequency range 80−281 GHz. We identified more than 700 rotational transitions of these molecules, including lines from the vibrational state ν2 = 1 of SO2 and the isotopologue SO17O, detected for the first time in the interstellar medium. This large sample has let us improve our knowledge about the physical and chemical conditions in Orion KL, especially due to the observation of a large number of SO2 transitions at high energies. The analysis of SO and SO2 was carried out using an LTE and LVG radiative transfer model, taking the physical structure of the source into account (hot core, compact ridge, extended ridge, and plateau components).
First, we fit SO and SO2 lines with Gaussian profiles to obtain an approximate Trot value in each component. We detected a dip at ~15 km s-1 in most of the lines and an emission peak centered on 20.5 km s-1. For the dip at 15 km s-1, we discarded self-absorption as a possible cause, concluding instead that the weak emission is due to the sum of small contributions coming from the HVP and from the 20.5 km s-1 feature, which corresponds to an unresolved component (~5″ diameter), with line width of ~7.5 km s-1 and with an especially high column density of SO in comparison to SO2. Its rotational temperature is 50 ± 10 K from SO lines and 90 ± 20 K from SO2 lines. For the rest of the components, the rotational temperatures obtained from SO2 lines are: plateau (PL) = 120 ± 20 K, hot core (HC) = 190 ± 60 K, (HVP) = 110 ± 20 K, compact ridge (CR) = 80 ± 30 K, and extended ridge (ER) = 83 ± 40. The results from SO lines are: (PL) = 130 ± 20Ã K, (HC) = 288 ± 90 K, (HVP) = 111 ± 15 K, and (ER) = 107 ± 40 K.
The second part of the analysis was carried out using a radiative transfer code. For the case of SO, we analyzed its non-LTE excitation, however, for SO2 we assumed LTE excitation due to the lack of collisional rates for energies higher than 90 K (we observe SO2 lines with energies up to 1500 K). We found that most of the emission of SO2 and SO arises from the HVP, with column densities of N(SO2) = (1.3 ± 0.3) × 1017 cm-2 and N(SO) = (5 ± 1) × 1016 cm-2, respectively, and from the hot core, in particular in the case of SO2, whose column density is similar to that obtained in the HVP. These values are up to three orders of magnitude higher than the column densities obtained for the ridge components. These results let us conclude that SO and SO2 are good tracers not only of shock-affected areas, but also of hot dense gas. In addition, from the ratios 34SO/34SO2, 33SO/33SO2, and S18O/SO18O2 in the different components of the cloud, we observe that in the HVP (region affected by shocks) sulfur dioxide is up to five times more abundant than SO. The same trend is found in the hot core.
We have also carried out 2′ × 2′ mapping around Orion IRc2 in a number of lines of SO, SO2, and their 34S isotopologues. In Sect. 3.4 we presented maps of three transitions of SO2 (Fig. 7), two transitions of SO (Fig. 6), one transition of 34SO and one of 34SO2 (Fig. 8). We plotted different velocity ranges for each transition to explore the spatial distribution of the emission. In agreement with our column density results, we found the maximum integrated intensities in the range containing the hot core (3−7 km s-1) and in the range 10−14 km s-1 (corresponding to the HVP), whose emission peak is centered approximately 4″ to the southwest of IRc2. In all mapped transitions, but especially in those of SO and 34SO, we observe an elongation of the gas along the NE-SW direction. In these maps, we also detected a strong emission in the velocity range located at 20.5 km s-1. From the spatial distribution of this feature and from the analysis of the line profiles, we suggest that this emission is probably related to shocks associated to the BN source or to a gas cloudlet ejected in the explosive event that could have taken place in Orion KL.
In this paper, we have also demonstrated the need to consider a temperature and density gradient in the hot core of Orion KL, with a comparison between fits of SO2 line profiles at high energies, assuming two different temperatures (TK = 220 K and TK = 280 K) in the hot core. Only with the low temperature it was not possible to obtain good line fits for E > 700 K, without avoiding overestimation for lines with intermediate energies. In addition, the large difference between the rotational temperatures in the hot core and the need to consider a large contribution to the SO2 isotopologue emission in the extended ridge support the conclusion of the presence of temperature and density gradients in Orion KL. However, it would be necessary to also consider emission lines (mainly from isotopologues) spanning a wider frequency range with observations from other telescopes, such as APEX, in order to determine these gradients accurately. Moreover, to describe this molecular cloud in greater detail while avoiding spectral confusion would require interferometric observations with higher spectral resolution and higher sensitivity (such as those provided by ALMA).
Online material
Appendix A: Figures and tables
SO emission line parameters obtained from Gaussian fits.
SO2 parameters from Gaussian fits (lines at 1.3 mm).
SO2 parameters from Gaussian fits (lines at 2−3 mm).
Rotational temperatures, Trot, and column densities, N, obtained from rotational diagrams.
Isotopologue ratios and molecular ratios.
Molecular abundances, X.
Column density upper limits for undetected sulfur-bearing molecules in Orion KL.
 |
Fig. A.1 Rotational diagrams for the plateau, high-velocity plateau, and hot core components. Black dots for SO2 and green dots for SO. The black and green lines are the best linear fits to the SO2 and SO points, respectively. |
 |
Fig. A.2 Rotational diagrams for the compact ridge, extended ridge, and 20.5 km s-1 component. Black dots for SO2 and green dots for SO. The black and green lines are the best linear fits to the SO2 and SO points, respectively. |
 |
Fig. A.3 Observed lines of 33SO (black histogram) and best fit LVG model results (red). |
 |
Fig. A.4 Observed lines of S18O (black histogram) and best fit LVG model results (red). |
 |
Fig. A.5 Observed lines of 33SO2 (black histogram) and best fit LTE model (red). Boxes in black, blue, and green correspond to frequencies at 1.3, 2, and 3 mm, respectively. |
 |
Fig. A.6 Observed lines of SO18O (black histogram) and best fit LTE model (red). |
 |
Fig. A.7 Observed lines of SO17O (black histogram) and best fit LTE model (red). |
 |
Fig. A.8 Observed lines of 34SO2ν2 = 1 (black histogram) and best fit LTE model (red). |
Observed lines of SO and its isotopologues.
Observed lines of SO2, its isotopologues, and vibrationally excited states.
Spectroscopic parameters for SO (dipole moment μ = 1.535 D) have been obtained from Clark & DeLucia (1976), Tiemann (1982), Lovas et al. (1992), Cazzoli et al. (1994), Klaus et al. (1996), Bogey et al. (1997), Powell & Lide (1964), and Martin-Drumel (2012). For 34SO and S18O (μ = 1.535 D) from Tiemann (1974), Tiemann (1982), Lovas et al. (1992), Klaus et al. (1996), Bogey et al. (1982), and Powell & Lide (1964). And for 33SO (μ = 1.535 D) from Klauss et al. (1996), Lovas et al. (1992), and Powell & Lide (1964). In the case of SO2 and 33SO2 (μ = 1.633 D), the spectroscopic parameters were taken from Müller et al. (2000) and Patel et al. (1970). For 34SO2 (μ = 1.633 D) from Belov et al. (1998) and Patel et al. (1979). For the isotopologue SO18O (μa = 0.0328 D, μb = 1.633 D) obtained from Belov et al. (1998) and for SO17O (μa = 0.02 D, μb = 1.633 D) from Müller et al. (2000). For the vibrational state SO2ν2 = 1, (μ = 1.626 D) from Müller & Brünken (2005) and from Patel et al. (1979), and for 34SO2ν2 = 1, (μ = 1.626 D) from Maki & Kuritsyn (1990).
In fact, interferometric maps of 34SO in Orion KL reveal emission only from 1 to 15 km s-1 (Beuther et al. 2005), indicating that the emission from the 20 km s-1 component has probably been filtered out by the interferometer. Given the minimum baseline of the interferometric observations (Beuther et al. 2005), the largest angular scale detectable is ~6″ (following the Appendix in Palau et al. 2010), similar to the size adopted in this work for the 20.5 km s-1 component.
Acknowledgments
We thank the Spanish MICINN for funding support through grants AYA2006-14876, AYA2009-07304, and CSD2009-00038. J.R.G. is supported by a Ramón y Cajal research contract. A.P. is supported by a JAE-Doc CSIC fellowship co-funded with the European Social Fund under the program “Junta para la Ampliación de Estudios”, by the Spanish MICINN grant AYA2011-30228-C03-02 (co-funded with FEDER funds), and by the AGAUR grant 2009SGR1172 (Catalonia). T.A.B. is supported by a JAE-Doc research contract.
References
- Anders, E., & Gevesse, N. 1989, GeCoA, 53, 197 [Google Scholar]
- Bachiller, R. 1996, A&A, 34, 111 [Google Scholar]
- Bak, B., Nielsen, J., & Svanholt, H. 1978, J. Mol. Spectrosc., 69, 401 [Google Scholar]
- Barnes, I., Becker, K. H., & Patroescu, I. 1994, GeoRL, 21, 2389 [NASA ADS] [Google Scholar]
- Behrend, J., Mittler, P., Winnewisser, G., & Yamada, K. M. T. 1990, J. Mol. Espectrosc., 141, 265 [Google Scholar]
- Belov, S. P., Tretyakov, M. Y., Kozin, I. N., et al. 1998, J. Mol. Espectrosc., 191, 17 [Google Scholar]
- Benedettini, M., Yates, J. A., Viti, S., & Codella, C., et al. 2006, MNRAS, 370, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Zhang, Q., & Greenhill, L. J., et al. 2005, ApJ, 632, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, G., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Bogey, M. 1982, Chem. Phys., 66, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bogey, M., Civis, S., Delcroix, B., et al. 1997, J. Mol. Spectrosc., 182, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Cludi, L., Cotti, G., et al. 1994, J. Mol. Spectrosc., 167, 468 [Google Scholar]
- Cernicharo, J. 1985, ATM, A Program to compute atmospheric absorption for frequencies below 1000 GHz, IRAM Internal Report No. 52 [Google Scholar]
- Cernicharo, J. 2012, in ECLA-2011: Proc. Eur. Conf. Lab. Astrophys. EAS PS, 2012 [Google Scholar]
- Chernin, L. M., Masson, C. R., & Fuller, G. A. 1994, ApJ, 436, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, F. O., & Johnson, D. R. 1974, ApJ, 191, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, W. W., & DeLucia, F. C. 1976, J. Mol. Spectrosc., 60, 332 [Google Scholar]
- Codella, C., & Bachiller, R. 1999, A&A, 350, 659 [NASA ADS] [Google Scholar]
- Codella, C., & Scappini, F. 2003, MNRAS, 344, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Dreizler, H., & Dendl, G. 1964, Naturforsch. 19a, 512 [Google Scholar]
- Fuente, A., Rodríguez-Franco, A., García-Burillo, S., et al. 2003, A&A, 406, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gezari, D. Y., Backman, D. E., & Werner, M. W. 1998 ApJ, 509, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., Cernicharo, J., Lerate, M. R., et al. 2006, ApJ, 641, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, L., Rodríguez, L. F., Loinard, L., & Lizano, S. 2005, ApJ, 635, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., & Ball, J. A. 1973, ApJ, 184, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Guélin, M., Brouillet, N., Cernicharo, J., et al. 2008, Ap&SS, 313, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., Thompson, M. A., Millar, T. J., & MacDonald, G. H. 1998, A&A, 338, 713 [NASA ADS] [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., Rodríguez-Franco, A., & Martín, S. 2005, ApJ, 627, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Joo, D. L., Clouthier, D. J., Chan, C. P., et al. 1995, J. Mol. Spectrosc., 171, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Joo, D. L., Harjanto, H., & Clouthier, D. J. 1996, J. Mol. Spectrosc., 178, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchhoff, W. H. 1969, J. Am. Chem. Soc., 91, 2437 [CrossRef] [Google Scholar]
- Klaus, Th., Saleck, A. H., Belov, S. P., et al. 1996, J. Mol. Spectrosc., 180, 197 [Google Scholar]
- Lattanzi, V., Gottlieb, C. A., Thaddeus, P., et al. 2011, A&A, 533, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, C. F., Hasegawa, T. I., Hirano, N., Palau, A., et al. 2010, ApJ, 713 [Google Scholar]
- Lique, F., & Spielfiedel, A. 2007, AA, 462, 1179 [Google Scholar]
- Lique, F., Spielfiedel, A., Dhont, G., & Feautrier, N. 2006, A&A, 458, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovas, F. J., Suenram, R. D., Ogata, T., & Yamamoto, S. 1992, ApJ, 399, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Maki, & Kuritsyn, 1990, J. Mol. Spectrosc., 144, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M. L., Mendis, D. A., Mitchell, D. L., et al. 1991, ApJ, 378, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Margules, L., et al. 2010, J. Mol. Spectrosc., 260, 23 [Google Scholar]
- Martin-Drumel, M. A. 2012, Ph.D. Thesis, Paris University [Google Scholar]
- Mauersberger, R., Henkel, C., Langer, N., & Chin, Y. N. 1996, A&A, 313, L1 [NASA ADS] [Google Scholar]
- McCarthy, M. C., Thorwirth, S., Gottlieb, C. A., & Thaddeus, P. 2004a, J. Chem. Phys. 126, 4096 [Google Scholar]
- McCarthy, M. C., Thorwirth, S., Gottlieb, C. A., & Thaddeus, P. 2004b, J. Chem. Phys. 121, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meschi, D. J., & Myers, R. J. 1959, J. Mol. Spectrosc., 3, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., & Brünken, S. 2005, J. Mol. Spectrosc., 232, 213 [CrossRef] [Google Scholar]
- Müller, H. S. P., Farhoomand, J., Cohen, E. A., et al. 2000, J. Mol. Spectrosc., 232, 213 [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palau, A., Sánchez-Monge, Á., Busquet, G., et al. 2010, A&A, 510, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J. R., & Encrenaz, P. J., Berton, D. 2001, IAU Symp., 196, 255 [NASA ADS] [Google Scholar]
- Patel, D., Margolese, D., & Dykea, T. R. 1979, J. Chem. Phys., 70, 2740 [NASA ADS] [CrossRef] [Google Scholar]
- Penn, R. E., & Olsen, R. J. 1976, J. Mol. Spectrosc., 61, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Persson, C. M., Olofsson, A. O. H., Koning, N., et al. 2007, A&A, 476, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, JQSRT, 60, 5 [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., Welch, W. J., et al. 1982, ApJ, 259, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., Friedel, D. N., et al. 2009, ApJ, 704, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Powell, F. X., & Lide, D. R., et al. 1964, J. Chem. Phys., 41, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Rawling, J. M. C., & Yates, J. A. 2001, MNRAS, 326, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Benford, D. J., Hunter, T. R., et al. 2001, ApJ, 132, 281 [Google Scholar]
- Schultz, A. S. B., Colgan, S. W. J., Erickson, E. F., et al. 1999, ApJ, 511, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Kleinmann, S. G., Hall, D. N. B., & Ridgway, S. T. 1983, ApJ, 275, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Sedo, G., Schultz, J., & Leopold, K. R. 2008, J. Mol. Spectrosc., 251, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, AJSS, 97, 455 [CrossRef] [Google Scholar]
- Tafalla, M., Santiago-García, J., Hacar, A., & Bachiller, R. 2010, A&A, 522, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J. R., & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Vincent, L., Cernicharo, J., et al. 2011, A&A, 528, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorwirth, S., McCarthy, M. C., Gottlieb, C. A., et al. 2005, J. Chem. Phys., 123, 54326 [Google Scholar]
- Thorwirth, S., Theulé, P., Gottlieb, C. A., et al. 2006, J. Mol. Struc., 795, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Thorwirth, S., Mück, L. A., Gauss, F., et al. 2011, J. Chem. Phys. Lett., 2, 1228 [Google Scholar]
- Tiemann, E. 1974, J. Phys. Chem., 3, 259 [Google Scholar]
- Tiemann, E. 1982, J. Mol. Spectrosc., 91, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E. 1991, ApJ, 76, 617 [Google Scholar]
- Turner, B. E. 1994, ApJ, 430, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E., Chan, Kin-Wing, Green, S., & Lubowich, D. A. 1992, ApJ, 399, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Tyblewski, M., Ha, T. K., Bauder, A., et al. 1986, J. Mol. Spectrosc., 115, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., & Williams, D. A. 1999, MNRAS, 305, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Caselli, P., Hartquist, T. W., & Williams, D. A. 2001, A&A, 370, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viti, S., Collings, M. P., Dever, J. W., et al. 2004a, MNRAS, 354, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Codella, C., Benedettini, M., & Bachiller, R. 2004b, MNRAS, 350, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- White, G. J., & Phillips, J. P. 1983, MNRS, 203 [Google Scholar]
- Wilson, T. L., Gaume, R. A., Gensheimer, P., & Johnston, K. J. 2000, ApJ, 538, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Winnewisser, G., Winnewisser, M., & Gordy, W. 1966, Bull. Am. Phys. Soc., 11, 312 [Google Scholar]
- Wright, M. C. H., Plambeck, R. L., & Wilner, D. J. 1996, ApJ, 469, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Zapata, L. A., Schmid-Burgk, J., & Menten, K. M. 2011a, A&A, 529, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Column densities, N, for SO2 and its isotopologues, obtained from LTE model analysis.
Rotational temperatures, Trot, and column densities, N, obtained from rotational diagrams.
Column density upper limits for undetected sulfur-bearing molecules in Orion KL.
All Figures
 |
Fig. 1 Gaussian fits to the observed SO lines. Dashed line for the plateau, cyan (solid line) for the high-velocity plateau, black for hot core, green for extended ridge, and red for the contribution of the component at 20.5 km s-1. The total fit is shown in magenta. The data are the black histogram spectra. |
| In the text | |
 |
Fig. 2 Gaussian fits for the SO2 lines (2 mm data). The total fit is shown in magenta. Plateau is represented with the dashed line, high-velocity plateau in cyan (solid line), hot core in black, compact ridge in blue, extended ridge in green, and 20.5 km s-1 component in red. The data are the black histogram spectra. |
| In the text | |
 |
Fig. 3 Gaussian fits for the SO2 lines (1.3 mm data). The total fit is shown in magenta. Plateau is represented with the dashed line, high-velocity plateau in cyan (solid line), hot core in black, compact ridge in blue, extended ridge in green, and 20.5 km s-1 component in red. The data are the black histogram spectra. |
| In the text | |
 |
Fig. 4 Gaussian fits for the SO2 lines (3 mm data). The total fit is shown in magenta. Plateau is represented with the dashed line, high-velocity plateau in cyan (solid line), hot core in black, compact ridge in blue, extended ridge in green, and 20.5 km s-1 component in red. The data are the black histogram spectra. |
| In the text | |
 |
Fig. 5 Integrated line intensities of the 20.5 km s-1 component as a function of the line frequency for SO transitions. |
| In the text | |
 |
Fig. 6 SO-integrated intensity maps over different velocity ranges (indicated at the bottom of each panel in km s-1). Row 1 shows the transition 32−21 (Eup = 21.1 K, Aul = 1.1 × 10-5 s-1, S = 1.5). The interval between contours is 8 K km s-1 and the minimum contour is 15 K km s-1. Row 2 shows the transition 66−55 (Eup = 56.5 K, Aul = 2.2 × 10-4 s-1, S = 5.8). The interval between contours is 20 K km s-1 and the minimum contour is 15 K km s-1. The white cross indicates the position of the hot core and the black cross the position of the compact ridge. |
| In the text | |
 |
Fig. 7 SO2-integrated intensity maps over different velocity ranges (indicated at the bottom of each panel in km s-1). Row 1 shows the transition 4(2,2)−3(1,3) (energy Eup = 19 K, Einstein coefficient Aul = 7.7 × 10-5 s-1, and line strength S = 1.7), row 2 the transition 11(1,11)−10(0,10) (Eup = 60.4 K, Aul = 1.1 × 10-4 s-1, S = 7.7), and the last row shows the transition 14(3,11)−14(2,12) (Eup = 119 K, Aul = 1.1 × 10-4 s-1, S = 8.1). The interval between contours is 10 K km s-1, the minimum contour is 5 K km s-1 and the maximum 155 K km s-1. The white cross indicates the position of the hot core and the black cross the position of the compact ridge. |
| In the text | |
 |
Fig. 8 34SO and 34SO2-integrated intensity maps over different velocity ranges (indicated at the bottom of each panel in km s-1). Row 1 shows the transition 67−56 of 34SO (Eup = 46.7 K, Aul = 2.2 × 10-4 s-1). The contour interval is 7 K km s-1 and the minimum contour is 8 K km s-1. Row 2 shows the transition 28(3,25)−28(2,26) of 34SO2 (Eup = 402.1 K, Aul = 1.5 × 10-4 s-1). The interval between contours is 0.9 K km s-1, and the minimum contour is 1.2 K km s-1. The white cross indicates the position of the hot core and the black cross the position of the compact ridge. |
| In the text | |
 |
Fig. 9 Observed lines of SO (black histogram) and best fit LVG model results (red). |
| In the text | |
 |
Fig. 10 Observed lines of 34SO (black histogram) and best fit LVG model results (red). |
| In the text | |
 |
Fig. 11 Observed lines (black histogram) of SO2 with upper state energies lower than 400 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
| In the text | |
 |
Fig. 12 Observed lines of SO2 (black histogram) with upper state energies lower than 400 K (continued), ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
| In the text | |
 |
Fig. 13 Observed lines of SO2 (black histogram) with upper state energies between 400 K and 700 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
| In the text | |
 |
Fig. 14 Observed lines of SO2 (black histogram) with energies higher than 700 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results are overlaid in red. |
| In the text | |
 |
Fig. 15 Observed lines of 34SO2 (black histogram). Best fit LTE model results are shown in red. Boxes with black, blue and green borders correspond to lines observed at 1.3, 2, and 3 mm, respectively. |
| In the text | |
 |
Fig. 16 Observed lines of SO2ν2 = 1 (black histogram). Best fit LTE model results are shown in red. |
| In the text | |
 |
Fig. 17 Observed lines of SO2 (black histogram) with energies higher than 700 K, ordered by increasing energy from top left to bottom right. Best fit LTE model results considering a hot core at TK = 220 K (green curve) and with a hot core at TK = 280 K (red curve). |
| In the text | |
 |
Fig. 18 Ratio N(SO)/N(SO2) for each component and for the different isotopologues of SO and SO2. |
| In the text | |
 |
Fig. A.1 Rotational diagrams for the plateau, high-velocity plateau, and hot core components. Black dots for SO2 and green dots for SO. The black and green lines are the best linear fits to the SO2 and SO points, respectively. |
| In the text | |
 |
Fig. A.2 Rotational diagrams for the compact ridge, extended ridge, and 20.5 km s-1 component. Black dots for SO2 and green dots for SO. The black and green lines are the best linear fits to the SO2 and SO points, respectively. |
| In the text | |
 |
Fig. A.3 Observed lines of 33SO (black histogram) and best fit LVG model results (red). |
| In the text | |
 |
Fig. A.4 Observed lines of S18O (black histogram) and best fit LVG model results (red). |
| In the text | |
 |
Fig. A.5 Observed lines of 33SO2 (black histogram) and best fit LTE model (red). Boxes in black, blue, and green correspond to frequencies at 1.3, 2, and 3 mm, respectively. |
| In the text | |
 |
Fig. A.6 Observed lines of SO18O (black histogram) and best fit LTE model (red). |
| In the text | |
 |
Fig. A.7 Observed lines of SO17O (black histogram) and best fit LTE model (red). |
| In the text | |
 |
Fig. A.8 Observed lines of 34SO2ν2 = 1 (black histogram) and best fit LTE model (red). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


