| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321100 | |
| Published online | 25 July 2013 | |
Mass assembly in quiescent and star-forming galaxies since z ≃ 4 from UltraVISTA⋆,⋆⋆
1 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille), UMR 7326, 13388 Marseille, France
e-mail: olivier.ilbert@lam.fr
2 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
3 Spitzer Science Center, California Institute of Technology, Pasadena, CA 91125, USA
4 Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
5 Institute for Computational Cosmology, Durham University, South Road, Durham, DH1 3LE, UK
6 Argelander-Institute of Astronomy, Bonn University, Auf dem Hügel 71, 53121 Bonn, Germany
7 Dipartimento di Astronomia, Universita di Padova, vicolo dell’Osservatorio 2, 35122 Padua, Italy
8 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
9 Canada France Hawaii telescope corporation, 65-1238 Mamalahoa Hwy, Kamuela, Hawaii 96743, USA
10 AIM Unité Mixte de Recherche CEA CNRS, Université Paris VII, UMR n158, Paris, France
11 Partner Group of the Max-Planck-Institut für Astrophysik, National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
12 National Optical Astronomy Observatory, 950 North Cherry Avenue, Tucson, AZ 85719, USA
13 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Mariesvej 30, 2100 Copenhagen, Denmark
14 Laboratoire AIM, CEA/DSM/IRFU, CNRS, Université Paris-Diderot, 91190 Gif-sur-Yvette, France
15 Department of Physics, ETH Zurich, 8093 Zurich, Switzerland
16 CRAL, Université Lyon-1 and CNRS-UMR 5574, 9 avenue Charles André, 69561 Saint-Genis Laval Cedex, France
17 Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching bei München, Germany
18 Excellence Cluster, Boltzmann Strasse 2, 85748 Garching, Germany
19 Institute for Astronomy, 2680 Woodlawn Dr., University of Hawaii, 96822 Honolulu, Hawaii, USA
20 California Institute of Technology, MC 105-24, 1200 East California Boulevard, Pasadena, CA 91125, USA
21 Kavli Institute for the Physics and Mathematics of the Universe, Todai Institutes for Advanced Study, the University of Tokyo, 277-8583 Kashiwa, Japan
22 Research Center for Space and Cosmic Evolution, Ehime University, Bunkyo-cho 2–5, 790-8577 Matsuyama, Japan
23 INAF – IASFBO, via P. Gobetti 101, 40129 Bologna, Italy
Received: 14 January 2013
Accepted: 30 May 2013
We estimate the galaxy stellar mass function and stellar mass density for star-forming and quiescent galaxies with 0.2 < z < 4. We construct a large, deep (Ks < 24) sample of 220 000 galaxies selected using the new UltraVISTA DR1 data release. Our analysis is based on precise 30-band photometricredshifts. By comparing these photometric redshifts with 10,800 spectroscopic redshifts from the zCOSMOS bright and faint surveys, we find a precision of σΔz/(1 + z) = 0.008 at i+ < 22.5 and σΔz/(1 + z) = 0.03 at 1.5 < z < 4. We derive the stellar mass function and correct for the Eddington bias. We find a mass-dependent evolution of the global and star-forming populations, with the low-mass end of the mass functions evolving more rapidly than the high-mass end. This mass-dependent evolution is a direct consequence of the star formation being “quenched” in galaxies more massive than ℳ ≳ 1010.7 − 10.9ℳ⊙. For the mass function of the quiescent galaxies, we do not find any significant evolution of the high-mass end at z < 1; however we observe a clear flattening of the faint-end slope. From z ~ 3 to z ~ 1, the density of quiescent galaxies increases over the entire mass range. Their comoving stellar mass density increases by 1.6 dex between z ~ 3 and z ~ 1 and by less than 0.2 dex at z < 1. We infer the star formation history from the mass density evolution. This inferred star formation history is in excellent agreement with instantaneous star formation rate measurements at z < 1.5, while we find differences of 0.2 dex at z > 1.5 consistent with the expected uncertainties. We also develop a new method to infer the specific star formation rate from the mass function of star-forming galaxies. We find that the specific star formation rate of 1010 − 10.5ℳ⊙ galaxies increases continuously in the redshift range 1 < z < 4. Finally, we compare our results with a semi-analytical model and find that these models overestimate the density of low mass quiescent galaxies by an order of magnitude, while the density of low-mass star-forming galaxies is successfully reproduced.
Key words: galaxies: distances and redshifts / galaxies: evolution / galaxies: formation / galaxies: star formation / galaxies: stellar content
Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO programme ID 179.A-2005 and on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium.
Catalogues are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/556/A55
© ESO, 2013
1. Introduction
The galaxy stellar mass function (MF) is a fundamental indicator of the physical processes that regulate mass assembly in galaxies across cosmic time. Stellar mass assembly in galaxies is believed to result from several physical processes such as star formation from in-situ or accreted gas as well as from major or minor mergers. The star formation may also be stopped, or “quenched”, by external process such as “feedback” in active galactic nuclei (AGN) for galaxies residing in more massive dark matter haloes, or by other processes such as supernovae-driven winds in less massive haloes. The relative contribution and operating timescales of these different processes are still a matter of debate.
The evolutionary tracks of the MF as a function of look-back time reveal the major paths taken by different galaxy populations across cosmic time. Despite the considerable progress made over the last decade, our understanding of the early evolution of stellar mass growth is still incomplete and several puzzling issues have yet to be resolved: (i) The stellar mass density of the most massive galaxies (1011.7ℳ⊙) at z ~ 3 is almost identical to the local measurement (Perez-Gonzalez et al. 2008). This result requires a powerful feedback mechanism in order to halt star formation in massive galaxies, like AGN feedback (e.g. Bower et al. 2006; Croton et al. 2006). However, numerous systematic uncertainties could still be hiding an evolution of the high-mass end (Marchesini et al. 2009). In particular, if both random and systematic errors are considered, Marchesini et al. (2009) “can not exclude a strong evolution (by as much as a factor of ~50) in the number density of the most massive galaxies (>1011.5 ℳ⊙) from z = 4.0 to z = 1.3”. (ii) The stellar mass density of the most massive quiescent galaxies undergoes little evolution (less than 0.2 dex) from z ~ 1 to z ~ 0.1 (Arnouts et al. 2007; Pozzetti et al. 2010; Ilbert et al. 2010). Therefore, major merger activity must be relatively limited for this population since z ~ 1, in agreement with galaxy merger rate measurements (e.g. Lopez-Sanjuan et al. 2012). (iii) The stellar mass density increases continuously with cosmic time. The star formation rate (SFR) integrated along cosmic time and the stellar mass density evolution should provide a coherent picture (Arnouts et al. 2007; Boissier et al. 2010), but are still difficult to reconcile unless the initial mass function (IMF) changes with time, as advocated by several authors (e.g. Wilkins et al. 2008; Lu et al. 2012). A significant uncertainty remains on the contribution of low mass galaxies which could impact the global stellar mass density at z > 2 (Mortlock et al. 2011; Santini et al. 2012). (iv) Red galaxies are created very efficiently at 1 < z < 2 (Cirasuolo et al. 2007; Arnouts et al. 2007; Ilbert et al. 2010; Cassata et al. 2011). This implies that the quenching of star forming galaxies must be extremely efficient at z > 1. Arnouts et al. (2007), Ilbert et al. (2010) and Kajisawa et al. (2011) found that the stellar mass density of quiescent galaxies increased by roughly one order of magnitude from z ~ 2 to z ~ 1 (2.5 Gyr) as star-formation stops in galaxies which then migrate into the “red sequence” of passively evolving galaxies. But the amount of evolution is still debated. Brammer et al. (2011) find also an evolution of the quiescent population at 1 < z < 2, but at a smaller rate of 0.5 dex for the massive population. Ilbert et al. (2010) identify z ~ 1 as a transition epoch in the assembly of the most massive quiescent galaxies (the density of the most massive galaxies ceases to increase at z < 1). But from the Brammer et al. (2011) study, no clear transition occurs at z ~ 1. Therefore, a key point is to consolidate these measurements at z < 2 and follow the growth of the quiescent population to even earlier times.
Beyond z ~ 1 observations are challenging, and are currently limited either by depth or small numbers of objects in relatively small fields, making the computation of the massive end of the MF sensitive to cosmic variance and the lower mass end difficult to constrain. The identification of a robust quiescent galaxy sample requires accurate photometric redshifts with a low number of catastrophic failures. A field of at least one square degree or more is necessary to provide a large volume and minimise cosmic variance. Moreover, samples need to be deep enough to probe the low-mass end of the MF beyond z ~ 2. The availability of deep wide field near-IR multi-band photometry is essential. Spectral features like the D4000 or Balmer break move into the near-IR at z > 1.5, and several near-IR bands are required to properly sample the spectral energy distribution (SED) and enable a stable photometric redshift and type classification from SED-fitting techniques.
The COSMOS field is one of the best available fields to derive the MF thanks to the large area (2 deg2) and the large amount of deep (IAB ~ 26.5) multi-wavelength data available (more than 35 bands). Several papers showing the MF evolution in the COSMOS field have been published (Drory et al. 2009; Ilbert et al. 2010; Pozzetti et al. 2010; Dominguez-Sanchez et al. 2011). New photometric and spectroscopic datasets have been obtained in the last two years which allow us to greatly reduce the systematic uncertainties in the MF estimate at z > 1. The first UltraVISTA DR1 data release1 (McCracken et al. 2012) covers 1.5 deg2 in four near-infrared filters Y, J, H and Ks. The DR1 data are at least one magnitude deeper than previous COSMOS near-infrared datasets (McCracken et al. 2010) and also provide new Y-band photometric information. Since the Balmer break lies between UltraVISTA filters at z > 1.3, we can now derive photometric redshifts which are more robust at high redshift. Secondly, almost 35 000 new spectra are now available in the COSMOS field. This sample includes 9900 spectroscopic redshifts at z > 1, including extremely faint objects. Such a spectroscopic sample is essential to ensure that our analysis can be extended at high redshift. New near-IR spectroscopic samples (WFMOS and MOIRCS on Subaru and WFC3/HST grism data) contain spectroscopic redshifts for the quiescent and the dusty populations at z > 1.5. Therefore, we can ensure that our photo-z are robust at z > 1 and we are now able to extend MF measurements to z = 4 and to lower stellar masses than previous studies in the same field.
In this paper, we extend MF and stellar mass density measurements out to z = 4 and for stellar masses down to 1010.3ℳ⊙ for the global population. The new data sets are introduced in Sect. 2. The photometric redshifts and associated physical properties are discussed in Sect. 3. The method used to estimate the MF and the associated uncertainties is given in Sect. 4. We present the measured MF and stellar mass density for the full, star-forming and quiescent galaxy samples in Sect. 5. Results are discussed and compared to semi-analytical models in Sect. 6. In particular, we investigate systematic uncertainties linked to the choice of the star formation histories in our models. Throughout this paper, we use the standard cosmology (Ωm = 0.3, ΩΛ = 0.7 with H0 = 70 km s-1 Mpc-1). Magnitudes are given in the AB system (Oke 1974). The stellar masses are given in units of solar masses (ℳ⊙) for a Chabrier (2003) IMF.
Characteristics of the spectroscopic redshift samples and photometric redshift accuracy.
2. Data description
2.1. Preparation of stacked images and confidence maps
Our photometric catalogue comprises near-infrared data taken with the VIRCAM (Emerson & Sutherland 2010) on the VISTA telescope as part of the UltraVISTA project and optical broad and intermediate-band data taken with the SUPRIME camera on Subaru in support of the COSMOS project (Capak et al. 2007). The near-infrared data we use here corresponds to the UltraVISTA DR1 data release fully described in McCracken et al. (2012).
To construct our multi-band catalogue, we first downloaded all COSMOS tiles and confidence maps from theIRSA2COSMOS archive, choosing where possible the “best” seeing images. Since the IRSA tiles have the same tangent point and pixel scale as UltraVISTA DR1, they may be simply “pasted together” (i.e., without image resampling) using the swarp software to produce a single, large image which is pixel-matched to UltraVISTA DR1. Catalogues can then be simply generated using SExtractor (Bertin & Arnouts 1996) in “dual-image” mode, using matched apertures on each image. The list of broad and intermediate band / narrow band images used is as follows: u∗, BJ, VJ, r+, i+, z +, IA484, IA527, IA624, IA679, IA738, IA767, IA427, IA464, IA505, IA574, IA709, IA827, NB711, NB816. Table 1 in Ilbert et al. (2009) lists the effective wavelengths of each of these filters (note that we do not use the Subaru g-band data as this has particularly poor seeing). All four UltraVISTA bands are used: Y, J, H, Ks; the depths for the UltraVISTA DR1 are given in Table 1 of McCracken et al. (2012).
Before catalogue extraction, we must first take into account the large variation in seeing between different COSMOS images and also within the UltraVISTA stacks themselves. As already documented in McCracken et al. (2012), in the UltraVISTA H and Ks stacks there are “columns” of different seeing as a consequence of the different VISTA pawprints contained in the final stacks being taken under different seeing conditions. To correct for this, we first construct for each H and Ks stack six separate stacks comprising the six individual VISTA “pawprints”. We then measure the average seeing on each of six pawprints using the PSFex software (Bertin et al. 2011), which corresponds to a fit of a Moffat (1969) profile. Next, the individual pawprints are convolved by a Gaussian profile calculated to bring the point spread function (PSF) on the final images to 1.1″. A similar procedure is adopted to homogenise the COSMOS broad and intermediate-band images: the seeing is measured on each stack and the images are then convolved with a Gaussian profile to bring the final image to 1.1″ which is the worst PSF among all bands (the Y band from ultraVISTA).
2.2. IRAC observations
The IRAC data consist of all cryogenic data (Sanders et al. 2007) and the data from the Warm mission SEDS program (Fazio et al. 2012) covering ~0.1 deg2 in the center of the field. The data were reduced with theMOPEX3software package. Photometric measurements were made using SExtractor in dual image mode with the Subaru i-band image as a detection image and the IRAC image for measurement. This improves photometric accuracy when optical sources are close to each other by making use of the SExtractor aperture de-blending routines. As in described in Sanders et al. (2007) photometric measurements were made in a 3.8′′ diameter aperture and corrected to pseudo-total using a statistical aperture correction. We adopt a 3.8′′ aperture which is a good trade-off between a small aperture which limits the noise created by blending, and a large aperture which reduces the correction needed to estimate the total fluxes of bright galaxies. A comparison between these IRAC fluxes in the i- and IRAC selected catalogues (Ilbert et al. 2010) shows only a small systematic offset which is to be expected as a consequence of the update to the IRAC calibration.
2.3. Source catalogue extraction and merged catalogue creation
In extracting our source catalogues using SEXtractor, the choice of the detection image is important. Our scientific objectives drive us to use the longest possible wavelengths in order to reliably detect galaxies at intermediate to high redshifts. On the other hand, we also want a sample which is as complete as possible to the faintest possible limits in stellar mass. We construct a detection image using SWarp (Bertin et al. 2002) from the chi-squared sum of the (non-convolved) UltraVISTA DR1 YJHKs images, following the techniques outlined in Szalay et al. (1999). This ensures that all sources detected in at least one VISTA band are included in the final catalogue.
With this detection image and a set of PSF-homogenised images in hand, we can proceed to catalogue extraction. In order to make reliable magnitude error estimates on stacked, convolved data which has a non-negligible amount of correlated noise we use for each Subaru band pre-computed effective gain values (Capak et al. 2007) in combination with the MAP_RMS confidence maps supplied by IRSA. This is particularly important for the shorter wavelength data which saturates at relatively bright magnitudes. For the UltraVISTA data, where we use weight maps as opposed to RMS-maps we set the SEXtractor option RESCALE_WEIGHTS to N to ensure that image convolution has no effect on image noise measurement and that the weight-maps are not rescaled automatically as is normally the case in SExtractor. To account for additional noise sources not accounted for in the RMS maps such as errors in the background subtraction, zero-point errors, confusion, morphological aperture corrections, and other effects the errors were multiplied by a factor of 1.5 to match the measured noise on the extracted photometry.
For each detected source we measure aperture magnitudes into a 3″ diameter circle, and “pseudo-total” “Kron” magnitudes (Kron 1980), corresponding to SExtractor’s MAG_APER and MAG_AUTO respectively. Next, catalogues from each band were merged together into a single FITS table and galactic extinction values computed at each object position using the Schlegel et al. (1998) dust maps were added. In addition object mask flags indicating bad regions in optical and near-infrared bands were included, and saturated pixels in the optical bands were flagged by using the appropriate FLAG_MAPs at the extraction stage.
In each band, for the purposes of photometric redshift measurements, aperture magnitudes are corrected to pseudo-total magnitudes using a band-dependent aperture correction computed using a stellar curve-of-growth method (although the images are PSF-homogenised, there are still small residual PSF variations band-to-band). The SED fitting is performed on these magnitudes. However, this aperture correction is not enough to capture the total flux of large and bright galaxies. As a consequence, we would underestimate the stellar masses of these galaxies. To get the correct stellar masses, we compute an average transformation between these aperture corrected magnitudes and SExtractor’s MAG_AUTO over all broad-band filters for each object and then apply this adjustment to the stellar masses.
The i-selected catalogue from Capak et al. (2007) was cross-matched to the near-infrared UltraVISTA catalogue. This i-selected catalogue contains GALEX UV magnitudes computed by Zamojski et al (2007). GALEX fluxes were measured using PSF fitting method.
This i-selected catalogue contains also the IRAC fluxes as described above. Some red galaxies could be too faint to be detected in the i-band selected catalogue (e.g. quiescent galaxies at z > 2). Nevertheless, such galaxies could be detected in the IRAC images. For these sources, we include the 3.8′′ aperture fluxes from the IRAC selected catalogue of Ilbert et al. (2010).
Finally, a significant fraction of the objects (2%) were flagged as power-law sources using the criteria established by Donley et al. (2012). Since in these cases the IRAC flux could be dominated by AGN emission, we do not use the IRAC flux for this population.
 |
Fig. 1 Photometric redshifts versus spectroscopic redshifts. Only secure spectroscopic redshifts at Ks < 24 are considered. Different symbols correspond to the spectroscopic samples labelled in the right. |
3. Photometric redshifts and physical parameters
3.1. Photometric redshift estimation
We derive our photometric redshifts following the recipes outlined in Ilbert et al. (2009). The photometric redshifts are derived using “Le Phare” (Arnouts et al. 2002; Ilbert et al. 2006). Ilbert et al. (2009) used 31 templates including elliptical and spiral galaxies from the Polletta et al. (2006) library and 12 templates of young and blue star-forming galaxies generated with Bruzual and Charlot stellar population synthesis models (2003, hereafter BC03). Using a spectroscopic sample of quiescent galaxies, Onodera et al. (2012) showed that the estimate of the photo-z for the quiescent galaxies in Ilbert et al. (2009) were underestimated at 1.5 < z < 2. We improve the photo-z for this specific population by adding two new templates of elliptical galaxies generated with BC03. These two new templates are generated assuming an exponentially declining SFR with a short timescale τ = 0.3 Gyr and two different metallicities (Z = 0.008 and Z = 0.02 i.e. Z⊙). They include 22 ages well sampled between 0.5 Gyr and 4 Gyr old. Thanks to a better sampling of younger ages than our previous library, they improve the photo-z for the quiescent population at z > 1.5.
Extinction is added as a free parameter (E(B − V) < 0.5) and several extinction laws are considered (Calzetti et al. 2000; Prevot 1984 and a modified version of the Calzetti laws including a bump at 2175 Å). We do not add any extinction for the templates redder than S0. We also do not allow additional extinction for the templates redder than Sc (the Sa, Sb, Sc templates from Polletta et al. 2007, already include some extinction). Emission lines are added to the templates using an empirical relation between the UV light and the emission line fluxes (Ilbert et al. 2009). By contrast with Ilbert et al. (2009), we assign the redshift using the median of the marginalised probability distribution function rather than the minimum χ2. While the results are broadly similar between the two methods, using the median has the advantage of producing more reliable error bars for the photometric redshifts4 and reducing the effect of aliasing in the photometric redshift space.
We combine several spectroscopic samples to test the accuracy of the photometric redshifts, including zCOSMOS-bright with 20700 bright VIMOS/VLT spectra selected at i+ < 22.5 (Lilly et al. 2007), zCOSMOS faint with 9500 faint VIMOS/ VLT spectra selected at 1.5 < z < 3 (Lilly et al., in prep.), 2300 DEIMOS/Keck redshifts which combined several selected sub-populations of blue star-forming and infrared galaxies at 0.5 < z < 6 (Kartaltepe et al., in prep., Capak et al., in prep.), 835 FORS2/VLT redshifts at 0.6 < z < 1.8 (Comparat et al., in prep.), 138 FMOS/Subaru redshifts at 1.4 < z < 1.8 (Silverman et al., in prep.), 18 faint quiescent galaxies at z < 1.9 obtained with MOIRCS/Subaru (Onodera et al. 2012) and 16 faint quiescent galaxies at 1.85 < z < 2.6 obtained with the WFC3 grism observations from the 3D-HST survey (Krogager et al., in prep.). We keep only the most secure spectroscopic redshifts (e.g. flag 3 and 4 for zCOSMOS) at Ks < 24 which reduces to 12482 the number of spectroscopic redshifts used for the comparison. The comparison between photometric and spectroscopic redshifts is shown in Fig. 1 and the accuracy obtained for each spectroscopic sample is listed in Table 1. The fraction of catastrophic failures η is defined as | zphot − zspec | /(1 + zspec) > 0.15. The redshift accuracy σΔz/(1 + zs) is computed using the normalised median absolute deviation (Ilbert et al. 2006).
Figure 1 shows that the photometric redshift accuracy has two regimes. At z < 1.5, the Balmer break falls between the intermediate band filters. In this regime, the spectroscopic sample is dominated by the zCOSMOS bright sample selected at i+ < 22.5 (blue crosses). The precision is better than 1% with less than 1% of catastrophic failures. Even as faint as i+ ~ 24, comparisons with the DEIMOS sample show a better than 3% precision at z < 1.5 (green crosses). At intermediate redshifts 1.4 < z < 2, the FMOS sample from Silverman et al. shows an excellent precision of 0.026. However we note that Hα is identified in the near-IR spectra from a knowledge of photo-z which could explain the low failure rate. At higher redshifts 1.5 < z < 4 the accuracy of the photo-z has been tested against the zCOSMOS faint sample and faint DEIMOS spectra. Here the precision is around 3%, showing that we can safely extend our analysis at z > 1.5 for faint star-forming galaxies. Thanks to new near-IR spectroscopic samples, we can now test the accuracy of the photo-z for the quiescent population at z > 1.5. We combine the quiescent sample of Onodera et al. (2012) and Krogager et al. (in prep.). These galaxies are extremely faint with a median i+ band magnitude of 24.5 and a median redshift of 1.8. We have only one outlier in 30 galaxies. The precision is as good as σΔz/(1 + zs) = 0.056. We still detect a small bias with median(zp − zs) = −0.1, which does not have significant impact on our work.
We also compute the best-fitting χ2 using the stellar library. The sources are classified as stars when the χ2 obtained with the star library is lower than the one obtained with the galaxy library. Since near-infrared data are available, such criterion is effective in isolating the stars.
 |
Fig. 2 Stellar masses versus redshift for the KAB < 24 selected sample. The top and bottom panels correspond to the full sample and the quiescent population, respectively. Black points correspond to the measured stellar masses. The brown points correspond to ℳlimit which is the lowest mass which could be observed for a given galaxy for a limit at KAB = 24. The blue circles correspond to the completeness limit chosen in this study. The red and green curves correspond to the two extreme templates with τ = 0.1 Gyr and τ = 30 Gyr, respectively. We show 3 ages which are 0.9, 2 and 5 Gyr (from the bottom to the top, respectively). The dashed lines correspond to an extinction of E(B − V) = 0.2. If the lines are not drawn, it means that either the age is older than the age of the Universe or that the condition age/τ > 4 implies a small extinction. We indicate at the top of each panel the percentage of galaxies detected at 3.6 μm (top line) and in at least four bands (detection thresholds at >2σ and >5σ for the middle and bottom lines, respectively). |
3.2. Stellar masses and associated completeness
We turn now to the estimation of physical properties based on these photometric redshifts, first estimating galaxy stellar masses. We rely on a model to convert the galaxy luminosity into stellar mass. We generate a library of synthetic spectra normalised at one solar mass. These synthetic spectra are fitted to the multi-colour photometry described above using Le_Phare. The physical parameter called “stellar mass” in this paper corresponds to the median of the stellar mass probability distribution marginalised over all other parameters. The library of synthetic spectra is generated using the Stellar Population Synthesis (SPS) model of Bruzual & Charlot (2003). Several other models are available in the literature (e.g. Fioc & Rocca-Volmerange 1997; Maraston 2005; Bruzual 2007; Conroy et al. 2009). The stellar masses could vary by 0.1–0.15 dex depending on the considered SPS model (e.g. Walcher et al. 2011). For consistency, we use the same default library as Ilbert et al. (2010): we assume the Calzetti (2000) extinction law; emission line contributions are included using an empirical relation between the UV light and the emission line fluxes (Ilbert et al. 2009); we used three different metallicities (Z = 0.004, Z = 0.008, Z = 0.02 i.e. Z⊙); the star formation history declines exponentially following τ-1e− t/τ. We considered nine possible τ values ranging from 0.1 Gyr to 30 Gyr. We will test the systematic uncertainties linked to our choice of star formation history in Sect. 6.4. Following Fontana et al. (2006), Pozzetti et al. (2007), Ilbert et al. (2010), we impose the prior E(B − V) < 0.15 if age/τ > 4 (a low extinction is imposed for galaxies having a low SFR).
Figure 2 shows the stellar masses as a function of redshift. We can detect galaxies with masses as low as ℳ ~ 1010 ℳ⊙ at z = 4. The mass limit depends on the mass-to-light ratio of the considered template. Figure 2 shows the stellar mass limit that can be reached for different templates. For clarity, we show only two extreme templates in terms of star formation history (τ = 0.1 Gyr and τ = 30 Gyr), with solar metallicity and we select three ages. Oldest galaxies have the highest stellar mass limit. We follow a procedure similar to Pozzetti et al. (2010) to define the stellar mass completeness limit. We base our estimate on the 90% of the templates which are the most often fitted. In practice, we compute the lowest stellar mass which could be detected for a galaxy with log (ℳlimit) = log (ℳ) + 0.4(K − 24), given a sample selected at K < 24 (brown points). At a given redshift, the stellar mass completeness limit corresponds to the mass with 90% of the galaxies having their ℳlimit below the stellar mass completeness limit. Following this procedure, not more than 10% of the galaxies could be missed in the lowest mass end of the mass function.
At z > 2, galaxies could be too faint to be detected in optical and we need to rely on optical upper-limits and near-IR fluxes to estimate the photo-z. Photometric redshifts with a precision of 5% are routinely computed with four bands (e.g. Ilbert et al. 2006). Therefore, we checked that most of the galaxies are detected in four bands at least, to allow a robust photo-z estimate. The fraction of galaxies detected in a minimum of four bands at 2 and 5 σ are given in Fig. 2. This fraction is always above 95% at z < 2 even if we consider a 5σ detection limit. At z > 2, the fraction stays higher than 80% (90%) for a 5σ (2σ) detection limit, except at 2.5 < z < 3 for the quiescent (still 91% have their magnitudes measured in a minimum of 4 bands, with a detection limit better than 2σ). Moreover, as indicated in Fig. 2, more than 75% of sources show a 5σ detection at 3.6 μm even at the highest redshift bin.
 |
Fig. 3 Two-colour selection of the quiescent population. The galaxies above the black line in the top left are selected as quiescent. The fraction (in %) of log (sSFR) < −11 galaxies selected by the two-colour selection box is the top number in each panel. The fraction of galaxies with log (sSFR) > −11 within the two-colour box is the bottom number. |
3.3. Galaxy classification
In order to divide the sample into quiescent and star-forming galaxies, we use a slightly modified version of the two-colour selection technique proposed by Williams et al. (2009). Following Ilbert et al. (2010), we use the rest-frame two-colour selection NUV − r+ versus r+ − J instead of U − V versus V − J. In fact, NUV − r+ is a better indicator of the current versus past star formation activity (e.g. Martin et al. 2007; Arnouts et al. 2007)5. Moreover, the dynamical range covered by the NUV − r+ rest-frame colour is larger than the one covered by U − V, making the NUV − r+ rest-frame colour less sensitive to uncertainties linked to observations. Finally, the NUV rest-frame is still sampled by optical data at z > 2 which is no longer true for the rest frame U band.
Figure 3 shows the two-colour criterion used to select the quiescent population. Galaxies with MNUV − Mr > 3(Mr − MJ) + 1 and MNUV − Mr > 3.1 are considered as quiescent. The advantage of this classification is that it avoids a mix between dusty star-forming galaxies and quiescent galaxies: extinction moves star-forming galaxies along a diagonal axes from the bottom left to the top right of Fig. 3. We derive the absolute magnitudes with the method of Ilbert et al. (2005) which minimises the k-correction dependency6.
The specific star formation rate (sSFR, estimated in yr-1 throughout the paper) is the ratio between the instantaneous SFR and the stellar mass obtained from the best-fit template. In Ilbert et al. (2010) and Domínguez Sánchez et al. (2011), we considered that a galaxy was quiescent when log (sSFR) < −11. The fraction of galaxies with log (sSFR) < −11 in the selection box is given in each panel of Fig. 3. Over the full redshift range, ~90% of the galaxies with log (sSFR) < −11 are in the selection box. We also indicate the fraction of galaxies with log (sSFR) > −11 in the selection box. The fraction of galaxies with log (sSFR) > −11 increases from 20% at z < 1 to 60% at 2 < z < 2.5. Therefore, both classifications provide similar results at z < 1. But the classification based on the sSFR is more conservative at high redshift.
Best-fit parameters for the full sample, for the quiescent galaxies classified with the two-colour criteria and for the star-forming galaxies.
4. Method used to estimate the Galaxy Stellar Mass Function
We use the tool ALF (Ilbert et al. 2005) to derive the galaxy stellar mass functions. This tool includes three non-parametric estimators (Vmax, SWML, C+) detailed in Appendix A.2 of Ilbert et al. (2005). We limit our analysis to above the stellar mass limit given in Table 2 (Col. 4), as defined in Sect. 3.2. We verified that the three non-parametric estimators are in good agreement over the considered mass ranges. As shown in Ilbert et al. (2004), the estimators behave differently if a galaxy population is missing and diverge below a given mass limit when a significant population is no longer present. The good agreement between the three estimators confirm that our stellar mass limits are well established.
4.1. Associated uncertainties
Our error budget includes the Poissonian errors, the photo-z redshift uncertainties, and the uncertainties in the mass estimations.
We estimate the cosmic variance with the public tool getcv provided by Moster et al. (2011). The square root of the cosmic variance for galaxies is computed as the product of the galaxy bias and the dark matter root cosmic variance. The dark matter cosmic variance is computed for a field of 1.5 deg2. Moster et al. (2011) provide an estimate of the bias as a function of redshift and stellar mass. The fractional error in density is shown in the top panel of Fig. 4. This uncertainty increases with the mass since the massive galaxies are more biased than lower mass galaxies. The error associated to the cosmic variance is always larger than 5% at low mass and reaches 30% at high mass.
In order to take into account the uncertainties generated by the template-fitting procedure (photo-z and stellar mass), we created a set of 30 mock catalogues by perturbing each flux point according to its formal error bar. We scatter the photometric redshifts according to their 1σ error provided by Le_Phare. For each realisation, we recompute the stellar masses, and perform again the galaxy classification and recompute the MFs. We compute the 1σ dispersion in density at a given mass and redshift. The evolution of this dispersion is shown in Fig. 4. These uncertainties are below 2% at low masses and z < 2. In this regime, the cosmic variance dominates the error budget. At high masses ℳ > 1011ℳ⊙, the errors associated with the template fitting procedure reach 30–40% and become as important as the cosmic variance.
In order to obtain the total errors, we add in quadrature the errors due to the galaxy cosmic variance (errcosmic_var), the ones linked to the template-fitting procedure (errfit) and the Poissonian errors (errpoisson): 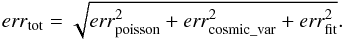 (1)Since errcosmic_var and errfit are derived as a function of the mass and the redshift, it is straightforward to associate the total errors to the non-parametric MF data points.
(1)Since errcosmic_var and errfit are derived as a function of the mass and the redshift, it is straightforward to associate the total errors to the non-parametric MF data points.
4.2. Fit of the stellar mass function and Eddington bias
We fit a parametric form over the Vmax non-parametric data. The choice of the non-parametric estimator has no impact on our results since we work in a mass range where the three non-parametric estimators are consistent. Following Pozzetti et al. (2010), we use a double Schechter function, defined as: ![\begin{equation} \phi({\cal M}){\rm d}{\cal M}={\rm e}^{-\frac{{\cal M}}{{\cal M}^*}}\left[\phi^*_1\left(\frac{{\cal M}}{{\cal M}^*}\right)^{\alpha_1}+\phi^*_2\left(\frac{{\cal M}}{{\cal M}^*}\right)^{\alpha_2}\right]\frac{{\rm d}{\cal M}}{{\cal M}^*} \end{equation}](/articles/aa/full_html/2013/08/aa21100-13/aa21100-13-eq249.png) (2)with ℳ∗ the characteristic stellar mass, α1 and α2 are the slopes which need to satisfy the following criteria α2 < α1, and
(2)with ℳ∗ the characteristic stellar mass, α1 and α2 are the slopes which need to satisfy the following criteria α2 < α1, and 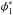 and
and 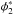 correspond to the normalisation. For the global and star-forming populations, we arbitrary set the slope at α2 = −1.6 at z > 1.5 since this parameter is no longer constrained. For the quiescent population, we use a simple Schechter function at z > 0.5 since we do not detect any upturn at the low-mass end given our survey limit. At 0.2 < z < 0.5, we still need to use a fit with a double Schechter function.
correspond to the normalisation. For the global and star-forming populations, we arbitrary set the slope at α2 = −1.6 at z > 1.5 since this parameter is no longer constrained. For the quiescent population, we use a simple Schechter function at z > 0.5 since we do not detect any upturn at the low-mass end given our survey limit. At 0.2 < z < 0.5, we still need to use a fit with a double Schechter function.
 |
Fig. 4 Fractional error in density as a function of the stellar mass and redshift. The top panel shows the errors due to the cosmic variance. The middle and bottom panels are the errors associated to the template fitting procedure (photo-z and stellar mass) for the full sample and the quiescent population, respectively. Results are shown only in the mass range covered by our dataset. |
Below the stellar mass limit ℳcomplete given in Table 2 (see Sect. 3.2), the Vmax estimator underestimates the true MF (Ilbert et al. 2004). Therefore, we use the Vmax measurements below ℳcomplete as a lower bound in the fitting procedure.
A crucial step in our fitting procedure is to account for the uncertainties in the stellar mass. These uncertainties could bias our estimate of the high-mass end (Caputi et al. 2011). Since the galaxy density exponentially decreases towards massive galaxies, errors in the stellar mass scatters more galaxies into the massive end than the reverse (Eddington 1913). Our procedure to avoid this bias is detailed in Appendix A. First, we find that the stellar mass uncertainties are well characterised by the product of a Lorentzian distribution 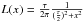 with τ = 0.04(1 + z) and a Gaussian distribution G with σ = 0.5. Then, we convolve the double Schechter function φ by the stellar mass uncertainties: φconvolved = φ ∗ (L × G). Finally, we fit φconvolved to the Vmax non-parametric data. Therefore, the best-fit parameters that we provide in Table 2 are deconvolved by the expected stellar mass uncertainties and do not suffer from Eddington bias.
with τ = 0.04(1 + z) and a Gaussian distribution G with σ = 0.5. Then, we convolve the double Schechter function φ by the stellar mass uncertainties: φconvolved = φ ∗ (L × G). Finally, we fit φconvolved to the Vmax non-parametric data. Therefore, the best-fit parameters that we provide in Table 2 are deconvolved by the expected stellar mass uncertainties and do not suffer from Eddington bias.
5. Results: evolution of the galaxy stellar mass function and stellar mass density
The galaxy stellar mass functions are computed with a sample of 220 000 galaxies selected at Ks < 24. We keep only the sources in areas with good image quality, representing an area of 1.52 deg2. We remove the stars and X-ray detected AGNs (Brusa et al. 2007). Figures 5 and 6 show the galaxy stellar mass functions for the full sample, the quiescent and the star-forming populations. The best fit parameters are given in Table 2. In this section, we describe our results out to z = 4.
 |
Fig. 5 Galaxy stellar mass function up to z = 4 for the full sample. Each colour corresponds to different redshift bins of variable step size. Fits are shown in the mass range covered by our dataset. The filled areas correspond to the 68% confidence level regions, after accounting for Poissonian errors, the cosmic variance and the uncertainties created during the template fitting procedure. The open triangles and squares correspond to the local estimates by Moustakas et al. (2013) and Baldry et al. (2012), respectively. |
 |
Fig. 6 Galaxy stellar mass function up to z = 4 for the star-forming population (top panel) and for the quiescent population (middle panel). Symbols are the same as Fig. 5. The bottom panel shows the percentage of quiescent galaxies as a function of stellar mass in the same redshift bins. |
5.1. Evolution of the full sample
Figure 5 shows the evolution of the MFs for the full sample. A first option is to consider a pure evolution in stellar mass. In this case, we assume that only star formation drives the MF evolution (no galaxy can be created or destroyed). We find that the evolution is strongly mass-dependent, with the low-mass end evolving more rapidly than the high-mass end. For instance, the stellar mass of a 109.8 ℳ⊙ galaxy increases by 0.9 dex between 1.5 < z < 2 and 0.2 < z < 0.5, while the stellar mass of a 1011.6 ℳ⊙ galaxy increases by only 0.2 dex in the same time interval. Therefore, we conclude that the evolution is strongly mass-dependent, in agreement Marchesini et al. (2009). A second option is to consider a pure density evolution. A constant increase in density by 0.3–0.4 dex, independent of the mass, is sufficient to match the 1.5 < z < 2 and the 0.2 < z < 0.5 MFs. However such a pure density evolution scenario is not applicable to the full sample: it would mean that new galaxies which were not present in a given redshift appear in the next redshift bin. Major mergers are not an option for a pure increase in density with cosmic time: for a α = −1.4 MF slope, the density of low mass galaxies would decrease by 0.16 dex if we assume that all galaxies encounter a major merger since z = 27.
In Fig. 7, we compare our results with several MF estimates published since 2008. We find an excellent agreement with the various MFs from the literature. Still, the differences in normalisation are as large as 0.2 dex in certain bins (e.g. 0.5 < z < 0.8 with Kajisawa et al. (2009) and Pérez-González et al. (2008); at 2 < z < 2.5 with Santini et al. (2012) which could be explained by known groups at z ~ 2.2−2.3). We also find that the extrapolation of our MF slope is flatter than data from Santini et al. (2012), but our sample does not reach a similar depth as this study.
 |
Fig. 7 UltraVISTA global stellar mass functions (open black circles and solid lines) compared with several measurements from the literature published since 2008 (labelled in the bottom right). Each panel corresponds to a redshift bin. The literature MF measurements are converted to the same cosmology and IMF as used in this study (H0 = 70 km s-1 Mpc-1 and Chabrier 2003 IMF). |
We derive the stellar mass density by integrating the best-fit double Schechter functions over the mass range 108 to 1013ℳ⊙. Since our mass limits are above 1010ℳ⊙ at z > 2 (see Table 2), our mass density estimates rely on the slope extrapolation for low mass galaxies. Since the slope is arbitrary set at α2 = −1.6 at z > 1.5, we allow α2 to vary in the range − 1.9 < α2 < − 1.4 to compute the mass density uncertainties. The results are shown in Fig. 8 (black circles). We fit the stellar mass density by the parametric form ρ∗(z) = a × e− bzc. Our best fit function is shown with a dashed line in Fig. 8 for the best fitting parameters 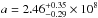 ,
, 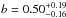 and
and 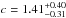 . We find that the global stellar mass density increases by 1.1 dex between 3 < z < 4 and 0.8 < z < 1.1 (a factor 13 in 4.2 Gyr). The evolution is much smaller at z < 1 with an increase of 0.2 dex between 0.8 < z < 1.1 and the local estimate (a factor 1.6 in 6 Gyr). Therefore, the stellar mass is assembled twice as fast at 1 < z < 4 (14% of the local stellar mass density per Gyr) than at z < 1 (6% of the local stellar mass density per Gyr).
. We find that the global stellar mass density increases by 1.1 dex between 3 < z < 4 and 0.8 < z < 1.1 (a factor 13 in 4.2 Gyr). The evolution is much smaller at z < 1 with an increase of 0.2 dex between 0.8 < z < 1.1 and the local estimate (a factor 1.6 in 6 Gyr). Therefore, the stellar mass is assembled twice as fast at 1 < z < 4 (14% of the local stellar mass density per Gyr) than at z < 1 (6% of the local stellar mass density per Gyr).
 |
Fig. 8 Stellar mass density as a function of cosmic time (redshift is given in the top label). Black and red points correspond to the full and quiescent populations, respectively. The circles correspond to our new results using UltraVISTA. Solid and open red circles correspond to the two-colour and sSFR selected quiescent galaxies, respectively. The green shaded area corresponds to the cosmic SFR compiled by Behroozi et al. (2013) and integrated over cosmic time as described in Sect. 6.1. The dashed line corresponds to the best fit over the mass density data. |
Figure 8 shows an excellent agreement between the various estimates from the literature, in particular at high redshift with the previous results from Caputi et al. (2011), Pérez-González et al. (2008) and Marchesini et al. (2009). We derive stellar mass densities which are lower by 0.2–0.3 dex at z > 2 in comparison with Santini et al. (2012). They find a slope much steeper than ours (α < − 1.8) which explains this difference. Their steep slopes are explained by a steep upturn in their faintest bins in stellar mass (see the red triangles in Fig. 7). Our MF and mass density are in good agreement if we limit the comparison to the mass range common to both studies. Santini et al. use a HAWK-I Ks selected sample which is 1.5 mag deeper than our sample and we are not able to reach the stellar mass limit at which this upturn occurs.
5.2. Evolution of the quiescent population
Middle panel of Fig. 6 shows the MF evolution of quiescent galaxies. The MF evolution of the quiescent population is clearly mass dependent at z < 1. In this redshift range, we do not find any significant evolution of the high-mass end while we observe a clear flattening of the faint-end slope. Between 0.8 < z < 1.1 and 0.2 < z < 0.5, the density of galaxies more massive than 1011.2 ℳ⊙ does not increase, while galaxies are continuously “quenched” at the low-mass end. For instance, the density of 109.5 ℳ⊙ galaxies increases by a factor of >5 between 0.8 < z < 1.1 and 0.2 < z < 0.5.
At 1 < z < 3, we find a rapid increase in density of all quiescent galaxies. In contrast with the result at z < 1, the evolution is no longer mass dependent. The most massive galaxies evolve as fast as intermediate mass galaxies. The density of 1011ℳ⊙ galaxies increases by 1.4 dex (factor 25) between 2.5 < z < 3 and 0.8 < z < 1.1. The normalisation parameter 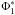 increases continuously between z ~ 3 and z ~ 1. We consider a pure density evolution for the quiescent MF rather than a pure mass evolution. Indeed, new quiescent galaxies are created along cosmic time by quenching of star-forming galaxies. Moreover, an isolated quiescent galaxy grows by less than 0.03 dex in 6 Gyr (since log (sSFR) < −11) due to its own star-formation.
increases continuously between z ~ 3 and z ~ 1. We consider a pure density evolution for the quiescent MF rather than a pure mass evolution. Indeed, new quiescent galaxies are created along cosmic time by quenching of star-forming galaxies. Moreover, an isolated quiescent galaxy grows by less than 0.03 dex in 6 Gyr (since log (sSFR) < −11) due to its own star-formation.
 |
Fig. 9 Stellar mass density as a function of cosmic time. Black open circles, red solid circles and blue pentagons correspond to the full, quiescent and star-forming galaxies, respectively. |
Figures 8 and 9 show the evolution of the stellar mass density for the quiescent population. The stellar mass density increases by 1.6 dex between 2.5 < z < 3 and 0.8 < z < 1.1. Again, we find a change of regime around z ~ 1 with the mass assembly slowing down at z < 1. We find that the stellar mass assembly is faster at 1 < z < 3 for the quiescent population than for the global population which evolves by 0.8 dex in the same redshift range. For the massive quiescent galaxies (ℳ > 1011ℳ⊙), Brammer et al. (2011) find an evolution of 0.5 dex between z = 2.1 and z = 1. But their mass density drops quickly at z > 2.1. Their evolution reaches 1 dex if we consider the redshift range z = 2.3 and z = 1, which is really close to our value of 1.1 dex. We find a slightly slower evolution compared to Ilbert et al. (2010). However, our conclusion depends on the method used to classify the quiescent population. If we use a classification based on the sSFR, as in Ilbert et al. (2010), the stellar mass densities are consistent between both studies. The sSFR classification is more restrictive than the two-colour selection (see Sect. 3.3).
5.3. Evolution of the star-forming population
The top panel of Fig. 6 shows the stellar mass function of the star-forming galaxies. We can divide this evolution in two regimes: above and below 1010.7 − 10.9ℳ⊙. If we consider only the low mass regime, the faint-end slope remains steep over the full redshift range. We do not detect any significant trend in the slope evolution over the stellar mass range covered by our dataset. We observe a strong evolution of low-mass galaxies, especially at z > 2. For the MF at 2 < z < 2.5 to match that at 1.5 < z < 2 requires the stellar mass of a 1010.3ℳ⊙ galaxy to increase by around 0.4 dex. We discuss in Sect. 6.2 how such evolution could be interpreted in term of sSFR. If we consider now the evolution of the high-mass end, we do not detect an evolution of the density of the most massive galaxies 1011.6 − 11.8ℳ⊙. Since these star-forming galaxies are forming new stellar populations, these massive star-forming galaxies are necessarily quenched along cosmic time, as we will discuss in Sect. 6.3.
Figure 9 shows the evolution of the stellar mass density for star-forming galaxies. As for the quiescent population, we also observe two regimes with a faster evolution at 1 < z < 4 than at z < 1. We observe an evolution of 0.5 dex between 2.5 < z < 3 and 0.8 < z < 1.1, while the quiescent galaxies evolve by 1.6 dex in the same period. Therefore, quiescent galaxies are building faster at this epoch. We also observe that the stellar mass density of quiescent and star-forming galaxies are comparable at z < 1, while star-forming galaxies dominate the stellar mass budget at higher redshift.
6. Discussion
 |
Fig. 10 A comparison between the star formation history inferred from the UltraVISTA mass density (black solid line and dashed area corresponding to 1σ errors) and literature determinations including: direct measurements of the SFR density compiled by Behroozi et al. (2013) (red solid line with dashed lines for the associated uncertainties); star formation histories derived from the UV and IR luminosity functions from Cucciati et al. (2012) and Gruppioni et al. (2013) (brown triangles and green squares, respectively); and finally radio estimates from Karim et al. (2011) updated using the mass functions presented in this paper (blue circles). |
6.1. Inferred star formation history
Following Wilkins et al. (2008), we can link the mass density evolution and the star formation history using ![\begin{equation} \label{rhoeq} \rho_*(t)=\int^t_0 {\it SFRD}(t')(1-f_r[t-t']){\rm d}t' \end{equation}](/articles/aa/full_html/2013/08/aa21100-13/aa21100-13-eq293.png) (3)where SFRD corresponds to the star formation rate density and fr is the stellar mass loss depending on the age of the stellar populations (Renzini & Buzzoni 1986). We adopt the parametrisation of the stellar mass loss provided by Conroy & Wechsler (2009) for a Chabrier (2003) IMF fr(t − t′) = 0.05ln(1 + (t − t′)/0.3 Myr).
(3)where SFRD corresponds to the star formation rate density and fr is the stellar mass loss depending on the age of the stellar populations (Renzini & Buzzoni 1986). We adopt the parametrisation of the stellar mass loss provided by Conroy & Wechsler (2009) for a Chabrier (2003) IMF fr(t − t′) = 0.05ln(1 + (t − t′)/0.3 Myr).
Wilkins et al. (2008) found that the star formation history inferred from the mass density measurements is not consistent with SFRD observations. We re-investigate this problem using our own mass density measurements. We fit the UltraVISTA mass density data using Eq. (3) and the the parameterisation of the star formation history of Behroozi et al. (2013): 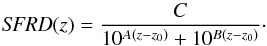 (4)The resulting best fit parameters are
(4)The resulting best fit parameters are 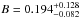 ,
, 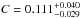 and
and 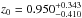 . We set A = −1 as Behroozi et al. (2013). Our inferred star formation history and the associated uncertainties are shown with the black solid line and the shaded area in Fig. 10. The inferred star formation history is compared with the data compiled by Behroozi et al. (2013) and the most recent measurements of the SFRD at 0 < z < 4 based on UV (Cucciati et al. 2012), IR (Gruppioni et al. 2013) and radio data (Karim et al. 2011)8. This inferred star formation history is in excellent agreement with SFRD measurements at z < 1.5, while we find differences of 0.2 dex at z > 1.5. However, such offset is well within the expected SFRD uncertainties (see the large scatter between the various SFRD measurements at z > 2 depending on the wavelength used to trace the SFR in Fig. 10) and the mass density uncertainties created by the slope extrapolation at the low mass end (e.g. Mortlock et al. 2011; Santini et al. 2012).
. We set A = −1 as Behroozi et al. (2013). Our inferred star formation history and the associated uncertainties are shown with the black solid line and the shaded area in Fig. 10. The inferred star formation history is compared with the data compiled by Behroozi et al. (2013) and the most recent measurements of the SFRD at 0 < z < 4 based on UV (Cucciati et al. 2012), IR (Gruppioni et al. 2013) and radio data (Karim et al. 2011)8. This inferred star formation history is in excellent agreement with SFRD measurements at z < 1.5, while we find differences of 0.2 dex at z > 1.5. However, such offset is well within the expected SFRD uncertainties (see the large scatter between the various SFRD measurements at z > 2 depending on the wavelength used to trace the SFR in Fig. 10) and the mass density uncertainties created by the slope extrapolation at the low mass end (e.g. Mortlock et al. 2011; Santini et al. 2012).
We also derive the mass density evolution expected from the star formation history compilation of Behroozi et al. (solid green line and shaded area in Fig. 8). We find that the expected mass density is systematically higher by 0.05–0.2 dex than our data, while still consistent with the expected uncertainties. The discrepancy between direct and inferred mass densities reaches 0.2 dex at z ~ 1.5, and decreases at lower redshift. We note that we would not observe this decrease at z < 1.5 using a constant return fraction.
 |
Fig. 11 Cumulative MF of star-forming galaxies at t2 in red (lowest redshift bin) and at t1 in black (highest redshift bin). The contribution of galaxies quenched between t1 and t2 is removed from the cumulative MF at t1. The dashed lines correspond to the uncertainties. The shifts Δlog ℳ used to estimate the sSFR are shown with the horizontal arrows at four reference masses: ℳR = 1010, 1010.25, 1010.5, 1010.75ℳ⊙ in blue, green, brown and orange, respectively. |
6.2. Inferred specific star formation rates
We now consider an admittedly over-simplistic scenario in which evolution of star-forming galaxies is driven only by star formation (i.e. we consider that mergers do not significantly change the galaxy distribution between two redshift bins, see Sect. 4.3 of Boissier et al. 2010). Given this assumption, the stellar masses increase by ![\hbox{${\cal M}(t_2)-{\cal M}(t_1)=\int^{t_2}_{t_1} {\it SFR}(t')(1-f_r[t_2-t']){\rm d}t'$}](/articles/aa/full_html/2013/08/aa21100-13/aa21100-13-eq310.png) between t1 and t2 (t1 < t2), with fr corresponding to the stellar mass loss (see Sect. 6.1). Assuming that the SFR remains constant over the considered time interval and over the mass range [ℳ(t1),ℳ(t2)], we obtain the specific SFR:
between t1 and t2 (t1 < t2), with fr corresponding to the stellar mass loss (see Sect. 6.1). Assuming that the SFR remains constant over the considered time interval and over the mass range [ℳ(t1),ℳ(t2)], we obtain the specific SFR: 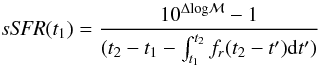 (5)with Δlog ℳ = log ℳ(t2) − log ℳ(t1). The shift Δlog ℳ is directly derived from the MF evolution of star forming galaxies between t1 and t2.
(5)with Δlog ℳ = log ℳ(t2) − log ℳ(t1). The shift Δlog ℳ is directly derived from the MF evolution of star forming galaxies between t1 and t2.
Star-forming galaxies could be quenched and move to the quiescent population in the time interval t2 − t1. Since we want to compute Δlog ℳ for the same galaxy population at t1 and t2, we need to remove the contribution of the galaxies quenched between t1 and t2. This contribution is simply the difference between the quiescent MF (hereafter MFQ) estimated at t2 and t1. Therefore, the MF of star-forming galaxies without the contribution of the galaxies quenched between t1 and t2 is computed as MFSF − Q(t1) = MFSF(t1) − MFQ(t2) + MFQ(t1).
We measure the shifts Δlog ℳ required to superimpose the cumulative MFSF − Q(t1) and of the cumulative MFSF(t2). These shifts are indicated with horizontal arrows in Fig. 11. Since the sSFR could depend on the mass (e.g. Dunne et al. 2009; Karim et al. 2011), we measure Δlog ℳ at four reference masses (ℳR = 1010, 1010.25, 1010.5 and 1010.75ℳ⊙). We do not consider ℳR < 1010ℳ⊙ to limit the impact of the slope extrapolation at low masses. The top label of Fig. 12 shows the evolution of the sSFR estimated at the four reference masses in our analysis. We find consistent sSFR for the three reference masses lower than ℳ < 1010.75ℳ⊙. In the bottom panel of Fig. 12, we focus on the sSFR evolution measured for ℳR = 1010ℳ⊙, which depends less on the removal of quenched galaxies. The sSFR increases from z = 1 to z = 4 (blue circles). The sSFR computed with this indirect method are compared with direct measurement of the sSFR from the literature. Given the size of the uncertainties, our inferred sSFR is in good agreement with literature measurements. At z > 2.5, we obtain a sSFR larger than the compilation from Behroozi et al. (2013). However, recent studies taking into account the contribution of nebular emission lines show that the sSFR at z > 2 could be higher than previously found (e.g. de Barros et al. 2012; Stark et al. 2013). Still, we obtain a value at z ~ 3.5 which is higher than Gonzalez et al. (2012) which takes nebular emission lines into account. We also apply the same method with the MFs computed by Caputi et al. (2011) to derive the sSFR at z ~ 4 (grey star in Fig. 6.2). Given the mass limit of this study, we adopt a reference mass of ℳR = 1010.5ℳ⊙. Despite large error bars, our sSFR values are in excellent agreement.
 |
Fig. 12 Evolution of the sSFR (SFR/ℳ) derived from the UltraVISTA mass functions. Top panel: sSFR measured at different masses using the shifts Δlog ℳ shown in Fig. 11. The sSFR computed at four reference masses ℳR = 1010, 1010.25, 1010.5, 1010.75ℳ⊙ are shown with blue circles, green squares, brown stars and orange triangles, respectively. We also added with a grey star the sSFR measured using the same method using the MF of Caputi et al. (2011). The brown and red shaded areas for Karim et al. (2011) correspond to the mass bins 1010.2 − 1010.6ℳ⊙ and 1010.6 − 1011ℳ⊙, respectively. Bottom panel: sSFR estimated at 1010ℳ⊙ compared with direct measurements from the literature. The purple solid line (dashed lines showing the uncertainties) correspond to the compilation by Behroozi et al. (2013) at the mass 1010ℳ⊙, respectively. The other points are a compilation by Stark et al. (2013) including also data from Dunne et al. (2009) and Reddy et al. (2012) at log (ℳ) ~ 9.7. The red pentagon corresponds to the Gonzalez et al. (2012) value at log (ℳ) ~ 9.7. The open green squares correspond to Noeske et al. (2007) at log (ℳ) ~ 10. |
Finally, we note that our method is more robust at z > 1.5 than at lower redshift, as shown by the size of the error bars. Indeed, the contribution of the quiescent galaxies to the global population is below 40% at z > 1.5 and is restricted to the massive population (bottom panel of Fig. 6). Therefore, residual uncertainties on the removal of the quenched population has a small impact on the analysis. At z < 1.5, the quiescent galaxies are built very fast and their contributions to the global MF reaches 80% at 0.8 < z < 1.1. Therefore, the uncertainties on MFQ generated by cosmic variance have a strong impact on our density estimate of the quenched population between t1 and t2.
6.3. Quenching processes
Newly quenched galaxies and major mergers drive the evolution in density of the quiescent MF, since by definition a quiescent galaxy grows by less than 0.03 dex in 6 Gyr by star formation. Therefore, the efficiency of quenching with cosmic time can be directly estimated from the MF evolution of the quiescent and star-forming galaxies. In this section we discuss our results in term of quenching efficiency, and we summarise our interpretation with a synthetic scheme (Fig. 13).
As we discuss in Sect. 6.2, the evolution of the low-mass star-forming galaxies at z > 2 is consistent with the expected sSFR while the lack of evolution of the massive end implies that massive star-forming galaxies are necessarily quenched. Our data are deep enough at z < 3 to show that the slope of the star-forming sample is steeper than the slope of the quiescent population (see Fig. 6). If the quenching processes acted with the same efficiency at all masses, the MF of the quiescent population should have the same slope as the star-forming MF. We conclude that the physical process which quenches star formation is necessarily more efficient above ℳ ≳ 1010.7−10.9ℳ⊙, i.e. the maximum in density of the quiescent MF9. This scenario is fully consistent with the model proposed in Peng et al. (2010) who introduce a “mass quenching” process which is independent of environment for the massive galaxies. We show that this mass quenching has been active since z = 3. This mass quenching process must have been efficient at 1 < z < 3 to rapidly build up the quiescent population (left panel of Fig. 13). For instance, around 30% of the star-forming galaxies with ℳ ~ 1011ℳ⊙ should be quenched between 2.5 < z < 3 and 2 < z < 2.5 to explain a density increase by 0.25 dex of massive quiescent galaxies. While we can see that this quenching process is extremely efficient above a given mass, we cannot infer the physical nature of the quenching process. AGN feedback or major mergers (or both) are possible candidates (e.g. Hopkins et al. 2006).
Since the star-forming galaxies dominate the high-mass end of the global MF at z > 1 (bottom panel of Fig. 6), an efficient “mass quenching” process is rapidly transitioning them into passive systems. If the “mass quenching” process depletes more rapidly the reservoir of massive star-forming galaxies than new star formation is able to replenish it, we reach an epoch where the quenching is no longer a channel to create new massive quiescent galaxies. By z ~ 1 the supply of massive star forming galaxies has dwindled to the point that few new galaxies are being quenched. Figure 5 shows that >70% of the galaxies more massive than ℳ > 1011ℳ⊙ are quiescent at z < 1.1. Moreover, the sSFR estimated from the literature decreases by a factor 15 between z ~ 1.5 and z ~ 0.6 as shown by the green arrows in Fig. 13 (e.g. Noeske et al. 2007; Daddi et al. 2007; Elbaz et al. 2007; Karim et al. 2011). Since the massive galaxy population is already dominated by quiescent galaxies at z < 1 and since the growth rate of star-forming galaxies is no longer sufficiently efficient to generate numerous massive star-forming galaxies (middle panel of Fig. 13), the quenching of massive star-forming galaxies can not modify significantly the high-mass end of the quiescent MF at z < 1.
 |
Fig. 13 A possible scenario showing how sSFR and quenching impact the star-forming MF (blue lines) and quiescent MF (red lines), similar to Peng et al. (2010). The large arrows represent quenching. The green arrows correspond to the mass increase expected in 2 Gyr, by taking the sSFR values compiled by Stark et al. (2013). The left panel corresponds to the high redshift bin 2.5 < z < 3, where we show the mass quenching process which is more efficient at high mass. The middle panel corresponds to the redshift bin 1.1 < z < 1.5 when the quiescent galaxies starts to dominate the high-mass end. The right panel corresponds to the redshift bin 0.2 < z < 0.5, when environment quenching generates new low mass quiescent galaxies. |
The flattening of the faint-end slope of the quiescent MF at z < 1 (see Sect. 5.2) shows that the quenching starts to be efficient at low masses (right panel of Fig. 13). As shown by Bezanson et al. (2012), such flattening of the slope is easily obtained by quenching a small fraction (between 1 and 10%) of the star-forming galaxies. Using the COSMOS sample, Scoville et al. (2013) find that low-mass quiescent galaxies appear in high density environment at z < 1. Peng et al. (2010) proposed the “environment quenching” process which mainly affects the satellite galaxies as large-scale structure develop. Gabor & Davé (2012) find a similar quenching process using an hydronamical simulation. Therefore, we interpret the flattening of the slope of the quiescent MF as an environmentally driven process, even if our results alone can not demonstrate it.
6.4. Impact of the assumed star formation histories
We derive the stellar masses assuming an exponentially declining SFR for the stellar population synthesis models. However, numerous studies pointed out that such star formation histories could be inappropriate at z > 1 (e.g. Maraston et al. 2010; Pacifici et al. 2013). Therefore, we investigate how this choice impacts our conclusions.
We derive the MF using two other libraries: one library based on delayed star formation histories and another using a composite of various star formation histories (see Sect. 3.2). We generate the second library based on delayed star formation histories following a law in τ-2te− t/τ. The maximum SFR peak could be delayed by 0.1, 0.5, 1, 2 or 3 Gyr and we consider three different metallicities (Z = 0.004, Z = 0.008, Z = 0.02). We generate a third composite library including various combinations: three templates with an exponentially declining SFR (τ = 0.1,1, 5 Gyr), two templates with a delayed star formation history (maximum peak at 1 and 3 Gyr). For each of these templates, we allow a possible second burst 3 Gyr after the peak in SFR. The amplitude of this second burst could be 0.25 or 0.5 times the maximum of the first burst. This second burst is generated using a constant SFR. We derive the MFs with these three libraries (called hereafter exponential, delayed and composite libraries). Still, we do not test the impact of stochastic star formation histories.
Figures 14 and 15 show the MFs of the star-forming and quiescent galaxies, respectively. The MFs based on the exponential, delayed and composite libraries are shown with red squares, blue triangles and green crosses, respectively. We do not detect any significant difference between the MFs. Therefore, all our conclusions are equally valid for any of these three libraries.
In detail, we find that quiescent galaxies are almost always fitted with a delayed SFR history peaking after 0.1 or 0.5 Gyr, which is close to an exponentially declining history. For the star forming galaxies, the templates are uniformly distributed between the five delayed star formation histories. By comparing the best-fit ages and the τ values of the delayed templates, 30% of star-forming galaxies at z > 2 are fitted with a template in the rising part of the star formation history. The dispersion between the stellar masses computed with the exponential and delayed libraries is lower than 0.06 dex out to z < 4, with no systematic difference. This explains why the delayed and exponential MFs are similar. For the composite library, the templates with an exponentially declining star formation history are selected in 87% of the case, with a possible small second burst. This explains why we obtain almost the same results between the composite and the exponential libraries.
 |
Fig. 14 Galaxy stellar mass functions of the star-forming sample. The points correspond to the Vmax estimator (we do not show the other estimators for clarity) and error bars include cosmic variance, Poissonian errors and photo-z/stellar mass uncertainties. The red squares, the blue triangles and the green crosses correspond to the MFs computed using the exponential, delayed and composite libraries. The red solid line is the best-fitted double-Schechter function. The black solid, dashed and dotted lines correspond to the MFs predicted by the semi-analytical model, assuming no error on the stellar masses, an error evolving as described in appendix A (using the product of a Lorentzian and Gaussian distribution), and a Gaussian with a σ = 0.2 dex. |
 |
Fig. 15 Galaxy stellar mass functions of the quiescent sample for selected using a two-colour technique. Symbols are the same as Fig. 14. The short dashed brown lines correspond to quiescent galaxies with a bulge-to-disc ratio greater than 0.5. The long dashed cyan lines correspond to the central galaxies in the models. |
6.5. Comparison with the semi-analytical models
We now compare our mass function measurements with the predictions of semi-analytical models. The mock catalogues are based on ΛCDM simulations from Wang et al. (2008) with the cosmological parameters derived from the third-year WMAP data (H0 = 74.3 km s-1, ΩM = 0.226 and ΩΛ = 0.774). The light cone survey covers an area of 1.4 × 1.4 deg2 similar to COSMOS. Galaxy properties were generated using the galaxy formation model, as detailed in De Lucia & Blaizot (2007) and Wang & White (2008). Since the redshift and the galaxy stellar masses are available for all galaxies in the simulation, we can directly compute the predicted MFs. We use our standard cosmology (H0 = 70 km s-1, ΩM = 0.3 and ΩΛ = 0.7) to renormalise the predicted stellar mass counts by the comoving volume. We isolate the quiescent population in the simulations. We try three different criteria: a red clump criteria using rest-frame UV − r versus r − K colours, a cut in log (sSFR) < −11 and a cut in B − I corrected for dust extinction. The quiescent MFs are almost identical regardless of selection criteria.
The comparison between the observed and predicted MFs is shown in Fig. 14 for the star-forming sample. First, we find that the predicted and observed faint-end slopes are in good agreement at least up to z = 2. Secondly, the model under-predicts the density of massive galaxies. The mismatch between the observed and predicted high-mass end increases with redshift. If we add a 1σ error of 0.2 dex to the stellar masses, as commonly assumed in the literature (e.g. Cattaneo et al. 2006; Bower et al. 2012), we reduce the tension between model and observation (dotted lines in Fig. 14). We point out that the 0.2 dex uncertainty commonly associated to the stellar mass is mostly explained by systematic uncertainties (choice of the IMF, adopted population synthesis models) and should not be applied to the stellar masses. For a given library, the statistical errors are much smaller. Moreover, we already deconvolved the fit by the expected statistical errors in the stellar masses (see Sect. 4). Therefore, the red solid line is directly comparable to the model prediction, showing that the predicted high-mass end is underestimated. Several factors could explain this mismatch: 1) we do not consider stochastic star formation histories to estimate the stellar masses, while such histories are common for simulated galaxies in semi-analytical models. Such difference could create an intrinsic scatter which could justify a Gaussian smoothing of the observed MF; 2) our high redshift sample is contaminated by low redshift galaxies (i.e. catastrophic failures in the photo-z); however Fig. 1 do not show such contamination with our current spectroscopic sample; 3) some assumed physical laws (e.g. IMF) evolve with redshift which generate redshift dependent biases in our stellar mass estimates; 4) the models do not generate enough massive galaxies at z = 3−4. The last option would require that the models generate 1011.5 ℳ⊙ galaxies in less than two Gyr. Then, these galaxies should stop to grow on a very short timescale by having their star formation activity drastically reduced or quenched.
Figure 15 shows the comparison between observed and predicted MFs for the quiescent population. The mismatch between the observed and predicted faint end slopes is dramatic. At 9.5 < log (ℳ) < 10 and 0.5 < z < 0.8, the model overestimates the low-mass end by a factor 10. Such an effect has been already noticed by Cucciati et al. (2012) in the VVDS field based on the B-band luminosity function. Wang & White (2008), Bielby et al. (2012), Bower et al. (2012), Guo et al. (2011) show that the models overproduce the density of low-mass galaxies for the full population. In this paper, we show that the origin of this discrepancy is the high density of low-mass quiescent galaxies, since the faint end slope of the star-forming galaxies is correctly predicted at z < 2. Information such as the host halo mass, the galaxy location in the halo (central or satellite) and the galaxy morphology are kept in the simulation. We use this information to investigate in more detail the properties of the quiescent galaxies overproduced by the models. We first keep only bulge-dominated quiescent galaxies with a bulge-to-disc ratio greater than 0.5 (brown short dashed lines). The slopes are in much better agreement with the data. Therefore, the model is able to generate a reasonable amount of quiescent galaxies when the quenching is associated to a process which makes the galaxy dominated by a bulge. Indeed, Ilbert et al. (2010) showed that between 40 and 70% of the quiescent galaxies have an elliptical morphology at z < 0.8 and 9.5 < log (ℳ) < 10, while in the model, 20% of the quiescent galaxies are bulge dominated in the same mass range. We also show the predicted MF of central quiescent galaxies (cyan long dashed lines). It appears that the low-mass quiescent simulated galaxies are mostly dominated by satellite/orphans galaxies. One possible interpretation of the mismatch between the faint-end slopes is an over-quenching of the star formation in satellite galaxies and/or an over-quenching of the star-formation in disc galaxies.
7. Conclusions
We study the stellar mass assembly out to z = 4 with a unique sample of 220 000 galaxies selected at Ks < 24 in the COSMOS field. Galaxies are selected using the new UltraVISTA DR1 near-infrared data release, which reaches between one and two magnitudes deeper than previous COSMOS near-infrared data. Fluxes are measured on PSF-homogenised images in 25 bands including optical broad and intermediate-band Subaru data taken for the COSMOS project. We also add four bands at 3.6 − 8 μm from S-COSMOS and the GALEX NUV band. We keep only the sources at Ks < 24 located in areas with a good image quality, which represents an effective area of 1.52 deg2.
The photometric redshifts are derived using Le_Phare following a procedure similar to Ilbert et al. (2009). Our photometric redshifts have two regimes: at 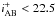 (zmed ~ 0.5), precision 1% with less than 1% of catastrophic failures. In the high redshift range 1.5 < z < 4, the precision of the photo-z is tested against the zCOSMOS faint sample, and is 3% for
(zmed ~ 0.5), precision 1% with less than 1% of catastrophic failures. In the high redshift range 1.5 < z < 4, the precision of the photo-z is tested against the zCOSMOS faint sample, and is 3% for 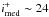 galaxies. We estimate the galaxy stellar masses using a library of synthetic spectra generated using the SPS model of Bruzual & Charlot (2003). We show that our results are independent of the assumed star-formation history (among our tested star-formation histories, i.e. exponentially decreasing, delayed or a possible second burst).
galaxies. We estimate the galaxy stellar masses using a library of synthetic spectra generated using the SPS model of Bruzual & Charlot (2003). We show that our results are independent of the assumed star-formation history (among our tested star-formation histories, i.e. exponentially decreasing, delayed or a possible second burst).
We find that the evolution of the global stellar mass function is strongly mass-dependent. The low-mass end evolves more rapidly than the high-mass end. If we consider an evolution purely driven by star formation, the low-mass galaxies evolve by almost 1 dex between 1.5 < z < 2 and 0.2 < z < 0.5, while the stellar mass of the most massive galaxies increases by less than 0.2 dex in the same time interval. The lack of evolution of the massive end can be interpreted as a direct consequence of star formation being drastically reduced or quenched when a galaxy becomes more massive than ℳ > 1010.7 − 10.9ℳ⊙. We derive the comoving stellar mass density of the full sample from z = 4 to z = 0.2. We find that the stellar mass is assembled twice as fast at 1 < z < 4 (14% of the local stellar mass density per Gyr) than at z < 1 (6% of the local stellar mass density per Gyr).
We isolate the quiescent population using a classification based on the rest-frame colours NUV − r+ and r+ − J. This classification separates cleanly dusty star-forming galaxies and quiescent galaxies. We find that the MF evolution of the quiescent population is definitively mass-dependent at z < 1, confirming the trend shown in Ilbert et al. (2010). We do not find any significant evolution of the high-mass end at z < 1 (any evolution being limited to ΔM < 0.2 dex), while we observe a clear flattening of the slope in the same redshift range. We interpret this evolution of the low-mass end of the MF as arising from continuous quenching of galaxies between z ~ 1 and z ~ 0.1, probably by physical processes related to environment.
The UltraVISTA data now allows us to trace the growth in stellar mass density in quiescent galaxies from z ~ 3 to the present day. From z ~ 3 to z ~ 1 we find a rapid increase in the stellar mass density of all quiescent galaxies, independent of stellar mass. We confirm that the steep rise of more than one order of magnitude of this population between 1 < z < 2 observed in previous works (Arnouts et al. 2007; Ilbert et al. 2010) follows an earlier rise by a factor ~3 in 2 < z < 3.5. In total, we find that the density of 1011ℳ⊙ galaxies is continuously increasing, reaching a factor ~40 between 2.5 < z < 3 and 0.8 < z < 1.1. This must indicate that a fraction of star-forming galaxies is continuously quenched at z > 1. Because of the different faint-end slopes of the MF between the quiescent and global populations at z < 3, we infer that the physical processes which quench the star formation are more efficient above ℳ ≳ 1010.7 − 10.9ℳ⊙ (the maximum in density of the quiescent MF). This scenario is consistent with the model proposed by Peng et al. (2010) who introduce a “mass quenching” process. Since the high-mass end of the quiescent MF stops evolving at z < 1, we conclude that: 1) star formation is not efficient enough at z < 1 to produce new massive star-forming galaxies, which could be quenched later; 2) major mergers between massive galaxies are not sufficiently frequent at z < 1 to increase significantly the density of massive quiescent galaxies.
We infer the star formation history from the mass density evolution following the formalism of Wilkins et al. (2008). We find that the inferred star formation history is in excellent agreement with SFRD data at z < 1.5 but under-predict them by 0.2 dex at z > 1.5. However, considering the size of the uncertainties at z > 1.5, the SFRD and mass density data still provide a consistent picture of the star formation history.
We also develop a new method to estimate the sSFR from the mass function evolution. By comparing the star-forming MFs at two different epochs (after having removed the contribution of galaxies quenched during the considered time interval), we derive the sSFR from z ~ 0.5 up to z < 4. We find that the sSFR increases continuously at 1 < z < 4 for our considered mass range 1010ℳ⊙ ≤ ℳ ≤ 1010.5ℳ⊙. This new method is complementary to direct sSFR measurements at z > 2, which are very sensitive to dust extinction (e.g. Bouwens et al. 2009) or SED modelling (e.g. Stark et al. 2013).
Finally, we compare our data with the predictions of the semi-analytical model of De Lucia & Blaizot (2007) as described in Wang et al. (2008). We find that the model under-predicts the density of massive galaxies for quiescent and star-forming galaxies. The tension between model and observations at the high-mass end can be alleviated if scatter in the modelled stellar masses errors is a 1σ of 0.2 dex. When we compare the observed and predicted MFs for the quiescent population, the difference in the slope is striking. At log (ℳ) ~ 10 and z < 0.8, the model overestimates the low-mass end by a factor 10. On the other hand, the model successfully reproduce the faint-end slope of the star-forming population. This indicates that recipes to quench satellite and/or disc galaxies within semi-analytical models are still incomplete and will need to be modified.
The COSMOS field will be observed during five years for the UltraVISTA survey, allowing to obtain near-IR data two magnitudes deeper. In the meantime, the SPLASH program (Capak et al., in prep.) will observe the COSMOS field with IRAC, allowing a gain of 1.5 mag at 3.6 μm. The combination of this new data will allowed to extend this work at 4 < z < 7 and better constrain the contribution of low-mass galaxies.
Acknowledgments
We are grateful to the referee for a careful reading of the manuscript and useful suggestions. The authors thank M. Kajisawa, L. Pozzetti, P. Pérez-González and P. Santini for providing their estimates of the mass function. We also thanks P. Behroozi for his useful suggestions. The authors thank J. Donley for providing her catalogue of IRAC power-laws. We gratefully acknowledge the contributions of the entire COSMOS collaboration consisting of more than 100 scientists. The HST COSMOS program was supported through NASA grant HST-GO-09822. More information on the COSMOS survey is available at http://www.astro.caltech.edu/cosmos. H.J. McCracken acknowledges support from the “Programme national cosmologie et galaxies”. J.S.D. acknowledges the support of the European Research Council through an Advanced grant, and the support of the Royal Society via a Wolfson Research Merit Award. S. Toft acknowledges support from the Lundbeck foundation. The Dark Cosmology Centre is funded by the Danish National Research Foundation. This paper is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO programme ID 179.A-2005 and on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium. This work is based in part on archival SEDS data obtained with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA. This research has made use of the NASA/ IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. The Dark Cosmology Centre is funded by the Danish National Research Foundation. B.M.J. acknowledges support from the ERC-StG grant EGGS-278202.
References
- Arnouts, S., Moscardini, L., Vanzella, E., et al. 2002, MNRAS, 329, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, 770, 57 [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Wolf, C., Meisenheimer, K., et al. 2004, ApJ, 608, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, Astronomical Data Analysis Software and Systems XI, 281, 228 [NASA ADS] [Google Scholar]
- Bezanson, R., van Dokkum, P., & Franx, M. 2012, ApJ, 760, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissier, S., Buat, V., & Ilbert, O. 2010, A&A, 522, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borch, A., Meisenheimer, K., Bell, E. F., et al. 2006, A&A, 453, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., & Crain, A. 2012, MNRAS, 422, 2816 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., Whitaker, K. E., van Dokkum, P. G., et al. 2011, ApJ, 739, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Zamorani, G., Comastri, A., et al. 2007, ApJS, 172, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, A. G. 2007, in From Stars to Galaxies: Building the Pieces to Build Up the Universe, eds. A. Vallenari et al., ASP Conf. Ser., 374, 303 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Abraham, R. G., Ellis, R. S., et al. 2007, ApJS, 172, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K. I., Cirasuolo, M., Dunlop, J. S., et al. 2011, MNRAS, 413, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Giavalisco, M., Guo, Y., et al. 2011, ApJ, 743, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Dekel, A., Devriendt, J., Guiderdoni, B., & Blaizot, J. 2006, MNRAS, 370, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cirasuolo, M., McLure, R. J., Dunlop, J. S., et al. 2007, MNRAS, 380, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & Wechsler, R. H. 2009, ApJ, 696, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Gunn, J. E., & White, M. 2009, ApJ, 699, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., De Lucia, G., Zucca, E., et al. 2012, A&A, 548, 108 [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- de Barros, S., Schaerer, D., & Stark, D. P. 2012, submitted [arXiv:1207.3663] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domínguez Sánchez, H., Pozzi, F., Gruppioni, C., et al. 2011, MNRAS, 417, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Drory, N., Bundy, K., Leauthaud, A., et al. 2009, ApJ, 707, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Dunne, L., Ivison, R. J., Maddox, S., et al. 2009, MNRAS, 394, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emerson, J. P., & Sutherland, W. J. 2010, in Proc. SPIE, 7733, 773306 [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fontana, A., Pozzetti, L., Donnarumma, I., et al. 2004, A&A, 424, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontana, A., Salimbeni, S., Grazian, A., et al. 2006, A&A, 459, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabor, J. M., & Davé, R. 2012, MNRAS, 427, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, V., Bouwens, R., Illingworth, G., et al. 2012, ApJ, submitted [arXiv:1208.4362] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Ilbert, O., Tresse, L., Arnouts, S., et al. 2004, MNRAS, 351, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Kajisawa, M., Ichikawa, T., Tanaka, I., et al. 2009, ApJ, 702, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Kajisawa, M., Ichikawa, T., Yoshikawa, T., et al. 2011, PASJ, 63, 403 [NASA ADS] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lu, Y., Mo, H. J., Katz, N., & Weinberg, M. D. 2012, MNRAS, 421, 1779 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C., Pforr, J., Renzini, A., et al. 2010, MNRAS, 407, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., van Dokkum, P. G., Förster Schreiber, N. M., et al. 2009, ApJ, 701, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Wyder, T. K., Schiminovich, D., et al. 2007, ApJS, 173, 342 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Capak, P., Salvato, M., et al. 2010, ApJ, 708, 202 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Mortlock, A., Conselice, C. J., Bluck, A. F. L., et al. 2011, MNRAS, 413, 2845 [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H. 2011, ApJ, 731, 113 [Google Scholar]
- Moustakas, J., Coil, A., Aird, J., et al. 2013, ApJ, 767, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Onodera, M., Renzini, A., Carollo, M., et al. 2012, ApJ, 755, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1974, ApJS, 27, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pacifici, C., Kassin, S. A., Weiner, B., Charlot, S., & Gardner, J. P. 2013, ApJ, 762, 15 [Google Scholar]
- Peng, Y. J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Villar, V., et al. 2008, ApJ, 675, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Reddy, N. A., Pettini, M., Steidel, C. C., et al. 2012, ApJ, 754, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Buzzoni, A. 1986, Spectral Evolution of Galaxies, 122, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2012, A&A, 538, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Arnouts, S., Aussel, H., et al. 2013, ApJS, 206, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D., Schenker, M. A., Ellis, R., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, J., Groves, B., Budavari, T., & Dale, D. 2011, ApSS, 331, 1 [Google Scholar]
- Wang, J., De Lucia, G., Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS, 384, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., et al. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Trentham, N., & Hopkins, A. M. 2008, MNRAS, 385, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Szalay, A. S., Connolly, A. J., & Szokoly, G. P. 1999, AJ, 117, 68 [Google Scholar]
- Zamojski, M. A., Schiminovich, D., Rich, R. M., et al. 2007, ApJS, 172, 468 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Treatment of the Eddington bias
Caputi et al. (2011) outlined that a bias (Eddington 1913) could affect the estimate of the high-mass end of the stellar mass function. The uncertainties on the stellar masses scatter the galaxies from one stellar mass bin to another. In the case of the stellar mass function, the density exponentially decreases toward massive galaxies. The stellar mass scattering therefore moves more galaxies into the massive end than the reverse. As a consequence, we overestimate the density of massive galaxies.
Caputi et al. (2011) estimated that the Eddington bias could affect the density by up to 0.13 dex for the most massive galaxies. In this paper, we go one step further and we deconvolve the density estimate by the stellar mass uncertainties. The first step is to characterise the stellar mass uncertainties. We do not consider here systematic errors linked to the choice of the stellar synthesis models or to the IMF. We consider only the uncertainties linked to the photometry and to the photometric redshifts. We generate a “noisy” sample by adding noise to the apparent magnitudes and to the photometric redshifts using their associated error bars. Then, we recompute the stellar masses with this “noisy” catalogue. Figure A.1 shows the difference between the original masses and the ones obtained on this “noisy”catalogue at ℳ > 1010.5ℳ⊙. The red histogram shows the cumulative distribution of these differences. We first model the stellar mass uncertainties using a Gaussian distribution 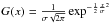 as it is commonly assumed (e.g. Cattaneo et al. 2006; Bower et al. 2012). The dotted lines correspond to a Gaussian distribution with σ = 0.04(1 + z). The fraction of galaxies with a difference larger than 0.1 dex is underestimated and the Gaussian distribution is not a good representation of the main peak at z > 2.5. We also model the distribution by using a Lorentzian distribution
as it is commonly assumed (e.g. Cattaneo et al. 2006; Bower et al. 2012). The dotted lines correspond to a Gaussian distribution with σ = 0.04(1 + z). The fraction of galaxies with a difference larger than 0.1 dex is underestimated and the Gaussian distribution is not a good representation of the main peak at z > 2.5. We also model the distribution by using a Lorentzian distribution 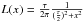 with τ = 0.04(1 + z) (short dashed lines in Fig. A.1). This parametrisation of the stellar mass uncertainties produces too many galaxies with differences larger than 0.2 dex. Finally, we adopt a function which is the product between a Lorentzian distribution with τ = 0.04(1 + z) and a Gaussian distribution with σ = 0.5. This distribution is shown with the long dashed lines in Fig. A.1 and provides the best representation of the stellar mass uncertainties.
with τ = 0.04(1 + z) (short dashed lines in Fig. A.1). This parametrisation of the stellar mass uncertainties produces too many galaxies with differences larger than 0.2 dex. Finally, we adopt a function which is the product between a Lorentzian distribution with τ = 0.04(1 + z) and a Gaussian distribution with σ = 0.5. This distribution is shown with the long dashed lines in Fig. A.1 and provides the best representation of the stellar mass uncertainties.
 |
Fig. A.1 The red histogram show the cumulative distribution of the difference between the original stellar masses and the ones obtained with a “noisy” catalogues (redshifts and magnitudes are scattered according to the expected errors) at ℳ > 1010.5ℳ⊙. The dotted, short-dashed and long-dashed lines correspond to a Gaussian distribution with σ = 0.04(1 + z), a Lorentzian distribution with τ = 0.04(1 + z), and the product of a Lorentzian and a Gaussian distributions with τ = 0.04(1 + z) and σ = 0.5. |
 |
Fig. A.2 Global stellar mass function in several redshift bins. The open circles correspond to the Vmax non-parametric estimates. The thick black solid lines correspond to the double-Schechter fit deconcolved by the stellar mass uncertainties. The green thin solid lines correspond to the simple fit without deconvolution. The pink dotted lines, the short-dashed blue lines and the long dashed red lines correspond to the fiducial mass function (black solid lines) convolved with G(σ = 0.04(1 + z)), L(τ = 0.04(1 + z))G(σ = 0.5), L(τ = 0.04(1 + z))G(σ = 1), respectively. |
The second step is to take into account the stellar mass uncertainties when we derive the stellar mass function. We deconvolve only the parametric fit of the stellar mass function by the stellar mass uncertainties (not the non-parametric estimates). As described in Sect. 4, we fit a double-Schechter function φ(ℳ) to the Vmax non-parametric data. In order to take into account the stellar mass uncertainties, we convolve the double Schechter function by our modelled stellar mass uncertainties 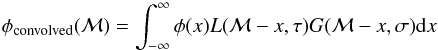 (A.1)with τ = 0.04(1 + z) and σ = 0.5. We fit the convolved double Schechter function to the Vmax non parametric data. Figure A.2 shows the result of this convolution at z > 0.8 for the global sample. The thick solid black lines show the best fit double-Schechter function, deconvolved by the stellar mass uncertainties (our fiducial measurement used in this paper). The difference between the best-fit double-Schechter functions with and without the deconvolution (black and green lines, respectively) is significant only at the high-mass end and remains below 0.1 dex. The blue solid dashed lines correspond to the fiducial MF convolved by the G × L functions. By construction, the blue dashed line provides a good fit of the Vmax non parametric data points. The pink dotted lines correspond to the fiducial MF convolved by a simple Gaussian with σ = 0.04(1 + z). As seen in the 0.8 < z < 1.1 redshift bin, a convolution by a Gaussian does not explain the presence of some massive galaxies, which is well explained if we use the G × L convolution functions. If we allow more extreme errors in the stellar mass estimate, using for instance a convolution by the same Lorentzian function multiplied by a Gaussian with σ = 1, we would observe a larger population of massive galaxies (red long dashed line).
(A.1)with τ = 0.04(1 + z) and σ = 0.5. We fit the convolved double Schechter function to the Vmax non parametric data. Figure A.2 shows the result of this convolution at z > 0.8 for the global sample. The thick solid black lines show the best fit double-Schechter function, deconvolved by the stellar mass uncertainties (our fiducial measurement used in this paper). The difference between the best-fit double-Schechter functions with and without the deconvolution (black and green lines, respectively) is significant only at the high-mass end and remains below 0.1 dex. The blue solid dashed lines correspond to the fiducial MF convolved by the G × L functions. By construction, the blue dashed line provides a good fit of the Vmax non parametric data points. The pink dotted lines correspond to the fiducial MF convolved by a simple Gaussian with σ = 0.04(1 + z). As seen in the 0.8 < z < 1.1 redshift bin, a convolution by a Gaussian does not explain the presence of some massive galaxies, which is well explained if we use the G × L convolution functions. If we allow more extreme errors in the stellar mass estimate, using for instance a convolution by the same Lorentzian function multiplied by a Gaussian with σ = 1, we would observe a larger population of massive galaxies (red long dashed line).
All Tables
Characteristics of the spectroscopic redshift samples and photometric redshift accuracy.
Best-fit parameters for the full sample, for the quiescent galaxies classified with the two-colour criteria and for the star-forming galaxies.
All Figures
 |
Fig. 1 Photometric redshifts versus spectroscopic redshifts. Only secure spectroscopic redshifts at Ks < 24 are considered. Different symbols correspond to the spectroscopic samples labelled in the right. |
| In the text | |
 |
Fig. 2 Stellar masses versus redshift for the KAB < 24 selected sample. The top and bottom panels correspond to the full sample and the quiescent population, respectively. Black points correspond to the measured stellar masses. The brown points correspond to ℳlimit which is the lowest mass which could be observed for a given galaxy for a limit at KAB = 24. The blue circles correspond to the completeness limit chosen in this study. The red and green curves correspond to the two extreme templates with τ = 0.1 Gyr and τ = 30 Gyr, respectively. We show 3 ages which are 0.9, 2 and 5 Gyr (from the bottom to the top, respectively). The dashed lines correspond to an extinction of E(B − V) = 0.2. If the lines are not drawn, it means that either the age is older than the age of the Universe or that the condition age/τ > 4 implies a small extinction. We indicate at the top of each panel the percentage of galaxies detected at 3.6 μm (top line) and in at least four bands (detection thresholds at >2σ and >5σ for the middle and bottom lines, respectively). |
| In the text | |
 |
Fig. 3 Two-colour selection of the quiescent population. The galaxies above the black line in the top left are selected as quiescent. The fraction (in %) of log (sSFR) < −11 galaxies selected by the two-colour selection box is the top number in each panel. The fraction of galaxies with log (sSFR) > −11 within the two-colour box is the bottom number. |
| In the text | |
 |
Fig. 4 Fractional error in density as a function of the stellar mass and redshift. The top panel shows the errors due to the cosmic variance. The middle and bottom panels are the errors associated to the template fitting procedure (photo-z and stellar mass) for the full sample and the quiescent population, respectively. Results are shown only in the mass range covered by our dataset. |
| In the text | |
 |
Fig. 5 Galaxy stellar mass function up to z = 4 for the full sample. Each colour corresponds to different redshift bins of variable step size. Fits are shown in the mass range covered by our dataset. The filled areas correspond to the 68% confidence level regions, after accounting for Poissonian errors, the cosmic variance and the uncertainties created during the template fitting procedure. The open triangles and squares correspond to the local estimates by Moustakas et al. (2013) and Baldry et al. (2012), respectively. |
| In the text | |
 |
Fig. 6 Galaxy stellar mass function up to z = 4 for the star-forming population (top panel) and for the quiescent population (middle panel). Symbols are the same as Fig. 5. The bottom panel shows the percentage of quiescent galaxies as a function of stellar mass in the same redshift bins. |
| In the text | |
 |
Fig. 7 UltraVISTA global stellar mass functions (open black circles and solid lines) compared with several measurements from the literature published since 2008 (labelled in the bottom right). Each panel corresponds to a redshift bin. The literature MF measurements are converted to the same cosmology and IMF as used in this study (H0 = 70 km s-1 Mpc-1 and Chabrier 2003 IMF). |
| In the text | |
 |
Fig. 8 Stellar mass density as a function of cosmic time (redshift is given in the top label). Black and red points correspond to the full and quiescent populations, respectively. The circles correspond to our new results using UltraVISTA. Solid and open red circles correspond to the two-colour and sSFR selected quiescent galaxies, respectively. The green shaded area corresponds to the cosmic SFR compiled by Behroozi et al. (2013) and integrated over cosmic time as described in Sect. 6.1. The dashed line corresponds to the best fit over the mass density data. |
| In the text | |
 |
Fig. 9 Stellar mass density as a function of cosmic time. Black open circles, red solid circles and blue pentagons correspond to the full, quiescent and star-forming galaxies, respectively. |
| In the text | |
 |
Fig. 10 A comparison between the star formation history inferred from the UltraVISTA mass density (black solid line and dashed area corresponding to 1σ errors) and literature determinations including: direct measurements of the SFR density compiled by Behroozi et al. (2013) (red solid line with dashed lines for the associated uncertainties); star formation histories derived from the UV and IR luminosity functions from Cucciati et al. (2012) and Gruppioni et al. (2013) (brown triangles and green squares, respectively); and finally radio estimates from Karim et al. (2011) updated using the mass functions presented in this paper (blue circles). |
| In the text | |
 |
Fig. 11 Cumulative MF of star-forming galaxies at t2 in red (lowest redshift bin) and at t1 in black (highest redshift bin). The contribution of galaxies quenched between t1 and t2 is removed from the cumulative MF at t1. The dashed lines correspond to the uncertainties. The shifts Δlog ℳ used to estimate the sSFR are shown with the horizontal arrows at four reference masses: ℳR = 1010, 1010.25, 1010.5, 1010.75ℳ⊙ in blue, green, brown and orange, respectively. |
| In the text | |
 |
Fig. 12 Evolution of the sSFR (SFR/ℳ) derived from the UltraVISTA mass functions. Top panel: sSFR measured at different masses using the shifts Δlog ℳ shown in Fig. 11. The sSFR computed at four reference masses ℳR = 1010, 1010.25, 1010.5, 1010.75ℳ⊙ are shown with blue circles, green squares, brown stars and orange triangles, respectively. We also added with a grey star the sSFR measured using the same method using the MF of Caputi et al. (2011). The brown and red shaded areas for Karim et al. (2011) correspond to the mass bins 1010.2 − 1010.6ℳ⊙ and 1010.6 − 1011ℳ⊙, respectively. Bottom panel: sSFR estimated at 1010ℳ⊙ compared with direct measurements from the literature. The purple solid line (dashed lines showing the uncertainties) correspond to the compilation by Behroozi et al. (2013) at the mass 1010ℳ⊙, respectively. The other points are a compilation by Stark et al. (2013) including also data from Dunne et al. (2009) and Reddy et al. (2012) at log (ℳ) ~ 9.7. The red pentagon corresponds to the Gonzalez et al. (2012) value at log (ℳ) ~ 9.7. The open green squares correspond to Noeske et al. (2007) at log (ℳ) ~ 10. |
| In the text | |
 |
Fig. 13 A possible scenario showing how sSFR and quenching impact the star-forming MF (blue lines) and quiescent MF (red lines), similar to Peng et al. (2010). The large arrows represent quenching. The green arrows correspond to the mass increase expected in 2 Gyr, by taking the sSFR values compiled by Stark et al. (2013). The left panel corresponds to the high redshift bin 2.5 < z < 3, where we show the mass quenching process which is more efficient at high mass. The middle panel corresponds to the redshift bin 1.1 < z < 1.5 when the quiescent galaxies starts to dominate the high-mass end. The right panel corresponds to the redshift bin 0.2 < z < 0.5, when environment quenching generates new low mass quiescent galaxies. |
| In the text | |
 |
Fig. 14 Galaxy stellar mass functions of the star-forming sample. The points correspond to the Vmax estimator (we do not show the other estimators for clarity) and error bars include cosmic variance, Poissonian errors and photo-z/stellar mass uncertainties. The red squares, the blue triangles and the green crosses correspond to the MFs computed using the exponential, delayed and composite libraries. The red solid line is the best-fitted double-Schechter function. The black solid, dashed and dotted lines correspond to the MFs predicted by the semi-analytical model, assuming no error on the stellar masses, an error evolving as described in appendix A (using the product of a Lorentzian and Gaussian distribution), and a Gaussian with a σ = 0.2 dex. |
| In the text | |
 |
Fig. 15 Galaxy stellar mass functions of the quiescent sample for selected using a two-colour technique. Symbols are the same as Fig. 14. The short dashed brown lines correspond to quiescent galaxies with a bulge-to-disc ratio greater than 0.5. The long dashed cyan lines correspond to the central galaxies in the models. |
| In the text | |
 |
Fig. A.1 The red histogram show the cumulative distribution of the difference between the original stellar masses and the ones obtained with a “noisy” catalogues (redshifts and magnitudes are scattered according to the expected errors) at ℳ > 1010.5ℳ⊙. The dotted, short-dashed and long-dashed lines correspond to a Gaussian distribution with σ = 0.04(1 + z), a Lorentzian distribution with τ = 0.04(1 + z), and the product of a Lorentzian and a Gaussian distributions with τ = 0.04(1 + z) and σ = 0.5. |
| In the text | |
 |
Fig. A.2 Global stellar mass function in several redshift bins. The open circles correspond to the Vmax non-parametric estimates. The thick black solid lines correspond to the double-Schechter fit deconcolved by the stellar mass uncertainties. The green thin solid lines correspond to the simple fit without deconvolution. The pink dotted lines, the short-dashed blue lines and the long dashed red lines correspond to the fiducial mass function (black solid lines) convolved with G(σ = 0.04(1 + z)), L(τ = 0.04(1 + z))G(σ = 0.5), L(τ = 0.04(1 + z))G(σ = 1), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


