| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220271 | |
| Published online | 18 June 2013 | |
Planck intermediate results
IX. Detection of the Galactic haze with Planck
1 APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
2 Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
3 African Institute for Mathematical Sciences, 6–8 Melrose Road, Muizenberg, Cape Town, South Africa
4 Agenzia Spaziale Italiana Science Data Center, c/o ESRIN, via Galileo Galilei, Frascati, Italy
5 Agenzia Spaziale Italiana, Viale Liegi 26, Roma, Italy
6 Astrophysics Group, Cavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge CB3 0HE, UK
7 CITA, University of Toronto, 60 St. George St., Toronto, ON M5S 3H8, Canada
8 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
9 California Institute of Technology, Pasadena, California, USA
10 Centre of Mathematics for Applications, University of Oslo, Blindern, Oslo, Norway
11 Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza San Juan, 1, planta 2, 44001 Teruel, Spain
12 Computational Cosmology Center, Lawrence Berkeley National Laboratory, Berkeley, California, USA
13 Consejo Superior de Investigaciones Científicas (CSIC), Madrid, Spain
14 DSM/Irfu/SPP, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
15 DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
16 Département de Physique Théorique, Université de Genève, 24, Quai E. Ansermet, 1211 Genève 4, Switzerland
17 Departamento de Física Fundamental, Facultad de Ciencias, Universidad de Salamanca, 37008 Salamanca, Spain
18 Departamento de Física, Universidad de Oviedo, Avda. Calvo Sotelo s/n, Oviedo, Spain
19 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
20 Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, British Columbia, Canada
21 Department of Physics and Astronomy, Dana and DavidDornsife College of Letter, Arts and Sciences, University of Southern California, Los Angeles, CA 90089, USA
22 Department of Physics, Gustaf Hällströmin katu 2a, University of Helsinki, Helsinki, Finland
23 Department of Physics, Princeton University, Princeton, New Jersey, USA
24 Department of Physics, University of California, Berkeley, California, USA
25 Department of Physics, University of California, One Shields Avenue, Davis, California, USA
26 Department of Physics, University of California, Santa Barbara, California, USA
27 Department of Physics, University of Illinois at Urbana-Champaign, 1110 West Green Street, Urbana, Illinois, USA
28 Department of Statistics, Purdue University, 250 N. University Street, West Lafayette, Indiana, USA
29 Dipartimento di Fisica e Astronomia G. Galilei, Università degli Studi di Padova, via Marzolo 8, 35131 Padova, Italy
30 Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, via Saragat 1, 44122 Ferrara, Italy
31 Dipartimento di Fisica, Università La Sapienza, P. le A. Moro 2, Roma, Italy
32 Dipartimento di Fisica, Università degli Studi di Milano, via Celoria, 16, Milano, Italy
33 Dipartimento di Fisica, Università degli Studi di Trieste, via A. Valerio 2, Trieste, Italy
34 Dipartimento di Fisica, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, Roma, Italy
35 Dipartimento di Matematica, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, Roma, Italy
36 Discovery Center, Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
37 Dpto. Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
38 European Space Agency, ESAC, Planck Science Office, Camino bajo del Castillo, s/n, Urbanización Villafranca del Castillo, Villanueva de la Cañada, Madrid, Spain
39 European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
40 Haverford College Astronomy Department, 370 Lancaster Avenue, Haverford, Pennsylvania, USA
41 Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University of Helsinki, Helsinki, Finland
42 INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78, Catania, Italy
43 INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, Padova, Italy
44 INAF – Osservatorio Astronomico di Roma, via di Frascati 33, Monte Porzio Catone, Italy
45 INAF – Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, Trieste, Italy
46 INAF Istituto di Radioastronomia, via P. Gobetti 101, 40129 Bologna, Italy
47 INAF/IASF Bologna, via Gobetti 101, Bologna, Italy
48 INAF/IASF Milano, via E. Bassini 15, Milano, Italy
49 INFN, Sezione di Roma 1, Università di Roma Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy
50 INRIA, Laboratoire de Recherche en Informatique, Université Paris-Sud 11, Bâtiment 490, 91405 Orsay Cedex, France
51 IPAG: Institut de Planétologie et d’Astrophysique de Grenoble, Université Joseph Fourier, Grenoble 1/CNRS-INSU, UMR 5274, 38041 Grenoble, France
52 ISDC Data Centre for Astrophysics, University of Geneva, ch. d’Ecogia 16, Versoix, Switzerland
53 IUCAA, Post Bag 4, Ganeshkhind, Pune University Campus, 411 007 Pune, India
54 Imperial College London, Astrophysics group, Blackett Laboratory, Prince Consort Road, London, SW7 2AZ, UK
55 Infrared Processing and Analysis Center, California Institute of Technology, Pasadena, CA 91125, USA
56 Institut Néel, CNRS, Université Joseph Fourier Grenoble I, 25 rue des Martyrs, Grenoble, France
57 Institut Universitaire de France, 103, bd Saint-Michel, 75005 Paris, France
58 Institut d’Astrophysique Spatiale, CNRS (UMR 8617), Université Paris-Sud 11, Bâtiment 121, Orsay, France
59 Institut d’Astrophysique de Paris, CNRS (UMR 7095), 98 bis Boulevard Arago, 75014 Paris, France
60 Institute for Space Sciences, Bucharest-Magurale, Romania
61 Institute of Astronomy and Astrophysics, Academia Sinica, Taipei, Taiwan
62 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
63 Institute of Theoretical Astrophysics, University of Oslo, Blindern, Oslo, Norway
64 Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, Tenerife, Spain
65 Instituto de Física de Cantabria (CSIC-Universidad de Cantabria), Avda. de los Castros s/n, Santander, Spain
66 Istituto di Fisica del Plasma, CNR-ENEA-EURATOM Association, via R. Cozzi 53, Milano, Italy
67 Jet PropulsionLaboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California, USA
68 Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
69 Kavli Institute for Cosmology Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
70 Kavli Institute for Theoretical Physics, University of California, Santa Barbara Kohn Hall, Santa Barbara, CA 93106, USA
71 LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
72 LERMA, CNRS, Observatoire de Paris, 61 Avenue de l’Observatoire, Paris, France
73 Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS – Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
74 Laboratoire Traitement et Communication de l’Information, CNRS (UMR 5141) and Télécom ParisTech, 46 rue Barrault 75634 Paris Cedex 13, France
75 Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de Grenoble, 53 rue des Martyrs, 38026 Grenoble Cedex, France
76 Laboratoire de Physique Théorique, Université Paris-Sud 11 & CNRS, Bâtiment 210, 91405 Orsay, France
77 Lawrence Berkeley National Laboratory, Berkeley, California, USA
78 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
79 National University of Ireland, Department of Experimental Physics, Maynooth, Co. Kildare, Ireland
80 Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
81 Observational Cosmology, Mail Stop 367-17, California Institute of Technology, Pasadena, CA, 91125, USA
82 Optical Science Laboratory, University College London, Gower Street, London, UK
83 SISSA, Astrophysics Sector, via Bonomea 265, 34136 Trieste, Italy
84 School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff, CF24 3AA, UK
85 Space Sciences Laboratory, University of California, Berkeley, California, USA
86 Stanford University, Dept of Physics, Varian Physics Bldg, 382 via Pueblo Mall, Stanford, California, USA
87 UPMC Univ Paris 06, UMR 7095, 98 bis Boulevard Arago, 75014 Paris, France
88 Universität Heidelberg, Institut für Theoretische Astrophysik, Albert-Überle-Str. 2, 69120 Heidelberg, Germany
89 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
90 University of Granada, Departamento de Física Teórica y del Cosmos, Facultad de Ciencias, Granada, Spain
91 University of Miami, Knight Physics Building, 1320 Campo Sano Dr., Coral Gables, Florida, USA
92 Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478 Warszawa, Poland
Received: 22 August 2012
Accepted: 5 April 2013
Using precise full-sky observations from Planck, and applying several methods of component separation, we identify and characterise the emission from the Galactic “haze” at microwave wavelengths. The haze is a distinct component of diffuse Galactic emission, roughly centered on the Galactic centre, and extends to | b | ~ 35−50° in Galactic latitude and | l | ~ 15−20° in longitude. By combining the Planck data with observations from the Wilkinson Microwave Anisotropy Probe, we were able to determine the spectrum of this emission to high accuracy, unhindered by the strong systematic biases present in previous analyses. The derived spectrum is consistent with power-law emission with a spectral index of −2.56 ± 0.05, thus excluding free-free emission as the source and instead favouring hard-spectrum synchrotron radiation from an electron population with a spectrum (number density per energy) dN/dE ∝ E-2.1. At Galactic latitudes | b | < 30°, the microwave haze morphology is consistent with that of the Fermi gamma-ray “haze” or “bubbles”, while at b ~ −50° we have identified an edge in the microwave haze that is spatially coincident with the edge in the gamma-ray bubbles. Taken together, this indicates that we have a multi-wavelength view of a distinct component of our Galaxy. Given both the very hard spectrum and the extended nature of the emission, it is highly unlikely that the haze electrons result from supernova shocks in the Galactic disk. Instead, a new astrophysical mechanism for cosmic-ray acceleration in the inner Galaxy is implied.
Key words: Galaxy: nucleus / ISM: structure / ISM: bubbles / radio continuum: ISM
© ESO, 2013
1. Introduction
The initial data release from the Wilkinson Microwave Anisotropy Probe (WMAP) revolutionised our understanding of both cosmology (Spergel et al. 2003) and the physical processes at work in the interstellar medium (ISM) of our own Galaxy (Bennett et al. 2003). Some of the processes observed were expected, such as the thermal emission from dust grains, free-free emission (or thermal bremsstrahlung) from electron/ion scattering, and synchrotron emission due to shock-accelerated electrons interacting with the Galactic magnetic field. Others, such as the anomalous microwave emission now identified as spinning dust emission from rapidly rotating tiny dust grains (Draine & Lazarian 1998a,b; de Oliveira-Costa et al. 2002; Finkbeiner et al. 2004; Hinshaw et al. 2007; Boughn & Pober 2007; Dobler & Finkbeiner 2008b; Dobler et al. 2009), were more surprising. But perhaps most mysterious was a “haze” of emission discovered by Finkbeiner (2004) that was centred on the Galactic centre (GC), appeared to be almost spherically symmetric in profile, fell off approximately as the inverse distance from the GC, and was of unknown origin. This haze was originally characterised as free-free emission by Finkbeiner (2004) because of its apparently very hard spectrum, although it was not appreciated at the time how significant the systematic uncertainty in the measured spectrum was.
An analysis of the three-year WMAP data by Dobler & Finkbeiner (2008a, hereafter DF08) identified a source of systematic uncertainty in the determination of the haze spectrum that remains the key to determining the origin of the emission. This uncertainty is due to residual foregrounds contaminating the cosmic microwave background (CMB) radiation estimate used in the analysis, and arises as a consequence of chance morphological correlations between the CMB and the haze itself. Nevertheless, the spectrum was found to be significantly softer than free-free emission, and also significantly harder than the synchrotron emission observed elsewhere in the Galaxy as traced by the low-frequency synchrotron measurements of Haslam et al. (1982, see also Reich & Reich 1988; Davies et al. 1996; Kogut et al. 2007; Strong et al. 2011; Kogut 2012). Finally, it was noted by DF08 that this systematic uncertainty could be almost completely eliminated with data from the Planck1 mission, which would produce estimates of the CMB signal that were significantly less contaminated by Galactic foregrounds.
The synchrotron nature of the microwave haze was substantially supported by the discovery of a gamma-ray counterpart to this emission by Dobler et al. (2010) using data from the Fermi Gamma-ray Space Telescope. These observations were consistent with an inverse Compton (IC) signal generated by electrons with the same spectrum and amplitude as would yield the microwave haze at WMAP wavelengths. Further work by Su et al. (2010) showed that the Fermi haze appeared to have sharp edges and it was renamed the “Fermi bubbles”. Subsequently, there has been significant theoretical interest in determining the origin of the very hard spectrum of progenitor electrons. Suggestions include enhanced supernova rates (Biermann et al. 2010), a Galactic wind (Crocker & Aharonian 2011), a jet generated by accretion onto the central black hole (Guo & Mathews 2012; Guo et al. 2012), and co-annihilation of dark matter (DM) particles in the Galactic halo (Hooper et al. 2007; Lin et al. 2010; Dobler et al. 2011). However, while each of these scenarios can reproduce some of the properties of the haze/bubbles well, none can completely match all of the observed characteristics (Dobler 2012a).
Moreover, despite the significant observational evidence, there have been suggestions in the literature that the microwave haze is either an artefact of the analysis procedure (Mertsch & Sarkar 2010) or not synchrotron emission (Gold et al. 2011). The former conclusion was initially supported by alternative analyses of the WMAP data that found no evidence of the haze (Eriksen et al. 2006; Dickinson et al. 2009). However, more recently Pietrobon et al. (2012) showed that these analyses, while extremely effective at cleaning the CMB of foregrounds and identifying likely contaminants of a known morphology (e.g., a low-level residual cosmological dipole), typically cannot separate the haze emission from a low-frequency combination of free-free, spinning dust, and softer synchrotron radiation. The argument of Gold et al. (2011) that the microwave haze is not synchrotron emission was based on the lack of detection of a polarised component. This criticism was addressed by Dobler (2012a), who showed that, even if the emission is not depolarised by turbulence in the magnetic field, such a polarised signal is not likely to be seen with WMAP given the noise in the data.
With the Planck data, we now have the ability not only to provide evidence for the existence of the microwave haze with an independent experiment, but also to eliminate the uncertainty in the spectrum of the emission, which has hindered observational and theoretical studies for nearly a decade. In Sect. 2 we describe the Planck data as well as some external templates we used in our analysis. In Sect. 3 we describe the two most effective component separation techniques for studying the haze emission in temperature. In Sect. 4 we discuss our results on the morphology and spectrum of the haze, before summarising in Sect. 5.
2. Planck data and templates
Planck (Tauber et al. 2010; Planck Collaboration 2011a) is the third-generation space mission to measure the anisotropy of the CMB. It observes the sky in nine frequency bands covering 30–857 GHz with high sensitivity and angular resolution from 31′ to 5′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20 K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1 K. Polarisation is measured in all but the highest two bands (Leahy et al. 2010; Rosset et al. 2010). A combination of radiative cooling and three mechanical coolers produces the temperatures needed for the detectors and optics (Planck Collaboration 2011b). Two data processing centres (DPCs) check and calibrate the data and make maps of the sky (Planck HFI Core Team 2011b; Zacchei et al. 2011). Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for galactic and extragalactic astrophysics as well as cosmology. Early astrophysics results are given in Planck Collaboration VIII–XXVI 2011, based on data taken between 13 August 2009 and 7 June 2010. Intermediate astrophysics results are now being presented in a series of papers based on data taken between 13 August 2009 and 27 November 2010.
We took both the WMAP and Planck bandpasses into account when defining our central frequencies. However, throughout we refer to the bands by the conventional labels of 23, 33, 41, 61, and 94 GHz for WMAP and 30, 44, 70, 100, 143, 217, 353, 545, and 857 GHz for Planck; the central frequencies are 22.8, 33.2, 41.0, 61.4, and 94.0 GHz, and 28.5, 44.1, 70.3, 100.0, 143.0, 217.0, 353.0, 545.0, and 857.0 GHz. In each case, the central frequency represents the convolution of the bandpass response with a CMB spectrum and so corresponds to the effective frequency for emission with that spectrum. For emission with different spectra, the effective frequency is slightly shifted, but the effects are at the few percent level and do not significantly affect our conclusions.
Our analysis also requires the use of external templates to morphologically trace emission mechanisms within the Planck data. All the data are available in the HEALPix2 scheme (Górski et al. 2005). In each case, we used maps smoothed to 1° angular resolution.
Thermal and spinning dust.
For a template of the combined thermal and spinning dust emission, we used the 100 μm all-sky map from Schlegel et al. (1998) evaluated at the appropriate textitPlanck and WMAP frequencies using Model 8 from Finkbeiner et al. (1999, FDS99). This is a sufficiently good estimate of the thermal emission for our purposes, although it is important to note that the morphological correlation between thermal and spinning dust is not well known.
Free-free.
The free-free template adopted in our analysis is the Hα map assembled by Finkbeiner (2003)3 from three surveys: the Wisconsin Hα Mapper (Haffner et al. 2003), the Southern Hα Sky Survey Atlas (Gaustad et al. 2001), and the Virginia Tech Spectral-Line Survey (Dennison et al. 1998). The map was corrected for line-of-sight dust absorption assuming uniform mixing between gas and dust, although we masked some regions based on the predicted total dust extinction where the correction to the Hα emission was deemed unreliable.
Soft synchrotron.
Since synchrotron intensity rises with decreasing frequency, the 408 MHz full-sky radio continuum map (Haslam et al. 1982) provides a reasonable tracer of the soft synchrotron emission. While there is a very small contribution from free-free emission to the observed intensity, particularly in the Galactic plane, the bulk of the emission traces synchrotron radiation from supernova shock-accelerated electrons that have had sufficient time to diffuse from their source. In addition, as pointed out by Dobler (2012a), the propagation length for cosmic-ray electrons in the disk is energy-dependent and therefore the 408 MHz map (which is dominated by synchrotron emission from electrons with a lower energy than in the situation at 20–100 GHz) will be more spatially extended than the synchrotron at Planck frequencies (see Mertsch & Sarkar 2010). This can result in a disk-like residual when using the 408 MHz map as a tracer of synchrotron at higher frequencies, which could be confused with the haze emission. We used an elliptical Gaussian disk template (σl = 20° and σb = 5°) for this residual, though in practice this results in only a very small correction to our results, which use a larger mask than (Dobler 2012a, see below).
The haze.
Although a measurement of the precise morphology of the microwave haze is yet to be determined, an estimate of the morphology is necessary to reduce bias in template fits for the following reason: when using templates to separate foregrounds, the amplitudes of the other templates may be biased to compensate for the haze emission present in the data unless an appropriate haze template is used to approximate the emission. Following Dobler (2012a), we used an elliptical Gaussian template with σl = 15° and σb = 25°. A map of the Fermi gamma-ray haze/bubbles cannot be used to trace the emission for two reasons. First, as pointed out by Dobler et al. (2011), the morphology of the gamma-ray emission is uncertain at low latitudes. Second, the synchrotron morphology depends sensitively on the magnetic field while the gamma-ray morphology depends on the interstellar radiation field. Therefore, while the same cosmic-ray population is clearly responsible for both, the detailed morphologies are not identical4.
Mask.
As noted above, the effect of dust extinction requires careful treatment of the Hα map when using it as a tracer of free-free emission. Therefore, we masked out all regions where dust extinction at Hα wavelengths is greater than 1 mag. We also masked out all point sources in the WMAP and Planck ERCSC (30–143 GHz) catalogues. Several larger-scale features where our templates are likely to fail were masked as well: the Large and Small Magellanic Clouds, M31, Orion-Barnard’s Loop, Cen A, and ζ Oph. Finally, since the Hα-to-free-free ratio is a function of gas temperature, we masked pixels whose Hα intensity was greater than 10 rayleigh to minimise the bias due to strong spatial fluctuations in gas temperatures. This mask covers 32% of the sky and is shown in Fig. 2.
3. Component separation methods
We applied two methods for separating the Galactic emission components in the Planck data. The first one, used in the original WMAP haze analyses, is a simple regression technique in which the templates described in the previous section are directly fitted to the data. This “template fitting” method is relatively simple to implement and its results are easy to interpret. Furthermore, the noise characteristics are well understood and additional components not represented by the templates are readily identifiable in residual maps. The second technique, a powerful power-spectrum estimation and component-separation method based on Gibbs sampling, uses a Bayesian approach and combines pixel-by-pixel spectral fits with template amplitudes. One of the significant advantages of this approach is that, instead of assuming an estimate for the CMB anisotropy, a CMB map is generated via joint sampling of the foreground parameters and Cℓs of cosmological anisotropies; this reduces the bias in the inferred foreground spectra.
3.1. Template fitting
The rationale behind the simple template fitting technique is that there are only a few physical mechanisms in the ISM that generate emission at microwave wavelengths, and these emission mechanisms are morphologically traced by maps at other frequencies at which they dominate. We followed the linear regression formalism of Finkbeiner (2004), Dobler & Finkbeiner (2008a), and Dobler (2012a) and solved the relation 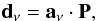 (1)where dν is a data map at frequency ν, P is a matrix of the templates defined in Sect. 2, and aν is the vector of scaling amplitudes for this set of templates. The least-squares solution to this equation is
(1)where dν is a data map at frequency ν, P is a matrix of the templates defined in Sect. 2, and aν is the vector of scaling amplitudes for this set of templates. The least-squares solution to this equation is 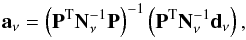 (2)where Nν is the noise covariance matrix at frequency ν. In practice, for our template fits we used the mean noise per band (i.e., we set Nν = ⟨ Nν ⟩ for all pixels), which is appropriate when the dominant uncertainty is the quality with which the templates trace the foregrounds, as is the case here. To the extent that the templates morphologically match the actual foregrounds, the solutions
(2)where Nν is the noise covariance matrix at frequency ν. In practice, for our template fits we used the mean noise per band (i.e., we set Nν = ⟨ Nν ⟩ for all pixels), which is appropriate when the dominant uncertainty is the quality with which the templates trace the foregrounds, as is the case here. To the extent that the templates morphologically match the actual foregrounds, the solutions 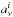 for template i as a function of frequency represent a reasonable estimate of the spectrum over the fitted pixels.
for template i as a function of frequency represent a reasonable estimate of the spectrum over the fitted pixels.
There are two important features of this approach to template fitting that must be addressed. First, there is an implicit assumption that the spectrum of a given template-correlated emission mechanism does not vary across the region of interest, and second, an estimate for the CMB must be pre-subtracted from the data. The former can be validated by inspecting a map of the residuals, which can reveal where this assumption fails, and as a consequence of which the sky can easily be subdivided into regions that can be fitted independently. The latter involves the complication that no CMB estimate is completely clean of the foregrounds to be measured, which therefore introduces a bias (with the same spectrum as the CMB) in the inferred foreground spectra. As shown by DF08, this bias becomes increasingly stronger with frequency and renders an exact measurement of the haze spectrum that is impossible with WMAP alone. This “CMB bias” is the dominant source of uncertainty in all foreground analyses. However, DF08 also pointed out that, because the haze spectrum becomes fainter with frequency, the high-frequency data from Planck can be used to generate a CMB estimate that is nearly completely free from haze emission. Thus, pre-subtraction of this estimate should result in an essentially unbiased estimate of the haze spectrum. The CMB estimate that we used consists of a “Planck HFI internal linear combination” (PILC) map, formed from a minimum-variance linear combination of the Planck HFI 143–545 GHz data after pre-subtracting the thermal dust model of FDS99 at each frequency5. Defining pν and tν to be the Planck maps and FDS99 prediction (respectively) at frequency ν, the PILC in ΔTCMB is given by 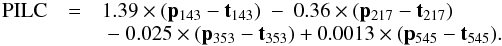 (3)The weights were determined by minimising the the variance over unmasked pixels of the PILC while maintaining a unity response to the CMB spectrum.
(3)The weights were determined by minimising the the variance over unmasked pixels of the PILC while maintaining a unity response to the CMB spectrum.
Although no constraint is made on the spectral dependence of the template coefficients in Eq. (2), the fit does assume that the spectrum is constant across the sky. While this assumption is quite good outside our mask (as we show below), it is known to be incorrect in detail. As such, in addition to full (unmasked) sky fits, we also performed template fits on smaller sky regions and combined the results to form a full composite map. The subdivisions were defined by hand to separate the sky into regions with particularly strong residuals in a full-sky fit and are listed in Table 1 and shown in Fig. 1.
3.2. Gibbs sampling: commander
An alternative method for minimising the CMB bias is to generate a CMB estimate from the data while simultaneously solving for the parameters of a Galactic foreground model. Within the Bayesian framework it is possible to set stronger priors on the CMB parameterisation (i.e., Cℓs), taking advantage not only of the frequency spectrum of the CMB (a blackbody), but also of the angular power spectrum of the fluctuations. Even for relatively simple foreground models, the dimensionality of parameter space is quite large, which makes uniform sampling on a grid not feasible.
Jewell et al. (2004) and Wandelt et al. (2004) first discussed the application of Gibbs sampling algorithms (a variant of MCMC sampling) in this context. These algorithms have been further improved (Eriksen et al. 2004, 2007; O’Dwyer et al. 2004; Chu et al. 2005; Jewell et al. 2009; Rudjord et al. 2009; Larson et al. 2007) and packaged into the Commander code.
Gibbs sampling is particularly suitable for component separation since it samples from the conditional distribution along perpendicular directions in parameter space, updating the distribution with each sample. This approach has been advocated in Eriksen et al. (2007, 2008a) and Dickinson et al. (2009) and has been applied recently to the WMAP 7-year data in Pietrobon et al. (2012). A detailed description of the algorithm and its validation on simulated data was provided in Eriksen et al. (2008b, and references therein).
The outputs of the sampling are a map-based CMB estimate and the parameters of a foreground model, which can either be template-based, pixel-based, or a combination of the two. We performed the analysis at HEALPix resolution Nside = 128. The choice of the foreground model is limited by the number of frequency channels observed since it sets the number of constraints on the model when fitting spectra for each pixel. We separated our results in the following section into two categories, fits using Planck data only, and fits using Planck data plus ancillary data sets.
For the Planck-only fits, our model consists of a single power law T ∝ ν βS describing the effective low-frequency emission (with a prior on spectral index, βS = − 3.05 ± 0.3), a grey-body for the thermal dust emission that dominates at high frequencies (with a temperature and emissivity prior given by the results of Planck Collaboration 2011c, where mean values of TD ≃ 18 K and ϵD = 1.8 were measured), and a CO spectrum. The CO spectrum was assumed to be constant across the sky and normalised to 100 GHz. The relative strength of the J = 2 → 1 (~217 GHz) and J = 3 → 2 (~353 GHz) transition lines with respect to the J = 1 → 0 transition were computed by taking into account the specifications of the HFI detectors and calibrated by means of the available survey (Dame et al. 2001). The relative ratios in the 100, 217, and 353 GHz bands are 1.0, 0.35, and 0.12 respectively. We checked the robustness of the result against a plausible variation of the line ratios of ~10%. (A more detailed discussion of the CO analysis that we performed can be found in Planck Collaboration 2011c.) We normalised the thermal dust component at 353 GHz and the low-frequency power law at 33 GHz. Hence, we solved for two spectral indices together with the corresponding amplitudes as well as a CO amplitude, with the dust temperature fixed at a value of 18 K. The current Commander implementation allows for the determination of residual monopole and dipole contributions, as may result from the calibration and map-making procedures. This fit is referred to as CMD1 throughout. It is interesting to note that, given the noise in the data, this highly over-simplified model is sufficient to describe the total Galactic emission (see Sect. 4.1). However, it is well established that the low-frequency emission consists of multiple components. Following Pietrobon et al. (2012), our procedure for separating these components was to perform a template fit as specified in Eq. (2) on the Commander solution for the low-frequency amplitude (i.e., replacing dν with the low-frequency amplitude map). Pietrobon et al. (2012) showed that applying this “post-processing” template regression procedure is effective in extracting the haze from the Commander solution.
Adding the WMAP channels allowed us to refine the foreground model even more, separating the multiple contributions in the frequency range 23–70 GHz. Moreover, including the 408 MHz data improved the characterisation of the synchrotron component and allowed us to investigate the spatial variations of its spectral index (see Sect. 4.2). The Commander fit, CMD2, is based on 13 frequency maps (seven Planck channels from 30 to 353 GHz, five from WMAP, and Haslam 408 MHz), and allows a modification of the foreground model to encompass two low-frequency power-law components – one soft component with a fixed spectral index βS = − 3.05 to describe the soft synchrotron emission6 and one with a spectral index βH with prior βH = − 2.15 ± 0.3 to capture both the hard synchrotron haze and the free-free emission. With this model, the low-frequency part of the spectrum is more easily resolved into physically meaningful components.
In addition, we parameterised a joint thermal and spinning-dust model by ![\begin{equation} D_{\rm jd}(\nu) = \left(\frac{\nu}{\nu_0}\right)^{1+\epsilon} \frac{B(\nu, T)}{B(\nu_0, T)} + {\rm e}^\alpha {\rm e}^{-[(\nu-\nu_1)/b]^{2}/2}. \end{equation}](/articles/aa/full_html/2013/06/aa20271-12/aa20271-12-eq55.png) (4)This is the sum of a grey-body spectrum for the thermal dust, and a Gaussian profile to mimic the spinning dust SED. The latter is a purely phenomenological model selected on the basis of its straightforward numerical implementation. However, we established its effectiveness in describing well-known spinning dust regions in the Gould Belt. The thermal dust pivot frequency ν0 was set to 353 GHz and the spinning dust peak frequency ν1 to 20 GHz. The remaining parameters (the amplitude of the joint spectrum, the relative amplitude of the spinning dust contribution, and the width of the spinning dust bump) were constrained by the Gibbs sampling procedure. As before, we also adopted a spectrum for the CO emission.
(4)This is the sum of a grey-body spectrum for the thermal dust, and a Gaussian profile to mimic the spinning dust SED. The latter is a purely phenomenological model selected on the basis of its straightforward numerical implementation. However, we established its effectiveness in describing well-known spinning dust regions in the Gould Belt. The thermal dust pivot frequency ν0 was set to 353 GHz and the spinning dust peak frequency ν1 to 20 GHz. The remaining parameters (the amplitude of the joint spectrum, the relative amplitude of the spinning dust contribution, and the width of the spinning dust bump) were constrained by the Gibbs sampling procedure. As before, we also adopted a spectrum for the CO emission.
4. Results
As described above, we performed four different types of haze extraction:
-
1.
A masked full-sky (FS) template fit for eachinput frequency band.
-
2.
Template fits over subsections of the sky (RG) that were combined to give a full-sky haze map for each input frequency band.
-
3.
A Commander fit (CMD1) with a simple two-component foreground model, using Planck 30–353 GHz data.
-
4.
A comprehensive Commander fit (CMD2) including thermal and spinning dust models, a soft power-law component, and a hard power-law component, using Planck 30–353 GHz, WMAP 23–94 GHz, and Haslam 408 MHz data sets.
Below, we first discuss our results from the template fitting and Gibbs sampling analyses derived from the Planck data alone (using methods 1, 2, and 3), then proceed to include external data sets in the analysis (using methods 1, 2, and 4). A direct comparison of the results between the template fits and Commander haze extraction methods boosts our confidence that not only are the components appropriately separated, but the spectrum is relatively free from bias.
4.1. Planck-only results
4.1.1. Template fitting
 |
Fig. 2 Templates and full-sky template fitting model (see Sect. 4.1). Top left: the Haslam et al. (1982) 408 MHz map. Top middle: the Finkbeiner (2003) Hα map. Top right: the Finkbeiner et al. (1999) dust prediction at the Planck 30 GHz channel. Middle left: the elliptical Gaussian haze template. Center: the elliptical Gaussian disk template. Middle right: the mask used in the fit. Bottom left: the best-fit template linear combination model at Planck 30 GHz. Bottom middle: the CMB-subtracted Planck data at 30 GHz. Bottom right: the Planck 30 GHz data minus the 30 GHz model with the haze template component added back into the map. |
 |
Fig. 3 Left column: Planck haze (i.e., the same as the bottom right panel of Fig. 2), for the Planck 30 and 44 GHz channels using a full-sky template fit to the data. A scaling of ν2.5 yields roughly equal brightness residuals, indicating that the haze spectrum is roughly Tν ∝ ν-2.5, implying that the electron spectrum is a very hard dN/dEe ∝ E-2. Note that the haze appears more elongated in latitude than longitude by a factor of two, which is approximately consistent with the Fermi gamma-ray haze/bubbles (Dobler et al. 2010). For frequencies above ~40 GHz, striping in the HFI channels (which contaminates our CMB estimate) begins to dominate over the haze emission. Right column: the same but for the “regional” fits described in Sect. 4.1. The overall morphology of the haze is the same, but the residuals near the mask and in the Ophiuchus complex in the north GC are improved. |
Figure 2 presents the templates and mask used for the Planck analysis, together with the CMB-subtracted data and best-fit template model at 30 GHz. We also show the full-sky (i.e., unrestricted in l and b) haze residual, defined as 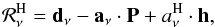 (5)where h is the haze template defined in Sect. 2. The haze is clearly present in the Planck data set and, as illustrated in Fig. 3 (left column), scaling each residual by ν2.5 yields an approximately equal brightness per frequency band, indicating that the spectrum is approximately
(5)where h is the haze template defined in Sect. 2. The haze is clearly present in the Planck data set and, as illustrated in Fig. 3 (left column), scaling each residual by ν2.5 yields an approximately equal brightness per frequency band, indicating that the spectrum is approximately 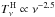 . A more detailed measurement of the spectrum is given in Sect. 4.3. It is also interesting to note that the morphology does not change significantly with frequency (although striping in the Planck HFI maps used to form the CMB estimate is a significant contaminant at frequencies above ~40 GHz) indicating that the spectrum of the haze emission is fairly constant with position.
. A more detailed measurement of the spectrum is given in Sect. 4.3. It is also interesting to note that the morphology does not change significantly with frequency (although striping in the Planck HFI maps used to form the CMB estimate is a significant contaminant at frequencies above ~40 GHz) indicating that the spectrum of the haze emission is fairly constant with position.
The haze residual is most clearly visible in the southern GC region, but we note that our assumption of uniform spectra across the sky does leave some residuals around the edge of the mask and in a few particularly bright free-free regions. However, while our imperfect templates and assumptions about uniform spectra have isolated the haze emission very well (96% of the total variance is removed in the fit at Planck 30 GHz), we can more effectively isolate the haze by subdividing the sky into smaller regions as described in Sect. 3.1. The resulting full-sky haze residual is shown in Fig. 3. With this fit, the residuals near the mask are cleaner and we improved fitting the difficult Ophiuchus region in the northern GC, though striping again becomes a major contaminant for frequencies above ~40 GHz.
4.1.2. Commander
 |
Fig. 4 Left column, top: recovered amplitude of the low-frequency component at 23 GHz from our simplest Commander fit to the Planck data alone, CMD1. As shown in Pietrobon et al. (2012), while this model provides an excellent description of the data, this low-frequency component is a combination of free-free, spinning dust, and synchrotron emission (top). Left column, middle: four-component template model of this component (see Table 2). Left column, bottom: haze residual. The residuals are low outside the haze region, indicating that the templates are a reasonable morphological representation of the different components contained in the Commander solution. The haze residual is strikingly similar to that found for the template-only approach in Fig. 3 (though there does seem to be a residual dipole in the Commander solution). Right column: the same, but for the CMD2 low-frequency, hard spectrum component. While there is still some leakage of dust-correlated emission in the solution, the softer synchrotron emission (mostly correlated with the 408 MHz template see, Fig. 7) has been separated by Commander. The resulting map is dominated by free-free and the haze emission, and the regressed haze residual (bottom panel) shows a morphology very similar to both the template fitting and CMD1 results, indicating that the haze has been effectively isolated. |
Figure 4 presents the results of our CMD1 Commander fit and the subsequent post-processing. As noted previously, this very simple model provides an adequate description of the data with a highest χ2 of 18.4 (7 d.o.f.) outside the mask, even though the low-frequency component is really an aggregate of several different emission mechanisms, as shown by Pietrobon et al. (2012). Clearly, the low-frequency amplitude is highly correlated with thermal dust emission in some regions, suggesting a dust origin for some of this emission (e.g., spinning dust). Finally, features that are well-known from low-frequency radio surveys, such as Loop I, are also visible, implying a synchrotron origin with a spectral index closer to βS = − 3. The coefficients of the post-processing template-based fit described in Sect. 3.2 are given in Table 2 and show a strong positive correlation with each template.
As with the template fitting case, we see from Fig. 4 that the post-processing residuals for the low-frequency CMD1 component are low except towards the GC where the haze is clearly present, implying that it is emission with a distinct morphology compared to the dust, free-free, and soft synchrotron emission. Furthermore, the morphology is strikingly similar to the template fitting, indicating strong consistency between the results. Since an analogous regression cannot be performed on the spectral-index map, a more flexible foreground model must be implemented to isolate the haze spectrum. However, the additional model parameters require the use of external data sets.
4.2. Results from Planck plus external data sets
4.2.1. Template fitting
Regression coefficients of the Commander foreground amplitude maps.
 |
Fig. 5 Microwave haze at WMAP and Planck frequencies using a full-sky template fit to the data. The morphology of the haze is remarkably consistent from band to band and between data sets, implying that the spectrum of the haze does not vary significantly with position. Furthermore, the ν2.5 scaling again yields about equal-brightness residuals, indicating that the haze spectrum is roughly Tν ∝ ν-2.5 through both the Planck and WMAP channels. In addition, while striping is negligible at low frequencies, above ~40 GHz it becomes comparable with, or brighter than, the haze emission (see text). |
 |
Fig. 6 Same as Fig. 5, but using the regions defined in DF08. Clearly, the residuals near the mask are significantly reduced, although, as with the full-sky fits, striping in the HFI channels (which leaks into the CMB estimate) becomes significant above ~40 GHz. |
To further our understanding of the spectrum and morphology of the microwave haze component, we augmented the Planck data with the WMAP seven-year data set (covering the frequency range 23–94 GHz) and the 408 MHz data. Including the new data in the template-fitting method is trivial since Eq. (2) does not assume anything about the frequency dependence of the spectrum and each map is fitted independently. The results for the full sky and for smaller regional fits are shown in Figs. 5 and 6. The haze residual is present in both the WMAP and Planck data, and the morphology and spectrum appear to be consistent between data sets. As before, scaling each residual by ν2.5 yields a roughly equal brightness per band from 23 GHz to 61 GHz. Including the WMAP data also confirms that the morphology does not change significantly with frequency, which implies a fairly constant haze spectrum with position.
4.2.2. Commander
 |
Fig. 7 Left: soft synchrotron component at 408 MHz from the Commander CMD2 analysis. The map is strikingly similar to the Haslam map (see Fig. 2), indicating that soft synchrotron emission has a very uniform spectrum from 408 MHz to 60 GHz through all data sets. Right: difference between the Haslam map and the Commander solution. This is consistent with noise across almost the entire sky with the exception of a few bright free-free clouds that are present in the Haslam data at the ~10% level. The lack of significant haze emission in the difference map (particularly in the south) is a strong indication that the haze region consists of both a hard and a soft component, and does not have a simple spatially variable spectral index. |
Comparing the low-frequency hard-spectral index Commander solution at 23 GHz obtained with this model with our previous (less flexible) parameterisation, we find that the residuals correlated with the Haslam 408 MHz map are significantly reduced, as shown in Fig. 4. Table 2 lists the fit coefficients in this case, and we now find no significant correlation with the Haslam map. As before, a template regression illustrates that the haze residual is significant and our hard-spectrum power law contains both free-free and haze emission7. Furthermore, Fig. 7 illustrates that the fixed βS = − 3.05 power law provides a remarkably good fit to the 408 MHz data. Indeed, subtracting this soft-spectrum component from the map yields nearly zero residuals outside the mask, except for bright free-free regions, which contaminate the Haslam et al. (1982) map at the ~10% level. It is interesting to note that this residual (as well as the negligible Haslam-correlation coefficient in Table 2) implies that fits assuming a constant spectral index across the sky for this correlated emission are reasonable. Physically, this means that electrons do diffuse to a steady-state spectrum that is very close to dN/dE ∝ E-3 (in agreement with the propagation models of Strong et al. 2011).
Taken together, Figs. 4 and 7 imply that not only is the 408 MHz-correlated soft synchrotron emission consistent with a spectral index of − 3.05 across the entire sky (outside our mask) from 408 MHz to 60 GHz, but the haze region consists of both a soft and a hard component. That is, the haze is not a simple variation of spectral index from 408 MHz to ~20 GHz. The map of the harder spectral index would ideally be a direct measurement of the haze spectrum. However, the signal-to-noise ratio is only sufficient to accurately measure the spectrum in the very bright free-free regions (e.g., the Gum Nebula). In the fainter haze region, the spectral index is dominated by noise in the maps.
4.3. Spectrum and morphology
 |
Fig. 8 Left: spectrum measured from the residual in Fig. 6 in the region | l | < 35°, − 35° < b < − 10°. The haze spectrum is very nearly a power law with spectral index βH = − 2.56, while the total synchrotron emission in the region has a spectral index of βS = − 3.1 (see Sect. 4.3), significantly softer than the haze emission. This spectrum should be free from biases caused by template uncertainties. Middle and right: scatter plots (shown in contours) for both the haze (dotted) and total synchrotron (solid) emission using WMAP 23–33 GHz and Planck 30 GHz. |
While a pixel-by-pixel determination of the haze spectrum is not possible given the relatively low signal-to-noise ratio per pixel of the haze emission, we can obtain a reliable estimate of its mean behaviour from the template fitting residuals in Fig. 6. The majority of previous haze studies have estimated the haze spectrum via the template coefficients aν for the haze template. However, as noted in Dobler (2012a), such an estimate is not only affected by the CMB bias (which we have effectively minimised by using the PILC), but may also be biased by the effect of imperfect template morphologies. The argument is as follows: consider a perfectly CMB-subtracted map that consists of the true haze h′ plus another true foreground component f′, which we are approximating by templates h and f. Our template fit approach can be written as 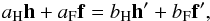 (6)where we are solving for aH and aF while bH and bF are the true amplitudes. The aH solution to this equation is
(6)where we are solving for aH and aF while bH and bF are the true amplitudes. The aH solution to this equation is 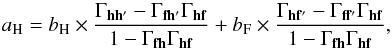 (7)where, for example, Γhf′ ≡ ⟨ hf′ ⟩ / ⟨ h2 ⟩, and the mean is over unmasked pixels. Thus, if h = h′ and f = f′ then aH = bH and we recover the correct spectrum. However, if h ≠ h′ the spectrum is biased, and if f ≠ f′, it is biased and dependent upon the true spectrum of the other foreground, bF.
(7)where, for example, Γhf′ ≡ ⟨ hf′ ⟩ / ⟨ h2 ⟩, and the mean is over unmasked pixels. Thus, if h = h′ and f = f′ then aH = bH and we recover the correct spectrum. However, if h ≠ h′ the spectrum is biased, and if f ≠ f′, it is biased and dependent upon the true spectrum of the other foreground, bF.
We emphasise that this bias is dependent on the cross-correlation of the true foregrounds with the templates (which is unknown) and that we assumed a perfectly clean CMB estimate (which is not possible to create) and did not discuss the impact of striping or other survey artefacts (which Figs. 5 and 6 show are present). Given this, a much more straightforward estimate of the haze spectrum is to measure it directly from ℛH in a region that is relatively devoid of artefacts or other emission. We measured the spectrum in the GC south region | l | < 35° and − 35° < b < − 10° by performing a linear fit (slope and offset) over unmasked pixels and converted the slope measurement to a power law given the central frequencies of the Planck and WMAP data (see Fig. 8). Specifically, we fitted 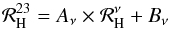 (8)over unmasked pixels in this region for Aν and Bν, and calculated the haze spectral index, βH = log (Aν)/log (ν/23GHz), for each ν. This spectrum should now be very clean and – given our use of the PILC – reasonably unbiased.
(8)over unmasked pixels in this region for Aν and Bν, and calculated the haze spectral index, βH = log (Aν)/log (ν/23GHz), for each ν. This spectrum should now be very clean and – given our use of the PILC – reasonably unbiased.
A measurement of the spectrum of the haze emission is shown in Fig. 8. It is evident that the WMAP and Planck bands are complementarily located in log-frequency space and the two experiments together provide significantly more information than either one alone8. In the left panel we plot 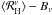 (where the mean is derived over the unmasked pixels in the region given above and the errors are their standard deviation). The haze spectrum is measured to be Tν ∝ ν βH with βH = − 2.56 ± 0.05. This spectrum is a nearly perfect power law from 23 to 41 GHz. Furthermore, if we form the total synchrotron residual,
(where the mean is derived over the unmasked pixels in the region given above and the errors are their standard deviation). The haze spectrum is measured to be Tν ∝ ν βH with βH = − 2.56 ± 0.05. This spectrum is a nearly perfect power law from 23 to 41 GHz. Furthermore, if we form the total synchrotron residual, 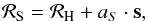 (9)where s is the Haslam map, and measure its spectrum in the south GC, we again recover a nearly perfect power law with βS = − 3.1. Our conclusion is that the haze, which is not consistent with free-free emission, arises from synchrotron emission with a spectral index that is significantly harder than elsewhere in the Galaxy. Within the haze region, this component represents ~33% of the total synchrotron and 23% of the total Galactic emission at 23 GHz (WMAP K-band), while emissions correlated with Haslam, Hα, and FDS contribute 43%, 4%, and 30%.
(9)where s is the Haslam map, and measure its spectrum in the south GC, we again recover a nearly perfect power law with βS = − 3.1. Our conclusion is that the haze, which is not consistent with free-free emission, arises from synchrotron emission with a spectral index that is significantly harder than elsewhere in the Galaxy. Within the haze region, this component represents ~33% of the total synchrotron and 23% of the total Galactic emission at 23 GHz (WMAP K-band), while emissions correlated with Haslam, Hα, and FDS contribute 43%, 4%, and 30%.
The βH = − 2.56 spectral index of the haze is strongly indicative of synchrotron emission from a population of electrons with a spectrum that is harder than elsewhere in the Galaxy. The other possible origins of the emission in this frequency range (free-free and spinning dust) are strongly disfavoured for several reasons. First, the spinning dust mechanism is very unlikely since there is no corresponding feature in thermal dust emission at HFI frequencies. While it is true that environment can have an impact on both the grain size distribution and relative ratio of spinning to thermal dust emission (thus making the FDS models an imperfect tracer of spinning dust, e.g., Ysard et al. 2011), to generate a strong spinning dust signal at LFI frequencies while not simultaneously producing a thermal signal a highly contrived grain population would be required, in which small grains survive but large grains are completely destroyed. Furthermore, the FDS thermal predictions yield very low dust-correlated residuals (see Fig. 6), indicating a close correspondence between thermal and spinning-dust morphology. Finally, this spectrum is significantly softer than free-free emission, which has a characteristic spectral index ≈− 2.15. Since the Hα to free-free ratio is temperature-dependent, the possibility exists that the haze emission represents some mixture of synchrotron and free-free without yielding a detectable Hα signal. However, to obtain a measured spectral index of βH ≈ − 2.5 from 23 to 41 GHz, free-free emission could only represent 50% of the emission if the synchrotron component had a spectral index ≈− 3. Since such a steep spectral index is ruled out by the lack of a strong haze signal at 408 MHz, the synchrotron emission must have a harder spectrum and the free-free component (if it exists) must be subdominant9. These considerations, coupled with the claimed inverse-Compton signal with Fermi (see Dobler et al. 2010; Su et al. 2010), strongly indicate a separate component of synchrotron emission.
4.4. Spatial correspondence with the Fermi haze/bubbles
 |
Fig. 9 Left: southern Planck 30 GHz haze from Fig. 6. Right: the same but with contours of the Fermi gamma-ray haze/bubbles (Su et al. 2010) overlaid in white. Above b = − 35° (orange dashed line), the morphological correspondence is very strong, suggesting that the two signals are generated by the same underlying phenomenon. |
 |
Fig. 10 Left: a high southern latitude (b < −35°) view of the Galactic haze at Planck 30 GHz smoothed to 2°. There is a clear spatial correspondence between the haze and the Fermi bubbles shown in Dobler et al. (2010) and Su et al. (2010) including an edge at high latitudes (the green line arc roughly represents the southern Fermi bubble edge). Plotting the brightness in both the Fermi bubble and Planck haze as a function of the distance from the bubble center (taken to be (ℓ,b)cen = (−4.5°, −35.0°)) by integrating over angular bins as shown by the dotted lines reveals an unambiguous detection of an edge in the Planck haze (middle panel red and green lines) that is spatially coincident with the bubble edge in the Fermi data (middle panel blue line). This emission is consistent with an almost flat profile (purple line) at r ~ 17° from the bubble center. In addition, by integrating over radial bins and plotting as a function of angular bin for two ranges of r (right panel), there is a clear excess of emission inside compared to outside of the bubble in both the Planck and Fermi data. |
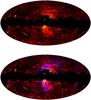 |
Fig. 11 Top: microwave haze at Planck 30 GHz (red, −12 μK < ΔTCMB< 30 μK) and 44 GHz (yellow, 12 μK < ΔTCMB< 40 μK). Bottom: the same, but including the Fermi 2–5 GeV haze/bubbles of Dobler et al. (2010) (blue, 1.05 < intensity (keV cm-2 s-1 sr-1) < 1.25; see their Fig. 11). The spatial correspondence between the two is excellent, particularly at low southern Galactic latitude, suggesting that this is a multi-wavelength view of the same underlying physical mechanism. |
The gamma-ray emission from the Fermi haze/bubbles (Dobler et al. 2010; Su et al. 2010) is consistent with the inverse-Compton emission from a population of electrons with the energy spectrum required to reproduce the βH = 2.56 haze emission measured in this paper. Furthermore, the Fermi haze has a very strong spatial coincidence with the Planck microwaves at low latitude (below | b | ~ 35°), as we show in Fig. 9. This suggests a common physical origin for these two measurements, with the gamma-ray contribution extending to b ≈ − 50°, while the microwaves decrease quickly below b ≈ −35°. As in Dobler (2012a), the interpretation is that the magnetic field within the haze/bubbles sharply decreases above ~5 kpc from the Galactic plane, while the cosmic-ray distribution extends to ~10 kpc and continues to generate gamma-ray emission (e.g., by inverse Compton scattering CMB photons).
Nevertheless, Dobler (2012b) has recently reported the detection of a sharp “edge” in the microwave haze using the WMAP seven-year data. This edge is spatially coincident with the edge in the Fermi bubbles at b ~ − 50°. We repeated the analysis described in that paper by smoothing the Planck data to 2° and binning the extreme high southern latitudes (b < − 35°) into polar bins centered on the southern Fermi bubble ((ℓ,b)cen = ( − 4.5°, − 35.0°) Su et al. 2010). As shown in Fig. 10, the haze below b = − 35° is clearly detected and, visually, the emission appears to have a sharp edge at precisely the location of the Fermi bubble edge. To assess the statistical significance of this feature in the Planck data, we plotted the intensity of the Planck haze as a function of distance from the bubble center by integrating over angular bins (see Fig. 10) and found that both the Planck and Fermi data are consistent with an infinitely sharp edge at a distance of r ~ 17° from the bubble center. Furthermore, by plotting as a function of polar angle for two different ranges of r (i.e., inside and outside the edge), we found an excess of haze emission inside compared to outside the bubble for all angles. As in Dobler (2012b), we found an “arm” of emission for polar angles less than ~20° in the Planck data that is not present in Fermi, though it is less pronounced than reported by Dobler (2012b) using the WMAP K-band data.
Finally, to illustrate the morphological correspondence between the two observations at low and high Galactic latitude, we show a full-sky representation of the Planck haze emission overlaid with the Fermi gamma-ray haze/bubbles from Dobler et al. (2010) in Fig. 11.
5. Summary
We have identified the presence of a microwave haze in the Planck LFI data and performed a joint analysis with the seven-year WMAP data. Our findings verify not only that the haze is real, but also that it is consistent in amplitude and spectrum in these two different experiments. Furthermore, we used Planck HFI maps to generate a CMB estimate that is nearly completely clean of haze emission, implying that we have reduced systematic biases in the inferred spectrum to a negligible level. We found that the unbiased haze spectrum is consistent with a power law of spectral index βH = − 2.56 ± 0.05, ruling out free-free emission as a possible explanation, and strengthening the possibility of a hard synchrotron component origin. The spectrum of softer synchrotron emission found elsewhere in the Galaxy is βS = − 3.1, consistent with a cosmic-ray electron population that has been accelerated in supernova shocks and diffused throughout the Galaxy. This spectrum is significantly softer than the haze emission, which is not consistent with supernova shock acceleration after taking into account energy losses from diffusion effects.
The microwave haze is detected in the Planck maps with both simple template regression against the data and a more sophisticated Gibbs sampling analysis. The former provides an excellent visualisation of the haze at each wavelength on large scales, while the latter allows a pixel-by-pixel analysis of the complete data set. While the template analysis allowed us to derive the βH = − 2.56 spectrum with high confidence, the spectral determination with the Gibbs approach is more difficult because noise must be added to the analysis to ensure convergence in the sampling method, and because a significantly more flexible model is used (specifically, one in which the spectrum of synchrotron is allowed to vary with each pixel). However, the spatial correspondence of the haze derived with the two methods is excellent, indicating that this component of the emission was successfully separated from other Galactic emissions.
Lastly, we showed that there is a strong morphological correspondence between the microwave haze and the recently discovered Fermi gamma-ray haze/bubbles, including a sharp edge in the microwave data at high southern galactic latitudes (b ~ − 50°) that is spatially coincident with the edge of the southern Fermi bubble. This last finding strongly supports the conclusion that the haze and the bubbles are a multi-wavelength view of the same structure, and that the microwave haze is a distinct component of Galactic synchrotron emission and not a spatial variation of the spectral index of synchrotron from the Galactic disk.
Although a detection of the haze in polarization with WMAP remains unlikely considering the noise level of the data (Dobler 2012a), future work with Planck will concentrate on using its enhanced sensitivity to search for this component.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Our specific choice of the Finkbeiner (2003) Hα template does not have a strong impact on results. We repeated our analysis using the Dickinson et al. (2003) Hα map and found differences at the few percent level that are not spatially correlated with haze emission.
We performed our fits using the uniform “bubbles” template given in Su et al. (2010) and the morphology of the haze excess (see Sect. 4) is not significantly changed.
Pre-subtracting the FDS99 prediction for the thermal dust is not meant to provide a perfect model for the thermal dust, but rather a reasonable model. The goal is to minimise variance in the PILC and it is more effective to do so by pre-subtracting the dust model. This allows the fit to manage the CO contamination present at various HFI frequency channels more effectively (although there is still some leakage, see Sect. 4.1). We tested a PILC that does not subtract the thermal dust, and the morphology and amplitude of the recovered haze signal are similar.
This value represents the spectral index of the large Loop I feature that is a prominent supernova remnant visible at both 408 MHz and microwave frequencies in the northern Galactic hemisphere. We repeated our analysis varying this index by δβ = 0.1 and found no significant difference in our results.
A close comparison between the CMD1 and CMD2 results suggests that the haze amplitude is slightly lower in the latter. However, due to the flexibility of the CMD2 model (specifically because the model allows for the unphysical case of non-zero spinning dust in regions of negligible thermal dust), it is very likely that some of the haze emission is included in the spinning dust component.
In addition, the lack of a bremsstrahlung signal in X-rays requires a fine tuning of the gas temperature to ~106 K, a temperature at which the gas has a very short cooling time. This also argues against a free-free explanation as described in McQuinn & Zaldarriaga (2011).
Acknowledgments
The development of Planck has been supported by ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and DEISA (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.rssd.esa.int/Planck. Part of the research described in this publication was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. G. Dobler has been supported by the Harvey L. Karp Discovery Award. Some of the results in this paper have been derived using the HEALPix (Górski et al. 2005) package.
References
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biermann, P. L., Becker, J. K., Caceres, G., et al. 2010, ApJ, 710, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Boughn, S. P., & Pober, J. C. 2007, ApJ, 661, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Chu, M., Eriksen, H. K., Knox, L., et al. 2005, Phys. Rev. D, 71, 103002 [NASA ADS] [CrossRef] [Google Scholar]
- Crocker, R. M., & Aharonian, F. 2011, Phys. Rev. Lett., 106, 101102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. D., Watson, R. A., & Gutierrez, C. M. 1996, MNRAS, 278, 925 [NASA ADS] [CrossRef] [Google Scholar]
- de Oliveira-Costa, A., Tegmark, M., Finkbeiner, D. P., et al. 2002, ApJ, 567, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Dennison, B., Simonetti, J. H., & Topasna, G. A. 1998, PASA, 15, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Dickinson, C., Eriksen, H. K., Banday, A. J., et al. 2009, ApJ, 705, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G. 2012a, ApJ, 750, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G. 2012b, ApJ, 760, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008a, ApJ, 680, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008b, ApJ, 680, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Draine, B., & Finkbeiner, D. P. 2009, ApJ, 699, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Finkbeiner, D. P., Cholis, I., Slatyer, T., & Weiner, N. 2010, ApJ, 717, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Cholis, I., & Weiner, N. 2011, ApJ, 741, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998a, ApJ, 494, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998b, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., O’Dwyer, I. J., Jewell, J. B., et al. 2004, ApJS, 155, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Dickinson, C., Lawrence, C. R., et al. 2006, ApJ, 641, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Huey, G., Saha, R., et al. 2007, ApJ, 656, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Dickinson, C., Jewell, J. B., et al. 2008a, ApJ, 672, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Jewell, J. B., Dickinson, C., et al. 2008b, ApJ, 676, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Langston, G. I., & Minter, A. H. 2004, ApJ, 617, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Gaustad, J. E., McCullough, P. R., Rosing, W., & Van Buren, D. 2001, PASP, 113, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., & Mathews, W. G. 2012, ApJ, 756, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., Mathews, W. G., Dobler, G., & Oh, S. P. 2012, ApJ, 756, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Haffner, L. M., Reynolds, R. J., Tufte, S. L., et al. 2003, ApJS, 149, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hinshaw, G., Nolta, M. R., Bennett, C. L., et al. 2007, ApJS, 170, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, D., Finkbeiner, D. P., & Dobler, G. 2007, Phys. Rev. D, 76, 083012 [NASA ADS] [CrossRef] [Google Scholar]
- Jewell, J., Levin, S., & Anderson, C. H. 2004, ApJ, 609, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jewell, J. B., Eriksen, H. K., Wandelt, B. D., et al. 2009, ApJ, 697, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A. 2012, ApJ, 753, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Dunkley, J., Bennett, C. L., et al. 2007, ApJ, 665, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, D. L., Eriksen, H. K., Wandelt, B. D., et al. 2007, ApJ, 656, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, T., Finkbeiner, D. P., & Dobler, G. 2010, Phys. Rev. D, 82, 023518 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- McQuinn, M., & Zaldarriaga, M. 2011, MNRAS, 414, 3577 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, A., Bersanelli, M., Butler, R. C., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mertsch, P., & Sarkar, S. 2010, JCAP, 10, 19 [Google Scholar]
- O’Dwyer, I. J., Eriksen, H. K., Wandelt, B. D., et al. 2004, ApJ, 617, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrobon, D., Górski, K. M., Bartlett, J., et al. 2012, ApJ, 755, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reich, P., & Reich, W. 1988, A&AS, 74, 7 [NASA ADS] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudjord, Ø., Groeneboom, N. E., Eriksen, H. K., et al. 2009, ApJ, 692, 1669 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Orlando, E., & Jaffe, T. R. 2011, A&A, 534, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wandelt, B. D., Larson, D. L., & Lakshminarayanan, A. 2004, Phys. Rev. D, 70, 083511 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Juvela, M., & Verstraete, L. 2011, A&A, 535, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Regions used in our multi-region RG template fits (see Sect. 3.1 and Table 1). |
| In the text | |
 |
Fig. 2 Templates and full-sky template fitting model (see Sect. 4.1). Top left: the Haslam et al. (1982) 408 MHz map. Top middle: the Finkbeiner (2003) Hα map. Top right: the Finkbeiner et al. (1999) dust prediction at the Planck 30 GHz channel. Middle left: the elliptical Gaussian haze template. Center: the elliptical Gaussian disk template. Middle right: the mask used in the fit. Bottom left: the best-fit template linear combination model at Planck 30 GHz. Bottom middle: the CMB-subtracted Planck data at 30 GHz. Bottom right: the Planck 30 GHz data minus the 30 GHz model with the haze template component added back into the map. |
| In the text | |
 |
Fig. 3 Left column: Planck haze (i.e., the same as the bottom right panel of Fig. 2), for the Planck 30 and 44 GHz channels using a full-sky template fit to the data. A scaling of ν2.5 yields roughly equal brightness residuals, indicating that the haze spectrum is roughly Tν ∝ ν-2.5, implying that the electron spectrum is a very hard dN/dEe ∝ E-2. Note that the haze appears more elongated in latitude than longitude by a factor of two, which is approximately consistent with the Fermi gamma-ray haze/bubbles (Dobler et al. 2010). For frequencies above ~40 GHz, striping in the HFI channels (which contaminates our CMB estimate) begins to dominate over the haze emission. Right column: the same but for the “regional” fits described in Sect. 4.1. The overall morphology of the haze is the same, but the residuals near the mask and in the Ophiuchus complex in the north GC are improved. |
| In the text | |
 |
Fig. 4 Left column, top: recovered amplitude of the low-frequency component at 23 GHz from our simplest Commander fit to the Planck data alone, CMD1. As shown in Pietrobon et al. (2012), while this model provides an excellent description of the data, this low-frequency component is a combination of free-free, spinning dust, and synchrotron emission (top). Left column, middle: four-component template model of this component (see Table 2). Left column, bottom: haze residual. The residuals are low outside the haze region, indicating that the templates are a reasonable morphological representation of the different components contained in the Commander solution. The haze residual is strikingly similar to that found for the template-only approach in Fig. 3 (though there does seem to be a residual dipole in the Commander solution). Right column: the same, but for the CMD2 low-frequency, hard spectrum component. While there is still some leakage of dust-correlated emission in the solution, the softer synchrotron emission (mostly correlated with the 408 MHz template see, Fig. 7) has been separated by Commander. The resulting map is dominated by free-free and the haze emission, and the regressed haze residual (bottom panel) shows a morphology very similar to both the template fitting and CMD1 results, indicating that the haze has been effectively isolated. |
| In the text | |
 |
Fig. 5 Microwave haze at WMAP and Planck frequencies using a full-sky template fit to the data. The morphology of the haze is remarkably consistent from band to band and between data sets, implying that the spectrum of the haze does not vary significantly with position. Furthermore, the ν2.5 scaling again yields about equal-brightness residuals, indicating that the haze spectrum is roughly Tν ∝ ν-2.5 through both the Planck and WMAP channels. In addition, while striping is negligible at low frequencies, above ~40 GHz it becomes comparable with, or brighter than, the haze emission (see text). |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but using the regions defined in DF08. Clearly, the residuals near the mask are significantly reduced, although, as with the full-sky fits, striping in the HFI channels (which leaks into the CMB estimate) becomes significant above ~40 GHz. |
| In the text | |
 |
Fig. 7 Left: soft synchrotron component at 408 MHz from the Commander CMD2 analysis. The map is strikingly similar to the Haslam map (see Fig. 2), indicating that soft synchrotron emission has a very uniform spectrum from 408 MHz to 60 GHz through all data sets. Right: difference between the Haslam map and the Commander solution. This is consistent with noise across almost the entire sky with the exception of a few bright free-free clouds that are present in the Haslam data at the ~10% level. The lack of significant haze emission in the difference map (particularly in the south) is a strong indication that the haze region consists of both a hard and a soft component, and does not have a simple spatially variable spectral index. |
| In the text | |
 |
Fig. 8 Left: spectrum measured from the residual in Fig. 6 in the region | l | < 35°, − 35° < b < − 10°. The haze spectrum is very nearly a power law with spectral index βH = − 2.56, while the total synchrotron emission in the region has a spectral index of βS = − 3.1 (see Sect. 4.3), significantly softer than the haze emission. This spectrum should be free from biases caused by template uncertainties. Middle and right: scatter plots (shown in contours) for both the haze (dotted) and total synchrotron (solid) emission using WMAP 23–33 GHz and Planck 30 GHz. |
| In the text | |
 |
Fig. 9 Left: southern Planck 30 GHz haze from Fig. 6. Right: the same but with contours of the Fermi gamma-ray haze/bubbles (Su et al. 2010) overlaid in white. Above b = − 35° (orange dashed line), the morphological correspondence is very strong, suggesting that the two signals are generated by the same underlying phenomenon. |
| In the text | |
 |
Fig. 10 Left: a high southern latitude (b < −35°) view of the Galactic haze at Planck 30 GHz smoothed to 2°. There is a clear spatial correspondence between the haze and the Fermi bubbles shown in Dobler et al. (2010) and Su et al. (2010) including an edge at high latitudes (the green line arc roughly represents the southern Fermi bubble edge). Plotting the brightness in both the Fermi bubble and Planck haze as a function of the distance from the bubble center (taken to be (ℓ,b)cen = (−4.5°, −35.0°)) by integrating over angular bins as shown by the dotted lines reveals an unambiguous detection of an edge in the Planck haze (middle panel red and green lines) that is spatially coincident with the bubble edge in the Fermi data (middle panel blue line). This emission is consistent with an almost flat profile (purple line) at r ~ 17° from the bubble center. In addition, by integrating over radial bins and plotting as a function of angular bin for two ranges of r (right panel), there is a clear excess of emission inside compared to outside of the bubble in both the Planck and Fermi data. |
| In the text | |
 |
Fig. 11 Top: microwave haze at Planck 30 GHz (red, −12 μK < ΔTCMB< 30 μK) and 44 GHz (yellow, 12 μK < ΔTCMB< 40 μK). Bottom: the same, but including the Fermi 2–5 GeV haze/bubbles of Dobler et al. (2010) (blue, 1.05 < intensity (keV cm-2 s-1 sr-1) < 1.25; see their Fig. 11). The spatial correspondence between the two is excellent, particularly at low southern Galactic latitude, suggesting that this is a multi-wavelength view of the same underlying physical mechanism. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


