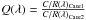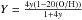| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321387 | |
| Published online | 06 May 2013 | |
He i in the central giant H ii region of NGC 5253
A 2D observational approach to collisional and radiative transfer effects⋆
1 Instituto de Astrofísica de Andalucía (CSIC), C/ Camino Bajo de Huétor, 50, 18008 Granada, Spain
e-mail: ami@iaa.es
2 European Southern Observatory, Karl-Schwarzschild Strasse 2, 85748 Garching bei München, Germany
Received: 1 March 2013
Accepted: 19 March 2013
Context. NGC 5253 is a nearby peculiar blue compact dwarf (BCD) galaxy that, on account of its proximity, provides an ideal laboratory for detailed spatial study of starburst galaxies. An open issue not addressed so far is how the collisional and self-absorption effects on He i emission influence the determination of the He+ abundance in 2D and what is the relation to the physical and chemical properties of the ionised gas.
Aims. A 2D, imaging spectroscopy, study of the spatial behaviour of collisional and radiative transfer effects in He+ and their impact on the determination of He+ abundance is presented for the first time in a starburst galaxy.
Methods. The He i lines were analysed based on previously presented integral field spectroscopy (IFS) data, obtained with FLAMES at the VLT and lower resolution gratings of the Giraffe spectrograph, as well as with GMOS at Gemini and the R381 grating.
Results. Collisional effects reproduce the electron density (ne) structure. They are negligible (i.e. ~0.1–0.6%) for transitions in the singlet cascade but relatively important for those in the triplet cascade. In particular, they can contribute up to 20% of the flux in the He iλ7065 line. Radiative transfer effects are important over an extended and circular area of ~30 pc in diameter centred on the super star clusters (SSCs). The singly ionised helium abundance, y+, has been mapped using extinction-corrected fluxes of six He i lines, realistic assumptions for electron temperature (Te), ne, and the stellar absorption equivalent width, as well as the most recent emissivities. We find a mean(± standard deviation) of 103y+ ~ 80.3( ± 2.7) over the mapped area. The relation between the excitation and the total helium abundance, ytot, is consistent with no abundance gradient. Uncertainties in the derivation of helium abundances are dominated by the adopted assumptions. We illustrate the difficulty of detecting a putative helium enrichment owing to the presence of Wolf-Rayet (WR) stars in the main GH iiR. Data are marginally consistent with an excess in the N/He ratio in the nitrogen-enriched area. This excess would be close to both the atmospheric N/He ratios in WR stars and the uncertainties estimated for the N/He ratios. We explored the influence of the kinematics in the evaluation of the He i radiative transfer effects. Our data empirically support the use of the traditional assumption that motions in an extragalactic H ii region have a negligible effect in the estimation of the global optical depths. Individually, the broad kinematic component (associated with an outflow) is affected by radiative transfer effects in a much more significant way than the narrow one. We find a relation between the amount of extra nitrogen and the upper limit of the contribution from radiative transfer effects that requires further investigation. We suggest that the electron temperature could be a common agent causing this relation.
Key words: galaxies: starburst / galaxies: dwarf / galaxies: individual: NGC 5253 / galaxies: ISM / galaxies: abundances / galaxies: kinematics and dynamics
© ESO, 2013
1. Introduction
At a distance of 3.8 Mpc (Sakai et al. 2004), NGC 5253, in the Centaurus A/M 83 group (Karachentsev et al. 2007), is one of the closest blue compact dwarf (BCD) galaxies. This galaxy is well known for presenting several peculiarities, whose detailed study are closely connected to its proximity and high surface brightness. For example, it contains a deeply embedded very dense compact H ii region at its nucleus (hereafter, “the supernebula”), detected in the radio at 1.3 cm and 2 cm (Turner et al. 2000) that host two very massive super star clusters (SSCs, Alonso-Herrero et al. 2004) and is embedded in a larger (i.e. ~100 pc × 80 pc) giant H ii region (hereafter, the central GH iiR). Recently, mid-infrared observations have shown how its kinematics is compatible with a model for the supernebula in which gas flows out from the molecular cloud (Beck et al. 2012). Indeed, the whole central region of the galaxy is dominated by an intense burst of star formation in the form of a large collection of compact young (~1–12 Myr) star clusters (e.g. Harris et al. 2004). In contrast to this, the main body of NGC 5253 resembles that of a dwarf elliptical galaxy and recently, three potentially massive (≳105 M⊙) and old (1–2 Gyr) star clusters have been found on the outskirts of the galaxy (Harbeck et al. 2012). Finally, NGC 5253 is best known for being one of the few examples (and the closest) of a galaxy presenting a confirmed local excess in nitrogen (see e.g. Walsh & Roy 1989).
We are carrying out a detailed study of this galaxy using integral field spectroscopy (IFS). The results so far have further highlighted its peculiar nature. In Monreal-Ibero et al. (2010, hereafter Paper I), we found that the emission line profiles were complex and consistent with an scenario where the two SSCs produce an outflow (see also Beck et al. 2012). Also, we delimited the area polluted with extra nitrogen very precisely. Moreover, we detected nebular He iiλ4686 in several locations, some associated with WN-type Wolf-Rayet (WR) stars (as traced by the blue bump at around 4680 Å) and some not, but not necessarily coincident with the area exhibiting extra nitrogen. In Monreal-Ibero et al. (2012, hereafter Paper II), we studied the 2D distribution of the main physical (electron temperature (Te), and density, (ne), degree of ionization) and chemical properties (metallicity and relative abundances of several light elements) of the ionised gas. A new area of enhanced nitrogen abundance at ~130 pc from the main area of enhancement and not reported so far was found. In Westmoquette et al. (2013, hereafter Paper III) several locations showing emission characteristic of WC-type WR stars (via the red bump at around 5810 Å) were identified. That WR stars are spread over ~350 pc gives an idea of the area over which the recent starburst has occurred. The chemical analysis was extended with the finding that, with the exception of the aforementioned localised N excess, the O/H and N/H distributions are flat within the whole central 250 pc.
An issue not addressed in detail so far in NGC 5253 is the 2D determination and distribution of the He+ abundance. In a cosmological context, this is particularly relevant since the joint determination of metallicity (as traced by the O/H abundance) and 4He abundance (Y1) for extragalactic H ii regions and star-forming galaxies at low-metallicity was proposed as a means to estimate the primordial helium abundance, YP (Peimbert & Torres-Peimbert 1976; Pagel et al. 1986) serving as a test-bench for the standard hot big band model of nucleosynthesis. However, the density of baryonic matter depends weakly on YP. Therefore, to put useful constrains on YP, 4He abundance of individual objects has to be determined with accuracies ≲1%. Nowadays, emission line flux data of this quality can be achieved and, indeed, the astronomical community is actively working on getting and improving the estimation of YP (see e.g. Aver et al. 2010; Izotov & Thuan 2010; Fukugita & Kawasaki 2006; Peimbert et al. 2002, 2007; Izotov et al. 2007; Olive & Skillman 2001, for recent estimations by the different groups). However, He abundance determinations are influenced by several effects and systematic errors which are not, in principle, straightforward to quantify and correct (see for example Olive & Skillman 2001). Specifically, the intensity of He i emission lines may intrinsically deviate from the recombination values due to collisional and radiative transfer effects. Moreover, the emitted spectrum also depends on the physical conditions of the ionised gas (e.g. Te, ne and ionization structure). Also, on top of these specific properties of the H ii region, extinction by dust and a possible underlying stellar absorption component can also affect the observed spectrum. All these effects contribute to the uncertainties associated with the estimation of ionised helium abundance (y+ = He+/H+). A final extra source of uncertainty is associated with the estimation of the amount of existing neutral helium (i.e. the estimation of the ionization correction factor, icf(He)) and the calculation of the total helium abundance, y = ytot = icf(He) × y+.
Tentative values for y+ were presented in Paper I based on the He iλ6678 line, which is almost insensitive to collisional and self-absorption effects. However, 2D distributions of all the relevant physical properties for the ionised gas were not available at that time. Moreover, other He i lines, in particular He iλ7065, can indeed be affected by collisional and self-absorption effects, specially in conditions of relatively high Te and ne, as it is the case in the main GH iiR of NGC 5253. Supporting this expectation, long-slit measurements predict too high He+ abundances from the He iλ7065 when only recombination effects are taken into account (Sidoli 2010) and a non-negligible optical depth τ(3889) when the He+ abundance is derived using several emission lines in a consistent manner (López-Sánchez et al. 2007).
At present, a complete 2D characterization of the physical properties of the ionised gas in the main GH iiR of NGC 5253 is available. Therefore, we are in an optimal situation for both mapping the collisional and radiative transfer effects in 2D, and re-visiting the derivation of the He+ abundance map taking many He i lines into account. This will be the main purpose of this work. Given that the metallicity of the object (12 + log (O/H) = 8.26, Paper II) is only moderately low, our focus will not be on achieving the ≲1% accuracy required in the determination of the primordial He abundance, but to explore the effects of a parameter not taken into account so far: namely spatial resolution. In addition, we will explore the 2D relationship between the properties of the ionised gas derived so far and the He i collisional and self-absorption effects. To our knowledge this work constitutes the first attempt to study in 2D the collisional and self-absorption effects in He i in any extra-galactic object. Moreover, irrespective of the spatial resolution, due to the characteristics inherent in IFS data, there is the guarantee that the set of ~100 spectra utilized in this work have been processed in a homogeneous manner all the way from the observations (i.e. a given observable was taken with the same observing conditions for the whole set of data) to the final y+ and ytot derivations.
The paper is structured as follows: Sect. 2 describes the characteristics of the data utilized in our analysis; Sect. 3 contains an evaluation of the He i collisional and self-absorption effects in 2D as well as the derivation of the y+ and y maps. Sect. 4 discusses the relation between radiative transfer effects and other quantities (e.g. kinematics of the gas, relative N/O abundance). Our main conclusions are summarised in Sect. 5.
2. The data
We focus our study on the area associated with the main GH iiR in NGC 5253 (see Fig. 1). This is a portion of the full area studied in Paper I and the location where: i) the gas presents relatively high Te and ne, and therefore, important collisional and radiative transfer effects are expected; and ii) several helium lines can be detected over a relatively large area with sufficient quality, and therefore a 2D analysis based on the information in individual spaxels is feasible. The utilized data were collected during several observing runs using the FLAMES-Argus and the GMOS integral field units (IFUs) and together cover the whole optical spectral range. In the following, we briefly describe the basic instrumental characteristics of each set of data and compile the information that was extracted.
 |
Fig. 1 Left: false colour image in filters F658N (Hα, cyan channel), F550M (V, yellow channel), and F814W (I, magenta channel) for the central part of NGC 5253 using the HST-ACS images (programme 10608, P.I.: Vacca). The area studied here is marked with a black rectangle. Right: ionised gas distribution as traced by the extinction-corrected Hβ map derived from a portion of the original FLAMES data. The position of the two main peaks of continuum emission are marked with crosses. The map is presented in logarithmic scale in order to emphasize the relevant morphological features and cover a range of 2.0 dex. Flux units are arbitrary. Note the existence of three dead spaxels at |
 |
Fig. 2 Extinction-corrected flux maps normalized to Hβ for the lines utilized in this work. The position of the two main peaks of continuum emission are marked with crosses in this and all subsequent maps. We marked in white the areas where a given line was not observed. Specifically, for the He iλ6678, He iλ4922 and He iλ7065, they correspond to dead fibres. For He iλ5876, He iλ4471 and He iλ3889, these areas were not covered by the corresponding GMOS or FLAMES-Argus field of view. |
2.1. FLAMES-Argus data
Data were obtained with FLAMES (Pasquini et al. 2002) at VLT UT2 in Paranal. We used the Argus IFU with the sampling of 0.52′′/lens, covering a field of view (f.o.v.) of 11 5 × 7
5 × 7 3, and four low resolution gratings (LR1, LR2, LR3, and LR6). All together, they offer a spectral coverage of 3610 − 5070 Å plus 6440 − 7180 Å at a dispersion of 0.2 Å pix-1. Details of the observations, data reduction, and cube processing, as well as maps for most of the physical and chemical properties utilized in this work, have already been presented in Papers I and II. Maps for the helium lines were derived by independently fitting in each spaxel the He i line profiles with a single Gaussian function with MPFITEXPR (Markwardt 2009). For the particular case of He iλ3889, which is blended with H8 at our spectral resolution, we created an extinction-corrected map by subtracting from the H8+He iλ3889 map, a map of 0.659× the H7 map. This H8 line intensity is that predicted by Storey & Hummer (1995) for Case B, Te = 104 K and ne = 100 cm-3. The final set of FLAMES-Argus maps utilized here are:
3, and four low resolution gratings (LR1, LR2, LR3, and LR6). All together, they offer a spectral coverage of 3610 − 5070 Å plus 6440 − 7180 Å at a dispersion of 0.2 Å pix-1. Details of the observations, data reduction, and cube processing, as well as maps for most of the physical and chemical properties utilized in this work, have already been presented in Papers I and II. Maps for the helium lines were derived by independently fitting in each spaxel the He i line profiles with a single Gaussian function with MPFITEXPR (Markwardt 2009). For the particular case of He iλ3889, which is blended with H8 at our spectral resolution, we created an extinction-corrected map by subtracting from the H8+He iλ3889 map, a map of 0.659× the H7 map. This H8 line intensity is that predicted by Storey & Hummer (1995) for Case B, Te = 104 K and ne = 100 cm-3. The final set of FLAMES-Argus maps utilized here are:
-
i)
an extinction map derived from the Hα/Hβ lineratio;
-
ii)
a map for the Hβ equivalent width (EW(Hβ));
-
iii)
a map of Te as derived from the [O iii]λλ4959,5007/ [O iii]λ4363 line ratio: Te([O iii]). In those spaxels where no determination of Te([O iii]) was available, we assumed Te([O iii]) = 10 500 K (see Paper II, for typical Te([O iii]) values outside the main GH iiR);
-
iv)
a map for ne as derived from the [S ii]λ6717/ [S ii]λ6731 line ratio;
-
v)
maps for the O+/H+, O/H and S+/H+ abundances, as derived from collisional lines using the direct method, to estimate the icf(He);
-
vi)
maps for different tracers of the excitation degree (i.e. [S ii]λλ6717,6731/Hα and [O iii]λ5007/Hβ line ratio) to be used in the estimation of the icf(He) at those locations where no measure of the O+/H+, O/H and S+/H+ abundances is available and to explore the dependence of y+ and ytot on the excitation;
-
vii)
a map of the relative abundance of nitrogen, N/O, as derived from collisional lines using the direct method;
-
viii)
maps for the λ3889, λ4471, λ4922, λ6678, λ7065 He i equivalent widths and extinction-corrected line fluxes using our extinction map and the extinction curve of Fluks et al. (1994). The extinction corrected line flux maps normalized to Hβ are presented in Fig. 2. Note that in order to minimize uncertainties associated to aperture matching, absolute flux calibration and extinction, lines were measured relative to a bright Balmer line observed simultaneously with a given helium line. Then, we assumed the theoretical Balmer line intensities obtained from Storey & Hummer (1995) for Case B, Te = 104 K and ne = 100 cm-3. Additional He i lines were covered by the FLAMES set-up but not used here. Specifically, He iλ5016 and He iλ4713 emission lines were detected over most of the FLAMES f.o.v. He iλ5016 is relatively close to the much brighter (i.e. ~150–400 times) [O iii]λ5007 line and, in the main GH iiR, the wings of the [O iii] line profile prevented us from measuring a reliable line flux. Regarding the relatively weak λ4713 line, at the spectral resolution of these data, this line is strongly blended with [Ar iv]λ4711 and the uncertainties associated with the deblending of these lines in the GH iiR are relatively large due to the existence of several distinct kinematic components (see Papers I, III);
-
ix)
maps with the extinction-corrected line fluxes in λ6678, λ7065 He i and Hα, for the different kinematic components presented in Paper I.
2.2. GMOS data
The Gemini-South Multi-Object Spectrograph (GMOS) data were taken using the one-slit mode of its IFU (Allington-Smith et al. 2002). In this mode, the IFU covers a f.o.v. of 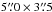 sampled by 500 contiguous hexagonal lenslets of 0
sampled by 500 contiguous hexagonal lenslets of 0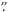 2 diametre. The utilized grating (R381) gives a spectral coverage of 4750 − 6850 Å at a dispersion of 0.34 Å pix-1, thus complementing the FLAMES-Argus data. We refer to Paper III for further details on the observations and data reduction. The product of the reduction is a datacube per pointing with a uniformly sampled grid of 0
2 diametre. The utilized grating (R381) gives a spectral coverage of 4750 − 6850 Å at a dispersion of 0.34 Å pix-1, thus complementing the FLAMES-Argus data. We refer to Paper III for further details on the observations and data reduction. The product of the reduction is a datacube per pointing with a uniformly sampled grid of 0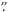 1. In this work, we utilized the two pointings (out of four) that mapped the central GH iiR. As we did with the FLAMES’s data, in each spaxel all the lines of interest were independently fitted with a single Gaussian function with MPFITEXPR. The final set of GMOS maps utilized here are:
1. In this work, we utilized the two pointings (out of four) that mapped the central GH iiR. As we did with the FLAMES’s data, in each spaxel all the lines of interest were independently fitted with a single Gaussian function with MPFITEXPR. The final set of GMOS maps utilized here are:
-
i)
maps for Hα and Hβ fluxes. Theseimages were utilized to check the consistency between theFLAMES and GMOS data, both in terms of observed structureand derived extinction map, to estimate the offset and rotation thatwas necessary to be applied to the GMOS data, and to correct forextinction the He iλ5876 map;
-
ii)
a map for He iλ5876 flux. This is the strongest He i line and therefore, one of the key observables for the present study;
-
iii)
equivalent widths and extinction-corrected line flux maps of He iλ5876 flux normalized to Hβ. These were derived from the maps previously mentioned and were rotated and reformatted to match the FLAMES data using the drizzle task of the Space Telescope Science Data Analysis System (STSDAS) package of IRAF2. They were the only GMOS maps utilized jointly with the FLAMES’s maps. The flux map is shown in Fig. 2 together with the other He i line flux maps.
3. Results
3.1. Collisional effects as traced by the theoretical C/R ratio
Collisional excitation in hydrogen can be important in regions of very low metallicities (Z ≲ 1/6 Z⊙) due to their relatively high temperatures (Luridiana 2009). However, for the typical temperatures and densities found in H ii regions in general, and in the main GH iiR of NGC 5253 in particular, the collisional excitation in hydrogen is negligible in comparison with recombination (see e.g. Fig. 9 of Aver et al. 2010). This is not the case for helium. The He i 23S level (see Fig. 1 in Benjamin et al. 1999, for a representation of the Grotian diagram for He i singlet and triplet ladders) is highly metastable, and collisional transition from it can be important (Osterbrock & Ferland 2006). Specifically, at relatively high densities this level can be depopulated via collisional transitions to the 23P0, 21P0 and 21S and, to a lesser extent, to higher singlets and triplets (mainly 33P0). The effect on the observed He i emission lines is always an increase in the observed flux. The relative importance of the collisional effects on a given emission line is characterized by the C/R factor, i.e. the ratio of the collisional component to that arising from recombination which is given by: 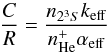 (1)where n23S, and
(1)where n23S, and 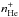 are the densities of the 23S state and He+ respectively, αeff is the effective recombination coefficient for the line, and keff is the effective collisional rate coefficient.
are the densities of the 23S state and He+ respectively, αeff is the effective recombination coefficient for the line, and keff is the effective collisional rate coefficient.
Here, we will estimate the 2D contribution to the collisional component using the relations derived by Porter et al. (2007), where theoretical C/R factors are calculated as functions of ne and Te, and assuming that the density from [S ii] traces well that from helium. Plasma temperatures as traced by helium lines can typically be ~50% of those traced by oxygen in planetary nebulae (Zhang et al. 2005). For H ii regions the situation is not so clear. For the specific case of NGC 5253, values between 82% and 96% have been reported in specific apertures (López-Sánchez et al. 2007). We made two assumptions for the Te:
-
Case 1: the temperature from oxygen traces well that fromhelium: Te(He i) = Te([O iii]);
-
Case 2: the temperature from helium is proportional to the temperature from oxygen, with the constant of proportionality estimated as the mean of the ratios between both temperatures provided by López-Sánchez et al. (2007): Te(He i) = 0.87 Te([O iii]).
Maps for the C/R factors using the first assumption are presented in Fig. 3 whilst the ratio between the two estimations is presented in Fig. 4. This is the first time that collisional effects for a set of helium lines have been mapped in an extragalactic source. Several results can be extracted from these maps.
Firstly, all the C/R maps display the same structure. That is: higher ratios at the peak of emission for the ionised gas and towards the northwest half of the GH iiR and a decrease of the collisional contribution outwards. This reproduces the observed density structure (see e.g. Fig. 6 in Paper I).
 |
Fig. 3 Collisional effects as traced by the C/R ratio for the He i lines utilized in this work. Note that a common scale was used for all the lines in order to facilitate comparison of the relative effects between the different lines. Also, a logarithmic colour stretch is used to emphasize the variations within the region for a given line. |
 |
Fig. 4 Maps for the ratio between the C/R factors derived for two assumptions of the Te(He i): |
Secondly, lines corresponding to transitions in the singlet cascade have a negligible contribution from collisional effects (e.g. C/R factor for λ4922 varies between ~0.001–0.006) whilst for those lines in the triplet cascade (λ7065, λ5876, λ4471, and λ3889), the contributions from collisional effects can be important. In particular, the C/R factor for λ7065 ranges between ~0.02 and ~0.22, meaning it reaches ~20% in the nucleus of the galaxy.
Thirdly, the assumed temperature has some influence in the estimation of the collisional effects. In our particular case the assumed temperature in Case 2 was only ~15% smaller than that in Case 1. However, this implies a smaller contribution of the collisional effects by ~25–30% for λ7065 and ~30–35% for λ3889 (the two lines most affected by collisional effects) and up to ~50% for the other lines under study. Interestingly, areas of lower temperature are more sensitive to the assumption on Te. It is important to note that the uncertainties associated to the errors due to the measurement of the line fluxes involved in the determination of Te([O iii]) were typically ≲1000 K (Paper II). This is smaller than the difference in the assumed temperature between the two reasonable assumptions, Cases 1 and 2, which range between ~1500 K at the peak of emission to ~1300 K in the areas of lowest surface brightness. This implies that, at this level of data quality, more than errors associated to line fluxes, it is systematic errors associated with assumptions in density and temperature that dominate the uncertainties in the evaluation of the collisional effects.
3.2. Radiative transfer effects as traced by τ(3889) and derivation of He+ abundance
Single ionised helium abundance, y+, can be calculated as follows: 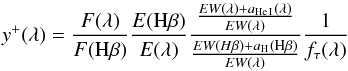 (2)where F(λ)/F(Hβ) is the extinction-corrected flux for the He i line scaled to Hβ, E(Hβ) and E(He i) are the theoretical emissivities; fτ(λ) is a factor that takes radiative transfer effects into account. The remaining term in Eq. (2), with a(λ) being the equivalent width in absorption, takes the effect of the underlying stellar population into account. In the following, we will describe how each of these terms were evaluated.
(2)where F(λ)/F(Hβ) is the extinction-corrected flux for the He i line scaled to Hβ, E(Hβ) and E(He i) are the theoretical emissivities; fτ(λ) is a factor that takes radiative transfer effects into account. The remaining term in Eq. (2), with a(λ) being the equivalent width in absorption, takes the effect of the underlying stellar population into account. In the following, we will describe how each of these terms were evaluated.
3.2.1. Calculation of the emissivities
For Hβ emissivities, we utilized the function from Storey & Hummer (1995) which is, in units of 1025 erg cm-3 s-1: 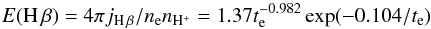 (3)with te = Te/104. For the He i lines, we utilized those emissivities originally provided by Porter et al. (2012) and recently corrected by Porter et al. (2013). These are the most recent He i emissivities, and the collisional effects are included. Therefore, there was no need to include an extra term in Eq. (2) to take collisional effects into account. They are tabulated for discrete values of ne and Te. However, the ne in the main GH iiR varies between ≲100 cm-3 and ~660 cm-3 and Te ranges between ~9000 K and ~12 000 K. Therefore, to evaluate the emissivities at each individual spaxel, we fitted the values provided for ne = 100 cm-3 and 1000 cm-3 and Te ranging from 5000 K to 25 000 K to functions with the same parametrization as E(H β),
(3)with te = Te/104. For the He i lines, we utilized those emissivities originally provided by Porter et al. (2012) and recently corrected by Porter et al. (2013). These are the most recent He i emissivities, and the collisional effects are included. Therefore, there was no need to include an extra term in Eq. (2) to take collisional effects into account. They are tabulated for discrete values of ne and Te. However, the ne in the main GH iiR varies between ≲100 cm-3 and ~660 cm-3 and Te ranges between ~9000 K and ~12 000 K. Therefore, to evaluate the emissivities at each individual spaxel, we fitted the values provided for ne = 100 cm-3 and 1000 cm-3 and Te ranging from 5000 K to 25 000 K to functions with the same parametrization as E(H β), 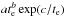 , and then interpolated on a logarithmic scale as follows:
, and then interpolated on a logarithmic scale as follows: 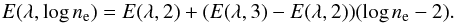 (4)The coefficients and standard deviations of the fits are compiled in Table 1 whilst Fig. 5 shows a comparison between the fitted function and the discrete values provided by Porter et al. (2012) for the range of densities and temperatures covered in the GH iiR. A comparison between this figure and Fig. 3 shows the correspondence between the degree of dependence on the density and the contribution of the collisional effects.
(4)The coefficients and standard deviations of the fits are compiled in Table 1 whilst Fig. 5 shows a comparison between the fitted function and the discrete values provided by Porter et al. (2012) for the range of densities and temperatures covered in the GH iiR. A comparison between this figure and Fig. 3 shows the correspondence between the degree of dependence on the density and the contribution of the collisional effects.
 |
Fig. 5 Fitted functions to the Porter et al. (2013) emissivities. The black lines are the functions for ne = 100 cm-3 (continuous line) and for ne = 1000 cm-3 (long dashed line). The intermediate short dashed lines represent the interpolated emissivities for log (ne) = 2.2,2.4,2.6,2.8. Discrete values listed by Porter et al. (2013) are overplotted with blue triangles (log (ne) = 2) and orange circles (log (ne) = 3). |
Coefficients for the equations fitted to the Porter et al. (2013) Table 2.
3.2.2. Correction for underlying stellar population
To take the effect of the underlying stellar population into account, it is necessary to estimate the equivalent width both in emission and absorption for Hβ and the helium lines. The equivalent width of Hβ in emission (not shown) ranges typically from ~240 Å at the peak of emission for the ionised gas to ~65 Å in the most outer regions of the area sampled here. We assumed a component in absorption of 2 Å, which is adequate for very young starbursts, as the one at the nucleus of NGC 5253 (e.g. González Delgado et al. 2005; Alonso-Herrero et al. 2010). This implies a correction for Hβ in absorption from a negligible value (i.e. ≲1%) at the peak of emission to ~4% in the outer parts of the covered area.
The correction due to the underlying stellar population is not straightforward to estimate for the helium lines. As explained in Paper II, for the data obtained with FLAMES Giraffe and the LR1 or LR2 gratings, the contribution of the stellar population was separated from that of the gas using the STARLIGHT code (Cid Fernandes et al. 2005, 2009) to match the stellar continuum. Therefore, we can assume aHe I(λ4471) = aHe I(λ3889) = 0. For the other lines, a common approach assumes identical stellar equivalent widths for all the helium lines. However, He i lines are produced by the bluest stars. Therefore, in the context of a galaxy suffering a burst of star formation on top of an older population, redder lines should have smaller equivalent widths in absorption, since older stars contribute more to the stellar continuum. Specifically, typical estimations of the equivalent width in absorption for redder lines would be ~40–80% that of aHe i(λ4471) (Aver et al. 2010). This is one of the lines observed with the LR2+FLAMES configuration for which nebular and stellar information have been disentangled. Therefore aHe i(λ4471) could be measured from our emission line free cube. Typical values were extremely low (i.e. ~0.11 ± 0.03 Å) and without any obvious variation following the structure of the GH iiR or the location of the SSCs. Taking this as reference, and the relative values between the different aHe i(λ)’s reported by Aver et al. (2010), which were in turn derived using the models presented by González Delgado et al. (2005) and Martins et al. (2005), we assumed aHe i(λ) = 0.09, 0.08, 0.06 and 0.05 Å for λ4922, λ5876, λ6678, λ7065, respectively. Equivalent widths for the λ4922, λ5876, λ6678, λ7065 He i emission lines were ~0.3–4 Å, ~20–60 Å, ~3–20 Å, and ~3–35 Å, respectively. With these values, the largest correction for absorption was for He iλ4922, with typical values between 3% and 6%. However, corrections in the most external spaxels could reach up to ~25%. For the other lines the correction was more moderate, with values between ~1% and ≲8% for He iλ5876 and comparable to the correction in Hβ for the He iλ6678 and He iλ7065 lines. This is illustrated in Fig. 6.
 |
Fig. 6 Maps of the correction factor due to a component in absorption in the He i lines. Different scales were utilized in the different maps to emphasize the structure. The corresponding map for the Hβ correction factor (not shown) is similar to those for λ6678 and λ7065. |
3.2.3. Estimation of radiative transfer effects
Radiative transfer effects can be important in recombination radiation. Given the metastable character of the 23S level, under certain conditions, the optical depths in lower 23S–n3P0 lines imply non-negligible effects on the emission line strengths (Osterbrock & Ferland 2006). Specifically λ10 830 photons are only scattered, but absorbed photons, corresponding to transitions to higher levels, can be converted to several photons of lower energy. The most prominent example is λ3889 photons that can be converted to λ4.3 μm 33S–33P0, plus λ7065 23S–33P0, plus λ10 830 23S–23P0. The net effect is that lines associated with transitions from the 23P level upwards (e.g. λ3889) are weakened by self-absorption, whilst lines associated with several transitions from higher levels (e.g. λ7065) are strengthened by resonance fluorescence. Contrary to collisional effects, radiative transfer effects do not affect photons in the singlet cascade. The relative importance of radiative transfer effects is quantified by a correction factor, fτ(λ), for each line which is a function of the optical depth at λ3889, τ(3889). Here, we parametrized these factors by fitting the values provided by Robbins (1968) to a non-expanding nebula to the functional form fτ(λ)ω = 0 = 1 + aτb. The corresponding functions for the lines utilized in this work are:
![\begin{eqnarray} \label{eqfac7065}&&f_\tau(7065)_{\omega\,=\,0} = 1 + 0.741\tau^{0.341} \\[2.5mm] \label{eqfac6678}&&f_\tau(6678)_{\omega\,=\,0} = 1 \\[2.5mm] \label{eqfac5876}&&f_\tau(5876)_{\omega\,=\,0} = 1 + 0.0126\tau^{0.496} \\[2.5mm] \label{eqfac4922}&&f_\tau(4922)_{\omega\,=\,0} = 1 \\[2.5mm] \label{eqfac4471}&&f_\tau(4471)_{\omega\,=\,0} = 1 + 0.0022\tau^{0.728} \\[2.5mm] \label{eqfac3889}&&f_\tau(3889)_{\omega\,=\,0} = 1 - 0.261\tau^{0.305}. \end{eqnarray}](/articles/aa/full_html/2013/05/aa21387-13/aa21387-13-eq111.png) Note that no values were provided for He iλ4922 in the original work of Robbins (1968). However, as it happens for He iλ6678, this is a singlet line, and therefore fτ(4922) = 1 can be assumed.
Note that no values were provided for He iλ4922 in the original work of Robbins (1968). However, as it happens for He iλ6678, this is a singlet line, and therefore fτ(4922) = 1 can be assumed.
Typically, optical depth (τ(3889)) and He i abundance (y+) (and other parametres) are determined simultaneously by minimizing χ2, defined as the difference between each helium line’s abundance (weighted according to a reasonable criterion like the line flux) and the average. In this methodology it is implicit that all the lines trace the same location in the nebula/galaxy. However, the area under study in this work suffers from heavy extinction (see Fig. 3 in Paper I). Therefore, a priori, it is not possible to assume that all the lines equally penetrate the nebula interior and that bluer and redder lines trace zones with the same y+. Because of that, we grouped the lines in two sets according to their wavelengths, called hereafter the blue (λ3889, λ4471, λ4922) and red (λ5876, λ6678, λ7065) sets, which will be analysed independently. Each set is made out of: i) a line from the singlet cascade, and therefore not affected by radiative transfer effects; ii) a line from the triplet cascade highly sensitive to radiative transfer effects; iii) a line from the triplet cascade mildly sensitive to radiative transfer effects.
 |
Fig. 7 Maps for y+ derived from lines of the singlet cascade for the blue (left) and red (right) sets. A common scale was used in both maps to facilitate comparison between them. |
A first estimation of the y+ abundance structure as traced by the red and blue lines can be obtained from the singlet lines, since they are not affected by radiative transfer effects. This is shown in Fig. 7. The mean (± standard deviation) are 80.7(±5.1) and 76.8(±1.8) for the λ4922 and λ6678 lines averaged over the mapped area. These values indicate that even if the red and blue lines are not tracing exactly the same gas columns, at least they sample areas with a the same y+ within ~5%.
A comparison of the initial y+ maps with those obtained from a line highly sensitive to radiative transfer effects in each set (λ3889 and λ7065), allowed us to determine the respective fτ(λ) map for each set, which can, in turn, be converted into τ(3889) maps. These are shown in Fig. 8. The optical depth has the same structure in both maps, with the peak at the SSC(s). The shape of the area presenting τ(3889) > 0 is circular but resolved. With a FWHM = 1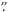 6 ~ 30 pc, this is larger than the seeing (~0
6 ~ 30 pc, this is larger than the seeing (~0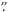 9). This is consistent with a picture where high optical depths are not restricted to the deepest core of the galaxy, associated with the supernebula, but extend over a larger region. Also, the fact that the optical depths derived from the red set of lines are larger than those derived from the blue set is in harmony with a picture where deeper layers in the nebula, which we interpreted as denser and hotter (Monreal-Ibero et al. 2012; see also Beck et al. 2012), suffer from larger radiative transfer effects and suggests a link between He i optical depth and dust optical depth.
9). This is consistent with a picture where high optical depths are not restricted to the deepest core of the galaxy, associated with the supernebula, but extend over a larger region. Also, the fact that the optical depths derived from the red set of lines are larger than those derived from the blue set is in harmony with a picture where deeper layers in the nebula, which we interpreted as denser and hotter (Monreal-Ibero et al. 2012; see also Beck et al. 2012), suffer from larger radiative transfer effects and suggests a link between He i optical depth and dust optical depth.
 |
Fig. 8 Maps for τ(3889) as derived from the λ4922 and λ3889 (left) and the λ6678 and λ7065 (right) emission lines. |
3.2.4. Final derivation of He+ abundance
Finally for both sets, the information of the mildly sensitive line was added and abundances from each line were recalculated using their corresponding τ(3889). The final abundance maps for each set were made using a weighted average. We used the mean fluxes of the He i in the utilized area to determine the respective weights. These were 3:1:1 for the λ5878:λ6678:λ7065 and 25:5:1 for λ3889:λ4471:λ4922. The mean (±standard deviation) for the red and blue sets for y+ are 79.3(±2.5) and 82.0(±3.8), i.e., results from the red and the blue sets agree to within ~3%. Since differences between the maps derived from the blue and red sets are consistent with tracing the same y+ per spaxel, we derived a final map using the information of all the lines by averaging these two maps with a blue:red weight of 0.8:1.0, the mean ratio between the brightest lines in the blue and red sets (i.e. λ3889 and λ5876). This is shown in Fig. 9. The mean (±standard deviation) is 80.3(±2.7). This value compares well with other values of y+ reported in the literature for this area (Kobulnicky et al. 1997; López-Sánchez et al. 2007; Sidoli 2010).
 |
Fig. 9 Final map for y+ derived from a weighted average of those derived for the lines in the blue and red sets. Note we used a different scale than in Fig. 7 to increase the contrast and emphasize the structure following the excitation structure. Instead, the scale is common with that in the right column of Fig. 12 to make easier the comparison between total and ionic helium abundances. |
To estimate the emissivities, the calculation of these abundances was made with assumed ne([S ii]) and Te(He i) = Te(H i) = Te([O iii]). As for the mapping of the collisional effects, in order to evaluated the influence of the selection of Te, the derivation presented here was repeated assuming Te(He i) = Te(H i) = 0.87 Te([O iii]) and finding a mean (±standard deviation) of 79.4(±3.0). This implies that the precise selection of Te has a small effect (~1%) in the determination of y+, in comparison to other factors like e.g. the correction for absorption or radiative transfer effects, as long as one keeps this selection within reasonable values.
Finally, it is worth mentioning that throughout all the derivation of y+, we have assumed that He i singlets are formed under Case B conditions (i.e. lines are formed in the limit of infinite Lyman line optical depth and there is no optical depth in transitions arising from excited states). This is the standard framework for the derivation of helium abundances. However, under certain conditions, helium Lyαλ584 (and higher Lyman transitions) may be attenuated due to two effects: absorption of the helium Lyα line by dust and hydrogen absorption (Ferland 1980; Shields 1993). If these effects were important, the Case B assumption would no longer be applicable. The fact that we have recovered similar helium abundances from the two sets of lines supports the Case B assumption.
3.3. Determination of He abundance
The favourite scenario to explain the extra nitrogen found within the area studied here is that this has been produced by Wolf-Rayet stars and presumedly those at the two SSCs. In this scenario, as it happens with the nitrogen, an overabundance of helium is also expected to be observed. Specifically, typical stellar atmospheric N/He ratios would be ~3 × 10-3 and ~5 × 10-4 for WN and WC stars, respectively (Smith & Willis 1982). This could be used as a reference for the expected N/He ratios of the material newly incorporated into the warm ISM. Are our data supporting an enrichment in helium abundance compatible with these ratios and, therefore, supporting the Wolf-Rayet stars hypothesis?
 |
Fig. 10 He+ abundance vs. [O iii]λ5007/Hβ. The first-degree polynomial fit is shown with a black line. The 1-σ and 3-σ levels are marked with thick and thin red lines respectively. Mean and standard deviation of each 0.05 dex bin in log ([O iii]λ5007/Hβ) are shown with blue diamonds and error bars respectively. The green horizontal dashed line shows the mean value. Data points corresponding to spaxels with log (N/O) > − 1.3 have been marked with orange circles. |
As can be clearly seen in Fig. 9, the y+ map presents some structure that follows the excitation, even if the standard deviation for y+ is small (~4% of the mean value). This is better seen in Fig. 10 which is an updated version of Fig. 14 in Paper I but restricted to the area studied here. The figure presents y+ for each individual spaxel versus a tracer of the excitation, in this case [O iii]λ5007/Hβ. For each bin of 0.05 dex, we overplotted the mean and standard deviation of y+ values and fitted all our data points with a first-degree polynomial. Considering that if we find ⟨ y+ ⟩ in the bin of highest [O iii]λ5007/Hβ to be larger than ⟨ y+ ⟩ + σ(y+) in the bin of lowest [O iii]λ5007/Hβ indicates the presence of a gradient, then this plot is consistent with a positive gradient in y+. Moreover, spaxels with an extra amount of nitrogen have, on average higher y+. Is this increase due only to variations in the ionization structure or are we witnessing an enrichment in the helium abundance? To answer this question, one needs to estimate and correct for the unseen neutral helium, removing in this way, the dependence on the excitation. This is not straight forward as examplified by previous studies (e.g. Viegas et al. 2000; Sauer & Jedamzik 2002; Gruenwald et al. 2002).
 |
Fig. 11 Maps for the ionic abundances utilized in the derivation of the ionization correction factors. Left: O+/H+. Right: S+/H+ |
Within the spirit of keeping the analysis simple, here we compare the results using three approaches. The first two make use the icf’s proposed by Kunth & Sargent (1983) and Peimbert & Torres-Peimbert (1977):
![\begin{eqnarray} && \rm icf(He)_{K\&S83} = (1 - 0. 25\,O^+ / O)^{-1} \label{eqks83} \\[2.5mm] && \rm icf(He)_{P\&TP77} = (1 - 0. 35\,O^+ / O- 0.65\,S^+ / S)^{-1}. \label{eqptp77} \end{eqnarray}](/articles/aa/full_html/2013/05/aa21387-13/aa21387-13-eq123.png) For the third one, we assumed a priori a functional form similar to that of Kunth & Sargent (1983) and iteratively determined the required coefficients to obtain a relation consistent with no gradient of helium abundance. This would represent the case of largest reasonable correction for unseen helium:
For the third one, we assumed a priori a functional form similar to that of Kunth & Sargent (1983) and iteratively determined the required coefficients to obtain a relation consistent with no gradient of helium abundance. This would represent the case of largest reasonable correction for unseen helium: 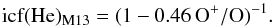 (13)These icf’s depend on the ionic and total abundances of oxygen and sulphur. A map for the total abundance of oxygen was presented in Paper II. We utilized a constant sulphur abundance determined as the mean of those presented in Paper III. Regarding the ionic abundances of oxygen and sulphur, they were derived as part of the work presented in Paper II. However, maps were not included there and are displayed in Fig. 11 for completeness. An extra assumption is needed to calculate the icf’s in those areas where no measurement for the ionic abundance is available. For that, we utilized the information in the other spaxels to fit a first-degree polynomial to the relation between the [S ii]λλ6717,6731/Hα line ratio and icf(He):
(13)These icf’s depend on the ionic and total abundances of oxygen and sulphur. A map for the total abundance of oxygen was presented in Paper II. We utilized a constant sulphur abundance determined as the mean of those presented in Paper III. Regarding the ionic abundances of oxygen and sulphur, they were derived as part of the work presented in Paper II. However, maps were not included there and are displayed in Fig. 11 for completeness. An extra assumption is needed to calculate the icf’s in those areas where no measurement for the ionic abundance is available. For that, we utilized the information in the other spaxels to fit a first-degree polynomial to the relation between the [S ii]λλ6717,6731/Hα line ratio and icf(He): ![\begin{eqnarray} && \rm icf(He)_{K\&S83} \!=\! (0.354\pm0.012) \mathrm{[S\,\textsc{ii}]/H}\alpha + (1.033\pm0.002)~~~~~~~~~~ \\[2.5mm] && \rm icf(He)_{P\&TP77} \!=\! (0.447\pm0.026) \mathrm{[S\,\textsc{ii}]/H}\alpha + (1.054\pm0.003) \\[2.5mm] && \rm icf(He)_{M13} \!=\! (0.763\pm0.025) \mathrm{[S\,\textsc{ii}]/H}\alpha + (1.057\pm0.004). \end{eqnarray}](/articles/aa/full_html/2013/05/aa21387-13/aa21387-13-eq125.png) The maps for the three icf(He) estimations are presented in the left column of Fig. 12. In all three cases, the icf is smallest at the peak of emission for the ionised gas and increases outwards, following the ionization structure.
The maps for the three icf(He) estimations are presented in the left column of Fig. 12. In all three cases, the icf is smallest at the peak of emission for the ionised gas and increases outwards, following the ionization structure.
 |
Fig. 12 Left: maps for the icf(He) as estimated from the expressions proposed by Kunth & Sargent (1983, top, Peimbert & Torres-Peimbert (1977, centre and assuming no gradient in helium abundance bottom. Right: corresponding helium abundance maps. |
 |
Fig. 13 Helium abundance as derived using the icf(He) proposed by Kunth & Sargent (1983, top, Peimbert & Torres-Peimbert (1977, centre and assuming no gradient in helium abundance (bottom) vs. [O iii]λ5007/Hβ. Symbol and colour codes are as in Fig. 10. |
The icf(He) values are close to one another but variable within a range ~1.04–1.09, ~1.06–1.12 and ~1.09–1.20 when using Eqs. (11)–(13), respectively. The corresponding maps with the total helium abundance are presented in the right column of this figure, whilst the dependence on the excitation is presented in Fig. 10. Note that, when using the Kunth & Sargent (1983) and Peimbert & Torres-Peimbert (1977) icf’s, the slope of the relation between y and [O iii]λ5007/Hβ is slightly positive within the errors of the fit. However, according to the criterion presented for the y+ vs. [O iii]λ5007/Hβ relation, the derived helium abundance for these icf’s would be effectively consistent with no positive gradient. The mean total helium abundance ranges between 0.086 and 0.091, depending on the assumed icf. This range is larger by a factor ~2 than the uncertainties due to the measurements (assumed to be traced by the standard deviation). This implies that the main source of uncertainty is still in the assumptions taken on the way to the derivation of the final abundance and highlight how, even with a level of data quality as high as those utilized here (i.e. data allowing to determine locally the physical conditions of the gas, the fluxes of several helium lines and estimations of the contribution of underlying stellar populations), achieving an uncertainty ≲1% is extremely difficult.
The main conclusion of Fig. 13 is that the relation between the total helium abundance, ytot, and the excitation of the gas, as traced by [O iii]λ5007/Hβ is consistent with a lack of gradient in helium abundance. However, if the extra helium were produced by the Wolf-Rayet stars, the required amount to be detected would be tiny in comparison to the pre-existing helium. This implies that a positive slope in Fig. 13 consistent with this enrichment would be indistinguishable of the presented fits. Exploiting these data to their limits, we can derive the average excess in N/He, by comparing the mean abundances in the N-enriched and non N-enriched areas. A map for the N/H abundance can be derived using the O/H and N/O maps presented in Paper II. Assuming a value of log (N/O) = −1.3 as the limit above which the interstellar medium is enriched in nitrogen, we find a mean N/H of 8.4 × 10-6 and 17.4 × 10-6 in the spaxels without and with enrichment. This implies a flux weighted excess in nitrogen of (N/H)exc = 8.9 × 10-6. Proceeding in the same manner with the different estimations of the total helium abundance, we find mean He/H values ranging between 8.49 × 10-2 and 9.05 × 10-2 for the non-enriched spaxels and between 8.68 × 10-2 and 9.14 × 10-2 for the enriched ones, depending on the assumed icf(He). Differences in helium abundances between the enriched and non-enriched zones are ~0.9–1.9 × 10-3. The lowest value was derived using our largest icf(He) (i.e. Eq. 13) which, by construction, was defined to minimize any helium abundance gradient. The highest value is at the limit of the uncertainties (~2 × 10-3 assumed to be traced by the standard deviation for the spaxels under consideration in each separate group) and implies a (N/He)exc ~ 4 × 10-3. This value compares well with the stellar atmospheric N/He ratios for an N-type Wolf-Rayet star (e.g. Smith & Willis 1982). Therefore, these data appear to be marginally in accord with the hypothesis of a putative enrichment of helium due to the Wolf-Rayet population in the main H ii region, but more importantly, they stress the difficulties in pushing this methodology further in order to confirm this contamination without doubt.
4. Discussion
4.1. Kinematics and radiative transfer effects
The standard approach in the literature to estimate radiative transfer effects assumes a negligible influence of the movements of the gas in the H ii region. i.e. a static nebula (ω = v/vth = 0, in the formalism presented by Robbins 1968). This is the approach utilized in Sect. 3.2. The general use of this assumption is motivated by the difficulty of obtaining data of sufficient quality to allow, on top of measuring the flux of several helium lines with good signal to noise, tracing their profiles and clearly identify the different kinematic components in a consistent manner in all of them. However, it is not unusual for starburst galaxies or H ii regions to present velocity gradients and/or relatively high velocity dispersion that can be attributed to outflows (or expanding structures). In particular, the kinematic study presented in Papers I and III showed that movements in this H ii region are significant and can indeed be attributed to an outflow caused by the two embedded SSCs. Specifically, in Paper I, we detected a relatively static (i.e. small velocity gradient) narrow component on top of a much broader component (σ ~ 20 − 25 km s-1) with a velocity gradient of Δv ~ 70 km s-1. An additional component was also detected with the higher resolution GMOS data (Paper III). Therefore, these data provide a very good opportunity to explore what is the impact of the kinematics in the derivation of the optical depths from an empirical point of view.
Since this is only an exploratory analysis and a consistent approach based on the identification and modeling of multiple kinematic components in several emission lines would be more complex (and not supported by the signal-to-noise of all the He i data) than the one presented in Sect. 3.2, we opt for a simpler analysis based on the He iλ6678 and He iλ7065 lines. These were the pair of lines utilized to estimate τ(3889) in the red set. Also both were observed with the same instrumental set-up, which was the same as for Hα in the multicomponent analysis presented in Paper I. Therefore, we could link on a spaxel-by-spaxel basis the multicomponent analysis utilized in Paper I to similar components in He iλ6678 and He iλ7065. The contribution to the total flux from each component varies from spaxel to spaxel as well as with the line in consideration. Specifically, the broad component presents a higher contribution (i.e. ~35–60%) to He iλ7065 than to He iλ6678 (~30–50%). This implies different correction factors, fτ(7065), for the narrow and broad component that can be converted into optical depths as in Sect. 3.2. Given the velocity gradient and the velocity dispersion measured for the broad component, values for ω = v/vth = 3 are more appropriate for this component. Fitting the same functional form as in Eqs. (5)–(10) to the values reported in Robbins (1968) for ω = v/vth = 3 and Te = 10 000 K, we derived the following relation: 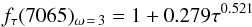 (17)The structure of the derived optical depth for both the narrow and the broad components is shown in Fig. 14 and several conclusions can be drawn from this figure. Firstly, a comparison between the left panel of this figure with those presented in Fig. 8 highlights the similarity between the optical depth maps derived for the narrow component and for the line integrated analysis. To our knowledge, this is the first empirical evidence supporting the traditional assumption that movements in extragalactic H ii regions with a known outflow have a negligible effect in the estimation of the global optical depth.
(17)The structure of the derived optical depth for both the narrow and the broad components is shown in Fig. 14 and several conclusions can be drawn from this figure. Firstly, a comparison between the left panel of this figure with those presented in Fig. 8 highlights the similarity between the optical depth maps derived for the narrow component and for the line integrated analysis. To our knowledge, this is the first empirical evidence supporting the traditional assumption that movements in extragalactic H ii regions with a known outflow have a negligible effect in the estimation of the global optical depth.
Secondly, a comparison between the two maps in Fig. 14 shows how the structure of the two τ(3889) is different: whilst the narrow component τ(3889) displays a clear peak associated with the peak of emission for the GH iiR and decreases outwards, the broad component remains relatively high over a large area of ~4′′ × 2′′ (~74 pc × 37 pc) centred on the double cluster.
 |
Fig. 14 τ(3889) for the two main kinematic components presented in Fig. 19 of Paper I derived from the fits to relations presented by Robbins (1968) for Te = 10 000 K. Left: narrow kinematic component and ω = 0. Right: broad kinematic component and ω = 3. The τ(3889) map for this component using the relation for ω = 0 (not shown) displays the same structure but with values ~4–6 times lower. |
Thirdly, the comparison between the specific values displayed in these two graphics shows that the broad component suffers from radiative transfer effects to a higher degree than the narrow one. This is a consequence of the adopted relation between fτ(7065) and τ(3889), which is motivated by our kinematic results. If we had used Eq. (5) (i.e. assuming ω = 0 for the broad component), we would have obtained comparable values for the τ(3889) in both components (although, still, with a different structure since this is determined by the fτ(7065) itself, which in turns depends on the relative flux between He iλ6678 and He iλ7065).
There is certainly room for improvement in this analysis. For example, although the multicomponent analysis treats in a consistent way the line profiles of He iλ6678 and He iλ7065, the same physical conditions (i.e. Te, ne, extinction) had to be assumed for both components. Moreover, we used here only two helium lines, in contrast with the more canonical methodology for determining helium abundances based in a larger set of helium lines. These improvements suggest a new approach to the study of the helium content in galaxies with IFS. Specifically, the 2D analysis presented in the previous sections together with the separate analysis of different kinematic components along the line of sight (i.e. in a given spaxel) constitute a 3D view of the radiative transfer effects in the nebula.
4.2. Relation between collisional and radiative transfer effects and other properties of the ionised gas
We have evaluated locally both collisional and radiative transfer effects in the helium lines, as well as several important physical conditions (ne, Te, excitation) and chemical properties (i.e. relative abundance N/O) of the ionised gas. Therefore, the central part of NGC 5253 constitutes a good case study to explore whether there is a (strong) spatial relation of collisional and/or radiative transfer effects with other gas properties.
As discussed in Sect. 3.1, theory predicts a strong dependence of the collisional effects on ne and, to a lesser extent, on Te. This implies a strong spatial correlation with the these properties. Indeed, when all the spaxels in the area under study are considered, the relations between C/R(λ7065) vs. ne and Te have Pearson’s correlation coefficients of 0.99 and 0.71, respectively. Regarding the other two properties, Fig. 15 presents the relation between the collisional effects (as traced by C/R(7065)) and the excitation (as traced by [O iii]λ5007/Hβ) and the relative abundance of nitrogen: N/O. The excitation presents a degree of correlation similar to ne. The correlation for N/O is not as strong as that for ne but still comparable to that for Te.
 |
Fig. 15 Relation between collisional effects as traced by the C/R ratio for the λ7065 line and the excitation (left) and relative abundance of nitrogen, N/O (right). The Pearson’s correlation coefficients are indicated in the corners of the individual plots. |
 |
Fig. 16 Relation between the self-absorption effects as traced by τ(3889) and different physical and chemical properties in NGC 5253. From left to right and from top to bottom, these are electron density and temperature, excitation and relative abundance of nitrogen, N/O. The correlation coefficients are indicated in the corners of the individual plots. |
Likewise, Fig. 16 shows the relation between radiative transfer effects, as traced by τ(3889) and different properties of the gas. As expected, there is a good correlation with ne. For Te lower than ~10 700 K, He i emission lines do not suffer from radiative transfer effects in a significant way. However, above this threshold there is a clear correlation between the temperature and the relevance of the radiative transfer effects.
More interestingly, as happened with the collisional effects, there is a good correlation between the excitation and the relevance of radiative transfer effects (lower left panel in Fig. 16). It is not clear why the excitation should correlate with the contribution of collisional effects (mainly) or the radiative transfer effects (to a lesser extent).
Something similar occurs with the relative abundance, N/O. At the typical log (N/O) values for this galaxy (≲− 1.3), He i radiative transfer effects appear to be negligible. However, those locations displaying extra nitrogen appear to show significant radiative transfer effects. Rather than a discernible correlation between individual spaxels, there appears a correlation between the upper limit to the contribution of the radiative transfer effects and the amount of extra nitrogen. To our knowledge, there is no reason to link these two properties from the theoretical point of view. The fact that both the relations with Te and N/O present bimodal behaviour (i.e. with “turning points”), and that there is a similar structure for the electron temperature and relative abundance (Paper II), implying a good correlation (i.e. r = 0.91) between Te and N/O, points towards the local electron temperature as a common cause.
5. Conclusions
This is the fourth in a series of articles that make use of IFS-based data to study in detail the 2D physical and chemical properties of the gas in the main GH iiR of the nearby BCD NGC 5253. The main goal of this article was to estimate the contribution of the collisional and radiative transfer effects on the helium emission lines and to map, in turn, the helium abundance. The major conclusions can be summarised as follows:
-
1.
The collisional effects on the different helium transitions havebeen mapped for the first time in an extragalactic object. Asexpected, they reproduce the ne structure. They are negligible (i.e.~0.1–0.6%) for transitions in the singlet cascade whilst relativelyimportant for those transitions in the triplet cascade. In particular,they can contribute up to 20% of the flux in theHe iλ7065 line.
-
2.
The contribution of the collisional effects is sensitive to the assumed Te for helium. Specifically, we found differences ~25–35% for the λ3889 and λ7065 lines two reasonable assumptions for the Te sensitivity. Relative differences for the other lines were larger. However, this does not have important consequences since the contribution of the collisional effect to the observed spectrum for these lines is negligible.
-
3.
We present a map for the optical depth at λ3889 in the main GH iiR of NGC 5253. τ(3889) is elevated over an extended and circular area of ~30 pc in diametre, centred on the SSC(s), where it reaches its maximum.
-
4.
The singly ionised helium abundance, y+, has been mapped using extinction-corrected fluxes of six He i lines, realistic assumptions for Te, ne, and the stellar absorption equivalent width as well as the most recent emissivities. We found a mean(±standard deviation) of 103y+ ~ 80.3( ± 2.7) over the mapped area.
-
5.
We derived total helium abundance maps using three possible icf(He)’s. The relation between the excitation and the total helium abundances is consistent with no abundance gradient. Differences between the derived total abundances according to the three methods are larger than statistical errors associated with the data themselves, emphasising how uncertainties in the derivation of helium abundances are dominated by the adopted assumptions.
-
6.
We illustrated the difficulty of detecting a putative helium enrichment owing to the presence of WR stars in the main GH iiR. This is due to the comparatively large amount of preexisting helium. The data are marginally consistent with an excess in the N/He ratio in the nitrogen-enriched area similar to the atmospheric N/He ratios in WR stars. However, this excess is also of the same order of the uncertainty estimated for the N/He ratios in the nitrogen enriched and non-enriched areas.
-
7.
We explored the influence of the kinematics on the evaluation of the He i radiative transfer effects. Our data empirically support the use of the traditional assumption that motions in an extragalactic H ii region have a negligible effect on the estimation of the global optical depths. However, individually, the broad kinematic component (associated with an outflow) is affected by radiative transfer effects in a much more significant way than the narrow one.
-
8.
The local relationships between the contribution of collisional and radiative transfer effects to the helium lines and different physical and chemical properties of the gas have been explored. Interestingly, we found a relation between the amount of extra nitrogen and the upper limit of the contribution from radiative transfer effects that requires further investigation. We suggest that the electron temperature could be a common agent causing this relation.
Acknowledgments
We are very grateful to the referee for the careful and diligent reading of the manuscript as well as for the useful comments that helped us to clarify and improve the first submitted version of this paper. Also, we thank R. L. Porter for advice on use of his tabulated He i emissivities and for so promptly informing us of the Corrigendum. Based on observations carried out at the European Southern Observatory, Paranal (Chile), programmes 078.B-0043(A) and 383.B-0043(A). This paper uses the plotting package jmaplot, developed by Jesús Maíz-Apellániz, http://dae45.iaa.csic.es:8080/~jmaiz/software. This research made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. A.M.-I. is supported by the Spanish Research Council within the program JAE-Doc, Junta para la Ampliación de Estudios, co-funded by the FSE. A.M.-I. is also grateful to ESO – Garching, where part of this work was carried out, for their hospitality and funding via their visitor program. This work has been partially funded by the Spanish PNAYA, project AYA2010-21887 of the Spanish MINECO. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (/FP7/2007-2013/) under grant agreement No 229517.
References
- Allington-Smith, J., Murray, G., Content, R., et al. 2002, PASP, 114, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Takagi, T., Baker, A. J., et al. 2004, ApJ, 612, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., García-Marín, M., Rodríguez Zaurín, J., et al. 2010, A&A, 522, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aver, E., Olive, K. A., & Skillman, E. D. 2010, J. Cosmology Astropart. Phys., 5, 3 [Google Scholar]
- Beck, S. C., Lacy, J. H., Turner, J. L., et al. 2012, ApJ, 755, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Skillman, E. D., & Smits, D. P. 1999, ApJ, 514, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Schoenell, W., Gomes, J. M., et al. 2009, in Rev. Mex. Astron. Astrofis., 35, 127 [Google Scholar]
- Ferland, G. J. 1980, MNRAS, 191, 243 [NASA ADS] [Google Scholar]
- Fluks, M. A., Plez, B., The, P. S., et al. 1994, A&AS, 105, 311 [NASA ADS] [Google Scholar]
- Fukugita, M., & Kawasaki, M. 2006, ApJ, 646, 691 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, R. M., Cerviño, M., Martins, L. P., Leitherer, C., & Hauschildt, P. H. 2005, MNRAS, 357, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gruenwald, R., Steigman, G., & Viegas, S. M. 2002, ApJ, 567, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Harbeck, D., Gallagher, J., & Crnojević, D. 2012, MNRAS, 422, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., Calzetti, D., Gallagher, III, J. S., Smith, D. A., & Conselice, C. J. 2004, ApJ, 603, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2010, ApJ, 710, L67 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Tully, R. B., Dolphin, A., et al. 2007, AJ, 133, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., Skillman, E. D., Roy, J.-R., Walsh, J. R., & Rosa, M. R. 1997, ApJ, 477, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Sargent, W. L. W. 1983, ApJ, 273, 81 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, Á. R., Esteban, C., García-Rojas, J., Peimbert, M., & Rodríguez, M. 2007, ApJ, 656, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Luridiana, V. 2009, Ap&SS, 324, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in ASP Conf. Ser. 411, eds. D. A. Bohlender, D. Durand, & P. Dowler, 251 [Google Scholar]
- Martins, L. P., González Delgado, R. M., Leitherer, C., Cerviño, M., & Hauschildt, P. 2005, MNRAS, 358, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Monreal-Ibero, A., Vílchez, J. M., Walsh, J. R., & Muñoz-Tuñón, C. 2010, A&A, 517, A27 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monreal-Ibero, A., Walsh, J. R., & Vílchez, J. M. 2012, A&A, 544, A60 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olive, K. A., & Skillman, E. D. 2001, New A, 6, 119 [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei [Google Scholar]
- Pagel, B. E. J., Terlevich, R. J., & Melnick, J. 1986, PASP, 98, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Ávila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Peimbert, M., & Torres-Peimbert, S. 1976, ApJ, 203, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., & Torres-Peimbert, S. 1977, MNRAS, 179, 217 [NASA ADS] [Google Scholar]
- Peimbert, A., Peimbert, M., & Luridiana, V. 2002, ApJ, 565, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Luridiana, V., & Peimbert, A. 2007, ApJ, 666, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, R. L., Ferland, G. J., & MacAdam, K. B. 2007, ApJ, 657, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, R. L., Ferland, G. J., Storey, P. J., & Detisch, M. J. 2012, MNRAS, L487 [Google Scholar]
- Porter, R. L., Ferland, G. J., Storey, P. J., & Detisch, M. J. 2013, MNRAS, accepted [arXiv:1303.5115] [Google Scholar]
- Robbins, R. R. 1968, ApJ, 151, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, S., Ferrarese, L., Kennicutt, Jr., R. C., & Saha, A. 2004, ApJ, 608, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Sauer, D., & Jedamzik, K. 2002, A&A, 381, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shields, J. C. 1993, ApJ, 419, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Sidoli, F. 2010, Ph.D. Thesis, University of London, UK [Google Scholar]
- Smith, L. J., & Willis, A. J. 1982, MNRAS, 201, 451 [NASA ADS] [Google Scholar]
- Storey, P. J., & Hummer, D. G. 1995, MNRAS, 272, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., Beck, S. C., & Ho, P. T. P. 2000, ApJ, 532, L109 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Viegas, S. M., Gruenwald, R., & Steigman, G. 2000, ApJ, 531, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. R., & Roy, J.-R. 1989, MNRAS, 239, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Westmoquette, M. S., James, B., Monreal-Ibero, A., & Walsh, J. R. 2013, A&A, 550, A88 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y., Liu, X.-W., Liu, Y., & Rubin, R. H. 2005, MNRAS, 358, 457 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: false colour image in filters F658N (Hα, cyan channel), F550M (V, yellow channel), and F814W (I, magenta channel) for the central part of NGC 5253 using the HST-ACS images (programme 10608, P.I.: Vacca). The area studied here is marked with a black rectangle. Right: ionised gas distribution as traced by the extinction-corrected Hβ map derived from a portion of the original FLAMES data. The position of the two main peaks of continuum emission are marked with crosses. The map is presented in logarithmic scale in order to emphasize the relevant morphological features and cover a range of 2.0 dex. Flux units are arbitrary. Note the existence of three dead spaxels at |
| In the text | |
 |
Fig. 2 Extinction-corrected flux maps normalized to Hβ for the lines utilized in this work. The position of the two main peaks of continuum emission are marked with crosses in this and all subsequent maps. We marked in white the areas where a given line was not observed. Specifically, for the He iλ6678, He iλ4922 and He iλ7065, they correspond to dead fibres. For He iλ5876, He iλ4471 and He iλ3889, these areas were not covered by the corresponding GMOS or FLAMES-Argus field of view. |
| In the text | |
 |
Fig. 3 Collisional effects as traced by the C/R ratio for the He i lines utilized in this work. Note that a common scale was used for all the lines in order to facilitate comparison of the relative effects between the different lines. Also, a logarithmic colour stretch is used to emphasize the variations within the region for a given line. |
| In the text | |
 |
Fig. 4 Maps for the ratio between the C/R factors derived for two assumptions of the Te(He i): |
| In the text | |
 |
Fig. 5 Fitted functions to the Porter et al. (2013) emissivities. The black lines are the functions for ne = 100 cm-3 (continuous line) and for ne = 1000 cm-3 (long dashed line). The intermediate short dashed lines represent the interpolated emissivities for log (ne) = 2.2,2.4,2.6,2.8. Discrete values listed by Porter et al. (2013) are overplotted with blue triangles (log (ne) = 2) and orange circles (log (ne) = 3). |
| In the text | |
 |
Fig. 6 Maps of the correction factor due to a component in absorption in the He i lines. Different scales were utilized in the different maps to emphasize the structure. The corresponding map for the Hβ correction factor (not shown) is similar to those for λ6678 and λ7065. |
| In the text | |
 |
Fig. 7 Maps for y+ derived from lines of the singlet cascade for the blue (left) and red (right) sets. A common scale was used in both maps to facilitate comparison between them. |
| In the text | |
 |
Fig. 8 Maps for τ(3889) as derived from the λ4922 and λ3889 (left) and the λ6678 and λ7065 (right) emission lines. |
| In the text | |
 |
Fig. 9 Final map for y+ derived from a weighted average of those derived for the lines in the blue and red sets. Note we used a different scale than in Fig. 7 to increase the contrast and emphasize the structure following the excitation structure. Instead, the scale is common with that in the right column of Fig. 12 to make easier the comparison between total and ionic helium abundances. |
| In the text | |
 |
Fig. 10 He+ abundance vs. [O iii]λ5007/Hβ. The first-degree polynomial fit is shown with a black line. The 1-σ and 3-σ levels are marked with thick and thin red lines respectively. Mean and standard deviation of each 0.05 dex bin in log ([O iii]λ5007/Hβ) are shown with blue diamonds and error bars respectively. The green horizontal dashed line shows the mean value. Data points corresponding to spaxels with log (N/O) > − 1.3 have been marked with orange circles. |
| In the text | |
 |
Fig. 11 Maps for the ionic abundances utilized in the derivation of the ionization correction factors. Left: O+/H+. Right: S+/H+ |
| In the text | |
 |
Fig. 12 Left: maps for the icf(He) as estimated from the expressions proposed by Kunth & Sargent (1983, top, Peimbert & Torres-Peimbert (1977, centre and assuming no gradient in helium abundance bottom. Right: corresponding helium abundance maps. |
| In the text | |
 |
Fig. 13 Helium abundance as derived using the icf(He) proposed by Kunth & Sargent (1983, top, Peimbert & Torres-Peimbert (1977, centre and assuming no gradient in helium abundance (bottom) vs. [O iii]λ5007/Hβ. Symbol and colour codes are as in Fig. 10. |
| In the text | |
 |
Fig. 14 τ(3889) for the two main kinematic components presented in Fig. 19 of Paper I derived from the fits to relations presented by Robbins (1968) for Te = 10 000 K. Left: narrow kinematic component and ω = 0. Right: broad kinematic component and ω = 3. The τ(3889) map for this component using the relation for ω = 0 (not shown) displays the same structure but with values ~4–6 times lower. |
| In the text | |
 |
Fig. 15 Relation between collisional effects as traced by the C/R ratio for the λ7065 line and the excitation (left) and relative abundance of nitrogen, N/O (right). The Pearson’s correlation coefficients are indicated in the corners of the individual plots. |
| In the text | |
 |
Fig. 16 Relation between the self-absorption effects as traced by τ(3889) and different physical and chemical properties in NGC 5253. From left to right and from top to bottom, these are electron density and temperature, excitation and relative abundance of nitrogen, N/O. The correlation coefficients are indicated in the corners of the individual plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{${\sim}[5\farcs0,-1\farcs0]$}](/articles/aa/full_html/2013/05/aa21387-13/aa21387-13-eq28.png)