| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 32 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220948 | |
| Published online | 23 April 2013 | |
Chemical enrichment and physical conditions in I Zw 18⋆
1
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot DAPNIA/Service
d’Astrophysique, Bât. 709, CEA-Saclay,
91191
Gif-sur-Yvette Cedex,
France
e-mail:
vianney.lebouteiller@cea.fr
2
Laboratory of Astronomy and Solar Physics,
NASA Goddard Space Flight
Center, Greenbelt,
MD
20771,
USA
3
Department of Astronomy and Steward Observatory, University of
Arizona, Tucson,
AZ
85721,
USA
4
Institut d’Astrophysique, Paris, 98bis boulevard Arago, 75014
Paris,
France
Received:
18
December
2012
Accepted:
4
February
2013
Context. Low-metallicity star-forming dwarf galaxies are prime targets to understand the chemical enrichment of the interstellar medium. The H i region contains the bulk of the mass in blue compact dwarfs, and it provides important constraints on the dispersal and mixing of heavy elements released by successive star-formation episodes. The metallicity of the H i region is also a critical parameter to investigate the future star-formation history, as metals provide most of the gas cooling that will facilitate and sustain star formation.
Aims. Our primary objective is to study the enrichment of the H i region and the interplay between star-formation history and metallicity evolution. Our secondary objective is to constrain the spatial- and time-scales over which the H i and H ii regions are enriched, and the mass range of stars responsible for the heavy element production. Finally, we aim to examine the gas heating and cooling mechanisms in the H i region.
Methods. We observed the most metal-poor star-forming galaxy in the Local Universe, I Zw 18, with the Cosmic Origin Spectrograph onboard Hubble. The abundances in the neutral gas are derived from far-ultraviolet absorption-lines (H i, C ii, C ii*, N i, O i, ...) and are compared to the abundances in the H ii region. Models are constructed to calculate the ionization structure and the thermal processes. We investigate the gas cooling in the H i region through physical diagnostics drawn from the fine-structure level of C+.
Results. We find that H i region abundances are lower by a factor of ~2 as compared to the H ii region. There is no differential depletion on dust between the H i and H ii region. Using sulfur as a metallicity tracer, we calculate a metallicity of 1/46 Z⊙ (vs. 1/31 Z⊙ in the H ii region). From the study of the C/O, [O/Fe], and N/O abundance ratios, we propose that C, N, O, and Fe are mainly produced in massive stars. We argue that the H i envelope may contain pockets of pristine gas with a metallicity essentially null. Finally, we derive the physical conditions in the H i region by investigating the C ii* absorption line. The cooling rate derived from C ii* is consistent with collisions with H0 atoms in the diffuse neutral gas. We calculate the star-formation rate from the C ii* cooling rate assuming that photoelectric effect on dust is the dominant gas heating mechanism. Our determination is in good agreement with the values in the literature if we assume a low dust-to-gas ratio (~2000 times lower than the Milky Way value).
Key words: galaxies: abundances / HII regions / galaxies: individual: I Zw 18 / galaxies: ISM / galaxies: star formation / galaxies: evolution
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Numerical simulations by Cen & Ostriker (1999), predicting the evolution of the metal content of the Universe, show that metallicity is a stronger function of density than age. It is therefore plausible that gas-rich dwarf galaxies in the Local Universe may remain in an early stage of chemical enrichment, possibly preserving pockets of pristine gas (Kunth & Sargent 1986; Kunth et al. 1994). Blue compact dwarf (BCD) galaxies represent a major testbed as they include the most-metal poor star-forming galaxies known (Kunth & Östlin 2000). Among these, I Zw 18 (Mrk 116) continues to attract considerable interest and to feed intense debates in extragalactic research. For more than three decades, I Zw 18, discovered by Zwicky (1966) and first studied by Sargent & Searle (1970) held the record as the most metal-deficient galaxy known, with an oxygen abundance 12 + log (O/H) = 7.17 ± 0.011 in its NW component and 7.22 ± 0.02 in its SE component (Izotov et al. 1999). Only recently has it been displaced by two more metal-deficient BCDs, SBS 0335–052W with 12 + log (O/H) = 7.12 ± 0.03 (Izotov et al. 2005) and DDO 68 with 12 + log (O/H) = 7.14 ± 0.03 (Izotov & Thuan 2007).
It was postulated that the difficulty of finding more metal-poor objects could be explained by thorough local mixing of the metals produced and released over a single starburst episode (Kunth & Sargent 1986). This hypothesis, implying the existence of quasi-pristine gas beforehand, has been since challenged by observations of uniform abundances in disconnected star-forming regions within a single dwarf galaxy (e.g., Skillman & Kennicutt 1993; Kobulnicky & Skillman 1997; Noeske et al. 2000). Although evidence of local metal enrichment has already been observed (e.g., Walsh & Roy 1993), it is usually associated with the presence of Wolf-Rayet (WR) stars (Walsh & Roy 1989; Thuan et al. 1996; Lopez Sanchez et al. 2007). This hypothesis was later confirmed by Brinchmann et al. (2008), with the study of a large sample of WR galaxies from the Sloan Digital Sky Survey.
Chemical abundances and metallicity are key parameters for the evolution of galaxies. Abundances in BCDs are usually probed in the ionized gas of the H ii regions, as derived from optical emission-lines. While H ii regions correspond to the present star-formation episode, they can also be related to previous episodes via the triggered star-formation mechanism, in which star formation take place following compression of molecular clouds by massive stellar winds and supernovae (e.g., Vanhala & Cameron 1998; Bhattal et al. 1998; Fukuda & Hanawa 2000; Pustilnik et al. 2001; Lee & Chen 2007; Elmegreen 2011). H ii regions represent however a small fraction of the galaxy in mass as compared to the surrounding H i region (Thuan & Martin 1981).
The H i region provides another way of measuring the metallicity, which accounts for the bulk of the mass of a galaxy. The H i region sets a reference abundance pattern, caused by metal enrichment over long time scales and large spatial scales, that needs to be understood and constrained. With this in mind, the comparison of abundances between the H i region and the H ii regions allows us to examine the dispersal and mixing of heavy elements from recent starburst episodes, and to constrain stellar evolution models. Furthermore, since future star formation thrives on the H i gas reservoir, the H i region makes it possible to study the interplay between star-formation history and metallicity. While past and present star-formation episodes enrich the interstellar medium (ISM) in heavy elements, the latter are, in turn, able to facilitate and sustain star-formation through several gas cooling mechanisms (e.g., [C ii] 157 μm, CO, and dust radiative cooling). The main questions that drive the studies of the H i region in BCDs are the following. (1) What mechanisms control the H i region metallicity? (2) What is the influence of metallicity on the star-formation history?
BCDs are ideal targets because they display large amounts of H i gas (Thuan & Martin 1981) and because the massive stars provide a strong far-ultraviolet (FUV) continuum on which absorption-lines from neutral species located along the line of sight are superimposed. Kunth et al. (1994) used the GHRS instrument on board the Hubble Space Telescope (HST) to observe interstellar absorption lines toward the many massive stars in I Zw 18. The authors detected the O i line at 1302.2 Å and, together with the neutral hydrogen content measured from the 21 cm line, they estimated the metallicity of the neutral envelope to be at least 10 times lower than that of the ionized gas in the H ii regions. Later, Thuan et al. (1997) obtained a GHRS spectrum for SBS 0335–052E and found the metallicity of the neutral gas to be similar to that of the ionized gas. These results remained however inconclusive because of possible saturation effects of the O i absorption line (Pettini & Lipman 1995).
A further step forward was then achieved with the launch of the Far Ultraviolet Spectroscopic Explorer (FUSE; Moos et al. 2000), which allowed the observation of H i absorption-lines together with many metallic species such as N i, O i, Si ii, P ii, Ar i, and Fe ii. The spectral resolution of FUSE (λ / Δλ ~ 20 000) and its sensitivity made it possible to detect numerous absorption-lines, some of them apparently not saturated. The neutral gas chemical composition was derived in several BCDs, spanning a wide range in ionized gas metallicity, from 1/30 to 1/3 Z⊙, with I Zw 18 (Aloisi et al. 2003, hereafter A03; Lecavelier des Etangs et al. 2004, hereafter L04), SBS 0335–052 (Thuan et al. 2005), I Zw 36 (Lebouteiller et al. 2004), Pox 36 (Lebouteiller et al. 2009), Mark 59 (Thuan et al. 2002), NGC 625 (Cannon et al. 2005), and NGC 1705 (Heckman et al. 2001; Lee & Skillman 2004). These investigations showed that the neutral gas of BCDs is not pristine; it has already been enriched with metals, with a minimal metallicity of ~1/50 Z⊙ (see the FUSE sample analysis in Lebouteiller et al. 2009). The second most important result is that the metallicity of the neutral gas is generally lower than that of the ionized gas − except for the two lowest-metallicity BCDs, I Zw 18 and SBS 0335–052E − implying that the H i region has been probably less processed than the H ii region.
However the interpretation of these results has been limited by the lack of constraints on the properties of the gas detected in absorption in the FUV (physical location along the line of sight, density structure, temperature). FUV observations select out dust-free lines of sight toward the massive stars, and the intervening gas might have peculiar properties as compared to the global ISM. Uncertainties also remain in deriving column densities from absorption-lines in complex systems. Most FUSE studies of BCDs assumed a single absorption component arising from a single homogeneous line of sight with the exception of Mark 59 (Thuan et al. 2002; see also Lebouteiller et al. 2006 for the giant H ii region NGC 604 in M 33). A more realistic approach would be to consider multiple lines of sight toward massive stars, each line of sight intersecting clouds with possibly different physical conditions (such as turbulent and radial velocity) and chemical properties. Whenever individual absorption components are unresolved, it is almost impossible to tell whether they are saturated, in which case the column density inferred from the global absorption line can be severely underestimated (see e.g., Lebouteiller et al. 2006). Following the suggestion of Kunth & Sargent (1986), Bowen et al. (2005) got around the problem by deriving the abundances in the neutral gas of the dwarf spiral galaxy SBS 1543+593 along a quasar line of sight. The authors found that the abundances agree with those in the ionized gas of the brightest H ii region in the arms, contrasting with the FUSE results in BCDs.
With the advent of the HST/Cosmic Origins Spectrograph (COS; Green et al. 2011) we have the opportunity to look anew at the problem of
the chemical discontinuity between the ionized and neutral gas in BCDs, with in particular
the observation of the S ii multiplet, which Pettini & Lipman (1995) have proposed as a tracer of the neutral gas
enrichment. The cornerstone galaxy I Zw 18 is therefore once again put to the test, not only
because of its extremely low metallicity content. As it turns out this object has led to
discordant analysis of the same dataset obtained with FUSE by two independent groups of
scientists. A03 used an individual line fitting method and found abundances globally lower
in the neutral gas as compared to the ionized gas, while L04 find no significant difference
between the two phases. L04 find O i/H i =
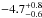 ,
which is consistent with the O/H ratio observed in the H ii regions (−4.83 ± 0.03;
Izotov et al. 1999), while A03 report a
significantly different value with O i/H i = −5.4 ± 0.3, a discrepancy
with the former result that awaits clarification. This is indeed worrisome since this object
has also a considerable weight in the study of depletion and that of a possible threshold
for chemical enrichment. Most importantly, the discrepancy between the observational results
complicates the interpretation of chemical evolution models. Recchi et al. (2004) found that abundances in the H i medium
(defined by a temperature lower than 7000 K) should be similar to those in the H ii
gas. A definitive observational constraint is needed to challenge the models.
,
which is consistent with the O/H ratio observed in the H ii regions (−4.83 ± 0.03;
Izotov et al. 1999), while A03 report a
significantly different value with O i/H i = −5.4 ± 0.3, a discrepancy
with the former result that awaits clarification. This is indeed worrisome since this object
has also a considerable weight in the study of depletion and that of a possible threshold
for chemical enrichment. Most importantly, the discrepancy between the observational results
complicates the interpretation of chemical evolution models. Recchi et al. (2004) found that abundances in the H i medium
(defined by a temperature lower than 7000 K) should be similar to those in the H ii
gas. A definitive observational constraint is needed to challenge the models.
While providing accurate measurements of chemical abundances in the neutral gas, the COS observations also shed a new light on the physical conditions and thermal processes in the H i region. The absorption line C ii* λ1335.7, arising from the fine-structure level of C+, is intimately related to the far-IR cooling line [C ii] 157 μm that was recently detected in I Zw 18 with the Herschel Space Telescope (Lebouteiller et al., in prep.). We investigate in the present study the heating and cooling mechanisms in the H i region in order to understand the present and future star-formation history of the galaxy.
Our study is organized as follows. We present the observations in Sect. 2. Column densities are determined in Sect. 3. After the description of the nebular models in Sect. 4, we examine the physical conditions in the H i region in Sect. 5. We then derive and interpret elementary abundances in Sect. 6. Finally, we discuss chemical evolution scenarios in Sect. 7.
2. Observations and data processing
2.1. Datasets
 |
Fig. 1 HST/ACS image of I Zw 18 (main body), with RBG colors defined as I, V, and B filters. Images were downloaded from the Hubble Legacy Archive (http://hla.stsci.edu/) and later combined. The green contours show the H i column density distribution from Lelli et al. (2012) with 2′′ resolution (beam size in the bottom left). Contours are drawn for 3 (dashed), 6, 9, 12, and 15 × 1021 cm-2. The COS observation, represented by the black circle (2.5″ diameter), is centered on the NW star cluster. |
To first approximation, I Zw 18 is composed of two young, massive star clusters, NW and SE, which ionize the surrounding medium. We used COS on the HST to observe the brightest region in the FUV, NW, in April 2010 (program 11 523) and later in December 2010 (program 12 028). Both observations were made with the circular aperture, with a diameter D ~ 2.5″, corresponding to ~230 pc at the distance of I Zw 18 (≈19 Mpc; Aloisi et al. 2007). Observations were centered on NW (see Fig. 1 and the observation log in Table 1). Target acquisition consisted of a slew to the specified coordinates of NW followed by a peak-up in ultraviolet light. Although both observing programs made use of the FUV gratings G130M and G160M, the two sets of exposures cover somewhat different wavelength range. Together, they span ~1135–1760 Å. We also use the archival dataset from program 11 579 which observed with the G130M grating (~1132–1433 Å). No peak-up was performed for the latter observation and the telescope was slewed to the requested coordinates of NW. The G185M spectrum was not used because of the low data quality2.
COS datasets.
 |
Fig. 2 Processing of the observed spectrum a) consists of correcting for reddening and for Lyα absorption in the Milky Way and in the high-velocity cloud b); fitting and removing Lyα from I Zw 18 c); and normalizing the spectrum d). The residual emission at Lyα wavelength is due to geocoronal H i. |
The pipeline reduction procedure is continually being improved, and we obtained our spectra well after the observations were made (July 2011) from the Hubble Data Archive, which makes an “on-the-fly” reduction using the best calibrations available. We combined exposures from a given program to form a single, co-added spectrum. We did not merge the spectra from the three programs because the pointing was slightly different. This results in differences in the spectra, with for instance the C ivλ1548, λ1550 doublet, which is formed in stellar winds and in the H ii region.
Among the 3 available datasets, the 11 579 observation has the longest exposure time below ~1433 Å, while the 12 028 observation has the longest exposure time above (Table 1). The 12 028 observations should be superior to the 11 523 observations by virtue of their longer exposure times. Indeed, the higher signal-to-noise ratio (S/N) in the 12 028 spectra enabled us to discern broad, shallow stellar absorption lines that we had not detected before in the other datasets. Also, the 12 028 observations were accomplished in a single 5-orbit visit, so we are assured of a constant telescope pointing throughout the visit, whereas in program 11 523, the G130M exposures and G160M exposures were obtained in different visits.
In some exposures, geocoronal emission (in particular from the O i 1302,1305,1306 Å multiplet) is contaminating the interstellar line profiles. We ignored the corresponding exposures for the wavelength range around the geocoronal emission.
As a preparation for the fitting of the interstellar lines, we prepared each COS spectrum in several steps as illustrated in Fig. 2. In the four steps, we:
-
Corrected the observed spectrum for foreground Galactic extinction by dust, using the color excess E(B − V) = 0.032 (Schlegel et al. 1998). This correction is used for the normalization by the stellar model (see below);
-
Corrected for Lyα absorption in the galaxy and for Lyα absorption by the high-velocity cloud in the line of sight to I Zw 18, following Kunth et al. (1994);
-
Measured the column density of Lyα in I Zw 18 and removed Lyα (Sect. 3.4);
-
Normalized by the stellar spectrum (continuum and absorption in photospheres; Sect. 2.2). Figure 3 shows the spectra along with the normalized stellar model. Final spectra are shown in the Appendix.
 |
Fig. 3 COS spectra of I Zw 18. The Lyα absorption (from I Zw 18, the Milky Way, and the high-velocity cloud) was removed and the flux was normalized to the local continuum. The numerous absorption features often come in pairs: the weaker − redshifted − absorption feature is from I Zw 18; the stronger feature arises in the Galaxy. A non-LTE, photospheric model spectrum (no winds) of the stellar population (10 Myr age with a continuous star formation hypothesis) and log (Z / Z⊙) = −1.7 is shown in blue. While many features such as C iiiλ1175 and the Si ivλ1400 doublet appear to be well matched by the stellar model, other high-ionization features such as He iiλ1640 and the C ivλ1549 doublet are not well matched. The origin of these lines (e.g., WR stars, H ii region...) is unclear. |
2.2. Contamination by stellar absorption
The FUV spectrum of I Zw 18 is clearly composite, with contributions from stars, H ii region, and H i region. Absorption in stellar photospheres needs to be removed since they may contaminate interstellar absorption-lines. We calculated model spectra of young stellar populations using grids of high-resolution (0.2 Å) non-LTE photospheric spectra (900–2000 Å) by Lanz & Hubeny (2003, 2007) and Geneva evolutionary tracks (Lejeune & Schaerer 2001).
High-resolution imaging studies (Hunter & Thronson 1995; Heap et al. 2013) indicate that I Zw 18 is undergoing continuous star formation rather than an instantaneous burst. Also, it is clear from deep HST/ACS observations that I Zw 18 has a widely extended, older stellar population (Aloisi et al. 2007; Contreras Ramos et al. 2011). However, it is equally clear that young, massive stars are the dominant contributors to the UV flux of the NW component. Observations of individual stars in I Zw 18 with WFC2 (Hunter & Thronson 1995) and STIS (Brown et al. 2002; Heap et al. 2013) on HST indicate that the NW massive star cluster has a range of ages. The brightest stars in the UV are also the youngest, and their inferred masses range up to 150 M⊙. We therefore assumed continuous star formation and a Salpeter initial mass function with lower and upper mass limits, 1–150 M⊙, to calculate the spectrum of the stellar population for ages (i.e., the duration of star formation up until now) ranging from 0 to 100 Myr. We then convolved each calculated spectrum with a rotational broadening function (vsini = 150 km s-1) and with the instrumental function (Sect. 3.2). From a comparison of these models to photospheric lines in the COS spectrum, we derive a continuous-star-formation age of 10–15 Myr and a stellar metallicity log (Z / Z⊙) ~ −1.7.
Using the age and metallicity derived above, we calculated the overall spectral energy distribution (SED) of stars in the NW component using the grids of low-resolution, LTE spectra by Castelli & Kurucz (2003). This grid and the TLUSTY/synspec grid only cover effective temperatures up to 50 000 K, somewhat lower than the highest temperatures of massive stars on the zero-age main sequence (65 000 K), and definitely lower than highly evolved stars such as WR stars. It is therefore likely that our model SED underestimates the ionizing flux of the stellar population.
Figure 3 shows the stellar models overplotted on each dataset. We find that the contamination from stellar lines is negligible for most of the interstellar lines from I Zw 18 and also from the local absorption systems (Sect. 3.1). One exception is the contamination of S iiλ1250.6 in the Milky Way by the stellar C iii line. The stellar model was used to normalize the observed spectrum so as to isolate the purely interstellar absorption.
3. Column density determination
3.1. Method
Once the spectrum has been corrected for stellar absorption (Sect. 2.2), several interstellar absorption line systems can be distinguished along the line of sight to the massive stars in I Zw 18 (Table 2). The main interstellar lines are listed in Table 3. The atomic data, in particular the oscillator strength values, were taken from Morton (2003), except for P ii and S ii for which we used Federman et al. (2007) and Podobedova et al. (2009) respectively. The I Zw 18 component is visible at a velocity of ≈755 km s-1. Two local components are required at ≈−10 km s-1 and ≈−90 km s-1. In addition, a component at ≈−60 km s-1 is detected that corresponds to ionized species in the Milky Way. Finally, the high-velocity cloud “A vi” in complex A is detected at ≈−171 km s-1 (Hulsbosch & Wakker 1988; Wakker & van Woerden 1997).
Absorption systems.
Main interstellar lines used in this study.
Radial velocities (2σ error bars).
We noticed a relative shift in the velocity of the neutral component within I Zw 18 between the datasets: 756 ± 3 km s-1 for 12 028, 750 ± 2 km s-1 for 11 523, and 768 ± 3 km s-1 for 11 579 (Table 4). The same relative shifts are observed for the Milky Way component, suggesting an instrumental origin. We attribute this difference to a different distribution of the UV flux in and outside the aperture. As a comparison to our velocity determinations, the Hα observation of the NW component, probing the ionized gas in the H ii region, is 742 ± 7 km s-1 (Petrosian et al. 1997) while the H i 21 cm line has a velocity of ≈740 km s-1 (Lelli et al. 2012). Table 4 also shows the radial velocities inferred from each species individually.
The column densities were calculated with the line fitting routine Owens (Lemoine et al. 2002). Owens was originally developed to solve the complexity of many interleaved absorption systems in the FUSE spectra. Although line blending is not a significant issue in the COS spectrum of I Zw 18, we used Owens because of its ability to perform a simultaneous fit of the absorption line profiles from any number of absorption systems. Each gaseous system is defined by (1) a radial velocity vrad; (2) a temperature T; (3) a turbulent velocity b, and (4) a set of column densities from selected species. In practice, the species within a given absorption system are assumed to share the same set of parameters (vrad, T, b).
We assume in the following that the absorption arises from a single broad component as opposed to a collection of narrow components. Within this hypothesis, the column density determined from saturated lines highly depends on the b parameter. Systematic uncertainties on b include errors on the instrumental resolution (Sect. 3.2) or the fact that species in the neutral gas might not share exactly the same b value. If we choose to neglect these systematic uncertainties, the simultaneous fit of lines with a wide range of optical depths provides constraints on both b and the column density. We verified that the additional presence of saturated lines in the simultaneous fit does not bias the column density determination if the column density is otherwise already well constrained by weak lines.
Other effects might also be at work that introduce systematic errors on the column density. For example, the velocity distribution could include a number of individual narrow absorption components that we cannot resolve. The integrated, unresolved, line profile may appear optically thin even though narrow components are saturated (the so-called “hidden saturation”). Although the absorption spectra of metal-poor objects, with their low metal column densities, is in principle less affected than more metal-rich sources, the hidden saturation effect is non-linear and can result in underestimating the total column density by several factors (e.g., Lebouteiller 2005; Lebouteiller et al. 2006). Observationally, this effect can be minimized by including lines with a low oscillator strength f (e.g., C ii*, S ii, P ii in our spectra). Another method is to verify that, for a given species, lines with a wide range of f values can be fitted by a single column density and that the apparent optical depth scales with f (e.g., N i, S ii, Fe ii in our spectra). Nevertheless, the column density of some other species was determined only from strong lines. We note in particular C iiλ1334.5 (optical depth in the line center τ0 ≈ 76), O iλ1302.2 (τ0 ≈ 34), and all the Si ii lines, with the weakest being λ1526.7 (τ0 ≈ 9). For these species, we rely on the hypothesis that the absorption does not arise from a collection of narrow components, and we keep in mind that the quoted errors could be underestimated.
The absorption lines from the various systems are blended with each other throughout the COS range. The following lines in I Zw 18 are contaminated by local absorption systems, Fe iiλ1142.4, Si iiλ1190.4, λ1193.3, Mn iiλ1199.4, and S iiλ1250.6. The Owens algorithm allows us to use these lines to determine column densities under certain conditions, either other lines from the same species are isolated and/or the column density of the local component is well constrained by other lines. In the FUV spectrum of I Zw 18, Fe ii, Si ii, Mn ii, and S ii have other isolated lines and the local absorption systems are well constrained by a variety of lines throughout the COS range.
In order to derive column densities, Owens performs a χ2 minimization over a number of spectral windows containing one or several lines. While Owens enables the parametrization of the local continuum around the lines, the normalization we performed (Sect. 2.1) results in a flat continuum that does not need to be further parametrized. For each specie, we included every line in the COS wavelength domain. This includes the lines that are not detected, since the latter help providing a reliable upper limit to the column density. The fits were performed on the 3 observation sets separately because of possible systematic differences in the spectra.
3.2. Line broadening
The observed line width is a combination of the intrinsic broadening (thermal and turbulent) with the instrumental line spread function. The latter is a critical parameter upon which the b value determination relies. Systematic errors on the line spread function could lead to wrong diagnostics on the line saturation and, therefore, to unreliable column density determinations.
In the case of a point-source well-centered in the aperture, the instrumental full width at half maximum (FWHM) is ≈0.08 Å. If the source has extended emission or if it is a collection of point-sources, the spectral resolution is significantly degraded3. Depending on the source distribution in the aperture, the line profiles might be shifted and/or skewed, but we found the lines to be Gaussian and symmetric, suggesting a rather uniformly distributed light in the aperture.
We estimated the effective instrumental spectral resolution in two ways. First, we measured the one-dimensional flux profile of stars in the NW component as derived from a FUV image obtained by Brown et al. (2002). The profile looks roughly Gaussian with a FWHM = 1.25″, i.e., half the size of the COS aperture. The flat-topped profile of geocoronal Lyα emission, which uniformly fills the COS aperture, has a FWHM = 0.84 Å, so the expected instrumental profile is expected to have a FWHM = 0.4 Å. The second estimate of the spectral resolution makes use of the data itself. For this, we considered the sharpest lines in the COS spectrum and also the line blends for which the 2 lines are barely separated (in particular at ≈1134 Å and ≈1260 Å). These profiles give a reliable constraint on the instrumental FWHM, ≈0.45−0.50 Å. We use 0.50 Å (≈90 km s-1) for the line fitting of the 11 523 and 12 028 datasets (Sect. 3.1). A slightly larger FWHM was required for the 11 579 dataset, 0.55 Å, which could be due to pointing jitter over the long exposure time. For comparison, the point-like source FWHM with the FUSE telescope is 20 km s-1 (Hébrard et al. 2002; Wood et al. 2002).
We used the instrumental resolution above to calculate the intrinsic line broadening. For the latter, we could not distinguish between the thermal and turbulent components. We assumed that turbulence is the dominant source of broadening by setting the temperature to 1000 K, corresponding to a thermal broadening of ≲1 km s-1. The turbulent velocity value we determine for I Zw 18 is b ≈ 17.8 ± 3 km s-1 for the 12 028 dataset, and 18.2 ± 8 km s-1 for the 11 579 dataset, in good agreement with the value 17.3 ± 5 km s-1 found by L04. The 11 523 dataset did not converge on a well constrained b value, which is likely due to the relatively low S/N ratio of this observation and also to the presence of spurious features. We forced the b value in the 11 523 dataset to be ≈17.8 ± 3 km s-1.
3.3. Heavy elements
Column densities.
The fitting of the absorption line profiles is shown in the Appendix. Final column
densities are given in Table 5. The error bars were
calculated by using the Δχ2 method, which gives the variation
of 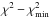 , where
, where
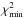 is the lowest
χ2 value corresponding to the global minimum over the entire
parameter space. Since we use the information from all available lines in the wavelength
range, the error bar can be significantly smaller than when considering a single line. We
refer to L04 and Lebouteiller et al. (2006, 2009) for more details. The comparison between the
column densities we derive and the FUSE results asks for caution. The large FUSE aperture
(30″ × 30″) includes the entire main body of I Zw 18 while COS only observed the NW
component. However, most of the UV-bright stars are located toward NW (Brown et al. 2002), and the corresponding lines of
sight presumably dominated the FUSE spectral continuum. Therefore, we do not expect large
differences between the column densities derived with COS and with FUSE. In the following
we provide individual comments for each species.
is the lowest
χ2 value corresponding to the global minimum over the entire
parameter space. Since we use the information from all available lines in the wavelength
range, the error bar can be significantly smaller than when considering a single line. We
refer to L04 and Lebouteiller et al. (2006, 2009) for more details. The comparison between the
column densities we derive and the FUSE results asks for caution. The large FUSE aperture
(30″ × 30″) includes the entire main body of I Zw 18 while COS only observed the NW
component. However, most of the UV-bright stars are located toward NW (Brown et al. 2002), and the corresponding lines of
sight presumably dominated the FUSE spectral continuum. Therefore, we do not expect large
differences between the column densities derived with COS and with FUSE. In the following
we provide individual comments for each species.
The C ii column density is not well constrained because the only C ii line, λ1334.4, is heavily saturated. Our determination relies on the confidence that the b value is well constrained by other lines from other species included in the fitting and on the fact that hidden saturation effects are negligible (Sect. 3.1). The column density of C ii* is much better determined. C i and C i* lines could be present in our spectra but they are either barely detected or not detected. The contribution from C i and C i* to the total C column density is negligible.
The N iλ1134 triplet, observed in the 11 579 dataset, is not saturated (see also L04), while the λ1200 triplet is close to saturation. The N i column density determination from the 3 datasets are in good agreement. They fall somewhat above the value from L04 and agree well with that from A03.
O i is observed in the λ1302.2 line (oscillator strength f = 0.048) in the 11 523 and 11 579 datasets and in the λ1355.6 line (oscillator strength f = 10-6) in all datasets. The former line is contaminated by geocoronal O i emission (Sect. 2.1), and, although the contaminated exposures were ignored, we cannot exclude that a weak contamination remains in the other exposures. The λ1355.6 line is never detected and provides a large upper limit to the O i column density. L04 and A03 measured different O i column densities from the same spectrum, mostly because of the set of O i lines used for the fitting. L04 ignored the λ1039 line because of contamination by a terrestrial airglow and because of the line saturation. Our O i column density determination is closer to that of A03, but we consider our value as highly uncertain because of saturation.
Aluminum has a single strong line in the COS range at 1670.8 Å. The line is unfortunately saturated, and the Al ii column density determination relies on the constraints on the b value. We adopt an average column density from the datasets 11 523 and 12 028.
All the Si ii lines are saturated. The Si ii column determination is thus relatively uncertain since it depends strongly on the b value determination and on the assumption that absorption arises from a single broad component (Sect. 3.1). We use both 12 028 and 11 579 datasets for the Si ii column density determination, and ignore the 11 523 dataset because of its relatively lower S/N. Our adopted column density is somewhat lower than the FUSE measurements by L04 and A03. We thus keep in mind that our Si ii column density might be underestimated and adopt a large error bar that reconciles our value with the FUSE values.
The strongest P ii line (λ1152.8) is barely detected. Our column density determination falls well below the upper limit from A03. The strongest P i line at 1381.5 Å is not detected, and the contribution from P i to the total P column density is negligible.
S ii is observed in the λ1250.8, λ1253.8, and λ1259.5 lines. The main constraint on the S ii column density is given by the weakest line, λ1253.8. It is well detected in the 12 028 dataset, while the profile is more noisy in the 2 other datasets, especially in 11 579. We adopt an average column density between the 11 523 and 12 028 datasets.
Chlorine is expected as Cl i and Cl ii in the neutral phase. Cl ii has no lines in the COS range and it was not detected in the FUSE spectra. Cl i has numerous lines below ~1400 Å with the strongest at 1347.24 Å. The latter is however not detected in any of the datasets.
Manganese is observed via several Mn ii lines with strong oscillator strengths. Unfortunately all the lines are heavily blended with saturated (or close to being saturated) N i lines from I Zw 18 and from the Milky Way. Therefore, we consider that the Mn ii column density is highly uncertain and may be affected by systematic uncertainties.
Iron is observed via several Fe ii lines spanning a wide range of oscillator strengths. The presence of weak lines should result in a reliable Fe ii column density determination. Our column density determination falls between the value from L04 and A03. It agrees slightly better with L04 while it is not compatible within errors with the value from A03. The difference between L04 and A03 is due to the lower b value (<8 km s-1) assumed by A03 for the Fe ii lines.
Nickel is observed via many weak Ni ii lines, most of which are not detected. We stress that the column density determination of Ni ii is better than 5σ because it uses the information from all the lines we included in the fitting. The column density determination from the 3 datasets are in remarkable agreement.
3.4. Hydrogen
The column density of H i is an important quantity since metal abundances are tied to it. However, it is a difficult parameter to measure correctly. The blue wing of the Lyα profile is contaminated by numerous metal lines and by Lyα absorption from the Galaxy and from a high-velocity cloud along the line of sight to I Zw 18 (Sect. 3.1). Furthermore, the red wing of Lyα is contaminated by nebular continuum emission (2-photon and Balmer continuum) arising in the H ii region of I Zw 18 and by the N vλ1238, λ1240 wind lines from the ionizing stars in I Zw 18. Finally, the continuum level is uncertain, because Lyα is such a broad line. In principle, both red and blue wings can be contaminated by stellar Lyα absorption, but this contamination turns out to be insignificant (see also Lebouteiller et al. 2008).
We worked with the COS spectrum processed through step 3 (i.e., corrected for Lyα in the Milky Way and in the high-velocity cloud; Sect. 2.1). We measured the Lyα column density in I Zw 18 by multiplying the observed spectrum by eτ, with τ = N(H i) × 10-19.37 × (λ − λ0)-2 (Jenkins 1971). The column density that best canceled the observed absorption is N(H i) = 2.2 × 1021 cm-2. We find a similar value for the 3 datasets. We list in Table 6 the various H i column density determinations in the literature, either derived in absorption from the Lyman series or in emission using the hyperfine-structure 21 cm line. Note that the comparison between observations in absorption and in emission should account for the simple geometrical effect that the absorption only probes the gas in the foreground of the UV-bright stars.
The H i spatial distribution observed by Lelli et al. (2012) is particularly informative. The high-spatial resolution (2″ beam) reveals that the NW region lies in a H i hole (see also Fig. 1). The NW region is located between the southeast H i peak, with N(H i) ≈ 1.5 × 1022 cm-2, and a region to the north with a rather flat column density distribution (≈6 × 1021 cm-2). Interpolating between these 2 values, we would expect an H i column density of ~1022 cm-2 toward NW, which is significantly larger than our observed value. As discussed in Lelli et al. (2012), the young stellar cluster in NW likely created an H i hole, either due to ionization or to a blow out of the ISM. Assuming the H i hole is due to ionization, the column density of ionized hydrogen should be on first approximation 1022−2.2 × 1021 = 7.8 × 1021 cm-2. We discuss further the distribution of ionized gas in Sect. 4.
H i column density determinations.
4. Nebular models
4.1. Geometry and physical conditions
 |
Fig. 4 Electron temperature (top) and density (bottom) profile of the simple model approximation of I Zw 18. The abscissa is the radial distance from the ionizing stars in cm. |
 |
Fig. 5 Cloudspec model spectra. Top: stellar and nebular (H i and H ii region) component normalized to the stellar continuum (blue) and emission component (red). Both component spectra have been convolved with a Gaussian line-spread function having a FWHM = 0.5 Å to simulate the observations. Major absorption lines formed in the H i region are labeled on top. Most other strong lines, e.g. the Si ivλ1400 doublet, C ivλ1549 doublet, are higher ionization lines formed in the H ii region. The absorption component of Lyα completely erases the Lyα emission formed in the H ii region. Bottom: simple model spectrum for the case CF × AF = 0.1 (top) and for CF × AF = 0.4 (bottom), with CF the covering fraction and AF the aperture fraction (see text). The dotted line is the absorption spectrum, and the bold line is the net spectrum. The component and net spectra have been convolved with a Gaussian line-spread function having a FWHM = 0.5 Å. |
Models were constructed to compute the ionization structure of the nebula and the relative emission and absorption strength of the intervening medium along the line of sight to UV bright stars. We made the following simplifying assumptions: (1) the ionizing stars of NW can be treated as a single, central source; (2) nebular emission arises over the whole volume of H ii region, but nebular absorption arises only in material along the line of sight to the central source; and (3) there is a clear-cut boundary between the H ii and H i regions. The latter assumption is problematic. The photoionization model of I Zw 18 by Péquignot (2008) indicates that the covering fraction of the H ii region is only 40%, so the bulk of the photoionizing radiation must escape into the H i region, and deep observations of I Zw 18 show Hα emission in arcs outside the star-forming region and in a diffuse halo 3 kpc across (Dufour & Hester 1990).
Spectral analysis of the H i cloud of I Zw 18 is much more complicated than for normal (i.e., star-less) damped Lyα systems (DLAs). For example, the spectral profile of the C ii 1334-5 resonance doublet is formed by absorption by relatively lower-mass and/or cooler young stars, and by emission from the outer parts of the H ii region, as well as by absorption in the H i cloud. Even Lyα, nominally formed in the H i cloud is not immune to contamination. Balmer continuum emission and 2-photon emission from the H ii region affect the long-wavelength side of the line, and absorption by H0 atoms in the atmospheres of cool stars can affect both the short- and long-wavelength wings of Lyα (Sect. 3.4).
We used the software package, cloudspec (Hubeny et al. 2000), which combines the photoionization code Cloudy (Ferland et al. 1998) with the spectral-synthesis code synspec (Hubeny & Lanz 1995) to compute the emission and absorption spectrum of an object. The physical model is a medium photoionized by a central source and the cosmic background. Cloudy computes the ionization structure and emission spectrum (both lines and continuum) of the medium. The synspec part of cloudspec then calculates the level populations and the attenuation spectrum produced by such a medium along the line of sight toward the central ionizing source.
We ran cloudspec through the H ii region and into the H i region until the H i column density reached its observed value toward the NW component, 2.2 × 1021 cm-2 (Sect. 3.4). Figure 4 shows the radial profile of the electron temperature and density and the sharp change in the physical conditions between the H ii and the H i region. Close in to the ionizing stars, the nebula is quite hot, due to the low abundance of oxygen, the main element for collisional cooling in the ionized gas. The electron temperature decreases outward from the ionizing stars with an abrupt drop near the edge of the H ii region, and outside the Strömgren sphere, the temperature reaches down to 100 K. The electron density drops by 3 orders of magnitude at the edge of the Strömgren sphere, because most of the free electrons supplied by hydrogen are no longer available.
The NW component is dominated by the H ii region which sits an H i hole either due to hydrogen ionization or to a blow out of the ISM (Lelli et al. 2012). In our model, we find that the column density of ionized hydrogen should be log N(H i) = 21.79, i.e., almost a factor 3 larger than the observed H i column density. Following the hypothesis that the total (ionized+neutral) hydrogen column density is flat across the main body of I Zw 18, we would expect the ionized hydrogen column density toward NW to be around log N(H i) ~ 21.89 in order to compensate for the relatively lower H i column density (Sect. 3.4). Our models are in good agreement with this value and support the idea that the gas was not blown out but mainly ionized.
In assuming spherical symmetry, the models are highly simplistic. The ionizing stars in I Zw 18 are offset from Hα emission shell (Hunter & Thronson 1995; Brown et al. 2002), and the H ii region has a knot of high density. Nevertheless, the models help us to understand important physical processes operating in I Zw 18 (Sect. 5) and to guide the abundance analysis of the H i region (Sect. 6).
4.2. Spectral line formation in the H II region
Singly ionized ions are formed by recombination of higher ionization stages inside the H ii region near the edge of the Strömgren sphere. Recombination and subsequent cascade down to the ground state in the H ii region creates emission that works to reduce the apparent strength of absorption lines arising in the H i region.
Figure 5a shows the emission and absorption components of the model line spectrum as derived by cloudspec. The observed spectrum is the net. As can be seen from the figure, the emission is strong relative to the absorption for C ii* λ1335.7. How important is contamination by emission lines? The answer depends on two factors: the covering fraction of the H ii region, CF, and the fraction of the H ii emission region subtended by the entrance aperture to the spectrograph, AF. Péquignot (2008) estimates the covering fraction of the H ii region in I Zw 18 at CF = 0.4, based on the strength of Hβ emission to Lyman continuum flux of the model best fitting the observations. The COS aperture fraction is not known, but is certainly much less than 1. Figure 5b compares a segment of the model UV spectrum for two cases, CF × AF = 0.1 (top) and CF × AF = 0.4 (bottom). It is clear that the latter case disagrees with observation by generally overestimating the strength of emission, making the ground-state absorption lines too weak, and the fine-structure lines appearing in emission (particularly C ii* and Si ii*). The agreement is much better for the case where CF × AF = 0.1. In our abundance analysis, we have therefore neglected the effects of emission except for the C ii doublet at 1334-5 Å.
Contamination by emission cannot always be neglected. In fact, the spectra of star-forming galaxies at high-redshift often show emission in the fine-structure lines (Pettini et al. 2000; Shapley et al. 2003). This emission is easily identifiable because these galaxies have outflows. The H i region is expanding with respect to the central, ionizing stars, so the absorption component, which arises along the line of sight to the stars, is blue-shifted. The emission component is formed over the outermost shell within the H ii region, so it is centered on the stellar radial velocity. Expansion of the H ii region simply broadens the line. Thus, the red half of the emission reaches the observer unscathed, but the blue half of the emission is at least partially nullified by the blue-shifted absorption component. The net profile looks like a P Cygni profile. The emission spectrum of I Zw 18 is as real as in high-redshift, star-forming galaxies. The difference is that there is no detectable velocity gradient in I Zw 18, so the emission is not separable from the absorption component.
While the emission component in the H ii region is negligible for most lines, absorption can also arise from the H ii region. A few resonant lines originating in the ionized gas are seen in absorption in the FUV spectra of I Zw 18 and provide an independent, direct, estimate of the ionization structure of the nebula. For instance, A03 measured the Fe iiiλ1122 line in the FUSE spectrum of I Zw 18 and set an upper limit to the fraction of Fe ii in the ionized gas of 5%. A03 also cautioned that a large fraction of Si ii absorption might arise in the ionized gas. We are now able to test this hypothesis, with the Si iiiλ1206.5 line, which we detect at a velocity of ~755 ± 50 km s-1 in the COS spectra. This line partly originates from stellar atmospheres and partly from the H ii region. The observed profile of the Si iii line is complex and it depends on the stellar contribution that was removed (Sect. 2.2). The column density determination also depends on the b value for which we have little information in the ionized gas. Assuming that the line is not saturated, we find a consistent Si iii column density in the 3 datasets with ~2 × 1013 cm-2. What is the fraction of the Si ii column density we measured (3.3 × 1014 cm-2) arising in the ionized gas? In the warm ionized medium in the Milky Way, about 90% of silicon is expected into Si ii and 10% into Si iii (Sembach et al. 2000). Assuming this result is applicable to I Zw 18, we find that only ~40% of the measured Si ii column density might arise from the neutral gas. However, the situation is likely different in I Zw 18 where silicon in the ionized gas is expected mostly into higher ionization stages (Sect. 6.1; see also A03). We assume in the following that most of Si ii should lie in the H i region gas.
Unfortunately, no S iii line could be used to perform a similar analysis with sulfur. The brightest S iii line, λ1190, is blended with Si ii. Nevertheless, we consider that the ionization correction smaller than for Si and that most of S ii lies in the H i region.
5. Physical conditions and thermal equilibrium in the H I region
The C ii* column density represents only ≈3% of the total carbon column density (Table 5), yet C ii* is key to understanding the physical conditions, in particular the thermal processes toward the NW region. The ground state of C+ is split into the fine-structure levels 2P1/2 and 2P3/2. The absorption line C iiλ1334.5 originates from the 2P1/2 level while C ii* λ1335.7 originates from 2P3/2. The upper level is populated by collisions with H0, H2, and e−. The spontaneous emission between the two fine-structure levels is observed in the far-IR emission line [C ii] 157 μm and dominates over collisional de-excitation as long as the density is lower than the transition critical density.
5.1. Electron fraction in the H I region
The population of the C+ fine-structure level constrains the electron density
toward the NW region. Following Jenkins et al.
(2000a), the volume-density ratio
n(C+ ∗) / n(C+)
provides the electron density as long as collisions with electrons dominate the population
of the fine-structure level. Collisions with H2 should be unimportant in
I Zw 18 given the lack of diffuse H2 (Vidal-Madjar et al. 2000). Furthermore, the collision strength with
e− is larger than the collision strength with H atoms by a factor of ≈150 for
T = 6000 K. Collisions with e− will therefore dominate as
long as ne / nH
remains larger than ~0.75% (e.g., Lehner et al.
2004). Potential sources of free electrons are soft X-rays, cosmic rays, and
ionization of C0. We approximate the number density ratio
n(C+ ∗) / n(C+)
with the column density ratio
RCII = n(C+ ∗) / n(C+)
and, by assuming that electrons are the dominant collision partners, we derive an upper
limit on the electron density 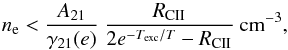 (1)where
A21 is the radiative decay probability from the
fine-structure level from the 2P3/2 level to the
2P1/2, Texc is the
2P3/2 level excitation temperature (≈91 K),
T is the electron temperature and
γ21(e) is the collisional deexcitation rate
coefficient, which we take from Goldsmith et al.
(2012).
(1)where
A21 is the radiative decay probability from the
fine-structure level from the 2P3/2 level to the
2P1/2, Texc is the
2P3/2 level excitation temperature (≈91 K),
T is the electron temperature and
γ21(e) is the collisional deexcitation rate
coefficient, which we take from Goldsmith et al.
(2012).
For a temperature range of [1000−8000] K, we find
ne ≲ [10−20] RCII cm-3.
Using the observed column density ratio
RCII = 2.8 × 10-2, we calculate
ne ≲ 0.4 cm-3. Since the C ii
absorption-line is saturated, we also checked that the result holds when using
S ii as a replacement for C ii. The S ii lines are not prone
to saturation, and both S ii and C ii are the dominant ionization stages
in the H i region, so we expect the ionization fractions of S into S+
and C into C+ to be well correlated over a wide range of conditions. Carbon is
more readily depleted on dust grains than sulfur (Sofia
et al. 1997, 1998), but rather than
assuming a depletion factor, we assume that the abundance ratio in the neutral gas equates
that in the ionized gas (C/S)H ii ≈ 0.98 (Péquignot 2008). The latter assumption also implies that C and S
disperse and mix in the ISM over similar timescales (Sect. 6.4). We can then approximate RCII with
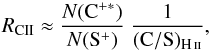 (2)from which we derive a
somewhat lower upper limit of ne ≲ 0.2 cm-3.
(2)from which we derive a
somewhat lower upper limit of ne ≲ 0.2 cm-3.
On the one hand, the upper limit on the electron density we determine is significantly lower than the value measured in the ionized gas of the star-forming regions derived in Dufour & Hester (1990) and in the Hα arc derived by Izotov et al. (2001a), on the order of 10 cm-3. This suggests that C ii* arises in the diffuse ionized gas or in the H i region. On the other hand, the upper limit on ne is significantly larger than the electron density in the H i region inferred from our Cloudy models (~0.01 cm-3; Sect. 4). The models suggest that the C ii* emission component can be neglected and thus does not impact our estimate of RCII (Sect. 4.2). However, it is plausible that collisions partners other than e− contribute to populating the C+ fine-structure level, in particular H atoms. We can use the same method as Eq. (1) to derive an upper limit on the hydrogen density, i.e., assuming that hydrogen atoms are the dominant collision partners. For a temperature range of [100−1000] K, we find nH ≲ [30−40] cm-3.
If we assume that the H i region has a density around or lower than 10 cm-3, we must conclude that the electron fraction in the H i region is likely significant, possibly reaching a few percents. Such values would lie many orders of magnitude above the fraction of electrons provided by ionization of C0 alone (equal to the carbon abundance relative to hydrogen), suggesting that the H i region is partially ionized, with electrons created by UV photons, soft X-rays, or cosmic rays originating from the star-forming regions. We investigate further the electron fraction in Sect. 5.2.
5.2. Theoretical cooling rate from the H I envelope
In order to examine further the physical conditions in the H i region, we now
compare the observed cooling rate to the theoretical rate expected from the H i
envelope, with H atoms and free electrons as collisions partners. The observed cooling
rate per H atom is calculated following Pottasch et al.
(1979) and Gry et al. (1992), with
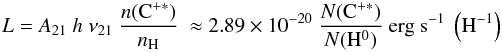 (3)where
ν21 is the transition frequency and where we have again
approximated the number density ratio with the column density ratio. We find
LCOS ≈ 8 × 10-28 erg
s-1 (H-1). We can rewrite the cooling rate per surface unit of the
galaxy,
(3)where
ν21 is the transition frequency and where we have again
approximated the number density ratio with the column density ratio. We find
LCOS ≈ 8 × 10-28 erg
s-1 (H-1). We can rewrite the cooling rate per surface unit of the
galaxy, 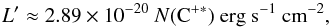 (4)which leads to
(4)which leads to
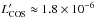 erg
s-1 cm-2. Assuming the source is extended, the intensity per
surface unit of the galaxy is the same as the intensity per surface unit on the detector,
so we can directly relate L′ to the corresponding
157 μm emission intensity I(157 μm)
in erg s-1 cm-2 sr-1 via:
erg
s-1 cm-2. Assuming the source is extended, the intensity per
surface unit of the galaxy is the same as the intensity per surface unit on the detector,
so we can directly relate L′ to the corresponding
157 μm emission intensity I(157 μm)
in erg s-1 cm-2 sr-1 via:
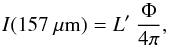 (5)where Φ is the
fraction of the beam filled with [C ii] emission. Assuming Φ = 1, we find
ICOS(157 μm) ~ 1.5 × 10-7 erg s-1 cm-2 sr-1 = 1.5 × 10-10 W m-2 sr-1.
This is the observed cooling rate toward the NW component.
(5)where Φ is the
fraction of the beam filled with [C ii] emission. Assuming Φ = 1, we find
ICOS(157 μm) ~ 1.5 × 10-7 erg s-1 cm-2 sr-1 = 1.5 × 10-10 W m-2 sr-1.
This is the observed cooling rate toward the NW component.
For the theoretical cooling rate in the H i envelope, we consider a medium with
most free electrons produced by cosmic rays, soft X-rays, or escaping UV photons (see
Sect. 5.1). Following Crawford et al. (1985) and Madden et
al. (1993), the cooling rate expressed in W m-2 sr-1 can
be written as 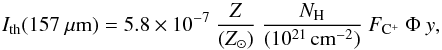 (6)where
Z is the abundance of carbon relative to the solar value
(C/H = 2.69 × 10-4; Asplund
et al. 2009), NH is the hydrogen nuclei column
density, FC+ is the fraction of carbon into
C+ ions along the line of sight, Φ is the fraction of the beam filled by
C+ gas, and y is the dimensionless factor defined as
(6)where
Z is the abundance of carbon relative to the solar value
(C/H = 2.69 × 10-4; Asplund
et al. 2009), NH is the hydrogen nuclei column
density, FC+ is the fraction of carbon into
C+ ions along the line of sight, Φ is the fraction of the beam filled by
C+ gas, and y is the dimensionless factor defined as
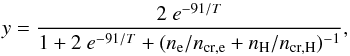 (7)where
ncr,e and
ncr,H are the critical densities for
collisions with electrons and hydrogen (which we take from Goldsmith et al. 2012). We assume in the following
FC+ = 1 and we define x as the
electron fraction
x = ne / nH.
Figure 6 provides
Ith(157 μm) as a function of density for
various temperatures and electron fractions. When the ionization fraction is large, proton
impact could contribute to the 2P3/2 level
excitation, but here we neglect this contribution since we focus on the H i
region. It can be seen that Ith(157 μm)
flattens for densities >10 cm-3 for large
x values (medium significantly ionized), and
>103 cm-3 for low x
values (purely neutral medium), which is a consequence of the critical densities for
collisions with electrons and hydrogen atoms.
Ith(157 μm) depends little on temperature
for T greater than a few hundreds K.
(7)where
ncr,e and
ncr,H are the critical densities for
collisions with electrons and hydrogen (which we take from Goldsmith et al. 2012). We assume in the following
FC+ = 1 and we define x as the
electron fraction
x = ne / nH.
Figure 6 provides
Ith(157 μm) as a function of density for
various temperatures and electron fractions. When the ionization fraction is large, proton
impact could contribute to the 2P3/2 level
excitation, but here we neglect this contribution since we focus on the H i
region. It can be seen that Ith(157 μm)
flattens for densities >10 cm-3 for large
x values (medium significantly ionized), and
>103 cm-3 for low x
values (purely neutral medium), which is a consequence of the critical densities for
collisions with electrons and hydrogen atoms.
Ith(157 μm) depends little on temperature
for T greater than a few hundreds K.
 |
Fig. 6 The 157 μm cooling line intensity is calculated from Eq. (6) and is plotted as a function of the hydrogen number density and of the electron fraction (x = ne / nH). Note that the result should be scaled by the fraction of carbon in C+. The result should also be scaled by the carbon abundance with respect to the solar value and by the column density of hydrogen nuclei in units of 1021 cm-2. For temperatures 50 K and 100 K, only the curve for x = 0 is shown. |
In I Zw 18, the abundance of carbon relative to solar is Z = 10-2, where we have used sulfur abundance as a substitute and assumed the C/S ratio in the ionized gas (see Sect. 5.1). We first consider a mostly neutral medium, with T ~ 1000 K and use the H i column density derived in Sect. 3.4 (1021.34 cm-2). From Fig. 6, we calculate that the observed cooling rate ICOS(157 μm) can be reproduced by a wide range of conditions, from purely neutral with nH ≈ 15 cm-3, to a medium with a significant electron fraction with nH ≈ 5 cm-3 and x ≈ 2%. Assuming a homogenous medium with a low clumping factor, such number densities imply small H i scales on the order of ≳100 pc, which is compatible with an H i shell, left over after the NW star cluster blew out and ionized the pre-existing cloud (Sect. 4.2).
For larger electron fractions, the medium is diffuse and ionized and we need to account for the column density of H+. Following the hypothesis that the total hydrogen column density toward NW is ≈1022 cm-2 (Sect. 3.4), we find that the cooling rate can be reproduced by an electron density of ne ≈ 0.04 cm-3. However, such a low number density would result in an unrealistic nebula size (>50 kpc).
In summary, although the lack of knowledge on the hydrogen number density in the H i region prevents us from deriving a precise electron fraction, our results are compatible with most of the C ii* absorption arising in the H i region with likely a significant electron fraction.
How does the cooling rate derived from C ii* compare with the predicted value from the Cloudy models? The models (Sect. 4) predict that radiative de-excitation of the C+ fine-structure level dominates the cooling in the H i region, with Lmodel ≈ 3.5 × 10-28 erg s-1 (H-1), which is a factor of ≈2 lower than the observed value LCOS ≈ 8 × 10-28 erg s-1 (H-1). While we assumed a constant hydrogen density of 10 cm-3 in the models, a lower density would result in a higher temperature, with other coolants contributing significantly to the total cooling rate, such as [O i] 63 μm or [Si ii] 35 μm. This would suggest that the total cooling rate in the models is likely underestimated by several factors. Since our models assume a thermal equilibrium, the heating rate is also underestimated by the same amount. We discuss in Sect. 5.4 the heating mechanisms and how to reconcile the models with the observed C ii* cooling rate.
5.3. Cooling rate and SFR
The observed cooling rate derived from Eq. (3) is LCOS ≈ 8 × 10-28 erg
s-1 (H-1). This value is significantly lower than in the diffuse
medium of our galaxy (≈10-26−10-25 erg
s-1 (H-1); Lehner et al.
2004) or in other nearby galaxies (e.g., Madden
et al. 1993), but it is close to the average cooling rate in DLAs
(≈10-27 erg s-1 (H-1); Wolfe et al. 2003a). Assuming that the photoelectric effect on dust is the
dominant gas heating mechanism (see Sect. 5.4), the
cooling rate scales with the dust-to-gas ratio (D/G), the photoelectric efficiency, and
the FUV field. Since the latter is a good gauge of the star-formation rate (SFR) per unit
physical area, the similar cooling rate between I Zw 18 and DLAs could in principle imply
a similar surface SFR density (Wolfe et al.
2003b). Following Bowen et al. (2005), we can
estimate the SFR from C ii* by using the Milky Way (MW) as a reference
![\begin{equation} \Sigma_{\rm SFR} ({\rm I\,Zw\,18}) \approx [Z]^{-1}\ \frac{L_{\rm COS}}{L ({\rm MW})}\ \Sigma_{\rm SFR} ({\rm MW}), \end{equation}](/articles/aa/full_html/2013/05/aa20948-12/aa20948-12-eq358.png) (8)where ΣSFR is
the SFR per unit area and [Z] represents the D/G normalized to the MW
value. While [Z] should in principle scale with the gas metallicity, we
use instead the D/G as measured with the Herschel Space Telescope
(
(8)where ΣSFR is
the SFR per unit area and [Z] represents the D/G normalized to the MW
value. While [Z] should in principle scale with the gas metallicity, we
use instead the D/G as measured with the Herschel Space Telescope
(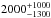 times lower than the MW value; Rémy et al., in prep.). We assume
ΣSFR(MW) ≈ 4 × 10-3 M⊙ yr-1 kpc-2
(Rana 1991) and
L(MW) ≈ 2 × 10-26 erg s-1 (H)-1 (Lehner et al. 2004), and we finally obtain
ΣSFR(I Zw 18) ~ 0.3 ± 0.2 M⊙ yr-1 kpc-2.
As an alternative measurement of the SFR, we use the empirical relation between the gas
surface density Σgas and ΣSFR (e.g., Kennicutt 1998). The H i column density is used as a tracer of
Σgas, with a correction factor of ~4 due to the ionized gas along the line of
sight (Sect. 4.1). We find
Σgas ≈ 87.6 M⊙ pc-2 and
times lower than the MW value; Rémy et al., in prep.). We assume
ΣSFR(MW) ≈ 4 × 10-3 M⊙ yr-1 kpc-2
(Rana 1991) and
L(MW) ≈ 2 × 10-26 erg s-1 (H)-1 (Lehner et al. 2004), and we finally obtain
ΣSFR(I Zw 18) ~ 0.3 ± 0.2 M⊙ yr-1 kpc-2.
As an alternative measurement of the SFR, we use the empirical relation between the gas
surface density Σgas and ΣSFR (e.g., Kennicutt 1998). The H i column density is used as a tracer of
Σgas, with a correction factor of ~4 due to the ionized gas along the line of
sight (Sect. 4.1). We find
Σgas ≈ 87.6 M⊙ pc-2 and
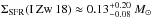 yr-1 kpc-2.
Both these determinations are close to the values found by Aloisi et al. (1999), with
10-2−10-1 M⊙ yr-1 kpc-2,
and Petrosian et al. (1997), with
0.14 M⊙ yr-1 kpc-2 (corrected to a
distance of 19 Mpc). The slightly higher SFR found from the C ii* cooling rate,
if genuine, might be due to an underestimated D/G because of the presence of metal-free
gas on the line of sight (Sect. 7.1) and/or to a
larger photoelectric efficiency in I Zw 18 as compared to the MW (see also Sect. 5.4).
yr-1 kpc-2.
Both these determinations are close to the values found by Aloisi et al. (1999), with
10-2−10-1 M⊙ yr-1 kpc-2,
and Petrosian et al. (1997), with
0.14 M⊙ yr-1 kpc-2 (corrected to a
distance of 19 Mpc). The slightly higher SFR found from the C ii* cooling rate,
if genuine, might be due to an underestimated D/G because of the presence of metal-free
gas on the line of sight (Sect. 7.1) and/or to a
larger photoelectric efficiency in I Zw 18 as compared to the MW (see also Sect. 5.4).
5.4. Heating mechanisms
In the warm ionized medium, photoionization of H should dominate the heating (see Péquignot 2008 for I Zw 18), with likely extra heating from photoelectric effect on dust and from dissipation of interstellar turbulence (Reynolds et al. 1999). The heating mechanisms in the H i region are comparatively much less constrained. The gas heating rate in the ISM of our Galaxy is dominated by photoelectrons ejected from polycyclic aromatic hydrocarbons (PAHs) and small dust grains (Wolfire et al. 1995; Weingartner & Draine 2001), but low metallicity environments could show fundamental differences, with for instance the low PAH abundance of PAHs (e.g., Wu et al. 2006).
Ultraviolet photons escaping the H ii region play an important role in the H i gas heating through photoionization and through the photoelectric effect. Dufour & Hester (1990) discovered a faint halo of Hα emission extending at least 2.7 kpc from the star-forming massive star clusters of I Zw 18. Furthermore, Péquignot (2008) found that only 30–40% of ionizing photons from the NW and SE massive star clusters is absorbed by surrounding H ii regions. The leakage of ionizing photons into the neutral medium should result in a heating effect, affecting the relative population of the ground and fine-structure levels of C ii, as well as the strength of the C ii* λ1335 fine-structure line.
The total heating rate predicted by the Cloudy models in the
H i region (Sect. 4) is dominated by
cosmic rays, and amounts to Γ ~ 3.5 × 10-27 erg s-1 cm-3.
Photoelectric effect heating is comparatively negligible, with ~2% of the total heating
rate4. However, our simple model has important
limitations. First, the heating rate is likely underestimated by several factors
(Sect. 5.3), which could be due an underestimated
photoelectric effect heating rate. The latter is highly dependent on the model geometry
and parameters since it is proportional to the incident UV radiation field, the
photoelectric efficiency, and the D/G ratio (e.g., Bakes
& Tielens 1994; Weingartner &
Draine 2001). Apart from the remarkably low D/G in I Zw 18 (Rémy et al., in
prep.), the low photoelectric heating rate predicted by our models is due to the
relatively weak radiation field in the H i region
(G0 < 100, expressed in Habing
units; Habing 1968), and to the low photoelectric
efficiency, due to the large grain charging parameter
(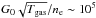 K1/2 cm3).
The photoelectric effect might become the dominant heating mechanism in the models if a
more realistic approach was taken. We list below some of the most important
parameters,
K1/2 cm3).
The photoelectric effect might become the dominant heating mechanism in the models if a
more realistic approach was taken. We list below some of the most important
parameters,
-
The radiation field in theH i region depends on theISM topology and in particular on the coveringfactor of the H ii region. The UVphotons likely escape the star-forming region to reach and heatthe gas on large spatial scales across the galaxy.
-
The electron density in the models might be underestimated (Sect. 5.1). A larger electron density will increase the photoelectric efficiency, resulting in a larger heating rate.
-
The grain size distribution could be biased toward the smallest sizes in low-metallicity dwarf galaxies (e.g., Galliano et al. 2005), with likely a significant impact in the gas heating rate and efficiency.
-
The D/G ratio is uncertain, between 700 and 3000 times lower than the MW value.
The study of the far-IR [C ii] line and its relation to the IR luminosity will be important to confirm the importance of dust in the gas heating process (Lebouteiller et al., in prep.).
 |
Fig. 7 Effect of extra heating in the H i region. The electron temperature (top panel) and the fraction of C ii and C ii* to total carbon (middle panel) are shown as a function of radius to the ionizing stars. The predicted line strength is shown in the bottom panel. The models assume unity for both the covering fraction of the H ii region and the fraction of the emission subtended by the COS aperture (see Sect. 4.2). |
Since our model appears to underestimate the heating rate (Sect. 5.3), we explored further the heating of the H i gas through the use of the “extra heating” parameter in Cloudy. The extra heating represents all heating sources that are not well constrained or not modeled (e.g., escaping ionizing photons, compressional heating, dissipation of turbulence, mechanical energy transfer from stellar winds and supernovae...). We assumed no radial dependence for this parameter. Figure 7 shows that the electron temperature, initially at 100 K in absence of extra heating, jumps from 300 K to 7000 K when the extra heating rate is increased from 10-27 to 10-25 erg s-1 cm-3. The higher temperature brings increased collisional excitation of C+ to the fine-structure level, and hence, stronger absorption of C ii* λ1335.7. As expected, the strengths of the emission components to the C ii doublet are hardly affected. The emission appears very strong − enough to overwhelm the absorption component of C iiλ1334.5, but the COS aperture only subtended a small fraction of the H ii region, so the emission components are significantly weaker (see Sect. 4.2). Nevertheless, the unknown strength of the emission component adds to the uncertainty on the heating rate as derived from the observed C ii* profile.
 |
Fig. 8 Cloudy model spectral energy distribution of I Zw 18. The flux distribution of the stellar population incident on the inner edge of the H ii region is shown in white, the stellar flux transmitted to the H i region in gray. The wavelength of the ionization edge of relevant species is given along the top of the figure. The H ii region absorbs virtually all the H i Lyman continuum and converts it to H i Lyα, nebular continuum, and line emission (all shown in red). |
Assuming an extra heating rate of ~10-25.8 erg s-1 cm-3, we are able to reconcile our models with the cooling rate derived from C ii* (Sect. 5.3). The electron temperature Te in the H i region with such extra heating increases from 100 K to 1000 K. The electron temperature is unfortunately difficult to measure observationally, and, although the column density ratio N(Si+∗)/N(C+∗) provides in principle the gas kinetic temperature (Howk et al. 2005), our upper limit on the Si ii* column density is too large to provide any constraint.
By including the extra heating, the main IR cooling lines predicted by the models are [C ii] (~40% of the total cooling rate), [O i] 63 μm (~30%), and [Si ii] 35 μm (~26%). We wish to recall here that these values correspond to the diffuse medium, and that far-IR emission-line intensities might include other components (e.g., photodissociation regions). The O i* λ1304.9 absorption-line, arising from the 3P1 fine-structure level of O0, is unfortunately undetected. Following Eq. (3), we calculate an upper limit on the [O i] cooling of <10-26 erg s-1 (H-1), which is significantly larger than the cooling by [C ii] inferred from C ii* (Sect. 5.3). Therefore, we cannot examine in detail the effect of extra heating on the relative cooling line contributions. At best, the large upper limit on the cooling by [O i] is compatible with the extra heating.
6. Chemical abundances
6.1. Dominant ionization stages in the H I region
In order to calculate the abundances relative to atomic hydrogen, all the ionization stages in the neutral phase should be accounted for. Fortunately, the COS range gives access to the lines of the dominant ionization stages in the neutral gas, namely C ii, N i, O i, Mg ii, Si ii, P ii, S ii, Mn ii, Fe ii, and Ni ii. Only chlorine is expected about equally between Cl i and Cl ii. Most studies of DLAs assume that singly ionized metals such as C, Al, Si, S, Fe, and Ni reside exclusively in the H i region so that elemental abundances can be obtained from the ratio of the ion column density to the H i column density (e.g., Pettini et al. 2000). However, this assumption is not always correct for H i clouds with embedded star-forming regions. To illustrate, we have constructed a simple Cloudy model of the gaseous medium surrounding the ionizing stars (Sect. 4). The model is simplistic in having a constant total hydrogen density, 10 cm-3, but in other respects − metallicity, ionizing radiation field, star-formation rate, and H i column density − the model is appropriate for I Zw 18.
Figure 8 compares the model spectral energy distribution of the ionizing stars incident on the surrounding gaseous medium and after passage through the H ii region. No H-, N-, or O-ionizing radiation gets through to the H i region, so oxygen and nitrogen are neutral in the H i region. However, stellar radiation longward of the H i Lyman limit, although diluted by distance from ionizing stars, has basically the same relative flux distribution except for the addition of very strong Lyα and other, much weaker nebular features. Hence, other elements such as C, Al, Ni, Mg, Fe, Si, S, and Cl will be ionized in the H i region.
 |
Fig. 9 Ionization structure of the simple model approximation of I Zw 18 NW. The abscissa is the radial distance from the ionizing stars in cm. Ionization stages are identified by their color: dark blue (V), cyan (IV), green (III), orange (II), red (I). See Fig. 4 for the corresponding electron temperature and density profiles. |
From Fig. 9, we can see that in the H i region, the dominant ionization state of metals with ionization edges longward of the H i Lyman limit is singly ionized. We use the column densities of the corresponding species to determine the total abundance. A fraction of these species also arises in the H ii region where it can lead to emission (recombination of higher stages; Sect. 4.2) and absorption.
A caveat should be that partially-ionized regions might exist on the lines of sight that our model cannot account for. The existence of such regions might affect the ionization structure of species with a large photoionization cross-sections (PiCS). Even if the ionization potential is greater than 13.6 eV, the PiCS can be large enough for ionization to occur while hydrogen remains atomic. This effect is unimportant for thick clouds well shielded from the FUV radiation, but becomes significant for thin clouds or clouds embedded in a diffuse UV field. Among the species observed in absorption in galaxies, Ar i is the species the most affected because of its large PiCS (e.g., Sofia & Jenkins 1998; Jenkins 2013). More relevant to our study, N i and O i also have a PiCS larger than that of H i (Verner et al. 1996), but also lower than that of Ar i by a factor of ≳3, so we expect a much smaller correction than for Ar. Most importantly, the ionization fraction of N and O are coupled to the ionization fraction of H via resonant charge exchange reactions (see also Jenkins et al. 2000b). For all the other species5, the first ionization potential is lower than 13.6 eV, and the second ionization potential is well above, so we always expect them as single-charged ions in the neutral phase even in partially-ionized regions.
In the following, we compare our abundances to the solar values from Asplund et al. (2009) except for argon for which we
choose Lodders (2003). For the H ii region
abundances, we use the results of Péquignot (2008)
and adopt error bars that encompass the determinations by Izotov et al. (1999). Following Lebouteiller et
al. (2004), we define the abundance difference between the H ii and
H i region as: 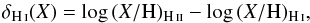 (9)where
(X / H)H ii and
(X / H)H i are the abundances of
the element X in the H ii region and H i region
respectively. We also define the abundance relative to the solar value as:
(9)where
(X / H)H ii and
(X / H)H i are the abundances of
the element X in the H ii region and H i region
respectively. We also define the abundance relative to the solar value as:
![\begin{equation} [{X/Y}] = \log\,({X}/{Y}) - \log\,({X}/{Y})_\odot, \end{equation}](/articles/aa/full_html/2013/05/aa20948-12/aa20948-12-eq394.png) (10)where
(X / Y)⊙ is the solar
abundance reference.
(10)where
(X / Y)⊙ is the solar
abundance reference.
Figure 10 shows the abundances in the neutral gas (see Table 7 and Sect. 6) as compared those in the ionized gas. The line fits are shown in the appendix, including the line profiles as they would appear if the H i region abundances would be similar to those in the H ii region.
Chemical abundances.
L04 and A03 examined the same FUSE spectrum and the differences are due to a different method of measuring the column densities and also to the choice of lines (Sect. 3.3). Our method is similar to L04’s method, i.e., a simultaneous fit of the lines. The differences in the abundances between our study and L04 and A03 directly reflect the differences in the metal column density determinations since our H i column density is similar to their’s and since no ionization correction was used in our study nor in L04 and A03.
 |
Fig. 10 Abundance of each element in the H i region and in the H ii region. Elements are ordered by increasing condensation temperature (temperature for which 50% of an element is removed from the gas phase). The horizontal lines show the metallicity for each phase based on [O/H]. For the H i region, S is used to estimate O (Sect. 6.2). |
6.2. O/H and the α-elements
α-elements are produced in short-lived high-mass stars and are often used to trace the metallicity of galaxies. The majority of oxygen is produced by He and Ne burning during the hydrostatic burning phase with negligible contribution from the explosive stages. Silicon is produced by O burning (hydrostatic and explosive) and Ne burning, while sulfur is produced by O burning. Since the α-elements are made in the same massive stars that make oxygen, the abundance ratio between two α-elements should depend little on metallicity (see Izotov et al. 1999).
The sulfur abundance is tightly correlated with that of oxygen in BCDs (Izotov et al. 1999). The S/O ratio in the ionized gas of I Zw 18 is identical the solar ratio, with [S/O] = −0.07 ± 0.08. Within the error bars, we find that S is barely underabundant in the neutral phase with δH i(S) ≈ 0.18 ± 0.11. Figure A.2 shows that the line profiles are not consistent with the H ii region abundance. Sulfur is not expected to be depleted on dust (except in molecular clouds) and ionization corrections are negligible (Sect. 6.1), so we consider that this result implies a genuine underabundance of sulfur in the neutral gas. In other words, the metallicity of the neutral gas is between 51% and 85% that of the H ii region.
The silicon abundance determination is fairly uncertain in the H ii region, with the values from Péquignot (2008) and Izotov et al. (1999) differing by almost a factor 2. Taking at face the value from Péquignot (2008), Si/O in the ionized gas is in good agreement with the solar ratio, with [Si/O] = −0.14 ± 0.33. Considering the similar nucleosynthesis process of these elements, this indicates little or no depletion of Si on dust grains in the H ii region. It must be noted that Peimbert & Peimbert (2010) used the relatively smaller silicon abundance found by Garnett et al. (1995) to conclude that ~39% of Si might be locked in dust in I Zw 18. The silicon abundance in the H i region is uncertain because of the Si ii line saturation; our determination is somewhat lower than the column density derived by both L04 and A03 (Table 5). Within errors, we find that silicon is underabundant in the neutral gas with respect to the ionized gas, although with a large uncertainty, with δH i(Si) ≈ 0.71 ± 0.42. Figures A.2, A.3 show that the line profiles are not consistent with the H ii region abundance. Silicon can be affected by depletion on dust in the neutral phase, but this turns out to be a negligible effect (Sect. 6.7). Furthermore, although a fraction of Si ii could originate in the diffuse ionized gas (Sect. 4.2), it would only increase the discrepancy between the silicon abundance in the two phases. The Si/S ratio in the ionized gas is solar ([Si/S] = −0.08 ± 0.30), while it is somewhat sub-solar in the neutral gas ([Si/S] = −0.60 ± 0.32). Assuming that [Si/S] should also be ≈0 in the neutral gas, we consider that our silicon abundance might be somewhat underestimated. This hypothesis seems to be confirmed in Fig. 11, which shows that our observed [Si/O] lies below the predicted value from massive star yields (Woosley & Weaver 1995).
Comparison between abundances in the H i and H ii region.
 |
Fig. 11 Abundance ratios calculated from the stellar yields of Woosley & Weaver (1995). Yields are plotted for two mass ranges, 11–25 M⊙ (open symbols) and 30–40 M⊙ (filled symbols), and two metallicities, 0.1 Z⊙ (diamonds) and 0.01 Z⊙ (squares). The grey stripe shows the observed values. The horizontal black line shows the average ratio observed in the H ii region of BCDs (Izotov et al. 1999). |
The oxygen abundance is widely used as a metallicity tracer. However the O i lines in the COS spectra are either too weak to provide a useful upper limit or too strong to provide a reliable column density determination (Sect. 3.3). To circumvent this issue, we can use silicon or sulfur as a replacement. Sulfur is a better candidate because the S ii lines are not prone to saturation. Bowen et al. (2005) find that S ii traces well H i in a diffuse slab over a wide range of ionization parameter (see also Sect. 6.1). Sulfur is thus a reliable substitute for oxygen and a useful metallicity tracer. Assuming that the S/O ratio in the ionized phase of I Zw 18 (−1.64) also holds in the neutral phase, we find (OS/H) ≈ 7.03 ± 0.15. This value is barely in agreement with the O/H ratio measured in the ionized gas, leading to δH i(OS) ≈ 0.18 ± 0.16. Our indirect determination of the oxygen abundance lies between the FUSE value of L04, who found similar O/H between the two phases (although with large error bars), and the value of A03, who, despite using the same spectrum as L04, found δH i(O) ≈ 0.54 (Sect. 3.3).
6.3. The odd-Z elements
Although Al and P are not α-elements, they are thought to be produced the same massive stars that make oxygen. No significant amount should be produced in the explosive phases and the yields are expected to be metallicity dependent because of the odd-even effect (Woosley & Weaver 1995). Aluminum is produced by C and Ne burning while phosphorus is produced during Ne burning. Lebouteiller et al. (2005) found that P ii and O i column densities trace well each other over a wide range of environments as long as ionization corrections are not a major issue. Depletion on dust grains affects P more than O (Jenkins 2009), so part of the dispersion observed by Lebouteiller et al. (2005) could also be due to a differential depletion factor.
In this section, we discuss the abundances of P and Al relative to α-elements since there is no measurement of P or Al abundance in the ionized gas. Assuming a solar P/O ratio we estimate (OP/H) ~ 6.86 ± 0.33. This value agrees within errors with the oxygen abundance (OS/H) ≈ 7.05 ± 0.15 (Sect. 6.2). Figure 11 shows that the expected yields from massive stars are also close to the solar P/O ratio.
The Al/S ratio in the neutral gas is remarkably lower than the solar value, with [Al/S] = −0.74 ± 0.32. Aluminum abundance is determined using a single Al ii line that is unfortunately saturated. However, the saturation of the Al ii line is not as strong as C ii or Si ii lines, so we consider that saturation cannot explain the entire difference. It is also unlikely that there is a significant contribution from Al i given its extremely low ionization potential of 5.99 eV. The low [Al/S] ratio could be due to a relatively stronger depletion of Al on dust grains as compared to S. The depletion of Al in the Local Interstellar Cloud is ~0.9 dex relative to O in the WNM (Kimura et al. 2003). Such a factor would be more than enough to reconcile our Al/S ratio with the solar ratio. However, we investigate further the hypothesis of dust depletion in Sect. 6.7 and find that depletion alone cannot explain the low [Al/S] ratio. The Al/S ratio in the neutral gas, although sub-solar, is in fact consistent with expected yields from massive stars (Fig. 11). We therefore conclude that aluminum in the H i region is not deficient with respect to the α-elements.
6.4. Carbon
Carbon is produced in intermediate- and high-mass stars by He burning. During the early stages of a galaxy evolution, carbon is released mostly by the same young stars that make oxygen, so it is expected that C/O traces the yield ratio from massive stars. As galaxies evolve, older stellar population will contribute to the total carbon abundance, and a rise in C/O is expected (e.g., Izotov & Thuan 1999).
In the ionized gas of I Zw 18, [C/O] = −0.40 ± 0.17, which is somewhat lower than more metal-rich BCDs, suggesting that C mostly comes from massive stars, as proposed in Izotov & Thuan (1999). Note that the C/O measured by Izotov et al. (1999), −0.77 ± 0.10, is slightly lower than both the value in Garnett et al. (1997), −0.63 ± 0.10, and than the value in Péquignot (2008), ≈−0.66. Garnett et al. (1997) found that C/O in I Zw 18 is larger than expected from massive star nucleosynthesis and attribute the discrepancy to C enrichment by a lower mass stellar population.
The carbon abundance in the H i region is somewhat lower than in the H ii region. Using sulfur to trace oxygen in the neutral gas (Sect. 6.2), we find [C/OS] = −0.77 ± 0.33, which falls somewhat below, although compatible with, the ionized gas value. We also note that [C/OS] appears to be compatible with expected massive stars yields (Fig. 11).
6.5. Nitrogen
The nucleosynthesis of nitrogen is not as well understood as for carbon or oxygen. Nitrogen can be produced in the CNO cycle by any stars more massive than 1.5 M⊙. The observation of a N/O plateau at low-metallicity in BCDs (e.g., Izotov & Thuan 1999; Nava et al. 2006) leads to the conclusion that nitrogen is produced as a primary element, i.e., using the C and O produced in situ (since little C is available when the stars form). At higher metallicities (12 + log (O/H) ≳ 8.3), secondary nitrogen production (from C and O from older generations) dominates. The origin of the N/O scatter at low-metallicity is still debated. If it is dominated by measurement errors, then nitrogen, like oxygen, is likely produced in short-lived massive stars (Nava et al. 2006). The spread could also be intrinsic, due to the delayed injection of N from intermediate-mass stars. The observed scatter is theoretically explained either by effective yield variations and/or different star-formation history (Henry et al. 2000, 2006; Meynet & Maeder 2002b). The results of Henry et al. also show that nitrogen production in massive stars is possible.
The N/O ratio in the ionized gas of I Zw 18, −1.61 ± 0.06, is compatible with the low-metallicity BCD plateau located at ≈−1.60 (Izotov & Thuan 1999). In the neutral gas, nitrogen is somewhat deficient, with δH i(N) ≈ 0.39 ± 0.11. This translates into a N/O ratio of N/OS = −1.84 ± 0.19 which is only somewhat lower than the ionized gas ratio. Following the N/O plateau paradigm, we conclude that the ISM was enriched on large scales by the same stellar population. Assuming the lower N/O in the H i region is genuine, it could be that intermediate-mass stars have contributed to the nitrogen enrichment in the H i region, or that nitrogen abundance was enhanced by massive stars in the H ii region (see also Sect. 7.2).
6.6. The iron group elements
The iron group elements are particularly important because they could be released in the ISM on longer timescales than α-elements. Iron is produced partly in massive stars and in SNe Ia. A useful quantity to disentangle the two origins is [α/Fe]. The [α/Fe] ratio should increase with the progenitor mass (Woosley & Weaver 1995). If star formation is stopped, SNe II contribute no more to the Fe enrichment and SNe Ia could become important. Our Fe abundance is the same as the value determined by L04 using FUSE, and both values hint at a lower Fe abundance in the neutral gas as compared to the ionized gas. However, our value remains compatible with the ionized gas value within errors, with δH i(Fe) ≈ 0.24 ± 0.28. We find that [OS/Fe] in the neutral gas is 0.45 ± 0.25, as compared to 0.37 ± 0.21 in the ionized gas. It is thus likely that the enrichment from SNe Ia, if any, is identical in the H i phase and in the H ii phase. This value of [OS/Fe] lies between 0 (solar O/Fe ratio) and the value in Galactic halo stars (Barbuy 1988) and in metal-poor stars in the solar neighborhood (Jonsell et al. 2005), suggesting an early enrichment by high-mass stars (see Izotov & Thuan 1999).
Nickel and manganese both belong to the iron group. The depletion strength of Ni is similar to that of Fe while Mn is less depleted than Fe by a factor ≲0.5 dex (Jenkins 2009). Manganese is mostly made in explosive Si burning while nickel is produced mostly by neutron capture on the iron-peak elements in SNe Ia. It should be noticed that Ni and Fe are among the most heavily depleted elements in the ISM (e.g., Savage & Sembach 1996). We discuss the influence of depletion on dust grains in Sect. 6.7. The Ni/Fe ratio in the neutral gas of I Zw 18 is solar, with [Ni/Fe] = −0.05 ± 0.23. We note that [Ni/Fe] remains essentially null over a wide range of metallicities in nearby stars (also in DLAs; Izotov et al. 2001b) while at the same time [α/Fe] increases at low-metallicity (Jonsell et al. 2005). This implies that Ni and Fe evolve in parallel, and it is therefore not surprising that we also find a solar ratio in I Zw 18. Since we already suggested that iron might be produced mainly in massive stars, the same result should apply to nickel. Concerning manganese, its abundance is uncertain, and we measure a Mn/Fe ratio slightly above the solar ratio, with [Mn/Fe] = 0.32 ± 0.51.
6.7. Depletion on dust grains
We observe a small abundance discontinuity between the H i and the H ii region (Sect. 6). Could part of the discontinuity be explained by a differential depletion factor on dust grains? Volatile elements such as sulfur and chlorine provide us with a way of estimating the fraction of the underabundance in the neutral gas that is not due to depletion on dust. Unfortunately, Cl is expected both as Cl i and Cl ii in the neutral phase so our upper limit on Cl abundance is not useful. On the other hand, sulfur is our best metallicity estimator since little or no S is expected to be locked in dust. We found that S/H is at least ~15% lower than in the ionized gas, implying that depletion alone cannot explain the lower metallicity of the neutral gas.
We then examine whether depletion could explain the abundance discontinuity observed for
the refractory elements. For this, we calculate the mass of each element in the
H i region locked in dust that would be required to explain the observed
abundance discontinuity between the H i and the H ii region. Given the
small mass fraction of ionized gas in I Zw 18 (e.g., Petrosian et al. 1997), we expect most of the dust mass to lie in the
H i region and we therefore ignore the depletion in the H ii region.
Dust extinction toward I Zw 18 is mostly Galactic, and the dust mass in I Zw 18 is
exceptionally low. Using data from the Spitzer Space Telescope, Galliano et al. (2008) found an upper limit of
<2000 M⊙, while Herschel
data constrains for the first time the dust mass, with
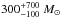 (Rémy et al., in
prep.). We assume that the metals are well mixed in the H i region and express
the mass locked in dust md(X) as:
(Rémy et al., in
prep.). We assume that the metals are well mixed in the H i region and express
the mass locked in dust md(X) as:
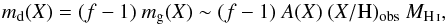 (11)where
md(X) is the mass locked into dust,
mg(X) is the observed abundance in the
neutral gas, f is the total mass (dust+gas) divided by the mass in the
gas, A(X) is the atomic mass,
(X / H)obs is the observed abundance ratio,
and MH i is the H i mass. The total
H i mass in I Zw 18 is
MH i = 6.9 × 107 M⊙,
38% of which (2.6 × 107 M⊙) coming from the main
H i component associated with the star-forming regions (Lequeux & Viallefond 1980; van
Zee et al. 1998).
(11)where
md(X) is the mass locked into dust,
mg(X) is the observed abundance in the
neutral gas, f is the total mass (dust+gas) divided by the mass in the
gas, A(X) is the atomic mass,
(X / H)obs is the observed abundance ratio,
and MH i is the H i mass. The total
H i mass in I Zw 18 is
MH i = 6.9 × 107 M⊙,
38% of which (2.6 × 107 M⊙) coming from the main
H i component associated with the star-forming regions (Lequeux & Viallefond 1980; van
Zee et al. 1998).
Mass estimates of elements locked in dust.
The mass of each element in the gas phase is tabulated in Table 9. We also list the mass required in the dust phase to reach the corresponding abundance in the H ii region. For Al, P, and Cl, whose abundances are not constrained in the ionized gas, we estimate the mass required to obtain a solar proportion with oxygen, i.e., [X/O] = 0. The mass of elements locked into the dust can be then compared to the dust mass measured by Herschel. Since we ignore the dust in the H ii region, the dust mass derived from Herschel is an upper limit to the available dust in the H i region. We find that depletion alone cannot explain the underabundance of C and Si in the neutral gas. Even though the required mass of N, Al, and S into dust is below the observed dust mass, altogether they represent at least half of the available dust, requiring unlikely dust compounds composition. We thus conclude that depletion on dust cannot explain the observed underabundances in the neutral gas.
Since there is little dust available to remove elements from the gas phase, we also find that the abundance ratios are not affected by depletion on dust. As an illustration, there is not enough dust to reconcile O/Fe with the solar ratio (Sect. 6.6). Similarly, we find that the low Al/S and Si/S ratio (Sects. 6.3, 6.2) cannot be explained by aluminum and silicon locked in dust.
7. Discussion
The H i region of I Zw 18 is not pristine; it has already been enriched in metals. We also find that all the elemental abundances, in particular for Al, S, P, Fe, and Ni, are consistent with production in massive stars (Sect. 6). Our best tracer of the enrichment in the H i region by massive stars is sulfur (Sect. 6.2). By using the solar sulfur abundance from Asplund et al. (2009), we estimate the metallicity of the neutral phase to be ≈1/46 Z⊙, as compared to ≈1/31 Z⊙ for the H ii region. Depletion on dust grains should have a negligible impact in both phases considering the low dust mass in the galaxy (Sect. 6.7). We now discuss the enrichment of the H i and H ii regions.
7.1. Abundance discontinuity H I–H II
The ionized gas in I Zw 18 is more metal-rich than the neutral gas, with abundances higher by ≈0.18–0.77 dex depending on the element. Our results are a priori compatible with either (1) the H ii region being enriched by the present or recent star-formation episode(s) or (2) the presence of extremely low-metallicity clouds in the H i region diluting the observed abundances.
The elements synthesized and released by the current burst are expected to lie at first in a hot phase (106 K) and mixing timescales could be as long as 109 yr. Hot gas outflows have been observed through the O vi FUV doublet in starburst galaxies, including a few dwarf galaxies (e.g., Grimes et al. 2009). However, there is no evidence that I Zw 18 developed such an outflow, even though the non-detection of the O vi doublet could be due to the low oxygen abundance in this object (Heckman et al. 2002). Furthermore, Chandra X-ray observations of SBS 0335-052W, SBS 0335-052E, and I Zw 18 also failed to reveal any sign of hot gas breaking out from the stellar body implying that the galactic fountain scenario may not be valid in BCDs (Thuan et al. 2004; see also Sect. 7.3).
As first hypothesized by Kunth & Sargent (1986), the H ii region could be self-enriched, with a fraction of the newly produced heavy elements dispersing on small spatial scales and mixing on short timescales (few Myrs). This would naturally explain the H i-H ii region abundance discontinuity. Legrand et al. (2000) find that abundances are remarkably uniform in the ionized gas of I Zw 18, with a dispersion of ≲0.1 dex on scales of several hundreds of parsecs, which seems to go against the fast and local enrichment hypothesis in the H ii regions. We recall that our H i region abundances are measured toward the NW region, and compared to the H ii region abundances in that region. The NW region is where the youngest stars are located, which in principle provides us with the best chance of observing a local enrichment from the recent star-formation episode(s). The most significant abundance discontinuities H i-H ii we calculate are for N and Si, with δH i(N) = 0.39 ± 0.14 and δH i(Si) = 0.71 ± 0.42 respectively (Sects. 6.5, 6.2), which is significantly larger than the abundance dispersion across the galaxy in its ionized gas. Although nitrogen abundance might be enhanced by very massive, rotating, stars in the H ii region (e.g., Meynet & Maeder 2002a; Hunter et al. 2008; Maeder & Meynet 2012), local enrichment by massive stars does not explain the abundance enhancement of the other elements in the H ii region.
Another possibility to explain a metal deficiency in the neutral gas is to invoke the
presence of extremely metal-poor regions along the lines of sight, such as the
low-metallicity high-velocity clouds infalling on the Milky Way. The H i envelope
in I Zw 18 extends as much as ~13 kpc away from the star-forming regions (Lelli et al. 2012), and it is possible that the −
presumably lower density − outskirts are not as enriched in heavy elements as the
immediate surroundings of the H ii regions. In order to estimate the mass of this
relatively metal-poor H i gas, we tentatively assume that the H i medium
can be separated into two components, one (hereafter HI-sf) is spatially
associated with the star-forming region and another component (HI-ex) is
more extended and possibly less enriched. In the following, we neglect the size and mass
of the H ii region. We further assume that the mixing of metals is uniform in the
vicinity of the H ii region, i.e., abundances are similar in the H ii
region and in HI-sf. The metal abundance in the H i region can
then be written as 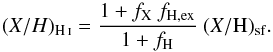 (12)And the
underabundance δH i(X) in the
neutral gas becomes:
(12)And the
underabundance δH i(X) in the
neutral gas becomes: ![\begin{equation} \delta_{\rm \ion{H}{I}} ({X})= -\log\ [ (1-f_{\rm H}) + f_{\rm X}\ f_{\rm H,ex} ], \end{equation}](/articles/aa/full_html/2013/05/aa20948-12/aa20948-12-eq569.png) (13)where
fX = (X / H)ex / (X / H)sf
is the relative abundance ratio of a given element between HI-ex and
HI-sf and fH is the fraction of the total
H i along the line of sight in the HI-ex component.
Figure 12 shows the variations of
δH i(X) with
fH and fX.
(13)where
fX = (X / H)ex / (X / H)sf
is the relative abundance ratio of a given element between HI-ex and
HI-sf and fH is the fraction of the total
H i along the line of sight in the HI-ex component.
Figure 12 shows the variations of
δH i(X) with
fH and fX.
Taking sulfur as a metallicity tracer (X = S), it can be seen that if HI-ex is pristine (fS = 0), the observed sulfur deficiency is compatible with ≈10–45% of hydrogen into HI-ex along the line of sight. Assuming a spherical distribution with constant hydrogen volume density, this represents a factor [1 − (1 − fH)3] in mass, translating to ~25–80% of the total H i mass in HI-ex. In other words, about half the mass of the H i envelope in I Zw 18 could be pristine. This scenario is therefore not compatible with a small number of low column density H i clouds such as the high-velocity clouds observed in the Milky Way. If the observed H i-H ii region abundance discontinuity is caused by the presence of pristine gas, the latter should represent a significant mass fraction of the galaxy (whose baryonic mass budget is dominated by H i gas).
We can then assume that the HI-ex component has also been somewhat enriched (fS > 0). Considering that the H i mass in HI-ex is diluted over a larger volume, the aperture fraction is probably very small, and we can reasonably assume that the fraction of hydrogen in the HI-ex component is less than 75%. For such a value of fH, the observed sulfur deficiency is compatible with the sulfur abundance in HI-ex being ≈40–80% of the value in HI-sf, and thus also of the value in the H ii region. This would imply a metallicity as low as ~1/70 Z⊙ in the outskirts of the galaxy. These results could put galaxy evolution scenarios to the test, with in particular the hypothesis of a minimal enrichment level at a given redshift (Sect. 7.3). Does a metallicity of ~1/70 Z⊙ correspond to the minimal enrichment at redshift z = 0? Deep H i surveys such as ALFALFA (Giovanelli et al. 2005), and later SKA, should identify large numbers of optically-faint H i clouds in the Local Universe that will test the hypothesis of a minimal enrichment level at z = 0. We also wish to emphasize that the hypothetical presence of metal-free gas has important consequences on the interpretation of the integrated D/G ratio, in particular if the latter does not scale linearly with metallicity.
 |
Fig. 12 Metal deficiency in the H i region δH i as a function of the fraction of hydrogen present in the HI-ex component defined as the extended H i component that may be less enriched in metals as compared to HI-sf (the H i component associated to the star-forming regions). We assume that the HI-sf component has the same metallicity as the H ii region and calculate δH i for several values of the sulfur abundance ratio between HI-ex and HI-sf. The horizontal dashed line and the grey stripe indicates illustrate the sulfur deficiency, δH i(S) = 0.18 ± 0.11. |
7.2. Comparison with the sample of BCDs
 |
Fig. 13 Top: comparison of the N/O ratio between the H i and H ii region for the sample of BCDs studied with FUSE, and for I Zw 18 with COS. The labels are defined as 1a) I Zw 18 (L04), 1b) I Zw 18 (A03), 1c) I Zw 18 (this study, with S as a tracer of O; Sect. 6.2), 2) NGC 1705 (Heckman et al. 2001), 3) SBS 0335-052 (Thuan et al. 2005), 4) Mark 59 (Thuan et al. 2002), 5) NGC 625 (Cannon et al. 2005), 6) I Zw 36 (Lebouteiller et al. 2004), 7) Pox 36 (Lebouteiller et al. 2009), 8) NGC 604 (Lebouteiller et al. 2006), 9) SBS 1543+593 (Bowen et al. 2005; Schulte Ladbeck et al. 2004). Bottom: ratio of the average metal abundance [M / H] = ⟨ [X / H] ⟩ between the H i and H ii regions. [M/H] is calculated two ways, averaging all elements observed in each phase (small diamonds), and averaging only the elements observed in both phases (large diamonds). |
We now compare our results on I Zw 18 to the sample of BCDs whose neutral gas has been investigated with the FUSE telescope. First, we examine the N/O abundance ratio as it potentially holds clues as to the stellar population responsible for enriching the ISM. Nitrogen can be synthesized in a wider range of stellar masses than oxygen, and rapidly rotating massive stars can potentially enrich the ISM on short timescales (Sect. 6.5). In contrast, oxygen and the α-elements are produced exclusively in massive stars and are released within a few Myrs through SNe (Sect. 6.2). Figure 13a compares the N/O ratio in the H i and in the H ii region of BCDs. The N/O ratio is similar in both phases for the highest metallicity objects. There might be a hint of a lower N/O in the H i region for the lowest-metallicity objects (I Zw 18, SBS 0335-052, and I Zw 36), but the result is inconclusive within error bars. We conclude that the stars producing N have the same mass range in both phases, which argues for an enrichment of the ISM before the present starburst episode.
The hypothesis of relatively metal-poor outskirts (Sect. 7.1) can also be put to the test in the BCD sample. Lebouteiller et al. (2009) summarized the FUSE results and showed that the metallicity in the H i region in BCDs was equal (I Zw 18, SBS 0335-052) or lower (I Zw 36, Mark 59, Pox 36, NGC 625, NGC 1705) than that in the H ii region. A trend might exist, with the discontinuity being essentially null for the lowest metallicity objects, and then constant around ~1 dex for metallicities ≳1/6 Z⊙ (value in the ionized gas). However, if nitrogen is used as a metallicity tracer instead of oxygen, the results could also be interpreted as a constant discontinuity independent on metallicity. The lowest-metallicity object, I Zw 18, is key to conclude on the ubiquity of the abundance discontinuity H i-H ii region. While the result for I Zw 18 was at the time inconclusive because of the discrepancy between A03 and L04, our study suggests that the abundance discontinuity in I Zw 18 is rather small, smaller than what is observed in other BCDs. We now revisit the findings of Lebouteiller et al. (2009) by including this new measurement, and by calculating the average metal abundance [M / H] = ⟨ [X / H] ⟩ in the H i and H ii regions (Fig. 13b). The choice of averaging the abundances is motivated by (1) possible systematic problems in the abundance determination of some elements (hidden saturation, stellar contamination, atomic data...); and (2) the fact that there is so far no clear evidence of a different nucleosynthesis origin of elements in both phases. Figure 13b shows that the abundance discontinuity is around 0.7 dex for most objects, with no clear correlation as a function of metallicity. This implies that the chemical enrichment H i and H ii region is disconnected in most objects, with the H i region systematically more metal-poor than the H ii region. Applying the results of Sect. 7.1 to the sample of BCDs, Fig. 12 shows that for δH i ~ 0.7 dex, the HI-ex component (extended H i envelope) would have a metallicity between 0% and 30% that of the HI-sf component (associated to the H ii region), and would represent more than 75% of the H i mass. This result is relevant in particular for SBS 0335-052, which, despite a metallicity close to I Zw 18, shows a discontinuity of ≈0.7 dex (Fig. 13b). For SBS 0335-052, the H i envelope could be as metal-poor as ~1/150 Z⊙. New abundance determinations in this object by COS should bring a definitive answer (James et al., in prep.).
7.3. Enrichment of the H I region
7.3.1. Cosmic evolution
Despite the weak discontinuity between the abundances of the H i and H ii regions of I Zw 18, the ISM is fairly well mixed on kiloparsec scales, with the metallicity of the neutral gas at least ≈50% of that in the ionized gas (most likely value of 66%). How was the ISM, and in particular the H i region, enriched? Considering the relatively uniform abundances, at least half of the metallicity in the H i region was presumably set before the current starburst episode. A major uncertainty concerns the genuine age of the galaxy as compared to its chemical age. The latter is probed by the metallicity parameter, which is determined by a complex interplay between successive star-formation episodes and external gas flow exchanges (outflow of enriched material and infall of metal-poor gas).
Although the age of the oldest stars in I Zw 18 is still subject to debate (see Papaderos & Östlin 2012), stars as old as the Hubble time (Aloisi et al. 2007; Contreras Ramos et al. 2011) might be present, suggesting that I Zw 18 is not genuinely young, and therefore that its present-day metallicity is the result of the mechanisms mentioned above over cosmic times. For this reason, the comparison between I Zw 18 and high-z objects is relevant and instructive. The intergalactic medium (IGM) was already enriched to metallicities similar to that of the H i region of I Zw 18 at z ~ 1.6−2.9 (Telfer et al. 2002). Hence it is possible that I Zw 18 was assembled from a collection of low column-density clouds in the IGM a few Gyrs after the Big Bang, and experienced little enrichment since then. The metallicity of the H i envelope of I Zw 18 is also typical of DLAs at z > 2 (Rafelski et al. 2012), again compatible with a slow chemical enrichment. The lack of strong constraints on the mass of DLAs makes the comparison with I Zw 18 relatively uncertain within the chemical downsizing scenario in which galaxies with different mass have different star-formation efficiencies (e.g., Brooks et al. 2007). Nevertheless, the lack of nearby galaxies as metal-poor as high-z DLAs (~1/100 Z⊙; e.g., Prochaska & Wolfe 1999; Rafelski et al. 2012) implies that nearby BCDs, including I Zw 18, have experienced a slow, minimal, enrichment over several Gyr. Legrand et al. (2000) suggested that I Zw 18 went through a mild continuous star-formation rate (SFR), ~10-4 M⊙ yr-1, over several Gyrs as opposed to a series of violent short bursts separated by relatively longer quiescent eras. Metal enrichment in BCDs through a series of violent star-formation episodes is an unlikely process as galaxies with different star-formation histories would result in different metallicities, thus including a class of nearby galaxies with no starburst episodes and an extremely low-metallicity, which is not confirmed by observations.
The relation between stellar mass and metallicity in galaxies (e.g., Tremonti et al. 2004) suggests that star formation proceeds slowly at low metallicity. However, the mass-metallicity relation can also be understood as a lower star-formation efficiency at low mass, with a relatively more efficient ejection of enriched material, or by a metallicity increase through star-formation triggered by infalling gas. Mannucci et al. (2010) showed that a more fundamental relation exists between stellar mass, metallicity, and SFR, where downsizing, outflows, and infalls are the major actors.
Accretion of inflowing cold gas triggers a transient phase in which (1) metallicity is diluted by the injection of significant amounts of low-metallicity gas; (2) the SFR increases through the Schmidt-Kennicutt law; and (3) metallicity increases again as star formation proceeds. Although H i companions are often observed around star-forming dwarf galaxies (e.g., Taylor 1997; Ramya et al. 2009; Pustilnik et al. 2001), their accretion and the consequence on star formation is not definitive (e.g., Telles & Maddox 2000). Gas inflow is expected to play a more important role at high-z. The cosmological inflow from the cosmic web could have been so high at high-z that star-formation could not catch up in the least massive haloes like I Zw 18 (Krumholz & Dekel 2012). This metallicity-dependent quenching would result in a growth of the H i envelope, the latter still being observed today. Only at z < 2 could a low-mass galaxy like I Zw 18 start to build up its metallicity. Such a scenario remains compatible with the presence of old stars in I Zw 18.
Alternatively (or possibly in parallel), galactic winds could expel most of the metals into the IGM through multiple supernovae explosions, effectively keeping the ISM metallicity to low levels (e.g., Recchi et al. 2004). The most active star-forming regions would be responsible for those winds. A major uncertainty remains however on the fate of the metals observed in galactic outflows, since the superbubble expansion might decelerate, and the outflowing material might cool down and return to the ISM instead of escaping the gravitational well (e.g., Tenorio-Tagle et al. 1999; Mac Low & Ferrara 1999; Rieschick 2003). Despite the current starburst episode in I Zw 18, there is no evidence of outflowing hot gas (Sect. 7.1). Furthermore, we note that outflows would play a more important role in galaxies whose star-formation history is dominated by a series of violent bursts, which has probably not been the case in I Zw 18 (Legrand et al. 2000).
In summary, although gas flows play a major role in the cosmic evolution of galaxies, their effects in I Zw 18 are not yet fully constrained and understood. A combination of metal-poor gas infall in the early stages of the galaxy, and a chemical downsizing could be responsible for the extremely low-metallicity observed today in the H i and H ii regions. Finally, our results do not allow putting constraints on the reasons of the current starburst episode in I Zw 18, which has been ~10–100 times relatively stronger over the past ~50 Myr (Aloisi et al. 1999; Legrand et al. 2000). The sudden onset of star formation could have been triggered by gas compression from merging events. The disturbed H i morphology suggests that several small structures might have been interacting (Lelli et al. 2012). Such structures could have been gas-rich dwarf galaxies or sub-DLAs. From the radial velocity of the neutral metals observed with COS, we did not find any evidence of infalling material on the NW region itself; the H i gas is, if anything, outflowing from the H ii region with a velocity of ~20 km s-1 (see also A03; L04). However, Lelli et al. (2012) found a radial inflow/outflow motion on the order of ~15 km s-1 on larger scales and concluded that interactions or mergers are the most likely explanation for the current starburst episode. In general, the FUSE results for other BCDs show blue shifts of at most 10–20 km s-1 (e.g., Lebouteiller et al. 2009; Cannon et al. 2005), confirming that slow radial flows of H i gas might be frequent.
7.3.2. Local conditions for star formation
We now discuss the star-formation process itself, and the influence of metallicity in the ability of clouds to form stars in an environment as metal-poor as I Zw 18. Our present study puts strong constraints on the metallicity of the H i region, which constitutes the bulk of the mass of the galaxy. The H i region is thus key to understand the past star-formation efficiency.
First, the fact that stars of all masses have formed for several Gyrs has some implications for the early metallicity evolution of the galaxy. Bromm & Loeb (2003) showed that when the metallicity reaches more than 10-4−10-3 Z⊙, the cooling by the far-IR fine-structure lines [C ii] 157 μm and [O i] 63 μm enables cloud fragmentation and therefore low-mass star-formation. No dust or molecules were considered for this calculation and we note that H2 could provide the most efficient cooling at even lower metallicity (e.g., Omukai et al. 2005). However, the lack of diffuse H2 in I Zw 18 (Vidal-Madjar et al. 2000) suggests that H2 cooling is not significant in our practical study, except if present in small dense clumps where H2 might be more abundant (see Thuan et al. 2005). We thus get the picture of I Zw 18 forming stars of all masses only a few Gyrs after the Big Bang, when its metallicity reached ≳10-4 Z⊙. The oldest stars in I Zw 18 could be the remnants of the star-formation episode following this early enrichment. The existence of a metallicity threshold for low-mass star-formation is however still debated and we note that the presence of dust to shield UV photons, and the D/G ratio, ultimately related to metallicity via the evolution of the dust-to-metal ratio, may be the most important parameters governing the star formation process (Schneider et al. 2012; Glover & Clark 2012).
The importance of the ISM metallicity is fundamental for the ability of clouds to form stars, and it may well regulate the SFR as long as external gas flows are unimportant. Although the observed SFR in BCDs is ~10-2−10 M⊙ yr-1, this corresponds to the current starburst episode, and a much milder SFR could have dominated beforehand. For example, in I Zw 18 the past SFR could have been as low as ~10-4 M⊙ yr-1; e.g., Legrand et al. 2000). It seems at first contradictory with Mannucci et al. (2010) who finds that for a given stellar mass, the SFR is anti-correlated with metallicity. The fundamental metallicity relation found by Mannucci et al. (2010) is, however, biased toward emission-line galaxies, and a “pre-starburst” I Zw 18 would not have been selected by their survey. Furthermore, as discussed in the following, it is possible that the extremely low-metallicity of this galaxy has a major impact on the star-formation process itself.
The temperature and density of the ISM are essential parameters for star formation. The latter can be inhibited by the inability of the gas to cool down enough for removing thermal pressure and for creating gravitational instabilities. The warm temperature in a metal-poor ISM is due to the paucity of efficient cooling mechanisms, such as molecules or the far-IR fine-structure line [C ii], which dominates the cooling in the diffuse atomic clouds. Krumholz (2012) showed that the thermal equilibrium timescale is more important than the timescale for conversion of atomic to molecular gas in a low-metallicity gas. Star formation could proceed before the medium becomes molecular when the metallicity reaches below a few percents solar. The metallicity threshold above which thermal equilibrium is reached before a few free-fall timescales (once the gas becomes gravitationally unstable) thus depends mostly on the ability of the gas to cool down. The H i region of I Zw 18 is an ideal testbed for star-formation timescales in a low-metallicity atomic gas, since molecular gas has yet to be detected. The model in Krumholz (2012) highly depends on the heating mechanisms and their metallicity dependence, and the uncertain heating mechanisms in the H i region of galaxies such as I Zw 18 (Sect. 5.4) add to the uncertainty on the threshold metallicity and thermal equilibrium timescale. Following the method in Krumholz (2012), we use our determination of the heating rate in the H i region, and an initial gas density and temperature of ~10 cm-3 and ~1000 K, respectively. We find that thermal equilibrium is reached before a few free-fall timescales only for a metallicity greater than ~1/100 Z⊙. A lower threshold metallicity would be obtained if we consider a significant clumping factor. Hence we see that widespread star formation is possible in the H i region of I Zw 18, currently holding a metallicity of ≈1/46 Z⊙. If such physical conditions prevail in objects as metal-poor as ≲1/100 Z⊙, the thermal equilibrium timescales are rather long and the ability to form stars ultimately depends on the survival of the clouds. I Zw 18 might have kept a low metallicity because its ISM remained warm on long timescales. A major uncertainty remains on the presence of small cold clumps (cold neutral medium phase) in which star formation would be more efficient. The mixing factor of the warm neutral medium and cold dense clumps in the FUV absorption lines is difficult to quantify. Moreover the ISM pressure in I Zw 18 might be too low to maintain a multi-phase ISM, so that the neutral gas we characterized in this study might be the only thermally-stable phase. The temperature from this phase could thus be a crucial parameter to understand the star-formation process on large spatial scales and over cosmic times.
8. Conclusions
We present a comprehensive investigation of the H i envelope of I Zw 18. The H i region holds several fundamental clues to the chemical evolution of galaxies. The metallicity of the H i region is set by the successive star-formation episodes over the galaxy history, and is modulated by outflows of supernovae products and hypothetical inflows of quasi-pristine gas from the cosmic web. The abundance of metals in the H i region is also a critical parameter to understand the present and the future star-formation history, as metals provide most of the cooling in the H i gas reservoir to facilitate and sustain the star-formation process. Our objectives are to characterize the H i region by (1) its physical conditions and (2) its chemical abundances. We compare the abundances to those derived in the H ii region (from optical emission-lines), and discuss the enrichment history of the galaxy.
The H i envelope of I Zw 18 was observed toward the NW young stellar cluster in the FUV with the COS instrument on HST. The massive stars provide the FUV continuum over which absorption-lines from neutral species are superimposed. We modeled the stellar absorption in order to remove its contribution and isolate the interstellar absorption. We derived the column density of H i and of heavy elements (C ii, C ii*, N i, O i, Al ii, Si ii, P ii, S ii, Mn ii, Fe ii, Ni ii). Models were constructed to compute the ionization structure of the nebula. Our models predict a large ionized gas volume in the H ii region, suggesting that the H i cavity observed at 21 cm toward NW is due to ionization by the stellar cluster as opposed to blow-out by stellar winds and supernovae. We study potential emission components in the H ii region that could work out to reduce the apparent optical depth of absorption lines.
The physical conditions in the H i region are drawn from the study of the C ii* absorption-line.
-
The population of the fine-structure level of C+ toward NW is compatible with collisions with H0 atoms, implying that C ii* arises in the H i envelope.
-
We determine observationally that the electron fraction in the H i region is less than ~2%; our models predict ~0.1%.
-
From C ii* we derive a cooling rate that is larger than the models. An extra heating source is required in the models to reconcile them with the observations, leading to an elevated electron temperature in the H i region of ~1000 K.
-
The cooling rate inferred from C ii* is used to calculate the star-formation rate. Our value agrees with other determinations in the literature, although on the high-end. The D/G ratio used for this calculation is a factor of ~2000 times lower than the Milky Way value, i.e., a factor of ~60 times lower than what is expected if we simply scale D/G with metallicity.
We then infer the dominant ionization stages in the H i region from the models and calculate the chemical abundances in the H i region.
-
We find that sulfur is less abundant in the H i region as compared to the H ii region, by a (log) factor of 0.18 ± 0.11.
-
Nitrogen, and possibly carbon, are also underabundant in the H i region.
-
The P/S ratio is solar while Al/S is consistent with yields from massive stars. The Fe abundance is the same in the 2 phases within errors. The [α/Fe] ratio is consistent with production in massive stars.
-
Depletion on dust grains is unlikely to explain the observed abundance discontinuity between the H i and H ii regions. This is due to the low dust mass available.
Finally, we discuss possible scenarios concerning the abundance difference in the gas phases, and concerning the enrichment of the H i region.
-
Local enrichment in the H ii regions could explain the enhanced N abundance but fails to explain other results, especially for S.
-
The presence of relatively lower metallicity outskirts in the H i region is discussed. As much as 50% of the H i mass could be pristine.
-
The metallicity of the H i region is not null, it is compatible with the IGM metallicity at z = 1.6−2.9. I Zw 18 could be considered as an old DLA with little recent star formation. The presence of old stars confirm that I Zw 18 is not a genuinely young galaxy. The inflow of quasi-pristine gas from the cosmic web for a few Gyrs after the Big Bang could explain the massive H i envelope and the quenched star-formation in the early stages of the galaxy evolution.
-
The current onset of star formation could be a due the merging of dwarfs or sub-DLAs, as suggested by the disrupted H i morphology.
The sample of BCDs whose neutral gas has been investigated by FUSE and COS shows that a systematic discontinuity exists between the H i and H ii region abundances. I Zw 18 is the object with the lowest discontinuity. Another BCD, SBS 0335-052, despite having a metallicity similar to I Zw 18 does show a significant discontinuity which could translate in the H i region being as metal-poor as 1/150 Z⊙.
Online material
Appendix A: Line fitting
 |
Fig. A.1 Line profile fitting for the 11 523 (top), 12 028 (middle), and 11 579 datasets (bottom). For display purposes, only the strongest lines from I Zw 18 (component 1, also indicated by the vertical dotted lines), from the Milky Way (component 2), and from the high-velocity cloud (component 3) are labeled. The thin green line shows the individual line profiles. The solid thick red line shows the fit to the data while the dotted red line shows the line profiles assuming the H i region abundances are equal to the H ii region abundances. |
 |
Fig. A.2 See Fig. A.1 for the plot description. The unlabelled line on the far right is Si iiiλ1206.5 arising in I Zw 18. |
This translates into a metallicity of ≈ 1/31 Z⊙ with the solar oxygen abundance taken from Asplund et al. (2009).
The G185M spectrum contains in particular the Si iiλ1808.0 line, with an oscillator strength about 50 times lower than the weakest Si ii line in our study, λ1546.7. However, the low S/N of the spectrum, due to the almost fully illuminated aperture (Sect. 3.2) and to cross-contamination between the spectral stripes of the grating on the detector, does not allow setting a useful constraint on the Si ii column density.
COS instrument handbook, http://www.stsci.edu/hst/cos, Sect. 5.9.
Acknowledgments
V.L. is supported by a CEA/Marie Curie Eurotalents fellowship. We would like to thank Aurélie Rémy for the Herschel dust mass measurements. Based on observations obtained with the NASA/ESA Hubble Space Telescope, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. S.R.H. and I.H. gratefully acknowledge support by the NASA Cosmic Origins Spectrograph program at the University of Colorado, Boulder.
References
- Aloisi, A., Tosi, M., & Greggio, L. 1999, AJ, 118, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Aloisi, A., Savaglio, S., Heckman, T. M., et al. 2003, ApJ, 595, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Aloisi, A., Annibali, F., Mack, J., et al. 2007, Stellar Populations as Building Blocks of Galaxies, 241, 310 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Barbuy, B. 1988, A&A, 191, 121 [NASA ADS] [Google Scholar]
- Bhattal, A. S., Francis, N., Watkins, S. J., & Whitworth, A. P. 1998, MNRAS, 297, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Bowen, D. V., Jenkins, E. B., Pettini, M., & Tripp, T. M. 2005, ApJ, 635, 880 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Brinchmann, J., Kunth, D., & Durret, F. 2008, A&A, 485, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Heap, S. R., Hubeny, I., Lanz, T., & Lindler, D. 2002, ApJ, 579, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, J. M., Skillman, E. D., Sembach, K. R., & Bomans, D. J. 2005, ApJ, 618, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, ApJ, 210 [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 519, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras Ramos, R., Annibali, F., Fiorentino, G., et al. 2011, ApJ, 739, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, M. K., Genzel, R., Townes, C. H., & Watson, D. M. 1985, ApJ, 291, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Dufour, R. J., & Hester, J. J. 1990, ApJ, 350, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 2011, ApJ, 51, 59 [Google Scholar]
- Federman, S. R., Brown, M., Torok, S., et al. 2007, ApJ, 660, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Fukuda, N., & Hanawa, T. 2000, ApJ, 533, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J. P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Skillman, E. D., Dufour, R. J., et al. 1995, ApJ, 443, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Skillman, E. D., Dufour, R. J., & Shields, G. A. 1997, ApJ, 481, 174 [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Kent, B. R., et al. 2005, AJ, 130, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 116 [NASA ADS] [Google Scholar]
- Goldsmith, P. F., Langer, W. D., Pineda, J. L., & Velusamy, T. 2012, ApJS, 203, 13 [Google Scholar]
- Green, J. C., Froning, C. S., Osterman, S., et al. 2011, ApJ, 744, 60 [Google Scholar]
- Grimes, J. P., Heckman, T., Aloisi, A., et al. 2009, ApJ, 181, 272 [Google Scholar]
- Gry, C., Lequeux, J., & Boulanger, F. 1992, A&A, 266, 457 [NASA ADS] [Google Scholar]
- Habing, H. J. 1968, ApJ, 19, 421 [Google Scholar]
- Heap, S., Malumuth, E., Landsman, W., & Lindler, D. 2013, ApJ, submitted [Google Scholar]
- Hébrard, G., Lemoine, M., Vidal-Madjar, A., et al. 2002, ApJ, 140, 103 [Google Scholar]
- Heckman, T. M., Sembach, K. R., Meurer, G. R., et al. 2001, ApJ, 554, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Norman, C. A., Strickland, D. K., & Sembach, K. R. 2002, ApJ, 577, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., Edmunds, M. G., & Koppen, J. 2000, ApJ, 541, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., Nava, A., & Prochaska, J. X. 2006, ApJ, 647, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Howk, J. C., Wolfe, A. M., & Prochaska, J. X. 2005, ApJ, 622, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hubeny, I., Heap, S. R., & Lanz, T. M. 2000, AAS 197th meeting, 32, 718 [Google Scholar]
- Hulsbosch, A. N. M., & Wakker, B. P. 1988, ApJ, 75, 191 [Google Scholar]
- Hunter, D. A., & Thronson, H. A. J. 1995, ApJ, 452, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Brott, I., Lennon, D. J., et al. 2008, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 1999, ApJ, 511, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2007, ApJ, 665, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1997, ApJ, 108, 1 [NASA ADS] [Google Scholar]
- Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 1999, ApJ, 527, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 2001a, ApJ, 560, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., & Charbonnel, C. 2001b, ApJ, 549, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Guseva, N. G. 2005, ApJ, 632, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 1971, ApJ, 169, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2013, ApJ, 764, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B., Gry, C., & Dupin, O. 2000a, A&A, 354, 253 [NASA ADS] [Google Scholar]
- Jenkins, E. B., Oegerle, W. R., Gry, C., et al. 2000b, ApJ, 538, L81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jonsell, K., Edvardsson, B., Gustafsson, B., et al. 2005, ApJ, 440, 321 [Google Scholar]
- Kennicutt, Jr, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., Mann, I., & Jessberger, E. K. 2003, ApJ, 582, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Skillman, E. D. 1997, ApJ, 489, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2012, ApJ, 759, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Dekel, A. 2012, ApJ, 753, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Östlin, G. 2000, A&ARv, 10, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Sargent, W. L. W. 1986, ApJ, 300, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., Lequeux, J., Sargent, W. L. W., & Viallefond, F. 1994, A&A, 282, 709 [NASA ADS] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJ, 146, 417 [NASA ADS] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJ, 169, 83 [Google Scholar]
- Lebouteiller, V. 2005, Ph.D. Thesis [Google Scholar]
- Lebouteiller, V., Kunth, D., Lequeux, J., et al. 2004, A&A, 415, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebouteiller, V., Kuassivi, & Ferlet, R. 2005, A&A, 443, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebouteiller, V., Kunth, D., Lequeux, J., et al. 2006, A&A, 459, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebouteiller, V., Bernard-Salas, J., Brandl, B., et al. 2008, ApJ, 680, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Kunth, D., Thuan, T. X., & Désert, J.-M. 2009, A&A, 494, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Etangs, A., Désert, J.-M., Kunth, D., et al. 2004, A&A, 413, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, H. T., & Chen, W. P. 2007, ApJ, 657, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H., & Skillman, E. D. 2004, ApJ, 614, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Legrand, F., Kunth, D., Roy, J.-R., Mas-Hesse, J. M., & Walsh, J. R. 2000, A&A, 355, 891 [NASA ADS] [Google Scholar]
- Lehner, N., Wakker, B. P., & Savage, B. D. 2004, ApJ, 615, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Lejeune, T., & Schaerer, D. 2001, ApJ, 366, 538 [Google Scholar]
- Lelli, F., Verheijen, M., Fraternali, F., & Sancisi, R. 2012, A&A, 537, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemoine, M., Vidal-Madjar, A., Hébrard, G., et al. 2002, ApJ, 140, 67 [Google Scholar]
- Lequeux, J., & Viallefond, F. 1980, A&A, 91, 269 [NASA ADS] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez Sanchez, A. R., Esteban, C., Garcia Rojas, J., Peimbert, M., & Rodriguez, M. 2007, ApJ, 656, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M. M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2012, ApJ, 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Geis, N., Genzel, R., et al. 1993, ApJ, 407, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2002a, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2002b, A&A, 381, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moos, H. W., Cash, W. C., Cowie, L. L., et al. 2000, ApJ, 538, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, D. C. 2003, ApJ, 149, 205 [NASA ADS] [Google Scholar]
- Nava, A., Casebeer, D., Henry, R. B. C., & Jevremovic, D. 2006, ApJ, 645, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Guseva, N. G., Fricke, K. J., et al. 2000, A&A, 361, 33 [NASA ADS] [Google Scholar]
- Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Papaderos, P., & Östlin, G. 2012, A&A, 537, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peimbert, A., & Peimbert, M. 2010, ApJ, 724, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Péquignot, D., 2008, A&A, 478, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrosian, A. R., Boulesteix, J., Comte, G., Kunth, D., & Lecoarer, E. 1997, A&A, 318, 390 [NASA ADS] [Google Scholar]
- Pettini, M., & Lipman, K. 1995, A&A, 297, L63 [Google Scholar]
- Pettini, M., Steidel, C. C., Adelberger, K. L., Dickinson, M., & Giavalisco, M. 2000, ApJ, 528, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Podobedova, L. I., Kelleher, D. E., & Wiese, W. L. 2009, J. Phys. Chem. Ref. Data, 38, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Pottasch, S. R., Wesselius, P. R., & van Duinen, R. J. 1979, A&A, 74, L15 [NASA ADS] [Google Scholar]
- Prochaska, J. X., & Wolfe, A. M. 1999, ApJ, 121, 369 [Google Scholar]
- Pustilnik, S. A., Brinks, E., Thuan, T. X., Lipovetsky, V. A., & Izotov, Y. I. 2001, AJ, 121, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Wolfe, A. M., Prochaska, J. X., Neeleman, M., & Mendez, A. J. 2012, ApJ, 755, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Ramya, S., Kantharia, N. G., & Prabhu, T. P. 2009, ASP Conf. Ser., 407, 114 [NASA ADS] [Google Scholar]
- Rana, N. C. 1991, ARA&A, 29, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Matteucci, F., D’Ercole, A., & Tosi, M. 2004, A&A, 426, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieschick, A. 2003, ApJ, 284, 861 [Google Scholar]
- Sargent, W. L. W., & Searle, L. 1970, ApJ, 162, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Güsten, R., Tremblin, P., et al. 2012, A&A, 542, L18 [Google Scholar]
- Schulte Ladbeck, R. E., Rao, S. M., Drozdovsky, I. O., et al. 2004, ApJ, 600, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Sembach, K. R., Howk, J. C., Ryans, R. S. I., & Keenan, F. P. 2000, ApJ, 528, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, E. D., & Kennicutt, R. C. J. 1993, ApJ, 411, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., & Jenkins, E. B. 1998, ApJ, 499, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Cardelli, J. A., Guerin, K. P., & Meyer, D. M. 1997, ApJ, 482, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Fitzpatrick, E. L., & Meyer, D. M. 1998, ApJ, 504, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, C. L. 1997, ApJ, 480, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Telfer, R. C., Kriss, G. A., Zheng, W., Davidsen, A. F., & Tytler, D. 2002, ApJ, 579, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Telles, E., & Maddox, S. 2000, MNRAS, 311, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G., Silich, S. A., Kunth, D., Terlevich, E., & Terlevich, R. 1999, MNRAS, 309, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., & Izotov, Y. I. 2005, ApJ, 161, 240 [Google Scholar]
- Thuan, T. X., & Martin, G. E. 1981, ApJ, 247, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1996, ApJ, 463, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1997, ApJ, 477, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Lecavelier Des Etangs, A. L. d., & Izotov, Y. I. 2002, ApJ, 565, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Bauer, F. E., Papaderos, P., & Izotov, Y. I. 2004, ApJ, 606, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Lecavelier des Etangs, A., & Izotov, Y. I. 2005, ApJ, 621, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L., Westpfahl, D., & Haynes, M. P. 1998, AJ, 115, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Vanhala, H. A. T., & Cameron, A. G. W. 1998, ApJ, 508, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Kunth, D., Lecavelier Des Etangs, A. L. d., et al. 2000, ApJ, 538, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & van Woerden, H. 1997, ARA&A, 35, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. R., & Roy, J.-R. 1989, MNRAS, 239, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. R., & Roy, J.-R. 1993, MNRAS, 262, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 134, 263 [Google Scholar]
- Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2003a, ApJ, 593, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Prochaska, J. X., & Gawiser, E. 2003b, ApJ, 593, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Wood, B. E., Linsky, J. L., Hébrard, G., et al. 2002, ApJ, 140, 91 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJ, 101, 181 [Google Scholar]
- Wu, Y., Charmandaris, V., Hao, L., et al. 2006, ApJ, 639, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1966, ApJ, 143, 192 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 HST/ACS image of I Zw 18 (main body), with RBG colors defined as I, V, and B filters. Images were downloaded from the Hubble Legacy Archive (http://hla.stsci.edu/) and later combined. The green contours show the H i column density distribution from Lelli et al. (2012) with 2′′ resolution (beam size in the bottom left). Contours are drawn for 3 (dashed), 6, 9, 12, and 15 × 1021 cm-2. The COS observation, represented by the black circle (2.5″ diameter), is centered on the NW star cluster. |
| In the text | |
 |
Fig. 2 Processing of the observed spectrum a) consists of correcting for reddening and for Lyα absorption in the Milky Way and in the high-velocity cloud b); fitting and removing Lyα from I Zw 18 c); and normalizing the spectrum d). The residual emission at Lyα wavelength is due to geocoronal H i. |
| In the text | |
 |
Fig. 3 COS spectra of I Zw 18. The Lyα absorption (from I Zw 18, the Milky Way, and the high-velocity cloud) was removed and the flux was normalized to the local continuum. The numerous absorption features often come in pairs: the weaker − redshifted − absorption feature is from I Zw 18; the stronger feature arises in the Galaxy. A non-LTE, photospheric model spectrum (no winds) of the stellar population (10 Myr age with a continuous star formation hypothesis) and log (Z / Z⊙) = −1.7 is shown in blue. While many features such as C iiiλ1175 and the Si ivλ1400 doublet appear to be well matched by the stellar model, other high-ionization features such as He iiλ1640 and the C ivλ1549 doublet are not well matched. The origin of these lines (e.g., WR stars, H ii region...) is unclear. |
| In the text | |
 |
Fig. 4 Electron temperature (top) and density (bottom) profile of the simple model approximation of I Zw 18. The abscissa is the radial distance from the ionizing stars in cm. |
| In the text | |
 |
Fig. 5 Cloudspec model spectra. Top: stellar and nebular (H i and H ii region) component normalized to the stellar continuum (blue) and emission component (red). Both component spectra have been convolved with a Gaussian line-spread function having a FWHM = 0.5 Å to simulate the observations. Major absorption lines formed in the H i region are labeled on top. Most other strong lines, e.g. the Si ivλ1400 doublet, C ivλ1549 doublet, are higher ionization lines formed in the H ii region. The absorption component of Lyα completely erases the Lyα emission formed in the H ii region. Bottom: simple model spectrum for the case CF × AF = 0.1 (top) and for CF × AF = 0.4 (bottom), with CF the covering fraction and AF the aperture fraction (see text). The dotted line is the absorption spectrum, and the bold line is the net spectrum. The component and net spectra have been convolved with a Gaussian line-spread function having a FWHM = 0.5 Å. |
| In the text | |
 |
Fig. 6 The 157 μm cooling line intensity is calculated from Eq. (6) and is plotted as a function of the hydrogen number density and of the electron fraction (x = ne / nH). Note that the result should be scaled by the fraction of carbon in C+. The result should also be scaled by the carbon abundance with respect to the solar value and by the column density of hydrogen nuclei in units of 1021 cm-2. For temperatures 50 K and 100 K, only the curve for x = 0 is shown. |
| In the text | |
 |
Fig. 7 Effect of extra heating in the H i region. The electron temperature (top panel) and the fraction of C ii and C ii* to total carbon (middle panel) are shown as a function of radius to the ionizing stars. The predicted line strength is shown in the bottom panel. The models assume unity for both the covering fraction of the H ii region and the fraction of the emission subtended by the COS aperture (see Sect. 4.2). |
| In the text | |
 |
Fig. 8 Cloudy model spectral energy distribution of I Zw 18. The flux distribution of the stellar population incident on the inner edge of the H ii region is shown in white, the stellar flux transmitted to the H i region in gray. The wavelength of the ionization edge of relevant species is given along the top of the figure. The H ii region absorbs virtually all the H i Lyman continuum and converts it to H i Lyα, nebular continuum, and line emission (all shown in red). |
| In the text | |
 |
Fig. 9 Ionization structure of the simple model approximation of I Zw 18 NW. The abscissa is the radial distance from the ionizing stars in cm. Ionization stages are identified by their color: dark blue (V), cyan (IV), green (III), orange (II), red (I). See Fig. 4 for the corresponding electron temperature and density profiles. |
| In the text | |
 |
Fig. 10 Abundance of each element in the H i region and in the H ii region. Elements are ordered by increasing condensation temperature (temperature for which 50% of an element is removed from the gas phase). The horizontal lines show the metallicity for each phase based on [O/H]. For the H i region, S is used to estimate O (Sect. 6.2). |
| In the text | |
 |
Fig. 11 Abundance ratios calculated from the stellar yields of Woosley & Weaver (1995). Yields are plotted for two mass ranges, 11–25 M⊙ (open symbols) and 30–40 M⊙ (filled symbols), and two metallicities, 0.1 Z⊙ (diamonds) and 0.01 Z⊙ (squares). The grey stripe shows the observed values. The horizontal black line shows the average ratio observed in the H ii region of BCDs (Izotov et al. 1999). |
| In the text | |
 |
Fig. 12 Metal deficiency in the H i region δH i as a function of the fraction of hydrogen present in the HI-ex component defined as the extended H i component that may be less enriched in metals as compared to HI-sf (the H i component associated to the star-forming regions). We assume that the HI-sf component has the same metallicity as the H ii region and calculate δH i for several values of the sulfur abundance ratio between HI-ex and HI-sf. The horizontal dashed line and the grey stripe indicates illustrate the sulfur deficiency, δH i(S) = 0.18 ± 0.11. |
| In the text | |
 |
Fig. 13 Top: comparison of the N/O ratio between the H i and H ii region for the sample of BCDs studied with FUSE, and for I Zw 18 with COS. The labels are defined as 1a) I Zw 18 (L04), 1b) I Zw 18 (A03), 1c) I Zw 18 (this study, with S as a tracer of O; Sect. 6.2), 2) NGC 1705 (Heckman et al. 2001), 3) SBS 0335-052 (Thuan et al. 2005), 4) Mark 59 (Thuan et al. 2002), 5) NGC 625 (Cannon et al. 2005), 6) I Zw 36 (Lebouteiller et al. 2004), 7) Pox 36 (Lebouteiller et al. 2009), 8) NGC 604 (Lebouteiller et al. 2006), 9) SBS 1543+593 (Bowen et al. 2005; Schulte Ladbeck et al. 2004). Bottom: ratio of the average metal abundance [M / H] = ⟨ [X / H] ⟩ between the H i and H ii regions. [M/H] is calculated two ways, averaging all elements observed in each phase (small diamonds), and averaging only the elements observed in both phases (large diamonds). |
| In the text | |
 |
Fig. A.1 Line profile fitting for the 11 523 (top), 12 028 (middle), and 11 579 datasets (bottom). For display purposes, only the strongest lines from I Zw 18 (component 1, also indicated by the vertical dotted lines), from the Milky Way (component 2), and from the high-velocity cloud (component 3) are labeled. The thin green line shows the individual line profiles. The solid thick red line shows the fit to the data while the dotted red line shows the line profiles assuming the H i region abundances are equal to the H ii region abundances. |
| In the text | |
 |
Fig. A.2 See Fig. A.1 for the plot description. The unlabelled line on the far right is Si iiiλ1206.5 arising in I Zw 18. |
| In the text | |
 |
Fig. A.3 See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. A.4 See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. A.5 See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. A.6 See Fig. A.1 for the plot description. |
| In the text | |
 |
Fig. A.7 See Fig. A.1 for the plot description. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


