| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 15 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201220899 | |
| Published online | 06 May 2013 | |
Opposite polarity field with convective downflow and its relation to magnetic spines in a sunspot penumbra
1 Institute for Solar Physics, Royal Swedish Academy of Sciences, AlbaNova University Center, 10691 Stockholm, Sweden
e-mail: scharmer@astro.su.se
2 Stockholm Observatory, Dept. of Astronomy, Stockholm University, AlbaNova University Center, 10691 Stockholm, Sweden
3 Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
Received: 13 December 2012
Accepted: 6 March 2013
We discuss NICOLE inversions of Fe i 630.15 nm and 630.25 nm Stokes spectra from a sunspot penumbra recorded with the CRISP imaging spectropolarimeter on the Swedish 1-m Solar Telescope at a spatial resolution close to 0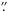 15. We report on narrow, radially extended lanes of opposite polarity field, located at the boundaries between areas of relatively horizontal magnetic field (the intra-spines) and much more vertical field (the spines). These lanes harbor convective downflows of about 1 km s-1. The locations of these downflows close to the spines agree with predictions from the convective gap model (the “gappy penumbra”) proposed six years ago, and more recent three-dimensional magnetohydrodynamic simulations. We also confirm the existence of strong convective flows throughout the entire penumbra, showing the expected correlation between temperature and vertical velocity, and having vertical root mean square velocities of about 1.2 km s-1.
15. We report on narrow, radially extended lanes of opposite polarity field, located at the boundaries between areas of relatively horizontal magnetic field (the intra-spines) and much more vertical field (the spines). These lanes harbor convective downflows of about 1 km s-1. The locations of these downflows close to the spines agree with predictions from the convective gap model (the “gappy penumbra”) proposed six years ago, and more recent three-dimensional magnetohydrodynamic simulations. We also confirm the existence of strong convective flows throughout the entire penumbra, showing the expected correlation between temperature and vertical velocity, and having vertical root mean square velocities of about 1.2 km s-1.
Key words: Sun: atmosphere / Sun: magnetic topology / convection / magnetic fields / magnetohydrodynamics (MHD) / sunspots
© ESO, 2013
1. Introduction
The strong, nearly horizontal and radial outflows discovered more than 100 years ago (Evershed 1909), have inspired 1-dimensional (1D) numerical modeling of the penumbral filaments as flux tubes, with a siphon flow indirectly driven by the assumed difference in magnetic field strength between the ascending (in the penumbra) and descending (outside the penumbra) parts of magnetic flux tubes (Meyer & Schmidt 1968; Montesinos & Thomas 1989, 1997). Schlichenmaier et al. (1998a,b) instead modeled these flows as transient flows triggered by heating of thin flux tubes embedded in a convectively unstable penumbral atmosphere of given properties.
In parallel to the development of the theoretical models described above, spectropolarimetric data, initially at only 1′′ spatial resolution, were used to develop a plethora of 1-component (with vertical gradients) and 2-component (without vertical gradients) empirical models of flux tubes and similar models of the penumbral magnetic field and flows (cf. Solanki & Montavon 1993; Schlichenmaier & Collados 2002; Müller et al. 2002; Bellot Rubio et al. 2003, 2004; Borrero et al. 2005, 2007; Borrero 2007; Puschmann et al. 2010). The ability of these simplified models to represent observed data (most of which were recorded at low spatial resolution), as well as their apparent consistency with the simulations of Schlichenmaier et al. (1998b,a) was interpreted to validate both the theoretical and observationally based models.
However, neither of the above models can provide the overall heat flux needed to explain the radiative losses of the penumbra (Schlichenmaier & Solanki 2003; Spruit & Scharmer 2006). For this, efficient convection is needed, with vertical root mean square (rms) velocities comparable to those of the quiet Sun. Spruit & Scharmer (2006), Scharmer & Spruit (2006), and Scharmer (2009) concluded that the penumbral filamentary structure and complex magnetic field topology must be the result of convection opening up radially aligned essentially field-free gaps, just below the visible surface. Sánchez Almeida (2005) and Sánchez Almeida & Ichimoto (2009) proposed to explain observed penumbral Stokes profiles in terms of spatially unresolved fluctuations in velocity and magnetic field, the micro-structured magnetic atmospheres (MISMAs).
Recent simulations (Heinemann et al. 2007; Rempel et al. 2009; Rempel 2011, 2012) clearly support the presence of strong penumbral convection at observable scales, and lead to the surprising conclusion that the Evershed flow corresponds to the horizontal and radially outward component of this convection (Scharmer et al. 2008b; Rempel et al. 2009). This interpretation of penumbral fine structure is however not without controversy, the main argument being that observational evidence for convective downflows well inside the outer boundary of the penumbra is missing (Franz & Schlichenmaier 2009; Franz 2011). Recently, such evidence was reported in the C i 538.03 nm line (Scharmer et al. 2011; Joshi et al. 2011) and the Fe i 630.15 nm line (Scharmer & Henriques 2012), based on observations with the Swedish 1-m Solar Telescope (SST; Scharmer et al. 2003) and its imaging spectropolarimeter CRISP (Scharmer 2006; Scharmer et al. 2008a). Synthetic spectra calculated from simulations (Rempel 2011) confirm that such downflows should be visible in the C i 538.03 nm line at the spatial resolution of the SST (Bharti et al. 2011).
An important question in the context of the present work concerns the existence of opposite polarity field in the penumbra. The existence of such field can be taken as strong evidence of (convective) downflows, dragging down some of the field. Franz (2011) investigated spectropolarimetric Hinode data from a sunspot close to disk center and concluded that 36% of all penumbral downflows give rise to Stokes V profiles showing an additional 3rd lobe in the red wing of the 630.25 nm line, indicating a hidden opposite polarity. However, nearly all the downflow pixels found by him are located at the outermost parts of the penumbra, where downflows are ubiquitous. The question of whether or not there is convection in the main body of the penumbra can therefore not be addressed with these data. Recently, Scharmer et al. (2012)1 and Ruiz Cobo & Asensio Ramos (2013) reported the detection of opposite polarity field also in the interior of the penumbra, thus providing independent support to earlier evidence demonstrating that the penumbra is fully convective (Scharmer et al. 2011; Joshi et al. 2011; Scharmer & Henriques 2012).
In the present paper, we apply Stokes inversions jointly to Fe i 630.15 nm and 630.25 nm spectra, recorded with CRISP/SST close to the diffraction limit of 0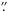 15. We describe the data reduction, the rationale for straylight compensation, and the determination of the CRISP transmission profile in Sect. 2. In Sect. 3, we describe the NICOLE inversions (Socas-Navarro et al. 2000; Socas-Navarro 2011), allowing for gradients in both the line-of-sight (LOS) velocities and the magnetic field, and using an individual spectral transmission profile for each pixel. We validate the inversions of our Stokes spectra in Sect. 4, and use the inversions in Sect. 5 to establish the locations of opposite polarity patches and their association with magnetic spines in the deep layers of a sunspot penumbra. We then analyze the azimuthal variations of the observed LOS velocities at the opposite polarity patches, and draw conclusions about their vertical and radial velocities.
15. We describe the data reduction, the rationale for straylight compensation, and the determination of the CRISP transmission profile in Sect. 2. In Sect. 3, we describe the NICOLE inversions (Socas-Navarro et al. 2000; Socas-Navarro 2011), allowing for gradients in both the line-of-sight (LOS) velocities and the magnetic field, and using an individual spectral transmission profile for each pixel. We validate the inversions of our Stokes spectra in Sect. 4, and use the inversions in Sect. 5 to establish the locations of opposite polarity patches and their association with magnetic spines in the deep layers of a sunspot penumbra. We then analyze the azimuthal variations of the observed LOS velocities at the opposite polarity patches, and draw conclusions about their vertical and radial velocities.
2. Observations and data reduction
The observed data analyzed are of a reasonably symmetric sunspot at approximately 15° heliocentric distance, obtained on 23 May 2010 with the SST and its imaging spectropolarimeter CRISP. These data have been described before (Scharmer et al. 2011; Scharmer & Henriques 2012), but here we extend the analysis by including 15 wavelengths scanned in the 630.25 nm line and a continuum wavelength 60 pm redward of this line, in addition to the 15 wavelengths scanned for the Fe i 630.15 line and analyzed by Scharmer & Henriques (2012). A complete scan of the two Fe i lines required only 16.5 s observing time.
We first compensated the images for darks and the “raw” flats similar to as described by Schnerr et al. (2011), and then compensated the images for residual low-order aberrations with the multi-object multi-frame blind deconvolution (MOMFBD) code of van Noort et al. (2005). This was followed by a small-scale dewarping (small-scale geometric distortion correction) of the images to remove remaining alignment errors from high-altitude seeing at arc second scale, which cannot be compensated for by the 4″ × 4″ subfield MOMFBD processing (Henriques 2012).
We also re-determined the polarization properties of the SST, using calibration data obtained with a 1-m rotating linear polarizer mounted in front of the SST in May, June and October 2011. After demodulation of the MOMFBD restored images with an improved version of the polarization model of Selbing (2005), we checked the data for residual cross-talk from I to Q, U and V and from V to Q and U using methods similar to those described by Schlichenmaier & Collados (2002). The cross-talk found was 0.3% or less from I to Q, U and V, 2.7% from V to U, and much smaller from V to Q. These cross-talks were compensated for.
The wavelength scale (used for establishing the LOS velocity reference) was set by comparing the observed line profiles for granulation surrounding the sunspot and void of strong fields, with those of 3D simulations (de la Cruz Rodríguez et al. 2011). With this calibration, we found an average velocity of the umbra to be 60 m s-1 at τc = 0.95 and − 80 m s-1 at τc = 0.01 from the inversions (described in Sect. 3), such that this wavelength scale can be considered quite accurate.
2.1. Determination of the CRISP transmission profile
We derived the transmission profile of CRISP and the pre-filter at each pixel, as well as a “true” flat-field image at each wavelength, by comparing the observed flat-field spectra, obtained close to disk center, to the FTS atlas spectrum (Brault & Neckel 1987; see Neckel 1999). Our fits go beyond the determination of “cavity maps” (Scharmer et al. 2008a), which characterize the transmission profile only in terms of a pure wavelength shift, by allowing also for variable asymmetries in the transmission profile over the field-of-view (FOV). Such asymmetries come from relative wavelength shifts of the transmission profiles of the two etalons. We implemented our fitting procedure using analytical expressions for the transmission profiles of the two etalons (cf. Scharmer 2006). The free parameters of the fit are the wavelength shifts of the two etalons, the reflectivity of the high-resolution (HR) etalon and the parameters of an assumed linear variation of the pre-filter transmission with wavelength (correcting for any deviations from the assumed theoretical shape, corresponding to a 2-cavity interference filter). Due to the low reflectivity of the low-resolution (LR) etalon (83.9%), its reflectivity variations over the FOV have a negligible impact on the combined transmission profile of the two etalons, and this parameter was held constant at its nominal value. Our initial fits returned an average HR reflectivity that was somewhat below that given by the manufacturer of the etalon coating (93.56%), suggesting the presence of spectral straylight of approximately 1%. This is because spectral straylight results in a spectral line profile with reduced depth, which is compensated for in our fits by a widened transmission profile, i.e. a reduced reflectivity. However, including the first side lobe on each side of the peak for the HR etalon transmission profile returned excellent fits and an average reflectivity (93.44%) that is very close to that expected (93.56%). Our fits therefore give no reason for suspecting significant levels of spectral straylight beyond the approximately 0.8% contributed from the first side lobes of the combined transmission profile. From the fits, we also determined and compensated for the telluric blend in the red wing of the 630.25 nm line, as follows: we first removed the telluric line from the FTS solar atlas and replaced it with a “modeled” narrow Lorentzian line profile of unknown strength and width, located at an unknown wavelength. To fit the parameters of this Lorentzian, we shifted the wavelength scales of all flat-field spectra in the FOV to a common wavelength scale according to the measured cavity errors. Using the spectra with their shifted wavelengths, and convolving the synthetic FTS spectrum (including the modeled telluric line), we then iteratively fitted all these spectra to a single Lorentzian profile, characterized by its strength, width and center wavelength. A similar procedure was applied to the science data since the strength and wavelength (relative to the 630 nm lines) of the telluric line changes during the day. In general, the fits of the observed CRISP profiles to the convolved FTS spectrum are excellent, as illustrated in Fig. 1.
Our characterization of the CRISP transmission profile allows the inversions to take into account any asymmetries in the transmission profile resulting from the relative wavelength shifts of the peak transmissions of the two Fabry-Perot etalons. In particular, such asymmetries could otherwise lead to errors in the LOS velocity gradient.
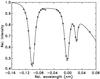 |
Fig. 1 Observed flatfield spectrum for a pixel near the center of the FOV (circles). The solid line shows the FTS atlas spectrum for the same wavelength range, convolved with the fitted CRISP transmission profile and multiplied with the fitted pre-filter transmission curve. The strength and position of the telluric blend have been determined in a separate fit (see text). |
2.2. Straylight compensation
As the final step of our pre-processing, we compensated the data for straylight. The need and rationale for such compensation has been discussed extensively in previous publications (Scharmer et al. 2011; Narayan 2011; Scharmer & Henriques 2012). Here, we summarize the arguments and some of the results, but do not repeat the detailed analysis presented earlier (Scharmer et al. 2011, their Supporting Online Material, SOM2).
Recent measurements of the Hinode/SOT point spread function (PSF) and rms granulation contrasts from Hinode clearly demonstrate consistency with 3D simulations (Wedemeyer-Böhm 2008; Danilovic et al. 2008; Wedemeyer-Böhm & Rouppe van der Voort 2009; Mathew et al. 2009), leading to the conclusion that there is no scientific ground for questioning the theoretically obtained granulation contrast. This implies that actual measurements of the granulation contrast can be used to constrain the PSF of other telescopes. For telescope diameters larger than approximately 0.5 m, almost all contributions to the granulation contrast come from spatial frequencies well within the diffraction limit, such that the obtained granulation contrast is determined (primarily) by the wings of the PSF, referred to below as “straylight”, rather than by its core. This is not surprising, since granules have typical diameters of 1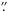 4. The present SST data contain both (nearly) non-magnetic granulation and a sunspot within the same FOV. The minimum umbra intensity in the sunspot provides a second important constraint on the width and strength of the wings of the PSF for our data.
4. The present SST data contain both (nearly) non-magnetic granulation and a sunspot within the same FOV. The minimum umbra intensity in the sunspot provides a second important constraint on the width and strength of the wings of the PSF for our data.
A detailed analysis of the CRISP data obtained in the C i 538.03 nm line (Scharmer et al. 2011, SOM) shows that the overall straylight must be more than 50% at this wavelength to explain the granulation contrast. On the other hand, the measured minimum umbra intensity of only 15.6% excludes the possibility that this straylight comes primarily from a PSF with very wide wings. In particular, the analysis excludes a PSF with Lorentzian wings, since that leads to negative intensities in the umbra when deconvolving the CRISP data. Trial deconvolutions with PSF’s having Gaussian shapes lead to the result that the full width at half maximum of such a PSF must be less than about 2 4 in order to reproduce the expected granulation contrast of 17% at this wavelength and to give a minimum umbra intensity of more than 6% (Scharmer et al. 2011, SOM, Table S2). We cannot exclude the possibility of a quite narrow Gaussian straylight PSF from our data, however that would imply that the straylight fraction must be much higher than 50%, which seems unlikely. Our analysis of the C i 538.03 nm data led us to adopt a straylight fraction of 58% and a full width at half maximum (FWHM) of 1
4 in order to reproduce the expected granulation contrast of 17% at this wavelength and to give a minimum umbra intensity of more than 6% (Scharmer et al. 2011, SOM, Table S2). We cannot exclude the possibility of a quite narrow Gaussian straylight PSF from our data, however that would imply that the straylight fraction must be much higher than 50%, which seems unlikely. Our analysis of the C i 538.03 nm data led us to adopt a straylight fraction of 58% and a full width at half maximum (FWHM) of 1 2 at that wavelength, but assuming a somewhat wider PSF of 1
2 at that wavelength, but assuming a somewhat wider PSF of 1 8 and a straylight fraction of about 54% would reproduce the synthetic C i 538.03 nm data just as well.
8 and a straylight fraction of about 54% would reproduce the synthetic C i 538.03 nm data just as well.
The origin of this straylight has not been established with certainty, but is now strongly suspected to be mainly from phase errors (aberrations), such as residuals from MOMFBD processing, high-altitude seeing and possibly fixed high-order aberrations in the adaptive mirror or other optics (Scharmer et al. 2010; Löfdahl & Scharmer 2012). In particular, we note that MOMFBD processing (image restoration jointly of images recorded at many wavelengths) leads to only a marginal increase in the rms granulation contrast, whereas speckle and multi-frame blind deconvolution (MFBD) processing (image restoration of images recorded at a single wavelength) lead to significantly stronger contrast enhancement (Puschmann & Beck 2011). In addition, MOMFBD image reconstruction is always limited to accounting for a small number of atmospheric aberration modes (for our data, only 36 modes), leading to a tail of uncorrected high-order aberrations that gives a PSF with enhanced wings, qualitatively similar to the PSF modeled here (Scharmer et al. 2010; Löfdahl & Scharmer 2012).
We therefore compensate the present 630.15 nm and 630.25 nm data for straylight, using the same procedure as applied previously to the 538.03 nm data (Scharmer et al. 2011) and 630.15 nm data (Scharmer & Henriques 2012). We assume the following relation between the observed Io and “true” It intensities at any wavelength and polarization state: 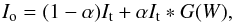 (1)where α is the straylight fraction, “*” denotes convolution, and G is a Gaussian straylight PSF, having a full width at half maximum of W. For the present inversions, we set W to 1
(1)where α is the straylight fraction, “*” denotes convolution, and G is a Gaussian straylight PSF, having a full width at half maximum of W. For the present inversions, we set W to 1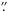 8 and α to 0.4, rather than to 1
8 and α to 0.4, rather than to 1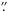 2 and 0.5 respectively, as used previously for the 630.15 nm data (Scharmer & Henriques 2012). Note that our model for the straylight is such that the diffraction limited core of the PSF is not compensated for beyond that already made in MOMFBD processing. In particular, straylight compensation, as described above, with a relatively wide PSF does not selectively amplify the high spatial frequencies of the images.
2 and 0.5 respectively, as used previously for the 630.15 nm data (Scharmer & Henriques 2012). Note that our model for the straylight is such that the diffraction limited core of the PSF is not compensated for beyond that already made in MOMFBD processing. In particular, straylight compensation, as described above, with a relatively wide PSF does not selectively amplify the high spatial frequencies of the images.
Before straylight compensation our data give a granulation rms contrast in the continuum of 7.5% and a minimum umbra intensity of 18.4%. Our present choice of straylight parameters increases the rms contrast to 11.7%, and reduces the minimum umbra intensity to 14.9%, whereas our previous choice of setting W to 1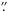 2 and α to 0.5 gave 12.5% and 14.7%, respectively. The present choice of straylight parameters gave fewer failures with the inversion code and less noisy maps for the inverted parameters, but otherwise very similar results as with the previously used values, justifying our choice. We note that our straylight compensation gives a granulation rms contrast that is significantly below that obtained from simulations (14–14.5%), such that the presently used data are under-compensated for straylight.
2 and α to 0.5 gave 12.5% and 14.7%, respectively. The present choice of straylight parameters gave fewer failures with the inversion code and less noisy maps for the inverted parameters, but otherwise very similar results as with the previously used values, justifying our choice. We note that our straylight compensation gives a granulation rms contrast that is significantly below that obtained from simulations (14–14.5%), such that the presently used data are under-compensated for straylight.
As mentioned earlier, telecentric Fabry-Perot systems, such as CRISP, give rise to wavelength shifts of the transmission profile over the FOV. Individual Stokes images recorded in the wings of a spectral line therefore show intensity variations that are in part of solar origin and in part artificial from wavelength shifts of the transmission profile. To avoid amplifying any such artificial structures by straylight compensation, we used the cavity map to first shift each profile to a common wavelength grid, employing Hermitian interpolation (Hill 1982). We then applied the straylight compensation to the data, and shifted back the profiles to the original wavelength grid. In the first interpolation, we expanded the wavelength grid by a factor 4 to ensure that the forward-backward interpolation did not introduce errors. This was checked by applying the forward-backward interpolation to the data without any straylight compensation.
We finally comment that straylight compensation of spectropolarimetric data has been implemented using widely different approaches in the past. For example, Borrero & Solanki (2008) used an average global Stokes I profile (ignoring polarized straylight) averaged from non-magnetic granulation outside the spot. The relative contribution of this straylight profile to the measured profile in the sunspot was a free parameter of the inversions, fitted separately for each pixel. Orozco Suárez et al. (2007a,b) instead employed a local (unpolarized) straylight profile, obtained independently from 1 × 1′′ boxes surrounding each pixel. Our approach is distinctly different from their approaches in that we use fixed and identical straylight parameters for all pixels within the FOV and that we deconvolve all 4 Stokes images at each wavelength for the assumed straylight PSF. The observed granulation contrast and minimum umbra intensity do not allow us to firmly establish the strength and shape for the SST straylight PSF.
 |
Fig. 2 Panels a)–c) show the temperature at τc = 0.95, 0.05 and 0.01, clipped at (5500, 6700), (4600, 5300), and (4300, 5200) K resp., for inversions made assuming depth-independent magnetic field and LOS velocity, and in panels d)−f) the corresponding temperatures obtained with 2 nodes for the velocity and 3 nodes for BLOS. Note the absence of inverse granulation in panel b). Panels g) and h) show the LOS velocity at τc = 0.95 and τc = 0.05 from the inversions corresponding to panels d)−f), and in panel i the LOS velocity from the inversions assuming constant LOS velocity (panels a)−c)). The LOS velocities have been clipped at (− 4.5, 4.5), (− 2.3, 2.3) and (− 2.3, 2.3) km s-1. The bottom row (panels j)−l)) show the LOS magnetic field (with 3 nodes for BLOS) at τc = 0.95, 0.05 and 0.01, clipped at (− 1000, 1500) G. Note the increasing area coverage (expansion with height) of the network field at smaller optical depths. The FOV shown is 25 × 18″. |
3. Inversions
The inversions were applied jointly to the two Fe i lines. Inversions were made assuming a single atmospheric component in each pixel, excluding straylight compensation beyond that of the pre-processing (Sect. 2). We used the inversion code NICOLE, which is an improved implementation of the inversion code of Socas-Navarro et al. (2000). NICOLE was modified to accept a separate transmission profile for each pixel. In order to carry out the convolution with the CRISP transmission profile, the synthetic Stokes spectra were calculated with a 4 times denser wavelength grid than that of the CRISP data. Our version of NICOLE computes the emerging intensity vector using a quadratic DELO-Bezier solution to the radiative transfer equation (de la Cruz Rodríguez & Piskunov 2013), which improves the accuracy of the synthetic spectra and response functions.
NICOLE was applied iteratively to the data with an increasing number of nodes, similar to as described by Socas-Navarro (2011). We used the following final number of nodes: 3 each for temperature (using the HSRA model as the initial estimate) and the LOS magnetic field BLOS, 2 each for the LOS velocity and the transverse components of the magnetic field, and 1 for the micro-turbulence (in total 13 free parameters). Initially, we made the inversions with 2 nodes for BLOS, but decided to use 3 nodes for BLOS instead in order to ensure that the inferred polarity reversals (Sect. 5) at continuum optical depth τc = 0.95, are robust results. We also made one inversion as above but with 3 nodes for the LOS velocity (and without micro-turbulence). The resulting velocity maps look good but are visibly noisier than with 2 nodes. We use that inversion only to verify one of our results obtained with 2 nodes. Unless otherwise stated, the results presented are based on inversions with 3 nodes for BLOS and 2 nodes for the LOS velocity. Note that NICOLE models the global variations of the atmospheric properties as being constant when using 1 node, as being linear in log τc when using 2 nodes, and as being quadratic in log τc when using 3 nodes.
We note that the final number of nodes for our inversions is smaller than used by Socas-Navarro (2011). This is a direct consequence of the spectral resolution of CRISP (about 6 pm at 630 nm) being smaller than for his Hinode/SOT data, reducing the “height” resolution along the LOS for our data through the broadening of the radiative transfer contribution functions within the passband of CRISP. We made a total of 49 inversion experiments in order to explore the effects of improvements in the pre-processing of the data and changes in the number of nodes, and to verify the robustness of our results. However, these experiments do not allow us to draw firmer conclusions about the optimum choice of the straylight parameters than given by the constraints discussed in Sect. 2.2.
Abundances and atomic parameters used are identical to those of Socas-Navarro (2011).
Using the angle between solar North and disk center and the heliocentric distance of the spot, we transformed the magnetic field to the local frame. We resolved the 180 degree ambiguity by defining an approximate center for the sunspot and choosing the azimuth angle offset (0 or 180 deg) for which the horizontal field at τc = 0.09 is directed more outward than inward from the spot center. As discussed in Sect. 4.3, the so obtained penumbra field in the local frame on the average appears well aligned with the penumbral filaments, strongly indicating that the telescope polarization model and demodulation of the Stokes data gives good estimates of the direction of the transverse field. The procedure used for resolving the 180 degree ambiguity is of course inappropriate outside the sunspot and probably also in the lightbridge.
4. Validation of inversions
To evaluate the quality of our inversions, we first discuss maps for the temperature, velocity and magnetic field returned by NICOLE over a 25″ × 18″ FOV, showing quiet Sun granulation and network field. We compare our inversion results to those of earlier high-resolution observations and to simulations showing both field-free convection and network fields. We also validate our obtained LOS magnetic field gradients from the overall penumbra spine structure, the light bridge, some of the brighter umbral dots and the surroundings of a pore close to the sunspot.
4.1. Temperature structure and velocity field
Figure 2 shows in the top two rows the temperature of field-free granulation and patches of network field at τc = 0.95, 0.05 and 0.01. These maps were obtained from inversions obtained without (panels a−c) and with allowance for gradients in the LOS velocity and magnetic field (panels d−f). The latter inversions (panels d−f) show reverse granulation at small optical depths, which is consistent with both observations in the wing of the Ca ii H-line for the same FOV (Henriques 2012, his Fig. 7), and numerical simulations of convection showing reverse granulation above τc = 0.1 (Cheung et al. 2007). The absence of reverse granulation in the temperature maps obtained without allowance for gradients in the LOS velocity can be attributed to the intensities in the line wings depending strongly on a complicated correlation between temperature and LOS velocity at different heights. In the deep photosphere, this correlation is in the sense expected for convection. Above τc = 0.1 this correlation reverses such that intergranular lanes (having downflows also at this height) are brighter than the interiors of granules, where overshooting convective upflows maintain their presence (Cheung et al. 2007). When the radiative response function peaks for the deeper layers, this enhances the granulation contrast in the red wing of strong spectral lines, whereas in the blue wing the intensity fluctuations from temperature and Doppler shifts largely cancel. Sufficiently close to line center, this pattern reverses. Without properly modeling both the gradients of the temperature and the LOS velocity, this leads to strong cross-talks and errors, in particular for the temperature stratifications in the upper layers of the atmosphere.
Based on comparisons with both independent observations and simulations (Leenaarts & Wedemeyer-Böhm 2005; Cheung et al. 2007; Rutten et al. 2011; Henriques 2012), Fig. 2 therefore demonstrates that we can have reasonable confidence in the stratifications and spatial variations of the temperature obtained from inversions allowing for LOS gradients in the Doppler velocity (and magnetic field). However, close inspection of panels e and f shows that this comes at the prize of enhanced noise in the measured temperatures in the upper layers of the photosphere. Using inversions with only 2 nodes for temperature instead of 3 nodes (these inversions are not shown in any of our figures) removes this noise, but unfortunately also removes the inverse granulation pattern at τc = 0.05. The conclusion is that 3 nodes are needed for temperature and 2 nodes for the LOS velocity in order to disentangle LOS velocity and temperature gradients in the observed layers.
Figure 2 also shows the LOS velocity at τc = 0.95 and 0.05 from inversions allowing for gradients (panels g−h), and without allowance for such gradients (panel i). Note that the clippings are different for panel g and for panels h and i, and are scaled according to their rms values (1.79 km s-1 at τc = 0.95; 0.94 km s-1 at τc = 0.05; and 0.93 km s-1 for panel i. The rms velocity at τc = 0.95 is very close to the value obtained from numerical simulations (1.78 km s-1Scharmer et al. 2011, their Table S2 in SOM). Figure 2 also demonstrates that the LOS velocity field at τc = 0.05 is morphologically very similar to that at τc = 0.95, but reduced in strength by nearly a factor of 2. This morphological similarity between the flow field at τc = 0.95 and τc = 0.05 is also consistent with numerical simulations of convection (Cheung et al. 2007). This comparison validates the magnitudes of the LOS velocities inferred from our inversions, and qualitatively the variation of these velocities with optical depth. Finally, this figure demonstrates that making inversions that assume a constant LOS velocity (a Milne-Eddington like inversion) returns a velocity that corresponds to the velocity at τc ≈ 0.05 when allowing for gradients in the LOS velocity. This is in agreement with earlier comparisons between Milne-Eddington techniques and the SIR technique (Stokes Inversion based on Response Functions, Ruiz Cobo & del Toro Iniesta 1992; Westendorp Plaza et al. 1998).
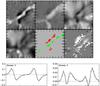 |
Fig. 3 Top row of panels: LOS magnetic field at τc = 0.95, and 0.09 (both clipped at (− 1500, 2000) G), and the LOS velocity at τc = 0.95, clipped at (− 3.0, 2.0) km s-1, from a 2′′ × 2′′ subfield showing a sheet-like network patch located in the lower-left corner of Figs. 4, 6 and 11. Second row: temperature at τc = 0.95, the green and red pixels used to produce the plots in the lower part of the figure, and the Stokes V area asymmetry (∫V dλ/∫ | V | dλ), clipped at (− 0.5, 0.5). Note the presence of strong opposite polarity field at τc = 0.95, the virtual absence of such field at τc = 0.09 and the strongly increased width of the LOS magnetic field with height. Short tick marks are separated by 0 |
4.2. LOS magnetic field
4.2.1. Network
We now turn to evaluating the measured LOS magnetic field. In panels j−l of Fig. 2 we show BLOS at τc = 0.95, 0.05 and 0.01. About a dozen of the flux concentrations shown in Fig. 2 reach a peak LOS magnetic field stronger than 1.5 kG at τc = 0.95, which is in good agreement with the field strengths for network field obtained from Sunrise data, about 1.45 kG (Lagg et al. 2010). The average LOS magnetic field for these pixels is 1.7, 1.3 and 1.1 kG at τc = 0.95, 0.05 and 0.01, respectively. Near the boundaries of these flux concentrations we find many examples where the LOS field increases in strength by more than 300 G from τc = 0.95 to τc = 0.05. This is evident from the increasing size and “fuzzier” appearance of these concentrations at decreasing optical depths. The variations of BLOS with optical depth both near the centers and boundaries of these flux concentrations are thus consistent with canopy fields expanding with height, as demonstrated indirectly from the center-to-limb variations of the LOS magnetic field of network field by Pietarila et al. (2010) and from Sunrise data by Martínez González et al. (2012).
At the boundaries of a few of the larger flux concentrations, we see also tiny narrow sheets and small patches with opposite polarity field. Most Stokes V profiles at these locations are normal with 2 lobes, but show strong asymmetries with a weak red lobe. However, we also find a few extreme examples with abnormal V profiles having 3 lobes, as shown in Fig. 3. This figure also demonstrates that our inversions give good fits even to abnormal V profiles. The canonic interpretation of 2-lobed asymmetric V profiles (Martínez González et al. 2012, and references therein) is that the canopy fields expanding with height produce a discontinuity in the magnetic field (the magnetopause), the height of which increases with increasing distance from the flux concentration. The field-free gas below the canopy flows downward, explaining the asymmetric V profile. Our inversions, which assume a continuous variation of the magnetic field with height, indicate in some cases the existence of opposite polarity field at deep layers adjacent to parts of some of the flux concentrations. We note that such opposite polarity field adjacent to small flux tubes and flux sheets can be found also in 3D magnetohydrodynamic (MHD) simulations (Yelles Chaouche et al. 2009, their Figs. 4 and 10).
 |
Fig. 4 Panels a) and b) show the LOS magnetic field (in the observers frame) at τc = 0.95, for inversions made allowing for respectively 2 and 3 nodes for the LOS magnetic field, 2 nodes for the LOS velocity field and 3 nodes for the temperature. Panels c) and d) show the LOS magnetic field at τc = 0.09 and 0.01 with 3 nodes for the LOS magnetic field. Note the presence of opposite polarity field at τc = 0.95 in the penumbra, and the virtual absence of such opposite polarity field at smaller depths. The scaling of the magnetic field (in G) is according to the grayscale bar shown in panel a and is the same for panels a)−d). The FOV shown is 35 × 35′′. The plus symbols indicate the first and last pixels of the plots shown in Fig. 5. The long white arrow points in the direction of disk center, the shorter arrows to a pore discussed in Sect. 4.2.4. |
 |
Fig. 5 LOS magnetic field (in the observers frame) along the line defined by the two plus symbols in Fig. 4 at τc = 0.95, 0.09 and 0.01. Note the omnipresence of opposite polarity field at τc = 0.95 and the virtual absence of such field in the upper layers. |
4.2.2. Sunspot
Figure 4 shows the sunspot LOS magnetic field obtained from the inversions. Panels a and b show the LOS field at τc = 0.95, obtained with 2 nodes for BLOS (linear variation with log τc) and 3 nodes (allowing for also a quadratic variation with log τc), respectively. In panels c and d are shown the LOS magnetic field at τc = 0.09 and τc = 0.01, respectively, obtained with inversions made with 3 nodes for BLOS. We note that the strong spine structure (the bright “spokes” in the penumbra LOS magnetic field maps) appears fundamentally different at τc = 0.95 and 0.01. In the deep layers, the penumbra shows numerous narrow radial structures, many of which are flanked with opposite polarity field. This spine structure is very distinct and “sharp”. In the higher layers, most of the opposite polarity structures in the penumbra are absent, and the spines are wider and more fuzzy. Several intra-spines (the areas between two spines) can be seen to narrow strongly at small optical depths, and even disappear entirely at τc = 0.01, especially in the innermost penumbra. It is also evident from Fig. 4 that the strength of the LOS field in the spines weakens with height. To further quantify these variations with height, we show in Fig. 5 plots of the LOS magnetic field (in the observers frame) across several filaments at the disk center side of the inner penumbra.
The presence of opposite polarity field only in the deep layers is obvious from these plots, as is the overall weakening of the strength and the fluctuations of the field in the upper layers. The detection of opposite polarity field in the deep layers of the inner parts of the penumbra is a fundamental result of our investigation. It is intriguing to note that the spine structure at τc = 0.95 actually is even sharper and more well defined with 3 nodes than with 2 nodes for BLOS. We are confident that the detection of these opposite polarity patches well inside the penumbra is a robust result. However, the inversions with 3 nodes for BLOS show enhanced levels of random noise. We discuss in the following only the results obtained with 3 nodes for BLOS.
Noting that the spines represent azimuthal structures with much stronger vertical field than in the intra-spines, as first described by Lites et al. (1993), the observed spatial and LOS variations of the LOS magnetic field are perfectly understandable. The more vertical field in the spines expands with height to match the decreasing gas pressure. The weaker spine field seen at smaller optical depths is qualitatively consistent with flux conservation of such structures spreading out with height. The “sharp” spine structures seen in the deep photosphere can be explained as (convective) flows shaping these structures. In the upper layers, the morphology of the spines can qualitatively be explained as a potential field “extrapolation” of this field structure controlled from below, such that the spine field folds over the intra-spines. Such field topologies in the penumbra were proposed by Spruit & Scharmer (2006); Scharmer & Spruit (2006), and inferred from Hinode data by Borrero et al. (2008).
4.2.3. Umbral dots and lightbridge
Figure 4 shows several examples of umbral dots that have strongly reduced LOS magnetic field at τc = 0.95, whereas at τc = 0.01 these signatures are absent entirely. Evidently, the LOS magnetic field increases in strength with height (as earlier described by Riethmüller et al. 2008). In Fig. 6 a few bright umbral dots (indicated with circles) can be seen that have strongly reduced transverse field at their limb sides. These observed properties are consistent with a field that wraps around and closes above structures that have weak field, or are nearly field-free, deeper down. For many of the brighter umbral dots, we find upflows in the deepest layers. Similar upflows in the deep layers of peripheral (but not central) umbral dots have earlier been reported from Hinode data at lower spatial resolution than here (Riethmüller et al. 2008), and from SST observations of umbral dots (Ortiz et al. 2010; Watanabe et al. 2012) and numerical umbra simulations (Schüssler & Vögler 2006). However, we find no clear evidence of the expected downflows surrounding the upflows, as was the case also for the data of Riethmüller et al. (2008). Ortiz et al. (2010) and Watanabe et al. (2012) reported evidence of such downflows but Watanabe et al. (2012) found only patchy downflows in some cases and no downflows at all for many umbral dots.
The inner part of the light bridge shows a narrow irregular ridge with patches of opposite polarity field at τc = 0.95; this feature is almost absent at τc = 0.01. At these locations, panel d in Fig. 6 shows downflows. The transverse field is weak or absent at the limb side of this part of the light bridge, but not on its disk center side. As is the case for the umbral dots discussed previously, this is consistent with a (convective) field-free structure protruding into a magnetic field that closes over this structure higher up.
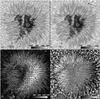 |
Fig. 6 Panels a)–d) show the temperature (in K) at τc = 0.95 and 0.09, the transverse magnetic field (in G) at τc = 0.09, and the LOS velocity (in km s-1) at τc = 0.95, respectively. In panel c) is shown also the direction of the horizontal field (in the solar frame) at τc = 0.09 for every 20th pixel. The FOV shown is 35 × 35′′. The circles mark examples of umbral dot-like structures that show strongly reduced transverse field on their limb sides, consistent with a magnetic field folding over the dots. The long black arrow points in the direction of disk center, the shorter white and black arrows to a pore discussed in Sect. 4.2.4. |
4.2.4. Pore
The lower-left part of the FOV in Fig. 6 shows a pore-like structure. Along its magnetic boundary, which is well outside the visible boundary in the temperature map at τc = 0.95, Fig. 4 shows several patches of opposite polarity field, one of which is outlined with an arrow. These opposite polarity patches are absent at τc = 0.09 and 0.01. Figure 6 (panel d) shows strong downflows at the same locations, in agreement with earlier observations of downflows adjacent to pores (Keil et al. 1999; Hirzberger 2003) as well as with simulations (Cameron et al. 2007), and leading to the interpretation that some of the field is dragged down by the downflows. A high-quality movie of the same spot shows vigorous convection in the region between the pore and the sunspot, and also intensity patterns suggesting inflows toward the pore (as reported earlier by e.g. Sobotka et al. 1999; Roudier et al. 2002), consistent with the (strong) downflows seen at its perimeter. Panel c in Fig. 6 shows a ring of transverse field surrounding the pore, indicating a strongly inclined field (a canopy) at the locations of these downflows. This transverse field is stronger on the limb side than on the disk center side of the pore, as is generally also the case for the sunspot penumbra, which is in agreement with expectations.
In the interior of the pore is a bright granular-like structure. The LOS magnetic field is strongly reduced near its center at τc = 0.95, but at τc = 0.01 the LOS magnetic field is almost the same as in the surroundings. This is consistent with a magnetic field folding over this “granule”, having (strongly) reduced field strength in the deeper layers, as is the case for the umbral dots in the sunspot umbra and the light bridge.
4.3. Orientation of the horizontal magnetic field
Figure 6c shows the magnitude of the transverse field (in the observers frame) and orientation of the horizontal field (in the local frame) for every 20th pixel. As is evident, the horizontal field is approximately parallel to the penumbral filaments and there are no indications of major systematic errors from the calibration of, and compensation for, the telescope polarization.
 |
Fig. 7 Masks used to divide the penumbra into 6 radial zones, with the temperature at τc = 0.95 superimposed. |
 |
Fig. 8 Histograms of the magnetic field inclination angle in the entire penumbra except the outermost radial zone (shown in Fig. 7) at τc = 0.95 (full), 0.09 (dashed), and 0.01 (dotted). The distributions are bimodal, with peaks at approx. 45° and 80°. We define spines/intra-spines as having inclinations smaller/larger than 60°. The histograms have been smoothed over 3°. |
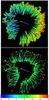 |
Fig. 9 LOS velocity at τc = 0.95 inferred from the inversions for intra-spines (top), and spines (bottom). The LOS velocities are color coded such that red and blue corresponds to velocities away from and toward the observer respectively, and are clipped at (− 3.0, 3.0) km s-1. The absence of systematic differences in LOS velocities between the disk center (direction of arrow) and limb sides of the penumbra demonstrates that the radial Evershed flow is absent in the spines, as expected from the more vertical field there. The FOV is ~35 × 35′′ and corresponds to that shown in Figs. 4 and 6. Tick marks are at 1′′ intervals. |
5. Properties of penumbral convection
5.1. Convective flows in spines and intra-spines
Figure 7 shows the temperature at τc = 0.95 overlaid by a mask identifying the penumbral part of the sunspot, and subdividing this into 6 radial zones, counting from the innermost zone and outwards. Figure 8 shows a histogram of the magnetic field inclinations in the radial zones 1–5, excluding the end points of filaments protruding into the surrounding quiet Sun. The histogram is clearly bimodal, with peaks at approximately 45° and 80°, suggesting the existence of two components with fundamentally different properties. This is in agreement with simulations, showing a similar bimodal distribution of field inclinations with peaks around 45° and 85° (Rempel, priv. comm.). In the following, we identify the magnetic spines and intra-spines as having inclinations less than and larger than 60°, respectively.
Figure 9 shows the LOS velocities obtained with NICOLE at τc = 0.95 in the intra-spines (top) and spines (bottom). Within the intra-spines, the LOS velocity shows a clear signature of horizontal (Evershed) flows: blue-shifts in the disk center direction and red-shifts in the limb direction. This signature appears entirely absent in the intra-spines. Thus it is clear that the flow properties of spines and intra-spines must be fundamentally different for this sunspot, as found already by Scharmer et al. (2011) and Scharmer & Henriques (2012), using a spatially high-pass filtered LOS magnetic field map to identify spines and intra-spines. That the Evershed flow resides in the nearly horizontal component of the penumbral magnetic field is consistent with earlier direct measurements (e.g. Title et al. 1993) and inferences from 2-component inversions of spectropolarimetric data obtained at much lower spatial resolution than here (e.g. Solanki & Montavon 1993; Martínez Pillet 2000; Schlichenmaier & Collados 2002; Bellot Rubio et al. 2003, 2004; Borrero et al. 2007; Tritschler et al. 2007). Here, we distinguish between spines and intra-spines using measurements of the field inclination from spectropolarimetric data recorded at extremely high spatial resolution, by relying on 1-component inversions with NICOLE.
To quantify properties of the vertical and radial flows in the spines and intra-spines, we follow the approach of Scharmer et al. (2011) and Scharmer & Henriques (2012) and fit the variations of the LOS velocity vLOS with the azimuth angle φ (set to zero in the disk center direction) to 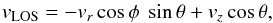 (2)(Plaskett 1952), where vr and vz are the radial and vertical velocities and θ the heliocentric distance (for this sunspot, 15°). The sign conventions are that outward radial flows, downward flows, and LOS flows away from the observer are counted positive. Applying a high-pass spatial filter to the temperature map at τc = 0.95, we remove any large-scale radial and azimuthal variations in temperature and obtain a map showing only small-scale “local” temperature fluctuations, δT. We divide these data into 5 temperature bins and make the azimuthal fits separately for each temperature bin and radial zone. The corresponding fitted data show large scatter (see Scharmer & Henriques 2012, their Fig. 7, for plots showing similar data), but the fitted parameters in Eq. (2) are well determined, as demonstrated in particular by the smoothness of their radial variations. The results are summarized in Fig. 10, showing the variation of the vertical (left column) and radial (right column) average velocities with δT for radial zones 2–5. The corresponding average velocity obtained when including all pixels in each radial zone is shown with dashed lines.
(2)(Plaskett 1952), where vr and vz are the radial and vertical velocities and θ the heliocentric distance (for this sunspot, 15°). The sign conventions are that outward radial flows, downward flows, and LOS flows away from the observer are counted positive. Applying a high-pass spatial filter to the temperature map at τc = 0.95, we remove any large-scale radial and azimuthal variations in temperature and obtain a map showing only small-scale “local” temperature fluctuations, δT. We divide these data into 5 temperature bins and make the azimuthal fits separately for each temperature bin and radial zone. The corresponding fitted data show large scatter (see Scharmer & Henriques 2012, their Fig. 7, for plots showing similar data), but the fitted parameters in Eq. (2) are well determined, as demonstrated in particular by the smoothness of their radial variations. The results are summarized in Fig. 10, showing the variation of the vertical (left column) and radial (right column) average velocities with δT for radial zones 2–5. The corresponding average velocity obtained when including all pixels in each radial zone is shown with dashed lines.
 |
Fig. 10 Variation of vertical (left column) and radial outflow (right column) velocities with local (high-pass spatially filtered) temperature fluctuations, obtained by fitting the azimuthal variations of the inferred LOS velocities at τc = 0.95, and shown for radial zones 2–5. The vertical velocities show the expected convective signature: the relatively cool component has downflows of up to 1.2 km s-1, the relatively hot gas upflows of up to − 1.3 km s-1. Radial velocities are strong in the intra-spines (circles) and weak in the spines (X-symbols), but the hottest spine structures show radial outflows in excess of 3 km s-1. |
The results agree qualitatively with those found earlier (Scharmer et al. 2011; Scharmer & Henriques 2012). The vertical flows show a clear convective signature everywhere in the penumbra, cool structures on the average show downflows and hot structures upflows. These signatures are similar for spines and intra-spines, except that the hottest structures show stronger upflows in spines than in intra-spines. The radial flows are strong in intra-spines and very weak in spines, as expected from Fig. 9, except that the hottest structures in the spines show radial velocities that are nearly as strong as in the intra-spines. However, the overall variations in vertical velocity with temperature are smaller than found earlier (Scharmer et al. 2011; Scharmer & Henriques 2012). Redoing the NICOLE inversions with 3 nodes for velocity instead of 2 nodes shows stronger downflows and upflows, clearly suggesting that using only 2 nodes for the velocity leads to underestimates of the LOS velocities in the deep layers of the penumbra. However, using 3 nodes also leads to strongly enhanced noise in the obtained LOS velocities, such that we restrict most of the following analysis to inversions made with 2 nodes for the LOS velocity.
The azimuthal fits also allow an estimate of the rms vertical convective velocities in the penumbra. Removing the contributions from the fitted radial velocities in Eq. (2), gives 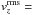 (1.1, 1.1, 1.1, 1.2, 1.4, 1.4) km s-1 in the intra-spines, and (0.7, 1.1, 1.4, 1.5, 1.6, 1.6) km s-1 in the spines, for radial zones 1–6, respectively. These rms convective velocities are similar to our previous estimate of 1.2 km s-1 and certainly sufficiently large to heat the penumbra (Scharmer et al. 2011). The larger rms velocities found in the spines come from the contributions of the very strong LOS velocities in the hottest structures.
(1.1, 1.1, 1.1, 1.2, 1.4, 1.4) km s-1 in the intra-spines, and (0.7, 1.1, 1.4, 1.5, 1.6, 1.6) km s-1 in the spines, for radial zones 1–6, respectively. These rms convective velocities are similar to our previous estimate of 1.2 km s-1 and certainly sufficiently large to heat the penumbra (Scharmer et al. 2011). The larger rms velocities found in the spines come from the contributions of the very strong LOS velocities in the hottest structures.
 |
Fig. 11 Composite masks showing the magnetic field with inclination less than 60° at τc = 0.95 (in the solar frame) in green and vertical field in the solar frame of less than − 100 G (opposite polarity field) in red. In the penumbra, the green color corresponds to the magnetic spines, and the black and red colors correspond to the intra-spines. The opposite polarity field in the penumbra is mostly found adjacent to the spines. Opposite polarity field is found also near some strong flux concentrations (plage and pores), and in a few cases near network field. Areas with field strength smaller than 350 G are shown black. The FOV is 35 × 35′′ and corresponds to that shown in Figs. 4 and 6. Tick marks are at 1′′ intervals. |
5.2. Spatial locations of penumbral opposite polarity field
The histogram for τc = 0.95 in Fig. 8 shows an extended tail for inclinations larger than 90°, corresponding to a significant fraction of opposite polarity field in the penumbra. We find that (28, 20, 19, 26, 38, 47) percent of the pixels in the intra-spines have an inclination larger than 95°, and (21, 14, 13, 19, 31, 40) percent larger than 100° in radial zones 1–6 resp. Note that these percentages exclude pixels corresponding to the spines.
Figure 11 shows in red color locations where Bz < − 100 G at τc = 0.95, i.e. corresponds to opposite polarity field in the solar frame. In green color, we show also the magnetic field for which the inclination is less than 60°, corresponding to our definition of the magnetic spines. In the quiet Sun, the noise in the Stokes Q and U data results in a mean strength of the horizontal field of nearly 200 G.
Figure 11 shows many examples of opposite polarity field far inside the outer boundary of the penumbra. Away from the outermost parts of the penumbra, it is evident that most of these opposite polarity patches are located close to and are aligned with the boundaries of the penumbral spines.
Figure 12 shows the opposite polarity field in the observers frame, i.e., before transforming the field to the solar frame. Green pixels show locations where BLOS at τc = 0.95 is larger than 1 kG, red pixels where BLOS is less than − 150 G, i.e., has opposite polarity. Also on the disk center side penumbra, many spines are flanked by (small) patches of opposite polarity field, and we must conclude that some of this opposite polarity field dives down at a rather steep angle with respect to the horizontal plane.
5.3. Vertical and radial flows in opposite polarity patches
Figure 13 summarizes the results of azimuthal fits made for opposite polarity patches having a vertical field (in the solar frame) of less than − 100 G (corresponding to opposite polarity field), shown in red color in Fig. 11. The results obtained with inversions using 2 nodes for the LOS velocity are shown in the left column, and with 3 nodes in the right column. We show the average vertical and radial velocities and the average flow field inclination for these patches (circles) and for all remaining intra-spine pixels in each radial zone (plus symbols). Relative to the average vertical velocity for each radial zone, the opposite polarity patches show downflows of about 0.6–1.3 km s-1 in all radial zones. We note that our wavelength calibration (Sect. 2) gives average velocities for the umbra that are only 60 m s-1 at τc = 0.95, such that this is a robust result. The bottom panels in Fig. 13 shows that the opposite polarity downflows are directed more downward by about 10–20° relative to their surroundings, except in the outermost radial zone. The outward radial velocities of the opposite polarity patches are very similar to those of the surroundings.
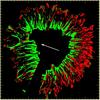 |
Fig. 12 Composite masks showing the vertical magnetic field with BLOS > 1 kG at τc = 0.95 in the observers frame shown in green, and the field with BLOS − 150 G (opposite polarity field) in red. Note that opposite polarity field is seen adjacent to the spines also in many locations at the disk center side. Tick marks are at 1′′ intervals. |
 |
Fig. 13 Average flow properties of opposite polarity patches in the penumbra, obtained by making azimuthal fits of the inferred LOS velocities at τc = 0.95 within the red patches (circles), and for all other (i.e., excluding the opposite polarity field) intra-spine pixels (plus symbols) shown in Fig. 11. The left column shows the results obtained with inversions using 2 nodes for the LOS velocity, the right column with 3 nodes. The penumbra is divided into 6 radial zones, where zone 1 corresponds to the innermost penumbra. On the average, the opposite polarity patches show genuine downflows throughout the penumbra, corresponding to a downflow of 0.6–1.3 km s-1 relative to the average of all intra-spine pixels, and an increased inclination by 10–20°, compared to the intra-spines. The radial outflow velocity of the opposite polarity field is similar to that of other intra-spine pixels. |
 |
Fig. 14 Properties of the limb-side penumbra (excluding the outermost penumbra) at τc = 0.95. Pixels with opposite polarity field in the solar frame are indicated with red color. Panel a) shows the LOS velocity (clipped at (− 2.5, 2.5) km s-1), panel b) the temperature (clipped at (4500, 6500) K), panel c) the vertical magnetic field (in the solar frame; clipped at (− 1000, 2200) G), and panel d) the horizontal magnetic field strength (in the solar frame; clipped at 1500 G. The FOV shown is 8 × 20′′. Tick marks are at 1′′ intervals. |
 |
Fig. 15 Observed (solid) and fitted synthetic (dashed) 630.15/ 630.25 nm Stokes profiles from within the limb side penumbra shown in Fig. 14. The left column shows the averaged profiles from all opposite polarity pixels (marked with red color in Fig. 14). Note the abnormal Stokes V profile with 3 lobes, where the third “extra” lobe appears in the red wings of the lines, and that the abnormal Stokes V profile is fitted reasonably well by the inversions. The right column shows the averaged profiles from all other pixels within the same subfield, for which the average Stokes V profile is normal. The line profiles (plotted side by side) are normalized to the average continuum intensity outside the spot. |
 |
Fig. 16 Upper 4 panels: observed (dashed) and fitted synthetic (solid) Stokes profiles from the pixel marked with “+” in Fig. 14. This pixel is adjacent to a spine and associated with a strong redshift (4 km s-1 at τc = 0.95). Note the abnormal Stokes V profile with 3 lobes. The synthetic fitted profile shows the correct shape, but does not reproduce all details of the observed profile. The 630.15/630.25 nm line profiles (plotted side by side) are normalized to the average continuum intensity outside the spot. Lower 4 panels: variations with continuum optical depth of the temperature, LOS velocity, and vertical and horizontal magnetic field (in the solar frame) returned by NICOLE. |
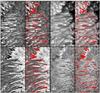 |
Fig. 17 Properties of the disk center side penumbra (excluding the outermost penumbra) at τc = 0.95. Pixels with opposite polarity field in the solar frame are indicated with red color. Panel a) shows the LOS velocity (clipped at (–4.0, 2.5) km s-1), panel b) the temperature (clipped at (4500, 6500) K), panel c) the vertical magnetic field (in the solar frame; clipped at (–1000, 2200) G), and panel d) the horizontal magnetic field strength (in the solar frame; clipped at 1500 G). The FOV shown is 8 × 15′′. Tick marks are at 1′′ intervals. |
We note that the inclination of the opposite polarity downflows is around 100–120° in the mid and outer penumbra, such that they are well aligned with our LOS angle of 105° on the limb-side penumbra (at this heliocentric angle of 15°). In addition, upflows show a strongly reduced LOS velocity at the limb side. This makes the limb side ideal for seeing opposite polarity patches harboring downflows. Figure 14 shows in panel a the LOS velocity at τc = 0.95, without (left) and with (right) the red mask showing the locations of the opposite polarity field. It is obvious that the opposite polarity patches are located in narrow radially extended downflow lanes, as confirmed by the azimuthal variations of their LOS velocities. The vertical magnetic field map (panel c) shows the strong tendency of these opposite polarity patches (and thus also the downflow lanes) to be adjacent to the spines. Panel b illustrates that opposite polarity patches cannot easily be associated with cold or hot structures at τc = 0.95, rather they seem to be located at flanks of the filamentary structures. Finally, panel c shows the absence of spine structure in the horizontal magnetic field map.
In Fig. 15 we show the average Stokes profiles for all opposite polarity patches (left column) and all remaining pixels (right column), within the FOV in Fig. 14. The Stokes V profile is weak and abnormal in the opposite polarity patches, and has a third “extra” lobe in the red wings of both lines. Figure 15 also shows (as dashed lines) the correspondingly averaged fitted synthetic profiles returned by NICOLE3. Quite evidently, the fitted profiles reproduce even the observed abnormal V profiles rather well.
Figure 16 shows the observed and fitted synthetic Stokes profiles for a downflow lane pixel marked with “+” in Fig. 14. The Stokes V profile is abnormal with 3 lobes instead of 2, but is nevertheless fitted by the variations of the LOS velocity and vertical magnetic field (in the local frame) with τc, shown in the lower panels. The polarity of the vertical magnetic field reverses below τc = 0.1, and the magnitude of the horizontal field increases with height.
Abnormal and 3-lobed penumbral Stokes V profiles have been reported recently (cf. Franz 2011; Franz & Schlichenmaier 2013), and were found to be associated with downflows and opposite polarity field in the deep layers, but most such profiles were found in the outermost parts of the penumbra and none in the inner penumbra. Here, we find clear evidence of opposite polarity field even in the innermost penumbra.
Figure 17 shows the same layout as in Fig. 14, but for the disk center side of the spot. This confirms the strong tendency for the opposite polarity patches to be located adjacent to the boundaries of the spines. The strongest Doppler signatures at the disk center sides are from the bright upflows, and panel a shows several examples where the opposite polarity field is located at the sides (flanks) of the bright upflows, which is according to expectations.
6. Conclusions
By calibrating the SST/CRISP transmission profile, and feeding this information pixel by pixel to the inversion code NICOLE, we have been successful in simultaneously estimating the LOS velocity, the magnetic field vector and their gradients in a sunspot penumbra from combined 630.15 nm and 630.25 nm Stokes spectra, at a spatial resolution close to 0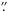 15. The inversions return good fits to the observed Stokes profiles, even when the V profiles are abnormal with 3 lobes.
15. The inversions return good fits to the observed Stokes profiles, even when the V profiles are abnormal with 3 lobes.
Using these data, we validate the inversions through the returned variations of temperature, LOS velocity and magnetic field with optical depth for different magnetic and non-magnetic structures within the FOV. We find that that the magnetic field in the penumbral spines expands over the intra-spines with height, in agreement with predictions of the convective gap model (Spruit & Scharmer 2006; Scharmer & Spruit 2006) and numerical simulations (Rempel 2012, his Fig. 22). Moreover, our data show the ubiquitous presence of narrow and radially extended opposite polarity patches in the entire penumbra. We find that these patches are located in the intra-spines (where the magnetic field is nearly horizontal), and predominantly close to the boundaries to the magnetic spines, where the magnetic field has a strong vertical component. Franz & Schlichenmaier (2013) recently reported on penumbral opposite polarity field that appears “patchy” rather than radially elongated, and considered this to support an interpretation of the associated flows in terms of arching magnetic flux tubes. Our finding that the opposite polarity patches are radially extended and preferentially located close to the magnetic spines rules out such an explanation.
Analyzing the azimuthal variations of the LOS velocity for the opposite polarity patches, we find that they harbor downflows of typically 1 km s-1 near τc = 0.95, consistent with convective downflows dragging down some field-lines. The locations of the opposite polarity downflows agree perfectly with predictions of the convective gap model (Scharmer & Spruit 2006) and recent simulations (Rempel 2012, his Fig. 22).
The horizontal field inferred from our data is found to be nearly as strong in the intra-spines as in the spines. This is in agreement with the simulations of Rempel (2012), showing a layer of strong horizontal magnetic field near τc = 1, and weak-field gaps located below the visible surface. Neither these nor other observations allow conclusions about the sub-photospheric layers, but the distinctly different morphologies of the penumbral vertical and horizontal magnetic field at the limb side, shown in Figs. 4 and 6, are remarkably similar to those of the simulations (Rempel 2012, his Figs. 6b and c).
Our results also confirm earlier measurements in the deeply formed C i line (Scharmer et al. 2011) and the Fe i 630.15 nm line (Scharmer & Henriques 2012). Throughout the entire penumbra, we detect a vertical velocity field that shows the expected correlation with temperature: hot gas moves up and cool gas down. Removing the contribution from the radial flows to the measured LOS velocities, we estimate an rms velocity of 1.2 km s-1 at τc = 0.95 for this vertical component of the penumbral convection. These vertical velocities are sufficiently large to explain the penumbral radiative heat loss (Scharmer et al. 2011).
Acknowledgments
We thank an anonymous referee for valuable comments and suggestions. The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics of the Royal Swedish Academy of Sciences in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
References
- Bellot Rubio, L. R., Balthasar, H., Collados, M., & Schlichenmaier, R. 2003, A&A, 403, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R., Balthasar, H., & Collados, M. 2004, A&A, 427, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bharti, L., Schüssler, M., & Rempel, M. 2011, ApJ, 739, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M. 2007, A&A, 471, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., & Solanki, S. K. 2008, ApJ, 687, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Lagg, A., Solanki, S. K., & Collados, M. 2005, A&A, 436, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Bellot Rubio, L. R., & Müller, D. A. N. 2007, ApJ, 666, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Lites, B. W., & Solanki, S. K. 2008, A&A, 481, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007, A&A, 467, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., Kiselman, D., & Carlsson, M. 2011, A&A, 528, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evershed, J. 1909, MNRAS, 69, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Franz, M. 2011, Ph.D. Thesis [arXiv:1107.2586] [Google Scholar]
- Franz, M., & Schlichenmaier, R. 2009, A&A, 508, 1453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franz, M., & Schlichenmaier, R. 2013, A&A, 550, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinemann, T., Nordlund, Å., Scharmer, G. B., & Spruit, H. C. 2007, ApJ, 669, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, V. M. J. 2012, A&A, 548, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, G. 1982, Publications of the Dominion Astrophysical Observatory Victoria, 16, 67 [NASA ADS] [Google Scholar]
- Hirzberger, J. 2003, A&A, 405, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J., Pietarila, A., Hirzberger, J., et al. 2011, ApJ, 734, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Keil, S. L., Balasubramaniam, K. S., Smaldone, L. A., & Reger, B. 1999, ApJ, 510, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Lagg, A., Solanki, S. K., Riethmüller, T. L., et al. 2010, ApJ, 723, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., & Wedemeyer-Böhm, S. 2005, A&A, 431, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., Elmore, D. F., Seagraves, P., & Skumanich, A. P. 1993, ApJ, 418, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 2012, A&A, 537, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Bellot Rubio, L. R., Solanki, S. K., et al. 2012, ApJ, 758, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V. 2000, A&A, 361, 734 [NASA ADS] [Google Scholar]
- Mathew, S. K., Zakharov, V., & Solanki, S. K. 2009, A&A, 501, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, F., & Schmidt, H. U. 1968, Mitteilungen der Astronomischen Gesellschaft Hamburg, 25, 194 [NASA ADS] [Google Scholar]
- Montesinos, B., & Thomas, J. H. 1989, ApJ, 337, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Montesinos, B., & Thomas, J. H. 1997, Nature, 390, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D. A. N., Schlichenmaier, R., Steiner, O., & Stix, M. 2002, A&A, 393, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, G. 2011, A&A, 529, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2007a, ApJ, 662, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007b, ApJ, 670, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, A., Bellot Rubio, L. R., & Rouppe van der Voort, L. 2010, ApJ, 713, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Pietarila, A., Cameron, R., & Solanki, S. K. 2010, A&A, 518, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plaskett, H. H. 1952, MNRAS, 112, 414 [NASA ADS] [Google Scholar]
- Puschmann, K. G., & Beck, C. 2011, A&A, 533, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010, ApJ, 720, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2011, ApJ, 729, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2012, ApJ, 750, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009, Science, 325, 171 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., & Lagg, A. 2008, ApJ, 678, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Roudier, T., Bonet, J. A., & Sobotka, M. 2002, A&A, 395, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz Cobo, B., & Asensio Ramos, A. 2013, A&A, 549, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., Leenaarts, J., Rouppe van der Voort, L. H. M., et al. 2011, A&A, 531, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Almeida, J. 2005, ApJ, 622, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., & Ichimoto, K. 2009, A&A, 508, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B. 2006, A&A, 447, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B. 2009, Space Sci. Rev., 144, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., & Henriques, V. M. J. 2012, A&A, 540, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., & Spruit, H. C. 2006, A&A, 460, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Bjelksjö, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, in SPIE Conf. Ser. 4853, eds. S. L. Keil, & S. V. Avakyan, 341 [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008a, ApJ, 689, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Nordlund, Å., & Heinemann, T. 2008b, ApJ, 677, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Löfdahl, M. G., van Werkhoven, T. I. M., & de la Cruz Rodríguez, J. 2010, A&A, 521, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Henriques, V. M. J., Kiselman, D., & de la Cruz Rodríguez, J. 2011, Science, 333, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., de la Cruz Rodríguez, J., Sütterlin, P., & Henriques, V. M. J. 2012 [arXiv:1211.5776v1] [Google Scholar]
- Schlichenmaier, R., & Collados, M. 2002, A&A, 381, 668 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichenmaier, R., & Solanki, S. K. 2003, A&A, 411, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichenmaier, R., Jahn, K., & Schmidt, H. U. 1998a, ApJ, 493, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichenmaier, R., Jahn, K., & Schmidt, H. U. 1998b, A&A, 337, 897 [NASA ADS] [Google Scholar]
- Schnerr, R. S., de La Cruz Rodríguez, J., & van Noort, M. 2011, A&A, 534, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., & Vögler, A. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Selbing, J. 2005, Master’s Thesis, Stockholm University [Google Scholar]
- Sobotka, M., Vázquez, M., Bonet, J. A., Hanslmeier, A., & Hirzberger, J. 1999, ApJ, 511, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2011, A&A, 529, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Ruiz Cobo, B. 2000, ApJ, 530, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Montavon, C. A. P. 1993, A&A, 275, 283 [NASA ADS] [Google Scholar]
- Spruit, H. C., & Scharmer, G. B. 2006, A&A, 447, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Title, A. M., Frank, Z. A., Shine, R. A., et al. 1993, ApJ, 403, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Tritschler, A., Müller, D. A. N., Schlichenmaier, R., & Hagenaar, H. J. 2007, ApJ, 671, L85 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, H., Bellot Rubio, L. R., de la Cruz Rodríguez, J., & Rouppe van der Voort, L. 2012, ApJ, 757, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 1998, ApJ, 494, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Yelles Chaouche, L., Solanki, S. K., & Schüssler, M. 2009, A&A, 504, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Observed flatfield spectrum for a pixel near the center of the FOV (circles). The solid line shows the FTS atlas spectrum for the same wavelength range, convolved with the fitted CRISP transmission profile and multiplied with the fitted pre-filter transmission curve. The strength and position of the telluric blend have been determined in a separate fit (see text). |
| In the text | |
 |
Fig. 2 Panels a)–c) show the temperature at τc = 0.95, 0.05 and 0.01, clipped at (5500, 6700), (4600, 5300), and (4300, 5200) K resp., for inversions made assuming depth-independent magnetic field and LOS velocity, and in panels d)−f) the corresponding temperatures obtained with 2 nodes for the velocity and 3 nodes for BLOS. Note the absence of inverse granulation in panel b). Panels g) and h) show the LOS velocity at τc = 0.95 and τc = 0.05 from the inversions corresponding to panels d)−f), and in panel i the LOS velocity from the inversions assuming constant LOS velocity (panels a)−c)). The LOS velocities have been clipped at (− 4.5, 4.5), (− 2.3, 2.3) and (− 2.3, 2.3) km s-1. The bottom row (panels j)−l)) show the LOS magnetic field (with 3 nodes for BLOS) at τc = 0.95, 0.05 and 0.01, clipped at (− 1000, 1500) G. Note the increasing area coverage (expansion with height) of the network field at smaller optical depths. The FOV shown is 25 × 18″. |
| In the text | |
 |
Fig. 3 Top row of panels: LOS magnetic field at τc = 0.95, and 0.09 (both clipped at (− 1500, 2000) G), and the LOS velocity at τc = 0.95, clipped at (− 3.0, 2.0) km s-1, from a 2′′ × 2′′ subfield showing a sheet-like network patch located in the lower-left corner of Figs. 4, 6 and 11. Second row: temperature at τc = 0.95, the green and red pixels used to produce the plots in the lower part of the figure, and the Stokes V area asymmetry (∫V dλ/∫ | V | dλ), clipped at (− 0.5, 0.5). Note the presence of strong opposite polarity field at τc = 0.95, the virtual absence of such field at τc = 0.09 and the strongly increased width of the LOS magnetic field with height. Short tick marks are separated by 0 |
| In the text | |
 |
Fig. 4 Panels a) and b) show the LOS magnetic field (in the observers frame) at τc = 0.95, for inversions made allowing for respectively 2 and 3 nodes for the LOS magnetic field, 2 nodes for the LOS velocity field and 3 nodes for the temperature. Panels c) and d) show the LOS magnetic field at τc = 0.09 and 0.01 with 3 nodes for the LOS magnetic field. Note the presence of opposite polarity field at τc = 0.95 in the penumbra, and the virtual absence of such opposite polarity field at smaller depths. The scaling of the magnetic field (in G) is according to the grayscale bar shown in panel a and is the same for panels a)−d). The FOV shown is 35 × 35′′. The plus symbols indicate the first and last pixels of the plots shown in Fig. 5. The long white arrow points in the direction of disk center, the shorter arrows to a pore discussed in Sect. 4.2.4. |
| In the text | |
 |
Fig. 5 LOS magnetic field (in the observers frame) along the line defined by the two plus symbols in Fig. 4 at τc = 0.95, 0.09 and 0.01. Note the omnipresence of opposite polarity field at τc = 0.95 and the virtual absence of such field in the upper layers. |
| In the text | |
 |
Fig. 6 Panels a)–d) show the temperature (in K) at τc = 0.95 and 0.09, the transverse magnetic field (in G) at τc = 0.09, and the LOS velocity (in km s-1) at τc = 0.95, respectively. In panel c) is shown also the direction of the horizontal field (in the solar frame) at τc = 0.09 for every 20th pixel. The FOV shown is 35 × 35′′. The circles mark examples of umbral dot-like structures that show strongly reduced transverse field on their limb sides, consistent with a magnetic field folding over the dots. The long black arrow points in the direction of disk center, the shorter white and black arrows to a pore discussed in Sect. 4.2.4. |
| In the text | |
 |
Fig. 7 Masks used to divide the penumbra into 6 radial zones, with the temperature at τc = 0.95 superimposed. |
| In the text | |
 |
Fig. 8 Histograms of the magnetic field inclination angle in the entire penumbra except the outermost radial zone (shown in Fig. 7) at τc = 0.95 (full), 0.09 (dashed), and 0.01 (dotted). The distributions are bimodal, with peaks at approx. 45° and 80°. We define spines/intra-spines as having inclinations smaller/larger than 60°. The histograms have been smoothed over 3°. |
| In the text | |
 |
Fig. 9 LOS velocity at τc = 0.95 inferred from the inversions for intra-spines (top), and spines (bottom). The LOS velocities are color coded such that red and blue corresponds to velocities away from and toward the observer respectively, and are clipped at (− 3.0, 3.0) km s-1. The absence of systematic differences in LOS velocities between the disk center (direction of arrow) and limb sides of the penumbra demonstrates that the radial Evershed flow is absent in the spines, as expected from the more vertical field there. The FOV is ~35 × 35′′ and corresponds to that shown in Figs. 4 and 6. Tick marks are at 1′′ intervals. |
| In the text | |
 |
Fig. 10 Variation of vertical (left column) and radial outflow (right column) velocities with local (high-pass spatially filtered) temperature fluctuations, obtained by fitting the azimuthal variations of the inferred LOS velocities at τc = 0.95, and shown for radial zones 2–5. The vertical velocities show the expected convective signature: the relatively cool component has downflows of up to 1.2 km s-1, the relatively hot gas upflows of up to − 1.3 km s-1. Radial velocities are strong in the intra-spines (circles) and weak in the spines (X-symbols), but the hottest spine structures show radial outflows in excess of 3 km s-1. |
| In the text | |
 |
Fig. 11 Composite masks showing the magnetic field with inclination less than 60° at τc = 0.95 (in the solar frame) in green and vertical field in the solar frame of less than − 100 G (opposite polarity field) in red. In the penumbra, the green color corresponds to the magnetic spines, and the black and red colors correspond to the intra-spines. The opposite polarity field in the penumbra is mostly found adjacent to the spines. Opposite polarity field is found also near some strong flux concentrations (plage and pores), and in a few cases near network field. Areas with field strength smaller than 350 G are shown black. The FOV is 35 × 35′′ and corresponds to that shown in Figs. 4 and 6. Tick marks are at 1′′ intervals. |
| In the text | |
 |
Fig. 12 Composite masks showing the vertical magnetic field with BLOS > 1 kG at τc = 0.95 in the observers frame shown in green, and the field with BLOS − 150 G (opposite polarity field) in red. Note that opposite polarity field is seen adjacent to the spines also in many locations at the disk center side. Tick marks are at 1′′ intervals. |
| In the text | |
 |
Fig. 13 Average flow properties of opposite polarity patches in the penumbra, obtained by making azimuthal fits of the inferred LOS velocities at τc = 0.95 within the red patches (circles), and for all other (i.e., excluding the opposite polarity field) intra-spine pixels (plus symbols) shown in Fig. 11. The left column shows the results obtained with inversions using 2 nodes for the LOS velocity, the right column with 3 nodes. The penumbra is divided into 6 radial zones, where zone 1 corresponds to the innermost penumbra. On the average, the opposite polarity patches show genuine downflows throughout the penumbra, corresponding to a downflow of 0.6–1.3 km s-1 relative to the average of all intra-spine pixels, and an increased inclination by 10–20°, compared to the intra-spines. The radial outflow velocity of the opposite polarity field is similar to that of other intra-spine pixels. |
| In the text | |
 |
Fig. 14 Properties of the limb-side penumbra (excluding the outermost penumbra) at τc = 0.95. Pixels with opposite polarity field in the solar frame are indicated with red color. Panel a) shows the LOS velocity (clipped at (− 2.5, 2.5) km s-1), panel b) the temperature (clipped at (4500, 6500) K), panel c) the vertical magnetic field (in the solar frame; clipped at (− 1000, 2200) G), and panel d) the horizontal magnetic field strength (in the solar frame; clipped at 1500 G. The FOV shown is 8 × 20′′. Tick marks are at 1′′ intervals. |
| In the text | |
 |
Fig. 15 Observed (solid) and fitted synthetic (dashed) 630.15/ 630.25 nm Stokes profiles from within the limb side penumbra shown in Fig. 14. The left column shows the averaged profiles from all opposite polarity pixels (marked with red color in Fig. 14). Note the abnormal Stokes V profile with 3 lobes, where the third “extra” lobe appears in the red wings of the lines, and that the abnormal Stokes V profile is fitted reasonably well by the inversions. The right column shows the averaged profiles from all other pixels within the same subfield, for which the average Stokes V profile is normal. The line profiles (plotted side by side) are normalized to the average continuum intensity outside the spot. |
| In the text | |
 |
Fig. 16 Upper 4 panels: observed (dashed) and fitted synthetic (solid) Stokes profiles from the pixel marked with “+” in Fig. 14. This pixel is adjacent to a spine and associated with a strong redshift (4 km s-1 at τc = 0.95). Note the abnormal Stokes V profile with 3 lobes. The synthetic fitted profile shows the correct shape, but does not reproduce all details of the observed profile. The 630.15/630.25 nm line profiles (plotted side by side) are normalized to the average continuum intensity outside the spot. Lower 4 panels: variations with continuum optical depth of the temperature, LOS velocity, and vertical and horizontal magnetic field (in the solar frame) returned by NICOLE. |
| In the text | |
 |
Fig. 17 Properties of the disk center side penumbra (excluding the outermost penumbra) at τc = 0.95. Pixels with opposite polarity field in the solar frame are indicated with red color. Panel a) shows the LOS velocity (clipped at (–4.0, 2.5) km s-1), panel b) the temperature (clipped at (4500, 6500) K), panel c) the vertical magnetic field (in the solar frame; clipped at (–1000, 2200) G), and panel d) the horizontal magnetic field strength (in the solar frame; clipped at 1500 G). The FOV shown is 8 × 15′′. Tick marks are at 1′′ intervals. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


