| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220818 | |
| Published online | 29 March 2013 | |
Fluctuations of the intergalactic ionization field at redshift z ~ 2
1 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
2 Ioffe Physical-Technical Institute, Polytekhnicheskaya Str. 26, 194021 St. Petersburg, Russia
e-mail: ira@astro.ioffe.rssi.ru
3 St. Petersburg Electrotechnical University “LETI”, Prof. Popov Str. 5, 197376 St. Petersburg, Russia
4 Center for Astrophysics and Space Science, University of California, San Diego, CA 92093-0424, USA
Received: 29 November 2012
Accepted: 19 February 2013
Aims. To probe the spectral energy distribution (SED) of the ionizing background radiation at z ≲ 2 and to specify the sources contributing to the intergalactic radiation field.
Methods. The spectrum of a bright quasar HS 1103+6416 (zem = 2.19) contains five successive metal-line absorption systems at zabs = 1.1923, 1.7193, 1.8873, 1.8916, and 1.9410. The systems are optically thin and reveal multiple lines of different metal ions with the ionization potentials lying in the extreme ultraviolet (EUV) range (~1 Ryd to ~0.2 keV). For each system, the EUV SED of the underlying ionization field is reconstructed by means of a special technique developed for solving the inverse problem in spectroscopy. For the zabs = 1.8916 system, the analysis also involves the He i resonance lines of the Lyman series and the He iλ504 Å continuum, which are seen for the first time in any cosmic object except the Sun.
Results. From one system to another, the SED of the ionizing continuum changes significantly, indicating that the intergalactic ionization field at z ≲ 2 fluctuates at the scale of at least Δz ~ 0.004. This is consistent with Δz ≲ 0.01 estimated from He ii and H i Lyman-α forest measurements between the redshifts 2 and 3. A radiation intensity break by approximately an order of magnitude at E = 4 Ryd in SEDs restored for the zabs = 1.1923, 1.8873, 1.8916, and 1.9410 systems points to quasars as the main sources of the ionizing radiation. The SED variability is mostly caused by a small number of objects contributing at any given redshift to the ionizing background; at scales Δz ≳ 0.05, the influence of local radiation sources becomes significant. A remarkable SED restored for the zabs = 1.7193 system, with a sharp break shifted to E ~ 3.5 Ryd and a subsequent intensity decrease by ~1.5 dex, indicates a source with comparable inputs of both hard (active galactic nuclei, AGN) and soft (stellar) radiation components. Such a continuum can be emitted by (ultra) luminous infrared galaxies, many of which reveal both a strong AGN activity and intense star formation in the circumnuclear regions.
Key words: line: profiles / methods: observational / techniques: spectroscopic / quasars: absorption lines
© ESO, 2013
1. Introduction
Lines of different ions observed in spectra of extragalactic sources indicate that the intergalactic medium (IGM) is kept ionized. Fractions of individual ions are determined by the spectral energy distribution (SED) of the ionizing continuum; hence, a particular shape of the SED must be known to transform the measured line intensities into absolute element abundances. Another reason to study the SED is that it provides information about the inputs of hard (active galactic nuclei/quasars, AGNs/QSOs) and soft (star-forming galaxies) radiation emitters. Thus it can help to specify the relative contributions of different sources to the integrated ionizing continuum.
The spectral range considered in the present paper is the extreme ultraviolet (EUV), defined as energies between the hydrogen ionization potential at 1 Ryd (13.6 eV) and ~0.2 keV (15 Ryd), where the soft X-ray band begins. The SED in the EUV range is still poorly known since direct observations are difficult due to several technical and physical limitations. However, the EUV SED can be probed indirectly by using spectral lines of different ions observed in the absorption spectra of distant quasars, i.e., by solving the inverse problem when the shape of the underlying ionizing continuum is restored from the measured column densities (which are proportional to the ion fractions). The simplest (coarse) SED reconstruction involving only the ratio of the radiation intensities at 4 and 1 Ryd (so-called hardness of the spectrum) can be performed on the basis of the column densities of He ii and H i lines detected in the Ly-α forest. Up to now, such measurements have been carried out for the H i and He ii lines between redshifts z ~ 2 and ~ 3 along two different lines of sight (toward HE 2347–4342 and HS 1700+6416), and it was found that the parameter η = He ii/H i fluctuates from one spatial coordinate to another with a characteristic small scale of Δz ≲ 0.01 (Reimers et al. 1997; Zheng et al. 2004; Shull et al. 2004, 2010; Fechner et al. 2006, 2007). This was interpreted as a result of a variable hardness of the ionizing radiation caused by diversity of the radiation sources coupled with radiation transfer effects in the non-uniform IGM. The discovery of foreground quasars located transverse to the line of sight just at the positions where the He ii/H i ratios show their lowest values supports the assumption that the metagalactic ionizing radiation is strongly affected by local sources (Jakobsen et al. 2003; Worseck et al. 2007).
A finer reconstruction of the SED requires the use of metal absorption lines (C ii–C iv, Si ii–Si iv, N ii–N v, O i–O vi, etc.), ionization potentials of which sample the EUV range of the ionizing continuum with a quite small step. An important fact is that at z ≲ 2 the metal lines are the sole means to probe the continuum shape since with modern facilities the He ii Ly-α forest can be studied only at z > 2. Different variants of the SED reconstruction procedure and its application to the analysis of specific quasar absorption-line systems are described in Agafonova et al. (2005), Levshakov et al. (2008, 2009), and Fechner (2011).
In the present work we restore the SED of the ionizing background for absorption-line systems detected toward a bright quasar HS 1103+6416 with zem = 2.19 (Reimers et al. 1995). To reconstruct the SED from metal lines, one generally needs special absorbers: optically thin systems with lines of successive ions of the same element (e.g., C ii–C iii–C iv, Si ii–Si iii–Si iv). However, they are not often found in quasar spectra. Thus the quasar HS 1103+6416 is one of the most favorable objects since its spectrum contains just several systems suitable for the SED reconstruction and detached from each other by Δz ~ 0.004 − 0.17, i.e., by the redshift interval comparable with that in the He ii Ly-α forest studies. An additional advantage is that the observational data are available in a broad wavelength range from 1400 Å to 5700 Å, which provides a large variety of ionic transitions and, hence, improves the accuracy of the results.
The paper is structured as follows: the computational method used to reconstruct the continuum shape of the ionization field is described in Sect. 2. Section 3 deals with the observational data with attention to the consistency of the wavelength calibration in different parts of the spectrum. In Sect. 4, individual absorption systems are analyzed and the results obtained are discussed in Sect. 5. Our conclusions are given in Sect. 6.
2. Computational method
The computational procedure used to reconstruct the SED of the background ionizing radiation from metal lines was considered in detail in Agafonova et al. (2005). Here we describe it briefly to explain the basic principles of the analysis.
The true shape of the incident radiation can be restored from absorption systems that are optically thin in the Lyman continuum both in H i and He ii, i.e., from those with column densities N(H i)< 2 × 1017 cm-2 and N(He ii)< 1018 cm-2. Another requirement is that the absorbing gas should be in the thermal and ionization equilibrium, i.e., its ionization structure is determined entirely by the SED of the ionizing radiation and the ionization parameter U ≡ nph/ngas, where nph and ngas are, respectively, the local densities of the ionizing photons and of the gas. Figure 1 shows continuum shapes commonly used to approximate the EUV range: a simple power law, an AGN spectrum of Mathews & Ferland (1987), and an SED of the intergalactic ionization field at z < 2 calculated by, e.g., Haardt & Madau (1996) or Fardal et al. (1998). In this figure, tick marks indicate the ionization thresholds of ions usually observed in quasar absorption spectra. The column densities of these ions are proportional to their fractions Υi, which in turn are determined by the SED above the corresponding ionization thresholds. Thus, having the column densities of ions with ionization potentials sampling some energy interval of the ionizing continuum, we can try to solve the inverse problem: namely, to reconstruct the SED in this interval. The procedure is iterative and consists of the following steps.
 |
Fig. 1 Continuum shapes used to approximate the SED in the EUV (1 Ryd–0.2 keV) range: a simple power law (blue dotted line), an AGN continuum by Mathews & Ferland (1987) (blue line), an ionizing spectrum of the metagalactic radiation field at redshift z ~ 2 by Haardt & Madau (1996) (black line), and its approximation by a broken power law (red line). All the SEDs are normalized so that Jν(hν = 1 Ryd) = 1. The positions of ionization thresholds of different ions are indicated by tick marks. |
Firstly, the shape of an SED should be parameterized, i.e., described by a set of parameters (also called factors). As seen from Fig. 1, in the EUV range the intensity Jν can be well fitted by a simple/broken power law, i.e., by a set of n power-law indices αi (Jν ∝ ν− αi) and breaking points νi, i = 1,...,n. The number and definition of factors depend on how many lines of different ions are available in the absorption system: it is clear that with only a couple of lines the continuum shape cannot be reconstructed in great detail, i.e., the fewer the lines the fewer the factors. With some initial guesses for the adopted factors, a trial SED is computed and inserted into the photoionization code CLOUDY (ver.07.02.01, last described by Ferland et al. 1998). The ionization parameter U at this stage of the analysis is assumed constant within the absorber and is commonly estimated by ratio(s) of column densities of two or more subsequent ions of the same element (Si ii–Si iii–Si iv, or C ii–C iii–C iv). If for this value of U the trial SED cannot reproduce the column densities of all ions observed in the system or some other peculiarities arise (like abundance pattern well beyond observational and theoretical constraints), then it is considered as inadequate and has to be adjusted. To evaluate the goodness of a trial continuum shape, we need to choose some quantitative measure (“response”). The choice is performed rather heuristically and accounts for both the information obtained with the tried SED and for any other a priori available information. If, for example, the trial SED gives a lower than the observed ratio of Si ii/Si iv at U corresponding to the observed C ii/C iv ratio, then the factor values should be varied in a way to produce SEDs that will give a higher Si ii/Si iv. In addition, a trial SED can possibly reproduce well the observed column densities of silicon and carbon ions, but only at the expense of an extremely high relative overabundance of silicon to carbon, [Si/C] > 0.3, which is neither predicted for nor measured in intergalactic absorbers. In this case the adjustment should go toward the continuum shapes reducing the [Si/C] value to the acceptable level of [Si/C] ≲ 0.3. When the SED is parameterized by a single factor (simple power law Jν ∝ ν− α), then the adjustment can easily be performed by a trial-and-error procedure. In case of multiple factors, the direction (in the factor space) toward the desired response is found by means of a special randomization technique for the factor values based on the experimental design methodology (details are given in Agafonova et al. 2005). The adjustment of an initial SED occurs by stepwise movement along this direction until the SED that produces the required response is found.
Now with the found SED as an input, CLOUDY is used to calculate the ionization curves for all ions detected in the absorption system. The ionization curves are then inserted in the Monte Carlo inversion (MCI) code, which is a solver for the inverse problem in spectroscopy based on a model of line formation in clumpy stochastic media, i.e., in the gas with fluctuating density and velocity fields (full description is given in Levshakov et al. 2000). The MCI reconstructs the distributions of the gas density (and hence of the ionization parameter) and the velocity along the line of sight and estimates the element abundances (assumed to be constant within the absorber) by fitting the synthetic line profiles to the observed ones, i.e., it works directly with the intensities at every point within the line profiles. Compared with the estimates based solely on column densities, the abundances obtained by the MCI are more accurate and robust, especially in case of complex line profiles, i.e., when significant density and velocity gradients are expected (see Eq. (15) in Levshakov et al. 2000). Another advantage of the MCI is the treatment of blends: supposing that all lines arise in the same gas, we restore the underlying gas density and velocity distributions using firstly the lines with clear profiles and then reconstructing the profiles of blended lines on the basis of these distributions and ionization curves for the corresponding ions. The important point here is that this approach also allows us to check (and to correct) the eventual shifts of absorption lines caused by errors in wavelength calibration (Levshakov et al. 2009). If with a newly found SED we can self-consistently describe the profiles of all observed lines, i.e., obtain χ2 ≲ 1 (per degree of freedom) for individual lines along with acceptable element abundances, then calculations are finished. Otherwise, the next iteration of the SED adjustment is performed, eventually with a different response function.
3. Observational data
Details of the observations and data reduction are given in Köhler et al. (1999). Here we repeat only what is relevant for the present study. A high resolution (FWHM ~ 8 km s-1) optical spectrum of HS 1103+6416 was obtained in the wavelength coverage of 3180–5800 Å with the HIRES spectrograph (Vogt et al. 1994) on the Keck 10 m telescope. Low-resolution spectra in the UV range were taken with the FOS and the GHRS onboard the Hubble Space Telescope (HST). Depending on the wavelength range, the spectral resolution was 0.77 Å (grating G140L, Δλ = 1415 − 1700 Å), 1.44 Å (G190H, Δλ = 1572 − 2311 Å), and 2 Å (G270H, Δλ = 2223 − 3277 Å), which is equivalent to velocity resolutions (FWHM) of 136–163 km s-1, 186–275 km s-1, and 183–270 km s-1, respectively.
 |
Fig. 2 Calibration-induced shifts of the observed profiles illustrated by spectral lines from different absorption systems. The velocity structure is estimated on the basis of lines from the high-resolution (Keck/HIRES) part of the HS 1103+6416 spectrum and then applied to calculate the profiles from low-resolution (HST) parts. The synthetic profiles are shown by red, the vertical ticks mark positions of sub-components. ΔV indicates the velocity shift applied to the observed profile to align it with a reference line from the Keck spectrum. |
Since the data were obtained with different instruments, offsets in the wavelength calibration between the corresponding parts of the spectrum are possible. In our analysis of an absorption-line system, all transitions are fitted with the same model of the underlying density-velocity field and artificial (calibration-induced) velocity shifts between the absorption lines can negatively affect the final result. To reveal the eventual offsets, we used several absorption systems with strong hydrogen and metal lines throughout the whole available spectral range. The velocity structure was estimated by fitting the line profiles from the high-resolution Keck spectra to a number of Gaussian component. The synthetic profiles of low-resolution lines were then calculated by convolving the obtained velocity structure with a FWHM at the position of a given line and adjusting the column density to comply with the observed line intensities. The calibration shifts were evaluated by cross-correlation of synthetic and observed profiles.
Some examples are shown in Fig. 2. For the system at z = 0 (probably a DLA), the velocity structure was estimated on the basis of the doublet Ca iiλλ3439,3969 Å in the Keck spectrum and then transferred to other ions assuming purely turbulent broadening (i.e., the Doppler b-parameters for all ions were identical). For the systems at z = 1.1923 and 1.8916, the lines of ions with close ionization potentials and close atomic weights (e.g., C iv and O iv, Si ii and S ii) were selected. For the system at z = 0.7129, a weak H i Lyman limit is present in the G140 part of the spectrum, which allows us to estimate the H i column density as N(H i)= (1.0−1.5) × 1016 cm-2, i.e., the system is optically thin. The b-parameter for H i lines in this system was calculated from the b-parameter of Mg ii doublet in the Keck spectrum assuming a purely thermal broadening.
 |
Fig. 3 High-resolution hydrogen and metal absorption lines associated with the zabs = 1.9410 system toward HS 1103+6416 (black curves). The synthetic profiles calculated with the UV SEDs shown by the shadowed area in Fig. 5 are plotted by red curves. The zero radial velocity is fixed at z = 1.9410. The inserted figures in Si iv panels display the synthetic spectra (blue curves) calculated with the first-guess SED (red dotted line in Fig. 5). |
 |
Fig. 4 Low-resolution lines (HST) from the zabs = 1.9410 system. The vertical ticks in the H i panels indicate the positions of individual Voigt components. The profiles of metal ions are calculated using the velocity-density distributions restored on the basis of high-resolution lines shown in Fig. 3. The red synthetic profiles in the O iii and O iv panels are calculated for two oxygen abundances [O/C] = 0.2 and 0.3 (see text for details). |
Calculated column densities (in cm-2) for atoms and ions in systems used to reconstruct the SED of the underlying ionizing continuum.
It is seen from Fig. 2 that the calibration in the G270 part either complies with that in the Keck spectrum (e.g., Mg iλ2852 Å at z = 0) or demonstrates a negative offset of ~–10 km s-1 (Fe iiλλ2600,2586 Å at z = 0, O iiλ834 Å at z = 1.8916). In G190, the offsets relative to the Keck spectrum are much larger (~ 40 km s-1) and change only slowly with wavelength (S iiλ764 Å at z = 1.8916, O iv λ787 Å at z = 1.1923). Contrary to this, the calibration in G140 is quite irregular and lines detached in the spectrum only by a few angstroms can be either coherent with the Keck spectrum (Fe iiλ1608 Å at z = 0, H iλ937 Å at z = 0.7129) or significantly shifted (Si iiλ1526 Å at z = 0, H iλ930 Å at z = 0.7129).
The absorption lines in the Keck spectrum are also not free from calibration errors. For example, in the system at z = 0, the Ca iiλ3969 Å line is offset by 1.5 km s-1 relative to Ca iiλ3934 Å, while in the system at z = 0.7129, the Mg iiλ2803 Å line is shifted by − 1.3 km s-1 relative to Mg iiλ2796 Å. The calibration of lines of the same ion can be easily checked by a simple cross-correlation of the line profiles. To reveal possible calibration shifts between lines of different ions, several trial MCI runs are required. We found that the Si iv λ1393 Å line in the z = 1.8916 system was offset by 2.0 km s-1 relative to both low (Si ii, C ii) and high ionization lines (C iv), i.e., its shift was caused not by a kinematical segregation but by miscalibration of the wavelength scale. In general, we confirm the results of Griest et al. (2010) that calibration errors in Keck spectra are quite common and can reach a value of ~0.5 pixel size (~ 2 km s-1).
For calculations described below, all revealed calibration shifts were corrected, i.e., positions of lines in each absorption system were set according to a coherent wavelength calibration.
4. Analysis of individual systems
All calculations throughout the paper are performed with laboratory wavelengths and oscillator strengths taken from Morton (2003) for λ > 912 Å, except for the ion Si iii, and from Verner et al. (1994) for λ < 912 Å. For Si iii, the adopted laboratory wavelength is 1206.51 Å and not 1206.50 Å as Morton’s (for explanation, see Sect. 2 in Levshakov et al. 2009). The Lyman series limit for He i, λc = 504.2593 Å, is taken from the database of NIST. We use element abundances of the solar photosphere as given in Asplund et al. (2009) and Grevesse et al. (2010). The abundance ratio [X/Y] means log (NX/NY) − log (NX/NY)⊙, while [X] = log (NX) − log (NX)⊙.
4.1. Absorption system at z = 1.9410
The high-resolution (Keck) spectrum of HS 1103+6416 contains the H i Ly-α line and lines of subsequent ions of both carbon, C iiλ1334 Å, C iv λλ1548,1550 Å, and silicon, Si iiλ1260 Å, Si iiiλ1206 Å, Si iv λλ1393,1402 Å (Fig. 3, observed profiles are shown by black). There are absorption features at the expected positions of the N v λλ1238,1242 Å lines, but their profiles are inconsistent with each other, probably because of blending with some forest lines. In any case, they can be used to set an upper limit on the nitrogen abundance. Clearly present in the UV part of the spectrum are strong lines O iiiλλ832,702,507 Å, O iv λλ608,553,554 Å, and C iiiλ977 Å (Fig. 4).
 |
Fig. 5 SEDs complying with the line profiles from the zabs = 1.9410 system: yellow cone plots simple power laws, Jν ∝ ν− α, with α = 1.5–1.7; grey shadowed area marks broken power laws with a break at 4 Ryd. The black dotted line shows an initial shape used in the SED adjustment procedure. |
The column densities for metal ions from the optical (Keck) spectrum that can be calculated by a simple Voigt profile fitting are given in Table 1. The column densities for lines from the UV part cannot be estimated a priori due to low resolutions (FWHM > 200 km s-1) and, as a consequence, possible blending of many lines within one profile, but they can be calculated at the next stages of the SED reconstruction employing the gas density and velocity distributions derived by the MCI procedure.
The ion fractions depend strongly on the input metal abundances, so that for accurate analysis we need to know the H i content as well. In Fig. 3, a neighboring system, which is seen mainly in the C iv absorption, is clearly visible at radial velocity v ≃ 115 km s-1, i.e., the observed profile of H i Ly-α is formed by a superposition of two saturated lines. Using H i lines from the low-resolution (HST) spectrum of HS 1103+6416, we deconvolve this H i profile into two sub-components, with N(H i)= (2.5 − 3.0) × 1015 cm-2 (b = 33.1 km s-1) for the z = 1.9410 system and N(H i)= (0.8 − 1.1) × 1015 cm-2 (b = 32.6 km s-1) for the neighbor (Fig. 4).
Firstly, simple power laws, Jν ∝ ν− α, with the index α ranging from 0.6 to 1.8 were tried as a continuum shape in the EUV range. At U determined by the measured ratio of N(C iv)/N(C ii), the column densities of silicon ions are reproduced with power-law continua having indices α = 1.5 − 1.7, with the element abundances estimated as [C] = −0.3 − −0.4 and [Si/C] ~ 0.0−0.05. However, these continua predict small fractions of O iii, and one needs a rather strong overabundance of oxygen, [O/C] ~ 0.5, to describe the observed profiles of the O iii lines. Such an overabundance is only marginally consistent with measurements both in metal-rich stars (metal content Z ≳ 0.5 Z⊙) and in high-metallicity H ii regions that usually show [O/C] < 0.3 (Akerman et al. 2004; Garcia-Rojas et al. 2004; Bensby & Feltzing 2006; Bresolin 2007; Esteban et al. 2009). That is why more complex continuum shapes were tried as well: namely, broken power laws defined by three indices and two breaking points (five factors) in the range 1 Ryd < E < 15 Ryd (Fig. 5). The boundary to the soft X-ray range was fixed at 0.2 keV (14.7 Ryd) and α = 1.8 at E > 0.2 keV (this last setting is arbitrary since it does not affect the fractions of ions relevant for the present study).
At U corresponding to the measured ratio of N(C iv)/N(C ii), the first-guess SED (dotted line in Fig. 5) underproduced the measured N(Si iv)/N(Si iii) (corresponding Si iv profiles are shown in the inserts in Fig. 3). The latter was chosen as a response function and the search in the five-factor space was performed for the direction toward SEDs with a higher response. Moving along this direction in steps, we found the range of SEDs reproducing both the observed N(C iv)/N(C ii) and N(Si iv)/N(Si iii). However, for some SEDs from this range we obtained a negative abundance ratio [Si/C] < 0. Such an underabundance of silicon can occur in the gas enriched mostly by the AGB stars (Garnett et al. 1995; Agafonova et al. 2011), but it is coupled both with a high (solar to oversolar) content of carbon and a relative overabundance of C to oxygen, [C/O] > 0 (Kingsburgh & Barlow 1999). In the present system, carbon abundance for any type of the ionizing spectrum does not exceed half-solar value. However, to describe the profiles of the strong O iiiλλ832,702,507 Å lines, the relative oxygen content should always be at least not lower than that of carbon, i.e., [O/C] > 0. Thus, we can exclude here AGB stars as a prevalent enrichment source and set zero as a lower limit for the relative abundance of silicon to carbon: [Si/C] > 0. Using this condition as a new response function, we performed a second iteration of the continuum shape adjustment.
 |
Fig. 6 Observed flux of HS 1103+6416 obtained with the FOS and GHRS onboard the HST. The arrows mark the H i Lyman limits for the z = 1.8916 and z = 1.7193 systems. |
The range of acceptable SEDs finally obtained, i.e., those that allow us to describe self-consistently all observed profiles along with reasonable abundance ratios, is shown by the shadowed area in Fig. 5. The physical parameters derived with SEDs from this range are listed in Table 2. The corresponding synthetic absorption-line profiles are plotted by red in Figs. 3 and 4. Compared to pure power laws, the SEDs with a break at E ~ 4 Ryd give a fraction of O iii that is almost twice as large, so that now the observed intensities of O iii lines can be well reproduced with a moderate oxygen-to-carbon overabundance ratio, [O/C] = 0.2–0.3. This behavior of the O iii fraction is easy to explain: the ionization potential of O iii is 4.038 Ryd and a sharp decrease of the number density of the ionizing photons just above this energy hampers the transition from O iii to O iv, thus retaining the oxygen in the double-ionized stage.
 |
Fig. 7 He i Lyman limit at z = 1.8916 and the identified He i Lyman series lines. The H i Lyman limit at z = 0.7129 and the O iiiλ507.388 Å line at z = 1.8916 are also indicated. The latter is blended with He i Ly-θ (λ507.718 Å) and Ly-ι (λ507.058 Å) lines. |
 |
Fig. 8 High-resolution lines observed in the z = 1.8916 system. Brackets indicate the sub-systems A, B, C, and D with strong lines, vertical ticks in the C iv panels point to superimposed sub-systems with weak absorption lines. The synthetic profiles for metal ions (red) in the sub-system A are calculated with broken power-law SEDs from the grey shadowed area in Fig. 10. The black line in the O i panel is a restored profile from the forest absorption shown in the insert. The black and blue curves in the insert are the original and deconvolved profiles, respectively. |
4.2. Absorption complex at z = 1.8916
This system was described in detail by Köhler et al. (1999). Here we re-analyze it with the aim of restoring the continuum shape of the UV ionizing radiation.
The available UV parts of the HS 1103+6416 spectrum contain clear Lyman limits for both H i and He i, making it possible to measure the corresponding column densities1: N(H i)= (2.87 ± 0.03) × 1017 cm-2 (Fig. 6) and N(He i)= (1.5 ± 0.3) × 1016 cm-2 (Fig. 7). We note that this is the first discovery of the He i continuum in any cosmic object except the Sun. The spread of the N(H i) values is determined by the uncertainty in the emission profile of the blend O ii+O iii+Fe iii blueward of the H i Lyman edge and for N(He i) by the noise in the spectrum. The ratio N(He i)/N(H i) is sensitive to the radiation intensity ratio at 1 Ryd and 1.8 Ryd (Lyman limit for He i) and in principle could be used to estimate the slope of the continuum spectrum in this energy range, similar to the way N(He ii)/N(H i) is used to probe the J1/J4 ratio in the H i+He ii Ly-α forest measurements. But for a given ionization spectrum, the value of N(He i)/N(H i) depends strongly on the ionization parameter, i.e., any estimation of this ratio can be made only by involving metal lines.
The absorption lines of metal ions detected in the Keck spectrum are shown in Fig. 8. Essential for the SED reconstruction are weak but clearly present lines of Fe iiλ1608 Å (other Fe ii transitions are beyond the observed range) and O iλ1302 Å. The latter is blended with an H i line from the Ly-α forest, but the component that falls into the blue wing of H i can be deconvolved. Although the complex represents a superposition of several individual absorbers (marked by the letters A,B,C, and D in Fig. 8), they can be separated if we compare the relative strengths of their C ii, C iv, Si ii, Si iii, and Si iv lines: strong C ii, Si ii along with weak C iv, Si iv lines characterize the gas in the absorber A; comparably strong pairs C ii, C iv, and Si ii, Si iv are revealed in the absorber B; and lines of highly ionized species C iv and Si iv are slightly stronger than low-ionization C ii, Si ii in the absorbers C and D. A significantly different metal content in the sub-systems C and D is conceivable. Additionally, there are superimposed absorbers seen mostly in weak C iv (in some cases also in Si iv) transitions (indicated by vertical ticks in Fig. 8).
In order to distribute between the individual absorbers the total column density N(H i) measured from the optical depth at the Lyman edge, we fit all available H i lines to the sum of Voigt components, each of which is described by three parameters: the line center, the broadening b-parameter, and the column density. However, unlike the previous system at z = 1.9410, which consists of two well-separated absorbers with the total N(H i)~ 5 × 1015 cm-2, we have here at least four close and partially overlapping absorbers with the total N(H i)~ 3 × 1017 cm-2. Coupled with a low resolution (FWHM ~ 200 km s-1) of higher Lyman series lines of H i, this makes the deconvolution procedure numerically unstable (ill-posed), which results in multiple solutions (i.e., in significantly different column densities for the same component, depending on model, initial guesses, exit conditions, etc.), even if the total N(H i) remains constant.
A common approach to regularizing an ill-posed problem is to place some a priori known constraints on the fitting parameters. In the present case such constraints can be derived from metal lines: the absorber B has N(Si ii)= 2.2 × 1013 cm-2 and N(Si iv)= 2.1 × 1013 cm-2 (Table 2 in Köhler et al. 1999). The Si iiiλ1206 Å line is saturated (Fig. 8) and hence should have N(Si iii)~ 1014 cm-2. The line is in the Ly-α forest and in principle could be blended with some forest feature. However, any strong Ly-α blend with N(H i)~ 1014 cm-2 is excluded by the continuum window at the expected position of Ly-βλ1025 Å, and there are no candidate systems that could produce strong metal lines at the position of Si iii. Thus the observed saturation is indeed due to absorption in Si iiiλ1206 Å, although contamination with a weak, N(H i)~ 1013 cm-2, hydrogen line (or lines) cannot be excluded (see the synthetic Si iii profile in Fig. 8). The silicon ion fractions depend quite strongly on the gas metallicity Z, and trial calculations with CLOUDY have shown that for a wide range of shapes of the ionizing continua the required large fraction of Si iii at Si ii/Si iv ~ 1 can be realized only if [Z] ≲ − 0.4. Similarly, in the absorber D the column density of the double-ionized silicon N(Si iii)~ (3 − 4) × 1013 cm-2 at N(Si iv)/N(Si ii) ≳ 3 is reproduced only at low gas metalicities, [Z] ≲ − 1.0. It follows from these conditions that the sub-systems B and D should have N(H i)~ 1017 cm-2. Compared to the absorber B, the absorber C reveals two times lower column densities of Si ii and C ii, but almost similar N(Si iv) and N(C iv) (Köhler et al. 1999). Assuming for C the same metallicity as in B (which looks plausible taking into account the closeness and similarity of line profiles), we estimate for it N(H i)~ 5 × 1016 cm-2. These constraints on the H i column densities, along with setting the bounds for the component centers close to the position of the strongest metal absorption, allow us to stabilize the H i deconvolution and to obtain the parameters listed in Table 3. The synthetic H i profiles calculated with these parameters are shown by red curves in Fig. 9.
The sub-system A is optically thin both in H i, N(H i)~ 4 × 1016 cm-2 and He ii, N(He ii)~ 2 × 1017 cm-2; with its great diversity of ionic transitions, this sub-system is suitable for the SED reconstruction. The measured column densities are listed in Table 1. The red wings of several lines in the sub-system A are blended with corresponding components from the other sub-systems (Fig. 8), but Si ii and Si iv are affected only weakly and can be used to estimate the ionization parameter. The power-law SEDs with α = 0.9−1.2 reproduce the column densities of all ions with the following abundances: [C] = −0.45−− 0.55, [Al, Si, Fe/C] = 0.0–0.1, [O/C] = 0.0–0.3, which are consistent with standard models of chemical enrichment. The profiles of both C ivλ1548 Å and C ivλ1550 Å lines come out slightly underestimated, but they might be blended with components from weak-C iv sub-systems like those seen at v = −120 or −90 km s-1 (tick marks in the C iv panels in Fig. 8). However, these power laws also significantly underproduce C iv profiles in the adjacent system B, which are much stronger and, hence, less affected by possible blends. Thus pure power-law continua are probably not the best choice for the present absorber.
Softer power laws (α ~ 1.5), like those considered for the z = 1.9410 system, reproduce all ions including C iv, but only at the expense of high overabundances of O and Fe relative to C: [C] = −0.6−− 0.7, [Si/C] = 0.15–0.20, [O,Fe/C] > 0.5. A simultaneous overabundance of both iron and α-elements (O, Si) to carbon at a quite high carbon content is neither predicted nor observed. Besides, the total column densities of C ii and O ii, N(C ii)= 3.3 × 1014 cm-2 and N(O ii)= (8.5−9.0) × 1014 cm-2 (see Fig. 2), do not indicate a high oxygen overabundance. Thus, we can conclude that pure power-law SEDs, if adopted as the ionizing continua, are significantly different at z = 1.8916 and 1.9410.
The continuum shape from the previous z = 1.9410 system (upper boundary of the shadowed region in Fig. 5) was tried as an initial guess for a broken power-law SED. With this SED, the Fe iiλ1608 Å and O iλ1302 Å lines can also be reproduced with [O,Fe/C] > 0.5. In general, ion fractions of Fe ii and O i are only weakly influenced by the continuum shape at E > 1 Ryd and depend mostly on the ionization parameter U, which starts to decrease sharply at lgU ≳ −4. Thus, to obtain reasonable relative abundances of Fe and O, we have to modify the initial continuum shape so that the measured ratio N(Si ii)/N(Si iv) (along with a sufficient amount of C iv) will be achieved at a possible low U.
The range of the broken power-law SEDs acceptable for the present system is shown by the shadowed area in Fig. 10, with the synthetic line profiles plotted in red in Fig. 8 and the estimated abundances given in Table 2. These continua are very hard, with a slope between 1 Ryd and 4 Ryd corresponding to α = 0.5−0.6 (cf. with α = 1.3−1.5 at z = 1.9410). We note that Köhler et al. (1999), in spite of their quite different approach, also proposed a continuum shape with α = 0.5 and an order of magnitude break in the intensity at 4 Ryd as a favorable SED for the present system.
Such hard slopes at E > 1 Ryd are indeed observed in some AGNs (Scott et al. 2004; Shull et al. 2012). This type of objects includes a well-known quasar HE 2347–4342 (toward which the He ii Ly-α forest was firstly resolved); according to Telfer et al. (2002) it should have α = 0.56.
 |
Fig. 9 Low-resolution H i and He i lines from the z = 1.8916 system. Tick marks indicate the positions of individual sub-components in the H i profile deconvolution. The synthetic profiles are shown by red and the observed ones by black curves. |
Now, using the H i column densities for the individual components (Table 3), the restored SED, and the column densities for metal ions from Köhler et al. (1999) to estimate the ionization parameters in the sub-systems A, B, C and D, we can calculate the total amount of He i and compare it with the value given by the He i Lyman limit optical depth. Assuming the helium abundance (in number) of 0.083, we obtain N(He i)A = (2.5−3.0) × 1015 cm-2, N(He i)B = (5.0−6.0) × 1015 cm-2, N(He i)C = (2.0−2.5) × 1015 cm-2, and N(He i)D = (2.5−3.0) × 1015 cm-2, which results in the total N(He i)tot = (1.2−1.5) × 1016 cm-2 complying well with the value estimated from the He i Lyman edge.
The G140 part of the HS 1103+6416 spectrum also contains a series of He i Lyman lines. To model these lines with a sum of components, we need a broadening parameter for each component. For the component A, we obtain bHe I = 15 km s-1 from the comparison of the He i synthetic profile calculated with the density-velocity distributions estimated from metal lines and a single Voigt profile with the same N(He i). This means that the broadening is dominated by turbulent effects. Assuming the same ratio (~ 0.9) between the b-parameters of the H i and He i lines in the components B,C, and D, we model the He i profiles as the sum of four Gaussians convolved with the instrumental function. The synthetic He i profiles are shown by red curves in the right-hand panels in Fig. 9.
4.3. Absorption system at z = 1.8873
The system is detached from the z = 1.8916 absorber by only 450 km s-1, which corresponds to ~2.2 Mpc if the offset is purely cosmological.
The metal ions are represented by lines of C ivλ1548 Å (C ivλ1550 Å is blended with C ivλ1548 Å from the z = 1.8916 system ) and Si iiiλ1206 Å, Si ivλλ1393,1402 Å (Fig. 11). There is a weak absorption at the position of C iiλ1334 Å, but it is not clear whether it is indeed C ii or some forest feature since the spectrum of HS 1103+6416 contains many weak and unidentified lines in the vicinity of this wavelength. In the UV part, a continuum window seen at the position of the O ivλ553 Å line and weak absorption at the position of N ivλ765 Å can be used to set upper limits on their column densities. The hydrogen content was estimated in the previous section and is given in Table 3 (component No. 1); the column densities for metal ions are listed in Table 1.
Power-law SEDs with α > 1.6 reproduce the measured ion ratios with [C] ~ −1.0 and relative underabundance of silicon, [Si/C] < 0, and thus can be ruled out for the same reasons as in Sect. 4.1. Power laws with α = 1.6 − 1.8 give [C] ~ −1.2 and [Si/C] ~ 0−0.2, i.e., C and Si abundances are in line with standard chemical enrichment. However, under the assumption of [O/C] ~ 0.2−0.3, which is also in line with standard enrichment, these SEDs predict quite a large column density of N(O iv)= (5.0 − 6.0) × 1014 cm-2, which is only marginally consistent with the noisy continuum at the expected position of O ivλ553 Å.
Broken power-law SEDs reconstructed for the previous z = 1.8916 system are definitely inconsistent with lines in the present absorber: at U estimated from the condition N(Si iv) = N(Si iii), the predicted intensity of the C iiλ1334 Å line significantly overestimates the observed profile; besides, the measured N(C iv) requires the abundance ratio [Si/C] ~ − 0.5. Thus, we can conclude that the SED at z = 1.8873 in any case differs from that at z = 1.8916.
Due to a small number of available lines at z = 1.8873, it is not possible to restrict the range of appropriate continuum shapes as was done in Sects. 4.1 and 4.2. A large plurality of SEDs consistent both with the measured column densities and with standard chemical enrichment (i.e., delivering [O, Si/C] > 0 at [C] ~ −1.0) can be proposed; two examples are shown in Fig. 12 by solid lines. It is seen that the SEDs at z = 1.8873 are considerable softer, either only at E > 4 Ryd or in the whole EUV range, than the ionizing continuum at z = 1.8916.
 |
Fig. 10 SEDs complying with the lines observed in the z = 1.8916 system: yellow cone plots simple power laws, Jν ∝ ν− α, with α = 0.9–1.2; grey shadowed area indicates broken power laws with a break at 4 Ryd. The black dotted line shows an initial shape used in the SED adjustment procedure; here it is chosen as an upper bound of the broken power-law SEDs restored for the z = 1.9410 system (grey shadowed area in Fig. 5). |
4.4. Absorption system at z = 1.7193
The system is detached by 17 400 km s-1, or ~90 Mpc, from the previous z = 1.8873 absorber. In the Keck spectrum, the H iλ1215 Å, C ivλλ1548,1550 Å, Si iiiλ1206 Å, Si ivλλ1393,1402 Å lines are present, with continuum windows at the expected positions of Si iiλ1260 Å, Al iiλ1670 Å, and N vλ1242 Å (Fig. 13). The C iiλ1334 Å line is blended with a strong forest line, and it is unclear whether there is a corresponding absorption or not. The UV spectrum contains a series of H i Lyman lines up to the Lyman limit at 2479 Å (marked by the arrow in Fig. 6). Fitting the H i profiles to the three component model, we obtain N(H i)= (1.5 − 1.6) × 1016 cm-2 for the total hydrogen and N(H i)= (1.4 − 1.5) × 1016 cm-2 for the central component exhibiting metal lines. The column densities measured from the Si iiiλ1206 Å, Si ivλλ1393,1402 Å, and C ivλλ1548,1550 Å profiles are given in Table 1. A highly unusual ratio Si iv/C iv ~ 0.5 at log U ~ −2 (determined by Si iii/Si iv ~ 2 and Si iv/Si ii> 13) is found: in the systems at z = 1.9410 and z = 1.8873 with comparable ionization states of the absorbing gas, the Si iv/C iv ratio is only ~0.06 and 0.03, respectively. The measured ratios Si ii/Si iv, Si iii/Si iv, and Si iv/C iv are neither reproduced by simple power-law SEDs (α = 0.5 − 1.9) nor by any of the broken power laws restored from the previous absorption systems. Besides, the element abundances compliant with the Si iv/C iv ratio require [Si/C] > 0.6 at [C] < − 2.0. However, at such a low [C], the overabundance of Si to C is well constrained by [Si/C] ≲ 0.3 (Erni et al. 2006; Cooke et al. 2011). The search for direction (in five-factor space) toward SEDs ensuring both the measured ionic ratios and [Si/C] ≲ 0.3 was performed with the same initial guess as for the z = 1.9410 system (Fig. 5) and with the response function defined as a [Si/C] value (first iteration) and a Si iv/Si ii ratio (second iteration). The resulting range is shown by the shadowed area in Fig. 12; the upper envelope gives [Si/C] ~ 0.3 and the lower one is determined from the condition [Si/C] ~ 0. The physical parameters obtained with SEDs from the shadowed area are listed in Table 2 and the synthetic spectra are shown by red curves in Fig. 13.
 |
Fig. 11 Absorption lines observed in the z = 1.8873 system. The synthetic profiles (red) are calculated with the SEDs shown in Fig. 12. |
The restored SEDs differ considerably from those derived from the previous absorption systems as they are much softer and, most striking, have a sharp break shifted to lower energies. Since this shift is a decisive argument in the further interpretation of SEDs, it is important to ascertain that it is not a computational artefact. The relative Si abundance is calculated as [Si/C] =log (Si iv/C iv)+ log (ΥC IV/ΥSi IV) −log (Si/C)⊙, i.e., to ensure [Si/C] ~ 0.3 the ionizing continuum should provide at U determined by Si iii/Si iv ~2 at least two times lower ratio log (ΥC IV/ΥSi IV) as compared to the initially tried SEDs. It is clear that to increase the fraction of Si iv we have to simultaneously push the ionization of Si iii (i.e., increase the number of photons with E > 2.46 Ryd, the ionization potential of Si iii) and suppress the ionization of Si iv (decrease the number of photons with E > 3.32 Ryd, the ionization potential of Si iv). At the same time, the ionization of C iii (the ionization potential 3.52 Ryd) should also be suppressed to decrease the fraction of C iv. Figure 14 shows photoionization cross sections for C iii, C iv, Si iii, and Si iv as they are used in CLOUDY to calculate the ion fractions (Υi): C iii has the highest cross section with a strong gradient, whereas the cross sections of Si iii and Si iv are smaller and more mildly sloping. This explains why the fractions of C iii and C iv are extremely sensitive to the distribution of energy in the range 3.5–4.0 Ryd, whereas the fractions of Si iii and Si iv demonstrate a significantly weaker dependence. As a result of such behavior, the ratio ΥC IV/ΥSi IV can be lowered by two times only if the ionizing energy is strongly suppressed starting at the ionization threshold of C iii, i.e., at E ~ 3.5 Ryd.
In this regard we note that the modeling of metagalactic ionizing continua produced by the quasar radiation transferred through the IGM predicts at redshifts z < 2 that the He ii breaks also shifted to lower energies (to the same 3.5 Ryd) due to the Hubble expansion (Haard & Madau 1996; Fardal et al. 1998). However, these breaks occur smeared out, and the corresponding SEDs cannot ensure ΥC IV/ΥSi IV low enough to obtain [Si/C] ~ 0.3 for the measured Si iv and C iv column densities. For example, the ionizing continuum of Haard & Madau (1996) shown in Fig. 12 gives [Si/C] ~ 0.55.
The absorber at z = 1.7193 is optically thin in the H i Lyman continuum but opaque in He ii. Due to the softness of the ionizing continuum, the estimated N(He ii) ranges from 2.5 × 1018 cm-2 (upper envelope) to 6.0 × 1018 cm-2 (lower envelope). This means that the incident radiation is attenuated within the absorber and is probably slightly harder at E > 4 Ryd than the one restored from the absorption lines. However, local processes in the absorber itself do not affect the energy range below 4 Ryd and thus cannot be responsible for the intensity suppression at 3.5 Ryd.
4.5. Absorption system at z = 1.1923
Moving from the z = 1.7193 system down the redshift scale, the next system with metal lines is found only at z = 1.1923, i.e., it is detached by ~ 900 Mpc (or ~ 0.3c in the velocity space). Some lines from this system were used to probe the wavelength calibration of the HS 1103+6416 spectrum and are shown in Fig. 2. The presence of several strong Lyman series lines (H iλλ1025,972 Å) and a very shallow Lyman limit allow us to estimate the hydrogen content as N(H i)~ 5 × 1015 cm-2. Except for the C iv doublet, all other expected metal lines, C iiiλ977 Å, O iiiλλ832,702 Å, O ivλ787 Å, Si iiiλ1206 Å, and Si ivλ1393 Å, fall in the low-resolution part of the spectrum. Their column densities can be estimated using the radial velocity structure found from the analysis of the C iv lines (see Sect. 3) and, hence, they are not very accurate. Besides, at FWHM ~ 200 km s-1, it is always possible that some intervening absorption lines also contributed to the observed profile. However, with N(C iv)= 2.2 × 1014 cm-2, we can expect the same order of magnitude column densities for C iii, O iii, and O iv, so that their possible blending with a weak Ly-α with N(H i)~ 1013 cm-2 (stronger hydrogen lines are excluded by continuum windows at the corresponding positions of Ly-β) will not significantly affect the measured column densities. Unlikely C iii, O iii, and O iv, lines of silicon ions with expected column densities of ~ 1013 cm-2 fall in the absorption troughs and their column densities cannot be even roughly estimated. The measured column densities of N(O iii)~ (4.0 − 5.0) × 1014 cm-2, N(C iii)~ (1.5 − 2.0) × 1014 cm-2, and N(O iv)~ (1.0 − 1.5) × 1015 cm-2 are sufficient to rule out both the power laws and soft SEDs of a type recovered at z = 1.7193 (i.e., with a sharp break shifted to E ≤ 3.5 Ryd) as an ionizing continuum for the present system. At U determined by the ratio N(C iv)/N(C iii)≥ 1.0, all these SEDs produce a small fraction of O iii and, as a result, a large ratio N(O iv)/N(O iii)≥ 10, which significantly exceeds the observed N(O iv)/N(O iii)~ 3. The ionizing spectra with a break at 4 Ryd similar to those shown in Figs. 5, 10, and 12 seem to be more appropriate because they provide N(O iv)/N(O iii)~ 3 − 5.
5. Discussion
Using lines of diverse metal ions, we reconstruct the SED of the environmental radiation field that ionizes absorption systems at z = 1.9410,1.8916,1.8873,1.7193, and 1.1923. The SED differs significantly from system to system, so that we can conclude that the ionization field fluctuates at the redshift scale of at least Δz ~ 0.004. This is comparable with Δz ≲ 0.01 revealed from joint observations of He ii and H i Ly-α forest at 2.0 < z < 2.9 (Shull et al. 2004, 2010). Figure 16 shows η ≡ N(He ii)/N(H i), the parameter used in the forest studies to probe fluctuations of the ionizing background with z. The curves η(U) are calculated with CLOUDY for a range of SEDs restored for a given system and for the gas metallicity [Z] = − 1.0 (arbitrarily chosen since η-values are very weakly affected by metallicity). It is seen that while moving from z = 1.9410 to z = 1.8916, η decreases from ~ 40 to ~ 10 (for lgU > − 2 relevant for the majority of the forest absorbers) and then increases at z = 1.8874 to ~ 30 − 50. In the vicinity of z = 1.7193, the η-values reach several hundreds due to a sharp decrease in the number of photons with energies E ≳ 4 Ryd in the ionizing continuum and, as a consequence, the impossibility to ionize He ii. At z = 1.1923, where the preferable SEDs return to the range detected between z = 1.9410 and 1.8873, η will be again about a few tens. The He ii/H i forest studies have shown a slow evolution of η toward smaller values at lower redshift, with the mean 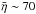 at z = 2.9 and
at z = 2.9 and 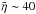 at z = 2.0 (Zheng et al. 2004; Fechner et al. 2006). Our values are in line with these results.
at z = 2.0 (Zheng et al. 2004; Fechner et al. 2006). Our values are in line with these results.
 |
Fig. 12 SEDs restored for the z = 1.8873 system: yellow cone plots simple power laws, Jν ∝ ν− α, with α = 1.6–1.8; red and blue lines show two examples of broken power laws. The black dotted line indicates the SED restored for the previous z = 1.8916 system; this SED does not comply with the lines observed at z = 1.8873. |
Further on, the restored continuum shapes allow us to identify the main sources contributing to the ionizing background. At z = 1.9410,1.8916,1.8873, and 1.1923, these are definitely the AGNs. In all systems, simple power-law SEDs are only marginally consistent with the observed lines, whereas a more appropriate continuum shape corresponds to a broken power law with an intensity break of an order of magnitude at 4 Ryd. Such an SED is usually attributed to absorption in the He ii Lyman continuum occurring when quasar radiation, which is assumed to have a simple power-law SED, passes through the IGM (Haard & Madau 1996, 2012; Giroux & Shull 1997). However, studying the so-called associated systems (absorbers located in the physical vicinity of quasars), we found that they were ionized by a continuum that already had a pronounced break at 4 Ryd (Levshakov et al. 2008), i.e., He ii absorption occurred not outside, but within the radiation-generating structures. A generally accepted mechanism of the majority of the quasar continuum is photon emission by geometrically thin but optically thick accretion disc. That optically thick structures are indeed involved is verified observationally by detecting the hydrogen Balmer edge in the spectra of several quasars (Kishimoto et al. 2003, 2004; Hu & Zhang 2012). It is important that the corresponding Lyman break at 1 Ryd (3.3 × 1015 Hz) is not observed, and this is just what the non-LTE models of accretion discs predict (Hubeny et al. 2000; Blaes et al. 2001). The break is reduced and smeared out both by relativistic effects (Doppler shifts) and by summing over H i emission and absorption edges from different parts of the disc. If the disc is optically thick in H i, it will be opaque in He ii as well, and it is clear that a real depth of the He ii Lyman break at 4 Ryd in the emerging disc spectrum will be affected by the same processes as the H i Lyman break, primarily by a combination of the He ii emission and absorption. However, at energies close to and above 4 Ryd, the thermal accretion disc already loses its validity as a model for quasar continuum. At high frequencies (soft and hard X-ray bands) radiation is generated by other, still poorly understood, mechanisms; this means that calculations of the He ii emission/absorption balance become highly uncertain. Depending on the parameters, the resulting SEDs demonstrate at E ≳ 4 Ryd a variety of shapes, from a sharp flux decrease to an almost complete reduction of a flux discontinuity (Hubeny et al. 2000, 2001). As already mentioned in Sect. 1, quasar spectra between ~ 3 Ryd and the soft X-ray band (0.2 keV) are completely absorbed, so that the observational data cannot be used to distinguish between the model predictions. Thereby it seems quite plausible that the integrated spectrum of all radiation-generating quasar structures retains a flux break at 4 Ryd. This break can be further enhanced if the central engine is accompanied by a so-called warm absorber, a circumnuclear gas responsible for broad absorption features in the X-ray spectra and detected in ~ 50% of AGNs (Piconcelli et al. 2005). With a total hydrogen column density N(H)~ 1022−1023 cm-2, the ionization parameter U ~ few units, and the standard helium abundance Z = 0.083, the predicted (by CLOUDY) column density of He ii is ~1017 − 1018 cm-2. Hence, it noticeably softens the radiation at E > 4 Ryd. Thus, broken power-law SEDs restored for the z = 1.9410,1.8916,1.8873, and 1.1923 systems most probably represent intrinsic AGN spectra as only weakly attenuated, if at all, by the IGM.
 |
Fig. 13 Absorption lines observed in the z = 1.7193 system. The synthetic profiles (red) are calculated with SEDs from the shadowed area in Fig. 15. |
In this regard the differences between SEDs at z = 1.9410 and z = 1.8916 (cf. SEDs in Figs. 5 and 10) can be a consequence of different spectral shapes of the ionizing radiation from the contributing sources. It is well established that both the AGN space density and their cumulative luminosity peak around z ~ 2 (Assef et al. 2011, and references therein). To make some quantitative estimates, we employ the probability that a line of sight intersects a “sphere of influence” of an AGN in redshift interval Δz at redshift z (Peebles 1993): 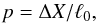 (1)which is the ratio of the physical path length
(1)which is the ratio of the physical path length 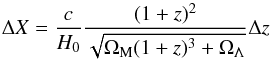 (2)and the mean free path between the spheres
(2)and the mean free path between the spheres 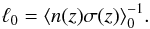 (3)Here n(z) and σ(z) are, respectively, the comoving number density of AGNs and cross section of the sphere of influence, c is the speed of light, H0 is the Hubble constant, and ΩM, ΩΛ are dimensionless density parameters (we adopt the flat ΛCDM cosmology with H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7).
(3)Here n(z) and σ(z) are, respectively, the comoving number density of AGNs and cross section of the sphere of influence, c is the speed of light, H0 is the Hubble constant, and ΩM, ΩΛ are dimensionless density parameters (we adopt the flat ΛCDM cosmology with H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7).
The cross section of the sphere of influence is defined by a radius 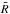 at which the AGN radiation flux at 1 Ryd,
at which the AGN radiation flux at 1 Ryd, 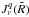 , becomes equal to the mean background metagalactic flux,
, becomes equal to the mean background metagalactic flux, 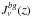 . At redshift z = 1.9, the value of
. At redshift z = 1.9, the value of 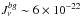 erg cm-2 s-1 Hz-1 sr-1 at 1 Ryd was measured in Tytler et al. (2004), Bolton et al. (2005), and Dall’Aglio et al. (2008). Taking the AGN comoving space density at this redshift from Wolf et al. (2003) and Croom et al. (2009) and choosing Δz = 0.05, we calculate the intersection probability p depending on the source absolute magnitude MB (blue curve in Fig. 17)2. The red curve in Fig. 17 indicates the comoving AGN emissivity, ε, at 1 Ryd. It is seen that bright sources with MB < − 24 (quasars) contribute the majority (~80%) of all ionizing photons, and at the same time their spheres of influence are the most probable candidates for intersection. Since the space number density of such quasars is low (at z ~ 2, n < 5 objects per cube of 100 Mpc side), only a small number of them contribute to the ionizing background at every given point along the line of sight. In addition, the diversity of their intrinsic SEDs just causes the variations in the spectral shape of the resulting ionizing radiation.
erg cm-2 s-1 Hz-1 sr-1 at 1 Ryd was measured in Tytler et al. (2004), Bolton et al. (2005), and Dall’Aglio et al. (2008). Taking the AGN comoving space density at this redshift from Wolf et al. (2003) and Croom et al. (2009) and choosing Δz = 0.05, we calculate the intersection probability p depending on the source absolute magnitude MB (blue curve in Fig. 17)2. The red curve in Fig. 17 indicates the comoving AGN emissivity, ε, at 1 Ryd. It is seen that bright sources with MB < − 24 (quasars) contribute the majority (~80%) of all ionizing photons, and at the same time their spheres of influence are the most probable candidates for intersection. Since the space number density of such quasars is low (at z ~ 2, n < 5 objects per cube of 100 Mpc side), only a small number of them contribute to the ionizing background at every given point along the line of sight. In addition, the diversity of their intrinsic SEDs just causes the variations in the spectral shape of the resulting ionizing radiation.
The mean free path ℓ0 for all objects with MB < −21 is ℓ0 = 1.5 Gpc (comoving). Thus, the probability of intersecting a sphere of influence of at least one quasar in the redshift interval Δz ~ 0.05 at z ~ 1.9 (ΔX = 0.6 Gpc) is p ≃ 0.4 (it may be even higher if obscured quasars are taken into account). This probability is sufficient to suggest that at least in one of the three close systems (z = 1.9410,1.8916,1.8873) the ionizing radiation is dominated by a local source, i.e., by a quasar located transverse to the line of sight.
The estimate of p can be directly tested against observations. Searching for “quasars near quasars”, i.e., for foreground quasars located within 30′ from the line of sight to a background quasar, Worseck et al. (2008) detected 7 QSOs per 18 lines of sight in the range 1.89 < z < 1.94, among them one pair of QSOs separated by Δz < 0.05. We note here that in general such pairs are not extremely rare since the survey by Worseck et al. contains many other examples at different redshifts. Thus, it is not unlikely that local sources affect the mean metagalactic SED even in more than one system between z = 1.94 and 1.89.
 |
Fig. 14 Photoionization cross sections for the Si iii, Si iv, C iii, and C iv ions used in CLOUDY. |
 |
Fig. 15 Range of SEDs of the ionizing UV radiation (shadowed area) reconstructed from absorption lines at zabs = 1.7193. The initial guess SED is plotted by the dotted line. For comparison, the model metagalactic SED of Haardt & Madau (1996) is shown by red. |
 |
Fig. 16 Parameter η = He ii/H i as a function of the ionization parameter U calculated for the SEDs restored at z = 1.9410 (dark grey), 1.8916 (yellow), 1.8874 (light grey), and 1.7193 (blue). |
 |
Fig. 17 Blue curve: the probability for a given line of sight to intersect the sphere of influence of an AGN with an absolute magnitude MB; red curve: comoving AGN emissivity at 1 Ryd. Both curves are calculated for z = 1.9. |
 |
Fig. 18 Simultaneous UV and soft X-ray Swift observations by Grupe et al. (2010) of two AGN sources Mkn 335 and Mkn 876 (blue and red stars, respectively). Mkn 335 is a pure AGN without significant star-formation activity, whereas Mkn 876 demonstrates both strong AGN activity and intense circumnuclear star formation. The original data by Grupe et al. are (i) corrected for Galactic absorption using the X-ray cross section from Morrison & McCammon (1983) and N(H) from Table 1 in Grupe et al.; (ii) transferred from coordinates log (νLν) vs. log ν to log (Lν) vs. log E; (iii) normalized by Lν at 1 Ryd, which is found by linear extrapolation of the UV data to 1 Ryd with spectral indices reported for Mkn 335 and Mkn 876 in Shull et al. (2012). The solid lines in the X-ray range are the power laws with indices given in Table 4 in Grupe et al.The dotted lines show the SEDs restored for the z = 1.9410 (blue) and 1.7193 (red) systems. |
The spectral shape of the ionizing radiation can also be altered due to absorption in the intervening systems, primarily by strong absorbers with N(H i)> 1017 cm-2. The common assumption is that such systems are directly related to galaxies and originate in galactic halos at different impact parameters. Then the mean free path between the halos is given by (e.g., Burbidge et al. 1977): ![\begin{equation} \ell_0 = [\sigma_\ast \phi_\ast \Gamma(1+s+2\beta)]^{-1} , \label{Eq8} \end{equation}](/articles/aa/full_html/2013/04/aa20818-12/aa20818-12-eq312.png) (4)where Γ(x) is the gamma function. For the parameters of Eq. (4) the following values are taken:
(4)where Γ(x) is the gamma function. For the parameters of Eq. (4) the following values are taken: 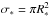 with R∗ ≈ 100 kpc, β ≈ 0.35 (e.g., Matejek & Simcoe 2012), φ∗ ≃ 2 × 10-3 Mpc-3 (corresponding to
with R∗ ≈ 100 kpc, β ≈ 0.35 (e.g., Matejek & Simcoe 2012), φ∗ ≃ 2 × 10-3 Mpc-3 (corresponding to 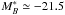 at z ~ 2) and s ≃ −1.25 (Poli et al. 2003; Gabasch et al. 2004). This provides ℓ0 ≃ 8 Gpc. Given ℓ0 = 1.5 Gpc for AGNs, the probability of intersecting a galactic halo at an impact parameter ≲100 kpc is several times lower as compared to the sphere of influence of an AGN.
at z ~ 2) and s ≃ −1.25 (Poli et al. 2003; Gabasch et al. 2004). This provides ℓ0 ≃ 8 Gpc. Given ℓ0 = 1.5 Gpc for AGNs, the probability of intersecting a galactic halo at an impact parameter ≲100 kpc is several times lower as compared to the sphere of influence of an AGN.
Thus, it is more likely that differences in the SEDs between the z = 1.9410 and 1.8916 systems are indeed due to SEDs in QSOs but not due to the effects of radiative transfer in the IGM. We note that this is an additional argument supporting the intrinsic nature of the intensity break at 4 Ryd in the outcoming AGN spectrum.
Of course, the above consideration does not exclude that in some cases the shape of the ionizing background radiation can be attenuated by the intervening systems. For example, if we assume that the systems at z = 1.8916 and z = 1.8876 are illuminated by the same transverse quasar, then the softer SED in the latter case may indicate the presence of a strong absorber with N(H i)> 5 × 1016 cm-2 between this system and the quasar.
As for the SED at z = 1.7193, the footprint of a local source is quite certain: a deep intensity drop at E > 3.5 Ryd points to a substantial input from a soft (galactic, i.e., stellar) component (see, e.g., Fig. 1 in Giroux & Shull 1997). In a quasar-dominated field of metagalactic ionizing radiation, which is relatively hard at E > 4 Ryd, such spectral shapes can be sensed only in the vicinity of the source itself. Possible emitters of radiation with this type of SED are the so-called (ultra) luminous infrared galaxies, (U)LIRGs, which in many cases show spectra powered by a mixture of AGN and starburst activity (Sanders et al. 1988). The (U)LIRGs that host AGNs also reveal large-scale gas outflows (Alexander et al. 2010; Harrison et al. 2012). At low z (~0.05), it is even possible to resolve multiple star clusters with a young stellar population (Mazzarella et al. 2012) and superbubbles in the blowout phase, which are believed to form as a result of giant supernova explosions (Lipari et al. 2005, 2009). In addition, the z = 1.7193 absorber could be an outflow from a transverse (U)LIRG because the overabundance of α-elements and general low metallicity of the gas are typical for the enrichment by massive star(s) exploded as core-collapse supernova (SN II).
The difference in the high-frequency range of the SED between pure AGN and AGN+starburst sources is illustrated in Fig. 18, which shows observations by Grupe et al. (2010) that were taken with Swift simultaneously in the optical/UV and soft X-ray bands. Blue stars indicate data for Mkn 335, which is a classical AGN with no star-forming activity, and red stars show data for Mkn 876, a galaxy with both strong AGN activity and intense circumnuclear star formation (Shi et al. 2007; Sani et al. 2010). The latter SED is appreciably softer in the X-ray band. For comparison, SEDs restored for the z = 1.9410 and 1.7193 systems are also shown by dotted lines. It is seen that they fit well in the gap between the UV and X-ray points.
6. Summary
The spectrum of bright quasar HS 1103+6416 (zem = 2.19) available in the wavelength coverage from 1400 Å to 5700 Å contains between the redshifts z = 1.19 and 1.94 five successive absorption systems detached by the redshifts intervals Δz ~ 0.004−0.5. These systems are optically thin both in H i and in He ii and reveal multiple lines of different metal ions, the ionization potentials of which sample the EUV range (1 Ryd–0.2 keV) of the ionizing radiation with a fairly small step. Such properties make it possible to solve with sufficient accuracy the inverse problem of spectroscopy: namely, to estimate the physical parameters of the absorbing medium simultaneously with the reconstruction of the SED in the underlying ionizing continuum. We note that metal absorption systems in quasar spectra are the only means to probe observationally the SED of the ionizing radiation at redshifts z ≲ 2. The results obtained are as follow.
-
1.
The SED changes significantly from one system to another, i.e.,the intergalactic ionization field fluctuates at the scale of at least Δz ~ 0.004.This is consistent with Δz ≲ 0.01 estimated from He ii andH i Lyman-α forest measurements betweenredshifts 2 and 3.
-
2.
In all systems, pure power-law SEDs of the type Jν ∝ ν− α are not or only marginally consistent with the observed line profiles. A more preferable continuum shape is a broken power-law with the break at E 4 Ryd, which likely represents an intrinsic SED of the outcoming AGN radiation.
-
3.
The SEDs restored for the zabs = 1.1923, 1.8873, 1.8916, and 1.9410 systems point to AGNs/QSOs as the main source of the ionizing radiation. The SED variability is mostly caused by a small number of QSOs contributing at any given redshift to the ionizing background. At scales Δz ≳ 0.05 the influence of local sources (foreground quasars located transverse to the line of sight) becomes significant. This can be tested observationally by a search for QSOs close to the line of sight as done by Worseck et al. (2008).
-
4.
A remarkable type of SED is restored for the zabs = 1.7193 system. It demonstrates a sharp break shifted to E ~ 3.5 Ryd with a subsequent intensity decrease by ~1.5 dex, suggesting comparable inputs from both hard (AGNs/QSOs) and soft (young stars) radiation components. In a quasar-dominated ionizing radiation field, such a soft continuum can survive only in the vicinity of the radiation source itself. For the given system this source is probably one of the (U)LIRGs, many of which reveal both strong AGN activity and intense star formation in the circumnuclear regions.
The photoionization cross section for the He i continuum is taken from Samson et al. (1994).
Acknowledgments
I.I.A. and S.A.L. are grateful for the kind hospitality of Hamburger Sternwarte, where this work has been done. We also thank an anonymous referee for the useful comments received. The work of I.I.A. and S.A.L. is supported by DFG Sonderforschungsbereich SFB 676 Teilprojekt C4 and, in part, by the State Program “Leading Scientific Schools of Russian Federation” (grant NSh 4035.2012.2).
References
- Agafonova, I. I., Centurión, M., Levshakov, S. A., & Molaro, P. 2005, A&A, 441, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agafonova, I. I., Molaro, P., Levshakov, S. A., & Hou, J. L. 2011, A&A, 529, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akerman, C. J., Carigi, L., Nissen, P. E., Pettini, M., & Asplund, M. 2004, A&A, 414, 93 [Google Scholar]
- Alexander, D. M., Swinbank, A. M., Smail, I., McDermid, R., & Nesvalda, N. P. H. 2010, MNRAS, 402, 2211 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Assef, R. J., Kochanek, C. S., Ashby, M. L. N., et al. 2011, ApJ, 728, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., & Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O., Hubeny, I., Agol, E., & Krolik, J. H. 2001, ApJ, 563, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F. 2007, ApJ, 656, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., Haehnelt, M. G., Viel, M., & Springel, V. 2005, MNRAS, 357, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Burbidge, G., O’Dell, S. L., Roberts, D. H., & Smith, H. E. 1977, ApJ, 218, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R., Pettini, M., Steidel, C. C., Rudie, G. C., & Nissen, P. E. 2011, MNRAS, 417, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Richards, G. T., Shanks, T., et al. 2009, MNRAS, 399, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Aglio, A., Wisotzki, L., & Worseck, G. 2008, A&A, 491, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erni, P., Richter, P., Ledoux, C., & Petitjean, P. 2006, A&A, 451, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esteban, C., Bresoli, F., Peimbert, M., et al. 2009, ApJ, 700, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Fardal, M. A., Giroux, M. L., & Shull, J. M. 1998, AJ, 115, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Fechner, C. 2011, A&A, 532, 62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fechner, C., & Reimers, D. 2007, A&A, 461, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fechner, C., Reimers, D., Songaila, A., et al. 2006, A&A, 455, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Gabasch, A., Bender, R., Seitz, S., et al. 2004, A&A, 421, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Rojas, J., Esteban, C., Peimbert, M., et al. 2004, ApJS, 153, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Dufour, R. J., Peimbert, M., et al. 1995, ApJ, 449, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Giroux, M. L., & Shull, J. M. 1997, AJ, 113, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., Sauval, A. J., & Scott, P. 2010, Ap&SS, 328, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Griest, K., Whitmore, J. B., Wolfe, A. M., et al. 2010, ApJ, 708, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, ApJS, 187, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Haard, F., & Madau, P. 1996, ApJ, 461, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Haard, F., & Madau, P. 2012, ApJ, 746, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Swinbank, A. M., et al. 2012, MNRAS, 426, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, R., & Zhang, S.-N. 2012, MNRAS, 426, 2847 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Agol, E., Blaes, O., & Krolik, J. H. 2000, ApJ, 533, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Blaes, O., Krolik, J. H., & Agol, E. 2001, ApJ, 559, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsen, P., Jansen, R. A., Wagner, S., & Reimers, D. 2003, A&A, 397, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kingsburgh, R. L., & Barlow, M. J. 1999, MNRAS, 271, 257 [Google Scholar]
- Kishimoto, M., Antonucci, R., & Blaes, O. 2003, MNRAS, 345, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Antonucci, R., Boisson, C., & Blaes, O. 2004, MNRAS, 354, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, S., Reimers, D., Tytler, D., et al. 1999, A&A, 342, 395 [NASA ADS] [Google Scholar]
- Levshakov, S. A., Agafonova, I. I., & Kegel, W. H. 2000, A&A, 360, 833 [NASA ADS] [Google Scholar]
- Levshakov, S. A., Agafonova, I. I., Reimers, D., et al. 2008, A&A, 483, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Agafonova, I. I., Molaro, P., Reimers, D., & Hou, J. 2009, A&A, 507, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lipari, S., Terlevich, R., Zheng, W., et al. 2005, MNRAS, 360, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Lipari, S., Sanchez, S. F., Bergmann, M., et al. 2009, MNRAS, 392, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Matejek, M. S., & Simcoe, R. A. 2012, ApJ, 761, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, D. C. 2003, ApJS, 149, 205 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peebles, P. J. E. 1993, Principles of Physical Cosmology (Princeton: Princeton University Press) [Google Scholar]
- Piconcelli, E., Jimenez-Bailon, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poli, F., Giallongo, E., Fontana, A., et al. 2003, ApJ, 593, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D., Rodriguez-Pascual, P., Hagen, H.-J., & Wisotzki, L. 1995, A&A, 293, L21 [NASA ADS] [Google Scholar]
- Reimers, D., Kohler, S., Wisotzki, L., et al. 1997, A&A, 327, 890 [NASA ADS] [Google Scholar]
- Samson, J. A. R., He, Z. X., Yin, L., & Haddad, G. N. 1994, J. Phys. B, 27, 887 [CrossRef] [Google Scholar]
- Sanders, D. B., Soifer, B. T., Elias, J. H., Neugebauer, G., & Matthews, K. 1988, ApJ, 328, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Sani, E., Lutz, D., Risaliti, G., et al. 2010, MNRAS, 403, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J. E., Kriss, G. A., Brotherton, M., et al. 2004, ApJ, 615, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Ogle, P., Rieke, G., et al. 2007, ApJ, 669, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., Tumlison, J., Giroux, M. L., Kriss, G. A., & Reimers, D. 2004, ApJ, 600, 768 [Google Scholar]
- Shull, J. M., France, K., Danforth, C., Smith, B., & Tumlison, J. 2010, ApJ, 722, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., Stevans, M., & Danforth, C. W. 2012, ApJ, 752, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Tytler, D., Kirkman, D., O’Meara, J. M., et al. 2004, ApJ, 617, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Barthel, P. D., & Tytler, D. 1994, A&AS, 108, 287 [NASA ADS] [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, Proc. SPIE, 2198, 362 [Google Scholar]
- Wolf, C., Wisotzki, L., Borch, A., et al. 2003, A&A, 408, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worseck, G., Fechner, C., Wisotzki, L., & Dall’Aglio, A. 2007, A&A, 473, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zheng, W., Kriss, G. A., Deharveng, J.-M., et al. 2004, ApJ, 605, 631 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Calculated column densities (in cm-2) for atoms and ions in systems used to reconstruct the SED of the underlying ionizing continuum.
All Figures
 |
Fig. 1 Continuum shapes used to approximate the SED in the EUV (1 Ryd–0.2 keV) range: a simple power law (blue dotted line), an AGN continuum by Mathews & Ferland (1987) (blue line), an ionizing spectrum of the metagalactic radiation field at redshift z ~ 2 by Haardt & Madau (1996) (black line), and its approximation by a broken power law (red line). All the SEDs are normalized so that Jν(hν = 1 Ryd) = 1. The positions of ionization thresholds of different ions are indicated by tick marks. |
| In the text | |
 |
Fig. 2 Calibration-induced shifts of the observed profiles illustrated by spectral lines from different absorption systems. The velocity structure is estimated on the basis of lines from the high-resolution (Keck/HIRES) part of the HS 1103+6416 spectrum and then applied to calculate the profiles from low-resolution (HST) parts. The synthetic profiles are shown by red, the vertical ticks mark positions of sub-components. ΔV indicates the velocity shift applied to the observed profile to align it with a reference line from the Keck spectrum. |
| In the text | |
 |
Fig. 3 High-resolution hydrogen and metal absorption lines associated with the zabs = 1.9410 system toward HS 1103+6416 (black curves). The synthetic profiles calculated with the UV SEDs shown by the shadowed area in Fig. 5 are plotted by red curves. The zero radial velocity is fixed at z = 1.9410. The inserted figures in Si iv panels display the synthetic spectra (blue curves) calculated with the first-guess SED (red dotted line in Fig. 5). |
| In the text | |
 |
Fig. 4 Low-resolution lines (HST) from the zabs = 1.9410 system. The vertical ticks in the H i panels indicate the positions of individual Voigt components. The profiles of metal ions are calculated using the velocity-density distributions restored on the basis of high-resolution lines shown in Fig. 3. The red synthetic profiles in the O iii and O iv panels are calculated for two oxygen abundances [O/C] = 0.2 and 0.3 (see text for details). |
| In the text | |
 |
Fig. 5 SEDs complying with the line profiles from the zabs = 1.9410 system: yellow cone plots simple power laws, Jν ∝ ν− α, with α = 1.5–1.7; grey shadowed area marks broken power laws with a break at 4 Ryd. The black dotted line shows an initial shape used in the SED adjustment procedure. |
| In the text | |
 |
Fig. 6 Observed flux of HS 1103+6416 obtained with the FOS and GHRS onboard the HST. The arrows mark the H i Lyman limits for the z = 1.8916 and z = 1.7193 systems. |
| In the text | |
 |
Fig. 7 He i Lyman limit at z = 1.8916 and the identified He i Lyman series lines. The H i Lyman limit at z = 0.7129 and the O iiiλ507.388 Å line at z = 1.8916 are also indicated. The latter is blended with He i Ly-θ (λ507.718 Å) and Ly-ι (λ507.058 Å) lines. |
| In the text | |
 |
Fig. 8 High-resolution lines observed in the z = 1.8916 system. Brackets indicate the sub-systems A, B, C, and D with strong lines, vertical ticks in the C iv panels point to superimposed sub-systems with weak absorption lines. The synthetic profiles for metal ions (red) in the sub-system A are calculated with broken power-law SEDs from the grey shadowed area in Fig. 10. The black line in the O i panel is a restored profile from the forest absorption shown in the insert. The black and blue curves in the insert are the original and deconvolved profiles, respectively. |
| In the text | |
 |
Fig. 9 Low-resolution H i and He i lines from the z = 1.8916 system. Tick marks indicate the positions of individual sub-components in the H i profile deconvolution. The synthetic profiles are shown by red and the observed ones by black curves. |
| In the text | |
 |
Fig. 10 SEDs complying with the lines observed in the z = 1.8916 system: yellow cone plots simple power laws, Jν ∝ ν− α, with α = 0.9–1.2; grey shadowed area indicates broken power laws with a break at 4 Ryd. The black dotted line shows an initial shape used in the SED adjustment procedure; here it is chosen as an upper bound of the broken power-law SEDs restored for the z = 1.9410 system (grey shadowed area in Fig. 5). |
| In the text | |
 |
Fig. 11 Absorption lines observed in the z = 1.8873 system. The synthetic profiles (red) are calculated with the SEDs shown in Fig. 12. |
| In the text | |
 |
Fig. 12 SEDs restored for the z = 1.8873 system: yellow cone plots simple power laws, Jν ∝ ν− α, with α = 1.6–1.8; red and blue lines show two examples of broken power laws. The black dotted line indicates the SED restored for the previous z = 1.8916 system; this SED does not comply with the lines observed at z = 1.8873. |
| In the text | |
 |
Fig. 13 Absorption lines observed in the z = 1.7193 system. The synthetic profiles (red) are calculated with SEDs from the shadowed area in Fig. 15. |
| In the text | |
 |
Fig. 14 Photoionization cross sections for the Si iii, Si iv, C iii, and C iv ions used in CLOUDY. |
| In the text | |
 |
Fig. 15 Range of SEDs of the ionizing UV radiation (shadowed area) reconstructed from absorption lines at zabs = 1.7193. The initial guess SED is plotted by the dotted line. For comparison, the model metagalactic SED of Haardt & Madau (1996) is shown by red. |
| In the text | |
 |
Fig. 16 Parameter η = He ii/H i as a function of the ionization parameter U calculated for the SEDs restored at z = 1.9410 (dark grey), 1.8916 (yellow), 1.8874 (light grey), and 1.7193 (blue). |
| In the text | |
 |
Fig. 17 Blue curve: the probability for a given line of sight to intersect the sphere of influence of an AGN with an absolute magnitude MB; red curve: comoving AGN emissivity at 1 Ryd. Both curves are calculated for z = 1.9. |
| In the text | |
 |
Fig. 18 Simultaneous UV and soft X-ray Swift observations by Grupe et al. (2010) of two AGN sources Mkn 335 and Mkn 876 (blue and red stars, respectively). Mkn 335 is a pure AGN without significant star-formation activity, whereas Mkn 876 demonstrates both strong AGN activity and intense circumnuclear star formation. The original data by Grupe et al. are (i) corrected for Galactic absorption using the X-ray cross section from Morrison & McCammon (1983) and N(H) from Table 1 in Grupe et al.; (ii) transferred from coordinates log (νLν) vs. log ν to log (Lν) vs. log E; (iii) normalized by Lν at 1 Ryd, which is found by linear extrapolation of the UV data to 1 Ryd with spectral indices reported for Mkn 335 and Mkn 876 in Shull et al. (2012). The solid lines in the X-ray range are the power laws with indices given in Table 4 in Grupe et al.The dotted lines show the SEDs restored for the z = 1.9410 (blue) and 1.7193 (red) systems. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


