| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220227 | |
| Published online | 07 February 2013 | |
Doppler imaging of stellar surface structure
XXIV. The lithium-rich single K-giants DP Canum Venaticorum and DI Piscium⋆,⋆⋆,⋆⋆⋆
1 Konkoly Observatory of the Hungarian Academy of Sciences, Konkoly Thege út 15–17, 1121, Budapest, Hungary
e-mail: kovari@konkoly.hu
2 Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 København Ø, Denmark
3 Centre for Star and Planet Formation, Natural History Museum of Denmark, University of Copenhagen, Øster Voldgade 5–7, 1350 København Ø, Denmark
4 Leibniz Institute for Astrophysics (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
5 Institute of Astronomy of the Russian Academy of Sciences, Pyatnitskaya 48, 119017 Moscow, Russia
Received: 14 August 2012
Accepted: 23 December 2012
Aims. We present the first Doppler imaging study of the two rapidly rotating, single K-giants DP CVn and DI Psc in order to study the surface spot configuration and to pinpoint their stellar evolutionary status.
Methods. Optical spectroscopy and photometry were used to determine the fundamental astrophysical properties. Doppler imaging was applied to recover the surface temperature distribution for both stars, while photometric light-curve inversions were carried out for studying the long-term changes of the surface activity of DP CVn. Surface differential rotation of DP CVn was estimated from cross-correlating the available subsequent Doppler reconstructions separated by roughly one rotation period.
Results. Both stars appear to have higher than normal lithium abundance, LTE log n of 2.28 (DP CVn) and 2.20 (DI Psc), and are supposed to be located at the end of the first Li dredge-up on the RGB. Photometric observations reveal rotational modulation with a period of 14.010 d (DP CVn) and 18.066 d (DI Psc). Doppler reconstructions from the available mapping lines well agree in the revealed spot patterns, recovering rather low latitude spots for both stars with temperature contrasts of ΔT ≈ 600−800 K below the unspotted photospheric background. Spots at higher latitudes are also found but either with less contrast (DP CVn) or with smaller extent (DI Psc). A preliminary antisolar-type differential rotation with α = −0.035 is found for DP CVn from cross-correlating the subsequent Doppler images. Long-term photometric analysis supports the existence of active longitudes, as well as the differential rotation.
Key words: stars: activity / stars: imaging / stars: late-type / starspots / stars: individual: DP CVn / stars: individual: DI Psc
Based on observations obtained at the Kitt Peak National Observatory, USA, and at the Canada-France-Hawaii Telescope, USA.
Tables 1 and 2 are only available in electronic form at http://www.aanda.org
Photometric data summarized in Table 2 are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A2
© ESO, 2013
1. Introduction
The surface lithium abundance is a crucial diagnostic mark for studying stellar structure and evolution. The 7Li isotope, which represents the vast majority of the solar Li, is destroyed through proton capture at the temperatures of ~3 MK (Lugaro & Chieffi 2011). This means that the stellar surface layers are progressively depleted of lithium through material transportation to the deeper, hotter layers by convective motions, turbulent diffusion and meridional flows. Therefore, the surface lithium abundance can in principle be used as an age indicator but, in reality, the situation is more complex.
Comparison of Li lines observed from the quiet Sun and sunspot umbrae shows that the Li lines are enhanced in sunspots (e.g., Grevesse 1968; Giampapa 1984). This is due to the lower temperature of the spots. Giampapa (1984) suggested that this effect could possibly also be seen in disk-integrated stellar spectra and that the strength of the lithium line in stars could be greatly affected by cool spots. On the other hand, the solar lithium abundance is lower in hot plage regions. This effect could compensate the effect of the apparent Li enhancement from cool spots, when looking at disk integrated spectra. Several studies of the relation of Li abundance with stellar activity were published. These studies had different results though, from a clear correlation (e.g., Jeffries et al. 1994; Fernández & Miranda 1998; Neuhäuser et al. 1998) to no relation at all, even in the presence of very strong starspot activity (e.g., Pallavacini et al. 1993; Mallik 1998; Berdyugina et al. 1998).
In a statistical analysis De Medeiros et al. (2000) tested the possible connection between rotation and Li abundance in single F, G and K-giants. Their result showed a link between the rotation-rate discontinuity at spectral type G0III and the Li abundance near the same spectral type. Giants cooler than G0III are generally very slow rotators (a mean of the vsini value of 2 km s-1) and generally also show low Li abundances, while the giants warmer than G0 are fast rotators and have higher Li abundances. Just recently, Strassmeier et al. (2012) found a trend of increased Li abundance with rotation period but with a dispersion of up to 3–4 orders of magnitude. In this study, stars in binaries appear to exhibit 0.25 dex less surface lithium than singles, as one would expect if the depletion mechanism is rotation dependent. On the other hand, there is a small group of single K-giants which show rapid rotation and also larger than expected Li abundances (e.g., Reddy & Lambert 2005; Drake et al. 2002; Fekel & Balachandran 1993, and references therein). Charbonnel & Balachandran (2000) concluded that relatively high Li abundance is not abnormal for a low-mass star on the red-giant branch (RGB). They identified two distinct evolutionary episodes on the RGB in which extra mixing of Li may cause an unusual high surface abundance. Both episodes are related to the close vicinity of the bottom of the convective envelope to the hydrogen-burning shell. Rotational mixing will likely play an important role in bringing Li-rich material into the convective mantle (cf. Lugaro & Chieffi 2011). Per definition, we call a red-giant star “Li-rich” once it has evolved through the first dredge-up and still has a logarithmic surface abundance greater than 1.5.
Attention to DP CVn (HD 109703) and DI Psc (HD 217352) was drawn in the Vienna-KPNO Doppler-imaging candidate survey (Strassmeier et al. 2000). According to this database, the stars are rapidly rotating single K-giants, having projected rotational velocities of ≈ 35 km s-1 (with 2–4 km s-1 estimated errors). Charbonnel & Balachandran (2000) pointed out that these two stars are new candidates for the small group of rapidly-rotating Li-rich giants that appear at or very near the RGB bump and already exhibit freshly synthesized lithium. Preliminary determinations of the Li abundances yielded log n(Li) of 2.82 and 2.64 for DP CVn and DI Psc, respectively (Strassmeier et al. 2000).
In this paper, we redetermine the absolute dimensions (see Sect. 3) and the lithium abundance of these two giant stars (Sect. 3.3). We show them to have indeed a constant radial velocity within our precision limits, thus are single stars (Sect. 2.1). In Sect. 4, we study the surface spot configuration and evolution by means of Doppler imaging and complement this in Sect. 5 with a long-term photometric spot analysis. Finally, Sect. 6 concludes on our results.
2. Observations
2.1. Spectroscopy and radial velocities
Most spectroscopic observations were obtained at Kitt Peak National Observatory (KPNO) with the 0.9-m coudé feed telescope between March 29 and May 9, 2000 (summarized in Table 1). The F3KB 3k-CCD was used together with grating A, the long collimator and a 280 μm slit. This configuration allows a resolving power of R ≈ 28 000 at a dispersion of 4.81 km s-1/pixel. The full wavelength coverage was 300 Å and the spectra were centered at 6490 Å. The exposure time was typically 4500 s for DP CVn and 1800 s for DI Psc, giving average signal-to-noise ratios (S/N) of 130:1 and 160:1, respectively.
Six high resolution spectra were obtained with the 3.6 m Canada-France-Hawaii telescope (CFHT) during May 18 and 19, 2000. The Gecko spectrograph was used with the 316 l/mm grating in 8th order and provided a resolution of R ≈ 120 000. The 4.4k × 2k 13.5 μm-pixel EEV1E CCD gives a ≈ 10 nm wide wavelength range centered at the Li-6708 line.
Data reductions were done using the NOAO/IRAF software package and followed our standard procedure for coudé spectra (see, e.g., Weber & Strassmeier 2001). Nightly observations of various radial-velocity standards were used to obtain the radial velocities for DP CVn and DI Psc (Table 1). For DP CVn we used mostly 16 Vir (K0.5III, vr = + 36.48 km s-1) as the standard except for the spectra at HJDs 2 451 632.65 and 2 451 633.77 when β Gem (K0III, vr = + 3.23 km s-1) was used and HJDs 2 451 663.75 and 2 451 670.84 when HD 145001 (G8III, vr = −10.33 km s-1) was used. For DI Psc we used mostly β Oph (K2III, vr = −12.18 km s-1) except for HJD 2 451 672.96 where we used HD 145001, and for the three CFHT spectra where we used γ Ser (F6IV, vr = + 6.58 km s-1) and β CVn (G0V, vr = + 6.33 km s-1) (velocity standards are taken from Scarfe et al. 1990). There appears to be a zero-point shift of 2 km s-1 of the DI Psc velocities between KPNO and CFHT data, which we interpret to be mostly due to the use of β Oph as the KPNO template star. Fekel (2004, private communication) obtained five more velocities of DI Psc with the coudé feed telescope at KPNO and got an average velocity of − 18.1 km s-1, in agreement with our CFHT velocities. We therefore assumed the CFHT velocities to be correct and accordingly shifted the KPNO data by 2.0 km s-1. The average radial velocity values of DP CVn from a total of 23 measurements is − 29.6 ± 0.5 (rms) km s-1, while from 18 measurements the average value for DI Psc is − 18.3 ± 0.7 (rms) km s-1. The small rms values suggest that both stars are single.
A summary of the spectroscopic observations is given in Table 1.
2.2. Photometry
Photometric observations of DP CVn and DI Psc were obtained with Wolfgang and Amadeus, the two 0.75-m twin automatic photoelectric telescopes (APTs) of the Leibniz-Institute for Astrophysics Potsdam (formerly owned by the University of Vienna) at Fairborn observatory in Arizona (Strassmeier et al. 1997). Amadeus is optimized for red wavelengths and used Johnson-Cousins VIC filters while Wolfgang is optimized for blue wavelengths and used Strömgren by filters. All the measurements were done differentially in respect to HD 109529 for DP CVn and to HD 217019 for DI Psc. Check stars were HD 108400 and HD 217590, respectively. For further details on the observing procedure and data reduction we refer to Strassmeier et al. (1997) and Granzer et al. (2001). The observations of DP CVn consist of a total of 1627 data points, with the largest number of data points (617) in the V band. For DI Psc we have in total 329 measurements with the largest number (121) in the y band. Mean photometric errors by bandpasses are 0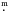 006 (V), 0
006 (V), 0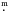 007 (IC), 0
007 (IC), 0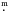 004 (b), and 0
004 (b), and 0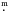 003 (y) for both stars in this paper. A summary of the photometric observations is given in Table 2.
003 (y) for both stars in this paper. A summary of the photometric observations is given in Table 2.
3. Stellar parameters
3.1. Absolute dimensions
Hipparcos measured parallaxes for DP CVn and DI Psc of 3.35 ± 0.99 mas and 5.27 ± 0.73 mas, respectively (van Leeuwen 2007). This translates into distances of 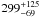 pc for DP CVn and
pc for DP CVn and 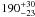 pc for DI Psc. Table 3 gives a summary of the astrophysical data of both systems.
pc for DI Psc. Table 3 gives a summary of the astrophysical data of both systems.
The brightest observed V and IC magnitudes for DP CVn are 8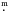 50 and 7
50 and 7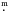 42 respectively, and for DI Psc 7
42 respectively, and for DI Psc 7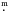 10 and 5
10 and 5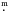 95. Due to the relatively large distances, interstellar reddening has to be taken into account before using absolute magnitudes. The galactic coordinates of DP CVn and DI Psc are ℓ = 128.61 b = + 65.45 and ℓ = 78.90 b = −47.96, respectively. We infer the reddening to these directions from the dust maps by Schlegel et al. (1998) and find E(B − V) ≈ 0
95. Due to the relatively large distances, interstellar reddening has to be taken into account before using absolute magnitudes. The galactic coordinates of DP CVn and DI Psc are ℓ = 128.61 b = + 65.45 and ℓ = 78.90 b = −47.96, respectively. We infer the reddening to these directions from the dust maps by Schlegel et al. (1998) and find E(B − V) ≈ 0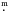 014 for DP CVn and E(B − V) ≈ 0
014 for DP CVn and E(B − V) ≈ 0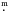 073 for DI Psc. Using the transformations given by Schlegel et al. this translates to
073 for DI Psc. Using the transformations given by Schlegel et al. this translates to  and
and 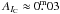 for DP CVn, and
for DP CVn, and 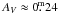 and
and 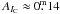 for DI Psc. Together with the Hipparcos distance this yields an absolute visual magnitude
for DI Psc. Together with the Hipparcos distance this yields an absolute visual magnitude  and the de-reddened V − IC color of 1
and the de-reddened V − IC color of 1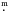 06 for DP CVn, and
06 for DP CVn, and 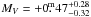 and V − IC=1
and V − IC=1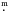 05 for DI Psc. It has to be noted that Schlegel et al.’s dust maps give the interstellar reddening throughout the entire Milky Way, which means that the adopted reddening could be exaggerated in our case. Nevertheless, the target stars are located at such distances and positions that they are likely above most of the dust, and the expected errors are well within the errors caused by the uncertainties in other parameters.
05 for DI Psc. It has to be noted that Schlegel et al.’s dust maps give the interstellar reddening throughout the entire Milky Way, which means that the adopted reddening could be exaggerated in our case. Nevertheless, the target stars are located at such distances and positions that they are likely above most of the dust, and the expected errors are well within the errors caused by the uncertainties in other parameters.
Summary of astrophysical data.
The de-reddened V − IC color can be used to estimate the effective temperature of our stars, e.g., with the empirical formula given by McWilliam (1990) and the transformation of Bessell (1979). For both stars, we obtain Teff = 4600 ± 100 K. This is in agreement with an independent estimation from our b − y data. The bluest observed b − y colors are 0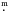 70 and 0
70 and 0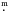 71 for DP CVn and DI Psc, respectively, and, with the calibration of Clem et al. (2004), suggest Teff = 4550 ± 100 K for log g = 2.5 for both stars, in agreement with the estimate from V − IC within its uncertainties. This gives a bolometric correction of –0.53 (Flower 1996) and bolometric absolute brightness of
71 for DP CVn and DI Psc, respectively, and, with the calibration of Clem et al. (2004), suggest Teff = 4550 ± 100 K for log g = 2.5 for both stars, in agreement with the estimate from V − IC within its uncertainties. This gives a bolometric correction of –0.53 (Flower 1996) and bolometric absolute brightness of 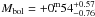 (DP CVn) and
(DP CVn) and 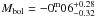 (DI Psc). The logarithmic luminosity (
(DI Psc). The logarithmic luminosity (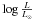 ) of DP CVn is
) of DP CVn is 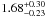 and of DI Psc is
and of DI Psc is 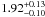 , based on an absolute bolometric magnitude of the Sun of
, based on an absolute bolometric magnitude of the Sun of  (Cox 2000).
(Cox 2000).
Morel et al. (2004) determined temperatures from the excitation equilibrium of Fe i lines of 13 active binaries and found only fair agreement with the temperature from B − V color, but even cooler by 200 K on average from V − R and V − I. Despite that the temperatures from these three indices agree within their errors in case of our two active stars, we employed the line-ratio calibration for giants by Strassmeier & Schordan (2000). This is normally not done because our Doppler-imaging stars have rather strong rotational broadening that makes it virtually impossible to measure accurate line-ratios but may serve as an independent cross check for the photometric temperatures. Altogether, eight line ratios between 6405 Å and 6460 Å were measured for both stars and, following the procedure suggested by Strassmeier & Schordan (2000, their Fig. 18) for V − I only, convert to average effective temperatures of 4530 ± 75 K and 4580 ± 75 K for DP CVn and DI Psc, respectively. Note that the DP CVn line ratios appear 0–3% larger than for DI Psc, which is reflected in the different effective temperatures. However, the expected external uncertainties due to the large line broadening are at least of the same order. We conclude that the line-ratio method at least agrees with the previous temperature determinations but fails to improve the accuracy.
 |
Fig. 1 Observed positions of DP CVn and DI Psc in the Hertzsprung-Russell diagram. The post-main-sequence tracks for 1.5, 1.8, 2.0, 2.3, 2.5 and 3.0 solar masses are shown (cf. Granzer et al. 2000). These tracks suggest masses of 1.8 M⊙ and 2.3 M⊙ for DP CVn and DI Psc, respectively. Both stars appear on the RGB at the end of the first Li dredge-up phase, which is marked by the dashed lines taken from Charbonnel & Balachandran (2000). |
The positions of DP CVn and DI Psc in the Hertzsprung-Russell (H-R) diagram are shown in Fig. 1. We have computed new post main sequence evolutionary tracks with the Kippenhahn code with up-to-date input physics (as described in Granzer et al. 2000). No overshooting was assumed though. The comparison with these tracks for solar metallicity suggests masses of approximately 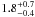 M⊙ (DP CVn) and
M⊙ (DP CVn) and 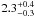 M⊙ (DI Psc). We placed our stars also on the color–magnitude diagram constructed with the Padova stellar evolution code (Bertelli et al. 2008) (considering overshooting) which yielded slightly lower values but still within the given error boxes, i.e.,
M⊙ (DI Psc). We placed our stars also on the color–magnitude diagram constructed with the Padova stellar evolution code (Bertelli et al. 2008) (considering overshooting) which yielded slightly lower values but still within the given error boxes, i.e., 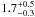 M⊙ for DP CVn and
M⊙ for DP CVn and 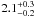 M⊙ for DI Psc. This result places both stars quite high up on the RGB and very close to the end of the first dredge-up phase. DP CVn has basically already passed this phase. During the first dredge-up the Li abundance at the surface gets diluted as Li-free material from the stellar interior is brought to the surface, i.e., both stars should have low Li abundance.
M⊙ for DI Psc. This result places both stars quite high up on the RGB and very close to the end of the first dredge-up phase. DP CVn has basically already passed this phase. During the first dredge-up the Li abundance at the surface gets diluted as Li-free material from the stellar interior is brought to the surface, i.e., both stars should have low Li abundance.
3.2. Rotational properties
 |
Fig. 2 ΔV and Δy magnitudes and periodograms from the APT data of DP CVn (top) and DI Psc (bottom). The vertical grey stripes indicate the time of our Doppler imaging data. The photometric periods adopted for this work are 14.010 d (DP CVn) and 18.066 d (DI Psc, but see also Sect. 3.2 for details). |
 |
Fig. 3 Folded light curves of DI Psc for four observing runs between HJD 2 451 098.7 and HJD 2451825.8 (S1-S4 from top to bottom panels, respectively), assuming rotation period of either 9.0358 d (left panels) or 18.066 d (right panels), according to the power spectrum in Fig. 2 bottom. Note that using 18.066 d yields less scattered light curves. For a quantitative comparison see Sect. 3.2. |
The rotation period of DP CVn and DI Psc was determined from our photometric observations using the frequency analysis program package MuFrAn by Kolláth (1990), see Fig. 2. For both of the stars V and y observations were used together, as this gave the largest amount of data points for the analysis. The most significant period found in the DP CVn observations was 14.010 ± 0.040 days. In the DI Psc data two similarly significant periods were found: 9.0358 ± 0.060 d and 18.066 ± 0.088 d. Although, the shorter period is the more significant one, after a careful investigation the longer period was adopted. The reasons for this are manifold: earlier period analysis (Strassmeier et al. 2000) indicates a period of 18.4 d, two other period analysis methods, the Lomb-method (Press et al. 1992) and the three stage period analysis (TSPA, Jetsu & Pelt 1999) also favor the longer period. In addition, the individual light curves (S1-S4) in Fig. 3 show less scatter when phasing them with the longer period. For a quantitative test we apply spot model fits for the seasonal light curves (SpotModeL by Ribárik et al. 2003) to compare the sum of squares of residuals, assuming either Prot of 9.0358 d or 18.066 d. Unambiguously, systematic improvement of the fits is found when using the longer period, resulting in 53% (S1), 30% (S2), 89% (S3) and 12% (S4) less residuals. Finally, we note that in a situation where there are two spot groups separated by approximately half a rotation, many period search methods would prefer the period which is half of the real one.
Rotational phases were calculated using the following ephemerides: ![\begin{eqnarray} \label{eqdpcvn} \rm{HJD}&=& 2\,451\,632.63084 + 14.010(40) \times {\rm E}, \ \ \ (\text{\dpcvn}), \\[2mm] \label{eqdipsc} \rm{HJD}&=& 2\,451\,639.00330 + 18.066(88) \times {\rm E}, \ \ \ (\text{\dipsc}) \end{eqnarray}](/articles/aa/full_html/2013/03/aa20227-12/aa20227-12-eq81.png) where the epoch is the time of the first spectroscopic observation in the data set and the period is the photometric period. The errors of the period determinations are estimated by increasing the residual scatter of the nonlinear least-squares solutions a certain degree, which corresponds to 10% of the accuracy of our photometric data (cf. Oláh et al. 2003).
where the epoch is the time of the first spectroscopic observation in the data set and the period is the photometric period. The errors of the period determinations are estimated by increasing the residual scatter of the nonlinear least-squares solutions a certain degree, which corresponds to 10% of the accuracy of our photometric data (cf. Oláh et al. 2003).
Our Doppler imaging analysis (Sect. 4) helped us to determine the projected rotational velocities (vsini) and the inclination angles i from goodness-of-fit landscapes (see Fig. 6). When we combine the resulting vsini of 39.0 ± 1.0 km s-1 for DP CVn and 42.0 ± 1.0 km s-1 for DI Psc with above rotational periods, the minimum radii of our stars are 10.7 ± 0.3 R⊙ and 15.0 ± 0.4 R⊙, respectively. Doppler imaging constraints the inclination to 35° ± 10° for DP CVn and 50° ± 10° for DI Psc, giving absolute radii of 18.7 R⊙ and 19.6 R⊙, respectively (see also Table 3). We note, that within the given errors, the radii and masses from Table 3 are in agreement with the adopted log g value.
3.3. Lithium abundances
Top panel of Fig. 4 shows a high-resolution spectrum of the exceptionally strong Li i 6708Å line for both stars in comparison with the inactive K0.5III star 16 Vir (otherwise an IAU velocity standard; see, e.g., Strassmeier et al. 1998; Weber & Strassmeier 2001; Strassmeier et al. 2011, etc.). The measured equivalent widths are 316 ± 7 mÅ (DP CVn) and 328 ± 5 mÅ (DI Psc). The corresponding equivalent width (EW) of the sum of the lines that would appear as blends within the Li line width, as measured in 16 Vir, is 39.8 ± 3 mÅ. The uncertainty of just 5–7 mÅ is estimated from different types of fits to the line profile, e.g. with a Gaussian profile of variable width where only the profile points of the red profile wing are used for the least-squares fit, from a normal Gaussian fit or from a simple profile-area integration. The final Li EWs for the two target stars are obtained by subtracting the 16 Vir contribution and are 277 mÅ for DP CVn and 288 mÅ for DI Psc.
Next we fit synthetic (LTE) spectra to the Li line profiles. Synthetic spectra were calculated and matched to the observed spectra by adjusting the Li abundance to fit the 6707.8 Å feature. We used the VALD database (Piskunov et al. 1995; Kupka et al. 1999) and Kurucz’s CD-ROM No. 23 for the numerous atomic and molecular lines. Its log gf values were slightly tuned using a spectrum of β Gem, while we adopted (and fixed) the values from Reddy et al. (2002) with the component structure of the Li resonance doublet from Hobbs et al. (1999). We assume that Li is purely 7Li.
 |
Fig. 4 Top panel: Li i 6708 Å spectra of DI Psc (top) and DP CVn (shifted by –0.2). Also shown is a spectrum of the inactive K0.5III giant 16 Vir (shifted to bottom) for comparison purpose. The measured equivalent width of the lithium line of DI Psc and DP CVn is 328 ± 5 mÅ and 316 ± 7 mÅ, respectively. Bottom panels: Li i 6708 Å line fitted by synthetic spectra for DP CVn (left) and DI Psc (right), resulting in logarithmic abundances of log n(Li) = 2.28, and of 2.20, respectively. |
Bottom panels of Fig. 4 show comparisons of the observed and synthetic spectra for both stars. Li abundances derived from our LTE analysis are equal to 2.28 for DP CVn and 2.20 for DI Psc. Small perturbations of the observed profiles are due to spots on the stellar surfaces which may influence the abundance value. Note that 100 K uncertainty in Teff yields ≈ 0.2 dex.
Tests with changes of the continuum level of 2% resulted in abundance changes of 0.10–0.12 dex. In our case the continuum level of the observed spectra was obtained iteratively from a comparison with calculated spectra including rotationally broadening. Notice a 4% depression of the continuum in the bottom panels of Fig. 4 due to the rotational convolution with several absorption blends. We did not carry out a full abundance analysis and thus assumed solar abundances for all other elements except Li and C, N, O. As our target stars likely belong to the “bump” clan (Charbonnel & Balachandran 2000) corresponding values of C, N, O abundances were used in our calculations.
Non-LTE corrections interpolated from the results by Carlsson et al. (1994) were found to be small ( < 0.03 dex) and comparable to its uncertainties and methods of interpolation. Therefore, we refrain from giving non-LTE abundances. However, we note that the non-LTE curves of growth of Pavlenko & Magazzú (1996) for a 4600 K/log g = 2.5 model convert the EWs measured into a Li abundance of 2.37 ± 0.05 (DP CVn) and 2.40 ± 0.05 (DI Psc), both on the log n(H) = 12.00 scale, i.e., larger by 0.1–0.2 dex than our LTE values.
 |
Fig. 5 Hα line profiles of DP CVn (left) and of DI Psc (right). In the top panels the observations are plotted together, while in the bottom panels the corresponding averages are subtracted to emphasize the nightly variations. Note the telluric water lines, especially at around 6552.5 Å, 6557 Å, and 6564 Å, as well as the sporadic cosmic peaks. |
 |
Fig. 6 Dependency of the normalized goodness-of-fit (χ2) of our Doppler maps over the vsini − i parameter plane. Best values for DP CVn (left) are vsini of 39.0 ± 1.0 km s-1 with i ≈ 35° ± 10° and for DI Psc (right) are 42.0 ± 1.0 km s-1 with 50° ± 10°, respectively. |
 |
Fig. 7 Surface temperature distribution maps of DP CVn for the two available data subsets taken in April 2000 (ser1, top row) and in May 2000 (ser2, bottom row), using Ca i 6439 Å, Fe i 6430 Å, Fe i 6421 Å, and Fe i 6400 Å mapping lines. The temperature maps are presented in a pseudo-Mercator projection from latitude − 35° to +90°. The phases of the observations are marked by arrows underneath. Below surface temperature reconstructions, in the middle panels the fitted line profiles are shown. Small dashes represent the data points and measure the ± 1-σ errors. Simultaneous light curves in Strömgren b and y are plotted in the bottom panels with their respective fits. |
The position in the H-R diagram in Fig. 1 and the large Li abundance places both stars at the end of the first dredge up according to the models of Charbonnel & Balachandran (2000). Thus, they are truly Li-rich stars. They even clump together with stars having freshly synthesized Li on their surface, such as the super-meteoritic Li stars HD 9746 and HD 233517 (Fekel & Balachandran 1993).
3.4. Hα line profiles
In both stars Hα appears as a relatively stable absorption line without periodic variations from one spectrum to the next (see Fig. 5), suggesting a rather homogeneous chromosphere made up of symmetrically distributed emission regions, comparable to a more active version of the solar chromospheric network. The averaged EWs are 1.183 Å for DP CVn and 1.369 Å for DI Psc, virtually without any significant phase dependency. The only markable phase independent change is seen in three spectra of DP CVn taken in three subsequent nights from HJD 2 451 636.657 (φ = 0.288) through HJD 2 451 637.745 (φ = 0.365, with EW of 1.526 at maximum) to HJD 2 451 638.698 (φ = 0.433). The line is broadened asymmetrically toward the blue wing, however, the feature did not return during the next rotation cycle. Such a nonrecurring phenomenon can be caused by an erupting coronal prominence. A similar change in the Hα line was reported e.g., for the effectively single G8-giant CM Cam by Strassmeier et al. (1998).
4. Doppler imaging
4.1. The TempMap inversion code
A full description of the TempMap code can be found in Rice et al. (1989), Rice & Strassmeier (2000) and in Rice (2002). The program performs a full LTE spectrum synthesis by solving the equation of transfer through a set of ATLAS-9 (Kurucz 1993) model atmospheres at all aspect angles and for a given set of chemical abundances. Atomic line parameters are obtained from VALD (Piskunov et al. 1995; Kupka et al. 1999). Spectra were calculated for temperatures ranging from 3500 K to 5500 K in steps of 250 K and with solar abundances. Simultaneous inversions of the usual mapping lines as well as of the photometric light variations in two photometric bandpasses are then carried out using maximum-entropy regularization.
A large number of trial inversions helped us to fine-tune some input parameters, and led us to the final values for the projected rotational velocity veqsini and the inclination i, which were determined with test runs by minimizing the χ2, i.e., the goodness-of-fit of the Doppler reconstructions (for the χ2 definition see Rice & Strassmeier 2000). The goodness-of-fit landscape in Fig. 6 demonstrates the change of χ2 over a meaningful domain of the veqsini − i parameter plane for both stars. Best values for veqsini were 39.0 ± 1.0 km s-1 (DP CVn) and 42.0 ± 1.0 km s-1 (DI Psc), and for the inclination were 35° ± 10° (DP CVn) and 40° ± 10° (DI Psc). The best combinations are listed also in Table 3.
4.2. Doppler reconstructions for DP CVn
Data for this star were taken in the modus of 12 nights on, 16 nights off, 13 nights on, i.e., approximately two rotation cycles were covered by the observations, with one rotation between them. This enabled two independent data sets with one spectrum per night and a total of 10 spectra for the first rotation (ser1, note that one Ca i 6439 Å spectrum was omitted due to probable cosmic noise) and 14 for the second rotation (ser2). Four nights were lost during the first rotation due to bad weather, the second rotation was covered completely.
The sampling of our spectra allowed ≈ 23 pixels across the full width of a given spectral line and the S/N per pixel is between 100:1 to 150:1 as measured with IRAF. Additionally, there are 17 simultaneous two-color photometric data points in Strömgren b and y.
Maps for the two data subsets taken in Apr. 2000 (ser1) and in May 2000 (ser2) are shown in Fig. 7 for Ca i 6439 Å, Fe i 6430 Å, Fe i 6421 Å, and Fe i 6400 Å, our most commonly used absorption lines with well-known formation physics and mostly free of telluric blends. (Surface reconstruction from Li cannot be done because we have only one high-resolution Li spectrum.) Also shown are the simultaneously fitted light curves in b and y. The individual reconstructions agree quite well, revealing dominant spots at lower latitudes with ≈ 700 K below Teff, as well as some high-latitude features but mostly with lesser contrast. Note also, that the minimum temperature value of the Ca-maps in Fig. 7 is set to 4200 K, i.e., 300 K hotter than that of the Fe-maps. The less contrast of the Ca-line reconstruction is probably due to the fact that the Ca line has broader equivalent width and also is more sensitive to temperature changes than the iron lines. On the other hand, smaller differences could occur through the relatively low S/N of the spectra. The agreement of the individual reconstructions can be demonstrated by comparing them with their averages (see Fig. 8). Markedly, most of the noticeable features in the contemporaneous individual maps in Fig. 7 can be identified in the corresponding combined map.
4.2.1. Searching for surface differential rotation
 |
Fig. 8 Combined images of DP CVn for the two data subsets ser1 (top) and ser2 (bottom). The maps are presented in a pseudo-Mercator projection from latitude − 35° to +90°. The phases of the observations are marked by arrows below the maps. Note, that even if the individual reconstructions show differences (cf. Fig. 7), the average maps still retain most of the traits. |
 |
Fig. 9 Cross-correlation function (CCF) map for DP CVn. The image is the average of four CCF maps obtained from cross-correlating the individual Doppler reconstructions (i.e., Ca i 6439 Å, Fe i 6430 Å, Fe i 6421 Å, and Fe i 6400 Å maps) taken in Apr. (ser1) and May (ser2). Dots with error bars are the Gaussian-fitted correlation peaks per 5° latitude bin. The best fit suggests an anti-solar differential rotation function (solid line) and corresponds to a surface shear α of − 0.035. |
 |
Fig. 10 Reconstructed Doppler maps of DI Psc for Ca i 6439 Å, Fe i 6430 Å, and Fe i 6400 Å mapping lines. The maps are presented in a pseudo-Mercator projection from latitude − 50° to +90°. The phases of the observations are marked by arrows underneath. Below surface temperature reconstructions the fitted line profiles are shown, where small dashes represent the data points and measure the ± 1-σ errors. |
Latitude dependency of the spot displacements from the first subset (ser1) in Apr 2000 to the second one (ser2) in May 2000 can be assigned as a trace of surface differential rotation. Such a dependency is suspected when looking at Fig. 7, e.g., where the spots near the equator seem to be shifted mostly backwards in longitude, unlike spots at higher (>45°) latitudes. Differential rotation can be measured by cross-correlating subsequent Doppler images (Donati & Collier Cameron 1997). We apply the cross-correlation method called ACCORD, as described recently in Kővári et al. (2012). We cross-correlate the corresponding longitude strips of the subsequent Doppler maps for each latitude value (in practice in bins of 5° width) for the four available individual reconstructions. This way, we get four cross-correlation function (CCF) maps. Then, the CCF maps are combined to achieve the average correlation pattern, wherein the sign of the differential rotation is expected to be intensified as a common feature of the individual CCF maps. Finally, the best correlated pattern is fitted by a solar-like differential rotation law, assuming the usual quadratic form of Ω(β) = Ωeq − ΔΩsin2β, where Ωeq is the angular velocity at the equator and ΔΩ = Ωeq − Ωpole is the difference between the equatorial and the polar angular velocity. The dimensionless surface shear parameter is expressed as α = ΔΩ/Ωeq.
In Fig. 9 the best-fit rotation law to the correlation peaks per latitude bin (represented by fitted Gaussian maxima and their errorbars) is plotted. The relevant part of the correlation pattern extends from −25° to +40°, and is strongest at around 30°, i.e., the latitude belt that rotates with the disk-integrated photometric period. This is not surprising because below the equator the inclination angle limits the visibility while at higher latitudes the lack of strong surface features that are jointly present on the corresponding maps yields weak and slurred correlation. Note that at even higher latitudes, close to the visible pole, the geometric singularity makes “correlation” comparably meaningless. The resulting fit indicates antisolar-type differential rotation, i.e. equatorial deceleration, with Ωeq = 25.336 ± 0.044°/day and ΔΩ = 0.875 ± 0.411°/day or α = −0.035 ± 0.016 (errors are estimated from the FWHMs and amplitudes of the Gaussian profiles). We note, that considering the moderate significance, the surface shear parameter needs further validation from better quality data.
4.3. Doppler reconstructions for DI Psc
Our observations allow for one Doppler reconstruction from data taken between HJD 2 451 661.00 and HJD 2 451 673.99, i.e. covering 13 nights, or 72% of one rotation cycle. Unfortunately, no simultaneous photometric data were available (but see Strassmeier et al. 1993 on the role of photometry in TempMap). Figure 10 shows the Ca i 6439 Å, Fe i 6430 Å, and Fe i 6400 Å images along with the corresponding spectroscopic data and their respective fits.
 |
Fig. 11 Combined image of DI Psc from the available three individual Doppler reconstructions. The map is presented in a pseudo-Mercator projection from latitude − 50° to +90°. The phases of the observations are marked by arrows below the map. |
Attempts to use other mapping lines from the observed spectral region, i.e. Fe i 6421 Å, Fe i 6411 Å or Fe i 6393 Å led to unacceptable results probably due to unknown blends (atomic and molecular), to uncertain turbulence parameters, etc. Note that the available Li spectra of DI Psc are insufficient for Doppler reconstruction.
The Ca i 6439 Å map reveals cool spots at high latitudes as well as spots at lower latitudes, but with lesser contrast. Similarly, the Fe i 6430 Å, and Fe i 6400 Å maps show cool polar features, but dominant spots appear also at latitudes below ≈ 40°, forming a belt-like structure. The temperature scale is different, typically ranging from ΔT ≈ 800 K in the Ca map up to 1300 K in the iron maps. Aside from that and from minor dissimilarities (most likely due to the moderate quality of the data and the uncovered phase gap from ≈ 340° to ≈ 80°), the agreement is still acceptable, as shown in Fig. 11 where an average map is combined from the individual reconstructions. It is clearly worth to revisit this star with instruments with larger wavelength coverage and further explore its surface inhomogeneity.
 |
Fig. 12 Light-curve inversions for DP CVn. Darker regions indicate larger spot filling factors. The grid in the maps indicates the equator and four longitudes separated by 90°. The observations (crosses) and calculated V and y light curves (solid lines) are also presented. Note that for convenience reasons we use 2 451 250.99805 as the zero phase in the plot, i.e., the time of the first photometric observation we have, yielding a phase shift of +0.240 as compared to the Doppler maps in Sect. 4.2). |
5. Long-term photometry of DP CVn
5.1. Spot evolution
The spot evolution was investigated first by plotting the maximum, minimum and mean magnitudes in V and y at different observing periods against the amplitude. No systematic trend in the mean magnitude with amplitude is seen, while the maximum and minimum magnitudes are systematically higher and lower, respectively, when the amplitude increases. We conclude that on DP CVn the light-curve variations are caused by a rather symmetrical rearrangement of a more or less constant amount of dark spots. This is consonant with the results from Doppler imaging (Sect. 4.2), where the most dominant spots are located within a belt below ≈ 40° and distributed more or less evenly (see Fig. 8).
5.2. Active longitudes
The photometric dataset of DP CVn is suitable for carrying out a more detailed analysis of the spot evolution through the 6 year-long observing range. For this purpose the V and y observations were divided into 16 subsets. These individual light curves were then used for obtaining spot filling factor maps of the stellar surface. For the inversions we use the Occamian approach method (Berdyugina 1998; but see also Lanza et al. 1998). The stellar surface was divided into areas of 10° × 10°. The temperatures for the unspotted surface and the spots were fixed to 4600 K and 4000 K, respectively, based on the Doppler maps (see Sect. 4.2). The limb-darkening coefficient for the V band for the unspotted surface was estimated to be 0.802 from the results by Al-Naimiy (1978) and the same value was also adopted for the spotted areas. As unspotted magnitude we used 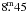 as an estimation from the brightest observed magnitude of
as an estimation from the brightest observed magnitude of 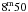 .
.
The inversions of the individual light curves covering the interval 1999–2005 are presented in Fig. 12 together with the light curves themselves. As can be seen, the maps usually show two active regions which often are extended or even merged. Also, these active regions seem to be quite stably separated by half of the phase. This kind of activity pattern has been found on many active stars (see, e.g., Oláh et al. 1991; Henry et al. 1995; Jetsu 1996; Berdyugina & Tuominen 1998, etc.), and may bear also some evidence for the existence of a flip-flop phenomenon, where the dominant part of the spot activity shifts 180° in longitude over a short period of time and remains at this new active longitude for some time, usually a few years (see e.g., Jetsu et al. 1993; Berdyugina & Tuominen 1998; Korhonen et al. 2001).
5.3. Differential rotation
Differential rotation can be assessed from seasonal photometric period changes, since the current period depends on the stellar latitude of the spots that produce rotational modulation. Therefore, we derived rotation periods for the ten available observing seasons (cf. Fig. 2). The values fall between  d (2nd season) and
d (2nd season) and 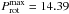 d (7th season). A rough guess of the surface shear parameter α can be estimated from ΔP/P, getting ≈ 0,06. We underline nonetheless, that the sign of the surface shear (i.e., solar-type equatorial acceleration, or opposite) cannot be determined without additional information. This result is quite close to the value derived from spectroscopy. On the other hand, the typical error of the period determination of 0.36 d for such short intervals makes this determination ambiguous.
d (7th season). A rough guess of the surface shear parameter α can be estimated from ΔP/P, getting ≈ 0,06. We underline nonetheless, that the sign of the surface shear (i.e., solar-type equatorial acceleration, or opposite) cannot be determined without additional information. This result is quite close to the value derived from spectroscopy. On the other hand, the typical error of the period determination of 0.36 d for such short intervals makes this determination ambiguous.
To perform a more reliable analysis we divided the whole photometric dataset into two parts. During the first half of the observing range (1st–5th seasons) the seasonal amplitudes were smaller, while the mean brightness level was higher, as compared to the second half (6th–10th seasons) where the amplitudes were increased and the mean brightness was decreased. This change can be interpreted by shifting dominant spotted region(s) toward lower latitudes. If so, we would expect longer rotation period for the second half of the dataset when assuming antisolar-type differential rotation. Fourier analysis resulted in 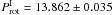 d for the first term (1st–5th seasons), and
d for the first term (1st–5th seasons), and 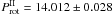 d for the second term (6th–10th seasons), implying a minimum shear of α = −0.01. We conclude that such an overall period change is in agreement with the proposed antisolar-type differential rotation law for DP CVn in Sect. 4.2.1.
d for the second term (6th–10th seasons), implying a minimum shear of α = −0.01. We conclude that such an overall period change is in agreement with the proposed antisolar-type differential rotation law for DP CVn in Sect. 4.2.1.
6. Conclusions
The revised Hipparcos parallax places both DP CVn and DI Psc at a position in the H-R diagram where a deep convective envelope coexists with a hydrogen-burning shell. In that evolutionary phase, rapid redistribution of the moment of inertia must occur or had occurred (e.g. do Nascimento et al. 2000) and is likely to be a time of high dynamo activity due to the extra shear forces. Indeed, a number of overactive single giants were identified from their unusual high Li abundance (e.g. Brown et al. 1989; Fekel & Balachandran 1993). Therefore, these stars seem to have already experienced their first Li dredge-up according to the models of Charbonnel & Balachandran (2000). Both stars of the present study likely have developed a degenerate helium core, and will later undergo a He-flash, and will evolve on to the early asymptotic giant branch and experience a second Li dredge-up.
The surface spot distribution in both stars is rather unspectacular in that there is no large polar cap, or a single high-latitude feature or any other dominating feature. This is qualitatively in agreement with the absence of rotational modulation in Hα at that time (for both stars, see Sect. 3.4), and suggestive of an atmosphere probably entirely penetrated and saturated by magnetic fields. However, this may not be the case at all times, as shown by the light-curve inversion for DP CVn in 2002.26, when spots were concentrated just in one hemisphere.
Both stars are very similar to the single high-Li K2-giant HD 31993 (Strassmeier et al. 2003) in that they are very active and in an evolutionary episode where we might expect a relation between its magnetic surface activity and the Li abundance. Knowing the surface Li distribution and its relation to chromospheric activity indicators would be most useful for abundance determinations. Our Doppler maps of HD 31993 and the two stars in this paper may support the analogy with the Li enhancement in sunspots, i.e., that the high Li abundance of these stars is related to the increased and nearly isotropic spottedness. Unfortunately, the quality of our spectra is only moderate and higher S/N ratio and higher spectral resolution are warranted. Also, further Doppler images of Li-rich stars are needed to quantitatively elaborate on such a speculation.
Online material
Summary of the spectroscopic observations for DP CVn and DI Psc.
Photometric observation of DP CVn and DI Psc obtained with the Wolfgang and Amadeus APTs. Data available in electronic form at the CDS.
Acknowledgments
Authors wish to thank an anonymous referee for his/her valuable comments. We thank Thomas Hackman for analysing DI Psc photometry using TSPA period analysis method, Katalin Oláh for the useful discussions on MuFrAn and Krisztián Vida for his help in applying Lomb-method. Z.s.K. and L.K. are grateful to the Hungarian Science Research Program (OTKA) for support under the grant K-81421. This work is supported by the “Lendület-2009” Young Researchers’ Program of the Hungarian Academy of Sciences and by the HUMAN MB08C 81013 grant of the MAG Zrt. H.K. acknowledges the support from the European Commission under the Marie Curie Intra-European Fellowship. The authors acknowledge the support of the German Deutsche Forschungsgemeinschaft, DFG through projects KO 2320/1 and STR645/1. K.G.S. acknowledges the generous allotment of telescope time at KPNO as well as the access to the Canadian CFHT time. This study was supported by the Ministry of Education of the Russian Federation through the Federal Targeted program “Scientific and Pedagogical Staff of Innovative Russia” for 20092013 (state contract 14.740.11.0084).
References
- Al-Naimiy, H. M. 1978, Ap&SS, 53, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 1998, A&A, 338, 97 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., Jankov, S., Ilyin, I. V., et al. 1998, A&A, 334, 863 [NASA ADS] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell M. S. 1979, PASP 91, 589 [Google Scholar]
- Brown, J. A., Sneden, C., Lambert, D. L., & Dutchover, E. 1989, ApJS, 71, 293 [CrossRef] [Google Scholar]
- Carlsson, M., Rutten, R. J., Bruls, J., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
- Charbonnel, C., & Balachandran, S. C. 2000, A&A, 359, 563 [NASA ADS] [Google Scholar]
- Clem, J. L., VandenBerg, D. A., Grundahl, F., & Bell, R. A. 2004, AJ, 127, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N., ed. 2000, Allen’s Astrophysical Quantities (New York: Springer) [Google Scholar]
- De Medeiros, J. R., do Nascimento, J. D., Jr.,Sankarankutty, J., et al. 2000, A&A, 363, 239 [NASA ADS] [Google Scholar]
- do Nascimento, J. D., Charbonnel, C., Lébre, A., et al. 2000, A&A 357, 931 [Google Scholar]
- Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, N. A., de la Reza, R., da Silva, L., & Lambert, D. L. 2002, AJ, 123, 2703 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., & Balachandran, S. C. 1993, ApJ, 403, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, M., & Miranda, L. F. 1998, A&A, 332, 629 [NASA ADS] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Giampapa, M. S. 1984, ApJ, 277, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, T., Schüssler, M., Caligari, P., & Strassmeier, K. G. 2000, A&A, 355, 1087 [NASA ADS] [Google Scholar]
- Granzer, T., Reegen, P., & Strassmeier, K. G. 2001, AN, 322, 325 [Google Scholar]
- Grevesse, N. 1968, Sol. Phys., 5, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Hackman, T., Jetsu, L., & Tuominen, I. 2001, A&A, 374, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, G. W., Eaton, J. A., Hamer, J., & Hall, D. S. 1995, ApJS, 97, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., Thorburn, J. A., & Rebull, L. M. 1999, ApJ, 523, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Byrne, P. B., Doyle, G., et al. 1994, MNRAS, 270, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Jetsu, L. 1996, A&A, 314, 153 [NASA ADS] [Google Scholar]
- Jetsu, L., & Pelt, J. 1999, A&AS, 139, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jetsu, L., Pelt, J., & Tuominen, I. 1993, A&A, 278, 449 [NASA ADS] [Google Scholar]
- Kolláth, Z. 1990, The program package MuFrAn, Occ. Techn. Notes of Konkoly Obs., No. 1 [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Strassmeier, K. G., & Tuominen, I. 2001, A&A, 379, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Korhonen, H., Kriskovics, L., et al. 2012, A&A, 539, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., et al. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. L. 1993, ATLAS-9, CD No. 13 [Google Scholar]
- Lanza, A. F., Catalano, S., Cutispoto, G., et al. 2002, A&A, 332, 541 [Google Scholar]
- Lugaro, M., & Chieffi, A. 2011, Lect. Notes Phys., 812, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Mallik, S. V. 1998, A&A, 338, 623 [NASA ADS] [Google Scholar]
- McWilliam, A. 1990, ApJS, 74, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, T., Micela, M., Favata, F., & Katz, D. 2004, A&A, 426,1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neuhäuserer, R., Wolk, S. J., Torres, G., et al. 1998, A&A, 334, 873 [NASA ADS] [Google Scholar]
- Oláh, K., Hall, D. S., & Henry, G. W. 1991, A&A, 251, 531 [NASA ADS] [Google Scholar]
- Oláh, K., Jurcsik, J., & Strassmeier, K. G. 2003, A&A, 410, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pallavacini, R., Cutispoto, G., Randich, S., & Gratton, R. 1993, A&A, 267, 145 [NASA ADS] [Google Scholar]
- Pavlenko, Ya. V., & Magazzú, A. 1996, A&A 311, 961 [Google Scholar]
- Piskunov, N. E. 1991, in: The Sun and Cool Stars, IAU Collq. 130, eds. I. Tuominen, D. Moss, & G. Rüdiger (Heidelberg: Springer-Verlag), 309 [Google Scholar]
- Piskunov, N. E., Tuominen, I., & Vilhu, O. 1990, A&A, 230, 363 [NASA ADS] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., et al. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Plez, B. 1998, A&A, 337, 495 [NASA ADS] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical Recipes in FORTRAN - The Art of Scientific Computing, 2nd edn. (New York: Cambridge University Press), 569 [Google Scholar]
- Reddy, B. E., & Lambert, D. L. 2005, AJ, 129, 2831 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., Laws, C., et al. 2002, MNRAS, 335, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ribárik, G., Oláh, K., & Strassmeier, K. G. 2003, AN, 324, 202 [Google Scholar]
- Rice, J. B. 2002, AN, 323, 220 [Google Scholar]
- Rice, J. B., & Strassmeier, K. G. 2000, A&AS, 147, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, J. B., Wehlau, W. H., & Khokhlova, V. L. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]
- Scarfe, C. D., Batten, A. H., & Fletcher, J. M. 1990, Publ. Dominion Astron. Obs. Victoria 18, 21 [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Strassmeier, K. G., & Schordan, P. 2000, AN, 321, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Rice, J. B., Wehlau, W. H., et al. 1993, A&A, 268, 671 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Bartus, J., Kővári, Zs., et al. 1998, A&A, 336, 587 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Washuettl, A., Granzer, T., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Kratzwald, L., & Weber, M. 2003, A&A, 408, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Carroll, T. A., Weber, M., et al. 2011, A&A, 535, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Weber, M., Granzer, T., & Järvinen, S. 2012, AN, 333, 663 [Google Scholar]
- Valenti, J., Piskunov, N., & Johns-Krull, C. 1998, ApJ, 498, 851 [Google Scholar]
- Van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 2001, A&A, 373, 974 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Photometric observation of DP CVn and DI Psc obtained with the Wolfgang and Amadeus APTs. Data available in electronic form at the CDS.
All Figures
 |
Fig. 1 Observed positions of DP CVn and DI Psc in the Hertzsprung-Russell diagram. The post-main-sequence tracks for 1.5, 1.8, 2.0, 2.3, 2.5 and 3.0 solar masses are shown (cf. Granzer et al. 2000). These tracks suggest masses of 1.8 M⊙ and 2.3 M⊙ for DP CVn and DI Psc, respectively. Both stars appear on the RGB at the end of the first Li dredge-up phase, which is marked by the dashed lines taken from Charbonnel & Balachandran (2000). |
| In the text | |
 |
Fig. 2 ΔV and Δy magnitudes and periodograms from the APT data of DP CVn (top) and DI Psc (bottom). The vertical grey stripes indicate the time of our Doppler imaging data. The photometric periods adopted for this work are 14.010 d (DP CVn) and 18.066 d (DI Psc, but see also Sect. 3.2 for details). |
| In the text | |
 |
Fig. 3 Folded light curves of DI Psc for four observing runs between HJD 2 451 098.7 and HJD 2451825.8 (S1-S4 from top to bottom panels, respectively), assuming rotation period of either 9.0358 d (left panels) or 18.066 d (right panels), according to the power spectrum in Fig. 2 bottom. Note that using 18.066 d yields less scattered light curves. For a quantitative comparison see Sect. 3.2. |
| In the text | |
 |
Fig. 4 Top panel: Li i 6708 Å spectra of DI Psc (top) and DP CVn (shifted by –0.2). Also shown is a spectrum of the inactive K0.5III giant 16 Vir (shifted to bottom) for comparison purpose. The measured equivalent width of the lithium line of DI Psc and DP CVn is 328 ± 5 mÅ and 316 ± 7 mÅ, respectively. Bottom panels: Li i 6708 Å line fitted by synthetic spectra for DP CVn (left) and DI Psc (right), resulting in logarithmic abundances of log n(Li) = 2.28, and of 2.20, respectively. |
| In the text | |
 |
Fig. 5 Hα line profiles of DP CVn (left) and of DI Psc (right). In the top panels the observations are plotted together, while in the bottom panels the corresponding averages are subtracted to emphasize the nightly variations. Note the telluric water lines, especially at around 6552.5 Å, 6557 Å, and 6564 Å, as well as the sporadic cosmic peaks. |
| In the text | |
 |
Fig. 6 Dependency of the normalized goodness-of-fit (χ2) of our Doppler maps over the vsini − i parameter plane. Best values for DP CVn (left) are vsini of 39.0 ± 1.0 km s-1 with i ≈ 35° ± 10° and for DI Psc (right) are 42.0 ± 1.0 km s-1 with 50° ± 10°, respectively. |
| In the text | |
 |
Fig. 7 Surface temperature distribution maps of DP CVn for the two available data subsets taken in April 2000 (ser1, top row) and in May 2000 (ser2, bottom row), using Ca i 6439 Å, Fe i 6430 Å, Fe i 6421 Å, and Fe i 6400 Å mapping lines. The temperature maps are presented in a pseudo-Mercator projection from latitude − 35° to +90°. The phases of the observations are marked by arrows underneath. Below surface temperature reconstructions, in the middle panels the fitted line profiles are shown. Small dashes represent the data points and measure the ± 1-σ errors. Simultaneous light curves in Strömgren b and y are plotted in the bottom panels with their respective fits. |
| In the text | |
 |
Fig. 8 Combined images of DP CVn for the two data subsets ser1 (top) and ser2 (bottom). The maps are presented in a pseudo-Mercator projection from latitude − 35° to +90°. The phases of the observations are marked by arrows below the maps. Note, that even if the individual reconstructions show differences (cf. Fig. 7), the average maps still retain most of the traits. |
| In the text | |
 |
Fig. 9 Cross-correlation function (CCF) map for DP CVn. The image is the average of four CCF maps obtained from cross-correlating the individual Doppler reconstructions (i.e., Ca i 6439 Å, Fe i 6430 Å, Fe i 6421 Å, and Fe i 6400 Å maps) taken in Apr. (ser1) and May (ser2). Dots with error bars are the Gaussian-fitted correlation peaks per 5° latitude bin. The best fit suggests an anti-solar differential rotation function (solid line) and corresponds to a surface shear α of − 0.035. |
| In the text | |
 |
Fig. 10 Reconstructed Doppler maps of DI Psc for Ca i 6439 Å, Fe i 6430 Å, and Fe i 6400 Å mapping lines. The maps are presented in a pseudo-Mercator projection from latitude − 50° to +90°. The phases of the observations are marked by arrows underneath. Below surface temperature reconstructions the fitted line profiles are shown, where small dashes represent the data points and measure the ± 1-σ errors. |
| In the text | |
 |
Fig. 11 Combined image of DI Psc from the available three individual Doppler reconstructions. The map is presented in a pseudo-Mercator projection from latitude − 50° to +90°. The phases of the observations are marked by arrows below the map. |
| In the text | |
 |
Fig. 12 Light-curve inversions for DP CVn. Darker regions indicate larger spot filling factors. The grid in the maps indicates the equator and four longitudes separated by 90°. The observations (crosses) and calculated V and y light curves (solid lines) are also presented. Note that for convenience reasons we use 2 451 250.99805 as the zero phase in the plot, i.e., the time of the first photometric observation we have, yielding a phase shift of +0.240 as compared to the Doppler maps in Sect. 4.2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


