| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A147 | |
| Number of page(s) | 26 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220678 | |
| Published online | 16 January 2013 | |
Chemical evolution of the Galactic bulge as traced by microlensed dwarf and subgiant stars⋆,⋆⋆
V. Evidence for a wide age distribution and a complex MDF
1
Lund ObservatoryDepartment of Astronomy and Theoretical
physics, PO Box
43, 221 00
Lund, Sweden
e-mail: tbensby@astro.lu.se
2
Department of Astronomy, Ohio State University,
140 W. 18th Avenue,
Columbus, OH
43210,
USA
3
Palomar Observatory, Mail Stop 249-17, California Institute of
Technology, Pasadena,
CA
91125,
USA
4
Research School of Astronomy & Astrophysics, Mount Stromlo
Observatory, Cotter Road, Weston
Creek, 2611
ACT,
Australia
5
Departamento de Astronomia do IAG/USP, Universidade de São
Paulo, Rua do Matão
1226, 05508-900
São Paulo,
Brasil
6
INAF – Astronomical Observatory of Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
7
Department of Physics, Chungbuk National University,
361-763
Cheongju, Republic of
Korea
8
Carnegie Observatories, 813 Santa Barbara Street, Pasadena, CA
91101,
USA
9
Department of Particle Physics and Astrophysics, Weizmann
Institute of Science, 76100
Rehovot,
Israel
10
Warsaw University Observatory, A1. Ujazdowskie 4, 00-478, Warszawa, Poland
11
University of Notre Dame, Notre Dame, IN
46556,
USA
12
Institute for Information and Mathematical Sciences, Massey
University, 1330
Auckland, New
Zealand
13
Department of Earth and Space Science, Osaka
University, 560-0043
Osaka,
Japan
14
Solar-Terrestrial Environment Laboratory, Nagoya
University, 464-8601
Nagoya,
Japan
15
Mt. John Observatory, PO Box 56, 8770
Lake Tekapo, New
Zealand
16
Department of Physics, Faculty of Science, Kyoto Sangyo
University, 603-8555
Kyoto,
Japan
Received: 31 October 2012
Accepted: 28 November 2012
Based on high-resolution spectra obtained during gravitational microlensing events we present a detailed elemental abundance analysis of 32 dwarf and subgiant stars in the Galactic bulge. Combined with the sample of 26 stars from the previous papers in this series, we now have 58 microlensed bulge dwarfs and subgiants that have been homogeneously analysed. The main characteristics of the sample and the findings that can be drawn are: (i) the metallicity distribution (MDF) is wide and spans all metallicities between [Fe/H] = −1.9 to +0.6; (ii) the dip in the MDF around solar metallicity that was apparent in our previous analysis of a smaller sample (26 microlensed stars) is no longer evident; instead it has a complex structure and indications of multiple components are starting to emerge. A tentative interpretation is that there could be different stellar populations at interplay, each with a different scale height: the thin disk, the thick disk, and a bar population; (iii) the stars with [Fe/H] ≲ −0.1 are old with ages between 10 and 12 Gyr; (iv) the metal-rich stars with [Fe/H] ≳ −0.1 show a wide variety of ages, ranging from 2 to 12 Gyr with a distribution that has a dominant peak around 4−5 Gyr and a tail towards higher ages; (v) there are indications in the [α/Fe]−[Fe/H] abundance trends that the “knee” occurs around [Fe/H] = −0.3to −0.2, which is a slightly higher metallicity as compared to the “knee” for the local thick disk. This suggests that the chemical enrichment of the metal-poor bulge has been somewhat faster than what is observed for the local thick disk. The results from the microlensed bulge dwarf stars in combination with other findings in the literature, in particular the evidence that the bulge has cylindrical rotation, indicate that the Milky Way could be an almost pure disk galaxy. The bulge would then just be a conglomerate of the other Galactic stellar populations (thin disk, thick disk, halo, and ...?), residing together in the central parts of the Galaxy, influenced by the Galactic bar.
Key words: gravitational lensing: micro / Galaxy: bulge / Galaxy: formation / Galaxy: evolution / stars: abundances
Based on data obtained with the European Southern Observatory telescopes (Proposal ID:s 87.B-0600, 88.B-0349, 89.B-0047, and 90.B-0204), the Magellan Clay telescope at the Las Campanas observatory, and the Keck I telescope at the W.M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration.
Tables 2–5 are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/549/A147
© ESO, 2013
1. Introduction
Galactic bulges are emerging as inherently complex features in spiral galaxies and are a defining component of many spiral and disk galaxies (Kormendy & Kennicutt 2004; Athanassoula 2005). Numerous studies have shown them to have several spatial structures overlaying each other. The Milky Way is no different and over the last decades studies of the Galactic bulge have revealed an increasingly complex, and not always consistent, picture of the stellar population present in the innermost few kpc of our Galaxy. The formation of this central concentration of stars is not fully understood and if the observed spatial structures are uniquely related to dynamical and chemical features is a very actively studied field. New surveys such as the VISTA Variables in the Via Lactea (VVV) public survey (Saito et al. 2010) are looking into this intriguing Galactic component. Several outstanding questions remain un-resolved including the true shape of the metallicity distribution function (MDF) and how the MDF is connected to different spatial and kinematical structures. A recent discussion of these issues can be found in, e.g., Babusiaux et al. (2010).
A number of formation scenarios for the Galactic bulge have been proposed and were first summarised by Wyse & Gilmore (1992) and set out in greater detail in later works (e.g., Kormendy & Kennicutt 2004; Athanassoula 2005). The first major scenario is in situ star formation from primordial gas in the gravitational collapse (e.g., Eggen et al. 1962; Matteucci & Brocato 1990), or merging of clumps within the disk at high redshift (e.g., Noguchi 1999; Bournaud et al. 2009). Historically, this has been thought to be the major component of the Galactic bulge, and bulges in general, and is referred to as a classical bulge. However, in the Milky Way it now seems that the spherical component that should form from an initial collapse is after all a rather small component. The mass of the classical bulge might be less than 8% of the mass of the disk (Shen et al. 2010).
Instead, the scenario that is currently emerging as the most compelling is secular evolution in which a bulge and bar forms from buckling instabilities in the disk (e.g., Combes et al. 1990; Kormendy & Kennicutt 2004; Athanassoula 2005; Ness et al. 2012). Bars are common in other galaxies and the existence of a bar in the Milky Way in addition to its classical, spherical bulge has been debated for some time. Star counts have shown that there definitely is a bar (Stanek et al. 1994; McWilliam & Zoccali 2010; Saito et al. 2011, 2012). Studies of the stellar kinematics show that a large fraction of the stars exhibit cylindrical rotation (e.g., Shen et al. 2010; Howard et al. 2009; Sumi et al. 2003) which is indicative of a boxy bulge, i.e., one with a bar (Athanassoula 2005). Thus both star counts as well as the stellar kinematics unambiguously show the presence of a bar. Since the bar forms from buckling instabilities in a disk, there may be a strong connection between the Galactic stellar disk and the bar population.
A realistic approach could be a mixed scenario encompassing two or more formation scenarios. Mixed formation has been observed in other galaxies (e.g., Prugniel et al. 2001) and a mixed origin of the Galactic bulge is explored by a number of theoretical studies predicting both the shape of the MDF as well as the elemental abundance trends that should be expected (e.g., Tsujimoto & Bekki 2012; Grieco et al. 2012). The presence of the first stars in the Galactic bulge as predicted in, e.g., Wyse & Gilmore (1992) who discuss the possibility of merging of dwarf satellite galaxies that sink into the Galactic bulge, have been further developed within the context of cosmological simulations (Tumlinson 2010).
Elemental abundances in stars are able to provide vital clues to the formation time scales involved in the stellar population(s) present in the Galactic bulge as well as to constrain the shape of the MDF and slope of the IMF (e.g., Ballero et al. 2007; Tsujimoto & Bekki 2012). Initial studies of red giants revealed the Galactic bulge to be relatively metal-rich but with a wide metallicity distribution (e.g., McWilliam & Rich 1994; Zoccali et al. 2008). It also appeared enhanced in the α-elements, indicative of a short formation time (McWilliam & Rich 1994; Fulbright et al. 2006, 2007). The elevated levels of α-elements continued to super-solar metallicities, thus setting the bulge stellar population apart from what was found in the solar neighbourhood, i.e., with solar levels of most elements at these metallicities (e.g., Edvardsson et al. 1993). As the bulge is far away the stars are faint and hence these studies were and, essentially are, confined to the most luminous giants. Results based on giant spectra are not trivial to interpret. Physical processes within giant stars also erase some original abundance signatures. This is the case for C, N, and Li in all giants, and for O, Na, Mg, and Al in some cases (e.g., Kraft et al. 1992). Additionally, although recent differential analysis of giant stars in the bulge and disk have achieved high precision (Alves-Brito et al. 2010), the situation at high metallicities is still unclear due to heavy blending, as the cool atmospheres of giants, rich in molecules, are difficult to analyse (e.g., Lebzelter et al. 2012).
The spectra of dwarfs, even metal-rich ones, are fairly straightforward to analyse and are the best tracers of galactic chemical evolution (Edvardsson et al. 1993). The dwarf stars are also unique in that they give star-by-star age information and not just the bulk age-information available through analysis of colour magnitude diagrams. Normally dwarf stars in the bulge are too faint to be observed with high-resolution spectrographs. However, during microlensing events they can brighten by several magnitudes and during the last few years there have been several studies that have utilised this phenomenon and obtained spectra that allowed detailed elemental abundance analysis of bulge dwarf stars. In total there have been 26 bulge dwarfs observed (Cavallo et al. 2003; Johnson et al. 2007, 2008; Cohen et al. 2008, 2009; Bensby et al. 2009; Epstein et al. 2010; Bensby et al. 2010b, 2011) all homogeneously analysed in Bensby et al. (2011). These studies have revitalised the study of chemical evolution and structure of the bulge.
For instance, the microlensed dwarf stars (Bensby et al. 2010b, 2011) as well as of red giant branch (RGB) stars (Hill et al. 2011; Uttenthaler et al. 2012) have revealed a dual-component bulge MDF – one metal-poor component around [Fe/H] ≈ −0.6 and one metal-rich component around [Fe/H] ≈ +0.3. There has also been considerable evidence that secular evolution of the thick disk may have played a large role in the origin and evolution of the bulge. This is based on the apparent similarity of the [α/Fe]−[Fe/H] abundance trends in the bulge at sub-solar metallicities (e.g., Meléndez et al. 2008; Bensby et al. 2010b; Alves-Brito et al. 2010; Gonzalez et al. 2011) and those of the nearby thick disk (e.g, Bensby et al. 2007a; Fuhrmann 2008; Reddy et al. 2006). Also, the metal-poor peak in the bi-modal bulge MDF appears to coincide with the MDF for the thick disk and considering that the age structure of the metal-poor bulge dwarfs is the same as for the thick disk, i.e., mainly old, it might well be that the bulge and the thick disk have had similar or even shared chemical histories (Meléndez et al. 2008; Alves-Brito et al. 2010; Bensby et al. 2010b, 2011; Gonzalez et al. 2011). Of course, the comparisons between the bulge and the thick disk have mainly used nearby thick disk samples, and if the bulge partly originated through secular evolution of the thick disk it would be desirable to compare with thick disk stellar samples located in situ in the inner Galactic disk. The only such study is the Bensby et al. (2010a) study of 44 red giants, located between galactocentric radii 4−7 kpc and up to 3−4 kpc from the Galactic plane. Those results show that the inner disk region has a similar abundance structure as seen in the solar neighbourhood, i.e., a thin disk-thick disk dichotomy, and that the similarities between the bulge and the thick disk persist when comparing to an inner disk sample.
A recent controversy is the overall age distribution in the bulge. Photometric observations of different bulge fields point to an exclusively old stellar population with ages greater than 10 Gyr (Zoccali et al. 2003; Clarkson et al. 2008; Brown et al. 2010; Clarkson et al. 2011). In addition to the very old stars, the observations of microlensed bulge dwarf stars have revealed a significant fraction of stars with ages between 3−7 Gyr (Bensby et al. 2010b, 2011). Nataf & Gould (2012) tried to reconcile the dilemma of the young bulge dwarfs by showing that a factor of 2 discrepancy between spectroscopic and photometric age determinations of the Galactic bulge main-sequence turnoff possibly can be explained if the Galactic bulge is helium-enhanced relative to that assumed by standard isochrones. An intriguing recent result, based on spectra of 575 bulges from the Sloan Digital Sky Survey, is that barred galaxies show a stellar age distribution with a young stellar component not present in unbarred galaxies (Coelho & Gadotti 2011).
Another intriguing result is the multi-component (>4) MDF proposed by Ness et al. (submitted) based on low/intermediate-resolution spectra of 28 000 RGB stars at different longitudes and latitudes in the bulge. Whether these proposed multiple bulge components are real and where they come from needs to be investigated.
Summary of the 32 microlensed bulge dwarf stars new in this study (sorted by observation date).
In this work we present a detailed elemental abundance analysis of 32 new microlensing events towards the Galactic bulge. Together with the previous 26 events homogeneously analysed in Bensby et al. (2011), the sample now contains 58 microlensed dwarf and subgiant stars in the bulge.
 |
Fig. 1 Light curves for the first 16 of the 32 new microlensing events. Each plot has a zoom window, showing the time intervals when the source stars were observed with high-resolution spectrographs. In each plot the un-lensed magnitude of the source star is also given (IS). |
 |
Fig. 2 Light curves for the remaining 16 of the 32 new microlensing events. Each plot has a zoom window, showing the time intervals when the source stars were observed with high-resolution spectrographs. In each plot the un-lensed magnitude of the source star is also given (IS). |
2. Observations and data reduction
Dwarf and main sequence turn-off stars in the Galactic bulge have V magnitudes around 19−20 (e.g., Feltzing & Gilmore 2000), which is far too faint to observe under normal circumstances even with today’s 8−10 m class telescopes. To obtain a decent high-resolution spectrum (S/N > 50 and R > 40 000) of V = 19−20 star would require more than 50 hours of exposure time with an instrument such as UVES on VLT. To the rescue, gravitational microlensing has surfaced as nature’s golden magnifying glass to study dwarf stars in the bulge. Gravitational microlensing occurs whenever a compact object, by chance, passes the line of sight between an observer and a distant object. The brightness of the distant object can then be magnified by factors of several hundred. However, as microlensing events are completely random it is impossible to predict when and where they will happen. The search for microlensing events in the bulge is today mainly done by the MOA and OGLE surveys, which monitor the bulge every night. The OGLE survey is carried out primarily in the I band using 1.3 m Warsaw Telescope at Las Campanas, Chile and detects roughly 1700 events per year (Udalski et al. 1994; Udalski 2003). The MOA survey is carried out primarily in a broad R/I filter using the 1.8 m telescope at Mt. John, New Zealand, and detects roughly 650 events per year (Bond et al. 2001; Sumi et al. 2011). For a small subset of these events the background source stars are both (1) dwarfs (or subgiants); and (2) magnified highly enough to allow us to obtain a high-resolution high-S/N spectrum in a few hours. To find these spectroscopy targets, we perform real-time modelling of OGLE and MOA data as they are updated, and also acquire additional data on promising targets using the ANDICAM camera on the 1.3 m SMARTS telescope at Cerro Tololo Interamerican Observatory (CTIO) in Chile. We also use the SMARTS telescope to measure the (V − I) colours of most events when they are near peak brightness.
Due to the unpredictability of microlensing events it is impossible to have a standard observing program, which is allocated specific nights in visitor mode or put in queue service mode. Hence, starting in the ESO observing period P82 we have been running Target-of-Opportunity (ToO) programs using UVES (Dekker et al. 2000) on the VLT allowing us to trigger observations with only a few hours notice. Up until now, including the second of five triggers in P90, we have submitted 52 triggers with the result of 47 successfully acquired spectra of dwarf stars in the bulge. Of the five “failures” there were two events for which the predicted magnification was much higher than the actual one, resulting in too low S/N and spectra useless for abundance analysis, one event turned out to be a red giant and will be published in another paper, one spectrum was obtained when only the UVES blue arm was available resulting in very low S/N and short wavelength coverage, and deemed useless, and one event turned out to be a nova towards the bulge (see Wagner et al. 2012). The ToO observations with VLT have been augmented with a few observations obtained with the MIKE spectrograph (Bernstein et al. 2003) on Magellan or the HIRES spectrograph (Vogt et al. 1994) on Keck. The spectra have resolutions between R ≈ 40 000−90 000 (see Table 1).
Our goal has been to observe the targets as close to peak brightness as possible, and to observe targets that reach at least I ≈ 15.0 during the observations. With a 1′′ wide slit this means that the spectra should have a minimum signal-to-noise ratio of around S/N ≈ 50−60 and a resolution of R ≈ 42 000 in the UVES 760 nm setting (according to the UVES exposure time calculator). However, sometimes the observed microlensing light curve does not follow the predicted one, meaning that the obtained spectra could be better or worse than predicted. Also, observing conditions (seeing and clouds) have severely affected the quality of some of the observations. Hence, the signal-to-noise ratios vary between S/N ≈ 30−100 (see Table 1) and for a few events the S/N is even lower than 20. Figure 1 shows the light curves for the 32 new events (light curves for the first 26 events are published in Bensby et al. 2009, 2010b, 2011). In each plot the time interval when the spectroscopic observations were carried out has been marked (see insets in each panel). Generally, we were able to catch many objects very close to peak brightness, but in a few cases we were less lucky. Especially interesting is the observation of MOA-2012-BLG-532S (Fig. 2). This event suddenly entered a caustic crossing resulting in a strong a sudden increase in brightness. We managed to submit a trigger and start observations. However, its brightness started to decrease again sooner than expected, resulting in most of the two hour exposure being executed when it had dropped 2 magnitudes in brightness. Hence, the spectrum for MOA-2012-BLG-532S is of lower quality.
 |
Fig. 3 Comparison of stellar parameters before and after implementation of NLTE corrections for Fe i lines. The differences are NLTE values minus LTE values and mean differences and σ are indicated in each panel. |
Data reductions of the UVES spectra were carried out with the UVES pipeline (Ballester et al. 2000) versions 4.9.0 through 5.0.7, depending on when the event was observed. The MIKE spectra were reduced with the Carnegie Observatories python pipeline1, and the reduction of the HIRES spectrum follows the procedure outlined in Cohen et al. (2008).
3. Analysis
3.1. Stellar parameters – with Fe I NLTE corrections
Non-local thermodynamic equilibrium (NLTE) corrections for Fe i are now included in the analysis compared to the analysis of the previous sample of 26 microlensed dwarf stars from Bensby et al. (2010b, 2011). As the inclusion of NLTE corrections for Fe i lines impacts the final values of the stellar parameters, those 26 stars have been re-analysed, ensuring a homogeneous treatment of the full sample. The NLTE corrections are implemented on a line-by-line basis using an IDL script kindly provided by Karin Lind (Lind et al. 2012). Fe ii lines are on the other hand not sensitive to NLTE effects (e.g., Thévenin & Idiart 1999; Lind et al. 2012), and need not be corrected. Apart from the implementation of Fe i NLTE corrections, the methodology to find the stellar parameters is the same as before and is fully described in Bensby et al. (2009, 2010b, 2011). In brief, the analysis is based on standard 1D plane-parallel MARCS model stellar atmospheres (Gustafsson et al. 1975; Edvardsson et al. 1993; Asplund et al. 1997), and abundances are calculated with the Uppsala EQWIDTH program using equivalent widths measured by hand using the IRAF task SPLOT. The effective temperatures were determined from excitation balance of NLTE corrected abundances from Fe i lines, surface gravities from ionisation balance between NLTE corrected Fe i abundances and abundances from Fe ii lines, and the microturbulence parameters by requiring that the NLTE corrected Fe i abundances are independent of line strength.
As demonstrated by Lind et al. (2012) the NLTE effects are very small, being smallest for the most metal-rich stars (generally below 0.01 dex) and increasing for lower metallicities, and for stars with lower surface gravities. Figure 3 shows comparisons of effective temperatures, metallicities, and microturbulence velocities for all 58 stars with and without the inclusion of Fe i NLTE corrections, and as can be seen the effects are truly minuscule for the type of stars analysed here (mostly metal-rich F and G dwarfs).
Uncertainties in stellar parameters and elemental abundances were, as for the previous sample of 26 stars (Bensby et al. 2011), calculated according to the method outlined in Epstein et al. (2010). This method takes into account the uncertainties in the four observables used to find the stellar parameters, i.e. the uncertainty of the slope in the graph of Fe i abundances versus lower excitation potential; the uncertainty of the slope in the graph of Fe i abundances versus reduced line strength; the uncertainty in the difference between Fe i and Fe ii abundances; and the uncertainty in the difference between input and output metallicities. The method also accounts for abundance spreads (line-to-line scatter) as well as how the average abundances for each element reacts to changes in the stellar parameters (see also comments in Bensby et al. 2011).
Figure 4 shows the location in the log g − Teff plane, for all 58 stars in the microlensed bulge dwarf sample over-plotted on the α-enhanced isochrones from Demarque et al. (2004). A majority of the stars are located either on the main-sequence turn-off or the subgiant branch. Three or four stars have started to ascend the giant branch but not far enough to have the chemical composition of their atmospheres altered. The fact that most of the stars are either turn-off or subgiant stars, and that the uncertainties in the stellar parameters are well-constrained with usually small uncertainties, means that it is possible to determine relative ages accurately. Stellar ages, masses, luminosities, absolute I magnitudes (MI), and colours (V − I) were estimated from Y2 isochrones (Demarque et al. 2004) by maximising probability distribution functions as described in Bensby et al. (2011).
We have also double-checked the analysis of the previous 26 events and revised some equivalent width measurements. This lead to changes in the stellar parameters and abundance ratios for a few stars. Also, the inclusion of NLTE corrections for Fe i lead to some, although small, changes. Therefore, equivalent width measurements and abundances for individual lines are given in Table 2 for all 58 stars, and stellar parameters, stellar ages, and elemental abundances in Tables 3−5, for all 58 stars, i.e., all tables include the revised values for the 26 stars in Bensby et al. (2010b, 2011). All abundances have been normalised to the Sun on a line-by-line basis using our own solar analysis as reference (see also Bensby et al. 2011).
3.2. (V – I) colours from spectroscopy and microlensing techniques
The (V − I)0 colour and the MI magnitude can be estimated from microlensing techniques (Yoo et al. 2004) assuming that the reddening towards the microlensed source is the same as towards the red clump in the same field, that (V − I)0 and MI of the bulge red clump is known, and (for MI) that the distance to the source and the red clump is the same. The de-reddened magnitude and colour of the source can then be derived from the offsets between the microlensing source and the red clump in the instrumental colour-magnitude diagram. The microlensing values for MI and (V − I) given in Table 5 are based on the assumption that the bulge red clump has (V − I)0 = 1.06 (as determined in Bensby et al. 2011) and MI = −0.12 (Nataf & Gould 2012). For 55 of the 58 events, Fig. 5 shows comparisons between the spectroscopic MI magnitudes and (V − I) colours (see Sect. 3.1) to those determined from microlensing techniques. Two events from Bensby et al. 2011 and one of the new events do not have any estimates of (V − I)0 from microlensing techniques (see Table 5). The first thing to notice is that there appears to be a slope present between the colour difference (Δ(V − I)) and the spectroscopic Teff (see red line in Fig. 5). The question is whether this trend is due to uncertainties in the spectroscopic analysis or due to the microlensing assumptions?
 |
Fig. 4 All 58 microlensed dwarf stars plotted on the α-enhanced isochrones from Demarque et al. (2004). The metallicity of the stars in each panel is within ±0.05 dex of the isochrone metallicity. In each plot the solid lines represent isochrones with ages of 0.1, 5, 10, 15, and 20 Gyr. Dotted lines are isochrones in steps of 1 Gyr. Error bars represent the uncertainties in Teff and log g as given in Table 4. Note that the age determinations reported in Table 5 are based on probability distribution functions as described in Bensby et al. (2011). |
The bulge is known to have patchy and irregular reddening. Nataf et al. (2012) measured reddening and differential reddening for more then 9000 sight lines towards the bulge. Figure 6 shows the differential reddening along the sight lines to the individual microlensing events in this study versus the absolute value of the Δ(V − I). While there is no one-to-one relationship between these two parameters it is evident that there are very few events with large colour discrepancies that at the same time have low differential reddening values (i.e., in the lower right corner of the Fig. 6). Note that the Nataf & Gould (2012) differential-reddening dispersions are systemically larger than the offsets between the colours determined from microlensing and spectroscopy. For example, when Nataf estimates δE(V − I) ≈ 0.15, the microlensing offset averages about 0.06. The reason for this apparent discrepancy is that to estimate the microlensing (V − I)0, we consider the minimum possible area around the source needed to determine the colour of the bulge clump, whereas Nataf & Gould (2012) use a robust algorithm that chooses a larger area, in order to minimise failures among their 9000 automated determinations.
In any case, Fig. 6 gives a hint that differential reddening could play a rôle in explaining the discrepancies between spectroscopic and microlensing (V − I) colours. However, differential reddening cannot cause the (2σ statistically significant) slope in the Δ(V − I) − Teff diagram. The only assumptions being made are that the extinction is the same (on average) between the red clump and the source, and that the bulge clump (V − I) colour is known. While either of these assumptions might be violated, it is hard to seen why, e.g., the bulge red clump should be redder in fields with reddish subgiants than turnoff stars, or why there should be systematically more differential reddening (relative to the mean of that field) for fields containing reddish subgiants compared to turnoff stars.
Measured equivalent widths and calculated elemental abundances for all 58 microlensed bulge dwarfs.
Elemental abundance ratios, errors in the abundance ratios, and number of lines used, for all 58 microlensed dwarf stars.
Stellar parameters and radial velocities for all 58 stars (sorted by metallicity).
Stellar ages, masses, and colours as determined from spectroscopy and microlensing techniques for all 58 stars.
 |
Fig. 5 a) Difference between microlensing colours and the spectroscopic colours versus spectroscopic Teff. b) Difference between the absolute I magnitudes from microlensing techniques and from spectroscopy versus stellar mass (derived from spectroscopy). Error bars represent the uncertainties in the spectroscopic values. The microlensing values used in the plots are based on the assumption that the bulge red clump has (V − I)0 = 1.06 and MI = −0.12. Stars with Teff > 5500 K are marked by filled circles, otherwise by open circles. |
 |
Fig. 6 Differential reddening versus the absolute value of the difference between microlensing colours and spectroscopic colours. The differential reddening values for the individual sight lines are taken from Nataf et al. (2012). Stars with Teff > 5500 K are marked by filled circles, otherwise by open circles. |
So, that turns the focus to the spectroscopic colours. As explained by Yi et al. (2001), the Y2 isochrones come with two different Teff-to-colour transformations employed: either the one by Green et al. (1987) or the one by Lejeune et al. (1998). As also pointed out by Yi et al. (2001), while the two sets of colour transformations agree fairly well for main sequence dwarf stars, there are large differences for giant stars. The version of the Y2 isochrones that we used for the microlensed dwarf sample utilises the colour transformation from Lejeune et al. (1998). Figure 7a shows the spectroscopic (V − I) (black filled circles) and the microlensing ones (open circles). Overplotted are three sets of Teff-colour transformations for [Fe/H] = 0 and three surface gravities log g = 3.5, 4.0, 4.5: Lejeune et al. (1998), Green et al. (1987), and Casagrande et al. (2010), which have no dependence on log g. Figures 7b and c then show the differences between the Casagrande-Lejeune and Green-Lejeune transformations, respectively. What is interesting here is that the Lejeune and Casagrande transformations are nearly identical for Teff > 5500 K, and that there is an offset between Green and Lejeune that varies with log g but which is nearly constant for Teff > 5500 K. However, for Teff ≲ 5500 the three sets of transformations differ, and increasingly more for lower Teff. The points in Figs. 7b and c show the corrections that would have to be applied to the microlensed dwarf stars if we were to change from the Lejeune transformation to any of the other two. Generally, stars with Teff ≳ 5500 would be more or less untouched while the cooler stars would get higher (V − I) colours. This is a frustrating finding as it means that the slope seen in Fig. 5 would become steeper with the Casagrande and Green Teff-colour transformations!
 |
Fig. 7 a) Filled black circles mark the spectroscopic values, open circles microlensing values. Dash-dotted blue line show the Casagrande et al. (2010)Teff-colour transformation, dashed green lines the Green et al. (1987) transformation (for three different log g), and the solid red lines the Lejeune et al. (1998) transformation (for three different log g). b) Differences between Casagrande et al. (2010) and Lejeune et al. (1998). c) Differences between Green et al. (1987) and Lejeune et al. (1998). The markers in b) and c) show the differences that should be applied to the microlensed dwarfs if the Casagrande et al. (2010) and Green et al. (1987) trandformations had been applied instead of the one from Lejeune et al. (1998). |
However, from Fig. 7 it is apparent that the agreement between the three calibrations is good for hotter stars. Even though the Green et al. (1987) transformations will show offsets depending on log g, it will be a constannt offset and no slope will be introduced. As further investigations into the field of Teff-colour transformations is beyond the scope of the current paper, we will, for now, restrict ourselves to stars with Teff ≳ 5500 K when comparing spectroscopic and microlensing colours. These stars are marked by filled circles in Fig. 5. The difference in the (V − I) colour is now 0.00 ± 0.07 mag (while if we were to include all stars, i.e., also those with Teff < 5500 K, the difference would be +0.03 ± 0.08 mag). Our conclusion is that the colour of the bulge red clump should remain at (V − I)0 = 1.06.
3.3. Comparisons to the Balmer Hα line
To further check the effective temperatures of the microlensed dwarf stars we have calculated synthetic spectra with the SME (Spectroscopy Made Easy, v. 2011-12-05, Valenti & Piskunov 1996) for the 32 new microlensing events. Figure 8 shows comparisons of the synthetic Hα line profiles to the observed Hα line profiles the spectroscopic temperatures (blue lines). There is generally very good agreement between synthetic and observed spectra for the spectroscopic effective temperatures. Hence, we believe that the effective temperatures we have determined should be good.
 |
Fig. 8 Illustration to see how well the spectroscopic temperatures (full blue lines) and temperatures from microlensing techniques (dashed red lines) reproduce the observed wing profiles of the Hα line at 6563 Å for the 32 new microlensed bulge dwarfs. Note that no estimate of the temperature from microlensing techniques is available for OGLE-2011-BLG-1410S. The stars are sorted by metallicity. |
For the 55 stars that have (V − I)0 colours from microlensing techniques we calculate effective temperatures using the Casagrande et al. (2010)Teff-colour calibration. These temperatures are on average 105 K higher than the spectroscopic ones. If we restrict ourselves to stars with (spectroscopic) Teff > 5500 the spectroscopic temperatures are on average higher, but only by 10 K. The dispersion in both cases is around 230 K.
Figure 8 also shows synthetic spectra based on temperatures from the microlensing (V − I)0 colours (red dashed lines). It is clear that the microlensing temperatures produce spectra that do not match for a few cases (e.g., MOA-2011-BLG-090S and MOA-2012-BLG-410S). The Hα wing profile for the star with the largest colour discrepancy between spectroscopic and microlensing temperature, MOA-2009-BLG-259S, is shown in Fig. 3 of Bensby et al. (2011). From that figure it is clear that the spectroscopic temperature is the better match. However, this star has Teff = 4915 K and log g = 3.3, which is in a region where the Teff-colour calibrations appear to be very uncertain (see Fig. 7), meaning that the colour-Teff transformation could be substantially affected.
3.4. A few special cases
 |
Fig. 9 Fitting of the Hα wing profiles to find the effective temperatures for OGLE-2011-BLG-0969S and OGLE-2012-BLG-1156S. The insets show the summed absolute values of the residuals that was minimised to find the best fitting temperature. |
The combination of low metallicity and low S/N of the observed spectra of
OGLE-2011-BLG-0969S and OGLE-2012-BLG-1156S meant that very few equivalent widths could be
measured for these stars. Hence, the effective temperatures and the microturbulence
parameters for these two stars could not be constrained in the standard way, through
excitation and ionisation balance, as described above. As an alternative, the effective
temperatures were constrained by fitting the wing profiles of the Balmer
Hα line at 6563 Å for these two stars (as described in Sect. 3.2). This gives an effective temperature of around
6150 K for OGLE-2011-BLG-0969S and around 6200 K for OGLE-2012-BLG-1156S (see Fig. 9). This in fair agreement with the temperatures that can
be estimated from microlensing techniques for these two stars, 6283 K and 6012 K,
respectively (see Sect. 3.2). The surface gravities
were set based on microlensing techniques to log g = 4.14 for
OGLE-2011-BLG-0969S and log g = 4.25 for OGLE-2012-BLG-1156S. First,
(V − I)0 and I0
are determined from the offset to the bulge red clump.
(V − I)0 is then transferred to
(V − K)0 using the calibration by Bessell & Brett (1988). Combining
(V − K)0 with
V0 = (V − I)0 + I0
give θstar using the calibration by Kervella et al. (2004). We then assume that the microlensing source is
at same distance as the red clump given by Nataf et al.
(2012). The radius of the star is then
rstar = Dsource·θstar.
Finally, we assume that the stellar mass is
Mstar = 1 M⊙, so the gravity
is given by 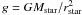 . We estimate the uncertainty in the
distance to be 15% (0.3 mag), and the mass uncertainty to be about 10%. Hence, the
dominant error is in the distance (because it enters as the square), imply that the error
in log g using this method is about 0.1 dex. The microturbulence
parameter was set to ξt = 1.5 km s-1 for
both stars using the empirical calibration by M. Bergemann (private communication)2.
. We estimate the uncertainty in the
distance to be 15% (0.3 mag), and the mass uncertainty to be about 10%. Hence, the
dominant error is in the distance (because it enters as the square), imply that the error
in log g using this method is about 0.1 dex. The microturbulence
parameter was set to ξt = 1.5 km s-1 for
both stars using the empirical calibration by M. Bergemann (private communication)2.
 |
Fig. 10 Positions on the sky for the microlensed dwarf sample. The bulge contour lines based on observations with the COBE satellite are shown as solid lines (Weiland et al. 1994). The positions of Baade’s window (BW), the Galactic centre (GC), and three of the ARGOS survey fields (see Ness et al. 2012) are delineated. The dotted lines are concentric circles in steps of 2°. |
Following the standard procedure to determine the stellar parameters (see above) for MOA-2011-BLG-104S we get a microturbulence value of ξt = 2.7 km s-1. This value seems too high for these types of stars. According to the empirical calibration by Bergemann, stars with similar stellar parameters (Teff = 6106 K, log g = 4.4, and [Fe/H] = −0.88) have microturbulence values around 1.5 km s-1. Also, the discrepancy between the spectroscopic temperature and the temperature deduced from microlensing techniques is unusually large for this star (~500 K). Hence, we believe that due to the quite low metallicity of this star, combined with a relatively low signal-to-noise ratio of the observed spectrum (S/N ≈ 25), the stellar parameters have been poorly constrained from the Fe i balance plots.
The discrepancies indicate that it is likely that the temperature should be lower than the 6100 K derived from excitation balance. However, based on the Balmer Hα line profile it should probably not be as low as the temperature deduced from the microlensing techniques (5644 K, see Table 5 and Fig. 8). Hence, for MOA-2011-BLG-104S, we set the temperature to 5900 K. Following the empirical calibration by M. Bergemann we set the microturbulence to 1.3 km s-1. To get ionisation balance between Fe i and Fe ii abundances the surface gravity needs to be set to log g = 4.15. The effect on the metallicity for MOA-2011-BLG-104S, when changing the temperature from 6100 K to 5900 K is only −0.03 dex (down from [Fe/H] = −0.88 to −0.85). The age of the star increased from 8.7 Gyr to 10.2 Gyr (which is more in line with ages seen for the other metal-poor stars).
4. Results
4.1. Positions on the sky
Figure 10 shows the positions on the sky for the 58 microlensed dwarf stars. Except for the first three detections at positive latitudes, essentially all stars are located between 2° to 5° below the the Galactic plane and mainly at positive longitudes. This distribution is a reflection of the locations of the fields surveyed by MOA and OGLE. At the distance of the bulge, 8.2 kpc (e.g., Nataf et al. 2012), 2° to 5° corresponds to a vertical distance of 150 to 750 pc, respectively, below the plane.
4.2. Radial velocities – bulge membership
Radial velocities can help constraining dynamical models of the bulge. The BRAVA survey (see, Kunder et al. 2012, for latest release) presents radial velocities for ~10 000 red giant stars covering −10 < l < 10 and −8 < b < −4. They find that the rotation curves at l = −4, −6 and −8 almost perfectly follow the cylindrical rotation models by Shen et al. (2010). The velocity dispersion varies from around 100 km s-1 at (l, b) = (0, −4) to around 80 km s-1 at (l, b) = (±10, −4).
We correct our measured heliocentric radial velocities for the microlensed bulge dwarfs to the Galactic centre using the relation3vGC = vr, HC + 232sin(l)cos(b) + 9cos(l)cos(b) + 7sin(b) which takes the motion of the relative to the local standard of rest (LSR), and the motion of the LSR relative to the Galactic centre, into account. Figure 11 then shows the galactocentric radial velocities versus l and b for the microlensed dwarf sample (grey circles) as well as the results from the BRAVA survey in different l and b bins (as indicated in the figure; red, cyan, and green). The black circles mark the mean velocity and the rms dispersion around the mean the microlensed dwarf stars, binned into 3° wide bins. The average velocities as well as the dispersions for the microlensed dwarf stars follow nicely the results from the BRAVA survey, especially versus l. Given that the BRAVA sample is representative of the bulge population, this shows that the radial velocities and the velocity dispersion seen in the microlensed dwarf sample are at the expected levels if they belong to a bulge population.
 |
Fig. 11 Galactocentric velocity versus Galactic longitude and latitude for the microlensed dwarf sample (grey circles). The black circles represent the mean radial velocity and the 1σ rms dispersion for the microlensed bulge dwarfs, binned into 3° wide bins. The results from the BRAVA survey (Rich et al. 2007; Kunder et al. 2012) have been over-plotted, and the different colours (red, cyan, and green) represent the values at different l and b as given in the plots. |
4.3. Metallicity distribution
 |
Fig. 12 a) Metallicity distribution for the microlensed dwarf sample (white dashed line shows the distribution of the 26 microlensed dwarf stars from Bensby et al. 2011); b) 166 red giant stars in Baade’s window from Hill et al. (2011); c) 220 red clump stars in Baade’s window from Hill et al. (2011); d) 1813 red giant stars with from the ARGOS survey fields at (l,b) = (0, −5), (5, −5), (−5, −5) from Ness et al. (submitted). e) 363 red giants at (l,b) = (0, −10) from Uttenthaler et al. (2012); The curved lines in a)–d) represent generalised histograms. Dotted vertical lines mark the peaks claimed by Ness et al. (submitted) in d). |
 |
Fig. 13 Cumulative histograms and the Kolmogorov-Smirnow tests between the microlensed dwarf sample and the giant star samples shown in Fig. 12. The solid thicker red line shows the microlensed bulge dwarfs, (b) the RGB sample from Hill et al. (2011), (c) the red clump sample from Hill et al. (2011), (d) the red clump sample from ARGOS (Ness et al., submitted), and (e) the RGB sample from Uttenthaler et al. (2012). |
 |
Fig. 14 a) and b) show the MDFs when the microlensed dwarf sample is split into stars farther from the plane (|b| ≳ 3), and closer to the plane (|b| < 3), respectively. c)–d) the MDFs when sample is split into stars farther from the centre (|l| > 2), and closer to the centre (|l| ≲ 2), respectively. The curved lines represent generalised histograms. |
Figure 12a shows the metallicity distribution for the microlensed dwarf sample. The finding from Bensby et al. (2011), that the MDF is bi-modal, with a paucity of stars around solar metallicity, is weakened as we now have several stars with metallicities within ±0.1 dex of the Sun. One of those stars, MOA-2010-BLG-523S, was already published in Bensby et al. (2011) but has now been revised 0.08 dex lower metallicity following the current analysis (see Sect. 3.1).
A major issue in Bensby et al. (2011) was the apparent discrepancy between the microlensed dwarf star MDF, which was clearly bi-modal, and the red giant MDF in Baade’s window by Zoccali et al. (2008), which then did not appear bi-modal. Since then, the Zoccali et al. (2008) RGB sample has been re-analysed by Hill et al. (2011) with the result that the RGB sample shrank from 213 stars to 166 stars and that the MDF now appears bi-modal (see Fig. 12b). With the current microlensed dwarf sample, and the re-analysed RGB sample, the two distributions are quite similar. A two-sided KS test yields a p-value of 0.17 (see Fig. 13), i.e., the hypothesis that the two samples have been drawn from the same underlying population cannot be rejected.
Hill et al. (2011) also presented a sample of 220 red clump giants in Baade’s window. The MDF of these red clump stars (Fig. 12c) is similar to the RGB sample, and a two-sided KS test between the red clump sample and the microlensed dwarf sample yields a p-value of 0.06 (see Fig. 13). Hence, the conclusions are the same as for the RGB sample.
Furthermore, ARGOS (Abundances and Radial velocity Galactic Origins Survey) observed 28 000 stars, mostly red clump giants, in 28 fields of the Galactic bulge. In Fig. 12d we show the MDF for the 1813 red clump giants that are located in the three ARGOS fields at (l,b) = (0, −5), (5, −5), (− 5, −5) (the fields are delineated out in Fig. 10). The internal random uncertainty in [Fe/H] for individual stars in ARGOS is 0.13 dex (Ness et al. submitted). By fitting Gaussians to the MDF, Ness et al. claim detection of three components at [Fe/H] = +0.14, −0.23, −0.60, and possibly another two at [Fe/H] = −1.24, −1.7. The peaks are indicated by the vertical dotted lines in Fig. 12. It is interesting to see that the three metal-rich ARGOS peaks more or less coincide with the “bumps” in the generalised dwarf star MDF in Fig. 12a. There might be a slight offset, but the three peaks are clearly within 0.1 dex of the “bumps”. It is also interesting to note that the ARGOS MDF does not show the relatively large fraction of metal-rich stars ([Fe/H] > +0.3) seen in the microlensed dwarf sample and the RGB and RC samples in Baade’s window. Since the ARGOS fields are slightly farther from the Galactic plane than the other samples, this trend could be explained if there were a metal-rich population that drops off very rapidly with distance from the plane. The MDF of 363 RGB stars at (l,b) = (0, −10) by Uttenthaler et al. (2012) in Fig. 12e shows a more dominant metal-poor peak, possibly confirming the drop-off with |b| for the metal-rich peak. However, contrary to the ARGOS MDF, the b = −10° MDF by Uttenthaler et al. (2012) contains a larger fraction of metal-rich stars ([Fe/H] > +0.3). Since it is located even farther from the plane than the ARGOS fields it could mean that the ARGOS study suffers from a systematic shift in [Fe/H] (i.e., it should be moved to higher [Fe/H]).
Regarding the regions closer to the plane, both Ramírez et al. (2000) and Rich et al. (2012) used infrared spectroscopy to study M giants in several fields in the innermost 600 pc between Baade’s window and ~150 pc (i.e., 4° to 1°) below the plane. Neither of these two studies find a major vertical abundance or composition gradient. Hence, if there is a gradient, or gradual change of stellar populations, it appears to disappear close to the plane. What is intriguing about the Rich et al. (2012) study is that the M giant MDFs peak at [Fe/H] ≈ −0.2 at all latitudes, and that there are essentially no M giants with [Fe/H] > 0. This is in stark contrast to the findings from both the microlensed bulge dwarf sample as well as the RGB and RC samples in Baade’s window from Hill et al. (2011), which all see a large fraction of stars at super-solar metallicities. The reason might be that very metal-rich M stars actually never reach the RGB phase due to strong stellar winds (see discussion in, e.g., Cohen et al. 2008), or that the metallicities of M giants may be systematically underestimated. In any case, the metal-rich stars are lacking from studies that probe the MDF using M giants
To further investigate the variation of the MDF we split the microlensed dwarf sample in latitude and then in longitude. Figures 14a and b show the MDFs when the microlensed dwarf sample is divided into two samples: one with stars closer than 3° to the plane, and one with stars farther than 3° from the plane. A two-sided KS-test (prob = 0.32, and D = 0.24) shows that the hypothesis that the two subsamples have been drawn from the same underlying distribution cannot be rejected. However, to the eye, two distributions appear to have distinctly different features, and not just a systematic shift which would as in the case of a vertical metallicity gradient. The outer sample appears bi-modal with a paucity of stars around solar metallicities. The inner sample on the other hand contain many stars around solar values. Both MDFs span the same metallicity range, but with different peaks, indicating a gradual change with b of the fraction of the different stellar population components (see also discussion in Babusiaux et al. 2010). When going towards the plane, the fraction of metal-poor and metal-rich stars drops off while the fraction of solar metallicity stars increases. The fraction of metal-poor stars appears to drop faster than the fraction of metal-rich stars. A tentative interpretation could be that there are three populations with different scale heights; could it be the thin disk, the thick disk, and a bar population? This interpretation would be in line with the results by Ness et al. (submitted) of their multicomponent MDF (see Fig. 12d). They interpret their [Fe/H] = +0.14 peak as belonging to the thin disk surrounding the bulge, the [Fe/H] = −0.23 peak as the true boxy/peanut bulge, and the [Fe/H] = −0.60 peak as the old thick disk, maybe being part of the bulge.
Figure 14e−f shows the MDFs for the microlensed dwarf stars split in two subsamples: one with |l| > 2 and one with |l| ≲ 2, respectively. The two-sided KS-test yields a similar result (prob = 0.32, and D = 0.24) as when splitting the sample in latitude, i.e. it is not possible by statistics to reject the claim that the two subsamples have been drawn from the same underlying distribution.
 |
Fig. 15 Age versus [Fe/H] for the microlensed dwarf sample. |
4.4. Stellar ages
Figure 15 shows the age–metallicity diagram for the microlensed bulge dwarfs. The metal-poor stars below [Fe/H] ≈ −0.4 are consistently old with ages around 10 to 12 Gyr. The metal-rich stars on the other hand show a large dispersion, with ages ranging from a few billion years up to ~13 Gyr.
The varying age distribution is further highlighted in Fig. 16 which shows the summed age distribution functions (ADF) from the individual stars in different metallicity bins (an ADF for an individual star include all possible ages from the isochrones that are encompassed by the uncertainties of the stellar parameters). The summed ADF of the most metal-rich population ([Fe/H] > 0.3) is dominated by young stars and peaks around 3−4 Gyr with a long tail towards higher ages. The ADF of the most metal-poor stars ([Fe/H] < −0.5) is on the other hand dominated by stars older that 10−12 Gyr. The ADF for the stars with −0.5 < [Fe/H] < 0 shows a mixed age structure with a broad peak around 5−9 Gyr. The ADF for the stars with −0.5 < [Fe/H] < 0 divides into two peaks, one coinciding with the metal-rich ADF (~4 Gyr) and one coinciding with the metal-poor ADF (10−12 Gyr).
 |
Fig. 16 Sums of individual age probability distribution functions for the microlensed dwarf sample for four metallicity bins (as indicated). |
4.5. On the presence of young stars in the bulge
 |
Fig. 17 Y2 isochrone plots for different metallicities. Four different ages are plotted (1, 5, 10, and 15 Gyr). In each plot, all 58 stars in microlensed dwarf sample are included, and those with [Fe/H] within ±0.25 dex of the isochrone metallicity have been marked by bigger red circles. |
The microlensed dwarf sample signals the existence of a significant fraction of low- and intermediate age stars in the bulge. As deep colour magnitude diagrams of the Galactic bulge (e.g., Holtzman et al. 1993; Ortolani et al. 1995; Feltzing & Gilmore 2000; Zoccali et al. 2003; Clarkson et al. 2011; Brown et al. 2010) show a faint red turn-off, indicative of an exclusively old and metal-rich population, this is a surprising result. For instance, the Clarkson et al. (2011) study of blue stragglers concluded that no more than 3% of the bulge population could be younger than 5 Gyr. In our sample of microlensed dwarf stars 13 out of 58 stars (23%) have ages lower than 5 Gyr. However, if the claimed age uncertainties are taken into account, we only have 3 stars out of 58 (~5%) that within 1σ have an age lower than 5 Gyr, which is more or less in agreement with the estimate from Clarkson et al. (2011). It should be noted that our sample does indeed contain 13 stars out of 58 (23%) that have an upper age limit below 9 Gyr, i.e. taking the age uncertainties into account these stars are for certain younger than 9 Gyr, pointing to a significant intermediate-age population of stars in the bulge. While it is feasible to hide a small number of metal-rich and young stars “inside” a red and old turn-off, but this cannot be large.
In Fig. 17 we show the microlensed dwarf stars plotted on top of isochrones with five different metallicities (as indicated on the top of the figure). Each plot contains all 58 microlensed dwarf stars, with the stars that have [Fe/H] within ±0.25 dex of the isochrone metallicity highlighted in red. It is evident that a single set of isochrones cannot be used for all stars. Especially at low metallicity, many of the stars that have higher metallicities fall outside the isochrones. If we were to assign a single set of isochrones to the sample, say the [Fe/H] = −0.2 set of isochrones, it would be difficult to claim a significant intermediate-age population in the bulge. As we have no stars in the upper left corner of the CMD, i.e., within the 1 to 5 Gyr isochrones, one would be tempted to claim that the bulge turn-off is around 10 Gyr and that the bulge population is all old. This is not the case, as can be seen in panel with the [Fe/H] = +0.3, many stars fall on young isochrones, stars that would be classified as old on a set of more metal-poor isochrones. This illustrates the importance of metallicity as a key ingredient in the determination of the age of the bulge. In many cases, such as in photometric studies, the metallicities of the stars are lacking, and a metallicity has to be assumed. The microlensed stars show that even though it is very difficult to claim stars younger than say 3−4 Gyr, it is clear that there is a substantial fraction of intermediate age (5 to 8 Gyr).
Nataf et al. (2011) found evidence from studying the red giant branch bump that the bulge should be enriched in helium. This led to an attempt by Nataf & Gould (2012) to reconcile the age situation by suggesting that the reason for the apparent miss-match in age between spectroscopic and photometric results can be related to an enhanced He/metals content, Y/Z, in the bulge as opposed to that in the Sun. As the stellar isochrones used to infer the ages are calculated using the standard He abundance the resulting spectroscopic ages might be erroneously too low. They discuss two systematic effects that arise as a consequence of an age offset that should be a function of the evolutionary state of the star. The first prediction was that this age offset, when applying standard log g − Teff isochrones, should be maximised on the subgiant branch and minimised around the main-sequence turn-off. The second prediction was that the difference between the true absolute magnitude and the spectroscopically inferred absolute magnitude should correlate positively with the spectroscopically inferred stellar mass. Using the, at the time, 26 available microlensed bulge dwarfs in Bensby et al. (2010b, 2011) they found a positive correlation between the difference in absolute magnitude and stellar mass for the stars with [Fe/H] > 0. This led Nataf & Gould (2012) to tentatively claim that the Y abundance should be higher in the bulge than in the Sun.
The plots in Fig. 19 are reproductions of the bottom plots in Figs. 2 and 3 of Nataf & Gould (2012) but with the now much expanded sample of 58 microlensed bulge dwarfs. Figures 18a and b show the stellar age versus log g for the metal-poor and the metal-rich bulge dwarfs, respectively. Figures 18c and d show the difference between the absolute I magnitude inferred from microlensing techniques and spectroscopy versus the spectroscopically inferred stellar mass for the metal-poor and metal-rich bulge dwarfs, respectively. It is clear that the trend with stellar mass that was found for the metal-rich bulge dwarfs is no longer present. Also, for the stars with sub-solar [Fe/H], where they found a negative trend with stellar mass, there is now a positive trend. If anything, this shows that a statistically significant sample of microlensed bulge dwarf stars is needed to firmly establish whether there are any trends or not.
 |
Fig. 18 a) and b) show the spectroscopic ages as a function of spectroscopic surface gravity for the metal-poor and metal-rich bulge dwarfs, respectively. c) and d) show the difference between absolute magnitude inferred from microlensing techniques and from spectroscopy as a function of inferred spectroscopic mass for the metal-poor and metal-rich bulge dwarfs, respectively. (Compare Figs. 2 and 3 in Nataf & Gould 2012). |
 |
Fig. 19 a) shows the predicted ratios (taken from Table 1 in Nataf & Gould (2012) for a true age of 10 Gyr) between the inferred spectroscopic age and the true age versus surface gravity for four different increases of the He abundance (ΔY, as indicated on the right-hand side). b) shows the age distribution for the microlensed dwarf sample. c) − e) show how the age distribution changes with ΔY if the ages are corrected following the relationships in a). |
Figure 19a shows the Nataf & Gould (2012) prediction (their Table 1) of the ratio between the spectroscopically inferred age to a “true” age versus surface gravity in the case of a true age of 10 Gyr. As can be seen it would be possible to derive a too low He abundance in the models responsible for some of the young stars we see in the bulge. For instance, old ages could be recovered for some of the stars with ages less the 5 Gyr that have log g ≲ 3.8 or log g ≳ 4.5 if the He abundance were increased by 0.1 or more. However, this is a dramatic change, and there would still be stars with ages around, or less than, 5 Gyr between 4 ≲ log g ≲ 4.3, where an increase in the He abundance will not have an equally large impact on the spectroscopically inferred stellar ages. In Fig. 19b we show the age distribution for the 58 micro lensed dwarf stars and Figs. 19c−e then show how this age distribution changes when the effects predicted in Fig. 19a are applied to the stars. Even though there are stars that become substantially older, it is not enough, even in the extreme case of ΔY = +0.098, to to contradict the conclusion that the age distribution has a substantial fraction of young and intermediate age stars.
There is other evidence, from AGB stars, of an intermediate age population in the bulge (e.g., van Loon et al. 2003; Cole & Weinberg 2002; Uttenthaler et al. 2007). van Loon et al. (2003) used near infrared CMDs from DENIS and ISOGAL to simultaneously derive the extinction, metallicity and age of individual stars. They found that the inner region (the inner 10°) are dominated by an old population (>7 Gyr), but that an intermediate age population is also present. This is consistent with their finding of a few hundred AGB stars with heavy mass loss. Using data from 2MASS, Cole & Weinberg (2002) were able to identify a population of carbon stars in the Galaxy that traced the bar. Their analysis finds that these stars very likely are of intermediate age. Uttenthaler et al. (2007) find evidence for Tc in a sub-sample of their pulsating AGB stars, indicative of third dredge up and a minimum stellar mass of 1.5 M⊙ which implies an upper age limit of 3 Gyr. Groenewegen & Blommaert (2005) also found Mira variables with ages of only 1−3 Gyr at latitudes between −1.2° to −5.8°. That stars have formed recently “around” the bar is not unexpected (e.g., Sánchez-Blázquez et al. 2011). Cole & Weinberg (2002) discuss the possibility that the carbon stars have wandered in to the bulge/bar region, but are unable to draw firm conclusions.
4.6. The Amax puzzle
 |
Fig. 20 [Fe/H] versus Amax for the microlensed dwarf sample. |
Using at the time 16 available microlensing events Cohen et al. (2010) reported an unexpected correlation between the metallicity of the microlensed star and the maximum magnification of the microlensing event in the sense that metal-rich stars had higher maximum magnifications than metal-poor ones. Several possibilities were investigated but none could satisfactory resolve the situation.
Figure 20c shows [Fe/H] versus Amax for the now much larger sample of microlensed dwarf stars. Compared to when the analysis by Cohen et al. (2010) was done, the sample now contains high-magnification events at low metallicities and low-magnification events at high metallicities. However, looking at the histograms in Figs. 20a and b, it is clear that the metal-rich part of the sample contains a higher fraction of high-magnification events than the metal-poor part. Classifying a microlensing event with Amax ≥ 70 as a high-magnification event, and otherwise a low-magnification event (vertical dotted line in Fig. 20), the metal-rich sample contain 84% high-mag events, compared to 51% for the metal-poor stars. As it is highly unlikely that the maximum magnification should have any dependence on the chemical composition of the background star, this correlation must be a result of some selection bias or being due to that the environment of the metal-rich stars is different from the environment of the metal-poor stars. In the following section we will investigate how big such a bias might be and whether the differences in the Amax distributions between the metal-rich and metal-poor samples can be accounted for.
4.7. Sampling bias?
The selection of candidate microlensed bulge dwarfs for spectroscopy is made from the OGLE and MOA surveys, which image through I and R/I filters, respectively. The cutoff in brightness for effective high dispersion spectroscopy even with 8−10 m telescopes, given that target of opportunity observations cannot exceed 1 or 2 h, is I brighter than about 15.0 mag.
We attempt to model our sampling process to look for selection effects. We assume a distance to the bulge of 8.2 kpc and a mean extinction of AI ≈ 1.0. We adopt version 2 of the Yale-Yonsei evolutionary tracks and isochrones (Yi et al. 2003; Demarque et al. 2004) and select five representative choices of [Fe/H], −0.90, −0.43, +0.05, +0.39, and +0.60 dex. Stars with subsolar metallicities are assumed to have [α/Fe] = +0.3, while higher metallicity stars have no α-enhancement. We adopt the Salpeter IMF.
These isochrones are normalized to have 1000 stars in their initial mass function with masses between 0.5 and 1.0 M⊙. The summed stellar mass for each our five metallicity choices for isochrones with age 4 Gyr was compared; there is a total range of 2%, which we can ignore for present purposes.
If we assume that all the bulge stars have the same age, irrespective of metallicity, then at ages older than ~5 Gyr, the main sequence turnoff is ~0.4 mag fainter for bulge dwarfs with [Fe/H] super-solar than it is for dwarfs with −0.9 ≲ [Fe/H] ≲ −0.5. This would suggest that in the microlensed sample, the intrinsically fainter high-metallicity dwarfs would be under-represented.
However, a key result of this paper is the apparent dependence of mean age of the bulge dwarfs with metallicity (see Fig. 15). If we adopt this as true, and allow the stellar mean age to decrease as the metallicity increases, with the most metal-poor stars having an age of 12 Gyr and the most metal-rich ones 4 Gyr, a different result emerges; the younger population of super-solar metal-rich bulge dwarfs then has a main sequence turnoff that is essentially identical to that of the more metal-poor, older bulge populations, with a substantial blue hook as is shown in Fig. 21. This is manifested in the star counts in the regime 2.2 < MI < 3.8, which are dominated by the youngest, most metal-rich bulge turnoff region stars. In this regime, the star counts from this young population are a factor of ~2 or more higher than those from populations with ages of 10 to 12 Gyr (see Fig. 22).
 |
Fig. 21 Y2 isochrones for five different metallicities with different mean ages that decrease with increasing metallicity. |
 |
Fig. 23 Number of stars along the isochrones shown in Fig. 21, but now with microlensing of the sample included. |
When we simulate lensing of this sample, this difference of a factor of two is smoothed out somewhat, but is still present (see Fig. 23). At MI(lensed) = −0.6, corresponding to the limiting magnitude of our spectroscopic sample, the youngest, most metal-rich population has star counts which are about 50% higher than those of any of the older, more metal-poor populations with the same total stellar mass. Hence we would overestimate the fractional contribution to the total bulge population of young, metal-rich stars. For a system of uniform age 10 Gyr, the super-solar stars would be under-represented in the lensed star counts by about a factor of 30%, and would then be more difficult to detect in our microlensed bulge dwarf sample.
Thus, assuming the adopted metallicity – age relation shown in Fig. 15 is valid, the fraction of the bulge stellar population which is metal-rich and young is over-estimated in our current microlensed bulge dwarf sample of 58 stars by ~50%. Note that a turnoff star from the lower metallicity populations with MI ≈ +3.8 has to be lensed by a factor of 55 to be bright enough to be included in the spectroscopic microlensed bulge stellar sample.
Next, we simulate the distribution of Amax in an attempt to determine whether selection effects arising from the age–metallicity relation of Fig. 15 could be producing the apparent deficiency of low metallicity, high Amax stars seen in Fig. 20.
Our simulation for Amax is shown in Fig. 24. We find that there is a strong trend for the young, metal-rich population to dominate over the more metal-poor and older populations which is strongest at the lowest magnifications and decreases towards higher magnification. Since there are more intrinsically luminous stars in the former, they will dominate at the lower magnification levels. At high magnification, the main sequence turnoff can be boosted into the observed sample for the entire range of metallicities probed, and hence the bias favoring the highest metallicity young population is reduced. We thus deduce that our sample of microlensed bulge dwarfs is biased in favor of high-metallicity young stars, and hence our derived MDF is also biased. However, it does not appear possible to reproduce the apparent relative absence of low-metallicity high magnification events with our simulation.
4.8. Abundance trends
 |
Fig. 25 Abundance trends with Fe as reference element for the microlensed dwarf sample. Circles have been scaled with the ages of the stars. |
 |
Fig. 26 Abundance trends with Mg as reference element for the microlensed dwarf sample. Circles have been scaled with the ages of the stars. |
 |
Fig. 27 Abundance trends for the α-elements Mg, Si, Ca, and Ti. Left-hand-side panels show [X/Fe] versus [Fe/H], and right-hand panels show [Fe/X] versus [X/H]. Filled grey circles mark the microlensed bulge dwarfs and the red and blue circles are nearby thick and thin disk dwarf stars, respectively (from Bensby et al. 2003, 2005, and in prep.). |
4.8.1. General appearance for 12 elements
The plots in Figs. 25 and 26 show the abundance trends for O, Na, Mg, Al, Si, Ca, Ti, Cr, Ni, Fe, Zn, Y, and Ba for the 58 microlensed bulge dwarfs. In Fig. 25 Fe is the reference element and in Fig. 26 Mg is the reference element. In all plots the sizes of the circles have been scaled with the ages of the stars (larger circles equal higher ages). The α-element plots in Fig. 25 (i.e., [O, Mg, Si, Ca, Ti] versus [Fe/H]) show a plateau of elevated [α/Fe] abundance ratios at metallicities below [Fe/H] ≈ −0.4, signalling fast chemical enrichment by massive stars. These stars are all old. The α-trends then decline towards solar values, and even though most of the stars are old, there are one or two that start to show up with lower ages. At super-solar metallicities the trends generally level out, meaning that there is some kind of equilibrium between SN II and SN Ia enrichment. The age structure is also very complex with a mix of stars at all ages, 2 to 15 Gyr. What is notable is that the abundance trends are very well-defined and generally have very low scatter.
By using an α-element that mainly comes from a single source (in this case core-collapse supernovae), one might get a clearer picture on the chemical history of a stellar population. The “x-axis” could then be interpreted as a proxy for time. Hence, Fig. 26 shows the abundance trends again, but now with Mg as the reference element. Especially interesting plots are now the Fe, Cr, and Ni plots where we can see flat, under-abundant, [(Fe, Ni, Cr)/Mg] trends for low [Mg/H] values. This is consistent with rapid enrichment by massive stars. The [(Fe, Ni, Cr)/Mg] ratios start to increase around [Mg/H] ≈ −0.2 to −0.1, signalling that low-mass stars are becoming the dominant source for chemical enrichment of the interstellar medium.
4.8.2. Fast enrichment − revising the position of the knee
In Bensby et al. (2010b) we noted that even though the metal-poor bulge dwarf stars generally follow the abundance trends outlined by the thick disk it was also apparent that they were slightly more α-enhanced, mainly being located on the upper rim of the thick disk abundance trends. Figure 27 shows the abundance trends for the α-elements Mg, Si, Ca, and Ti with the nearby thick disk stars from (Bensby et al. 2003, 2005, and in prep.) included for comparison purposes. As found by Bensby & Feltzing (2012), discriminating between thin and thick disk stars based on stellar age appears to produce “cleaner” results when applied to local samples, and we have therefore marked stars with ages greater than 9 Gyr (and age uncertainties less than 4 Gyr) as thick disk stars (red circles), and stars with ages less than 7 Gyr (and age uncertainties less than 4 Gyr) as thin disk stars (blue dots).
At low [Fe/H], the metal-poor bulge dwarfs show an α-to-iron ratio that is similar to what is seen the nearby thick disk (which also is similar to what is observed in the stellar halo, see, e.g., Nissen & Schuster 2010). However, it is possible that the declining [α/Fe] ratios (or rising [Fe/α] ratios) occur at slightly higher [Fe/H] (or [α/H]) than for the local thick disk. As we now have many more microlensed dwarf stars around and slightly below solar [Fe/H], where the thick disk [α/Fe] trends decline, we are more confident to claim that this slight shift might be real. This slight shift in the position of the “knee” is clearly evident in Mg and Ti, slightly less in Si, and barely in Ca. If it is real it can be interpreted as being due to the bulge having experienced a faster enrichment than the local thick disk, leading to the onset of enrichment from low-mass stars occur at higher metallicities.
Does this mean that the possible connection between the bulge and the thick disk becomes weaker? As of now we are only able to compare the bulge with the thick disk in the solar neighbourhood while it would be desirable to compare with the thick disk in the inner regions of the Galaxy. The only such study to date is the one by Bensby et al. (2010a) but their sample of 44 red giants is unfortunately too small to whether or not the inner thick disk is different from the nearby thick disk. If there is a radial metallicity gradient in the thick disk it would mean that the inner thick disk regions have experienced a more rapid evolution, and hence pushed the “knee” to higher metallicities. What we see in the bulge is a “knee” that starts to decline perhaps 0.1 dex higher in [Fe/H] than seen in the nearby thick disk.
5. Discussion
The first microlensed dwarf stars that were studied provided a real surprise, an MDF heavily skewed to super-solar metallicities and significantly different from what had been found from giants (Johnson et al. 2007; Cohen et al. 2008). The difference was somewhat elevated by the very first of our VLT ToO observations from which we found many of the microlensed dwarfs to have super-solar metallicities. But as the number of microlensing events grew we started to also get metal-poor dwarfs in larger numbers, and a clearly bi-modal MDF emerged (Bensby et al. 2010b, 2011). That MDF was still very different from the best MDF from high-resolution spectra of a representative sample of bulge giants (Zoccali et al. 2008). A recent re-analysis of the Zoccali et al. (2008) data by Hill et al. (2011) and further increased number statistics of the microlensed dwarf stars has changed this, and there is now good agreement between the overall appearance of the MDFs traced by microlensed dwarfs and the giant stars in the Galactic bulge (see Figs. 12 and 13).
The MDF is an important constraint to models of galactic chemical evolution (e.g., Matteucci & Francois 1989). The MDF of the Galactic bulge is best probed through the detailed elemental abundances of stars. Most studies use the intrinsically bright red giant stars for this. The first studies showed a metal-rich population with a somewhat broadened distribution of [Fe/H]. Coupled with the high α abundances this pointed to a short formation time-scale (Rich 1988; McWilliam & Rich 1994; Fulbright et al. 2007). However, the mean [Fe/H] changed between these studies leaving substantial room for interpretation. Recently, with the arrival of the multi-fibre spectrograph FLAMES (Pasquini et al. 2002) on the VLT, it has become feasible to probe further down the red giant branch and reach warmer stars that are less prone to evolutionary effects (compare lack of metal-rich M giants in Rich et al. 2012) and also to the red clump which should give a reliable tracer of the MDF.
Chemical evolution models have been created to attempt to explain the broad spread in [Fe/H] and to explain the fact that the bulge appears to have two populations: one with a low mean [Fe/H] and one with super-solar [Fe/H]. For example, the two-component chemical evolution model by Tsujimoto & Bekki (2012) is able to explain the [Ba/Mg] versus [Fe/H] pattern seen in the dwarf stars (Fig. 28) as well as a bi-modal MDF. They also find that a top-heavy IMF is essential to explain the high metallicity of the metal-rich component of the MDF.
 |
Fig. 28 [Ba/Mg] versus [Fe/H] for the microlensed dwarf sample. The two-component bulge model by Tsujimoto & Bekki (2012) is shown (blue dashed line is the first component that forms quickly, and red solid line is the second component that forms from pre-enriched gas). |
Grieco et al. (2012) also explores a multi-component model of the chemical evolution of the Galactic bulge. They model a two component bulge with one representing the classical bulge and the other the pseudo-bulge (bar population?). One prediction from their model is that there could be an abundance gradient within the classical, spherical bulge but that also the differences between the chemical evolution of the spherical component and the bar component could be (erroneously) interpreted as a gradient.
In simulations of the formation and evolution of the Milky Way in a cosmological context, the star formation of the bulge lasts for longer than a single starburst (Rahimi et al. 2010; Kobayashi & Nakasato 2011; Scannapieco et al. 2011; Doménech-Moral et al. 2012). For example, while most of the bulge stars in Kobayashi & Nakasato (2011) are old (80% > 10 Gyr, and 90% > 8 Gyr), 10% of stars form later, at super-solar metallicities. While Kobayashi & Nakasato (2011) simulated a single history for a MW-like galaxy, Scannapieco et al. (2011) and Doménech-Moral et al. (2012) each modelled several halo histories. The galaxies showed different star formation histories for all components, and it is therefore likely that star formation histories are not universal in each galaxy type. However, several of their simulationsshow extended star formation histories for the bulge, although the interpretation of Scannapieco et al. (2011) is complicated by the fact that their “inner spheroid” extends ~10 kpc. While it is not yet clear how well these simulations model the behaviour of baryons through their sub-grid physics, that some fraction of the bulge consists of stars younger than 8 Gyr is not surprising within the framework of current theories.
So what is the bulge?
Where do all the observational evidence point to? One thing is clear, there is overwhelming evidence for more than one population in the bulge. Whether it is two, or even more, it is a fact that the inner region of the Galaxy is where the major Galactic stellar populations (if they all exist in this region) should meet and overlap. For instance, the interpretation by Ness et al. (submitted) of their multicomponent MDF is that the [Fe/H] = +0.14 peak belongs to the thin disk surrounding the bulge, the [Fe/H] = −0.23 peak is the true boxy/peanut bulge, and the [Fe/H] = −0.60 peak is the old thick disk, which may or may not be part of the bulge. Adding the Galactic bar (possibly formed from disk stars), and the influence that it has on its surroundings, the situation is truly intricate. However, at the same time the metal-poor bulge shows abundance trends that are very well-defined with low scatter, which could argue against a bulge composed of more than two populations (as proposed by Ness et al., submitted, see Fig. 12d).
As noted in Sect. 4.8.2, the α-element trends for the metal-poor bulge dwarfs now appear to be slightly different from those of the nearby thick disk, possibly implying that the metal-poor bulge population experienced a somewhat more intense star formation than the local thick disk. This does not necessarily weaken a possible connection between the metal-poor bulge component and the thick disk. It might just instead be a reflection of the more intense star formation in the inner regions of the Galaxy than in and around the solar circle.
The abundance trends seen for the metal-rich bulge is partly consistent with what is seen for metal-rich nearby thin disk dwarf stars (e.g., Bensby et al. 2003, 2005; Reddy et al. 2006; Bensby et al. 2007b), although disk stars with metallicities higher than [Fe/H] ≳ +0.4 are rarely seen. Given the wide range in ages, the metal-rich bulge could be the most complex region in the Galaxy, possibly hosting stars from several populations.
A bimodal age distribution in the bulges of external spirals galaxies with bars has been recently found through a stellar population synthesis analysis by Coelho & Gadotti (2011), with mean ages of 4.7 and 10.4 Gyr. Interestingly, unbarred galaxies do not show this bimodal distribution, perhaps implying that bars have the effect of rejuvenating bulges. The above results are in line with our findings based on Galactic bulge dwarf stars, and a larger sample will allow us to obtain firmer results for comparison with external bulges.
6. Summary
In this study we have presented a detailed elemental abundance analysis of 32 microlensed dwarf and subgiant stars in the bulge. Together with the previous sample of 26 microlensed bulge dwarfs from Bensby et al. (2010b, 2011) the sample now contains 58 stars. In summary, the findings and main results from this data set are:
-
The metallicities span the full range between [Fe/H] = −2 to +0.6. The MDF that appeared clearly bi-modal, even with a paucity of stars around [Fe/H] = 0, when based on the 26 stars in Bensby et al. (2011), is now less so. The overall shape of the MDF is now similar to the MDF in Baade’s window found by Hill et al. (2011), as traced by both red giants and red clump giants. Furthermore, signatures of more than two components is starting to emerge in the microlensed dwarf star MDF.
-
The microlensed dwarf stars more metal-poor than [Fe/H] ≲ −0.4 are all old with ages around or greater than 10 Gyr. The more metal-rich stars, on the other hand, have a wide age distribution with a significant fraction of stars having ages lower than 5 to 6 Gyr, and quite a large number of stars with intermediate ages around 5−7 Gyr. These are essentially indistinguishable from an old turn-off when the metallicities are unknown. We have investigated in some detail whether an He enriched bulge, as proposed by Nataf & Gould (2012), could explain the large fraction of young stars in the microlensed dwarf sample, but the effects are not large enough. We have also investigated sampling biases and find that our microlensed dwarf sample could be biased in the sense that the number of young metal-rich stars is over-estimated (perhaps by as much as 50%). In any case, neither sampling bias, nor a He enriched bulge, can fully account for the large fraction of young and intermediate age stars in the microlensed bulge dwarf star sample.
-
With the now much expanded sample of 58 stars we see that the metal-poor bulge population have abundance trends slightly different from what is observed in the nearby Galactic thick disk. The “knee” in the [α/Fe] − [Fe/H] trends occurs at a slightly higher metallicity in the bulge, indicating that the metal-poor bulge component has experienced a somewhat faster star formation rate.
-
The microlensed bulge dwarfs with solar [Fe/H] show abundance trends similar to what is seen in the nearby thin and (metal-rich) thick disks. If the bar population is formed from disk material, this is what could be expected. The very metal-rich bulge dwarfs ([Fe/H] ≳ +0.35) are difficult to compare to disk stars, as essentally no disk stars have been observed at such high metallicities. They do, however, appear to follow an extension of the abundance trends outlined by the metal-rich disk stars.
Even though it is difficult to pinpoint the exact origin of the bulge, observational evidence now clearly indicates that the bulge has a complex structure with wide age and metallicity distributions. Combined with the cylindrical rotation of the bulge, the bulge appears to be a conglomerate of Galactic stellar populations under the influence of the bar.
Available at http://obs.carnegiescience.edu/Code/mike
The empirical microturbulence relation by Maria Bergemann was derived for the Gaia-ESO public spectroscopic survey (Gilmore et al. 2012) and will be published in one of her first science papers based on Gaia-ESO data.
Obtained from http://leda.univ-lyon1.fr.
Acknowledgments
We are grateful to and thank Patrick Baumann who obtained the MIKE spectrum for MOA-2011-BLG-234S, Julio Chaname who obtained the MIKE spectrum for MOA-2011-BLG-278S, G.W. Marcy who obtained the HIRES spectra for MOA-2011-BLG-191S and OGLE-2012-BLG-0816S, and Elizabeth Wylie and Mario Mateo who obtained the MIKE spectrum for OGLE-2012-BLG-1279S. We would also like to thank Bengt Gustafsson, Bengt Edvardsson, and Kjell Eriksson for usage of the MARCS model atmosphere program and their suite of stellar abundance programs. T.B. was funded by grant No. 621-2009-3911 from The Swedish Research Council. S.F. was partly funded by grant No. 2008-4095 from The Swedish Research Council. Work by J.C.Y. was supported by an SNSF Graduate Research Fellowship under Grant No. 2009068160. A.G. and J.C.Y. acknowledge support from NSF AST-1103471. M.A. gratefully acknowledges funding from the Australian Research Council (FL110100012). J.L.C. is grateful to NSF award AST-0908139 for partial support. S.L. reasearch is partially supported by the INAF PRIN grant “Multiple populations in Globular Clusters: their role in the Galaxy assembly” J.M. thanks support from FAPESP (2010/50930-6), USP (Novos Docentes) and CNPq (Bolsa de produtividade). A.G.-Y. acknowledges support by the Lord Sieff of Brimpton Fund. The OGLE project has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement No. 246678 to AU. Work by C.H. was supported by the Creative Research Initiative Program (2009-0081561) of National Research Foundation of Korea. T.B, S.F., and J.A.J. are grateful to the Aspen Center for Physics and the NSF Grant 1066293 for hospitality during the “Galactic bulge and bar” workshop in August 2011, where many inspiring discussions were held.
References
- Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Gustafsson, B., Kiselman, D., & Eriksson, K. 1997, A&A, 318, 521 [NASA ADS] [Google Scholar]
- Athanassoula, E. 2005, MNRAS, 358, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballero, S. K., Kroupa, P., & Matteucci, F. 2007, A&A, 467, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballester, P., Modigliani, A., Boitquin, O., et al. 2000, The Messenger, 101, 31 [NASA ADS] [Google Scholar]
- Bensby, T., & Feltzing, S. 2012, in Eur. Phys. J. Web Conf., 19, 4001 [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Oey, M. S., Feltzing, S., & Gustafsson, B. 2007a, ApJ, 655, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Zenn, A. R., Oey, M. S., & Feltzing, S. 2007b, ApJ, 663, L13 [CrossRef] [Google Scholar]
- Bensby, T., Johnson, J. A., Cohen, J., et al. 2009, A&A, 499, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D., & Meléndez, J. 2010a, A&A, 516, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Johnson, J. A., et al. 2010b, A&A, 512, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernstein, R., Shectman, S. A., Gunnels, S. M., Mochnacki, S., & Athey, A. E. 2003, in Proc. SPIE, 4841, eds. M. Iye, & A. F. M. Moorwood, 1694 [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Sahu, K., Anderson, J., et al. 2010, ApJ, 725, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavallo, R. M., Cook, K. H., Minniti, D., & Vandehei, T. 2003, in SPIE Conf. Ser. 4834, ed. P. Guhathakurta, 66 [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W. I., Sahu, K. C., Anderson, J., et al. 2011, ApJ, 735, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, P., & Gadotti, D. A. 2011, ApJ, 743, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Huang, W., Udalski, A., Gould, A., & Johnson, J. A. 2008, ApJ, 682, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Thompson, I. B., Sumi, T., et al. 2009, ApJ, 699, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Gould, A., Thompson, I. B., et al. 2010, ApJ, 711, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A., & Weinberg, M. D. 2002, ApJ, 574, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, Proc. SPIE 4008, 534 [Google Scholar]
- Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Doménech-Moral, M., Martínez-Serrano, F. J., Domínguez-Tenreiro, R., & Serna, A. 2012, MNRAS, 421, 2510 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, C. R., Johnson, J. A., Dong, S., et al. 2010, ApJ, 709, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Feltzing, S., & Gilmore, G. 2000, A&A, 355, 949 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, E. M., Demarque, P., & King, C. R. 1987, The revised Yale isochrones and luminosity functions [Google Scholar]
- Grieco, V., Matteucci, F., Pipino, A., & Cescutti, G. 2012, A&A, 548, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., & Blommaert, J. A. D. L. 2005, A&A, 443, 143 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, A. 1975, A&A, 42, 407 [NASA ADS] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holtzman, J. A., Light, R. M., Baum, W. A., et al. 1993, AJ, 106, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, C. D., Rich, R. M., Clarkson, W., et al. 2009, ApJ, 702, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Gal-Yam, A., Leonard, D. C., et al. 2007, ApJ, 655, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Gaudi, B. S., Sumi, T., Bond, I. A., & Gould, A. 2008, ApJ, 685, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, C., & Nakasato, N. 2011, ApJ, 729, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Sneden, C., Langer, G. E., & Prosser, C. F. 1992, AJ, 104, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Kunder, A., Koch, A., Rich, R. M., et al. 2012, AJ, 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lebzelter, T., Heiter, U., Abia, C., et al. 2012, A&A, 547, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Brocato, E. 1990, ApJ, 365, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Zoccali, M. 2010, ApJ, 724, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Nataf, D. M., & Gould, A. P. 2012, ApJ, 751, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Udalski, A., Gould, A., & Pinsonneault, M. H. 2011, ApJ, 730, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2012, ApJ, submitted [arXiv:1208.1263] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2012, ApJ, 756, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noguchi, M. 1999, ApJ, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Prugniel, P., Maubon, G., & Simien, F. 2001, A&A, 366, 68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahimi, A., Kawata, D., Brook, C. B., & Gibson, B. K. 2010, MNRAS, 401, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., Stephens, A. W., Frogel, J. A., & DePoy, D. L. 2000, AJ, 120, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M. 1988, AJ, 95, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Reitzel, D. B., Howard, C. D., & Zhao, H. 2007, ApJ, 658, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2012, ApJ, 746, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, R., Hempel, M., Alonso-García, J., et al. 2010, The Messenger, 141, 24 [NASA ADS] [Google Scholar]
- Saito, R. K., Zoccali, M., McWilliam, A., et al. 2011, AJ, 142, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, R. K., Minniti, D., Dias, B., et al. 2012, A&A, 544, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Ocvirk, P., Gibson, B. K., Pérez, I., & Peletier, R. F. 2011, MNRAS, 415, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., White, S. D. M., Springel, V., & Tissera, P. B. 2011, MNRAS, 417, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., Rich, R. M., Kormendy, J., et al. 2010, ApJ, 720, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Mateo, M., Udalski, A., et al. 1994, ApJ, 429, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Eyer, L., & Woźniak, P. R. 2003, MNRAS, 340, 1346 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Kamiya, K., Bennett, D. P., et al. 2011, Nature, 473, 349 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thévenin, F., & Idiart, T. P. 1999, ApJ, 521, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, T., & Bekki, K. 2012, ApJ, 747, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J. 2010, ApJ, 708, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Udalski, A., Szymanski, M., Kaluzny, J., et al. 1994, Acta Astron., 44, 227 [NASA ADS] [Google Scholar]
- Uttenthaler, S., Hron, J., Lebzelter, T., et al. 2007, A&A, 463, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uttenthaler, S., Schultheis, M., Nataf, D. M., et al. 2012, A&A, 546, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loon, J. T., Gilmore, G. F., Omont, A., et al. 2003, MNRAS, 338, 857 [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in SPIE Conf. Ser. 2198, eds. D. L. Crawford, & E. R. Craine, 362 [Google Scholar]
- Wagner, R. M., Dong, S., Bensby, T., et al. 2012, ATel, 4157, 1 [NASA ADS] [Google Scholar]
- Weiland, J. L., Arendt, R. G., Berriman, G. B., et al. 1994, ApJ, 425, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, R. F. G., & Gilmore, G. 1992, AJ, 104, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Summary of the 32 microlensed bulge dwarf stars new in this study (sorted by observation date).
Measured equivalent widths and calculated elemental abundances for all 58 microlensed bulge dwarfs.
Elemental abundance ratios, errors in the abundance ratios, and number of lines used, for all 58 microlensed dwarf stars.
Stellar parameters and radial velocities for all 58 stars (sorted by metallicity).
Stellar ages, masses, and colours as determined from spectroscopy and microlensing techniques for all 58 stars.
All Figures
 |
Fig. 1 Light curves for the first 16 of the 32 new microlensing events. Each plot has a zoom window, showing the time intervals when the source stars were observed with high-resolution spectrographs. In each plot the un-lensed magnitude of the source star is also given (IS). |
| In the text | |
 |
Fig. 2 Light curves for the remaining 16 of the 32 new microlensing events. Each plot has a zoom window, showing the time intervals when the source stars were observed with high-resolution spectrographs. In each plot the un-lensed magnitude of the source star is also given (IS). |
| In the text | |
 |
Fig. 3 Comparison of stellar parameters before and after implementation of NLTE corrections for Fe i lines. The differences are NLTE values minus LTE values and mean differences and σ are indicated in each panel. |
| In the text | |
 |
Fig. 4 All 58 microlensed dwarf stars plotted on the α-enhanced isochrones from Demarque et al. (2004). The metallicity of the stars in each panel is within ±0.05 dex of the isochrone metallicity. In each plot the solid lines represent isochrones with ages of 0.1, 5, 10, 15, and 20 Gyr. Dotted lines are isochrones in steps of 1 Gyr. Error bars represent the uncertainties in Teff and log g as given in Table 4. Note that the age determinations reported in Table 5 are based on probability distribution functions as described in Bensby et al. (2011). |
| In the text | |
 |
Fig. 5 a) Difference between microlensing colours and the spectroscopic colours versus spectroscopic Teff. b) Difference between the absolute I magnitudes from microlensing techniques and from spectroscopy versus stellar mass (derived from spectroscopy). Error bars represent the uncertainties in the spectroscopic values. The microlensing values used in the plots are based on the assumption that the bulge red clump has (V − I)0 = 1.06 and MI = −0.12. Stars with Teff > 5500 K are marked by filled circles, otherwise by open circles. |
| In the text | |
 |
Fig. 6 Differential reddening versus the absolute value of the difference between microlensing colours and spectroscopic colours. The differential reddening values for the individual sight lines are taken from Nataf et al. (2012). Stars with Teff > 5500 K are marked by filled circles, otherwise by open circles. |
| In the text | |
 |
Fig. 7 a) Filled black circles mark the spectroscopic values, open circles microlensing values. Dash-dotted blue line show the Casagrande et al. (2010)Teff-colour transformation, dashed green lines the Green et al. (1987) transformation (for three different log g), and the solid red lines the Lejeune et al. (1998) transformation (for three different log g). b) Differences between Casagrande et al. (2010) and Lejeune et al. (1998). c) Differences between Green et al. (1987) and Lejeune et al. (1998). The markers in b) and c) show the differences that should be applied to the microlensed dwarfs if the Casagrande et al. (2010) and Green et al. (1987) trandformations had been applied instead of the one from Lejeune et al. (1998). |
| In the text | |
 |
Fig. 8 Illustration to see how well the spectroscopic temperatures (full blue lines) and temperatures from microlensing techniques (dashed red lines) reproduce the observed wing profiles of the Hα line at 6563 Å for the 32 new microlensed bulge dwarfs. Note that no estimate of the temperature from microlensing techniques is available for OGLE-2011-BLG-1410S. The stars are sorted by metallicity. |
| In the text | |
 |
Fig. 9 Fitting of the Hα wing profiles to find the effective temperatures for OGLE-2011-BLG-0969S and OGLE-2012-BLG-1156S. The insets show the summed absolute values of the residuals that was minimised to find the best fitting temperature. |
| In the text | |
 |
Fig. 10 Positions on the sky for the microlensed dwarf sample. The bulge contour lines based on observations with the COBE satellite are shown as solid lines (Weiland et al. 1994). The positions of Baade’s window (BW), the Galactic centre (GC), and three of the ARGOS survey fields (see Ness et al. 2012) are delineated. The dotted lines are concentric circles in steps of 2°. |
| In the text | |
 |
Fig. 11 Galactocentric velocity versus Galactic longitude and latitude for the microlensed dwarf sample (grey circles). The black circles represent the mean radial velocity and the 1σ rms dispersion for the microlensed bulge dwarfs, binned into 3° wide bins. The results from the BRAVA survey (Rich et al. 2007; Kunder et al. 2012) have been over-plotted, and the different colours (red, cyan, and green) represent the values at different l and b as given in the plots. |
| In the text | |
 |
Fig. 12 a) Metallicity distribution for the microlensed dwarf sample (white dashed line shows the distribution of the 26 microlensed dwarf stars from Bensby et al. 2011); b) 166 red giant stars in Baade’s window from Hill et al. (2011); c) 220 red clump stars in Baade’s window from Hill et al. (2011); d) 1813 red giant stars with from the ARGOS survey fields at (l,b) = (0, −5), (5, −5), (−5, −5) from Ness et al. (submitted). e) 363 red giants at (l,b) = (0, −10) from Uttenthaler et al. (2012); The curved lines in a)–d) represent generalised histograms. Dotted vertical lines mark the peaks claimed by Ness et al. (submitted) in d). |
| In the text | |
 |
Fig. 13 Cumulative histograms and the Kolmogorov-Smirnow tests between the microlensed dwarf sample and the giant star samples shown in Fig. 12. The solid thicker red line shows the microlensed bulge dwarfs, (b) the RGB sample from Hill et al. (2011), (c) the red clump sample from Hill et al. (2011), (d) the red clump sample from ARGOS (Ness et al., submitted), and (e) the RGB sample from Uttenthaler et al. (2012). |
| In the text | |
 |
Fig. 14 a) and b) show the MDFs when the microlensed dwarf sample is split into stars farther from the plane (|b| ≳ 3), and closer to the plane (|b| < 3), respectively. c)–d) the MDFs when sample is split into stars farther from the centre (|l| > 2), and closer to the centre (|l| ≲ 2), respectively. The curved lines represent generalised histograms. |
| In the text | |
 |
Fig. 15 Age versus [Fe/H] for the microlensed dwarf sample. |
| In the text | |
 |
Fig. 16 Sums of individual age probability distribution functions for the microlensed dwarf sample for four metallicity bins (as indicated). |
| In the text | |
 |
Fig. 17 Y2 isochrone plots for different metallicities. Four different ages are plotted (1, 5, 10, and 15 Gyr). In each plot, all 58 stars in microlensed dwarf sample are included, and those with [Fe/H] within ±0.25 dex of the isochrone metallicity have been marked by bigger red circles. |
| In the text | |
 |
Fig. 18 a) and b) show the spectroscopic ages as a function of spectroscopic surface gravity for the metal-poor and metal-rich bulge dwarfs, respectively. c) and d) show the difference between absolute magnitude inferred from microlensing techniques and from spectroscopy as a function of inferred spectroscopic mass for the metal-poor and metal-rich bulge dwarfs, respectively. (Compare Figs. 2 and 3 in Nataf & Gould 2012). |
| In the text | |
 |
Fig. 19 a) shows the predicted ratios (taken from Table 1 in Nataf & Gould (2012) for a true age of 10 Gyr) between the inferred spectroscopic age and the true age versus surface gravity for four different increases of the He abundance (ΔY, as indicated on the right-hand side). b) shows the age distribution for the microlensed dwarf sample. c) − e) show how the age distribution changes with ΔY if the ages are corrected following the relationships in a). |
| In the text | |
 |
Fig. 20 [Fe/H] versus Amax for the microlensed dwarf sample. |
| In the text | |
 |
Fig. 21 Y2 isochrones for five different metallicities with different mean ages that decrease with increasing metallicity. |
| In the text | |
 |
Fig. 22 Number of stars along the isochrones shown in Fig. 21. |
| In the text | |
 |
Fig. 23 Number of stars along the isochrones shown in Fig. 21, but now with microlensing of the sample included. |
| In the text | |
 |
Fig. 24 Simulated magnification distribution for the isochrones shown in Fig. 21. |
| In the text | |
 |
Fig. 25 Abundance trends with Fe as reference element for the microlensed dwarf sample. Circles have been scaled with the ages of the stars. |
| In the text | |
 |
Fig. 26 Abundance trends with Mg as reference element for the microlensed dwarf sample. Circles have been scaled with the ages of the stars. |
| In the text | |
 |
Fig. 27 Abundance trends for the α-elements Mg, Si, Ca, and Ti. Left-hand-side panels show [X/Fe] versus [Fe/H], and right-hand panels show [Fe/X] versus [X/H]. Filled grey circles mark the microlensed bulge dwarfs and the red and blue circles are nearby thick and thin disk dwarf stars, respectively (from Bensby et al. 2003, 2005, and in prep.). |
| In the text | |
 |
Fig. 28 [Ba/Mg] versus [Fe/H] for the microlensed dwarf sample. The two-component bulge model by Tsujimoto & Bekki (2012) is shown (blue dashed line is the first component that forms quickly, and red solid line is the second component that forms from pre-enriched gas). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


