| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219038 | |
| Published online | 26 October 2012 | |
The Swift X-ray Telescope Cluster Survey: data reduction and cluster catalog for the GRB fields⋆
1
INAF, Osservatorio Astronomico di Trieste, via G.B. Tiepolo
11,
34131
Trieste,
Italy
e-mail: tundo@oats.inaf.it
2
INAF, Osservatorio Astronomico di Brera, via Brera 28,
20121
Milano,
Italy
3
INFN – National Institute for Nuclear Physics,
via Valerio 2,
34127
Trieste,
Italy
4
ESO, Karl-Schwarzchild Strasse 2, 85748
Garching,
Germany
5 INAF, Osservatorio Astronomico di Brera, via Bianchi 46,
23807 Merate ( LC), Italy
Received: 14 February 2012
Accepted: 31 July 2012
Aims. We present a new sample of X-ray selected galaxy groups and clusters serendipitously observed with the X-ray Telescope (XRT) on board of the Swift satellite. Using the XRT archive as of April 2010, we searched for extended sources among 336 gamma-ray burst (GRB) fields with galactic latitude |b| > 20°. Our selection algorithm provides us with a flux-limited sample of 72 X-ray groups and clusters with a well defined selection function and an expected negligible contamination. The sky coverage of the survey goes from the total 40 deg2 to 1 deg2 at a flux limit of 10-14 erg s-1 cm-2 (0.5−2 keV). This paper provides a description of the XRT data processing, the statistical calibration of the survey, and the catalog of detected cluster candidates.
Methods. All the X-ray sources are detected in the Swift/XRT soft (0.5−2 keV) images with the algorithm wavdetect. A size parameter defined as the half power radius (HPR) measured inside a box of 45 × 45 arcsec, is assigned to each source. We select extended sources by applying a threshold on the HPR. Thanks to extensive simulations, we are able to calibrate the threshold value, which depends on the measured net counts inside the box and on the image background, in order to identify all the sources with a probability ≃ 99% of being extended. The net counts associated to each extended source are then computed by simple aperture photometry.
Results. We compute the log N–log S of our sample, finding very good agreement with previous deep cluster surveys. We did not find any correlation between the cluster and the GRB positions. A cross correlation with published X-ray catalogs shows that only 9 sources were already detected, none of them as extended. Therefore, ~90% of our sources are new X-ray detections. We also cross correlated our sources with optical catalogs, finding 20 previously identified clusters. Overall, about ~65% of our sources are new detections, both as X-ray sources and as clusters of galaxies.
Conclusions. The XRT follow-up observation of GRBs is providing an excellent serendipitous survey for groups and clusters of galaxies, mainly thanks to the low background of XRT and its constant angular resolution across the field of view. A significant fraction of the sample (~33%) has spectroscopic or photometric redshift thanks to a cross-correlation with public optical surveys.
Key words: galaxies: clusters: general / galaxies: high-redshift / cosmology: observations / X-rays: galaxies: clusters / surveys / catalogs
Table 2 (catalog) and Fig. 16 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
X-ray observations of clusters of galaxies over a significant range of redshifts have been used to investigate the chemical and thermodynamical evolution of the X-ray emitting intra cluster medium (ICM, see Ettori et al. 2004; Balestra et al. 2007; Maughan et al. 2008; Anderson et al. 2009), and to constrain the cosmological parameters and the spectrum of the primordial density fluctuations (Rosati et al. 2002a; Schuecker 2005; Voit 2005; Borgani 2008; Vikhlinin et al. 2009; Mantz et al. 2010; Allen et al. 2011). In this respect, X-ray surveys of clusters of galaxies represent a key tool for cosmology and the physics of large scale structure. The need of assembling larger and larger X-ray selected cluster samples with well defined completeness criteria is one of the critical issues of present-day cosmology. To build statistically complete cluster catalogs, a wide and deep coverage of the X-ray sky is mandatory.
Flux limited X-ray cluster surveys.
To date, there is a remarkable lack of recent wide area X-ray surveys suitable to this scope. Most of the existing cluster surveys are based on source samples selected by ROSAT, and confirmed through optical imaging and spectroscopic observations. The most recent constraints on cosmological parameters from X-ray clusters are based on the Chandra follow-up of 400 deg2 ROSAT serendipitous survey and of the All-Sky Survey (Vikhlinin et al. 2009; Mantz et al. 2010). Renewed interest in the field of cosmological tests with clusters has been recently provided by Sunyaev-Zel’dovich (SZ) surveys from the South Pole Telescope Survey (Reichardt et al. 2012) and the Atacama cosmology project (Sehgal et al. 2011). At present, only modest improvements have been obtained with respect to constraints from WMAP7 plus baryonic acoustic oscillations plus Type Ia supernova. The future of SZ cluster surveys is very promising, but at present an X-ray follow-up of SZ clusters is still needed, either for narrowing down the uncertainties on the cluster mass, or to firmly evaluate purity and completeness of the sample. For example, a large effort is being invested in the X-ray follow-up with Chandra (PI B. Benson) of SZ selected clusters from the South Pole Telescope Survey. This follow-up will provide the X-ray data for 80 massive clusters spread over 2000 deg2 in the redshift range 0.4 < z < 1.2.
New X-ray surveys of clusters of galaxies in the Chandra and XMM-Newton era are based on the compilation of serendipitous medium and deep-exposure extragalactic pointings not associated to previously known X-ray clusters. Among these, one of the first survey was assembled by Boschin (2002), who found 36 clusters (among them 28 new detections) in 5.55 deg2 of surveyed area. Eventually, the Chandra multiwavelength project (ChaMP) Serendipitous Galaxy Cluster Survey (Barkhouse et al. 2006) identified about 50 cluster and group candidates from 130 archival Chandra pointings covering 13 deg2. Of the 50 clusters, about 16 are expected to have redshift z > 0.5.
More effort is devoted to the XMM-Newton archival data, also motivated by the larger solid angle and the nominal larger sensitivity. The XMM-Newton distant cluster project (XDCP, Fassbender et al. 2011) take advantage of an optical and IR follow-up of extended source candidate in XMM images, to identify high-z clusters. So far, the XDCP survey has yielded 22 spectroscopically confirmed clusters in the redshift range 0.9 < z ≲ 1.6. A key step in XDCP is the identification of high-z candidates based on optical and NIR photometric technique,as well as extensive spectroscopic work. In this respect, it currently provides the largest sample of confirmed galaxy clusters at z > 0.8, and the purity of the sample is extremely high. Another small survey (2.1 deg2) conducted using XMM archival data is SEXCLAS (Kolokotronis et al. 2006), which includes 19 serendipitous detections down to 6 × 10-15 erg s-1 cm-2.
The largest project based on the entire XMM archive is the XMM Clusters Survey (XCS, Romer et al. 2001; Lloyd-Davies et al. 2011), with about 1000 cluster candidates over a solid angle of 410 deg2 (the largest based on current X-ray facilities). Recently, about 500 clusters have been optically identified out of ~1000 candidates (Mehrtens et al. 2012). Another survey based on the XMM archive is XCLASS, which is limited to brighter sources and aims at constraining cosmological parameters on the basis of the X-ray information only (Clerc et al. 2012). Finally, a survey combining 41.2 deg2 of XMM and Chandra overlapping archival data, plus 122.2 deg2 of Chandra only, has been presented in Peterson et al. (2009), for a total of 462 new serendipitous sources. Clearly, there is a significant overlap among the cluster samples derived from serendipitous XMM/Chandra surveys.
In addition, there are also ongoing dedicated, contiguous surveys. The cluster survey in the Subaru-XMM Deep Field (SXDF) reaches a depth of 2 × 10-15 erg s-1 cm-2 over 1.3 deg2 with 57 X-ray clusters identified with the red-sequence technique (Finoguenov et al. 2010). Similar depth has been reached in the COSMOS field over 2 deg2, for a total of 72 clusters (Finoguenov et al. 2007). The XMM-Newton-Blanco Cosmology Survey project (XMM-BCS, Šuhada et al. 2012) is a multiwavelength X-ray, optical and mid-infrared cluster survey covered also by the South Pole Telescope and the Atacama Cosmology Telescope with the aim of studying the cluster population in a 14 deg2 field. The analysis of the first 6 deg2 provided a sample of 46 clusters. Finally, the largest contiguous survey is the XMM Large Scale Structure Survey (XMM-LSS, Pierre et al. 2007) which is covering a region of 11 deg2 with the aim of tracing the large scale structure of the Universe out to a redshift of z ~ 1. At present, a first data release from an area of 6 deg2 consists in 66 spectroscopically confirmed clusters with 0.05 < z < 1.5 (Adami et al. 2011).
One of the most important goal of these surveys is to find massive clusters at high z. Clearly, tracing the most massive, gravitationally bound structures in the Universe up to the highest possible redshift is of paramount importance for structure formation and for cosmology. While the redshift limit for X-ray selected clusters is z ~ 1.57 (in XDCP), extended X-ray emission has been detected in optical and IR selected clusters at z = 1.75 (Stanford et al. 2012), z = 2.07 (Gobat et al. 2011), with an extreme candidate at z ~ 2.2 (see Andreon & Huertas-Company 2011).
The present situation is summarized in Table 1. This picture is not expected to change significantly in the next years, with a modest increase in the source statistics and in the quality of the X-ray data. In particular, the study of distant (z ≥ 1) clusters relies almost exclusively on time-expensive follow-up with Chandra. In the case of Chandra, the process of assembling a wide and deep survey is slow due to the small field of view (FOV) and the low collecting area. In the case of XMM-Newton the collecting area is significantly higher, but the identification of extended sources, in particular at medium and high redshift, is more difficult due to the larger size of the point spread function (PSF, whose half energy width is 15′′ at the aimpoint) and its degradation as a function of the off-axis angle. This is not an issue for nearby or medium redshift clusters and groups, but it becomes a problem at z > 1, where the optical and IR data play a dominat role in cluster identifications. In addition, the relatively high and unstable background may hamper the proper characterization of low surface brightness sources. In conclusion, while their design is optimized to obtain detailed images of isolated sources to explore the deep X-ray sky, a substantially different mission strategy is required for surveys.
In this work we present a new X-ray cluster survey using the rich archive of the X-ray Telescope (XRT) on board of the Swift satellite (Burrows et al. 2005) which has never been used for the detection of extended sources. Despite its low collecting area (about one fifth of that of Chandra at 1 keV, see Fig. 1), XRT has two characteristics which are optimal for X-ray cluster surveys: a low background and an almost constant PSF across the FOV (Moretti et al. 2007). Moreover, almost all the Swift/XRT pointings can be used to build a serendipitous survey. In fact, the operation mode of the XRT observations considered in this work, consists of a prompt follow-up of fields centered on gamma ray bursts (GRB) detected by Swift. As we will show in Sect. 6, the GRBs do not show any correlation with our extended sources. Therefore, despite its small size, the XRT can be successfully used to build an unbiased cluster survey.
 |
Fig. 1 Effective area of XRT (green solid line) as a function of the energy compared with that of the Chandra satellite (red dotted and cyan dashed lines for Chandra ACIS-I and ACIS-S, respectively). |
The catalog of extended sources presented in this paper constitutes the Swift X-ray Cluster Survey (SXCS) and it is based on the 336 GRB fields with galaxtic latitude |b| > 20° present in the XRT archive as of April 2010. The sources are identified thanks to a very simple but effective algorithm to select extended X-ray sources in the XRT soft band images. In this paper we adopt a conservative detection threshold which guarantees very low contamination and a well defined completeness function. This catalog is complementary to the catalog of point sources identified in the GRB fields of XRT by Puccetti et al. (2011), which focus on the study of the active galactic nuclei (AGN) population.
The paper is organized as follows. In Sect. 2 we provide a description of the principal characteristics of the XRT. In Sect. 3 we describe the field selection and the data reduction. In Sect. 4 we describe the detection algorithm and the selection of the extended source candidates. In Sect. 5 we describe how we performed extended source photometry. In Sect. 6 we present the final list of groups and clusters in our sample, compute the sky coverage and the Log N–Log S, and check for possible selection bias. In Sect. 7 we correlate our catalog with existing databases to identify previously known sources and collect the spectroscopic or photometric redshifts of member galaxies available in the literature. In Sect. 8 we discuss our results in the context of current and future X-ray surveys. Finally, in Sect. 9 we summarize our conclusions.
2. XRT characteristics
The XRT is part of the scientific payload of the Swift satellite (Gehrels et al. 2004), a mission dedicated to the study of GRBs and their afterglows operating since January 20051. GRBs are detected and localized by the Burst Alert Telescope (BAT, Barthelmy et al. 2005), in the 15−300 keV energy band and followed-up at X-ray energies (0.3−10 keV) by the X-ray Telescope. The XRT (Burrows et al. 2005) is an X-ray CCD imaging spectrometer which utilizes the third flight mirror module originally developed for the JET-X program (Citterio et al. 1994). The mirror module focuses X-rays (0.2−10 keV) onto a XMM-Newton/EPICMOS CCD detector consisting of 600 × 600 pixels, with a nominal plate scale of 2.36 arcseconds per pixel, which provides an effective FOV of the system of ~24 arcmin. The PSF, similar to XMM-Newton, is characterized by an half energy width (HEW) of ~18 arcsec at 1.5 keV Moretti et al. (2007). The PSF dependence on the off-axis angle is very weak. This is due to the fact that the CCD is intentionally slightly offset along the optical axis from the best on-axis focus in order to have a uniform PSF over a large fraction of the FOV, with a negligible dependence on the photon energy. To show the remarkably flat behavior of the PSF, we show in Fig. 2 the measured half power radius (HPR) within a box of 45 × 45 arcsec as a function of the off-axis angle for all the sources detected in the XRT fields used in this work. The PSF can be analytically described by a King function with slope β ~ 1.45 and core radius rc ~ 5.3 arcsec (Moretti et al. 2007).
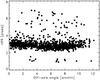 |
Fig. 2 Measured HPR within a box of 45 × 45 arcsec as a function of the off-axis angle for all the sources detected in the XRT fields used in this work. |
One of the most relevant aspect for our purposes is the low level and the high reproducibility of the background not associated to astronomical sources (NXB). Due to the low orbit and short focal length, the NXB is the lowest among the currently operating X-ray telescopes (see Hall et al. 2007). As a reference, the NXB of XRT calculated per solid angle and normalized by the effective area is a factor ~7 lower than Chandra in the 0.5−7.0 keV energy band (Moretti et al., in prep.).
3. Fields selection and data reduction
We consider the entire Swift/XRT archive from February 2005 to April 2010, including 502 fields in the corresponding GRB positions, distributed in the sky as shown in Fig. 3. We select the fields with Galactic latitude |b| > 20°, to avoid crowded fields and strong Galactic absorption. This selection provides us with 336 fields which we use to search for extended sources.
 |
Fig. 3 Distribution on the sky (Aitoff projection) of the GRB fields in the XRT archive as of April 2010 (red dots). The fields selected in our survey are those outside the Galactic plane (shaded area). |
In this paper we use photon counting mode data with the standard grade selection (grade 0−12) reduced by means of the xrtpipeline task of the current release of the HEADAS software (version v6.8) with the most updated calibration at the time of writing (CALDB version 20111031, Nov. 2011). More detail on the standard data reduction can be found in the instrument user guide2. Then, we proceed with a customized data reduction, aimed at optimizing our data to the detection of extended sources. First we exclude the external CCD columns (corresponding to the detector coordinates Detx < 90 and Detx > 510) which are affected by the presence of out-of-time events from corner calibration sources (see Moretti et al. 2009, for a detailed map of the CCD and a discussion on the XRT background). The corrected FOV, after removal of the external CCD columns, is 16.5′ × 18.9′ (0.087 deg2) for each pointing. Different observations of the same object and corresponding exposure maps are merged by means of the the extractor and farith tasks of the HEADAS software, respectively.
To further reduce the background, we investigate the background light curves in the soft image of each field. At the beginning of each observation, corresponding to the maximum emission from the GRB, the background on the entire image is significantly larger than the typical, quiescent value. Actually it was previosly known (Moretti et al. 2009) that for very high fluences3, about 5% of the GRB X-ray emission is scattered across the image.
We effectively tested that by removing all the data taken before the epoch T0 + 0.1 × texp, where T0 is the epoch of the beginning of the observation, and texp is the total effective exposure time, the average background on a typical image can be reduced by ~5%. This empiric rule is motivated by the fact that the total exposure time of a typical GRB follow-up observation is set by the GRB emission itself, therefore brighter GRBs will have larger observation length and therefore larger time intervals removed. In addition, note that the time interval 0.1 × texp does not correspond to 10% of the exposure time, since this is distributed over several orbits, each one with an observability time of 1500 s over a total orbit period of 5400 s. Figure 4 shows an example of a typical light curve, where the time interval that has been removed is shown in gray. The removal of the data up to the time T0 + 0.1 × texp corresponds typically to the first two or three orbits. On average, the time interval 0.1 × texp corresponds to 2−3% of the effective exposure time, since this is distributed over several days with 10−20 ks observed every day. We also note that removing the first orbits has the effect of reducing the non-homogeneity of the background caused by the GRB emission, which would have affected the detection of extended sources. In Fig. 5 we show the distribution of the effective exposure times of the XRT fields after this correction.
 |
Fig. 4 Light curve of the background of the field of GRB 051008 plotted as a function of the time elapsed from the GRB trigger. The saw-tooth appearance is due to the orbits of Swift (one orbit lasts 90 minutes). The removed time interval below the epoch T0 + 0.1 × texp is shown in gray. |
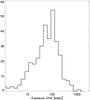 |
Fig. 5 Distribution of the exposure times in ks for the 336 selected GRB fields. |
4. Selection of extended-source candidates
4.1. Initial source detection
The identification of the X-ray sources is performed with the standard algorithm wavdetect within the CIAO software used successfully on Chandra and XMM-Newton images (Lloyd-Davies et al. 2011). We run the algorithm on the images obtained in the soft (0.5−2 keV) band using a set of six wavelet scales corresponding to 2, 4, 8, 16 and 32 image pixels. We use a mild selection threshold corresponding to the wavdetect threshold parameter 10-6. Despite not guaranteeing a high completeness nor high purity, this choice is motivated by the fact that the selection of extended sources will be based on the growth curve method, and that only relatively high S/N sources will be selected as we will show in Sect. 4.5. Therefore the wavdetect threshold parameter has no effects on our final cluster candidates list.
The soft band is optimal to identify extended ICM emission, since in this band XRT has the highest effective area and the lowest instrumental background. In this way we maximize our sensitivity in the detection of extended source powered by thermal bremsstrahlung, whose soft band emission has a small K-correction up to z ~ 1, at least for hot clusters (kT > 3 keV). We also considered modifications to the standard soft band in order to find the energy range optimal for cluster detection, similarly to what has been done for Chandra and XMM-Newton (Scharf 2002). We explored the use of a narrower energy band in order to reduce the effect of the Galactic background, which rapidly grows below 1 keV. We found that a narrower energy band would have a minor positive effect on the detection of clusters, while negatively affecting the detection of low temperature groups whose emission is below 2 keV. We also explored the use of a larger upper energy value, but the poor photons statistics for thermal spectra at high energies and the rapidly increasing hard background nullify any advantage for values above 2 keV. Since the small, positive effects we found in changing the energy band are also significantly dependent on the temperature of the ICM, we decide to maintain the standard 0.5−2 keV band.
Incidentally, we notice that, given the sensitivity at high energies of the XRT, it is possible in principle to use also the hard band (2−7 keV) to disentangle thermal emission from power-law emission typical of AGN, on the basis of the source hardness ratio. The hardness ratio is defined as HR = (H−S)/(H + S), where H and S are the hard band and soft band counts respectively, corrected for vignetting. In Fig. 6 we show the hardness ratio as a function of redshift expected for groups and clusters at different temperatures, compared to the hardness ratio of AGN with different intrinsic absorption NH. Values for clusters and AGN are taken using Xspec v12.6.0 assuming in the first case an absorbed thermal model with a mean Galactic absorption of NH = 3 × 1020 cm-2, and in the second case assuming an absorbed power law with an intrinsic redshifted absorption. We find that only nearby, strongly absorbed AGN have hardness ratio values clearly different from those of the ICM. We conclude that the hard band does not provide a relevant information for the detection of groups and clusters. Therefore we will use only the soft band in this work. The full band will be used for the spectral analysis of the brightest sources in a companion paper (Moretti et al., in prep.).
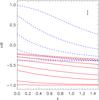 |
Fig. 6 Hardness ratios modeled for XRT as a function of redshift for groups and clusters with several temperatures (red continuous lines, kT respectively equal to 0.5, 1.0, 2.0, 3.0, 5.0, 7.0, 10.0 and 12.0 keV from the bottom to the top) and for AGN with different intrinsic absorption (blue dashed lines, NH respectively equal to 0.01, 0.1, 0.3, 1.0, 3.0 and 10.0 × 1022 cm-2 from the bottom to the top). In the top right, we show the typical error bar on HR for a source with 200 total net counts. |
Since the algorithm wavdetect has never been tested thoroughly on XRT images, we cannot immediately associate an expected contamination level to the threshold value of 10-6. In any case, at this stage we are mostly interested in collecting all the possible extended-source candidates, while the contamination level will be estimated during our selection process. This step leads us to identify a total of ~104 sources in the 336 GRB fields. This number is somewhat lower than that expected on the basis of the Swift serendipitous survey (Swift FT, see Puccetti et al. 2011) which was based on a ~20% smaller field selection. The lowest number of net photons in our total source list is as low as 5. Despite the low background, Poisson fluctuations may appear as spurious sources at such a low signal. However, we do not apply any filter to this parent list, since much more stringent thresholds will be applied when selecting extended sources, as described in the next subsection.
 |
Fig. 7 Distribution of the measured HPR within a 45 × 45 arcsec box for simulated unresolved sources as a function of the soft counts within the box. The same range of exposure times and backgrounds present in the real data has been adopted in the simulations. The continuous line shows the 99% confidence level envelope of the source distribution. |
4.2. Source extent determination
For each source we consider a 60 × 60 pixels box centered around the source. In each of these boxes, we mask the other sources whose emission can overlap with the central one, by removing a PSF image. The PSF is accurately fitted with a King profile normalized to each source photometry assuming a core radius of rc = 5.3 arcsec and a β = 1.45. These values are valid at energies ~1.5 keV and have been recomputed in-flight by fitting the many high S/N sources observed by XRT, therefore updating the values in Moretti et al. (2005) and Moretti et al. (2007). This gives us a sub-image cleaned from point-like sources, with the considered source at its center. To account for defects due to missing columns or removed pixels in the CCD, we divide this image by the corresponding soft exposure map. Then, we compute the growth curve of the source within a box of 45 × 45 arcsec. This region corresponds to 2.5 times the HEW (which is 18 arcsec) and includes 80% of the flux of a point source. From the growth curve within this region, we measure the HPR, effectively defined as the 50% encircled energy radius within a box of 45 × 45 arcsec. Note that the HPR is smaller than the HEW, since it refers to only 80% of the total flux. The choice of a restricted regions is motivated by the need of sampling the growth curve with a good signal-to-noise ratio (S/N) for the majority of the sources in the initial list. This choice does not affect by any means the final total flux, which will be computed according to a different procedure as shown in the next subsections, and it is used only to classify extended versus unresolved sources.
4.3. Point source simulation, and determination of threshold parameters
Extensive simulations spanning all the parameter range found in the survey (in particular source fluxes and background levels) have been used to estimate the expected distribution of the HPR for point sources. The input flux distribution for unresolved sources is consistent with the number counts obtained by Puccetti et al. (2011) and with the deeper CDFS counts (Rosati et al. 2002b), while the fluxes for clusters are distributed according with the number counts obtained in the ROSAT Deep Cluster Survey (Rosati et al. 2002a).
The distribution of the measured HPR in the simulations as a function of the source counts within the 45 × 45 arcsec box is shown in Fig. 7. The simulations (including only point sources) are used to define the threshold values HPRth above which a source is inconsistent with being unresolved at the 99% level (see red line in Fig. 7). This criterion is extremely simple and it does not depend on the off-axis angle θ, thanks to the flat PSF. However, HPRth is a function of the source counts measured within the 45 × 45 arcsec box, in particular it increases significantly below 60 counts. Above this value, HPRth ranges between 3 and 4 image pixels (equal to 7.1−9.4 arcsec for a pixel size of 2.36 arcsec). Instead of using a single HPRth based on the entire simulation, we compute HPRth for a set of different background values, finding a significant dependence which will be taken into account in the source selection. By directly applying this criterion, we expect to have a number of spurious sources equal to 1% of the total source number. We remark that the counts within the 45 × 45 arcsec box can be much lower than the total net counts, particularly for extended sources.
This procedure is applied to all sources detected with wavdetect. Figure 8 shows the distribution of the HPR of the detected point sources (gray dots) versus the source counts measured inside the HPR, with the extended source candidates marked as black and red big dots. Note that extended source candidates are selected on the basis of a HPRth value which depends also on the background (tied to the exposure of the image). The HPRth for different exposures are shown in Fig. 8 as solid lines ranging from 1 ks (orange line) to 1 Ms (blue line). The number of extended source candidates grows rapidly when the number of detected counts within the box decreases toward low values. The inclusion of all the candidates in our survey clearly would imply a large number of spurious sources, given the large total number of sources (~104). We finally apply the threshold on the total number of counts to be >100 in the extraction radius (defined as the circular region where the source surface brightness is larger than the background level). The red big dots indicate the candidate extended sources matching all our selection thresholds.
 |
Fig. 8 Distribution of the measured HPR within a box of 45 × 45 arcsec for all the sources detected in the XRT fields as a function of the soft counts measured within the HPR. All possible extended source candidates are marked with black big dots, while red big dots indicate sources with >100 soft net counts from the aperture photometry in the extraction radius (see Sect. 5) and are therefore included in the cluster candidate list. The continuous lines show the typical 99% confidence level envelope for different exposures, from 1 ks (orange line) to 1 Ms (blue line). |
The sharp threshold on the soft net counts allows us to compute directly a sky coverage as a function of the source flux within the extraction region (see Sect. 6). Clearly, the sky coverage information would be sufficient to compute the log N−log S only in absence of any morphology bias. Actually, we do miss a fraction of extended sources, mostly due to the wide range of intrinsic morphologies. The completeness of our survey is then estimated as described in the next subsection.
4.4. Completeness and contamination level
To properly characterize the quality of our sample we need to assess the completeness, defined as the fraction of extended sources actually selected as extended by our procedure as a function of their soft net counts. To estimate the completeness, we realize another set of simulations with a different strategy. We simulated a few thousand extended sources, spanning a wide range of fluxes consistent with the number counts measured in the ROSAT Deep Cluster Survey (Rosati et al. 1998).
Our extended sources are modeled starting from ten real cluster images originally obtained with the Chandra satellite (therefore with a resolution much higher that that of XRT), cloned at a typical redshift and resampled at the XRT resolution. This cloning procedure, already used to investigate the evolution of cool core clusters at high redshift (see Santos et al. 2008, 2010) allows us to measure our completeness for a realistic range of surface brightness profiles, representing the local population of groups and clusters of galaxies: temperatures go from 2 keV to 8 keV, the redshift of the clusters are all below 0.2, and half of the clusters have a cool core. Clearly, the limited set of group/cluster templates, and the assumption of no evolution in the surface brightness properties with redshift, may introduce some difference with respect to the actual cluster population. The impact of the intrinsic morphologies on the source selection is properly taken into account as long as the morphologies of the simulated sources are representative of the real sources. This is admittedly a limitation of the present approach. Still, this procedure is the most accurate with the present knowledge. The simulated clusters are positioned randomly on real XRT images and the fluxes are converted into count rate using the response function of the instrument, including vignetting effects. We run our detection procedure on the simulated images, and compute the completeness as the recovered source fraction (i.e., the fraction of sources detected and characterized as extended with our criterion) as a function of the input counts. As shown in Fig. 9, we reach a completeness level ~70% for sources above our threshold of ~100 net counts within the extraction regions. This level increases to ~90% for sources with ~200 net counts, and reach a completeness level of >95% for sources with ~300 net counts. We will use this information to correct the log N−log S of our sample in Sect. 6. We remark that this completeness function is by no means general: it depends, in fact, on the intrinsic properties of the survey, on the exposure time distribution, and on the source selection and classification method. We are actually aiming at increasing the completeness down to a threshold of ~50 net counts, while maintaining a low contamination level, thanks to a different detection algorithm based on Voronoi tessellation (Liu et al., in prep.).
Finally, our simulations allow us to estimate also the contamination level. This is obtained directly by averaging the number of spurious sources surviving our selection criteria in all our survey realizations. The average expected number of spurious sources in the SXCS survey turns out to be ~5. The contamination is due to Poisson noise in the measured parameters (HPR, photometry) and to blending. We neglect any spatial correlation which, however, is expected to give a negligible enhancement to the contamination level.
4.5. Final sample selection
Our algorithm identified 87 candidate extended sources with ≥ 100 soft net counts. We proceeded to a careful visual inspection of these candidates, including a look through the optical images taken from the DSS and from the SDSS when available. This visual inspection allows us to remove 3 sources which are identified with stars4. In addition, 3 sources are removed since they are identified with nearby large galaxies. Note that all these sources are correctly identified as extended by our algorithm.
We also remove 6 sources since they are easily recognized as blended by visual inspection. This effect was included in the simulations which predicted a number of spurious sources equal to 5. We argue that our visual inspection actually remove most of the spurious detections. The visual inspection is made possible thanks to the limited size of our sample. For larger samples, a more efficient, self-consistent detection algorithm would be needed to keep the contamination level under control down to lower fluxes, without recurring to time-consuming visual inspections.
Another 3 sources are found to be very close to the edge of the XRT images, where the gradient of the exposure map significantly affects the photometry. We remove them since their photometry would necessarily rely on a substantial extrapolation of their properties. The final sample includes 72 extended sources. Figure 10 shows a typical example of a GRB field imaged by XRT. In this case (GRB 050505) three extended sources, highlighted by green circles, have been selected by our algorithm.
 |
Fig. 9 Completeness level, expressed as the ratio of recovered extended sources on the number of simulated extended sources as a function of the input soft counts. |
 |
Fig. 10 XRT smoothed image of the GRB050505 field in the soft (0.5−2.0 keV) band; the exposure time is ~170 ks, and the image size is ~24 × 24 arcmin. The three clusters in the fields are highlighted by the green cicles. The bright source at the center is the GRB. |
5. Extended sources photometry
The measured net counts from each source are computed by aperture photometry up to an extraction radius Rext, after removing the emission associated to point sources included in this region. Rext is defined as the radius where the surface brightness profile of the source reaches the background level. The total net counts are finally obtained by accounting for the missed flux beyond Rext. To measure the lost signal, we fit the surface brightness SB of every extended source with a King profile modeled as SB ∝ (1 + (r/rc)2)3β−1/2 (Cavaliere & Fusco-Femiano 1978) leaving both rc and β free to vary. Then, we extend the surface brightness profile up to 2 × Rext. The typical ratio of the total estimated flux to that actually measured within Rext is cf = 1.05−1.10. Extrapolating the profile to larger radii has a modest effect on the final results. We also checked that the errors on the rc and β parameters affect the correction factor cf only at a 10% level, and therefore constitute a negligible uncertainty for the final source flux.
The net count rate measured for each source is obtained dividing the net counts by the exposure time, after correcting for vignetting effects in the soft (0.5−2 keV) band. The average vignetting correction in the extraction region is estimated by the ratio of the photon-weighted average value of the soft exposure map within Rext to the value of the soft exposure map at the aimpoint. From the corrected net count rate, the energy flux is computed simply by multiplying it by the energy conversion factor (ECF) computed at the aimpoint for a suitable spectral model.
The ECF for thermal X-ray emission from the ICM is computed assuming a mekal model within XSPEC. Since we do not know a priori the temperature of our sources, we explore a range of temperatures from 1 to 12 keV, and a redshift range from 0 to 1.5. The corresponding ECF values in the soft band are shown in Fig. 11 for a typical Fe abundance of 0.3 Z⊙ in units of Anders & Grevesse (1989). We note that the ECFs vary less than 2% for kT > 3 keV at any redshift. The largest changes are found for lower temperatures, up to a maximum of 8% for kT = 1 keV. However, given the average L − T relation measured locally, and considering that it is approximately constant with redshift (Reichert et al. 2011; Branchesi et al. 2007; Maughan et al. 2006; Ettori et al. 2004; Mushotzky & Scharf 1997), we can derive a minimum temperature detectable at a given redshift for our flux limit. If we set Flim ~ 10-14 erg s-1 cm-2, we find that clusters and groups with kT < 2 keV can be observed only for z < 0.5. This allows us to conclude that the maximum variation is below 4%, and that this number is little affected by the actual ICM metallicity. Therefore we assume an average ECF of 2.35 × 10-11 erg s-1 cm-2/(cts s-1) with a maximum systematic uncertainty of 0.1 × 10-11 erg s-1 cm-2/(cts s-1).
 |
Fig. 11 Energy conversion factor (ECF) as a function of the ICM temperature for different redshifts. Here we assumed no Galactic absorption. |
The ECFs, however, have a more significant dependence on the Galactic absorption. This can be estimated thanks to the Galactic NH values measured in the radio survey in the Leiden/Argentine/Bonn survey (Kalberla et al. 2005). As shown by the histogram in Fig. 12, the distribution of Galactic NH for our sources implies changes up to the order of 30%. Therefore we use for each detected source the ECF appropriate to the corresponding field. We note that self shielding of molecular hydrogen from ambient UV radiation is expected to occur for NH > 5 × 1020 cm-2 (Arabadjis & Bregman 1999), and this molecular gas absorbs also X-rays. Therefore for this NH values X-ray fluxes are slightly underestimated. We do not correct for this effect (see also Lloyd-Davies et al. 2011).
To summarize, the total unabsorbed, soft fluxes, including the correction up to 2 Rext, are measured as: 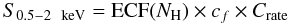 (1)where ECF(NH) is the energy conversion factor, which accounts for the Galactic absorption (see Fig. 12), cf is the correction factor for the flux between 2 × Rext and Rext, and Crate is the soft band count rate mesured within Rext and corrected for vignetting effects.
(1)where ECF(NH) is the energy conversion factor, which accounts for the Galactic absorption (see Fig. 12), cf is the correction factor for the flux between 2 × Rext and Rext, and Crate is the soft band count rate mesured within Rext and corrected for vignetting effects.
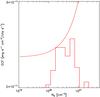 |
Fig. 12 Energy conversion factor (ECF) as a function of the Galactic NH for a typical cluster (kT = 5 keV, z = 0.4). The histogram shows the distribution of Galactic NH in our cluster sample. |
6. Cluster catalog and number counts
Table 2, available at the CDS, contains the aperture photometry within Rext and total energy flux for all the sources of our sample. The net counts error is obtained from the Poissonian error on the numbers of net photons. We remark that, as explained in detail in the previous section, the photometry of our extended sources refers to the extraction radius Rext defined as the radius where the fitted surface brightness falls below the measured local background, while the total energy flux include the correction factor cf for the flux lost beyond Rext. In Table 2, Col. 1 reports the SXCS name of the source, Cols. 2 and 3 give the coordinates of the sources in degrees, Col. 4 the exposure time corrected for vignetting, Col. 5 reports the Galatic absorption, Col. 6 the extraction radius Rext in arcsec, Cols. 7 and 8 the Soft net counts with their uncertainties, Col. 9 the Soft Signal to Noise Ratio, Cols. 10 and 11 the Soft Flux with associated uncertainties.
To compute the number counts for our cluster sample, we need to derive the sky coverage of our survey. The sky coverage is determined by the sharp limit in the total net photons. For each field we compute a flux-limit map obtained as ECF(NH) × 100/Expmap(t), where Expmap(t) is the exposure map in units of effective time, therefore including the effect of vignetting. Then, the solid angle covered by the survey above a given flux is obtained by measuring the total solid angle where the flux-limit is lower than a given flux. In Fig. 13 we show the resulting sky coverage Ω(S) and compare it with the sky coverage of the 400 Square Degree ROSAT PSPC Galaxy Cluster Survey by Burenin et al. (2007) and with the sky coverage of the ROSAT Deep Cluster Survey (RDCS) by Rosati et al. (1998). Unfortunately, sky coverage curves for other on-going XMM/Chandra surveys have not been published. The cumulative number counts for sources brighter than a given flux S is therefore given by 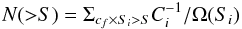 (2)where S is the total flux, Si is the soft flux within Rext of the ith source, cf is the correction factor for the flux outside Rext and Ω(Si) is the solid angle corresponding to Si. Finally, Ci is the completeness factor plotted in Fig. 9 which depends on the net detected photons of the ith source. In this way, each source is weighted with a factor inversely proportional to the survey completeness which depends only on source photometry.
(2)where S is the total flux, Si is the soft flux within Rext of the ith source, cf is the correction factor for the flux outside Rext and Ω(Si) is the solid angle corresponding to Si. Finally, Ci is the completeness factor plotted in Fig. 9 which depends on the net detected photons of the ith source. In this way, each source is weighted with a factor inversely proportional to the survey completeness which depends only on source photometry.
 |
Fig. 13 Solid angle Ω covered by our survey as a function of the soft flux. As a comparison, we show also the sky coverage of the 400 Square Degree Survey (Burenin et al. 2007, blue dashed line) and the sky coverage of the RDCS (Rosati et al. 1998, green dotted line). |
An alternative procedure to correct for completeness is obtained by randomly extracting the missing sources and computing their average effect. The procedure consists in dividing the sources in 3 bins of net photons (100−150, 150−200, 200−300). Then, in each bin we randomly add a number of sources drawn from a Poissonian distribution centered on the expected number of missed sources according to Fig. 9. Finally we assign a random exposure and ECF among those in the survey to each mock source, and compute its energy flux. Finally the log N−log S is recomputed for each Monte Carlo realization. The average log N−log S obtained with this procedure with 104 realizations is in very good agreement with that obtained with Eq. (2), therefore confirming that our treatment of the completeness is robust.
 |
Fig. 14 Cumulative number counts, corrected for completeness, with 1σ confidence level for SXCS (red area), compared to the log N−log S derived from the ROSAT Deep Cluster Survey (cyan area), Rosati et al. (1998). Dot-dashed and dashed lines show the fit to the 400 d (Burenin et al. 2007) and to the COSMOS (Finoguenov et al. 2007) number counts, respectively. |
 |
Fig. 15 Positions of our sources with respect to the GRB position (set to 0, 0). |
Our log N−log S is shown in Fig. 14 with its 68% confidence limits (shaded red region). The confidence limits are computed with Monte Carlo realizations. We re-extract the flux of each source times assuming its Poissonian uncertainties on the net detected counts, including the systematic uncertanty on the ECFs, obtaining 104 realizations of the log N−log S. Then, at each flux, we compute the 68% confidence interval around the mean value.
Our results are consistent with the log N−log S measured with the ROSAT Deep Cluster Survey (RDCS, Rosati et al. 1998), shown in Fig. 14 as the cyan region, down to fluxes ~10-14 erg s-1 cm-2. We are also consistent with the the log N−log S measured in the 400 deg2 survey (Burenin et al. 2007) and in the COSMOS field (Finoguenov et al. 2007), shown as the dash-dotted and dotted lines respectively.
The good agreement with previous results confirm the proper characterization of our sample. Nevertheless, we also perform a test against a possible correlation between the GRB position and the position of our sources, since the detection of an enhanced density of clusters and groups toward the position of GRB would bias our survey. In Fig. 15 we plot the positions of the sources in our sample with respect to the GRB positions (set to 0, 0). We do not find any hint of an increasing surface density of extended sources toward the GRB position. We also tested for such a possible bias by measuring the log N−log S for the sources whose distance is, respectively, below 400 arcseconds from the GRB and between 400 and 800 arcsec from the GRB. The two log N−log S agree with each other within the uncertainties, showing that there is no correlation between GRB and clusters (see also Berger et al. 2007). We can safely assume that our field selection is unbiased with respect to X-ray clusters.
List of counterparts of SXCS sources.
To check whether we properly treated the effect of the Galactic absorption, we split the survey into two segments according to the Galactic absorption, above and below NH = 3 × 1020 cm-2. We find that the log N−log S computed in the two cases are in very good agreement, and therefore we conclude that our flux measurements do not appear to suffer any bias from Galactic absorption.
To summarize, the sources included in the SXCS catalog represent a sample of group and cluster candidates with a negligible contamination, a well defined selection function and a robustly estimated completeness, spanning two orders of magnitude in flux, and reaching the flux limit of ~10-14 erg s-1 cm-2.
7. Cross-correlation with X-ray and optical catalogs
We checked for counterparts both in previous X-ray surveys and in optical cluster surveys, assuming a search radius of 1 arcmin from our X-ray centroid. The results are shown in Table 3. We find 9 X-ray counterparts to our sources in ROSAT, ASCA and Chandra catalogs, none of them characterized as extended and none of them with a published redshift. We also find a total of 20 previously known, optically identified clusters. Among them, 6 are found in the Wen+Han+Liu cluster sample (WHL, Wen et al. 2009), which is an optical catalog of galaxy clusters obtained from an adaptive-matched filter finder applied to Sloan Digital Sky Survey DR6. We find 4 clusters in the Szabo et al. (2011) catalog (AMF) based on a similar method in the SDSS DR6.
We also report one cluster from the Gaussian mixture brightest cluster galaxy (GMBCG, Hao et al. 2010) based on SDSS DR7, which is an extension of the maxBCG cluster catalog (Koester et al. 2007) to redshift beyond 0.3 and on a slightly larger sky area (~8000 deg2), and one cluster in the MaxBCG catalog itself.
Finally, we find 3 clusters in the Abell catalog (Abell et al. 1989), two cluster in the Northern Sky optical Cluster Survey (NSCS, Gal et al. 2003; Lopes et al. 2004), and one cluster in each of the following catalogs: the Zwicky Cluster Catalog (CGCG, Zwicky et al. 1963), the Sloan Digital Sky Survey C4 Cluster Catalog (SDSS-C4-DR3, based on DR3, Miller et al. 2005; von der Linden et al. 2007), the Edinburgh-Durham Southern Galaxy Catalogue (EDCC, Lumsden et al. 1992). Three out of twenty clusters also have an X-ray counterpart.
To increase the number of available redshifts, we also search for galaxies with published redshift not associated to previously known clusters, within a search radius of 7 arcsec from the X-ray centroid of our sources. In Table 3 we report 11 galaxies with redshift, within a search radius of 7 arcsec, as a complement to the redshift of the cluster counterpart. The redshift of the central galaxy candidate is always consistent with the photometric redshift of the optical cluster counterpart when present. In the 4 cases where no optical cluster counterpart is found, we tentatively assign the galaxy redshift to our X-ray source. We note that both cluster and central galaxy counterparts have been found by adopting a simple matching criterion. A more refined analysis of the optical data covering our survey is under way (Tundo et al., in prep.).
To summarize, we have 24 optical redshifts (spectroscopic or photometric) published in the literature and associated to our cluster candidates. Overall, 46 sources in our catalog are new detections, both as X-ray sources and as clusters of galaxies. Finally, we remark that a total of 32 SXCS sources fall in SDSS fields. Thanks to the SDSS depth, we expect to increase the identification of our cluster candidates. In particular we expect to be able to identify at least the brightest cluster galaxy up to z ≤ 1 for those cluster candidates which are not already included in the SDSS catalogs. This will also provide an estimate of the photometric redshift of the host cluster. Figure 16 shows a selection of SDSS r-band images of SXCS fields, with X-ray contours overlaid in green.
We stress that we can also attempt a measure of the source redshift through the X-ray spectral analysis for a significant fraction of the sample. The requirements for a successfull identification of the redshifted Kα Fe line, shown in Yu et al. (2011) for Chandra, do not apply to most of the SXCS sources. However the lower background and the flatter effective area of XRT may allow X-ray redshift measurements in a lower S/N regime. A preliminary result indicates that the X-ray redshift zX of about 30% of the SXCS sources can be successfully measured. This is an important aspect since the measure of zX will complement the photometric and spectroscopic redshifts obtained with optical follow-up with the aim of using the cluster sample for cosmological tests. We will present the spectral analysis in a companion paper (Moretti et al., in prep.).
8. Future prospects
SXCS data have different properties from Chandra and XMM-Newton data as described in Sect. 2 and Sect. 3, and therefore SXCS extended sources have a different selection function. For these reasons the SXCS is a valuable touchstone to the cluster catalogs obtained from XMM-Newton and Chandra. The full SXCS survey (Liu et al., in prep.) is expected to cover a larger solid angle especially at bright fluxes, and to be at least a factor of two deeper. The exploitation of the Chandra and XMM archives is still far from being concluded, and we expect to see the number of high-z clusters (z > 1) to double in the next years, and in particular to see the increase of the sample of clusters at z > 1.5 which are being found only recently. However, a major breakthrough in the field of cluster surveys can be achieved only with a survey dedicated mission.
The planned eROSITA satellite (Predehl et al. 2010; Cappelluti et al. 2011) and the proposed WFXT mission (Rosati et al. 2011; Murray et al. 2010) can provide a large number of new detections and X-ray spectra for a large number of them. The eROSITA mission is expected fo fly in the near future, and it will finally provide an all-sky survey almost two orders of magnitude deeper than the last one performed by the ROSAT satellite (Voges et al. 1999), filling a gap of almost 20 years. Unfortunately, eROSITA will be confusion limited in the flux regime where the majority of the high-z clusters are expected. In addition, the low hard-band sensitivity (the effective area decreases an order of magnitude5 from 1 keV to 4 keV) hampers a measure of the temperature for hot clusters, limiting cosmological studies.
The WFXT is the only X-ray mission optimized for efficient wide-area surveys, with a design which yields good angular resolution and a constant image quality across a large (1 deg2) FOV (see Rosati et al. 2011). These aspects, coupled with a large effective area, will provide not only a survey more than one order of magnitude deeper than eROSITA, but a direct measurement of global temperatures, density profiles and redshifts for a significant fraction of the cluster sample, thus allowing cosmological studies independently of optical and spectroscopic follow-up (Borgani et al. 2011). Simulations based on the original WFXT design (Tozzi et al. 2011) show that such a mission is able to match in depth, survey volume and angular resolution surveys at other wavelengths which are planned for the next decade.
9. Conclusions
We present a new sample of X-ray selected groups and clusters of galaxies obtained with the X-ray Telescope (XRT) on board of the Swift satellite. We search for extended sources among 336 GRB fields imaged with XRT with galactic latitude |b| > 20° (available in the archive as of April 2010). We identify extended sources with a simple criterion based on the measurement of the HPR within a box of 45 × 45 arcsec of the source image. We apply a sharp threshold of 100 net soft counts within the extraction radius Rext to select reliable extended sources. Extensive simulations showed that our method, despite being very simple, provide us with an X-ray sample with an expected high completeness and a low contamination, also thanks to a careful a posteriori visual inspection. Our final group and cluster catalog consists of 72 X-ray sources6.
The sky coverage of the survey goes from the total 40 deg2 to 1 deg2 at a flux limit of about 10-14 erg s-1 cm-2. The corresponding log N−log S is in very good agreement with previous deep surveys.
We directly verified that there is no correlation between the position of the clusters and that of the GRBs. In other words, selecting our cluster sample from XRT GRB fields does not result in any spatial bias with respect to the GRB positions.
A cross correlation with X-ray catalogs shows that only 9 SXCS sources were previously identified in the X-ray band, none of them classified as extended. A search in optical databases (mostly based on SDSS data) allows us to find the counterparts of 20 clusters. In addition, 4 galaxies with redshift have been found to be within 7 arcsec from the X-ray centroid, and therefore they are considered as possible identification of the central galaxy of the group/cluster candidate. Overall, only 20 sources are confirmed as clusters using data from the literature, while 30 sources have some counterpart in the NASA Extragalactic Database, and, finally, 42 sources are newly identified.
We estimate that about one third of the sample is detected with a S/N high enough to allow the measure of the redshift from the X-ray spectral analysis (see Yu et al. 2011), as we will show in a companion paper (Moretti et al., in prep.). Thanks to the quality of our X-ray data, and thanks to the synergy with other surveys, specifically the SDSS, we are able to provide a X-ray cluster sample with a well established completeness function down to a flux limit comparable to that of the deepest cluster surveys based on ROSAT data (RDCS, see Rosati et al. 1998), and with a comparable statistics. In addition, we expect to detect a few clusters with redshift z ≥ 1. Overall, the SXCS is expected to give a significant contribution in the field of X-ray clusters surveys also thanks to its peculiar properties of a low background and a constant PSF. These properties are two key requirements for future wide-area, X-ray surveys, as foreseen by proposed future missions aiming at bringing the X-ray sky to the same depth and richness of the optical and IR sky in the next decade. A deeper, extended release of the SXCS based on a new detection algorithm tailored to XRT images is currently undergoing (Liu et al., in prep.).
Online material
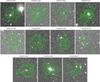 |
Fig. 16 Selection of SXCS cluster candidates imaged by the Sloan Digital Sky Survey (SDSS) with X-ray contours overlaid in green. The image size is 3 × 3 arcmin. The X-ray contours are computed on XRT images in the 0.5−2 keV energy band with the Chandra Ciao software, and the contours are drawn at respectively 9, 15, 30, 50, 90, 160 and 300σ, where σ is given by the local background level. |
SXCS sources.
Catalog and data products of SXCS, constantly updated, are made available to the public through the website http://adlibitum.oats.inaf.it/sxcs
Acknowledgments
We acknowledge support from ASI-INAF I/088/06/0 and ASI-INAF I/009/10/0. PT aknowledges support under the grant INFN PD51. GT and SC acknowledge support from ASI-INAF I/011/07/0. We thank the anonymous referee for helping us to improve sgnificantly our paper with extremely detailed and useful comments. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Abell, G. O., Corwin, Jr., H. G., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Mazure, A., Pierre, M., et al. 2011, A&A, 526, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Anderson, M. E., Bregman, J. N., Butler, S. C., & Mullis, C. R. 2009, ApJ, 698, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., & Huertas-Company, M. 2011, A&A, 526, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arabadjis, J. S., & Bregman, J. N. 1999, ApJ, 510, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barkhouse, W. A., Green, P. J., Vikhlinin, A., et al. 2006, ApJ, 645, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Shin, M.-S., Mulchaey, J. S., & Jeltema, T. E. 2007, ApJ, 660, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Borgani, S. 2008, in A Pan-Chromatic View of Clusters of Galaxies and the Large-Scale Structure, eds. M. Plionis, O. López-Cruz, & D. Hughes, Lect. Notes Phys. (Berlin: Springer Verlag), 740, 287 [Google Scholar]
- Borgani, S., Rosati, P., Sartoris, B., Tozzi, P., & Giacconi, R. 2011, Mem. Soc. Astron. It. Supp., 17, 36 [Google Scholar]
- Boschin, W. 2002, A&A, 396, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Branchesi, M., Gioia, I. M., Fanti, C., & Fanti, R. 2007, A&A, 472, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Predehl, P., Boehringer, H., et al. 2011, Mem. Soc. Astron. It. Supp., 17, 159 [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1978, A&A, 70, 677 [NASA ADS] [Google Scholar]
- Citterio, O., Conconi, P., Ghigo, M., et al. 1994, in SPIE Conf. Ser. 2279, eds. R. B. Hoover, & A. B. Walker, 480 [Google Scholar]
- Clerc, N., Sadibekova, T., Pierre, M., et al. 2012, MNRAS, 423, 3561 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Tozzi, P., Borgani, S., & Rosati, P. 2004, A&A, 417, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fassbender, R., Böhringer, H., Nastasi, A., et al. 2011, New J. Phys., 13, 125014 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [Google Scholar]
- Finoguenov, A., Watson, M. G., Tanaka, M., et al. 2010, MNRAS, 403, 2063 [NASA ADS] [CrossRef] [Google Scholar]
- Gal, R. R., de Carvalho, R. R., Lopes, P. A. A., et al. 2003, AJ, 125, 2064 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Daddi, E., Onodera, M., et al. 2011, A&A, 526, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, D., Holland, A., & Turner, M. 2007, in SPIE Conf. Ser., 6686 [Google Scholar]
- Hao, J., McKay, T. A., Koester, B. P., et al. 2010, ApJS, 191, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Kolokotronis, V., Georgakakis, A., Basilakos, S., et al. 2006, MNRAS, 366, 163 [NASA ADS] [Google Scholar]
- Lloyd-Davies, E. J., Romer, A. K., Mehrtens, N., et al. 2011, MNRAS, 418, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Lopes, P. A. A., de Carvalho, R. R., Gal, R. R., et al. 2004, AJ, 128, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Nichol, R. C., Collins, C. A., & Guzzo, L. 1992, MNRAS, 258, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2010, MNRAS, 406, 1759 [NASA ADS] [Google Scholar]
- Maughan, B. J., Jones, L. R., Ebeling, H., & Scharf, C. 2006, MNRAS, 365, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2008, ApJS, 174, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Mehrtens, N., Romer, A. K., Hilton, M., et al. 2012, MNRAS, 423, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, C. J., Nichol, R. C., Reichart, D., et al. 2005, AJ, 130, 968 [Google Scholar]
- Moretti, A., Campana, S., Mineo, T., et al. 2005, in SPIE Conf. Ser. 5898, ed. O. H. W. Siegmund, 360 [Google Scholar]
- Moretti, A., Perri, M., Capalbi, M., et al. 2007, in SPIE Conf. Ser., 6688 [Google Scholar]
- Moretti, A., Pagani, C., Cusumano, G., et al. 2009, A&A, 493, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, S. S., Giacconi, R., Ptak, A., et al. 2010, in SPIE Conf. Ser., 7732 [Google Scholar]
- Mushotzky, R. F., & Scharf, C. A. 1997, ApJ, 482, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, J. R., Jernigan, J. G., Gupta, R. R., Bankert, J., & Kahn, S. M. 2009, ApJ, 707, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Chiappetti, L., Pacaud, F., et al. 2007, MNRAS, 382, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., Böhringer, H., Brunner, H., et al. 2010, in AIP Conf. Ser., 1248, eds. A. Comastri, L. Angelini, & M. Cappi, 543 [Google Scholar]
- Puccetti, S., Capalbi, M., Giommi, P., et al. 2011, A&A, 528, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2012, ApJ, submitted [arXiv:1203.5775] [Google Scholar]
- Reichert, A., Böhringer, H., Fassbender, R., & Mühlegger, M. 2011, A&A, 535, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romer, A. K., Viana, P. T. P., Liddle, A. R., & Mann, R. G. 2001, ApJ, 547, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., della Ceca, R., Norman, C., & Giacconi, R. 1998, ApJ, 492, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Borgani, S., & Norman, C. 2002a, ARA&A, 40, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Tozzi, P., Giacconi, R., et al. 2002b, ApJ, 566, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Borgani, S., Gilli, R., et al. 2011, Mem. Soc. Astron. It. Supp., 17, 8 [Google Scholar]
- Santos, J. S., Rosati, P., Tozzi, P., et al. 2008, A&A, 483, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, J. S., Tozzi, P., Rosati, P., & Böhringer, H. 2010, A&A, 521, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharf, C. 2002, ApJ, 572, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Schuecker, P. 2005, in Rev. Mod. Astron., 18, ed. S. Röser, 76 [Google Scholar]
- Sehgal, N., Trac, H., Acquaviva, V., et al. 2011, ApJ, 732, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, S. A., Brodwin, M., Gonzalez, A. H., et al. 2012, ApJ, 753, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Šuhada, R., Song, J., Böhringer, H., et al. 2012, A&A, 537, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabo, T., Pierpaoli, E., Dong, F., Pipino, A., & Gunn, J. 2011, ApJ, 736, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., Santos, J., Yu, H., et al. 2011, Mem. Soc. Astron. It. Supp., 17, 24 [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Best, P. N., Kauffmann, G., & White, S. D. M. 2007, MNRAS, 379, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2009, ApJS, 183, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., Tozzi, P., Borgani, S., Rosati, P., & Zhu, Z.-H. 2011, A&A, 529, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwicky, F., Herzog, E., & Wild, P. 1963, Catalogue of galaxies and of clusters of galaxies, 2 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Effective area of XRT (green solid line) as a function of the energy compared with that of the Chandra satellite (red dotted and cyan dashed lines for Chandra ACIS-I and ACIS-S, respectively). |
| In the text | |
 |
Fig. 2 Measured HPR within a box of 45 × 45 arcsec as a function of the off-axis angle for all the sources detected in the XRT fields used in this work. |
| In the text | |
 |
Fig. 3 Distribution on the sky (Aitoff projection) of the GRB fields in the XRT archive as of April 2010 (red dots). The fields selected in our survey are those outside the Galactic plane (shaded area). |
| In the text | |
 |
Fig. 4 Light curve of the background of the field of GRB 051008 plotted as a function of the time elapsed from the GRB trigger. The saw-tooth appearance is due to the orbits of Swift (one orbit lasts 90 minutes). The removed time interval below the epoch T0 + 0.1 × texp is shown in gray. |
| In the text | |
 |
Fig. 5 Distribution of the exposure times in ks for the 336 selected GRB fields. |
| In the text | |
 |
Fig. 6 Hardness ratios modeled for XRT as a function of redshift for groups and clusters with several temperatures (red continuous lines, kT respectively equal to 0.5, 1.0, 2.0, 3.0, 5.0, 7.0, 10.0 and 12.0 keV from the bottom to the top) and for AGN with different intrinsic absorption (blue dashed lines, NH respectively equal to 0.01, 0.1, 0.3, 1.0, 3.0 and 10.0 × 1022 cm-2 from the bottom to the top). In the top right, we show the typical error bar on HR for a source with 200 total net counts. |
| In the text | |
 |
Fig. 7 Distribution of the measured HPR within a 45 × 45 arcsec box for simulated unresolved sources as a function of the soft counts within the box. The same range of exposure times and backgrounds present in the real data has been adopted in the simulations. The continuous line shows the 99% confidence level envelope of the source distribution. |
| In the text | |
 |
Fig. 8 Distribution of the measured HPR within a box of 45 × 45 arcsec for all the sources detected in the XRT fields as a function of the soft counts measured within the HPR. All possible extended source candidates are marked with black big dots, while red big dots indicate sources with >100 soft net counts from the aperture photometry in the extraction radius (see Sect. 5) and are therefore included in the cluster candidate list. The continuous lines show the typical 99% confidence level envelope for different exposures, from 1 ks (orange line) to 1 Ms (blue line). |
| In the text | |
 |
Fig. 9 Completeness level, expressed as the ratio of recovered extended sources on the number of simulated extended sources as a function of the input soft counts. |
| In the text | |
 |
Fig. 10 XRT smoothed image of the GRB050505 field in the soft (0.5−2.0 keV) band; the exposure time is ~170 ks, and the image size is ~24 × 24 arcmin. The three clusters in the fields are highlighted by the green cicles. The bright source at the center is the GRB. |
| In the text | |
 |
Fig. 11 Energy conversion factor (ECF) as a function of the ICM temperature for different redshifts. Here we assumed no Galactic absorption. |
| In the text | |
 |
Fig. 12 Energy conversion factor (ECF) as a function of the Galactic NH for a typical cluster (kT = 5 keV, z = 0.4). The histogram shows the distribution of Galactic NH in our cluster sample. |
| In the text | |
 |
Fig. 13 Solid angle Ω covered by our survey as a function of the soft flux. As a comparison, we show also the sky coverage of the 400 Square Degree Survey (Burenin et al. 2007, blue dashed line) and the sky coverage of the RDCS (Rosati et al. 1998, green dotted line). |
| In the text | |
 |
Fig. 14 Cumulative number counts, corrected for completeness, with 1σ confidence level for SXCS (red area), compared to the log N−log S derived from the ROSAT Deep Cluster Survey (cyan area), Rosati et al. (1998). Dot-dashed and dashed lines show the fit to the 400 d (Burenin et al. 2007) and to the COSMOS (Finoguenov et al. 2007) number counts, respectively. |
| In the text | |
 |
Fig. 15 Positions of our sources with respect to the GRB position (set to 0, 0). |
| In the text | |
 |
Fig. 16 Selection of SXCS cluster candidates imaged by the Sloan Digital Sky Survey (SDSS) with X-ray contours overlaid in green. The image size is 3 × 3 arcmin. The X-ray contours are computed on XRT images in the 0.5−2 keV energy band with the Chandra Ciao software, and the contours are drawn at respectively 9, 15, 30, 50, 90, 160 and 300σ, where σ is given by the local background level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


