| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219000 | |
| Published online | 17 October 2012 | |
The “toothbrush-relic”: evidence for a coherent linear 2-Mpc scale shock wave in a massive merging galaxy cluster?
1
Leiden Observatory, Leiden University,
PO Box 9513
2300 RA,
Leiden
The Netherlands
e-mail: rvanweeren@cfa.harvard.edu
2
Netherlands Institute for Radio Astronomy (ASTRON),
Postbus 2, 7990 AA
Dwingeloo, The
Netherlands
3
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
4
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA
22903-2475,
USA
5
Minnesota Institute for Astrophysics, University of
Minnesota, 116 Church St.
S.E., Minneapolis,
MN
55455,
USA
6
Jacobs University Bremen, PO Box 750561, 28725
Bremen,
Germany
7
Hamburger Sternwarte, Gojenbergsweg 112,
21029
Hamburg,
Germany
8
Thüringer Landessternwarte Tautenburg, Sternwarte 5,
07778
Tautenburg,
Germany
Received: 9 February 2012
Accepted: 3 September 2012
Some merging galaxy clusters host diffuse extended radio emission, so-called radio halos and relics, unrelated to individual galaxies. The origin of these halos and relics is still debated, although there is compelling evidence now that they are related to cluster merger events. Here we present detailed Westerbork Synthesis Radio Telescope (WSRT) and Giant Metrewave Radio Telescope (GMRT) radio observations between 147 MHz and 4.9 GHz of a new radio-selected galaxy cluster 1RXS J0603.3+4214, for which we find a redshift of 0.225. The cluster is detected as an extended X-ray source in the ROSAT All Sky Survey with an X-ray luminosity of LX, 0.1−2.4 keV ~ 1 × 1045 erg s-1. The cluster hosts a large bright 1.9 Mpc radio relic, an elongated ~2 Mpc radio halo, and two fainter smaller radio relics. The large radio relic has a peculiar linear morphology. For this relic we observe a clear spectral index gradient from the front of the relic towards the back, in the direction towards the cluster center. Parts of this relic are highly polarized with a polarization fraction of up to 60%. We performed rotation measure (RM) synthesis between 1.2 and 1.7 GHz. The results suggest that for the west part of the large relic some of the Faraday rotation is caused by the intracluster medium and not only due to galactic foregrounds. We also carried out a detailed spectral analysis of this radio relic and created radio color–color diagrams. We find (i) an injection spectral index of −0.6 to −0.7; (ii) steepening spectral index and increasing spectral curvature in the post-shock region; and (iii) an overall power-law spectrum between 74 MHz and 4.9 GHz with α = −1.10 ± 0.02. Mixing of emission in the beam from regions with different spectral ages is probably the dominant factor that determines the shape of the radio spectra. Changes in the magnetic field, total electron content, or adiabatic gains/losses do not play a major role. A model in which particles are (re)accelerated in a first order Fermi process at the front of the relic provides the best match to the observed spectra. We speculate that in the post-shock region particles are re-accelerated by merger induced turbulence to form the radio halo as the relic and halo are connected. The orientation of the bright relic and halo indicate a north-south merger event, but the peculiar linear shape and the presence of another relic, perpendicular to the bright relic, suggest a more complex merger event. Deep X-ray observations will be needed to determine the merger scenario.
Key words: radio continuum: galaxies / galaxies: active / galaxies: clusters: individual: 1RXS J0603.3+4214 / large-scale structure of Universe
© ESO, 2012
GMRT observations.
1. Introduction
Radio halos and relics are diffuse sources found in galaxy clusters that show signs of an ongoing merger event (see Feretti 2005; Ferrari et al. 2008; Brüggen et al. 2011, for an overview). These sources reveal the presence of relativistic particles and cluster-wide magnetic fields (e.g., Jaffe 1977) within the intracluster medium (ICM). In the hierarchical model of structure formation galaxy cluster form through a sequence of mergers with smaller substructures. These merger events create shocks and turbulence in the ICM and could amplify magnetic fields. Several models have been put forward which link the presence of these diffuse radio sources to cluster merger events (e.g., Enßlin et al. 1998; Brunetti et al. 2001; Petrosian 2001; Cassano & Brunetti 2005; Keshet 2010; Enßlin et al. 2011).
Radio halos are smooth extended radio sources that roughly follow the X-ray emission from the ICM. They are typically unpolarized and have an extent of about a Mpc. There are two main classes of models proposed to explain the origin of radio halos: (1) relativistic electrons in the ICM are re-accelerated in-situ through interaction with turbulence generated in the ICM by cluster-cluster mergers (Brunetti et al. 2001; Petrosian 2001), or (2) the energetic electrons are secondary products of proton-proton collisions (e.g., Dennison 1980; Blasi & Colafrancesco 1999; Dolag & Enßlin 2000; Miniati et al. 2001; Keshet & Loeb 2010; Enßlin et al. 2011). In addition, models using a combination of the two mechanisms have been considered (Brunetti & Blasi 2005; Dolag et al. 2008; Brunetti & Lazarian 2011).
Radio relics are usually divided up into three different classes (see Kempner et al. 2004, for an overview). (1) Radio gischt are large extended sources mostly found in the outskirts of galaxy clusters. They are proposed to trace shock waves (Enßlin et al. 1998; Miniati et al. 2001), in which particles are accelerated by the diffusive shock acceleration mechanism (DSA; e.g., Krymskii 1977; Axford et al. 1977; Bell 1978a,b; Blandford & Ostriker 1978; Drury 1983; Blandford & Eichler 1987; Jones & Ellison 1991; Malkov & O’C Drury 2001) in a first-order Fermi process. However, the efficiency with which collisionless shocks can accelerate particles is unknown and may not be enough to produce the observed radio brightness of relics. A closely linked scenario is that of shock re-acceleration of pre-accelerated electrons in the ICM, which is a more efficient mechanism for weak shocks (e.g., Markevitch et al. 2005; Giacintucci et al. 2008; Kang & Ryu 2011; Kang et al. 2012). (2) Active galactic nucleus (AGN) relics trace old radio plasma from previous episodes of AGN activity. (3) Radio phoenices are AGN relics that have been compressed adiabatically by merger shock waves boosting the radio emission (Enßlin & Gopal-Krishna 2001; Enßlin & Brüggen 2002). The radio spectra of these sources should be steep (α ≲ −1.5, Fν ∝ να, where α is the spectral index) and curved due to synchrotron and Inverse Compton (IC) losses.
A different model for radio relics (radio gischt) and halos has been proposed by Keshet (2010). It is based on a secondary cosmic ray electron model, where the time evolution of the magnetic fields and cosmic ray distribution are taken into account to explain both halos and gischt. For the outer edges of relics it is predicted that the spectral index should be α ≃ −1. In addition, the magnetic fields (B) are expected to be strong, with B ≳ BCMB > 3 μGauss, and BCMB the equivalent magnetic field strength of the cosmic microwave background.
Although there is now substantial evidence that radio relics and halos are related to galaxy cluster mergers (e.g., Cassano et al. 2010), the detailed physics are still not understood. Radio spectra are a crucial way to separate between the physical models for the origin of radio relics and halos. Obtaining high-quality spectra is however difficult as these sources are extended and have a low surface brightness. In particular, spectral curvature provides important information about the underlying physical processes. However, curvature in the synchrotron spectrum is only observable if the observed frequency range is wide enough. In addition, obtaining images at matched resolutions over a wide-frequency range is often not possible.
We carried out an observing campaign to search for new diffuse radio sources in clusters (van Weeren et al. 2011c,b). By inspecting the WENSS (Rengelink et al. 1997) and NVSS (Condon et al. 1998) surveys we came across the complex radio source B3 0559+422B. The radio source roughly coincided with an extended X-ray source in the ROSAT All Sky Survey. In addition, an overdensity of galaxies following the X-ray emission, was visible in 2MASS images. The diffuse radio source, extended X-ray emission and galaxy overdensity strongly suggested the presence of a previously unidentified galaxy cluster located at moderate redshift. In this paper we present detailed radio observations of this new galaxy cluster 1RXS J0603.3+4214 and investigate the spectral and polarimetric properties of the diffuse emission.
The layout of this paper is as follows. In Sect. 2 we give an overview of the observations and the data reduction. The Westerbork Synthesis Radio Telescope (WSRT) and Giant Metrewave Radio Telescope (GMRT) images are presented in Sect. 3. The radio spectra and polarization data are analyzed in Sects. 4 to 6. We end with a discussion and conclusions in Sects. 7 and 8.
Throughout this paper we assume a ΛCDM cosmology with H0 = 71 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. All images are in the J2000 coordinate system.
2. Observations and data reduction
2.1. GMRT observations
GMRT observations were taken using the GMRT software backend (GSB; Roy et al. 2010). An overview of the observations is given in Table 1.
The data were reduced with the NRAO Astronomical Image Processing System (AIPS) package. The data were visually inspected for the presence of radio frequency interference (RFI) which was subsequently removed. For the 147 and 241 MHz data, RFI was fitted and subtracted using the technique described by Athreya (2009), implemented in Obit (Cotton 2008). Standard bandpass and gain calibration were carried out, followed by several rounds of phase self-calibration and two final rounds of amplitude and phase self-calibration. The fluxes for the calibrator sources were set by the Perley & Taylor (1999) extension to the Baars et al. (1977) scale. Images were made using “briggs” weighting (Briggs 1995), see Table 1. were cleaned down to 2 times the rms noise level (2σrms) within the clean boxes and corrected for the primary beam attenuation1. For more details about the data reduction see van Weeren et al. (2011d). The 147 MHz data were further calibrated for ionospheric phase distortions, as these can become quite severe at this frequency, with the SPAM package (Intema et al. 2009). At 325 MHz we removed several sources using the “peeling”-method (e.g., Noordam 2004). We assume a 5% uncertainty in the calibration of the absolute flux-scale (Chandra et al. 2004).
2.2. WSRT observations
WSRT observations.
WSRT observations of 1RXS J0603.3+4214 were taken in the L-band, 13cm and 6cm bands, see Table 2 for details. The data were calibrated with the CASA2 package. We first removed time ranges affected by shadowing and RFI. The data were then calibrated for the bandpass response and subsequent gain solutions were transferred to the target source. Channel dependent leakage terms were found using an unpolarized calibrator source and the polarization angles were determined from 3C 286. The fluxes for the calibrator sources were set by the Perley & Taylor (1999) extension to the Baars et al. (1977) scale. The data were exported into AIPS for several rounds of phase self-calibration, followed by two rounds of amplitude and phase self-calibration, see also van Weeren et al. (2011d). Images were cleaned with manually placed clean boxes and corrected for the primary beam attenuation. A deep image was created by combining the images from individual IF’s from the 18, 21, and 25 cm bands. The images were convolved to the same resolution and combined with a spectral index scaling of −1. The resolution of this combined image is 29″ × 19″. We assume a 5% uncertainty in the calibration of the absolute flux-scale.
We used the WSRT L-band observations to perform rotation measure (RM) synthesis (see Sect. 6.2). For this, we created full polarization maps of every two neighboring frequency channels (i.e., the image bandwidth is 62.5 kHz). We inspected all these images and removed maps that had high noise levels, were affected by RFI or had other artifacts. In the end, 280 channels maps between 1170 and 1786 MHz were retained for RM-synthesis.
2.3. WHT spectroscopy and imaging
Optical images of 1RXS J0603.3+4214 were taken with the PFIP camera on the 4.2 m William Herschel Telescope (WHT) between 15 and 19 April, 2009 with V, R and I filters. The seeing varied between 1.0′′ and 1.5′′ and the total integration time was 1500 s per filter. The data were reduced with IRAF (Tody 1986, 1993) and the mscred package (Valdes 1998). Images were flat-fielded and corrected for the bias offset. R and I band images were also fringe corrected. The individual exposures were averaged, with pixels being rejected above 3.0σrms to remove cosmic rays and other artifacts. The optical images were strongly affected by the bright star BD+42 1474 (Vmag = 8.62), see Fig. 1.
To determine the redshift of the cluster, WHT ISIS spectra of galaxies located on the optical images were taken on 10 and 11 February, 2011. For the blue arm we used the R300B grating and for the red arm the R316R grating. The slit-width was 1.5′′. Flat-fielding, bias correction, and wavelength calibration were performed in IDL3. The total exposure time per galaxy was 1500 s in both the blue and red arms. In the end, the spectra for the blue and red arm were merged into single spectrum for each galaxy.
3. Results: redshift, X-rays, and radio continuum maps
3.1. Redshift of 1RXS J0603.3+4214
The brightest cluster members are visible in the 2MASS survey images (Skrutskie et al. 2006) and some of them are also listed in the 2MASS Extended sources catalog (Skrutskie et al. 2003). The cluster is not listed in NED or SIMBAD and probably remained unidentified because it is located relatively close to the galactic plane at a galactic latitude b = 9.4° and nearby the bright star BD+42 1474.
No published redshifts are available for any of the galaxies in the cluster. Galaxies for which WHT ISIS spectra were obtained are listed in Table 3 and the spectra are shown in Fig. 2. The spectra are typical for passive red elliptical galaxies mostly found in clusters. We find that the five galaxies are located at 0.220 ≤ z ≤ 0.228. Taking the average value we adopt z = 0.225 ± 0.04 for the cluster, with the uncertainty in the redshift given by the standard deviation.
 |
Fig. 1 WHT V, R, I color image. Yellow contours are from the GMRT 610 MHz image (Fig. 4) and drawn at levels of [1,2,4,8,...] × 0.15 mJy beam-1. Galaxies for which spectra were obtained are marked with red circles, see also Table 3 and Fig. 2. The spiral pattern (yellow contours) at the bottom right is due to residual calibration errors around the source B3 0559+422A. |
Redshifts.
3.2. X-ray emission from the ICM
1RXS J0603.1+4214 is seen the ROSAT All-Sky Survey as an extended source and listed as 1RXS J060313.4+421231, 1RXS J060322.3+421305, and 1RXS J060314.8+421439 (Voges et al. 1999, 2000), see Fig. 3 (left panel). Using the redshift and ROSAT count rate (0.21 PSPC cts s-1) we find an X-ray luminosity (LX, 0.1−2.4 keV) of ~1 × 1045 erg s-1. The X-ray emission is extended in the north-south direction. Additional emission extends to the east and west of the main X-ray peak. The high X-ray luminosity and extended emission are consistent with a massive cluster undergoing a major merger event.
 |
Fig. 2 Rest-frame WHT ISIS spectra for the galaxies listed in Table 3. The order (from top to bottom) is the same as in Table 3. Various absorption features are indicated. |
 |
Fig. 3 Left: X-ray emission from ROSAT. The image from the ROSAT All Sky Survey was smoothed with a 200′′ FWHM Gaussian and is shown in orange colors. Solid contours are from the WSRT L-band image and drawn at levels of [1,2,4,8,...] × 0.15 mJy beam-1. Right: WSRT L-band image (1160–1780 MHz) with sources labelled. Contour levels are drawn at [1,2,4,8,...] × 80 μJy beam-1. The beam size is 29″ × 19″ and indicated in the bottom left corner of the image. |
 |
Fig. 4 GMRT 610 MHz image. Contour levels are drawn at |
3.3. Radio continuum maps
The WSRT L-band map is displayed in Fig. 3. We labeled some of the most prominent sources in this image. The GMRT 147, 241, 325, 610, 1280 MHz, and WSRT 21 and 13 cm images are shown in Figs. 4 to 6 (for the 4.9 GHz image see Fig. 17). The properties of the diffuse source in the cluster are summarized in Table 4.
Source A (B3 0559+422A) is a compact flat spectrum source with a flux of 0.29 Jy at 1.4 GHz (Jackson et al. 2007; Beasley et al. 2002; Marecki et al. 1999; Patnaik et al. 1992). The radio source is associated with a star-like object in the WHT images and listed as a quasar by Andrei et al. (2009), but no redshift is reported. Source F is a compact source (but resolved in the 1280 and 610 MHz images) and has an optical counterpart in the WHT images.
The most prominent source in the GMRT and WSRT images is B3 0559+422B (source B). The source is also visible in the 74 MHz VLSS survey (Cohen et al. 2007) and listed as VLSS J0603.2+4217. In the L-band image, the source has a largest angular size of 8.7′, which corresponds to a physical size of almost 1900 kpc. The source consists of a bright western part (B1) and a fainter linear extension to the northeast (B2, B3). The radio emission brightens and fades two times along this extension, while the width of the source also varies. In the high-resolution 1280, 610, and 325 MHz images, the source displays a complex filamentary morphology. Some “streams” of emission extent from the northern part of B1 to the south. The northern boundary of the source is sharp, while the emission fades more slowly at the southern part. We classify source B as a radio relic because of the lack of optical counterparts, its polarization and spectral properties (see Sects. 4 to 6), and the large physical elongated size and peripheral location in the cluster.
Extending from B1 to the south, there is a patch of low surface brightness emission (C: subdivided into C1and C2). A hint of emission is visible north of B1 in the L-band and 325 MHz images, possibly associated with C1. The surface brightness decreases more rapidly at the south side of C (C2) than at the east and west sides. If we consider the faint emission north of B1 to be part of C then the source has a largest angular size of about 10′ (i.e., a physical extent of 2.1 Mpc). Only counting the emission south of B1 the source extends about 8′. We classify source C as the giant elongated radio halo because it roughly follows the X-ray emission from the ICM and has different spectral index properties than source B. The radio power of 6.8 × 1024 W Hz-1 falls on the LX–P1.4 GHz correlation for giant radio halos (e.g., Liang et al. 2000; Cassano et al. 2006). However, at the most southern part of C2 the surface brightness increases slightly. This is best seen in the 147 and 241 MHz images (Fig. 6). The southern end of C2 could therefore be the “counter” radio relic of B1 (see Sect. 7). Although, we can also not exclude the possibility that it is part of the radio halo.
Another diffuse elongated source is located to the east of C1. The source consist of two parts, E1 and E2. We classify source E as a radio relic because we could not find an optical counterpart associated with it and it is located at the eastern boundary of the X-ray emission. The extent of E is 4′ which corresponds to 860 kpc. Source D is another diffuse source without any optical counterpart in the WHT images, which we also classify as a radio relic. It has a largest angular size of 1.0′ in the GMRT 610 MHz image and displays hints of a complex morphology (Fig. 5), very different from a typical radio galaxy.
4. Radio spectra
4.1. Spectral index maps
We created radio spectral index maps using the GMRT and WSRT data. We first made radio maps at roughly the same resolution applying suitable tapers in the uv-plane and using uniform weighting. We discarded data below 0.25 kλ to select only common inner uvranges. The maps were then convolved to the same resolution. A high-resolution (7.9″ × 6.2″) spectral index map between 610 and 325 MHz is shown in Fig. 7. Pixels with values below 5σrms were blanked. A medium-resolution (20″ × 18″) spectral index map between 2272 and 147 MHz was also made by fitting a second order polynomial in log (S) − log (ν) space through the flux measurements at 2272, 1714, 1382, 1221, 610, 325, 241, and 147 MHz, see Fig. 8 (left panel). Pixels with values below 1.5σrms were blanked. To map the spectral index across the low surface brightness halo emission in the cluster, we also made a low-resolution spectral index map. We convolved the eight maps with a 35″ FWHM Gaussian (giving a resolution of approximately 40′′) and fitted a power-law spectral index to minimize the number of fitted parameters. Pixels with a spectral spectral index error >0.7 were blanked (Fig. 8, right panel). The errors in the spectral index maps are computed on the basis of the σrms values for the individual maps at the various frequencies and the reported flux calibration uncertainties in Sect. 2. When maps at more than two frequencies are used, it is assumed that the adopted fitting function provides a good physical description of the spectral shape. Figures displaying the corresponding errors in the spectral maps are show in Appendix A.
The spectral index across relic B displays a clear north-south gradient, with a spectral index of about −0.6 to −0.75 on the north side of the relic, steepening to ~−1.9 at the south side of B2 and B3 and to ≲ −2.5 for B1. The spectral index gradient is visible over the entire length of the relic. The high-resolution 610–325 MHz spectral index map reveals the same general trends for relic B as in the medium-resolution map. However, the SNR on the spectral index is somewhat lower, mainly because of the smaller frequency span. We note that the spectral index at the front of B2 and B3 has a steeper spectral index (about −0.9 to −1.1) in the region where the surface brightness drops (i.e., at the intersection B1, B2 and B2, B3).
 |
Fig. 6 GMRT 150, 241, 325, 1280 MHz and WSRT 1382 and 2272 MHz images. Contour levels are drawn at [1,2,4,8,...] × 4σrms. Negative −3σrms contours are shown by the dotted lines. The beam size is shown in the bottom left corner of the images. |
The spectral index across Relic E varies mostly between −1.0 to −1.2. There are no systematic trends visible across the relic, except that the north part of E3 has a somewhat flatter spectral index, see Fig. 8. The spectral index for relic D steepens from −1.0 to −1.3 from south to north. The spectral index across the radio halo (C) is difficult to determine as the SNR is low, but it roughly varies between −1.5 and −0.8 with an average of −1.1. There is a hint of spectral flattening for the center of the halo, while to the north and south of it the spectral index is steeper on average.
4.2. Integrated radio spectra
We determined the integrated radio spectra of the components, taking the same maps which were used to create the medium-resolution (20″ × 18″) spectral index map to minimize the effects of different uv-coverage. In addition, we added flux measurements at 74 MHz and 4.9 GHz for relic B from the VLSS survey and the WSRT observations. The radio spectrum is shown in Fig. 9 and is well fitted by a single power-law with α = −1.10 ± 0.02 between 74 and 4900 MHz. For relics D and E we find integrated spectral indices of −1.10 ± 0.05 and −1.0 ± 0.2. For source C we find α = −1.15 ± 0.06. The integrated radio spectra do not show clear evidence for spectral breaks or turnovers, although the radio spectrum for E is poorly determined.
Diffuse radio sources in 1RXS J0603.3+4214.
 |
Fig. 7 GMRT 610–325 MHz spectral index map. Contour levels from the GMRT 325 MHz image are drawn at [1,4,16,64,...] × 6σrms and the spectral index map has a resolution of 7.9″ × 6.2″. Pixels below 5σrms are blanked. |
 |
Fig. 8 Left: fitted spectral index map between 2272 and 147 MHz. The spectral index map was made by fitting a second order polynomial in log (S) − log (ν) for each pixel in the maps at 2272, 1714, 1382, 1221, 610, 325, 241 and 147 MHz. Contour levels are drawn at [1,2,4,8,...] × 0.175 mJy beam-1 and are from the L-band image in Fig. 3. The spectral index map has a resolution of 20″ × 18″ and pixels below 1.5σrms were blanked. Right: fitted spectral index (2272 and 147 MHz) for each pixel in the maps at 2272, 1714, 1382, 1221, 610, 325, 241 and 147 MHz. The individual maps were convolved with Gaussians of 35″ FWHM and pixels with a spectral index error >0.7 were blanked, contours are drawn as in the left panel. |
5. Radio color–color diagrams
We investigated the detailed spectral shape of the relic emission. We first divided the relic into two parts, B1 and B2+B3, which we analyzed separately. These parts were further subdivided into regions (αref) within a specific spectral index range of 0.1 units, using the spectral index map from Fig. 8 (left panel). The resulting spectra, including first order polynomial fits (in log (I) − log (ν) space) through the data points are shown in Fig. 13. The fluxes were normalized by dividing by the number of pixels found in each region, i.e., we work in surface brightness units. Each spectra thus corresponds to a region from the spectral index map where αref − 0.05 < αref < αref + 0.05, with αref = −0.65, −0.75, −0.85, etc. We limited αref to −1.85 and −1.65 for B1 and B2+B3, respectively, to retain sufficient SNR at the highest frequency map (at 2272 MHz). We use these spectra as a starting point for creating the radio color–color diagrams.
5.1. Spectral models
In the model put forward by Enßlin et al. (1998), relics trace shock waves in which particles are accelerated by the DSA mechanism. Without projection effects and mixing of emission, and all properties of the shock remaining constant, the spectra at the different locations should simply reflect the energy losses of the radiating particles. Assuming an edge-on planar shock-wave, the time since acceleration for particles at a given location behind the front of the relic is simply l/vd, with l the distance from the front of the shock and vd the shock downstream velocity. According to DSA-theory, the injection spectral index αinj is linked to the Mach number (ℳ) of the shock by (e.g., Blandford & Eichler 1987) 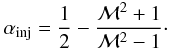 (1)The integrated spectral index is steeper by about 0.5 units compared to αinj for a simple shock model where the electron cooling time is much shorter than the lifetime of the shock (Miniati 2002). Most of the synchrotron radiation we observe comes from the “critical” frequency νc
(1)The integrated spectral index is steeper by about 0.5 units compared to αinj for a simple shock model where the electron cooling time is much shorter than the lifetime of the shock (Miniati 2002). Most of the synchrotron radiation we observe comes from the “critical” frequency νc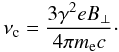 (2)Directly behind the front of the shock, the spectra should have a power-law shape of the form I(ν) = I0ναinj, under the usual assumption that one starts with a power-law distribution of relativistic electrons N(E) = N0E−s, where s = 1−2αinj.
(2)Directly behind the front of the shock, the spectra should have a power-law shape of the form I(ν) = I0ναinj, under the usual assumption that one starts with a power-law distribution of relativistic electrons N(E) = N0E−s, where s = 1−2αinj.
Synchrotron spectra can be calculated using the standard formula (Pacholczyk 1970) 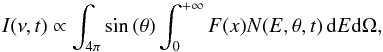 (3)where N(E,θ,t) is the electron energy distribution, θ the pitch angle between the electron velocity and magnetic field vectors, x = ν/νc, and
(3)where N(E,θ,t) is the electron energy distribution, θ the pitch angle between the electron velocity and magnetic field vectors, x = ν/νc, and 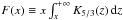 , with K5/3(z) an irregular modified Bessel function. Synchrotron and IC (radiation) losses change the electron energy distribution over time at a rate
, with K5/3(z) an irregular modified Bessel function. Synchrotron and IC (radiation) losses change the electron energy distribution over time at a rate 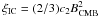 (4)The IC losses are given by
(4)The IC losses are given by 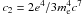 and the quantity
and the quantity 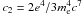 is a constant defined by (Pacholczyk 1970). Two main expressions for ξsyn exist.
is a constant defined by (Pacholczyk 1970). Two main expressions for ξsyn exist.
The Jaffe-Perola (JP) model takes into account that the pitch angles of the synchrotron emitting electrons are continuously isotropized on a timescale shorter than the radiative timescale (Jaffe & Perola 1973)  (5)For the Kardashev-Pacholczyk (KP) model, the pitch angle of the electrons remains in its original orientation with respect to the magnetic field
(5)For the Kardashev-Pacholczyk (KP) model, the pitch angle of the electrons remains in its original orientation with respect to the magnetic field 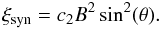 (6)The JP model is more realistic from a physical point of view, as an anisotropic pitch angle distribution will become more isotropic due to changes in the magnetic field strength between different regions and scattering by self-induced Alfvén waves (e.g., Carilli et al. 1991; Tribble 1993; Slee et al. 2001). The JP and the KP models assume a single impulsive injection that produces a power-law distribution of relativistic electrons. At t = 0, N(E) = N0E−s and at some later time (t)
(6)The JP model is more realistic from a physical point of view, as an anisotropic pitch angle distribution will become more isotropic due to changes in the magnetic field strength between different regions and scattering by self-induced Alfvén waves (e.g., Carilli et al. 1991; Tribble 1993; Slee et al. 2001). The JP and the KP models assume a single impulsive injection that produces a power-law distribution of relativistic electrons. At t = 0, N(E) = N0E−s and at some later time (t) 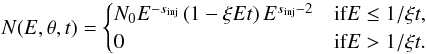 (7)With this equation for N(E,θ,t) and Eq. (3) the synchrotron spectrum can be computed. The result is that the energy losses (both for the JP and KP models) cause the radio spectrum to steepen (see Fig. 11) above a break frequency (νbrk), with
(7)With this equation for N(E,θ,t) and Eq. (3) the synchrotron spectrum can be computed. The result is that the energy losses (both for the JP and KP models) cause the radio spectrum to steepen (see Fig. 11) above a break frequency (νbrk), with ![\begin{equation} \nu_{\rm{brk}} \propto \frac{B}{\left(\left[B^2 + B^{2}_{\rm{CMB}}\right]t\right)^2 } \cdot \end{equation}](/articles/aa/full_html/2012/10/aa19000-12/aa19000-12-eq133.png) (8)JP-spectra have an exponential high-frequency cutoff above νbrk. KP-spectra steepen to a power-law with a slope (4/3)αinj − 1 above νbrk, because there are always some high energy electrons with low pitch angles to radiate at high frequencies in the KP case.
(8)JP-spectra have an exponential high-frequency cutoff above νbrk. KP-spectra steepen to a power-law with a slope (4/3)αinj − 1 above νbrk, because there are always some high energy electrons with low pitch angles to radiate at high frequencies in the KP case.
In addition to the above mentioned JP and KP models, where all particles are injected in one single burst and then simply age, there is the continuous injection (CI) model (Pacholczyk 1970), i.e., a fresh supply of particles is injected continuously and the so-called KGJP or KGKP models (Komissarov & Gubanov 1994), where particles are injected for a fixed period of time after which the supply of newly injected electrons is switched off. This results in different expressions for N(E,θ,t), see Eq. (6) from Komissarov & Gubanov (1994). CI and KGJP/KP spectra are basically summations of individual JP and KP spectra with different amounts of spectral ageing. Examples of resulting spectral shapes used in this work are shown in Fig. 11.
5.2. Effect of resolution on surface brightness
If radiative losses are the dominant effect then all spectra for different parts of the relic should line up at some fiducial low energy/frequency where radiation losses are not important. The spectra displayed in Fig. 13 should therefore all line up at low enough frequencies. Part of such a trend is indeed visible. However, the spectra with αref = −0.65, −0.75 have a lower surface brightnesses than we naively expect. We attribute this to the fact that the pixels, from which these spectra are determined, are all located on the sharp outer edge of the relic, where the emission drops abruptly to zero within a single beam element. Since the resolution of the spectral index map is only about 20′′ and there are about 4 pixels per beam, the regions with the flattest spectral index are all located on pixels where the surface brightness drops at the front of the relic due to the finite beam size. This can be seen by looking at the black contours in Fig. 8, i.e., the surface brightness does not peak at the region with the flattest spectral index. Comparing these contours to the higher resolution images in Figs. 4 and 6, we find however that the outer rim of the relic is indeed the brightest part of the relic. The lower surface brightness for the αref = −0.65, −0.75 regions is thus caused by the low spatial resolution of the spectral index map. This is also confirmed by the high-resolution 325–610 MHz spectral index map, see Fig. 7.
 |
Fig. 9 Integrated radio spectrum for radio relic B. |
 |
Fig. 10 Integrated radio spectra for sources C (left), D (middle), and E (right). The lines are fitted straight power-laws with indices given in Table 4. |
 |
Fig. 11 Overview of the spectral models used in this work (left) and corresponding radio color–color corves (right) to highlight differences in the spectral shapes. All spectral models have αinj = 0.6. Solid grey line and filled grey circle (in the color–color diagram): power-law spectrum without any ageing, solid black line: KP, dotted line: CI, dash-dotted line: KGJP, dashed line: JP. Note that a power-law spectrum will translate in a single point on a color–color diagram. The αlow−frequency = αhigh−frequency line divides concave and convex spectral shapes between the frequencies where the spectral index is computed. |
It is interesting to note that the spectra for the regions with a flattest spectral index are all relatively straight and show little deviations from a pure power-laws (Fig. 13). Going to the regions with a steeper αref, the spectral shapes change and display signs of curvature at the higher frequencies. These changes happens gradually from the regions with a flat αref to a steeper αref.
5.3. Color–color diagrams
To better investigate the spectral shape we use so called three frequency “color–color” diagrams for which the spectral indices for different region of the source can all be put in a single diagram (Katz-Stone et al. 1993). On the x-axis we plot the low- frequency spectral index and on the y-axis the high-frequency one. Color–color diagrams are particularly useful to discriminate between theoretical synchrotron spectral models, such as the JP, KP, CI, KGJP, KGKP models described before, see Fig. 11 for several examples.
Another advantage of color–color diagrams is that the shapes traced out in the diagrams are conserved for changes in the magnetic field, adiabatic expansion or compression, and the radiation losses, for standard spectral models. We observe a different portion of the spectrum for each different frequency or source physical condition (e.g., local B field). We can thus use the observed curve to constrain the different models (JP, CI, KP, etc.) and injection spectral indices. Mixing of emission, for example from regions with different B strengths or radiation losses, due the finite resolution of the observations or projection effects, will lead to different curves in the color–color diagrams. If a global spectral shape exists, it also allows for a better effective frequency sampling and provides sampling of a larger range of electrons energies.
5.3.1. Color–color diagrams for B1 and B2+B3
The color–color diagrams for B1 and B2+B3 are shown in Fig. 14 (left and right panels, respectively). The points in the color–color diagrams seem to trace out single curves. This suggests the existence of a global spectral shape for these regions. The curves are similar for the B1 and B2+B3 regions, but they slightly differ for αref ≲ −1.4.
Tracing the curves back to the 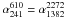 (i.e., power-law) line gives the injection spectral index. In both cases we find αinj is about −0.6 to −0.7 for B1 and B2+B3, in agreement with the spectral index maps. The color–color diagrams highlight the trend of increasing spectral curvature, i.e., distance from the power-law line, with decreasing αref (Fig. 13). The spectra for αref = −0.65, −0.75 are power-laws. We also indicated various spectral models in the diagrams. We compare the observed curves in the color–color diagrams to the some of the standard spectral models.
(i.e., power-law) line gives the injection spectral index. In both cases we find αinj is about −0.6 to −0.7 for B1 and B2+B3, in agreement with the spectral index maps. The color–color diagrams highlight the trend of increasing spectral curvature, i.e., distance from the power-law line, with decreasing αref (Fig. 13). The spectra for αref = −0.65, −0.75 are power-laws. We also indicated various spectral models in the diagrams. We compare the observed curves in the color–color diagrams to the some of the standard spectral models.
The observed curve is clearly different from the continuous injection spectral model. The CI model only steepens to α = αinj − 0.5 (Pacholczyk 1970). The KP model (with αinj = −0.6) roughly follows the data for flat αref, but deviates for αref ≲ −1. In the end the KP curve bends back and returns to the 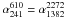 line. We do not see evidence for a turn back to the
line. We do not see evidence for a turn back to the 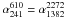 line in the data, although we do not sample this part of the diagram well because of insufficient SNR at high-frequencies. As mentioned previously, a KP model is rather unphysical. However, it sometimes provides a good fit to observed radio spectra because it is similar to the shapes caused by losses in a randomly varying magnetic field (Tribble 1993).
line in the data, although we do not sample this part of the diagram well because of insufficient SNR at high-frequencies. As mentioned previously, a KP model is rather unphysical. However, it sometimes provides a good fit to observed radio spectra because it is similar to the shapes caused by losses in a randomly varying magnetic field (Tribble 1993).
The JP model (plotted for αinj = −0.6 and −0.7) follows the KP model for flat αref. Instead of turning back to the 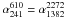 line, the spectral curvature keeps increasing. The data also show this trend of increasing curvature, but less quickly than the JP curve. A KGJP model with αinj = −0.7 matches the data for B2+B3 very well. The KGJP curves in Fig. 14 are for particles injected continuously for about 0.6 × 108 yr and B = 9 μGauss (see Sect. 7.3). The KGJP model also provides a better match for the B1 region compared to the KP and JP curves. Although, in the regions with the steepest αref values the KGJP model still overestimates the amount of curvature. A KGJP model can be thought of as an integration of JP spectra with a range of spectral ages, up to the oldest population of electrons. At first, the KGJP model follows the CI model until at some point in time the supply of newly injected electrons is shut off. Our injection time of 0.6 × 108 yr leads to a distribution of spectral ages in each αref region that is 0.6 × 108 yr wide at maximum, i.e., it represents the amount of mixing encountered in each αref region. It should not be interpreted as the total injection time for the relic. This value thus depends on the resolution of the spectral maps and unavoidable projection effects.
line, the spectral curvature keeps increasing. The data also show this trend of increasing curvature, but less quickly than the JP curve. A KGJP model with αinj = −0.7 matches the data for B2+B3 very well. The KGJP curves in Fig. 14 are for particles injected continuously for about 0.6 × 108 yr and B = 9 μGauss (see Sect. 7.3). The KGJP model also provides a better match for the B1 region compared to the KP and JP curves. Although, in the regions with the steepest αref values the KGJP model still overestimates the amount of curvature. A KGJP model can be thought of as an integration of JP spectra with a range of spectral ages, up to the oldest population of electrons. At first, the KGJP model follows the CI model until at some point in time the supply of newly injected electrons is shut off. Our injection time of 0.6 × 108 yr leads to a distribution of spectral ages in each αref region that is 0.6 × 108 yr wide at maximum, i.e., it represents the amount of mixing encountered in each αref region. It should not be interpreted as the total injection time for the relic. This value thus depends on the resolution of the spectral maps and unavoidable projection effects.
5.3.2. The effect of resolution and mixing
One important effect is mixing of emission within the beam. Each beam samples superpositions of regions with potentially physical different conditions. To investigate the effect of resolution in the color–color diagrams, we decreased the resolution of the spectral index maps by convolving them with Gaussians of 60′′ FWHM. The data for the lower resolution maps are also displayed in Fig. 14. The effect of the lower resolution is that the curve ends up closer to the 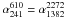 line. This is expected because the total integrated spectrum of the relic has a power-law shape (Fig. 9).
line. This is expected because the total integrated spectrum of the relic has a power-law shape (Fig. 9).
We also investigated for B1, the effect of a possible underlying flux component from the radio halo C. For this, we determined the average spectrum of the radio halo and subtracted this flux contribution at each frequency. This however did not substantially change the resulting color–color diagram for B1 because the surface brightness of the relic is much higher than that of the radio halo.
Our conclusion is that mixing of emission (from regions with different B-fields or different electron energy distributions, spectral ages, etc.) pushes the spectra closer to power-law shapes. The spectral curvature we find can thus be regarded as a lower limit on the actual curvature and it is therefore important that when searching for spectral curvature one retains sufficient spatial resolution (enough to properly resolve the spectral variations).
5.4. Global spectrum
Since the data points trace out a well defined curve in the color–color diagrams, we have attempted to map the flux measurements onto a single spectral shape using the “shift-technique” described by Katz-Stone et al. (1993); Rudnick & Katz-Stone (1996); Rudnick (2001). This allows for a much better sampling in frequency, and maps out the spectrum over a larger range of electron energies. The idea is that the individual radio spectra for different αref regions each trace some part of the “global spectrum” (or electron energy distribution) of the source, depending on the energy losses, and magnetic fields in these regions. The shifts (in log (I)-log (ν) space) remove the effects of possible different local magnetic field strengths, electron densities, radiative energy losses, and adiabatic energy gains/losses.
We shifted the spectra, displayed Fig. 13, in log (I)–log (ν) space and tried to line them all up. This went remarkably well, indicating we indeed have a single electron energy distribution (or global spectral shape) that is consistent with the spectra for each individual region. The two resulting spectra (for B1 and B2+B3) are displayed in Fig. 15. As can be seen it allows for an almost continuous sampling of the radio relic spectrum over about 4 orders of magnitude in frequency (two orders of magnitude in energy, see Eq. (2)).
Similar to the color–color diagrams we find that the low-frequency part of the global spectrum has a power-law shape, with α = −0.6 to −0.7. At higher frequencies the spectrum steepens. We also compare the global spectra with some of the standard models in Fig. 15. The results are the same as for the color–color diagrams, i.e., the best match we find for a KGJP model and for B1 the KGJP spectral curvature is somewhat too high for νeff ≳ 20 GHz.
5.4.1. Shift diagrams
Interestingly, the shifts made to align up all the individual radio spectra to create Fig. 15 provide information about changes in the underlying physical parameters (Katz-Stone & Rudnick 1994). The shifts made in the frequency direction (log (ν)), to line up the spectra, are related to γ2B. The shifts in log (I) are related to NTB, where NT is the total number of relativistic electrons in the volume determined by the beam size.
 |
Fig. 12 Schematic representation of two radio spectra with different spectral ages (break frequencies). To align the red spectrum to the black one in log-log space, a shift in the frequency direction is required to match up the break frequencies. The red spectrum then falls below the injection power-law spectrum and needs to be shifted upwards. The slope Δlog (I)/Δlog (ν) equals the injection spectral index in this case (see the main text). |
By plotting the shifts which we needed to align up the individual spectra (log (ν) shifts against log (I) shifts), we can investigate the contributions of the above mentioned quantities, i.e., which quantities cause the spectra to differ from region to region. The shift diagrams are shown in Fig. 16. For example, a slope (δlog (I)/δlog (ν)) of +1 indicates mainly variations in the magnetic field strength, a slope of infinity indicates density variations, and a slope of zero energy variations. If every line of sight samples the same physical conditions (i.e., the same magnetic field, path length through the source, number of relativistic particles at some fiducial low energy), then ageing alone would give a slope equal to the injection spectral index, see Fig. 12. This can be seen as follows: one needs to shift the red spectrum in Fig. 12 in log (ν) space to match up the break frequency of the black spectrum, but then the red spectrum will fall below the initial power-law injection spectrum, so a shift (up) in log (I) is also required. For the shift in log (ν) 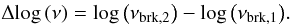 (9)For the shift in log I we have
(9)For the shift in log I we have![\begin{eqnarray} \Delta\!\log{(I)} &=& \log{\left(I_0 \nu_{\rm{brk,2}}^{\alpha_{\rm{inj}}} \right)} - \log{\left(I_0 \nu_{\rm{brk,1}}^{\alpha_{\rm{inj}}} \right)}\nonumber \\ &=& \alpha_{\rm{inj}}\left[ \log{\left(\nu_{\rm{brk,2}}\right)} - \log{\left(\nu_{\rm{brk,1}}\right)} \right] \end{eqnarray}](/articles/aa/full_html/2012/10/aa19000-12/aa19000-12-eq161.png) (10)}and thus the slope in the shift diagram is Δlog (I)/Δlog (ν) = αinj.
(10)}and thus the slope in the shift diagram is Δlog (I)/Δlog (ν) = αinj.
We find slopes of −0.83 and −0.67 in the shifts diagrams for B1 and B2+B3, respectively. We did not include the first three (B1) and two (B2+B3) points for fitting the slope. This because the log (I)-shifts for these points are affected by the reduced surface brightness at the outer edge of the relic, see Sect. 5.2. The slopes are close to the injection spectral indices of −0.6 to −0.7 we found from the color–color diagrams. The slope for B1 deviates a little more, but overall the shift diagrams indicate that spectral ageing is likely the dominant factor in explaining the different spectral shapes from region to region. Apparently, the magnetic field and total number of number of relativistic electrons remain more or less constant for the different αref regions.
 |
Fig. 13 Normalized radio spectra for relic B1 (top) and B2+B3 (bottom). Each spectrum corresponds to a region from the spectral index map where αref − 0.05 < αref < αref + 0.05, with αref = −0.65, −0.75,..., −1.85 for B1, and αref = −0.75, −0.85,..., −1.65 for B2+B3. The spectra are plotted in log ν − log (νI) space to emphasize the differences between the spectra. First order polynomial fits, done in log (I) − log (ν) space, are shown by the solid lines to emphasize possible deviations from power-law radio spectra. Colors correspond to the different αref and go from black, blue, purple, red, to orange. |
 |
Fig. 14 Color–color diagrams for B1 (left) and B2+B3 (right). Black data points are from the spectra displayed in Fig. 13. The solid black (slightly curved) line is a JP model with αinj = −0.6, the dashed black line a JP model with αinj = −0.7, the solid red line a KP model with αinj = −0.6, the dashed red line a CI model with αinj = −0.6, and the blue line a KGJP model with αinj = −0.7. The grey data points are for the same data as the black points, except the maps were smoothed with a 60′′ FWHM Gaussian. The |
 |
Fig. 15 “Global” radio spectra for B1 (left) and B2+B3 (right). The spectrum for each αref spectral region from Fig. 13 has been shifted in log (I) − log (ν) space to create the “global” spectral shape. Fourth order polynomial fits through these data points are shown by solid thin black lines. JP (red), KP (black) and KGJP (blue) models are shown by the dashed lines. The color coding, based on the αref regions, is the same as in Fig. 13. |
 |
Fig. 16 Shifts in log (I) − log (ν) space, for B1 (left) and B2+B3 (right), needed to line up the radio spectra displayed in Fig. 15. A line is fitted through the data points, excluding the first three (B1) or two (B2 + B3) points. Color coding for the αref regions is the same as in Fig. 13. |
6. RM-synthesis and polarization maps
6.1. Polarization maps
The distribution of the polarization E-vectors at 4.9 and 1.382 GHz are shown in Fig. 17. In the 4.9 GHz map, we find the relic to be polarized over its entire length (in the region with sufficient SNR). The E-vectors are mainly perpendicular to the relic’s orientation, except at the eastern end of B1 (where the relic bends and is connected to the linear eastward extension B2). The polarization fraction across the relic varies between 10 and 60%, where it can be measured. At the front of B1, the polarization fraction is mostly between 15 and 30%, while at the front of B2 the fraction is 50% or higher. In the 4.9 GHz map we cannot determine the polarization fraction for B3 because the attenuation of the primary beam. It should be noted that the spatially averaged polarization fractions are lower.
At 1382 MHz the polarization fraction drops significantly for B1 and B2, compared to at 4.9 GHz. For region B3 we measure a polarization fraction as high as 40%, while for the brightest part of B2 it is about 5%, and for B1 it drops below 1%. The average polarization fractions and depolarization properties for relic B are described in Sect. 6.3.
 |
Fig. 17 Left: WSRT 4.9 GHz polarization E-vector map. Total polarized intensity is shown as grayscale image. Vectors depict the polarization E-vectors, their length represents the polarization fraction. The length of the E-vectors are corrected for Ricean bias (Wardle & Kronberg 1974). A reference vector for a polarization fraction of 100% is shown in the bottom left corner. No vectors were drawn for pixels with a SNR < 3 in the total polarized intensity image. Contour levels are drawn at [1,4,16,64,...] × 3σrms and are from the Stokes I image. The beam size is 7.0″ × 4.7″ and indicated in the bottom left corner of the image. Right: WSRT 1382 MHz polarization E-vector map made with natural weighting. Total polarized intensity is shown as grayscale image. No vectors were drawn for pixels with a SNR <4 in the total polarized intensity image. Contour levels are drawn at [1,4,16,64,...] × 0.18 mJy beam-1. and are from the Stokes I image. |
6.2. RM-synthesis
Faraday rotation changes the intrinsic polarization angle (χ0) depending on the wavelength (λ) or frequency of the radiation. The Faraday depth (φ) is related to the properties of the plasma causing the Faraday rotation (Burn 1966; Brentjens & de Bruyn 2005) ![\begin{equation} \phi ({\vec r}) = 0.81 \int_{\mathrm{source}}^{\mathrm{telescope}} n_{\mathrm{e}}{\vec B} \cdot \, {\rm d}{\vec r} \mbox{ } [\mbox{rad m}^{-2} ] , \end{equation}](/articles/aa/full_html/2012/10/aa19000-12/aa19000-12-eq176.png) (11)where dr is an infinitesimal path length in parsec along the line of sight, B the magnetic field in μGauss and ne the electron density in cm-3. The sign is defined to be positive for a magnetic field pointing towards the observer. The rotation measure (RM) is defined as
(11)where dr is an infinitesimal path length in parsec along the line of sight, B the magnetic field in μGauss and ne the electron density in cm-3. The sign is defined to be positive for a magnetic field pointing towards the observer. The rotation measure (RM) is defined as 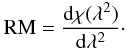 (12)If there is only one source along the line of sight (without internal Faraday rotation), the Faraday depth is equal the rotation measure (RM) at all wavelengths. In other words, all polarized emission is observed at a single Faraday depth φ. The observed polarization angle (χ) is then
(12)If there is only one source along the line of sight (without internal Faraday rotation), the Faraday depth is equal the rotation measure (RM) at all wavelengths. In other words, all polarized emission is observed at a single Faraday depth φ. The observed polarization angle (χ) is then 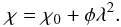 (13)In more complicated situations this relation is not valid (e.g., Vallee 1980; Sokoloff et al. 1998). By expressing the polarization as a complex vector P = pe2iχ = Q + iU, with p the intrinsic polarization Burn (1966) showed that
(13)In more complicated situations this relation is not valid (e.g., Vallee 1980; Sokoloff et al. 1998). By expressing the polarization as a complex vector P = pe2iχ = Q + iU, with p the intrinsic polarization Burn (1966) showed that 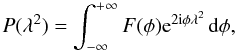 (14)where F(φ) is the Faraday dispersion function, i.e., the complex polarized surface brightness per unit Faraday depth. Equation (14) is invertible if the intrinsic polarization angle χ0 is constant as function of λ, then F(φ) can be found by measuring P(λ2)
(14)where F(φ) is the Faraday dispersion function, i.e., the complex polarized surface brightness per unit Faraday depth. Equation (14) is invertible if the intrinsic polarization angle χ0 is constant as function of λ, then F(φ) can be found by measuring P(λ2) 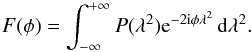 (15)With modern correlator backends, such as the one at the WSRT or EVLA, P(λ2) can measured over a large number of frequency channels. If φδλ2 ≪ 1, with δλ2 the channel width in wavelength squared, Brentjens & de Bruyn (2005) showed that Eq. (15) can be approximated as
(15)With modern correlator backends, such as the one at the WSRT or EVLA, P(λ2) can measured over a large number of frequency channels. If φδλ2 ≪ 1, with δλ2 the channel width in wavelength squared, Brentjens & de Bruyn (2005) showed that Eq. (15) can be approximated as 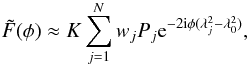 (16)with wj being some weights and K a normalization factor
(16)with wj being some weights and K a normalization factor 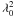 (17)As explained by Brentjens & de Bruyn, adding the term
(17)As explained by Brentjens & de Bruyn, adding the term 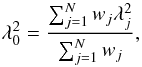 in the exponent of Eq. (16) results in a better sidelobe pattern for the rotation measure spread function (RMSF), with
in the exponent of Eq. (16) results in a better sidelobe pattern for the rotation measure spread function (RMSF), with 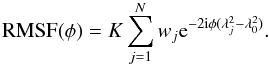 (18)and the RMSF given by
(18)and the RMSF given by 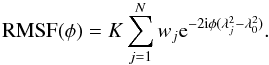 (19)Because P is not measured for every possible
(19)Because P is not measured for every possible 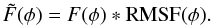 , the true Faraday depth function is related to Eq. (16) by a convolution
, the true Faraday depth function is related to Eq. (16) by a convolution 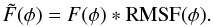 (20)Depending on the sidelobe structure of the RMSF (which can be adjusted by choosing the weights wj) a brighter component can contaminate the response of fainter components in
(20)Depending on the sidelobe structure of the RMSF (which can be adjusted by choosing the weights wj) a brighter component can contaminate the response of fainter components in 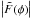 and therefore deconvolution might be necessary. The one-dimensional deconvolution algorithm which has been used is a simple extension of Högbom (1974) RM-CLEAN algorithm to the complex domain as described by Brentjens (2007), see also Heald et al. (2009). It works as follows:
and therefore deconvolution might be necessary. The one-dimensional deconvolution algorithm which has been used is a simple extension of Högbom (1974) RM-CLEAN algorithm to the complex domain as described by Brentjens (2007), see also Heald et al. (2009). It works as follows:
-
1.
For a spatial pixel the maximum of
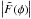 is found and the location ofthe peak is stored (φpeak).
is found and the location ofthe peak is stored (φpeak). -
2.
If this maximum value is higher than a user defined cutoff, the RMSF is shifted to the location of the peak (φpeak) and a scaled version (i.e., using a gain of 0.1) is subtracted from
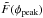 . Since the RMSF is complex, a multiplication with a phase factor is needed which depends on the phase of
. Since the RMSF is complex, a multiplication with a phase factor is needed which depends on the phase of 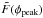 .
. -
3.
The complex scaling factor, which was used to shift and subtract the RMSF, is stored as a clean component.
-
4.
Steps 2–4 are repeated until a user defined threshold is reached or the number of iterations has reached a predefined maximum.
-
5.
Optionally, the clean components are restored with Gaussians with a FWHM matched to that of the RMSF. The Gaussians are again shifted to their respective locations (φpeak), and since this happens in the complex domain, multiplied by a phase factor (i.e., the complex part of the clean component). The restored Gaussians are added to the residual from step 4. If there are multiple RM components within the beam it is however not a good idea to reconvolve the spectra with the RMSF if one wants to investigate the depolarization properties. This is related to the fact that the clean components are complex numbers and can interfere with each other (Farnsworth et al. 2011).
-
6.
The algorithm then continues with the next spatial pixel.
The above described RM-synthesis technique works better than linear fitting techniques (e.g., Ruzmaikin & Sokoloff 1979; Dolag et al. 2005; Vogt et al. 2005), which break down in low signal to noise regimes and do not apply to more complex situations when Eq. (13) is not valid.
The RM-synthesis technique (i.e., Eq. (16)) and RM-CLEAN algorithm were implemented in IDL.
 |
Fig. 18 RMSF from the 25, 21, 18 cm bands WSRT data. The solid line is the overall amplitude of the complex RMSF. Dotted line depicts the Real part of the RMSF and the dashed line the Imaginary part. The FWHM of the RMSF is 88 rad m-2. |
 |
Fig. 19 Faraday depth value of the peak in F(φ). Contours are from the WSRT 1382 MHz image and drawn at levels of [1,3,9,27,...] × 0.225 mJy beam-1. |
 |
Fig. 20 Left: Gaussian restored |F(φ)| spectra of compact sources. B3 0559+422A black solid line, NVSS J060406+422125 blue dashed line, NVSS J060416+422110 (south component) blue solid line, NVSS J060416+422110 (north component) dashed-dotted blue line, NVSS J060231+422811 (west component) red dashed line, NVSS J060231+422811 (east component) red solid line, and NVSS J060206+422045 black dashed line. The high “residuals” for B3 0559+422A are an artifact due to remaining calibration errors. Right: |F(φ)| spectra, consisting of clean components, extracted at three different positions from relic B. The positions are indicated by the circles drawn in Fig. 19. Red line: position B3, blue line: position B2, and black line: position B1 (see also Fig. 3). |
6.2.1. Application to the L-band WSRT data
We performed RM-synthesis on the WSRT 25, 21 and 18 cm data using cubes of Stokes Q and U images with a resolution of 40″ × 28″, see also Sect. 2.2. These data give a sensitivity to polarized emission up to a maximum Faraday depth of 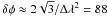 rad m-2 (Brentjens & de Bruyn 2005). The three bands provide a resolution of
rad m-2 (Brentjens & de Bruyn 2005). The three bands provide a resolution of 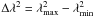 rad m-2, with
rad m-2, with 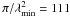 the total bandwidth in wavelength squared. The maximum scale in φ space to which the sensitivity has dropped to 50% is approximately
the total bandwidth in wavelength squared. The maximum scale in φ space to which the sensitivity has dropped to 50% is approximately 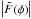 rad m-2. The RMSF is shown in Fig. 18. Since the first sidelobe of the RMSF is about 65% of the main lobe, we used the RM-CLEAN algorithm, cleaning down to a threshold of 0.12 mJy beam-1 RMSF-1. The distribution of the peak of
rad m-2. The RMSF is shown in Fig. 18. Since the first sidelobe of the RMSF is about 65% of the main lobe, we used the RM-CLEAN algorithm, cleaning down to a threshold of 0.12 mJy beam-1 RMSF-1. The distribution of the peak of  , the so-called “rotation measure map” (or Faraday depth map), is shown in Fig. 19.
, the so-called “rotation measure map” (or Faraday depth map), is shown in Fig. 19.
We extracted the location of the peak in the Faraday depth (φpeak) for all compact sources within 0.5° radius of the cluster. In total for 17 sources we find an outlier-resistant mean of +11.7 ± 3.0 rad m-2, clipping values more than two standard deviations away from the median, with the uncertainty the standard deviation of the mean of the φpeak distribution. This is in agreement with the value of 11 rad m-2 from Taylor et al. (2009) derived from NVSS data measured over scales of 8°. The  spectra for seven compact sources are displayed in Fig. 20 (left panel).
spectra for seven compact sources are displayed in Fig. 20 (left panel).
For the relic, φpeak values vary spatially from about −53 to +55 rad m-2. For B3, φpeak is about 10 rad m-2, similar to the compact sources in the field. For B2, we find a strong gradient from −10 to +55 rad m-2 from east to west. For B1, φpeak varies between −10 and −53 rad m-2. The “clean component” spectra are clearly resolved, see Fig. 20 (right panel).
Interestingly, the φpeak values for B1 and B2 deviate from the average galactic foreground of +11.7 ± 3.0 rad m-2, indicating that some of the Faraday rotation is probably caused by the ICM. The φpeak value for B3 indicates it is located in the cluster outskirts and the line of sight towards it does not pass deep into the ICM. B2 and B1 seem to be located progressively deeper into the ICM of the cluster (or more behind it) given the larger φpeak deviation from the galactic foreground. Although the number of counts is low in the ROSAT image (Fig. 3), it is indeed expected that 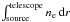 increases from B3, B2, to B1.
increases from B3, B2, to B1.
6.3. The depolarization properties of the radio relic
Our observations show a significant decrease in the polarization fraction towards lower frequencies. There are several factors that can cause such an effect. We rule out the effect of bandwidth depolarization, as the frequency resolution of the observations is sufficient to detected polarized emission with a Faraday depth >104 rad m-2 using RM-synthesis. A second possibility is beam depolarization due to multiple RM components within the beam (spatially varying). These different RM components can be caused by variations of the magnetic field and/or electron density. The spatially averaged polarization fraction over B1 and B2 is about 13% at 4.9 GHz, 1.6% at 1714 MHz cm and <1% at 1382 and 1221 MHz. We excluded B3 from the analysis because the SNR is too low at 4.9 GHz due to the primary beam attenuation.
Two types of depolarization, internal and external, have been identified (Burn 1966; Tribble 1991). Internal depolarization takes place within the radio source itself, while external depolarization takes place in a medium between the source and the observer, e.g., the ICM or magnetized plasma from our own galaxy. A simple case of internal depolarization is for a uniform magnetic field and electron density within the source. In this slab model (Burn 1966), the fractional polarization as function of λ2 is given by a sinc-function. From this, the extent in Faraday depth of the source can be estimated. Observations indicate that the uniform slab model does not fit the data for the radio relics in A2256 and the Coma cluster (Brentjens 2008; Pizzo 2010).
For B1 and B2 there is a clear trend of depolarization towards higher λ2. The only way to get depolarization as a function of wavelength is to have multiple RM components within the beam, either across it or along it – external –, or mixed with the synchrotron emitting plasma – internal. Therefore, the Faraday spectrum must be resolved wherever there is depolarization. In practice, because of the finite width of the RMSF, it may not always be possible to see these multiple RM components, even though they are depolarizing. In the case of B1 and B2, the spectra are indeed clearly resolved, consistent with the high amount of depolarization found for these regions. It cannot be directly determined whether this is due to beam depolarization (spatially varying RM components) or due to multiple RM components along the line of sight. In the first case, the depolarization should vanish when going to high enough spatial resolution. The fact that the RM varies spatially from beam to beam across B1 and B2 makes it very likely that at least a significant part of the depolarization is indeed caused beam depolarization.
The trend from east to west over the relic of (i) a larger φpeak deviation from the galactic foreground, and (ii) an increasing depolarization towards higher λ2, suggest that most of the depolarization is probably due to the ICM of the cluster itself and not due to internal depolarization.
7. Discussion
The complex diffuse radio emission and extended X-ray emission give strong support for the fact that the cluster is currently undergoing a merger event. There are however a few puzzling aspects to the diffuse emission in this cluster. The linear extension of relic B to the east is quite peculiar. Usually shock surfaces are curved and not very linear over distances of more than a Mpc (e.g., Hoeft et al. 2008; Battaglia et al. 2009; Vazza et al. 2009; Skillman et al. 2011). The ongoing merger event for 1RXS J0603.3+4214 is probably more complex than the “simple” binary merger events that are thought to give rise to symmetric double radio relics (e.g., Roettiger et al. 1999; van Weeren et al. 2011a). Deep X-ray observations will be needed to investigate whether the relic is indeed associated with such a linear shock front.
Relic E could also trace a shock wave with DSA, given its large extent and relatively flat integrated spectral index. The nature of relic D remains unclear, its small size and morphology would suggest a radio phoenix scenario, but the integrated spectral index of −1.10 ± 0.05 is not consistent with this interpretation. Higher-resolution observations (~1″) would be helpful to better delineate the morphology.
An interesting point is the relation between relic B and the radio halo C. The radio halo is located directly south of B1, the brightest part of relic B. The halo and relic are connected by a region with α ≲ −2, but then the spectral index flattens to α ~−1.2 and increases a bit towards the center of the halo. We speculate that relativistic particles, previously accelerated at the shock front, are re-accelerated due to merger induced turbulence and then form the radio halo. Another interesting feature of the halo is the increased surface brightness at its southern end. Why does the surface brightness increase here? For a binary cluster merger event one expects two shock waves to form traveling diametrically outwards (e.g., Roettiger et al. 1999). If relic B traces the main shock wave one could also expect a second shock waves at the south side of the cluster center. This could be the region of increased surface brightness at the southern end of C. Although, this remains somewhat speculative, also because the merger event seems to be complex given the peculiar linear extension of relic B. X-ray observations could reveal whether the south part of radio halo C is associated with a shocked region with a higher ICM temperature.
There is also a possibility that source C is not a radio halo, but another relic seen close to face-on, because the surface brightness does not clearly peak at the location of the ROSAT X-ray peak. However, the radio power of source C is in agreement with the LX–P1.4 GHz correlation. Also, the brightness distribution over C is regular and quite smooth, which argues against a relic interpretation. Relics are often composed of smaller filamentary structures (e.g., Clarke & Enßlin 2006). We note that source C is somewhat similar to the diffuse emission seen between the relics in CIZA J2242.8+5301 (van Weeren et al. 2010).
7.1. Relic spectra
The analysis of the radio spectra for radio relic B are consistent with the existence a two global spectral shapes, one that describes the spectrum for the east part and one for the west part. This because it is possible to line up all radio spectra onto a single shape with shifts along log (I) and log (ν).
The spectral shapes of the west (B1) and east (B2+B3) regions only differ in regions in the spectral index map with α ≲ −1.4 (e.g., see Fig. 14). At the front part of the relic we find power-law radio spectra, consistent with an injection spectral index of −0.6 to −0.7. The injection spectral index is also consistent with the total integrated spectral index of −1.1, i.e., the integrated spectral index should be −0.5 units steeper than the injection spectral index (e.g., Miniati 2002; Bagchi et al. 2002) for a simple shock model (with the properties of the shock not changing over time). We also find that the shape of the radio spectra are mostly governed by the effects of spectral ageing, by looking at the shifts made to align up all individual spectra to the global spectral shape (see Sect. 5.4.1). Changes in the magnetic field, total electron content, or electron energy (except energy changes due to ageing) do not seem to play a major role.
The observed radio spectra are not consistent with a JP model (which consists of a single burst of injection and spectral ageing). Instead, we find that the KGJP model, which consist of a sum of individual JP spectra with different amounts of ageing, provides a good match to the spectrum of the east part of the relic. This can be thought of as mixing of emission, most likely because of projection effects. For the west part of the relic (in the regions with the steepest spectral index), we find deviations from the KGJP model. We speculate that additional mixing of emission takes place here, or the spectra are contaminated by the emission from radio halo C (although we attempted to subtract this emission).
The KGJP spectra indicate that (1) at the front of the relic we see freshly injected radio plasma, giving a power-law spectrum. Little mixing of emission takes place here. (2) For the middle part of the relic (the region −0.9 ≲ α ≲ −1.1 from the spectral index map), we observe a mix of radio aged radio plasma and freshly injected radio plasma. For the back part of the relic (the region with α ≲ −1.1), we see a mix of aged radio plasma, but no freshly injected plasma.
Mixing of emission thus seems to be an important factor determining the spectral shape. This suppresses spectral curvature and pushes back the radio spectra to power-law shapes. It is therefore crucial that this effect is considered. The lack of spectral curvature does therefore not directly imply spectral ageing is not important.
An injection spectral index of −0.6 in combination with DSA, implicates a Mach number between 4.6, quite high. The minimum allowed injection spectral index of −0.7, gives a Mach number of 3.3. Instead of DSA, another possibility is shock re-acceleration of fossil electrons. In practice, these radio spectra will probably be indistinguishable from DSA (Markevitch et al. 2005). The ℳ > 3 we find is interesting. Simulations indicate that merger shocks with these Mach numbers are rare (e.g., Vazza et al. 2011; Araya-Melo et al. 2012). Deep all-sky radio surveys are therefore very important to pinpoint these extreme cluster merger shocks.
7.2. Alternative models to explain the relativistic electrons from the radio relic
An alternative explanation for radio relics, based on a secondary cosmic ray electron model, has been proposed by Keshet (2010). This model predicts a spectral index of −1 at the front of the relic. We do not observe this, although there is a hint of a steeper spectral index at the front of B1 at some places in the 325–610 MHz spectral index map. However, this could be an artifact, as edge pixels is the spectral index map are not reliable. Also these steeper regions are smaller than the beam size. We do not find indications of magnetic field changes across the relic from the shifts needed to align up the spectra from individual regions. On the other hand, in the images we see a morphological connection between the radio relic and halo, these halo-relic “bridges” are included in the model from Keshet (2010).
Enßlin & Gopal-Krishna (2001) and Enßlin & Brüggen (2002) proposed that (some) radio relics could be the result of adiabatically compressed fossil radio plasma due to a shock wave. This could boost the radio luminosity by about two orders of magnitude. The question is whether the large relic in 1RXS J0603.3+4214 can be explained in this way. The model of Enßlin & Gopal-Krishna (2001) consist of five phases: (1) injection by a radio galaxy; (2) expansion of the radio cocoon, during this phase the cocoon becomes undetectable; (3) the “lurking”-phase, when pressure equilibrium is reached and the volume of the cocoon remains constant. Due to significant adiabatic losses most of the electrons reside at low energies which reduces the radiation losses. The losses can be further reduced by a low-magnetic field. (4) Adiabatic compression of the cocoon, the radio emission is boosted so it becomes visible again and the break frequency moves upwards. (5) The radio emission fades away due to synchrotron and IC losses.
In the case of 1RXS J0603.3+4214, the fossil plasma should be quite old (≳1 Gyr) as it takes a considerable amount of time for a radio galaxy to move over a distance of 2 Mpc and dump the radio plasma. The change in the break frequency from the adiabatic compression is (Giacintucci et al. 2008) 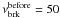 (21)Adopting a reasonable value of
(21)Adopting a reasonable value of 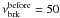 MHz for 1 Gyr old fossil radio plasma (e.g., Enßlin & Gopal-Krishna 2001), we would need a ℳ > 8 shock to push
MHz for 1 Gyr old fossil radio plasma (e.g., Enßlin & Gopal-Krishna 2001), we would need a ℳ > 8 shock to push 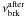 above 4 GHz. For more realistic Mach numbers of ℳ ≲ 4 we should thus observe steep and curved radio spectra. This contradicts the flat spectral indices of α = −0.6 we find and the straight power-law integrated radio spectrum.
above 4 GHz. For more realistic Mach numbers of ℳ ≲ 4 we should thus observe steep and curved radio spectra. This contradicts the flat spectral indices of α = −0.6 we find and the straight power-law integrated radio spectrum.
Only in the unlikely scenario that the plasma is about 0.1 Gyr old, before it is compressed by the shock, the break frequency could be pushed up to a few GHz. We also note that to produce a spectral index gradient a high mass load is required, which would allow the shock wave to successively compress the radio plasma. In the case of a high mass load due to undetectable cool gas, a shock forms and the adiabatic gains are restricted due to the limited compression factor of such a shock wave (Enßlin & Gopal-Krishna 2001).
7.3. Magnetic field
The RM for the west part of the main relic (B1) deviates from the foreground RM, determined from compact sources in the field around the cluster. This suggests that the west part of the relic is located deeper into the ICM, also consistent with the higher amount of depolarization found for that part of the relic. A constant magnetic field of 1 μGauss, ne = 1 × 10-4 cm-3 and a path length 500 kpc, will give a Faraday depth of about 40 rad m-2. The observed difference of about 60 rad m-2, compared to the galactic foreground value, suggests a relatively high magnetic field (B ≳ 1 μGauss). Also because the magnetic field topology is likely more complex, i.e., the magnetic field could have reversals along the line of sight.
We estimate the magnetic field at the front of relic B1 by assuming minimum energy densities in the relics (e.g., Govoni & Feretti 2004) and using the same procedure as described in van Weeren et al. (2009). We take k = 100, i.e, the ratio of energy in relativistic protons to that in electrons, 250 kpc for the depth (d) along the line of sight, a spectral index of −0.6, and a surface brightness of 0.205 mJy arcsec-2 at 610 MHz. We use low and high energy cutoffs (γmin and γmax, with γmin ≪ γmax) instead of low and high frequency cutoffs (Beck & Krause 2005; Brunetti et al. 1997), giving the so-called “revised” equipartition magnetic strength (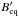 ). For γmin = 100 this gives
). For γmin = 100 this gives 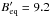 μGauss. If we take γmin = 5000 we get
μGauss. If we take γmin = 5000 we get 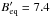 μGauss. The revised equipartition magnetic field strength scales with (1 + k)1/(3 − α).
μGauss. The revised equipartition magnetic field strength scales with (1 + k)1/(3 − α).
Both the polarization and equipartition results indicate a relatively high magnetic field strength. These relatively high values have also been found for other relics by Finoguenov et al. (2010); van Weeren et al. (2010) using limits on the IC X-ray emission or modeling the relic’s brightness profile.
8. Conclusions
We presented detailed GMRT and WSRT radio observations of a newly discovered cluster of galaxies at z = 0.225. We find the cluster to host three radio relics and also a giant ~2 Mpc radio halo. The radio power follows the LX–P1.4 GHz correlation for giant radio halos. The extended X-ray emission and complex diffuse radio emission indicate we are witnessing an ongoing cluster merger event.
The WSRT observations reveal that the front of the relic is highly polarized, with a polarization fraction of up to ~60% at 4.9 GHz. At lower frequencies (in the L-band), the polarization fraction drops considerably, as has been seen for other well studies relics, e.g., in A2256 (Brentjens 2008) and A2255 (Pizzo et al. 2011). The observed depolarization and Faraday depth suggest that the west part of the main relic is located deeper into the ICM of the cluster. Using equipartition argument we find a high magnetic field strength of about 7–9 μGauss for the bright relic.
For the radio halo we find a spectral index of α = −1.15 ± 0.06. The spectrum for the bright radio relic is a power-law between 74 MHz and 4.9 GHz with α = −1.10 ± 0.02. If this relic traces a shock, where particles are accelerated by the DSA mechanism, then the injection spectral index of −0.7 to −0.6 would imply a Mach number of 3.3 to 4.6. The spectral index steepens systematically across the width of the relic from about −0.6 to ~−2. For the bright western part of the relic we can trace the spectral steepening to α < −2.5. The radio spectrum at the front of the relic has a power-law shape with α = −0.6 to −0.7, while the amounts of spectral curvature increases gradually towards the back of the relic.
We analyzed the radio spectra making use of color–color and shift diagrams (Katz-Stone et al. 1993; Katz-Stone & Rudnick 1994) and divided the relic into an eastern and western part. Both parts were further divided into smaller regions based on the spectral index map in Fig. 8 (left panel). We found that the individual radio spectra in each region could all be lined up. This implies the existence of a single global electron energy distribution. The shifts needed to align up the individual spectra, indicate that spectral ageing is the dominant factor explaining the changes in the spectra from one region to another. Changes in the magnetic field, total number of electrons, or adiabatic expansion/compression do not seem to be important.
In addition, we find evidence for mixing of radio emission with different amounts of spectral ageing within the beam. The amount of mixing increases away from the front of the relic. A so-called KGJP model (see Sect. 5.1), which can be thought of as a mix of spectra with different ages, describes the global spectral shape for the east part of the relic. For the west part of the relic, in particular the region with the steepest spectral index, we find a small deviation from this shape, possibly because the amount of mixing increases here.
The effects of spectral curvature are suppressed by mixing and this pushes the radio spectra closer towards power-law shapes. This means that if a spectral index gradient is seen, but no spectral curvature (or only very little), this does not necessarily imply that the spectral index gradient is not related to spectral ageing.
We conclude that the color–color and shift diagrams provide a powerful tool to constrain physical conditions that shape the radio spectra. In the future we plan (i) to expand the color–color analyses to smaller regions, by obtaining higher resolution maps; (ii) increase the frequency range to <150 MHz or >3 GHz; and (iii) apply the technique to other radio relics and halos.
For the origin of the relativistic electrons (in the bright relic), the results favor a scenario where particles are accelerated or re-accelerated in a shock. Interesting is the high Mach number we found, simulations indicate that merger shocks with these Mach numbers are rare. A crucial test would be the to measure the Mach number directly from the jump conditions and compare this with αinj. Deep X-ray observations of this cluster and simulations are also needed to constrain the merger scenario and determine the dynamical state of the cluster.
 |
Fig. A.1 Spectral index error map corresponding to Fig. 4. The map is computed on the basis of σrms values for the individual maps and the uncertainties in the absolute flux scale. |
 |
Fig. A.2 Left: spectral index error map corresponding to Fig. 8 (left panel). Right: spectral index error map corresponding to Fig. 8 (right panel). |
Acknowledgments
We would like to thank the anonymous referee for useful comments. We thank the staff of the GMRT who have made these observations possible. The GMRT is run by the National Centre for Radio Astrophysics of the Tata Institute of Fundamental Research. The Westerbork Synthesis Radio Telescope is operated by ASTRON (Netherlands Institute for Radio Astronomy) with support from the Netherlands Foundation for Scientific Research (NWO). The William Herschel Telescope are operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. Support for this work was provided by NASA through Einstein Postdoctoral grant number PF2-130104 awarded by the Chandra X-ray Center, which is operated by the Smithsonian Astrophysical Observatory for NASA under contract NAS8-03060. R.J.v.W. acknowledges funding from the Royal Netherlands Academy of Arts and Sciences. M.B. and M.H. acknowledges support by the research group FOR 1254 funded by the Deutsche Forschungsgemeinschaft. LR acknowledges support from the US National Science Foundation, under grant AST0908668 to the University of Minnesota. H.T.I. is Jansky Fellow of the National Radio Astronomy Observatory. R.J.v.W. would like to thank C. Pfrommer for discussions and G. Heald for his explanation of the RM-CLEAN algorithm.
References
- Andrei, A. H., Souchay, J., Zacharias, N., et al. 2009, A&A, 505, 385 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Araya-Melo, P. A., Aragón-Calvo, M. A., Brüggen, M., & Hoeft, M. 2012, MNRAS, 3005 [Google Scholar]
- Athreya, R. 2009, ApJ, 696, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Axford, W. I., Leer, E., & Skadron, G. 1977, in Int. Cosmic Ray Conf., 11, 132 [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Bagchi, J., Enßlin, T. A., Miniati, F., et al. 2002, New Astron., 7, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, N., Pfrommer, C., Sievers, J. L., Bond, J. R., & Enßlin, T. A. 2009, MNRAS, 393, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Beasley, A. J., Gordon, D., Peck, A. B., et al. 2002, ApJS, 141, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Blasi, P., & Colafrancesco, S. 1999, Astroparticle Physics, 12, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A. 2007, Ph.D. Thesis, Rijksuniversiteit Groningen, The Netherlands [Google Scholar]
- Brentjens, M. A. 2008, A&A, 489, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briggs, D. S. 1995, Ph.D. Thesis, New Mexico Institute of Mining Technology, Socorro, New Mexico, USA [Google Scholar]
- Brüggen, M., Bykov, A., Ryu, D., & Röttgering, H. 2011, Space Sci. Rev., 138 [Google Scholar]
- Brunetti, G., & Blasi, P. 2005, MNRAS, 363, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Lazarian, A. 2011, MNRAS, 410, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Setti, G., & Comastri, A. 1997, A&A, 325, 898 [NASA ADS] [Google Scholar]
- Brunetti, G., Setti, G., Feretti, L., & Giovannini, G. 2001, MNRAS, 320, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Perley, R. A., Dreher, J. W., & Leahy, J. P. 1991, ApJ, 383, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., & Brunetti, G. 2005, MNRAS, 357, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Brunetti, G., & Setti, G. 2006, MNRAS, 369, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Ettori, S., Giacintucci, S., et al. 2010, ApJ, 721, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, P., Ray, A., & Bhatnagar, S. 2004, ApJ, 612, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, T. E., & Enßlin, T. A. 2006, AJ, 131, 2900 [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D. 2008, PASP, 120, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Dennison, B. 1980, ApJ, 239, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., & Enßlin, T. A. 2000, A&A, 362, 151 [NASA ADS] [Google Scholar]
- Dolag, K., Vogt, C., & Enßlin, T. A. 2005, MNRAS, 358, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Bykov, A. M., & Diaferio, A. 2008, Space Sci. Rev., 134, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O. 1983, Rep. Progr. Phys., 46, 973 [Google Scholar]
- Enßlin, T. A., & Brüggen, M. 2002, MNRAS, 331, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Gopal-Krishna 2001, A&A, 366, 26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T., Pfrommer, C., Miniati, F., & Subramanian, K. 2011, A&A, 527, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T. A., Biermann, P. L., Klein, U., & Kohle, S. 1998, A&A, 332, 395 [NASA ADS] [Google Scholar]
- Farnsworth, D., Rudnick, L., & Brown, S. 2011, AJ, 141, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L. 2005, Adv. Space Res., 36, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Sarazin, C. L., Nakazawa, K., Wik, D. R., & Clarke, T. E. 2010, ApJ, 715, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Venturi, T., Macario, G., et al. 2008, A&A, 486, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Int. J. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Braun, R., & Edmonds, R. 2009, A&A, 503, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoeft, M., Brüggen, M., Yepes, G., Gottlöber, S., & Schwope, A. 2008, MNRAS, 391, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Högbom, J. A. 1974, A&AS, 15, 417 [NASA ADS] [Google Scholar]
- Intema, H. T., van der Tol, S., Cotton, W. D., et al. 2009, A&A, 501, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, N., Battye, R. A., Browne, I. W. A., et al. 2007, MNRAS, 376, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. J. 1977, ApJ, 212, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. J., & Perola, G. C. 1973, A&A, 26, 423 [NASA ADS] [Google Scholar]
- Jones, F. C., & Ellison, D. C. 1991, Space Sci. Rev., 58, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., & Ryu, D. 2011, ApJ, 734, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., Ryu, D., & Jones, T. W. 2012, ApJ, 756, 97 [Google Scholar]
- Katz-Stone, D. M., & Rudnick, L. 1994, ApJ, 426, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Katz-Stone, D. M., Rudnick, L., & Anderson, M. C. 1993, ApJ, 407, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Kempner, J. C., Blanton, E. L., Clarke, T. E., et al. 2004, in The Riddle of Cooling Flows in Galaxies and Clusters of galaxies, eds. T. Reiprich, J. Kempner, & N. Soker, 335 [Google Scholar]
- Keshet, U. 2010 [arXiv:1011.0729] [Google Scholar]
- Keshet, U., & Loeb, A. 2010, ApJ, 722, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., & Gubanov, A. G. 1994, A&A, 285, 27 [NASA ADS] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Liang, H., Hunstead, R. W., Birkinshaw, M., & Andreani, P. 2000, ApJ, 544, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., & O’C Drury, L. 2001, Rep. Progress Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Marecki, A., Falcke, H., Niezgoda, J., Garrington, S. T., & Patnaik, A. R. 1999, A&AS, 135, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markevitch, M., Govoni, F., Brunetti, G., & Jerius, D. 2005, ApJ, 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F. 2002, MNRAS, 337, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F., Jones, T. W., Kang, H., & Ryu, D. 2001, ApJ, 562, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Noordam, J. E. 2004, in SPIE Conf. Ser. 5489, ed. J. M. Oschmann, Jr., 817 [Google Scholar]
- Pacholczyk, A. G. 1970, Radio astrophysics. Nonthermal processes in galactic and extragalactic sources, Series of Books in Astronomy and Astrophysics (San Francisco: Freeman) [Google Scholar]
- Patnaik, A. R., Browne, I. W. A., Wilkinson, P. N., & Wrobel, J. M. 1992, MNRAS, 254, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. T., & Taylor, G. B. 1999, VLA Calibrator Manual, Tech. rep., NRAO [Google Scholar]
- Petrosian, V. 2001, ApJ, 557, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzo, R. F. 2010, Ph.D. Thesis, Rijksuniversiteit Groningen, The Netherlands [Google Scholar]
- Pizzo, R. F., de Bruyn, A. G., Bernardi, G., & Brentjens, M. A. 2011, A&A, 525, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roettiger, K., Burns, J. O., & Stone, J. M. 1999, ApJ, 518, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, J., Gupta, Y., Pen, U., et al. 2010, Exp. Astron., 28, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rudnick, L. 2001, in Particles and Fields in Radio Galaxies Conference, eds. R. A. Laing, & K. M. Blundell, ASP Conf. Ser., 250, 372 [Google Scholar]
- Rudnick, L., & Katz-Stone, D. 1996, Powerful diagnostics of Cygnus A’s relativistic electrons, eds. C. L. Carilli, & D. E. Harris, 158 [Google Scholar]
- Ruzmaikin, A. A., & Sokoloff, D. D. 1979, A&A, 78, 1 [NASA ADS] [Google Scholar]
- Skillman, S. W., Hallman, E. J., O’Shea, B. W., et al. 2011, ApJ, 735, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2003, VizieR Online Data Catalog, VII/233 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Slee, O. B., Roy, A. L., Murgia, M., Andernach, H., & Ehle, M. 2001, AJ, 122, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Stil, J. M., & Sunstrum, C. 2009, ApJ, 702, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1986, in SPIE Conf., 627, ed. D. L. Crawford, 733 [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser. 52, 173 [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 250, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1993, MNRAS, 261, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F. G. 1998, in Astronomical Data Analysis Software and Systems VII, eds. R. Albrecht, R. N. Hook, & H. A. Bushouse, ASP Conf. Ser., 145, 53 [Google Scholar]
- Vallee, J. P. 1980, A&A, 86, 251 [NASA ADS] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Bagchi, J., et al. 2009, A&A, 506, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Brüggen, M., & Hoeft, M. 2010, Science, 330, 347 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Weeren, R. J., Brüggen, M., Röttgering, H. J. A., & Hoeft, M. 2011a, MNRAS, 418, 230 [Google Scholar]
- van Weeren, R. J., Brüggen, M., Röttgering, H. J. A., et al. 2011b, A&A, 533, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Hoeft, M., Röttgering, H. J. A., et al. 2011c, A&A, 528, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., & Brüggen, M. 2011d, A&A, 527, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brunetti, G., & Gheller, C. 2009, MNRAS, 395, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Dolag, K., Ryu, D., et al. 2011, MNRAS, 418, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 2000, IAU Circ., 7432, 1 [NASA ADS] [Google Scholar]
- Vogt, C., Dolag, K., & Enßlin, T. A. 2005, MNRAS, 358, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 WHT V, R, I color image. Yellow contours are from the GMRT 610 MHz image (Fig. 4) and drawn at levels of [1,2,4,8,...] × 0.15 mJy beam-1. Galaxies for which spectra were obtained are marked with red circles, see also Table 3 and Fig. 2. The spiral pattern (yellow contours) at the bottom right is due to residual calibration errors around the source B3 0559+422A. |
| In the text | |
 |
Fig. 2 Rest-frame WHT ISIS spectra for the galaxies listed in Table 3. The order (from top to bottom) is the same as in Table 3. Various absorption features are indicated. |
| In the text | |
 |
Fig. 3 Left: X-ray emission from ROSAT. The image from the ROSAT All Sky Survey was smoothed with a 200′′ FWHM Gaussian and is shown in orange colors. Solid contours are from the WSRT L-band image and drawn at levels of [1,2,4,8,...] × 0.15 mJy beam-1. Right: WSRT L-band image (1160–1780 MHz) with sources labelled. Contour levels are drawn at [1,2,4,8,...] × 80 μJy beam-1. The beam size is 29″ × 19″ and indicated in the bottom left corner of the image. |
| In the text | |
 |
Fig. 4 GMRT 610 MHz image. Contour levels are drawn at |
| In the text | |
 |
Fig. 5 GMRT 610 MHz cutout around sources D and E. Contours are drawn as in Fig. 4. |
| In the text | |
 |
Fig. 6 GMRT 150, 241, 325, 1280 MHz and WSRT 1382 and 2272 MHz images. Contour levels are drawn at [1,2,4,8,...] × 4σrms. Negative −3σrms contours are shown by the dotted lines. The beam size is shown in the bottom left corner of the images. |
| In the text | |
 |
Fig. 7 GMRT 610–325 MHz spectral index map. Contour levels from the GMRT 325 MHz image are drawn at [1,4,16,64,...] × 6σrms and the spectral index map has a resolution of 7.9″ × 6.2″. Pixels below 5σrms are blanked. |
| In the text | |
 |
Fig. 8 Left: fitted spectral index map between 2272 and 147 MHz. The spectral index map was made by fitting a second order polynomial in log (S) − log (ν) for each pixel in the maps at 2272, 1714, 1382, 1221, 610, 325, 241 and 147 MHz. Contour levels are drawn at [1,2,4,8,...] × 0.175 mJy beam-1 and are from the L-band image in Fig. 3. The spectral index map has a resolution of 20″ × 18″ and pixels below 1.5σrms were blanked. Right: fitted spectral index (2272 and 147 MHz) for each pixel in the maps at 2272, 1714, 1382, 1221, 610, 325, 241 and 147 MHz. The individual maps were convolved with Gaussians of 35″ FWHM and pixels with a spectral index error >0.7 were blanked, contours are drawn as in the left panel. |
| In the text | |
 |
Fig. 9 Integrated radio spectrum for radio relic B. |
| In the text | |
 |
Fig. 10 Integrated radio spectra for sources C (left), D (middle), and E (right). The lines are fitted straight power-laws with indices given in Table 4. |
| In the text | |
 |
Fig. 11 Overview of the spectral models used in this work (left) and corresponding radio color–color corves (right) to highlight differences in the spectral shapes. All spectral models have αinj = 0.6. Solid grey line and filled grey circle (in the color–color diagram): power-law spectrum without any ageing, solid black line: KP, dotted line: CI, dash-dotted line: KGJP, dashed line: JP. Note that a power-law spectrum will translate in a single point on a color–color diagram. The αlow−frequency = αhigh−frequency line divides concave and convex spectral shapes between the frequencies where the spectral index is computed. |
| In the text | |
 |
Fig. 12 Schematic representation of two radio spectra with different spectral ages (break frequencies). To align the red spectrum to the black one in log-log space, a shift in the frequency direction is required to match up the break frequencies. The red spectrum then falls below the injection power-law spectrum and needs to be shifted upwards. The slope Δlog (I)/Δlog (ν) equals the injection spectral index in this case (see the main text). |
| In the text | |
 |
Fig. 13 Normalized radio spectra for relic B1 (top) and B2+B3 (bottom). Each spectrum corresponds to a region from the spectral index map where αref − 0.05 < αref < αref + 0.05, with αref = −0.65, −0.75,..., −1.85 for B1, and αref = −0.75, −0.85,..., −1.65 for B2+B3. The spectra are plotted in log ν − log (νI) space to emphasize the differences between the spectra. First order polynomial fits, done in log (I) − log (ν) space, are shown by the solid lines to emphasize possible deviations from power-law radio spectra. Colors correspond to the different αref and go from black, blue, purple, red, to orange. |
| In the text | |
 |
Fig. 14 Color–color diagrams for B1 (left) and B2+B3 (right). Black data points are from the spectra displayed in Fig. 13. The solid black (slightly curved) line is a JP model with αinj = −0.6, the dashed black line a JP model with αinj = −0.7, the solid red line a KP model with αinj = −0.6, the dashed red line a CI model with αinj = −0.6, and the blue line a KGJP model with αinj = −0.7. The grey data points are for the same data as the black points, except the maps were smoothed with a 60′′ FWHM Gaussian. The |
| In the text | |
 |
Fig. 15 “Global” radio spectra for B1 (left) and B2+B3 (right). The spectrum for each αref spectral region from Fig. 13 has been shifted in log (I) − log (ν) space to create the “global” spectral shape. Fourth order polynomial fits through these data points are shown by solid thin black lines. JP (red), KP (black) and KGJP (blue) models are shown by the dashed lines. The color coding, based on the αref regions, is the same as in Fig. 13. |
| In the text | |
 |
Fig. 16 Shifts in log (I) − log (ν) space, for B1 (left) and B2+B3 (right), needed to line up the radio spectra displayed in Fig. 15. A line is fitted through the data points, excluding the first three (B1) or two (B2 + B3) points. Color coding for the αref regions is the same as in Fig. 13. |
| In the text | |
 |
Fig. 17 Left: WSRT 4.9 GHz polarization E-vector map. Total polarized intensity is shown as grayscale image. Vectors depict the polarization E-vectors, their length represents the polarization fraction. The length of the E-vectors are corrected for Ricean bias (Wardle & Kronberg 1974). A reference vector for a polarization fraction of 100% is shown in the bottom left corner. No vectors were drawn for pixels with a SNR < 3 in the total polarized intensity image. Contour levels are drawn at [1,4,16,64,...] × 3σrms and are from the Stokes I image. The beam size is 7.0″ × 4.7″ and indicated in the bottom left corner of the image. Right: WSRT 1382 MHz polarization E-vector map made with natural weighting. Total polarized intensity is shown as grayscale image. No vectors were drawn for pixels with a SNR <4 in the total polarized intensity image. Contour levels are drawn at [1,4,16,64,...] × 0.18 mJy beam-1. and are from the Stokes I image. |
| In the text | |
 |
Fig. 18 RMSF from the 25, 21, 18 cm bands WSRT data. The solid line is the overall amplitude of the complex RMSF. Dotted line depicts the Real part of the RMSF and the dashed line the Imaginary part. The FWHM of the RMSF is 88 rad m-2. |
| In the text | |
 |
Fig. 19 Faraday depth value of the peak in F(φ). Contours are from the WSRT 1382 MHz image and drawn at levels of [1,3,9,27,...] × 0.225 mJy beam-1. |
| In the text | |
 |
Fig. 20 Left: Gaussian restored |F(φ)| spectra of compact sources. B3 0559+422A black solid line, NVSS J060406+422125 blue dashed line, NVSS J060416+422110 (south component) blue solid line, NVSS J060416+422110 (north component) dashed-dotted blue line, NVSS J060231+422811 (west component) red dashed line, NVSS J060231+422811 (east component) red solid line, and NVSS J060206+422045 black dashed line. The high “residuals” for B3 0559+422A are an artifact due to remaining calibration errors. Right: |F(φ)| spectra, consisting of clean components, extracted at three different positions from relic B. The positions are indicated by the circles drawn in Fig. 19. Red line: position B3, blue line: position B2, and black line: position B1 (see also Fig. 3). |
| In the text | |
 |
Fig. A.1 Spectral index error map corresponding to Fig. 4. The map is computed on the basis of σrms values for the individual maps and the uncertainties in the absolute flux scale. |
| In the text | |
 |
Fig. A.2 Left: spectral index error map corresponding to Fig. 8 (left panel). Right: spectral index error map corresponding to Fig. 8 (right panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$\sqrt{[1, 2, 4, 8, \ldots]} \times 4\sigma_{\mathrm{rms}}$}](/articles/aa/full_html/2012/10/aa19000-12/aa19000-12-eq52.png)