| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219262 | |
| Published online | 01 August 2012 | |
Can grain growth explain transition disks?
1
University Observatory Munich, Scheinerstr. 1, 81679
München, Germany
e-mail: til.birnstiel@lmu.de
2
Excellence Cluster Universe, Technische Universität
München, Boltzmannstr.
2, 85748
Garching,
Germany
3
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street, Cambridge, MA
02138,
USA
Received:
21
March
2012
Accepted:
21
June
2012
Aims. Grain growth has been suggested as one possible explanation for the diminished dust optical depths in the inner regions of protoplanetary “transition” disks. In this work, we directly test this hypothesis in the context of current models of grain growth and transport.
Methods. A set of dust evolution models with different disk shapes, masses, turbulence parameters, and drift efficiencies is combined with radiative transfer calculations in order to derive theoretical spectral energy distributions (SEDs) and images.
Results. We find that grain growth and transport effects can indeed produce dips in the infrared SED, as typically found in observations of transition disks. Our models achieve the necessary reduction of mass in small dust by producing larger grains, yet not large enough to be fragmenting efficiently. However, this population of large grains is still detectable at millimeter wavelengths. Even if perfect sticking is assumed and radial drift is neglected, a large population of dust grains is left behind because the time scales on which they are swept up by the larger grains are too long. This mechanism thus fails to reproduce the large emission cavities observed in recent millimeter-wave interferometric images of accreting transition disks.
Key words: accretion, accretion disks / protoplanetary disks / stars: pre-main sequence / planets and satellites: formation / circumstellar matter
© ESO, 2012
1. Introduction
The evolution of circumstellar disks, the birthplaces of planets, is still enigmatic, even though the pioneering theoretical work on this topic was started almost 40 years ago by Lynden-Bell & Pringle (1974). Viscous and/or gravitational stresses are the drivers of the disk accretion flows, which can be traced indirectly by the observed disk lifetimes and accretion rates (e.g., Hartmann et al. 1998; Sicilia-Aguilar et al. 2006; Hernández et al. 2007; Fedele et al. 2010).
While the general trends of declining accretion rates and disk masses can be explained by viscous evolution, a sub-set of objects called transition disks remain mysterious. These objects appear dust-depleted in their inner regions, while the outer regions resemble normal circumstellar disks (Strom et al. 1989; Skrutskie et al. 1990; Calvet et al. 2002; Espaillat et al. 2007, 2010; Andrews et al. 2011). The sizes of the dust cavities range from a few to more than 70 AU (e.g., Piétu et al. 2006; Hughes et al. 2007; Brown et al. 2008; Hughes et al. 2009; Andrews et al. 2009; Brown et al. 2009; Isella et al. 2010a; Andrews et al. 2010; Isella et al. 2010b; Andrews et al. 2011). The gas content of the cavities is still largely unknown. It may also be reduced compared to the outer disk regions as found for example by Najita et al. (2010), Dutrey et al. (2008), or Lyo et al. (2011); yet other works such as Pontoppidan et al. (2008) or Salyk et al. (2011) do detect gas inside the dust cavities.
The time scale of this transition phase of disk evolution is estimated to be of the order of a few times 105 years (Skrutskie et al. 1990; Hartigan et al. 1990). This estimate, however, is based on the transition disk frequency, which is still only a lower limit due to the lack of spatial resolution. Classifying transition disks only based on the spectral energy distribution (SED) can be misleading because steep decreases in the dust surface density can easily be missed due to the presence of small dust particles. Some mechanisms proposed to explain observations of transition disks include planet-disk interactions (e.g., Rice et al. 2003; Zhu et al. 2011), or photo-evaporation (Clarke et al. 2001; Alexander et al. 2006; Ercolano et al. 2008). Recent imaging of disks by Andrews et al. (2011) revealed a higher fraction (>20%) of disks with large cavities for the mm-brightest sources. Higher fractions of transition disks, indicating longer disk clearing time scales, are more difficult to explain by photoevaporation. However, the dust emission signature of photoevaporating disks has not yet been self-consistently modeled, treating grain growth physics and dust-gas feedback. It is therefore unclear whether photoevaporating disks leave a dust rich or a completely dust and gas free cavity behind (e.g., Alexander & Armitage 2007; Garaud 2007).
The formation of large disk cavities by viscous evolution is generally problematic, even with the assumption that photoevaporation or some other mechanism is able to decouple the outer and inner disc at larger radii. Indeed the viscous time at 35 AU for typical values for the viscosity parameter1 is 3.4 Myr. On the other hand, even at 35 AU, the time scales for grain growth and radial drift are only a couple of thousand years. Any mechanism that triggers significant changes in the dust evolution (e.g., the emergence of a pressure maximum, see Pinilla et al. 2012a) could therefore quickly induce observational signatures. The fact that grains grow and consequently become more mobile due to radial drift is likely an important part of the solution to this problem.
Recent observations by Kraus & Ireland (2012) found a possible planetary-mass companion inside the cavity of the LkCa 15 transition disk. It remains to be shown whether planets cause gaps/pressure bumps or vice versa (e.g., Kretke & Lin 2007; Brauer et al. 2008; Pinilla et al. 2012b). Determining the origin of transition disks is therefore one of the most fundamental issues in our efforts to forge a better understanding of planet formation.
It has been suggested, although not demonstrated in any detail, that the growth and radial transport of dust could potentially explain the observed signatures of transition disks with large inner holes (e.g., Dullemond & Dominik 2005; Tanaka et al. 2005; Najita et al. 2008; Pontoppidan et al. 2008). The observations indicate a decreased optical depth in the inner regions of transition disks both in the IR as well as in mm-observations, which does not necessarily imply diminished dust densities. Grain growth therefore offers two (related) pathways towards this end. First, particles decouple from the gas as they grow, which causes them to spiral inwards (Weidenschilling 1977; Nakagawa et al. 1986). This way, the dust optical depths are reduced by the actual removal of dust mass. Second, grain growth itself causes a decrease in the dust opacities, since larger particles emit less efficiently, which also decreses the otpical depth. Dust grains of sizes beyond a few centimeters become basically invisible to observations. However, the edges of transition disks seem to be relatively abrupt; they have been modeled as step functions (Andrews et al. 2011; Isella et al. 2012) or steep power-law profiles Isella et al. (2010b, 2012). This suggests that the environment for grain evolution must abruptly change at this point in the disk. Pressure bumps or even gaps opened by planets might be possible explanations (Lin & Papaloizou 1986; Zhu et al. 2011). Another possibility could be the outer edges of dead-zones (Gammie 1996). Dead zones are regions where the ionization fraction of the disk drops below the critical value needed to drive the magneto-rotational instability (MRI, Balbus & Hawley 1991), the widely accepted source of turbulent viscosity.
In this work, we want to investigate whether grain growth and transport – either alone or aided by a dead zone – can be the cause of the observed transition disk signatures. In Sect. 2 we will discuss some of the equations which are crucial for the understanding of our modeling results. Section 3 describes the model setups and assumptions. The resulting simulation outcomes and simulated observations are shown and explained in Sect. 4. Our findings are discussed and summarized in Sect. 5.
2. Background
In the following section, we will summarize some of the results of Birnstiel et al. (2012, hereafter BKE12, which motivated the simulations presented in this paper and will help to
understand the results. It was found in BKE12 that
the upper end of the grain size distribution can be limited by two effects, namely
fragmentation and radial drift. In the former case, due to the fact that typical impact
velocities increase with grain size, the grains can only grow until they reach a size at
which fragmentation sets in. The size limit for turbulent relative velocities was found to
be 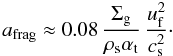 (1)Here,
uf denotes the fragmentation threshold velocity and
ρs the specific density of the dust grains. Σg is
the gas surface density, cs the sound speed and
αt the turbulent viscosity parameter (Shakura & Sunyaev 1973). The other size limit is due to radial
drift: grains can only exist at a given radius if growth from smaller sizes resupplies them
as fast as radial drift removes them. In this case, the upper end of the size distribution
can be approximated by (see BKE12)
(1)Here,
uf denotes the fragmentation threshold velocity and
ρs the specific density of the dust grains. Σg is
the gas surface density, cs the sound speed and
αt the turbulent viscosity parameter (Shakura & Sunyaev 1973). The other size limit is due to radial
drift: grains can only exist at a given radius if growth from smaller sizes resupplies them
as fast as radial drift removes them. In this case, the upper end of the size distribution
can be approximated by (see BKE12) 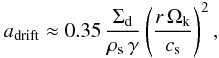 (2)where Σd
is the dust surface density, Ωk the Keplerian frequency and γ
the absolute value of the power law index of the gas pressure P,
(2)where Σd
is the dust surface density, Ωk the Keplerian frequency and γ
the absolute value of the power law index of the gas pressure P,
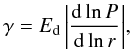 (3)and we have introduced a
parameter for the efficiency of radial drift, Ed where
Ed = 1 corresponds to the fiducial literature value. In the
limit
afrag < adrift,
fragmentation of the dust grains is the relevant size limit. In this case, small dust is
constantly resupplied in the form of fragments. In the opposite case, when the radial drift
barrier is the growth limiting factor, grains are removed by radial drift even before they
reach sizes at which fragmentation starts to become important.
(3)and we have introduced a
parameter for the efficiency of radial drift, Ed where
Ed = 1 corresponds to the fiducial literature value. In the
limit
afrag < adrift,
fragmentation of the dust grains is the relevant size limit. In this case, small dust is
constantly resupplied in the form of fragments. In the opposite case, when the radial drift
barrier is the growth limiting factor, grains are removed by radial drift even before they
reach sizes at which fragmentation starts to become important.
From Eqs. (1) and (2), it can be seen that the quantities which most clearly determine the time evolution of the size limits are Σg and Σd, respectively, because the other quantities are not expected to change by orders of magnitude with time at a given radius. However, it should be noted that in this study, we do not track the viscous evolution of the gas surface density. This would lead to a further reduction of the maximum grain size. A fixed gas surface density is therefore in tune with having a best-case scenario to test the potential of the proposed mechanism. The fact that radial drift causes the dust surface density to decrease faster than the gas surface density, even if viscous evolution were to be included, means that the drift limit can become more important as the disk evolves.
The dependence of Eqs. (1) and (2) on Σg and Σd also causes both size limits to decrease with radius, as observed by Banzatti et al. (2011) and Guilloteau et al. (2011). If the largest grain size at a given radius is limited by radial drift, dust collision velocities are not high enough to cause fragmentation (BKE12). The drifting grains therefore sweep up the small dust without resupplying it by fragmentation. This means that drift-limited grain growth could naturally lead to conditions where the inner regions are devoid of small dust (due to lack of fragmentation), while small grains are still present in the outer disk (due to lower grain size limits in the outer regions).
The most important and uncertain parameters are uf, the collision velocity at which fragmentation sets in, and the turbulent state of the disk, which is described by the parameter αt. Estimates for uf range from a few up to 35 m s-1 (see, Wada et al. 2008; Paszun & Dominik 2009; Blum & Wurm 2008, and references therein). We use values of 3 and 10 m s-1, because icy aggregates are expected to fragment only at larger velocities compared to the ~1 m s-1, found for silicate dust grains (Blum & Muench 1993; Blum & Wurm 2008).
 |
Fig. 1 Initial conditions of the simulations without a dead zone. Solid and dashed lines denote the gas and dust surface density in g cm-2, respectively. The dash-dotted line denotes the mid-plane temperature. |
3. Modeling approach
3.1. Dust evolution
In this work, we use a vertically averaged dust evolution code which tracks the radial and size evolution of the dust surface density of the disk. Effects of coagulation, fragmentation, and cratering as well as radial drift, gas drag, and turbulent mixing are taken into account. For any details of the dust evolution model, we refer to Birnstiel et al. (2010).
We model both active disks, where the complete disk is MRI active as well as disks with MRI-inactive regions, the so-called dead zones. The properties and even the mere existence of dead zones is still an active matter of debate. In order to investigate whether a dead-zone can produce the observational appearance of a protoplanetary disk, we have to make some simplifications and assumptions. Therefore, we include the two most prominent effects of a dead zone which can alter the evolution of dust, namely the decreased amount of turbulence and increased gas surface density in the MRI inactive regions.
For the gas disk, we use a fixed surface density profile with a constant mass accretion
rate up to a characteristic radius rc, 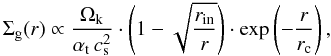 (4)where
rin is the innermost radius of the disk. In order to mimic
the effects of a dead zone, we use an alpha profile of
(4)where
rin is the innermost radius of the disk. In order to mimic
the effects of a dead zone, we use an alpha profile of 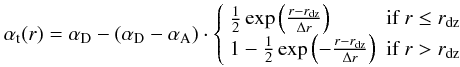 (5)which
represents a smooth transition at rdz from the turbulence
parameter in the dead zone αD to the active
one αA over a transition width Δr, which we
arbitrarily set to 1 AU. This jump in αt causes also a jump in
the gas surface density profile, as can be seen from Eq. (4).
(5)which
represents a smooth transition at rdz from the turbulence
parameter in the dead zone αD to the active
one αA over a transition width Δr, which we
arbitrarily set to 1 AU. This jump in αt causes also a jump in
the gas surface density profile, as can be seen from Eq. (4).
The initial condition for the dust surface density is given by a constant dust-to-gas ratio in μm sized grains. The temperature profile is derived from two-dimensional radiative transfer calculations (see Sect. 3.3) and is kept fixed throughout the simulation. As an example, the initial gas and dust surface densities and the initial temperature profile of simulation A2 is shown in Fig. 1.
3.2. Vertical structure
Following the results from Dubrulle et al. (1995), the grain evolution code used in this work assumes a Gaussian vertical distribution for the dust, where the scale heights depend on the grain size (see Birnstiel et al. 2010). This assumption is very accurate at the mid-plane, but it deviates in the surface layers of the disk. It can therefore be used for the dust size evolution, which mostly depends on the mid-plane values. However, to derive proper observables from the simulation outcome, the two-dimensional dust density distribution needs to be reconstructed from the dust surface densities.
To this end, the vertical structure is assumed to be stationary and isothermal and we
solve numerically for the equilibrium between vertical mixing and dust settling,
![\begin{equation} \frac{\del \rhodust}{\del t} = - \frac{\del}{\del z} \left[ \rhodust \, u_\mathrm{sett} - D_\mathrm{d} \, \rhogas \frac{\del}{\del z} \left(\frac{\rhodust}{\rhogas}\right) \right] = 0, \label{eq:settling_mixing} \end{equation}](/articles/aa/full_html/2012/08/aa19262-12/aa19262-12-eq20.png) (6)where
ρd and ρg are the dust and gas
densities,
(6)where
ρd and ρg are the dust and gas
densities, 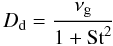 (7)is
the dust diffusivity (Youdin & Lithwick
2007); we assume that the gas diffusivity equals the gas viscosity
νg. St is the particle Stokes number and
(7)is
the dust diffusivity (Youdin & Lithwick
2007); we assume that the gas diffusivity equals the gas viscosity
νg. St is the particle Stokes number and 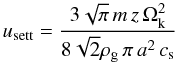 (8)is
the settling velocity for spherical grains in the Epstein regime (Nakagawa et al. 1986). We denote the grain masses and radii as
m and a, respectively. The resulting two-dimensional
density distribution of each grain size is then used in the radiative transfer
calculations.
(8)is
the settling velocity for spherical grains in the Epstein regime (Nakagawa et al. 1986). We denote the grain masses and radii as
m and a, respectively. The resulting two-dimensional
density distribution of each grain size is then used in the radiative transfer
calculations.
Parameters and initial conditions of the simulations.
3.3. Radiative transfer calculations
The dust evolution models described above need to be converted into synthetic data products to assess how well they can reproduce the key observational properties of transition disks. For each model, we compute a broadband SED and high resolution millimeter-wave continuum image following the basic procedures outlined by (Andrews et al. 2009, 2011). The dust density structure ρd for each grain size a was re-sampled onto a fixed grid in spherical coordinates, with high resolution refinements near the disk midplane and around regions of strong optical depth gradients (i.e., at the inner edge near 0.1 AU and the outer boundary of the dead zone). Absorption and scattering opacities for each grain size were calculated with a Mie code, assuming a population of segregated spheres with the optical constants and material compositions advocated by Pollack et al. (1994, see also Andrews et al. 2012). We assume that stellar irradiation is the only relevant heating source, and set the stellar photosphere to have properties that are representative of typical transition disk hosts: Teff = 4300 K, R∗ = 2.5 R⊙ (implying L∗ ≈ 2 L⊙), and M∗ = 1 M⊙.
The two-dimensional Monte Carlo radiative transfer code RADMC (Dullemond & Dominik 2004) was used to simulate the propagation of radiation through each model structure and compute an internally-consistent temperature structure. That process was iterated with the dust evolution code for each model so adjustments could be made to the vertical distribution of particles of a given size. We adopted a simple convergence criterion such that the midplane temperatures did not change more than ~10% between iterations (in practice, this amounted to only 1 or 2 iterations). A ray tracing algorithm was then used on the final model structure to construct a theoretical SED and 880 μm continuum image for a given disk viewing geometry and distance. For simplicity, we fixed representative values for the latter; d = 140 pc, a disk inclination i = 35°, and major axis position angle of 155° (measured east of north). The 880 μm model image is used to synthesize a simulated interferometric image like those observed by the Submillimeter Array (for examples, see Andrews et al. 2011).
3.4. Shortcomings of the modeling approach
A vertically integrated coagulation code combined with a vertical settling-mixing equilibrium calculation is a good approximation of the vertical dust structure, as long as the disk is not layered, as it is in the presence of a dead zone. For example, a small amount of the mid-plane dust could reach the surface layers and be fragmented due to the high degree of turbulence in the active regions. Furthermore, turbulent transport in these regions can be much stronger than in the mid-plane (Turner et al. 2010). Due to the fact that our model only uses the (possibly very low) mid-plane turbulence parameter, this model represents a “best case” scenario in favor of the removal of small grains. For simplicity, the evolution of the gas surface density and also the dependence of the MRI turbulence on the dust distribution (e.g., Sano et al. 2000) are not treated in this work.
It is important to note that other obstacles for particle growth at smaller sizes have been suggested, e.g., bouncing (Güttler et al. 2010; Zsom et al. 2010) or charging effects (Okuzumi 2009). Observations, however, do find ample evidence of the presence of both large (Testi et al. 2001; Natta et al. 2004; Rodmann et al. 2006; Ricci et al. 2010) and small grains (e.g., Watson et al. 2007, and references therein) in protoplanetary disks, which suggest that these barriers have been overcome. The question remains whether the radial drift and the fragmentation barrier are indeed the upper limits of the size distribution. At least fragmentation seems necessary in order to explain the observed presence of small dust (see Dullemond & Dominik 2005), however the expected rate of radial drift is too high to account for the observed disk lifetimes (Weidenschilling 1977; Brauer et al. 2007). On the other hand, different sizes as well as different profiles of the dust and the gas disk (Panić et al. 2009; Andrews et al. 2012) are indicating that to some extent radial drift is at work in circumstellar disks. Possibly reduced drift rates (e.g., Johansen et al. 2006) or pressure traps (Pinilla et al. 2012a) are needed to reconcile theory and observations. To account for these open issues, we will also present models with reduced or without radial drift and without fragmentation (see Sect. 4.1).
4. Results
In this section we will discuss the results of two parameter studies: one of entirely MRI-active disks with varied levels of turbulence, and another which mimics MRI-inactive regions (dead zones) in which we vary the turbulence in both the MRI-active and dead regions as well as the efficiency of radial drift. A summary of the models and parameters is given in Table 1.
 |
Fig. 2 Vertically integrated dust surface density distribution after 5 Myr of evolution for the simulations without a dead zone, A2 (top) to A5 (bottom). The parameters for the simulations are shown in Table 1. The solid red line denotes the growth barrier set by grain fragmentation, the dashed red line the size limit due to radial drift. |
4.1. Growth and transport in smooth disk profiles
4.1.1. Evolution of the dust distribution
In this first parameter study, we investigate how the possible transition from a fragmentation dominated (af < ad) to a drift dominated (ad < af) size distribution is reflected in the SED of a typical disk profile. To this end we set up different simulations with the same initial conditions and vary the constant turbulence parameter αt from 10-2 to 10-5 in simulations A2 to A5, respectively. According to Eq. (1), this variation in αt shifts the fragmentation barrier with respect to the drift barrier (Eq. (2)) by three orders of magnitude in size. Thus the maximum size of the dust grains in the simulation with the highest αt value of 10-2 (i.e., simulation A2) is set by fragmentation, while the drift limit becomes more important as we go to lower turbulence values. In this parameter study, we vary only the turbulence parameter, however it is important to note that the same or similar effects can be achieved by varying the initial dust-to-gas mass ratio Σd/Σg (for Σd ≪ Σg), or the fragmentation velocity uf, since these parameters determine the initial ratio of the size limits (Eqs. (1) and (2)). Changing these parameters, a drift-limited size distribution can be achieved, even for a disk with relatively strong turbulence.
Figure 2 shows
σ(r,a), the dust surface density distributions as
function of grain size and radius for the active disk simulations, A2 through A5, after
5 Myr of evolution. The quantity σ(r,a) is defined as
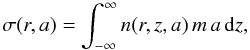 (9)where
m = 4π/3 ρs a3
is the particle mass, and n(r,z,a) is the dust number
density distribution as a function of radius r, height above the
mid-plane z, and grain size a. Integration of
σ(r,a) over ln(a) gives the dust
surface density Σd(r). The solid red line in Fig. 2 denotes the fragmentation limit (cf. Eq. (1)), the dashed red line the drift size limit
(cf. Eq. (2)).
(9)where
m = 4π/3 ρs a3
is the particle mass, and n(r,z,a) is the dust number
density distribution as a function of radius r, height above the
mid-plane z, and grain size a. Integration of
σ(r,a) over ln(a) gives the dust
surface density Σd(r). The solid red line in Fig. 2 denotes the fragmentation limit (cf. Eq. (1)), the dashed red line the drift size limit
(cf. Eq. (2)).
Going from simulation A2 to A5 (see Fig. 2), it is evident that the small grain population becomes increasingly depleted. The reason for this behaviour is the following: radial drift causes the dust surface density to be decreased on shorter time scales than the gas surface density. The dust-to-gas ratio is therefore decreasing with time. The ratio of the two growth barriers, which in this study is initially set by the choice of αt, therefore shifts with time from a fragmentation limited distribution towards a drift limited one. As described in BKE12, for a drift limited size distribution, dust collision velocities induced by radial drift decrease with the dust-to-gas ratio. Therefore, at later times, the low collision velocities prevent grain fragmentation. Consequently, small dust particles are not reproduced by fragmentation anymore, but are rather swept up by the inward-drifting population of larger grains.
The time scale of this sweep-up can be estimated in the context of the drift-dominated
two-population model of BKE12 (see Appendix A) as 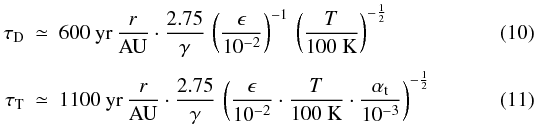 where
ϵ is the dust-to-gas mass ratio, τD and
τT are the sweep-up time scales for drift and turbulence
induced collision velocities. The dependence on temperature T and
γ is not relevant, considering that these values do not change
drastically with time or radius and the dependence on T is weak. The
sweep-up time scale is therefore set by the quantities r,
ϵ, and αt. The late stages of disk
evolution after 5 Myr in Fig. 2 are typically
paired with dust-to-gas mass ratios of 10-5 to a few times 10-4,
quite irrespective of αt.2 The radial dependence and time evolution of the dust to gas ratio is very
similar to the results shown in Fig. 8 of BKE12.
Therefore, the sweep-up time scales approach ~Myr values beyond about 10 AU. This
explains why dust at these radii is not swept up quickly. The linear dependence with
r means that the clearing of dust in this picture proceeds from
inside-out, as typically associated with other disc-clearing mechanisms (e.g., Ercolano et al. 2011). In the innermost regions, the
drift size limit approaches the fragmentation limit. This causes some fragmentation of
the largest particles, which is the source of the small dust population inside of
~0.5 AU for simulation A5 and inside of ~1 AU for simulation A4.
where
ϵ is the dust-to-gas mass ratio, τD and
τT are the sweep-up time scales for drift and turbulence
induced collision velocities. The dependence on temperature T and
γ is not relevant, considering that these values do not change
drastically with time or radius and the dependence on T is weak. The
sweep-up time scale is therefore set by the quantities r,
ϵ, and αt. The late stages of disk
evolution after 5 Myr in Fig. 2 are typically
paired with dust-to-gas mass ratios of 10-5 to a few times 10-4,
quite irrespective of αt.2 The radial dependence and time evolution of the dust to gas ratio is very
similar to the results shown in Fig. 8 of BKE12.
Therefore, the sweep-up time scales approach ~Myr values beyond about 10 AU. This
explains why dust at these radii is not swept up quickly. The linear dependence with
r means that the clearing of dust in this picture proceeds from
inside-out, as typically associated with other disc-clearing mechanisms (e.g., Ercolano et al. 2011). In the innermost regions, the
drift size limit approaches the fragmentation limit. This causes some fragmentation of
the largest particles, which is the source of the small dust population inside of
~0.5 AU for simulation A5 and inside of ~1 AU for simulation A4.
4.1.2. Evolution of the SED
The resulting SEDs and 880 μm intensity profiles for all the MRI-active disk simulations are shown in Fig. 4, where the panels from left to right show the time evolution of the different models. It can be seen that the mid-IR emission of A2 and A3 are comparable up to about 20 μm, because even at 5 Myr the fragmentation barrier in both cases is still at similar or even smaller grains sizes than the drift limit. Going to the lower αt values of A4 and A5 causes an ever stronger reduction of the mid-IR emission, due to the fact that the drift limit becomes significantly smaller than the fragmentation limit and the small dust grains in the hot inner regions are swept up by the drifting grains.
The outer regions show a similar effect: the emission beyond about 30 μm stays high in the case of A2 due to the fact that the strong level of turbulence prevents the formation of larger grains. The dust grains in this case are so small that they are well coupled to the gas. Hence, the dust is not strongly drifting, which means that more mass is retained in the outer regions and the emission therefore stays at a high level. Reducing the turbulence strength in the fragmentation limited case leads to larger particles which start to attain significant inward drift velocities. The far-IR flux is therefore decreased, because less dust mass is retained in the outer regions of the disk. This explains the strong difference between the SEDs of model A2 compared to the other models.
4.1.3. Evolution of the (sub-)mm brightness
The shape of the final radial intensity profiles in the 10–100 AU range can be
understood by approximating
Iν ∝ T Σd κν.
For simulations A3, A4, and A5, the largest grain size between about 7 and 50 AU is
given by the drift-limit Eq. (2) and at
the same time is larger than
880 μm/(2π). This means that
the opacity κ880 is roughly
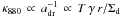 . The intensity
then becomes
Iν ∝ T2 γ r,
which for a temperature profile
T ~ r−1/2 leads to
a flat intensity profile. The entire disk of model A2 is fragmentation-dominated. This
gives rise to a steeper intensity profile because the presence of large amounts of small
dust means the opacity does not depend as strongly on the largest grain size. For a
typical size distribution in the fragmentation case, we get
. The intensity
then becomes
Iν ∝ T2 γ r,
which for a temperature profile
T ~ r−1/2 leads to
a flat intensity profile. The entire disk of model A2 is fragmentation-dominated. This
gives rise to a steeper intensity profile because the presence of large amounts of small
dust means the opacity does not depend as strongly on the largest grain size. For a
typical size distribution in the fragmentation case, we get
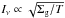 which explains the slope of model A2.
which explains the slope of model A2.
4.1.4. Conclusions for the smooth disk models
Even though the SED signatures of the low turbulence simulations do resemble the ones of typical transition disks, there is an important drawback of this mechanism when it comes to disks with resolved holes in the (sub-)millimeter wavelength range: as pioneered by Brown et al. (2009) and confirmed by other studies such as Andrews et al. (2011), many of the transition disks (but also some of the disks without typical transition disk-like SEDs) were found to have inner dust cavities with sizes up to 70 AU. While it is easy to “hide” such cavities in the SED by relatively small amounts of small dust, the resolved optically thin (sub-)millimeter observations unambiguously reveal these features, as shown e.g., by Isella et al. (2010b) and Andrews et al. (2011).
The mechanism presented here is able to remove the small dust population; however, it does so by locking it up in a non-fragmenting population of larger dust particles. This population of grains contains still enough particles of ~centimeter sizes such that they clearly show up in the (sub-)millimeter images. So even in the best case (model A4), no cavity is seen in the simulated images (Fig. 4, bottom row). The size of the largest particles scale with the gas surface density; however, we chose a very high disk mass (20% of the mass of the central star) in order to reach the largest possible sizes for the given disk model. Even in this case, the images shown in Fig. 4 do not resemble the observational data of e.g., Brown et al. (2009). In the following section, we will investigate how far this mechanism can be pushed by including effects which might be caused by a layered structure of the disk.
4.2. Beyond standard dust modeling
4.2.1. Including effects of a layered disk structure
So far, we have shown that the mechanism presented in this paper is able to strongly deplete the inner regions of disks in small dust grains and that a mid-IR dip in the SED, as found by observations (e.g. Skrutskie et al. 1990; Calvet et al. 2002; Espaillat et al. 2007, 2010) can be produced. In order to resemble the resolved (sub-)mm observations such as Brown et al. (2009), Andrews et al. (2011), or Lyo et al. (2011), two further features are required. First, the dust cavities also need to be observed in the (sub-)mm, i.e. for larger grains. The absence of a cavity in the simulated images of Fig. 4 indicates that the grain sizes found in our simulations are not large enough. Larger surface densities or larger fragmentation thresholds can be considered. The former option, however, is restricted by the total mass of the disk. Second, in our simulations, the dust surface density and the largest grain sizes are smooth functions of the radius, giving rise to a flat intensity profile (cf. the estimate in Sect. 4.1). This is in contrast with the observed dust cavities. These facts motivate a model which allows for higher gas surface densities and steep changes in the maximum grain size at the cavity edge.
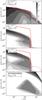 |
Fig. 3 Vertically integrated dust surface density distribution after 5 Myr of evolution for simulations D23_M05 (top), D25_M05 (second panel), LDE (third panel) and COAG (bottom panel). The corresponding parameters are shown in Table 1. The solid red line denotes the growth barrier set by grain fragmentation, the dashed red line the size limit due to radial drift. |
One candidate for this behavior could be disks with dead zones, regions of low ionization which are not MRI-active. The inactive regions transport angular momentum less efficiently (Armitage 2011), which is why they can accumulate large amounts of mass, while the outer, active regions still resemble normal disks. This way, the inner, MRI-dead regions can have higher surface densities, while the transition from MRI-active to MRI-dead gives rise to strong changes in the turbulence parameter αt (e.g. Dzyurkevich et al. 2010).
In this section, we therefore take these two effects into account without any detailed modeling of the dead zone. This means that neither the vertical structure nor the viscous evolution of the dead zone are considered; only the reduced αt and the increased gas surface density Σg are treated. This is a valid approach because we are considering this as a best-case model. Other effects such as fragmentation and enhanced radial mixing in the active surface layers are working against the presented mechanism by replenishing small dust grains.
The situation where αt is higher in the outer parts of the disk and lower inside the dead zone can cause the dust distribution to be fragmentation limited outside and drift limited inside the dead zone. Models D23_M05 and D25_M05 simulate such a situation for rdz = 35 AU, but for different contrasts between the active and the dead region. The size of the dead zone is not physically motivated, but rather chosen from the typical size of the observed transition disk cavities. However, the theoretical models of Bai (2011) can account for dead zones of sizes up to 20 AU.
A comparison of the SEDs for model D23_M05 (Fig. 5, purple SED) and A2 (Fig. 4, purple SED) highlights how the contrast of one order of magnitude in αt changes the long wavelength emission in the SED. For our choice of parameters, the outer regions start to be effected by drift, but fragmentation stays active throughout the disk. Only at 5 Myr, between around 10 AU and the outer edge of the dead zone, the drift barrier drops slightly below the fragmentation barrier, causing a minor reduction of small grains.
We also compared models with different disk masses (not shown), but no significant differences were found for changes within a factor of a few. Going to very low disk masses of 0.005 M⊙ further reduces the maximum grain size, which is producing relatively more mm- and IR emission in the inner regions. Severe changes are found if the contrast in αt between the active and the dead regions is increased, because this changes the relative importance of the fragmentation and the drift barrier, as already discussed in the previous section. The simulated images in Fig. 5 (bottom row), however, do not show any signs of a cavity. The reason for this is that the peak of the size distribution reaches sizes of around a centimeter and larger only within a few AU (see third plot from top of Fig. 3). Therefore, the surface density of dust smaller than ~1 cm only decreases smoothly inwards of 3–8 AU, depending on the age of the disk.
 |
Fig. 4 Spectral energy distributions (top row), normalized radial surface brightness profiles at 880 μm (middle row), and synthesized 880 μm images (bottom row) corresponding to the Submillimeter Array setup of Andrews et al. (2011) for the active disk models. The line colors correspond to models A2 to A5 and model COAG, as labeled in the left panels. The dashed grey line in the SEDs represents the stellar photosphere. The columns from left to right correspond to 0, 1, 2, and 5 Myr of evolution. The shaded areas in the central row depict the resolution limits of current (pre-ALMA) interferometers. Only the results for model A4 are shown in the synthesized images, where the contours correspond to 10% levels of the peak brightness and the bar and dashed oval represent the size scale and the beam size, respectively. |
 |
Fig. 5 Same as Fig. 4 but for the models which include dead-zones, corresponding to the simulations labeled in the left panels. The dashed vertical line in the central row marks the dead zone radius rdz. The synthesized images in the bottom row correspond to model D25_M05. |
In order to confirm this trend, we carried out simulations in which the size limits are pushed to even larger values. One reason for larger grains can be the efficiency of radial drift: simulations by Johansen et al. (2006) and Bai & Stone (2010) showed that the radial drift velocity in the case of a turbulent environment can be reduced compared to the laminar, single-size results of Weidenschilling (1977) and Nakagawa et al. (1986). In order to artificially change the efficiency of radial drift, we have introduced the efficiency factor Ed in Eq. (3). From Eq. (2), it follows that adrift then becomes inversely proportional to the drift efficiency. This means that if radial drift is only Ed = 0.1 times as fast as the classical value, afrag became 1/Ed = 10 times larger3.
Our simulation results with reduced drift efficiency (cf. model LDE in Table 1) show that particles do reach larger sizes in the dead zone (see third panel from top in Fig. 3). Still, the grain size is a smooth function of radius inside the dead zone. We found that going from 20 to 1 AU, the total surface density of grains smaller than one centimeter decreases only smoothly by two orders of magnitude. This means that the cavities in the mm-images cannot be explained with this mechanism. In addition to that, the reduced drift speed also increases the time scale on which small dust is swept up (cf. Eq. (11)). This results in much larger amounts of small dust being left over, as can be seen by comparing the second and third panel in Fig. 3. It also explains the less pronounced infrared dip in the SEDs (cf. Figs. 4 and 5).
The intensity shapes inside the dead zones can be understood as in the previous subsection: for all models but D23_M05, we recover a rather flat intensity profile due to the presence of large grains and a drift limited distribution. In model D23_M05, the effective fragmentation causes a steep increase in the inner regions, as in model A3. This increase is mostly caused by changes in the opacity due to the presence of large amounts of small dust.
4.2.2. Growth through all barriers
It is a valid question to ask what disks would look like if our current understanding of the growth barriers and radial drift is entirely wrong. For this reason we simulated a case where grain growth is not inhibited by either fragmentation or radial drift. That is, we consider perfect sticking (without any fragmentation) and in addition, dust is only allowed to be diffused or dragged along by the gas, but not to drift (i.e., Ed = 0). Apart from those changes, all other parameters of this model are identical to A55 (see model COAG in Table 1). The resulting grain size distribution is plotted in the bottom panel of Fig. 3 and the resulting SEDs and brightness profiles are shown in Fig. 4.
In Fig. 4, it can be seen that for perfect sticking, the IR dip in the SED forms very quickly and is very pronounced, as also found by Dullemond & Dominik (2005). While the inner parts are cleared of small dust, the growing dust particles are not able to sweep up all smaller dust further out in the disk, a population of small dust remains, as seen in the bottom panel of Fig. 3. We calculated the time scale for the small dust sweep-up in such a scenario (see Appendix A), which is proportional to the planetesimal size and to the quantity r/(Σdcs) and for our setup exceeds 1 Myr beyond 10 AU. This approximation does not include a reproduction of small dust, as would be expected for a distribution of planetesimals, which would further increase the time scale. Therefore, even a scenario with perfect sticking and no radial drift is not able to reproduce the observed large cavities in transition disks.
5. Discussion and conclusions
In this paper, we have investigated the ability of models of dust evolution to explain transition disks. We calculated simulated SEDs and 880 μm images from the output produced by a dust evolution code for a variety of different initial conditions. For clarity, we only considered effects directly induced by growth, fragmentation and transport of dust, without pressure traps or planet induced gaps. The models were chosen to represent best-case scenarios for this mechanism to work, i.e. large gas disk masses and no viscous evolution were assumed. The only extensions to this model we have considered here are the ones which influence the grain size limits, i.e., the strength of turbulence and the gas surface density. We found that effects of grain growth can indeed produce dips in the SED such as found for many transition disks (see also Dullemond & Dominik 2005), however they fail to reproduce the cavities in the (sub-)millimeter images such as found by Brown et al. (2009); Andrews et al. (2011); Lyo et al. (2011). Even in the extreme case where growth proceeds without any barriers and radial drift is switched off, no large inner cavities can be formed within 5 Myr of evolution.
This leads to the conclusion that disks with large inner holes cannot be caused by grain growth alone. Due to the fact that current models of disk photoevaporation (e.g. Owen et al. 2010) also fail to explain the inner cavities in the accreting objects, we propose that a combination of dust evolution with other effects such as pressure bumps, spiral arms or planet induced gaps could be the solution of the problem (see Pinilla et al. 2012b). Important questions to be answered from the observational side are: apart from the size of the cavity, is there a distinct difference between disks with small and large cavities? What is the gas content inside the cavities? And do different sizes of dust show different cavity shapes in the same object (see Dong et al. 2012)? Theoretical models will need to investigate the trapping mechanisms which effectively shepherd the dust outside the cavity, irrespective of the particle sizes.
Our findings can be summarized as follows:
-
A grain size distribution for which the drift-induced grain sizelimit is smaller than the fragmentation induced size limitbecomes inefficient in replenishing small dust due to a lack offragmenting collisions.
-
The time scale on which the remaining small dust is swept up by the largest, inward drifting grains is proportional to the distance to the central star and depends also on the dust-to-gas mass ratio and the turbulence strength. The dispersal of small dust is therefore from the inside out.
-
Small amounts of small dust can be retained for several million years in the outer parts of the disk (≳ 10 AU) if the dust-to-gas mass ratio is lower than a few times 10-4.
-
Even if the inner regions are cleared of small dust via grain growth, most of the dust mass is still detectable by millimeter observations. Furthermore, the grain size is a smooth function of the stellocentric radius which means that the “observable” dust surface density decreases only slightly and the brightness profile stays approximately flat. This mechanism thus fails to reproduce the strong drop in millimeter emission which is typically observed in disks with large cavities.
-
The model does not resemble the observations of large cavities, even if perfect sticking and no radial drift is assumed. The observed, sharp division between the inner and the outer regions call for a severe change in the disk properties. Pressure bumps that are strong enough to decouple both large and small dust from the accretion flow are most likely necessary to explain the observations.
As long as the dust distribution becomes drift dominated, this leads to a self-regulating process: radial drift removes dust mass, thus lowering the dust-to-gas ratio. As the dust-to-gas ratio drops, the growth time scale and therefore also the drift time scale increases. Hence, the evolutionary time scale of the dust-to-gas ratio depends on the dust-to-gas ratio itself, and to reach a dust evolution time scale of a few Myr, the dust-to-gas ratio needs to be in the range of 10-5 to some 10-4.
It should be noted that in the fragmentation dominated limit (afrag < adrift), the drift velocity of the largest particles is decreased if Ed is decreased while the particle size does not change. In the drift limit (adrift < afrag), the situation is reversed: the largest particles will grow to larger sizes until their drift time scale again equals the growth time scale. Thus the particle size is increased while the drift velocity of the largest particles is unchanged as long as their Stokes number is below unity.
Acknowledgments
We like to thank Kees Dullemond, Chris Ormel, James Owen, and Satoshi Okuzumi for stimulating discussions. We also thank the anonymous referee for his/her very constructive and helpful criticism.
References
- Alexander, R. D., & Armitage, P. J. 2007, MNRAS, 375, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., Clarke, C., & Pringle, J. E. 2006, MNRAS, 369, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., et al. 2012, ApJ, 744, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bai, X.-N. 2011, ApJ, 739, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2010, ApJ, 722, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Testi, L., Isella, A., et al. 2011, A&A, 525, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Muench, M. 1993, Icarus, 106, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., Johansen, A., et al. 2007, A&A, 469, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Henning, T., & Dullemond, C. P. 2008, A&A, 487, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., Dullemond, C. P., & Wilner, D. J. 2008, ApJ, 675, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., D’Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C., Gendrin, A., & Sotomayor, M. 2001, MNRAS, 328, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., Rafikov, R., Zhu, Z., et al. 2012, ApJ, 750, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Dubrulle, B., Morfill, G. E., & Sterzik, M. F. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., Guilloteau, S., Piétu, V., et al. 2008, A&A, 490, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, T. 2010, A&A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ercolano, B., Drake, J. J., Raymond, J. C., & Clarke, C. C. 2008, ApJ, 688, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Clarke, C. J., & Hall, A. C. 2011, MNRAS, 410 [Google Scholar]
- Espaillat, C., Calvet, N., D’Alessio, P., et al. 2007, ApJ, 664, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Fedele, D., van den Ancker, M. E., Henning, T., Jayawardhana, R., & Oliveira, J. M. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P. 2007, ApJ, 671, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güttler, C., Blum, J., Zsom, A., Ormel, C. W., & Dullemond, C. P. 2010, A&A, 513, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartigan, P., Hartmann, L., Kenyon, S. J., Strom, S. E., & Skrutskie, M. F. 1990, ApJ, 354, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495 [Google Scholar]
- Hernández, J., Hartmann, L., Megeath, T., et al. 2007, ApJ, 662 [Google Scholar]
- Hughes, A. M., Wilner, D. J., Calvet, N., et al. 2007, ApJ, 664, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, A. M., Andrews, S. M., Espaillat, C., et al. 2009, ApJ, 698, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2010a, ApJ, 714, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Natta, A., Wilner, D., Carpenter, J. M., & Testi, L. 2010b, ApJ, 725, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Pérez, L. M., & Carpenter, J. M. 2012, ApJ, 747, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Klahr, H., & Henning, T. 2006, ApJ, 636 [Google Scholar]
- Kraus, A. L., & Ireland, M. J. 2012, ApJ, 745 [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2007, ApJ, 664 [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Lyo, A.-R., Ohashi, N., Qi, C., Wilner, D. J., & Su, Y.-N. 2011, AJ, 142, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Crockett, N., & Carr, J. S. 2008, ApJ, 687, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Carr, J. S., Strom, S. E., et al. 2010, ApJ, 712, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., Neri, R., Shepherd, D. S., & Wilner, D. J. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okuzumi, S. 2009, ApJ, 698, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Cuzzi, J. N. 2007, A&A, 466, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Panić, O., Hogerheijde, M. R., Wilner, D., & Qi, C. 2009, A&A, 501, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paszun, D., & Dominik, C. 2009, A&A, 507, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piétu, V., Dutrey, A., Guilloteau, S., Chapillon, E., & Pety, J. 2006, A&A, 460, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012a, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Benisty, M., Birnstiel, T. 2012b, A&A, accepted [Google Scholar]
- Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., van Dishoeck, E. F., et al. 2008, ApJ, 684, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., Wood, K., Armitage, P. J., Whitney, B. A., & Bjorkman, J. E. 2003, MNRAS, 342, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rodmann, J., Henning, T., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2011, ApJ, 743, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Sano, T., Miyama, S. M., Umebayashi, T., & Nakano, T. 2000, ApJ, 543, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L. W., Fürész, G., et al. 2006, AJ, 132, 2135 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Dutkevitch, D., Strom, S. E., et al. 1990, AJ, 99, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, K. M., Strom, S. E., Edwards, S., Cabrit, S., & Skrutskie, M. F. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Himeno, Y., & Ida, S. 2005, ApJ, 625, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2001, ApJ, 554, 1087 [Google Scholar]
- Turner, N. J., Carballido, A., & Sano, T. 2010, ApJ, 708, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2008, ApJ, 677, 1296 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, A., Stapelfeldt, K., Wood, K., & Ménard, F. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 523 [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Hartmann, L., Espaillat, C., & Calvet, N. 2011, ApJ, 729, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Estimation of the sweep-up time scales
To estimate the time scale on which small dust is swept up by larger, drifting particles,
we consider the two-population model of BKE12
according to which the grain size of the drifting particles is given by 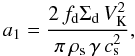 (A.1)where
fd = 0.55 and VK is the
Keplerian velocity. The drift velocity of the largest grains is then given by
(A.1)where
fd = 0.55 and VK is the
Keplerian velocity. The drift velocity of the largest grains is then given by
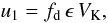 (A.2)where
ϵ is the dust-to-gas mass ratio. Assuming that the large particles
contain most of the mass of the system (Σ1 ≃ Σd), and that the small
particles are well mixed with the gas (St1 ≲ αt),
we can write the change of the surface number density of small particles
N0 as (see, Birnstiel et al.
2010, Appendix A.2.)
(A.2)where
ϵ is the dust-to-gas mass ratio. Assuming that the large particles
contain most of the mass of the system (Σ1 ≃ Σd), and that the small
particles are well mixed with the gas (St1 ≲ αt),
we can write the change of the surface number density of small particles
N0 as (see, Birnstiel et al.
2010, Appendix A.2.) 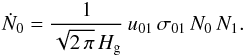 (A.3)Approximating the
relative velocity u01 between the two species by the drift
velocity of the large grains and the collision cross section by
(A.3)Approximating the
relative velocity u01 between the two species by the drift
velocity of the large grains and the collision cross section by
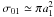 , we can
derive the time scale for the sweep-up of small dust by drift-induced collisions
, we can
derive the time scale for the sweep-up of small dust by drift-induced collisions
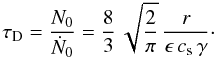 (A.4)The same
calculation but using the turbulent relative velocities between the largest and smallest
grains
(A.4)The same
calculation but using the turbulent relative velocities between the largest and smallest
grains 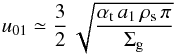 (A.5)according
to Ormel & Cuzzi (2007) yields the sweep-up
time of small particles where collisions are driven by turbulence,
(A.5)according
to Ormel & Cuzzi (2007) yields the sweep-up
time of small particles where collisions are driven by turbulence, 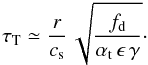 (A.6)Comparing Eqs. (A.4) and (A.6) shows that the sweep-up of the small dust is driven by turbulent
velocities, as long as
(A.6)Comparing Eqs. (A.4) and (A.6) shows that the sweep-up of the small dust is driven by turbulent
velocities, as long as 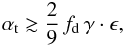 (A.7)which is in our
models approximately gives
(A.7)which is in our
models approximately gives 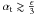 .
.
A similar calculation can be done for the small dust in a distribution which is dominated
by planetesimals of size a1. Using Eq. (A.3) with the cross section
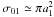 and the
relative velocities from the head wind
and the
relative velocities from the head wind 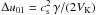 , we derive
, we derive 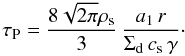 (A.8)For the values of
our simulations (model COAG) and a1 = 104 cm, we
find that τP ≃ 1 Myr at 10 AU and increases steeply with
radius. This agrees well with the fact that the planetesimals cannot efficiently sweep up
the small grains beyond a few AU, as seen in the bottom panel of Fig. 3.
(A.8)For the values of
our simulations (model COAG) and a1 = 104 cm, we
find that τP ≃ 1 Myr at 10 AU and increases steeply with
radius. This agrees well with the fact that the planetesimals cannot efficiently sweep up
the small grains beyond a few AU, as seen in the bottom panel of Fig. 3.
All Tables
All Figures
 |
Fig. 1 Initial conditions of the simulations without a dead zone. Solid and dashed lines denote the gas and dust surface density in g cm-2, respectively. The dash-dotted line denotes the mid-plane temperature. |
| In the text | |
 |
Fig. 2 Vertically integrated dust surface density distribution after 5 Myr of evolution for the simulations without a dead zone, A2 (top) to A5 (bottom). The parameters for the simulations are shown in Table 1. The solid red line denotes the growth barrier set by grain fragmentation, the dashed red line the size limit due to radial drift. |
| In the text | |
 |
Fig. 3 Vertically integrated dust surface density distribution after 5 Myr of evolution for simulations D23_M05 (top), D25_M05 (second panel), LDE (third panel) and COAG (bottom panel). The corresponding parameters are shown in Table 1. The solid red line denotes the growth barrier set by grain fragmentation, the dashed red line the size limit due to radial drift. |
| In the text | |
 |
Fig. 4 Spectral energy distributions (top row), normalized radial surface brightness profiles at 880 μm (middle row), and synthesized 880 μm images (bottom row) corresponding to the Submillimeter Array setup of Andrews et al. (2011) for the active disk models. The line colors correspond to models A2 to A5 and model COAG, as labeled in the left panels. The dashed grey line in the SEDs represents the stellar photosphere. The columns from left to right correspond to 0, 1, 2, and 5 Myr of evolution. The shaded areas in the central row depict the resolution limits of current (pre-ALMA) interferometers. Only the results for model A4 are shown in the synthesized images, where the contours correspond to 10% levels of the peak brightness and the bar and dashed oval represent the size scale and the beam size, respectively. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 but for the models which include dead-zones, corresponding to the simulations labeled in the left panels. The dashed vertical line in the central row marks the dead zone radius rdz. The synthesized images in the bottom row correspond to model D25_M05. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


