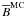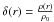EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 542 (June 2012) A&A, 542 (2012) A34 Full HTML
Free Access
Issue
A&A
Volume 542, June 2012
Article Number A34
Number of page(s) 11
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201118017
Published online 01 June 2012

© ESO, 2012

1. Introduction

Before recombination, the energy of photons is high enough to avoid the formation of neutral hydrogen atoms. This means that baryons and photons are coupled through Compton scattering and electromagnetic interaction between protons and electrons, forming a plasma. In this fluid, two phenomena act in opposite directions: gravitational forces tend to compress the plasma around high density regions, while radiation pressure tends to dilute any such over-density. The combination of both in the presence of any initial inhomogeneity gives rise to acoustic waves propagating in the baryon-photon plasma. This phenomenon ends abruptly at the epoch of recombination, when the temperature drops sufficiently to allow hydrogen atoms to form, and therefore radiation decouples from the baryons.

Baryon acoustic oscillations (BAO) are therefore due to the propagation of these sound waves in the baryon-photon plasma in the early universe (Peebles & Yu 1970; Hu et al. 1997; Eisenstein & Hu 1998; Bassett & Hlozek 2010). Any primordial over-density in the early universe produces a spherical acoustic wave in the baryon-photon plasma, travelling outwards: the radiation pressure drags the baryons that are coupled to the photons, and compensates the gravity force that pulls all matter towards the centre. Dark matter, however, is totally decoupled from the photons, and therefore its density at the centre continues growing. About 380   000 years after the Big Bang, the temperature drops so that photons and baryons decouple, and the scale of the baryon shells freezes. After this time, both the central over-density and the shell grow gravitationally, accreting both dark matter and baryons. The result at late times is a large over-density at the position of the original perturbation, surrounded by a faint spherical shell on a fixed co-moving scale (Eisenstein et al. 2007).

The BAO scale is fixed by the sound horizon at decoupling because it is the distance that the expanding acoustic shells can travel before decoupling. It has been accurately measured by the study of the anisotropies in the cosmic microwave background (CMB) to be (Komatsu et al. 2009) rs = 153.3  ±  2.0   Mpc = 110.4  ±  1.4   h-1   Mpc (where we take h = 0.72, Freedman et al. 2001)1. Therefore, this scale, once measured, could be used as a standard ruler to measure the Hubble expansion rate H(z) and the angular diameter distance DA(z) as function of redshift (Cooray et al. 2001; Blake & Glazebrook 2003; Seo & Eisenstein 2005).

The BAO should appear as a series of damping wiggles in the matter power spectrum, with the locations of the peaks and troughs in k-space being a function of rs and other cosmological parameters (Eisenstein & Hu 1998). All the harmonics sum up to the same peak in the galaxy correlation function ξ(r) on the scale rs, and therefore it seems more appropriate to use this statistic to detect the BAO feature in the available galaxy redshift surveys encompassing large volumes of the universe (Sánchez et al. 2008).

The first detection of BAO (at about the 3σ level) was reported in an analysis of the correlation function (Eisenstein et al. 2005) of the Sloan Digital Sky Survey (SDSS, York et al. 2000) luminous red galaxies (LRG) sample (Eisenstein et al. 2001), and later in the power spectrum (Cole et al. 2005) of the Two-degree Field Galaxy Redshift Survey (2dFGRS) (Colless et al. 2001). However, this is certainly a controversial topic. Cabré & Gaztañaga (2011) are not finding such level of detection using a data set twice as large in both volume and number of galaxies. They do not claim that this result contradicts the standard Λ – cold dark matter (ΛCDM) model, but instead that it is a consequence of insufficient data. One of the arguments in Cabré & Gaztañaga (2011) is that mixing model selection with parameter determination can lead to some confusion in interpreting the results and their significance. Different authors use different criteria to assess the significance of their BAO detection. For example, when Eisenstein et al. (2005) affirm that the baryon signature was detected at 3.4σ (or at 3.0σ when including only data points between 60 and 180 h-1 Mpc), they compare their results of the SDSS-LRG correlation function with those expected for the best-fit pure CDM model and different BAO models. The most robust BAO detection up to now (Percival et al. 2010) was obtained by studying the combined power spectrum of the LRG and the “main” (Strauss et al. 2002) samples of SDSS, together with the 2dFGRS sample, and is at the  ~ 3.6σ level. The authors explicitly state that since this number is obtained by comparing to an arbitrary smooth model, the significance cannot be directly compared with the one reported in Eisenstein et al. (2005). This is a clear example of different authors using different ways to assess the significance of their results that in practice are not comparable. Hütsi (2006) calculated the redshift space power spectrum of the SDSS-LRG sample drawn from the data release 4. He concludes that BAO models are more likely by 3.3σ over the corresponding models without any oscillatory behaviour in the power spectrum.

Percival et al. (2007) detected BAO in the clustering of the combined 2dFGRS and SDSS galaxy samples, and used their measurements to constrain cosmological models, in particular a given combination of the angular diameter distance DA(z) and the Hubble parameter H(z). Cabré & Gaztañaga (2009a,b) studied the LRG anisotropic redshift-space correlation function ξ(σ,π), where π is the line-of-sight or radial separation and σ is the transverse separation. Moreover, Gaztañaga et al. (2009) illustrated how H(z) could be constrained using the correlations in the radial direction. Kazin et al. (2010a) found similar results for the correlation measurements and uncertainties, but manifest disagreement in the interpretation of the results regarding the detection of a line-of-sight baryon acoustic feature.

More recent studies (Martínez et al. 2009; Cabré & Gaztañaga 2009a; Sánchez et al. 2009; Kazin et al. 2010b) have confirmed this detection in the last data release (DR7, Abazajian et al. 2009) of the SDSS-LRG, containing twice as many galaxies as the original sample, although the observed peak is in these cases wider than that observed in the original detection – an issue that needs further explanation. These measurements of the BAO scale at low redshift, combined with other cosmological probes, have been used to place stringent constraints on the values of cosmological parameters (Tegmark et al. 2006; Percival et al. 2007; Sánchez et al. 2009; Percival et al. 2010; Reid et al. 2010; Kazin et al. 2010a).

While Bassett & Afshordi (2010) argue that low-level detections may be insufficient to robustly estimate the cosmological parameters, Cabré & Gaztañaga (2011) show instead that it is still possible – assuming a model – to locate the BAO position with data providing very low significant BAO detection.

It is important, therefore, to find evidence of BAO in the galaxy distribution based on complementary methods. A step further is to search for real structures in the galaxy distribution that are responsible for the BAO feature in these second-order statistics. The detection of these structures would confirm the existence of the baryon acoustic phenomenon. Moreover, if we were able to localise these structures in configuration space, this would allow us to study in more detail the properties of the BAO.

In this paper, we introduce a new method for the detection of BAO that is closely tied to the underlying physics of the process, and apply it to a sample drawn from the SDSS catalogue. This method (described in Sect. 2) is based on analysing directly the three-dimensional (3D) galaxy distribution using a very specific wavelet function (which we called “BAOlet”), which is especially well-suited to searching for BAO features. The method makes use of two different tracers, one to map the overall density field (including the BAO shells), and the other to locate the position of the largest over-densities, which should correspond to the centres of the shells. As we directly study the galaxy distribution in configuration space, this method also allows us to identify regions of space where the BAO signal is either stronger or fainter. We describe the expected signal in the ΛCDM model in Sect. 3, using both an analytical prediction and a N-body simulation catalogue. We describe the samples used in the case of SDSS in Sect. 4. In Sect. 5, we show the results obtained in this case. We also perform a test to assess the significance of these results, and explore the implications of this analysis regarding the localisation of BAO structures. Finally, we summarise our conclusions and discuss possibilities for future work in Sect. 6.

2. The wavelet detection method

The basis of the new BAO detection method is to focus on the positions of massive dark matter haloes, which correspond to the location of large initial perturbations, and to search for structures resembling the acoustic shells around these. Once we locate the positions of the large over-densities, we need to study the density field to identify the structures corresponding to the acoustic shells around these centres. An appropriate method for identifying structures in continuous fields is a wavelet analysis (Martínez et al. 1993; Starck & Murtagh 2006; Jones 2009). Wavelet transforms are widely used in many areas, especially in image analysis (Mallat 2008; Starck et al. 2010). They are especially suited to the analysis of data on different scales, and the identification of characteristic patterns or structures. Wavelets have been used in cosmology to analyse large-scale structure and CMB anisotropies (Martínez et al. 1993; Rauzy et al. 1993; Vielva et al. 2004; Starck et al. 2006; Saar 2009).

Standard wavelet functions such as the Mexican hat are, however, unsuitable for the detection of shells. We need instead a family of wavelets whose shape matches the type of structures we wish to find in our data. We use therefore a especially designed wavelet (the “BAOlet”), which is well adapted to the search of BAO features – shell-like structures around our selected centres. We design this new family of wavelet functions as a transformation of the wide-used B-spline wavelets (Saar 2009). These ψR,s(x) functions are spherically symmetric, and their radial profiles are defined as ψR,s(r)=αR,s4πr2[2B3(2r−Rs)−B3(r−Rs)],\begin{equation} \psi_{R,s}(r) = \frac{\alpha_{R,s}}{4\pi r^2} \left[ 2B_3\left( 2\frac{r - R}{s} \right) - B_3\left(\frac{r-R}{s}\right)\right], \label{eq:baodef} \\ \end{equation}(1)where R and s are the two parameters that define the scale and width of the BAOlet function, αR,s is the normalisation constant defined so that ||ψR,s||2≡∫|ψR,s(x)|2dx=1,\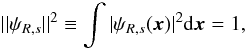begin{equation} ||\psi_{R,s}||^2 \equiv \int |\psi_{R,s}(\vec{x})|^2{\rm d}\vec{x} = 1, \label{eq:wavenorm} \\ \end{equation}(2)and B3(x) is the box spline of the third degree, defined by 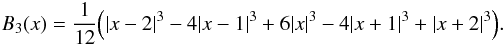B3(x)=112(|x−2|3−4|x−1|3+6|x|3−4|x+1|3+|x+2|3).\begin{eqnarray*} B_3(x) = \frac{1}{12} \Big(\vert x-2 \vert^3 - 4\vert x-1 \vert^3+6\vert x \vert^3-4 \vert x+1 \vert^3+\vert x+2 \vert^3 \Big). \\ \end{eqnarray*}The BAOlet function is shown in Fig. 1. It can be thought of as a spherical shell of radius R and width s, with zero amplitude at its centre and therefore adapted to the detection of spherical shells of a given radius. This specific choice is motivated by the integrated profile being the widely used one-dimensional (1D) “B-spline” wavelet function that has a null mean and compact support [ − 2,2] . These properties directly translate into the BAOlet, which also has a null mean – a requirement for any wavelet function – if R > 2s, and takes non-zero values only for R − 2s ≤ |x| ≤ R + 2s.

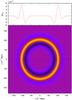thumbnail Fig. 1

The BAOlet function. Here we show a two-dimensional (2D) plot (bottom) of the wavelet ψR,s(x) used in the analysis, as defined by Eq. (1). The top panel shows a 1D slice along the dashed-dotted axis. The wavelet is plotted here for R = 105   h-1   Mpc, s = 30   h-1   Mpc. The red dot marks the centre of the wavelet. This function has a null mean (provided that R > 2s), and compact support. It takes non-zero values only for R − 2s ≤ |x| ≤ R + 2s.

We describe the density field using the density contrast δ(x), defined as 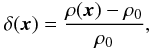δ(x)=ρ(x)−ρ0ρ0,\begin{eqnarray*} \delta(\vec{x}) = \frac{\rho(\vec{x}) - \rho_0}{\rho_0}, \end{eqnarray*}where ρ(x) is the density field, and ρ0 is its mean. Then, given a density contrast map δ(x), properly normalised as in Eq. (2), we can construct, for each point in the parameter space (R,s), a BAOlet coefficient map as the convolution of our density field with the corresponding wavelet 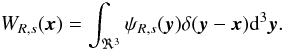WR,s(x)=∫ℜ3ψR,s(y)δ(y−x)d3y.\begin{equation} W_{R,s}(\vec{x}) = \int_{\Re^3} \psi_{R,s}(\vec{y}) \delta(\vec{y} - \vec{x}) {\rm d}^3\vec{y}. \label{eq:coeff} \end{equation}(3)The BAOlet acts as a matched filter, which is sensitive to data containing shells of different radii and different widths. Its property of zero mean is also of high importance since it makes the statistics derived from the BAOlet coefficients independent of the background level. It is indeed obvious that any constant added to the input data would not change the BAOlet coefficients. In comparison, the estimation of this baseline level is a very delicate aspect of the BAO detection in the two-point correlation function.

Owing to the properties of the wavelet, the coefficient maps WR,s(x) should have a null mean when averaged over all points in the volume considered. Equivalently, if we sampled these maps at N random points uniformly distributed in the volume (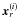x(i)r\hbox{$\vec{x}_r^{(i)}$}), the expected value of the average of the coefficients would be zero 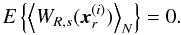E{⟨WR,s(x(i)r)⟩N}=0.\begin{equation} E\left\lbrace \left \langle W_{R,s}(\vec{x}_r^{(i)}) \right\rangle_N \right\rbrace = 0. \label{eq:E0} \end{equation}(4)This condition holds even in the presence of shell-like structures in the density field. Of course, for such structures the value of WR,s(xc) (xc is the centre of the shell) is positive, and remains positive in nearby points. For an ideal δ(r − R) density shell, the radius of the region around the centre where the wavelet amplitude is positive, is s; the positive signal in this region is compensated by negative amplitudes around |x| = R. However, if we are able to identify the positions of N massive haloes in the same volume (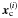x(i)c\hbox{$\vec{x}_{\rm c}^{(i)}$}), we can define a new statistic B(R,s) as the mean value of the coefficients WR,s(x) at these positions 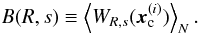B(R,s)≡⟨WR,s(x(i)c)⟩N.\begin{equation} B(R,s) \equiv \left\langle W_{R,s}(\vec{x}_{\rm c}^{(i)})\right\rangle_N. \label{eq:Bstat} \end{equation}(5)If there are indeed shell-like structures around the selected density maxima 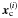x(i)c\hbox{$\vec{x}_{\rm c}^{(i)}$}, as expected for baryon acoustic structures, we should find positive values of B(R,s) with the maximum of B at the (R,s) values characterising these shells.

We can obtain further information from the wavelet coefficients WR,s(x), as we have information on the actual dependence of the signal picked up by the BAOlet function on the position. In particular, fixing a set of parameters of interest (Ri,si), we could use the coefficients WRi,si(xc) to identify which of the selected massive haloes produce the strongest signal for these shell characteristics. In the context of BAO, the parameters Ri, si can be chosen a priori using a theoretical model, or a posteriori using the parameters for which the function B(R,s) attains its maximum. In this way, we can localise in configuration space the structures responsible for the largest BAO signal in a given sample.

For our calculation of B(R,s), we sample the (R,s) parameter space on a grid. For each point (R,s), we calculate the coefficient map WR,s(x) as the convolution of the BAOlet with the density field (Eq. (3)). We perform the convolution in Fourier space using a fast Fourier transform (FFT) technique. To avoid problems with the FFT, we zero-pad a large region around our density cube. To obtain B(R,s), we sample WR,s(x) at the position of the N selected centres, and calculate the average value (Eq. (5)).

Therefore, to apply this method, we need a way to map the overall density field δ(x), but also to locate the positions of the massive matter haloes 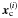x(i)c\hbox{$\vec{x}_{\rm c}^{(i)}$}. We have to use two different populations of mass tracers, so that they play the appropriate role in the detection algorithm. The idea of using two different tracer sets, one for the small perturbations and another for the high peaks, in a cross-correlation analysis was anticipated by Eisenstein et al. (2007). We implement here a similar idea, but applying a wavelet tool directly to the density field. As detailed below, we use galaxies from the “main” and LRG samples of SDSS in this case. However, this choice depends on the kind of data available in each case.

3. Prediction from ΛCDM

To illustrate our method more clearly, we show here the results we would expect according to the ΛCDM model, and the effect of BAO in our new statistic B(R,s). For this aim, we use both the analytical approximation to the transfer function of Eisenstein & Hu (1998), and the results from the MareNostrum Institut de Ciències de l’Espai (MICE) simulation (Fosalba et al. 2008).

In the first place, we use the ΛCDM transfer function, which allow us to study directly the effect of the BAO. However, in this case, we must make a series of approximations in order to derive a prediction for B(R,s). We wish to predict the typical result for the wavelet coefficient WR,s at the position of massive matter haloes xc, as a function of R,s. From Eq. (3), we see that this is equivalent to studying the typical density profile around these haloes, δ(y − xc). The ΛCDM transfer function allows us to calculate this profile, provided that we know the initial perturbation corresponding to the selected haloes. We make here the simple approximation of considering that these initial perturbations are point-like and spherically symmetric, and can thus be simply described by a Dirac delta function in configuration space. This corresponds to a constant value in Fourier space. As the transfer function T(k) describes the relative evolution of the different Fourier modes, the present-day radial density profile corresponding to this initial perturbation is given simply by (Eisenstein et al. 2007) 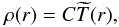ρ(r)=C􏽥T(r),\begin{equation} \rho(r) = C \widetilde{T}(r), \label{eq:tf} \end{equation}(6)where 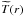􏽥T(r)\hbox{$\widetilde{T}(r)$} is the Fourier transform of the transfer function T(k), and C is a normalisation constant that depends on both the details of the initial perturbation and the cosmic growth function D1(z). From Eqs. (3) and (5), we see that the effect of C is just to change the normalisation of our statistic B(R,s).

We use the fitting formulae to the transfer function T(k) of Eisenstein & Hu (1998), and obtain the expected WR,s at a large over-density using Eqs. (6) and (3). To highlight the particular signature of BAO, we also calculate WR,s using the “no wiggle” transfer function formula, in which the BAO have been removed. We use here the values ΩM = 0.25, ΩΛ = 0.75, Ωb = 0.044, and h = 0.7 for the cosmological parameters, to allow a direct comparison with the MICE simulation. Following Eisenstein & Hu (1998), the sound horizon scale in this case is rs = 109.3   h-1   Mpc. The results in both cases are shown in Fig. 2. In the plot, we mask the region R < 2s, as for these values of the parameters our BAOlet is not compensated (its mean is different from 0). Comparing both panels of the figure, we see clearly the effect of the presence of BAO in our statistic B(R,s). In the case without BAO, WR,s is always negative, and has a smooth gradient across the (R,s) plane. This gradient is due to the overall shape of the radial profile (Eq. (6)). However, in the presence of BAO, WR,s has a prominent peak with positive values. This clearly illustrates the concept behind the B(R,s) statistic. The BAOlet ψR,s acts as a matched filter with a shape adapted to detecting BAO shells. Therefore, the positive values in the coefficients WR,s correspond to the cases in which the radial profile is matched by the BAOlet shape. The values at which WR,s attains its absolute maximum, Rmax = 110   h-1   Mpc and smax = 22   h-1   Mpc, thus correspond to the characteristics of the shell that most closely match the observed profile around the selected centres.

thumbnail Fig. 2

Values of the BAOlet coefficients WR,s expected at the positions of large initial point-like perturbations, as a function of the BAOlet parameters (R,s). The bottom panel shows the result using a standard ΛCDM transfer function, while the top panel shows the result using a transfer function with the BAO wiggles edited out (Eisenstein & Hu 1998). The normalisation is arbitrary. The contours are drawn in steps of 1000 for WR,s < 0 (dotted), WR,s = 0 (solid), and WR,s > 0 (dashed). The map attains a maximum at R = 110   h-1   Mpc, s = 22   h-1   Mpc.

To test the reliability of the method, and this ΛCDM prediction, we calculate the B(R,s) for a halo catalogue drawn from the MICE simulations. We use the publicly available halo catalogue from the “MICE3072” run (Crocce et al. 2010). This particular run contains 20483 particles in a box of side 3072   h-1   Mpc, therefore covers a volume of 29   h-3   Gpc3. Crocce et al. performed the simulation with the GADGET-2 code (Springel 2005), assuming a ΛCDM model with the parameters mentioned above. The haloes in the simulation were selected using a friends-of-friends (FoF) algorithm.

We use the resulting halo catalogue at z = 0, which contains a total of 2   819   031 haloes containing 143 or more particles. This corresponds to haloes with masses  ≥ 3.35  ×  1013   h-1   M⊙. The halo number density is thus 9.72  ×  10-5   h3   Mpc-3. We use the full halo catalogue as a tracer of the overall density field. We then select as centres for the calculation of B(R,s) in Eq. (5) only the haloes with a mass  ≥ 1.76  ×  1014   h-1   M⊙. We choose this mass threshold in order to select approximately the 10% most massive haloes in the simulation box. This choice is somewhat arbitrary, but serves for the purpose of testing the BAOlet method and illustrating the expected result.

Figure 3 shows the BAOlet result B(R,s) for these MICE samples, compared to the theoretical results obtained above from the Eisenstein & Hu (1998) transfer functions. We obtain a result very similar to that of Fig. 2, as B(R,s) has a clear peak, and attains its absolute maximum for Rmax = 108   h-1   Mpc and smax = 28   h-1   Mpc. This indicates that our BAOlet method can be applied to two sets of mass tracers, although the details of the tracers used here are very different from the ones we use later on with the SDSS samples. This also confirms the expected effect of the presence of BAO in the B(R,s) function, namely a large peak with positive values of B, located approximately at the values of R and s corresponding to the radius and width of the acoustic shells. That we obtain here slightly different values for Rmax and smax than those predicted above may be due to non-linear evolution effects, which slightly reduce the radius and increase the width of the shells. A similar effect is present in the correlation function (see e.g. Crocce & Scoccimarro 2008).

thumbnail Fig. 3

The BAOlet statistic B calculated for the MICE simulation sample described in the text as a function of the parameters (R,s) (bottom panel). The contours are drawn in steps of 5 for B < 0 (dotted), B = 0 (solid), and B > 0 (dashed). This function attains its maximum for R = 108   h-1   Mpc, s = 28   h-1   Mpc. The top two panels show cuts at the values s = 28   h-1   Mpc (top) and s = 22   h-1   Mpc (middle), marked with grey horizontal lines in the 2D panel. In each case, the solid blue line corresponds to the value obtained from MICE, the dashed red line corresponds to the theoretical expectation from the Eisenstein & Hu (1998) transfer function (bottom panel of Fig. 2), and the dotted green line to the theoretical expectation using the “no wiggle” transfer function (top panel of Fig. 2). These theoretical predictions have been re-normalised to get the same value at the maximum in B(R,s).

We also use this halo catalogue from MICE to make a qualitative estimation of how different observational effects would affect the BAOlet result. In the first place, we study the effect of redshift-space distortions. To this end, we calculate the redshift-space positions of all haloes taking into account their peculiar velocities, as given by the simulation, and considering an observer located in one of the vertices of the simulation cube. The result for B(R,s) in this case is shown in the top panel of Fig. 4, where it is compared to the real-space result discussed above. As can be seen from the figure, although small differences appear between the real- and redshift-space results, the main features of the B(R,s) prediction remain the same, with the position of the maximum changing by only  ~1   h-1   Mpc.

In the second case, we add the effect of a decreasing radial selection function across the sample. We model this selection as an exponential decay function, such that the final number of haloes used to trace the overall density field is  ~20% of the total. In our calculations, we then weight each halo by the inverse of the mean density at its redshift, as we do later for the SDSS data. We do not apply any selection function to the centres. The results for B(R,s) obtained in this case (including also the redshift-space effects) are shown in the bottom panel of Fig. 4. As above, these observational effects do not significantly change the overall behaviour of B(R,s), or the location of the maximum of the peak. Overall, although the MICE catalogue used does not mimic the characteristics of our SDSS samples, we can be confident that neither redshift-space distortions nor a radial selection function (when it is taken into account in the calculation) should significantly bias our results.

thumbnail Fig. 4

The BAOlet statistic B for the MICE simulation when some observational effects are taken into account. In the top panel, we show the B(R,s) obtained when redshift-space distortions are included in the simulation. In the bottom panel, we show the result when a radial selection function is applied to the halo catalogue. In both cases, the contours are drawn in steps of 5 in B. Solid contours correspond to the results with the observational effects included. The dashed contours correspond to the original real-space result without selection, i.e., they are identical to those in the bottom panel of Fig. 3.

4. SDSS samples used

We use data from two different samples of the DR7 of the spectroscopic SDSS. On the one hand, we use the “main” galaxy sample (Strauss et al. 2002) as mass tracers to reconstruct the overall density field δ(x). On the other hand, we use the LRG as tracers of the central over-densities, and therefore use them as the selected centres 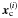x(i)c\hbox{$\vec{x}_{\rm c}^{(i)}$} to compute B(R,s).

LRG were selected by the SDSS team using several colour and magnitude cuts to obtain a highly biased sample extending to high redshift (Eisenstein et al. 2001). The galaxies selected in this way are known to reside near the centres of massive dark matter haloes (Zheng et al. 2009) and are thus adequate tracers for the centres of baryon acoustic structures. We apply an extra cut in the K-corrected, evolved, g-band absolute magnitude of  −23.2 < Mg <  −21.2, as in the previous BAO analysis by Eisenstein et al. (2005). This results in an approximately volume-limited sample in the redshift range 0.15 < z < 0.30.

“Main” galaxies in the SDSS constitute a much denser sample, and are therefore more suitable to map small density changes such as BAO shells. We use the “main” sample from the Value-Added Galaxy Catalogue (Blanton et al. 2005), which constitutes a magnitude-limited sample in the r band, with r < 17.6. We apply an extra simple cut, Mr <  −20.

For the conversion of angles and redshifts into co-moving distances, we use a fiducial cosmology with the parameters ΩM = 0.25, ΩΛ = 0.75. In our analysis, we use distances in units of h-1   Mpc, so that they do not depend on the specific value of h. We convert the distribution of the “main” galaxies into a density field δ(x) binning it into a grid with cubic pixels of 3   h-1   Mpc side. We correct for the selection effects by weighting each galaxy by the inverse of the average density at its redshift. As explained below, we performed some tests by slightly changing this weighting scheme. Although this weighting may not be optimal, it should not significantly affect our results, given that the wavelet method does not depend on the local background level. We used the density field constructed in this way for the calculation of the BAOlet coefficients following Eq. (3).

In our calculations, we could only use the region in which these two samples overlap, which corresponds to the redshift limits 0.15 < z < 0.26. To minimise border effects in the B(R,s) calculation, we defined a buffer region of rbuff = 175   h-1   Mpc from any of the borders of the “main” sample volume. As centres, we use only the LRG in the inner volume. This allows us to use the density field, as traced by the “main” sample galaxies, from z > 0.09. To minimise angular selection effects and border effects, we use a compact area of the sky where the angular completeness is nearly uniform. This area covers 5511deg2 and is defined, in the SDSS survey coordinates (Stoughton et al. 2002), by the limits  −31.25° < η < 28.75°,  −54.8° < λ < 51.8°. This results in finally using the density field in a volume of 2.2  ×  108   h-3   Mpc3, as traced by NMain = 198   342 galaxies. The number of LRG used as centres (avoiding the buffer region) is NLRG = 1599.

In Fig. 5, we show a slice of this survey showing both the “main” galaxies and the LRG. We show how, given the buffer used, the LRG used as centres are located in only an inner volume of the larger “main” sample. To illustrate the idea of the method, we show a zoom around a given LRG galaxy. Even for this single centre, a slight over-density of “main” galaxies is seen at the radii of 105 − 110 h-1   Mpc.

thumbnail Fig. 5

The SDSS catalogues used. We show a six-degree thick slice drawn from the catalogues used in our analysis. The red points are the LRG galaxies, which form a nearly volume-limited sample at z > 0.15. The “main” galaxies of the SDSS are depicted in blue. As shown, we use the “main” galaxies from z > 0.09, and we use only the LRG in an inner volume, allowing for a buffer region of rbuff = 175   h-1   Mpc from any of the borders of the “main” sample volume. For our analysis, we use the samples covering a total area of 5511deg2. The radius of a typical BAO shell is shown as a segment. At the top insets, we show two orthogonal slices of width 20   h-1   Mpc, centred on a particular LRG. The BAOlet coefficient map WR,s(x) has a large value at the position of this centre (for Rmax,smax), thus we expect to find a strong BAO signal. The two circles have the radii of 100 and 110 h-1   Mpc, respectively. This is a single BAO shell where the over-density can be appreciated by eye on the right scale.

As the structures we search for are huge, with radii of about 100   h-1   Mpc, we have to consider the effect of the assumed cosmology (different comoving distances) on our result. To estimate the distance differences, we compare the distances in our adopted MICE cosmology (ΩM = 0.25, ΩΛ = 0.75) with those in the WMAP seven-year cosmological model (Komatsu et al. 2011), ΩM = 0.271, ΩΛ = 0.729. We fixed the redshift difference δz = 0.07 that corresponds approximately to our shell diameter of 200   h-1   Mpc, and found that this gives distance differences of only a 0.3 and 0.8 per cent at the near and far borders of our sample (the MICE distances are larger than the WMAP7 ones in each case). Hence, for our nearby volume, the effect is small, and does not influence our results given that the statistical uncertainties are much larger (see next section). However, this effect will be significant for deep samples.

5. Results for the SDSS samples

We perform the calculation of B(R,s) for the SDSS in an analogous way to the case of the MICE simulation, using the samples defined in Sect. 4. Our results are shown in Fig. 6. As above, we mask the region R < 2s. As we do not introduce any border correction when calculating the B(R,s) statistic, we also mask the region corresponding to the values R > rbuf − s. Values obtained at such large values of R could contain some spurious signals, as the calculation of WR,s would rely on the density field in regions outside the survey boundaries.

thumbnail Fig. 6

The BAOlet statistic B calculated for SDSS data as a function of the parameters (R,s). The bottom panel shows the results in the full parameter space considered, where we sampled both R and s at intervals of 1   h-1   Mpc. We mask two areas, at the upper right and left corners, where our results are not reliable (see details in the text). The contours are drawn in steps of 5 for B < 0 (dotted), B = 0 (solid), and B > 0 (dashed). The top two panels show cuts at the arbitrarily chosen values s = 36   h-1   Mpc (top) and s = 20   h-1   Mpc (middle), marked with grey horizontal lines in the 2D panel. In these panels, the blue line is B(R,s), while the green line and the red band show the mean (BMC\hbox{$\overline{B}^{\rm MC}$}) and 1-σMC interval for the Monte Carlo realisations of random centres. We obtain a clear significant peak at different values of s, with a maximum for R = 116   h-1   Mpc, s = 36   h-1   Mpc.

The resulting B(R,s) map is qualitatively very similar to that expected, either using an analytical ΛCDM model (Fig. 2) or the MICE simulation (Figs. 3 and 4). This indicates that the observed pattern does not originate from spurious features in the SDSS but is closely related to the large-scale structure and more specifically the BAO. The B(R,s) attains a maximum at Rmax = 116   h-1   Mpc, smax = 36   h-1   Mpc. This maximum is clearly related to the characteristics of the BAO structures present in our samples. We studied the robustness of this result by changing the weighting scheme applied to construct the density map (see Sect. 4). We do so by capping at different maximum values the possible weights associated with each galaxy, and repeating the calculation of B(R,s) in each case. The results are qualitatively similar, a peak in B(R,s) being obtained in all cases. However, the position of the peak changes in each case, with maximum changes of the order of  ± 5   h-1   Mpc in Rmax, and  ± 10   h-1   Mpc in smax. Therefore, the difference between the position of the peak obtained from the SDSS data and that given by the MICE simulation is not significant. In any case, we cannot use the scale and the width of the observed maximum of B(R,s) as direct estimates of the radius or width of the shells, especially given that our analysis of the possible observational biases (Fig. 4) was only qualitative.

To assess the significance of the BAO detection with this method, we focused on the value of B(R,s) obtained at the maximum, Bmax = B(Rmax,smax) = 22.9  ±  3.72. A more thorough analysis would model the B(R,s) statistic in the full parameter space. However, given the large covariances between measurements at different values of (R,s) we do not expect there to be a large difference from the simple case we consider. We assess the probability of finding such a maximum in the case in which there are no baryon acoustic structures present in our sample. We model this null hypothesis by using randomly distributed centres for the calculation of B(R,s) in Eq. (5), instead of LRG. Even using the WR,s(x) coefficients from the observed density field (traced by SDSS “main” galaxies), the expected value of B(R,s) in this case is 0 (see Eq. (4)), and we expect to obtain a significantly stronger signal in the data. In this way, we test the null hypothesis that, either there are no shell-like structures in the density field traced by the “main” sample, or these shell-like structures are not found preferentially around LRG centres. In either case, that would mean that there are no BAO-like structures present in our sample.

To perform the significance test, we generate 105 random realisations of a Poisson process, with the mean number of points NLRG, in the same volume as the LRG considered in the calculation (i.e. taking into account the buffer zone). For a realisation j, we use the generated points as our centres 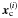x(i)c\hbox{$\vec{x}_{\rm c}^{(i)}$} to compute the B(R,s) statistic following Eq. (5), using the WR,s(x) coefficients obtained from the data. We can then obtain the mean value 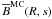BMC(R,s)\hbox{$\overline{B}^{\rm MC}(R,s)$}, and the standard deviation σMC(R,s) of the Monte-Carlo realisations of the centres. We show 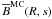BMC(R,s)\hbox{$\overline{B}^{\rm MC}(R,s)$} and a band of 1σMC(R,s) around it in the top panels of Fig. 6.

We now calculate our signal-to-noise ratio at the maximum as SNRmax≡Bmax/σMC[(Rmax,smax)]=6.60\hbox{$SNR_{\rm max} \equiv B_{\rm max}/\left[\sigma^{\rm MC}(R_{\rm max},s_{\rm max})\right] = 6.60$}, and assess the probability of finding such a large value of SNRmax anywhere in the parameter space for the Monte Carlo realisations. We use SNRmax instead of directly using Bmax because for some regions of parameter space, especially at low s, σMC(R,s) is extremely large. Therefore, if we used Bmax, we would need to arbitrarily restrict the parameter space studied, thus possibly introducing a posteriori bias. When using SNRmax, we sample the full parameter space considered in the calculations (as shown in Fig. 6). 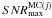We compute the maximum value of SNR for each realisation j in the full (R,s) range, SNRmaxMC(j)\hbox{$SNR^{{\rm MC}(j)}_{\rm max}$}. The distribution of the values of 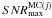SNRmaxMC(j)\hbox{$SNR^{{\rm MC}(j)}_{\rm max}$} is shown in Fig. 7, where it is compared to the value of SNRmax obtained in the real data. We find that only one of the realisations give a value of 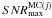SNRmaxMC(j)\hbox{$SNR^{{\rm MC}(j)}_{\rm max}$} larger than SNRmax. Thus, the probability of obtaining such a large maximum value of SNR in the absence of baryon acoustic structures (our null hypothesis) is p ≃ 10-5, equivalent to a  ~4.4σ detection in the Gaussian case.

However, we emphasise that the significance found in this work cannot be compared directly to other detection levels found in the literature, as it has been stated in the introduction. In particular, we do not compare our results with an analytical no-BAO model of B(R,s) (such as that shown in the top panel of Fig. 2), since to do so would require the detailed modelling of all the selection effects affecting the two samples used.

thumbnail Fig. 7

Histogram showing the distribution of the maximum SNR values obtained, in the full (R,s) space, for the 105 Monte Carlo realisations of Poisson-distributed centres (SNRmaxMC(j)\hbox{$SNR^{{\rm MC}(j)}_{\rm max}$}). This histogram has a mean of 3.72 and a standard deviation of 0.46. We show as a dashed vertical line the value obtained from the data (using the LRG as centres), SNRmax = 6.60. Only one of the Monte Carlo realisations give a maximum value larger than SNRmax.

thumbnail Fig. 8

A 2D projection of the distribution in redshift space of the LRG used in the analysis (i.e. inside our buffer region)3.

Table 1

Basic characteristics (J2000 sky coordinates, redshift and redshift uncertainty) of the 10 LRG with the larger values of the BAOlet coefficient at the maximum Wmax.

As explained in Sect. 2, we can extract more information about the BAO phenomenon in our samples by making further use of the BAOlet coefficient maps WR,s(x). Here, we use the coefficient values at the positions of the LRG for the parameters Rmax, smax, which correspond to the characteristics of the BAO shells present in our samples. In this way, the values Wmax ≡ WRmax,smax are a measure of the strength of the signal coming from a BAO shell around a given point, and in particular, a given LRG. Therefore, using Wmax we can localise in configuration space the regions of the volume covered by our samples where the BAO signal mostly originates.

We illustrate this idea in Fig. 8, where we plot a 2D projection of the distribution of the LRG used as centres in our analysis. We also show the value of Wmax for each of them according to a colour gradient, the highest values of Wmax corresponding to the red points in the plot.

In Table 1, we provide the 10 LRG used as centres with the larger values of Wmax. The whole catalogue of the NLRG = 1599 LRG used as our centres, and the value of Wmax obtained for each of them is available on-line. This catalogue could be used to study the relation of the BAO signal at a given LRG to its properties or the environment. It could also be used to select LRG centres with strong signal, and use them to refine the measurements of the BAO characteristics.

As an illustration of this later use, we show a simple way to study the overall properties of the BAO structures, its shape and scale. We select the centres that we know display a prominent acoustic feature, i.e., those for which Wmax > 0. This leaves us with Nr = 809 centres. To improve the signal-to-noise ratio in this illustration when studying the BAO structures, we stack together the 3D density maps around the Nr selected LRG. In doing so, we keep the line-of-sight direction aligned for all the centres, as this direction defines the possible anisotropies in the distribution. We show a 3D view and a 2D cut of this stacked density map in Fig. 9. Thanks to this selection, the characteristic elements of the BAO are amplified, namely on the one hand, a central bump of high density corresponding to the massive halo traced by the LRG, and on the other hand, the shell surrounding it of scale  ~109   h-1   Mpc, which corresponds to a fainter over-density. We also observe the anisotropic nature of these structures. This is a combination of our working in redshift space, and the redshift-dependent selection function for “main” galaxies.

thumbnail Fig. 9

Stacked 3D and 2D density fields. In the top three panels, we show the density field after stacking the Nr centres with WRmax,smax > 0. We show surfaces encompassing the regions above different thresholds in density after an isotropic Gaussian smoothing with σ = 10   h-1   Mpc. The density threshold decreases from top to bottom, with values of δ = 1.24,1.18,1.13 (δ is the density relative to the average density of the sample). We show only the bottom half of the density field for clarity. It can be seen that the acoustic shell clearly appears around the central over-density at the detected horizon scale. A 2D slice of this density field is shown in the bottom panel. Here, the dotted line is a circle whose radius corresponds to the one we measure for the BAO shells, rmax = 109.5   h-1   Mpc, and the arrow marks the direction of the line of sight.

A simpler view can be obtained by calculating the average radial density profile ρ(r) around the Nr centres. The resulting profile, shown in Fig. 10, has the same features as the 3D view, namely a high bump on short scales and a clear peak on about the acoustic scale, with a maximum at rmax = 109.5  ±  3.9   h-1   Mpc. The error in rmax was estimated using bootstrap realisations (Lupton 1993). This scale gives the radius of the baryon acoustic shells, and is therefore a good estimator of the acoustic scale in the sample. We also show in Fig. 10 the radial profiles restricted to different regions of the sphere, to better characterise the anisotropy of the distribution. We define two cones with a width of 45° with respect to the line-of-sight in each direction (we call these “near” and “far” regions), and a “transverse” region covering the belt between the cones. We obtain for each of these regions qualitatively similar results. As expected, we see how the “near” and “far” sub-samples are more strongly affected by observational effects, such as redshift-space distortions, which are more significant along the line of sight. In contrast, the result for the “transverse” sub-sample matches, within the errors, that for the full sphere. We note that the value of rmax is slightly larger for the “far” sample than for the “near” one.

We emphasise that this approach would be impossible with any statistical BAO detection method used this far, since the spatial localisation of the shells is completely lost in either the correlation function or the power spectrum, while the local nature of the wavelet approach has allowed us to identify the positions of the most representative structures in our sample. Moreover, we measure the acoustic scale at positions selected for their low contamination from other structures, which is not the case when averaging over the full sample. In this way, we maximise the BAO signal, while minimising the effect of signals coming from different large-scale structures.

thumbnail Fig. 10

Average radial profiles. We show the radial density profile averaged over the Nr centres with WRmax,smax > 0. We plot δ(r)=ρ(r)ρ0\hbox{$\delta(r) = \frac{\rho(r)}{\rho_0}$}, where ρ0 is the average density of the sample. The continuous line with a red error band shows the radial profile for the full sphere. We also show the error bands for the radial profile restricted to regions of the sphere, as defined in the text: the “near” region (green), the “far” region (orange), and the “transverse” region (blue). The arrow signals the location of the maximum, rmax = 109.5   h-1   Mpc. The error band corresponds to the 1-σ dispersion of 1000 bootstrap realisations. The profiles were estimated using a B3 kernel of width h = 4   h-1   Mpc in the radial coordinate, but similar results are obtained when using slightly different widths or shapes of the kernel.

6. Discussion and conclusions

We have designed a new method to detect BAO in the galaxy distribution and to localise, in configuration space, the structures responsible for them. This method is based on the use of a specially designed wavelet applied directly to the density field. Our approach also relies on the use of two different tracers: one for the overall density distribution, and the other for the central over-densities of the baryon acoustic structures.

After testing the method with simulations, we have applied this method to the detection of baryon acoustic structures in a sample drawn from the SDSS. In this case, we have used galaxies from the “main” catalogue to trace the overall density field, and galaxies from the LRG catalogue to trace the location of massive dark matter haloes. We clearly detected BAO in the sample providing a confirmation of the detection obtained previously using general two-point statistics (the power spectrum and correlation function). Our approach provides an independent method for the detection. Finally, we showed how this method allows us, through the use of Wmax(x), to localise in configuration space the actual structures responsible for the BAO signal obtained. This is a consequence of using a wavelet acting directly on the density field. We illustrated the utility of this approach by showing the density distribution stacked around a set of centres known to show the BAO feature given their Wmax value.

Recent works have proposed alternative methods to study the BAO based on wavelets (Xu et al. 2010; Tian et al. 2011). In particular, Tian et al. use a Mexican hat wavelet function with two parameters, conceptually similar to ours. They use it to search for a peak in the two point correlation function of the “main” SDSS sample, obtaining a detection with a p-value p = 0.002 (equivalent to 3.1σ in the Gaussian case). As in our case, this shows the utility of using the “main” sample to reduce the shot noise in the calculation and obtain significant detections. However, these works apply the wavelet to the measured two-point correlation function, instead of directly to the density field. In this way, these studies take advantage of the capabilities of the wavelets to characterise accurately the BAO signal (in terms of radius and width), but are unable to get any information about the localisation of these structures in space.

The use of wavelets directly in the density field isolates valuable information about the baryon acoustic structures that is hidden in the standard two-point statistics. In particular, it gives us information, in terms of the coefficients WR,s(x), to localise regions in the sampled volume containing either the strongest or weakest signal. We expect that this new method for studying BAO will be of much use to ongoing and planned surveys, such as the WiggleZ Survey (Drinkwater et al. 2010), the Baryon Oscillation Spectroscopic Survey (BOSS, Eisenstein et al. 2011), or the Physics of the Accelerating Universe (PAU) Survey (Benítez et al. 2009), which will cover a much larger volume than studied here and explore higher redshifts.

1

h is the Hubble constant in units of 100   km   s-1   Mpc-1.

2

This error in Bmax is obtained from the variance in the coefficients at the NLRG different LRG. However, our significance test is independent of this error value.

3

The data shown correspond to a slice of a width of  ≃8° in declination, which contains  ~40% of the LRG. The colour and size of each point corresponds to the value of Wmax at this LRG position.

Acknowledgments

This work has been supported by the European Research Council grant SparseAstro (ERC 228261), by the Spanish CONSOLIDER projects AYA2006-14056, CSD2007-00060 and AYA2010-22111-C03-02, including FEDER contributions, by the Generalitat Valenciana project of excellence PROMETEO/2009/064, and by the Estonian grants SF0060067s08 and ETF8005. P.A.M. was supported by the Spanish Ministerio de Educación through a FPU grant, and by an ERC StG Grant (DEGAS-259586). We acknowledge the use of data from the MICE simulations, publicly available at http://www.ice.cat/mice. We also acknowledge the use of public data from SDSS. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.

References

  1. Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bassett, B. A., & Afshordi, N. 2010 [arXiv:1005.1664] [Google Scholar]
  3. Bassett, B. A., & Hlozek, R. 2010, in Dark Energy: Observational and Theoretical Approaches, ed. P. Ruiz-Lapuente (Cambridge: Cambridge University Press), 246 [Google Scholar]
  4. Benítez, N., Gaztañaga, E., Miquel, R., et al. 2009, ApJ, 691, 241 [NASA ADS] [CrossRef] [Google Scholar]
  5. Blake, C., & Glazebrook, K. 2003, ApJ, 594, 665 [NASA ADS] [CrossRef] [Google Scholar]
  6. Blanton, M. R., Schlegel, D. J., Strauss, M. A., et al. 2005, AJ, 129, 2562 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cabré, A., & Gaztañaga, E. 2009a, MNRAS, 393, 1183 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cabré, A., & Gaztañaga, E. 2009b, MNRAS, 396, 1119 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cabré, A., & Gaztañaga, E. 2011, MNRAS, 412, L98 [NASA ADS] [Google Scholar]
  10. Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
  11. Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cooray, A., Hu, W., Huterer, D., & Joffre, M. 2001, ApJ, 557, L7 [NASA ADS] [CrossRef] [Google Scholar]
  13. Crocce, M., & Scoccimarro, R. 2008, Phys. Rev. D, 77, 023533 [NASA ADS] [CrossRef] [Google Scholar]
  14. Crocce, M., Fosalba, P., Castander, F. J., & Gaztañaga, E. 2010, MNRAS, 403, 1353 [Google Scholar]
  15. Drinkwater, M. J., Jurek, R. J., Blake, C., et al. 2010, MNRAS, 401, 1429 [Google Scholar]
  16. Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
  17. Eisenstein, D. J., Seo, H., & White, M. 2007, ApJ, 664, 660 [NASA ADS] [CrossRef] [Google Scholar]
  18. Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
  19. Eisenstein, D. J., Annis, J., Gunn, J. E., et al. 2001, AJ, 122, 2267 [NASA ADS] [CrossRef] [Google Scholar]
  20. Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fosalba, P., Gaztañaga, E., Castander, F. J., & Manera, M. 2008, MNRAS, 391, 435 [NASA ADS] [CrossRef] [Google Scholar]
  22. Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gaztañaga, E., Cabré, A., & Hui, L. 2009, MNRAS, 399, 1663 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hu, W., Sugiyama, N., & Silk, J. 1997, Nature, 386, 37 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hütsi, G. 2006, A&A, 449, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Jones, B. J. T. 2009, in Data Analysis in Cosmology, ed. V. J. Martínez, E. Saar, E. Martínez-González, & M. J. Pons-Bordería (Berlin: Springer Verlag), Lect. Notes Phys., 665, 3 [Google Scholar]
  27. Kazin, E. A., Blanton, M. R., Scoccimarro, R., McBride, C. K., & Berlind, A. A. 2010a, ApJ, 719, 1032 [Google Scholar]
  28. Kazin, E. A., Blanton, M. R., Scoccimarro, R., et al. 2010b, ApJ, 710, 1444 [NASA ADS] [CrossRef] [Google Scholar]
  29. Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  30. Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lupton, R. 1993, Statistics in Theory and Practice (Princeton, New Jersey: Princeton University Press) [Google Scholar]
  32. Mallat, S. 2008, A Wavelet Tour of Signal Processing, The Sparse Way, 3rd edn. (Academic Press) [Google Scholar]
  33. Martínez, V. J., Paredes, S., & Saar, E. 1993, MNRAS, 260, 365 [NASA ADS] [Google Scholar]
  34. Martínez, V. J., Arnalte-Mur, P., Saar, E., et al. 2009, ApJ, 696, L93; Erratum: 2009, 703, L184 [NASA ADS] [CrossRef] [Google Scholar]
  35. Peebles, P. J. E., & Yu, J. T. 1970, ApJ, 162, 815 [NASA ADS] [CrossRef] [Google Scholar]
  36. Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  37. Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
  38. Rauzy, S., Lachieze-Rey, M., & Henriksen, R. N. 1993, A&A, 273, 357 [NASA ADS] [Google Scholar]
  39. Reid, B. A., Percival, W. J., Eisenstein, D. J., et al. 2010, MNRAS, 404, 60 [NASA ADS] [CrossRef] [Google Scholar]
  40. Saar, E. 2009, in Data Analysis in Cosmology, ed. V. J. Martínez, E. Saar, E. Martínez-González, & M. J. Pons-Bordería (Berlin: Springer Verlag), Lect. Notes Phys., 665, 523 [Google Scholar]
  41. Sánchez, A. G., Baugh, C. M., & Angulo, R. 2008, MNRAS, 390, 1470 [NASA ADS] [Google Scholar]
  42. Sánchez, A. G., Crocce, M., Cabré, A., Baugh, C. M., & Gaztañaga, E. 2009, MNRAS, 400, 1643 [NASA ADS] [CrossRef] [Google Scholar]
  43. Seo, H.-J., & Eisenstein, D. J. 2005, ApJ, 633, 575 [NASA ADS] [CrossRef] [Google Scholar]
  44. Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  45. Starck, J.-L., & Murtagh, F. 2006, Astronomical Image and Data Analysis (Springer), 2nd edn. [Google Scholar]
  46. Starck, J., Moudden, Y., Abrial, P., & Nguyen, M. 2006, A&A, 446, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Starck, J.-L., Murtagh, F., & Fadili, M. 2010, Sparse Image and Signal Processing (Cambridge University Press) [Google Scholar]
  48. Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
  49. Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
  50. Tegmark, M., Eisenstein, D. J., Strauss, M. A., et al. 2006, Phys. Rev. D, 74, 123507 [Google Scholar]
  51. Tian, H. J., Neyrinck, M. C., Budavári, T., & Szalay, A. S. 2011, ApJ, 728, 34 [NASA ADS] [CrossRef] [Google Scholar]
  52. Vielva, P., Martínez-González, E., Barreiro, R. B., Sanz, J. L., & Cayón, L. 2004, ApJ, 609, 22 [NASA ADS] [CrossRef] [Google Scholar]
  53. Xu, X., White, M., Padmanabhan, N., et al. 2010, ApJ, 718, 1224 [NASA ADS] [CrossRef] [Google Scholar]
  54. York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [Google Scholar]
  55. Zheng, Z., Zehavi, I., Eisenstein, D. J., Weinberg, D. H., & Jing, Y. P. 2009, ApJ, 707, 554 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Basic characteristics (J2000 sky coordinates, redshift and redshift uncertainty) of the 10 LRG with the larger values of the BAOlet coefficient at the maximum Wmax.

In the text

All Figures

thumbnail Fig. 1

The BAOlet function. Here we show a two-dimensional (2D) plot (bottom) of the wavelet ψR,s(x) used in the analysis, as defined by Eq. (1). The top panel shows a 1D slice along the dashed-dotted axis. The wavelet is plotted here for R = 105   h-1   Mpc, s = 30   h-1   Mpc. The red dot marks the centre of the wavelet. This function has a null mean (provided that R > 2s), and compact support. It takes non-zero values only for R − 2s ≤ |x| ≤ R + 2s.
In the text
thumbnail Fig. 2

Values of the BAOlet coefficients WR,s expected at the positions of large initial point-like perturbations, as a function of the BAOlet parameters (R,s). The bottom panel shows the result using a standard ΛCDM transfer function, while the top panel shows the result using a transfer function with the BAO wiggles edited out (Eisenstein & Hu 1998). The normalisation is arbitrary. The contours are drawn in steps of 1000 for WR,s < 0 (dotted), WR,s = 0 (solid), and WR,s > 0 (dashed). The map attains a maximum at R = 110   h-1   Mpc, s = 22   h-1   Mpc.
In the text
thumbnail Fig. 3

The BAOlet statistic B calculated for the MICE simulation sample described in the text as a function of the parameters (R,s) (bottom panel). The contours are drawn in steps of 5 for B < 0 (dotted), B = 0 (solid), and B > 0 (dashed). This function attains its maximum for R = 108   h-1   Mpc, s = 28   h-1   Mpc. The top two panels show cuts at the values s = 28   h-1   Mpc (top) and s = 22   h-1   Mpc (middle), marked with grey horizontal lines in the 2D panel. In each case, the solid blue line corresponds to the value obtained from MICE, the dashed red line corresponds to the theoretical expectation from the Eisenstein & Hu (1998) transfer function (bottom panel of Fig. 2), and the dotted green line to the theoretical expectation using the “no wiggle” transfer function (top panel of Fig. 2). These theoretical predictions have been re-normalised to get the same value at the maximum in B(R,s).
In the text
thumbnail Fig. 4

The BAOlet statistic B for the MICE simulation when some observational effects are taken into account. In the top panel, we show the B(R,s) obtained when redshift-space distortions are included in the simulation. In the bottom panel, we show the result when a radial selection function is applied to the halo catalogue. In both cases, the contours are drawn in steps of 5 in B. Solid contours correspond to the results with the observational effects included. The dashed contours correspond to the original real-space result without selection, i.e., they are identical to those in the bottom panel of Fig. 3.
In the text
thumbnail Fig. 5

The SDSS catalogues used. We show a six-degree thick slice drawn from the catalogues used in our analysis. The red points are the LRG galaxies, which form a nearly volume-limited sample at z > 0.15. The “main” galaxies of the SDSS are depicted in blue. As shown, we use the “main” galaxies from z > 0.09, and we use only the LRG in an inner volume, allowing for a buffer region of rbuff = 175   h-1   Mpc from any of the borders of the “main” sample volume. For our analysis, we use the samples covering a total area of 5511deg2. The radius of a typical BAO shell is shown as a segment. At the top insets, we show two orthogonal slices of width 20   h-1   Mpc, centred on a particular LRG. The BAOlet coefficient map WR,s(x) has a large value at the position of this centre (for Rmax,smax), thus we expect to find a strong BAO signal. The two circles have the radii of 100 and 110 h-1   Mpc, respectively. This is a single BAO shell where the over-density can be appreciated by eye on the right scale.
In the text
thumbnail Fig. 6

The BAOlet statistic B calculated for SDSS data as a function of the parameters (R,s). The bottom panel shows the results in the full parameter space considered, where we sampled both R and s at intervals of 1   h-1   Mpc. We mask two areas, at the upper right and left corners, where our results are not reliable (see details in the text). The contours are drawn in steps of 5 for B < 0 (dotted), B = 0 (solid), and B > 0 (dashed). The top two panels show cuts at the arbitrarily chosen values s = 36   h-1   Mpc (top) and s = 20   h-1   Mpc (middle), marked with grey horizontal lines in the 2D panel. In these panels, the blue line is B(R,s), while the green line and the red band show the mean (BMC\hbox{$\overline{B}^{\rm MC}$}) and 1-σMC interval for the Monte Carlo realisations of random centres. We obtain a clear significant peak at different values of s, with a maximum for R = 116   h-1   Mpc, s = 36   h-1   Mpc.
In the text
thumbnail Fig. 7

Histogram showing the distribution of the maximum SNR values obtained, in the full (R,s) space, for the 105 Monte Carlo realisations of Poisson-distributed centres (SNRmaxMC(j)\hbox{$SNR^{{\rm MC}(j)}_{\rm max}$}). This histogram has a mean of 3.72 and a standard deviation of 0.46. We show as a dashed vertical line the value obtained from the data (using the LRG as centres), SNRmax = 6.60. Only one of the Monte Carlo realisations give a maximum value larger than SNRmax.
In the text
thumbnail Fig. 8

A 2D projection of the distribution in redshift space of the LRG used in the analysis (i.e. inside our buffer region)3.
In the text
thumbnail Fig. 9

Stacked 3D and 2D density fields. In the top three panels, we show the density field after stacking the Nr centres with WRmax,smax > 0. We show surfaces encompassing the regions above different thresholds in density after an isotropic Gaussian smoothing with σ = 10   h-1   Mpc. The density threshold decreases from top to bottom, with values of δ = 1.24,1.18,1.13 (δ is the density relative to the average density of the sample). We show only the bottom half of the density field for clarity. It can be seen that the acoustic shell clearly appears around the central over-density at the detected horizon scale. A 2D slice of this density field is shown in the bottom panel. Here, the dotted line is a circle whose radius corresponds to the one we measure for the BAO shells, rmax = 109.5   h-1   Mpc, and the arrow marks the direction of the line of sight.
In the text
thumbnail Fig. 10

Average radial profiles. We show the radial density profile averaged over the Nr centres with WRmax,smax > 0. We plot δ(r)=ρ(r)ρ0\hbox{$\delta(r) = \frac{\rho(r)}{\rho_0}$}, where ρ0 is the average density of the sample. The continuous line with a red error band shows the radial profile for the full sphere. We also show the error bands for the radial profile restricted to regions of the sphere, as defined in the text: the “near” region (green), the “far” region (orange), and the “transverse” region (blue). The arrow signals the location of the maximum, rmax = 109.5   h-1   Mpc. The error band corresponds to the 1-σ dispersion of 1000 bootstrap realisations. The profiles were estimated using a B3 kernel of width h = 4   h-1   Mpc in the radial coordinate, but similar results are obtained when using slightly different widths or shapes of the kernel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.