| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 57 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201118158 | |
| Published online | 07 March 2012 | |
Present-day cosmic abundances
A comprehensive study of nearby early B-type stars and implications for stellar and Galactic evolution and interstellar dust models⋆,⋆⋆
1 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
2 Dr. Karl Remeis-Sternwarte & ECAP, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
e-mail: Maria-Fernanda.Nieva@sternwarte.uni-erlangen.de; Norbert.Przybilla@sternwarte.uni-erlangen.de
Received: 27 September 2011
Accepted: 21 December 2011
Context. Early B-type stars are ideal indicators for present-day cosmic abundances since they preserve their pristine abundances and typically do not migrate far beyond their birth environments over their short lifetimes, in contrast to older stars like the Sun. They are also unaffected by depletion onto dust grains, unlike the cold/warm interstellar medium (ISM) or H ii regions.
Aims. A carefully selected sample of early B-type stars in OB associations and the field within the solar neighbourhood is studied comprehensively. Quantitative spectroscopy is used to characterise their atmospheric properties in a self-consistent way. Present-day abundances for the astrophysically most interesting chemical elements are derived in order to investigate whether a present-day cosmic abundance standard can be established.
Methods. High-resolution and high-S/N FOCES, FEROS and ELODIE spectra of well-studied sharp-lined early B-type stars are analysed in non-LTE. Line-profile fits based on extensive model grids and an iterative analysis methodology are used to constrain stellar parameters and elemental abundances at high accuracy and precision. Atmospheric parameters are derived from the simultaneous establishment of independent indicators, from multiple ionization equilibria and the Stark-broadened hydrogen Balmer lines, and they are confirmed by reproduction of the stars’ global spectral energy distributions.
Results. Effective temperatures are constrained to 1–2% and surface gravities to less than 15% uncertainty, along with accurate rotational, micro- and macroturbulence velocities. Good agreement of the resulting spectroscopic parallaxes with those from the new reduction of the Hipparcos catalogue is obtained. Absolute values for abundances of He, C, N, O, Ne, Mg, Si and Fe are determined to better than 25% uncertainty. The synthetic spectra match the observations reliably over almost the entire visual spectral range. Three sample stars, γ Ori, o Per and θ1 Ori D, are identified as double-lined, indicating the presence of an early/mid B-type companion.
Conclusions. A present-day cosmic abundance standard is established from a sample of 29 early B-type stars, indicating abundance fluctuations of less than 10% around the mean. Our results (i) resolve the long-standing discrepancy between a chemical homogeneous gas-phase ISM and a chemically inhomogeneous young stellar component out to several hundred parsec from the Sun, (ii) facilitate the amount of heavy elements locked up in the interstellar dust to be constrained precisely – the results imply that carbonaceous dust is largely destroyed inside the Orion H ii region, unlike the silicates, and that graphite is only a minority species in interstellar dust –, (iii) show that the mixing of CNO-burning products in the course of massive star evolution follows tightly the predicted nuclear path, (iv) provide reliable present-day reference points for anchoring Galactic chemical evolution models to observation, and (v) imply that the Sun has migrated outwards from the inner Galactic disk over its lifetime from a birthplace at a distance around 5−6 kpc from the Galactic Centre; a cancellation of the effects of Galactic chemical evolution and abundance gradients leads to the similarity of solar and present-day cosmic abundances in the solar neighbourhood, with a telltaling signature of the Sun’s origin left in the C/O ratio.
Key words: stars: abundances / stars: early-type / stars: fundamental parameters / stars: evolution / ISM: abundances / Galaxy: evolution
Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max- Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC), proposals H2001-2.2-011 and H2005-2.2-016. Based on observations collected at the European Southern Observatory, Chile, ESO 074.B-0455(A). Based on spectral data retrieved from the ELODIE archive at Observatoire de Haute-Provence (OHP).
Tables 5 and 6 are also available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/539/A143 Figures 4, 7, 8–11 and Tables 7, 8 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The formation and evolution of galaxies, stars, interstellar gas and dust, planetary systems, and even life are tightly related to the origin and evolution of the chemical elements, and therefore to the cosmic cycle of matter. Theories that aim at explaining these phenomena need to be anchored to reference values for chemical abundances. The most appropriate source of reference abundances for the chemical composition of cosmic matter is a topic of vivid discussion.
The chemical composition of most astronomical objects is traditionally compared to that of the Sun because it is the closest star and therefore its chemical abundances can be determined with high accuracy and precision from application of various techniques to observations of very high quality. The solar photosphere, its chromosphere and corona can be studied remotely via spectroscopy. Particle collection techniques from space also allow in-situ measurements of the chemical composition of the solar wind and of solar energetic particles. Moreover, mass spectroscopy of CI-chondrites facilitates the pristine composition of the solar nebula to be accessed (except for a few volatile elements). The wealth of data gave rise to the solar abundance standard, which has been subject of active research in the past decades and it is still subject of continuous revision and improvement based on the modeling of its convective outer envelope and the radiative transfer in 3D models (e.g. Asplund et al. 2009; Lodders et al. 2009; Caffau et al. 2010, and references therein).
Conceptually, the chemical composition of the Sun constitutes an excellent reference for numerous astrophysical studies, of e.g. low-mass stars’ interiors and atmospheres, the Galactic chemical evolution of “older” star populations, or of solar twins (with and without planets), to mention only few among many other applications. In doing this, one supposes that the Sun is a typical, middle-aged low-mass star. However, the concept faces complications as different sets of reference values for the Sun are discussed in the literature. Objective criteria that allow one to decide which is the most appropriate on a level where the details matter do not exist, as each of them may reproduce one or another aspect of observations better1. Because of this we will refer to the generic solar values henceforth as the “solar standard” and specify individual sources where relevant.
There are also examples where the Sun is considered as a reference because of the lack of another reliable standard, despite its chemical composition may not be representative for the objects of study, e.g. whenever a local and present-day reference is required. This is because the Sun can a priori not be assumed to provide a standard for the chemical composition at present-day. The reason for this is that Galactic chemical evolution has proceeded for the 4.56 Gyr since the formation of the Sun, enriching the interstellar medium (ISM) in heavy elements. For instance, structure and evolution models of massive stars anchor their initial composition to the solar standard despite these young stars are formed from the present-day ISM. Similarly, the solar standard is used to constrain the amount of heavy elements locked up in the dust-phase of the present-day ISM. Galactic chemical evolution models also consider the solar chemical abundances as representative for the “local” Galactic neighbourhood of the Sun2 while it was possibly formed nowhere near its current Galactocentric position. Moreover, Galactic chemical evolution models anchor the present-day composition of the solar neighbourhood to the solar standard in aiming to reproduce present-day Galactic abundance gradients. These are only a few among many other applications. Establishing an appropriate abundance standard for the present-day in our local Galactic environment would be highly valuable either to verify whether the assumption that the solar standard is indeed representative, or to constrain various theories in the astrophysical context more tightly.
Present-day chemical abundances in the solar neighbourhood can be accessed relatively easily from absorption line studies of the cold/warm ISM or from emission line spectroscopy of the Orion nebula. In particular the H ii regions are regarded as privileged sites for the determination of chemical abundances over large distances, even in other galaxies. Unfortunately, the composition of the neutral and the ionized ISM gas is altered by depletion onto dust grains. In order to access the actual chemical composition accurately, an a-priori knowledge of the composition of the dust-phase is required, which, however, is lacking. Further complications for H ii region studies are the dependence of the derived abundances on the indicators employed in the analysis3, fluctuations of the electron temperature throughout the nebula, and ionization correction factors, which can be substantial for some chemical species.
An ideal alternative to find a reference for the chemical composition of cosmic matter are normal unevolved early B-type stars of ~8–18 M⊙, which can provide simultaneously temporal (present-day) and local (birth place) information on chemical abundances. They can be observed not only in the solar neighbourhood, but also at larger distances in the Milky Way and in other galaxies. Their composition is unaffected by depletion onto dust grains, unlike the cool/warm ISM and the H ii regions. In contrast to cooler and lower mass stars they are so short lived (typically ~107 yrs) that they have no time to travel far from their birth place, except for the occasional runaway star. From an analysis perspective, spectroscopic studies of early B-type stars are relatively simple because their photospheres are not affected by strong stellar winds, unlike their hotter and more luminous siblings, or by convection and chromospheres, unlike the cool stars, which furthermore pose more challenges because of severe line blending in their crowded optical spectra. The atmospheres of unevolved early B-type stars are well represented by classical hydrostatic, plane-parallel 1D-models in radiative and local thermodynamic equilibrium (LTE; Nieva & Przybilla 2007, henceforth abbreviated NP07) – though deviations from LTE (non-LTE effects) need to be accounted for properly in line-formation calculations (Przybilla et al. 2011). Moreover, they are typically unaffected by atomic diffusion that gives rise to peculiarities of elemental abundances in many mid B- to A-type stars (e.g. Smith 1996). In slowly-rotating stars the photosphere should also be essentially unaffected by rotational mixing with CNO-cycled matter from the stellar core (except for some fast rotators seen pole-on), i.e. they should retain their pristine chemical surface composition throughout their main-sequence phase.
Despite the relatively simple physics, spectral analyses of main sequence B-stars have turned out to provide inconclusive results over the past decades, i.e. large uncertainties in basic stellar parameters, a tendency towards a metal-poor composition with respect to older stars like the Sun and an overall enormous range in derived elemental abundances, challenging predictions of stellar and Galactic evolution models. For a discussion on these topics see e.g. the reviews of Herrero (2003), Herrero & Lennon (2004), Przybilla (2008) and Morel (2009).
In order to improve the quantitative analysis of this type of stars we have extensively updated the spectral modelling by constructing robust model atoms for non-LTE line-formation calculations and implemented a powerful self-consistent analysis technique, which brings numerous spectroscopic parameter and abundance indicators into agreement simultaneously, starting with H, He and C (Nieva 2007). First applications of our method to carbon abundances in a small sample of stars in the solar neighbourhood (Nieva & Przybilla 2008, NP08) provided an unprecedented small scatter and an absolute average abundance similar to the solar value by Asplund et al. (2005), solving for the first time the above mentioned problems. Our efforts, also on other metals (Przybilla et al. 2008c, PNB08), have provided highly-promising results so far, i.e. a drastic reduction of statistical and systematic errors in stellar parameters and chemical abundances: uncertainties as low as ~1% in effective temperature, ~10% in surface gravity and ~10–20% in elemental abundances have been achieved – compared to ~5–10%, ~25% and a factor ~2, respectively, using standard methods4. The initial sample of 6 stars from OB associations and the field in the solar neighbourhood covering a broad parameter range turned out to be chemically homogeneous on the 10% level, corroborating earlier findings from analyses of the ISM gas-phase (PNB08). Yet, the sample size was arguably small.
In this work we therefore present a comprehensive study of a sample of initially 27 early B-type stars from the solar neighborhood, aiming to re-investigate our previous findings (from a sub-sample of only 6 stars) on a solid statistical basis. The stars span about 20 000 K in effective temperature and ~0.7 dex in surface gravities, from the zero-age main sequence (ZAMS) to close to the end of the core hydrogen burning phase. Seven stars from the original sample had to be excluded from the analysis for various reasons. In order to compensate for this loss, nine additional stars from the Ori OB1 association analysed in an identical way (Nieva & Simón-Díaz 2011, NS11) were included in the derivation of the proposed cosmic abundance standard.
The paper is organised as follows. Particular attention is paid to the selection criteria for the star sample and of the special care taken to obtain observations of high quality in Sect. 2. The computations of extensive grids of synthetic spectra and the implementation of a semi-automatic analysis technique are discussed in Sect. 3, which facilitates the same quality of the analyses to be achieved as in our previous work (Sect. 4). A comprehensive characterisation of the atmospheric properties of the sample stars and related quantities is provided in Sect. 5. Then, the resulting present-day cosmic abundance standard for the solar neighbourhood is discussed in Sect. 6. Our results are put in the broader astrophysical context in Sect. 7, concentrating on ISM science, and stellar and Galactic chemical evolution. Finally, a summary is given in Sect. 8.
 |
Fig. 1 Distribution of the sample stars in the solar neighbourhood. Upper panel: galactic plane projection, the Galactic centre lies in direction of the bottom of the panel. Lower panel: rotational plane projection, the Northern Galactic Pole lies in direction of the top of the panel. The sample stars that are analysed quantitatively here are marked by dots, open boxes mark candidate SB2 systems and open circles stars that were excluded from the analysis because of other peculiarities. Numbers/letters correspond to those of our internal numbering in the tables. Error bars are of spectroscopic distances (stars 1–20, see Table 5) and of measured parallaxes (objects A–G). The position of the Sun is marked by ⊙ . |
2. The star sample
2.1. Primary target selection
An investigation of the present-day chemical composition of the solar neighbourhood requires a careful selection of the star sample to minimise observationally-induced systematic bias. We took advantage of previous studies of early B-type stars (Grigsby et al. 1992; Gies & Lambert 1992; Kilian 1992; Cunha & Lambert 1994; Andrievsky et al. 1999; Adelman et al. 2002; Lyubimkov et al. 2004; Morel et al. 2006) to compile our target list. Criteria were the stars to be
-
i)
bright:early B-type stars near the main sequence of magnitude V < 6 mag are located at distances < 500 pc, with such a brightness limit facilitating high-quality spectra to be obtained with relative ease;
-
ii)
sharp lined:low (projected) rotational velocities vsini ≲ 40 km s-1 allow spectral line analyses to be done at highest precision, maximising the chances to identify line blends and to place the continuum unambiguously;
-
iii)
single:this is to prevent systematic errors in the analysis as second light from a companion distorts the ratio of line- to continuum-fluxes; objects in SB1 systems with much fainter companions or individual components in a visual binary can therefore still qualify as targets; and
-
iv)
chemically inconspicuous:the CP phenomenon is rare among early B-stars (e.g. Smith 1996) but spectroscopically classified He-weak or He-strong stars need to be excluded as segregation processes in their atmospheres have rendered them useless to trace the pristine chemical composition.
The distribution of the sample stars in the solar neighbourhood is visualised in Fig. 1 (anticipating distance determinations in Sect. 5). The stars delineate Gould’s Belt both in the Galactic plane projection as well as in the vertical cut through the Galactic disk, with few outliers. They are highly concentrated towards the disk plane, with few objects located beyond a vertical distance z > 100 pc. Members of the two most prominent star-forming regions in the solar vicinity are included in the sample, object C is one of the Orion Trapezium stars, objects 5 and 6 are members of the Sco-Cen association. The asymmetry of the star distribution is because our main observing program utilised telescopes on the northern hemisphere (the celestial equator is roughly spanned by the connecting line between objects E and 9).
2.2. Observations and data reduction
High-resolution échelle spectra at very high signal-to-noise (S/N) ratio – ranging from 250 up to over 800 in B – and wide wavelength coverage for 27 objects were obtained, either by own observations, or from archives. A summary of the star sample and observational details are given in Table 1. Object identifications include our own numbering scheme (to facilitate easy identification in the figures and other tables), HD and HR numbers and names of the stars. Spectral types are given and an indication of variability, basically divided in β Cephei types and slowly-pulsating B-stars (SPB)5. Membership to one of the nearby OB associations or to the field population is indicated. Photometric information covers observed Johnson V-magnitudes and colors B − V. Observational details like the date of observation, the number of individual exposures per object N, the total exposure time and the resulting S/N-ratio in the B band of the coadded spectrum are also indicated. Our philosophy for coaddition of data aims at obtaining a “snapshot” of the stellar spectrum, even for variable stars. Consequently, only exposures taken during a small fraction of the same night were coadded, with the one exception of a non-variable star. The analysis will thus yield meaningful time-invariant quantities like elemental abundances or fundamental stellar parameters even for variable stars, while atmospheric parameters like effective temperature and surface gravity will be valid only for the moment of observation. The observational material divides into three subsets.
The first subset includes stars 1–6, for which spectra were obtained with Feros (Fiberfed Extended Range Optical Spectrograph, Kaufer et al. 1999) on the ESO 2.2 m telescope in La Silla/Chile. Feros provides a resolving power of R = λ/Δλ ≈ 48 000, with 2.2 pixels covering a Δλ resolution element. Of the entire Feros wavelength range, only the part between ~3800 and 8000 Å meets our quality criteria for detailed analysis. The stars have already been subject to investigation in Nieva & Przybilla (2006, NP06), NP07, NP08 and PNB08. Nevertheless, they are included here as many details of the analysis were unreported previously. We refer the reader to NP07 for details of the observations and the data reduction.
 |
Fig. 2 Examples of prominent spectral lines of the newly identified candidate SB2 systems in our sample, HD 22951 (B0.5 V), HD 35468 (B2 III) and HD 37023 (B0.5 V). For comparison the corresponding spectral lines in the single star HD 36822 (B0 III) are shown as well. The emission peak in He i λ6678 of the Trapezium star HD 37023 in Orion is of nebular origin. |
Thirteen stars (7–16, A–C) compose the second subset, which were observed with Foces (Fibre Optics Cassegrain Échelle Spectrograph, Pfeiffer et al. 1998) on the 2.2 m telescope at Calar Alto/Spain. With the instrument configuration chosen a 2-pixel resolution of R ≈ 40 000 was obtained, providing wavelength coverage from ~3900 to 9500 Å. Data reduction was performed using the Foces data reduction software (Pfeiffer et al. 1998), comprising the usual steps of bad pixel and cosmic correction, bias and dark current subtraction, removal of scattered light, optimum order extraction, flatfielding, wavelength calibration using Th-Ar exposures, rectification, and merging of the échelle orders. A major advantage related to the Foces design is that the order tilt for normalisation is much more homogeneous than in similar spectrographs. This facilitates a more robust continuum rectification than feasible usually, even in the case of broad features like the hydrogen Balmer lines, which can span more than one échelle order (see Korn 2002). Finally, multiple exposures of individual stars were coadded and the spectra were shifted to rest wavelength by cross-correlation with appropriate synthetic spectra.
Spectra for the third subset of stars (eight stars: 17–20, D−G) were extracted from the Elodie archive (Moultaka et al. 2004). Elodie was an échelle spectrograph mounted on the 1.93 m telescope of the Observatoire de Haute-Provence/France, covering a wavelength range from ~4000 to 6800 Å at R ≈ 42 000 (see Baranne et al. 1996). The reduced spectra from the archive needed to be normalised as a last step of post-processing. We used a spline function to carefully selected continuum points for this purpose, in analogy to our procedure for the Feros data. Unfortunately, a reliable normalisation of broad lines in the blue like Hγ and Hδ turned out difficult, such that they were not considered for the analysis. After normalisation, the individual spectra of one object were coadded in order to obtain a combined spectrum of improved S/N.
In addition to the spectra, which constitute the principal data for the analysis, various (spectro-)photometric data were adopted from the literature for constructing spectral energy distributions (SEDs). Main sources of Johnson UBVRIJHK-photometry were Mermilliod (1991), Morel & Magnenat (1978) and Ducati (2002), and some JHK-magnitudes (only those with a quality marker “A”) were adopted from the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006). Additionally, flux-calibrated spectra for 15 objects as observed with the International Ultraviolet Explorer (IUE) were extracted from the MAST archive6. Only spectra acquired using a large aperture were considered to avoid light loss. Preference was given to low-dispersion data, except for a few cases where only high-dispersion spectra were available. These data cover the range from 1150 to 1980 Å for the short (SW) and from 1850 to 3290 Å for the long wavelength (LW) range camera. Typically, both wavelength ranges were observed the same day. A summary of the individual spectra used in the present work (data ID number and observation date) is given in Table 2.
The observational material comprises one of the highest quality for the quantitative study of elemental abundances from early B-type stars in the solar neighbourhood so far. Observational bias should thus be reduced to a minimum.
IUE spectra used in this study.
2.3. Stars excluded from the analysis
Once the spectra were reduced we undertook visual inspections of the data in the course of the quality assessment. Four objects were immediately found conspicuous, while three more were found to be problematic in the analysis. About a quarter of the carefully pre-selected sample turned out as candidate binaries or as chemically peculiar. In the following we want to briefly address the reasons why these cases (stars A–G in Table 1) needed to be removed from our sample.
A: HD22951.
The object is a so far unrecognised candidate SB2 system. All the stronger sharp lines in the spectrum show weaker and broader absorption dips as well, shifted blueward from the primary’s features. Examples are given in Fig. 2, where the corresponding lines in one of the single stars of our sample are also shown for comparison. The secondary of the system is a cooler main-sequence star, of spectral type about B2. All the signatures can be viewed as undetectable at the resolution of classification spectra. The secondary’s light renders the spectrum unsuited for our analysis technique and the star is therefore excluded from further analysis.
B: HD35468 (Bellatrix).
The star was considered a reference for the definition of spectral type B2 III by Walborn (1971). However, our spectrum shows that γ Ori is a candidate SB2 system composed of two very similar components, see Fig. 2. This resolves the apparent overluminosity of the star found by Schröder et al. (2004) from an evaluation of its Hipparcos parallax.
C: HD37023.
The case resembles that of HD 22951, see Fig. 2. The companion of HD 37023 is of slightly earlier type than that of HD 22951, as its contribution to the spectrum is stronger. Note that while HD 37023 is a known spectroscopic binary (see Vitrichenko 2002, for a discussion) the direct detection of a companion in the spectrum7 offers the possibility to put much tighter constraints on the system, such that follow-up observations are recommended, like for the two previous cases.
D: HD11415.
A preliminary analysis of the star yielded several inconsistencies, which either relate to unrecognised problems with the Elodie spectrum (in particular to the continuum normalisation) or to some peculiarity of the star. A closer inspection of the literature revealed that it is listed in the catalogue of Be-stars of Jaschek & Egret (1982). All Balmer lines and in particular Hα are in absorption in the available spectrum, but we cannot rule out low-level emission filling in the inner line wings (imitating normalisation problems). Moreover, Leone et al. (1995) describe HD 11415 as CP star of the He-weak type. These factors prompted us to exclude HD 11415 from the detailed analysis.
E: HD163472.
A preliminary analysis of the star indicated inconsistencies of the solution, which were unexpected in view of the “normal” appearance implied by the analysis of Morel et al. (2006). However, a detailed study by Neiner et al. (2003) found HD 163472 to be chemically peculiar, in particular it is a He-strong star. Diffusion in the magnetic atmosphere renders this otherwise highly interesting star useless for our purpose.
F: HD214993.
The star is one of the most intensely studied β Cephei pulsators (Desmet et al. 2009, and references therein). Our preliminary modelling encounters difficulties, which may be resolved assuming helium-enrichment of the atmosphere. This requires further investigation and in consequence we exclude the star from the present work program.
G: HD218376.
The star shows conspicuously broad lines. Whether this may be interpreted as unresolved binarity – requiring two about similar components – or whether a different explanation needs to be found has to be decided by further investigations.
3. Spectrum synthesis in non-LTE
The non-LTE line-formation computations follow the methodology discussed in detail in our previous studies for H and He in NP07, for C in NP06 and NP08, and for N, Ne, Mg, Si and Fe in PNB08. In brief, a non-LTE approach is employed to solve the restricted non-LTE problem on the basis of prescribed LTE atmospheres. This technique provides an efficient way to compute realistic synthetic spectra in all cases where the atmospheric structure is close to LTE, like for the early B-type main sequence stars analysed here (see NP07). The computational efforts can thus be focussed on robust non-LTE line-formation calculations. The validity of the approach was recently verified by direct comparison with hydrodynamic line-blanketed non-LTE model atmospheres (NS11). This approach has been equally successful in improving model fits beyond the field of massive B-type stars, e.g. in low-mass subdwarf B-stars (Przybilla et al. 2006b) and B-type extreme helium stars (Przybilla et al. 2005, 2006c).
3.1. Models and programs
The model atmospheres were computed with the Atlas9 code (Kurucz 1993b) which assumes plane-parallel geometry, chemical homogeneity, as well as hydrostatic, radiative and local thermodynamic equilibrium (LTE). Line blanketing was realised here by means of opacity distribution functions (ODFs, Kurucz 1993a). Solar abundances of Grevesse & Sauval (1998) were adopted in all computations. The model atmospheres were held fixed in the non-LTE calculations. Non-LTE level populations and model spectra were obtained with recent versions of Detail and Surface (Giddings 1981; Butler & Giddings 1985, both updated by Butler). The coupled radiative transfer and statistical equilibrium equations were solved with Detail, employing an accelerated lambda iteration scheme of Rybicki & Hummer (1991). This allowed even complex ions to be treated in a realistic way. Synthetic spectra were calculated with Surface, using refined line-broadening theories. Continuous opacities due to hydrogen and helium were considered in non-LTE and line blocking was accounted for in LTE via Kurucz’ ODFs. Microturbulence was considered in a consistent way throughout all computation steps: in the selection of appropriate ODFs for realising line blanketing and line blocking in the atmospheric structure and non-LTE level populations determination, and for the formal solution.
Model atoms for non-LTE calculations.
Non-LTE level populations and the synthetic spectra of all elements were computed using our most recent model atoms listed in Table 3. Updates of some of the published models were carried out introducing improved oscillator strengths and collisional data. These models were previously tested in NP08 and PNB08 for early B-type stars covering a wide parameter range. A problem with the line-formation calculations for Fe iii was identified in the course of the present work. Several high-lying energy levels were previously erroneously treated in LTE in the formal solution with Surface, despite correct non-LTE level populations were provided by Detail. Higher iron abundances for the hotter objects (e.g. by 0.16 dex for τ Sco and ≲ 0.05 dex for the majority of stars) result after implementing the corrected Fe model atom, removing a slight artificial trend with temperature found previously.
3.2. Grids of synthetic spectra
For the present work a set of grids of synthetic spectra was computed with Atlas9, Detail and Surface following the same procedure as in our previous papers. Large independent grids of H/He, C, N, O, Mg and Si encompass effective temperatures from 15 000 to 35 000 K in steps of 1000 K, surface gravities log g from 3.0 to 4.5 (cgs units) in steps of 0.1 dex, microturbulences from 0 to 12 km s-1 in steps of 2 km s-1 and metal abundances within 1 dex centered on the B-star abundance values of PNB08 in steps of 0.1 dex. Hydrogen and helium abundances are set to the values derived by PNB08. The lower limit of the surface gravity for each value of temperature/microturbulence is constrained by the convergence of Atlas9. All grids have been successfully tested by reproducing results from PNB08. For Ne and Fe (the computationally most demanding species) microgrids – varying abundance only – were computed per star once all stellar parameters were determined with the larger pre-computed grids.
4. Spectral analysis
Our analysis method is based on the simultaneous reproduction of all spectroscopic indicators (Sect. 4.2) via an iterative line-fitting procedure aiming to derive atmospheric parameters and chemical abundances self-consistently. In contrast to common strategies in stellar spectroscopy, this analysis technique takes full advantage of the information encoded in the line profiles at different wavelength ranges simultaneously. Integrated quantities like equivalent widths Wλ are not measured in this approach. The stellar parameters primarily derived here are the effective temperature Teff, surface gravity log g, microturbulence ξ, (radial-tangential) macroturbulence ζ, projected rotational velocity v sin i and elemental abundances ε(X) = log (X/H) + 12.
4.1. Semi-automation of the analysis procedure
The basic analysis methodology was introduced and applied to a strategically chosen star sample covering a broad parameter range in Nieva (2007), NP07 and NP08. A major complication in that work was that both the model atom for carbon and the stellar parameters had to be constrained simultaneously. Thus, one global problem needed to be solved – to select among the available atomic data the one combination that facilitated reproduction of the observed lines throughout the entire sample equally well – and many individual problems – the determination of atmospheric models that described the sample stars best. The only way to realise this was via the computation of numerous small grids per star for different sets of stellar parameters and atomic data, and interactive work to decide how to improve based on the quality of match between the models and observation. Over 100 interactive iterations were needed to find a self-consistent solution, i.e. selection of the best atomic data and determination of stellar parameters and carbon abundances for six stars covering a broad temperature range. The benefit from this time-consuming approach was twofold: first, a highly robust model atom was provided for further applications, and second, copious experience was gained in the identification of sources of systematic error that helps to minimise such uncertainties in work thereafter. This lead, e.g. to updates of model atoms for other elements, see PNB08 and Table 3. All in all, a solid basis for highly accurate (reduction of systematic uncertainty to the greatest possible extent) and precise (low statistical uncertainties) analyses was thus laid.
Once the global problem of the model atom construction and testing is solved, one is faced with the much easier task that only stellar parameters and elemental abundances need to be constrained. The basic analysis methodology is outlined in Fig. 3. The individual steps could be realised in form of small grid computations like outlined before, but this is too inefficient for investigating larger star samples. We have therefore replaced the calculation of dedicated small grids of synthetic spectra (comprising the boxes “Model Atmosphere”, “Model Atom” and “Non-LTE Spectrum Synthesis” in Fig. 3) by a pre-computed comprehensive grid of models (in total of the order ~ 100 000 synthetic spectra), as described in Sect. 3.2. The second new ingredient for the present work was the adaptation of a powerful fitting routine for the semi-automatic comparison of observed and theoretical spectra (the box “Quantitative Analysis” in Fig. 3). Spas8 provides the means to interpolate between model grid points for up to three parameters simultaneously and allows to apply instrumental, rotational and (radial-tangential) macrobroadening functions to the resulting theoretical profiles. The program uses the downhill simplex algorithm (Nelder & Mead 1965) to minimise χ2 in order to find a good fit to the observed spectrum.
Interactive work in some decisive steps on the analysis with Spas paid off as much more accurate results could be obtained. Crucial was the selection of the appropriate spectroscopic indicators (Sect. 4.2) for the parameter determination which may vary from star to star upon availability of specific spectral lines (depending on stellar temperature, spectrum quality and the observed wavelength coverage). All spectral lines unsuited for analysis because of e.g. blends, low S/N, uncorrectable normalisation problems, incomplete correction of cosmics, or known shortcomings in the modelling needed to be excluded. Also a verification and, possibly, correction of the automatic continuum placement lead to a gain in precision. Every element was analysed independently (passing through the loop procedure in Fig. 3) and some interactive iterations for fine-tuning the parameter determination were needed in order to find a unique solution that reproduces all indicators simultaneously. This facilitated also to derive realistic uncertainties for the stellar parameters, as the formal errors determined by Spas (via bootstrapping) were unrealistically low. Instead, the standard deviations around the average parameter values were adopted, as derived from the various independent spectral indicators. Likewise, uncertainties of elemental abundances were determined from the line-to-line scatter found from the analysis of the individual features.
Finally, it was thus possible to derive a simultaneous, self-consistent solution for atmospheric parameters and chemical abundances, and also to quantify their statistical uncertainties. The novel approach provides results meeting the same quality standard as our previous work (for test purposes and consistency checks we therefore included the previously analysed objects in the present sample, stars 1–6 in the tables). Its advantages are a higher degree of objectivity than “by eye” fits and a far higher efficiency, hence allowing larger star samples to be analysed.
4.2. Stellar parameter and abundance determination
Special emphasis was given to use multiple indicators in order to minimise the chance of the stellar atmospheric parameters and chemical abundance determination being biased by residual systematic errors. The following spectroscopic indicators were utilised in the quantitative analysis:
-
Teff: all available H and He lines, and multiple independent ionization equilibria; confirmation via spectral energy distributions (SEDs);
-
log g: wings of all available hydrogen lines and multiple ionization equilibria; confirmation via Hipparcos distances;
-
ξ: several elements with spectral lines of different strength enforcing no correlation between ε(X) and the strength of the lines (equivalent to ε(X) being independent of Wλ);
-
vsini and ζ: metal line profiles;
-
ε(X): a comprehensive set of metal lines.
The parameter determination started with the analysis of the hydrogen and helium lines. When a good simultaneous fit to most H and He lines was achieved – Teff and log g were then typically constrained to better than ~5% and 0.1–0.2 dex, respectively, for this high-quality set of stellar spectra – the procedure commenced to consider lines of other elements. Ionization equilibria, i.e. the requirement that lines from different ions of an element have to indicate the same chemical abundance, facilitated a fine-tuning of the previously derived parameters. The selection of ionization equilibria to be analysed depends primarily on Teff. Table 4 summarises the spectroscopic indicators employed for the Teff and log g determination of each sample star, sorted by temperature. Elements that show lines of three ionization stages simultaneously in the spectrum are most valuable as they can in principle constrain both Teff and log g at once. Examples are C ii/iii/iv or Si ii/iii/iv9 in early B-type stars. When lines from only two ionization stages of an element are present in the spectra, then more indicators are required for the parameter determination. Usually in the literature, a few hydrogen lines are analysed and one ionization equilibrium is established. On the other hand, we try to establish typically 4–5 independent ionization equilibria in addition to fitting all available hydrogen lines, which is unprecedented. Finally, the resulting model fluxes were compared with the observed SEDs. While such a high accuracy in the Teff-determination as with our spectroscopic approach can not be achieved by SED fitting alone, it provides a valuable consistency check, which can also facilitate the detection of otherwise unrecognised cooler companions.
Spectroscopic indicators for for Teff and log g determination.
Microturbulence was for a long time an ad-hoc fit parameter that was employed to remove correlations of abundance with Wλ, and often a different ξ was adopted for different elements. Only recently, a physical explanation for the phenomenon of microturbulence in hot stars was suggested, likely being a consequence of subsurface convection (Cantiello et al. 2009), similar to the case of solar-type stars. Microturbulence needs to be constrained simultaneously along with Teff and log g, such that its determination was a crucial part of our iteration procedure. The reason for this is that an inappropriately chosen microturbulence may lead to substantial shifts in Teff from the ionization equilibria analysis, see Fig. 5 in Nieva & Przybilla (2010b), which may remain unnoticed in the usual approach of using a minimum set of indicators for the parameter determination. Consequently, several elements were analysed for deriving the microturbulent velocity. Our primary indicators were the Si, O and C lines, but the results were checked for consistency with the lines from the other elements as well.
The detailed analysis of line profiles shows that rotational broadening alone is often not sufficient to explain the observed line shapes in hot stars. Agreement can be achieved when introducing a radial-tangential anisotropic macroturbulence (Gray 2005, p. 433f) as additional broadening agent, see e.g. Fig. 11 of Przybilla et al. (2006a). Consideration of macroturbulence is therefore essential for meaningful line-fits using χ2-minimisation. A physical explanation of macroturbulence in hot stars was also only recently suggested, likely being a collective effect of (non-radial) pulsations (Aerts et al. 2009).
Usually in stellar analyses, once the stellar parameters are fixed one commences with the abundance determination, treating this as an essentially independent step. In our approach the abundance and stellar parameter determination are tightly related because of the use of ionization equilibria. In consequence, only few species (those not appearing as ionization equilibria in Table 4) are left to finalise the analysis. Another difference to typical literature studies is the large number of spectral lines evaluated by us per species, and the consistency achieved from the different ionization stages of the various elements. All the various improvements in observations, modelling and analysis methodology facilitated analyses at much higher precision and accuracy to be achieved than possible in standard works. The quality of the analyses could be retained over a large parameter space, spanning nearly 20 000 K in Teff and ranging from close to the zero-age main sequence (ZAMS) to the giant stage. Consequently, an excellent match of the computed and the observed spectra is achieved globally and in the details, see the end of Sect. 5 for a discussion.
Stellar parameters of the program starsa.
5. Results
5.1. Stellar parameters
Table 5 summarises the stellar parameters derived from the quantitative spectral analysis. This includes the atmospheric parameters effective temperature Teff, surface gravity log g, microturbulence ξ, projected rotational velocity v sin i and macroturbulent velocity ζ. Additional quantities include the computed colour excess E(B − V) of the sample stars, their de-reddened apparent magnitude V0, evolutionary masses Mev, spectroscopic distances dspec and Hipparcos distances dHIP.
Effective temperatures are constrained to 1–2% and surface gravities to less than 15% (1σ uncertainties). It is unlikely that these values are subject to larger residual systematics10, as they are constrained by the simultaneous match of many independent indicators. Even changes of the underlying physical models, like a use of hydrostatic non-LTE model atmospheres (Nieva 2007) or hydrodynamic non-LTE model atmospheres (NS11), have been shown to have only small effects (i.e. agreement of stellar parameters and elemental abundances is obtained with the different models, within the stated statistical 1σ-uncertainties and without systematic trends). Overall, this is a major improvement over other literature studies, where the uncertainties can amount to ~5–10% for effective temperature and ~25% for surface gravity. In consequence, all quantities depending on temperature and gravity (e.g. reddening, evolutionary masses, spectroscopic distances) also show reduced uncertainties. A slight degeneracy of line profile variations to simultaneous changes of v sin i and ζ prevents one to achieve very tight constraints on these quantities individually.
A noteworthy result is the finding that one value of microturbulent velocity is derived from the different chemical species, after several iterations in all variables of the spectral fitting procedure. This was often not the case in previous studies, likely being a consequence of adopting ill-chosen atmospheric parameters or of shortcomings in the modelling, e.g. the assumption of LTE or the use of limited sets of atomic data for non-LTE line-formation calculations.
 |
Fig. 5 The sample stars in the Teff–log g plane. 1σ-uncertainties are shown. Numbering according to Table 1. Overlaid are evolution tracks for non-rotating stars of metallicity Z = 0.02 from Meynet & Maeder (2003, full lines) and Schaller et al. (1992, dotted lines). See Sect. 5.1 for a discussion. |
A comparison of the resulting model fluxes with the observed spectral energy distributions (where available) shows good agreement, see Fig. 4 (available online only). Our values for effective temperature derived via multiple independent ionization equilibria are thus further verified11. The photometric data was converted into fluxes using zeropoints of Bessell et al. (1998) for Johnson photometry and of Heber et al. (2002) for the 2MASS photometry. All observed fluxes were de-reddened using an interstellar reddening law according to Cardelli et al. (1989), adopting colour excesses E(B − V) as indicated in Fig. 4 and a ratio of total-to-selective extinction RV = AV/E(B − V) = 3.1. Note that the E(B − V) values used in Fig. 4 may differ slightly (on average by ~0.02 mag, which is within the mutual uncertainties) from those in Table 5, which were calculated from the difference between the observed and the computed Atlas9 model colour. As IUE spectrophotometry was not available for all the sample stars, we decided to use the homogeneously derived E(B − V) data in Table 5 to determine V0.
Evolutionary masses of the sample stars were determined by comparison of the objects’ positions in an effective temperature Teff vs. surface gravity log g diagram with stellar evolution models from Meynet & Maeder (2003), see Fig. 5. Tracks for non-rotating stars with “solar” metallicity Z = 0.02 were adopted. As several stars are less massive than the lower mass limit of this grid, additional tracks from Schaller et al. (1992) were adopted, which however show a small offset with respect to the more modern data, see the 9 M⊙ models. For consistency, we applied corresponding offsets to the lower-mass objects in order to derive homogeneous Mev values in Table 5. Note that some systematic offsets will result due to difference between the model (Z = 0.02) and our derived metallicities (Z = 0.014). One consequence will be a shift of the zero-age main sequence towards higher gravities, such that the high-gravity objects 6, 11 and 19 will fall on the ZAMS. We neglect this in the following, as the effects on the further discussion are small.
Metal abundances for the sample stars.
Once these parameters are constrained, it is possible to determine spectroscopic distances dspec of the sample stars using a formula by Ramspeck et al. (2001)![\begin{equation} d_\mathrm{spec}=7.11\times10^4\,\sqrt{M_\mathrm{ev}\,H_{\nu}\,10^{(0.4V_0-\log g)}}~[{\rm pc}], \end{equation}](/articles/aa/full_html/2012/03/aa18158-11/aa18158-11-eq66.png) (1)where Mev is expressed in units of M⊙, the Eddington flux at the effective wavelength of the V filter Hν in erg cm-2 s-1 Hz-1 (derived here from the Atlas9 models), V0 in mag and log g in cgs units. The formula uses a flux calibration of Vega according to Heber et al. (1984). The most crucial input quantity in the distance determination is the surface gravity. This opens up a possibility to independently verify our log g determination via comparison of the spectroscopic with Hipparcos distances as derived from parallaxes π from the new reduction of the Hipparcos catalogue (van Leeuwen 2007), see Fig. 6. Lutz-Kelker corrections (Lutz & Kelker 1973; Smith 2003) have not been adopted to refine the Hipparcos parallaxes, as they should not be applied to measurements of individual stars (van Leeuwen 2007, p. 87). Their potential impact is nevertheless rather small for the present sample stars, as visualised in Fig. 6. Overall, good agreement of the spectroscopic and Hipparcos distances is found within the uncertainties, except for the objects 9, 18 and 20, which, however, are still within the 3σ limits. An apparent systematic trend of increasing difference dspec − dHIP with increasing distance (lower panel of Fig. 6) becomes marginal when only one object, #9, is disregarded, i.e. the regression line is then compatible with slope and offset zero.
(1)where Mev is expressed in units of M⊙, the Eddington flux at the effective wavelength of the V filter Hν in erg cm-2 s-1 Hz-1 (derived here from the Atlas9 models), V0 in mag and log g in cgs units. The formula uses a flux calibration of Vega according to Heber et al. (1984). The most crucial input quantity in the distance determination is the surface gravity. This opens up a possibility to independently verify our log g determination via comparison of the spectroscopic with Hipparcos distances as derived from parallaxes π from the new reduction of the Hipparcos catalogue (van Leeuwen 2007), see Fig. 6. Lutz-Kelker corrections (Lutz & Kelker 1973; Smith 2003) have not been adopted to refine the Hipparcos parallaxes, as they should not be applied to measurements of individual stars (van Leeuwen 2007, p. 87). Their potential impact is nevertheless rather small for the present sample stars, as visualised in Fig. 6. Overall, good agreement of the spectroscopic and Hipparcos distances is found within the uncertainties, except for the objects 9, 18 and 20, which, however, are still within the 3σ limits. An apparent systematic trend of increasing difference dspec − dHIP with increasing distance (lower panel of Fig. 6) becomes marginal when only one object, #9, is disregarded, i.e. the regression line is then compatible with slope and offset zero.
 |
Fig. 6 Results of the distance determination. Upper panel: comparison of spectroscopic and Hipparcos distances. 1σ-uncertainties are shown. Numbering according to Table 1. The 1:1 relation is indicated by the dashed line. Lower panel: percent difference of the two distance indicators. Open circles mark the data if corrected for Lutz-Kelker bias. See Sect. 5.1 for a discussion. |
5.2. Chemical abundances
Metal abundances of the sample stars are summarised in Table 6, where also the standard deviation from the line-to-line scatter and the number of analysed lines are indicated. The values are averages over all lines of a given species, giving each line in the different ions equal weight. A precision of the results of better than 25% is indicated typically. The individual line abundances are listed in Table 7, where further details on the line formation calculations are also given: central wavelengths λ of the spectral lines, excitation energy of the lower level χ, oscillator strengths log gf and the accuracy and source of the oscillator strengths.
We deviated from the above procedure for the derivation of the helium abundances. Helium is the second most abundant element and therefore cannot be treated as a trace element: changes in its abundance modify the mean molecular weight of the atmospheric plasma and thus can affect the atmospheric structure noticeably. However, the comparison of the observed with the computed spectra showed that the sample stars are indeed well-described by a (protosolar) ε(He) = 10.99 ± 0.05 (except for object 4, with a – still compatible – ε(He) = 10.94 ± 0.05).
The metal abundances show a small scatter around the average sample abundances, which is visualised later, in Fig. 12. The only peculiarities are enhanced nitrogen abundances in several sample stars, which can be understood in the framework of mixing of CN-cycled material into the atmospheric layers (see e.g. Przybilla et al. 2010). The silicon abundance in object 5 is also conspicuously low, which may be an indicator for the onset of chemical differentiation in the otherwise normal star. We decided to discard these peculiarities from further analysis.
 |
Fig. 12 Abundance distributions for the astrophysically most relevant chemical species as derived from early B-type stars in the solar neighbourhood. Red histograms: present work, establishing the cosmic abundance standard. Black histograms: literature data. Photospheric and protosolar abundances from AGSS09 are also indicated, the bars representing the range spanned by the ± 1σ-uncertainties. See Sect. 6 for details. |
The most relevant sources of systematic uncertainties in the chemical abundances that arise from the spectral modelling, analysis and observations in our approach have already been discussed in a series of papers. We refer to the work summarised in Table 3 for estimates of effects and systematics due to uncertainties in the atomic input data. Systematics due to basic model atmosphere input physics were investigated in particular by NP07 and NS11, while systematics due to details of analysis strategies were discussed by Nieva (2007) and Nieva & Przybilla (2010a,b).
Since our observational material leaves little room for observational bias we concentrate here only in quantifying the systematic effects on chemical abundances as introduced by uncertainties in the stellar parameters. We exemplify the effects of independent effective temperature, surface gravity and microturbulence variations on oxygen and silicon abundances (the most sensitive among the elements in this parameter range) for the star #7 (HD 886, γ Peg) in Table 8. Two cases are investigated, for our and also for typical values in the literature. Note that this case represents our largest relative uncertainty in Teff, one of the largest in Δξ/ξ, and typical uncertainty in log g, such that the example constrains the maximum systematic effects expected for our sample stars. As correlations exist between parameters – e.g. a higher Teff implies a higher log g in analyses – the true systematic uncertainties are hard to quantify in detail. Based on the given example and previous experience we estimate systematic uncertainties of the elemental abundances in our sample stars, accounting for all factors, to be about 0.15 dex at maximum, with the majority being accurate to within better than about 0.10 dex. In comparison the systematics due to stellar parameter variations for typical uncertainties from the literature are much higher (Table 8), amounting to a factor ~2 in individual cases. Usually, uncertainties in Teff are the most critical, but note the high sensitivity of the (rather strong) silicon lines to microturbulence variations.
A test for residual systematics can be made by searching for trends among the elemental abundances as a function of atmospheric parameters. Figure 7 (available online only) displays metal abundances from the present work and from nine additional Orion OB1 stars of NS11 (analysed in the same manner) as a function of Teff and log g. All data points cluster tightly around the average sample values and the respective 1σ-error margins (see Table 9), except for the few cases discussed earlier, mostly for nitrogen. No significant trends either with Teff or log g are found.
Finally, we want to briefly comment on several potential sources of systematic uncertainties due to non-standard input physics in the context of model atmospheres. Potential weak stellar winds present have a negligible effect on the photospheric line spectrum, as the effects of the velocity field on the atmospheric stratification become noticeable only outside the line-formation region. Wind variability by larger amounts than the mass loss-rates of Ṁ ≲ 10-8 M⊙ typical for B-type main-sequence stars has no effects on the metal line spectrum in supergiants (e.g. Schiller & Przybilla 2008). Systematic effects on the abundance analysis due to the presence of magnetic fields are also not expected. Only three sample stars have a confirmed magnetic field, β Cep (Henrichs et al. 2000), ζ Cas (Neiner et al. 2003) and τ Sco (Donati et al. 2006). To date, none of these shows observational evidence for abundance spots or vertical chemical stratification.
5.3. Global spectrum synthesis
Stellar parameters in Table 5 in combination with averaged chemical abundances in Table 6 were used to compute global synthetic spectra to visualize the quality of the analysis procedure. Overall, excellent agreement is found for all stars over the entire observed spectral regions. Examples for four stars with spectral types B3 III (#15 HD 209008, 18 Peg), B2 IV (#7 HD 886, γ Peg), B1 V (#1, HD 36591, HR 1861) and B0.2 V (#6 HD 149438, τ Sco) are shown in Figs. 8a–11e.
Chemical composition of different object classes in the solar neighbourhood.
It is worth to notice that it is relatively simple to achieve reasonable fits of models to lower resolution spectra and data at lower S/N over limited wavelength regions, i.e. whenever the observational details tend to be washed out. High-resolution and high-S/N observations spanning a large wavelength range are much more challenging to be reproduced with synthetic spectra based on physical models at once. This is feasible only if the models match the global physics (i.e. the atmospheric structure) and details of individual features (i.e. the lines) equally well. We consider our success as a strong support for the absence of any significant systematics from our analysis. We thus complement the probably most comprehensive benchmark test for stellar atmosphere modelling of OB stars to date by Marcolino et al. (2009, at about the upper Teff.
The locations of numerous spectral lines that are considered in our line-formation computations are indicated in the upper parts of the individual panels in Figs. 8a–11e in order to facilitate an evaluation of their presence/absence for a given set of stellar parameters12. These include many more features (also from additional chemical species) than those analysed quantitatively in the present work (the latter are marked in the lower parts of the panels). We thereby show that even complex blend features like e.g. around He i λ4120 Å or around O ii/C iii λ4650 Å can be reproduced well.
There are still some residual minor shortcomings. As can be seen from the comparison of observation with theory the continuum normalisation could be improved globally. However, we have corrected for this by adjusting the continuum locally when analysing individual wavelength regions, such that this would be rather a cosmetic improvement. Our compromise to fit the five displayed Balmer lines, Hϵ to Hα, results in a slight mismatch in some of the Balmer line wings because of the imperfect normalisation, but the effect is well within the uncertainties of the log g-determination. The cores of the Balmer lines for the hot star τ Sco (and just visible in HR 1861) are not matched well because non-LTE effects on the atmospheric structure are likely to affect the outer photosphere, i.e. the core-formation region for the strongest lines, gradually with increasing temperature. Moreover, Hα is expected to be influenced by the weak stellar wind, which is unaccounted for by our hydrostatic modelling. The unavailability of realistic broadening data is an issue for some lines, e.g. for He i λ3926 Å.
Several (high-excitation) spectral lines of the elements from Table 3 and some elements/ions are still not incorporated in our non-LTE spectral synthesis. On the other hand, we have included Al iii and S ii/iii in the calculations, adopting model atoms of Dufton et al. (1986) and Vrancken et al. (1996), respectively, and assuming solar abundances of Asplund et al. (2009). However, we do not consider these elements for the analysis as several shortcomings have been identified in the model atoms. In consequence, not all of the computed lines of these two elements give a good match to the observed spectra. A thorough verification and improvement of the model atoms for aluminium and sulphur is beyond the scope of the present paper, as is the inclusion of the missing lines from other chemical species. We will report on our efforts for achieving completion of the non-LTE spectrum synthesis in forthcoming papers.
6. Present-day cosmic abundances
The high degree of chemical homogeneity of the sample stars (Table 6) encourages us to identify the average abundances with the long-sought cosmic abundance standard (CAS) for the present-day chemical composition of the cosmic matter in the solar neighbourhood. As statistical significance does matter for such a claim, we seek to compensate for the seven stars that were removed from our initial sample in order to avoid observational biases. We therefore adopt abundance data for 9 additional early B-type stars from the Ori OB1 association13 (NS11), which were derived using the same models and analysis techniques as applied here. The stars meet the same observational selection criteria (i-iv in Sect. 2.1) as our core sample. The spectra were obtained with Fies on the 2.5 m Nordic Optical Telescope (La Palma), covering the wavelength range of 3700–7300 Å at R = 46 000 and S/N > 250 (Simón-Díaz 2010).
Distribution functions for the individual elemental abundances in the star sample are displayed in Fig. 12 (red histograms). The data are normalised by the number of sample members, with the maximum value set to 1. The bin width is chosen as the standard deviation of the individual distributions. Note that only 20 stars are considered in the histograms for N – the atmospheres of nine stars are mixed with CN-processed material – and 28 for Si – one star is Si peculiar – as we are interested in the pristine abundances for constraining the CAS (see Table 6 for an identification of the data removed from the discussion here).
Very tight distributions are found, described by a standard deviation of typically ~10%. Mean abundances together with the standard deviations (of the sample) are given in Table 9, which summarises also data on present-day abundances in the solar neighbourhood from other object classes, and the Sun. Resulting mass fractions for hydrogen (X), helium (Y) and the metals (Z) are indicated in Table 10. In addition to the metals investigated here – which cover the most abundant ones in the cosmos –, data for all other metals up to zinc was considered for constraining Z, using solar meteoritic values of Asplund et al. (2009), except for chlorine and argon, where abundances from the Orion nebula were adopted (Esteban et al. 2004). Any deviations of this auxiliary data from the “true” cosmic values will be absorbed by the error margins of Z due to their small contribution.
This finding of homogeneity is in analogy to PNB08, but on a statistically much more significant basis and corrected for slight systematics in the iron abundances (see Sect. 3.1). The same degree of chemical homogeneity is recovered as for the gas-phase of the diffuse ISM out to distances of 1.5 kpc from the Sun (Sofia & Meyer 2001), see also Table 9, though different absolute abundance values for many elements are found because of depletion onto dust grains (see Sect. 7.3).
However, the finding is at odds with practically all previous work on early B-type stars in the solar neighbourhood. We concentrate on literature data from homogeneously analysed samples of more than 10 stars for the comparison with the present work, as a comprehensive review of all available data is beyond the scope of this paper. Therefore, abundances from the studies of Kilian (1992, 1994), Gies & Lambert (1992) – excluding bright giants and supergiants –, Cunha & Lambert (1994), Daflon et al. (1999, 2001a,b, 2003), Cunha et al. (2006), Morel & Butler (2008) and Lyubimkov et al. (2004, 2005) are adopted, essentially applying the same distance cut as in our sample selection. These abundances were derived from high-resolution spectra using comparable non-LTE techniques as utilised here: either hybrid non-LTE or full non-LTE modelling under consideration of metal line blanketing. The only exception are iron abundances, which were determined in LTE in these studies. The combined distribution functions14 for the individual elemental abundances from the literature are also displayed in Fig. 12 (black histograms). Much broader distributions are indicated, with typical standard deviations of about 0.2 dex. This is a factor ~5 larger than in the present work, despite our sample is a representative sub-set of the previously investigated stars, see Sect. 2.1.
Mass fractions for hydrogen, helium and metals.
It is extremely difficult to trace the discrepancies in stellar parameters and elemental abundances of individual stars from the various investigations, as differences exist at all levels: the quality of the observational material, the methodologies of stellar parameter determination, the choice of analysed lines, the input atomic data, the computer codes and assumptions used for the modelling, among many other details that differ from study to study. A combination of several factors is most likely responsible for the discrepancies. We do not aim at resolving these discrepancies in detail case by case as little can be learned in terms of the objective of the present work. Moreover, the overall picture can actually be understood rather well from some basic considerations.
Any abundance determination using a method with finite precision will yield an abundance distribution with a larger dispersion than the true one. Broad distributions like those derived from the literature data can result from underlying tight distributions. Actually, the finding of such broad distributions is expected, given that the statistical 1σ-uncertainties in the literature data alone can amount to 0.2 to 0.3 dex and systematic uncertainties result in shifts of the derived abundance distributions of the individual studies relative to each other (see Fig. 2 of PNB08 for a visualisation). A full spread of the literature data over 1 dex and a shift in mean abundances is therefore hardly surprising.
Finally, Fig. 12 allows also a comparison of the abundance distributions for the B-stars with the solar standard to be made. Photospheric abundances of Asplund et al. (2009) are chosen as a representative for the type of data that is typically adopted in all kinds of astrophysical literature, and protosolar values from the same source as a representative for the bulk composition of the Sun (correcting for a ~0.04 dex depletion of the photosphere due to diffusion). Interestingly, similarities are found for some elements and differences for others, which will be discussed further in Sect. 7.5. Note that the 1σ-uncertainties of the solar abundances are about the same as the B-star sample standard deviations. Technically, the fact that a larger number of B-stars is considered for the determination of the CAS – in contrast to one star defining the solar standard –, means that the uncertainties of the CAS-values can be expressed via the respective standard error of the mean, which amounts to 0.01 dex for all metals studied here. However, we prefer to assign the standard deviation of the sample as conservative error margins for the CAS.
In our quest to reduce systematic errors to a minimum we cannot ignore possible bias introduced by other factors than stellar atmospheres alone. When considering an extended region like the solar neighbourhood (in our definition), effects from Galactic chemical evolution may also come into play. The presence of Galactic abundance gradients implies a decrease of metal abundances with increasing Galactocentric radius. To verify this, we checked for correlations of the stellar abundances with the spatial positions of the stars. An example for oxygen is shown in Fig. 13. No correlations are found, neither with Galactocentric distance nor with distance from the Galactic plane. We conclude that signatures of Galactic chemical evolution are insignificant on scales of ~ 500 pc, providing no bias to the CAS on the level of precision achieved with our analysis methodology.
 |
Fig. 13 Spatial distribution of oxygen abundances in the sample stars, in analogy to Fig. 1. Open circles represent objects from NS11. The symbol size encodes the abundance according to the figure legend. |
In summary, it emerges from our previous discussion that the drastic reduction of many systematic uncertainties in our analysis procedure is the key for understanding the derived small dispersion in the elemental abundances of the sample stars. For the first time the true abundance distributions of the young stellar population in our Galactic vicinity are approximated, which appear intrinsically tight. At the same time, the overall match of a large number of independent observational constraints and the successful passing of numerous tests for remaining biases puts confidence in the accuracy of the results. This allows an accurate and precise cosmic abundance standard to be established. We expect that the true abundance distributions for our B-star sample will be in fact tighter than derived here because they are subject to analysis with a methodology of finite precision. Therefore, our study gives only a upper limit on the true degree of chemical homogeneity of the present-day cosmic matter in the solar neighbourhood. Given the current state of input physics for the models, it will be highly costly to improve the analysis inventory to a degree where much tighter constraints can be achieved.
7. Implications
In the following we want to investigate what implications the use of the cosmic abundance standard instead of the solar standard has on various astrophysical fields. We concentrate on the impact of our sample data and the resulting CAS values for the evolution of massive stars, for ISM science and for Galactic chemical evolution. Finally, we briefly comment on the origin of the Sun and its relation to its present Galactic neighbourhood.
 |
Fig. 14 Observational constraints on mixing of CNO-burning products in massive stars. Mass ratios N/C over N/O are displayed. Black dots: present data; black circles: 9 additional objects from NS11. Data from previous non-LTE analyses are given as grey symbols (green online) – plus signs: Kilian (1992); triangles: Gies & Lambert (1992); diamonds: Cunha & Lambert (1994), Daflon et al. (1999, 2001a,b); squares: Morel et al. (2008); crosses: Hunter et al. (2009). The predicted nuclear paths assuming initial CAS abundances (red star) and solar abundances ( ⊙ ) of Asplund et al. (2009) are indicated by the long-dashed and dotted lines, respectively. Statistical uncertainties of 0.2 dex in each element – which are typical for previous literature data – result in an error bars more than twice as large than those from the present data. |
7.1. Stellar evolution: the initial chemical composition
The initial chemical composition has a profound influence on the structure and evolution of stars because of its effect on opacities and mean molecular weight. We have addressed the effect of a metallicity reduced from the so far canonical value Z⊙ = 0.02 to ZCAS = 0.014 in the discussion of Fig. 5. The shift of the ZAMS towards higher gravities will also be accompanied by a shift of the evolution tracks towards higher effective temperatures. But, would there be a significant effect if the CAS or modern solar abundances at about the same Z (see Table 10) were used? In terms of the position of the tracks in the Hertzsprung-Russell diagram – probably not; however, in terms of observable tracers for rotational mixing, certainly yes.
Energy production in massive stars is governed by the CNO cycles throughout most of their lifetime and the nuclear-processed material may reach their surface layers through rotational mixing already during their main sequence phase (e.g. Maeder & Meynet 2000; Heger & Langer 2000), opening up a very powerful diagnostic to test models of stellar evolution. The changes of the CNO surface abundances reflect the actions of the dominating CN-cycle initially, following a well-defined nuclear path. This can be analytically approximated by a straight line in the diagnostic N/C–N/O-diagram (see Fig. 14), with a slope defined solely by the initial CNO abundances (Przybilla et al. 2010), regardless of the mass, initial velocity or other model details.
The present analysis of our sample stars (and the additional nine objects from NS11) facilitates the predicted trend to be recovered for a statistically significant sample for the first time, see Fig. 14. Most of our objects cluster around the pristine CAS values, i.e. they are unmixed, while about 1/3 of the stars show a mixing signature of varying magnitude, following the predicted nuclear path with d(N/C)/d(N/O) = 4.6 (for initial CAS abundances) tightly. Stellar evolution models based e.g. on the solar values by AGSS09 would predict a different nuclear path (with slope ~3.0) despite a rather similar bulk metallicity.
The large scatter found by previous non-LTE analyses of early B-type stars in the solar neighbourhood (many objects are in common with our sample) and additionally in three Galactic clusters is also likely a consequence of the lower accuracy and precision achieved in these studies, as argued in Sect. 6. Most data points are in fact consistent with the predictions because of the larger error bars, but they are of limited use for testing stellar evolution models stringently.
Further consequences of the use of different individual abundances will be modified yields. As these are key input for Galactic chemical evolution models, they have to be determined as realistically as possible.
7.2. Chemical homogeneity: early B-type stars vs. ISM
From studies of interstellar absorption lines of the cold gas it is known for a long time that the local ISM out to 1.5 kpc from the Sun is chemically homogeneous, to the 10%-level (Sofia & Meyer 2001). This can be understood as a natural consequence of turbulent mixing acting on all scales, which is due to the large density variations of the gas, generated by a complex interaction of many factors like momentum injection by stellar winds and supernova shocks, magnetic fields and self-gravity. Theoretical investigations of metal abundance fluctuations in the ISM have until recently been based on order of magnitude arguments involving characteristic spatial scales and timescales for various turbulent mixing processes, see e.g. Roy & Kunth (1995), and Scalo & Elmegreen (2004) for a review. More recently, sophisticated 3D (magneto-)hydrodynamic simulations of the local ISM at high resolution (e.g. de Avillez & Breitschwerdt 2007) support the view of an efficient mixing of metals at wide ranges of scales, driven by turbulence.
The young stars in the solar neighbourhood are expected to follow the chemical characteristics of the matter from which they were formed. Indeed, the present study shows that, independent of the location of the sample stars in the solar neighbourhood (see Fig. 13) – whether they reside in OB associations or in the field –, and also independent of their mass (~6 to 20 M⊙) and hence their life-time (~5 × 107 to 5 × 106 yr, respectively), all stars show practically the same chemical composition. The fluctuations around the mean are ~10%, and probably less. This independent verification of the results from investigations of the ISM gas is achieved for the first time.
The huge advantage of studying early-type stars is that the entire metal content can be determined using quantitative spectroscopy, with no material hidden in an observationally inaccessible reservoir like the dust-phase in the ISM. This opens up the possibility to determine the chemical composition of the dust in an indirect way, see the next sub-section.
Moreover, our results put constraints on the injection and mixing timescales of metals in the local Galactic ISM, and therefore on the hydrodynamics of the ISM. It appears that fresh nucleosynthesis products from supernovae and AGB (super-)winds or infall of pristine material onto the Galactic disk are unlikely to lead to a noticeable (at the level of the present abundance determination precision) local enrichment or depletion in a high-metallicity environment like the solar neighbourhood over a timescale of several 107 yr. Or, in other words, the interaction of hydrodynamic mixing on the one hand and viscosity and molecular diffusion on the other is highly efficient, such that the medium is homogenised quickly.
 |
Fig. 15 Comparison of the stellar O abundance distribution as derived in the present work (red histogram) with gas-phase abundances along different sightlines of the diffuse ISM (thin blue histogram, Cartledge et al. 2004), in analogy to Fig. 12. Mean abundances are indicated. |
7.3. Dust composition of the local ISM
An important open question in our understanding of the ISM is the chemical composition of the dust particles. The amount of metals incorporated into dust cannot be derived directly from observations. Only an indirect determination is feasible, from the comparison of the ISM gas-phase abundances and a suitable reference that is unaffected by depletion onto dust grains. There is an ongoing debate which kind of objects provide the reference suited best for the comparison: young B-type stars, young F&G-type stars, or the Sun (Sofia & Meyer 2001).
 |
Fig. 16 Observational constraints on the chemical evolution of Galactic CNO abundances: abundance ratios log (C/O) and log (N/O) vs. O abundance. Left panels: black triangles: early B-stars from the literature extracted from Fig. 12. Data for low-mass stars are displayed as grey symbols (green in the online edition) – squares: Gustafsson et al. (1999, solar-type dwarfs); crosses: Fabbian et al. (2009, solar-type dwarfs and subgiants); diamonds: Spite et al. (2005, unmixed cool giants); plus signs: Israelian et al. (2004, unevolved solar-type stars). Solar abundance ratios of Asplund et al. (2009) are also indicated ( ⊙ ). Right panels: black dots: unmixed objects from the present work, black circles: unmixed stars from NS11. Data from the literature like in the left panels. The CAS is also indicated (red star). Error bars (statistical 1σ-uncertainties) typical for individual stars in the present study are shown. |
We argue here that the CAS values as established from the analysis of early B-type stars provide the long-sought reference, unprecedented in precision and accuracy. Most notable is that the same degree of chemical homogeneity is found for both, the CAS reference and the gas-phase abundances of the diffuse ISM (see Table 9). The abundance distributions are very similar, see Fig. 15 for the example of oxygen (the gas-phase abundance distribution is based on 37 diffuse sightlines of Cartledge et al. 2004). From this it follows immediately that the dust-phase is chemically also rather homogeneous, what can be expected if mixing processes are highly efficient within the ISM (Sect. 7.2).
We derive a similar chemical composition for the dust grains as PNB08, but at much higher statistical significance and with two exceptions (see Table 9). The Fe abundance is higher due to the identification and removal of residual systematics in the line-formation computations for that element (Sect. 3.1). For carbon, a recent investigation by Sofia et al. (2011) raises doubts about the precision of weak-line analyses based on the C ii] λ2325 Å transition (see Sofia 2004, for a discussion), possibly related to a systematically underestimated oscillator strength. We therefore adopt a mean abundance from five sightlines of the strong-line analysis of Sofia et al. (2011), which is compatible with data from the [C ii] λ158 μm line by Dwek et al. (1997).
Overall, the results indicate a silicate/oxide-rich and relatively carbon-poor composition for the local ISM gas phase. In particular, the CAS provides sufficient oxygen to sustain the values required by magnesium, silicon and iron to be locked up by vast majority in silicates (plus a small fraction in metal oxides) in the diffuse ISM. Using a reasonable dust composition (Draine 2003) this amounts to about 140–150 ppm of oxygen for the given abundances of the refractory elements in the dust, in good agreement with the observed value (Table 9), with some additional oxygen possibly incorporated in organic compound material. About 60% of the total carbon resides in the dust phase. Despite a higher abundance of carbon is found in the dust in absolute terms relative to PNB08, this falls still somewhat short of the demands of most dust models, see e.g. the discussions by Snow & Witt (1995) and Zubko et al. (2004).
Finally, we want to comment on the cosmic abundance standard in the context of gas- and dust-phase abundances in the Orion nebula. Further information for the general picture can be gained under the – not unlikely – assumption that the Orion giant molecular cloud formed out of material typical for the diffuse ISM, with subsequent chemical processing taking place in the cloud core.
A comparison of the CAS with gas-phase abundances (Esteban et al. 2004; Simón-Díaz & Stasińska 2011) implies that the H ii region is devoid of carbonaceous dust. From observations of the photodissociation region in the Orion nebula it is known that polycyclic aromatic hydrocarbons (PAHs) disappear as the gas becomes ionized (e.g. Tielens 2008). Our results imply that photoevaporation affects all carbon-bearing dust particles in a similar manner, indicating that little carbon was incorporated initially in graphite (the most stable form of carbon under interstellar conditions), in line with the findings of Amari et al. (1990) from laboratory studies of meteorites. Also, amorphous carbon dust grains15 are either efficiently destroyed inside the ionized region, or they were a minority species initially as well. On the other hand, there is only weak evidence for the destruction of silicate grains from the numbers in Table 9 – the abundances of oxygen and of the refractory elements in the Orion nebula dust-phase are compatible with the ISM dust data within the (large) error bars. Unfortunately, a more direct verification of the carbon-poorness of dust within the H ii region via e.g. the extinction properties is complicated, as most of the extinction towards Orion occurs in the neutral medium surrounding the H ii gas (Baldwin et al. 1991).
The combined evidence from abundances in the ISM and in the Orion H ii region indicates that dust models considering silicates, PAHs, organic refractory material and possibly amorphous carbon, but not graphite, should be investigated more closely. Models in analogy to the COMP-NC-type or COMP-AC-type models of Zubko et al. (2004) look highly promising for future studies in view of abundance demands and the ability to match other observational constraints like extinction and emission properties of the dust. We are confident that the tight observational constraints provided by the CAS will facilitate a better understanding of the nature of dust and grain structure to be developed.
7.4. Galactochemical evolution: present-day abundances
Nucleosynthesis in successive generations of stars has enriched the cosmic matter with heavy elements ever since the first Population III stars were born. Studies of various objects like (Galactic and extragalactic) stars and H ii regions, or the ISM in damped Lyα (DLAs) systems allow the cosmic enrichment history to be traced and the specific production sites of individual elements to be constrained. The CAS provides valuable input for the comparison of models with observations, as it marks the present-day endpoint of galactochemical evolution, in particular for a typical spiral galaxy like the Milky Way. We put CAS values into the context of the evolution of the five most important chemical species, the light elements CNO, magnesium as a typical tracer of the α-process in core-collapse supernovae and iron as tracer of iron-peak nucleosynthesis in supernovae of type Ia.
 |
Fig. 17 Evolution of Galactic α-process vs. iron-group elements: log (Mg/Fe) as a function of Fe abundance. Literature data on solar-type stars are displayed as grey symbols (green online) – squares: Fuhrmann (1998, 2004); triangles: Edvardsson et al. (1993). All other symbols as in Fig. 16. |
Observational constraints on the interlinked evolution of CNO are displayed in Fig. 16. Abundances from early B-type stars are compared to data from solar-type stars in the Galactic thin and thick disk, and in the halo. Typical statistical accuracies for abundances in solar-type stars are ~0.05–0.10 dex for LTE analyses, similar to the present work. Note, however, that systematic uncertainties due to non-LTE and 3D effects (and additionally due to the presence of magnetic field and stellar activity/chromospheres) can be substantial for solar-type stars, but are not understood comprehensively at present16. The comparison of literature data for the B-stars in the left panels and our data in the right panels shows once more which improvements in the precision and accuracy of the analyses were achieved.
In terms of the investigation of the cosmic chemical evolution the current focus of studies in the literature lies on the early phases at low metallicity. The interpretation of the data comes from the comparison with Galactic chemical evolution (GCE) models, which have to match the present-day composition as a boundary condition. It is therefore important for the entire modelling which reference values are used, solar or CAS abundances. In particular the differences in the C/O ratio are appreciable, also with respect to the majority of nearby solar-type stars, amounting to almost 50%. Taken at face value this difference indicates that the C/O enrichment of the ISM in the present-day solar neighbourhood occurred slower than at the Sun’s place of birth (see Sect. 7.5). No such conclusions could be drawn from the available literature data on early B-type stars so far.
Note that the Sun may be viewed as an extreme but still compatible case in terms of the distribution of the stars from the present sample in the log O–log C/O diagram, but the absolute values for the carbon abundance differ significantly. The solar and CAS data on N/O are rather compatible on the other hand. A systematic investigation of nitrogen abundances in high-metallicity solar-type stars would be desirable for further comparisons.
The occurrence of α-enhancement in the old stars of the halo and of the thick disk, Fig. 17, is well understood in terms of the different evolution timescales of supernovae of type Ia and II. The CAS Mg/Fe-ratio is compatible with the data from the Sun and from nearby solar-type stars, though it is somewhat low. Metal-poor objects among the solar-type stars are easily explained by their large lifetimes. However, metal-rich stars are absent among the young stars from the present sample, while they are common among the solar-type stars. Finding a reason for this is not straightforward in terms of standard GCE (metallicity is supposed to increase in time), but see the discussion in Sect. 7.5 related to radial migration. Again, data on early B-type stars from the literature were inconclusive in these terms.
Overall, it is astonishing how different and at the same time how similar the young and old star populations in the solar neighbourhood are. It is for the first time that this is elaborated, as the lack of high precision and accuracy in many previous studies of early B-type stars prevented any meaningful conclusions to be drawn.
In addition, reference abundances are not only of interest in terms of the temporal evolution of elemental abundances, but also for the spatial distribution, in particular for the interpretation of Galactic abundance gradients. The current sample is not useful for deriving abundance gradients per se because of the small baseline spread in terms of Galactocentric radius (about 400 pc). However, the CAS provides a highly robust anchor point for theoretical models at the solar circle, implying agreement with the solar standard for some elements, but also systematic shifts of various degrees for other elements.
7.5. The Sun: an immigrant to its current neighbourhood
In a strict sense, comparisons of the CAS and the solar chemical composition discussed in the previous sections are meaningful in terms of GCE only when there is a causal relationship of the 4.56 Gyr old solar matter and the present-day material in its surroundings. In other words, the question is whether the matter that we see in the nearby new-born stars, as represented in particular by the early B-type stars, and in the local ISM has chemically evolved from the matter that was around at the birth of the Sun. The existence of such a relationship is a strong assumption for most previous and current GCE modelling17.
Chemical tagging of the Sun’s place of birth.
Unfortunately, the birth-place of the Sun is unknown and tracing its orbit back is a highly complex task. Passages near other stars or molecular clouds, which are a stochastic process, and dynamical interactions with spiral arms prevent a straightforward integration of the Sun’s orbit in the Galactic potential backward in time from being successful. Improvements in our detailed understanding of the relevant processes affecting the motions of stars will certainly result from the Gaia mission in the future. But for the moment, we can rely only on a statistical approach, using the theoretical framework of Galactic dynamics and kinematics (e.g. Wielen et al. 1996; Sellwood & Binney 2002) that predict that old stars like the Sun are able to migrate up to several kiloparsecs radially through the Galactic disk over their lifetime. It is therefore possible that the Sun was born away from the present solar circle. Chemical abundances can provide valuable additional constraints.
The radial migration of stars within the Galaxy has been incorporated in Galactic chemical evolution calculations for the first time by Schönrich & Binney (2009). This kind of models constitutes a more realistic theoretical frame that could be used to refine the previous estimations (e.g. Wielen et al. 1996) of the solar place of origin. It is important, though, to bear in mind that details in the model input like e.g. the adoption of different yields or abundance gradients along the Galactic disk may have a non-negligible effect in such estimations (Schönrich, priv. comm.). The required systematic studies are beyond the scope of the present paper, but we can provide some qualitative evaluation, which is illustrated by Table 11.
In order to make a meaningful comparison of metal abundances in terms of Galactic chemical evolution, CAS values need to be compared to the bulk composition of the Sun (i.e. protosolar values18), corrected for the effects of GCE. The required abundance enrichments due to GCE are difficult to be quantified, as they depend on many model details like e.g. the adopted star-formation history and yields. Crucial is that enrichment is expected to occur, not depletion. In view of the previous discussion in this section and in Sect. 7.4, it is therefore in fact the similarities of the solar values and the present-day CAS, which are astonishing, and less the differences.
Let us elaborate the argument in more detail: assume that the protosolar nebula would not have collapsed to the Protosun (with elemental abundances according to Cols. 2 and 3 of Table 11). Instead, the gas would have been enriched in metal content over the past 4.56 Gyrs as predicted by GCE models for the present solar vicinity, leading to the formation of the Sun at the present day, with abundances according to Cols. 4 and 5. The Sun would appear significantly more metal rich than its surroundings, represented by the CAS (Col. 6).
A different birth place of the Sun than around the solar circle could resolve this apparent contradiction. Higher abundance values have been characteristic for the inner disk of the Milky Way for a long time over Galactic history. This does not only apply to individual metal abundances, the argument is further sustained by the presence of a higher C/O ratio in the Sun than in the CAS (independent of the reference of solar abundances). The inner disk shows a higher C/O ratio, which is supported both by an observationally derived negative radial C/O gradient (Esteban et al. 2005) and some GCE models (e.g. Carigi et al. 2005).
In order to further constrain the origin of the Sun, we have to correct the CAS data for the effects of Galactic abundance gradients19 (Col. 7 in Table 11), which were derived from a carefully analysed sample of H ii regions (Esteban et al. 2005; Carigi et al. 2005) and the modelling of the Cepheid data of Andrievsky et al. (2004, and references therein) by Cescutti et al. (2007). From our own experience, we consider these works as sources of reliable data on this topic, see Przybilla (2008) and Firnstein (2010) for a discussion. The results from the gradient-corrected CAS values at Galactocentric radii Rg of 6 and 5 kpc are shown in Cols. 8 and 9 of Table 11.
The comparison of the GCE-corrected protosolar abundances with the gradient-corrected CAS values suggests that the birthplace of the Sun was located at a Rg between 5 to 6 kpc (depending on the solar standard reference, which introduces another uncertainty to the previous considerations). We conclude that the Sun – and probably many other nearby older and metal-rich stars – are immigrants to the present solar neighbourhood, supporting views that stellar radial migration is essential for understanding Galactic evolution (Schönrich & Binney 2009). It would be highly interesting though difficult to investigate the details of the Sun’s migration to its current location close to the Galactic co-rotation radius, which is so favourable for the existence of life on Earth (Leitch & Vasisht 1998).
8. Summary
With the present work we have established a new benchmark for analyses of early B-type stars, demonstrating that practically the entire observed spectra can be reproduced reliably. It was shown that by the combined use of sophisticated models and of a thorough analysis methodology on high-quality spectra absolute stellar parameters and elemental abundances for early-type stars can be determined with a precision rivaling that of differential studies of solar-type stars. The successful simultaneous match of many independent observational indicators like the Balmer line wings, multiple ionization equilibria, SEDs and the agreement of spectroscopic and Hipparcos distances indicates that high accuracy was achieved at the same time, facilitated by the minimisation of systematic errors wherever they could be identified.
Overall, our analysis methodology provides both the accuracy and precision to use early B-type stars as versatile tools for astrophysics, besides our immediate objective here. Some conclusions from earlier applications get even strengthened in retrospect by the present work: e.g. on chemical tagging in order to determine population membership of hypervelocity stars (Przybilla et al. 2008a; Tillich et al. 2009), the investigation of subtle abundance signatures to constrain supernova nucleosynthesis from binary supernova runaways (Przybilla et al. 2008b; Irrgang et al. 2010), or on coupling quantitative spectroscopy with asteroseismic analysis of pulsating OB stars observed with CoRoT (Briquet et al. 2011). And, the methodology offers a high potential for future applications, that may facilitate many more facets of astrophysics to be studied at high confidence.
The principal application of our novel analysis methodology here was on a larger sample of nearby apparently slowly-rotating early B-type stars that were cleaned from peculiar objects. This confirmed that the young stellar component of the solar neighbourhood is chemically homogeneous to better than 10%, in accordance to studies of the local ISM abundances – the material out of which the stars formed. This in turn allowed us to establish a present-day cosmic abundance standard (CAS), which has the advantage of redundancy when compared to the solar standard, as it is based on an entire sample of stars instead of one object alone. So far, information for the most abundant chemical species have been provided, with log ε ≥ 7.50.
First implications of the existence of a present-day cosmic abundance standard were outlined here. The CAS represents the recommended initial chemical composition for stellar structure and evolution calculations, in particular for short-lived massive stars. Observationally, nitrogen enrichment in about 1/3 of the sample objects indicates mixing of the surface layers with CN-processed material from the stellar core, with the abundance ratios for the light elements carbon, nitrogen and oxygen following tightly the predicted nuclear path of the CNO cycles.
The CAS provides the to date most authoritative reference for constraining the chemical composition of the ISM dust-phase. A silicate-rich and relatively carbon-poor nature of the local ISM dust is inferred, challenging many contemporary dust models. In combination with the finding that carbonaceous dust is practically absent inside the Orion H ii region this implies that the dust in the ISM is in its majority composed of silicates, PAHs, organic refractory material and possibly amorphous carbon, with only little carbon incorporated in graphite.
The CAS provides tight reference points for anchoring models of the chemical evolution of the Milky Way, constraining the present-day endpoint of Galactic nucleosynthesis in the solar neighbourhood in the course of the cosmic matter cycle. We discussed in particular the examples of the light elements CNO, and the Mg/Fe ratio as a tracer for the α/Fe ratio. While the CAS indicates a surprisingly good agreement with most inferences from the solar abundances, a striking difference is found for the C/O ratio, amounting to almost 50% between cosmic and solar values. Intriguingly, early B-type stars with super-solar metallicity are absent in the solar neighbourhood, while several nearby solar-type stars show super-solar metallicities. This can be interpreted as a consequence of radial migration of stars within the Galactic disk.
Finally, the comparison of the CAS with the solar standard in view of Galactic chemical evolution (GCE) shows that the highly successful use of the Sun as proxy for cosmic abundances is somewhat coincidental. Radial migration outward from its birth place in the inner disk at ~ 5–6 kpc Galactocentic distance (where higher metallicity values were reached earlier in cosmic history) over its lifetime to its current neighbourhood has compensated for the expected metal enrichment in the course of GCE. A telltaling signature is left only in the C/O ratio. The present work provides the so far most stringent evidence in terms of chemical signature that the Sun – like many other solar-type stars – is an immigrant to its current Galactic neighbourhood.
Online material
 |
Fig. 4 Comparison between synthetic fluxes based on Teff and log g values from multiple ionization equilibria to observed spectral energy distributions for the sample stars with available IUE data. Displayed are wavelength-weighted fluxes λFλ from the far-UV to the near-IR in the K-band. Observations consist of IUE spectra (black lines), Johnson UBVRIJHK photometry (boxes) and 2MASS JHK photometry (circles). Model fluxes are indicated by red lines. The observations have been dereddened adopting colour excesses as indicated and the model fluxes have been normalised with respect to the observations in V. Some fluxes have been scaled for clarity, as indicated. |
 |
Fig. 7 Metal abundances as a function of effective temperature (left) and of surface gravity (right). Sample stars from the present work are indicated by dots, data from NS11 by open circles. Error bars are statistical 1σ-uncertainties. Average abundances from the combined samples are indicated by the dashed line, the dotted lines delineate the 1σ-scatter around the average value. See Sect. 5.2 for a discussion. |
 |
Fig. 8a Comparison between global synthetic and observed spectrum for the B3 III-type star #15 = 18 Peg (Teff = 15 800 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
 |
Fig. 9a Comparison between global synthetic and observed spectrum for the B2 IV-type star #7 =γ Peg (Teff = 22 000 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
 |
Fig. 10a Comparison between global synthetic and observed spectrum for the B1 V-type star #1= HR 1861 (Teff = 27 000 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
 |
Fig. 11a Comparison between global synthetic and observed spectrum for the B0.2 V-type star #6 = τ Sco (Teff = 32 000 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
Spectral line analysis of the program stars.
Example of abundance changes caused by atmospheric parameter variations for HD 886.
The contemporarily most prominent example may be the so-called solar composition problem (Basu & Antia 2008), the mismatch of solar interior models based on modern (lower) solar abundances with helioseismic observations, whereas consensus was established with previous higher metallicity values of Grevesse & Sauval (1998).
Recombination or collisionally excited lines can indicate rather discrepant results (see e.g. Simón-Díaz & Stasińska 2011).
Note that typical uncertainties for effective temperature given in the literature are ≤ 3–5%, however these do not take into account the large discrepancies – up to ~4000 K – that exist between different temperature determination methods, see Sect. 5.2 of NP08 for a discussion. In the extremes, error estimates of up to 40–60% in surface gravity and a factor 3–5 in elemental abundances are found in the literature (e.g. Hunter et al. 2007; Trundle et al. 2007).
The presence of light from a companion in the spectrum of HD 37023 was indicated recently also by Simón-Díaz (2010, his footnote 3), however without giving further details.
Spectrum Plotting and Analysing Suite, Spas (Hirsch 2009).
Note that we analyse Si iii/iv lines only because the model atom employed here underestimates silicon abundances derived from Si ii lines, see Simón-Díaz (2010) for a discussion.
This is strictly valid only for the time of observation, see Sect. 2.2. The variable stars are expected to show (correlated) changes of Teff and log g, (de Ridder et al. 2002; Catanzaro & Leone 2008), which may exceed the given uncertainties in Table 5. Average atmospheric parameters as derived from the analysis of time-series observations may be more appropriate in this context, however our approach recovers the time-invariant quantities like elemental abundances, which is the main topic of the present work.
More comprehensive line identifications for early B-type stars are provided e.g. by Kilian et al. (1991) for the optical blue spectral region, or by Gummersbach & Kaufer, online via http://www.lsw.uni-heidelberg.de/cgi-bin/websynspec.cgi
Amorphous carbon is considered the predominant grain material produced by C-type asymptotic giant branch stars, the main source of carbonaceous dust (e.g. Wallerstein & Knapp 1998).
Approximate corrections for such effects may e.g. reproduce the upturn in the C/O ratio at low O as indicated by the (non-LTE) data of Fabbian et al. (2009) also in the data of Spite et al. (2005). However, we prefer to display uncorrected values, as these are likely more realistic in view of more recent investigations (M. Spite, priv. comm.).
Over the lifetime of the Sun, the combined effects of thermal diffusion, gravitational settling and radiative acceleration have lead to a build-up of helium and metal abundances below the convection zone, such that the photospheric abundances are not representative for the bulk composition of the Sun.
Data are for the present-day, but GCE models suggest that the flattening of Galactic abundance gradients over the lifetime of the Sun are insignificant for our considerations (Marcon-Uchida et al. 2010).
Acknowledgments
We wish to thank M. Firnstein and T. Kupfer for help with the reduction of Foces spectra, K. Butler for providing Detail/Surface, H. Hirsch for making Spas available and E. Niemczura for computations of Atlas9 models. We are grateful to M. Asplund, U. Heber, G. Meynet, R. Schönrich, S. Simón-Díaz, E. Ntormousi and the MPA SAGA-group for fruitful discussions, and the referee for valuable suggestions. We thank the staff at Calar Alto for performing observations in the service run of 2005. Some of the data presented in this paper were obtained from the Multimission Archive at the Space Telescope Science Institute (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NAG5-7584 and by other grants and contracts. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. Travel to the Calar Alto Observatory/Spain in 2001 was supported by DFG under grant PR 685/1-1.
References
- Adelman, S. J., Pintado, O. I., Nieva, M. F., Rayle, K. E., & Sanders, S. E., Jr. 2002, A&A, 392, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C., Puls, J., Godart, M., & Dupret, M.-A. 2009, A&A, 508, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amari, S., Anders, A., Virag, A., & Zinner, E. 1990, Nature, 345, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Andrievsky, S. M., Korotin, S. A., Luck, R. E., & Kostynchuk, L. Y. 1999, A&A, 350, 598 [NASA ADS] [Google Scholar]
- Andrievsky, S. M., Luck, R. E., Martin, P., & Lépine, J. R. D. 2004, A&A, 413, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Ser., 336, 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 (AGSS09) [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Martin, P. G., et al. 1991, ApJ, 374, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, D., & Damgaard, A. 1949, Phil. Trans. R. Soc. London, Ser. A, 242, 101 [Google Scholar]
- Becker, S. R. 1998, ASP Conf. Ser., 131, 137 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1988, A&A, 201, 232 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1989, A&A, 209, 244 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1990, A&A, 235, 326 [NASA ADS] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 337, 321 [NASA ADS] [Google Scholar]
- Briquet, M., Aerts, C., Baglin, et al. 2011, A&A, 527, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, K., & Giddings, J. R. 1985, in Newsletter of Analysis of Astronomical Spectra, No. 9 (Univ. London) [Google Scholar]
- Butler, K., Mendoza, C., & Zeippen, C. J. 1993, J. Phys. B, 26, 4409 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2010, Sol. Phys., 268, 255 (CLSFB10) [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carigi, L., Peimbert, M., Esteban, C., & García-Rojas, J. 2005, ApJ, 623, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Cartledge, S. I. B., Lauroesch, J. T., Meyer, D. M., & Sofia, U. J. 2004, ApJ, 613, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Cartledge, S. I. B., Lauroesch, J. T., Meyer, D. M., & Sofia, U. J. 2006, ApJ, 641, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Catanzaro, G., & Leone, F. 2008, MNRAS, 389, 1414 [NASA ADS] [CrossRef] [Google Scholar]
- Cescutti, G., Matteucci, F., François, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Romano, D., & Matteucci, F. 2003, MNRAS, 339, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., & Lambert, D. L. 1994, ApJ, 426, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Hubeny, I., & Lanz, T. 2006, ApJ, 647, 143 [Google Scholar]
- Daflon, S., Cunha, K., & Becker, S. R. 1999, ApJ, 522, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., Becker, S. R., & Smith, V. V. 2001a, ApJ, 552, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., Butler, K., & Smith, V. V. 2001b, ApJ, 563, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., Smith, V. V., & Butler, K. 2003, A&A, 399, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2007, ApJ, 665, 35 [Google Scholar]
- de Ridder, J., Dupret, M.-A., Neuforge, C., & Aerts, C. 2002, A&A, 385, 572 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmet, M., Briquet, M., Thoul, A., et al. 2009, MNRAS, 396, 1460 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog, 2237 [Google Scholar]
- Dufton, P. L., Brown, P. J. F., Lennon, D. J., & Lynas-Gray, A. E. 1986, MNRAS, 222, 713 [NASA ADS] [Google Scholar]
- Dwek, E., Arendt, R. G., Fixsen, D. J., et al. 1997, ApJ, 475, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Esteban, C., Peimbert, M., García-Rojas, J., et al. 2004, MNRAS, 355, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., García-Rojas, J., Peimbert, M., et al. 2005, ApJ, 618, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbian, D., Nissen, P. E., Asplund, M., Pettini, M., & Akerman, C. 2009, A&A, 500, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Firnstein, M. 2010, Ph.D. Thesis, University of Erlangen-Nuremberg [Google Scholar]
- Froese Fischer, C., & Tachiev, G. 2004, At. Data Nucl. Data Tables, 87, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C., Tachiev, G., & Irimia, A. 2006, At. Data Nucl. Data Tables, 92, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhr, J. R., & Wiese, W. L. 1998, in CRC Handbook of Chemistry and Physics, 79th edn., ed. D. R. Lide (Boca Raton: CRC Press) [Google Scholar]
- Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. & Chem. Ref. Data, 17, 4 [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Giddings, J. R. 1981, Ph.D. Thesis, University of London [Google Scholar]
- Gies, D. R., & Lambert, D. L. 1992, ApJ, 387, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres, 3rd edn. (Cambridge University Press, Cambridge) [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 (GS98) [NASA ADS] [CrossRef] [Google Scholar]
- Grigsby, J. A., Morrison, N. D., & Anderson, L. S. 1992, ApJS, 78, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Karlsson, T., Olsson, E., Edvardsson, B., & Ryde, N. 1999, A&A, 342, 426 [NASA ADS] [Google Scholar]
- Heber, U., Hunger, K., Jonas, G., & Kudritzki, R. P. 1984, A&A, 130, 119 [NASA ADS] [Google Scholar]
- Heber, U., Moehler, S., Napiwotzki, R., Thejll, P., & Green, E. M. 2002, A&A, 383, 938 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Henrichs, H. F., de Jong, J. A., Donati, J.-F., et al. 2000, ASP Conf. Ser., 214, 324 [NASA ADS] [Google Scholar]
- Herrero, A. 2003, ASP Conf. Ser., 304, 10 [NASA ADS] [Google Scholar]
- Herrero, A., & Lennon, D. J. 2004, in Stellar Rotation, ed. A. Maeder, & P. Eenens (San Francisco: ASP), 209 [Google Scholar]
- Hirsch, H. 2009, Ph.D. Thesis, University of Erlangen-Nuremberg [Google Scholar]
- Hoffleit, D., & Jaschek, C. 1982, The Bright Star Catalogue, 4th edn. (New Haven: Yale University Observatory) [Google Scholar]
- Hunter, I., Dufton, P. L., Smartt, S. S., et al. 2007, A&A, 466, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irrgang, A., Przybilla, N., Heber, U., et al. 2010, ApJ, 711, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Israelian, G., Ecuvillon, A., Rebolo, R., et al. 2004, A&A, 421, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaschek, M., & Egret, D. 1982, in Be Stars, ed. M. Jaschek, & H.-G. Groth, 261 [Google Scholar]
- Jensen, A. G., Rachford, B. L., & Snow, T. P. 2007, ApJ, 654, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, ESO Messenger, 95, 8 [NASA ADS] [Google Scholar]
- Kilian, J. 1992, A&A, 262, 17 [Google Scholar]
- Kilian, J. 1994, A&A, 282, 867 [NASA ADS] [Google Scholar]
- Kilian, J., Montenbruck, O., & Nissen, P. E. 1991, A&AS, 88, 101 [NASA ADS] [Google Scholar]
- Korn, A. J. 2002, in Scientific Drivers for ESO Future VLT/VLTI Instrumentation, ed. J. Bergeron, & G. Monnet (Berlin: Springer), 199 [Google Scholar]
- Kurucz, R. L. 1993a, CD-ROM No. 2–12 (Cambridge, Mass: SAO) [Google Scholar]
- Kurucz, R. L. 1993b, CD-ROM No. 13 (Cambridge, Mass: SAO) [Google Scholar]
- Kurucz, R. L., & Bell, B. 1995, CD-ROM No. 23 (Cambridge, Mass: SAO) [Google Scholar]
- Leitch, E. M., & Vasisht, G. 1998, New A, 3, 51 [Google Scholar]
- Leone, F., Lanzafame, A. C., & Pasquini, L. 1995, A&A, 293, 457 [NASA ADS] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, in Landolt-Börnstein, New Series VI/4B, ed. J. E. Trümper (Berlin: Springer) [Google Scholar]
- Lutz, T. E., & Kelker, D. H. 1973, PASP, 85, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubimkov, L. S., Rostopchin, S. I., & Lambert, D. L. 2004, MNRAS, 351, 745 [Google Scholar]
- Lyubimkov, L. S., Rostopchin, S. I., Rachkovskaya, T. M., et al. 2005, MNRAS, 358, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Mar, S., Pérez, C., González, V. R., et al. 2000, A&AS, 144, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcolino, W. L. F., Bouret, J.-C., Martins, F., et al. 2009, A&A, 498, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcon-Uchida, M. M., Matteucci, F., & Costa, R. D. D. 2010, A&A, 520, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matheron, P., Escarguel, A., Redon, R., Lesage, A., & Richou, J. 2001, J. Quant. Spec. Radiat. Transf., 69, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza, C., Eissner, W., LeDourneuf, M., & Zeippen, C. J. 1995, J. Phys. B, 28, 3485 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J. C. 1991, Catalogue of Homogeneous Means in the UBV System, Institut d’Astronomie, Universite de Lausanne [Google Scholar]
- Meyer, D. M., Cardelli, J. A., & Sofia, U. J. 1997, ApJ, 490, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 411, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, M., & Magnenat, P. 1978, A&AS, 34, 477 [NASA ADS] [Google Scholar]
- Morel, T. 2009, CoAst, 158, 122 [Google Scholar]
- Morel, T., & Butler, K. 2008, A&A, 487, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Butler, K., Aerts, C., et al. 2006, A&A, 457, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Hubrig, S., & Briquet, M. 2008, A&A, 481, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N. 2002, At. Data Nucl. Data Tables, 80, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Neiner, C., Henrichs, H. F., Floquet, M., et al. 2003, A&A, 411, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Computer Journal, 7, 308 [CrossRef] [Google Scholar]
- Nieva, M. F. 2007, Ph.D. Thesis, Univ. Erlangen-Nuremberg and Obs. Nacional/MCT (Berlin: Verkannten Verlag) [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2006, ApJ, 639, L39 (NP06) [NASA ADS] [CrossRef] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2007, A&A, 467, 295 (NP07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2008, A&A, 481, 199 (NP08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2010a, ASP Conf. Ser., 425, 146 [NASA ADS] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2010b, EAS Publ. Ser., 43, 167 [Google Scholar]
- Nieva, M. F., & Simón-Díaz, S. 2011, A&A, 532, A2 (NS11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nussbaumer, V. H. 1986, A&A, 155, 205 [NASA ADS] [Google Scholar]
- Pfeiffer, M. J., Frank, C., Baumüller, D., Fuhrmann, K., & Gehren, T. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N. 2005, A&A, 443, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N. 2008, Rev. Mod. Astron., 20, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., & Butler, K. 2001, A&A, 379, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., & Butler, K. 2004, ApJ, 609, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Butler, K., Becker, S. R., et al. 2000, A&A, 359, 1085 [NASA ADS] [Google Scholar]
- Przybilla, N., Butler, K., & Kudritzki, R. P. 2001, A&A, 369, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Butler, K., Heber, U., & Jeffery, C. S. 2005, A&A, 443, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P., 2006a, A&A, 445, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Nieva, M. F., & Edelmann, H. 2006b, Balt. Astron., 15, 107 [Google Scholar]
- Przybilla, N., Nieva, M. F., Heber, U., & Jeffery, C. S. 2006c, Balt. Astron., 15, 163 [Google Scholar]
- Przybilla, N., Nieva, M. F., Heber, U., et al. 2008a, A&A, 480, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Nieva, M. F., Heber, U., & Butler, K. 2008b, ApJ, 684, L103 [Google Scholar]
- Przybilla, N., Nieva, M. F., & Butler, K. 2008c, ApJ, 688, L103 (PNB08) [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Nieva, M. F., & Butler, K. 2011, J. Phys.: Conf. Ser., 328, 012015 [NASA ADS] [CrossRef] [Google Scholar]
- Ramspeck, M., Heber, U., & Moehler, S. 2001, A&A, 378, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, J.-R., & Kunth, D. 1995, A&A, 294, 432 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Scalo, J., & Elmegreen, B. G. 2004, ARA&A, 42, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schiller, F., & Przybilla, N. 2008, A&A, 479, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, S. E., Kaper, L., Lamers, H. J. G. L. M., & Brown, A. G. A. 2004, A&A, 428, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S. 2010, A&A, 510, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., & Stasińska, G. 2011, A&A, 526, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. C. 1996, Ap&SS, 237, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H., Jr. 2003, MNRAS, 338, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & Witt, A. N. 1995, Science, 270, 1455 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sofia, U. J. 2004, ASP Conf. Ser., 309, 393 [Google Scholar]
- Sofia, U. J., & Meyer, D. M. 2001, ApJ, 554, L221 (SM01) [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Parvathi, V. S., Babu, B. R. S., & Murthy, J. 2011, AJ, 141, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trundle, C., Dufton, P. L., Hunter, I., et al. 2007, A&A, 471, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tillich, A., Przybilla, N., Scholz, R.-D., & Heber, U. 2009, A&A, 507, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the new reduction of the raw data (Dordrecht: Springer) [Google Scholar]
- Vitrichenko, E. A. 2002, Astron. Lett., 28, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Vrancken, M., Butler, K., & Becker, S. R. 1996, A&A, 311, 66 [Google Scholar]
- Walborn, N. R. 1971, ApJS, 23, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., & Knapp, G. R. 1998, ARA&A, 36, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R., Fuchs, B., & Dettbarn, C. 1996, A&A, 314, 438 [NASA ADS] [Google Scholar]
- Wiese, W. L., Smith, M. W., & Miles, B. M. 1969, Nat. Stand. Ref. Data Ser., Nat. Bur. Stand. (U.S.), NSRDS-NBS 22, Vol. I [Google Scholar]
- Wiese, W. L., Fuhr, J. R., & Deters, T. M. 1996, J. Phys. & Chem. Ref. Data, Mon., 7 [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Example of abundance changes caused by atmospheric parameter variations for HD 886.
All Figures
 |
Fig. 1 Distribution of the sample stars in the solar neighbourhood. Upper panel: galactic plane projection, the Galactic centre lies in direction of the bottom of the panel. Lower panel: rotational plane projection, the Northern Galactic Pole lies in direction of the top of the panel. The sample stars that are analysed quantitatively here are marked by dots, open boxes mark candidate SB2 systems and open circles stars that were excluded from the analysis because of other peculiarities. Numbers/letters correspond to those of our internal numbering in the tables. Error bars are of spectroscopic distances (stars 1–20, see Table 5) and of measured parallaxes (objects A–G). The position of the Sun is marked by ⊙ . |
| In the text | |
 |
Fig. 2 Examples of prominent spectral lines of the newly identified candidate SB2 systems in our sample, HD 22951 (B0.5 V), HD 35468 (B2 III) and HD 37023 (B0.5 V). For comparison the corresponding spectral lines in the single star HD 36822 (B0 III) are shown as well. The emission peak in He i λ6678 of the Trapezium star HD 37023 in Orion is of nebular origin. |
| In the text | |
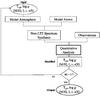 |
Fig. 3 Schematic diagram of our analysis method. See Sect. 4.1 for details. |
| In the text | |
 |
Fig. 5 The sample stars in the Teff–log g plane. 1σ-uncertainties are shown. Numbering according to Table 1. Overlaid are evolution tracks for non-rotating stars of metallicity Z = 0.02 from Meynet & Maeder (2003, full lines) and Schaller et al. (1992, dotted lines). See Sect. 5.1 for a discussion. |
| In the text | |
 |
Fig. 6 Results of the distance determination. Upper panel: comparison of spectroscopic and Hipparcos distances. 1σ-uncertainties are shown. Numbering according to Table 1. The 1:1 relation is indicated by the dashed line. Lower panel: percent difference of the two distance indicators. Open circles mark the data if corrected for Lutz-Kelker bias. See Sect. 5.1 for a discussion. |
| In the text | |
 |
Fig. 12 Abundance distributions for the astrophysically most relevant chemical species as derived from early B-type stars in the solar neighbourhood. Red histograms: present work, establishing the cosmic abundance standard. Black histograms: literature data. Photospheric and protosolar abundances from AGSS09 are also indicated, the bars representing the range spanned by the ± 1σ-uncertainties. See Sect. 6 for details. |
| In the text | |
 |
Fig. 13 Spatial distribution of oxygen abundances in the sample stars, in analogy to Fig. 1. Open circles represent objects from NS11. The symbol size encodes the abundance according to the figure legend. |
| In the text | |
 |
Fig. 14 Observational constraints on mixing of CNO-burning products in massive stars. Mass ratios N/C over N/O are displayed. Black dots: present data; black circles: 9 additional objects from NS11. Data from previous non-LTE analyses are given as grey symbols (green online) – plus signs: Kilian (1992); triangles: Gies & Lambert (1992); diamonds: Cunha & Lambert (1994), Daflon et al. (1999, 2001a,b); squares: Morel et al. (2008); crosses: Hunter et al. (2009). The predicted nuclear paths assuming initial CAS abundances (red star) and solar abundances ( ⊙ ) of Asplund et al. (2009) are indicated by the long-dashed and dotted lines, respectively. Statistical uncertainties of 0.2 dex in each element – which are typical for previous literature data – result in an error bars more than twice as large than those from the present data. |
| In the text | |
 |
Fig. 15 Comparison of the stellar O abundance distribution as derived in the present work (red histogram) with gas-phase abundances along different sightlines of the diffuse ISM (thin blue histogram, Cartledge et al. 2004), in analogy to Fig. 12. Mean abundances are indicated. |
| In the text | |
 |
Fig. 16 Observational constraints on the chemical evolution of Galactic CNO abundances: abundance ratios log (C/O) and log (N/O) vs. O abundance. Left panels: black triangles: early B-stars from the literature extracted from Fig. 12. Data for low-mass stars are displayed as grey symbols (green in the online edition) – squares: Gustafsson et al. (1999, solar-type dwarfs); crosses: Fabbian et al. (2009, solar-type dwarfs and subgiants); diamonds: Spite et al. (2005, unmixed cool giants); plus signs: Israelian et al. (2004, unevolved solar-type stars). Solar abundance ratios of Asplund et al. (2009) are also indicated ( ⊙ ). Right panels: black dots: unmixed objects from the present work, black circles: unmixed stars from NS11. Data from the literature like in the left panels. The CAS is also indicated (red star). Error bars (statistical 1σ-uncertainties) typical for individual stars in the present study are shown. |
| In the text | |
 |
Fig. 17 Evolution of Galactic α-process vs. iron-group elements: log (Mg/Fe) as a function of Fe abundance. Literature data on solar-type stars are displayed as grey symbols (green online) – squares: Fuhrmann (1998, 2004); triangles: Edvardsson et al. (1993). All other symbols as in Fig. 16. |
| In the text | |
 |
Fig. 4 Comparison between synthetic fluxes based on Teff and log g values from multiple ionization equilibria to observed spectral energy distributions for the sample stars with available IUE data. Displayed are wavelength-weighted fluxes λFλ from the far-UV to the near-IR in the K-band. Observations consist of IUE spectra (black lines), Johnson UBVRIJHK photometry (boxes) and 2MASS JHK photometry (circles). Model fluxes are indicated by red lines. The observations have been dereddened adopting colour excesses as indicated and the model fluxes have been normalised with respect to the observations in V. Some fluxes have been scaled for clarity, as indicated. |
| In the text | |
 |
Fig. 7 Metal abundances as a function of effective temperature (left) and of surface gravity (right). Sample stars from the present work are indicated by dots, data from NS11 by open circles. Error bars are statistical 1σ-uncertainties. Average abundances from the combined samples are indicated by the dashed line, the dotted lines delineate the 1σ-scatter around the average value. See Sect. 5.2 for a discussion. |
| In the text | |
 |
Fig. 8a Comparison between global synthetic and observed spectrum for the B3 III-type star #15 = 18 Peg (Teff = 15 800 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
| In the text | |
 |
Fig. 8b Same as Fig. 8a in the spectral range λλ 4500–5100 Å. |
| In the text | |
 |
Fig. 8c Same as Fig. 8a in the spectral range λλ 5100–5700 Å. |
| In the text | |
 |
Fig. 8d Same as Fig. 8a in the spectral range λλ 5700–6300 Å. |
| In the text | |
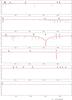 |
Fig. 8e Same as Fig. 8a in the spectral range λλ 6300–6880 Å. |
| In the text | |
 |
Fig. 9a Comparison between global synthetic and observed spectrum for the B2 IV-type star #7 =γ Peg (Teff = 22 000 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
| In the text | |
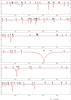 |
Fig. 9b Same as Fig. 9a in the spectral range λλ 4500–5100 Å. |
| In the text | |
 |
Fig. 9c Same as Fig. 9a in the spectral range λλ 5100–5700 Å. |
| In the text | |
 |
Fig. 9d Same as Fig. 9a in the spectral range λλ 5700–6300 Å. |
| In the text | |
 |
Fig. 9e Same as Fig. 9a in the spectral range λλ 6300–6880 Å. |
| In the text | |
 |
Fig. 10a Comparison between global synthetic and observed spectrum for the B1 V-type star #1= HR 1861 (Teff = 27 000 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
| In the text | |
 |
Fig. 10b Same as Fig. 10a in the spectral range λλ 4500–5100 Å. |
| In the text | |
 |
Fig. 10c Same as Fig. 10a in the spectral range λλ 5100–5700 Å. |
| In the text | |
 |
Fig. 10d Same as Fig. 10a in the spectral range λλ 5700–6300 Å. |
| In the text | |
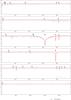 |
Fig. 10e Same as Fig. 10a in the spectral range λλ 6300–6880 Å. |
| In the text | |
 |
Fig. 11a Comparison between global synthetic and observed spectrum for the B0.2 V-type star #6 = τ Sco (Teff = 32 000 K) in the spectral range λλ 3900–4500 Å. See Sect. 5.3 for details. |
| In the text | |
 |
Fig. 11b Same as Fig. 11a in the spectral range λλ 4500–5100 Å. |
| In the text | |
 |
Fig. 11c Same as Fig. 11a in the spectral range λλ 5100–5700 Å. |
| In the text | |
 |
Fig. 11d Same as Fig. 11a in the spectral range λλ 5700–6300 Å. |
| In the text | |
 |
Fig. 11e Same as Fig. 11a in the spectral range λλ 6300–6880 Å. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


