| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 19 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117661 | |
| Published online | 01 February 2012 | |
Improved achromatization of phase mask coronagraphs using colored apodization
1
Laboratoire d’Astrophysique de Marseille, Université d’Aix-Marseille
& CNRS, UMR 7326,
38 rue Frédéric Joliot-Curie,
13388
Marseille Cedex 13,
France
e-mail: mamadou.ndiaye@oamp.fr; kjetil.dohlen@oamp.fr
2
Instituto de Astronomía, Universidad Nacional Autónoma de México
(UNAM), Apartado Postal 70-264 Ciudad Universitaria, 04510
México D.F.,
Mexico
3
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
4
Centro de Ciencias Aplicadas y Desarrollo Tecnológico, UNAM,
Apartado Postal 70-186 Ciudad Universitaria, 04510
México D.F.,
Mexico
5
Groupement d’Intérêt Scientifique PHASE (Partenariat Haute Résolution
Angulaire Sol-Espace), France
Received: 8 July 2011
Accepted: 3 November 2011
Context. For direct imaging of exoplanets, a stellar coronagraph helps to remove the image of an observed bright star by attenuating the diffraction effects caused by the telescope aperture of diameter D. The dual zone phase mask (DZPM) coronagraph constitutes a promising concept since it theoretically offers a small inner working angle (IWA ~ λ0/D where λ0 denotes the central wavelength of the spectral range Δλ), good achromaticity, and high starlight rejection, typically reaching a 106 contrast at 5 λ0/D from the star over a spectral bandwidth Δλ/λ0 of 25% (similar to H-band). This last value proves to be encouraging for broadband imaging of young and warm Jupiter-like planets.
Aims. Contrast levels higher than 106 are, however, required for observing older and/or less massive companions over a finite spectral bandwidth. An achromatization improvement of the DZPM coronagraph is therefore mandatory to reach such good performance.
Methods. In its design, the DZPM coronagraph uses a gray (or achromatic) apodization. We replaced it by a colored apodization to increase the performance of this coronagraphic system over a wide spectral range. This innovative concept, called colored apodizer phase mask (CAPM) coronagraph, is defined to reach the highest contrast in the exoplanet search area. Once this has been done, we study the performance of the CAPM coronagraph in the presence of different errors to evaluate the sensitivity of our concept.
Results. A 2.5 contrast gain is estimated from the performance provided by the CAPM coronagraph with respect to that of the DZPM coronagraph. A 2.2 × 10-8 intensity level at 5 λ0/D separation is then theoretically achieved with the CAPM coronagraph in the presence of a clear circular aperture and a 25% bandwidth. In addition, our studies show that our concept is less sensitive to low than to high-order aberrations for a given value of rms wavefront errors.
Key words: methods: numerical / techniques: high angular resolution / instrumentation: high angular resolution / telescopes
© ESO, 2012
1. Introduction
Recently, direct imaging of several exoplanets has been made possible (Kalas et al. 2008; Marois et al. 2008; Lagrange et al. 2010) by their youth (tens of Myr), their high mass (a few Jupiter masses), or their wide apparent distance from their host star (farther than 1 arcsec). For imaging older, less massive, or less separated planetary companions while enabling their spectroscopic observations, achromatic high-contrast imaging techniques are required. However, large broadband imaging of these exoplanets is extraordinarily challenging in the visible and near-infrared bands because of the high flux ratio (107 to 1010) and the small angular separation (less than 1 arcsec) between them and their host star (Traub & Oppenheimer 2010).
This detection requires the combination of different methods, such as extreme adaptive optics (XAO), stellar coronagraphy, and post processing techniques, to enhance the exoplanet image (Oppenheimer & Hinkley 2009). XAO systems on ground-based telescopes (Macintosh et al. 2008; Sauvage et al. 2010; Guyon et al. 2010b; Hinkley et al. 2011) will compensate for the effects of the atmospheric turbulence to provide high angular resolution images at a very high Strehl ratio. A stellar coronagraph (Guyon et al. 2006) will mostly help suppress the diffraction effects of the telescope aperture. In addition, post-processing techniques (e.g. Marois et al. 2000; Sparks & Ford 2002; Marois et al. 2006; Lafrenière et al. 2007; Mugnier et al. 2008; Vigan et al. 2008) will allow us to remove the speckles caused by the XAO residual aberrations and the slow variations in the physical conditions of a telescope.
The current limits of all these methods need to be pushed further to expect to image the exoplanets mentioned above. In particular, increasing the performance of the current coronagraphs is mandatory for reaching an excellent polychromatic removal of the star diffraction pattern and image the faintest substellar mass companions in white light. The resulting, innovative coronagraphs will find their place in the exoplanet imagers planned to follow the upcoming Palomar P1640 (Hinkley et al. 2011), VLT-SPHERE (Beuzit et al. 2008), Gemini Planet Imager (Macintosh et al. 2008), and Subaru HiCIAO (Hodapp et al. 2008): e.g., EPICS (Kasper et al. 2008) for the European Extremely Large Telescope (E-ELT) on the ground or possible 1–2 m off-axis telescopes in space (Galicher et al. 2010; Trauger et al. 2010; Guyon et al. 2010c).
Many coronagraphic designs have been proposed these past few years, most of them reported in Guyon et al. (2006). We are here particularly interested in the broadband behavior of coronagraphs, and although a complete review of the broadband performance of all the existing coronagraphs is not within the scope of this paper, we provide here some numbers from the literature allowing the presented work to be situated in the context of the state of the art, with λ0 and D denoting the central wavelength of the spectral range Δλ and the telescope aperture diameter.
The achromatic interfero coronagraph (Gay & Rabbia 1996) was the first attempt to make a concept able to image faint substellar mass companions close to the star in white light. This device can theoretically offer an intensity level of 1.6 × 10-5 at a distance of λ0/D from the star over a bandwidth (Δλ/λ0) of 18% (Baudoz et al. 2000). The apodized pupil Lyot coronagraph (Aime et al. 2002; Soummer et al. 2003a), a more recent concept, is one of the most popular designs, which was adopted for the forthcoming generation of exoplanet imagers (e.g. VLT-SPHERE, Gemini Planet Imager, Palomar P1640). It can theoretically reach an intensity level lower than 10-7 at 5 λ0/D over a bandwidth of 20%, in the presence of a telescope aperture with central obstruction (Aime 2005; Soummer 2005; Soummer et al. 2011). Band-limited coronagraphs (Kuchner & Traub 2002; Kuchner et al. 2005) also represent encouraging solutions for producing very high-contrast performance over wide spectral bands. Recent studies predict, for instance, that those concepts that use hybrid metal-dielectric masks and are combined with a deformable mirror, which is set to generate a dark half field in the image plane, can provide an intensity level of 4.9 × 10-10 at 3.5 λ0/D within this dark region, over a bandwidth of 20% (Moody et al. 2008). The phase induced amplitude apodization (PIAA, Guyon 2003) and its avatars (Guyon et al. 2005; Martinache et al. 2006; Pluzhnik et al. 2006; Guyon et al. 2010a) constitute some of the most promising solutions for Earth-like planet detection. Indeed, an intensity level of 10-10 at 1.5 λ0/D over a 21% bandwidth is predicted with a hybrid coronagraph composed of PIAA with a classical apodization (Pluzhnik et al. 2006).
Stellar coronagraphs using a phase mask in the focal plane represent some encouraging solutions for achieving the requested contrast levels, either in the form of sectorized masks (four quadrant phase mask, FQPM, Rouan et al. 2000; and eight octant phase mask, Murakami et al. 2008) or circular masks (Roddier & Roddier 1997; Soummer et al. 2003b). These systems are characterized by their very small inner working angles (IWAs) and good starlight rejection capabilities.
Achromatization of these phase mask coronagraphs has been intensively studied in the past few years to improve the capability of these concepts to work in broad spectral bands. For sectorized phase masks, the use of achromatic half-wave plates leads to intensity levels of 5 × 10-5 at 2.5 λ0/D from the star over a 20% bandwidth (Mawet et al. 2006).
Derived from the FQPM concept, the vector vortex coronagraph (Mawet et al. 2005, 2010) also provides achromatic solutions. Using liquid crystal polymers (LCP) for the manufacturing of such phase mask, intensity levels lower than 1.4 × 10-7 at 3 λ0/D for a 15% bandwidth can theoretically be reached (Mawet et al. 2005), and further improvements are expected using a 3-layer LCP structure (Mawet et al. 2010).
Achromatization of circular phase mask coronagraphs by the use of dual zone phase structures has also been studied (Soummer et al. 2003b), leading to intensity levels of 10-6 at 3 λ0/D for a 20% bandwidth. We report on further improvements to this concept in the following.
We focus here on stellar coronagraphs with circular axi-symmetrical phase masks (Roddier & Roddier 1997; Soummer et al. 2003b). This is a promising concept, because well suited to any arbitrary aperture (clear aperture, centrally obstructed circular pupil, diluted pupil, etc.) and free of blind axes in the coronagraphic images. Roddier & Roddier (1997) proposed the first design, referred to here as the Roddier & Roddier phase mask (RRPM), which was later improved by adding an entrance pupil apodizer (Guyon & Roddier 2000; Soummer et al. 2003a). The corresponding system, called apodized pupil Roddier & Roddier phase mask (ARPM) coronagraph, can theoretically achieve perfect starlight extinction at a single wavelength. Unfortunately, its performance decreases strongly in broadband observation. This loss of coronagraphic performance comes from chromatism effects related to the inherent properties of the RRPM.
Soummer et al. (2003b) proposed an improvement of the ARPM coronagraph to overcome the problem of chromaticity, replacing the simple phase mask of the Roddier coronagraph with a double phase mask, named dual zone phase mask (DZPM). With this innovative coronagraph, which also includes pupil apodization, they showed that an intensity level of ~10-6 can theoretically be reached at a 3 λ0/D angular distance from the star. These promising results were achieved both for a clear circular aperture and for an entrance pupil with a 14% central obscuration ratio, in both cases considering a 20% bandwidth. Although encouraging, the performance of this coronagraphic system needs to be enlarged so as to realize spectro-imaging observations of the faintest close-in companions with this concept. The DZPM coronagraph was originally designed with a gray (or achromatic) entrance pupil apodization. This component then applies the same transmission function to the incident beam over the whole spectral bandwidth of study. The apodization shape is possibly not optimal at all the wavelengths of study.
The aim of this paper is twofold. First of all, we investigate the possibility of using a colored (or chromatic) instead of a gray apodization to improve the contrast gain delivered by the DZPM coronagraph over the whole spectral bandwidth. This innovative concept will be named colored apodizer phase mask (CAPM) coronagraph. Secondly, once the apodization parameters are optimized, we propose to analyze the sensitivity of the CAPM coronagraph by estimating the impact of different effects that may alter its performance in a realistic case.
In Sect. 2, we briefly review the principle of the DZPM coronagraph and state the possibility of upgrading this concept with the use of a colored apodization. The methodology, applied to numerically optimizing the parameters of the CAPM coronagraph, is thereafter described in Sect. 3. We present the theoretical performance achieved by this coronagraphic device for different spectral bandwidths and a clear circular aperture in Sect. 4. In addition, manufacturing aspects are addressed in Sect. 5 with the development of a physical design for the colored apodization and the performance study for the CAPM coronagraph in the presence of this component. The sensitivity of the CAPM coronagraph to different errors is thereafter analyzed in Sect. 6.
2. The CAPM coronagraph
The principle of the DZPM coronagraph is recalled in the following before introducing our proposal, the CAPM coronagraph, and its colored apodization. We then explain its formalism of the last.
2.1. Principle of the DZPM coronagraph
An illustration of the DZPM coronagraphic layout is given in Fig. 1, detailing the typical four planes of Lyot style coronagraphs. The DZPM coronagraph combines an apodization in the entrance pupil plane A, a DZPM in the next focal plane B, and a Lyot stop in the re-imaged pupil plane C. The coronagraphic image forms in the final image plane D in which a detector is located. The optical design is such that the complex amplitudes of the electric field in two successive planes are related to each other by a Fourier transform operation.
The DZPM is designed as a circular phase disk of diameter d1 surrounded by an annular phase ring of diameter d2, see Fig. 2. Each diameter is equal to a very precise fraction of the size of the Airy disk. The inner and outer parts of the mask introduce some phase shifts ϕ1 and ϕ2 respectively, to the incoming wavefront in the focal plane B. As the wavelength increases, ϕ1 and ϕ2 decrease and the stellar diffraction pattern expands. This combination of effects leads to a decrease in the relative flux passing through the inner zone, while the flux passing through the annular zone increases. At a given wavelength, the complex amplitude of the field in the relayed pupil plane C corresponds to the result of the interference between the direct wave with the waves delayed by the two phase shift zones of the DZPM. This sum of wavefronts varies with the wavelength since ϕ1, ϕ2 and the areas of the diffraction pattern covered by the mask also evolve with the wavelength. With an adequate choice of the DZPM parameters, the recombination of these three wavefronts in plane C generates destructive interferences inside the geometric pupil for a wide range of wavelengths. The light is rejected outside of this relayed pupil and blocked by a Lyot stop, leading to a broadband suppression of the star image at the detector in plane D.
In addition, the presence of an entrance pupil apodization in plane A allows us to match the direct wave with the waves diffracted by the DZPM. It results in improved destructive interference over the relayed pupil. A lower amount of the residual starlight is then found inside this pupil, and a better starlight extinction is therefore observed in the final image plane D. As was shown by Soummer et al. (2003b), further improvements can be achieved by adding a slight defocus of the coronagraph mask, which is equivalent to allocating a complex term in our apodization.
 |
Fig. 1 Scheme of the coronagraphic layout. |
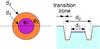 |
Fig. 2 Schematic representation of the DZPM. The dimensions are not at scale in this drawing. |
2.2. Replacement of the gray by a colored apodization
A complex apodization in the coronagraphic scheme allows the direct wave and the waves diffracted by the DZPM to match within the geometric pupil image and interfere destructively over it. In their design, Soummer et al. (2003b) considered a gray version of the complex apodization. Since the waves diffracted by the mask evolve with the wavelength, they do not match the direct wave at all wavelengths. Ideally, a complex apodization has to be found for each wavelength to obtain an achromatic nulling recombination of the direct with the diffracted waves.
The design improvement proposed here from the DZPM coronagraph is similar to the approach developed by Aime (2005) for the Prolate apodized Lyot coronagraph. The idea consists in replacing the gray by a colored apodization in our coronagraphic system. This colored apodization constitutes an amplitude apodization, hence intensity apodization variable with the wavelength. This change in apodization leads to the design of CAPM coronagraph that combines a colored apodization, a DZPM in the following focal plane, and a Lyot stop in the relayed pupil plane. With this innovative coronagraphic system, we expect to reach higher contrast levels than those achieved by the DZPM coronagraph over a finite spectral bandwidth.
2.3. Formalism
In the following, the formalism common to DZPM and CAPM coronagraphs is given. For the sake of clarity, we omit the position vector r, its modulus r and the wavelength λ in the equations below, and ℱ symbolizes the Fourier transform operator in which we include the Fourier optics scaling factor 1/λf, with f the telescope focal length (Goodman 1996).
The complex amplitude of the field ΨA at the aperture is given by 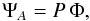 (1)in which P defines the telescope aperture shape, whereas Φ denotes the complex apodization.
(1)in which P defines the telescope aperture shape, whereas Φ denotes the complex apodization.
The DZPM is located in the following focal plane B. Its amplitude transmission function t can be written as 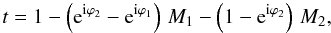 (2)in which M1 and M2 define the top-hat functions of the inner and outer parts of the DZPM; they are equal to 1 for |r| < d1/2 and |r| < d2/2, respectively, and 0 otherwise. We recall that ϕ1 and ϕ2 represent the phase shifts introduced by the mask in its inner and outer parts, respectively, at a given wavelength.
(2)in which M1 and M2 define the top-hat functions of the inner and outer parts of the DZPM; they are equal to 1 for |r| < d1/2 and |r| < d2/2, respectively, and 0 otherwise. We recall that ϕ1 and ϕ2 represent the phase shifts introduced by the mask in its inner and outer parts, respectively, at a given wavelength.
The complex amplitude of the field ΨB after the mask is then given by ![\begin{equation} \Psi_B=\left [1 - \left({\rm e}^{\rm i\varphi_2}- {\rm e}^{\rm i\varphi_1}\right)\,M_1\, - \left(1- {\rm e}^{\rm i\varphi_2}\right)\,M_2 \right ]\,\mathcal{F}[\Psi_A] . \label{eq:amplitude_B} \end{equation}](/articles/aa/full_html/2012/02/aa17661-11/aa17661-11-eq44.png) (3)The DZPM and CAPM coronagraphs belong to the class of the Lyot-style coronagraphs, which consist in a succession of binary filters (pupil, finite-size focal plane mask, Lyot stop). We then adopt the semi-analytical approach suggested by Soummer et al. (2007) in the case of a Lyot-style coronagraph for a better understanding of the interference effects occurring in the pupil plane C. The complex amplitude after the Lyot stop ΨC is expressed as follows:
(3)The DZPM and CAPM coronagraphs belong to the class of the Lyot-style coronagraphs, which consist in a succession of binary filters (pupil, finite-size focal plane mask, Lyot stop). We then adopt the semi-analytical approach suggested by Soummer et al. (2007) in the case of a Lyot-style coronagraph for a better understanding of the interference effects occurring in the pupil plane C. The complex amplitude after the Lyot stop ΨC is expressed as follows: ![\begin{eqnarray} \label{eq:ampltude_C} \Psi_C = & \,\Psi_A\,L \notag \\ &&- ({\rm e}^{\rm i\varphi_2}- {\rm e}^{\rm i\varphi_1})\,\mathcal{F}\left [\mathcal{F}[\Psi_A]M_1 \right ]\,L\notag \\ && - (1- {\rm e}^{\rm i\varphi_2})\,\mathcal{F} \left [\mathcal{F}[\Psi_A]M_2 \right ]\,L , \end{eqnarray}](/articles/aa/full_html/2012/02/aa17661-11/aa17661-11-eq46.png) (4)in which L denotes the index function of the Lyot stop, and ΨC is the sum of three terms that represent the direct wave ΨA and the sum of the waves diffracted by the inner and outer parts of the DZPM. As mentioned above, perfect starlight cancellation is achieved if the sum of the waves diffracted by the DZPM matches the direct wave inside the geometric pupil perfectly.
(4)in which L denotes the index function of the Lyot stop, and ΨC is the sum of three terms that represent the direct wave ΨA and the sum of the waves diffracted by the inner and outer parts of the DZPM. As mentioned above, perfect starlight cancellation is achieved if the sum of the waves diffracted by the DZPM matches the direct wave inside the geometric pupil perfectly.
The coronagraphic amplitude ΨD in the image plane D is finally obtained with ![\begin{equation} \Psi_D=\mathcal{F}[\Psi_C] . \label{eq:ampltude_D} \end{equation}](/articles/aa/full_html/2012/02/aa17661-11/aa17661-11-eq49.png) (5)The corresponding intensity ID of the polychromatic coronagraphic image is given by
(5)The corresponding intensity ID of the polychromatic coronagraphic image is given by 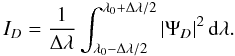 (6)We recall that Δλ defines the spectral range of study centered at the wavelength λ0.
(6)We recall that Δλ defines the spectral range of study centered at the wavelength λ0.
3. Methodology
In this section, we describe the methodology used to realize our numerical simulations of the CAPM coronagraph. We also explain the optimization criteria for determining its parameters.
3.1. Parameters of the CAPM coronagraph
Several parameters are involved in the CAPM coronagraph. d1, d2, and the phase steps, expressed in optical path differences OPD1 and OPD2, correspond to the characteristics related to the DZPM. The other parameters refer to the complex apodization Φ, which can be decomposed into the product of an amplitude and a phase apodizations Φa and Φw, respectively: 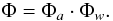 (7)Following the indications of Soummer et al. (2003b), the transmission function chosen for Φa is a radial symmetric fourth-order polynomial, while Φw is in the form of a defocus of the mask. This amplitude transmission function finds its maximum value at the pupil center in the case of a clear aperture and at the edge of the central obscuration for a centrally obstructed circular aperture. For a given central obscuration ratio η (null for a clear aperture), the amplitude apodization Φa can be written as
(7)Following the indications of Soummer et al. (2003b), the transmission function chosen for Φa is a radial symmetric fourth-order polynomial, while Φw is in the form of a defocus of the mask. This amplitude transmission function finds its maximum value at the pupil center in the case of a clear aperture and at the edge of the central obscuration for a centrally obstructed circular aperture. For a given central obscuration ratio η (null for a clear aperture), the amplitude apodization Φa can be written as 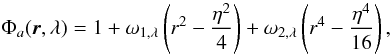 (8)where ω1,λ and ω2,λ denote the colored parameters related to the amplitude apodization Φa. In addition, the phase apodization Φw is expressed as
(8)where ω1,λ and ω2,λ denote the colored parameters related to the amplitude apodization Φa. In addition, the phase apodization Φw is expressed as 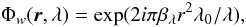 (9)where βλ is a chromatic parameter associated with the phase apodization. The chromatic longitudinal defocus Δz is related to βλ by the expression
(9)where βλ is a chromatic parameter associated with the phase apodization. The chromatic longitudinal defocus Δz is related to βλ by the expression 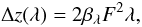 (10)where F denotes the focal ratio of the optical system. The manufacturing aspects on the chromatic defocus are discussed below in Sect. 5. As mentioned above, ω1,λ, ω2,λ, and βλ are chromatic parameters since we deal here with a colored apodization. They will be optimized at each wavelength of the spectral bandwidth with the criteria given below. We note that the previous expressions of apodization are still valid for the DZPM coronagraph, with ω1,λ, ω2,λ, and βλ remaining constant over the spectral bandwidth.
(10)where F denotes the focal ratio of the optical system. The manufacturing aspects on the chromatic defocus are discussed below in Sect. 5. As mentioned above, ω1,λ, ω2,λ, and βλ are chromatic parameters since we deal here with a colored apodization. They will be optimized at each wavelength of the spectral bandwidth with the criteria given below. We note that the previous expressions of apodization are still valid for the DZPM coronagraph, with ω1,λ, ω2,λ, and βλ remaining constant over the spectral bandwidth.
3.2. Numerical simulations using ultrafast Fourier transforms
We give here the computation of the amplitudes ΨC and ΨD, respectively based on a semi-analytical approach and a novel method providing fast computation of high-resolution Fourier transform.
3.2.1. Computation of the amplitude in plane C
The complex amplitude ΨC in pupil plane C is computed following Eq. (4). This semi-analytical expression is advantageous in terms of computation time since Fourier transform operations are only required within the mask area of width ~λ0/D in the focal plane B and within the Lyot stop area in plane C. No zero-padding is required in this case so we can use arrays of width equal to the mask diameter to which we apply the matrix Fourier transform (MFT) as proposed by Soummer et al. (2007) to compute these truncated Fourier transform and evaluate ΨC.
3.2.2. Computation of the amplitude in plane D
The complex amplitude ΨD in image plane D is obtained with a Fourier transform of the complex amplitude ΨC, see Eq. (5). We want to evaluate this complex amplitude over a large field of view (FoV), typically from 50 to 200 λ0/D width with good sampling. This can be seen as a truncated Fourier transform within the area of interest (here, FoV) as in the case of ΨB, and the MFT can be used again. However, the computation proves to be slow since an array much larger than used in plane B is involved. While this increase in computation time is not dramatic in the monochromatic case, it becomes important when we consider a broadband image for which several monochromatic images are computed and summed.
For fast computation of ΨD from ΨC, we apply a novel method based on a succession of fast Fourier transforms (FFTs) instead of the MFT. By this method, already experimented in the context of James Webb Space Telescope PSF calculation (Zamkotsian & Dohlen 2004), the diameter in pixels of the geometric pupil in plane C is assumed to be equal to NC0, and ΨC is represented in an array C0 with dimensions NC0 × NC0. In the following, we describe the successive steps used for the computation of ΨD and illustrated in Fig. 3:
-
1)
FFT of the array C0. This leads to an array D1 that contains ΨD over a certain FoV of width ND1 λ/D where ND1 = NC0;
-
2)
selection of a central subarray of D1 to restrict the FoV to the area of interest of width ND2 λ/D. The dimensions of this new array D2 are ND2 × ND2 with ND2 ≤ ND1. It contains ΨD in a smaller FoV than in D1;
-
3)
inverse FFT of the array D2. It results in an array C2 of same size as D2 containing a miniature version of the pupil;
-
4)
use of the zero padding technique with the insertion of C2 in a larger array C3 of dimensions NC3 × NC3;
-
5)
FFT of the array C3. The result of this operation is an array D3, with the same dimensions as C3, containing the final complex amplitude ΨD in plane D.
Thanks to these successive operations, a fast computation of ΨD is achieved. To check the accuracy of our method, we compared the monochromatic intensity |ΨD|2 obtained with our ultrafast Fourier transform method and with a simple FFT (steps 1 to 3 are skipped here). We work with NC0 = 390 and ND3 = 10 NC0 so the element resolution λ/D is sampled every ten pixels in the image plane. This leads to an absolute difference less than 2 × 10-15. This numerical noise remains largely below all the contrast values that we are considering here, and therefore it does not have any influence on the analysis of our results. This test allows us to confirm the accuracy of our ultrafast Fourier transform proposed here. In the following, we apply this algorithm to estimating ΨD.
 |
Fig. 3 Schematic illustration of the method used for computating ΨD. |
3.3. Optimization criteria
In their study, Soummer et al. (2003b) optimized the parameters of the DZPM coronagraph to achieve the best on-axis extinction of the stellar diffraction pattern in the image plane. We decide here to optimize the CAPM coronagraph parameters in order to reach the best off-axis cancellation of the star image. This will yield minimal starlight pollution in the search area in which exoplanets are expected to be found. The search area is defined by an annulus of width between 2 λ0/D and 10 λ0/D from the main optical axis in the image plane.
We average the intensity of the monochromatic coronagraphic image over this search area. This calculus is performed at five different wavelengths uniformly distributed within the spectral bandwidth. Once this is done, we compute a merit function M to estimate the quadratic sum of the mean intensities reached at each wavelength λ: 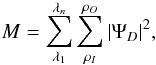 (11)where ρI and ρO are the inner and outer radii of the search area, and λ1 and λn represent the first and nth wavelengths of study within the spectral bandwidth. For our optimization, five wavelengths from λ1 to λ5 have been considered within the spectral bandwidth Δλ, centered on λ3 = λ0, and equally spaced from one to another by Δλ/5, see Fig. 4. Some test optimizations have also been run with an eleven wavelengths gridding for 25% and 50% bands, showing no improvement in the coronagraph performance with respect to the five wavelength samplings.
(11)where ρI and ρO are the inner and outer radii of the search area, and λ1 and λn represent the first and nth wavelengths of study within the spectral bandwidth. For our optimization, five wavelengths from λ1 to λ5 have been considered within the spectral bandwidth Δλ, centered on λ3 = λ0, and equally spaced from one to another by Δλ/5, see Fig. 4. Some test optimizations have also been run with an eleven wavelengths gridding for 25% and 50% bands, showing no improvement in the coronagraph performance with respect to the five wavelength samplings.
A numerical least-squares method is used to obtain the CAPM coronagraph parameters (d1, d2, ϕ1, ϕ2, ω1,λ, ω2,λ, βλ) that minimize our merit function and therefore achieve the lowest averaged intensity over the search area for all wavelengths simultaneously.
 |
Fig. 4 Schematic illustration of the wavelengths and bandwidth of study. λI and λO represent the limit wavelengths of the spectral bandwidth. |
 |
Fig. 5 a) Radial profile of the colored intensity apodization for the CAPM coronagraph at different wavelengths λ; b) radial profiles of the difference between the intensity apodization at a given wavelength λ and at the central wavelength λ0 (here 1.650 μm); c) and d) reproduce panels a) and b) respectively, for the phase given by the phase apodization Φw. |
3.4. Computation of the broadband image in plane D
Once the parameters are optimized, we can calculate the broadband image obtained with the CAPM coronagraph using Eq. (6). Since ω1,λ, ω2,λ, and βλ are estimated for five wavelengths, the monochromatic images at those wavelengths can be computed. To sum more than five frames for our final broadband image, we need to know the parameter values at other wavelengths. An interpolation of the values is realized for each apodization parameter. After several tests, we decided to use a second-degree polynomial function to fit the parameter values, which is more representative of the behavior of actual materials than higher order functions. In the following, all our interpolations are performed with a second-degree polynomial function. Once this is defined, we can estimate the values of the parameter at a given wavelength and compute its frame. We then sum several monochromatic images with a small spectral separation between two successive frames and obtain our broadband image in plane D.
4. Performance over large spectral bandwidths
In this section, we study the behavior of the CAPM coronagraph and its theoretical performance for different spectral bandwidths. This investigation is made for a clear circular aperture but it can be generalized to any kind of entrance pupil geometry. The current study will be particularly interesting in the context of some exoplanet imagers under consideration, such as 1–2 m class off-axis space telescopes equipped with an internal coronagraph (see e.g., Galicher et al. 2010; Trauger et al. 2010; Guyon et al. 2010c). In addition, the results reached with our concept are compared to those previously achieved by Soummer et al. (2003b) with the DZPM coronagraph. This allows us to underline the contrast gain obtained with the use of a colored apodization instead of a gray one.
4.1. Colored apodization
We first observe the shape of the apodization reached for the CAPM coronagraph at different wavelengths. Figure 5 panel (a) shows the radial intensity profiles of the colored apodization at five wavelengths for a 25% bandwidth (H-band). We can notice the similarity between all the displayed profiles. To disentangle them, the difference between the transmission functions at a given wavelength λ and at λ0 has been drawn on the panel (b), emphasizing small differences in absolute value existing between different profiles. The intensity difference is not greater than 3% of the normalized intensity peak, but it reveals the chromatic aspect of our apodization used for the CAPM coronagraph. The apodization throughput evolves slightly from 57.9% (λ = 1.485 μm) to 55.3% (λ = 1.815 μm).
Panels (c) and (d) of Fig. 5 show the phase ϕ of the phase apodization Φw = eiϕ in a similar way. The phase difference between the phases at a given wavelength λ and at λ0 is not larger than 0.1 rad but it emphasizes the chromatic aspect of the phase apodization Φw in the CAPM coronagraph.
4.2. Residual intensity
Much information can be extracted from the monochromatic intensity profiles in the Lyot and image planes, see Fig. 6. These curves have been obtained by considering the optimized apodizer showed in Fig. 5. The minimization of the residual broadband intensity inside the search area (2–10 λ0/D range) has driven the optimization of our CAPM concept, leading to coronagraphic images with high intensity peak and low sidelobe level, see the bottom plot of Fig. 6. In parallel, the energy distribution inside the Lyot stop exhibits apodized intensity profiles, see the top plot of Fig. 6. Observing all the wavelengths, we note that the brightness of the sidelobes beyond 6 λ0/D angular separation follows the intensity value found at the pupil’s edge. For sidelobes in the 2–6 λ0/D range, this assertion is no longer valid because of the combination of several effects, including oscillations of the amplitude for some wavelengths in the Lyot plane and a phase apodization in the entrance pupil.
 |
Fig. 6 Radial profiles of the residual intensity with the CAPM coronagraph, within the re-imaged pupil in plane C (top) and in the final image plane D (bottom) at different wavelengths λ. Profiles have been normalized at the origin to directly read the coronagraphic extinction ratio at a given angular distance from the on-axis star image. |
4.3. Optimized parameters
Following our optimization criteria, we estimate the different parameters of the CAPM coronagraph for different spectral bandwidths. The obtained values are given in Table 1. In addition, the colored apodization parameters ω1,λ, ω2,λ, and βλ are plotted as a function of the wavelength for different bandwidths in Fig. 7.
 |
Fig. 7 Optimized values of the amplitude apodization parameter ω1,λ (top plot), ω2,λ (middle) and the phase apodization parameter βλ (bottom) as a function of the wavelength for different bandwidths. A second-degree polynomial interpolation of the points is represented for each parameter and bandwidth. |
4.4. Contrast results and discussion
In Fig. 8, we draw the radial intensity profile of the images achieved with the CAPM coronagraph for different spectral bandwidths. The plotted curves are extracted from polychromatic images computed with N = 1 + 100 Δλ/λ0 monochromatic frames with a separation corresponding to a 1% band. The values of the averaged intensities reached for each band and at several angular separations are given in Table 1. Averaged intensities of 2.2 × 10-7 and 2.2 × 10-8 are theoretically reached at 3 λ0/D and 5 λ0/D, respectively, with our coronagraphic device for a 25% bandwidth. As we can notice in Fig. 7, the interpolation function is not optimal for the largest bands, leading to a loss of coronagraph performance when the optimized parameters are replaced by the interpolated values: the averaged intensity at 5 λ0/D degrades from 3.8 × 10-8 and 7.1 × 10-8 to 5.0 × 10-8 and 1.3 × 10-7 for the 40% and 50% bands, respectively.
To go further in the analysis, we also determine the averaged intensity at 5 λ0/D achieved by the coronagraph at each wavelength of a given spectral bandwidth case, see Fig. 9. Each curve is plotted with the same 1% sampling as described above. It can be noticed from this plot that a 2 × 10-8 averaged intensity at ~λ0 can theoretically be achieved in the case of a 25% bandwidth. Another interesting aspect about reachable averaged intensities concerns the spectral range. As the bandwidth decreases below 20%, a single hole in the intensity curve appears around λ0, surrounded by increasingly steep edges. In the monochromatic case, the coronagraph becomes identical to the ARPM coronagraph as we could expect.
Finally in Fig. 10, we compare the results achieved with the CAPM coronagraph with those obtained by Soummer et al. (2003b) with the DZPM coronagraph. A ~2.5 contrast gain at 3 λ0/D is reached with our device compared with the first DZPM coronagraph design for a 20% and a 40% bandwidths. Similar improvements of the reachable averaged intensities have been observed at other angular separations (5 and 7 λ0/D), confirming the substantial gain obtained for the CAPM coronagraph by replacing the gray by a colored apodization.
 |
Fig. 8 Radial intensity profile of the coronagraphic images achieved with the CAPM coronagraph for different sizes of the spectral bandwidth. |
 |
Fig. 9 Theoretical averaged intensity at 5 λ0/D obtained with the CAPM coronagraph as a function of the wavelength for different bandwidths. |
 |
Fig. 10 Theoretical averaged intensity achieved at different angular separations from the main optical axis with the DZPM and CAPM coronagraphs as a function of the bandwidth. |
Values of the CAPM coronagraph parameters optimized for different spectral bandwidths and averaged intensity results at different separations.
5. Design proposal for the colored apodization
The realization of a colored apodizer is a key point for the implementation of the CAPM coronagraph. This requires careful control of the transmission function of the apodizer both spatially across the pupil and spectrally over a wide range of wavelengths. We describe here some of the options currently considered for manufacturing this chromatic apodization.
One option consists of using an absorbing material with an appropriate chromatic variation in the absorption coefficient, for instance a colored-glass filter. The required transmission function for the apodizer is obtained at all the wavelengths by careful thickness control of the absorbing material. An appropriate material choice would lead to a negative lens of up to a few mm edge thickness. The optical power of this lens could possibly be included in the optical design of the instrument, but in a more general option it would need to be compensated for by a positively powered non-absorbing lens.
Another approach for the colored apodizer that we have considered is to use a thin film of a highly absorbing material such as metal, deposited with an appropriate radial thickness profile onto a silica substrate. The chromaticity of the apodizer is now related to the chromatic variation of the complex refractive index of the material.
Solutions based on metallic thin film, alloy layer, or else high-energy beam sensitive (HEBS) glass have already been investigated to produce achromatic band-limited masks in the visible (Sidick 2007; Moody et al. 2008; Balasubramanian 2008) or manufacture achromatic apodizers of the APLC coronagraph for VLT-SPHERE (Guerri et al. 2008, 2011; Carbillet et al. 2011) and Gemini Planet Imager (Soummer et al. 2009; Sivaramakrishnan et al. 2009). Our study is focused here on the search for metals to design chromatic components instead of gray masks.
In the following, we explain this approach for the realization of the colored apodization. The performance of the CAPM coronagraph is estimated with this physical design and then compared to the results with the theoretical model of colored apodizer described above. We assume a clear circular aperture and a 25% bandwidth centered at λ0 = 1.65 μm (H-band) for our optimization.
5.1. Assembly based on a metallic thin film on a silica substrate
To manufacture our colored amplitude apodization Φa, we investigated an assembly based on a metallic thin film deposited on a silica substrate with complex refractive index Nm and Ns, see Fig. 11. At the boundaries of our assembly, we consider an absorption-free medium of refractive index N0. The assembly is assumed to work in transmission at normal incidence.
The substrate is supposed to be an absorption-free medium, thick enough to neglect the internal reflections. Referring to the metallic thin film, the refractive index Nm presents a complex part, called extinction coefficient k, which is related to the absorption αm within the metal layer by αm = 4πk/λ. Increasing the metal thickness leads to a combined enhancement of the absorption and reflection of the assembly, hence a reduction in its transmission. Careful control of the metallic thin film thickness allows us to adjust the amplitude transmission function of our assembly. The chromaticity of the amplitude apodization is mainly due to the dependence on wavelength of the metal extinction coefficient.
For the present concept, the amplitude transmission function of our assembly Φb is defined as the product of the transmittances through the metallic thin film and the substrate τm and τs. The amplitude apodization can therefore be written as 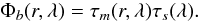 (12)For the sake of clarity, we omit the dependence on wavelength of the refractive indices and the parameters B, C, and δm, which appear in the following equations. The transmittances in amplitude τm and τs can be expressed as
(12)For the sake of clarity, we omit the dependence on wavelength of the refractive indices and the parameters B, C, and δm, which appear in the following equations. The transmittances in amplitude τm and τs can be expressed as 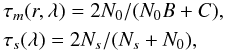 (13)where B and C can be identified as the normalized electric and magnetic field amplitudes at the front interface respectively (MacLeod 1991). In our case, B and C can be calculated with the following equation:
(13)where B and C can be identified as the normalized electric and magnetic field amplitudes at the front interface respectively (MacLeod 1991). In our case, B and C can be calculated with the following equation: 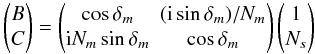 (14)with δm(r,λ) = 2πNmt(r)/λ the phase shift experienced by the wave as it traverses a distance t normal to the substrate boundary.
(14)with δm(r,λ) = 2πNmt(r)/λ the phase shift experienced by the wave as it traverses a distance t normal to the substrate boundary.
The complex apodization Φ of the CAPM coronagraph with the physical design writes as 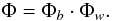 (15)The metallic thin film also induces a radially variable phase delay, leading to complex values evolving with r for the transmission function Φb. Since our concept of CAPM coronagraph also contains a phase apodization Φw, the total phase of the complex apodization Φ in the entrance pupil plane A will be the combination of the phase terms of Φw and Φb.
(15)The metallic thin film also induces a radially variable phase delay, leading to complex values evolving with r for the transmission function Φb. Since our concept of CAPM coronagraph also contains a phase apodization Φw, the total phase of the complex apodization Φ in the entrance pupil plane A will be the combination of the phase terms of Φw and Φb.
 |
Fig. 11 Schematic illustration of the assembly, composed of a metallic thin film deposited on a substrate. The scheme is not to scale. |
 |
Fig. 12 Transmission values in intensity obtained for the theoretical model and the assembly with different metals as a function of the wavelength. Values are provided for different normal radial distances. Thickness for each material and radial distance are given in Table 2. |
5.2. Choice of the metal
Preliminary studies have been realized to choose the metal for the physical model, see Fig. 12. Five metals (gold, silver, aluminum, nickel, and chromium) were considered for this purpose, while five radial distances were investigated to determine the optimal thickness of the metallic thin film at different positions in the pupil. For each metal and radial distance, the thickness of the metallic thin film was estimated such that the assembly reaches the same intensity transmission as the theoretical model at λ0 observed in Fig. 5. Bulk refractive indices for the metal layer, obtained from Palik (1985), were used for implementing our simulations. The thicknesses reached for each metal and radial distance are given in Table 2.
Using silver or nickel provides the best fits to the theoretical model at small or large radial distances. However, even with those metals, the theoretical profile of the colored apodization is not reached at all the wavelengths under study. In the following, we re-optimize the CAPM coronagraph, using a nickel apodizer.
With reference to the apodizer model of Eq. (8), the thickness profile t of the metal is optimized using the expression ![\begin{equation} t(r)= t_c \left [\chi_{1}\left (r^2-\frac{\eta^2}{4}\right ) + \chi_{2}\left (r^4-\frac{\eta^4}{16}\right ) \right ] , \label{eq:thickness_2} \end{equation}](/articles/aa/full_html/2012/02/aa17661-11/aa17661-11-eq178.png) (16)where tc = 1 nm is the reference thin film thickness, and χ1 and χ2 are the parameters related to the terms in r2 and r4, respectively, of the thickness profile. This assembly provides a maximum amplitude transmission at the center of the pupil or at the edge of the central obscuration for η ≠ 0.
(16)where tc = 1 nm is the reference thin film thickness, and χ1 and χ2 are the parameters related to the terms in r2 and r4, respectively, of the thickness profile. This assembly provides a maximum amplitude transmission at the center of the pupil or at the edge of the central obscuration for η ≠ 0.
Values of the parameters for the CAPM coronagraph optimized with an assembly using nickel thin film for the colored apodization.
5.3. Results
The optimized parameters for the phase mask and apodizer are reported in Table 3, while the resulting thickness profile t of the nickel film and the parameter βλ associated to the phase apodization are plotted in Fig. 13. Regarding t displayed in the top plot, a maximum thickness of 9.1 nm is reached at the pupil edge for the metal layer, proving to be consistent with the 9.7 nm value observed at r = 0.5 in the tests for the choice of the metal and reported in Table 2. Concerning the βλ curve in the bottom plot, we note some discrepancy between the values obtained for the CAPM coronagraphs working with the theoretical model and the physical design. This difference can be explained by the presence of the additional phase shifting introduced by the metallic thin film of the assembly, leading to a readjustment of the parameter βλ of the chromatic defocus during the optimization of the CAPM coronagraph with the physical design.
The radial intensity profiles of the apodizer for a 25% bandwidth (H-band) are represented at five wavelengths in Fig. 14 panel (a). While the profiles are quite similar to the profiles shown in Fig. 5, the difference between them, shown in panel (b), is smaller than for the optimal profiles. The apodization throughput of the assembly ranges from 59.5% (λ = 1.485 μm) to 58.8% (λ = 1.815 μm), which is slightly higher than the theoretical colored apodizer. The phase profiles, shown in panel (c), are somewhat different from those of the optimal apodizer in Fig. 5, indicating the presence of a fourth-order term (spherical aberration) in addition to the second-order term. The differential phase profiles in panel (d) are remarkably similar to those of the optimal apodizer, both in shape and amplitude.
In Fig. 15, we represent the intensity profiles obtained with the CAPM coronagraph in the presence of the theoretical colored apodizer and our physical design. The profiles are almost identical, underlining the relevance of using a nickel layer to realize our colored amplitude apodization. The intensity levels estimated at different separations from the star are thus very close for the two models of colored amplitude apodization, see Table 4. For instance, the intensity levels at 5 λ0/D are 2.6 × 10-8 and 2.2 × 10-8. An optimized design using a nickel thin film therefore allows us to reproduce the contrast results obtained for the optimal CAPM coronagraph. The nickel layer presents a maximum thickness of 9.1 nm with an accurate control at atomic level. To manufacture such a design, atomic layer deposition (ALD) represents a very attractive technique, which is widely used in microelectronics, since it enables the production of very thin, conformal film with thickness control and composition of the films at the atomic level for a wide range of materials (Leskel & Ritala 2002).
Further studies and tests will be required for manufacturing such chromatic apodizers. Finally, options based on more elaborate, radially variable thin film stacks, possibly containing both dielectric and metallic materials, are also being considered.
Intensity values provided by the CAPM coronagraph with the theoretical model and the physical design for the colored apodization, for a 25% bandwidth centered at λ0 = 1.650 μm (H-band).
 |
Fig. 13 Top: thickness profile of the nickel layer as a function of the wavelength. Bottom: optimized values of the phase apodization parameter βλ for the CAPM coronagraph in the presence of the theoretical model and the physical design as a colored amplitude apodization. |
 |
Fig. 14 a) Radial intensity profile of the colored apodizer, made with an assembly using nickel layer, for the CAPM coronagraph at different wavelengths λ; b) radial profiles of the difference between the intensity apodization at a given wavelength λ and that obtained at the central wavelength λ0 (here 1.650 μm); c) and d) reproduce a) and b) respectively for the phase given by the phase apodization Φw. |
 |
Fig. 15 Radial intensity profile of the coronagraphic images achieved with the CAPM coronagraph using the theoretical model and the physical design for the colored apodizer. |
5.4. Implementation of the chromatic defocus
The colored apodizer also includes phase apodization Φw with a chromatic parameter βλ. While gray phase apodization can be realized simply by defocusing the mask, we address here the possibility of producing a chromatic defocus. Our numerical optimization shows that parameter βλ varies as λ2 for the theoretical model and our physical design, see Fig. 13. A possible way to realize a second-degree polynomial chromatic defocus consists in using a powerless doublet at the entrance pupil plane. This doublet will present the following characteristics: infinite focal length at λ0, a null first-order chromatic dispersion and a constant and non null second-order chromatic dispersion, also called anomalous dispersion. This can be achieved by combining glasses that have the same refractive indices n1 and n2, the same Abbe numbers ν1 and ν2, but different partial dispersions. This work follows Duplov (2006), who has recently studied apochromatic lens design by considering the partial dispersion properties of materials from standard glass catalogs rather than special anomalous-dispersion glasses. We performed preliminary tests of this approach in the visible range using ZEMAXR◯ ray-tracing code and tabulated glass data. Encouraging results for the realization of our phase apodization were found with a combination of Schott glass materials N-FK9 and K5, see Fig. 16. Indeed, chromatic behavior in λ2 is obtained with this doublet, corresponding to the chromatic defocus expected for the phase apodization of our CAPM coronagraph. Combination of other glass materials are currently under study to achieve adequate chromatic defocus in other spectral bands.
 |
Fig. 16 Top: design of a lens doublet combining Schott glass materials N-FK9 and K5. Bottom: focal shift versus wavelength. This result has been obtained assuming a longitudinal focal shift reached in the visible range with our values of βλ. A second-order polynomial chromatic focal shift with a 5 mm amplitude range has been achieved. |
6. Sensitivity analysis
After optimizing the CAPM coronagraph for achromatization, we investigate here several effects that may alter the performance provided by this coronagraphic system. In the following sensitivity analysis, we consider a CAPM coronagraph optimized for a 25% bandwidth (H-band) observing a point-like source, except for the star angular size study, in the case of a clear circular aperture.
6.1. Performance criteria
Contrast performance is judged by the averaged intensity estimated at 5 λ0/D from the main optical axis in the image plane and for an annulus of width λ0/D. The inner working angle (IWA) is often used to quantify the capacity to work close to the star, defining the minimum angular distance at which the throughput of a companion is more than 50%. Phase mask coronagraphs offer very small IWA, typically ~λ0/D, as recalled for instance by Martinez et al. (2008). This is the case for the CAPM coronagraph as illustrated in Fig. 17. Unfortunately, IWA is not related to the notion of contrast, so the intensity of close-in companions detectable at a given angular distance from the star cannot be determined with this benchmark.
We propose a new criterion, called inner detectability angle (IDA), which represents the compromise between IWA and achievable contrast. IDA is defined as the minimum angular distance α from the main optical axis for which the ratio between the normalized intensity of our coronagraphic star image and the planet transmission flux Tp is less than a given value, here set to 10-6: 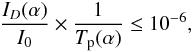 (17)where I0 denotes the intensity peak value in the absence of coronagraph mask. In Fig. 17, we plot the planet transmission profile as a function of the planet position in the presence of a CAPM coronagraph optimized for a 25% bandwidth. From this curve, we deduce that the planet transmission can reasonably be taken equal to one for distances greater than 1.5 λ0/D. IDA is expected to be larger than IWA, but estimating IDA allows us to know at which angular distance companions, 10-6 fainter than their host star, could be detected with our CAPM coronagraph. We study the evolution of IDA for the different cases described below.
(17)where I0 denotes the intensity peak value in the absence of coronagraph mask. In Fig. 17, we plot the planet transmission profile as a function of the planet position in the presence of a CAPM coronagraph optimized for a 25% bandwidth. From this curve, we deduce that the planet transmission can reasonably be taken equal to one for distances greater than 1.5 λ0/D. IDA is expected to be larger than IWA, but estimating IDA allows us to know at which angular distance companions, 10-6 fainter than their host star, could be detected with our CAPM coronagraph. We study the evolution of IDA for the different cases described below.
 |
Fig. 17 Planet transmission profile achieved with the CAPM coronagraph as a function of the planet position. |
6.2. Effects of aberrations
Wavefront errors constitute a major problem for stellar coronagraphs because they limit the performance provided by these diffraction suppression systems. This crucial point of aberrations then has to be addressed in the framework of a coronagraphic planet imager. In the case of a ground-based telescope with an XAO system, as in the case of a well-corrected space instrument, the residual quasi-static instrumental aberrations are known to affect the intensity level reached by a downstream coronagraphic device. A performance estimate of the CAPM coronagraph in the presence of aberrations is therefore required to know the sensitivity of our device. In the following, we describe the behavior of our coronagraphic concept in the presence of low-order aberrations (tip-tilt, defocus, astigmatism, coma, and spherical aberration) since they represent the main contribution in terms of wavefront errors. In addition, we analyze the impact of random aberrations caused by real optical elements on the CAPM coronagraph performance. This aims to determine the limits of our system in the presence of light scattered by the surface roughness of optical elements.
The low-order aberrations are decomposed here following the Zernike polynomial basis. Their amount is expressed in Zernike rms coefficients and given in λ0 units. The random aberrations considered here are related to the wavefront errors introduced by real optical elements. Good quality optical surfaces are found to exhibit a power spectral density (PSD) function proportional to ν-2 where ν denotes the spatial frequency in the pupil, as recalled for instance by Roddier & Roddier (1997). To succeed at our study with random aberrations, we introduced numerically a randomly aberrated phase screen following this PSD, in the entrance pupil plane A of our coronagraph.
6.2.1. Qualitative analysis
Figure 18 shows a set of simulated CAPM coronagraphic images. These frames are represented for different values of rms wavefront errors and each aberration considered here. The shape of the coronagraphic image modifies and evolves quickly as the amount of the rms wavefront errors increases.
 |
Fig. 18 Set of coronagraphic images achieved with the CAPM coronagraph and computed numerically for different aberrations. All the images are normalized to the peak of the noncoronagraphic image. The pixel scale is the same for all the images, and the field of view is represented with a linear range of 22 λ0/D. |
In Fig. 19, we draw the radial intensity profiles of the coronagraphic images obtained with the CAPM coronagraph for different rms wavefront error values of defocus (top plot), spherical aberration (middle plot) and random aberration (bottom plot). Through the evolution of the profile with the amount of a given aberration, one can appreciate the variation in the IDA and the intensity level reached with the CAPM coronagraph. A dashed line representing the 10-6 intensity level set for IDA is also displayed on the plot.
We note that, while both low-order and random aberrations affect all angular separations, the low-order profiles remain parallel with the nonaberrated profile, following an α-3 law, as in the case of the classical Airy pattern. In the random aberrations case, on the other hand, the profile changes towards an α-2 profile, corresponding to the PSD profile defined above. We conclude that mechanism leading to performance degradation is different in the two cases. While edge diffraction dominates in the low-order case, wavefront diffraction, as modeled by a sum of phase gratings (Goodman 1996) dominates in the random case.
6.2.2. Intensity at 5 λ0/D & IDA
In the top plot of Fig. 20, we represent the averaged intensity at 5 λ0/D achieved by the CAPM coronagraph as a function of the rms wavefront error value. The averaged intensity goes beyond a 10-7 value for rms wavefront error values over ~3 × 10-3 λ0 and ~9 × 10-4 λ0 for low-order and random aberrations, respectively. At the highest aberration values, the reachable averaged intensity increases approximately as a second-degree polynomial function for all the aberrations.
We note that, in the case of a spherical aberration, a small and local improvement of the coronagraph performance is observed for a wavefront error of ~7 × 10-4 λ0 rms with respect to the reference averaged intensity value in the absence of aberration. We deduce that an additional phase apodization in the form of spherical aberration can slightly improve the contrast gain provided by this device, but the investigation of this effect is not within the scope of this paper. However, the gain at 5 λ0/D implies an undesirable increase in intensity of the first Airy ring, see the 10-3 λ0 rms profile in the middle plot of Fig. 19.
To complete the analysis, we represent the IDA theoretically achieved with the CAPM coronagraph as a function of the rms wavefront error value, see the bottom plot of Fig. 20. IDA remains below 3 λ0/D for rms wavefront errors lower than 3 × 10-3 λ0 and 2 × 10-3 λ0 for the low-order and random aberrations, respectively. At higher values, the IDA evolves approximately as a 2/3- and a second-degree polynomial function for the low-order and random aberrations, respectively.
6.2.3. Discussion
The intensity level and IDA provided by CAPM coronagraph are all the more altered as the aberration order is higher. These results show that at a given value of rms aberration, the sensitivity of our coronagraph increases with the order of the aberration. They also underline the necessity of working with very high-quality optical elements, typically better than 10-3 λ0 rms wavefront error, to enable high performance of the CAPM coronagraph for a very high-contrast imaging, as well as a very small IDA.
Several studies of sensitivity to low-order aberrations have been performed for different kinds of coronagraph (e.g. Shaklan & Green 2005; Sivaramakrishnan et al. 2005; Belikov et al. 2006; Mawet et al. 2010). No general behavior of the coronagraphs to low-order aberrations emerge from the previous analysis since each concept presents a specific response to these wavefront errors. In addition and to the best of our knowledge, no advanced study has been reported on the response of circular phase mask coronagraphs to low-order aberrations.
 |
Fig. 19 Radial intensity profiles of the coronagraphic images theoretically achieved with the CAPM coronagraph for different rms wavefront errors values of defocus (top plot), spherical aberration (middle), and random aberration with PSD defined above (bottom). |
 |
Fig. 20 Theoretical averaged intensity at 5 λ0/D (top plot) and IDA (bottom plot) achieved with the CAPM coronagraph for different aberrations. |
6.3. Effects of mask imperfections
6.3.1. Mask roughness
The effects of the mask roughness have to be analyzed since they could alter the performance of the CAPM coronagraph. Many glass substrates with excellent flatness (better than λ/20, see for instance NewportR ◯10QW40-30 glass) are available and useful for our DZPM manufacturing. For this study, we therefore assumed a perfectly smooth substrate, affected by surface roughness only within the phase mask, which is assumed to be tooled into the surface, typically by ion beam techniques.
In the top plot of Fig. 21, we draw the radial profile of the coronagraphic image for different values of rms mask roughness. All the coronagraphic profiles follow an α-3 law as does the Airy diffraction pattern and their intensity level increases with the amount of rms mask roughness. Following this result, we also represent the averaged intensity at 5 λ0/D reached by the CAPM coronagraph as a function of the rms mask roughness, see Fig. 22 top plot. It can be noticed that a 10-7 intensity level is provided with the CAPM coronagraph for rms mask roughness values lower than ~0.12 λ0. Beyond this value, the intensity increases and follows the behavior of a second-degree polynomial function until it reaches a plateau at 2 × 10-5, corresponding to the noncoronagraphic case, for roughness greater than 1.00 λ0 rms.
In addition, the IDA profile is displayed in Fig. 22 bottom plot. A 3 λ0/D IDA is preserved for rms mask roughness value lower than 0.15 λ0. For larger roughness values, the IDA increases and follows a first degree polynomial function, again reaching a plateau at 1.00 λ0 rms.
For 0.12 λ0 rms mask roughness, the corresponding values are 198.0 nm and 76.0 nm at λ0 = 1650 nm (H-band) and at λ0 = 633 nm (visible) respectively. As a reference, the roughness obtained with our second-generation RRPM is 0.8 nm rms (N’Diaye et al. 2010). Since the same accuracy can be obtained for the manufacturing of DZPM as for that of the RRPM, we can deduce that mask roughness will not constitute a major issue for the CAPM coronagraph.
6.3.2. Mask transition zone width
The DZPM is theoretically a hard-edge mask. However, in practice, some transition zone widths are found in a manufactured prototype as noticed with the second-generation RRPM (N’Diaye et al. 2010). We propose to study the impact of the DZPM transition width on the CAPM coronagraph performance by replacing vertical transitions by slopes in the mask shape. The same width is assumed here for the inner and outer parts of the DZPM and expressed in the mask’s outer part diameter d2. The transition zone is illustrated in Fig. 2.
Radial profiles of the coronagraphic images are displayed for different mask transition widths in the lower plot of Fig. 21. All the profiles evolve as a third-degree polynomial function like the Airy diffraction pattern. As expected, the intensity values of the coronagraphic image increase as the DZPM transition zone width becomes larger.
In the top plot of Fig. 22, we display the averaged intensity at 5 λ0/D provided by the CAPM coronagraph as a function of the DZPM transition zone width. An intensity level of 10-7 is preserved for a mask transition width smaller than 0.014 d2. At larger widths, the averaged intensity increases but more slowly than a second-degree polynomial function.
The bottom plot of Fig. 22 shows the evolution of IDA achieved with the CAPM coronagraph as a function of the mask transition width. We notice that IDA remains below 3 λ0/D for a mask transition width lower than 0.028 d2. Beyond this value, IDA evolves as a half-degree polynomial function, showing the low sensitivity of this criteria to an increase in the mask transition width.
As a summary, a 1% mask transition width allows us to preserve a 10-7 intensity level and good IDA with the CAPM coronagraph. This value is similar to the one measured for the second-generation RRPM, which was less than 1% of the mask diameter (N’Diaye et al. 2010) and below 1 μm. The same accuracy is expected for the manufacturing of the DZPM. A 1% mask transition width corresponds physically to 1 μm for a 100 μm DZPM diameter. As a result, the focal ratio F of the coronagraphic layout will range as follows: F ~ 61 at λ = 1.65 μm, F ~ 100 at λ = 1 μm, and F ~ 200 at λ = 0.5 μm. Below a 1 μm wavelength, F constitutes a severe constraint on the design of a planet imager working in the visible and in which a CAPM coronagraph could be inserted. To overcome focal ratio issues in the visible spectral range, manufacturing DZPM with a diameter and mask transition width smaller than 100 μm and 1 μm respectively is required.
 |
Fig. 21 Radial intensity profiles of the coronagraphic images theoretically achieved with the CAPM coronagraph for different rms values of mask roughness (top plot) and for different sizes of mask transition width, expressed in DZPM diameter d2 (bottom). |
 |
Fig. 22 Theoretical averaged intensity (top plot) and IDA (bottom plot) achieved with the CAPM coronagraph as a function of the size of the mask transition zone (bottom axis) and the mask roughness (top axis). |
6.4. Lyot stop size and misalignment
6.4.1. Lyot stop size
Pupil undersizing in the Lyot plane is often required in the context of instrument design to allow alignment and manufacturing tolerance. The sensitivity of the CAPM coronagraph to this parameter therefore has to be taken into account. We analyze the impact of a Lyot stop (LS) size reduction on the contrast provided by the CAPM coronagraph. Two CAPM coronagraphs optimized with a 90% and a 100% LS are considered here.
In Fig. 23, the averaged intensity at 5 λ0/D achieved by the CAPM coronagraph is represented as a function of the pupil size for both designs. In each case, the best contrast provided by the CAPM coronagraph is almost obtained for the LS size for which the coronagraphic device has been optimized. However, the behavior of the CAPM coronagraphs differs. In the case of the CAPM coronagraph optimized with a 100% LS, the intensity level increases from 2 × 10-8 to 2 × 10-7 because we reduce the size of the LS from 1 D to 0.85 D. In contrast, in the case of the CAPM coronagraph optimized with a 90% LS, the intensity level varies slowly from 3 × 10-8 to 5 × 10-8 for LS sizes diverging from 0.93 D. A gray area in the plot underlines the range of Lyot stop sizes for which weak fluctuations of the coronagraph performance are observed. The CAPM coronagraph optimized with 90% LS is less sensitive to Lyot stop reduction than is the one optimized with 100% LS.
Pupil undersizing weakly alters the CAPM coronagraph performance if this coronagraphic system has been optimized considering the Lyot stop size. We notice that for a Lyot stop size larger than the geometric pupil diameter, the performance of the CAPM coronagraph decreases quickly as expected since the rejected starlight is found there.
 |
Fig. 23 Theoretical averaged intensity at 5 λ0/D achieved with the CAPM coronagraph as a function of the Lyot stop (LS) size. The dashed line represents the edge of the geometrical relayed pupil. The gray area represents the tolerance range, defined in the text, for the CAPM coronagraph optimized with 90% LS. |
6.4.2. Lyot stop misalignment
Lyot stop misalignment has been identified as one of the problems for the coronagraphs on the VLT-SPHERE. A misalignment less than 0.2% of the pupil diameter has been imposed on the selected coronagraphs for the instrument requirements (Beuzit et al. 2006). In the following, we analyze the impact of the Lyot stop misalignment with respect to the geometric pupil on the CAPM coronagraph performance. The LS size is taken here as equal to 90% of the relayed pupil diameter D. Once again, we consider two CAPM coronagraphs: optimized with a 90% and a 100% LS.
In Fig. 24, the averaged intensity at 5 λ0/D provided by the DZPM coronagraph is represented as a function of the Lyot stop misalignment. In the absence of pupil misalignment, the intensity level achieved by the CAPM coronagraph optimized with a 90% LS and a 100% LS are about 4 × 10-8 and 8 × 10-8 respectively. The result achieved by the CAPM coronagraph optimized to 90% LS is better than the one optimized to 100% LS, since we are facing a 90% LS in the coronagraphic scheme as mentioned above.
As the pupil misalignment increases up to 0.05 D, the intensity level provided by the CAPM coronagraph does not really change significantly. Clearly, the CAPM coronagraph is not sensitive to pupil misalignment for a LS remaining completely inside the geometric pupil. Beyond a 0.05 D pupil misalignment, the Lyot stop starts to go outside the geometric pupil image where most of the rejected starlight is found. It results in a very high increase in the averaged intensity and an expected dramatic decrease in performance for the CAPM coronagraph.
 |
Fig. 24 Theoretical averaged intensity at 5 λ0/D achieved with the CAPM coronagraph and a 90% Lyot stop, as a function of the Lyot stop misalignment. The dashed line represents the edge of the geometric relayed pupil. These results are obtained in the presence of a clear circular aperture. |
 |
Fig. 25 Radial intensity profiles of the coronagraphic images theoretically achieved with the CAPM coronagraph for different stellar radii. |
6.5. Star angular size
A Sun-like star at 10 pc is 1 milliarcsec across, corresponding to 0.024 λ0/D and 0.125 λ0/D in the H-band for an 8 m-class telescope and the E-ELT, respectively. Since phase mask coronagraphs are quite sensitive to star size (Guyon et al. 2006), we analyzed the impact of this on the performance of our concept.
In Fig. 25, we plot the azimuthally averaged intensity profiles with the CAPM coronagraph for different star angular radii θ. All the profiles follow a α-3 law like the Airy diffraction pattern and the intensity values increase with θ, as expected. In the top and bottom plots of Fig. 26, we represent the averaged intensity at 5 λ0/D and IDA, respectively, as a function of the star angular radius. In the top plot, the intensity level goes beyond 10-7 for θ larger than 0.018 λ0/D. At larger angular radii, the intensity level increases as θ2. In the bottom plot, a 3 λ0/D IDA is preserved for θ lower than 0.025 λ0/D. At higher values, IDA evolves as θ.
As a consequence, the finite size of the Sun-like star at 10 pc has little impact on the CAPM coronagraph when observed through an 8 m-class telescope. However, for a 40 m-class telescope, the finite size of this star clearly limits the coronagraphic performance. These results confirm the limitations observed by Guyon et al. (2006) in the circular phase mask coronagraphs for the direct imaging of extrasolar terrestrial planets. To use the CAPM coronagraph at its optimal performance with an ELT, it is therefore more appropriate to observe more compact or more distant stellar objects.
 |
Fig. 26 Theoretical averaged intensity at 5 λ0/D (top plot) and IDA (bottom plot) achieved with the CAPM coronagraph for different stellar radii. |
7. Conclusion
The CAPM coronagraph is an original concept composed of a colored pupil apodization, a DZPM in the following focal plane and a Lyot stop in the re-imaged pupil plane. This diffraction suppression system constitutes an improved version of the DZPM coronagraph (Soummer et al. 2003b) in which the gray apodization has been replaced by a colored one. This change allows us to increase the achromaticity of circular phase mask coronagraphs; indeed, a 2.5 contrast gain for the CAPM coronagraph is achieved with respect to the DZPM coronagraph. In addition, an intensity level of 2.2 × 10-7 at 3 λ0/D and 2.2 × 10-8 at 5 λ0/D from the observed bright star are expected with the CAPM coronagraph, for a clear aperture and a 25% bandwidth. This performance situates the concept in an excellent position with respect to similar concepts reviewed in the introduction to this paper.
Manufacturing aspects of the colored apodizer were also addressed, leading to a promising solution for realizing our CAPM coronagraph with a nickel thin film for the colored amplitude apodizer. Optimizing the metallic layer thickness and mask parameters, we obtained the ultimate performance of the CAPM coronagraph. We consider using a lens doublet by combining two glasses with the same refractive index, the same Abbe number, and different anomalous dispersions to produce colored phase apodization. An encouraging solution has been found for the visible range and studies continue to address other spectral bands with the same concept.
A sensitivity analysis of the CAPM coronagraph to different errors was also performed, leading to the determination of the error level which can be accepted before the performance of the device is altered. We find in particular that, for a given amount of rms wavefront errors, the concept is less sensitive to low-order than to high-order aberrations. While an intensity level at 5 λ0/D of 10-7 is ensured for about 6 × 10-3 λ0 of tilt or defocus, the same intensity level requires spherical aberration below 3 × 10-3 λ0. In the case of random aberrations with a ν-2 PSD distribution, this intensity level requires wavefront errors below 10-3 λ0. Similar observations were made in the case of close-in imaging capabilities, quantified by the inner detectability angle (IDA).
Constraints on DZPM design are quite relaxed at level of mask roughness (76 nm rms in the visible spectral range). However, they can prove to be critical in the case of the mask transition width where a value over 1 μm is required if one wants to use our CAPM coronagraph within an exoplanet imager with a reasonable focal ratio (F less than 100) in the visible. Technological improvements of mask manufacturing are under development, and some first prototypes are expected to be tested in our laboratory soon. In addition, we show that an optimization of the CAPM coronagraph with a 90% Lyot stop is helpful for this device to be less sensitive to pupil stop misalignments. Furthermore, the averaged intensity at 5 λ0/D remains lower than 10-7 with our concept for a stellar angular size below 0.018 λ0/D.
Central obstruction and spiders effects have not been addressed here. They will be presented in a future paper with a design study and performance analysis of the CAPM coronagraph in the framework of the E-ELT.
Finally, the CAPM coronagraph constitutes a very attractive concept for the planet imagers of the next decade thanks to its small inner working angle, its great ability to suppress broadband starlight and the relative simplicity of its design. The next step will now consist in manufacturing all the components of the CAPM coronagraph and performing an experimental demonstration of the concept. We are currently preparing a visible coronagraph testbed at LAM in Marseilles for this purpose.
References
- Aime, C. 2005, PASP, 117, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Aime, C., Soummer, R., & Ferrari, A. 2002, A&A, 389, 334 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balasubramanian, K. 2008, Appl. Opt., 47, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Baudoz, P., Rabbia, Y., & Gay, J. 2000, A&AS, 141, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belikov, R., Kasdin, N. J., & Vanderbei, R. J. 2006, ApJ, 652, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2006, The Messenger, 125, 29 [NASA ADS] [Google Scholar]
- Beuzit, J., Feldt, M., & Dohlen, K. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Carbillet, M., Bendjoya, P., Abe, L., et al. 2011, Exper. Astron., 30, 39 [Google Scholar]
- Duplov, R. 2006, Appl. Opt., 45, 5164 [NASA ADS] [CrossRef] [Google Scholar]
- Galicher, R., Baudoz, P., Boccaletti, A., et al. 2010, in SPIE Conf. Ser., 7731 [Google Scholar]
- Gay, J., & Rabbia, Y. 1996, Académie des Sciences Paris Comptes Rendus Série B Sciences Physiques, 322, 265 [Google Scholar]
- Goodman, J. W. 1996, Introduction to Fourier Optics, 2nd ed. (New York, MA: The McGraw-Hill companies) [Google Scholar]
- Guerri, G., Robbe-Dubois, S., Daban, J.-B., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Guerri, G., Daban, J.-B., Robbe-Dubois, S., et al. 2011, Exper. Astron., 30, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O. 2003, A&A, 404, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guyon, O., & Roddier, F. J. 2000, in Interferometry in Optical Astronomy, ed. P. J. Lena, & A. Quirrenbach, SPIE Conf., 4006, 377 [Google Scholar]
- Guyon, O., Pluzhnik, E. A., Galicher, R., et al. 2005, ApJ, 622, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Pluzhnik, E. A., Kuchner, M. J., Collins, B., & Ridgway, S. T. 2006, ApJS, 167, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Guyon, O., Martinache, F., Belikov, R., & Soummer, R. 2010a, ApJS, 190, 220 [Google Scholar]
- Guyon, O., Martinache, F., Garrel, V., et al. 2010b, in SPIE Conf. Ser., 7736 [Google Scholar]
- Guyon, O., Shaklan, S., Levine, M., et al. 2010c, in SPIE Conf. Ser., 7731 [Google Scholar]
- Hinkley, S., Oppenheimer, B. R., Zimmerman, N., et al. 2011, PASP, 123, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Hodapp, K. W., Suzuki, R., Tamura, M., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasper, M. E., Beuzit, J.-L., Verinaud, C., et al. 2008, in SPIE Conf., 7015 [Google Scholar]
- Kuchner, M. J., & Traub, W. A. 2002, ApJ, 570, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, M. J., Crepp, J., & Ge, J. 2005, ApJ, 628, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leskel, M., & Ritala, M. 2002, Thin Solid Films, 409, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B. A., Graham, J. R., Palmer, D. W., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- MacLeod, H. A. 1991, Thin-Film Optical Filters, ed. H. A. MacLeod [Google Scholar]
- Marois, C., Doyon, R., Racine, R., & Nadeau, D. 2000, PASP, 112, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Martinache, F., Guyon, O., Pluzhnik, E. A., Galicher, R., & Ridgway, S. T. 2006, ApJ, 639, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, P., Boccaletti, A., Kasper, M., et al. 2008, A&A, 492, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mawet, D., Riaud, P., Absil, O., & Surdej, J. 2005, ApJ, 633, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Mawet, D., Riaud, P., Baudrand, J., et al. 2006, A&A, 448, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mawet, D., Pueyo, L., Moody, D., Krist, J., & Serabyn, E. 2010, in SPIE Conf., 7739 [Google Scholar]
- Moody, D. C., Gordon, B. L., & Trauger, J. T. 2008, in SPIE Conf. Ser., 7010 [Google Scholar]
- Mugnier, L. M., Sauvage, J.-F., Fusco, T., Cornia, A., & Dandy, S. 2008, Opt. Exp., 161, 18406 [Google Scholar]
- Murakami, N., Uemura, R., Baba, N., et al. 2008, PASP, 120, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- N’Diaye, M., Dohlen, K., Cuevas, S., et al. 2010, A&A, 509, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppenheimer, B. R., & Hinkley, S. 2009, ARA&A, 47, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Palik, E. 1985, Handbook of Optical Constants of Solids (Academic Press), 1 [Google Scholar]
- Pluzhnik, E. A., Guyon, O., Ridgway, S. T., et al. 2006, ApJ, 644, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, F., & Roddier, C. 1997, PASP, 109, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Rouan, D., Riaud, P., Boccaletti, A., Clénet, Y., & Labeyrie, A. 2000, PASP, 112, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Sauvage, J.-F., Fusco, T., Petit, C., et al. 2010, in SPIE Conf. Ser., 7736 [Google Scholar]
- Shaklan, S. B., & Green, J. J. 2005, ApJ, 628, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Sidick, E. 2007, Appl. Opt., 46, 7485 [NASA ADS] [CrossRef] [Google Scholar]
- Sivaramakrishnan, A., Soummer, R., Sivaramakrishnan, A. V., et al. 2005, ApJ, 634, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Sivaramakrishnan, A., Soummer, R., Carr, G. L., et al. 2009, in SPIE Conf. Ser., 7440 [Google Scholar]
- Soummer, R. 2005, ApJ, 618, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Aime, C., & Falloon, P. E. 2003a, A&A, 397, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soummer, R., Dohlen, K., & Aime, C. 2003b, A&A, 403, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soummer, R., Pueyo, L., Sivaramakrishnan, A., & Vanderbei, R. J. 2007, Opt. Exp., 15, 15935 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Sivaramakrishnan, A., Oppenheimer, B. R., et al. 2009, in SPIE Conf. Ser., 7440 [Google Scholar]
- Soummer, R., Sivaramakrishnan, A., Pueyo, L., Macintosh, B., & Oppenheimer, B. R. 2011, ApJ, 729, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Traub, W. A., & Oppenheimer, B. R. 2010, Direct Imaging of Exoplanets, ed. S. Seager, 111 [Google Scholar]
- Trauger, J., Stapelfeldt, K., Traub, W., et al. 2010, in SPIE Conf. Ser., 7731 [Google Scholar]
- Vigan, A., Langlois, M., Moutou, C., & Dohlen, K. 2008, A&A, 489, 1345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zamkotsian, F., & Dohlen, K. 2004, in SPIE Conf. 5487, ed. J. C. Mather, 635 [Google Scholar]
All Tables
Values of the CAPM coronagraph parameters optimized for different spectral bandwidths and averaged intensity results at different separations.
Values of the parameters for the CAPM coronagraph optimized with an assembly using nickel thin film for the colored apodization.
Intensity values provided by the CAPM coronagraph with the theoretical model and the physical design for the colored apodization, for a 25% bandwidth centered at λ0 = 1.650 μm (H-band).
All Figures
 |
Fig. 1 Scheme of the coronagraphic layout. |
| In the text | |
 |
Fig. 2 Schematic representation of the DZPM. The dimensions are not at scale in this drawing. |
| In the text | |
 |
Fig. 3 Schematic illustration of the method used for computating ΨD. |
| In the text | |
 |
Fig. 4 Schematic illustration of the wavelengths and bandwidth of study. λI and λO represent the limit wavelengths of the spectral bandwidth. |
| In the text | |
 |
Fig. 5 a) Radial profile of the colored intensity apodization for the CAPM coronagraph at different wavelengths λ; b) radial profiles of the difference between the intensity apodization at a given wavelength λ and at the central wavelength λ0 (here 1.650 μm); c) and d) reproduce panels a) and b) respectively, for the phase given by the phase apodization Φw. |
| In the text | |
 |
Fig. 6 Radial profiles of the residual intensity with the CAPM coronagraph, within the re-imaged pupil in plane C (top) and in the final image plane D (bottom) at different wavelengths λ. Profiles have been normalized at the origin to directly read the coronagraphic extinction ratio at a given angular distance from the on-axis star image. |
| In the text | |
 |
Fig. 7 Optimized values of the amplitude apodization parameter ω1,λ (top plot), ω2,λ (middle) and the phase apodization parameter βλ (bottom) as a function of the wavelength for different bandwidths. A second-degree polynomial interpolation of the points is represented for each parameter and bandwidth. |
| In the text | |
 |
Fig. 8 Radial intensity profile of the coronagraphic images achieved with the CAPM coronagraph for different sizes of the spectral bandwidth. |
| In the text | |
 |
Fig. 9 Theoretical averaged intensity at 5 λ0/D obtained with the CAPM coronagraph as a function of the wavelength for different bandwidths. |
| In the text | |
 |
Fig. 10 Theoretical averaged intensity achieved at different angular separations from the main optical axis with the DZPM and CAPM coronagraphs as a function of the bandwidth. |
| In the text | |
 |
Fig. 11 Schematic illustration of the assembly, composed of a metallic thin film deposited on a substrate. The scheme is not to scale. |
| In the text | |
 |
Fig. 12 Transmission values in intensity obtained for the theoretical model and the assembly with different metals as a function of the wavelength. Values are provided for different normal radial distances. Thickness for each material and radial distance are given in Table 2. |
| In the text | |
 |
Fig. 13 Top: thickness profile of the nickel layer as a function of the wavelength. Bottom: optimized values of the phase apodization parameter βλ for the CAPM coronagraph in the presence of the theoretical model and the physical design as a colored amplitude apodization. |
| In the text | |
 |
Fig. 14 a) Radial intensity profile of the colored apodizer, made with an assembly using nickel layer, for the CAPM coronagraph at different wavelengths λ; b) radial profiles of the difference between the intensity apodization at a given wavelength λ and that obtained at the central wavelength λ0 (here 1.650 μm); c) and d) reproduce a) and b) respectively for the phase given by the phase apodization Φw. |
| In the text | |
 |
Fig. 15 Radial intensity profile of the coronagraphic images achieved with the CAPM coronagraph using the theoretical model and the physical design for the colored apodizer. |
| In the text | |
 |
Fig. 16 Top: design of a lens doublet combining Schott glass materials N-FK9 and K5. Bottom: focal shift versus wavelength. This result has been obtained assuming a longitudinal focal shift reached in the visible range with our values of βλ. A second-order polynomial chromatic focal shift with a 5 mm amplitude range has been achieved. |
| In the text | |
 |
Fig. 17 Planet transmission profile achieved with the CAPM coronagraph as a function of the planet position. |
| In the text | |
 |
Fig. 18 Set of coronagraphic images achieved with the CAPM coronagraph and computed numerically for different aberrations. All the images are normalized to the peak of the noncoronagraphic image. The pixel scale is the same for all the images, and the field of view is represented with a linear range of 22 λ0/D. |
| In the text | |
 |
Fig. 19 Radial intensity profiles of the coronagraphic images theoretically achieved with the CAPM coronagraph for different rms wavefront errors values of defocus (top plot), spherical aberration (middle), and random aberration with PSD defined above (bottom). |
| In the text | |
 |
Fig. 20 Theoretical averaged intensity at 5 λ0/D (top plot) and IDA (bottom plot) achieved with the CAPM coronagraph for different aberrations. |
| In the text | |
 |
Fig. 21 Radial intensity profiles of the coronagraphic images theoretically achieved with the CAPM coronagraph for different rms values of mask roughness (top plot) and for different sizes of mask transition width, expressed in DZPM diameter d2 (bottom). |
| In the text | |
 |
Fig. 22 Theoretical averaged intensity (top plot) and IDA (bottom plot) achieved with the CAPM coronagraph as a function of the size of the mask transition zone (bottom axis) and the mask roughness (top axis). |
| In the text | |
 |
Fig. 23 Theoretical averaged intensity at 5 λ0/D achieved with the CAPM coronagraph as a function of the Lyot stop (LS) size. The dashed line represents the edge of the geometrical relayed pupil. The gray area represents the tolerance range, defined in the text, for the CAPM coronagraph optimized with 90% LS. |
| In the text | |
 |
Fig. 24 Theoretical averaged intensity at 5 λ0/D achieved with the CAPM coronagraph and a 90% Lyot stop, as a function of the Lyot stop misalignment. The dashed line represents the edge of the geometric relayed pupil. These results are obtained in the presence of a clear circular aperture. |
| In the text | |
 |
Fig. 25 Radial intensity profiles of the coronagraphic images theoretically achieved with the CAPM coronagraph for different stellar radii. |
| In the text | |
 |
Fig. 26 Theoretical averaged intensity at 5 λ0/D (top plot) and IDA (bottom plot) achieved with the CAPM coronagraph for different stellar radii. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


