| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117655 | |
| Published online | 09 February 2012 | |
Dark matter subhaloes as gamma-ray sources and candidates in the first Fermi-LAT catalogue
1 University of Hamburg, Institut für Experimentalphysik, Luruper Chaussee 149, 22761 Hamburg, Germany
e-mail: hzechlin@physik.uni-hamburg.de
2 University of Würzburg, Institut für Theoretische Physik und Astrophysik, Am Hubland, 97074 Würzburg, Germany
Received: 7 July 2011
Accepted: 3 November 2011
The standard paradigm of hierarchical structure formation in a ΛCDM universe predicts the presence of dark matter subhaloes, hosted by Milky Way-sized galaxies. Anticipated subhalo masses range from 1010 down to a cut-off mass between 10-3 and 10-11 M⊙. If dark matter is composed of heavy self-annihilating or decaying particles, these subhaloes could be visible in the γ-ray band as faint and temporally constant sources without astrophysical counterparts. Based upon realistic subhalo models and current observational constraints on annihilating dark matter scenarios, we predict that one massive Galactic subhalo between 106 and 108 M⊙ may already be present in the 11-month catalogue of Fermi-LAT. Indeed, at least twelve objects in the first Fermi catalogue qualify as candidates. The most promising object, 1FGL J0030.7+0724, is investigated in detail using a dedicated Swift X-ray follow-up observation and a refined positional analysis of the 24-month Fermi-LAT data. With the new observations, seven point-like X-ray sources have been discovered, of which SWIFT J003119.8+072454, which coincides with a faint radio source (12 mJy at 1.4 GHz), serves as a counterpart candidate of 1FGL J0030.7+0724. The broad-band spectral energy distribution is consistent with a high-energy-peaked blazar. However, flux and extent of 1FGL J0030.7+0724 may also be compatible with a dark matter subhalo. Detection of temporal variability or improved astrometry of 1FGL J0030.7+0724 are necessary to rule out or confirm an astrophysical origin. We discuss strategies to identify γ-ray sources that are associated with self-annihilating dark matter subhaloes.
Key words: dark matter / Galaxy: halo / Galaxy: structure / gamma rays: general
© ESO, 2012
1. Introduction
Several astrophysical observations indicate that in the early as well as in the present Universe a non-baryonic form of dark matter (DM) prevails over the baryonic matter content. Structure formation favours a cold dark matter (CDM) scenario (for recent reviews see, e.g., Bertone et al. 2005; D’Amico et al. 2009; Bertone 2010). However, the nature of DM remains unknown. A class of promising candidates for CDM are stable, weakly interacting, massive particles (WIMPs) with masses between 10 and 105 GeV, predicted by theories that extend the standard model of particle physics. The most prominent extensions encompass those based on supersymmetry and universal extradimensions, which were invented to solve inconsistencies of the standard model at high energy scales [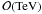 ], and which deliver adequate DM candidates in this way. These particles can self-annihilate or decay, producing detectable signatures in the final states such as energetic photons (γ rays), antimatter, and leptons.
], and which deliver adequate DM candidates in this way. These particles can self-annihilate or decay, producing detectable signatures in the final states such as energetic photons (γ rays), antimatter, and leptons.
Unravelling the nature of DM remains a challenging problem for astronomy and particle physics, and a variety of attempts to detect signals have been made, using both direct and indirect detection techniques. For instance, multi-wavelength observations of astrophysical targets have constrained the self-annihilation rate of DM, which is related to the thermally averaged annihilation cross section. In particular, regions with high DM densities such as the Galactic Centre (Aharonian et al. 2006a,b; Morselli et al. 2010; Abramowski et al. 2011b), Galactic Ridge (Aharonian et al. 2006d), dwarf spheroidal galaxies (dSphs; Colafrancesco et al. 2007; Albert et al. 2008b; Aharonian et al. 2008, 2009; Aliu et al. 2009; Aharonian et al. 2010; Abdo et al. 2010c; Acciari et al. 2010; Aleksić et al. 2011, H.E.S.S. Collaboration 2011), as well as globular (Colafrancesco et al. 2006; Wagner 2009; Abramowski et al. 2011a) and galaxy clusters (Aleksić et al. 2010; Ackermann et al. 2010) serve as excellent targets. Furthermore, DM annihilation in the entire Galactic halo as well as its subhalo population produces a diffuse γ-ray flux, which contributes to the overall diffuse signal of the Galaxy. Comparatively stringent upper limits on the annihilation cross section have been obtained from the combination of both dedicated observations and bounds obtained from the diffuse γ-ray flux (Abazajian et al. 2010; Cirelli et al. 2010; Meade et al. 2010; Papucci & Strumia 2010; Zaharijas et al. 2010).
Based on the theory of hierarchical structure formation, DM haloes of Milky Way-sized galaxies are anticipated to host numerous DM subhaloes with masses between a cut-off scale 10-11−10-3 and 1010 M⊙ (e.g., Bringmann 2009), where M⊙ denotes the solar mass. This expectation is a consequence of the early collapse of overdensities in the expanding Universe (Diemand et al. 2005), leading to the formation of initially low-mass haloes, which subsequently serve as building-blocks for larger haloes by merging at later times. Besides analytical calculations (e.g., Berezinsky et al. 2003, 2006, 2008), recent numerical high-resolution N-body simulations of structure formation in a ΛCDM cosmology (Komatsu et al. 2011), such as the Aquarius Project (Springel et al. 2008a,b) or the Via Lactea II simulation (Diemand et al. 2008b; Zemp et al. 2009), allow us to study substructures in detail. For a Milky Way-type galaxy, these simulations predict a large number of subhaloes (up to 1016) with masses distributed following a power law, dN/dM ∝ M − α, where α ∈ [1.9;2.0] . The DM density profiles of large-mass subhaloes are found to be similar to the host’s, which results in high central densities (Springel et al. 2008a). The spatial distribution of subhaloes is “anti-biased”, i.e., the dominant fraction is placed far away from the host-halo’s centre.
In self-annihilating DM scenarios, subhaloes are expected to appear as weak point-like or moderately extended γ-ray sources, and a small fraction of them could be detectable with current high- or very high-energy (VHE) γ-ray telescopes (e.g., Pieri et al. 2005, 2008, 2011; Springel et al. 2008b; Kuhlen et al. 2008; Ando 2009; Buckley & Hooper 2010; Brun et al. 2011; Zechlin et al. 2011). Examples for currently operating telescopes are the Fermi-LAT (20 MeV−300 GeV, Atwood et al. 2009) and imaging air Cherenkov telescopes (IACTs; E ≳ 100 GeV) such as H.E.S.S. (Aharonian et al. 2006c), MAGIC (Albert et al. 2008a; Tridon et al. 2010), and VERITAS (Weekes et al. 2002). In the near future, a significant improvement in the overall sensitivity and lower energy threshold will be achieved by upcoming experiments such as H.E.S.S.-II (Vincent 2005) and CTA (Hermann 2010; the CTA consortium 2010; Doro 2011). Such instruments are possibly sufficiently sensitive to detect nearby large-mass subhaloes of  within distances of
within distances of 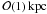 .
.
This paper consists of two separate parts, which can in principle be read independently. The first part (Sects. 2 to 4) investigates the detectability of subhaloes with Fermi-LAT, where the basic framework for predicting the γ-ray properties of subhaloes is laid out in Sects. 2 and 3. In Sect. 4, properties of detectable subhaloes are investigated by means of a fiducial source. In the second part, Sect. 5 discusses the search for DM subhaloes in the first Fermi-LAT point-source catalogue (1FGL) and subsequent multi-wavelength studies of the most promising candidate, 1FGL J0030.7+0724. A discussion of the physical origin of 1FGL J0030.7+0724 and prospects for IACTs are presented in Sect. 6.
Throughout this paper, Hubble’s constant is H0 = 73 km s-1 Mpc-1, yielding the present value of the Universe’s critical density 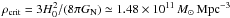 , where GN denotes Newton’s gravitational constant (e.g., Spergel et al. 2007).
, where GN denotes Newton’s gravitational constant (e.g., Spergel et al. 2007).
2. Gamma rays from DM subhaloes
In the following, the γ-ray flux from DM subhaloes will be derived, based upon current theoretical models of the corresponding radial density distribution.
With respect to undisturbed, isolated galactic haloes, henceforth field haloes, the general formation history of (embedded) subhaloes differs significantly. Analytical models and numerical N-body simulations of structure formation found their physical properties to depend on particular evolutionary conditions, i.e., formation time, evolution, and orbit (see Diemand et al. 2007, 2008a, and references therein). Tidal interaction with the gravitational potential of the host halo leads to tidal stripping and heating, and can therefore truncate the outer region of subhaloes. In the following, two different approaches will be discussed. On the one hand, subhaloes are modelled assuming negligible tidal effects and are therefore considered to be in a genuine virialised state. Because this approximation is (at least) valid for field haloes, this model will be tagged as field-halo model (FHM). On the other hand, a second and more realistic model is considered to account for subhalo evolution, henceforth referred to as subhalo model (SHM).
2.1. Density profile
The subhalo’s DM density profile ρ(r) is assumed to follow 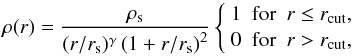 (1)where r denotes the distance to the subhalo’s centre. In general, the profile cuts at an outer radius rcut, which is the virial or tidal radius (Rvir or Rt), respectively. Given γ = 1.0 for the remainder, the profile follows the universal spherically symmetric Navarro-Frenk-White (NFW) profile, well-fitting haloes resolved in numerical simulations1 (Navarro et al. 1997). The profile is defined by two parameters: a characteristic inner radius rs, where the effective logarithmic slope of the profile is − 2, and an inner density ρs = 4ρ(rs). In case of FHM haloes, which are not subject to tides, both parameters are related to each other by the virial halo mass Mvir. This quantity is defined as the mass inside the sphere of radius Rvir, which encloses a mean density of Δc times the critical density of the Universe at the considered redshift z (Navarro et al. 1997; Bullock et al. 2001),
(1)where r denotes the distance to the subhalo’s centre. In general, the profile cuts at an outer radius rcut, which is the virial or tidal radius (Rvir or Rt), respectively. Given γ = 1.0 for the remainder, the profile follows the universal spherically symmetric Navarro-Frenk-White (NFW) profile, well-fitting haloes resolved in numerical simulations1 (Navarro et al. 1997). The profile is defined by two parameters: a characteristic inner radius rs, where the effective logarithmic slope of the profile is − 2, and an inner density ρs = 4ρ(rs). In case of FHM haloes, which are not subject to tides, both parameters are related to each other by the virial halo mass Mvir. This quantity is defined as the mass inside the sphere of radius Rvir, which encloses a mean density of Δc times the critical density of the Universe at the considered redshift z (Navarro et al. 1997; Bullock et al. 2001), 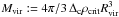 . The virial overdensity at z = 0 is Δc ≈ 100, as suggested by models of the dissipationless spherical top-hat collapse (Eke et al. 1996; Bryan & Norman 1998) and assuming present concordance cosmology. In general, the subhalo mass M is given by a volume integration of Eq. (1), revealing
. The virial overdensity at z = 0 is Δc ≈ 100, as suggested by models of the dissipationless spherical top-hat collapse (Eke et al. 1996; Bryan & Norman 1998) and assuming present concordance cosmology. In general, the subhalo mass M is given by a volume integration of Eq. (1), revealing 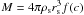 , where f(c) ≡ ln(1 + c) − c/(1 + c) and c denotes the concentration parameter of the subhalo. For non-disturbed haloes, the concentration is then given by the virial concentration cvir ≡ Rvir/rs. Generally, the concentration depends on the subhalo mass and redshift, c = c(M,z), where lighter haloes have higher concentrations (Navarro et al. 1996, 1997; Bullock et al. 2001). Since observational estimates are lacking (see Sect. 2.2.1 in Lavalle et al. 2008, and references therein), c(M) is adopted from N-body simulations. For the FHM, the toy model of Bullock et al. (2001)2 is used, where the halo’s (average) virial concentration at redshift z is connected with the density of the Universe at the halo’s (mass-dependent) collapse redshift zc(M), cvir = K(1 + zc)/(1 + z). The contraction parameter K is constant and independent of cosmology. To determine the mass dependence of zc and, therefore, of cvir at z = 0, the low-mass extrapolation of the Bullock model by Lavalle et al. (2008) is adapted. Because cvir implicitly depends on Δc (see also Sect. 2.2), a conversion of cvir to Δc = 100 was applied3 with the relation of Hu & Kravtsov (2003). The concentration-to-mass relation is well-fitted by the polynomial form
, where f(c) ≡ ln(1 + c) − c/(1 + c) and c denotes the concentration parameter of the subhalo. For non-disturbed haloes, the concentration is then given by the virial concentration cvir ≡ Rvir/rs. Generally, the concentration depends on the subhalo mass and redshift, c = c(M,z), where lighter haloes have higher concentrations (Navarro et al. 1996, 1997; Bullock et al. 2001). Since observational estimates are lacking (see Sect. 2.2.1 in Lavalle et al. 2008, and references therein), c(M) is adopted from N-body simulations. For the FHM, the toy model of Bullock et al. (2001)2 is used, where the halo’s (average) virial concentration at redshift z is connected with the density of the Universe at the halo’s (mass-dependent) collapse redshift zc(M), cvir = K(1 + zc)/(1 + z). The contraction parameter K is constant and independent of cosmology. To determine the mass dependence of zc and, therefore, of cvir at z = 0, the low-mass extrapolation of the Bullock model by Lavalle et al. (2008) is adapted. Because cvir implicitly depends on Δc (see also Sect. 2.2), a conversion of cvir to Δc = 100 was applied3 with the relation of Hu & Kravtsov (2003). The concentration-to-mass relation is well-fitted by the polynomial form ![\begin{equation} \label{eq:cvir_lavalle} \ln (c^{\rm FHM}_{\rm vir}) = \sum_{i=0}^{4} c^{\rm FHM}_i \times \left[ \ln \left( \frac{M}{{M}_\odot} \right) \right]^i, \end{equation}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq56.png) (2)
(2)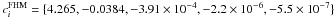 . Note that this model almost equals the relation derived by Pieri et al. (2011) for a cosmology as used in the Aquarius simulation. Regarding the concentration of SHM haloes, the low-mass extrapolation of the Bullock model provides a conservative estimate (cf., Pieri et al. 2008).
. Note that this model almost equals the relation derived by Pieri et al. (2011) for a cosmology as used in the Aquarius simulation. Regarding the concentration of SHM haloes, the low-mass extrapolation of the Bullock model provides a conservative estimate (cf., Pieri et al. 2008).
 |
Fig. 1 Concentration-to-mass relation for subhaloes at z = 0. The dashed blue line depicts the concentration predicted by the Bullock model (FHM), while its corresponding scatter is given by the blue-shaded area. The mean concentration corrected for subhalo evolution (SHM) is shown by the solid red line for a galactocentric distance of 74 kpc, the average distance of the dSph galaxies included from Abdo et al. (2010c) (black triangles). For comparison, the concentration derived for Aquarius subhaloes is indicated by the dot-dashed dark green line within its validity range, the low/high-mass extrapolation by the double-dotted green line. The black filled circle marks the virial concentration of the MW. |
However, because subhalo formation differs from that of field haloes and includes tidal truncation at Rt, the virial concentration is not well defined for subhaloes4 (Diemand et al. 2007). Therefore, the SHM incorporates an empirical correction of cvir. Indicated by numerical simulations, the concentration of subhaloes increases with decreasing distance to the host’s centre Dgc, 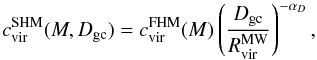 (3)see Diemand et al. (2007, 2008a) and Kuhlen et al. (2008). The galactocentric distance is
(3)see Diemand et al. (2007, 2008a) and Kuhlen et al. (2008). The galactocentric distance is 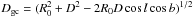 , where D denotes the subhalo’s distance to the Sun, (l,b) its position in galactic coordinates, and R0 = (8.28 ± 0.29) kpc the Sun’s distance to the Galactic Centre (Catena & Ullio 2010). The virial radius of the Milky Way (MW) is
, where D denotes the subhalo’s distance to the Sun, (l,b) its position in galactic coordinates, and R0 = (8.28 ± 0.29) kpc the Sun’s distance to the Galactic Centre (Catena & Ullio 2010). The virial radius of the Milky Way (MW) is 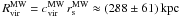 , where
, where 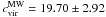 and
and 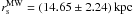 (Catena & Ullio 2010). The power-law slope αD = 0.237 is adopted as fitting subhaloes resolved in the Aquarius simulation (Pieri et al. 2011).
(Catena & Ullio 2010). The power-law slope αD = 0.237 is adopted as fitting subhaloes resolved in the Aquarius simulation (Pieri et al. 2011).
Intrinsic to the stochastic process of halo formation, the concentration of individual haloes scatters around the median 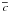 provided by the quantities
provided by the quantities 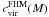 and
and 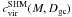 , respectively. The corresponding probability distribution follows a lognormal,
, respectively. The corresponding probability distribution follows a lognormal, ![\begin{equation} \label{eq:scatter} P(c,\overline{c}) = \frac{\log_{10} e}{\sqrt{2 \pi} \sigma_{\log_{10} c} \,c} \exp \left[ -\frac{1}{2} \left( \frac{\log_{10} c - \log_{10} \overline{c}}{\sigma_{\log_{10} c}} \right)^2 \right], \end{equation}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq72.png) (4)where σlog 10c = 0.14 (Bullock et al. 2001; Wechsler et al. 2002).
(4)where σlog 10c = 0.14 (Bullock et al. 2001; Wechsler et al. 2002).
The concentration-to-mass relations are shown in Fig. 1. For the FHM, the scatter is also depicted (68% c.l. of log 10c), see Eq. (4). In addition to the concentration of the MW, Fig. 1 contains a selection of eight dSphs that are associated with sufficiently precise stellar data, which allow a conclusive modelling of the DM distribution (see Abdo et al. 2010c). Each dSph is modelled with a NFW profile with parameters chosen to fit measurements of stellar line-of-sight velocities and their distributions (see also Martinez et al. 2009). The dSph’s virial concentration is given by its characteristic density, ![\hbox{$\rho_{\rm s}=\Delta_{\rm c} \rho_{\rm crit} c_{\rm vir}^3/[3f(c_{\rm vir})]$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq75.png) , where tidal effects on the inner system are assumed to be negligible. The SHM is depicted for Dgc = 74 kpc, the average galactocentric distance of the dSph subset. Additionally, the models are confronted with direct predictions of the Aquarius simulation, derived from scaling relations fitting subhaloes observed in the simulation. Details are provided in Appendix A.
, where tidal effects on the inner system are assumed to be negligible. The SHM is depicted for Dgc = 74 kpc, the average galactocentric distance of the dSph subset. Additionally, the models are confronted with direct predictions of the Aquarius simulation, derived from scaling relations fitting subhaloes observed in the simulation. Details are provided in Appendix A.
Within its scatter, the concentration model of FHM haloes consistently describes the DM profile of dSph galaxies and the MW itself. However, the median values 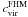 underpredict dSphs, whereas the subhalo model SHM provides convincing agreement (as expected by N-body simulations). The concentration derived directly from the Aquarius simulation confirms the SHM within the validity range, see Fig. 1. Note that the mean distance of subhaloes resolved in Aquarius is 64 kpc.
underpredict dSphs, whereas the subhalo model SHM provides convincing agreement (as expected by N-body simulations). The concentration derived directly from the Aquarius simulation confirms the SHM within the validity range, see Fig. 1. Note that the mean distance of subhaloes resolved in Aquarius is 64 kpc.
2.2. DM annihilation in subhaloes
For self-annihilating particles, the total rate of photons (or particles) emitted by a DM subhalo with energy E in the interval [E1;E2] is 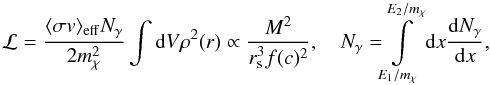 (5)where ⟨ σv ⟩ eff is the thermally averaged annihilation cross section times the relative velocity, mχ the WIMP mass, and dNγ/dx, x ≡ E/mχ, denotes the differential spectrum of photons per annihilation. Assuming rs ≪ D, the produced photon flux is given by φ = ℒ/(4πD2). The solution of the integral holds for γ = 1.0 and c ≫ 1. In Eq. (5), a small, flat core replacing the unphysical singularity at the halo centre (Berezinsky et al. 1992) is safely neglected (given the NFW profile used here). For γ = 1.0, Eq. (5) simplifies via
(5)where ⟨ σv ⟩ eff is the thermally averaged annihilation cross section times the relative velocity, mχ the WIMP mass, and dNγ/dx, x ≡ E/mχ, denotes the differential spectrum of photons per annihilation. Assuming rs ≪ D, the produced photon flux is given by φ = ℒ/(4πD2). The solution of the integral holds for γ = 1.0 and c ≫ 1. In Eq. (5), a small, flat core replacing the unphysical singularity at the halo centre (Berezinsky et al. 1992) is safely neglected (given the NFW profile used here). For γ = 1.0, Eq. (5) simplifies via ![\hbox{$r_{\rm s} = [ 3 M/(4\pi \Delta_{\rm c} \rho_{\rm crit} c_{\rm vir}^3) ]^{1/3}$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq88.png) :
: 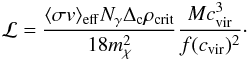 (6)For a γ = 1.2 profile (Eq. (1)) the photon rate increases by a factor of ~1.5 for subhaloes above 103 M⊙. DM annihilation in subhaloes may be additionally boosted by sub-substructure populations (see Strigari et al. 2007; Kuhlen et al. 2008; Martinez et al. 2009). Conveniently, the value of ⟨ σv ⟩ eff is normalised to the value ⟨ σv ⟩ 0 = 3 × 10-26 cm3 s-1, which leads to the correct relic density. An increase of the annihilation rate, a so-called boost factor ⟨ σv ⟩ eff/ ⟨ σv ⟩ 0, could in principle be related to the underlying particle physics framework (e.g., Fornengo et al. 2004) and effects such as Sommerfeld enhancement (e.g., Arkani-Hamed et al. 2009; Kuhlen et al. 2009).
(6)For a γ = 1.2 profile (Eq. (1)) the photon rate increases by a factor of ~1.5 for subhaloes above 103 M⊙. DM annihilation in subhaloes may be additionally boosted by sub-substructure populations (see Strigari et al. 2007; Kuhlen et al. 2008; Martinez et al. 2009). Conveniently, the value of ⟨ σv ⟩ eff is normalised to the value ⟨ σv ⟩ 0 = 3 × 10-26 cm3 s-1, which leads to the correct relic density. An increase of the annihilation rate, a so-called boost factor ⟨ σv ⟩ eff/ ⟨ σv ⟩ 0, could in principle be related to the underlying particle physics framework (e.g., Fornengo et al. 2004) and effects such as Sommerfeld enhancement (e.g., Arkani-Hamed et al. 2009; Kuhlen et al. 2009).
We considered DM to be composed of self-annihilating heavy WIMPs of mass mχ = 500 GeV and investigated three distinct annihilation models: two of them with total annihilation in heavy quarks or gauge bosons ( and W + W − ) and a model with total annihilation in the leptons τ + τ − . Additionally, we considered WIMPs of mχ = 150 GeV for annihilation in τ + τ − final states. Particles of this type are, for instance, provided by supersymmetric theories, e.g., manifested in the neutralino. The WIMP masses chosen are compatible with WIMPs which might explain the recently observed cosmic-ray electron and positron excess, see, e.g., Meade et al. (2010). In general, heavy WIMPs are also supported by collider searches such as the non-detection of supersymmetric particles in the 7 TeV run of the Large Hadron Collider (for an integrated luminosity of 35 pb-1) (Aad et al. 2011; CMS Collaboration 2011, and references therein).
and W + W − ) and a model with total annihilation in the leptons τ + τ − . Additionally, we considered WIMPs of mχ = 150 GeV for annihilation in τ + τ − final states. Particles of this type are, for instance, provided by supersymmetric theories, e.g., manifested in the neutralino. The WIMP masses chosen are compatible with WIMPs which might explain the recently observed cosmic-ray electron and positron excess, see, e.g., Meade et al. (2010). In general, heavy WIMPs are also supported by collider searches such as the non-detection of supersymmetric particles in the 7 TeV run of the Large Hadron Collider (for an integrated luminosity of 35 pb-1) (Aad et al. 2011; CMS Collaboration 2011, and references therein).
 |
Fig. 2 Differential γ-ray energy spectra |
Given these final annihilation states, hadronisation and the subsequent decay of π0-mesons lead to a continuous γ-ray spectrum. The resulting photon spectra dNγ/dx were modelled using parametrisations provided by Fornengo et al. (2004), see Fig. 2. Note that photons produced by final state radiation (FSR) and virtual internal bremsstrahlung (VIB) (Bergström et al. 2005a,b; Bringmann et al. 2008) are neglected, because a significant contribution of FSR is only expected for W + W − at high energies (E > 0.6 mχ) and possible contributions of VIB are highly model-dependent.
3. Candidate gamma-ray sources
Given a high WIMP mass, a DM subhalo will show up as steady (very) high-energy γ-ray source. The differential photon spectrum follows a hard power law (index Γ ≲ 1.5) that cuts off exponentially at energies beyond 10 GeV, see Fig. 2.
Candidate sources are selected according to their possibility to originate from DM subhaloes based on their observational quantities flux and angular extent. Note that the detailed spectral shape of faint sources is observationally rather unconstrained. Via Eq. (6), the effective self-annihilation cross section ⟨ σv ⟩ eff required to obtain a given flux φ for the intrinsic source extent θs is determined by ℒ = 4πD2φ, where θs constrains the distance D to the subhalo. For feasible candidate sources the required ⟨ σv ⟩ eff should comply with current observational constraints.
Conveniently, the characteristic profile radius rs (see Eq. (1)) traces the intrinsic extent of a DM subhalo, because for an NFW profile 87.5% of the total luminosity is produced within rs (see Table 1 for values of rs). Therefore, the distance to the subhalo is D ≈ rs/θs, where θs denotes the angle corresponding to rs. Owing to the centrally peaked profile, about 68% of the total luminosity is emitted within the angle θ68 ≃ 0.46 θs. The following relations are given with respect to θs and can easily be adjusted for θ68, which is more convenient for a comparison with observational data. With ![\hbox{$r_{\rm s} = [ 3 M/(4\pi \Delta_{\rm c} \rho_{\rm crit} c_{\rm vir}^3)]^{1/3}$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq114.png) , the distance to a subhalo with given θs is related to its mass and concentration. In the FHM,
, the distance to a subhalo with given θs is related to its mass and concentration. In the FHM, 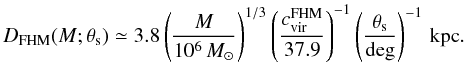 (7)Note that the concentration depends on the subhalo mass via Eq. (2) as well as, in the SHM, on the object’s position (l,b).
(7)Note that the concentration depends on the subhalo mass via Eq. (2) as well as, in the SHM, on the object’s position (l,b).
 |
Fig. 3 Effective self-annihilation cross section ⟨ σv ⟩ eff required for a moderately extended, faint Fermi-LAT source to originate from a DM subhalo of mass M. Assumed source parameters are φ(10−100 GeV) = 1.6 × 10-10 cm-2 s-1, an intrinsic extent θs = 1° (θ68 ≈ 0.5°), and the Galactic position (l,b) = (114°, −55°). The dashed blue and solid red lines indicate the average prediction considering the FHM and SHM, respectively. The intrinsic SHM scatter is shown by the red-shaded area and the dotted red lines. The left panel depicts WIMPs of mχ = 500 GeV totally annihilating in |
For a given WIMP model ⟨σv⟩eff is then fully determined by the subhalo mass (Eq. (6)) and the observed quantities flux and extent: 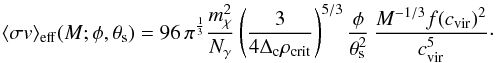 (8)Additional contributions to the DM signal from annihilation in the smooth halo as well as the entire subhalo population were neglected5. The required ⟨ σv ⟩ eff is highly sensitive to the (observationally unconstrained) concentration, because Eq. (8) roughly depends on
(8)Additional contributions to the DM signal from annihilation in the smooth halo as well as the entire subhalo population were neglected5. The required ⟨ σv ⟩ eff is highly sensitive to the (observationally unconstrained) concentration, because Eq. (8) roughly depends on 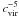 .
.
4. Interpretation of Fermi sources as DM subhaloes
Based on the study of a fiducial candidate source in Sect. 4.1, the properties of Fermi-LAT detectable subhaloes are investigated in Sect. 4.2.
4.1. A fiducial candidate
4.1.1. Observational properties
In combination with improving (integrated) sensitivity at high energy (Atwood et al. 2009, and cf., Fig. 7), the expected energy spectrum of DM subhaloes (Sects. 2 and 3) favours a detection at the high-energy band of Fermi-LAT. In Appendix B, we investigate the detection sensitivity for faint, moderately extended (θs ≲ 1°, corresponding to θ68 ≲ 0.5°), and high-latitude (|b| > 20°) sources between 10 and 100 GeV in detail. We find that a spectrally hard high-energy source with a flux φ(10−100 GeV) = 1.4 × 10-10 cm-2 s-1 and moderate extent6θs = 1° can be detected as a point-source with a reconstructed flux φp(10−100 GeV) = 0.9 × 10-10 cm-2 s-1, with a sky-survey exposure of one year. With respect to the true flux φ emitted by the entire source, the reconstructed flux φp fitted by the point-source analysis in general decreases with increasing θs. To account for this effect, the scaling relation φ(θs) = h(θs) φp is used in Eq. (8), where h(θs) = 1 for θs ≪ 2 σPSF and h(θs) ≈ 0.72(θs/deg) + 0.89 for extended sources up to ~1° (see Appendix B for details).
The high-energy flux of the fiducial source above 10 GeV has been chosen to be at the level of the detection sensitivity, 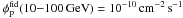 , assuming an extent of
, assuming an extent of 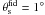 . Given the dependence of the SHM concentration on the galactocentric distance (see Eq. (3)), the fiducial source is placed on a particular line-of-sight chosen to match the location of 1FGL J0030.7+0724 (investigated in Sect. 5). In general, this line-of-sight serves as an appropriate (conservative) benchmark, because it points to (anticentric) positions where the majority of subhaloes is located.
. Given the dependence of the SHM concentration on the galactocentric distance (see Eq. (3)), the fiducial source is placed on a particular line-of-sight chosen to match the location of 1FGL J0030.7+0724 (investigated in Sect. 5). In general, this line-of-sight serves as an appropriate (conservative) benchmark, because it points to (anticentric) positions where the majority of subhaloes is located.
4.1.2. Subhalo interpretation
Adopting the properties of the fiducial source, Fig. 3 depicts the effective enhancement factors ⟨ σv ⟩ eff/ ⟨ σv ⟩ 0 required to generate the emission 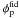 by DM annihilation (obtained via Eq. (8)). In the left panel, WIMPs of mχ = 500 GeV are considered to totally annihilate in
by DM annihilation (obtained via Eq. (8)). In the left panel, WIMPs of mχ = 500 GeV are considered to totally annihilate in 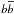 , while the right panel assumes mχ = 150 GeV and annihilation in τ + τ − . For a given WIMP model, the resulting enhancement factors of the FHM and SHM are widely different. With respect to the FHM, much less enhancement is required in the SHM, which is manifested in generically higher concentrations of SHM subhaloes. Within the scatter of the concentration intrinsic to the stochastic nature of halo formation (Eq. (4)), which is shown for the SHM, the necessary enhancement spans about one order of magnitude. Only moderate enhancement is required for massive subhaloes between 106 and 107 M⊙, where the lowest ⟨ σv ⟩ eff is needed for mχ = 150 GeV and τ + τ − final states (amongst the WIMP models considered here). The lowest possible enhancement factors within the concentration scatter of a 106 M⊙ subhalo are listed in Table 1 for the different subhalo and the WIMP models of Sect. 2.
, while the right panel assumes mχ = 150 GeV and annihilation in τ + τ − . For a given WIMP model, the resulting enhancement factors of the FHM and SHM are widely different. With respect to the FHM, much less enhancement is required in the SHM, which is manifested in generically higher concentrations of SHM subhaloes. Within the scatter of the concentration intrinsic to the stochastic nature of halo formation (Eq. (4)), which is shown for the SHM, the necessary enhancement spans about one order of magnitude. Only moderate enhancement is required for massive subhaloes between 106 and 107 M⊙, where the lowest ⟨ σv ⟩ eff is needed for mχ = 150 GeV and τ + τ − final states (amongst the WIMP models considered here). The lowest possible enhancement factors within the concentration scatter of a 106 M⊙ subhalo are listed in Table 1 for the different subhalo and the WIMP models of Sect. 2.
The distance to the fiducial candidate anticipated in the FHM and the SHM is shown in Fig. 4. The intrinsic concentration scatter implies a corresponding distance scatter for a given halo mass and angular extent. Note that a similar scatter is present for the FHM, but is not shown in the figure. Compared with the FHM, tidal effects lead to higher concentrated subhaloes. This in turn favours a closer distance at the same mass and angular extent for SHM subhaloes than for FHM.
Enhancement factors ⟨ σv ⟩ eff/ ⟨ σv ⟩ 0 required to explain the fiducial γ-ray source with a DM subhalo of 106 M⊙.
4.1.3. Consistency with observational constraints
The resulting values of ⟨ σv ⟩ eff can now be checked for consistency with the diffuse extragalactic γ-ray background (EGB; Abdo et al. 2010b). Fermi-LAT measurements of the overall diffuse γ-ray flux allow the derivation of the isotropic high-energy EGB, which is shown to be compatible with a featureless power-law spectrum (Γ = 2.41 ± 0.05) and integrated diffuse flux φEGB(>100 MeV) = (1.03 ± 0.17) × 10-5 cm-2 s-1 sr-1 (Abdo et al. 2010b). The diffuse γ-ray flux anticipated from DM annihilation in the Galactic halo as well as the entire subhalo population is shown in Fig. 5 (see Appendix C for details), in comparison with the EGB. Both FHM and SHM subhaloes are depicted for mχ = 150 GeV and annihilation in τ+τ − . In this model, the nearly isotropic diffuse flux from the subhalo population contributes about 1% to the EGB (assuming SHM subhaloes and no sub-substructure) and is fainter than the contribution of the smooth halo (≳3%). Note that the flux from the extragalactic halo population is lower than the contribution of Galactic subhaloes, see, e.g., Abazajian et al. (2010).
The contribution from the smooth halo peaks at the Galactic Centre, where a high astrophysical foreground is also present, and can therefore not be isotropic. Given that the EGB has been derived assuming isotropy, the most robust upper limits on ⟨ σv ⟩ eff are determined by the subhalo contribution and are listed in Table 2, depending on the WIMP model and cut-off mass. The bounds were obtained requiring that the specific intensity of the subhalo population ⟨ Iν(180°,E) ⟩ does not exceed the EGB, where ⟨ Iν(ψ,E) ⟩ depends on the angle ψ between the Galactic Centre direction and line-of-sight, and the γ-ray energy E (see Appendix C).
 |
Fig. 4 Distance to the fiducial subhalo in the FHM (dashed blue line) and SHM (solid red line), respectively, as function of the subhalo mass M. The scatter of the SHM distance is indicated by the red-shaded area. An extent of θs = 1° (θ68 ≈ 0.5°) and a source position (l,b) = (114°, −55°) are assumed. |
However, more stringent constraints have been provided by a more detailed modelling of the EGB, including all DM components. To evaluate a possible DM origin of the fiducial source, the results of Abazajian et al. (2010) and Papucci & Strumia (2010)7 are included in Fig. 3. As stated in the introduction, competitive and similar constraints have been also provided by the non-detection of various objects with high (central) DM densities. Note, for instance, that the constraints used here are consistent with recent bounds from dSph galaxies (Abdo et al. 2010c).
 |
Fig. 5 Average diffuse γ-ray flux from DM annihilation in the Galaxy as function of the angle between the observational and Galactic Centre direction ψ. The fluxes from the host halo (double-dot-dashed magenta line), FHM (dashed blue line), and SHM subhaloes (solid red line) are depicted. Each curve was derived at the peak energy of νIν(E) (40 GeV) assuming total annihilation in τ+τ− with mχ = 150 GeV and ⟨ σv ⟩ eff = ⟨ σv ⟩ 0. The minimum subhalo mass used was Mmin = 10-6 M⊙ (see Appendix C). The EGB at 40 GeV is shown by the dotted black line. |
Upper limits on ⟨ σv ⟩ eff/ ⟨ σv ⟩ 0 from the EGB.
4.2. Fermi-LAT detectable subhaloes
4.2.1. Expected number
Integrating over the mass and spatial distribution (Eq. (C.2)) reveals the total number of detectable subhaloes with masses MI ∈ [M;M + ΔM] , solar distances DI ∈ [D;D + ΔD] , concentrations cI ∈ [c;c + Δc] , galactic latitudes bI ∈ [b,b + Δb] , and galactic longitudes l ∈ [0;2π] , N = N(MI,DI,cI,bI), 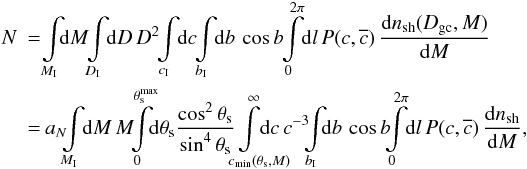 (9)using D = rs/tanθs (see Sect. 3) and aN ≡ 3/(4πΔcρcrit). Parameters defining the subhalo distribution were taken to match the Aquarius simulation (Appendix C). In total, this resulted in about 6.4 × 1014 Galactic subhaloes residing in the Galaxy. For every single θs and M, the integral counts detectable subhaloes only, i.e., their concentration is sufficiently high to ensure their ⟨ σv ⟩ eff to be smaller than the observational constraints (cf., Fig. 3). Therefore, the lower bound of the concentration integral cmin(θs,M) is determined via Eq. (8), choosing the instrument’s sensitivity and constraints from Abazajian et al. (2010) and Papucci & Strumia (2010), respectively. To account for the fact that highly extended objects will be hardly detectable (see Appendix B), we conservatively chose
(9)using D = rs/tanθs (see Sect. 3) and aN ≡ 3/(4πΔcρcrit). Parameters defining the subhalo distribution were taken to match the Aquarius simulation (Appendix C). In total, this resulted in about 6.4 × 1014 Galactic subhaloes residing in the Galaxy. For every single θs and M, the integral counts detectable subhaloes only, i.e., their concentration is sufficiently high to ensure their ⟨ σv ⟩ eff to be smaller than the observational constraints (cf., Fig. 3). Therefore, the lower bound of the concentration integral cmin(θs,M) is determined via Eq. (8), choosing the instrument’s sensitivity and constraints from Abazajian et al. (2010) and Papucci & Strumia (2010), respectively. To account for the fact that highly extended objects will be hardly detectable (see Appendix B), we conservatively chose 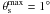 . For the SHM, Fig. 6 shows the number of detectable subhaloes per mass decade expected in one year of data taking while considering subhaloes at galactic latitudes |b| ≥ 20° only (cf., Sect. 5). Given the dependence of cmin on the WIMP model, the results for the
. For the SHM, Fig. 6 shows the number of detectable subhaloes per mass decade expected in one year of data taking while considering subhaloes at galactic latitudes |b| ≥ 20° only (cf., Sect. 5). Given the dependence of cmin on the WIMP model, the results for the 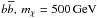 model are compared to the τ + τ − , mχ = 150 GeV scenario.
model are compared to the τ + τ − , mχ = 150 GeV scenario.
 |
Fig. 6 Expected number of one-year detectable subhaloes per mass decade at |b| ≥ 20°. The subhaloes′ mass and spatial distributions were adopted from Aquarius (Appendix C) while the SHM concentration was used. Mmin = 10-6 M⊙. The number corresponding to the |
Considering the constraints found by Abazajian et al. (2010) for the 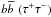 model, on average 0.4 (0.2) subhaloes within 105 and 108 M⊙ are anticipated for detection with Fermi-LAT in one year. Given the Poisson distribution of N, this means that up to one massive subhalo is expected in the one-year data set (at 95% confidence). Comparable results have been claimed by other authors, e.g., Baltz et al. (2008), Kuhlen et al. (2008), Pieri et al. (2008, 2011), and Anderson et al. (2010).
model, on average 0.4 (0.2) subhaloes within 105 and 108 M⊙ are anticipated for detection with Fermi-LAT in one year. Given the Poisson distribution of N, this means that up to one massive subhalo is expected in the one-year data set (at 95% confidence). Comparable results have been claimed by other authors, e.g., Baltz et al. (2008), Kuhlen et al. (2008), Pieri et al. (2008, 2011), and Anderson et al. (2010).
In general, note that numerical simulations like Aquarius and Via Lactea II neglect the influences of baryonic matter distributed in galactic disks. A recent study by D’Onghia et al. (2010) indicates that a baryonic disk may reduce the number of (massive) subhaloes in the inner galaxy by a factor of 2 to 3.
4.2.2. Properties
Given a particular γ-ray source (such as the fiducial of Sect. 4.1), massive subhaloes between about 105 and 108 M⊙ require a minimally enhanced annihilation cross section ⟨ σv ⟩ eff, see Fig. 3. Consistently, the probability for these objects to appear in current data sets peaks for high subhalo masses (Fig. 6). Therefore, subhalos with masses of 105 up to 108 M⊙ in corresponding distances from 0.5 to 10 kpc (Fig. 4) are favoured for detection with Fermi-LAT as faint and moderately extended sources. Although for the FHM a DM origin of the fiducial source is excluded, within the scatter of the more realistic SHM cross sections required for sources with φ(10 − 100 GeV) ≈ 10-10 cm-2 s-1 and angular extents up to ~1° are well consistent with observational constraints. The presence of sub-substructure will even lower ⟨ σv ⟩ eff by a mass-dependent factor of ~2 to 3 for massive subhaloes (Kuhlen et al. 2008; Martinez et al. 2009). In case of a cuspier profile (γ = 1.2), the required cross section is lowered by an additional factor of 1.5. At least for WIMPs of mχ = 150 GeV annihilating to τ + τ − , this leads to a required enhancement of the order of unity within the scatter. Summarising, in optimistic but realistic scenarios a γ-ray emitter at the (one year) detection level of Fermi-LAT with a measured extent θ68 of about 0.5° might be consistent with a subhalo driven by self-annihilating DM.
In the next years, Fermi-LAT will provide deeper observations with increased observation time Tobs. This will improve the sensitivity by roughly 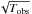 , leading to a factor of about 2 lower values of the minimum detectable flux for the five-year catalogue. This in turn will allow us to detect fainter subhaloes with a correspondingly reduced minimum ⟨ σv ⟩ eff. The average number of detectable subhaloes within five years is about 1.3 (0.8) for the
, leading to a factor of about 2 lower values of the minimum detectable flux for the five-year catalogue. This in turn will allow us to detect fainter subhaloes with a correspondingly reduced minimum ⟨ σv ⟩ eff. The average number of detectable subhaloes within five years is about 1.3 (0.8) for the 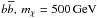 (τ + τ − , mχ = 150 GeV) scenario.
(τ + τ − , mχ = 150 GeV) scenario.
Via Eq. (8), a comparison with observational constraints on ⟨ σv ⟩ eff allows to estimate the maximum flux subhalo candidates are expected to have. The catalogued flux is 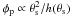 , which is quadratic for θs ≪ 0.3° and linear in the limit of large θs. The increase with θs originates from decreasing subhalo distance. Because massive subhaloes require minimum ⟨ σv ⟩ eff, a subhalo of 106 M⊙ is assumed below. Within the concentration scatter, the maximum flux between 10 and 100 GeV expected for a source with θs = 1° is
, which is quadratic for θs ≪ 0.3° and linear in the limit of large θs. The increase with θs originates from decreasing subhalo distance. Because massive subhaloes require minimum ⟨ σv ⟩ eff, a subhalo of 106 M⊙ is assumed below. Within the concentration scatter, the maximum flux between 10 and 100 GeV expected for a source with θs = 1° is 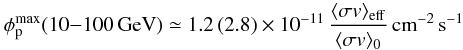 (10)in the
(10)in the 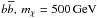 and τ + τ − , mχ = 150 GeV scenario, respectively. Given the observational constraints of Abazajian et al., the high-energy flux of catalogued candidates should not exceed
and τ + τ − , mχ = 150 GeV scenario, respectively. Given the observational constraints of Abazajian et al., the high-energy flux of catalogued candidates should not exceed 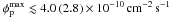 .
.
5. Searches for DM subhaloes in the 1FGL
In the previous section we demonstrated that DM subhaloes could appear in γ-ray catalogues of sufficient sensitivity as faint, non-variable, and moderately extended objects without astrophysical counterparts. The 11-month8 point-source catalogue of Fermi-LAT (1FGL, Abdo et al. 2010a) lists 1451 sources significantly detected above 100 MeV (test statistic TS ≥ 25, corresponding to a significance S = 4.1σ), together with the flux in five discrete energy bins (up to 100 GeV), position, significance of variability, and spectral curvature. Source spectra have been fitted with power laws. Among the sources, 630 objects9 are not confidently associated with known sources at other wavelengths.
Although sophisticated methods have been applied to find multi-wavelength associations for unidentified sources, all algorithms suffer from lacking sensitivity or incomplete sky-coverage of current surveys. Therefore, the sample of unassociated high-latitude Fermi-LAT sources is expected to be composed of several source classes, among them faint AGN (Active Galactic Nuclei), galaxy clusters, and new exotic sources like DM subhaloes (Stephen et al. 2010; Mirabal et al. 2010, and references therein). Concerning the 1FGL catalogue, improved association methods recently presented by Mirabal et al. (2010) revealed that ≲20% of all unassociated 1FGL sources with |b| ≥ 15° may contain new γ-ray emitters.
To single out possible subhalo candidates within the sample of unassociated sources (cf., Buckley & Hooper 2010), we searched the sample for non-variable10 sources detected between 10 and 100 GeV. Requiring a detection at high energy provides subhalo candidates driven by heavy WIMPs and avoids confusion with high-energy pulsars11. Furthermore, the candidate’s location was constrained to galactic latitudes |b| ≥ 20° to avoid a general confusion with Galactic sources. Additionally, the lower Galactic foreground improves the detection sensitivity of Fermi-LAT at high latitudes (Atwood et al. 2009).
Applying all cuts, twelve unassociated sources remain. The twelve sources are listed in Table 4 together with additional information from the catalogue. With the exception of 1FGL J0614.1-3328, the sample consists of sources at the faint end of the entire 1FGL sample. Given the result of Mirabal et al. (2010), the sample should statistically contain two to three subhaloes at most, consistent with the estimate discussed previously (Fig. 6). The expectation of the sample consisting mostly of AGN is met by applying the same cuts to all AGN detected by Fermi-LAT. A comparison with the sample of unassociated sources reveals similar cut efficiencies (5% vs. 11%, see Table 3), indicating that the two populations share common properties. Note that for the AGN the variability cut has subdominant influence as well, see Table 3. Except for three, all AGN that passed the cuts have been classified as BL Lac.
Cut efficiencies on the sample of unassociated sources and AGN.
Even though the twelve candidate objects are listed in the 1FGL catalogue as unassociated, we extended the counterpart search to a wider choice of astronomical catalogues. Table 4 lists the classifications of counterpart candidates in the 68% confidence regions around the most likely 1FGL positions, retrieved from the NASA/IPAC Extragalactic Database (NED). In particular, possible associatons are provided by radio and X-ray sources, since most of the selected γ-ray sources are expected to be AGN. Given that no detailed association study was conducted, some of the tabulated sources might be by-chance associations.
Unassociated, non-variable 1FGL sources at high galactic latitudes.
Governed by lacking association, faintness, and spectral shape, this study focusses on the most promising candidate, 1FGL J0030.7+0724. Within the errors, its high-energy flux and spectral index are well-compatible with a self-annihilating DM scenario. The source has only been detected between 10 and 100 GeV, see Fig. 7.
5.1. Multi-wavelength properties of 1FGL J0030.7+0724
5.1.1. Catalogued data
No counterpart candidate was found within the positional uncertainty of the γ-ray source at a 68% confidence level (Table 4). In the 95% confidence region, the faint radio object NVSS J003030+072132 is located (f1.4 GHz = (3.5 ± 0.4) mJy; Condon et al. 1998). However, no conclusive infrared (2MASS, Skrutskie et al. 2006) or optical (USNO B1.0, Monet et al. 2003) association of the NVSS source is known so far12. Note that no dSph galaxy is located in the source region (NED). ROSAT (0.1−2.4 keV; Voges et al. 1999) observations of the region with an exposure of about 170 s revealed no X-ray source down to an energy-flux level of ~10-12 erg cm-2 s-1 (Borm 2010).
We emphasise that the orphaned faint radio source is likely located in the uncertainty region of 1FGL J0030.7+0724 by chance, because about 0.7 NVSS sources are expected by statistics.
 |
Fig. 7 Energy spectrum of 1FGL J0030.7+0724 as given in the first Fermi-LAT catalogue between 100 MeV and 100 GeV (filled circles). The solid red line depicts the (catalogued) power law fitting the data. Only the highest energy bin has been significantly detected, while for the low-energy bins upper limits are shown (95% c.l.). |
5.1.2. Fermi-LAT data
By analysing the 24-month public archival data between 10 and 100 GeV, updated results on 1FGL J0030.7+0724 will be provided. For the same energy range, a reanalysis of the 11-month data is presented for comparison. Particular focus will be drawn on positional properties, the high-energy flux, and the photon distribution, which allows us to investigate possible counterparts, temporal variability, and the angular extent.
The data analysis was performed with the latest public version of the Fermi science tools (v9r18p6)13 along with recommended options and the set of instrument-response functions P6_V3_DIFFUSE (Rando 2009). Throughout the analysis, the optimiser MINUIT was used. For reliable results, photons of event class 3 (Diffuse) and 4 (DataClean) within a radius of 10°, centred on the nominal position of 1FGL J0030.7+0724, were selected. Given that most of the photons are at highest energies (Fig. 7), only events between 10 and 100 GeV were selected to minimise the background and ensure a narrow PSF. The data were processed using gtselect, gtmktime, gtltcube, gtexpmap, and unbinned gtlike. To compute the most likely position and its corresponding uncertainty on basis of the 10–100 GeV photon sample, we used gtfindsrc. For the purpose of detailed counterpart searches, the two-dimensional likelihood function L(RA,Dec) was computed, which provides the 95% uncertainty contour by 2 Δ(log L) = 6.18 (2 degrees of freedom).
Positional and spectral properties of 1FGL J0030.7+0724 as given in the catalogue (11 months) and by the (re-)analysis of the first 11 and 24-month data sets.
The source model for the data analysis contains all 1FGL sources within the region of interest (ROI, radius 10°). Their parameters were taken as catalogued and we used the latest Galactic (gll_iem_v02.fit) and extragalactic (isotropic_iem_v02.txt) diffuse background models. All parameters but those of 1FGL J0030.7+0724 were kept fixed. Furthermore, the catalogued power-law index of 1FGL J0030.7+0724 was used while fitting the flux between 10 and 100 GeV. Although the exposure of the 24-month data has almost doubled with respect to the catalogue, the use of the catalogued properties for sources within the ROI will not affect the analysis between 10 and 100 GeV: The three nearby sources, i.e., 1FGL J0022.5+0607, 1FGL J0030.4+0451, and 1FGL J0023.5+0930, are not only more than 2° away from 1FGL J0030.7+0724, but they are also not significantly detected between 10 and 100 GeV. Furthermore, visual inspection does not reveal any other relevant source within this nearby region.
High-energy photons detected from 1FGL J0030.7+0724 within 0.5°.
The analysis of the 11-month data reproduces the catalogued values well (Table 5). After 11 (24) months, five (six) photons between 10 and 100 GeV have been detected within a radius of 0.5° around the nominal position, listed in Table 6. Except one, all photons are classified as class 4 events and are therefore very likely signal events. The Galactic foreground and the extragalactic background at the source position are negligible with respect to the signal, with an expected total number of background photons Nbg = 0.6 (1.2) within the considered region of 0.5°. For comparison, the predicted number of signal events is Nsig = 4.9 (5.8) after 11 (24) months. According to the 11-month data set, the (10–100 GeV) best-fit position shifts by about 2.5′. The small positional error of the sixth photon also accounts for the increase of the source’s positional uncertainty, see Fig. 8.
The average flux over the entire data set has decreased by a factor of roughly 1.5 with respect to the first 11 months (Table 5). To judge on the variability of 1FGL J0030.7+0724, its temporal photon distribution (Table 6) was tested for compatibility with a constant flux, using an unbinned Kolmogorov-Smirnov (KS) test (Press et al. 2007). The KS test is already valid for low photon counts, unlike the binned chi-square method used by the catalogue. The KS test confirms the null-hypothesis of non-variability with a probability of about 0.7 (0.5) for the 11 (24) months data set. The varying exposure on the region was taken into account by examining the photon distribution of the bright pulsar nearby (1FGL J0030.4+0451).
 |
Fig. 8 Celestial region of 1FGL J0030.7+0724, 25′ × 13′. The catalogued position is indicated by the red + , while the dashed red ellipse borders its uncertainty (95% c.l.). The black × marks the 24-month position, the solid black contour its uncertainty at 95% confidence. Photons detected by Swift-XRT (10.1 ks) are mapped by the back-image, which is smoothed with a Gaussian (7′′). The positions of NVSS radio sources are given by the darkgreen boxes, the two NVSS sources discussed in the text are named. In this region, seven X-ray sources have been discovered, indicated by the blue arrows (see Table 7). Note that the boxes’ size is chosen arbitrarily. |
The analysis of the (intrinsic) spatial extent of the source is based upon a likelihood-ratio test, using all photons listed in Table 6. The corresponding statistical measure is given by ![\hbox{$L(\theta_{\rm s}) = -2 \sum_{i=1}^N \ln [p_{\rm det}({\vec x}_i-\overline{\vec x};\theta_{\rm s}) + b]$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq274.png) , where pdet(x;θs) is the probability distribution function for a photon detected at x,
, where pdet(x;θs) is the probability distribution function for a photon detected at x,  denotes the best-fit position (Table 5), and b incorporates the flat background. For a spatially extended γ-ray emitter pdet = pPSF ∗ pint, the (two dimensional) convolution of the Fermi-LAT PSF (P6_v3, diffuse class) with the intensity profile of the emitter. In the subhalo case, the intensity profile follows the line-of-sight integral of the squared NFW profile (Eq. (1)). The quantity ΔL = L − Lmin follows a chi-square distribution with one degree of freedom, with additional terms of the order of 1/N1/2, which are important for a small number of counts (Wilks 1938; Cash 1979). The likelihood is minimised (Lmin) for the intrinsic extension parameter fitting the photon distribution best. Examining the 11-month data, the test shows the source to be consistent with a point source, implying that the intrinsic extent is smaller than the (average) PSF (about 0.15°). The 24-month data favour a moderate extent
denotes the best-fit position (Table 5), and b incorporates the flat background. For a spatially extended γ-ray emitter pdet = pPSF ∗ pint, the (two dimensional) convolution of the Fermi-LAT PSF (P6_v3, diffuse class) with the intensity profile of the emitter. In the subhalo case, the intensity profile follows the line-of-sight integral of the squared NFW profile (Eq. (1)). The quantity ΔL = L − Lmin follows a chi-square distribution with one degree of freedom, with additional terms of the order of 1/N1/2, which are important for a small number of counts (Wilks 1938; Cash 1979). The likelihood is minimised (Lmin) for the intrinsic extension parameter fitting the photon distribution best. Examining the 11-month data, the test shows the source to be consistent with a point source, implying that the intrinsic extent is smaller than the (average) PSF (about 0.15°). The 24-month data favour a moderate extent 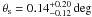 , which is, however, not significant. Upper limits on the extension parameter are θs ≤ 0.54 (0.72) deg at 95% confidence level, derived from the 11 (24) months data set. Since the low statistics affect the chi-square distribution, note that the confidence level is not precisely defined (Cash 1979; Mattox et al. 1996). Furthermore, we point out that the PSF of Fermi-LAT (P6_v3) may be underestimated14 and changes will have an impact on the fitted extent.
, which is, however, not significant. Upper limits on the extension parameter are θs ≤ 0.54 (0.72) deg at 95% confidence level, derived from the 11 (24) months data set. Since the low statistics affect the chi-square distribution, note that the confidence level is not precisely defined (Cash 1979; Mattox et al. 1996). Furthermore, we point out that the PSF of Fermi-LAT (P6_v3) may be underestimated14 and changes will have an impact on the fitted extent.
5.1.3. Swift-XRT data
The field was successfully proposed for observation with the X-ray telescope (XRT, 0.2–10 keV) onboard the Swift satellite (Gehrels et al. 2004, 2005). The observations (Obs. ID 00041265001) were carried out on 10 November, 2010, between 00:23:46 and 19:52:56 UT with a total effective exposure of 10.1 ks. Observations with the XRT were performed in photon-counting (PC) mode. The XRT data were calibrated and selected with standard screening criteria (xrtpipeline), using the HEAsoft 6.10 package for data reduction with the current version of calibration files available (release 2010-09-30). For the analysis, events with grades 0–12 (Burrows et al. 2005) were used. The spectral analysis was carried out with Xspec (12.6.0, Arnaud 1996), using the PC grade 0–12 response matrix swxpc0to12s6_20070901v011.rmf with the ancilliary response function generated by xrtmkarf for PSF correction and the position of the source considered. The on-source region was selected to contain about 90% of the PSF (≈47′′). For background subtraction, an off-source region with radius of about 4′ was used. To ensure a spectral fit of sufficient quality, the spectra were rebinned to a minimum of 10 events per bin (with grppha). Owing to the low statistics accumulated, the C-statistic was used for spectral fitting.
In the field-of-view (FoV) of XRT, seven new X-ray sources were discovered with a probability of being background fluctuations smaller than 10-6. We show them in Fig. 8. Their positional properties, measured flux, and the flux corrected for photoelectric absorption between 0.2 and 2 keV are listed in Table 7. The spectra of the two brightest sources are well-fitted by an absorption corrected power-law model, fixing the hydrogen column density NH to the nominal Galactic value. The power-law index for the faint sources was fixed to 2.0. The Galactic hydrogen column density was obtained from the LAB HI survey (Kalberla et al. 2005) for the corresponding celestial positions.
Associations.
The newly discovered X-ray sources were studied for possible associations in other accessible wavelengths. Multi-wavelength surveys covering the region are the NVSS in the radio, the 2MASS in the infrared, and the USNO B1.0 and SDSS DR7 catalogues for the optical band. For every Swift source we found at least one SDSS source to be positionally coincident (Table 8), with apparent magnitudes between 21m and 17m. Owing to insufficient sensitivity, the very faint SDSS sources have not been detected by USNO.
X-ray sources detected with the Swift-XRT.
6. Discussion
6.1. An AGN origin of 1FGL J0030.7+0724
The γ-ray signal of 1FGL J0030.7+0724 can be explained by a conventional AGN. With respect to the unified scheme for the spectral energy distribution (SED) of AGN (namely Flat Spectrum Radio Quasars (FSRQs) and blazars), see, e.g., Donato et al. (2001), the hard spectral index of 1FGL J0030.7+0724 (Γ ≈ 1.7) is compatible with a high-energy-peaked blazar (HBL). Within the updated positional uncertainty of 1FGL J0030.7+0724 derived from the 24-month data (Fig. 8), the most likely radio counterpart is NVSS J003119+072456 (f1.4 GHz = (11.6 ± 0.6) mJy), which positionally coincides with the newly discovered hard X-ray source SWIFT J003119.8+072454 (Γ ≈ 1.6). Note that corresponding to the notation of Table 7, the Swift source is flagged with a G in Fig. 8. The energy flux observed between 0.2 and 2 keV is ~2 × 10-13 erg cm-2 s-1 (Table 7). Additionally, an optical counterpart of the radio and X-ray source is listed in the SDSS catalogue (r = 17.4m), see Table 8. In Fig. 9 we show an empirical model for the average SED of HBLs, which is based on the bolometric luminosity distribution of FSRQs and blazars (Fossati et al. 1997, 1998; Donato et al. 2001). The SED is normalised to the radio flux of NVSS J003119+072456 (at 5 GHz). For comparison, the spectral measurements of the optical and X-ray counterparts are presented as well. Within the observational errors and assuming temporal variability, the γ-ray spectrum of 1FGL J0030.7+0724 is consistent with the model prediction. Furthermore, the spectral index of the X-ray source agrees with an HBL, while its flux is fainter than predicted for an (average) HBL. This might be also explainable by temporal variability (the radio, X-ray, and γ-ray observations were not taken simultaneously), and blazars are well known to be variable in all wavelength bands, where the amplitude of variability increases with energy (Ulrich et al. 1997).
The other fainter objects in the uncertainty region (the radio source NVSS J003030+072132 and the two X-ray sources E and F, see Fig. 8) are less likely to be associated with 1FGL J0030.7+0724, but cannot be excluded. For NVSS J003030+072132, no X-ray association was detected with Swift-XRT at the level of 2 × 10-14 erg cm-2 s-1. No conclusive optical counterpart is catalogued (above ~26m, see Sect. 5.1.1). With respect to the comparatively high γ-ray signal (cf., Fig. 9), this source therefore fails to provide a convincing counterpart for 1FGL J0030.7+0724. Similarly, the lacking radio detection as well as energy fluxes (~4 × 10-14 erg cm-2 s-1), which are much fainter than the HBL prediction, disfavour a coincidence of the X-ray sources E and F with 1FGL J0030.7+0724.
 |
Fig. 9 Energy spectra of 1FGL J0030.7+0724 (solid red line) and the favoured radio (filled black triangle), optical (violet crosses, dereddened ugriz magnitudes), and X-ray (solid blue line) counterparts, together with the SED of an average HBL (solid black line). The SED was adapted from Donato et al., assuming the average redshift of known HBLs z = 0.25 (Donato et al. 2001), and is normalised to the radio flux of NVSS J003119+072456. The frequency-dependent energy flux νfν is given in the observer’s frame. Note that the statistical errors of the radio and optical data points are too low to be resolved in the figure. Statistical uncertainties of the X- and γ-ray spectra are indicated by the corresponding shaded areas, which we derived with Eq. (1) in Abdo et al. (2009b). The filled red circle indicates the catalogued high-energy flux from Fermi-LAT. Observations with ROSAT provide an upper limit on the X-ray flux at the nominal position of 1FGL J0030.7+0724 between 0.1 and 2.4 keV, which is depicted by the green square (95% c.l., assuming Γ = 2.0, Borm 2010). |
6.2. A DM subhalo origin of 1FGL J0030.7+0724
Without a clear indication for variability, it remains plausible that the γ-ray emission of 1FGL J0030.7+0724 originates from a DM subhalo. The analysis of the arrival times of the source photons (Sect. 5.1.2) is consistent with a temporally constant source of moderate spatial extent. The reconstructed high-energy flux within the statistical errors is φp(10 − 100 GeV) ≳ 5 × 10-11 cm-2 s-1, while the upper limit on the extent is θs ≲ 0.7°, corresponding to θ68 ≲ 0.3°. As shown in Sect. 4, in realistic WIMP scenarios the high effective self-annihilation cross section required to explain the source with DM annihilation in a FHM subhalo is hardly compatible with current observational constraints (see Fig. 3 and Table 1). However, given the more realistic SHM, flux and extent of 1FGL J0030.7+0724 are consistent with a subhalo of mass between 106 and 108 M⊙. Assuming a DM subhalo of 106 M⊙, the resulting distance would be 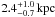 , given the concentration scatter of the SHM model. For a WIMP of 500 GeV annihilating to
, given the concentration scatter of the SHM model. For a WIMP of 500 GeV annihilating to 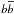 , the required minimum effective enhancement is 7 for a high-concentrated SHM subhalo with a corresponding distance of 1.7 kpc, while it increases to 31 for an average-concentrated subhalo with a corresponding distance of 2.4 kpc. Note that h(0.7°) ≈ 1.4. An even lower boost factor is required for a lighter WIMP of 150 GeV which predominantly annihilates to τ+τ−: 3 (13) for a high-concentrated (average-concentrated) SHM subhalo. Further decrease of the necessary boost may be provided by sub-substructure and cuspier profiles (Sect. 4).
, the required minimum effective enhancement is 7 for a high-concentrated SHM subhalo with a corresponding distance of 1.7 kpc, while it increases to 31 for an average-concentrated subhalo with a corresponding distance of 2.4 kpc. Note that h(0.7°) ≈ 1.4. An even lower boost factor is required for a lighter WIMP of 150 GeV which predominantly annihilates to τ+τ−: 3 (13) for a high-concentrated (average-concentrated) SHM subhalo. Further decrease of the necessary boost may be provided by sub-substructure and cuspier profiles (Sect. 4).
In addition to theoretical uncertainties on halo properties and their expected scatter (Sect. 2.1), observational uncertainties affect the distance and boost factor estimates. The uncertainties on the flux directly change the boost, while uncertainties on the most crucial measurement, the angular extent θs, affect both the required boost and the distance estimate (Sect. 3). The discussed object 1FGL J0030.7+0724 serves as an appropriate benchmark, because the corresponding uncertainties are representative for a typical DM subhalo source. The observational uncertainties are of similar magnitude as the theoretical ones.
6.3. Remarks and prospects for IACTs
The 28-month data of Fermi-LAT contains no additional photon detected around the nominal position. This lowers the probability of steadiness to ~25% and may indicate variability, which supports a BL Lac scenario. Vice versa, such a behaviour would also be anticipated by a selection bias: If the true flux is lower than the value found in the discovery data set, the discovery condition would only allow for the detection of sources where the photon number has been fluctuating upwards. Poisson fluctuations of this faint signal could have accounted for a detection with the LAT even if the true flux had remained below the detection sensitivity.
It is instructive to note that with regard to a definite identification of a counterpart (or ruling out a candidate) from observations in other wavelength regimes the limiting factor is the accuracy of the Fermi-LAT source position (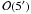 , cf., Table 4) and PSF. With just six detected photons, probably including one background photon, the source is close to the confusion limit. This situation can only be resolved by future instruments with much larger effective areas, such as the proposed CTA, which will probe deep into the expected population of subhaloes. The much larger number of photons would help to infer significantly improved source positions. Furthermore, for detecting a spectral cut-off and in case of heavy WIMPs (mχ > 1 TeV), observations in the VHE range with IACTs are favoured. For the particular DM scenarios proposed for 1FGL J0030.7+0724, fluxes anticipated in the energy ranges accessible for MAGIC and H.E.S.S., φ(>50 GeV) and φ(>300 GeV), respectively, are listed in Table 9 (given by φ(>E) ∝ Nγ(>E)/Nγ(10−100 GeV), see Eq. (8)). Additionally, flux estimates for WIMPs with mχ = 1 TeV were derived. Note that the required effective cross sections (see Sect. 6.2) increase by a factor of 2.3, because
, cf., Table 4) and PSF. With just six detected photons, probably including one background photon, the source is close to the confusion limit. This situation can only be resolved by future instruments with much larger effective areas, such as the proposed CTA, which will probe deep into the expected population of subhaloes. The much larger number of photons would help to infer significantly improved source positions. Furthermore, for detecting a spectral cut-off and in case of heavy WIMPs (mχ > 1 TeV), observations in the VHE range with IACTs are favoured. For the particular DM scenarios proposed for 1FGL J0030.7+0724, fluxes anticipated in the energy ranges accessible for MAGIC and H.E.S.S., φ(>50 GeV) and φ(>300 GeV), respectively, are listed in Table 9 (given by φ(>E) ∝ Nγ(>E)/Nγ(10−100 GeV), see Eq. (8)). Additionally, flux estimates for WIMPs with mχ = 1 TeV were derived. Note that the required effective cross sections (see Sect. 6.2) increase by a factor of 2.3, because 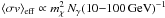 . Also note that fluxes expected for VERITAS are comparable to those for H.E.S.S.
. Also note that fluxes expected for VERITAS are comparable to those for H.E.S.S.
Fluxes above the energy thresholds of MAGIC and H.E.S.S., predicted by a DM scenario of 1FGL J0030.7+0724.
The low energy threshold of MAGIC leads to comparatively high integrated VHE fluxes for mχ < 1 TeV. The flux prediction for MAGIC is of 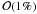 of the Crab Nebula’s for the favoured τ+τ−,mχ = 150 GeV and W+W−,mχ = 1 TeV model. With MAGIC, 50 h of observation are necessary to detect this source with more than 5σ. For comparison, predicted fluxes for H.E.S.S. are not higher than 0.2% Crab for these models, which requires a few hundred hours of observation (Aharonian et al. 2006c). We remark that advanced analysis methods improve the sensitivity of H.E.S.S. by a factor of 2 (de Naurois & Rolland 2009). In the near future, an additional telescope (H.E.S.S.-II) will lower the energy threshold of H.E.S.S. to about 25–50 GeV. For the corresponding flux level of 1% Crab, the required observation time for H.E.S.S.-II and MAGIC will be similar. Furthermore, the planned CTA observatory will be able to detect such a source in about 50 h (the CTA consortium 2010).
of the Crab Nebula’s for the favoured τ+τ−,mχ = 150 GeV and W+W−,mχ = 1 TeV model. With MAGIC, 50 h of observation are necessary to detect this source with more than 5σ. For comparison, predicted fluxes for H.E.S.S. are not higher than 0.2% Crab for these models, which requires a few hundred hours of observation (Aharonian et al. 2006c). We remark that advanced analysis methods improve the sensitivity of H.E.S.S. by a factor of 2 (de Naurois & Rolland 2009). In the near future, an additional telescope (H.E.S.S.-II) will lower the energy threshold of H.E.S.S. to about 25–50 GeV. For the corresponding flux level of 1% Crab, the required observation time for H.E.S.S.-II and MAGIC will be similar. Furthermore, the planned CTA observatory will be able to detect such a source in about 50 h (the CTA consortium 2010).
7. Summary and conclusions
Hierarchical structure formation predicts Milky Way-sized galaxies to host numerous DM subhaloes with masses ranging from 1010 down to a cut-off scale of 10-3 − 10-11 M⊙. Given standard WIMP scenarios, e.g., motivated by supersymmetry, we have demonstrated that DM subhaloes are detectable with the currently operating γ-ray telescope Fermi-LAT. Based upon state-of-the-art models, detectable subhaloes would observationally appear as faint high-energy γ-ray sources between 10 and 100 GeV with a flux at the sensitivity level of Fermi-LAT (~10-10 cm-2 s-1 between 10 and 100 GeV for one year). The observable γ-ray emission exhibits a moderate spatial extent below ~0.5°. Subhaloes favoured for detection are massive (105−108 M⊙) at distances of 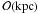 , while low-mass subhaloes are not detectable. Within the intrinsic halo-to-halo scatter, only a moderate enhancement of the self-annihilation cross section preferred by standard cosmology, ⟨ σv ⟩ 0 = 3 × 10-26 cm3 s-1, between 3 and 12 is necessary (dependent on the WIMP model), which is consistent with current observational constraints. Increasing sensitivity for a data-taking period of five years will allow us to resolve subhaloes requiring a cross section enhanced by a factor between 1.3 and 5. Additional sub-substructure within a subhalo may lower the required enhancement. Within statistics, one massive subhalo could be detectable with Fermi-LAT in one year and might appear in the first-year catalogue (1FGL), assuming a subhalo population predicted by numerical N-body simulations. Regarding the 1FGL, the high-energy flux (10 − 100 GeV) of subhalo candidates should be fainter than ~4 × 10-10 cm-2 s-1 (for the WIMP scenarios considered here).
, while low-mass subhaloes are not detectable. Within the intrinsic halo-to-halo scatter, only a moderate enhancement of the self-annihilation cross section preferred by standard cosmology, ⟨ σv ⟩ 0 = 3 × 10-26 cm3 s-1, between 3 and 12 is necessary (dependent on the WIMP model), which is consistent with current observational constraints. Increasing sensitivity for a data-taking period of five years will allow us to resolve subhaloes requiring a cross section enhanced by a factor between 1.3 and 5. Additional sub-substructure within a subhalo may lower the required enhancement. Within statistics, one massive subhalo could be detectable with Fermi-LAT in one year and might appear in the first-year catalogue (1FGL), assuming a subhalo population predicted by numerical N-body simulations. Regarding the 1FGL, the high-energy flux (10 − 100 GeV) of subhalo candidates should be fainter than ~4 × 10-10 cm-2 s-1 (for the WIMP scenarios considered here).
Intensive searches for subhaloes in the 1FGL reveal twelve candidates, which are unassociated, non-variable, high-latitude sources detected above 10 GeV. The physical origin of the most promising object selected by lacking association, faintness, and spectral index, 1FGL J0030.7+0724, was investigated by analysing the 24-month data set of Fermi-LAT. With dedicated Swift-XRT observations (10.1 ks), seven X-ray sources were discovered around 1FGL J0030.7+0724. Located within the positional uncertainty of the γ-ray source, a radio source positionally coincident with a newly discovered X-ray source hints at a conventional HBL origin of 1FGL J0030.7+0724. However, owing to a large positional uncertainty and the lacking detection of variability, the possibility of a dark nature remains. The measured high-energy flux and spatial extent of the source is compatible with a DM subhalo between 106 and 108 M⊙ in a distance of about 2 kpc, driven by a 500 (150) GeV WIMP self-annihilating to 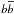 (τ + τ − ). In this case, the required enhancement of ⟨ σv ⟩ 0 is 7 (3) within the intrinsic scatter of the subhalo model, given a subhalo of 106 M⊙.
(τ + τ − ). In this case, the required enhancement of ⟨ σv ⟩ 0 is 7 (3) within the intrinsic scatter of the subhalo model, given a subhalo of 106 M⊙.
Establishing the – probably more likely – HBL scenario of 1FGL J0030.7+0724 requires a significant detection of γ-ray variability and a confirmation of the radio as well as X-ray counterparts. Vice versa, a steady γ-ray flux with a spectral shape predicted by self-annihilating WIMPs would hint at a DM nature of the object. This validates the necessity of additional intense and long multi-wavelength observations. In particular, IACTs offer a unique capability to reduce the positional uncertainty of faint LAT sources and to detect a spectral cut-off in the VHE range. A detection of the subhalo candidate 1FGL J0030.7+0724 may be possible with telescope systems like H.E.S.S.-II, MAGIC, and CTA within about 50 h of observation.
Our results encourage the search for more subhalo candidates in current and upcoming (very-)high-energy data releases. However, even in optimistic scenarios the expected number of LAT-detectable subhaloes is small. Furthermore, a longer exposure time – while certainly helpful with regard to the single candidate discussed in this work – will not neccessarily remedy the general problem of the γ-ray photon count that limits the positional accuracy and therefore the chance of identifying counterparts. Given mχ < 1 TeV, acquiring a sufficiently large number of detections which may solve the subhalo problem requires higher sensitivity in the high-energy range.
Note that details on the very inner slope of halo profiles remain to be clarified, by simulations as well as observationally (e.g., Walker et al. 2011; Salucci et al. 2007).
This model extends a proposal by Navarro et al. (1997).
Lavalle et al. chose Δc = 81.6.
In general, the physical subhalo radius Rt is smaller than the formally defined virial radius Rvir, implying the physical subhalo mass Mt to be smaller than Mvir. For massive subhaloes, the Mt(Mvir) relation is approximately linear, where Mt/Mvir ≈ 0.2 (see Appendix A). Given the empirical model correction discussed below, the formal virial quantities will be used in the remainder of the paper.
For the fiducial candidate in Sect. 4 this additional contribution is less than 1%.
In comparison with the point spread function of Fermi-LAT, θs = 1° (as implying θ68 ≈ 0.5°) corresponds to about 3 σPSF, where σPSF ≈ 0.15° for energies beyond 10 GeV (see http://www-glast.slac.stanford.edu/software/IS/glast_lat_performance.htm).
In comparison with Papucci & Strumia, the work by Abazajian et al. includes a fore- and background subtraction. Note that the MW halo parameters used by Abazajian et al. are similar to those adopted in this work (see Sect. 2.1).
The spectral properties of γ-ray pulsars can mimic the spectra of DM subhaloes, see Baltz et al. (2007). However, spectral cut-off energies of γ-ray pulsars are well below 5 GeV (Abdo et al. 2009a), excluding a detection above 10 GeV.
Within the 2σ positional uncertainty of NVSS J003030+072132, a very faint optical SDSS (Sloan Digital Sky Survey) source is located (26.0m) – SDSS J003031.22+072132.2 (SDSS DR7, Abazajian et al. 2009). However, this object was observed with the edge of the plated SDSS camera. Therefore, this detection is probably spurious.
Fermi Science Support Center, http://fermi.gsfc.nasa.gov/ssc/
Acknowledgments
We kindly acknowledge helpful discussions with our colleagues Katharina Borm, Torsten Bringmann, Wilfried Buchmüller, Frederike Jäger, Andrei Lobanov, and Martin Raue. We kindly acknowledge the Swift PI Neil Gehrels and his team for the prompt response to our ToO request and the corresponding observations. The help of the Fermi HelpDesk is kindly acknowledged. We kindly thank the anonymous referee for useful comments. This work was supported through the collaborative research center (SFB) 676 “Particles, Strings, and the Early Universe” at the University of Hamburg. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This publication makes use of data from the Sloan Digital Sky Survey (SDSS). Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Aad, G., Abbott, B., Abdallah, J., et al. 2011, Eur. Phys. J. C, 71, 1682 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K. N., Agrawal, P., Chacko, Z., & Kilic, C. 2010, J. Cosmology Astropart. Phys., 11, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 707, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 712, 147 [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2011a, ApJ, 735, 12 [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2011b, Phys. Rev. Lett., 106, 161301, H.E.S.S. Collaboration [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Acciari, V. A., Arlen, T., Aune, T., et al. 2010, ApJ, 720, 1174 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2010, J. Cosmology Astropart. Phys., 5, 25 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, Phys. Rev. Lett., 97, 221102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, Phys. Rev. Lett., 97, 249901 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006c, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006d, Nature, 439, 695 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2008, Astropart. Phys., 29, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., de Almeida, U. B., et al. 2009, ApJ, 691, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2010, Astropart. Phys., 33, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008a, ApJ, 674, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008b, ApJ, 679, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2010, ApJ, 710, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2011, J. Cosmology Astropart. Phys., 6, 35 [Google Scholar]
- Aliu, E., Anderhub, H., Antonelli, L. A., et al. 2009, ApJ, 697, 1299 [Google Scholar]
- Anderson, B., Kuhlen, M., Diemand, J., Johnson, R. P., & Madau, P. 2010, ApJ, 718, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Ando, S. 2009, Phys. Rev. D, 80, 023520 [NASA ADS] [CrossRef] [Google Scholar]
- Arkani-Hamed, N., Finkbeiner, D. P., Slatyer, T. R., & Weiner, N. 2009, Phys. Rev. D, 79, 015014 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Baltz, E. A., Taylor, J. E., & Wai, L. L. 2007, ApJ, 659, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Baltz, E. A., Berenji, B., Bertone, G., et al. 2008, J. Cosmology Astropart. Phys., 7, 13 [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V. S., Gurevich, A. V., & Zybin, K. P. 1992, Phys. Lett. B, 294, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V., Dokuchaev, V., & Eroshenko, Y. 2003, Phys. Rev. D, 68, 103003 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V., Dokuchaev, V., & Eroshenko, Y. 2006, Phys. Rev. D, 73, 063504 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V., Dokuchaev, V., & Eroshenko, Y. 2008, Phys. Rev. D, 77, 083519 [NASA ADS] [CrossRef] [Google Scholar]
- Bergström, L., Bringmann, T., Eriksson, M., & Gustafsson, M. 2005a, Phys. Rev. Lett., 95, 241301 [NASA ADS] [CrossRef] [Google Scholar]
- Bergström, L., Bringmann, T., Eriksson, M., & Gustafsson, M. 2005b, Phys. Rev. Lett., 94, 131301 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, G. 2010, Nature, 468, 389 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bertone, G., Hooper, D., & Silk, J. 2005, Phys. Rep., 405, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Borm, K. 2010, Research on a Possible Dark Matter Substructure within the Galactic Halo, Bachelor thesis, University of Hamburg, Germany [Google Scholar]
- Bringmann, T. 2009, New J. Phys., 11, 105027 [NASA ADS] [CrossRef] [Google Scholar]
- Bringmann, T., Bergström, L., & Edsjö, J. 2008, J. High Energy Phys., 1, 49 [Google Scholar]
- Brun, P., Moulin, E., Diemand, J., & Glicenstein, J. 2011, Phys. Rev. D, 83, 015003 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Buckley, M. R., & Hooper, D. 2010, Phys. Rev. D, 82, 063501 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Catena, R., & Ullio, P. 2010, J. Cosmology Astropart. Phys., 8, 4 [Google Scholar]
- Cirelli, M., Panci, P., & Serpico, P. D. 2010, Nucl. Phys. B, 840, 284 [Google Scholar]
- CMS Collaboration 2011, JHEP, 6, 93 [Google Scholar]
- Colafrancesco, S., Profumo, S., & Ullio, P. 2006, A&A, 455, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colafrancesco, S., Profumo, S., & Ullio, P. 2007, Phys. Rev. D, 75, 023513 [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- D’Amico, G., Kamionkowski, M., & Sigurdson, K. 2009 [arXiv:0907.1912] [Google Scholar]
- de Naurois, M., & Rolland, L. 2009, Astropart. Phys., 32, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., & Moore, B. 2011, Adv. Science Lett., 4, 297 [Google Scholar]
- Diemand, J., Moore, B., & Stadel, J. 2005, Nature, 433, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Kuhlen, M., & Madau, P. 2007, ApJ, 667, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Kuhlen, M., & Madau, P. 2008a, ApJ, 679, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Kuhlen, M., Madau, P., et al. 2008b, Nature, 454, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Donato, D., Ghisellini, G., Tagliaferri, G., & Fossati, G. 2001, A&A, 375, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Onghia, E., Springel, V., Hernquist, L., & Keres, D. 2010, ApJ, 709, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Doro, M. 2011, Nuclear Instruments and Methods in Physics Research A, 630, 285, for the CTA Consortium [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J. 1965, Trudy Inst. Astroz. Alma-Ata, 51, 87 [Google Scholar]
- Eke, V. R., Cole, S., & Frenk, C. S. 1996, MNRAS, 282, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Fornengo, N., Pieri, L., & Scopel, S. 2004, Phys. Rev. D, 70, 103529 [Google Scholar]
- Fossati, G., Celotti, A., Ghisellini, G., & Maraschi, L. 1997, MNRAS, 289, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2005, ApJ, 621, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Green, A. M., Hofmann, S., & Schwarz, D. J. 2005, J. Cosmology Astropart. Phys., 8, 3 [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hermann, G. 2010, Nuclear Instruments and Methods in Physics Research A, 623, 408, for the CTA Collaboration [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration: Abramowski, A., Acero, F., Aharonian, F., et al. 2011, Astropart. Phys., 34, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Kravtsov, A. V. 2003, ApJ, 584, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, N., Battye, R. A., Browne, I. W. A., et al. 2007, MNRAS, 376, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhlen, M., Diemand, J., & Madau, P. 2008, ApJ, 686, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhlen, M., Madau, P., & Silk, J. 2009, Science, 325, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalle, J., Yuan, Q., Maurin, D., & Bi, X. 2008, A&A, 479, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lupton, R., Gunn, J. E., Ivezić, Z., Knapp, G. R., & Kent, S. 2001, in Astronomical Data Analysis Software and Systems X, ed. F. R. Harnden Jr., F. A. Primini, & H. E. Payne, ASP Conf. Ser., 238, 269 [Google Scholar]
- Maddox, S. J., Efstathiou, G., Sutherland, W. J., & Loveday, J. 1990, MNRAS, 243, 692 [NASA ADS] [Google Scholar]
- Martinez, G. D., Bullock, J. S., Kaplinghat, M., Strigari, L. E., & Trotta, R. 2009, J. Cosmology Astropart. Phys., 6, 14 [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., Murphy, T., Buttery, H. J., et al. 2003, MNRAS, 342, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Meade, P., Papucci, M., Strumia, A., & Volansky, T. 2010, Nuclear Physics B, 831, 178 [Google Scholar]
- Mirabal, N., Nieto, D., & Pardo, S. 2010 [arXiv:1007.2644] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Morselli, A., Canadas, B., & V. Vitale on behalf of the Fermi LAT collaboration. 2010, in SciNeGHE 2010, to appear in Il Nuovo Cimento C – Colloquia on physics [arXiv:1012.2292] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, L., Bertone, G., & Branchini, E. 2008, MNRAS, 384, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Papucci, M., & Strumia, A. 2010, J. Cosmology Astropart. Phys., 3, 14 [Google Scholar]
- Pieri, L., Branchini, E., & Hofmann, S. 2005, Phys. Rev. Lett., 95, 211301 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, L., Lavalle, J., Bertone, G., & Branchini, E. 2011, Phys. Rev. D, 83, 023518 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes: The Art of Scientific Computing, 3rd edn. (Cambridge University Press) [Google Scholar]
- Rando, R. 2009, in Proc. 31st ICRC, Łódź, Poland, for the Fermi LAT Collaboration [arXiv:0907.0626] [Google Scholar]
- Salucci, P., Lapi, A., Tonini, C., et al. 2007, MNRAS, 378, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008a, MNRAS, 391, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Frenk, C. S., et al. 2008b, Nature, 456, 73 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stephen, J. B., Bassani, L., Landi, R., et al. 2010, MNRAS, 408, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Strigari, L. E., Koushiappas, S. M., Bullock, J. S., & Kaplinghat, M. 2007, Phys. Rev. D, 75, 083526 [NASA ADS] [CrossRef] [Google Scholar]
- The CTA Consortium. 2010 [arXiv:1008.3703] [Google Scholar]
- Tridon, D. B., Schweizer, T., Goebel, F., Mirzoyan, R., & Teshima, M. 2010, Nuclear Instruments and Methods in Physics Research A, 623, 437, for the MAGIC Collaboration [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, M., Maraschi, L., & Urry, C. M. 1997, ARA&A, 35, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, P. 2005, in International Cosmic Ray Conference, 5, 163 [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Wagner, R. G. 2009, in Proc. 31st ICRC, Łódź, Poland, for the VERITAS Collaboration [arXiv:0910.4563] [Google Scholar]
- Walker, M. G., Combet, C., Hinton, J. A., Maurin, D., & Wilkinson, M. I. 2011, ApJ, 733, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Weekes, T. C., Badran, H., Biller, S. D., et al. 2002, Astropart. Phys., 17, 221 [Google Scholar]
- Wilks, S. S. 1938, Ann. Math. Statist., 9, 60 [Google Scholar]
- Zaharijas, G., Cuoco, A., Yang, Z., & Conrad, J. 2010, in Proc. IDM 2010 conference, Montpellier, France, published online at http://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=110 [Google Scholar]
- Zechlin, H.-S., Fernandes, M. V., Elsaesser, D., & Horns, D. 2011, in 2011 Fermi Symposium proceedings - eConf C110509 [arXiv:1110.6868] [Google Scholar]
- Zemp, M., Diemand, J., Kuhlen, M., et al. 2009, MNRAS, 394, 641 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Concentration of Aquarius subhaloes
The Aquarius simulation provides results on the profile parameters of resolved subhaloes, taking tidal interaction into account (Springel et al. 2008a). These results are used to derive the distance-averaged virial concentration of subhaloes to confront it with the toy-model predictions used here.
Following up on Eq. (1), the tidal concentration ct ≡ Rt/rs is introduced (cf., Ando 2009), where Rt denotes the tidal and therefore physical radius of a subhalo. For an NFW-type mass density profile, ct = exp [W( − e − a) + a] − 1, 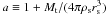 , where W(x) denotes Lambert’s W-function and Mt the tidal subhalo mass. In numerical simulations, the directly “observable” quantities of (sub)haloes are related to the dynamics of the halo system, including the maximum velocity Vmax and the distance rmax where Vmax is reached. To recover the canonical parameters rs and ρs related to the density profile, we use approximate relations 2 [Vmax/(H0rmax)] 2 ≃ 5.80 × 104 [Mt/(108 M⊙)] -0.18 and Mt ≃ 3.37 × 107 [Vmax/(10 km s-1)] 3.49 M⊙, fitting the results of the simulation (Springel et al. 2008a; Ando 2009). Given analytical relations between (rmax,Vmax) and (rs,ρs) for the NFW profile (e.g., Eq. (8) in Kuhlen et al. 2008), this yields
, where W(x) denotes Lambert’s W-function and Mt the tidal subhalo mass. In numerical simulations, the directly “observable” quantities of (sub)haloes are related to the dynamics of the halo system, including the maximum velocity Vmax and the distance rmax where Vmax is reached. To recover the canonical parameters rs and ρs related to the density profile, we use approximate relations 2 [Vmax/(H0rmax)] 2 ≃ 5.80 × 104 [Mt/(108 M⊙)] -0.18 and Mt ≃ 3.37 × 107 [Vmax/(10 km s-1)] 3.49 M⊙, fitting the results of the simulation (Springel et al. 2008a; Ando 2009). Given analytical relations between (rmax,Vmax) and (rs,ρs) for the NFW profile (e.g., Eq. (8) in Kuhlen et al. 2008), this yields ![\hbox{$r^{\rm Aq}_{\rm s}(M_{\rm t}) \simeq 0.094\,[ M_{\rm t}/(10^6\,{M}_\odot) ]^{0.38}\,{\rm kpc}$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq390.png) and
and ![\hbox{$\rho^{\rm Aq}_{\rm s}(M_{\rm t}) \simeq 9.6 \times 10^5 \rho_{\rm crit}\,[ M_{\rm t}/(10^6\,{M}_\odot) ]^{-0.18}$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq391.png) . Therefore, the tidal concentration
. Therefore, the tidal concentration 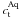 is determined via aAq ≃ 1 + 0.66 [Mt/(106 M⊙)] 0.04, which is valid for masses above the resolution limit of the simulation, Mt ≳ 3.2 × 104 M⊙.
is determined via aAq ≃ 1 + 0.66 [Mt/(106 M⊙)] 0.04, which is valid for masses above the resolution limit of the simulation, Mt ≳ 3.2 × 104 M⊙.
The virial concentration of Aquarius subhaloes is given by ![\hbox{$c_{\rm vir}^{\rm Aq}(M_{\rm vir}) = [3 M_{\rm vir}/(4\pi \Delta_{\rm c} \rho_{\rm crit})]^{1/3}/r^{\rm Aq}_{\rm s}(M_{\rm vir})$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq395.png) , where the characteristic radius as function of the virial subhalo mass is obtained from an empirical relation mapping Mvir to Mt. Based on
, where the characteristic radius as function of the virial subhalo mass is obtained from an empirical relation mapping Mvir to Mt. Based on 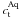 and assuming the FHM virial concentration-to-mass relation (Eq. (2)), the relative tidal mass is
and assuming the FHM virial concentration-to-mass relation (Eq. (2)), the relative tidal mass is ![\hbox{$M_{\rm t}/M_{\rm vir} \approx f[c^{\rm Aq}_{\rm t}(M_{\rm t})]/f[c^{\rm FHM}_{\rm vir}(M_{\rm vir})]$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq396.png) , since
, since 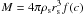 . Hereby, we have assumed that tidal effects on inner subhalo parts are negligible: ρs(Mvir)rs(Mvir)3 ≈ ρs(Mt)rs(Mt)3. With
. Hereby, we have assumed that tidal effects on inner subhalo parts are negligible: ρs(Mvir)rs(Mvir)3 ≈ ρs(Mt)rs(Mt)3. With 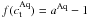 , the distance-averaged Mt-Mvir relation is
, the distance-averaged Mt-Mvir relation is 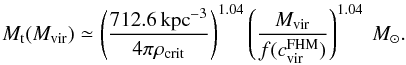 (A.1)For massive subhaloes ( ≳ 104 M⊙),
(A.1)For massive subhaloes ( ≳ 104 M⊙),  is well fit by a power law,
is well fit by a power law, ![\hbox{$f[c^{\rm FHM}_{\rm vir}(M_{\rm vir})]^{-1.04} \approx 0.34\,[M_{\rm vir}/(10^6\,{M}_\odot)]^{0.02}$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq403.png) , yielding Mt/Mvir ≈ 0.23 [Mvir/(106 M⊙)] 0.06 for Mt ≳ 3.2 × 104 M⊙. This reveals
, yielding Mt/Mvir ≈ 0.23 [Mvir/(106 M⊙)] 0.06 for Mt ≳ 3.2 × 104 M⊙. This reveals ![\hbox{$r^{\rm Aq}_{\rm s}(M_{\rm vir}) \simeq 0.054\,[ M_{\rm vir}/(10^6\,{M}_\odot) ]^{0.40}\,{\rm kpc}$}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq405.png) and, therefore, the distance-averaged virial concentration of subhaloes
and, therefore, the distance-averaged virial concentration of subhaloes 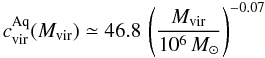 (A.2)for Mvir ∈ [1.5 × 105; ~ 1010] M⊙.
(A.2)for Mvir ∈ [1.5 × 105; ~ 1010] M⊙.
Appendix B: Moderately extended Fermi sources
For γ-ray catalogues such as 1FGL, instrument data have been analysed assuming sources to be point-like. Given that detectable subhaloes would appear as moderately extended according to the PSF of Fermi-LAT (see Sect. 4.1.1, σPSF ≈ 0.15° for E = 10 GeV), we investigated the effect of the 1FGL point-source-analysis framework on extended sources.
To study the high-energy flux φp(10−100 GeV) reconstructed by the point-source analysis for a given intrinsic (subhalo) extent θs, a Monte-Carlo (MC) simulation dedicated to the particular source 1FGL J0030.7+0724 was used. Based on the 11-month data set (see Sect. 5.1.2 for details), the celestial coordinates of each of the five source photons between 10 and 100 GeV were re-simulated. The intensity profile was assumed to follow the line-of-sight integral over the (squared) NFW profile of a subhalo for the given θs (peaking at the nominal source position). Other observational photon parameters, such as energy, inclination, detection time, conversion type, and event class (see Table 6), were kept fixed. Subsequently, detectional influences were accounted for by smoothing with the PSF. For each θs, 500 iterations were analysed with the framework described in Sect. 5.1.2 (gtfindsrc and gtlike) according to flux and significance (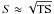 , where TS denotes the test statistic of the analysis). All other sources within the ROI were kept fixed. The study is restricted to the signal-dominated regime chosen to be θs ≲ 1° given the low background Nbg. Since θ68 ≈ 0.46°, this corresponds to ~3σPSF. Justified by the low background, all photons were treated as signal events.
, where TS denotes the test statistic of the analysis). All other sources within the ROI were kept fixed. The study is restricted to the signal-dominated regime chosen to be θs ≲ 1° given the low background Nbg. Since θ68 ≈ 0.46°, this corresponds to ~3σPSF. Justified by the low background, all photons were treated as signal events.
 |
Fig. B.1 Average (solid lines) and rms (shaded areas) of φp(10 − 100 GeV) (upper panel), TS (middle panel), and the scaling h(θs) (lower panel) as function of the intrinsic angular extent θs. For each θs, a sample of 500 simulations of the 1FGL J0030.7+0724 photon distribution between 10 and 100 GeV assuming a DM subhalo intensity profile was analysed with the 1FGL point-source-analysis framework. |
The θs dependence of the sample-averaged reconstructed flux φp(10 − 100 GeV) and corresponding test statistic TS is shown in the two upper panels of Fig. B.1. For large θs, the probability of photons to be located far away from their central position increases. Therefore, both φp and TS decrease because of a minor contribution of outer photons to the point-source region (defined by the PSF). For θs ≈ 1°, the average significance drops below the detection criterion (TS ≥ 25). Note that TS ≥ 25 still holds for about 35% of the simulated samples.
In terms of Eq. (8), appropriate investigation of candidates provided by point-source catalogues is therefore admitted by a scaling h(θs), which allows us to map the catalogued flux φp to the true flux φ of the entire source. The angular dependence of h is shown in the lower panel of Fig. B.1. Given φ = h(θs) φp, the factor was derived by defining h(0°) = 1. Conservatively, the complete MC sample was used to derive h(θs), including realisations with TS < 25 15. As expected in the signal-dominated regime, the increase of h with increasing θs is comparatively slight, while it is fairly linear in the background-dominated regime. Note again that this result holds for sources similar to 1FGL J0030.7+0724 at high galactic latitudes only, while in general h = h(l,b,θs).
Vice versa, Fig. B.1 states a reasonable (but conservative) value of the sensitivity of Fermi-LAT for hard sources of similar type: φp(10−100 GeV) ≈ 10-10 cm-2 s-1. Note that this value is similar to the point-source sensitivity stated in Atwood et al. (2009).
Appendix C: Subhalo-induced diffuse flux
In the following, the diffuse flux of the subhalo population is derived using a prescription by Ando (2009), which is extended to include the probability distribution of the concentration parameter c (see Eq. (4)). Numerical N-body simulations have demonstrated that the differential subhalo number density 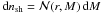 follows a power-law in subhalo mass M. Following standard assumptions, the number density
follows a power-law in subhalo mass M. Following standard assumptions, the number density 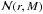 factorises such that
factorises such that 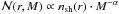 , where α = 1.9 and r is the distance to the host’s centre. In simulations, the spatial density distribution nsh(r) is consistently found to be “anti-biased” and, e.g., nsh(r) ∝ ρEin(r) (Springel et al. 2008a), where ρEin(r) denotes the Einasto profile (Einasto 1965)
, where α = 1.9 and r is the distance to the host’s centre. In simulations, the spatial density distribution nsh(r) is consistently found to be “anti-biased” and, e.g., nsh(r) ∝ ρEin(r) (Springel et al. 2008a), where ρEin(r) denotes the Einasto profile (Einasto 1965) ![\appendix \setcounter{section}{3} \begin{equation} \rho_{\rm Ein}(r) \propto \exp\left\{-\frac{2}{\alpha_{\rm E}} \left[ \left( \frac{r}{r_{-2}} \right)^{\alpha_{\rm E}} - 1 \right] \right\}. \end{equation}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq429.png) (C.1)For a Milky Way-sized halo, the best-fit parameters for the subhaloes’ spatial distribution ρEin(r) have been found to be αE = 0.68 and
(C.1)For a Milky Way-sized halo, the best-fit parameters for the subhaloes’ spatial distribution ρEin(r) have been found to be αE = 0.68 and 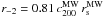 (Springel et al. 2008a), where
(Springel et al. 2008a), where 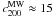 (Catena & Ullio 2010). Using
(Catena & Ullio 2010). Using  normalised to represent a probability density function in M, the differential density is
normalised to represent a probability density function in M, the differential density is 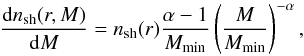 (C.2)where Mmin ≪ Mmax are the minimum and maximum mass of Galactic subhaloes, respectively. The normalisation of the subhalo number density nsh(r) is chosen such that the fraction of the host’s mass distributed in subhaloes
(C.2)where Mmin ≪ Mmax are the minimum and maximum mass of Galactic subhaloes, respectively. The normalisation of the subhalo number density nsh(r) is chosen such that the fraction of the host’s mass distributed in subhaloes 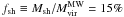 for the cut-off scale Mmin = 10-6 M⊙, where
for the cut-off scale Mmin = 10-6 M⊙, where 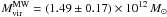 (Catena & Ullio 2010). The chosen value of fsh is consistent with recent estimates fsh = 10 − 50% (Diemand et al. 2005; Diemand & Moore 2011; Diemand et al. 2008b; Springel et al. 2008b). The total mass contained in subhaloes is given by
(Catena & Ullio 2010). The chosen value of fsh is consistent with recent estimates fsh = 10 − 50% (Diemand et al. 2005; Diemand & Moore 2011; Diemand et al. 2008b; Springel et al. 2008b). The total mass contained in subhaloes is given by 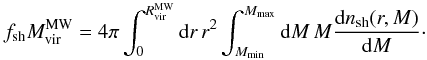 (C.3)Solving for an Einasto-type profile and α ≠ 2 yields
(C.3)Solving for an Einasto-type profile and α ≠ 2 yields ![\appendix \setcounter{section}{3} \begin{eqnarray} n_{\rm sh}(r) & = & \frac{f_{\rm sh} M^{\rm MW}_{\rm vir}}{2\pi r^3_{-2} M_{\rm min}} \left( \frac{2}{\alpha_{\rm E}} \right)^{3/\alpha_{\rm E}-1} \Gamma \left[ \frac{3}{\alpha_{\rm E}}, \frac{2}{\alpha_{\rm E}} \left( \frac{R^{\rm MW}_{\rm vir}}{r_{-2}} \right)^{\alpha_{\rm E}}\right]^{-1} \nonumber \\ & \quad \times & \frac{2-\alpha}{(\alpha-1) (\Lambda^{2-\alpha}-1)} \exp \left[ -\frac{2}{\alpha_{\rm E}} \left( \frac{r}{r_{-2}} \right)^{\alpha_{\rm E}} \right], \end{eqnarray}](/articles/aa/full_html/2012/02/aa17655-11/aa17655-11-eq441.png) (C.4)where Γ(a,x) is the lower incomplete gamma function and Λ = Mmax/Mmin.
(C.4)where Γ(a,x) is the lower incomplete gamma function and Λ = Mmax/Mmin.
The minimum mass Mmin of subhaloes is governed by the details of kinetic decoupling of WIMPs in the early Universe (Berezinsky et al. 2003, 2006; Green et al. 2005; Bringmann 2009). Depending upon the mass and composition of, e.g., the neutralino, a wide range of minimal subhalo masses has been considered in the literature, namely Mmin ∈ [10-11;10-3] M⊙. Here, two benchmark cases are considered for Mmin, i.e., 10-10 and 10-6 M⊙, bracketing the 500 GeV neutralino scenario discussed by Bringmann (2009). The upper mass limit was fixed to 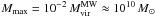 . Results do not depend on the exact value chosen for Mmax.
. Results do not depend on the exact value chosen for Mmax.
Using ℒ(M,D) (Sects. 2.1 and 2.2), the average specific intensity from a subhalo population with extended, isotropic emissivity profiles is given towards a galactic direction 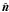 by
by 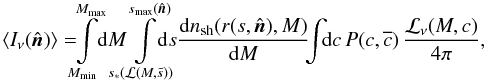 (C.5)assuming that the spatial extent of each subhalo is much smaller than the scale on which the subhalo distribution changes significantly. The total photon rate ℒν is given by Eq. (6) with the substitution Nγ → E dNγ/dE. Furthermore, ℒν(M) is required to be one-to-one. The galactocentric radius corresponding to the position
(C.5)assuming that the spatial extent of each subhalo is much smaller than the scale on which the subhalo distribution changes significantly. The total photon rate ℒν is given by Eq. (6) with the substitution Nγ → E dNγ/dE. Furthermore, ℒν(M) is required to be one-to-one. The galactocentric radius corresponding to the position  is
is 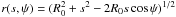 , where ψ denotes the angle between
, where ψ denotes the angle between 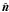 and
and 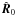 (
(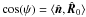 ). Subhaloes bright enough to be detected as individual sources are not considered to contribute to the diffuse emission. Therefore, the lower limit of the line-of-sight integral is set by the detection criterion
). Subhaloes bright enough to be detected as individual sources are not considered to contribute to the diffuse emission. Therefore, the lower limit of the line-of-sight integral is set by the detection criterion 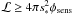 , where φsens denotes the flux sensitivity for a detection in one year with Fermi-LAT, see Sect. 4. Since R0 ≪ Rvir, the upper bound of the s-integral
, where φsens denotes the flux sensitivity for a detection in one year with Fermi-LAT, see Sect. 4. Since R0 ≪ Rvir, the upper bound of the s-integral 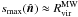 . The SHM photon rate is a function of both M and s, and therefore s∗ also depends slightly on s. Conservatively,
. The SHM photon rate is a function of both M and s, and therefore s∗ also depends slightly on s. Conservatively, 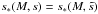 ,
, 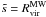 , revealing a lower bound on s∗.
, revealing a lower bound on s∗.
All Tables
Enhancement factors ⟨ σv ⟩ eff/ ⟨ σv ⟩ 0 required to explain the fiducial γ-ray source with a DM subhalo of 106 M⊙.
Positional and spectral properties of 1FGL J0030.7+0724 as given in the catalogue (11 months) and by the (re-)analysis of the first 11 and 24-month data sets.
Fluxes above the energy thresholds of MAGIC and H.E.S.S., predicted by a DM scenario of 1FGL J0030.7+0724.
All Figures
 |
Fig. 1 Concentration-to-mass relation for subhaloes at z = 0. The dashed blue line depicts the concentration predicted by the Bullock model (FHM), while its corresponding scatter is given by the blue-shaded area. The mean concentration corrected for subhalo evolution (SHM) is shown by the solid red line for a galactocentric distance of 74 kpc, the average distance of the dSph galaxies included from Abdo et al. (2010c) (black triangles). For comparison, the concentration derived for Aquarius subhaloes is indicated by the dot-dashed dark green line within its validity range, the low/high-mass extrapolation by the double-dotted green line. The black filled circle marks the virial concentration of the MW. |
| In the text | |
 |
Fig. 2 Differential γ-ray energy spectra |
| In the text | |
 |
Fig. 3 Effective self-annihilation cross section ⟨ σv ⟩ eff required for a moderately extended, faint Fermi-LAT source to originate from a DM subhalo of mass M. Assumed source parameters are φ(10−100 GeV) = 1.6 × 10-10 cm-2 s-1, an intrinsic extent θs = 1° (θ68 ≈ 0.5°), and the Galactic position (l,b) = (114°, −55°). The dashed blue and solid red lines indicate the average prediction considering the FHM and SHM, respectively. The intrinsic SHM scatter is shown by the red-shaded area and the dotted red lines. The left panel depicts WIMPs of mχ = 500 GeV totally annihilating in |
| In the text | |
 |
Fig. 4 Distance to the fiducial subhalo in the FHM (dashed blue line) and SHM (solid red line), respectively, as function of the subhalo mass M. The scatter of the SHM distance is indicated by the red-shaded area. An extent of θs = 1° (θ68 ≈ 0.5°) and a source position (l,b) = (114°, −55°) are assumed. |
| In the text | |
 |
Fig. 5 Average diffuse γ-ray flux from DM annihilation in the Galaxy as function of the angle between the observational and Galactic Centre direction ψ. The fluxes from the host halo (double-dot-dashed magenta line), FHM (dashed blue line), and SHM subhaloes (solid red line) are depicted. Each curve was derived at the peak energy of νIν(E) (40 GeV) assuming total annihilation in τ+τ− with mχ = 150 GeV and ⟨ σv ⟩ eff = ⟨ σv ⟩ 0. The minimum subhalo mass used was Mmin = 10-6 M⊙ (see Appendix C). The EGB at 40 GeV is shown by the dotted black line. |
| In the text | |
 |
Fig. 6 Expected number of one-year detectable subhaloes per mass decade at |b| ≥ 20°. The subhaloes′ mass and spatial distributions were adopted from Aquarius (Appendix C) while the SHM concentration was used. Mmin = 10-6 M⊙. The number corresponding to the |
| In the text | |
 |
Fig. 7 Energy spectrum of 1FGL J0030.7+0724 as given in the first Fermi-LAT catalogue between 100 MeV and 100 GeV (filled circles). The solid red line depicts the (catalogued) power law fitting the data. Only the highest energy bin has been significantly detected, while for the low-energy bins upper limits are shown (95% c.l.). |
| In the text | |
 |
Fig. 8 Celestial region of 1FGL J0030.7+0724, 25′ × 13′. The catalogued position is indicated by the red + , while the dashed red ellipse borders its uncertainty (95% c.l.). The black × marks the 24-month position, the solid black contour its uncertainty at 95% confidence. Photons detected by Swift-XRT (10.1 ks) are mapped by the back-image, which is smoothed with a Gaussian (7′′). The positions of NVSS radio sources are given by the darkgreen boxes, the two NVSS sources discussed in the text are named. In this region, seven X-ray sources have been discovered, indicated by the blue arrows (see Table 7). Note that the boxes’ size is chosen arbitrarily. |
| In the text | |
 |
Fig. 9 Energy spectra of 1FGL J0030.7+0724 (solid red line) and the favoured radio (filled black triangle), optical (violet crosses, dereddened ugriz magnitudes), and X-ray (solid blue line) counterparts, together with the SED of an average HBL (solid black line). The SED was adapted from Donato et al., assuming the average redshift of known HBLs z = 0.25 (Donato et al. 2001), and is normalised to the radio flux of NVSS J003119+072456. The frequency-dependent energy flux νfν is given in the observer’s frame. Note that the statistical errors of the radio and optical data points are too low to be resolved in the figure. Statistical uncertainties of the X- and γ-ray spectra are indicated by the corresponding shaded areas, which we derived with Eq. (1) in Abdo et al. (2009b). The filled red circle indicates the catalogued high-energy flux from Fermi-LAT. Observations with ROSAT provide an upper limit on the X-ray flux at the nominal position of 1FGL J0030.7+0724 between 0.1 and 2.4 keV, which is depicted by the green square (95% c.l., assuming Γ = 2.0, Borm 2010). |
| In the text | |
 |
Fig. B.1 Average (solid lines) and rms (shaded areas) of φp(10 − 100 GeV) (upper panel), TS (middle panel), and the scaling h(θs) (lower panel) as function of the intrinsic angular extent θs. For each θs, a sample of 500 simulations of the 1FGL J0030.7+0724 photon distribution between 10 and 100 GeV assuming a DM subhalo intensity profile was analysed with the 1FGL point-source-analysis framework. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.