| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117209 | |
| Published online | 13 February 2012 | |
A dynamical explanation for a long-term modulation in the light curve of FS Aurigae
A possible triple cataclysmic variable system
1 Instituto de Astronomia, Universidad Nacional Autonoma de Mexico, Apdo. Postal 877, Ensenada, 22800 Baja California, Mexico
e-mail: carlosepech@astrosen.unam.mx; gag@astrosen.unam.mx; zhar@astrosen.unam.mx; aguilar@astrosen.unam.mx
2 AAVSO Headquarters, 49 Bay State Rd., Cambridge, MA 02138, USA
Received: 6 May 2011
Accepted: 8 December 2011
Aims. FS Aur is an unusual cataclysmic variable, which in addition to its spectroscopically determined orbital period of 85.7 min exhibits spectroscopic and photometric periods of 147 and 205 min, correspondingly, which are attributed to the period of the fast rotating and freely precessing magnetic white dwarf. We aim to study the origin of a very long term variability observed in the light curve of FS Aur accumulated by us and in the AAVSO International Database over the past thirteen years.
Methods. Discrete Fourier transform algorithm and Scargle-Lomb least-squares spectral analysis were used for the period analysis of the observational data. A 12th-order Runge-Kutta-Nyström integrator was used to conduct numerical simulations of a three-body system that is invoked to explain the observed long-term variability in the FS Aur light curve, which is probably periodic.
Results. We report here a newly discovered ~2-mag modulation of the light curve of FS Aur with a ~900-day period. The huge disparity with the previous periods makes this difficult to explain within the confines of the binary system. We propose a mechanism for this longer period: a modulation in the binary eccentricity, produced by the gravitational perturbation of a third object on a larger orbit. We first explore orbits with a period equal to the ~900-day modulation and a high eccentricity that can produce a direct perturbation in the close binary system, and conclude that the shape of the time response does not match the observed light curve. However, putting the perturber on a circular, shorter period orbit at the proper location can induce a long-term secular modulation.
Conclusions. There is a tight correlation between the perturber mass and orbital radius with the induced long-term modulation in the central binary. To explain the observed ~900-day period, the perturber must be a substellar mass object with a probable mass between 25 to 64 times that of Jupiter. The presence of the third body in this system may be a clue for understanding other observational peculiarities.
Key words: novae, cataclysmic variables / binaries: close / planets and satellites: dynamical evolution and stability
© ESO, 2012
1. Introduction
Cataclysmic variables are close binary stars composed of a late-type main-sequence star that fills its Roche lobe, losing matter to the more massive white dwarf companion. The transferred mass forms an accretion disk around the white dwarf and is often so bright that it outshines both stars of the system. Cataclysmic variables exhibit several periodic signals related to the binary period, the spin period, variabilities caused by to the presence of bright spots and precession effects in the accretion disk (superhumps), but all these periods are equal to, very close to, or much shorter than, the orbital period of the system. The outburst activity in CVs has a cyclic nature with multiple time scales, but it is not periodic. FS Aur is a CV with an 85.7 min orbital period (OP) (Thorstensen et al. 1996) and, a so far poorly understood 205.5 min long photometric period (LPP) (Tovmassian et al. 2003). The LPP, coupled with the long, 147 min spectroscopic period (LSP) detected in the wings of the emission lines at a beat frequency with the OP (Tovmassian et al. 2007), is thought to be the result of a spot in the inner parts of the accretion disk, induced by the precession of a fast rotating magnetic white dwarf. Here we show that in addition to these periods, FS Aur also exhibits a much longer ~900-days photometric period (VLPP). We show that this extremely long periodicity may be result of the presence of a massive planet, or a very late brown dwarf, on a circumbinary orbit. This solution not only provides an explanation for the VLPP, but it also may give a plausible answer for other observed peculiarities of FS Aur. Moreover, it offers a new possibility for detecting planets in accretion disk environments, where most of the usual methods fail1. The discovery of a planet, or a third component of substellar mass, around a cataclysmic variable is important also in the context of stellar evolution, since such a system should have undergone a common envelope stage and a drastic reduction of distance between the stellar components. It adds facts to our poor understanding of extra-solar planet formation and survivability.
Summary of AAVSO data of FS Aur in quiescence (<15.2 mag).
In Sect. 2, we review observational data of FS Aur to show the temporal behavior of the object on different time scales. We provide observational examples demonstrating the presence of a variety of periods in its light curve, culminating with the newly discovered very long photometric period. In Sect. 3.1, we discuss a first possible dynamical scenario that depends on the direct perturbation of FS Aur by a third object on an orbit whose period matches the observed long-term periodicity, and show that the outcome does not match the observations. In Sect. 3.2, we examine a second scenario, where the perturber moves on a circular orbit whose period is much shorter than the long period, and yet produces a binary eccentricity variation with the latter period. The range and properties of the allowed solutions are shown. In Sect. 4 we discuss the implications that the third body may have on a CV system and its observational imprint on FS Aur’s features. Finally, our conclusions are presented in Sect. 5.
2. The complex photometric behavior of FS Aur
The long-term variability of FS Aur became apparent after Tovmassian et al. (2003) pointed out the presence of the LPP in its light curve and drew the attention of the amateur community to this star. Long monitoring and relatively dense coverage helped to reveal a large amplitude variability of the object in quiescence. This work is based on a wealth of observational data accumulated thanks to many amateur observers. We used the AAVSO International Database “American Association of Variable Star Observers”, which contains contributions of many observers worldwide. A significant part of the data in the AAVSO archives is contributed by members of the “Center for Backyard Astrophysics” (CBA), a global network of small telescopes dedicated to photometry of cataclysmic variables. Our own observations presented in Tovmassian et al. (2003) were added to the dataset. The data were obtained principally in the V-band or undefined band (NA in AAVSO tables). Data obtained exclusively with CCD cameras was used in the analysis. In Table 1 we present statistics of the analyzed data. The table shows the distribution of the data by bandpasses (after eliminating measurements with magnitudes brighter than 15.2, corresponding to the outburst activity), the average magnitude in each band, the scatter of data and a correction (described in the text below), which was applied to the measurements in each band to normalize them to a common V magnitude. As was mentioned above, the bulk of homogeneously distributed data was obtained in V and NA bands and the difference in average magnitudes between these two is negligible compared to the amplitude of variability that we are going to discuss. The latter reaches 2 mag and greatly surpasses the amplitude of nightly variations, which are also fairly large (up to 0.5 mag). The average V magnitude of the data obtained in Observatorio Astronómico de San Pedro Martír (OAN SPM) by ourselves is considerably fainter (see Table 1), but the data obtained there, although numerous, are concentrated in an brief stretch of time, when the object was experiencing a low state. Similarly, the data in CV are limited in time and their average magnitude is different from that of in V, but the bandpasses are not so significantly different that we would need to apply any correction there. It is noteworthy that the color indexes of (B − V) and (V − R) or (g − r) determined from the data obtained simultaneously in different epochs (Tovmassian et al. 2003; Neustroev et al. 2005) are no higher than ≤ 0.3 mag. The color differences of data obtained quasi-simultaneously in AAVSO dataset are similarly small compared to the variability of the object on different time scales. Since it is impossible to exactly correct the fluxes obtained in a variety of different bandpasses, we conducted the time analysis of the combined data ignoring the band differences, and also introduced a rough color correction according to numbers in the last column of Table 1 before the analysis.
 |
Fig. 1 Long-term light curve of FS Aur. The data set includes exclusively CCD observations and is obtained predominately in the V-band (green circles) for the last 4000 days. The black symbols correspond to the data for which there is no information of the bandpass, but their average value is very close to the V-band. The data obtained in B and R filters are marked by blue and red circles, respectively. The open symbols corresponds to outbursts, which were duly separated using a V > 15.2 mag threshold. |
In the lower panel of Fig. 1 the original dataset is displayed by points marked in different colors according to the bands in which they were obtained. This panel shows that the large amplitude and large time-scale variability in quiescence far exceeds any color differences. Therefore, combining data obtained in different filters should not have a strong impact on the result of the time analysis. In the upper panel the same data are shown after the color correction. The data were also processed in order to eliminate short, unevenly distributed outbursts by filtering any points brighter than 15.2 mag. These points corresponding to the outbursts are marked by open symbols in the bottom panel and are eliminated in the upper panel and from the subsequent considerations. Certainly, this does not clean the data of all outburst events, since some take place during the low quiescent levels, but their number and influence on the time analysis is negligible.
The data considered here were collected on more than 5000 days and include ~11 500 measurements of AAVSO data only. The AAVSO data are publicly available and can be quickly looked up or downloaded from the AAVSO.
The discovered phenomenon is unprecedented. It involves cyclical variations of light on such a long base and large amplitude that it is easily recognized even in by-eye examination. We present the time analysis of the data in the next section, but because of the limited time coverage, the precision of the deduced period remains very low and its stability uncertain. The short-term variabilities of the object (OP, LTP, LSP, white dwarf spin period (SP) and stochastic) are not the subject of this study and are presented only to illustrate observational features of FS Aur, which makes it stand out among other CVs. The period search for short-term variations (of hours, comparable to the orbital period) was conducted on data obtained in one filter and normalized to the nightly averaged magnitude. This avoids long-term trends characteristic of CVs and particularly of this object. Below, we briefly review all previously detected variabilities of the object with the corresponding references, before revealing the VLPP at the end of this section. We point out features that are un-common for CVs and earlier attempts to explain them.
2.1. Orbital period (OP)
The OP of FS Aur was determined from spectroscopy. Thorstensen et al. (1996) first reported a spectroscopic period Porb = 0.05954 ± 0.00012 d (=85.73 ± 0.17 min). Neustroev (2002) confirmed that period spectroscopically, but pointed out that photometric variability has a duration much longer than the spectroscopic period, and that the orbital period is not detected in the light curve. Ten years of monitoring the orbital period of FS Aur spectroscopically did not reveal any measurable change2. An attempt to measure the OP from photometry was made by Howell & Szkody (1988), but the large range they report on their period determination (87–105 min) probably disqualifies it from consideration. The first long-term and systematic study of the photometric variability of FS Aur was conducted by Tovmassian et al. (2003), and no variability with orbital period was detected. Instead, a long photometric period was discovered, which we will discuss in Sect. 2.2.
Monitoring of FS Aur during a long time span reveals, however, that its photometric behavior during quiescence is more complicated than was previously thought. For example, the orbital period can be seen at some epochs, but completely disappears at others. There is no good statistics to know how often this happens, or whether it depends on anything else. In Fig. 2 a portion of the light curve of FS Aur from 2004 (JD 2 453 348–2 453 358) with dense observational coverage is presented along with the corresponding power spectrum, which shows a peak at a frequency (16.78 day-1), coinciding within errors with the spectroscopic orbital period. Power spectra were obtained using the discrete Fourier transform algorithm (DFT). Comparison of the power spectrum from Fig. 2 with the one presented in Fig. 3 or Fig. 6 of Tovmassian et al. (2003), where the peak at the frequency corresponding to the orbital period is completely absent, demonstrates that it is not always detected. Generally, a lot of transient peaks of significant power are detected in the light curves of FS Aur at higher frequencies, which sometimes persist only one night (Neustroev et al. 2005). Appearance and complete disappearance of variability with the orbital period in the light curves of CVs, however, is a very unusual phenomenon.
2.2. 205.5 min long photometric period (LPP)
There is a 205.5 min photometric period (LPP), persistently observed in the course of ~10 years of monitoring. It appears to be a permanent feature with a stable period. However, its amplitude is not constant. The LPP is often observed as a smooth sinusoidal signal, as can be seen in the left panel of Fig. 3, where a few selected nights are presented. The power spectrum in Fig. 3 was generated applying the DFT to the data spanning from JD 2 451 161 to 2 452 261. But in other cases it is contaminated by the orbital period in the photometric data, as we already demonstrated in Fig. 2). On many occasions, it is also overlapped with a strong, erratic variability with an amplitude on the order of 0.5 mag, producing a quiescent light curve unlike any other known CV (discussed in Sect. 2.3; Fig. 4). But regardless of what else shows up in the light curve, the 205.5 min LPP signal is always there.
 |
Fig. 2 Portions of the light curve from the 2004 observations (left panels) and its power spectrum. The power spectrum is obtained from a larger data set spanning from JD 2 453 348 to 2 453 361. The highest peak of the power spectrum at fLPP = 7.0079 day-1 corresponds to the long photometric period (s. 2.2). The peak at fOP = 16.78 day-1 is, within errors, the orbital period determined from spectroscopy. The rest of the peaks in the power spectrum are either transient, or aliases, like the one at 2 × fLPP = 14.1. The lines on the light curve are sinusoidal fits of OP (dot-dashed; magenta), LPP (dotted; cyan) and the sum of both (black). |
 |
Fig. 3 Selected portions of the light curve from different epochs in which the LPP is the dominating periodicity are presented in the left panel. The curve is a sinusoidal fit to the data, confirming phase stability of the periodicity from year to year. Similar light curves can be found in earlier observations (Tovmassian et al. 2003). The power spectrum calculated over a huge 1100-day time period shows a strong, single peak at the LPP frequency and its nightly aliases. |
 |
Fig. 4 Examples of FS Aur photometry. The two lower panels show cases of large, ~0.5 mag bulges in the light curve. The left upper panel is simply a zoom of the central part of the lower panel, where we have overlapping data obtained from two different sites (solid and open points). The high-frequency oscillations are a good example of flickering. The solid black line is the sum of OP and LPP. The dotted cyan curve is a fit to the LPP and it is a continuation of the same curve as presented in Fig. 2. The dash-dotted magenta curve is a fit to the OP and it is seen only in certain epochs. The upper panels on right side are portions of the light curve well fitted with the sum of the OP and LPP periods. |
Inspection of the profiles of emission lines of FS Aur demonstrates that their wings are not symmetric (Neustroev 2002). Tovmassian et al. (2003) have found a peak in the power spectrum of radial velocity (RV) variations at the frequency corresponding to the beat period between OP and LPP. Later, on one occasion, Tovmassian et al. (2007) were able to detect this long spectroscopic period (LSP) visually in the wings of the emission lines of FS Aur, in addition to the OP easily detected in the core of the lines. The LSP = 147 ± 5 min was found to be at exactly the beat period between the orbital and the long photometric period PLSP ≈ 1/85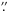 7−1/205
7−1/205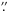 5 = 1/147
5 = 1/147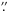 0. This exceptional feature, a second period in the wings of emission lines, has been observed only in another unique CV: V455 And (also known as HS2331+3905, Araujo-Betancor et al. 2005). This object is also known to have a mildly magnetic WD (as an intermediate polar) that spins rapidly: Pspin = 67 s. Based on these facts, Tovmassian et al. (2007) came up with the hypothesis that the long periods in these systems were the result of precession of a magnetic white dwarf, which induces a bright spot on the inner rim of the accretion disk. That spot co-rotates with the precession axes of the WD and gives rise to the long period in the wings of emission lines. But in V455 And, the period appears to be not very stable (Araujo-Betancor et al. 2005), and efforts to find out if it changes, and by how much, were thwarted by a super-outburst in 2007, after which the period in the wings of the lines disappeared altogether. On the other hand, the efforts to prove that FS Aur contains a magnetic (intermediate polar strength) fast rotating, asynchronous WD were not conclusive (Neustroev et al. 2005).
0. This exceptional feature, a second period in the wings of emission lines, has been observed only in another unique CV: V455 And (also known as HS2331+3905, Araujo-Betancor et al. 2005). This object is also known to have a mildly magnetic WD (as an intermediate polar) that spins rapidly: Pspin = 67 s. Based on these facts, Tovmassian et al. (2007) came up with the hypothesis that the long periods in these systems were the result of precession of a magnetic white dwarf, which induces a bright spot on the inner rim of the accretion disk. That spot co-rotates with the precession axes of the WD and gives rise to the long period in the wings of emission lines. But in V455 And, the period appears to be not very stable (Araujo-Betancor et al. 2005), and efforts to find out if it changes, and by how much, were thwarted by a super-outburst in 2007, after which the period in the wings of the lines disappeared altogether. On the other hand, the efforts to prove that FS Aur contains a magnetic (intermediate polar strength) fast rotating, asynchronous WD were not conclusive (Neustroev et al. 2005).
2.3. Stochastic variability and flickering
The bulk of light in the optical and UV range from CVs is produced in an accretion disk and its luminosity fluctuates because of viscosity, turbulence, uneven distribution of matter in the disk and accretion of matter on the surface of the WD. So, in addition to strictly periodic phenomena (like the orbital period, variations caused by bright spots, eclipses, elliptically distorted stellar shapes, etc., and different manifestations of the spin period, or effects induced by tidal forces), there are short duration and small amplitude flux variations such as quasi-periodic oscillations (QPOs) or flickering. The latter is clearly observed in FS Aur and must not be confused with much larger nightly variability, both in terms of duration and amplitude. This variability in terms of amplitude and duration in FS Aur is really untraceable; sometimes it contaminates the light curves to such a degree that it is difficult to see the periodic LPP or OP variabilities described in the previous sections; sometimes it is mild and unobtrusive. On the left side of Fig. 4 we present a piece of the light curve obtained simultaneously from two different observatories. Strong, 0.5 mag humps of erratic nature and irregular forms prevail in the light curve. On top of it, the flickering is observed with amplitudes reaching 0.2 mag. The perfect coincidence of every flicker recorded from different observatories illustrates the precision of the observations and authenticity of the variability with different scales. If the flickering is a usual phenomenon and its magnitude and temporal behavior are very similar to other CVs, the large amplitude and irregular variability is peculiar of this object and can hardly be matched by any other system in the diverse zoo of CVs. The stochastic variability has no repetitive or definite structure to be quantified, but the typical timescale of such large irregular humps that appear in the light curve are on the order of 8 − 12 × 103 s. In the right panels of Fig. 4 more examples of light curves are presented. The two upper right panels show light curves in which both the LPP and OP have similar strength and can be fitted relatively well by two sinusoids, but the bottom panel exhibits a portion of light curve obtained just a day apart, with a bulge in it too strong to be ignored, or to be found in light curves of other DNe.
 |
Fig. 5 Power spectrum of the quiescent light curve of FS Aur (left panel) and its corresponding spectral window (right). The strongest peak in the window at fY = 0.00274 day-1 corresponds to the yearly observational cycle. The fVLPP = 0.001114 ± 0.00015 day-1 frequency corresponding to VLPP is the second-highest peak in the power spectrum, with the strongest peak being falias = 0.00114 + 0.00274 = 0.00388 day-1, an alias created by the beat between fVLPP and f1y. |
Summary of periodicities detected in FS Aur.
2.4. Very long photometric period (VLPP)
The quiescent light curve of FS Aur observed over a decade exhibits drops and rises of brightness, unlike any other CV. An inconstant quiescent level is not unusual in itself: there are CVs that have low and high states like some magnetic systems, or anti-outbursts like VY Scl systems, and Z Cam-type standstills, when the system remains at some intermediate level between the maximum of outburst and quiescence. Usually these quiescent level changes are step-like. But in the case of FS Aur it is a smoother wavelike variability with sharp dips of quite high amplitude of ~2 mag. The modulation appears to be periodic on eye inspection, which is confirmed by a Fourier analysis. The power spectrum of the data displayed in the upper panel of Fig. 1 is presented in Fig. 5 (left panel). The data set spans over 13 years and fully six periods of ~900 days, peaking in the periodogram at the 0.001114 day-1 frequency. Naturally, the error in the period determination is large, but its presence is very significant. The other low-frequency peak of similar strength at f = 0.004 day-1 is probably an alias related to the one year observational cycle, since it is a beat period with the VLPP (1/897 + 1/365 ≈ 1/258). The spectral window (Fourier transformation of the time sampling) presented in the right panel of Fig. 5 confirms the alias nature of the f = 0.004 day-1 peak, since the window peaks at 0.00274 days-1, corresponding to a yearly observational cycle. The distribution of the data is very uneven, and the shape of the light curve folded with the VLPP is not sinusoidal, which badly reflects on the Fourier analysis. Therefore, we applied a Scargle-Lomb (Scargle 1982) least-squares spectral analysis, which is similar to the Fourier analysis, but mitigates the long-periodic noise in long gapped records. The result is shown in Fig. 6, where two curves show the periodogram calculated for data without color correction and with the correction applied. It once again confirms that neither small differences in magnitudes in different bandpasses, nor time distribution of the data really affect the outcome of the period analysis and that the cyclic luminosity dips in the light curve are fairly periodic.
Our aim is not the determination of a precise VLPP, because this cannot be done with a few cycles anyway (there are very few points in the first two cycles, so the period comes out mostly in the last four cycles), the purpose of this study is to show that FS Aur has a very long period modulation of its quiescent light curve, and to offer a possible explanation for this behavior. In the subsequent analysis and calculations we use an average value of PVLPP = 875 ± 50 days, since the exact period is not well established.
As we mentioned in the introduction, periods much longer than the orbital period are not common for CVs. The existence of multiple long periods, seemingly unrelated and of very different time scales (see the summary of periods detected in FS Aur in Table 2) begs for a universal explanation. Below we present a new hypothesis involving a third body, possibly a super-massive planet, or substellar companion, which may explain many features of FS Aur that are incomprehensible within the standard CV configuration.
 |
Fig. 6 Periodograms calculated by the Scargle-Lomb method for the set of data obtained in different filters (dashed line) and after color correction (solid). The strongest peak in both cases coincides with the peak in the power spectrum obtained by the Fourier method. |
3. FS Aurigae as a triple system: a dynamical solution
A CV is a system in a very stable configuration (Frank et al. 2002, pp. 53, 54). If we disturb the system even slightly, it tends to compensate and adjusts its parameters to return to equilibrium. However, the secondary star in a CV is a late main-sequence star that fills its Roche lobe and its surface is near the inner Lagrangian point L1. While maintaining equilibrium, the secondary loses matter, since any small perturbation pushes matter over the L1 Lagrangian point into the gravitational pull of the primary. This balance is maintained either by a containing evolutionary expansion of the secondary star, or by shrinkage of the binary via angular momentum loss. The secondary has to adjust its structure so that its radius moves in step with the Roche lobe size. Angular momentum loss is governed by magnetic braking for the systems with orbital periods longer than three hours and by gravitational waves emission for those shorter than two hours. The lack of an angular momentum-removing mechanism for periods between 2–3 h is believed to be the reason that the mass transfer ceases, which significantly reduces the number of observed CVs with such periods. Matter lost through the L1 point orbits the more massive WD, forming an accretion disk around it (Ritter 2008, and references therein). As mentioned in the introduction, the accretion disk is the most luminous component of a CV. Its brightness is proportional to the mass transfer or mass accretion rate. Any change in mass transfer rate will be directly reflected by the system brightness. Thus, any perturbation of the position of the Lagrangian point will affect the mass transfer rate and consequently the system brightness.
Given the huge disparity between the VLPP and all other periods, we should probably seek the cause of variable mass transfer rate, and therefore of the disk brightness variability, outside the binary. Below we will consider two distinct scenarios exploring the origin of the VLPP by the presence of a third hypothetical body in this system and by taking into account possible effects inflicted by tidal interaction among the components of the triple system. In all numerical integrations in the subsequent subsections, we used the high-order Runge-Kutta-Nyström RKN 12(10) 17M integrator of Brankin et al. (1989) for the full equations of motion of the full three-body problem in the barycenter inertial frame. The adopted total mass of the system is MT = M1 + M2 + M3 = 0.84 M⊙ with M1 = 0.75 ± 0.05 M⊙, M2 = 0.09 ± 0.02 M⊙3 and M3 = 1 MJ (where MJ is one Jupiter mass). Total energy is monitored and it is conserved to 10-5, or better, for all experiments. At each time step, the instantaneous eccentricity of the binary is computed using the osculating ellipse approximation (Murray & Dermott 2000, Eq. (2.135)). Stellar finite size effects and the effect of the accretion disk were not included in the calculations.
Point masses, particularly for the inner binary, should be used with some caution. It may be important to take the tidal deformation of the stars in the close binary into account when studying three-body effects. As has been demonstrated by a number of authors (Soderhjelm 1984; Kiseleva et al. 1998; Eggleton et al. 1998; Borkovits et al. 2004), the eccentricity variations calculated for a mass-point system may be appreciably diminished by tidal effects. For a three-body effect to have a 900 d period, any tidal apsidal motion must be much slower. For a synchronous rotating secondary (which is the case of CV’s) we have according to Warner (1978)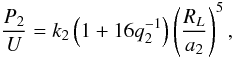 (1)where P2 = OP denotes the period of the close binary, U is the apsidal period of the system owing to the tidal deformation of the secondary, k2 is the apsidal coefficient of the secondary, q2 is the mass ratio between the white dwarf and the secondary (q2 = M2/M1), a2 is the semi-major axis of the inner binary, RL is the mean radius of a lobe-filling secondary. The apsidal motion constant k2 is a function of the internal structure of the secondary star and basically quantifies the extent to which the mass is concentrated toward the center of the star. This constant is k2 = 0 for a point mass and has the value of k2 = 0.75 for a uniform mass density sphere. For main-sequence stars, k2 is on the order of ~10-2.
(1)where P2 = OP denotes the period of the close binary, U is the apsidal period of the system owing to the tidal deformation of the secondary, k2 is the apsidal coefficient of the secondary, q2 is the mass ratio between the white dwarf and the secondary (q2 = M2/M1), a2 is the semi-major axis of the inner binary, RL is the mean radius of a lobe-filling secondary. The apsidal motion constant k2 is a function of the internal structure of the secondary star and basically quantifies the extent to which the mass is concentrated toward the center of the star. This constant is k2 = 0 for a point mass and has the value of k2 = 0.75 for a uniform mass density sphere. For main-sequence stars, k2 is on the order of ~10-2.
Our justification in using the point mass approximation and ignoring the finite size effects on apsidal motion is based on the fact that the secondary stars in CVs are different from their main-sequence counterparts (Patterson 1984; Baraffe & Kolb 2000; Knigge et al. 2011). The difference is caused by the nuclei of a bloated, Roche-lobe filling secondary star being denser and more massive than it should be for a regular star of corresponding type (Baraffe & Kolb 2000). Indeed, Warner (1978) empirically estimated the k2 constant using cyclic changes in the eclipse (O–C) diagram for two nova-like CVs and established that their values are approximately a few 10-4. FS Aur has a much shorter orbital period than the objects considered by Warner (1978), the secondary star in a OP = 85.7 min CV probably has a mass below 0.1 M⊙. The stars with M ~ 0.4 M⊙ become fully convective as the mass decreases, the density increases and the internal temperature decreases, leading to a partial degeneracy of the core. Around a mass 0.08 M⊙ stars reach the minimum mass required to sustain nuclear burning. Approaching the minimum hydrogen-burning mass, the increasing electron degeneracy induces structural changes on the secondary. The secondary star in FS Aur is very close, or is in a regime of the highest density (see Fig. 1 in Chabrier et al. 2009), therefore the core of the secondary star must be highly degenerate, containing the larger part of the mass. As a result, any long-term variations caused by the apsidal motion would be significantly longer than the ~900-day period observed in FS Aur.
A first natural scenario is to perturb the binary orbit with a recurrent perturber. Assuming that the ~900-day modulation in the light curve is caused by a periodic variation in the rate of mass transfer in the close binary through the inner Lagrangian point, a variation in the binary orbit could be the origin of this period (King 1988).
3.1. The third body with an orbital period of ~900 days.
Because of the unique one-to-one relationship between orbital period and semi-major axis in Keplerian orbits, Kepler’s third law gives us the semi-major axis of the perturber to explain the 900-day light curve modulation as the result of the direct gravitational perturbation of a third object, 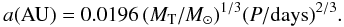 (2)The third-body orbital period of P3 = 875 days results in a semi-major axis for the third object equal to a3 = 1.692 AU, which is around 600 times longer than the binary separation inferred from the 85.7 min period. We performed a series of numerical experiments with a perturber of one Jupiter mass (MJ) and fixed semi-major axis (1.69 AU) at increasing eccentricities, and measured the resulting effect on the binary eccentricity (e2). For a perturber on such a high large to have a direct effect on the binary, it must have a very high orbital eccentricity (e3), for its periastron to take it close to the binary.
(2)The third-body orbital period of P3 = 875 days results in a semi-major axis for the third object equal to a3 = 1.692 AU, which is around 600 times longer than the binary separation inferred from the 85.7 min period. We performed a series of numerical experiments with a perturber of one Jupiter mass (MJ) and fixed semi-major axis (1.69 AU) at increasing eccentricities, and measured the resulting effect on the binary eccentricity (e2). For a perturber on such a high large to have a direct effect on the binary, it must have a very high orbital eccentricity (e3), for its periastron to take it close to the binary.
 |
Fig. 7 Effect on the binary eccentricity of a close encounter with a third object on a high-eccentricity (e3 = 0.95) orbit with an 875d period. The perturbation occurs within a ~10d interval and leads to a persistent effect. The horizontal axis is in units of the third-body period (875d). |
 |
Fig. 8 Summary of our results: the upper panel shows the period of the long-term modulation in binary eccentricity as a function of the perturber mass (in Jupiter masses). Each curve corresponds to different P3/P2 ratios taken from 12 to 48 (lower and upper curves, respectively). The thick horizontal line shows the observed value of the VLPP. Only solutions that cross this line can explain the VLPP. The middle panel shows the perturber mass and orbital radius combinations that result in a long-term modulation of the binary orbit equal to the VLPP. The lower panel shows the amplitude of the binary eccentricity perturbation for those solutions. |
Figure 7 presents the resulting perturbation in the binary eccentricity for an extreme value of the perturber eccentricity of e3 = 0.95. Lower values do not result in a measurable effect. One can argue that a stronger response can be attained with a more massive perturber. However, it is clear from the figure that any such attempt is futile, since the form of the time variation induced in e2 does not match the observed light curve: the driven modulation is confined to a narrow 10-day window, whereas the observed light curve does not vary abruptly. Furthermore, although low, the perturbation leaves a residual effect which, upon repeated encounters, will lead to a secular effect that would end up changing the parameters of the system significantly. A perturber like this will either collide, or will be expelled from the system in ~107 encounters (2.4 × 107 years) in the e3 = 0.95 case. Third bodies with greater eccentricities would have even shorter life-spans.
3.2. The third body on a close near-circular orbit
In hierarchical triple systems a third light-weight body can produce a perturbation on a central binary, perturbation with a much longer period compared to the orbital period of the perturber (e.g. Mazeh & Shaham 1979; Soderhjelm 1982, 1984; Georgakarakos 2002, 2009). A third companion prevents the complete circularization of the orbit of a binary system by inducing a long-term eccentricity modulation. As shown e.g. in (Soderhjelm 1984), the amplitude of such an eccentricity-variation can be estimated from 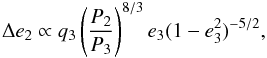 (3)where P3 is the period of the third body around central binary, e3 is the ellipcity of its orbit and q3 ≡ M3/(M1 + M2 + M3). We will use this equation in the next subsections after defining possible triple configurations responsible for VLPP.
(3)where P3 is the period of the third body around central binary, e3 is the ellipcity of its orbit and q3 ≡ M3/(M1 + M2 + M3). We will use this equation in the next subsections after defining possible triple configurations responsible for VLPP.
Here we explore this effect on FS Aur. The basic setup is a binary formed by two point masses initially in circular orbit. We used the same masses for the binary components as in the previous section, with the orbital period P2 equal to the OP. A third point mass (perturber) moves initially on its own circular orbit, farther away and in the same plane. Its mass M3 and orbital period P3 are changed across an ensemble of numerical experiments.
To test our numerical integrations, we ran some experiments to compare with the results of Georgakarakos (2002), whose set-up is very similar to ours. He studied the eccentricity modulation of a binary in a hierarchical triple system, where all orbits are coplanar and initially circular. He used the perturbation theory to derive a formula that can be used to estimate the magnitude of the effect for various mass ratios. Specifically, we reproduced his Figs. 2 and 3, which show the binary eccentricity modulation during one perturber period, and Fig. 5, for timescales of a few hundreds of such periods. In all cases our results differ from those of the Georgakarakos (2002) numerical experiments by no more than 1%. We also compared our calculations to the analytical approximation of Georgakarakos (2002) and also found deviations well within his quoted precision. We now turn to our experiments that simulate FS Aur.
The top panel of Fig. 8 shows the resulting periods of the long-term modulation of the binary eccentricity as a function of the mass of the perturber. The thick horizontal line corresponds to the VLPP value. For perturbers whose orbital period is less than 13.4 binary periods, no solution is possible, because their respective curves do not reach the VLPP value. For perturbers with periods longer than that, but shorter than 23 orbital periods, two solutions are possible: one at low mass and another at an increasingly larger mass. Finally, perturbers with longer periods produce only one solution at the large mass range.
The curve in the middle panel of Fig. 8 presents the perturber orbit semi-major axis for the solutions that result in the binary system eccentricity modulation of period equal to the observed VLPP value, i.e solutions that cross the solid line on the upper panel. The lower panel shows the amplitude of the eccentricity perturbation for the corresponding solutions presented in the middle panel. The maximum amplitude is achieved for systems that harbor a third body with M3 = 48 MJ.
We point out that the binary eccentricity is modulated at three different scales, not only the long period we are interested in. Figure 9 shows the behavior of the binary eccentricity at different time scales, for a solution near the maximum amplitude eccentricity modulation (M3 = 48 MJ and P3/P2 = 13.4): e2 is forced to oscillate at three different timescales, the period of the binary P2, that of the perturber P3, and a much longer period (PVLPP).
 |
Fig. 9 Perturbation of the binary eccentricity caused by a perturber on a distant, circular orbit. The perturber has a mass of 48 MJ and its orbital period is 13.4 times that of the binary. The three panels show that the perturbation occurs at three different timescales: that of the binary P2 (0.0595d) panel a), that of the perturber (0.7975d) panel b), and a much longer modulation (875d) panel c). |
 |
Fig. 10 In the upper panel, the relative amplitude of the low frequency to the high frequency e2 modulations (Θ), see main text for definition, is plotted vs. the mass of the perturber. The higher Θ, the higher is the probability to detect the long-term modulation of the eccentricity. To show the effect on the shape of the resulting e2 modulation, three extreme cases are presented in the bottom panels: 1) a low-mass solution, with M3 = 2 MJ and P3/P2 = 23; 2) the solution with maximum eccentricity amplitude, with M3 = 48 MJ and P3/P2 = 13.4; 3) a high-mass solution, with M3 = 152 MJ and P3/P2 = 36. |
The relative amplitudes of these three modulations depend on the mass and size of the orbit of the perturber. In the lower panel of Fig. 10 the modulation of the binary eccentricity is presented for three distinct cases: low, intermediate and high perturber mass (left to right panels). The amplitude of the low-frequency modulation Δel, which basically corresponds to the VLPP, is estimated using the maximum to minimum difference of the outline of the corresponding curves. The amplitude of the high-frequency modulation Δeh, is determined from the width of the strip forming the curves. The measure of relative amplitudes is expressed as the ratio of these amplitudes (Θ = Δel/Δeh). The upper panel of Fig. 10 shows the continuous dependence of the amplitude ratio, Θ, on the mass of the perturber. The three particular cases shown at the bottom of the figure are marked on the curve. Evidently, the amplitude of the low-frequency eccentricity variation is the highest, compared to that of the high frequency, when the perturber’s mass hovers around 50 Jupiter masses. The amplitude of the low-frequency modulation becomes dominant (Θ ≥ 1.0) in the range of masses for the third body of 25 MJ < M3 < 65 MJ.
The shape of the calculated long-term modulation of the binary eccentricity is remarkably similar to the form of the VLPP, as can be seen in Fig. 11 (upper panel). Here we replaced long nightly observational runs with a single point averaged over the night to make the light curve less crowded. Another question is whether the amplitude of the binary eccentricity modulation is sufficient to drive the observed long-term variation in the light curve of FS Aur. Here it is necessary to consider the physical mechanisms that link orbital variation to mass transfer variation, and this in turn to the overall luminosity. It is possible to derive a relation between the rates of mass transfer and eccentricity variations using Eq. (9.4b) of Warner (1995), Eq. (2.135) of Murray & Dermott (2000) and additionally, assuming that the entire mass lost by the secondary star is accreted by the primary, so Ṁ1 + Ṁ2 = 0: 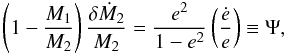 (4)where
(4)where 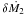 is the change in the mass transfer rate caused by a Ψ eccentricity variation of the binary system. Thus, we obtain qualitatively a direct relation between orbital eccentricity and mass transfer. However, description of this link in detail, or performing quantitative estimates of the luminosity variation is beyond the scope of this work. We used Eq. (4) only to provide a suggested link between our results in binary eccentricity modulation time and the observed long-term variation of the light curve of FS Aur. Specifically, we show in Fig. 11 the binary eccentricity e2 for the case M3 = 48 MJ and P3/P2 = 13.4 (panel b) along the light curve of FS Aur folded with PVVLP (top panel). The corresponding variation of the Ψ parameter is shown in the panel c. Finally, in the bottom of Fig. 11 we show the percentage change in the position of the inner Lagrangian point of the binary.
is the change in the mass transfer rate caused by a Ψ eccentricity variation of the binary system. Thus, we obtain qualitatively a direct relation between orbital eccentricity and mass transfer. However, description of this link in detail, or performing quantitative estimates of the luminosity variation is beyond the scope of this work. We used Eq. (4) only to provide a suggested link between our results in binary eccentricity modulation time and the observed long-term variation of the light curve of FS Aur. Specifically, we show in Fig. 11 the binary eccentricity e2 for the case M3 = 48 MJ and P3/P2 = 13.4 (panel b) along the light curve of FS Aur folded with PVVLP (top panel). The corresponding variation of the Ψ parameter is shown in the panel c. Finally, in the bottom of Fig. 11 we show the percentage change in the position of the inner Lagrangian point of the binary.
We point out that we have monitored our numerical experiments for changes in the binary orbital period caused by the third object. For all cases we studied here, the changes are negligibly small, with no secular trend and within the uncertainty in the determination of the OP.
 |
Fig. 11 Light curve of FS Aur folded with the 875-day period (top panel). The number of points is reduced compared to Fig. 1 by averaging long nightly sequences to one point. In the second panel from the top, the eccentricity modulation is shown for the best solution to explain the VLPP (M3 = 48 MJ and P3/P2 = 13.4). The next panel depicts the variation of the Ψ parameter (see Eq. (4)). The percentual change in the position of inner Lagrangian point of the close binary is shown in the bottom panel. All curves are repeated for two periods for better visual presentation. |
The calculations above are made for initially circular orbits, but the modulation of the close binary eccentricity can be enhanced in a triple system (P3/P2 ≤ 50) if the third body (Eq. (3)) has an eccentric orbit. Our results for a circular outer orbit correspond to e3 around 0.01 in Eq. (3). Even a mild e3 around 0.1 would give a ten times larger modulation of the binary eccentricity, which is clearly not observed. Therefore, the outer eccentricity clearly has to be very low, and the circular case studied here is a realistic one. The basic parameters of triple systems regarding the mass of the third body or its period are very similar to the case of circular orbits.
4. Discussion
We have shown that a massive planet, or a substellar object, on a circumbinary circular orbit introduces perturbations into the eccentricity of a close binary orbit on several frequencies. Specifically, a third body with an orbital period of P3 ≈ 20 h and mass M3 ≈ 50 MJ, produces oscillations of the binary eccentricity with time scales similar to P2, P3 and PVVLP. This is precisely on the order detected in FS Aur. Moreover, the form of the eccentricity modulation closely resembles the form of the light curve folded with the estimated period of 875 days, as shown in Fig. 11. The error in the determination of the VLPP is large, though, and the best estimate has been changing slightly with the arrival of new data points in the course of this study. However, it is on the order of 850–900 days and neither the folded light curve, nor other important conclusions in this paper are really affected by the lack of a precise value. The uncertainty range in the VLPP period determination is narrow relative to the amplitude of the phenomenon, as can be seen from Fig. 8.
We suggest that the brightness of the system during quiescence varies smoothly with the variable mass transfer rate triggered by the low-frequency modulation of the eccentricity of the binary orbit. The variable eccentricity directly translates into a variable size of the Roche lobe of the secondary star. Note that a change of the L1 position by 5 × 10-3 percent is equivalent to a shrinkage of the Roche lobe radius by a few thousand kilometers. The range in the size of third-body orbits, which may be responsible for a periodic eccentricity variation on the order of ~900 days, is quite narrow (between 0.016–0.032 AU), although the range in the mass of the perturber is large (between 1.7–150 MJ), but the highest amplitude modulation in absolute terms, and in terms of relative amplitude (ratio of low-frequency modulation amplitude to those of high frequency), point to the most probable value of the mass of the third body in the range 25 MJ < M3 < 65 MJ. Thus the mass of the third body in FS Aur is found at the borderline between planets and very late brown dwarfs. We made a quick estimate of fluxes of FS Aur in the far-IR (the object was observed by Spitzer; Program ID 2314 PI D. Hoard). The far-IR points form a smooth power law slope in the SED when combined with the UV-optical-NIR points corresponding to the object. Hence, we found no flux excess in IR, which indicates a presence of large late star in the system. The distance to FS Aur is not known, but it is apparent that it has quite a luminous accretion disk for a 85.7 min DN.
However, it is necessary to keep in mind that the bulk of light in the optical and UV range from CVs is produced in an accretion disk where the luminosity fluctuates because of various reasons, such as viscosity, turbulence, uneven distribution of matter in the disk and accretion of matter on the surface of the WD. The entire internal structure of the disk undergoes violent shake-up during outbursts. So, the mass transfer from the donor star is important, but not the only factor influencing the brightness of the disk. Hence, it would be naive to expect that the brightness of the disk strictly adheres to the periodic modulation of the binary orbit eccentricity and the light curve to exactly repeat itself from cycle to cycle of the VLPP. Only time will show how stable and repetitive the VLPP is. However, at this point it is clear that no other dwarf nova has been found to show such strong and cyclical variability in quiescence, and our hypothesis is a viable solution for FS Aur. It is also a possibility that should be explored regarding other close binaries with luminous disks, where radial velocity and eclipse detection methods would fail in search of planets and third bodies.
We note that the presence of the third object in a circular orbit around the central binary, within the range of orbital radius for our proposed mechanism is possible on dynamical grounds because Pichardo et al. (2005) have demonstrated that there are circular, stable orbits around a binary with the characteristics of the system studied here (see their Fig. 3). In their notation, our system corresponds to a mass ratio of q = m2/(m1 + m2) = 0.11, eccentricity zero and orbital radius for the perturber of r3/r12 between 6 and 12).
Finally, we also note that the presence of a third object in orbit around close binary systems, like CV’s, has been previously suggested, based on light time effects in short-period eclipsing binaries (e.g. Guinan & Ribas 2001; Pribulla et al. 2005; Kundra & Hric 2010; Beuermann et al. 2011).
A satisfactory explanation of the VLPP is not the only outcome of the proposed hypothesis. FS Aur has a number of peculiarities and we now address them, although some of our conceptions are purely speculative.
Stochastic variability. The object is known for showing a large amplitude variability in addition to various periods detected in its light curve. A modulated mass transfer rate has been proposed at previous times as a mechanism to explain diverse phenomena, from DN outbursts (Bath 1973; Lanzafame 2008) and superhumps in SU UMa objects (Mineshige 1988) to QPOs (Godon 1995; Kluzniak et al. 2007). While each of these phenomena has an alternative, and often broadly accepted explanation, it is clear from these papers and references therein that modulated mass transfer may cause instabilities in the disk, which produces luminosity modulations that are comparable in amplitude and duration with the stochastic variability we observe in FS Aur. Bath et al. (1974) showed that in a close binary with a WD primary and a disk temperature on the order of 105, the dissolution time of spots triggered by inhomogeneous structure in the accretion disk is about 2 × 103 s, which is comparable to the duration of irregular humps in the light curve of FS Aur. However, since the amplitude of this stochastic variability in FS Aur is highly variable and cannot be analyzed methodically in the available data sampled, we cannot dwell on these theories, but simply speculate that the non-periodical, atypical light curve variability of this object might be the result of the disk response to the high-frequency modulation of mass transfer. The amplitude of the high-frequency eccentricity modulation has a smaller amplitude than that of the low-frequency modulation causing the VLPP in the preferred range of solutions, but it cannot be ignored.
Photometric orbital period. In previously published papers, particularly in Tovmassian et al. (2003), we reported detection of the LPP, which often appeared to be the only, fairly sinusoidal flux variability. However, because the data were continuously increasing, new details surfaced. We began to see the orbital period in the light curves at some epochs, and sometimes the OP signal will exceed that of LPP. The most probable source of light modulation by the orbital period in low-inclination FS Aur is the “bright spot”. What influences the brightness of that spot, which is the area of impact of mass transfer matter with the accretion disk? The mass transfer rate, of course. But based on the available data, it is very difficult to systematize appearances and disappearances of one or another light modulation, and hence find the correlation with the long time behavior. On top of that, there is irregular variability discussed in the previous subsection and there are nights when it is practically impossible to separate all these different variabilities.
The 205.5m LPP. The LPP is the best established period in FS Aur apart from the OP, and it has no direct relation to the possible triplicity of this system. However, assuming that the hypothesis of the precessing WD in FS Aur, proposed by Tovmassian et al. (2007) is still valid, we may argue that a perturbing third body on a circumbinary orbit may be a good reason why the WD in this particular system is precessing. Precession is observed routinely in solid bodies of the solar system and it has been invoked to explain number of phenomena observed in pulsars (i.e. Breton et al. 2008). White dwarfs also have been considered as possible candidates of precessing stellar objects (Leins et al. 1992). In a slowly rotating compact stars, the precession period is extremely long and the amplitude of precession is small. However, in rapid rotating neutron stars and white dwarfs, the precession period is still within reasonable observational limits and can explain observed periodicities exceeding spin period by several times. For triple systems the precessional effects might be amplified, since the compact object, a fast rotating gyroscope, will be found in a variable gravitational field of the second and third bodies and will precess according to classical physics (Goldstein et al. 2002; Bohigas et al. 1994).
Evolutionary considerations. It is not clear how a triple system involving a CV may be formed. Close binaries consisting of a WD and a MS star undergo a common envelope (CE) phase to spin down and end up in orbits with roughly the size of the Sun (Yorke et al. 1995). The presence of a third body seems problematic at first sight. However, very recently there was a report of the detection of a massive planet around another CVs (Qian et al. 2010; Beuermann et al. 2011) based on more direct evidence than presented here. A planet may be formed after the CE phase. For FS Aur the favored mass estimates of the third body are a bit higher than the upper mass limit of a planet, as defined by the Working Group on Extrasolar Planets. But there are claims of planet discoveries with masses to up to 22 MJ (Butler et al. 2006), for FS Aur solutions with M3 < 25 MJ are not excluded. On the other hand, there are also observations of a giant K star with two brown dwarfs orbiting it (Niedzielski et al. 2009), which might be a good progenitor candidate for a system such as FS Aur.
Alternative solutions. An alternative solution to the VLPP we can think of is the effects of magnetic activity on the surface of the secondary, similar to the solar cycles. Indeed, Richman et al. (1994) surveyed possible CV systems known to have long-term variability and concluded that this explanation is plausible. But these cycles did not show any strict periodicity and are decades long. A similar possibility was explored for low mass X-ray binaries (Kotze & Charles 2010). The spectral class of the secondary star in FS Aur is not known, but is expected to be a very late M-dwarf, or even brown dwarf. The cycle length of these late dwarfs due to the magnetic activity is not known, but we find it to be a very improbable explanation for the observed phenomena in FS Aur.
5. Conclusions
We discovered that the brightness of the cataclysmic variable FS Aur in quiescence varies within a wide range (17.4–15.2 mag), and that this variability is strongly modulated. The period of this variability, ~900 days, is determined on the basis of only a few observed cycles in the course of the last 10 years, and is therefore not very precise. In addition to this VLPP, FS Aur is known to exhibit a number of other observational peculiarities. We propose that FS Aur is a triple system, containing a substellar mass companion that perturbs the eccentricity of the close CV binary. Extensive numerical integrations show that a third component on a circular circumbinary orbit may produce these modulations on time scales as long as the VLPP. The range of possible masses for the perturber spans a wide range, from a massive planet to another red dwarf in this system. However, solutions where the binary eccentricity modulation has a period equal to the VLPP define a narrow set of solutions. Those with a perturber with a mass within 25 MJ < M3 < 65 MJ are considered the more plausible, since in this range the amplitude of the long period modulation dominates that of the rapid variability, with periods corresponding to the orbital periods of the binary or the perturber. The eccentricity variability of the binary affects the mass transfer rate, which is responsible for the brightness of the accretion disk and is the most luminous component of the system. We suggest that the mass transfer variability on short time scales is the cause of the complex, highly variable form of the light curve on a nightly basis. The proposed triplicity of FS Aur should be confirmed by additional photometric monitoring of the system and observations of more ~900-day cycles, to make sure it is certainly periodic and to establish the precise period. Our calculations demonstrate the possibility of the detection of triple systems containing close binaries with mass exchange and dominating accretion powered luminosity.
Recently there were claims of a planet discovery in other CVs by traditional methods by Qian et al. (2010); Beuermann et al. (2011).
Typical masses for a system with the orbital period of FS Aur (Knigge 2006; Knigge et al. 2011).
Acknowledgments
We thank all the amateur observers who do a tremendous job in collecting professional grade data with persistence and zeal. We are particularly indebted to Joe Patterson, who guides the amateur community engaged in CV monitoring and who made possible the dense observational coverage of FS Aur, and CBA member Jerry Foote, who actually observed this object extensively and kindly offered us his data. G.T. acknowledges CONACyT grant #45847 and PAPIIT #101506. C.C. and L.A. were supported by DGAPA/PAPIIT grant IN112210. C.C. thanks the CONACyT postdoctoral program for its financial support. We appreciate the extended comments by the referee Staffan Söderhjelm, which helped us to greatly improve the quality of our analysis.
References
- Araujo-Betancor, S., Gänsicke, B. T., Hagen, H.-J., et al. 2005, A&A, 430, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., & Kolb, U. 2000, MNRAS, 318, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Bath, G. T. 1973, Nature, 246, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Bath, G. T., Evans, W. D., & Papaloizou, J. 1974, MNRAS, 167, 7 [NASA ADS] [Google Scholar]
- Beuermann, K., Buhlmann, J., Diese, J., et al. 2011, A&A, 526, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohigas, J., Lopez, J. A., & Aguilar, L. 1994, A&A, 291, 595 [NASA ADS] [Google Scholar]
- Borkovits, T., Forgács-Dajka, E., & Regály, Z. 2004, A&A, 426, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brankin, R. W., Glaswell, I., Dormand, J. R., Prince, P. J., & Seward, W. L. 1989, ACM Trnas. Math. Soft., 15, 31 [Google Scholar]
- Breton, R. P., Kaspi, V. M., Kramer, M., et al. 2008, Science, 321, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Baraffe, I., Leconte, J., Gallardo, J., & Barman, T. 2009, in AIP Conf. Ser. 1094, ed. E. Stempels, 102 [Google Scholar]
- Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition, ed. J. Frank, A. King, & D. J. Raine [Google Scholar]
- Georgakarakos, N. 2002, MNRAS, 337, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakarakos, N. 2009, MNRAS, 392, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P. 1995, MNRAS, 274, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H., Poole, C., & Safko, J. 2002, Classical mechanics, ed. H. Goldstein, C. Poole, & J. Safko [Google Scholar]
- Guinan, E. F., & Ribas, I. 2001, ApJ, 546, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S., & Szkody, P. 1988, PASP, 100, 224 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R. 1988, QJRAS, 29, 1 [NASA ADS] [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Mikkola, S. 1998, MNRAS, 300, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Kluzniak, W., Abramowicz, M. A., Bursa, M., & Török, G. 2007, in Rev. Mex. Astron. Astrofis., 27, 18 [Google Scholar]
- Knigge, C. 2006, MNRAS, 373, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kotze, M. M., & Charles, P. A. 2010, MNRAS, 402, L16 [NASA ADS] [Google Scholar]
- Kundra, E., & Hric, L. 2010, Ap&SS, 228 [Google Scholar]
- Lanzafame, G. 2008, PASJ, 60, 259 [NASA ADS] [Google Scholar]
- Leins, M., Soffel, M. H., Lay, W., & Ruder, H. 1992, A&A, 261, 658 [NASA ADS] [Google Scholar]
- Mazeh, T., & Shaham, J. 1979, A&A, 77, 145 [Google Scholar]
- Mineshige, S. 1988, ApJ, 335, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 2000, Solar System Dynamics, ed. C. D. Murray, & S. F. Dermott [Google Scholar]
- Neustroev, V. V. 2002, A&A, 382, 974 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neustroev, V. V., Zharikov, S., Tovmassian, G., & Shearer, A. 2005, MNRAS, 362, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Niedzielski, A., Nowak, G., Adamów, M., & Wolszczan, A. 2009, ApJ, 707, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J. 1984, ApJS, 54, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Pichardo, B., Sparke, L. S., & Aguilar, L. A. 2005, MNRAS, 359, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Pribulla, T., Chochol, D., Tremko, J., & Kreiner, J. M. 2005, in The Light-Time Effect in Astrophysics: Causes and cures of the O–C diagram, ed. C. Sterken, ASP Conf. Ser., 335, 103 [Google Scholar]
- Qian, S., Liao, W., Zhu, L., et al. 2010, MNRAS, 401, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Richman, H. R., Applegate, J. H., & Patterson, J. 1994, PASP, 106, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H. 2008 [arXiv:0809.1800] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Soderhjelm, S. 1982, A&A, 107, 54 [NASA ADS] [Google Scholar]
- Soderhjelm, S. 1984, A&A, 141, 232 [NASA ADS] [Google Scholar]
- Thorstensen, J. R., Patterson, J. O., Shambrook, A., & Thomas, G. 1996, PASP, 108, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Tovmassian, G., Zharikov, S., Michel, R., et al. 2003, PASP, 115, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Tovmassian, G. H., Zharikov, S. V., & Neustroev, V. V. 2007, ApJ, 655, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1978, Acta Astron., 28, 303 [NASA ADS] [Google Scholar]
- Warner, B. 1995, Cataclysmic variable stars, Cambridge Astrophys. Ser. (Cambridge, New York: Cambridge University Press) [Google Scholar]
- Yorke, H. W., Bodenheimer, P., & Taam, R. E. 1995, ApJ, 451, 308 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Long-term light curve of FS Aur. The data set includes exclusively CCD observations and is obtained predominately in the V-band (green circles) for the last 4000 days. The black symbols correspond to the data for which there is no information of the bandpass, but their average value is very close to the V-band. The data obtained in B and R filters are marked by blue and red circles, respectively. The open symbols corresponds to outbursts, which were duly separated using a V > 15.2 mag threshold. |
| In the text | |
 |
Fig. 2 Portions of the light curve from the 2004 observations (left panels) and its power spectrum. The power spectrum is obtained from a larger data set spanning from JD 2 453 348 to 2 453 361. The highest peak of the power spectrum at fLPP = 7.0079 day-1 corresponds to the long photometric period (s. 2.2). The peak at fOP = 16.78 day-1 is, within errors, the orbital period determined from spectroscopy. The rest of the peaks in the power spectrum are either transient, or aliases, like the one at 2 × fLPP = 14.1. The lines on the light curve are sinusoidal fits of OP (dot-dashed; magenta), LPP (dotted; cyan) and the sum of both (black). |
| In the text | |
 |
Fig. 3 Selected portions of the light curve from different epochs in which the LPP is the dominating periodicity are presented in the left panel. The curve is a sinusoidal fit to the data, confirming phase stability of the periodicity from year to year. Similar light curves can be found in earlier observations (Tovmassian et al. 2003). The power spectrum calculated over a huge 1100-day time period shows a strong, single peak at the LPP frequency and its nightly aliases. |
| In the text | |
 |
Fig. 4 Examples of FS Aur photometry. The two lower panels show cases of large, ~0.5 mag bulges in the light curve. The left upper panel is simply a zoom of the central part of the lower panel, where we have overlapping data obtained from two different sites (solid and open points). The high-frequency oscillations are a good example of flickering. The solid black line is the sum of OP and LPP. The dotted cyan curve is a fit to the LPP and it is a continuation of the same curve as presented in Fig. 2. The dash-dotted magenta curve is a fit to the OP and it is seen only in certain epochs. The upper panels on right side are portions of the light curve well fitted with the sum of the OP and LPP periods. |
| In the text | |
 |
Fig. 5 Power spectrum of the quiescent light curve of FS Aur (left panel) and its corresponding spectral window (right). The strongest peak in the window at fY = 0.00274 day-1 corresponds to the yearly observational cycle. The fVLPP = 0.001114 ± 0.00015 day-1 frequency corresponding to VLPP is the second-highest peak in the power spectrum, with the strongest peak being falias = 0.00114 + 0.00274 = 0.00388 day-1, an alias created by the beat between fVLPP and f1y. |
| In the text | |
 |
Fig. 6 Periodograms calculated by the Scargle-Lomb method for the set of data obtained in different filters (dashed line) and after color correction (solid). The strongest peak in both cases coincides with the peak in the power spectrum obtained by the Fourier method. |
| In the text | |
 |
Fig. 7 Effect on the binary eccentricity of a close encounter with a third object on a high-eccentricity (e3 = 0.95) orbit with an 875d period. The perturbation occurs within a ~10d interval and leads to a persistent effect. The horizontal axis is in units of the third-body period (875d). |
| In the text | |
 |
Fig. 8 Summary of our results: the upper panel shows the period of the long-term modulation in binary eccentricity as a function of the perturber mass (in Jupiter masses). Each curve corresponds to different P3/P2 ratios taken from 12 to 48 (lower and upper curves, respectively). The thick horizontal line shows the observed value of the VLPP. Only solutions that cross this line can explain the VLPP. The middle panel shows the perturber mass and orbital radius combinations that result in a long-term modulation of the binary orbit equal to the VLPP. The lower panel shows the amplitude of the binary eccentricity perturbation for those solutions. |
| In the text | |
 |
Fig. 9 Perturbation of the binary eccentricity caused by a perturber on a distant, circular orbit. The perturber has a mass of 48 MJ and its orbital period is 13.4 times that of the binary. The three panels show that the perturbation occurs at three different timescales: that of the binary P2 (0.0595d) panel a), that of the perturber (0.7975d) panel b), and a much longer modulation (875d) panel c). |
| In the text | |
 |
Fig. 10 In the upper panel, the relative amplitude of the low frequency to the high frequency e2 modulations (Θ), see main text for definition, is plotted vs. the mass of the perturber. The higher Θ, the higher is the probability to detect the long-term modulation of the eccentricity. To show the effect on the shape of the resulting e2 modulation, three extreme cases are presented in the bottom panels: 1) a low-mass solution, with M3 = 2 MJ and P3/P2 = 23; 2) the solution with maximum eccentricity amplitude, with M3 = 48 MJ and P3/P2 = 13.4; 3) a high-mass solution, with M3 = 152 MJ and P3/P2 = 36. |
| In the text | |
 |
Fig. 11 Light curve of FS Aur folded with the 875-day period (top panel). The number of points is reduced compared to Fig. 1 by averaging long nightly sequences to one point. In the second panel from the top, the eccentricity modulation is shown for the best solution to explain the VLPP (M3 = 48 MJ and P3/P2 = 13.4). The next panel depicts the variation of the Ψ parameter (see Eq. (4)). The percentual change in the position of inner Lagrangian point of the close binary is shown in the bottom panel. All curves are repeated for two periods for better visual presentation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


