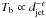| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117705 | |
| Published online | 10 January 2012 | |
Relativistic outflow drives γ-ray emission in 3C 345
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
e-mail: schinzel@mpifr-bonn.mpg.de
2
Department of Physics and Astronomy, University of New
Mexico, Albuquerque
NM, 87131, USA
3
Institute for Astrophysical Research, Boston
University, Boston,
MA
02215,
USA
4
Also an adjunct astronomer at the National Radio Astronomy
Observatory
5
St. Petersburg State University, St. Petersburg,
Russia
Received:
14
July
2011
Accepted:
29
October
2011
Aims. On the basis of the first 20 months of Fermi-LAT data and optical monitoring, the quasar 3C 345 has been identified as a γ-ray emitter. We investigate whether there is a connection between the γ-ray and optical variability of 3C 345 and the properties of its parsec-scale radio emission.
Methods. We combined the Fermi-LAT data of 3C 345, covering an energy range of 0.1–300 GeV, with 32 Very Long Baseline Array observations of the object made at 43.2 GHz in the period of January 2008–March 2010.
Results. The VLBA data reveal the morphology and kinematics of the flow on scales of up to ≈5 milliarcseconds (deprojected linear distances of 380 parsecs). The brightness temperature, Tb(r), measured along the jet first decreases with distance ∝ r−(0.95 ± 0.69) and later exhibits a break at ≈ 0.3 milliarcseconds (mas), with Tb(r) ∝ r−(4.11 ± 0.85) at larger separations. Variations in the γ-ray, optical, and parsec-scale radio emission display a similar long-term trend that persists during the entire VLBA monitoring period. The γ-ray and optical variations on shorter timescales are related to structural changes in the jet on scales of ≈ 0.3 mas ( ≈ 23 parsecs, deprojected), with the γ-ray and optical flares possibly being related to the evolution of four distinct superluminal components identified in the flow.
Conclusions. The observations indicate that both the quiescent and flaring components of the γ-ray emission are produced in a region of the jet that extends up to ~23 pc. This region may correspond to the Compton-loss dominated zone of the flow and its large extent may favor the synchrotron self-Compton mechanism for γ-ray production in the relativistic jet of the quasar 3C 345.
Key words: galaxies: jets / galaxies: active / radio continuum: galaxies / gamma rays: galaxies / Galaxy: nucleus / galaxies: individual: 3C 345
© ESO, 2012
1. Introduction
Observations of high-energy emission (keV – TeV range) provide important insights into the physical properties of active galactic nuclei (AGN), in particular for the subgroup of quasars. However, high energy production scenarios remain heavily debated with many possibilities continuing to be discussed (e.g., Böttcher et al. 2009; Dermer et al. 2009; Błażejowski et al. 2004). Most of these physical models depend on the emission site, and in particular its distance from the central engine. A connection between the cm-/mm-radio and high energy emission of quasars was proposed by Valtaoja & Teräsranta (1996), Jorstad et al. (2001), and references therein. To investigate this connection, the variability of AGN have been studied in coordinated multi-wavelength observation campaigns covering radio to γ-ray wavelengths. Their results, especially for archetypal sources, have been essential to improving our physical understanding of the emission processes in AGN up to the highest energies (cf. Longair 2011). These observations, in particular simultaneous high-resolution very long baseline interferometry (VLBI) observations at mm-wavelengths, have provided new constraints on the parameter space of proposed emission models, placing constraints on the size, energetics, and locations of the emission regions.
The archetypal quasar 3C 345 is one of the best studied “superluminal” radio sources, whose parsec-scale radio emission has been monitored over the past 30 years, in particular with VLBI (e.g.: Biretta et al. 1986; Baath et al. 1992; Lobanov 1996; Zensus et al. 1995; Ros et al. 2000; Klare 2004; Jorstad et al. 2007). On the basis of previous observations, spectral index and turnover frequency distributions have been obtained (Lobanov 1996, 1998a; Ros et al. 2000), the spectral evolution of the jet has been studied (Lobanov & Zensus 1999), the properties of the radio and X-ray emission have been related (Unwin et al. 1997; Lobanov & Roland 2005), the dynamics of the central region has been investigated (Lobanov & Roland 2005) and opacity in the nuclear region has been used to determine the physical properties and matter composition of the compact jet (Lobanov 1998b; Hirotani 2005). Quasi-periodic variations in the emission have been detected in the optical (Babadzhanyants & Belokon 1984; Kidger & Takalo 1990) and radio (Aller et al. 1996; Teräsranta et al. 1998; Lobanov & Zensus 1999) regimes with a possible periodicity of 3.5–4.5 years and major flares occurring every 8–10 years. A new cycle of enhanced nuclear activity began in early 2008 (Larionov et al. 2009).
The identification of 3C 345 as a γ-ray source was unclear during the EGRET-era (1991–2000; Thompson et al. 1993) with a possible weak detection between April and May, 1996 (Casandjian & Grenier 2008). The γ-ray emission detected by the Large Area Telescope (LAT), on board the Fermi satellite, in the vicinity of 3C 345 was initially associated with another quasar in the region, B3 1640+396 with low confidence, based on the 3 months of data (August–October, 2008) collected (Abdo et al. 2009). However, with 20 months (August 2008–April 2010) of LAT monitoring data, 3C 345 was identified as a γ-ray source at GeV energies, based on multi-wavelength counterpart localizations and correlated variability (Schinzel et al. 2011).
This paper presents the results of a coordinated observational campaign targeting 3C 345 and combining the 20-month Fermi-LAT γ-ray monitoring data (Schinzel et al. 2011) with monthly VLBI observations made at 43.2 GHz (7 mm wavelength) at the VLBA1. Section 2 discusses the observations and data reduction methods applied to obtain calibrated datasets for further analysis. It discusses in particular the criteria that were developed to determine the statistical significance of the two-dimensional Gaussian models (modelfits) applied to the observed radio brightness distribution. In Sect. 3, we present kinematics of the pc-scale radio jet and flux density evolution, and a possible connection with the high energy γ-ray emission. Section 4 discusses the findings of this paper and in Sect. 5 our conclusions are drawn from the results presented here.
Throughout this paper, a flat ΛCDM cosmology is assumed, with H0 = 71 km s-1 Mpc-1 and ΩM = 0.27. At the redshift z = 0.593 (Marziani et al. 1996) of 3C 345, this relates to a luminosity distance DL = 3.47 Gpc, a linear scale of 6.64 pc mas-1, and a proper motion scale of 1 mas year-1 corresponding to 34.5 c.
2. Observations and data analysis
2.1. Fermi-LAT
The Fermi-LAT (Atwood et al. 2009) is a pair conversion telescope designed to cover the energy band from 20 MeV to greater than 300 GeV. It is the product of an international collaboration between NASA and DOE in the U.S. and many scientific institutions across France, Italy, Japan, and Sweden.
The γ-ray emission of 3C 345 was identified based on correlations found between the optical variability and major γ-ray events observed by Fermi LAT between August 2008 and April 2010. The γ-ray counterpart of 3C 345 was localized to RA 16h43m0.24s, Dec + 39°48′22.7′′ (Schinzel et al. 2011). For this paper, a light curve for which the γ-ray monitoring data was split into regular time intervals, each integrating over periods of 7 days and an energy range of 0.1–300 GeV, was obtained in the fashion described in Schinzel et al. (2011). The position of the γ-ray counterpart was fixed to the radio localization of 3C 345. For the spectral shape of the γ-ray emission of 3C 345, a power-law was used with the spectral index fixed to its 20-month average value of Γ = 2.452. The particular time binning of 7 days in this case provides the optimal trade-off between time resolution and signal-to-noise ratio (SNR). This yielded a light curve with 81 significant detections and five 2σ upper limit time intervals (JD 2 454 756, 2 454 826, 2 454 903, 2 454 945, 2 455 155), in total this covers a time period of 602 days (20 months). To homogenize the light curve, 2σ upper limits were used as values with their error estimate for that interval replaced with half the difference between that upper limit and its value determined through the unbinned spectral likelihood analysis. This method was applied to the calculation of the variability index in Schinzel et al. (2011) and Abdo et al. (2010).
2.2. Very Long Baseline Array (VLBA)
Following the onset of a new period of flaring activity in 2008, we initiated a dedicated monthly monitoring campaign, using the VLBA to monitor the radio emission of 3C 345 at 43.2, 23.8, and 15.4 GHz (VLBA project codes: BS193, BS194). In this paper, we discuss only the 43.2 GHz observations continuing our analysis of the 15.4 and 23.8 GHz data. The observations were made with a bandwidth of 32 MHz (total recording bit rate 256 Mbits s-1). A total of 12 VLBA observations were completed, with about 4.5 h at 43.2 GHz spent on 3C 345 during each observation. Scans on 3C 345 were interleaved with observations of J1310+3233 (amplitude check, EVPA calibrator), J1407+2827 (D-term calibrator), and 3C 279 (amplitude check, EVPA calibrator). The VLBA data were correlated at the NRAO VLBA hardware correlator (Benson 1995) and starting from December 2009 the new VLBA-DiFX correlator was employed (Deller et al. 2011). Analysis was done with NRAO’s Astronomical Image Processing System (AIPS) and Caltech’s Difmap (Shepherd et al. 1995) software for imaging and modeling. Corrections were applied to both the parallactic angle and the Earth orientation parameters used by the VLBA correlator. Fringe fitting was used to calibrate the observations for group delay and phase rate. A summary of all the observations is presented in Table 1. We present the data for the 12 epochs of this dedicated monitoring campaign, and combine them with 20 VLBA observations from the blazar monitoring program of Marscher et al. (VLBA project codes BM256, S1136) available online3. The combined data (see Table 1) cover a period from January 2008 to March 2010, with observations spaced roughly at monthly intervals or shorter.
Summary of VLBA observations.
The brightness distribution of the radio emission was modelfitted by multiple Gaussian components providing positions, flux densities, and sizes of distinct emitting regions in the jet. Figure 1 illustrates the observed radio structure and the Gaussian-modelfit representation. In the following, we interpret the eastern-most Gaussian-modelfit component obtained from the VLBI map, hereafter labeled Q0 (see Fig. 1), as the base (or “core”) of the radio jet at 43.2 GHz. The remaining features might represent either perturbations or shocks developing in the jet. Locations and proper motions of these jet features are determined with respect to Q0.
To find the optimal description of the observed brightness distribution, compact emission in the nuclear region ( ≤ 0.15 mas from Q0) was fitted by using four different approaches: 1) single circular Gaussian; 2) single elliptical Gaussian; 3) two circular Gaussian; and 4) three circular Gaussian. In the following discussion, these modelfitting approaches we designate as 1C, 1E, 2C, and 3C, respectively.
The criterion for significant improvement between two modelfits was developed using a
ratio of reduced χ2 parameters
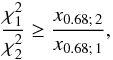 (1)where the subscripts
refer to the two modelfits that we compared. The order is defined by the number of degrees
of freedom n of the individual modelfits with the condition
n1 < n2. The parameter
x0.68 is obtained by solving the equation of the cumulative
distribution function (CDF) of the χ2 distribution
(1)where the subscripts
refer to the two modelfits that we compared. The order is defined by the number of degrees
of freedom n of the individual modelfits with the condition
n1 < n2. The parameter
x0.68 is obtained by solving the equation of the cumulative
distribution function (CDF) of the χ2 distribution
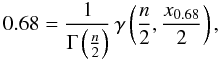 (2)where Γ denotes Euler’s
Gamma function and γ represents the lower incomplete Gamma function. The
number of degrees of freedom, n, depends on the number of modelfit
parameters, since
(2)where Γ denotes Euler’s
Gamma function and γ represents the lower incomplete Gamma function. The
number of degrees of freedom, n, depends on the number of modelfit
parameters, since 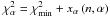 , where
α describes the significance level (α = 0.68, in our
case). The proof and application of this property are discussed in Avni (1976).
, where
α describes the significance level (α = 0.68, in our
case). The proof and application of this property are discussed in Avni (1976).
Figure 2 compares the χ2 parameters of each modelfit, normalized to the χ2 values of the 1C (top panel), 1E (middle panel), and 2C (bottom panel). The horizontal lines in the plots represent the upper thresholds for significant improvement over the labeled Gaussian model. Relative to the 1E and 2C models, the 1C models have the respective threshold values of 0.77 and 0.82. Relative to 2C models the 1E models have a threshold value of 0.91, and relative to those of 3C models, 2C needs to improve by a ratio of 0.86 or less. For some of the observations, the representation of the nuclear region by 1E is comparable to 2C. However, to form a consistent dataset, we adopt the representation of 2C providing the optimal ratio of χ2 to the number of model parameters for all epochs.
 |
Fig. 1 VLBA image of the total brightness distribution of 3C 345 at 43.2 GHz made from observations on Nov. 30, 2009. Open crossed circles show the FWHM of eight Gaussian components applied to fit the structure observed. The shaded ellipse, in the lower left corner, represents the FWHM of the restoring beam. The image peak flux density is 2.1 Jy beam-1 and the RMS noise is 1 mJy beam-1. The contour levels are (–0.15, 0.15, 0.3, 0.6, 1.2, 2.4, 4.8, 9.6, 19, 38, 77)% of the peak flux density. Here the nuclear region is modeled by two circular Gaussian components (Q0, Q11) identified as the best representation of the observed brightness distribution. |
 |
Fig. 2 Reduced χ2 parameters of the modelfit representations
of the core region. The top panel shows the resulting
|
The errors in the derived modelfit parameters were estimated from the image plane,
following analytical approximations introduced by Fomalont
(1999) and Lobanov (2005) with
modifications to account for the strong side-lobe case inherent to VLBI observations. For
each component in the model, the root-mean-square (RMS) noise
(σp) was determined by measuring around its position in the
residual image. The respective component was then removed from the Gaussian model and the
modified model was subtracted from the data, yielding an image that contained only the
contribution from the investigated component. The flux density
(Sp) was measured at the peak position of the Gaussian.
Additional input values were the observation beam size
(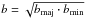 ),
component total flux density (St), component
distance (r), position angle (Φ), and size (d). The
errors in the model fit parameters were calculated to be
),
component total flux density (St), component
distance (r), position angle (Φ), and size (d). The
errors in the model fit parameters were calculated to be
 These
error estimates only reflect the statistical image errors and are assumed to be
uncorrelated. No additional systematic errors were taken into account, such as errors in
the amplitude calibration that could add additional uncertainty to the determined flux
density values.
These
error estimates only reflect the statistical image errors and are assumed to be
uncorrelated. No additional systematic errors were taken into account, such as errors in
the amplitude calibration that could add additional uncertainty to the determined flux
density values.
3. Results
In this section we present the flux and spatial evolution of the pc-scale radio emission of 3C 345 between 2008 and 2010. Special attention is given to the determination of kinematics and ejection epochs, as well as the dominant emission loss mechanisms. In the end, the information that is collected on the radio jet is compared to the observed γ-ray emission from 3C 345.
3.1. Evolution of the radio emission in the nuclear region
Comparisons of the component positions, flux densities, and sizes determined from the Gaussian-modelfits revealed a new moving emission region, labeled Q9, first detected in the VLBA image from June 16, 2008, followed by detections of another new component on January 24, 2009 (Q10), a third one on July 27, 2009 (Q11), and a fourth on November 28, 2009 (Q12). In the following, the components Q9, Q10, Q11, and Q12 (Fig. 1) observed within a distance of 0.5 mas from the core Q0 are referred to as the “jet”.
3.1.1. Kinematics
 |
Fig. 3 Evolution of the radial separations from the core of components Q12, Q11, Q10, Q9 and Q8. Q12-Q9 are related to the radio variability since 2008, Q8 is related to a previous radio flare observed in 2007. The lines are the results of polynomial fits to x(t) and y(t) directions separately. The dashed lines are the results of linear fits to x(t) and y(t) to determine ejection epochs and speeds for the two cases discussed in Sect. 3.1.2. |
Measured and derived physical parameters for radio emission regions in the inner jet ≤ 0.7 mas (4.6 pc).
We determine the kinematics of individual features from their relative positional offsets with respect to Q0. The temporal evolution of the measured offsets is plotted in Fig. 3. The component Q8, which was first observed in 2007, is also included for the purpose of comparison.
The motions in the jet of 3C 345 are investigated using the RA, Dec (x, y) positions of a jet component relative to the core component (Q0) over the observed periods, fitting them separately using polynomials of different order (cf. Zensus et al. 1995) and applying the following procedure:
-
1.
The first order polynomial is fitted to the trajectory using thenonlinear least-squares Marquardt-Levenberg algorithm (asimplemented by gnuplot).
-
2.
The second order polynomial is fitted to the trajectory and if the improvement of the reduced χ2 satisfies the criterion described in Sect. 2.2, the fit is accepted.
-
3.
The order of the fit polynomial is increased until no improvement according to the χ2 statistics is achieved.
Using this approach, we find that it is sufficient to represent the trajectories of
components Q8, Q11, and Q12 by linear fits in both the x and
y directions. In the case of components Q9 and Q10, a second order
polynomial represents the best-fit model to the observed data in the
x direction, implying that there is some apparent acceleration. In the
y direction, a linear fit is sufficient. The resulting fitted radial
separations, 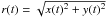 ,
are drawn in Fig. 3. For each component, the fits
yield the average proper motion and the mean angular speed ⟨ μ ⟩ and
the average direction of motion ⟨ Φ ⟩ . The kinematic properties thus derived for the
jet components indicate that Q9 and Q10 underwent a clear phase of apparent acceleration
over a period of 1.5 years and over a distance of ~ 0.3 mas (2 pc). No
statistically significant acceleration was observed for Q8, Q11, and Q12. The observed
values for ⟨ μ ⟩ are in the range of 0.25–0.42 mas year-1
and for ⟨ Φ ⟩ in the range of − 96 to − 120° (see also Table 2). Jorstad et al. (2005)
previously reported apparent jet component speeds of 0.29–0.69 mas year-1 and
a jet position angle of − 66 − − 95°. Using ⟨ μ ⟩ , the average
apparent speed
,
are drawn in Fig. 3. For each component, the fits
yield the average proper motion and the mean angular speed ⟨ μ ⟩ and
the average direction of motion ⟨ Φ ⟩ . The kinematic properties thus derived for the
jet components indicate that Q9 and Q10 underwent a clear phase of apparent acceleration
over a period of 1.5 years and over a distance of ~ 0.3 mas (2 pc). No
statistically significant acceleration was observed for Q8, Q11, and Q12. The observed
values for ⟨ μ ⟩ are in the range of 0.25–0.42 mas year-1
and for ⟨ Φ ⟩ in the range of − 96 to − 120° (see also Table 2). Jorstad et al. (2005)
previously reported apparent jet component speeds of 0.29–0.69 mas year-1 and
a jet position angle of − 66 − − 95°. Using ⟨ μ ⟩ , the average
apparent speed 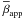 and the
speed in the source frame (deprojected)
and the
speed in the source frame (deprojected) 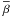 are
derived from
are
derived from 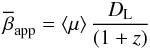 (10)and
(10)and
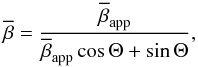 (11)where
DL is the luminosity distance, z is the
redshift, and Θ is the jet angle to the line of sight (viewing angle).
(11)where
DL is the luminosity distance, z is the
redshift, and Θ is the jet angle to the line of sight (viewing angle).
As a final step, the physical parameters, Doppler factor δ, Lorentz
factor Γ, and viewing angle Θ of each jet component are derived. For the following
calculations, we assume that the jet emission is dominated by radiative losses (see
e.g., Jorstad et al. 2005) and consists of
optically thin shocked gas, α = −0.7 (i.e.
Sν ∝ R-1.633·ν + α,
where R is the size of the emitting region in the rest-frame of the
jet and ν the frequency in the observer’s frame (Marscher & Gear 1985). The variability Doppler factor is then
derived as 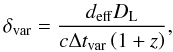 (12)where
DL is the luminosity distance and
deff is the effective angular size of a spherical region
(i.e. the measured FWHM of the component multiplied by a factor of 1.8; cf. Pearson 1999). The flux variability timescale is
defined as
Δtvar = dt/ln(S1/S2).
The value of S1 was the measured maximum component flux
density, while S2 was the minimum component flux density
selected at the time of maximum absolute value of the time derivative of the flux
density. It is then possible to calculate bulk Lorentz factors by combining the derived
δvar with
βapp
(12)where
DL is the luminosity distance and
deff is the effective angular size of a spherical region
(i.e. the measured FWHM of the component multiplied by a factor of 1.8; cf. Pearson 1999). The flux variability timescale is
defined as
Δtvar = dt/ln(S1/S2).
The value of S1 was the measured maximum component flux
density, while S2 was the minimum component flux density
selected at the time of maximum absolute value of the time derivative of the flux
density. It is then possible to calculate bulk Lorentz factors by combining the derived
δvar with
βapp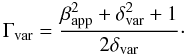 (13)Combining the derived
values for all components, a mean Lorentz factor of 12.5 and a mean Doppler factor
of 14.4 were obtained (see Table 2).
(13)Combining the derived
values for all components, a mean Lorentz factor of 12.5 and a mean Doppler factor
of 14.4 were obtained (see Table 2).
An upper limit to the viewing angle Θ can immediately be determined using the average
apparent component speed 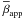 and the
relation
and the
relation 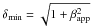 .
This combined with the equation
.
This combined with the equation 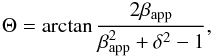 (14)yields
Θ ≤ 5.2°. Using the variability timescale argument and the derived values of
δvar from above, the values Θvar for each
component were obtained, which together have a mean Θvar of
4.7°
(14)yields
Θ ≤ 5.2°. Using the variability timescale argument and the derived values of
δvar from above, the values Θvar for each
component were obtained, which together have a mean Θvar of
4.7°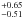 ,
consistent with our upper limit. Pushkarev et al.
(2009) obtained a similar value of Θ = 5.1°, which was determined by combining
the component speeds at 15 GHz and variability Doppler factors derived from single-dish
observations at 37 GHz. Earlier, Jorstad et al.
(2005) obtained a smaller viewing angle of 2.7° ± 0.9° using VLBI data at
43.2 GHz alone. In the following discussion, we adopted Θ = 5°.
,
consistent with our upper limit. Pushkarev et al.
(2009) obtained a similar value of Θ = 5.1°, which was determined by combining
the component speeds at 15 GHz and variability Doppler factors derived from single-dish
observations at 37 GHz. Earlier, Jorstad et al.
(2005) obtained a smaller viewing angle of 2.7° ± 0.9° using VLBI data at
43.2 GHz alone. In the following discussion, we adopted Θ = 5°.
3.1.2. Ejection epochs
With the kinematics determined in Sect. 3.1.1, it is possible to estimate the time at which a moving jet feature passes the VLBI core at 43 GHz. These passages are referred to as ejection epochs. The ejection epoch also marks the time at which a new jet feature begins to contribute to the observed radio emission.
As a first approach to determine the ejection epochs, we assumed that the jet is optically thin all the way to the core and the features already travel at the observed average speed while passing through the VLBI core. Under these assumptions, the ejection epoch is determined by back-tracing the fitted linear trajectories. The resulting ejection epochs for all features are also listed in Table 2. This approach provides reasonable estimates of the ejection epochs for non-accelerating features, while for the apparently accelerating components Q9 and Q10 a different approach is required.
Looking at the radial separations of Q9 and Q10 in Fig. 3, the acceleration is most evident for the time before 2009.6. An upper limit to the ejection epoch can be determined using a linear fit to the data points after 2009.5 for Q9 and 2009.4 for Q10 (τupper in Table 2). Similarly, lower limits, τlower, to the ejection epochs of Q9 and Q10 were obtained by considering only data points before 2009.5 and 2009.4, respectively.
3.1.3. Jet intensity gradient
In flat spectrum radio quasars (FSRQs), such as 3C 345, the component flux decay is
commonly driven by radiative losses (Lobanov &
Zensus 1999; Jorstad et al. 2005), which
was assumed in Sect. 3.1.1 without any additional
justification. To test this, the maximum component brightness temperature needs to be
calculated as a measure for the emission intensity of each component, using
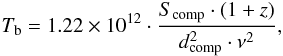 (15)where
Scomp is the component flux density in Jansky,
z the redshift of the source, dcomp the
FWHM size of the circular Gaussian in mas and ν the observing frequency
in GHz. In Fig. 4, the brightness temperatures for
components Q9, Q10, and Q11 are plotted as a function of the radial separation from the
core.
(15)where
Scomp is the component flux density in Jansky,
z the redshift of the source, dcomp the
FWHM size of the circular Gaussian in mas and ν the observing frequency
in GHz. In Fig. 4, the brightness temperatures for
components Q9, Q10, and Q11 are plotted as a function of the radial separation from the
core.
In the common picture of the shock-in-jet model, a relativistic shock propagates down a
conical jet, slowly expanding adiabatically albeit maintaining shock conditions. In this
scenario, we assumed a power-law electron energy distribution
(N(E) dE ∝ E − s dE),
a power-law magnetic field evolution (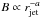 ),
and a constant jet opening angle with the jet transverse size proportional to the
distance along the jet
(djet ∝ rjetsinΘ). While the
shock continues to travel down the jet, it undergoes three major evolutionary stages
dominated by Compton, synchrotron, and adiabatic energy losses (Marscher et al. 1992). From this it follows that the brightness
temperature decays as a power-law,
),
and a constant jet opening angle with the jet transverse size proportional to the
distance along the jet
(djet ∝ rjetsinΘ). While the
shock continues to travel down the jet, it undergoes three major evolutionary stages
dominated by Compton, synchrotron, and adiabatic energy losses (Marscher et al. 1992). From this it follows that the brightness
temperature decays as a power-law, 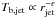 ,
where rjet is the distance in the jet at which
Tb,jet is measured. The value of ϵ can be
derived from the spectral evolution of the radio emission (Lobanov & Zensus 1999), assuming
,
where rjet is the distance in the jet at which
Tb,jet is measured. The value of ϵ can be
derived from the spectral evolution of the radio emission (Lobanov & Zensus 1999), assuming
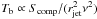 and
the Doppler factor δ = const.
and
the Doppler factor δ = const.
For Compton (ϵc), synchrotron
(ϵs), and adiabatic (ϵa)
losses, ϵ are calculated as ![\begin{eqnarray} \epsilon_\mathrm{c} &=& \left[\left(s+5\right)+a\left(s+1\right)\right]/8,\\ \epsilon_\mathrm{s} &=& \left[4\left(s+2\right)+3a\left(s+1\right)\right]/6,\\ \epsilon_\mathrm{a} &=& \left[ 2 \left(2s+1\right) + 3a \left(s + 1\right) \right]/6, \end{eqnarray}](/articles/aa/full_html/2012/01/aa17705-11/aa17705-11-eq124.png) with
a typical value of s = 2.0 (corresponding to a synchrotron spectral
index α = −0.5;
Sν ∝ ν + α)
and a = 1 (dominant transverse magnetic field),
ϵc = 10/8 = 1.25,
ϵs = 25/6 ≈ 4.17, and
ϵa = 19/6 ≈ 3.17. For the slopes to be shallower than these
derived values, acceleration resulting in increasing Doppler factors of
with
a typical value of s = 2.0 (corresponding to a synchrotron spectral
index α = −0.5;
Sν ∝ ν + α)
and a = 1 (dominant transverse magnetic field),
ϵc = 10/8 = 1.25,
ϵs = 25/6 ≈ 4.17, and
ϵa = 19/6 ≈ 3.17. For the slopes to be shallower than these
derived values, acceleration resulting in increasing Doppler factors of
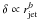 may be
considered. For a moderate acceleration (i.e. b = 0.1 − 0.2), a value
ϵc ≈ 0.13 is obtained assuming s = 2 and
with a longitudinal magnetic field (a = 2).
may be
considered. For a moderate acceleration (i.e. b = 0.1 − 0.2), a value
ϵc ≈ 0.13 is obtained assuming s = 2 and
with a longitudinal magnetic field (a = 2).
The brightness temperature gradient along the jet, shown in Fig. 4, reveals a possible broken power-law behavior of the jet intensity gradient with a break distance of ~0.3 mas and the two slopes ϵ1 = 0.95 ± 0.69 and ϵ2 = 4.11 ± 0.85. The value of ϵ1 is consistent with ϵc, with the possible indication of a mild change in δ, and ϵ2 is consistent with the derived ϵs. However, at the ~1σ level, ϵ2 is also consistent with ϵa. Using the spectral evolution of a jet component, Lobanov & Zensus (1999) found evidence of a change from the synchrotron to the adiabatic stage at a distance of 1.2–1.5 mas from the core. This suggests that the transition from Compton to synchrotron stage was indeed observed. Future investigations on the spectral evolution of the jet will be able to provide additional constraints on the transition regions between the Compton, synchrotron, and adiabatic stages.
 |
Fig. 4 Component brightness temperatures against radial separation from the VLBI core
(Q0), representing the emission intensity gradient along the jet. Points with
arrows are 1σ upper limits. Two lines are fitted to the data to
determine the power-law indices ϵ
( |
3.2. Radio-γ-ray correlation
 |
Fig. 5 top: Fermi LAT 7-day binned γ-ray light curve of 3C 345 for the energy range of 0.1–300 GeV. bottom: VLBA 7 mm component flux densities for the modelfitted to the VLBI core and inner jet, represented by up to five circular Gaussian components (Q0, Q12, Q11, Q10, Q9). The component labeled Q0 is the east-most component (see Fig. 1) and represents the compact “core” or base of the jet. The black curve plots the sum of the flux densities of all four components. |
The correlation between radio and optical emission was studied in Schinzel et al. (2011) for identification of γ-ray emission from 3C 345. Here the connection between the synchrotron radio emission and γ-ray emission was investigated. To quantify a possible connection, the correlation between the γ-ray and the radio light curve was calculated. For this, we used the discrete correlation function presented by Edelson & Krolik (1988), which works well for unevenly sampled data. No statistically significant correlation was found, although around 2009.4, a rapid change in VLBI flux densities by ~1.5 Jy within only 4 days coincided well with a γ-ray flare (also see Fig. 5).
The top panel of Fig. 5 plots the weekly averaged γ-ray light curve of 3C 345. From it, a seemingly long-term trend was seen, which was most evident between 2008.7 and 2009.4. After 2009.4, an increase in short-time variability was observed, followed by a slightly decreasing trend after 2009.8. The measured γ-ray flux increases by a factor of 2–3 between 2008.6 and 2009.5. A long-term trend in the light curve of the radio jet features is even more clearly evident (bottom panel of Fig. 5), as follows from the sum of the flux density of the individual jet components. The optical R band data presented in Schinzel et al. (2011) similarly showed a rising trend for the same time period. This dataset is added for comparison.
To quantify this relation, the light curves were first rescaled so that the zero flux represents their respective mean value. The radio flux density of the jet has a mean value of 3.60 Jy and corresponds to the emission from the jet of an apparent size of ≤ 2 pc (excluding the core). The core has a mean flux density of 1.5 Jy and an apparent size of ~0.3 pc. We note that the jet flux density is by a factor of 2.4 stronger than that of the core. The average γ-ray flux was 1.8 × 10-7 ph cm-2 s-1. Observations at optical R band had an average magnitude of 16.6, which corresponds to a flux density of 7.7 × 10-4 Jy.
In the final step, the rescaled light curves were de-trended using cubic spline
interpolations over 0.4 year bins (Press et al.
1992). The extracted long-term trends are shown in Fig. 6. From these, it is immediately evident that a similar trend is
obtained for the radio jet and the γ-rays, whereas the core does not show
a significant trend. This discrepancy of the first 0.4 years of data is caused by the lack
of γ-ray monitoring before 2008.6 and a flare immediately after 2008.6
(see Fig. 5). The trend of the optical emission shows
a similar behavior relative to the γ-ray and radio trends, although it is
more peaked. Comparing trend amplitudes, the amplitude of the variation in the optical is
four times greater than in the γ-rays. The radio shows a factor of two
higher amplitude for the variation than γ-rays. On the basis of the peak
values of these trends, the radio leads the γ-ray trend by
31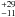 days
and the optical leads the γ-ray trend by
1.1
days
and the optical leads the γ-ray trend by
1.1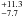 days.
Altogether this is consistent with an almost zero time lag between the observed long-term
trends.
days.
Altogether this is consistent with an almost zero time lag between the observed long-term
trends.
The observed emission from the radio jet responsible for the matching trend is most of the time dominated by the jet component closest to the core. At the beginning of the monitoring period, this is Q9 and Q10 and by the end of 2010 they are replaced by Q11 and Q12. This connects the emission from the radio jet with that observed at optical and γ-ray energies and places the site of the underlying multi-wavelength emission within the resolved 43 GHz radio jet. The very region that was shown to be dominated by Compton losses in Sect. 3.1.3.
 |
Fig. 6 Long-term trends of the radio jet, radio core flux densities, optical R band flux (Schinzel et al., in prep.) and the γ-ray flux relative to their respective mean values (radio jet: 3.6 Jy, radio core: 1.5 Jy, optical R: 16.6m (7.7 × 10-4 Jy), γ-ray: 1.8 × 10-7 ph cm-2 s-1). The trend was extracted fitting cubic splines with 0.4 year bins. The relative radio flux density was scaled by a factor of 2:1 with respect to the relative γ-ray flux, the optical flux density was scaled by a factor of 4:1, and the data points match the sampling of the original light curves. |
4. Discussion
Monitoring of the fine structure of the jet in 3C 345 reveals a wealth of morphological and kinematic features of the flow. In particular, we have found compelling evidence of a stationary feature in the parsec-scale radio jet of 3C 345. This stationary feature is located at a distance of ~0.1 mas (~0.7 pc) from the core. The kinematics of a large sample of relativistic jets, obtained through the MOJAVE survey4, revealed that stationary features are frequently observed (Lister et al. 2009). In particular, in the jets of γ-ray blazars, observed at 22 and 43 GHz, stationary features within a distance of 2 pc (projected) from the core are commonly observed (Jorstad et al. 2001). Stationary jet features were previously investigated in more detail in the cases of 3C 390.3 (Arshakian et al. 2010), a nearby double-peaked radio galaxy at z = 0.0561, and the Seyfert galaxy 3C 120 (z = 0.033; León-Tavares et al. 2010). For these two sources, stationary features were found at distances of ~0.4 pc (3C 390.3) and ~1.3 pc (3C 120) from the core at 15 GHz. Their physical origin was associated with that of standing shocks. A more detailed investigation of the spectral evolution of a radio flare in CTA 102, a highly polarized quasar at z = 1.037, revealed supporting evidence of a shock-shock interaction scenario, providing a physical description of stationary features interacting with traveling shocks (Fromm et al. 2011).
The moving plasma condensations (components) are most likely generated near the base of the jet of 3C 345, but can only be reliably monitored after they pass through the location of the stationary feature. The nucleus of the jet lies at a distance of ~ 7 pc upstream from the 43 GHz VLBI core (Lobanov 1998b, in press). After the passage of the stationary feature, the superluminal components in 3C 345 undergo an apparent acceleration from ~5 to ~15 c over a distance of 0.3 mas in extent (~23 pc deprojected). This acceleration seems to be a commonly observed feature of many objects in the MOJAVE sample, where a statistically significant tendency for acceleration in the base of jets is found (Homan et al. 2009). Previously, Lobanov & Roland (2005) discussed the observed acceleration of a different component in 3C 345, testing the case of a substantially curved three-dimensional path, causing the observed dramatic change in the apparent component speed. They concluded that the observed acceleration is not likely to be a geometrical effect, but should reflect the physical acceleration of plasma. The possibility of the intrinsic acceleration of jet features on parsec scales was discussed by Vlahakis & Königl (2004). There it was specifically argued that the acceleration observed in 3C 345 is not purely hydrodynamic, but can be attributed to magnetic driving. They showed that the observed acceleration is consistent with an acceleration from Γ ~ 5 to Γ ~ 10 over a linear distance of ~3 to ~ 20 pc. The results presented here are consistent with these findings.
The times of passage of knots Q10, Q11, and Q12 through the 43 GHz VLBI core coincide with short-term increases in the γ-ray flux (see Fig. 5, with times listed in Table 2). In a similar case, PKS 1510-089 showed, in addition to the appearance of a new VLBI component, a rapid rotation in the optical linear polarization just prior to the components passage through the core. This was explained by the feature following a spiral path through a toroidal field until it crosses a standing shock in the 43 GHz core (Marscher et al. 2010).
A γ-ray flare centered on 2009.4 may be related to the brightening of radio structure at distances of 0.12–0.20 mas from the core (0.8–1.3 pc), corresponding to a deprojected distance of ~9–15 pc. Interestingly, this includes the region for which the presence of a standing shock is suggested by the observations presented in Sect. 3.1.1. Radio flares in the compact jet downstream of the VLBI core are known to occur (e.g., Wehrle et al. 2001). Furthermore, Jorstad et al. (2001, 2010) found that γ-ray flares often occur after superluminal knots have separated away from the VLBI core. The results presented here support the inference that γ-ray emission still occurs parsecs downstream of the central engine, in contrast to conclusions based on theoretical arguments (e.g., Tavecchio et al. 2010; Poutanen & Stern 2010). These arguments place the γ-ray emission zones within the broad-line region (BLR) at distances of ≲ 1 pc from the central engine. Within this region, a large number of optical-UV photons are produced (e.g. Kaspi et al. 2007), providing ideal conditions for inverse Compton scattering with relativistic electrons from the jet (e.g. Arshakian et al. 2012; Dermer et al. 1997). In addition, the observed variability timescales place constraints on the size of the emitting region owing to causality arguments. Usually this size is related to the jet cross-section, implying that the emission region is located close to the black hole. However, these standard assumptions do not necessarily need to be true.
In Sect. 3.2, we have shown that long-term trends observed at γ-ray and optical energies correlate with those of the radio emission at VLBI scales, which imply a common emission region. This emission region is related to the inner jet, extending over a distance of up to 23 pc from the VLBI core, which is at a distance of ≫ 1 pc from the central engine, well beyond the BLR. The mechanism for the emission at radio and optical wavelengths is therefore dominated by the synchrotron emission from the relativistic jet itself. The simultaneity of γ-ray emission implies that there is an inverse Compton upscattering of synchrotron photons produced in the jet. The relative increase in the of optical and radio emission relative to γ-ray emission is a factor of two larger in the radio and even a factor of four larger in the optical emission, which is consistent with the mechanism of synchrotron self-Compton. An external contribution of “seed” photons, as proposed by external Compton scenarios (e.g. Tavecchio et al. 2010), is not required to produce the amount of the observed γ-ray emission. Additionally, we have found that the properties of the emission in this region are consistent with the Compton-loss stage of a shock (Sect. 3.1.3). Altogether, this contradicts the common theoretical high-energy production scenario described in the previous paragraph. Observations of TeV emission from FSRQs (e.g. Aleksić et al. 2011) would not have been possible if the high energy emission site were within the BLR, which is expected to be opaque to γ-rays at TeV energies owing to γγ interactions.
The observed kinematics of the jet is now combined with the rise times of the radio, optical, and γ-ray emission. The component Q9 is the first new component identified in 2008 and is most likely to be the emission region responsible for the initial flux increase. Using the long-term trends extracted, the distance at which Q9 was located during the onset of the flaring period in 2008 is ~0.05 mas from the VLBI core. This marks the region between the stationary feature and the core at 43 GHz. Instead of using the combined flux trend that is related to the sum of the radio emission regions, we calculated the time between the peak brightness of Q9 (2009.40) and the first γ-ray flare observed (2008.73). If we use the average component speed and assume no acceleration, the distance at which Q9 might have been during the first observed γ-ray flare is consistent with the position of the radio core at 43 GHz. This finding strongly supports the interpretation that the parsec-scale jet is responsible for driving the observed high energy emission.
Agudo et al. (2011) reported the location of a γ-ray flare in OJ 287, which was identified at a distance of more than 14 pc from the central engine. They proposed a model for the multi-wavelength emission where the high energy emission could be explained by the synchrotron self-Compton process or inverse Compton scattering of infrared radiation from a hot dusty torus, although it was concluded that the hot dusty torus scenario is less likely. In the case of 3C 345, it seems to be clear that multiple compact emission features are responsible for the observed variability and what seems to be a reasonable model for the case of OJ 287, might also be applicable to 3C 345. In these cases, a new plasma disturbance passes through a first conical shock in the core and produces a rapid rise in high energy emission; as it continues to propagate down the jet, it continues to produce high energy emission.
5. Summary and conclusions
On the basis of 32 VLBA observations of 3C 345 at 43.2 GHz, we have investigated the structure and evolution of the radio emission and related this to variations in the γ-ray and optical emission observed 2008–2010 by Fermi-LAT and a number of optical observatories.
We have identified and analyzed four new moving emission features (jet components) in the radio jet of 3C 345. These regions are found to move at apparent speeds of 9–15 c, with the corresponding Doppler and Lorentz factors derived to be in the ranges of 12–23 and 12–15, respectively. The kinematic data strongly favor a viewing angle of 4.7° between the jet axis and the line of sight.
We have presented evidence of the γ-ray emission to be produced not in a compact region near the central engine of the AGN, but in the Compton-loss dominated zone of the parsec-scale jet extending to r ≈ 0.3 mas, corresponding to a deprojected linear extent of ≈ 23 pc (accounting for the source distance and jet orientation). This zone is delineated by a break in the evolution of the brightness temperature, Tb, of the radio emission, with Tb ∝ r − (0.95 ± 0.69) at r ≤ 0.3 mas and Tb ∝ r − (4.11 ± 0.85) at larger separations. Ejections of new superluminally moving and apparently accelerating features in the jet are linked to the flaring component of the γ-ray and optical emission.
These findings imply that the synchrotron self-Compton mechanism is responsible for the high-energy emission production, but place in doubt the entire class of models that propose that the high energy emission site is within 1 pc of the central engine of AGN, with external seed photons for inverse Compton scattering from the accretion disk or broad-line-region. They also imply that a significant part of the γ-ray emission is generated by highly-relativistic electrons propagating at a large bulk speed in the jet. In the context of newly emerging results, stimulated by Fermi data, more detailed analytical and numerical descriptions of this scenario are clearly needed to explain the observed connection between radio and γ-ray variability. At the same time, continued monitoring and more densely sampled VLBI observations of well-studied, bright blazar radio jets represent an essential requirement for improving the degree of detail and statistical accuracy of the correlation reported and improving the spatial localization of individual flares in relativistic jets.
Acknowledgments
We thank Nicola Marchili for providing us with his implementation of the cubic spline de-trending algorithm. We thank the anonymous referee for valuable comments. Frank Schinzel was supported for this research through a stipend from the International Max-Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. We thank NASA for support under FERMI grant GSFC #21078/FERMI08-0051. The research at Boston University was supported in part by NASA through Fermi Guest Investigator grants NNX08AJ64G, NNX08AU02G, NNX08AV61G, and NNX08AV65G, and by National Science Foundation grant AST-0907893. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This work made use of the Swinburne University of Technology software correlator, developed as part of the Australian Major National Research Facilities Programme and operated under licence. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of NASA’s Astrophysics Data System.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 700, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Jorstad, S. G., Marscher, A. P., et al. 2011, ApJ, 726, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2011, ApJ, 730, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, H. D., Aller, M. F., & Hughes, P. A. 1996, in Blazar Continuum Variability, ed. H. R. Miller, J. R. Webb, & J. C. Noble, ASP Conf. Ser., 110, 208 [Google Scholar]
- Arshakian, T. G., León-Tavares, J., Lobanov, A. P., et al. 2010, MNRAS, 401, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Arshakian, T. G., León-Tavares, J., Böttcher, M., et al. 2012, A&A, 537, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y. 1976, ApJ, 210, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Baath, L. B., Rogers, A. E. E., Inoue, M., et al. 1992, A&A, 257, 31 [NASA ADS] [Google Scholar]
- Babadzhanyants, M. K., & Belokon, E. T. 1984, Astrophys., 20, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, J. M. 1995, in Very Long Baseline Interferometry and the VLBA, ed. J. A. Zensus, P. J. Diamond, & P. J. Napier, ASP Conf. Ser., 82, 117 [Google Scholar]
- Biretta, J. A., Moore, R. L., & Cohen, M. H. 1986, ApJ, 308, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Błażejowski, M., Siemiginowska, A., Sikora, M., Moderski, R., & Bechtold, J. 2004, ApJ, 600, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., Reimer, A., & Marscher, A. P. 2009, ApJ, 703, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Casandjian, J.-M., & Grenier, I. A. 2008, A&A, 489, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deller, A. T., Brisken, W. F., Phillips, C. J., et al. 2011, PASP, 123, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Sturner, S. J., & Schlickeiser, R. 1997, ApJS, 109, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Finke, J. D., Krug, H., & Böttcher, M. 2009, ApJ, 692, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Fomalont, E. B. 1999, in Synthesis Imaging in Radio Astronomy II, ed. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 301 [Google Scholar]
- Fromm, C. M., Perucho, M., Ros, E., et al. 2011, A&A, 531, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirotani, K. 2005, ApJ, 619, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Kadler, M., Kellermann, K. I., et al. 2009, ApJ, 706, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Mattox, J. R., et al. 2001, ApJS, 134, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Smith, P. A., Larionov, V. M., & I., A. 2010, in Fermi meets Jandky – AGN in Radio and Gamma Rays, ed. T. Savolainen [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Stevens, J. A., et al. 2007, AJ, 134, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Brandt, W. N., Maoz, D., et al. 2007, ApJ, 659, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Kidger, M., & Takalo, L. 1990, A&A, 239, L9 [NASA ADS] [Google Scholar]
- Klare, J. 2004, Ph.D. Thesis, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, Germany [Google Scholar]
- Larionov, V. M., Villata, M., Raiteri, C. M., et al. 2009, The Astronomer’s Telegram, 2222, 1 [NASA ADS] [Google Scholar]
- León-Tavares, J., Lobanov, A. P., Chavushyan, V. H., et al. 2010, ApJ, 715, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1996, Ph.D. Thesis, New Mexico Institute of Mining & Technology, Socorro, NM, US [Google Scholar]
- Lobanov, A. P. 1998a, A&AS, 132, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobanov, A. P. 1998b, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lobanov, A. P. 2005, unpublished [arXiv:astro-ph/0503225] [Google Scholar]
- Lobanov, A. P., & Roland, J. 2005, A&A, 431, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 1999, ApJ, 521, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, S. M. 2011, High Energy Astrophysics (Cambridge University Press) [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Gear, W. K., & Travis, J. P. 1992, in Variability of Blazars, ed. E. Valtaoja, & M. Valtonen, 85 [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Larionov, V. M., et al. 2010, ApJ, 710, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS, 104, 37 [Google Scholar]
- Pearson, T. J. 1999, in Synthesis Imaging in Radio Astronomy II, ed. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 335 [Google Scholar]
- Poutanen, J., & Stern, B. 2010, ApJ, 717, L118 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, ed. W. H. Press, S. A. Teukolsky, W. T. Vetterling, & B. P. Flannery [Google Scholar]
- Pushkarev, A. B., Kovalev, Y. Y., Lister, M. L., & Savolainen, T. 2009, A&A, 507, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ros, E., Zensus, J. A., & Lobanov, A. P. 2000, A&A, 354, 55 [NASA ADS] [Google Scholar]
- Schinzel, F. K. 2011, Ph.D. Thesis, University of Cologne [Google Scholar]
- Schinzel, F. K., Sokolovsky, K. V., D’Ammando, F., et al. 2011, A&A, 532, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1995, BAAS 27, ed. B. J. Butler, & D. O. Muhleman, 903 [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Ghirlanda, G. 2010, MNRAS, 405, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Teräsranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, D. J., Bertsch, D. L., Fichtel, C. E., et al. 1993, ApJS, 86, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Unwin, S. C., Wehrle, A. E., Lobanov, A. P., et al. 1997, ApJ, 480, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Valtaoja, E., & Teräsranta, H. 1996, A&AS, 120, C491 [NASA ADS] [Google Scholar]
- Vlahakis, N., & Königl, A. 2004, ApJ, 605, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Wehrle, A. E., Piner, B. G., Unwin, S. C., et al. 2001, ApJS, 133, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Zensus, J. A., Cohen, M. H., & Unwin, S. C. 1995, ApJ, 443, 35 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Measured and derived physical parameters for radio emission regions in the inner jet ≤ 0.7 mas (4.6 pc).
All Figures
 |
Fig. 1 VLBA image of the total brightness distribution of 3C 345 at 43.2 GHz made from observations on Nov. 30, 2009. Open crossed circles show the FWHM of eight Gaussian components applied to fit the structure observed. The shaded ellipse, in the lower left corner, represents the FWHM of the restoring beam. The image peak flux density is 2.1 Jy beam-1 and the RMS noise is 1 mJy beam-1. The contour levels are (–0.15, 0.15, 0.3, 0.6, 1.2, 2.4, 4.8, 9.6, 19, 38, 77)% of the peak flux density. Here the nuclear region is modeled by two circular Gaussian components (Q0, Q11) identified as the best representation of the observed brightness distribution. |
| In the text | |
 |
Fig. 2 Reduced χ2 parameters of the modelfit representations
of the core region. The top panel shows the resulting
|
| In the text | |
 |
Fig. 3 Evolution of the radial separations from the core of components Q12, Q11, Q10, Q9 and Q8. Q12-Q9 are related to the radio variability since 2008, Q8 is related to a previous radio flare observed in 2007. The lines are the results of polynomial fits to x(t) and y(t) directions separately. The dashed lines are the results of linear fits to x(t) and y(t) to determine ejection epochs and speeds for the two cases discussed in Sect. 3.1.2. |
| In the text | |
 |
Fig. 4 Component brightness temperatures against radial separation from the VLBI core
(Q0), representing the emission intensity gradient along the jet. Points with
arrows are 1σ upper limits. Two lines are fitted to the data to
determine the power-law indices ϵ
( |
| In the text | |
 |
Fig. 5 top: Fermi LAT 7-day binned γ-ray light curve of 3C 345 for the energy range of 0.1–300 GeV. bottom: VLBA 7 mm component flux densities for the modelfitted to the VLBI core and inner jet, represented by up to five circular Gaussian components (Q0, Q12, Q11, Q10, Q9). The component labeled Q0 is the east-most component (see Fig. 1) and represents the compact “core” or base of the jet. The black curve plots the sum of the flux densities of all four components. |
| In the text | |
 |
Fig. 6 Long-term trends of the radio jet, radio core flux densities, optical R band flux (Schinzel et al., in prep.) and the γ-ray flux relative to their respective mean values (radio jet: 3.6 Jy, radio core: 1.5 Jy, optical R: 16.6m (7.7 × 10-4 Jy), γ-ray: 1.8 × 10-7 ph cm-2 s-1). The trend was extracted fitting cubic splines with 0.4 year bins. The relative radio flux density was scaled by a factor of 2:1 with respect to the relative γ-ray flux, the optical flux density was scaled by a factor of 4:1, and the data points match the sampling of the original light curves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.