| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116825 | |
| Published online | 27 July 2011 | |
Mixed modes in red-giant stars observed with CoRoT⋆,⋆⋆
1
LESIA, CNRS, Université Pierre et Marie Curie, Université Denis Diderot, Observatoire de Paris, 92195 Meudon Cedex, France
e-mail: benoit.mosser@obspm.fr
2
Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
3
Instituut voor Sterrenkunde, K. U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
4
School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
5
Institut d’Astrophysique Spatiale, UMR 8617, Université Paris XI, Bâtiment 121, 91405 Orsay Cedex, France
6
Astronomical Institute “Anton Pannekoek”, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
Received: 3 March 2011
Accepted: 31 May 2011
Context. The CoRoT mission has provided thousands of red-giant light curves. The analysis of their solar-like oscillations allows us to characterize their stellar properties.
Aims. Up to now, the global seismic parameters of the pressure modes have been unable to distinguish red-clump giants from members of the red-giant branch. As recently done with Kepler red giants, we intend to analyze and use the so-called mixed modes to determine the evolutionary status of the red giants observed with CoRoT. We also aim at deriving different seismic characteristics depending on evolution.
Methods. The complete identification of the pressure eigenmodes provided by the red-giant universal oscillation pattern allows us to aim at the mixed modes surrounding the ℓ = 1 expected eigenfrequencies. A dedicated method based on the envelope autocorrelation function is proposed to analyze their period separation.
Results. We have identified the mixed-mode signature separation thanks to their pattern that is compatible with the asymptotic law of gravity modes. We have shown that, independent of any modeling, the g-mode spacings help to distinguish the evolutionary status of a red-giant star. We then report the different seismic and fundamental properties of the stars, depending on their evolutionary status. In particular, we show that high-mass stars of the secondary clump present very specific seismic properties. We emphasize that stars belonging to the clump were affected by significant mass loss. We also note significant population and/or evolution differences in the different fields observed by CoRoT.
Key words: stars: oscillations / stars: interiors / stars: mass-loss / methods: data analysis
The CoRoT space mission, launched 2006 December 27, was developed and is operated by the CNES, with participation of the Science Programs of ESA, ESAŠs RSSD, Austria, Belgium, Brazil, Germany, and Spain.
Apeendix A is available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The CoRoT and Kepler missions have revealed solar-like oscillation in thousands of red-giant stars. This gives us the opportunity to test this important phase of stellar evolution and provides new information in stellar and galactic physics (Miglio et al. 2009; Bedding et al. 2011). Thanks to the dramatic increase in information recently made available (De Ridder et al. 2009; Hekker et al. 2009; Mosser et al. 2010; Kallinger et al. 2010; Huber et al. 2010), we now have a precise view of pressure modes (p modes) corresponding to oscillations propagating essentially in the large convective envelopes. Gravity modes (g modes) may exist in all stars with radiative regions. They result from the trapping of gravity waves, with buoyancy as a restoring force. In red giants, gravity waves propagating in the core have high enough frequencies to be coupled to pressure waves propagating in the envelope (Dupret et al. 2009). The trapping of such waves with mixed pressure and gravity character gives the so-called mixed modes. The coupling insures non-negligible oscillation amplitudes in the stellar photosphere, hence possible detection of these mixed modes.
Observationally, mixed modes were first identified in white-dwarf oscillation spectra (Winget et al. 1991). They have also been observed in subgiant stars, first with ground-based observations (Carrier et al. 2005; Bedding et al. 2007, 2010b), then recently in Kepler and CoRoT fields (Chaplin et al. 2010; Deheuvels et al. 2010). In red giants, they were first suspected by Bedding et al. (2010a). Their presence significantly complicates the fit of the p modes observed in CoRoT giants (Hekker et al. 2010; Barban et al. 2010), and they were identified as outliers to the universal red-giant oscillation spectrum (Mosser et al. 2011). Recent modeling of a giant star observed by the Kepler mission had to take their presence into account (Di Mauro et al. 2011). Finally, they have been firmly identified in Kepler data (Beck et al. 2011), making the difference clear between giants burning hydrogen in shell or helium in the core (Bedding et al. 2011).
The theoretical analysis of these mixed modes in red giants has been performed prior to observations (Dziembowski et al. 2001; Christensen-Dalsgaard 2004; Dupret et al. 2009). Using a non-radial, non-adiabatic pulsation code including a non-local, time-dependent treatment of convection and a stochastic excitation model, Dupret et al. (2009) have computed the eigenfrequencies and the mode heights in several red-giant models. They have shown that mixed modes have much higher mode inertias than p modes, hence present longer lifetimes and smaller linewidths. They were able to identify different regimes, depending on the location of the models on the red-giant branch (RGB). Recently, Montalbán et al. (2010) propose using the oscillation spectrum of dipole modes to distinguish between the RGB and central-He burning (clump) evolutionary phases of red giants. This illustrates that observing p-g-mixed modes and identifying their properties give us a unique opportunity to analyze the cores of red giants, since the g component is highly sensitive to the core condition (Dupret et al. 2009).
In this paper, we present and validate an alternative method to Bedding et al. (2011) to detect and identify mixed modes in red giants. We use it to analyze red-giant stars in two different fields observed by CoRoT and show that they present different properties: mixed modes not only allow us to distinguish different evolutionary status, but can also show different population characteristics. We also assess clear observational differences between the fundamental and seismic properties of the red-giant stars, depending on their evolutionary status. We show for instance that the observation of mixed modes opens a new way to study the mass loss at the tip of the RGB. We also have a clear indication that mixed modes in red giants are sensitive to chemical composition gradients in the deep interior, as they are in SPB and γ Doradus stars (Miglio et al. 2008). Their study will definitely boost both stellar and galactic physics.
 |
Fig. 1 Power density spectra of three CoRoT targets (ID given on the right side), with shaded regions of these bar code spectra that reproduce the universal red-giant oscillation pattern and identify the location of the different harmonic degrees; the denser the background, the higher the probability of having the short-lived p mode realized there. Black dashes in the ℓ = 1 ridges indicate the asymptotic spacing of the mixed modes as derived from Eq. (2). They do not give their exact eigenfrequencies, since the asymptotic relation does not account for the mode bumping of mixed modes. |
2. Analysis
2.1. Mixed-mode pattern
According to Dupret et al. (2009), each ℓ = 1 ridge is composed of a pressure mode surrounded by mixed modes with a pattern mostly dominated by the g-mode component. According to the asymptotic description (Tassoul 1980), both p modes and g modes present well-organized patterns. For p modes, the organization is a comb-like structure in frequency, and for g modes, regularity is observed in period. Mixed modes in giants are supposed to exhibit the well-organized pattern of g modes. To detect them in an automated way, we searched for this asymptotic pattern: ![\begin{equation} \per_{\ng, \ell} = {2\pi^2 (\ng + \alpha_\ell) \over \sqrt{\ell (\ell +1)}} \ \left[ \int_{\mathrm{core}} \!\!{{\NBV \over r}\; \diff r } \right]^{-1} = {(\ng + \alpha_\ell)\ \Delta T\ind{g} \over \sqrt{\ell (\ell +1)}} \label{tassoulg} \end{equation}](/articles/aa/full_html/2011/08/aa16825-11/aa16825-11-eq3.png) (1)with ng the gravity radial order, αℓ an unknown constant, and NBV the Brunt-Väisälä frequency. The period spacing ΔTg is the equivalent for g modes of the large separation for p modes.
(1)with ng the gravity radial order, αℓ an unknown constant, and NBV the Brunt-Väisälä frequency. The period spacing ΔTg is the equivalent for g modes of the large separation for p modes.
2.2. Periodic spacings
We first restricted our attention to ℓ = 1 modes since mixed modes with ℓ = 2 are not supposed to be as clearly visible (Dupret et al. 2009). Furthermore, the close proximity of ℓ = 2 modes to radial modes complicates the analysis. For the ℓ = 1 mixed modes, the periodic pattern simply becomes ![\begin{equation} \per_{\ng, 1} = \left[ \ng + \alpha_1 \right] \tgun , \hbox{ with \ } \tgun= \Delta T\ind{g} / \!\sqrt{2} . \label{tassoul_un} \end{equation}](/articles/aa/full_html/2011/08/aa16825-11/aa16825-11-eq9.png) (2)The period spacing ΔT1, linked to the integral of the Brunt-Väisälä frequency by Eq. (1), can be deduced from the frequency spacing in the Fourier spectrum. To measure this spacing, we need to focus on the mixed modes. We are able to do this using the method introduced in Mosser et al. (2011), which allows a complete and automated mode identification. We then use the envelope autocorrelation function (Mosser & Appourchaux 2009) to derive the period spacing. The method is described in the Appendix. Owing to the bumping of mixed modes, the method derives a period ΔTobs less than ΔT1, as in Bedding et al. (2011). We have estimated that, for the 5-month long CoRoT time series, we measure ΔTobs ≃ ΔT1/1.15 (see Appendix).
(2)The period spacing ΔT1, linked to the integral of the Brunt-Väisälä frequency by Eq. (1), can be deduced from the frequency spacing in the Fourier spectrum. To measure this spacing, we need to focus on the mixed modes. We are able to do this using the method introduced in Mosser et al. (2011), which allows a complete and automated mode identification. We then use the envelope autocorrelation function (Mosser & Appourchaux 2009) to derive the period spacing. The method is described in the Appendix. Owing to the bumping of mixed modes, the method derives a period ΔTobs less than ΔT1, as in Bedding et al. (2011). We have estimated that, for the 5-month long CoRoT time series, we measure ΔTobs ≃ ΔT1/1.15 (see Appendix).
Typical parameters of mixed modes.
2.3. Positive detection
The analysis was performed on CoRoT red giants previously analyzed in Hekker et al. (2009) and Mosser et al. (2010). These stars were observed continuously during five months in two different fields centered on the Galactic coordinates (37°, −07°45′) and (212°, −01°45′). Targets with too low a signal-to-noise ratio were excluded (see the Appendix). We therefore only considered stars with accurate global seismic parameters and labeled as the 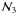 set in Mosser et al. (2010).
set in Mosser et al. (2010).
Thanks to the method explained in the Appendix, we analyzed all red-giant spectra in an automated way. We then checked all results individually. This allowed us to discard a few false positive results and then to verify that the asymptotic expansion of the g modes (Eq. (2)) gives an accurate description of the mixed modes since it is able to reproduce their spacings. The irregularities of the spacings are discussed in Sect. 3.1 and in the Appendix. A few examples are given in Fig. 1: we overplotted the expected location of the p-mode pattern derived from Mosser et al. (2011) on red-giant oscillation spectra and indicated the frequency separation of the mixed modes derived from the asymptotic description. Because of the mode bumping due to coupling, the g-mode asymptotic expression is not able to derive the exact location of the mixed-mode eigenfrequencies, but we see that the spacings reproduce the observations. This agreement is certainly related to measuring very high values of the gravity radial orders, typically above 60 and up to 400 (Table 1). We were then able to provide a diagram representing the period separation ΔTobs of the mixed modes as a function of the large frequency separation Δν of the pressure modes (Fig. 2).
The five-month long CoRoT time series provide a frequency resolution of about 0.08 μHz, which is accurate enough for detecting the mixed modes in the red clump, but it limits their possible detection at a lower frequency. Therefore, we took care of possible artefacts. We excluded the region of the ⟨ Δν ⟩ –ΔTobs diagram limited by the frequency resolution (Fig. 2). We also took care of the possible confusion with the small separation δν02, since in given frequency ranges its signature can mimic a g-mode spacing (Fig. 2). Due to the low visibility of ℓ = 3 modes, it appeared useless to test the influence of their pattern combined with radial or dipole modes.
The criterion of a positive detection of the mixed modes in at least two frequency ranges allowed us to distinguish regular period spacings from regular frequency spacings as caused by rotation. We also examined the possible confusion with the ragged, speckle-like appearance of the structure due to the limited lifetime of the modes. Simulations have shown that the threshold level provided by the method (Mosser & Appourchaux 2009), combined with the detection in multiple frequency ranges excludes spurious signature.
 |
Fig. 2 Period separation of mixed modes ΔTobs as a function of the mean frequency separation of the pressure modes ⟨ Δν ⟩ . Blue (purple) crosses represent the targets observed in the center (anticenter) direction. The dashed line indicates the frontier below which the frequency resolution is not fine enough for deriving ΔTobs and the dotted line represents the location of the spurious signature that would correspond to the small separation δν02 (Mosser et al. 2011). The two separate domains correspond to the location of ΔT1 observed by Bedding et al. (2011) and theoretically expected (Montalbán et al., in prep.). The vertical thick line indicates the mean 1-σ error bars (the error bar on the large separation Δν is in fact very small). |
Finally, we identified an ℓ = 1 mixed-modes pattern in about 42% of the targets (387 out of a total of 929) and for more than 75% of the stars with an R magnitude brighter than 13. The few remaining bright stars do not present a reliable signature, either because their spectrum is free of mixed modes or because the signature was not found reliable according to the threshold detection level. When detected, the pattern closely follows both the asymptotic expression of gravity modes (Tassoul 1980) and the description by Dupret et al. (2009). The peaks generating these spacings are visible in a frequency range of about 0.25 Δν around the expected pure p-mode eigenfrequencies νn,ℓ = 1. This typically represents, at the peak of the red clump distribution (Δν ≃ 4 μHz and νmax ≃ 32 μHz), from two to ten mixed modes (Table 1). Owing to the frequency dependence derived from Eq. (2), the number of observable modes varies very rapidly, as observed by Beck et al. (2011) and made explicit in Table 1.
 |
Fig. 3 Échelle diagrams around νmax for different targets sorted by increasingly large separations. The red squares indicate the observed peaks, selected with a height-to-background ratio above 6. Dark blue crosses indicate the expected location of the ℓ = 1 mixed modes strictly following the asymptotic expression; light blue diamonds are for ℓ = 2. Similarly to Fig. 1, crosses and diamonds indicate the mean spacing of the mixed modes only, not their exact location. |
According to Dupret et al. (2009), ℓ = 2 mixed modes are expected to be much more damped than ℓ = 1 modes. However, their presence is clearly identified for about a third of the targets (Fig. 3). The agreement of their mean separation with 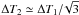 (Eq. (1)) is clear enough to be disentangled from the speckle-like aspect of short-lived modes. Their observation will give strong constraints on the inner envelope, where g modes are coupled to p modes, because the coupling is highly sensitive to the respective location of the Brunt-Väisälä and ℓ = 2 Lamb frequency. The high density of mixed modes makes it possible to achieve this high-resolution analysis, thanks to the high values of the radial gravity orders observed. We observe in most cases groups of only two ℓ = 2 mixed modes, rarely three, spread in a frequency range of about 0.04 Δν. A further consequence of the observation of ℓ = 2 mixed modes is correction to the asymptotic laws reported for the small separation δν02 by Huber et al. (2010) and Mosser et al. (2011); they are correct, but only indicative of the barycenter of the ℓ = 2 modes if mixed.
(Eq. (1)) is clear enough to be disentangled from the speckle-like aspect of short-lived modes. Their observation will give strong constraints on the inner envelope, where g modes are coupled to p modes, because the coupling is highly sensitive to the respective location of the Brunt-Väisälä and ℓ = 2 Lamb frequency. The high density of mixed modes makes it possible to achieve this high-resolution analysis, thanks to the high values of the radial gravity orders observed. We observe in most cases groups of only two ℓ = 2 mixed modes, rarely three, spread in a frequency range of about 0.04 Δν. A further consequence of the observation of ℓ = 2 mixed modes is correction to the asymptotic laws reported for the small separation δν02 by Huber et al. (2010) and Mosser et al. (2011); they are correct, but only indicative of the barycenter of the ℓ = 2 modes if mixed.
3. Discussion
3.1. Period spacing
The measurement of mixed-mode spacings varying as 1/ν2 (Eq. (A.2)) validates the use of the asymptotic law of g modes, even if a detailed view of the mixed modes indicates irregularities in their spacings (Fig. 3). These shifts may be interpreted as a modulation due to the structure of the core with a sharp density contrast compared to the envelope, as observed in white dwarfs. The determination of ΔT1 will allow modelers to define the size of the radiative core region. The direct measurement of the individual shifts ΔT1(ng) will give access to the core stratification (Miglio et al. 2008), as well as allowing the observation (or not) of ℓ = 2 mixed modes that test a different cavity.
The method developed in this paper presents many interesting characteristics compared to the method used by Bedding et al. (2011). First, it is directly applicable in the Fourier spectrum and does not require the power spectrum to be expressed in period. The method is fully automated, since it is coupled to the identification of the spectrum based on the universal pattern, and it includes a systematic search of periodic spacings that are not related to the p-mode pattern. Since it is based on an H0 test, it intrinsically includes a statistical test of reliability. This test defines a threshold level that makes the method efficient even at a low signal-to-noise ratio. Its most interesting property certainly consists in its ability to derive the measurement of the variation of ΔT1 with frequency, as the EACF method used for p modes (Mosser & Appourchaux 2009; Mosser 2010). In fact, the method was developed in parallel to the one mainly presented in Bedding et al. (2011), and it gave similar results, so it confirmed the detection of mixed modes in Kepler giants.
3.2. Red-clump and red-giant branch stars
Red-clump stars have been characterized in previous work (e.g. Fig. 5 of Mosser et al. 2010). They contribute to a distribution in Δν with a pronounced accumulation near 4 μHz (equivalent to the accumulation near νmax ≃ 32 μHz). However, population analysis made by Miglio et al. (2009) has shown that this population of stars with Δν ≃ 4 μHz effectively dominated by red-clump stars also contains a non-negligible fraction ( ≃ 30 %) of RGB stars. None of the global parameters of p mode (neither Δν nor νmax) is able to distinguish between RGB and red-clump stars. However, as shown by Bedding et al. (2011) with Kepler data, the examination of the relation between the p-mode and g-mode spacings shows two regimes (Fig. 2). The signature of the red-clump stars piling up around ⟨ Δν ⟩ ≃ 4 μHz is visible with ΔTobs ≃ 250 s. Another group of stars has ΔTobs values lower than 100 s. Regardless of any modeling, this gives a clear signature of the difference between red-clump stars that burn helium in their core and stars of the RGB that burn hydrogen in a shell (Montalbán et al. 2010).
The contribution of the red-clump stars in the Δν-ΔTobs diagram presented in Fig. 2 is unambiguous. Stars with large separations larger than the clump value (about 4 μHz) are located on the ascending RGB or are members of the secondary clump (Girardi 1999; Miglio et al. 2009). At a lower frequency than the clump, using mixed modes to disentangle the evolutionary status is more difficult. According to the identification of the clump provided by the distributions of the large separation (Mosser et al. 2010), we assume that the giants with Δν ≤ 3.5 μHz and ΔTobs ≥ 200 s belong to the RGB. The following analysis shows other consistent indications.
We finally note that the detection of RGB stars having a large separation similar to the peak of the clump stars ( ≃ 4 μHz) is only marginally possible, because of insufficient frequency resolution. According to Table 1, more than 200 days are needed to resolve the mixed modes, while CoRoT runs are limited to about 150 days.
3.3. Mode lifetimes and heights
We have pointed out that, as predicted by Dupret et al. (2009), the lifetimes of the mixed modes trapped in the core are much longer than the lifetimes of radial modes (Fig. 1). In most cases, the mixed modes are not resolved. When the mixed modes are identified, they correspond in most cases to a comb-like pattern of thin peaks, without a larger and broader peak that could correspond to the pure ℓ = 1 pressure mode. However, since mixed modes are only detected for a limited set of stars, one cannot exclude some red giants only showing pure ℓ = 1 pressure modes.
 |
Fig. 4 Asteroseismic mass as a function of the asteroseismic radius, with an indication of the evolutionary status derived from the mixed-mode spacing: blue squares for RGB stars, red diamonds for clump stars. Stars without clear measurement of ΔTobs are marked with a small cross. The rectangle indicates the mean 1-σ error bars. The dotted lines at 1 and 1.8 M⊙ correspond to the limits defined in the text. |
 |
Fig. 5 Mean mode height as a function of νmax. Same color code as in Fig. 4. The rectangle indicates the mean 1-σ error bars. |
 |
Fig. 6 Proxy of the number of observable modes, given by the ratio δνenv/Δν, as a function of νmax. Same color code as in Fig. 4. The rectangle indicates the mean 1-σ error bars. |
3.4. Mass-radius relation
The possibility of distinguishing the evolutionary status allows us to refine the ensemble asteroseismic analysis made on CoRoT red giants, especially the mass and radius distributions (Figs. 12 and 13 of Mosser et al. 2010). Benefitting from the same calibration of the asteroseismic mass and radius determination, we investigated the mass-radius relation, keeping in mind that, without information of the evolutionary status, there is no clear information (Hekker et al. 2011b).
We note here that the mass distribution is almost uniform in the RGB, in contrast to clump stars (Fig. 4). The number of high-mass stars in the RGB, above 1.8 M⊙ as defined in Bedding et al. (2011), is about half those in the clump, consistent with their expected more rapid evolution. Similarly, stars with masses below 1 M⊙ are significantly rarer (by a factor of six to one) in the RGB than in the clump. If we assume that the scaling relations, which are valid along the whole evolution from the main sequence to the giant class, remain valid after the tip of the RGB, this comparative study proves that low-mass stars present in the clump but absent in the branch have lost a substantial fraction of their mass because of stellar winds when ascending up to the tip of the RGB. Therefore, after the helium flash, these stars show lower mass. The quantitative study of this mass loss will require a careful, unbiased analysis, which is beyond the scope of this paper. In contrast, high-mass stars, even if they lost mass too, can be observed as clump stars since they spend a much longer time in the core-helium burning phase than while ascending the RGB. Most of these stars belong to the secondary red clump (Girardi 1999; Bedding et al. 2011). We note that the secondary-clump stars present a wider spread in the mass-radius distribution, certainly because those stars that have not undergone the helium flash present different interior structures. On the other hand, the low-mass stars of the clump present a clear mass-radius relation: the helium flash will have made their core largely homologous.
3.5. Mode amplitudes and number of modes
We also address the influence of the evolutionary status on the energetic parameters of the red-giant oscillation spectrum. When plotting the mean height of the excess power Gaussian envelope as a function of the frequency νmax, we notice that clump stars and RGB stars present very similar heights for νmax less than 40 μHz. However, above 40 μHz, the oscillations in clump stars present systematically lower heights than RGB stars (Fig. 5). The contrast is more than a factor of 2. On the other hand, the number of modes, estimated from the ratio δνenv/Δν where δνenv is the full width at half-maximum of the total oscillation excess power envelope, is similar below 40 μHz, but more than 30% more for clump stars above this limit (Fig. 6). Despite the somewhat arbitrary limit in νmax, we see here evidence of the secondary clump (Girardi 1999), which consists of He-core burning stars that are massive enough to have ignited He in nondegenerate conditions. These stars have, at νmax > 40 μHz, similar radii to RGB stars, and higher masses. As a result, they have a smaller L/M ratio, so that the excitation of oscillation is expected to be weaker. With a larger νmax, they also present a solar-like oscillation spectrum with modes excited in a broader frequency range.
We suggest that, in case the measurement of ΔTobs is made difficult by a low signal-to-noise ratio, the oscillation amplitude and the size of the Gaussian envelope with noticeable amplitude may be used to help the determination of the evolutionary status. Finally, we note that the secondary-clump population is certainly underestimated, because the low amplitudes make their detection quite complex in CoRoT data. In fact, such stars are observed with a low signal-to-noise ratio since their Fourier spectra are dominated by a white-noise contribution.
3.6. Different populations
The number of detections of solar-like oscillations in the anticenter direction is lower than towards the center, due to a lower red-giant density in the outer galactic regions and to dimmer magnitudes (Mosser et al. 2010). This means that the number of reliable measurements of ΔTobs is lower too, but with the same proportion of 40 %. The sample is large enough to make sure that the difference between the distributions is significant (Fig. 2).
The anticenter field shows a significant deficit of red-clump stars below Δν = 3.8 μHz, e.g. with low mass. Another such deficit is observed at low frequency in the RGB, and it should indicate populations with different ages. We also note that secondary-clump stars of the anticenter direction present slightly higher g-mode spacings, which should indicate populations with different mass distributions. This illustrates the interest in comparing the different fields in order to analyze different populations (Miglio et al., in prep.).
4. Conclusion
Clear identification of the p-mode oscillation pattern has allowed us to identify in CoRoT observations the pattern of mixed modes behaving as gravity modes in the core and pressure modes in the envelope. We verified that this pattern is very close to the asymptotic expression of g modes. Benefitting from the identification of ℓ = 1 mixed modes, we also measured ℓ = 2 mixed modes. The presence or absence of these mixed modes will allow us to study the deep envelope surrounding the core.
We verified that the mean large period separation of the mixed modes gives a clear indication of the evolution of the
star. Assuming the validity of the asteroseismic scalings laws for the stellar mass and radius, we showed that the mass distribution of the RGB is much more uniform than in the red clump. Asteroseismology confirms that these red-clump stars have undergone a significant mass loss. Furthermore, red-giant low-mass stars after the helium flash present homologous interiors and a clear mass-radius relation, in contrast to stars in the secondary clump. Longer time series recorded with Kepler will allow us to investigate this relation in more detail. Benefitting from the fact that CoRoT provides observations in two fields, towards the Galactic center and in the opposite direction, we now have a performing indicator for making the population study more precise. This will be done in future work.
These data confirm the power of red-giant asteroseismology, because we have access to the direct measure of the radiative central regions. Even if observations only deliver a proxy of the large period separation, comparison with modeling will undoubtedly be very fruitful. In a next step, the dedicated analysis of the best signal-to-noise ratio targets will allow us to sound the red-giant core in detail. Modulation of the large period spacing, observed in many targets, will give a precise view of the core layers.
Online material
Appendix A: Method
Identifying ℓ = 1 mixed modes first requires one to aim at them precisely. This first step is achieved by the method presented in Mosser et al. (2011), which is able to mitigate the major sources of noise that perturb any measurement of the large separation Δν and then to derive the complete identification of the p-mode oscillation pattern. Complete identification means that all eigenfrequencies, their radial order, and their degree are unambiguously identified, such as the expected frequencies of the pure pressure ℓ = 1 modes: ![\appendix \setcounter{section}{1} \begin{equation} \label{ridge} \nu_{n,\ell=1} = [n+1/2+\varepsilon(\Dnu) - d_{01}] \;\Dnu, \end{equation}](/articles/aa/full_html/2011/08/aa16825-11/aa16825-11-eq59.png) (A.1)with ε(Δν) representing the surface term and d01 accounting for the small separation of ℓ = 1 pure p modes.
(A.1)with ε(Δν) representing the surface term and d01 accounting for the small separation of ℓ = 1 pure p modes.
The frequency spacings of the mixed modes are then analyzed with the envelope autocorrelation function (EACF) based on narrow filters centered on the frequencies νn,1 in the vicinity of the frequency νmax of maximum oscillation amplitude (Mosser & Appourchaux 2009). We deliberately chose the EACF method since it has proved to be efficient at a very low signal-to-noise ratio (Mosser et al. 2009; Gaulme et al. 2010; Hekker et al. 2011a), thanks to a statistical test of reliability based on the null hypothesis.
In order to only select mixed modes, the full width at half-maximum of the filter is fixed to Δν/2 (Fig. A.1). From the differentiation of the relation between period and frequency, the regular spacing of Eq. (2) in period translates into spacings varying with frequency as 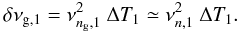 (A.2)For an individual measure centered on a given p mode, the frequency spacings selected by the narrow filter can be considered as uniform, since the ratio Δng/ng that represents the relative variation in the gravity radial order within the filter is less than about 1/25 (Table 1). Then, when comparing the different measures around different pressure radial orders, obtaining mean frequency spacings varying as
(A.2)For an individual measure centered on a given p mode, the frequency spacings selected by the narrow filter can be considered as uniform, since the ratio Δng/ng that represents the relative variation in the gravity radial order within the filter is less than about 1/25 (Table 1). Then, when comparing the different measures around different pressure radial orders, obtaining mean frequency spacings varying as 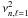 validates the hypothesis of a Tassoul-like g-mode pattern (Fig. A.2).
validates the hypothesis of a Tassoul-like g-mode pattern (Fig. A.2).
We have checked that the method can operate with a filter narrow enough to isolate the mixed modes. This is clearly a limit, since the performance of the EACF varies directly with the width of the filter (Mosser & Appourchaux 2009). We have also checked that such a filter is able to derive the signature of ℓ = 1 mixed modes in a frequency range as wide as possible, without significant perturbation of possible ℓ = 2 mixed modes. Because filters with a narrower width focus too much on the region where, due to the vicinity of the ℓ = 1 pure pressure mode,
bumped mixed modes present a narrower period spacing than what is expected from Eq. (2), we consider the Δν/2 width to be the best compromise.
Since measurements can be verified in different frequency ranges (Figs. A.1 and A.2), we have chosen a threshold value corresponding to the rejection of the H0 hypothesis at the 10% level. For the characteristics of mixed modes, which are different from the characteristics of the p modes considered in Mosser & Appourchaux (2009), this corresponds to a normalized EACF of about 4.5 at νmax. In practice, stellar time series with a low signal-to-noise ratio are excluded by this threshold value. For reliable detection, error bars can be derived following Eq. (A.8) of Mosser & Appourchaux (2009).
The measurement of the g-mode frequency spacing δνg,1 is not only validated by a correlation signal that is greater than the threshold level: we only selected results with δνg,1 measured in at least two frequency ranges and verified Eq. (A.2) within 20%. This flexibility allows us to account for a possible discrepancy to the exact asymptotic relation (Eq. (2)), as produced by the avoided crossings resulting from coupling of the p mode in the stellar envelope to the g modes in the core. It also accounts for the possible modulation of the period caused by a composition gradient in the core (Miglio et al. 2008).
 |
Fig. A.1 Zoom on the bar code spectrum of the target CoRoT 100752538, with the large separation provided by the adjustment derived from the red-giant oscillation universal pattern. Different narrow filters centered on different pure ℓ = 1 pressure modes are indicated with different line styles. They allow us to measure a local g-mode frequency spacing in each filter. |
Deriving an estimate ΔTobs of ΔT1 from the spacings δνg,1 is then direct. Owing to avoided crossings, ΔTobs is close to but less than ΔT1 (Althaus et al. 2010; Beck et al. 2011; Bedding et al. 2011). This is called mode bumping and results from the fact that the mixed modes around νn,1 present necessarily smaller spacings than pure g modes since the mixing of the g modes with one p mode gives one supernumerary mixed mode per Δν frequency interval, as shown in Beck et al. (2011). The ratio ΔT1/ΔTobs ≃ 1.15 is derived from the examination, when possible, of the g-mode spacing far from the expected p mode, assuming as in Bedding et al. (2011) that this spacing is unperturbed by the mode bumping and corresponds to the asymptotic g-mode spacing. The ratio differs from the value obtained with the Kepler data, since the frequency resolutions and the analysis methods are different. First, the frequency resolution is 2.5 times less fine for CoRoT data; as a consequence, the influence of the mode bumping is smoother. Second, and more important, the envelope autocorrelation method is able to derive a mean value of the spacing in a wider frequency range than the method given in Bedding et al. (2011) thanks to the Δν/2-broad filter used to select the mixed modes. This helps to enhance the contribution of non-bumped mixed modes.
When relaxing the condition expressed by Eq. (A.2), the method can be applied to search for rotational splittings, with ultra-narrow filters centered on individual mixed modes. This search was unfortunately negative for CoRoT red-giant spectra.
 |
Fig. A.2 Mean period spacings measured around the expected pure ℓ = 1 pressure modes of the target CoRoT 100752538. Vertical lines indicate the error bars on each individual measurement. |
Acknowledgments
This work was supported by the Centre National d’Études Spatiales (CNES). It is based on observations with CoRoT. The research made use of the Exo-Dat database, operated at LAM-OAMP, Marseille, France, on behalf of the CoRoT/Exoplanet program. K.B. acknowledges financial support from CNES. S.H. acknowledges financial support from the Netherlands Organization for Scientific Research (NWO). P.B. received funding from the European Community’s 7th Framework Program, ERC grant n227224 (PROSPERITY).
References
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Barban, C., Baudin, F., Mosser, B., et al. 2010, Astron. Nachr., 331, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Arentoft, T., et al. 2007, ApJ, 663, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Huber, D., Stello, D., et al. 2010a, ApJ, 713, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Campante, T. L., et al. 2010b, ApJ, 713, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carrier, F., Eggenberger, P., & Bouchy, F. 2005, A&A, 434, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., Appourchaux, T., Elsworth, Y., et al. 2010, ApJ, 713, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2004, Sol. Phys., 220, 137 [NASA ADS] [CrossRef] [Google Scholar]
- De Ridder, J., Barban, C., Baudin, F., et al. 2009, Nature, 459, 398 [Google Scholar]
- Deheuvels, S., Bruntt, H., Michel, E., et al. 2010, A&A, 515, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Mauro, M. P., Cardini, D., Catanzaro, G., et al. 2011 [arXiv:1105.1076] [Google Scholar]
- Dupret, M., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., Deheuvels, S., Weiss, W. W., et al. 2010, A&A, 524, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L. 1999, MNRAS, 308, 818 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hekker, S., Kallinger, T., Baudin, F., et al. 2009, A&A, 506, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Barban, C., Baudin, F., et al. 2010, A&A, 520, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Elsworth, Y., De Ridder, J., et al. 2011a, A&A, 525, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Gilliland, R. L., Elsworth, Y., et al. 2011b, MNRAS, 414, 2594 [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2010, ApJ, 723, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Mosser, B., Hekker, S., et al. 2010, A&A, 522, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Montalbán, J., Baudin, F., et al. 2009, A&A, 503, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., Scuflaire, R., & Ventura, P. 2010, ApJ, 721, L182 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B. 2010, Astron. Nachr., 331, 944 [Google Scholar]
- Mosser, B. & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Appourchaux, T., et al. 2009, A&A, 506, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M. J., et al. 2011, A&A, 525, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1991, ApJ, 378, 326 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Power density spectra of three CoRoT targets (ID given on the right side), with shaded regions of these bar code spectra that reproduce the universal red-giant oscillation pattern and identify the location of the different harmonic degrees; the denser the background, the higher the probability of having the short-lived p mode realized there. Black dashes in the ℓ = 1 ridges indicate the asymptotic spacing of the mixed modes as derived from Eq. (2). They do not give their exact eigenfrequencies, since the asymptotic relation does not account for the mode bumping of mixed modes. |
| In the text | |
 |
Fig. 2 Period separation of mixed modes ΔTobs as a function of the mean frequency separation of the pressure modes ⟨ Δν ⟩ . Blue (purple) crosses represent the targets observed in the center (anticenter) direction. The dashed line indicates the frontier below which the frequency resolution is not fine enough for deriving ΔTobs and the dotted line represents the location of the spurious signature that would correspond to the small separation δν02 (Mosser et al. 2011). The two separate domains correspond to the location of ΔT1 observed by Bedding et al. (2011) and theoretically expected (Montalbán et al., in prep.). The vertical thick line indicates the mean 1-σ error bars (the error bar on the large separation Δν is in fact very small). |
| In the text | |
 |
Fig. 3 Échelle diagrams around νmax for different targets sorted by increasingly large separations. The red squares indicate the observed peaks, selected with a height-to-background ratio above 6. Dark blue crosses indicate the expected location of the ℓ = 1 mixed modes strictly following the asymptotic expression; light blue diamonds are for ℓ = 2. Similarly to Fig. 1, crosses and diamonds indicate the mean spacing of the mixed modes only, not their exact location. |
| In the text | |
 |
Fig. 4 Asteroseismic mass as a function of the asteroseismic radius, with an indication of the evolutionary status derived from the mixed-mode spacing: blue squares for RGB stars, red diamonds for clump stars. Stars without clear measurement of ΔTobs are marked with a small cross. The rectangle indicates the mean 1-σ error bars. The dotted lines at 1 and 1.8 M⊙ correspond to the limits defined in the text. |
| In the text | |
 |
Fig. 5 Mean mode height as a function of νmax. Same color code as in Fig. 4. The rectangle indicates the mean 1-σ error bars. |
| In the text | |
 |
Fig. 6 Proxy of the number of observable modes, given by the ratio δνenv/Δν, as a function of νmax. Same color code as in Fig. 4. The rectangle indicates the mean 1-σ error bars. |
| In the text | |
 |
Fig. A.1 Zoom on the bar code spectrum of the target CoRoT 100752538, with the large separation provided by the adjustment derived from the red-giant oscillation universal pattern. Different narrow filters centered on different pure ℓ = 1 pressure modes are indicated with different line styles. They allow us to measure a local g-mode frequency spacing in each filter. |
| In the text | |
 |
Fig. A.2 Mean period spacings measured around the expected pure ℓ = 1 pressure modes of the target CoRoT 100752538. Vertical lines indicate the error bars on each individual measurement. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


