| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116825 | |
| Published online | 27 July 2011 | |
Online material
Appendix A: Method
Identifying ℓ = 1 mixed modes first requires one to aim at them precisely. This first step is achieved by the method presented in Mosser et al. (2011), which is able to mitigate the major sources of noise that perturb any measurement of the large separation Δν and then to derive the complete identification of the p-mode oscillation pattern. Complete identification means that all eigenfrequencies, their radial order, and their degree are unambiguously identified, such as the expected frequencies of the pure pressure ℓ = 1 modes:  (A.1)with ε(Δν) representing the surface term and d01 accounting for the small separation of ℓ = 1 pure p modes.
(A.1)with ε(Δν) representing the surface term and d01 accounting for the small separation of ℓ = 1 pure p modes.
The frequency spacings of the mixed modes are then analyzed with the envelope autocorrelation function (EACF) based on narrow filters centered on the frequencies νn,1 in the vicinity of the frequency νmax of maximum oscillation amplitude (Mosser & Appourchaux 2009). We deliberately chose the EACF method since it has proved to be efficient at a very low signal-to-noise ratio (Mosser et al. 2009; Gaulme et al. 2010; Hekker et al. 2011a), thanks to a statistical test of reliability based on the null hypothesis.
In order to only select mixed modes, the full width at half-maximum of the filter is fixed to Δν/2 (Fig. A.1). From the differentiation of the relation between period and frequency, the regular spacing of Eq. (2) in period translates into spacings varying with frequency as 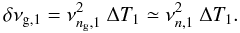 (A.2)For an individual measure centered on a given p mode, the frequency spacings selected by the narrow filter can be considered as uniform, since the ratio Δng/ng that represents the relative variation in the gravity radial order within the filter is less than about 1/25 (Table 1). Then, when comparing the different measures around different pressure radial orders, obtaining mean frequency spacings varying as
(A.2)For an individual measure centered on a given p mode, the frequency spacings selected by the narrow filter can be considered as uniform, since the ratio Δng/ng that represents the relative variation in the gravity radial order within the filter is less than about 1/25 (Table 1). Then, when comparing the different measures around different pressure radial orders, obtaining mean frequency spacings varying as 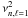 validates the hypothesis of a Tassoul-like g-mode pattern (Fig. A.2).
validates the hypothesis of a Tassoul-like g-mode pattern (Fig. A.2).
We have checked that the method can operate with a filter narrow enough to isolate the mixed modes. This is clearly a limit, since the performance of the EACF varies directly with the width of the filter (Mosser & Appourchaux 2009). We have also checked that such a filter is able to derive the signature of ℓ = 1 mixed modes in a frequency range as wide as possible, without significant perturbation of possible ℓ = 2 mixed modes. Because filters with a narrower width focus too much on the region where, due to the vicinity of the ℓ = 1 pure pressure mode,
bumped mixed modes present a narrower period spacing than what is expected from Eq. (2), we consider the Δν/2 width to be the best compromise.
Since measurements can be verified in different frequency ranges (Figs. A.1 and A.2), we have chosen a threshold value corresponding to the rejection of the H0 hypothesis at the 10% level. For the characteristics of mixed modes, which are different from the characteristics of the p modes considered in Mosser & Appourchaux (2009), this corresponds to a normalized EACF of about 4.5 at νmax. In practice, stellar time series with a low signal-to-noise ratio are excluded by this threshold value. For reliable detection, error bars can be derived following Eq. (A.8) of Mosser & Appourchaux (2009).
The measurement of the g-mode frequency spacing δνg,1 is not only validated by a correlation signal that is greater than the threshold level: we only selected results with δνg,1 measured in at least two frequency ranges and verified Eq. (A.2) within 20%. This flexibility allows us to account for a possible discrepancy to the exact asymptotic relation (Eq. (2)), as produced by the avoided crossings resulting from coupling of the p mode in the stellar envelope to the g modes in the core. It also accounts for the possible modulation of the period caused by a composition gradient in the core (Miglio et al. 2008).
 |
Fig. A.1
Zoom on the bar code spectrum of the target CoRoT 100752538, with the large separation provided by the adjustment derived from the red-giant oscillation universal pattern. Different narrow filters centered on different pure ℓ = 1 pressure modes are indicated with different line styles. They allow us to measure a local g-mode frequency spacing in each filter. |
| Open with DEXTER | |
Deriving an estimate ΔTobs of ΔT1 from the spacings δνg,1 is then direct. Owing to avoided crossings, ΔTobs is close to but less than ΔT1 (Althaus et al. 2010; Beck et al. 2011; Bedding et al. 2011). This is called mode bumping and results from the fact that the mixed modes around νn,1 present necessarily smaller spacings than pure g modes since the mixing of the g modes with one p mode gives one supernumerary mixed mode per Δν frequency interval, as shown in Beck et al. (2011). The ratio ΔT1/ΔTobs ≃ 1.15 is derived from the examination, when possible, of the g-mode spacing far from the expected p mode, assuming as in Bedding et al. (2011) that this spacing is unperturbed by the mode bumping and corresponds to the asymptotic g-mode spacing. The ratio differs from the value obtained with the Kepler data, since the frequency resolutions and the analysis methods are different. First, the frequency resolution is 2.5 times less fine for CoRoT data; as a consequence, the influence of the mode bumping is smoother. Second, and more important, the envelope autocorrelation method is able to derive a mean value of the spacing in a wider frequency range than the method given in Bedding et al. (2011) thanks to the Δν/2-broad filter used to select the mixed modes. This helps to enhance the contribution of non-bumped mixed modes.
When relaxing the condition expressed by Eq. (A.2), the method can be applied to search for rotational splittings, with ultra-narrow filters centered on individual mixed modes. This search was unfortunately negative for CoRoT red-giant spectra.
 |
Fig. A.2
Mean period spacings measured around the expected pure ℓ = 1 pressure modes of the target CoRoT 100752538. Vertical lines indicate the error bars on each individual measurement. |
| Open with DEXTER | |
© ESO, 2011
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


