Probing the dust properties of galaxies up to submillimetre wavelengths

M. Galametz; S. C. Madden; F. Galliano; S. Hony; G. J. Bendo; M. Sauvage

doi:10.1051/0004-6361/201014904

Home

All issues

Volume 532 (August 2011)

A&A, 532 (2011) A56

Full HTML

Free Access

Issue		A&A Volume 532, August 2011


Article Number		A56
Number of page(s)		18
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/201014904
Published online		21 July 2011

A&A 532, A56 (2011)

II. Dust-to-gas mass ratio trends with metallicity and the submm excess in dwarf galaxies

M. Galametz¹, S. C. Madden¹, F. Galliano¹, S. Hony¹, G. J. Bendo² and M. Sauvage¹

¹ Laboratoire AIM, CEA, Université Paris Diderot, IRFU/Service d’Astrophysique, Bât. 709, 91191 Gif-sur-Yvette, France
e-mail: mgalamet@ast.cam.ac.uk
² Jodrell Bank Centre for Astrophysics, University of Manchester, Alan Turing Building, Manchester, M13 9PL, UK

Received: 30 April 2010
Accepted: 4 April 2011

Abstract

Aims. We are studying the effects of submm observations on the total dust mass and thus dust-to-gas mass ratio measurements.

Methods. We gather a wide sample of galaxies that have been observed at submillimeter (submm) wavelengths to model their spectral energy distributions using submm observations (>160 μm) and then without submm observational constraints in order to quantify the error on the dust mass when submm data are not available. Our model does not make strong assumptions on the dust temperature distribution to precisely avoid submm biaises in the study. Our sample includes 52 galaxies observed at submm wavelengths. Out of these, 9 galaxies show an excess in submm which is not accounted for in our fiducial model, most of these galaxies being low-metallicity dwarfs. We chose to add an independant very cold dust component (T = 10 K) to account for this excess.

Results. We find that metal-rich galaxies modelled with submm data often show lower dust masses than when modelled without submm data. Indeed, these galaxies usually have dust SEDs that peaks at longer wavelengths and require constraints above 160 μm to correctly position the peak and sample the submillimeter slope of their SEDs and thus correctly cover the dust temperature distribution. On the other hand, some metal-poor dwarf galaxies modelled with submm data show higher dust masses than when modelled without submm data. Using submm constraints for the dust mass estimates, we find a tightened correlation of the dust-to-gas mass ratio with the metallicity of the galaxies. We also often find that when there is a submm excess present, it occurs preferentially in low-metallicity galaxies. We analyse the conditions for the presence of this excess and find a relation between the 160/850 μm ratio and the submm excess.

Key words: galaxies: ISM / galaxies: dwarf / infrared: ISM / dust, extinction

© ESO, 2011

1. Introduction

Interstellar medium (ISM) dust is formed in the ejected elements of dying stars. The location of the actual formation of dust grains, whether in the ejecta or farther away in the ISM, is still debated. Within the ISM, dust undergoes constructive processes of accretion or coagulation (Stepnik et al. 2003; Hirashita & Omukai 2009) or destructive/disruptive processes of vaporisation, fragmentation, erosion and shattering (Jones et al. 1994, 1996). Dust grains are, moreover, incorporated in the formation of new stars through gravitational collapse of gas and dust clouds. Dust grains also participate in the synthesis of molecules on their surface (e.g. Hasegawa & Herbst 1993; Vidali et al. 2004), leading to the formation of giant molecular clouds within the galaxy. Dust finally plays a key role in the overall emission of a galaxy since it absorbs stellar and ionized gas radiation to re-emit it from infrared (IR) to submillimeter (submm) wavelengths, thus shaping its overall spectral energy distibution (SED). Dust thus enables us to have access to the most embedded star forming regions of a galaxy which makes it an indirect but reliable tracer of its star formation. Dust grains are thus, at the same time, relics as well as engines of the evolution of the galaxy.

The ISO and Spitzer telescopes have, in the last few years, opened up the view of the interstellar dust in mid-infrared (mid-IR) to far-infrared (far-IR) wavelengths. They enabled us to improve our knowledge of the dust properties of the ISM such as the distribution of the different dust components (polycyclic aromatic hydrocarbons (PAHs), silicate, graphite) and how they are affected by metallicity (Galliano et al. 2008; Engelbracht et al. 2008; Bendo et al. 2008; Muñoz-Mateos et al. 2009).

Many studies have also been performed to investigate the relation between the dust-to-gas mass ratio (D/G) and metal enrichment of galaxies, the D/G of a galaxy being the main output of dust evolution models and a crucial key to understand the cycle of matter within galaxies. Early studies suggested that the D/G should be proportional to the metallicity of the galaxy (Franco & Cox 1986). Investigations in the Milky Way (MW) found a D/G of ~ 10^-2 for our galaxy (Sodroski et al. 1997). Further analysis into depletion of metals from the ISM or into comparisons of dust extinction versus hydrogen column densities have both shown that the D/G of the MW falls within the range of 1 − 5 × 10^-2 (see Whittet 2003; Krügel 2003, 2008, for more complete details). To investigate the relation between the metallicity and the D/G, Lisenfeld & Ferrara (1998) studied a broad sample of dwarf irregular (dIrrs) and blue compact dwarfs (BCDs) from InfraRed Astronomical Satellite (IRAS) observations at 60 and 100 μm. A logarithmic correlation between D/G and the oxygen abundance was found for the dIrrs: 12 + log (O/H) ∝ (0.52 ± 0.25) × log (M_dust/M_HI), but no relation was found for the BCDs which are more actively forming stars. Therefore, they observed that metals are less effectively incorporated into dust in dwarf galaxies than in more metal-rich galaxies. Using the Spitzer Infrared Nearby Galaxies Survey sample (SINGS), Engelbracht et al. (2008) also found a steep decrease of the D/G from solar metallicity to a metallicity of 8 and note that the D/G seems to flatten out at low metallicity. With the same sample, Muñoz-Mateos et al. (2009) showed that the D/G decreases with galactocentric radius. Bendo et al. (2010) also compare radial variations in the D/G with the oxygen abundance gradients and found a good correspondence, although the D/G radial variations seems to be steeper. Recent studies in the low-metallicity Magellanic Clouds have shown that their D/G are lower than that estimated for more metal-rich environments (Bernard et al. 2008; Gordon et al. 2009), consistent with what should be expected from the previous relation between the D/G and the metallicity.

James et al. (2002), using JCMT/SCUBA observations at 850 μm observations, concluded that the fraction of metals incorporated into dust was a universal constant, that is to say similar for dwarf and giant galaxies, which was in contradiction to the Lisenfeld & Ferrara (1998) conclusions. They also noted that their D/G mass ratios estimated with submm observations are usually higher than those previously estimated by Lisenfeld & Ferrara (1998) for the same galaxies. Galliano et al. (2003, 2005) also showed that taking the very cold dust traced in some low metallicity galaxies by SCUBA or MAMBO, the dust-to-metals ratios are closer to the Galactic value. Galametz et al. (2009) present the SED models of 4 low-metallicity galaxies observed with the APEX/LABOCA instrument at 870 μm and noticed that the dust masses estimated from their models increase when using the submm constraints. On the contrary, Draine et al. (2007) found that the dust masses of the subset of their SINGS sample observed with SCUBA, which are metal-rich galaxies, are rather unaffected by submm constraints and that omitting the submm data only moderately increases the D/G. Nevertheless, Vlahakis et al. (2005) used the SCUBA Local Universe Galaxy Survey (SLUGS) to confirm that most of the dust mass of their galaxies was contained in cold grains. Willmer et al. (2009) completed the coverage of the far-IR/submm SED of the SLUGS sample with Spitzer data and found that these galaxies show flatter νF_ν(160 μm)/νF_ν(850 μm) slopes than the SINGS sample in which galaxies with large amounts of cold dust seem to be under-represented.

Many issues thus still remain open to correctly characterize the D/G with metallicity, among which is the basic question of the accurate quantification of the total dust mass of a galaxy and the real impact of submm constraints in the assessment of this mass. To complicate the mass determination issue, there have been findings of excess emission in the submm wavelength regime (Galliano et al. 2003; Dumke et al. 2004; Galliano et al. 2005; Bendo et al. 2006a; Marleau et al. 2006; Galametz et al. 2009; Grossi et al. 2010; O’Halloran et al. 2010; Israel et al. 2010; Bot et al. 2010, among others).

Several hypotheses have be studied to explain this excess by a variation of the dust emissivity in that submm regime:

Models of Meny et al. (2007) and observations of Dupac et al. (2003) found an effective decrease in the submm emissivity index as the dust temperature increases. Shetty et al. (2009), however, express caution in the inverse temperature – β interpretation, showing that flux uncertainties, especially in the Rayleigh-Jeans regime, can affect the results for the SED fits as far as temperature and emissivity are concerned. It is still not clear what would be the nature of this new grain population or which processes could lead to their predominance in dwarf galaxies. Recently, Paradis et al. (2009) interpreted the increase of the far-IR emissivity in molecular clouds of the Milky Way containing cold dust by fractal aggregates of individual amorphous grains. They note that an increase of a factor of 3 − 4 in the dust emissivity is required to explain the unusually low dust temperatures observed by dust aggregation. This explanation of a submm excess by grain coagulation was already suggested by Bazell & Dwek (1990) (theorethical approach) and Stepnik et al. (2001) (using the baloon-borne experiment ProNaos). We note that this study is limited to solar metallicity environments for now. Serra Díaz-Cano & Jones (2008) also note that graphite can not reproduce the carbonaceous grain sputtering in interstellar shock waves and cautionned the use of graphite in dust models. They proposed that hydrogenated amorphous carbon could be the most probable form of carbonaceous grain material. Amorphous carbons have a lower emissivity index which could be responsible for a flattening of the SED at submm wavelength compared to current SED models using graphite (i.e. Meixner et al. 2010; Galametz et al. 2010). This scenario alone would nevertheless be unable to reproduce the knee observed in the submm regime of the SEDs of some low-metallicity galaxies observed at 450 and 850 μm such as II Zw 40 (see Fig. 3).

Other explanations try to explain the excess usually observed beyond 400 μm by a different population of grains:

Lisenfeld et al. (2001) and studies of Zhu et al. (2009) on extreme extragalactic environments suggested that the submm excess could originate from an enhanced very small grain abundance with an emissivity index β = 1. Ferrara & Dettmar (1994) showed that “spinning dust” located in the ionized gas of many galaxies were producing radio emission. Studies by Anderson & Watson (1993), Draine & Lazarian (1998), Hoang et al. (2010), Silsbee et al. (2011) or the recent Planck results (Planck Collaboration 2011a) aimed to characterise this component which explains most of the 10 − 100 GHz emission, also called the anomalous foreground. Ysard & Verstraete (2010) recently suggested that their peak frequency could depend on different parameters (radiation field intensity, size distribution of the dust species, dipole moment distribution, physical parameters of the gas phases etc.) and thus that spinning dust emission could be responsible for the excess at submm wavelengths observed in some galaxies, as recently suggested by Bot et al. (2010) for the Large Magellanic Cloud. Spinning dust emission being generated by very rapidly spinning and assymetric small dust grains, PAHs are often proposed as possible carriers. However, this assumption seems to be in contradiction with the lack of PAH features observed in low-metallicity galaxies in which submm excess is usually detected.

This excess could finally be interpreted as a very cold ( ≤ 10 K) dust component (e.g. Galliano et al. 2003, 2005; Galametz et al. 2009). This latter hypothesis could explain the break observed in the submm regime of some SEDs, especially in low-metallicity galaxies. However, its use in SED models usually implies a significant increase of the total dust mass, with more than 50% of the total dust mass residing in this very cold component, leading to unrealistic D/G in some galaxies (e.g. Dumke et al. 2004; Bendo et al. 2006b), if we are taking into account the total gas reservoir detected.

The ISO and Spitzer telescopes offered a vision of the IR emission limited to 160 μm and thus do not place constraints on the bulk of the coldest (<15 K) dust of the galaxies, that could represent a large amount of the dust mass of galaxies. For many galaxies, the Herschel telescope, more specifically the SPIRE instrument observing from 250 to 500 μm, will better constrain the submm slope and thus help to disentangle between those scenarios. The issues discussed here will continue to be of concern throughout the Herschel, Planck and ALMA era, especially for low-metallicity objects not detected. Thus, this study lays the ground work for an eventual broader study from which these future data can build on.

We perform a systematic study of the dust SEDs of galaxies spanning of a wide range of metallicities with the following objectives:

1)
compare the estimates of the total dust mass of the galaxieswhen the SED modelling has submm constraints, to the dustmasses determined when the submm observations are not used(as if they are not available);
2)
using only the sample modeled with submm data, to have a reliable dust mass, determine the D/G as a function of metallicity and compare with chemical evolution models;
3)
identify the galaxies of the sample which show a submm excess.

This paper is organised as follows: in Sect. 2, we describe the preliminary study we perform on the D/G as a function of metallicity by gathering dust and gas masses from the literature for a large sample of galaxies. in Sect. 3, we describe the common SED modelling technique we apply to remodel a subsample of these galaxies in a unique way with and without submm constraints. Finally, in Sect. 4, we analyse the differences obtained in the dust masses found with or without submm constraints and analyse the conditions under which a submm excess is found in galaxies and relate this to the metallicity. We finally summarize the main conclusions of the study in Sect. 5.

2. Genesis of our study

For this section, we perform a preliminary study based on data directly taken from the literature, in particular, the dust masses.

2.1. The sample

We have gathered published dust and gas masses of a broad sample of galaxies, some of them observed with submm telescopes, to study the relation of D/G with metallicity. The dust and gas masses used in this preliminary study are published in:

Lisenfeld & Ferrara (1998): this sample groups together dwarf irregular galaxies (dIrrs) and BCDs. Their SEDs were performed using only IRAS data and a single temperature, modified black body model. Their dust mass estimates are thus considered as lower limits to the total dust masses of the galaxies.
James et al. (2002): in this sample, the submm observations were performed with JCMT/SCUBA at 850 μm. They fitted their data with the Dunne & Eales (2001) two-component modified blackbodies to derive the total dust mass of their galaxies.
Hirashita et al. (2008): this sample of eight low-metallicity galaxies was observed with AKARI at 65, 90, 140 and 160 μm. They derived a total mass of dust for their galaxies from the far-IR emission using a single temperature modified blackbody model, using the mass absorption coefficient of dust grains taken from Hildebrand (1983).
Draine et al. (2007): their sample (SINGS, see Kennicutt et al. 2003) includes spirals, ellipticals, starburst galaxies and both metal-rich and metal-poor galaxies. Their dust SED modelling use the Li & Draine (2001) dust properties and is performed with Spitzer IRAC and MIPS data, with some of their galaxies observed with SCUBA at 450 or/and 850 μm.
Engelbracht et al. (2008): their galaxies, observed with Spitzer, cover a wide range of metallicity values (from 12 + log (O/H) = 7.1 for SBS 0335-052 to 8.85 for IC 342). Their dust masses are estimated using the standard formula and the absorption coefficients from Li & Draine (2001).
Galliano et al. (2008): a subset of their sample had been observed with SCUBA 450 μm and/or 850 μm. All of their SED models included either the Spitzer/IRS spectra or the ISOCAM spectra for optimum contraints in the mid-IR. Their model includes a detailed decomposition of dust emission into its gas-phase components.
Galametz et al. (2009): their sample contains 3 low-metalllicity sources observed with the Spitzer telescope and LABOCA, a 870 μm multi-channel bolometer array available on the APEX telescope in Chile.

In these papers, the gas masses are estimated using Hi 21 cm line measurements and the H₂ mass determined from CO observations, when available.

Fig. 1

Dust-to-gas mass ratio as a function of oxygen abundance. Black crosses show the Lisenfeld & Ferrara (1998) sample of blue compact galaxies and dwarf irregulars. Purple asterisks show the Engelbracht et al. (2008) sample using Spitzer data. Blue squares indicate the James et al. (2002) galaxies. Green circles show the galaxies of the SINGS survey (Draine et al. 2007) for which metallicity is already published. Orange upward triangles are the Galliano et al. (2008) sample, blue downward triangles are the Hirashita et al. (2008) sample. Stars finally indicate the location of the three low-metallicity galaxies Haro 11, NGC 1705 and Mrk 1089 of Galametz et al. (2009). Filled triangles, squares, circles or stars indicate when submm data were used in the SED modelling to estimate the total dust mass of the SED. The solid line and the dotted line are the predictions of the dust formation models from Edmunds (2001): the solid line shows a model in which dust is produced in low and intermediate mass stars while the dotted line shows the model in which supernovae play an important role in the production of dust. The gray stripe is the expectation of the one-zone, single-phase chemical evolution model of Dwek (1998) presented in Galliano et al. (2008). The dashed line shows the linear regression of the whole sample. The D/G errors can be significant for many galaxies but should not exceed ± 50% (the ± 50% error bars are plotted on the bottom right part of the plot).

2.2. The relation between the dust-to-gas ratio and metallicity

Figure 1 shows the D/G of these galaxies as a function of metallicity. We overlay several chemical evolution models on this figure: the one-zone single-phase chemical evolution model of Dwek (1998) presented in Galliano et al. (2008) and the dust formation models of Edmunds (2001). Edmunds (2001) note that they adopt a less detailed quasi-analytic model compared to Dwek (1998). Their models include mantle growth in the ISM and take into account the grain core production in both supernovae and giant stars. These two modes of dust formation are plotted in Fig. 1. The solid line corresponds to dust produced in low and intermediate mass stars and the dotted line corresponds to dust production strongly affected by the role of supernovae.

The filled symbols localise the galaxies for which dust masses are estimated using submm constraints. These galaxies tend to follow the Edmunds (2001) and Dwek (1998) models and clearly differ from the linear regression performed with the whole sample (dashed line), i.e. which also include galaxies that were not observed at submm wavelengths. We particularly noticed that low-metallicity galaxies (12 + log (O/H) < 8.5) whose dust masses were estimated with submm constraints (filled symbols) have higher D/G than galaxies modelled without submm constraints (empty symbols, crosses or asterisks). This could imply that for dwarf galaxies, the use of submm constraints leads to higher dust mass predictions. We further investigate this behaviour in this study.

2.3. The limitations of the samples

Of course, these various samples do not necessarily have any selection criteria in common. Some of the surveys were deliberately targeting dwarf galaxies yet others are covering a wider variety of galaxies. For instance, the SINGS sample is designed with a broad range of galaxies evenly filling a three-parameter space defined by morphology, infrared luminosity and L_FIR/L_optical. The dust models and SED fitting procedure used to derive D/G are different from one sample to another, which could lead to biases in the analysis and interpretation. Moreover, all of the galaxies used in this broad sample have not been observed at submm wavelengths, data that are necessary to put constraints on the coldest phases of the dust which could represent a large amount of the total dust mass. Such a global study should quantify the total gas mass in a uniform manner. We discuss this issue in Sect. 4.2.1.

In conclusion, analyzing the dust and gas masses of these galaxies directly given by the literature as one broad collection should be limited. We decided 1) to reprocess this analysis using a common realistic SED model to avoid biases in comparing galaxies analysed with different SED models; 2) to restrict our study to galaxies observed at submm wavelengths to determine, for a set of fixed dust properties (emissivity, composition), the influence of submm constraints on the estimates of the total dust mass of the galaxies. Thus we use a subsample of the galaxies from Fig. 1 in the following study, namely galaxies which have submm observations.

3. The SED models

3.1. The wavelength coverage

From the previous full sample described in Sect. 2, we only keep galaxies for which submm data are available, namely observational constraints beyond 200 μm. The restricted sample is presented in Table 1 and gathers subsamples of the James et al. (2002), Draine et al. (2007), Galliano et al. (2008) and Galametz et al. (2009) samples.

Metallicities, distances and submm 450 and/or 850 (or 870) μm observations for this subsample are summarized in Table 1.

Table 1

Description of the sample and dust mass estimates with and without submm data.

3.1.1. Submm flux densities

Most of the submm data we used are flux densities at 450 and/or 850 μm from SCUBA or 870 μm from LABOCA. A few galaxies of our sample were not observed with SCUBA or LABOCA but with other submm instruments. M 83 was observed at 540 μm with the 4-m telescope at Cerro Tololo Inter American Observatory (Hildebrand et al. 1977). NGC 1068 was observed at 350 μm and 390 μm, respectively with the Submm High Angular Resolution Camera (SHARC) (Benford 1999) and with the University of Hawaii 2.2-m telescope at the Mauna Kea Observatory (Hildebrand et al. 1977). NGC 891 was observed at 350 and 1300 μm, with the 3-m Infrared Telescope Facility (IRTF) and the 88′′ telescope of the University of Hawaii on Mauna Kea (Chini et al. 1986). Finally, IC 342 was observed at 1mm with the Palomar 5-m telescope (Elias et al. 1978). Only an upper limit was derived for this galaxy.

We would also like to warn the reader about the quality of the submm fluxes derived for some of the SINGS galaxies used in this paper. Indeed, Draine et al. (2007) warned that the galaxy NGC 6946 was scan mapped with SCUBA and that the data processing could have removed some extended emission for this galaxy, leading to an underestimate of submm fluxes. Furthermore, in the case of NGC 1097, SCUBA observations only cover the galaxy center and the total submm fluxes were estimated by inferring how much flux resides in the outer regions not observed, assuming a constant MIPS-to-submm ratio (Dale et al. 2007). This assumption could be incorrect if radial color variations are present. SCUBA maps of NGC 3521, NGC 3627, NGC 4536 and NGC 7331 also have small field of views. The submm fluxes presented in Dale et al. (2007) should therefore be used with caution in a global analysis of the galaxies.

3.1.2. Optical and infrared flux densities

2MASS data constrain the stellar contribution of the SEDs. 2MASS flux densities are taken from the 2MASS Large Galaxy Atlas (Jarrett et al. 2003), Galametz et al. (2009) and Dale et al. (2007). Spitzer/IRAC and MIPS flux densities are used to sample the infrared part of the SED, when available. The Spitzer flux densities used in the following study are also given in Dale et al. (2007), Engelbracht et al. (2008) and Galametz et al. (2009). For the SINGS galaxies used in this paper and for which far-IR data are critical when submm data are not available, the Spitzer data enable us to sample both the peak position and the beginning of the submm slope. For the Galliano et al. (2008) sample, Spitzer/IRS spectral information is, in most cases, available and used in our modelling. These spectra are presented in Galliano et al. (2008).

We use the best available IRAS fluxes. The IRAS flux densities of the Draine et al. (2007) galaxies were obtained from SCANPI and the IRAS High Resolution Image Restoration Atlas (HIRES; Surace et al. 2004). Those of the James et al. (2002) sample are coming from the IRAS Revised Bright Galaxy Sample (Sanders et al. 2003), HIRES for the galaxies NGC 3994 and NGC 3995 and from the IRAS Faint Source Catalog (Moshir & et al. 1990) for NGC 4670. The IRAS flux densities of Galliano et al. (2008) and Galametz et al. (2009) galaxies are finally obtained from the IRAS Faint Source catalogue and the IRAS catalog of Point Sources (IPAC 1986). The choice of the IRAS data is of little influence on the dust masses we derive from the SED models. We finally note that there is no systematic difference between the wavelength coverage of dwarf galaxies compared to higher metallicity galaxies.

3.2. The building blocks of our fiducial SED model

The SED of a galaxy synthesizes the emission at each wavelength of its different components: H ii regions, molecular clouds, diffuse ISM etc. The SED fits obtained from any model are dependant on the assumptions we make a priori about parameters such as radiation field or dust properties. Despite this dependance, valuable comparisons can be made from the study of different galaxies using the same SED modelling method.

We first consider that the sources of IR emission are the dust grains (PAHs, silicate, graphite) and the stellar continuum. Our SED modelling approach uses realistic intrinsic dust properties and is commonly used in the litterature (Dale & Helou 2002; Paradis et al. 2009; Whaley et al. 2009). The properties of silicate and grapite grains, namely their size distribution and chemical composition, are the standard and up-to-date properties of the Bare-Gr-S dust model Zubko et al. (2004). We emphasis that this model is consistent with the recent results of Draine et al. (2007) and the DustEM model of Compiègne et al. (2011).We assume that the dust particles are thus a mixture of grains with solar depletion constraints. The optical properties of the silicate and graphite grains are taken from Weingartner & Draine (2001) and Laor & Draine (1993) respectively¹. In order to better constrain the SED in the mid-IR range, we introduce two free parameters to model the PAH emission: the PAH charge fraction (f_PAH +) and the PAH-to-dust mass ratio (f_PAH), normalised to the Galactic value of 0.046. The PAH and PAH+ properties (e.g. the absorption efficiencies) are taken from Draine & Li (2007). When observations are lacking 8 μm measures and to avoid a degeneracy in the modelling, this f_PAH parameter is fixed to 0.5 (which means half the Galactic value). This choice does not significantly influence the total dust mass derived from the models. The total mass of dust M_dust is a free parameter of our modelling.

Fig. 2

Emission of silicate, graphite, neutral and ionized PAHs for different values of U.

We adopt the spectral shape of the Galactic diffuse ISM interstellar radiation field (ISRF) determined by Mathis et al. (1983). Previous studies have shown that the form of the global ISRF is different from normal or dusty galaxies to low-metallicity galaxies (e.g. Madden et al. 2006), an effect attributed to the lower dust attenuation and thus the larger mean free path length of the ionizing photons in low-metallicity ISM and the predominance of massive stars in those environments. Nevertheless, the shape of the ISRF does not influence the far-IR to submm regime of the SED and thus the total dust mass derived (see Galametz et al. 2009). The radiation field indeed mainly affects the emission of the non-equilibrium grains that do not significantly contribute to the dust mass.

The SED is multiplied by a dimensionless scaling factor U, with U = 1 corresponding to a radiation field of the local solar neighborhood value of 2.17 × 10^-5 W m^-2 (Mathis et al. 1983). To describe the various environments within which the various components of the ISM reside, we combine the individual SEDs using the prescription defined in Dale et al. (2001). This parametrisation of the analytical form of the temperature distribution has been widely adopted to describe the ISRF in galaxies, for example by Dale & Helou (2002), Galliano et al. (2008), Paradis et al. (2009), among others. It assumes a power-law distribution of the dust mass over a wide range of interstellar radiation heating intensities and conservatively links the hot and cold emission in galaxies: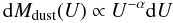 $d M_{dust} (U) \propto U^{- α} d U$ $\begin{equation} {\rm d}M_{\rm dust}({\it U}) \propto {\it U} ^{-\alpha}{\rm d}U \end{equation}$ (1)where M_dust is the dust mass heated by the radiation field, U its intensity and α the coefficient of the power law describing the contributions of the individual SEDs (also a free parameter of our model).

Radiation field intensities are ranging between the two free parameters U_min and U_max. The behavior of the emission of the different dust components as a function of U are plotted in Fig. 2. We note that Draine et al. (2007) used a similar parametrisation but add a “diffuse ISM” component with a unique intensity factor U = U_min. They choose to restrain this parameter to values ≥ 0.7 as an ad hoc measure to avoid invoking large dust masses when the submm slope of the SED is not constrained. This assumption is further discussed in Sect. 4.1.

Finally, we subtract the stellar contribution to the SED in the mid-IR using 2MASS and the Spitzer/IRAC 3.6 μm bands. We model the contribution of old stars using the stellar evolution program PEGASE (Fioc & Rocca-Volmerange 1997), assuming that the stellar population has undergone an instantaneous burst 5 Gyr ago. We adopt the Salpeter Initial Mass Function: N(M) dM ∝ M^-1.35 dM (Salpeter 1955), and an initial metallicity of Z = Z_⊙. The mass of old stars M_oldstars is a free parameter of our modelling. The choice of the IMF does not particularly influence our study since we are only fitting the IR and do not want to necessarily quantify the mass of old stars. We finally note that no radio component was introduced in the modelling compared to the similar model of Galliano et al. (2008).

In summary, the free parameters of our modelling are:

M_dustthe total mass of dust;
f_PAHthe PAHs-to-dust mass ratio (normalised to the Galactic value);
f_PAH +the ionized PAHs-to-total PAHs mass ratio;
αthe index describing the fraction of dust exposed to a given intensity;
U_minthe minimum heating intensity;
U_maxthe maximum heating intensity;
M_oldstarthe mass of old stars.

The overall modelling is an iterative process. We compute the temperature distribution of the dust grains heated by the absorption of the stellar radiation. The IR emission is then precalculated for each dust grain (different sizes, different properties) and each intensity U. The sum of these discrete contributions leads to a global SED model of the galaxy: 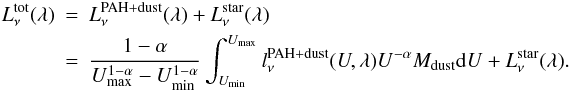$\begin{matrix} L_{ν}^{tot} (λ) & = & L_{ν}^{PAH + dust} (λ) + L_{ν}^{star} (λ) \\ = & \frac{1 - α}{U_{\max}^{1 - α} - U_{\min}^{1 - α}} \int_{U_{\min}}^{U_{\max}} l_{ν}^{PAH + dust} (U,λ) U^{- α} M_{dust} d U + L_{ν}^{star} (λ) . \end{matrix}$ $\begin{eqnarray} L^{\rm tot}_{\nu} (\lambda) & =& L^{\rm PAH+dust}_{\nu} (\lambda) + L^{\rm star}_{\nu}(\lambda) \nonumber \\ & =& \frac{1-\alpha}{U_{\rm max}^{1-\alpha}-U_{\rm min}^{1-\alpha}}\int_{U_{\rm min}}^{U_{\rm max}} l^{\rm PAH+dust}_{\nu}(U,\lambda)U^{-\alpha}M_{\rm dust}{\rm d}U+L^{\rm star}_{\nu}(\lambda). \end{eqnarray}$ (2)with $\begin{matrix} l_{ν}^{PAH + dust} (U,λ) & = & f_{PAH} [L_{ν}^{PA H^{0}} (U,λ) (1 - f_{PAH +}) \\ + L_{ν}^{PAH +} (U,λ) f_{PAH +}] \\ + L_{ν}^{graphites} (U,λ) + L_{ν}^{silicates} (U,λ) . \end{matrix}$ $\begin{eqnarray} l^{\rm PAH+dust}_{\nu}(U,\lambda) & =& f_{\rm PAH}[L^{PAH^0}_{\nu}(U,\lambda)(1-f_{\rm PAH+})\nonumber \\ &&\quad+ L^{\rm PAH+}_{\nu}(U,\lambda)f_{\rm PAH+}] \nonumber \\ & &\quad + L^{\rm graphites}_{\nu}(U,\lambda)+L^{\rm silicates}_{\nu}(U,\lambda). \end{eqnarray}$ (3)Both IRAS and Spitzer bands are color-corrected. The IRAS fluxes are corrected using a ν × F_ν convention. The Spitzer bands are corrected using the convention described on the Spitzer website².

Finally, all data are weighted with respect to the density of their neighbours. The model obtained is integrated within each filter and compared to observed values using a χ² minimisation based on the Levenberg-Marquardt algorithm (least squares fitting routines): $χ^{2} = \sum_{i} (\frac{λ_{i + 1} - λ_{i - 1}}{2 λ_{i}}) {[\frac{L_{ν}^{obs} (λ_{i}) - L_{ν} (λ_{i})}{Δ L_{ν}^{obs} (λ_{i}) / 2}]}^{2}$ $\begin{equation} {\chi^2}=\sum_i\left(\frac{ \lambda_{i+1}-\lambda_{i-1}}{2\lambda_i}\right)\left[\frac{ L_{\nu}^{\rm obs}(\lambda_i)-L_{\nu}(\lambda_i)}{\Delta L_{\nu}^{\rm obs}(\lambda_i)/2}\right]^2 \end{equation}$ (4)where $Δ L_{ν}^{obs}$ $\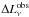hbox{$\Delta L _{\nu}^{\rm obs}$}$ (λ_i) is the error on the luminosity at a given wavelength.

3.3. Modelling the submm excess

Most of the galaxies of our sample can be fit with our SED model up to submm wavelengths. Nevertheless, for 9 galaxies (namely NGC 1569, NGC 1140, He 2-10, II Zw 40, NGC 4303, NGC 2903, NGC 7674, NGC 1705 and Haro 11), our model can not fit together the far-IR measures and the elevated submm fluxes and an excess at submm wavelengths is detected. Those galaxies are mostly low-metallicity dwarf galaxies. Such excess is often reported while modelling the SEDs of low-metallicity galaxies (Galliano et al. 2003; Dumke et al. 2004; Galliano et al. 2005; Bendo et al. 2006a; Marleau et al. 2006; Galametz et al. 2009; Grossi et al. 2010; O’Halloran et al. 2010; Israel et al. 2010; Bot et al. 2010).

We note that Li & Draine (2001) modified the standard silicate emissivity at λ > 250 μm in order to match the average high Galactic latitude dust emission and the Galactic “submm excess” observed with DIRBE/FIRAS. In this paper, we use the Zubko et al. (2004) model that fits the same constraints. The submm excess detected in our 9 galaxies may have the same origin as the Galactic submm excess, but the amplitude of the excess observed in the Milky Way is much smaller than observed in dwarf galaxies.

This paper will assume that the excess is due to cold dust and explore the consequences of this hypothesis on the global properties (total dust mass and D/G) of those 9 galaxies.For these 9 galaxies, we thus add an independent thermal cold dust component to our fiducial model. The luminosity of the cold dust component is calculated using: $\begin{matrix} L_{ν}^{CD} (λ) & = & M_{CD} κ_{ν, CD} {(\frac{λ_{0}}{λ})}^{β} (4 π B_{ν} (λ, T_{CD})) \\ = & M_{CD} \frac{(π a^{2} Q_{0})}{(4 / 3 π a^{3} ρ)} {(\frac{λ_{0}}{λ})}^{β} (4 π B_{ν} (λ, T_{CD})) \\ = & M_{CD} 3 π (\frac{1}{ρ}) (\frac{Q_{0}}{a}) λ_{0}^{β} [λ^{- β} B_{ν} (λ, T_{CD})^{]} \end{matrix}$ $\begin{eqnarray} L_{\nu}^{\rm CD}(\lambda) & = & M_{\rm CD} ~ \kappa_{\nu,{\rm CD}} ~ \left(\frac{\lambda_0}{\lambda}\right)^{\beta} ~ (4 \pi B_{\nu}(\lambda,T_{\rm CD})) \nonumber \\ & = & M_{\rm CD} ~ \frac{( \pi a^2 Q_0 )}{(4/3~\pi a^3 \rho)} ~ \left(\frac{\lambda_0}{\lambda}\right)^{\beta} (4 \pi B_{\nu}(\lambda,T_{\rm CD})) \nonumber \\ & = & M_{\rm CD} ~ 3 \pi ~ \left(\frac{1}{\rho}\right) ~\left(\frac{Q_0}{a}\right) ~ \lambda_0^{\beta} ~ \left[\lambda^{- \beta} B_{\nu}(\lambda,T_{\rm CD})\right] \end{eqnarray}$ (5)where B_ν is the Planck function, T_CD the cold dust temperature, β the emissivity coefficient. We adopt λ₀ = 100 μm for the reference wavelength. We assume graphitic values for the mass density of the grains ρ = 2.5 × 10³ kg m^-3 (close to the mass density of carbonaceous grains of 2.2 × 10³ kg m^-3 of Draine & Li 2007) and the absorption coefficient Q₀/a = 150 cm^-1 at λ₀, with a, the radius of the grain. We are studying an effect which is difficult to constrain completely with one or two submm fluxes.

Fig. 3

SED models of the galaxies for which an excess at submm wavelengths is detected. The SEDs modelled with submm data are indicated by the black lines while the dashed black lines indicates the model obtained when submm data are omitted in the modelling. Observational constraints are superimposed (filled circles). When the error bars are not shown, the errors are smaller than symbols. The thick orange line shows the IRS spectrum used in the SED modelling when available. The open circles indicate the expected modelled fluxes integrated over the instrumental bands. The green, red and blue lines respectively distinguish the stellar, the warm dust and the cold dust contributions to the SED determined with submm data.

Fig. 3

continued.

The lack of constraints forces us to fix the temperature and the dust emissivity index of this blackbody to conservative values.

Temperature –Galliano et al. (2003, 2005) and Marleau et al. (2006) suggest that their submm excess observed in low-metallicity galaxies could be explained by the presence of cold dust distributed in small and dense clumps and modelled the excess with an independant cold dust component with temperatures between 5 and 10 K. We tried modeled the 9 galaxies with a cold dust component with T > 10 K (ex: 15 K). In most cases, this leads to fits with higher chi-square values. When the 450 μm measure is available, the model has difficulty to fit the peak of the SED and the 450 μm data together and usually leads to a SED model that overestimates the 450 μm data. The temperature choice influences the dust mass derived from our modelling and we decide to fix the cold dust component temperature to 10 K. Using 10 K (and not < 10 K) dust also prevents us from requiring excessive cold dust.

Emissivity –A flattening of the submm slope is often observed when 450 + 850 or 870 μm measurements are available (see Fig. 3). As suggested by several hypothesis to explain the submm excess and reviewed in the introduction of this paper, an increase of the emissivity at submm wavelengths is expected to explain the flattening of the submm slope. Moreover, Galliano et al. (2003, 2005) and Galametz et al. (2009) modeled the submm excess they detected with a very cold dust component and found that an emissivity index of 2, as commonly used to describe the submm slope of SEDs (i.e. Dunne & Eales 2001; Draine & Li 2007) leads to unrealistically high dust masses. (For instance, Galametz et al. 2009,found that dust masses were multiplied by a factor of 6 − 7 when using β = 2 in lieu of 1.) We conservatively adopt the value β = 1. We fix our absorption to the model of Li & Draine (2001), which may deviate when a dust emissivity index of 1 (and not the standard emissivity of 2) is used. We assume that this value would still be applicable here.

The SEDs of the 9 galaxies showing a submm excess and modelled with an extra cold dust component are presented in Fig. 3. We already want to note that those galaxies only constitute a small subset of our sample and global relations studied in the following should not be affected by those objects. Those galaxies are marked by red symbols in the following plots.

Fig. 4

a) Total dust mass estimated with submm observations versus total mass of dust estimated without submm observations. The line shows the 1:1 relation. Squares indicate the James et al. (2002) galaxies. Circles indicate the galaxies of the SINGS survey (Draine et al. 2007) for which metallicity is already published. Triangles are the Galliano et al. (2008) sample and stars indicate the location of the three galaxies Haro 11, NGC 1705 and Mrk 1089 of Galametz et al. (2009). Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added. b) Evolution of the ratio of the total mass of dust estimated with and without submm data as a function of the oxygen abundance of the galaxy.

4. Analysis

4.1. Dust mass estimates with submm observations

We apply our SED modelling technique to the observational constraints we gathered. We derive dust mass estimates with all the data including the submm data, and another time omitting the submm data, which normally means that the observations stop at 160 μm. To quantify the errors on our dust masses for each SED solution, we produce a grid of 100 randomly modified observational constraints, allowing the observational fluxes to vary within their error bars, following a Gaussian distribution around their reference value. Dust masses and errors are summarized in the last column of Table 1.

We also test the presence of the mid-IR spectroscopic observations (e.g. ISO or Spitzer IRS) on the dust mass deduced without submm, to study the influence of submm data on the submm slope. We run our model with and without the mid-IR spectrum and without data beyond 200 μm. We find no strong differences nor systematic increase or decrease of the total dust mass deduced when a mid-IR spectrum is added to constrain the SED, as long as there are at least a few observations at mid-IR wavelengths (i.e. IRAC and MIPS 24 μm or IRAS 25 μm).

In Fig. 4a, we show the values of the dust mass estimated with submm data vs. the dust mass estimated without submm data. Figure 4b presents the ratio of these two quantities as a function of metallicity. Both figures demonstrate that, for dusty massive galaxies, the dust mass tends to be higher when submm measures are omitted. We also note that errors on the dust mass of galaxies (as given in Table 1) can be significant when submm data are omitted, especially for dustier galaxies.

In the case when submm data is lacking, there is indeed a risk that the SED procedure invokes a large mass of cool dust. Fig. 5 illustrates this effect on the galaxy NGC 337 modelled with (solid line) and without (dashed line) the 850 μm SCUBA flux. The submm slope of the SED is reasonably sampled when the submm flux is available and the total dust mass decreases by a factor of 8 for this galaxy. This systematic overestimate of the dust masses mostly affects metal-rich galaxies. Indeed, their SEDs usually peak at longer wavelengths compared to the low-metallicity galaxies. The 160 μm flux is thus no longer sufficient to fully sample the dust SED peak and constrain the submm slope.

Fig. 5

Total SED of the galaxy NGC 337 using the 850 μm SCUBA flux (solid line) and not using the submm information (dashed line). Observational constraints are superimposed (filled circles). Open circles are the expected modelled fluxes integrated over the instrumental bands. Green and red lines respectively distinguish the stellar and the dust contributions of the SED.

The SCUBA/LABOCA fluxes constrain the submm slope of our SEDs and more particularly the minimum intensity U_min. This parameter is directly linked to the cold dust mass (see Fig. 2 and the influence of ⟨ U ⟩ in the emission of silicate and graphite) and thus significantly influences the total dust mass derived. An overestimate of U_min will systematically lead to an underestimate of the dust mass. Figure 6 shows the evolution of U_min parameter if submm observations are used in the modelling. The galaxies showing a submm excess do not appear on this plot. We observe a tighter dispersion of this parameter when submm data are used in the modelling. The small values of this parameter when submm observations are omitted lead to the high dust mass we derive in some cases. A similar study on the U_min parameter has been performed by Draine et al. (2007). They found that the dust masses of their SINGS-SCUBA sample is rather unaffected by the use of submm constraints. For the same galaxies, we find, on the contrary, that the dust masses we derive without using submm data can be significantly higher than those obtained using submm data. Our model assumes a power-law distribution of the dust mass over interstellar radiation heating intensities. The SED model used in Draine et al. (2007) includes both this parametrisation and a “diffuse” dust component heated by a single radiation field with an intensity of U = U_min which describes most of the far-IR/submm emission of their galaxies. They also chose to restrict their radiation fields to intensities U_min ≥ 0.7 as an ad hoc measure to avoid their model invoking a large mass of cold dust heated by weak starlight when submm observations are not available. The boundaries of the minimum heating intensity range chosen by Draine et al. (2007) are shown in the shaded region in Fig. 6. The restriction of the U_min interval seems to be consistent with their objects, and for most of the metal-rich galaxies of our sample.

Fig. 6

Minimum heating intensity derived from the SED model using submm data compared to minimum heating intensity determined without submm data. The orange line indicates the 1:1 relation. The dashed lines define the limits Draine et al. (2007) used as boundaries for their minimum heating intensity U_min. We remind the reader that our model solutions are obtained with U_min as a free parameter. For convention on symbols, see Fig. 4. Limiting U_min to 0.7 avoids an overestimate of the dust mass but removes the possibility of low temperature radiation fields.

However, as noted in the Draine et al. (2007) study, the SINGS-SCUBA galaxy sample could be biased in favor of increased dust mass and associated star formation. The restriction on the U_min parameter would not be valid in systems containing a large amount of cold dust heated by weaker stellar light. This assumption could lead, in a systematic way, to an underestimate of the dust mass of those environements when submm data are not available and should be used with caution in some galaxies.

Indeed, we find that for some low-metallicity galaxies of our sample, the dust masses estimated without submm observations are, on the contrary, lower than those determined with submm data (Fig. 4b). This increase of the total dust mass while using submm data was already discussed in James et al. (2002). They observed some of the galaxies presented in Lisenfeld et al. (2001) with SCUBA and noticed an increase of the total dust mass of their galaxies when submm data are used. Indeed, the Lisenfeld et al. (2001) study was performed based on IRAS 60/100 μm fluxes only and could have missed cold dust at longer wavelengths and thus underestimated the total dust mass. For most of the low-metallicity galaxies of our sample, the restriction of the U_min parameter when submm data are not available is an unsatisfactory solution, since such a bias leads to an underestimate of the total dust mass. In those environments, submm data are crucial to trace the coldest phases of dust and also detect, if present, a possible submm excess.

In conclusion, when comparing the results unconstrained to those with the proper submm data, we find that the uncertainty on the dust mass is non-trivial and systematic, depending on metallicity of the object. Without submm constraints, our fit of the SEDs will give higher mass for metal-rich galaxies and lower masses for low-metallicity galaxies.

In Fig. 4, we finally note that our modelling of the submm excess (which includes a modified blackbody with T = 10 K – red symbols) does not systematically lead to an increase of the dust mass estimate of a galaxy compared to that estimated omitting submm data . The slope of the trend (i.e. the correlation coefficients) observed in Fig. 4b is, furthermore, not affected by the addition of galaxies in which a submm excess is detected.

4.2. The dust-to-gas mass ratio relation with metallicity

4.2.1. The gas masses and metallicities

Values and references of the gas masses of our galaxies are given in Table 1. Both atomic and molecular gas masses are given when available in the literature and gas masses were evaluated using the same distances as those used to derive the dust masses and quoted in Table 1. We determine the molecular gas masses using the canonical galactic X_CO factor of 2.3 × 10²⁰ cm^-2/K km s^-1 of Strong et al. (1988) (Table 1, Value _Gal). The conversion factor from CO to H₂ (X_CO) in galaxies depends on the metallicity (Wilson 1995; Israel 1997, 2000; Barone et al. 2000; Boselli et al. 2002; Strong et al. 2004; Leroy et al. 2005). Boselli et al. (2002) studied X_CO in normal late-type galaxies and derived X_CO factors ranging from 10²⁰ cm^-2/K km s^-1 in giant spirals to 10²¹ cm^-2/K km s^-1 in dwarf irregulars. They conclude that using a constant X_CO factor to derive the molecular gas mass from CO observations could lead to an underestimation of a factor ~ 10. We use the relation from Boselli et al. (2002) to estimate X_CO for each galaxy depending on its metallicity and rescale the molecular gas masses (Table 1, Value _B02): 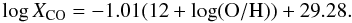$\log X_{CO} = - 1.01 (12 + \log (O / H)) + 29.28.$ $\begin{equation} \log X_{\rm CO} = -1.01 (12 + \log({\rm O/H})) + 29.28. \end{equation}$ (6)The metallicities of the galaxies are given in Table 1 and were estimated in the different papers using standard R₂₃ methods³, except in some cases discussed in Sect. 4.2.2. We would like to warn the reader about the current debate on the correct way to estimate the metallicity of a galaxy. For instance, Pilyugin & Thuan (2005) discuss the problem of empirical calibrations performed with strong oxygen line intensities-oxygen abundances and propose revised methods to estimate the metallicity (see Moustakas et al. 2010, for applications on the Spitzer/SINGS sample). These different methods will not affect the general trend of our sample but could, nevertheless, introduce a systematic offset in our metallicity values.

Fig. 7

a) Dust-to-gas mass ratio as a function of oxygen abundance for our restricted sample of galaxies that were observed at submm wavelengths. For the convention on symbols, refer to Fig. 4. Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added. In this plot, the dust masses of the galaxies are derived from our SED models without introducing submm observational constraints. The solid line and the dotted line are the predictions of the dust formation models from Edmunds (2001). The gray stripe is the expectation of the one-zone, single-phase chemical evolution model of Dwek (1998) presented in Galliano et al. (2008). Both models are presented in Sect. 2. The dashed line is the linear regression of the broad sample of Sect. 2 where all galaxies, including those without submm data, are used. b) Same but the dust masses of the galaxies are derived from our SED models using submm observational data. Labeled galaxies are discussed in Sect. 4.1. Error bars refer to errors in the dust mass estimates and do not take the gas mass errors into account. c) We gather the two previous plots to emphasize how the D/G “moves” (dot-dash vertical lines) in the diagram when submm data are used to estimate the dust mass in the SED modelling.

4.2.2. A revised D/G relation

Figure 7 shows the D/G as a function of oxygen abundance. More precisely, the D/G is estimated using the dust masses calculated without submm fluxes in Fig. 7a and then recalculated using the submm data in Fig. 7b. The error bars indicate the errors on the dust masses. We separate the two plots for clarity. Figure 7c gathers information from Figs. 7a and b. The dot-dash vertical lines indicate how galaxies “move” on the D/G axis when submm measures are used in the dust mass estimation and clearly show that for dustier galaxies, submm data significantly affect the total dust mass estimates by shifting the dust masses to lower values. The predictions of the Edmunds (2001) and Dwek (1998) models presented in Sect. 2 are indicated on the plots. We also overlay the linear regression (dashed line) which was determined from our original broad sample of galaxies (Sect. 2 and Fig. 1).

Our sample restricted to galaxies observed at submm wavelength does not follow the regression of the original big sample presented in Fig. 1. The D/G vs. metallicity relation, in fact, now tends to flatten toward lower metallicity when submm data are used in the dust mass estimates, with D/G values of low-metallicity galaxies systematically higher using submm data than those determined without submm data. Furthermore, the use of submm data significantly tightens the D/G vs. metallicity relation. In order to quantify the scatter in both plots, we calculate the standard deviation of log(D/G) in the three metallicity bins Z = [8.2, 8.5], Z = [8.5, 8.8] and Z = [8.8, 9.1]. The standard deviation is equal to 0.55, 0.44 and 0.72 in those different metallicity bins when submm data are omitted in the SED modelling to determine the total dust mass. Those values decrease to 0.34, 0.32 and 0.5 if submm data are used, consistent with the visual impression of a tightening in the D/G vs. metallicity relation.

We note that galaxies modeled with an extra cold dust component (red symbols) do not affect the global relation. Unfortunately, the current observations are still not sufficient to discriminate between the two models of Edmunds (2001), mainly due to the lack of low-metallicity galaxies observed at submm wavelengths because of the difficulty to perform such observations. Submm observations from Planck and newly available ground based submm instruments (e.g. SCUBA-2, LABOCA) will be necessary to observe more low-metallicity environments at better sensitivty. Furthermore, the Herschel Guarantee Time Key Program, Dwarf Galaxy Survey (PI: S. Madden), is dedicated to the observation of a wide range of low-metallicity environments with the far-IR to submm PACS and SPIRE instruments. These observations will enable us to extend our knowledge on the D/G vs. metallicity relation to lower metallicities, using 70 to 500 μm data to constrain the peak and the submm slope of the SEDs.

4.2.3. Outlying galaxies

In this section, we focus on the galaxies that deviate from the relation between the D/G and oxygen abundance.

MCG+02-04-025 – The H₂ mass could not be estimated for the galaxy due to the lack of CO observations for this galaxy. The estimated D/G is thus an upper limit.

M 51 – This galaxy has an unusually “cold” global SED (Fig. 8). Applying only IRAS data, the SED modelling gives much lower total mass of dust but the use of Spitzer data, especially the 160 μm of MIPS already significantly increases the dust mass, thus increases the D/G. There are still difficulties in estimating an average metallicity due to the extension of the galaxy and the fact that metallicity usually varies as a function of radius for spiral galaxies (e.g. Phillipps & Edmunds 1991; Issa et al. 1990). For M51, Moustakas & Kennicutt (2006) also estimated the metallicity to be 12 + log (O/H) = 8.7 using Pilyugin & Thuan (2005) but their estimate reaches 9.2 using the McGaugh (1991) strong-line calibration of the R₂₃. A higher metallicity would, in fact, make the galaxy move rightward, close to the James et al. (2002) relationship but we prefer to keep the value 8.7 estimated by Bresolin et al. (2004), which is based on high-quality Hii region observations and calculated in the arms of the galaxy, where star-forming regions are concentrated. Nevertheless, M 51 could have a strong gradient of metallicity that affects its position on this plot.

Fig. 8

SED models of the galaxies M 51, M 83, IC 342 and NGC 3190. The SEDs modelled with submm data are indicated by the black lines. Dashed lines indicates the model obtained when submm data are omitted. Observational constraints are superimposed (filled circles). When the error bars are not shown, the errors are smaller than symbols. The thick orange line shows the IRS spectrum used in the SED modelling when available. The open circles indicate the expected modelled fluxes integrated over the instrumental bands. The green and red lines respectively distinguish the stellar and dust contributions.

M83 – The SED of this galaxy is plotted in Fig. 8. This galaxy is surrounded by a very large Hi envelope, with a radius > 125 kpc – 6.5 times the optical radius (Huchtmeier & Bohnenstengel 1981). The total Hi mass of this envelope was estimated to be 2 × 10¹⁰ M_⊙ (Tilanus & Allen 1993). The Hi mass of Table 1 only accounts for that included in the photometric apertures used to estimate the fluxes we use in the SED modelling to derive the total mass of dust. The low D/G we derive is thus not due to an overestimation of the Hi mass. Lundgren et al. (2004) studied the kinematics of molecular gas of this galaxy with CO observations performed at the SEST and estimate the total gas mass, including H₂ and Hi to be ~ 7.8 × 10⁹ M_⊙, close to that used by Galliano et al. (2008) for the D/G estimate plotted in Fig. 7. The metallicity used in this paper (12 + log (O/H) = 9.2) was determined by Webster & Smith (1983) using the R₂₃ method used in our study. Engelbracht et al. (2008) recently re-estimated the oxygen abundance of M 83 with the direct electron-temperature (Te) method applied to individual H ii regions (Skillman et al. 1998) and found 12 + log (O/H) = 8.62. This metallicity would thus bring the galaxy closer to the model predictions.

IC 342 – The submm constraint we used is the 1 mm flux and is an upper limit (Fig. 8), meaning that the dust mass we estimated is also an upper limit too. The location of IC 342 at low Galactic latitudes makes it difficult to study because of its large extent. It is affected by foreground extinction due to our Galaxy and the background subtraction issues it generates. This galaxy possesses a very peculiar optical/near-infrared shape (Galliano et al. 2008).

He 2-10 – This Blue Compact Dwarf (BCD) differs from other BCDs because of its near solar metallicity (Kobulnicky et al. 1999) and contains a relatively large amount of molecular gas (Meier et al. 2001), which is unusual for low-metallicity dwarf galaxies. Nevertheless, the metallicity of the galaxy is rather uncertain due to the lack of measured [O III] λ4363.

NGC 3190 – No H₂ mass estimates have been obtained in NGC 3190. The value presented on the plot is thus an upper limit. An amount of molecular gas equivalent to that of the Hi mass would lead to a higher D/G. The SED of this galaxy is plotted in Fig. 8.

Haro 11 – Using Spitzer data, Engelbracht et al. (2008) note that Haro 11 possesses an intriguing SED, dominated by the mid-IR emssion and showing weak emission at 70 μm. A D/G of ~10^-3 would be expected, using the Galliano et al. (2008) chemical model, for a galaxy with such metallicity (12 + log (O/H) = 7.9). We find an unusually high dust/Hi mass ratio < 2 × 10^-1, using the Hi mass upper limit of 10⁸ M_⊙ given by Bergvall et al. (2000). This high value could suggest that the scenario of cold dust may be physically inappropriate for this galaxy if the totalgas reservoir is estimated correctly. In the particular case of Haro 11, Galametz et al. (2009) show that, even taking all the possible upper limits of gas into account in the total gas mass estimate (H₂ derived from CO(1 − 0) observations in Bergvall & Östlin 2002; or from [CII] measurement in Bergvall et al. 2000; ionized gas mass estimate in Östlin et al. 1999), the galaxy is an outlier of the Schmidt law (Kennicutt 1998), relation which relates the star formation rate of a galaxy to its total IR luminosity. They derived a “missing gas mass” of ~10¹⁰M_⊙, a value consistent with that independantly derived using the dust mass. A large amount of gas is thus not “detected” by current observations in Haro 11.

The molecular gas mass, commonly inferred from the CO tracer, is very difficult to estimate in low-metallicity galaxies. The CO to H₂ conversion factor is usually calibrated with cold ( ≈ 12 K) Galactic clouds (solar metallicity) and may not necessarily resemble the physical conditions of low-metallicity objects. Some studies show that this conversion factor can be far higher in low-metallicity environments than in metal-rich ones (Wilson 1995; Madden et al. 1997; Leroy et al. 2005, 2007). Due to the high excitation and the paucity of the dust in low-metallicity environments, CO is generally a poor tracer of molecular gas. The opacity of the H₂ and CO lines can create a condition where the molecules are self-shielded, an effect which can be efficient for hiding H₂ in regions where CO is photodissociated. Cold dust could reside in small shielded molecular/cold dust cores embedded in [CII] emitting envelopes where UV radiation would hardly penetrate. High values of L([CII])/L(CO) have indeed been found in low-metallicity galaxies sometimes up to 10 times higher than normal dusty starbursts or spirals (Poglitsch et al. 1995; Madden et al. 1997; Madden 2000; Hunter et al. 2001; Galliano et al. 2003). This high ratio of observed L([CII])/L(CO) generally suggests a clumpy ISM. It is, for instance, the case in the galaxy Haro 11 discussed above, with L([CII])/L(CO) ≥ 10⁵ (Bergvall et al. 2000). CO is also known to be a poor tracer of dense gas. Further observations of the far-IR fine structure lines will be done with the Herschel Dwarf Galaxy Survey (PI: S. Madden) to obtain a more accurate estimate of the gas content of dwarf galaxies.

4.3. Conditions for submm excess

We find that for 9 galaxies of our sample, a submm excess is detected (Fig. 3). To study the physical conditions leading to an excess emission at submm wavelengths, we plot the 850 μm flux as a function of the 160 μm flux (Fig. 9a). When the 160 μm or 850 μm fluxes are not directly observed, values are derived from the SED models we generated. Red symbols indicate galaxies where a submm excess is detected (SEDs modelled with an additional very cold dust component). While other galaxies follow a tight correlation, galaxies with submm excess show a 160 − 850 correlation that seems to be shifted. Figure 9b shows the 160 μm/850 μm flux density ratios as a function of metallicity. The 160 μm to 850 μm flux ratio is lower for galaxies in which a submm excess is detected (most of the time below ~65, see the red symbols) but no clear correlation is found at this point with metallicity. Nevertheless, the sample is clearly lacking very low-metallicity galaxies (12 + log (O/H) < 7.9), which prevents us from studying the submm excess with an unbiaised metallicity coverage.

We also note that a submm excess is detected in dustier galaxies (NGC 4303 and NGC 2903). In NGC 4303, the lack of far-IR measures between 100 and 450 μm does not enable us to correctly sample the peak of the dust SED and the submm slope. Observations sampling this wavelength range (with Herschel for instance) would be required to confirm the excess in this galaxies. The dwarf galaxy He 2-10, which has a nearly solar metallicity, also shows a submm excess. We note that our fit has difficulties to fit the 100 and 160 μm fluxes for this galaxy as well as for NGC 2903. However, the 850 μm flux clearly exhibits an excess compared to the submm slope sampled by the 160 and 450 μm fluxes.

Fig. 9

a) Correlation between the 160 μm and the 850 μm fluxes of the galaxies. A linear regression is overlaid (dashed line). When the galaxies do not possess an observational constraint at 850 μm, the flux value was deduced from the SED model. b) 160 μm/850 μm flux density ratios as a function of metallicity. For convention on colors and symbols, see Fig. 4. Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added.

Submm excess is most evidently detected in low-metallicity galaxies. If we assume that this excess is due to very cold dust, could it be possible that very cold dust is more apparent in dwarf galaxies compared to more metal rich galaxies? Indeed, on average, global SEDs of blue compact galaxies generally peak at relatively short wavelengths (30 − 60 μm), compared to more quiescent, higher metallicity sources. For a metal-rich galaxy, peaking around 100 μm for example, the submm emission at 870 μm should be very difficult to distinguish from the emission of warm grains while in the case of a low-metallicity galaxy peaking shortward, the separation between two types of grain population temperatures, one warm and one very cold, may be easier to detect. We test this idea by modelling four galaxies with different metallicities (M 51, M 82, SBS 0335-052, Haro 11) with an independent very cold dust component, supposing that the mass and the properties (β, T) of the very cold dust (VCD) is the same, thus M_VCD/M_dust = const. These tests lead to the inverse conclusion. The difference between the temperature of dust grains and the very cold grains is smaller in galaxies having higher metallicities. With a constant mass ratio, the emissivity ratio between the two components is thus higher in the dustier galaxies than in low-metallicity galaxies. If a very cold dust component exists with the same characteristics, our test here implies that it should be more evident as submm excess in dustier galaxies rather than in low-metallicity galaxies.

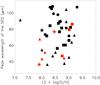Fig. 10

Wavelength of the peak of the dust emission as a function of metallicity. For convention on colors and symbols, see Fig. 4. Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added.

The SEDs of low-metallicity galaxies usually show relatively “warm” (f₇₀/f₁₆₀ > 1) dust temperatures. For these “warm” galaxies, the temperature of the SED is then well constrained but the flux at 870 μm will significantly influence the total amount of dust while in “colder” galaxies (f₇₀/f₁₆₀ < 1), the SED model without submm data already leads to a large amount of dust. We plotted the ratio of the dust mass obtained with submm data over the dust mass without submm observations as a function of f₇₀/f₁₆₀ but did not find any correlation for our galaxies. We also plot the wavelength of the IR peak as a function of metallicity in Fig. 10. We do not clearly detect a correlation between the position of the dust emission peak and the metallicity of the galaxy. However, we note that a submm excess is not detected when the SED peaks above 85 μm. In some galaxies, the fact that a submm excess is not detected could also be due to an underestimate of the submm fluxes due to background subtraction issues (e.g. NGC 6946) or a lack of coverage of the complete emission in the submm observations (e.g. NGC 1097). Having several observational constraints in the submm slope of the SED would also help us to be more confident in the presence of submm excess: as shown in Fig. 3, most of the galaxies where submm excess was detected were actually observed at different submm wavelengths (at 450 and 850 μm). The addition of observational constraints will be a solution to avoid biases and sample a possible knee in the submm emission or a smoothness of the far-IR/submm slope, that could favor one of the two possible theories to explain the excess: a cold dust population or a change in the dust emissivity.

Herschel is currently observing in the 70 to 500 μm wavelength range and will not only bring the lacking data to sample the SED but also the high resolution crucial to understand the origin of cold dust emission in galaxies. Herschel is also probing the coldest phases of dust in high-z galaxies. Santini et al. (2010) recently found that the dust content of their high-z submillimeter galaxies appears to be far higher than that expected from their metallicity, probably revealing different dust properties or dust growth mechanism in those environments. We caution the accuracy of dust masses estimates made without rest-frame submm observations. Accurate dust mass estimates in high-z galaxies are necessary to enable us to study the evolution of metals through cosmic time.

5. Discussion and conclusions

We have gathered observational constraints of a large sample of galaxies from low-metallicity to metal-rich environments to study the influence of submm measurements on the total dust mass estimates and the consequences on the D/G. We use mid-IR and far-IR data from the literature. Our second sample is confined to galaxies having submm data beyond 160 μm, namely 850 or 870 μm, and sometimes 450 μm, leading to a broad sample of 52 galaxies with submm observations. Submm observations probe the coldest dust grain emission of galaxies, a component that could account for a significant fraction of the total dust mass of galaxies.

We model the SEDs of our sample and derive their total dust masses with and without submm fluxes to determine the importance of submm data in determining the dust SEDs. We find that submm data are crucial to accurately determine the dust masses. The error bars on the total dust mass estimates significantly decrease when using submm constraints. We show that submm data systematically affect the dust mass derived for our galaxies for different reasons: a) for dustier galaxies for which the SED usually peaks at longer wavelengths, submm fluxes are crucial to position the peak and the Rayleigh-Jeans slope of their SED and avoid an overestimation of the total dust mass of the galaxy usually observed when the SED modelling is performed using data at wavelengths only as long as 160 μm; b) the submm wavelength domain sometimes harbours an excess that may imply a large amount of very cold dust. The lack of submm constraints will lead, in those cases, to an underestimate of the total dust mass of the galaxies. We caution the estimate of dust masses made without submm observations.

We find that for 9 galaxies of our sample, mostly low-metallicity galaxies, our fiducial model can not fit the mid-IR to submm observational constraints and a submm excess is detected. We model this excess with a very cold dust component, using a temperature of 10 K and a dust grain emissivity index of 1. The early results of Herschel also highlight a submm excess in dwarf galaxies (O’Halloran et al. 2010; Grossi et al. 2010). First results based on observations with the Planck mission in nearby galaxies have also lead to evidence of cold dust (Planck Collaboration 2011c). In the Magellanic Clouds, Planck Collaboration (2011b) have lead to the detection of an excess at submm/mm wavelengths. Average emissivity indexes β of 1.5 and 1.2 were found for the LMC and SMC respectively, so flatter than observed in the Milky Way. Even taking the flatter slope into account, there is still evidence for a further flattening in the submm regime for the SMC, that has been modeled with a combination of thermal and spinning dust emission.

Gathering the gas mass information for our galaxies, we estimate the D/G of our sample. We find a tightened relation between the D/G and the metallicity of the galaxies when the models take into account submm observations. This effect is present in spite of our model assumption of cold dust for the submm excess.

More submm observations of low-metallicity galaxies, which will be obtained with Herschel and Planck will extend the coverage to a broader range of metallicity and enable us to study how the D/G evolves in more metal poor environements. The spatial resolution and sensitivity of Herschel combined with current ground based instruments (for example, JCMT/SCUBA-2; APEX/Laboca) and ALMA will help us probe the submm emission of nearby galaxies in detail to better isolate the excess emission and understand the physics of the coldest phases of dust and the chemical enrichment thus drawing the global picture of the dust distribution within galaxies. While presently the nature of this submm excess seen in low metallicity environments is still not understood, the higher spatial resolution submm observations will help us disentangle the different scenarios: emission from very cold dust, possible changes in the dust grain emissivity, spinning dust etc.

¹

We also refer to Draine & Li (2007) and http://www.astro.princeton.edu/~draine/dust/dust.html where dust properties can be found.

²

IRAC: http://ssc.spitzer.caltech.edu/irac/ iracinstrumenthandbook/21/ MIPS: http://ssc.spitzer.caltech.edu/mips/mipsinstrumenthandbook/51/

³

The oxygen abundance, commonly used to estimate the metallicity, can be derived from the bright line observations and depends on the quantity [Oii]λ3727+[Oiii]λ4959,λ5007/Hβ, also called the R₂₃ parameter (Pagel et al. 1979).

Acknowledgments

We thank the referee for her/his useful comments, which helped to improve the content of this paper. We would also like to thank John Moustakas for his advice on the metallicity of some of the Spitzer SINGS galaxies and Eli Dwek for useful discussion on this work.

References

Anderson, N., & Watson, W. D. 1993, A&A, 270, 477 [NASA ADS] [Google Scholar]
Appleton, P. N., Davies, R. D., & Stephenson, R. J. 1981, MNRAS, 195, 327 [NASA ADS] [CrossRef] [Google Scholar]
Barone, L. T., Heithausen, A., Hüttemeister, S., Fritz, T., & Klein, U. 2000, MNRAS, 317, 649 [NASA ADS] [CrossRef] [Google Scholar]
Bazell, D., & Dwek, E. 1990, ApJ, 360, 142 [NASA ADS] [CrossRef] [Google Scholar]
Bendo, G. J., Dale, D. A., Draine, B. T., et al. 2006a, ApJ, 652, 283 [NASA ADS] [CrossRef] [Google Scholar]
Bendo, G. J., Buckalew, B. A., Dale, D. A., et al. 2006b, ApJ, 645, 134 [NASA ADS] [CrossRef] [Google Scholar]
Bendo, G. J., Draine, B. T., Engelbracht, C. W., et al. 2008, MNRAS, 389, 629 [NASA ADS] [CrossRef] [Google Scholar]
Bendo, G. J., Wilson, C. D., Warren, B. E., et al. 2010, MNRAS, 402, 1409 [NASA ADS] [CrossRef] [Google Scholar]
Benford, D. J. 1999, Ph.D. Thesis, California Institute of Technology [Google Scholar]
Bergvall, N., & Östlin, G. 2002, A&A, 390, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bergvall, N., Masegosa, J., Östlin, G., & Cernicharo, J. 2000, A&A, 359, 41 [NASA ADS] [Google Scholar]
Bernard, J.-P., Reach, W. T., Paradis, D., et al. 2008, AJ, 136, 919 [NASA ADS] [CrossRef] [Google Scholar]
Bernloehr, K. 1993, A&A, 270, 20 [NASA ADS] [Google Scholar]
Bettoni, D., Galletta, G., & García-Burillo, S. 2003, A&A, 405, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonatto, C. J., & Pastoriza, M. G. 1990, ApJ, 353, 445 [NASA ADS] [CrossRef] [Google Scholar]
Boselli, A., Lequeux, J., & Gavazzi, G. 2002, A&A, 384, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bresolin, F., Garnett, D. R., & Kennicutt, Jr., R. C. 2004, ApJ, 615, 228 [NASA ADS] [CrossRef] [Google Scholar]
Chini, R., Kreysa, E., Kruegel, E., & Mezger, P. G. 1986, A&A, 166, L8 [NASA ADS] [Google Scholar]
Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dahlem, M., Aalto, S., Klein, U., et al. 1990, A&A, 240, 237 [NASA ADS] [Google Scholar]
Dahlem, M., Ehle, M., & Ryder, S. D. 2001, A&A, 373, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
Dale, D. A., Helou, G., Contursi, A., Silbermann, N. A., & Kolhatkar, S. 2001, ApJ, 549, 215 [NASA ADS] [CrossRef] [Google Scholar]
Dale, D. A., Gil de Paz, A., & Gordon, K. D. 2007, ApJ, 655, 863 [NASA ADS] [CrossRef] [Google Scholar]
Dean, J. F., & Davies, R. D. 1975, MNRAS, 170, 503 [NASA ADS] [Google Scholar]
Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]
Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
Dumke, M., Krause, M., & Wielebinski, R. 2004, A&A, 414, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dunne, L., & Eales, S. A. 2001, MNRAS, 327, 697 [NASA ADS] [CrossRef] [Google Scholar]
Dunne, L., Eales, S., Edmunds, M., et al. 2000, MNRAS, 315, 115 [NASA ADS] [CrossRef] [Google Scholar]
Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dutil, Y., & Roy, J.-R. 1999, ApJ, 516, 62 [NASA ADS] [CrossRef] [Google Scholar]
Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
Edmunds, M. G. 2001, MNRAS, 328, 223 [NASA ADS] [CrossRef] [Google Scholar]
Elias, J. H., Ennis, D. J., Gezari, D. Y., et al. 1978, ApJ, 220, 25 [NASA ADS] [CrossRef] [Google Scholar]
Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]
Ferrara, A., & Dettmar, R. 1994, ApJ, 427, 155 [NASA ADS] [CrossRef] [Google Scholar]
Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
Franco, J., & Cox, D. P. 1986, PASP, 98, 1076 [NASA ADS] [CrossRef] [Google Scholar]
Galametz, M., Madden, S., Galliano, F., et al. 2009, A&A, 508, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Galametz, M., Madden, S., Galliano, F., et al. 2010, A&A, 518, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J.-P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
Gerin, M., Combes, F., & Nakai, N. 1988, A&A, 203, 44 [NASA ADS] [Google Scholar]
Gonzalez-Delgado, R. M., Perez, E., Diaz, A. I., et al. 1995, ApJ, 439, 604 [NASA ADS] [CrossRef] [Google Scholar]
Gordon, K. D., Bot, C., Muller, E., et al. 2009, ApJ, 690, L76 [NASA ADS] [CrossRef] [Google Scholar]
Grossi, M., et al. 2010, A&A, in press [Google Scholar]
Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
Heckman, T. M., Robert, C., Leitherer, C., Garnett, D. R., & van der Rydt, F. 1998, ApJ, 503, 646 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Helfer, T. T., Thornley, M. D., Regan, M. W., et al. 2003, ApJS, 145, 259 [NASA ADS] [CrossRef] [Google Scholar]
Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
Hildebrand, R. H., Whitcomb, S. E., Winston, R., et al. 1977, ApJ, 216, 698 [NASA ADS] [CrossRef] [Google Scholar]
Hirashita, H., & Omukai, K. 2009, MNRAS, 399, 1795 [NASA ADS] [CrossRef] [Google Scholar]
Hirashita, H., Kaneda, H., Onaka, T., & Suzuki, T. 2008, PASJ, 60, 477 [Google Scholar]
Hoang, T., Draine, B. T., & Lazarian, A. 2010, ApJ, 715, 1462 [NASA ADS] [CrossRef] [Google Scholar]
Hopkins, A. M., Schulte-Ladbeck, R. E., & Drozdovsky, I. O. 2002, AJ, 124, 862 [NASA ADS] [CrossRef] [Google Scholar]
Huchtmeier, W. K., & Bohnenstengel, H.-D. 1981, A&A, 100, 72 [NASA ADS] [Google Scholar]
Hunt, L., Bianchi, S., & Maiolino, R. 2005, A&A, 434, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hunter, D. A., van Woerden, H., & Gallagher, III, J. S. 1994, ApJS, 91, 79 [NASA ADS] [CrossRef] [Google Scholar]
Hunter, D. A., Kaufman, M., Hollenbach, D. J., et al. 2001, ApJ, 553, 121 [NASA ADS] [CrossRef] [Google Scholar]
Israel, F. 2000, in Molecular Hydrogen in Space, ed. F. Combes & G. Pineau Des Forets, 293 [Google Scholar]
Israel, F. P. 1997, A&A, 328, 471 [NASA ADS] [Google Scholar]
Israel, F. P. 2005, A&A, 438, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Israel, F. P., Wall, W. F., Raban, D., et al. 2010, A&A, 519, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Issa, M. R., MacLaren, I., & Wolfendale, A. W. 1990, A&A, 236, 237 [NASA ADS] [Google Scholar]
Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 500, 188 [NASA ADS] [CrossRef] [Google Scholar]
Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 1999, ApJ, 527, 757 [NASA ADS] [CrossRef] [Google Scholar]
James, A., Dunne, L., Eales, S., & Edmunds, M. G. 2002, MNRAS, 335, 753 [NASA ADS] [CrossRef] [Google Scholar]
Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]
Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
Klaas, U., Haas, M., Müller, S. A. H., et al. 2001, A&A, 379, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kobulnicky, H. A., & Skillman, E. D. 1997, ApJ, 489, 636 [NASA ADS] [CrossRef] [Google Scholar]
Kobulnicky, H. A., Kennicutt, Jr., R. C., & Pizagno, J. L. 1999, ApJ, 514, 544 [NASA ADS] [CrossRef] [Google Scholar]
Krügel, E. 2003, The physics of interstellar dust, ed. E. Kruegel [Google Scholar]
Krügel, E. 2008, An introduction to the physics of interstellar dust, ed. E. Krügel [Google Scholar]
Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
Leroy, A., Bolatto, A. D., Simon, J. D., & Blitz, L. 2005, ApJ, 625, 763 [NASA ADS] [CrossRef] [Google Scholar]
Leroy, A., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
Lisenfeld, U., & Ferrara, A. 1998, ApJ, 496, 145 [NASA ADS] [CrossRef] [Google Scholar]
Lisenfeld, U., Sievers, A., Israel, F., & Stil, J. 2001, Ap&SS, 277, 105 [Google Scholar]
Lundgren, A. A., Olofsson, H., Wiklind, T., & Rydbeck, G. 2004, A&A, 422, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Madden, S. C. 2000, New Astron. Rev., 44, 249 [NASA ADS] [CrossRef] [Google Scholar]
Madden, S. C., Poglitsch, A., Geis, N., Stacey, G. J., & Townes, C. H. 1997, ApJ, 483, 200 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marleau, F. R., Noriega-Crespo, A., Misselt, K. A., et al. 2006, ApJ, 646, 929 [NASA ADS] [CrossRef] [Google Scholar]
Mas-Hesse, J. M., & Kunth, D. 1999, A&A, 349, 765 [NASA ADS] [Google Scholar]
Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
McGaugh, S. S. 1991, ApJ, 380, 140 [NASA ADS] [CrossRef] [Google Scholar]
Meier, D. S., Turner, J. L., Crosthwaite, L. P., & Beck, S. C. 2001, AJ, 121, 740 [NASA ADS] [CrossRef] [Google Scholar]
Meier, D. S., Turner, J. L., & Beck, S. C. 2002, AJ, 124, 877 [NASA ADS] [CrossRef] [Google Scholar]
Meijerink, R., Tilanus, R. P. J., Dullemond, C. P., Israel, F. P., & van der Werf, P. P. 2005, A&A, 430, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Meixner, M., Galliano, F., Hony, S., et al. 2010, A&A, 518, L71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Meny, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]
Meurer, G. R., Freeman, K. C., Dopita, M. A., & Cacciari, C. 1992, AJ, 103, 60 [NASA ADS] [CrossRef] [Google Scholar]
Meurer, G. R., Staveley-Smith, L., & Killeen, N. E. B. 1998, MNRAS, 300, 705 [NASA ADS] [CrossRef] [Google Scholar]
Moshir, M., Kopan, G., Conrow, T., et al. 1990, in IRAS Faint Source Catalogue, version 2.0 [Google Scholar]
Moustakas, J., & Kennicutt, Jr., R. C. 2006, ApJ, 651, 155 [NASA ADS] [CrossRef] [Google Scholar]
Moustakas, J., Kennicutt, Jr., R. C., & Tremonti, C. A. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2009, ApJ, 701, 1965 [NASA ADS] [CrossRef] [Google Scholar]
O’Halloran, B., Galametz, M., Madden, S. C., et al. 2010, A&A, 518, L58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ondrechen, M. P., van der Hulst, J. M., & Hummel, E. 1989, ApJ, 342, 39 [NASA ADS] [CrossRef] [Google Scholar]
Östlin, G., Amram, P., Masegosa, J., Bergvall, N., & Boulesteix, J. 1999, A&AS, 137, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Otte, B., Reynolds, R. J., Gallagher, III, J. S., & Ferguson, A. M. N. 2001, ApJ, 560, 207 [NASA ADS] [CrossRef] [Google Scholar]
Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
Paradis, D., Bernard, J., & Mény, C. 2009, A&A, 506, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pérez-Montero, E., & Díaz, A. I. 2003, MNRAS, 346, 105 [NASA ADS] [CrossRef] [Google Scholar]
Petrosian, A. R., & Burenkov, A. N. 1993, A&A, 279, 21 [NASA ADS] [Google Scholar]
Phillipps, S., & Edmunds, M. G. 1991, MNRAS, 251, 84 [NASA ADS] [Google Scholar]
Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Planck Collaboration 2011a, A&A, accepted [arXiv:1101.2031] [Google Scholar]
Planck Collaboration 2011b, A&A, accepted [arXiv:1101.2046] [Google Scholar]
Planck Collaboration 2011c, A&A, accepted [arXiv:1101.2045] [Google Scholar]
Poglitsch, A., Krabbe, A., Madden, S. C., et al. 1995, ApJ, 454, 293 [NASA ADS] [CrossRef] [Google Scholar]
Ravindranath, S., & Prabhu, T. P. 2001, Ap&SS, 276, 593 [NASA ADS] [CrossRef] [Google Scholar]
Reif, K., Mebold, U., Goss, W. M., van Woerden, H., & Siegman, B. 1982, A&AS, 50, 451 [Google Scholar]
Sage, L. J., Salzer, J. J., Loose, H.-H., & Henkel, C. 1992, A&A, 265, 19 [NASA ADS] [Google Scholar]
Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
Santini, P., Maiolino, R., Magnelli, B., et al. 2010, A&A, 518, L154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sauvage, M., Thuan, T. X., & Lagage, P. O. 1997, A&A, 325, 98 [NASA ADS] [Google Scholar]
Serra Díaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
Silsbee, K., Ali-Haimoud, Y., & Hirata, C. M. 2011, MNRAS, 411, 2750 [NASA ADS] [CrossRef] [Google Scholar]
Skillman, E. D., Terlevich, E., & Terlevich, R. 1998, Space Sci. Rev., 84, 105 [NASA ADS] [CrossRef] [Google Scholar]
Smith, P. A., Brand, P. W. J. L., Puxley, P. J., Mountain, C. M., & Nakai, N. 1990, MNRAS, 243, 97 [NASA ADS] [Google Scholar]
Sodroski, T. J., Odegard, N., Arendt, R. G., et al. 1997, ApJ, 480, 173 [NASA ADS] [CrossRef] [Google Scholar]
Staveley-Smith, L., & Davies, R. D. 1987, MNRAS, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2001, in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, ed. T. Montmerle, & P. André, ASP Conf. Ser., 243, 47 [Google Scholar]
Stepnik, B., Abergel, A., Bernard, J., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Stevens, J. A., Amure, M., & Gear, W. K. 2005, MNRAS, 357, 361 [NASA ADS] [CrossRef] [Google Scholar]
Stil, J. M., & Israel, F. P. 2002, A&A, 392, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Storchi-Bergmann, T., Kinney, A. L., & Challis, P. 1995, ApJS, 98, 103 [NASA ADS] [CrossRef] [Google Scholar]
Strong, A. W., Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]
Strong, A. W., Moskalenko, I. V., Reimer, O., Digel, S., & Diehl, R. 2004, A&A, 422, L47 [Google Scholar]
Struck, C., & Smith, B. J. 2003, ApJ, 589, 157 [NASA ADS] [CrossRef] [Google Scholar]
Surace, J. A., Sanders, D. B., & Mazzarella, J. M. 2004, AJ, 127, 3235 [NASA ADS] [CrossRef] [Google Scholar]
Thuan, T. X., Hibbard, J. E., & Lévrier, F. 2004, AJ, 128, 617 [NASA ADS] [CrossRef] [Google Scholar]
Tilanus, R. P. J., & Allen, R. J. 1993, A&A, 274, 707 [NASA ADS] [Google Scholar]
van Zee, L., Westpfahl, D., Haynes, M. P., & Salzer, J. J. 1998, AJ, 115, 1000 [NASA ADS] [CrossRef] [Google Scholar]
Vidali, G., Roser, J. E., Manicó, G., & Pirronello, V. 2004, J. Geophys. Res. (Planets), 109, 7 [Google Scholar]
Vlahakis, C., Dunne, L., & Eales, S. 2005, MNRAS, 364, 1253 [NASA ADS] [CrossRef] [Google Scholar]
Walter, F., Weiss, A., & Scoville, N. 2002, ApJ, 580, L21 [NASA ADS] [CrossRef] [Google Scholar]
Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
Webster, B. L., & Smith, M. G. 1983, MNRAS, 204, 743 [NASA ADS] [Google Scholar]
Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
Whaley, C. H., Irwin, J. A., Madden, S. C., Galliano, F., & Bendo, G. J. 2009, MNRAS, 395, 97 [NASA ADS] [CrossRef] [Google Scholar]
Whittet, D. C. B. 2003, Dust in the galactic environment (Bristol: Institute of Physics (IOP) Publishing) [Google Scholar]
Williams, B. A., McMahon, P. M., & van Gorkom, J. H. 1991, AJ, 101, 1957 [NASA ADS] [CrossRef] [Google Scholar]
Willmer, C. N. A., Rieke, G. H., LeFloc’h, E., et al. 2009, AJ, 138, 146 [NASA ADS] [CrossRef] [Google Scholar]
Wilson, C. D. 1995, ApJ, 448, L97 [NASA ADS] [CrossRef] [Google Scholar]
Ysard, N., & Verstraete, L. 2010, A&A, 509, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Yun, M. S., & Hibbard, J. E. 2001, ApJ, 550, 104 [NASA ADS] [CrossRef] [Google Scholar]
Zhu, M., Papadopoulos, P. P., Xilouris, E. M., Kuno, N., & Lisenfeld, U. 2009, ApJ, 706, 941 [NASA ADS] [CrossRef] [Google Scholar]
Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Description of the sample and dust mass estimates with and without submm data.

In the text

All Figures

Fig. 1

Dust-to-gas mass ratio as a function of oxygen abundance. Black crosses show the Lisenfeld & Ferrara (1998) sample of blue compact galaxies and dwarf irregulars. Purple asterisks show the Engelbracht et al. (2008) sample using Spitzer data. Blue squares indicate the James et al. (2002) galaxies. Green circles show the galaxies of the SINGS survey (Draine et al. 2007) for which metallicity is already published. Orange upward triangles are the Galliano et al. (2008) sample, blue downward triangles are the Hirashita et al. (2008) sample. Stars finally indicate the location of the three low-metallicity galaxies Haro 11, NGC 1705 and Mrk 1089 of Galametz et al. (2009). Filled triangles, squares, circles or stars indicate when submm data were used in the SED modelling to estimate the total dust mass of the SED. The solid line and the dotted line are the predictions of the dust formation models from Edmunds (2001): the solid line shows a model in which dust is produced in low and intermediate mass stars while the dotted line shows the model in which supernovae play an important role in the production of dust. The gray stripe is the expectation of the one-zone, single-phase chemical evolution model of Dwek (1998) presented in Galliano et al. (2008). The dashed line shows the linear regression of the whole sample. The D/G errors can be significant for many galaxies but should not exceed ± 50% (the ± 50% error bars are plotted on the bottom right part of the plot).

In the text

	Fig. 2 Emission of silicate, graphite, neutral and ionized PAHs for different values of U.
In the text

Fig. 3

SED models of the galaxies for which an excess at submm wavelengths is detected. The SEDs modelled with submm data are indicated by the black lines while the dashed black lines indicates the model obtained when submm data are omitted in the modelling. Observational constraints are superimposed (filled circles). When the error bars are not shown, the errors are smaller than symbols. The thick orange line shows the IRS spectrum used in the SED modelling when available. The open circles indicate the expected modelled fluxes integrated over the instrumental bands. The green, red and blue lines respectively distinguish the stellar, the warm dust and the cold dust contributions to the SED determined with submm data.

In the text

	Fig. 3 continued.
In the text

Fig. 4

a) Total dust mass estimated with submm observations versus total mass of dust estimated without submm observations. The line shows the 1:1 relation. Squares indicate the James et al. (2002) galaxies. Circles indicate the galaxies of the SINGS survey (Draine et al. 2007) for which metallicity is already published. Triangles are the Galliano et al. (2008) sample and stars indicate the location of the three galaxies Haro 11, NGC 1705 and Mrk 1089 of Galametz et al. (2009). Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added. b) Evolution of the ratio of the total mass of dust estimated with and without submm data as a function of the oxygen abundance of the galaxy.

In the text

	Fig. 5 Total SED of the galaxy NGC 337 using the 850 μm SCUBA flux (solid line) and not using the submm information (dashed line). Observational constraints are superimposed (filled circles). Open circles are the expected modelled fluxes integrated over the instrumental bands. Green and red lines respectively distinguish the stellar and the dust contributions of the SED.
In the text

Fig. 6

Minimum heating intensity derived from the SED model using submm data compared to minimum heating intensity determined without submm data. The orange line indicates the 1:1 relation. The dashed lines define the limits Draine et al. (2007) used as boundaries for their minimum heating intensity U_min. We remind the reader that our model solutions are obtained with U_min as a free parameter. For convention on symbols, see Fig. 4. Limiting U_min to 0.7 avoids an overestimate of the dust mass but removes the possibility of low temperature radiation fields.

In the text

Fig. 7

a) Dust-to-gas mass ratio as a function of oxygen abundance for our restricted sample of galaxies that were observed at submm wavelengths. For the convention on symbols, refer to Fig. 4. Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added. In this plot, the dust masses of the galaxies are derived from our SED models without introducing submm observational constraints. The solid line and the dotted line are the predictions of the dust formation models from Edmunds (2001). The gray stripe is the expectation of the one-zone, single-phase chemical evolution model of Dwek (1998) presented in Galliano et al. (2008). Both models are presented in Sect. 2. The dashed line is the linear regression of the broad sample of Sect. 2 where all galaxies, including those without submm data, are used. b) Same but the dust masses of the galaxies are derived from our SED models using submm observational data. Labeled galaxies are discussed in Sect. 4.1. Error bars refer to errors in the dust mass estimates and do not take the gas mass errors into account. c) We gather the two previous plots to emphasize how the D/G “moves” (dot-dash vertical lines) in the diagram when submm data are used to estimate the dust mass in the SED modelling.

In the text

Fig. 8

SED models of the galaxies M 51, M 83, IC 342 and NGC 3190. The SEDs modelled with submm data are indicated by the black lines. Dashed lines indicates the model obtained when submm data are omitted. Observational constraints are superimposed (filled circles). When the error bars are not shown, the errors are smaller than symbols. The thick orange line shows the IRS spectrum used in the SED modelling when available. The open circles indicate the expected modelled fluxes integrated over the instrumental bands. The green and red lines respectively distinguish the stellar and dust contributions.

In the text

Fig. 9

a) Correlation between the 160 μm and the 850 μm fluxes of the galaxies. A linear regression is overlaid (dashed line). When the galaxies do not possess an observational constraint at 850 μm, the flux value was deduced from the SED model. b) 160 μm/850 μm flux density ratios as a function of metallicity. For convention on colors and symbols, see Fig. 4. Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added.

In the text

	Fig. 10 Wavelength of the peak of the dust emission as a function of metallicity. For convention on colors and symbols, see Fig. 4. Red symbols show the galaxies that present a submm excess and for which a cold dust (10 K) component with an emissivity β = 1 is added.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Anderson, N., & Watson, W. D. 1993, A&A, 270, 477 [NASA ADS] [Google Scholar]

[2] Appleton, P. N., Davies, R. D., & Stephenson, R. J. 1981, MNRAS, 195, 327 [NASA ADS] [CrossRef] [Google Scholar]

[3] Barone, L. T., Heithausen, A., Hüttemeister, S., Fritz, T., & Klein, U. 2000, MNRAS, 317, 649 [NASA ADS] [CrossRef] [Google Scholar]

[4] Bazell, D., & Dwek, E. 1990, ApJ, 360, 142 [NASA ADS] [CrossRef] [Google Scholar]

[5] Bendo, G. J., Dale, D. A., Draine, B. T., et al. 2006a, ApJ, 652, 283 [NASA ADS] [CrossRef] [Google Scholar]

[6] Bendo, G. J., Buckalew, B. A., Dale, D. A., et al. 2006b, ApJ, 645, 134 [NASA ADS] [CrossRef] [Google Scholar]

[7] Bendo, G. J., Draine, B. T., Engelbracht, C. W., et al. 2008, MNRAS, 389, 629 [NASA ADS] [CrossRef] [Google Scholar]

[8] Bendo, G. J., Wilson, C. D., Warren, B. E., et al. 2010, MNRAS, 402, 1409 [NASA ADS] [CrossRef] [Google Scholar]

[9] Benford, D. J. 1999, Ph.D. Thesis, California Institute of Technology [Google Scholar]

[10] Bergvall, N., & Östlin, G. 2002, A&A, 390, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[11] Bergvall, N., Masegosa, J., Östlin, G., & Cernicharo, J. 2000, A&A, 359, 41 [NASA ADS] [Google Scholar]

[12] Bernard, J.-P., Reach, W. T., Paradis, D., et al. 2008, AJ, 136, 919 [NASA ADS] [CrossRef] [Google Scholar]

[13] Bernloehr, K. 1993, A&A, 270, 20 [NASA ADS] [Google Scholar]

[14] Bettoni, D., Galletta, G., & García-Burillo, S. 2003, A&A, 405, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[15] Bonatto, C. J., & Pastoriza, M. G. 1990, ApJ, 353, 445 [NASA ADS] [CrossRef] [Google Scholar]

[16] Boselli, A., Lequeux, J., & Gavazzi, G. 2002, A&A, 384, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[17] Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Bresolin, F., Garnett, D. R., & Kennicutt, Jr., R. C. 2004, ApJ, 615, 228 [NASA ADS] [CrossRef] [Google Scholar]

[19] Chini, R., Kreysa, E., Kruegel, E., & Mezger, P. G. 1986, A&A, 166, L8 [NASA ADS] [Google Scholar]

[20] Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[21] Dahlem, M., Aalto, S., Klein, U., et al. 1990, A&A, 240, 237 [NASA ADS] [Google Scholar]

[22] Dahlem, M., Ehle, M., & Ryder, S. D. 2001, A&A, 373, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[23] Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]

[24] Dale, D. A., Helou, G., Contursi, A., Silbermann, N. A., & Kolhatkar, S. 2001, ApJ, 549, 215 [NASA ADS] [CrossRef] [Google Scholar]

[25] Dale, D. A., Gil de Paz, A., & Gordon, K. D. 2007, ApJ, 655, 863 [NASA ADS] [CrossRef] [Google Scholar]

[26] Dean, J. F., & Davies, R. D. 1975, MNRAS, 170, 503 [NASA ADS] [Google Scholar]

[27] Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]

[28] Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]

[29] Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]

[30] Dumke, M., Krause, M., & Wielebinski, R. 2004, A&A, 414, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[31] Dunne, L., & Eales, S. A. 2001, MNRAS, 327, 697 [NASA ADS] [CrossRef] [Google Scholar]

[32] Dunne, L., Eales, S., Edmunds, M., et al. 2000, MNRAS, 315, 115 [NASA ADS] [CrossRef] [Google Scholar]

[33] Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[34] Dutil, Y., & Roy, J.-R. 1999, ApJ, 516, 62 [NASA ADS] [CrossRef] [Google Scholar]

[35] Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]

[36] Edmunds, M. G. 2001, MNRAS, 328, 223 [NASA ADS] [CrossRef] [Google Scholar]

[37] Elias, J. H., Ennis, D. J., Gezari, D. Y., et al. 1978, ApJ, 220, 25 [NASA ADS] [CrossRef] [Google Scholar]

[38] Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]

[39] Ferrara, A., & Dettmar, R. 1994, ApJ, 427, 155 [NASA ADS] [CrossRef] [Google Scholar]

[40] Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]

[41] Franco, J., & Cox, D. P. 1986, PASP, 98, 1076 [NASA ADS] [CrossRef] [Google Scholar]

[42] Galametz, M., Madden, S., Galliano, F., et al. 2009, A&A, 508, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[43] Galametz, M., Madden, S., Galliano, F., et al. 2010, A&A, 518, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[44] Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[45] Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J.-P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[46] Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]

[47] Gerin, M., Combes, F., & Nakai, N. 1988, A&A, 203, 44 [NASA ADS] [Google Scholar]

[48] Gonzalez-Delgado, R. M., Perez, E., Diaz, A. I., et al. 1995, ApJ, 439, 604 [NASA ADS] [CrossRef] [Google Scholar]

[49] Gordon, K. D., Bot, C., Muller, E., et al. 2009, ApJ, 690, L76 [NASA ADS] [CrossRef] [Google Scholar]

[50] Grossi, M., et al. 2010, A&A, in press [Google Scholar]

[51] Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]

[52] Heckman, T. M., Robert, C., Leitherer, C., Garnett, D. R., & van der Rydt, F. 1998, ApJ, 503, 646 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[53] Helfer, T. T., Thornley, M. D., Regan, M. W., et al. 2003, ApJS, 145, 259 [NASA ADS] [CrossRef] [Google Scholar]

[54] Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]

[55] Hildebrand, R. H., Whitcomb, S. E., Winston, R., et al. 1977, ApJ, 216, 698 [NASA ADS] [CrossRef] [Google Scholar]

[56] Hirashita, H., & Omukai, K. 2009, MNRAS, 399, 1795 [NASA ADS] [CrossRef] [Google Scholar]

[57] Hirashita, H., Kaneda, H., Onaka, T., & Suzuki, T. 2008, PASJ, 60, 477 [Google Scholar]

[58] Hoang, T., Draine, B. T., & Lazarian, A. 2010, ApJ, 715, 1462 [NASA ADS] [CrossRef] [Google Scholar]

[59] Hopkins, A. M., Schulte-Ladbeck, R. E., & Drozdovsky, I. O. 2002, AJ, 124, 862 [NASA ADS] [CrossRef] [Google Scholar]

[60] Huchtmeier, W. K., & Bohnenstengel, H.-D. 1981, A&A, 100, 72 [NASA ADS] [Google Scholar]

[61] Hunt, L., Bianchi, S., & Maiolino, R. 2005, A&A, 434, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[62] Hunter, D. A., van Woerden, H., & Gallagher, III, J. S. 1994, ApJS, 91, 79 [NASA ADS] [CrossRef] [Google Scholar]

[63] Hunter, D. A., Kaufman, M., Hollenbach, D. J., et al. 2001, ApJ, 553, 121 [NASA ADS] [CrossRef] [Google Scholar]

[64] Israel, F. 2000, in Molecular Hydrogen in Space, ed. F. Combes & G. Pineau Des Forets, 293 [Google Scholar]

[65] Israel, F. P. 1997, A&A, 328, 471 [NASA ADS] [Google Scholar]

[66] Israel, F. P. 2005, A&A, 438, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[67] Israel, F. P., Wall, W. F., Raban, D., et al. 2010, A&A, 519, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[68] Issa, M. R., MacLaren, I., & Wolfendale, A. W. 1990, A&A, 236, 237 [NASA ADS] [Google Scholar]

[69] Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 500, 188 [NASA ADS] [CrossRef] [Google Scholar]

[70] Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 1999, ApJ, 527, 757 [NASA ADS] [CrossRef] [Google Scholar]

[71] James, A., Dunne, L., Eales, S., & Edmunds, M. G. 2002, MNRAS, 335, 753 [NASA ADS] [CrossRef] [Google Scholar]

[72] Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]

[73] Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]

[74] Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]

[75] Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]

[76] Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]

[77] Klaas, U., Haas, M., Müller, S. A. H., et al. 2001, A&A, 379, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[78] Kobulnicky, H. A., & Skillman, E. D. 1997, ApJ, 489, 636 [NASA ADS] [CrossRef] [Google Scholar]

[79] Kobulnicky, H. A., Kennicutt, Jr., R. C., & Pizagno, J. L. 1999, ApJ, 514, 544 [NASA ADS] [CrossRef] [Google Scholar]

[80] Krügel, E. 2003, The physics of interstellar dust, ed. E. Kruegel [Google Scholar]

[81] Krügel, E. 2008, An introduction to the physics of interstellar dust, ed. E. Krügel [Google Scholar]

[82] Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]

[83] Leroy, A., Bolatto, A. D., Simon, J. D., & Blitz, L. 2005, ApJ, 625, 763 [NASA ADS] [CrossRef] [Google Scholar]

[84] Leroy, A., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]

[85] Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]

[86] Lisenfeld, U., & Ferrara, A. 1998, ApJ, 496, 145 [NASA ADS] [CrossRef] [Google Scholar]

[87] Lisenfeld, U., Sievers, A., Israel, F., & Stil, J. 2001, Ap&SS, 277, 105 [Google Scholar]

[88] Lundgren, A. A., Olofsson, H., Wiklind, T., & Rydbeck, G. 2004, A&A, 422, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[89] Madden, S. C. 2000, New Astron. Rev., 44, 249 [NASA ADS] [CrossRef] [Google Scholar]

[90] Madden, S. C., Poglitsch, A., Geis, N., Stacey, G. J., & Townes, C. H. 1997, ApJ, 483, 200 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[91] Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[92] Marleau, F. R., Noriega-Crespo, A., Misselt, K. A., et al. 2006, ApJ, 646, 929 [NASA ADS] [CrossRef] [Google Scholar]

[93] Mas-Hesse, J. M., & Kunth, D. 1999, A&A, 349, 765 [NASA ADS] [Google Scholar]

[94] Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]

[95] McGaugh, S. S. 1991, ApJ, 380, 140 [NASA ADS] [CrossRef] [Google Scholar]

[96] Meier, D. S., Turner, J. L., Crosthwaite, L. P., & Beck, S. C. 2001, AJ, 121, 740 [NASA ADS] [CrossRef] [Google Scholar]

[97] Meier, D. S., Turner, J. L., & Beck, S. C. 2002, AJ, 124, 877 [NASA ADS] [CrossRef] [Google Scholar]

[98] Meijerink, R., Tilanus, R. P. J., Dullemond, C. P., Israel, F. P., & van der Werf, P. P. 2005, A&A, 430, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[99] Meixner, M., Galliano, F., Hony, S., et al. 2010, A&A, 518, L71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[100] Meny, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]

[101] Meurer, G. R., Freeman, K. C., Dopita, M. A., & Cacciari, C. 1992, AJ, 103, 60 [NASA ADS] [CrossRef] [Google Scholar]

[102] Meurer, G. R., Staveley-Smith, L., & Killeen, N. E. B. 1998, MNRAS, 300, 705 [NASA ADS] [CrossRef] [Google Scholar]

[103] Moshir, M., Kopan, G., Conrow, T., et al. 1990, in IRAS Faint Source Catalogue, version 2.0 [Google Scholar]

[104] Moustakas, J., & Kennicutt, Jr., R. C. 2006, ApJ, 651, 155 [NASA ADS] [CrossRef] [Google Scholar]

[105] Moustakas, J., Kennicutt, Jr., R. C., & Tremonti, C. A. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]

[106] Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2009, ApJ, 701, 1965 [NASA ADS] [CrossRef] [Google Scholar]

[107] O’Halloran, B., Galametz, M., Madden, S. C., et al. 2010, A&A, 518, L58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[108] Ondrechen, M. P., van der Hulst, J. M., & Hummel, E. 1989, ApJ, 342, 39 [NASA ADS] [CrossRef] [Google Scholar]

[109] Östlin, G., Amram, P., Masegosa, J., Bergvall, N., & Boulesteix, J. 1999, A&AS, 137, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[110] Otte, B., Reynolds, R. J., Gallagher, III, J. S., & Ferguson, A. M. N. 2001, ApJ, 560, 207 [NASA ADS] [CrossRef] [Google Scholar]

[111] Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]

[112] Paradis, D., Bernard, J., & Mény, C. 2009, A&A, 506, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[113] Pérez-Montero, E., & Díaz, A. I. 2003, MNRAS, 346, 105 [NASA ADS] [CrossRef] [Google Scholar]

[114] Petrosian, A. R., & Burenkov, A. N. 1993, A&A, 279, 21 [NASA ADS] [Google Scholar]

[115] Phillipps, S., & Edmunds, M. G. 1991, MNRAS, 251, 84 [NASA ADS] [Google Scholar]

[116] Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[117] Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[118] Planck Collaboration 2011a, A&A, accepted [arXiv:1101.2031] [Google Scholar]

[119] Planck Collaboration 2011b, A&A, accepted [arXiv:1101.2046] [Google Scholar]

[120] Planck Collaboration 2011c, A&A, accepted [arXiv:1101.2045] [Google Scholar]

[121] Poglitsch, A., Krabbe, A., Madden, S. C., et al. 1995, ApJ, 454, 293 [NASA ADS] [CrossRef] [Google Scholar]

[122] Ravindranath, S., & Prabhu, T. P. 2001, Ap&SS, 276, 593 [NASA ADS] [CrossRef] [Google Scholar]

[123] Reif, K., Mebold, U., Goss, W. M., van Woerden, H., & Siegman, B. 1982, A&AS, 50, 451 [Google Scholar]

[124] Sage, L. J., Salzer, J. J., Loose, H.-H., & Henkel, C. 1992, A&A, 265, 19 [NASA ADS] [Google Scholar]

[125] Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]

[126] Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]

[127] Santini, P., Maiolino, R., Magnelli, B., et al. 2010, A&A, 518, L154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[128] Sauvage, M., Thuan, T. X., & Lagage, P. O. 1997, A&A, 325, 98 [NASA ADS] [Google Scholar]

[129] Serra Díaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[130] Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]

[131] Silsbee, K., Ali-Haimoud, Y., & Hirata, C. M. 2011, MNRAS, 411, 2750 [NASA ADS] [CrossRef] [Google Scholar]

[132] Skillman, E. D., Terlevich, E., & Terlevich, R. 1998, Space Sci. Rev., 84, 105 [NASA ADS] [CrossRef] [Google Scholar]

[133] Smith, P. A., Brand, P. W. J. L., Puxley, P. J., Mountain, C. M., & Nakai, N. 1990, MNRAS, 243, 97 [NASA ADS] [Google Scholar]

[134] Sodroski, T. J., Odegard, N., Arendt, R. G., et al. 1997, ApJ, 480, 173 [NASA ADS] [CrossRef] [Google Scholar]

[135] Staveley-Smith, L., & Davies, R. D. 1987, MNRAS, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]

[136] Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2001, in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, ed. T. Montmerle, & P. André, ASP Conf. Ser., 243, 47 [Google Scholar]

[137] Stepnik, B., Abergel, A., Bernard, J., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[138] Stevens, J. A., Amure, M., & Gear, W. K. 2005, MNRAS, 357, 361 [NASA ADS] [CrossRef] [Google Scholar]

[139] Stil, J. M., & Israel, F. P. 2002, A&A, 392, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[140] Storchi-Bergmann, T., Kinney, A. L., & Challis, P. 1995, ApJS, 98, 103 [NASA ADS] [CrossRef] [Google Scholar]

[141] Strong, A. W., Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]

[142] Strong, A. W., Moskalenko, I. V., Reimer, O., Digel, S., & Diehl, R. 2004, A&A, 422, L47 [Google Scholar]

[143] Struck, C., & Smith, B. J. 2003, ApJ, 589, 157 [NASA ADS] [CrossRef] [Google Scholar]

[144] Surace, J. A., Sanders, D. B., & Mazzarella, J. M. 2004, AJ, 127, 3235 [NASA ADS] [CrossRef] [Google Scholar]

[145] Thuan, T. X., Hibbard, J. E., & Lévrier, F. 2004, AJ, 128, 617 [NASA ADS] [CrossRef] [Google Scholar]

[146] Tilanus, R. P. J., & Allen, R. J. 1993, A&A, 274, 707 [NASA ADS] [Google Scholar]

[147] van Zee, L., Westpfahl, D., Haynes, M. P., & Salzer, J. J. 1998, AJ, 115, 1000 [NASA ADS] [CrossRef] [Google Scholar]

[148] Vidali, G., Roser, J. E., Manicó, G., & Pirronello, V. 2004, J. Geophys. Res. (Planets), 109, 7 [Google Scholar]

[149] Vlahakis, C., Dunne, L., & Eales, S. 2005, MNRAS, 364, 1253 [NASA ADS] [CrossRef] [Google Scholar]

[150] Walter, F., Weiss, A., & Scoville, N. 2002, ApJ, 580, L21 [NASA ADS] [CrossRef] [Google Scholar]

[151] Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]

[152] Webster, B. L., & Smith, M. G. 1983, MNRAS, 204, 743 [NASA ADS] [Google Scholar]

[153] Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]

[154] Whaley, C. H., Irwin, J. A., Madden, S. C., Galliano, F., & Bendo, G. J. 2009, MNRAS, 395, 97 [NASA ADS] [CrossRef] [Google Scholar]

[155] Whittet, D. C. B. 2003, Dust in the galactic environment (Bristol: Institute of Physics (IOP) Publishing) [Google Scholar]

[156] Williams, B. A., McMahon, P. M., & van Gorkom, J. H. 1991, AJ, 101, 1957 [NASA ADS] [CrossRef] [Google Scholar]

[157] Willmer, C. N. A., Rieke, G. H., LeFloc’h, E., et al. 2009, AJ, 138, 146 [NASA ADS] [CrossRef] [Google Scholar]

[158] Wilson, C. D. 1995, ApJ, 448, L97 [NASA ADS] [CrossRef] [Google Scholar]

[159] Ysard, N., & Verstraete, L. 2010, A&A, 509, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[160] Yun, M. S., & Hibbard, J. E. 2001, ApJ, 550, 104 [NASA ADS] [CrossRef] [Google Scholar]

[161] Zhu, M., Papadopoulos, P. P., Xilouris, E. M., Kuno, N., & Lisenfeld, U. 2009, ApJ, 706, 941 [NASA ADS] [CrossRef] [Google Scholar]

[162] Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]