| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 38 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015830 | |
| Published online | 06 January 2011 | |
HIFLUGCS: Galaxy cluster scaling relations between X-ray luminosity, gas mass, cluster radius, and velocity dispersion⋆
1
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71, 53121
Bonn, Germany
e-mail: yyzhang@astro.uni-bonn.de
2
National Astronomical Observatories, Chinese Academy of
Sciences, Beijing
100012, PR
China
3
Departamento de Astronomía, Universidad de
Guanajuato, AP 144,
Guanajuato
CP
36000,
Mexico
4
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße, 85748
Garching,
Germany
5
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85741
Garching,
Germany
6
Kavli Institute for Cosmology, Cambridge and Institute of
Astronomy, Madingley
Road, Cambridge,
CB3 0HA,
UK
7
Dipartimento di Fisica dell’ Universitá degli Studi di Trieste
Sezione di Astronomia, via Tiepolo
11, 34143
Trieste,
Italy
8
INAF Osservatorio Astronomico di Trieste, via Tiepolo
11, 34143
Trieste,
Italy
Received:
28
September
2010
Accepted:
10
November
2010
We present relations between X-ray luminosity and velocity dispersion (L − σ), X-ray luminosity and gas mass (L − Mgas), and cluster radius and velocity dispersion (r500 − σ) for 62 galaxy clusters in the HIFLUGCS, an X-ray flux-limited sample minimizing bias toward any cluster morphology. Our analysis in total is based on ~1.3 Ms of clean X-ray XMM-Newton data and 13439 cluster member galaxies with redshifts. Cool cores are among the major contributors to the scatter in the L − σ relation. When the cool-core-corrected X-ray luminosity is used the intrinsic scatter decreases to 0.27 dex. Even after the X-ray luminosity is corrected for the cool core, the scatter caused by the presence of cool cores dominates for the low-mass systems. The scatter caused by the non-cool-core clusters does not strongly depend on the mass range, and becomes dominant in the high-mass regime. The observed L − σ relation agrees with the self-similar prediction, matches that of a simulated sample with AGN feedback disregarding six clusters with <45 cluster members with spectroscopic redshifts, and shows a common trend of increasing scatter toward the low-mass end, i.e., systems with σ ≤ 500 kms-1. A comparison of observations with simulations indicates an AGN-feedback-driven impact in the low-mass regime. The best fits to the L − Mgas relations for the disturbed clusters and undisturbed clusters in the observational sample closely match those of the simulated samples with and without AGN feedback, respectively. This suggests that one main cause of the scatter is AGN activity providing feedback in different phases, e.g. during a feedback cycle. The slope and scatter in the observed r500 − σ relation is similar to that of the simulated sample with AGN feedback except for a small offset but still within the scatter.
Key words: cosmology: observations / dark matter / galaxies: clusters: general / methods: data analysis / surveys / X-rays: galaxies: clusters
Appendices A–G are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Galaxy clusters have been suggested as a potential probe of the dark energy equation of state parameter (w = p/ρ, where ρ is the energy density and p is the pressure), through the evolution of the mass function (e.g., Schuecker et al. 2003; Predehl et al. 2007; Henry et al. 2009; Vikhlinin et al. 2009a,b; Mantz et al. 2010). Observational surveys select galaxy clusters by their observables rather than by their mass. Therefore, a relationship between the cluster total mass and an observable such as X-ray luminosity is required to recover the selection function of an X-ray survey in terms of cluster masses and predict the cluster mass, hence the cluster mass function. During the past, there have been a large number of studies of X-ray luminosity scaling relations along with their applications to constrain cosmological parameters in galaxy cluster surveys and the physical state of the hot intracluster medium (ICM) in galaxy clusters (e.g., Henry & Tucker 1979; Henry & Arnaud 1991; Edge & Stewart 1991; David et al. 1993; Fabian et al. 1994; Girardi et al. 1996; Mushotzky & Scharf 1997; Cavaliere et al. 1997; White et al. 1997; Markevitch 1998; Wu et al. 1998, 1999; Allen & Fabian 1998; Arnaud & Evrard 1999; Reiprich & Böhringer 2002; Ota et al. 2006; Chen et al. 2007; Zhang et al. 2006, 2008; Pratt et al. 2009; Leauthaud et al. 2010; Stanek et al. 2010). Large X-ray cosmology surveys, e.g., by eROSITA, are expected to substantially improve cosmological constraints using a large number of galaxy clusters. For eROSITA, the use of X-ray mass proxies has been proposed, specifically X-ray luminosity, to infer the total mass and construct the selection function in the forthcoming wide survey of the satellite (Predehl et al. 2007). The superb quality X-ray data in the XMM-Newton archive provide us with an excellent opportunity to calibrate the luminosity scaling relations and more clearly understand the X-ray selection method.
Simulations show that the formation of galaxy clusters is not a purely gravitational process; The galaxy velocity dispersions of clusters appear to indicate that heating is present when compared to the cold dark matter (CDM) velocity dispersion normalized to the WMAP and large-scale structure (LSS) distributions (Evrard et al. 2008). Cluster mergers not only change the cluster X-ray luminosity (e.g., Ricker & Sarazin 2001; Poole et al. 2006), but also affect the properties of the cluster galaxies (e.g., Sun et al. 2007; Smith et al. 2010). Although the hot gas and galaxies are not pure tracers of the gravitational potential of galaxy clusters, they are indeed sensitive probes of the dynamical properties of galaxy clusters, and react on different timescales during a merger in simulations (e.g. Roettiger et al. 1999). In particular, the optical information about the line-of-sight velocity of cluster galaxies complements X-ray information about the cluster morphology projected onto the sky. The luminosity – velocity dispersion (L − σ) relation of galaxy clusters is thus crucial to understanding the dynamical properties of galaxy clusters and their impact on the scaling relations and possibly the X-ray selection bias (e.g., Wu et al. 1999; Ortiz-Gil et al. 2004).
To carry out the L − σ studies, one requires a representative sample with a well-defined selection function and minimal bias toward any cluster morphology, as well as superb quality X-ray data and large amount of cluster galaxy redshifts. The HIghest X-ray FLUx Galaxy Cluster Sample (HIFLUGCS, Reiprich & Böhringer 2002) of 64 galaxy clusters selected from the ROSAT All-Sky Survey (RASS; Ebeling et al. 2000; Böhringer et al. 2004) is such a sample. In the HIFLUGCS, we analyzed all available X-ray data in the XMM-Newton archive for 63 clusters which represents nearly 4 Ms of data. After cleaning and selecting the longest observation closest to the cluster center for clusters with multiple observations, we still have ~1.3 Ms XMM-Newton data for 59 clusters. For 62 clusters in the HIFLUGCS, we obtained a sum of 13 439 cluster member galaxies based on spectroscopic redshifts and performed a careful exclusion of non-members. In the end, we were able to measure X-ray observables, combining XMM-Newton and ROSAT data, and velocity dispersion, based on 13 439 cluster members, to make a cross-calibration for 62 out of 64 clusters in the HIFLUGCS.
The outline of this paper is as follows. We describe the data analysis in Sect. 2, present the scaling relations of the 62 clusters in the HIFLUGCS in Sect. 3, compare the observational and simulated samples in Sect. 4, discuss the systematic errors in determining the velocity dispersion in Sect. 5, and summarize our conclusions in Sect. 6. Our Appendix provides extra information on the cross-calibration between XMM-Newton and ROSAT, the iron abundance versus (vs.) temperature correlation, results using either the 0.5–2 keV X-ray luminosity corrected for the presence of a cool core (≤0.2r500), or the luminosity including or excluding the cluster core, the XMM-Newton 0.7–2 keV images, and the figures illustrating systematic errors in estimates of σ. Throughout the paper, we assume that Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s-1 Mpc-1. Confidence intervals correspond to the 68% confidence level. Unless explicitly stated otherwise, we apply the BCES regression fitting method taking into account measurement errors in both variables (Akritas & Bershady 1996).
2. Data analysis
2.1. Optical data analysis and velocity dispersion
We draw the velocity of the cluster galaxies from the literature (updated until March 2010, including the compilation in Andernach et al. 2005). When there is more than one velocity per galaxy, we calculate an average1 of the measurements, excluding discordant values and those with large errors when more than one measurement is available.
Brightest cluster galaxies (BCGs) in galaxy clusters are almost invariably giant ellipticals and are more luminous than normal galaxies. The BCGs have line-of-sight velocities that are similar to the mean of their host clusters and extended stellar envelopes. We identify the BCG on the basis of its apparent magnitude and spectroscopic confirmation as a cluster member. To define a BCG position for every HIFLUGCS cluster, we made the following choices for clusters without a single dominant BCG. A0400 and A2065 have dumbbell BCGs, and A3158 and A2256 have BCG pairs, for which we place the BCG positions in the middle of the two components of indistinguishable brightness. A3266, A3391, A0576, A2634, MKW8, and IIIZw54 have dumbbell BCGs, and Coma and Hydra (A1060) have two brightest galaxies of similar brightness, for which we place the BCG position on the brighter component as the difference in the brightness is measurable. A2199 has multiple nuclei, and we place the BCG position at the brightest nucleus. We list the BCG positions in Table 1.
Offset between the X-ray flux-weighted cluster center and BCG position, velocity dispersion, and X-ray bolometric luminosity.
As most BCGs are located very near the X-ray flux-weighted cluster centers (definition see Sect. 2.3.1), we select preliminarily galaxies with spectroscopic redshifts in each cluster within an aperture of at least 1.2 Abell radius, i.e., 2.57 Mpc, centered on the BCG. For each cluster, we plot the line-of-sight velocity of the selected galaxies as a function of their projected distance from the BCG, and locate the caustic, a trumpet-shaped region, which efficiently excludes interlopers (e.g., Diaferio 1999; Katgert et al. 2004; Popesso et al. 2005; Rines & Diaferio 2006). We consider only the galaxies inside the caustic as cluster members, and exclude the others from subsequent analysis. More than 80% of the clusters have a clearly evident caustic shape. In Fig. 1, we show as an example the caustic and sky positions of the cluster galaxies in Coma, and as a poor example in S1101. There are eight clusters that have fewer than 45 cluster members with spectroscopic redshifts in the HIFLUGCS. We excluded 2A0355 and RXCJ1504 from our study since both have at most three redshifts each. We still consider the remaining six systems (i.e., A0478, NGC 1550, EXO0422, HydraA, S1101, and A2597) with >12 but <45 cluster members with spectroscopic redshifts, and highlight them in our results. We gathered a total of 13 439 cluster-member galaxies based on spectroscopic redshifts and a careful exclusion of non-members, which gives a median value of 185.5 per cluster.
 |
Fig. 1 Line-of-sight velocity vs. projected radius (left panels) and sky positions (right panels) of the selected galaxies in a rich cluster, i.e., Coma (top panels) and in a poor cluster, i.e., S1101 (bottom panels). |
For the galaxies selected as cluster members we apply the bi-weight estimator (e.g., Beers et al. 1990) to measure the velocity dispersion. The errors are estimated through 1000 bootstrap simulations. We list the number of cluster members (ngal) and the velocity dispersion (σ) of the cluster for 62 clusters in the HIFLUGCS in Table 1. The systematic errors in the determination of the velocity dispersion are discussed in Sect. 5.
2.2. X-ray data analysis
There are 63 clusters in the HIFLUGCS in the XMM-Newton archive. Only A2244 has not yet been observed. We analyzed 150 XMM-Newton observations, which give 3.90 Ms for MOS1, 3.97 Ms for MOS2, and 3.68 Ms for pn, respectively. To filter flares, we apply iterative screening similar to Zhang et al. (2006) using both the soft (0.3–10 keV) band and the hard (10–12 keV for MOS, 12–14 keV for pn) band but with a 3.3-σ clipping. We found that the XMM-Newton observations of four clusters (i.e., A0401, A0478, A1736, A2163) are flared. For clusters with multiple observations, we select the longest observation of which the pointing position is the closest to the cluster center. Since 2A0355 and RXCJ1504 have at most three redshifts each, we exclude these two clusters, and end up with nearly 1.3 Ms of XMM-Newton data of 57 clusters for a more detailed analysis.
For the four flared clusters (i.e., A0401, A0478, A1736, A2163), as well as for A2244, the X-ray quantities are derived from ROSAT pointed observations. The X-ray quantities for the remaining 57 clusters in the HIFLUGCS are derived from combined XMM-Newton and ROSAT data. We note that the XMM-Newton observations only cover an incomplete sector of A2142, such that we have to use the ROSAT data to derive its surface brightness profile. The XMM-Newton observations of A2142 are only used to measure the global temperature and iron abundance. We describe in detail the procedures we adopted to detect and subtract point-like sources and for background treatment in Sects. 2 and 3 of Zhang et al. (2009). Significant substructure features clearly detected in the image are excised before we perform the spectral and surface brightness analysis. We note that the surface brightness analysis is slightly different from that in Sect. 4 of Zhang et al. (2009) in that we directly convert the ROSAT surface brightness profile to the XMM-Newton count rate using the best-fit spectral model obtained from the XMM-Newton data. We then combine the XMM-Newton surface brightness profile within the truncation radius, where the XMM-Newton signal-to-noise ratio is ~3, with the ROSAT converted surface brightness profile beyond the truncation radius for further analysis. We list the properties of the XMM-Newton observations, redshift, hydrogen column density, gas mass, X-ray morphology, and presence of a cool core of each cluster in Table 2.
XMM-Newton observations and cluster properties.
2.2.1. Cluster radius, i.e., r500
X-ray quantities have to be derived consistently within a certain cluster radius, e.g., r500, the radius within which the mass density is 500 times of the critical density2, at the cluster redshift. The quantity r500 can be measured from the X-ray measured mass distribution derived under the assumption of hydrostatic equilibrium as we did in Zhang et al. (2009). Observations have found evidence of deviations from hydrostatic equilibrium (e.g., Zhang et al. 2008, 2010; Mahdavi et al. 2008). The cross-calibration between weak lensing masses and X-ray observables instead uncovers a tight scaling relation between gas mass and cluster total mass (e.g., Okabe et al. 2010). We therefore use the gas mass to infer the cluster mass and r500. Our sample occupies a wide mass range with the gas masses from 1.74 × 1011 M⊙ to 2.12 × 1014 M⊙, which is similar to the mass range of the extended sample in Pratt et al. (2009) consisting of 41 groups and clusters collected from Vikhlinin et al. (2006), Arnaud et al. (2007), Böhringer et al. (2007), and Sun et al. (2009). We thus adopt their relation E1.5(z)ln(Mgas,500/M500) = −2.37 + 0.21ln(M500/2 × 1014 M⊙) to derive the cluster mass and radius (r500) from our gas mass estimate.
2.2.2. X-ray luminosity
The X-ray luminosity is estimated by integrating the X-ray surface brightness. At 3σ significance, the surface brightness profiles are detected out to at least r500 for all 62 clusters combining XMM-Newton and ROSAT data (see Zhang et al. 2009). In practice, we estimate the total count rate from the background-subtracted, flat-fielded, point-source-subtracted, and point-spread-function (PSF) corrected surface brightness profile in the 0.7–2 keV band, and convert this to X-ray luminosity using the best-fit “mekal”3 model given by the spectra in XSPEC in the aperture covering all annuli defined in Sect. 3.2 in Zhang et al. (2009). We note that we do not study the temperature scaling relations for this sample here because of the inhomogeneous range of projected distances used to measure the cluster temperature.
We show the XMM-Newton-ROSAT vs. ROSAT-only measured X-ray luminosity in the 0.1–2.4 keV band in Fig. A.1 in Appendix A. The XMM-Newton-ROSAT to ROSAT-only measured X-ray luminosity ratio is (92 ± 2)% with (0.07±0.01) dex scatter. The faint point sources subtracted from the XMM-Newton data may account for a small fraction of the difference. A systematic difference in the flux calibration between ROSAT and XMM-Newton might play a major role in the 8% difference in the X-ray luminosity (e.g., Snowden 2002). A good fraction of the scatter may be introduced by the varying amounts of point sources and, especially, substructures that get excluded in the ROSAT and XMM-Newton analysis.
In addition, there are some low-temperature systems (i.e., NGC 507, Fornax, NGC 1550, MKW4, NGC 4636, NGC 5044, and A3581; kT < 2 keV) in the sample. To examine whether the line emission becomes important and boosts the X-ray luminosity for those systems, we show the iron abundance vs. temperature relation for the 62 clusters in Fig. B.1 in Appendix B. The best fit is Z/Z⊙ = 10−(0.323±0.061)(kT/keV)−(0.324±0.098) using the bisector method and Z/Z⊙ = 10−(0.325±0.043)(kT/keV) − (0.320±0.068) using the orthogonal method, respectively. This is consistent with the results found in Balestra et al. (2007) but for clusters at higher redshifts (z ≥ 0.3) and in a higher temperature range (3–15 keV), though their clusters show a steeper slope than that for our nearby clusters. The iron abundance vs. temperature correlation indicates that a flux-limited sample tends to include low-mass systems with high iron abundance, of which the X-ray luminosity is in part boosted by the line emission. This may modify the scaling relations at the low-mass end in terms of the mass dependence of the slope and the intrinsic scatter.
Fabian et al. (1994) pointed out that some clusters are significantly above the best fit of the luminosity scaling relation because of the presence of cool cores. This motivates the cluster core correction in deriving the X-ray luminosity (e.g., Markevitch 1998). We focus on the results using the X-ray luminosity corrected for the cluster core (hereafter Lco) by assuming a constant value in the cluster core equal to the value at 0.2r500, SX(R < 0.2r500) = SX(0.2r500) (Zhang et al. 2007). We note that this correction is only applied in determining the X-ray luminosity, not the gas mass. The bolometric luminosity corrected for the cluster core is listed in Table 1, and the bolometric luminosity within r500 (hereafter Lin) and in the [0.2 − 1.0] r500 radial range (hereafter Lex) are listed in Table C.1. To examine the scatter in the scaling relations caused by the presence of cool cores, we also compare the results using Lco with those using Lin (Appendix C) and Lex (Appendix D), respectively.
Since the soft band X-ray luminosity is widely used in studies of the scaling relations, we calibrate the luminosity scaling relations using both the bolometric luminosity in the 0.01–100 keV band (Lbol) and the soft band luminosity in the 0.5–2 keV band (L0.5 − 2 keV, see also Appendix E).
2.3. Quantification of the cluster dynamical state
2.3.1. Offset between the X-ray flux-weighted center and BCG position
The X-ray flux-weighted center of each cluster is listed in Cols. 2–3 of Table 1, which is determined based on XMM-Newton data as described in Sect. 2.3 in Zhang et al. (2010). Our choice of the BCG position (Cols. 4–5 of Table 1) is explained in Sect. 2.1. The angular separation between the X-ray flux-weighted center and BCG position is converted into the physical separation at the cluster redshift, and is listed in Table 1, in units of both kpc (doffset) and r500 (doffset/r500).
The offsets between the X-ray flux-weighted centers and BCG positions for the 62 clusters closely follow a log-normal Gaussian distribution (Fig. 2, left panel). The best fit of log 10(doffset/r500) gives a mean value of −(1.93 ± 0.06) and σ = (0.50 ± 0.06). Forty-six clusters show ≤0.037r500 offsets, within 1σ of the mean value. The remaining 16 clusters are sparsely spread over the range of [0.037 − 1] r500. The best fit of log 10(doffset/kpc) gives a mean value of (1.03 ± 0.06) and σ = (0.55 ± 0.06). Forty-seven clusters show ≤38 kpc offsets, within 1σ of the mean value. The remaining 15 clusters are sparsely spread over the range of [38 − 1000] kpc. Thirteen of those 16 clusters with large offsets between the X-ray flux-weighted centers (see Table 1) and BCG positions are disturbed clusters (see Table 2 and Sect. 2.3.3).
 |
Fig. 2 Histogram of the offset between the X-ray flux-weighted center and BCG position (left panel) and central cooling time vs. offset (right panel). |
2.3.2. Central cooling time
The central cooling time can be more accurately estimated from Chandra data because of its smaller PSF. We thus use the central cooling time calculated at 0.004r500 from Eq. (15) in Sect. 2.6 in Hudson et al. (2010) to divide the sample of the 62 clusters into 26 cool-core clusters (i.e., “SCC” in Hudson et al. 2010) and 36 non-cool-core clusters (i.e., “NCC” and “WCC” in Hudson et al. 2010) as listed in Table 2. Interestingly, we also found a correlation between the central cooling time and the offset between the cluster center and BCG position (Fig. 2, right panel). The best power-law fit to the relation between the offset and central cooling time is  and
and  .
.
2.3.3. X-ray morphology
The combined MOS and pn images in the 0.7–2 keV band are shown in Appendix F. According to their X-ray flux images, Vikhlinin et al. (2009a) divide the 62 clusters into 41 undisturbed clusters and 21 disturbed clusters listed in Table 2.
3. Results for the observational sample
We investigate the three scaling relations between the luminosity and velocity dispersion, luminosity and gas mass, and cluster radius and velocity dispersion, respectively, for the 62 clusters in the HIFLUGCS. To examine possible systematic uncertainties due to the choice of the fitting method, we apply the BCES bisector and orthogonal methods. For all 62 clusters, the best power-law fits of all studied relations given by the bisector and orthogonal methods are consistent (Table 3). We therefore focus on the best fits given by one of the two methods, i.e., the BCES bisector method, to illustrate the results.
Power-law fit, log 10(Y) = A + Blog 10(X), to the scaling relations of the observational sample.
3.1. L − σ relation
We summarize the best power-law fits of the L − σ relations using the X-ray bolometric luminosity (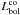 ) and 0.5–2 keV luminosity (
) and 0.5–2 keV luminosity ( ), respectively, in Table 3. In Fig. 3, we show the
), respectively, in Table 3. In Fig. 3, we show the  relation of the 62 clusters.
relation of the 62 clusters.
 |
Fig. 3 X-ray bolometric luminosity vs. velocity dispersion with luminosity corrected for the cluster core ( |
 |
Fig. 4 Top-left: histogram of residuals in logarithmic space from the best-fit |
The slope for the 62 clusters, i.e., (4.02 ± 0.33), agrees with the self-similar prediction (L ~ σ4). The slopes for the undisturbed clusters, disturbed clusters, cool-core clusters, and non-cool-core clusters are statistically indistinguishable. Ignoring their measurement uncertainties, both slopes for disturbed and undisturbed clusters are steeper than for the combined sample. This is because most disturbed clusters are below the best-fit relation, most undisturbed clusters are above, and hardly any low-mass clusters are flagged as disturbed. The slope for the combined sample is thus influenced by a number of low-mass systems, which are all undisturbed clusters. The normalization for the undisturbed clusters is ~60% higher than for the disturbed ones.
The intrinsic scatter (Table 3) of the undisturbed clusters and cool-core clusters is only slightly larger than that of the disturbed clusters and non-cool-core clusters. The clusters with more morphological substructure do not show larger scatter than those with less substructure. This indicates that the scatter driven by the presence of cool cores is comparable to that driven by substructure using Lco. The increasingly large scatter toward the low-mass end is caused by the systems with <45 cluster members with spectroscopic redshifts. In Sect. 5, we will discuss the systematic uncertainties in the velocity dispersion measurements due to the limited number of cluster members.
The top-left panel of Fig. 4 shows the histogram of residuals in logarithmic space from the Lbol, 500 − σ relation. The best Gaussian fit gives  dex scatter, dominated by the intrinsic scatter, i.e., (0.27 ± 0.03) dex. We note that the histogram does not closely follow a symmetric Gaussian distribution, which may slightly underestimate the scatter. The top-right, bottom-left, and bottom-right panels of Fig. 4 show the residuals as a function of the offset between the X-ray flux-weighted center and BCG position, luminosity fraction within 0.2r500, and central cooling time, respectively. There are very weak correlations caused mainly by the systems that have fewer than 45 cluster members with spectroscopic redshifts, for which the measurement uncertainties in the velocity dispersion can be large and in part account for the scatter.
dex scatter, dominated by the intrinsic scatter, i.e., (0.27 ± 0.03) dex. We note that the histogram does not closely follow a symmetric Gaussian distribution, which may slightly underestimate the scatter. The top-right, bottom-left, and bottom-right panels of Fig. 4 show the residuals as a function of the offset between the X-ray flux-weighted center and BCG position, luminosity fraction within 0.2r500, and central cooling time, respectively. There are very weak correlations caused mainly by the systems that have fewer than 45 cluster members with spectroscopic redshifts, for which the measurement uncertainties in the velocity dispersion can be large and in part account for the scatter.
As shown in Fig. 3, the normalization of the L − σ relation for the sample in Wu et al. (1999) is slightly higher than that of our sample. For Lin, the two samples are in better agreement (see Fig. C.1 in Appendix C). Therefore, the core correction applied when deriving the X-ray luminosity for our sample accounts for the normalization difference between our sample and the sample of Wu et al. (1999) in Fig. 3. The different slopes between two samples may be due to their different selection functions as the sample in Wu et al. (1999) is not a flux-limited sample.
The presence of cool cores is one of the main causes of the scatter in the L − σ relation as the scatter using Lin for the non-cool-core clusters is ~20% smaller than that for the cool-core clusters (Appendix C). When the X-ray luminosity corrected for the central region (<0.2r500) is used, the intrinsic scatter is smaller by ~0.05 dex equaling (0.27 ± 0.03) dex for the sample of 62 clusters. The intrinsic scatter in the L − σ relation is similar using Lco and Lex (Appendix D). The residuals of  are more strongly correlated with the luminosity fraction within 0.2r500 than the residuals of both
are more strongly correlated with the luminosity fraction within 0.2r500 than the residuals of both  and
and  . The best-fit relation is ΔlgL = (0.52 ± 0.10) + (0.51 ± 0.09)log 10(Lbol,0.2r500/Lbol,500) with its correlation coefficient of 0.44. Correcting or excluding the central emission therefore efficiently reduces the intrinsic scatter.
. The best-fit relation is ΔlgL = (0.52 ± 0.10) + (0.51 ± 0.09)log 10(Lbol,0.2r500/Lbol,500) with its correlation coefficient of 0.44. Correcting or excluding the central emission therefore efficiently reduces the intrinsic scatter.
3.2. L – Mgas relation
We summarize the best power-law fits of the L − Mgas relations using the X-ray bolometric luminosity (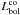 ) and 0.5–2 keV luminosity (
) and 0.5–2 keV luminosity ( ), respectively, in Table 3. In Fig. 5, we present the
), respectively, in Table 3. In Fig. 5, we present the  relation of the 62 clusters. The slope of the best-fit power-law for the 62 clusters is (1.29 ± 0.05). The slopes for the undisturbed and disturbed clusters are statistically identical. The slope for the non-cool-core clusters, i.e., (1.42 ± 0.05), is steeper than that for the cool-core clusters, i.e., (1.24 ± 0.06). The intrinsic scatter of those subsamples is comparable.
relation of the 62 clusters. The slope of the best-fit power-law for the 62 clusters is (1.29 ± 0.05). The slopes for the undisturbed and disturbed clusters are statistically identical. The slope for the non-cool-core clusters, i.e., (1.42 ± 0.05), is steeper than that for the cool-core clusters, i.e., (1.24 ± 0.06). The intrinsic scatter of those subsamples is comparable.
 |
Fig. 5 X-ray bolometric luminosity vs. gas mass with luminosity corrected for the cluster core ( |
The top-left panel of Fig. 6 shows the histogram of residuals in logarithmic space from the best-fit 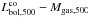 relation for the 62 clusters using the BCES bisector method. The best Gaussian fit gives (0.07 ± 0.01) dex scatter in logarithmic space, comparable to the intrinsic scatter. We note that the histogram does not closely follow a symmetric Gaussian distribution, which may slightly underestimate the scatter. The top-right, bottom-left, and bottom-right panels of Fig. 6 show the residuals as a function of the offset between the cluster X-ray flux-weighted center and BCG position, luminosity fraction within 0.2r500, and central cooling time, respectively. We do not observe as clearly evident correlations as for the
relation for the 62 clusters using the BCES bisector method. The best Gaussian fit gives (0.07 ± 0.01) dex scatter in logarithmic space, comparable to the intrinsic scatter. We note that the histogram does not closely follow a symmetric Gaussian distribution, which may slightly underestimate the scatter. The top-right, bottom-left, and bottom-right panels of Fig. 6 show the residuals as a function of the offset between the cluster X-ray flux-weighted center and BCG position, luminosity fraction within 0.2r500, and central cooling time, respectively. We do not observe as clearly evident correlations as for the  relation in Fig. C.1 in Appendix C. This indicates that the cluster core correction may sufficiently suppress the scatter caused by the presence of cool cores.
relation in Fig. C.1 in Appendix C. This indicates that the cluster core correction may sufficiently suppress the scatter caused by the presence of cool cores.
 |
Fig. 6 Top-left: histogram of residuals in logarithmic space from the best-fit |
The intrinsic scatter in logarithmic space of the L − Mgas relation using Lco is similar to that using Lex (Appendix D), but is 0.05 dex lower than that using Lin (Appendix C). The cluster core correction in deriving the X-ray luminosity significantly reduces the intrinsic scatter in the L − Mgas relation.
We note that both quantities are derived from the X-ray surface brightness distribution in the soft band. If the gas is clumped, the emission measure can be overestimated by 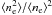 , which results in overestimation of both the X-ray luminosity and the gas mass. Therefore, one possibly underestimates the scatter in the relation.
, which results in overestimation of both the X-ray luminosity and the gas mass. Therefore, one possibly underestimates the scatter in the relation.
3.3. r500 – σ relation
In Fig. 7, we present the relation between the velocity dispersion and cluster radius, the latter being determined from the mass vs. gas-mass relation (see Sect. 2.2.1). In Table 3, we summarize the best power-law fits. The slopes for the undisturbed clusters, disturbed clusters, cool-core clusters, and non-cool-core clusters are statistically indistinguishable.
Surprisingly the intrinsic scatter in logarithmic space (Table 3) for the cool-core clusters is about a factor of two larger than for the non-cool-core clusters. Since most undisturbed clusters are cool-core clusters, the undisturbed clusters exhibit significantly larger intrinsic scatter than the disturbed clusters. This indicates that the presence of cool cores is the main driver of the scatter instead of the morphological substructure. We note that the scatter becomes increasingly large toward the low-mass end, which is coincidentally again caused by the systems that have fewer than 45 cluster members with spectroscopic redshifts.
The top-left panel of Fig. 8 shows the histogram of the residuals in logarithmic space from the r500 − σ relation. The best Gaussian fit gives ( ) scatter in logarithmic space, comparable to the intrinsic scatter. We note that the histogram has a strong asymmetric shape, such that the Gaussian distribution slightly underestimates the scatter. The top-right, bottom-left, and bottom-right panels of Fig. 8 show the residuals as a function of the offset between the X-ray flux-weighted cluster center and BCG position, the luminosity fraction within 0.2r500, and the central cooling time, respectively. The residuals are not very tightly correlated with any of these three parameters. However, 20 of the 26 cool-core clusters are above the best fit, and two thirds of the non-cool-core clusters are below the best fit. The undisturbed and disturbed clusters display homogeneously distributed residuals. This confirms that the presence of cool cores is the main cause of the intrinsic scatter in the r500 − σ relation.
) scatter in logarithmic space, comparable to the intrinsic scatter. We note that the histogram has a strong asymmetric shape, such that the Gaussian distribution slightly underestimates the scatter. The top-right, bottom-left, and bottom-right panels of Fig. 8 show the residuals as a function of the offset between the X-ray flux-weighted cluster center and BCG position, the luminosity fraction within 0.2r500, and the central cooling time, respectively. The residuals are not very tightly correlated with any of these three parameters. However, 20 of the 26 cool-core clusters are above the best fit, and two thirds of the non-cool-core clusters are below the best fit. The undisturbed and disturbed clusters display homogeneously distributed residuals. This confirms that the presence of cool cores is the main cause of the intrinsic scatter in the r500 − σ relation.
 |
Fig. 7 Gas-mass-determined cluster radius vs. velocity dispersion. The colors, lines, and symbols have the same meaning as those in Fig. 3. |
4. Simulated vs. observational samples
To understand the cluster physics behind the observed scaling relations, it is crucial to compare observational samples to representative samples in simulations. Our analysis of our sample shows that the presence of cool cores is one of the main causes of the scatter. In addition, it has become increasingly clear that active galactic nuclei (AGN) play an important role in understanding the properties of clusters (e.g., McNamara & Nulsen 2007) and their scaling relations. We therefore investigated how well simulations can explain the observed results by comparing our observational measurements to those for a sample of 21 clusters and groups simulated at a very high resolution both with and without AGN feedback (Puchwein et al. 2008). The AGN feedback model that was employed resolves some of the long-standing problems that hydro-dynamical simulations of galaxy clusters typically have, i.e. excessive overcooling within the densest cluster regions and too bright and too blue central galaxies. The AGN feedback model also brings the simulated X-ray luminosity-temperature scaling relation into excellent agreement with the observational one. We note that simulations with different cluster physics (e.g., Borgani et al. 2004; Evrard et al. 2008) may give different predictions about the normalization, slope, and scatter of the scaling relations.
4.1. A sample drawn from simulations
Puchwein et al. (2008) carried out a set of high-resolution hydrodynamical re-simulations of clusters selected from the Millennium simulation with and without AGN feedback (for the AGN feedback model see Sijacki et al. 2007), and present the corresponding L − T relation. In Puchwein et al. (2010), they also show the properties of the stellar components and halo baryon fractions for the same sample. Their simulations have high enough resolution to accurately resolve galaxy populations down to the smallest galaxies that are expected to contribute significantly to the stellar mass budget. We select a sample of 21 galaxy clusters from their simulations, whose gas masses span a similar range as our observational sample, i.e., (2.95 × 1011−1.10 × 1014) M⊙ for the case without AGN feedback and (0.74 × 1011−1.23 × 1014) M⊙ for the case with AGN feedback. The gas masses for the same sample of 21 simulated clusters but with AGN feedback expand to a broader range due to the feedback.
4.2. Analyzing the sample from simulations
Both X-ray bolometric luminosity (also corrected for the cluster core) and velocity dispersion are derived in the same manner as for the observational sample of the 62 clusters except that we do not use the caustic method to identify interlopers since they are known in simulations. In determining the velocity dispersion, we exclude sub-halos that do not contain any stellar components and should thus not be considered as galaxies.
In the simulations, the virialized region of every cluster is known. We derive both the velocity dispersion using those galaxies within a projected radius of 1.2 Abell radii (hereafter σdirty), and the velocity dispersion using those galaxies not only within a projected radius of 1.2 Abell radii, but also within the virialized region of the cluster (hereafter σclean)4. In the σclean case, nearby galaxies and interlopers are completely removed. Therefore, σclean gives a reliable estimate of the velocity dispersion. We note that even σdirty contains only interlopers that are very close to the cluster center since they are all within the high resolution region of the cluster re-simulation, which typically extends to five times the cluster virial radius or somewhat farther depending on its exact geometry.
 |
Fig. 8 Top-left: histogram of residuals in logarithmic space from the best-fit r500 − σ relation for the 62 clusters using the BCES bisector method. Top-right: residual vs. offset between the X-ray flux-weighted center and BCG position. Bottom-left: residual vs. fraction of the X-ray luminosity within 0.2r500. Bottom-right: residual vs. central cooling time. The colors and symbols have the same meaning as those in Fig. 3. |
 |
Fig. 9 Top-left: velocity dispersion within a projected radius of R normalized by the velocity dispersion within 1.2 Abell radii as a function of the projected radius. We do not include the values for the clusters having fewer than 10 members within the projected radius we are interested. Top-right: normalized velocity dispersion within a projected radius of r500 vs. velocity dispersion. Bottom-left: normalized velocity dispersion within a projected radius of r500 vs. offset between the X-ray flux-weighted center and BCG position. Bottom-right: normalized velocity dispersion within a projected radius of r500 vs. central cooling time. The results are only based on the observational sample of the 62 clusters. The colors and symbols have the same meaning as those in Fig. 3. The curves are the local regression non-parametric fits. |
4.3. L relation
relation
The 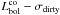 relation is slightly shallower than the
relation is slightly shallower than the  relation for the simulated sample (Fig. 3). This may suggest that interlopers bias the velocity dispersion estimates toward lower values, which might be the case for the six clusters that have fewer than 45 cluster members with spectroscopic redshifts in the observational sample. We discuss this further in Sect. 5. The scatter in the L − σ relation of the simulated sample is larger for the run with AGN feedback.
relation for the simulated sample (Fig. 3). This may suggest that interlopers bias the velocity dispersion estimates toward lower values, which might be the case for the six clusters that have fewer than 45 cluster members with spectroscopic redshifts in the observational sample. We discuss this further in Sect. 5. The scatter in the L − σ relation of the simulated sample is larger for the run with AGN feedback.
The shape and scatter of the L − σ relation of the simulated sample with AGN feedback is comparable to that of the cool-core clusters in the observational sample, disregarding the six clusters with <45 cluster members with spectroscopic redshifts. AGN feedback suppresses cool cores, thus reduces the X-ray luminosity in simulations. AGN feedback also significantly lowers halo gas mass fractions in low-mass systems. We therefore find that the scatter becomes larger toward the low-mass end, i.e., systems with σ ≤ 500 km s-1, which is also present in our observations. The observational sample, disregarding the six clusters with <45 cluster members with spectroscopic redshifts, gives a best fit of  , which closely follows the simulated sample with AGN feedback.
, which closely follows the simulated sample with AGN feedback.
In the high-mass regime, the observational sample shows that non-cool-core clusters are the main driver of the scatter. Since most non-cool-core clusters are disturbed clusters, their substructures cause overestimations of the σ values (see Figs. 6 and 9 in Biviano et al. 2006). Different fractions of substructures therefore translate into scatter in the L − σ relation, which is exactly what we find in the observational sample. The scatter in the L − σ relation of the simulated sample is smaller than that of the observational sample in the high-mass regime since the simulated sample does not predominantly contain mergers. In part, this difference might also be due to too few massive clusters in our simulations, i.e., six systems with σclean > 500 km s-1. Forthcoming simulations of much larger cosmic volumes will be very useful in differentiating the scatter in the L − σ relation caused by measurement systematics from that attributable to cluster physics and achieving a clearer understanding of the cluster dynamics and gas physics in the high-mass regime.
4.4. L – Mgas relation
The intrinsic scatter in the L − Mgas relation is small for both the observational sample and the simulated sample. AGN feedback mainly tends to move clusters downward along the L − Mgas relation rather than strongly changing the relation because removing gas from within r500 also significantly reduces the X-ray luminosity. Hence, AGN feedback does not produce significant scatter in the L − Mgas relation found in simulations. Nevertheless, the simulated sample with AGN feedback has a slightly steeper slope than that of the case without AGN feedback. The difference between the simulated samples without and with AGN feedback is still small, and comparable to the intrinsic scatter. There is a good agreement between the L − Mgas relations from observations and simulations as shown in Fig. 5. Interestingly, the best fits of the disturbed clusters and undisturbed clusters in the observational sample closely match the simulated samples with and without AGN feedback, respectively. This suggests that one of the main causes of the scatter could be AGN activities providing feedback in different phases, e.g. during a feedback cycle.
4.5. r500 − σ relation
As shown in Fig. 7, the slope of the r500 − σ relation for the observational sample is similar to that of the simulated sample with AGN feedback, disregarding the clusters again that have fewer than 45 cluster members with spectroscopic redshifts. For the simulated sample, the fraction of gas removed by AGN feedback becomes significant toward low-mass systems. As a consequence, their DM distributions expand slightly. Both the removal of gas and the expansion of the DM distribution result in increasingly smaller cluster radii with decreasing mass in the simulated sample with AGN feedback compared to the simulated sample without AGN feedback. The simulated sample with AGN feedback thus has a slightly steeper slope than that of the sample without AGN feedback. For the observational sample, the subsample of the undisturbed clusters exhibit a steeper slope than that of the subsample of the disturbed clusters. This is consistent with the scenario that incorporates AGN activities in the undisturbed clusters (mostly cool-core clusters).
 |
Fig. 10 Velocity dispersion measured by the galaxies within a projected radius of R normalized by the velocity dispersion within 1.2 Abell radii as a function of the projected radius for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 3. The curves are the local regression non-parametric fits. We do not include the values for the clusters having fewer than 10 members within the projected radius we are interested. The black circles highlight the derived velocity dispersion with <45 cluster members. |
There is some offset in the normalization between the simulated sample and the observational sample, which is however still within the scatter. X-ray masses are lower than the true masses in numerical simulations (e.g., Evrard 1990; Lewis et al. 2000; Rasia et al. 2006; Nagai et al. 2007; Piffaretti & Valdarnini 2008; Jeltema et al. 2008; Lau et al. 2009; Meneghetti et al. 2010). This may in part account for the offset in the normalization, which relies on the total mass vs. gas mass calibration. The galaxy selection is complete for the simulated cluster. However, we have no homogeneous photometry data to constrain the completeness for the clusters in the observational sample. Differences in the selection of galaxies used to compute the σ may also in part cause this offset.
5. Systematic errors in estimates of σ
5.1. Galaxy selection by projected radial distance
Most velocity dispersion profiles of galaxy clusters become flat beyond 1 h-1 Mpc which suggests that the measured velocity dispersion within a larger radius is more representative of the total kinetic energy of the cluster galaxies (e.g., Fadda et al. 1996; den Hartog & Katgert 1996; Biviano & Girardi 2003; Boschin et al. 2010).
We test how the radial selection of cluster members affects the velocity dispersion estimates of the observational sample as follows. We measure the velocity dispersion within [0.5,1.0,1.5,2.0,2.5] × r500, and normalize it to the value measured within 1.2 Abell radii (top-left panel of Fig. 9). On average, the velocity dispersion measured within small radii, i.e., [0.5,1.0] × r500, is ~10% larger than the one measured within larger radii. This is consistent with den Hartog & Katgert (1996) finding that more clusters with relatively large velocity dispersion than small when measuring velocity dispersion close to the cluster center. We also note that the scatter in the measured velocity dispersion within small radii is ~3 times that measured within 2.5r500.
In the top-right panel of Fig. 9, we show the normalized velocity dispersion measurements within r500 as a function of the velocity dispersion measured within 1.2 Abell radii. For systems of velocity dispersion greater than 500 km s-1, there is on average less than 10% difference between the velocity dispersion measurements within r500 and within 1.2 Abell radii. The difference becomes larger for low-mass systems, and is up to ~30% on average for our sample. The scatter in the ratio of the velocity dispersion measurements within r500 and to those within 1.2 Abell radii is almost independent of the absolute value of the velocity dispersion, at ~25%.
In the bottom panels of Fig. 9, we also show the normalized velocity dispersion measurements within r500 as a function of the offset between the X-ray flux-weighted cluster center and BCG position and the central cooling time. For clusters with a smaller offset between the X-ray flux-weighted cluster center and BCG position or shorter central cooling time, the velocity dispersion measurements within r500 are significantly larger than the values measured within 1.2 Abell radii.
We note that interlopers introduce uncertainties in the above tests, particularly for the six systems with <45 cluster members with spectroscopic redshifts. We therefore also carried out tests using the simulated sample as shown in Figs. 10, 11.
 |
Fig. 11 Velocity dispersion measured by the galaxies within a projected radius of r500 normalized by the velocity dispersion within 1.2 Abell radii as a function of velocity dispersion for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
The trends of velocity dispersion decrease with increasing radius agree between the simulated sample and the observational sample. In Fig. 10, the simulated sample shows that AGN feedback does not clearly affect the velocity dispersion estimates. However, interlopers increase both the amplitude and the scatter in the deviations of the σ estimates as a function of projected cluster-centric distance. The average deviation for the simulated sample without interlopers is similar to that of the observational sample. However, the scatter for the simulated sample with interlopers is comparable to that of the observational sample. This indicates interlopers may affect the velocity dispersion estimates for a few but not the majority of systems in the observational sample.
 |
Fig. 12 Velocity dispersion measured by the n most massive galaxies normalized by the velocity dispersion within 1.2 Abell radii as a function of the fraction of galaxies for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
 |
Fig. 13 Line-of-sight velocity vs. projected radius of the 30 brightest member galaxies (left panels) and all members within 1.2 Abell radii (right panels), respectively, for a simulated cluster (without AGN feedback) having 40 cluster galaxies when excluding interlopers. The top panels correspond to σdirty, and the bottom panels correspond to σclean. |
As shown in Fig. 10, the velocity dispersion within 1.2 Abell radii for two groups in the simulated sample is ~30% larger than that within smaller cluster-centric radii. One group is in a strongly clustered region with several group-size objects within 1.2 Abell radius in projection. In particular, one of the group-size objects has a similar mass to the group we analyzed. The other group is in the process of merging, which biases the σ estimate toward larger values (see also Biviano et al. 2006).
In Fig. 11, the simulated sample without interlopers confirms that systems with velocity dispersions greater than 500 km s-1 have <10% difference between the velocity dispersion measurements within r500 and within 1.2 Abell radii. The results for the simulated sample also indicates that interlopers can boost the scatter in the bias for the low-mass systems of velocity dispersion <500 km s-1. For the low-mass systems, the uncertainties in the velocity dispersion estimates may indeed be as large as 40%, disregarding the radial selection. We have to keep this in mind when we consider the six clusters with <45 cluster members with spectroscopic redshifts in the observational sample.
5.2. Mass selection
For the observational sample, we collected cluster galaxy redshifts from the literature. This may introduce a bias in the velocity dispersion estimates because brighter cluster galaxies may be more likely to have published redshifts than fainter ones. This bias becomes less significant when many cluster galaxies with spectroscopic redshifts are available. Since our observed sample of cluster galaxies is incomplete, we test how the mass selection of cluster members affects the velocity dispersion estimates using the simulated sample, which is homogeneous in terms of cluster galaxies. In Fig. 12, we display the velocity dispersion determined for a fraction of cluster members at the massive end for the 21 simulated clusters5.
AGN feedback does not have an obvious effect on the velocity dispersion estimates. For the simulated sample, the local regression non-parametric fit illustrates that the velocity dispersion estimate tends to be increasingly biased toward smaller values with decreasing fraction of cluster members. The bias on average is within a few per cent as long as more than 10% of the cluster members at the massive end are used. The scatter in the velocity dispersion also increases as a smaller fraction of cluster galaxies are used, and is within 10% when at least 50% cluster members at the massive end are used. The scatter is slightly smaller when there are no interlopers. As shown in Figs. G.1–G.2, when we consider only 45 of the most massive cluster members, the uncertainties in the velocity dispersion estimates can be up to 40% for some low-mass systems (σ < 500 km s-1).
5.3. Interlopers
Except for one system in the simulated sample, interlopers always bias the measurements of the velocity dispersion toward smaller values (see also Biviano et al. 2006). A significant fraction of galaxies (up to ~50% of ngal) within 1.2 Abell radii are not in the virialized region for poor systems. This is not the case for massive systems. As shown in Fig. 13, a caustic cannot efficiently exclude interlopers at larger radii, i.e., [1 − 2.5] r500, and may significantly bias the measurements of the velocity dispersion toward smaller values for poor systems. The σclean is a far more robust indicator of the cluster mass than the σdirty for poor systems.
We note that σdirty for the simulated sample only contains interlopers very close to the cluster. In the observations, there may be more distant interlopers for poor systems. As shown in Fig. 10 in Biviano et al. (2006), unrecognized interlopers that are outside the virial radius but dynamically linked to the host cluster and do not form major substructures, bias the σ estimate toward smaller values than cluster galaxies.
6. Conclusions
We have presented the L − σ, L − Mgas, and r500 − σ relations for the 62 clusters in the HIFLUGCS, a purely X-ray flux-limited sample selected to minimize bias toward any cluster morphology. The systems in this sample span a broad range of morphological substructure, central cooling time, and offset between the X-ray flux-weighted cluster center and BCG position, respectively. Owing to our representative, statistically large sample, with ~1.3 Ms of clean X-ray XMM-Newton data and 13 439 spectroscopically confirmed cluster members for 62 clusters, we have been able to minimize our measurement uncertainties in both X-ray observables and velocity dispersion. Our main results are as follows:
-
The luminosity vs. velocity dispersion relation agrees with the self-similar prediction. The presence of cool cores is one of the major contributors to the scatter in the L − σ relation. Correcting the central region in deriving the X-ray luminosity reduces the intrinsic scatter from 0.33 dex to 0.27 dex. Even after correcting the X-ray luminosity for the cool core, the scatter caused by cool cores becomes increasingly large toward the low-mass end. The scatter caused by the non-cool-core clusters does not strongly depend on the mass range, but becomes dominant for massive systems. The intrinsic scatter for the non-cool-core clusters, 0.25 dex, is statistically indistinguishable from that of the cool-core clusters, 0.28 dex, after correcting the central region when deriving the X-ray luminosity.
-
The presence of cool cores is also one of the major contributors to the scatter in the L − Mgas relation. Using the X-ray luminosity corrected for the cool core, the disturbed clusters with significant X-ray substructures exhibit similar scatter as the undisturbed clusters, partly because of the preponderance of cool-core clusters in the undisturbed subsample.
-
The shape of the Lco − σ relation in simulations with AGN feedback matches the observational sample, specifically the cool-core clusters, disregarding the clusters that have fewer than 45 cluster members with spectroscopic redshifts. A common trend in both observations and simulations is that the scatter becomes larger toward the low-mass end, i.e., systems with σ ≤ 500 km s-1. The shape and intrinsic scatter in the Lco − σ relation of the observational sample closely matches that of the simulated sample for the low-mass clusters indicating that AGN feedback operates there. In the high-mass regime, the observational sample shows that non-cool-core clusters (their substructures) are the main driver of the scatter. The scatter in the L − σ relation at the high-mass end is larger than the scatter in the simulated sample. This may be in part because there are too few massive clusters and no significantly disturbed clusters in the simulated sample.
-
Interestingly, the best fits of the luminosity vs. gas mass relations for the disturbed clusters and undisturbed clusters in the observational sample closely match those of the simulated samples with and without AGN feedback, respectively. This suggests that one of the main causes of the scatter could be AGN providing feedback in different phases, e.g. during a feedback cycle.
-
The r500 − σ relation of the observational sample is similar to that of the simulated sample, disregarding the clusters with <45 cluster members with spectroscopic redshifts. For the simulated sample, the fraction of gas removed by AGN feedback becomes significant toward low-mass systems, which makes their potential wells shallower. The slope for the simulated sample with AGN feedback is thus steeper than that for the sample without AGN feedback. For the observational sample, the subsample of the undisturbed clusters exhibits a steeper r500 − σ relation than that of the subsample of the disturbed clusters. This suggests that there is AGN activity in the undisturbed clusters, which are mostly cool-core clusters.
-
Both the selections of the aperture and mass limit of the cluster members and interlopers cause systematic uncertainties in estimating the velocity dispersion. For the observational sample, the scatter in the velocity dispersion measured within small radii, i.e., [0.5,1.0] × r500 is ~3 times that measured within 2.5r500. The analysis of the simulated sample indicates that interlopers bias the velocity dispersion estimates toward smaller values. The interlopers increase both the amplitude and the scatter in the bias, which is particularly significant for low-mass systems (σ < 500 km s-1). The scatter in the bias of the velocity dispersion estimates increases as the fraction of cluster galaxies used decreases. The scatter is slightly smaller when there are no interlopers.
Online material
Appendix A: Luminosity cross-calibration
 |
Fig. A.1 XMM-Newton-ROSAT vs. ROSAT-only measured luminosity in the 0.1–2.4 keV band within r500. The dashed line denotes 1:1. With a fixed slope to 1, the best-fit normalization of the XMM-Newton-ROSAT vs. ROSAT-only measured luminosity for the 62 clusters is 0.92 shown in solid line. The colors and symbols have the same meaning as those in Fig. 3. |
To cross-calibrate the XMM-Newton-ROSAT with the ROSAT-only measured X-ray luminosity, we re-derived the X-ray luminosity from ROSAT within r500 given in Sect. 2.2.1 by using the gas mass from the current work and the mass vs. gas mass relation in Pratt et al. (2009). The same spectral model was used to derive the X-ray luminosity using both ROSAT data alone and a combination of XMM-Newton and ROSAT data. The comparison between the XMM-Newton-ROSAT and ROSAT-only measured luminosity in the 0.1–2.4 keV band is shown in Fig. A.1.
The XMM-Newton-ROSAT to ROSAT-only measured luminosity ratio is (92 ± 2)%. The intrinsic scatter is (0.07 ± 0.01) dex. This was found for the REFLEX-DXL sample of 14 massive galaxy clusters at z ~ 0.3 in Zhang et al. (2006) and the REXCESS sample of 31 nearby galaxy clusters in Pratt et al. (2009,  ). The difference between the XMM-Newton-ROSAT and ROSAT-only measured luminosity is well within the intrinsic scatter.
). The difference between the XMM-Newton-ROSAT and ROSAT-only measured luminosity is well within the intrinsic scatter.
Appendix B: Iron abundance vs. temperature
 |
Fig. B.1 Iron abundance vs. temperature for the 62 clusters. The black line denotes our best power-law fit using the bisector method. The dot-dashed line is the best fit in Balestra et al. (2007) for clusters at higher redshifts (z ≥ 0.3) and in a higher temperature range (3–15 keV). The colors and symbols have the same meaning as those in Fig. 3. |
Appendix C: Scaling relations using Lin
In Table C.1, we present the X-ray bolometric luminosity within r500 ( ). We list the best fits to the corresponding scaling relations using the bolometric and 0.5–2 keV band luminosity in Table C.2, and show those plots using the bolometric luminosity in Figs. C.1–C.2, which helps us to understand the scatter driven by the presence of cool cores.
). We list the best fits to the corresponding scaling relations using the bolometric and 0.5–2 keV band luminosity in Table C.2, and show those plots using the bolometric luminosity in Figs. C.1–C.2, which helps us to understand the scatter driven by the presence of cool cores.
X-ray bolometric luminosity within r500, Lin, and in the [0.2 − 1] r500 annulus, Lex.
Power-law fit, log 10(Y) = A + Blog 10(X), to the scaling relations for the observational sample using Lin.
 |
Fig. C.1 Upper panel: X-ray bolometric luminosity vs. velocity dispersion with luminosity derived from all emission interior to r500 ( |
 |
Fig. C.2 Upper panel: X-ray bolometric luminosity vs. gas mass with luminosity derived from all emission interior to r500 ( |
Appendix D: Scaling relations using Lex
Since the luminosity derived in the [0.2–1] r500 radial range is widely used to reduce the scatter caused by the presence of cool cores, we also present the X-ray bolometric luminosity in the [0.2–1] r500 radial range ( ) in Table C.1. We also list the best fits to the corresponding scaling relations using the bolometric and 0.5–2 keV band luminosity derived in the [0.2–1] r500 radial range in Table D.1, and show the plots using
) in Table C.1. We also list the best fits to the corresponding scaling relations using the bolometric and 0.5–2 keV band luminosity derived in the [0.2–1] r500 radial range in Table D.1, and show the plots using  in Figs. D.1–D.2.
in Figs. D.1–D.2.
Power-law fit, log 10(Y) = A + Blog 10(X), to the scaling relations for the observational sample using Lex.
 |
Fig. D.1 Upper panel: X-ray bolometric luminosity vs. velocity dispersion with luminosity derived from emission in the [0.2 − 1.0] r500 aperture ( |
 |
Fig. D.2 Upper panel: X-ray bolometric luminosity vs. gas mass with luminosity derived from emission in the [0.2 − 1.0] r500 aperture ( |
Appendix E: Scaling relations using 
We present the corresponding scaling relations using the 0.5–2 keV band luminosity corrected for the cluster central regions,  , in Figs. E.1–E.2. The best fits are listed in Table 3.
, in Figs. E.1–E.2. The best fits are listed in Table 3.
 |
Fig. E.1 Upper panel: X-ray luminosity in the 0.5–2 keV band vs. velocity dispersion with luminosity corrected for the cluster core ( |
 |
Fig. E.2 Upper panel: X-ray luminosity in the 0.5–2 keV band vs. gas mass with luminosity corrected for the cluster core ( |
Appendix F: XMM-Newton images of the sample
As the soft band is insensitive to the cluster temperature and has data of high signal-to-noise ratio, we use the MOS and pn combined image in the 0.7–2 keV band to illustrate the X-ray morphological substructure of each cluster (Figs. F.1–F.5). X-ray point-like sources are identified and subtracted. The holes, where the point-like sources were, are re-filled with the Chandra CIAO routine “dmfilth” using randomization based on the surface brightness distribution around the holes. We only use this image to demonstrate the existence of morphological substructure in the cluster. Significant substructure features shown in the image are excised before we perform the spectral and surface brightness analysis.
As addressed in Sect. 2.3, 13 of the 16 clusters with large offsets between the X-ray flux-weighted centers (see Table 1) and BCG positions are disturbed clusters (see Table 2). We now comment on these 13 clusters. The BCGs in A0399 and A1736 are slightly offset from the main X-ray emission. The ICM in A3376, A0754, A2256, and A3667 exhibits a comet-like tail, and their BCGs are at the opposite end from the X-ray centers probably because of their on-going dynamical activity. A3395s is the south component of a bi-cluster, and its BCG is at an X-ray weak bright peak. The ICM in A1367 has multi-peaks, and the BCG is at the northwest X-ray peak, which is not the brightest one. The BCG in A2163 (A2255) is not a dominant BCG, which sits slightly east (west) of the X-ray center. This also applies but less significantly to some more clusters in the sample. The ICM in Coma, A3558, and A2065 shows some weakly disturbed features, and their BCGs are only 40–60 kpc away from the X-ray centers. A3158, A3391, and A0576 are relaxed clusters, and their BCGs are ≳40 kpc away from the X-ray centers.
 |
Fig. F.1 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
 |
Fig. F.2 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
 |
Fig. F.3 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
 |
Fig. F.4 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
 |
Fig. F.5 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
Appendix G: Systematic errors in estimates of σ
 |
Fig. G.1 Velocity dispersion measured by the 45 most massive galaxies normalized by the velocity dispersion within 1.2 Abell radii as a function of the fraction of galaxies for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
 |
Fig. G.2 Velocity dispersion measured by the 45 most massive galaxies normalized by the velocity dispersion within 1.2 Abell radii as a function of velocity dispersion for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
For A0401, A0478, A1736, A2163, and A2244, which have no XMM-Newton data, we extracted the temperature from Vikhlinin et al. (2009a) assuming 0.3 Z⊙ iron abundance.
More precisely, we include only galaxies that are part of the friends-of-friends (FoF) group of the cluster in calculating σclean. The FoF group is computed using a linking length of 0.2 times the mean inter-particle distance, and extends to roughly ~1.7r200 which corresponds to ~1.2 Abell radii for clusters with a virial mass of 2.7 × 1014 M⊙/h. For more massive clusters, the FoF group is of course larger, while it is significantly smaller for poor groups.
Acknowledgments
The XMM-Newton project is an ESA Science Mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). The XMM-Newton project is supported by the Bundesministerium für Wirtschaft und Technologie/Deutsches Zentrum für Luft- und Raumfahrt (BMWI/DLR, FKZ 50 OX 0001) and the Max-Planck Society. We acknowledge the anonymous referee for suggestions that improved the disucssion of the results. Y.Y.Z., H.A., and T.H.R. acknowledge support by the DFG through Emmy Noether Research Grant RE 1462/2 and by the German BMBF through the Verbundforschung under grant 50 OR 0601 and 50 OR 1005, and T.H.R. in addition acknowledges DFG Heisenberg Grant RE 1462/5. H.A. and C.A.C. acknowledge support from Mexican CONACyT grant 50921-F, and H.A. in addition benefited from CONACyT grants 81356 and 118295. Y.Y.Z. acknowledges A. Babul, A. Biviano, S. Borgani, and R. Piffaretti for useful discussions.
References
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., & Fabian, A. C. 1998, 297, L57 [Google Scholar]
- Andernach, H., Tago, E., Einasto, M., Einasto, J., & Jaaniste, J. 2005, in Nearby Large-Scale Structures and the Zone of Avoidance, ed. A. P. Fairall, & P. Woudt, San Francisco: Astronomical Society of the Pacific, ASP Conf. Ser., 329, 283 [Google Scholar]
- Arnaud, M., & Evrard, A. E. 1999, MNRAS, 305, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2007, A&A, 474, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., & Girardi, M. 2003, ApJ, 585, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Murante, G., Borgani, S., et al. 2006, A&A 456, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgani, S., Murante, G., Springel, V., et al. 2004, MNRAS, 348, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Boschin, W., Barrena, R., & Girardi, M. 2010, A&A, 521, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavaliere, A., Menci, N., & Tozzi, P. 1997, 484, L21 [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y.-Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, L. P., Slyz, A., Jones, C., Forman, W., & Vrtilek, S. D. 1993, ApJ, 412, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A. 1999, MNRAS, 309, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A.C., Allen, S. W., et al. 2000, MNRAS, 365, 1021 [Google Scholar]
- Edge, A. C., & Stewart, G. C. 1991, MNRAS, 252, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., 1990, ApJ, 363, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., Bialek, J., Busha, M., et al. 2008, ApJ, 672, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Crawford, C. S., Edge, A. C., & Mushotzky, R. F. 1994, MNRAS, 267, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Fadda, D., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 457, 61 [NASA ADS] [CrossRef] [Google Scholar]
- den Hartog, R., & Katgert, P. 1996, MNRAS, 279, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P., & Tucker, W. 1979, ApJ, 229, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P., & Arnaud, K. A. 1991, ApJ, 372, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P., Evrard, A. E., Hoekstra, H., Babul, A., & Mahdavi, A. 2009, ApJ, 691, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, D. S., Mittal, R., Reiprich, T. H., et al. 2010, A&A, 513, 437 [Google Scholar]
- Jeltema, T. E., Hallman, E. J., Burns, J. O., & Motl, P. M. 2008, ApJ, 681, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Katgert, P., Biviano, A., & Mazure, A. 2004, ApJ, 600, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Nagai, D., & Vikhlinin, A. 2005, ApJ, 625, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, G. F., Babul, A., Katz, N., et al. 2000, ApJ, 536, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Finoguenov, A., Kneib, J. P., et al. 2010, ApJ, 709, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., & Henry, J. P. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2010, MNRAS, 406, 1759 [NASA ADS] [Google Scholar]
- Markevitch, M. 1998, ApJ, 504, 27 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, 93 [Google Scholar]
- Mushotzky, R. F., & Scharf, C. A. 1997, ApJ, 482, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Zhang, Y.-Y., Finoguenov, A., et al. 2010, ApJ, 721, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-Gil, A., Guzzo, L., Schuecker, P., Böhringer, H., & Collins, C. A. 2004, MNRAS, 348, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, N., Kitayama, T., Masai, K., & Mitsuda, K. 2006, ApJ, 640, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 373, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H., 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., Andritschke, R., Bornemann, W., et al. 2007, Proc. of the SPIE, 6686, pp. 668617-668617-9 [Google Scholar]
- Puchwein, E., Sijacki, D., & Springel, V. 2008, ApJ, 687, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Puchwein, E., Springel, V., Sijacki, D., & Dolag, K. 2010, MNRAS, 406, 936 [NASA ADS] [Google Scholar]
- Rasia, E., Moscardini, L., Mazzotta, P., et al. 2006, MNRAS, 369, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Sarazin, C. L. 2001, ApJ, 561, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., & Diaferio, A. 2006, ApJ, 132, 1275 [Google Scholar]
- Roettiger, K., Burns, J. O., & Stone, J. M. 1999, ApJ, 518, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Schuecker, P., Böhringer, H., Collins, C. A., & Guzzo, L. 2003, A&A, 398, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sijacki, D., Springel, V., Di Matteo, T., & Hernquist, L. 2007, MNRAS, 380, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. P., Haines, C. P., Pereira, M. J., et al. 2010, A&A, 518, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snowden, S. L. 2002, proc. of ESTEC Symposium: New Visions of the X-ray Universe in the XMM-Newton and Chandra Era [arXiv:0203311] [Google Scholar]
- Stanek, R., Rasia, E., Evrard, A. E., Pearce, F., & Gazzola, L. 2010, ApJ, 715, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Donahue, M., & Voit, G. M. 2007, ApJ, 671, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009a, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009b, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- White, D. A., Jones, C., & Forman, W. 1997, MNRAS, 292, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-P., Fang, L.-Z., & Xu, W. 1998, A&A, 338, 813 [NASA ADS] [Google Scholar]
- Wu, X.-P., Xue, Y.-J., & Fang, L.-Z. 1999, ApJ, 524, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Böhringer, H., Finoguenov, A., et al. 2006, A&A, 456, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y.-Y., Finoguenov, A., Böhringer, H., et al. 2007, A&A, 467, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y.-Y., Finoguenov, A., Böhringer, H., et al. 2008, A&A, 482, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y.-Y., Reiprich, T. H., Finoguenov, A., Hudson, D. S., & Sarazin, C. L. 2009, ApJ, 699, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Okabe, N., Finoguenov, A., et al. 2010, ApJ, 711, 1033 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Offset between the X-ray flux-weighted cluster center and BCG position, velocity dispersion, and X-ray bolometric luminosity.
Power-law fit, log 10(Y) = A + Blog 10(X), to the scaling relations of the observational sample.
X-ray bolometric luminosity within r500, Lin, and in the [0.2 − 1] r500 annulus, Lex.
Power-law fit, log 10(Y) = A + Blog 10(X), to the scaling relations for the observational sample using Lin.
Power-law fit, log 10(Y) = A + Blog 10(X), to the scaling relations for the observational sample using Lex.
All Figures
 |
Fig. 1 Line-of-sight velocity vs. projected radius (left panels) and sky positions (right panels) of the selected galaxies in a rich cluster, i.e., Coma (top panels) and in a poor cluster, i.e., S1101 (bottom panels). |
| In the text | |
 |
Fig. 2 Histogram of the offset between the X-ray flux-weighted center and BCG position (left panel) and central cooling time vs. offset (right panel). |
| In the text | |
 |
Fig. 3 X-ray bolometric luminosity vs. velocity dispersion with luminosity corrected for the cluster core ( |
| In the text | |
 |
Fig. 4 Top-left: histogram of residuals in logarithmic space from the best-fit |
| In the text | |
 |
Fig. 5 X-ray bolometric luminosity vs. gas mass with luminosity corrected for the cluster core ( |
| In the text | |
 |
Fig. 6 Top-left: histogram of residuals in logarithmic space from the best-fit |
| In the text | |
 |
Fig. 7 Gas-mass-determined cluster radius vs. velocity dispersion. The colors, lines, and symbols have the same meaning as those in Fig. 3. |
| In the text | |
 |
Fig. 8 Top-left: histogram of residuals in logarithmic space from the best-fit r500 − σ relation for the 62 clusters using the BCES bisector method. Top-right: residual vs. offset between the X-ray flux-weighted center and BCG position. Bottom-left: residual vs. fraction of the X-ray luminosity within 0.2r500. Bottom-right: residual vs. central cooling time. The colors and symbols have the same meaning as those in Fig. 3. |
| In the text | |
 |
Fig. 9 Top-left: velocity dispersion within a projected radius of R normalized by the velocity dispersion within 1.2 Abell radii as a function of the projected radius. We do not include the values for the clusters having fewer than 10 members within the projected radius we are interested. Top-right: normalized velocity dispersion within a projected radius of r500 vs. velocity dispersion. Bottom-left: normalized velocity dispersion within a projected radius of r500 vs. offset between the X-ray flux-weighted center and BCG position. Bottom-right: normalized velocity dispersion within a projected radius of r500 vs. central cooling time. The results are only based on the observational sample of the 62 clusters. The colors and symbols have the same meaning as those in Fig. 3. The curves are the local regression non-parametric fits. |
| In the text | |
 |
Fig. 10 Velocity dispersion measured by the galaxies within a projected radius of R normalized by the velocity dispersion within 1.2 Abell radii as a function of the projected radius for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 3. The curves are the local regression non-parametric fits. We do not include the values for the clusters having fewer than 10 members within the projected radius we are interested. The black circles highlight the derived velocity dispersion with <45 cluster members. |
| In the text | |
 |
Fig. 11 Velocity dispersion measured by the galaxies within a projected radius of r500 normalized by the velocity dispersion within 1.2 Abell radii as a function of velocity dispersion for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
| In the text | |
 |
Fig. 12 Velocity dispersion measured by the n most massive galaxies normalized by the velocity dispersion within 1.2 Abell radii as a function of the fraction of galaxies for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
| In the text | |
 |
Fig. 13 Line-of-sight velocity vs. projected radius of the 30 brightest member galaxies (left panels) and all members within 1.2 Abell radii (right panels), respectively, for a simulated cluster (without AGN feedback) having 40 cluster galaxies when excluding interlopers. The top panels correspond to σdirty, and the bottom panels correspond to σclean. |
| In the text | |
 |
Fig. A.1 XMM-Newton-ROSAT vs. ROSAT-only measured luminosity in the 0.1–2.4 keV band within r500. The dashed line denotes 1:1. With a fixed slope to 1, the best-fit normalization of the XMM-Newton-ROSAT vs. ROSAT-only measured luminosity for the 62 clusters is 0.92 shown in solid line. The colors and symbols have the same meaning as those in Fig. 3. |
| In the text | |
 |
Fig. B.1 Iron abundance vs. temperature for the 62 clusters. The black line denotes our best power-law fit using the bisector method. The dot-dashed line is the best fit in Balestra et al. (2007) for clusters at higher redshifts (z ≥ 0.3) and in a higher temperature range (3–15 keV). The colors and symbols have the same meaning as those in Fig. 3. |
| In the text | |
 |
Fig. C.1 Upper panel: X-ray bolometric luminosity vs. velocity dispersion with luminosity derived from all emission interior to r500 ( |
| In the text | |
 |
Fig. C.2 Upper panel: X-ray bolometric luminosity vs. gas mass with luminosity derived from all emission interior to r500 ( |
| In the text | |
 |
Fig. D.1 Upper panel: X-ray bolometric luminosity vs. velocity dispersion with luminosity derived from emission in the [0.2 − 1.0] r500 aperture ( |
| In the text | |
 |
Fig. D.2 Upper panel: X-ray bolometric luminosity vs. gas mass with luminosity derived from emission in the [0.2 − 1.0] r500 aperture ( |
| In the text | |
 |
Fig. E.1 Upper panel: X-ray luminosity in the 0.5–2 keV band vs. velocity dispersion with luminosity corrected for the cluster core ( |
| In the text | |
 |
Fig. E.2 Upper panel: X-ray luminosity in the 0.5–2 keV band vs. gas mass with luminosity corrected for the cluster core ( |
| In the text | |
 |
Fig. F.1 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
| In the text | |
 |
Fig. F.2 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
| In the text | |
 |
Fig. F.3 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
| In the text | |
 |
Fig. F.4 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
| In the text | |
 |
Fig. F.5 Combined MOS and pn images of the clusters in the 0.7–2 keV band, where point sources have been excised and refilled with values from neighboring pixels. |
| In the text | |
 |
Fig. G.1 Velocity dispersion measured by the 45 most massive galaxies normalized by the velocity dispersion within 1.2 Abell radii as a function of the fraction of galaxies for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
| In the text | |
 |
Fig. G.2 Velocity dispersion measured by the 45 most massive galaxies normalized by the velocity dispersion within 1.2 Abell radii as a function of velocity dispersion for the simulated sample. The results are only based on the simulated sample of the 21 clusters. The colors and symbols have the same meaning as those in Fig. 10. The curves are the local regression non-parametric fits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.










