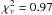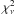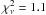| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015147 | |
| Published online | 18 November 2010 | |
A translucent interstellar cloud at z = 2.69
CO, H2, and HD in the line-of-sight to SDSS J123714.60 + 064759.5⋆
1
Departamento de AstronomíaUniversidad de Chile,
Casilla 36-D,
Santiago,
Chile
e-mail: pasquier@das.uchile.cl; slopez@das.uchile.cl
2
Université Paris 6, Institut d’Astrophysique de Paris, CNRS UMR
7095, 98bis bd
Arago, 75014
Paris,
France
e-mail: petitjean@iap.fr
3
European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla 19001,
Santiago 19,
Chile
e-mail: cledoux@eso.org
4
Inter-University Centre for Astronomy and Astrophysics,
Post Bag 4,
Ganeshkhind, 411
007
Pune,
India
e-mail: anand@iucaa.ernet.in
5
Université Paris 7, APC, CNRS UMR 7164,
10 rue Alice Domon et Léonie
Duquet, 75205
Paris Cedex 13,
France
6
GEPI, Observatoire de Paris, CNRS UMR 8111,
5 place Jules
Janssen, 92195
Meudon,
France
e-mail: vergani@apc.univ-paris7.fr
Received:
3
June
2010
Accepted:
2
August
2010
We present the analysis of a sub-damped Lyman-α system with neutral
hydrogen column density,
log N(H0) (cm-2) = 20.0 ± 0.15 at
zabs = 2.69 toward SDSS J123714.60 + 064759.5
(zem = 2.78). Using the VLT/UVES and X-shooter
spectrographs, we detect H2, HD, and CO molecules in absorption with
log N(H2, HD,
CO) (cm-2) = 19.21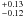 , 14.48 ± 0.05 and 14.17 ± 0.09 respectively. The overall
metallicity of the system is super-solar ([Zn/H] = +0.34 relative to solar) and iron is
highly depleted ([Fe/Zn] = −1.39), revealing metal-rich and dusty gas. Three
H2 velocity components spanning ~125 km s-1 are detected. The
strongest H2 component, at zabs = 2.68955,
with log N(H2) = 19.20, does not coincide
with the centre of the H i absorption. This implies that the molecular fraction
in this component,
fH2 = 2N(H2)/(2N(H2)+N(H0)),
is higher than the mean molecular fraction
⟨fH2⟩ = 1/4 in the system. We also found the
Cl0 associated with this H2 component to have
N(Cl0)/N(Cl+) > 0.4,
which points in the same direction. Cl0 is tied to H2 by charge
exchange reactions, this means that the molecular fraction in this component is not far
from unity. The kinetic temperature derived from the J = 0 and 1
rotational levels of H2 is
, 14.48 ± 0.05 and 14.17 ± 0.09 respectively. The overall
metallicity of the system is super-solar ([Zn/H] = +0.34 relative to solar) and iron is
highly depleted ([Fe/Zn] = −1.39), revealing metal-rich and dusty gas. Three
H2 velocity components spanning ~125 km s-1 are detected. The
strongest H2 component, at zabs = 2.68955,
with log N(H2) = 19.20, does not coincide
with the centre of the H i absorption. This implies that the molecular fraction
in this component,
fH2 = 2N(H2)/(2N(H2)+N(H0)),
is higher than the mean molecular fraction
⟨fH2⟩ = 1/4 in the system. We also found the
Cl0 associated with this H2 component to have
N(Cl0)/N(Cl+) > 0.4,
which points in the same direction. Cl0 is tied to H2 by charge
exchange reactions, this means that the molecular fraction in this component is not far
from unity. The kinetic temperature derived from the J = 0 and 1
rotational levels of H2 is 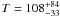 K and the particle density derived from the C0
ground-state fine structure level populations is
nH0 ~ 50–60 cm-3. We derive an electronic
density <2 cm-3 for a UV field similar to the Galactic
one and show that the carbon-to-sulphur ratio in the cloud is close to the solar ratio.
The size of the molecular cloud is probably smaller than 1 pc. Both the
CO/H2 = 10-5 and CO/C0 ~ 1 ratios for
fH2 > 0.24 indicate that the
cloud classifies as translucent, i.e., a regime where carbon is found
both in atomic and molecular form. The corresponding extinction,
AV = 0.14, albeit lower than the definition of a translucent
sightline (based on extinction properties), is high for the observed
H0 column density. This means that intervening clouds with similar local
properties but with higher column densities (i.e. larger physical extent) could be missed
by current magnitude-limited QSO surveys. The excitation of CO is dominated by radiative
interaction with the cosmic microwave background radiation (CMBR) and we derive
Tex(CO) = 10.5
K and the particle density derived from the C0
ground-state fine structure level populations is
nH0 ~ 50–60 cm-3. We derive an electronic
density <2 cm-3 for a UV field similar to the Galactic
one and show that the carbon-to-sulphur ratio in the cloud is close to the solar ratio.
The size of the molecular cloud is probably smaller than 1 pc. Both the
CO/H2 = 10-5 and CO/C0 ~ 1 ratios for
fH2 > 0.24 indicate that the
cloud classifies as translucent, i.e., a regime where carbon is found
both in atomic and molecular form. The corresponding extinction,
AV = 0.14, albeit lower than the definition of a translucent
sightline (based on extinction properties), is high for the observed
H0 column density. This means that intervening clouds with similar local
properties but with higher column densities (i.e. larger physical extent) could be missed
by current magnitude-limited QSO surveys. The excitation of CO is dominated by radiative
interaction with the cosmic microwave background radiation (CMBR) and we derive
Tex(CO) = 10.5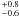 K when
TCMBR(z = 2.69) = 10.05 K is expected. We
measure
N(HD) / 2N(H2) = 10-5.
This is about 10 times higher than what is measured in the Galactic ISM for
fH2 = 1/4 but similar to what
is measured in the Galactic ISM for higher molecular fractions. The astration factor of
deuterium with respect to the primordial D/H ratio is only about 3. This can be the
consequence of accretion ofunprocessed gas from the intergalactic medium onto the
associated galaxy. In the future, it will be possible to search efficiently for
molecular-rich DLAs/sub-DLAs with X-shooter, but detailed studies of the physical state of
the gas will still need UVES observations.
K when
TCMBR(z = 2.69) = 10.05 K is expected. We
measure
N(HD) / 2N(H2) = 10-5.
This is about 10 times higher than what is measured in the Galactic ISM for
fH2 = 1/4 but similar to what
is measured in the Galactic ISM for higher molecular fractions. The astration factor of
deuterium with respect to the primordial D/H ratio is only about 3. This can be the
consequence of accretion ofunprocessed gas from the intergalactic medium onto the
associated galaxy. In the future, it will be possible to search efficiently for
molecular-rich DLAs/sub-DLAs with X-shooter, but detailed studies of the physical state of
the gas will still need UVES observations.
Key words: cosmology: observations / galaxies: ISM / quasars: absorption lines / quasars: individual: SDSS J123714.60 + 064759.5
© ESO, 2010
1. Introduction
Studies of the interstellar medium (ISM) in the local Universe have shown that the neutral ISM presents a complex structure, with cold and dense clouds immersed in a warmer and more diffuse medium. These different ISM phases should be detectable at high redshift by their absorption signatures in damped Lyman-α (DLA) systems observed in quasar spectra (Petitjean et al. 1992). However, although there is evidence of the multiphase nature of DLA systems (e.g. Wolfe et al. 2004), most of the intervening DLAs probe only warm (T ≳ 3000 K) and diffuse (nH < 1 cm-2) atomic gas (e.g. Petitjean et al. 2000; Kanekar & Chengalur 2003). The reason is that the cross-sections of the different phases are quite different and it is not possible to sample them equally well.
Journal of observations.
Searching for molecular hydrogen in high-redshift DLAs (Ledoux et al. 2003; Petitjean et al. 2006; Noterdaeme et al. 2008a) is an efficient way of detecting colder and denser neutral gas and to probe its physical conditions (e.g. Reimers et al. 2003; Cui et al. 2005; Hirashita & Ferrara 2005; Srianand et al. 2005; Ledoux et al. 2006b; Noterdaeme et al. 2007a,b). Past studies have shown that molecular hydrogen is confined in small clouds (pc-sized) with densities n ~ 1–100 cm-3 and temperatures T ~ 70–200 K. The filling factor of H2-bearing clouds in DLAs is much less than one, and only 10% of the lines of sight through a DLA galaxy do intercept H2-bearing clouds down to a limit of N(H2) ~ 1014 cm-2 (Noterdaeme et al. 2008a). H2-bearing clouds in DLAs have small physical extents. Direct evidence for this is that the intervening H2-bearing gas does not completely fill the beam from the broad line region of the quasar Q 1232+082 (Ivanchik et al. 2010; Balashev et al. 2010). Nonetheless, the molecular fraction in DLAs remains small and typical of what is seen in Galactic diffuse atomic gas with fH2 = 2N(H2) / (2N(H2) + N(H0)) < 0.1 and often much lower than this (Ledoux et al. 2003; Noterdaeme et al. 2008a).
Snow & McCall (2006) have classified Galactic interstellar clouds into the following categories: (i) diffuse atomic, with low molecular fractions; (ii) diffuse molecular, where the fraction of hydrogen in molecules becomes substantial (fH2 > 0.1) but carbon is still mainly in ionised form (C+); (iii) translucent (first introduced by van Dishoeck & Black 1989), where the carbon makes the transition to molecular; and (iv) dense molecular, where both hydrogen and carbon are fully molecular. As discussed above, most of the H2-bearing DLAs detected so far are part of the first, and maybe for some of them, part of the second categories. The fourth category may be difficult to detect in absorption because of the high extinction such a cloud produces on the background source.
Despite their highly interesting chemistry and their close connection with star formation, we know very little about translucent clouds (i.e., the third category) at high redshift. The small cross-section of these clouds and/or the induced extinction of the light from the background sources can probably explain the absence of detection in more than three decades of QSO absorption-line research. However, observing molecular-rich gas in absorption should be possible by selecting sightlines passing through or starting from star-forming regions.
Since long-duration gamma-ray bursts (GRBs) are known to occur within star-forming regions, absorption lines at the host-galaxy redshifts which are imprinted in GRB optical afterglow spectra (e.g., Fynbo et al. 2009) are obvious targets towards this goal. Nevertheless, current samples are characterised by a general lack of H2 detection (e.g., Fynbo et al. 2006; Tumlinson et al. 2007). This is probably due to the still limited sample sizes as well as to a bias against dusty – molecular-rich – lines of sight (Ledoux et al. 2009; Fynbo et al. 2009). The first detection of both H2 and CO in the low-resolution spectrum of a highly reddened GRB afterglow (Prochaska et al. 2009) seems to confirm this scenario. Moreover, the observed molecular excitation is high in this case, indicating strong UV pumping from the GRB afterglow itself.
With the large number of quasar spectra available in the Sloan Digital Sky Survey (SDSS), it becomes possible to select the rare sightlines passing through intervening molecular-rich gas. However, due to the small cross-section of such clouds, an efficient selection must be applied. In the local ISM, carbon is found to transition from an ionised state (C+) to neutral (C0) and molecular form (CO) from the most superficial to the deepest parts of the clouds (e.g. Snow & McCall 2006; Burgh et al. 2010). From our Very Large Telescope (VLT) survey for H2 in DLAs (Ledoux et al. 2003; Noterdaeme et al. 2008a), it appears that C0 is generally observed in the same components as H2. This is because the photo-ionisation potential of C0 is similar to the energy of photons that dissociate H2. However, the neutral fraction of carbon is generally low, probably because the gas is not completely shielded. This explains the non-detection of CO in these H2-bearing DLAs, even down to N(CO) ~ 1012 cm-2 (e.g. Petitjean et al. 2002). Searching for systems with high column densities of neutral carbon could be an efficient way to select more shielded gas where other molecules can survive, without relying on a pre-selection based on the H0 column density (i.e. the absorbers need not be DLAs). Because several C i lines are located redwards of the Lyman-α forest, it is possible to search for strong C i absorptions directly in SDSS spectra with automatic procedures. We therefore initiated a programme to survey specifically these sightlines with the VLT. Our selection has been very successful and already allowed us to detect carbon monoxide along QSO sightlines for the first (Srianand et al. 2008b) and second times (Noterdaeme et al. 2009a). We present here the third detection of CO, at z = 2.69 towards SDSS J123714.60 + 064759.5 (zem = 2.78, hereafter called J 1237 + 0647). This is a beautiful and peculiar case, for which a xdetailed analysis of the physical properties of the gas is possible. We present the observations in Sect. 2, the measurement and results in Sect. 3 and provide some discussion in Sect. 4. We summarise our findings in Sect. 5.
2. Observations
2.1. X-shooter observations
We are conducting an observing campaign with X-shooter mounted on the Cassegrain focus of the VLT Unit 2-Kueyen telescope to study the molecular content of our complete sample of C0 absorbers. As a test case for the sensitivity of X-shooter in the blue we observed J 1237 + 0647 (g = 19.2) twice in service mode on February 24 (airmass 1.2; seeing 1.4″) and March 3, 2010 (airmass 1.3; seeing 1.2″), using a slit width of 1″ in the UVB arm. Each observation run consisted in 1 h exposure taken in staring mode (see Table 1). This yields the nominal resolution power of R = 5100 in the UVB arm and a signal-to-noise ratio of about 50 at ~500 nm. Data were reduced with version 0.9.5 of the preliminary ESO X-shooter pipeline (Goldoni et al. 2006) and the appropriate calibration data. The two individual spectra were then combined weighting each pixel by the inverse of the error variance. A portion of the X-shooter spectrum featuring CO is shown in Fig. 1, where several electronic bands of CO are clearly detected. These bands are resolved into individual rotational levels in the UVES spectrum obtained with 8.5 h of exposure time (inset figures). From this, it is apparent that X-shooter is the most efficient instrument to survey a complete sample of candidates down to quasar magnitudes as faint as r ~ 21.5, whereas using UVES would be excessively time consuming. Then, but only in the case of detection, higher spectral resolution is needed to make a detailed analysis of the physical state of the gas as done in the following.
 |
Fig. 1 Portion of X-shooter spectrum in the UVB. The inset figures show 5 Å-wide portions of the UVES spectrum around the position of the detected electronic bands of CO. |
2.2. UVES observations
The quasar J 1237 + 0647 was observed in visitor mode on March 27 and 29, 2009 and April 27, 2009 with the Ultraviolet and Visual Echelle Spectrograph (UVES, Dekker et al. 2000), mounted at the Nasmyth B focus of VLT-UT2. The total exposure time on-source is 8.5 h (see Table 1). We used two dichroic settings (4 × 5400 s with 390+564 and 2 × 4500 s with 390+775) to cover the wavelength range 3300–9600 Å with small gaps at 4517–4621, 5597–5677 and 7764–7809 Å. The CCD pixels were binned 2 × 2 and the slit width adjusted to 1″, yielding a resolving power of ~50 000 under seeing conditions of 0.9–1″. Individual science spectra were reduced with the ESO UVES pipeline, which performs accurate sky subtraction while removing cosmic ray impacts at the same time. The spectra were then combined with a dedicated IDL routine by weighting each pixel by the inverse of the error variance in that pixel and clipping residual cosmic ray impacts that remained after the cleaning of 2D spectra.
3. Analysis
The system at z = 2.69 towards J 1237 + 0647 features numerous absorption lines from atomic (H0, O0, C0, Mg0, Cl0 and S0), singly-ionised (Fe+, Si+, Zn+, Ni+, S+, C+), and molecular species (two isotopomers of molecular hydrogen: H2 and HD; as well as carbon monoxide: CO).
 |
Fig. 2 Measurement of the total column density of neutral atomic hydrogen at z = 2.69 towards J 1237 + 0647. The solid line represents the best one-component fit to the data. The centroid of the profile is indicated by a dotted vertical line. Uncertainties on the column density measurement are illustrated by the shaded area. The short tick marks indicate the position of the three H2-bearing components, the reddest of which also features CO and HD absorptions. The origin of the velocity scale for this figure and all following ones is defined at the position of the CO-bearing component at zabs = 2.68957. |
We analysed the UVES spectrum using standard Voigt profile fitting techniques. The fits were performed through χ2-minimisation with the code FITLYMAN (Fontana & Ballester 1995) which is available as a context of the ESO-MIDAS data analysis software. The spectrum was normalised in the wavelength ranges of interest by fitting spline functions to regions free from absorption lines. Atomic data were taken from Morton (2003) for metal lines, unless otherwise specified. Wavelengths and oscillator strengths were taken from Morton & Noreau (1994) and Eidelsberg & Rostas (2003) for CO and from Abgrall & Roueff (2006) for HD. Updated wavelengths of H2 Lyman and Werner bands were taken from Bailly et al. (2010), with oscillator strengths from the Meudon group1, based on calculations described in Abgrall et al. (1994). Photospheric solar abundances are taken from Asplund et al. (2009).
 |
Fig. 3 Fit to metal lines. The origin of the velocity scale is set at the redshift of the CO absorption (z = 2.68957). The positions of the three H2 components are indicated by short tick marks. The absorption seen at v = + 55 kms-1 in the Zn iiλ2026 panel (in blue) is due to Mg iλ2026 while that at v = − 110 kms-1 on the Si iiλ1808 panel is due to S iλ1807. Note that both S ii lines are affected by blends. Finally Si iiλ1304 reveals the presence of additional weak components that are not fitted (see text). |
3.1. Atomic hydrogen
From the damped Lyman-α absorption line (see Fig. 2) we measured the total column density of atomic hydrogen to be log N(H0) (cm-2) = 20.00 ± 0.15, which agrees with the value measured automatically by Noterdaeme et al. (2009b) from the low resolution SDSS spectrum (20.15 ± 0.28). The centroid of the H i profile is well constrained by the Lyman-β and Lyman-γ absorption lines. The large Doppler parameter (b ~ 100 km s-1) required to fit the Lyman-β and Lyman-γ lines is a consequence of the presence of multiple components as testified by the clumpy profile of the O iλ1302 absorption line spread over ~350 km s-1 (see Fig. 2). We recall that O0 closely follows H0 because of favourable charge-exchange reaction. Unfortunately, because of strong saturation and blending effects, it is impossible to derive column densities in individual components and only the total H0 column density along the line of sight is accessible.
In Fig. 2 and subsequent figures and tables, the zero of the velocity scale is taken at the position of the CO component (zabs = 2.68957, see Sect. 3.5) and the centroid of the three detected H2 components at zabs = 2.68801, 2.68868 and 2.68955 (Δv = − 127, − 73, − 1.6 km s-1, see Sect. 3.3) are indicated by short vertical marks. Interestingly, the centroid of the atomic hydrogen absorption profile (vertical dotted line in Fig. 2 at zabs = 2.69063) is shifted by about + 86 ± 10 km s-1 relative to the CO absorption feature. This, the clumpy O i profile, and the high value of the b-parameter of the H i lines all indicate that a significant fraction of the atomic gas is not associated with the molecular gas. We will discuss this below in more detail.
3.2. Metal content
3.2.1. Singly ionised species
Absorption lines from detected low-ionisation species are spread over about 350 km s-1 around the strongest component, which is also the component where CO and HD are detected. We used non-saturated transitions to derive accurate column densities for Fe+, Ni+, S+, and Zn+. Lines from other species (C+, O0, N0) are heavily saturated, which prevented us to derive any meaningful value of the corresponding column densities. It is however possible to perform an accurate measurement of the Si+ column density from the simultaneous use of Si ii λ1808, which is very weak (below the 3σ detection level), and Si iiλ1304, which is close to saturation. Note that although the strong Si iiλ1304 line reveals additional weak components, their contribution to the overall column density is negligible. The result of the Voigt-profile fitting is shown in Fig. 3 with the corresponding parameters in Table 2. Both the S iiλ1253 and S iiλ1259 profiles are partially blended. Unfortunately, S iiλ1250 falls in a gap of the spectrum. Therefore, we provide only upper-limits for the blended components in Table 2. 3-σ upper-limits on the column densities of Ni+ and Zn+ for the undetected components are provided in the table. Finally, we measure log N(Cr+) < 12.2 at 3σ from the non-detection of Cr iiλ2056.
Column densities of metal species.
Total column densities and corresponding mean metallicities in the gas relative to solar are given in Table 3. Note that we do not apply ionisation correction because the presence of neutral and molecular species in the strongest components indicates that the effect of ionisation on the overall abundances should be negligible. Indeed, even in the general population of absorbers, the ionisation correction is only about 0.1 dex for N(H0) = 1020 cm-2 (Péroux et al. 2007). The metallicity is super-solar with [Zn/H] = + 0.34 and [S/H] = + 0.15. Other species are depleted ([Fe/Zn] = −1.39, [Si/Zn] = −0.82). This indicates that a significant fraction of the refractory species is locked in solid phase onto dust grains. The presence of dust and its consequences are discussed in more detail in Sect. 4.2.
Summary of overall gas-phase abundances.
 |
Fig. 4 Portions of the J 1237 + 0647 UVES spectrum around C i absorption lines. The short vertical marks in each panel represent the positions of absorption lines from the ground state (3P0), the first excited level (3P1) and the second excited level (3P2) from top to bottom, respectively. The component where CO is detected (at zabs = 2.68957) is marked in red. |
Column densities of neutral carbon in fine-structure levels.
3.2.2. Neutral carbon
Because the ionisation potential of neutral carbon (C0) is similar to the energy of the photons that destroy H2, C i is usually a good tracer of the presence of H2 (Srianand et al. 2005). The expected positions of several C i lines usually fall out of the Lyman-α forest. We therefore initiated a programme to search for molecules along QSOs selected upon the presence of C i, as seen in the low-resolution SDSS spectra. Because of this selection, it is not surprising to detect strong C i lines in the UVES spectrum of J 1237 + 0647. The profile of C i absorption lines is complex and results from the blending of absorption lines from different components seen in different excitation levels (ground state: 3P0, first excited level: 3P1 and second excited level: 3P2). Nevertheless, the high signal-to-noise and high spectral resolution allow us to clearly identify eight components. Most of them are also detected in the first excited level, while only the strongest two are detected in the second excited level. The fit to C i lines is shown in Fig. 4, with the corresponding parameters given in Table 4. We considered all optically thin absorption lines but did not include in the fit weak absorption lines in the region around C i λ1277 where the placement of the continuum was uncertain. The main uncertainty in determining the C0 column densities comes from the uncertainties on the oscillator strengths. As in previous works from our group (e.g. Noterdaeme et al. 2007a,b; Srianand et al. 2008b) and others in the field (Jorgenson et al. 2009), we used the f-values from Morton (2003). Using the oscillator strengths from Jenkins & Tripp (2001) results in column densities that are 2 to 3 times lower.
The relative populations of the fine-structure levels of neutral carbon depend on the gas pressure. Because the kinetic temperature of the gas can be derived from the the relative populations of the low rotational levels of H2 (see Sect. 3.3), it is possible to measure the volumic density of the gas. From Fig. 2 of Silva & Viegas 2002 (see also Srianand et al. 2000) and taking into account excitation by collisions and by the Cosmic Microwave Background radiation, we can see that the measured ratios log N(C0, J = 1)/N(C0, J = 0) = − 0.2 and log N(C0, J = 2)/N(C0, J = 0) = − 1 in the main component, which coincides with the position of the CO component, correspond to a volumic density of the order of nH0 ~ 50–60 cm-3 for T ~ 110 K (see Sect. 3.3). Other components have similar fine-structure ratios, which indicate a similar thermal pressure. The kinetic temperature is probably higher in all other components (which is verified at least for the two other H2-bearing components, see Table 6), which implies lower densities (e.g. nH0 ~ 1–10 cm-3 in the component at v = − 127 kms-1).
3.2.3. Neutral sulphur
Because the first ionisation potential of sulphur is 10.36 eV, this element is usually observed in its first ionised state (S+) in damped Lyman-α systems. In turn, sulphur is expected to be found in neutral form (S0) inside molecular clouds, where the surrounding UV field has been strongly attenuated. To date, S0 has been detected only in QSO absorbers where CO absorption is seen as well: in the systems at z = 2.42 towards SDSS J143912.04 + 111740.5 (hereafter J 1439 + 1117; Srianand et al. 2008b) and at z = 1.64 towards SDSS J160457.50 + 220300.5 (Noterdaeme et al. 2009a).
Absorption lines from eight transitions of neutral sulphur are detected in the UVES spectrum of J 1237 + 0647. This strengthens the claim that the presence of neutral sulphur flags molecular gas. Just like the presence of neutral carbon is a good indicator of that of H2 (Srianand et al. 2005, albeit with generally modest molecular fractions, Noterdaeme et al. 2008a), S i lines might well indicate the presence of CO. This is however of little practical use for pre-selecting CO-bearing DLAs from the low resolution SDSS spectra, because S i and CO lines are located in the same spectral region and have similar strengths.
We used all detected S i lines to constrain the column density and
b parameter. Two components are needed to properly fit the data, with
resulting  . The b-value obtained is less than
1 km s-1 for the main component, i.e., well below the spectral resolution
(~6 km s-1). However, b is well constrained, thanks to
the relatively wide range that is spanned by the oscillator strength values. However,
the fit is sensitive to the exact value of the spectral resolution. Therefore, to add
confidence to the b and N measurements, we built the
curve of growth for the detected S i lines, which does not depend on the
spectral resolution (see Fig. 6). The error on the
equivalent width measurements are conservative and take into account uncertainties in
the continuum placement. From this figure, we confirm the small Doppler parameter. The
measured column density nicely matches the sum of the individual column densities in the
two components derived from the Voigt-profile fitting.
. The b-value obtained is less than
1 km s-1 for the main component, i.e., well below the spectral resolution
(~6 km s-1). However, b is well constrained, thanks to
the relatively wide range that is spanned by the oscillator strength values. However,
the fit is sensitive to the exact value of the spectral resolution. Therefore, to add
confidence to the b and N measurements, we built the
curve of growth for the detected S i lines, which does not depend on the
spectral resolution (see Fig. 6). The error on the
equivalent width measurements are conservative and take into account uncertainties in
the continuum placement. From this figure, we confirm the small Doppler parameter. The
measured column density nicely matches the sum of the individual column densities in the
two components derived from the Voigt-profile fitting.
S0 column densities.
 |
Fig. 5 Fit to S i absorption lines. Results of the best model fit with two
components is overplotted ( |
 |
Fig. 6 Curve of growth analysis of S i absorption lines. Left:
curve of growth. Right: confidence interval. Minimum
|
H2 column densities and excitation temperatures.
3.2.4. Neutral chlorine
Chlorine, with an ionisation potential of 12.97 eV, is a unique species among those that can be photoionised by photons with energy hν < 13.6 eV. The dominant form of chlorine is Cl+ when hydrogen is mostly in the atomic form. However, neutral chlorine (Cl0) results from rapid exothermic ion-molecule reaction between singly-ionised chlorine (Cl+) and H2 when H2 is optically thick (Jura 1974). Therefore, the presence of neutral chlorine in the ISM is expected to be a good indicator of the presence of molecular gas.
Cl0 is clearly detected at zabs = 2.689560, associated with the strongest H2 component. We measure log N(Cl0) = 13.01 ± 0.02 from the fit to the Cl iλ1347 absorption line, with b = 4.5 ± 0.4 km s-1 (see Fig. 7). From the non-detection of Cl iiλ1071 we derive log N(Cl + ) < 13.4 at the 3 σ confidence level, which translates to fCl0 ≡ N(Cl0) / (N(Cl0) + N(Cl + )) > 0.3. As the fraction of chlorine in neutral form is expected to follow approximately that of hydrogen in molecular form (Jura & York 1978; see also Sonnentrucker et al. 2002), the lower limit on fCl0 indicates that hydrogen could be mostly molecular at the place where we detect Cl0. We indeed show in the next section that the molecular fraction is particularly high in this component.
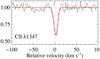 |
Fig. 7 Cl iλ1347 absorption at zabs = 2.68960. A single component fit is overplotted. |
 |
Fig. 8 Portion of the UVES spectrum of J 1237 + 0647 covering the (1–0) Lyman band of H2. The labels indicate the branches (“R”, “P” for ΔJ = − 1, + 1, respectively) and the rotational levels of the lower states. Absorptions from different components are indicated by different label colours (#1: blue, #2: green, #3: red). |
3.3. Molecular hydrogen
Molecular hydrogen is detected in three components at
zabs = 2.68801, 2.68868 and 2.68955, spread over
~125 km s-1. The strongest component at
zabs = 2.68955 also features HD and CO absorption lines. The
UVES spectrum covers numerous Lyman bands (B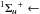 X
X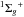 ) as well as some Werner bands (C
) as well as some Werner bands (C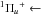 X
X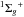 ), which allows for an accurate measurement of the
H2 column densities in each component and in different rotational levels. A
portion of the UVES spectrum covering the H2 Lyman (1–0) band is shown in
Fig. 8, while the full velocity plots for different
rotational levels are shown in Figs. 16 to 21. The measured column densities and corresponding
excitation temperatures are given in Table 6. Below
we refer to these components as #1, #2 and #3 from the bluest to the reddest.
), which allows for an accurate measurement of the
H2 column densities in each component and in different rotational levels. A
portion of the UVES spectrum covering the H2 Lyman (1–0) band is shown in
Fig. 8, while the full velocity plots for different
rotational levels are shown in Figs. 16 to 21. The measured column densities and corresponding
excitation temperatures are given in Table 6. Below
we refer to these components as #1, #2 and #3 from the bluest to the reddest.
Component #1 has a similar width in all rotational levels and requires a single Doppler parameter to describe the profiles of the H2J = 0 to J = 3 absorption lines. The Doppler parameter (b ~ 3 km s-1) is likely to be dominated by turbulent motions.
Component #2 presents a broadening of the profiles with increasing rotational level and requires different Doppler parameters. This behaviour has already been observed in the Galactic ISM (e.g. Jenkins & Peimbert 1997; Lacour et al. 2005b) but also in high-redshift damped Lyman-α systems (Noterdaeme et al. 2007a). Doppler parameters can be accurately measured even when they are significantly smaller than the spectral resolution thanks to the presence of numerous transitions with different oscillator strengths. However, the measurement of b in the first rotational level (J = 0) remains difficult because of the small number of unblended absorption lines (see Table 6). However, there are enough transitions from the J = 0 and 1 levels together to ascertain that the Doppler parameter of the transitions from these two levels is very small, of the order of b ~ 1 km s-1. This is consistent with thermal excitation with a temperature of Tk ~ 120 K, which is similar to what is measured from T01.
The reddest component (#3) is very strong, with damping wings seen for rotational levels up to J = 3, which allows for accurate measurement of the column densities. Non-saturated lines for J = 4 and 5 also allow for accurate measurements in these rotational levels. Component #3 is particularly interesting not only because of its high H2 column density, but because it also contains deuterated molecular hydrogen, carbon monoxide as well as neutral sulphur and neutral chlorine, all of which have been very rarely detected at high redshift. Because the column density of H2 is high, the J = 0 and J = 1 levels are self-shielded and the collisional time-scale is much shorter than the photo-dissociation time-scale. Therefore, the N(J = 1)/N(J = 0) ratio is maintained at the Boltzmann equilibrium value. This means that T01 provides a robust measurement of the kinetic temperature. We measure T01 = Tkin ~ 110 K, which is similar to the temperature in the local interstellar medium (Tkin ~ 80 K, Savage et al. 1977).
We measure a total column density log N(H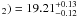 in the sub-DLA system with far the most important
contribution coming from the CO-bearing component (component #3). This corresponds to a
large mean molecular fraction
in the sub-DLA system with far the most important
contribution coming from the CO-bearing component (component #3). This corresponds to a
large mean molecular fraction 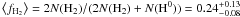 . However, the centre of the H i
Lyman-α absorption line is clearly shifted from component #3 by more
than 50 km s-1 (see Fig. 2). This means
that the amount of atomic hydrogen in the CO-bearing cloud is much smaller than
log N(H0) = 20, and the value given above should be
considered as a lower limit on the actual molecular fraction in the CO-bearing cloud (i.e.
fH2 > 1/4).
As noticed in the previous section from the presence of Cl0 absorption
associated with #3, the molecular fraction in the component #3 is probably not far from
unity.
. However, the centre of the H i
Lyman-α absorption line is clearly shifted from component #3 by more
than 50 km s-1 (see Fig. 2). This means
that the amount of atomic hydrogen in the CO-bearing cloud is much smaller than
log N(H0) = 20, and the value given above should be
considered as a lower limit on the actual molecular fraction in the CO-bearing cloud (i.e.
fH2 > 1/4).
As noticed in the previous section from the presence of Cl0 absorption
associated with #3, the molecular fraction in the component #3 is probably not far from
unity.
HD column densities.
3.4. HD and the D/H ratio
Several Lyman-band HD lines from the first two rotational levels are detected in the UVES spectrum (see Fig. 9). Unfortunately, J = 1 lines are either severely blended or redshifted in regions of bad signal-to-noise ratio and we can only derive an upper limit on the column density for this rotational level. We measured the HD column density in the J = 0 rotational level from fitting the HD L5R0 and HD L8R0 lines, which are unblended. Measurements are summarised in Table 7.
We measured N(HD) / 2N(H2) = 0.95 × 10-5. This is about 10 times higher than what is measured in the Galactic ISM (Lacour et al. 2005a) for f = 0.24. Because this ratio is known to increase with the molecular fraction (Lacour et al. 2005a), HD/2H2 might provide a lower limit on D/H for fH2 < 1. If, as discussed previously, the actual molecular fraction in the HD-bearing cloud towards J 1237 + 0647 is higher than 0.25, both HD and H2 could be self-shielded and HD / 2H2 ~ D0/H0. The value we obtain is then consistent with the D0 / H0 ratio measured in the Galactic disc (Linsky et al. 2006). This corresponds to an astration factor of ~3 when comparing to the primordial value as measured in low-metallicity absorption systems (D/H = 2.82 ± 0.2 × 10-5, Pettini et al. 2008; Ivanchik et al. 2010; see however Srianand et al. 2010) or derived from the baryon density parameter (Steigman 2007).
Note that all five high-redshift HD detections to date yield relatively high D/H values despite significant metal enrichment: N(HD)/2N(H2) = 1.5 × 10-5, 3.6 × 10-5, 7.9 × 10-5 and 1.6 × 10-5 towards, J 1439 + 1117 (Noterdaeme et al. 2008b), Q 1232 + 082 (Ivanchik et al. 2010), J 2123-0500 and FJ 0812+32 (Tumlinson et al. 2010). Because deuterium is easily destroyed as interstellar gas is cycled through stars, large deuterium abundances are difficult to reproduce with closed-box models. However, these are well explained by models including infall of primordial gas (e.g. Prodanović & Fields 2008). If the velocity-metallicity correlation found by Ledoux et al. (2006a) is the consequence of an underlying mass-metallicity relation, we can expect that a high astration of deuterium in high metallicity systems is roughly compensated by a strong infall of primordial material onto massive galaxies. However, Tumlinson et al. (2010) noted that HD/2H2 ratios in high-z absorption systems lie in a narrow range well above the value measured in the Galaxy, while these systems present a broad diversity in terms of metallicities and molecular fractions. This puzzling behaviour led them to conclude that it could be premature to use the HD/2H2 ratio to derive Ωb, given our actual understanding of interstellar chemistry. In addition, we note that for QSO absorbers, we only have access to the properties of the gas (metallicities, molecular fractions) averaged over the line of sight. These may not be representative of the actual chemical abundances in the HD-bearing cloud. Indeed, only the total N(H0) can usually be measured and the metal components are blended into a smooth absorption profile. It is therefore necessary to be careful and to study each system in detail (e.g. Balashev et al. 2010) to derive the local chemical and physical conditions in the cloud.
 |
Fig. 9 Fit to HD J = 0 lines. The blue profile is the contribution from HD while the red profile represents H2. The velocity of the H2 detected components are indicated by vertical dotted lines. |
 |
Fig. 10 Fit to CO lines ( |
3.5. Carbon monoxide
Absorptions from eight A1Π(ν′) ← X1Σ + (ν = 0) bands of CO (from AX (0–0) to AX (7–0)), the C1Σ(ν′ = 0) ← X1Σ + (ν = 0) Rydberg band and the d3Δ(ν′ = 5) ← X1Σ + (ν = 0) inter-band system are detected at zabs = 2.68957 towards J 1237 + 0647, see Fig. 10. Each band produces a complex absorption profile, which results from superposition of absorption lines from different rotational levels in the P and R branches. The resolving power (R ~ 50000) and the signal-to-noise ratio (SNR ~ 28) of the UVES spectrum are high enough to individually measure the column densities in rotational levels up to J = 3. In addition, the J = 4 level is probably detected in the P branch of CX (0–0). We used the AX and dX bands that fall outside of the Lyman-α forest to measure the column densities in rotational levels up to J = 3. The AX (3–0) band is affected by a spike that is likely due to a cosmic ray impact at the position of the R branch, and this region is therefore not considered when fitting the profile. In addition, we use the CX(0–0) band up to J = 4. This band is the strongest one available but the corresponding rest wavelength (1088 Å) makes it redshifted in the Ly-α forest. Fortunately, only the R branch is blended but the P branch is free from any blend. Moreover, the CX rotational levels are well separated at the UVES spectral resolution.
The results of the fit are presented in Table 8. Two errors are quoted in this table for the column densities: the first one is the rms error on the fit, while the second one reflects the uncertainties resulting from the continuum placement. The latter uncertainties were estimated by changing the normalisation by plus or minus 0.5σ (i.e. about ± 2% for SNR = 28) around the best continuum fit. The total CO column density we derive is log N(CO) = 14.17 ± 0.09, implying a high CO to H2 ratio of N(CO)/N(H2) = 10-5. This is typical of what is seen in translucent clouds (see Burgh et al. 2010).
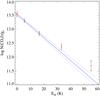 |
Fig. 11 Excitation diagram of CO rotational levels. Errors on the column densities from fitting the lines are represented by the small red error bars while the long black error bars take into account the uncertainty in the continuum placement. The plain line represents the linear regression fit using J = 0 to J = 2 measurements and the best continuum fit. 1σ errors are represented by dashed lines. |
CO column densities and excitation temperatures.
In Fig. 11 we show the excitation diagram of CO. It
is clear that the population of the first three rotational levels can be reproduced with a
single excitation temperature. We measure this excitation temperature by performing a
linear fit of
log N(CO, J) / gJ
vs. the energy of the levels (E0J). The fit
and 1σ range in Fig. 11 corresponds
to the best-fit continuum. In order to estimate the effect of the continuum placement, we
repeated the linear fit for each set of continua and took the extrema as representative of
the range of possible values for Tex(CO). This gives
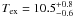 . Note that the effect of the continuum placement is mainly
a change in the total CO column density, while little change on the slope of the linear
fit (i.e. the excitation temperature). The CO excitation temperature is well below the
kinetic temperature of the gas. This means that the gas density is low enough so that
radiative processes are likely to dominate the downwards cascade, as predicted in diffuse
molecular and translucent clouds (e.g. Warin et al.
1996). Indeed, the population ratios of the neutral carbon fine-structure levels
indicate a volumic density of the order of
nH0 ~ 50 cm-3, which is well below the
critical density at which the collisional de-excitation rate of
CO(J = 1–0) equals that of the spontaneous emission
(ncrit ~ 1000 cm-3, Snow & McCall 2006). Indeed, in terms of density and molecular
fraction, the CO-bearing system presented here is very similar to that presented in Srianand et al. (2008b) where we concluded that
collisional excitation of CO is negligible. Note however that the fine-structure levels of
C0 only give the average volumic density. The actual local volumic density in
the CO-bearing cloud could be higher. A small shift (~1 km s-1) is measured
between the strongest C i feature and the CO component. This may indicate that
the two species are not completely co-spatial.
. Note that the effect of the continuum placement is mainly
a change in the total CO column density, while little change on the slope of the linear
fit (i.e. the excitation temperature). The CO excitation temperature is well below the
kinetic temperature of the gas. This means that the gas density is low enough so that
radiative processes are likely to dominate the downwards cascade, as predicted in diffuse
molecular and translucent clouds (e.g. Warin et al.
1996). Indeed, the population ratios of the neutral carbon fine-structure levels
indicate a volumic density of the order of
nH0 ~ 50 cm-3, which is well below the
critical density at which the collisional de-excitation rate of
CO(J = 1–0) equals that of the spontaneous emission
(ncrit ~ 1000 cm-3, Snow & McCall 2006). Indeed, in terms of density and molecular
fraction, the CO-bearing system presented here is very similar to that presented in Srianand et al. (2008b) where we concluded that
collisional excitation of CO is negligible. Note however that the fine-structure levels of
C0 only give the average volumic density. The actual local volumic density in
the CO-bearing cloud could be higher. A small shift (~1 km s-1) is measured
between the strongest C i feature and the CO component. This may indicate that
the two species are not completely co-spatial.
 |
Fig. 12 Excitation temperature of CO as a function of the total CO column density. Black error bars are measurements at z = 0 from Burgh et al. (2007). The red filled circle with error bars is our measurement at z = 2.7 towards J 1237 + 0647 while the blue square represents the measurement at z = 2.4 towards J 1439 + 1117 (Srianand et al. 2008b). Only a large range on Tex (6–16 K) could be determined for the system at z = 1.64 towards SDSS J160457.50 + 220300.5 (Noterdaeme et al. 2009a), and is therefore not represented in the figure. The vertical dotted line is indicative of a change of behaviour: below this limit there is no correlation between N(CO) and Tex(CO). |
From the radiative code RADEX (van der Tak et al. 2007) we expect the excitation temperature of CO to be about one degree higher than the expected temperature of the cosmic microwave background (CMB) radiation (TCMB(z = 2.69) = 10.05 K) as soon as the collision partner (H0, H2 and He) density is higher than 50 cm-3. This explains that the excitation temperature we measure is slightly higher than what is expected from excitation by the CMB radiation alone.
In Fig. 12 we compare the excitation temperature of CO at high redshift with that in the local Universe. In the local ISM, the temperature is seen a few degrees above TCMB at low CO column densities and rises for column densities above N(CO) = 2 × 1015 cm-2. This is due to the increased importance of photon trapping at higher column densities (Burgh et al. 2007). The values observed at high redshift are significantly higher than the local ones, despite similar N(CO) and kinetic temperatures. This clearly means that the main physical difference between high redshift and local lines of sight is the higher CMB temperature at high redshift. This provides a strong positive test of the hot Big-Bang theory. Another consequence of Fig. 12 is that only CO-bearing systems with log N(CO) < 15 – for which there is no correlation between N(CO) and Tex(CO) – are good places to measure the evolution of TCMB with cosmic time.
Interestingly, although the differences are small and within errors, we measure a
systematic trend,
T04 ≳ T03 ≳ T02 ≳ T01,
regardless of the exact continuum placement. This indicates that while CMB photons
dominate the rotational excitation of CO, other mechanisms are at play. We fail to
reproduce the increasing temperature with increasing rotational level with RADEX. However,
this behaviour has already been noticed in the local ISM (Sonnentrucker et al. 2007; Sheffer et al.
2008) and could be explained by the selective self-shielding of low rotational
lines for log N(CO) > 14 (Warin et al. 1996). The self-shielding of far-UV Rydberg bands of CO
(those relevant to the photo-destruction process) could be more effective than previously
thought (Sheffer et al. 2003). In addition, the
presence of H2 lines in the same spectral region can contribute to an effective
shielding of CO lines. Finally, radiative pumping from CO emission lines due to nearby
dense molecular clouds could contribute to populate the higher rotational levels in the
absorbing cloud (Wannier et al. 1997). If the
increasing temperature with increasing rotational level is physical, then
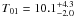 K could better represent the excitation by the CMB alone.
K could better represent the excitation by the CMB alone.
4. The nature of the absorbing cloud
4.1. Summary of the physical properties in the CO component
In the previous sections we derived physical properties of the gas associated to the molecular absorptions seen at zabs ~ 2.68957 towards J 1237 + 0647.
From the analysis of Cl0, we derived that the molecular fraction, 2N(H2)/(2N(H2)+N(H0)), in the CO component is larger than 1/4 for a super-solar metallicity: Z(Zn, S) = +0.34, +0.15. From the populations of the C0 ground-state fine structure levels, we found that the particle density is of the order of ~50 cm-3. The analysis of the H2 rotational levels yields a kinetic temperature of ~100 K and CO is mainly excited by radiative interaction with the CMBR.
We can have an indication of the electronic density in the cloud thanks to the
S0/S+ ratio. Assuming that the mean ratio can be derived using the
column densities in the strongest components we measure:
log N(S0)/N(S+) = − 1.72. The
electronic density, ne, is derived from the ionisation
equilibrium between the two species
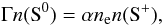 (1)where Γ is the photoionisation rate of
S0 and α the combination rate of S+. Taking the
ratio in diffuse gas of the Galaxy
(Γ / α ~ 95 cm-3, Péquignot & Aldrovandi 1986; see also Table 8 of Welty et al. 1999b) we derive
ne ~ 1.85 (Γ/α/95) cm-3.
Note that this is an average value in the strongest metal component. Because S0
and S+ are not co-spatial – as indicated by the different Doppler-parameters –
the electron density derived here should be considered as an upper limit in the molecular
gas.
(1)where Γ is the photoionisation rate of
S0 and α the combination rate of S+. Taking the
ratio in diffuse gas of the Galaxy
(Γ / α ~ 95 cm-3, Péquignot & Aldrovandi 1986; see also Table 8 of Welty et al. 1999b) we derive
ne ~ 1.85 (Γ/α/95) cm-3.
Note that this is an average value in the strongest metal component. Because S0
and S+ are not co-spatial – as indicated by the different Doppler-parameters –
the electron density derived here should be considered as an upper limit in the molecular
gas.
We could apply the same reasoning to carbon, but we cannot measure the C+
column density because C iiλ1334 is highly saturated. In turn we
can derive N(C+) from the sulphur electronic density
measurement. We find 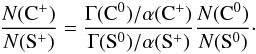 (2)Using
Γ(C0)/α(C+) = 32 cm-3
yields log N(C+)/N(S+) = 1.26,
which is close to the solar ratio.
(2)Using
Γ(C0)/α(C+) = 32 cm-3
yields log N(C+)/N(S+) = 1.26,
which is close to the solar ratio.
4.2. Dust content
Figure 13 shows the distribution of g − r colours for 650 non-BAL quasars with redshifts similar to J 1237 + 0647 (Δz = 0.1). The median g − r value of the distribution is 0.16 with a standard deviation of 0.11. This dispersion reflects the colour variation from one QSO to the other and is not due uncertainties in the SDSS photometric measurements (which are better than 0.03 mag). This implies that the colour excess of J 1237 + 0647 (g − r = 0.59) is significant at the 3.9σ level. This significance increases to 4.9σ if we consider a Gaussian fit to the distribution. Indeed, there is a tail towards large colour excesses, which shows the existence of a population of reddened quasars. J 1237 + 0647 is among the reddest 1.5% quasars with g − r > 0.5.
 |
Fig. 13 Distribution of SDSS photometric g − r values for a sample of 650 non-BAL QSOs at 2.681 < z < 2.881. The arrow indicates the position of J 1237 + 0647. |
The observed flux-calibrated SDSS spectrum of J 1237 + 0647 is matched by the QSO composite spectrum from Vanden Berk et al. (2001) reddened by a SMC-like extinction law with E(B − V) = 0.05 ± 0.01. The spectrum together with the fit is shown in Fig. 14. Note that because we are only interested in the slope of the continuum of J 1237 + 0647 and the strength of emission lines varies strongly from one quasar to the other, we do not include emission line regions in our fit. Absorption lines were also ignored during the fit as well as the wavelength range bluewards of the Ly-α emission.
In order to further estimate the probability that the above reddening might be due to a peculiar intrinsic QSO shape, we used a technique described in Srianand et al. (2008a) and Noterdaeme et al. (2009a): we repeated the spectral slope fitting assuming an absorber at z = 2.69 for a control sample of 82 non-BAL QSOs with similar emission redshifts (2.76 < zem < 2.80) and spectra with i-band S/N ratios higher than5. We find that the continuum slope of J 1237 + 0647 deviates at the 98% confidence level from the mean slope of other quasars. Below we will therefore consider that the colour excess of J 1237 + 0647 is owing to the presence of dust at zabs = 2.69.
 |
Fig. 14 SDSS spectrum of J 1237 + 0647 (black). The orange dashed spectrum is the unreddened SDSS QSO composite spectrum (Vanden Berk et al. 2001). The red spectrum is the composite spectrum reddened by a SMC extinction law with E(B − V) = 0.053 (i.e. AV = 0.14, in the rest-frame of the absorber). The fit was performed using an IDL code based on MPFIT (Markwardt 2009). |
Our best-fit model predicts J = 16.9, H = 16.3, K = 15.5 (with typical errors of 0.2 mag), while the observed Two Micron All Sky Survey (2MASS) magnitudes are J = 16.8 ± 0.2, H = 15.7 ± 0.2, and K > 15.0. The agreement is reasonable although not perfect in the H-band. Indeed, the 2MASS magnitudes come from Point Source Reject Table for objects with very low SNR. These measurements are known to suffer from flux overestimation, which can easily explain the discrepancy between predicted and measured H-band magnitudes. In addition, the presence of the H-β emission line in the H-band increases the uncertainty of our estimate. This together with the fact that the 2MASS and SDSS observations were taken five years apart, makes our predicted magnitudes consistent with the 2MASS data. Unfortunately, there are no SDSS measurements at different epochs for this object to monitor any variation in the QSO flux.
The measured reddening, although significant, is marginally higher than what is seen in the general population of DLAs (E(B − V) ~ 0.04, Ellison et al. 2005). Interestingly, the integrated extinction-to-gas ratio measured towards J 1237 + 0647, A(V)/N(H0) = 1.5 × 10-21 mag cm2 is 20 times higher that the average value for the SMC (7.5 × 10-23 mag cm2, Gordon et al. 2003) and about 50 times higher than the mean value measured in high redshift DLAs (2–4 × 10-23 mag cm2, Vladilo et al. 2008). This means that if the H0 column density were higher, the extinction induced would have been so high that the QSO would have been missed by the SDSS target selection2. Note that the moderate extinction AV = 0.14 in the rest-frame of the absorber, already produces an extinction of nearly 1 mag in the g-band. This further supports the possibility that current surveys can miss a large number of cold clouds (Noterdaeme et al. 2009a). If, as discussed before, a large fraction of the atomic hydrogen is not associated with the molecular component, then the extinction-to-gas ratio in the molecular component is even higher. The line-of-sight to J 1237 + 0647 probably passes through a relatively thin slab of dusty gas. This is also supported by the high depletion factors measured in the CO-bearing component ([Fe/Zn] ~ −2.0, [Ni/Zn] ~ − 1.6, [Si/Zn] ~ −1.7, [Cr/Zn] < −1.6). This abundance pattern is typical of what is seen in cold gas of the Galactic disc (Welty et al. 1999a).
If we consider the extinction only, then the sightline studied in this paper is not translucent. Indeed, the historical definition of translucent corresponds to 1 < AV < 5. However, as noted by Rachford et al. (2002), even translucent sightlines can result from the concatenation of multiple diffuse clouds along the line-of-sight. This kind of scenario has already been advocated to explain the bimodal distribution in the log N(H2) distribution for a given column density of dust (Noterdaeme et al. 2008a). Therefore extinction may not be the best parameter to define translucent clouds. Rachford et al. (2002) and Snow & McCall (2006) have proposed that the definition of translucent clouds should be based on the local properties of the gas rather than on the integrated properties along the line-of-sight. Following this suggestion, Burgh et al. (2010) have presented a definition based on the abundance of hydrogen and carbon in molecular forms. These authors noted that with this definition, translucent clouds do not necessarily produce strong reddening.
 |
Fig. 15 N(CO)/N(H2) and N(CO)/N(C0) versus the molecular fraction, fH2. The red filled circle with error bars is our measurement at z = 2.7 towards J 1237 + 0647, while the blue square represents the measurement at z = 2.4 towards J 1439 + 1117 (Srianand et al. 2008b). Other points represent measurements in the Galactic ISM with three outliers represented in grey (Burgh et al. 2010). These are peculiar systems with uncertain measurements by the same authors. The horizontal dotted line marks the limit between diffuse and translucent clouds, while the two vertical dotted lines mark the transition range between these two regimes. Note that the molecular fraction we indicates toward J 1237 + 0647 is a lower limit. In order to facilitate the comparison with local values, we use N(C0) measured with the f-values from Jenkins & Tripp (2001). |
 |
Fig. 16 Fit to H2(J = 0) lines. The blue profile is the contribution from HD. |
 |
Fig. 17 Fit to H2(J = 1) lines. |
 |
Fig. 18 Fit to H2(J = 2) lines. |
 |
Fig. 19 Fit to H2(J = 3) lines. |
 |
Fig. 20 Fit to H2(J = 4) lines. |
 |
Fig. 21 Fit to H2(J = 5) lines. |
4.3. The molecular fractions of H and C
In Fig. 15 we plot the ratios N(CO)/N(H2) and N(CO)/N(C0) versus the hydrogen molecular fraction, fH2, for the two systems towards J 1237 + 0647 (this work) and J 1439+1117 (Srianand et al. 2008) together with measurements in the ISM of the Galaxy (Burgh et al. 2010). The latter authors define translucent clouds as clouds with CO)/H2 > 10-6 and CO/C0 > 1.0 for fH2 > 0.4. In the cloud toward J 1237 + 0647, we find N(CO)/N(H2) = 10-5 for ⟨fH2⟩ = 0.24. However, as discussed previously, the hydrogen molecular fraction in the CO-bearing cloud is higher than this. In addition, the amount of carbon in CO molecules is about that in atomic form3. We therefore conclude that the cloud in front of J 1237 + 0647 is indeed a translucent cloud, an ideal laboratory for probing astrochemistry at high redshift.
5. Conclusion
From our VLT survey for H2 in DLAs it appears that neutral carbon is generally observed in the same components that feature H2 (Srianand et al. 2005; Noterdaeme et al. 2008a). We therefore selected the rare SDSS lines of sight in which C i absorptions are present. From UVES follow-up observations we have detected strong absorptions from H2, HD and CO along SDSS J123714.60 + 064759.5. This is a beautiful and peculiar case where detailed analysis of the physical properties of the gas is possible.
The H0 column density is low, log N(H0) = 20.00 ± 0.15 and corresponds to what is usually called a sub-DLA (Péroux et al. 2002). The corresponding overall metallicity is super solar with [Zn/H] = +0.34 and [S/H] = +0.15. The system features three H2 components that span ~125 km s-1, the strongest of which, with log N(H2) = 19.20, does not coincide with the centre of the H i absorption. This means that the molecular fraction in this component is higher than the mean molecular fraction ⟨fH2⟩ = 1 / 4 in the system.
From the populations of the low H2 rotational levels we measured the kinetic temperature of the gas to be around 100 K in the strongest component, where HD and CO are also detected. The detection of S0 and C0 implies that the gas is shielded from the surrounding far-UV radiation field.
The relative populations of the C0 fine structure levels yield an estimate of the average hydrogen density in the main component of about 50–60 cm-3. At these densities collisions are not frequent enough to dominate the rotational excitation of CO molecules, and radiative processes are likely to determine the CO rotational populations. The excitation temperature we measure (Tex(CO) = 10.5 K) is significantly higher than that measured in the local ISM (Tex(CO) ~ 3.5 K) for similar CO column densities, molecular fractions, and kinetic temperatures. We show that the higher rotational excitation of CO towards J 1237 + 0647 results from the higher temperature of the cosmic microwave background at the redshift of the absorber, TCMB(z = 2.69) = 10.05 K. This provides a strong positive test of the hot Big-Bang theory.
Small velocity shifts (of the order of 1 km s-1) are observed between the different neutral and molecular species in the main component. For H2, the shift might appear more important but this is rather because the H2 component is a blend of several sub-components. Neutral chlorine is likely a better indicator of the strongest molecular component (Sonnentrucker et al. 2006). Srianand et al. (2010) recently observed similar small velocity shifts between H2 and 21-cm absorption in a high redshift DLA which also testifies to the presence of inhomogeneities of the ISM on very small scales. In turn, because the distribution of H0 and O0 are expected to follow each other closely, the O iλ1302 absorption profile indicates that atomic hydrogen is distributed over the full ~400 km s-1 velocity range over which metals are observed. This explains the large velocity shift between the centroid of H i and molecular lines.
All this reinforces the view that the ISM is patchy, with small and dense molecular cloudlets (probably with an onion-like structure) immersed in a warmer diffuse atomic medium (see e.g. Petitjean et al. 1992). We can derive an upper limit on the size of the molecular-rich region along the line-of-sight by considering that all H0 is associated with the main velocity component of density nH = 50 cm-3. The corresponding characteristic length is l = N(H0) / nH0 ≃ 0.6 pc. A lower-limit can be given using Eq. (A7) of Jura & York (1978; see also Sonnentrucker et al. 2002) and the observed molecular and neutral chlorine fractions. This gives l > 0.05 pc. The molecular region of the system has therefore a very small size and hence small cross-section. It is therefore not surprising that detections of translucent clouds were elusive till now. Studying the frequency of CO absorbers would give an idea of the filling factor of the molecular-rich gas, but requires more extended statistics. Small physical extents could yield partial covering of the background source by the cloud. This may happen in particular if some absorption lines are redshifted on top of emission lines from the extended QSO broad line region, as seen in the case of Q 1232+082 (Ivanchik et al. 2010; Balashev et al. 2010).
Interestingly, the conclusion that the ISM at high redshift is made of small cold cloudlets immersed in warmer diffuse medium has been reached by Gupta et al. (2009) while considering the distribution of cold gas detected in 21-cm absorption. Note that J 1237 + 0647 is detected in the radio domain by FIRST. However, the low radio flux (2.3 mJy) prevents any spectroscopic study with current radio-telescopes.
Several chemical reactions can take place in this cloud. Indeed, three molecular species are detected, while the presence of neutral chlorine suggests chemical reactions involving HCl and HCl+ (e.g. Dalgarno et al. 1974; Neufeld & Wolfire 2009). The DLA system toward J 1237 + 0647 is therefore an excellent candidate to target with future extremely large telescopes (ELTs) to detect other molecular species like C2, CH, OH and study astrochemistry in the interstellar medium of high-redshift galaxies. Given the expected attenuation of the quasar by CO-bearing clouds, X-shooter, with its high throughput and medium resolution, is the best instrument to survey carefully selected DLA/sub-DLA candidates for CO absorptions and build a sample of molecular-rich clouds at high redshift, which may then be studied in details in the optical and sub-millimeter ranges with future facilities like ELTs and ALMA.
Note that we use here log N(C0,J = 0,1,2) = 14.39 ± 0.10 derived using f-values from Jenkins & Tripp (2001) to enable comparison with the work by Burgh et al. (2010).
Acknowledgments
P.N. is supported by a CONICYT/CNRS fellowship and gratefully acknowledges the European Southern Observatory for hospitality during part of the time this work was done. S.L. is supported by FONDECYT grant No. 1100214. We thank Alain Smette for helpful discussions and an anonymous referee for helpul comments and suggestions that improved the content and presentation of the paper. We thank A. Peter for smoothing out the English. We acknowledge the use of the Sloan Digital Sky Survey.
References
- Abgrall, H., & Roueff, E. 2006, A&A, 445, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., & Roncin, J.-Y. 1994, Can. J. Phys., 72, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bailly, D., Salumbides, E. J., Vervloet, M., & Ubachs, W. 2010, Molec. Phys., in press [Google Scholar]
- Balashev, S. A., Petitjean, P., Ivanchik, A. V., et al. 2010, MNRAS, submitted [Google Scholar]
- Burgh, E. B., France, K., & McCandliss, S. R. 2007, ApJ, 658, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Burgh, E. B., France, K., & Jenkins, E. B. 2010, ApJ, 708, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Bechtold, J., Ge, J., & Meyer, D. M. 2005, ApJ, 633, 649 [Google Scholar]
- Dalgarno, A., de Jong, T., Oppenheimer, M., & Black, J. H. 1974, ApJ, 192, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, ed. M. Iye, A. F. Moorwood, Proc. SPIE, 4008, 534 [Google Scholar]
- Eidelsberg, M., & Rostas, F. 2003, ApJS, 145, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Hall, P. B., & Lira, P. 2005, AJ, 130, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Fontana, A., & Ballester, P. 1995, The Messenger, 80, 37 [NASA ADS] [Google Scholar]
- Fynbo, J. P. U., Starling, R. L. C., Ledoux, C., et al. 2006, A&A, 451, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fynbo, J. P. U., Jakobsson, P., Prochaska, J. X., et al. 2009, ApJS, 185, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, in SPIE Conf. Ser., 6269 [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, N., Srianand, R., Petitjean, P., Noterdaeme, P., & Saikia, D. J. 2009, MNRAS, 398, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., & Ferrara, A. 2005, MNRAS, 356, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanchik, A. V., Petitjean, P., Balashev, S. A., et al. 2010, MNRAS, 404, 1583 [NASA ADS] [Google Scholar]
- Jenkins, E. B., & Peimbert, A. 1997, ApJ, 477, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B., & Tripp, T. M. 2001, ApJS, 137, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgenson, R. A., Wolfe, A. M., Prochaska, J. X., & Carswell, R. F. 2009, ApJ, 704, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Jura, M. 1974, ApJ, 190, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Jura, M., & York, D. G. 1978, ApJ, 219, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N., & Chengalur, J. N. 2003, A&A, 399, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., André, M. K., Sonnentrucker, P., et al. 2005a, A&A, 430, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Ziskin, V., Hébrard, G., et al. 2005b, ApJ, 627, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Petitjean, P., & Srianand, R. 2003, MNRAS, 346, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006a, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ledoux, C., Petitjean, P., & Srianand, R. 2006b, ApJ, 640, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Vreeswijk, P. M., Smette, A., et al. 2009, A&A, 506, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., Draine, B. T., Moos, H. W., et al. 2006, ApJ, 647, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
- Morton, D. C. 2003, ApJS, 149, 205 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morton, D. C., & Noreau, L. 1994, ApJS, 95, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2009, ApJ, 706, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., et al. 2007a, A&A, 474, 393 [Google Scholar]
- Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C., & Le Petit, F. 2007b, A&A, 469, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., & Srianand, R. 2008a, A&A, 481, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Ledoux, C., Srianand, R., & Ivanchik, A. 2008b, A&A, 491, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Srianand, R., Petitjean, P., & Lopez, S. 2009a, A&A, 503, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Ledoux, C., & Srianand, R. 2009b, A&A, 505, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Péquignot, D., & Aldrovandi, S. M. V. 1986, A&A, 161, 169 [NASA ADS] [Google Scholar]
- Péroux, C., Dessauges-Zavadsky, M., Kim, T., McMahon, R. G., & D’Odorico, S. 2002, Ap&SS, 281, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Dessauges-Zavadsky, M., D’Odorico, S., Kim, T.-S., & McMahon, R. G. 2007, MNRAS, 382, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Petitjean, P., Bergeron, J., & Puget, J. L. 1992, A&A, 265, 375 [NASA ADS] [Google Scholar]
- Petitjean, P., Srianand, R., & Ledoux, C. 2000, A&A, 364, L26 [NASA ADS] [Google Scholar]
- Petitjean, P., Srianand, R., & Ledoux, C. 2002, MNRAS, 332, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Petitjean, P., Ledoux, C., Noterdaeme, P., & Srianand, R. 2006, A&A, 456, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettini, M., Zych, B. J., Murphy, M. T., Lewis, A., & Steidel, C. C. 2008, MNRAS, 391, 1499 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Prochaska, J. X., Sheffer, Y., Perley, D. A., et al. 2009, ApJ, 691, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Prodanović, T., & Fields, B. D. 2008, J. Cosmol. Astro-Part. Phys., 9, 3 [Google Scholar]
- Rachford, B. L., Snow, T. P., Tumlinson, J., et al. 2002, ApJ, 577, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D., Baade, R., Quast, R., & Levshakov, S. A. 2003, A&A, 410, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Federman, S. R., & Andersson, B. 2003, ApJ, 597, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, A. I., & Viegas, S. M. 2002, MNRAS, 329, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Friedman, S. D., Welty, D. E., York, D. G., & Snow, T. P. 2002, ApJ, 576, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Friedman, S. D., & York, D. G. 2006, ApJ, 650, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Welty, D. E., Thorburn, J. A., & York, D. G. 2007, ApJS, 168, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Srianand, R., Petitjean, P., & Ledoux, C. 2000, Nature, 408, 931 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Srianand, R., Petitjean, P., Ledoux, C., Ferland, G., & Shaw, G. 2005, MNRAS, 362, 549 [Google Scholar]
- Srianand, R., Gupta, N., Petitjean, P., Noterdaeme, P., & Saikia, D. J. 2008a, MNRAS, 391, L69 [NASA ADS] [Google Scholar]
- Srianand, R., Noterdaeme, P., Ledoux, C., & Petitjean, P. 2008b, A&A, 482, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srianand, R., Gupta, N., Petitjean, P., Noterdaeme, P., & Ledoux, C. 2010, MNRAS, 405, 1888 [NASA ADS] [Google Scholar]
- Steigman, G. 2007, Ann. Rev. Nucl. Part. Sci., 57, 463 [Google Scholar]
- Tumlinson, J., Prochaska, J. X., Chen, H.-W., Dessauges-Zavadsky, M., & Bloom, J. S. 2007, ApJ, 668, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Malec, A. L., Carswell, R. F., et al. 2010, ApJ, 718, L156 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1989, ApJ, 340, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vladilo, G., Prochaska, J. X., & Wolfe, A. M. 2008, A&A, 478, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wannier, P., Penprase, B. E., & Andersson, B. 1997, ApJ, 487, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Warin, S., Benayoun, J. J., & Viala, Y. P. 1996, A&A, 308, 535 [NASA ADS] [Google Scholar]
- Welty, D. E., Frisch, P. C., Sonneborn, G., & York, D. G. 1999a, ApJ, 512, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Welty, D. E., Hobbs, L. M., Lauroesch, J. T., et al. 1999b, ApJS, 124, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Howk, J. C., Gawiser, E., Prochaska, J. X., & Lopez, S. 2004, ApJ, 615, 625 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Portion of X-shooter spectrum in the UVB. The inset figures show 5 Å-wide portions of the UVES spectrum around the position of the detected electronic bands of CO. |
| In the text | |
 |
Fig. 2 Measurement of the total column density of neutral atomic hydrogen at z = 2.69 towards J 1237 + 0647. The solid line represents the best one-component fit to the data. The centroid of the profile is indicated by a dotted vertical line. Uncertainties on the column density measurement are illustrated by the shaded area. The short tick marks indicate the position of the three H2-bearing components, the reddest of which also features CO and HD absorptions. The origin of the velocity scale for this figure and all following ones is defined at the position of the CO-bearing component at zabs = 2.68957. |
| In the text | |
 |
Fig. 3 Fit to metal lines. The origin of the velocity scale is set at the redshift of the CO absorption (z = 2.68957). The positions of the three H2 components are indicated by short tick marks. The absorption seen at v = + 55 kms-1 in the Zn iiλ2026 panel (in blue) is due to Mg iλ2026 while that at v = − 110 kms-1 on the Si iiλ1808 panel is due to S iλ1807. Note that both S ii lines are affected by blends. Finally Si iiλ1304 reveals the presence of additional weak components that are not fitted (see text). |
| In the text | |
 |
Fig. 4 Portions of the J 1237 + 0647 UVES spectrum around C i absorption lines. The short vertical marks in each panel represent the positions of absorption lines from the ground state (3P0), the first excited level (3P1) and the second excited level (3P2) from top to bottom, respectively. The component where CO is detected (at zabs = 2.68957) is marked in red. |
| In the text | |
 |
Fig. 5 Fit to S i absorption lines. Results of the best model fit with two
components is overplotted ( |
| In the text | |
 |
Fig. 6 Curve of growth analysis of S i absorption lines. Left:
curve of growth. Right: confidence interval. Minimum
|
| In the text | |
 |
Fig. 7 Cl iλ1347 absorption at zabs = 2.68960. A single component fit is overplotted. |
| In the text | |
 |
Fig. 8 Portion of the UVES spectrum of J 1237 + 0647 covering the (1–0) Lyman band of H2. The labels indicate the branches (“R”, “P” for ΔJ = − 1, + 1, respectively) and the rotational levels of the lower states. Absorptions from different components are indicated by different label colours (#1: blue, #2: green, #3: red). |
| In the text | |
 |
Fig. 9 Fit to HD J = 0 lines. The blue profile is the contribution from HD while the red profile represents H2. The velocity of the H2 detected components are indicated by vertical dotted lines. |
| In the text | |
 |
Fig. 10 Fit to CO lines ( |
| In the text | |
 |
Fig. 11 Excitation diagram of CO rotational levels. Errors on the column densities from fitting the lines are represented by the small red error bars while the long black error bars take into account the uncertainty in the continuum placement. The plain line represents the linear regression fit using J = 0 to J = 2 measurements and the best continuum fit. 1σ errors are represented by dashed lines. |
| In the text | |
 |
Fig. 12 Excitation temperature of CO as a function of the total CO column density. Black error bars are measurements at z = 0 from Burgh et al. (2007). The red filled circle with error bars is our measurement at z = 2.7 towards J 1237 + 0647 while the blue square represents the measurement at z = 2.4 towards J 1439 + 1117 (Srianand et al. 2008b). Only a large range on Tex (6–16 K) could be determined for the system at z = 1.64 towards SDSS J160457.50 + 220300.5 (Noterdaeme et al. 2009a), and is therefore not represented in the figure. The vertical dotted line is indicative of a change of behaviour: below this limit there is no correlation between N(CO) and Tex(CO). |
| In the text | |
 |
Fig. 13 Distribution of SDSS photometric g − r values for a sample of 650 non-BAL QSOs at 2.681 < z < 2.881. The arrow indicates the position of J 1237 + 0647. |
| In the text | |
 |
Fig. 14 SDSS spectrum of J 1237 + 0647 (black). The orange dashed spectrum is the unreddened SDSS QSO composite spectrum (Vanden Berk et al. 2001). The red spectrum is the composite spectrum reddened by a SMC extinction law with E(B − V) = 0.053 (i.e. AV = 0.14, in the rest-frame of the absorber). The fit was performed using an IDL code based on MPFIT (Markwardt 2009). |
| In the text | |
 |
Fig. 15 N(CO)/N(H2) and N(CO)/N(C0) versus the molecular fraction, fH2. The red filled circle with error bars is our measurement at z = 2.7 towards J 1237 + 0647, while the blue square represents the measurement at z = 2.4 towards J 1439 + 1117 (Srianand et al. 2008b). Other points represent measurements in the Galactic ISM with three outliers represented in grey (Burgh et al. 2010). These are peculiar systems with uncertain measurements by the same authors. The horizontal dotted line marks the limit between diffuse and translucent clouds, while the two vertical dotted lines mark the transition range between these two regimes. Note that the molecular fraction we indicates toward J 1237 + 0647 is a lower limit. In order to facilitate the comparison with local values, we use N(C0) measured with the f-values from Jenkins & Tripp (2001). |
| In the text | |
 |
Fig. 16 Fit to H2(J = 0) lines. The blue profile is the contribution from HD. |
| In the text | |
 |
Fig. 17 Fit to H2(J = 1) lines. |
| In the text | |
 |
Fig. 18 Fit to H2(J = 2) lines. |
| In the text | |
 |
Fig. 19 Fit to H2(J = 3) lines. |
| In the text | |
 |
Fig. 20 Fit to H2(J = 4) lines. |
| In the text | |
 |
Fig. 21 Fit to H2(J = 5) lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.