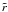| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200913934 | |
| Published online | 05 November 2010 | |
An all-sky catalogue of cold cores observed with Planck-HFI: simulation and colour detection algorithms
1
Université de Toulouse, UPS, CESR,
9 avenue du colonel
Roche,
31028
Toulouse Cedex 4,
France
e-mail: montier@cesr.fr
2
CNRS, UMR5187, 31028
Toulouse,
France
3 Helsinki University Observatory, Tahtitorninmaki,
University of Helsinki, PO Box 14, Finland
Received: 21 December 2010
Accepted: 26 June 2010
Context.Planck will provide an unprecedented view of the (cold dust in both diffuse regions and dense cores and associated gas in the Galaxy), resulting in the observation of a large number of cold objects. Understanding the processes acting at the very earliest stages of star formation requires a detailed study of these cold cores.
Aims. We present an algorithm which is able to compile a reliable catalogue of cold cores from the Planck High Frequency Instrument (HFI) data. We construct models of the cold cores and validate the extraction algorithm on simulated Planck data.
Methods. We model cold cores along with their warmer envelopes which are then injected into a full sky simulation of Planck HFI data. These cold cores are mostly embedded in the relatively warmer Galactic background, in particular in the plane where there is a high level of confusion. We have developed two detection algorithms which make use of the colour of the cores rather than simply extracting compact sources from the individual frequency maps. The cold sources present a relative emission excess at wavelengths longer than 350 μm (i.e. 857 GHz), and thus provide the necessary signature to separate them from the diffuse Galactic emission and warmer cores. Furthermore, using an optimised photometry algorithm for embedded cold sources, reliable fluxes can be extracted.
Results. We recover nearly 3% of our input sources, with 60% completeness at high latitude. This suggests that we will be able to compile a catalogue of nearly 5000 objects over the entire sky with a reliability of 98%. These detections cover the entire simulated mass range from 0.4 to 10 000 solar masses and cover the entire sky, including a small number of sources on the far side of the Galaxy.
Conclusions. This algorithm is ready to be applied on Planck HFI data, and will be able to produce a reliable catalogue of sources ready for follow up observations, in particular for the Herschel open-time key-program on Galactic cold cores.
Key words: infrared: ISM / ISM: clouds / methods: data analysis / submillimeter: ISM
© ESO, 2010
1. Introduction
The fundamental aspects of star formation (stellar mass distribution, formation efficiency, clustered or isolated modes, evolution timescales, spontaneous/triggered mechanisms) are closely linked to the initial conditions in cold and dense molecular clouds. However, the properties of these objects are still poorly known, mainly because of the observational difficulty to explore the submillimeter domain: in a cold cloud, most of the dust mass is colder than 12 K, leading to an emission peak in the wavelength range 200–300 μm. Therefore, cores have remained undetected in the Infrared Astronomical Satellite (IRAS, Neugebauer et al. 1984) maps (λ ≤ 100 μm) and will be very faint (or swamped in warmer component) even in the Akari (Pearson et al. 2004) and Spitzer MIPSGal surveys (Carey et al. 2009) (λ ≲ 160 μm). Over the past decade, the development of ground-based observations in the mm-submm range has allowed important progress in the analysis of dark cloud properties of nearby star forming regions (Bergin & Tafalla 2007). In particular, the studies have shown that the core mass distribution follows a power law with a slope close to the initial mass function (IMF), supporting the theoretical prediction that the IMF is largely determined during the pre-stellar cores fragmentation (Motte et al. 1998; Johnstone et al. 2000; Onishi et al. 2002; Alves et al. 2007; Enoch et al. 2008). Understanding the processes acting at the very earliest stages of star formation requires a statistical and detailed study of the cold and dense cores at large scale in the Galaxy. One must investigate what is generating the cores and controlling their evolution, as well as their variation with the Galactic environment.
Until recently the most effective way of detecting compact clouds at large scale in the Galaxy was to look for them on photographic plates, as optical extinction features. From these studies, the total number of Galactic globules and small clouds has been estimated to be around 3 × 105 (Clemens et al. 1991). A new population consisting of thousands of cold dark clouds was discovered by means of mid-infrared absorption towards the bright background emission of the Galactic plane, cf. the Midcourse Space Experiment (MSX, Egan et al. 1998; Price 1995) and the Infrared Space Observatory (ISOGAL, Perault et al. 1996) surveys. These clouds are massive and dense ( > 1021 cm-2), with sizes of a few arcminutes and distances up to a few kiloparsecs (Egan et al. 1998; Perault et al. 1996). More than 12 000 so-called infrared dark cloud (IRDC) cores have been identified (see the catalogue by Simon et al. 2006a), and a large number have been characterized in detail with follow-up observations, in particular in terms of mass spectrum and galactic distribution (Simon et al. 2006b; Rathborne et al. 2006; Marshall et al. 2009). However, many cores have escaped detection using this extinction signature, especially at high latitudes where the stellar density and diffuse background levels are low. In this case, emission is a better tracer of the cores: the Cosmic Background Explorer (COBE, Boggess et al. 1992) satellite revealed in the Galaxy a widely-distributed cold dust component that extends to high Galactic latitudes (Lagache et al. 1998). This could be a sign of a number of compact cold objects, but the coarse resolution impeded detection of individual sources. Higher resolution was provided by the ISO satellite and the balloon-borne telescope PRONAOS (PROgramme NAtional d’Observations Submillimetriques, Serra et al. 2001). With a detection limit of ~ 1 Jy at 170 μm and a sky coverage of 15%, the ISO serendipity survey detected more than one hundred cold cores (Stickel et al. 2007). PRONAOS discovered similarly cold condensations not only in star forming regions but also in cirrus type clouds (Bernard et al. 1999; Ristorcelli et al. 1998; Dupac et al. 2003; Stepnik et al. 2003), with typical characteristics of Tdust = 12 K, D = 0.1–1 pc, and M = 5–30 M⊙. More recently, hundreds of very cold sources (from 18 K down to 7 K) have been detected with the Archeops balloon-borne experiment, see Fig. 5 of Désert et al. (2008). Observations have revealed a number of low mass stars that evidently have formed at high Galactic latitudes (Martin & Kun 1996; Magnani et al. 1995; Hearty et al. 2000). Furthermore, whereas detection methods based on extinction are biased towards near distances, methods based on emission should, in principle, be able to detect them also at large distances, with some limitation due to resolution, sensitivity and Galactic confusion.
Exploring the sub-mm domain with unique sensitivity, angular resolution, spectral and spatial coverage, Planck and Herschel will provide an unprecedented view of the cold component in the Galaxy. A large number of cold objects is expected to be revealed, with their primary properties: temperature, spectral index, distance, and associated mass. This will offer the best opportunity to address a number of key questions: What are the characteristics of the total population of cold cores in the Galaxy? How are they distributed? Are they concentrated in the molecular cloud rings and spiral arms? How are they correlated with star forming regions and other Galactic large-scale structures seen in the FIR images of IRAS (FIR loops, bubbles, shells, filaments, etc.)? What are their characteristics as a function of Galactic environment? It will be possible to study in detail the physical properties of the cores in the various environments of the ISM and to investigate the possible role of large-scale triggering mechanisms in their formation.
The first step of this study will be to yield an unbiased catalogue of Galactic cold cores detected in the Planck all-sky survey. Herschel can then be used for more detailed studies. The much better angular resolution and the extended spectral coverage offered by its instruments, the Spectral and Photometric Imaging REceiver (SPIRE) and the Photodetector Array Camera and Spectrometer (PACS), will allow the study of the density structure and temperature distributions of the Planck cores. In the sub-mm bands, Planck has a resolution of 5′ and a very high sensitivity to dust emission that corresponds to a column density of ~ 5 × 1018 H2 / cm2 (1-σ) or a visual extinction of AV ~ 0.005m. However, the major limitation for the cold cores detection will be due to the background confusion: the emission from the cold core will be mixed with various dust emission components along the line of sight, with a main contribution of the warm dust emission arising from the molecular cloud surrounding the core. The core emission may be a very small fraction of the total surface brightness rendering direct detection by standard process possible only for the strongest sources. The confusion level is expected to be particularly high in the Galactic plane. For this reason, we have developed dedicated detection algorithms based on the typical colour signature of cold cores, gathered into a common facility: the Colour Cold Core Detection Tool (CoCoCoDeT). In this paper we present various methods prepared, tested and optimised on simulated Planck maps that include a population of Galactic cold cores. This analysis is required for performance evaluation, especially in terms of reliability. The same kind of detection method applied on Herschel data will be very powerful, especially in the plane, and will present a natural extension to this work.
In the following we describe the data sets developed to test the methods: our modelling of the cold cores’ properties (Sect. 2), the simulation of the corresponding Galactic catalogue (Sect. 3) and of the all-sky emission in the Planck wavelength bands (Sect. 4). The main methods and algorithms are presented in Sect. 5, and the comparative results are given in Sect. 6. Based on these results, we present the best method, and provide predictions for the achievable detection efficiency as a function of Galactic latitude.
2. Cold core modelling
In the following, we model the cold cores along with their associated warmer envelope. Two approaches have been used to model the brightness emission of these objects, depending on their mass: for medium mass objects, a Bonnor-Ebert model has been used, and for high mass objects an isothermal model has been applied, ensuring flux continuity between both.
2.1. Medium size cold cores
The density distribution of our spherically symmetric model clouds follows the Bonnor-Ebert solution (Bonnor 1956; Ebert 1955; Fischera & Dopita 2008). The model clouds are close to being critically stable, with the dimensionless stability parameter ξmax = 7.0. Models of different mass are obtained by varying the external pressure that is part of the Bonnor-Ebert model. The simulation results are not sensitive to the assumed density profiles because the sources are mostly small compared to the Planck beam size. On the other hand, the total column density of the models is a crucial parameter that determines the range of dust temperatures and, thus the integrated spectrum of the sources.
We use the dust model of Ossenkopf & Henning (1994), where, at a density of 106 cm-3 and over a time of 105 years, dust has undergone coagulation and has acquired thin ice mantles. The dust emission in the sub-millimeter results from the energy absorbed at shorter wavelengths, even in the UV regime. In the radiative transfer modelling we follow the prescription of Stamatellos & Whitworth (2003) to derive opacities at shorter wavelengths.
In the case of the Ossenkopf & Henning dust model only dust equilibrium temperature is calculated. Therefore, the results cannot be used to make predictions of dust emission at or below λ ~ 100 μm, where transiently heated grains would stand for a significant fraction of the observed intensity. The surface brightness of the cores has been calculated with radiative transfer modelling (Juvela 2005). In this work we limit the study to wavelengths longer than λ ~ 100 μm. where the stochastic heating of small grains need not be taken into account.
 |
Fig. 1 Typical profiles of the medium size cold cores. Density (top) as a function of the radius for 0.4, 5, and 20 solar masses, Temperature (middle), and Surface Brightness at 857 GHz (bottom). |
2.2. High mass cold cores
The transition between medium and high mass cold cores is given by the limitation of the Bonnor-Ebert Model described above. The inner core temperature of the Bonnor-Ebert modelled “cold cores” increases with mass, and becomes greater than 14 K for a cloud mass over 20 M⊙, as shown in Fig. 1. For our purposes we do not consider this to be “cold” anymore. Above a certain mass, the clouds consist not only of a single core, but a few cores linked together, leading to clumpy clouds. Each core inside this bigger structure has a cold temperature lower than 13 K, so that the entire cloud does not exceed a temperature of around 14 K (Sakai et al. 2008; Pillai et al. 2006; Sridharan et al. 2005). We model this kind of high mass object as an isothermal cloud at 14 K, adopting a mass limit of 20 M⊙ between the Bonnor-Ebert and isothermal models.
Furthermore, the isothermal model has to be constrained in terms of radius and extended with a warm envelope; such properties have already been included in the Bonnor-Ebert model. For our purpose we have used the Simon et al. (2006b) catalogue of 313 IRDCs, that provides mass and size properties. These IRDCs have been selected from a larger catalogue of IRDC candidates (Simon et al. 2006a) detected with MSX in extinction. The distance of these objects has been derived from the CO J = 1–0 molecular line emission, leading to an estimate of the size and mass. We emphasize that these objects have been detected in extinction, and that the derived size traces the inner and denser part of the clouds. We have fitted a power law over the Simon et al. (2006b) catalogue size-mass relation and obtained: 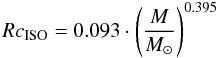 (1)where RcISO is the core radius in pc for the Isothermal model, and M is the mass. On the other hand, we define the core radius in the Bonnor-Ebert case RcBE as the domain in which the temperature remains flat: thus RcBE is the radius at which the temperature becomes greater than 1.02 times the central temperature. The continuity between the two definitions of core radius at M = 20 M⊙ is shown on the upper panel of Fig. 3 where RcBE is plotted as a red dashed line and RcISO as a red solid line. Finally the total radius of the cores is defined as the sum of the core radius and the warm envelope. As a first approximation, we can consider that the extent of the warmer dust and gas surrounding the cores remains unchanged when clouds become clumpy. The amount of warm gas depends only on the cold cores inside, and is given by the properties of these inner cores. Thus we have chosen a constant envelope radius over the whole range of high mass, set to the size of the envelope at 20 M⊙ given by the Bonnor-Ebert model. The total radius is shown by the black solid line in the upper panel of Fig. 3.
(1)where RcISO is the core radius in pc for the Isothermal model, and M is the mass. On the other hand, we define the core radius in the Bonnor-Ebert case RcBE as the domain in which the temperature remains flat: thus RcBE is the radius at which the temperature becomes greater than 1.02 times the central temperature. The continuity between the two definitions of core radius at M = 20 M⊙ is shown on the upper panel of Fig. 3 where RcBE is plotted as a red dashed line and RcISO as a red solid line. Finally the total radius of the cores is defined as the sum of the core radius and the warm envelope. As a first approximation, we can consider that the extent of the warmer dust and gas surrounding the cores remains unchanged when clouds become clumpy. The amount of warm gas depends only on the cold cores inside, and is given by the properties of these inner cores. Thus we have chosen a constant envelope radius over the whole range of high mass, set to the size of the envelope at 20 M⊙ given by the Bonnor-Ebert model. The total radius is shown by the black solid line in the upper panel of Fig. 3.
 |
Fig. 2 Surface Brightness Spectra of medium size cold cores as a function of the mass: 0.4, 5 and 20 solar Masses. The typical cirrus galactic brightness emission (red dashed-dot line) is modelled as a grey body at 17K with a spectral index β = 2. The averaged Galactic plane emission, over-plotted in red dash-dot-dot-dot line, gives an estimate of the background Galactic confusion level. The more massive the cold cores are, the more warmer they appear, and the less detectable they are. |
The surface brightness of the high mass objects is computed as the sum of two components: the isothermal cold core and the warm envelope. The isothermal intensity is given by a grey body model: 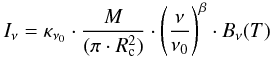 (2)where Iν is the surface Brightness, κ the dust opacity per unit of mass (gas plus dust), M is the gas mass, Rc is the core radius, T is the temperature (set to 14 K), Bν is the Planck function, ν0 is the frequency reference and β the emissivity index of the grey body law. Following Ossenkopf & Henning (1994), we adopt for κν0 a value of 8 × 10-3 cm2g-1 at ν0 = 250 GHz, and a value of 2 for the emissivity index β. The intensity of the envelope is extrapolated from the averaged intensity of the envelope estimated on the Bonnor-Ebert model at M = 20 M⊙. The resulting mean intensity at 857GHz is shown in the middle panel of Fig. 3 as a function of the mass. The continuity between the Bonnor-Ebert and the isothermal models is obvious, but one remarks a sharp transition with two opposite trends: the intensity of medium mass objects decreases when mass increases, because the temperature increases with the mass (cf. Figs. 2 and 1) and the warm envelope becomes more extended. On the other hand, the intensity of the high mass objects increases with mass, because the proportion of cold gas increases with the mass compared to the warm envelope. This sharp transition could represent an issue by introducing a deficit in the simulated catalogue of intermediate masses around M = 20 M⊙, but the integrated flux over the core and its envelope placed at a typical distance of 1 kpc (see lower panel of Fig. 3) has a very smooth behaviour from low to high masses, ensuring the continuity between the two models.
(2)where Iν is the surface Brightness, κ the dust opacity per unit of mass (gas plus dust), M is the gas mass, Rc is the core radius, T is the temperature (set to 14 K), Bν is the Planck function, ν0 is the frequency reference and β the emissivity index of the grey body law. Following Ossenkopf & Henning (1994), we adopt for κν0 a value of 8 × 10-3 cm2g-1 at ν0 = 250 GHz, and a value of 2 for the emissivity index β. The intensity of the envelope is extrapolated from the averaged intensity of the envelope estimated on the Bonnor-Ebert model at M = 20 M⊙. The resulting mean intensity at 857GHz is shown in the middle panel of Fig. 3 as a function of the mass. The continuity between the Bonnor-Ebert and the isothermal models is obvious, but one remarks a sharp transition with two opposite trends: the intensity of medium mass objects decreases when mass increases, because the temperature increases with the mass (cf. Figs. 2 and 1) and the warm envelope becomes more extended. On the other hand, the intensity of the high mass objects increases with mass, because the proportion of cold gas increases with the mass compared to the warm envelope. This sharp transition could represent an issue by introducing a deficit in the simulated catalogue of intermediate masses around M = 20 M⊙, but the integrated flux over the core and its envelope placed at a typical distance of 1 kpc (see lower panel of Fig. 3) has a very smooth behaviour from low to high masses, ensuring the continuity between the two models.
 |
Fig. 3 Continuity between medium size and high mass models. Top: core radius as a function of the mass, following the Simon et al. (2006b) catalogue distribution (triangles) for high masses. The red line gives the core size model adopted for high masses, when the dash red line is an estimate of the cold inner core for small masses. The black full line stands for the sum of inner core and envelope radius. Middle: associated surface brightness at 857 GHz averaged over the cold core surface including the envelope. Bottom: flux integrated over the core plus the envelope placed at a typical distance of 1 kpc. |
3. Catalogue simulation
We detail here the method we have developed to simulate a realistic catalogue of cold-cores on the entire Galactic sky. We describe the parameters of the simulation, and the algorithms used to generate the catalogue.
3.1. Spatial and mass distribution
The intrinsic 3D distribution of the cold cores inside the Galaxy is assumed to be radially symmetric with respect to the Galactic Center and symmetric with respect to the Galactic plane. In order to mimic the overall distribution of the cold cores, we have correlated the core distribution with the molecular phase of the gas at large scale. Thus we reproduce the global structure of the molecular ring, as has also been observed by Simon et al. (2006b), but not smaller structures of the Galaxy such as asymmetries due to the bar or the spiral arms. This gives a realistic view of the overall cold core distribution. We define the probability Pr of a cold core to be present at the radius R from the Galactic center as follows: 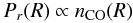 (3)where nCO is the number density of H2 as a function of radius R in kpc given by Bronfman et al. (1988), Rmin = 0 kpc and Rmax = 17 kpc define the radius range of the Galaxy. The probability Pz of a cold core to be present at an altitude z is given by:
(3)where nCO is the number density of H2 as a function of radius R in kpc given by Bronfman et al. (1988), Rmin = 0 kpc and Rmax = 17 kpc define the radius range of the Galaxy. The probability Pz of a cold core to be present at an altitude z is given by: 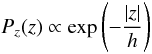 (4)where h = 0.1 kpc is approximately the scale height of the Galactic disk (Marshall et al. 2006; Drimmel & Spergel 2001). The 3D probability P3D of the cold cores to be present at a distance R from the Galactic center, and at a height z becomes:
(4)where h = 0.1 kpc is approximately the scale height of the Galactic disk (Marshall et al. 2006; Drimmel & Spergel 2001). The 3D probability P3D of the cold cores to be present at a distance R from the Galactic center, and at a height z becomes: 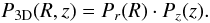 (5)This probability defines the modelled distribution of the cold cores over the Galaxy. We will detail in Sect. 3.2 how it is modulated by the observational bias in the case of Planck.
(5)This probability defines the modelled distribution of the cold cores over the Galaxy. We will detail in Sect. 3.2 how it is modulated by the observational bias in the case of Planck.
It has been shown that the cold core mass spectrum is approximatively given by a power law with index α: (dN / dM) ∝ M − α. We adopt here the value of Rathborne et al. (2006) who derived an index α of 2.1 ± 0.4 on a subset of 140 cores of the Simon et al. (2006b) catalogue observed in the millimeter continuum. Simon et al. (2006b) obtained a value of α = 1.97 over the 313 IRDCs observed in CO lines. These values of α are bracketed by the index of the stellar Initial Mass Function (IMF) that is about α = 2.35 (Salpeter 1955), and the index of the clump mass spectrum for molecular clouds spanning from 1.6 to 1.9 (Kramer et al. 1998; Simon et al. 2001). Thus the probability PM of a cold core to have the mass M is defined as follows: 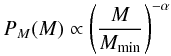 (6)where α = 2.1 and the mass M is bracketed between Mmin = 0.4 M⊙ and Mmax = 10000 M⊙.
(6)where α = 2.1 and the mass M is bracketed between Mmin = 0.4 M⊙ and Mmax = 10000 M⊙.
3.2. Catalogue generation
There are some practical problems connected with the creation of a complete simulated cold cores catalogue. Considering that the mass distribution is a power law with an index of 2.1, and the wide range of masses explored, the resulting catalogue would include a large amount of very small objects, even at large distances from the Sun. Furthermore many of them would be completely undetectable due to resolution and sensitivity limitations. We therefore take into account the characteristics of the instrument used to observe these objects. In our case, the simulated catalogue will be adapted to the Planck-HFI instrument, and the objects that are below its intrinsic detection limit are rejected. This implies that the initial symmetrical 3D distribution introduced in Sect. 3.1 is now broken.
The generation algorithm is divided into 3 steps: i) the position of the object is randomly chosen in the Galaxy following the 3D probability P3D; ii) the mass of the object is randomly chosen following the mass probability PM; iii) the object is kept in the catalogue if its observed intensity at the frequency ν integrated in the Planck beam is higher than the instrument sensitivity. The threshold has been set to Imin = 1.95 × 104 Jy / sr at 857 GHz, inside a beam of 5 arcmin, deduced from Lamarre et al. (2010). We stress that the last step of the catalogue generation implies that the cold core brightness model described in Sect. 2 has a significant impact on the resulting catalogue.
3.3. The normalisation issue
The number of objects Ncc that should be included in the catalogue is still uncertain. Concerning the purpose of this paper, which is dedicated to detection methods, we are principally interested in the statistical distribution of the objects over the sky and over the mass range. We wish to reproduce the large variety of detection configurations, from the confusion inside the Galactic disk, to cirrus confusion and low background level at high latitude. Thus the chosen number of simulated objects has to be high enough to properly cover all these different situations. We have first chosen to simulate Ncc = 105 objects in our catalogue. This number of cold cores already takes into account the sensitivity of Planck-HFI, so that all objects of the simulated catalogue are theoretically visible by Planck, i.e. above the sensitivity threshold.
The recent detection of cold sources in the Archeops data (Désert et al. 2008) represents an opportunity to verify this result. The balloon-borne experiment Archeops (Benoît et al. 2002) has been developed as a prototype of the Planck-HFI instrument, and has a similar architecture, although both its resolution and its sensitivity are much lower than the ones Planck will achieve. The cold core emission model described in Sect. 2 has been applied to the 105 objects of our simulated catalogue to get an estimate of the surface brightness at 353 GHz as observed by Archeops. It appears that only 70 of the simulated clouds have a flux greater than the Archeops sensitivity limit at 353 GHz ( ~ 12.1 Jy, Macías-Pérez et al. 2007) over the 30% of the sky covered by Archeops data, instead of the 304 detections of Désert et al. (2008). Nevertheless, among the Archeops point sources, 58 have been identified as UCHII regions. This leaves us with 246 sources, compared to the 70 we detected, suggesting that we would need ~ 3.5 × 105 simulated clouds to be in agreement with Archeops detections.
However, from the subset of 153 Archeops point sources for which a temperature has been derived using the 60 μm and 100 μm IRAS bands, only 114 have a temperature below 14 K, which is the cut in temperature of our simulated catalogue of cold cores (see Sect. 2). As we are interested in the colder clouds, we have finally adopted a number Ncc = 1.6 × 105 cold cores to match better the observations in emission delivered by the Archeops experiment.
4. Emission maps
4.1. Resulting catalogue
The resulting cold core catalogue contains 160000 objects. The a-priori flux selection performed during step iii) of the catalogue generation (see Sect. 3.2) leads to a solar concentrated 3D-distribution, see Fig. 10. The longitude histogram of Fig. 12 clearly shows the correlation of the cold cores with the molecular ring. We also emphasize that many cores are present at high latitude, and not only in the thin disk of the Galaxy. This will allow us to test the robustness of the detection algorithm with respect to other point sources such as extra-galactic objects present at high latitude, which we will discuss in Sect. 6.2. The mass-distance diagram (see Fig. 11) shows that the more massive cores are also visible quite far from the Sun, whereas many small objects have been rejected due to the sensitivity threshold. Accordingly, the mass histogram shown in the lower panel of Fig. 12 presents a cut around 40 M⊙. Above this mass limit the distribution follows the requested power-law (red line).
Sensitivity levels of Planck-HFI high frequency channels and IRAS.
4.2. Galactic and cold cores emission maps
From the coordinates, distance, size and mass properties of the 160000 objects of the simulated catalogue, we are able to produce simulated all-sky maps of the cold core emission in the Planck-HFI Bands. A spherical symmetry was assumed for the cores, and the brightness modelling described in Sect. 2 has been applied on each object. We produced all-sky maps of the cold cores emission at 2997 GHz, 857 GHz, 545 GHz and 353 GHz to simulate respectively the 100 μm IRAS maps, and the three highest frequency bands of Planck-HFI. A resolution of 5 arcmin was used at all frequencies. Under these conditions, about 0.17% of the objects are not point sources, but slightly extended sources spanning up to 30 arcmin of FWHM. The maps have been built in the HEALPIX Format (Górski et al. 2005), used for Planck-HFI Data storage, at the resolution of the Planck-HFI maps (nside = 2048, i.e. pixels of 1.7 arcmin).
Onto these pure cold cores emission all-sky maps, we have added the other various Galactic components predicted by the Planck Sky Model (hereafter PSM). This all-sky model contains the following components: the thermal emission from dust, the free-free emission from ionized gas, the synchrotron emission, and the Cosmic Microwave Background. It also includes a set of source catalogues: HII sources, radio sources and galaxy clusters seen by their Sunyaev-Zeldovitch effect, but no cold cores. For our purpose, we only detail here the dust model of Finkbeiner et al. (1999) included in the PSM, because we are especially interested in the high frequency channels where dust emission is dominant. This model contains two components: an amorphous silicate-like component at ⟨ T ⟩ ≈ 9.5K and emissivity ν1.7, and a carbonaceous component at ⟨ T ⟩ ≈ 16K and emissivity ν2.7. This non-physical model is in very good agreement with the FIRAS and DIRBE data and provides a good approximation of the FIR emission. We just have to keep in mind that a fraction of the PSM emission already has a very low temperature component, that could limit the efficiency of the detection method based on the colour properties of the cold cores, presented in Sect. 5.
The noise model we have added to the simulated data consists in a first component of white noise corresponding to the instrument sensitivity, and a second component of white noise proportional to the signal. The sensitivities of Planck-HFI and IRIS (Miville-Deschênes & Lagache 2005) are compiled in Table 1. The proportional component of the noise is mainly due to the uncertainty in the pointing. We investigated the impact of a 1-σ pointing error on the flux estimate of extended sources inside a beam of 5 arcmin. We found that for a 1-σ error of 5 arcsec (Planck requirement, private communication), the 1-σ error is about 0.1% of the signal. Thus we integrated a white noise with a level proportional to 0.1% of the input signal of the maps, i.e. thermal dust emission of the Galaxy and cold cores.
 |
Fig. 4 All sky Emission Maps. Top: Planck Sky Model brightness emission map at 545 GHz with Cold Cores. Bottom: cold cores emission map at 545 GHz. |
The resulting map at 545 GHz is shown in the upper panel of Fig. 4, and the cold core component in the lower panel. The cold core sources are hidden in the warm thermal dust component. This can be attributed to two causes: firstly the cold cores are very faint compared to the Galactic thermal dust component, and secondly they are hidden in the highly varying structures of the Galaxy. This Galactic confusion leads to the defeat of the classical methods of point sources detection inside the Galactic disk.
5. Detection algorithms
The originality of the detection algorithms we present here is above all the use of elaborated input maps rather than the simple frequency maps, in order to benefit from the cold signature of the objects we are interested in. We describe the 3 types of input maps investigated in this paper in Sect. 5.1: the Direct, Colour Ratio or Warm Background Subtracted maps. We detail in Sect. 5.2 the various steps of the detection processing we applied to these input maps.
5.1. Input maps
5.1.1. Direct map: MD
The direct map is simply the input map Iν at each frequency: 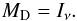 (7)This is our reference case, used to quantify the benefits of taking into account the colour properties of the objects in order to detect them. A typical case is shown in the frequency domain in Fig. 5 to illustrate the advantage the colour signature could give. We consider the spectrum of a point source at four characteristic temperatures (7K, 14K, 20K and 30K) added to the spectrum of the warm Galactic background typical of a cirrus at 17K (red line). We observe that at each Planck-HFI frequency the level of the point source appears higher than the background. Thus the use of the Direct map clearly deals with all kinds of point sources, and does not discriminate between cold and warm objects, HII or radio sources. In consequence, the cross-correlation with other existing catalogues becomes crucial to characterize the sample of detected sources, as detailed in Sect. 6.2.
(7)This is our reference case, used to quantify the benefits of taking into account the colour properties of the objects in order to detect them. A typical case is shown in the frequency domain in Fig. 5 to illustrate the advantage the colour signature could give. We consider the spectrum of a point source at four characteristic temperatures (7K, 14K, 20K and 30K) added to the spectrum of the warm Galactic background typical of a cirrus at 17K (red line). We observe that at each Planck-HFI frequency the level of the point source appears higher than the background. Thus the use of the Direct map clearly deals with all kinds of point sources, and does not discriminate between cold and warm objects, HII or radio sources. In consequence, the cross-correlation with other existing catalogues becomes crucial to characterize the sample of detected sources, as detailed in Sect. 6.2.
 |
Fig. 5 Illustration of the Direct method. The vertical dark grey band is the 2997 GHz IRAS band, and the 3 clear-grey bands are the 3 Planck-HFI bands (857 GHz, 545 GHz and 353 GHz). The red line represents the spectrum of the warm background cirrus, on which is added the spectrum of point sources at various temperatures: 7K, 14K, 20K and 30K. In the Direct method, the detection is performed at each frequency separately, and the method deals with all types of sources above the background level. |
 |
Fig. 6 Same as Fig. 5, in the case of the CR input maps. Each spectrum has been normalized by its value at 2997 GHz. The colour signature inside the Planck-HFI bands shows a clear excess over the background (red line) for cold sources. |
5.1.2. Colour ratio map: MCR
The cores we are looking for are cold compared to the warmer background of the Galaxy, and they present a relative emission excess at wavelengths above 350 μm (i.e. 857 GHz), as illustrated in Fig. 6. We see that normalizing each spectrum by its value at 2997 GHz clearly separates the warm and cold spectra: the cold ones present an excess compared to the background (red line), whereas the warm ones present a deficiency. Thus, mapping the ratio of the intensities Iν1 / Iν2 with ν1 < ν2 traces this characteristic excess used to optimise the detection processing. The Colour Ratio Map consists in that kind of ratio between the initial frequency map and a reference frequency map that should trace the warm background: 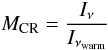 (8)where Iν is the intensity map at the frequency ν and Iνwarm is the intensity map of the warm component. The frequency νwarm is chosen to be reasonably free of emission from cold dust. In our case, we have chosen either the 2997 GHz of IRAS (i.e. 100 μm) or the 857 GHz band of Planck-HFI, that are dominated by the thermal emission of big grains at temperatures from 18 K to 30 K. The two options will be discussed later in Sect. 6. We would like to stress that using this kind of input maps is very sensitive to the noise level of the reference warmtemplate map, due to the use of a ratio, and even more at high latitude where the signal could be very close to zero.
(8)where Iν is the intensity map at the frequency ν and Iνwarm is the intensity map of the warm component. The frequency νwarm is chosen to be reasonably free of emission from cold dust. In our case, we have chosen either the 2997 GHz of IRAS (i.e. 100 μm) or the 857 GHz band of Planck-HFI, that are dominated by the thermal emission of big grains at temperatures from 18 K to 30 K. The two options will be discussed later in Sect. 6. We would like to stress that using this kind of input maps is very sensitive to the noise level of the reference warmtemplate map, due to the use of a ratio, and even more at high latitude where the signal could be very close to zero.
5.1.3. Warm background subtracted map: MWBS
 |
Fig. 7 Same as Fig. 5, in the case of the WBS input maps. The warm spectrum extrapolated from the 2997 GHz has been removed, so that cold sources (7K and 14K) appear positive with respect to the background (red line) while the warmer sources are negative. |
For the warm background subtracted map, we use the same colour property of the cold cores, but instead of looking at the ratio, we look at the cold residual once the warm component has been subtracted from the map. This warm component at the frequency ν is extrapolated from our reference warm frequency, using the average colour of the background. This colour background is computed at each pixel as the median of the colour ratio map between frequencies ν and νwarm inside an annulus spanning from 4 arcmin to 15 arcmin around the central pixel. Thus we get an estimate of the emission of the warm dust component IWν at frequency ν by: ![\begin{equation} IW_{\nu} = {\rm med} \left( \frac{I_{\nu}}{I_{\nu_{\rm warm}}} \right)_{\rm [ann]} \cdot I_{\nu_{\rm warm}} \label{eq_warmcomponent} \end{equation}](/articles/aa/full_html/2010/14/aa13934-09/aa13934-09-eq121.png) (9)where med(..) [ ann ] stands for the median inside an annulus around each target pixel. The use of the median is more robust here than the standard average, and allows the removal of sources and non Gaussian discrepancies inside the background annulus. The size of the annulus has been optimised to get a good estimate of the warm background level, i.e. far enough from the central pixel to avoid any contamination from cold emission, yet not too large in order to avoid any kind of local structure bias. The cold residual map is finally given by:
(9)where med(..) [ ann ] stands for the median inside an annulus around each target pixel. The use of the median is more robust here than the standard average, and allows the removal of sources and non Gaussian discrepancies inside the background annulus. The size of the annulus has been optimised to get a good estimate of the warm background level, i.e. far enough from the central pixel to avoid any contamination from cold emission, yet not too large in order to avoid any kind of local structure bias. The cold residual map is finally given by: 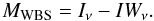 (10)Once again, the reference frequency for warm emission could be either the 2997 GHz of IRAS or the 857 GHz band of Planck-HFI. Figure 7 illustrates how the cold residual spectra remains positive over the warm background, whereas the spectra of the two warm sources result in negative features.
(10)Once again, the reference frequency for warm emission could be either the 2997 GHz of IRAS or the 857 GHz band of Planck-HFI. Figure 7 illustrates how the cold residual spectra remains positive over the warm background, whereas the spectra of the two warm sources result in negative features.
5.2. Detection processing
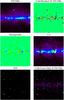 |
Fig. 8 Illustration of the warm background subtraction detection processing on a Galactic patch of 10° × 10° centered on ( − 40°, 0°). The upper left map is the original 545 GHz map, from 0 to 500 MJy/sr. In the right upper panel is the cold residual at 545 GHz after subtraction of the warm component extrapolated from the 2997 GHz. From the cold residual map are then computed the background and 1-σ maps, respectively left and right middle panels, plotted from − 5 MJy/sr to 5 MJy/sr. The signal-to-noise map S/N is given in the lower left panel, plotted in the range 4 to 10. The simulated cold cores only map is shown at 545 GHz in the lower right panel, with a colour scale ranging from 0 to 5 MJy/sr. We observe a good agreement between detections and real positions of cold cores. |
The detection processing is performed directly on the sphere, using the HEALPIX pixelization scheme, instead of working on small projected patches. This choice has been motivated by several reasons: i) the computing time is divided by a factor 10 at least; ii) we do not introduce any projection artifacts; iii) many border-effects are avoided when working on the sphere as a whole. The detection algorithm is divided into the following steps, illustrated in Fig. 8:
-
1.
Noise reduction: we use the so-called “a trous wavelet”algorithm (Starck et al. 1997) toclean our input maps. We select only the smallest scales, from1′ to 5′, and remove the noise component. This first step allows to throw out a fraction of the spurious structures such as strong stripes or borders of maps that could perturb the point source detection. This cleaning process has a negligible impact on point sources and larger structures, because it is only effective at very small scales, even lower than the beam, i.e. map artifacts.
-
2.
Input maps: we have investigated 3 types of input maps listed in Sect. 5.1. Thus we apply the same detection processing on the following inputs: the frequency map (MD), as a reference case, the colour map (MCR), and the warm background subtracted map (MWBS).
-
3.
Local background filtering: a local estimate of the background is calculated for each pixel of the input map, using a median filter inside an annulus of a given radius. The size of this annulus is adapted to the point spread function of the input data, so that any point source present at the central pixel does not enter into the background estimate: this leads to an inner-radius of 5 arcmin in the case of Planck-HFI (Maffei et al. 2010). The width of the annulus has been optimised to integrate enough data for the median computation and to avoid any kind of bias due to large scale structures of the Galaxy. This finally leads to an outer-radius of 15 arcmin. This local background map MBKG is then subtracted from the input map M, providing a local filtering of large scales in order to focus on point sources or slightly extended structures only.
-
4.
Local signal-to-noise estimate: the local dispersion is computed for each pixel inside the same annulus defined for the background estimate, using the median absolute deviation (MAD). The 1-σ rms obtained with the MAD method is given by σ = 1.4826·med( | x − med(x) | ). It provides a robust estimate of the rms, even in the presence of close point sources or non gaussian structures. The signal-to-noise map of the detection MSN is then given by:
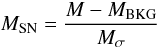 (11)where Mσ is the robust estimate of the local discrepancy. We emphasize that the local background and dispersion are estimated over the same annulus around each pixel.
(11)where Mσ is the robust estimate of the local discrepancy. We emphasize that the local background and dispersion are estimated over the same annulus around each pixel. -
5.
Deblending: the last step of the detection processing consists of searching the local maxima in the signal-to-noise detection map MSN over a given threshold (S / N)th. We define a minimum distance between two maxima, set to 5 arcmin, and a threshold (S / N)th = 4. This method allows the detection of any type of source and not only point sources. This last point is very important in the case of the cold cores, because they are often embedded in larger cold structures, such as filaments or extended molecular clouds.
6. All-Sky comparative results
We have applied a set of 13 methods on the simulated all-sky maps introduced in Sect. 4, containing all Galactic components plus a realistic catalogue of 160 000 cold cores, at four frequencies: 2997 GHz, 857 GHz, 545 GHz and 353 GHz. We now describe the efficiency of the various algorithms, and how we can get an optimised method based on the following criteria: completeness, reliability, and association with other point sources catalogues.
6.1. Signal-to-noise threshold optimisation
The 13 methods investigated are based on the 3 main algorithms listed above: the direct detection, the colour ratio method, and the warm background subtraction method (hereafter “D”, “CR”, and “WBS” respectively) applied on the Planck and IRAS bands. Thus we have 3 Direct methods D857, D545 and D353 respectively on the 857 GHz, 545 GHz and 353 GHz maps; 2 colour ratio methods using the highest frequency band at 857 GHz of Planck-HFI as a warm reference: CR 545/857, CR 353/857; 3 colour ratio methods using the IRIS 100 μm (=2997 GHz) reference map as a warm template, leading to: CR 857/2997, CR 545/2997, and CR 353/2997; 2 warm background subtraction methods using the highest frequency band at 857 GHz of Planck-HFI as a warm reference, leading to: WBS 545-857, and WBS 353-857; 3 Warm Background Subtraction methods using the IRIS 100 μm map: WBS 857-2997, WBS 545-2997, and WBS 353-2997.
We define the completeness of the detection catalogue as: 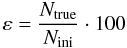 (12)where Ntrue is the number of correct detections of the resulting catalogue, and Nini is the number of cold cores initially injected in the catalogue. The reliability is an estimator of the confidence we can have in our detection catalogue, given by:
(12)where Ntrue is the number of correct detections of the resulting catalogue, and Nini is the number of cold cores initially injected in the catalogue. The reliability is an estimator of the confidence we can have in our detection catalogue, given by: 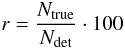 (13)where Ndet is the total number of detected objects, including spurious detections.
(13)where Ndet is the total number of detected objects, including spurious detections.
The optimisation of the cold core catalogue is first based on a robust reliability. The method consists in first setting a goal of the reliability r, then computing the appropriate signal-to-noise threshold (S / N)th requested to reach this goal for each method, and finally obtaining the completeness of the resulting catalogue. We have performed this optimisation for each method as a function of the latitude. The results are compiled in Table 2 and show for each of the 6 latitude bins, the completeness and signal-to-noise threshold obtained for a requested 98% reliability.
We first emphasize the very poor efficiency of the Direct method: less than 0.08% completeness for | b | < 5°. As mentioned before, this kind of method does not discriminate between cold sources and others, leading to an extremely high signal-to-noise threshold required to remove spurious detections: (S / N)th ~ 13 in the Galactic plane, and up to (S / N)th ~ 300 for | b | > 30°. We will see in Sect. 6.2 that the results are not better when we take into account the knowledge of the point sources already present in the maps.
The global completeness for the other methods is less than ~ 1% within the Galactic plane, a result that could appear disappointing. Nevertheless the population of cold cores is concentrated inside the Galactic disk, and even a detection rate of 1% in that region represents about 500 detections.
We also observe that the WBS and CR methods are less efficient when the 353 GHz band is used. This may be due to the lower brightness intensity of the cold cores at this frequency, compared to the 545 GHz band where the cold signature is also more obvious and detectable.
Furthermore the WBS methods globally have a slightly higher efficiency than the CR methods for most of the sky ( | b | < 30°). At higher latitude the CR 857/2997 method results in a completeness of 30%, when the other methods provide very poor results due to a high spurious rate, and even no detection at all under the 98% reliability requirement. This underlines the robustness of the CR methods on spurious detections compared to the WBS method, as detailed below.
Optimised completeness ε and signal-to-noise threshold (S / N)th for a requested reliability r = 98%.
 |
Fig. 9 Optimised signal-to-noise threshold (S/N)th of the detection process as a function of the latitude, and under the given constraint of 98% reliability. This latitude-dependence is shown for the 3 best selected methods: CR 545-2997, WBS 545-2997 and WBS 545-857 (numbers taken from Table 3 after cross-correlation with known point sources). |
One important result of this study is the dependence of the signal-to-noise threshold with latitude that allows optimisation of the detection processing. As an example, the (S/N)th range spans from 4.6 to 48.33 between the Galactic disk and pole, in the WBS 857-2997 case, leading to a completeness of 0.46% to 16.44% respectively. Choosing the extreme value 48.33 of the signal-to-noise threshold for the whole range of latitude would be catastrophic to the efficiency within the disk, and, conversely, choosing the lowest value 4.6 even at high latitude would result in too many spurious detections. The choice of the optimised (S/N)th per latitude bin is very method-dependent, as shown in Fig. 9 for the 3 best cases CR 545/2997, WBS 545-857 and WBS 545-2997 after taking into account the cross-correlation with known point sources as described in the following Sect. 6.2.
6.2. Cross-correlation with point source catalogues
Fraction of detections that are not cold cores but real point sources from other catalogues.
In order to increase the reliability, we perform a cross-correlation with catalogues of point sources. In the context of these simulations we have access to the entire knowledge of the various populations of point sources already present in the simulated maps, from the disk to higher latitude: HII regions, IR point sources such as nearby galaxies, Radio Galaxies, Galaxy Clusters. Thus the number of spurious detections Nspu( = Ndet − Ntrue) can be divided into two components: the number of real false detections Nfalse and the number of detected point sources that are not cold cores but other types of sources Nps, Nspu = Nfalse + Nps. Once the true detections of point sources that are not cold cores have been removed from the detected catalogue, a cross-checked reliability is defined as follows:  (14)The same optimisation of the signal-to-noise threshold (S / N)th described in Sect. 6.1 is performed using a criteria on the cross-checked reliability
(14)The same optimisation of the signal-to-noise threshold (S / N)th described in Sect. 6.1 is performed using a criteria on the cross-checked reliability 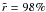 . The results are compiled in Table 3. The fraction of detected point sources rejected from the catalogue by this ideal cross-correlation processing is given for each method and latitude bin in Table 4.
. The results are compiled in Table 3. The fraction of detected point sources rejected from the catalogue by this ideal cross-correlation processing is given for each method and latitude bin in Table 4.
As expected, the fraction of spurious detections that are in fact real point sources from another type is very large for the Direct methods, and varies from 1% in the Galactic plane to 50% at higher latitude. This explains the poor efficiency of these methods before cross-correlation. Nevertheless, even after this catalogue cross-correlation processing, the completeness achieved by the Direct methods remain much lower than for the other methods: < 0.1% for 1° < | b | < 30° (cf. Table 4). At higher latitude, | b | > 30°, the efficiency is about 50%, in accordance with the other algorithms, but the proportion of “not cold cores” point sources could reach 50%, implying that the quality of the cold core catalogue is dependent on the completeness of other point source catalogues. The same high level of “not cold cores” point sources detections is observed for the D methods using the 353 GHz, explaining the poor results provided by this kind of methods.
The completeness achieved for the WBS and the CR algorithms is much higher after the cross-correlation processing, especially at medium and high latitudes, leading to 1% to 10% completeness in the latitude range 1° < |b| < 10°, and up to 61.60% at high latitude for the WBS 545-2997 method.
Looking at the thin Galactic plane, the completeness results have not been significantly affected by the cross-correlation processing. The “not cold cores” point sources already present in the maps are naturally rejected by the first processing of optimisation of the signal-to-noise threshold, without any use of external point sources catalogues. This reinforces the independence of this kind of algorithm to other a-priori knowledge.
6.3. Methods comparison and combination
We have optimised the detection algorithm in two ways: optimisation of the signal-to-noise threshold as a function of the latitude bin, and cross-correlation with existing point sources catalogues. After this processing, two main approaches have been identified.
In the first one, we assume that we have a good a-priori knowledge of the existing point sources catalogues, and we try to maximise the number of true detections after having performed the cross-correlation processing. In that case the WBS 545-857 method provides the best completeness over the whole latitude range, leading to 5370 detections, i.e. an averaged completeness of 3.36% with a 98% reliability. However the fraction of ’not cold cores’ point sources ranges from 1% in the thin Galactic disk to 15% at high latitude.
In the second approach, we base the optimisation only on the a-priori colour information, remaining as independent as possible from other point sources catalogues. The best compromise between completeness and reliability is obtained for two methods: the WBS 545-2997 method has a spurious rate (cf. Table 4) about half that of the WBS 545-857 method, and provides 4626 detections, i.e. 2.89% completeness; the CR 545/2997 method presents an even lower spurious rate by a factor of 20% to 50% depending on the latitude bin, and leads to 3727 detections, or 2.33% completeness. Moreover the results of the CR 545/2997 method are only slightly improved by the cross-correlation processing below | b | = 30°. This proves the robustness of the algorithm to spurious detections once again. The WBS 545-2997 method shows the same robustness on a more restricted region, below | b | = 10°. More generally the WBS method is less sensitive to noise features in the warm template than the CR method because the colour is computed on the background and not pixel by pixel. Thus the WBS method should be more robust to stripes and map-making artifacts. According to this last remark, a set of WBS methods using the same 100 μm reference warm template will be applied on real Planck-HFI data, taking advantage of the redundancy over frequencies and the robustness to maps artifacts.
The associated optimised signal-to-noise threshold (S / N)th for the 3 methods selected above are shown in Fig. 9.
6.4. Statistical analysis
We now compare the statistical properties of the input and detection catalogues, in terms of Galactic, mass and distance distributions. The global completeness does not exceed 3.4% in the best case, but we observe in the upper panel of Fig. 12 that this is mainly due to the loss of detections in the Galactic plane, where the completeness falls under 1% for all plotted detection methods (see caption). It is not surprising as the average level of the Galactic emission is a few hundred MJy/sr in the plane whereas the integrated surface brightness of a typical cold core of M = 10 M⊙ is a few MJy/sr. On the contrary, at high latitude, we obtain a very good completeness level that can reach 60%. This confusion issue leads to a concentration of the detections around the Sun, as shown in Fig. 10. The flatness of the longitude distribution profile is also explained by the fact that we are exploring the solar neighborhood, and we do not see any correlation with the molecular ring, as in the simulated catalogue (see middle panel of Fig. 12).
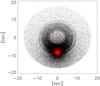 |
Fig. 10 Galactic distribution around the Galactic center of the input cold core simulated catalogue (black points) and of the resulting detection catalogue (red points) obtained by the WBS 545-857 algorithm. |
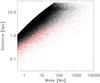 |
Fig. 11 Mass-distance diagram of the input simulated catalogue of cold cores (black points), and of the resulting detection catalogue (red points) obtained by the WBS 545-857 algorithm. |
The mass-distance diagram (see Fig. 11) illustrates the same feature: the black points are the initial cold cores of the simulated catalogue and in red are the detected ones with the WBS 545-857 method. The sensitivity limit of Planck-HFI is visible here by the straight upper boundary of the black cloud, but another boundary appears in red that is a result of the confusion. Moreover we notice in Fig. 12 that the 3 selected detection algorithms present the same properties in latitude and longitude distribution. Nevertheless the mass histogram (see lower panel of Fig. 12) shows an interesting discrepancy between the WBS and the CR methods: whereas the completeness for high masses (M > 20 M⊙) is roughly the same for all 3 methods, the efficiency is about twice better in the WBS case than in the CR one for the low mass objects (M < 20 M⊙). Thus the WBS algorithms are better suited to explore the less massive objects, that are also the coldest ones.
We would like to stress that the overall properties of the detection algorithm described above could be significantly improved by the use of high resolution data such as Herschel observations, especially in terms of completeness. Whereas the beam dilution effect lowers the efficiency of the detection method in the plane for Planck-HFI, the resolution of Herschel (5 to 36 arcsec) will probe objects deeper in the plane using the colour detection algorithm. We expect to detect a much larger amount of cold sources with Herschel data than with Planck when applying the CoCoCoDeT method on the same region, exploring even fainter, colder and less massive objects.
 |
Fig. 12 Catalogue distribution in latitude (top), longitude (middle) and mass (bottom). The distribution of the input simulated catalogue is plotted as a solid line. The statistics of the output detection catalogue is given for the 3 best methods: CR 545/2997 (dot dot dot dash), WBS 545-2997 (dash) and WBS 545-857 (long dash). The red line in the bottom panel indicates the input power law of the mass distribution with an index α = 2.1. |
 |
Fig. 13 Recovered flux versus true flux [Jy] at 545 GHz applied on the 4626 detections delivered by the WBS 545-2997 method. |
6.5. Photometry
We address here the complex issue of the photometry of such cold cores embedded in larger structures. A classical aperture photometry would lead in this case to an overestimation of the flux, due to the pollution by the warm background component. The first idea consists in computing the flux inside a given radius and subtracting the background level estimated on an annulus outside the core. However this method provides poor results due to the high level of confusion in the Galactic plane, leading to more than 40% error. Thus we have developed a photometry estimate based on the colour properties of these objects. Following the same approach used for the Warm Background Subtraction, we first estimate the warm background component that we subtract from the map at each frequency, and we focus the photometry estimate on the cold residual. The difficulty of such a technique is the warm template that is extrapolated to each frequency, because this warm template could already contain a cold part and thus lead to an underestimation of the flux at the extrapolated frequencies. We present here the algorithm performed on mini-maps of 1° × 1° centered around the detected point sources:
-
1.
Get spatial properties: they are derived from an ellipticalgaussian fit performed on the colour map857 GHz / 2997 GHz centered on the detected source, leading to the following quantities: galactic coordinates (glon, glat), angular extensions along long axis and short axis (σx, σy), and orientation given by the rotation angle α. We stress that some of the sources can be extended, and computing the flux estimate using a simple Point Spread Function could lead to major errors.
-
2.
Estimate of the flux at 2997 GHz: the amplitude of the central elliptical gaussian is fitted on the 2997 GHz map using the spatial properties provided by step 1, after removing a polynomial surface of 5th order fitted on the background simultaneously inside an area of 30 arcmin radius.
-
3.
Correct warm template: the corrected warm template at 2997 GHz is obtained by subtracting, at the centre, the flux estimate obtained during step 2 from the initial mini-map at 2997 GHz.
-
4.
Cold residual estimate at each ν: the same algorithm presented in Eq. (9) is applied here to extrapolate the warm component from the reference frequency νwarm = 2997 GHz to the frequency ν and is then subtracted from the initial mini-map to get the cold residual only.
-
5.
Flux estimate at each ν: the amplitude of the elliptical gaussian of step 1 is fitted on the cold residual map. The flux (in Jy) is finally computed as the integral of the intensity map (in MJy/sr) inside the elliptical gaussian solid angle.
We show in Fig. 13 the agreement between the recovered fluxes and the initial fluxes at 545 GHz of the detected sources provided by the WBS 545-2997 method. The median of the relative error is about 20% as illustrated in Fig. 14, which is better by a factor 2 than a classical aperture photometry inside a disk of 5 arcmin of radius (dotted line in the histogram of the error). The same gain on the flux estimate is observed at the other frequencies when using the WBS photometry instead of the aperture method.
 |
Fig. 14 Histogram of the relative error on the recovered flux at 545 GHz obtained by applying the WBS photometry estimate (full line) and an aperture photometry inside a 5 arcmin radius disk (dotted line). The vertical full and dotted lines stand for the median of the error for the WBS and aperture method respectively. |
7. Conclusion
We have described a complete algorithm to build an all-sky simulated catalogue of cold cores. We have simulated their emission properties including the cold core (from 7 K to 14 K) and the warm envelope in a unified and continuous model from 0.4 M⊙ to 1000 M⊙, by using a Bonnor-Ebert modelling for low masses until 20 M⊙, and an isothermal model for higher masses. The distribution of these objects over the sky has been chosen to statistically match the molecular phase as a function of the altitude and the distance to the Galactic center. We have adapted the initial power-law mass distribution as a function of the distance to the Sun in order to take into account the sensitivity limit of any dedicated instrument. This ensures the completeness of the simulated cold core catalogue without inclusion of many undetectable objects.
We have applied this algorithm in the frame of the Planck mission to get a simulated catalogue of cold cores adapted to the Planck resolution and sensitivity. Particular attention has been given to the normalisation of this simulated catalogue using the Archeops Point Source Catalogue (Désert et al. 2008), and focusing on the population of cold cores. The result is a catalogue of 1.6 × 105 objects in the Planck simulated cold core catalogue, containing longitude, latitude, distance, mass and size information. All-sky maps have been built in the Planck bands, including all Galactic components and point sources, and cold core sources.
These simulated maps have been used to investigate the extraction of the cold cores with Planck. Three detection methods have been explored: the classical thresholding detection method at each frequency, and two other methods based on the colour signature of the cold cores, the colour ratio and the warm background subtraction methods. The principle of the first colour method is to perform the detection on the colour map, i.e. the ratio of two frequency maps. Concerning the second method, the extraction is performed on the cold residual map obtained after subtraction of an extrapolated warm template. We have shown that where the classical method fails due to Galactic confusion, the colour methods remain more efficient and ensure a higher reliability. The best results have been obtained with the warm background subtraction method using the Planck-HFI 545 GHz and the IRAS 2997 GHz as a warm reference map, leading to a completeness of 2.89% (4626 objects) and a reliability of 98%. We stress that the reliability of our detected catalogue is the most important criteria, and that it has been used as a guide to optimise the signal-to-noise threshold of the detection as a function of Galactic latitude. The recovered distribution of the detections spans all masses, and covers the whole sky, even if the detected objects are mostly located in the solar neighbourhood and near the Galactic plane.
Furthermore we have developed an original photometry algorithm, based on the colour properties of this kind of objects, to get the flux estimate of the cold part only. The idea consists in removing the warm background extrapolated from a warm template for each source and computing the flux inside an elliptical gaussian (2 × FHWM area) on the cold residual. This technique increases the quality of the recovered flux by a factor of 2, compared to classical aperture photometry.
The Planck survey will allow the first all-sky study of the cold cores statistics, and should provide thousands of detections with a high quality of flux recovery, leading to a first estimate of their temperature and of their physical properties: temperature, emissivity, column density and mass when distance can be derived (using kinematic and extinction based methods, Marshall et al. 2009) Herschel provides further perspectives for these studies. In an already accepted Herschel Open Time Key Programme, follow-up observations will be carried out on 150 cold core candidates detected by Planck (Juvela et al. 2010). On the other hand, the methods described in this paper can directly be applied on Herschel data, especially in the Galactic plane where the HiGal Project (Molinari et al. 2010) will cover a region 2 by 120 degrees. This will allow an investigation of the cold core population in the plane with high resolution and sensitivity.
Acknowledgments
The authors acknowledge the use of the Planck Sky Model, developed by the Component Separation Working Group (WG2) of the Planck Collaboration. M. Juvela acknowledges the financial support of the Academy of Finland through grants 127015, 105623, 115056. We acknowledge the french spatial agency, the Centre National d’Etude Spatiale, that have funded D.J. Marshall. We would like to thank the referee for his constructive remarks that have improved this work.
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benoît, A., Ade, P., Amblard, A., et al. 2002, Astropart. Phys., 17, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J. P., Abergel, A., Ristorcelli, I., et al. 1999, A&A, 347, 640 [NASA ADS] [Google Scholar]
- Boggess, N. W., Mather, J. C., Weiss, R., et al. 1992, ApJ, 397, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Bronfman, L., Cohen, R. S., Alvarez, H., May, J., & Thaddeus, P. 1988, ApJ, 324, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, D. P., Yun, J. L., & Heyer, M. H. 1991, ApJS, 75, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, F., Macías-Pérez, J. F., Mayet, F. M., et al. 2008, A&A, 481, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Dupac, X., Bernard, J., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebert, R. 1955, Zeitschrift fur Astrophysik, 37, 217 [Google Scholar]
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Fischera, J., & Dopita, M. A. 2008, ApJS, 176, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hearty, T., Fernández, M., Alcalá, J. M., Covino, E., & Neuhäuser, R. 2000, A&A, 357, 681 [NASA ADS] [Google Scholar]
- Johnstone, D., Wilson, C. D., Moriarty-Schieven, G., et al. 2000, ApJ, 545, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M. 2005, A&A, 440, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Montier, L., et al. 2010, A&A, 518, L93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
- Lagache, G., Abergel, A., Boulanger, F., & Puget, J. 1998, A&A, 333, 709 [NASA ADS] [Google Scholar]
- Lamarre, J. M., Puget, J. L., Ade, P., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macías-Pérez, J. F., Lagache, G., Maffei, B., et al. 2007, A&A, 467, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maffei, B., Noviello, F., Murphy, J. A., et al. 2010, A&A, 520, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnani, L., Caillault, J., Buchalter, A., & Beichman, C. A. 1995, ApJ, 96, 159 [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, D. J., Joncas, G., & Jones, A. P. 2009, ApJ, 706, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, E. L., & Kun, M. 1996, A&AS, 116, 467 [Google Scholar]
- Miville-Deschênes, M., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Tachihara, K., & Fukui, Y. 2002, ApJ, 575, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pearson, C. P., Shibai, H., Matsumoto, T., et al. 2004, MNRAS, 347, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Perault, M., Omont, A., Simon, G., et al. 1996, A&A, 315, L165 [NASA ADS] [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, S. D. 1995, Space Sci. Rev., 74, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Ristorcelli, I., Serra, G., Lamarre, J. M., et al. 1998, ApJ, 496, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, T., Sakai, N., Kamegai, K., et al. 2008, ApJ, 678, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Serra, G., Giard, M., Bernard, J., Stepnik, B., & Ristorcelli, I. 2001, C. R. Acad. Sci. Ser. IV, 1, 1215 [Google Scholar]
- Simon, R., Jackson, J. M., Clemens, D. P., Bania, T. M., & Heyer, M. H. 2001, ApJ, 551, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Jackson, J. M., Rathborne, J. M., & Chambers, E. T. 2006a, ApJ, 639, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Rathborne, J. M., Shah, R. Y., Jackson, J. M., & Chambers, E. T. 2006b, ApJ, 653, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Saito, M., Wyrowski, F., & Schilke, P. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2003, A&A, 407, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J., Siebenmorgen, R., & Gredel, R. 1997, ApJ, 482, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stickel, M., Krause, O., Klaas, U., & Lemke, D. 2007, A&A, 466, 1205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Optimised completeness ε and signal-to-noise threshold (S / N)th for a requested reliability r = 98%.
Fraction of detections that are not cold cores but real point sources from other catalogues.
All Figures
 |
Fig. 1 Typical profiles of the medium size cold cores. Density (top) as a function of the radius for 0.4, 5, and 20 solar masses, Temperature (middle), and Surface Brightness at 857 GHz (bottom). |
| In the text | |
 |
Fig. 2 Surface Brightness Spectra of medium size cold cores as a function of the mass: 0.4, 5 and 20 solar Masses. The typical cirrus galactic brightness emission (red dashed-dot line) is modelled as a grey body at 17K with a spectral index β = 2. The averaged Galactic plane emission, over-plotted in red dash-dot-dot-dot line, gives an estimate of the background Galactic confusion level. The more massive the cold cores are, the more warmer they appear, and the less detectable they are. |
| In the text | |
 |
Fig. 3 Continuity between medium size and high mass models. Top: core radius as a function of the mass, following the Simon et al. (2006b) catalogue distribution (triangles) for high masses. The red line gives the core size model adopted for high masses, when the dash red line is an estimate of the cold inner core for small masses. The black full line stands for the sum of inner core and envelope radius. Middle: associated surface brightness at 857 GHz averaged over the cold core surface including the envelope. Bottom: flux integrated over the core plus the envelope placed at a typical distance of 1 kpc. |
| In the text | |
 |
Fig. 4 All sky Emission Maps. Top: Planck Sky Model brightness emission map at 545 GHz with Cold Cores. Bottom: cold cores emission map at 545 GHz. |
| In the text | |
 |
Fig. 5 Illustration of the Direct method. The vertical dark grey band is the 2997 GHz IRAS band, and the 3 clear-grey bands are the 3 Planck-HFI bands (857 GHz, 545 GHz and 353 GHz). The red line represents the spectrum of the warm background cirrus, on which is added the spectrum of point sources at various temperatures: 7K, 14K, 20K and 30K. In the Direct method, the detection is performed at each frequency separately, and the method deals with all types of sources above the background level. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, in the case of the CR input maps. Each spectrum has been normalized by its value at 2997 GHz. The colour signature inside the Planck-HFI bands shows a clear excess over the background (red line) for cold sources. |
| In the text | |
 |
Fig. 7 Same as Fig. 5, in the case of the WBS input maps. The warm spectrum extrapolated from the 2997 GHz has been removed, so that cold sources (7K and 14K) appear positive with respect to the background (red line) while the warmer sources are negative. |
| In the text | |
 |
Fig. 8 Illustration of the warm background subtraction detection processing on a Galactic patch of 10° × 10° centered on ( − 40°, 0°). The upper left map is the original 545 GHz map, from 0 to 500 MJy/sr. In the right upper panel is the cold residual at 545 GHz after subtraction of the warm component extrapolated from the 2997 GHz. From the cold residual map are then computed the background and 1-σ maps, respectively left and right middle panels, plotted from − 5 MJy/sr to 5 MJy/sr. The signal-to-noise map S/N is given in the lower left panel, plotted in the range 4 to 10. The simulated cold cores only map is shown at 545 GHz in the lower right panel, with a colour scale ranging from 0 to 5 MJy/sr. We observe a good agreement between detections and real positions of cold cores. |
| In the text | |
 |
Fig. 9 Optimised signal-to-noise threshold (S/N)th of the detection process as a function of the latitude, and under the given constraint of 98% reliability. This latitude-dependence is shown for the 3 best selected methods: CR 545-2997, WBS 545-2997 and WBS 545-857 (numbers taken from Table 3 after cross-correlation with known point sources). |
| In the text | |
 |
Fig. 10 Galactic distribution around the Galactic center of the input cold core simulated catalogue (black points) and of the resulting detection catalogue (red points) obtained by the WBS 545-857 algorithm. |
| In the text | |
 |
Fig. 11 Mass-distance diagram of the input simulated catalogue of cold cores (black points), and of the resulting detection catalogue (red points) obtained by the WBS 545-857 algorithm. |
| In the text | |
 |
Fig. 12 Catalogue distribution in latitude (top), longitude (middle) and mass (bottom). The distribution of the input simulated catalogue is plotted as a solid line. The statistics of the output detection catalogue is given for the 3 best methods: CR 545/2997 (dot dot dot dash), WBS 545-2997 (dash) and WBS 545-857 (long dash). The red line in the bottom panel indicates the input power law of the mass distribution with an index α = 2.1. |
| In the text | |
 |
Fig. 13 Recovered flux versus true flux [Jy] at 545 GHz applied on the 4626 detections delivered by the WBS 545-2997 method. |
| In the text | |
 |
Fig. 14 Histogram of the relative error on the recovered flux at 545 GHz obtained by applying the WBS photometry estimate (full line) and an aperture photometry inside a 5 arcmin radius disk (dotted line). The vertical full and dotted lines stand for the median of the error for the WBS and aperture method respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.