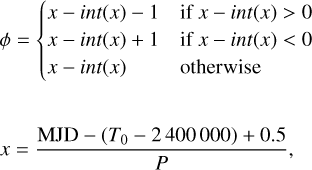EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 678 (October 2023) A&A, 678 (2023) A195 Full HTML
Open Access
Issue
A&A
Volume 678, October 2023
Article Number A195
Number of page(s) 21
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202346982
Published online 24 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Radial and azimuthal metallicity gradients (with respect to the galactic center and to the galactic plane, respectively) are crucial diagnostics for tracing the chemical enrichment history of individual galactic components (Lemasle et al. 2013, 2018; Genovali et al. 2014, 2015; da Silva et al. 2016, 2022). The radial variation of different heavy elements is produced either by Type Ia supernovae (SN Ia) or by massive and asymptotic giant branch (AGB) stars or by more exotic objects (e.g., neutron star mergers). It provides fundamental constraints on chemical evolution models (Cavichia et al. 2014; Schönrich & McMillan 2017; Grisoni et al. 2018; Prantzos et al. 2018; Matteucci et al. 2020; Spitoni et al. 2022; Tsujimoto 2023). Several stellar tracers, covering a broad range in stellar ages – old stars: RR Lyrae, blue horizontal branch, and globular clusters; intermediate age-stars: red clump stars and anomalous Cepheids; and young stars: red and blue supergiants, classical Cepheids (CCs), and open clusters (OCs) – allows us to investigate the role that galaxy mergers, stellar migrations, and kinematics play in the formation and evolution of galaxies. In addition to these indisputable advantages, radial metallicity gradients allow us to trace the coupling among star-forming regions (Genovali et al. 2014), spiral structure (Lemasle et al. 2022), and geometrical complexity (warps, flares, and streams; Feast et al. 2014; Matsunaga et al. 2018; Chen et al. 2019; Skowron et al. 2019; Dehnen et al. 2023).

Dating back to more than half a century ago (Kraft 1966), CCs have been widely used to trace the variation in iron as a function of the galactocentric distance. The key advantage of using CCs to trace young stellar populations is manifold: i) CCs are very solid primary-distance indicators, and their individual distances can be estimated with an accuracy better than 3% on average. ii) They are associated with central helium-burning phases (blue loop) of intermediate-mass stars (from ~3 to ~10 M⊙). This means that they are quite common and ubiquitous across the Galactic thin disk. iii) CCs have low surface gravities, and their spectra are quite rich in absorption lines. Long-period Cepheids are characterized by strong molecular bands. The main drawback is that the variation in the physical properties throughout the pulsation cycle requires a solid approach for estimating the effective temperature, surface gravity, and microturbulent velocity. Moreover, different lines might also vary significantly during the pulsation cycle, and therefore, they need to be properly identified. A detailed and more quantitative discussion of these issues is provided by da Silva et al. (2022).

The empirical scenario emerging from the recent paramount spectroscopic effort on CCs is that all the investigated elements (iron peak, α, and neutron capture) display a well-defined radial gradient, with the exception of barium (Andrievsky et al. 2013). In spite of this global agreement, some problems emerge. The current estimates of the global metallicity gradient very often differ in zeropoint, as expected, because the assumptions on the solar abundances and on the approach adopted to estimate the atmospheric parameters are different. Moreover, a difference is also quite often seen in the slope of the radial metallicity gradient, which is commonly associated with the adopted line list. Several atomic lines from both neutral and ionized species are affected by nonlocal thermodynamical equilibrium (NLTE) effects, and this dependence changes as a function of surface gravity, effective temperature, and iron abundance. This means that in the estimate of the mean abundance based on different lines, a significant fraction of possible systematic errors is summed.

Finally, it is worth mentioning that the slope is also tightly correlated with the rate at which the individual elements are enriched. For this main reason, the iron radial gradient is typically steepest, not only among the iron-peak elements, but also among the α and neutron-capture elements. Iron is produced by both SN Ia and massive stars, with the former enriching the interstellar medium on longer timescales (about some billion years). In a recent investigation based on more than 400 high-resolution spectra with a high signal-to-noise ratio (S/N) for two dozen calibrating Cepheids (da Silva et al. 2022), we found preliminary evidence that the slope of the sulfur radial gradient is steeper than that found for iron abundances. To further investigate this crucial issue, we performed the same measurements plus those of another α-element (oxygen) over a significantly larger sample of CCs (more than 350 variables). To provide a comprehensive analysis of Galactic CCs, we also reanalyzed literature data. In passing, we also mention that recent findings indicate that stellar metallicities measured in extragalactic systems in general agree with the nebular abundances based on the analysis of the auroral lines (Bresolin et al. 2009, 2022; Gazak et al. 2015; Liu et al. 2022). Studies of H II regions and luminous young stars in local disk galaxies show a significant gas metallicity gradient (−0.04 to −0.06 dex kpc−1), that is, a strong decrease in the abundances from the center to the outskirts of the galaxy (Zaritsky et al. 1994; Sánchez-Blázquez et al. 2014; Bresolin et al. 2012, 2016; Kudritzki & Urbaneja 2018). The same outcome applies to the α-element abundance gradients (Urbaneja et al. 2005). However, many disks are surrounded by huge areas of neutral hydrogen with constant low metallicity and a low star formation rate (Bresolin et al. 2012; Kudritzki et al. 2014, and references therein).

The main aim here is to determine and compare the iron, sulfur, and oxygen radial abundance gradients throughout the Galactic thin disk. The paper is therefore organized as follows. In Sect. 2, we introduce the spectroscopic data and the properties of our sample of classical Cepheids and open clusters. In Sect. 3, we describe how we derived the atmospheric parameters and the abundances. Section 4 shows the Galactic radial gradients that we obtained for different abundance ratios, together with their dependence on the stellar age. In Sects. 5 and 6 we compare our results with those from the literature derived from both observations and theory. A summary of our results together with some final considerations is provided in Sect. 7.

2 Observations and sample properties

2.1 Sample of classical Cepheids

The sample of classical Cepheids investigated in the current study is the result of a compilation of several subsamples for which high-resolution spectra with an high S/N are available in different databases. These spectra were collected using four high-resolution spectrographs: the High Accuracy Radial velocity Planet Searcher spectrograph (HARPS; Mayor et al. 2003) mounted at the 3.6 m telescope of the European Southern Observatory (ESO) at La Silla (Chile), the Fiber-fed Extended Range Optical Spectrograph (FEROS; Kaufer et al. 1999) installed at the 2.2 m MPG/ESO, the Ultraviolet and Visual Echelle Spectrograph (UVES; Dekker et al. 2000) at the Very Large Telescope of ESO at Paranal (Chile), and the STELLar Activity (STELLA) Echelle Spectrograph (SES; Strassmeier et al. 2004, 2010) mounted at the 1.2 m telescope of the Izána Observatory located in Tenerife, Spain. The spectral resolution achieved for the instrument settings we used is R ~ 40 000 for UVES spectra, R ~ 115 000 for HARPS, R ~ 48 000 for FEROS, and R ~ 55 000 for STELLA. For details about the wavelength ranges, we refer to Proxauf et al. (2018) and Crestani et al. (2021).

Our spectroscopic sample includes proprietary data and spectra downloaded from the ESO and the STELLA archives: 183 HARPS spectra of 10 stars, 339 FEROS spectra of 161 stars, 363 UVES spectra of 215 stars, and 400 STELLA spectra of 64 stars (the spectra for some of the stars were collected with more than one instrument) for a total of 1285 spectra of 379 stars. The S/N is at least 100 for more than 80% of these spectra. For 1118 spectra of 356 stars, we were able to derive all the stellar atmospheric parameters required for abundance determination (effective temperature, surface gravity, microturbulent velocity, and metallicity). For reasons discussed in the next section, only the effective temperature was derived for 167 spectra of 23 stars. In this context, it is worth mentioning that the abundance estimates based on high-resolution spectra for 70 out of the 356 CCs are provided here for the first time. The complete sample of 379 stars is listed in Table 1. A more detailed discussion of the classification of our sample as classical Cepheids is provided in Appendix A.

Table 1

Excerpt from the list of our sample of 379 Galactic classical Cepheids.

2.2 Sample of open clusters

We complemented our sample of classical Cepheids with a sample of open clusters from Randich et al. (2022), which includes 62 open clusters observed by the Gaia-ESO Survey (GES) plus 18 retrieved from the ESO archive. We refer to Viscasillas Vâzquez et al. (2022) for the general characteristics of the sample and the selection criteria of members in each cluster. Briefly, the sample covers a range in age from 1.4 Myr to 6.8 Gyr, in galactocentric distances from 5.8 to 20.6 kpc, and in metallicity from −0.45 to 0.27 dex.

For the sample clusters, we adopted the [O/H] ratios from Magrini et al. (2023). The abundance of O was computed using the forbidden [O I] line at 6300.3 Å in the LTE approximation (see Tautvaišienė et al. 2015, for details). For S, to be consistent with the spectral analysis done on the CCs, we remeasured the abundance using only the S I triplet at 6757 Å. We then computed the mean [S/H] for each cluster.

2.3 Spatial distribution in the thin disk

The heliocentric distances of our Cepheids were estimated based on four different diagnostics, listed here in priority order: 1) Gaia Early Data Release 3 (Gaia EDR3) distances from parallaxes within the external.gaiaedr3_distance table (Bailer-Jones et al. 2021); 2) W1-band period-luminosity relation (PL; calibrated from Galactic CCs by Wang et al. 2018); 3) K-band PL (calibrated on Galactic CCs by Ripepi et al. 2020); and 4) J-band PL (calibrated from CCs in the Large Magellanic Cloud – LMC – by Ripepi et al. 2022). We adopted the Gaia distances only for Cepheids with parallax_over_error > 10 and ruwe < 1.4. The first condition is self-explanatory, whereas the second was included because ruwe is an estimate of the goodness of the astrometric solution for single stars. A value of 1.4 is a typical threshold adopted to separate single detections from multiple-detection candidates (or problematic solutions). For the other Cepheids, we adopted the PL relations using 2MASS and WISE magnitudes. We ruled out all the magnitudes with poor photometric quality (X, U, or E) from both surveys. The apparent magnitudes were dereddened by using E(B – V) from Schlafly & Finkbeiner (2011) and the reddening law by Cardelli et al. (1989), extended to the mid-infrared (MIR) by Madore et al. (2013). We finally had 282 CCs with distances from Gaia and 115, 12, and 3 from W1-, K-, and J-band PLs.

After deriving the heliocentric distances, we used the Gaia coordinates to estimate the galactocentric Cartesian coordinates (X, Y, Z) and the galactocentric distance on the plane 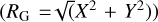(RG=√(X2+Y2))$\left( {{R_{\rm{G}}} = \surd \left( {{X^2} + {Y^2}} \right)} \right)$. For these calculation, a distance of 8.127 kpc from the Galactic center was assumed (GRAVITY Collaboration 2018). Figure 1 shows the radial distribution of the entire spectroscopic sample projected onto the Galactic plane. The symbols are color-coded according to the distance from the Galactic plane (the absolute value of Z). The data plotted in this figure display several interesting findings that we discuss in more detail below.

  1. Galactocentric distances. The Cepheid galactocentric distances cover almost 25 kpc, ranging from about 5 kpc for stars in the inner disk to almost 30 kpc for stars in the outer disk. The current sample for the first time includes eight Cepheids with galactocentric distances larger than 18 kpc.

  2. Height from the Galactic plane. The distances from the Galactic plane for the bulk of the spectroscopic sample are smaller than 500 pc, as expected for typical disk stellar populations. Interestingly enough, Cepheids located at galactocentric distances larger than 12 kpc display a systematic drift toward negative Z values and approach Z = −1.5 kpc for RG~ 17–18 kpc. This trend and the increase at even larger galactocentric distances are associated with the Milky Way (MW) warp. There is only one exception: the Cepheid V1253 Cen (X = −7.73, Y = 3.63 kpc) is located across the solar circle, but its height above the Galactic plane is ~4 kpc. This circumstantial evidence indicates that this variable does not appear to be a typical disk star, and is in turn a typical CCs. In passing, we note that in a recent investigation, Gaia Collaboration (2023) called attention to the fact that a large sample of Galactic field stars included in the Gaia DR3 display a strong vertical asymmetry of the thin disk. The conclusions of this investigation are independent of the inclusion of this object, and it was neglected. However, it is worth keeping this Cepheid under special surveillance.

  3. Distribution across the disk. The current sample covers the four quadrants, and, in particular, the third and fourth quadrant. Interestingly enough, the spatial distribution agrees quite well with high-mass star-forming regions observed by Reid et al. (2019). The agreement is further supported by the comparison with the spiral arms identified by these authors, and it applies not only to the main arms (Sgr-Car, Perseus, Norma, and Sct-Cen), but to the Local arm as well. However, there is evidence that the Norma-Outer arm has a larger pitch angle in the third quadrant. The separation among the different arms is not very sharp due to the presence of several interarm objects, but the overdensities trace the main arms quite well.

  4. Orbital properties. We also investigated the orbital properties of the current sample of Galactic Cepheids. In particular, we computed the circularity of the orbits, defined as the angular momentum JZ around the short Z-axis, normalized by the maximum angular momentum of a circular orbit with the same binding energy E: λZ = JZ/Jmax(E). The orbits were split into four components (Zhu et al. 2018; Santucci et al. 2023): a cold component with near circular orbits (λZ > 0.8) typical of the thin disk, a hot component with near radial orbits (−0.25 < λZ < 0.25) typical of the bulge, a warm component (0.25 < λZ < 0.8) typical of the thick disk, and a counter-rotating component (λZ < −0.25). To integrate the orbits, we used the galpy code (Bovy 2015), modeling the potential of the Galaxy by means of the MWPotential2014 implementation, which is composed of a power law with an exponential cutoff for the bulge, a Miyamoto & Nagai (1975) disk, and a Navarro et al. (1996) halo1. To perform the orbit integration, we used the Dormand & Prince (1980) integration method (by setting the option method = dopr54_c in galpy). We integrated the orbits for 10 Gyr, starting from the current position and velocity of the variables. We found that the bulk of the current spectroscopic sample has cold orbits typical of thin-disk stars. The same outcome applies to the Cepheids with larger heights above the disk. The fraction of objects with warm orbits typical of the thick disk is about 1%. The orbital and kinematic properties of Galactic Cepheids will be addressed in a forthcoming investigation (Zocchi et al., in prep.).

thumbnail Fig. 1

Radial distribution of the current Cepheid sample (colored circles) projected onto the Galactic plane. The symbols are color-coded (see the color bar on the right side) according to the distance from the Galactic plane. The dotted annuli display muliples of 5 kpc of the distances from the Galactic center. The position adopted for the Sun is at X = 0 and Y = 8.127 kpc (GRAVITY Collaboration 2018). The colored diamonds show the locations of highmass star-forming regions used by Reid et al. (2019) to fit the spiral arms. They are color-coded according to the spiral arm association. The long bar of the inner part of the Galaxy is indicated with a shaded ellipse (Wegg et al. 2015). The solid curved lines trace the Milky Way spiral arms from Reid et al. (2019) and from Sun et al. (2015, Outer, Scutum, and Centaurus arms).

3 Atmospheric parameters and abundances

The effective temperature (Teff), surface gravity (log g), micro-turbulent velocity (υt), and metallicity ([Fe/H]) for our sample of classical Cepheids were derived using pyMOOGi2, a Python version of the MOOG code (Sneden 2002). The model atmospheres, interpolated in the grid of Castelli & Kurucz (2004), and the equivalent widths (EWs), measured using ARES (Sousa et al. 2007, 2015), were taken as input by the code. The atomic data for the Fe I and Fe II lines were the same as were adopted by da Silva et al. (2022), who created a clean and homogeneous line list with revised atomic parameters. The procedure was the same as adopted in our previous works, which is described in detail in Proxauf et al. (2018). In this procedure, first we derived the Teff for each spectrum using the line-depth ratio (LDR) method (Kovtyukh 2007, and references therein). Then, keeping Teff fixed, the three other parameters were iteratively changed until convergence. A solution for the surface gravity was accepted only if the ionization equilibrium of Fe I and Fe II lines was achieved. An accepted value for the microturbulent velocity was obtained only if the abundances from the Fe I lines did not depend on their EWs within the errors. The metallicity passed as input to our algorithm was updated constantly, and the final iron abundance we adopted was the mean value computed from individual Fe I lines. Table 2 lists the atmospheric parameters derived for each spectrum of each star in our sample. Table 3 lists the mean abundances of Fe, O, and S calculated for each star together with the number of lines used and the number of spectra available.

After we computed the stellar parameters, we derived the S abundances by performing line profile fitting of the S I triplet at 6757 Å, adopting the same model atmospheres. This line has been proven to be unblended and relatively strong in our sample stars (Duffau et al. 2017). We computed synthetic profiles using the Python version the code Spectroscopy Made Easy (SME; Piskunov & Valenti 2017), made available by A. Wehrhahn3 (Wehrhahn 2021). The adopted line list, covering 15 Å around the S I triplet, was retrieved from VALD4 using the “extract stellar” option and including hyperfine or isotopic splitting information when available. We updated the atomic parameters for the line under scrutiny in this study following Duffau et al. (2017). We refer to that paper for further details and an extensive discussion of the 3D NLTE effects of sulfur lines. Here we briefly recall that the lines in Multiplet 8 differ only very little (up to 0.1 dex) from the LTE approximation (see also Takeda et al. 2005; Korotin 2009). We also adopted the same solarabun-dance of A(S)⊙ = 7.16 dex as Duffau et al. (2017). To evaluate systematic effects due to the different code and line list with respect to da Silva et al. (2022), we reanalyzed the 20 calibrating Cepheids published in our previous work and found a mean difference of +0.03 ± 0.02 dex, which is well within the observational uncertainties.

Oxygen abundances were derived via spectral synthesis of the [O I] forbidden line at 6300.3 Å, for which NLTE departures are negligible. We analyzed a UVES solar spectrum, finding A(O)⊙ = 8.78, which is the value we adopted as reference abundance throughout this work. Atomic parameters for the blending Ni I line at 6300.37 were adopted such that the excitation potential EP = 4.266 eV and the log gf = −2.11 (see also Caffau et al. 2015). Telluric lines affecting this spectral region around the oxygen line were removed using a synthetic template computed with the updated version of the TELFIT code (Gullikson et al. 2014).

Internal errors were computed considering the best-fit uncertainties as given by SME (see Piskunov & Valenti 2017 for further details) and errors in atmospheric stellar parameters. These were estimated in the standard way, that is, by changing one parameter at a time and computing the corresponding variations in abundance. The different contributions were then added in quadrature (we refer to our previous works, e.g., D’Orazi et al. 2020).

Figure B.1 shows examples of spectral synthesis fit around the sulfur line at 6757 Å for HARPS, FEROS, UVES, and STELLA spectra. Figure C.1 shows a comparison of the atmospheric parameters and abundances derived in the present work with the data available in the literature for a set of stars in common. Figure D.1 shows O and S abundances as a function of the pulsation phase for a subsample of CCs with multiple spectra collected during the pulsation cycle (see da Silva et al. 2022). Similarly to the results we published previously for iron and α elements, this figure clearly shows that there is no significant correlation of the [O/H] and [S/H] abundance ratios with the pulsation cycle.

Table 2

Excerpt from the list of atmospheric parameters and Fe, O, and S abundances for each spectrum in our sample.

Table 3

Excerpt from the list of Fe, O, and S abundances derived for each star in our sample.

thumbnail Fig. 2

Abundance ratios as a function of the galactocentric distance. Our sample of Cepheids (blue circles) is compared with our sample of open clusters (symbols color-coded according to the stellar age). The Fe and O abundance ratios are taken from Magrini et al. (2023), whereas the S abundances are taken from the present work. The black line displays a linear regression fitted to Cepheids in the range of galactocentric distance from 4 to 12.5 kpc, and the dashed line is the extrapolation up to 17 kpc. The red line shows a logarithmic fit over the whole range of galactocentric distances. The corresponding equations are also shown. The shaded area shows one standard deviation around the running mean, weighted with a Gaussian function taking the errors into account.

4 Galactic radial gradients

4.1 [Fe/H] and [α/H] radial gradients

Figure 2 displays the radial gradients for the derived iron, oxygen, and sulfur. The corresponding coefficients of both linear (for RG within 12.5 kpc) and logarithmic (for the whole range of RG) regressions are listed in Table 4. The data plotted in this figure disclose several interesting new findings that we list below.

  1. Slope of the iron radial gradient. Dating back to Twarog et al. (1997) and Caputo et al. (2001), it has been suggested that the radial gradient, based either on classical Cepheids or on open clusters, shows a change in the slope across the solar circle, even though only a few data are available for radii above ~12 kpc (see, e.g., Magrini et al. 2017). To support this preliminary evidence, a few authors suggested that this variation might be associated with a resonance in the spiral arm (Lépine et al. 2011, 2017). However, from a more detailed analysis of the radial distribution of Galactic Cepheids in the thin disk, and using a more detailed algorithm to constrain the clustering of these stars, Genovali et al. (2014) instead found a linear radial gradient from the inner to the outer disk. Moreover, they also suggested that the dispersion at a fixed galactocentric distance is mainly caused by a spread in chemical composition inside the same Cepheid group. This finding was soundly and independently supported in a recent and more sophisticated approach reported by Lemasle et al. (2022), who took the disk flare into account.

    The data plotted in the top panel of Fig. 2 show that the radial metallicity gradient is almost linear for galactocentric distances smaller than ~12 kpc, but it becomes significantly flatter for RG larger than 15 kpc. By performing a number of numerical fits using different analytical functions, we found that a logarithmic fit can account for the steepening of the gradient when it approaches the inner disk and for the flattening when it approaches the outer disk. We also performed a linear fit for Cepheids with galactocentric distances smaller than 12.5 kpc. The current estimate agrees quite well with similar estimates available in the literature (Magrini et al. 2023). The flattening in the outer disk fully supports preliminary results based on both CCs and OCs (Carraro et al. 2007; Yong et al. 2012; Donor et al. 2020). In passing, we note that the current empirical evidence for the linearity is based on the largest and most homogeneous sample of Galactic Cepheids.

    On the other hand, Twarog et al. (1997) used a large sample of open clusters and found evidence of a metallicity discontinuity located at RG ~10 kpc. They suggested a two-zone model for the chemical enrichment of the Galactic thin disk. This working hypothesis was also supported by Caputo et al. (2001) by using photometric metallicities for a large sample of Galactic CCs. This empirical evidence was interpreted by Lépine et al. (2017) as a possible corotation resonance of the Galactic thin disk. It was also questioned by Genovali et al. (2014) because the residuals of the iron gradients appeared to be correlated with the location of the spiral arms. These authors suggested that the evidence of a possible change in the slope and dip in the rotation curve of the Galactic thin disk between 9 and 10 kpc (Sofue 2013) might be associated with the Perseus arm. More recently, by analyzing a larger sample of CCs, Trentin et al. (2023) also found some evidence of a possible change in the slope at RG ~ 9.25 kpc. They performed linear regressions to the entire dataset and to the data obtained by binning the CCs into 12 radial intervals of 1.33 kpc each. Similar fits to individual objects and to the binned data were also performed for galactocentric distances smaller and larger than 9.25 kpc. They found that one single fit to the entire sample can account for both inner and outer disk Cepheids. However, the possible presence of a break in the radial gradient could not be excluded on the basis of their dataset. The current data indicate a departure from linearity for galactocentric distances larger than 12–14 kpc, but a more quantitative analysis requires a larger sample and a more detailed statistical approach (Lemasle et al., in prep.) to confirm whether the radial gradient shows either a break at a given galactocentric distance or a smooth change with distance, as suggested by the logarithmic fit.

  2. Comparison with the iron gradient of open clusters. To investigate the impact that age has on the radial metallicity gradient, we performed a detailed comparison with our sample of Galactic open clusters. CCs cover a limited range in age, from a few dozen million years (long period) to a few hundred million years (short period). Therefore, we took advantage of the homogeneous abundance estimates recently provided by the last GES data release. The key advantage of this sample is that in addition to the homogeneous abundances, it also has homogeneous estimates of individual distances and ages from isochrone fitting of their members detected in Gaia DR2 (Cantat-Gaudin et al. 2020). Furthermore, the GES sample of OCs covers a broad range in galactocentric distances (RG ~ 6–20 kpc), and their cluster ages range from a few million years (i.e., even younger than the youngest CCs) to almost 7 Gyr. The data plotted in Fig. 2 (see also Table 4) show that CCs and OCs display a similar iron radial gradient from the inner to the outer disk. Moreover, the OCs do not show any clear variation in the zeropoint and in the slope as a function of the cluster age. The cluster ages of the GES sample changes by more than one order of magnitude, but their distribution is similar within the errors. This agrees with what was found in Magrini et al. (2023) for the radial gradient of several elements belonging to different nucleosynthesis channels, whereby a limited temporal evolution is observed in the age range covered by open clusters. The similarity of the CC and OC iron radial gradients is soundly supported by the similarity of the zeropoint and slope of the linear fits listed in Table 4. However, it is worth noting that only a few of the clusters are older than 3 Gyr (~10 clusters), which limits the conclusions we can draw concerning the old-age tail. The flattening of the radial gradient in the outermost disk regions is only partially supported by OCs because the galactocentric distance for most of them are smaller than ~15 kpc and only one cluster is located at 20 kpc.

  3. Slope of the oxygen radial gradient. The oxygen abundances plotted in Fig. 2 display quite clearly that the oxygen radial gradient is shallower than the iron gradient. The slope of the linear fit is 25% shallower, whereas the logarithmic fit can be barely compared because oxygen abundances in the outermost disk regions are missing. CCs and OCs once again display very similar radial trends without a clear dependence on the cluster age. The comparison with similar estimates available in the literature based on CCs indicates that the current slope is shallower. In particular, it is shallower than the slope obtained by Trentin et al. (2023) using a sample of 65 CCs plus literature data (−0.029 ± 0.006 vs. −0.046 ± 0.002 dex kpc−1) and by Luck & Lambert (2011) using a sample of 313 CCs (−0.056±0.003 dex kpc−1). This comparison should be treated with caution because the different lines that were used for measuring oxygen abundances might have an effect on them, and more in general, the details of the spectroscopic analyses were different (e.g., code, model atmospheres, and atmospheric parameters). Using data provided by Magrini et al. (2023), we performed an independent fit of the OCs following the same approach as we adopted for CCs. We found that the two gradients agree within the errors (−0.029 ±0.006 vs. −0.040± 0.009 dex kpc−1), thus supporting the idea that the oxygen radial gradients of CCs and OCs are similar.

    The oxygen abundances provided by Luck & Lambert (2011) and by Trentin et al. (2023) are based on a combination of the 6156–8 triplet and the [O I] forbidden line at 6300.3 Å, whereas the cluster abundances (Magrini et al. 2023; Randich et al. 2022) are only based on the line at 6300.3 Å. Similarly, we only adopted the forbidden line at 6300.3 Å because it is stronger than the 6156–8 triplet in all our sample stars.

  4. Slope of the sulfur radial gradient. The data plotted in the bottom panel of Fig. 2 highlight the key role that sulfur can play, which can help us to better understand the chemical enrichment of the Galactic thin disk. This key role has two parts: a) The slope of the sulfur radial gradient based on the linear fit is steeper by a factor of two than the slope of the iron gradient. The difference in the logarithmic fit is about 0.7 dex (log kpc)−1. The latter fit ranges from the inner disk to the outskirts of the thin disk. This finding supports preliminary results obtained by da Silva et al. (2022), although the significance of those results was hampered by the sample size. The sulfur radial gradients for both CCs and OCs agree quite well. The zeropoints and the slopes of the linear fits are very similar within the errors (see Table 4). It is also worth mentioning that the current data show no evidence of an abrupt change in the slope from the inner to the outer disk. b) The standard deviation of sulfur abundances at a fixed galactocentric distance is smaller than the dispersion of the oxygen and iron abundances, thus suggesting that the spectroscopic diagnostic we adopted is also minimally affected by possible changes in effective temperature, surface gravity, or microturbulent velocity. To our knowledge, this is the very first time in which there is solid evidence of an α-element gradient that is steeper than the iron gradient. This paves the way to a new empirical framework for the role played by massive stars in the chemical enrichment of both iron and sulfur.

It is worth noting that the slope of the sulfur gradient provided by Trentin et al. (2023) is shallower by about 25% (−0.060 ± 0.006 dex kpc−1 ), but it is based on three S I lines, namely λ = 6743.585, 6748.153, and 6757.153 Å. However, we cannot ascertain whether each line of the multiplet has been measured in all their Cepheids. On the other hand, in all our sample stars, only the strongest line at 6757 Å can be useful for an abundance determination (see the similar discussion in Duffau et al. 2017). The slope provided by Luck (2018) is slightly shallower (−0.0693 ± 0.0035 dex kpc−1 ), but information on which lines they used is missing.

In passing, we also note that the current slope for the [S/H] radial gradient is similar within the errors to the estimate provided by Perdigon et al. (2021, −0.050±0.025 dex kpc−1) based on a large sample of field stars with galactocentric distances between 6 and 10 kpc, and it is steeper than the radial gradient provided by Arellano-Córdova et al. (2020, −0.035 ± 0.006 dex kpc−1 ) using H II regions with galactocentric distances ranging from 7 to 14 kpc. The comparison with similar estimates available in the literature should be considered as a global validation test because when CC are compared with field stars, they cover a well-defined range in age and are associated with a specific evolutionary channel.

To further investigate the difference between the two α elements studied in the present work, Fig. 3 shows the S-O relation for both classical Cepheids and open clusters. The data plotted in this figure indicate that in the metal-poorer regime, S and O display the same trend within the errors. These objects are located, as expected, in the outer disk (see the color bar on the right). Interestingly enough, the main finding emerging from the current analysis is that CCs and OCs are more oxygen enhanced at a fixed sulfur abundance. The distribution across the one-to-one liner relation is asymmetrical, and a good fraction of CCs and the large majority of OCs are located below the dashed line. The trend becomes even clearer for sulfur abundances close to solar, where the oxygen abundances are 0.1–0.2 dex more enhanced on average. This may be explained by the fact that oxygen is only produced by massive stars (see, e.g., Matteucci 2021), while a non-negligible fraction of sulfur is also produced on longer timescales by SNe Ia (e.g., Leung & Nomoto 2018, 2020).

Table 4

Slopes and zeropoints of the abundance gradients as a function of the galactocentric distance.

thumbnail Fig. 3

[S/H] as a function of the [O/H] abundances. Our sample of Cepheids, color-coded according to the distance from the Galactic center (see the color bar on the right side), is compared with the same open clusters as plotted in Fig. 2. The dashed gray line is the 1:1 linear relation.

4.2 [α/Fe] radial gradients

Figure 4 shows the α-to-iron abundance ratio as a function of the galactocentric distance. In the top panel, the oxygen-to-iron abundance ratio ([O/Fe]) is almost constant over the entire range of distances, as expected. The slope is quite flat and agrees with similar estimates of the [α/Fe] radial gradients available in the literature within the errors. In a recent investigation, Santos-Peral et al. (2021) found a [Mg/Fe] radial gradient of 0.025 ± 0.009 dex kpc−1 using field stars with galactocentric distances between 6 and 11 kpc.

In the bottom panel of the same figure, the sulfur-to-iron abundance ratio ([S/Fe]) shows a well-defined negative gradient that is supported by the linear and logarithmic regressions. The quoted evidence is somewhat puzzling because a similar estimate reported by Perdigon et al. (2021), based on a large sample of field stars, indicated a flat [S/Fe] radial gradient between 6 and 10 kpc (0.004±0.006 dex kpc−1). The comparison with similar estimates available in the literature should be treated with caution because field stars cover a broad range in age and in evolutionary phases.

Oxygen and magnesium are mainly produced in hydrostatic nucleosynthesis of massive stars (McWilliam et al. 2008; Kobayashi et al. 2020). Sulfur has a mixed origin because it is produced during the final evolutionary phases of massive (M ≥ 20 M⊙) stars, but it is also produced during Type II SNe explosions (Limongi & Chieffi 2003). Sulfur therefore has a key advantage over other α-elements.

The range in iron abundance covered by the current sample of CCs, and for which we were able to measure the oxygen abundance, is about 0.7 dex. In this range, the [O/Fe] abundance ratio is constant, but the [S/Fe] ratio shows a steady decrease from the inner (more metal-rich) to the outer (more metal-poor) disk. The depletion in sulfur is already about 0.2 dex at RG ~ 12.5 kpc and becomes about 0.5 dex in the outermost disk regions.

The physical reasons driving the difference in the abundance ratios of these two α-elements are not clear. It would be quite interesting to investigate the abundance ratios of the other explosive α-elements (Si, Ca, and Ti) to provide a more complete analysis of their enrichment in the Milky Way. Sulfur can play a key role in this context because it is a moderately volatile element and is therefore not blocked into the dust grains of the interstellar medium. For this reason, the S abundance in stars can be directly compared with abundances in H II regions, supernovae remnants, planetary nebulae (P Ne; Henry et al. 2004), damped Ly-α systems and, in general, high-redshift galaxies (Vladilo et al. 2018; Dessauges-Zavadsky et al. 2007), and active galactic nuclei (AGN; Liu et al. 2015; Mizumoto et al. 2023).

thumbnail Fig. 4

Abundance ratios as a function of the Galactocentric distance. Same as in Fig. 2 but showing the [O/Fe] and the [S/Fe] abundance ratios.

4.3 Dependence on the age of classical Cepheid abundances

To further investigate the difference in the slope between iron and α-elements, the left panels of Fig. 5 show the same abundance ratios as plotted in Fig. 2, but as a function of the logarithmic pulsation period. As already mentioned in Sects. 1 and 4, the pulsation period is a solid diagnostic for the individual age of CCs (Bono et al. 2005). The abundances plotted in the top and bottom panels show for the first time that CCs with periods shorter than ~4 days (log P ≲ 0.6, older ages) are also poorer in iron and sulfur. In the middle panel, the trend is different, but only because oxygen abundances are missing in a good fraction of the metal-poor CCs. This is a spectroscopic validation of an intrinsic property of CCs. Their period distribution systematically shifts toward shorter periods in the metal-poor regime. This circumstantial evidence was only based on the difference in the period distribution of CCs in the Small Magellanic Cloud (SMC) and the LMC so far (Soszyński et al. 2017; Pietrukowicz et al. 2021; Bono et al. 2023). The drift toward shorter periods is observed in metal-poor Galactic CCs for the first time here.

The right panels of Fig. 5 display the element-to-iron abundance ratios as a function of the logarithmic pulsation period. The linear regressions show that the slope of the [O/Fe] ratio is steeper than the [S/Fe] and [((O+S)/2)/Fe] slopes. Moreover, the spread in the range of short periods clearly increases.

This empirical evidence indicates that both O and S are overabundant in very young (long-period) Cepheids. However, this plain physical argument is hampered by the fact that the α-elements are typically produced on a timescale of some dozen million years, whereas iron-peak elements, if we assume that they are mainly produced by Type Ia SNe, are produced on a timescale of a few billion years.

5 Comparison with literature data

The top left panel of Fig. 6 shows the [O/Fe] abundance ratio as a function of the iron abundance for both the CC and OC samples. The data plotted in this figure display that for Fe abundances that are more metal poor than solar, the O abundance is overabundant on average. In particular, CCs and OCs for [Fe/H] ≲ −0.3 show a well-defined O enhancement. The data plotted in the bottom panel display that the S abundance is underabundant on average. The abundance ratio attains solar values only in the metal-rich regime ([Fe/H] ≥ 0). Trumpler 20, one of the open clusters observed by Lucertini et al. (2023), agrees quite well with the current sample of OCs and CCs, whereas Trumpler 5 shows a well-defined enhancement in sulfur. In passing, we also note that the abundance ratios are independent of the age because CCs and OCs display similar variations.

The right panels of Fig. 6 show the same comparison, but with thin- and thick-disk field stars observed by GES and with bulge field stars observed by Lucertini et al. (2023). The [O/Fe] abundance ratio is enhanced in the metal-poor regime and becomes underabundant in the metal-rich regime, as expected. CCs display a remarkable agreement when compared with thin- and thick-disk stars. This suggests that the O abundance of metal-poor CCs is expected to be enhanced in the metal-poor regime and depleted in the metal-rich regime (Romaniello et al. 2022).

The variation in the [S/Fe] as a function of the iron abundance for CCs is far from being linear. The ratio attains solar values in the metal-poor ([Fe/H] ~ −0.6) and in the metal-rich ([Fe/H] ≥ 0) regimes, but shows a parabolic trend for intermediate iron abundances. The parabolic trend is less clear in OCs because the current sample only includes a few OCs located in the outer disk and with accurate S abundances.

Thin-disk stars agree quite well with CCs, but thick-disk stars are systematically enhanced when compared with classical Cepheids. The bulge stars attain solar ratios only in the very metal-rich ([Fe/H] ≥ 0.2) regime, whereas in the more metal-poor regime, the ratio is systematically enhanced, suggesting a different chemical enrichment compared with young thin-disk stars. However, it is worth noting that while thick, thin, and bulge stellar abundances indicate evolutionary trends of individual MW components (see the time-delay model, e.g., Matteucci 2021), CCs display present-day frames of different regions with diverse histories of star formation. Therefore, caution must be taken when comparing these different datasets.

To further constrain the variation in the abundance ratios, Fig. 7 shows the same data for CCs plotted in Fig. 6, but color-coded according to the galactocentric distance. The data plotted in the left panel show that the [O/Fe] is solar in the solar neighborhood and in the inner disk, as expected, whereas it becomes enhanced in the more metal-poor regions of the outer disk. The transition from the inner to outer disk is even more clearly traced by the [S/Fe] abundance ratios plotted in the right panel of the same figure. The CCs located inside the solar circle display solar values, whereas those located at larger galactocentric distances appear to be underabundant and approach solar values once again in the outermost regions. The number of stars approaching solar abundance at low metallicities is quite small for firm conclusions, but the data plotted in the bottom panel of Fig. 4 and in the right panel of Fig. 7 indicate that the sulfur abundances do not follow the iron abundances for galactocentric distances larger than ~ 12–13 kpc. This behavior could be supported by a S production that is variable with distance. This working hypothesis is discussed on a more quantitative basis in the next section.

thumbnail Fig. 5

Abundance ratios as a function of the logarithmic pulsation period. The black line shows a linear regression fit to the current Cepheid sample. The corresponding equation is also shown.

6 Comparison between theory and observations

To investigate the impact of the observed CCs abundance gradients on the Milky Way disk evolution on a more quantitative basis, we compared them with the results of detailed Galactic chemical evolution models. The starting point was the best-fit model recently provided by Palla et al. (2020). The model is a revised version of the two-infall paradigm (see also Spitoni et al. 2019) in which two consecutive gas accretion episodes, separated by an age gap of at least 3 Gyr, form the so-called high-α and low-α sequences observed in the Galactic disk. For the second gas-infall episode forming the low-α sequence, the timescale for gas accretion increases with radius according to the inside-out scenario. In addition, inward radial gas flows with a constant velocity (of 1 km s−1 ) and a star formation efficiency (SFE) for the Schmidt-Kenicutt law5 that is variable with radius (with values between ν = 5 and 0.1 Gyr−1 ), act together with the inside-out mechanism. A more detailed discussion of the physical assumptions is given in Palla et al. (2020).

This model accounts for radial abundance gradients based either on CC or on OC observational programs (Luck & Lambert 2011; Genovali et al. 2015; Magrini et al. 2017) as well as on gas, stellar, and star formation rate (SFR) density gradients (see, e.g., Nakanishi & Sofue 2003, 2006; Stahler & Palla 2005; Green 2014) in the Galactic thin disk. Moreover, the model setup allows us to reproduce the so-called α-dichotomy/bimodality in [α/Fe] versus [Fe/H] trends by the APOGEE survey at different galactocentric distances (see, e.g., Queiroz et al. 2020).

Figure 8 shows the comparison between the observed abundance gradients for Fe, O, and S with the best-fit model of Palla et al. (2020). Starting from Fe, the model by Palla et al. (2020) underestimates the present-day [Fe/H] abundance in the outermost radii (RG ≳ 12 kpc). The same seems to happen for the [O/H] gradient, even though the number of stars in outer regions (~10 with RG > 13 kpc) is too limited for firm conclusions. To reproduce the radial trends, we ran another chemical evolution model with modified prescriptions relative to the best-fit model by Palla et al. (2020). In particular, we relaxed the condition of a variable SFE for RG > 12 kpc by fixing its value to the one at RG = 12 kpc (ν = 0.5 Gyr−1 ). This new model agrees quite well with the observed abundance plateau at large galactocentric distances, and at the same time, it does not significantly affect the predicted [α/Fe] radial trends, as can be seen in the right panels for both O and S.

The bending of the slope of sulfur (see also Fig. 2) at large radii should also agree with our modified model, which shows a plateau at RG>12 kpc. However, the lower panels of Fig. 8 highlight an overestimation of the observed [S/H] and [S/Fe] by the modified model in the outer regions, whereas present-day abundances within the solar ring (RG < 8 kpc) are generally reproduced. This indicates that the greater steepness of the sulfur gradient (see the slope coefficients in Figs. 2 and 4 or in Table 4) is not captured by the current models.

This discrepancy may be explained by the nucleosynthesis prescriptions for sulfur. This element is also synthesized by Type II SN explosive nucleosynthesis (see also Sect. 4.2), and it has a more uncertain outcome than the synthesis of purely hydrostatic elements, such as oxygen (Woosley & Weaver 1995; Nomoto et al. 2013; Limongi & Chieffi 2018). Moreover, the comparison with stellar abundances in the [S/Fe] versus [Fe/H] diagram is often hampered by the difficulty of obtaining reliable and homogeneous stellar abundances over a broad range in iron abundances (see Romano et al. 2010; Kobayashi et al. 2020, and references therein). Therefore, we decided to change the stellar yield prescriptions adopted in Palla et al. (2020). In particular, we multiplied the CC-SN yields by Kobayashi et al. (2006, 2011) by a scaling factor K. It is worth noting that even though it is also not negligibly produced by Type Ia SNe, we kept the S yield prescriptions by Iwamoto et al. (1999) fixed. The variations in [S/Fe] that can be obtained by changing the plethora of Type Ia SN models available in the literature is ~0.1 dex (see Palla 2021), which is much smaller than the difference in [S/Fe] at different galactocentric distances (~0.3 dex).

Figure 9 shows the results of this test. Together with the modified model presented in Fig. 8, we also plot an analogous model in which the CC-SN sulfur yield is multiplied by a factor K = 0.25. This model clearly recover the agreement with the data in the outer regions for both the [S/H] and [S/Fe] but it underestimates the observed values for radii within the solar ring, as expected. For this reason, we also show in Fig. 9 a third model for which the K factor changes with radius, from K = 1 at 4 kpc to K = 0.25 from 12 kpc onward. This toy model, as we called it, reproduces the observed trends for both [S/H] and [S/Fe] very well and highlights the necessity of a source of production for sulfur that varies in its contribution with the galactocentric radius.

It is beyond the scope of this work to determine whether this might be the contribution by stellar populations with different typical rotational velocity (e.g., Limongi & Chieffi 2018), a different binary fraction (Farmer et al. 2023), or combined effects (including the contribution by different Type Ia SNe progenitors). A much larger number of chemical elements are needed to perform such a study.

The new spectroscopic sample for Galactic CCs presented in this work points toward a revision in the prescriptions adopted by chemical evolution models aiming at reproducing Galactic radial gradients (e.g., Grisoni et al. 2018; Palla et al. 2020). This is mainly driven by the much larger statistical significance of the data for the outermost regions of the Galactic thin disk. Several previous OCs catalogs also suggested the possibility of a change in the slope between inner and outer disk (e.g., Yong et al. 2012; Magrini et al. 2023), however, uncertainties affecting individual distances, the limited number of objects located in the outermost regions, and the possibility that the change in the slope was driven by an age effect prevented firm conclusions. In passing, we also note that the different scenarios in the modeling of radial gradients have a marginal impact on the fit of the observed α-bimodality within the two-infall paradigm (e.g., Spitoni et al. 2019, 2021; Palla et al. 2022). The galactocentric distances of the stellar data adopted for these analyses are smaller than 12–14 kpc because those from outer regions are significant severely limited in number (see, e.g., Spitoni et al. 2021). Next-generation spectroscopic surveys focusing on the outer Galaxy (e.g., WEAVE; Dalton et al. 2020, and 4MOST; de Jong et al. 2019) may help to increase the number of field stars with abundance ratios in the outer regions significantly, and thus provide simultaneous constraints to probe Galactic evolutionary models.

Finally, the detection of the significant difference between the sulfur gradient and gradients from other elements underlines the importance of obtaining data for the largest number of chemical elements because this highlights features of nucleosynthetic processes that are hidden when the oxygen and iron gradients alone are considered. Therefore, we plan to extend the analysis for other chemical elements in order to unveil the causes of the different gradient behaviors.

thumbnail Fig. 6

Abundance ratios as a function of the iron abundance. Left panels: same data as in Fig. 2, but comparing the [O/Fe] (top) and [S/Fe] (bottom) ratios for our samples of classical Cepheids and open clusters. The bottom panel also shows the abundance ratios for the open clusters (Trumpler 5 and Trumpler 20) provided by Lucertini et al. (2023). Right panels: [O/Fe] and [S/Fe] ratios for Galactic Cepheids compared with thin-and thick-disk stars provided by the GES (DR5.0) collaboration and with thin-disk, thick-disk, and bulge field stars provided by Lucertini et al. (2022, L22a).
thumbnail Fig. 7

Abundance ratios as a function of the iron abundance. The [O/Fe] and [S/Fe] ratios for the current CC sample are color-coded according to their galactocentric distance.

7 Summary and final remarks

We present the largest (1285 spectra) and most homogeneous spectroscopic sample for Galactic classical Cepheids (379 objects). For a significant fraction of them (1118 spectra, 356 objects) we measured the abundances of iron and of two α-elements (O and S). The new abundances are based on optical spectra with high S/N collected with a variety of high-resolution spectrographs. The current sample, when compared with similar estimates available in the literature, has several key advantages: New accurate abundances are provided for the first time for 70 CCs in our sample. The current CC sample ranges from the inner (RG ~ 5 kpc) to the outer (RG ~ 25–30 kpc) disk, and they are distributed across the four quadrants. The spectroscopic sample includes both short- (old) and long-period (young) CCs. The sample includes CCs that pulsate in the fundamental mode, in first overtone, in mixed mode, and in double mode. A number of acid tests have been performed to remove possible contamination either from old (Type II Cepheids) or intermediate-age (anomalous Cepheids) tracers or from geometrical (binaries) variables. We also investigated the orbital properties of the current spectroscopic sample and found that the bulk of them have orbits typical of thin-disk stars.

The objects vary steadily in their physical properties because of radial oscillations. We therefore paid special care to estimating the atmospheric parameters (effective temperature, surface gravity, and microturbulent velocity). They were often verified using different approaches and/or diagnostics. The internal consistency and the accuracy of the atmospheric parameters and of the adopted line list were investigated in a previous study (da Silva et al. 2022) by using two dozen calibrating Cepheids for which high-resolution spectra cover the entire pulsation cycle.

Classical Cepheids are excellent standard candles. The individual distances that we estimated are based either on Gaia DR3 trigonometric parallaxes or on near- and mid-infrared period-luminosity relations (Ripepi et al. 2022). The latter were estimated by using individual color excesses from Schlafly & Finkbeiner (2011) and the reddening law by Cardelli et al. (1989) and by Madore et al. (2013, MIR).

In order to constrain the sensitivity of the radial gradients to the age, we took advantage of a sample of 62 open clusters collected by the Gaia-ESO survey (Randich et al. 2022) and complemented with 18 OCs available in the ESO archive. The key advantage of this sample is that homogeneous estimates of their abundances (Fe and O) were already available together with homogeneous cluster parameters (cluster age, distance, and reddening). Furthermore, we measured S abundances with the same diagnostics. All in all, the current OC sample covers galactocentric distances similar to the CC sample, but the age distribution ranges from a few million years to about 7 Gyr. The main results concerning the radial abundance gradients are listed below.

Slope of the radial gradients. The iron and sulfur radial gradients based on both CCs and OCs display a well-defined departure from linearity from the inner to the outer disk. The oxygen radial gradient shows a similar trend, but the flattening at large galactocentric distance is partially hampered by the lack of measurements for RG ≥ 19 kpc. We found that logarithmic regressions account for the variation in [X/H] abundances from the inner to the outer disk. This is a solid finding because we individually checked CCs located at large galactocentric distances by using pulsation observables (I-band amplitude, Fourier parameters) and the height above the Galactic plane.

Difference in the slope between iron and α-elements. The slope of the S radial gradient is steeper than the Fe slope. The difference is approximately a factor of two for the linear fit (−0.081 vs. −0.041 dex kpc−1) and changes from −1.62 to −0.91 in the logarithmic distance. The OCs fully support the difference we found for CCs. It is worth mentioning that the current finding is minimally affected by the spread in iron and in sulfur abundances at fixed galactocentric distance. The uncertainty on individual measurements is significantly smaller. The linear fit to the oxygen radial gradient is similar to the iron radial gradient, as expected, whereas the logarithmic fit is slightly shallower.

Difference between O and S. Empirical evidence indicates that S (explosive nucleosynthesis) is underabundant when compared with O on average (hydrostatic nucleosynthesis). The difference becomes clearer in the metal-poor regime, and clearer still for the [O/Fe] and [S/Fe] abundance ratios. The former regime shows either a flat distribution or a tiny positive slope. On the other hand, the [S/Fe] abundance ratio displays a well-defined negative gradient, suggesting that sulfur is under-abundant compared with iron over a substantial fraction of the Galactic thin disk. In this context, it is worth mentioning that OCs display either a flat distribution or a mild difference when compared with CCs. The OCs for galactocentric distances larger than 10 kpc attain solar [S/Fe] abundance ratios.

Age effects. 1) The current abundances and the element-to-iron abundance ratios display positive gradients when plotted as a function of the logarithmic period. More metal-poor CCs display a systematic drift toward shorter periods, as expected on the basis of theoretical and empirical evidence. Circumstantial evidence indicates that very young CCs are overabundant in O and in S. The difference is mainly a consequence of the fast chemical enrichment of α-elements when compared with iron-peak elements. 2) Radial gradients and abundance ratios do not appear to be correlated with age. CCs together with young and old open clusters display similar variations from the inner to the outer disk and from more metal-poor to more metal-rich regimes. In this context, it is worth mentioning that dating back to Carraro et al. (2007) and to Friel et al. (2010), a flattening of the radial gradients based on OCs has already been suggested in the literature. However, this variation was interpreted as an age effect in the sense that an increase in cluster age caused a flattening of the radial gradients. CCs, being systematically younger than 250 Myr, trace the present-day radial gradient. This means that when we assume that the average galactocentric velocity is about a few km/sec (Tian et al. 2017; López-Corredoira et al. 2019), a CC that was born at a galactocentric distance of 10 kpc moved 1 kpc at most after 200 Myr. The consequence of this plain evidence is that the flattening is associated with the physical properties of the outer disk.

To investigate the impact that the current radial abundance gradients have on the chemical evolution of the Galactic thin disk on a more quantitative basis, we also performed a detailed comparison between theory and observations. We adopted the best-fit model recently provided by Palla et al. (2020) and found that a constant star formation efficiency for galactocentric distances larger than 12 kpc can account for the flattening observed in iron and in α-elements.

Moreover, we developed a toy model to investigate the impact that current predictions concerning S yields for massive stars have on the radial abundance gradients. We found that inside the solar circle, the current [S/H] and [S/Fe] gradients are well reproduced by the canonical yield prescriptions by Kobayashi et al. (2006, 2011). The same comparison indicates that the flattening in the outermost regions requires a decrease of a factor of four in the current S predictions. This indicates a substantial decrease in the S yields in the more metal-poor regime.

The current findings open the path to a few key pieces of evidence that are worth being discussed in more detail. Biochemistry mainly relies on six crucial elements: carbon, hydrogen, oxygen, nitrogen, phosphorus, and sulfur (CHONPS). This means that molecules containing these key elements played a key role in prebiotic chemistry and in the origins of life on Earth. The overabundance of sulfur in the solar circle and in the inner disk seems a good viaticum for the identification of prebiotic molecules.

Moreover, sulfur in contrast with other α-elements is a volatile element. This means that stellar sulfur abundances can be directly compared with nebular sulfur abundances in external galaxies. There is mounting evidence that both barred and unbarred galaxies display a flattening in the metallicity gradients at large radial distances, as discussed, for instance, by Sánchez-Menguiano et al. (2016). These authors also found that the outer flattening regions contain a relatively high metallicity that can barely be explained in the framework of a canonical inside-out scenario with a constant SFR. Many mechanisms have been suggested to explain this trend, and in particular, the role played by a bar and/or spiral arms (Minchev et al. 2011; Spitoni et al. 2019), minor mergers of satellites (Quillen et al. 2009), and “wind recycling” accretions (Oppenheimer & Davé 2008). The preliminary findings brought forward by this investigation indicate that the MW radial gradients traced by young stellar populations show a similar trend. This means that they are a fundamental laboratory for investigating here and now the physical mechanisms driving the flattening.

Finally, the possibility of comparing sulfur abundances in external galaxies appears even more promising because the strong emission lines of the S abundances can be measured even at high redshifts in Seyfert galaxies (see Mizumoto et al. 2023; Dors et al. 2023, and references therein) and in damped Lyman-α systems (see Gioannini et al. 2017, and references therein).

thumbnail Fig. 8

Predicted [X/H] and [X/Fe] radial gradients compared with the Cepheid data presented in this work (blue points with error bars). The black lines are from the best-fit model presented by Palla et al. (2020), and the red lines are from a model with analogous setup, but with a flattened profile for the efficiency of star formation ν in the outer Galactic regions (RG > 12 kpc).
thumbnail Fig. 9

Effect of the S yield for massive stars on the [S/H] and [S/Fe] radial gradients for the model with a flattened star formation efficiency profile for the outer regions. The solid red line shows the model with standard yield prescriptions (from Kobayashi et al. 2006, 2011), the dashed red line shows the model with the S yield reduced by a factor 4, and the dash-dotted green line displays a model with scaling factor for the S yields that is variable with radius. The symbols are the same as in Fig. 8.

Acknowledgements

We thank the reviewer for their positive words and constructive suggestions concerning an earlier version of the present paper, which improved its content and readability. We acknowledge financial support from the ASI-INAF agreement no. 2022-14-HH.0. V.K. is grateful to the Vector-Stiftung at Stuttgart, Germany, for support within the program “2022-Immediate help for Ukrainian refugee scientists” under grant P2022-0064. M.B. is supported through the Lise Meitner grant from the Max Planck Society. We acknowledge support by the Collaborative Research Centre SFB 881 (projects A5, A10), Heidelberg University, of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and by the European Research Council (ERC) under the European Unionâs Horizon 2020 research and innovation programme (grant agreement 949173). M.P. acknowledges funding support from ERC starting grant 851622 Dust Origin. M.M. thanks financial support from the Spanish Ministry of Science and Innovation (MICINN) through the Spanish State Research Agency, under Severo Ochoa Programe 2020-2023 (CEX2019-000920-S), and from the Agencia Estatal de Investigación del Ministerio de Ciencia e Innovación (MCINN/AEI) under the grant “RR Lyrae stars, a lighthouse to distant galaxies and early galaxy evolution” and the European Regional Development Fun (ERDF) with reference PID2021-127042OB-I00. R.P.K. acknowledges support by the Munich Excellence Cluster Origins, funded by the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) under Germany’s Excellence Strategy EXC-2094 390783311. This paper is partially supported by the Fondazione ICSC, Spoke 3 Astrophysics and Cosmos Observations, National Recovery and Resilience Plan (Piano Nazionale di Ripresa e Resilienza, PNRR) Project ID CN00000013 Italian Research Center on High-Performance Computing, Big Data and Quantum Computing funded by MUR Missione 4 Componente 2 Investimento 1.4: Potenziamento strutture di ricerca e creazione di campioni nazionali di R&S (M4C2-19) – Next Generation EU (NGEU). G.B. thanks the partial support by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP), which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311.

Appendix A Pulsation type classification

By considering the position of our CCs in the MW, we found 12 objects that needed further investigation in order to validate our results. More specifically, the distances of 11 CCs from the Galactic center are larger than 17 kpc, and the height from the Galactic plane of 2 CCs is larger than 3 kpc (see Fig. A.1, panel a). With the aim at separating different types of pulsating variables, we therefore verified their positions in diagrams that are commonly used for variable star classification, namely, the Bailey diagram (panel b of the same figure) and the Fourier parameters plotted as a function of the logarithmic pulsation period (panels c and d).

Comparing our sample of CCs with bona fide CCs from the OGLE survey (including the LMC, SMC, the disk, and the bulge sample), we found that only the two fundamental-mode CCs with a large Z (i.e., the two triangles) occupy anomalous positions in some of these diagram. More specifically, the star ASAS J062939-1840.5 (the one at Rg~29 kpc and with pulsation period ~ 17 days) is slightly outside of the main sequence of fundamental CCs in both the Bailey and the R21 plots. V1253Cen (RG~8.5 kpc and P~4 days) instead is outside the locus of fundamental CCs only in the R21 versus log P diagram. All the other CCs in our sample are well within the loci of both fundamental and first-overtone CCs.

thumbnail Fig. A.1

Height from the Galactic plane, Bailey diagram, and Fourier parameters. Panel a) Distance from the Galactic plane as a function of the galactocentric distance for the current sample of 379 classical Cepheids. Panel b) Bailey diagram: I-band luminosity amplitude as a function of the logarithmic pulsation period. The gray and cyan dots display the fundamental (FU) and first overtone (FO) Galactic CCs, respectively, collected by OGLE IV. The red triangles indicate two of our Cepheids for which only the V-band light curves are available (Jayasinghe et al. 2021, ASAS-SN V) and that were transformed into the I band using an amplitude ratio of 1.61 (see Klagyivik & Szabados 2009). The red and blue circles display FU and FO Cepheids located in the outermost disk region. Panels c) and d) Same as in panel (b), but showing the R21 and the φ31 Fourier parameters. For the two CCs with V-band light curves alone, the Fourier parameters were transformed into the I band using the empirical relations from Ngeow et al. (2003).

Appendix B Spectral synthesis examples for sulfur

Figure B.1 shows the comparison between observed spectra and the best-fit synthetic models for a sample of four stars, acquired with different spectrographs, in the sulfur line region at 6757 Å. Specifically, the HARPS spectrum (R~ 115 000) is for the star ζ Gem (Teff = 5617 K, log g = 1.2 dex, [Fe/H] = 0.02 dex, vt = 3.4 km s−1, A(S) = 7.13 ±0.03 dex); the FEROS spectrum (R~48 000) is for TVel (Teff = 5721 K, log g = 1.6 dex, [Fe/H] = −0.06 dex, vt = 3.3 km s−1, A(S) = 7.02±0.05 dex); the UVES spectrum (R~40 000) is for XX Sgr (Teff = 6259 K, log g = 1.3 dex, [Fe/H] = −0.06 dex, vt = 2.9 km s−1 , A(S) = 7.05 ± 0.05 dex); and the STELLA spectrum (R~55 000) is for the star VZCyg (Teff = 6169 K, log g = 1.3 dex, [Fe/H] = −0.02 dex, vt = 2.9 km s−1, A(S) = 7.03 ± 0.04 dex).

thumbnail Fig. B.1

Examples of spectral synthesis for the S I line at 6757 A. The observed (HARPS, FEROS, UVES, and STELLA) and best-fit synthetic spectra are plotted as black points and magenta solid lines, respectively. The line of interest is marked as the green area.

Appendix C Comparison with stars in common

Figure C.1 shows a comparison of the atmospheric parameters and the O and S abundances for Cepheids in common in our sample and the literature (Luck et al. 2011; Trentin et al. 2023). The differences are close to zero within the errors for most of the comparisons. The surface gravity and the microturbulent velocity are systematically higher in Luck et al. (2011), which might be due to differences in the line lists used. Sulfur abundances are systematically overabundant in both literature works compared to our estimates. Again, the line list differences likely play an important role. Our measurements are based on one single line of sulfur, whereas those authors used additional S lines in their estimates.

thumbnail Fig. C.1

Comparison with literature of the atmospheric parameters and abundances estimated in the current work. The panels shows the differences as a function of the effective temperature for stars in common in the current study (TS) and data from Luck et al. (2011, L11) and Trentin et al. (2023, T23).

Appendix D Abundances in the pulsation cycle

Figure D.1 shows the O and S abundances plotted as a function of the pulsation phase for the 20 calibrating CCs provided by da Silva et al. (2022). This is a selection of Cepheids from our sample for which high-resolution spectra cover either the entire cycle or a significant portion of the pulsation cycle.

The phases (φ) in the pulsation cycle were calculated by using the following equation and the ephemerides that we previously published in da Silva et al. (2022):

ϕ={ x−int(x)if x−int(x)>0x−int(x)if x−int(x)<0x−int(x)otherwise x=MJD−(T0−2400000)+0.5P,$\matrix{ {\phi = \left\{ {\matrix{ {x - int\left( x \right)} \hfill &amp; {{\rm{if}}\,x - int\left( x \right) &gt; 0} \hfill \cr {x - int\left( x \right)} \hfill &amp; {{\rm{if}}\,x - int\left( x \right) &lt; 0} \hfill \cr {x - int\left( x \right)} \hfill &amp; {{\rm{otherwise}}} \hfill \cr } } \right.} \cr {x = {{{\rm{MJD}} - \left( {{T_0} - 2400000} \right) + 0.5} \over P},} \cr }$(D.1)

where MJD is the modified Julian date from their Table 4, while T0 (as defined in that paper) and the pulsation period (P) are from their Table 5. For Cepheids for which more than one value of T0 was available, we adopted the first one (ephemeris source = 0). We note that a shift was applied to the phases of VY Sgr (−0.05), RZ Vel (+0.03), and WZ Sgr (−0.03) for the reasons mentioned in the notes to Table 5. Finally, we mention that the oxygen abundance for the variable Y Oph was not included in our current study. Although the S/N of the spectra available for this variable is quite high (from ~70 to more than 180), there are several emission features close to the oxygen line at 6300.3 Å. This means that the position of the continuum could not be assessed accurately. This oxygen line is relatively weak, which makes the abundance measurements very sensible to the continuum definition. The observed features might be related to airglow emission lines (see Noll et al. 2012), which may affect some of the spectra adopted in our analysis.

thumbnail Fig. D.1

Abundance ratios as a function of the pulsation phase. Measurements from different spectrographs are indicated with different colors and symbols. The error bars are smaller than the symbol size in some cases. The weighted mean (dashed line) and the standard error of the abundances are also shown, together with the pulsation period.

References

  1. Andrievsky, S. M., Lépine, J. R. D., Korotin, S. A., et al. 2013, MNRAS, 428, 3252 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arellano-Córdova, K. Z., Esteban, C., García-Rojas, J., & Méndez-Delgado, J. E. 2020, MNRAS, 496, 1051 [Google Scholar]
  3. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  4. Bono, G., Marconi, M., Cassisi, S., et al. 2005, ApJ, 621, 966 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bono, G., Braga, V., Pietrinferni, A., et al. 2023, TAAR, submitted [Google Scholar]
  6. Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bresolin, F., Kennicutt, R. C., & Ryan-Weber, E. 2012, ApJ, 750, 122 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bresolin, F., Kudritzki, R.-P., Urbaneja, M. A., et al. 2016, ApJ, 830, 64 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bresolin, F., Kudritzki, R.-P., & Urbaneja, M. A. 2022, ApJ, 940, 32 [NASA ADS] [CrossRef] [Google Scholar]
  11. Caffau, E., Ludwig, H. G., Steffen, M., et al. 2015, A & A, 579, A88 [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cantat-Gaudin, T., Anders, F., Castro-Ginard, A., et al. 2020, A & A, 640, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Caputo, F., Marconi, M., Musella, I., & Pont, F. 2001, A & A, 372, 544 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  15. Carraro, G., Geisler, D., Villanova, S., Frinchaboy, P. M., & Majewski, S. R. 2007, A & A, 476, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Castelli, F., & Kurucz, R. L. 2004, ArXiv Astrophysics e-prints [astro-ph/8485887] [Google Scholar]
  17. Cavichia, O., Mollá, M., Costa, R. D. D., & Maciel, W. J. 2014, MNRAS, 437, 3688 [NASA ADS] [CrossRef] [Google Scholar]
  18. Chen, B., Stoughton, C., Smith, J. A., et al. 2001, ApJ, 553, 184 [Google Scholar]
  19. Chen, X., Wang, S., Deng, L., et al. 2019, Nat. Astron., 3, 320 [NASA ADS] [CrossRef] [Google Scholar]
  20. Crestani, J., Braga, V. F., Fabrizio, M., et al. 2021, ApJ, 914, 10 [NASA ADS] [CrossRef] [Google Scholar]
  21. da Silva, R., Lemasle, B., Bono, G., et al. 2016, A & A, 586, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. da Silva, R., Crestani, J., Bono, G., et al. 2022, A & A, 661, A104 [CrossRef] [EDP Sciences] [Google Scholar]
  23. Dalton, G., Trager, S., Abrams, D. C., et al. 2020, SPIE Conf. Ser., 11447, 1144714 [NASA ADS] [Google Scholar]
  24. de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
  25. Dehnen, W., Semczuk, M., & Schönrich, R. 2023, MNRAS, 523, 1556 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, Proc. SPIE, 4008, 534 [Google Scholar]
  27. Dessauges-Zavadsky, M., Calura, F., Prochaska, J. X., D’Odorico, S., & Matteucci, F. 2007, A & A, 470, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Donor, J., Frinchaboy, P. M., Cunha, K., et al. 2020, AJ, 159, 199 [NASA ADS] [CrossRef] [Google Scholar]
  29. D’Orazi, V., Oliva, E., Bragaglia, A., et al. 2020, A & A, 633, A38 [CrossRef] [EDP Sciences] [Google Scholar]
  30. Dormand, J., & Prince, P. 1980, J. Comput. Appl. Math., 6, 19 [CrossRef] [MathSciNet] [Google Scholar]
  31. Dors, O. L., Valerdi, M., Riffel, R. A., et al. 2023, MNRAS, 521, 1969 [NASA ADS] [CrossRef] [Google Scholar]
  32. Duffau, S., Caffau, E., Sbordone, L., et al. 2017, A & A, 604, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Farmer, R., Laplace, E., Ma, J.-Z., de Mink, S. E., & Justham, S. 2023, ApJ, 948, 111 [NASA ADS] [CrossRef] [Google Scholar]
  34. Feast, M. W., Menzies, J. W., Matsunaga, N., & Whitelock, P. A. 2014, Nature, 509, 342 [Google Scholar]
  35. Friel, E. D., Jacobson, H. R., & Pilachowski, C. A. 2010, AJ, 139, 1942 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gaia Collaboration (Katz, D., et al.) 2018, A & A, 616, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gaia Collaboration (Recio-Blanco, A., et al.) 2023, A & A, 674, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Gazak, J. Z., Kudritzki, R., Evans, C., et al. 2015, ApJ, 805, 182 [NASA ADS] [CrossRef] [Google Scholar]
  39. Genovali, K., Lemasle, B., Bono, G., et al. 2014, A & A, 566, A37 [CrossRef] [EDP Sciences] [Google Scholar]
  40. Genovali, K., Lemasle, B., da Silva, R., et al. 2015, A & A, 580, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gioannini, L., Matteucci, F., Vladilo, G., & Calura, F. 2017, MNRAS, 464, 985 [CrossRef] [Google Scholar]
  42. GRAVITY Collaboration (Abuter, R., et al.) 2018, A & A, 615, A15 [CrossRef] [EDP Sciences] [Google Scholar]
  43. Green, D. A. 2014, Supernova Environmental Impacts, eds. A. Ray, & R. A. McCray, IAU Symposium, 296, 188 [NASA ADS] [Google Scholar]
  44. Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
  45. Gullikson, K., Dodson-Robinson, S., & Kraus, A. 2014, AJ, 148, 53 [NASA ADS] [CrossRef] [Google Scholar]
  46. Henry, R. B. C., Kwitter, K. B., & Balick, B. 2004, AJ, 127, 2284 [CrossRef] [Google Scholar]
  47. Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
  48. Jayasinghe, T., Kochanek, C. S., Stanek, K. Z., et al. 2021, MNRAS, 503, 200 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
  50. Kennicutt, Robert C. J. 1998, ARA & A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
  51. Klagyivik, P., & Szabados, L. 2009, A & A, 504, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [Google Scholar]
  54. Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020, ApJ, 900, 179 [Google Scholar]
  55. Korotin, S. A. 2009, Astron. Rep., 53, 651 [Google Scholar]
  56. Kovtyukh, V. V. 2007, MNRAS, 378, 617 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kraft, R. P. 1966, AJ, 71, 166 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kudritzki, R., & Urbaneja, M. A. 2018, arXiv e-prints [arXiv:1818.81182] [Google Scholar]
  59. Kudritzki, R.-P., Urbaneja, M. A., Bresolin, F., Hosek, Matthew, W. J., & Przybilla, N. 2014, ApJ, 788, 56 [NASA ADS] [CrossRef] [Google Scholar]
  60. Lemasle, B., François, P., Genovali, K., et al. 2013, A & A, 558, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Lemasle, B., Hajdu, G., Kovtyukh, V., et al. 2018, A & A, 618, A160 [CrossRef] [EDP Sciences] [Google Scholar]
  62. Lemasle, B., Lala, H. N., Kovtyukh, V., et al. 2022, A & A, 668, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Lépine, J. R. D., Roman-Lopes, A., Abraham, Z., Junqueira, T. C., & Mishurov, Y. N. 2011, MNRAS, 414, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  64. Lépine, J. R. D., Michtchenko, T. A., Barros, D. A., & Vieira, R. S. S. 2017, ApJ, 843, 48 [CrossRef] [Google Scholar]
  65. Leung, S.-C., & Nomoto, K. 2018, ApJ, 861, 143 [Google Scholar]
  66. Leung, S.-C., & Nomoto, K. 2020, ApJ, 888, 80 [Google Scholar]
  67. Limongi, M., & Chieffi, A. 2003, ApJ, 592, 404 [CrossRef] [Google Scholar]
  68. Limongi, M. & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  69. Liu, G., Arav, N., & Rupke, D. S. N. 2015, ApJS, 221, 9 [NASA ADS] [CrossRef] [Google Scholar]
  70. Liu, C., Kudritzki, R.-P., Zhao, G., et al. 2022, ApJ, 932, 29 [NASA ADS] [CrossRef] [Google Scholar]
  71. López-Corredoira, M., Sylos Labini, F., Kalberla, P. M. W., & Allende Prieto, C. 2019, AJ, 157, 26 [CrossRef] [Google Scholar]
  72. Lucertini, F., Monaco, L., Caffau, E., Bonifacio, P., & Mucciarelli, A. 2022, A & A, 657, A29 [CrossRef] [EDP Sciences] [Google Scholar]
  73. Lucertini, F., Monaco, L., Caffau, E., et al. 2023, A & A, 671, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Luck, R. E. 2018, AJ, 156, 171 [Google Scholar]
  75. Luck, R. E., & Lambert, D. L. 2011, AJ, 142, 136 [Google Scholar]
  76. Luck, R. E., Andrievsky, S. M., Kovtyukh, V. V., Gieren, W., & Graczyk, D. 2011, AJ, 142, 51 [NASA ADS] [CrossRef] [Google Scholar]
  77. Madore, B. F., Hoffman, D., Freedman, W. L., et al. 2013, ApJ, 776, 135 [Google Scholar]
  78. Magrini, L., Randich, S., Kordopatis, G., et al. 2017, A & A, 603, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Magrini, L., Viscasillas Vâzquez, C., Spina, L., et al. 2023, A & A, 669, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Matsunaga, N., Bono, G., Chen, X., et al. 2018, Space Sci. Rev., 214, 74 [NASA ADS] [CrossRef] [Google Scholar]
  81. Matteucci, F. 2021, A & ARv, 29, 5 [NASA ADS] [Google Scholar]
  82. Matteucci, F., Vasini, A., Grisoni, V., & Schultheis, M. 2020, MNRAS, 494, 5534 [Google Scholar]
  83. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  84. McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, AJ, 136, 367 [NASA ADS] [CrossRef] [Google Scholar]
  85. Minchev, I., Famaey, B., Combes, F., et al. 2011, A & A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
  87. Mizumoto, M., Sameshima, H., Kobayashi, N., et al. 2023, ApJ, submitted [Google Scholar]
  88. Nakanishi, H., & Sofue, Y. 2003, PASJ, 55, 191 [Google Scholar]
  89. Nakanishi, H., & Sofue, Y. 2006, PASJ, 58, 847 [NASA ADS] [Google Scholar]
  90. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
  91. Ngeow, C.-C., Kanbur, S. M., Nikolaev, S., Tanvir, N. R., & Hendry, M. A. 2003, ApJ, 586, 959 [NASA ADS] [CrossRef] [Google Scholar]
  92. Noll, S., Kausch, W., Barden, M., et al. 2012, A & A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA & A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
  94. Oppenheimer, B. D., & Davé, R. 2008, MNRAS, 387, 577 [NASA ADS] [CrossRef] [Google Scholar]
  95. Palla, M. 2021, MNRAS, 503, 3216 [Google Scholar]
  96. Palla, M., Matteucci, F., Spitoni, E., Vincenzo, F., & Grisoni, V. 2020, MNRAS, 498, 1710 [Google Scholar]
  97. Palla, M., Santos-Peral, P., Recio-Blanco, A., & Matteucci, F. 2022, A & A, 663, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Perdigon, J., de Laverny, P., Recio-Blanco, A., et al. 2021, A & A, 647, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Pietrukowicz, P., Soszyński, I., & Udalski, A. 2021, Acta Astron., 71, 205 [NASA ADS] [Google Scholar]
  100. Piskunov, N., & Valenti, J. A. 2017, A & A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [Google Scholar]
  102. Proxauf, B., da Silva, R., Kovtyukh, V. V., et al. 2018, A & A, 616, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Queiroz, A. B. A., Anders, F., Chiappini, C., et al. 2020, A & A, 638, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Quillen, A. C., Minchev, I., Bland-Hawthorn, J., & Haywood, M. 2009, MNRAS, 397, 1599 [NASA ADS] [CrossRef] [Google Scholar]
  105. Randich, S., Gilmore, G., Magrini, L., et al. 2022, A & A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
  107. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [Google Scholar]
  108. Ripepi, V., Catanzaro, G., Molinaro, R., et al. 2020, A & A, 642, A230 [CrossRef] [EDP Sciences] [Google Scholar]
  109. Ripepi, V., Chemin, L., Molinaro, R., et al. 2022, MNRAS, 512, 563 [NASA ADS] [CrossRef] [Google Scholar]
  110. Romaniello, M., Riess, A., Mancino, S., et al. 2022, A & A, 658, A29 [CrossRef] [EDP Sciences] [Google Scholar]
  111. Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A & A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Sánchez-Blázquez, P., Rosales-Ortega, F. F., Méndez-Abreu, J., et al. 2014, A & A, 570, A6 [CrossRef] [EDP Sciences] [Google Scholar]
  113. Sánchez-Menguiano, L., Sânchez, S. F., Pérez, I., et al. 2016, A & A, 587, A70 [CrossRef] [EDP Sciences] [Google Scholar]
  114. Santos-Peral, P., Recio-Blanco, A., Kordopatis, G., Fernândez-Alvar, E., & de Laverny, P. 2021, A & A, 653, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Santucci, G., Brough, S., van de Sande, J., et al. 2023, MNRAS, 521, 2671 [NASA ADS] [CrossRef] [Google Scholar]
  116. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  117. Schönrich, R., & McMillan, P. J. 2017, MNRAS, 467, 1154 [NASA ADS] [Google Scholar]
  118. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
  119. Skowron, D. M., Skowron, J., Mróz, P., et al. 2019, Science, 365, 478 [Google Scholar]
  120. Sneden, C. 2002, The MOOG code, http://www.as.utexas.edu/~chris/moog.html [Google Scholar]
  121. Sofue, Y. 2013, PASJ, 65, 118 [NASA ADS] [Google Scholar]
  122. Soszyński, I., Udalski, A., Szymański, M. K., et al. 2017, Acta Astron., 67, 103 [NASA ADS] [Google Scholar]
  123. Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A & A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A & A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  125. Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019, A & A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A & A, 647, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Spitoni, E., Aguirre Børsen-Koch, V., Verma, K., & Stokholm, A. 2022, A & A, 663, A174 [CrossRef] [EDP Sciences] [Google Scholar]
  128. Stahler, S. W., & Palla, F. 2005, The Formation of Stars (Wiley) [Google Scholar]
  129. Strassmeier, K. G., Granzer, T., Weber, M., et al. 2004, Astron. Nachr., 325, 527 [NASA ADS] [CrossRef] [Google Scholar]
  130. Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 970306 [CrossRef] [Google Scholar]
  131. Sun, Y., Xu, Y., Yang, J., et al. 2015, ApJ, 798, L27 [Google Scholar]
  132. Takeda, Y., Hashimoto, O., Taguchi, H., et al. 2005, PASJ, 57, 751 [NASA ADS] [Google Scholar]
  133. Tautvaišienė, G., Drazdauskas, A., Mikolaitis, Š., et al. 2015, A & A, 573, A55 [CrossRef] [EDP Sciences] [Google Scholar]
  134. Tian, H.-J., Liu, C., Wan, J.-C., et al. 2017, Res. Astron. Astrophys., 17, 114 [Google Scholar]
  135. Trentin, E., Ripepi, V., Catanzaro, G., et al. 2023, MNRAS, 519, 2331 [Google Scholar]
  136. Tsujimoto, T. 2023, MNRAS, 518, 3475 [Google Scholar]
  137. Twarog, B. A., Ashman, K. M., & Anthony-Twarog, B. J. 1997, AJ, 114, 2556 [NASA ADS] [CrossRef] [Google Scholar]
  138. Urbaneja, M. A., Herrero, A., Bresolin, F., et al. 2005, ApJ, 622, 862 [Google Scholar]
  139. Viscasillas Vázquez, C., Magrini, L., Casali, G., et al. 2022, A & A, 660, A135 [CrossRef] [EDP Sciences] [Google Scholar]
  140. Vladilo, G., Gioannini, L., Matteucci, F., & Palla, M. 2018, ApJ, 868, 127 [NASA ADS] [CrossRef] [Google Scholar]
  141. Wang, S., Chen, X., de Grijs, R., & Deng, L. 2018, ApJ, 852, 78 [NASA ADS] [CrossRef] [Google Scholar]
  142. Wegg, C., Gerhard, O., & Portail, M. 2015, MNRAS, 450, 4050 [NASA ADS] [CrossRef] [Google Scholar]
  143. Wehrhahn, A. 2021, in The 20.5th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS20.5), 1 [Google Scholar]
  144. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [Google Scholar]
  145. Yong, D., Carney, B. W., & Friel, E. D. 2012, AJ, 144, 95 [Google Scholar]
  146. Zaritsky, D., Kennicutt, Robert C. J., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
  147. Zhu, L., van den Bosch, R., van de Ven, G., et al. 2018, MNRAS, 473, 3000 [Google Scholar]
1

We assumed the position of the Sun in the Galaxy adopted by Gaia Collaboration (2018): a height above the Galactic plane Z⊙ = 27 pc (Chen et al. 2001), a distance from the Galactic center <ieq/> kpc, and a circular velocity at the solar radius Vc = 240 km s−1 (Reid et al. 2014). We also adopted the solar reflex motion components from Schönrich et al. (2010), that is, U⊙, V⊙, and W⊙ of 11.1, 12.24, and 7.25 km s−1.

5

We adopted ∑SFR=v∑gask${\sum _{{\rm{SFR}}}} = v\sum _{{\rm{gas}}}^k$ (Kennicutt 1998), with k = 1.5.

All Tables

Table 1

Excerpt from the list of our sample of 379 Galactic classical Cepheids.

In the text
Table 2

Excerpt from the list of atmospheric parameters and Fe, O, and S abundances for each spectrum in our sample.

In the text
Table 3

Excerpt from the list of Fe, O, and S abundances derived for each star in our sample.

In the text
Table 4

Slopes and zeropoints of the abundance gradients as a function of the galactocentric distance.

In the text

All Figures

thumbnail Fig. 1

Radial distribution of the current Cepheid sample (colored circles) projected onto the Galactic plane. The symbols are color-coded (see the color bar on the right side) according to the distance from the Galactic plane. The dotted annuli display muliples of 5 kpc of the distances from the Galactic center. The position adopted for the Sun is at X = 0 and Y = 8.127 kpc (GRAVITY Collaboration 2018). The colored diamonds show the locations of highmass star-forming regions used by Reid et al. (2019) to fit the spiral arms. They are color-coded according to the spiral arm association. The long bar of the inner part of the Galaxy is indicated with a shaded ellipse (Wegg et al. 2015). The solid curved lines trace the Milky Way spiral arms from Reid et al. (2019) and from Sun et al. (2015, Outer, Scutum, and Centaurus arms).
In the text
thumbnail Fig. 2

Abundance ratios as a function of the galactocentric distance. Our sample of Cepheids (blue circles) is compared with our sample of open clusters (symbols color-coded according to the stellar age). The Fe and O abundance ratios are taken from Magrini et al. (2023), whereas the S abundances are taken from the present work. The black line displays a linear regression fitted to Cepheids in the range of galactocentric distance from 4 to 12.5 kpc, and the dashed line is the extrapolation up to 17 kpc. The red line shows a logarithmic fit over the whole range of galactocentric distances. The corresponding equations are also shown. The shaded area shows one standard deviation around the running mean, weighted with a Gaussian function taking the errors into account.
In the text
thumbnail Fig. 3

[S/H] as a function of the [O/H] abundances. Our sample of Cepheids, color-coded according to the distance from the Galactic center (see the color bar on the right side), is compared with the same open clusters as plotted in Fig. 2. The dashed gray line is the 1:1 linear relation.
In the text
thumbnail Fig. 4

Abundance ratios as a function of the Galactocentric distance. Same as in Fig. 2 but showing the [O/Fe] and the [S/Fe] abundance ratios.
In the text
thumbnail Fig. 5

Abundance ratios as a function of the logarithmic pulsation period. The black line shows a linear regression fit to the current Cepheid sample. The corresponding equation is also shown.
In the text
thumbnail Fig. 6

Abundance ratios as a function of the iron abundance. Left panels: same data as in Fig. 2, but comparing the [O/Fe] (top) and [S/Fe] (bottom) ratios for our samples of classical Cepheids and open clusters. The bottom panel also shows the abundance ratios for the open clusters (Trumpler 5 and Trumpler 20) provided by Lucertini et al. (2023). Right panels: [O/Fe] and [S/Fe] ratios for Galactic Cepheids compared with thin-and thick-disk stars provided by the GES (DR5.0) collaboration and with thin-disk, thick-disk, and bulge field stars provided by Lucertini et al. (2022, L22a).
In the text
thumbnail Fig. 7

Abundance ratios as a function of the iron abundance. The [O/Fe] and [S/Fe] ratios for the current CC sample are color-coded according to their galactocentric distance.
In the text
thumbnail Fig. 8

Predicted [X/H] and [X/Fe] radial gradients compared with the Cepheid data presented in this work (blue points with error bars). The black lines are from the best-fit model presented by Palla et al. (2020), and the red lines are from a model with analogous setup, but with a flattened profile for the efficiency of star formation ν in the outer Galactic regions (RG > 12 kpc).
In the text
thumbnail Fig. 9

Effect of the S yield for massive stars on the [S/H] and [S/Fe] radial gradients for the model with a flattened star formation efficiency profile for the outer regions. The solid red line shows the model with standard yield prescriptions (from Kobayashi et al. 2006, 2011), the dashed red line shows the model with the S yield reduced by a factor 4, and the dash-dotted green line displays a model with scaling factor for the S yields that is variable with radius. The symbols are the same as in Fig. 8.
In the text
thumbnail Fig. A.1

Height from the Galactic plane, Bailey diagram, and Fourier parameters. Panel a) Distance from the Galactic plane as a function of the galactocentric distance for the current sample of 379 classical Cepheids. Panel b) Bailey diagram: I-band luminosity amplitude as a function of the logarithmic pulsation period. The gray and cyan dots display the fundamental (FU) and first overtone (FO) Galactic CCs, respectively, collected by OGLE IV. The red triangles indicate two of our Cepheids for which only the V-band light curves are available (Jayasinghe et al. 2021, ASAS-SN V) and that were transformed into the I band using an amplitude ratio of 1.61 (see Klagyivik & Szabados 2009). The red and blue circles display FU and FO Cepheids located in the outermost disk region. Panels c) and d) Same as in panel (b), but showing the R21 and the φ31 Fourier parameters. For the two CCs with V-band light curves alone, the Fourier parameters were transformed into the I band using the empirical relations from Ngeow et al. (2003).
In the text
thumbnail Fig. B.1

Examples of spectral synthesis for the S I line at 6757 A. The observed (HARPS, FEROS, UVES, and STELLA) and best-fit synthetic spectra are plotted as black points and magenta solid lines, respectively. The line of interest is marked as the green area.
In the text
thumbnail Fig. C.1

Comparison with literature of the atmospheric parameters and abundances estimated in the current work. The panels shows the differences as a function of the effective temperature for stars in common in the current study (TS) and data from Luck et al. (2011, L11) and Trentin et al. (2023, T23).
In the text
thumbnail Fig. D.1

Abundance ratios as a function of the pulsation phase. Measurements from different spectrographs are indicated with different colors and symbols. The error bars are smaller than the symbol size in some cases. The weighted mean (dashed line) and the standard error of the abundances are also shown, together with the pulsation period.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.