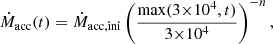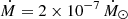| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346148 | |
| Published online | 26 September 2023 | |
Effects of accretion on the structure and rotation of forming stars
1
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris, Sorbonne Paris Cité, 91191 Gif-sur-Yvette, France
e-mail: louis.amard@cea.fr
2
University of Exeter, Physics and Astrophysics dept, Stoker Road, EX44QL Exeter, UK
Received:
15
February
2023
Accepted:
12
June
2023
Context. Rotation period measurements of low-mass stars show that the spin distributions in young clusters do not exhibit the spin-up expected due to contraction in the phase when a large fraction of stars is still surrounded by accretion discs. Many physical models have been developed to explain this feature based on different types of star-disc interactions alone. In this phase, the stars accrete mass and angular momentum and may experience accretion-enhanced magnetised winds. The stellar structure and angular momentum content thus strongly depend on the properties of the accretion mechanism. At the same time, the accretion of mass and energy has a significant impact on the evolution of the stellar structure and the moment of inertia. Our understanding of the spin rates of young stars therefore requires a description of how accretion affects the stellar structure and angular momentum simultaneously.
Aims. We aim to understand the role of accretion to explain the observed rotation-rate distributions of forming stars.
Methods. We computed evolution models of accreting very young stars and determined in a self-consistent way the effect of accretion on stellar structure and the angular momentum exchanges between the stars and their disc. We then varied the deuterium content, the accretion history, the entropy content of the accreted material, and the magnetic field as well as the efficiency of the accretion-enhanced winds.
Results. The models are driven alternatively both by the evolution of the momentum of inertia and by the star-disc interaction torques. Of all the parameters we tested, the magnetic field strength, the accretion history, and the deuterium content have the largest impact. The injection of heat plays a major role only early in the evolution.
Conclusions. This work demonstrates the importance of the moment of inertia evolution under the influence of accretion for explaining the constant rotation-rate distributions that are observed during the star-disc interactions. When we account for rotation, the models computed with the recently calculated torque along with a consistent structural evolution of the accreting star are able to explain the almost constant spin evolution for the whole range of parameters we investigated, but it only reproduces a narrow range around the median of the observed spin rate distributions. Further development, including for example more realistic accretion histories based on dedicated disc simulations, are likely needed to reproduce the extremes of the spin rate distributions.
Key words: accretion / accretion disks / stars: formation / stars: rotation / stars: low-mass / stars: pre-main sequence
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Understanding the formation stage of low-mass stellar system is of crucial importance for both planetary and stellar science. The early pre-main sequence (PMS) is the stage for many important events in a stellar system and is still poorly understood, despite many efforts to solve the questions in the past few decades. The total angular momentum of the system is particularly important because it is a main driver of the early stellar evolution and the formation of the proto-planetary disc.
During the first stages of its evolution, classical stellar evolution theory predicts that the star contracts while it relaxes to a stable state, and thus should spin up. In addition, the accretion of material coming from the inner edge of the proto-planetary disc should increase the stellar angular momentum. Following these basic assumption, the presence of a disc around a forming star should in theory be associated with a very fast stellar rotation rate. However, observations of stars in clusters younger than ∼10 Myr show that the distributions of the rotation rates are approximately constant in time, or are at least inconsistent with the systematic spinning-up that is expected. Furthermore, stars that are currently surrounded by accretion discs do not systematically exhibit faster rotation than those without. These apparent paradoxes are often described using a pseudo-explanation called “disc locking,” which refers to a highly simplified concept according to which the presence of a disc causes a star to remain locked to a constant rotation rate during its evolution (Koenigl 1991; Edwards et al. 1993; Bouvier et al. 1993, 2007, 2014; Rebull et al. 2004; Kennedy & Kenyon 2009; Davies et al. 2014; Venuti et al. 2017; Rebull et al. 2018, 2020, 2022). To describe the observed behaviour, several theoretical explanations for extracting angular momentum from the systems have been proposed. They include the X-winds model (Shu et al. 1994; Ferreira et al. 2000), the accretion-powered stellar winds (APSW, Matt & Pudritz 2005, 2008), or the magnetospheric ejections (Zanni & Ferreira 2009, 2013). While almost none of these mechanisms are exclusive by essence, they have rarely been studied together (Gallet et al. 2019). In addition, the systems are very dynamic and complicated, so that many variable parameters must be considered simultaneously, and ideally, self-consistently. Theoretical models for angular momentum transfer between the star and its environment (accretion discs and/or winds) show that the net torque on the star can be either negative or positive, and that the value depends on stellar and environmental properties that are themselves evolving with time. Therefore, an understanding of the evolution of stellar angular momentum requires a description of several properties evolving together.
The modelling of low-mass rotational evolution has been steadily and consistently improved over the past decade (Gallet & Bouvier 2013, 2015; Lanzafame & Spada 2015; Amard et al. 2016; Somers & Pinsonneault 2016; Amard & Matt 2020; Spada & Lanzafame 2020). However, very little work has been dedicated to the very early evolution, when the star still has a disc and appears to maintain an almost constant rotation rate. All the models listed above assume a constant rotation rate for a given duration, which is associated with the time of interaction with the surrounding proto-planetary disc. A few groups have studied the effect of a variable duration of this star-disc interaction (SDI) phase to reproduce the rotation periods on a longer timescale (Vasconcelos & Bouvier 2015; Coker et al. 2016; Roquette et al. 2021). Siess & Livio (1997) described the role of a reduced convective mixing to explain the very slow rotation in young clusters, and Batygin & Adams (2013) reported on the link between rotation rates during the SDI phase and misalignment of close-in Jupiter-mass planets. Finally, a few rotation evolution models have accounted for a physical evolution during the SDI phase, but required extreme stellar properties to explain the distributions (Matt et al. 2010, 2012b; Gallet et al. 2019) or remained empirical (Johnstone et al. 2014).
Because of the stellar contraction, the typical rotational evolution of young stars is strongly influenced by the evolution of the moment of inertia. In order to account for its variation, rotation evolution models make use of stellar evolution tracks to follow the evolution of the stellar structure. The models start the evolution around 1 Myr or after the disc-coupling phase. Thus, the early structure evolution is often neglected. The community has been using models that do not account for an accretion process such as those described by either Baraffe et al. (1998) or Siess et al. (2000). The radius and thus the moment of inertia can be drastically affected by accretion of material with different composition and thermodynamic properties (Siess et al. 1997; Baraffe et al. 2009; Hosokawa et al. 2011; Kunitomo et al. 2017, 2018).
Another element for which SDI has been shown to play a role is the amount of lithium observed in young clusters and metal-poor old stars. It was shown by Bouvier et al. (2018) to already be connected to the rotation rates of PMS stars before the first five million years. Eggenberger et al. (2012) showed that a longer disc-coupling time generates a stronger shear at the base of the convective zone, which would then efficiently transport the lithium to deeper part of the star where it can be burnt. Baraffe et al. (2017) showed for the lithium evolution that the entropy content of the accreted material affects the temperature at the base of the convective region, and thus the amount of lithium burnt during the PMS. Tognelli et al. (2020, 2021) tested the impact of several accretion scenarios on the abundance of lithium and more generally, of light elements.
In addition, accretion leaves a mark on the stellar structure that can remain for several tens of million years. Its impact on the stellar pulsation spectra of δScuti stars was estimated by Steindl et al. (2021, 2022a,b).
The early PMS is a highly dynamical phase and is therefore hard to model on evolutionary timescales. A common approach is to start from short time-span multidimensional MHD simulations (Matt & Pudritz 2005, 2008; Romanova et al. 2013, 2018, 2021; Zanni & Ferreira 2009, 2013; Pantolmos et al. 2020; Ireland et al. 2021, 2022) and to derive scaling laws to use in 1D evolution models on a longer timescale. We here use the results from the star-disc PLUTO simulations by Ireland et al. (2022) and implement them in the STAREVOL evolution code.
The model and the implementation are described in Sect. 2. Section 3 presents some non-rotating accreting models to validate the evolution compared to other recent work. In Sect. 4 we discuss the rotational evolution and test various parameters of the torque laws that we finally compare to the rotation rate distribution in open clusters. Finally, in Sect. 5, we recall the limitations of the model, draw conclusions, and discuss further possibilities.
2. Description of the model
2.1. Stellar evolution model: STAREVOL with accretion
2.1.1. Standard case
We used the 1D stellar evolution code STAREVOL (Siess et al. 2000; Palacios et al. 2006; Lagarde et al. 2012; Amard et al. 2019 and refer to these papers for the specific details of the code). Our models were computed for 1D single stars without a magnetic field, but under the influence of rotation and accretion, starting from a small initial seed. STAREVOL solves the structure equations and assumes hydrostatic equilibrium at each time step, assuming that the effects of rotation on the structure are treated as a perturbation in the hydrostatic and radiative equilibrium equations (for more details, see Endal & Sofia 1976; Meynet & Maeder 1997). This assumption is valid in a relatively slowly rotating regime with respect to the break-up velocity. All the models we considered remained below half of the break-up velocity and mostly were about 10 to 20% of this velocity. This led to an increase in the radius of a few percent at most. We patched atmospheric T(τ) relations from Krishna Swamy (1966) from τ = 0.005 to τ = 100. We kept this set of models for numerical stability reasons, but verified in advance that the results were qualitatively similar to PHOENIX atmosphere models as in Amard et al. (2019). The temperature gradient was computed following the mixing-length theory (MLT; Cox & Giuli 1968), with a fixed parameter αMLT = 2.173 that reproduced the solar luminosity and radius at 4.57 Gyr. The internal chemical composition changed with the nuclear reactions and the diffusion in the convective envelope given by the MLT. We did not account for any overshooting or microscopic diffusion. Although STAREVOL is capable of computing differentially rotating models by solving the full set of angular momentum equations (Zahn 1992; Mathis & Zahn 2004; Palacios et al. 2003; Decressin et al. 2009), as a first step, we kept the star as a solid body in the radiative and convective regions. The effect of differential rotation will be investigated in further work. Since the star is in a state of solid-body rotation, there is no chemical transport by shear mixing, and the transport associated with the meridional circulation is negligible in the current case. Similarly, we did not account for any transport by magnetic instabilities or by waves. While we considered a magnetic field to compute the spin evolution, the effects of magnetism on the structure (Somers & Pinsonneault 2015) or the internal transport of angular momentum (Eggenberger et al. 2022) were neglected in the current case.
The initial composition was set as given in Asplund et al. (2021), except for the fraction of deuterium, which was variable. As was emphasised by Kunitomo et al. (2017), deuterium is the main nuclear driver of the evolution during the early PMS, in particular in the case of low-entropy accretion. However, its initial value is still relatively uncertain, and values in the literature vary between 10 ppm and 40 ppm (Hébrard et al. 2005; Linsky et al. 2006). Because of how quickly the deuterium is consumed, we accounted for diffusion when solving the associated nuclear reactions to determine the deuterium profile.
2.1.2. Accretion
Stellar evolution may drastically change when material is accreted. Accretion modifies the stellar structure by bringing mass, energy, and new chemicals to the star. Some energy is kept by the star (as thermal energy), and some is directly radiated away. The question of the deposition of the accreted material in the star is very important for the evolution (see Siess & Forestini 1996; Siess et al. 1997; Hartmann et al. 1998; Baraffe et al. 2009; Kunitomo et al. 2017 for detailed discussions of the physics of accretion in stellar evolution models). We followed the simpler description by Hartmann et al. (1998) that we recall below.
We parametrised the heat injected by the accreted material into the forming star as
where M⋆ and R⋆ are the mass and radius of the central star, respectively, Ṁacc is the accretion rate, and ξ is the accretion efficiency, such that 0 ≤ ξ ≤ 0.5. We set the upper limit at 0.5 and not 1 to account for the radiative cooling from the disc surface and the geometry of the problem. The star only accrets on a small surface, generally, at mid latitude.
An additional term is added to the energy equation to account for the accreted material. We again followed Kunitomo et al. (2018), and the energy was only deposited in the upper layer of the star with a fractional mass of mke. We then have the expression of the energy deposited per unit mass,
with Mr the mass coordinate, and mke is a fraction of the total mass. We assumed mke = 0.02. Although it is much more simplistic, this somewhat mimics the energy deposition in the upper layer given by the more physical formalism by Siess & Forestini (1996) and confirmed by the 2D MUSIC simulations of accreting stars (Geroux et al. 2016).
Finally, we note that Kunitomo & Guillot (2021) recently explored the effect of an increasing metallicity as the disc is being more structured and found that a more realistic chemical evolution of the accreted material could explain the structure of the modern Sun. However, this level of detail is beyond the scope of the present work and adds a parameter. We therefore set the accreted material with the exact same composition as the central initial seed for now and did not change it as the disc evolved.
2.2. Angular momentum evolution
The PMS evolution is highly dynamic, and the angular momentum exchanges are mostly driven by the interactions with the disc. Thus, 1D evolutionary models cannot capture all the details of the accretion phase. Only multidimensional MHD models may be able to estimate the dynamics and the overall physical trends that can then be input in 1D models. We relied on the 2.5D PLUTO simulations by Pantolmos et al. (2020), Ireland et al. (2021), Ireland et al. (2022). These simulations model the magnetised wind of a star that is accreting from a disc. The authors were able to extract some simplified expressions describing the fluxes of angular momentum that leave or impinge onto the stellar surface as a function of physical parameters. During the star-disc interaction phase, the torque can be separated into three components. The first component is due to the accretion by the star of material that is incoming from the inner edge of the disc. The second component is due to a magnetised stellar wind, similar to the wind in the main sequence (Matt et al. 2012a; Réville et al. 2015; Finley et al. 2018), but with some modifications arising from the presence of the disc and the accretion of material. The last component of the torque is related to the large bubbles of plasma that leave the star-disc system as a result of the large-scale magnetic reconnection close to the stellar surface. These so-called magnetospheric ejections (MEs) remain magnetically tied to the star and may either spin the star up or down, depending on the accreting state.
The three components of the torque have indeed been conveniently expressed so that only one parameter governs the change from one state to the next: the ratio of the truncation radius Rt of the disc to the co-rotation radius Rco (i.e. where the Keplerian orbital rate is equal to the angular rotation rate of the star). In state 1, Rt/Rco < 0.433, and the star is accreting from closer in, where the orbiting material has less angular momentum, and thus, the spin-up torque is weakened. However, the MEs spin up the star as well because the disc material brought by the magnetic field lines to the star comes from within the corotation radius, where it spins faster than the surface. State 2 can be seen as a transition stage. When 0.433 < Rt/Rco < 1, the system becomes more complex. In the simulations, the stellar magnetic field now connects to the disc beyond the co-rotation radius, and thus, the MEs may spin the star up or down, depending on the extent of the field line and the stellar rotation (the transition from spin-up to spin-down occurs at intermediate values in the range of Rt/Rco). Finally, state 3 is when Rt/Rco > 1. At this point, the system enters the so-called propeller regime, where the star alternates between being able and unable to accrete on timescales of days to weeks. This is associated with fast rotation and/or a strong magnetic field, leading to a very dynamical situation. In this state, the MEs are maximally efficient at extracting angular momentum, while the accretion torque is largely decreased.
We relied on Ireland et al. (2022) to describe the loss and gain of angular momentum of the star with a surrounding disc. We describe these torque formulations below, and we also adopt the fitted values of Ireland et al. (2022) for each of their formulation parameters (see Table 1). However, the sign changes compared to their formulation. In our case, a positive torque added angular momentum to the star, and therefore spins it up. In addition, the mass accretion rate Ṁacc and mass-loss rate Ṁw are given in terms of absolute values. This again leaves the sign out.
Parameters used for the SDI torque.
2.2.1. Truncation radius
The torques depend on the inner radius of the disc, or in other words, on the truncation radius, where the force exerted by the stellar magnetosphere disrupts the disc structure. Based on time-averaged values for all simulations, Ireland et al. (2022) reported an expression for computing the location of the truncation radius,
with 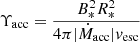 as the disc magnetisation parameter (Matt & Pudritz 2005; Bessolaz et al. 2008). The constants Kt, 1, Kt, 2, mt, 1, mt, 2, and mt, 3 were set according to the simulation of Ireland et al. (2022). f is the fraction of the equatorial surface velocity relative to the break-up speed. vesc is the escape velocity, and B* is the surface dipole strength. The two cases allow for a transition between state 1, where the truncation radius varies as a simple power law in the magnetisation parameter, and states 2 and 3, where Rt is much closer to the co-rotation radius and the centrifugal barrier starts to hinder the accretion. In the case of high accretion rates (or more generally, low disc magnetisation values), the truncation radius can approach the stellar surface. To be able to model the extreme case in which the disc reaches the surface of the star, we further imposed the condition that Rt ≥ R⋆.
as the disc magnetisation parameter (Matt & Pudritz 2005; Bessolaz et al. 2008). The constants Kt, 1, Kt, 2, mt, 1, mt, 2, and mt, 3 were set according to the simulation of Ireland et al. (2022). f is the fraction of the equatorial surface velocity relative to the break-up speed. vesc is the escape velocity, and B* is the surface dipole strength. The two cases allow for a transition between state 1, where the truncation radius varies as a simple power law in the magnetisation parameter, and states 2 and 3, where Rt is much closer to the co-rotation radius and the centrifugal barrier starts to hinder the accretion. In the case of high accretion rates (or more generally, low disc magnetisation values), the truncation radius can approach the stellar surface. To be able to model the extreme case in which the disc reaches the surface of the star, we further imposed the condition that Rt ≥ R⋆.
2.2.2. SDI torque
The first torque that needs to be considered because it is associated with the SDI clearly comes from the angular momentum brought in by the material accreted from the truncation radius Rt. It follows
with Ṁacc the accretion rate, G the gravitational constant, and R⋆ and M⋆ the radius and mass of the star.
The second SDI torque we considered comes from the magnetospheric ejections (ME). They are an outflow caused by the reconnection and expansion of the magnetic field lines that couple the star and the disc. Because of the interaction between the two systems, the mid-latitude regions of the dipole are highly dynamic and reconnect occasionally. This causes some outflows that separate from the stellar magnetosphere and the system. Depending on the regime and the extent of the magnetic field with regard to the co-rotation radius, they spin the star either up or down (Zanni & Ferreira 2013; Gallet et al. 2019; Ireland et al. 2021, 2022). Ireland et al. (2022) found that the spin-up torque varies with the accretion torque, such that
The spin-down torque associated with the MEs depends on the differential rotation between the stellar surface and the MEs connected to the disc. Assuming a dipolar magnetosphere, Ireland et al. (2022) found
with Rin = max(Rco, Rt).
The torque associated directly with the SDI can be written as the sum of the accretion torque and the ME torque, depending on the accretion state in which the system is at a given time. According to the simulations of Ireland et al. (2022), the net SDI torque can be expressed as
2.2.3. Spin-down torque: Winds
Finally, the magnetospheric accretion and the presence of the disc perturb the large-scale magnetic field of the star and allow for more lines to be open. This globally increases the specific (per mass-loss rate) torque compared to a wind from a star without a disc. In addition, the hypothesis of accretion-powered stellar winds posits a wind mass-loss rate Ṁwind that is a fraction of the accretion rate, generally less than ∼10% (Matt & Pudritz 2005), but more likely with an upper limit of about 1% (Zanni & Ferreira 2011),
Here, f is the ratio of the stellar surface rotational velocity to the break-up speed, and KA, 1, KA, 2, KΦ, mA, mΦ, 1, and mΦ, 2 are constant, again calibrated on MHD simulations and presented in Table 1. We only considered a surface dipole here because this geometry was chosen for the simulations of Ireland et al. (2022), and thus, α = 2.
2.3. Initial conditions and reference model
2.3.1. Initial model
We obtained the initial model by removing the external layers of a 0.1 M⊙ polytrope and then relaxed the remaining seed for about 1000 yr with STAREVOL. We verified that the resulting seed was not dependent on these assumptions, and finally worked with an initial seed of 0.01 M⊙ for a radius of about 1.5 R⊙, similarly to Stahler et al. (1980), Hosokawa et al. (2011), and Kunitomo et al. (2017). Our initial seed is slightly larger than the second Larson core (e.g. Larson 1969; Vaytet et al. 2013) and corresponds to a case with relatively high initial entropy (Baraffe et al. 2009; Kunitomo et al. 2017). We note that 3D MHD numerical simulations of star-forming cores seem to indicate a much larger radius for this mass and at this stage (Bhandare et al. 2020), which is indicative of an extremely high accretion rate with very little radiative losses. The accretion history as well as the physics in these models are quite different from what we used. In addition, it has not yet been confirmed by observations, and we therefore kept a smaller initial radius.
2.3.2. Accretion characteristics and assumptions for the reference case
We set a reference case in order to test the different parameters of the model. All the inputs are summarised in Table 2. For simplicity and to focus on the effect of the torque on the rotational evolution, we chose to use an analytical form for the accretion rate. We acknowledge more realistic modelling in which the accretion rates come from accretion disc simulations by Gehrig et al. (2022), for instance (see also Baraffe et al. 2017; Jensen & Haugbølle 2018; Miley et al. 2021; Kunitomo & Guillot 2021). In these simulations, the accretion histories are highly variable (episodic) and create very bumpy evolutionary paths in the HR diagram. In the current case, the evolution of the accretion rate is smooth and defined by a simple function allowing for a well-defined path. We started the evolution with a strong constant accretion rate Ṁacc,ini for 3 × 104 yr. After that time, the accretion rate decayed as a power law with index n based on the observation in young accreting stars. We thus have
Reference model and explored parameter range.
where n has typical values between 1.2 and 2. We set a disc duration time of 10 Myr for all models, after which time, the accretion rate drops to zero. For each value of n we explored, we set the value of Ṁacc,ini such that a total of 99% M⊙ was accreted by the end of the accretion phase, bringing the final stellar mass to 1 M⊙. In each case, Ṁacc,ini had a value around ∼10−5 M⊙ yr−1 (see Table 2). The three decaying accretion rate histories are displayed in Fig. 1. In addition, we also present a case of constant accretion at Ṁ = 2 × 10−7 M⊙ yr−1 for 5 Myr. To account for the mass added to the star, we neglected the mass loss from stellar winds.
 |
Fig. 1. Evolution of the accretion rates as a function of time for the four cases studied in Sect. 3.3. The orange, magenta (reference), and grey tracks show the power-law decays with indexes 2.0, 1.5, and 1.2, respectively. The black line shows the constant accretion rate at |
The composition of the disc may evolve with time and become quite different as the gas-grain ratio changes with the disc structure. While the gas is first accreted or blown away by the winds, the heavier elements have condensed into grains and start to form small pebbles. They can then chemically enrich the accreted material and create long-time effects on the stellar structure (Kunitomo et al. 2018). In the current case, we kept a constant chemical composition identical to the initial proto-stellar seed. The initial amount of deuterium was set to 28 ppm, which is close to the value obtained from meteorites (Asplund et al. 2009).
Following Hartmann et al. (1997), we assumed that most of the entropy is radiated away as the material reaches the surface. The specific entropy of the accreted material is therefore about the same as the stellar surface. The accretion efficiency parameter ξ was fixed at 0.1 for the reference model, which means that only 10% of the heat of the infalling material is absorbed by the star. This corresponds to a relatively cool accretion. Hartmann et al. (1998) and Kunitomo et al. (2017) showed that this value was able to explain the broadening of the sequence observed in the HR diagram of very young open clusters. Finally, the energy and accreted mass were deposited in the upper 2% of the star (see Sect. 2.1.2) before they were transported by the convective motions.
3. Stellar evolution with accretion and without rotation
3.1. Reference case
Figure 2 shows the evolution of our reference case compared to a classical model for solar mass PMS evolution. The starting point is clearly very cold, and despite its relatively large radius, it remains faint compared to the solar mass evolution. During the early evolution, the accretion rate is very high, and the stellar structure quickly reacts to the large amount of accreted energy by strongly increasing the model radius from 1.5 to more than 2.5 R⊙ in a few iterations. Figure 3 shows the evolution of stellar radius for the reference model (magenta line) compared to the classical (non-accreting) model (dashed red line), starting from an age of 10 kyr. The radius (and the temperature) and thus the luminosity continue to increase as the mass increases to reach about 4.0 R⊙ (3600 K) before the accretion rate starts to decrease at 30 000 yr.
 |
Fig. 2. Hertzsprung-Russel diagram of a 1 M⊙ pre-main-sequence star starting from 1 M⊙ (without accretion, black) and from 0.01 M⊙ with accretion, our reference case (magenta). The green, red, and cyan diamonds indicate the end of the constant high-accretion rate, the end of the accretion phase, and the onset of deuterium burning, respectively. |
 |
Fig. 3. Radius as a function of time for models accreting material with XD = 10 ppm (green), XD = 28 ppm (magenta), and XD = 10 ppm (blue), and a non-accreting models with an initial abundance of XD = 28 ppm (dark red). |
Around 7 × 104 yr, the temperature has increased enough in the inner region (around 10% in mass) to ignite the burning of deuterium. As the reactions begin, a convective layer develops deep in the star and reconnects with the upper convective envelope, suddenly increasing the radius and the luminosity of the star at log(Teff)∼3.6. At this point, the star has a mass of about half solar and is fuelled by the accreted deuterium. It continues its evolution in the HR diagram (Fig. 2) close to the path of the non-accreting PMS model of the same mass. However, in our case, the deuterium burning still contributes to the stellar luminosity until the end of the SDI phase, thereby increasing the radius of the star to the point that it is slightly larger than the non-accreting case beyond about 1 Myr.
3.2. Deuterium abundance
As of today, the initial amount of deuterium present in the Sun is still poorly constrained. It cannot be tracked from the current abundance, and the spectroscopic analysis of meteoritic rocks gives a value that only constrains the region of the disc in which the meteorite material was formed. Deuterium is the only element that can be burnt to counteract the gravitational contraction during the PMS. It is therefore crucial to test its influence on the evolution. If the amount of deuterium is fixed from the starting point, its combustion will last a few hundred thousand years. However, if it is being constantly refuelled by newly accreted material, it has a long-lasting effect on the structure. Figure 3 shows the radius evolution for different deuterium mass fractions from 10 ppm to 50 ppm. We recall that we assumed the same composition for the initial seed as for the accreted material. As expected, the evolution is the same in all cases before the onset of deuterium burning at about 60 000 yr. Then, most of the luminosity comes from the nuclear reactions, and because most of the deuterium is consumed, the larger the mass fraction of deuterium, the higher the luminosity and the larger the radius. For example, at 2 × 105 yr, the radius of the high-deuterium model (XD = 50 ppm) is larger by a factor 1.4 than in the low-deuterium case (XD = 10 ppm). During the later stages (1–10 Myr), the difference is much smaller, but remains qualitatively the same: the larger the fraction of deuterium that fuels the star, the stronger the limitation on the contraction. This radius evolution differs from Fig. 2 of Kunitomo et al. (2017), essentially because they considered a cold case (ξ = 0) while we worked with warm accretion (ξ = 0.1).
3.3. Accretion history
We mentioned in the introduction that the accretion rate is quite variable during the evolution (Baraffe & Chabrier 2010), and here we only reproduce some global trends. As the disc becomes thinner and more structured, the accretion rate also becomes generally lower. The slope of the decay timescale is not strongly constrained by observations. Some studies use isochronal ages to estimate the evolution of accretion rates with time (e.g. Caratti o Garatti et al. 2012), but at this stage of the evolution, the uncertainties in age are very large, up to a factor of more than 2 per open clusters (e.g. Bell et al. 2013; Cao et al. 2022), and even more when we consider an internal age spread (Getman et al. 2018). We considered four different simple accretion histories: one constant accretion rate at Ṁacc = 2 × 10−7 M⊙ yr−1, and three power-law decaying accretion rates of the form Ṁacc = Ṁini 10−nt with n = [1.2, 1.5, 2.0]. In order for all models to reach a mass of one solar mass by the end of the accretion phase, we shifted the initial accretion rate, as described in Sect. 2.3.2 (see Table 2 and Fig. 1). Finally we used a non-accreting model of 1 M⊙ for comparison purposes. In this case, the evolution started with a one solar mass polytrope similar to what is typically used in rotation evolution models. The initial radius of ∼10 R⊙ is larger than what is expected on the birthline (Stahler & Palla 2004) because our model starts before the birthline, which is reached at about 105 yr.
Figure 4 shows the radial evolution of models with each of the varied accretion rates, compared to a 1 M⊙ non-accreting case. The first thing we note is that the higher the initial accretion rate, the larger the stellar radius, likely because the amount of energy that is deposited by the accretion in the upper layer of the star is higher. Even though the n = 1.2 case has the higher accretion rate already at 0.15 Myr, the total mass remains much lower, and at this point of the evolution, deuterium burning has taken over the accretion in terms of input of energy. Thus, for the trend to reverse, we need to wait for another ∼1 Myr when the radius of the higher accretor is again largest (n = 1.2 case). The constant-accretion rate case is somewhat special. It is comparatively very low at first, with a mass accretion rate that is almost two orders of magnitude lower than in the other models and becomes one to three orders of magnitude higher during the later evolution. This leads to a very cold and compact evolution early on because only little mass is accumulated. The star then accumulates 80% of its mass from 1 Myr to the end of the disc phase, and thus continues to gain energy from accretion and fresh deuterium to burn, and the star puffs up accordingly.
 |
Fig. 4. Evolution of the radius for the four different accretion rates histories as well as the non-accreting case. |
3.4. Accreted energy
The entropy of the accreted material was shown to drastically affect the evolution (e.g. Hartmann et al. 1998). A few elements have to be considered here. First, the material comes in with its own entropy, which is generally similar to the stellar surface value. This is called warm accretion (cold when the entropy is equal). Thus, we considered that most (but not all) of the kinetic energy of the accreted material has been radiated away before it is deposited in the star. Furthermore, we considered that the accreted heat is only injected in the upper layers mke of the star (as a fraction of mass) before it is transported by the convective motions to the deeper layers. The depth that is reached by the energy and chemicals is expected to change according to the physical and chemical properties of the accreted material, as shown by Siess et al. (1997) and confirmed by the simulations of Geroux et al. (2016). We only considered a fixed mke to keep the lowest possible number of parameters for the study. However, as the energy and material penetrate the star more deeply, the effect of the heat content of the accreted material becomes more important and may prevent an early expansion. Figure 5 shows the radius evolution for three cases from very cool accretion (ξ = 0.02, blue) to hot accretion (ξ = 0.50, cyan) with intermediate warm accretion (reference case; ξ = 0.10, magenta). The lower heat content reduces the inflation during the early evolution, while the hot accretion model expands to a very large radius that even approaches the non-accreting case. Kunitomo et al. (2017) pointed out that the heat injection is likely the most important parameter during the first growing phase. We confirm that the differences are quite striking, even more than in the cases of different accretion histories or deuterium contents (for the particular ranges of parameters explored here). However, after about 1 Myr, the structures have converged despite a very different initial evolution.
 |
Fig. 5. Evolution of the radius for three models with different entropy content in the accreted material. |
4. Evolution with accretion and rotation
The novelty of this work is that we simultaneously and semi-consistently consider the rotation and the stellar structure evolution during the accretion phase. We showed in the previous section that the stellar structure is strongly affected by the accretion of material and that different assumptions on the accretion properties lead to a widely different evolution of the structure and thus of the moment of inertia. In this section, we study the evolution of the surface rotation of these models when their angular momentum content is driven by the exchange with the surrounding proto-planetary disc. To compute the SDI and wind torques, we need to set the properties of the magnetic field as well as the mass-loss rate. For the reference model, we used a 1kG dipole and a mass-loss rate equal to 5% of the mass-accretion rate. We then proceeded to broaden this range of magnetic field strength and explored a lower mass-loss rate ratio that may be closer to what we can expect.
The initial rotation period often has a very high uncertainty. However, for models that accrete mass and angular momentum, varying the initial velocity does not make a difference because the moment of inertia of the initial seed is so small compared to that of the final object. The amount of angular momentum of the initial seed is negligible compared to the angular momentum brought in by the SDI torque (see Fig. 6). We thus arbitrarily chose an initial surface velocity of 4 km s−1 for the initial seed, which corresponds to a period of about 20 days. Finally, because we did not consider any internal redistribution of the angular momentum, all our models spin up faster than what the observations show after the disc-coupling phase.
 |
Fig. 6. Torques guiding the evolution of the stellar angular momentum as a function of time for the reference model in g cm2 s−2. The upper (lower) part of the diagram shows a spin-up (spin-down) torque applied on the star. The total torque is shown by the solid black line, the stellar wind torque is plotted as the dashed red line, and the torque due to the SDI interaction (sum of the accretion and ME torques) is shown by the dotted blue line. |
4.1. Reference model
4.1.1. Evolution of the different torques
The evolution of the total torque is rather complex, with intermittent phases of net positive or net negative torque as the system evolves. Figure 6 shows the torques exerted on the star by the SDI (i.e. the sum of the accretion and the ME torque) and the magnetised stellar winds in the reference case as a function of time. The torques change by more than four orders of magnitude between the beginning and end of the disc phase. Nevertheless, the SDI torque approximately mirrors the enhanced stellar wind torque, and therefore, the total change in angular momentum is much smaller than either of the two torques and is alternatively led by one of the two components. Figure 7 helps to visualise the effect of each torque on the stellar spin evolution. Because the spin rate is also affected by the change in the moment of inertia, we added the relative variation in Ω due to the change in inertia over the course of the disc-coupling phase. The latter can be compared to the rotational change due to the sum of the two magnetic torques (SDI+winds; magenta line in Fig. 7). It is clear that the rotational evolution of the star is quite complex and undergoes intermittent phases in which the spin evolution is dominated by the net torque, dominated by the changing moment of inertia, or set by a combination of these factors.
 |
Fig. 7. Variation in the rotation rate associated with each torque as a fraction of the current rotation rate per year. The upper (lower) part of the diagram shows a spin-up (spin-down) of the star. The actual change in the rotation rate is shown as a solid black line. The changes associated with the stellar wind and the SDI torque are plotted as dashed red and dotted blue lines, respectively. The variation due to a change in the moment of inertia is shown as the orange line. The background colours indicate the state of the star-disc interaction. States 1 and 2 are shown in purple and green, respectively. The light blue region with a gradient indicates a long-lived phase when the system remains close to the transition between states 1 and 2 and switches frequently between the two states. This model does not reach state 3. |
At first, when the accretion rate is very high ( ∼ 10−5 M⊙ yr−1), the star gains angular momentum very rapidly. At this stage, the truncation radius of the disc is limited by the surface of the star, and the star thus accretes through boundary layer accretion. As the star rotates more rapidly and the accretion rate decreases, both the wind and the MEs weaken. At the same time, the radius of the star expands very rapidly because of the energy that is brought in by the accreted material. In this situation, the mass as well as well as the gyration radius (Rucinski 1988) increase strongly. For example, even though the radius shrinks from 30 to 60 kyr as the accretion rate starts to decrease, the moment of inertia still grows due to the expansion of the convective region. Overall, the stellar moment of inertia therefore still grows and acts to spin down the star, as shown in Fig. 7. Around 7 × 104 yr, deuterium burning starts in the deeper layer of the star (see Sect. 3.1).
Soon after, around 8 × 104 yr, the deep convective layer connects to the base of the convective zone, bringing the freshly accreted deuterium down to regions in which it can be burnt. The release of energy hence puffs the star up. As a consequence, the star reaches state 1, and the SDI torque (blue in Figs. 6 and 7) becomes a pure spin-up torque, thus losing the spin-down torque associated with the MEs. During the whole time the star spent in state 1, the spin evolution is dominated by the change in the moment of inertia (dI/dt is higher than the SDI+wind torque). Although the SDI torque is stronger (blue line on Figs. 7 and 6), the sudden increase in radius keeps the star in a spin-down state for about 100 000 yr. As the radius inflation stops, the moment of inertia starts to decrease and spins the star up, with a little help from the accretion torque.
Finally, between about 4 × 105 yr and 2 × 106 yr, the truncation radius stays very close to 0.433 times the co-rotation radius, which marks the boundary between states 1 and 2. The star oscillates between state 1 and 2 on a timescale of about 100 yr at first up to 1000 yr as the accretion rate decreases, and the evolutionary time-step then becomes very small to follow this phase. This results in an overall loss of angular momentum from the star. After 2 Myr, the star is clearly in state 2 as the mass accretion rate becomes increasingly lower and the MEs start to efficiently remove angular momentum from the star. Figures 6 and 7 show that the combined SDI and wind torques then spin the star down, but the mild contraction of the star causes the star to slowly spin up from about 4 Myr to the end of the disc-coupling phase at 10 Myr.
Figures 6 and 7 only display the evolution of the torque and spin evolution of the reference case. The other cases with different physical assumptions discussed in Sect. 3 all show qualitative similarities. Each shows varying epochs of spin up and down due to varying balances between the torques and the structure evolution. For the sake of brevity, we do not discuss them here.
4.1.2. Comparisons to observations
Covey et al. (2005) published the projected surface velocity (v sin i) for 38 Class I objects. However, the exact evolutionary stage is not well constrained. Their v sin i ranges from 10 to 60 km s−1, with a median projected velocity of 38 km s−1.
The lack of information about the rotation of Class I young stellar objects limits the possibility of constraining our model in the earliest phases of the evolution. To test our models against observations, we therefore selected the younger clusters of Gallet & Bouvier (2015, also present in Gallet et al. 2019) and NGC 2264 from Venuti et al. (2017) as a comparison point (see Table 3). Their rotation period distributions are similar. Each exhibits a broad range of rotation rates within a similar range, between ∼1 and ∼10 days. The large uncertainty in their ages therefore does not strongly affect their quality as indicators.
Ages and reference for the relevant open clusters and associations.
Figure 8 shows the rotation period evolution for all models with different input physics. In the background, we display the rotation period distribution of 1 ± 0.1 M⊙ stars in six young clusters from the ONC (1.5 Myr) to hPer (13 Myr), as listed in Table 3. In addition, we show the median, 25th, and 90th percentile for the clusters with a sufficient number of datapoint (Gallet & Bouvier 2013, 2015; Gallet et al. 2019).
 |
Fig. 8. Evolution of the surface rotation period as a function of time when the amount of deuterium in the accreted material (top), the entropy in the accreted material (middle), and the mass accretion history (bottom) are varied. The black crosses show observed rotation periods in very young open clusters. The red, green, and blue diamonds indicate the 25th percentile, the median, and the 90th percentile of each distribution with a sufficient number of stars (see text for details). |
First, the non-accreting model with one solar mass undergoing only a pure contraction predicts a very steep spin-up during the entire PMS evolution. We started this model with an extremely slow spin rate, just so that the rotation period at the ZAMS would be reasonable, for illustration purposes. None of the accreting models undergoes such a strong systematic spin-up between 0.1 Myr and the end of the disc phase.
We saw in Sect. 3 that accreting models start with a much smaller radius and thus contract much less, also because deuterium is continuously refuelled by the accreted material. The slower contraction prevents a strong spin up that would naturally come from the global conservation of angular momentum.
The reference model (in magenta in Fig. 8) falls close to the median of the data. There is a little offset (∼0.2 dex) towards a faster rotation, depending on the considered cluster. We then varied the same physical ingredients as in Sect. 3 as well as the dipole magnetic strength and the efficiency of the accretion powered stellar winds.
4.2. Exploring varying accretion assumptions
Figure 8 presents the rotation period evolution during the SDI phase for models with different accretion physics. The top panel shows the evolution for three different amounts of deuterium in the accreted material. Deuterium does not directly affect the SDI torque or the wind torque. However, as we saw in the previous section, it inflates the star while it is burning, and thus increases the radius and the moment of inertia. As a consequence, as soon as the deuterium burning begins (in these models, at around 70 000 yr), the rotation rate rapidly decreases at a rate that depends on the amount of deuterium that is accreted by the star. This establishes a difference in rotation rate between the models that last as long as the star accretes, although its effects lessen as the accretion rate decreases over time.
In the same fashion, the middle panel compares the rotation period evolution with different heat injection by the accreted material. This parameter does not directly affect the torque, but again changes the radius of the star. However, this time, the change in radius occurs from the start of the evolution. A hot accretion leads to a large radius very early in the evolution, which limits the spin up during this phase because 1) the moment of inertia increases and 2) the larger radius and longer rotation period lead to a high ratio R*/Rco during the early evolution. However, between 1 and 2 Myr, the tracks converge towards the same rotational evolution. At this point, the accretion energy becomes minimal compared to energy brought by the deuterium burning and the gravitational contraction. Their structures therefore become very similar (see Fig. 5). The injection of non-thermalised material therefore only changes the evolution during the first million years of the evolution and does not seem to play at role at a later time, at least in our reference setup. This may suggest that the stellar rotation is driven to a quasi-equilibrium spin rate by the various torques and structural evolution on a short timescale, and that this equilibrium is independent of their past evolution.
The last panel shows the rotational evolution for different accretion histories. All models accrete the same amount of mass, but not at the same time. In this case, the change in accretion rate modifies both the moment of inertia and the torques themselves. Thus, the trends are no longer monotonous. For example, the grey, magenta, and orange tracks represent models with an accretion rate that decays more (orange) or less (grey) quickly from the end of the early strong accretion phase to the end of the disc-coupling phase at 10 Myr. We saw in the previous section that the radius of the orange (grey) model with Ṁ ∝ t−2 (Ṁ ∝ t−1.2) is larger (smaller) at the beginning of the evolution. The larger expansion leads to a longer rotation period compared to the intermediate reference case. However, the lower accretion rate at later ages leads to a lower torque, which allows the contraction to spin the star up more strongly as the model reaches the end of the disc-coupling phase. The unrealistic constant accretion model (Ṁ = 2 × 10−7 M⊙ yr−1) has a wild rotational evolution that reflects its structural evolution. The total mass of this model remains much lower than the reference case until the end of the disc phase (at 5 Myr for this specific model). As a consequence, the radius remains much smaller, even though the star gains angular momentum and thus spins up to very fast rotation before 1 Myr. At this time, the model slowly starts to expand as the mass increases, and the accreted energy and deuterium are injected at a medium but steady rate. The model finally is the largest at the end of the disc phase (at 5 Myr for this model), but with a similar rotation period as the others. The ensuing contraction towards the zero-age main-sequence makes it the fastest rotator at the end of the PMS by a factor of five.
4.3. Exploring the accreted-to-ejected mass ratio and dipole strength
The torques depend on two additional parameters that we vary in this section: the magnetic strength, which we take as a fixed value at the stellar pole, and the ratio of the mass-loss rate and the mass accretion rate. In Fig. 9 we present three models with dipole strengths between 750 and 2000 G, which is comparable to values observed in T Tauri stars. As expected, increasing the dipolar magnetic field strength enhances the spin-down torque associated both with the enhanced winds and the SDI (see Eqs. (6) and (8)). This spread in magnetic field strengths alone allows us to cover about a quarter of the spread in velocity displayed by the observations (on a logarithmic scale).
Figure 10 shows computations with two different values for the ratio Ṁwind/Ṁacc, but even though the two cases vary by a factor of 5, both spin evolutions remain very close to each other. The difference only appears towards the end of the disc phase, when the wind torque dominates the torque over the SDI (see Fig. 6). Thus, the case with a higher Ṁwind/Ṁacc ratio keeps a slower rotation rate because it counteracts the effect of the contraction on the spin more efficiently.
5. Discussion and conclusion
Previous stellar evolution models that included the effects of accretion were shown to reproduce the spread observed in colour-magnitude diagrams of young clusters (Hartmann et al. 1998; Siess et al. 1999; Baraffe et al. 2009; Hosokawa et al. 2011; Kunitomo et al. 2017). We used the most recent SDI torques from 2.5D MHD simulations and stellar evolution models that include the effects of both accretion and rotation to model the rotation period distributions of these very young open clusters. We showed in particular in Figs. 8–10 that their rotational evolutions roughly track the middle of the rotation rate distributions measured in open clusters during the last few million years of the accretion phase and that they evolve in a way that is similar (within the large scatter) to the observed distributions. These physics-based models provide a more meaningful interpretation of the observed spin distributions than the large class of spin-evolution models that artificially enforce a constant rotation rate to avoid the strong spin-up predicted by non-accreting models. In agreement with Gallet et al. (2019), we showed that the SDI torques issued from MHD simulations can prevent a spin up during the disc-coupling phase. However, in contrast to their conclusions, we show that this can be achieved without relying on extremely massive stellar winds or very low accretion rates. Our study of this phase indeed revealed that the structural evolution is a critical factor that significantly alters both the moment of inertia and the external torques related to the star-disc interaction. Therefore, in order to model the early spin evolution, it is necessary to take all of these effects into account in a self-consistent way.
The changes associated with deuterium burning are particularly important because the continuous refuelling means that its effects last for the whole accretion phase. In addition, in agreement with what was found in some early works on stellar formation, the complex processes involving burning of newly added deuterium significantly alter the moment of inertia of a star compared to the expectation from non-accreting models, for example, by preventing the star from becoming fully convective. We find that with a larger deuterium content, the star is spun down more efficiently during the disc-coupling phase, without affecting the rotation on the ZAMS. In other words, changing the deuterium content mostly changes the rotation rate during the star-disc interaction phase, without changing the final angular momentum content. Similarly, the accretion rate history plays a critical role in shaping the rotational evolution of the star. We showed that an initially higher accretion rate brings the star to a slower rotation rate because the inflation of the star is increased. Later, as the accretion rate decays to zero, the steeper the slope of decay, the stronger the tendency for a star to spin up with time.
We also showed that changing the heat content of the accreted material strongly affects the early evolution. As previously shown by Kunitomo et al. (2017), for example, a colder accretion leads to a more compact star early on, and therefore, in our case, to a faster rotator. This difference in evolution does not continue after 106 yr for the cases we tested. At this point, the thermal energy brought by the accretion becomes negligible, and thus the structure is expected to be independent of the differences in the accreted heat content (see Fig. 5) and to be driven instead by the burning of deuterium. Interestingly, despite being very different at 105 yr, at 106 yr, the rotation period is driven to an equilibrium by the various torques on a short timescale. This has some important consequence for observations because it suggests that the type of accretion (hot or cold) probably does not affect the current rotation of observed T Tauri stars, unless some other parameters are added (e.g. a very low deuterium content may leave the larger role to the heat injection parameter at a later time).
The variations we explored in the accretion- and SDI-related parameters predicted a spread in the modelled rotation rates that covered the central regions of the observed distributions. Our design was to explore a relatively extreme range, close to the observationally constrained boundaries for each parameter. Between ages of 1.5 and 5 Myr, the predicted rotation range covered by the models extends from about 2 to 8 days. In comparison, the rotation rates in the observational datasets we used range from less than one day to 11 days. A first possibility to explain this discrepancy would be to hypothesise even more extreme values in the parameter ranges, but more extreme values may be unrealistic. For example, while a 5 kG dipole could easily explain the slowest rotators, a strong field like this has never been observed on T Tauri stars. Another option is to combine the various parameter ranges. For example, a model with both a lower magnetic field and a lower deuterium should predict a faster rotation rate than the range of models shown. Testing this will require computing a large grid of models and requires significant computational resources, such as was done recently by Steindl et al. (2022a,b) for the case of non-rotating accreting stars to explore the seismic signature of accretion. Finally, we can also consider additional processes that are missing in our model, such as a variation in the duration of the accretion phase (we already know that most stars do not retain a disc for 10 Myr from Roquette et al. 2021), or possible dynamical encounters between stars.
While these models are an improvement over previous models, they still lack some important elements that could play a significant role in the structural and rotational evolution. For example, the evolution of accretion does not follow a smooth trend. Instead, all dedicated simulations show that the accretion rate can be quite variable, with short episodes of accretion that are hundreds of times more important (Baraffe et al. 2009; Hosokawa et al. 2011; Audard et al. 2014; Vorobyov & Basu 2015; Vorobyov et al. 2017). The coupling of these accretion rate leads to a choppy evolution in the HR diagram, but the global evolution is not too different, regardless of whether a smooth trend or an episodic accretion is chosen (Baraffe et al. 2017; Jensen & Haugbølle 2018; Miley et al. 2021; Kunitomo & Guillot 2021; Steiner et al. 2021; Steindl et al. 2022a). Recently, Gehrig et al. (2022, 2023) and Gehrig & Vorobyov (2023) have shown that the rotational evolution can also be reproduced in these conditions. While the evolution model uses a smooth accretion rate, the SDI torques as well as the wind torque we used come from a largely episodic and dynamical evolution on short timescales that were averaged over approximately ten rotation periods (Ireland et al. 2021, 2022).
Modelling the effects of magnetic fields remains a challenge in stellar evolution because it is intrinsically a 3D problem, and stellar evolution models have to be 1D to be efficient enough to compute on timescales of billions of years. The large-scale magnetic fields of very young stars may be explained by fast rotation and very large convective cells (Emeriau-Viard & Brun 2017; Zaire et al. 2017, 2022), or they might be fossil remnants from the tendency for magnetic flux conservations during the protostellar cloud collapse (e.g. Hennebelle et al. 2020), so that even the origin and time-evolution of these fields are poorly understood. In addition, only an aligned dipole was considered in the simulations of Ireland et al. (2022). In the case of misalignment between the magnetic field and the rotation axis, simulations of protoplanetary discs show that the inner region of the disc warps and may separate from the rest due to a precessing torque from the star, and lead to a two discs system (Takaishi et al. 2020; Romanova et al. 2021) or other complications. The SDI could exhibit additional 3D processes, such as interactions between accretion flows and turbulent and conical disc winds (Takasao et al. 2022). The effects of tilted and more complex stellar magnetic fields, as well as other 3D processes in the SDI, might result in significantly different torque scalings from those we have adopted here. Internal magnetic fields can also inhibit convective motions and have an impact on the stellar structure by expanding the size of the convective cells and thus the stellar radius (Feiden & Chaboyer 2014; Browning et al. 2016; Ireland & Browning 2018). Finally, although the origin of the fields is still unclear, we do not expect them to keep a fixed value in time, as we have assumed in the present work.
Most of the models we presented possess a radiative core at all times. In these stably stratified regions, the redistribution of angular momentum occurs on longer timescales than in the convective zones, and the assumption of instantaneous transport may break down. The timescale of angular momentum transport depends on the (magneto-)hydrodynamic instability that can develop in the radiative regions, such as hydrodynamic instabilities (Zahn 1992; Mathis & Zahn 2004; Prat & Lignières 2014), magnetic instabilities (Bugnet et al. 2021; Takahashi & Langer 2021; Petitdemange et al. 2023; Eggenberger et al. 2022), or internal gravity waves (Charbonnel et al. 2013; Ahuir et al. 2021), but generally, the star reaches a state of differential rotation. These instabilities should thus be considered.
The deposition of mass and energy by the accreted material is likely to vary during the evolution. During the early accretion phase, material likely falls directly onto the star, rather than being channelled into magnetic accretion columns. Bhandare et al. (2020) showed that during the strong accretion phase, most of the accreted energy is kept by the star and is not radiated away because of the very important opacity of the infalling material, which should lead to a very large stellar radius. Moreover, Siess et al. (1997) showed that in the case of a boundary layer accretion, the mixing in the star depends on the entropy of the accreted material, with lower-entropy material diving deeper, in agreement with the simulations of Geroux et al. (2016).
Finally, the chemical composition of the disc evolves spatially and in time as the star evolves (e.g. Miley et al. 2021). When this is considered, this effect can impact the stellar structure on the main sequence and help to reconcile the helioseismic and spectroscopic properties of the Sun by changing the composition of the core (Zhang et al. 2019; Kunitomo & Guillot 2021). Gehrig et al. (2022, 2023) showed the importance of the composition when considering rotating stars during the accretion phase and its role on the disc. They find for example that metal-poor stars have shorter disc lifetimes with much less efficient torques that allow the star to spin up significantly during the disc-coupling phase. In general, for further progress, future improvements to the models should consider the above effects.
Acknowledgments
We would like to thank the anonymous referee for their relevant comments and suggestions. LA would like to thank Lionel Siess and Isabelle Baraffe for fruitful discussions at the beginning of this work. LA acknowledges funding from CNES via an AIM/PLATO grant. LA and SPM acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 682393 AWESoMeStars). SPM also thanks the University of Washington Astronomy Department for hosting him, as well as the Simons Foundation Flatiron Institute Center for Computational Astrophysics for hosting and support, during part of this work.
References
- Ahuir, J., Mathis, S., & Amard, L. 2021, A&A, 651, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amard, L., & Matt, S. P. 2020, ApJ, 889, 108 [Google Scholar]
- Amard, L., Palacios, A., Charbonnel, C., Gallet, F., & Bouvier, J. 2016, A&A, 587, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amard, L., Palacios, A., Charbonnel, C., et al. 2019, A&A, 631, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audard, M., Ábrahám, P., Dunham, M. M., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 387 [Google Scholar]
- Baraffe, I., & Chabrier, G. 2010, A&A, 521, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [Google Scholar]
- Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Pratt, J., Goffrey, T., et al. 2017, ApJ, 845, L6 [Google Scholar]
- Batygin, K., & Adams, F. C. 2013, ApJ, 778, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bessolaz, N., Zanni, C., Ferreira, J., Keppens, R., & Bouvier, J. 2008, A&A, 478, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhandare, A., Kuiper, R., Henning, T., et al. 2020, A&A, 638, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Cabrit, S., Fernandez, M., Martin, E. L., & Matthews, J. M. 1993, A&A, 272, 176 [NASA ADS] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 479 [Google Scholar]
- Bouvier, J., Matt, S. P., Mohanty, S., et al. 2014, Protostars and Planets VI, 433 [Google Scholar]
- Bouvier, J., Barrado, D., Moraux, E., et al. 2018, A&A, 613, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, M. K., Weber, M. A., Chabrier, G., & Massey, A. P. 2016, ApJ, 818, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Bugnet, L., Prat, V., Mathis, S., et al. 2021, A&A, 650, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, L., Pinsonneault, M. H., Hillenbrand, L. A., & Kuhn, M. A. 2022, ApJ, 924, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Caratti o Garatti, A., Garcia Lopez, R., Antoniucci, S., et al. 2012, A&A, 538, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., Decressin, T., Amard, L., Palacios, A., & Talon, S. 2013, A&A, 554, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coker, C. T., Pinsonneault, M., & Terndrup, D. M. 2016, ApJ, 833, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Covey, K. R., Greene, T. P., Doppmann, G. W., & Lada, C. J. 2005, AJ, 129, 2765 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- Davies, C. L., Gregory, S. G., & Greaves, J. S. 2014, MNRAS, 444, 1157 [Google Scholar]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwards, S., Strom, S. E., Hartigan, P., et al. 1993, AJ, 106, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Haemmerlé, L., Meynet, G., & Maeder, A. 2012, A&A, 539, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Moyano, F. D., & den Hartogh, J. W. 2022, A&A, 664, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emeriau-Viard, C., & Brun, A. S. 2017, ApJ, 846, 8 [Google Scholar]
- Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Feiden, G. A., & Chaboyer, B. 2014, ApJ, 789, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., Pelletier, G., & Appl, S. 2000, MNRAS, 312, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, A. J., Matt, S. P., & See, V. 2018, ApJ, 864, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., Zanni, C., & Amard, L. 2019, A&A, 632, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrig, L., & Vorobyov, E. I. 2023, A&A, 673, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrig, L., Steiner, D., Vorobyov, E. I., & Güdel, M. 2022, A&A, 667, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrig, L., Steindl, T., Vorobyov, E. I., Guadarrama, R., & Zwintz, K. 2023, A&A, 669, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geroux, C., Baraffe, I., Viallet, M., et al. 2016, A&A, 588, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Getman, K. V., Feigelson, E. D., Kuhn, M. A., et al. 2018, MNRAS, 476, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Cassen, P., & Kenyon, S. J. 1997, ApJ, 475, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [Google Scholar]
- Hébrard, G., Tripp, T. M., Chayer, P., et al. 2005, ApJ, 635, 1136 [CrossRef] [Google Scholar]
- Henderson, C. B., & Stassun, K. G. 2012, ApJ, 747, 51 [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Charnoz, S. 2020, A&A, 635, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hosokawa, T., Offner, S. S. R., & Krumholz, M. R. 2011, ApJ, 738, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, L. G., & Browning, M. K. 2018, ApJ, 856, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, L. G., Zanni, C., Matt, S. P., & Pantolmos, G. 2021, ApJ, 906, 4 [Google Scholar]
- Ireland, L. G., Matt, S. P., & Zanni, C. 2022, ApJ, 929, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, in IAU Symposium, eds. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, 258, 363 [NASA ADS] [Google Scholar]
- Jensen, S. S., & Haugbølle, T. 2018, MNRAS, 474, 1176 [Google Scholar]
- Johnstone, C. P., Jardine, M., Gregory, S. G., Donati, J. F., & Hussain, G. 2014, MNRAS, 437, 3202 [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2009, ApJ, 695, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Koenigl, A. 1991, ApJ, 370, L39 [Google Scholar]
- Krishna Swamy, K. S. 1966, ApJ, 145, 174 [Google Scholar]
- Kunitomo, M., & Guillot, T. 2021, A&A, 655, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunitomo, M., Guillot, T., Takeuchi, T., & Ida, S. 2017, A&A, 599, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunitomo, M., Guillot, T., Ida, S., & Takeuchi, T. 2018, A&A, 618, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzafame, A. C., & Spada, F. 2015, A&A, 584, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [Google Scholar]
- Linsky, J. L., Draine, B. T., Moos, H. W., et al. 2006, ApJ, 647, 1106 [Google Scholar]
- Littlefair, S. P., Naylor, T., Mayne, N. J., Saunders, E. S., & Jeffries, R. D. 2010, MNRAS, 403, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005, ApJ, 632, L135 [Google Scholar]
- Matt, S., & Pudritz, R. E. 2008, ApJ, 678, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., Pinzón, G., de la Reza, R., & Greene, T. P. 2010, ApJ, 714, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012a, ApJ, 754, L26 [Google Scholar]
- Matt, S. P., Pinzón, G., Greene, T. P., & Pudritz, R. E. 2012b, ApJ, 745, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 1997, A&A, 321, 465 [NASA ADS] [Google Scholar]
- Miley, J. M., Panić, O., Booth, R. A., et al. 2021, MNRAS, 500, 4658 [Google Scholar]
- Moraux, E., Artemenko, S., Bouvier, J., et al. 2013, A&A, 560, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Talon, S., Charbonnel, C., & Forestini, M. 2003, A&A, 399, 603 [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pantolmos, G., Zanni, C., & Bouvier, J. 2020, A&A, 643, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petitdemange, L., Marcotte, F., & Gissinger, C. 2023, Science, 379, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Prat, V., & Lignières, F. 2014, A&A, 566, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebull, L. M., Wolff, S. C., & Strom, S. E. 2004, AJ, 127, 1029 [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Cody, A. M., et al. 2018, AJ, 155, 196 [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Cody, A. M., et al. 2020, AJ, 159, 273 [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Hillenbrand, L. A., et al. 2022, AJ, 164, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Réville, V., Brun, A. S., Matt, S. P., Strugarek, A., & Pinto, R. F. 2015, ApJ, 798, 116 [Google Scholar]
- Rodríguez-Ledesma, M. V., Mundt, R., & Eislöffel, J. 2009, A&A, 502, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2013, MNRAS, 430, 699 [Google Scholar]
- Romanova, M. M., Blinova, A. A., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2018, New Astron., 62, 94 [Google Scholar]
- Romanova, M. M., Koldoba, A. V., Ustyugova, G. V., et al. 2021, MNRAS, 506, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Roquette, J., Matt, S. P., Winter, A. J., Amard, L., & Stasevic, S. 2021, MNRAS, 508, 3710 [NASA ADS] [CrossRef] [Google Scholar]
- Rucinski, S. M. 1988, AJ, 95, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [Google Scholar]
- Siess, L., & Forestini, M. 1996, A&A, 308, 472 [NASA ADS] [Google Scholar]
- Siess, L., & Livio, M. 1997, ApJ, 490, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Forestini, M., & Bertout, C. 1997, A&A, 326, 1001 [NASA ADS] [Google Scholar]
- Siess, L., Forestini, M., & Bertout, C. 1999, A&A, 342, 480 [NASA ADS] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Somers, G., & Pinsonneault, M. H. 2015, ApJ, 807, 174 [Google Scholar]
- Somers, G., & Pinsonneault, M. H. 2016, ApJ, 829, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., & Lanzafame, A. C. 2020, A&A, 636, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stahler, S. W., & Palla, F. 2004, The Formation of Stars [CrossRef] [Google Scholar]
- Stahler, S. W., Shu, F. H., & Taam, R. E. 1980, ApJ, 242, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Steindl, T., Zwintz, K., Barnes, T. G., Müllner, M., & Vorobyov, E. I. 2021, A&A, 654, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steindl, T., Zwintz, K., & Müllner, M. 2022a, A&A, 664, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steindl, T., Zwintz, K., & Vorobyov, E. 2022b, Nat. Commun., 13, 5355 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, D., Gehrig, L., Ratschiner, B., et al. 2021, A&A, 655, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, K., & Langer, N. 2021, A&A, 646, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takaishi, D., Tsukamoto, Y., & Suto, Y. 2020, MNRAS, 492, 5641 [NASA ADS] [CrossRef] [Google Scholar]
- Takasao, S., Tomida, K., Iwasaki, K., & Suzuki, T. K. 2022, ApJ, 941, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., Degl’Innocenti, S., Salaris, M., & Cassisi, S. 2020, A&A, 638, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tognelli, E., Degl’Innocenti, S., Prada Moroni, P. G., et al. 2021, Front. Astron. Space Sci., 8, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Vasconcelos, M. J., & Bouvier, J. 2015, A&A, 578, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaytet, N., Chabrier, G., Audit, E., et al. 2013, A&A, 557, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Bouvier, J., Cody, A. M., et al. 2017, A&A, 599, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2015, ApJ, 805, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., Elbakyan, V., Hosokawa, T., et al. 2017, A&A, 605, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zaire, B., Guerrero, G., Kosovichev, A. G., Smolarkiewicz, P. K., & Landin, N. R. 2017, in Living Around Active Stars. eds. D. Nandy, A. Valio, & P. Petit, 328, 30 [NASA ADS] [Google Scholar]
- Zaire, B., Jouve, L., Gastine, T., et al. 2022, MNRAS, 517, 3392 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., & Ferreira, J. 2009, A&A, 508, 1117 [CrossRef] [EDP Sciences] [Google Scholar]
- Zanni, C., & Ferreira, J. 2011, ApJ, 727, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., & Ferreira, J. 2013, A&A, 550, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Q.-S., Li, Y., & Christensen-Dalsgaard, J. 2019, ApJ, 881, 103 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Evolution of the accretion rates as a function of time for the four cases studied in Sect. 3.3. The orange, magenta (reference), and grey tracks show the power-law decays with indexes 2.0, 1.5, and 1.2, respectively. The black line shows the constant accretion rate at |
| In the text | |
 |
Fig. 2. Hertzsprung-Russel diagram of a 1 M⊙ pre-main-sequence star starting from 1 M⊙ (without accretion, black) and from 0.01 M⊙ with accretion, our reference case (magenta). The green, red, and cyan diamonds indicate the end of the constant high-accretion rate, the end of the accretion phase, and the onset of deuterium burning, respectively. |
| In the text | |
 |
Fig. 3. Radius as a function of time for models accreting material with XD = 10 ppm (green), XD = 28 ppm (magenta), and XD = 10 ppm (blue), and a non-accreting models with an initial abundance of XD = 28 ppm (dark red). |
| In the text | |
 |
Fig. 4. Evolution of the radius for the four different accretion rates histories as well as the non-accreting case. |
| In the text | |
 |
Fig. 5. Evolution of the radius for three models with different entropy content in the accreted material. |
| In the text | |
 |
Fig. 6. Torques guiding the evolution of the stellar angular momentum as a function of time for the reference model in g cm2 s−2. The upper (lower) part of the diagram shows a spin-up (spin-down) torque applied on the star. The total torque is shown by the solid black line, the stellar wind torque is plotted as the dashed red line, and the torque due to the SDI interaction (sum of the accretion and ME torques) is shown by the dotted blue line. |
| In the text | |
 |
Fig. 7. Variation in the rotation rate associated with each torque as a fraction of the current rotation rate per year. The upper (lower) part of the diagram shows a spin-up (spin-down) of the star. The actual change in the rotation rate is shown as a solid black line. The changes associated with the stellar wind and the SDI torque are plotted as dashed red and dotted blue lines, respectively. The variation due to a change in the moment of inertia is shown as the orange line. The background colours indicate the state of the star-disc interaction. States 1 and 2 are shown in purple and green, respectively. The light blue region with a gradient indicates a long-lived phase when the system remains close to the transition between states 1 and 2 and switches frequently between the two states. This model does not reach state 3. |
| In the text | |
 |
Fig. 8. Evolution of the surface rotation period as a function of time when the amount of deuterium in the accreted material (top), the entropy in the accreted material (middle), and the mass accretion history (bottom) are varied. The black crosses show observed rotation periods in very young open clusters. The red, green, and blue diamonds indicate the 25th percentile, the median, and the 90th percentile of each distribution with a sufficient number of stars (see text for details). |
| In the text | |
 |
Fig. 9. Same as Fig. 8 for models with different dipolar magnetic field strengths. |
| In the text | |
 |
Fig. 10. Same as Fig. 8 for models with a different Ṁw/Ṁacc ratio. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



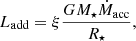
![$$ \begin{aligned} \varepsilon _{\rm add} = \frac{L_{\rm add}}{M_\star }\times \mathrm{Max}\left[0;\frac{2}{m_{ke}^2}\left(\frac{M_r}{M_\star }-1 + m_{ke}\right)\right], \end{aligned} $$](/articles/aa/full_html/2023/10/aa46148-23/aa46148-23-eq2.gif)
![$$ \begin{aligned} \frac{R_t}{R_*} = \mathrm{min} \left[ K_{t,1} \Upsilon ^{m_{t,1}}_{\rm acc}, \; K_{t,2} \Upsilon ^{m_{t,2}}_{\rm acc}f^{m_{t,3}}\right] ,\end{aligned} $$](/articles/aa/full_html/2023/10/aa46148-23/aa46148-23-eq3.gif)
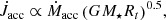
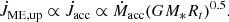
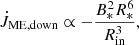
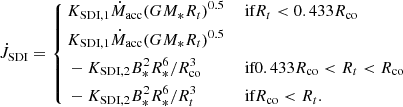
![$$ \begin{aligned} \begin{aligned}&\dot{J}_{\rm wind} = - K_{A,1}^2(\alpha \pi K_{\Phi })^{4 m_A} |\dot{M}_{\rm acc}|\sqrt{GM_\star R_\star } \left(\frac{\dot{M}_{\rm wind}}{\dot{M}_{\rm acc}}\right)^{1-2 m_A}\\&f^{1+4m_Am_{\Phi ,2}}\left[1+\left(\frac{f}{ K_{A,2}}\right)^2\right]^{- m_A}\left(\frac{R_t}{R_\star }\right)^{4 m_Am_{\Phi ,1.}} \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/10/aa46148-23/aa46148-23-eq9.gif)