| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142345 | |
| Published online | 27 April 2022 | |
A “no-drift” runaway pile-up of pebbles in protoplanetary disks
II. Characteristics of the resulting planetesimal belt
1
ISAS/JAXA,
Sagamihara,
Kanagawa,
Japan
e-mail: hyodo@elsi.jp
2
Earth-Life Science Institute, Tokyo Institute of Technology,
Meguro-ku,
Tokyo
152-8550,
Japan
3
Université Côte d’Azur, Laboratoire J.-L. Lagrange, CNRS, Observatoire de la Côte d’Azur,
06304
Nice,
France
Received:
1
October
2021
Accepted:
8
February
2022
Context. Forming planetesimals from pebbles is a major challenge in our current understanding of planet formation. In a protoplanetary disk, pebbles drift inward near the disk midplane via gas drag and they may enter a zone of reduced turbulence (dead zone). In this context, we identified that the backreaction of the drag of pebbles onto the gas could lead to a runaway pile-up of pebbles, the so-called no-drift mechanism for the formation of planetesimals.
Aims. We improve upon the previous study of planetesimal formation from accumulating pebbles via the no-drift mechanism by investigating the nature and characteristics of the resultant planetesimal belt.
Methods. We performed 1D diffusion-advection simulations of drifting pebbles in the outer region of a modeled dead zone by including a pebble-gas backreaction to the radial drift of pebbles and including planetesimal formation via the streaming instability. We independently considered the parameters that regulate gas accretion (αacc) and vertical stirring of pebbles in the disk midplane (αmid). In this study, the pebble-to-gas mass flux (Fp/g) was fixed as a parameter.
Results. We find that, for a constant Fp/g, after the criteria of the no-drift mechanism are satisfied, planetesimals initially form within a narrow ring whose width expands as accumulating pebbles radially diffuse over time. The system finally reaches a steady-state where the width of the planetesimal belt no longer changes, followed by a continuous formation of planetesimals. A non-negligible total mass of planetesimals (more than one Earth mass) is formed via the no-drift mechanism for a disk having Fp/g ≳ 0.1 for more than ~10–100 kyr with nominal parameters: a gas mass flux of ≳10−8 M⊙ yr−1, τs ≃ 0.01−0.1, αmid ≲ 10−4, and αacc ≃ 10−3−10−2 at r ≲ 10 au, where r, τs, αmid, and αacc are the heliocentric distance, the Stokes number, and the parameters in a dead zone controlling the efficiencies of vertical turbulent diffusion of pebbles (i.e., scale height of pebbles) and gas accretion of the α-disk (i.e., gas surface density), respectively.
Key words: accretion, accretion disks / planets and satellites: formation / protoplanetary disks / planet-disk interactions
© ESO 2022
1 Introduction
Planetesimals, measuring a subkilometer to several hundred kilometers, are fundamental building blocks of planets and small bodies (Safronov 1972; Hayashi et al. 1985). It is thought that planetesimals form from micron-sized dust in protoplanetary disks.
However, forming planetesimals from small dust through all intermediate sizes via pairwise collisions is still challenging. Two theoretical challenges exist − the growth barrier and the radial drift barrier. The growth barrier is caused by the fact that approximately centimeter-sized icy particles become too large to grow further due to fragmentation or bouncing during their high-speed collisions (Blum & Wurm 2000; Zsom et al. 2010). The radial drift barrier arises because the radial drift due to gas drag becomes too fast for meter-sized particles to grow to planetesimals before they fall onto the host star (Whipple 1972; Weidenschilling 1977).
An alternative idea is gravitational collapse for the planetes-imal formation from small particles (typically micron-sized dust and/or millimeter- to decimeter-sized pebbles). A gravitational instability (hereafter GI; Goldreich & Ward 1973; Youdin & Shu 2002; Gerbig et al. 2020) and/or the streaming instability (hereafter SI; Youdin & Goodman 2005; Johansen & Youdin 2007) are possible mechanisms that can avoid the above challenges and that can lead to planetesimal formation without a step-by-step gradual growth, although a high spatial particle concentration within the gas disk is required for triggering these mechanisms (Carrera et al. 2015; Yang et al. 2017; Youdin & Shu 2002; Gerbig et al. 2020).
In this study, a follow-up study of the no-drift (hereafter ND) mechanism was performed. The ND mechanism is a newly reported physical mechanism that causes a traffic jam of pebbles and that leads to a runaway accumulation of pebbles in disks, thus favoring the formation of planetesimals by SI or GI (Hyodo et al. 2021b, hereafter Paper I). The ND mechanism differs from other mechanisms in that it does not require a pressure bump, snow line, and pebble growth and/or fragmentation.
The main drivers of the ND mechanism are (1) a pebble-gas friction, backreaction, that slows down the radial drift of pebbles as its spatial concentration to that of the gas increases, and (2) different α-parameters for the gas accretion, αacc, and for the midplane turbulence, αmid, that regulates the pebble vertical scale height. Such a condition should occur when the gas accretion is regulated by a different mechanism from that for the vertical turbulence near the disk midplane − for example, a layered disk with a disk wind could trigger the gas accretion only near the disk surface (e.g., Armitage 2011; Bai & Stone 2013; Lee et al. 2021).
Paper I analytically and numerically investigated the aerody-namically coupled 1D system of drifting pebbles and gas within an outer part of a dead zone, assuming the gas profile is described by the classical α-accretion disk model (i.e., the gas surface density 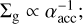 Shakura & Sunyaev 1973; Lynden-Bell & Pringle 1974) and the vertical turbulent αmid decreases with decreasing r (i.e., the outer region of a dead zone). For a large αacc, Σg decreases and correspondingly the midplane pebble-to-gas ratio increases. For a small αmid, the scale height of pebbles decreases and correspondingly the radial backreaction more efficiently slows down the radial drift of pebbles as the midplane pebble-to-gas ratio increases.
Shakura & Sunyaev 1973; Lynden-Bell & Pringle 1974) and the vertical turbulent αmid decreases with decreasing r (i.e., the outer region of a dead zone). For a large αacc, Σg decreases and correspondingly the midplane pebble-to-gas ratio increases. For a small αmid, the scale height of pebbles decreases and correspondingly the radial backreaction more efficiently slows down the radial drift of pebbles as the midplane pebble-to-gas ratio increases.
It showed that a runaway accumulation of pebbles (i.e., no-drift), positive feedback, occurs when the pebble-to-gas mass flux, Fp/g, is large enough and when drifting pebbles entering a dead zone reach a critical level of low-turbulence (i.e., a critical small αmid/αacc which depends on Fp/g). This occurs because of the traffic jam effect - that is, at large orbital distances (corresponding to a large αmid), pebbles drift inward efficiently, whereas the pebble drift is progressively seized in the dead zone (where αmid becomes small) via the backreaction effect, leading to a runaway accumulation of pebbles.
Paper I, however, did not include the physics of planetesimal formation after the point where pebbles accumulate in a runaway fashion due to the ND mechanism, that is, pebble surface density and local spatial density simply kept increasing (see their Fig. 2). In reality, GI or SI would then operate to form planetesimals. The resultant planetesimal distribution should be characterized by the balance between the rate of pebble pile-up by the ND mode and that of planetesimal formation from pebbles by GI or SI1.
In this study, an analytical algorithm that forms planetes-imals from accumulating pebbles via SI was implemented in our 1D numerical code to further study the ND mechanism. We address (1) the resultant planetesimal belt, (2) its dependencies on different physical parameters, and (3) the rate of planetesimal formation by the ND mode.
The structure of this paper is as follows: in Sect. 2, we introduce concepts and formulae of our numerical approach. Section 3 presents some fiducial simulation results and discusses its dependencies. Section 4 discusses possible applications of the ND mechanism. Our findings are summarized in Sect. 5.
2 Concepts and formulae of our numerical approach
The numerical approach is the same as Paper I except for additional consideration of planetesimal formation from accumulating pebbles via SI. Below, we briefly explain the concepts and formulae of our numerical approach.
2.1 Disk structure
A 1D radial protoplanetary disk, a function of the distance to the central star r, was constructed using the classical α-accretion disk model (Shakura & Sunyaev 1973; Lynden-Bell & Pringle 1974). The surface density of gas in a steady accretion disk is given by
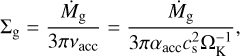 (1)
(1)
where Mg and 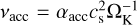 are the gas mass accretion rate and the effective viscosity, respectively (cs being the gas sound velocity and ΩK being the Keplerian orbital frequency).
are the gas mass accretion rate and the effective viscosity, respectively (cs being the gas sound velocity and ΩK being the Keplerian orbital frequency).
The disk radial structure is characterized by its radial pressure gradient using Cη as
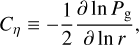 (2)
(2)
where Pg is the gas pressure which depends on the disk temperature profile, T(r) (e.g., Cη = 11/8 for T ∝ r−1/2).
In this study, we considered a dead zone in the disk midplane (Sect. 2.4) and the above smooth gas disk structure was fixed throughout the simulations assuming that the efficient gas accretion is driven by, for example, disk winds in the upper layers. In reality, a coupled simulation including protoplanetary disk evolution is required to address the fate of a specific system (Sect. 4).
2.2 Pebble radial drift
The driver of the ND mechanism is the radial backreaction, inertia, that slows down the radial velocity of pebbles for high values of the midplane pebble-to-gas ratio. Including backreaction, the radial velocity of pebbles, vp, is given as (Ida & Guillot 2016; Schoonenberg & Ormel 2017)
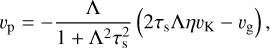 (3)
(3)
where Λ = ρg/(ρg + ρp) = 1/(1 + Z) characterizes the strength of the backreaction due to the pile-up of pebbles (Z = ρp/ρg being the midplane pebble-to-gas spatial density ratio). Here, a negative value indicates radial drift to the central star. 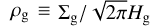 and
and 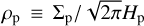 where Σg, Σp, Hg, and Hp being the surface densities and scale heights of gas and pebbles, respectively. vK and η = Cη(Hg/r)2 are the Keplerian velocity and the degree of deviation of the gas rotation frequency from that of Keplerian, respectively. vg = −3vacc/(2r) is the gas accretion velocity.
where Σg, Σp, Hg, and Hp being the surface densities and scale heights of gas and pebbles, respectively. vK and η = Cη(Hg/r)2 are the Keplerian velocity and the degree of deviation of the gas rotation frequency from that of Keplerian, respectively. vg = −3vacc/(2r) is the gas accretion velocity.
In this study, pebbles were considered to be decoupled from the gas with a Stokes number τs = 0.01−0.1 (e.g., Okuzumi et al. 2012; Ida et al. 2016). Changing τs linearly changes the critical value of Fp/g for the ND mode to be triggered (Eq. (16) in Paper I, see also Eq. (11)).
2.3 Scale height of pebbles
Another essential feature of the ND process is the midplane pebbles-to-gas concentration of the spatial density (i.e., Z = ρp/ρg) that directly affects Λ through Z (Eq. (3)). As ρp ∝ 1/Hp, a small scale height of pebbles elevates the midplane pebble-togas density ratio, leading to a less efficient radial drift of pebbles via the radial backreaction. In this study, for Hp, the larger of the two − Hp,tur and Hp,KH − was adopted as
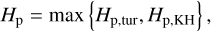 (4)
(4)
where Hp,tur is regulated by the midplane vertical turbulence and Hp,KH is regulated by a vertical shear Kelvin-Helmholtz (KH) instability.
When the midplane vertical turbulence (∝ αmid) regulates the vertical scale height of pebbles, it is given as (Hyodo et al. 2019)
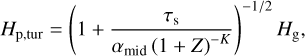 (5)
(5)
where a coefficient K characterizes the strength of the backreac-tion onto the diffusivity and K = 1 is used.
When the turbulent α-parameter, αmid, is very small, a KH instability may prevent a further decrease in the pebble scale height. Thus, the minimum scale height, Hp,KH (Ri = 0.5), is defined as
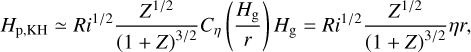 (6)
(6)
which is generally valid for Z ≲ 1, and Z ≫ 1 indicates a gravitational collapse (Hyodo et al. 2021a). We note that Chiang (2008) solved the particle height distribution function and derived zmax where the particle distribution is truncated. Their distribution function has a cusp for Z ≳ 1 and the cusp becomes sharper as Z increases. Our definition of Hp,KH is based on the root mean square of the heights of the particle distribution. The difference between zmax of Chiang (2008) and our Hp,KH becomes larger as Z increases, while they are similar (only differ by 2) for Z ≪ 1 (see more details in Hyodo et al. 2021a). For αmid = 10−4, Hp,tur > Hp,KH and thus Hp = Htur. For αmid < 10−4, Hp = Hp,KH depending on Z during the evolution (Fig. 1). Here, to be consistent with the settings in Paper I and Fig. 1, we used Eq. (4) in our numerical simulations. We used αmid ≥ 10−4 and thus our choise of Hp,KH does not affect our numerical results.
 |
Fig. 1 Midplane pebble-to-gas ratio Z = ρp /ρg in the αmid/αacc − Fp/g space (Eq. (10)). Top and bottom panels correspond to αacc = 10−2 and αacc = 10−3, respectively. Left and right panels correspond to τs = 0.01 and τs = 0.1, respectively. The color contours are obtained by directly solving Eq. (10). The red-colored regions indicate the “no-drift” runaway pile-up (i.e., ρp/ρg goes to infinity; no-solution). The calculations correspond to r = 5 au, but the results depend very weakly on the radial distance to the star. The ND mode can occur irrespectively of the radial shape and position of a dead zone (see more details in Paper I). We note that the physics of planetesimal formation is not included here. |
2.4 Midplane turbulent structure
In our numerical approach, we used a nondimensional midplane turbulent α-parameter, αmid, which differs from α-parameter that characterizes the gas accretion, αacc (Eq. (1)). We adopted a dead zone in the inner region of the disk midplane modeled as
![${\alpha_{{\rm{mid}}}}(r) = {\alpha_{{\rm{dead}}}} + \left({{{{\alpha_{{\rm{acc}}}} - {\alpha_{{\rm{dead}}}}} \over 2}} \right)\left[{{\rm{erf}}\left({3 + {{6(r - r*)} \over {\Lambda {r_{{\rm{tra}}}}}}} \right) + 1} \right],$](/articles/aa/full_html/2022/04/aa42345-21/aa42345-21-eq11.png) (7)
(7)
where αacc and αdead are turbulence parameters outside and inside the dead zone. r* is the innermost radial distance where αmid = αacc. Δrtra is the radial width of the transition from αmid = αacc to αmid = αdead. Although it is still under intense research and depends on the detailed settings of the hydrodynamics simulations, αacc could be up to αacc ~ 10−2 in well-ionized gas (e.g., Flock et al. 2017, 2019), while αdead ~ 10−5−10−3 (e.g., Okuzumi & Hirose 2011; Mori et al. 2019). The radial width of the transition from an active zone to a dead zone (i.e., Δrtra) could be ≳10 au (e.g., Dzyurkevich et al. 2013) or as small as the local scale height (~0.1 au; Okuzumi personal communication). We used r*, Δrtra, αacc, and αdead as parameters in this study (Table 1 and see Pinilla et al. 2016 for similar settings; Fig. 2 top panels). Our chosen parameters triggered the ND mechanism at r ≲ 10 au for Fp/g ≳ 0.1.
As shown in Paper I, the ND mode occurs for an arbitrary choice of the dead zone’s radial structure, that is, irrespective of a sharp or a smooth change between the active and dead zones (i.e., arbitrary choice of αdead, αacc, r*, and ∆rtra) as long as αmid is smaller than a threshold value (Eq. (11); derived in Paper I).
 |
Fig. 2 Overall results of our numerical simulations for different combinations of the disk structure and Fp/g. Top panels: given disk structures (the black lines; see Table 1). Middle panels: resultant midplane pebble-to-gas ratio of the spatial density, ρp/ρg. Bottom panels: resultant planetesimal surface density formed by the ND mode and SI (Eq. (8)). The blue, green, and red lines indicate time evolution. By t ≃ 1 × 105 yr, the system reaches a steady-state in ρp/ρg and then planetesimals keep forming in a steady width. The dashed gray lines in the top panels represent analytically derived critical αmid/αacc for a given Fp/g (Eq. (11)), indicating that disks of smaller αmid/αacc than this critical value develop the ND mode. The gray lines in the middle panels represent the critical ρp/ρg above which the ND mode occurs (i.e., ρp/ρg = 1). Here, αacc = 10−2, τs = 0.1, Mg = 10−8 M⊙ yr−1, and kSI = 10−3 are used. |
2.5 From pebbles to planetesimals
The above settings and models are the same as those in Paper I. In this follow-up study, we additionally included a toy model of planetesimal formation via SI in which a fraction of pebbles are converted to planetesimals.
When Z ≥ 1 and τs ≥ 0.01 are locally satisfied, pebbles lead to the formation of planetesimals as (Drążkowska et al. 2016)
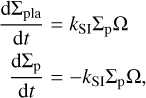 (8)
(8)
where Σpla is the surface density of planetesimals. kSI is a coefficient that characterizes the efficiency of conversion from pebbles to planetesimals. It can be rewritten as kSI = ζτs (a coefficient ζ = 0.1 was used in e.g., Stammler et al. 2019; Miller et al. 2021). Thus, for τs = 0.1, ζ = 0.1 corresponds to kSI = 10−2. We used kSI = 10−2−10−4.
2.6 Numerical settings and parameters
We performed 1D diffusion-advection simulations that included the backreaction to radial drift of pebbles that slows down the pebble drift for an elevated midplane pebble-to-gas concentration. For the gas accretion, αacc = 1 × 10−3, 3 × 10−3, and 1 × 10−2 were used. The governing equation of pebbles is given as (Desch et al. 2017)
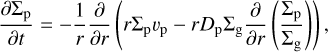 (9)
(9)
where 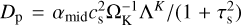 is the radial diffusivity of pebbles. Here, the diffusivity included the effects of the back-reaction with K = 1 (Hyodo et al. 2021b). The temperature profile was T (r) = 150K× (r/3 au)−1/2. This leads to Cη = 11/8 and Σg ∝ r−1. The central star had the mass of the Sun, M⊙. The gas molecular weight was μg = 2.34. Mg = 10−9,10−8, and 10−7 M⊙ yr−1 were adopted.
is the radial diffusivity of pebbles. Here, the diffusivity included the effects of the back-reaction with K = 1 (Hyodo et al. 2021b). The temperature profile was T (r) = 150K× (r/3 au)−1/2. This leads to Cη = 11/8 and Σg ∝ r−1. The central star had the mass of the Sun, M⊙. The gas molecular weight was μg = 2.34. Mg = 10−9,10−8, and 10−7 M⊙ yr−1 were adopted.
At the beginning of the 1D simulations, we set the pebble-togas mass flux Fp/g = Mp/Mg (where Mp is the pebble mass flux) at the outer boundary, rout (typically rout = 30 au). Fp/g at rout was fixed throughout the simulations. We set Fp/g ~ 0.1–0.5 as a typical value. With this value of Fp/g, Mp ~ 10−4−10−3M⊙ yr−1 corresponds to Mg ~ 10−9−10−7M⊙ yr−1, where M⊕ is the Earth-mass. This is consistent with Drążkowska et al. (2021) (see their case with αmid = 10−4 and including pebble fragmentation). When pebble fragmentation is not effective, Fp/g could become about the order of unity for αmid ~ 10−4 and Mg ~ 10−8 M⊙ yr−1 (Ida et al. 2016).
In this study, planetesimals do not interact with disks and pebbles, and the growth of planetesimals is not considered. The pebble/planetesimal-to-planet formation (e.g., Ormel & Klahr 2010; Lambrechts & Johansen 2014; Liu et al. 2019; Lichtenberg et al. 2021) in the context of the ND mechanism should be studied in the future.
3 Results
Below, we show our numerical results as well as analytical estimates. First, we present overall parameters in the αmid/αacc - Fp/g space where the ND mechanism is triggered (Sect. 3.1). Second, including planetesimal formation, we introduce overall numerical results which demonstrate that the resultant planetesimal belts formed by the ND mechanism could be diverse in terms of their widths and profiles (Sect. 3.2). Third, we show the dependencies on different parameters (e.g., kSI and Mg; Sects. 3.3 and 3.4). Fourth, we discuss the inner and outer edges of the planetes-imal belts (Sect. 3.5). Fifth, the rate of planetesimal formation via the ND mode is presented (Sect. 3.6). Sixth, the dependence on the Stokes number, τs, is discussed (Sect. 3.7). Finally, the dependence on αacc is discussed (Sect. 3.8).
3.1 Parameters triggering the ND mechanism
Here, before performing the 1D numerical simulations that include planetesimal formation, we first present the overall parameters in the αmid/αacc − Fp/g space where the ND mechanism is triggered (Fig. 1). The arguments are made by directly solving Eq. (10) for αacc = 10−3 and 10−2 with τs = 0.01 and 0.1 to find parameter sets for the ND mode to be triggered. This is originally demonstrated in Paper I, although it was limited to τs = 0.1.
The concentration of pebbles at the midplane is written as
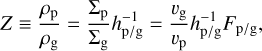 (10)
(10)
where hp/g = Hp/Hg. Equation (10) indicates the existence of a positive feedback. When vp decreases, Z increases and then vp further decreases due to the radial backreaction (Eq. (3)). This feedback can be triggered when hp/g decreases (i.e., Z increases and thus vp decreases) as pebbles enter a dead zone.
Now, Eq. (10) can be solved (i.e., solve for Z) for a given combination of Fp/g and αmid. The color contours in Fig. 1 show the values of Z obtained in a steady-state with a red-shaded region indicating that no steady-state solution is found due to the development of the ND mechanism (i.e., Z goes to infinity). The horizontal boundary of the ND region is due to the fact that the minimum scale height is regulated by the KH instability, independently of αmid (Eq. (6)). The diagonal boundary is a function of αmid (Eq. (5)). For the analytical derivations of these boundaries, we refer to Paper I.
The parameters controlling the ND instability are as follows. A larger αacc yields a smaller gas surface density in a steady accretion disk (Eq. (1)), thus leading to a higher solid-to-gas ratio for a fixed τs and favoring the ND mechanism. Alternatively, for a fixed αacc, a smaller τs leads to a less efficient radial drift of pebbles, leading to a higher concentration of pebbles in the disk midplane, also favoring the ND mechanism. These arguments help to account qualitatively for the variations of the extent of the ND instability space in Fig. 1. We note that the analytical predictions from Eq. (11) (see also Eq. (20) in Paper I) for αacc = 10−2 and τs = 0.01 slightly deviate from the direct solutions (see the top left panel of Fig. 1). This is because the analytical arguments were derived based on the assumption of αacc ≪ τs (see more details in Paper I), while here αacc = τs.
Our numerical simulations including a modeled dead zone with the pebble drift can correspond to Fig. 1 in the following way: First, in a steady accretion disk, the pebble-to-gas mass flux, Fp/g, is conserved without sublimation and condensation. Then, when drifting pebbles enter a dead zone, αmid/αacc decreases (i.e., Eq. (7)). Thus, a given pebbles flux (i.e., pebbles) moves horizontally from right to left in Fig. 1. When pebbles cross the diagonal boundary into the red-shaded region in Fig. 1, the ND mechanism is triggered (Here, Z = 1 is critical for driving the ND mechanism; see Paper I). This is the reason why the critical condition - the on/off of the ND mechanism − does not depend on the radial shape of a dead zone (Paper I).
3.2 Planetesimal belt formed by the ND mechanism
Figure 2 shows the disk structures (top panels), the midplane pebble-to-gas ratio (middle panels), and the resultant planetesi-mal surface density formed by the ND mode (bottom panels) for different combinations of disk structures (Table 1) and Fp/g. All cases developed the ND mode and formed planetesimals. The dashed gray lines in the top panels show the analytically derived critical αmid/αacc for a given Fp/g (Eq. (11)), indicating that disks having smaller αmid/αacc than the critical values are expected to develop the ND mode. The critical αmid/αacc is analytically given as (Paper I, their Eq. (22)–(23)).
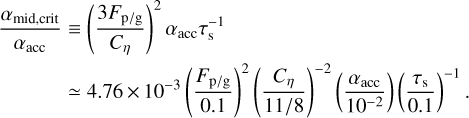 (11)
(11)
This criterion is in very good accordance with the numerical simulations. The gray lines in the middle panel show the critical ρp/ρg = 1 above which the ND mode is developed. We note that Eq. (11) is derived under the assumption of αacc ≪ τs.
The resultant planetesimal belts have diverse widths and profiles depending on the disk structure and the value of Fp/g (Fig. 2). The leftmost and rightmost two panels have the same Fp/g but have different disk structures, respectively. The middle two panels have the same disk structure but have different Fp/g.
Early in its evolution when the ND mode has just begun, the pile-up of pebbles and thus planetesimal formation start only at the vicinity of the critical radial distance where the ND occurs for a given Fp/g (Eq. (11), that is, the radial distance where the dashed gray line and the black line intersect in the top panels in Fig. 2). As pile-up continues, diffusion of pebbles enlarges its width and thus the resultant width of the planetesimal belt correspondingly stretches.
Because Fp/g is kept constant at the outer boundary in our simulation, the system eventually reaches a steady-state in ρp/ρg (middle panels) and reaches a steady width of planetesimal belt for a given combination of disk structure and Fp/g value (time-evolutions are indicated by colors in Fig. 2). After the system reaches a steady-state in ρp/ρg, planetesimals keep forming within a fixed radial width.
The dependence on the disk structure (compare leftmost and/or rightmost two panels in Fig. 2) is as follow. When the disk has a radially sharper dead zone (i.e., αmid/αacc changes abruptly with radial direction), the resultant planetesimal belt becomes narrower and its surface density becomes more peaked.
Regarding the Fp/g dependence (compare the middle panels of Fig. 2), a greater Fp/g leads to a wider planetesimal belt. The timescale to reach a steady-state solution for the width of plan-etesimals belt is longer for a greater Fp/g. The reason for this is discussed in Sect. 3.5.
The steady-state ρp/ρg value also depends on the disk structure and Fp/g. For the streaming instability to operate, ρp/ρg ≥ 1 is required (Eq. (8)). The timescale to reach a steady-state and the steady-state solution itself are regulated by a complex interplay between the inclusion of new drifting pebbles, the radial diffusion of pebble pile-ups, and the conversion from pebbles to planetesimals via SI (Eq. (8)). Thus, whether steady-state values of ρp/ρg become >1 depends on these conditions, kSI, and τs (see Sects. 3.3 and 3.7).
 |
Fig. 3 Dependence of the resultant planetesimal belt on kSI. Left and right panels: cases of different given disk structures (Disk 2 and Disk 3, respectively; Table 1). Top panels: given disk structures. Bottom three panels: the same combination of Fp/g and the disk structure but different kSI. The dashed gray lines in the top panels show the analytically derived critical αmid/αacc for a given Fp/g, indicating that disks having smaller αmid/αacc than the critical one are expected to develop the ND mode (no dependence on kSI; Eq. (11)). The blue, green, red, and black lines represent time evolution. By t ≃ 3 x 105 years, all cases reach a steady-state in ρp/ρg and the planetesimals keep forming in a ring with a constant width. The gray lines represent the midplane pebble-togas ratio, ρp/ρg, at the steady-state shown in the right axis. Here, τs = 0.1 and Mg = 10−8 M⊙ yr−1 are used. |
3.3 Dependence on kSI
The efficiency of planetesimal formation via the streaming instability, that is, the ratio of pebbles that are turned to planetesimals within one orbital period, is characterized by the kSI coefficient as defined in Eq. (8). Here, we show the dependence of the resultant planetesimal belt on kSI.
Without any planetesimal formation, a runaway pile-up of pebbles (i.e., ND mode) starting at a critical radial distance continuously propagates radially outward (see Fig. 2 in Paper I). Including planetesimal formation via SI would change this picture as the final pile-up would be regulated by the relative efficiency of planetesimal formation via SI and that of the pile-up of pebbles via ND mode.
Figure 3 shows the dependence of the resultant planetesimal belt formed via SI on kSI. The left and right panels are the cases of Disk 2 and Disk 3, respectively (Table 1). Disk 2 case has a sharper radial change in αacc/αmid than that of Disk 3 (top panels). Here, Fp/g = 0.47 is used for both cases. The results of the kSI dependence can be categorized into two types.
First, the results can be converged for a large kSI case depending on the disk structure (see cases of Disk 3 with kSI = 10−2 and kSI = 10−3). In this case, the timescale of planetesimal formation is shorter than that of pile-up by the ND mechanism to reach ρp/ρg > 1. Thus, the steady-state in the midplane pebble-to-gas ratio is ρp/ρg ~ 1, which is the minimum value required for the SI to operate we set in this study (the gray lines in Fig. 3). Thus, for high-enough kSI values, the results are independent of kSI.
Second, the widths of planetesimal belt and the timescales to reach a steady-state in ρp/ρg become wider and longer for a smaller kSI (see cases of Disk 2 with kSI = 10−2,10−3, and 10−4, and cases of Disk 3 with kSI = 10−3 and 10−4). In this case, the timescale of planetesimal formation is longer than that of pile-up to reach ρp/ρg = 1 depending on the kSI value. Thus, for smaller kSI values, the steady-state value of ρp/ρg becomes larger than unity (i.e., ρp/ρg > 1; the gray lines in Fig. 3).
 |
Fig. 4 Dependence of the resultant planetesimal belt on Ṁg. Left to right panels are the cases of Ṁg=10−9,10−8, and 10−7 M⊙ yr−1, respectively. The gray lines represent the surface density of solids in the classical minimum mass solar nebula model (MMSN; Σpla = 30(r/1 au)−3/2 gcm−2) of Weidenschilling (1977) for reference. By t ≃ 1 × 105 yr, the system reaches a steady-state in ρp/ρg and width of the planetesimal ring. Here, αacc = 10−2, τs = 0.1, and kSI = 10−3 are used. |
3.4 Dependence on Ṁg
In this subsection, we study the dependence on Ṁg in the resultant planetesimal belt. Using the classical α-disk model and Fp/g, the pebble surface density is characterized by Σp ∝ Fp/g × Ṁg. Thus, a higher value of Ṁg also yields a larger absolute amount of pebbles in the disk.
The criteria and conditions of the ND mechanism are described in nondimensional forms by using Fp/g = Ṁp/Ṁg (see Eq. (11)). Thus, the resultant absolute planetesimal surface density linearly scales with Ṁg as Σpla ∝ Σp ∝ Ṁp ∝ Fp/g × Ṁg.
Figure 4 shows the resultant planetesimal belts for cases with the same Fp/g value and disk structure but for different Ṁg values. As discussed above, a larger amount of planetesimals is formed for a larger Ṁg, and it scales with Ṁg; the profile and width are the same but only the absolute value scales with Ṁg.
3.5 Edges of the planetesimal belt
In the previous subsections, we discussed the dependences of the widths and profiles of the planetesimal belts formed by the ND mechanism on kSI and Ṁg. We numerically demonstrated that the resultant planetesimal distribution finally reaches a steady-state to have a fixed width for a constant Fp/g.
One may notice that the inner edge of the planetesimal belt is nearly independent on kSI and Ṁg for a given disk structure (Figs. 3 and 4). The inner edge is characterized by the disk structure; it is located at the vicinity of the outermost radial distance where αmid/αacc no longer decreases with decreasing r.
The ND pile-up starts at a greater radial distance, defined by rND,start (i.e., characterized by Eq. (11) where a critical αmid/αacc is a function of Fp/g,given we set at the outer boundary). Because accumulating pebbles radially diffuse, a fraction of pebbles diffuse inward and the pebble mass flux at r < rND,start smoothly propagates to have Fp/g < Fp/g,given. At r < rND,start, the required Fp/g for the ND mode to develop is smaller as αmid/αacc decreases with decreasing r and thus the ND mode smoothly keeps being developed at r < rND,start until αmid/αacc reaches its minimum value.
The outer edge of the planetesimal belt depends on kSI and the disk structure (Figs. 2 and 3). Smoother radial change in αmid/αacc and/or smaller kSI leads to the outer edges of the planetesimal belt more radially distant for a given Fp/g as accumulating pebbles more efficiently diffuse outward while turning into planetesimals. The radial change in αmid results in an additional diffusion flux to the case of a constant diffusiv-ity (see Eq. (9) which includes the term of the dependence on (∂Dp(αmid)/∂r) × (∂ZΣ/∂r) where ZΣ = Σp/Σg). A smaller value of kSI indicates a less effective conversion from accumulating pebbles to planetesimals, and thus the pebble pile-up propagates outward.
3.6 Cumulative planetesimal mass formed by the ND mode
Here, we aim to understand the total mass of planetesimals contained within the belt. Below, we first analytically derive the rate of planetesimal formation when the system reaches a steady-state in ρp/ρg. Then, the validity of our analytical arguments is checked by comparing them with the numerical simulations (Fig. 5).
Following the discussion in Sect. 3.5, a reduced pebble mass flux propagates continuously inward from the radial point where the Nd mechanism initially takes place at r = rND,start for a given Fp/g,given. The development of the ND mode correspondingly propagates inward because αmid/αacc decreases with decreasing r. The ND mode develops until it reaches the minimum αmid/αacc point (i.e., the minimum midplane turbulence of αmid,min). At this radial distance, Fp/g becomes its minimum for the ND mode to develop. This minimum value, Fp/g,ND,min is given from Eq. (11) as
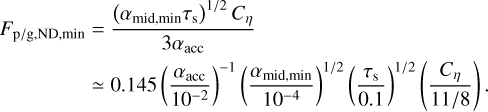 (12)
(12)
Therefore, the pebble mass flux is reduced from Fp/g = Fp/g,given at the outer boundary to Fp/gND,min This difference leads to the rate of pebble pile-up and is eventually converted to planetesimals via SI. To estimate the rate of planetesimal formation via the ND mechanism, the following mass balance is considered. From the outer region of the disk, pebbles with Fp/g,given are supplied to the ND region within a dead zone, and a fraction of the supplied pebbles are flowed out further inward from the ND region with Fp/g,ND,min. Thus, the cumulative mass of planetesimals formed by the ND mode during the time interval of Δt is given as
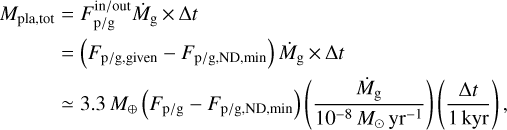 (13)
(13)
where 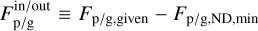 is the net mass flux supplied to the ND region.
is the net mass flux supplied to the ND region.
Importantly, this analytical estimation indicates that the total mass of planetesimals formed via the ND mechanism through SI is independent on the disk’s radial structure and kSI, that is, irrespective of the smooth or sharp radial change in αmid/αacc. Instead, it is characterized by Fp/g,given, the minimum value of αmid/αacc through Fp/g,ND,min (Eq. (12)), and Mg.
The maximum total mass of planetesimals should be regulated by the mass budget of solid in a disk. Considering a disk having a disk-to-star mass ratio of fdisk/star and a disk’s solid-to-gas mass ratio of fsolid/gas, the maximum solid mass is MSolid = fdisk/starfsolid/gas M⊙ ≃ 3 × 105fdisk/starfsolid/gas M⊕ for solar mass star. Using the efficiency of the planetesimal formation in Eq. (13), the maximum total planetesimal mass, Mpla;max, is given as
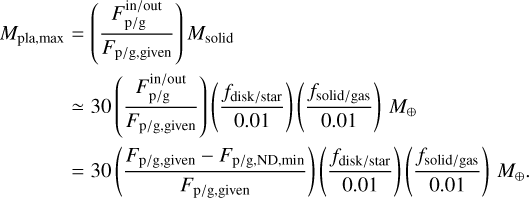 (14)
(14)
Accordingly, for the classical minimum mass solar nebula (MMSN) model of fdisk/star ~ 0.01 (Weidenschilling 1977) and for the interstellar medium value of fsolid/gas ~ 0.01 (Bohlin et al. 1978), Mpia,max ~ 20 M⊕ and ~4.5 M⊕ for Fp/g,given = 0.47 and 0.17 with αacc = 10−2 and αmid = 10−4, respectively. We note that the MMSN (i.e., Msolid ≃ 30 M⊕) is just a single benchmark in the limit of the smallest mass budget. The ND mechanism works better for a larger mass budget. Recent studies in the context of drifting pebbles (e.g., Lambrechts & Johansen 2014; Ida et al. 2016; Bitsch et al. 2019; Drążkowska et al. 2021) considered the cases of a more abundant solid mass budget (e.g., Msolid ≃ 650 M⊕ in Drążkowska et al. 2021), where more planetesimals are expected to be formed by the ND mechanism.
Figure 5 shows the cumulative mass of planetesimals, Mpla,tot, formed by the ND as a function of time. Here, t = 0 is set to be the point where Mpla,tot = 0 in the numerical simulations, that is, the time at which ρd/ρg exceeds 1, which should depend on the parameters in the numerical simulations, is always shifted to t = 0. The thin dashed lines are the analytical estimates (Eq. (13)) and the thick solid lines are numerical results. The rate of planetesimal formation seen in the numerical simulations can be divided into two phases − the early nonlinear phase and the successive linear phase.
In the early stage of the evolution (during the first ~10–100 kyr after the start of planetesimal formation for kSI ≳ 10−3), deviations are seen between analytical estimates and numerical results with an early evolution that is nonlinear. During this early phase, the width of the planetesimal belt changes as pebbles affected by the ND mechanism diffuse radially inward and outward, thus affecting the pebble surface density profile (e.g., Fig. 2). A fraction of incoming pebbles are used to increase the pebble surface density in the ND region toward a steady-state, while only a fraction of pebbles are used to form planetesimals. The efficiency of the planetesimal formation can then be significantly smaller than that predicted in steady-state by Eq. (13). Accretion peaks (with high Fp/g values) that are too short (∆t ≪ 10–100 kyr) hence would not yield an efficient formation of planetesimals.
After about 10–100 kyr since the start of planetesimal formation, the system reaches a steady-state and the efficiency of the planetesimal formation is linear and can be described by Eq. (13). A small mismatch is still seen even after the system reaches the steady-state for the Fp/g = 0.17 cases (middle panel). This is probably because this value is close to Fp/g,ND,min≃ 0.15 so that even a small error in the analytical estimation of Fp/gND,min (e.g., neglecting the effects of diffusion) may lead to a noticeable difference. We confirmed that this deviation becomes smaller for greater Fp/g values.
A non-negligible total mass of planetesimals (more than Earth mass) could be formed for a disk having Fp/g ≳ 0.1 for a duration ≳ 10–100 kyr and a gas mass flux of ≳ 10−8 M⊙ yr−1, and αmid/αacc ≃ 10−2 with αacc = 10−2 at r ≲ 10 au. Dependencies on the other factors are discussed below.
At the steady-state, as expected from the analytical estimation, the total mass of planetesimals formed within the planetesimal belt does not depend on the width and profile of the belt (i.e., irrespective of the dead zone structure and of kSI). Conversely, in the early nonlinear phase of the evolution before reaching the steady-state in ρp/ρg (when the width of the planetesimal belt is still changing; see Figs. 2–4), the rate of planetesimal formation depends on the disk structures and kSI (see also discussion of the outer edge of the planetesimal belt in Sect. 3.5).
The dependencies on Ṁg, Fp/g, and kSI are as follows. (1) The total planetesimal mass is linearly scaled with Ṁg (left panel in Fig. 5; see also Sect. 3.4). (2) A greater Fp/g results in a larger amount of total planetesimal mass (middle panel in Fig. 5; see also Sect. 3.5). (3) For a smaller SI efficiency (i.e., smaller kSI), the timescale to reach the steady-state in ρp/ρg with a fixed width of planetesimal belt is longer (right panel in Fig. 5; see also Sect. 3.3 and Fig. 3).
 |
Fig. 5 Cumulative mass of planetesimals, Mpla,tot, formed by the ND mechanism as a function of time. The thin dashed lines are analytically derived cumulative masses of planetesimals (Eq. (13)). The thick solid lines are the results of numerical simulations. Here, we sorted numerical data so that planetesimal formation starts at t = 0 kyr (i.e., the time at which ρd/ρg exceeds 1, which should depend on the parameters in the numerical simulations, is always shifted to t = 0 kyr). Left panel: dependence on Ṁg where Ṁg(= 10−7, 10−8, and 10−9 M⊙ yr−1) are a variable while the disk structure (Disk 3) and Fp/g = 0.47 are kept the same. Middle panel: dependence on disk structure and Fp/g where disk structure (Disk 1 or Disk 3; see Table 1) and Fp/g(= 0.17 or 0.47) are variables while keeping the same Ṁg = 10−8 M⊙ yr−1. Right panel: dependence on kSI where kSI = 10−2,10−3, and 10−4 while having the same disk structure (Disk 2), Fp/g = 0.47, and Ṁg = 10−8 M⊙ yr−1. After around ~10–100 kyr, depending on the parameters, the rate of planetesimal formation can be described by the analytical arguments (dashed lines); that is, the system reaches a steady width of the planetesimal belt (Sect. 3.6). In this study, Fp/g is kept constant (i.e., infinite solid mass budget). We note, however, that the maximum total mass of planetesimals in a real system should be regulated by the mass budget of solids (see Sect. 3.6). Here, αacc = 10−2 and τs = 0.1 are used. |
 |
Fig. 6 Dependence of the resultant planetesimal belt on the Stokes number, τs (blue for τs = 0.01, green for τs = 0.03, and red for τs = 0.1, respectively). Left panel: resultant midplane pebble-to-gas ratio of the spatial density, Z = ρp/ρg, after the establishment of the steady-state. Middle panel: resultant planetesimal surface density at t = 100 kyr since the start of planetesimal formation. The gray line is the classical minimum mass solar nebula model (MMSN; Σpla = 30(r/1 au)−3/2 g cm−2) of Weidenschilling (1977). Right panel: cumulative mass of planetesimals, Mpla,tot, formed by the ND mechanism since the start of planetesimal formation. The thin dashed line is analytically derived cumulative mass of planetesimals with τs = 0.1. Here, Disk 2, αacc = 10−2, Ṁg = 10−8 M⊙ yr−1, Fp/g = 0.47, and kSI = 10−3 are used. |
3.7 Dependence on τs
So far, we have considered that pebbles were characterized by a Stokes parameter of τs = 0.1. Here, we additionally considered τs = 0.01 and 0.03.
From analytical considerations, the critical αmid below which the ND runaway pile-up occurs depends on 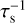 (Eq. (11)). Alternatively, the critical Fp/g above which the ND mode takes place depends on
(Eq. (11)). Alternatively, the critical Fp/g above which the ND mode takes place depends on 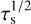 (Eq. (11)). Thus, a larger αmid (or a smaller Fp/g) satisfies the ND criterion for a smaller τs. This is because, for αacc ≲ τs, a smaller τs increases the pebble surface density
(Eq. (11)). Thus, a larger αmid (or a smaller Fp/g) satisfies the ND criterion for a smaller τs. This is because, for αacc ≲ τs, a smaller τs increases the pebble surface density 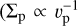 and Eq. (3)), while its scale height is independently regulated by αmid. Its dependence on τs is weaker (Eq. (5)).
and Eq. (3)), while its scale height is independently regulated by αmid. Its dependence on τs is weaker (Eq. (5)).
Figure 6 shows the numerical results and dependence of the resultant planetesimal belt on the Stokes number (τs = 0.01, 0.03, and 0.1 with Disk-2, Ṁg = 10−8 M⊙ yr−1, Fp/g = 0.47, αacc = 10−2, and kSI = 10−3). Although a smaller τs more easily satisfies the ND criterion (i.e., with a smaller Fp/g), the early-phase efficiency of planetesimal formation before the steady-state decreases and the timescale of the pebble pile-up becomes longer (~10 kyr for τs = 0.1 and ~100 kyr for τs = 0.01). This is because the efficiency of the pebble pile-up is regulated by the balance between the continuous accumulation of pebbles by absorbing inwardly drifting pebbles, the radial diffusion of the piled-up pebbles, and the conversion from pebbles to planetesi-mals via Si. For a smaller τs, the inward drift of pebbles becomes less efficient (Eq. (3)).
The similarity seen in the resultant radial extent of the plan-etesimal belt can be understood from the leftmost panel of Fig. 6: it shows that the steady-state ρp/ρg is constant and ≃1 independently of τs for small τs values. Such a similarity is also seen in Fig. 3 for large kSI values (see the middle panels in Fig. 3). This is because a smaller τs requires a longer timescale to pile up as the drift velocity decreases. Its timescale becomes longer than that of the planetesimal formation via SI, settling to ρp/ρg ≃ 1, which is the value required for the SI to operate. Finally, we note that 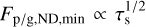 (Eq. (12)) and thus the total mass of planetesimals weakly depends on τs (Eq. (13)).
(Eq. (12)) and thus the total mass of planetesimals weakly depends on τs (Eq. (13)).
 |
Fig. 7 Same as Fig. 6, but for different αacc (blue for αacc = 1 × 10−3, green for αacc = 3 × 10−3, and red for αacc = 1 × 10−2, respectively). Here, Disk 2, τs = 0.01, Ṁg = 10−8M⊙ yr−1, Fp/g = 0.47, and kSI = 10−3 are used. A large deviation between the analytical estimation (blue dashed line) and the simulation (blue solid line) for αacc = 1 × 10−3 is seen in the right panel (see texts for the potential reason). |
3.8 Dependence on αacc
In this subsection, we present the dependence on αacc. Here, αacc = 1 × 10−3, 3 × 10−3, and 1 × 10−2 were used with τs = 0.01. Figure 7 shows the dependence of the resultant planetesimal belt on αacc. Because we used τs = 0.01, the timescale to reach a steady-state becomes longer than with τs = 0.1 (~100 kyr; see the right panel in Fig. 7; see also Sect. 3.7).
A larger αacc yields a smaller gas surface density (Eq. (1)). This leads to a larger ratio of pebbles to gas midplane density. Thus, the critical αmid for the ND to be triggered becomes larger (Eq. (11)), that is, the ND starts at a larger radial distance for the same dead zone structure. Also, as Z becomes globally higher, the width of the planetesimal formation becomes larger (see the left and middle panels in Fig. 7). The rate of planetesimal formation during the early (nonlinear) phase also depends on αacc (the panel in Fig. 7). This would be because the drift velocity of pebbles is smaller for a smaller αacc and thus the absorption of drifting pebbles into the pebble pile-up is less efficient, delaying the entrance into the steady-state regime.
For the cases of αacc = 10−2 and 3 × 10−3, the rate of plan-etesimal formation in steady-state are relatively well described by the analytical relations (see the red and green lines in the right panel of Fig. 7 and Eq. (13)). A small deviation is probably related to the fact that Eq. (13) assumes αacc ≪ τs while here αacc ~ τs. For αacc = 10−3, a large deviation between the analytical estimation (the blue dashed line) and the numerical simulation (the blue solid line) is seen. This would be because Fp/g,ND,min ≃ 0.46 is very close to Fp/g,given = 0.47 for αacc = 1 × 10−3 with τs = 0.01 − the same as cases of Fp/g,given = 0.17 seen in the middle panel of Fig. 5 − and the analytical estimation of Fp/gND,min does not fully include the effects of backreaction and diffusion. This potentially leads to a noticeable difference even from a small error in Fp/gNDmin because Fp/g,given − Fp/g,ND,mid is used to calculate Mpia,tot (see Eq. (13)).
4 Discussion
4.1 Comparison to other pile-up mechanisms
Depending on the disk structures as well as the physicochemical properties of the solids, different mechanisms may be responsible for trapping drifting particles. Here, we compare the ND mechanism with other mechanisms that can potentially pile up solids in disks.
Pressure bumps, radial maxima in the disk gas pressure, naturally lead to convergent motions of solid particles and their pile-up (Whipple 1972; Kretke & Lin 2007; Pinilla et al. 2012; Chatterjee & Tan 2014; Desch et al. 2018; Dullemond et al. 2018). These pressure bumps may be preferentially formed at the snow line (e.g., Müller et al. 2021; Charnoz et al. 2019, 2021) or at the outer edge of a dead zone due to the change of the α-viscosity (Pinilla et al. 2016). However, it is still questionable how the pressure bump is efficiently preserved against the backreaction of the solid pile-up (e.g., Taki et al. 2016; Kanagawa et al. 2018).
The pressure bump found by Pinilla et al. (2016) at the edge of a dead zone is caused by the evolution of a standard α-disk. However, the evolution of non-standard disk models, such as when including disk winds and accounting for vertical variations of angular momentum transport, do not necessarily lead to the formation of such a pressure bump, even in the presence of a dead zone. Also, the feedback, backreaction, from the accumulating pebbles to the gas may smooth out a bump structure. Our study shows that even without a pressure bump, particle pile-up may occur (for appropriate change in the vertical turbulence and pebble-to-gas mass flux) through the ND mechanism. Although this should be studied through dedicated simulations including disk evolution and backreaction effects, in the presence of a pressure bump, the ND mechanism should combine to convergent motions of particles to lead to a more pronounced pile-up of pebbles.
Other mechanisms leading to a pile-up of particles require efficient particle growth and/or fragmentation combined to the backreaction. If these lead to a strong enough modification of the gas profile, dust particles may pile up (e.g., Gonzalez et al. 2017; Gárate et al. 2020). The inner region of disks may also be a favorable location for solids to pile up via a traffic-jam effect, if the fragmentation is efficient enough at a small radial distance where the Keplerian velocity is high (e.g., Birnstiel et al. 2012; Laibe et al. 2012; Drążkowska et al. 2016). Finally, sublimation and re-condensation of particles, that is, recycling of materials, around the snow line may trigger the solid pile-ups (e.g., Stevenson & Lunine 1988; Ciesla & Cuzzi 2006; Birnstiel et al. 2010; Ros & Johansen 2013; Morbidelli et al. 2015; Estrada et al. 2016; Armitage et al. 2016; Schoonenberg & Ormel 2017; Drążkowska & Alibert 2017; Ida & Guillot 2016; Ida et al. 2021; Hyodo et al. 2019, Hyodo et al. 2021a).
The ND mechanism differs from the above mechanisms in that it does not require a pressure bump, snow line, and pebble growth and/or fragmentation. Instead, it requires an increase in αmid/αacc with radial distance combined to the backreaction of solids to the gas that slows down the radial velocity of pebbles. The ND mechanism may be favored during the early phase of the disk evolution when the solid mass budget is large enough (i.e., a large Fp/g) (Drążkowska et al. 2021) and when an efficient gas accretion may take place with a dead zone (i.e., a small αmid/αacc) (Lee et al. 2021). Our results highlight the importance of better observational constraints of gas and diffusion structure to understand whether the ND mechanism is indeed responsible for the dust trapping and formation of planetesimals (see also Sect. 4.2).
4.2 Application to evolving protoplanetary disks
In this study, using local simulations, Fp/g was set as a fixed constant at the outer boundary and the gas surface density was described by the classical α-disk model 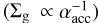 . This approach helped us to understand the nature and essence of the ND mechanism and the resultant planetesimal belt.
. This approach helped us to understand the nature and essence of the ND mechanism and the resultant planetesimal belt.
In reality, however, protoplanetary disks and Fp/g evolve as a function of time and the radial distance (e.g., Drążkowska et al. 2021). Discrete accretion episodes may exist (e.g., Armitage et al. 2001; Zhu et al. 2009) and Fp/g could be time-dependent. Indeed, Elbakyan et al. (2020) demonstrated short-period discrete accretion fluxes of pebbles at the early stages in the disk evolution (see also Ida et al. 2021).
If the change in Fp/g is slow compared to the timescale to reach a steady width of the planetesimal belt (e.g., ≃ 10 kyr for τs = 0.1 and ≃ 100 kyr for τs = 0.01 at r ≲ 10 au; Fig. 5), the outcomes would be similar to those observed in the late epochs in the simulations when planetesimals keep being formed within a fixed width (e.g., Fig. 2). In this case, the analytical estimations (e.g., Eq. (13)) can be used to predict the rate of planetesimal formation which does not depend on the radial structure of the dead zone and on kSI (see Sect. 3.5).
If it is the other way around, the width and profile of the planetesimal belt are time-dependent (e.g., when Fp/g changes within ~ 10 kyr for τs = 0.1; Fig. 5). In this case, the rate of planetesimal formation depends on the disk radial structure (i.e., dead zone structure) and kSI. Such a case could be inferred by the lines in the early phase of the evolutions in Figs. 2–5 where the width is changing (see the lines in different colors in Figs. 2–5). The exact timescale to reach a steady width of the planetesimal belt depends on the dead zone structure in the radial direction, kSI, and τs (Figs. 5 and 6).
The values of the gas accretion parameter (αacc) and of the parameter controlling the effect of vertical stirring of solid particles in the midplane (αmid) are poorly known. Variations of the stellar accretion rate with age, the disk lifetime, and the extent of protoplanetary disks point to a disk evolution that should proceed with an effective viscosity parameter αacc ~ 10−3−10−2 (Hueso & Guillot 2005; Hartmann et al. 2016). Separately, although it is an indirect estimation and thus one should be cautious interpreting data, dust settling compatible with ALMA observations seems to indicate a turbulence level of αmid ~ (0.1−1) × 10−3 (Mulders & Dominik 2012; de Juan Ovelar et al. 2016; Pinte et al. 2016). Measurements of nonthermal gas motions point to similarly low turbulence values, a potential indication of αmid ~ 10−3 or less (Boneberg et al. 2016; Flaherty et al. 2020).
Our chosen parameters of αacc and αmid are within the range of the estimated values above. However, a deeper investigation of the disk structures, including the radial structure and Fp/g, both from theoretical and observational sides are required to further test the applicability of the ND mechanism.
4.3 Application to planet formation
As discussed hereafter, planetesimal formation via the no-drift mechanism may prevent pebbles from drifting further inward and lead to the formation of seed planetesimals that would then grow by successive pebble accretion waves.
First, in the ND scenario, pebbles drift inward from the outer disk region, entering a dead zone. As a consequence of the ND mechanism, the pebble mass flux that is propagated interior to the ND zone is reduced from Fp/g outside the dead zone to approximately Fp/gND,min inside the dead zone, as estimated from Eq. (12). This indicates the partial blocking of pebbles from flowing further inward.
A stopping of drifting water-rich pebbles may be needed to avoid too much “wetting” of the inner planets, such as the terrestrial planets, to explain their observed water contents. The efficiency of pebble retention via the ND mechanism is proportional to the minimum 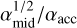 value (Eq. (12)). Fp/g,ND,min/Fp/g,given is the fraction of pebbles that passes through the ND region. The other possible filtering mechanisms are the presence of pressure bumps, the growth of a large planetary core (Guillot et al. 2014; Morbidelli et al. 2016; Bitsch et al. 2021), and/or the early consumption of solid materials in small size disks (Ida et al. 2019).
value (Eq. (12)). Fp/g,ND,min/Fp/g,given is the fraction of pebbles that passes through the ND region. The other possible filtering mechanisms are the presence of pressure bumps, the growth of a large planetary core (Guillot et al. 2014; Morbidelli et al. 2016; Bitsch et al. 2021), and/or the early consumption of solid materials in small size disks (Ida et al. 2019).
Second, because the ND mechanism operates only while the criterion defined by Eq. (11) is satisfied (see also Paper I), the total mass of planetesimals depends on how long this condition is fulfilled (Sect. 3.6). As discussed in Sect. 4.2, the duration of the relatively high Fp/g for the ND mode to operate may be short. In this case, the total amount of planetesimals formed by the ND mechanism might be inadequate to fully form a giant planet (Fig. 5).
In this study, we assumed that pebbles whose Stokes number is τs ~ 0.01−0.1 so that pebbles are decoupled from the gas. Very small dust particles are well coupled with the gas and are thus not subject to the SI. Now, classically, pebbles are expected to be larger outside the snow line, due to more efficient sticking properties for ice than for rock (e.g., Blum & Wurm 2000). This would imply that the ND mechanism with the SI may be favored at a greater radial distance than the snow line. Recent studies of material sticking properties, however, challenged this conventional view (e.g., Kimura et al. 2015; Gundlach et al. 2018; Musiolik & Wurm 2019; Steinpilz et al. 2019). In that case, rocky pebbles may also potentially experience the ND mode to form rocky planetesimals, if the criteria are satisfied (e.g., Fig. 1 and Eq. (11)).
Such considerations lead us to envision that the combination of planetesimal seeds formation via the ND mechanism with SI and successive pebble accretion (e.g., Ormel & Klahr 2010; Lambrechts & Johansen 2014; Liu et al. 2019) could lead to the formation of a large planetary core, even if the ND mode itself forms only a limited amount of planetesimals. We leave consideration of the pebble/planetesimal-to-planet formation in the context of the ND mechanism for future study.
Lastly, even if particles are too small for the SI to operate (e.g., τs < 0.01; Kataoka et al. 2017) but when the ND mode develops with small τs, planetesimals may be formed via GI of runaway piling-up small dust particles. Studying GI in the context of the ND mechanism for small dust particles is beyond the scope of this paper and we leave that for future work.
5 Summary
The no-drift (ND) mechanism is a newly identified instability mode in which a runaway pile-up of pebbles results from a variation of the vertical turbulence in the disk (Hyodo et al. 2021b, Paper I). This process requires (1) the pebble-gas back-reaction that slows down the radial velocity of pebbles and (2) a disk structure whose αmid/αacc decreases with decreasing r, where αacc and αmid independently characterize the gas accretion (i.e., the surface density of gas) and the vertical turbulence (i.e., the scale height of pebbles), respectively. Such a nonuniform turbulent disk structure is motivated by recent nonideal magneto-hydrodynamics (MHD) simulations of a dead zone and a disk wind. Contrary to other planetesimal formation mechanisms, the ND mechanism does not require a pressure bump, snow line, and pebble growth and/or fragmentation.
In this study, we numerically modeled that pebbles drift inward from the outer region of a dead zone (r ≲ 10 au), where the scale height of pebbles becomes smaller with decreasing r (i.e., αmid decreases with decreasing r). The gas surface density was independently controlled by αacc in a classical α-disk model.
Once the ND mode develops, the pile-up of pebbles continues in a runaway fashion for a fixed Fp/g without any consideration of planetesimal formation from accumulating pebbles Paper (I). In reality, however, planetesimals would form via the streaming instability as the midplane pebble-to-gas ratio of the spatial density becomes larger than unity via the ND mode.
Here, we additionally included a prescription of the streaming instability in our 1D numerical code assuming a fixed Fp/g and using a modeled dead zone to study the resultant planetesi-mal belt formed by the ND mechanism and SI. The main findings are as follows:
After pebbles enter a ND mode, planetesimals start to form via SI initially within a narrow ring whose width expands as accumulating pebbles radially diffuse over time (i.e., the radial width of the ND mode expands). The system finally reaches a steady-state in ρp/ρg, where the width of the plan-etesimal belt no longer changes, followed by continuous formation of planetesimals within a fixed width for a given fixed Fp/g and disk structure (Sect. 3.2 and Fig. 2).
Planetesimal formation by the ND mechanism results from a complex interplay between a pile-up of pebbles drifting inward more slowly due to the backreaction effect, an absorption of inward-drifting pebbles, a radial diffusion of piled-up pebbles, and the conversion from pebbles to plan-etesimals via SI (Eq. (8)). Thus, the width and profile of the planetesimal belt depend on the disk structure and kSI value. The smoother radial change in αmid/αacc and/or smaller kSI result in more radially-extended planetesimal belts (Figs. 2 and 3). Correspondingly, the timescale to reach a fixed width becomes longer (Fig. 5) and so does for a smaller τs (Fig. 6).
Once the planetesimal formation reaches a steady-state in ρp/ρg with a fixed radial width for a given constant Fp/g, the rate of planetesimal formation within the belt does not depend on the disk’s radial structure and kSI, but it is regulated by Fp/g and the minimum value of αmid/αacc (Sect. 3.6, Fig. 5, and Eq. (13)).
For our nominal settings (Ṁg ≳ 10−8 M⊙ yr−1, Fp/g ≳ 0.1, τs ≃ 0.01−0.1, αmid ≲ 10−4, and αacc ≃ 10−3−10−2 at r ≲ 10 au with kSI ≳ 10−3), a non-negligible total mass of plan-etesimals (more than Earth mass) is formed within about 10–100 kyr via the no-drift mode.
This study focused on the physics of the no-drift mechanism and the nature of the resultant planetesimal belt. To fully address the fate of a specific system where the ND is possibly occurring, we need full global simulations that include pebble growth and the disk viscous evolutions, and that self-consistently solve the dead zone structure. Such a completely self-consistently coupled numerical approach is conceptually and numerically challenging at this moment which will be the subject of future work.
Acknowledgements
R.H. acknowledges the financial support of JSPS Grants-in-Aid (JP17J01269, 18K13600). R.H. also acknowledges JAXA’s International Top Young program. S.I. acknowledges the financial support (JSPS Kakenhi 15H02065), MEXT Kakenhi 18H05438). T.G. thanks the University of Tokyo and ELSI for their hospitality during 2019-2020 and acknowledges support from JSPS (long-term fellowship L19506). We thank the anonymous referee for thought-provoking comments which substantially improved the presentation of this manuscript.
References
- Armitage, P. J. 2011, ARA&A, 49, 195 [Google Scholar]
- Armitage, P. J., Livio, M., & Pringle, J. E. 2001, MNRAS, 324, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., Eisner, J. A., & Simon, J. B. 2016, ApJ, 828, L2 [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 769, 76 [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Izidoro, A., Johansen, A., et al. 2019, A&A, 623, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Raymond, S. N., Buchhave, L. A., et al. 2021, A&A, 649, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
- Boneberg, D. M., Panic, O., Haworth, T. J., Clarke, C. J., & Min, M. 2016, MNRAS, 461, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Johansen, A., & Davies, M. B. 2015, A&A, 579, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnoz, S., Pignatale, F. C., Hyodo, R., et al. 2019, A&A, 627, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnoz, S., Avice, G., Hyodo, R., Pignatale, F. C., & Chaussidon, M. 2021, A&A, 652, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatterjee, S., & Tan, J. C. 2014, ApJ, 780, 53 [Google Scholar]
- Chiang, E. 2008, ApJ, 675, 1549 [CrossRef] [Google Scholar]
- Ciesla, F. J., & Cuzzi, J. N. 2006, Icarus, 181, 178 [NASA ADS] [CrossRef] [Google Scholar]
- de Juan Ovelar, M., Pinilla, P., Min, M., Dominik, C., & Birnstiel, T. 2016, MNRAS, 459, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J., Estrada, P. R., Kalyaan, A., & Cuzzi, J. N. 2017, ApJ, 840, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J., Kalyaan, A., & O’DAlexander, C. M. 2018, ApJS, 238, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Drążkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [Google Scholar]
- Drążkowska, J., Alibert, Y., & Moore, B. 2016, A&A, 594, A105 [Google Scholar]
- Drążkowska, J., Stammler, S. M., & Birnstiel, T. 2021, A&A, 647, A15 [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Dzyurkevich, N., Turner, N. J., Henning, T., & Kley, W. 2013, ApJ, 765, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Elbakyan, V. G., Johansen, A., Lambrechts, M., Akimkin, V., & Vorobyov, E. I. 2020, A&A, 637, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Estrada, P. R., Cuzzi, J. N., & Morgan, D. A. 2016, ApJ, 818, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K., Hughes, A. M., Simon, J. B., et al. 2020, ApJ, 895, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Nelson, R. P., Turner, N. J., et al. 2017, ApJ, 850, 131 [Google Scholar]
- Flock, M., Turner, N. J., Mulders, G. D., et al. 2019, A&A, 630, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gárate, M., Birnstiel, T., Drążkowska, J., & Stammler, S. M. 2020, A&A, 635, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerbig, K., Murray-Clay, R. A., Klahr, H., & Baehr, H. 2020, ApJ, 895, 91 [CrossRef] [Google Scholar]
- Goldreich, P., & Ward, W. R. 1973, ApJ, 183, 1051 [Google Scholar]
- Gonzalez, J. F., Laibe, G., & Maddison, S. T. 2017, MNRAS, 467, 1984 [NASA ADS] [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gundlach, B., Schmidt, K. P., Kreuzig, C., et al. 2018, MNRAS, 479, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [Google Scholar]
- Hayashi, C., Nakazawa, K., & Nakagawa, Y. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews, 1100 [Google Scholar]
- Hueso, R., & Guillot, T. 2005, A&A, 442, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hyodo, R., Ida, S., & Charnoz, S. 2019, A&A, 629, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hyodo, R., Guillot, T., Ida, S., Okuzumi, S., & Youdin, A. N. 2021a, A&A, 646, A14 [EDP Sciences] [Google Scholar]
- Hyodo, R., Ida, S., & Guillot, T. 2021b, A&A, 645, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Guillot, T. 2016, A&A, 596, L3 [EDP Sciences] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., Yamamura, T., & Okuzumi, S. 2019, A&A, 624, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., Guillot, T., Hyodo, R., Okuzumi, S., & Youdin, A. N. 2021, A&A, 646, A13 [EDP Sciences] [Google Scholar]
- Johansen, A., & Youdin, A. 2007, ApJ, 662, 627 [Google Scholar]
- Kanagawa, K. D., Muto, T., Okuzumi, S., et al. 2018, ApJ, 868, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Tsukagoshi, T., Pohl, A., et al. 2017, ApJ, 844, L5 [Google Scholar]
- Kimura, H., Wada, K., Senshu, H., & Kobayashi, H. 2015, ApJ, 812, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2007, ApJ, 664, L55 [CrossRef] [Google Scholar]
- Laibe, G., Gonzalez, J. F., & Maddison, S. T. 2012, A&A, 537, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., Charnoz, S., & Hennebelle, P. 2021, A&A, 648, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lichtenberg, T., Drążkowska, J., Schönbächler, M., Golabek, G. J., & Hands, T. O. 2021, Science, 371, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Ormel, C. W., & Johansen, A. 2019, A&A, 624, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Miller, E., Marino, S., Stammler, S. M., et al. 2021, MNRAS, 508, 5638 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bitsch, B., Crida, A., et al. 2016, Icarus, 267, 368 [Google Scholar]
- Mori, S., Bai, X.-N., & Okuzumi, S. 2019, ApJ, 872, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A&A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, J., Savvidou, S., & Bitsch, B. 2021, A&A, 650, A185 [Google Scholar]
- Musiolik, G., & Wurm, G. 2019, ApJ, 873, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., & Hirose, S. 2011, ApJ, 742, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Flock, M., Ovelar, M. D. J., & Birnstiel, T. 2016, A&A, 596, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [Google Scholar]
- Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safronov, V. S. 1972, Evolution of the protoplanetary cloud and formation of the earth and planets [Google Scholar]
- Schoonenberg, D., & Ormel, C. W. 2017, A&A, 602, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stammler, S. M., Drążkowska, J., Birnstiel, T., et al. 2019, ApJ, 884, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Steinpilz, T., Teiser, J., & Wurm, G. 2019, ApJ, 874, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J., & Lunine, J. I. 1988, Icarus, 75, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Taki, T., Fujimoto, M., & Ida, S. 2016, A&A, 591, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
- Whipple, F. L. 1972, in From Plasma to Planet, ed. A. Elvius, 211 [Google Scholar]
- Yang, C. C., Johansen, A., & Carrera, D. 2017, A&A, 606, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Youdin, A. N., & Shu, F. H. 2002, ApJ, 580, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Gammie, C., & McKinney, J. C. 2009, ApJ, 701, 620 [CrossRef] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Midplane pebble-to-gas ratio Z = ρp /ρg in the αmid/αacc − Fp/g space (Eq. (10)). Top and bottom panels correspond to αacc = 10−2 and αacc = 10−3, respectively. Left and right panels correspond to τs = 0.01 and τs = 0.1, respectively. The color contours are obtained by directly solving Eq. (10). The red-colored regions indicate the “no-drift” runaway pile-up (i.e., ρp/ρg goes to infinity; no-solution). The calculations correspond to r = 5 au, but the results depend very weakly on the radial distance to the star. The ND mode can occur irrespectively of the radial shape and position of a dead zone (see more details in Paper I). We note that the physics of planetesimal formation is not included here. |
| In the text | |
 |
Fig. 2 Overall results of our numerical simulations for different combinations of the disk structure and Fp/g. Top panels: given disk structures (the black lines; see Table 1). Middle panels: resultant midplane pebble-to-gas ratio of the spatial density, ρp/ρg. Bottom panels: resultant planetesimal surface density formed by the ND mode and SI (Eq. (8)). The blue, green, and red lines indicate time evolution. By t ≃ 1 × 105 yr, the system reaches a steady-state in ρp/ρg and then planetesimals keep forming in a steady width. The dashed gray lines in the top panels represent analytically derived critical αmid/αacc for a given Fp/g (Eq. (11)), indicating that disks of smaller αmid/αacc than this critical value develop the ND mode. The gray lines in the middle panels represent the critical ρp/ρg above which the ND mode occurs (i.e., ρp/ρg = 1). Here, αacc = 10−2, τs = 0.1, Mg = 10−8 M⊙ yr−1, and kSI = 10−3 are used. |
| In the text | |
 |
Fig. 3 Dependence of the resultant planetesimal belt on kSI. Left and right panels: cases of different given disk structures (Disk 2 and Disk 3, respectively; Table 1). Top panels: given disk structures. Bottom three panels: the same combination of Fp/g and the disk structure but different kSI. The dashed gray lines in the top panels show the analytically derived critical αmid/αacc for a given Fp/g, indicating that disks having smaller αmid/αacc than the critical one are expected to develop the ND mode (no dependence on kSI; Eq. (11)). The blue, green, red, and black lines represent time evolution. By t ≃ 3 x 105 years, all cases reach a steady-state in ρp/ρg and the planetesimals keep forming in a ring with a constant width. The gray lines represent the midplane pebble-togas ratio, ρp/ρg, at the steady-state shown in the right axis. Here, τs = 0.1 and Mg = 10−8 M⊙ yr−1 are used. |
| In the text | |
 |
Fig. 4 Dependence of the resultant planetesimal belt on Ṁg. Left to right panels are the cases of Ṁg=10−9,10−8, and 10−7 M⊙ yr−1, respectively. The gray lines represent the surface density of solids in the classical minimum mass solar nebula model (MMSN; Σpla = 30(r/1 au)−3/2 gcm−2) of Weidenschilling (1977) for reference. By t ≃ 1 × 105 yr, the system reaches a steady-state in ρp/ρg and width of the planetesimal ring. Here, αacc = 10−2, τs = 0.1, and kSI = 10−3 are used. |
| In the text | |
 |
Fig. 5 Cumulative mass of planetesimals, Mpla,tot, formed by the ND mechanism as a function of time. The thin dashed lines are analytically derived cumulative masses of planetesimals (Eq. (13)). The thick solid lines are the results of numerical simulations. Here, we sorted numerical data so that planetesimal formation starts at t = 0 kyr (i.e., the time at which ρd/ρg exceeds 1, which should depend on the parameters in the numerical simulations, is always shifted to t = 0 kyr). Left panel: dependence on Ṁg where Ṁg(= 10−7, 10−8, and 10−9 M⊙ yr−1) are a variable while the disk structure (Disk 3) and Fp/g = 0.47 are kept the same. Middle panel: dependence on disk structure and Fp/g where disk structure (Disk 1 or Disk 3; see Table 1) and Fp/g(= 0.17 or 0.47) are variables while keeping the same Ṁg = 10−8 M⊙ yr−1. Right panel: dependence on kSI where kSI = 10−2,10−3, and 10−4 while having the same disk structure (Disk 2), Fp/g = 0.47, and Ṁg = 10−8 M⊙ yr−1. After around ~10–100 kyr, depending on the parameters, the rate of planetesimal formation can be described by the analytical arguments (dashed lines); that is, the system reaches a steady width of the planetesimal belt (Sect. 3.6). In this study, Fp/g is kept constant (i.e., infinite solid mass budget). We note, however, that the maximum total mass of planetesimals in a real system should be regulated by the mass budget of solids (see Sect. 3.6). Here, αacc = 10−2 and τs = 0.1 are used. |
| In the text | |
 |
Fig. 6 Dependence of the resultant planetesimal belt on the Stokes number, τs (blue for τs = 0.01, green for τs = 0.03, and red for τs = 0.1, respectively). Left panel: resultant midplane pebble-to-gas ratio of the spatial density, Z = ρp/ρg, after the establishment of the steady-state. Middle panel: resultant planetesimal surface density at t = 100 kyr since the start of planetesimal formation. The gray line is the classical minimum mass solar nebula model (MMSN; Σpla = 30(r/1 au)−3/2 g cm−2) of Weidenschilling (1977). Right panel: cumulative mass of planetesimals, Mpla,tot, formed by the ND mechanism since the start of planetesimal formation. The thin dashed line is analytically derived cumulative mass of planetesimals with τs = 0.1. Here, Disk 2, αacc = 10−2, Ṁg = 10−8 M⊙ yr−1, Fp/g = 0.47, and kSI = 10−3 are used. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but for different αacc (blue for αacc = 1 × 10−3, green for αacc = 3 × 10−3, and red for αacc = 1 × 10−2, respectively). Here, Disk 2, τs = 0.01, Ṁg = 10−8M⊙ yr−1, Fp/g = 0.47, and kSI = 10−3 are used. A large deviation between the analytical estimation (blue dashed line) and the simulation (blue solid line) for αacc = 1 × 10−3 is seen in the right panel (see texts for the potential reason). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


