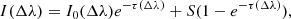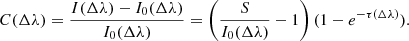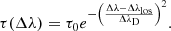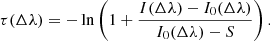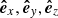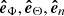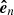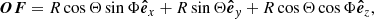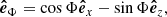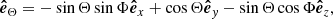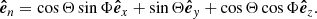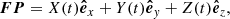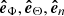| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A172 | |
| Number of page(s) | 18 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202450099 | |
| Published online | 07 October 2024 | |
A fast-filament eruption observed in the Hα spectral line
I. Imaging spectroscopy diagnostic
1
Institute for Space-Earth Environmental Research, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, Aichi 464-8601, Japan
2
Astronomical Observatory, Kyoto University, Kitashirakawa-Oiwake-Cho, Sakyo-Ku, Kyoto 606-8502, Japan
3
National Institute of Information and Communications Technology, Nukui-Kitamachi, Koganei, Tokyo 181-8795, Japan
4
School of Science and Engineering, Doshisha University, Kyotonabe, Kyoto 610-0394, Japan
Received:
23
March
2024
Accepted:
28
June
2024
Context. Solar filament eruptions usually appear to occur in association with the sudden explosive release of magnetic energy accumulated in long-lived arched magnetic structures. The released energy occasionally drives fast-filament eruptions that can be the source regions of coronal mass ejections. A quantitative analysis of high-speed filament eruptions is thus essential to help elucidate the formation and early acceleration of coronal mass ejections.
Aims. The goal of this paper is to investigate the dynamic processes of a fast-filament eruption by using unprecedented high-resolution full-disk Hα imaging spectroscopy observations.
Methods. The whole process of the eruption was captured in a wide spectral window of the Hα line (±9.0 Å), which allowed for the detection of highly Doppler-shifted plasma. By applying the “cloud model” and obtaining two-dimensional optical thickness spectra, we derived the Doppler velocity; the true eruption profiles (height, velocity, and acceleration); and the trajectory of the filament eruption in 3D space.
Results. The Doppler velocity maps show that the filament was predominantly blueshifted. During the main and final process of the eruption, strongly blueshifted materials manifest, traveling with velocities exceeding 250 km s−1. The spectral analysis further revealed that the erupting filament is made of multiple components, some of which were Doppler-shifted approximately to −300 km s−1. We found that the filament eruption attains a maximum true velocity and acceleration of about 600 km s−1 and 2.5 km s−2, respectively, and its propagation direction deviates from the radial direction. On the other hand, downflows manifested as redshifted plasma close to the footpoints of the erupting filament move with velocities of 45–125 km s−1. We interpret these redshifted signatures as draining material and therefore as mass loss of the filament, which has implications for the dynamic and the acceleration process of the eruption. Furthermore, we have estimated the total mass of the Hα filament, resulting in ∼5.4 × 1015 g.
Key words: radiative transfer / techniques: imaging spectroscopy / Sun: chromosphere / Sun: coronal mass ejections (CMEs) / Sun: filaments / prominences
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Solar filaments are dense and cool “magnetic clouds” immersed in the chromosphere and hot corona. They are seen as dark elongated structures against the bright solar disk and are also referred to as prominences when they are projected above the solar limb as bright standing-up strands. Filaments are best observed in cool spectral lines, such as hydrogen and helium, that originate at chromospheric temperatures. This indicates that filaments are made of relatively low temperature (∼104 K) and high density (∼1011 cm−3) plasma, that is, about two orders of magnitude cooler and denser than the surrounding tenuous coronal environment. Depending on the morphology, dynamic properties, and their relative location on the solar disk, filaments are generally classified into three categories: quiescent, intermediate, and active region filaments (Mackay et al. 2010; Engvold 2015, and references therein).
Because quiescent filaments form along the magnetic polarity inversion line and are confined only in some specific regions of the solar atmosphere (Martin et al. 1994; Tandberg-Hanssen 1995), it is believed that they are sustained in equilibrium against gravity by the horizontal component of the ambient magnetic field and are thermally shielded from the encompassing hot corona (Tandberg-Hanssen 1970, 1995; Engvold 2015; Hillier 2018). This means that any change or reconfiguration of the magnetic field harboring a filament may lead to the loss of equilibrium and the eventual eruption of the filament. On the other hand, mass unloading, or mass draining, has also been pointed to as an important factor that could induce the loss of equilibrium and the subsequent eruption of filaments. Observational evidence of mass unloading before a filament eruption has been presented in early works (e.g., Seaton et al. 2011; Huang et al. 2014; Li et al. 2017; Jenkins et al. 2018; Doyle et al. 2019), and quite recently analytical and numerical studies have also been conducted (e.g., Vršnak 2019; Tsap et al. 2019; Fan 2020). Accordingly, it is reasonable to believe that the mass drainage that could appear during filament and prominence eruptions may also exert influences on the acceleration process.
In many cases, observations have revealed that during the preeruption stage, filaments exhibit signs of activation followed by a slow rise and a gentle expansion; thereafter, at a certain point when the filament enters an eruption stage, it experiences a drastic transition from slow to fast expansion (e.g., Kahler et al. 1988). Particularly in the latter stage, the system becomes very dynamic, where a large amount of the filament material is strongly accelerated upward to velocities over 100 km s−1. Filament eruptions can be accompanied by solar flares and coronal mass ejections (CMEs), but interestingly most of the erupting filaments are directly associated with the occurrence of CMEs (e.g., Gilbert et al. 2000; Forbes et al. 2006; Gopalswamy 2015, and references therein). Therefore, understanding the initiation and acceleration processes of filament and prominence eruptions can provide reliable clues on the formation, development, and launch of CMEs. In this respect, we can mention the new results about eruptive events and CMEs reported by Russano et al. (2024) based on observations of the Metis coronagraph (Antonucci et al. 2020) on board Solar Orbiter (Müller et al. 2020).
Several works have dealt with the problem of acceleration of filament eruptions by trying to qualitatively elucidate the governing physical processes involved in the eruptions (e.g., Gilbert et al. 2000; Vršnak 2001; Gallagher et al. 2003; Török & Kliem 2005; Williams et al. 2005; Schrijver et al. 2008; Cheng et al. 2020, and references therein). In these works, the authors used different fitting models, such as linear, nonlinear, or composite models, to replicate the eruption profiles inferred from observations. Although in most case studies the main acceleration phase could be satisfactorily characterized with exponential forms, it has been found that polynomial and power-law functions can also yield reliable results (Priest & Forbes 2002; Schrijver et al. 2008). It is thus clear that different driving processes are at work during the eruptions, which also means that the mechanism responsible for filament eruptions may vary from event to event. We leave the theoretical aspects of filament eruptions and results of numerical modeling to Cabezas et al. (in prep., hereafter Paper II).
Quantifying the real magnitude of filaments and prominence eruptions requires an accurate determination of the actual propagation speed. However, at present, most studies still make use of the projected motion in the plane of sky as the main parameter, and in some cases assumptions are imposed to estimate the true motion of the erupting material while paying no attention to the line of sight component (i.e., directed toward the Earth). Therefore, caution should be taken because quite often only the plane of sky component has been used to draw conclusions and adopted in the majority of models to predict the propagation of CMEs. Although we should make a distinction between eruptions occurring on disk and off limb (or at the solar limb). If an off limb eruption has a strong radial velocity component, then its actual propagation speed could be constrained mainly by its apparent motion in the plane of sky. However, the situation of on disk eruptions requires appropriate treatments because they can be strongly affected by the line of sight component.
The difficulties in deriving the true motion of erupting filaments and prominences lie mainly in the limited spectral window of conventional instruments, the small field of view in the case of large-aperture telescopes, and the scanning time across the full-disk image in the case of spectrographs. These limitations prevent the detection of large Doppler-shifted plasma and tracking of the whole evolution of the eruption. Here it is worth mentioning the work by Li et al. (2005), who based on Hα spectroscopic observations reported an extreme blueshift of a filament eruption exceeding 480 km s−1, and the calculated true velocity of the eruption was ∼700 km s−1. Similarly, Penn (2000) presented observations of a filament eruption and showed that the He I line (10830 Å) was strongly blueshifted to velocities 200–300 km s−1. Recently, Liu et al. (2015) and Zhang et al. (2019) also found large Doppler-shifted prominence eruptions in spectroscopic observations. On the other hand, some efforts have been made to recover the true velocity and three-dimensional trajectory of filament and prominence eruptions by employing spectroscopic observations (Zapiór & Rudawy 2010, 2012; Schmieder et al. 2017; Sakaue et al. 2018) and multiwavelength imaging observations (Morimoto & Kurokawa 2003; Chae et al. 2006; Cabezas et al. 2017; Gutierrez et al. 2021). Alternatively, there are a few reports in which the velocity components of the filament and prominence eruptions have been estimated by using stereoscopic observations (e.g., Bemporad 2009; Li et al. 2010; Bemporad et al. 2011; Rees-Crockford et al. 2020; Janvier et al. 2023; Russano et al. 2024), but these kinds of observations are still very sporadic.
In this paper, we report on a remarkable fast-filament eruption detected in a broad range of the Hα spectral profile by the Solar Dynamics Doppler Imager (SDDI; Ichimoto et al. 2017) on board the Solar Magnetic Activity Research Telescope (SMART; UeNo et al. 2004). This novel observing system provides high-resolution full-disk filtergrams in a wide spectral window of the Hα line, and it is particularly suitable for performing imaging spectroscopy analysis of filament and prominence eruptions that may emerge from any location of the solar disk. We focus on the different aspects of the filament eruption, with particular emphasis on the detection of highly Doppler-shifted plasma, the time development of the true velocity and acceleration profiles, and the trajectory of the eruption. Numerical modeling for the filament eruption is presented in Paper II of this series. The initial results based on SDDI observations can be found in Seki et al. (2017, 2019), where the increase in the amplitude of the Doppler velocity is discussed as a possible precursor of filament eruptions. Sun-as-a-star analysis of the SDDI Hα spectra was performed for a number of events by Otsu et al. (2022), and a statistical analysis of flare energies and mass ejections has recently been conducted by Kotani et al. (2023).
2. Observations
2.1. The Solar Dynamics Doppler Imager
SMART located at the Hida Observatory of Kyoto University consists of four refractive telescopes (e.g., UeNo et al. 2004; Ishii et al. 2013; Nagata et al. 2014; Kawate et al. 2016). SMART/T1 telescope designed to map full-disk solar images in the Hα line had an observing system covering a short set of wavelengths (± 1.2 Å) around the line center (6562.8 Å), which only permitted detections of relatively small Doppler velocity of filament and prominence eruptions. Since 2016, the observing system of SMART/T1 has been upgraded with a new Hα imaging instrument named Solar Dynamics Doppler Imager (SDDI: Ichimoto et al. 2017). This unique instrument consisting of a Lyot type birefringent tunable filter incorporates liquid-crystal variable retarders and is capable of recording successively high-resolution full-disk solar images at 73 positions (wavelengths) of the Hα spectral profile, spanning −9 to +9 Å from the line center with a wavelength step of 0.25 Å. This characteristic makes the SDDI a relevant instrument that allows not only imaging analysis to be performed but also spectroscopy diagnostics of flares and high-speed mass motions with large Doppler velocities (±400 km s−1) and the precise derivation of the velocity vectors in 3D space. The spatial sampling and time cadence of SDDI is 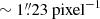 and 12 s (for the 73 wavelengths, 15 s before July 2018), respectively, and the field of view covered by the detector of the high-speed CMOS camera is 2520 × 2520 arcsec2.
and 12 s (for the 73 wavelengths, 15 s before July 2018), respectively, and the field of view covered by the detector of the high-speed CMOS camera is 2520 × 2520 arcsec2.
Before proceeding with the analysis of the filament presented in this paper, we performed standard data calibration by applying dark-current subtraction and flat-field gain corrections. Here it is important to mention that because the flat-pattern is wavelength-dependent of the tunable filter, we implemented individual flat-field images for each of the SDDI 73 spectral images following the method of Kuhn-Lin-Loranz (Kuhn et al. 1991), see also Ichimoto et al. (2017).
2.2. Overview of the event
On 2017 April 23, SDDI detected a filament eruption that occurred in association with a B-class solar flare at the heliographic coordinates N16 E41 (X = −605″, Y = 335″), near NOAA active region 12652. The filament eruption produced a narrow fast CME traveling with a plane of sky velocity of about 955 km s−11. The whole process of the filament eruption was captured by SDDI in the full set of wavelengths with a time cadence of 15 seconds. Figure 1 shows a full-disk solar image in the Hα line taken at 05:10:36 UT, where the white box encloses the filament that lies on a quiescent region. In the bottom panel we present the SDDI Hα spectral profile of a quiet-sun region (X = −580″, Y = 148″) corresponding to the intensity emerging at μ ≈ 0.78 (cosine of the heliocentric angle). The Atlas solar spectrum (Kurucz et al. 1984) normalized to the continuum level is also shown, as well as the convolution of the Atlas spectrum with the SDDI filter transmission profile. Also, it is plotted an example of a strongly blueshifted spectral profile obtained from the lateral part of the filament eruption at 05:44:50 UT.
 |
Fig. 1. Overview of the studied filament and Hα spectral profiles. Panel (a): Solar disk in the Hα line (6562.8 Å) captured by the Solar Dynamics Doppler Imager (SDDI) shortly before the filament eruption. The white box encloses the filament and outlines the field of view (FOV) of the images presented in Fig. 2. The small red box (50″ × 50″) surrounds a quiet-sun region from which the spectral profile is obtained and plotted in panel (b) by the red curve. The slit S1 is positioned in the direction of the leading part of the eruption (filament apex), whereas the slit S2 is used to track the lateral part of the eruption. Panel (b): Atlas solar spectrum of the Hα line (gray normalized to the continuum level) and convolution of the Atlas spectrum with the SDDI filter transmission profile (black). The quiet-sun SDDI spectral profile (see panel a) at μ ≈ 0.78 is also shown (red dots with spline interpolation), and an example of a strongly blueshifted profile (blue dots with spline interpolation) from the lateral part of the filament eruption at 05:44:50 UT (see Fig. 2). In the SDDI spectral profiles each dot represents the wavelength offset λs from the line center λ0 (6562.8 Å) at which SDDI performs regular observations. |
 |
Fig. 2. Eruption process of the filament captured in a wide range of the Hα spectral line. The maps are Dopplergrams wherein the blueshifted (dark) and redshifted (bright) features of the erupting material have manifested. The black lines labeled S1 and S2 on the map at 05:37:47 UT represent the artificial slits, and the green curved dashed-line outlines the arc-shaped filament (∼ 1.8 × 1010 cm). The orange arched line at 05:41:42 UT depicts the filament footpoint separation (∼1.6 × 1010 cm). During the eruption a large amount of the filament material is blueshifted up to 4.0 Å from the line center, also blobs-like structures are further blueshifted over 6.25 Å (red arrows). The symbol ‘+’ at 05:44:50 UT indicates the region from which a strongly blueshifted spectral profile is obtained and shown in Fig. 1. The bottom panels show blueshifted and redshifted spectral profiles from the regions outlined with blue and red circle marks (upper panels), the black profiles are from a quiet region. The redshifted profile (red plot) is caused by downflows close to the filament footpoint (see the text). The background hatched rectangles highlight the wavelength range of the Dopplergrams presented in each column of the upper panels. An animation of this figure is available online. |
Signatures of activation and slow-rising of the filament are observed approximately from 05:10–05:25 UT. By 05:30 UT, an arc-shaped structure already formed and started to grow rapidly becoming these characteristics more noticeable in the blue wing of Hα (e.g., 0.25–2.0 Å). The growing up and rapid expansion of the filament lasted for a few minutes, then at around 05:37 UT the filament apex is fragmented and a large amount of the erupting material is expelled into the outer space (see Fig. 2 and the associated animation). What is interesting but not surprising is that the footpoints of the filament remained rooted to the solar surface and the material contained in the filament legs exhibited signs of untwisting motions. During the late phase of the eruption, that is, from 05:50 UT onward, fragments of the ejected filament fall back onto the solar surface but a great portion persists ascending, later on, the filament simply fades out and disappears from the Hα images around 06:24 UT. The disappearance of the filament in the Hα line suggests that the material possibly reached high altitudes of the solar atmosphere, also because in the course of the eruption both the increase of the temperature and the diminution of the density contribute to the ionization (cf. Athay & Illing 1986), the hot ascending plasma is no longer visible in cool spectral lines like Hα.
A time series of the filament eruption captured by SDDI is presented in Fig. 2. The images are Dopplergrams resulting from the difference between mean-intensity maps recorded in the blue and red wings of the Hα line, that is, blue minus red mean-intensity maps in the wavelengths range: Hα ± (0.25:2.0 Å), Hα ± (2.25:4.0 Å), Hα ± (4.25:6.0 Å), and Hα ± (6.25:8.0 Å), respectively. The Dopplergrams illustrate the overall evolution of the filament eruption wherein the material directed toward the Earth is observed as dark structures (blueshift), while the component moving in the opposite direction is seen as bright structures (redshift). From 05:41 UT onward, highly blueshifted material can be identified even at very far-wing wavelengths (6.25:8.0 Å), which are indicated by the red arrows (see also the animation). This suggests that the broken parts of the filament are ejected exceeding a line of sight velocity of about 285 km s−1. A detailed analysis of the highly blueshifted filament material caused by the eruption is carried out in Sects. 3.2 and 3.3. Figure 2 (panel at 05:37:47 UT) also shows the positions of the artificial slits (S1, S2) used to make the time-distance diagrams, and the green dashed-line outlines the apparent length of the arc-shaped erupting filament (∼1.8 × 1010 cm). In the second column of Fig. 2 (panel at 05:41:42 UT) the orange arched line depicts the filament footpoint separation (∼1.6 × 1010 cm). The footpoint separation and the filament apex height are important parameters used to characterize the stability and acceleration process of arched magnetic flux ropes (e.g., Chen 1989; Vršnak 1990; Cargill et al. 1994; Olmedo & Zhang 2010, see also Paper II). Selected blueshifted and redshifted spectral profiles obtained from specific regions of the erupting filament are also shown in the bottom panels of Fig. 2. Here we remark the profile redshifted to 1.0–2.75 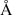 (second column) observed at the filament footpoint. This redshifted signature could be related to downflows or material precipitating down to the solar surface. Details of the detected redshifted features are discussed in Sect. 4.4.
(second column) observed at the filament footpoint. This redshifted signature could be related to downflows or material precipitating down to the solar surface. Details of the detected redshifted features are discussed in Sect. 4.4.
3. Analysis and results
3.1. Dynamical evolution and apparent motion
In Sect. 2.2 we mentioned that by 05:30 UT the formed arc-shaped filament exhibited a rapid ascending motion leading to the eruption. The dynamical evolution of the filament can be visualized as intensity variation in the multiwavelength time-distance diagrams made from Hα imaging spectroscopy observations. Results of the multiwavelength time-distance diagrams obtained along the filament apex (slit S1), namely, the leading part of the eruption, are presented in Fig. 3. Here it is important to mention that the vertical axes of Fig. 3 denote the apparent vertical distance in the plane of sky measured along the artificial slit from the initial position of the filament apex. In principle, the diagrams allow the apparent motion of the erupting filament in the plane of sky to be traced. However, because SDDI records filtergrams at multiple positions on both sides of the Hα line, the obtained diagrams also provide insights into the line of sight component. From the figure it is evident that depending on the wavelength range at which the time-distance plots are performed, particular characteristics of the erupting material are distinguished. In the diagram Hα ± (0.25:2.0 Å), the slow-ascending, the onset, and the main phase of the eruption are observed. At more far-wing wavelengths, that is, in the diagrams Hα ± (2.25:4.0 Å) and Hα ± (4.25:6.0 Å), the fast components of the eruption become visible at greater distances. Figure 3d shows a composite time-distance diagram resulting from the combination of the diagrams shown in panels (a), (b), and (c) – that is, including observations in the range Hα ± (0.25:6.0 Å). The composite diagram illustrates the complete picture of the eruption and demonstrates that as the eruption develops, not only does the filament’s apparent motion (plane of sky velocity) increase as a function of distance and time but also the line of sight velocity. Particularly during the late phase, the erupting filament exhibits a large line of sight velocity. Additionally, an exponential model fitting applied to the measured positions along the erupting feature in the plane of sky is overlaid on the composite diagram. This was done to highlight that the evolution of the filament eruption approximates to an exponential function. The measured positions were also used to estimate the plane of sky velocity of the eruption, which in combination with the line of sight velocity (see Sect. 3.4) allowed us to derive the true eruption profiles of the filament (velocity, height, and acceleration).
 |
Fig. 3. Multiwavelength time-distance diagrams of the filament eruption obtained along the slit S1 (filament apex). The vertical axes denote the apparent vertical distance in the plane of sky measured from the initial position of the filament apex. Panels (a), (b), and (c) show different characteristics of the eruption that become more evident at specific wavelengths. At Hα ± (0.25:2.0 Å) the slow-rising phase and the initial acceleration are observed, at Hα ± (2.25:4.0 Å) the main phase and fast acceleration have manifested, and at Hα ± (4.25:6.0 Å) the fastest-ascending phase is visible. Panel (d) is a composite time-distance diagram, which helps visualize the complete picture of the eruption and demonstrates that the line of sight velocity of the erupting filament also increases as a function of distance and time. The inset color-bar depicts the corresponding line of sight velocity of the wavelength range indicated in panels (a), (b), and (c). The dashed line is the fitting of an exponential function to the selected points along the erupting feature in the plane of sky. |
For comparison, time-distance diagrams were also obtained from He II (304 Å) images taken by the Atmospheric Imaging Assembly (AIA: Lemen et al. 2012) on board the Solar Dynamics Observatory (Pesnell et al. 2012). Figure 4 shows the filament eruption in the He II line, where on the map captured at 05:42:05 UT (panel a) the slit S1 (same as for Hα) from which we extracted the intensity variation is depicted. In the He II time-distance diagram (panel b), the eruption appears much more complex where two main branches become visible. One evolves ahead (filament apex), while the other lags behind. In the diagram, the yellow dotted-line represents the fitting of the measured points along the leading part of the eruption in the plane of sky, while the red dashed-line is the fitting result presented in the Hα time-distance diagram (see Fig. 3). Here we note that the slow-rise and main phase of the eruption in the He II diagram is well fitted with an exponential function, whereas the late phase of the eruption is fitted with a quadratic polynomial form. By comparing the evolution of the filament eruption in the Hα and He II diagrams, we found that the erupting features evolve quasi-identically, although the material seen in He II attains a greater distance (∼320 Mm) and is visible for a more extended period. In Hα, the maximum apparent distance attained by the eruption (filament apex) is ∼170 Mm; this happens at 05:41 UT, which is the instance at which the erupting material practically becomes invisible in the Hα diagram (see Fig. 3). On the other hand, the filament eruption also exhibits signs of unwinding (untwisting) motions. As shown in panel (c) of Fig. 4, such a manifestation is more pronounced during the main and fast-ascending phases of the eruption. In the following, we focus on these two phases of the filament eruption, that is, the period in which the eruption is well observed in Hα. This is also because we aim to calculate the true eruption profiles using imaging spectroscopy observations (see Sect. 3.4).
 |
Fig. 4. Observations of the filament eruption in the He II line (304 Å) and light curve of the associated solar flare. Panel (a): Main phase of the filament eruption, where the straight line labeled S1 outlines the artificial slit positioned along the filament apex (same as for Hα in Fig. 2). The curved cyan line depicts the filament footpoints separation, while the ‘×’ symbols outline the erupting material. Panel (b): Time-distance diagram extracted from the slit S1. The diagram shows a complex eruption, wherein at around 05:38 UT the erupting material splits into two main branches. The yellow dotted profile is the fitting curve applied to the selected positions along the erupting feature in the plane of sky, while the red dashed plot is the fitting curve applied to Hα data shown in Fig. 3. Panel (c): Running difference time-distance diagram showing the apparent unwinding motion of the erupting filament (see the text). As in Fig. 3, the vertical axis of panels (b) and (c) denote the apparent vertical distance in the plane of sky from the initial position of the filament apex. For context, the soft X-ray light curve of the B-class flare is also plotted in panel (d). The temporal evolution of the profiles in panel (b) suggests that the eruption of the filament started before the soft X-ray flux enhancement. |
3.2. Doppler velocity based on the cloud model
The classical “cloud model” introduced by Beckers (1964) is an effective tool to derive the physical properties of filaments and prominences, as well as of fine structures in the solar chromosphere. In the model such structures are considered as plasma “clouds” located above the solar surface, which absorb and scatter the incident radiation coming from the solar surface behind. The process in which the incident radiation passes through and emerges from the cloud structure is well described by the radiative transfer equation. The simplified form of the solution of the radiative transfer equation is
where I(Δλ) represents the observed intensity, I0(Δλ) the background incident radiation, τ(Δλ) the optical thickness, and S the source function. Equation (1) arises from the assumption that the cloud structure is fully isolated from the underlying surface, the source function, Doppler width, and the absorption coefficient are constant along the line of sight (see Tziotziou 2007; Heinzel 2015, for comprehensive reviews). From Eq. (1) the contrast profile C(Δλ) is defined as
We note that the variables on the left side of Eq. (2) can independently be determined from the observations. Furthermore, for practical reasons we assumed that the optical thickness of the cloud follows a Gaussian profile
Here, τ0 is the optical thickness at the line center, Δλ = λ − λ0 is the wavelength displacement from the Hα line core λ0, ΔλD is the Doppler width, and Δλlos = λ0υlos/c is the Doppler shift of the line due to the line of sight motion of the cloud υlos being c the speed of light.
Applying the above definitions to the SDDI imaging spectroscopy data, we obtained a series of two-dimensional physical properties of the filament eruption including the Doppler shift relative to the line center. From the Doppler shift we directly derived Doppler velocity maps that are presented in Fig. 5. Following the convention, negative Doppler velocity corresponds to blueshift (toward the observed), while positive Doppler velocity to redshift (away from the observer). The velocity maps illustrate in great detail the Doppler characteristics of the filament eruption, where the color-code highlights the velocity distribution of the plasma contained in the ejecta, that is, redshifted and blueshifted patterns in relation to the observer. During the initial phase of the eruption, from 05:20–05:34 UT (see the associated animation), it is noted a moderated increase of the Doppler velocity (blueshift) up to several tens of kilometers per second. Subsequently, there is a drastic increment in the velocity due to the strong blueshifted plasma. The most remarkable change in the filament configuration and its velocity is visualized from 05:38:17 UT, the time when the filament apex is fragmented and the erupted material starts to exhibit redshifted and particularly highly blueshifted characteristics. During this period, which corresponds to the main phase of the eruption, a great amount of the filament material is launched with a line of sight velocity larger than −100 km s−1. Redshifted structures also appear predominantly in the filament upper leg, which suggests that downflows manifest as the filament expands upward. Shortly after, from 05:42–05:49 UT blob-like structures are ejected with even larger velocities – most of the blobs approach −300 km s−1 (see the animation of Fig. 5). The characteristics of large Doppler velocity detected during the filament eruption are investigated further in the next section.
 |
Fig. 5. Velocity maps based on the cloud model illustrating the Doppler characteristics of the filament eruption (blue colors toward the Earth). Shortly after the filament disruption, which happens at around 05:38 UT, a large amount of the filament material is launched with velocities of about −100 km s−1 (blueshifted). Redshifted structures corresponding to the material moving in opposite direction are also observed close to the footpoints of the erupting filament. This suggests that downflows are driven during the eruption and could be related to the mass loss (see the text). In the latter phase of the eruption, blob-like structures traveling with velocities exceeding −250 km s−1 also can be identified. An animation of this figure is available online. |
3.3. Spectral diagnostic and multiple velocity components
Here we investigate the spectral characteristics of the filament eruption focusing on the highly Doppler-shifted material detected at the apex and the lateral part of the eruption. To this end, we take advantage of the SDDI high-resolution full-disk spectral images that allow us to obtain two-dimensional spectra and profiles from any given position and extent on the solar disk.
In order to get a more physically meaningful quantity from our observation, we rewrite Eq. (2) as
Thus, using Eq. (4) the optical thickness can be calculated. Except for the source function S all quantities in Eq. (4) can be inferred from the observation. We use two-dimensional spectra as inputs for I0(Δλ) and I(Δλ) obtained along the slits S1 (filament apex) and S2 (lateral part of the eruption), respectively. Post-eruption spectra at 06:10:03 UT along the corresponding slits are considered as background radiation I0(Δλ), and we set S = 0.1 expressed in units of the disk-center continuum intensity around the Hα line (4.077 × 10−5 erg s−1 cm−2 sr−2 Hz−1). It should be mentioned that increasing or decreasing S in Eq. (4) produces minimal effect in the final result, for instance, only a small variation in the amplitude if one calculates optical thickness profiles (see discussion Sect. 4.2). In this way, we computed two-dimensional optical thickness spectra in which the erupting material can be traced more effectively in space (slit), time (t), and wavelength (Δλ). Furthermore, we applied deconvolution to the optical thickness spectra with the theoretical transmission profile of the Lyot filter to recover the true optical thickness profiles. Thereafter, we reconstructed a series of optical thickness spectra (distance along the slit and Δλ) by assembling the deconvolved profiles.
Examples of two-dimensional optical thickness resulting from deconvolution are presented in Figs. 6 and 7 (upper panels) for the slits S1 and S2, respectively. In the optical thickness spectra the erupting material is observed as dark elongated structures departing from the line center (see the associated animations). These characteristics indicate that the eruption is made up predominantly of blueshifted plasma. In the course of time, the dark structures become faint, which suggests that the erupting material reached high altitudes of the solar atmosphere, it started to get ionized due to the temperature enhancement and/or density reduction. Because in the two-dimensional spectral image the highly blueshifted plasma can be tracked more effectively, optical thickness profiles are obtained at three positions across the erupting material, namely, fast (leading), main (core), and slow (following) components (Figs. 6, 7 lower panels). The profiles help visualize more characteristics of the erupting material, for example, the profiles have no symmetric shapes nor single peaks. In addition to the main blueshifted peak, there exist multiple peaks or subcomponents that have manifested, and they exhibit different behaviors during the filament eruption.
 |
Fig. 6. Optical thickness spectra of the filament apex (slit S1) extracted from the SDDI Hα filtergrams (see Fig. 2). Upper panels: Two-dimensional spectra wherein the erupting filament is visible as dark elongated structures extending upward from the central part of the spectra. We applied deconvolution to recover the instrumental broadening in our observations (see the text). The horizontal green, black, and red lines are used to track the fast (leading), main (core), and slow (following) components of the eruption, respectively. We note that the negative values in the optical thickness spectra are related to some errors (bias) in the estimates arising from the noise in the data. Lower panels: Optical thickness profiles obtained from the horizontal lines shown in the upper panels. The profiles show different characteristics of the erupting material, for example, multiple peaks and large Doppler shifts. An animation of this figure is available online. |
 |
Fig. 7. Same as in Fig. 6 but for the lateral part of the filament eruption that crosses the slit S2 (see Fig. 2). What is remarkable here is the detection of strongly blueshifted plasma contained in the filament. Again, the optical thickness profiles help visualize in more detail the characteristics of the fast, main, and slow components of the erupting material. An animation of this figure is available online. |
We further characterize the optical thickness profiles with multiple Gaussian fits by employing Eq. (3) as a model fitting. The Doppler width in Eq. (3) is related to the mass of the hydrogen atom mH ≃ 1.67 × 10−24 g and the unknown kinetic temperature T and micro-turbulent velocity ξ due to the nonthermal motions. Given that the Doppler velocity υlos is a measurable quantity from our observation and assuming that the temperature of the erupting filament (cloud) is about T ≈ 104 K, we created synthetic optical thickness profiles by applying the model fitting. The fitting results provide us with better estimates of the model coefficients, such as the peak velocity υpeak, the optical thickness at the line center τ0, and ξ for each synthetic profile. The combination of the synthetic profiles yields the composite fitting curves for the observed optical thickness profiles. In Fig. 8 we present selected optical thickness profiles of the filament eruption (apex and the lateral part) along with the fitting results of the multiple Gaussian model. It is also shown the individual synthetic profiles to highlight the multi-component characteristics of the filament eruption. The profiles clearly show that the erupting filament has a main peak velocity and multiple subcomponents, some profiles exhibit strong blueshift denoting the presence of large Doppler velocity. This means that during the eruption there exists a main bulk moving with an average velocity determined by the peak of the distribution and the other subcomponents or unresolved structures moving ahead and behind the main bulk with distinct velocities. The multiple peaks that appear in the profiles could be related to the presence of internal motions inside the erupting filament (see discussion in Sect. 4).
 |
Fig. 8. Selected optical thickness profiles of the fast and main components at the apex (top panels) and lateral part (bottom panels) of the filament eruption, respectively. The time of the profiles are nearly the same as the two-dimensional spectra shown in Figs. 6 and 7. The colored profiles highlight the subcomponents resulting from the Gaussian fitting model, while the solid gray profiles are composite fitting results by combining the multiple subcomponents. It is also shown the peak velocity υpeak (km s−1) of the composite profiles and the estimated micro-turbulent velocity ξ (km s−1) of each subcomponent (see the text). |
3.4. Velocity distribution and true eruption profiles
The optical thickness profiles described in the previous section were also used to infer the distribution of the line of sight velocity. Because the optical thickness is a function of wavelength τ(Δλ), it can conveniently be expressed in terms of velocity. Figure 9 presents the distribution and time-variation of the optical thickness profiles corresponding to the fast and main components at the apex of the erupting filament. By fast and main components we mean the profiles obtained from the leading and the central part of the erupting feature identified in a series of the deconvolved two-dimensional optical thickness spectra (e.g., Fig. 6). In Fig. 9 the concentrated points shown as enhanced regions correspond to the highest peaks of the optical thickness profiles. The distribution plots illustrate that during the initial period, the highest values of the optical thickness congregate, on average, below −10 km s−1, indicating a small Doppler shift. From 05:25 UT, the peak values of the optical thickness are blueshifted to relatively high velocities, and after 05:35 UT, the peaks of the optical thickness start to become shifted to even larger velocities, with some peaks approaching −300 km s−1 in the latter phase. Starting from 05:37 UT onward, a high-velocity dispersion can be seen, suggesting the existence of multiple components that are predominantly manifested during the final episode of the filament eruption. Figure A.1 presents the optical thickness distribution of the lateral part of the filament eruption also obtained from a sequence of two-dimensional spectra as shown in Fig. 7.
 |
Fig. 9. Distribution of the optical thickness profiles obtained from the filament apex. Panel (a) shows the distribution of the fast component, while panel (b) the distribution of the main component. The fast and main components refer to the measurements obtained from the leading and the central part of the erupting feature, respectively, detected in the optical thickness spectra (see the text). The enhanced regions correspond to the multiple peaks of the profiles that are Doppler-shifted to large velocities during the filament eruption. The blue profiles are the line of sight velocity υlos of the fast and main components calculated by tracking the enhanced regions. For comparison, it is also plotted the plane of sky velocity profile υpos (black) calculated from the time-distance diagrams presented in Fig. 3. |
Given the optical thickness distribution, we calculated the line of sight velocity profiles of the fast and main components by approximately tracking at each time step the central part of the congregated optical thickness peaks. We note that in the optical thickness distribution (Fig. 9), evidence of larger Doppler shifts does exist, identified as weak enhancements at far distances from the central part. In our analysis, we consider the derived velocity profiles as representative line of sight velocity υlos of the fast and main components at the apex of the filament eruption. The combination of υlos with the plane of sky velocity υpos obtained at nearly the same location along the slit S1, yields the true velocity profiles at the apex of the erupting filament, that is, 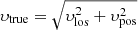 . By integrating and differentiating the velocity profiles, we calculated the true height and acceleration profiles, respectively. It is noteworthy here that the true height refers to the actual propagation distance of the filament eruption measured along the slit S1 from the initial position of the filament apex. Figure 10 presents the true eruption profiles of the fast (hf, υf, af) and main (hm, υm, am) components. The eruption profiles show interesting characteristics of the filament dynamics, for example, a large propagation distance, high propagation speed, and fast acceleration. These aspects make the filament eruption under study a relevant phenomenon that is not often observed. Comparing the velocity and acceleration profiles of the main and fast components, we observe that they evolve almost identically during the initial and ascending phase of the eruption until about 05:35 UT. Subsequently, the profiles deviate from each other, that is, the fast component accelerates impulsively while the main component experiences a gradual increase and then it steeply drops. These findings are further investigated by performing numerical simulations in Paper II of this series.
. By integrating and differentiating the velocity profiles, we calculated the true height and acceleration profiles, respectively. It is noteworthy here that the true height refers to the actual propagation distance of the filament eruption measured along the slit S1 from the initial position of the filament apex. Figure 10 presents the true eruption profiles of the fast (hf, υf, af) and main (hm, υm, am) components. The eruption profiles show interesting characteristics of the filament dynamics, for example, a large propagation distance, high propagation speed, and fast acceleration. These aspects make the filament eruption under study a relevant phenomenon that is not often observed. Comparing the velocity and acceleration profiles of the main and fast components, we observe that they evolve almost identically during the initial and ascending phase of the eruption until about 05:35 UT. Subsequently, the profiles deviate from each other, that is, the fast component accelerates impulsively while the main component experiences a gradual increase and then it steeply drops. These findings are further investigated by performing numerical simulations in Paper II of this series.
 |
Fig. 10. True eruption profiles (height, velocity, and acceleration) of the filament apex fast and main components. We note that the profiles in panel (a) show the actual propagation distance of the filament eruption measured from the initial position of the filament apex (see the text). The eruption profiles reveal that the filament attains a large propagation distance (panel a), high propagation speed (panel b), and fast acceleration (panel c). Of note regarding the velocity and acceleration profiles is that the fast and main components evolve identically until 05:35 UT, thereafter the profiles deviate from each other, that is, one accelerates impulsively while the other undergoes a rapid diminution. |
3.5. Propagation direction of the filament
The propagation direction of the filament eruption in 3D space is examined here by considering the velocity vectors derived from our observation. Figure 11 shows a schematic representation of the Sun, where (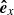 ,
, 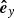 ,
, 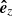 ) defines the right-handed Cartesian coordinate system (observer’s reference frame) with the axes centered at the Sun’s center and orthogonal to each other. The
) defines the right-handed Cartesian coordinate system (observer’s reference frame) with the axes centered at the Sun’s center and orthogonal to each other. The 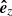 axis is aligned with the line of sight direction, while
axis is aligned with the line of sight direction, while 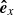 and
and 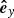 span the plane of sky with
span the plane of sky with 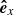 pointing toward the solar west and
pointing toward the solar west and 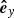 toward the solar north. The vector OF denotes the position of the filament before its eruption, Θ = 16deg and Φ = −41deg are the heliographic latitude and longitude of F, respectively. On the other hand, an instantaneous position of the erupting filament is denoted by P and its velocity components in the plane of sky υpos and in the line of sight υlos, and the true velocity υtrue are represented by the gray arrows. The propagation direction of the eruption relative to the Sun-Earth line is given by the angle δ, while ϑ is the angle that the eruption makes with the local solar normal
toward the solar north. The vector OF denotes the position of the filament before its eruption, Θ = 16deg and Φ = −41deg are the heliographic latitude and longitude of F, respectively. On the other hand, an instantaneous position of the erupting filament is denoted by P and its velocity components in the plane of sky υpos and in the line of sight υlos, and the true velocity υtrue are represented by the gray arrows. The propagation direction of the eruption relative to the Sun-Earth line is given by the angle δ, while ϑ is the angle that the eruption makes with the local solar normal 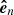 (see below). Based on the geometric relations these angles are given by:
(see below). Based on the geometric relations these angles are given by: 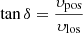 and
and 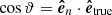 , where
, where 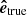 refers to the unit vector parallel and in the direction of the true velocity.
refers to the unit vector parallel and in the direction of the true velocity.
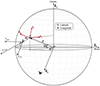 |
Fig. 11. Geometry of the Sun and representation of the velocity vectors related to the filament eruption. The axes ( |
To calculate the three-dimensional trajectory of the filament eruption with respect to the solar surface, we define a local coordinate system (local reference frame) determined by the unit vectors (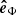 ,
, 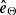 ,
, 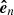 ) fixed at point F (see Fig. 11). Here
) fixed at point F (see Fig. 11). Here 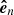 is a normal vector perpendicular to the plane tangential to the solar surface and,
is a normal vector perpendicular to the plane tangential to the solar surface and, 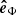 and
and 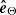 are tangent vectors directed toward the solar west and north, respectively. The unit vectors (
are tangent vectors directed toward the solar west and north, respectively. The unit vectors (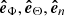 ) are calculated as follows. From the geometry the position vector OF is written as
) are calculated as follows. From the geometry the position vector OF is written as
where R represents the solar radius. Since the position vector OF is parallel to the unit vector 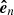 , meaning that both are perpendicular to the tangential plane at point F, we find that
, meaning that both are perpendicular to the tangential plane at point F, we find that 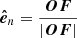 . Moreover, from the geometrical relations and calculating the cross-product,
. Moreover, from the geometrical relations and calculating the cross-product, 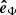 and
and 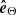 can be easily derived. Therefore, the unit vectors belonging to the local reference frame are given by
can be easily derived. Therefore, the unit vectors belonging to the local reference frame are given by
Next, we define the position vector of the erupting filament with respect to point F to describe the trajectory of the eruption. This vector can be written in terms of the observer’s and the local reference frames, respectively, as
where (X(t),Y(t),Z(t)) refer to the coordinates in the observer’s reference frame, while (α(t),β(t),γ(t)) the coordinates in the local reference frame. We can relate Eqs. (9) and (10) through the following transformation matrix equation
Equation (11) allows for the conversion of the observer’s coordinate into the local coordinate system. We note that X(t) and Y(t) are the positions of the filament apex in the plane of sky, while it is very close to the slit S1 as a result. Z(t) is obtained from the time integral of υlos(t) profile of the apex main component.
 |
Fig. 12. Trajectory of the filament eruption projected in 3D space calculated with Eq. (11). The axes (α, β, γ) refer to the local coordinates system determined by the unit vectors ( |
The trajectory of the filament eruption (apex) calculated with Eq. (11) is presented in Fig. 12. Panels (a) and (b) show different perspectives of the 3D space, which reveal that the filament propagates making a pronounced angle with the local vertical (γ-axis) and travels more or less inclined toward the solar surface (see also the associated animation). Panel (b) shows that during the initial process of the eruption (05:10–05:25 UT), the filament experiences small variations in its propagation direction, thereafter, the filament gradually recovers its ascending motion but proceeds maintaining a relatively large inclination angle with respect to the local vertical. These findings demonstrate that the studied filament erupted following a nonradial direction and markedly deviated from the local vertical direction. Cabezas et al. (2017), using multiwavelength imaging observation in the Hα line, also reported on a filament that erupted nearly horizontally exhibiting variations of the inclination angle.
4. Discussion
4.1. Fast-filament eruption
The filament eruption introduced in this paper occurred in a spotless region associated with a weak B-class solar flare. The derived maximum true velocity 600 km s−1 and acceleration 2.5 km s−2 are considerably larger than the commonly reported in previous works. This kind of observation represents a challenge for interpreting and modeling because the common thought is that active region filaments are subject to experience fast acceleration. Focusing on the Doppler velocity, Li et al. (2005) reported on a complex filament eruption in the Hα line blueshifted over 400 km s−1. Similarly, Kleint et al. (2015) investigated a fast-filament eruption observed in transition region spectral lines and obtained a maximum Doppler velocity of about 600 km s−1. The common aspect of the two mentioned fast eruptions is that both originated from complex active regions and were associated with X-class flares. According to the general picture, solar eruptions predominantly occur in magnetically complex active regions and the accumulated magnetic energy associated with nonpotential fields constitutes the primary source to power the eruptions. The studied filament eruption, however, cannot adequately be explained with the above standard view.
If, however, we consider the unwinding characteristics of the filament eruption that was revealed by the observation (see Fig. 4, also the associated animation of Fig. 2), we can hypothesize that the filament was strongly twisted during the preeruption stage. Theoretical models of solar eruptions also invoke that the twisting mechanism can be a source of energy injection (Sakurai 1976), and highly twisted flux ropes rise much faster, releasing a large amount of energy (e.g., Amari et al. 2003; Williams et al. 2005). For example, Nishida et al. (2013) performed a three-dimensional MHD simulation that showed that the strongly twisted flux rope experiences a high ejection speed, allowing for a rapid acceleration. On the other hand, Kurokawa et al. (1987) examined a high-speed filament eruption in which unwinding and rotation characteristics were observed in Hα filtergrams and concluded that the eruption process can be explained with the magnetic twist model proposed by Shibata & Uchida (1986). It has been also shown by Moore (1988) that the expansion and unwinding of the field lines in and around the erupting filaments are directly related to the release of magnetic energy, which can supply enough power to drive the eruptions. Therefore, we argue that the high-speed of the studied filament eruption can be a consequence of the initially strong twist and the release of a considerable amount of accumulated energy (see Sect. 4.3). It is important to note here that other mechanisms, such as magnetic reconnection, could also contribute because it has been found that mass acceleration and the reconnection rate are well correlated (e.g., Qiu et al. 2004; Lynch et al. 2008).
4.2. Doppler-shifted components and velocity distribution
The Hα optical thickness profiles revealed that the erupting filament is made of multiple subcomponents that are manifested showing discrete peaks in the profiles (see Fig. 8). As the eruption develops, between 05:32–05:37 UT the main peak (main bulk) of the fast (leading) and main (core) components at the filament apex (upper panels in Fig. 8) are blueshifted from about −30 to −145 km s−1 and from −36 to −102 km s−1, respectively. Similarly at the lateral part of the erupting filament (lower panels in Fig. 8), between 05:41–05:44 UT, the main peak of the fast (leading) and main (core) components are blueshifted from about −72 to −265 km s−1 and from −70 to −184 km s−1, respectively. The abrupt change in the velocity mentioned above happened exceptionally fast, within ∼5 minutes. In the meantime, some subcomponents that appear ahead of the main bulk are shifted even to much higher velocities, for example to nearly −400 km s−1 at 05:36:44 (apex fast) and 05:44:19 UT (lateral fast). The profiles of the subcomponents are rather narrow than the profiles of the main bulk, and their corresponding micro-turbulent velocities ξ inferred from the model fitting (see Sect. 3.3) differ from each other. We note that in some cases the fitting results yield large micro-turbulent velocities beyond those expected for quiescent filaments and prominences (e.g., Molowny-Horas et al. 1999; Schwartz et al. 2019; Okada et al. 2020; Yamasaki et al. 2023), even over the estimates of previous studies for the case of eruptive events (e.g., Labrosse & McGlinchey 2012; Heinzel et al. 2016; Zhang et al. 2019). One must note, however, that in the case of filament and prominence eruptions significant nonthermal motions should be expected due to more turbulent plasma that could broaden the profiles. Regarding our observation, we argue that the pronounced turbulent velocity could occur because of the filament fast expansion and the superposition of unresolved structures moving with distinct velocities. On the other hand, as it is also noted in Figs. 9 and A.1 the line of sight velocity distribution is greatly enhanced in the late phase of the eruption and the presence of subcomponents becomes more conspicuous. Wang et al. (2022) also reported enhancements of the line of sight velocity distribution of an erupting filament, but only up to about −22 km s−1.
The characteristics described above indicate that complex plasma motions originate as a consequence of the fast eruption, leading the individual blob-like structures to expand rapidly with random velocities. These findings also suggest that high-velocity dispersion manifests during the main and final episodes of the eruption that could be related to the internal motions. A likely explanation for the appearance of the subcomponents or blobs moving with distinct velocities is that internal structures existed in the filament body before the eruption, and the filament disruption allowed these confined structures to escape and flow abruptly with high velocities. These characteristics are also well observed in the Doppler velocity maps (see Fig. 5 and the animation) where most of the subcomponents or blob-like structures are ejected with supersonic velocities. Although we cannot confirm in our data the existence of internal structures in the filament body before its eruption, previous high-resolution observations showed evidence of complex internal structures right before the filament eruptions (e.g., Sasso et al. 2011; Schwartz et al. 2019), and also manifestations of internal motions in the spectral profiles during a filament eruption (Penn 2000).
Another aspect that we would like to mention here concerns the fixed source function adopted to calculate the optical thickness of the filament eruption in Sect. 3.3. It has been shown by Heinzel & Rompolt (1987) that for prominence-like structures located at greater heights above the solar surface and moving with large vertical velocities, the Hα source function can substantially change due to the so-called Doppler brightening effect (DBE). In other words, there is a velocity effect on the Hα line source function (cf. Heinzel et al. 1999). To evaluate quantitatively the influence of DBE on our fast-moving filament, we consider the height and velocity presented in Fig. 10 and calculate the source function following Heinzel (2015) and Heinzel et al. (2015). In the case of filaments seen in absorption against the background solar disk, the source function is mostly controlled by the photon scattering, so one can approximate S ≈ WI0, where W is the geometrical dilution factor that decreases with increasing height, and I0 is the incident radiation expressed in terms of the central depression of the Hα line 0.17 multiplied by the disk-center continuum intensity 4.077 × 10−5 erg s−1 cm−2 sr−1 Hz−1 (see David 1961; Heinzel et al. 1999). Focusing on the main phase of the eruption (see Fig. 10), at 05:35 UT the filament is traveling with a velocity of about 150 km s−1 located at a height of 5 × 104 km. For this height, we find that the intensity of the incident radiation illuminating the moving cloud (filament) is diluted by a factor of 0.32 (see Eq. (7) in Heinzel et al. 2015). In addition, for the height and velocity mentioned previously, DBE approaches a factor of about 1.85 (see Fig. 11 in Heinzel & Rompolt 1987). Therefore, the source function influenced by DBE and normalized to the continuum level is S = 0.1. This result is the same as our assumed value in Sect. 3.3. We note that our choice of considering the results given in Fig. 11 of Heinzel & Rompolt (1987) is also because the computation was done for the case of a large micro-turbulent velocity, such as what we found in our observation. To summarize, if DBE is neglected when calculating the source function, the result obtained above is reduced by a factor of two, and if large DBE factors (and thus high velocities) are included in the computation, the source function is moderately enhanced. However, as already mentioned in Sect. 3.3 our results of the optical thickness obtained with Eq. (4) are not very sensitive to the variation of the source function, so even if the source function varies, the determination of the Doppler-shifted plasma in the optical thickness spectra, and thus the velocity (i.e., the quantity that is our primary focus), is not affected.
4.3. Filament mass
Filament mass is an important physical quantity for considerations related to its formation, stability and dynamics. Here we discuss on the probable total mass contained in the studied filament and provide a quantitative estimate. We take into account the filament geometry and the line center optical thickness τ0 calculated with the fitting model in Sect. 3.3, as well as the non-LTE theoretical relations given in Heinzel et al. (1994). If we approximate the filament body to a cylindrically symmetric flux tube, the filament length and the diameter of its corresponding cross-sectional area at 05:37:47 UT (see first column of Fig. 2) are ∼ 1.8 × 1010 cm and ∼ 1.3 × 109 cm, respectively. At this time the optical thickness of the filament apex main component is τ0 ≃ 0.13 (see Fig. 8). On the other hand, the filament density can be calculated with ρm = 1.4mHnH, where mH represents the mass of the hydrogen atom and nH is the number density of the hydrogen including neutral atoms and protons (cf. Heinzel et al. 2003). Using the correlation-plots given in Figs. 5, 8, and 23 of Heinzel et al. (1994), for log(τ0)≃0.13 we get the line integrated emission log(EHα)≃5.0, the electron density log(ne)≃11.0, and then the total hydrogen density log(nH)≃10.9, respectively. With the calculated nH the filament density is ρm ≃ 2.12 × 10−13 g cm−3. Finally, considering the geometry and the dimensions given above the filament mass is ∼5.4 × 1015 g. This result indicates that the studied filament is rather a relatively massive erupting structure. Grechnev et al. (2014) investigated a filament eruption in the Hα line that exhibited similar morphological characteristics to our filament and obtained a filament mass comparable to our result.
Furthermore, taking into account the estimated filament mass we can also gain insights about the energy involved in the eruption. Considering the scaling relations between mass ejection and flare energy given in Fig. 6b of Kotani et al. (2023), we can argue that the total flare energy associated with the filament eruption could be of the order of ∼1031 erg. If we compare our estimated filament mass and the associated flare energy with the results shown in Fig. 3 of Namekata et al. (2021) for the case of solar filament eruptions, we can see that our values lie above the results of previous studies. In Paper II, we provide further discussions about the filament total mass and the associated energetics.
4.4. Downflows driven by the filament eruption
We have identified intermittent downflows as redshifted plasma close to the footpoints of the erupting filament whose corresponding velocities range from 45–125 km s−1 (see lower panels of Fig. 2). Our interpretation is that the observed redshifted signatures are caused by plasma flows along the filament legs that are precipitating down to the solar surface. The downward-moving plasma represents drainage of the filament material, which evidently has direct consequences on the dynamics of the filament. The downflow velocity we found is larger than in previous studies. For example, Doyle et al. (2019) using Hα ± 1.38 Å observations found downflows along the legs of an erupting filament redshifted up to 45 km s−1. Guo et al. (2023) also detected downward plasma flows during a filament eruption redshifted to about 20 km s−1. These authors concluded that the redshifted plasma was due to mass draining toward the solar surface. The high velocity we detected in our data is simply because the spectral coverage of our instrument is sufficient enough to capture high-speed structures associated with the filament eruption. Relatively high velocity of mass drainage in erupting filaments was also reported. Dai et al. (2021) found velocities in the range of 35–85 km s−1 of draining material, although these measurements were obtained based on the projected motion in the plane of sky. We conclude that the observed downflows that appear during the filament eruption constitute mass loss of the filament that might have contributed to the triggering of the fast acceleration. A model of an expanding magnetic loop that incorporates the temporal variation of the Hα spectrum was developed by Ikuta & Shibata (2024) recently. This model can be suitable to describe the appearance of downflows in erupting filaments, such as what we found in our observation. Alternatively, the redshifted plasma flows detected close to the footpoints of the filament eruption could be further enhanced due to the expansion and helical motions of the erupting material (Otsu & Asai 2024).
4.5. Implication for models
One of the important results of this work was the detection of highly Doppler-shifted plasma that accompanied the filament eruption. The large blueshifted plasma (see Figs. 5, 9) indicates that the filament material was launched into the outer space having a significant line of sight component. This result is a clear example that the actual velocity and propagation direction of filament eruptions could be greatly influenced by the line of sight component and the fact of not including it in the computations would certainly yield inaccurate results. This is also an important issue for modeling solar eruptions. Since in our current understanding erupting filaments and prominences form part of the flux rope embedded in the CMEs core (e.g., Shibata & Magara 2011; Webb 2015; Heinzel et al. 2016; Wood et al. 2016; Chen 2017; Green et al. 2018, and references therein), models attempting to predict the early propagation of CMEs will have to include as initial boundary conditions accurate estimates taking into account the contributions of all velocity components (e.g., tree-dimensional velocity field). Another important point to mention here is that filaments and prominences do not always erupt in the radial direction or perpendicular to the solar surface, though this has been assumed in many models. This is a subject of great importance that is not often discussed. As shown in Fig. 12 (see also Fig. 6 in Cabezas et al. 2017), filaments can significantly deviate from the radial direction. In the case of the studied filament, we speculate that the erupting material possibly experienced a change in its rise direction when interacting with the overlying asymmetric magnetic field and its surroundings. Other case studies showing that the trajectory of erupting prominences is generally not in the radial direction were presented by Zapiór & Rudawy (2010) and Zapiór & Martínez Gómez (2016). Indeed, the change in the propagation direction of filament and prominence eruptions may also have implications for the initial trajectory of CMEs (e.g., Lugaz et al. 2011; Kliem et al. 2012; Guo et al. 2023), which we do not address in this article.
On the other hand, the derived maximum true velocity and acceleration (Fig. 10) may have been even much larger. As shown in Fig. 4b, in the He II line the filament continues ascending to greater distances even after it has disappeared in Hα. However, we cannot confirm the actual velocity of the eruption beyond 05:40 UT because of the lack of spectroscopy observations in spectral lines other than Hα. Looking at the time-distance profile (yellow plot) we suggest that during the final stage of the eruption the filament apparently underwent a drastic diminution in the velocity, meaning that the main acceleration process occurred earlier than 05:40 UT, that is, the period at which the event is well observed in Hα. Hence, the true eruption profiles obtained solely based on Hα data are adequate to explain most characteristics of the studied filament eruption. Nevertheless, it would be advantageous to have simultaneous full-disk imaging spectroscopy observations in various spectral lines, for instance, Hα and He I (10830 Å), which could provide a better picture of erupting filaments at different heights of the solar atmosphere, also it would be beneficial for modeling.
Last, numerical modeling will certainly be important to deepen our understanding of the physics behind the fast eruptions. In Paper II, we discuss details about the necessary energy to power the studied fast-filament eruption, the action of the driving forces, and the influence of the mass loss on the acceleration process of the filament.
5. Conclusions
In this paper, we have investigated a fast-filament eruption that occurred on 2017 April 23. We used Hα imaging spectroscopy observations provided by SMART/SDDI, which allowed us to characterize the whole eruption process in detail. Results of the cloud model fitting and spectral diagnostics revealed that the filament was ejected with a line of sight velocity exceeding −250 km s−1. This is an important finding and demonstrates that high-resolution full-disk imaging spectroscopy observations are essential to detect high-speed mass motions ejected from the Sun that could potentially impact the space environment at Earth. Most existing solar instruments generally miss high line of sight velocities of filament and prominence eruptions, partly due to their limited spectral coverage or small field of view.
The spectral analysis showed that the erupting filament is composed of multiple subcomponents moving with discrete velocities. This suggests that internal complex structures exist before the filament eruption. Sub-arcsecond resolution observations are necessary to reach conclusions on the relation between the subcomponents and the detected high velocity. On the other hand, the distribution of the optical thickness profiles allowed us to apply a different approach in order to calculate the line of sight velocity profiles, enabling us to derive the true velocity and acceleration profiles of the filament eruption. This alternative method may be suitable for obtaining time velocity profiles of filament and prominence eruptions captured in spectroscopic observations. Moreover, thanks to the velocity vectors, it was also possible to reveal that the filament erupted making a pronounced angle with the local vertical direction.
Finally, in the context of space weather, the continuous monitoring of potential source regions on the solar disk and the building of procedures to accurately infer their physical properties (e.g., absolute velocity and propagation direction) are crucial. Such collected and inferred information can eventually be used as initial conditions to predict, for example, the initial propagation of a solar eruption and Earth-directed CMEs. In line with the above statements, the Astronomical Observatory of Kyoto University is leading and promoting the Continuous H-Alpha Imaging Network (CHAIN; UeNo et al. 2007) project that aims to obtain continuously synoptic Doppler maps and provide the three-dimensional velocity field of filament and prominence eruptions and associated events (e.g., Cabezas et al. 2017, 2019; Seki et al. 2019; Gutierrez et al. 2021). Currently, three instruments of the CHAIN project are in operation at three strategic locations around the globe: SMART/SDDI at Hida Observatory (Japan) and two Flare Monitoring Telescopes (FMTs), one located at San Luis Gonzaga National University (Ica, Peru) and the other at King Saud University (Saudi Arabia). It is also important to mention that several efforts are going in the same direction, such as the next-generation GONG network (Pevtsov et al. 2022), the project of Synoptic Solar Observations at NAOJ (Hanaoka et al. 2020), and the recently launched space mission Chinese H-alpha solar explorer (CHASE; Li et al. 2022).
Movies
Movie 1 associated with Fig. 6 Access here
Movie 2 associated with Fig. 2 Access here
Movie 3 associated with Fig. 5 Access here
Movie 4 associated with Fig. 12 Access here
Movie 5 associated with Fig. 7 Access here
Data availability
Movies associated to Figs. 2, 5–7, 12 are available at https://www.aanda.org
Acknowledgments
The authors are grateful to the staff members of Hida Observatory for the operation and continuous solar observations with SMART/SDDI. D.P.C. is thankful to Shin-ichi Nagata, Yuwei Huang, Takako T. Ishii, and Kumi Hirose for fruitful discussions, He also thanks KD Leka for insightful comments and discussions. D.P.C gratefully acknowledges support from Kyoto University during the post-doctoral fellowship at Hida Observatory. This work is supported by the Institute for Space-Earth Environmental Research (ISEE), Nagoya University. This work was also supported by JSPS KAKENHI grant Nos. JP24K07093 (PI: A. A.) JP21H01131 (PI: K. S.), and JP24K00680 (PI: K. S.). AIA data products are courtesy of NASA/SDO science team, a mission for NASA’s Living With a Star program. In this research we have made use of Python packages SunPy, Astropy, Scipy, Matplotlib, and Numpy. Additionally, we used the Solarsoft library. Finally, we appreciate the constructive comments and suggestions of the anonymous referee that helped improve the clarity and presentation of this work.
References
- Amari, T., Luciani, J. F., & Aly, J. J. 2003, ApJ, 585, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, E., Romuli, M., Andretta, V., et al. 2020, A&A, 642, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athay, G. R., & Illing, R. M. 1986, J. Geophys. Res., 91, 961 [NASA ADS] [Google Scholar]
- Beckers, J. M., 1964 Ph.D. Thesis, Utrecht University, The Netherlands [Google Scholar]
- Bemporad, A. 2009, ApJ, 701, 298 [Google Scholar]
- Bemporad, A., Mierla, M., & Tripathi, D. 2011, A&A, 531, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, D. P., Martínez, L. M., Buleje, Y. J., et al. 2017, ApJ, 836, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Cabezas, D. P., Asai, A., Ichimoto, K., et al. 2019, ApJ, 883, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Chen, J., & Garren, D. A. 1994, ApJ, 423, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Park, Y.-D., & Park, H.-M. 2006, Sol. Phys., 234, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J. 1989, ApJ, 338, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J. 2017, Phys. Plasmas, 24, 090501 [Google Scholar]
- Cheng, X., Zhang, J., Kliem, B., et al. 2020, ApJ, 894, 85 [Google Scholar]
- Dai, J., Zhang, Q., Zhang, Y., et al. 2021, ApJ, 923, 74 [NASA ADS] [CrossRef] [Google Scholar]
- David, K.-H. 1961, Z. Astrophys., 53, 37 [NASA ADS] [Google Scholar]
- Doyle, L., Wyper, P. F., Scullion, E., et al. 2019, ApJ, 887, 246 [Google Scholar]
- Engvold, O. 2015, Astrophys. Space Sci. Lib., 415, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2020, ApJ, 898, 34 [Google Scholar]
- Forbes, T. G., Linker, J. A., Chen, J., et al. 2006, Space Sci. Rev., 123, 251 [Google Scholar]
- Gallagher, P. T., Lawrence, G. R., & Dennis, B. R. 2003, ApJ, 588, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H. R., Holzer, T. E., Burkepile, J. T., & Hundhausen, A. J. 2000, ApJ, 537, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N. 2015, Astrophys. Space Sci. Lib., 415, 381 [Google Scholar]
- Green, L. M., Török, T., Vršnak, B., et al. 2018, Space Sci. Rev., 214, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Uralov, A. M., Slemzin, V. A., et al. 2014, Sol. Phys., 289, 318 [Google Scholar]
- Guo, J. H., Qiu, Y., Ni, Y. W., et al. 2023, ApJ, 956, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Gutierrez, M. V., Otsuji, K., Asai, A., et al. 2021, PASJ, 73, 394 [CrossRef] [Google Scholar]
- Hanaoka, Y., Sakurai, T., Otsuji, K., Suzuki, I., & Morita, S. 2020, J. Space Weather Clim., 10, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P. 2015, Astrophys. Space Sci. Lib., 415, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., & Rompolt, B. 1987, Sol. Phys., 110, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Gouttebroze, P., & Vial, J.-C. 1994, A&A, 292, 656 [NASA ADS] [Google Scholar]
- Heinzel, P., Mein, N., & Mein, P. 1999, A&A, 346, 322 [NASA ADS] [Google Scholar]
- Heinzel, P., Anzer, U., Schmieder, B., & Schwartz, P. 2003, Proc. ISCS 2003 Symposium Solar Variability as an Input to the Earth’s Environment, ESA SP-535 (Noordwijk: ESA Publications Division) [Google Scholar]
- Heinzel, P., Gunár, S., & Anzer, U. 2015, A&A, 579, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Susino, R., Jejčič, S., et al. 2016, A&A, 589, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, A. 2018, Rev. Mod. Plasma Phys., 2, 1 [Google Scholar]
- Huang, Z., Madjarska, M. S., Koleva, K., et al. 2014, A&A, 566, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ichimoto, K., Ishii, T. T., Otsuji, K., Kimura, G., et al. 2017, Sol. Phys., 292, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ikuta, K., & Shibata, K. 2024, ApJ, 963, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Ishii, T., Kawate, T., Nakatani, Y., Morita, S., et al. 2013, PASJ, 65, 39 [CrossRef] [Google Scholar]
- Janvier, M., Mzerguat, S., & Young, P. R. 2023, A&A, 677, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. M., Long, D. M., van Driel-Gesztelyi, L., & Carlyle, J. 2018, Sol. Phys., 293, 7 [Google Scholar]
- Kahler, S. W., Moore, R. L., Kane, S. R., Zirin, H., et al. 1988, ApJ, 328, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Kawate, T., Ishii, T. T., Nakatani, Y., et al. 2016, ApJ, 833, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Kleint, L., Battaglia, M., Reardon, K., et al. 2015, ApJ, 806, 9 [Google Scholar]
- Kliem, B., Török, T., & Thompson, W. T. 2012, Sol. Phys., 281, 137 [NASA ADS] [Google Scholar]
- Kotani, Y., Shibata, K., Ishii, T. T., et al. 2023, ApJ, 943, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, J. R., Lin, H., & Loranz, D. 1991, PASP, 103, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Kurokawa, H., Hanaoka, Y., Shibata, K., & Uchida, Y. 1987, Sol. Phys., 108, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 to 1300 nm (New Mexico: National Solar Observatory) [Google Scholar]
- Labrosse, N., & McGlinchey, K. 2012, A&A, 537, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemen, J. R., Title, A., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Li, J., Mickey, D. L., & LaBonte, B. J. 2005, ApJ, 620, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T., Zhang, J., Zhao, H., & Yang, S. 2010, ApJ, 720, 144 [CrossRef] [Google Scholar]
- Li, Q., Deng, N., Jing, J., & Wang, H. 2017, ApJ, 841, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Fang, C., & Li, Z. 2022, Sci. China Phys. Mech. Astron., 65, 289602 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., De Pontieu, B., Vial, J.-C., et al. 2015, ApJ, 803, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Antiochos, S. K., DeVore, C. R., et al. 2008, ApJ, 683, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaz, N., Downs, C., Shibata, K., et al. 2011, ApJ, 738, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D., Karpen, J., Ballester, J., et al. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F., Bilimoria, R., Tracadas, P. W., et al. 1994, Magnetic Field Configurations Basic to Filament Channels and Filaments (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Molowny-Horas, R., Heinzel, P., Mein, P., & Mein, N. 1999, A&A, 345, 618 [NASA ADS] [Google Scholar]
- Moore, R. L. 1988, ApJ, 324, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Morimoto, T., & Kurokawa, H. 2003, PASJ, 55, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D., St. Cyr, O. C., & Zouganelis, I. 2020, A&A, 642, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagata, S.-I., Morita, S., Ichimoto, K., Nishida, K., et al. 2014, PASJ, 66, 45 [CrossRef] [Google Scholar]
- Namekata, K., Maehara, H., Honda, S., et al. 2021, Nature, 6, 241 [NASA ADS] [Google Scholar]
- Nishida, K., Nishizuka, N., Shibata, K., et al. 2013, ApJ, 775, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Okada, S., Ichimoto, K., Machida, A., et al. 2020, PASJ, 72, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Olmedo, O., & Zhang, J. 2010, ApJ, 718, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Otsu, T., & Asai, A. 2024, ApJ, 964, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Otsu, T., Asai, A., Ichimoto, K., et al. 2022, ApJ, 939, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Penn, M. J. 2000, Sol. Phys., 197, 313 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Pevtsov, A. A., Martinez-Pillet, V., & Gilbert, H. 2022, ArXiv e-prints [arXiv:2211.06712] [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2002, A&ARv, 10, 313 [Google Scholar]
- Qiu, J., Wang, H., Cheng, C. Z., et al. 2004, ApJ, 604, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Rees-Crockford, T., Bloomfield, D. S., Scullion, E., & Park, S.-H. 2020, ApJ, 897, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Russano, G., Andretta, V., De Leo, Y., et al. 2024, A&A, 683, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakaue, T., Tei, A., Asai, A., et al. 2018, PASJ, 70, 99 [Google Scholar]
- Sakurai, T. 1976, PASJ, 21, 177 [NASA ADS] [Google Scholar]
- Sasso, C., Lagg, A., & Solanki, S. K. 2011, A&A, 526, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seaton, D. B., Mierla, M., Berghmans, D., et al. 2011, ApJ, 727, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Seki, D., Otsuji, K., Isobe, H., et al. 2017, ApJ, 843, L23 [Google Scholar]
- Seki, D., Otsuji, K., Isobe, H., et al. 2019, PASJ, 71, 56 [CrossRef] [Google Scholar]
- Shibata, K., & Magara, T. 2011, Liv. Rev. Sol. Phys., 8, 6 [Google Scholar]
- Shibata, K., & Uchida, Y. 1986, Sol. Phys., 103, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Zapiór, M., López Ariste, A., et al. 2017, A&A, 606, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrijver, C. J., Elmore, C., Kliem, B., et al. 2008, ApJ, 674, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, P., Gunár, S., Jenkins, J. M., et al. 2019, A&A, 631, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tandberg-Hanssen, E. 1970, Sol. Phys., 15, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Tandberg-Hanssen, E. 1995, The Nature of Solar Prominences (Dordrecht: Kluwer Academic Publishers) [CrossRef] [Google Scholar]
- Török, T., & Kliem, B. 2005, A&A, 630, L97 [Google Scholar]
- Tsap, Y. T., Filippov, B. P., & Kopylova, Y. G. 2019, Sol. Phys., 294, 35 [CrossRef] [Google Scholar]
- Tziotziou, K. 2007, ASP Conf. Ser., 368, 217 [NASA ADS] [Google Scholar]
- UeNo, S., Nagata, S.-I., Kitai, R., Kurokawa, H., & Ichimoto, K. 2004, Proc. SPIE, 5492, 958 [NASA ADS] [CrossRef] [Google Scholar]
- UeNo, S., Shibata, K., Kimura, G., et al. 2007, Bull. Astron. Soc. India, 35, 697 [NASA ADS] [Google Scholar]
- Vršnak, B. 1990, Sol. Phys., 129, 295 [CrossRef] [Google Scholar]
- Vršnak, B. 2001, J. Geophys. Res., 106, 25249 [CrossRef] [Google Scholar]
- Vršnak, B. 2019, Front. Astron. Space Sci., 6, 28 [CrossRef] [Google Scholar]
- Wang, S., Jenkins, J. M., & Muglach, K. 2022, ApJ, 926, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, D. F. 2015, Astrophys. Space Sci. Lib., 415, 381 [CrossRef] [Google Scholar]
- Wood, B. E., Howard, R. A., & Linton, M. G. 2016, ApJ, 816, 67 [Google Scholar]
- Williams, D. R., Török, T., Démoulin, P., et al. 2005, ApJ, 628, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Yamasaki, D., Huang, W. Y., Hashimoto, Y., Cabezas, D. P., et al. 2023, PASJ, 75, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Zapiór, M., & Martínez Gómez, D. 2016, ApJ, 817, 123 [CrossRef] [Google Scholar]
- Zapiór, M., & Rudawy, P. 2010, Sol. Phys., 267, 95 [CrossRef] [Google Scholar]
- Zapiór, M., & Rudawy, P. 2012, Sol. Phys., 280, 445 [CrossRef] [Google Scholar]
- Zhang, P., Buchlin, É., & Vial, J.-C. 2019, A&A, 624, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Distribution of the optical thickness at the lateral part of the filament eruption
 |
Fig. A.1. Same as in Fig. 9 but for the lateral part of the filament eruption (main and fast components). The distribution plots in panel (a) clearly show that the erupting material is blueshifted to velocities of about −300 km s−1. |
All Figures
 |
Fig. 1. Overview of the studied filament and Hα spectral profiles. Panel (a): Solar disk in the Hα line (6562.8 Å) captured by the Solar Dynamics Doppler Imager (SDDI) shortly before the filament eruption. The white box encloses the filament and outlines the field of view (FOV) of the images presented in Fig. 2. The small red box (50″ × 50″) surrounds a quiet-sun region from which the spectral profile is obtained and plotted in panel (b) by the red curve. The slit S1 is positioned in the direction of the leading part of the eruption (filament apex), whereas the slit S2 is used to track the lateral part of the eruption. Panel (b): Atlas solar spectrum of the Hα line (gray normalized to the continuum level) and convolution of the Atlas spectrum with the SDDI filter transmission profile (black). The quiet-sun SDDI spectral profile (see panel a) at μ ≈ 0.78 is also shown (red dots with spline interpolation), and an example of a strongly blueshifted profile (blue dots with spline interpolation) from the lateral part of the filament eruption at 05:44:50 UT (see Fig. 2). In the SDDI spectral profiles each dot represents the wavelength offset λs from the line center λ0 (6562.8 Å) at which SDDI performs regular observations. |
| In the text | |
 |
Fig. 2. Eruption process of the filament captured in a wide range of the Hα spectral line. The maps are Dopplergrams wherein the blueshifted (dark) and redshifted (bright) features of the erupting material have manifested. The black lines labeled S1 and S2 on the map at 05:37:47 UT represent the artificial slits, and the green curved dashed-line outlines the arc-shaped filament (∼ 1.8 × 1010 cm). The orange arched line at 05:41:42 UT depicts the filament footpoint separation (∼1.6 × 1010 cm). During the eruption a large amount of the filament material is blueshifted up to 4.0 Å from the line center, also blobs-like structures are further blueshifted over 6.25 Å (red arrows). The symbol ‘+’ at 05:44:50 UT indicates the region from which a strongly blueshifted spectral profile is obtained and shown in Fig. 1. The bottom panels show blueshifted and redshifted spectral profiles from the regions outlined with blue and red circle marks (upper panels), the black profiles are from a quiet region. The redshifted profile (red plot) is caused by downflows close to the filament footpoint (see the text). The background hatched rectangles highlight the wavelength range of the Dopplergrams presented in each column of the upper panels. An animation of this figure is available online. |
| In the text | |
 |
Fig. 3. Multiwavelength time-distance diagrams of the filament eruption obtained along the slit S1 (filament apex). The vertical axes denote the apparent vertical distance in the plane of sky measured from the initial position of the filament apex. Panels (a), (b), and (c) show different characteristics of the eruption that become more evident at specific wavelengths. At Hα ± (0.25:2.0 Å) the slow-rising phase and the initial acceleration are observed, at Hα ± (2.25:4.0 Å) the main phase and fast acceleration have manifested, and at Hα ± (4.25:6.0 Å) the fastest-ascending phase is visible. Panel (d) is a composite time-distance diagram, which helps visualize the complete picture of the eruption and demonstrates that the line of sight velocity of the erupting filament also increases as a function of distance and time. The inset color-bar depicts the corresponding line of sight velocity of the wavelength range indicated in panels (a), (b), and (c). The dashed line is the fitting of an exponential function to the selected points along the erupting feature in the plane of sky. |
| In the text | |
 |
Fig. 4. Observations of the filament eruption in the He II line (304 Å) and light curve of the associated solar flare. Panel (a): Main phase of the filament eruption, where the straight line labeled S1 outlines the artificial slit positioned along the filament apex (same as for Hα in Fig. 2). The curved cyan line depicts the filament footpoints separation, while the ‘×’ symbols outline the erupting material. Panel (b): Time-distance diagram extracted from the slit S1. The diagram shows a complex eruption, wherein at around 05:38 UT the erupting material splits into two main branches. The yellow dotted profile is the fitting curve applied to the selected positions along the erupting feature in the plane of sky, while the red dashed plot is the fitting curve applied to Hα data shown in Fig. 3. Panel (c): Running difference time-distance diagram showing the apparent unwinding motion of the erupting filament (see the text). As in Fig. 3, the vertical axis of panels (b) and (c) denote the apparent vertical distance in the plane of sky from the initial position of the filament apex. For context, the soft X-ray light curve of the B-class flare is also plotted in panel (d). The temporal evolution of the profiles in panel (b) suggests that the eruption of the filament started before the soft X-ray flux enhancement. |
| In the text | |
 |
Fig. 5. Velocity maps based on the cloud model illustrating the Doppler characteristics of the filament eruption (blue colors toward the Earth). Shortly after the filament disruption, which happens at around 05:38 UT, a large amount of the filament material is launched with velocities of about −100 km s−1 (blueshifted). Redshifted structures corresponding to the material moving in opposite direction are also observed close to the footpoints of the erupting filament. This suggests that downflows are driven during the eruption and could be related to the mass loss (see the text). In the latter phase of the eruption, blob-like structures traveling with velocities exceeding −250 km s−1 also can be identified. An animation of this figure is available online. |
| In the text | |
 |
Fig. 6. Optical thickness spectra of the filament apex (slit S1) extracted from the SDDI Hα filtergrams (see Fig. 2). Upper panels: Two-dimensional spectra wherein the erupting filament is visible as dark elongated structures extending upward from the central part of the spectra. We applied deconvolution to recover the instrumental broadening in our observations (see the text). The horizontal green, black, and red lines are used to track the fast (leading), main (core), and slow (following) components of the eruption, respectively. We note that the negative values in the optical thickness spectra are related to some errors (bias) in the estimates arising from the noise in the data. Lower panels: Optical thickness profiles obtained from the horizontal lines shown in the upper panels. The profiles show different characteristics of the erupting material, for example, multiple peaks and large Doppler shifts. An animation of this figure is available online. |
| In the text | |
 |
Fig. 7. Same as in Fig. 6 but for the lateral part of the filament eruption that crosses the slit S2 (see Fig. 2). What is remarkable here is the detection of strongly blueshifted plasma contained in the filament. Again, the optical thickness profiles help visualize in more detail the characteristics of the fast, main, and slow components of the erupting material. An animation of this figure is available online. |
| In the text | |
 |
Fig. 8. Selected optical thickness profiles of the fast and main components at the apex (top panels) and lateral part (bottom panels) of the filament eruption, respectively. The time of the profiles are nearly the same as the two-dimensional spectra shown in Figs. 6 and 7. The colored profiles highlight the subcomponents resulting from the Gaussian fitting model, while the solid gray profiles are composite fitting results by combining the multiple subcomponents. It is also shown the peak velocity υpeak (km s−1) of the composite profiles and the estimated micro-turbulent velocity ξ (km s−1) of each subcomponent (see the text). |
| In the text | |
 |
Fig. 9. Distribution of the optical thickness profiles obtained from the filament apex. Panel (a) shows the distribution of the fast component, while panel (b) the distribution of the main component. The fast and main components refer to the measurements obtained from the leading and the central part of the erupting feature, respectively, detected in the optical thickness spectra (see the text). The enhanced regions correspond to the multiple peaks of the profiles that are Doppler-shifted to large velocities during the filament eruption. The blue profiles are the line of sight velocity υlos of the fast and main components calculated by tracking the enhanced regions. For comparison, it is also plotted the plane of sky velocity profile υpos (black) calculated from the time-distance diagrams presented in Fig. 3. |
| In the text | |
 |
Fig. 10. True eruption profiles (height, velocity, and acceleration) of the filament apex fast and main components. We note that the profiles in panel (a) show the actual propagation distance of the filament eruption measured from the initial position of the filament apex (see the text). The eruption profiles reveal that the filament attains a large propagation distance (panel a), high propagation speed (panel b), and fast acceleration (panel c). Of note regarding the velocity and acceleration profiles is that the fast and main components evolve identically until 05:35 UT, thereafter the profiles deviate from each other, that is, one accelerates impulsively while the other undergoes a rapid diminution. |
| In the text | |
 |
Fig. 11. Geometry of the Sun and representation of the velocity vectors related to the filament eruption. The axes ( |
| In the text | |
 |
Fig. 12. Trajectory of the filament eruption projected in 3D space calculated with Eq. (11). The axes (α, β, γ) refer to the local coordinates system determined by the unit vectors ( |
| In the text | |
 |
Fig. A.1. Same as in Fig. 9 but for the lateral part of the filament eruption (main and fast components). The distribution plots in panel (a) clearly show that the erupting material is blueshifted to velocities of about −300 km s−1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.