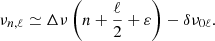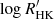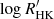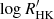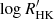| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | L16 | |
| Number of page(s) | 10 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202449197 | |
| Published online | 26 March 2024 | |
Letter to the Editor
Expanding the frontiers of cool-dwarf asteroseismology with ESPRESSO
Detection of solar-like oscillations in the K5 dwarf ϵ Indi
1
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: tiago.campante@astro.up.pt
2
Departamento de Física e Astronomia, Faculdade de Ciências da Universidade do Porto, Rua do Campo Alegre, s/n, 4169-007 Porto, Portugal
3
Stellar Astrophysics Centre (SAC), Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
4
Institute for Astronomy, University of Hawai‘i, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
5
INAF – Osservatorio Astrofisico di Catania, Via S. Sofia 78, 95123 Catania, Italy
6
Sydney Institute for Astronomy (SIfA), School of Physics, University of Sydney, Sydney, NSW 2006, Australia
7
Department of Chemistry and Physics, Florida Gulf Coast University, 10501 FGCU Blvd. S., Fort Myers, FL 33965, USA
8
School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
9
Université Paris-Saclay, Université Paris Cité, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
10
White Dwarf Research Corporation, 9020 Brumm Trail, Golden, CO 80403, USA
11
INAF – Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, Italy
Received:
9
January
2024
Accepted:
5
March
2024
Fuelled by space photometry, asteroseismology is vastly benefitting the study of cool main-sequence stars, which exhibit convection-driven solar-like oscillations. Even so, the tiny oscillation amplitudes in K dwarfs continue to pose a challenge to space-based asteroseismology. A viable alternative is offered by the lower stellar noise over the oscillation timescales in Doppler observations. In this Letter we present the definite detection of solar-like oscillations in the bright K5 dwarf ϵ Indi based on time-intensive observations collected with the ESPRESSO spectrograph at the VLT, thus making it the coolest seismic dwarf ever observed. We measured the frequencies of a total of 19 modes of degree ℓ = 0–2 along with νmax = 5305 ± 176 μHz and Δν = 201.25 ± 0.16 μHz. The peak amplitude of radial modes is 2.6 ± 0.5 cm s−1, or a mere ∼14% of the solar value. Measured mode amplitudes are ∼2 times lower than predicted from a nominal L/M scaling relation and favour a scaling closer to (L/M)1.5 below ∼5500 K, carrying important implications for our understanding of the coupling efficiency between pulsations and near-surface convection in K dwarfs. This detection conclusively shows that precise asteroseismology of cool dwarfs is possible down to at least the mid-K regime using next-generation spectrographs on large-aperture telescopes, effectively opening up a new domain in observational asteroseismology.
Key words: asteroseismology / techniques: radial velocities / stars: late-type / stars: oscillations / stars: individual: ϵ Indi A
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Asteroseismology has seen remarkable advances thanks to missions such as Convection, Rotation and planetary Transits (CoRoT; Baglin et al. 2006) and Kepler/K2 (Borucki et al. 2010; Howell et al. 2014). These missions have provided exquisite space photometry, enabling the detailed study of the interiors of solar-type and red-giant stars, which exhibit convection-driven solar-like oscillations (for a recent review, see Aerts 2021). The ongoing Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015), along with the upcoming PLAnetary Transits and Oscillations of stars (PLATO; Rauer et al. 2014) and Nancy Grace Roman (Spergel et al. 2015) space telescopes, are set to revolutionise the field as they are expected to raise the yield of known solar-like oscillators to a few million stars, or by two orders of magnitude over previous missions combined (Gould et al. 2015; Miglio et al. 2017; Hon et al. 2021; Goupil et al. 2024).
Despite this success story, space-based asteroseismology faces a challenge regarding K dwarfs. Owing to the low luminosities of K dwarfs, their oscillation amplitudes are extremely small (below a few parts per million or, equivalently, 10 cm s−1; Kjeldsen et al. 2008; Verner et al. 2011; Corsaro et al. 2013) and thus hard to detect, even with multi-year Kepler photometry (e.g., Kepler-444; Campante et al. 2015). As a result, only a few dwarfs cooler than the Sun have detected solar-like oscillations to date, and none cooler than ∼5000 K (see Fig. 1).
 |
Fig. 1. Stellar radius–effective temperature diagram highlighting seismic detections from Kepler and TESS photometry (blue circles; Mathur et al. 2017; Hatt et al. 2023), and radial-velocity campaigns (red diamonds; see e.g., Arentoft et al. 2008; Kjeldsen et al. 2008, and references therein). The stellar background sample (grey dots) is taken from the TESS Input Catalog (TIC; Stassun et al. 2019). The Sun is represented by its usual symbol. Approximate spectral type ranges (F, G, and K) are delimited by the vertical dashed lines. ϵ Indi (K5 V) is the coolest seismic dwarf observed to date (its interferometric radius and effective temperature were used to place it in the diagram; Rains et al. 2020). |
A viable alternative to space photometry is offered by Doppler observations. Stellar noise due to non-oscillatory fluctuations associated with activity and granulation is substantially lower in Doppler than it is in photometry (Harvey 1988). Consequently, radial-velocity (RV) observations have a higher signal-to-noise ratio (S/N) over the typical timescales of the oscillations (by an order of magnitude in power for the Sun; Grundahl et al. 2007). This motivated a number of pre-Kepler ground-based campaigns on cool dwarfs with the state-of-the-art spectrographs such as the High Accuracy Radial velocity Planet Searcher (HARPS; Mayor et al. 2003) and the Ultraviolet and Visual Echelle Spectrograph (UVES; Dekker et al. 2000). Observing runs like those on τ Ceti (G8 V; Teixeira et al. 2009), 70 Ophiuchi A (K0 V; Carrier & Eggenberger 2006), and α Centauri B (K1 V; Kjeldsen et al. 2005) are the epitome of such efforts, having helped set a lower effective temperature (Teff) bound on cool-dwarf asteroseismology. However, long readout times and/or relatively small apertures meant that these early campaigns would remain limited to the very brightest dwarfs.
K dwarfs have since become a primary focus in searches for potentially habitable planets (Lillo-Box et al. 2022; Mamajek & Stapelfeldt 2023). Moreover, owing to their ubiquity and long lives, they are unique probes of local Galactic chemical evolution (Adibekyan et al. 2012; Delgado Mena et al. 2021). The time is thus ripe to systematically extend asteroseismology to these cooler dwarfs via ultra-high-precision RV observations that make use of next-generation spectrographs on large-aperture telescopes. The combination of a large collecting area, instrumental stability, and high spectral resolution makes the Echelle SPectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO; Pepe et al. 2021), mounted on the Very Large Telescope (VLT) at the European Southern Observatory (ESO), Paranal, Chile, particularly suitable for this purpose.
An exploratory campaign on the seventh magnitude K3 dwarf HD 40307 was conducted in December 2018 as part of the ESPRESSO Guaranteed Time Observations (GTO), as described in Sect. 5.3.2 of Pepe et al. (2021). However, due in part to the target’s relative faintness, only a tentative claim of p-mode detection (at the level of 3–4 cm s−1) could be made. In this Letter we overcome this drawback as we report on the recent campaign conducted with ESPRESSO on the fourth magnitude K5 dwarf ϵ Indi A (HD 209100, HR 8387; hereafter ϵ Indi), a target providing a nearly ten times greater flux than HD 40307. We are able to firmly establish the presence of solar-like oscillations in the RV data of ϵ Indi, thus making it the coolest seismic dwarf observed to date.
2. Observations and data reduction
ϵ Indi is a nearby (d = 3.64 pc), bright (V = 4.69), and metal-poor ([Fe/H] = −0.17 ± 0.05 dex; Gomes da Silva et al. 2021) K5 dwarf (interferometry-based Teff = 4649 ± 84 K; Rains et al. 2020). It hosts a cold Jupiter (ϵ Indi Ab) on a 45 yr period orbit detected in RV and astrometric data (Feng et al. 2019). ϵ Indi further hosts a brown dwarf binary (ϵ Indi Ba, Bb) in a wide orbit with a projected separation of ∼1500 AU (McCaughrean et al. 2004). This system hence provides a benchmark for the study of the formation of gas-giant planets and brown dwarfs (e.g., Pathak et al. 2021; Viswanath et al. 2021; Chen et al. 2022; Šubjak et al. 2023).
We observed ϵ Indi for six consecutive half nights with ESPRESSO in September 2022. Observations were carried out in single Unit Telescope (single-UT) high-resolution (1 × 1 binning and fast readout) mode. Weather conditions were generally favourable, with photometric and/or clear skies over the first two nights, and spells of thin cirrus clouds and relatively high winds during the remaining nights. We obtained 2084 spectra with a fixed exposure time of 25 s and a median cadence of one exposure every 60 s (which corresponds to a Nyquist frequency of 8.3 mHz). The spectra were subsequently reduced using version 3.0.0 of the ESPRESSO data reduction software (DRS), having adopted a K6 stellar binary mask to compute cross-correlation functions (CCFs), from which RVs and associated CCF parameters (see Appendix A) were derived.
The resulting (raw) RVs are shown in the top panel of Fig. 2. The slow modulation of the time series is likely a manifestation, as seen in this short-duration data set, of the 18-day signal (corresponding to half the rotation period) due to rotational activity variations identified by Feng et al. (2019). Moreover, the time series displays intranight trends, presumably due to a combination of instrumental drift and stellar convection. To remove the slow modulation and intranight trends, we high-pass filtered the time series one night at a time using a triangular smoothing function (∼2 h cutoff). The detrended time series thus obtained is shown in the middle panel of Fig. 2. Its dispersion (rms scatter) is 30 cm s−1 and greater than the photon noise, which we attribute to the presence of oscillations (the average photon-noise uncertainty per data point is ⟨σRV⟩ = 22 cm s−1; see bottom panel of Fig. 2).
 |
Fig. 2. Time series of ESPRESSO radial-velocity measurements of ϵ Indi. Top: raw time series (after removal of a constant RV offset). The solid red curves represent smoothing functions applied on a nightly basis (see text for details). Middle: detrended time series (after high-pass filtering). Bottom: internal (photon-noise limited) RV precision as returned by the ESPRESSO DRS. The horizontal dotted line represents the instrumental noise level of 10 cm s−1 quoted by Pepe et al. (2021). |
3. Asteroseismic data analysis
3.1. Computation of the power spectrum
We based our analysis of the power spectrum on the discrete Fourier transform (DFT) of the detrended RV time series. This involved using the measurement uncertainties, σRV, i, as statistical weights in calculating the power spectrum (according to 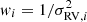 ). In order to optimise the noise floor in the power spectrum, these weights were further adjusted to account for a small fraction of bad data points (37 data points, or ∼2% of the total, were removed) as well as night-to-night variations in the noise level. We followed a well-tested procedure in adjusting the weights (for details, see e.g., Bedding et al. 2004; Arentoft et al. 2008).
). In order to optimise the noise floor in the power spectrum, these weights were further adjusted to account for a small fraction of bad data points (37 data points, or ∼2% of the total, were removed) as well as night-to-night variations in the noise level. We followed a well-tested procedure in adjusting the weights (for details, see e.g., Bedding et al. 2004; Arentoft et al. 2008).
The resulting noise-optimised power spectrum is shown in Fig. 3, which displays a clear power excess due to solar-like oscillations centred just above 5 mHz (typical periods of ∼3 min). This is in agreement with the predicted frequency of maximum oscillation amplitude, νmax = νmax, ⊙ (g/g⊙) (Teff/Teff, ⊙)−1/2 ∼ 5.2 mHz, scaled by solar values (Brown et al. 1991; Kjeldsen & Bedding 1995), where g is the surface gravity (log g = 4.61 ± 0.29 dex; Gomes da Silva et al. 2021). We proceeded to measure νmax based on a heavily smoothed version of the power spectrum (see Sect. 3.3 for details). After correcting for the background noise in the power spectrum, an estimate νmax = 5305 ± 176 μHz was obtained.
 |
Fig. 3. Noise-optimised power spectrum of ϵ Indi. The power spectrum has been oversampled for visual purposes. A clear power excess due to solar-like oscillations can be seen centred just above 5 mHz. The vertical dashed line represents the measured νmax (see text for details). The inset shows the spectral window, with prominent sidelobes (daily aliases) due to the single-site nature of the observations. |
The spectral window is shown as an inset in Fig. 3, and reveals prominent sidelobes caused by the daily gaps in the RV data. The average photon-noise level in the amplitude spectrum, as measured at high frequencies (above 6.5 mHz, i.e., beyond the frequency range occupied by the p modes), is 0.94 cm s−1. For comparison, the high-frequency noise level reported for the observations of α Centauri B is 1.39 cm s−1 (Kjeldsen et al. 2005).
3.2. Oscillation frequencies
The frequencies of acoustic (p) modes of high radial order, n, and low angular degree, ℓ, are well approximated by the asymptotic relation (Tassoul 1980):
Here Δν is the large separation between modes of like degree and consecutive order, being a probe of the mean stellar density; δν0ℓ is the small separation between modes of different degree and is sensitive to variations in the sound speed gradient near the core in main-sequence stars; and the dimensionless offset, ε, is determined by the reflection properties of the surface layers. Observed solar-like oscillations in main-sequence stars are expected to follow this relation closely. We thus used this prior information to guide the mode identification and extraction (as described below), bearing in mind the presence of daily aliases in the power spectrum (appearing at splittings of ±11.57 μHz, or ±1 cycle per day, about genuine peaks).
Extracted mode frequencies are listed in Table 1 and displayed in échelle format in the top panel of Fig. 4. Owing to the short duration of the RV time series, individual modes are only partially resolved (see also Sect. 3.4). Modes were thus extracted using a standard iterative sine-wave fitting procedure, also known as prewhitening (e.g., Bedding et al. 2010). A total of 19 modes of degree ℓ = 0–2 were extracted across seven orders down to S/N = 2.5. The full procedure for identifying and extracting oscillation frequencies consisted in the following steps:
 |
Fig. 4. Outcome of the mode identification and extraction procedure. Top: replicated échelle diagram displaying the mode frequencies extracted for ϵ Indi (cf. Table 1). The smoothed power spectrum is shown in grey scale. The vertical dashed line gives the measured Δν value. Bottom: likelihood-weighted histogram of ε Δν for the models in the grid (see text for details). The observed ε Δν is represented by a vertical dotted line. |
Oscillation frequencies for ϵ Indi (in μHz).
1. We measured the strongest peak (5121.61 μHz) within the frequency range occupied by the p modes and used it to compute a modified comb response (e.g., Kjeldsen et al. 1995) over a range of trial large separations. The comb response peaks at ∼201.3 μHz, which we adopted as a first estimate of Δν.
2. Guided by this estimate, we identified the sequence of (nearly) regularly spaced peaks below and above the dominant mode at 5121.61 μHz (and hence sharing the same ℓ). We measured seven such modes, based on which the large separation, Δν = 201.25 ± 0.16 μHz, was computed. Based on the value for Δν and the frequency of the dominant mode, we inferred ε = 1.451 ± 0.019, consistent with the empirical results in the literature obtained for other cool dwarfs (cf. White et al. 2011a,b, 2012; Lund et al. 2017), and hence with these being radial (ℓ = 0) modes.
3. We extracted these modes from the time series through iterative sine-wave fitting. By collapsing the resulting prewhitened power spectrum about the position of the ℓ = 0 ridge, we saw a power excess at lower frequencies, which we assigned to the ℓ = 2 ridge, being able to resolve the small separation (δν02 ∼ 14.5 μHz). Guided by this, we then identified a sequence of five quadrupole (ℓ = 2) modes in the prewhitened power spectrum, based on which we obtained δν02 = 15.28 ± 0.45 μHz. We note that δν02 is a decreasing function of frequency (or n), as expected (e.g., Lund et al. 2017).
4. Finally, we collapsed the power spectrum about the midpoint between consecutive radial modes. A clear power excess corresponding to the ℓ = 1 ridge could be seen below the midpoint frequency (δν01 ∼ 4.4 μHz). Guided by this, we identified a sequence of seven dipole (ℓ = 1) modes, providing a direct measurement of the small separation, δν01 = 3.46 ± 1.48 μHz. We estimated the power ratio between the ℓ = 1 and 0 ridges to be ∼1.3, in accordance with the predicted spatial response of Doppler observations (Kjeldsen et al. 2008; Schou 2018).
Figure B.1 shows the prewhitened power spectrum after extracting all 19 identified modes, where it can be seen that they account for most of the power within the p-mode frequency range.
The problem of mode identification, in the sense of assigning a pair (n, ℓ) to the extracted frequencies, may not be a trivial one to solve. There are numerous instances of seismic studies that led to uncertainty on the mode identification (e.g., Carrier & Eggenberger 2006; Appourchaux et al. 2008; Bedding et al. 2010), which is made worse in the case of single-site ground-based observations. As an additional check on the above observational procedure, we adopted a model-based approach to mode identification based upon the work of White et al. (2011a,b), in order to verify whether the observed position of the ℓ = 0 ridge in the échelle diagram is consistent with expectations from stellar models. Based on the stellar model grid of Li et al. (2023), we calculated, for each model in that grid, a likelihood function, 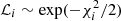 , where the discrepancy function,
, where the discrepancy function, 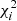 , is given by the sum of the error-normalised discrepancies for Teff, [Fe/H], and Δν, adopted as observational constraints. We next computed a model prediction of the quantity ε Δν, which gives the absolute position of the ℓ = 0 ridge in an échelle diagram (cf. Eq. (1)). This was simply done by constructing a likelihood-weighted histogram of ε Δν for the models in the grid (see bottom panel of Fig. 4). According to this, the power ridge just below 100 μHz in the top panel of Fig. 4 should correspond to ℓ = 2, 0 (rather than ℓ = 1), thus providing support to our adopted mode identification. We note the presence of a small offset between the model-based and observed (shown as a vertical dotted line) ε Δν. This is to be expected, and is due to the fact that model frequencies were not corrected for the surface effect (see e.g., Ball & Gizon 2014). We will be investigating the magnitude of the surface effect in this Teff regime in a follow-up study.
, is given by the sum of the error-normalised discrepancies for Teff, [Fe/H], and Δν, adopted as observational constraints. We next computed a model prediction of the quantity ε Δν, which gives the absolute position of the ℓ = 0 ridge in an échelle diagram (cf. Eq. (1)). This was simply done by constructing a likelihood-weighted histogram of ε Δν for the models in the grid (see bottom panel of Fig. 4). According to this, the power ridge just below 100 μHz in the top panel of Fig. 4 should correspond to ℓ = 2, 0 (rather than ℓ = 1), thus providing support to our adopted mode identification. We note the presence of a small offset between the model-based and observed (shown as a vertical dotted line) ε Δν. This is to be expected, and is due to the fact that model frequencies were not corrected for the surface effect (see e.g., Ball & Gizon 2014). We will be investigating the magnitude of the surface effect in this Teff regime in a follow-up study.
3.3. Oscillation amplitudes
The measured amplitudes of individual modes are affected by the stochastic nature of the excitation and damping. We hence followed the procedure described in Kjeldsen et al. (2005, 2008) to measure the oscillation amplitude envelope in a way that is independent of these effects. In short, we heavily smoothed the power spectrum by convolving it with a Gaussian having a full width at half maximum (FWHM) of 4 Δν; converted to power density; fitted and subtracted the background noise; and multiplied by Δν/c and took the square root, thus converting to amplitude per radial mode (a value of c = 4.09 was adopted, representing the effective number of modes per order for full-disk velocity observations, normalised to the amplitudes of radial modes; Kjeldsen et al. 2008).
The envelope peak amplitude thus obtained is vosc = 2.6 ± 0.5 cm s−1, or a mere ∼14% of the solar value (vosc, ⊙ = 18.7 cm s−1, as measured using stellar techniques and averaged over one full solar cycle; Kjeldsen et al. 2008). The associated uncertainty was estimated as the standard deviation resulting from having applied the above procedure to the power spectra of 2000 artificial time series, generated using the asteroFLAG Artificial DataSet Generator, version 3 (AADG3; Ball et al. 2018). Each simulated time series contained as input all extracted mode frequencies (cf. Table 1), with mode lifetimes allowed to vary across simulations, and was sampled adopting the ϵ Indi observing window. A fixed νmax and amplitude per radial mode were assumed based on the corresponding measured quantities. The reported error bar thus takes into account different sources of uncertainty, namely realisation noise, the stochastic nature of the oscillations, and the white-noise level (whose input value was subject to a 10% perturbation). Owing to the single-epoch nature of the observations, no attempt was made to quantify the uncertainty related to potential variations induced by the stellar activity cycle (see Fig. C.1).
Figure 5 shows the amplitude per radial mode as a function of Teff (colour-coded according to the chromospheric emission ratio, 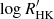 ) for ϵ Indi and a number of cool dwarfs with published measurements. We note that the amount of smoothing of the power spectrum affects the exact height of the smoothed amplitude envelope, and hence the estimate of vosc. Measurements for the Sun and α Centauri A and B (Kjeldsen et al. 2008), as well as for τ Ceti (Teixeira et al. 2009) were obtained following the same procedure as described above. The value plotted for 70 Ophiuchi A (Carrier & Eggenberger 2006) corresponds to the upper bound on the amplitudes of the highest mode peaks detected and has no associated uncertainty, while an estimate (no error provided) of the mode amplitudes for the solar twin 18 Scorpii is given in Bazot et al. (2011). Finally, our reanalysis of the ESPRESSO GTO radial-velocity data of HD 40307 showed no p-mode detection (see Appendix D), and so the plotted value corresponds to an upper limit.
) for ϵ Indi and a number of cool dwarfs with published measurements. We note that the amount of smoothing of the power spectrum affects the exact height of the smoothed amplitude envelope, and hence the estimate of vosc. Measurements for the Sun and α Centauri A and B (Kjeldsen et al. 2008), as well as for τ Ceti (Teixeira et al. 2009) were obtained following the same procedure as described above. The value plotted for 70 Ophiuchi A (Carrier & Eggenberger 2006) corresponds to the upper bound on the amplitudes of the highest mode peaks detected and has no associated uncertainty, while an estimate (no error provided) of the mode amplitudes for the solar twin 18 Scorpii is given in Bazot et al. (2011). Finally, our reanalysis of the ESPRESSO GTO radial-velocity data of HD 40307 showed no p-mode detection (see Appendix D), and so the plotted value corresponds to an upper limit.
 |
Fig. 5. Amplitude per radial mode as a function of Teff for ϵ Indi and a number of cool dwarfs with published measurements. Reported statistical uncertainties for the mode amplitudes are comparable in size to the plotted symbols. Data points are colour-coded according to the corresponding |
Based on calculations by Christensen-Dalsgaard & Frandsen (1983), Kjeldsen & Bedding (1995) suggested a scaling of the oscillation amplitudes of p modes in Doppler velocity of the form vosc ∝ (L/M)s, with s = 1, and where L and M are respectively the stellar luminosity and mass. The numerical value of the exponent s has since been revised theoretically, based on models of main-sequence stars, and found to lie in the range 0.7–1.5 (see e.g., Houdek et al. 1999; Samadi et al. 2005, 2007). On the other hand, observational1 studies based on large ensembles of main-sequence and subgiant Kepler stars have constrained s to the approximate range2 0.5–1.0, depending on Teff (Verner et al. 2011; Corsaro et al. 2013).
We show, in Fig. 5, two scalings of the mode amplitudes corresponding to the extrema of the theoretical range in s (i.e., s = 0.7 and 1.5). The displayed mode amplitude measurements hint at a transition to a scaling closer to (L/M)1.5 below ∼5500 K (cf. Verner et al. 2011, where a negative ds/dTeff gradient was determined). This is supported by the mode amplitudes measured herein for ϵ Indi and the upper limit on the mode amplitudes obtained for HD 40307. The fraction of magnetically active stars among K dwarfs is higher than among G dwarfs (e.g., Jenkins et al. 2011; Gomes da Silva et al. 2021). At the same time, increasing levels of activity are known to suppress the amplitudes of solar-like oscillations (García et al. 2010; Chaplin et al. 2011; Bonanno et al. 2014; Campante et al. 2014), which could therefore be the underlying cause for the apparent transition between scaling relations when moving down in Teff in Fig. 5. We find no significant correlation between 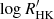 and Teff (Spearman’s rank correlation coefficient, ρ = −0.17, and large p-value, p ≫ 0.05) for the displayed cool-dwarf sample. However, given the limited size of this sample, we refrain from making more general considerations regarding the role of activity in this context, and advocate for the inclusion of its effect in the calibration of the mode-amplitude scaling in this Teff regime as more targets are observed. Finally, it is worth noting that ϵ Indi (
and Teff (Spearman’s rank correlation coefficient, ρ = −0.17, and large p-value, p ≫ 0.05) for the displayed cool-dwarf sample. However, given the limited size of this sample, we refrain from making more general considerations regarding the role of activity in this context, and advocate for the inclusion of its effect in the calibration of the mode-amplitude scaling in this Teff regime as more targets are observed. Finally, it is worth noting that ϵ Indi (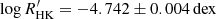 ; see Appendix C) and 70 Ophiuchi A (
; see Appendix C) and 70 Ophiuchi A (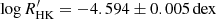 ; Gomes da Silva et al. 2021) are the only relatively active stars in a sample otherwise biased toward inactive stars (
; Gomes da Silva et al. 2021) are the only relatively active stars in a sample otherwise biased toward inactive stars (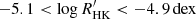 ).
).
3.4. Oscillation lifetimes
Solar-like oscillations are stochastically excited and damped by near-surface convection. The power spectrum of a single mode that is observed for long enough will appear as an erratic function concealing a Lorentzian profile, the width of which indicates the mode lifetime (e.g., Anderson et al. 1990). If, as in the present case, the observations are not long enough to fully resolve the Lorentzian profile, then the effect of the finite mode lifetime is to randomly shift each mode peak from its true position by a small amount (e.g., Bedding et al. 2004; Kjeldsen et al. 2005). Measuring this scatter provides an opportunity to infer the mode lifetimes in ϵ Indi.
We inferred the mode lifetimes by measuring the scatter of the observed frequencies of radial modes (which are not impacted by rotation) about their power ridge in the échelle diagram and comparing with simulations (see Appendix E). The top panel of Fig. E.1 shows the outcome of this calibration procedure for the ϵ Indi observing window. Although an upper bound on the mode lifetimes is weakly constrained, it is safe to say that lifetimes are at least a few days long (≳3 d). For context, the average mode lifetime in the Sun, measured in the range 2.8–3.4 mHz, is 2.88 ± 0.07 d (Chaplin et al. 1997), being slightly longer than for τ Ceti (1.7 ± 0.5 d; Teixeira et al. 2009), and in line with that measured for α Centauri B (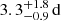 at 3.6 mHz and
at 3.6 mHz and 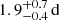 at 4.6 mHz; Kjeldsen et al. 2005).
at 4.6 mHz; Kjeldsen et al. 2005).
4. Conclusion and outlook
In this Letter we have presented the definite detection of solar-like oscillations in the bright K5 dwarf ϵ Indi based on radial-velocity observations carried out with the ESPRESSO spectrograph. This campaign hence unambiguously demonstrates the potential of ESPRESSO for cool-dwarf asteroseismology, effectively opening up a new observational domain in the field.
Measured mode amplitudes for ϵ Indi are approximately two times lower than predicted from a nominal L/M scaling relation, favouring a scaling closer to (L/M)1.5 below ∼5500 K. A calibration of the mode-amplitude scaling relation in this Teff regime is thus called for as more targets are observed for asteroseismology. Mode amplitudes are determined by a delicate balance between the energy supply and the mode damping, both being directly connected to the turbulent velocity field associated with convection (Houdek & Dupret 2015). The measurement of oscillation modes in K dwarfs will hence allow us to constrain the dynamical coupling between pulsations and near-surface convection in a regime yet unexplored. Moreover, measured mode amplitudes, used in combination either with 1D non-local time-dependent convection models (Chaplin et al. 2005) or with state-of-the-art 3D stellar atmosphere simulations (Zhou et al. 2021), will enable predictions of amplitudes in photometry. This information is key to accurately estimating the PLATO seismic yield (Miglio et al. 2017; Goupil et al. 2024) and can potentially influence the PLATO pipeline development strategy (Cunha et al. 2021).
Furthermore, ϵ Indi is the only known system containing T-type brown dwarfs for which a test of substellar cooling with time and a coevality test of model isochrones are both made possible (Chen et al. 2022). These tests would greatly benefit from having a precise seismic age for the host star, as it still remains a major source of uncertainty in the evolutionary and atmospheric modelling of the system. We display, in Fig. 6, the location of ϵ Indi in a C-D diagram (Christensen-Dalsgaard 1984), showing δν02 versus Δν. Inspection of this diagram implies a seismic stellar age < 4 Gyr, consistent with most literature measurements (see Chen et al. 2022, and references therein), which include activity-based estimates, as well as ages from kinematics and isochrone fitting. Detailed asteroseismic modelling of ϵ Indi will be the subject of a follow-up study.
 |
Fig. 6. C–D diagram, showing δν02 vs. Δν. Models from the grid of Li et al. (2023) are colour-coded according to age (left) and mass (right). The location of ϵ Indi is indicated by the black symbol in both panels. The error on Δν is too small to be discerned. |
Observational results draw mostly from studies conducted in photometry. Photometric mode amplitudes, once corrected to bolometric amplitudes, are expected to scale as 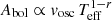 (with r = 1.5 if assuming adiabatic oscillations; Kjeldsen & Bedding 1995), thus allowing for conversion between photometric and Doppler observations.
(with r = 1.5 if assuming adiabatic oscillations; Kjeldsen & Bedding 1995), thus allowing for conversion between photometric and Doppler observations.
The procedure described in Kjeldsen et al. (2005, 2008) has been widely implemented in automated analysis pipelines with the goal of calibrating scaling relations. Corsaro et al. (2013) make exclusive use of amplitudes derived following this procedure. Verner et al. (2011) compare different analysis pipelines, several of which adopt this procedure; for the sake of homogeneity, we consider only the latter pipelines here (i.e., Huber et al. 2009; Hekker et al. 2010; Mathur et al. 2010).
An edge-on configuration (i.e. a stellar inclination angle i = 90°) is assumed here for illustrative purposes only, as it maximises the relative visibility of the two sectoral modes in a dipole triplet. We note that the best orbital solution of Feng et al. (2019) is instead characterised by 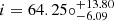 .
.
The rotation period estimate adopted throughout this work, 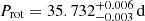 , is from Feng et al. (2019). The authors argue that this estimate, which is derived from a relatively large data set of high-precision RVs and multiple activity indicators, is a more reliable estimate than the 22-day rotation period quoted by Saar & Osten (1997). A 37.2-day estimate based on an unpublished ZDI analysis is quoted by Vidotto et al. (2016).
, is from Feng et al. (2019). The authors argue that this estimate, which is derived from a relatively large data set of high-precision RVs and multiple activity indicators, is a more reliable estimate than the 22-day rotation period quoted by Saar & Osten (1997). A 37.2-day estimate based on an unpublished ZDI analysis is quoted by Vidotto et al. (2016).
Acknowledgments
We thank the anonymous referee for their valuable comments and attention to detail. Based on observations collected at the European Southern Observatory under ESO programmes 109.236P.001 (ϵ Indi; PI: Campante) and 0102.D-0346(A) (HD 40307; PI: Bouchy). We thank François Bouchy for having shared with us the ESPRESSO GTO data of HD 40307 when these data were not yet public. This work was supported by Fundação para a Ciência e a Tecnologia (FCT) through research grants UIDB/04434/2020 and UIDP/04434/2020. Co-funded by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. Funding for the Stellar Astrophysics Centre (SAC) was provided by the Danish National Research Foundation (grant agreement no.: DNRF106). TLC is supported by FCT in the form of a work contract (CEECIND/00476/2018). AMS acknowledges support from FCT through fellowship 2020.05387.BD. TRB is supported by the Australian Research Council (FL220100117). DLB gratefully acknowledges support from NASA (NNX16AB76G, 80NSSC22K0622) and the Whitaker Endowed Fund at Florida Gulf Coast University. MSC acknowledges support from FCT/MCTES through grants 2022.03993.PTDC and CEECIND/02619/2017. RAG acknowledges support from the GOLF and PLATO grants from Centre National d’Études Spatiales (CNES). MSL acknowledges support from VILLUM FONDEN (research grant 42101) and The Independent Research Fund Denmark’s Inge Lehmann programme (grant agreement no.: 1131-00014B).
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
- Anderson, E. R., Duvall, T. L., Jr, & Jefferies, S. M. 1990, ApJ, 364, 699 [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arentoft, T., Kjeldsen, H., Bedding, T. R., et al. 2008, ApJ, 687, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in The CoRoT Mission Pre-Launch Status - Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA Special Publ., 1306, 33 [NASA ADS] [Google Scholar]
- Ball, W. H., & Gizon, L. 2014, A&A, 568, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, W. H., Chaplin, W. J., Schofield, M., et al. 2018, ApJS, 239, 34 [Google Scholar]
- Bazot, M., Ireland, M. J., Huber, D., et al. 2011, A&A, 526, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Butler, R. P., et al. 2004, ApJ, 614, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Campante, T. L., et al. 2010, ApJ, 713, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, A., & Corsaro, E. 2022, ApJ, 939, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, A., Corsaro, E., & Karoff, C. 2014, A&A, 571, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [Google Scholar]
- Campante, T. L., Chaplin, W. J., Lund, M. N., et al. 2014, ApJ, 783, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T. L., Barclay, T., Swift, J. J., et al. 2015, ApJ, 799, 170 [Google Scholar]
- Carrier, F., & Eggenberger, P. 2006, A&A, 450, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 1997, MNRAS, 288, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Houdek, G., Elsworth, Y., et al. 2005, MNRAS, 360, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Bedding, T. R., Bonanno, A., et al. 2011, ApJ, 732, L5 [Google Scholar]
- Chen, M., Li, Y., Brandt, T. D., et al. 2022, AJ, 163, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 1984, in Space Research in Stellar Activity and Variability, eds. A. Mangeney, & F. Praderie, 11 [Google Scholar]
- Christensen-Dalsgaard, J., & Frandsen, S. 1983, Sol. Phys., 82, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Corsaro, E., & De Ridder, J. 2014, A&A, 571, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corsaro, E., Fröhlich, H. E., Bonanno, A., et al. 2013, MNRAS, 430, 2313 [Google Scholar]
- Cunha, M. S., Roxburgh, I. W., Aguirre Børsen-Koch, V., et al. 2021, MNRAS, 508, 5864 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, G. R., Handberg, R., Miglio, A., et al. 2014, MNRAS, 445, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 534 [Google Scholar]
- Delgado Mena, E., Adibekyan, V., Santos, N. C., et al. 2021, A&A, 655, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, F., Anglada-Escudé, G., Tuomi, M., et al. 2019, MNRAS, 490, 5002 [Google Scholar]
- García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [Google Scholar]
- Gomes da Silva, J., Figueira, P., Santos, N., & Faria, J. 2018, J. Open Source Softw., 3, 667 [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Adibekyan, V., et al. 2021, A&A, 646, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A., Huber, D., Penny, M., & Stello, D. 2015, J. Korean Astron. Soc., 48, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M. J., Catala, C., Samadi, R., et al. 2024, A&A, 683, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grundahl, F., Kjeldsen, H., Christensen-Dalsgaard, J., Arentoft, T., & Frandsen, S. 2007, Commun. Asteroseismol., 150, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. W. 1988, in Advances in Helio- and Asteroseismology, eds. J. Christensen-Dalsgaard, & S. Frandsen, 123, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Hatt, E., Nielsen, M. B., Chaplin, W. J., et al. 2023, A&A, 669, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Broomhall, A. M., Chaplin, W. J., et al. 2010, MNRAS, 402, 2049 [NASA ADS] [CrossRef] [Google Scholar]
- Hon, M., Huber, D., Kuszlewicz, J. S., et al. 2021, ApJ, 919, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G., & Dupret, M.-A. 2015, Liv. Rev. Sol. Phys., 12, 8 [Google Scholar]
- Houdek, G., Balmforth, N. J., Christensen-Dalsgaard, J., & Gough, D. O. 1999, A&A, 351, 582 [NASA ADS] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
- Huber, D., Stello, D., Bedding, T. R., et al. 2009, Commun. Asteroseismol., 160, 74 [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability, International Series of Monographs on Physics (Clarendon Press) [Google Scholar]
- Jenkins, J. S., Murgas, F., Rojo, P., et al. 2011, A&A, 531, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Viskum, M., & Frandsen, S. 1995, AJ, 109, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Butler, R. P., et al. 2005, ApJ, 635, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Arentoft, T., et al. 2008, ApJ, 682, 1370 [Google Scholar]
- Li, Y., Bedding, T. R., Stello, D., et al. 2023, MNRAS, 523, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Lillo-Box, J., Santos, N. C., Santerne, A., et al. 2022, A&A, 667, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017, ApJ, 835, 172 [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [Google Scholar]
- Mamajek, E., & Stapelfeldt, K. 2023, Am. Astron. Soc. Meet. Abstr., 55, 116.07 [NASA ADS] [Google Scholar]
- Mathur, S., García, R. A., Régulo, C., et al. 2010, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Huber, D., Batalha, N. M., et al. 2017, ApJS, 229, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McCaughrean, M. J., Close, L. M., Scholz, R. D., et al. 2004, A&A, 413, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Chiappini, C., Mosser, B., et al. 2017, Astron. Nachr., 338, 644 [Google Scholar]
- Pathak, P., Petit dit de la Roche, D. J. M., Kasper, M., et al. 2021, A&A, 652, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rains, A. D., Ireland, M. J., White, T. R., Casagrande, L., & Karovicova, I. 2020, MNRAS, 493, 2377 [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Saar, S. H., & Osten, R. A. 1997, MNRAS, 284, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Samadi, R., Goupil, M. J., Alecian, E., et al. 2005, J. Astrophys. Astron., 26, 171 [Google Scholar]
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J. 2018, A&A, 617, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spergel, D., Gehrels, N., Baltay, C., et al. 2015, arXiv e-prints [arXiv:1503.03757] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Šubjak, J., Lodieu, N., Kabáth, P., et al. 2023, A&A, 671, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
- Teixeira, T. C., Kjeldsen, H., Bedding, T. R., et al. 2009, A&A, 494, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, A. H., & Preston, G. W. 1980, PASP, 92, 385 [Google Scholar]
- Verner, G. A., Elsworth, Y., Chaplin, W. J., et al. 2011, MNRAS, 415, 3539 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Donati, J. F., Jardine, M., et al. 2016, MNRAS, 455, L52 [Google Scholar]
- Viswanath, G., Janson, M., Dahlqvist, C.-H., et al. 2021, A&A, 651, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011a, ApJ, 742, L3 [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011b, ApJ, 743, 161 [Google Scholar]
- White, T. R., Bedding, T. R., Gruberbauer, M., et al. 2012, ApJ, 751, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y., Nordlander, T., Casagrande, L., et al. 2021, MNRAS, 503, 13 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Radial velocities and associated CCF parameters
Spectra were reduced using the ESPRESSO DRS (version 3.0.0). We searched for correlations between the RVs and a number of activity proxies derived concurrently from the CCFs, namely the full width at half maximum (FWHM), contrast, bisector span (BIS), and asymmetry. From Fig. A.1, no obvious correlations can be seen (also supported by the correlation coefficients displayed in each panel). A trend in the different CCF metrics is nevertheless evident throughout the observing run.
 |
Fig. A.1. Derived radial velocities vs activity proxies. The raw time series (after removal of a constant RV offset) is shown in the leftmost column. A ∼20 min gap in the data collection is apparent toward the end of night 2, which resulted from an interruption of the corresponding observation block. The remaining columns show the relationship (on a nightly basis) between the RVs and associated CCF parameters (FWHM, contrast, BIS, and asymmetry). Each panel is supplemented by Pearson’s correlation coefficient, R. |
Appendix B: Power spectrum prewhitening
The outcome of the iterative prewhitening procedure (after extraction of all 19 identified modes) is illustrated in Fig. B.1. The bottom panel shows the raw power spectrum (i.e. before prewhitening). The two panels immediately above the bottom panel display the prewhitened (or residual) power spectrum and the extracted modes (along with their aliases). The top panel shows a reconstructed power spectrum where the effect of the spectral window has been deconvolved.
 |
Fig. B.1. Power spectrum prewhitening. The outcome of having extracted all 19 identified modes is illustrated (see text for details). |
Appendix C: Chromospheric emission and magnetic activity cycle
Characterised by a median chromospheric emission level of 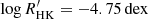 (Gomes da Silva et al. 2021), ϵ Indi is more active than the Sun (
(Gomes da Silva et al. 2021), ϵ Indi is more active than the Sun (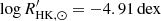 ; Mamajek & Hillenbrand 2008). It lies close to the Vaughan–Preston gap (Vaughan & Preston 1980), identified as a dearth of stars in the distribution of
; Mamajek & Hillenbrand 2008). It lies close to the Vaughan–Preston gap (Vaughan & Preston 1980), identified as a dearth of stars in the distribution of 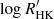 for main-sequence stars at about −4.75 dex. Moreover, ϵ Indi has an activity dispersion of log σ(R5) = − 0.84 dex, where
for main-sequence stars at about −4.75 dex. Moreover, ϵ Indi has an activity dispersion of log σ(R5) = − 0.84 dex, where 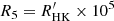 , hence displaying a typical activity variability for a K dwarf (Gomes da Silva et al. 2021).
, hence displaying a typical activity variability for a K dwarf (Gomes da Silva et al. 2021).
Based on 4293 HARPS archival observations obtained between 2003 and 2016, binned to 112 nights, we extracted the Ca II H&K index using ACTIN 2 (Gomes da Silva et al. 2018, 2021) and converted it to 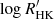 following Gomes da Silva et al. (2021). We next modelled the activity cycle of ϵ Indi, as traced by
following Gomes da Silva et al. (2021). We next modelled the activity cycle of ϵ Indi, as traced by 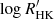 , assuming a simple sinusoidal behaviour. Figure C.1 shows the long-term variation of
, assuming a simple sinusoidal behaviour. Figure C.1 shows the long-term variation of 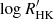 phase-folded onto the estimated (from a periodogram analysis) cycle period, Pcyc, of ∼2600 days (or ∼7 yr). The scatter of the HARPS observations about the activity cycle model is caused by rotational activity variations. We note that a period of about 2500 days for the primary magnetic cycle is reported by Feng et al. (2019), in good agreement with the value estimated here.
phase-folded onto the estimated (from a periodogram analysis) cycle period, Pcyc, of ∼2600 days (or ∼7 yr). The scatter of the HARPS observations about the activity cycle model is caused by rotational activity variations. We note that a period of about 2500 days for the primary magnetic cycle is reported by Feng et al. (2019), in good agreement with the value estimated here.
 |
Fig. C.1. Activity cycle of ϵ Indi as traced by |
We used the ESPRESSO spectra obtained herein to compute 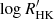 following the same procedure as above, having determined a mean chromospheric emission level of
following the same procedure as above, having determined a mean chromospheric emission level of 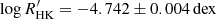 (blue square in Fig. C.1). The ESPRESSO emission level is very close to the value predicted by our simple model. Moreover, it is apparent that the ESPRESSO observations were obtained during the descending phase of the cycle, following the last maximum of activity in 2021.
(blue square in Fig. C.1). The ESPRESSO emission level is very close to the value predicted by our simple model. Moreover, it is apparent that the ESPRESSO observations were obtained during the descending phase of the cycle, following the last maximum of activity in 2021.
Based on the activity cycle period, Pcyc, estimated above and the rotation period estimate, Prot, from Feng et al. (2019), we evaluated the corresponding rates as ωcyc ≡ 2π/Pcyc and Ω ≡ 2π/Prot, yielding log ωcyc ≃ − 2.62 and logΩ ≃ − 0.76. When placed in the context of the correlation between activity cycle and rotation rates recently analysed by Bonanno & Corsaro (2022) for an extended Mt. Wilson sample of 67 stars, ϵ Indi appears to belong to what is called the upper branch, consisting of stars for which ωcyc increases with increasing Ω. According to the same study, stars belonging to the upper branch tend to be more metal-poor than stars in the lower branch (to which the Sun belongs), in line with the subsolar metallicity of ϵ Indi. ϵ Indi is thus likely characterised by an αΩ type of dynamo action in which global stellar rotation plays a primary role in setting the efficiency of the dynamo process since, according to mixing-length theory, a reduced metallicity enhances the eddy diffusivity of the plasma in the outer convection zone.
Appendix D: Revisiting HD 40307
With the goal of reassessing the tentative claim of p-mode detection for HD 40307 (Pepe et al. 2021), we re-reduced the 2018 ESPRESSO GTO data using the latest version (3.0.0) of the DRS, having computed a noise-optimised power spectrum in the same manner as described in Sect. 3.1. We next fitted a background profile plus a Gaussian envelope to the power spectrum using the high-DImensional And multi-MOdal NesteD Sampling (DIAMONDS; Corsaro & De Ridder 2014) Bayesian software. The Gaussian envelope is used to describe a possible power excess due to solar-like oscillations and was centred at different proxies for νmax in the range 3–6 mHz. Finally, we computed the Bayes factor (B) in favour of a model containing the envelope (over a model without the envelope) to test the statistical significance of the presence of a power excess. The resulting logarithmic factor of lnB < − 2 (irrespective of the νmax proxy adopted) provides strong evidence (Jeffreys 1961) against the detection of p modes, at odds with the findings of Pepe et al. (2021).
The average photon-noise level in the amplitude spectrum, as measured in the range3 1.5–3 mHz, is 4.93 cm s−1, which we adopt as an upper limit on the mode amplitude. The factor of ∼5 difference in the photon-noise level relative to that measured for ϵ Indi (0.94 cm s−1) is mostly accounted for by the nearly ten times lower brightness of HD 40307 and shorter effective length of its observing campaign (1150 spectra with a fixed exposure time of 30 s). We further note that the blue detector of ESPRESSO was prone to, at the time the observations of HD 40307 were collected, a known RV systematic effect4 with periodicities of five and seven minutes caused by a temperature instability in the blue cryostat, which may also be contributing to the overall noise budget in this frequency range.
Appendix E: Mode lifetime calibration
We conducted simulations following Kjeldsen et al. (2005), having made use of AADG3 (Ball et al. 2018) to generate artificial time series. Each simulation contains a single input frequency of varying mode lifetime (0.3, 0.6, 0.8, 1, 1.5, 2, 3, 10, and 30 days) and S/N, and was sampled adopting the ϵ Indi observing window. Simulations were run considering both radial (which are not impacted by rotation) and dipole modes. The ℓ = 1 simulations also included rotational splittings assuming an edge-on configuration5 and a rotation period6 of 36 days. Mode lifetimes may then be inferred, for a given fiducial S/N level, by comparing7 the simulated frequency scatter with the scatter of the observed frequencies about the asymptotic values given by Eq. (1). Figure E.1 shows the outcome of this calibration procedure for radial (top panel) and dipole (bottom panel) modes.
 |
Fig. E.1. Mode lifetime calibration (top: radial modes; bottom: dipole modes) for the ϵ Indi observing window. The solid lines are the result of simulations (see text for details) and show frequency scatter vs S/N for a range of input mode lifetimes. The measured frequency scatter is represented by a black symbol in both panels, placed at a fiducial S/N = 3.5 level (corresponding to the typical S/N of radial modes near νmax). |
We explored possible physical causes for the enhanced scatter about the ℓ = 1 power ridge (apparent in the top panel of Fig. 4 and made more evident in the bottom panel of Fig. E.1), a feature that we find not to be reproduced by model frequencies; the same models rule out undetected ℓ = 3 modes as the cause since they are expected to lie farther away from the ridge than implied by the observed scatter. Based on the simulation results, the observed scatter of dipole modes is too large to be explained by a combination of mode damping and rotational splittings. If, however, a strong dipole magnetic field is present, this could in principle lead to extra damping of the ℓ = 1 modes (with respect to the ℓ = 0 modes). The unpublished, single-epoch Zeeman–Doppler imaging (ZDI) map from Vidotto et al. (2016) is indeed dominated by a strong dipole field (56% of the field energy is in the dipole component, according to their Table 2). A similar field, if concurrent with the ESPRESSO observations, could partially account for the enhanced scatter about the ℓ = 1 ridge.
All Tables
All Figures
 |
Fig. 1. Stellar radius–effective temperature diagram highlighting seismic detections from Kepler and TESS photometry (blue circles; Mathur et al. 2017; Hatt et al. 2023), and radial-velocity campaigns (red diamonds; see e.g., Arentoft et al. 2008; Kjeldsen et al. 2008, and references therein). The stellar background sample (grey dots) is taken from the TESS Input Catalog (TIC; Stassun et al. 2019). The Sun is represented by its usual symbol. Approximate spectral type ranges (F, G, and K) are delimited by the vertical dashed lines. ϵ Indi (K5 V) is the coolest seismic dwarf observed to date (its interferometric radius and effective temperature were used to place it in the diagram; Rains et al. 2020). |
| In the text | |
 |
Fig. 2. Time series of ESPRESSO radial-velocity measurements of ϵ Indi. Top: raw time series (after removal of a constant RV offset). The solid red curves represent smoothing functions applied on a nightly basis (see text for details). Middle: detrended time series (after high-pass filtering). Bottom: internal (photon-noise limited) RV precision as returned by the ESPRESSO DRS. The horizontal dotted line represents the instrumental noise level of 10 cm s−1 quoted by Pepe et al. (2021). |
| In the text | |
 |
Fig. 3. Noise-optimised power spectrum of ϵ Indi. The power spectrum has been oversampled for visual purposes. A clear power excess due to solar-like oscillations can be seen centred just above 5 mHz. The vertical dashed line represents the measured νmax (see text for details). The inset shows the spectral window, with prominent sidelobes (daily aliases) due to the single-site nature of the observations. |
| In the text | |
 |
Fig. 4. Outcome of the mode identification and extraction procedure. Top: replicated échelle diagram displaying the mode frequencies extracted for ϵ Indi (cf. Table 1). The smoothed power spectrum is shown in grey scale. The vertical dashed line gives the measured Δν value. Bottom: likelihood-weighted histogram of ε Δν for the models in the grid (see text for details). The observed ε Δν is represented by a vertical dotted line. |
| In the text | |
 |
Fig. 5. Amplitude per radial mode as a function of Teff for ϵ Indi and a number of cool dwarfs with published measurements. Reported statistical uncertainties for the mode amplitudes are comparable in size to the plotted symbols. Data points are colour-coded according to the corresponding |
| In the text | |
 |
Fig. 6. C–D diagram, showing δν02 vs. Δν. Models from the grid of Li et al. (2023) are colour-coded according to age (left) and mass (right). The location of ϵ Indi is indicated by the black symbol in both panels. The error on Δν is too small to be discerned. |
| In the text | |
 |
Fig. A.1. Derived radial velocities vs activity proxies. The raw time series (after removal of a constant RV offset) is shown in the leftmost column. A ∼20 min gap in the data collection is apparent toward the end of night 2, which resulted from an interruption of the corresponding observation block. The remaining columns show the relationship (on a nightly basis) between the RVs and associated CCF parameters (FWHM, contrast, BIS, and asymmetry). Each panel is supplemented by Pearson’s correlation coefficient, R. |
| In the text | |
 |
Fig. B.1. Power spectrum prewhitening. The outcome of having extracted all 19 identified modes is illustrated (see text for details). |
| In the text | |
 |
Fig. C.1. Activity cycle of ϵ Indi as traced by |
| In the text | |
 |
Fig. E.1. Mode lifetime calibration (top: radial modes; bottom: dipole modes) for the ϵ Indi observing window. The solid lines are the result of simulations (see text for details) and show frequency scatter vs S/N for a range of input mode lifetimes. The measured frequency scatter is represented by a black symbol in both panels, placed at a fiducial S/N = 3.5 level (corresponding to the typical S/N of radial modes near νmax). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.