| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202349004 | |
| Published online | 02 July 2024 | |
Kaleidoscope of irradiated disks: MUSE observations of proplyds in the Orion Nebula Cluster
I. Sample presentation and ionization front sizes
1
European Southern Observatory,
Karl-Schwarzschild-Strasse 2,
85748
Garching bei München, Germany
e-mail: mariliis.aru@eso.org
2
Astronomy Unit, School of Physics and Astronomy, Queen Mary University of London,
London
E1 4NS, UK
3
Dipartimento di Fisica, Università degli Studi di Milano,
Via Celoria 16,
20133
Milano, Italy
4
Centre for Extragalactic Astronomy, Department of Physics, Durham University,
South Road,
Durham
DH1 3LE, UK
5
Department of Physics, Institute for Computational Cosmology, University of Durham,
South Road,
Durham
DH1 3LE, UK
6
Space Telescope Science Institute,
3700 San Martin Dr,
Baltimore, MD
21218, USA
7
Johns Hopkins University,
3400 N. Charles Street,
Baltimore, MD
21218, USA
8
Instituto de Astrofísica e Ciências do Espaco, Universidade de Lisboa, OAL, Tapada da Ajuda,
1349-018
Lisboa, Portugal
9
Université Cote d’Azur, Observatoire de la Cote d’Azur, CNRS, Laboratoire Lagrange,
06300
Nice, France
10
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
11
NASA Headquarters,
300 E Street SW,
Washington, DC
20546, USA
Received:
18
December
2023
Accepted:
2
April
2024
In the Orion Nebula Cluster (ONC), protoplanetary disks exhibit ionized gas clouds in the form of a striking teardrop shape as massive stars irradiate the disk material. We present the first spatially and spectrally resolved observations of 12 such objects, known as proplyds, using integral field spectroscopy observations performed with the Multi-Unit Spectroscopic Explorer (MUSE) instrument in Narrow Field Mode (NFM) on the Very Large Telescope (VLT). We present the morphology of the proplyds in seven emission lines and measure the radius of the ionization front (I-front) of the targets in four tracers, covering transitions of different ionization states for the same element. We also derive stellar masses for the targets. The measurements follow a consistent trend of increasing I-front radius for a decreasing strength of the far-UV radiation as expected from photoevaporation models. By analyzing the ratios of the I-front radii as measured in the emission lines of Hα, [O I] 6300 A, [O II] 7330 A, and [O III] 5007 A, we observe the ionization stratification, that is, the most ionized part of the flow being the furthest from the disk (and closest to the UV source). The ratios of ionization front radii scale in the same way for all proplyds in our sample regardless of the incident radiation. We show that the stratification can help constrain the densities near the I-front by using a 1D photoionization model. We derive the upper limits of photoevaporative mass-loss rates (Ṁloss) by assuming ionization equilibrium, and estimate values in the range 1.07–94.5 × 10−7 M⊙ yr−1, with Ṁloss values decreasing towards lower impinging radiation. We do not find a correlation between the mass-loss rate and stellar mass. The highest mass-loss rate is for the giant proplyd 244–440. These values of Ṁloss, combined with recent estimates of the disk mass with ALMA, confirm previous estimates of the short lifetime of these proplyds. This work demonstrates the potential of this MUSE dataset and offers a new set of observables to be used to test current and future models of external photoevaporation.
Key words: protoplanetary disks / stars: formation / stars: pre-main sequence / HII regions
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Protoplanetary disks, composed of gas and dust, emerge as a consequence of the star formation process, and provide the birthplaces of planetary systems. The evolutionary pathways of protoplanetary disks and their ability to form planets are expected to differ depending on the surrounding environment, with disks undergoing rapid changes in the presence of massive stars (for a recent review see Parker 2020 and Reiter & Parker 2022). In massive clusters near OB-type stars, UV radiation can externally photoevaporate disks and severely diminish their size, mass, and survival timescale (e.g., Winter & Haworth 2022).
The effect of external photoevaporation can be studied in the act in the Orion Nebula Cluster (ONC), where the primary UV source is the O6V star θ1 Ori C (O’Dell et al. 2017). These systems of ionized protoplanetary disks, known as “proplyds”, were first imaged with the Hubble Space Telescope (HST), exhibiting ionization fronts, disk silhouettes, and comet-like tails pointing away from the UV source (O’Dell et al. 1993; O’Dell & Wen 1994; McCaughrean & O’Dell 1996; Ricci et al. 2008).
Proplyds are detected in strong Ha emission, which serves as a signature of ionized gas near the ionization front, where UV radiation effectively ionizes the wind from the disk. The Hα surface brightness was first employed by Laques & Vidal (1979) to estimate the electron density of the gas in proplyds, which at the time were proposed to be partially ionized globules. Subsequently, Henney et al. (1997) introduced the first theoretical models, which reproduced the emission line profiles. Expanding on the latter study, Henney & O’Dell (1999) compared the models with high-resolution spectroscopy measurements of four proplyds acquired with the HIRES spectrograph on the Keck Telescope, and analyzed the spatial profiles of Ηα, Hβ, and forbidden lines, such as those of oxygen, sulfur, and nitrogen ions. Forbidden lines have been the key tool to probe the density, temperature, and ionization state of the gas in proplyds (Mesa-Delgado et al. 2012). Furthermore, forbidden lines of for instance, [Fe II] and [S II] have traced the supersonic jets and winds from proplyds (Bally & Reipurth 2001; Kirwan et al. 2023).
The characteristic cometary or teardrop shape of proplyds is created by the outflow of neutral gas from the disk as extreme-and far-UV energy photons heat the surface material and drive thermal winds. The neutral gas becomes photoionized as it expands and interacts with stellar UV radiation. The external photoevaporation of disk material leads to mass loss, estimated to be in the range from 10−8 to 10−6 M⊙ yr−1 for proplyds within 0.3 pc of θ1 Ori C, based on values inferred from observations (Henney & Arthur 1998; Henney & O’Dell 1999; Henney et al. 2002) and theory (Johnstone et al. 1998; Storzer & Hollenbach 1999; Richling & Yorke 2000). Recent ALMA Band 3 (3.1 mm) observations of a dozen proplyds in the ONC found values in the order of 10−7 M⊙ yr−1 (Ballering et al. 2023).
Submillimeter wavelength observations with ALMA confirm that the gas disks in the ONC are compact in comparison with the disks studied in environments where negligible UV radiation is present (Mann et al. 2014; Eisner et al. 2018; Boyden & Eisner 2020; van Terwisga & Hacar 2023; Ballering et al. 2023). Similarly, low disk dust masses are found in regions with weaker, but still relevant, UV radiation, such as the inner ~0.5 pc of the σ-Orionis cluster (Ansdell et al. 2017; Maucó et al. 2023). The extreme environment may dramatically alter the initial conditions for emerging planets, as the total disk mass limits the mass available for planet formation.
The majority of the past studies of proplyds were carried out with HST imaging in a limited number of filters, and spectroscopic analysis is available for only a few proplyds (e.g., Henney & O’Dell 1999). The Multi-Unit Spectroscopic Explorer (MUSE) is an integral field unit (IFU) spectrograph on the ESO Very Large Telescope (VLT). Used in the narrow-field mode (NFM), MUSE allows for the first time to both spatially and spectrally resolve the structure of proplyds in the ONC, as demonstrated by Kirwan et al. (2023) and Haworth et al. (2023b). The IFU data provides spectroscopy covering a wealth of emission lines at each position in the proplyds, and sub-arcsec spatial resolution of the objects.
Here, we present the morphology of 12 objects in seven emission lines, including Ηα, and forbidden oxygen, sulfur, and nitrogen lines. We measure the radius of the ionization front of proplyds, a key ingredient for estimating the mass-loss rate, in Ηα and forbidden oxygen lines. Using the forbidden oxygen lines in addition to the traditional tracer Ηα is important for gaining a more comprehensive understanding of the physical and chemical processes occurring in these systems. From the spectra, we also measure the stellar properties of the targets.
The paper is structured as follows. In Sect. 2, we describe the MUSE observations and data reduction. The sample with the morphology of individual proplyds is presented in Sect. 3, and the outline of the analysis steps is given in Sect. 4. We summarize the results in Sect. 5, and further discuss them in Sect. 6.
2 Observations and data reduction
The targets in our sample were chosen to cover a large range of distances from θ1 Ori C, covering different levels of the incident radiation field and thus ionization. Furthermore, the targets were selected to have an overlap with ALMA observations, providing disk mass and size (Mann et al. 2014; Eisner et al. 2018; Boyden & Eisner 2020).
Observations were carried out with the MUSE integral-field spectrograph (Bacon et al. 2010), which is mounted on the Unit Telescope 4 (UT4) at the VLT. MUSE was operated in the Narrow Field Mode (NFM), which covers 4750–9350 Å in a smaller field of view (FOV) of ~7.5″ × 7.5″. On this FOV, the AO-correction is enhanced by the Laser Tomography Adaptive Optics (LTAO) mode leading to near diffraction limited images with a sampling of 0.025″ per spatial pixel. In all the observations, the Natural Guide Star (NGS) was chosen to be the target, and was thus on-axis.
The observations presented here were carried out in three different observing programs between October 2019 and November 2022, always in Service Mode. The observations for the proplyds 244–440 (see Kirwan et al. 2023), 168–328, and 177–341W were taken in October 2019 (program ID 104.C-0963(A), PI: C. F. Manara), and those for the rest of the sample in January and February 2021 (program ID 106.218X.001, PI: C. F. Manara). Finally, we also include here the data taken in November 2022 during the Director Discretionary Time program 110.259E.001 (PI T. J. Haworth) for the proplyd 203–504, which are presented in Haworth et al. (2023b). MUSE was operated under clear sky conditions, and the full AO system was employed, using the stars at the center of our targets as NGS to achieve the best possible correction. The log file, including the airmass-corrected seeing and turbulence parameters are listed in Table D.1.
The observations were generally composed by three dithered exposures. In each observation, the telescope was offset by 0.2″ and 0.1″ in the second and third exposures, respectively, and turned by 90 degrees with respect to the previous exposure to achieve the best possible corrections for bad pixels and instrumental effects. The exposure time in each exposure is reported in Table D.1.
Data reduction was carried out with the MUSE pipeline v2.8 (Weilbacher et al. 2020) run in the ESO Reflex (Freudling et al. 2013) environment. The pipeline carries out the classical data reduction steps, including bias, dark, flat computation and correction, wavelength calibration, flux calibration, sky subtraction, and exposure alignment and combination. The only steps that required non-standard settings were the alignment and combination of the cubes. Obtaining a satisfactory alignment was complicated due to only a small number of stars being present in the observed FOV. For that reason, some of the final cubes are obtained by combining a smaller set of dithering/rotation exposures (see Table D.1). Having a few stars available in the FOV can also decrease the accuracy of the coordinates, and the coordinates of the central stars are retrieved relative to those catalogued following the process described in Sect. 4.1. The final, wavelength calibrated data-cubes are in barycentric velocities, and the wavelength scale is in air wavelengths. The spectral resolution is R ≈ 2000–4000, corresponding to 170−90 km s−1 from blue to red. We measure the spatial resolution of the images in the range FWHM≈0.065−0.080″ at ~6760 Å in our observations.
Continuum subtraction was then performed on sub-cubes spanning ~100 Å to only include the spectral emission regions of interest. Each sub-cube was continuum-subtracted by fitting a second-order polynomial to the spectrum at each spatial pixel (spaxel) in the sub-cube. This procedure was performed using the Python package MUSE Python Data Analysis Framework (mpdaf1, Piqueras et al. 2017), in particular the function spec.poly_spec. After this step, the sub-cubes were divided into smaller slabs with individual lines only, again using mpdaf.
 |
Fig. 1 RGB images (insets) of continuum subtracted, single line integrated flux images of the sample acquired with MUSE. In each inset, a variety of emission lines are combined to highlight the morphology of the proplyd. The background image is a Hubble optical image of the Orion Nebula Cluster (Credit: NASA, ESA, M. Robberto (Space Telescope Science Institute/ESA) and the Hubble Space Telescope Orion Treasury Project Team). |
3 Morphology of observed proplyds
An overview of the ONC with the observed proplyds is presented in Fig. 1. The view includes RGB images of nine proplyds: 154–346, 167–325, 170–249, 170–337, 173–236, 174–414, 177–341W, 203–504, and 244–440. In addition, there are proplyds in the background of several images: 168–326, 170–334, and 171–340. The coordinates of the targets are given in Table 1. The lines associated with the RGB colors are chosen for each target to show the morphological characteristics described in this section.
A collage of each proplyd is shown in Figs. A.1 and A.2 in the following emission lines: Hα, [O I] 6300 Å, [O II] 7330 Å, [O III] 5007 Å, [S II] 6731 Å, [N II] 5755 Å, and [N II] 6584 Å. These lines are selected to show the various components of the systems, including the ionization front, the disk, the cusp, and the tail, as seen as an example based on proplyd 177–341W in Fig. 2. The detailed analysis of these and other emission lines is deferred to forthcoming papers, while here we focus only on the measurement of the ionization front size, well traced by the Hα and oxygen emission lines.
We first describe the morphology of the well-detected proplyds, targets for which the ionization front, the disk, and the tail can be distinguished. These targets appear with the classic teardrop shape and the elongated tail, covering ~ 1.2–4″ in the FOV, except for 244–440 which spans over ~6.4″. We then give an overview of the fainter objects, which cover <1″ in the FOV, and the non-detections.
 |
Fig. 2 Continuum subtracted, single line integrated flux images of proplyd 177–341W. The panels show which parts of the system are visible in given emission lines. |
Coordinates and projected separations of the detected proplyds.
3.1 Well-detected proplyds
3.1.1 170–249
The proplyd 170–249 has an elongated tail in the north direction. This tail is visible in Hα, forbidden sulfur species, and [N II] 6584 Å lines. The cusp and the ionization front are bright in most of the emission lines, while the disk is traced in the [O I] 6300 Å and [S II] 6312 Å lines.
In the FOV, the bright central region of a second object is visible in [O I] 6300 Å and [N II] 5755 Å lines to the southwest of 170–249 (not shown in the RGB image in Fig. 1); no tail is distinguished.
3.1.2 170–337
The proplyd 170–337 exhibits the elongated tail in the southeast direction, visible in [S II] 6731 Å and [N II] 6584 Å emission. The disk can be distinguished in Ha and [O I] 6300 Å lines. The cusp and the ionization front are bright in most of the emission lines.
The FOV of 170–337 is rich with more targets:
-
In the southeast direction of 170–337, a well-resolved proplyd, designated 171–340, is visible with a round, extended cloud of ionized gas surrounding the disk. The proplyd differs from other objects by bearing a dark core, which may be a disk seen in silhouette against the background nebular light. The structure resembles the case of proplyd HST-10, also designated as 182–413 (O’Dell et al. 1993).
A long tail is not visible, but the proplyd is extended in the direction opposite the UV source. The proplyd is bright in [S II] 6731 Å and [N II] 6584 Å lines. The central region appears bright in [S II] 6731 Å.
In the upper part of the cube in the northeast from 170–337, the cusp of the proplyd 170–334 is bright in most emission lines. The classic tail shape is visible in Hα, and it is aligned with the one of 170–337.
There is a very small proplyd, 169–338, visible to the west of 170–337. We do not include it in the analysis as it is unresolved.
Although 171–340 and 170–334 are smaller than the central target 170–337, it is possible to measure their ionization front radius.
3.1.3 173–236
The proplyd 173–236 exhibits an elongated tail in the northeast direction. The star-disk region is traced by [O I] 6300 Å and [S II] 6731 Å lines. With a small, bright central part visible in Ha. There is a bubble-like structure southeast from the center of the FOV, which is most prominent in [S II] 6731 Å emission (not shown in Fig. 1).
3.1.4 177–341W
The RGB image of proplyd 177Å341W, shows both a bright cusp and a highly elongated tail in the southeast direction, which is brightest in [S II] and [N II] emission lines. Each emission line traces the cusp with the ionization front. The disk can be distinguished in the [O I] 6300 Å emission line, oriented perpendicular to the cusp, in a northwest to southeast direction.
3.1.5 244–440
Proplyd 224–440 is one of the largest in the ONC, spanning about 6.4″ from the tip of the longest tail to the ioniza-tion front. The tail structure is more complex compared to the other proplyds, resembling a tooth-like shape with two to three tail components depending on the observed wavelength; a JWST/NIRCam view is shown by Habart et al. (2024).
The morphology is striking with different emission lines tracing a variety of the system’s components: the cusp and the tail being visible in different ionization states of forbidden oxygen, sulfur, and nitrogen; the disk is bright in [O I] 6300 Å. The jet is visible in the MUSE data in the [O I] 6300 Å and various [Fe II] lines (Kirwan et al. 2023).
3.1.6 203–504
The proplyd 203Å504 is coincident with the Orion Bar, which lies approximately 112″ to the southeast of the Trapezium. The teardrop shape is less elongated and more oval compared to the targets close to θ1 Ori C, and the morphology is bright in Hα and [N II] 5755 Å. The cusp is brightest in Hα, [N II] 5755 Å, while the disk region is traced in the forbidden oxygen lines. Haworth et al. (2023b) discusses the target in depth. This is the only proplyd in our sample which is directly irradiated only by θ2 Ori A.
3.2 Faint proplyds
3.2.1 154–346
The star-disk region of proplyd 154–346 is visibly bright in each emission listed above, except for [O III] 5007 Å and [N II] 5755 Å. The proplyd makes up a small part of the FOV and the classic drop-like shape can be distinguished faintly.
3.2.2 167–325 and its FOV
The proplyd 167–325 is closest to θ1 Ori C (0.009 pc) in our field. Only the star-disk region of the system is visible, traced in [N II] 6584 Å line and faintly in forbidden sulfur species. In the same FOV, there are three objects:
Two proplyds appear very close to each other in the southeast direction of the central target; the classic shape of the foreground proplyd (168–326) is visible while only a part of the background proplyd can be distinguished. The tail of 168–326 is visible in [N III] 6584 Å line. The star-disk region is traced by Hα, [O II] 7320 Å, [O III] 5007 Å, and [S II] 9068 Å lines.
There is another proplyd in the south of 167Å325 and 168–326. It is much smaller, and its ionization front size is not measured.
3.2.3 174–414
The proplyd 174–414 appears at the very edge of the cube which was planned to be an observation of HST-10. The teardrop shape is visible faintly in Hα and [N II] 6584 Å. The central part is bright in [O I] 6300 Å, [O II] 7320 Å and forbidden nitrogen and sulfur lines.
3.3 Non-detections
The proplyds 142–301, 167–231, and HST-10 were targeted on our MUSE programs, but not detected.
In the case of proplyd 159–350, the pointing was not accurate and the observation of this proplyd was not acquired; instead, the pointing was centered at the nearby proplyd 154–346.
 |
Fig. 3 Method for measuring the ionization front radius of a proplyd. Top panel: the intensity cut is taken along the diagonal line. The red line marks our identification of the ionization front. Bottom panel: intensity cut along the diagonal line marked in the top panel. |
4 Analysis
4.1 Measurement of the ionization front radius
Our goal is to study the radius of the ionization front (I-front) as a function of the incident radiation field. Here, we focus on measuring the I-front radius for four lines: Hα, [O I] 6300 Å, [O II] 7330 Å, and [O III] 5007 Å. The Ha line allows us to detect the region where ionized gas transitions to neutral gas; this has been used as the tracer of the ionization front in past studies (e.g., Henney & Arthur 1998; Henney & O’Dell 1999). The forbidden oxygen lines allow us to additionally trace the ionization structure for different ionization states.
We located the I-front at the bright cusp on the side closer to the UV source. The main UV influx comes from θ1 Ori C for all proplyds except 203–504 and 244–440, which appear to be primarily irradiated by θ2 Ori A (O’Dell et al. 2017; Haworth et al. 2023b).
As the coordinates of the stars in the MUSE cubes might not directly correspond to those catalogued because of poor astrometric calibrations of our dataset (described in Sect. 2), we determined the coordinates of the central stars in the MUSE data directly. We created a sub-cube with continuum emission only, that is, a region free of lines, at 6740–6780 Å. We located the peak of the continuum emission by using the mpdaf function peak in the region of the star. The coordinates of the peak were used as the location of the star for the following steps and the following measurements were always carried out using relative distances (Fig. 3).
We then retrieved a radial cut of the proplyd intensity profile in each of the investigated lines by tracing a 6″ line centered at the coordinates of the central star. We set the position angle of the radial cut in the direction between the central star and the peak of the emission in the ionization front, which in turn is in the direction of the ionizing star in all cases, with the exception of 244–440 and 203–504. For 203–504, the angle between the proplyd and θ2 Ori A was calculated based on their catalogued coordinates. The intensity profile along the line was extracted by using cubic interpolation with the scipy function map_coordinates. The location of the I-front was determined relative to the line’s center, the ~ 0″ mark on the x-axis of the intensity profile. For the majority of the sample, an intensity peak corresponding to the I-front, a bright region in the direction of the UV source, lies at a small offset from the center. This offset is the radius of the I-front.
The I-front radius value measured from the intensity profile overlaps roughly with the brightest area visible on the image of each proplyd; the scale parameters of the image can slightly change the boundary of the brightest area. An example of the measurement method is shown in Fig. 3.
We estimated the uncertainty by repeating the measurement for two more position angles (±15°), and calculating the percentage change between the values of I-front radii. The typical uncertainty in the cases of good detection is 10% (see Table 2).
Proplyds 154–346, 167–325, 170–334, and 174–414 make up a much smaller part in the FOV compared to the well-detected targets. In those cases, no distinct peak is visible in the intensity profile and we estimated the I-front’s position based on locating the outer part of the bright center of the target. This is the lower limit of the I-front.
The identification of the I-front was straightforward for the Ha lines of each well-detected proplyd. The I-front was fainter and less clear to distinguish the oxygen lines of several proplyds. There were two intensity peaks for the oxygen lines compared to the single peak in Ha intensity profiles: the higher peak coincided with the star’s location, and the smaller peak coincided with the I-front. The principle of the measurement remained the same. The measured I-front radii in the various lines are reported in Table 2.
Measured values for the observed proplyds.
4.2 Stellar parameters
The MUSE data allow us to determine the stellar parameters of the central objects for the observed proplyds. We extracted the spectra of the stars using a circular aperture of 0.05″–0.075″ depending on the target and an annulus of 0.075″–0.175″ to estimate the sky emission. The spectra for 167–325 and for 168–326 could not be extracted as the S/N ratio of the continuum is too low.
The spectra were then compared with the set of pre-main-sequence empirical templates from Manara et al. (2013, 2017a), and Claes et al. (in prep.) to determine the spectral type (SpT) and extinction (AV). The latter was determined assuming the reddening law by Cardelli et al. (1989) and a value RV=3.1. Typical uncertainties on these derived parameters are of 1–2 sub-classes for the SpT and of 0.5 mag on AV, but they depend on the quality of the spectrum in the redder part (λ >750 nm) which is sometimes suboptimal for several reasons, including strong emission lines and telluric absorption. The SpT was converted into effective temperatures (Teff) using the relation by Herczeg & Hillenbrand (2014). From the J–band magnitude (Robberto et al. 2010), we then estimated the stellar luminosity (L*) using the bolometric correction by Herczeg & Hillenbrand (2014), to finally derive a stellar mass (M*) using the evolutionary tracks by Siess et al. (2000). The latter was used because most of the targets appear to be located on the Hertzsprung-Russel Diagram above the 1 Myr isochrone, not covered by other tracks, as expected due to their young age.
The derived parameters are reported in Table 3, and the best fits are shown in Fig. C.1. We compare the derived values with Fang et al. (2021), but only a sub-sample of our targets are covered by that study, and they show a good agreement within one subclass with our estimates.
5 Results
5.1 Ionization front radius
The ionization front radius of proplyds enables us to infer the mass-loss rate of proplyds, which is a critical factor in the evolution of protoplanetary disks. The radii of targets irradiated by θ1 Ori C are shown as a function of the projected distance from the massive star in Fig. 4. We note that given the distance to the ONC and the generally high optical extinctions towards the region, the Gaia parallaxes for our targets are not always available, or they are too uncertain to provide reliable individual distances to the targets. For this reason, we assume a common distance of 400 pc for the targets in our sample, and only consider projected separations from the ionizing stars in our analysis. In the panel of Ha emission, we compare the measurements with predicted values for a set of mass-loss rates, as described in Sect. 5.3.
Figure 4 shows that the I-front radius is generally larger at lower ionization rates, that is, at larger projected distance, in all tracers discussed here. The proplyds with more uncertain measurements do not however typically follow the trend. The proplyds with more uncertain measurements are small and faint compared to the rest of the sample, and the I-front measurement could not be carried out with the same approach.
To explore the significance of the relation between I-front radii (RIF) and projected distance (dp), we carried out two analyses similarly to McLeod et al. (2021). Firstly, we tested the null-hypothesis that there is no relation between the parameters. We used a bootstrap sampling method with 104 iterations, where we randomized the x-axis values and computed the Spearman correlation coefficient (rs). By calculating the σ distribution of the data, we can exclude the null-hypothesis with a larger than 2σ confidence in all cases (p < 0.05). Secondly, we assessed the uncertainty of the correlation coefficient by bootstrapping with 104 iterations while varying the y-axis values within their respective uncertainties. We adopted a truncated Gaussian distribution to model the uncertainty for the lower limits values in the RIF measurements. In those cases, the bootstrapping was selected within this truncated Gaussian distribution with a standard deviation of 20% of the lower limit value. Both of these tests were then compared with the actual coefficient rs. We also report the p-value of the null hypothesis randomizing the x-axis values. The p-value was calculated as the number of correlation coefficients larger (for positive correlation) than 1σ of bootstrapped observations, and divided by the number of iterations. We excluded proplyd 244–440 from the given test and those which follow.
We found p-value ≃ 0.02 and rs ≃ 0.62, indicating a positive relation (Fig. B.1a).
The sub-cube was too noisy for the measurement of RIF in the case of 167–325 at [O II] 7330 Å and [O III] 5007 Å, and for proplyds 174–414 and 203–504 at [O III] 5007 Å; they are not included in Fig. 4.
In Fig. 5, we show the comparison between our measurements of Rif and those from the literature. The I-front radii of proplyds 154–346, 168–326, 170–337, 170–334, and 177–341W were derived by Henney & Arthur (1998), who fit models to observed Ha intensity profiles. Proplyd 168–326 is within the uncertainties of the literature values; proplyd 154–346 is a factor ~3.5 lower in the literature, and the rest are higher. The differences in the measured values could be explained by the measurement approaches.
Vicente & Alves (2005) measured the “chord diameters” of a sample of proplyds, in which 244–440 is common with our sample. The chord diameter is defined as the diameter of a circle fitted to the contour of the proplyd cusp boundary, plus ~30% the average background intensity. This approach places the I-front radius higher than our value, roughly at 2.8″ or 1120 au; the measurement is not shown in Fig. 5 due to the great difference in size compared to the rest of the targets.
Recently, Ballering et al. (2023) estimated the I-front radii of proplyds 170–249, 170–337, 173–236, and 177–341W marking the disk center and the outer edge of the ionization front on surface brightness cuts of ALMA Band 3 images. Our values are systematically lower compared to the ALMA study, because the I-front marker was positioned past the peak’s inflection point, not on the peak.
 |
Fig. 4 Ionization front radius versus the projected separation from θ1 Ori C. Squares mark proplyds for which the I-front measurement has a higher uncertainty. The radii of the ionization fronts increase with larger projected distances from the UV source. Due to noisy subcubes, measurements were not taken for proplyd 167–325 (closest to the UV source) in the bottom panels. For the same reason, the panel of [O III] 5007 Å excludes the radii of several targets. |
Stellar parameters derived for the sampled proplyds.
 |
Fig. 5 Ionization front sizes from literature (Henney & Arthur 1998; Ballering et al. 2023) versus as measured with MUSE IFU data. We note that the measurement methods differ slightly from each other. |
5.2 Ionization front radius and incident radiation field strength
The strength of the FUV environment is described in the units of the Habing radiation field; 1 G0 = 1.6 × 10−3 erg cm−2 s−1 (Habing 1968). We calculate the strength of the incident radiation field using the following adimensional parameter:
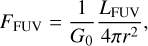 (1)
(1)
where the far-UV (FUV) luminosity LFUV is derived from the values of FUV radiation reported as a function of stellar mass by Winter & Haworth (2022). Thestellarmass was consideredtobe 45 M⊙ for θ1 Ori C and 39 M⊙ for θ2 Ori A (Simón-Díaz et al. 2006). The ionizing radiation strength for our sample spans from 105–107 G0 over projected distances of 0.009–0.31 pc. These values are consistent with the literature: the FUV field incident upon most of the proplyds in the vicinity of θ1 Ori C is estimated to be FFUV ≥ 106. For 244–440, the value is estimated to be on the order of 105G0 assuming irradiation by θ2 Ori A, which agrees with the value found by Vicente (2009). However, O’Dell et al. (2017) note that the proplyd may be ionized by both θ1 Ori C and θ2 Ori A, which would increase the radiation strength.
In Fig. 6, the I-front radii of the proplyds irradiated by θ1 Ori C, as well as proplyd 203–504 irradiated by θ2 Ori A, are plotted as a function of the incident UV radiation field. The I-front radii are larger at lower incident fields. We repeat the statistical test described above, and find rs ≃ -0.65, indicating a negative relation (Fig. B.1b), and p-value ≃ 0.02.
The proplyd 203–504, irradiated by θ2 Ori A, follows very well the trend of the proplyds irradiated by θ1 Ori C. The proplyd 244–440 appears to be much larger than any other proplyd, and it is not included in the figure.
To compare the different levels of ionization, we show the ratios of RIF for the Ηα line and for different forbidden oxygen lines as a function of the UV field in Fig. 7. We calculate the mean and its standard deviation for the following ratios. The ionization front radius increases for tracers that are more ionized: Rif[O III]/Rif[O I] ≃ 1.22±0.06 > Rif[O II]/Rif[O I] ≃ 1.12±0.06. We see an increasing trend as expected, but the statistical significance is limited by the small sample size. More data would be needed for a firm confirmation. The same applies to the following case: RifHα/RIF[O III] ≃ 0.95±0.05.
5.3 Mass-loss rate
In Fig. 4 (panel of Ηα), the measured values of I-front radii are compared with predicted ionization front radii based on a set of mass-loss rates described by the following equation from Winter & Haworth (2022):
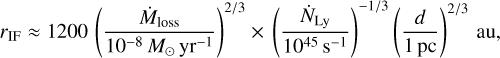 (2)
(2)
where Ṁloss is the mass-loss rate of the proplyd, d the projected separation from an irradiation source emitting 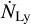 ionizing photons per second. For θ1 Ori C, we use
ionizing photons per second. For θ1 Ori C, we use 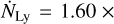 1049 photons s−1, and
1049 photons s−1, and 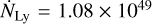 photons s−1 for θ2 Ori A, based on the values of stellar EUV luminosity as a function of stellar mass from Winter & Haworth (2022).
photons s−1 for θ2 Ori A, based on the values of stellar EUV luminosity as a function of stellar mass from Winter & Haworth (2022).
In the panel of Ηα, of Fig. 4, curves for three different mass-loss rate values are partly overlapping with the data points, with Ṁloss decreasing over larger projected distances, as expected from theoretical models of disk photoevaporation (e.g., Johnstone et al. 1998; Storzer & Hollenbach 1999). Four of the proplyds are at the curve marking 6 × 10−7 M⊙ yr−1, while the rest of the proplyds vary slightly more, falling between 1 × 10−6 and 3 × 10−7 M0 yr−1. The inferred Ṁloss values are reported in Table 2.
The comparison of our estimates of Ṁloss with values reported in the literature is shown in Fig. 8. The values are very consistent, except for 244–440 which has the highest Ṁloss value in our sample, ~8.06 × 10−6 M⊙ yr−1. We discuss the values of Ṁloss and the comparison with literature further in Sect. 6.3, and the case of 244–440 in Sect. 6.3.1.
To analyze how the estimated Ṁloss of proplyds depends on the strength of the ionizing field, we plot the Ṁloss values as a function of the incident UV radiation field in Fig. 9. This shows an increasing trend for Ṁloss for the proplyds irradiated by θ1 Ori C, moving from 106 to 107 G0. Proplyd 203–504 also follows the trend relatively well. The proplyds with uncertain measurements of the I-front radii have a systematically lower value of Ṁloss, but the uncertainty in the measurement does not allow further considerations. We assessed the trend between Ṁloss and G0 with the statistical analysis described in the previous section. The Spearman correlation coefficient rs ≃ 0.84, indicating a strong positive relation (Fig. B.1c), and p-value ≃ 0.001, which indicates a very significant correlation.
 |
Fig. 6 Ionizing radiation strength as a function of the ionization front radius. The diamond marks proplyd 203–504. irradiated mainly by θ2 Ori A. For the rest of the targets (dots and squares), the UV source is θ1 Ori C. Squares mark proplyds for which the I-front measurement has a higher uncertainty. 244–440 is not included in this figure due to the stark difference in size compared to the rest of the sample. |
 |
Fig. 7 Ratios of ionization front sizes of Hα, [O III], [O II], and [O I] as a function of the incident UV field. The empty diamond marks 244–440, and the empty triangle marks 203–504. The mean and SEM are marked in violet. |
6 Discussion
6.1 Ratios of ionization front sizes
We have analyzed the MUSE IFU data of 12 proplyds to measure the I-front radii in four emission lines. The I-front radii as measured in different tracers reflect the ionization stratification in photoevaporating flow models (Henney & Arthur 1998), with the highest ionized flow spanning the furthest from the disk and closest to the UV source. Figure 7 underlines this ionization structure as RIF[O III] > RIF[O I], and Rif[O III]/Rif[O I] > Rif[O II]/Rif[O I]. However, the statistical significance is limited by the small sample size.
We observe no dependency of the ratios on the impinging radiation, which indicates that the distribution of ionization front sizes of proplyds in the sample is self-similar: they have the same relative sizes at all levels of ionization, independently of the incident radiation. We provide a simple explanation of why this is expected, as follows.
Assuming equilibrium between ionizing flux from a massive star at distance d and gas recombinations, another way to express RIF, following the analytic treatment of flows by Johnstone et al. (1998), is:
![${r_{{\rm{IF}}}} = {\left[ {{{\alpha r_0^4n_0^2} \over 3}{{4\pi {d^2}} \over {{{\dot N}_i}}}} \right]^{1/3}}$](/articles/aa/full_html/2024/07/aa49004-23/aa49004-23-eq6.png) (3)
(3)
where α is the recombination coefficient for the given ionized species, r0 is the disk outer radius, n0 is the density of neutral material at the disk surface, and 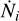 the ionizing photon count. When considering the ratio between I-front radii of two emission lines, the influence of distance becomes negligible, and the ratio depends on α, and
the ionizing photon count. When considering the ratio between I-front radii of two emission lines, the influence of distance becomes negligible, and the ratio depends on α, and 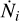 . Considering the same UV source, the ratio for [O I] and [O II], for example, would simplify as
. Considering the same UV source, the ratio for [O I] and [O II], for example, would simplify as
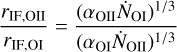 (4)
(4)
In the case of a θ1 Ori C like object, with  ,
, 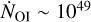 , αOI 3.25 × 10−13, αOII 1.99 × 10−12 (recombination coefficients from Draine (2011)) the ratio is ~9, so while it is expected to be insensitive to the distance of the proplyd from the UV source, the predicted magnitude of the ratio is too high from this simple analysis. The reason for this is that the above argument assumes a spherically diverging (R−2) scaling of the density at all distances from the disk. In reality, at the hydrogen ionization front (which coincides closely with the singly ionized oxygen front) there is a sharp jump in temperature from tens/hundreds of Kelvin to ~104 K. That temperature jump is associated with a sharp increase in the flow velocity and a sharp decrease in the gas density (easily an order of magnitude). Furthermore, if material is being accumulated in a shell within the proplyd cusp then the density contrast between the proplyd and surrounding H II region can be even higher, which we explore below with a basic numerical photoionization calculation.
, αOI 3.25 × 10−13, αOII 1.99 × 10−12 (recombination coefficients from Draine (2011)) the ratio is ~9, so while it is expected to be insensitive to the distance of the proplyd from the UV source, the predicted magnitude of the ratio is too high from this simple analysis. The reason for this is that the above argument assumes a spherically diverging (R−2) scaling of the density at all distances from the disk. In reality, at the hydrogen ionization front (which coincides closely with the singly ionized oxygen front) there is a sharp jump in temperature from tens/hundreds of Kelvin to ~104 K. That temperature jump is associated with a sharp increase in the flow velocity and a sharp decrease in the gas density (easily an order of magnitude). Furthermore, if material is being accumulated in a shell within the proplyd cusp then the density contrast between the proplyd and surrounding H II region can be even higher, which we explore below with a basic numerical photoionization calculation.
 |
Fig. 8 Mass-loss rates of MUSE compared with the values reported by Henney & O’Dell (1999); Ballering et al. (2023). |
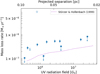 |
Fig. 9 Mass-loss rate vs incident radiation field. The dots represent well-detected proplyds, and the squares denote the proplyds with higher uncertainty. The diamond (244–440) and the triangle (203–504) mark proplyds irradiated by θ2 Ori A. The dashed purple line represents a model prediction for disks with a radius of 40 au (Storzer & Hollenbach 1999). |
6.2 Photoionization models of the ionization front structure
The structure of the H II region around a θ1 Ori C type star is well understood to have an inner zone of more highly ionized species such as O III and He II surrounded by a zone where hydrogen is still ionized but, for example there is neutral helium and only singly ionized oxygen (e.g. O’Dell 2001; O’Dell et al. 2017). In the case of the proplyds, the transition from [O III], to [O II] to [O I] is very sharp, as shown in Sect. 6.1, suggesting that the density is substantially higher than the ambient H II region.
Here we build a simple set of models to estimate the required density near the I-front in the proplyds. The purpose of these models is purely to determine the density of gas required to make the separation between the different oxygen emission features as small as observed. We are not aiming at producing a detailed model of the structure of the proplyds.
We ran 1D spherical photoionization equilibrium calculations with the TORUS Monte Carlo Radiative Transfer code (Haworth & Harries 2012; Harries et al. 2019). This included polychromatic radiation, the diffuse field. The species included are hydrogen, helium, oxygen, carbon, nitrogen, neon and sulfur. We set the dust abundance to a negligible value in these calculations.
Our model consists of a star with Teff = 39 000 K and radius R* 10.6 R⊙. The inner portion of the 1D spherical grid was then modeled to be representative of the “normal” H II region, in which the gas density is 100 mH cm−3. If the medium were all at that density, the H II region would extend to around 3.3 pc. We then imposed a density enhancement at 0.1 pc from the UV source that is supposed to represent the denser medium associated with the proplyd cometary cusp. The increased density is then a free parameter of the models and we study the location of the oxygen ionization fronts. We note that it is not an issue if the separation between ionization fronts is not significantly smaller than the radius of curvature of the object in the 1D spherical model, since the required thickness for that to be the case would be inconsistent with the observed thickness for the real proplyds.
Figure 10 shows the oxygen ionization fractions as a function of distance from the density enhancement (i.e., the distance outside of the normal H II region and into the “proplyd”) for different densities. At low densities the spacing between the different oxygen emitting zones is far larger than the extent of proplyds. At higher densities, at around a few ×105 cm−3, the model results in a spatial distribution of ionization states of oxygen consistent with what is typical for the observed proplyds.
It is possible to broadly encapsulate the behavior here with the width of the O II zone. Figure 11 shows the scaling of that width as a function of the density enhancement beyond 0.1 pc. The scaling is approximately linear in log space, of the form
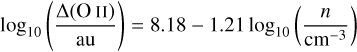 (5)
(5)
Although this was derived for a proplyd at 0.1 pc from θ1 Ori C, this distance is quite representative for our sample, as the projected separation are lower limits of the real distances. Furthermore, if the proplyd is closer, the proplyd would have to be even denser than predicted by Eq. (5) to achieve the same O II width. The same would be the case if the H II region density were lower. Overall these combine to make Eq. (5) a lower limit, in such a way that the empirical scaling of Eq. (5) could be applied to give rough representative values of the density of cometary cusps across the ONC, which results in the typical values being ~2–3 × 105 cm−3. More detailed modeling is needed to precisely determine densities in proplyds using this approach, and we defer this analysis to future work. The densities predicted close to the I-front in our model are consistent with the electron density estimates inferred from radio continuum observations of ONC proplyds by Ballering et al. (2023).
 |
Fig. 10 Example profiles of the oxygen ionization state as a function of distance from the density enhancement in the H II region (distance from the star of the proplyd cusp). The upper and lower panels are for densities of 3 × 104 cm−3 and 3 × 105 cm−3 respectively. |
 |
Fig. 11 Distance between the O III-O II transition and the O II-O I transition for a proplyd at a distance of 0.1 pc from a θ1 Ori C like star, as a function of the density in the cometary cusp of the proplyd. For densities ~ 2–3 × 105 cm−3 the thickness of the O II layer is consistent with our observations of ONC proplyds. |
6.3 Mass-loss rate
Our estimates of the mass-loss rate employ the I-front radius, measured from the Ha line emission, following Eq. (2). The latter provides an upper limit on the mass-loss rate, since it neglects any possible extinction between the irradiating star and the pro-plyd. Indeed, clumps of dust between the ionizing source and the young stars can cause a total shielding of the ambient radiation field, as in the case of object 204–506, which does not show a cocoon of ionized material unlike the nearby 203–504 proplyd (Haworth et al. 2023b).
Figure 9 shows a decrease in the mass-loss rate with a smaller incident UV radiation field. This is in agreement with photodissociation models (Storzer & Hollenbach 1999), which consider that Ṁloss is a slowly decreasing function of the UV field strength. The theoretical expectation is marked with the dashed line in Fig. 9. This prediction reproduces the increase of Ṁloss with incident radiation observed in our measurements, but at lower Ṁloss values. The offset is likely due to several assumptions, such as dust extinction, the outflow velocity, and the disk radius. The latter has a value of 6 × 1014 cm (40 au) in the plotted curve.
Proplyd 244–440 stands out as an outlier in Fig. 9 with Ṁloss nearly an order and a half of magnitude larger than for the nearby proplyd 203–504. We discuss the properties of this object in the next subsection.
6.3.1 The curious case of 244–440
Proplyd 244–440 exhibits the widest cusp observed in the Trapezium. Past studies note that the giant proplyd is possibly irradiated by both θ2 Ori A and θ1 Ori C (O’Dell et al. 2017), evident from its multiple tails, although five times further from the latter (see Fig. 1). The complex environment might play a role in the unusual shape of 244–440; Haworth et al. (2023b) showed that the ONC is an environment where two YSOs can appear extremely different from each other regardless of their proximity.
The disk diameter of 244–440 has been estimated to be 387 au from HST-WFPC2 images (Vicente & Alves 2005).
Using the higher spatial resolution observation of MUSE, the disk is roughly 300 au in diameter in the [O I]λ6300 Å line. This is a particularly large size for disks in the ONC, smaller than the giant disk 114–426 (e.g., Miotello et al. 2012) but much larger than any other disk in this region, typically smaller than ~60 au in radius (Eisner et al. 2018). For a disk size of that order, exposed to a high UV radiation field (> 105G0), the models predict mass-loss rate >10−6 M⊙ yr−1 (Haworth et al. 2023a), consistent with our estimation.
Despite standing out from the sample with its large I-front radius and high mass loss rate, 244–440 follows the same behavior as the rest of the objects in Fig. 7, with the ratios of its I-front radius being similar to the rest of the sample. This confirms a similar effect of the irradiation from the massive star(s) on the relative sizes of the I-fronts, as expected by the fact that they depend mainly on physical constants and, to a lesser extent, on the densities in the systems (see Sects. 6.1 and 6.2).
Given the rapid mass-loss rate, 244–440 is a unique object to be observed before its dispersal. Future observations with ALMA would clarify the disk properties and give insight into the evolution of the proplyd.
6.3.2 Dependence of the mass-loss rate on stellar mass
We have determined the stellar parameters for 10 targets in our sample. One half of the sample is classified as M spectral type (M0 and M5), and the other half is classified as mid-late K spectral type. The stellar masses range from 0.2 to ~1 M⊙.
It is known that, in such a stellar mass range, several disk, accretion, and wind properties have a steep scaling with stellar mass (e.g., Manara et al. 2023). Although this sample is small, a correlation between Ṁloss and stellar mass would be expected if the mass loss rate was driven by other processes than the irradiation from the ionizing stars, or if the stellar mass was a significant factor in setting the strength of the photoevaporating wind.
We explore the relation between Ṁloss and stellar mass and find no correlation or dependence between the two parameters, which implies that mass loss is driven by the external UV source and depends on other properties, such as disk radii, but not (significantly) on the stellar mass. On the other hand, it is known that, in low-mass star-forming regions, the disk radii typically scale with stellar mass (e.g., Hendler et al. 2020). This is not the case in the ONC. Indeed, Vicente & Alves (2005) presented the disk diameter as a function of the SpT in a sample of 52 sources, and found no obvious correlation between the two.
Recently, Maucó et al. (2023) observed that the depletion of disk masses in the vicinity of the massive star σ-Ori is more pronounced for disks around stars with stellar masses higher than ~0.4 M⊙. Our sample is too small to firmly confirm or dispute this finding, but we do not find any significant difference in the measured Ṁloss for the disks around stars more massive than 0.4 M⊙. The reason could be a combination of the location and impinging radiation onto the disks, or the lack of a dependence on stellar mass. Future studies measuring both Ṁloss and stellar masses should further explore this possibility.
6.4 Proplyd lifetime
The external photoevaporation process erodes material from the outer part of protoplanetary disks at a rate calculated here for our sample as Ṁloss. Here we investigate how long the disks we have observed can appear to survive under the effect of this process. In Fig. 12, we show Ṁloss as a function of the disk masses measured with ALMA from continuum emission for seven pro-plyds from Mann et al. (2014; reported as 100 × dust mass) and Ballering et al. (2023). The disk masses in the literature have been estimated by using different dust temperatures: Mann et al. (2014) assumed 40 K, while Ballering et al. (2023) computed the disk masses at both 20 K, and at temperatures that take external heating (Haworth 2021) by θ1 Ori C into account for each pro-plyd in their sample. The values of disk masses for our targets are lower than typical disk populations in nearby low-mass star-forming regions. Indeed, the relation between disk masses and the projected separation from θ1 Ori C have been studied by for example, Mann & Williams (2010), who found that the disks located within 0.3 pc from the massive star have lower masses. The low disk masses close to the UV source is also consistent with studies in different regions with lower but not negligible UV field, such as σ Orionis (Ansdell et al. 2017; Maucó et al. 2023) and NGC 2024 (Mann et al. 2015; van Terwisga et al. 2020). Interestingly, also in the latter region proplyds were observed with HST (Robberto et al. 2024). The Ṁloss values are within the same order of 10−7 M⊙ yr−1 for the available disk masses (10−4 M⊙–10−1 M⊙).
The ratio between the disk mass and Ṁloss gives an estimate of the expected lifetime of these systems, assuming that a constant Ṁloss will affect them during their lifetime. Since other processes, such as accretion onto the star or internal winds, are predicted to remove mass from the disk at a rate that is orders of magnitudes lower (e.g., Alcalá et al. 2017; Manara et al. 2017b; Nisini et al. 2018), this ratio is the most constraining for the disk lifetime. Observational studies report mass loss (10−7−10−6 M⊙ yr−1 ) similar to our estimates, and lifetimes <1 Myr (e.g., Storzer & Hollenbach 1999; Henney et al. 2002; Ballering et al. 2023) for the proplyds. Here we have a larger sample of proplyds with both measured Ṁloss and disk mass, and we derive photoevaporative timescale t = Mdisk/Ṁloss in the range from 2.4 to 130 kyr (Fig. 12). These values are very short compared to the age of the region, making it peculiar that these objects are observed just before their final dispersal. Given these derived values, our results are in agreement with the literature values, conforming to this “proplyd lifetime problem”.
Multiple works have explored solutions to the lifetime problem. Storzer & Hollenbach (1999) suggested that disks can survive much longer if they have radial orbits, and experience the highest mass-loss rate when they are closer to the ionizing stars, when they fly by in their vicinity. However, the dynamical models of the ONC were not found to be consistent with the suggestion (Scally & Clarke 2001).
The theoretical study by Winter et al. (2019) explored the survival of disks in the ONC by implementing a one-dimensional viscous evolution model, and highlighted that the mass loss rates inferred from observations of proplyds in the ONC are preferentially high, representing the most extreme values. Their model predicts Ṁloss to be a factor of 2–3 lower for the majority of proplyds in their sample. The study also shows that part of the solution involves accounting for the age spread present in the stellar population of the ONC (e.g., Hillenbrand 1997; Palla & Stahler 1999; Da Rio et al. 2010; Jeffries et al. 2011; Beccari et al. 2017). In this scenario, the strongly irradiated stars are also the youngest and therefore have the greatest mass reservoir remaining. This represents a natural mechanism by which disks in the ONC can survive until the present day. Wilhelm et al. (2023) focused on modeling the radiation shielding by gas in massive star-forming regions, and showed that the disk lifetime could be extended by an order of magnitude by such shielding, making the lifetime problem milder. In the context of recent observational analysis, Ballering et al. (2023) suggested that disk masses are underestimated as a result of the ALMA emission being optically thick, which could play a role in solving the proplyd lifetime problem. Therefore, there are multiple factors to take into account when estimating the lifetimes of proplyds.
 |
Fig. 12 Mass-loss rates measured from the ionization front radius as a function of disk mass. The disk masses found by Mann et al. (2014) partly overlap with those reported by Ballering et al. (2023). Each colour represents a different assumed dust temperature: T = 20 K, T = 40 K, and Td = 62–108 K, and diagonal lines mark lifetimes. |
7 Conclusions
We have presented the first spatially and spectrally resolved observations of 12 proplyds in the Orion Nebula Cluster using MUSE NFM. We have characterized their morphology in different emission lines commonly associated with ionized gas, measured the size of the ionization front in different ionization tracers, and measured their stellar properties. This has allowed us to estimate physical parameters and draw comparisons with photoevaporation models. Our main conclusions are as follows:
The ionization front radius traced by different emission lines (Hα, [O I], [O II], and [O III]) increases with decreasing strength of the FUV radiation field, as expected by photoevaporation models;
The ratios of the ionization front radii for the emission lines of Hα, [O I] 6300 Å, [O II] 7330 A, and [O III] 5007 A, shows the expected ionization stratification: the most ionized part of the flow is located closest to the UV source;
The ratios of ionization fronts at the different ionization states explored in this work scale in the same way for all pro-plyds in our sample regardless of the incident radiation. This indicates that the ratio of ionization front sizes at different ionization states of proplyds is self-similar;
Mass-loss rates, estimated based on the Ha emission, are of the order of 1.07–94.5 × 10−7 M⊙ yr−1. Higher Ṁloss is observed at higher FUV field strengths, in line with general expectations from models. No dependence is observed with the stellar mass;
The density of cometary cusps across the ONC should have typical values ~2–3×105 cm−3 to explain the observed spatial distribution of ionization states of oxygen in proplyds;
Observationally, the proplyd lifetime problem still holds even after new measurements of disk masses and mass loss rates have been performed.
This work sets the stage for identifying firm signatures associated with external photoevaporation, which would open the possibility of confirming whether disks located in more massive and distant star-forming regions undergo the effect. Moreover, the characterization of external photoevaporation is fundamental to constraining planet formation models.
Future work will involve analyzing line ratios as the tracers of electron density and temperature. Determining the physical properties of the proplyds will allow for a more precise measurement of the mass-loss rate. Additionally, the identification of new emission lines will be explored.
Acknowledgements
We thank the anonymous referee for the insightful review that improved our study. M.L.A., K.M., and C.F.M. acknowledge funding from the European Union (ERC, WANDA, 101039452). S.F. is funded by the European Union (ERC, UNVEIL, 101076613) and by the grant PRIN-MUR 2022YP5ACE. G.P.R. is funded by the Fondazione Cariplo, grant no. 2022-1217, and the European Union (ERC, DiscEvol, 101039651). T.J.H. acknowledges funding from a Royal Society Dorothy Hodgkin Fellowship and UKRI guaranteed funding for a Horizon Europe ERC consolidator grant (EP/Y024710/1). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
Appendix A MUSE NFM images of ONC proplyds
Figures A.1 and A.2 show each proplyd in a collage of the following emission lines: Ha, [O I] 6300 Å, [O II] 7330 Å, [O III] 5007 Å, [S II] 6731 Å, [N II] 5755 Å, and [N II] 6584 Å. These lines are selected to show the various components of the systems.
 |
Fig. A.1 MUSE NFM observations of proplyds in seven emission lines. The last column is an RGB image combining [N II] 6548 Å, Ha, and [O III] 5007 Å emission lines. |
 |
Fig. A.2 MUSE NFM observations of proplyds in seven emission lines. The last column is an RGB image combining [N II] 6548 Å, Ha, and [O III] 5007 Å emission lines. |
Appendix B Statistical test
To asses the statistical significance of the relations in our small sample, we carry out two analyses for the following: ionization front radius (RIF) and projected separation (d); RIF with UV radiation (G0); and mass-loss rate (Ṁloss) with G0.
Firstly, we test the null-hypothesis that there is no relation between the independent variable on the x-axis and the dependent variable on the y-axis. We use a bootstrap sampling method with 104 iterations, where we randomize the x values and compute the Spearman correlation coefficient. Secondly, we assess the uncertainty of the correlation coefficient by bootstrapping with 104 iterations while varying the y-axis values within their respective uncertainties taken as the standard deviation of a Gaussian distribution of random points. We adopt a truncated Gaussian distribution to model the uncertainty for the lower limits values in the RIF, and thus also Ṁloss, measurements. In those cases, the bootstrapping is selected within this truncated Gaussian distribution with a standard deviation of 20% of the lower limit value. Both of these tests are then compared with the actual Spearman correlation coefficient rs. The results are presented in Fig. B.1.
 |
Fig. B.1 Correlation coefficient analysis for: (a) the ionization front radii and projected separation relation; (b) the ionization front radii and UV radiation relation; (c) mass-loss rate and UV radiation relation. The violet histogram corresponds to the bootstrapped randomized x-axis values; the dashed purple lines mark the 2σ ranges of the realizations. The blue histogram results from bootstrapping the y-axis values within the respective error bars, and the 1σ ranges of the bootstrap are shown with cyan line. We show that Spearman correlation coefficient for the measured data (orange line), which is outside 2σ of the randomized distribution. |
Appendix C Best fit of the stellar spectra
As described in Sect. 4.2, the extracted stellar spectra for the proplyds are compared with templates of young stellar objects to determine their spectral type and extinction. The best fit of the spectra are presented in Fig. C.1.
 |
Fig. C.1 Best fit of the stellar spectra of the proplyds studied in this work |
Appendix D Observations
The details concerning the MUSE NFM observations are given in Table D.1.
Information about the observations taken with MUSE NFM.
References
- Alcalá, J. M., Manara, C. F., Natta, A., et al. 2017, A&A, 600, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, SPIE Conf. Ser., 7735, 773508 [Google Scholar]
- Ballering, N. P., Cleeves, L. I., Haworth, T. J., et al. 2023, ApJ, 954, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., & Reipurth, B. 2001, ApJ, 546, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., O’Dell, C. R., & McCaughrean, M. J. 2000, AJ, 119, 2919 [NASA ADS] [CrossRef] [Google Scholar]
- Beccari, G., Petr-Gotzens, M. G., Boffin, H. M. J., et al. 2017, A&A, 604, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyden, R. D., & Eisner, J. A. 2020, ApJ, 894, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Da Rio, N., Gouliermis, D. A., & Gennaro, M. 2010, ApJ, 723, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Eisner, J. A., Arce, H. G., Ballering, N. P., et al. 2018, ApJ, 860, 77 [CrossRef] [Google Scholar]
- Fang, M., Kim, J. S., Pascucci, I., & Apai, D. 2021, ApJ, 908, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Peeters, E., Berné, O., et al. 2024, A&A, 685, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Harries, T., Haworth, T., Acreman, D., Ali, A., & Douglas, T. 2019, Astron. Comput., 27, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J. 2021, MNRAS, 503, 4172 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., & Harries, T. J. 2012, MNRAS, 420, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., Coleman, G. A. L., Qiao, L., Sellek, A. D., & Askari, K. 2023a, MNRAS, 526, 4315 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., Reiter, M., O’Dell, C. R., et al. 2023b, MNRAS, 525, 4129 [NASA ADS] [CrossRef] [Google Scholar]
- Hendler, N., Pascucci, I., Pinilla, P., et al. 2020, ApJ, 895, 126 [Google Scholar]
- Henney, W. J., & Arthur, S. J. 1998, AJ, 116, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Henney, W. J., & O’Dell, C. R. 1999, AJ, 118, 2350 [CrossRef] [Google Scholar]
- Henney, W. J., Meaburn, J., Raga, A. C., & Massey, R. 1997, Optical Emission Line Profiles of the LV Knots (Proplyds) in Orion, Tech. rep. [Google Scholar]
- Henney, W. J., O’Dell, C. R., Meaburn, J., Garrington, S. T., & Lopez, J. A. 2002, ApJ, 566, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [Google Scholar]
- Jeffries, R. D., Littlefair, S. P., Naylor, T., & Mayne, N. J. 2011, MNRAS, 418, 1948 [Google Scholar]
- Johnstone, D., Hollenbach, D., & Bally, J. 1998, ApJ, 499, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Kirwan, A., Manara, C. F., Whelan, E. T., et al. 2023, A&A, 673, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laques, P., & Vidal, J. L. 1979, A&A, 73, 97 [NASA ADS] [Google Scholar]
- Manara, C. F., Testi, L., Rigliaco, E., et al. 2013, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Frasca, A., Alcalá, J. M., et al. 2017a, A&A, 605, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Testi, L., Herczeg, G. J., et al. 2017b, A&A, 604, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Ansdell, M., Rosotti, G. P., et al. 2023, Protostars and Planets VII, 534, 539 [NASA ADS] [Google Scholar]
- Mann, R. K., & Williams, J. P. 2010, ApJ, 725, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, R. K., Di Francesco, J., Johnstone, D., et al. 2014, ApJ, 784, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, R. K., Andrews, S. M., Eisner, J. A., et al. 2015, ApJ, 802, 77 [Google Scholar]
- Maucó, K., Manara, C. F., Ansdell, M., et al. 2023, A&A, 680, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCaughrean, M. J., & O’Dell, C. R. 1996, AJ, 111, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Ali, A. A., Chevance, M., et al. 2021, MNRAS, 508, 5425 [NASA ADS] [CrossRef] [Google Scholar]
- Mesa-Delgado, A., Núñez-Díaz, M., Esteban, C., et al. 2012, MNRAS, 426, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Miotello, A., Robberto, M., Potenza, M. A. C., & Ricci, L. 2012, ApJ, 757, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Nisini, B., Antoniucci, S., Alcalá, J. M., et al. 2018, A&A, 609, A87 [EDP Sciences] [Google Scholar]
- O’Dell, C. 2001, PASP, 113, 29 [CrossRef] [Google Scholar]
- O’Dell, C. R., & Wen, Z. 1994, ApJ, 436, 194 [CrossRef] [Google Scholar]
- O’Dell, C. R., Wen, Z., & Hu, X. 1993, ApJ, 410, 696 [CrossRef] [Google Scholar]
- O’Dell, C. R., Kollatschny, W., & Ferland, G. J. 2017, ApJ, 837, 151 [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J. 2020, Roy. Soc. Open Sci., 7, 201271 [NASA ADS] [CrossRef] [Google Scholar]
- Piqueras, L., Conseil, S., Shepherd, M., et al. 2017, arXiv e-prints [arXiv:1710.03554] [Google Scholar]
- Reiter, M., & Parker, R. J. 2022, Eur. Phys. J. Plus, 137, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Robberto, M., & Soderblom, D. R. 2008, AJ, 136, 2136 [CrossRef] [Google Scholar]
- Richling, S., & Yorke, H. W. 2000, ApJ, 539, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Robberto, M., Soderblom, D. R., Scandariato, G., et al. 2010, AJ, 139, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Robberto, M., Gennaro, M., Da Rio, N., et al. 2024, ApJ, 960, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Scally, A., & Clarke, C. 2001, MNRAS, 325, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Simón-Díaz, S., Herrero, A., Esteban, C., & Najarro, F. 2006, A&A, 448, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storzer, H., & Hollenbach, D. 1999, ApJ, 515, 669 [CrossRef] [Google Scholar]
- van Terwisga, S. E., & Hacar, A. 2023, A&A, 673, A2 [Google Scholar]
- van Terwisga, S. E., van Dishoeck, E. F., Mann, R. K., et al. 2020, A&A, 640, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vicente, S. M. H. 2009, Physical properties and evolution of protoplanetary disks in stellar clusters:planet formation in harsh environments, PhD thesis, University of Lisbon, Portugal [Google Scholar]
- Vicente, S. M., & Alves, J. 2005, A&A, 441, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilhelm, M. J. C., Portegies Zwart, S., Cournoyer-Cloutier, C., et al. 2023, MNRAS, 520, 5331 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, A. J., & Haworth, T. J. 2022, Eur. Phys. J. Plus, 137, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, A. J., Clarke, C. J., Rosotti, G. P., Hacar, A., & Alexander, R. 2019, MNRAS, 490, 5478 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 RGB images (insets) of continuum subtracted, single line integrated flux images of the sample acquired with MUSE. In each inset, a variety of emission lines are combined to highlight the morphology of the proplyd. The background image is a Hubble optical image of the Orion Nebula Cluster (Credit: NASA, ESA, M. Robberto (Space Telescope Science Institute/ESA) and the Hubble Space Telescope Orion Treasury Project Team). |
| In the text | |
 |
Fig. 2 Continuum subtracted, single line integrated flux images of proplyd 177–341W. The panels show which parts of the system are visible in given emission lines. |
| In the text | |
 |
Fig. 3 Method for measuring the ionization front radius of a proplyd. Top panel: the intensity cut is taken along the diagonal line. The red line marks our identification of the ionization front. Bottom panel: intensity cut along the diagonal line marked in the top panel. |
| In the text | |
 |
Fig. 4 Ionization front radius versus the projected separation from θ1 Ori C. Squares mark proplyds for which the I-front measurement has a higher uncertainty. The radii of the ionization fronts increase with larger projected distances from the UV source. Due to noisy subcubes, measurements were not taken for proplyd 167–325 (closest to the UV source) in the bottom panels. For the same reason, the panel of [O III] 5007 Å excludes the radii of several targets. |
| In the text | |
 |
Fig. 5 Ionization front sizes from literature (Henney & Arthur 1998; Ballering et al. 2023) versus as measured with MUSE IFU data. We note that the measurement methods differ slightly from each other. |
| In the text | |
 |
Fig. 6 Ionizing radiation strength as a function of the ionization front radius. The diamond marks proplyd 203–504. irradiated mainly by θ2 Ori A. For the rest of the targets (dots and squares), the UV source is θ1 Ori C. Squares mark proplyds for which the I-front measurement has a higher uncertainty. 244–440 is not included in this figure due to the stark difference in size compared to the rest of the sample. |
| In the text | |
 |
Fig. 7 Ratios of ionization front sizes of Hα, [O III], [O II], and [O I] as a function of the incident UV field. The empty diamond marks 244–440, and the empty triangle marks 203–504. The mean and SEM are marked in violet. |
| In the text | |
 |
Fig. 8 Mass-loss rates of MUSE compared with the values reported by Henney & O’Dell (1999); Ballering et al. (2023). |
| In the text | |
 |
Fig. 9 Mass-loss rate vs incident radiation field. The dots represent well-detected proplyds, and the squares denote the proplyds with higher uncertainty. The diamond (244–440) and the triangle (203–504) mark proplyds irradiated by θ2 Ori A. The dashed purple line represents a model prediction for disks with a radius of 40 au (Storzer & Hollenbach 1999). |
| In the text | |
 |
Fig. 10 Example profiles of the oxygen ionization state as a function of distance from the density enhancement in the H II region (distance from the star of the proplyd cusp). The upper and lower panels are for densities of 3 × 104 cm−3 and 3 × 105 cm−3 respectively. |
| In the text | |
 |
Fig. 11 Distance between the O III-O II transition and the O II-O I transition for a proplyd at a distance of 0.1 pc from a θ1 Ori C like star, as a function of the density in the cometary cusp of the proplyd. For densities ~ 2–3 × 105 cm−3 the thickness of the O II layer is consistent with our observations of ONC proplyds. |
| In the text | |
 |
Fig. 12 Mass-loss rates measured from the ionization front radius as a function of disk mass. The disk masses found by Mann et al. (2014) partly overlap with those reported by Ballering et al. (2023). Each colour represents a different assumed dust temperature: T = 20 K, T = 40 K, and Td = 62–108 K, and diagonal lines mark lifetimes. |
| In the text | |
 |
Fig. A.1 MUSE NFM observations of proplyds in seven emission lines. The last column is an RGB image combining [N II] 6548 Å, Ha, and [O III] 5007 Å emission lines. |
| In the text | |
 |
Fig. A.2 MUSE NFM observations of proplyds in seven emission lines. The last column is an RGB image combining [N II] 6548 Å, Ha, and [O III] 5007 Å emission lines. |
| In the text | |
 |
Fig. B.1 Correlation coefficient analysis for: (a) the ionization front radii and projected separation relation; (b) the ionization front radii and UV radiation relation; (c) mass-loss rate and UV radiation relation. The violet histogram corresponds to the bootstrapped randomized x-axis values; the dashed purple lines mark the 2σ ranges of the realizations. The blue histogram results from bootstrapping the y-axis values within the respective error bars, and the 1σ ranges of the bootstrap are shown with cyan line. We show that Spearman correlation coefficient for the measured data (orange line), which is outside 2σ of the randomized distribution. |
| In the text | |
 |
Fig. C.1 Best fit of the stellar spectra of the proplyds studied in this work |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


