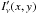| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322574 | |
| Published online | 14 January 2014 | |
Online material
Appendix A: Line profiles and slit loss
In our dataset, we found clear variations in the shape of line profiles observed at
different position angles. These variations are due to the relative size of the slit and
the disc on the sky (Fig. 1). At the distance of
HD 100546 (103 pc), a slit width of 0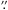 2 corresponds to a
width of about 20 AU. This is coincidentally close to the diameter of the disc wall.
Figure 1 shows how varying the position angle of
the slit results in losing parts of the emission originating at the disc wall (10–13
AU). Thus different slit position angles will lead to different profile shapes. For
HD 100546 the resulting line profiles should show double peaks at PA = 145°
and PA = 325°, while showing flat topped profiles at PA = 55° and
PA = 235°.
2 corresponds to a
width of about 20 AU. This is coincidentally close to the diameter of the disc wall.
Figure 1 shows how varying the position angle of
the slit results in losing parts of the emission originating at the disc wall (10–13
AU). Thus different slit position angles will lead to different profile shapes. For
HD 100546 the resulting line profiles should show double peaks at PA = 145°
and PA = 325°, while showing flat topped profiles at PA = 55° and
PA = 235°.
With a slit width that barely includes most of the disc wall, a poorly centred slit can affect the shape of the lines. If the slit is offset to one side, we lose emission from the velocity channels falling outside the slit.
These important effects need to be considered in both our observational analysis and in our modelling efforts.
Appendix A.1: Observed line profiles
 |
Fig. A.1
Averaged line profile at PA = 145° for lines observed on the 29th, for each v level separately. The lines included are those listed in Table 2. The dotted lines are the normalized individual transitions and the red line is the median average of all these lines. |
| Open with DEXTER | |
Table 2 presents a full listing of our selected unblended and clean CO ro-vibrational lines. For all these CO ro-vibrational transitions, line profiles (flux as a function of velocity) have been extracted. To investigate whether we can build high resolution average line profiles, we checked the data for shape variations as a function of v,J, PA, and different nights.
The individual line profiles are normalized by their fitted continuum, shifted to zero continuum, and the line profile is then normalized to the maximum flux value. Profiles are then combined to median average profiles.
The profile shapes vary between the two nights and also between the four/eight different position angles. We find no significant variations when comparing v-levels and wavelength settings (see Fig. A.1 for an example at PA = 145° for the night of the 29th). For a more quantitative view, the FWHM and the peak separations, vsep, for PA = 145° are shown for all v-bands in Table A.1. The average for each v-band is build over the individual J transitions at that v-band. The 1σ standard deviation listed in the table is the deviation of the values at each J-level from the mean. The average from all v-bands agree with each other within 1σ.
The difference between line shapes observed at the same PA on the 29th and on the 30th could be explained by different pointing offsets present for each night. Within the individual position angles there are no shape variations during one night, i.e. data from different wavelength settings taken at different times with same PA are very similar.
The above found stability of the line profile shapes justifies building averaged line profiles over velocity for each PA and each night (independent of v,J). These co-added line profiles are shown in Fig. A.2. For the 29th, we find double peaked profiles at both PA = 145° and PA = 325°, as we would expect given the disc itself has a position angle of 145°. At PA = 55° and PA = 235°, we find single peaked asymmetric profiles, indicating an offset (with no offset we should find flat topped profiles). The profiles for the anti-parallel positions PA = 55° and PA = 235°, though very similar, do not match exactly but lean in opposite directions, which should not be the case for a true antiparallel case. For the 30th, the four repeated position angles (PA = 55°, PA = 235°, PA = 145°, and PA = 325°) show slightly altered shapes indicating a change in the offset with respect to the first night. The four new position angles (PA = 10°, PA = 190°, PA = 100°, and PA = 280°) all show asymmetric single peaks with a hint of a shoulder.
 |
Fig. A.2
Averaged line profiles at eight different position angles containing transitions from all v-levels observed on the 29th and 30th, listed in Table 2. The dotted lines are the normalized individual transitions and the red line is the median of all these lines. The upper four panels show the line profiles collected at PA = 55°/145°/235°/325° on the 29th. The middle four panels show the line profiles collected at PA = 55°/145°/235°/325° on the 30th. The lower four panels show the line profiles collected at PA = 10°/100°/190°/280° on the 30th. |
| Open with DEXTER | |
FWHM and peak separation of the average line profiles.
 |
Fig. A.3
Output from the IDL slit filtering tool, showing the unfiltered normalized line
profile (red line) and the slit filtered normalized line profile (black line)
for three different pointing offsets (from the top first frame:
0′′, second frame:
0 |
| Open with DEXTER | |
 |
Fig. A.4
Flux versus wavelength comparing the slit filtered model to the non slit filtered model for all lines observed on the 29th at PA = 145° listed in Table 2. The slit filtered modelled fluxes are shown as diamonds and the modelled fluxes without slit filter are shown as stars. The different vibrational bands are colour coded: v = 1–0 is black, v = 2–1 is blue, v = 3–2 is green and v = 4–3 is red. |
| Open with DEXTER | |
Appendix A.2: Modelled line profiles
ProDiMo outputs line data cubes for each chosen CO ro-vibrational transition. Each cube contains a 201 × 201 pixel coordinate grid in units of AU and the spectral intensity in [erg/cm2/s/Hz/sr] at every spatial position in the described coordinate grid for each of the 91 velocity channels, covering –20 km s-1 to +20 km s-1 and the continuum (see Appendix B). From this cube we create line images, profiles, and flux tables. They are our modelled “observations”.
Appendix A.2.1: Applying a slit filter to line data cubes
The line cubes do not contain any observational or instrumental effects. Hence, they need to be convolved with the instrumental PSF (we approximate the PSF by a Gaussian), rotated to the position angle of the disc on the sky and corrected for slit loss and pointing offsets before comparison with the actual observations. Each cube is therefore piped through a slit filtering IDL procedure (Carmona et al. 2011) adapted for the purposes in this paper. The slit filter applies the described corrections and produces line profiles that can be directly compared to our observed data.
Each spectral slice of the ProDiMo data cube is convolved in the spatial
(x,y) direction with a Gaussian two dimensional PSF using a FWHM
of 0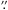 169 and
the idl routines “convolve.pro” and “psf_gaussian.pro”). In the spectral direction,
the cube is convolved with the CRIRES instrumental resolution
(R = 90 000) using the routine “gaussfold.pro”. We rotate the
cube in the x,y, direction to match the position angle of HD 100546
by 145 degrees using the routine “rot.pro” and cubic interpolation with an
interpolation parameter of –0.6.
169 and
the idl routines “convolve.pro” and “psf_gaussian.pro”). In the spectral direction,
the cube is convolved with the CRIRES instrumental resolution
(R = 90 000) using the routine “gaussfold.pro”. We rotate the
cube in the x,y, direction to match the position angle of HD 100546
by 145 degrees using the routine “rot.pro” and cubic interpolation with an
interpolation parameter of –0.6.
Each spectral slice of the data cube is now covered with a two dimensional mask (x,y) representing the spectrograph slit (with arbitrary orientation and/or offset from the disc centre and centred on x0, slit, y0, slit). From the resulting signal we calculate the line profile and astrometric signal (SPP and FWHM). The SPP is calculated as the shortest distance between the centre of mass (centroid) of the CO + continuum emission and a line perpendicular to the slit running through the slit origin. The FWHM is calculated from a Gaussian fit to the CO + continuum emission. Figure A.3, shows for three different offsets the effect that slit filtering has on a line profile, together with a sketch of the slit on disc. The line profiles are normalized in the same way as the observed profiles (see Sect. A.1).
To asses the importance of slit loss and telescope effects, we have also compared the unfiltered model line fluxes to the slit filtered model line fluxes (Fig. A.4). We find that the slit affects all transitions in the same way and flux ratios are conserved through the slit filtering. This was expected, because the spatial profiles of the line emission are very similar.
Because our observed line profiles change on very short time scales (see Appendix A.1) it is virtually impossible to explain the shape asymmetries and variations with disc asymmetries alone and this calls for the shape variations to be caused by pointing offsets.
To explore the variety in line profiles due to varying PA and pointing offsets, we
select a representative line, v(2–1)R06, and study seven different
offsets (–0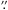 20;
–0
20;
–0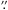 15;
–0
15;
–0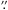 10;
–0
10;
–0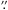 06;
–0
06;
–0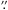 03;
0′′; 0
03;
0′′; 0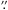 10; and
0
10; and
0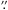 20),
measured along the semi-major axis of the disc (positive to the right) while varying
the slit position angle from 15° to 175° with a step size of
10°. The full parameter grid of line profile shapes is presented in
Fig. A.5. These tests show that the shape
variations seen in our observed data are fully consistent with the variations from a
combination of PA and/or offset covered in our theoretical grid. From our
theoretical grid we furthermore derive the plots shown in Figs. A.6 and A.7. Here the
pointing offsets needed to explain our observed line profile variations are plotted
as a function of Time and PA these figures reveal that a pointing offset of
–0
20),
measured along the semi-major axis of the disc (positive to the right) while varying
the slit position angle from 15° to 175° with a step size of
10°. The full parameter grid of line profile shapes is presented in
Fig. A.5. These tests show that the shape
variations seen in our observed data are fully consistent with the variations from a
combination of PA and/or offset covered in our theoretical grid. From our
theoretical grid we furthermore derive the plots shown in Figs. A.6 and A.7. Here the
pointing offsets needed to explain our observed line profile variations are plotted
as a function of Time and PA these figures reveal that a pointing offset of
–0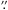 06 would
be an appropriate assumption for most position angles. This offset was imposed on
the slit filtering procedure for the simulated lines of the night of the 29th and
30th. For our full selection of lines the slit filtering procedure is run for
various position angles based on the settings and the PSF of the observations made
on the 29th and 30th of March 2010, listed in Table 1.
06 would
be an appropriate assumption for most position angles. This offset was imposed on
the slit filtering procedure for the simulated lines of the night of the 29th and
30th. For our full selection of lines the slit filtering procedure is run for
various position angles based on the settings and the PSF of the observations made
on the 29th and 30th of March 2010, listed in Table 1.
For comparison purposes, the final modelled line profiles are normalized co-added and averaged for each PA setting separately, following the exact same scheme as the combining of the observed line profiles (see Appendix A.1 for more details). These normalized combined line profiles are shown in Fig. 6 with the corresponding average observed line profiles overplotted. Table 5 lists the line fluxes and continuum fluxes for each modelled slit filtered line at one particular position angle (PA = 145°).
The upper frame of Fig. 6 shows that the line
shape variations, that we see in our observations from the 29th, cannot be explained
well by a single slit pointing offset of –0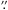 06 (the line
profile collected at PA = 235° is leaning toward the wrong side). The
middle and lower frame of Fig. 6 show that the
line shape variations observed on the 30th could in principle be explained by one
single consistent pointing offset: The slit filtered model (with a pointing offset
of –0
06 (the line
profile collected at PA = 235° is leaning toward the wrong side). The
middle and lower frame of Fig. 6 show that the
line shape variations observed on the 30th could in principle be explained by one
single consistent pointing offset: The slit filtered model (with a pointing offset
of –0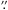 6)
reproduces the observed line shapes reasonably well.
6)
reproduces the observed line shapes reasonably well.
 |
Fig. A.5
Parameter exploration made with our slit filtering tool. The position angle
of the slit was varied from 0° to 175° in steps of
10°. The offset values are
–0 |
| Open with DEXTER | |
 |
Fig. A.6
Derived offset versus time for our individual observed spectra collected on the 29th. Time moves forward along the positive direction of the x-axis. Along the x-axis the position angle of each individual spectrum is written. |
| Open with DEXTER | |
 |
Fig. A.7
Derived offset versus time for our individual observed spectra collected on the 30th. Time moves forward along the positive direction of the x-axis. Along the x-axis the position angle of each individual spectrum is written. |
| Open with DEXTER | |
Appendix B: A flux-conserving scheme to convert images in polar coordinates to regular Cartesian grids
Continuum images and channel maps in ProDiMo are initially calculated on a polar grid
(see Thi et al. 2011 for details) with
roughly2 logarithmic equidistant radial grid
points
{ ri | i ∈ [0...Nr] }
and linear equidistant angular grid points
{ θj | j ∈ [0...Nθ] }.
This is necessary to resolve the tiny inner disc rim (important for the short
wavelengths) as well as resolving the outer regions (important for the long wavelengths)
at the same time. The polar intensities
Iν(i,j) have associated
areas in the image plane as 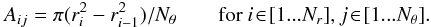 (B.1)The
intensities are assumed to be constant on the polar “pixels”, i.e. the area
Aij bracketed by
ri,
ri−1,
θj and
θj−1, see Fig. B.1.
(B.1)The
intensities are assumed to be constant on the polar “pixels”, i.e. the area
Aij bracketed by
ri,
ri−1,
θj and
θj−1, see Fig. B.1.
 |
Fig. B.1
Conversion from polar intensities
Iν(r,θ) to a
regular Cartesian grid |
| Open with DEXTER | |
 |
Fig. B.2
Rotational diagram for each of the first four v levels made from observational data gathered on the 29th. In each plot, data from two position angles are plotted for comparison (PA = 55° shown as red squares and PA = 145° shown as blue triangles). A linear fit to find Trot is made separately for each PA The fitted values are printed on the plots together with their formal error bars. However, we expect a somewhat larger error from the limited J range. |
| Open with DEXTER | |
We seek a fast numerical method to convert these polar images onto a regular grid with
equidistant Cartesian image coordinates
(xn, n ∈ [0...Nx])
and
(yk, k ∈ [0...Ny])
with associated pixel areas  (B.2)The
method is flux-conservative if
(B.2)The
method is flux-conservative if  (B.3)where
(B.3)where
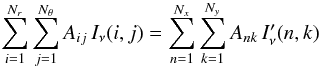 are the desired intensities
on the regular Cartesian pixels. The exact solution of this problem would be to
calculate the overlap areas,
O(Ank,Aij),
between the regular pixels Ank and any
polar pixel Aij, then sum up the fluxes and
divide by the pixel area as
are the desired intensities
on the regular Cartesian pixels. The exact solution of this problem would be to
calculate the overlap areas,
O(Ank,Aij),
between the regular pixels Ank and any
polar pixel Aij, then sum up the fluxes and
divide by the pixel area as 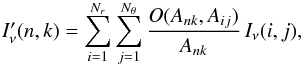 (B.4)but
to calculate those overlap areas is painful, see Fig. B.1. A more practical idea is to create a Cartesian rectangular area that
exactly contains the polar pixel, see Fig. B.1, by
taking the minimum and maximum of the four corner points of
Aij
(B.4)but
to calculate those overlap areas is painful, see Fig. B.1. A more practical idea is to create a Cartesian rectangular area that
exactly contains the polar pixel, see Fig. B.1, by
taking the minimum and maximum of the four corner points of
Aij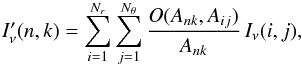 (B.5)The
area of this rectangular pixel,
(B.5)The
area of this rectangular pixel,
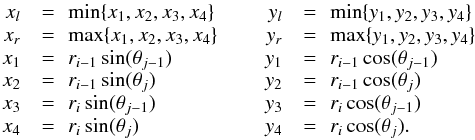 (B.6)is
always larger than the area of the original polar pixel
Aij, resulting in a correction factor
in Eq. (B.7) below. The area overlaps
between Ank and
(B.6)is
always larger than the area of the original polar pixel
Aij, resulting in a correction factor
in Eq. (B.7) below. The area overlaps
between Ank and
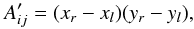 are now
easy to calculate, and the resulting conversion formula is
are now
easy to calculate, and the resulting conversion formula is 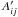 (B.7)The
area coverage Cnk is close, but not exactly
equal to Ank, because some regular pixels
will be slightly oversampled by the polar pixels, and others slightly under sampled, and
this effect is automatically corrected for in Eq. (B.7). This conversion method is fast, reliable, and exactly flux
conservative. However, the resulting spatial resolution in the regular image will suffer
somewhat in areas where the rectangular pixels
(B.7)The
area coverage Cnk is close, but not exactly
equal to Ank, because some regular pixels
will be slightly oversampled by the polar pixels, and others slightly under sampled, and
this effect is automatically corrected for in Eq. (B.7). This conversion method is fast, reliable, and exactly flux
conservative. However, the resulting spatial resolution in the regular image will suffer
somewhat in areas where the rectangular pixels 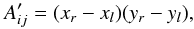 , as constructed
from the polar pixels Aij, are larger than
the regular pixels Ank. Here, the
simulation can be improved by introducing polar sub-pixels in the first place, i.e. by
subdividing large polar pixels into a suitable number of smaller polar sub-pixels,
equally spaced in r and θ, assuming the intensities to
be constant over all sub-pixels, before applying Eqs. (B.5) to (B.7).
, as constructed
from the polar pixels Aij, are larger than
the regular pixels Ank. Here, the
simulation can be improved by introducing polar sub-pixels in the first place, i.e. by
subdividing large polar pixels into a suitable number of smaller polar sub-pixels,
equally spaced in r and θ, assuming the intensities to
be constant over all sub-pixels, before applying Eqs. (B.5) to (B.7).
 |
Fig. B.3
Rotational diagram for each of the first four v levels made from observational data gathered on the 30th. In each plot, data from two position angles are plotted for comparison (PA = 55° shown as red squares and PA = 145° shown as blue triangles). A linear fit to find Trot is made separately for each PA The fit is strongly affected by the limited line sample. To visualize this effect the rotational diagrams from the 29th are overplotted in black. |
| Open with DEXTER | |
Appendix C: Population diagrams
Appendix C.1: Observed rotational diagrams
Rotational diagrams were compiled, for each vibrational level, using the integrated line fluxes derived from the CRIRES data separating data from different position angles and observing nights. We note that in our sample the most optically thick lines, like the v = 1–0 low J lines, are missing (these lines coincide with strong telluric absorption features and are therefore excluded). The rotational diagrams are shown in Figs. B.2 and B.3. The details of the equations and quantities used are described in Sect. 4.1. We see that there is no big variation between the fit for two position angles taken on the same night. The rotational temperatures found from each of the two observing nights are different, but this is mainly caused by a narrower fitting range in J levels for the second night. The v = 2–1 and v = 4–3 rotational diagrams are to sparsely populated and no v = 1–0 lines were collected in the second night. For the first observing night the v = 2–1 rotational diagram shows a Trot ~ 1100 K and the v = 3–2 rotational diagram shows a Trot ~ 1300 K. And for the second night the v = 3–2 rotational diagram shows a Trot ~ 1100/1200 K. In these diagrams, the individual lines all fall on a curve typically seen in the presence of optical depth and non-LTE effects, making a linear fit questionable. Thi et al. (2013) showed that it is hard to fit a single temperature and that the real rotational temperature can be found in a “second” turn over at higher J levels. We do not have a wide enough J range for this. The formal error bars for the rotational temperatures are printed on the rotational diagrams but we expect that there is a somewhat larger error from the limited J range.
Appendix C.2: Modelled rotational diagrams
As described for the observational data, rotational diagrams were produced for the modelled line transitions (comparable to the data collected on the 29th) for two orthogonal position angles separately. The rotational diagrams are shown in Fig. C.1 and the details of derivations are described in Sect. 4.1. The rotational temperatures found from the modelled lines are higher than those observed, but the lines fall on a curve and it is hard to get a good linear fit. The fit depends heavily on the range of lines included.
 |
Fig. C.1
Rotational diagram of the lowest four v levels for the modelled line sample. The fitting is done with the exact same range and line selection as the observational data set collected on the 29th, see Table 2. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.