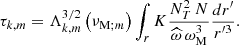| Issue |
A&A
Volume 694, February 2025
|
|
|---|---|---|
| Article Number | A173 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202452066 | |
| Published online | 11 February 2025 | |
Non-linear internal waves breaking in stellar-radiation zones
Parametrisation for the transport of angular momentum: Bridging geophysical-to-stellar fluid dynamics
Université Paris-Saclay, Université Paris Cité, CEA, CNRS, AIM, F-91191 Gif-sur-Yvette, France
⋆ Corresponding author; stephane.mathis@cea.fr
Received:
30
August
2024
Accepted:
18
November
2024
Context. Internal gravity waves (IGWs) are one of the mechanisms that can play a key role in efficiently redistributing angular momentum in stars along their evolution. The study of IGWs is thus of major importance since space-based asteroseismology reveals a transport of angular momentum in stars, which is stronger by two orders of magnitude than the one predicted by stellar models ignoring their action or those of magnetic fields.
Aims. IGWs trigger angular momentum transport when they are damped by heat or viscous diffusion, when they meet a critical layer where their phase velocity in the azimuthal direction equals the zonal wind or when they break. Theoretical prescriptions have been derived for the transport of angular momentum induced by IGWs because of their radiative and viscous dampings and of the critical layers they encounter along their propagation. However, none have been proposed for the transport of angular momentum triggered by their non-linear breaking. In this work, we aim to derive such a physical and robust prescription, which can be implemented in stellar structure and evolution codes.
Methods. We adapted an analytical saturation model – which has been developed for IGWs’ nonlinear convective breaking in the Earth’s atmosphere and has been successfully compared to in situ measurements in the stratosphere – to the case of deep spherical stellar interiors. This allowed us to derive the saturated amplitude of the velocity of IGWs breaking in stellar radiation zones through convective overturning of the stable stratification or the instability of the vertical shear of IGWs motion and of the angular momentum transport they trigger. In a first step, we neglected the modification of IGWs by the Coriolis acceleration and the Lorentz force, which are discussed and taken into account in a second step.
Results. We derive a complete semi-analytical prescription for the transport of angular momentum by IGWs that takes into account both their radiative damping and their potential nonlinear breaking because of their convective and vertical shear instabilities. We show that the deposit of angular momentum by breaking waves increases with their latitudinal degree, the ratio of the Brunt-Vaïsälä frequency and the wave frequency; and when the density decreases or the Doppler-shifted frequency vanishes. This allows us to bring the physical prescription for the interactions between IGWs and the differential rotation to the same level of realism as the one used in global circulation models for the atmosphere.
Key words: waves / methods: analytical / stars: evolution / stars: rotation
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Internal gravity waves (IGWs) are waves that propagate in stably stratified stellar-radiation zones. Their restoring force is the buoyancy force. For more than 40 years, they have been identified as one of the key mechanisms able to efficiently transport angular momentum and chemicals in these regions (e.g. Press 1981; Schatzman 1993b; Zahn et al. 1997). Their study is thus of major importance within the ongoing probe of the internal transport of angular momentum in the Sun and in stars thanks to space-based helioseismology and asteroseismology (e.g. García et al. 2007; Mosser et al. 2012, 2024; Deheuvels et al. 2014, 2015, 2020; Van Reeth et al. 2016; Aerts et al. 2017; Li et al. 2020, 2024). It reveals that the solar and stellar interiors are the place of a strong extraction of angular momentum, more intense by two orders of magnitude than what is predicted by the stellar structure and evolution codes including the transport mechanisms related to differential rotation (e.g. vertical and horizontal shear instabilities and meridional circulation; Zahn 1992; Maeder & Zahn 1998; Mathis & Zahn 2004; Mathis et al. 2018) but neglecting IGWs and magnetic fields (Marques et al. 2013; Ceillier et al. 2013; Cantiello et al. 2014; Ouazzani et al. 2019). In this framework, IGWs are, along with magnetic fields, the best candidates to explain the extraction of angular momentum from the radiative core of solar-type stars and their internal mixing (e.g. Montalbán & Schatzman 2000; Charbonnel & Talon 2005; Talon & Charbonnel 2005), in sub-giant stars (Pinçon et al. 2017) and in early-type stars (Rogers 2015; Rogers & McElwaine 2017; Neiner et al. 2020; Varghese et al. 2023).
In this context, the key theoretical challenge is to provide the most realistic and robust prescription possible for the extraction or deposit of angular momentum by IGWs to be implemented in stellar structure and evolution (SSE) codes, which compute the evolution of rotating stars (e.g. Meynet & Maeder 2000; Palacios et al. 2003; Marques et al. 2013). An IGW has three channels to transport momentum and matter: through i) viscous friction or heat diffusion (e.g. Press 1981; Schatzman 1993b; Zahn et al. 1997; Vadas & Fritts 2005); ii) critical layers, which are the place of a resonance between an IGW and a large-scale (zonal) flow (e.g. Booker & Bretherton 1967; Alvan et al. 2013); and iii) non-linear breaking because of IGWs’ convective or shear instabilities (e.g. Lindzen 1981; Sutherland 2001; Barker & Ogilvie 2010; Barker 2011). While the physical description of the transport of angular momentum by IGWs because of their radiative damping has become the standard way of implementing it in SSE (e.g. Talon & Charbonnel 2005; Fuller et al. 2014), IGWs breaking in stars came to the forefront in several configurations. First, Press (1981) pointed out that progressive IGWs can break near the centre of solar-type stars because of their geometrical focusing. This breaking is one of the main sources of the dissipation of tidal gravity waves triggered by close-in massive planets in solar-type stars (e.g. Barker & Ogilvie 2010; Barker 2011), which drives their orbital evolution (Lazovik 2021). In early-type stars, IGWs excited by their convective core can break near their surface because of the low density there (Rogers et al. 2013; Rogers 2015). In these configurations, specific physical modelling must be developed to evaluate angular momentum transport triggered by breaking IGWs, while the standard formalism of linear IGWs damped by radiative damping is not physically appropriate anymore.
Such a theoretical modelling has been developed in the case of the atmosphere of the Earth for convectively excited IGWs (Lindzen 1981; Holton & Zhu 1984; Lott et al. 2012; Lott & Guez 2013) to compute their impact on the general atmospheric circulation. The derived prescriptions are then implemented in global circulation models (GCMs), where small-scale transport and mixing processes are not solved directly but parameterised (e.g. Ribstein et al. 2022; Achatz et al. 2024), which is a situation similar to that of SSE codes. The predictions of these prescriptions have been successfully compared to Reynolds stresses measured in the Earth’s atmosphere by stratospheric balloons (Lott et al. 2023). However, this modelling for the Earth has been built in local Cartesian shallow-water models, which are not adapted to global spherical shells such as stellar radiative zones. In this work, we revisited the formalism developed in geophysics to adapt it to the case of stars and provide the relevant prescription for SSE codes. In Sect. 2, we recall the basics of the mathematical modelling of the adiabatic and dissipative propagation of low-frequency IGWs, which transport angular momentum. In Sect. 3, we detail the conditions for the convective and shear-induced breaking of IGWs, and we derive the triggered vertical transport of energy and angular momentum. To obtain these results, we adapted the saturation scheme (built in the case of the Earth’s atmosphere) to the case of spherically thick stellar radiation zones. In Sect. 4, we discuss the impact of the Coriolis acceleration and of the Lorentz magnetic force on IGW breaking. Finally, in Sect. 5, we present the conclusions and the perspectives of this work.
2. Propagation of low-frequency internal gravity waves
Internal gravity waves that transport angular momentum efficiently are low-frequency progressive waves (e.g. Schatzman 1993b; Zahn et al. 1997). To study their non-linear breaking following the path of what has been done in atmospheric physics by Lindzen (1981), Lott et al. (2012), and Lott & Guez (2013), the first step is to recall the formalism to model their propagation.
2.1. Adiabatic propagation
We expand the macroscopic velocity in stellar radiation zones as follows:
where 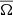 is the rotation angular velocity, which is assumed here to be shellular (Zahn 1992), and u is the velocity field of IGWs. We introduce the spherical coordinates {r,θ,φ} and the corresponding unit vector basis
is the rotation angular velocity, which is assumed here to be shellular (Zahn 1992), and u is the velocity field of IGWs. We introduce the spherical coordinates {r,θ,φ} and the corresponding unit vector basis 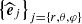 .
.
We adopted the so-called shellular rotation approximation, where the rotation only (or mainly) varies with r the radius, since our objective in this work is to provide prescriptions for state-of-the-art 1D stellar-structure and evolution codes. These codes, when taking transport and mixing processes’ parametrisations into account, are working in this theoretical framework since the work by Zahn (1992) (e.g. Talon et al. 1997; Meynet & Maeder 2000; Palacios et al. 2003; Talon & Charbonnel 2005; Marques et al. 2013; Charbonnel et al. 2013; Mathis et al. 2013; Cantiello et al. 2014; Fuller et al. 2014). This implicitly assumes that a strong transport of angular momentum is ongoing along the horizontal direction and enforcing a weak latitudinal variation of the angular velocity in stellar radiation zones. In a hydrodynamical theoretical framework, this may be due to hydrodynamical shear instabilities of the horizontal differential rotation (e.g. Zahn 1992; Maeder 2003; Mathis et al. 2004, 2018; Park et al. 2021) or the action of IGWs (e.g. Mathis 2009). In a magneto-hydrodynamical (MHD) theoretical framework, this may be due to MHD instabilities and potential resulting dynamo action (e.g. Spruit 2002; Fuller et al. 2019; Petitdemange et al. 2023). The shellular approximation has also been strengthened by the results obtained by the helioseismic inversions of the rotation profile of the Sun that revealed a quasi-uniform rotation of the solar radiative core until 0.25 R⊙, where R⊙ is the radius of the Sun (e.g. Thompson et al. 2003; García et al. 2007). A similar trend is obtained by an asteroseismic probe of the internal rotation of stars in the whole Hertzsprung-Russell diagram; this reveals only a weak radial differential rotation in stellar radiative zones, which is in agreement with what has been observed in the solar case (e.g. Deheuvels et al. 2012, 2014, 2015, 2020; Kurtz et al. 2014; Saio et al. 2015; Murphy et al. 2016; Aerts et al. 2017, and references therein).
We solve the linearised momentum equation
and continuity equation
where 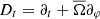 , ρ and p are the density and the pressure, respectively, and g is the gravity. Each thermodynamic quantity X (density, pressure, entropy, temperature) is expended as
, ρ and p are the density and the pressure, respectively, and g is the gravity. Each thermodynamic quantity X (density, pressure, entropy, temperature) is expended as 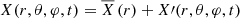 , where
, where 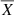 is its hydrostatic value and X′ its perturbation. For low-frequency IGWs, we can adopt the Cowling approximation (Cowling 1941) and neglect the fluctuation of the gravity.
is its hydrostatic value and X′ its perturbation. For low-frequency IGWs, we can adopt the Cowling approximation (Cowling 1941) and neglect the fluctuation of the gravity.
Finally, we introduce the equation for the transport of heat in the adiabatic limit
where 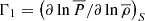 is the adiabatic exponent at a fixed macroscopic entropy S.
is the adiabatic exponent at a fixed macroscopic entropy S.
Each thermodynamic quantity is expended on spherical harmonics and as Fourier series in time:
where ωin is the wave frequency in an inertial reference frame. The wave velocity field is projected on vectorial spherical harmonics as defined in Rieutord (1987):
where
with the following orthogonality relationships: 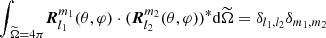 and
and 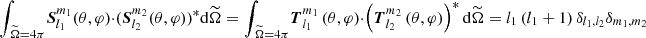 , where
, where 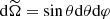 ,
, 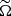 is the solid angle and designates the complex conjugate. We introduced the usual Kronecker symbol δi, j = 1 if i = j, and that vanishes otherwise. Within this framework, prograde waves are such that m < 0, while retrograde waves are such that m > 0.
is the solid angle and designates the complex conjugate. We introduced the usual Kronecker symbol δi, j = 1 if i = j, and that vanishes otherwise. Within this framework, prograde waves are such that m < 0, while retrograde waves are such that m > 0.
We obtain the system of equations for the radial functions derived from the projection of the momentum equation on the vectorial spherical harmonics:
from the projection of the equation-of-mass conservation on spherical harmonics:
and of the equation for the transport of energy in the adiabatic limit:
where 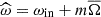 is the Doppler-shifted frequency. We introduced the total squared Brunt-Vaïsälä frequency N2, which is related to the combination of the entropy stratification and of the chemical stratification (Zahn et al. 1997). It can be decomposed as
is the Doppler-shifted frequency. We introduced the total squared Brunt-Vaïsälä frequency N2, which is related to the combination of the entropy stratification and of the chemical stratification (Zahn et al. 1997). It can be decomposed as
where
and
We introduced the pressure height scale 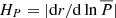 ; the gradients
; the gradients 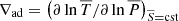 ,
, 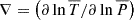 , and
, and 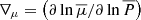 with S the macroscopic entropy, T the temperature, and μ the mean molecular weight; and the thermodynamics coefficients
with S the macroscopic entropy, T the temperature, and μ the mean molecular weight; and the thermodynamics coefficients 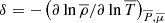 and
and 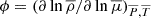 (Maeder & Zahn 1998).
(Maeder & Zahn 1998).
Hereafter, we focus on low-frequency IGWs. This means that we consider progressive IGWs and not standing gravity modes. Progressive IGWs are damped because of their thermal damping (or breaking) before being able to reach the second turning point after their excitation (i.e. the turning point close to the centre of the star for a late-type star with an outer convective envelope and the one close to the surface for an early-type star with a convective core). On the one hand, they are not able to form standing gravity modes. On the other hand, they deposit angular momentum where they are damped or where they break (e.g. Zahn et al. 1997). The analytical expression for the critical frequency (ωc), below which IGWs are progressive, was derived in Alvan et al. (2015) and is given by
where rt; 1 and rt; 2 are the two turning points in the considered radiation zone at which ω = N and K is the heat diffusivity. We thus considered frequencies such that ω < ωc. In addition, we know that the radiative damping of progressive IGWs scales as NNT2/ω4 (e.g. Zahn et al. 1997, and Eq. (21)). As a consequence, the larger the ratio N/ω, the stronger the damping and the transport of angular momentum triggered by IGWs. In addition, when N/ω > > 1, the JWKB asymptotic method (Fröman & Fröman 2005) can be used to solve the radial ODE (Eq. (15)) describing the radial propagation of a progressive IGW of given latitudinal and azimuthal orders l and m. As a consequence, by low-frequency waves we mean progressive IGWs, such that ω < ωc and ω < < N. In the case of main-sequence stars, these frequency hierarchies also allow us to filter out acoustic waves, which are at higher frequencies, within the framework of the anelastic approximation.
Then, the system given by Eqs. (8-9-10) reduces to the Schrödinger-like propagation equation (e.g. Press 1981; Zahn et al. 1997):
where
and
When 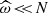 , one can provide an asymptotic solution to Eq. (15) using the JWKB solution (Fröman & Fröman 2005):
, one can provide an asymptotic solution to Eq. (15) using the JWKB solution (Fröman & Fröman 2005):
where AΨ is an amplitude coefficient. The parameter ε ≡ ±1 determines if the phase of the wave is propagating outward (ε = −1; the energy then propagates inward; this corresponds to the excitation of IGWs by an external convective envelope in solar-type stars) or inward (ε = 1; the energy then propagates outward; this corresponds to the excitation of IGWs by a convective core). Using Eq. (16), we obtain the JWKB expression of the radial component of the velocity:
where r0 is the excitation radius of the considered IGW.
2.2. Quasi-adiabatic propagation
As recalled in the introduction, the current way to model the transport of angular momentum and the mixing of chemicals by IGWs in SSE is to take into account their radiative damping. Their viscous damping is generally neglected since the Prandtl number comparing the viscosity (ν) to heat diffusion (K) is small in stellar radiation zones (e.g. of the order of 10−6 in the solar radiative core; Brun & Zahn 2006). In this framework, it is assumed that the heat diffusion acts as a first-order perturbation of the adiabatic propagation of IGWs (e.g. Press 1981; Schatzman 1993b; Zahn et al. 1997). The vertical wave number used in the JWKB regime has a small imaginary part 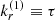 , and the quasi-adiabatic JWKB solution for each thermodynamic quantity or component of the velocity (noted as
, and the quasi-adiabatic JWKB solution for each thermodynamic quantity or component of the velocity (noted as 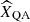 ) is expressed as
) is expressed as
where 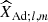 is the corresponding adiabatic JWKB value and
is the corresponding adiabatic JWKB value and
is the damping rate.
3. Non-linear wave breaking
As in planetary atmospheres, IGWs can break non-linearly in stellar interiors. The two main sources of non-linear breaking are IGW-driven shear and convective instabilities (see Press 1981; Lindzen 1981; Sutherland 2001, respectively).
3.1. Convective wave breaking
The first missing piece in stellar modelling is the breaking induced by the local convective overturning of the stable stratification (Barker & Ogilvie 2010). This phenomenon has never been modelled analytically in stellar physics.
To improve the situation, the best strategy is then to turn to the literature of atmospheric physics. Indeed, this community has to model small-scale transport and mixing processes such as turbulence and IGWs in global circulation models (hereafter GCMs), which are used to predict the long-term evolution of the climate. Because of the broad range of space and timescales that have to be considered, the equations for the small-scale processes cannot be directly solved in the GCMs, and they have to be parametrised (Ribstein et al. 2022). We also wish to address this issue in stellar physics; that is, we want to evaluate the impact of the transport of momentum and chemicals in SSE codes, which allow us to compute the long-term structural, chemical, and rotational evolution of stars. In this regard, relevant theoretical formalism has been developed by Lott et al. (2012) and Lott & Guez (2013) to evaluate the modification of atmospheric zonal mean flows by convectively excited breaking IGWs. In their model, IGWs excited by convective turbulence –for instance at the top of clouds– non-linearly break, which triggers a convective instability and overturns the stable stratification. After a transient, the instability saturates, and Lott et al. (2012) and Lott & Guez (2013) proposed a scheme to compute the transported momentum. The great interest of the parametrisation they obtained for the wave-triggered Reynolds stresses is that its prediction has been successfully compared to those observed in situ in the Earth’s atmosphere by stratospheric balloons (Lott et al. 2023).
This methodology can be applied to the case of stellar interiors. However, it has to be adapted to the spherical geometry of the problem because the Lott et al. (2012) and Lott & Guez (2013) formalism was developed to be used in local Cartesian shallow-water models relevant for the thin atmosphere of the Earth.
3.1.1. Convective breaking and saturation scheme
We introduce the macroscopic entropy S definition
where T is the temperature and CP is the heat capacity at constant pressure; we recall that ∇ad = (∂lnT/∂lnP)S = cst. For low-frequency IGWs, we can assume the anelastic approximation where acoustic waves are filtered out. In this framework, the linearised equation for the transport of heat
reduces to
When an IGW propagates in the direction of a critical layer (at which 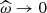 and kr → ∞), the gradient of the temperature fluctuation increases (since it scales as kr in the JWKB regime). At the so-called braking radius rb (derived in the next section), its amplitude reaches the value of the gradient of the background temperature (as represented in Fig. 1):
and kr → ∞), the gradient of the temperature fluctuation increases (since it scales as kr in the JWKB regime). At the so-called braking radius rb (derived in the next section), its amplitude reaches the value of the gradient of the background temperature (as represented in Fig. 1):
 |
Fig. 1. Principle of convective wave breaking: an IGW is excited at r = r0. When propagating towards a critical layer located at r = rc, the radial gradient of its temperature fluctuation grows with kr until it overturns the stable equilibrium entropy stratification at the breaking radius r = rb. This triggers a convective instability. |
The breaking IGW thus overturns the stable stratification leading to a convective instability (Lindzen 1981; Sutherland 2001).
At this point, the radial velocity of the IGW reaches its maximum value, which we call the saturated value following Lott et al. (2012) and Lott & Guez (2013). To derive its amplitude, we used the heat transport equation (Eq. (24)) that leads to
Using 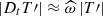 and |∂rT′| ≈ kr|T′|, we obtain
and |∂rT′| ≈ kr|T′|, we obtain
where we used the IGW dispersion relation 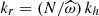 with
with 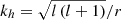 . We thus recovered one of the usual criteria for defining the breaking of waves that states it occurs when the wave velocity reaches the wave phase velocity (e.g. Banner & Peregrine 1993; Stansell & Macfarlane 2002). Using the asymptotic relation uh = (kr/kh)ur, that leads to
. We thus recovered one of the usual criteria for defining the breaking of waves that states it occurs when the wave velocity reaches the wave phase velocity (e.g. Banner & Peregrine 1993; Stansell & Macfarlane 2002). Using the asymptotic relation uh = (kr/kh)ur, that leads to
for the horizontal component.
It is interesting to note that these predictions are also in agreement with the criteria for the threshold for IGW non-linear breaking introduced by Press (1981), which stated that 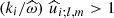 with i ≡ {r,h}.
with i ≡ {r,h}.
The condition for wave breaking is that 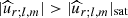 . Using Eq. (19), this means that the waves have been excited with an initial amplitude, such that
. Using Eq. (19), this means that the waves have been excited with an initial amplitude, such that
Therefore, for a given value of 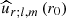 , this equation implicitly determines the value of rb.
, this equation implicitly determines the value of rb.
3.1.2. Saturated vertical flux of energy and angular momentum
Using Eqs. (8) and (10), assuming that 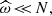 and employing the anelastic approximation, we express the pressure fluctuation as a function of the vertical velocity:
and employing the anelastic approximation, we express the pressure fluctuation as a function of the vertical velocity:
This allows us to compute the saturated transported monochromatic flux of energy for convective wave breaking (CWB):
where 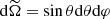 is the elementary solid angle, Re is the real part, and * is the complex conjugate; while
is the elementary solid angle, Re is the real part, and * is the complex conjugate; while 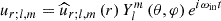 ,
, 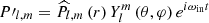 with
with 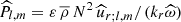 where
where 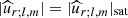 (Eqs. (30) and (27), respectively). In the case of a solar-type star with an external convective envelope, we find that the energy is injected inward with ε = −1. In the case of an early-type star with a convective core, it is injected outward with ε = 1. This allows us to derive the triggered flux of angular momentum:
(Eqs. (30) and (27), respectively). In the case of a solar-type star with an external convective envelope, we find that the energy is injected inward with ε = −1. In the case of an early-type star with a convective core, it is injected outward with ε = 1. This allows us to derive the triggered flux of angular momentum:
When taking this expression and applying it in a local Cartesian plane, we recover the expression derived by Lott et al. (2012) and Lott & Guez (2013). We recall the interest of their parametrisation, which has been validated by in situ measurements of wave-induced Reynolds stresses in the Earth’s atmosphere by stratospheric baloons (Lott et al. 2023). In the case of a solar-type star for which ε = −1, we find that a retrograde wave (m > 0) is extracting angular momentum from the radiative core, while a prograde one (m < 0) is depositing angular momentum there. The situation is the opposite in the case of an early-type star for which ε = 1.
It is important to examine the physical behaviour of the transported flux of angular momentum. First, as expected, it vanishes when the IGWs propagate very close to a critical layer where 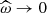 . This means that the angular momentum is deposited very efficiently close to this layer. Next, we see that the higher the latitudinal degree l, the stronger the deposit. Such a behaviour is similar to the case of the deposit through the radiative damping, which is also more efficient for high-degree IGWs.
. This means that the angular momentum is deposited very efficiently close to this layer. Next, we see that the higher the latitudinal degree l, the stronger the deposit. Such a behaviour is similar to the case of the deposit through the radiative damping, which is also more efficient for high-degree IGWs.
The transported flux diminishes with the strength of the stratification quantified by N, which means a more efficient deposit. This can be understood as, at a fixed 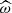 , the strongest N, the strongest the vertical wave number kr, and as a consequence the vertical gradient of the wave triggered temperature fluctuation that overcomes the stable equilibrium entropy gradient. In the specific case where N → 0, as in the centre of solar-type stars, the asymptotic relation
, the strongest N, the strongest the vertical wave number kr, and as a consequence the vertical gradient of the wave triggered temperature fluctuation that overcomes the stable equilibrium entropy gradient. In the specific case where N → 0, as in the centre of solar-type stars, the asymptotic relation 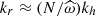 cannot be used anymore since we lose the frequency hierarchy
cannot be used anymore since we lose the frequency hierarchy 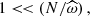 and specific prescriptions must be derived. In this case, the radial buoyancy force vanishes and any motion potentially leads to a convective instability (e.g. Barker & Ogilvie 2010).
and specific prescriptions must be derived. In this case, the radial buoyancy force vanishes and any motion potentially leads to a convective instability (e.g. Barker & Ogilvie 2010).
Finally, a vanishing density (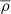 ) also leads to a flux that vanishes and an efficient deposit of angular momentum. This corresponds, for instance, to the case of layers close to the surface of early-type stars where such an efficient momentum deposit could drive matter ejection, as in active Be stars (Rogers et al. 2013; Rogers 2015; Neiner et al. 2020).
) also leads to a flux that vanishes and an efficient deposit of angular momentum. This corresponds, for instance, to the case of layers close to the surface of early-type stars where such an efficient momentum deposit could drive matter ejection, as in active Be stars (Rogers et al. 2013; Rogers 2015; Neiner et al. 2020).
3.2. Breaking due to IGW shear instabilities
The great interest of the method proposed by Lott et al. (2012) and Lott & Guez (2013) is that it allows us to derive the transported fluxes of energy and angular momentum by IGW convective breaking by calculating the saturated value of their velocity from the convective instability criteria.
Since IGWs can also break because of the vertical shear instability of their own velocity (Garcia Lopez & Spruit 1991), we can apply the methodology of Lott et al. (2012) and Lott et al. (2023) to this instability. We first consider the simplest case where the action of the heat diffusion, which weakens the action of the restoring buoyancy force, is ignored. Following Alvan et al. (2013), the Richardson criteria for the vertical shear instability of an IGW is given by
and Ri; c is the critical Richardson number. The geometrical factor βl, m comes from the derivation of the Taylor Goldstein Synge equation for IGWs propagating in vertically sheared shellular rotation projected on spherical harmonics in spherical geometry (Alvan et al. 2013). Since we considered low-frequency IGWs for which asymptotic JWKB solutions apply, we have 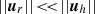 , where
, where 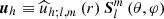 is their horizontal component; we introduced the horizontal average over the sphere
is their horizontal component; we introduced the horizontal average over the sphere 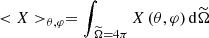 , where we recall that
, where we recall that 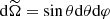 is the elementary solid angle element. The introduction of this horizontal average is motivated by our goal to evaluate horizontal averages of the transported fluxes of energy and angular momentum. It is thus more appropriate than a purely local criteria that may be only applied at a given co-latitude. Using the JWKB identity d/dr ∝ i ε kr, Eq. (33) can be written as
is the elementary solid angle element. The introduction of this horizontal average is motivated by our goal to evaluate horizontal averages of the transported fluxes of energy and angular momentum. It is thus more appropriate than a purely local criteria that may be only applied at a given co-latitude. Using the JWKB identity d/dr ∝ i ε kr, Eq. (33) can be written as
Using the JWKB polarisation relation uh ≈ (kr/kh) ur with kh = [l(l+1)]1/2/r, this leads to the corresponding criterion for the vertical velocity:
As in the case of the convective breaking, we recover a criteria whereby the component of the velocity field have to overcome the corresponding component of the wave phase velocity. These equations allow us to derive the explicit expression for the saturated value for the squared amplitude of the vertical component of IGWs:
This allows us to obtain the saturated amplitudes of the flux of energy,
and angular momentum,
along the radial direction, respectively, in the case of shear-driven wave breaking (SWB).
Given the similar form of the saturated velocity when compared to the convective breaking, we obtain the same dependences of the flux of angular momentum as a function of 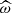 , l, N, and
, l, N, and 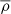 . We note a supplementary dependence on m2 due to the geometrical factor βl, m. The larger m is, the stronger the deposit of angular momentum. We note, however, that this dependence on m2 does not introduce a supplementary bias between prograde and retrograde waves. Finally, the deposit of angular momentum is more efficient for high values of the critical Richardson number (Ri; c). This can be understood by looking at Eq. (33): a higher Ri; c diminishes the instability threshold N2/(Ri; cβl, m).
. We note a supplementary dependence on m2 due to the geometrical factor βl, m. The larger m is, the stronger the deposit of angular momentum. We note, however, that this dependence on m2 does not introduce a supplementary bias between prograde and retrograde waves. Finally, the deposit of angular momentum is more efficient for high values of the critical Richardson number (Ri; c). This can be understood by looking at Eq. (33): a higher Ri; c diminishes the instability threshold N2/(Ri; cβl, m).
However, the action of heat diffusion is of great importance in stellar interiors, because it favours the development of vertical shear instabilities (Townsend 1958; Zahn 1992; Lignières 1999; Prat & Lignières 2013, 2014). The vertical shear instability criterion becomes
where we identify the Peclet number 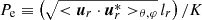 , which evaluates the ratio between heat vertical advection and diffusion. At the saturation level for IGWs for which we reach the instability threshold, we can identify the radial characteristic length scale lr to 1/kr. This allows us to derive the scalings for the saturated values of the vertical components of IGWs’ velocities:
, which evaluates the ratio between heat vertical advection and diffusion. At the saturation level for IGWs for which we reach the instability threshold, we can identify the radial characteristic length scale lr to 1/kr. This allows us to derive the scalings for the saturated values of the vertical components of IGWs’ velocities:
energy flux
and angular momentum
The key modification in this case is the dependence of the saturated velocity and of the transported fluxes on the heat diffusivity (K). The stronger the heat diffusion, the more efficient the deposit of angular momentum. This can be understood since the heat diffusion diminishes the stability of a vertically sheared flow that favours the IGW shear-instability-driven breaking. The modified form of the stability equation is the reason for the modification of the dependence of the flux on 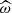 , l, m, and N. If the involved powers are higher, the trends are, however, the same as in the case where the action of heat diffusion was neglected.
, l, m, and N. If the involved powers are higher, the trends are, however, the same as in the case where the action of heat diffusion was neglected.
3.3. Modelling angular-momentum transport
The computed transported flux of angular momentum allows us to evaluate its evolution (e.g. Zahn et al. 1997; Mathis 2009):
From the previous section, we know that the flux cannot exceed its value in the saturated regime when IGW non-linear breaking occurs. We can thus model the transported flux of angular momentum as
where the first flux in the brackets corresponds to its standard quasi-adiabatic modelling (e.g. Schatzman 1993b; Zahn et al. 1997). This expression is the generalisation of the expression derived in Lott et al. (2012), Lott & Guez (2013), and Ribstein et al. (2022) for the studied case of deep spherical stellar regions taking into account both the convective- and vertical-shear-driven breakings. Its analytical form makes it ready to be implemented in 1D SSE numerical codes.
4. Taking into account the Coriolis and Lorentz forces
Early-type stars and young late-type stars are rapid rotators (e.g. Gallet & Bouvier 2013; Aerts & Tkachenko 2024). In addition, stellar-radiation zones can be the place of magnetic fields (stable or unstable) inherited from previous convective phases where dynamo action has generated magnetic energy (e.g. Braithwaite & Spruit 2004; Duez & Mathis 2010; Arlt 2014; Emeriau-Viard & Brun 2017; Bugnet et al. 2021). As a consequence, low-frequency IGWs that transport angular momentum can be simultaneously modified by the Coriolis acceleration and the Lorentz force and become magneto-gravito-inertial waves (MGIWs; Kumar et al. 1999; MacGregor & Rogers 2011; Mathis & de Brye 2011, 2012; Rui et al. 2024).
In the case where the Archimedean force is larger than the radial components of the Coriolis acceleration and of the Lorentz force, the dynamics of MGIWs can be modelled semi-analytically using the traditional approximation for rotation and magnetism (TARM; e.g. Mathis & de Brye 2011; Rui et al. 2024).
We now analyse the most advanced semi-analytical model for the transport of angular momentum by MGIWs in stellar radiation zones developed by Mathis & de Brye (2012). In this model, we consider, as a first step, a rotation profile:
which is the sum of a global solid rotation Ωs and of a weak radial differential rotation δΩ. Next, we choose a purely axisymmetric azimuthal magnetic field defined as in Malkus (1967):
corresponding to a constant Alfvén frequency ωA. If this magnetic topology is a very specific simplified one, it allows us to explore the dynamics of the waves within the radiation zone as a function of the frequency hierarchies between N, Ωs, and ωA when {ωA,2Ωs} < < N when taking into account both the Coriolis acceleration and the Lorentz force in a non-perturbative way. The interesting point is that more complex models considering more general axisymmetric differential rotation and magnetic field (e.g. Dhouib et al. 2022; Rui et al. 2024) show similar behaviours to this simplified model, which thus constitutes an interesting first laboratory.
Within this simplified model, Mathis & de Brye (2011) and Mathis & de Brye (2012) identified a key modified frequency,
and the magnetic spin control parameter
which allowed us to model the propagation of MGIWs in a theoretical formalism similar to the non-rotating non-magnetic case. The only difference is that the associated Legendre polynomial of the spherical harmonics is replaced by a so-called Hough function Θk, m (cos θ;νM) with an associated horizontal eigenvalue Λk, m(νM) that reduces to l(l+1) when Ωs and ωA vanish. We refer the reader to Hough (1898), Longuet-Higgins (1968), Lee & Saio (1997), and Townsend (2003, 2020) for their detailed properties. In this framework, the MGIW-JWKB dispersion relation becomes
The place where ωM vanishes corresponds to a magnetic critical layer where MGIWs become trapped by the magnetic field and cannot propagate anymore (e.g. Schatzman 1993a; MacGregor & Rogers 2011; Mathis & de Brye 2011). As a consequence, the transport of angular momentum by MGIWs vanishes.
In the following, we focus on the impact of the Coriolis and Lorentz forces on the convective breaking of MGIWs. Indeed, to our knowledge, there is no available general criterion for the instability of a radial shear in the presence of both rotation and magnetic field (e.g. Salhi & Cambon 2010; Lecoanet et al. 2010). Inserting the dispersion relation for MGIWs into the heat transport equation, where we neglect the effects of the Ohmic heating, the amplitude of the saturated velocity becomes
Using the polarisation relation (Eq. (30)) within the TARM, we derive the monochromatic transported flux of angular momentum:
where 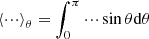 . Since the horizontal eigenvalue Λk, m is larger than l(l+1) while
. Since the horizontal eigenvalue Λk, m is larger than l(l+1) while 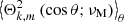 is smaller than the latitudinal average of the corresponding associated Legendre polynomial when the rotation and the magnetic field vanish, FJ; breaking diminishes in the presence of rotation and magnetism. This can be understood since we are considering the convective overturning of the stable stratification here, while rotation and magnetic field are known to potentially decrease the efficiency of convection for its mode transporting the most heat (e.g. Stevenson 1979; Augustson & Mathis 2019). When ωM vanishes, meaning that the IGW meets a critical magnetic layer, we find that the flux of angular momentum vanishes.
is smaller than the latitudinal average of the corresponding associated Legendre polynomial when the rotation and the magnetic field vanish, FJ; breaking diminishes in the presence of rotation and magnetism. This can be understood since we are considering the convective overturning of the stable stratification here, while rotation and magnetic field are known to potentially decrease the efficiency of convection for its mode transporting the most heat (e.g. Stevenson 1979; Augustson & Mathis 2019). When ωM vanishes, meaning that the IGW meets a critical magnetic layer, we find that the flux of angular momentum vanishes.
Following the same methodology as in the non-rotating and non-magnetic case, we obtain the parametrisation of the angular momentum transport:
where we recall the value of the thermal damping in the rotating magnetic case as derived in Mathis & de Brye (2012):
5. Conclusion and perspectives
In this work, we studied the non-linear breaking of IGWs and the transport of angular momentum it triggers. We took advantage of theoretical progress for its modelling in the Earth’s atmosphere, which were achieved ten years ago in local Cartesian models (Lott et al. 2012; Lott & Guez 2013) and implemented in global circulation models (e.g. Ribstein et al. 2022) and whose predictions have been successfully compared to in situ measurements of Reynolds stresses triggered by IGWs by stratospheric balloons (Lott et al. 2023).
First, we considered the non-rotating and non-magnetic case. We identified the conditions in which the temperature fluctuation of an IGW is able to overturn the surrounding stable stratification or its velocity becomes unstable because of its vertical shear. We derived the IGW amplitude for which convective or vertical shear instabilities occur and the corresponding breaking radius, even though we should remember that once turbulence is developing, such a local criterion is an approximation of the reality. From the instability criteria, we derived the values of the saturated wave velocity necessary to trigger them. This allowed us to derive the value of the transported flux of energy and angular momentum. We show that the deposit of angular momentum by breaking waves increases with their latitudinal degree, the ratio of the Brunt-Vaïsälä frequency and the wave frequency, and when the density decreases or the Doppler-shifted frequency vanishes.
As in geophysics, we thus obtain a theoretical, semi-analytical prescription for the wave-mean differential rotation interaction, which takes into account the smooth thermal damping of IGWs and their non-linear breaking simultaneously. In this vision, IGWs break before reaching critical layers and this is the reason why the prescription derived in Alvan et al. (2013) is not taken into account. Such a prescription thus allows us to bring the modelling of the transport of angular momentum by waves over long timescales in stellar structure and evolution numerical codes to the same level of realism as in global circulation models for the Earth’s atmosphere and the prediction of climate evolution.
Second, we considered the case of rotating magnetised stellar-radiation zones in which the non-perturbative actions of the Coriolis acceleration and of the Lorentz force on IGWs must be taken into account. With simplified assumptions of a weak, radial differential rotation and an azimuthal magnetic topology that corresponds to a constant Alfvén frequency, we generalised the results we obtained in the case where the modification of IGWs by the Coriolis acceleration and the Lorentz force are ignored. We considered the regime of the traditional approximation for rotation and magnetism (TARM) where the radial component of the Coriolis acceleration and of the Lorentz force are dominated by the buoyancy Archimedean force. In this case, a semi-analytical approach is still possible, and we see that the transported flux of angular momentum by IGWs’ convective breaking will diminish when compared to the non-rotating and non-magnetic case. This can be understood as a consequence of the fact that rotation and magnetism can inhibit the efficiency of convection for its mode transporting more heat.
The perspectives of this work can be structured along three axes. The first one will be to implement the obtained prescription in stellar structure and evolution numerical codes, where physical prescriptions for the transport of angular momentum are implemented, and to explore different stellar masses and evolutionary stages (e.g. Charbonnel & Talon 2005; Talon & Charbonnel 2005). Next, more general differential rotation (Mathis 2009; Dhouib et al. 2021) or magnetic topologies (Dhouib et al. 2022; Rui et al. 2024) can be considered. For instance, asteroseismology does not yet provide any constraint on the latitudinal variation of differential rotation in stellar radiation zones, while their interfaces with adjacent convective regions (i.e. stellar tachoclines) can be the seat of strong horizontal shears because of the transition between a differential rotation that varies both in radius and latitude in convection zones and a weaker differential rotation in stellar radiative regions (e.g. Spiegel & Zahn 1992; Brun et al. 2005, 2011, 2017, 2022). Moreover, the 2D stellar structure and evolution code ESTER predicts a possible 2D angular velocity profile in the external radiative envelope of rapidly rotating early-type stars (e.g. Espinosa Lara & Rieutord 2013; Rieutord et al. 2016; Mombarg et al. 2023). In these configurations, within the framework of the TARM, generalised Hough functions describing the latitudinal behaviour of IGWs replace the standard Hough functions, but the main trends described here with our simplifying assumptions should be conserved. Finally, because of the rapid rotation of young late-type stars and the rapid rotation and weaker stratification in early-type stars, it will be necessary to go beyond the TARM and take into account the full Coriolis acceleration and Lorentz force (e.g. Dintrans & Rieutord 2000; Gerkema & Shrira 2005; Mathis et al. 2014; Mirouh et al. 2016).
Acknowledgments
S.M. thanks the referee for her/his careful reading of the manuscript and for her/his constructive and precise comments, which have allowed him to improve the initial version of the article. S.M. acknowledges support from the European Research Council (ERC) under the Horizon Europe programme (Synergy Grant agreement 101071505: 4D-STAR), from the CNES SOHO-GOLF and PLATO grants at CEA-DAp, and from PNPS (CNRS/INSU). While partially funded by the European Union, views and opinions expressed are however those of the author only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
References
- Achatz, U., Alexander, M. J., Becker, E., et al. 2024, J. Atmos. Sci., 81, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., & Tkachenko, A. 2024, A&A, 692, R1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C., Van Reeth, T., & Tkachenko, A. 2017, ApJ, 847, L7 [Google Scholar]
- Alvan, L., Mathis, S., & Decressin, T. 2013, A&A, 553, A86 [CrossRef] [EDP Sciences] [Google Scholar]
- Alvan, L., Strugarek, A., Brun, A. S., Mathis, S., & Garcia, R. A. 2015, A&A, 581, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlt, R. 2014, in Putting A Stars into Context: Evolution, Environment, and Related Stars, eds. G. Mathys, E. R. Griffin, O. Kochukhov, et al., 93 [Google Scholar]
- Augustson, K. C., & Mathis, S. 2019, ApJ, 874, 83 [Google Scholar]
- Banner, M. L., & Peregrine, D. H. 1993, Ann. Rev. Fluid Mech., 25, 373 [Google Scholar]
- Barker, A. J. 2011, MNRAS, 414, 1365 [Google Scholar]
- Barker, A. J., & Ogilvie, G. I. 2010, MNRAS, 404, 1849 [NASA ADS] [Google Scholar]
- Booker, J. R., & Bretherton, F. P. 1967, J. Fluid Mech., 27, 513 [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2004, Nature, 431, 819 [Google Scholar]
- Brun, A. S., & Zahn, J. P. 2006, A&A, 457, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brun, A. S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2011, ApJ, 742, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Strugarek, A., Varela, J., et al. 2017, ApJ, 836, 192 [Google Scholar]
- Brun, A. S., Strugarek, A., Noraz, Q., et al. 2022, ApJ, 926, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bugnet, L., Prat, V., Mathis, S., et al. 2021, A&A, 650, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [Google Scholar]
- Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [Google Scholar]
- Charbonnel, C., Decressin, T., Amard, L., Palacios, A., & Talon, S. 2013, A&A, 554, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Eggenberger, P., et al. 2020, A&A, 641, A117 [EDP Sciences] [Google Scholar]
- Dhouib, H., Prat, V., Van Reeth, T., & Mathis, S. 2021, A&A, 656, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dhouib, H., Mathis, S., Bugnet, L., Van Reeth, T., & Aerts, C. 2022, A&A, 661, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dintrans, B., & Rieutord, M. 2000, A&A, 354, 86 [NASA ADS] [Google Scholar]
- Duez, V., & Mathis, S. 2010, A&A, 517, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emeriau-Viard, C., & Brun, A. S. 2017, ApJ, 846, 8 [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröman, N., & Fröman, P. O. 2005, Physical Problems Solved by the Phase-Integral Method (Cambridge University Press) [Google Scholar]
- Fuller, J., Lecoanet, D., Cantiello, M., & Brown, B. 2014, ApJ, 796, 17 [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia Lopez, R. J., & Spruit, H. C. 1991, ApJ, 377, 268 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005, J. Fluid Mech., 529, 195 [Google Scholar]
- Holton, J. R., & Zhu, X. 1984, J. Atmos. Sci., 41, 2653 [NASA ADS] [CrossRef] [Google Scholar]
- Hough, S. S. 1898, Phil. Trans. R. Soc. London Ser. A, 191, 139 [Google Scholar]
- Kumar, P., Talon, S., & Zahn, J.-P. 1999, ApJ, 520, 859 [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [Google Scholar]
- Lazovik, Y. A. 2021, MNRAS, 508, 3408 [NASA ADS] [CrossRef] [Google Scholar]
- Lecoanet, D., Zweibel, E. G., Townsend, R. H. D., & Huang, Y.-M. 2010, ApJ, 712, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U., & Saio, H. 1997, ApJ, 491, 839 [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [Google Scholar]
- Li, G., Deheuvels, S., & Ballot, J. 2024, A&A, 688, A184 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lignières, F. 1999, A&A, 348, 933 [NASA ADS] [Google Scholar]
- Lindzen, R. S. 1981, J. Geophys. Res., 86, 9707 [NASA ADS] [CrossRef] [Google Scholar]
- Longuet-Higgins, M. S. 1968, Phil. Trans. R. Soc. London Ser. A, 262, 511 [CrossRef] [Google Scholar]
- Lott, F., & Guez, L. 2013, J. Geophys. Res. (Atmos.), 118, 8897 [NASA ADS] [CrossRef] [Google Scholar]
- Lott, F., Guez, L., & Maury, P. 2012, Geophys. Res. Lett., 39, L06807 [Google Scholar]
- Lott, F., Rani, R., Podglajen, A., et al. 2023, J. Geophys. Res., Atmos.), 128, e2022JD037585 [CrossRef] [Google Scholar]
- MacGregor, K. B., & Rogers, T. M. 2011, Sol. Phys., 270, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Malkus, W. V. R. 1967, Journal of Fluid Mechanics, 28, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & de Brye, N. 2011, A&A, 526, A65 [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & de Brye, N. 2012, A&A, 540, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J. P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Palacios, A., & Zahn, J. P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Decressin, T., Eggenberger, P., & Charbonnel, C. 2013, A&A, 558, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Neiner, C., & Tran Minh, N. 2014, A&A, 565, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Prat, V., Amard, L., et al. 2018, A&A, 620, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Mirouh, G. M., Baruteau, C., Rieutord, M., & Ballot, J. 2016, J. Fluid Mech., 800, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Mombarg, J. S. G., Rieutord, M., & Espinosa Lara, F. 2023, A&A, 677, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalbán, J., & Schatzman, E. 2000, A&A, 354, 943 [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Dréau, G., Pinçon, C., et al. 2024, A&A, 681, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [Google Scholar]
- Neiner, C., Lee, U., Mathis, S., et al. 2020, A&A, 644, A9 [EDP Sciences] [Google Scholar]
- Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Talon, S., Charbonnel, C., & Forestini, M. 2003, A&A, 399, 603 [CrossRef] [EDP Sciences] [Google Scholar]
- Park, J., Prat, V., Mathis, S., & Bugnet, L. 2021, A&A, 646, A64 [EDP Sciences] [Google Scholar]
- Petitdemange, L., Marcotte, F., & Gissinger, C. 2023, Science, 379, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Pinçon, C., Belkacem, K., Goupil, M. J., & Marques, J. P. 2017, A&A, 605, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, V., & Lignières, F. 2013, A&A, 551, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, V., & Lignières, F. 2014, A&A, 566, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H. 1981, ApJ, 245, 286 [Google Scholar]
- Ribstein, B., Millet, C., Lott, F., & de la Cámara, A. 2022, J. Adv. Model. Earth Syst., 14, e2021MS002563 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 1987, Geophys. Astrophys. Fluid Dyn., 39, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., Espinosa Lara, F., & Putigny, B. 2016, J. Comput. Phys., 318, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M. 2015, ApJ, 815, L30 [Google Scholar]
- Rogers, T. M., & McElwaine, J. N. 2017, ApJ, 848, L1 [CrossRef] [Google Scholar]
- Rogers, T. M., Lin, D. N. C., McElwaine, J. N., & Lau, H. H. B. 2013, ApJ, 772, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Rui, N. Z., Ong, J. M. J., & Mathis, S. 2024, MNRAS, 527, 6346 [Google Scholar]
- Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
- Salhi, A., & Cambon, C. 2010, Phys. Rev. E, 81, 026302 [CrossRef] [Google Scholar]
- Schatzman, E. 1993a, A&A, 271, L29 [NASA ADS] [Google Scholar]
- Schatzman, E. 1993b, A&A, 279, 431 [NASA ADS] [Google Scholar]
- Spiegel, E. A., & Zahn, J. P. 1992, A&A, 265, 106 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
- Stansell, P., & Macfarlane, C. 2002, J. Phys. Oceanogr., 32, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J. 1979, Geophys. Astrophys. Fluid Dyn., 12, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, B. R. 2001, J. Fluid Mech., 429, 343 [CrossRef] [Google Scholar]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., Zahn, J. P., Maeder, A., & Meynet, G. 1997, A&A, 322, 209 [NASA ADS] [Google Scholar]
- Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J. 2003, ARA&A, 41, 599 [Google Scholar]
- Townsend, A. A. 1958, J. Fluid Mech., 4, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D. 2003, MNRAS, 340, 1020 [Google Scholar]
- Townsend, R. H. D. 2020, MNRAS, 497, 2670 [NASA ADS] [CrossRef] [Google Scholar]
- Vadas, S. L., & Fritts, D. C. 2005, J. Geophys. Res. (Atmos.), 110, D15103 [NASA ADS] [CrossRef] [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varghese, A., Ratnasingam, R. P., Vanon, R., Edelmann, P. V. F., & Rogers, T. M. 2023, ApJ, 942, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J. P., Talon, S., & Matias, J. 1997, A&A, 322, 320 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1. Principle of convective wave breaking: an IGW is excited at r = r0. When propagating towards a critical layer located at r = rc, the radial gradient of its temperature fluctuation grows with kr until it overturns the stable equilibrium entropy stratification at the breaking radius r = rb. This triggers a convective instability. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



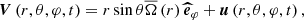
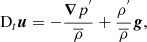
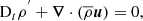
![$$ \begin{aligned} \frac{1}{\Gamma _1}\left[\frac{D_{t} P^{^{\prime }}}{\overline{P}}+u_r\frac{\mathrm{d}\ln {\overline{P}}}{\mathrm{d}r}\right]-\left[\frac{D_{t}\rho ^{^{\prime }}}{{\overline{\rho }}}+u_r\frac{\mathrm{d}\ln {\overline{\rho }}}{\mathrm{d}r}\right]=0, \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq9.gif)
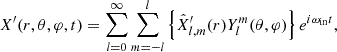
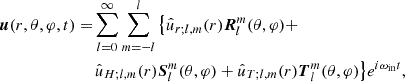
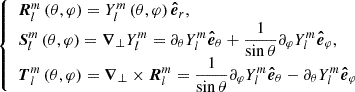
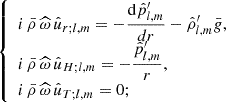
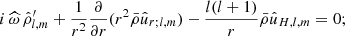
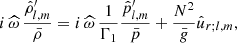
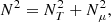
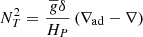
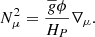
![$$ \begin{aligned} {\omega }_{c}=\left[l\left(l+1\right)\right]^{3/8}\left(\int _{r_{t;1}}^{r_{t;2}}K\frac{N\,N_{T}^{2}}{r^3}\mathrm{d}r\right)^{1/4}, \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq31.gif)
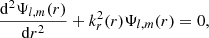
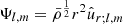
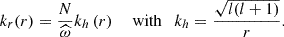
![$$ \begin{aligned} \Psi =\frac{A_{\Psi }}{\sqrt{k_r}}\exp \left[i\,{\varepsilon }\int _{r_0}^{r} k_r \mathrm{d}r^{\prime }\right], \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq36.gif)
![$$ \begin{aligned} {\widehat{u}}_{r;l,m}\left(r\right)&={\widehat{u}}_{r;l,m}\left(r_0\right)\left(\frac{{\overline{\rho }}\left(r_0\right)}{{\overline{\rho }}}\right)^{1/2}\left(\frac{r_0}{r}\right)^{3/2}\left(\frac{N\left(r_0\right)}{N}\right)^{1/2}\nonumber \\&\times \exp \left[i\,{\varepsilon }\int _{r_0}^{r} k_r \mathrm{d}r^{\prime }\right], \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq37.gif)
![$$ \begin{aligned} {\widehat{X}}_{\mathrm{QA};l,m}\left(r\right)={\widehat{X}}_{\mathrm{Ad};l,m}\left(r\right)\exp \left[\displaystyle {-\frac{\tau _{l,m}\left(r\right)}{2}}\right], \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq40.gif)
![$$ \begin{aligned} \tau _{l,m}\left(r\right)=\left[l\left(l+1\right)\right]^{3/2}\int _{r_{0}}^{r} K\frac{N\,N_{T}^2}{{\widehat{\omega }}^4}\frac{\mathrm{d}r^{\prime }}{r^{\prime 3}} \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq42.gif)
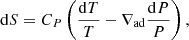
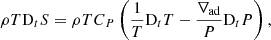
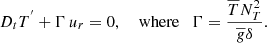
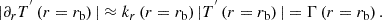
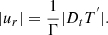
![$$ \begin{aligned} \vert {\widehat{u}}_{r;l,m} \vert _{\rm sat}=\frac{{\widehat{\omega }}}{k_r}=\frac{{\widehat{\omega }}^2}{N k_h}=\frac{1}{\left[l\left(l+1\right)\right]^{1/2}}\left(\frac{{\widehat{\omega }}}{N}\right)\left(r{\widehat{\omega }}\right), \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq50.gif)
![$$ \begin{aligned} \vert {\widehat{u}}_{h;l,m} \vert _{\rm sat}=\frac{{\widehat{\omega }}}{k_h}=\frac{1}{\left[l\left(l+1\right)\right]^{1/2}}\left(r{\widehat{\omega }}\right) \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq53.gif)
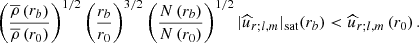
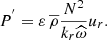
![$$ \begin{aligned}&{F_{\mathrm{E};l,m}^\mathrm{CWB}\left(r\right)=\frac{1}{4\pi }\int _{{\widetilde{\Omega }}=4\pi }\mathrm{Re}\left[P^{^{\prime }}_{l,m}\left(r,\theta ,\varphi ,t\right)\right]\mathrm{Re}\left[u^{*}_{r;l,m}\left(r,\theta ,\varphi ,t\right)\right]\mathrm{d}{\widetilde{\Omega }}}\nonumber \\&=\!\frac{1}{4\pi }\,\frac{1}{2}\,{\varepsilon }\,{\overline{\rho }}\,\frac{N^2}{k_r{\widehat{\omega }}}\left(\frac{{\widehat{\omega }}^2}{N k_h}\right)^2\!=\!\frac{1}{4\pi }\frac{1}{2}\frac{\varepsilon \,\overline{\rho }}{\left[l\left(l+1\right)\right]^{3/2}}\left(\frac{\widehat{\omega }}{N}\right)\left(r{\widetilde{\omega }}\right)^3, \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq60.gif)
![$$ \begin{aligned} F_{\mathrm{J};l,m}^\mathrm{CWB}\left(r\right)&=-\frac{m}{\widehat{\omega }}F_{\mathrm{E};l,m}^\mathrm{CWB}\left(r\right)\nonumber \\&=-\frac{1}{4\pi }\frac{1}{2}\frac{m\,{\varepsilon }\,{\overline{\rho }}}{\left[l\left(l+1\right)\right]^{3/2}}\left(\frac{\widehat{\omega }}{N}\right)\frac{\left(r{\widehat{\omega }}\right)^3}{\widehat{\omega }}. \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq66.gif)
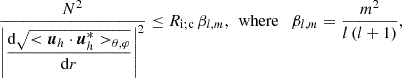
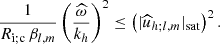
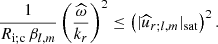
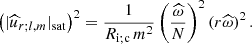
![$$ \begin{aligned} F_{\mathrm{E};l,m}^\mathrm{SWB}=\frac{1}{4\pi }\frac{1}{2}\frac{{\varepsilon }\,\overline{\rho }}{R_{\rm i;c}\,m^2\,\left[l\left(l+1\right)\right]^{1/2}}\left(\frac{\widehat{\omega }}{N}\right)\left(r{\widehat{\omega }}\right)^3 ,\end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq80.gif)
![$$ \begin{aligned} F_{\mathrm{J};l,m}^\mathrm{SWB}=-\frac{1}{4\pi }\frac{1}{2}\frac{m\,{\varepsilon }\,{\overline{\rho }}}{R_{\rm i;c}\,m^2\,\left[l\left(l+1\right)\right]^{1/2}}\left(\frac{\widehat{\omega }}{N}\right)\frac{\left(r{\widehat{\omega }}\right)^3}{\widehat{\omega }}, \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq81.gif)
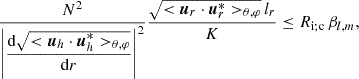
![$$ \begin{aligned} \vert {\widehat{u}}_{r;l,m}\vert _{\rm sat}=\frac{1}{R_{\rm i;c}\,\beta _{l,m}\,\left[l\left(l+1\right)\right]^{3/2}}\left(\frac{r^2\,N}{K}\right)\left(\frac{{\widehat{\omega }}}{N}\right)^4\left(r{\widehat{\omega }}\right), \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq86.gif)
![$$ \begin{aligned} F_{\mathrm{E};l,m}^\mathrm{SWB}=\frac{1}{4\pi }\frac{1}{2}\frac{\varepsilon \,{\overline{\rho }}}{R_{\rm i;c}^2\,\beta _{l,m}^{2}\,\left[l\left(l+1\right)\right]^{7/2}}\left(\frac{r^2\,N}{K}\right)^2\left(\frac{\widehat{\omega }}{N}\right)^{7}\left(r{\widehat{\omega }}\right)^3 ,\end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq87.gif)
![$$ \begin{aligned} F_{\mathrm{J};l,m}^\mathrm{SWB}=-\frac{1}{4\pi }\frac{1}{2}\frac{m\,{\varepsilon }\,{\overline{\rho }}}{R_{\rm i;c}^2\,\beta _{l,m}^{2}\,\left[l\left(l+1\right)\right]^{7/2}}\left(\frac{r^2\,N}{K}\right)^2\left(\frac{\widehat{\omega }}{N}\right)^{7}\frac{\left(r{\widehat{\omega }}\right)^3}{\widehat{\omega }}. \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq88.gif)
![$$ \begin{aligned} \left[{\overline{\rho }}\frac{\mathrm{d}\left(r^2{\overline{\Omega }}\right)}{\mathrm{d}t}\right]_{\rm IGWs}=-\frac{3}{2}\frac{1}{r^2}\partial _{r}\left[r^2\,F_{\rm J}\left(r\right)\right]. \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq90.gif)
![$$ \begin{aligned} F\left(r\right)&= \sum _{\omega _{\rm in},l,m}\mathrm{min}\left\{ -\frac{m}{\widehat{\omega }}F_{\mathrm{E};l,m}\left(r_0\right)\exp \left[-\tau _{l,m}\left(r\right)\right]\right.,\nonumber \\&-\frac{1}{4\pi }\frac{1}{2}\frac{m\,{\varepsilon }\,{\overline{\rho }}}{\left[l\left(l+1\right)\right]^{3/2}}\left(\frac{\widehat{\omega }}{N}\right)\frac{\left(r{\widehat{\omega }}\right)^3}{\widehat{\omega }},\nonumber \\&{\left.-\frac{1}{4\pi }\frac{1}{2}\frac{m\,{\varepsilon }\,{\overline{\rho }}}{R_{\rm i;c}^2\,\beta _{l,m}^{2}\,\left[l\left(l+1\right)\right]^{7/2}}\left(\frac{r^2\,N}{K}\right)^2\left(\frac{\widehat{\omega }}{N}\right)^{7}\frac{\left(r{\widehat{\omega }}\right)^3}{\widehat{\omega }}\right\} }, \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq91.gif)
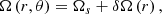
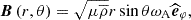
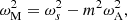
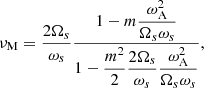
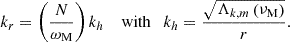
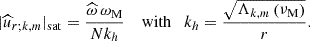
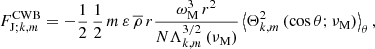
![$$ \begin{aligned} F\left(r\right)&=\sum _{\omega _{\rm in},k,m}\mathrm{min}\left\{ -\frac{m}{\widehat{\omega }}F_{\mathrm{E};k,m}\left(r_{0}\right)\exp \left[-\tau _{k,m}\left(r\right)\right]\right.,\nonumber \\&{\left. -\frac{1}{2}\,\frac{1}{2}\,m\,{\varepsilon }\,{\overline{\rho }}\,r \frac{\omega _{\rm M}^3\, r^2}{N \Lambda _{k,m}^{3/2}\left(\nu _{\rm M}\right)}\left<\Theta _{k,m}^{2}\left(\cos \theta ;\nu _{\rm M}\right)\right>_{\theta }\right\} }, \end{aligned} $$](/articles/aa/full_html/2025/02/aa52066-24/aa52066-24-eq101.gif)