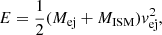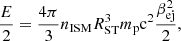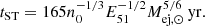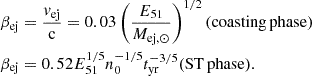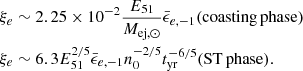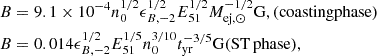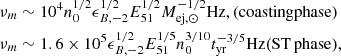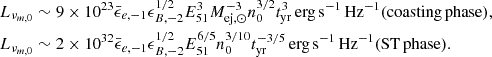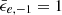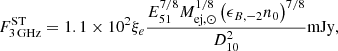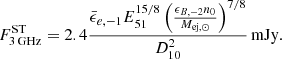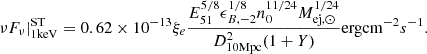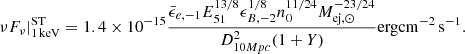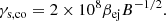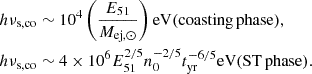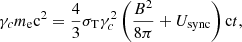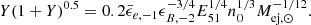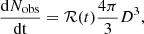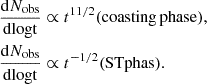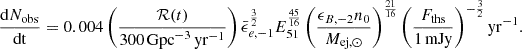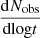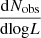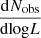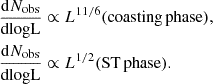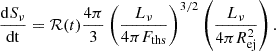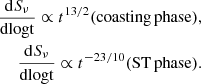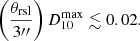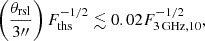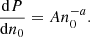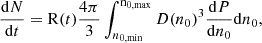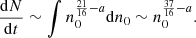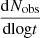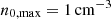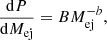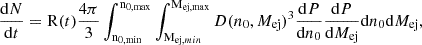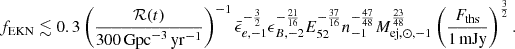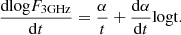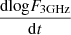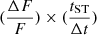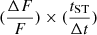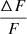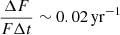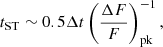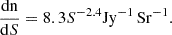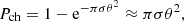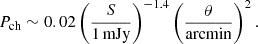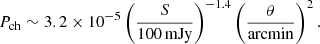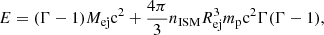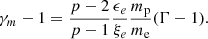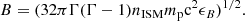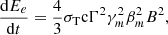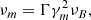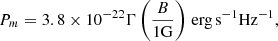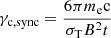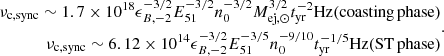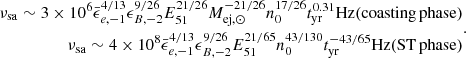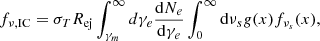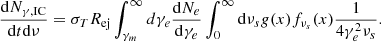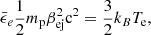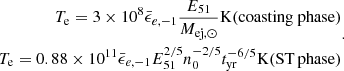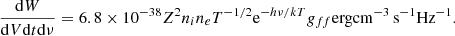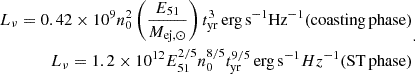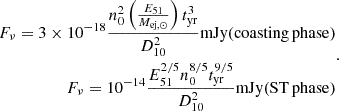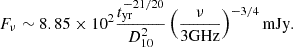| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202452290 | |
| Published online | 07 January 2025 | |
Features and prospects for kilonova remnant detection with current and future surveys
1
Astrophysics Research Center of the Open University, The Open University of Israel, Ra’anana, Israel
2
Department of Natural Sciences, The Open University of Israel, PO Box 808 Ra’anana 4353701, Israel
3
Department of Physics, The George Washington University, 725 21st Street NW, Washington, DC 20052, USA
4
Research Center for the Early Universe, Graduate School of Science, The University of Tokyo, Tokyo 113-0033, Japan
⋆ Corresponding author; sandeepkumaracharya92@gmail.com
Received:
18
September
2024
Accepted:
16
November
2024
We study the observable spectral and temporal properties of kilonova remnants (KNRs) analytically, and point out quantitative differences with respect to supernova remnants. We provide detection prospects of KNRs in the context of ongoing radio surveys. We find that there is a good chance to expect tens of these objects in future surveys with a flux threshold of ∼0.1 mJy. Kilonova remnants from a postulated population of long-lived supermassive neutron star remnants of neutron star mergers are even more likely to be detected, as they are extremely bright and peak earlier. For an ongoing survey with a threshold of ∼1 mJy, we expect to find tens to hundreds of such objects if they are a significant fraction of the total kilonova (KN) population. Considering that there are no such promising KN candidates in presently ongoing surveys, we constrain the fraction of these extreme KN to be no more than 30 percent of the overall KN population. This constraint depends sensitively on the details of ejecta mass and external density distribution.
Key words: stars: neutron / ISM: jets and outflows / ISM: supernova remnants
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Kilonovae (KNe) are transient events formed after the merger of binary neutron stars (Li & Paczyński 1998; Metzger et al. 2010; Rosswog 2015; Tanaka 2016; Fernández & Metzger 2016; Hotokezaka et al. 2018; Metzger 2019). Their emission initially peaks in the UV-optical-IR range and arises from heated ejecta material. The heat is generated from radioactive decay of heavy elements produced through r-process nucleosynthesis. The ejecta mass is expected to be in the range of 0.01 − 0.1 M⊙, with a total kinetic energy of ∼1051 erg. If the merger results in a long-lived rapidly spinning and highly magnetized neutron star (millisecond magnetar), then a large amount of energy (typically ∼5 × 1052 erg up to ∼2 × 1053 erg – limited primarily by the maximum possible rotation that the neutron star can attain before being torn apart, which is known as the mass-shedding limit; see, e.g. Giacomazzo & Perna 2013; Beniamini & Lu 2021) can be injected into the outflow. This can significantly enhance the brightness of the resulting KN (Yu et al. 2013; Metzger & Piro 2014; Kisaka et al. 2016; Ai et al. 2022; Wang et al. 2024).
In association with the gravitational-wave-detected neutron star merger, GW170817 (Abbott et al. 2017), a KN with ejecta of much lower kinetic energy, of the order of ∼1051 erg, has been observed with optical follow-up studies Coulter et al. (2017), Soares-Santos et al. (2017), Arcavi et al. (2017), Lipunov et al. (2017), Valenti et al. (2017), Troja et al. (2017), Kilpatrick et al. (2017), Smartt et al. (2017), Drout et al. (2017), Evans et al. (2017), suggesting a long-lived magnetar was not formed in this event. While supermassive neutron star (NS) formation might have been thought to be common based on considerations of total mass alone (e.g. Margalit & Metzger 2019), the occurrence rate of magnetar-boosted KNe (and the underlying long-lived central engines) is in practice strongly constrained by inferences based on observations. Relevant examples are (i) the analysis in Beniamini & Lu (2021), which is based on the typical durations and ejected energies of KN central engines as compared with the plateau-like features in short gamma-ray burst (sGRB) gamma-ray and X-ray observations; (ii) the long-term radio follow-up of low-redshift sGRBs (e.g. Horesh et al. 2016; Schroeder et al. 2020; Ricci et al. 2021), which puts limits on the kinetic energy of the outflow that are well below values expected for magnetar-boosted KNe (excluding the maximum ejecta energy of ≳5 × 1052 erg for Mej ≲ 0.05 M⊙, and constraining the fraction of short GRBs that produce stable remnants to ≲0.5); and (iii) the lack of bright transients in optical all-sky surveys such as Zwicky Transient Facility (ZTF; Bellm et al. 2019), which would naturally arise from magnetar-boosted KNe (Wang et al. 2024). The fraction of magnetar-boosted KNe is important for constraining the NS equation of state, because the latter is a major factor in determining the outcome of a NS merger (Shibata & Hotokezaka 2019).
While the optical transient from a KN substantially fades after a week or two, the ejecta continues to expand into the surrounding medium. As a result, a forward shock is driven into the surrounding material. This shock enhances the magnetic fields and accelerates electrons in the shocked medium, which then radiate their energy via synchrotron and synchrotron self-Compton. This can give rise to emission that is sometimes known as the ‘kilonova afterglow’ and can observationally manifest as approximately decades-long radio flares (Nakar & Piran 2011; Takami et al. 2014; Margalit & Piran 2015; Hotokezaka & Piran 2015; Kathirgamaraju et al. 2019). In the case of GW170817, the KN afterglow has not yet been observed even 7 years after the merger (e.g. Hajela et al. 2019; Balasubramanian et al. 2022).
Since the KN ejecta blast waves are expected to be mildly relativistic at most, the physics is essentially the same as in supernova remnants (SNRs). In analogy with the latter, this phase might also be dubbed the kilonova remnant (KNR; Beniamini & Lu 2021). Indeed, at times later than the ‘deceleration peak’ (also known as the Sedov time), the evolution depends only on the energy of the blastwave, and as such –considering the similarity between the energies of supernovae (SNe) and KNe–, it becomes challenging to distinguish between the two remnant types. The problem is compounded by the fact that the occurrence rate of SNe is about 300 times greater than that of KNe, and so SNRs are the major contaminant preventing potential identification of KNRs. Nevertheless, we show in the present work that there are important spectral, temporal, and environmental properties that can be used to distinguish KNRs from SNRs in observations.
In this paper, we perform an analytic study of the expected observable properties of KNRs and highlight their main differences from SNRs. In addition, we also focus on the class of highly energetic magnetar-boosted KN remnants (EKNRs), which, though expected to be rare, can be seen to much greater distances; therefore even a null detection of KNRs could strongly constrain their intrinsic occurrence rate. This paper is organised as follows. We start by presenting the dynamics of the ejecta of KNe in Sect. 2. We use Newtonian dynamics, which is relevant for our choice of fiducial parameters. However, we add a brief section (Appendix A) with fully relativistic expressions. In Sect. 3, we obtain expressions for the flux from emission originating from non-thermal electrons. We describe the combined spectrum due to synchrotron, bremsstrahlung, and synchrotron self-Compton emission and emphasise the differences between SNRs and KNRs. We predict the number of expected KNRs in radio surveys in Sect. 4 and show that we are likely to detect a candidate object with current (or future) facilities such as VLASS (Very Large Area Sky Survey) and VAST (Variables and Slow Transients). We are even more likely to detect an extreme KN, if they exist, due to the strong dependency of the observed flux on ejecta energy. As of yet, no such candidate object has been reported in the literature, which allows us to put moderate constraints on their abundance. In Sect. 5, we discuss how to extract the Sedov time from its observed light curve. For EKNRs, the Sedov time is of the order of 10–20 years, and therefore there is a good chance to obtain the Sedov time of extreme KNs with dedicated observations over a period of a few years. We also discuss how information about the host galaxies can be used to break degeneracies between KNRs and SNRs. We conclude in Sect. 6.
2. Ejecta dynamics
We compute the evolution of an ejecta (associated with either a KN or a SN) assuming it expands into a uniform surrounding medium in a spherically symmetric fashion. We assume Newtonian physics for the calculations shown here (see Appendix A for a fully relativistic treatment). The ejecta’s kinetic energy and velocity are connected via
where Mej is the ejecta mass and MISM is the mass of displaced surrounding gas with 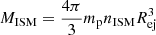 , mp is the mass of proton, nISM is the density of the surrounding gas and Rej is the size of expanding ejecta. The kinetic and the internal energy of the ejecta can be comparable. Therefore, if we were to use the total energy of ejecta in Eq. (1), it would roughly cancel the factor 1/2 on the right-hand side. We assume a uniform density profile without any spatial gradient. We normalise the physical parameters by defining,
, mp is the mass of proton, nISM is the density of the surrounding gas and Rej is the size of expanding ejecta. The kinetic and the internal energy of the ejecta can be comparable. Therefore, if we were to use the total energy of ejecta in Eq. (1), it would roughly cancel the factor 1/2 on the right-hand side. We assume a uniform density profile without any spatial gradient. We normalise the physical parameters by defining, 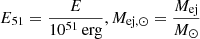 , and
, and 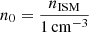 . During the initial phase, the ejecta expands freely into the medium (we call this the ‘coasting phase’ regime). This lasts until Mej ∼ MISM, when the ejecta starts decelerating and the evolution enters the Sedov-Taylor (ST) phase. The deceleration, or ST radius, RST can be obtained by solving
. During the initial phase, the ejecta expands freely into the medium (we call this the ‘coasting phase’ regime). This lasts until Mej ∼ MISM, when the ejecta starts decelerating and the evolution enters the Sedov-Taylor (ST) phase. The deceleration, or ST radius, RST can be obtained by solving
where vej = βejc. This simplifies to 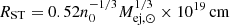 . The corresponding timescale is given by
. The corresponding timescale is given by
The velocity in each regime is
The radius of the ejecta is then Rej ≈ βejct in the coasting phase and 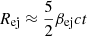 in the ST phase. We consider three classes of objects with fiducial physical parameters as stated in parentheses: a SNR (E51 = 1, Mej, ⊙ = 1, n0 = 1), a KNR (E51 = 1, Mej, ⊙ = 0.1, n0 = 0.1), and an EKNR (E51 = 10, Mej, ⊙ = 0.1, n0 = 0.1). We note that this implicitly assumes that, compared to SNRs, both KNRs and EKNRs occur in environments that exhibit less star formation and are therefore less dense. While this is true on average, it means that KNRs and EKNRs appear less bright than they would in a similar environment to a SNR, which is a topic we return to in Sect. 5.3.
in the ST phase. We consider three classes of objects with fiducial physical parameters as stated in parentheses: a SNR (E51 = 1, Mej, ⊙ = 1, n0 = 1), a KNR (E51 = 1, Mej, ⊙ = 0.1, n0 = 0.1), and an EKNR (E51 = 10, Mej, ⊙ = 0.1, n0 = 0.1). We note that this implicitly assumes that, compared to SNRs, both KNRs and EKNRs occur in environments that exhibit less star formation and are therefore less dense. While this is true on average, it means that KNRs and EKNRs appear less bright than they would in a similar environment to a SNR, which is a topic we return to in Sect. 5.3.
In these calculations, we have assumed that the external medium is undisturbed until the ejecta collides with it. However, relativistic jets from merging binaries can disturb the external medium before the ejecta. In that case, the early phase of the KNR emission could be suppressed due to the blast-wave passing through a region that was evacuated by the passage of the jet (Margalit & Piran 2020). The timescale of this suppression is related to tST by 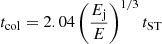 . For a jet with an isotropic equivalent energy of 1051 erg (Duran & Giannios 2015) and an opening angle of θj ∼ 0.2 radians, the energy of the jet
. For a jet with an isotropic equivalent energy of 1051 erg (Duran & Giannios 2015) and an opening angle of θj ∼ 0.2 radians, the energy of the jet 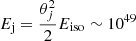 erg. For this case, we find that the suppression timescale is significantly shorter that the Sedov timescale. This means that propagation through the evacuated region typically only changes the KNR flux at early times, when the KNR is generally very dim. This conclusion is further enhanced in the case of EKNRs.
erg. For this case, we find that the suppression timescale is significantly shorter that the Sedov timescale. This means that propagation through the evacuated region typically only changes the KNR flux at early times, when the KNR is generally very dim. This conclusion is further enhanced in the case of EKNRs.
3. Synchrotron, synchrotron self-Compton, and Bremsstrahlung emission
The expanding ejecta shocks the surrounding medium, compressing it and accelerating the electrons. We assume that a fraction ϵe of the shock energy goes into accelerating electrons and a fraction ξe of electrons are accelerated to relativistic energies.
The relativistic electron Lorentz factor distribution is taken to be of the form
where γm is the minimal Lorentz factor. Integrating over γe and equating the electron number density to nISM, N0 = (p − 1)n0. The expression for γm in the bulk comoving frame is given by
where it is assumed that p > 2 with a fiducial value of p = 2.5 and Γ is the Lorentz factor of the shocked fluid. In the non-relativistic regime of expanding ejecta and defining 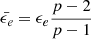 ,
, 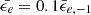 , the expression simplifies to,
, the expression simplifies to, 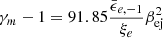 , or
, or
For a fixed ξe and at sufficiently late times, Eq. (7) would lead to γm − 1 ≪ 1, which will result in electrons being non-relativistic, at which point they cannot emit synchrotron photons at ν≳ GHz. The reason for this is straightforward: at such times, there is simply not enough energy to share between those electrons, while still allowing all of them to maintain relativistic velocities. This phase is known as the deep Newtonian phase. A natural resolution, which is consistent with giant flare outflows and GRB afterglows (Granot et al. 2006; Sironi & Giannios 2013), is to take γm to be the maximum between the value given in Eq. (7) and 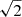 . The fraction of relativistic electrons then needs to be modified according to ξe = ξe, 0min[1, (βej/βdn)2] (Beniamini et al. 2022). In the analysis below, we assume ξe, 0 = 1. The expression for βdn is then
. The fraction of relativistic electrons then needs to be modified according to ξe = ξe, 0min[1, (βej/βdn)2] (Beniamini et al. 2022). In the analysis below, we assume ξe, 0 = 1. The expression for βdn is then 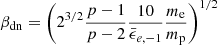 . Using p = 2.5 and
. Using p = 2.5 and 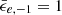 , βdn = 0.21. For our fiducial class of objects, we find that only the EKNRs transition to the deep Newtonian regime, while SNRs and KNRs are already in this regime in the coasting phase. As the ejecta transitions to the deep Newtonian regime in the ST era, requiring βej = βdn in Eq. (4), we obtain the transition timescale as,
, βdn = 0.21. For our fiducial class of objects, we find that only the EKNRs transition to the deep Newtonian regime, while SNRs and KNRs are already in this regime in the coasting phase. As the ejecta transitions to the deep Newtonian regime in the ST era, requiring βej = βdn in Eq. (4), we obtain the transition timescale as,
For E51 = 10, n0 = 0.1, and  , tdn ≈ 30 yr. The expression for ξe is given by
, tdn ≈ 30 yr. The expression for ξe is given by
3.1. Synchrotron emission
The energetic electrons in the presence of magnetic field emit synchrotron emission (Chevalier 1982, 1998; Frail et al. 2000). Assuming a fraction ϵB of shocked energy goes into amplifying the magnetic field, the comoving magnetic energy density in the non-relativistic regime is 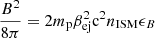 . Substituting the expression for βej (Eq. (4)), the expression for the magnetic field becomes
. Substituting the expression for βej (Eq. (4)), the expression for the magnetic field becomes
where ϵB ≡ 0.01ϵB, −2. The characteristic synchrotron frequency νm is given by νm = γm2νB, where 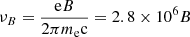 Hz is the cyclotron frequency. For our fiducial cases of SNR and KNR, the solutions are in the deep Newtonian regime, while for EKNR, γm ∼ 10 in the coasting phase (Eq. (7)) and the deep Newtonian regime is typically obtained in the ST phase. In the deep Newtonian regime, the expression for νm is given by
Hz is the cyclotron frequency. For our fiducial cases of SNR and KNR, the solutions are in the deep Newtonian regime, while for EKNR, γm ∼ 10 in the coasting phase (Eq. (7)) and the deep Newtonian regime is typically obtained in the ST phase. In the deep Newtonian regime, the expression for νm is given by
for slow-cooling electrons, or νm < νc, sync (Sari et al. 1998; Granot & Sari 2002), where νc, sync is the cooling frequency due to synchrotron losses alone (Appendix B). The power in the comoving frame due to one electron at the frequency νm is 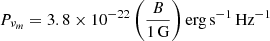 . The number of shocked electrons (which is a Lorentz invariant) within a dynamical time is
. The number of shocked electrons (which is a Lorentz invariant) within a dynamical time is 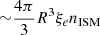 . Therefore, we multiply this number with the power per electron to obtain the maximum optically thin synchrotron luminosity,
. Therefore, we multiply this number with the power per electron to obtain the maximum optically thin synchrotron luminosity, 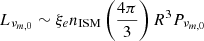 . All together,
. All together,
The equation above applies in the deep Newtonian regime. Furthermore, for the physical situation being discussed, we verified that νm < νsa < νc, sync, where νsa is the synchrotron self-absorption frequency (Appendix C). We caution that in this case, the luminosity at νm is not given by the expression given in Eq. (12). Nonetheless, as we are interested in luminosity or flux at ν > νsa > νm, we can still use these expressions to compute flux by extrapolation, as done below. We use the subscript ‘0’ in the expressions for Lνm, 0 and Fνm, 0 to clarify this difference. The spectral flux at a given observation frequency ν with νm < νsa < ν < νc, sync is given by 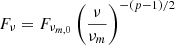 , which after substitution becomes
, which after substitution becomes
where we have assumed Euclidean geometry, as appropriate for distances of D ≲ 10 Mpc with 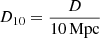 . We normalised the expression for flux with respect to the central frequency of VLASS (Gordon et al. 2023). In Fig. 1, we plot the observed flux for the three classes of objects considered in this work. The peak of the observed flux occurs at tST with a peak flux of ∼1 mJy (D = 10 Mpc) for both the SNR and KNR. EKNRs are significantly brighter and also have shorter tST. This will significantly impact the detection prospects for such extreme objects; we discuss this topic in subsequent sections. We have also included the corrections by Margalit & Piran (2020) in this figure, which are briefly discussed in Sect. 2. We note that the calculations discussed above are valid at t > tcol, while at t < tcol, there is an extremely sharp decrease in flux (∼t10) due to the decrease in external density caused by the previous propagation of the jet.
. We normalised the expression for flux with respect to the central frequency of VLASS (Gordon et al. 2023). In Fig. 1, we plot the observed flux for the three classes of objects considered in this work. The peak of the observed flux occurs at tST with a peak flux of ∼1 mJy (D = 10 Mpc) for both the SNR and KNR. EKNRs are significantly brighter and also have shorter tST. This will significantly impact the detection prospects for such extreme objects; we discuss this topic in subsequent sections. We have also included the corrections by Margalit & Piran (2020) in this figure, which are briefly discussed in Sect. 2. We note that the calculations discussed above are valid at t > tcol, while at t < tcol, there is an extremely sharp decrease in flux (∼t10) due to the decrease in external density caused by the previous propagation of the jet.
 |
Fig. 1. Flux at 3 GHz as a function of age and ejecta size with D = 10 Mpc for an SNR (E51 = 1, Mej, ⊙ = 1, n0 = 1), a KNR (E51 = 1, Mej, ⊙ = 0.1, n0 = 0.1), and a EKNR (E51 = 10, Mej, ⊙ = 0.1, n0 = 0.1). We have chosen |
3.1.1. Flux at tST
As objects have the highest detection probability when they are brightest, it is useful to have the expression for the peak flux, which occurs at tST (Fig. 1). Using the expression for tST (Eq. (3)) in the coasting phase solution for the observed flux (Eq. (13)), we have
where we we keep ξe explicit. Using the expression for ξe in the deep Newtonian regime (Eq. (9)),
The peak flux is a strong function of ejecta energy, which explains the dramatic boost to observed flux in the case of a EKNR. The peak flux is a degenerate combination of ϵB, −2, n0, and Mej, ⊙. This is visible in Fig. 1 for the SNR and KNR cases, which both have n0/Mej, ⊙ = 1.
3.1.2. Peak flux at X-ray frequency
We also compute the flux at tST in the X-ray band. The luminosity at 1 keV (or ν = 2.4 × 1017 Hz) with ν > νc is given by 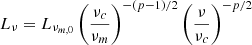 . At t = tST,
. At t = tST,
Using the expression for ξe in the deep Newtonian regime (Eq. (9)),
In the equation above, and in the full results shown in Fig. 2, we account for inverse-Compton losses affecting νc (Sect. 3.2). For our fiducial cases, Y ≲ 1, and so synchrotron self-Compton losses are a minor correction. The flux limit for eROSITA in the soft X-ray band (0.5–2 keV) is ∼10−15 − 10−14 erg cm−2 s−1 (Merloni et al. 2012). The ongoing Einstein probe (Yuan et al. 2022) has a similar energy band with slightly worse flux limit, which depends on the length of exposure. Therefore, we expect to see objects in X-rays up to distances of a few megaparsecs, which can complement radio observations. If synchrotron is the dominant process in X-rays (as indeed expected; see Sect. 3.2), we expect a correlation between radio and X-ray flux, as both arise from the same population of electrons.
 |
Fig. 2. νLν as a function of ν at tST for a SNR (black), a KNR (red), and a EKNR (blue). |
3.1.3. Synchrotron emission cutoff
We compute the synchrotron cutoff by requiring that the diffusion length scale of electrons, while gyrating in the magnetic field, be less than the size of the remnant. The diffusion coefficient in the Bohm limit is given by D = crg/3, where rg is the gyration radius, rg = γmec2/eB, which can be simplified to 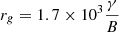 cm. Imposing the condition as stated above, we have Dt < βej2c2t2, or
cm. Imposing the condition as stated above, we have Dt < βej2c2t2, or 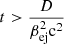 . We then use the synchrotron cooling timescale (Appendix B) in the expression to obtain
. We then use the synchrotron cooling timescale (Appendix B) in the expression to obtain
A more detailed calculation for the cutoff Lorentz factor is given by Zirakashvili & Aharonian (2007), which in the Bohm regime leads to a pre-factor of 3.6 × 107 instead of 2 × 108. Using the value from Zirakashvili & Aharonian (2007), the corresponding cutoff frequency is 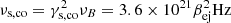 . Plugging in βej,
. Plugging in βej,
As βej is constant in the coasting phase, the corresponding expression gives a rough estimate at tST (at later times νs, co only declines). For SNRs, the expected cutoff is of the order of ∼10 keV, which becomes ∼100 keV – 1 MeV for our choice of KN parameters. Therefore, this feature, along with others (which we discuss later), can be used to separate SNRs from KNRs.
3.2. Synchrotron self-Compton emission
In addition to synchrotron, electrons also cool via Compton losses by the synchrotron photons, known as synchrotron self-Compton (SSC) loss. Therefore, Eq. (B.1) is modified as
where Usync is the energy density of the synchrotron photon spectrum. As a result, the cooling Lorentz factor is modified as 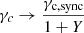 , where Y is the Compton parameter whose expression is given by Beniamini et al. (2015),
, where Y is the Compton parameter whose expression is given by Beniamini et al. (2015), 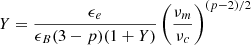 , where νc is the cooling frequency with the Compton correction included, that is, νc = νc, sync/(1 + Y)2, where νc, sync is the cooling frequency without SSC losses. Plugging in the expressions with p = 2.5, we have
, where νc is the cooling frequency with the Compton correction included, that is, νc = νc, sync/(1 + Y)2, where νc, sync is the cooling frequency without SSC losses. Plugging in the expressions with p = 2.5, we have
Using fiducial parameters, we obtain Y(1 + Y)0.5 ∼ 0.18, 0.24, and 0.43 for SNRs, KNRs, and EKNRs, respectively. Therefore, Compton cooling has a minor effect on the scenarios that we consider. However, if ϵB, −2 is much smaller than 1, then this effect is moderately important. Nevertheless, we include this effect in our calculation of the synchrotron spectrum as shown in Fig. 2. The Compton-scattered frequency corresponding to νc is given by νc, IC ∼ γc2νc ∼ γc4νB. The value of γc at tST is of the order of 105. Therefore, νc, IC ∼ 1024 Hz1. We solve for the SSC flux as a function of frequency, as explained in Appendix D.
In Fig. 2, we plot νLν for synchrotron, SSC, and bremsstrahlung at tST for our fiducial cases. We find that bremsstrahlung (Appendix E) is subdominant compared to the other channels over the entire frequency domain. For SNRs, with larger n0, bremsstrahlung may dominate over synchrotron in the X-ray band because it is highly sensitive to the value of the gas density. For our fiducial parameters of KNR, the synchrotron emission is further boosted compared to bremsstrahlung. Therefore, we expect the X-ray flux to be dominated by synchrotron, which may be a diagnostic tool to separate it from SNRs, especially with the synchrotron cut-off feature (Sect. 3.1.3). The SSC process completely dominates the emission in the gamma-ray band. For KNRs, the overall transition from synchrotron to SSC happens around 1-10 MeV. In this context, we briefly discuss γ-ray detectability with the Fermi gamma-ray burst monitor (Fermi-GBM). The sensitivity of this instrument is of the order of 0.5 cm−2 s−1 between 10 keV and 25 MeV. We note that this sensitivity is given in terms of photon flux, which is the number of photons per unit area per second. For the EKNR case in Fig. 2, the flux will be of the order of ∼10−7 cm−2 s−1 at 100 keV for an object located at D = 10 Mpc. Therefore, it would be difficult to detect features in the gamma-ray part of the spectrum. We also show the relevant energy range of ZTF in Fig. 2. Using its magnitude limit, we find that we can see objects up to a few megaparsecs. In subsequent sections, we concentrate on the radio part of spectrum and discuss how the light curves (Sect. 5.1) may help us distinguish KNRs from SNRs.
4. Number of detectable remnants
We now consider the detection prospects of KNRs with ongoing and future telescope surveys. The very large area sky survey (VLASS) is observing the entire sky north of −40° (33 885 deg2) in the 2 GHz ≲ ν ≲ 4 GHz band with an angular resolution of the order of 3 arcsec. The current sensitivity is of the order of 1 mJy (Gordon et al. 2021), which will eventually reach the level of 0.1 mJy. VLASS will cover its footprint over three epochs separated by 32 months. For the current flux threshold of ∼1 mJy, the expected distance up to which a KN can be seen is ∼10 Mpc (Fig. 1). For a generic flux threshold Fths, the maximum distance is given by Dmax = (L3 GHz/4πFths)1/2, which can be rewritten as 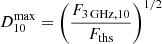 , where F3 GHz, 10 is the flux at 10 Mpc. Objects of a given age t are detected at a rate of
, where F3 GHz, 10 is the flux at 10 Mpc. Objects of a given age t are detected at a rate of
where ℛ(t) is the rate of formation of KNe per volume per time, which is ∼300 Gpc−3 yr−1 (Abbott et al. 2023). Substituting the numbers, we have, 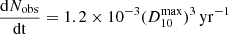 . For Lν ∝ tα,
. For Lν ∝ tα, 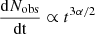 or equivalently
or equivalently 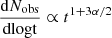 . While Eq. (22) is denoted in terms of the observer’s time, the luminosity is a function of the age of the system. In practice, we have many systems with different ages and we are averaging over their properties at a given observer time. Under our assumptions, this does not change our results. For the coasting phase regime, α = 3, while for the ST regime, α = −21/20 (Eq. (13)). Substituting, we have
. While Eq. (22) is denoted in terms of the observer’s time, the luminosity is a function of the age of the system. In practice, we have many systems with different ages and we are averaging over their properties at a given observer time. Under our assumptions, this does not change our results. For the coasting phase regime, α = 3, while for the ST regime, α = −21/20 (Eq. (13)). Substituting, we have
For the fiducial KNR parameters, 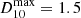 .
.
We expect the quantity 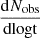 to be dominant at the Sedov time. At tST, we can use Eq. (15) to obtain the general expression,
to be dominant at the Sedov time. At tST, we can use Eq. (15) to obtain the general expression,
For our fiducial KNR case, tST ∼ 50 yr or 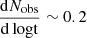 , meaning that there is a roughly 20% chance that such an object exists within the current VLASS dataset. In the future, with a reduction of the VLASS flux threshold to 0.1 mJy (Gordon et al. 2023), these numbers will be boosted by a factor of about 30. In Fig. 3, we plot
, meaning that there is a roughly 20% chance that such an object exists within the current VLASS dataset. In the future, with a reduction of the VLASS flux threshold to 0.1 mJy (Gordon et al. 2023), these numbers will be boosted by a factor of about 30. In Fig. 3, we plot 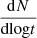 for SNRs, KNRs, and EKNRs with our choice of fiducial parameters. We also consider a few cases with a distribution over density and ejecta mass of EKNRs, which we describe below. We take the SN occurrence rate to be ∼105 Gpc−3 yr−1 (Li et al. 2011), which is approximately 300 times higher than the KN rate. A consistency check for the number of detectable SNRs given our assumptions is provided in Appendix F.
for SNRs, KNRs, and EKNRs with our choice of fiducial parameters. We also consider a few cases with a distribution over density and ejecta mass of EKNRs, which we describe below. We take the SN occurrence rate to be ∼105 Gpc−3 yr−1 (Li et al. 2011), which is approximately 300 times higher than the KN rate. A consistency check for the number of detectable SNRs given our assumptions is provided in Appendix F.
 |
Fig. 3. Abundance of SNR, KNR and EKNRs. Top: Number of systems observed by an all-sky radio survey per logarithmic unit of age, |
While Eq. (23) is written in terms of time, for an object at a known distance, the luminosity is directly inferred from observations. Therefore, it is useful to convert the expression into one in terms of luminosity using the relation, 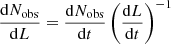 . Using the dependence of luminosity on time, we have
. Using the dependence of luminosity on time, we have 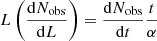 . In terms of luminosity,
. In terms of luminosity,
In the bottom panel of Fig. 3, we plot the same as in the upper panel but in terms of luminosity. We only consider the ST regime for this plot because 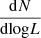 is a non-monotonic function of L and the number of objects in the ST regime dominates over the number of sources in the coasting phase (see the thin grey line in the figure).
is a non-monotonic function of L and the number of objects in the ST regime dominates over the number of sources in the coasting phase (see the thin grey line in the figure).
If we are able to spatially resolve the remnants, we can directly track their evolution in size as a function of time (see e.g. Barniol Duran et al. 2016). This provides additional information and can inform us as to whether the object is in the coasting or ST phase. In Fig. 1 (right panel), we plot the observed flux as a function of the size of the ejecta. We find that SNRs and KNRs are degenerate, with the Sedov radii of all three cases being similar. Nevertheless, observation of the ejecta evolution over time can help distinguish remnants from potential contaminants. The related observable is the surface brightness Sν given by 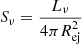 . The observed distribution of Sν is given by
. The observed distribution of Sν is given by
As the size of a KNR varies as t and t2/5 in blast-wave and ST-regime, respectively,
Given the flux sensitivity of a survey, we can see objects up to the maximum distance 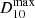 , as introduced above. The physical size of a resolvable object is given by
, as introduced above. The physical size of a resolvable object is given by 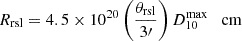 , where θrsl is the angular resolution of the survey, which we have normalised to 3 arcsec, for applicability to VLASS. As the Sedov radius of SNRs and KNRs are of the order of 1019 cm, in order to resolve a KNR, we have the relation
, where θrsl is the angular resolution of the survey, which we have normalised to 3 arcsec, for applicability to VLASS. As the Sedov radius of SNRs and KNRs are of the order of 1019 cm, in order to resolve a KNR, we have the relation
We can rewrite this equation in terms of Fths as
where we can use Eq. (15) for the expression of F3 GHz, 10 at tST. Assuming a conservative value of θrsl = 1″, we can resolve KNRs up to ∼600 kpc (Eq. (28)). We find the number of objects within 600 kpc to be 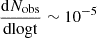 at tST, even when assuming ℛ(t) to be ten times higher than the assumed value in Eq. (22). Therefore, we do not expect to find a spatially resolvable KNR with a survey like VLASS.
at tST, even when assuming ℛ(t) to be ten times higher than the assumed value in Eq. (22). Therefore, we do not expect to find a spatially resolvable KNR with a survey like VLASS.
4.1. Extended distribution over density and ejecta mass
Up to this point, we have considered single values of the external density and ejecta mass for KNe. Here, we consider a distribution of external density, and we discuss the same for ejecta mass below. We assume the external density of EKNRs to be
The prefactor A is fixed by the normalisation 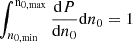 or A = (∫n0, minn0, maxn0−adn0)−1. The rate of detectable objects is
or A = (∫n0, minn0, maxn0−adn0)−1. The rate of detectable objects is
where D is a function of other ejecta parameters as well as the flux threshold, but we have suppressed them for brevity. We compute this quantity numerically to obtain the results shown in Fig. 4. Here, we give a simple estimate of how 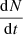 changes at tST depending on the value of a. As Lν ∝ n07/8 at tST (Eq. (15)) and the observable distance
changes at tST depending on the value of a. As Lν ∝ n07/8 at tST (Eq. (15)) and the observable distance 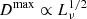 , the rate of detectable objects is
, the rate of detectable objects is
 |
Fig. 4. Dependence of EKNR abundance on surrounding density and mass distribution. Top: |
As tST ∼ n0−1/3, the number of detected objects at tST is approximately N ∼ n095/48 − a. We do not know the exact value of a at present. To motivate a guess for a, we assume n0, min = 10−3, n0, max = 1 cm−3 and require that the number of objects at n = 1 cm−3 is of the order of 1 percent of the population at n0 = 10−3 (this is guided by observations of short GRB afterglows by O’Connor et al. 2020, as well as by the inferred gravitational wave delay time distribution between formation and merger of binary neutron star mergers; see Beniamini & Piran 2024). This rough estimate gives a = 5/3. Incorporating this value into Eq. (32), the number of detectable objects goes as N ∝ n015/48. Therefore, a small number of objects with large external density can naturally dominate the number of detectable objects. The total number of detected objects depends on n0, min, n0, max, and a through the normalisation parameter A. We consider a few cases where we fix n0, max = 1 and vary a and n0, min such that the number of object at n = 1 cm−3 is of the order of 1 percent of the population at n0, min. We plot these cases in Fig. 4. We see that the number of detected objects depends sensitively on our choice of the density distribution.
We also consider a distribution of ejecta masses with,
where B is the normalisation parameter. We take the lower and upper limit of ejecta mass to be 0.01 and 0.1 M⊙, respectively. Without proper knowledge of the value of b, we choose b = 1, which corresponds to equal logarithmic contributions. Similar steps as above lead to
We solve this expression numerically and plot it in Fig. 4. We note that for extreme KNe with Mej, ⊙ = 0.01, the bulk velocity is mildly relativistic and we use the dynamical expressions provided in Appendix A. Still, some of the aspects can be understood from scaling relations obtained in the non-relativistic regime. While the flux at tST increases with decreasing Mej (Eq. (15)), the Sedov time itself is also a strong function of Mej (Eq. (3)). Therefore, the two effects compensate for each other in the quantity 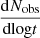 and the ejecta mass does not have a huge effect on the number of detectable objects at tST. Reducing Mej further has a much more drastic effect, with the ejecta moving at relativistic speeds, and causes a huge increase in the expected number of detected objects with extremely short tST.
and the ejecta mass does not have a huge effect on the number of detectable objects at tST. Reducing Mej further has a much more drastic effect, with the ejecta moving at relativistic speeds, and causes a huge increase in the expected number of detected objects with extremely short tST.
From the above calculations, we find that we should be in a position to detect a KNR in the near future with a VLASS-like survey with an achievable goal of Fths ∼ 0.1 mJy. Even more interestingly, if EKNRs constitute a significant population of all KNRs, we expect to find 10–100 such objects. If we do not find any in the survey, we should be able to put strong constraints on the population of EKNRs. As no such candidate objects are known in the literature to our knowledge, we take the conservative approach and obtain an upper limit on the abundance of EKNRs (Sect. 4.2). We discuss the potential signatures that can be used to differentiate these objects from SNRs in Sect. 5.
We also plot the areal density, or the number of objects per square degree, for the objects considered in Fig. 4. For the number of objects, we consider the peak of the distribution of 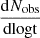 . The number of objects is proportional to (Dmax)3, which is turn is proportional to F−3/2 for an object of given luminosity. This gives rise to the qualitative behaviour seen in the bottom panel of Fig. 4.
. The number of objects is proportional to (Dmax)3, which is turn is proportional to F−3/2 for an object of given luminosity. This gives rise to the qualitative behaviour seen in the bottom panel of Fig. 4.
4.2. Constraints on extreme KN abundance
In order to constrain the abundance of EKNRs, we show presently available constraints from transient surveys in the bottom panel of Fig. 4. These are dedicated surveys that do not report a single KNR. Therefore, we use their results to put upper limits on the abundance of EKNRs. Presently, the strongest constraints come from the observations of Murphy et al. (2021), but they strongly depend on the assumed density and mass distribution of EKNRs, as can be seen in Fig. 4. For our fiducial case (E51 = 10, Mej, ⊙ = 0.1, n0 = 0.1), we find fEKN ≲ 0.3, where fEKN is the fraction of EKNRs with respect to the overall KNR population. As this constraint essentially depends on the value of 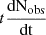 at tST, we derive a general expression using Eq. (24) and (3):
at tST, we derive a general expression using Eq. (24) and (3):
4.3. Future constraints
In Fig. 4, we also plot future constraints expected from VAST wide (Murphy et al. 2021) and VLASS (Mooley et al. 2016; Gordon et al. 2021). The expected areal densities from these surveys are 4 × 10−7 at 2.5 mJy (1.4 GHz) and 10−5 at 1 mJy (3 GHz), respectively. These surveys are expected to find EKNRs if they constitute a significant fraction of the total KNR population. If no candidate objects are found in these surveys, we should be able to put strong constraints on the occurrence rate of EKNRs irrespective of their assumed density and mass distribution.
5. Detection prospect of kilonova remnants
5.1. Estimating tST from the observed light curve
We turn next to the detection prospects for KNRs from the evolution of their light curves. The observed flux F3 GHz ∝ tα, where α is a constant, while observing deep within either the coasting or ST phases. The proportionality constant sets the overall magnitude of flux and depends on ejecta parameters and distance. By taking the derivative of the logarithm of the flux, the constant term drops out and we have
At t ≪ tST or t ≫ tST, the second term drops out with α = 3 or −21/20, respectively. In Fig. 5, we plot the discretised version of 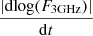 , assuming observation intervals of Δt = 5 years for our fiducial cases. Far from their respective Sedov time, it is not possible to differentiate the three objects, because the light curves approach the same (featureless) power-law scaling. However, most of the objects are expected to be detected in the Sedov-Taylor regime, because the objects spend most of their time in that domain.
, assuming observation intervals of Δt = 5 years for our fiducial cases. Far from their respective Sedov time, it is not possible to differentiate the three objects, because the light curves approach the same (featureless) power-law scaling. However, most of the objects are expected to be detected in the Sedov-Taylor regime, because the objects spend most of their time in that domain.
 |
Fig. 5. Detection prospects for KNRs from their temporal evolution information. Top: |
Assuming we detect an object around tST, we want to determine this timescale from the observed 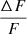 at intervals of Δt. From Fig. 5, we see that, at around tST,
at intervals of Δt. From Fig. 5, we see that, at around tST, 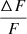 is higher for EKNRs, which is expected given that tST is smaller than for SNRs, and thus the flux changes faster. As the shape of the light curve is the same in all cases, in dimensionless units they must all be identical. As a visual demonstration, we plot
is higher for EKNRs, which is expected given that tST is smaller than for SNRs, and thus the flux changes faster. As the shape of the light curve is the same in all cases, in dimensionless units they must all be identical. As a visual demonstration, we plot 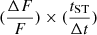 for our fiducial cases in the bottom panel of Fig. 5. We find that
for our fiducial cases in the bottom panel of Fig. 5. We find that 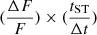 line up horizontally around their respective tST. As an example,
line up horizontally around their respective tST. As an example, 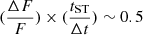 when the light curves are about to enter deep into the ST regime. Therefore, if we detect an object at this epoch, we can obtain an estimate for tST as,
when the light curves are about to enter deep into the ST regime. Therefore, if we detect an object at this epoch, we can obtain an estimate for tST as,
where 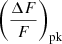 corresponds to the value close to the light curve peak. For EKNRs,
corresponds to the value close to the light curve peak. For EKNRs, 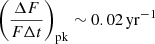 . By incorporating this value into Eq. 37, we have tST ∼ 25 years. We expect to detect a greater number of KNRs with higher external density (Sect. 4.1), which have even lower tST. If we find such an object at around its tST, 5–10 years of detailed observations with finer resolution in Δt could help to obtain a precise light curve, which would be helpful in distinguishing KNRs from SNRs and other contaminants. As an example, with finer resolution, we can reconstruct the feature that we see around tST. With coarse resolution, we may be unable to find this feature in the data as tST ∼ 20 yr for EKNRs.
. By incorporating this value into Eq. 37, we have tST ∼ 25 years. We expect to detect a greater number of KNRs with higher external density (Sect. 4.1), which have even lower tST. If we find such an object at around its tST, 5–10 years of detailed observations with finer resolution in Δt could help to obtain a precise light curve, which would be helpful in distinguishing KNRs from SNRs and other contaminants. As an example, with finer resolution, we can reconstruct the feature that we see around tST. With coarse resolution, we may be unable to find this feature in the data as tST ∼ 20 yr for EKNRs.
We should point out that observing such an object can be challenging, as ΔF/F ∼ 0.1 over a 5 yr time period can be confused with spatial variation of the surrounding gas density, scintillation, or calibration issues, and so on. As an example, Mooley et al. (2016) used the criteria of ΔF/F ≳ 0.3 at S/N ≳ 5. We note that the radio afterglow of GW170817 does not show a deviation of more than 30 percent from a power-law spectrum Mooley et al. (2018). In addition, the calibration error can also be of the order of 5 percent (Ofek et al. 2011). Therefore, one needs high-S/N events so that the observational uncertainty is < 10 percent. However, the fractional change we are discussing here is smooth, whereas fluctuations due to scintillation or density inhomogeneities will likely be stochastic. Furthermore, large sources at close distances –that is, with R ≳ 1019 cm at D < 100 Mpc, as in the remnants discussed here– will be resolved by the scintillation screen (see Kumar et al. 2024 for details) and as such are very weakly affected by scintillation.
5.2. Chance coincidence of KNR with other radio sources
As we expect the candidate KNRs to be point sources at distances of ∼10 Mpc (see Sect. 4), these can be confused with other radio sources. We compute the probability of a chance coincidence of a candidate source with another radio object. The source count at S > 40 μJy is given by (Richards 2000),
The source count of VLASS at a threshold of ∼1 mJy (Gordon et al. 2021) matches very well with a six-degree polynomial fit (Hopkins et al. 2003), which differs somewhat from the simple power-law fit at S > 0.1 mJy. For simplicity, we use the expression above for our estimation. The probability of a chance coincidence is given by (Bloom et al. 2002; Eftekhari & Berger 2017)
where σ is the number of sources per solid angle and θ can be the angular size of a source such as a galaxy. From Eq. (38), we obtain n(S) as a function of S. For a full sky survey, such as VLASS, we obtain σ ∼ 2 × 10−6 arcsec−2 at 1 mJy. In order to identify a source as a potential remnant candidate, we need to obtain its distance, and from that we should be able to identify the host galaxy. For a galaxy of ∼10 kpc in size at D ∼ 10 Mpc, the angular size is of the order of arcminutes. Putting everything together with appropriate normalisation, the probability of a chance coincidence is given by
For a galaxy of 10 kpc in size, we find that the probability of a chance coincidence can be of the order of a few percent. This might be an issue where the overall number of candidate objects is a few, but they may be distinguishable using spectral (Sect. 3) and light-curve information.
The EKNRs are expected to be much brighter with flux of ∼100 mJy (Fig. 1) at a distance of 10 Mpc. In that case, the probability of a chance coincidence is given by
In these expressions, we have considered all objects that are seen in the radio sky. However, we can use the flux variability information to reduce the chance coincidence even further. The authors in Becker et al. (2010), Bannister et al. (2011) and Croft et al. (2010) show that the number of variable sources on a timescale of 7–22 yr is of the order of a few percent. Using VLA and three epochs spanning 15 yr, Becker et al. (2010) show that the number of extragalactic sources with a variability of greater than 2 is less than 10 percent within the flux-density range of 1–100 mJy. Therefore, using the variability information we can increase the confidence of our detection even further.
5.3. Distinguishing between KNRs and SNRs with flux information
In the above sections, we discuss the importance of temporal measures such as the Sedov time in order to distinguish a KNR from a SNR. The measurement of flux at a given epoch may still be used for that purpose provided we know the density of the galaxy in which the KNR is located. The reader may notice that the peak flux for both SNRs and KNRs, assuming fiducial parameters, is the same in Fig. 1, which follows from Eq. (15). This may appear misleading, as the assumed external density encountered by KNRs is ten times smaller than that for SNRs. For a given density, the peak flux of a KNR is expected to be many times higher than that of a SNR, which becomes even more drastic in the case of EKNRs. Also, the spectral flux at different frequency bands (Fig. 2) will also be higher in the case of KNRs. In addition, the SNRs are expected to show distinctive line features (Woosley & Weaver 1986; Badenes et al. 2007) as well as morphologies (Lopez et al. 2009) in X-ray, which allows us to distinguish Type Ia from core-collapse supernovae. If we find a candidate object in an elliptical galaxy, we can almost certainly rule out a core-collapse supernova as the progenitor. Then, the non-detection of expected line features or morphology of Type Ia supernovae may help us in distinguishing a candidate KNR. Furthermore, as explained above, the peak luminosity for a KNR will be significantly larger. If we detect an object with L3 GHz ≳ 1027 erg s−1 Hz−1 associated with a remnant in an elliptical galaxy, this would be a very strong indication that the remnant is a KNR (or EKNR).
6. Discussion and conclusion
We have solved for the evolution of kilonova remnants (KNRs) and compare their light curves and spectral properties with supernova remnants (SNRs). While the physics is the same in both cases, we expect differences in quantitative properties due to different fiducial parameters, such as lower ejecta mass and lower external density in the KNR case. Spectral signatures such as the synchrotron cutoff, the correlation between radio and X-ray flux, and the transition from the synchrotron- to the SSC-dominated regime are features that can be used to distinguish KNRs from SNRs. As an example, around the peak of their flux, the synchrotron cutoff is of the order of 10 keV, 100 keV, and MeV for SNRs, KNRs, and EKNRs, respectively. We also note that despite the fact that most remnants are much older than the time at which their light curve peaks, due to the strong decrease in the luminosity with age during the decelerating phase, the observable sample is dominated by events observed close to their peak flux. However, as dN/dlog(t) ∼ t−1/2, one in three remnants will be approximately ten times older than tST, which is not insignificant.
For fiducial parameters (E51 = 1, Mej, ⊙ = 0.1, n0 = 0.1), we expect to detect KNRs in the near future using existing telescopes, such as VLASS. Due to the strong dependence of the observed flux on ejecta energy, extreme KNe (E51 = 10) are much easier to detect if they constitute a sizeable portion of the total KN population. As there have been no reported detections of EKNRs in the literature, we are able to put moderate constraints on their abundance relative to regular KNRs, with fEKN ≲ 0.3 assuming fiducial parameters. This constraint depends sensitively on the ejecta mass and external density distribution, as well as the neutron star merger rate, which is somewhat uncertain. We should be able to detect such objects or put strong constraints on their occurrence rate with ongoing surveys, such as VLASS and VAST, or future surveys with DSA-2000 and SKA (Hallinan et al. 2019; Braun et al. 2019).
The Sedov time for a EKNR is ∼20 years, which is at least an order of magnitude less than for a SNR. Depending on the external density, the Sedov time can be even shorter. If the remnants are detected deep in the Sedov-Taylor regime, we will not be able to easily distinguish KNRs from SNRs. However, if we do detect a remnant around its Sedov time, it may be possible to obtain a good estimate of tST with a few data points taken with a time interval of several years. A combination of estimated tST and corresponding spectral properties can provide strong evidence for the existence of a KNR. Also, if we find a candidate object in an elliptical galaxy, we can distinguish a KNR from a type Ia SNR using its brightness information or using line features and morphology in X-rays.
From the only robust KN identification to date, which is associated with the GW-detected NS merger GW170817, we can infer the ejecta mass and velocity for a given electron mass fraction Ye. Different choices of Ye can result in different interpretations of the properties of the ejecta (Metzger 2019). If we are able to infer ejecta mass and velocity from a remnant, we should be able to break the degeneracy and can independently infer Ye; this will have implications in terms of r-process nucleosynthesis and help us understand how much radioactive material was synthesised during the formation of the KN.
This is slightly below the Klein-Nishina cutoff in Fig. 2, but not by a large margin.
Acknowledgments
SKA is supported by ARCO fellowship. PB’s work was supported by a grant (no. 2020747) from the United States-Israel Binational Science Foundation (BSF), Jerusalem, Israel, by a grant (no. 1649/23) from the Israel Science Foundation and by a grant (no. 80NSSC 24K0770) from the NASA astrophysics theory program. KH’s work was supported by JSPS KAKENHI Grant-in-Aid for Scientific Research JP23H01169, JP23H04900, and JST FOREST Program JPMJFR2136.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Phys. Rev. Lett., 119, 161101 [Google Scholar]
- Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 011048 [NASA ADS] [Google Scholar]
- Ai, S., Zhang, B., & Zhu, Z. 2022, MNRAS, 516, 2614 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, M. M., Mooley, K. P., Hallinan, G., et al. 2020, ApJ, 903, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Arcavi, I., Hosseinzadeh, G., Howell, D. A., et al. 2017, Nature, 551, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Hughes, J. P., Bravo, E., & Langer, N. 2007, ApJ, 662, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Balasubramanian, A., Corsi, A., Mooley, K. P., et al. 2022, ApJ, 938, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bannister, K. W., Murphy, T., Gaensler, B. M., Hunstead, R. W., & Chatterjee, S. 2011, MNRAS, 412, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Barniol Duran, R., Whitehead, J. F., & Giannios, D. 2016, MNRAS, 462, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., Helfand, D. J., White, R. L., & Proctor, D. D. 2010, AJ, 140, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
- Beniamini, P., & Lu, W. 2021, ApJ, 920, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., & Piran, T. 2024, ApJ, 966, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Nava, L., Duran, R. B., & Piran, T. 2015, MNRAS, 454, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Gill, R., & Granot, J. 2022, MNRAS, 515, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Kulkarni, S. R., & Djorgovski, S. G. 2002, AJ, 123, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [Google Scholar]
- Braun, R., Bonaldi, A., Bourke, T., Keane, E., & Wagg, J. 2019, ArXiv e-prints [arXiv:1912.12699] [Google Scholar]
- Chevalier, R. A. 1982, ApJ, 259, 302 [Google Scholar]
- Chevalier, R. A. 1998, ApJ, 499, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Coulter, D. A., Foley, R. J., Kilpatrick, C. D., et al. 2017, Science, 358, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, S., Bower, G. C., Ackermann, R., et al. 2010, ApJ, 719, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Piro, A. L., Shappee, B. J., et al. 2017, Science, 358, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Duran, R. B., & Giannios, D. 2015, MNRAS, 454, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Eftekhari, T., & Berger, E. 2017, ApJ, 849, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Cenko, S. B., Kennea, J. A., et al. 2017, Science, 358, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, R., & Metzger, B. D. 2016, Ann. Rev. Nucl. Part. Sci., 66, 23 [CrossRef] [Google Scholar]
- Frail, D. A., Waxman, E., & Kulkarni, S. R. 2000, ApJ, 537, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Giacomazzo, B., & Perna, R. 2013, ApJ, 771, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, Y. A., Boyce, M. M., O’Dea, C. P., et al. 2021, ApJS, 255, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, Y. A., Rudnick, L., Andernach, H., et al. 2023, ApJS, 267, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Ramirez-Ruiz, E., Taylor, G. B., et al. 2006, ApJ, 638, 391 [CrossRef] [Google Scholar]
- Green, D. A. 2019, J. Astrophys. Astron., 40, 36 [Google Scholar]
- Hajela, A., Margutti, R., Alexander, K. D., et al. 2019, ApJ, 886, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Ravi, V., Weinreb, S., et al. 2019, Bull. Am. Astron. Soc., 51, 255 [Google Scholar]
- Hopkins, A. M., Afonso, J., Chan, B., et al. 2003, AJ, 125, 465 [Google Scholar]
- Horesh, A., Hotokezaka, K., Piran, T., Nakar, E., & Hancock, P. 2016, ApJ, 819, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Hotokezaka, K., & Piran, T. 2015, MNRAS, 450, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Hotokezaka, K., Beniamini, P., & Piran, T. 2018, Int. J. Mod. Phys. D, 27, 1842005 [Google Scholar]
- Kathirgamaraju, A., Giannios, D., & Beniamini, P. 2019, MNRAS, 487, 3914 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpatrick, C. D., Foley, R. J., Kasen, D., et al. 2017, Science, 358, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Kisaka, S., Ioka, K., & Nakar, E. 2016, ApJ, 818, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Beniamini, P., Gupta, O., & Cordes, J. M. 2024, MNRAS, 527, 457 [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Leaman, J., Chornock, R., et al. 2011, MNRAS, 412, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Lipunov, V. M., Gorbovskoy, E., Kornilov, V. G., et al. 2017, ApJ, 850, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Ramirez-Ruiz, E., Badenes, C., et al. 2009, ApJ, 706, L106 [Google Scholar]
- Margalit, B., & Metzger, B. D. 2019, ApJ, 880, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Margalit, B., & Piran, T. 2015, MNRAS, 452, 3419 [NASA ADS] [CrossRef] [Google Scholar]
- Margalit, B., & Piran, T. 2020, MNRAS, 495, 4981 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Metzger, B. D. 2019, Liv. Rev. Relativ., 23, 1 [NASA ADS] [Google Scholar]
- Metzger, B. D., & Piro, A. L. 2014, MNRAS, 439, 3916 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Martínez-Pinedo, G., Darbha, S., et al. 2010, MNRAS, 406, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Hallinan, G., Bourke, S., et al. 2016, ApJ, 818, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Frail, D. A., Dobie, D., et al. 2018, ApJ, 868, L11 [Google Scholar]
- Mooley, K. P., Margalit, B., Law, C. J., et al. 2022, ApJ, 924, 16 [CrossRef] [Google Scholar]
- Murphy, T., Kaplan, D. L., Stewart, A. J., et al. 2021, PASA, 38, e054 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Piran, T. 2011, Nature, 478, 82 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connor, B., Beniamini, P., & Kouveliotou, C. 2020, MNRAS, 495, 4782 [CrossRef] [Google Scholar]
- Ofek, E. O., Frail, D. A., Breslauer, B., et al. 2011, ApJ, 740, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, R., Troja, E., Bruni, G., et al. 2021, MNRAS, 500, 1708 [Google Scholar]
- Richards, E. A. 2000, ApJ, 533, 611 [Google Scholar]
- Rosswog, S. 2015, Int. J. Mod. Phys. D, 24, 1530012 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Esin, A. A. 2001, ApJ, 548, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [Google Scholar]
- Schroeder, G., Margalit, B., Fong, W.-F., et al. 2020, ApJ, 902, 82 [Google Scholar]
- Shibata, M., & Hotokezaka, K. 2019, Ann. Rev. Nucl. Part. Sci., 69, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., & Giannios, D. 2013, ApJ, 778, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Chen, T. W., Jerkstrand, A., et al. 2017, Nature, 551, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Soares-Santos, M., Holz, D. E., Annis, J., et al. 2017, ApJ, 848, L16 [CrossRef] [Google Scholar]
- Takami, H., Kyutoku, K., & Ioka, K. 2014, Phys. Rev. D, 89, 063006 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M. 2016, Adv. Astron., 2016, 634197 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Piro, L., van Eerten, H., et al. 2017, Nature, 551, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Sand, D. J., Yang, S., et al. 2017, ApJ, 848, L24 [CrossRef] [Google Scholar]
- Wang, H., Beniamini, P., & Giannios, D. 2024, MNRAS, 527, 5166 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1986, ARA&A, 24, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y.-W., Zhang, B., & Gao, H. 2013, ApJ, 776, L40 [CrossRef] [Google Scholar]
- Yuan, W., Zhang, C., Chen, Y., & Ling, Z. 2022, ArXiv e-prints [arXiv:2209.09763] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. 2007, A&A, 465, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Relativistic equations for dynamical properties of kilonovae
In this section we provide fully relativistic equations for the evolution of ejecta. For this work, we find that relativistic corrections are mildly important for some extreme parameter cases. For such cases, we directly solve these equations numerically. The dynamical equation for the ejecta can be written as
where E is the kinetic energy, Γ is the bulk Lorentz factor and Rej is the size of ejecta in observer frame. The ejecta size is related to the observed time as Rej = (1 + βej)Γ2βejct. The rest of the symbols have the same interpretation as in Sect. 2. In the coasting phase, 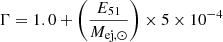 .
.
Assuming a fraction ϵe of the shocked energy is transferred to the electrons, by the same procedure as in Sect. 3, we obtain
The comoving magnetic energy density is given by
The synchrotron energy loss rate per electron in observer frame is given by
where Ee is the electron’s energy. The characteristic frequency in observer frame is given by
The power in observer frame is then
assuming βm → 1. The calculation of luminosity and flux follows the same way as in Sect. 3.1.
Appendix B: Cooling due to synchrotron
The Lorentz factor γc, sync for which the electrons cool within the timescale of expansion of the ejecta, i.e. the dynamical time, can be evaluated as, 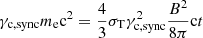 , or
, or
for γc, sync > > 1 which can be simplified to, 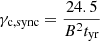 . The cooling frequency is given by, νc, sync = γc, sync2νB. In the coasting phase, B is constant, hence, νc, sync goes like
. The cooling frequency is given by, νc, sync = γc, sync2νB. In the coasting phase, B is constant, hence, νc, sync goes like 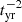 . Substituting the expression for B is ST regime, we have
. Substituting the expression for B is ST regime, we have
Appendix C: Synchrotron self-absorption frequency (νsa)
In the optically thin regime, the power per Hz at νm per steradian is given by
Assuming νsa > νm, the power at νsa is given by, 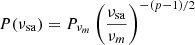 . The intensity at νsa is given by
. The intensity at νsa is given by
The intensity of a blackbody is given by
where kBT ∼ γsamec2 with 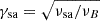 . Equating the two and using p = 2.5, the expression for νsa is given by
. Equating the two and using p = 2.5, the expression for νsa is given by
or νsa ∼ 8 × 109(B2.25R19n0ξe)1/3.25 Hz. Substituting the expressions for the physical parameters, we have
Appendix D: Computation of SSC flux
The number flux of inverse Compton photons is given by (Blumenthal & Gould 1970; Sari & Esin 2001)
where 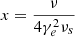 , g(x) = 1 + x − 2x2 + 2xlog(x) in Thomson approximation and
, g(x) = 1 + x − 2x2 + 2xlog(x) in Thomson approximation and 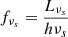 where Lνs is obtained in Sect. 3.1. Technically, the flux on both sides of the equation is at the location of shocked gas but they can be transformed to the observed flux with the same factor of
where Lνs is obtained in Sect. 3.1. Technically, the flux on both sides of the equation is at the location of shocked gas but they can be transformed to the observed flux with the same factor of 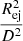 which cancels out. The factor g(x) has support only over 0 ≲ x ≲ 1 which effectively cuts off the νs integral for a given ν. Expanding the definition of the quantities, we have
which cancels out. The factor g(x) has support only over 0 ≲ x ≲ 1 which effectively cuts off the νs integral for a given ν. Expanding the definition of the quantities, we have
We solve this equation numerically and obtain the number flux which can be converted to Lν by multiplying hν. We compare synchrotron, SSC and bremsstrahlung flux for our fiducial cases in Fig. 2.
Appendix E: Bremsstrahlung emission
The thermal energy of electron is related to the shock energy via electron kinetic energy. Therefore, the temperature of electron is given by
which after substitution of βej becomes
The spectrum has a cutoff frequency 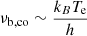 . The total emitted power per unit volume per frequency is given by
. The total emitted power per unit volume per frequency is given by
Assuming gff = 1 and hν ≲ kBT, the luminosity per frequency is given by
The corresponding flux is given by
Appendix F: Number of SNe in the Milky Way
In this work, we assume the volumetric rate of formation of supernova remnants to be 300 times greater than kilonova. Using this, the number density of SNRs ∼105 Gpc−3tyr where tyr is the age of SNRs and we have assumed that observed flux is not the limiting factor. We will compute the number of SNRs in the Milky Way and compare it with the number of detected objects which is ∼300 in Green (2019) as a consistency check. This is a revised catalogue of Galactic SNRs and for each SNR, Galactic coordinates, angular size, flux density, type of SNR and spectral index are provided. We find that most of the sources in the catalogue, have fluxes of the order of few Jy at ν ∼ GHz. Using the fiducial parameters, the flux in the ST regime in our model is given by (Eq. 13)
Assuming all SN are located at 10 kpc from us, 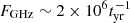 Jy. Therefore, most SN in the catalogue are 105 − 106 year old. To convert the volumetric formation rate to galactic rate, we use the number density of MW type galaxy ∼0.01 Mpc−3 (Hotokezaka et al. 2018). Combining these and assuming all remnants to be of the order of 105 years old, the expected SNRs in our galaxy turns out to be
Jy. Therefore, most SN in the catalogue are 105 − 106 year old. To convert the volumetric formation rate to galactic rate, we use the number density of MW type galaxy ∼0.01 Mpc−3 (Hotokezaka et al. 2018). Combining these and assuming all remnants to be of the order of 105 years old, the expected SNRs in our galaxy turns out to be 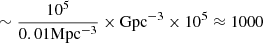 which gives roughly similar numbers to those in the catalogue.
which gives roughly similar numbers to those in the catalogue.
All Figures
 |
Fig. 1. Flux at 3 GHz as a function of age and ejecta size with D = 10 Mpc for an SNR (E51 = 1, Mej, ⊙ = 1, n0 = 1), a KNR (E51 = 1, Mej, ⊙ = 0.1, n0 = 0.1), and a EKNR (E51 = 10, Mej, ⊙ = 0.1, n0 = 0.1). We have chosen |
| In the text | |
 |
Fig. 2. νLν as a function of ν at tST for a SNR (black), a KNR (red), and a EKNR (blue). |
| In the text | |
 |
Fig. 3. Abundance of SNR, KNR and EKNRs. Top: Number of systems observed by an all-sky radio survey per logarithmic unit of age, |
| In the text | |
 |
Fig. 4. Dependence of EKNR abundance on surrounding density and mass distribution. Top: |
| In the text | |
 |
Fig. 5. Detection prospects for KNRs from their temporal evolution information. Top: |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.