| Issue |
A&A
Volume 692, December 2024
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202450490 | |
| Published online | 29 November 2024 | |
Chaotic magnetic disconnections trigger flux eruptions in accretion flows channeled onto magnetically saturated Kerr black holes
1
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
2
Astronomical Observatory, University of Warsaw, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
3
Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotnikow 32/46, 02-668 Warsaw, Poland
⋆ Corresponding author; knalew@camk.edu.pl
Received:
24
April
2024
Accepted:
8
October
2024
Context. Magnetized accretion flow onto a black hole (BH) may lead to the accumulation of poloidal magnetic flux across its horizon, which for high BH spin can power far-reaching relativistic jets. The BH magnetic flux is subject to a saturation mechanism by means of magnetic flux eruptions involving relativistic magnetic reconnection. Such accretion flows have been described as magnetically arrested disks (MAD) or magnetically choked accretion flows (MCAF).
Aims. The main goal of this work is to describe the onset of relativistic reconnection and initial development of magnetic flux eruption in accretion flow onto magnetically saturated BHs.
Methods. We analyzed the results of 3D general relativistic ideal magnetohydrodynamic (GRMHD) numerical simulations in the Kerr metric, starting from weakly magnetized geometrically thick tori rotating either prograde or retrograde. We integrated large samples of magnetic field lines in order to probe magnetic connectivity with the BH horizon.
Results. The boundary between magnetically connected and disconnected domains coincides roughly with enthalpy equipartition. The geometrically constricted innermost part of the disconnected domain develops a rigid structure of magnetic field lines – rotating slowly and insensitive to the BH spin orientation. The typical shape of innermost disconnected lines is a double spiral converging to a sharp inner tip anchored at the single equatorial current layer. The foot-points of magnetic flux eruptions are found to zip around the BH along with other azimuthal patterns.
Conclusions. Magnetic flux eruptions from magnetically saturated accreting BHs can be triggered by minor density gaps in the disconnected domain, resulting from the chaotic disconnection of plasma-depleted magnetospheric lines. Accretion flow is effectively channeled along the disconnected lines toward the current layer, and further toward the BH by turbulent cross-field diffusion. Rotation of flux eruption foot-points may contribute to the variability of BH crescent images.
Key words: accretion / accretion disks / black hole physics / magnetic fields / magnetic reconnection / magnetohydrodynamics (MHD) / relativistic processes
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Accretion onto black holes (BHs) is the engine of various astrophysical phenomena, including active galactic nuclei (AGNs), tidal disruption events (TDEs), gamma-ray bursts (GRBs), X-ray binaries (XRBs). Accretion flows have long been considered to be magnetized (Lynden-Bell 1969; Shakura & Sunyaev 1973), and even in very weakly magnetized accretion flows the magnetic field can play fundamental roles; e.g., magnetorotational instability (MRI) enables accretion by transporting angular momentum outward (Balbus & Hawley 1991). Accretion flows can also transport magnetic fields toward the BH, depending on the effective balance between advection and diffusion (Lubow et al. 1994). Advection of magnetic fields is more efficient for geometrically thick accretion flows; at low mass accretion rates (in terms of the Eddington luminosity) such flows are hot, radiatively inefficient (RIAF), and (heat-)advection dominated (ADAF) (Yuan & Narayan 2014).
As plasma is swallowed by the BH, it is separated from poloidal magnetic field, which accumulates across the BH outer horizon with unsigned magnetic flux ΦBH, easily overcoming the gravitational expulsion (Meissner) effect (e.g., Komissarov & McKinney 2007; James et al. 2024). The magnetic fields connected to the BH horizon form a highly magnetized, essentially force-free, bipolar BH magnetosphere. If the BH is spinning, such a magnetosphere induces an outward Poynting flux in the Blandford-Znajek mechanism (Blandford & Znajek 1977), which is the electromagnetic equivalent of the Penrose process (Lasota et al. 2014). Such Poynting flux is proportional to ΦBH2 and a function of the BH spin a (Tchekhovskoy et al. 2010; Camilloni et al. 2022). It drives a powerful outflow that gradually accelerates and collimates into a pair of relativistic jets (Begelman et al. 1984; Blandford et al. 2019).
Relativistic jets have dramatic observational manifestations. They are directly observed in ∼10% of AGNs belonging to the radio-loud group (e.g., Kellermann et al. 1998), which includes blazars (with huge relativistic luminosity boost due to jet orientation close to the line of sight) and radio galaxies (without strong luminosity boost) (Urry & Padovani 1995); and in certain low-mass XRBs (microquasars, Mirabel & Rodríguez 1999). Moreover, they are inferred indirectly due to the inevitability of relativistic beaming in all GRBs (Piran 2004; Zhang 2018) and some TDEs (Gezari 2021). Many relativistic jets dissipate very significant fractions of their power (Ghisellini et al. 2014) and are very efficient particle accelerators (Biteau et al. 2020; LHAASO Collaboration 2023), which makes blazars the dominant cosmic sources of energetic gamma-ray radiation (Ajello et al. 2015; Madejski & Sikora 2016). The most detailed observational picture of a relativistic jet, in particular of its gradual collimation and origin at the BH, is provided by one of the nearest radio galaxies, M87 (e.g., Junor et al. 1999; Hada et al. 2016; Walker et al. 2018; Kim et al. 2018; Lu et al. 2023).
A higher ΦBH allows for a more powerful jet, but it also means a stronger back-reaction of the BH magnetosphere on the accretion flow. There is an upper limit on the value of ΦBH (and hence on the power of relativistic jets driven by Poynting fluxes), roughly 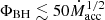 (in the natural Gaussian units with c = G = 1), where ṁacc is the mass-accretion rate (Tchekhovskoy et al. 2011); this limit depends moderately on the BH spin (Narayan et al. 2022; Zhang et al. 2024). Accretion flows interacting with such saturated magnetospheres were identified by Tchekhovskoy et al. (2011) as the magnetically arrested disks (MADs), referring to a model proposed by Narayan et al. (2003)1. Alternatively, they were described by McKinney et al. (2012) as the magnetically choked accretion flows (MCAF)2. In Sect. 4, we argue that at magnetic saturation the bulk of accretion flow is effectively “channeled” along regular magnetic fields and the equatorial current layer.
(in the natural Gaussian units with c = G = 1), where ṁacc is the mass-accretion rate (Tchekhovskoy et al. 2011); this limit depends moderately on the BH spin (Narayan et al. 2022; Zhang et al. 2024). Accretion flows interacting with such saturated magnetospheres were identified by Tchekhovskoy et al. (2011) as the magnetically arrested disks (MADs), referring to a model proposed by Narayan et al. (2003)1. Alternatively, they were described by McKinney et al. (2012) as the magnetically choked accretion flows (MCAF)2. In Sect. 4, we argue that at magnetic saturation the bulk of accretion flow is effectively “channeled” along regular magnetic fields and the equatorial current layer.
The saturation mechanism for BH magnetic flux involves episodic, relatively fast decreases of ΦBH with amplitudes up to roughly 50% of the preceding maximum levels. Magnetic-flux eruptions localized azimuthally (along coordinate ϕ), directed radially outwards along the equatorial plane, resulting in compact tubes of largely ‘vertical’ (perpendicular to the equatorial plane) magnetic fields ejected from the BH (Tchekhovskoy et al. 2011) are associated with such BH flux decreases. Signatures of magnetic-flux eruptions have also been seen in the 3D pseudo-Newtonian magnetohydrodynamical (MHD) simulations presented by Igumenshchev (2008) and Punsly et al. (2009).
Such magnetic flux eruptions may have various interesting consequences, including the ejection of magnetic-flux tubes orbiting the BH (applied to observations with the GRAVITY instrument at the Very Large Telescope Interferometer of hot-spots orbiting Sgr A*, the supermassive BH at the center of our Galaxy (Dexter et al. 2020; Porth et al. 2021), and flares of energetic radiation (Scepi et al. 2022; Hakobyan et al. 2023; Najafi-Ziyazi et al. 2024). Eruptions should also be particularly relevant for the substructure and variability of BH crescent images obtained by the Event Horizon Telescope (EHT) collaboration for M87* (the supermassive BH at the center of galaxy M87) (Event Horizon Telescope Collaboration 2019a) and Sgr A* (Event Horizon Telescope Collaboration 2022). A much higher BH mass for M87*, MM87* ≃ 6.5 × 109 M⊙, with M⊙ being the solar mass (Event Horizon Telescope Collaboration 2019d), implies a conveniently long dynamical timescale of GMM87*/c3 ≃ 9 h. The image of M87* obtained by the EHT suggests the presence of a distinct bright hot-spot in the ESE crescent sector (Nalewajko et al. 2020), which also appears to be strongly depolarized (Event Horizon Telescope Collaboration 2021a). Moreover, during the six-day EHT campaign in April, 2017, the image of M87* might have rotated counterclockwise by ≃23° (Event Horizon Telescope Collaboration 2019b), which coincides (Nalewajko 2023) with the rotation rate of the polarization vector for unresolved emission of M87* measured by ALMA (Goddi et al. 2021) and corrected for Faraday rotation. Although those results are not considered significant by the EHT collaboration, future millimeter-VLBI (very long baseline interferometry) monitoring campaigns should be able to measure coherent rotation patterns of substructures in the M87* crescent image. General relativistic magnetohydrodynamical (GRMHD) simulations predict a highly sub-Keplerian rotation rate of ∼1° per GM/c3 for ray-traced crescent image patterns, only very weakly depending on the BH spin or the sense of accretion flow angular momentum (prograde vs. retrograde) (Conroy et al. 2023).
The driving mechanism of the BH magnetic flux eruptions had been unclear – it has been interpreted as interchange modes (McKinney et al. 2012; Marshall et al. 2018), or as magneto-convection (Begelman et al. 2022). Recently, it was demonstrated as the large-scale relativistic magnetic reconnection by “extreme resolution” (effectively 5376 × 2304 × 2304 cells) 3D ideal GRMHD simulations (Ripperda et al. 2022). Extreme resolution allowed them to achieve thin current layers with sufficiently high Lundquist (magnetic Reynolds) numbers of S = vAL/η (with vA being the Alfvén speed, L the current layer length, and η the magnetic diffusivity); these are unstable to tearing modes and break into chains of magnetic-flux tubes (plasmoids) that determine a reconnection rate independent of the numerical magnetic diffusion. These authors also compared their main results with a “low-resolution” case (288 × 128 × 128 cells), providing several arguments against the reliability of the latter. In particular, a reconnection rate based on the numerical diffusion is significantly overestimated. On the other hand, strict adherence to conservation laws (energy, momentum, mass, magnetic flux) ensures that low-resolution results are qualitatively robust; i.e., many features of magnetic flux saturation and eruptions can be reproduced (e.g., flux saturation levels, depth of density gaps, relativistic temperature levels, and orbiting hot-spot trajectories), even at a “test resolution” of 72 × 64 × 64 (Nalewajko et al. 2024).
In this paper, we present the results of ideal GRMHD simulations of geometrically thick, hot, radiatively inefficient, weakly magnetized accretion flows with a ‘standard’ effective resolution of 288 × 256 × 256, similar to those presented in Janiuk & James (2022). Our analysis is focused on investigating the initiation mechanism of magnetic flux eruptions, a problem that does not depend on the formation of plasmoid chains, but is centered on the formation of magnetic X-points. In addition, we obtained qualitatively novel insights into the mechanism of regular accretion flows onto magnetically saturated BHs.
The 3D structure in quasi-spherical coordinates (r, θ, ϕ) of accretion flows onto magnetically saturated BHs and magnetic-flux eruptions cannot be captured by standard 2D maps in (r, θ) or (r, ϕ) coordinates. Although the innermost accretion flow is constricted into a narrow disk, the disk is not strictly aligned with the equatorial plane or intrinsically symmetric. For example, a slice along the equatorial plane may partially cross through a low-density magnetosphere bulging against a disk warp, which may be confused with a real density gap, or interpreted as signature of interchange instability (McKinney et al. 2012). Likewise, a latitudinal slice for constant ϕ cuts obliquely through the velocity and magnetic fields, making it very difficult to properly connect structures belonging to the same magnetic field line.
In order to obtain additional insight, we integrated large and complete samples of magnetic-field lines. Those lines can be divided into two fundamental classes: connected or disconnected from the BH horizon (hereafter, the terms “connected” and “disconnected” are used; accordingly, “connection” of a line means its transition from disconnected to connected, and “disconnection” means its transition from connected to disconnected). The disconnected lines are especially interesting, because they define a volume domain that is very flattened in the magnetically saturated BH state due to magnetic constriction, providing a fairly unobstructed view. We used such line samples to divide the volume around an accreting BH into the connected and disconnected domains. We identify the disconnected domain, which includes the entire accretion flow, winds, and ejected magnetic-flux tubes, as particularly useful to illustrate the initial development of magnetic-flux eruptions.
In Sect. 2, we describe the setup of GRMHD numerical simulations and our method of field-line integration. Simulation results are presented in Sect. 3 according to their distributions in Kerr-Schild coordinates (t, r, θ, ϕ), with Sect. 3.1 comparing time histories, Sect. 3.2 presenting detailed results for our reference prograde simulation, Sect. 3.3 presenting selected results for the retrograde simulation, Sect. 3.4 comparing (t, ϕ) diagrams of magnetic flux eruptions, and Sect. 3.5 comparing (r, θ) maps of parameters measuring the alignment between velocity and magnetic fields. The presentation of our reference simulation in Sect. 3.2 includes the following: maps in the (r, θ) coordinates (Sect. 3.2.1); maps in the (r, ϕ) coordinates (Sect. 3.2.2); 3D structures of magnetic field lines for regular accretion flow (Sect. 3.2.3), for magnetic-flux eruption (Sect. 3.2.4), and for short-term time sequences (Sect. 3.2.5). Section 4 presents the discussion and Sect. 5 the conclusions.
We used natural Heaviside-Lorentz (HL) units with c = G = 1 and with the 4π factors absorbed into the definition of magnetic field (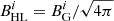 with BGi in Gaussian units)3. The BH mass is also set to unity M = 1 and sometimes omitted. Greek indices spanning {0, 1, 2, 3} are used for space-time forms (e.g., 4-vectors Xμ), and Latin indices spanning {1, 2, 3} are used for spatial forms (e.g., 3-vectors Xi).
with BGi in Gaussian units)3. The BH mass is also set to unity M = 1 and sometimes omitted. Greek indices spanning {0, 1, 2, 3} are used for space-time forms (e.g., 4-vectors Xμ), and Latin indices spanning {1, 2, 3} are used for spatial forms (e.g., 3-vectors Xi).
2. Methods
2.1. Setup of GRMHD simulations
We performed 3D ideal GRMHD numerical simulations in the Kerr spacetime using the public code Athena++ (Stone et al. 2020; White et al. 2016)4, which has been used to explore accretion flows on magnetically saturated BHs (White et al. 2019). This code solves covariant equations of continuity ∇μ(ρuμ) = 0, energy-momentum conservation ∇μTμν = 0, and Maxwell ∇μ*Fμν = 0. In the above, ∇μ is the covariant derivative, ρ is the plasma density, uμ is the four-velocity, Tμν = (w + b2)uμuν + (P + b2/2)gμν − bμbν is the energy-momentum tensor, w = ρ + [γ/(γ − 1)]P is the plasma enthalpy density, γ is the adiabatic index, P is the plasma pressure, bμ is the magnetic four-vector, b2 is the magnetic enthalpy density (b2/2 equals both the magnetic energy density and magnetic pressure), gμν is the inverse metric tensor, and *Fμν = bμuν − bνuμ is the dual electromagnetic field tensor. The magnetic four-vector bμ is related to the magnetic-field three-vector Bi via b0 = gμiuμBi (where gμν is the metric tensor) and bi = (Bi + uib0)/u0; hence, *Fi0 = biu0 − b0ui = Bi (Gammie et al. 2003)5. The code uses a constrained transport algorithm to clean the magnetic-field divergence (ensuring that ![$ \partial_i [\sqrt{-g}\,B^i] = 0 $](/articles/aa/full_html/2024/12/aa50490-24/aa50490-24-eq3.gif) , where g is the metric tensor determinant) (White et al. 2016).
, where g is the metric tensor determinant) (White et al. 2016).
The primitive parameters returned by the Athena++ code are plasma density ρ, plasma pressure P, three components of the fiducial velocity 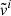 , and three components of the magnetic-field vector Bi. The fiducial velocity is a projection,
, and three components of the magnetic-field vector Bi. The fiducial velocity is a projection, 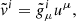 of the stationary four-velocity, uμ = dxμ/dτ (with τ being the proper time; satisfying gμνuμuν = −1), by the fiducial metric tensor
of the stationary four-velocity, uμ = dxμ/dτ (with τ being the proper time; satisfying gμνuμuν = −1), by the fiducial metric tensor 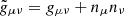 , with nμ = ( − α, 0, 0, 0) being the four-velocity of the fiducial observer and α = ( − g00)−1/2 the lapse. The stationary four-velocity is calculated from
, with nμ = ( − α, 0, 0, 0) being the four-velocity of the fiducial observer and α = ( − g00)−1/2 the lapse. The stationary four-velocity is calculated from 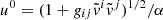 and
and 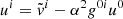 (Noble et al. 2006).
(Noble et al. 2006).
Simulations were performed in the horizon-penetrating quasi-spherical Kerr-Schild coordinates xμ = (t, r, θ, ϕ) for the spin of |a| = 0.9, for which the outer horizon radius is 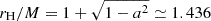 . The metric tensor gμν nonzero components are gtt = −1 + 2r/Σ, grr = 1 + 2r/Σ, gθθ = Σ, gϕϕ = (r2 + a2 + 2ra2sin2θ/Σ)sin2θ, gtr = grt = 2r/Σ, gtϕ = gϕt = −2arsin2θ/Σ, and grϕ = gϕr = −(1 + 2r/Σ)asin2θ, with Σ = r2 + a2cos2θ; the determinant of this metric is g = −Σ2sin2θ.
. The metric tensor gμν nonzero components are gtt = −1 + 2r/Σ, grr = 1 + 2r/Σ, gθθ = Σ, gϕϕ = (r2 + a2 + 2ra2sin2θ/Σ)sin2θ, gtr = grt = 2r/Σ, gtϕ = gϕt = −2arsin2θ/Σ, and grϕ = gϕr = −(1 + 2r/Σ)asin2θ, with Σ = r2 + a2cos2θ; the determinant of this metric is g = −Σ2sin2θ.
Our coordinate grid is uniform in ϕ, θ, and log r. We used static mesh refinement (SMR) in order to reduce resolution around the coordinate axis (θ ≃ 0, π). In our simulations, we used three levels of SMR, with the Level-3 grid of 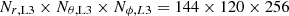 cells covering the region of rL3, min ≤ r ≤ rL3, max, θL3, min = (7/24)π = 52.5° ≤θ ≤ θL3, max = (17/24)π = 127.5°, 0 ≤ ϕ/π < 2. Radial vertices of the Level-3 grid are defined as
cells covering the region of rL3, min ≤ r ≤ rL3, max, θL3, min = (7/24)π = 52.5° ≤θ ≤ θL3, max = (17/24)π = 127.5°, 0 ≤ ϕ/π < 2. Radial vertices of the Level-3 grid are defined as ![$ r_{\mathrm{f}}[i] = r_{\mathrm{H}} (r_{\mathrm{max}}/r_{\mathrm{H}})^{(i-N_{\mathrm{H}})/(2N_{r,\rm L3}-N_{\mathrm{H}})} $](/articles/aa/full_html/2024/12/aa50490-24/aa50490-24-eq11.gif) for
for 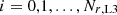 , where NH = 8 is the number of Level-3 cells inside the horizon6 and rmax = 500M is the maximum radius of the Level-0 grid; hence, rL3, min = rf[0]≃1.21M and
, where NH = 8 is the number of Level-3 cells inside the horizon6 and rmax = 500M is the maximum radius of the Level-0 grid; hence, rL3, min = rf[0]≃1.21M and ![$ r_{\mathrm{L3,max}} = r_{\mathrm{f}}[N_{r,\rm L3}] \simeq 24.6 M $](/articles/aa/full_html/2024/12/aa50490-24/aa50490-24-eq13.gif) .
.
Our simulations were initiated from an axisymmetric untilted torus in hydrodynamical equilibrium described by Fishbone & Moncrief (1976). For |a| = 0.9, we considered the prograde case (effective spin of a = 0.9) and the retrograde case (effective spin of a = −0.9). The torus extends from an inner radius rin (6M for a = 0.9; 11.25M for a = −0.9) to a fixed outer edge rout = 70M (the specific enthalpy satisfies h(6M) = h(rin) = h(rout); in the prograde case, rin = 6M; in the retrograde case, rin > 6M is another root of h). The density peak ρpeak = 1 (in code units) and the pressure peak Ppeak (0.0066 for a = 0.9; 0.0026 for a = −0.9) are located at the same radius, rpeak (13M for a = 0.9; 22.2M for a = −0.9), at which point the model evaluates the Keplerian specific angular momentum, lpeak = l(rpeak), which is assumed to be constant across the torus. The magnetic vector potential was set as Aϕ ∝ r5 max{ρ − ρmax/20, 0}, peaking at the amplitude of 2 × 10−7 in code units at the radius rpeak, A (34M for a = 0.9; 44M for a = −0.9); hence, at rpeak the plasma parameter is βpeak = 2Ppeak/bpeak2 (1920 for a = 0.9; 1150 for a = −0.9) with bpeak2 ≡ b2(rpeak). We also introduced, within the initial torus, a random perturbation to the radial component of fiducial four-velocity 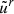 with an amplitude of ±5%.
with an amplitude of ±5%.
We also set numerical floor profiles of density ρfloor(r) = max{10−4r−1.5, 10−6} and pressure Pfloor(r) = max{10−6r−2.5, 10−8} and limits on the plasma parameter βmin = 10−3, magnetization σmax = 100, and bulk Lorentz factor umaxt = 50. The adiabatic index was set as γ = 13/9 (e.g., White et al. 2019).
In the configuration of the Athena++ code, we selected the Harten-Lax-van Leer-Einfeldt (HLLE) Riemann solver and the piecewise parabolic method (PPM) for the spatial reconstruction of primitive variables (White et al. 2019; Porth et al. 2019). For time integration, we selected the van Leer predictor-corrector scheme for long-term runs, and the fourth-order Runge-Kutta scheme for short-term runs with frequent output of full data cubes, in both cases setting the Courant-Friedrichs-Lewy parameter CFL = 0.5.
2.2. Magnetic-field-line integration
Magnetic-field lines were integrated in the Kerr-Schild coordinates (r, θ, ϕ) (with r in units of M and θ, ϕ in radians) using a fourth-order Runge-Kutta scheme. The input consists of data cubes for components of magnetic-field three-vector Bn1, n2, n3r, Bn1, n2, n3θ, Bn1, n2, n3ϕ at grid nodes (rn1, θn2, ϕn3). For every position of interest, local field components were calculated by trilinear interpolation using the eight grid nodes at the vertices of the volume cell including that position. Position xai would be advanced to xa + 1i = xai + (Bi/|B|) δl using a simplified norm, |B|2 = ∑i(Bi)2 (no difference was found when using the metric norm), and fixed integration step, δl = 0.02. We tested for accuracy against simple analytical solutions and for convergence in δl. Integration was performed within the Level-3 SMR region and over the radial range of rH < r < rmax, with rmax = 6M. Line samples were seeded from fixed positions at r = r0 (r0 = 5.9M for disconnected lines; r0 = 1.42M for doubly connected lines) and for every grid element in θL3, min < θ0 < θL3, max and 0 ≤ ϕ0 < 2π.
3. Results
3.1. Histories in (t)
Figure 1 presents long-term histories of the BH magnetic flux ΦBH and of its value normalized by the mass accretion rate 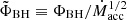 . In the prograde a = 0.9 case, the BH magnetic flux peaks at ΦBH, peak ≃ 28 at t ≃ 1500M; then, it settles to ΦBH ∼ 15 by t ≃ 5000M and remains roughly constant until at least t ∼ 30 000M. The normalized flux
. In the prograde a = 0.9 case, the BH magnetic flux peaks at ΦBH, peak ≃ 28 at t ≃ 1500M; then, it settles to ΦBH ∼ 15 by t ≃ 5000M and remains roughly constant until at least t ∼ 30 000M. The normalized flux 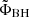 builds up much more slowly, achieving saturation at the level of
builds up much more slowly, achieving saturation at the level of 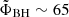 by t ∼ 14 000M. Relatively shallow magnetic-flux eruptions can be seen from t ∼ 18 000M.
by t ∼ 14 000M. Relatively shallow magnetic-flux eruptions can be seen from t ∼ 18 000M.
 |
Fig. 1. Long-term histories of BH magnetic flux ΦBH (upper panel) and its value normalized by the mass-accretion rate |
In the retrograde a = −0.9 case, the BH magnetic flux peaks at the ΦBH, peak ≃ 27 at t ≃ 3300M, followed by a slow decay. The normalized flux 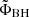 achieves saturation at the level of
achieves saturation at the level of 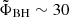 by t ∼ 14 000M7. Clear magnetic eruptions, deeper than in the prograde case, appear regularly after t ∼ 15 000M.
by t ∼ 14 000M7. Clear magnetic eruptions, deeper than in the prograde case, appear regularly after t ∼ 15 000M.
For a detailed analysis, we selected the magnetic-flux eruption beginning around t ∼ 19 500M in the prograde a = 0.9 case. The short-term history of ΦBH during that eruption is shown in Fig. 2. During this eruption, the BH magnetic flux decreases from ΦBH ≃ 17.6 at t ≃ 19 530M to ≃14.2 at t ≃ 19 825M, a decrease of ≃19% over Δt ≃ 300M. The flux decrease is not exactly uniform and monotonic. Further analysis was focused on two moments of time: at t = 19 594M, which has been identified as the actual onset of the eruption, and at t = 19 630M, in early advanced stage of the eruption.
 |
Fig. 2. Short-term histories of BH magnetic flux ΦBH during magnetic flux eruptions in the prograde a = 0.9 (red; time window from t0 = 19 500M to 20 000M) and retrograde a = −0.9 (blue; time window from t0 = 16 800M to 17 300M) cases. Two epochs of interest are indicated in the prograde case: the eruption onset at t = 19 594M and its advanced stage at t = 19 630M; one epoch is indicated in the retrograde case: the magnetic-flux peak at t = 17 050M. |
In the retrograde a = −0.9 case, we focused on the moment of peak ΦBH ≃ 17.3 at t = 17 050M. This is followed by a decrease to ΦBH ≃ 10.7 (≃38%) over Δt ≃ 165M, but it is preceded by rapid increase of ΦBH by ≃6.5%.
3.2. Reference prograde simulation
3.2.1. Maps in (r, θ) for slices in ϕ
Figure 3 shows overview maps in the (r, θ) coordinates within r ≤ 18M for the prograde a = 0.9 case at t = 19 594M. Two main regions can be distinguished: (1) geometrically thick (but converging to a thin nozzle near the BH) accretion flow centered around the equatorial plane θ = ±90°, characterized by negative radial velocity vr < 0, high plasma density (log10ρ > −3) and turbulent radial magnetic field Br (with multiple current layers); (2) paraboloidal (hourglass) bipolar magnetosphere centered around the polar axis θ = 0, 180°, characterized by positive radial velocity vr > 0, low plasma density (log10ρ < −3; mostly at the floor level), and ordered split-monopole radial magnetic field Br. A very strong density contrast means that the magnetosphere is relativistically magnetized (σ = b2/w > 1), with radial outflows accelerating over distance to relativistic speeds; it is destined to become collimated into relativistic jets.
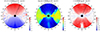 |
Fig. 3. Overview maps (r ≤ 18M) in Kerr-Schild (r, θ) coordinates of selected parameters for prograde a = 0.9 case at t = 19 594M. From the left, the first panel shows the radial component of magnetic-field three-vector Br (multiplied by r2), the second panel shows the plasma density ρ in log scale, and the third panel shows the radial component of velocity three-vector vr. The left and right sides of every panel show slices for opposite azimuths ϕL, ϕR indicated in the titles. The black circles mark the BH with horizon radius rH ≃ 1.436M. The coarse cells in the polar regions (|θ|< 30° and |θ|> 150°) result from the SMR. |
Figure 4 presents close-up (r, θ) maps (r ≤ 6M) of the same parameters (Br(×r2), log10ρ and vr). For t = 19 594M, we show the ϕ ≃ 90° slices (corresponding to the left halves of each panel in Fig. 3) with a mostly regular accretion flow that is relatively thick, dense, and cold. Nevertheless, the plasma density ρ distribution is significantly perturbed and not symmetric about the equatorial plane. The green contours of enthalpy equipartition (σ = 1) closely follow the density distribution. The boundary between magnetically connected and disconnected domains is roughly close to the σ = 1 lines with significant local departures. Hence, there are σ > 1 regions magnetically disconnected from the horizon and σ < 1 regions magnetically connected to the horizon. The boundary between positive and negative Br domains lies close to the equatorial plane, roughly midway across (latitudinally) the accretion flow; it is sharp, indicating a strong equatorial current layer. There are no signs of magnetic discontinuities (current layers) between the connected and disconnected domains. Similar structures can also be seen in (r, θ) maps of the Bϕ component, which is of comparable strength to Br. The Bθ component is weaker by an order of magnitude, and therefore disconnected field lines within r < 6M can be expected for form spirals with |Br|∼|Bϕ|≫|Bθ|.
 |
Fig. 4. Close-up maps (r ≤ 6M) in (r, θ) coordinates (with θ limited to the Level-3 SMR domain) of the same parameters as in Fig. 3 (from left to right) for the prograde a = 0.9 case at two epochs: t = 19 594M (upper row of panels) and t = 19 630M (lower row of panels). Each panel shows a slice for the azimuth ϕ indicated in its title (also marked in Fig. 5). The gray dashed circles mark the ergosphere boundary rE(θ), the black dashed lines mark the boundary of domain magnetically disconnected from the BH horizon, the green dashed lines mark equipartition between magnetic and plasma enthalpies (σ = b2/w = 1), and the magenta contours mark the relativistic temperature log10T = 0.5. |
For t = 19 630M, we present a different slice at ϕ ≃ 210° across an ongoing magnetic flux eruption. Here, the accretion flow extends only for r > 3.5M, showing a characteristic inner tip that we argue to be a magnetically arrested choke-point. However, the current layer extends all the way to the horizon. Its low-density inner section is immersed in a relatively thin layer of relativistic temperature (log10T > 0.5), which was limited to r < 2M at t = 19 594M. The boundary between magnetically connected and disconnected domains is broader than the equipartition line for 3.5M < r < 4M, which favors the presence of σ > 1 disconnected lines.
3.2.2. Maps in (r, ϕ) for statistics over θ
In Fig. 5, we present close-up maps (r ≤ 6M) in the (r, ϕ) coordinates of parameters: plasma density ρ, plasma temperature T = P/ρ (with P the plasma pressure), and radial component of the velocity three-vector vr. Recognizing from Fig. 4 that the innermost accretion flow is constricted to a thin disk that can be locally warped and azimuthally modulated, we do not simply slice the data cubes along the equatorial plane (θ = 90°). Instead, for each value of (r, ϕ), we calculated a parameter statistic over the range of θL3, min < θ < θL3, max. For the plasma density, we took the mean value, ρmean, which is dominated by the densest part of the accretion flow, but is also partially affected by the local flow thickness, and only in the gap regions does it approach the much lower floor values. For the plasma temperature, we took the maximum value, Tmax, which captures even very thin active current layers with relativistic heating due to magnetic reconnection. For the radial velocity, we take the minimum value vminr, which captures the regions in which radial outflow spans the entire range of θ; i.e., regions of completely reversed accretion.
 |
Fig. 5. Maps in (r, ϕ) coordinates of parameter statistics drawn from latitudinal arcs θL3, min < θ < θL3, max for the a = 0.9 case at two epochs: t = 19 594M (upper row of panels) and t = 19 630M (lower row of panels). From the left, the panels show (1) mean density ρmean in log scale, (2) maximum temperature Tmax in log scale, and (3) minimum radial velocity vminr. The black circles mark the BH with horizon radius rH ≃ 1.436M, the gray dashed circles mark the θ = 90° ergosphere boundary rE = 2M, the gray dashed lines in the upper panels mark the cutout ϕ sector in Figs. 6 and 7, and the black dashed lines mark the ϕ values for the (r, θ) maps presented in Fig. 4. |
At t = 19 594M, at the onset of magnetic-flux eruption, almost all ϕ sectors show high density (log10ρmean > −3), nonrelativistic temperature (log10Tmax < 0) and radial inflows (vminr < −0.1); i.e., a regular accretion flow that in principle can advect magnetic flux inward, supporting flux accumulation at the BH horizon (except that ΦBH is saturated). The line of ϕ = 90°, corresponding to the slices shown in the upper row of panels in Fig. 4, crosses through regions that are largely dense, cold, and accreting, except for a narrow spiral-density gap crossing that line for r < 2M, and a minor temperature enhancement at r ≃ 2M identified as the actual onset of magnetic flux eruption.
At t = 19 630M, a large region of relativistic temperature can be seen, touching the BH horizon over a range of 180° < ϕ < 300°, and extending to r ≃ 4M at ϕ ≃ 180°. This coincides with a deep density gap (log10ρmean ≃ −4), and with the presence of radial outflows for r > 3.5M along the spiral extension of the high-temperature patch. The line of ϕ = 210°, corresponding to the slices shown in the lower row of panels in Fig. 4, crosses through that eruption for r < 3.5M, touching the region of completely reversed accretion at r ≃ 3.5M.
3.2.3. Magnetic-field lines: Regular accretion flow
We now present a large sample of magnetic field lines in the prograde a = 0.9 case at t = 19 594M. In order to make the sample statistically complete, we seeded individual lines from a grid of fixed positions at r0 = 5.9M for every grid element in θL3, min < θ0 < θL3, max and 0 < ϕ0 < 2π. Depending on its minimum radius rmin, each line was classified as connected (rmin ≤ rH) or disconnected (rmin > rH). We also present a complete sample of doubly connected field lines, seeded just under the horizon at r0 = 1.42M and reaching a maximum radius satisfying rH < rmax < 6M.
Figure 6 presents the samples of connected lines for θ0 < 90° (upper panel) and all disconnected lines (lower panel), colored by the magnetization σ = b2/w. The distribution of connected lines appears somewhat untidy – a small number of individual connected lines can be seen sticking out in the foreground; they seem to navigate narrow channels within the disconnected domain. The disconnected lines appear more tidy – groups of neighboring lines form coherent flux tubes. The doubly connected lines form several short spiral loops. These are coherent but short-lived structures, collapsing toward the horizon along with the local accretion flow and slightly accelerated by the line tension. Additional animations show that they appear to form rather spontaneously.
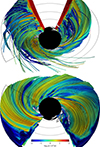 |
Fig. 6. Selected magnetic field lines within r ≤ 6M in prograde a = 0.9 case at onset of magnetic flux eruption (t = 19 594M), colored by the magnetization parameter σ = b2/w (line colors are also affected by shading, with lines seen at small angles rendered darker). Upper panel: Horizon-connected lines seeded at r0 = 5.9M for θL3, min < θ0 < 90°, seen from latitude θobs = 135°; lower panel: horizon-disconnected lines seeded at r0 = 5.9M for θL3, min < θ0 < θL3, max, seen from latitude θobs = 45°. In both panels, a small but (θ0, ϕ0)-complete sample of doubly connected lines (closed loops with max(r) < 6M) seeded at r0 = 1.42M (just under the horizon) are shown colored in white. Both images are seen from the same azimuth ϕobs = 180°; data for 150° < ϕ < 210° (except for the doubly connected lines) are cut out to reveal (r, θ) sections. Black spheres indicate the outer horizon at rH = 1.436M. The grid of arcs marks the radii r/M = 2, 3, 4, 5, 6 in the equatorial plane θ = 90° (gray) and in the ϕ = 90° quadrant spanning the latitudes θL3, min ≤ θ ≤ θL3, max (black). A small magenta patch just to the left of the horizon marks relativistic temperature (log10T ≥ 0.5). An associated movie is available online. |
Most of the disconnected lines are dominated by the plasma enthalpy (w ≫ b2; blue), and most of the connected lines are dominated by the magnetic enthalpy (b2 ≫ w; red). Such a distribution of σ reflects a strong latitudinal (along θ) stratification of the plasma density, ρ, which can be seen in the (r, θ) maps (Figs. 3 and 4). On the other hand, the magnetic enthalpy density b2 is roughly uniform in ϕ and θ (except for the equatorial current layer), and variations in the temperature T = P/ρ (affecting the relation between w and ρ) are less prominent.
The interface between the disconnected and connected domains is dominated by lines roughly in enthalpy equipartition (w ∼ b2; green). However, exceptions can be seen in the form of tubes of highly magnetized disconnected lines. We note that magnetization σ (like plasma density ρ) is fairly uniform along the field lines, but stratified across them. This reflects the ideal MHD principle that plasma is free to move along the magnetic field, but motions across the magnetic field are restricted, as they should be equivalent to transporting the field. Density redistribution is straightforward along individual field lines, but cross-field diffusion (motion between neighboring field lines) is only possible in regions where ideal MHD is violated due to numerical limitations.
One high-σ magnetic-flux tube approaches from behind the BH to a small relativistic-temperature patch (magenta) that can be seen in both panels across the ϕ = 90° quadrant at r < 2M and θ ≃ 90°. One can notice a corresponding gap of matching position and shape in (r, ϕ) in the sample of connected lines (upper panel of Fig. 6), where moderately magnetized lines (σ ∼ 1; green) are missing. Around this relativistically hot patch, disconnected field lines meet (and partially interlock) with a slightly twisted group of doubly connected lines. In Sect. 3.2.5, we demonstrate that those field lines are interacting dynamically.
Figure 7 presents the same disconnected lines colored by the radial component of plasma three-velocity vr = ur/ut. Blue regions indicate vr < 0; i.e., radial inflow or accretion. The disconnected domain is dominated by fast accretion with vr up to 0.3, especially along the equatorial plane. However, a small part of those field lines, especially those elevated furthest away from the equatorial plane in their outer sections (r > 4M), show vr > 0 (red); i.e., radial outflows. Those lines form a wind connected to the accretion flow often in its innermost regions (r < 2M).
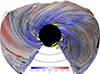 |
Fig. 7. Same as lower panel of Fig. 6, but with horizon-disconnected lines colored by the radial 3-velocity vr and doubly connected lines colored yellow. |
The distributions of σ and vr along individual disconnected and elevated field lines does not appear to be highly correlated. The most mass-depleted disconnected lines (orange on the log σ color-scale) might be expected to form an outflowing wind. Most of the elevated disconnected lines show stagnation points (white on the vr color scale) and an outflow (red) within r < 6M, regardless of their magnetization.
3.2.4. Magnetic field lines: Magnetic-flux eruption
Figure 8 shows disconnected magnetic field lines for the prograde a = 0.9 case at t = 19 630M, still in an early stage of that magnetic-flux eruption, colored by the magnetization σ (upper panel) or by the radial velocity vr (lower panel). An extended region of relativistic temperature can be seen around the front side of the BH horizon (while other sectors of the horizon are accreting regularly), which is strongly flattened along the equatorial plane. Considering that this scene is shown from the azimuth of ϕobs = 180°, this is consistent with the double-tongue-shaped region of relativistic temperature shown in the lower middle panel of Fig. 5. Parts of that relativistically hot region are filled with bunches of doubly connected field lines; other parts are filled with disconnected field lines, the remaining exposed gaps strongly suggest that antiparallel field lines from the upper and lower sides of the split-monopole horizon-connected magnetosphere come into direct contact (see the lower panels of Fig. 4). This results in relativistic reconnection with very weak guide field, which is optimal for efficient conversion of magnetic energy into heat, motion, and the nonthermal acceleration of particles (e.g., Werner & Uzdensky 2017). The magnetic-field lines crossing the region of relativistic temperature develop fast radial outflows that reach the r = 6M radius over a broad range of ϕ values. We also find much higher (compared with Fig. 6) magnetization values for horizon-disconnected field lines, not only for those connected to the main eruption region, but mainly for those most elevated from the equatorial plane. Those lines may have been depleted of mass while horizon-disconnected due to velocity divergence associated with stagnation; alternatively, they may have been depleted while horizon-connected and disconnected just a moment before.
 |
Fig. 8. Magnetic field lines disconnected from BH horizon within r ≤ 6M at a less advanced stage of magnetic flux eruption (t = 19 630M) in the prograde a = 0.9 case. Upper panel: Lines colored by magnetization parameter σ = b2/w; lower panel: lines colored by radial velocity vr. A sample of doubly connected lines seeded at r0 = 1.42M (just under the horizon) are shown colored in white (upper panel) or yellow (lower panel). The magenta patches mark regions of relativistic temperature (log10T ≥ 0.5). The view point is at θobs = 45°, ϕobs = 180°. Black sphere indicates the outer horizon at rH = 1.436M. The grid of black arcs marks the radii r/M = 2, 3, 4, 5, 6 in the equatorial plane θ = 90°, and in the ϕ = 210° quadrant spanning the latitudes θL3, min ≤ θ ≤ θL3, max. An associated movie is available online. |
3.2.5. Magnetic-field lines: Short-term dynamics
Figure 9 presents two short-term time sequences of zoomed-in views and cropped plots similar to Figs. 6 and 8, with disconnected magnetic-field lines colored by the magnetization σ. The first sequence covers the period of t = 19 592M − 19 596M with time resolution Δt = 1M. The third (middle) frame for t = 19 594M corresponds to Fig. 6 and is identified as the very onset of this magnetic flux eruption, for the reason that this is the first occurrence of a consistent patch of relativistic temperature. This hot patch appears between a small bundle of doubly connected field lines and a broad band of relatively highly magnetized disconnected lines. The second and third frames (t = 19 593M, 19 594M) show those groups of field lines partially interlocked. The doubly connected bundle appears to emerge spontaneously between the first (t = 19 592M) and second (t = 19 593M) snapshots. By the fifth (last) frame for t = 19 596M, the doubly connected field lines collapse into the BH, and the high-temperature patch appears attached to the horizon.
 |
Fig. 9. Time evolution of magnetic field lines during onset of magnetic-flux eruption in prograde a = 0.9 case. Horizon-disconnected lines are colored by the magnetization parameter σ = b2/w, and doubly connected lines are shown in white. The magenta patches mark the relativistic temperature (log10T ≥ 0.5). All images are seen from the latitude of θobs = 45° and the azimuth of ϕobs = 180°. Black spheres indicate the outer horizon at rH = 1.436M, and black arcs seen in most panels mark the radius r = 2M in the equatorial plane θ = 90°. The upper sequence covers the time period of t = 19 592M − 19 596M every Δt = 1M (the middle frame corresponds to Fig. 6). The lower sequence covers the time period of t = 19 602M − 19 630M every Δt = 7M (the last frame corresponds to Fig. 8). An associated movie is available online. |
The second sequence covers the period of t = 19 602M − 19 630M with the time resolution of Δt = 7M, showing further development of this magnetic-flux eruption. The fifth (last) frame for t = 19 630M corresponds to Fig. 8. The first two frames (t = 19 602M, 19 609M) show additional bundles of doubly connected field lines appearing at different azimuths along the equatorial part of the horizon followed by a more extended high-temperature region in the fourth frame (t = 19 623M). Isolated bands of very highly magnetized disconnected field lines appear in the third and fourth frames (t = 19 616M, 19 623M).
3.3. Magnetic-field lines: Retrograde case
Figure 10 presents a complete sample of disconnected magnetic field lines within r ≤ 6M colored by the magnetization σ in the retrograde a = −0.9 case at t = 17 050M (the peak of ΦBH indicated in Fig. 2). We also show a complete sample of doubly connected field lines. Those lines were seeded in the same way as in the prograde case presented in Fig. 6.
 |
Fig. 10. Magnetic-field lines disconnected from BH horizon within r < 6M in the retrograde a = −0.9 case at the peak of BH magnetic flux during the onset of magnetic flux eruption (t = 17 050M; cf. Fig. 2), with lines colored by the magnetization parameter σ = b2/w. A sample of doubly connected lines is shown in white. The small magenta patches mark regions of relativistic temperature (log10T ≥ 0.5). The viewpoint is at θobs = 0° , with ϕ measured counterclockwise from the right. The black sphere indicates the outer horizon at rH = 1.436M. The grid of black arcs marks the radii r/M = 2, 3, 4, 5, 6 in the equatorial plane θ = 90°. An associated movie is available online. |
The structure of disconnected field lines in the retrograde case is more complex than in the prograde case. The main difference is that the accretion flow has an opposite sense of angular momentum (in both cases, the BH spin vector points toward θ = 0; to the observer in Fig. 10). In the retrograde case, the angular momentum of the initial torus, and consequently of the magnetically disconnected accretion flow, points toward θ = 180° (away from the observer in Fig. 10).
The low-σ (blue) lines in Fig. 10 trace a regular accretion flow with azimuthal twist, such that BrBϕ > 0, which is opposite to the prograde case. The upper side of Fig. 10 (ϕ ∼ 90°) shows a bundle of high-σ (orange) lines forming a fan structure indicating a smoothly reversing azimuthal twist. In radial velocity, those reversing lines show stagnation or weak outflow (vr ≳ 0). A minor fan structure can also be seen rooted at ϕ ∼ 120°, with sparse high-σ (red) lines extending to the foreground. Most of the connected field lines show reversed azimuthal twist with BrBϕ < 0, as in the prograde case. Another band of high-σ lines can be seen rooted over the range of ϕ ∼ 60° −90° and swept to the right.
The right half of Fig. 10 (−90° < ϕ < 90°) shows more green and yellow color, which indicates log10σ ∼ 0 − 0.5. A minor patch or relativistic temperature seen just outside the horizon at ϕ ≃ 80° is the actual seed of magnetic-flux eruption that is going to develop intermittently (see the animated version of Fig. 10) and eventually engulf more than half of the horizon circumference (see the lower right panel of Fig. 11). The eruption trigger event is not as clean as the one in the prograde case illustrated in Fig. 9, since it was preceded by intermittent activity over at least Δt ∼ 170M, during which the global ΦBH remained roughly stable.
 |
Fig. 11. Spacetime diagrams in (t, ϕ) coordinates for parameters presented in Fig. 5; mean plasma density ρmean (left panels) and maximum plasma temperature Tmax (right panels), with statistics taken over θL3, min < θ < θL3, max at fixed radius r = 2M. The black contours indicate log10Tmax = 1. The white dashed lines mark linear rotation trends. The upper panels present the prograde a = 0.9 case in the time window 19 500M < t < 19 900M (trend with rotation period 85M); the lower panels present the retrograde a = −0.9 case in the time window 16 900M < t < 17 400M (trends with rotation periods −180M, 70M). |
On the opposite side of the BH, at ϕ ∼ 210°, a thick bundle of doubly connected lines wrap around a comparably thick tube of medium-σ (green) disconnected lines. The animated version of Fig. 10 shows that this is a final stage of rapid (Δt ∼ 5M) advection of a large concentration of magnetic flux into the BH, which is responsible for the sharp increase of ΦBH shown in Fig. 2 (directly preceding the blue circle).
In the lower right quadrant of Fig. 10, at r ≃ 2M and ϕ ≃ −45°, one can notice a warp in the distribution of disconnected lines, causing them to bend obliquely, not only in the equatorial plane, but also across. This pattern propagating retrograde with the accretion flow (see the animated version of Fig. 10) is likely an oblique shock (or at least a contact discontinuity). In the foreground of its left side (depressed under the equatorial plane) is a coherent tube of connected field lines (not shown here) oriented parallel to the discontinuity. Such structures appear to be more common in our retrograde simulations than in the prograde cases (including lower resolutions).
3.4. (t, ϕ) maps
Figure 11 shows spacetime diagrams of θ-averaged plasma density ρmean and θ-maximized plasma temperature Tmax extracted at radius r = 2M and presented as functions of coordinates (t, ϕ). This is based on the (r, ϕ) maps similar to those presented in Fig. 5, but for many additional time steps. We compare magnetic-flux eruptions in the prograde a = 0.9 and retrograde a = −0.9 cases.
The upper panels of Fig. 11 present an eruption in the prograde case in the time window 19 560M ≤ t ≤ 19 860M. We indicate two particular epochs (Fig. 2): the eruption onset at t = 19 594M and ϕ ≃ 90° (presented in Figs. 3 and 4 – upper panels; 5 – upper panels and, particularly, 6 and 7), and an early advanced eruption stage at t = 19 630M and 180° ≲ϕ ≲ 270° (presented in Figs. 4 – lower panels; 5 – lower panels; and, particularly, 8). The region of relativistic temperature coincides closely with the density gap. The main region of relativistic temperature exists for 19 620M < t < 19 760M and performs a coherent rotation by Δϕ = +480°. We present a trend line of linear rotation with the period of P = +85M, which also indicates a glitch at ϕ ≃ 30° for t ≃ 19 680M. Besides the eruption, the density map shows a large number of short-lived high-density filaments performing coherent rotations at similar rates.
The lower panels of Fig. 11 present an eruption in the retrograde case in the time window 17 030M ≤ t ≤ 17 330M. We indicate one particular epoch (Fig. 2) at t = 17 050M, which is presented in Fig. 10. In this case, the regions of relativistic temperature do not coincide with the density gap (they actually appear to avoid it). The main density gap performs a coherent rotation by Δϕ ≃ −525° over 17 070M < t < 17 370M. At the epoch of t = 17 050M, it appears to be limited to 270° ≲ϕ ≲ 360°, the lower right quadrant of Fig. 10 (including the warp at ϕ ≃ 320°). We plot a trend line of linear rotation toward decreasing ϕ (against the spacetime drag) with the period of −180M. This trend is similar to the rotation patterns of the high-density filaments. The regions of relativistic temperature do not follow such a rotation trend. The main hot region appears largely stationary in ϕ; however, some of its edges and other short-lived features suggest a fast rotation toward increasing ϕ (along the spacetime drag). We plot a second trend line for linear rotation toward increasing ϕ with the period of 70M. We suggest the following interpretation of these results: as the density gap corotates with the retrograde accretion flow, reconnection is triggered along the trailing edge of the gap and spreads along the magnetic-field lines rotating along the spacetime drag (field lines that have just disconnected from the BH horizon).
3.5. Alignment between velocity and magnetic fields
We decomposed velocity three-vectors v = v∥ + v⊥ into components parallel and perpendicular to the local magnetic-field three-vectors B, using the spatial metric dot product v ⋅ B = viBi = gijviBj and analogous vector norms |v|=(gijvivj)1/2 and |B|=(gijBiBj)1/2. We introduce the cosine of pitch angle μ(v, B) = (v ⋅ B)/(|v||B|) ∈ [ − 1 : 1] and calculate the parallel velocity v∥i = (v ⋅ B)Bi/|B|2 = μ(v, B) |v|Bi/|B| and the perpendicular velocity v⊥ = v − v∥. In ideal MHD, perpendicular velocity is a signature of electric fields.
Figure 12 presents, in the (r, θ) coordinates, the absolute value of pitch cosine |μ(v, B)|, as well as the total and perpendicular azimuthal velocities vϕ and v⊥ϕ, for both prograde and retrograde cases. In the high-density accretion flow, the values of |μ(v, B)| ≃ 1 indicate that the plasma velocity is closely parallel to the local magnetic field. The exception to this is that the values of |μ(v, B)| are low along the equatorial current layer. Thus, accreting plasma is generally forced to flow along the magnetic-field lines, except at their sharp inner tips rooted at the current layer. Because most disconnected field lines have a universal shape reflecting the dominance of Br, Bϕ components (see Fig. 13), plasma flowing radially inward (vr < 0; see Fig. 4) is channeled toward the equatorial current layer; this explains the strong radial stratification of plasma density. The inner tips of disconnected field lines might form obstacles (choke-points) for further accretion; however, the breaking of the ideal MHD flux-freezing condition, as well as stochastic variations in time (warping, flapping, etc.) of the current layer due to turbulent perturbations, allow for efficient cross-field diffusion.
 |
Fig. 12. Maps in (r, θ) coordinates showing the following (from the left): absolute value of the cosine of the pitch angle between the velocity three-vector vi and the magnetic-field three-vector Bi; azimuthal component of the velocity three-vector vi; azimuthal component of the velocity three-vector v⊥i perpendicular to the local Bi. Upper row of panels: prograde a = 0.9 case for t = 19 594M and ϕ ≃ 90°; lower row of panels: retrograde a = −0.9 case for t = 17 000M and ϕ ≃ 90°. |
The azimuthal component of perpendicular velocity v⊥ϕ is positive for almost every (r, θ), and significantly smaller in the disconnected accretion flow than in the equatorial current layer and in the connected magnetosphere. It is also significantly smaller in both regions than vϕ, which within the ergosphere approaches the BH angular velocity ΩH = a/(2rH) = 0.313 (for a = 0.9).
The disconnected field lines thus appear to be more static than the plasma flowing along them. The azimuthal component of perpendicular velocity indicates a slow rigid rotation, not sensitive to the differential rotation of spacetime in the vicinity of the ergosphere. The disconnected lines appear as stiff avenues for the accreting plasma; despite low σ and high β, they seem to rule the motion of plasma, rather than being advected and tangled by that motion. A major exception to this is the equatorial current layer, where ideal MHD conditions are violated and numerical cross-field diffusion prevents choking of the accretion flow.
In the retrograde case, accreting plasma with negative radial velocity vr < 0 flows along the disconnected magnetic-field lines with BrBϕ > 0, which implies negative azimuthal velocity: vϕ < 0. The perpendicular component v⊥ϕ for the accretion flow is also negative, but much closer to zero. In the magnetosphere, where BrBϕ < 0, the azimuthal velocity is positive vϕ > 0, while radial velocity transitions from an inflow (vr < 0) for r ≲ 3M (along the field lines) to an outflow (vr > 0) for r ≳ 3M (across the field lines).
4. Discussion
4.1. Magnetic arresting
In the model of magnetically arrested disk (MAD) (Narayan et al. 2003), strong latitudinal (‘vertical’) magnetic field, Bθ, forms a magnetic barrier across the equatorial plane that arrests the accretion flow. This model postulates a radial stratification of the plasma parameter β = P/Pmag and the ratio of plasma pressure P to the magnetic pressure Pmag = b2/2 at a certain magnetospheric radius Rm, such that β < 1 for r < Rm and β ≫ 1 for r > Rm (satisfying the balance of total pressure across Rm). The MAD model has been demonstrated in 2D (axisymmetric) simulations (e.g., Igumenshchev 2008; Chashkina et al. 2021), in which accretion states accumulating magnetic flux on the BH horizon alternate with eruption states ejecting BH magnetic flux via relativistic magnetic reconnection.
In the 3D case, Narayan et al. (2003) postulated that accretion could proceed through the magnetic barrier in the form of filaments resulting from the magnetic Rayleigh-Taylor (interchange) instability (e.g., Stone & Gardiner 2007). Such filaments can indeed be realized in a rigid dipolar magnetosphere rooted at a star (e.g., protostar or neutron star; Kulkarni & Romanova 2008; Zhu et al. 2024; Parfrey & Tchekhovskoy 2024) – such a magnetosphere forms a robust magnetic barrier. In the case of BH accretion, a proper context for the interchange modes are magnetic-flux tubes ejected by magnetic-flux eruptions, as was recently demonstrated by Zhdankin et al. (2023). The ejected-flux tubes are magnetically dominated (β < 1) structures of strong latitudinal field that locally arrest (or repel; Hakobyan et al. 2023) the plasma-dominated (β > 1) accretion flow, which results in the development of dense filaments within the flux tube.
Three-dimensional simulations of accretion onto magnetically saturated BHs also show strong azimuthal (along ϕ) structures in the form of ‘spiral arms’ of plasma density (e.g., McKinney et al. 2012). However, such structures are not consistent with interchange modes8: (1) the range of plasma parameter values is typically limited to β > 1; (2) radial velocity is roughly uniform across the density arms.
Most GRMHD simulations of magnetized accretion onto BHs (at least since the works of Gammie et al. 2003; De Villiers & Hawley 2003) have been initiated from geometrically thick toroidal hydrodynamical equilibria (Fishbone & Moncrief 1976; Chakrabarti 1985) seeded with weak magnetic fields (most often poloidal; but recently also toroidal, Liska et al. 2020), such that initial plasma β ≳ 100 and accretion results from the magnetorotational instability (MRI; Balbus & Hawley 1991). The inner parts of the poloidal field loops are advected onto the BH by largely stable and axisymmetric accretion flows maintaining high values of plasma β; i.e., flows dominated by plasma pressure. At no point is there an opportunity to develop a radial stratification of β and hence a synchronized magnetic barrier. The magnetic flux through the equatorial plane is much smaller than the magnetic flux collected across the BH horizon (Begelman et al. 2022). In our simulations, we also find that the latitudinal (vertical) magnetic-field component Bθ is typically one order of magnitude weaker than the radial and toroidal components Br, Bϕ, even when the BH is magnetically saturated and the inner accretion flow is geometrically thin.
Our simulations do not show any evidence of thin accretion flows breaking into azimuthal filaments. Such accretion flows pass smoothly all the way to the BH horizon, avoiding obstacles that might require developing instabilities such as interchange to be overcome. A potential choke-point upon approaching the equatorial current layer, where accreting plasma reaches the inner tip of its magnetic field line, can be avoided due to cross-field diffusion, which allows accretion to continue along the current layer.
The key to achieving a true MAD configuration in 3D appears to be synchronization of the magnetic barrier. Early simulations presented by Igumenshchev (2008) were initiated in 2D and continued only briefly in 3D, with a magnetic barrier established in the 2D stage. In longer 3D simulations of geometrically thick accretion flows (Tchekhovskoy et al. 2011; McKinney et al. 2012; Ripperda et al. 2022; and many other studies, including this work), ejected magnetic-flux tubes occasionally form temporary and localized magnetic barriers, which cannot be extended synchronously over all ϕ values. A true MAD appears to have been achieved in the radiative GRMHD simulations with poloidal magnetic fields described in the work of Liska et al. (2022), with radiative cooling resulting in vertical collapse of the initial geometrically thick torus into a geometrically thin Keplerian disk with the inner edge truncated at r ≃ 25M by a proper barrier of ‘vertical’ magnetic fields. This is not inconsistent with our interpretation of geometrically thick RIAFs.
4.2. Magnetic choking
The bulk of accretion flows onto magnetically saturated BHs do not appear to be magnetically choked in the sense proposed by McKinney et al. (2012). ‘Choked’ suggests that it is difficult for the accretion flow to proceed into a converging nozzle between two magnetospheres. This term can only be applied to the part of accretion flow directly upstream of a forming magnetic X-point. However, radial profiles of plasma density, averaged over t, θ, ϕ, in accretion flows onto magnetically saturated BHs, are consistent with a power law ρ ∝ r−1 (Begelman et al. 2022) and show no evidence of a break that would indicate an additional compression. Latitudinal stratification of plasma density appears to be regulated by the disconnected magnetic field lines. The disconnected lines are in direct contact and in latitudinal pressure balance with the connected lines of the magnetosphere, and yet they remain obliquely elevated from the densest layer of accreting plasma. There is a smooth continuity between the disconnected and connected lines, which together form a twisted split monopole. Hence, even in a saturated state the BH magnetosphere does not directly compress the accreting plasma.
Moreover, such accretion flows do not appear to be affected by an angular momentum barrier, since even in such narrow nozzles there is room for laminar winds that provide enough magnetic torque to maintain these flows in a sub-Keplerian plunge (Scepi et al. 2024; see also Manikantan et al. 2024). Magnetic flux eruptions also contribute to the outward angular momentum transport (Marshall et al. 2018), even for non-spinning BHs (Chatterjee & Narayan 2022). Sub-Keplerian rotation rates characterize the accreting plasma, and even more so the disconnected magnetic field lines (Sect. 3.5); they are reflected in the azimuthal patterns ray-traced into BH crescent images (Conroy et al. 2023).
4.3. Magnetic channeling
We find that in the narrow nozzle formed by two bulging connected magnetospheres, geometric constriction of MRI turbulence forces the disconnected magnetic-field lines to organize themselves into a rigid, slowly rotating structure. Once a saturated BH cannot accept additional flux, the pressure of connected field lines prevents further advection of disconnected lines. Additional analysis of trajectories of test particles (Appendix A) indicates that the disconnected lines channel the accretion flow toward the equatorial current layer, resulting in the latitudinal density stratification. The accretion flow does not stop at the current layer, but proceeds along it by turbulent cross-field diffusion. The equatorial current layer thus forms the ultimate channel for the accretion flow to reach the BH. Such accretion flows are thus effectively magnetically channeled onto the BH (see magnetic channeling into a jet or wind; Ferreira & Pelletier 1993).
4.4. Regularity of disconnected field lines
We find that the inner accretion flow is threaded by disconnected field lines attaining a universal shape illustrated in Fig. 13 – a double spiral with a sharp inner tip close to the equatorial plane, from which two branches extend outward, roughly symmetric with respect to the equatorial plane, systematically diverging away from that plane, and spiraling in the same azimuthal direction (reflecting the dominance of radial and toroidal components Br, Bϕ). A sharp tip means a sharp field gradient, and hence a strong electric current density. Most disconnected field lines are rooted along the single equatorial current layer. Accreting plasma is tied to those lines, forced to move parallel to them. The slowly rotating lines guide the plasma toward the current layer. This is consistent with the strong latitudinal density stratification, which is realized in our simulations instead of the radial stratification postulated by the MAD model. Should ideal MHD be satisfied strictly, the line tips would form choke-points for the plasma. However, if sufficient plasma density accumulates at those line tips, it would pull the line tip inward. On the other hand, a finite numerical resolution limits the field gradient and the sharpness of the line tip, i.e., the current density. Under finite resolution, ideal MHD must break down along the current layer, allowing the accumulated plasma to diffuse inward across the line tip (hence v⊥r < 0 along the current layer; Fig. 12). In addition, the equatorial current layer is not steady, but flapping and warping due to perturbations advected from the turbulent outer zones.
 |
Fig. 13. Examples of regular field lines disconnected from BH horizon, with inner tips at rmin ≃ 2M aligned in ϕ. Red dashed arrows illustrate the channeling effect of field lines on plasma motions (accretion, and for the most θ-elevated lines – outflows). |
This picture is consistent with the pattern of linear polarization observed in M87* by the Event Horizon Telescope (Event Horizon Telescope Collaboration 2021a), which was interpreted by Punsly & Chen (2021) in terms of a Parker spiral.
4.5. Triggering magnetic flux eruptions
We identified the trigger event for magnetic flux eruption as the activation of a pre-existing equatorial current layer due to the decrease of plasma density. A necessary but insufficient condition is the change of magnetic field topology (formation of magnetic X-points). This requires disconnection of a small group of field lines from the BH horizon. The spontaneous appearance of doubly connected field loops suggests that disconnection is chaotic (in the spirit of Lazarian & Vishniac 1999); this results from perturbations of the innermost geometrically constricted accretion flow, which are advected from larger radii where accretion is geometrically thick and MRI turbulence is fully developed. The disconnection of magnetospheric field lines introduces low-density plasma to the disconnected domain, from which it can be transmitted to an X-point.
This scenario is qualitatively similar to the scenarios proposed to explain analogous magnetic eruptions in other astrophysical environments. In the context of solar flares, it was demonstrated using ideal MHD simulations that gradual thinning of a current layer can nonlinearly accelerate reconnection (Jiang et al. 2021). In the context of Earth’s magnetotail region, in situ measurements by the Magnetospheric MultiScale (MMS) constellation of probes made it possible to attribute the onset of magnetic reconnection to the thinning of a current layer due to a transient thermal pressure pulse in the solar wind, rather than due to the loading of additional magnetic flux (Genestreti et al. 2023).
4.6. Self-organized criticality
In Sect. 3.2, we demonstrate the development of a full-scale magnetic-flux eruption from a very compact reconnection site related to a brief occurrence of a doubly connected field loop. We considered other examples of flux eruptions, large and small – they all start from similar conditions, essentially from scratch. At even lower resolutions, the initial phase of magnetic-flux eruption can be characterized as a self-similar growth of the relativistically hot density gap due to a positive feedback cycle (decreasing density → increasing temperature → radial acceleration → decreasing density) (Nalewajko et al. 2024). Most doubly connected field loops do not trigger an eruption, and there are clearly more small (failed) eruptions than large ones (Fig. 11). Such conditions are generally analogous to the solar and stellar flares (e.g., Lu & Hamilton 1991; Aschwanden & Güdel 2021; Feinstein et al. 2022), and it is reasonable to expect that BH flux eruptions are examples of the principle of self-organized criticality (a magnetic avalanche), in which small perturbations trigger events of unpredictable magnitude (Bak et al. 1988). This would predict that the magnetic energy released during BH flux eruptions should follow a power-law distribution N(ℰ)∝ℰ−p with the index p ≃ 1.5.
4.7. Rotation of flux eruption footpoints
Previous studies (Dexter et al. 2020; Porth et al. 2021) showed that magnetic-flux eruptions can eject compact tubes of vertical magnetic field orbiting the BH at radii r ∼ 10M, which have been applied to the flares of Sgr A* resolved by the GRAVITY instrument (GRAVITY Collaboration 2018). In Sect. 3.4, we show that systematic rotation can also be performed by the eruption foot-point measured at r ≃ 2M, and similar rotations can be demonstrated at radii of r ∼ 4M, contributing most directly to BH crescent images. However, low plasma density may cause the eruption foot-points to appear dark in crescent images. Even in such a case, an observation of coherently rotating dark band in future crescent images of M87*, correlated with other multiwavelength signatures, e.g., a TeV gamma-ray flare, or a helically propagating radio-VLBI feature, would be extremely useful to constrain the theoretical picture of BH-flux eruptions.
4.8. Prograde versus retrograde accretion flows
Prograde and retrograde cases for magnetically saturated BH accretion flows have been compared in several studies based on GRMHD simulations (Tchekhovskoy & McKinney 2012; Narayan et al. 2022; Zhang et al. 2024). Although various quantitative differences have been reported, the general picture is that such cases would be difficult to distinguish observationally. This was also the case in the interpretation of the BH crescent images obtained by the Event Horizon Telescope by comparing them with images produced from GRMHD simulations. In the case of M87*, both prograde and retrograde MAD models could satisfy the considered constraints (Event Horizon Telescope Collaboration 2019c), including linear polarization (Event Horizon Telescope Collaboration 2021b) and circular polarization (Event Horizon Telescope Collaboration 2023).
Our results presented in Sects. 3.3 and 3.4 suggest that the retrograde case is much more complex, including a chaotic transfer of magnetic field lines across a sharp shear layer. This should result in much more vigorous particle acceleration than in the prograde case, and potentially in distinct observational signatures. Global kinetic simulations using the general relativistic particle-in-cell (GRPIC) algorithm are necessary to verify this.
5. Conclusions
Using the results of 3D ideal GRMHD numerical simulations, we analyzed magnetic connectivity of magnetically saturated accreting Kerr BHs (also known as MAD or MCAF), focusing on the magnetic-field lines that are disconnected from the BH horizon (disconnected lines) and occupying the magnetically disconnected volume domain (disconnected domain), which separates two connected domains (bipolar split-monopole BH magnetosphere).
The inner part of the disconnected domain is geometrically constricted into a narrow nozzle, eventually restricting the outer magnetorotational turbulence to a single equatorial current layer, which is subject to significant fluctuations. Azimuthal sectors of the disconnected domain alternate between the states of magnetic-flux accumulation (regular accretion flow with low magnetization σ ≪ 1, strong latitudinal stratification, and inactive equatorial current layer) and magnetic-flux eruption (active equatorial current layer drives relativistic magnetic reconnection evidenced by relativistic temperature).
The surface regions of the disconnected domain are characterized by laminar magnetic fields transitioning into nonrelativistic outflows, potentially unbound winds (even ultrafast outflows; Scepi et al. 2024), with magnetization fluctuating around σ ∼ 1. The innermost disconnected magnetic field lines attain the regular shape of a double spiral that is elevated and converging to a sharp inner tip rooted at the equatorial current layer, reflecting the dominance of Br, Bϕ components over Bθ (twisted split monopole). Such field lines form a rigid structure, rotating at a slow sub-Keplerian rate insensitive to the sense of the BH spin (prograde vs. retrograde).
Plasma motions are well tied to the disconnected magnetic-field lines, which channel the accretion flow toward the equatorial current layer. The inner tips of the disconnected field lines do not choke the accretion flow, which proceeds further due to turbulent cross-field diffusion, channeled along the equatorial current layer toward the horizon, effectively plunging with sub-Keplerian azimuthal velocity vϕ.
In a magnetically saturated BH state, the magnetically disconnected domain acts like a “magnetic insulator” separating two connected magnetospheres “charged” with opposite field lines. The introduction of plasma-depleted field lines into the disconnected domain leads to its localized geometric thinning. A critically thin disconnected domain punctures locally, initiating magnetic reconnection between the connected domains and triggering a magnetic-flux eruption.
We identified the trigger event, i.e., the first consistent occurrence of relativistic temperature, for a moderate magnetic-flux eruption in our reference prograde case. The trigger is a magnetic X-point forming between a band of disconnected lines and a bundle of doubly connected loops. The frequent and abundant appearance of doubly connected magnetic field loops, short-lived features dynamically folding into the BH, is evidence of the chaotic disconnection of magnetospheric lines. In accordance with the principle of self-organized criticality, only some of those loops trigger eruptions of various magnitudes.
The retrograde case presents additional complication due to a strong shear between the accretion flow and the magnetosphere. The azimuthal twist of the disconnected magnetic-field lines advected by the accretion flow reverses due to spacetime rotation only once they unload their plasma into the BH and become highly magnetized connected field lines.
Magnetic-flux eruptions rotate systematically around the BH; this applies not only to the ejected-flux tubes (orbiting hot-spots at r ∼ 10M), but also to their foot-points (r ∼ 2M). In the prograde case, relativistic temperature coincides with the density gap. In the retrograde case, the relativistic temperature appears to corotate with the BH, while the density gap appears to corotate with the accretion flow. The disconnected magnetic-field lines rotate much more slowly than the accretion plasma, both in the prograde and retrograde cases. The rotation rate of those lines can explain9 the sub-Keplerian and spin-degenerate rotation speeds of azimuthal patterns imprinted on the simulated BH crescent images, in particular for the flux-eruption foot-points.
Data availability
Movies associated to Figs. 6, 8, 9, and 10 are available at https://www.aanda.org
McKinney et al. (2012) define magnetic choking as compression of the accretion flow by magnetic pressure of the BH magnetosphere, ‘analogous to chokes in man-made engines’.
An alternative 3+1 spacetime splitting convention has *Fi0 = Bi/α with α the lapse (Komissarov 2004).
The Level-0 grid has exactly 1 cell inside the horizon, in which we followed White et al. (2019) – this is limited to the polar regions (θ < 30° and θ > 150°) entirely within the magnetosphere; we performed full-resolution tests with up to eight Level-0 cells inside the horizon, the results of which show no significant differences outside the horizon.
Our flux-saturation levels are slightly higher than the results of longer simulations of comparable resolution reported in Narayan et al. (2022) – 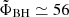 for a = 0.9 and
for a = 0.9 and 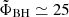 for a = −0.9.
for a = −0.9.
Geometrically thin accretion flows can be warped, hence a low-density magnetosphere may imprint an azimuthal structure in the equatorial plane that could be attributed to the interchange instability (this appears to be the case in Fig. 4 of McKinney et al. 2012). For this reason, our Fig. 5 presents (r, ϕ) maps of parameter statistics drawn from a range of θ values.
Acknowledgments
The authors benefited greatly from discussions with Marek Sikora, Marek Abramowicz, Mitch Begelman, Benoît Cerutti, Jonathan Ferreira, Nicolas Scepi, Alexander Philippov, Jordy Davelaar, Bart Ripperda, Vladimir Zhdankin, Gibwa Musoke. We gratefully acknowledge Poland’s high-performance Infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH, PCSS, CI TASK, WCSS) for providing computer facilities and support within computational grants no. PLG/2023/016444 and PLG/2024/017013, the Warsaw Interdisciplinary Center for Mathematical Modeling, and the Nicolaus Copernicus Astronomical Center for providing the Chuck cluster. Figs. 6–10 were created with the Mayavi (Ramachandran & Varoquaux 2011). This work was supported by the Polish National Science Centre grants 2021/41/B/ST9/04306, 2019/35/B/ST9/04000 and 2023/50/A/ST9/00527. KN acknowledges the hospitality of the Simons Foundation.
References
- Ajello, M., Gasparrini, D., Sánchez-Conde, M., et al. 2015, ApJ, 800, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Güdel, M. 2021, ApJ, 910, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bak, P., Tang, C., & Wiesenfeld, K. 1988, Phys. Rev. A, 38, 364 [CrossRef] [PubMed] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [Google Scholar]
- Begelman, M. C., Scepi, N., & Dexter, J. 2022, MNRAS, 511, 2040 [NASA ADS] [CrossRef] [Google Scholar]
- Biteau, J., Prandini, E., Costamante, L., et al. 2020, Nat. Astron., 4, 124 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Camilloni, F., Dias, O. J. C., Grignani, G., et al. 2022, JCAP, 2022, 032 [CrossRef] [Google Scholar]
- Chakrabarti, S. K. 1985, ApJ, 288, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chashkina, A., Bromberg, O., & Levinson, A. 2021, MNRAS, 508, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, K., & Narayan, R. 2022, ApJ, 941, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, N. S., Bauböck, M., Dhruv, V., et al. 2023, ApJ, 951, 46 [CrossRef] [Google Scholar]
- De Villiers, J.-P., & Hawley, J. F. 2003, ApJ, 589, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., Tchekhovskoy, A., Jiménez-Rosales, A., et al. 2020, MNRAS, 497, 4999 [Google Scholar]
- Event Horizon Telescope Collaboration 2019a, ApJ, 875, L1 [Google Scholar]
- Event Horizon Telescope Collaboration 2019b, ApJ, 875, L4 [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2019c, ApJ, 875, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2019d, ApJ, 875, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2021a, ApJ, 910, L12 [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2021b, ApJ, 910, L13 [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2022, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2023, ApJ, 957, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Feinstein, A. D., Seligman, D. Z., Günther, M. N., et al. 2022, ApJ, 925, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., & Pelletier, G. 1993, A&A, 276, 637 [NASA ADS] [Google Scholar]
- Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F., McKinney, J. C., & Tóth, G. 2003, ApJ, 589, 444 [Google Scholar]
- Genestreti, K. J., Farrugia, C. J., Lu, S., et al. 2023, JGRA, 128, e2023JA031758 [NASA ADS] [Google Scholar]
- Gezari, S. 2021, ARA&A, 59, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Maraschi, L., et al. 2014, Nature, 515, 376 [Google Scholar]
- Goddi, C., Martí-Vidal, I., Messias, H., et al. 2021, ApJ, 910, L14 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2016, ApJ, 817, 131 [Google Scholar]
- Hakobyan, H., Ripperda, B., & Philippov, A. A. 2023, ApJ, 943, L29 [Google Scholar]
- Igumenshchev, I. V. 2008, ApJ, 677, 317 [NASA ADS] [CrossRef] [Google Scholar]
- James, B., Janiuk, A., & Karas, V. 2024, A&A, 687, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janiuk, A., & James, B. 2022, A&A, 668, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, C., Feng, X., Liu, R., et al. 2021, Nat. Astron., 5, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Junor, W., Biretta, J. A., & Livio, M. 1999, Nature, 401, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Vermeulen, R. C., Zensus, J. A., et al. 1998, AJ, 115, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-Y., Krichbaum, T. P., Lu, R.-S., et al. 2018, A&A, 616, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komissarov, S. S. 2004, MNRAS, 350, 427 [Google Scholar]
- Komissarov, S. S., & McKinney, J. C. 2007, MNRAS, 377, L49 [Google Scholar]
- Kulkarni, A. K., & Romanova, M. M. 2008, MNRAS, 386, 673 [Google Scholar]
- Lasota, J.-P., Gourgoulhon, E., Abramowicz, M., et al. 2014, Phys. Rev. D, 89, 024041 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [Google Scholar]
- LHAASO Collaboration 2023, Science, 380, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Liska, M., Tchekhovskoy, A., & Quataert, E. 2020, MNRAS, 494, 3656 [Google Scholar]
- Liska, M. T. P., Musoke, G., Tchekhovskoy, A., et al. 2022, ApJ, 935, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, E. T., & Hamilton, R. J. 1991, ApJ, 380, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, R.-S., Asada, K., Krichbaum, T. P., et al. 2023, Nature, 616, 686 [CrossRef] [Google Scholar]
- Lubow, S. H., Papaloizou, J. C. B., & Pringle, J. E. 1994, MNRAS, 267, 235 [NASA ADS] [Google Scholar]
- Lynden-Bell, D. 1969, Nature, 223, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Madejski, G., & Sikora, M. 2016, ARA&A, 54, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Manikantan, V., Kaaz, N., Jacquemin-Ide, J., et al. 2024, ApJ, 965, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, M. D., Avara, M. J., & McKinney, J. C. 2018, MNRAS, 478, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [Google Scholar]
- Mirabel, I. F., & Rodríguez, L. F. 1999, ARA&A, 37, 409 [Google Scholar]
- Najafi-Ziyazi, M., Davelaar, J., Mizuno, Y., et al. 2024, MNRAS, 531, 3961 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K. 2023, The Sixteenth Marcel Grossmann Meeting, Published by World Scientific Publishing Co. Pte. Ltd. 339 https://doi.org/10.1142/9789811269776_0024 [CrossRef] [Google Scholar]
- Nalewajko, K., Sikora, M., & Różańska, A. 2020, A&A, 634, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nalewajko, K., Kapusta, M., & Janiuk, A. 2024, High Energy Phenomena in Relativistic Outflows VIII Published by Sissa Medialab https://doi.org/10.22323/1.461.0041 [Google Scholar]
- Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2003, PASJ, 55, L69 [NASA ADS] [Google Scholar]
- Narayan, R., Chael, A., Chatterjee, K., et al. 2022, MNRAS, 511, 3795 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Gammie, C. F., McKinney, J. C., et al. 2006, ApJ, 641, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Parfrey, K., & Tchekhovskoy, A. 2024, ApJ, 975, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Porth, O., Chatterjee, K., Narayan, R., et al. 2019, ApJS, 243, 26 [Google Scholar]
- Porth, O., Mizuno, Y., Younsi, Z., et al. 2021, MNRAS, 502, 2023 [NASA ADS] [CrossRef] [Google Scholar]
- Punsly, B., & Chen, S. 2021, ApJ, 921, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Punsly, B., Igumenshchev, I. V., & Hirose, S. 2009, ApJ, 704, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Ramachandran, P., & Varoquaux, G. 2011, IEEE Comput. Sci. Eng., 13, 40 [CrossRef] [Google Scholar]
- Ripperda, B., Liska, M., Chatterjee, K., et al. 2022, ApJ, 924, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Scepi, N., Dexter, J., & Begelman, M. C. 2022, MNRAS, 511, 3536 [NASA ADS] [CrossRef] [Google Scholar]
- Scepi, N., Begelman, M. C., & Dexter, J. 2024, MNRAS, 527, 1424 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stone, J. M., & Gardiner, T. 2007, ApJ, 671, 1726 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., Tomida, K., White, C. J., et al. 2020, ApJS, 249, 4 [Google Scholar]
- Tchekhovskoy, A., & McKinney, J. C. 2012, MNRAS, 423, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2010, ApJ, 711, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, R. C., Hardee, P. E., Davies, F. B., et al. 2018, ApJ, 855, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, G. R., & Uzdensky, D. A. 2017, ApJ, 843, L27 [NASA ADS] [CrossRef] [Google Scholar]
- White, C. J., Stone, J. M., & Gammie, C. F. 2016, ApJS, 225, 22 [NASA ADS] [CrossRef] [Google Scholar]
- White, C. J., Stone, J. M., & Quataert, E. 2019, ApJ, 874, 168 [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2018, The Physics of Gamma-Ray Bursts (Cambridge Univeristy Press) [Google Scholar]
- Zhang, G.-Q., Bégué, D., Pe’er, A., et al. 2024, ApJ, 962, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Zhdankin, V., Ripperda, B., & Philippov, A. A. 2023, Phys. Rev. Res., 5, 043023 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Stone, J. M., & Calvet, N. 2024, MNRAS, 528, 2883 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Magnetic pitch angles of accreting test particles
To illustrate channeling of accreting plasma along local magnetic field lines, and diffusion across the field lines, in Fig. A.1 we show a small representative sample of test plasma particles (∼40 out of a full sample of ∼15000, in order not to clutter the plot), the trajectories of which were integrated using the Euler method from 3-linearly interpolated full-resolution velocity field updated every dt = 0.1M, starting from their initial positions at r1 = 5M for a range of 70° < θ1 < 110° and 0 < ϕ1 < 360° values at t1 = 19500M (well before the onset of magnetic flux eruption) to their crossings of the BH horizon at r2 = rH at t2 < 19530M. While all trajectories are smooth in the (r, θ) plane (and also in the (r, ϕ) plane), the cosine of magnetic pitch angle μ(v,B) shows a variety of behaviors. Most plasma elements (especially those starting away from the accretion midplane) are found to follow their local magnetic field line at small pitch angle (|μ|≃1). However, some plasma elements show intermediate magnetic pitch angles – in some cases (those starting close to the midplane) over most of their way, in other cases they switch from following their local field line to diffusion shortly before reaching the horizon.
 |
Fig. A.1. Trajectories of test particles in the (r, θ) projection (upper panel), and cosines of their magnetic pitch angles μ(v,B) as function of r (lower panel). Line colors indicate the initial latitude, θ1. |
All Figures
 |
Fig. 1. Long-term histories of BH magnetic flux ΦBH (upper panel) and its value normalized by the mass-accretion rate |
| In the text | |
 |
Fig. 2. Short-term histories of BH magnetic flux ΦBH during magnetic flux eruptions in the prograde a = 0.9 (red; time window from t0 = 19 500M to 20 000M) and retrograde a = −0.9 (blue; time window from t0 = 16 800M to 17 300M) cases. Two epochs of interest are indicated in the prograde case: the eruption onset at t = 19 594M and its advanced stage at t = 19 630M; one epoch is indicated in the retrograde case: the magnetic-flux peak at t = 17 050M. |
| In the text | |
 |
Fig. 3. Overview maps (r ≤ 18M) in Kerr-Schild (r, θ) coordinates of selected parameters for prograde a = 0.9 case at t = 19 594M. From the left, the first panel shows the radial component of magnetic-field three-vector Br (multiplied by r2), the second panel shows the plasma density ρ in log scale, and the third panel shows the radial component of velocity three-vector vr. The left and right sides of every panel show slices for opposite azimuths ϕL, ϕR indicated in the titles. The black circles mark the BH with horizon radius rH ≃ 1.436M. The coarse cells in the polar regions (|θ|< 30° and |θ|> 150°) result from the SMR. |
| In the text | |
 |
Fig. 4. Close-up maps (r ≤ 6M) in (r, θ) coordinates (with θ limited to the Level-3 SMR domain) of the same parameters as in Fig. 3 (from left to right) for the prograde a = 0.9 case at two epochs: t = 19 594M (upper row of panels) and t = 19 630M (lower row of panels). Each panel shows a slice for the azimuth ϕ indicated in its title (also marked in Fig. 5). The gray dashed circles mark the ergosphere boundary rE(θ), the black dashed lines mark the boundary of domain magnetically disconnected from the BH horizon, the green dashed lines mark equipartition between magnetic and plasma enthalpies (σ = b2/w = 1), and the magenta contours mark the relativistic temperature log10T = 0.5. |
| In the text | |
 |
Fig. 5. Maps in (r, ϕ) coordinates of parameter statistics drawn from latitudinal arcs θL3, min < θ < θL3, max for the a = 0.9 case at two epochs: t = 19 594M (upper row of panels) and t = 19 630M (lower row of panels). From the left, the panels show (1) mean density ρmean in log scale, (2) maximum temperature Tmax in log scale, and (3) minimum radial velocity vminr. The black circles mark the BH with horizon radius rH ≃ 1.436M, the gray dashed circles mark the θ = 90° ergosphere boundary rE = 2M, the gray dashed lines in the upper panels mark the cutout ϕ sector in Figs. 6 and 7, and the black dashed lines mark the ϕ values for the (r, θ) maps presented in Fig. 4. |
| In the text | |
 |
Fig. 6. Selected magnetic field lines within r ≤ 6M in prograde a = 0.9 case at onset of magnetic flux eruption (t = 19 594M), colored by the magnetization parameter σ = b2/w (line colors are also affected by shading, with lines seen at small angles rendered darker). Upper panel: Horizon-connected lines seeded at r0 = 5.9M for θL3, min < θ0 < 90°, seen from latitude θobs = 135°; lower panel: horizon-disconnected lines seeded at r0 = 5.9M for θL3, min < θ0 < θL3, max, seen from latitude θobs = 45°. In both panels, a small but (θ0, ϕ0)-complete sample of doubly connected lines (closed loops with max(r) < 6M) seeded at r0 = 1.42M (just under the horizon) are shown colored in white. Both images are seen from the same azimuth ϕobs = 180°; data for 150° < ϕ < 210° (except for the doubly connected lines) are cut out to reveal (r, θ) sections. Black spheres indicate the outer horizon at rH = 1.436M. The grid of arcs marks the radii r/M = 2, 3, 4, 5, 6 in the equatorial plane θ = 90° (gray) and in the ϕ = 90° quadrant spanning the latitudes θL3, min ≤ θ ≤ θL3, max (black). A small magenta patch just to the left of the horizon marks relativistic temperature (log10T ≥ 0.5). An associated movie is available online. |
| In the text | |
 |
Fig. 7. Same as lower panel of Fig. 6, but with horizon-disconnected lines colored by the radial 3-velocity vr and doubly connected lines colored yellow. |
| In the text | |
 |
Fig. 8. Magnetic field lines disconnected from BH horizon within r ≤ 6M at a less advanced stage of magnetic flux eruption (t = 19 630M) in the prograde a = 0.9 case. Upper panel: Lines colored by magnetization parameter σ = b2/w; lower panel: lines colored by radial velocity vr. A sample of doubly connected lines seeded at r0 = 1.42M (just under the horizon) are shown colored in white (upper panel) or yellow (lower panel). The magenta patches mark regions of relativistic temperature (log10T ≥ 0.5). The view point is at θobs = 45°, ϕobs = 180°. Black sphere indicates the outer horizon at rH = 1.436M. The grid of black arcs marks the radii r/M = 2, 3, 4, 5, 6 in the equatorial plane θ = 90°, and in the ϕ = 210° quadrant spanning the latitudes θL3, min ≤ θ ≤ θL3, max. An associated movie is available online. |
| In the text | |
 |
Fig. 9. Time evolution of magnetic field lines during onset of magnetic-flux eruption in prograde a = 0.9 case. Horizon-disconnected lines are colored by the magnetization parameter σ = b2/w, and doubly connected lines are shown in white. The magenta patches mark the relativistic temperature (log10T ≥ 0.5). All images are seen from the latitude of θobs = 45° and the azimuth of ϕobs = 180°. Black spheres indicate the outer horizon at rH = 1.436M, and black arcs seen in most panels mark the radius r = 2M in the equatorial plane θ = 90°. The upper sequence covers the time period of t = 19 592M − 19 596M every Δt = 1M (the middle frame corresponds to Fig. 6). The lower sequence covers the time period of t = 19 602M − 19 630M every Δt = 7M (the last frame corresponds to Fig. 8). An associated movie is available online. |
| In the text | |
 |
Fig. 10. Magnetic-field lines disconnected from BH horizon within r < 6M in the retrograde a = −0.9 case at the peak of BH magnetic flux during the onset of magnetic flux eruption (t = 17 050M; cf. Fig. 2), with lines colored by the magnetization parameter σ = b2/w. A sample of doubly connected lines is shown in white. The small magenta patches mark regions of relativistic temperature (log10T ≥ 0.5). The viewpoint is at θobs = 0° , with ϕ measured counterclockwise from the right. The black sphere indicates the outer horizon at rH = 1.436M. The grid of black arcs marks the radii r/M = 2, 3, 4, 5, 6 in the equatorial plane θ = 90°. An associated movie is available online. |
| In the text | |
 |
Fig. 11. Spacetime diagrams in (t, ϕ) coordinates for parameters presented in Fig. 5; mean plasma density ρmean (left panels) and maximum plasma temperature Tmax (right panels), with statistics taken over θL3, min < θ < θL3, max at fixed radius r = 2M. The black contours indicate log10Tmax = 1. The white dashed lines mark linear rotation trends. The upper panels present the prograde a = 0.9 case in the time window 19 500M < t < 19 900M (trend with rotation period 85M); the lower panels present the retrograde a = −0.9 case in the time window 16 900M < t < 17 400M (trends with rotation periods −180M, 70M). |
| In the text | |
 |
Fig. 12. Maps in (r, θ) coordinates showing the following (from the left): absolute value of the cosine of the pitch angle between the velocity three-vector vi and the magnetic-field three-vector Bi; azimuthal component of the velocity three-vector vi; azimuthal component of the velocity three-vector v⊥i perpendicular to the local Bi. Upper row of panels: prograde a = 0.9 case for t = 19 594M and ϕ ≃ 90°; lower row of panels: retrograde a = −0.9 case for t = 17 000M and ϕ ≃ 90°. |
| In the text | |
 |
Fig. 13. Examples of regular field lines disconnected from BH horizon, with inner tips at rmin ≃ 2M aligned in ϕ. Red dashed arrows illustrate the channeling effect of field lines on plasma motions (accretion, and for the most θ-elevated lines – outflows). |
| In the text | |
 |
Fig. A.1. Trajectories of test particles in the (r, θ) projection (upper panel), and cosines of their magnetic pitch angles μ(v,B) as function of r (lower panel). Line colors indicate the initial latitude, θ1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.