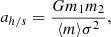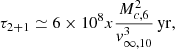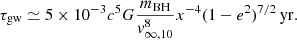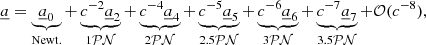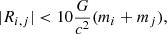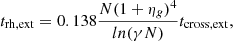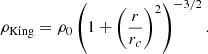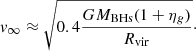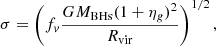EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A378 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A378
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202450770
Published online 22 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The existence of supermassive black holes (SMBHs) and their physical nature has been confirmed through different independent observations, including the orbits of the S2 stars near the center of the Milky Way with the GRAVITY instrument (GRAVITY Collaboration 2018), as well as observations of their shadows at the centers of M87 and Sagitarius A* (The Event Horizon Telescope Collaboration 2019, 2022). Observed through the detection of active galactic nuclei (AGN) at high redshift (e.g. Shankar et al. 2010), even at redshifts larger than z > 6, more than 300 quasars have been detected (e.g. Bañados et al. 2016; Inayoshi et al. 2020; Fan et al. 2023). These objects are very rare with number densities of 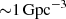∼ 1 Gpc − 3 $ {\thicksim}1\, \mathrm{Gpc}^{-3} $ and have been found so far in optical and infrared (IR) surveys that cover a large portion of the sky, such as the Sloan Digital Sky Survey (SDSS), the first survey to discover a high-redshift quasar (Fan et al. 2001). They are common in the centers of local galaxies (e.g. Ferrarese & Merritt 2000; Tremaine et al. 2002; Gültekin et al. 2009) and their masses are in the range of 106–1010 M⊙.

The most distant quasar detected so far was discovered by the James Webb Space Telescope (JWST) at a redshift of z ≈ 10.3 magnified by the cluster Abel 2744. The SMBH has a mass of ≈107–108 M⊙ assuming accretion at the Eddington limit (Bogdán et al. 2024).

In the local Universe, the rarest SMBHs are the so-called ultra-massive ones. Over the last decade, observations have established the existence of a few of these with masses ≳ 1010 M⊙ in some bright cluster galaxies (e.g. McConnell et al. 2011; Hlavacek-Larrondo et al. 2012; Wu et al. 2015; Schindler et al. 2020).

In the local Universe, galaxies have also been found to host nuclear star clusters (NSCs) at their centers (Neumayer et al. 2020). The most massive NSCs are the densest known stellar systems and can reach mass surface densities of ≈ 106 M⊙/pc2 or higher. Some important features of these objects and an important topic to study are their correlations with properties of their host galaxies, such as the tight correlations with the masses of their host galaxy (Wehner & Harris 2006; Rossa et al. 2006; Ferrarese et al. 2006). The correlation between the mass of the spheroidal component of the host galaxy and the mass of the SMBH, as well as that with the bulge velocity dispersion, is another crucial aspect to consider (Gültekin et al. 2009; Magorrian et al. 1998). There are a number of cases in which NSCs and SMBHs were found to co-exist (Filippenko & Ho 2003; Seth et al. 2008; Graham & Spitler 2009; Neumayer & Walcher 2012; Nguyen et al. 2019). Other nearby examples of SMBH detections within NSCs are M31 (Bender et al. 2005), M32 (Verolme et al. 2002; Nguyen et al. 2018), NGC 3115, and the Milky Way (Tonry 1984; Dressler & Richstone 1988; Richstone et al. 1990; Kormendy & Richstone 1992; van der Marel et al. 1994). The co-existence suggests that the build-up of NSCs and the growth of SMBHs are closely related (see also Escala 2021; Vergara et al. 2023). The high masses of the SMBHs at the early age of the Universe at which we observe these objects are a real challenge for theories of their formation. If we assume a constant accretion at the Eddington limit with only 10% of the matter falling into the black hole (BH) being radiated away, a stellar-mass BH with a mass of = 10 M⊙ requires a timescale of taccr ≈ 1 Gyr to reach the masses of SMBHs observed in the most massive AGN (Shapiro 2005). However, it is unlikely to grow so much because of the removal of the gas reservoir by ultraviolet (UV) radiation and supernova (SN) explosions of the Pop III stars in the shallow gravitational potential wells of minihalos (Johnson & Bromm 2007; Whalen et al. 2008; Milosavljević et al. 2009). This suggests that the seed BH must have formed at a redshift of z ≥ 15 with a mass of ≈105 M⊙, or that the BH seed had a lower mass but accreted very efficiently, or a combination of both.

One promising formation scenario is direct collapse (DC) (Latif et al. 2013, 2014), which involves the gravitational collapse of massive gas clouds in atomic cooling haloes (Tvir > 104 K, M ≈108 M⊙) at high redshift (Wise et al. 2019). It was suggested that this process forms SMBH seeds with masses around 103 − 5 M⊙. However, the presence of molecular hydrogen could lead to cloud fragmentation (Omukai et al. 2008; Suazo et al. 2019), preventing the formation of massive objects. Another scenario is associated with the dynamics within stellar clusters. Fragmentation at high density may give rise to the formation of ultradense clusters (Omukai et al. 2008; Devecchi & Volonteri 2009). Due to its high stellar density, this cluster can undergo runaway core collapse in a short time, forming a central intermediate-mass black hole (IMBH) with a mass of approximately 102 − 4 M⊙ (e.g. Portegies Zwart et al. 2004; Sakurai et al. 2017; Reinoso et al. 2018, 2020; Vergara et al. 2021, 2023). In this scenario, a newly born dense star cluster could still be embedded in gas, aiding in the formation of a massive BH seed through the inflow of gas into the cluster (Tagawa et al. 2020). This process increases the gravitational potential of the cluster, reduces the escapers, which we define as BHs with more kinetic than potential energy, and deepens the potential well of the cluster. Furthermore, in this scenario, the protostar may accrete gas, increasing its radius and, consequently, its cross section. Gas dynamical friction can drive a more efficient core collapse (e.g. Tagawa et al. 2020; Schleicher et al. 2022).

Dynamical friction can also cause massive objects to sink to the center of a star cluster, where at the end of their lifetime the massive objects will evolve into stellar mass BHs or neutron stars, forming a dark core. The dynamical evolution of such BH clusters has been examined by Quinlan & Shapiro (1987, 1989), who found that for typical parameters these clusters will dissolve due to the ejection of BHs as a result of three-body interactions (see also Chassonnery & Capuzzo-Dolcetta 2021). A solution to this problem has been proposed by Davies et al. (2011), showing that gas inflows after galaxy mergers could steepen the potential of the cluster, increase the velocity dispersion, and reduce the timescale for contraction due to gravitational wave (GW) emission in comparison to the three-body ejection timescale. Lupi et al. (2014) investigated the statistical implications of such a scenario by implementing it into a semi-analytic model of galaxy evolution, showing that this formation channel may contribute a substantial amount of seed BHs. In an independent investigation, Kroupa et al. (2020) found that the steepening of BH clusters through inflows of gas could explain the presence of SMBHs in high-redshift quasars.

In this paper, we investigate this scenario in more detail, exploring the evolution of a BH cluster in an external potential to determine under which conditions it can lead to the formation of an IMBH, as well as the efficiency of that process. In Section 2, we describe the model that forms the basis of our simulations. Section 3 outlines the methodology employed, along with the initial conditions for the simulations. In Section 4, we present the results of the evolution of the clusters, detailing the influence of the external potential and the post-Newtonian effects on the formation of massive objects. We explore mergers via GWs, the influence of escapers, and various properties of the binaries formed within the cluster. In Section 5, we provide a discussion of neglected effects including possible considerations for future research. Finally, in Section 6, we present our conclusions.

2. Model

The theoretical framework of this project is a variation of the model introduced in the previous section on runaway mergers in dense star clusters. The model considers mergers in dense BH clusters, following the framework of Davies et al. (2011). Due to mass segregation, the stellar mass BHs are assumed to have sunken to the center of the core of an NSC. In stellar systems there is a tendency toward equipartition of kinetic energies, so the most massive objects will tend to move more slowly on average and then massive objects fall deep into the potential well, while light objects tend to move fast and move out, and may reach the velocity necessary to escape. This instability is known as the equipartition instability or Spitzer instability, causing mass segregation and leading to the formation of a dark core.

We assume that the stars and other remnants in the core of the cluster can be ignored as their individual masses are much smaller than those of the stellar mass BHs, and thus they will be absorbed by the BHs or they may be pushed outside of the radius of the dark core (Banerjee & Kroupa 2011; Breen & Heggie 2013). The cluster, which is more than 50 Myr old, is assumed to consist of N equal mass stellar BHs, each with mass mBH. Some BH–BH interactions can lead to escapers but a significant fraction of the initial stellar mass BHs remains in the cluster (Mackey et al. 2007). For simplicity, we assume here that the BHs formed in the cluster do not grow during the initial 50 Myrs because of stellar feedback (radiation, winds, and SNe).

Binaries within the dark core stabilize the cluster against core collapse as the binaries are a heating source (Hills 1975; Heggie 1975; Coleman Miller & Hamilton 2002). Thus, the dark core evolves as the BH population self-depletes through the dynamical formation of BH binaries in triple encounters that, after their formation, may exchange energy with a third BH. Some of these interactions could lead to BH escapers though, due to the deep potential well, the cluster retains most of its BHs. According to the Hénon principle (Hénon 1961, 1975), the energy generation rate in the cluster core from encounters between single BHs or binaries with hard binaries is regulated by the mass of the system. Such encounters transform binding energy into kinetic energy, which supports the cluster against core collapse. While soft binaries will be split by interactions in binary-single encounters, hard binaries tend to harden in binary-single encounters. We introduce here the critical value of the semi-major axis describing the transition between soft and hard binary systems,

a h / s = G m 1 m 2 ⟨ m ⟩ σ 2 , $$ \begin{aligned} a_{h/s} = \frac{Gm_1m_2}{\langle m \rangle \sigma ^{2}}, \end{aligned} $$(1)

where m1 and m2 are the masses of the primary and secondary of the binary system, ⟨m⟩ describes the average BH mass in the cluster core, and σ the velocity dispersion. Binaries with semi-major axes of a > ah/s are then referred to as soft binaries and will be disrupted due to gravitationally encounters, while only hard binaries with a < ah/s can survive. The timescale of a binary within a cluster to gravitationally interact with another object is given by (Binney & Tremaine 2008)

τ 2 + 1 ≃ 6 × 10 8 x M c , 6 2 v ∞ , 10 3 yr , $$ \begin{aligned} \tau _{2+1} \simeq 6 \times 10^{8} x \frac{M_{c,6}^{2}}{{ v}_{\infty ,10}^3}\,\mathrm{yr} , \end{aligned} $$(2)

where Mc, 6 is the total mass of the cluster in units of 106 M⊙, x is the ratio of binary binding energy to kinetic energy, and v∞, 10 is the relative velocity at infinity in units of 10 km/s. In virial equilibrium, we have v∞, 10 ≈ 4.36 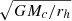G M c / r h $ \sqrt{GM_{c}/r_{h}} $ (Binney & Tremaine 2008), with rh is the cluster half-mass radius. Once the dark core reaches enough velocity dispersion (corresponding to a very large density), the dynamical binaries formed in the cluster will be sufficiently tight will quickly merge via GW emission, as then the timescale of GW emission will be equal to or shorter than the timescale of binary-single encounters. As the binding energy stored in the binaries is lost via GW emission, the binaries cease to be a source of heating for the cluster and core collapse takes place. The decay time of a BH binary with an initial separation, a, and eccentricity, e, is (Peters 1964)

τ gw ≃ 5 × 10 − 3 c 5 G m BH v ∞ , 10 8 x − 4 ( 1 − e 2 ) 7 / 2 yr . $$ \begin{aligned} \tau _{\rm gw} \simeq 5 \times 10^{-3} c^{5} G \frac{m_{\rm BH}}{{ v}_{\infty ,10}^{8}} x^{-4} (1-e^2)^{7/2}\,\mathrm{yr} . \end{aligned} $$(3)

The gravitational binary-single interactions will leave the binaries with a thermal distribution of the orbital eccentricities, where the median eccentricity is 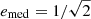e med = 1 / 2 $ e_{\mathrm{med}} = 1/\sqrt{2} $. This effect reduces the typical binary merger time by a factor ≈10. If τgr < τ2 + 1, binaries will merge, avoiding the transfer of their binding energy to kinetic energy via gravitational interactions, lose the energy that is stored in the binaries, and thus the binaries will not keep heating the cluster as a result. Then, the energy equilibrium breaks and core collapse is expected to happen.

This scenario thus requires a mechanism to shrink the radius of the cluster and/or increase its mass. The dark core thus needs to become more dense, so that the BHs may merge via runaway processes and stay within the cluster. In the scenario proposed by Mayer et al. (2010), the self-gravitating gas is subject to instabilities that funnel much of the low angular momentum gas to the center to scales of 0.2 pc or less. It is thus very efficient in contracting the core of the cluster, to increase the central densities and enhance the mass segregation, leading to fast interactions between stellar mass BHs that could lead to a quick coalescence and the formation of a massive BH seed. High-resolution cosmological simulations of galaxy formation by Bellovary et al. (2011) show a gaseous inflow due to a combination of matter accretion from the cosmic web filaments and mergers of galaxies, providing a significant inflow of gas comparable to or greater than the stellar mass in the cluster at high redshift (z > 10).

Independent of the primordial mass segregation, the inflow of gas into the cluster will make the BH cluster shrink given the steepening of the potential. This increases the interactions between the BHs, while the initial fraction of hard binaries also affects the re-expansion of the cluster due to their heating effect. In this scenario the gas only contributes to deepening the potential well, while we neglect here the dynamical friction that could make the cluster even more dissipative and further enhance the probability of forming a very massive object, as well as the formation of the gas itself (cooling, fragmentation, star formation) Kroupa et al. (2020) have further investigated this scenario, defining the gas mass that falls into the BH cluster as Mg = ηgNmBH. They find this scenario to be feasible for 0.1 < ηg < 1.0 with Rvir ≲ 1.5–4 pc and a total BH mass in the cluster of MBH ≳ 104 M⊙, where the cluster could reach a relativistic state (1% speed of light) within much less than a Gyr, while for ηg < 0.06 the BH cluster expands because the binary heating dominates over the gas drag. For large values such as ηg > 6, the BH cluster may even be in the relativistic regime from the beginning.

3. Simulations

To resolve the gravitational dynamics in the cluster, including post-Newtonian corrections, we used the NBODY6++GPU code (Wang et al. 2015). NBODY6++GPU uses a Hermite 4th order integrator method (Makino 1991). It also includes a set of routines to speed up the calculations such as using spatial and individual time steps and a spatial hierarchy that considers a list of neighbor particles inside a given radius to distinguish between the regular force and the irregular force (Ahmad & Cohen 1973). In this version, the gravitational forces are computed by graphics processing units (GPUs) (Wang et al. 2015; Nitadori & Aarseth 2012). It further uses an algorithm to regulate close encounters (Kustaanheimo et al. 1965). Finally, the code includes post-Newtonian effects, as is described below (Kupi et al. 2006).

As we saw above, NBODY6++GPU includes KS regularization (Kustaanheimo et al. 1965), and this algorithm starts to operate when two particles are tightly bound, replacing them with one particle and treating their orbit internally. This scheme was modified to allow for relativistic corrections to the Newtonian forces by expanding the accelerations in a series of powers of 1/c (Soffel 1989):

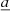a ̲ = a ̲ 0 ⏟ Newt . + c − 2 a ̲ 2 ⏟ 1 PN + c − 4 a ̲ 4 ⏟ 2 PN + c − 5 a ̲ 5 ⏟ 2.5 PN + c − 6 a ̲ 6 ⏟ 3 PN + c − 7 a ̲ 7 ⏟ 3.5 PN + O ( c − 8 ) , $$ \begin{aligned} \underline{a} = \underbrace{\underline{a}_{0} }_{\mathrm{Newt}.} + \underbrace{c^{-2}\underline{a}_2}_{1\mathcal{PN} } + \underbrace{c^{-4} \underline{a}_4}_{2\mathcal{PN} } + \underbrace{c^{-5} \underline{a}_5}_{2.5\mathcal{PN} } + \underbrace{c^{-6} \underline{a}_6}_{3\mathcal{PN} } + \underbrace{c^{-7} \underline{a}_7}_{3.5\mathcal{PN} } + \mathcal{O} (c^{-8}), \end{aligned} $$(4)

where a ̲ $ \underline{a} $ is the acceleration of particle one, 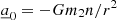a ̲ 0 = − G m 2 n / r 2 $ \underline{a}_0 = -Gm_2n/r^{2} $ is its Newtonian acceleration, and 1𝒫𝒩, 2𝒫𝒩, and 2.5𝒫𝒩 are the post-Newtonian corrections to the Newtonian acceleration, where 1𝒫𝒩 and 2𝒫𝒩 correspond to the pericenter shift and 2.5𝒫𝒩, 3𝒫𝒩, and 3.5𝒫𝒩 to the quadrupole gravitational radiation. The corrections were integrated into the KS regularization scheme as perturbations, similarly to what was done to account for passing stars influencing the KS pair (Brem et al. 2013).

Finally the criterion for particle mergers was calculated from their Schwarzschild radii as

| R i , j | < 10 G c 2 ( m i + m j ) , $$ \begin{aligned} |R_{i,j}| < 10\frac{G}{c^{2}} (m_i+m_j), \end{aligned} $$(5)

where G is the gravitational constant, c is the speed of light, and mi and mj are the mass of particles i and j, respectively, with |Ri, j| the distance between the particles in the binary system. This equation shows that the two BHs can merge only when their separation is smaller than five times the sum of their Schwarzchild radii. The mass of the new BH that forms is then given by the sum of the masses of the two merging BHs, considering a ideal case in which we neglect the mass loss due to GW radiation.

In this project, we used the model introduced in Sect. 2 to explore the evolution and formation of an SMBH seed in the dark core of a NSC. We performed a range of simulations to study how the presence of an external gas potential affects a dark core, the contraction of the dark core, and the growth of an SMBH seed via runaway mergers. The configurations that we considered to model the dark core of an NSC were a spherical cluster of N = 104 stellar mass BHs with identical BH masses of mBH = 10 M⊙ at the beginning of the simulations. The spatial distribution is an isotropic Plummer sphere (Plummer 1911) in virial equilibrium with a virial radius of Rv = 1.7Ra, with Ra = 0.59. The analytic potential is given by a Plummer distribution with a mass of Mgas = ηgMBH and the same virial radius of the cluster, where we varied the gas mass fraction of the cluster as ηg = 0.0,  0.1,  0.3,  0.5,  1.0.

Modeling such a cluster employing the physical velocity of light c = 3 × 105 km/s is computationally unfeasible as too many iterations would be required until the binaries evolve into a state in which the relativistic effects become important enough for the BH mergers to occur. Mergers via gravitational radiation are strongly dependent on the speed of light, as is seen in Eq. (3), and the timescale for GW emission is proportional to c5. Besides increasing the time for mergers, it also increases the time to solve the equation of motion, because as we see above in the Hermite scheme we need to compute not only the acceleration but also the derivative, and we need to do this for every factor of the post-Newtonian corrections, 1𝒫𝒩, 2𝒫𝒩, 2.5𝒫𝒩, 3𝒫𝒩, and 3.5𝒫𝒩. Simulations considering the real speed of light could take years to model the systems considered here. A simulation employing the real speed of light may not be feasible; however, one can employ a reduced speed of light, which makes the calculations computationally affordable and allows one to explore the behavior of the system. By exploring the dependence of the speed of light, we can then extrapolate the simulations outcome to the real value of c. We varied the speed of light as c = 103;  3 × 103;  6 × 103;  104,  3 × 104 km/s, which also affects the radii of the BHs in the cluster via the Schwarzschild radii and the criterion for the mergers. As we shall see in our results, for sufficiently high values of the speed of light, the dependence on this parameter in fact becomes relatively weak. The time evolution of all clusters was considered over a time of T = 1.4 Gyr. All configurations are given in Table 1. We conducted four simulations with different random seeds to ensure diverse initial conditions at the start of each simulation, corresponding to a total of 100 simulations. For these initial conditions, we estimated the range of root mean square (rms) velocities necessary for binary systems to efficiently merge via gravitational radiation before being ejected as a result of 2 + 1 encounters in Fig. 1. For the range of rms velocities in our simulations, the figure indeed shows that the timescale for GW emission becomes less than the timescale for 2 + 1 encounters for a speed of light of c = 3000 km/s, potentially enhancing the formation of a very massive object in this regime, while for larger values of the speed of light the mergers will be delayed, and escapers due to 2 + 1 interactions could play a certain role.

Table 1.

Initial conditions of the simulations.

thumbnail Fig. 1.

Different timescales in years: the timescale for binary-single encounters given by Eq. (2) (dashed lines) and gravitational radiation inspiral given by Eq. (3) (solid lines), considering a variation in the gas mass fraction between ηg = 0.0,  0.1,  0.3,  0.5,  1.0,  10.0, with the lowest value in the dashed blue line and the highest value in the violet. We also employed different values of the speed of light, from c = 103 km/s (dashed brown line) to the real value of c = 3 × 105 km/s (solid dark line). The vertical lines show the velocity dispersion given by v∞ for different gas mass fractions.

4. Results

In this section, we present the results of the simulations in which we explored the behavior of the BH clusters, taking into account the influence of an external gas potential as well as variations in the ratio of the gas mass over the total mass in BHs. Additionally, we consider the effects of varying the speed of light and how it affects the evolution and growth of the central object. The setups we considered are detailed in Table 1. In the next subsection, we focus on three specific clusters with IDs 1, 5, and 25, as is indicated in Table 1, corresponding to clusters with a low speed of light and no external potential, a low speed of light and high external potential, and a high speed of light with a high external potential.

4.1. Evolution of black hole clusters

The evolution of a BH cluster from birth to the moment of core collapse is described by Spitzer (1987), whereby the cluster evolves toward the collapse via two-body relaxations at the half-mass radius. This time tends to increase when the cluster is affected by a background potential (Reinoso et al. 2020) and is given by

t rh , ext = 0.138 N ( 1 + η g ) 4 l n ( γ N ) t cross , ext , $$ \begin{aligned} t_{\mathrm{rh,ext}} = 0.138\frac{N (1+\eta _{g})^{4}}{ln(\gamma N )} t_{\mathrm{cross,ext}}, \end{aligned} $$(6)

where N is the number of particles in the cluster, ηg is the fraction of gas mass, γ is equal to 0.4 for equal mass clusters, and tcross, ext is the time necessary for a BH to cross the cluster in the presence of an external potential.

In Fig. 2, we illustrate the evolution of the dark cluster without an external potential (i.e., ηg = 0.0) while considering a speed of light of 103 km/s. The crossing time of the cluster, assuming no external potential, is calculated to be 0.0482 Myr. Additionally, the half-mass relaxation time given by Eq. (6) is 166.38 tcross. The cluster reaches its highest density at 85.194 Myr or, in terms of the half-mass relaxation time, at 10.61 trh. The inner parts of the cluster measured via the 10% Lagrangian radius reach the highest density, 3.3 × 106 M⊙/pc3, at 0.144 pc.

thumbnail Fig. 2.

Evolution of the cluster in a simulation with speed of light c = 103km/s and an external potential of ηg = 0.0. The first two panels on the left present the results of our fit considering a King’s model. In the top left panel, we display the density of the core, while in the panel second from the left at the top, we illustrate the core radius of the cluster. In the bottom left panel, we show the Lagrangian radius for mass fractions between 1% and 90% of the total mass of the cluster. The top right panel shows the mergers of BHs in the cluster in bins of 5 Myr, in the middle right panel we show the growth in the mass of the most massive BH in the cluster. The bottom right panel shows the accumulative ejections in the cluster. The vertical line in the panels corresponds to the moment when the highest central density is reached.

In the first panel on the left we show the evolution of the core density and in the second panel we show the core radius evolution with time. The method used to obtain these results is explained in the next section. We note that before the core collapse, the density of the core of the cluster has a steep increase, reaching the maximum at ≈109 M⊙/pc3. At the same time, the core radius reaches the minimum at ≈0.01 pc when the core collapse occurs (vertical line), after which the cluster begins to expand, decreasing its density and increasing its core radius slowly. We can also note that the core density and core radius exhibit high dispersion in their trends, probably because almost all the mass in the core is within the massive BH seed at the center of the cluster. In the bottom left panel, we show the Lagrangian radius. We observe that the 1% Lagrangian radius post-core-collapse experiences the motion of the central object because the central object has more than 1% of the total mass of the cluster. The 5% Lagrangian radius shows a rebound and, approximately 50 Myr later, also shows similar behavior to a 1% Lagrangian radius. A similar phenomenon occurs with the 10% Lagrangian radius but with a longer delay in the collapse and subsequently the motion of the central object. Lagrangian radii greater than 10% are affected by the expansion of the cluster. The middle right panel depicts the growth in the mass of the central object and the beginning of massive BH formation. At the time when the highest density is reached, the growth becomes exponential, occurring in a short span of approximately 10 Myr, eventually reaching a mass of 10 770 M⊙ by the end of the simulation.

In the third panel, we show the evolution of BH escapers from the cluster with a similar peak when the highest density is reached, resulting in a total mass loss of 21% from the cluster. The fourth panel illustrates the evolution of mergers, with a peak of approximately ≈80 mergers in 5 Myr. There is a second peak occurring approximately ≈50 Myr later, with about ≈30 mergers, coinciding with the contraction of the 5% Lagrangian radius.

In Fig. 3, we show the evolution of the cluster considering an external potential of ηg = 1.0 and a speed of light of 103 km/s, The crossing time is 0.0241 Myr, and the half-mass relaxation time is 2662.149 tcross. The cluster experiences a high increase in the central density at 450 Myr or, in terms of the half-mass relaxation time, 7.010 trh. The density reached at the 10% Lagrangian radius is 1.23 × 106 M⊙/pc3, with a radius of 0.2 pc. The behavior of the cluster is remarkably similar to that of the cluster without an external potential. One of the differences is the delay in the contraction of the inner regions in the cluster and the lower contraction in the 10% Lagrangian radius; also, at the time of core collapse, the density and radius of the core exhibit even more abrupt changes considering a higher external potential, with a steep increase in the density of the core and the core radius. A higher merger rate is spread over a larger time interval, implying that the forming object becomes more massive. The amount of escapers is reduced by almost 5% compared to the cluster without external potential.

thumbnail Fig. 3.

Evolution of the cluster in a simulation with speed of light c = 103 km/s and an external potential of ηg = 1.0. The first two panels on the left present the results of our fit considering a King’s model. In the top left panel, we display the density of the core, while in the second panel from the left at the top, we illustrate the core radius of the cluster. In the bottom left panel, we show the Lagrangian radius for mass fractions between 1% and 90% of the total mass of the cluster. The top right panel shows the mergers of BHs in the cluster in bins of 5 Myr. In the middle right panel we show the growth in the mass of the most massive BH in the cluster. The bottom right panel shows the accumulative ejections in the cluster. The vertical line in the panels corresponds to the moment when the highest central density is reached.

Simulations with a higher speed of light tend to decrease the phase of oscillations in the inner regions of the clusters. Additionally, they tend to delay the core collapse, even when considering the same external potential. Moreover, the number of mergers decreases, resulting in lighter SMBH seeds. In Fig. 4, we illustrate the evolution of a BH cluster with an external potential of ηg = 1.0 and a speed of light of 3 × 104 km/s. The highest density that we computed, considering the 10% Lagrangian radius corresponding to a density peak of 1.92 × 107 M⊙/pc3, occurs at 1137 Myr or, in terms of relaxation time, 17.77 trh. As was mentioned previously, there is a delay in the core collapse compared to clusters with the same external potential but a lower speed of light. The core collapse appears to occur more smoothly compared to the case with a lower speed of light and is not as abrupt. Following the core collapse during the rebound process, the core density experiences a quick decrease. Additionally, the core radius undergoes a rapid increase, indicating that the rebound process is more prominent when the cluster has a higher speed of light. The contractions occur at the same time in the inner regions of the cluster, and prominent motion of the central object is only observed in the 1% Lagrangian radius. The number of escapers in the cluster is similar to the other clusters with the same external potential, with only 17% of BHs escaping.

thumbnail Fig. 4.

Evolution of the cluster in a simulation with speed of light c = 3 × 103 km/s and an external potential of ηg = 1.0. The first two panels on the left present the results of our fit considering a King’s model. In the top left panel, we display the density of the core, while in the second panel from the left at the top, we illustrate the core radius of the cluster. In the bottom left panel, we show the Lagrangian radius for mass fractions between 1% and 90% of the total mass of the cluster. The top right panel shows the mergers of BHs in the cluster in bins of 5 Myr. In the middle right panel, we show the growth in the mass of the most massive BH in the cluster. The bottom right panel shows the accumulative ejections in the cluster. The vertical line in the panels corresponds to the moment when the highest central density is reached.

4.2. Time dependence of core collapse

The most common way to determine whether a core collapse occurs in an N-body system is via the evolution of the core radius and the core density. An additional possibility involves considering the binding energy of binaries within the core of the cluster. During core collapse, binaries harden through three-body interactions until they possess enough energy for the core to bounce (Fujii & Portegies Zwart 2014). In the analysis presented here, we focus on the first possibility, the bounce of density and radius, as the density peak is significant enough to be visually observed. This is well justified as our model involves equal mass BHs, implying low values of fmax = mmax/⟨m⟩, while core collapse becomes more ambiguous for larger values of fmax (Fujii & Portegies Zwart 2014).

We estimated the core radius and core density by fitting a density profile according to King’s model (King 1962),

ρ King = ρ 0 ( 1 + ( r r c ) 2 ) − 3 / 2 . $$ \begin{aligned} \rho _{\rm King} = \rho _{0} \left( 1 + \left(\frac{r}{r_c} \right)^{2} \right)^{-3/2}. \end{aligned} $$(7)

This fitting is considering the cluster without the central massive object at the moment of core collapse. The massive object is not included as its increase in mass via collisions may contribute to an increase in central mass density, though our interest here is to determine whether there is a contraction of the central core. We determine the time of core collapse via the evolution of the peak density of the core.

As we increase the external potential, one of the significant differences is the time it takes for the contraction of the inner regions to occur. As was observed in the previous sections, there is a difference of more than 1 Gyr between the cluster without a gas potential and the one with an equal mass fraction of gas and BHs, considering a speed of light of 3 × 104 km/s. On the other hand, at a lower speed of light of 103 km/s, this difference in the time delay between the simulations with the highest and the lowest external potential corresponds to only about 450 Myr. For simplicity and to adopt a uniform approach between the simulations, we employed the 10% Lagrangian radius to determine the time of maximum contraction corresponding to the central density peak.

In Fig. 5, we show the time of the core collapse in the cluster in relaxation time given by Eq. (6) as a function of the external potential (ηg) at different speeds of light. The maximum central contraction is reached within 6–20 half-mass relaxation times, as is evident in Fig. 5. Assuming that core collapse is proportional to the relaxation time (Spitzer 1987), we can infer that the time of contraction of the inner regions is proportional to tcc ∝ (1 + ηg)4tcross, so the time of core contraction tends to be higher when the external potential increases (Reinoso et al. 2020). The linear trend suggests that clusters are more affected by gravitational radiation if the speed of light is reduced, making them more relativistic. In simulations in which the speed of light is particularly low – that is, less than 3 × 103 km/s – it is conceivable that the contraction time is even enhanced due to efficient GW emission. This is supported by simulations with a speed of light ≤3 × 103 km/s where the rms is larger than 1% of the value of the speed of light used in the simulation, implying that the BH cluster is in a relativistic state (Kupi et al. 2006). For instances in the cluster with c = 103 km/s, the rms velocity is higher than 1% of the speed of light that we consider in simulation IDs 1–5. Furthermore, the relativistic state is more prolonged for higher external potentials, as the rms speed increases with the external potential, affecting the cluster via strong relativistic effects, leading to the dissipation of kinetic energy into GWs. For speeds of light exceeding c = 3 × 103 km/s, we observe that the rms speed is slightly below 1% of the speed of light considered in this simulation (30 km/s), but it is very close. Consequently, we might expect that gravitational radiation is not exceptionally strong, but it is still sufficient to reduce the time for contraction of the cluster. On the other hand, the external potential increases the core collapse timescale. This is evident when examining the orange curve in Fig. 5. However, for higher speeds of light, gravitational radiation is not strong enough, leading to a delay in the contraction of the inner region.

thumbnail Fig. 5.

Core collapse time relative to the half-mass relaxation time as a function of the gas mass fraction of the cluster, denoted as ηg. Each curve represents a different value of the speed of light, c. The shadow zone is the error computed via the standard deviation from simulations with different initial conditions.

4.3. Binary population

Our simulations indicate that with respect to both the binary population and the mass of the cluster, the population of binary systems decreases when the cluster experiences a deeper external potential. This trend is primarily attributed to the disruption of soft binaries resulting from the increase in the velocity dispersion within the cluster. In dense star clusters, binaries are influenced by two-body encounters, leading to a drift due to mass segregation. This is primarily because binaries possess a larger mass relative to single stars. In denser regions, the semi-major axis of binary systems tends to decrease over time, which leads to an increase in their hardness or their disruption via encounters with single BHs. To provide a clearer view of the trends in the semi-major axis at different external potentials, we calculated the standard deviation of the semi-major axis of all binaries that are formed in the cluster via third-body BH interaction, finding an increase in the semi-major axis up to ηg = 0.1 (see Fig. 6). As the external potential increases, it becomes evident that binaries tend to become more tightly bound, resulting in a significant reduction in the spread of the semi-major axis, nearly by one magnitude, when ηg = 1.0. This trend is similar to the behavior of the number of escapers in the cluster, and could be a result of weak interactions increasing the kinetic energy enough to eventually escape from the cluster given the higher cross section of the binaries of cluster with higher external potential. For larger values of the speed of light, the semi-major axis tend to slightly decrease, as the evolution of the binaries via GW emission is decelerated.

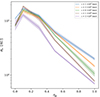thumbnail Fig. 6.

Root mean square dispersion of the semi-mayor axes of the binaries in the cluster as a function of the external potential (ηg). The different colors correspond to different speeds of light. The shadow regions correspond to the error associated with the random initial conditions.

4.4. Intermediate-mass black hole seed formation

The mass of the most massive object formed in the simulations is provided in Fig. 7 as a function of the ηg (left panel) and as a function of the speed of light, c (right panel). For speeds of light of 6 × 103 km/s or higher, the mass of the most massive object is essentially independent of ηg and in the range of 500–1500 M⊙,

thumbnail Fig. 7.

Mass of the most massive BH and the parameter α. In the top panels, we display the mass of the most massive BH in the cluster at the end of the simulation as a function of the external potential, ηg, (left) and as a function of the speed of light (right). In the bottom panels, we provide the parameter, α, as a function of the external potential, ηg, (left) and as a function of the speed of light (right). This parameter is defined as the ratio of total mergers in the cluster and the mass of the of the massive object, indicating how many merging objects contribute to the formation of the central object.

At least for ηg < 1.0, we can observe a slight decrease in the trend of the mass in the central object. This occurs as the time of contraction increases with higher external potential, as we can see Fig. 5, and the central object has less time post-core-collapse to increase its mass by mergers.

For lower speeds of light, the formation of the massive object has been considerably enhanced by stimulated GW emission, leading to masses of the most massive object on the order of 104 M⊙. A higher value of ηg further stimulates GW emission and enhances this effect. Looking at the mass of the most massive object as a function of c, we note that from the right panel of Fig. 7 the relation considerably flattens for speeds of light of 6 × 103 km/s or higher.

As is observed in Figs. 2 and 4, mergers of BHs can occur independently of the core contraction event. This suggests that the conditions for these mergers are not exclusively confined to the core contraction phase. Mergers can also occur after this contraction event due to the high density in the inner regions of the cluster. The presence of numerous binaries surrounding the central region and recently formed massive objects may enhance BH binary mergers via the Kozai-Lidov mechanism (Aarseth 2007; Sedda 2020). This mechanism involves the attainment of large eccentricities through third-body secular perturbations, and finally feeding the central object. Another speculative mechanism that could enhance the eccentricity of binaries in dense clusters is via perturbation of single objects passing near the binary system, driving the eccentricity to one (Reinoso et al. 2021).

Additionally, the external potential has a significant impact on the binary population by reducing the number of binaries available for mergers. This reduction in binaries could affect the mass of the central massive BH. Moreover, the external potential also delays the timing of core contraction. However, it is important to note that the density and velocity dispersion within the cluster are essential factors for the formation of “hard” binaries, which are more likely to merge due to gravitational radiation.

In Fig. 7, we further report the parameter, α, which corresponds to the ratio between the number of mergers and the mass of the most massive object, both as a function of ηg and c. For speeds of light of 6 × 103 km/s or less, the ratio, α, has only a weak dependence on ηg and is in the range of 0.85–1. In the simulations with higher speeds of light, α decreases with ηg, from values around 0.75 in the absence of an external potential to α ∼ 0.45 for ηg = 1. When we consider the dependence on the speed of light, we find a weak dependence on ηg for speeds of light below 3 × 103 km/s, as the efficient GW emission leads to a rapid contraction of the system. When c increases, there is more time for mergers among stellar mass BHs to occur, with a more significant spread and dependence on ηg. With further increasing values of c, α increases again for all values of ηg, as larger values of c also suggest a longer timescale for the merger of stellar mass BHs, while the timescale for the central collapse remains very similar.

The efficiency of the formation of the most massive object, defined as its final mass divided by the cluster mass in BHs, is provided in Fig. 8 as a function of the ratio of the rms velocity, v∞, at the time of core collapse divided by the speed of light adopted in the simulation. As a result, we find a clear relation, where the efficiencies are in the range of 0.001–0.004 for values of v∞/c < 0.0025. The efficiencies increase to 0.04–0.07 for v∞/c ∼ 0.005 and a further more moderate increase occurs for v∞/c ∼ 0.015, reaching efficiencies of 0.06–0.08. The dependence on the external potential is however nontrivial; we saw already above that the mass of the most massive object can either increase with ηg, stay constant or slightly decrease, leading here to a complex relation as a function of v∞/c. Fig. 8 nonetheless allows one to pursue a tentative extrapolation toward real systems, assuming BH clusters with velocity dispersion of 1000 km/s and 3000 km/s together with the physical speed of light. As is indicated within the figure, the latter corresponds to efficiencies of 0.004–0.05 and 0.05–0.07, respectively.

thumbnail Fig. 8.

BH formation efficiency of the clusters, defined as the mass of the most massive BH divided by the total BH mass of the cluster, as a function of the ratio between the rms velocity at the time of the core collapse and the speed of light (c) employed in the simulations. Different colors are used to denote varying external potentials, ηg. The vertical lines mark velocity ratios assuming the real value of the speed of light for clusters with an rms velocity of 1000 km/s and 3000 km/s.

4.5. Extrapolation to nuclear star clusters

After the tentative extrapolation of the efficiencies to real astrophysical systems in the previous subsection, we here aim to assess more quantitatively the masses of the most massive objects that could be formed via mergers in dense BH clusters as a function of the physical conditions. We showed in the previous subsection that a central parameter is the ratio v∞/c, as it allows one to characterize the relativistic state of the cluster and provides a good indication of the efficiency of the formation of a very massive BH.

As a first step, we thus aim to infer the rms velocities that can be expected in different clusters as a function of their mass and radius. For this purpose, we considered and distinguished two different cases. The first scenario assumes that the BHs in the cluster are in equipartition with their self-gravity and the external potential, as is intrinsically assumed in the simulations we presented here. In this case, we have

v ∞ ≈ 0.4 G M BHs ( 1 + η g ) R vir · $$ \begin{aligned} { v}_{\infty } \approx \sqrt{ 0.4 \frac{G M_{\rm BHs} (1+ \eta _{g})}{R_{\rm vir}}}\cdot \end{aligned} $$(8)

v∞, however, does not adequately account for the contraction of the BH cluster due to gas accretion. Therefore, the cluster is less dense than considered in the model proposed by Davies et al. (2011), in which gas accretion affects the density of the cluster and subsequently influences the rms velocity. A more accurate velocity dispersion for a cluster affected by gas accretion was derived by (Kroupa et al. 2020) as

σ = ( f v G M BHs ( 1 + η g ) 2 R vir ) 1 / 2 , $$ \begin{aligned} \sigma = \left( f_{ v} \frac{G M_{\rm BHs}(1+\eta _{g})^{2}}{ R_{\rm vir} } \right)^{1/2}, \end{aligned} $$(9)

where MBHs is the mass of BH in the cluster, Rvir is the virial radius, and fv ≈ 1 is a dimensionless factor that covers a departure from the virial equilibrium or a particular shape of the potential well. The corresponding velocity dispersion is given as a function of BH mass in the cluster and the cluster virial radius in Fig. 9, for both the case in which they are calculated via Eq. (8) and for Eq. (9). The behaviour in both cases is similar but the velocity dispersion is somewhat enhanced in the second case. Particularly high velocity dispersion occur when both the total mass in the cluster is high and the virial radius of the cluster is small. To obtain velocity dispersions on the order of 3000 km/s, implying relativistic clusters, it seems likely that cluster masses of 107 M⊙ or higher are required.

thumbnail Fig. 9.

RMS velocity of the cluster at different external potential. In the left panel, we show the rms contour lines of the velocity calculated via Eq. (8), providing its dependency on the virial radius and the total BH mass in the cluster. The contours illustrate the velocities at specific radii and masses. The bottom right panel provides contour lines of the velocity of the cluster defined by Eq. (9), assuming an additional contraction calculated by Kroupa et al. (2020). The different colors indicate various values of ηg.

The mass of the most massive object that forms in the two cases was finally estimated employing the efficiencies from Fig. 8. In the first case, in which the velocity was calculated assuming virial equilibrium Eq. (8), the resulting BH masses are provided as a function of the cluster mass and radius in Fig. 10, in which the different panels correspond to different values of ηg. In the case of BH clusters with masses of 105–106 M⊙, our model suggests that only BH seeds of moderate masses can be formed, roughly on the order of 103 M⊙. Black hole seeds of 104 M⊙ require clusters with at least ∼107 M⊙, which still needs to be sufficiently compact, with a virial radius of less than a parsec. The presence of an external potential potentially makes this more feasible, as it tends to increase the range of virial radii for which a massive object of significant mass can be produced for otherwise equal cluster parameters.

thumbnail Fig. 10.

Mass of the most massive BH estimated via the rms velocities calculated using Eq. (8) and their corresponding efficiencies depicted in Fig. 8. The clusters are within a range of virial radii from 0.1–2.0 pc and masses from 104–108 M⊙. The color represents the mass of the BH that forms. Each panel corresponds to a different value of the external potential.

We also provide the corresponding estimates for the scenario provided by Kroupa et al. (2020), with the estimated BH masses given in Fig. 11 for different values of ηg. The overall behavior is similar, but for a sensitive to the velocity dispersion of the cluster; however, we note a shift by about half an order of magnitude in the mass required for the cluster to form a seed BH of a certain stellar mass, which is dependent on the external potential. The decrease in the cluster radius and increase in its density as a result of the gas inflow is thus potentially relevant and may lead to the formation of more massive BH seeds under otherwise similar conditions.

thumbnail Fig. 11.

Mass of the most massive BHs that can form calculating the rms velocity using Eq. (9) from Kroupa et al. (2020) and the corresponding efficiency depicted in Fig. 8. The clusters are within a range of virial radii from 0.1–2.0 pc and masses from 104–108 M⊙. The color represents the mass of the BH that forms. Each panel corresponds to different external potentials.

5. Discussions

This investigation provides a clear insight into the formation of an IMBH in the dark core of an NSC. In a simplified model, we considered a cluster with equal mass BHs distributed according to a Plummer distribution. In our simulations, we formed two sets of BH seeds with approximately 104 M⊙ for clusters in a relativistic state and approximately 103 M⊙ for other clusters.

However, our models are affected by different assumptions. For instance, assuming equal-mass BHs in the cluster impacts mass segregation, leading to timescales for cluster evolution higher than in reality. Particularly, in clusters with a realistic stellar mass function, we have tcc ≃ 0.2trh (Zwart & McMillan 2002). Additionally, we neglected gas accretion onto the BHs, which further affects the timescale evolution, including the relaxation time (Leigh et al. 2013) and the mass distribution of the BHs in the cluster. Furthermore, gravitational recoil caused by GWs was not included in the simulations presented here. Studies such as Fragione & Silk (2020) provide a more extensive analysis of mergers and escapers considering recoils, with velocities up to a few thousand km/s, where the typical mass of an ejected massive BH is 400–500 M⊙. They also explore how the mass and density of the NSC influences the retention of massive BHs and the formation of binaries, in which the massive NSCs can more easily retain massive BHs but the formation of binaries requires longer timescales. Dense NSCs can both retain massive BHs and have a higher efficiency in forming binaries that merge through GW emission.

Regarding future work on the formation of an IMBH in a realistic NSC, Kroupa et al. (2020) demonstrate that for a high mass ratio of gas, ηg > 5.78, the cluster tends to expand for dark core masses < 107 M⊙. However, for a mass of the dark core > 107 M⊙, the cluster is already initially in a relativistic state. To form an IMBH, we could consider massive dark cores with either massive BHs > 10 M⊙ or a higher number of BHs in the cluster. But this is not enough to reach the core collapse with the methodology that we have used so far, as the relaxation timescales as ∝(1 + ηg)4, so for values of ηg higher than 2.0 the core collapse requires more than 1.4 Gyr. We further note that an initial mass distribution of the BHs reduces the time that the core collapse takes.

Of course, this is a recent investigation: our knowledge of the mass distribution of stellar mass BHs is still limited, and no model can fully reproduce the distribution of observed total masses. Nevertheless, the observations lie within the distribution of mass in the 1σ band of the Mmax = 50 M⊙, α = 2.35 model (Perna et al. 2019), which could be employed in follow-up calculations in the future. In future projects, it will also be important to understand resonant relaxation (or Kozai) effects, which could significantly increase the rate of inspiral and their relation with 𝒫𝒩1 and 𝒫𝒩2, affecting the precession and the impact of the number of captures (Hopman & Alexander 2006). Finally, the consideration of radiation recoil will give us a better understanding of the evolution and formation of IMBHs.

6. Conclusions

In this paper, we have explored the formation of seed BHs in dense BH clusters embedded in an external potential, with the goal of exploring the hypothesis of Davies et al. (2011) that relevant gas inflows into such compact clusters will significantly increase the velocity dispersion and help to make the timescale for GW emissions more relevant compared to the timescale for ejections via 2 + 1 encounters, thereby favoring the formation of a massive central object.

As the simulations of massive BH clusters incorporating post-Newtonian corrections with the real value of the speed of light are still computationally unfeasible, we have treated the speed of light as a free parameter to explore how the results of our simulations depend on the speed of light and more specifically also on the ratio of the velocity dispersion of the cluster divided by the speed of light. The latter allows us to test and explore the dependence on this parameter, including an extrapolation toward the parameters of real physical systems. We focused on BH clusters with 104 stellar mass BHs with each of them having 10 M⊙, a virial radius of 1 pc, ratios of gas mass to mass in BHs ranging from 0–1, as well as speed-of-light values ranging from 1000 km/s up to 3 × 104 km/s.

For speed-of-light values of 3000 km/s or less, we have found GW emission to be strongly enhanced, increasing even the contraction time of the cluster and favoring the formation of very massive objects of 104 M⊙ or more. For larger speed-of-light values, the sensitivity to this parameter significantly decreased as the timescale for GW emission was significantly enhanced, leading to typical seed masses in the range of 500–1500 M⊙. In particular, when considering the ratio of cluster rms velocity, v∞, divided by the speed of light, c, the latter provided a good relation with the efficiency of the formation of the most massive object, which we defined as the mass of the most massive object divided by the total mass in BHs. The latter has ranged from 0.001–0.004 for very low values of v∞/c to values in the range of 0.05–0.08 for v∞/c ∼ 0.005–0.015.

When extrapolating to real astrophysical systems, we have found that for BH clusters with masses in the range of 105–106 M⊙, this scenario may only be able to provide seed BHs of ∼103 M⊙. In clusters of 107 M⊙ that are more compact than a parsec, the formation of seed masses with ∼104 M⊙ is conceivable. The presence of an external potential also allows the formation of such objects in clusters of moderately increased size. If we adopt the formula provided by Kroupa et al. (2020) for the increase in the velocity dispersion as a result of the contraction due to the gas inflow, we further find that the required masses of the BH clusters decrease by roughly half an order of magnitude.

The astrophysical implications of the BHs formed via this mechanism will depend on their capability for subsequent growth. Even for accretion at a few percent of the Eddington rate, a strong radiatively driven wind could self-regulate BH growth. The physics of such radiatively driven winds has been explored; for example, by Thorne (1981) and Yamamoto & Fukue (2021), which might be complemented by radiation-driven disk winds as well (Giustini & Proga 2019). Observational evidence suggests that feedback via radiation-driven winds was more frequent and stronger in the early Universe (Bischetti et al. 2022) and may have been driven by the opacity from dust grains (Ishibashi 2019). In particular, winds from hot accretion flows were recently shown to be able to reach large scales (Cui & Yuan 2020), potentially expelling large fractions of the gas in the host galaxy (Brennan et al. 2018). Understanding the growth of seed BHs at early stages will therefore require further assessment of the operation of this feedback mechanism in their specific environment.

A particularly interesting place to study the origin of IMBHs may include low-metallicity dwarf galaxies in the metallicity range of 12 + log(O/H) = 7–9, which may more closely resemble the conditions corresponding to the early Universe. Enhanced X-ray activity has been found in several of these (e.g. Prestwich et al. 2013; Reefe et al. 2023; Cann et al. 2024), which could be due to an enhanced X-ray binary population but also an IMBH. These objects may include some interesting intermediate cases, as typically they do not necessarily show a fully established NSC in their center, but may include one or more globular-cluster-like objects, which potentially could be forming a dark core through the mechanism discussed above (e.g. Davies et al. 2011). Within these lower-mass environments, the evolution of the cluster would not necessarily lead to the formation of an IMBH, but could still be contributing to the X-ray excess found in observations.

The results we have derived here confirm important results from previous studies. In particular, it has been confirmed that higher BH formation efficiencies can be obtained when the cluster becomes relativistic; in other words, when the velocity dispersion corresponds to at least 1% of the speed of light. This assumption has already been employed in the investigation by Lupi et al. (2014) in the derivation of statistical predictions from this BH formation channel, with the conclusion that a significant amount of seed BHs may form in this way. Our results confirm these conclusions overall and suggest that the implications of this formation channel need to be taken into account in assessments of the formation history of SMBHs.

Acknowledgments

DRGS gratefully acknowledges support by the ANID BASAL projects ACE210002 and FB210003, via the Millenium Nucleus NCN19-058 (TITANs) and via Fondecyt Regular (project code 1201280). DRGS thanks for funding via the Alexander von Humboldt – Foundation, Bonn, Germany. BR acknowledges funding through ANID (CONICYT-PFCHA/Doctorado acuerdo bilateral DAAD/62180013), DAAD (funding program number 57451854), and the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg (IMPRS-HD). MF acknowledges funding through BASAL FB210003 and ACE210002. MCV acknowledges funding through ANID (Doctorado acuerdo bilateral DAAD/62210038) and DAAD (funding program number 57600326).

References

  1. Aarseth, S. J. 2007, MNRAS, 378, 285 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ahmad, A., & Cohen, L. 1973, J. Comput. Phys., 12, 389 [Google Scholar]
  3. Bañados, E., Venemans, B. P., Decarli, R., et al. 2016, ApJS, 227, 11 [Google Scholar]
  4. Banerjee, S., & Kroupa, P. 2011, ApJ, 741, L12 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bellovary, J., Volonteri, M., Governato, F., et al. 2011, ApJ, 742, 13 [Google Scholar]
  6. Bender, R., Kormendy, J., Bower, G., et al. 2005, ApJ, 631, 280 [NASA ADS] [CrossRef] [Google Scholar]
  7. Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
  8. Bischetti, M., Feruglio, C., D’Odorico, V., et al. 2022, Nature, 605, 244 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bogdán, Á., Goulding, A. D., Natarajan, P., et al. 2024, Nat. Astron., 8, 126 [Google Scholar]
  10. Breen, P. G., & Heggie, D. C. 2013, MNRAS, 432, 2779 [NASA ADS] [CrossRef] [Google Scholar]
  11. Brem, P., Amaro-Seoane, P., & Spurzem, R. 2013, MNRAS, 434, 2999 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brennan, R., Choi, E., Somerville, R. S., et al. 2018, ApJ, 860, 14 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cann, J. M., Weaver, K. A., Pfeifle, R. W., et al. 2024, ApJ, 961, 178 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chassonnery, P., & Capuzzo-Dolcetta, R. 2021, MNRAS, 504, 3909 [NASA ADS] [CrossRef] [Google Scholar]
  15. Coleman Miller, M., & Hamilton, D. P. 2002, MNRAS, 330, 232 [CrossRef] [Google Scholar]
  16. Cui, C., & Yuan, F. 2020, ApJ, 890, 81 [NASA ADS] [CrossRef] [Google Scholar]
  17. Davies, M. B., Miller, M. C., & Bellovary, J. M. 2011, ApJ, 740, L42 [NASA ADS] [CrossRef] [Google Scholar]
  18. Devecchi, B., & Volonteri, M. 2009, ApJ, 694, 302 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dressler, A., & Richstone, D. O. 1988, ApJ, 324, 701 [NASA ADS] [CrossRef] [Google Scholar]
  20. Escala, A. 2021, ApJ, 908, 57 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fan, X., Narayanan, V. K., Lupton, R. H., et al. 2001, ApJ, 122, 2833 [CrossRef] [Google Scholar]
  22. Fan, X., Bañados, E., & Simcoe, R. A. 2023, ARA&A, 61, 373 [NASA ADS] [CrossRef] [Google Scholar]
  23. Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [Google Scholar]
  24. Ferrarese, L., Côté, P., Bontà, E. D., et al. 2006, ApJ, 644, L21 [NASA ADS] [CrossRef] [Google Scholar]
  25. Filippenko, A. V., & Ho, L. C. 2003, ApJ, 588, L13 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fragione, G., & Silk, J. 2020, MNRAS, 498, 4591 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fujii, M. S., & Portegies Zwart, S. 2014, MNRAS, 439, 1003 [NASA ADS] [CrossRef] [Google Scholar]
  28. Giustini, M., & Proga, D. 2019, A&A, 630, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Graham, A. W., & Spitler, L. R. 2009, MNRAS, 397, 2148 [NASA ADS] [CrossRef] [Google Scholar]
  30. GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [Google Scholar]
  32. Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hénon, M. 1961, Ann. Astrophys., 24, 369 [Google Scholar]
  34. Hénon, M. 1975, Dynamics of the Solar Systems (Dordrecht, Boston: D. Reidel Pub. Co.) [Google Scholar]
  35. Hills, J. G. 1975, AJ, 80, 1075 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hlavacek-Larrondo, J., Fabian, A. C., Edge, A. C., & Hogan, M. T. 2012, MNRAS, 424, 224 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hopman, C., & Alexander, T. 2006, ApJ, 645, 1152 [NASA ADS] [CrossRef] [Google Scholar]
  38. Inayoshi, K., Visbal, E., & Haiman, Z. 2020, ARA&A, 58, 27 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ishibashi, W. 2019, MNRAS, 489, 5225 [NASA ADS] [CrossRef] [Google Scholar]
  40. Johnson, J. L., & Bromm, V. 2007, MNRAS, 374, 1557 [NASA ADS] [CrossRef] [Google Scholar]
  41. King, I. 1962, AJ, 67, 471 [Google Scholar]
  42. Kormendy, J., & Richstone, D. 1992, ApJ, 393, 559 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kroupa, P., Subr, L., Jerabkova, T., & Wang, L. 2020, MNRAS, 498, 5652 [Google Scholar]
  44. Kupi, G., Amaro-Seoane, P., & Spurzem, R. 2006, MNRAS, 371, L45 [NASA ADS] [Google Scholar]
  45. Kustaanheimo, P., Schinzel, A., Davenport, H., & Stiefel, E. 1965, Journal für die reine und angewandte Mathematik, 1965, 204 [CrossRef] [Google Scholar]
  46. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  47. Latif, M. A., Bovino, S., Grassi, T., Schleicher, D. R. G., & Spaans, M. 2014, MNRAS, 446, 3163 [Google Scholar]
  48. Leigh, N., Sills, A., & Böker, T. 2013, MNRAS, 433, 1958 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lupi, A., Colpi, M., Devecchi, B., Galanti, G., & Volonteri, M. 2014, MNRAS, 442, 3616 [NASA ADS] [CrossRef] [Google Scholar]
  50. Mackey, A. D., Wilkinson, M. I., Davies, M. B., & Gilmore, G. F. 2007, MNRAS, 379, L40 [NASA ADS] [CrossRef] [Google Scholar]
  51. Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, ApJ, 115, 2285 [CrossRef] [Google Scholar]
  52. Makino, J. 1991, ApJ, 369, 200 [Google Scholar]
  53. Mayer, L., Kazantzidis, S., Escala, A., & Callegari, S. 2010, Nature, 466, 1082 [Google Scholar]
  54. McConnell, N. J., Ma, C.-P., Gebhardt, K., et al. 2011, Nature, 480, 215 [NASA ADS] [CrossRef] [Google Scholar]
  55. Milosavljević, M., Bromm, V., Couch, S. M., & Oh, S. P. 2009, ApJ, 698, 766 [CrossRef] [Google Scholar]
  56. Neumayer, N., & Walcher, C. J. 2012, Adv. Astron., 2012, 709038 [NASA ADS] [Google Scholar]
  57. Neumayer, N., Seth, A., & Böker, T. 2020, A&ARv, 28, 4 [Google Scholar]
  58. Nguyen, D. D., Seth, A. C., Neumayer, N., et al. 2018, ApJ, 858, 118 [NASA ADS] [CrossRef] [Google Scholar]
  59. Nguyen, D. D., Seth, A. C., Neumayer, N., et al. 2019, ApJ, 872, 104 [Google Scholar]
  60. Nitadori, K., & Aarseth, S. J. 2012, MNRAS, 424, 545 [NASA ADS] [CrossRef] [Google Scholar]
  61. Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [Google Scholar]
  62. Perna, R., Wang, Y.-H., Farr, W. M., Leigh, N., & Cantiello, M. 2019, ApJ, 878, L1 [NASA ADS] [CrossRef] [Google Scholar]
  63. Peters, P. C. 1964, Phys. Rev., 136, B1224 [NASA ADS] [CrossRef] [Google Scholar]
  64. Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
  65. Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [Google Scholar]
  66. Prestwich, A. H., Tsantaki, M., Zezas, A., et al. 2013, ApJ, 769, 92 [NASA ADS] [CrossRef] [Google Scholar]
  67. Quinlan, G. D., & Shapiro, S. L. 1987, ApJ, 321, 199 [NASA ADS] [CrossRef] [Google Scholar]
  68. Quinlan, G. D., & Shapiro, S. L. 1989, ApJ, 343, 725 [NASA ADS] [CrossRef] [Google Scholar]
  69. Reefe, M., Satyapal, S., Sexton, R. O., et al. 2023, ApJ, 946, L38 [NASA ADS] [CrossRef] [Google Scholar]
  70. Reinoso, B., Schleicher, D. R. G., Fellhauer, M., Klessen, R. S., & Boekholt, T. C. N. 2018, A&A, 614, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Reinoso, B., Schleicher, D. R. G., Fellhauer, M., Leigh, N. W. C., & Klessen, R. S. 2020, A&A, 639, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Reinoso, B., Leigh, N. W. C., Barrera-Retamal, C. M., et al. 2021, MNRAS, 509, 3724 [NASA ADS] [CrossRef] [Google Scholar]
  73. Richstone, D., Bower, G., & Dressler, A. 1990, ApJ, 353, 118 [NASA ADS] [CrossRef] [Google Scholar]
  74. Rossa, J., van der Marel, R. P., Böker, T., et al. 2006, ApJ, 132, 1074 [CrossRef] [Google Scholar]
  75. Sakurai, Y., Yoshida, N., Fujii, M. S., & Hirano, S. 2017, MNRAS, 472, 1677 [NASA ADS] [CrossRef] [Google Scholar]
  76. Schindler, J.-T., Fan, X., Novak, M., et al. 2020, ApJ, 906, 12 [Google Scholar]
  77. Schleicher, D. R. G., Reinoso, B., Latif, M., et al. 2022, MNRAS, 512, 6192 [NASA ADS] [CrossRef] [Google Scholar]
  78. Sedda, M. A. 2020, ApJ, 891, 47 [CrossRef] [Google Scholar]
  79. Seth, A., Agüeros, M., Lee, D., & Basu-Zych, A. 2008, ApJ, 678, 116 [NASA ADS] [CrossRef] [Google Scholar]
  80. Shankar, F., Crocce, M., Miralda-Escudé, J., Fosalba, P., & Weinberg, D. H. 2010, ApJ, 718, 231 [NASA ADS] [CrossRef] [Google Scholar]
  81. Shapiro, S. L. 2005, ApJ, 620, 59 [NASA ADS] [CrossRef] [Google Scholar]
  82. Soffel, M. H. 1989, Relativity in Astrometry, Celestial Mechanics and Geodesy (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
  83. Spitzer, L. 1987, Dynamical Evolution of Globular Clusters (Princeton: Princeton University Press) [Google Scholar]
  84. Suazo, M., Prieto, J., Escala, A., & Schleicher, D. R. G. 2019, ApJ, 885, 127 [NASA ADS] [CrossRef] [Google Scholar]
  85. Tagawa, H., Haiman, Z., & Kocsis, B. 2020, ApJ, 898, 25 [NASA ADS] [CrossRef] [Google Scholar]
  86. The Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
  87. The Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
  88. Thorne, K. S. 1981, MNRAS, 194, 439 [NASA ADS] [Google Scholar]
  89. Tonry, J. L. 1984, ApJ, 279, 13 [NASA ADS] [CrossRef] [Google Scholar]
  90. Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
  91. van der Marel, R. P., Rix, H.-W., Carter, D., et al. 1994, MNRAS, 268, 521 [NASA ADS] [CrossRef] [Google Scholar]
  92. Vergara, M. Z. C., Schleicher, D. R. G., Boekholt, T. C. N., et al. 2021, A&A, 649, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Vergara, M. C., Escala, A., Schleicher, D. R. G., & Reinoso, B. 2023, MNRAS, 522, 4224 [NASA ADS] [CrossRef] [Google Scholar]
  94. Verolme, E. K., Cappellari, M., Copin, Y., et al. 2002, MNRAS, 335, 517 [NASA ADS] [CrossRef] [Google Scholar]
  95. Wang, L., Spurzem, R., Aarseth, S., et al. 2015, MNRAS, 450, 4070 [NASA ADS] [CrossRef] [Google Scholar]
  96. Wehner, E. H., & Harris, W. E. 2006, ApJ, 644, L17 [NASA ADS] [CrossRef] [Google Scholar]
  97. Whalen, D., O’Shea, B. W., Smidt, J., & Norman, M. L. 2008, ApJ, 679, 925 [NASA ADS] [CrossRef] [Google Scholar]
  98. Wise, J. H., Regan, J. A., O’Shea, B. W., et al. 2019, Nature, 566, 85 [NASA ADS] [CrossRef] [Google Scholar]
  99. Wu, X.-B., Wang, F., Fan, X., et al. 2015, Nature, 518, 512 [Google Scholar]
  100. Yamamoto, R., & Fukue, J. 2021, MNRAS, 502, 5797 [NASA ADS] [CrossRef] [Google Scholar]
  101. Zwart, S. F. P., & McMillan, S. L. W. 2002, ApJ, 576, 899 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Initial conditions of the simulations.

In the text

All Figures

thumbnail Fig. 1.

Different timescales in years: the timescale for binary-single encounters given by Eq. (2) (dashed lines) and gravitational radiation inspiral given by Eq. (3) (solid lines), considering a variation in the gas mass fraction between ηg = 0.0,  0.1,  0.3,  0.5,  1.0,  10.0, with the lowest value in the dashed blue line and the highest value in the violet. We also employed different values of the speed of light, from c = 103 km/s (dashed brown line) to the real value of c = 3 × 105 km/s (solid dark line). The vertical lines show the velocity dispersion given by v∞ for different gas mass fractions.
In the text
thumbnail Fig. 2.

Evolution of the cluster in a simulation with speed of light c = 103km/s and an external potential of ηg = 0.0. The first two panels on the left present the results of our fit considering a King’s model. In the top left panel, we display the density of the core, while in the panel second from the left at the top, we illustrate the core radius of the cluster. In the bottom left panel, we show the Lagrangian radius for mass fractions between 1% and 90% of the total mass of the cluster. The top right panel shows the mergers of BHs in the cluster in bins of 5 Myr, in the middle right panel we show the growth in the mass of the most massive BH in the cluster. The bottom right panel shows the accumulative ejections in the cluster. The vertical line in the panels corresponds to the moment when the highest central density is reached.
In the text
thumbnail Fig. 3.

Evolution of the cluster in a simulation with speed of light c = 103 km/s and an external potential of ηg = 1.0. The first two panels on the left present the results of our fit considering a King’s model. In the top left panel, we display the density of the core, while in the second panel from the left at the top, we illustrate the core radius of the cluster. In the bottom left panel, we show the Lagrangian radius for mass fractions between 1% and 90% of the total mass of the cluster. The top right panel shows the mergers of BHs in the cluster in bins of 5 Myr. In the middle right panel we show the growth in the mass of the most massive BH in the cluster. The bottom right panel shows the accumulative ejections in the cluster. The vertical line in the panels corresponds to the moment when the highest central density is reached.
In the text
thumbnail Fig. 4.

Evolution of the cluster in a simulation with speed of light c = 3 × 103 km/s and an external potential of ηg = 1.0. The first two panels on the left present the results of our fit considering a King’s model. In the top left panel, we display the density of the core, while in the second panel from the left at the top, we illustrate the core radius of the cluster. In the bottom left panel, we show the Lagrangian radius for mass fractions between 1% and 90% of the total mass of the cluster. The top right panel shows the mergers of BHs in the cluster in bins of 5 Myr. In the middle right panel, we show the growth in the mass of the most massive BH in the cluster. The bottom right panel shows the accumulative ejections in the cluster. The vertical line in the panels corresponds to the moment when the highest central density is reached.
In the text
thumbnail Fig. 5.

Core collapse time relative to the half-mass relaxation time as a function of the gas mass fraction of the cluster, denoted as ηg. Each curve represents a different value of the speed of light, c. The shadow zone is the error computed via the standard deviation from simulations with different initial conditions.
In the text
thumbnail Fig. 6.

Root mean square dispersion of the semi-mayor axes of the binaries in the cluster as a function of the external potential (ηg). The different colors correspond to different speeds of light. The shadow regions correspond to the error associated with the random initial conditions.
In the text
thumbnail Fig. 7.

Mass of the most massive BH and the parameter α. In the top panels, we display the mass of the most massive BH in the cluster at the end of the simulation as a function of the external potential, ηg, (left) and as a function of the speed of light (right). In the bottom panels, we provide the parameter, α, as a function of the external potential, ηg, (left) and as a function of the speed of light (right). This parameter is defined as the ratio of total mergers in the cluster and the mass of the of the massive object, indicating how many merging objects contribute to the formation of the central object.
In the text
thumbnail Fig. 8.

BH formation efficiency of the clusters, defined as the mass of the most massive BH divided by the total BH mass of the cluster, as a function of the ratio between the rms velocity at the time of the core collapse and the speed of light (c) employed in the simulations. Different colors are used to denote varying external potentials, ηg. The vertical lines mark velocity ratios assuming the real value of the speed of light for clusters with an rms velocity of 1000 km/s and 3000 km/s.
In the text
thumbnail Fig. 9.

RMS velocity of the cluster at different external potential. In the left panel, we show the rms contour lines of the velocity calculated via Eq. (8), providing its dependency on the virial radius and the total BH mass in the cluster. The contours illustrate the velocities at specific radii and masses. The bottom right panel provides contour lines of the velocity of the cluster defined by Eq. (9), assuming an additional contraction calculated by Kroupa et al. (2020). The different colors indicate various values of ηg.
In the text
thumbnail Fig. 10.

Mass of the most massive BH estimated via the rms velocities calculated using Eq. (8) and their corresponding efficiencies depicted in Fig. 8. The clusters are within a range of virial radii from 0.1–2.0 pc and masses from 104–108 M⊙. The color represents the mass of the BH that forms. Each panel corresponds to a different value of the external potential.
In the text
thumbnail Fig. 11.

Mass of the most massive BHs that can form calculating the rms velocity using Eq. (9) from Kroupa et al. (2020) and the corresponding efficiency depicted in Fig. 8. The clusters are within a range of virial radii from 0.1–2.0 pc and masses from 104–108 M⊙. The color represents the mass of the BH that forms. Each panel corresponds to different external potentials.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.