| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202450610 | |
| Published online | 04 October 2024 | |
The accreted galaxy: An overview of TESS metal-poor accreted star candidates
1
Instituto de Estudiols Astrofísicos, Facultad de Ingeniería y Ciencias, Univesidad Diego Portales,
Santiago de Chile,
Chile
2
Millennium Nucleus ERIS,
Santiago,
Chile
3
School of Physical and Chemical Sciences – Te Kura Matu, University of Canterbury,
Private Bag 4800,
Christchurch
8140,
New Zealand
4
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
5
Department of Astronomy, The University of Texas at Austin,
2515 Speedway Boulevard,
Austin,
TX
78712,
USA
6
Department of Physics, University of Surrey,
Stag Hill,
Guildford,
GU2 7XH
Guildford,
UK
★ Corresponding author; danielle.debrito@mail.udp.cl
Received:
4
May
2024
Accepted:
26
July
2024
The Milky Way is a mosaic of stars from different origins. In particular, metal-poor accreted star candidates offer a unique opportunity to better understand the accretion history of the Milky Way. In this work, we aim to explore the assembly history of the Milky Way by investigating accreted stars in terms of their ages, dynamical properties, and chemical abundances. We also aim to better characterize the impact of incorporating asteroseismic information on age and chemical abundance calculations of metal-poor accreted stars for which TESS data are available. In this study, we conducted an in-depth examination of 30 metal-poor accreted star candidates using TESS and Gaia data as well as MIKE spectra. We find satisfactory agreement between seismic surface gravity (log ɡ) values and values obtained using spectroscopy, demonstrating the reliability of spectroscopic data produced by our methodology. We find that while age determination is highly dependent on the log g and asteroseismic information used, the overall chemical abundance distributions are similar for different log ɡ. However, we find that calcium (Ca) abundances are more sensitive to the adopted log ɡ. Our study reveals that the majority of our stars have properties that are compatible with those reported for the Gai’a-Sausage-Enceladus, with a minority of stars that might be associated with Splash. We find an age distribution with a median of 11.3−4.1+1.3 Gyr when including asteroseismic information. Regarding some key chemical signatures, we note that these stars are metal poor ([Fe/H]) < −0.8), α rich ([α]/Fe] > 0.2), and copper poor ([Cu/Fe] < 0 ), with chemical abundances typical of accreted stars. These findings illustrate the importance of multidimensional analyses in unraveling the complex accretion history of the Milky Way.
Key words: stars: abundances / Galaxy: halo / Galaxy: stellar content
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Over the last few decades, evidence has been accumulating that the Milky Way was likely assembled through accretion and merger events (e.g., Searle & Zinn 1978; Nissen & Schuster 2010). This evidence is supported by Gaia survey data (Gaia Collaboration 2016; Brown et al. 2018, 2021), which is revolutionizing the investigation of the merger history of the Galaxy. In addition to Gaia, spectroscopic surveys such as the Apache Point Observatory Galactic Evolution Experiment (APOGEE; Abolfathi et al. 2018; Holtzman et al. 2018) and Galactic Archaeology with Hermes (GALAH; Buder et al. 2021) have also contributed providing information to unveiling the assembly of the Milky Way. Therefore, survey data are playing a key role in the exploration of the physical processes that led to the Milky Way as we know it today.
Numerous works in the literature have found stars attributed to different progenitors, and therefore formed ex situ, in contrast with the ones believed to be formed within the Milky Way (in situ). Belokurov et al. (2018) and Helmi et al. (2018) consolidated evidence for the relics of a fully disrupted galaxy lying in the midst of the inner stellar halo referred to as Gaia-Sausage-Enceladus (GES). Myeong et al. (2019) found evidence of a separate accreted system in the Milky Way halo composed of stars with very retrograde motions, and named this system Sequoia. Koppelman et al. (2019) reported possible progenitor galaxies, including evidence for Thamnos, a distinct structure in the low-energy part of the halo. Additionally, Horta et al. (2021) found evidence for a potential past accretion event – whose debris are currently found in the central bulge –, which they referred to as Heracles, while Kruijssen et al. (2020) reported Kraken based on properties of the Milky Way simulated globular clusters, which have similar properties to Heracles. Therefore, there are likely multiple accreted systems in the Galaxy and distinguishing among all of them represents a challenge that requires multidimensional data analysis.
In order to study the merger history of the Milky Way, there are three main ingredients necessary to understanding its past. The first ingredient is chemical abundances, because this is associated to the birth place of a star. The second ingredient is the dynamics, because stars with the same origin in general can have similar dynamical properties. The third ingredient is stellar age, as different structures of the Galaxy and substructures in the stellar halo have different age signatures.
The first ingredient, chemical abundances, plays a central role in Galactic Archaeology. By studying the chemical distribution of stars, it is possible to infer the star formation history of the Milky Way using elements synthesized by different nucleosynthetic channels (Freeman & Bland-Hawthorn 2002). For example, α elements such as magnesium (Mg), calcium (Ca), and silicon (Si) and Fe-peak elements such as manganese (Mn) trace the contribution of Type II and Type Ia (Iwamoto et al. 1999) supernovae, respectively, which provide information about the star formation rate of the Milky Way. Type II and Type Ia supernovae are also valuable for investigating the contribution of material from the explosion of high- and low-mass stars in the chemical evolution of a galaxy. Many authors have calculated chemical abundances of accreted stars using high-resolution spectroscopy techniques in order to shed light on the evolution of their progenitor galaxies (see e.g., Nissen & Schuster 2010; Aguado et al. 2021; Matsuno et al. 2022; Carrillo et al. 2022; Nissen et al. 2024; Ceccarelli et al. 2024).
Together with chemical abundances, the dynamics of stars is another valuable ingredient when attempting to understand the Milky Way. From dynamics it is possible to separate and characterize the different components of the Galaxy and to understand its structure. In particular, dynamics can help to distinguish the building blocks of the Milky Way and also to select accreted star candidates, as has been done using Gaia survey data since its launch, an approach illustrated by studies such as Koppelman et al. (2020); Naidu et al. (2020); Feuillet et al. (2021); Buder et al. (2022).
Stellar age is another very important ingredient that is required to unveil the past of the Galaxy, because by knowing stellar ages it is possible to understand the Galactic stellar formation timescales, the timescales of the Galactic merger history, and how the different stellar populations connect to the evolution of the Milky Way. In order to recover stellar ages, different techniques such as isochrone fitting and asteroseismology can be used, as illustrated in Das et al. (2020); Montalbán et al. (2021); Borre et al. (2022).
In the context of stellar ages, one survey with a great potential to aid in Galactic archaeology studies is the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014). The main objective of TESS is to find planets around bright stars close to the solar neighborhood. However, from the light curves provided by this survey it is also possible to calculate masses and therefore ages using seismic information.
TESS is an ongoing survey observing stars in its 26 sectors. As this survey focuses mostly on bright stars, the data obtained by it could be complemented by information from ground-based telescopes. This will allow targets from TESS to be characterized by other instruments, which again will contribute to the way we see the Galaxy, its stellar population content, and stellar formation timescales.
Considering how attractive TESS data can be for determining stellar ages using seismic information, data from this survey could also be of utmost importance in understanding the accretion timescales of the Milky Way. Unfortunately the bulk of TESS data are for metal-rich stars and seismic information for metal-poor objects is challenging to acquire. For this reason, only a limited number of works in the literature explore accreted stars – which are typically metal poor – using seismic information (e.g., Montalbán et al. 2021). Therefore, understanding the level of quality and the precision of ages and chemical abundances based on nonseismic information is fundamental when characterizing accreted stars. In this work, we aim to explore this problem.
In this study, we calculated detailed chemical abundances of elements from different nucleosynthetic channels in order to characterize a sample of metal-poor accreted star candidates observed as part of the TESS survey. The present paper is organized as follows: in Sect. 2 we describe our data, while in Sect. 3 we describe the methodology used to recover the atmospheric parameters, chemical abundances, dynamical properties, and ages of our stars. In Sect. 4 we present and discuss our results in the context of Galactic archaeology. In Sect. 5 we conclude and summarize our findings.
2 Data
2.1 TESS data
TESS is an all-sky survey designed to find transitioning exoplanets, and in particular exoplanets with periods of less than 13 days. TESS observes the sky in 26 segments and there are circular regions at the ecliptic poles where the segments overlap. In these regions, the TESS observing period is larger than 100 days, which contrasts with the regular 27.4 day observing period per segment and allows the discovery of longer-period planets. The overlap region in the South is named the TESS Southern Continuous Viewing Zone (SCVZ).
In Mackereth et al. (2021), the authors detected the frequency of maximum power (hereafter νmax) and the large frequency separation (hereafter Δν) for 6388 stars from the SCVZ sample and calculated ages for 1749 stars. We note that νmax refers to the frequency at which the peak power of the stellar oscillations occurs. Additionally, Δν refers to the average frequency difference between consecutive modes of oscillation with the same spherical degree in the oscillation spectrum of a star. Mackereth et al. (2021) determined seismic information using three different pipelines: BHM (Elsworth et al. 2020), A2Z (Mathur et al. 2010), and COR (Mosser & Appourchaux 2009). The authors also provided predicted values for νmax and Δν based on the Two Micron All Sky Survey (2MASS) photometry and Gaia DR2 parallax using the asteroestimate1 package, which is an implementation of the formalism presented in Chaplin et al. (2011), Campante et al. (2016), and Schofield et al. (2019), as explained in more detail in Mackereth et al. (2021).
2.2 Spectroscopic observations
In this work, we selected stars from the catalog of Mackereth et al. (2021), which contains 15 405 red giant stars brighter than G ≤ 11 that were targeted as part of the SCVZ. Our selection consisted of choosing only the stars with retrograde motions – following the methodology described in Sect. 3.1 – in order to select accreted star candidates. Several works in the literature (e.g.,Nissen & Schuster 2010; Belokurov et al. 2018; Helmi et al. 2018; Myeong et al. 2019) have shown that accreted stars tend to have retrograde motions. This characteristic can be caused by the angle at which the progenitor galaxy was disrupted and incorporated into the Milky Way. This resulted in a sample of 30 stars. Their identification number in different catalogs (Gaia ID and the ID adopted in this work), positions, and magnitudes are presented in Table 1. In order to make this selection, we used EDR3 data from the Gaia survey, because we observed the stars in January 2021.
We note that for the stars studied in this work there is good overall agreement on the parallax from the different Gaia data releases. Between Gaia DR2 and Gaia DR3, for example, the mean difference between the different parallax values is −0.04 mas with a standard deviation of 0.04 mas. The largest difference found was 0.14 mas, nevertheless all but one of the stars have differences of below 0.10 mas. There are only two stars in the sample where the two parallax values do not agree within 3 sigma: stars 419 and star 422. However, we did not find any relevant systematic effects associated with these objects in this work.
Among the chosen 30 stars, only two of them have ages provided by Mackereth et al. (2021), and 21 stars have νmax and Δν. Therefore, we used the νmax and Δν values provided to determine our own stellar ages, as described in Sect. 3.4. We also considered the νmax to derive surface gravity using scaling relations.
In order to determine chemical abundances, we took high-resolution (R ≈ 35 000) spectra using the Magellan Inamori Kyocera Echelle (MIKE) spectrograph on the 6.5 m Clay Telescope of Las Campanas Observatory in January 2021. The MIKE spectrograph is a double echelle spectrograph composed of a blue and a red arm. The blue arm provides a wavelength coverage from approximately 3350–5000 Å, while the red arm provides a wavelength coverage from approximately 4900–9500 Å. These spectra have an average signal-to-noise ratio of 100 pixel−1. The data were reduced using the pipeline for data reduction of the instrument: the Carnegie Python MIKE pipeline (Kelson 2003), hereafter CarPy. CarPy produces a science-ready 2D spectrum considering flats for slit distortion tracing and flat fielding, and Thorium-Argon arcs for wavelength solution. In case of multiple exposures of the same object, CarPy automatically co-adds the spectra of the same objects.
In order to stack the orders of the MIKE spectra, a step that is not performed during the data-reduction procedure of Carpy, we first normalized each order using splines of 3 degrees every 5 nm using the tool for the treatment and analysis of stellar spectra iSpec (Blanco-Cuaresma et al. 2014, Blanco-Cuaresma 2019). We then corrected the spectra using the radial velocity of the stars and using iSpec. To determine the radial velocity, we performed a cross-correlation between the observed spectrum and a spectrum of Arcturus from an Atlas provided with iSpec. The radial velocity correction was done order by order so as to avoid issues related to inaccurate wavelength calibration, as described in De Brito Silva et al. (2022). The subsequent combination of orders was done using the IRAF package (Tody 1993).
Only seven stars have a spectrum taken by APOGEE or GALAH, which have undertaken a follow-up campaign of the TESS-SCVZ field as well. We note that even though the 30 stars chosen in our selection were mostly not observed by spectroscopic surveys, other stars studied in Mackereth et al. (2021) with prograde motions are in the GALAH survey. The GALAH survey is a spectroscopic survey that delivers chemical abundances of up to 30 elements and we used its chemical abundances in this work as reference to discuss our findings when compared with the pro-grade sample presented in Mackereth et al. (2021). We also selected a sample of stars with retrograde motions in GALAH as an additional control sample.
Basic information about our sample of stars.
3 Methods
3.1 Kinematics
As we have Gaia DR3 data for our stellar sample, we have information about their total velocities. We calculated the velocities (U, V, W) adopting Galactic radius R⊙ = 8.2 Kpc (McMillan 2016) for the solar position and Galactic height of z⊙ = 0.0025 Kpc (Jurić et al. 2008) and (U, V, W)⊙ = (11.10, 247.97,7.25) km/s for the solar velocity relative to the Galactic Center, following Matsuno et al. (2020). We used the astropy package (Robitaille et al. 2013; Price-Whelan et al. 2018) for the task. Here we used Gaia DR3 positions, proper motions, parallaxes, and radial velocities. We adopted the following convention: U positive toward Galactic Center, V positive in the direction of Galactic rotation, and W positive toward the North Galactic Pole. The final velocity is assumed to be in the Galactic rest frame. Retrograde stars are those with V < 0.
We integrated the orbit of these stars and calculated the total energy (E), the angular momentum in the z direction (Lz), and the eccentricities (ecc) using the gala Python package (Price-Whelan et al. 2018). In the orbit integration, we adopted the default Milky Way potential and the Galactocentric coordinate frame built using the values described above.
3.2 Stellar parameters: Effective temperature and surface gravity
The effective temperature (Teff) was calculated using the InfraRed Flux Method (IRFM) as presented in Casagrande et al. (2021). The authors implement Gaia and 2MASS photometry (Skrutskie et al. 2006) in the IRFM and apply it to stars in GALAH DR3 considering different evolutionary stages, metallicities ([Fe/H]), and surface gravities (log ɡ). In order to calculate Teff, we applied the colte code2, the color–Teff relations from Casagrande et al. (2021), Gaia EDR3 and 2MASS photometry, as well as Gaia EDR3 (log ɡ) and [Fe/H]. As the colte code provided every permutation of the IRFM color combinations for the Teff, we calculated the mean absolute deviation (MAD) of all the values provided. We then multiplied the MAD value by 1.48 in order to obtain an approximation of the standard deviation. The typical uncertainty of Teff calculated with this approximation is of the order of 60 K. We then considered the standard deviation as the uncertainty of Teff.
Using our derived Teff, and the mean νmax calculated from all the available values from Mackereth et al. (2021) (see Sect. 2), we determined log ɡ using the scaling relation (Kjeldsen & Bedding 1994):
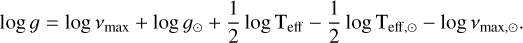 (1)
(1)
As not all stars have a value of νmax and Δν, we also considered other homogeneous determinations for log ɡ, namely one log ɡ using only the predicted νmax from Mackereth et al. (2021) and Eq. (1), and the log ɡ derived spectroscopically. The spectroscopic log ɡ was calculated using the iSpec code and their determination is better described in Sect. 3.3.
In summary, we have three different estimates of log ɡ: seismic (using the mean of νmax and Eq. (1)), predicted (using only the predicted νmax from Mackereth et al. 2021 and Eq. (1)), and spectroscopic (using MIKE spectral features). In Table 2, we present the values of Teff, seismic log ɡ, predicted log ɡ, spectroscopic log ɡ, [Fe/H], microturbulence velocity (vmic), νmax, and Δν for the stars studied in this work. We note that νmax and Δν are the values obtained after considering the quality criteria described in Sect. 4.2.
3.3 Spectroscopy
In order to calculate the chemical abundances, we followed the procedure presented in De Brito Silva et al. (2022), who determined parameters and abundances of an apparently high-mass accreted star candidate that might be the product of binary evolution using data from the MIKE spectrograph.
Briefly, we used iSpec for the chemical abundance determination. This method consists of fitting the chosen spectral regions on the fly until the synthetic spectrum agrees with the observed one. We used the spectral synthesis method for which we adopted the line list from the Gaia-ESO survey (Heiter et al. 2021), the solar abundances from Grevesse et al. (2007), the one-dimensional atmospheric models MARCS7 (Gustafsson et al. 2008), and the radiative transfer code TURBOSPECTRUM (Gray & Corbally 1994), which assumes local thermodynamical equilibrium (LTE).
With the aim of determining the spectroscopic log ɡ, we also used iSpec. We fixed the Teff at the value obtained using the IRFM, v sin i at 1.6 km/s, following Blanco-Cuaresma (2019), and vmac and vmic were determined from the same empirical relation used in Gaia-ESO. We let the metallicity be a free parameter. Only Fe I and Fe II lines were used to determine the spectroscopic log ɡ, applying the method of ionization and excitation balance (Gray 2005). We note that when the predicted or the seismic log ɡ were used, the metallicity was the only parameter let free.
The chemical abundances were determined line by line following the lines used in De Brito Silva et al. (2022), and low-quality results (i.e., chemical abundances with individual line uncertainties of higher than 0.40 dex) were discarded. We opted to analyze the different exposures of the spectra separately in order to obtain a greater number of measurements and assess our precision. We also evaluated the quality of our results by visually inspecting how well the synthetic spectrum represents the observed one. One example of the fit obtained is presented in Fig. 1. In this figure we show the observed spectrum in blue, the synthetic spectrum in orange, and the gray areas are the regions considered for the fit. The vertical lines indicate the center of the lines fitted inside each region. Our method was applied to the MIKE spectra, which allowed us to determine metallicities and chemical abundances of 15 elements (Ti, Ni, Ca, Si, Mg, Sc, Cr, Co, Mn, Ba, V, Y, Cu, Na and Al).
3.4 Age determination
We determined the stellar ages using the BAyesian STellar Algorithm (BASTA, Silva Aguirre et al. 2015; Aguirre Børsen-Koch et al. 2022)3. BASTA provides stellar properties by comparing a grid of stellar models with observational data. We calculated three stellar ages with BASTA based on the three different log ɡ we adopted in this work:
Seismic case: we provided BASTA with the following inputs: Teff, metallicity, [α/Fe], parallax, 2MASS photometry, Δν, and νmax.
Predicted case: we provided BASTA with the following inputs: Teff, metallicity, [α/Fe], parallax, 2MASS photometry, and predicted log ɡ.
Spectroscopic case: as input we used Teff, metallicity, [α/Fe], parallax, 2MASS photometry, and spectroscopic log ɡ.
The 2MASS photometry includes the magnitudes of the bands J, H, and Ks corrected for extinction using the dust map presented in Schlegel et al. (1998). We note that for the age calculation, [α/Fe] was approximated to be equal to [Mg/Fe].
Within BASTA, we used the updated Bag of Stellar Tracks and Isochrones (BASTI, Hidalgo et al. 2018; Pietrinferni et al. 2021) grid, which cover masses from 0.1 to 15 M⊙, [Fe/H] from −3.2 to 0.45 dex, and ages from 20 Myr to 14.5 Gyr. We defined an upper limit for the ages of 13.7 Gyr in order to avoid age solutions older than the age of the Universe. Following Borre et al. (2022), who calculated ages using BASTA for 23 ex situ stars using Kepler (Borucki et al. 2010; Koch et al. 2010) and K2 (Howell et al. 2014) seismic data, we adopted the Salpeter initial mass function (Salpeter 1955) in order to favor the presence of low-mass stars, because there is evidence that accreted stars are old objects (e.g., Das et al. 2020; Montalbán et al. 2021; Borre et al. 2022). Finally, we configured BASTA to account for both mass loss and diffusion. BASTA follows the mass-loss prescription described in Reimers (1975) and the diffusion described in Thoul et al. (1993).
Stellar and seismic parameters of our sample of stars.
4 Results and discussion
4.1 Dynamics
Studies in the literature have identified accreted stars within the Lz−E plane, associating different regions with various building blocks of the Milky Way. For instance, Koppelman et al. (2019) attributed regions in this diagram to stars originating from possible progenitor galaxies such as GES, Sequoia, Helmi Streams (Helmi & White 1999), Thamnos 1, and Thamnos 2. Additionally, Naidu et al. (2020) found four new substructures in the halo, possibly associated with different progenitor galaxies: Aleph, Arjuna, I’itoi, and Wukong. Furthermore, Horta et al. (2022) demonstrated the presence of Galactic substructures likely associated with different progenitor galaxies in the Lz −E plane, including regions likely linked to GES, Sequoia, and Heracles, among others.
Figure 2 shows the Lz–E plane for the stars studied here, represented as stellar markers, with stars from GALAH DR3 depicted in gray. In the upper panel, our stars are color-coded according to eccentricity, and in the lower panel they are color-coded according to metallicity. Notably, our stars predominantly cluster in a specific region with Lz close to zero, with two outliers.
We observe that the majority of the stars exhibit highly eccentric orbits, with ecc > 0.7 in most cases. However, each group contains one star with lower eccentricity, which is discussed in more detail in Sect. 4.6.
From a dynamical perspective, comparing regions within the Lz–E plane associated with different progenitor galaxies across various studies poses challenges due to variations in the solar velocities, Galactic height and radius, and the adopted Galactic potential. However, based on Koppelman et al. (2019) and Horta et al. (2022), the Lz, E, and eccentricity reported in the present work are consistent with those of accreted stars.
Based on the Lz–E plane, we identify that the majority of our stars are likely associated with GES, considering the Lz of close to zero, and high E. The two outlier stars may be remnants of the Sequoia galaxy, given their high E and low Lz. In Fig. 2 we show the approximate regions where GSE debris (green ellipse) and Sequoia debris (blue triangle) are believed to be located in the Lz–E plane. Furthermore, the prevalence of high-eccentricity orbits in our sample aligns with the notion that these stars are likely accreted and associated with GES and Sequoia. The low metallicity also agrees with the properties of accreted stars coming from dwarf galaxies reported so far in the literature.
 |
Fig. 1 Example region of stellar spectra. An example spectrum obtained with the MIKE spectrograph at the Clay Telescope at Las Campanas Observatory is shown in blue, and a synthetic spectrum built using iSpec (Blanco-Cuaresma et al. 2014; Blanco-Cuaresma 2019) is shown in orange. The gray regions were used to fit the observed spectra to obtain chemical abundances of different elements. |
 |
Fig. 2 Lɀ–E plane. Gray dots represent GALAH DR3 stars, while star markers denote the stars investigated in this study. The top panel displays the stars studied in this work color-coded according to eccentricity, while the bottom panel shows them color-coded according to [Fe/H], The approximate regions corresponding to GSE debris (green ellipse) and Sequoia debris (blue triangle) are indicated in the figure. |
4.2 The different log ɡ values
To investigate how similar the seismic, predicted, and spectroscopic log ɡ are and their impact on age and chemical abundance determinations (as discussed in more detail in the Sects. 4.3 and 4.4), we created a “golden” sample comprising 16 stars. The selection criteria used to produce the golden sample involve ensuring consistency in seismic log ɡ values either through agreement between at least two of the pipelines (COR, A2Z, and BHM) considering three sigmas or when a unique value from the A2Z pipeline was available. This golden sample is composed of the following stars: 405, 406, 407, 408, 409, 412, 413, 414, 415, 418, 419, 422, 424, 425, 426, and 430.
In the top panel of Fig. 3, we present the different log ɡ used in this work along with their uncertainties for each golden sample star. The seismic, predicted, and spectroscopic values are represented in gray, magenta, and blue, respectively. The bottom panel of the same figure illustrates the differences between seismic and predicted log ɡ values (magenta), as well as between seismic and spectroscopic log ɡ values (blue). We consider the uncertainties as the quadratic sum of the individual uncertainties in each case. The mean (µ) and standard deviation (σ) of the comparisons presented in the bottom panel are indicated in the label.
The mean (µ) difference between the seismic log ɡ and the predicted log ɡ is 0.07 dex with a standard deviation (σ) of 0.25 dex. Similarly, the mean difference between the seismic log ɡ and the spectroscopic log ɡ is 0.00 with a standard deviation of 0.30 dex. In the case of seismic versus predicted log ɡ, there are three cases (stars 405, 424, and 430) where the difference is not compatible with zero within 3 sigma. In the comparison between seismic and spectroscopic log ɡ, there are two cases (stars 415 and 430) where the differences exceed what can be explained by the uncertainties within 3 sigma. We note that the object 424 is a spectroscopic binary star (Pasquini & Lindgren 1994), and is therefore not further explored in this work. Consequently, we conclude that both the predicted and spectroscopic log ɡ are in agreement with the seismic log ɡ. However, we note that the golden sample was built in a way that facilitates the agreement between the seismic and predicted values.
The uncertainties associated with each log ɡ value vary depending on the method used to calculate it. Our seismic log ɡ values are the results with the highest precision, with uncertainties of the order of 0.01 dex, while the spectroscopic log ɡ values are the least precise results presented here, with mean uncertainties of 0.1 dex, which is ten times larger than the typical seismic uncertainties. The predicted log ɡ has a uncertainty distribution with a mean of 0.06 dex.
 |
Fig. 3 Comparison of different log ɡ. The top panel shows the values of seismic (gray), predicted (magenta), and spectroscopic (blue) log ɡ for each star, as well as their respective uncertainties. The bottom panel shows the difference between seismic and predicted log ɡ (magenta), as well as between seismic and spectroscopic log ɡ (blue). We consider as uncertainties the quadratic sum of the individual uncertainties of each case. The mean (µ) and standard deviation (σ) of the comparison presented in the bottom panel is shown in the label. |
4.3 Stellar ages
To assess the impact of the use of seismic information on age determination, we employed the BASTA code considering the three cases described in Sect. 3.4, namely seismic, predicted, and spectroscopic. From the 16 stars that have measured νmax and Δν and are part of our golden sample, only 13 have successfully measured ages in the three cases.
We identified the impact of using seismic information in the statistical uncertainties obtained in each case of study as provided by BASTA. When calculating ages using seismic information, the typical uncertainty found is of the order of 10.1 percent. When using the predicted log ɡ, the uncertainties represent about 18.5 percent. Finally, when using spectroscopic log ɡ, the typical uncertainty represents 28.6 percent of the measurement in this work. Therefore, our results suggest that using seismic information when calculating ages of metal-poor accreted star candidates can drastically improve the stellar age precision when considering statistical uncertainties, which illustrates the potential of TESS data for Galactic archaeology studies.
In Fig. 4 we compare the ages obtained when using seismic information (including νmax and Δν; top panel) and when using the predicted (middle panel) and the spectroscopic (lower panel) log ɡ. Additionally, the ages obtained for individual stars as well as their uncertainties considering the seismic, predicted, and spectroscopic log ɡ are provided in Table 3.
The age distribution for the seismic case goes from 4.5 to 13.1 Gyr, with a median of 11.3 Gyr, a lower uncertainty of 4.1 Gyr and an upper uncertainty of 1.3 Gyr. From the 13 stars considered, only two stars are younger than 7 Gyr. Therefore, considering asteroseismic information, 85 percent of our sample can be considered old, resulting in the age distribution presented in Fig. 4.
When considering the ages calculated using the predicted log ɡ, the distribution goes from 5.4 to 13.0 Gyr, with a median of 10.1 Gyr, a lower uncertainty of 2.9 Gyr, and an upper uncertainty of 1.8 Gyr. Repeating what was observed in the ages calculated using seismic information, 85 percent of our sample contains stars older than 7 Gyr according to our results.
The ages calculated using the spectroscopic log ɡ have a median of 9.3 Gyr, a lower uncertainty of 4.4 Gyr, and an upper uncertainty of 2.0 Gyr, and a range of between 2.9 and 12.8 Gyr. From the 13 stars, 6 have ages below 7 Gyr according to our analysis, and represent 46 percent of our sample. Considering the significant size of the young subsample, the age distribution appears to be bimodal.
Ages calculated using seismic information are generally higher than ages calculated using the predicted and the spectroscopic log ɡ. When compared with the age distribution calculated using the predicted log ɡ, seismic ages appear to be 1.2 Gyr older, while when compared with the age distribution calculated using spectroscopic log ɡ they appear to be 2.0 Gyr older. We note that the age distribution calculated using the predicted log ɡ is similar to the one computed with seismic information, which is because the νmax and Δν used in the seismic case are correlated with the predicted log ɡ (see Sects. 2 and 3.2.).
However, the difference in the median age in the three cases studied is small. Considering the uncertainties, we can consider the median ages are compatible within one sigma among all the three cases studied. We also note that the difference among the median values is of the order of the typical uncertainty of ages of the individual stars explored in this work, which mostly varies between 0.5 Gyr and 2.5 Gyr, indicating that the age resolution is currently insufficient to discern small variations in the median values of the distributions.
As an attempt to better discern the behavior of the three age distributions, we evaluated them using a Bayesian approach. In this method, we considered each individual age measurement as a Gaussian distribution and reassessed the overall age distribution. Using this Bayesian approach, we obtained a seismic distribution with a median of 10.2 Gyr and an uncertainty of 0.2 Gyr. The predicted distribution showed a median of 9.3 Gyr with an uncertainty of 0.3 Gyr. Finally, the spectroscopic distribution resulted in a median of 7.8 Gyr, with uncertainty of 0.4 Gyr. We observed that with the Bayesian approach, the median age is lower in all cases, and the uncertainties are smaller for all distributions; also, while the median ages are still compatible within three sigmas when considering the seismic and predicted cases, the spectroscopic median does not agree with the seismic median within three sigma.
The dominant old age distribution found in the seismic ages and the ages calculated using the predicted log ɡ agree well with previous works in the literature. As an example, Das et al. (2020) calculated ages using a Bayesian isochrone pipeline for a structure composed of accreted star candidates named the blob, and found an age span from 8–13 Gyr, which is comparable to results found in the present work. Montalbán et al. (2021) calculated the ages of [Mg/Fe]-poor stars with highly eccentric orbits that are accreted star candidates based on seismic data, and found a mean age distribution of 9.7 ± 0.6 Gyr. Feuillet et al. (2021) found a mean age distribution for accreted stars from the GES progenitor of 10–12 Gyr. As previously stated, Borre et al. (2022) calculated ages for accreted stars using Kepler and K2 data, and found an age distribution of 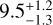 . We note that even though the ages calculated using the spectroscopic log ɡ appear to be younger than the other cases studied, 54 percent of that sample is composed of stars that appear to be old, which agrees with the literature.
. We note that even though the ages calculated using the spectroscopic log ɡ appear to be younger than the other cases studied, 54 percent of that sample is composed of stars that appear to be old, which agrees with the literature.
In our results, we find that about 15 percent of the ages calculated using the seismic information or the predicted log ɡ appear to be younger than 7 Gyr, in contrast with the 46 percent found when using the spectroscopic log ɡ. The young ages are in contrast with the low metallicity, because according to the delayed SNIa scenario, metal-poor stars tend to be older than metal-rich stars.
We note that Grunblatt et al. (2021) calculated ages of halo substructures using BASTA, among other codes. These authors studied ten red giant stars using kinematic, asteroseismic, and spectroscopic data, and a subsample of them were associated to GES. In that work, the probability density function of the age distribution obtained using BASTA spanned a wide range, going from 1 Gyr up to ages of as old as 13 Gyr. In comparison to their work, the results we find for ages calculated using seismic data appear to be older, but we also find a small population of young stars, similar to their work. However, we note that the setup used in this work to apply BASTA to our data is different from the one used in Grunblatt et al. (2021). Similarly, using data from the Large Sky Area Multi-Object Fibre Spectroscopic Telescope (LAMOST, Zhao et al. 2012), Horta et al. (2024) found a population of accreted stars with a mean age of 11.6 Gyr, but this was found to contain a tail of intermediate age stars with ages of between 6 and 9 Gyr. Therefore, accreted stars with lower ages have also been reported before in the literature.
Based on our results, we interpret that the use of seismic information impacts the age determination. Among the three studied age sets, seismic ages tend to be older. We note that this can be caused by the configuration chosen when using BASTA in this work. The age set calculated using seismic ages is the one providing older ages, and therefore this is the set we consider most trustworthy. While the impact of using (or not) seismic information on chemical abundance determinations is small (see Sect. 4.4 for details), the same is not true for ages. Therefore, age determination with or without seismic information requires careful determination.
In Fig. 5 we present a [Mg/Fe] versus [Fe/H] plane, with metal-rich stars from Mackereth et al. (2021) represented as teal dots and stars presented in this work represented as stellar symbols color-coded according to seismic stellar age. As a metal-poor control sample, we show the kernel density estimate of metal-poor stars with retrograde motions from GALAH DR3 survey, presented in Fig. 5 as contour lines; these have similar stellar parameters to those of the stars we studied in this work. The chemical abundances for the metal-rich stars from Mackereth et al. (2021) were obtained from GALAH DR3. As discussed above, our sample is composed of mostly old stars, with only two objects younger than 7 Gyr.
The stars that appear to be younger have a chemical pattern consistent with those of old stars. One possible scenario to explain the young ages is that the stars could be a product of binary evolution, following the discussion presented by De Brito Silva et al. (2022). The star could also be a young α-rich star (Chiappini et al. 2015; Martig et al. 2015; Jofré et al. 2016). Young α-rich stars are believed to be a product of binary evolution or stars formed near the Galactic bar corotation, which is a region where gas could be kept inert for long periods of time. More recent discussions on young α-rich stars can be found in Jofré et al. (2023); Cerqui et al. (2023); Grisoni et al. (2024). However, while this could possibly explain the two young stars found by calculating ages using seismic information and predicted log ɡ, the larger population of young stars found when using spectroscopic log ɡ is more likely to be explained by a necessity to include seismic information in order to better constrain the ages of these objects.
Ages of individual stars.
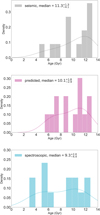 |
Fig. 4 Age distribution for the three cases studied in this work using BASTA. The top panel (gray) shows stellar ages calculated using the seismic information νmax and Δν. The middle panel (pink) shows stellar ages calculated using the predicted log ɡ. The bottom panel (blue) shows the stellar ages calculated using the spectroscopic log ɡ. Median values as well as lower and upper uncertainties are indicated in the label. |
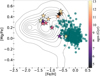 |
Fig. 5 [Mg/Fe] versus [Fe/H], The stars in this work are presented as stellar markers, while other stars from Mackereth et al. (2021) are represented as teal dots (from GALAH DR3 data). We also show as black contour lines the kernel density estimate of metal-poor stars with retrograde motion from GALAH DR3 survey. The stars presented in this work are color-coded according to BASTA seismic stellar ages. |
4.4 Chemical abundances based on different log ɡ
The top panel of Fig. 6 presents a comparison between the chemical abundance distribution obtained using seismic log ɡ and that obtained using the predicted log ɡ. Overall, we can deduce that the chemical abundance distribution is very similar when considering different log ɡ. However, we note that calcium (Ca) appears to be more affected by the choice of log ɡ.
The distribution of Ca also exhibits variations between the two results. Calcium determined with seismic log ɡ shows a broader, flatter distribution that covers a wider range compared to the distribution obtained using predicted log ɡ. Calcium abundances were determined using only neutral lines, but Ca is an element known to be highly influenced by surface gravity.
The bottom panel of Fig. 6 presents a comparison between the chemical abundances obtained using seismic log ɡ and those obtained using the spectroscopic log ɡ. Similar to the previous comparison, the overall shape and range of the chemical abundance distributions is the same whether we use the seismic log ɡ or the spectroscopic log ɡ. However, differences are observed in the distributions of Ca and Sc.
Ca, in this case, displays a two-peaked distribution, contrasting with the flatter and broader distribution obtained using seismic log ɡ. It is important to note that both distributions of Ca abundance were estimated using only neutral lines, highlighting the impact of surface gravity on this element. In the case of Sc, while the seismic distribution is narrow, the distribution of Sc determined with spectroscopic log ɡ is broader and shows a tail.
We also note that even though the range and general shape of the distribution of [Fe/H] is the same in the two chemical sets, the stars appear to be slightly metal poorer (about 0.1 dex) when the abundance is determined using the seismic log ɡ. When calculating [Fe/H], we used neutral and ionized lines, with neutral lines being the large majority.
Additionally, across all the chemical sets explored, distributions of Si, Co, Ni, Y, and Al consistently show two peaks. A few stars in the sample exhibit relatively high abundances of Mn and V, while the overall sample is rich in Ti. The stars also show a wide range of Mn abundances and low Cu abundances.
Considering the results from Sect. 4.2, where the seismic, predicted, and spectroscopic log ɡ values are generally compatible, it is not surprising that the overall chemical abundance distribution is similar to that seen in Fig. 6. To better assess the relationship between the difference in chemical abundances (Δ [X/Fe]) and the difference in log ɡ, we present Fig. 7, where we show Δ [X/Fe] as a function of the abundances estimated using the seismic log ɡ, with marker sizes proportional to the log ɡ difference for each case. The Δ [X/Fe] were calculated subtracting the chemical abundances determined using the predicted log ɡ from the ones estimated using the seismic log ɡ (magenta) and subtracting the chemical abundances determined adopting the spectroscopic log ɡ from the chemical abundances estimated adopting the seismic log ɡ (blue). We note that Δ [X/Fe] encompass all chemical elements studied in this work.
Figure 7 illustrates that the difference between the chemical abundances estimated using the predicted and spectroscopic log ɡ and the abundances determined using seismic log ɡ is correlated with the difference in log ɡ. Therefore, when the difference in log ɡ for a certain star is substantial, it results in a notable difference in chemical abundances. However, Δ [X/Fe] is mostly distributed within −0.1 < Δ [X/Fe] < 0.1 dex, which is usually small enough to be accounted for by the uncertainties in the chemical abundances.
We note that chemical abundances determined with or without seismic information are largely consistent, suggesting that the availability of seismic data for accreted stars does not significantly impact abundance determination using our methodology, at least when considering the chemical elements studied in this work. However, it is important to note that by using seismic information the uncertainty of log ɡ can be dramatically decreased. Nevertheless, minor impacts on the abundances of [Fe/H], [Ca/Fe], and [Sc/Fe] were observed, and therefore these chemical elements might require a more careful treatment.
 |
Fig. 6 Comparison of chemical abundance distribution obtained adopting the different log ɡ. The top panel shows the chemical distribution per element when using the seismic log ɡ (gray) and the predicted log ɡ (magenta). The bottom panel shows the chemical distribution per element when adopting the seismic log ɡ (gray) and the spectroscopic log ɡ (blue). The central dashed line represents the median of the distributions, while the other lines neighboring it show the data quartiles. The chemical abundances are ordered according to main nucleosynthetic channel: α-capture, iron peak, neutron-capture, and odd-Z. Within each nucleosynthetic channel, the chemical elements are organized according to atomic number. |
4.5 Chemical abundance distribution
Considering the satisfactory agreement among the different log ɡ and chemical abundances estimated using the different log ɡ previously discussed, we determined chemical abundances for the 29 stars in our sample using the spectroscopic log ɡ, excluding the spectroscopic binary 424. In Fig. 8, we present the distribution of the chemical abundances of the stars analyzed in this work, represented by blue stellar markers. Additionally, we include a control sample of GALAH DR3 prograde stars – shown as filled teal circles – that were also studied in Mackereth et al. (2021). We chose this set of stars as comparison because they are also TESS stars for which optical spectra are available; they are more metal rich, and their kinematics suggests that they were likely formed in situ. We also considered a metal-poor counter-rotating control sample of GALAH DR3 stars that have atmospheric parameters similar to the stars explored in this work. This allows us to compare the chemical pattern of stars born in situ and ex situ.
A significant portion of our stars display [Fe/H] < −0.8, which is consistent with the metal-poor nature of the majority of accreted stars, as reported in previous studies, such as Helmi et al. (2018); Matsuno et al. (2019); Das et al. (2020); Feuillet et al. (2021). Nonetheless, a minority of stars exhibit [Fe/H] > −0.8; these are the subject of further discussion in Sect. 4.6.
α elements such as Mg, Ca, Si, and Ti (which is not an α-capture element, but behaves like one) are good tracers of core collapse supernovae (Timmes et al. 1995; Kobayashi et al. 2006, 2020), because they are mostly produced in massive stars and later ejected by this kind of supernova. However, we note that about 22 percent of Si and 39 percent of Ca come from SN la, following the work of Kobayashi et al. (2020). Additionally, if other types of supernovae are considered (e.g., faint supernovae), it is possible that a larger fraction of α elements are produced by other mechanisms (Nomoto et al. 2009). Our stars present a high [α/Fe] abundance at low metallicities ([Fe/H] < −1.0), which is typical for halo and thick disk stars. There is one star in our sample with a lower enhancement of α-elements, which may suggest it originated in a lower-mass system than the Milky Way and was later accreted (Nissen & Schuster 2010). This star is discussed in more detail in Sect. 4.6. The generally high [α/Fe] values imply that the progenitor galaxy had the necessary mass and star formation rate to produce enhanced [α/Fe] abundances, consistent with findings in the literature regarding the abundance of α elements in GSE stars (see Helmi et al. 2018; Carrillo et al. 2022).
We observe that the stars are metal poor and [α/Fe] rich, indicating that if the stars are accreted objects, their progenitor galaxy was likely a massive system with a high star formation rate (SFR). Studies such as Tolstoy et al. (2009); Hill et al. (2019); Ji et al. (2019) showed that the chemical pattern of stars from dwarf galaxies varies according to the mass of the system, and that a similarly intense SFR might cause the gas to be enriched toward the metal-rich regime. Additionally, the high [α/Fe] abundance indicates numerous SNII events. While the typical abundance of α elements in metal-poor Milky Way halo and thick disk stars can be of the order of 0.4 dex (e.g.Ishigaki et al. 2012; Hawkins et al. 2015), the abundances of these elements can be much lower than this value in lower-mass galaxies.
In the Large Magellanic Clouds, the Fornax and Sculptor dwarf galaxies, for example, the abundances of α elements reported in works such as Shetrone et al. (2003); Letarte (2007); Van der Swaelmen et al. (2013); Hill et al. (2019) can be below zero for moderately metal-poor stars.
Iron-peak elements such as nickel (Ni), chromium (Cr), cobalt (Co), and manganese (Mn) are mostly produced by Type Ia supernovae (SNIa), making them valuable tracers of historic processes happening on longer timescales. In our sample, the [Ni/Fe] and [Co/Fe] distributions are generally flat around the solar value. [Cr/Fe] shows a slight increase with metallicity, which is in contrast to the slight decrease reported by Carrillo et al. (2022). This could be attributed to NLTE effects, because Cr is sensitive to these effects at low metallicities. We also observe an increase in Mn abundance with [Fe/H]. The metal-poor accreted star candidates show lower Mn abundances than the prograde stars, as expected due to the metallicity effect. We also note that the wide range of [Mn/Fe] abundance, with few stars that are Mn-rich, indicates a high SFR, because multiple SNIa may have enriched the gas from a low-Mn to a Mn-rich condition.
Neutron capture elements such as barium (Ba) and yttrium (Y) are very useful for Galactic archaeology as they reflect the impact of s-process chemical enrichment in the Milky Way chemical evolution. We do not find a Ba abundance variation associated with [Fe/H], and find a few mildly Ba-enhanced stars. Y shows a large spread, similar to what is observed for Ba, and two possible sequences are observed. However, these sequences may be influenced by our limited sample size. We also found a mildly Y-enhanced star.
The observed mild Ba enrichment implies that neutron-capture elements played a significant role in shaping the chemical evolution of the progenitor galaxy. The abundance patterns of these elements may provide valuable insights into the original environments of the progenitor galaxies, star formation timescales, and chemical evolution pathways.
Odd-Z and light elements such as vanadium (V), copper (Cu), scandium (Sc), sodium (Na), and aluminum (Al) are formed by different mechanisms and can provide important information for Galactic archaeology. We observe an increase in V and Cu with [Fe/H], along with a few stars that are strongly enrivhed with V, with abundances of [V/Fe] > 0.5 dex. The stars studied in this work appear to be Cu poor when compared with the stars likely formed in situ. Sc exhibits a slight decrease with [Fe/H], and our stars generally have high Al abundances, although three stars appear to be Al poor. This is interesting because many works in the literature use APOGEE to explore accreted stars (e.g., Das et al. 2020), which in general have low [Al/Fe], but we do not observe this trend in the optical. This could be due to systematic effects between the optical and the infrared caused by differences in the atomic data adopted.
Buder et al. (2022) studied accreted stars in GALAH and suggested the use of [Na/Fe] instead of [Al/Fe] in order to select accreted stars. In terms of [Na/Fe], some of our sample stars show subsolar abundances, while some are enriched, indicating that some of our sample stars have chemical abundances compatible with what is classically expected for accreted stars. However, we note that while low abundances of [Na/Fe] and [Al/Fe] might be a strong indicator that a star is accreted, there are overlaps in the higher abundance regime of these elements for in situ and ex situ stars. Therefore, a higher abundance of these elements does not discard the possibility that a star is accreted, as discussed in Buder et al. (2022). The depletion of [Cu/Fe] might be a chemical indicator that the stars are accreted, as depletion of this element has previously been reported for accreted stars both in the Milky Way (Nissen & Schuster 2010; Matsuno et al. 2021; Carrillo et al. 2022) and in the Small Magellanic Cloud (Mucciarelli et al. 2023).
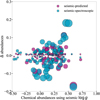 |
Fig. 7 Difference in chemical abundances for all elements (Δ [X/Fe]) as a function of chemical abundances determined adopting the seismic log ɡ. The difference between abundances estimated using seismic and predicted log ɡ is shown in magenta, while the difference between the abundances determined adopting seismic and spectroscopic log ɡ is shown in blue. The marker size is proportional to the difference between the log ɡ of each case. |
 |
Fig. 8 Chemical abundance distribution as a function of [Fe/H], Stars in blue are those studied in this work. The chemical abundances are those obtained using the spectroscopic log ɡ. The teal dots (prograde stars from Mackereth et al. 2021) and black contours (GALAH DR3 retrograde metal-poor stars) are the same control sample stars adopted in Fig. 5. The chemical elements are ordered according to their main nucleosynthetic channel: α-capture, iron peak, neutron-capture, and odd-Z. Within each nucleosynthetic channel, the chemical elements are organized according to atomic number. |
4.6 Peculiar stars
In this work, some peculiar stars were identified, and their characteristics warrant further examination. In Sect. 4.1 we present two stars in our sample with low eccentricity. Additionally, in Sect. 4.3 we find two stars with young ages in all three of the analyses we performed. In Sect. 4.5 we find three stars with high [Fe/H], a α-poor star, and three Al-poor stars.
The two stars with low-eccentricity orbits have standard low metallicities ([Fe/H] < −0.8) and do not have any peculiar chemical signature when compared with other accreted star candidates in our sample. Therefore, we conclude that they could be contaminants (stars formed in situ) in our sample.
The two stars that have young ages in the seismic analysis, are those with IDs 407 and 418, appear to be young in the other two analyses. Additionally, they appear to have low metallicities ([Fe/H] < −0.7) in all analyses and have highly eccentric orbits (ecc > 0.7), which agrees with the literature for accreted stars.
The three [Fe/H] -rich stars do not present any remarkable chemical difference compared to other stars in our sample, except that they are also α rich and have highly eccentric orbits.
These stars may potentially belong to the Splash (Belokurov et al. 2020) substructure, which is related to the thick disk of the Galaxy. The Splash stars have high-eccentricity orbits and have low angular momentum and in some cases retrograde orbits. They are believed to have formed in situ but to have had their orbits altered by a major merger event, possibly involving GES.
The α-poor star found is poor both in Ca and Mg and is the most metal-poor star in our sample. However, this star does not display any other significant chemical peculiarities, possibly because certain key elements such as Al, Ba, and Y could not be measured robustly. This star has a highly eccentric orbit and exhibits E and Lz compatible with those of GES stars, suggesting it might still share its origin with them. A detailed follow-up study of this object might shed light on its properties and history.
The Al-poor stars are also poor in Na, but apart from this observation, they do not have any other peculiar chemical signature that might indicate they come from a different progenitor galaxy than the other stars in our sample. They all have high eccentric orbits and E and Lz compatible with GES stars.
5 Summary and conclusion
In this work, we performed a comprehensive analysis of 30 metal-poor TESS accreted star candidates for which we obtained follow-up MIKE spectra. Given the limited number of metal-poor stars observed by TESS, it is crucial to improve our understanding of how the use of asteroseismic information impacts the characterization of these stars. Moreover, carefully characterizing accreted star candidates in terms of chemical abundances, dynamics, and ages is fundamental for improving our understanding of the Milky Way’s accretion history and the properties of its various building blocks.
In the literature, different works have associated different regions in the energy (E)–angular momentum (Lz) plane to different building blocks of the Milky Way. In order to characterize our sample of stars, we also studied them from a dynamical perspective using gala code. The majority of the stars occupy a region in the E–Lz plane that is consistent with GES stars. We identified two stars with very low Lz values that could potentially be associated with Sequoia debris. Additionally, we found that 28 of the 30 stars in our sample have highly eccentric orbits, typically with eccentricities exceeding 0.7, supporting their origins as accreted stars.
We also investigated the impact of different surface gravity (log ɡ) and the use of νmax and Δν on age and chemical abundance determinations. For our chemical abundance analysis, we adopted three different log ɡ values: seismic, predicted, and spectroscopic. The mean difference between seismic log ɡ and predicted log ɡ is 0.07 dex, with a standard deviation of 0.25 dex. Similarly, the mean difference between seismic log ɡ and spectroscopic log ɡ is 0.00 dex, with a standard deviation of 0.30 dex. In most cases, the differences in log ɡ values were well within the uncertainties, suggesting satisfactory overall agreement among the different log ɡ considered.
Next, we explored how the use of the predicted and spectroscopic log ɡ, as well as νmax and Δν, impacted the age determination. We used BASTA code to calculate the stellarages. Seismic ages (calculated using νmax and Δν) yield a median age of 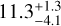 Gyr, with 15 percent of the sample found to be younger than 7 Gyr. Ages calculated using the predicted log ɡ result in slightly lower median age of
Gyr, with 15 percent of the sample found to be younger than 7 Gyr. Ages calculated using the predicted log ɡ result in slightly lower median age of 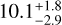 Gyr, also with 15 percent of the sample younger than 7 Gyr. Ages obtained using the spectroscopic log ɡ yield an even lower median age of
Gyr, also with 15 percent of the sample younger than 7 Gyr. Ages obtained using the spectroscopic log ɡ yield an even lower median age of 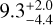 Gyr, with 46 percent of the sample younger than 7 Gyr according to our results. Additionally, statistical uncertainties found for the seismic, predicted, and spectroscopic cases are of the order of 10.1, 18.5, and 28.6 percent, respectively. Therefore, seismic ages tend to be slightly higher than those obtained using predicted or spectroscopic log ɡ values, and are also notably more precise according to our results. This study highlights the impact of seismic information on age determination, and in particular the potential of TESS data for Galactic archaeology studies.
Gyr, with 46 percent of the sample younger than 7 Gyr according to our results. Additionally, statistical uncertainties found for the seismic, predicted, and spectroscopic cases are of the order of 10.1, 18.5, and 28.6 percent, respectively. Therefore, seismic ages tend to be slightly higher than those obtained using predicted or spectroscopic log ɡ values, and are also notably more precise according to our results. This study highlights the impact of seismic information on age determination, and in particular the potential of TESS data for Galactic archaeology studies.
However, a different result was observed when evaluating the impact of different log ɡ in the chemical abundance determination when using the iSpec code. Comparing the chemical abundances calculated using the seismic and predicted log ɡ, we observe that the distributions are similar overall, but differences are observed for calcium (Ca). When comparing chemical abundances using the seismic and spectroscopic log ɡ, we also observe that the distributions are similar except for Ca and scandium (Sc) abundances. We note that Ca is very sensitive to log ɡ.
Finally, we studied the overall chemical distribution of our star sample, and our main findings are listed below:
The sample of stars studied here primarily exhibits high [α/Fe] abundances at low metallicities ([Fe/H] < −1.0), consistent with typical halo and thick disk stars. This suggests that if the stars are accreted, the progenitor galaxy had a high SFR and the necessary mass to produce enhanced [α/Fe] abundances.
Iron-peak elements, such as Ni, Cr, Co, and Mn, show abundance patterns that reflect the influence of Type Ia supernovae (SNIa) and suggest a high SFR with multiple SNIa events enriching the gas.
We identify some stars enhanced in Ba, indicating that neutron-capture enrichment played an important role in the chemical evolution of the environment in which they formed.
Odd-Z and light elements, such as vanadium (V), copper (Cu), scandium (Sc), sodium (Na), and aluminum (Al) exhibit varied abundance patterns, with V and Cu showing increases with [Fe/H]. The accreted star candidates appear to be poor in Cu when compared with stars likely formed in the Milky Way. Al is generally enhanced in the sample, but three stars appear to be Al poor.
Overall, the chemical abundance patterns of the stars studied here provide valuable insights into their origin and the processes that shaped the chemical evolution of their progenitor. These findings contribute to our understanding of the Milky Way’s assembly and the role of accretion events in building its stellar populations. We also show the importance of multidimensional analyses in unraveling the intricate nature of Galactic stars and the accretion history of the Milky Way.
Acknowledgements
We thank the anonymous referee, who provided valuable comments to improve this article. D.D.B.S. acknowledges ANID (Beca Doctorado Nacional, Folio 21220843) and Becas UDP for the financial support provided. D.D.B.S. also thanks Alexander Ji, Sara Vitali, Diane Feuillet and Henrique Reggiani for the valuable comments. P.J. acknowledges Fondo Nacional de Desarrollo Científico y Tecnológico (Fondecyt) Regular Number 1231057. D.D.B.S. and P.J. acknowledge Millennium Nucleus ERIS NCN2021_017. This paper includes data gathered with the 6.5 meter Magellan Telescopes located at Las Campanas Observatory, Chile. We also thank the staff of LCO for making the observation of these stars possible during the Covid-19 pandemic. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA Explorer Program. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. This work made use of the Third Data Release of the GALAH Survey (Buder et al. 2021). The GALAH Survey is based on data acquired through the Australian Astronomical Observatory, under programs: A/2013B/13 (The GALAH pilot survey); A/2014A/25, A/2015A/19, A2017A/18 (The GALAH survey phase 1); A2018A/18 (Open clusters with HERMES); A2019A/1 (Hierarchical star formation in Ori OB1); A2019A/15 (The GALAH survey phase 2); A/2015B/19, A/2016A/22, A/2016B/10, A/2017B/16, A/2018B/15 (The HERMES-TESS program); and A/2015A/3, A/2015B/1, A/2015B/19, A/2016A/22, A/2016B/12, A/2017A/14 (The HERMES K2-follow-up program). We acknowledge the traditional owners of the land on which the AAT stands, the Gamilaraay people, and pay our respects to elders past and present. This paper includes data that has been provided by AAO Data Central (datacentral.org.au). This research also made use of Matplotlib (Hunter 2007), NumPy (Walt et al. 2011), SciPy(Jones et al. 2001), Astropy (Robitaille et al. 2013; Price-Whelan et al. 2018) and seaborn (Waskom 2021).
References
- Abolfathi, B., Aguado, D., Aguilar, G., et al. 2018, ApJS, 235, 42 [Google Scholar]
- Aguado, D. S., Belokurov, V., Myeong, G. C., et al. 2021, ApJ, 908, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Aguirre Børsen-Koch, V., Rørsted, J., Justesen, A., et al. 2022, MNRAS, 509, 4344 [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N., Koposov, S., & Deason, A. 2018, MNRAS, 478, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Sanders, J. L., Fattahi, A., et al. 2020, MNRAS, 494, 3880 [Google Scholar]
- Blanco-Cuaresma, S. 2019, MNRAS, 486, 2075 [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [CrossRef] [EDP Sciences] [Google Scholar]
- Borre, C. C., Aguirre Børsen-Koch, V., Helmi, A., et al. 2022, MNRAS, 514, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Brown, A., Vallenari, A., Prusti, T., et al. 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, A. G., Vallenari, A., Prusti, T., et al. 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Lind, K., Ness, M. K., et al. 2022, MNRAS, 510, 2407 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T., Schofield, M., Kuszlewicz, J., et al. 2016, ApJ, 830, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Carrillo, A., Hawkins, K., Jofré, P., et al. 2022, MNRAS, 513, 1557 [CrossRef] [Google Scholar]
- Casagrande, L., Lin, J., Rains, A. D., et al. 2021, MNRAS, 507, 2684 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, E., Massari, D., Mucciarelli, A., et al. 2024, A&A, 684, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerqui, V., Haywood, M., Di Matteo, P., Katz, D., & Royer, F. 2023, A&A, 676, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Bedding, T. R., et al. 2011, ApJ, 732, 54 [CrossRef] [Google Scholar]
- Chiappini, C., Anders, F., Rodrigues, T. d. S., et al. 2015, A&A, 576, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Das, P., Hawkins, K., & Jofré, P. 2020, MNRAS, 493, 5195 [NASA ADS] [CrossRef] [Google Scholar]
- De Brito Silva, D., Jofré, P., Bourbert, D., et al. 2022, MNRAS, 509, 4637 [Google Scholar]
- Elsworth, Y., Themeßl, N., Hekker, S., & Chaplin, W. 2020, Res. Notes Astron. Astrophys. Soc., 4, 177 [Google Scholar]
- Feuillet, D. K., Sahlholdt, C. L., Feltzing, S., & Casagrande, L. 2021, MNRAS, 508, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
- Gray, R., & Corbally, C. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Grisoni, V., Chiappini, C., Miglio, A., et al. 2024, A&A, 683, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grunblatt, S. K., Zinn, J. C., Price-Whelan, A. M., et al. 2021, ApJ, 916, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawkins, K., Jofre, P., Masseron, T., & Gilmore, G. 2015, MNRAS, 453, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
- Helmi, A., & White, S. D. 1999, MNRAS, 307, 495 [CrossRef] [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Hidalgo, S. L., Pietrinferni, A., Cassisi, S., et al. 2018, ApJ, 856, 125 [Google Scholar]
- Hill, V., Skúladóttir, Á., Tolstoy, E., et al. 2019, A&A, 626, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holtzman, J. A., Hasselquist, S., Shetrone, M., et al. 2018, AJ, 156, 125 [Google Scholar]
- Horta, D., Ness, M. K., Lisanti, M., et al. 2024, arXiv e-prints [arXiv:2403.09777] [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2021, MNRAS, 500, 1385 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2022, arXiv e-prints [arXiv:2204.04233] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ishigaki, M. N., Chiba, M., & Aoki, W. 2012, ApJ, 753, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, A. P., Simon, J. D., Frebel, A., Venn, K. A., & Hansen, T. T. 2019, ApJ, 870, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Jofré, P., Jorissen, A., Van Eck, S., et al. 2016, A&A, 595, A60 [Google Scholar]
- Jofré, P., Jorissen, A., Aguilera-Gómez, C., et al. 2023, A&A, 671, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, online [Google Scholar]
- Juric, M., Ivezic, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D. 2003, PASP, 115, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1994, arXiv eprint [astro-ph/9403015] [Google Scholar]
- Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020, ApJ, 900, 179 [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019, A&A, 631, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koppelman, H. H., Bos, R. O., & Helmi, A. 2020, A&A, 642, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijssen, J. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [NASA ADS] [CrossRef] [Google Scholar]
- Letarte, B. 2007, Chemical Analysis of the Fornax Dwarf Galaxy (The Netherlands: University of Groningen) [Google Scholar]
- Mackereth, J. T., Miglio, A., Elsworth, Y., et al. 2021, MNRAS, 502, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Rix, H.-W., Aguirre, V. S., et al. 2015, MNRAS, 451, 2230 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R., Régulo, C., et al. 2010, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuno, T., Aoki, W., & Suda, T. 2019, ApJ, 874, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuno, T., Aoki, W., Casagrande, L., et al. 2020, arXiv e-prints [arXiv:2006.03619] [Google Scholar]
- Matsuno, T., Hirai, Y., Tarumi, Y., et al. 2021, A&A, 650, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuno, T., Koppelman, H. H., Helmi, A., et al. 2022, A&A, 661, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMillan, P. J. 2016, MNRAS, 465, 76 [Google Scholar]
- Montalbán, J., Mackereth, J. T., Miglio, A., et al. 2021, Nat. Astron., 5, 640 [Google Scholar]
- Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mucciarelli, A., Minelli, A., Bellazzini, M., et al. 2023, A&A, 671, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myeong, G., Vasiliev, E., Iorio, G., Evans, N., & Belokurov, V. 2019, MNRAS, 488, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Amarsi, A. M., Skúladóttir, Á., & Schuster, W. 2024, A&A, 682, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Moriya, T., & Tominaga, N. 2009, Proc. Int. Astron. Union, 5, 34 [CrossRef] [Google Scholar]
- Pasquini, L., & Lindgren, H. 1994, ASP Conf. Ser., 64, 453 [NASA ADS] [Google Scholar]
- Pietrinferni, A., Hidalgo, S., Cassisi, S., et al. 2021, ApJ, 908, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Sipocz, B., Günther, H., et al. 2018, AJ, 156, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, in Problems in Stellar Atmospheres and Envelopes (Berlin: Springer), 229 [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Robitaille, T. P., Tollerud, E. J., Greenfield, P., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Schofield, M., Chaplin, W. J., Huber, D., et al. 2019, ApJS, 241, 12 [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [Google Scholar]
- Shetrone, M., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [Google Scholar]
- Silva Aguirre, V., Davies, G., Basu, S., et al. 2015, MNRAS, 452, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1993, arXiv eprint [astro-ph/9304005] [Google Scholar]
- Timmes, F., Woosley, S., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1993, ASP Conf. Ser., 52, 173 [NASA ADS] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [Google Scholar]
- Van der Swaelmen, M., Hill, V., Primas, F., & Cole, A. 2013, A&A, 560, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walt, S. v. d., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Waskom, M. L. 2021, J. Open Source Softw., 6, 3021 [CrossRef] [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, RAA, 12, 723 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example region of stellar spectra. An example spectrum obtained with the MIKE spectrograph at the Clay Telescope at Las Campanas Observatory is shown in blue, and a synthetic spectrum built using iSpec (Blanco-Cuaresma et al. 2014; Blanco-Cuaresma 2019) is shown in orange. The gray regions were used to fit the observed spectra to obtain chemical abundances of different elements. |
| In the text | |
 |
Fig. 2 Lɀ–E plane. Gray dots represent GALAH DR3 stars, while star markers denote the stars investigated in this study. The top panel displays the stars studied in this work color-coded according to eccentricity, while the bottom panel shows them color-coded according to [Fe/H], The approximate regions corresponding to GSE debris (green ellipse) and Sequoia debris (blue triangle) are indicated in the figure. |
| In the text | |
 |
Fig. 3 Comparison of different log ɡ. The top panel shows the values of seismic (gray), predicted (magenta), and spectroscopic (blue) log ɡ for each star, as well as their respective uncertainties. The bottom panel shows the difference between seismic and predicted log ɡ (magenta), as well as between seismic and spectroscopic log ɡ (blue). We consider as uncertainties the quadratic sum of the individual uncertainties of each case. The mean (µ) and standard deviation (σ) of the comparison presented in the bottom panel is shown in the label. |
| In the text | |
 |
Fig. 4 Age distribution for the three cases studied in this work using BASTA. The top panel (gray) shows stellar ages calculated using the seismic information νmax and Δν. The middle panel (pink) shows stellar ages calculated using the predicted log ɡ. The bottom panel (blue) shows the stellar ages calculated using the spectroscopic log ɡ. Median values as well as lower and upper uncertainties are indicated in the label. |
| In the text | |
 |
Fig. 5 [Mg/Fe] versus [Fe/H], The stars in this work are presented as stellar markers, while other stars from Mackereth et al. (2021) are represented as teal dots (from GALAH DR3 data). We also show as black contour lines the kernel density estimate of metal-poor stars with retrograde motion from GALAH DR3 survey. The stars presented in this work are color-coded according to BASTA seismic stellar ages. |
| In the text | |
 |
Fig. 6 Comparison of chemical abundance distribution obtained adopting the different log ɡ. The top panel shows the chemical distribution per element when using the seismic log ɡ (gray) and the predicted log ɡ (magenta). The bottom panel shows the chemical distribution per element when adopting the seismic log ɡ (gray) and the spectroscopic log ɡ (blue). The central dashed line represents the median of the distributions, while the other lines neighboring it show the data quartiles. The chemical abundances are ordered according to main nucleosynthetic channel: α-capture, iron peak, neutron-capture, and odd-Z. Within each nucleosynthetic channel, the chemical elements are organized according to atomic number. |
| In the text | |
 |
Fig. 7 Difference in chemical abundances for all elements (Δ [X/Fe]) as a function of chemical abundances determined adopting the seismic log ɡ. The difference between abundances estimated using seismic and predicted log ɡ is shown in magenta, while the difference between the abundances determined adopting seismic and spectroscopic log ɡ is shown in blue. The marker size is proportional to the difference between the log ɡ of each case. |
| In the text | |
 |
Fig. 8 Chemical abundance distribution as a function of [Fe/H], Stars in blue are those studied in this work. The chemical abundances are those obtained using the spectroscopic log ɡ. The teal dots (prograde stars from Mackereth et al. 2021) and black contours (GALAH DR3 retrograde metal-poor stars) are the same control sample stars adopted in Fig. 5. The chemical elements are ordered according to their main nucleosynthetic channel: α-capture, iron peak, neutron-capture, and odd-Z. Within each nucleosynthetic channel, the chemical elements are organized according to atomic number. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


