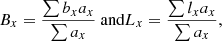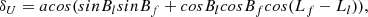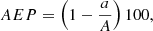| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A257 | |
| Number of page(s) | 6 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202450194 | |
| Published online | 14 October 2024 | |
Variation in the polarity separation of sunspot groups throughout their evolution
HUN-REN Institute of Earth Physics and Space Science, Csatkai Endre str. 6-8, 9400 Sopron, Hungary
Received:
31
March
2024
Accepted:
19
August
2024
During the emergence of sunspot groups, the footpoints of their leading and following parts move apart. This diverging motion results in the stretching of the active regions, which continues throughout the decay phase. The aim of the present work is to study the separation distance variations throughout the active region evolution on a large statistical sample. Altogether, we took more than 2000 individual sunspot groups into account. Our investigation is mainly based on data of the SoHO/MDI-Debrecen Sunspot Data (SDD) catalog, which covers the years 1996–2010, specifically, nearly the whole of solar cycle 23. For our check of the possible cyclical variation, we used Debrecen Photoheliographic Data (DPD), which contains data for solar cycles 20–24. The separation distance was calculated between the leading and following centers of mass, revealing that it starts to increase after the emergence and shows a plateau around the peak flux. The polarity separation reaches its maximum in the decay phase and then starts to decrease in the cases of the largest and midsize groups, but it does continue its rise in the case of the smallest groups. This decrease is caused by the eastward motion of the leading part, while the following part continues its backward motion. The separation distance is size-dependent, that is, the larger the sunspot group, the greater its extent. The cycles and cycle phase dependencies as well as related hemispheric connections have also been observed.
Key words: Sun: activity / Sun: magnetic fields / Sun: photosphere / sunspots
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Studies of the solar active region (AR) evolution are important regarding to the solar dynamo theories. The development and decay of the active region are governed by different mechanisms. While buoyancy is known to be responsible for the emergence, the decay is governed by the small-scale cancellation process that fragments and scatters the magnetic flux (van Driel-Gesztelyi & Green 2015). The statistical analysis carried out by Švanda et al. (2021) investigated the formation and decay of ARs and found that the decay is governed by an erosion process. Thus, their detailed study is vital to expanding our knowledge of the whole process at work. The emergence is a more widely known phenomenon in the sense of motion as well. Several works have studied the leading–following polarity separation of ARs. Gilman & Howard (1986) showed that the leading following sunspots can be characterized as a simple expansion along their major axis. Although Pevtsov et al. (2003) studied only six ARs, the image of the polarity separation continued to be refined thanks to this work. These authors found that the footpoint separation distances increase over time after the AR’s emergence and reach a plateau 1.5 days after the beginning of the emergence. Schunker et al. (2019) studied the motion of the opposite magnetic polarity regions of sunspot groups during their emergence. They pointed out that two phases of emergence can be distinguished. During the first phase, the polarity separation is accelerating, while during the second one is decelerating. The most striking feature is that the leading part moves towards the equator and westward, while the following one moves in the poleward and eastward direction. McClintock & Norton (2016) studied the variations among separation distances in sunspot groups of different sizes during their evolution, finding that the expansion behavior was different in sunspot groups of different sizes. Kosovichev & Stenflo (2008) studied 715 bipolar ARs from SOHO/MDI magnetograms and found that after the emergence of the ARs, the separation distance increases rapidly, but during the decay, it decreases. The process pointed out by Verma et al. (2016) is similar. They investigated the evolution of AR NOAA 12118 and pointed out its four phases: the initial separation of the two polarities followed by a rapid expansion phase, then the spread stalls, and the last phase, when the AR slowly shrinks. The separation rate is the highest in the initial stage, with a value of 0.26 km s−1, and after the halt of the separation, this rate decreases. The decay, namely, the last phase of the AR lifetime has also been investigated in several works. This specific phase lasts longer than the emerging phase (Javaraiah 2011) and differs in terms of the parameters related to the leading and following parts. Its rate was calculated in different studies, with some reporting the decay as a linear process (Bumba 1963; Gafeira et al. 2014; Muraközy 2020; Li et al. 2021; Muraközy 2021), while Solanki (2003) noted that linear decay law is appropriate for 95% of all of the sunspots, regardless whether the sunspot groups are recurrent or not. Other studies refer to decay as a parabolic process (Moreno-Insertis & Vazquez 1988; Martinez Pillet et al. 1993; Petrovay & van Driel-Gesztelyi 1997; Litvinenko & Wheatland 2015), where the temporal variation of the area is proportional to the square root of the area. Investigating sunspot groups of Cycle 23 Zharkova & Zharkov (2008) pointed out that the variations of polarity separation with latitude are in anti-phase with those of the tilts reaching a maximum at the latitude of 35°. Although, there are many studies on the leading-following separation distance, they mainly relate to the development phase of the ARs lifespan, and they are sparse during the decay phase. The present study offers a statistical investigation of the polarity separation of sunspot groups, as well as its possible hemispheric, cycle, and cycle phase dependencies on a large sample, using Debrecen sunspot databases.
2. Data and method
The Debrecen sunspot databases1 (Baranyi et al. 2016; Győri et al. 2017) offer a unique opportunity to study the evolution of sunspot groups in high temporal and spatial resolution. Thus, the growth and decay of sunspot groups and their leading and following parts can be tracked separately. This study uses two sunspot catalogs. The first is the SOHO-MDI/Debrecen Sunspot Data (hereafter, SDD), which contains data for the period 1996–2010, namely, solar cycle 23. The input of this database comes from the Solar and Heliospheric Observatory spacecraft and its Michelson Doppler Imager as a white light image and a magnetogram. The SDD’s temporal resolution is 1.5 h. Since the SDD contains magnetic data for each sunspot the two opposite polarity parts of the groups can be distinguished. Thus, by using the area, along with the latitudinal and longitudinal data of sunspots, the centers of mass of the leading and following polarities can be calculated. To take the area distributions of those parts into account the area-weighted latitude and longitude are calculated as
where x means the polarity and a denotes the area in millionth of solar hemisphere (MSH) corrected for foreshortening, while b and l indicate the latitude and longitude of the spots, respectively. The leading-following magnetic flux contents, and the sum of their absolute values (fU = |flU|+|ffU|), called the total unsigned flux, have been determined in Weber (unless otherwise stated). The flux is calculated for each sunspots and each observation time. Then the fluxes absolute values are summarized for the whole sunspot group and separately its leading and following parts. To check the possible cycle dependence of the polarity separation the tilt angle database (Baranyi 2015) of the so-called Debrecen Photoheliographic Data (DPD) sunspot catalog has been used. Its time span covers the period 1974–2018, covering solar cycles 20–24. The data of this catalog come from ground-based observations; thus, there is no magnetic data included and its temporal resolution is 1 day. For the present study, the DPD tilt angle database has been used because it contains the values of the leading and following parts’ centers of mass. Given the lack of magnetic data, the position of the leading and following parts is considered as the area-weighted position of those sunspots that precede and lag with respect to the center of mass of the whole sunspot group, respectively.
The polarity separation has been calculated as the spherical distance between the leading and following centers of mass:
where B and L indicate the area-weighted latitude and longitude of the leading and following parts (l and f lower indices), respectively. The separation distance is measured in degrees. Since the sunspot groups with different area evolve in different way and at different speed their areas must be eliminated to compare them. Therefore instead of time, the areal evolution phase (Muraközy 2022) is used:
where a is area of each sunspot group, while A is their peak area. For the growth and decay phases to be distinguished, the value of the AEP and FEP are multiplied by −1 for the growth. Thus, its value is negative during the growth phase of the group, positive if the group decays, and 0 at the time of the maximum area. The flux evolution phase (FEP) can be calculated similarly. These values are determined for each observational time of the groups by taking into account the umbral area or the flux. To extend the previously applied statistical sample (detailed in Muraközy 2022), we considered the sunspot groups that show a clear growth phase before and decay phase after the peak area at least 1 day. The number of sample selected such a way from the SDD is 1014, while altogether 1047 groups were studied from the DPD. The evolutionary process is tracked when the groups are within 0.75 of solar radius. Each active region is considered during one transit on the solar disk, regardless whether it is recurrent or not. In the present paper, only umbrae are taken into account, as denoted by the subscript U.
3. Results and discussion
In the prior work published on this topic (Muraközy 2022), the decay phase was studied on 142 selected and visually inspected sunspot groups. Although I also carried out the tests detailed below on the previous sample, only the results based on the extended sample are shown here. Otherwise, I confirm the results are similar for both data sets.
3.1. Magnetic flux
The evolution of an active region can be described by the variation of either the total umbral area or the total unsigned magnetic flux measured in the umbrae, at first their relationship is studied. Here, the total unsigned magnetic flux means the whole flux that is contained by the leading and following sunspots (fU=|flU|+|ffU|) regardless of their polarity. Figure 1 shows the total unsigned ubmral magnetic flux measured in Wb as a function of umbral area.
 |
Fig. 1. Total unsigned magnetic flux measured in Weber as a function of the area measured in millionths of solar hemisphere. The figure contains the data of all studied sunspot groups from SDD, each gray point marks a sunspot group. The linear fitted function is depicted with solid black line. Equation of the fitted linear function can be seen in the top-left corner. |
As the plot shows, their relationship is linear, namely: the higher the area, the higher its flux content. The equation of the fitted linear function can be seen in the figure. This relationship is previously investigated by Sheeley (1966) by considering eight sunspot groups and obtained that ϕ = 1.2A, where A is the area measured in 1018 cm2, and ϕ is expressed in 1021Mx. The result of the present study is ϕ = 1.47AU if AU and ϕ are expressed in the aforementioned units and are in good agreement with the results from Sheeley (1966).
The top panel of Figure 2 depicts the AEP-FEP relationship. The bulk of the sunspot groups are mostly located in two quadrants; namely: positive FEP and AEP or negative FEP and AEP. This means that sunspot groups are in their same phases (growth or decay) at the same time considering the area and flux. Some groups have different times of peak area and peak flux. The number of these cases is 379 while that of the coinciding peak times is 635 in the selected sample. The fitted linear function has an intercept on the vertical axis at −1.16 meaning that the majority of groups reach their peak area slightly earlier than their maximum flux. As the DPD does not contain magnetic polarity data, the AEP is used for comparison. In the bottom panel of Figure 2, we can see the connection between the FEPU and the time near the time of maximum flux. Since the sunspot groups with different peak area grow and decay in different ways (Muraközy et al. 2014; Muraközy 2020, 2021), here we consider three sets of area ranges of sunspot groups. Their peak sizes are smaller than 20 MSH, between 20 MSH and 60 MSH, and larger than 60 MSH (indicated in the panels). Each gray point marks a sunspot group in one observation time. The negative and positive values mean the growth and decay phases, respectively, the flux maximum is at the zero value of the time axis. Linear functions have been fitted to the growth and decay phases separately. Their equations are in the bottom right quadrant and the growth and decay periods calculated from those equations. Taking into account the peak area of sunspot groups, we can conclude that the mean period of the growth phase is shorter than the decay phase in each case. The growth phases are 2.56 ± 0.02 days, 3.69 ± 0.02 days and 4.96 ± 0.03 days for the smallest, midsized, and largest groups, respectively. While the decay phases are 2.72 ± 0.02 days, 4.13 ± 0.02 days, and 5.99 ± 0.02 days for the smallest, midsize, and largest groups, respectively. These are different representations of the asymmetric shape of the active region evolution which are referred to by several authors, including Javaraiah (2011).
 |
Fig. 2. Relationship of the area evolution phase and total unsigned flux evolution phase based on the SDD (top panel). Both of them are measured in percentage. Each gray point marks a sunspot group in one observation time. The linear fitted function is depicted with solid black line, its equation can be found in the upper left quadrant. Bottom panel: Umbral flux evolution phase as a function of time near the time of maximum flux measured in days for three sets of sunspot group sizes. The equations of the fitted regression lines and standard error values can be found in the bottom right quarter. The characters g and d mean the growth (negative values) and decay (positive values) phases of groups. The average growth and decay periods are calculated by using the equations of the fitted functions. |
3.2. Polarity separation
The separation distance is calculated between the area weighted positions of the centers of mass of sunspots with leading and following polarities by using Equation (2).
Figure 3 depicts the variation of the leading-following spherical distance as a function of FEP and AEP on the bottom and top axes, respectively. After the emergence the sunspot group starts expanding. This continues until the AEP phase of −40 where the expansion reaches a plateau that extends to somewhat beyond the maximum area (AEP = 0). After the peak area the separation distance increases again until about 60–70 % of the decay. At the end of the decay the polarity separation shows a conspicuous decrease. These results are in agreement with the previous studies on the emergence and decay of ARs. van Driel-Gesztelyi & Green (2015) summarized the process of the magnetic bipole emergence to the solar surface. When the tilted loop emerges as a result of the buoyancy, the footpoints are pushed apart, the legs of the Ω shape loop start to straighten, which cause the increase of the separation distance between the two legs (Caligari et al. 1995). The plateau is referred to as a stability plateau (Pevtsov et al. 2003; Norton et al. 2023) and Schunker et al. (2019) reported that this can be observed 2.5 days after the beginning of the emergence. In the present study, the beginning of the plateau is at −40% of AEP (30% of the entire lifetime), which corresponds to about 3 days in case of a lifetime of 10 days. The expansion process has also been pointed out by Kosovichev & Stenflo (2008), Verma et al. (2016).
 |
Fig. 3. Spherical leading-following distance vs. FEP (measured on the bottom axis) plotted with black dots and AEP (measured on the top axis) depicted by empty triangles. The mean values of separation distance with their standard errors are averaged over 10% bins of the umbral FEP (AEP). The data reported in this figure come from the SDD. |
Since the evolution of the active regions strongly depends on the peak area or peak flux, the variation in the separation distance was also analyzed by the area. Thus, the studied groups are divided into three classes according to their maximum umbral areas (AU): AU < 20 MSH, AU between 20 and 60 MSH and AU > 60 MSH (as in Figure 2). Figure 4 depicts these area divided data based on the SDD (top panel) and DPD (bottom panel). Sunspot groups of different areas evolve in different ways. The largest and middle size groups show the above mentioned path, while the leading – following separation of the smallest ones remains unchanged from the beginning of stable period and during the decay. The most pronounced decrease at the end of the decay phase is shown by the largest groups. The case is the same considering the DPD, although the plateaus in the growth phase are not as pronounced as in the case of the SDD, but the fallback in the end is much greater than that of the SDD’s groups. The development of the smallest groups is much more chaotic and does not show increasing polarity separation, and their errors are higher than that of the larger groups or that of the SDD groups. This may be explained by the lack of magnetic data in the DPD where the leading-following parts are distinguished by the Kodaikanal method, thus, these are the subgroups westward and eastward from the center of weight. However, Baranyi (2015) showed that under a certain size the sunspot groups are unipolar and the leading-following distinction is irrelevant. Since the leading-following expansion caused by the movement of the both parts their daily shift is also studied (Figure 5). The most conspicuous difference between the upper and lower panels of Figure 4 is that the distances measured after the 60% decay time decrease more steeply in the data of DPD than in the SDD. This can be explained by the lack of polarity data in the DPD because when the trailing spots gradually disappear the program is increasingly restricted to the remaining spots in the leading part which is not the case with SDD data.
 |
Fig. 4. Separation distance as a function of AEPU for three sets of sunspot groups considering their peak umbral area. The top panel concerns the SDD, the bottom panel concerns the DPD. The empty triangles mark the data calculated on the entire sample of the DPD (same as in Figure 3 for the SDD). The separation distances are averaged over 10% bins of the AEP, the error bars mark the standard error. |
The daily shift was determined as the difference between the latitudinal and longitudinal positions at two consecutive times extrapolated for 1 day. These shifts were averaged over 10% bins of AEP and calculated for the leading and following parts separately. The positive value of this shift concerns the forward and poleward motion. As one can see the following part mainly moves backward (i.e., its values are in the negative half) and poleward (its values are in the positive half of the diagram) regardless of the evolutionary phase of the group. This is not the case with respect to the leading part. This part mainly show equatorward motion during the emergence phase but then remains at that latitudinal position. The longitudinal shift of the leading part (bottom-right panel of Figure 5) shows the well-known forward motion during almost the entire life of the sunspot group, however, at the end of its decay, a pronounced backward motion can be observed. This means that the decrease in the separation distance at the end can be explained by the longitudinally backward motion and latitudinal immobility of the leading part. The biggest shift both in latitudinal and longitudinal directions is shown by the leading part at the beginning of the evolution. Similar findings have been reported by Schunker et al. (2019), who showed that the emergence consists of two parts. The first is a fast movement that lasts until about 1 day after the emergence where the polarity separation accelerates and this is followed by a decelerating phase. The movements of the two opposite polarity parts are also opposite, namely, the leading part moves forward and equatorward and the following part is shifted to backward and poleward directions.
 |
Fig. 5. Daily latitudinal shift (top row) and longitudinal shift (bottom row) of the leading part (right column, plotted with dots) and following part (left column, depicted by circles) versus AEP. The shifts are averaged over each 10% bin of AEP, the error bars mean the standard error. Positive and negative values of latitudinal shifts mean poleward/equatorward, and that of the longitudinal shifts concern forward and backward motion of sunspot groups. |
3.3. Long-term variation in the separation distance
The variation of the separation distance can also be studied on longer time intervals than half a solar rotation. At first, the DPD and SDD data of cycle 23 have been used with similar results, therefore, only the results from the SDD are presented here. The leading-following separation distance was calculated for all groups and, separately, for the growth, maximum, and decay phases. Figure 6 shows these variations. The mean separation distance is highest during the decay phase and lowest at the maximum phase. The rate of the separation distance during the growth is between them. After a peak at the beginning of the cycle the polarity separation starts to decrease until about the half of the cycle. Then a slow increase can be observed. This variation also shows that the polarity separation strongly depends on the area and the larger the area of the groups the higher the separation distance between its two parts. The fallback around the middle of the cycle is caused by the so-called Gnevyshev-gap when the area of the solar ARs decreases temporarily.
 |
Fig. 6. Separation distance versus cycle phase by using the SDD. The separation distances are averaged over 10% cycle phase bins and plotted to the center of each bin. The mean separation distance is calculated for the entire group (plotted by dots), their growth phase (triangles), maxima (asterisk), and decay (squares). The error bars mark the standard errors. |
The top panel of Figure 7 shows the hemispheric mean polarity separation averaged over the solar cycles by using the data from the DPD. The black dots mark the northern, while the empty circles depict the southern hemisphere’s values. The most striking feature of this plot is the alternating cyclic variation of the hemispheric separation distance. During solar cycle 20, the large errors and the high distance between the northern and southern values is caused by the small amount of data.
 |
Fig. 7. Hemispheric separation distances during SCs 20–24 (top panel). The separation distances are considered as their peak value and averaged over each solar cycle. Error bars represent the standard errors. Bottom panel: Maximum separation distances are averaged over solar cycles as a function of the cycle strengths. The latter is based on the yearly mean total sunspot number table created by WDC-SILSO, Royal Observatory of Belgium, Brussels. Error bars represent the standard errors, while the numbers mark the solar cycles. |
The bottom panel of Figure 7 depicts the cyclic mean separation distance as a function of the strength of the cycle. Each sunspot group was considered at the time of the peak polarity’s separation distance, thus, each group is considered only once. The cycle strength data are come from the yearly mean total sunspot number table of the Royal Observatory of Belgium2. To the clear view it should be mention that the data of cycle 20 is not reliable because the starting date of DPD is 1974, while that of cycle 21 is 1976; thus, there is a few data during cycle 20. The number of the studied distinct ARs is only 19 compared to that of the other cycles which is about 300. This data for solar cycle 24 is also low (89) and the standard error is relatively high; however, the data of DPD covers almost the entire cycle 24. If we take all cycles into account, the mean maximum separation distances does not show any correlation with the cycle strengths.
4. Summary and conclusion
The aim of this study is to investigate the variation among leading-following separation distances on as large a sample as possible and to check any plausible dependencies. Our results are summarized below.
-
The times of peak flux and peak area of the bulk of sunspot groups are the same, although there are some groups that have different peak flux and area times. In general the area of sunspot group reaches its peak value slightly earlier than its maximum flux. The growth phases last 2.56 ± 0.02 days, 3.69 ± 0.02 days, and 4.96 ± 0.03 days for the smallest, middle size, and the largest groups, respectively. While the decay phases are 2.72 ± 0.02 days, 4.13 ± 0.02 days, and 5.99 ± 0.02 days for the smallest, midsize, and largest groups, respectively (Figure 2).
-
The separation distance of leading-following subgroups has a plateau beginning at the 30% of the sunspot group lifetime. After the maximum an abrupt jump causes a higher plateau. This behavior is independent of the lifetime of the groups and it is exhibited in both the area and magnetic flux development phases (Figure 3).
-
At the end of the decay phase, a shrinking can be observed, which is mainly caused by the backward motion of the leading part. This decrease is more pronounced in the cases of the largest and midsized groups. It was not observed in the smallest groups (Figures 4 and 5).
-
The dependence of the separation distance on the area of ARs is strong, at the time of the Gnevyshev-gap, the separation distance decreases temporarily (Figure 6).
-
The sign of difference between the hemispheric polarity separations alternate by the consecutive cycles (Figure 7).
The emergence and decay of solar active regions have been investigated in several works but the majority of these studies is restricted to short timescales and a few solar ARs (Verma et al. 2016). Some investigations have used larger sample sizes, a few hundred sunspot groups (Kosovichev & Stenflo 2008; McClintock & Norton 2016; Schunker et al. 2019). Some of them, mainly, the more recent studies focus on SDO measurements covering one cycle or one-and-a-half cycles. The present uses the largest sample size on the longest time interval. Therefore, not only the peak area or flux dependence of the separation distance may be studied, but also its cycle phase and cycle variations. Cheung et al. (2010) used MHD simulation to find that during the magnetic flux emergence the convective cells are elongated due to the horizontal expansion of the rising plasma and the parts of sunspot group with opposite polarities diverge. Hartshorn (2012), van Driel-Gesztelyi & Green (2015) concluded that the peak separation follows the peak magnetic flux and, therefore, the peak area, which is also corroborated by our results.
McClintock & Norton (2016) assumed that larger sunspot groups are less influenced by the supergranular convection motion, while the smallest groups can not accumulate enough flux to prevail this disintegrating motion before their decay phase. The results in Figure 4 shows the separation distances of the smallest groups begin to increase after their peak area, while those of the largest groups increase already during the emergence. The poleward movement of the trailing parts observed mainly during the decay is in accordance with the flux transport dynamo theories. Cheung et al. (2010) pointed out theoretically that the flux transport rate is inversely proportional to the magnetic field strength. The reversal of the leading part at the end of the decay has also been found by Kosovichev & Stenflo (2008) but it will be investigated further. Verma et al. (2016) described the expansion of one studied AR with an initial separation rate followed by a rapid expansion phase and a time span when the spread stalls and after that the AR slowly shrinks toward the end of the decay phase. Figures 3 and 4 show these steps. At the beginning the speed of the separation is the fastest until AEP = −80%, which means about one day from the appearance of the group in the cases of the largest groups (bottom panel of Figure 2). During this period, the rising Ω loop expands, while the opposite polarity parts move apart. This phase is also described by Schunker et al. (2019), who reported that this first phase lasts until about 1 day. Then, the separation starts to slow down, this can be seen until about AEP = −40%, which corresponds to further two days in the largest groups. After the second phase, the increase of separation is dragged until a temporary state of rest at the peak area. Caligari et al. (1995) obtained the theoretical result that the emergence of an Ω loop to the surface is asymmetric, namely, the leading leg of the flux rope is more inclined from the vertical direction. Thus, we can suppose that the plateau can be observed when the leading leg becomes more vertical due to the buoyancy. The next step happens during the continuous expansion. Here, the disintegrating processes overcome the magnetic stability (McClintock & Norton 2016). The last phase of the sunspot group’s lifetime is a converging motion caused by the eastward shift of the leading center (Figure 5). Bray & Loughhead (1964) showed this phenomenon near the maximum area of sunspot groups. Its physical background is still unclear, as van Driel-Gesztelyi & Green (2015) discusses based on the summary of Fan (2009). According to McClintock & Norton (2016) the smallest groups cannot accumulate enough magnetic flux to resist the supergranular convection; thus, their separation increases throughout their whole lifetimes, in contrast to larger groups.
No clear relationship was distinguished between the cycle strength and separation distance on the studied sample (lower panel of Figure 7). This is also the case for the variation of the hemispheric separation distances if we consider the hemispheric strengths as the amplitudes of the corresponding cycle profiles (Muraközy 2016; Vernova et al. 2020). If the cycle strength is defined as the amplitude of the centers of mass of each solar cycle (Figures 5 and 8 in Muraközy 2016), a weak relationship can be found between them. The amplitude of the northern hemispheric activity and the separation distance were slightly higher during SCs 21 and 23, while the case was the opposite for SC 22. The possible nature of this hemispheric alternation of the leading-following separation distance is unclear; however, this two Schwabe-cyclicity resembles the α – Ω solar dynamo process, with its 22-year duration being the same as that assumed for the background of the Gnevyshev-Ohl rule (Nagovitsyn et al. 2024).
Schrijver & Zwaan (2008) showed that the lifetime of active regions is proportional to the magnetic flux and the rise time of the ARs decreases with the increasing area (van Driel-Gesztelyi & Green 2015). The rise time is found to be roughly 30% for ephemeral regions and 15% for large regions containing sunspots and living longer than a week. In our results the emerging phases are 48%, 47%, and 45% of the average lifetime of the studied groups from the smallest to the largest ones. Although the emergence phase of the sunspot groups is found to be shorter than the decay phase in the present study as well, but the relatively large discrepancy between the present results and those of Schrijver & Zwaan (2008) and van Driel-Gesztelyi & Green (2015) might be explained by a methodological difference. I note that the present study is focused on umbrae, while the cited authors considered the whole ARs, namely, sunspot groups with pores, faculae, and plages. These topics will be studied in greater detail, based on long-lived, recurrent sunspot groups and published in separate papers.
Acknowledgments
Thanks are due to the anonymous reviewer for her/his helpful advice. This research has received funding from National Research, Development and Innovation Office – NKFIH, 141895. The cycle strength data source is WDC-SILSO, Royal Observatory of Belgium, Brussels.
References
- Baranyi, T. 2015, MNRAS, 447, 1857 [NASA ADS] [CrossRef] [Google Scholar]
- Baranyi, T., Győri, L., & Ludmány, A. 2016, Sol. Phys., 291, 3081 [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1964, Sunspots [Google Scholar]
- Bumba, V. 1963, Bull. Astron. Inst. Czechoslovakia, 14, 91 [NASA ADS] [Google Scholar]
- Caligari, P., Moreno-Insertis, F., & Schussler, M. 1995, ApJ, 441, 886 [Google Scholar]
- Cheung, M. C. M., Rempel, M., Title, A. M., & Schüssler, M. 2010, ApJ, 720, 233 [Google Scholar]
- Fan, Y. 2009, Liv. Rev. Sol. Phys., 6, 4 [Google Scholar]
- Gafeira, R., Fonte, C. C., Pais, M. A., & Fernandes, J. 2014, Sol. Phys., 289, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, P. A., & Howard, R. 1986, ApJ, 303, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Győri, L., Ludmány, A., & Baranyi, T. 2017, MNRAS, 465, 1259 [Google Scholar]
- Hartshorn, A. J. 2012, Ph.D. Thesis, University College London, UK [Google Scholar]
- Javaraiah, J. 2011, Sol. Phys., 270, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G., & Stenflo, J. O. 2008, ApJ, 688, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Q., Zhang, L., Yan, X., et al. 2021, ApJ, 913, 147 [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Wheatland, M. S. 2015, ApJ, 800, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez Pillet, V., Moreno-Insertis, F., & Vazquez, M. 1993, A&A, 274, 521 [Google Scholar]
- McClintock, B. H., & Norton, A. A. 2016, ApJ, 818, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., & Vazquez, M. 1988, A&A, 205, 289 [NASA ADS] [Google Scholar]
- Muraközy, J. 2016, ApJ, 826, 145 [CrossRef] [Google Scholar]
- Muraközy, J. 2020, ApJ, 892, 107 [Google Scholar]
- Muraközy, J. 2021, ApJ, 908, 133 [Google Scholar]
- Muraközy, J. 2022, ApJ, 925, 87 [CrossRef] [Google Scholar]
- Muraközy, J., Baranyi, T., & Ludmány, A. 2014, Sol. Phys., 289, 563 [Google Scholar]
- Nagovitsyn, Y. A., Osipova, A. A., & Ivanov, V. G. 2024, Astron. Rep., 68, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A., Howe, R., Upton, L., & Usoskin, I. 2023, Space. Sci. Rev., 219, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovay, K., & van Driel-Gesztelyi, L. 1997, Sol. Phys., 176, 249 [Google Scholar]
- Pevtsov, A. A., Maleev, V. M., & Longcope, D. W. 2003, ApJ, 593, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2008, Solar and Stellar Magnetic Activity [Google Scholar]
- Schunker, H., Birch, A. C., Cameron, R. H., et al. 2019, A&A, 625, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheeley, N. R., Jr. 1966, ApJ, 144, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 2003, A&ARv., 11, 153 [Google Scholar]
- van Driel-Gesztelyi, L., & Green, L. M. 2015, Liv. Rev. Sol. Phys., 12, 1 [Google Scholar]
- Verma, M., Denker, C., Balthasar, H., et al. 2016, A&A, 596, A3 [Google Scholar]
- Vernova, E. S., Tyasto, M. I., Baranov, D. G., & Danilova, O. A. 2020, Sol. Phys., 295, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Švanda, M., Sobotka, M., Mravcová, L., & Výbošťoková, T. 2021, A&A, 647, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zharkova, V. V., & Zharkov, S. I. 2008, Adv. Space Res., 41, 881 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Total unsigned magnetic flux measured in Weber as a function of the area measured in millionths of solar hemisphere. The figure contains the data of all studied sunspot groups from SDD, each gray point marks a sunspot group. The linear fitted function is depicted with solid black line. Equation of the fitted linear function can be seen in the top-left corner. |
| In the text | |
 |
Fig. 2. Relationship of the area evolution phase and total unsigned flux evolution phase based on the SDD (top panel). Both of them are measured in percentage. Each gray point marks a sunspot group in one observation time. The linear fitted function is depicted with solid black line, its equation can be found in the upper left quadrant. Bottom panel: Umbral flux evolution phase as a function of time near the time of maximum flux measured in days for three sets of sunspot group sizes. The equations of the fitted regression lines and standard error values can be found in the bottom right quarter. The characters g and d mean the growth (negative values) and decay (positive values) phases of groups. The average growth and decay periods are calculated by using the equations of the fitted functions. |
| In the text | |
 |
Fig. 3. Spherical leading-following distance vs. FEP (measured on the bottom axis) plotted with black dots and AEP (measured on the top axis) depicted by empty triangles. The mean values of separation distance with their standard errors are averaged over 10% bins of the umbral FEP (AEP). The data reported in this figure come from the SDD. |
| In the text | |
 |
Fig. 4. Separation distance as a function of AEPU for three sets of sunspot groups considering their peak umbral area. The top panel concerns the SDD, the bottom panel concerns the DPD. The empty triangles mark the data calculated on the entire sample of the DPD (same as in Figure 3 for the SDD). The separation distances are averaged over 10% bins of the AEP, the error bars mark the standard error. |
| In the text | |
 |
Fig. 5. Daily latitudinal shift (top row) and longitudinal shift (bottom row) of the leading part (right column, plotted with dots) and following part (left column, depicted by circles) versus AEP. The shifts are averaged over each 10% bin of AEP, the error bars mean the standard error. Positive and negative values of latitudinal shifts mean poleward/equatorward, and that of the longitudinal shifts concern forward and backward motion of sunspot groups. |
| In the text | |
 |
Fig. 6. Separation distance versus cycle phase by using the SDD. The separation distances are averaged over 10% cycle phase bins and plotted to the center of each bin. The mean separation distance is calculated for the entire group (plotted by dots), their growth phase (triangles), maxima (asterisk), and decay (squares). The error bars mark the standard errors. |
| In the text | |
 |
Fig. 7. Hemispheric separation distances during SCs 20–24 (top panel). The separation distances are considered as their peak value and averaged over each solar cycle. Error bars represent the standard errors. Bottom panel: Maximum separation distances are averaged over solar cycles as a function of the cycle strengths. The latter is based on the yearly mean total sunspot number table created by WDC-SILSO, Royal Observatory of Belgium, Brussels. Error bars represent the standard errors, while the numbers mark the solar cycles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.