| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 20 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245635 | |
| Published online | 06 March 2024 | |
The influence of small bipolar magnetic regions on basic solar quantities
1
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, Göttingen, Germany
e-mail: hofer@mps.mpg.de
2
Institut für Astrophysik und Geophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, Göttingen, Germany
3
School of Space Research, Kyung Hee University, Yongin, Republic of Korea
Received:
7
December
2022
Accepted:
3
December
2023
Context. Understanding the evolution of the solar magnetic field is of great importance for heliosphere, dynamo, and irradiance studies, for example. While the contribution of the field in active regions (ARs) hosting sunspots to the Sun’s large-scale field has been extensively modelled, we still lack a realistic model of the contribution of smaller-scale magnetic regions such as ephemeral regions which do not contain any sunspots.
Aims. For this work, we studied the effect of small and large bipolar magnetic regions (BMRs) on the large-scale solar magnetic field.
Methods. The evolution of the total and open magnetic flux, the polar fields, and the toroidal flux loss since 1874 has been simulated with a surface flux transport model (SFTM) and the results were compared to analytical considerations and observational data. For this purpose, we constructed semi-synthetic BMR records using the international sunspot number as a proxy. We calculated the emergence rate of all BMRs from a single power-law size distribution, whose exponent varies with solar activity. The spatial distribution of the BMRs was calculated from statistical relationships derived from various solar observations. We included BMRs with a magnetic flux as low as 2 × 1020 Mx in our SFTM, corresponding to regions with lifetimes down to one day.
Results. We found a good agreement between the computed total magnetic flux and observations, even though we do not have a free parameter to adjust the simulated total flux to observations, as in earlier versions of the employed SFTM. The open flux, the polar fields, and the toroidal flux loss are also consistent with observations and independent reconstructions. In our model, small BMRs contribute about one-third of the total and open flux at activity maximum, while their contribution increases to roughly half at activity minimum. An even greater impact is found on the polar fields and the toroidal flux loss, for which the contribution of small BMRs is comparable to that of spot-containing ARs at all activity levels. Even so, smaller regions, not included in our simulations, do not seem to play a significant role due to their high tilt angle scatter. Our simulation results suggest that most of the statistical noise is caused by large ARs, while small BMRs have a stabilising effect on the magnetic flux evolution, especially for the polar field reversals.
Conclusions. We conclude that small BMRs (here, with magnetic fluxes between 2 × 1020 Mx and 3 × 1021 Mx) may also play an important role in the evolution of the solar magnetic field at large spatial scales. Their impact is largest at low solar activity, but it is also substantial during activity maxima, although the actual relative contributions by small and large regions depend on the steepness of their emergence rate distribution. The inclusion of small BMRs in SFTM simulations will allow the secular variability in solar irradiance to be better constrained and the generation of the poloidal field in the Babcock-Leighton dynamo to be better understood.
Key words: Sun: activity / Sun: evolution / Sun: heliosphere / Sun: magnetic fields / Sun: photosphere / solar-terrestrial relations
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
Understanding solar activity and variability is of great societal importance due to their potential to affect Earth, its climate, and life on it, as well as the heliosphere (Haigh 2007; Pulkkinen 2007; Gray et al. 2010; Temmer 2021). The driver of solar activity and variability is the magnetic field of the Sun, which is the product of the dynamo acting in its interior (e.g., Charbonneau 2020).
One of the proposed dynamo models is the Babcock–Leighton dynamo (Babcock 1961; Leighton 1964). In the Babcock–Leighton dynamo model, the toroidal magnetic field is generated from the poloidal field by rotational shear somewhere within the solar convection zone. This toroidal field then emerges at the solar surface in the form of tilted bipolar magnetic regions (BMRs). The BMRs are subjected to a combination of surface flows, most importantly the meridional circulation which transports the magnetic field on the surface to the poles, from where it is transported radially inwards and then towards the equator where rotational shear again converts it into toroidal fields emerging as BMRs. One prominent manifestation of the dynamo is the solar magnetic activity cycle (Hathaway 2015). Thus, emergence and evolution of BMRs, as well as the evolution of the global properties of the solar magnetic field are crucial for understanding the Babcock–Leighton mechanism, the solar cycle, and the dynamo action in general. This is also essential for long-term reconstructions of solar activity and irradiance (see, e.g. the reviews by Solanki et al. 2013; Usoskin 2017, and references therein).
The magnetic field on the solar surface appears in the form of a great variety of magnetic structures, which vary significantly both in size and the total magnetic flux content. The largest of these structures form active regions (ARs), BMRs which feature plage regions, pores, and sunspots (see e.g., van Driel-Gesztelyi & Green 2015). While sunspots have been observed and documented for centuries, smaller BMRs, without sunspots, are in fact much more frequent. Small BMRs keep emerging on the solar surface even when the Sun is comparatively quiet. BMRs with fluxes between roughly 3 × 1018 Mx and a few times 1020 Mx which do not form sunspots are called ephemeral regions (ERs; Harvey & Martin 1973; Harvey 1993; Hagenaar 2001; van Driel-Gesztelyi & Green 2015) due to their short lifetimes of typically just a few hours to one day. The emergence rate of ERs is several orders of magnitude higher than that of ARs so that, despite their short lifetimes and sizes, they are important for the total magnetic flux budget (Parnell et al. 2009; Thornton & Parnell 2011). It has also been shown that accounting for ERs is crucial for reconstructions of the secular variability of the solar total and open magnetic flux, as well as the irradiance (Solanki et al. 2000, 2002; Vieira & Solanki 2010; Krivova et al. 2007, 2010, 2021).
Solanki et al. (2002) were first to include the ERs into their comparatively simple model of the evolution of the solar open and total magnetic flux, which was then extended to also reconstruct the solar irradiance (Krivova et al. 2007, 2010; Vieira et al. 2011). In this original model, describing the evolution of the magnetic field using a set of ordinary differential equations, the emergence rate of BMRs on the solar surface was linearly linked to the sunspot number. The disadvantage of this assumption is that during grand minima of solar activity no magnetic flux is allowed to emerge, in contrast to the evidence coming from the data of radionuclide and magnetospheric phenomena (e.g., Beer et al. 1998; Fligge et al. 1999; Usoskin et al. 2001; Miyahara et al. 2004; Riley et al. 2015), as well as recent simulations (Saha et al. 2022).
Another approach to model the evolution of the Sun’s magnetic field is offered by the surface flux transport models (SFTMs; e.g., DeVore et al. 1985; Wang et al. 1989; Baumann et al. 2004). For example, Cameron et al. (2010) used an SFTM to simulate the evolution of the open magnetic flux, as well as the reversal times of the polar fields using the observed sunspot areas, latitudes, longitudes, and tilt angles as input. Jiang et al. (2011a,b) used the same model but with semi-synthetic sunspot records constructed using statistical properties of the observed sunspot records. The model was then extended by Dasi-Espuig et al. (2014, 2016) to also reconstruct the total solar irradiance back to 1700. However, using the SFTM, they could only simulate the evolution of the magnetic field in ARs, while the contribution of the ERs was then added from the simple model by Solanki et al. (2002), Vieira & Solanki (2010), and Krivova et al. (2010).
The inclusion of small ARs and ERs in SFTM simulations is challenging due to technical limitations, such as the spatial and temporal resolution and the sheer number of small regions. Among the few studies including ERs is Schrijver (2001), who modelled their magnetic flux by an ensemble of ER flux concentrations instead of tracking individual regions. Those ER flux concentrations were treated separately from ARs, with their own relationships describing the interaction between the flux concentrations when they encounter each other. Modelling the evolution of small BMRs individually remains challenging, however. Thus, there are still many unknowns surrounding the effects of ERs and small ARs on the evolution of the surface magnetic flux.
While ARs are produced by the global solar dynamo (Charbonneau 2020), internetwork features and maybe some of the smaller ERs are believed to be produced by a separate small-scale dynamo process (e.g., Borrero et al. 2017). Nevertheless, observations suggest that a substantial part of the ERs, especially the larger ones, is produced by the same global dynamo process as AR. For example, ERs are observed to follow a cyclic behaviour similar to ARs, although the ER cycle is more extended in time and the amplitude of their variability over a cycle is weaker than that of ARs (Harvey 1992, 1993; Hagenaar et al. 2003). Further, while ERs exhibit a much larger tilt angle scatter than ARs, they show a clear statistical tendency to follow Hale’s polarity law such as sunspot regions. In particular, 60% of ERs show a proper Hale orientation, which suggests that at least a part of the observed ERs must be linked to the global AR cycle (e.g., Harvey 1993; Hagenaar 2001). The fraction of ERs obeying Hale’s law increases for larger ERs, suggesting a smooth transition between large ERs and small ARs (e.g., Harvey 1993).
Combining high-resolution measurements of the emergence rate of small BMRs below ∼1018 Mx and the emergence rates of larger BMRs from previous studies with different methodologies, Thornton & Parnell (2011) found that the emergence rate of BMRs follows a single power-law distribution over nearly seven orders of magnitude in flux (1016–1023 Mx). It needs to be mentioned that combining different studies utilising different datasets and detection methods can lead to various cross-calibration issues. In particular, the number and the size (or the magnetic flux content) of BMRs detected in magnetograms heavily depend on the resolution of the data, the noise level, and the applied detection criteria. For example, the study by Zhou et al. (2013) reproduced the power-law exponent of the instantaneous magnetic flux in BMRs by Parnell et al. (2009; using the same detection method as Thornton & Parnell 2011), but their more sensitive detection algorithm measured about ten times more ERs. Further, detection algorithms tend to underestimate the smallest regions close to the resolution limit which can skew the observed distribution towards a flatter one. On the contrary, it is known that the magnetic flux in bigger sunspots measured in magnetograms is often underestimated (Liu et al. 2007), which would imply a flatter distribution for large ARs. All those uncertainties have led to somewhat contradictory results, with some studies finding a flatter distribution for large ARs (e.g., Wang & Sheeley 1989; Schrijver & Harvey 1994), and others suggesting a steepening towards larger regions instead (e.g., Muñoz-Jaramillo et al. 2015; Sakurai & Toriumi 2023). Unfortunately, the exact shape of the emergence rate distribution remains unclear. In this work, we use the distribution derived by Thornton & Parnell (2011), while we also discuss the effect of the slope of the distribution on the results.
Recently, Krivova et al. (2021) have included ERs into a simpler model using the disk-integrated emergence rate of all BMRs observed by Thornton & Parnell (2011). The inclusion of ERs greatly improved the reconstruction of the open and total magnetic flux during the grand minima around 1700. The next step is now to include such regions into a SFTM and therefore also take the spatial distribution of small BMRs on the solar surface into account.
The aim of this work is to study the effect of small BMRs (with fluxes as low as 2 × 1020 Mx) on various solar parameters describing the magnetic field on the Sun. For this, we simulated the solar surface magnetic field with a surface flux transport model, where the emergence of BMRs is described by a power-law size distribution as observed by Thornton & Parnell (2011). The simulation results are compared to independent observations or reconstructions of these quantities. We also discuss our results using analytical approximations and investigate how changing the slope of the emergence rate distribution would affect the simulation results.
The structure of the paper is as follows. In Sect. 2 we describe the various observational datasets used in this study. We then explain how we derived semi-synthetic data records from the relationships presented in Sect. 3. In Sect. 4 we describe the SFTM. The simulation results are presented in Sect. 5, and the analytical approximations are discussed in Sect. 6. Finally, we summarise and discuss our results and provide an outlook for future applications in Sect. 7.
2. Data
The SFTM, detailed in Sect. 4.1, describes the evolution and transport of the magnetic field emerging on the Sun. The emergence rates and patterns of the field need to be provided as input to the model. To construct an input record (as described in Sect. 3), we use the following datasets:
– the international sunspot number version 2.0 (ISN2.0), see Clette & Lefèvre (2016) and references therein;
– the ‘official’ dates of solar cycle minima and maxima as listed by the Sunspot Index and Long-term Solar Observations (SILSO) webpage1.
For comparison, we also consider the sunspot group records used in previous studies with the SFTM employed here (Baumann et al. 2006; Cameron et al. 2010; Jiang et al. 2011b; Jiang 2020), including:
– the combined Royal Greenwich Observatory (RGO) and USAF/NOAA SOON record2 featuring observed sunspot group areas and locations since 1874 (Hathaway 2015). We note that a newer and more consistent composite sunspot group catalogue3 has been developed more recently by Mandal et al. (2020). Since we use the sunspot group data only to compare with earlier results, we chose to employ the RGO/SOON record for consistency, as this is the same version as used in the above mentioned SFTM studies;
– the tilt angles for the RGO/SOON sunspot groups derived by Jiang et al. (2011a) from Mount Wilson and Kodaikanal images (Howard et al. 1984; Howard 1991; Sivaraman et al. 1993).
To evaluate the simulation results, we compare the model output to the following datasets:
– the observed total magnetic flux since 1967 from Wilcox Solar Observatory (WSO), National Solar Observatory at Kitt Peak (NSO KP), and Mount Wilson Observatory (MWO); see Arge et al. (2002) and Wenzler et al. (2006);
– the composite of the observed total magnetic flux since 1974 by Yeo et al. (2014, extended to 2020), derived from the Kitt Peak Vacuum Telescope (KPVT, Livingston et al. 1976; Jones & Duvall 1992), the Michelson Doppler Imager on board of Solar and Heliospheric Observatory (SoHO/MDI, Scherrer et al. 1995) and the Helioseismic and Magnetic Imager onboard the Solar Dynamics Observatory (SDO/HMI, Schou et al. 2012). The composite is on the HMI absolute scale, with the noise level of MDI being applied to all measurements. For comparison with the MWO data, we bring the composite to the MWO scale through a multiplicative factor, as suggested by Riley et al. (2014). The best agreement with the WSO–NSO–MWO level is found with the factor 3.7, which is close to the factor of roughly 4 found by Riley et al. (2014);
– the open magnetic flux reconstruction from the geomagnetic aa-index by Lockwood et al. (2022) since 1845, which is an update of the earlier versions (Lockwood et al. 1999, 2009, 2014);
– the in situ open magnetic flux measurements since 1998 from Owens et al. (2017);
– the line-of-sight polar field measurements from WSO4 since 1976 (Scherrer et al. 1977; Hoeksema et al. 1983).
3. Emergence of magnetic regions
3.1. Emergence rate
Combining high-resolution Hinode observations with earlier studies of magnetic field emergence on the solar surface, Thornton & Parnell (2011) found that the emergence rate of bipolar magnetic features on the Sun over a broad flux range is well represented by a power-law function:
where ϕ0 = 1016 Mx, n0 = 3.14 × 10−14 cm−2 day−1, m = −2.69, ϕ is the magnetic flux of the region and ϕ1 and ϕ2 are the upper and lower integration limits. Based on studies by Harvey (1993) (H93) and Harvey & Zwaan (1993), Krivova et al. (2021) have argued that the slope m of the distribution varies with solar activity. They described this change by a function of the sunspot number, SN, as follows:
where SN1 = 217, SN2 = 17, m1 = −2.5954, m2 = −2.7846 and p = 0.059 for the international sunspot number ISN2.0 used here. Note that Krivova et al. (2021) used the notation α instead of p.
In this work, we consider several populations of BMRs, depending on their sizes (or magnetic flux content), see also Krivova et al. (2021) and their Fig. 1. The boundaries between different BMR populations are rather approximate and the exact definitions can vary from study to study. van Driel-Gesztelyi & Green (2015) define large ARs containing sunspots as regions with total flux higher than 5 × 1021 Mx, small ARs forming only pores as regions with fluxes in the range 1020 − 5 × 1021 Mx, and ephemeral regions (ERs) as regions with fluxes 3 × 1018 − 1020 Mx. H93 classify the regions based primarily on their area, with the transition from ERs to ARs lying between 2.5 and 3.5 square degrees. The latter corresponds to a magnetic flux of roughly ≥4 × 1020 Mx. The smallest ERs considered by H93 correspond to about 3 × 1018 Mx.
Following H93 and Krivova et al. (2021), we also define ERs as regions with fluxes between 3 × 1018 Mx and 4 × 1020 Mx. BMRs with fluxes above 3 × 1021 Mx are defined here as large ARs – for large magnetic regions (LMRs hereafter). They are big enough to form spots. With this limit, the number of emerging LMRs is consistent with the number of sunspot groups in the RGO/SOON record. This allows a direct comparison of the simulation results based on the synthetic sunspot records (see Sect. 3) with those using direct observations. Since regions with magnetic flux close to the upper limit are extremely rare, if there are any at all, the exact value is not important, and we set it to 1023 Mx. This also corresponds to the upper limit of BMRs considered by Thornton & Parnell (2011). Typically, only one or two ARs with fluxes close to 1023 Mx emerge during a solar cycle. For example, the highest ever measured magnetic flux, 2 × 1023 Mx, was for the entire AR 12192 in 2014 (cycle 24), with the largest spot in it having the area of about 4300 msh (millionth of solar hemisphere) (Sun et al. 2015). The largest ever observed sunspot region in 1947 (Nicholson 1948; Taylor 1989) had an area of 5400 − 6000 msh, although no magnetic field measurements are available for it. To study the effect of smaller BMRs on the various magnetic field observables, we include in the simulations all regions with lifetimes of ≥1 day, which is currently the temporal resolution of the SFTM; see Sect. 4.1. The corresponding lower flux limit of 2 × 1020 Mx is lower than the AR limit in H93 and Krivova et al. (2021). By including the regions as small as 2 × 1020 Mx in this work, we thus consider all BMRs down to the biggest of the ERs. We refer to the regions with fluxes above this limit as all modelled regions (AMRs). BMRs with fluxes between 2 × 1020 Mx and 3 × 1021 Mx, that is all regions not covered by earlier SFTM simulations, are referred to as small magnetic regions (SMRs). It is important to note that SMRs still include mainly small ARs with either small spots or pores, while only the smallest regions of this population (between 2 and 4 × 1020 Mx) would qualify as ERs.
Even smaller (that is with fluxes below 3 × 1018 Mx) regions emerge on the solar surface, however a significant portion of their magnetic flux is believed to come from a separate small-scale dynamo and is unlikely to contribute to the Sun’s polar fields, open flux or toroidal flux loss, but it will affect the total amount of flux on the solar surface. We call the small ERs (below 2 × 1020 Mx) and even smaller internetwork fields (below 3 × 1018 Mx) not included in the model SSEs (Small-Scale Emergences). The observations of small ERs by H93, however, are still taken into account when constructing the synthetic input record as described in Sect. 3. Following Parnell et al. (2009), Thornton & Parnell (2011), and Krivova et al. (2021), the lower flux limit of SSEs is set to 1016 Mx. The definitions of the BMR populations and the abbreviation we use for them are summarised in Table 1.
Different BMR populations considered in this work.
3.2. Emergence patterns
The distribution of the newly emerging regions on the surface of the Sun generally depends on the size of the regions, as well as on the phase and the strength of the solar cycle (Harvey 1993; Jiang et al. 2014b; Hathaway 2015; van Driel-Gesztelyi & Green 2015). We build our input record of the spatial distribution of the emerging BMRs as a function of latitude and solar activity on the statistical studies by Jiang et al. (2011a, J11) and Jiang (2020, J20). J11 used the RGO/SOON sunspot group data, the Mount Wilson and Kodaikanal sunspot tilt angle records and the GSN to study the mean emergence latitude and its scatter, as well as the mean tilt angles of the regions between 1874 and 1976 (cycles 12–20). J20 have updated the relationships by using ISN2.0 over cycles 12–21. For our purpose, we partly revise and extend their relationships as described below.
3.2.1. Emergence latitudes
Using the records of sunspot observations, J11 and J20 divided each solar cycle into 30 equal phase bins between adjacent solar minima and calculated the mean emergence latitude for all cycles and phase bins. For the statistical analysis, they excluded the first and the last 3 bins to avoid distortion of the results due to an overlap between regions from two adjacent cycles emerging at high and low latitudes. They then derived a relationship between cycle phase “i” of cycle “n” and the mean latitude through a second order polynomial fit:
where 0 < i < 1 is the fraction of the solar cycle duration between adjacent minima, λn = 12.03 + 0.0015 Smax is the average latitude for cycle n for ISN2.0 (J20), ⟨λn⟩12 − 20 = 14.6° is the average over all cycles, and Smax is the maximum of the 13-month running average of the ISN2.0. The standard deviation of the latitude distribution is calculated as:
where 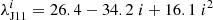 . Due to the removal of the bins at the beginning and the end of the cycle for the fits, the relationships by J11 and J20 do not account for the cycle overlap and thus potentially different parameters for the declining and rising phases of cycles (see Sect. 3.3). For example, according to Eq. (3), the mean latitude of the declining cycle would increase again after the cycle minimum, which is in contrast to observations. We consider each cycle individually, accounting for their overlap (see Sect. 3.3). Hence we replace the relationship given by Eq. (3) with an exponential fit to it, which steadily decreases towards zero after the cycle minimum:
. Due to the removal of the bins at the beginning and the end of the cycle for the fits, the relationships by J11 and J20 do not account for the cycle overlap and thus potentially different parameters for the declining and rising phases of cycles (see Sect. 3.3). For example, according to Eq. (3), the mean latitude of the declining cycle would increase again after the cycle minimum, which is in contrast to observations. We consider each cycle individually, accounting for their overlap (see Sect. 3.3). Hence we replace the relationship given by Eq. (3) with an exponential fit to it, which steadily decreases towards zero after the cycle minimum:
The mean latitude over one (extended) cycle described by Eq. (5) is shown in Fig. 1a, together with the original relationship from J11 and J20 for comparison.
 |
Fig. 1. Parameters describing the spatial distribution of emerging BMRs in our model (red) and as originally derived by Jiang et al. (2011a) (black, only in panels a and b). (a) Mean latitude. (b) Latitude scatter of spot-containing LMRs as a function of the solar cycle phase. (c) Correction factor to the latitude scatter depending on the magnetic flux content of a BMR. (d) Tilt angle scatter as a function of the total magnetic flux enclosed by a BMR. The vertical dashed lines in panels a and b mark the formal beginning and the end of the solar cycle (that is cycle minima). The horizontal bars in panels c and d mark the magnetic flux intervals from the fit, with their y-value being the observational mean value within the flux range (see also Table 2). |
The latitude scatter of large, spot-containing ARs from J11 and J20 (Eq. (4)) is shown in Fig. 1b by the black line. While decreasing after cycle maximum, it shows an opposite behaviour at the beginning of a cycle. For small BMRs during a cycle onset at high latitudes this would lead to no scatter. Instead, to extend the relationship to earlier cycle phases, we rely on the finding by Solanki et al. (2008) that the latitude scatter of sunspots is proportional to the mean latitude:
This roughly follows the latitude scatter of J11 and J20 over the declining phase of the cycle, but keeps the scatter steadily decreasing from the cycle’s dawn to its end; see the red curve in Fig. 1b.
The studies by J11, J20 and Solanki et al. (2008) have only considered large ARs with sunspots. However the latitude scatter also depends on the size of the regions. Thus, we introduce a multiplicative function flat that extrapolates the latitude scatter from J11 (Eq. (6)) to smaller BMRs. It has been observed by Harvey & Martin (1973), Harvey (1993), and Hagenaar et al. (2003) that the latitude scatter of ERs is significantly larger than that of ARs. In particular, H93 found that for ERs the standard deviation of their latitude distribution was roughly 20° (as estimated from Fig. 5 in her Chap. 5), while it was around 5 − 10° for ARs. The latter is roughly consistent with the latitude distribution described by Eq. (6) above. We took the value of ⟨σlat, LMR⟩ = 6.5°, which is the mean returned by Eq. (6) over the solar cycle, as the reference for LMRs, compared to the 20° for ERs. We then derived a relationship for the cycle-mean latitude scatter as a function of BMR size. To be consistent with observations, the scatter should change little for LMRs, while increasing faster for smaller regions. We assumed a log-square function, which fits this purpose well. The relationship was constrained such that the mean latitude scatter of ERs and LMRs was preserved to agree with H93’s observations. The function was then normalised by dividing by ⟨σlat, LMR⟩, which gives a factor of ∼1 for LMRs, and the best-fit was:
where ϕ* is the magnetic flux of the region in units of [1018 Mx]. The normalised size-dependent latitude scatter from Eq. (7) is shown in Fig. 1c. By multiplying the cycle phase-dependent latitude scatter from Eq. (6) with the normalised size-dependent latitude scatter from Eq. (7), we obtained the latitude scatter for all regions and cycle phases:
3.2.2. Tilt angles
Following J11 and J20, we assume that the mean tilt angle (αm) of a BMR, that is, the angle between the line connecting the two polarities and the equator, is proportional to the square root of the latitude λ:
The proportionality factor Tn = 1.72 − 0.0021Smax (for ISN2.0; J20) decreases for stronger cycles, consistent with the study by Dasi-Espuig et al. (2010), who found that stronger solar cycles tend to have smaller average tilt angles. We note that the tilt angles employed in this study are based on white-light observations by Kodaikanal and Mt. Wilson observatories, which tend to be systematically lower than the tilt angles derived from magnetograms (see e.g., Baranyi 2015; Wang et al. 2015). Part of the discrepancy comes from the fact that white-light observations lack information about the magnetic polarity and therefore contain small unipolar spots that skew the distribution. Filtering out such unipolar groups Jiao et al. (2021) found that the mean tilt angles increased by about 18% compared to those found by J20, in agreement with measurements from magnetograms. Furthermore, in contrast to white-light images, magnetograms also contain plage regions, which typically have higher tilt angles than sunspot groups (Howard 1996). At the same time, it is also known that tilt angles increase over time after a region has fully emerged at the solar surface (Schunker et al. 2020). Thus, since studies that derived the tilt angles did not distinguish between new and old regions and even considered same groups multiple times (Howard 1991; Li & Ulrich 2012), this would bias the distribution towards longer-living groups and thus towards higher tilt angles.
In our study, BMRs are injected into the SFTM at the stage of maximum development (see Sect. 4.1) and would therefore have on average smaller mean tilt angles than derived from observations. Yeates (2020) compared the output of a SFTM fed with ARs actually observed during cycle 24 to a run where these regions were approximated by BMRs with the same total magnetic flux and tilt angles calculated using the flux-weighted centroids of each magnetic polarity. They found that the latter overestimated the axial dipole at the end of the cycle by 24%. Reducing the tilt angles by ∼20% yielded the correct final dipole moment, although in this case the reversal time was slightly delayed. Due to the uncertainty in the true tilt angles and some controversy of the related results (see also van Driel-Gesztelyi & Green 2015), we have also run our simulations with the mean tilt angles increased by +20%, that makes them comparable to tilts derived from magnetogram observations. We saw that this worsened the overall agreement of the simulated open magnetic flux with observations and independent reconstructions and led to a smaller cycle amplitude of the open flux (cf., Cameron et al. 2010). Therefore, we choose to employ the tilt angles as given by J20 for our main analysis (see Sect. 5), while we also show the results obtained with the increased tilt angles in Appendix A for completeness.
The tilt angle scatter was not analysed by J11 and J20. As first shown by H93, the tilt angle scatter strongly depends on the region size, being small for large ARs and increasing for smaller BMRs. The tilt angles of smallest ERs are rather random. A number of more recent studies analysed the distribution of AR tilt angles, also using modern magnetograms (e.g., Tlatov et al. 2010; Stenflo & Kosovichev 2012; Jiang et al. 2014a; Wang et al. 2015; Jha et al. 2020; Schunker et al. 2020). The tilt angle distribution of the largest ARs generally shows a standard deviation of 10 − 15°, which increases to 20 − 30° for small ARs. In particular, Schunker et al. (2020) studied the standard deviation of the tilt angles of a sample of 153 emerging ARs with a median magnetic flux of 4.6 × 1021 Mx. Four days after emergence, they found a standard deviation of 30° for the tilt angles of all regions below the median value, 25° for the entire sample and 18° for all regions above the median. Although the magnetic flux of the smallest regions is not specified in Schunker et al. (2020), from Eq. (1) we find that the median value 4.6 × 1021 Mx would roughly correspond to the magnetic flux range from 1021 Mx to 1023 Mx. For ERs, we rely on the observations of H93 and Hagenaar (2001), who found that around 95% of ARs obeyed Hale’s polarity law while only about 60% of ERs did so. We use these numbers as a guidance for our model and assumed that the tilt scatter follows a Gaussian distribution with a variable standard deviation dependent on the region size. In this model, a BMR is considered to have an anti-Hale orientation if the tilt angle deviates by more than ±90° from the mean. Using the results from H93 and Hagenaar (2001) we estimate a standard deviation of 107° for the tilt angles of ERs and 46° for ARs. Together with the constraints from Schunker et al. (2020), this gives us a total of five magnetic flux ranges with the corresponding estimates of the standard deviation, summarised in Table 2. Assuming a log-square relationship between the region size and the tilt angle scatter, we find the following function to fit these constraints:
Mean standard deviations of the tilt angles of the emerging BMRs in our model.
Table 2 lists the values of the tilt scatter in the five flux ranges derived from observations and returned by the fit, and Fig. 1d shows the tilt scatter for the entire flux range.
3.2.3. Nesting
Sunspots show a tendency to emerge within the so-called activity nests, that is new magnetic regions tend to emerge in the vicinity of the existing regions more often than at random locations (see, e.g., Bumba & Howard 1965; Gaizauskas et al. 1983; Castenmiller et al. 1986; Bai 1988). The longitude distribution of BMRs is particularly important for the reconstruction of the open magnetic flux as it has been shown to be dominated by low-order multipoles which are strongly dependent on the randomness of the longitude distribution (Cameron et al. 2010). It has further been observed (Berdyugina & Usoskin 2003; Zhang et al. 2007) that activity nests preferably form in two persistent longitudes in opposite hemispheres separated by 180°. J11 argued that nesting can be accounted for by a linear combination of the magnetic field, Bcom, of two separate simulation runs: one with purely random longitudes, Bran, and one with all regions being ordered at 90° and 270° longitudes in the northern and southern hemisphere, respectively, Bord: Bcom = (1 − c)Bran + cBord. To describe the degree of nesting required to reproduce the open magnetic flux from Cameron et al. (2010), they introduced the parameter c, which was found to be c = 0.15. Since we reconstruct the open magnetic flux from the magnetograms with the same model as J11 (see Sect. 5.2) we adopt their approach.
3.3. Cycle overlap
It is well known that the magnetic activity of a given solar cycle n starts at high latitudes (∼50°) several years before the end of the previous cycle n − 1, apparently soon after the polar field reversal (see, e.g., Legrand & Simon 1981; Harvey 1993; Wilson et al. 1988; Tlatov et al. 2010; Hathaway 2015, and references therein). The first regions of a new cycle are typically small. The probably most complete study of BMR emergence available is that by H93, who analysed the emergence of regions as a function of their sizes, latitude and cycle phase in a systematic way. By analysing cycles 14–22, H93 noticed that the emergence onset of ERs started shortly after the polar field reversal, ∼0.5 − 1.5 years after the maximum of the activity cycle. It is worth noting, however, that due to limited spatial and temporal resolution of observations, small BMRs at high latitudes could easily escape notice. Thus, smaller regions might start emerging even earlier, possibly right after the polar field reversal.
The first (small) ARs are observed 2–4 years before the solar minimum or roughly 2 years after the polar field reversal, while larger ARs with sunspots emerge another 0.5–1.5 years later (see also the review by Hathaway 2015, and references therein). BMRs associated with cycle n also continue emerging for roughly two years after the “formal” beginning of the next cycle n + 1 (that is the minimum between cycles n and n + 1) close to the equator. This overlap, between what have been called extended activity cycles (Wilson et al. 1988), has important implications for the evolution of the solar magnetic flux. For example, it has been shown that such an overlap leads to a secular variability in the solar open and total magnetic flux (Solanki et al. 2000, 2002), which also has implications for reconstructions of past irradiance variations (Krivova et al. 2007, 2010; Wu et al. 2018).
To take the solar cycle overlap into account, we need to split the emergent BMRs between the subsequent cycles, n and n + 1. The simplest way of doing this would be to take a progressively large fraction of all emerging regions (see Eq. (1)) and place them at higher latitudes. However, it is important to remember that the size (or magnetic flux) distributions of the emerging regions belonging to the ongoing cycle n and the following, just starting, cycle n + 1 differ. At the onset of a new cycle (here n + 1), there are only few small regions emerging at high latitudes. At the same time, the ongoing cycle n is still close to its activity maximum and a lot of flux emerges in form of large ARs containing sunspots (the exponent m of the size distribution given by Eqs. (1) and (2) is higher at higher activity leading to a shallower distribution, see also Fig. 1 of Krivova et al. 2021). If we were to attribute a random sample of regions to the new cycle, we would greatly overestimate the amount of large, spot-containing, ARs at high latitudes. Therefore, we need to account for different slopes of the power law in Eq. (1) for the two cycles, such that the emergence rate for the new cycle matches the observed size distribution at low solar activity. To do this, we took observations by H93 as well as RGO/SOON sunspot group data as guidance and proceeded as described below, see also the illustration in Fig. 2.
 |
Fig. 2. (a) Power-law exponent calculated from the total SN (black), and from its portion belonging to the following cycle over the overlap period (the exponent fit in red and the linear transition in blue, see text for details). Only the solid lines were used for the calculation, and the transition between models is at solar minimum (dotted vertical line). (b) and (c) Exponential fit of the power-law exponent of cycles 21 and 22 in the overlap period with cycles 20 and 21, respectively. The “×” symbols are the estimated exponents from Table 3, based on the observations by Harvey (1993) and our analysis of the RGO/SOON record. The error-bars mark the uncertainty ranges in x (time) and y (exponent) directions, see text and Table 3 for details. The horizontal line is the power-law exponent m = −3.94 which corresponds to a SN of zero. |
As suggested by observations, we assumed that cycle n − 1 ends 2 years after the minimum between cycles n − 1 and n (in Fig. 2, activity minima are marked by vertical dotted lines). From this instant until the maximum of cycle n and the polar field reversal (shaded area in Fig. 2), only BMRs of cycle n emerge on the Sun. During this period, the exponent mn in Eq. (1) is determined directly from the SN as given by Eq. (2), see also Figs. 1 and 2 in Krivova et al. (2021). Shortly after the field reversal, cycle n + 1 starts. The exponent mn + 1 is infinitely low at this time but starts growing progressively until two years after the minimum between cycles n and n + 1, that is until the end of the extended cycle n (in Fig. 2, this period of time is left unshaded). From then until the maximum of cycle n + 1 the exponent mn + 1 is again defined by the instantaneous SN from Eq. (2). Thus, we need to describe the change of the exponent mn + 1 between the maximum and the end of cycle n (that is within the unshaded area). Thereby, we note that both the emergence onset and the pace of the emergence rate rise are observed to vary from cycle to cycle. We use the following observational constraints.
Firstly, at the minimum between cycles n and n + 1 we split the observed SN equally between the two cycles. Secondly, by analysing emergence latitudes and times of sunspot groups in the RGO/SOON record (which correspond to our LMRs) over cycles 12–24, we found that first LMRs of a new cycle n + 1 emerged on average about 1.5 years before its “formal” start at solar minimum tmin, n + 1, in good agreement with H93 and Hathaway (2015). The most extreme cases were −3.3 (cycle 21) and −0.3 years (cycle 19). Within one year before a minimum on average nine regions emerged, which we consider to roughly correspond to an emergence rate of ∼1/month or 12/year. The emergence rate drops to roughly 2/year and 0.5/year in the time intervals between 1 and 2 and 2 − 3 years before the minimum, respectively. This gives us “allowed” ranges for the possible time of emergence onset and for the emergence rate itself.
Thirdly, some BMRs of the new cycle, n + 1, emerge even earlier, that is more than 2–3 years before the minimum (e.g., H93). Normally, however, these are smaller regions, corresponding to our SMRs. To put constraints on the emergence of such regions prior to activity minimum, we relied on observations by H93, in particular her summary of the properties of 978 ARs from cycle 21 (also partly including regions from cycles 20 and 22, see Chap. 4 in H93), as well as her analysis of cycles 14–22 based on observations from various sources (her Chapter 11, see also Harvey 1992). Using these data, we estimated the emergence rate of SMRs to be about 1/year to 1/month roughly between 4 and 2 years prior to the minimum.
Finally, observations suggest that ERs start emerging at high latitudes shortly after the polar field reversal (Wilson et al. 1988; Harvey 1993; Tlatov et al. 2010; McIntosh et al. 2014). Being extremely difficult to observe, the emergence rate of ERs at the cycle onset is highly uncertain. Nevertheless, it is clear that the period shortly after the cycle maximum and field reversal, is dominated by regions from the ongoing cycle, and thus the fraction of BMRs of the new cycle is negligible. We set a rather arbitrary limit of one ER for the first year after the maximum. We note though that, being extremely low the exact value of the emergence rate of new ERs at this time has no effect on our results.
Table 3 summarises observational constraints on emergence rates of different BMRs during various phases of the cycle used by us to split the emergence rate of BMRs between two overlapping cycles, n and n + 1, as well as the derived values of the exponent mn + 1 during the respective phases of the activity cycle. To obtain the power-law exponent of the developing cycle throughout the overlap period, we fitted an exponential function to these points. Since estimates derived from observations are rather uncertain, we gave a higher weight to the last two points (that is the equal contribution from the two cycles at activity minimum and no “old” regions two years after the minimum). This fit was performed for each cycle separately. As an example, panels b and c of Fig. 2 show the fit for cycles 21 and 22.
Observational constraints on the emergence rate and the corresponding exponent m for BMRs of a newly starting cycle for different size ranges at different cycle phases.
The power-law exponent from the total instantaneous SN (mtot, black line), as well as the exponent fit of the new cycle n + 1 (mexp, n + 1, red line) for cycles 21 and 22 are shown in Fig. 2a. Although the exponent fit follows the trend of the new cycle n + 1 nicely, the exponent fit after minimum (red dashed) is occasionally higher than mtot. To account for the fact that the emergence rate for the new cycle n + 1 cannot be higher than the total emergence rate, we implemented a simple transition (blue line) from mexp, n + 1 at activity minimum to mtot at the end of cycle n. For this, we calculated the ratio between mexp, n + 1 and the 13-months mean of mtot at activity minimum n + 1 and progressively linearly reduced that ratio to unity, two year after the minimum. The power-law exponent of the new cycle n + 1 after minimum was then obtained by multiplying mtot with this factor. Just like the exponent fit, this linear transition was calculated separately for each cycle. The emergence of the new cycle n + 1 is then given by the exponent fit (solid red) before minimum and the linearly weighted transition (solid blue) after the minimum. To ensure that the observed total emergence rate of BMRs given by Eq. (1) is preserved at any given time we calculated the emergence rate for the ongoing cycle n during the overlap period as the difference between the total emergence and the emergence of the new cycle.
3.4. Final synthetic input records
We used four different types of records as input to the simulations, the observation-based RGO/SOON record and statistically generated AMR, LMR and SMR records (see Table 1). The RGO/SOON sunspot group record was used to compare the simulation results with those from Cameron et al. (2010). This was done as a test due to the modifications we applied to their SFTM, as described in Sect. 4.1. To obtain the AMR, LMR and SMR records, we first generated an input record for AMR (all modelled regions) from the ISN2.0 and the relationships derived in Sect. 3.2. The SMR and LMR records were then obtained from the AMR record by splitting and keeping only regions smaller or larger than 3 × 1021 Mx, respectively. For the synthetic input records (AMR, LMR and SMR), we generated 100 statistically independent realisations to allow an error estimate, see Sect. 4.4. To visualise the input records, Fig. 3 shows a butterfly diagram for one realisation. Colours indicate the monthly magnetic flux emergence rate within each 2° latitude bin; see figure caption for details.
 |
Fig. 3. Butterfly diagram for one realisation of the synthetic BMR input record. Different colours encode magnetic flux emerging in BMRs within one-month periods over 2° latitude bins. Blue corresponds to < 1 × 1021 Mx magnetic flux emerged in BMRs, green to 1 − 10 × 1021 Mx, black to 1 − 3 × 1022 Mx, red to 3 − 6 × 1022 Mx and yellow to > 6 × 1022 Mx. The vertical dashed lines mark cycle minima. |
4. Model
4.1. Surface flux transport model
We simulated the evolution of the large-scale radial magnetic field on the solar surface with a SFTM (see, e.g., DeVore et al. 1984, 1985; Wang et al. 1989). An SFTM describes the evolution of the radial magnetic field Br(θ, ϕ, t) on the solar surface with time, t, as a function of the heliocentric latitude θ and longitude ϕ. The flux emerging at the surface in the form of BMRs is represented by the source term S(θ, ϕ, t). Upon emergence, the flux is subject to the action of the differential rotation Ω(θ), the poleward meridional flow v(θ) (Babcock 1961) and the turbulent surface diffusivity ηh. The surface diffusivity is a result of convective plasma flows near the solar surface, in particular the supergranulation (Leighton 1964).
The original version of the SFTM used in this study was developed by Baumann et al. (2004). The evolution of the radial component of the magnetic induction is described as:
The additional decay term Dr(ηr) describes the radial decay of magnetic flux. It accounts for the 3D decay modes that cannot be captured by the 2D model and was first introduced by Baumann et al. (2006) to avoid a secular drift of the polar fields and obtain regular field reversals. We used the differential rotation profile introduced by Snodgrass (1983):
The meridional flow profile was taken from van Ballegooijen et al. (1998):
The model parameters were taken to be the same as in Cameron et al. (2010) and Jiang et al. (2011b), with ηh = 250 km2 s−1 and v0 = 11 m s−1. Following Jiang et al. (2011b), we also used the value of ηr = 25 km2 s−1 for the weak radial diffusion.
Following van Ballegooijen et al. (1998), emerging BMRs were represented by two Gaussian-like polarity patches with angular separation Δβ:
where Bamp is the initial amplitude of the magnetic flux density of the polarity patches, β±(θ, ϕ) are the heliocentric angles of the positive and negative polarity centres (θ±, ϕ±) and δinit = 0.4Δβ is the initial width of the polarity patches. This is different from the model by Baumann et al. (2004) and the subsequent versions by Cameron et al. (2010) and Jiang et al. (2011b), who injected the BMRs at a later stage of their development, when the polarity patches have diffused to the width of δ0 = 4° and the initial amplitude has been reduced by the factor (δinit/δ0)2. For small BMRs, this means that they were injected into the SFTM after several e-folding lifetimes and their contribution was essentially missed. This was accounted for by the (time-independent) free parameter Bmax, which was adjusted by comparing the computed total magnetic flux with observations. Having the initial shape described by Eq. (14) allows a more realistic description of small ERs, where the entire decay period of each BMR regardless of its size, starting from the time of its maximum development is included in the simulations.
We fixed the amplitude factor Bamp by comparing the decay rate of BMRs in the SFTM with their e-folding lifetimes derived from observations. Following Krivova et al. (2021), we estimated the lifetimes by dividing the instantaneous magnetic flux present in BMRs on the solar surface as observed by Parnell et al. (2009) by the BMR flux emergence rate derived by Thornton & Parnell (2011). The best agreement between the decay rate in SFTM and the estimated observed lifetimes was found for the value Bamp = 1000 G, with the magnetic flux content in BMRs of different sizes after one lifetime being within ±20% of the expected value.
The initial width of the polarity patches in Eq. (14) is linearly related to the angular separation between them. Hence, we can obtain the relationship between Δβ and the initial flux of the BMR ϕBMR (which is the sum of the unsigned fluxes from both polarity patches) directly, through numerical integration:
The smallest BMRs are initially too narrow to be resolved by the SFTM, which has a spatial resolution limit of 4°. The most straightforward approach would be to simply increase the spatial resolution. However, this is computationally very costly, as this is tied to a spherical harmonics decomposition needed to accurately calculate the effects of the radial diffusion and the meridional flow. Thus the total computing time increases exponentially with the highest order of the spherical harmonics. Fortunately, small BMRs are very compact during the initial stage of the emergence process and the effects of the meridional flow and the differential rotation are small in comparison to the turbulent diffusion which is faster for smaller regions. Thus, assuming that the early development of small regions is dominated by the turbulent diffusion allows us to separate such regions from the primary magnetogram (and the spherical harmonics decomposition) and account for the effect of turbulent diffusion alone in a separate secondary magnetogram (without spherical harmonics), until a region has diffused to a width that can be resolved by the SFTM, whereupon it is added to the primary magnetogram. The secondary magnetogram covers the entire surface and has the same resolution and time step as the primary magnetogram (see Sect. 4.4). The evolution of the region due to diffusion is calculated analytically and the rotation speed of the region is calculated only at the central latitude. Once the regions are added to the main magnetogram, their shape and treatment are identical to the SFTM versions by Baumann et al. (2004), Cameron et al. (2010), and Jiang et al. (2011b), except that they first appear in the main magnetogram with an up to one Carrington rotation delay (the time it would take for a point source to diffuse to a width of 4° in our model). At each time step, the solar quantities (total flux, open flux, polar fields, toroidal flux loss) are derived from the sum of the primary and the secondary magnetogram. In this way, the magnetic flux contributed by small BMRs is directly included into the simulation without the need for the free parameter Bmax to empirically adjust the magnetic flux amplitude of the BMRs to observations as done in previous versions of the SFTM. The overall approach is thus self-consistent, as we take the size distribution and lifetimes of BMRs in agreement with observations and calculate the total magnetic flux directly without an empirical adjustment.
4.2. Open flux calculation/CSSS
The SFTM only calculates the magnetic field on the solar surface. To extrapolate it into the heliosphere and calculate the open magnetic flux, we employ a current sheet source surface model (CSSS) (Zhao & Hoeksema 1995a,b). This model has earlier been shown to successfully reproduce the Ulysses open flux observations (Schüssler & Baumann 2006). The CSSS model has three parameters, a describing the thickness of the current sheet in the lower corona, Rcusp being the radius of the cusp surface where all field lines are open and Rsource the radius of the source surface where the magnetic field is fully controlled by the solar wind plasma. Following the previous SFTM versions by Cameron et al. (2010) and Jiang et al. (2011b) we take a = 0.2 R⊙ and Rsource = 10 R⊙, where R⊙ is the solar radius.
The best fit, with the lowest χ2-value, to the open magnetic flux from observations is found with a cusp radius of Rcusp = 1.4 R⊙. This best-fit Rcusp is however noticeably lower than in previous versions of the SFTM (1.55 R⊙, see Cameron et al. 2010), which is most likely because the BMRs in our semi-synthetic records have smaller angular separations compared to the regions in the RGO/SOON record and because of the introduction of a weak radial diffusion term with ηr = 25 km2 s−1; see Sect. 4.1. Observations suggest that cusp radius below 1.5 R⊙ would also lead to overly large open field areas and helmet streamers located too close to the solar surface (e.g., Koskela et al. 2019; Wang et al. 2022). Therefore we also ran the model with a more realistic Rcusp = 1.5 R⊙. We show the results of both runs in Sect. 5.2.
4.3. Toroidal flux loss calculation
The loss of toroidal flux inside the solar convection zone is linked to the emergence of BMRs. Following Cameron & Schüssler (2020, Eq. (11)) we calculated the toroidal flux loss during time interval Δt by adding up the contributions from all individual regions (i):
where Δφ = Δβ cos(αm) is the absolute value of the longitudinal polarity separation, ϕL is the magnetic flux of the loop equal to half of the total flux of the BMR, λ is the emergence latitude and γ is the fraction of magnetic flux emerging in regions following Hale’s polarity law (Hale et al. 1919; Hale & Nicholson 1925) minus the fraction disobeying it: γ(ϕ) = (ΦHale − Φnon-Hale)/(ΦHale + Φnon-Hale). In the SFTM, we set the time interval to one day and calculate the longitude separation Δφ by subtracting the position of the positive polarity patch from that of the negative one. Since Δφ can be positive or negative, this replaces the necessity of the factor γ and we can remove it from the equation. The total toroidal flux loss was calculated by summing up the absolute values for the northern and southern hemispheres:
4.4. Simulation setup
We ran the SFTM over the period from March 9, 1874, to December 31, 2019, (cycles 12–24) with a spatial resolution of 4° (lmax = 64 orders of spherical harmonics) on a 180 × 360 grid with a time step of one day and the model parameters as described in Sect. 4.1. We ran the SFTM for each of the 100 realisations of the AMR, LMR, and SMR records (see Sect. 3.4) and used their average as the result and the standard deviation as an uncertainty estimate.
For the RGO run, we used the same angular separation, tilt angles and the value of the free parameter Bmax = 374 G as in Cameron et al. (2010), but use Eq. (14) and Bamp = Bmax to calculate the polarity patches. We used Rcusp = 1.55 R⊙ for the open magnetic flux reconstruction of the RGO/SOON run and Rcusp = 1.4 R⊙ or Rcusp = 1.5 R⊙ for AMR, LMR and SMR. Since in the original SFTM version, BMRs were injected not until the polarity patches had diffused to the width of 4°, thus missing the initial phases of the evolution of the smaller ARs, we expect a slightly higher total magnetic flux even for the RGO/SOON in our simulation compared to Cameron et al. (2010).
5. Results
In this section we present our results from the SFTM and CSSS simulations of the evolution of the total (Sect. 5.1), open (Sect. 5.2) and polar (Sect. 5.3) magnetic field, as well as of the toroidal flux loss (Sect. 5.4). In the next section, we analyse the role of the small magnetic regions in the magnetic flux budget and its dependence on the steepness of the emergence rate distribution using analytical tools.
5.1. Total magnetic flux
We first look at the total magnetic flux computed from the simulated magnetograms. Figure 4 shows the results of the AMR run together with the total magnetic flux from three ground-based observatories (WSO, NSO KP and MWO, black line for the average and dark grey symbols for individual measurements, the latter only in panels a and b to avoid overloading panels c and d) and the KP–MDI–HMI magnetogram composite record from Yeo et al. (2014, green), see Sect. 2, for comparison. The KP–MDI–HMI composite has been brought from the HMI to the MWO scale by multiplying with a constant factor of 3.7 (see Sect. 2). When comparing simulations to observations, we need to keep the limitations of both the model and the observations in mind. In particular, observations are affected by magnetogram noise and have limited spatial resolution (Krivova & Solanki 2004). To account for this limited visibility, earlier studies (Solanki et al. 2002; Krivova et al. 2007, 2021; Dasi-Espuig et al. 2014, 2016) reduced the modelled contribution by ERs by a factor of 0.4 when comparing to observations. At the same time, our model does not include regions smaller than 2 × 1020 Mx. Thus for comparison purposes, to make the modelled and observed fluxes consistent, we accounted for both these effects. To compensate for the missing flux from SSEs (regions between 1016 and 2 × 1020 Mx, see Table 1) in the SFTM, we computed their contribution using the simpler approach of Solanki et al. (2002), Vieira & Solanki (2010), and Krivova et al. (2021) by solving a set of coupled ordinary differential equations. Specifically, we used the results from Krivova et al. (2021, grey line) as their BMR emergence model is consistent with ours, except that they only considered the disc-integrated quantities and did not account for the spatial distribution of BMRs. Since such small regions are distributed over the surface rather homogeneously, the effect of changes in their spatial distribution with activity is expected to be negligible. For comparison with observations we then added 0.4 times the SSE magnetic flux to the AMR run. This total magnetic flux is shown by the light blue line in panels a and b, whereas red and dark grey lines give the total magnetic flux from only AMRs or SSEs, respectively. We find that including all regions with lifetimes of more than one day in the AMR record accounts for most of the observed total magnetic flux. The measured flux (black and green) is only slightly higher, by roughly up to 10% at maxima, than the AMR flux (red). By adding 0.4 times the SSE flux, we get a yet better agreement with the observations during activity maxima. The reduced chi-squared values between the ground-based observations (MWO, WSO, NSO) and AMR plus 0.4 times the SSE flux (light blue line in panels a and b) is χ2 = 0.035. This is already an improvement compared to the previous version of the SFTM (Cameron et al. 2010) that uses only the RGO/SOON sunspot groups as input (χ2 = 0.069) and the simpler model by Krivova et al. (2021) (χ2 = 0.058; see also Table 4). We emphasise again that this was obtained without adjusting free parameters, as done by Krivova et al. (2021) or Cameron et al. (2010).
 |
Fig. 4. Comparison of the simulation results of the total magnetic flux with observations. (a) Evolution of the (3-months smoothed) total magnetic flux from AMRs over cycles 20–24 and comparison with observations. (b) Same as above but over the entire modelled period from 1874 to 2020. (c) and (d) Comparison of all the simulation runs with error estimates overplotted. Plotted quantities: The light blue line in panels a and b is the mean of 100 realisations used as input to the SFTM plus 0.4 times the contribution of SSEs estimated from ordinary differential equations following Krivova et al. (2021), see the main text for details. The total flux from SSEs is plotted in grey. As a comparison we plot the average (black line – all panels) and individual measurements (dark grey symbols – only panels a and b) of three ground based observatories (WSO, NSO KP, MWO). The total magnetic flux from the KP/MDI/HMI composite by Yeo et al. (2014) is shown in light green in all panels. AMR without SSEs is shown in red in panels a and b, and the means of the LMR and SMR runs in panels c and d are shown in blue and green, respectively. The difference between the AMR and LMR runs is shown by the darker green dot-dashed line (which is the lowest curve in in panels c and d). The shaded areas are the standard deviations. The results from the RGO/SOON record are shown by the dash-dotted purple line. |
Comparison of the modelled total and open magnetic flux to observations and independent reconstructions, quantified through their reduced χ2 values.
Figures 4c and d, show all simulation runs along with the measurements: AMR (red), LMR (blue), SMR (green) and RGO/SOON (dash-dotted purple line). We notice that the total flux of SMR and LMR does not add up exactly to AMR, as demonstrated by the dashed light-green line showing the difference between the AMR and LMR runs. This is the result of SMRs emerging inside the polarity patches of LMRs, which results in partial cancelling of the magnetic flux, see Nèmec et al. (2022). Due to the new SFTM setup (see Sect. 4.1), while keeping the value of the free parameter unchanged, the RGO/SOON run is about 5% higher during solar maximum than in the previous model by Cameron et al. (2010), and almost identical during solar minimum. Thus, the reduced chi-squared value between the ground based observations and the RGO/SOON run with the new setup (χ2 = 0.122, see Table 4) is slightly higher than with the old setup (χ2 = 0.069).
Comparing the contributions by SMRs and LMRs, we see that during activity maxima about two thirds of the total magnetic flux come from LMRs, while most of the remaining flux comes from SMRs (with only small contribution of yet smaller regions, SSEs). At activity minima, both LMR and SMR contribute roughly equally, while also the contribution of SSEs might play a role. (Note, however, that black lines in panels a and b show the entire expected SSE contribution, without accounting for their reduced visibility in the data due to the limited spatial resolution, that is without multiplying it with the factor 0.4.) We also see that the total flux from SMRs differs very weakly among the various realisations and thus most of the “noise” comes from large ARs.
5.2. Open magnetic flux
The modelled open magnetic flux (green, blue, red, and dot-dashed purple lines for SMRs, LMRs, AMRs and RGO, respectively) reconstructed with the CSSS extrapolation as described in Sect. 4.2 is compared to observations in Fig. 5. We compare the model output to the open flux reconstruction by Lockwood et al. (2022) from the geomagnetic aa-index (black) and the in situ measurements since 1998 by (Owens et al. 2017, dashed dark green). The top panels show the reconstruction with the best-fit Rcusp = 1.4 R⊙, where we find a good agreement of the AMR run with both datasets (χ2 = 0.195 for Lockwood et al. 2022 and 0.277 for Owens et al. 2017; see Table 4). This is similar to the results by Krivova et al. (2021, χ2 = 0.172 and 0.291, respectively) and by Cameron et al. (2010, χ2 = 0.156 and 0.242, respectively). Over the entire modelled period, the amplitude of the solar cycle variation in the best-fit open flux is in good agreement with the reconstruction by Lockwood et al. (2022) and the observation by Owens et al. (2017), lying within the uncertainty range for almost the entire interval. Only during the maximum of cycle 22, the computed AMR open flux is somewhat lower than in the reconstructions by Lockwood et al. (2022).
 |
Fig. 5. Comparison of the simulation results of the open magnetic flux with observations. The red, blue and green curves are the mean results of 100 realisations used as input to the SFTM for AMR, LMR and SMR, respectively. The top panels show the best-fit run with Rcusp = 1.4 R⊙ while the bottom panels show the run with Rcusp = 1.5 R⊙. The shaded areas are the standard deviations. The results from the RGO/SOON record are shown by the dash-dotted purple line. (a) and (c) Reconstruction of the (1-year smoothed) open magnetic flux from the CSSS model over cycles 20–24. The black line is the reconstruction from the geomagnetic aa-index by Lockwood et al. (2022) and the dark green dashed line shows the in-situ measurements by Owens et al. (2017). (b) and (d) Same but over the entire period from 1874 to 2020. |
The lower panels show the reconstruction with a higher Rcusp = 1.5 R⊙, yielding χ2 = 0.313 and 0.684 when compared to Lockwood et al. (2022) and Owens et al. (2017), respectively. As discussed in Sect. 4.2, this is the lowest cusp radius required to obtain open field areas consistent with observations (Koskela et al. 2019; Wang et al. 2022). The run with Rcusp = 1.5 R⊙ has a lower cycle amplitude than the best-fit run and as a result tends to underestimate the open flux during some periods, as compared to the reconstruction by Lockwood et al. (2022). Compared to Owens et al. (2017), the AR run is a good agreement during 2004 and 2013, although it is somewhat lower around the maxima of cycles 23 and 24. We recall, however, that our model does not include the contribution of the smallest regions and in contrast to the total magnetic flux, it is not straightforward to add it from another model, e.g., from Krivova et al. (2021), as we did for the total flux. Since the main goal of our study is to understand the role of the small magnetic regions in the overall magnetic flux budget of the Sun, and the latter appears consistent between the two runs, we do not go into detail regarding the potential improvements of the open flux modelling. This goes beyond the scope of this analysis.
The RGO/SOON run is mostly consistent with Lockwood et al. (2022) and Owens et al. (2017), and it tends to be slightly higher during maxima than the AMR run (especially for the Rcusp = 1.5 R⊙ case). However, for some mostly weak cycles the open flux from the RGO run is considerably weaker than in the empirical reconstruction and the AMR best-fit run, for example during cycles 15, 17 and 20. The reason could be that during weak cycles, the relative role of the smaller regions is higher than during high activity cycles. For both AMR reconstructions, we find that during some of the solar minima (e.g., in 1996), the open flux in our simulations is slightly delayed (by roughly a year or two). In Cameron et al. (2010) it was shown that the timing of the minima in the open flux is delayed for higher ηr. They found that ηr = 0 could reproduce the timing of the minima. Here we use a non-zero value of ηr to prevent a multi-cycle drift of the polar fields (Schrijver et al. 2002). This drift is possibly a consequence of the SFT model not being a full dynamo model and as such lacking any feedback mechanisms which might prevent such a drift. During the first two cycles covered by simulations, the computed open flux for both AMR runs and for the RGO/SOON run noticeably deviates from the reconstruction by Lockwood et al. (2022). This is because of our simple initial magnetic field configuration, taken from van Ballegooijen et al. (1998, see their Eq. (16)), and hence the results during these first two cycles should be taken with caution and are not used for the calculation of the χ2-values in Table 4.
Looking at the individual contributions by LMR and SMR we find that the LMR run follows a similar shape to the AMR run, although lower in amplitude. Interestingly, the timings of the peaks and troughs are more consistent with Lockwood et al. (2022). The timings of the SMRs are noticeably delayed, with the troughs in the open flux being close to solar maximum and the peaks in the declining phase of the cycle. The reason for this is that the open flux is dominated by a contribution of the axial and equatorial dipole moments. In the case of the LMRs, this balance is dominated by the equatorial dipole moment, which leads to the open flux peaking in phase with the solar cycle. In the LMR case, the equatorial dipole moment is made up of comparable contributions from the LMRs emerging at random longitudes and those emerging in nests (see Sect. 3.2.3). In the case of the SMRs, there are so many small emergences that the contribution from the random longitudes average out, and the only substantial contribution to the equatorial dipole moment is that due to nesting. Consequently the axial dipole moment plays a larger role and the minima of the open flux are moved closer to the polar field reversals. The SMR amplitude is comparable in amplitude to LMR during solar minimum, but only about one third of LMR during solar maximum. Similar to the total flux we find that the majority of the noise comes from large ARs, with only a small contribution by SMRs. The main contribution to the variation over the solar cycle is thus given by LMRs, however SMRs do give a significant contribution to the overall level of the open magnetic flux. Our simulations reproduce the high post-maximum peaks (see e.g., 1982, 1992, 2003, 2014) that can be seen in both records by Owens et al. (2017) and Lockwood et al. (2022). Such peaks in the open flux are commonly related to rapid strengthenings of the axial dipole moment, associated with “nesting” of large AR complexes. Looking at Fig. 5a, the same double peaks are seen during most of the maxima in the LMR simulation, while in SMRs only single peaks are seen. Due to the delayed occurrence of the SMR peaks during the declining phase, they may however contribute to the secondary peaks in the open flux.
5.3. Polar fields
In Fig. 6, we compare the simulated line-of-sight polar field above 55° latitude to the line-of-sight observations by WSO (black; Scherrer et al. 1977; Hoeksema et al. 1983). To bring the polar fields to the MWO scale, we multiply the WSO data with a conversion factor of 1.3, identical to Jiang et al. (2013). This is in good agreement with the factor of 1.26 found by Muñoz-Jaramillo et al. (2012) and the factor of 1.43 for the axial dipole term of the photospheric magnetic field between WSO and MWO data found by Virtanen & Mursula (2017). Again, the AMR run does not include the contribution by the smallest regions (SSEs, see Sect. 5.1). In contrast to the total magnetic flux, it is not straightforward to add this contribution separately. However, as discussed in Sect. 6.3, the contribution of yet smaller regions is expected to fall off rapidly, due to the increasing randomness in their tilt angles and so we do not expect a significant effect on the polar fields. We find a good agreement between the AMR run (red) and WSO amplitudes, except for the period between the maxima of cycles 23 and 24 (2000 − 2014) where the AMR run overestimates the amplitude by about a factor of 2. The same is seen for the RGO/SOON run, as well as in the study by Jiang et al. (2013, using the RGO/SOON record as SFTM input) who found that the polar field amplitude in the declining phase of cycle 23 (after year 2000) was too high compared to observations. This was caused by several large ARs close to the equator disobeying Joy’s law (Jiang et al. 2015). When using the observed tilt angles instead of the statistical ones, they found a good agreement with the WSO data.
 |
Fig. 6. Comparison of the simulation results of the line-of-sight polar magnetic field with observations. The red, blue and green curves are the mean results of the SFTM for 100 realisations used as input for AMR, LMR and SMR, respectively. The shaded areas are the standard deviations. The results from the RGO/SOON record are shown by the dashed-dotted purple line. (a) The line-of-sight polar field above 55° latitude from model runs and from the measurements from WSO (black) over cycles 20–24 multiplied by a factor 1.3. The northern polar fields are given by the solid lines, and southern polar fields are dot-dashed. (b) Same but over the entire modelled period from 1874 to 2020. |
Comparing the LMR and SMR runs, we find that their amplitudes are very similar throughout the entire interval. Therefore, the contribution by small regions in the AMR run is much higher for the polar fields than for the total and open magnetic flux. The higher importance of small BMRs for the polar fields could explain why the RGO/SOON run from our simulation has a similar amplitude to the AMR run, occasionally being even smaller than AMR, despite the total magnetic flux of RGO/SOON being consistently higher than AMR (see Fig. 4). The AMR, LMR and SMR runs all show regular polar reversals. However the reversals in cycles 21, 23 and 24 are delayed by about 1 year compared to the WSO measurements. The timing of the polar field (here poleward from λ| = 55°) reversals depends on the strength of the polar fields, the amount of flux carried past λ| = 55°, and ηr. Importantly, flux of both polarities is carried, so that the polar field can change sign several times before it finally reverses. The delay in cycles 21, 23 and 24 are within one standard deviation of the expectation value. We therefore suggest that the delay in the model for these cycles might be related to the scatter in the tilt angles at high-latitudes which affects the timing of the reversal but not the long-term strength of the polar fields. As with the total and open flux, we find that the polar field noise is dominated by LMRs.
5.4. Toroidal flux loss
The toroidal flux loss calculated from Eq. (17) for AMR (red) and LMR (blue) is shown in Fig. 7. Because the toroidal flux loss linearly depends on the magnetic flux emerging in BMRs (see Eq. (17)), its temporal profile is quite similar to that of the total magnetic flux. During solar maxima of cycles 21–24, we find between 2 and 5 × 1022 Mx year−1 for the toroidal flux loss for AMRs. This is in good agreement with the recent studies that found a toroidal flux loss of ≈4 × 1022 Mx year−1 in the same time period from WSO magnetograms (Jeffers et al. 2022) and the estimate by Cameron & Schüssler (2020). We find that contributions to the toroidal flux loss of both the LMR and SMR runs are similar during both activity minima and maxima, each contributing ≈50% to the AMR run. Thus, small regions have noticeably higher contribution to the toroidal flux loss than to the total magnetic flux. The toroidal flux loss noise is dominated by LMRs.
 |
Fig. 7. Comparison of the simulated toroidal flux loss with observations. The red, blue, and green curves are the mean results of 100 realisations used as input to the SFTM for AMR, LMR, and SMR, respectively. The shaded areas are the standard deviations. (a) 3-month smoothed sum of the absolute toroidal flux loss of both hemispheres over cycles 20–24. (b) 1-year smoothed sum of the absolute toroidal flux loss of both hemispheres over the entire simulated period from 1874 to 2020. |
6. Understanding the role of small BMRs
In Sect. 5, we showed that the simulated total and open magnetic flux, the polar fields and the toroidal flux loss are in good agreement with observations and/or other reconstructions. To better understand our results and the role of small BMRs (SMRs and even smaller BMRs such as ERs and internetwork features) we analytically analyse the governing equations of these solar quantities and compare the analytical results with those obtained from the simulations. We further discuss how the shape of the emergence rate distribution affects our results by flattening the distribution for large ARs (> 1022 Mx).
6.1. Flattening the emergence rate distribution
As discussed in Sect. 1, the exact shape of the emergence rate distribution is not very certain. In this study, we use the power-law size distribution as found by Thornton & Parnell (2011). However, some studies found evidence for flattening of the distribution for larger ARs (e.g., Wang & Sheeley 1989; Schrijver & Harvey 1994). To estimate how an uncertainty in the shape of the emergence rate distribution might influence the SFTM results, we conducted an additional simulation where we appled a simple modification to the power-law given by Eq. (1) to significantly increase the amount of large ARs (> 1022 Mx) in the simulation. Namely, for regions smaller than 1022 Mx, we kept the power-law unchanged, but for regions between 1022 and 1023 Mx, we changed the power-law exponent m2 to make the distribution less steep:
The modified power-law exponent m2 was calculated from the original exponent m (see Eq. (2)) as follows:
This increased the emergence rate of regions with 1023 Mx by five times compared to Eq. (2) and the average power-law exponent changed from −2.69 to −1.99, close to the value obtained by Schrijver & Harvey (1994). The factor C2 ensures that the two parts of Eq. (18) intersect at the transition point at 1022 Mx:
We note that the emergence rate from Eq. (18) simply yields an increased number of large regions with fluxes > 1022 Mx without modifying the distribution of the lower-flux regions so that in this case, the total magnetic flux in the simulation is higher than that from the measurements by Parnell et al. (2009) and the observations by WSO, NSO, and MWO. This also does not account for the possible steepening of the distribution for large ARs close to 1023 Mx as reported by Muñoz-Jaramillo et al. (2015) and Sakurai & Toriumi (2023). Thus the effect of larger regions is most likely overestimated. Nevertheless, this test allows us to estimate how the relative contribution of LMRs and SMRs to the studied solar quantities changes for flatter emergence rate distribution of larger BMRs. A comparison between the original simulation run (Sect. 5) and the additional simulation run with increased number of largs ARs (Sect. 6.1) is shown in Fig. 8. The panels on the left (a, c, e, g) display the relative contribution to the different solar quantities by LMRs (blue) and SMRs (green) from the original simulation, while the results from the additional run with modified emergence rate are shown on the right (b, d, f, h). The differences between the two simulations are discussed separately for each of the solar quantities in the respective following Sects. 6.2–6.5.
 |
Fig. 8. Relative contribution of LMRs and SMRs to the total flux, polar fields, toroidal flux loss, and the open flux. Left: Original setup from Sect. 5. Right: Increased emergence rate of large ARs (see Sect. 6.1). |
6.2. Total flux
The total magnetic flux is determined by the amount and size of magnetic flux elements present on the solar surface. Using high-resolution Hinode magnetograms, Parnell et al. (2009) found that the number of magnetic flux elements on the solar surface per area per magnetic flux follows a power-law size distribution:
where Nf = 3 × 10−4 cm−2, ϕ is the magnetic flux of the flux element in Mx and q = −1.85 (denoted as α in Parnell et al. 2009), c.f., Eq. (1) for the emergence rate. The total magnetic flux per area of all regions between magnetic flux limits ϕ1 and ϕ2 is calculated by integrating the product of the magnetic flux ϕ and Eq. (21):
The resulting exponent (q+2) = 0.15 is larger than 0, which means that the total flux should be dominated by large ARs. This is consistent with the simulation (see Fig. 4), showing that the LMR run contributes about two thirds to the total magnetic flux at activity maxima, while SMRs account for the remaining flux. As has been shown in Sect. 5.1, yet smaller BMRs not accounted by our model (that is ERs with fluxes below 2 × 1020 Mx) have an almost negligible effect on the total flux. Note though that at activity minima the contribution of SMRs is comparable to that of spot-containing LMRs. The exponent q in Eq. (21) was derived by Parnell et al. (2009) from the data without accounting for the activity level. If it varies with activity similarly to the exponent m in Eq. (1), the exponent (q+2) is getting closer to 0 at minima, in agreement with what we see in Fig. 4. If the number of large ARs is increased as described in Sect. 6.1, the contribution of LMRs, not unexpectedly, increases to about 75% during maxima and two thirds during minima (compare panels a and b in Fig. 8).
Assuming that the noise is Gaussian and that the individual emergences are independent of each other, the uncertainty (or noise) of the total flux is proportional to the square root of the number of magnetic flux elements:
The power-law exponent q/2 + 2 = 1.075 is significantly higher than zero, hence the noise must be dominated by large regions. This agrees with our simulations, as there is almost no observable variance between the SMR realisations and the noise of LMR and AMR runs is almost identical.
6.3. Polar fields
As described by Eq. (14), BMRs in the SFTM emerge as bipolar polarity patches with the same amount of positive and negative magnetic flux. As the BMR evolves, the polarities eventually cancel each other out by diffusion or after they are transported to the poles by the meridional flow. However, if a BMR is close to the equator, part of the magnetic flux can cross it and move to the other hemisphere before being cancelled out. This results in a change in the polar field strength. Petrovay et al. (2020, Eq. (24)) have derived this “transequatorial flux fraction” ftr for small latitude separations Δλ between the polarity patches as:
where λ is the emergence latitude and λR is the so-called dynamo effectivity range that depends on the SFTM model parameters. The latitude separation Δλ depends on the angular separation Δβ and hence on the square root of the magnetic flux of the BMR (see Eq. (15)):
The tilt angle is proportional to the square root of the emergence latitude (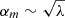 ) and the mean emergence latitude depends on the phase (time) in the cycle and the cycle strength, but both are independent of the BMR flux ϕ. Keeping in mind that even ERs show a tendency to obey Joy’s law – although with a much higher tilt scatter – we can employ Eq. (24) for all BMRs in our study. However, we need to consider that especially small BMRs may sometimes emerge with anti-Hale orientation which leads to a decrease in the polar field strength. This effect is described by the factor γ(ϕ) (see also Sect. 4.3) that varies between 1 and 0 and depends on the probability of a region emerging with proper Hale-orientation PHale, which depends on the tilt angle scatter σtilt; see Eq. (10). Using the definition of the normal distribution we calculate:
) and the mean emergence latitude depends on the phase (time) in the cycle and the cycle strength, but both are independent of the BMR flux ϕ. Keeping in mind that even ERs show a tendency to obey Joy’s law – although with a much higher tilt scatter – we can employ Eq. (24) for all BMRs in our study. However, we need to consider that especially small BMRs may sometimes emerge with anti-Hale orientation which leads to a decrease in the polar field strength. This effect is described by the factor γ(ϕ) (see also Sect. 4.3) that varies between 1 and 0 and depends on the probability of a region emerging with proper Hale-orientation PHale, which depends on the tilt angle scatter σtilt; see Eq. (10). Using the definition of the normal distribution we calculate:
where
denotes the error function. The probability of the region being anti-Hale oriented is 1 − PHale. Hence we can rewrite γ(σtilt) as:
The polar field strength now depends on the number of emerging regions (Eq. (1)) over the solar cycle times their magnetic flux times the fraction of that flux that crosses the equator (Eq. (24)) times the fraction of proper Hale-oriented regions:
where 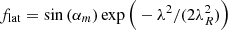 is independent of ϕ and m = −2.69 is the power-law exponent from Thornton & Parnell (2011). The average ⟨flat⟩ is calculated at an emergence latitude of λ = 15° and the mean tilt angle of αm = 5°. Equation (29) cannot be solved analytically, so instead we discuss the result by plotting the integrand in Fig. 9a. We find a concave function with the steepest (negative) slope at 1023 Mx. Integrating the tangent power law, we find the exponent of ∼ − 0.19, slightly lower than zero. However, due to the increasing number of anti-Hale regions for smaller BMRs, the steepness of the tangent power-law decreases and the exponent becomes positive for regions below 1.2 × 1020 Mx (just below the smallest regions included in our model). This means that the small BMRs included in our simulation should contribute a similar or slightly larger amount of flux to the poles as the large BMRs. We emphasise though that even smaller BMRs (ERs and internetwork features) are not expected to play a significant role to the polar fields. From Fig. 6, we find that the simulated polar fields from small regions in the SMR record are roughly as strong as in the LMR run, both during activity minima and maxima. However, if we increase the number of large ARs by flattening the power-law exponent (see Sect. 6.1), even the steepest exponent in Eq. (29) becomes distinctly positive (+0.51). In this case, the contribution by LMRs clearly dominates the polar field strength which is now about twice as large as that from SMRs in our simulations (compare Figs. 8c and d). The results might further be influenced by the angular separations used for the BMRs in our model. For example, Wang & Sheeley (1989) found that the angular separation of sunspots scales as ϕ0.77 rather than the ϕ0.5 as assumed in our study. Even without flattening the power-law, this would change the steepest exponent in Eq. (29) from me + 2.5 to me + 2.77 = +0.08, turning the exponent slightly positive. Based on Fig. 2 of Wang & Sheeley (1989), from which they derived the exponent of 0.77 using a linear fit, we note, however, that the fit is rather uncertain and the derived value of the exponent might be biased towards a higher value. While our results are sensitive to the assumptions discussed above, we find that SMRs provide a significant contribution to the polar field strength in all cases.
is independent of ϕ and m = −2.69 is the power-law exponent from Thornton & Parnell (2011). The average ⟨flat⟩ is calculated at an emergence latitude of λ = 15° and the mean tilt angle of αm = 5°. Equation (29) cannot be solved analytically, so instead we discuss the result by plotting the integrand in Fig. 9a. We find a concave function with the steepest (negative) slope at 1023 Mx. Integrating the tangent power law, we find the exponent of ∼ − 0.19, slightly lower than zero. However, due to the increasing number of anti-Hale regions for smaller BMRs, the steepness of the tangent power-law decreases and the exponent becomes positive for regions below 1.2 × 1020 Mx (just below the smallest regions included in our model). This means that the small BMRs included in our simulation should contribute a similar or slightly larger amount of flux to the poles as the large BMRs. We emphasise though that even smaller BMRs (ERs and internetwork features) are not expected to play a significant role to the polar fields. From Fig. 6, we find that the simulated polar fields from small regions in the SMR record are roughly as strong as in the LMR run, both during activity minima and maxima. However, if we increase the number of large ARs by flattening the power-law exponent (see Sect. 6.1), even the steepest exponent in Eq. (29) becomes distinctly positive (+0.51). In this case, the contribution by LMRs clearly dominates the polar field strength which is now about twice as large as that from SMRs in our simulations (compare Figs. 8c and d). The results might further be influenced by the angular separations used for the BMRs in our model. For example, Wang & Sheeley (1989) found that the angular separation of sunspots scales as ϕ0.77 rather than the ϕ0.5 as assumed in our study. Even without flattening the power-law, this would change the steepest exponent in Eq. (29) from me + 2.5 to me + 2.77 = +0.08, turning the exponent slightly positive. Based on Fig. 2 of Wang & Sheeley (1989), from which they derived the exponent of 0.77 using a linear fit, we note, however, that the fit is rather uncertain and the derived value of the exponent might be biased towards a higher value. While our results are sensitive to the assumptions discussed above, we find that SMRs provide a significant contribution to the polar field strength in all cases.
 |
Fig. 9. Estimating the polar field and the polar field noise. (a) Integrand of Eq. (29) (green solid), the tangent power law at the steepest point (blue dashed) and at the “reversal point” where the exponent of the integrated tangent power law becomes higher than zero (red dotted). (b) Same but for the integrant of Eq. (34). The vertical grey lines mark the lower flux limits of AMR and LMR. |
Now we consider the uncertainty of the polar fields, again by taking the square root of the number of emerging BMRs:
where SD[…] denotes the standard deviation. As described in Sect. 3, the standard deviations of the tilt angle and the emergence latitude are dependent on the regions size and they need to be considered in our calculation. The standard deviation of the sinusoidal function A = sin(αm) is calculated as:
where σtilt is given by Eq. (10). The standard deviation of the exponential function 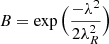 can be estimated as:
can be estimated as:
where σlat is given by Eq. (8) and λR = 7.5° for our SFTM setup. The combined standard deviation σAB is defined as:
Plugging into Eq. (30) we find:
Just as before, Eq. (34) does not have an analytical solution, and we discuss the integrand in Fig. 9b. The steepest slope of the concave function is 6 × 1022 Mx, where the integrated tangent power law has an exponent of ∼0.1. As this is higher than zero, and becomes even larger for smaller regions, we conclude that the uncertainty of the polar fields is dominated by large ARs. We note however, that if we choose an emergence latitude even closer to the equator (λ ≤ 15°), the tangent power law for the largest ARs is so steep that the exponent of the tangent power law becomes slightly negative. While this does not change the qualitative result that small BMRs have only a small contribution, it means that the contribution of the largest ARs (≥1022 Mx) this close to the equator is lower than that by small and medium LMRs (≤1022 Mx). This can be explained by the proximity to the equator, such that for very large spots parts of both polarity patches can cross, which leads to a stronger cancellation of the magnetic flux that is transported to the poles. Comparing the analytical results to the simulation (Fig. 6), we find that the LMR runs show a much greater variation between individual runs than SMR, which can in some cases lead to delayed or irregular polar field reversals. The contribution by small BMRs seem to stabilise the runs and lead to less variation between different realisations and more stable polar field reversals. Therefore the uncertainty of the polar fields in the simulation is dominated by LMRs.
6.4. Toroidal flux loss
The toroidal flux loss is calculated from Eq. (16), as described in Sect. 4.3. Plugging in the flux emergence rate from Eq. (1) we find:
This integral over ϕ cannot be solved analytically. As described in Sect. 6.3, γ(ϕ) describes the probability of a region emerging with proper Hale-orientation (see Eq. (28)). For the calculation we assume a typical mean tilt angle of αm = 5° at 15° latitude. The exact choice is not important as it has no significant effect on the results. The integrant is identical to Eq. (29) (except for the constant prefactors), and hence our result is identical to Sect. 6.3 for the polar fields. Therefore, small regions play a large role for the toroidal flux loss, comparable to that of large BMRs, while the contribution of ERs is expected to average out due to the large amount of anti-Hale regions. Indeed we find in the simulation that LMR and SMR contribute about equally to the total AMR toroidal flux loss (see also Fig. 8e), which suggests that the toroidal flux loss is dominated by both small and large ARs. If we employ an increased emergence rate of large ARs as described in Sect. 6.1, we find that the exponent of the tangent powerlaw is +0.51 at the upper flux limit of 1 × 1023 Mx, which means that LMRs dominate the toroidal flux loss. As we can see in Fig. 8f, in this case the contribution by LMRs is about twice as large as that from SMRs at all activity levels. Similar to the polar fields, we conclude that small BMRs play a significant role to the toroidal flux loss although the exact amount depends on the steepness of the emergence rate distribution.
The uncertainty of the toroidal flux loss depends on the square root of the number of emerging BMRs:
where σCD is the combination of the standard deviation of the cosine function C = cos(αm) and the standard deviation of the inverse cosine function D = cos−1(λ). The standard deviation of C is calculated as:
where we use αm = 5° and σtilt is given by Eq. (10). The standard deviation of D is calculated as:
where σlat is given by Eq. (8). The combined standard deviation is:
The integrand at emergence latitude 15° is plotted in Fig. 10b. We find a similar case to the polar field noise, where we find a concave function, and the exponent of the integral over ϕ of the steepest tangent power law at 2 × 1022 Mx is 0.22 > 0. At emergence latitudes ≤10°, the tangent power-law exponent becomes lower than zero, which diminishes the contribution by very large ARs (≥1022 Mx). We conclude that the toroidal flux loss noise is dominated by LMRs at medium to high emergence latitudes, and by small and medium LMRs (≤1022 Mx) at low latitudes. Comparing the result to the simulations in (Fig. 7), we find that most of the noise indeed comes from the LMRs which are included in both simulation runs.
 |
Fig. 10. Estimating the toroidal flux loss and the toroidal flux loss noise. (a) Integrand of Eq. (35) (green solid) and the tangent power law at the steepest point (blue dashed). (b) Same but for the integrand of Eq. (36). The vertical grey lines marks the lower flux limits of AMR and LMR. |
6.5. Open flux
Compared to the total flux, polar fields and toroidal flux loss, the open magnetic flux depends on a variety of factors, such as the degree of nesting, the fragmentation rate of ARs and the equatorial dipole moment. We were unable to construct a simple analytic power-law-like understanding of how the open flux depends upon the model parameters. Instead we compare our results to other studies and discuss the effects of flattening the emergence rate distribution for large ARs (see Sect. 6.1).
In our simulations (see Sect. 5.2), we find that the contribution to the open magnetic flux is dominated by LMRs. At solar maximum, LMRs contribute about two thirds of the open flux, while at solar minimum the contributions are almost equal. If we increase the number of large ARs (see Sect. 6.1), the contribution by LMRs increases to about 80% during maximum and about two thirds at solar minimum (compare Figs. 8g and h). As discussed in Sect. 5.2, we observe multiple peaks around and after solar maximum in the LMR simulation runs, while no such pattern is discernible in the SMRs. This is due to the large tilt scatters of the numerous small BMRs that average out the individual equatorial dipole moments. Hence we conclude that the main contribution to the variation of the open flux comes from large ARs, although small BMRs give a significant contribution to the overall level of the open magnetic flux.
Some earlier studies have suggested that large BMR might play an even bigger role than found in our simulation: Sheeley (1985) used over 2500 ARs with fluxes greater than a few times 1021 Mx as input to their flux transport model and found that only the largest ∼15% of their BMRs had a noticeable effect on the polarity pattern and strength of the mean field, despite contributing only about 50% of the total emerging flux. Wang & Sheeley (1991) found that more than half of the Sun’s axial dipole moment during cycle 21 was contributed by only 290 large ARs with fluxes > 1022 Mx. It is unclear whether this discrepancy comes from differences in the emergence rate or tilt angle scatter of BMRs, or if it is related to differences between the SFTMs.
The main contribution to the interplanetary magnetic field comes from the axisymmetric polar fields at solar minimum, which are build up by the cumulative axial dipole moments of the BMRs of the preceding cycle. Therefore, the steepness of the emergence rate distribution, as well as the question whether ERs and ARs follow the same distribution, is crucial to decide which regions dominate solar magnetic quantities such as the polar fields and the open magnetic flux. As our analysis has shown, increasing the number of large ARs has indeed a strong effect on the ratio between the contribution of LMR and SMRs for all the studied solar quantities. This highlights the importance of better constraining the still not fully understood transition between the distributions of ERs and ARs, in order to conclusively assess their respective importance to the evolution of the solar magnetic field.
7. Summary and conclusion
We have analysed the effect of small magnetic regions on basic solar quantities, including the total and open magnetic flux, the polar fields, and the toroidal flux loss. For this purpose, we simulated the Sun’s large-scale magnetic field since 1874 using an SFTM (Baumann et al. 2004; Cameron et al. 2010; Jiang et al. 2011b) to describe the evolution of BMRs on the solar surface upon their emergence, and we validated the results through their comparison with observations and analytical approximations. As input we used semi-synthetic BMR emergence records constructed from the international sunspot number (version2, ISN2.0). Compared to previous versions of the model (Cameron et al. 2010; Jiang et al. 2011b), we included not only large, spot-containing ARs, but also smaller BMRs with lifetimes of one day and longer.
To include smaller BMRs (that is those not represented by the historic sunspot observations) into the model, the emergence rate of all BMRs was taken to follow a single power-law size distribution, as derived from observations by Thornton & Parnell (2011), with the exponent varying with the sunspot number, following Krivova et al. (2021). To derive the mean and the scatter of the BMR emergence latitudes, as well as the mean and the scatter of the BMR tilt angles, we started with the empirical relationships from Jiang et al. (2011a); Jiang (2020), as well as Solanki et al. (2008). We have, however, partly revised and extended them to account for the overlap between solar cycles and the dependence of the latitude and tilt scatter on the size of BMRs, based on observations by Harvey (1993) and Schunker et al. (2020).
To incorporate the cycle overlap into the model, we used the observational results by Harvey (1993) and the RGO/SOON sunspot group data record to roughly estimate the emergence rate of BMRs of various sizes during different cycle phases. These constraints were then used to split the emerging BMRs between every pair of overlapping cycles. Thereby, we assumed that a new cycle starts (with a negligibly low emergence rate) at high latitudes soon after the polar field reversal around the maximum of the preceding cycle (Wilson et al. 1988; Harvey 1993; Tlatov et al. 2010; McIntosh et al. 2014) and it ends two years after the solar minimum, following Harvey (1993).
Using these emergence patterns, we synthesised a set of 100 independent realisations to estimate how the randomness of the statistical relationships affects the simulation results. We considered three types of input records, one with AMRs with lifetimes ≥1 day and magnetic flux ≥2 × 1020 Mx, with another one including only the LMRs with flux ≥3 × 1021 Mx, and a final one with only the SMRs with fluxes below 3 × 1021 Mx. The flux limit for LMRs was selected such as to make the LMR record consistent with the RGO/SOON sunspot group record used as input for the previous versions of the model, thus allowing a direct comparison.
To model the evolution of BMRs more realistically than in previous versions of the SFTM, we included all regions (regardless of their size) from the point of their maximum development, so that we always modelled the entire decay process in the SFTM. The angular separation between the emerging BMR polarity patches and the initial magnetic flux density were chosen such that the decay rate and the initial magnetic flux content of the BMRs were consistent with observations (Parnell et al. 2009; Thornton & Parnell 2011). Regions that are too narrow upon emergence to be spatially resolved in the SFTM were treated in separate, secondary magnetograms where they were only subjected to the effect of turbulent diffusion. The secondary magnetograms were then included in the total magnetic flux calculation at each time step, while the individual regions in the secondary magnetograms were added to the main magnetograms once they exceeded the resolution limit of the latter. Contrary to the previous version of the SFTM (Cameron et al. 2010; Jiang et al. 2011b), our new model does not require a free parameter to adjust the peak magnetic field strength of the BMRs to match observations of the total magnetic flux.
We compared the simulation results to various observations and reconstructions. Furthermore, to better understand the role of small BMRs on the evolution of global magnetic quantities, we analysed the governing equations of the total magnetic flux, the polar fields, and the toroidal flux loss and studied the effects of flattening the emergence rate distribution for large ARs (> 1022 Mx) by increasing the average power-law exponent from −2.69 to −1.99 (see Sect. 6.1). We summarise our results as follows:
-
The simulated total magnetic flux from the AMR run (that is, all modelled magnetic regions in the range 2 × 1020 − 1023 Mx) is in good agreement with the composite of measurements by NSO/KP, SoHO/MDI, and SDO/HMI as well as the ground-based observations by WSO, NSO, and MWO. The LMRs (large, spot-containing ARs with fluxes in the range 3 × 1021 − 1023 Mx) alone account for about two-thirds of the magnetic flux during activity maxima, while during minima LMRs and SMRs (small BMRs in the range 2 × 1020 − 3 × 1021 Mx) contribute roughly equally. Because we only included regions with lifetimes longer than one day into the simulations, small ERs and internetwork features with fluxes below 2 × 1020 Mx were not covered. We estimated their contribution to the measured magnetic flux using a simpler model by Krivova et al. (2021). Their inclusion slightly improved the agreement with the measured flux, but most of the total flux in the records we considered is well accounted for by AMRs alone (that is, all regions with fluxes above 2 × 1020 Mx). The agreement with the data is also better than in the previous models by Cameron et al. (2010) and Krivova et al. (2021), even though our model does not have the scaling-free parameter to adjust the computed flux to the observational level. When increasing the emergence rate of large ARs, the contribution of LMRs increased to 75% at solar activity maximum and to two-thirds at minimum.
-
The simulated open magnetic flux is in good agreement with satellite measurements (Owens et al. 2017) and the empirical reconstruction from the geomagnetic aa index (Lockwood et al. 2022), although this requires a very low cusp surface radius of Rcusp = 1.4 R⊙. With a more realistic radius of 1.5 R⊙, our reconstruction somewhat underestimates the open flux at solar maximum, which could be related to the smaller angular separations of our large BMRs compared to the previous models (Cameron et al. 2010; Krivova et al. 2021). We also miss the contribution by the smallest regions (below 2 × 1010 Mx) to the open flux. The simulated open flux is sometimes slightly delayed (by up to a year or two) compared to the aa-based reconstruction. SMRs contribute about one-third to the overall open magnetic flux at maxima and ≈40 − 50% at minima. Double peak structures around solar maxima similar to the observations are only seen in the LMR run, although the maximum in the flux of SMRs delayed with respect to the maximum in LMRs might contribute to the second peak. Flattening the slope for ARs increased the contribution of LMRs to 80% at maximum and two-thirds at minimum.
-
Both the AMR and LMR simulations return regular polar field reversals near solar maxima, in good agreement with the line-of-sight polar field measurements from WSO. The AMR polar field amplitude agrees reasonably with the WSO data, although it overestimates the polar field during cycle 23, similar to other studies with statistical BMR input; readers can refer to Jiang et al. (2013, 2015) for more details. The LMR and SMR runs each contributed equally to the total polar fields during both solar minimum and maximum. Though smaller regions are, however, not expected to play a significant role due to the increasing number of anti-Hale regions. The exact ratio between the contributions of LMRs and SMRs strongly depends on the steepness of the emergence rate distribution and the angular separation between polarity patches. Increasing the emergence rate of large ARs (≥1022 Mx) doubled the contribution by LMRs with respect to SMRs, although in all cases SMRs played a significant role in the polar field strength. The addition of SMRs leads to more consistent polar field reversals of the individual runs.
-
We find a total toroidal flux loss from AMRs of 2–5 × 1022 Mx yr−1 during the activity maxima of cycles 21–24. This is in good agreement with Jeffers et al. (2022) who found ∼4 × 1022 Mx yr−1 from WSO magnetograms in the same period of time. Just as for the polar fields, LMRs and SMRs contributed roughly equally to the AMR toroidal flux loss, both during minima and maxima, while smaller ERs are unlikely to have a strong influence on the results. Increasing the emergence rate of large ARs doubles the contribution of LMRs with respect to SMRs at all activity levels.
-
For all solar parameters (total flux, open flux, polar fields, and toroidal flux loss), the noise was dominated by LMRs. This is because due to the small number and large size of LMRs, individual regions can have a significant impact on the magnetic field, while the high number of SMRs smears out the contribution of each individual region.
To summarise, we find that SMRs are especially important for the polar field strength and the toroidal flux loss. In our simulation, the contribution of SMRs is comparable to that of LMRs, both during activity minima and maxima. The inclusion of even smaller ERs (< 2 × 1020 Mx) to the model would however only slightly increase the contribution of small regions to the polar fields and toroidal flux, due to the increasing number of anti-Hale regions. As shown in Sect. 6, the exact ratio between the contribution of large and small BMRs depends on the steepness of the emergence rate distribution. If the distribution flattens out for large ARs, we expect a noticeably smaller yet still significant contribution of small BMRs. Therefore, we require a better understanding of the emergence rate distribution and especially the transition between ERs and ARs to obtain a conclusive evaluation of the importance of small BMRs. In any case, our results suggest that small BMRs will be interesting for dynamo studies since the polar fields and their noise play a crucial role in the generation of the toroidal field of the next solar cycle and as such are crucial for understanding the solar dynamo (Cameron & Schüssler 2015). The same is true for the toroidal flux loss. The total and open magnetic flux at activity maxima are more strongly influenced by LMRs. At activity minima, small BMRs play a significant role in determining all solar quantities considered in this study: the total magnetic flux, open flux, polar fields, and toroidal flux loss. The noise for all these quantities is, however, dominated by large ARs. Since small BMRs are numerous and are widely spread over the solar surface, the contribution of individual small regions smears out.
We have included small ARs (those that are not covered by the historic sunspot records) and large ERs into the SFTM and studied their influence on the solar magnetic field. The inclusion of even smaller ERs (< 2 × 1020 Mx) into the model poses additional challenges. Firstly, the temporal and spatial resolution need to be further increased to accurately model the early evolution of small BMRs. Secondly, a much higher number of total regions would lead to a significantly higher part of the initial magnetic flux in the magnetograms being cancelled by overlapping polarity patches of neighbouring regions. The imposed shape of the BMRs however cannot be easily changed, as it is tied to the decay rate and a narrower shape would decrease the region lifetime. Therefore, we might require a separate treatment for the smallest of ERs. We note, however, that the smallest ERs have a much wider scatter in their tilt angles so that only a small fraction of them obey Hale’s polarity law. It is believed that a significant amount of this flux comes from a small-scale dynamo operating on the Sun (Cattaneo 1999; Cattaneo & Hughes 2001; Hagenaar 2001) and that it will not affect the open flux, polar field, or toroidal flux loss.
Simulated magnetograms of the type generated here are an important input to reconstructions of the past solar irradiance. Thus, Dasi-Espuig et al. (2014, 2016) used the previous version of the model, which employed only historic sunspot observations as input, to reconstruct the solar total and spectral irradiance back to 1878 and 1700, respectively. To include the contribution of the smaller regions, which is critical for an estimate of the secular irradiance variability, they had to add it separately from a simpler model (Solanki et al. 2002; Vieira & Solanki 2010; Krivova et al. 2007, 2010). The weakness of this approach lies therein that because the emergence rate of ERs was linked linearly to the emergence of ARs, the model returned zero magnetic flux at times when no sunspots emerged on the Sun for an extended period, which contradicts reconstructions of the open magnetic flux from radionuclide and magnetospheric phenomena data (e.g., Beer et al. 1998; Fligge et al. 1999; Usoskin et al. 2001; Miyahara et al. 2004; Riley et al. 2015) and recent simulations by Saha et al. (2022). This shortcoming is overcome by representing the BMR emergence rate by a single power-law distribution with an exponent depending on the solar activity, as used here (see also Krivova et al. 2021). The new model should thus allow a better constraint on the secular variability of solar irradiance.
Acknowledgments
We thank Kok Leng Yeo for providing the composite of total magnetic flux measurements and Mike Lockwood for providing the open magnetic flux reconstruction. We also thank the referee for the helpful comments. BH was supported by the International Max-Planck Research School (IMPRS) for Solar System Science at the University of Göttingen.
References
- Arge, C. N., Hildner, E., Pizzo, V. J., & Harvey, J. W. 2002, J. Geophys. Res. Space Phys., 107, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Bai, T. 1988, ApJ, 328, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Baranyi, T. 2015, MNRAS, 447, 1857 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. K. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumann, I., Schmitt, D., & Schüssler, M. 2006, A&A, 446, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beer, J., Tobias, S., & Weiss, N. 1998, Sol. Phys., 181, 237 [Google Scholar]
- Berdyugina, S. V., & Usoskin, I. G. 2003, A&A, 405, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Jafarzadeh, S., Schüssler, M., & Solanki, S. K. 2017, Space Sci. Rev., 210, 275 [Google Scholar]
- Bumba, V., & Howard, R. 1965, ApJ, 141, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., & Schüssler, M. 2015, Science, 347, 1333 [Google Scholar]
- Cameron, R. H., & Schüssler, M. 2020, A&A, 636, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Castenmiller, M. J. M., Zwaan, C., & van der Zalm, E. B. J. 1986, Sol. Phys., 105, 237 [CrossRef] [Google Scholar]
- Cattaneo, F. 1999, ApJ, 515, L39 [Google Scholar]
- Cattaneo, F., & Hughes, D. W. 2001, Astron. Geophys., 42,, 18 [Google Scholar]
- Charbonneau, P. 2020, Liv. Rev. Sol. Phys., 17, 4 [Google Scholar]
- Clette, F., & Lefèvre, L. 2016, Sol. Phys., 291, 2629 [Google Scholar]
- Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R., & Peñuela, T. 2010, A&A, 518, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasi-Espuig, M., Jiang, J., Krivova, N. A., & Solanki, S. K. 2014, A&A, 570, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasi-Espuig, M., Jiang, J., Krivova, N. A., et al. 2016, A&A, 590, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeVore, C. R., Boris, J. P., Sheeley, N. R. J., 1984, Sol. Phys., 92, 1 [NASA ADS] [CrossRef] [Google Scholar]
- DeVore, C. R., Boris, J. P., Young, T. R. J., Sheeley, N. R., & Harvey, K. L., 1985, Aust. J. Phys., 38, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Fligge, M., Solanki, S. K., & Beer, J. 1999, A&A, 346, 313 [NASA ADS] [Google Scholar]
- Gaizauskas, V., Harvey, K. L., Harvey, J. W., & Zwaan, C. 1983, ApJ, 265, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, L. J., Beer, J., Geller, M., et al. 2010, Rev. Geophys., 48, RG4001 [Google Scholar]
- Hagenaar, H. J. 2001, ApJ, 555, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Hagenaar, H. J., Schrijver, C. J., & Title, A. M. 2003, ApJ, 584, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Haigh, J. D. 2007, Liv. Rev. Sol. Phys., 4, 2 [Google Scholar]
- Hale, G. E., & Nicholson, S. B. 1925, ApJ, 62, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E., Ellerman, F., Nicholson, S. B., & Joy, A. H. 1919, ApJ, 49, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, K. L. 1992, ASP Conf. Ser., 27, 335 [NASA ADS] [Google Scholar]
- Harvey, K. L. 1993, PhD Thesis, University of Utrecht, The Netherlands [Google Scholar]
- Harvey, K. L., & Martin, S. F. 1973, Sol. Phys., 32, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, K. L., & Zwaan, C. 1993, Sol. Phys., 148, 85 [Google Scholar]
- Hathaway, D. H. 2015, Liv. Rev. Sol. Phys., 12, 4 [Google Scholar]
- Hoeksema, J. T., Wilcox, J. M., & Scherrer, P. H. 1983, J. Geophys. Res., 88, 9910 [CrossRef] [Google Scholar]
- Howard, R. F. 1991, Sol. Phys., 136, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. F. 1996, Sol. Phys., 169, 293 [NASA ADS] [Google Scholar]
- Howard, R., Gilman, P. I., & Gilman, P. A. 1984, ApJ, 283, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffers, S. V., Cameron, R. H., Marsden, S. C., et al. 2022, A&A, 661, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jha, B. K., Karak, B. B., Mandal, S., & Banerjee, D. 2020, ApJ, 889, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J. 2020, ApJ, 900, 19 [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011a, A&A, 528, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011b, A&A, 528, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2013, Space Sci. Rev., 176, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., & Schüssler, M. 2014a, ApJ, 791, 5 [Google Scholar]
- Jiang, J., Hathaway, D. H., Cameron, R. H., et al. 2014b, Space Sci. Rev., 186, 491 [Google Scholar]
- Jiang, J., Cameron, R. H., & Schüssler, M. 2015, ApJ, 808, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Jiao, Q., Jiang, J., & Wang, Z.-F. 2021, A&A, 653, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, H. P., Duvall, Thomas L. J., & Harvey, J. W., et al. 1992, Sol. Phys., 139, 211 [CrossRef] [Google Scholar]
- Koskela, J., Virtanen, I., & Mursula, K. 2019, A&A, 631, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., & Solanki, S. K. 2004, A&A, 417, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Balmaceda, L., & Solanki, S. K. 2007, A&A, 467, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Vieira, L. E. A., & Solanki, S. K. 2010, J. Geophys. Res., 115, A12112 [Google Scholar]
- Krivova, N. A., Solanki, S. K., Hofer, B., et al. 2021, A&A, 650, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Legrand, J. P., & Simon, P. A. 1981, Sol. Phys., 70, 173 [CrossRef] [Google Scholar]
- Leighton, R. B. 1964, ApJ, 140, 1547 [Google Scholar]
- Li, J., & Ulrich, R. K. 2012, ApJ, 758, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Norton, A. A., & Scherrer, P. H. 2007, Sol. Phys., 241, 185 [CrossRef] [Google Scholar]
- Livingston, W. C., Harvey, J., Pierce, A. K., et al. 1976, Appl. Opt., 15, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M., Owens, M., & Rouillard, A. P. 2009, J. Geophys. Res. Space Phys., 114, A11103 [Google Scholar]
- Lockwood, M., Nevanlinna, H., Barnard, L., et al. 2014, Annal. Geophys., 32, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M., Owens, M. J., Barnard, L. A., et al. 2022, Front. Astron. Space Sci., 9, 960775P [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, M., Stamper, R., & Wild, M. N. 1999, Nature, 399, 437 [Google Scholar]
- Mandal, S., Krivova, N. A., Solanki, S. K., Sinha, N., & Banerjee, D. 2020, A&A, 640, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McIntosh, S. W., Wang, X., Leamon, R. J., et al. 2014, ApJ, 792, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Miyahara, H., Masuda, K., Muraki, Y., et al. 2004, Sol. Phys., 224, 317 [Google Scholar]
- Muñoz-Jaramillo, A., Sheeley, N. R., Zhang, J., & DeLuca, E. E. 2012, ApJ, 753, 146 [CrossRef] [Google Scholar]
- Muñoz-Jaramillo, A., Senkpeil, R. R., Windmueller, J. C., et al. 2015, ApJ, 800, 48 [Google Scholar]
- Nèmec, N. E., Shapiro, A. I., Işık, E., et al. 2022, ApJ, 934, L23 [CrossRef] [Google Scholar]
- Nicholson, S. B. 1948, PASP, 60, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Owens, M. J., Lockwood, M., Riley, P., & Linker, J. 2017, J. Geophys. Res. Space Phys., 122, 980 [Google Scholar]
- Parnell, C. E., DeForest, C. E., Hagenaar, H. J., et al. 2009, ApJ, 698, 75 [Google Scholar]
- Petrovay, K., Nagy, M., & Yeates, A. R. 2020, J. Space Weather Space Clim., 10, 50 [EDP Sciences] [Google Scholar]
- Pulkkinen, T. 2007, Liv. Rev. Sol. Phys., 4, 1 [Google Scholar]
- Riley, P., Ben-Nun, M., Linker, J. A., et al. 2014, Sol. Phys., 289, 769 [Google Scholar]
- Riley, P., Lionello, R., Linker, J. A., et al. 2015, ApJ, 802, 105 [Google Scholar]
- Saha, C., Chandra, S., & Nandy, D. 2022, MNRAS, 517, L36 [CrossRef] [Google Scholar]
- Sakurai, T., & Toriumi, S. 2023, ApJ, 943, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Wilcox, J. M., Svalgaard, L., et al. 1977, Sol. Phys., 54, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schrijver, C. J. 2001, ApJ, 547, 475 [Google Scholar]
- Schrijver, C. J., & Harvey, K. L. 1994, Sol. Phys., 150, 1 [Google Scholar]
- Schrijver, C. J., De Rosa, M. L., & Title, A. M. 2002, ApJ, 577, 1006 [Google Scholar]
- Schunker, H., Baumgartner, C., Birch, A. C., et al. 2020, A&A, 640, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., & Baumann, I. 2006, A&A, 459, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheeley, N. R. J., DeVore, C. R., & Boris, J. P., 1985, Sol. Phys., 98, 219 [CrossRef] [Google Scholar]
- Sivaraman, K. R., Gupta, S. S., & Howard, R. F. 1993, Sol. Phys., 146, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Snodgrass, H. B. 1983, ApJ, 270, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Schüssler, M., & Fligge, M. 2000, Nature, 408, 445 [Google Scholar]
- Solanki, S. K., Schüssler, M., & Fligge, M. 2002, A&A, 383, 706 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., Wenzler, T., & Schmitt, D. 2008, A&A, 483, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., Krivova, N. A., & Haigh, J. D. 2013, ARA&A, 51, 311 [Google Scholar]
- Stenflo, J. O., & Kosovichev, A. G. 2012, ApJ, 745, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X., Bobra, M. G., Hoeksema, J. T., et al. 2015, ApJ, 804, L28 [Google Scholar]
- Taylor, P. O. 1989, JAVSO, 18, 65 [NASA ADS] [Google Scholar]
- Temmer, M. 2021, Liv. Rev. Sol. Phys., 18, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, L. M., & Parnell, C. E. 2011, Sol. Phys., 269, 13 [Google Scholar]
- Tlatov, A. G., Vasil’eva, V. V., & Pevtsov, A. A. 2010, ApJ, 717, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G. 2017, Liv. Rev. Sol. Phys., 14, 3 [Google Scholar]
- Usoskin, I. G., Mursula, K., & Kovaltsov, G. A. 2001, J. Geophys. Res., 106, 16039 [Google Scholar]
- van Ballegooijen, A. A., Cartledge, N. P., & Priest, E. R. 1998, ApJ, 501, 866 [Google Scholar]
- van Driel-Gesztelyi, L., & Green, L. M. 2015, Liv. Rev. Sol. Phys., 12, 1 [Google Scholar]
- Vieira, L. E. A., & Solanki, S. K. 2010, A&A, 509, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, L. E. A., Solanki, S. K., Krivova, N. A., & Usoskin, I. 2011, A&A, 531, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, I., & Mursula, K. 2017, A&A, 604, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y. M., & Sheeley, N. R., Jr 1989, Sol. Phys., 124, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. M., & Sheeley, N. R., Jr 1991, ApJ, 375, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. M., Nash, A. G., & Sheeley, Jr, N. R. 1989, Science, 245, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. M., Colaninno, R. C., Baranyi, T., & Li, J. 2015, ApJ, 798, 50 [Google Scholar]
- Wang, Y. M., Ulrich, R. K., & Harvey, J. W. 2022, ApJ, 926, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Wenzler, T., Solanki, S. K., Krivova, N. A., & Fröhlich, C. 2006, A&A, 460, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, P. R., Altrocki, R. C., Harvey, K. L., Martin, S. F., & Snodgrass, H. B. 1988, Nature, 333, 748 [Google Scholar]
- Wu, C.-J., Krivova, N. A., Solanki, S. K., & Usoskin, I. G. 2018, A&A, 620, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yeates, A. R. 2020, Sol. Phys., 295, 119 [Google Scholar]
- Yeo, K. L., Krivova, N. A., Solanki, S. K., & Glassmeier, K. H. 2014, A&A, 570, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, L. Y., Wang, H. N., Du, Z. L., Cui, Y. M., & He, H. 2007, A&A, 471, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, X., & Hoeksema, J. T. 1995a, AdSpR, 16, 181 [NASA ADS] [Google Scholar]
- Zhao, X., & Hoeksema, J. T. 1995b, J. Geophys. Res., 100, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G., Wang, J., & Jin, C. 2013, Sol. Phys., 283, 273 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Increased mean tilt angles
As discussed in Sect. 3.2.2, we use magnetic tilt angles based of white-light observations that are known to be systematically lower than the tilt angles derived from magnetograms. In this section, we analyse how increasing the mean tilt angles will affect the results of our simulation. For this purpose, we conducted a second simulation but with +20% increased mean tilt angles. For a full description of the SFTM setup and results, please refer to Sections 4 and 5.
A.1. Total flux
Starting with Fig. A.1, we find that the total magnetic flux is largely unaffected by the change in tilt angles compared to our results in Sect. 5.1. This was expected, since changing the tilt angle has no effect on the lifetime of BMRs.
A.2. Open flux
The open magnetic flux is plotted in Fig. A.2. We use the same CSSS model setup as described in Sect. 5.2, except that in this case the best-fit open flux is found with a slightly higher Rcusp = 1.45 R⊙. Both the best fit, and the run with Rcusp = 1.5 R⊙ show an overall worse agreement with both Lockwood et al. (2022) (χ2 = 0.303 and χ2 = 0.352) and Owens et al. (2017) (χ2 = 0.593 and χ2 = 0.814) than the original version without increased tilt angles (χ2 = 0.195 and χ2 = 0.313 for Lockwood et al. (2022) and χ2 = 0.277 and χ2 = 0.684 for Owens et al. (2017), respectively). Compared to the case with the original tilt angles (Fig. 5), we find that the best-fit run now overestimates the open flux during several solar minima (14, 15, 16, 18, 20, 21 and 24), as well as during maxima 17 and 20; see the upper panels of Fig. A.2. The open flux from the run with Rcusp = 1.5 R⊙ is slightly higher during all activity levels (lower panels of Fig. A.2), which improves the agreement with Lockwood et al. (2022) and Owens et al. (2017) during solar maximum (except for cycles 17, and 20, where we overestimate the open flux). However, we overestimate the open flux during cycles 14, 15, 16, 18, 20, 21 and 24 which leads to an overall worse agreement.
A.3. Polar field
The +20% mean tilt angles lead to a similar increase in the line-of-sight polar field strength of roughly 20% (see Fig. A.3) compared to Sect. 5.3 (see Fig. 6). The overall agreement of the AMR run with the WSO data is still good, except for cycle 20 (1976) where the AMR run now overestimates the polar field amplitude. Similar to Sect. 5.3 and Jiang et al. (2013), we overestimate the polar fields in cycle 23 by more than a factor of 2.
 |
Fig. A.3. Same as Fig. 6, but with +20% increased mean tilt angles. The WSO data were multiplied by a factor of 1.3 (see Sect. 5.3 for details). |
A.4. Toroidal flux loss
Similar to the total magnetic flux, there is almost no change in the toroidal flux loss from Sect. 5.4 (compare Fig. 7 and Fig. A.4). This is because the toroidal flux loss depends on the longitudinal separation between the polarity patches of BMRs (see Sect. 4.3), which has only a very weak dependence on the mean tilt angle (increasing the mean tilt angles by +20% leads to an increase of merely ∼0.1%).
All Tables
Observational constraints on the emergence rate and the corresponding exponent m for BMRs of a newly starting cycle for different size ranges at different cycle phases.
Comparison of the modelled total and open magnetic flux to observations and independent reconstructions, quantified through their reduced χ2 values.
All Figures
 |
Fig. 1. Parameters describing the spatial distribution of emerging BMRs in our model (red) and as originally derived by Jiang et al. (2011a) (black, only in panels a and b). (a) Mean latitude. (b) Latitude scatter of spot-containing LMRs as a function of the solar cycle phase. (c) Correction factor to the latitude scatter depending on the magnetic flux content of a BMR. (d) Tilt angle scatter as a function of the total magnetic flux enclosed by a BMR. The vertical dashed lines in panels a and b mark the formal beginning and the end of the solar cycle (that is cycle minima). The horizontal bars in panels c and d mark the magnetic flux intervals from the fit, with their y-value being the observational mean value within the flux range (see also Table 2). |
| In the text | |
 |
Fig. 2. (a) Power-law exponent calculated from the total SN (black), and from its portion belonging to the following cycle over the overlap period (the exponent fit in red and the linear transition in blue, see text for details). Only the solid lines were used for the calculation, and the transition between models is at solar minimum (dotted vertical line). (b) and (c) Exponential fit of the power-law exponent of cycles 21 and 22 in the overlap period with cycles 20 and 21, respectively. The “×” symbols are the estimated exponents from Table 3, based on the observations by Harvey (1993) and our analysis of the RGO/SOON record. The error-bars mark the uncertainty ranges in x (time) and y (exponent) directions, see text and Table 3 for details. The horizontal line is the power-law exponent m = −3.94 which corresponds to a SN of zero. |
| In the text | |
 |
Fig. 3. Butterfly diagram for one realisation of the synthetic BMR input record. Different colours encode magnetic flux emerging in BMRs within one-month periods over 2° latitude bins. Blue corresponds to < 1 × 1021 Mx magnetic flux emerged in BMRs, green to 1 − 10 × 1021 Mx, black to 1 − 3 × 1022 Mx, red to 3 − 6 × 1022 Mx and yellow to > 6 × 1022 Mx. The vertical dashed lines mark cycle minima. |
| In the text | |
 |
Fig. 4. Comparison of the simulation results of the total magnetic flux with observations. (a) Evolution of the (3-months smoothed) total magnetic flux from AMRs over cycles 20–24 and comparison with observations. (b) Same as above but over the entire modelled period from 1874 to 2020. (c) and (d) Comparison of all the simulation runs with error estimates overplotted. Plotted quantities: The light blue line in panels a and b is the mean of 100 realisations used as input to the SFTM plus 0.4 times the contribution of SSEs estimated from ordinary differential equations following Krivova et al. (2021), see the main text for details. The total flux from SSEs is plotted in grey. As a comparison we plot the average (black line – all panels) and individual measurements (dark grey symbols – only panels a and b) of three ground based observatories (WSO, NSO KP, MWO). The total magnetic flux from the KP/MDI/HMI composite by Yeo et al. (2014) is shown in light green in all panels. AMR without SSEs is shown in red in panels a and b, and the means of the LMR and SMR runs in panels c and d are shown in blue and green, respectively. The difference between the AMR and LMR runs is shown by the darker green dot-dashed line (which is the lowest curve in in panels c and d). The shaded areas are the standard deviations. The results from the RGO/SOON record are shown by the dash-dotted purple line. |
| In the text | |
 |
Fig. 5. Comparison of the simulation results of the open magnetic flux with observations. The red, blue and green curves are the mean results of 100 realisations used as input to the SFTM for AMR, LMR and SMR, respectively. The top panels show the best-fit run with Rcusp = 1.4 R⊙ while the bottom panels show the run with Rcusp = 1.5 R⊙. The shaded areas are the standard deviations. The results from the RGO/SOON record are shown by the dash-dotted purple line. (a) and (c) Reconstruction of the (1-year smoothed) open magnetic flux from the CSSS model over cycles 20–24. The black line is the reconstruction from the geomagnetic aa-index by Lockwood et al. (2022) and the dark green dashed line shows the in-situ measurements by Owens et al. (2017). (b) and (d) Same but over the entire period from 1874 to 2020. |
| In the text | |
 |
Fig. 6. Comparison of the simulation results of the line-of-sight polar magnetic field with observations. The red, blue and green curves are the mean results of the SFTM for 100 realisations used as input for AMR, LMR and SMR, respectively. The shaded areas are the standard deviations. The results from the RGO/SOON record are shown by the dashed-dotted purple line. (a) The line-of-sight polar field above 55° latitude from model runs and from the measurements from WSO (black) over cycles 20–24 multiplied by a factor 1.3. The northern polar fields are given by the solid lines, and southern polar fields are dot-dashed. (b) Same but over the entire modelled period from 1874 to 2020. |
| In the text | |
 |
Fig. 7. Comparison of the simulated toroidal flux loss with observations. The red, blue, and green curves are the mean results of 100 realisations used as input to the SFTM for AMR, LMR, and SMR, respectively. The shaded areas are the standard deviations. (a) 3-month smoothed sum of the absolute toroidal flux loss of both hemispheres over cycles 20–24. (b) 1-year smoothed sum of the absolute toroidal flux loss of both hemispheres over the entire simulated period from 1874 to 2020. |
| In the text | |
 |
Fig. 8. Relative contribution of LMRs and SMRs to the total flux, polar fields, toroidal flux loss, and the open flux. Left: Original setup from Sect. 5. Right: Increased emergence rate of large ARs (see Sect. 6.1). |
| In the text | |
 |
Fig. 9. Estimating the polar field and the polar field noise. (a) Integrand of Eq. (29) (green solid), the tangent power law at the steepest point (blue dashed) and at the “reversal point” where the exponent of the integrated tangent power law becomes higher than zero (red dotted). (b) Same but for the integrant of Eq. (34). The vertical grey lines mark the lower flux limits of AMR and LMR. |
| In the text | |
 |
Fig. 10. Estimating the toroidal flux loss and the toroidal flux loss noise. (a) Integrand of Eq. (35) (green solid) and the tangent power law at the steepest point (blue dashed). (b) Same but for the integrand of Eq. (36). The vertical grey lines marks the lower flux limits of AMR and LMR. |
| In the text | |
 |
Fig. A.1. Same as Fig. 4, but with +20% increased mean tilt angles. |
| In the text | |
 |
Fig. A.2. Same as Fig. 5, but with +20% increased mean tilt angles. |
| In the text | |
 |
Fig. A.3. Same as Fig. 6, but with +20% increased mean tilt angles. The WSO data were multiplied by a factor of 1.3 (see Sect. 5.3 for details). |
| In the text | |
 |
Fig. A.4. Same as Fig. 7, but with +20% increased mean tilt angles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



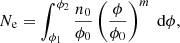
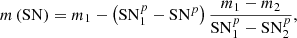
![$$ \begin{aligned} \lambda ^i_{n,\mathrm{J11} }[^\circ ] = \left( 26.4 {-} 34.2\;i + 16.1\;i^2 \right) \frac{\lambda _n}{\langle \lambda _n \rangle _{{12{-}20}}}, \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq3.gif)
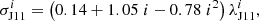
![$$ \begin{aligned} \lambda ^i_n[^\circ ] = \left( 31 \cdot 0.35^{i} - 5 \right) \; \frac{\lambda _n}{\langle \lambda _n \rangle _{{12{-}20}}}. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq6.gif)
![$$ \begin{aligned} \sigma _\mathrm{lat,ARs} [^\circ ] = 0.4\;\lambda ^i_n[^\circ ] + 1. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq7.gif)
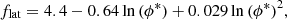
![$$ \begin{aligned} \sigma _\mathrm{lat} [^\circ ] = f_\mathrm{lat} \; \sigma _\mathrm{lat,ARs} . \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq9.gif)
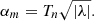
![$$ \begin{aligned} \sigma _\mathrm{tilt} [^\circ ] = 155 - 22.2\ln {(\phi ^*)} + 0.8\ln {(\phi ^*)}^2. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq11.gif)
![$$ \begin{aligned} \begin{aligned} \frac{\partial B_{\rm r}}{\partial t} =&- \Omega (\theta )\frac{\partial B}{\partial \phi } - \frac{1}{R_\odot \sin {(\theta )}} \frac{\partial }{\partial \theta } \left[ v(\theta ) B_{\rm r} \sin {(\theta )} \right] \\&+ \frac{\eta _h}{R_\odot ^2} \left[ \frac{1}{\sin {(\theta )}} \frac{\partial }{\partial \theta } \right( \sin {(\theta )} \frac{\partial B_r}{\partial \theta } \left) + \frac{1}{\sin ^2{(\theta )}} \frac{\partial ^2 B_r}{\partial \phi ^2} \right] \\&+ S(\theta ,\phi ,t) - D_{\rm r}(\eta _{\rm r}). \end{aligned} \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq12.gif)
![$$ \begin{aligned} \Omega (\theta ) = 13.38 - 2.30 \cos ^2{(\theta )} - 1.62 \cos ^4{(\theta )}\,[\mathrm {deg\,day}^{-1}]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq13.gif)
![$$ \begin{aligned} v(\theta )= {\left\{ \begin{array}{ll} v_0\sin {(\pi \lambda /\lambda _0)} \quad [\mathrm m\,s ^{-1}] \quad&|\lambda | \le \lambda _0 = 75^\circ \\ 0&\mathrm{otherwise.} \\ \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq14.gif)
![$$ \begin{aligned} B_{\rm r}^\pm (R_\odot ,\theta ,\phi ) = B_\mathrm{amp} \;\exp {\left\{ -\frac{2[1-\cos {\beta _\pm (\theta ,\phi )}]}{\delta _\mathrm{init} ^2} \right\} }, \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq15.gif)
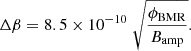
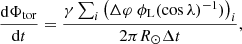
![$$ \begin{aligned} \left|\frac{\mathrm{d} \Phi _\mathrm{tor,hem} }{\mathrm{d} t}\right| = \frac{\left| \sum _i{\left( \Delta \varphi \;\phi _\mathrm{BMR} (\cos {\lambda )^{-1}}) \right)_i}\right|}{4\pi R_\odot } \quad [\mathrm{Mx\,day}^{-1}]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq18.gif)
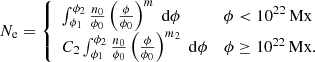
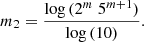
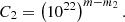
![$$ \begin{aligned} \frac{\mathrm{d} N_\mathrm{p} (\phi )}{\mathrm{d} \phi } = N_{\rm f} \; \phi ^{q} \; [\mathrm{Mx} ^{-1}\,\mathrm{cm} ^{-2}], \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq22.gif)
![$$ \begin{aligned} \Phi _\mathrm{total} = \int _{\phi _1}^{\phi _2} N_{\rm f} \; \phi ^{q}\;\phi \;\mathrm{d} \phi = \frac{N_{\rm f}}{(q+2)} \; \left[ \phi ^{q+2} \right]^{\phi _2}_{\phi _1} \, [\mathrm{G} ]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq23.gif)
![$$ \begin{aligned} \Phi _\mathrm{total} ^\mathrm{Noise} \sim \int _{\phi _1}^{\phi _2} \phi ^{q/2}\;\phi \;\mathrm{d} \phi \sim \left[ \phi ^{q/2+2} \right]^{\phi _2}_{\phi _1} \; [\mathrm{G} ]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq24.gif)
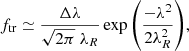
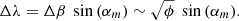
![$$ \begin{aligned} P_\mathrm{Hale}&= \int _{-90^\circ -\alpha _m}^{90^\circ -\alpha _m} \frac{\exp {\left(-\frac{x}{2\sigma _\mathrm{tilt} }\right)^2}}{\sqrt{2\pi }\;\sigma _\mathrm{tilt} } \;\mathrm{d} x \nonumber \\&= \frac{1}{2}\left[\mathrm{erf}{\left( \frac{\alpha _m+90^\circ }{\sqrt{2}\;\sigma _\mathrm{tilt} }\right)} - \mathrm{erf}{\left(\frac{\alpha _m-90^\circ }{\sqrt{2}\;\sigma _\mathrm{tilt} } \right)}\right], \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq28.gif)
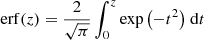
![$$ \begin{aligned} \gamma (\phi )&= P_\mathrm{Hale} -(1-P_\mathrm{Hale} ) = 2P_\mathrm{Hale} -1 \nonumber \\&= \left[\mathrm{erf}{\left( \frac{\alpha _m+90^\circ }{\sqrt{2}\;\sigma _\mathrm{tilt} }\right)} - \mathrm{erf}{\left(\frac{\alpha _m-90^\circ }{\sqrt{2}\;\sigma _\mathrm{tilt} } \right)}\right] -1. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq30.gif)
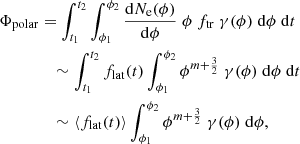
![$$ \begin{aligned} \Phi _\mathrm{polar} ^\mathrm{noise} \sim \int _{\phi _1}^{\phi _2} \mathrm{SD} \Big [\sin {(\alpha _m)}\;\exp {\Big (\frac{-\lambda ^2}{2\lambda _R^2}\Big )}\Big ] \; \phi ^{(m_\mathrm{e} +3)/2} \;\mathrm{d} \phi , \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq33.gif)
![$$ \begin{aligned} \sigma _A = \sqrt{\Big ( 1-\exp {(-\sigma _\mathrm{tilt} ^2)} \Big )\;\Big ( 1+\exp {(-\sigma _\mathrm{tilt} ^2)} \cos {(2\;\alpha _m)}\Big ) \;\Big /\; 2} \quad [\mathrm{rad} ], \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq34.gif)
![$$ \begin{aligned} \sigma _B \approx \frac{1}{2}\Big [\exp {\Big (-\Big (\frac{\lambda -\sigma _\mathrm{lat} }{\sqrt{2}\lambda _R}\Big )^2\Big )} - \exp {\Big (-\Big (\frac{\lambda +\sigma _\mathrm{lat} }{\sqrt{2}\lambda _R}\Big )^2\Big )}\Big ]\; \quad [\mathrm{rad} ], \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq36.gif)

![$$ \begin{aligned} \Phi _\mathrm{polar} ^\mathrm{noise} (\phi ) \sim \int _{\phi _1}^{\phi _2} \sigma _\mathrm{AB} \; \phi ^{(m_{\rm e}+3)/2} \; [\mathrm{cm} ^{-2}]\; \mathrm{d} \phi . \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq38.gif)
![$$ \begin{aligned} \Phi _\mathrm{tor}&= \int _{t_1}^{t_2} \int _{\phi _1}^{\phi _2} \frac{\mathrm{d} N_\mathrm{e} (\phi )}{\mathrm{d} \phi } \; \phi \; \frac{\gamma (\phi )\;\Delta \beta \;\cos {(\alpha _m)}}{2\pi R_\odot \;\cos {(\lambda )}} \;\mathrm{d} \phi \;\mathrm{d} t \nonumber \\&\quad \sim \int _{t_1}^{t_2} \frac{\cos {(\alpha _m)}}{\cos {(\lambda )}} \int _{\phi _1}^{\phi _2} \gamma (\phi )\; \phi ^{m_\mathrm{e} +\frac{3}{2}} \; [\mathrm{cm} ^{-2} \,\mathrm{s} ^{-1}]\; \mathrm{d} \phi \;\mathrm{d} t. \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq39.gif)
![$$ \begin{aligned} \Phi _\mathrm{tor} ^\mathrm{noise}&\sim \int _{\phi _1}^{\phi _2} \mathrm{SD} \Big [\frac{\cos {(\alpha _m)}}{\cos {(\lambda )}}\Big ] \; \phi ^{(m_{\rm e}+3)/2} \;\mathrm{d} \phi \nonumber \\&= \int _{\phi _1}^{\phi _2} \sigma _\mathrm{CD} \; \phi ^{(m_{\rm e}+3)/2} \;[\mathrm{cm} ^{-2} \,\mathrm{s} ^{-1}]\; \mathrm{d} \phi , \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq40.gif)
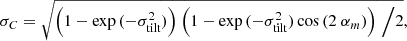
![$$ \begin{aligned} \sigma _D \approx \frac{1}{2}\Big |\Big (\cos {(\lambda )}+\mathrm{SD} \Big [\cos {(\lambda )}\Big ]\Big )^{-1}-\Big (\cos {(\lambda )}-\mathrm{SD} \Big [\cos {(\lambda )}\Big ]\Big )^{-1}\Big |, \end{aligned} $$](/articles/aa/full_html/2024/03/aa45635-22/aa45635-22-eq42.gif)
