| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A386 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202450036 | |
| Published online | 24 October 2024 | |
Spot modelling through multi-band photometry
Analysis of V1298 Tau
1
INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
2
Università degli Studi di Palermo, Dipartimento di Fisica e Chimica, Via Archirafi 36, Palermo, Italy
3
Dipartimento di Fisica e Astronomia, Università degli Studi di Firenze, Via Sansone, 150019 Sesto Fiorentino, FI, Italy
4
Osservatorio Polifunzionale del Chianti, Barberino Val d’Elsa, Florence, Italy
⋆ Corresponding author; alfredo.biagini@inaf.it
Received:
19
March
2024
Accepted:
11
September
2024
Context. Stellar activity is comprised of various phenomena, mainly spots and faculae. It is one of the main sources of noise in exoplanetary observations because it affects both spectroscopic and photometric observations. In studying young active planetary systems, we need to model the activity of the host stars to remove astrophysical noise from our observational data.
Aims. We model the contribution of stellar spots in photometric observations. Through the use of multi-band photometry, we aim to extract the geometric properties of the spots and constrain their temperatures.
Methods. We analysed multi-band photometric observations acquired with the 80 cm Marcon telescope of the Osservatorio Polifunzionale del Chianti of V1298 Tau, assuming the photometric modulation observed in different bands is attributed to cold spots.
Results We constrained the effective temperature of the active regions present on the surface of V1298 Tau, resulting from a combination of spots and faculae. We tested our hypothesis on solar data, verifying that we successfully measured the size of the dominant active region and its averaged effective temperature.
Key words: techniques: photometric / Sun: activity / stars: activity
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Stellar variability involves a variety of inhomogeneities on the stellar surface, produced by the magnetic activity of the interior of the star (Berdyugina 2005), which leads to a broad variety of phenomena, such as stellar spots (Solanki 2003), faculae, and flares (Ballerini et al. 2012). Their intrinsic evolution takes place across a broad range of timescales: minutes for flares, days for the evolution of the active regions (faculae and spots) on the stellar surface, years for active regions cycles, and billions of years for the evolution of the magnetic activity of the star (Berdyugina 2005). Analyses of stellar activity are crucial for understanding the interior processes of stars. Moreover, it is also fundamental for exoplanetary observations, since it is the main source of noise in both photometry and spectroscopy (e.g. Pont et al. 2008; Czesla et al. 2009; Sing et al. 2009, 2011a,b; Agol et al. 2010; Désert et al. 2011; Berta et al. 2011; Ballerini et al. 2012; Micela 2015; Scandariato & Micela 2015).
Stellar spots are regions with a lower temperature with respect to the quiet stellar surface because the local magnetic field configuration halts the convection process, leading to a local cooling of the stellar plasma together with a change in local gravity and magnetic field (Berdyugina 2005; Ballerini et al. 2012). The presence of stellar spots, for instance, can influence both spectroscopic and photometric observations: it can distort spectral lines, thus hampering accurate radial velocity estimations (Pont et al. 2008; Carleo et al. 2020; Damasso et al. 2023). It may also affect the photometric curve analysis by hiding or altering the signal of a transit in stellar light curves (Tsiaras et al. 2018). Furthermore, stellar activity could impact the extraction of the exoplanetary transmission spectra (Changeat et al. 2020), hampering the detection of atmospheric molecules and atmospheric features such as clouds (Pont et al. 2008; Ballerini et al. 2012; Micela 2015).
The modelling of the stellar inhomogeneities on the stellar surface could play a crucial role in the search and characterisation of exoplanetary atmosphere for such missions as the James Webb Space Telescope (JWST; Greene et al. 2016) and for the incoming Atmospheric Remote-Sensing Infrared Exoplanet Large-survey (ARIEL) mission (Tinetti et al. 2018), which is the M4-ESA mission dedicated to studying the exoplanetary atmospheres.
Stellar activity is a very common phenomenon among solar-type stars and it is due to the effects of the magnetic dynamo inside the star (Berdyugina 2005). Because stellar magnetic dynamos increase along with the stellar rotation (Pallavicini et al. 1981; Walter & Bowyer 1981; Pizzolato et al. 2003; Berdyugina 2005) and due to the typical age-rotation relation (Baliunas et al. 1995), we find that stellar activity is particularly strong for young stars (Baliunas et al. 1995; Berdyugina 2005). Despite this, in recent years, young stars have become targets of significant interest because they can provide valuable insights into the early stages of formation and evolution of exoplanetary systems (David et al. 2016; Carleo et al. 2020; Rizzuto et al. 2020; Plavchan et al. 2020; Damasso et al. 2023; Mantovan et al. 2024).
In recent years, ground- and space-based facilities have enabled us to discover thousands of exoplanets orbiting various types of stars, revealing a variety of these bodies with characteristics different from those of our own Solar System. To determine the properties of young planetary systems and analyse their planetary atmospheres, it is fundamental to understand the stellar activity of the host stars to remove its effects from the observational data or to study its impact on planets.
In this paper, we focus our work on the analysis of spots. In particular, we only study the change in temperature in the spots, with the hypothesis that local gravity and magnetic field changes of the spot have much more little effects on stellar observations.
Due to their lower temperature, the spot emission curve differs from that of the quiet photosphere, thereby altering the photometric signal with an effect that decreases along the wavelength observed. This may also distort the spectral lines of the star and lead to incorrect radial velocity measurements (Berdyugina 2005). For instance, during a photometric observation, the presence of a spot occulted by a transiting planet can produce bumps in the observed light-curve. This occurs because the planet obscures a region with a lower flux compared to the unspotted surface, thereby increasing the observed total intensity coming from the star (Czesla et al. 2009; Sing et al. 2011a). On the other hand, also an unocculted spot can affect the measurement of the transit depth (Czesla et al. 2009) since it can affect both photometric and spectroscopic in-transit observations without any clear signs of its presence, leading to incorrect estimations of the exoplanets parameters. In particular, the chromaticity of these effects leads to inaccurate measures of the planetary radius at different wavelengths. The presence of a spot can also mimic a transit and, as a consequence, more than one observation is needed to confirm the presence of a transiting planet.
To remove the effects of the spots on our data, we need to know their properties, positions, and temperature. For this reason, we have developed a method to model the spot configuration in active stars based on a multi-band photometry analysis. For this purpose, we used multiband photometric ground-based observations to model the spots of a very interesting young stellar object (YSO), V1298 Tau, which we describe in Sect. 2. In Sect. 3 we describe the methodology of our observations and in Sect. 4, we present our retrieval method. In Sect. 5 we will discuss the validation of our model using solar data. Our final results are discussed in Sect. 6.
2. Stellar target: V1298 Tau
V1298 Tau is a K0-K1.5 young star (∼20 Myr), with a mass about 1.1 M⊙ located at ∼108 pc from Earth. It is an ultra-fast rotator with a rotational period of less than 3 days (David et al. 2019a). In Table 1 we show the properties of V1298 Tau from the literature.
V1298 Tau properties.
V1298 Tau is one of the youngest stars known to host more than one transiting planet (Suárez Mascareño et al. 2021), which is not a very common occurrence (Latham et al. 2011). The star and its planets have already been studied through photometry, for example, by TESS (Transiting Exoplanet Survey Satellite, Feinstein et al. 2022), and through spectroscopic observations based on radial velocities, for example, by HARPS-N (High Accuracy Radial velocity Planet Searcher for the Northern Hemisphere, Suárez Mascareño et al. 2021).
We know also from previous studies, such as the spectral cross-correlation function (CCF) analysis from Di Maio et al. (2024), that the star shows large spots at high latitudes (> 60°) and smaller spots at low latitudes (< 40°), but the relation between the spectral distortion due to stellar activity and the photometric flux variations of the star is not clear and the spectral analysis of the spots has been based on the hypothesis of non-emitting spots (i.e. black spots, with surface regions with temperature of 0 K) that is not physically correct. In this paper, we are interested in modelling the activity of the star due to spots on the stellar surface using multi-band photometric data to better constrain their temperature and geometric parameters.
3. Observations and data analysis
Using the photometric light curve to model the spots leads to the so-called inverse light curve inversion problem (Luger et al. 2021), namely: we cannot directly see the spots and, as a result, we have many geometrical degeneracies in our models. For example, it is difficult to distinguish spots on each specific hemisphere of the star and we have a degeneracy between temperature, radius, and latitude of the spots. For isolated observations, we have also a degeneracy between the latitude and longitude of the spots that can be broken by observing the star multiple times during its rotation. We aim to break these degeneracies by monitoring the star for a few days through different photometric bands at the same time. We chose to use multi-band photometric observations because we want to take advantage of the chromaticity of the spot contribution to the stellar observation, in fact, we expect to have a different ratio between spots flux and stellar flux at different wavelengths because they correspond (in the first approximation) to two blackbodies with different temperatures. The difference between the spots and stellar flux should decrease at longer wavelengths, all the way to the IR band; for example, a star with T⊙ and a spot with a filling factor of 1% and a ΔT of 1250 K will present variations of 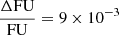 and
and 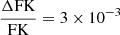 , respectively (Ballerini et al. 2012).
, respectively (Ballerini et al. 2012).
Through simultaneous multi-band photometric observations, we have aimed to estimate the temperature difference between the stellar surface (whose temperature is known from literature) and the spots. We organised multi-band photometric observing campaigns from Osservatorio Polifunzionale del Chianti (OPC) with a Ritchey-Chretien telescope with the following characteristics:
-
80 cm diameter;
-
f/8;
-
field of view (FoV) ∼ 20′ × 20′;
-
Johnson filters B − V − R − I.
Each observing campaign spanned between 3 and 5 days, namely, between one and slightly less than two rotational periods (about 2.8 days) of the star (see Table 2). The star’s location near the ecliptic during the period from October to March poses challenges with respect to coordinating observations for this target. Thus, in addition to the usual constraints arising from potential bad weather conditions, we also had to account for the lunar interference by avoiding days when the Moon passed near the target within a 60° range. Finally, to model the stellar photosphere, we avoided all the days with planetary transits for this target. In conclusion, we observed the star in three different periods: in February 2021, December 2021, and February 2022. We evaluated the best observing runs, selecting only observed sets with S/N > 20. Finally, to avoid problems due to possible spot evolution, we limited our analysis to maximum 3 days (see Sect. 4). We then obtained these final databases:
-
21-22-23, 22-23-24 and 23-24-25 (February 2021) with B, V, and R bands;
-
12-13-14 and 13-14-15 (December 2021) with B, V and R bands;
-
11-12-13 (December 2021) with V and R bands;
-
21-22-23 (February 2022) with V, R and I bands.
Scheme of our observing campaign of V1298 Tau.
We calibrated and analysed the images using AstroImageJ (a software developed by TESS collaboration, Collins et al. 2017) and we applied the so-called differential photometry method: we did not measure the absolute photometry of the target star, but its variability with respect to some carefully chosen stable check stars in the same field of view of V1298 Tau, used as reference. The choice of these check stars required a delicate compromise between the necessity of the highest number of them and the requirement of stability and comparable magnitude with respect to the target. In the FoV of the telescope (20′×20′) around the star, there were only a few stars and most of them were saturated, very faint or variable. Thus, in the end we found only six stable reference stars. We should note that we used the same reference stars for all the datasets.
Using this procedure, we obtained the light-curve of V1298 Tau in the selected photometric bands (shown in Fig. 1). To retrieve the rotational period of the star, we employed a sinusoidal function and an offset to fit the data. This function feeds the nested sampling algorithm Multinest v3.10 (Feroz et al. 2009) to derive parameters best-fit values and errors throughout the python package PyMultiNest v2.12 (Buchner et al. 2014) and with the following likelihood:
 |
Fig. 1. Data observed from OPC in the B, V, and R bands in February 2021 and December 2021 and in V, R, and I bands in February 2022. The plotted line is an estimation of the flux variation of the star obtained by fitting the data by using a sinusoidal function with an offset. For the observations of February 2022 and for the first day of observation of December 2021, B band data were discarded given their signal-to-noise ratio (S/N) of < 20. |
where yn and tn are, respectively, data fluxes and times, 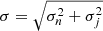 with σn as data errors and σj as the white noise jitter term, introduced to account for unknown source of errors. The algorithm was set to use 1000 live points, leaving all other parameters to their default values. This analysis allowed us to estimate the flux variations (see Table 3) of the star and verify the coherence in each observation.
with σn as data errors and σj as the white noise jitter term, introduced to account for unknown source of errors. The algorithm was set to use 1000 live points, leaving all other parameters to their default values. This analysis allowed us to estimate the flux variations (see Table 3) of the star and verify the coherence in each observation.
Flux variations of V1298 Tau.
Therefore, from Fig. 1, we can observe some variability in the amplitude of the sinusoidal fit, which (on average) tends to decrease at longer wavelengths, consistently with the assumption of a spot-dominated star. The results of this analysis are summarised in Table 3.
4. Forward model and retrieval
We modelled the spot properties (latitude, longitude, radius, and the temperature of the spots) following the approach of Cracchiolo et al. (2021a,b) and we imposed some assumptions:
-
Spots co-rotating with the stellar surface;
-
Non-evolving spots during a rotational period of the star;
-
Approximation of circular spots projected on the stellar surface;
-
Same temperature for all the spots.
With these hypotheses, we aimed to analyse flux variations of the star as generated by the luminosity contrast between the spots and the photosphere. Since the star has an inclination of nearly 90°, as we can see by combining the v sin i value of the star with its rotational period (see Table 1), we had a degeneration in latitude; this was because we could not distinguish the hemisphere the specific spot was located in. Instead, we removed the degeneracy in longitude for the spots thanks to the rotation of the star, so we could retrieve their longitude from the time variations of the stellar flux. We chose to analyse datasets of 3 consecutive days (about a rotational period of the star) in order to avoid relevant contributions from spots evolution. To build our forward model for the retrieval procedure, we divided the star into concentric rings, with a finer division near the limb of the stellar disk to better account for the effect of limb darkening. We also took into account the limb-darkening effect of the star with a linear approximation. We derived the limb darkening coefficients for each possible temperature of the stellar surface (and spots) and different wavelengths using ExoTETHyS package (Morello et al. 2020).
To retrieve the spots properties from our data we used the nested sampling algorithm MultiNest whose priors are shown in Table 4, setting 3000 live points to achieve high precision in the retrieval. It should be noted that spot temperature’s prior is set with a maximum temperature exceeding that estimated for the unspotted surface to include the possibility of retrieving a facula instead of a spot.
Priors on spot parameters for MultiNest retrieval procedure.
To fit the data, our forward model simulates the light curve of the star for each spot configuration tested, calculating at each temporal step the portion of the spotted and unspotted stellar surface visible from Earth. Using these simulated results, it estimates the contributions to the total stellar flux of the spotted and of the unspotted visible surface of the star using the method developed in Cracchiolo et al. (2021a), then it rotates the star of a given time step and uses this loop to calculate the lightcurve of the star. To estimate the fluxes of spots and stellar surface in the chosen range of temperatures (see Table 4), we used the Phoenix models (Claret et al. 2012; Husser et al. 2013) and applied the limb darkening coefficients derived by ExoTETHyS (Morello et al. 2020). Finally, MultiNest calculates the fit and Bayesian evidence to estimate the goodness of the fit and in the end the parameters of our model.
5. Results and discussion
5.1. One-band versus multi-band approach
Figure 2 shows some examples of results obtained from the analysis of single photometric band. It is clear that a degeneracy exists among the latitude of the spots, their radius, and their temperature, as we observe only the emission contrast between the spots and the stellar surface. These degeneracies lead to high uncertainties in spots parameters: in particular, we found a temperature error bar of several hundreds of K, while the latitude spans between 13° and 64° in the R band. By assuming that the stellar spots and the photosphere emit as star surfaces at different temperatures, the emission contrast should change at different wavelengths, producing a different flux variation across different spectral bands. Consequently, through the analysis of simultaneous multi-band photometric observations, we could be able to estimate the spots’ temperature, thereby breaking or at least reducing the degeneracy between the radius, temperature and latitude of the spots. Therefore, we performed a new retrieval procedure imposing for each 3 day sequence that all the bands share the same spot parameters, but different flux scales. We applied our model assuming the simultaneous presence of one, two, three, or four spots on the entire stellar surface. However, due to our temporal coverage and sampling, each model with more than one spot resulted in overfitting of our data, so we chose to model only one spot per dataset. Examples of the resulting corner plots are shown in Figs. 3, 4, and 5 and the retrieved spot temperatures are shown in Table 5. In comparison to the single band analysis, we found a more limited interval for spots temperature, with a decrease in the spot temperature uncertainty by a factor of two and a strong reduction of latitude uncertainties. The constraints on the spots parameters are typically wider when B filter data are not available, as in the observations of 11, 12, and 13 December, 2021 and 21, 22, and 23 February 2022. Finally, we checked for the consistency of the spot positions and geometry along each observing run, plotting all the configurations of the spots with weights (of MultiNest algorithm) over the 0.85 quantiles. The above selection guarantees that only high likelihood values are selected and subsequently shown.
Spot temperature range estimates.
 |
Fig. 2. Comparison of the retrieval posteriors of spots for V1298 Tau, obtained by OPC observations on 23-24-25/02/2021 through a separate analysis for data in B (top) and R (bottom) photometric bands. Blue lines (for the right) and red lines (for the left) mark median values, while black lines mark maximum probability (MAP) values for both images. |
 |
Fig. 3. Corner plot obtained by the retrieval procedure for the multi-band photometric data acquired by OPC in the first run of observation, specifically on February 23-24-25th, 2021. Next, σi represents the jitter parameters and γi the offsets of the forward model used in the retrieval for each band observed (B, V and R). Red lines mark median values, while green lines mark MAP values. |
For each observing run, we found a good compatibility between the radius and position of the retrieved spot, even if there were some hints of evolution on a timescale similar to the rotational period of the star, as we can see comparing the retrieved spots in different 3 day sequences. In each one, we had imposed the absence of evolution for the spot, but we can see how the same spot changes between different sequences of days in the same observing run. An example is shown in Fig. 6 for the best observing run (February 2021) results. The spot configurations here shown correspond to the same time of the star rotation as obtained using data by each 3 day sequence of this observing run. Comparing our results with those of Di Maio et al. (2024), obtained through a CCF analysis of V1298 Tau’s spectra with the hypothesis of non-emitting black spots, our method seems to be sensible only to bigger spots. Our retrieved spots’ projected filling factors range at their peak between 0.015 (February 2021) and 0.20 (December 2021 and February 2022), with respect to the distribution of filling factors of between 0 and 0.15 found showed in Fig. 13 from Di Maio et al. (2024). Our retrieved projected filling factors are higher than those retrieved through spot CCF, but still compatible. Moreover, our big spots are in the same range of latitude found for big spots using CCF. Our higher retrieved projected filling factors could be explained by our not-optimal time coverage that does not allow us to distinguish more than one active areas on the star. The retrieved filling factor is also compatible with results from Morris (2020), even if it is larger for the last set of data (February 2022).
 |
Fig. 6. V1298 Tau spots positions of the three observing sets of February 2021, given by the distribution of solutions of MultiNest retrieval. Each image shows the star as seen on the same day, February 23th 2021. The spots are shown both from a polar view (on the right) and from the equator, i.e. from Earth (on the left). |
The retrieved spot temperature intervals for each observing run are shown in Table 6. It is quite evident a decrease in the retrieved spots temperature between the first period of observations and the other two. A possible scenario is that in our approach we are measuring an effective temperature of the inhomogeneities of the stellar surface, which are more complex than simple spots and what we retrieve is in fact the whole active region of the star with properties that result from the average effect of little surface features (like spots and faculae). Then, our effective temperature should be sensitive, for example, to a change in the ratio between the filling factor of faculae and spots on the star.
Final spots temperature range estimates per observing run.
5.2. Interpretation of ‘spot temperature’
To verify the hypothesis that our analysis retrieves the properties of the complex dominant active region, we analysed the spectroscopic activity indicators of V1298 Tau to get some clues about a possible change of the stellar activity. In particular, we analysed HARPS-N (Cosentino et al. 2012) data acquired over a span of 4 years (2018–2023), using the method described in Di Maio et al. (2020). We looked for temporal variability of activity indicators such as CaII H and CaII K (Fig. 7) and Hα (Fig. 8). Vertical lines in the plots mark the periods of our observations. In Fig. 8, we can see a linear trend for the measured intensity that leads this line from absorption to emission; whereas, in Fig. 7, we can see an increase in the scatter of CaII H and K line intensities over time. These effects point towards a change in activity between the first and the second period of observations, with an increase in the ratio between Hα and CaII H + CaII K line intensities (Fig. 9). Our photometric observations support the reasoning that this evolution could result from a change in the ratio of stellar surface covered by spots and faculae.
 |
Fig. 7. CaII H + CaII K values obtained by HARPS-N for V1298 Tau. The colored lines correspond to our periods of observations: February 2021, December 2021, and February 2022. |
 |
Fig. 8. H alpha values obtained by HARPS-N for V1298 Tau. The colored lines correspond to our periods of observations: February 2021, December 2021, and February 2022. |
 |
Fig. 9. Ratio of Hα/(CaII H + CaII K) values obtained by HARPS-N spectrometer for V1298 Tau. The colored lines correspond to our periods of observations: February 2021, December 2021 and February 2022. |
5.3. Validation of the model: Solar case
For further validation, we tested the model using Sun observations, where photometric data can be directly compared with spatially resolved active regions present on its surface. We used the multi-band photometric data from VIRGO-SPM (Chaplin & Appourchaux 1999), the three-channel sun photometer (SPM) of the Variability of solar IRradiance and Gravity Oscillations (Fröhlich et al. 1997, VIRGO) experiment of the space mission Solar and Heliospheric Observatory (Domingo et al. 1995, SOHO). VIRGO-SPM observed the Sun from 11 April, 1996 until 30 March, 2014 with an image every 60 seconds in three narrow bands at 402, 500, and 862 nm with a bandwidth of about 5 nm.
In particular, we focused on the rotational period starting from 30 December, 2013, when the Sun exhibited a higher level of activity. This was evident through the presence of two large active regions separated by approximately 180° in longitude. We analysed the most active one fitting half period. Subsequently, we rebinned the data to obtain two data points per day (which is reasonable for observations of a long-period star like our Sun). We then applied our method to all three bands simultaneously, assuming one dominant spot. As priors for the retrieval model, we imposed a spot radius between 0 and 0.25 and a spot temperature between 3800 and 5900 K to include the possibility of retrieval of faculae instead of spots. The fit results for the first half-period analysed are shown in Fig. 10.
 |
Fig. 10. Posteriors of the retrieval procedure for the analysis of the active region properties on the Sun during the first half of the rotational period starting on 12/30/2013. Green lines mark MAP values, while red lines mark median values. |
Figure 11 shows the comparison between the simulation of the retrieved solar active region (left panel) and the actual contemporary image of the Sun (right panel), with its real spots, taken from Helioseismic and Magnetic Imager (Schou et al. 2012, HMI), while the bottom panel of the figure shows how our model fit the observed solar data in the three photometric bands. The comparison between the two upper panels of Fig. 11 shows that we were able to constrain with great precision the position of the active regions of the Sun breaking the degeneracy between their latitude and radius; whereas Fig. 10 shows that the degeneracy between active region’s latitude and temperature is also small and confined to a narrow parameter range. Moreover, we found that the retrieved radius encloses not only the main big spot but also all the smaller spots, penumbra areas, faculae, and some of the photosphere inside and around them, leading to very little contrast between the retrieved active region’s temperature and the photospheric temperature. This confirms our initial hypothesis that our procedure retrieves the average temperature of the entire active region of the star.
 |
Fig. 11. Simulated sunspot according to our model results, shown in Fig. 10 (top). Real image of the Sun during the period studied, from HMI (top-left). Bottom panel shows the best fit of our model compared to the observed data for the Sun in all the three bands, from left to right: the B, V, and R filters, shifted in time. |
6. Summary and conclusions
In conclusion, by modelling multi-band photometry and assuming a single spot-dominated surface, we measured an effective temperature of the active regions of V1298 Tau. This result is probably a weighted average of the temperature of the spots, faculae, and photosphere around them. Multi-band photometry allows us to estimate this property, with the bluest photometric bands that provide the strongest constraint. We may reduce the degeneracy between radius, latitude, and temperature of the active regions of the star, thanks to simultaneous multi-band data and, especially, by retrieving its geometric properties correctly (as verified on the Solar case). It is likely that more bands, especially bluer bands, and a denser temporal coverage would help reduce the temperature uncertainties, distinguish spots and other features of the surface, and better constraining their positions. Finally, we developed a method to characterise the surface inhomogeneities of quite active and young stars that has the advantage of using small and medium-sized telescopes over several days. Our results strongly suggest that the evolution of the effective temperature of the active regions may reflect the evolution of stellar activity, indicating the need to monitor the star across a range of timescales. In conclusion, we suggest that this method, together with ground-based high-resolution spectroscopy and photometric observations from space, could improve our understanding of the processes at work in active stars.
Acknowledgments
The authors thank the anonymous reviewer for his/her very useful comments and suggestions. The authors acknowledge the support of Osservatorio Polifunzionale del Chianti for the acquisition of the data. The authors acknowledge the support of the ASI-INAF agreement 2021-5-HH.0. Part of the research activities described in this paper were carried out with contribution of the Next Generation EU funds within the National Recovery and Resilience Plan (PNRR), Mission 4 – Education and Research, Component 2 – From Research to Business (M4C2), Investment Line 3.1 – Strengthening and creation of Research Infrastructures, Project IR0000034– “STILES – Strengthening the Italian Leadership in ELT and SKA”. AP and GM acknowledge the support of grant n. 2022J7ZFRA – Exo-planetary Cloudy Atmospheres and Stellar High energy (Exo-CASH) funded by MUR – PRIN 2022. AB and AP acknowledge the support from the INAF Minigrant of the RSN-2 nr. 16 “SpAcES: Spotting the Activity of Exoplanet hosting Stars” according to the INAF Fundamental Astrophysics funding scheme.
References
- Agol, E., Cowan, N. B., Knutson, H. A., et al. 2010, ApJ, 721, 1861 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [Google Scholar]
- Ballerini, P., Micela, G., Lanza, A. F., & Pagano, I. 2012, A&A, 539, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Berta, Z. K., Charbonneau, D., Bean, J., et al. 2011, ApJ, 736, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carleo, I., Malavolta, L., Lanza, A. F., et al. 2020, A&A, 638, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Changeat, Q., Edwards, B., Al-Refaie, A. F., et al. 2020, AJ, 160, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., & Appourchaux, T. 1999, MNRAS, 309, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collins, K. A., Kielkopf, J. F., Stassun, K. G., & Hessman, F. V. 2017, AJ, 153, 77 [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 84461V [Google Scholar]
- Cracchiolo, G., Micela, G., & Peres, G. 2021a, MNRAS, 501, 1733 [Google Scholar]
- Cracchiolo, G., Micela, G., Morello, G., & Peres, G. 2021b, MNRAS, 507, 6118 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., Huber, K. F., Wolter, U., Schröter, S., & Schmitt, J. H. M. M. 2009, A&A, 505, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damasso, M., Locci, D., Benatti, S., et al. 2023, A&A, 672, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, T. J., Conroy, K. E., Hillenbrand, L. A., et al. 2016, AJ, 151, 112 [NASA ADS] [CrossRef] [Google Scholar]
- David, T. J., Cody, A. M., Hedges, C. L., et al. 2019a, AJ, 158, 79 [NASA ADS] [CrossRef] [Google Scholar]
- David, T. J., Petigura, E. A., Luger, R., et al. 2019b, ApJ, 885, L12 [Google Scholar]
- Désert, J. M., Sing, D., Vidal-Madjar, A., et al. 2011, A&A, 526, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Maio, C., Argiroffi, C., Micela, G., et al. 2020, A&A, 642, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Maio, C., Petralia, A., Micela, G., et al. 2024, A&A, 683, A239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [Google Scholar]
- Feinstein, A. D., David, T. J., Montet, B. T., et al. 2022, ApJ, 925, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C., Andersen, B. N., Appourchaux, T., et al. 1997, Sol. Phys., 170, 1 [CrossRef] [Google Scholar]
- Greene, T. P., Line, M. R., Montero, C., et al. 2016, ApJ, 817, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latham, D. W., Rowe, J. F., Quinn, S. N., et al. 2011, ApJ, 732, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., Foreman-Mackey, D., Hedges, C., & Hogg, D. W. 2021, AJ, 162, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Mantovan, G., Malavolta, L., Desidera, S., et al. 2024, A&A, 682, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micela, G. 2015, Exp. Astron., 40, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Morello, G., Claret, A., Martin-Lagarde, M., et al. 2020, AJ, 159, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, B. M. 2020, ApJ, 893, 67 [Google Scholar]
- Pallavicini, R., Golub, L., Rosner, R., et al. 1981, ApJ, 248, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plavchan, P., Barclay, T., Gagné, J., et al. 2020, Nature, 582, 497 [Google Scholar]
- Pont, F., Knutson, H., Gilliland, R. L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [Google Scholar]
- Rizzuto, A. C., Newton, E. R., Mann, A. W., et al. 2020, AJ, 160, 33 [Google Scholar]
- Scandariato, G., & Micela, G. 2015, Exp. Astron., 40, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Sing, D. K., Désert, J. M., Lecavelier Des Etangs, A., et al. 2009, A&A, 505, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D. K., Pont, F., Aigrain, S., et al. 2011a, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Désert, J. M., Fortney, J. J., et al. 2011b, A&A, 527, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Suárez Mascareño, A., Damasso, M., Lodieu, N., et al. 2021, Nat. Astron., 6, 232 [Google Scholar]
- Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiaras, A., Waldmann, I. P., Zingales, T., et al. 2018, AJ, 155, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F. M., & Bowyer, S. 1981, ApJ, 245, 671 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Data observed from OPC in the B, V, and R bands in February 2021 and December 2021 and in V, R, and I bands in February 2022. The plotted line is an estimation of the flux variation of the star obtained by fitting the data by using a sinusoidal function with an offset. For the observations of February 2022 and for the first day of observation of December 2021, B band data were discarded given their signal-to-noise ratio (S/N) of < 20. |
| In the text | |
 |
Fig. 2. Comparison of the retrieval posteriors of spots for V1298 Tau, obtained by OPC observations on 23-24-25/02/2021 through a separate analysis for data in B (top) and R (bottom) photometric bands. Blue lines (for the right) and red lines (for the left) mark median values, while black lines mark maximum probability (MAP) values for both images. |
| In the text | |
 |
Fig. 3. Corner plot obtained by the retrieval procedure for the multi-band photometric data acquired by OPC in the first run of observation, specifically on February 23-24-25th, 2021. Next, σi represents the jitter parameters and γi the offsets of the forward model used in the retrieval for each band observed (B, V and R). Red lines mark median values, while green lines mark MAP values. |
| In the text | |
 |
Fig. 4. Same as Fig. 3, but in the case of B, V, and R bands on December 13-14-15, 2021. |
| In the text | |
 |
Fig. 5. Same as Fig. 3, but in the case of V, R, and I bands on February 21-22-23, 2022. |
| In the text | |
 |
Fig. 6. V1298 Tau spots positions of the three observing sets of February 2021, given by the distribution of solutions of MultiNest retrieval. Each image shows the star as seen on the same day, February 23th 2021. The spots are shown both from a polar view (on the right) and from the equator, i.e. from Earth (on the left). |
| In the text | |
 |
Fig. 7. CaII H + CaII K values obtained by HARPS-N for V1298 Tau. The colored lines correspond to our periods of observations: February 2021, December 2021, and February 2022. |
| In the text | |
 |
Fig. 8. H alpha values obtained by HARPS-N for V1298 Tau. The colored lines correspond to our periods of observations: February 2021, December 2021, and February 2022. |
| In the text | |
 |
Fig. 9. Ratio of Hα/(CaII H + CaII K) values obtained by HARPS-N spectrometer for V1298 Tau. The colored lines correspond to our periods of observations: February 2021, December 2021 and February 2022. |
| In the text | |
 |
Fig. 10. Posteriors of the retrieval procedure for the analysis of the active region properties on the Sun during the first half of the rotational period starting on 12/30/2013. Green lines mark MAP values, while red lines mark median values. |
| In the text | |
 |
Fig. 11. Simulated sunspot according to our model results, shown in Fig. 10 (top). Real image of the Sun during the period studied, from HMI (top-left). Bottom panel shows the best fit of our model compared to the observed data for the Sun in all the three bands, from left to right: the B, V, and R filters, shifted in time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \ln {p({y_n},{t_n},{\sigma },\theta )} = -1/2\sum _n \left[(y_n-F(t_n,\theta ))^2/\sigma ^2 + \ln 2 \pi \sigma ^2\right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa50036-24/aa50036-24-eq3.gif)