| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A201 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202449484 | |
| Published online | 10 October 2024 | |
Lifetime of starspots on detached eclipsing binaries: Detecting the effects of tides on stellar activity
1
School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2
School of Physics and Astronomy, China West Normal University, Nanchong 637002, China
3
Institute for Frontiers in Astronomy and Astrophysics, Beijing Normal University, Beijing 102206, China
4
Department of Astronomy, Beijing Normal University, Beijing 100875, China
5
Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China
Received:
4
February
2024
Accepted:
19
July
2024
Context. Tidal deformation breaks the axisymmetric structure of stars, and this may affect stellar activity. This effect has been demonstrated in theoretical analyses and simulations, but it lacks observational support. In this paper, we use spot-modulated detached binaries to study the effect of tides on stellar activity. We show this effect by analyzing the properties of the spot lifetime, the harmonic decay timescale, and the orbital parameters.
Aims. We aim to explore the differences in spot lifetimes between binaries and single stars, the main mechanisms of spot decay in binaries, and the correlation between orbital parameters and spot lifetimes. These differences will provide clues to the effect of tides on stellar activity.
Methods. We collected data of 311 spot-modulated detached binaries and 3272 single stars. The relative orbital parameters of the binaries were derived by combining Kepler photometry, stellar atmospheric parameters from LAMOST DR9 and Gaia DR3, and 2MASS photometry. We then used the ACF method to obtain the rotational periods, lifetimes, and harmonic decay timescales. Finally, we analyzed the correlation between the lifetime of spots and orbital parameters, explored the dominant decay mechanism of spots, and examined the differences in spots for binaries and single stars.
Results. The relative lifetime of a starspot is correlated with the sum of the fractional radii, the orbital eccentricity, and the synchronization ratio. Longer lifetimes are observed in close, circular, and synchronous binaries than in the other binaries. The main mechanism for the decay of star spots in binaries is large-scale convective motion. However, on close, cool, and fast-rotating binaries, horizontal diffusion or subphotospheric diffusion are dominant. Compared to single stars, the median lifetime of a starspot on binaries was found to be longer. Moreover, this difference decreases with rotation period. Additionally, it should be noted that spots on binaries experience increased horizontal or subphotospheric diffusion at the same rotation period and effective temperature.
Conclusions. According to the observation results, we conclude that the lifetime of starspots on detached close binaries is affected by tidal interactions.
Key words: stars: activity / binaries: eclipsing / stars: rotation / starspots
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Tidally locked stars maintain fast rotation in close binary systems (Lurie et al. 2017), and they thus sustain a high level of activity (Holzwarth & Schüssler 2003a). At the same time, tidal deformation can disrupt the axis symmetric structure of the star, which might affect convection and magnetic fields. This would also have some effects on the stellar activity. The theoretical analysis of Wei (2022) showed that the large-scale tidal flow can induce magnetic dynamo action on solar-like stars with an orbital period of 2 or 3 days. When the system is synchronized, the large-scale tidal flow vanish. However, the tidal deformation still affects the stellar activity. Holzwarth & Schüssler (2003b,a) analyzed the stability of magnetic flux tubes in the convection zone of stars under tidal deformation. They found that the nonlinear tidal effect caused some stable regions to become unstable, which increased the rise of a magnetic flux tube. While it rose, the tide caused the magnetic flux tube to cluster. This would cause the stellar activity to become more vigorous.
The activity index of photometry and chromosphere, preferential longitude, and the lifetime of a starspot on the binaries are observational clues for confirming the effect of the tide on stellar activity. Gaulme et al. (2020) found that the photometric activity indexes of binary red giants are larger by about one order of magnitude than those of single red giants when the rotational periods and stellar parameters were similar. This finding was further confirmed by the chromospheric indexes (Gehan et al. 2022). In addition to the activity index, binaries also exhibit differences in the preferred longitude of the starspot compared to that of the single star. The preferential longitude refers to the phenomenon that starspots occur more frequently or persist for longer periods at some longitudes. Observations of RS CVn, SS Boo, and MM HER indicated that as the orbital period increases from shorter than one day to over 10 days, which is the preferred longitude transition from a fixed longitude to a migrating longitude (Heckert & Ordway 1995). This suggests a correlation between tidal effects and starspot distribution (Holzwarth & Schüssler 2003b). Over the past 30 years, researchers have studied the active longitudes of roughly 20 modulated detached binaries through the light curves or Doppler images (Berdyugina 2005; Lanza et al. 2006; Savanov 2009; Zhang et al. 2014; Siltala et al. 2017; Green et al. 2019; Pan & Zhang 2023). The preferred longitude variations of these binaries are similar to the results of Heckert & Ordway (1995). Thus, the preferred longitude phenomenon is a good observational evidence for studying the tidal effects on starspots. It should be noted that for some binaries, the active longitudes are determined by a one or two spot model light curve. Basri & Shah (2020) have demonstrated that the light curves of complex spot distributions cannot be modeled with one or two spots. Consequently, it is difficult to determine a reliable preferred longitude from the light curves. This prevents us from using large samples of light curves to study the details of preferred longitude versus tide.
The spot lifetimes of binaries provide another clue for studying the tidal effect on stellar activity. Hussain (2002) found that the spot lifetimes of binaries are longer than those of single stars. Their spot lifetimes were derived from cross-correlating Doppler images between different epochs. Spot lifetimes can also be inferred from light curves. Giles et al. (2017) developed the auto-correlation function (ACF) method to derive the spot lifetimes from light curves. Santos et al. (2021) used simulations to show that the ACF method can estimate the lower limit of spot lifetimes. Pan et al. (2020) and Wang et al. (2022) used the ACF method to derive spot lifetimes for 15 binaries. Unfortunately, they did not find any obvious evidence for longer spot lifetimes in binaries.
Since observational evidence is rare, little is known about the effect of tides on stellar activity. A large sample of active binaries is useful to address this question and to study the interactions between tidal effects, convection, and magnetic fields. Of the three clues mentioned above, the lifetimes are easily obtained from the ACF of the light curves. In addition, spot decay mechanisms can be revealed from the light curve by the ratio of the harmonic decay timescales (Arkhypov et al. 2018). Therefore, to study the effect of tides on stellar activity, we derived the lifetimes and harmonic decay timescales of spots on detached binaries and single stars using Kepler light curves. To study more details, we need stellar atmospheres and orbital parameters. The Guoshoujing Telescope (The Large Sky Area Multi-Object Fiber Spectroscopic Telescope, LAMOST) performed the LAMOST-Kepler survey (De Cat et al. 2015; Ren et al. 2016; Zong et al. 2018, 2020; Fu et al. 2020), which made follow-up spectroscopic observations of as many objects as possible in the Kepler field. This survey provides stellar atmosphere parameters for binaries and single stars. Accurate orbital solutions require light curves and radial velocity curves. The LAMOST-Kepler survey provides radial velocity curves, but not in sufficient numbers. Fortunately, it is possible to obtain relative orbital solutions from the light curves. We combined Kepler photometry, LAMOST spectral data, Gaia DR3 data, and the Two Micron All-Sky Survey (2MASS) photometry to derive the relative orbital solution. These solutions and the starspot parameters were then combined to investigate the starspot properties.
We describe the sample and the data in Sect. 2. The binary modeling and starspot analysis are described in Sect. 3. The results are presented and discussed in Sects. 4 and 5, respectively. A conclusion is given in Sect. 6.
2. Sample selection and data
2.1. Samples
The spot-modulated binaries were selected from the catalog of (Lurie et al. 2017, hereafter L17), which identified 873 spot-modulated binaries among 2278 eclipsing binaries (EB) from the Kepler Eclipsing Binary Catalog1 (Prša et al. 2011; Kirk et al. 2016, KEBC). KEBC and L17 provided the orbital periods and the rotational periods for these sources, respectively. The range of orbital and rotational periods is [0.254, 958] and [0.45, 119] days, respectively. Lurie et al. (2017) pointed out that EBs with orbital periods exceeding 10 days are predominantly eccentric and unsynchronized. These EBs are also important for studying the tidal effect on the starspot. Thus, EBs with orbital periods longer than 10 days are required for this study. However, as the orbital period increases, the tidal force decreases rapidly. Thus, EBs with orbital periods shorter than 20 days may represent a suitable sample for investigating the effect of tides on starspots. Using this cutoff period, we obtained 692 EBs from L17. After cross-matching with the LAMOST DR9 LRS catalog (Wang et al. 1996; Su & Cui 2004; Cui et al. 2012; Zhao et al. 2012; Wu et al. 2010, 2014; Luo et al. 2004, 2012), we identified 268 sources in that catalog. Following a cross-match with Gaia DR3 (Gaia Collaboration 2023), 600 sources were identified, whereas 372 sources were only observed by Gaia DR3. A total of 640 sources with atmospheric parameters were obtained by combining these samples. The standard deviation of fitting residuals in this study is approximately 0.001. Therefore, a light curve with an eclipse depth more shallow than 0.001 cannot provide accurate parameters. We excluded 36 sources with such a shallow eclipsing depth. The total number of eclipsing binaries after the exclusion was 604. It should be noted that 199 sources exhibit no apparent secondary eclipsing, implying that either the secondary eclipses of these sources are obscured by the presence of starspots, or they do not exist. To identify the secondary eclipses of these sources, we applied the Gaussian process algorithm outlined in Sect. 3.1. As a result, only 55 sources were found to have detectable secondary eclipses. Finally, 460 sources were collected to create the sample, which is depicted in Fig. 1 with colored squares. In addition, the KEBC contains many overcontact and semidetached eclipsing binaries with short orbital periods (< a few days). L17 have identified contact binaries without well-defined eclipses and excluded them from the spot-modulated binaries. We fit the light curves with the detached eclipsing model. We then excluded the curves that did not fit the detached eclipsing model well (see Sect. 4.1). This further reduced the contamination from overcontact and semidetached eclipsing binaries.
To compare the properties of starspots on binary and single stars, it is necessary to use a sample of single stars. McQuillan et al. (2014) identified 34 030 single stars with starspot modulation and rotation periods ranging from 0.2 to 70 days. These sources consist of main-sequence stars and were observed by the Kepler mission. Through cross-matching with the LAMOST DR9 LRS catalog, we obtained 8035 sources with rotation periods shorter than 20 days. To minimize contamination from pulsations and binaries, we excluded them by consulting the Gaia DR3 catalog of variable stars (Gaia Collaboration 2022), the General catalog of Variable Stars (Kazarovets et al. 2022), KEBC, and the double-line spectroscopic binary catalog (Zhang et al. 2022). We finally had 5183 sources. They are shown in Fig. 1 with gray circles.
 |
Fig. 1. Sample of starspot-modulated binaries and single stars. The colored squares are binaries. The colors of the squares represent the orbital periods of the binaries. The gray circles represent single stars. |
2.2. Data collection
We used Kepler light curves in long-cadence (LC) mode with a sampling of 29.4 min between 2009 and 2013 (Prša et al. 2011; Slawson et al. 2011; Kirk et al. 2016) to obtain the binary orbital solution and to analyze the starspot modulations. The Kepler photometric data were downloaded from MAST2, which offers data that were preprocessed by the Presearch Data Conditioning (PDC) module (Stumpe et al. 2012) with discontinuities, systematic trends, and outliers corrected for the raw data. The PDC data were implemented in this study. However, the data still exhibit a long-term trend. Therefore, a polynomial was fit to the light curve of each quarter to correct for it. The time system used in Kepler data is BJD. KEBC provides linear ephemerides for EBs, including orbital period and BJD0. We calculated the phases of all the LC measurements with these ephemerides.
The stellar atmosphere parameters were obtained from the LAMOST DR9 LRS catalog and Gaia DR3 data. The parameters of the stellar atmosphere from the LAMOST DR9 LRS catalog were measured from three combined spectra taken over three successive epochs on the same night. For sources observed on different nights, the catalog provides the parameters for each night, and the mean value was adopted. The errors of Teff, log g, and [Fe/H] for most stars in the sample are smaller than 190 K, 0.32 dex, and 0.21 dex, respectively (Ren et al. 2016). The atmosphere parameters of Gaia DR3 were derived from the General Stellar Parameterizer from Photometry (GSP Phot). The typical biases of GSP Phot are 110 K for Teff and 0.2−0.25 dex for log g, and they strongly depend on the data quality (Andrae et al. 2023).
In order to estimate the radii of the binary components, the multiband photometric data consist of G, GBP, and GRP from Gaia DR3, and J, H, and Ks from 2MASS (Skrutskie et al. 2006) were adopted to construct the spectral energy distribution (SED) of binaries.
3. Method
3.1. Physical parameters of the binaries
The orbital solutions of binaries were obtained by fitting their light curves with forward detached eclipsing binary models generated by the code PHOEBE 2.4.73 (Prša & Zwitter 2005; Prša et al. 2016; Horvat et al. 2018; Jones et al. 2020; Conroy et al. 2020). In the absence of radial velocity curves, we only derived the relative orbital parameters, which include the temperature ratio T2/T1, the sum of the fractional radii (R1 + R2)/a, the radius ratio R2/R1, the inclination i, and the eccentricity e, where T1, T2, R1, R2, and a denote the temperatures of the primary and secondary, the radii of the primary and secondary, and the semimajor axis, respectively. To constrain the properties of the primary star, stellar atmosphere parameters from LAMOST or Gaia were used during the fitting process. The binary fitting is affected by spot modulation, so that the out-of-eclipse signals were modeled using the Gaussian process (GP) method (Rasmussen & Williams 2006), and spot signals in the eclipse phase were predicted by this GP model. The GP kernel developed by Angus et al. (2018), which is suitable for modeling the quasi-periodic signal, was used to fit the GP. This GP kernel is described as follows:
where ki, j is the covariance between the ith and the jth data. ti and tj are the epochs of the ith and the jth data, respectively. Here A, l, Γ, P, and σ are free parameters. The optimal parameters of GP model were derived with the PYTHON module SCIKIT-LEARN4 (Pedregosa et al. 2011). Then, we fit the binary to the light curve after subtracting the GP model. The process of binary fitting consists of two steps. First, a trial Markov chain Monte Carlo (MCMC) sampling was performed to find the initial parameters. Subsequently, based on these initial parameters, the optimal parameters were obtained using the least-squares method.
The out-of-eclipse signals consist of the spot signal, the ellipsoidal variation, and the reflection effect. To prevent GP from removing all the signals, an iteration procedure was performed after the first binary fit. GP fitting and binary fitting were performed alternately until the maximum relative errors of the orbital parameters between two successive iterations were smaller than 0.01. During the iteration process, the GP fit was performed on the out-of-eclipse signal after subtracting the PHOEBE model (see details about the iteration procedure in Wang et al. 2022). An example of the light-curve fitting is shown in Fig. 2. In the following, KIC 10935310 is used as an example to illustrate all the methods used in this work. The orbital parameters of KIC 10935310 are listed in Table 1.
 |
Fig. 2. The photometry and model of binary. (a) Binary modeling of KIC 10935310. The top panel shows the light curve and the Phoebe model. The blue points show observational data, and the red lines show the best-fitting model. The lower panel shows the residuals. The green points show the fitting residuals. (b) SED fit for KIC 10935310. The blue circles with error bars show observational data. The error bars from Gaia photometry are barely visible because their error is smaller than mmag. The green bands show the SED models. |
Physical parameters of the binaries.
The mass ratio plays a crucial role in tidal interactions and therefore is an important parameter to consider. However, without a radial velocity curve, it becomes challenging to accurately determine the mass ratio based on the light curve alone. Nonetheless, when the effective temperatures and radii of the components are known, we can estimate their masses using stellar models. To estimate the effective temperature of the primary, we relied on the LAMOST or Gaia atmospheric parameters. Similarly, the temperature of the secondary was estimated based on the temperature ratio. By fitting the multiband photometric data with an SED model, we obtained an estimate of radii. The SED fitting requires absolute magnitudes of the multiband data, which were derived by subtracting the distance modulus and extinction from the observed magnitudes. Gaia DR3 provides the distances needed for this calculation, and the extinction values were obtained from the Bayestar2019 3D dust map (Green 2018; Green et al. 2019). The SED models used in this study were generated with the code PHOEBE. The multiband data are the mean photometry from different epochs. While these values fall within the range of minimum and maximum magnitudes of the binary, they do not provide precise information about the epoch. As a result, the SED model is represented as a band between the minimum and maximum magnitudes, as shown in panel b of Fig. 2. During the SED fitting process, the orbital parameters and the effective temperatures were set to the values obtained from the light-curve fitting and the LAMOST or Gaia catalog, with the exception of the radius ratio. The radius ratio, the semimajor axis, and the reddening were allowed to vary within appropriate ranges based on the results derived from the light-curve fitting and dust maps. The fit was performed using the least-squares method. Figure 2 illustrates an example of the SED fitting result. Subsequently, the Padova stellar models5 (Girardi et al. 2000; Bressan et al. 2012) were used to estimate the masses based on the radii and effective temperatures of the components. The metallicity of the stellar model was set to the value obtained from the LAMOST or Gaia catalog. By applying this approach, we estimated the mass ratio.
3.2. Staspot analysis
Subtraction of the binary model from the light curves results in the starspot-modulation signal, as shown in Fig. 3. The rotational period and starspot decay timescale were determined using the autocorrelation function (ACF) of the starspot signal. Figure 3 shows that the interval between two consecutive peaks represents the rotational period, and the peak decay is caused by starspot decay and emergence. Giles et al. (2017) used an underdamped simple harmonic oscillator (uSHO) equation to depict the behavior in the first few periods of the ACF, and inferred the period and decay timescale by fitting the ACF with uSHO. Santos et al. (2021) illustrated that the exponential decay of uSHO may underestimate the decay timescale, suggesting that linear decay is more appropriate to evaluate the decay timescale. Therefore, we adopted the linear decay equation
 |
Fig. 3. Starspot analysis for KIC 10935310. (a) A segment of the starspot signal. (b) ACF of the starspot signal. The blue points show the ACFs. The red line shows the best-fitting linear decay model. (c) Time sequence of Am, E2. The first and second harmonic components are shown as blue and orange lines, respectively. (d) ACFs for panel c. The first and second harmonic components are shown as blue and orange dots, respectively. |
where τAR is the decay timescale [days] of the ACF, P is the stellar rotation period [days], A and B the amplitudes of the cosine terms, and y0 is the offset. The code EMCEE6 was used to perform the fitting in this work.
In addition to the decay timescale of the whole signal, the decay timescale of harmonics components also reveals the properties of starspot and convection, as shown by Arkhypov et al. (2018) and their series works. It was discovered that the decay timescales (τm, m is the harmonics number) of the square harmonic amplitude are related to the turnover time (τMLT) of a standard convection cell, and the derivative dτm/dm is related to the properties of turbulence, differential rotation, and horizontal diffusion process. To analyze these properties of the binary, the algorithm of Arkhypov et al. (2016) was employed to acquire these decay timescales. This algorithm is briefly described as follows (we refer to Arkhypov et al. 2015, 2016 for more details):
-
Performing the Fourier transform for the light curve of each cycle to obtain the amplitudes Am, E of the harmonics components, where E is the number of the cycle.
-
Calculating the autocorrelation function rm(Δt) of the time sequence of Am, E2, where Δt = E × P.
-
Calculating the harmonics decay timescale τm = −P/ln[rm(P)].
-
Calculating the derivative β21 = [∂log(τm)/∂log(m)]m = 2 ≈ log(τ2)−log(τ1).
The algorithm was performed for m = 1, 2. Figure 3 shows an example of the time sequence of Am, E2 and the corresponding ACF.
The root mean square (RMS) scatter of the normalized light curves was adopted by Giles et al. (2017) to represent the spot size. However, the amplitude of the photometric spot signal also depends on the inclination, spot temperature, and spot latitude. The amplitude of the photometric spot signal is positively correlated with the spot size and negatively correlated with the spot temperature, and the spot latitude and inclination change the project area of the spot to change the signal amplitude. In addition, the signal amplitude of an axisymmetric spot in the polar region is close to zero, regardless of the size and temperature of the spot. Although the amplitude or RMS of the spot signal is not a perfect representation of the size and temperature of the spot, it is the widely used photometric index of stellar activity (Mathur et al. 2014, 2023; Salabert et al. 2016; Karoff et al. 2018; Gaulme et al. 2020). We calculated the RMS of the binaries and single stars, which is used to avoid some possible biases in the comparative analyses (see Sect. 4.3).
4. Result
4.1. Result of modeling the binary
The outcome of modeling the binary was verified with the residual χ2. After applying the sigma-clipping technique, we eliminated sources with extreme χ2 values. The average χ2 of the remaining sources is approximately 15. Subsequently, we visually inspected the fit curve to eliminate unsuitable fits. Consequently, 318 sources successfully passed the check. Figure 4 displays the histograms of the orbital parameters of these sources. We defined the primary star as the hotter component of the binary. As a result, the temperature ratio does not exceed one. The orbital parameters of these sources are listed in Table 1.
 |
Fig. 4. Histograms of the orbital parameters: the orbital period Porb, the temperature ratio T1/T1, the sum of the fractional radii (R1 + R2)/a, the radius ratio R2/R1, the inclination, the eccentricity, and the mass ratio q. |
The accuracy of the fitting parameters had to be verified because we lack the radial velocity curve. To check the fit parameters, we adopted a reference sample of 15 starspot-modulated binaries collected by Wang et al. (2022), whose binary parameters were derived from a combination of light curves and radial velocity curves. The parameters collected from the original references are listed in Table A.1. The parameters of most sources in our sample fall within the range of the reference sample. A comparison of the parameters obtained in this study and those from the reference is presented in Fig. 5. The bias (i.e., the mean difference) and dispersion (i.e., the standard deviation of the differences) of these parameters are detailed in Table 2.
 |
Fig. 5. Comparison of the orbital parameters obtained here and in the references. The solid lines are the 1:1 diagonal lines. The error bars represent the errors of the parameters obtained from the references. The square indicates the outlier KIC 6859813. |
Bias and dispersion of the orbital parameters.
As depicted in Fig. 5, most sources exhibit consistent temperature ratios, with the exception of one source. When this outlier is excluded, the bias and dispersion of the temperature ratio are reduced to −0.013 and 0.031, respectively. This dispersion is comparable to the mean error of 0.023 given in the references. We then examined the outlier. The outlier has a high eccentricity of 0.3806. This orbit causes the secondary eclipse depth (0.0066) to be much smaller than the primary eclipse (0.1935), which caused our algorithm to misinterpret it as a low temperature ratio. As show in panel e of Fig. 5, our algorithm also underestimated the eccentricity of KIC 6859813 and the SED fit was unable to estimate the mass ratio of this source. However, the (R1 + R2)/a, R2/R1, and inclination are not affected by this high eccentricity. Our algorithm underestimated the exact eccentricity of 0.3806 to be 0.2429. If sources with an eccentricity estimated by our algorithm greater than 0.2429 had received a low temperature ratio and eccentricity estimate, approximately 2% of sources would have poor estimates of these two parameters. It is possible that this proportion may be smaller, as the eccentricity of KIC 6781535 (ecc = 0.2510) was obtained accurately. The values of (R1 + R2)/a are closely aligned with the references because they can be easily derived from the light curves. A significant dispersion is observed in R2/R1 due to the degeneracy between the radius ratio and the other parameters. The uncertainty of R2/R1 also impacts the accuracy of the inclination, with some sources exhibiting biases of approximately 1 degree in inclination. When the outlier is excluded, the bias and dispersion of the eccentricities are reduced to 0.0027 and 0.017, respectively. Sources with an eccentricity higher than 0.1 are rare. Similarly, our sample also shows a scarcity of sources with high eccentricities, as depicted in Fig. 4. Hence, estimating the uncertainty of eccentricity with the reference sample is feasible. The mass ratio derived from SED fitting exhibits a dispersion of 0.141, which is unexpectedly lower than that obtained for the radius ratio.
4.2. Properties of starspots on binaries
No ACF fitting result was obtained for 7 out of the 318 EBs. Consequently, a total of 311 sources were selected for the analysis of the starspot properties. The starspot parameters of these sources are listed in Table 3. Histograms depicting the rotational period, the decay timescale of starspots, the derivation of the harmonic decay timescale β21, and the RMS are shown in Fig. 6. The rotation periods range from 0.53 to 34.07 days, and most sources rotate faster than 10 days. The average decay timescale is approximately 144 days. The time baseline of a Kepler observation is about 1470 days. A decay timescale longer than 1000 days derived with ACF fitting should be considered with caution. The peak value for β21 is around −0.667. The mean RMS value for starspots is approximately 0.0088 mag.
Spot parameters.
 |
Fig. 6. Histograms of the starspot parameters, including the rotational periods, the decay timescale, the derivative of the harmonic decay timescale, and the RMS. |
The relative lifetime τ/Prot was employed by Basri et al. (2022) to investigate the decay of starspots on single stars. In order to facilitate a convenient comparison between the decay properties of starspots on binaries and those on single stars, this parameter was used here to explore the decay of starspots. The correlations between τ/Prot and orbital parameters are depicted in Fig. 7. For each orbital parameter, the sample was divided into ten bins based on the parameter value, with an equal number of sources in each bin. Subsequently, the median value of τ/Prot was calculated for each bin and is presented in Fig. 7. The Pearson correlation coefficient and p value are listed in Table 4.
 |
Fig. 7. Correlation between the orbital parameters and the relative decay timescale of starspots. Since the relative decay time crosses about 3 orders of magnitude, the logarithmic scale is used to display them. The blue dots show the data from the entire sample. The red dots and lines represent the median of τ/Prot in the orbital parameter bins. For panel e, because the circular sources are plotted in one bin, only six medians are shown in panel e. |
Correlation between the orbital and starspot parameters.
As displayed in panels a and b of Fig. 7, the temperature ratio and τ/Prot are not correlated, but the sum of the fractional radii (R1 + R2)/a is positively correlated with τ/Prot. The median values of R2/R1 exhibit a negative correlation with that of τ/Prot, which is obscured by the large standard deviation of R2/R1 as shown in panel c. The flat trend in the range 0.4 < R2/R1 < 1.1 shows that this correlation with should be treated with caution, however. The inclination correlates negatively with τ/Prot, demonstrated in panel d. The τ/Prot decreases with eccentricity until e = 0.036 and then increases, as shown in panel e. However, the p value for the increased segment is 0.33. This correlations is not credible. Moreover, the mass ratio is not correlated with τ/Prot. Although the correlation coefficient of their medians is −0.72, the significant fluctuations depicted in panel f cast doubt on the validity of this correlation. We investigated the correlation between the synchronization ratio of rsyn = Prot/Porb and τ/Prot. As rsyn approaches 1, τ/Prot increases. To highlight this trend, the asynchronized ratio is defined as 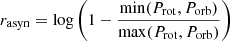 . Panel h reveals a negative correlation between τ/Prot and rasyn. All of these correlations indicate that starspots on circular, synchronized, and close binaries have a longer relative decay timescale.
. Panel h reveals a negative correlation between τ/Prot and rasyn. All of these correlations indicate that starspots on circular, synchronized, and close binaries have a longer relative decay timescale.
The timescale for the harmonic decay is proportional to mβ21, as demonstrated by Arkhypov et al. (2016). If the decay of starspots is driven by large-scale convective cells, β21 is equal to −2/3. When the decay is caused by horizontal diffusion, β21 has a value of −2. If subphotospheric diffusion causes decay, β21 is lower than −2.3 (Arkhypov et al. 2018). The change in decay mechanism is caused by the enhancement of convection suppression. The mean of β21 in this study is −1.03, indicating that the decay of most sources is dominated by the motion of large-scale convection. To explore the details, the sample was divided into different subsamples according to their rotation periods, (R1 + R2)/a, and effective temperatures. Figure 8 illustrates that systems with fast rotation (Prot < 3 days) have a mean β21 of −1.65, with the histogram peak close to −2. Close systems ((R1 + R2)/a ≥ 0.3) have a mean β21 of −2.00, whereas wide systems ((R1 + R2)/a < 0.3) have a mean β21 of −0.18. The mean β21 for cool sources (Teff < 5000) is −1.39, whereas for hotter sources, it is −0.96. These subsamples indicate that horizontal diffusion dominates the decay of starspots on fast-rotating, cool, and close binaries.
 |
Fig. 8. Histograms of β21. In the top panel, the blue and orange histograms are samples of wide ((R1 + R2)/a < 0.3) and close ((R1 + R2)/a ≥ 0.3) sources, respectively. In the bottom panel, the orange, green, and red histograms are samples of hot (Teff > 5000 K), cool (Teff ≤ 5000 K), and fast-rotating (Prot < 3 days) sources, respectively. The vertical solid and dashed lines label β21 of −2 and −2/3, respectively. |
4.3. Comparing starspots on binaries with those on single stars
The distributions of the starspot parameters on single stars as well as binaries are displayed in Fig. 9. Panel a shows that the RMS of numerous single stars is smaller by more than an order of magnitude than that of binaries. This significant dissimilarity can be attributed to the selection effect. We only selected binary systems whose starspot modulation can be distinguished from other variations, including the ellipsoidal variation and the reflection effect. Therefore, binaries have a larger RMS. To mitigate the potential comparison bias resulting from this selection effect, we removed single stars with an RMS lower than the minimum RMS of binaries. Ultimately, our selection process yielded 3272 single stars. The average relative decay timescale on single stars is 16.5. As the rotation period of most binaries within our sample is shorter than 10 days, we only compared sources with Prot < 10 days in both samples. For Prot < 10 days, the means τ/Prot are 29.2 and 74.6 for single stars and binaries, respectively. Starspots on binaries appear to have a longer lifetime than those on single stars. To obtain more details, the binaries were divided into ten bins according to rotation periods, and these bins had the same number of sources. Then, the means and 1σ errors of τ/Prot in each bin were calculated. According to the rotation period bins of the binary sample, the single-star samples were also divided into ten bins and the means and 1σ errors were calculated. The 1σ regions and the means are shown in panel b of Fig. 9. The means of the binaries are above the means of the single stars and close to the upper edge of the 1σ region of the single stars. The means of the single stars are close to the lower edge of the 1σ region of the binaries. The starspot of a binary has a longer relative decay timescale than that of a single star. We then analyzed the differences in mean τ/Prot between binaries and single stars. As the rotational period increases, the value of τ/Prot decreases by an order of magnitude. Therefore, it seems natural that the difference (i.e., Δτ/Prot) between binaries and single stars should decrease with increasing rotational period. To avoid this confusion, we used (Δτ/Prot)/(τ/Prot), that is, Δτ/τ, to measure the differences. These differences are shown at the bottom of panel b of Fig. 9. In the first bin, the period between 0.53143 and 0.894381 days, the relative difference is very small. These periods are in the saturated rotation–activity regime, as shown in Table 2 of Wright et al. (2011). This may cause the small relative difference. Starting from the second bin, the differences show a negative correlation with the rotation period. The Pearson correlation coefficient and the p value are −0.62 and 0.07, respectively. Since most binaries are close to synchronization, the rotation period is positively correlated with the orbital periods. Therefore, as the rotation period increases, the interaction of the binary decreases, and the lifetime of the starspot on the binary tends to be similar to that in the single star.
 |
Fig. 9. Comparisons of binaries and single stars. (a) Histograms of the RMS. The blue and orange histograms show the single stars and binaries, respectively. The number of single stars is 5183. In the following panels, we only show the single stars with large RMS, whose number is 3272. (b) Comparison of the relative lifetimes of starspots on single stars and binaries. The top panel shows the relative lifetimes. The gray squares and green dots represent single stars and binaries, respectively. The blue and red bands show the 1σ regions for single stars and binaries, respectively. The blue and red lines show the mean τ/Prot of single stars and binaries, respectively. The bottom panel shows the differences in mean τ/Prot between binaries and single stars. The vertical axis represents the differences normalized by the relative lifetime, which is (Δτ/Prot)/(τ/Prot) (i.e., Δτ/τ). (c) β21 of single sources. The blue, orange, green, and red histograms show the total sample, the hot subsample (Teff > 5000 and Prot < 10 days), the cool subsample (Teff ≤ 5000 K and Prot < 10 days), and the fast-rotating subsample (Prot < 3 days), respectively. |
The mean β21 of the single stars is −1.02 and the peak of its histogram is close to −2/3, as shown in panel c of Fig. 9. This agrees with the result of Arkhypov et al. (2016). For Prot < 10 days, the mean β21 is −0.99 and −1.16 for single stars and binaries, respectively. The latter seems to be more affected by the diffusive transport than the single stars. The fast-rotating sources (Prot < 3 days) have mean β21 of −1.35 and −1.65 for single stars and binaries, respectively. The peaks of the histograms of these two subsamples are −1 and −2, respectively. These differences indicate that the interaction of the binary may change the decay mechanism. The mean β21 of cool sources (Teff < 5000 K) are −1.39 and −1.49 for single star and binary, respectively. The mean β21 of hot sources are −1.01 and −1.09, respectively. The differences in mean β21 between cool and hot stars are similar for binaries and single stars, but the mean β21 of binaries are smaller. This situation suggests that the starspot decay is correlated with the binary interaction and the effective temperature, and these two factors are independent.
5. Discussion
5.1. Orbital parameters and starspot lifetime
Our result indicates that the lifetime of the starspot is influenced by binary interaction. In the case of a detached binary, the interaction is primarily due to the binary tidal effect. The tidal force is proportional to r/d3 (Hilditch 2001), where r is the distance of the point from the center of the nearby star, and d is the distance between the centers of the two stars. Therefore, the tidal force on the secondary can be estimated with R2/a3 and expanded as follows:
To discuss how (R1 + R2)/a and R2/R1 affect the tidal force, we first discuss the independence of (R1 + R2)/a, 1/(1 + R1/R2) and 1/a2. Because we cannot obtain the semimajor axis, we generated R1, R2 and a from the simulation to analyze the correlations between these three terms. The details of the simulation are described in Appendix B. The simulated parameters are shown in Fig. 10. The Pearson r correlation coefficients are listed in Table 5. We find that 1/(1 + R1/R2) is independent of (R1 + R2)/a and 1/a2. The medians of 1/(1 + R1/R2) and (R1 + R2)/a seem to show a positive correlation. However, the large scatter in each bin prevents us from being confident about this correlation. (R1 + R2)/a correlates with 1/a2. Nevertheless, (R1 + R2)/a3 increases monotonically with (R1 + R2)/a. We can therefore discuss how (R1 + R2)/a and R2/R1 affect the tidal force separately.
 |
Fig. 10. Correlations between the (R1 + R2)/a, 1/(1 + R1/R2), 1/a2, and (R1 + R2)/a3 from the simulation data. The blue dots show the simulation data, and the red dots and lines represent the medians of the parameters. |
Correlation between the simulation parameters.
Equation (3) shows that the tidal force on the secondary increases with (R1 + R2)/a. Similarly, the tidal force on the primary also increases with (R1 + R2)/a, which can be verified by exchanging R2 and R1 in Equation (3). Sect. 4.2 shows that the relative lifetime increases with (R1 + R2)/a. Therefore, the tidal interaction prolongs the lifetime of the starspot.
The tidal force on the secondary is also correlated with the radius ratio, as shown in Equation (3). However, Sect. 4.2 does not give a credible correlation with the radius ratio. According to Equation (3), the tidal effect on the secondary increases with R2/R1. Thus, the lifetime of the starspot on the secondary increases with R2/R1. However, these trends are reversed for the primary star. These two opposite trends cancel each other out. The large dispersion of the radius ratio makes the situation more complex. We therefore do not obtain a credible correlation between the radius ratio and the lifetime.
The tidal force is also proportional to the mass M of the companion. However, without the radial velocity curves, we cannot obtain the masses of the two components. We can only make a rough estimate of the mass ratio. In order to determine the correlation between the mass ratio and the tidal force, we used the simulation masses to determine the correlation between the mass ratio and the masses of the components. As shown in Fig. 11, the secondary mass M2 correlates positively with q, and the primary mass M1 has a week negative correlation with q. This means that the tidal force on the primary increases as q. However, in Sect. 4.2, no correlation of the mass ratio was obtained. Since the tidal force is affected by many factors, we discuss the correlation between the mass ratio and other factors. We verified the correlation between the mass ratio and the three terms in Equation (3). As shown in Figure 12, the mass ratio is negatively correlated with the term 1/(1 + R2/R1). For the tidal force on the primary star, we use the term 1/(1 + R2/R1). The positive correlation of M2 and the negative correlation of 1/(1 + R2/R1) cancel each other out, and we cannot obtain the correlation between the mass ratio and the tidal force. This is consistent with the observational result shown in Sect. 4.2.
 |
Fig. 11. Correlations between M1, M2, and q from the simulation data. The blue and orange dots show the primary and secondary masses, respectively. The green and red squares show the median of the primary and secondary masses, respectively. |
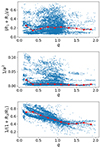 |
Fig. 12. Correlations between the q and (R1 + R2)/a, 1/(1 + R2/R1), and 1/a2 from the simulation data. The blue dots show the simulation data, and the red dots and lines represent the medians of the parameters. |
Section 4.2 showed that the decay scale is negatively correlated with the inclinations. This is an observational effect. The observable range of inclinations of eclipsing binaries is determined by the sum of their fractional radii. At low inclinations, only close eclipsing binaries (i.e., large (R1 + R2)/a binaries) can be observed. Close binaries have longer-living starspots. With increasing inclination, more and more wide binaries can be observed. Wide binaries have starspots with shorter lifetimes. Therefore, the lifetime decreases with increasing inclination.
Starspots in circular and/or synchronized systems have long lifetimes, as shown in Sect. 4.2. These systems are easily observed in close binaries because close systems have short circular and synchronous timescales. Thus, the long lifetime of starspots on these sources is attributed to the tidal effect at close distances.
5.2. Effect of the tides on the starspot lifetime
We have shown that the correlation between the orbital parameters and the relative lifetime is consistent with that between the orbital parameters and the tidal force. We therefore suggest that the lifetime of the starspot in the binary is affected by the tides. Furthermore, the tidal effect extends the lifetime of the starspot. Now the question arises how tides affect the lifetime of starspots. There is no theoretical or simulation work that specifically addresses this phenomenon. However, we can obtain some clues from references. Since the lifetime of a starspot is proportional to the area of the starspot (Gnevyshev 1938; Waldmeier 1955; Bradshaw & Hartigan 2014), the tides could increase the area of the starspot to extend the lifetime of the starspot. Our results show that the RMS of the binary starspot is larger than that of the single star, implying that the binary starspot has a larger area. On the other hand, our results indicate that binary-spot decays are largely accounted for by horizontal diffusion and subphotospheric diffusion, as opposed to single-star spot decays. Starspots that decay through these two mechanisms would last longer. Arkhypov et al. (2018) have shown that stars with saturated magnetism tend to have these decay mechanisms. The tides might therefore strengthen the magnetic field of the starspot to prolong its lifetime.
As shown by Holzwarth & Schüssler (2003a,b), a nonlinear perturbation of the tide would induce magnetic flux tube instabilities in the convection zone, which would then increase the emergence of magnetic flux tubes at the surface. As the flux tubes rise, the tidal force would cause them to cluster. These two effects strengthen the magnetic field of the active region or increase the area of the active region. However, there are some problems to note. First, the purpose of Holzwarth & Schüssler (2003a,b) was to study the preferred longitude of binary starspots, not the lifetime. Second, Holzwarth (2004) found that the flux tube cluster disappears in the giant companion. Finally, the flux tube cluster does not always strengthen the magnetic field of the active region or increases the area of the active region. If the flux tubes had opposite polarities, they would cancel each other out rather than strengthen. For the same reason, a high emergence rate could weaken the magnetic field. Işik et al. (2007) suggested that a high emergence frequency might cause the short lifetimes of starspots in low and medium latitudes. Therefore, this plausible mechanism should be investigated in further simulations.
Another clue is that the tidal effect induces secondary meridional circulation when the system is asynchronous (Tassoul & Tassoul 1990). In the spin-down case (Prot < Porb), the tidally induced meridional flow is poleward at the surface. Conversely, in the spin-up case, the flow is equatorward (Tassoul & Tassoul 1990). The poleward flow accelerates the primary meridional circulation, while the equatorward flow slows it down. The meridional flow transports the magnetic flux tube from low to high latitudes, supplying the polar active regions and extending their lifetime (Işik et al. 2007). Therefore, a spin-down star prolongs the lifetime of the starspot, while a spin up star shortens it. Figure 13 shows the details near the synchronous state, where the lifetime of the starspot on the spin-down star is slightly longer than that on the spin-up star. However, when the system reaches synchrony, the large-scale flow induced by tides disappears.
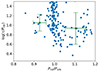 |
Fig. 13. Detail near the synchronous state. The error bars represent the means and 1σ regions of the lifetimes and synchronous rate of starspots on the spin-down stars (0.80 < Prot/Porb < 0.97) and the spin-up stars (1.03 < Prot/Porb < 1.20), respectively. The lifetime of the starspot on the spin-down star is slightly longer than that on the spin-up star. |
6. Conclusions
We investigated the lifetime of the starspot in detached eclipsing binaries. By combining the Kepler long-cadence photometric data with the stellar atmosphere parameters from LAMOST DR9/Gaia DR3, the relative orbital parameters of 318 detached eclipsing binaries were derived using the Phoebe model. The starspot signals were obtained after subtracting the binary models. We then used the ACF method to derive the rotational period, starspot lifetime, and harmonic decay timescales. The ratio of the second and first harmonic decay timescales can reveal the decay mechanism. To compare the starspot on the single star and binary, we also analyzed the starspot signals of 3272 single stars.
We find that the relative lifetime of the starspot is correlated with the sum of the fractional radii, the eccentricity, and the synchronization ratio. The starspot of the close, circular, and synchronised binary has a longer lifetime. The mechanism of starspot decay in the binary might be dominated by the large-scale convection motion. On the cool, close, and fast-rotating binary, the main decay mechanism is the horizontal diffusion or subphotospheric diffusion.
Compared with the single star, we find that the median lifetime of the starspot on the binary is longer than that on the single star. The difference in lifetime also decreases with the rotational period. For the same rotational period and effective temperature, our results indicate that binary spot decays are largely accounted for by horizontal diffusion and subphotospheric diffusion as opposed to single-star spot decays.
The correlation between the orbital parameters and the relative lifetime is consistent with that between the orbital parameters and the tidal force. Therefore, we suggest that the lifetime of the starspot in the binary is affected by the tides. To study more details of these interactions, more spot moduling of detached binary observations and magnetic convection simulations of binaries is required.
Data availability
Full Tables 1 and 3 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/690/A201
Acknowledgments
We acknowledge the support from the National Natural Science Foundation of China (NSFC) through grants 12203010, 12090040, 12090042, 12273002, 12203068, and 12105032, the Natural Science Foundation of Chongqing (CQCSTC) under grants No. CSTB2023NSCQ-MSX1048 and cstc2021jcyj-msxmX0481. The authors gratefully acknowledge the Kepler team and all who have contributed to making this mission possible. Funding for the Kepler mission is provided by NASA’s Science Mission Directorate. The LAMOST Telescope is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. JNF, WZ, JW acknowledge the science research grants from the China Manned Space Project.
References
- Andrae, R., Fouesneau, M., Sordo, R., et al. 2023, A&A, 674, A27 [CrossRef] [EDP Sciences] [Google Scholar]
- Angus, R., Morton, T., Aigrain, S., Foreman-Mackey, D., & Rajpaul, V. 2018, MNRAS, 474, 2094 [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Güdel, M., et al. 2015, A&A, 576, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Lammer, H., et al. 2016, ApJ, 826, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Lammer, H., et al. 2018, MNRAS, 473, L84 [CrossRef] [Google Scholar]
- Basri, G., & Shah, R. 2020, ApJ, 901, 14 [Google Scholar]
- Basri, G., Streichenberger, T., McWard, C., et al. 2022, ApJ, 924, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Bradshaw, S. J., & Hartigan, P. 2014, ApJ, 795, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Çakırlı, Ö., İbanoǧlu, C., & Sipahi, E. 2013, MNRAS, 429, 85 [CrossRef] [Google Scholar]
- Clark Cunningham, J. M., Rawls, M. L., Windemuth, D., et al. 2019, AJ, 158, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, K. E., Kochoska, A., Hey, D., et al. 2020, ApJS, 250, 34 [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, RAA, 12, 1197 [NASA ADS] [Google Scholar]
- De Cat, P., Fu, J. N., Ren, A. B., et al. 2015, ApJS, 220, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, J.-N., Cat, P. D., Zong, W., et al. 2020, RAA, 20, 167 [NASA ADS] [Google Scholar]
- Gaia Collaboration 2022, VizieR Online Data Catalog: I/358 [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaulme, P., Jackiewicz, J., Spada, F., et al. 2020, A&A, 639, A63 [EDP Sciences] [Google Scholar]
- Gehan, C., Gaulme, P., & Yu, J. 2022, A&A, 668, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giles, H. A. C., Collier Cameron, A., & Haywood, R. D. 2017, MNRAS, 472, 1618 [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gnevyshev, M. N. 1938, Izvestiya Glavnoj Astronomicheskoj Observatorii v Pulkove, 16, 36 [NASA ADS] [Google Scholar]
- Green, G. M. 2018, J. Open Source Softw., 3, 695 [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Han, E., Muirhead, P. S., Swift, J. J., et al. 2017, AJ, 154, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Han, E., Muirhead, P. S., & Swift, J. J. 2019, AJ, 158, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Heckert, P. A., & Ordway, J. I. 1995, AJ, 109, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Hełminiak, K. G., Ukita, N., Kambe, E., et al. 2016, MNRAS, 461, 2896 [CrossRef] [Google Scholar]
- Hełminiak, K. G., Ukita, N., Kambe, E., et al. 2017, MNRAS, 468, 1726 [CrossRef] [Google Scholar]
- Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge: Cambridge University Press) [Google Scholar]
- Holzwarth, V. 2004, Astron. Nachr., 325, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003a, A&A, 405, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003b, A&A, 405, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horvat, M., Conroy, K. E., Pablo, H., et al. 2018, ApJS, 237, 26 [Google Scholar]
- Hussain, G. A. J. 2002, Astron. Nachr., 323, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Işik, E., Schüssler, M., & Solanki, S. K. 2007, A&A, 464, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, D., Conroy, K. E., Horvat, M., et al. 2020, ApJS, 247, 63 [Google Scholar]
- Karoff, C., Metcalfe, T. S., Santos, Â. R. G., et al. 2018, ApJ, 852, 46 [Google Scholar]
- Kazarovets, E. V., Samus, N. N., & Durlevich, O. V. 2022, Astron. Rep., 66, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, B., Conroy, K., Prša, A., et al. 2016, AJ, 151, 68 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Piluso, N., Rodonò, M., Messina, S., & Cutispoto, G. 2006, A&A, 455, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luo, A. L., Zhang, Y.-X., & Zhao, Y.-H. 2004, Proc. SPIE, 5496, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, A. L., Zhang, H.-T., Zhao, Y.-H., et al. 2012, RAA, 12, 1243 [NASA ADS] [Google Scholar]
- Lurie, J. C., Vyhmeister, K., Hawley, S. L., et al. 2017, AJ, 154, 250 [Google Scholar]
- Mathur, S., Salabert, D., García, R. A., & Ceillier, T. 2014, J. Space Weather Space Clim., 4, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Claytor, Z. R., Santos, Â. R. G., et al. 2023, ApJ, 952, 131 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [Google Scholar]
- Pan, Y., & Zhang, X. 2023, AJ, 165, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, Y., Fu, J.-N., Zong, W., et al. 2020, ApJ, 905, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [Google Scholar]
- Prša, A., Batalha, N., Slawson, R. W., et al. 2011, AJ, 141, 83 [Google Scholar]
- Prša, A., Conroy, K. E., Horvat, M., et al. 2016, ApJS, 227, 29 [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning (MIT Press) [Google Scholar]
- Ren, A., Fu, J., De Cat, P., et al. 2016, ApJS, 225, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Salabert, D., García, R. A., Beck, P. G., et al. 2016, A&A, 596, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, A. R. G., Mathur, S., García, R. A., Cunha, M. S., & Avelino, P. P. 2021, MNRAS, 508, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Savanov, I. S. 2009, Astron. Rep., 53, 941 [CrossRef] [Google Scholar]
- Siltala, L., Jetsu, L., Hackman, T., et al. 2017, Astron. Nachr., 338, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Slawson, R. W., Prša, A., Welsh, W. F., et al. 2011, AJ, 142, 160 [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [Google Scholar]
- Su, D.-Q., & Cui, X.-Q. 2004, Chin. J. Astron. Astrophys., 4, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, J.-L., & Tassoul, M. 1990, ApJ, 359, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Waldmeier, M. 1955, Ergebnisse und Probleme der Sonnenforschung (Leipzig: Geest and Portig) [Google Scholar]
- Wang, S.-G., Su, D.-Q., Chu, Y.-Q., Cui, X., & Wang, Y.-N. 1996, Appl. Opt., 35, 5155 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fu, J., Niu, H., et al. 2021, MNRAS, 504, 4302 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fu, J., Zong, W., et al. 2022, MNRAS, 511, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, X. 2022, MNRAS, 513, 5474 [NASA ADS] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [Google Scholar]
- Wu, Y., Singh, H. P., Prugniel, P., Gupta, R., & Koleva, M. 2010, A&A, 525, 1 [Google Scholar]
- Wu, Y., Du, B., Luo, A., Zhao, Y., & Yuan, H. 2014, Proc. Int. Astron. Union, 10, 340 [CrossRef] [Google Scholar]
- Zhang, L.-Y., Pi, Q.-F., & Yang, Y.-G. 2014, MNRAS, 442, 2620 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Jing, Y.-J., Yang, F., et al. 2022, ApJS, 258, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, RAA, 12, 723 [Google Scholar]
- Zong, W., Fu, J.-N., De Cat, P., et al. 2018, ApJS, 238, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Zong, W., Fu, J.-N., De Cat, P., et al. 2020, ApJS, 251, 15 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The checked sample
The checked sample parameters collected from references.
Appendix B: The simulation of orbital parameters
It is nature to generate the simulation R1, R2 and a by drawing them from their distributions. However, the radius distribution is unknown. So this method is used instead of directly drawing radii. Firstly, we draw the stellar atmospheric parameters, temperature ratio, and orbital period from our sample. The atmospheric parameters are then given random fluctuations according to their errors. As the error of orbital periods is very small (approximately 10−5 days), we adopted an error of 0.1 * Porb to generate the random fluctuations of periods. Using the Padova stellar model, we obtain the mass M1, radius R1, and age based on the atmospheric parameters. According to the temperature ratio and its error, we construct the temperature ratio range [T2/T1 − σT2/T1, T2/T1 + σT2/T1]. Since the error in the temperature ratio is small, we took 0.1 * T2/T1 as the error. From this range we derived the effective temperature range of the secondary star. Based on the age of the primary star and the effective temperature range of the secondary star, we used the stellar model to derive the mass range of the secondary star. In this mass range we then draw the secondary mass M2 from the mass function of Kroupa (2001). This mass function is shown as follows.
The secondary radius R2 is calculated from the stellar model with the age of the primary star and the secondary mass M2. Finally, the semi major axis can be determined using the formula as follows.
Then, we use the Phoebe code to check the configure is reasonable or not. We simulated 10,000 sets of (R1,R2,a,M1,M2) using this described procedures.
All Tables
All Figures
 |
Fig. 1. Sample of starspot-modulated binaries and single stars. The colored squares are binaries. The colors of the squares represent the orbital periods of the binaries. The gray circles represent single stars. |
| In the text | |
 |
Fig. 2. The photometry and model of binary. (a) Binary modeling of KIC 10935310. The top panel shows the light curve and the Phoebe model. The blue points show observational data, and the red lines show the best-fitting model. The lower panel shows the residuals. The green points show the fitting residuals. (b) SED fit for KIC 10935310. The blue circles with error bars show observational data. The error bars from Gaia photometry are barely visible because their error is smaller than mmag. The green bands show the SED models. |
| In the text | |
 |
Fig. 3. Starspot analysis for KIC 10935310. (a) A segment of the starspot signal. (b) ACF of the starspot signal. The blue points show the ACFs. The red line shows the best-fitting linear decay model. (c) Time sequence of Am, E2. The first and second harmonic components are shown as blue and orange lines, respectively. (d) ACFs for panel c. The first and second harmonic components are shown as blue and orange dots, respectively. |
| In the text | |
 |
Fig. 4. Histograms of the orbital parameters: the orbital period Porb, the temperature ratio T1/T1, the sum of the fractional radii (R1 + R2)/a, the radius ratio R2/R1, the inclination, the eccentricity, and the mass ratio q. |
| In the text | |
 |
Fig. 5. Comparison of the orbital parameters obtained here and in the references. The solid lines are the 1:1 diagonal lines. The error bars represent the errors of the parameters obtained from the references. The square indicates the outlier KIC 6859813. |
| In the text | |
 |
Fig. 6. Histograms of the starspot parameters, including the rotational periods, the decay timescale, the derivative of the harmonic decay timescale, and the RMS. |
| In the text | |
 |
Fig. 7. Correlation between the orbital parameters and the relative decay timescale of starspots. Since the relative decay time crosses about 3 orders of magnitude, the logarithmic scale is used to display them. The blue dots show the data from the entire sample. The red dots and lines represent the median of τ/Prot in the orbital parameter bins. For panel e, because the circular sources are plotted in one bin, only six medians are shown in panel e. |
| In the text | |
 |
Fig. 8. Histograms of β21. In the top panel, the blue and orange histograms are samples of wide ((R1 + R2)/a < 0.3) and close ((R1 + R2)/a ≥ 0.3) sources, respectively. In the bottom panel, the orange, green, and red histograms are samples of hot (Teff > 5000 K), cool (Teff ≤ 5000 K), and fast-rotating (Prot < 3 days) sources, respectively. The vertical solid and dashed lines label β21 of −2 and −2/3, respectively. |
| In the text | |
 |
Fig. 9. Comparisons of binaries and single stars. (a) Histograms of the RMS. The blue and orange histograms show the single stars and binaries, respectively. The number of single stars is 5183. In the following panels, we only show the single stars with large RMS, whose number is 3272. (b) Comparison of the relative lifetimes of starspots on single stars and binaries. The top panel shows the relative lifetimes. The gray squares and green dots represent single stars and binaries, respectively. The blue and red bands show the 1σ regions for single stars and binaries, respectively. The blue and red lines show the mean τ/Prot of single stars and binaries, respectively. The bottom panel shows the differences in mean τ/Prot between binaries and single stars. The vertical axis represents the differences normalized by the relative lifetime, which is (Δτ/Prot)/(τ/Prot) (i.e., Δτ/τ). (c) β21 of single sources. The blue, orange, green, and red histograms show the total sample, the hot subsample (Teff > 5000 and Prot < 10 days), the cool subsample (Teff ≤ 5000 K and Prot < 10 days), and the fast-rotating subsample (Prot < 3 days), respectively. |
| In the text | |
 |
Fig. 10. Correlations between the (R1 + R2)/a, 1/(1 + R1/R2), 1/a2, and (R1 + R2)/a3 from the simulation data. The blue dots show the simulation data, and the red dots and lines represent the medians of the parameters. |
| In the text | |
 |
Fig. 11. Correlations between M1, M2, and q from the simulation data. The blue and orange dots show the primary and secondary masses, respectively. The green and red squares show the median of the primary and secondary masses, respectively. |
| In the text | |
 |
Fig. 12. Correlations between the q and (R1 + R2)/a, 1/(1 + R2/R1), and 1/a2 from the simulation data. The blue dots show the simulation data, and the red dots and lines represent the medians of the parameters. |
| In the text | |
 |
Fig. 13. Detail near the synchronous state. The error bars represent the means and 1σ regions of the lifetimes and synchronous rate of starspots on the spin-down stars (0.80 < Prot/Porb < 0.97) and the spin-up stars (1.03 < Prot/Porb < 1.20), respectively. The lifetime of the starspot on the spin-down star is slightly longer than that on the spin-up star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} k_{i,j}=A\mathrm{exp}\left[-\frac{(t_{i}-t_{j})}{2l^2}-\Gamma ^2\mathrm{sin}^2\left(\frac{\pi (t_{i}-t_{j})}{P}\right)\right]+\sigma ^2{\delta _{{ij}}}, \end{aligned} $$](/articles/aa/full_html/2024/10/aa49484-24/aa49484-24-eq1.gif)
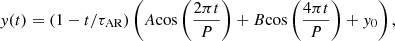
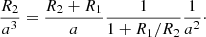
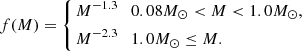
![$$ \begin{aligned} a=\left[\frac{G(M_1+M_2)P_{\rm orb}^2}{4\pi ^2}\right]^{1/3} \end{aligned} $$](/articles/aa/full_html/2024/10/aa49484-24/aa49484-24-eq6.gif)