EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 689 (September 2024) A&A, 689 (2024) A183 Full HTML
Open Access
Issue
A&A
Volume 689, September 2024
Article Number A183
Number of page(s) 24
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202450532
Published online 13 September 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Both telescopic observations and dynamical studies of Solar System small bodies imply that most meteorites and near-Earth objects (NEOs) originate from the main asteroid belt (Ceplecha 1961; Wisdom 1983; Binzel et al. 1996; Farinella et al. 1998; Morbidelli et al. 2002; Granvik et al. 2017; Nesvorný et al. 2023). Until recently, however, it has been an unsuccessful quest to unambiguously identify the origin of even the better-studied meteorite groups, with the exception of Lunar, Martian, and Ves-tian (HEDs) meteorites. The reason is pretty simple: Asteroids, as opposed to planets, are not unique in terms of composition and spectral properties (Vesta being an exception). It follows that there are several possible sources in the asteroid belt for a given meteorite class and for each compositional group of NEOs.

Two recent studies (Brož et al. 2024; Marsset et al. 2024) have provided a breath of fresh air to this quest, identifying the sources of the two main meteorite groups, H and L chondrites, representing ~ 70% of all falls. Specifically, H chondrites originate from two breakups related to (832) Karin and (158) Koronis, which occurred 5.7 and 7.6 Myr ago, whereas L chondrites originate from a cratering or reaccumulative event on (20) Massalia ~ 40 Myr ago. We summarise the implications of these studies that can be generalised to other classes of meteorites and NEOs hereafter:

  1. Faint (H ≳ 18.5 mag) asteroids are not distributed evenly in the main belt; instead, they are concentrated strongly around a few specific asteroid families. This is seen nicely in Fig. 1.

  2. The youngest (≲40 Myr) asteroid families are at the origin of the prominent dust bands observed at 1.4° (Massalia) and 2.1° (Karin, Koronis), highlighting that their size-frequency distribution (SFD) is steep and continuous from sub-kilometre asteroids to ~100-µm dust grains.

  3. Consequently, a sizeable breakup temporarily ‘overshoots’ the whole main belt population also at metre sizes.

  4. The background population must be a negligible source of meteorites, because both H and L chondrites exhibit unique radiometric features (Eugster et al. 2006; Swindle et al. 2014) for about half of all finds.

  5. The intervals of iridium or helium-3 excess found in terrestrial strata (Schmitz et al. 1997; Farley et al. 1998), which have a relatively short duration, confirm the transient nature of the extraterrestrial dust and meteoroid populations, created during breakups and sustained by a collisional cascade.

  6. Old families (Vesta, Flora, Eunomia, etc.) contribute significantly less than young ones to the meteorite flux because their SFD is ‘bent’ at sub-kilometre sizes due to a colli-sional cascade. They are, however, the primary source of D ≥ 1km NEOs. This difference is at the origin of the longtime meteorite–NEO conundrum (Vernazza et al. 2008).

  7. The Phocaea, Juno, and Flora families are the primary sources of H-, L-, and LL-like NEOs, respectively (Brož et al. 2024).

In this work, we present a follow-up study focusing on the source regions of carbonaceous chondrites (CCs) and CC-like NEOs. The CCs represent 4.4% of all falls (Gattacceca et al. 2022; see Table 1), whereas their parent bodies (C-complex asteroids along with K-type asteroids) represent more than 50% of the mass of the asteroid belt (DeMeo & Carry 2013). The discrepancy between CC falls and their abundance in the asteroid belt is at first order a direct consequence of their friable nature, which makes it more difficult for those types of materials to survive atmospheric entry (Borovička et al. 2019). One cannot exclude that most CCs actually reach the surface of the Earth in the form of micrometeorites or interplanetary dust particles (IDPs; Vernazza et al. 2015).

Table 1

Overview of carbonaceous chondrites classes.

2 Family identification

The first step of our work consisted of the identification and characterisation of CC-like families selected according to the following criteria: (i) abundance of small, faint bodies, as these are the most promising sources of meteorites (Fig. 1); (ii) abundance of large (D ≥ 1 km) bodies as these are the most promising sources of large NEOs; (iii) the slope of the SFD (Table C.1); (iv) the presence or absence of an associated dust band (Sykes 1990; Reach et al. 1997; Nesvorný et al. 2006; Planck Collaboration XIV 2014). We identified families using recent catalogues: Astorb (Moskovitz et al. 2019), AFP (Knežević & Milani 2003; Novaković & Radović 2019), Wise (Nugent et al. 2015), Akari (Usui et al. 2011), and SDSS (Parker et al. 2008); versions as of July 2023. They contained 1298281 orbits in total. We applied a hierarchical clustering (HCM; Zappalà et al. 1995) with a removal of interlopers. Specifically, family members had to fulfill several criteria. For C-type families, we assumed a geometric albedo of pV ∊ (0; 0.125) and an SDSS colour index of a* ∊ (−1; 0.1). Further, we used a magnitude criterion (Vokrouhlický et al. 2006): 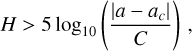H>5 log10(| a−ac |C),$H > 5{\log _{10}}\left( {{{\left| {a - {a_c}} \right|} \over C}} \right),$(1)

where ac is the centre and C is the extent of a family. Some families also contain sub-families (e.g. Beagle within Themis; Fig. B.1), which should be studied separately. For K-type families, we assumed a geometric albedo of pV > 0.075 and an SDSS colour index of a★ ∊ (−0.5; 0.5). For each family, we obtained the median albedo, diameters of all bodies, and observed SFDs (Fig. 2). Their well-defined slopes are provided in Table C.1. Some of the families are steep down to the observational limit (e.g. Veritas). On the other hand, none of the previously proposed old families (‘old Polana’, ‘Eulalia’, ‘Athor’) is relevant here, as they have too shallow (too depleted) SFDs.

thumbnail Fig. 1

‘Faint Main Belt’, showing only bodies with the absolute magnitude close to the limit of the Catalina Sky Survey, id est, H ≳ 19.25 + 5(log(2.2(l − 0.1)) + log(2.2 − 1))) − 5(log(a(l − e)) + log(a − 1))). The proper semimajor axis ap versus eccentricity ep (bottom) versus inclination sin ip (top) are plotted; together with locations of the mean-motion resonances (vertical lines), IRAS dust bands (horizontal lines), and known asteroid families (Nesvorný et al. 2015) (labels). Big and old ones are almost invisible here (e.g. ‘4’ Vesta). Small and young ones − having a steep SFD − are prominent. The distribution of faint bodies is surprisingly irregular. The concentrations are directly related to the sources of meteorites: L .. ‘20’ Massalia (Marsset et al. 2024), H .. ‘158’ Koronis (Brož et al. 2024), CM .. ‘490’ Veritas, CI.. ‘142’ Polana, CO/CV/CK .. ‘221’ Eos, M .. ‘293’ Brasilia, or M .. ‘606’ Brangäne (this work).
thumbnail Fig. 2

Observed SFDs of C-type asteroid families. The SFDs usually exhibit a steep slope q1 at sizes D ≳ 5 km and a shallow slope q2 at D ≲ 5 km. This break is often created in the course of collisonal evolution. An observational bias affects the SFDs at even smaller sizes (0.5–3 km), depending on the distance and albedo of the respective populations. Additionally, families of P, B, and M types were studied (together with 4 of unknown taxonomical classification).

3 Taxonomic classification

As a next step, we determined the meteoritic analogue of these CC-like main belt families as well as those of CC-like NEOs. We used publicly available colours in the optical domain (SDSS survey; Parker et al. 2008), visible spectra (SMASS and S3OS2 surveys; Bus & Binzel 2002b,a; Lazzaro et al. 2004), near-infrared spectra from the MITHNEOS survey (DeMeo et al. 2009; Binzel et al. 2019; Marsset et al. 2022), other sources from the literature (Fornasier et al. 2010, 2016; Masiero et al. 2015a; De Prá et al. 2020); and our own unpublished near-infrared spectra. We also used albedo information from WISE (Nugent et al. 2015) to distinguish chondrule-poor (CI/CM/C ungrouped/IDPs) from chondrule-rich (CO/CV/CK) carbonaceous materials and to ascertain our classification based on available spectrophotometric measurements. Typically, chondrule-poor materials possess a reflectance at 0.55 microns that falls in the 0.03–0.09 range, whereas chondrule-rich materials possess a reflectance at 0.55 microns that essentially falls in the 0.1-0.2 range. This dichotomy is well supported by albedo measurements (pV ≤ 0.1 and pV ≥ 0.1) of their carbonaceous parent bodies, for which a similar trend has been observed (Vernazza et al. 2021).

3.1 Families with pV ≤ 0.1

The vast majority of the families studied here possess low (pV ≤ 0.1) albedos (Masiero et al. 2015b). From a reflectance/albedo perspective, these families are suitable sources for at least four carbonaceous chondrite classes (CI, CM, CR, C ungrouped) as well as for IDPs.

Spectroscopy in the visible was particularly useful to distinguish CM as well as CR-like families from CI/C ungrouped/IDP-like ones. Indeed, all CM chondrites as well as a sizeable fraction of CR chondrites (e.g. Prestgard et al. 2023) possess spectral properties that are identical to those of Ch- and Cgh-type asteroids with the presence of an absorption feature at ~0.7 microns (see Vernazza et al. 2022 for a detailed review). CM/CR-like families comprise Adeona, Chloris, Dora, Veritas, Astrid, Vibilia, Erigone, Theobalda, and König.

Spectroscopy in the near-infrared was particularly useful to identify plausible sources of CI chondrites. Both the present study (see discussion) as well as previous studies (Bottke et al. 2020) have linked CI-like NEOs Ryugu and Bennu with the Polana family. Given that the spectrum of the Polana family (Pinilla-Alonso et al. 2016) is typical of those of C, Cb, Cg-type spectra, displaying a broad convex band centred around 1.1–1.3 micron, we assigned a CI-like analogue to all families with this convex feature (Hygiea, Themis, Euphrosyne, Nemesis, Polana, Clarissa, Ursula, Beagle, Hoffmeister).

At this stage, we were left with one B-type family (Alauda) and several P-type families (Misa, Elfriede, Naema, Lixiao-hua, Emma, Padua, and Sylvia). Given the B-type spectrum of NEO Bennu and its similarity to Ryugu, we also assigned a CI-like analogue to Alauda. P-types appear as natural sources for spectrally red and featureless meterorites such as Tagish Lake (Vernazza et al. 2013), a member of the C ungrouped class. It is interesting to note that other meteorites of the C ungrouped class appear spectrally similar to Tagish Lake (Applin et al. 2022). Meteorites such as Tagish Lake are, however, an unlikely analogue for many P-types, including Sylvia. Indeed, measurements in the mid-infrared suggest that many P and D-types are spectrally similar to anhydrous IDPs instead of aqueously altered meteorites such as Tagish Lake (Vernazza et al. 2013, 2015, 2022). In the absence of further measurements of P-type families in both the critical 3 micron and 7–25 micron regions (aside from Sylvia; Usui et al. 2019; Vernazza et al. 2015), and laboratory spectroscopic measurements in the visible and near-infrared range (0.4–4 microns) for IDPs (e.g. Bradley et al. 1996; Maupin et al. 2020), we cannot unambiguously identify their analogue. We consequently leave all possibilities open (C ungrouped, IDPs, CIs). We note that some prominent CI-like families such as Themis and Euphrosyne (Marsset et al. 2016; Yang et al. 2020a) show a mix of C and P-types, with objects filling the continuum between the two classes. Deciphering properly this spectral heterogeneity requires further measurements in the critical 3 micron and mid-infrared regions.

3.2 Families with pV ≥ 0.1

It has now been established for a long time that K-type asteroids (alike (221) Eos and its family) comprise the parent bodies of CV, CO, and CK meteorites (e.g. Bell 1988; Burbine et al. 2001; Clark et al. 2009; Mahlke et al. 2023). Recently, it has been demonstrated that Barbarians L-type asteroids alike (729) Wat-sonia are also plausible parent bodies for CO and CV chondrites (Mahlke et al. 2023).

For the Aeolia and Baptistina families, we were unable to identify a satisfactory match with any meteorite group. The spectra of both largest members (298 and 396) are characterised by the presence of a 1-micron feature and the absence of a 2-micron feature. Whereas this is very consistent with olivine being a substantial surface component, the band I centres are shifted towards lower values with respect to olivine (≈1.00 µm for asteroids, 1.05 µm for olivine). It follows that CO, CV or CK chondrites are unlikely analogues for both families. We also considered CR chondrites but these meteorites possess either a CM-like spectrum (Prestgard et al. 2023) or a spectrum with a 1-micron band located close to 0.9 µm. Similarly, ureilites are not convincing analogues for these two bodies.

We identified four families as plausible source of iron and/or metal-rich meteorites (Brasilia, Kalliope, Aëria, Brängane). The mean spectrum of two Brasilia family members (3985, 4461) displays a narrow ~0.9µm feature alike that seen in many M-type spectra although significantly deeper (Hardersen et al. 2005, 2011; Neeley et al. 2014) as well as a ~1.9µm feature, indicating the presence of low-Ca pyroxene. This spectrum appears consistent with the one of metal-rich chondrites (e.g. CH, CB; Dibb et al. 2022). In the case of (22) Kalliope, the asteroid with the highest density so far (Ferrais et al. 2022) and a differentiated metal-rich interior (Brož et al. 2022), radar measurements indicate a metal-poor surface (Shepard et al. 2015).

The mean spectra of asteroid families or of the largest family member are shown in Fig. 3.

4 Models

Unfortunately, observations of multi-km asteroids alone are not sufficient to identify the sources of meteorites. It is necessary to understand SFDs down to metre sizes, as well as the ages of families, because SFDs evolve considerably in the course of time. Eventually, meteoroid fluxes must be determined by transporting bodies from the main belt to the NEO space and by estimating collisional probabilities with the Earth.

4.1 Collisional model

In order to characterise the family SFDs, we used a statistical collisional model, described in detail in Brož et al. (2024). It is based on ‘Boulder’ (Morbidelli et al. 2009), with a number of subsequent improvements (Cibulková et al. 2016; Ševeček et al. 2017; Vernazza et al. 2018). The number of collisions is computed as: 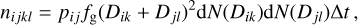nijkl=pijfg(Dik+Djl)2dN(Dik)dN(Djl)Δt,${n_{ijkl}} = {p_{ij}}{f_{\rm{g}}}{\left( {{D_{ik}} + {D_{jl}}} \right)^2}{\rm{d}}N\left( {{D_{ik}}} \right){\rm{d}}N\left( {{D_{jl}}} \right){\rm{\Delta }}t,$(2)

where i, j denote populations, k, I corresponding size bins, pij is the collisional probability (see Table C.3), fg, the gravitational focussing factor, Dik, Dji, corresponding sizes, dN(D), the differential distributions, and ∆t, the time step.

Fragmentation is determined by the specific energy of impact: 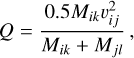Q=0.5Mikvij2Mik+Mjl,$Q = {{0.5{M_{ik}}\v _{ij}^2} \over {{M_{ik}} + {M_{jl}}}},$(3)

where Mik denotes the projectile mass, Mjl, the target mass, υij, the relative speed. We assumed a size-strength scaling law: 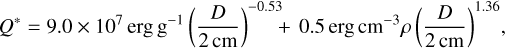Q∗=9.0×107erg g−1(D2 cm)−0.53+0.5 erg  cm−3ρ(D2 cm)1.36,${Q^ * } = 9.0 \times {10^7}{\rm{erg}}\,{{\rm{g}}^{ - 1}}{\left( {{D \over {2{\rm{cm}}}}} \right)^{ - 0.53}} + 0.5\,{\rm{erg}}\,\,{\rm{c}}{{\rm{m}}^{ - 3}}\rho {\left( {{D \over {2{\rm{cm}}}}} \right)^{1.36}},$(4)

which involves a strength (small D) and a gravity regimes (large D). Hereinafter, we assume a single law for the main belt population, even though S- and C-types might be different in terms of their rheology. Further relations for Mlr(Q), largest remnant mass, Mlf(Q), largest fragment mass, q(Q), slope of SFD of fragments, constrain the outcome of collisions.

For the decay time scale in the main belt, describing orbital dynamics, not collisions, we assumed the following analytical prescription (τ in Myr, D in km): τmb={ 30 for D<10−730(D/10−7)0.38D<0.0011000D<0.0031000(D/0.003)−0.58D<0.01500D<0.02500(D/0.02)0.86D<0.12000(D/0.1)0.30D<14000D0.41D<2013800(D/20)1.05D<10075000(D/100)1.30 otherwise,  ${\tau _{{\rm{mb}}}} = \left\{ {\matrix{ {30} \hfill & {{\rm{ for }}D < {{10}^{ - 7}}} \hfill \cr {30{{\left( {D/{{10}^{ - 7}}} \right)}^{0.38}}} \hfill & {D < 0.001} \hfill \cr {1000} \hfill & {D < 0.003} \hfill \cr {1000{{(D/0.003)}^{ - 0.58}}} \hfill & {D < 0.01} \hfill \cr {500} \hfill & {D < 0.02} \hfill \cr {500{{(D/0.02)}^{0.86}}} \hfill & {D < 0.1} \hfill \cr {2000{{(D/0.1)}^{0.30}}} \hfill & {D < 1} \hfill \cr {4000{D^{0.41}}} \hfill & {D < 20} \hfill \cr {13800{{(D/20)}^{1.05}}} \hfill & {D < 100} \hfill \cr {75000{{(D/100)}^{1.30}}} \hfill & {{\rm{ otherwise, }}} \hfill \cr } } \right.$(5)

which contains contributions from the diurnal Yarkovsky effect, the seasonal Yarkovsky effect, the YORP effect, spin-size dependence, conductivity-size dependence, or the Poynting-Robertson effect.

For the average lifetime in the NEO population (τ in Myr), we assumed: 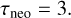τneo =3.${\tau _{{\rm{neo }}}} = 3.$(6)

It is shorter compared to Granvik et al. (2018), but closer to an average over all families. The two time scales cannot be easily separated from each other. The absolute NEO population is derived from the main-belt population by the ratio of τneo/τmb, assuming an equilibrium.

Our model was calibrated by: (i) the observed SFD of the asteroid belt (Bottke et al. 2015a) (Fig. B.2); (ii) the observed SFD of NEOs (Harris et al. 2015) (Fig. B.3); (iii) the Vesta family SFD; (iv) the Rheasylvia basin age (O’Brien et al. 2014); (v) (4) Vesta’s cratering record (Marchi et al. 2012).

Initial conditions for the Vesta family were as simple as possible, a single power-law N(>D) = CDq down to sub-kilometre sizes, with the initial slope q. The break at 4 km is created in the course of evolution by a collisional cascade. After approximately 1100 Myr, the slope q1 = q for D > 4 km remains steep, but the slope |q2| < |q1| for D < 4 km becomes shallow, which is in accord with the observed slopes (see again Fig. B.2). The break at 0.5 km, attributed to observational incompleteness, does not affect this calibration.

A similar approach was used for all other families, which led to an independent estimate of their ages (Table 2). It is based on the assumption that the break of the SFD at about 3 to 5 km has been created by the collisional cascade.

thumbnail Fig. 3

Mean spectra of asteroid families along with their classification. If only one spectrum (for the largest member) was available, the designation includes its number. If more spectra were available, but the mean was unreliable, spectra were plotted separately (blue, green).
Table 2

Ages of the C-type families estimated from our collisional model.

4.2 Backward integrations

For some of the ‘promising’ families, we tried to determine their ages independently by backward integrations of the orbits (Nesvorný et al. 2002, 2003). Our orbital model is based on a modified version of SWIFT (Levison & Duncan 1994; Brož et al. 2011), the symplectic integrator MVS2. It involves 5 massive bodies (Sun, Jupiter to Neptune), 100 mass-less asteroids, the Yarkovsky effect, and the YORP effect. The sampling time step of osculating elements was 1 y. On these, we applied filters A, A, B of Quinn et al. (1991), with the decimation factors 10, 10, 3, so that the output time step was 300 yr, which is sufficient to sample secular oscillations.

The thermal parameters were set up as follows: density p = 1.3 g cm−3, conductivity K = 10−3 Wm−1 K−1, capacity C = 680 J kg−1 K−1, the Bond albedo A = 0.1, emissivity ε = 0.9. For each asteroid, we created 20 clones with a uniform sampling of the obliquity (cos γ), in order to explore different Yarkovsky drift rates.

In the post-processing, we computed a differential precession ∆Ω with respect to the 1st body (unless its orbit is chaotic, e.g. (490) Veritas). At each time step and for each asteroid, we selected the best clone, that is, the clone with the smallest ∆Ω. The percentage of interlopers we removed from the output population varied from 0 to 50%, depending on the surrounding background population.

We determined either a precise age, when the orbits exhibit a convergence and then a divergence of ∆Ω, or a lower limit of the age t↓, when the orbits only converge, but then do not diverge, because there is always a clone which can reach zero ∆Ω.

The upper limit t↑ on the family age is given by the Yarkovsky semimajor axis drift (Nesvorný et al. 2015): 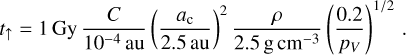t↑=1 GyC10−4 au(ac2.5 au)2ρ2.5 g cm−3(0.2pV)1/2.${t_ \uparrow } = 1{\rm{Gy}}{C \over {{{10}^{ - 4}}{\rm{au}}}}{\left( {{{{a_{\rm{c}}}} \over {2.5{\rm{au}}}}} \right)^2}{\rho \over {2.5{\rm{g}}{\rm{c}}{{\rm{m}}^{ - 3}}}}{\left( {{{0.2} \over {{p_V}}}} \right)^{1/2}}.$(7)

However, even t↑ is not a ‘hard’ limit, if the Yarkovsky drift is not nominal (e.g. due to different thermal parameters) oris modified (e.g. due to the stochastic YORP related to shape variations; Statler 2009; Bottke et al. 2015b).

A summary of our results is presented in Table 3. It is important to focus on the rows “young Ω”. From the point of convergence, the most promising C-type families seem to be: Aeolia, Misa, Elfriede, Hoffmeister, König, and, of course, Veritas (Carruba et al. 2017b).

An example of the König family is shown in Fig. 4. A clear convergence of Ω occurs either at 14.6, or 22.7 Myr, with a local uncertainty of 1 Myr. We will identify the correct solution soon (Sect. 4.3).

An independent argument is based on statistics. If there are breakups between 0–10 Myr (cf. Karin, Koronis2, and Veritas), there must be also some between 10–20 Myr, consequently, some of the convergences must be real.

4.3 Forward integrations

Again, for some of the ‘promising’ families we tried to determine their ages independently by forward integrations. Our orbital model is again based on a modified version of SWIFT (Levison & Duncan 1994; Brož et al. 2011), the symplectic integrator RMVS3. Hereinafter, we included 10 massive bodies (Sun, Mercury to Neptune, Ceres), about 1000 mass-less asteroids, the Yarkovsky effect, the YORP effect, and also collisional reorientations. The sampling time step was 1 yr. Mean elements were computed with the filters A, A, A, B, the factors 10, 10, 10, 3, the intermediate time step was 3000 yr; unless it was necessary to sample short-period oscillations. Proper elements were computed by the Fourier transform (Šidlichovský & Nesvorný 1996), out of 1024 samples, with an exclusion of planetary frequencies (𝑔, s). The output time step was 0.1 Myr. Thermal parameters were the same as above; the efficiency of YORP c = 0.33.

In the case of forward integrations, we needed a synthetic family, representing an initial configuration before dispersal. The geometry of individual impacts is presented in Table C.2. While the velocity field was isotropic, the distribution of a, e, i elements was determined by the true anomaly ƒ and the argument of perihelion ω. For example, ƒ = 0° (or 180°) corresponds to a narrow diagonal ellipse. We tested several combinations of ƒ, ω and selected suitable geometries. The uncertainty is typically of the order of 20°. A long-term evolution is chaotic, diffusive, i.e. irreversible, so that we must compare synthetic vs. observed distributions of a, e, i.

Perturbations, which actually allowed us to estimate the ages, included secular resonances, chaotic diffusion, (1) Ceres, or the YORP effect, i.e. a depletion of small bodies in the centre of the family. Again, a summary of our results is presented in Table 3. It is important to focus on the rows denoted “young e” or “young i”. The most promising C-type families are: Aeolia, Beagle, Brangäne, König, and Theobalda.

For example, the König family is perturbed by the 𝑔 − 𝑔5 + s − S6 secular resonance (Fig. 5). It evolves along the libration centre and subsequently, away from it. Starting from a simple isotropic field (ellipsoidal) ends up with a complex non-isotropic (‘criss-cross’). The best-fit age is (20 ± 5) Myr. Combined with the convergence of Ω (Sect. 4.2), the true age is 22 ± 2 Myr.

Taking the Astrid family as another example, it is affected by the 𝑔 − 𝑔C secular resonance with Ceres (Novaković et al. 2016; Tsirvoulis & Novaković 2016). This perturbation increases the spread of inclinations at a = 2.763 au; there is no spread without Ceres. According to Fig. B.4, the lower limit t↓ is 150 Myr. Importantly, the perturbations from Ceres allowed us to rule out the existence of a steep ‘tail’ of the SFD for Astrid, as well as for Aëria, Brasilia, or Hoffmeister. The argument is exactly the same as for Vesta (Sect. 4.1).

Other interesting examples of perturbations are shown in Figs. B.5, B.6.

Table 3

Ages of the C-type families estimated from our orbital model.

thumbnail Fig. 4

König family exhibits a convergence of nodes. The range of ΔΩ with respect to (3815) König (green; top) is plotted together with individual values (grey). For each body, we used a set of 20 clones with different Yarkovsky effect and we selected the best clone at each time step. Not all bodies converge, because some of them are interlopers. The temporal dependence ΔΩ(t) exhibits local minima, in particular, 14.6 Myr and 22.7 Myr seem to be possible ages. For 22.7 Myr, the converging orbits of the best clones were plotted (coloured; bottom). For 14.6 Myr, a different set of clones would have to be selected. The orbits often exhibit more than one differential-precession cycle. See also Fig. 5.
thumbnail Fig. 5

König family is 22 Myr old according to orbital evolution. The observed family (green) has a very peculiar structure in the proper semi-major axis ap versus the proper inclination sin ip. The synthetic family (blue; top) is initially distributed in a simple ‘ellipse’, created by an isotropic impact. The geometry of the impact was f = 85°, ω = 0°. In the course of evolution, the distribution is modified by the 𝑔 − 𝑔5 + s − s6 secular resonance. At the time (22 ± 2) Myr (bottom), it exactly corresponds to the observed distribution. Such a young age indicates that the SFD can still be steep.

4.4 Transport model

We constrained the transport from the family location to the near-Earth space by another set of orbital simulations. This time, we included 11 massive bodies (Sun, Mercury to Neptune, Ceres, Vesta), and about 1000 mass-less particles, which were initially located at the observed positions of the family members. The temporal decay of the populations is shown in Fig. B.7 the lifetime in the NEO space in Fig. B.8.

Assuming steady state (cf. the discussion in Brož et al. 2024), the NEO population can be estimated as: 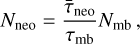Nneo=τ¯neoτmbNmb,${N_{{\rm{neo}}}} = {{{{\bar \tau }_{{\rm{neo}}}}} \over {{\tau _{{\rm{mb}}}}}}{N_{{\rm{mb}}}},$(8)

where τmb is the decay time scale in the main belt, 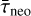τ¯neo${\bar \tau _{{\rm{neo}}}}$, the mean lifetime in the NEO region, and Nmb, the population in the main belt. A substantial number of families is too young or too small to contribute to the population of 1-km NEOs. Especially, if the families are located far from major resonances, there is no way how to transport bodies to the near-Earth space.

Regarding the transport of metre-sized bodies, we changed two important parameters, the conductivity K = 1 W m−1 K−1, corresponding to monoliths, and the tensile strength according to Holsapple (2007), which allows for fast-rotating bodies. This substantially suppresses the diurnal Yarkovsky effect (Vokrouhlický 1998). The outcomes are shown in Figs. B.9, B.10.

Using Eq. (8) is not sufficient though, because C-type families are found at very different locations. One has to compute collisional probabilities p with the Earth (Table C.4), and estimate the meteoroid flux (in 10−9 km−2 yr−1) as: 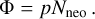Φ=pNneo .$\Phi = p{N_{{\rm{neo }}}}.$(9)

The populations and fluxes from individual sources are listed in Tables 4 and 5.

5 Results

The SFDs of individual families (Fig. 2) exhibit substantial differences in terms of observational bias, which occurs for diameters in the 1–3 km range. To make them comparable, we extrapolated SFDs from a multi-kilometer population consistently to 1 km. Most of the time, the extrapolation was straightforward (a straight line on a log-log plot). Sometimes, however, we had to use a collisional model (Sect. 4.1), because it turned out that the SFD was ‘bent’ already at multi-km sizes (e.g. Euphrosyne).

To further extrapolate these SFDs to metre sizes, the use of a collisional model was absolutely necessary (Fig. B.11). Moreover, SFDs evolve in the course of time and it is necessary to determine their current state. Regarding the transport from the main belt to the NEO space, our model is similar to Brož et al. (2024), with only a few exceptions (see Sect. 4.4).

A notable result is that the meteorite-NEO conundrum (Vernazza et al. 2008; Brož et al. 2024) is well present among carbonaceous bodies. Prominent sources for kilometre-sized bodies turn out in most cases to be irrelevant to modest sources for meteorites and vice versa. Hereafter, we describe in more detail the main respective source of kilometre- and metre-sized NEOs for the main CC compositional groups (CI/IDP/C-ungr., CM/CR, CO/CV/CK).

5.1 Source regions of kilometre-sized CC-like NEOs

The vast majority of kilometre-sized CI-like NEOs originate from three families: Polana (approximately 58 bodies), Euphrosyne (39), and also Themis (10) (Table 4, or percentages in Fig. 6). Regarding CM-like NEOs, the Adeona family is by far the main source (22), followed at a respectable distance by the Dora family (7). The Eos family alone is a sufficient source of CO/CV/CK NEOs. A subset of NEOs with a characteristic shallow 1.00-micron band is related to Baptistina, respectively.

Overall, CI-like NEOs are the dominant population among CC-like NEOs and they represent the vast majority (≈80 %) of low-albedo (pV ≤ 0.1) bodies that are either CI- or CM-like. In this context, the CI-like composition of Ryugu and Bennu (see discussion; Yokoyama et al. 2023), both with low (pV ≤ 0.06) albedos, is very consistent with our findings and actually not surprising. Finally, the relative abundance of the different compositional types predicted by our model are in excellent agreement with the observed ones (Fig. 6).

Table 4

Dynamical time scales and cumulative numbers of 1-km asteroids in the main belt (mb) and the near-Earth region (neo).

Table 5

Same as Table 4 for 1-m meteoroids.

thumbnail Fig. 6

Percentages of CM/CR- (blue), CI/IDP- (cyan), CO/CV/CK- (grey) and other carbonaceous-chondrite-like bodies of the synthetic main belt (left), of the synthetic NEO (middle) and the observed NEO (right) populations. These percentages are different for kilometre-sized (top) versus metre-sized (bottom) bodies, due to substantial differences in the SFDs of the source populations. The contributions of individual asteroid families are indicated within the respective pie charts. For comparison, the observed percentages of meteorite falls from https://www.lpi.usra.edu/meteor/, with respect to all classes, are as follows: HED 6.0%, OC 80%, CC 4.4%, irons 4.1%, enstatite chondrites 1.5%, aubrites 0.9%, mesosiderites 0.6%, ureilites 0.5%, pallasites 0.3%, acapulcoites 0.1%, lodranites 0.1%, respectively.

5.2 Source regions of carbonaceous chondrites

There are five families (Polana, Euphrosyne, Clarissa, Misa, Hoffmeister) that contribute to at least 10% of the incoming flux of CI chondrites (Table 5), with the Polana family being the most prominent source (approximately 80 × 10−9 km−2 yr−1). Its SFD is evolved and shallow at sub-kilometre sizes (Fig. 7).

On the contrary, the 8.3-Myr-old Veritas family (Nesvorný et al. 2003) still has a steep SFD (Fig. 8). It is by far the main source of CM chondrites (200 in the same units), followed by the König family (50). Overall, CM-like metre-sized bodies seem to be the dominant population over CI-like bodies, essentially because of the massive flux originating from the young Veritas family.

Of great interest, we identify Phaethon as the fourth most important source of CC meteorites, representing about 30 × 10−9 km−2 yr−1 of the incoming flux, provided its SFD is continuous from sub-kilometre asteroids to dust.

The Baptistina and Aeolia families, respectively, should also be sources of some meteorites, even though we were unable to identify an analogue. Their combined flux (≈30) is non-negligible, in comparison to other C-type families.

Finally, the Eos family is a viable source of CO/CV/CK chondrites. Its flux 5 × 10−9 km−2 yr−1 is sufficient, in comparison to the calibration, i.e. the Vesta family and HED meteorites (40 × 10−9km−2yr−1). This suggests that the denser (CO/CV/CK) carbonaceous bodies are much less affected by atmospheric or pre-atmospheric bias compared to less dense (CI/CM) bodies (see discussion). Quantitatively, CO/CV/CK-like meteoroids represent only about 1% of the incoming CC flux in our simulations, whereas they should represent more than 30% of all CC falls. Such a discrepancy between synthetic and observed CI/CM compositions versus CO/CV/CK ones is not observed at large kilometre sizes (see again Fig. 6), strengthening the likelihood of some sort of bias at small metre sizes.

thumbnail Fig. 7

Synthetic SFD of the Polana family derived from our collisional model. Initially, it was steep (Pantone 7633C, dashed), but since then it has evolved and it is now shallow (blue), in agreement with observations at kilometre sizes (grey, solid). For comparison, the main belt distribution is also plotted (cyan), as well as corresponding observations (Bottke et al. 2015a). Each model was run 10 times to account for stochasticity.

5.3 Source regions of other types of compositions

The majority of metal-rich (M-type) kilometre-sized NEOs originate from the Brasilia family (13 bodies), followed by the Tina family (4). The Kalliope, Aëria, and Brängane families are negligible source at kilometre sizes. The situation is more even at metre sizes, with all families contributing to the meteorite flux and the young Brangäne family being the most prominent source (about 10 × 10−9 km−2yr−1).

We further identified the Iannini family as the source of acapulcoite and lodranite meteorites. The match in terms of family age versus CRE ages of these meteorites is excellent, and the same can be said in terms of composition (pyroxene-rich). We note that the flux predicted from this family – in tandem with the flux predicted from the Vesta family – is consistent with meteorite falls statistics, acapulcoite and lodranite falls amounting to ≈ 0.2% and HED 6% of all falls (Table 5).

Finally, there is only one dedicated source of P-type kilometre NEOs, namely the Sylvia family. Nevertheless, P-type asteroids seem to be present also in the Euphrosyne and Themis families, at the levels of 20% (Yang et al. 2020b) and 50% (Marsset et al. 2016; Fornasier et al. 2016), respectively. These families therefore appear as the main sources of P-types.

6 Discussion

Our model (‘METEOMOD’1) for populations of meteoroids and NEOs, which has been constrained by the observed SFDs, can be compared to various types of other observations. We organise the discussion around three major science questions to which we attempt to provide elements of answer. Are our proposed source regions of CC meteorites compatible with laboratory and remote measurements? (Sects. 6.1, 6.2, 6.3, 6.4). Are CC meteorite fall statistics driven by atmospheric, thermal or collisional fragmentation? (Sects. 6.5, 6.6, 6.7). Is our synthetic population of kilometre-sized bodies compatible with spectroscopic observations? (Sects. 6.8, 6.9).

thumbnail Fig. 8

Same as Fig. 7 for the Veritas family. For a family as young as Veritas, however, the initially steep SFD is still preserved. In the future, it will become as shallow as Polana.

6.1 IRAS dust bands

The prominent 9.3° IRAS dust band is known to be associated with the CM-like Veritas family (Nesvorný et al. 2006). If the observed SFD is extrapolated with a −2.7 slope from kilometre sizes to 100 µm, it ‘hits’ the observed dust band abundance (see Fig. 9). If the SFD is interpolated to 1 m, it corresponds to the number of CM meteoroids in our model.

The inclinations of König (9.0°) and Brangäne (9.6°) are so similar to that of Veritas (9.3°) that their dust bands might be ‘hidden’ within that of Veritas. Since the band is more than several degrees wide, the model of Nesvorný et al. (2006) can surely be adapted to encompass all three families. Perhaps, there is another hidden band related to the Misa family (2.3°), contributing to the 2.1° band, even though its age indicates that the band must be ‘extinct’.

Fainter bands have imprecise inclinations (Fig. 1), the only exception being the 12.1° J/K band, associated to the family of (4562) Iannini (also denoted (1547) Nele; Carruba et al. 2018).

The ≈15° M/N dust band may be linked to the family of (293) Brasilia (also named after (1521) Seinajoki; Nesvorný et al. 2003) as its SFD is steep down to the observational limit. However, the effect of Ceres resonance indicates an age of 100 Myr, implying that the band should be more-or-less extinct. Nevertheless, having both prominent and extinct bands is expected.

thumbnail Fig. 9

Observed SFD of the Veritas family (grey, solid). Its extrapolation (dotted) is supported by the observed 9.3° IRAS dust band (Nesvorný et al. 2006), at approximately 30 µm (error bar). Moreover, the initial SFD (Pantone 7633C, dashed) is supported by the excess of extraterrestrial He-3 (Farley et al. 2006), which 8.3 Myr ago ‘overshot’ the background level by a factor of ~3. The interpolation to metre sizes (error bar) implies the abundance of CM chondrite meteoroids.

6.2 CRE ages

The CRE ages of CM chondrites (Krietsch et al. 2021; Fig. 10) indicate an onset at 8 to 9 Myr corresponding to the age of the Veritas family (8.3 Myr), in agreement with our model. The ages seem to indicate another onset at about 2 Myr. This may correspond to a secondary collision, which occur regularly in our collisional model.

CY (i.e. reclassified CI) chondrites (King et al. 2019) exhibit very short CRE ages (< 1.3 Myr). We did not find any CI-like family which could be so young. Instead, it is likely that CI-like meteoroids transported to the NEO space were thermally altered in a similar way as (3200) Phaethon (MacLennan & Granvik 2024) – due to its extreme eccentric orbit, high irradiation flux, leading to additional fragmentation (M. Granvik, priv. comm.), hence shortening of CRE ages.

The CO, CV, and CK chondrites (Scherer & Schultz 2000) exhibit a continuous distribution over the last 40 Myr, especially if all the three types are considered together. This corresponds to a typical collisional time scale, expected for old families like Eos. A similarity to the distribution of L or LL chondrites confirms this conclusion, as well as a similar strength to ordinary chondrites.

The CB chondrites are rare. Nevertheless, Gujba has an age (26 ± 7) Myr, Bencubbin ~ 27 Myr, Isheyevo ~ 34 Myr (Rubin et al. 2003; Ivanova et al. 2008), all of which might be compatible with the Brangäne family; even though we classified it rather as M-type. The CH chondrites are likely related to CB, having a similar formation age and environment (Ivanova et al. 2008; Wölfer et al. 2023), but their CRE ages are relatively short, 1 to 12 Myr (Eugster et al. 2006), indicating a distinct parent body.

thumbnail Fig. 10

CRE ages of CM chondrites (top) (Krietsch et al. 2021) exhibit an increase on a cumulative histogram, i.e. a peak on a differential histogram. On the contrary, CV, CO, and CK chondrites (Scherer & Schultz 2000) exhibit a continuous distribution over the last 40 Myr. This increase/peak corresponds to the late miocene peak of extraterrestrial helium-3 in terrestrial sediments (Farley et al. 2006) (middle) and to the age of the CM-like Veritas family, (8.3 ± 0.1) Myr, as confirmed by convergence of orbits (bottom). A plot with a sum of probability distributions presented in Krietsch et al. (2021), Fig. 9 is misleading; uncertainties of old CRE ages are large, the probability is low, it seems like there are ‘none’ meteorites having old CRE ages. On the contrary, our cumulative histogram demonstrates that there are numerous meteorites with old CRE ages.

6.3 Pre-atmospheric orbits of CM chondrites

Pre-atmospheric orbits of CM2 chondrites (Meier 2023; Fig. 11) are rare, but even with a limited sample of 3 orbits, it probably shows the most probable orbits from an underlying distribution. Orbits have low inclinations i ≲ 2°, semimajor axes up to a ≃ 2.6 au. These are important indicators, because some meteorites should be found close to their source.

According to Table 5, one of the promising sources could be the Astrid family, with i ≃ 0.6° and a ≃ 2.787 au. It readily produces low-inclination orbits of meteoroids and these have the largest collisional probability with the Earth. However, the respective SFD of Astrid is too shallow.

On the contrary, the SFD of Veritas is so steep that it should produce a much larger flux anyway (cf. Φ in Table 5). Some meteoroids from Veritas are indeed able to reach low-inclination orbits (see Fig. 11). This is even more common if the ejection velocity field from Veritas was more extended for metre-sized bodies than for kilometre ones. However, the size dependence of υ(D) can hardly be 1/D, because particles at 100 µm would be totally dispersed and we would see no dust bands. Instead, it could be proportional to 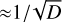≈1/D$ \approx 1/\sqrt D $.

thumbnail Fig. 11

Pre-atmospheric orbits of CM, C1-, and C2-ungrouped meteorites (Meier 2023; black crosses with error bars). Their maximum semimajor axis is well beyond the 3:1 mean-motion resonance (a ≲ 2.82 au) and their inclination is low (i ≲ 2°). For comparison, synthetic orbits of 1-m meteoroids from Veritas (top) and Astrid (bottom) are plotted, whenever an orbit is in the NEO region (a(1 + e) > 0.983 au Λ a(1 − e) < 1.3 au). Colours correspond to the lifetimes in the NEO region. It is difficult to scatter orbits from high → low inclinations, and vice versa. Low-inclination orbits also have much larger probability pi of collision with the Earth. Nevertheless, the flux Φ = PiNneo from Veritas is larger than from Astrid, according to our model. Consequently, we favour Veritas as the main source of CM chondrites.

6.4 Entry speeds from FRIPON

Since 2016, the worldwide FRIPON camera network (Colas et al. 2020) observes on a nightly basis incoming bolides, allowing the determination of their orbits and entry velocity, among other things. We considered detections of bolides recorded since 2016 by at least 3 stations. According to an ablation model, these events correspond to bolides with initial mass mi ≥ 10 g. We removed outliers, with uncertain values of mass, 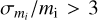σmi/mi>3${\sigma _{{m_i}}}/{m_{\rm{i}}} > 3$, or unrealistic values of the ablation parameter, B < 10−11 m2 J−1. From these 602 events, a histogram of entry speeds was constructed (Fig. 12). It is skewed towards low speeds (the minimum is the escape speed from Earth, 11.2 km s−1). At high speeds, there is no ‘cometary source’; all massive meteoroids seem to be asteroidal. The only prominent shower is Geminids, related to asteroid (3200) Phaethon (Whipple 1983; Hanuš et al. 2018; Battams et al. 2022; see Fig. 13). This NEO source was also added in Table 5.

A comparison with our model is not straightforward. Meteoroids from asteroid families have a range of speeds relative to Earth, typically between 20 to 30 km s−1 (cf. Figs. 12, B.13). Nevertheless, entry speeds must be properly weighted, since we compare it to observations of bodies entering the Earth’s atmosphere. Thus for each family j, we computed a histogram dNj(υ, υ + dυ) of υi values weighted by individual collisional probabilities pi (not the mean p, from Table C.4). Then we computed a sum of histograms, weighted by the corresponding meteoroid fluxes (from Table 5): 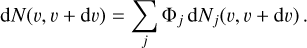dN(v,v+dv)=∑jΦj dNj(v,v+dv).${\rm{d}}N(\v ,\v + {\rm{d}}\v ) = \sum\limits_j {{\Phi _j}} {\rm{d}}{N_j}(\v ,\v + {\rm{d}}\v ).$(10)

The resulting histogram is surprisingly similar to the observations (Fig. 12). There are only minor differences, e.g. the synthetic histogram exhibits a bit narrower peak and a bit higher tail. Partly, this might be attributed to an observational bias, e.g. due to an instability of the ablation model (cf. outliers). Moreover, it is known that the mass determination from fireball data is especially difficult for higher speeds, or lower decelerations. Nevertheless, we consider our model (‘METEOMOD’) to be in agreement with bright bolides.

thumbnail Fig. 12

Histogram of entry speeds observed by FRIPON (grey) and computed from our model (‘METEOMOD’; violet), with appropriate weighting by collisional probabilities. For comparison, underlying (unweighted) distribution from the original families is plotted (dotted). The uncertainties were estimated as Poissonian. The total number of events was 602.
thumbnail Fig. 13

Same as Fig. 9 for (3200) Phaethon. Two additional NEOs were included in this SFD, (155140) and (225416); (MacLennan et al. 2021). Its extrapolation (dotted) is supported by the observed dust trail (Battams et al. 2022). Its interpolation (error bar) explains the abundance of Geminids (cf. Fig. 12).

6.5 Atmospheric fragmentation

We find that Cl-like and CM-like meteoroids should be nearly as abundant as ordinary chondrite (OC) like meteoroids at the top of the atmosphere. Yet, OCs are 40 times more abundant than CI and CM chondrites among falls. Hereafter, we explore the effects of various mechanisms that may explain this discrepancy between our model and observations.

Atmospheric entry has long been proposed as the main bias to explain the paucity of CI and CM falls with respect to OC falls, for instance, a consequence of their difference in terms of strength. Fragmentation of CC meteoroids occurs at a low dynamical pressure (10−2 MPa; Borovička et al. 2019). While this material (‘Original matrix’) cannot survive, fragments logically have a smaller volume, a lower number of flaws, and hence a higher strength, comparable to a typical peak dynamical pressure during an atmospheric entry (3 to 5 MPa; Borovička et al. 2019).

Of course, the strength of meteorites is generally different (Pohl & Britt 2020). If considering tensile strength, which is typically 10 times lower than the compressive strength, the mean values of meteorites classes are as follows: CI 2, CV 3.5, CM 7, LL 10, H 15, L 30, and irons 400 MPa. Fragments surviving the atmospheric entry do have strengths higher than the peak dynamical pressure. The key question, however, is not ‘at what pressure?’, but ‘into how many pieces?’, and eventually ‘how to find them?’. This determines whether a bolide will result in a fall.

Using a basic ablation model (Pecina & Ceplecha 1983; Brož & Šolc 2013) one can verify that the peak dynamical pressure p depends on the zenith angle ɀ2 (Fig. 14). If CC meteoroids have approximately 10 times lower strength than OC (as indicated above), they should only survive for trajectories with ɀ ≳ 85°. This amounts to a factor of 10 in the adjacent solid angle, ω = 2π(1 − cos ɀ).

An additional bias relates to entry speeds, which differ substantially for individual sources (Fig. B.13). Bodies with excessive speeds (≳30 km s−1) are eliminated by ablation. On the other hand, a low-speed part ≲20km s−1 of the distributions is strongly preferred. Surviving CM chondrites are thus likely related to low-speed Veritas meteoroids. Relatively, Polana (CI) is preferred over Euphrosyne, etc. This certainly contributes to the fact that OCs prevail over CCs, especially when Koronis (H) and Massalia (L) produce a lot of meteoroids with low speeds.

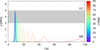thumbnail Fig. 14

Dynamical pressure p on a meteoroid during its atmospheric entry, depending on the zenith angle ɀ (in degrees). A basic ablation model was used, with the following parameters: initial mass m = 1000kg, entry speed υ = 20 km s−1, density ρ = 1700 kg m−3, ablation efficiency η = 0.02, specific heat l = 106 J kg−1, shape factor A = 1.22 (i.e. sphere), friction coefficient C = 0.5. The resulting terminal mass m′ = 0.3 kg. The strength of OC meteoroids (3 to 5 MPa; Borovička et al. 2019; grey area) is comparable to p. CC meteoroids (≈ 0.5 MPa; dotted line) are substantially weaker than p. If fragmentation occurs, the ablation process becomes much more efficient; CC meteorites only survive for trajectories with ɀ ≳ 85°.

6.6 Thermal cracking

Other mechanisms such as thermal cracking (Granvik et al. 2016), or water desorption (Granvik, priv. comm.) might be at play. In-situ observations of the asteroid Bennu (Delbo et al. 2022) revealed angular boulders and oriented cracks, induced by the diurnal cycle. This is a direct evidence of thermal cracking on metre scales.

On metre-sized bodies, a thermal stress of the order of MPa develops (Čapek & Vokrouhlický 2010), especially if the heliocentric distance is below 0.3 au, or the rotation frequency is below 1 Hz, or the obliquity γ ~ 90°, since then one hemisphere points towards the Sun for a long time. Evolution of the spin due to the YORP effect (Rubincam 2000; Čapek & Vokrouhlický 2004) might temporarily lead to conditions favouring disruptions. If carbonaceous bodies have strengths less than a MPa (Borovička et al. 2019), this should be commonplace and only strong bodies should enter the atmosphere. However, meteoroids like Geminids still exhibit low strengths (Henych et al. 2024), which is in contradiction with dispersal of weak bodies. Subsequently, these bodies might be disrupted by tides (Walsh & Richardson 2008; Granvik & Walsh 2024), if they encounter the Earth.

Regardless of CI and CM meteoroids being disrupted prior to or during atmospheric entry, they contribute to the abundance of interplanetary dust particles (IDPs), in particular, chondritic-smooth (CS), hydrous, asteroidal IDPs, which comprise about 50% of all IDPs at <50 µm (Bradley 2007).

Micrometeorites recovered in Antarctica (Genge et al. 2020) also indicate a comparable amount of C- vs. S-type asteroidal materials (60 vs. 40%) at sizes >300 µm. Chondritic-porous (CP), anhydrous, cometary IDPs are already negligible at these sizes. Given that the micrometeoroid flux is directly proportional to the metre-size flux, since the SFDs are in a collisional equilibrium, our model (Table 5) appears fully in agreement with this observation.

6.7 Collisional fragmentation

Alternatively, if C-types are less strong than S-types, their col-lisional evolution and their current SFD might be systematically different. If sub-kilometre C-type bodies are more easily disrupted than S-type bodies, the local slope of the SFD should be more shallow. Consequently, the population of metre-sized bodies should decrease, as well as that of 100 µm-sized dust grains.

However, this is in contradiction with the observations of dust bands, the 9.3° band being the most prominent one (see above). It follows that a collisional cascade cannot have destroyed all sub-kilometre C-type bodies; otherwise we would not observe this prominent dust band.

In fact, C-type asteroids represent the vast majority of sub-kilometre bodies in the asteroid belt (Marsset et al. 2022). It does not make sense to decrease the strength of the Veritas family, without decreasing the strength of ‘everything’ else. According to our tests, assuming a 10 times lower strength of all sub-kilometre bodies implies similar SFDs (relatively to each other; Veritas w.r.t. main belt) at sub-kilometre sizes. Consequently, collisional fragmentation on its own cannot explain the paucity of CC meteorites.

6.8 Taxonomy of NEO orbits

A comparison of our synthetic population of kilometre-sized CI- and CM-like NEOs with the observed orbital distribution is important, as it is a direct test of our transport model.

The orbits of CI- and CM-like NEOs (Fig. 15) exhibit an ‘extreme’ spread of inclinations up to 40°, and semima-jor axes up to 3.2 au. The distribution seems bimodal, with a low-inclination component (i ≲ 5°); and a more scattered high-inclination component (i ≳ 20°). According to our model (Table 4), most CI- and CM-like NEOs should originate from the Polana (3.3°) and Euphrosyne (26.5°) families; CM-like NEOs being significantly less abundant than CI-like ones. It follows that our model is in perfect agreement with observations.

Regarding B-type NEOs, a few of them possess a high albedo (pV ≥ 0.1) and do have high inclinations; these bodies ‘certainly’ originate from Pallas. However, the orbits of the low albedo B-type population are similar to those of CI- and CM-like NEOs, albeit without the low-inclination component from Polana (3.3°). These bodies must originate from other CI-like families, ergo, B-type being compositionally similar to C-types (e.g. Vernazza et al. 2015; Marsset et al. 2016).

CO/CV/CK-like NEOs (K-types), have medium- to high-inclination orbits. The only sizable family at the correct inclination is Eos (9.9°).

Bodies having a characteristic shallow 1.00-micron band, which are relatively rare, preferentially have low-inclination orbits, which cluster close to 2 au (Fig. 15). According to our model, they must originate from the Baptistina family (6.0°).

CH- and CB-like bodies are metal rich and they might appear as M-types. About 10 of them should be observable from Brasilia (15°). This seems to be compatible with the observed percentage of M-type NEOs (Marsset et al. 2022).

6.9 Common origin of Ryugu and Bennu

The JAXA Hayabusa 2 and NASA OSIRIS-Rex sample return missions have targeted two C-type NEOs, namely Ryugu and Bennu, respectively (Watanabe et al. 2019; Lauretta et al. 2019). Ongoing analysis of the object’ samples in terrestrial laboratories have revealed that CI chondrites are their closest analogues (Yokoyama et al. 2023).

Applying our model to Ryugu and Bennu, it appears that there is a ≳ 90% probability that both objects originate from the CI-like Polana family (Fig. 16). Even without a-priori knowledge of CI vs. CM classification, this is the only option, since Euphrosyne (CI) is too distant and Adeona (CM) is too inclined. It follows that these NEOs sample the same parent body. Our results are fully consistent with previous findings of Bottke et al. (2015b, 2020).

In case a future sample return mission aims to probe the diversity among CI-like asteroids, we suggest to target high-inclination CI-like NEOs originating from the Euphrosyne family. This will of course have a cost, due to a higher ∆υ.

7 Conclusions

In this work, we constructed a complex model linking NEOs and meteorites with their sources in the asteroid belt. Our approach is very different from previous works (e.g. Granvik & Brown 2018; Granvik et al. 2018; Nesvorný et al. 2023) because we use a-priori knowledge of families, their taxonomy and SFDs. Our sources correspond to individual families (not to resonances), because otherwise the ‘critical’ information about the original location (a, i) is lost. The taxonomy is important, because the orbital distributions for various classes do differ (cf. Figs. 11, 15). The SFD is equally important, because some sources dominate the others and they must serve as appropriate weights.

For kilometre-sized NEOs, our model indicates that most of them originate from just two families: Polana and Euphrosyne (Fig. 6). Their reflectance spectra are compatible with CI chondrites. Other primitive classes P and D do not have sufficient sources in the main belt, but they rather originate as comets (DeMeo & Binzel 2008).

On the other hand, the flux of metre-sized carbonaceous chondrites is dominated by just one family: Veritas (cf. Fig. 6). Its reflectance spectrum is compatible with CM chondrites. This certainly contributes to the prevalence of CM over CI chondrites. Even though the observed ratio CM/(CI+C-ungr.) ≃ 2 is higher than our prediction 1.6, it is still within uncertainties on the side of our model (i.e. a factor of two) and on the side of observations.

Regarding the total flux of meteorites, estimated to 740 × 10−9 km−2 yr−1 (Nesvorný et al. 2023) about half of it comes from S-types (Brož et al. 2024), the other half from C-types (this work). No other sources (e.g. comets) are needed to explain it.

However, the overall meteorite falls statistics (Gattacceca et al. 2022) shows different proportions of OC and CC meteorites: OC 80%, CC 4.4%. In particular, the observed ratio OC/(CM+CI+C-ungr.) ≃ 30 is too high compared to our prediction 1.3. This can only be explained by a difference in fragmentation in the upper atmosphere (Borovička et al. 2019) together with ablation at relatively high entry speeds (≳30 km s−1; cf. Fig. B.13), or by thermal fragmentation. Furthermore, there are substantial differences within carbonaceous classes; CO/CV/CK must be much stronger than CM, CI, C-ungr. On the other hand, our model does not indicate dramatic differences between CM, CI, C-ungr. classes in terms of fragmentation, since their proportions is largely a natural outcome of the sources, locations, and transport.

thumbnail Fig. 15

Observed orbital distributions of C/P-, B-, K/L-, Baptistina-like, D-, and M-type NEOs. The semimajor axis a versus inclination i plot is a good indicator of the source, because NEO orbits are initially close to their source, before they disperse due to planetary perturbations. For reference, the locations of selected asteroid families are indicated (‘K’ corresponds to König).
thumbnail Fig. 16

Same as Fig. 11 for the Polana (top) and Euphrosyne (bottom) families. Colours correspond to the numbers of orbits in bins. The orbits of both Ryugu and Bennu (crosses) are compatible with Polana. Even (3200) Phaethon on a high-eccentricity orbit (e = 0.89) is compatible with Polana.

Data availability

Movies are available at https://www.aanda.org/.

Movies

Movie 1 Access here

Movie 2 Access here

Movie 3 Access here

Movie 4 Access here

Movie 5 Access here

Acknowledgements

We thank an anonymous referee for a number of constructive comments. We thank Chrysa Avdellidou for providing spectroscopic observations of König. This work has been supported by the Czech Science Foundation through grant 21-11058S (M. Brož). The Chimera HPC cluster at Charles University (MFF UK) was used for computations. FRIPON3 is funded by the ANR grant N.13-BS05-0009-03, carried by the Paris Observatory, Muséum National d’Histoire Naturelle, Paris-Saclay University and Pythéas institute (LAM, CEREGE). Vigie-Ciel is part of the 65 Millions d’Observateurs project, carried by the Muséum National d’Histoire Naturelle, funded by the French Investissements d’Avenir program. FRIPON data are hosted and processed at Institut Pythéas IT department (SIP). A mirror is also hosted at IMCCE (Institut de Mécanique Céleste et de Calcul des Éphémérides).

Appendix A Enstatite chondrites and achondrites

When our model is consistently applied to E-type families (Nysa, Hungaria), it produces NEO and meteoroid populations which are compatible with the observed abundance of E-type NEOs as well as enstatite chondrites and achondrites, also known as aubrites (see Tabs. 4, 5). It is important to know that the spread of albedos in the Nysa family is huge (from 0.1 to 0.6). Approximately half of bodies have high albedos, pV > 0.3, i.e. characteristic of aubrites. At least a part of the other half might appear as EH- or EL-chondrite-like.4

For EL, EH chondrites, the CRE ages reach up to 40 My (Fig. A.1; Patzer & Schultz 2001), corresponding to a collisional cascade. This is compatible with Nysa (age ≫40My, presumably). The second onset coincides with the age of Veritas.

For aubrites (Keil 2010), the CRE ages reach up to ≈ 110 My, but an onset is observed at 60 My (Fig. A.1; Lorenzetti et al. 2003). This is fully compatible with the Hungaria family, which is more-or-less isolated from the asteroid belt; hence the collisional lifetime is long (Ćuk et al. 2014).

E-type NEOs, or more specifically Xe- or Xn-types, often exhibit a distinct spectral feature, which is characteristic of (44) Nysa. Those which are located at low inclinations (≈ 5°) ’certainly’ originate from the Nysa family (see Fig. A.2). The remaining population at high inclinations is easily explained by the Hungaria family.

thumbnail Fig. A.1

Same as Fig. 10 for enstatite chondrites (EC) and achondrites (Aub).
thumbnail Fig. A.2

Same as Fig. 15 for E-type NEOs.

Appendix B Supplementary figures

Apart from figures referred to in the main text, we show identified asteroid families in Fig. B.12 and histograms of entry speeds for individual families in Fig. B.13.

thumbnail Fig. B.1

Structure of the Themis family in the proper eccentricity ep versus proper inclination sin ip. Every asteroid is represented by a dot. Concentrations of dots indicate up to 7 sub-families. The most prominent one is related to (656) Beagle. The least prominent ones are very dispersed in the proper semimajor axis ap, due to the Yarkovsky effect. Nevertheless, it is a confirmation of an ongoing collisional cascade.
thumbnail Fig. B.2

SFDs of the main belt (blue) and the Vesta family (yellow), used for calibration of our collisional model. The observed SFDs (Bottke et al. 2015b; Harris et al. 2015 and this work) are in agreement with the synthetic SFDs, where the observational bias is negligible (D ≳ 1 km). At sub-kilometre sizes, the SFD of the Vesta family is shallow, similarly as the main belt, due to a collisional cascade. Additionally, the model is constrained by the observed SFD of NEOs, and cratering record at (4) Vesta.
thumbnail Fig. B.3

Same as Fig. B.2 for the NEOs.
thumbnail Fig. B.4

Astrid family is more than 150 My old according to orbital evolution. The observed family (green) has a substantial spread of inclinations sin ip below the semimajor axis ap = 2.763 au. The synthetic family (blue; top) is initially compact, in accord with a low escape speed (υesc ≐ 25 m s−1). In the course of evolution, it is modified by the 𝑔 − 𝑔C secular resonance with Ceres (Novaković et al. 2016). At the time ≳150 My (bottom), it corresponds to the observed distribution. Such an old age indicates that the SFD must already be shallow.
thumbnail Fig. B.5

Same as Fig. B.4 for the Misa family. Its orbital distribution indicates an age up to 100 My, due to interactions with the 11:4 mean-motion resonance with Jupiter.
thumbnail Fig. B.6

Brangäne family asteroids must have surfaces covered with regolith. The observed family (green) in the proper semimajor axis ap versus the proper eccentricity ep exhibits a depletion of small bodies in the centre. The synthetic family (blue) was initially more compact. After about 60 My of orbital evolution, it exhibits the same depletion due to the YORP effect (Vokrouhlický et al. 2006). The value of thermal conductivity was assumed low, K = 10−3W m−1 K−1, corresponding to regolith. An alternative model, assuming iron composition and no regolith (K = 40 W m−1 K−1), was excluded, because small bodies were not depleted, but spread due to chaotic diffusion in e. A suppression of the YORP effect was also excluded, because small bodies drifted towards small a, due to the seasonal variant of the Yarkovsky drift. The offset of (606) Brangäne with respect to other asteroids is most likely due to a random close encounter with (4) Vesta.

All other figures and tables are available on Zenodo, https://doi.org/10.5281/zenodo.12783392.

Appendix C Supplementary tables

We report properties of the observed SFDs in Tab. C.1, parameters of synthetic families in Tab. C.2, and intrinsic collisional probabilities in Tabs. C.3, C.4.

Appendix D Classification of NEOs

Several NEOs from MITHNEOS (Binzel et al. 2019; Marsset et al. 2022) were taxonomically reclassified in this work. In Table D.5, we provide our new classification of these objects within the Bus-DeMeo system (DeMeo et al. 2009). We introduce a new class, ‘298’, which stands for bodies spectrally analogue to (298) Baptistina and (396) Aeolia. Those bodies exhibit a single wide 1.00-µm absorption band but no 2-µm band. ‘U’ stands for unclassified/unknown.

In Table D.6, we classify B, C, and P-type NEOs into the two main groups of carbonaceous chondrites: CI (concave-up) and CM (concave-down). NEOs that could not be classified due to ambiguous spectra (e.g. low S/N) are not included in the table.

References

  1. Applin, D. M., Sch?ade?, D. L., Cloutis, E. A., Nakamura, T., & Matsuoka, M. 2022, in LPI Contributions, 2678, 53rd Lunar and Planetary Science Conference, 2218 [NASA ADS] [Google Scholar]
  2. Battams, K., Gutarra-Leon, A. J., Gallagher, B. M., et al. 2022, ApJ, 936, 81 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bell, J. F. 1988, Meteoritics, 23, 256 [NASA ADS] [Google Scholar]
  4. Binzel, R. P., Bus, S. J., Burbine, T. H., & Sunshine, J. M. 1996, Science, 273, 946 [NASA ADS] [CrossRef] [Google Scholar]
  5. Binzel, R. P., DeMeo, F. E., Turtelboom, E. V., et al. 2019, Icarus, 324, 41 [Google Scholar]
  6. Borovicka, J., Popova, O., & Spurný, P. 2019, Met. Planet. Sci., 54, 1024 [CrossRef] [Google Scholar]
  7. Bottke, W. F., Brož, M., O’Brien, D. P., et al. 2015a, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (University of Arizona Press), 701 [Google Scholar]
  8. Bottke, W. F., Vokrouhlický, D., Walsh, K. J., et al. 2015b, Icarus, 247, 191 [CrossRef] [Google Scholar]
  9. Bottke, W. F., Vokrouhlický, D., Ballouz, R. L., et al. 2020, AJ, 160, 14 [Google Scholar]
  10. Bradley, J. P. 2007, in Treatise on Geochemistry, 1 [Google Scholar]
  11. Bradley, J. P., Keller, L. P., Brownlee, D. E., & Thomas, K. L. 1996, Met. Planet. Sci., 31, 394 [Google Scholar]
  12. Brož, M., & Morbidelli, A. 2013, Icarus, 223, 844 [CrossRef] [Google Scholar]
  13. Brož, M., & Šolc, M. 2013, Fyzika slunecní soustavy (Matfyzpress) [Google Scholar]
  14. Brož, M., Vokrouhlický, D., Morbidelli, A., Nesvorný, D., & Bottke, W. F. 2011, MNRAS, 414, 2716 [Google Scholar]
  15. Brož, M., Ferrais, M., Vernazza, P., Ševecek, P., & Jutzi, M. 2022, A&A, 664, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Brož, M., Vernazza, P., Marsset, M., et al. 2024, Nature, submitted [Google Scholar]
  17. Burbine, T. H., Binzel, R. P., Bus, S. J., & Clark, B. E. 2001, Met. Planet. Sci., 36, 245 [CrossRef] [Google Scholar]
  18. Bus, S. J., & Binzel, R. P. 2002a, Icarus, 158, 146 [Google Scholar]
  19. Bus, S. J., & Binzel, R. P. 2002b, Icarus, 158, 106 [CrossRef] [Google Scholar]
  20. Capek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [CrossRef] [Google Scholar]
  21. Capek, D., & Vokrouhlický, D. 2010, A&A, 519, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Carruba, V. 2016, MNRAS, 461, 1605 [NASA ADS] [CrossRef] [Google Scholar]
  23. Carruba, V., & Morbidelli, A. 2011, MNRAS, 412, 2040 [NASA ADS] [CrossRef] [Google Scholar]
  24. Carruba, V., Novakovic, B., & Aljbaae, S. 2017a, MNRAS, 465, 4099 [NASA ADS] [CrossRef] [Google Scholar]
  25. Carruba, V., Vokrouhlický, D., & Nesvorný, D. 2017b, MNRAS, 469, 4400 [NASA ADS] [CrossRef] [Google Scholar]
  26. Carruba, V., Vokrouhlický, D., Nesvorný, D., & Aljbaae, S. 2018, MNRAS, 477, 1308 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ceplecha, Z. 1961, Bull. Astron. Inst. Czech., 12, 21 [NASA ADS] [Google Scholar]
  28. Cibulková, H., Durech, J., Vokrouhlický, D., Kaasalainen, M., & Oszkiewicz, D. A. 2016, A&A, 596, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Clark, B. E., Ockert-Bell, M. E., Cloutis, E. A., et al. 2009, Icarus, 202, 119 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cobb, A. K., & Pudritz, R. E. 2014, ApJ, 783, 140 [NASA ADS] [CrossRef] [Google Scholar]
  31. Colas, F., Zanda, B., Bouley, S., et al. 2020, A&A, 644, A53 [EDP Sciences] [Google Scholar]
  32. Consolmagno, G., Britt, D., & Macke, R. 2008, Chem. Erde/Geochemistry, 68, 1 [NASA ADS] [Google Scholar]
  33. Cuk, M., Gladman, B. J., & Nesvorný, D. 2014, Icarus, 239, 154 [NASA ADS] [CrossRef] [Google Scholar]
  34. De Prá, M. N., Pinilla-Alonso, N., Carvano, J., et al. 2020, A&A, 643, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Delbo, M., Walsh, K. J., Matonti, C., et al. 2022, Nat. Geosci., 15, 453 [NASA ADS] [CrossRef] [Google Scholar]
  36. DeMeo, F., & Binzel, R. P. 2008, Icarus, 194, 436 [NASA ADS] [CrossRef] [Google Scholar]
  37. DeMeo, F. E., & Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
  38. DeMeo, F. E., Binzel, R. P., Slivan, S. M., & Bus, S. J. 2009, Icarus, 202, 160 [Google Scholar]
  39. Dibb, S. D., Bell, J. F., & Garvie, L. A. J. 2022, Met. Planet. Sci., 57, 1570 [CrossRef] [Google Scholar]
  40. Eugster, O., Herzog, G. F., Marti, K., & Caffee, M. W. 2006, in Meteorites and the Early Solar System II, eds. D. S. Lauretta, & H. Y. McSween (University of Arizona Press), 829 [CrossRef] [Google Scholar]
  41. Farinella, P., Vokrouhlický, D., & Hartmann, W. K. 1998, Icarus, 132, 378 [NASA ADS] [CrossRef] [Google Scholar]
  42. Farley, K. A., Montanari, A., Shoemaker, E. M., & Shoemaker, C. S. 1998, Science, 280, 1250 [NASA ADS] [CrossRef] [Google Scholar]
  43. Farley, K. A., Vokrouhlický, D., Bottke, W. F., & Nesvorný, D. 2006, Nature, 439, 295 [Google Scholar]
  44. Ferrais, M., Jorda, L., Vernazza, P., et al. 2022, A&A, 662, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Fornasier, S., Clark, B. E., Dotto, E., et al. 2010, Icarus, 210, 655 [NASA ADS] [CrossRef] [Google Scholar]
  46. Fornasier, S., Lantz, C., Perna, D., et al. 2016, Icarus, 269, 1 [CrossRef] [Google Scholar]
  47. Gattacceca, J., McCubbin, F. M., Grossman, J., et al. 2022, Met. Planet. Sci., 57, 2102 [CrossRef] [Google Scholar]
  48. Genge, M. J., Van Ginneken, M., & Suttle, M. D. 2020, Planet. Space Sci., 187, 104900 [NASA ADS] [CrossRef] [Google Scholar]
  49. Granvik, M., & Brown, P. 2018, Icarus, 311, 271 [Google Scholar]
  50. Granvik, M., & Walsh, K. J. 2024, ApJ, 960, L9 [Google Scholar]
  51. Granvik, M., Morbidelli, A., Jedicke, R., et al. 2016, Nature, 530, 303 [Google Scholar]
  52. Granvik, M., Morbidelli, A., Vokrouhlický, D., et al. 2017, A&A, 598, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Granvik, M., Morbidelli, A., Jedicke, R., et al. 2018, Icarus, 312, 181 [CrossRef] [Google Scholar]
  54. Hanuš, J., Vokrouhlický, D., Delbo, M., et al. 2018, A&A, 620, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Hardersen, P. S., Gaffey, M. J., & Abell, P. A. 2005, Icarus, 175, 141 [NASA ADS] [CrossRef] [Google Scholar]
  56. Hardersen, P. S., Cloutis, E. A., Reddy, V., Mothé-Diniz, T., & Emery, J. P. 2011, Met. Planet. Sci., 46, 1910 [NASA ADS] [CrossRef] [Google Scholar]
  57. Harris, A. W., & Chodas, P. W. 2021, Icarus, 365, 114452 [NASA ADS] [CrossRef] [Google Scholar]
  58. Harris, A. W., Boslough, M., Chapman, C. R., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (University of Arizona Press), 835 [Google Scholar]
  59. Henych, T., Borovicka, J., Vojácek, V., & Spurný, P. 2024, A&A, 683, A229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Holsapple, K. A. 2007, Icarus, 187, 500 [NASA ADS] [CrossRef] [Google Scholar]
  61. Ivanova, M. A., Kononkova, N. N., Krot, A. N., et al. 2008, Met. Planet. Sci., 43, 915 [CrossRef] [Google Scholar]
  62. Keil, K. 2010, Chem. Erde/Geochemistry, 70, 295 [Google Scholar]
  63. King, A. J., Bates, H. C., Krietsch, D., et al. 2019, Chem. Erde/Geochemistry, 79, 125531 [Google Scholar]
  64. Kneževic, Z., & Milani, A. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Krietsch, D., Busemann, H., Riebe, M. E. I., et al. 2021, Geochim. Cos-mochim. Acta, 310, 240 [NASA ADS] [CrossRef] [Google Scholar]
  66. Lauretta, D. S., Dellagiustina, D. N., Bennett, C. A., et al. 2019, Nature, 568, 55 [NASA ADS] [CrossRef] [Google Scholar]
  67. Lazzaro, D., Angeli, C. A., Carvano, J. M., et al. 2004, Icarus, 172, 179 [NASA ADS] [CrossRef] [Google Scholar]
  68. Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
  69. Libourel, G., Beck, P., Nakamura, A. M., et al. 2023, Planet. Sci. J., 4, 123 [NASA ADS] [CrossRef] [Google Scholar]
  70. Lorenzetti, S., Eugster, O., Busemann, H., et al. 2003, Geochim. Cos-mochim. Acta, 67, 557 [NASA ADS] [CrossRef] [Google Scholar]
  71. Lowry, V. C., Vokrouhlický, D., Nesvorný, D., & Campins, H. 2020, AJ, 160, 127 [NASA ADS] [CrossRef] [Google Scholar]
  72. Macke, R. J., Britt, D. T., & Consolmagno, G. J. 2011, Met. Planet. Sci., 46, 311 [CrossRef] [Google Scholar]
  73. MacLennan, E., & Granvik, M. 2024, Nat. Astron., 8, 60 [Google Scholar]
  74. MacLennan, E., Toliou, A., & Granvik, M. 2021, Icarus, 366, 114535 [NASA ADS] [CrossRef] [Google Scholar]
  75. Mahlke, M., Esch?ig, J., Carry, B., Bonal, L., & Beck, P. 2023, A&A, 676, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Marchi, S., McSween, H. Y., O’Brien, D. P., et al. 2012, Science, 336, 690 [NASA ADS] [CrossRef] [Google Scholar]
  77. Marsset, M., Vernazza, P., Birlan, M., et al. 2016, A&A, 586, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Marsset, M., Brož, M., Vernazza, P., et al. 2020, Nat. Astron., 4, 569 [NASA ADS] [CrossRef] [Google Scholar]
  79. Marsset, M., DeMeo, F. E., Burt, B., et al. 2022, AJ, 163, 165 [NASA ADS] [CrossRef] [Google Scholar]
  80. Marsset, M., Vernazza, P., Brož, M., et al. 2024, Nature, submitted [Google Scholar]
  81. Masiero, J. R., Carruba, V., Mainzer, A., Bauer, J. M., & Nugent, C. 2015a, ApJ, 809, 179 [NASA ADS] [CrossRef] [Google Scholar]
  82. Masiero, J. R., DeMeo, F. E., Kasuga, T., & Parker, A. H. 2015b, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (University of Arizona Press), 323 [Google Scholar]
  83. Maupin, R., Djouadi, Z., Brunetto, R., et al. 2020, Planet. Sci. J., 1, 62 [NASA ADS] [CrossRef] [Google Scholar]
  84. Meier, M. 2023, https://www.meteoriteorbits.info/ [Google Scholar]
  85. Metzler, K., Hezel, D. C., Barosch, J., et al. 2021, Geochim. Cosmochim. Acta, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
  86. Morbidelli, A., Bottke, W. F., J., Froeschlé, C., & Michel, P. 2002, in Asteroids III, 409 [CrossRef] [Google Scholar]
  87. Morbidelli, A., Bottke, W. F., Nesvorný, D., & Levison, H. F. 2009, Icarus, 204, 558 [Google Scholar]
  88. Moskovitz, N., Schottland, R., Burt, B., et al. 2019, in EPSC-DPS Joint Meeting 2019, 2019, EPSC-DPS2019-644 [Google Scholar]
  89. Neeley, J. R., Clark, B. E., Ockert-Bell, M. E., et al. 2014, Icarus, 238, 37 [NASA ADS] [CrossRef] [Google Scholar]
  90. Nesvorný, D., Bottke, William F., J., Dones, L., & Levison, H. F. 2002, Nature, 417, 720 [CrossRef] [Google Scholar]
  91. Nesvorný, D., Bottke, W. F., Levison, H. F., & Dones, L. 2003, ApJ, 591, 486 [CrossRef] [Google Scholar]
  92. Nesvorný, D., Vokrouhlický, D., Bottke, W. F., & Sykes, M. 2006, Icarus, 181, 107 [CrossRef] [Google Scholar]
  93. Nesvorný, D., Brož, M., & Carruba, V. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (University of Arizona Press), 297 [Google Scholar]
  94. Nesvorný, D., Deienno, R., Bottke, W. F., et al. 2023, AJ, 166, 55 [CrossRef] [Google Scholar]
  95. Novakovic, B. 2010, MNRAS, 407, 1477 [CrossRef] [Google Scholar]
  96. Novakovic, B., & Radovic, V. 2019, in EPSC-DPS Joint Meeting 2019, EPSC-DPS2019-1671 [Google Scholar]
  97. Novakovic, B., Tsiganis, K., & Kneževic, Z. 2010, MNRAS, 402, 1263 [NASA ADS] [CrossRef] [Google Scholar]
  98. Novakovic, B., Tsirvoulis, G., Marò, S., Došovic, V., & Maurel, C. 2016, in Asteroids: New Observations, New Models, 318, eds. S. R. Chesley, A. Morbidelli, R. Jedicke, & D. Farnocchia, 46 [NASA ADS] [Google Scholar]
  99. Nugent, C. R., Mainzer, A., Masiero, J., et al. 2015, ApJ, 814, 117 [NASA ADS] [CrossRef] [Google Scholar]
  100. O’Brien, D. P., Marchi, S., Morbidelli, A., et al. 2014, Planet. Space Sci., 103, 131 [CrossRef] [Google Scholar]
  101. Parker, A., Ivezic, Ž., Juric, M., et al. 2008, Icarus, 198, 138 [NASA ADS] [CrossRef] [Google Scholar]
  102. Patzer, A., & Schultz, L. 2001, Met. Planet. Sci., 36, 947 [CrossRef] [Google Scholar]
  103. Pecina, P., & Ceplecha, Z. 1983, Bull. Astron. Inst. Czech., 34, 102 [NASA ADS] [Google Scholar]
  104. Pinilla-Alonso, N., de León, J., Walsh, K. J., et al. 2016, Icarus, 274, 231 [NASA ADS] [CrossRef] [Google Scholar]
  105. Planck Collaboration XIV. 2014, A&A, 571, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Pohl, L., & Britt, D. T. 2020, Met. Planet. Sci., 55, 962 [CrossRef] [Google Scholar]
  107. Prestgard, T., Beck, P., Bonal, L., et al. 2023, Met. Planet. Sci., 58, 1117 [CrossRef] [Google Scholar]
  108. Quinn, T. R., Tremaine, S., & Duncan, M. 1991, AJ, 101, 2287 [NASA ADS] [CrossRef] [Google Scholar]
  109. Reach, W. T., Franz, B. A., & Weiland, J. L. 1997, Icarus, 127, 461 [NASA ADS] [CrossRef] [Google Scholar]
  110. Rubin, A. E., Kallemeyn, G. W., Wasson, J. T., et al. 2003, Geochim. Cos-mochim. Acta, 67, 3283 [NASA ADS] [CrossRef] [Google Scholar]
  111. Rubincam, D. P. 2000, Icarus, 148, 2 [Google Scholar]
  112. Scherer, P., & Schultz, L. 2000, Met. Planet. Sci., 35, 145 [CrossRef] [Google Scholar]
  113. Schmitz, B., Peucker-Ehrenbrink, B., Lindström, M., & Tassinari, M. 1997, Science, 278, 88 [NASA ADS] [CrossRef] [Google Scholar]
  114. Ševecek, P., Brož, M., Nesvorný, D., et al. 2017, Icarus, 296, 239 [CrossRef] [Google Scholar]
  115. Shepard, M. K., Taylor, P. A., Nolan, M. C., et al. 2015, Icarus, 245, 38 [NASA ADS] [CrossRef] [Google Scholar]
  116. Šidlichovský, M. & Nesvorný, D. 1996, Celest. Mech. Dyn. Astron., 65, 137 [CrossRef] [Google Scholar]
  117. Statler, T. S. 2009, Icarus, 202, 502 [NASA ADS] [CrossRef] [Google Scholar]
  118. Swindle, T. D., Kring, D. A., & Weirich, J. R. 2014, Geol. Soc. Lond. Spec. Publ., 378, 333 [NASA ADS] [CrossRef] [Google Scholar]
  119. Sykes, M. V. 1990, Icarus, 85, 267 [NASA ADS] [CrossRef] [Google Scholar]
  120. Tsirvoulis, G., & Novakovic, B. 2016, Icarus, 280, 300 [NASA ADS] [CrossRef] [Google Scholar]
  121. Usui, F., Hasegawa, S., Ootsubo, T., & Onaka, T. 2019, PASJ, 71, 1 [NASA ADS] [CrossRef] [Google Scholar]
  122. Usui, F., Kuroda, D., Müller, T. G., et al. 2011, PASJ, 63, 1117 [Google Scholar]
  123. Vernazza, P., Binzel, R. P., Thomas, C. A., et al. 2008, Nature, 454, 858 [NASA ADS] [CrossRef] [Google Scholar]
  124. Vernazza, P., Fulvio, D., Brunetto, R., et al. 2013, Icarus, 225, 517 [Google Scholar]
  125. Vernazza, P., Marsset, M., Beck, P., et al. 2015, ApJ, 806, 204 [Google Scholar]
  126. Vernazza, P., Brož, M., Drouard, A., et al. 2018, A&A, 618, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Vernazza, P., Ferrais, M., Jorda, L., et al. 2021, A&A, 654, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Vernazza, P., Usui, F., & Hasegawa, S. 2022, in Vesta and Ceres. Insights from the Dawn Mission for the Origin of the Solar System, 3 [Google Scholar]
  129. Vokrouhlický, D. 1998, A&A, 335, 1093 [Google Scholar]
  130. Vokrouhlický, D., Brož, M., Bottke, W. F., Nesvorný, D., & Morbidelli, A. 2006, Icarus, 182, 118 [Google Scholar]
  131. Vokrouhlický, D., Nesvorný, D., Bottke, W. F., & Morbidelli, A. 2010, AJ, 139, 2148 [CrossRef] [Google Scholar]
  132. Walsh, K. J., & Richardson, D. C. 2008, Icarus, 193, 553 [NASA ADS] [CrossRef] [Google Scholar]
  133. Watanabe, S., Hirabayashi, M., Hirata, N., et al. 2019, Science, 364, 268 [NASA ADS] [Google Scholar]
  134. Whipple, F. L. 1983, IAU Circ., 3881, 1 [NASA ADS] [Google Scholar]
  135. Wisdom, J. 1983, Icarus, 56, 51 [NASA ADS] [CrossRef] [Google Scholar]
  136. Wölfer, E., Budde, G., & Kleine, T. 2023, Geochim. Cosmochim. Acta, 361, 288 [CrossRef] [Google Scholar]
  137. Yang, B., Hanuš, J., Brož, M., et al. 2020a, A&A, 643, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Yang, B., Hanuš, J., Carry, B., et al. 2020b, A&A, 641, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  139. Yokoyama, T., Nagashima, K., Nakai, I., et al. 2023, Science, 379, abn7850 [NASA ADS] [CrossRef] [Google Scholar]
  140. Zappalà, V., Bendjoya, P., Cellino, A., Farinella, P., & Froeschlé, C. 1995, Icarus, 116, 291 [CrossRef] [Google Scholar]
2

i.e. not the orbital inclination i; even high-i orbits enter the atmosphere at low-ɀ, and vice versa.

4

Additionally, a sizable M-type within the family is (135) Hertha.

All Tables

Table 1

Overview of carbonaceous chondrites classes.

In the text
Table 2

Ages of the C-type families estimated from our collisional model.

In the text
Table 3

Ages of the C-type families estimated from our orbital model.

In the text
Table 4

Dynamical time scales and cumulative numbers of 1-km asteroids in the main belt (mb) and the near-Earth region (neo).

In the text
Table 5

Same as Table 4 for 1-m meteoroids.

In the text

All Figures

thumbnail Fig. 1

‘Faint Main Belt’, showing only bodies with the absolute magnitude close to the limit of the Catalina Sky Survey, id est, H ≳ 19.25 + 5(log(2.2(l − 0.1)) + log(2.2 − 1))) − 5(log(a(l − e)) + log(a − 1))). The proper semimajor axis ap versus eccentricity ep (bottom) versus inclination sin ip (top) are plotted; together with locations of the mean-motion resonances (vertical lines), IRAS dust bands (horizontal lines), and known asteroid families (Nesvorný et al. 2015) (labels). Big and old ones are almost invisible here (e.g. ‘4’ Vesta). Small and young ones − having a steep SFD − are prominent. The distribution of faint bodies is surprisingly irregular. The concentrations are directly related to the sources of meteorites: L .. ‘20’ Massalia (Marsset et al. 2024), H .. ‘158’ Koronis (Brož et al. 2024), CM .. ‘490’ Veritas, CI.. ‘142’ Polana, CO/CV/CK .. ‘221’ Eos, M .. ‘293’ Brasilia, or M .. ‘606’ Brangäne (this work).
In the text
thumbnail Fig. 2

Observed SFDs of C-type asteroid families. The SFDs usually exhibit a steep slope q1 at sizes D ≳ 5 km and a shallow slope q2 at D ≲ 5 km. This break is often created in the course of collisonal evolution. An observational bias affects the SFDs at even smaller sizes (0.5–3 km), depending on the distance and albedo of the respective populations. Additionally, families of P, B, and M types were studied (together with 4 of unknown taxonomical classification).
In the text
thumbnail Fig. 3

Mean spectra of asteroid families along with their classification. If only one spectrum (for the largest member) was available, the designation includes its number. If more spectra were available, but the mean was unreliable, spectra were plotted separately (blue, green).
In the text
thumbnail Fig. 4

König family exhibits a convergence of nodes. The range of ΔΩ with respect to (3815) König (green; top) is plotted together with individual values (grey). For each body, we used a set of 20 clones with different Yarkovsky effect and we selected the best clone at each time step. Not all bodies converge, because some of them are interlopers. The temporal dependence ΔΩ(t) exhibits local minima, in particular, 14.6 Myr and 22.7 Myr seem to be possible ages. For 22.7 Myr, the converging orbits of the best clones were plotted (coloured; bottom). For 14.6 Myr, a different set of clones would have to be selected. The orbits often exhibit more than one differential-precession cycle. See also Fig. 5.
In the text
thumbnail Fig. 5

König family is 22 Myr old according to orbital evolution. The observed family (green) has a very peculiar structure in the proper semi-major axis ap versus the proper inclination sin ip. The synthetic family (blue; top) is initially distributed in a simple ‘ellipse’, created by an isotropic impact. The geometry of the impact was f = 85°, ω = 0°. In the course of evolution, the distribution is modified by the 𝑔 − 𝑔5 + s − s6 secular resonance. At the time (22 ± 2) Myr (bottom), it exactly corresponds to the observed distribution. Such a young age indicates that the SFD can still be steep.
In the text
thumbnail Fig. 6

Percentages of CM/CR- (blue), CI/IDP- (cyan), CO/CV/CK- (grey) and other carbonaceous-chondrite-like bodies of the synthetic main belt (left), of the synthetic NEO (middle) and the observed NEO (right) populations. These percentages are different for kilometre-sized (top) versus metre-sized (bottom) bodies, due to substantial differences in the SFDs of the source populations. The contributions of individual asteroid families are indicated within the respective pie charts. For comparison, the observed percentages of meteorite falls from https://www.lpi.usra.edu/meteor/, with respect to all classes, are as follows: HED 6.0%, OC 80%, CC 4.4%, irons 4.1%, enstatite chondrites 1.5%, aubrites 0.9%, mesosiderites 0.6%, ureilites 0.5%, pallasites 0.3%, acapulcoites 0.1%, lodranites 0.1%, respectively.
In the text
thumbnail Fig. 7

Synthetic SFD of the Polana family derived from our collisional model. Initially, it was steep (Pantone 7633C, dashed), but since then it has evolved and it is now shallow (blue), in agreement with observations at kilometre sizes (grey, solid). For comparison, the main belt distribution is also plotted (cyan), as well as corresponding observations (Bottke et al. 2015a). Each model was run 10 times to account for stochasticity.
In the text
thumbnail Fig. 8

Same as Fig. 7 for the Veritas family. For a family as young as Veritas, however, the initially steep SFD is still preserved. In the future, it will become as shallow as Polana.
In the text
thumbnail Fig. 9

Observed SFD of the Veritas family (grey, solid). Its extrapolation (dotted) is supported by the observed 9.3° IRAS dust band (Nesvorný et al. 2006), at approximately 30 µm (error bar). Moreover, the initial SFD (Pantone 7633C, dashed) is supported by the excess of extraterrestrial He-3 (Farley et al. 2006), which 8.3 Myr ago ‘overshot’ the background level by a factor of ~3. The interpolation to metre sizes (error bar) implies the abundance of CM chondrite meteoroids.
In the text
thumbnail Fig. 10

CRE ages of CM chondrites (top) (Krietsch et al. 2021) exhibit an increase on a cumulative histogram, i.e. a peak on a differential histogram. On the contrary, CV, CO, and CK chondrites (Scherer & Schultz 2000) exhibit a continuous distribution over the last 40 Myr. This increase/peak corresponds to the late miocene peak of extraterrestrial helium-3 in terrestrial sediments (Farley et al. 2006) (middle) and to the age of the CM-like Veritas family, (8.3 ± 0.1) Myr, as confirmed by convergence of orbits (bottom). A plot with a sum of probability distributions presented in Krietsch et al. (2021), Fig. 9 is misleading; uncertainties of old CRE ages are large, the probability is low, it seems like there are ‘none’ meteorites having old CRE ages. On the contrary, our cumulative histogram demonstrates that there are numerous meteorites with old CRE ages.
In the text
thumbnail Fig. 11

Pre-atmospheric orbits of CM, C1-, and C2-ungrouped meteorites (Meier 2023; black crosses with error bars). Their maximum semimajor axis is well beyond the 3:1 mean-motion resonance (a ≲ 2.82 au) and their inclination is low (i ≲ 2°). For comparison, synthetic orbits of 1-m meteoroids from Veritas (top) and Astrid (bottom) are plotted, whenever an orbit is in the NEO region (a(1 + e) > 0.983 au Λ a(1 − e) < 1.3 au). Colours correspond to the lifetimes in the NEO region. It is difficult to scatter orbits from high → low inclinations, and vice versa. Low-inclination orbits also have much larger probability pi of collision with the Earth. Nevertheless, the flux Φ = PiNneo from Veritas is larger than from Astrid, according to our model. Consequently, we favour Veritas as the main source of CM chondrites.
In the text
thumbnail Fig. 12

Histogram of entry speeds observed by FRIPON (grey) and computed from our model (‘METEOMOD’; violet), with appropriate weighting by collisional probabilities. For comparison, underlying (unweighted) distribution from the original families is plotted (dotted). The uncertainties were estimated as Poissonian. The total number of events was 602.
In the text
thumbnail Fig. 13

Same as Fig. 9 for (3200) Phaethon. Two additional NEOs were included in this SFD, (155140) and (225416); (MacLennan et al. 2021). Its extrapolation (dotted) is supported by the observed dust trail (Battams et al. 2022). Its interpolation (error bar) explains the abundance of Geminids (cf. Fig. 12).
In the text
thumbnail Fig. 14

Dynamical pressure p on a meteoroid during its atmospheric entry, depending on the zenith angle ɀ (in degrees). A basic ablation model was used, with the following parameters: initial mass m = 1000kg, entry speed υ = 20 km s−1, density ρ = 1700 kg m−3, ablation efficiency η = 0.02, specific heat l = 106 J kg−1, shape factor A = 1.22 (i.e. sphere), friction coefficient C = 0.5. The resulting terminal mass m′ = 0.3 kg. The strength of OC meteoroids (3 to 5 MPa; Borovička et al. 2019; grey area) is comparable to p. CC meteoroids (≈ 0.5 MPa; dotted line) are substantially weaker than p. If fragmentation occurs, the ablation process becomes much more efficient; CC meteorites only survive for trajectories with ɀ ≳ 85°.
In the text
thumbnail Fig. 15

Observed orbital distributions of C/P-, B-, K/L-, Baptistina-like, D-, and M-type NEOs. The semimajor axis a versus inclination i plot is a good indicator of the source, because NEO orbits are initially close to their source, before they disperse due to planetary perturbations. For reference, the locations of selected asteroid families are indicated (‘K’ corresponds to König).
In the text
thumbnail Fig. 16

Same as Fig. 11 for the Polana (top) and Euphrosyne (bottom) families. Colours correspond to the numbers of orbits in bins. The orbits of both Ryugu and Bennu (crosses) are compatible with Polana. Even (3200) Phaethon on a high-eccentricity orbit (e = 0.89) is compatible with Polana.
In the text
thumbnail Fig. A.1

Same as Fig. 10 for enstatite chondrites (EC) and achondrites (Aub).
In the text
thumbnail Fig. A.2

Same as Fig. 15 for E-type NEOs.
In the text
thumbnail Fig. B.1

Structure of the Themis family in the proper eccentricity ep versus proper inclination sin ip. Every asteroid is represented by a dot. Concentrations of dots indicate up to 7 sub-families. The most prominent one is related to (656) Beagle. The least prominent ones are very dispersed in the proper semimajor axis ap, due to the Yarkovsky effect. Nevertheless, it is a confirmation of an ongoing collisional cascade.
In the text
thumbnail Fig. B.2

SFDs of the main belt (blue) and the Vesta family (yellow), used for calibration of our collisional model. The observed SFDs (Bottke et al. 2015b; Harris et al. 2015 and this work) are in agreement with the synthetic SFDs, where the observational bias is negligible (D ≳ 1 km). At sub-kilometre sizes, the SFD of the Vesta family is shallow, similarly as the main belt, due to a collisional cascade. Additionally, the model is constrained by the observed SFD of NEOs, and cratering record at (4) Vesta.
In the text
thumbnail Fig. B.3

Same as Fig. B.2 for the NEOs.
In the text
thumbnail Fig. B.4

Astrid family is more than 150 My old according to orbital evolution. The observed family (green) has a substantial spread of inclinations sin ip below the semimajor axis ap = 2.763 au. The synthetic family (blue; top) is initially compact, in accord with a low escape speed (υesc ≐ 25 m s−1). In the course of evolution, it is modified by the 𝑔 − 𝑔C secular resonance with Ceres (Novaković et al. 2016). At the time ≳150 My (bottom), it corresponds to the observed distribution. Such an old age indicates that the SFD must already be shallow.
In the text
thumbnail Fig. B.5

Same as Fig. B.4 for the Misa family. Its orbital distribution indicates an age up to 100 My, due to interactions with the 11:4 mean-motion resonance with Jupiter.
In the text
thumbnail Fig. B.6

Brangäne family asteroids must have surfaces covered with regolith. The observed family (green) in the proper semimajor axis ap versus the proper eccentricity ep exhibits a depletion of small bodies in the centre. The synthetic family (blue) was initially more compact. After about 60 My of orbital evolution, it exhibits the same depletion due to the YORP effect (Vokrouhlický et al. 2006). The value of thermal conductivity was assumed low, K = 10−3W m−1 K−1, corresponding to regolith. An alternative model, assuming iron composition and no regolith (K = 40 W m−1 K−1), was excluded, because small bodies were not depleted, but spread due to chaotic diffusion in e. A suppression of the YORP effect was also excluded, because small bodies drifted towards small a, due to the seasonal variant of the Yarkovsky drift. The offset of (606) Brangäne with respect to other asteroids is most likely due to a random close encounter with (4) Vesta.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.